| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201731310 | |
| Published online | 05 October 2017 | |
Quiescent photometric modulations of two low-inclination cataclysmic variables KZ Geminorum and TW Virginis
1 Yunnan Observatories, Chinese Academy of Sciences, 396 Yangfangwang, Guandu District, 650216 Kunming, PR China
e-mail: zhibin_dai@ynao.ac.cn
2 Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 396 Yangfangwang, Guandu District, 650216 Kunming, PR China
3 Center for Astronomical Mega-Science, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, 100012 Beijing, PR China
4 University of Washington, Seattle, WA 98195, USA
5 Applied Sciences Department, Aqaba University College, Al-Balqa’ Applied University, PO Box 1199, 77110 Aqaba, Jordan
6 University of Notre Dame, Notre Dame, IN 46556, USA
7 Department of Physics, University College Cork, Cork, Ireland
Received: 3 June 2017
Accepted: 10 August 2017
Aims. The quiescent periodic photometric modulations of two low-inclination cataclysmic variables observed in Kepler K2 Campaigns 0 and 1, KZ Gem and TW Vir, are investigated.
Methods. A phase-correcting method was successfully used to detect the orbital modulations of KZ Gem and TW Vir and improve their orbital periods. The light curve morphologies of both CVs were further analyzed by defining flux ratios and creating colormaps.
Results. KZ Gem shows ellipsoidal modulations with an orbital period of 0.22242(1) day, twice the period listed in the updated RK catalogue (Edition 7.24). With this newly determined period, KZ Gem is no longer a CV in the period gap, but a long-period CV. A part of the quiescent light curve of TW Vir that had the highest stability was used to deduce its improved orbital period of 0.182682(3) day. The flat patterns shown in the colormaps of the flux ratios for KZ Gem demonstrate the stability of their orbital modulations, while TW Vir show variable orbital modulations during the K2 datasets. In TW Vir, the single versus double-peaked nature of the quiescent orbital variations before and after superoutburst may be related to the effect of the superoutburst on the accretion disk.
Key words: binaries close / novae, cataclysmic variables / stars: individual: KZ Gem / stars: individual: TW Vir
© ESO, 2017
1. Introduction
Cataclysmic variables (CVs) are close binary systems in which a white dwarf (WD) primary accretes matter from a Roche-lobe filling late-type star via the inner Lagrangian point (CVs are reviewed in Warner 1995). Unless the magnetic field of the white dwarf is in the MG regime, the matter accumulates in an accretion disk surrounding the white dwarf and a hot spot is created where the mass transfer stream intersects the accretion disk. The low-inclination CVs show no eclipses and lack easily detected photometric orbital modulations caused by a changing view of the hot spot during their orbit. To detect small (<1 mag) optical modulation features requires high signal-to-noise and a long time base (e.g. Szkody et al. 1992; Taylor et al. 1999; Patterson et al. 2003). Hence, it is difficult to find suitable data on many low-inclination CVs at quiescence. Considering that flickering is one of the most striking photometric characteristics common to all CVs and has an amplitude of a few hundredths of a magnitude up to more than an entire magnitude (Bruch 1991, 1992), the low-amplitude orbital modulations in faint low-inclination CVs may be completely overwhelmed. For example, data on QZ Vir (Dai et al. 2016) do not show a distinct orbital modulation due to possible large-amplitude flickering. The large scatter shown in the phased light curves of RZ Leo and FO Aqr derived by Dai et al. (2016) and Kennedy et al. (2016), respectively, indicates that effects from the white dwarf spin can also complicate the extraction of an orbital modulation.
Comparison of light curve data obtained at different times shows that flickering and orbital modulations are variable and the appearance in the measured light curve obviously depends on the exposure times and binning of the data (Szkody et al. 2016; Dai et al. 2016). The unprecedented light curves from the Kepler K2 mission (Howell et al. 2014), with nearly continuous photometric coverage for 1−3 months at different pointings (Campaigns) along the ecliptic provide an excellent database to study low-amplitude photometric variations in faint low-inclination CVs. K2 Campaign 0 (K2-C0) was an engineering test in the early stage of the K2 program and the telescope did not have pointing stability during the 35-day campaign. K2 Campaign 1 (K2-C1) was the first campaign with fine pointing and it covers 80 days.
In this paper, we analyze two CV light curves in detail KZ Gem was observed in long cadence (LC; 30 min sampling) during K2-C0 and and TW Vir in short cadence (SC; 1 min sampling) during K2-C1. Both CVs listed in Table 1 are considered low-inclination systems due to the lack of detected eclipses. We apply a phase-correcting method to the quiescent light curves of KZ Gem and TW Vir to refine their orbital periods and study their orbital modulations.
The two low-inclination CVs.
2. K2 light curve extractions
The K2 data are stored in the original Target Pixel Files (TPFs) provided by the Mikulski Archive for Space Telescopes (MAST). Dai et al. (2016) presented the light curve extractions for TW Vir, but there was only a featureless light curve for the faint CV KZ Gem, extracted by using the program PyKE developed by the Guest Observer Office (Still & Barclay 2012) and the pipeline presented by Dai et al. (2016). Since the “self-flat-fielding” (SFF) method proposed by Vanderburg & Johnson (2014) and Vanderburg (2014) was claimed to improve the K2 light curves by removing the effect of the trends, the SFF corrected light curves of KZ Gem was used for our further analysis. Note that the SFF corrected data are described by the normalized flux. Although the K2 light curve shown in Fig. 1 does not show any visible periodic modulation, the results from Lomb-Scargle periodogram (LSP; Lomb 1976; and Scargle 1982) and phase dispersion minimization (PDM; Stellingwerf 1978) found a modulation period from its K2 data.
3. Analysis methods
3.1. Phase-correcting Method
The methods of LSP and PDM are generally used to search for periods in time series data, but they are not ideal for finding variable or unstable modulations. Although a 2D power spectrum analysis can help with this problem, it may only show a rough period with low precision. Thus, based on a preliminary period P0 derived from the above period finding methods or an existing radial velocity result, we attempted to apply a phase-correcting method to improve the precision of the observed period. Since P0 is a key parameter for the success of our phase-correcting method, it is necessary to make a precise estimation as soon as possible by using the LSP and PDM, which are powerful to find periods in data sets with highly non-regular timing.
The K2 continuous time series data were separated into several sections for phasing the light curve on the starting period P0, with each section maintaining the same data length, Ns, which is measured in units of the cycles. A standard phase (e.g., the light minimum at phase 0 or maximum at phase 0.5) was fixed to be a reference phase. Based on this reference phase, the small and imperceptible discrepancy from the starting period P0 (the average phase uncertainty is on the order of tens of seconds for both CVs discussed in this paper) can then be accumulated and amplified to be a measurable parameter accompanying the increased cycles. In principle, the shifting phases of all sections show a linear curve with a constant shift rate Sphase derived by a decent linear fit. This discrepancy can be deduced as 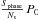 . The resulting modulation period Pb can be described by the following formula, i.e.,
. The resulting modulation period Pb can be described by the following formula, i.e., 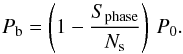 (1)The data length Ns is a key parameter for this phase-correcting method. An appropriate Ns should not only satisfy the minimal length for folding the light curve, but also guarantee enough number of sections for deducing the shift rate Sphase, which determines the precision of the final measured modulation period Pb. After several tries, we determined that the best Ns should be 10 and 5 for the LC and SC data, respectively. The orbital periods of the two CVs improved by using this method are discussed in detail in Sect. 4.
(1)The data length Ns is a key parameter for this phase-correcting method. An appropriate Ns should not only satisfy the minimal length for folding the light curve, but also guarantee enough number of sections for deducing the shift rate Sphase, which determines the precision of the final measured modulation period Pb. After several tries, we determined that the best Ns should be 10 and 5 for the LC and SC data, respectively. The orbital periods of the two CVs improved by using this method are discussed in detail in Sect. 4.
This method is suitable for analyzing data where the periodic variation is close to a simple harmonic model. Particularly, it is good at accurately finding modulations which undergo amplitude changes during a long data string. By separating a complete time series into many sections, it is easy to figure out when the modulations begin to become unstable, indicated by the first chaotic section. Thus, the part of the light curve with the highest stability can be picked out to derive the modulation period by using this method. And the modulation can be visualized by phasing the stable part of the light curve. TW Vir as a good example is presented at length in Sect. 4.2.1. Note that this method depends on an implicit assumption that the phase of the variability is not intrinsically variable during the time span of the data.
3.2. Flux ratios
For a double-hump light curve, the hump at the higher flux level is defined as the primary peak, and the lower flux hump is the secondary peak. Similarly, the light minimum at the lower flux level is the primary dip, and the other minimum is the secondary dip. Taking advantage of the continuous high-precision K2 data, these peaks and dips can be used to describe the light-curve morphologies. Although the K2 data are not absolutely calibrated, the relative flux changes with time can be determined. We use four flux ratios that are defined by the following formulas, 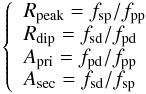 (2)where fsp, fsd, fpp and fpd are the flux at the secondary peak, secondary dip, primary peak and primary dip, respectively. An accurate modulation period and a parabolic least-square fitting method are used to extract the flux at the peaks and dips. The latter can largely eliminate the effects from discrepant data points and possible random drifts with time. Rpeak and Rdip indicate the flux ratios of two peaks and dips, respectively. Apri and Asec denote the primary and secondary amplitudes of the modulations, respectively. Since both a strengthening of a peak flux or a weakening of a dip flux can give rise to a variation in the hump amplitude, the two parameters Apri and Asec are not enough to completely describe the variations in the light curve. By combining these two ratios with the other two flux ratios Rpeak and Rdip, the variations in peaks and dips can be distinguished. This method is mainly considers the effects on the flux from cycle-to-cycle variations, flickering, and observational errors.
(2)where fsp, fsd, fpp and fpd are the flux at the secondary peak, secondary dip, primary peak and primary dip, respectively. An accurate modulation period and a parabolic least-square fitting method are used to extract the flux at the peaks and dips. The latter can largely eliminate the effects from discrepant data points and possible random drifts with time. Rpeak and Rdip indicate the flux ratios of two peaks and dips, respectively. Apri and Asec denote the primary and secondary amplitudes of the modulations, respectively. Since both a strengthening of a peak flux or a weakening of a dip flux can give rise to a variation in the hump amplitude, the two parameters Apri and Asec are not enough to completely describe the variations in the light curve. By combining these two ratios with the other two flux ratios Rpeak and Rdip, the variations in peaks and dips can be distinguished. This method is mainly considers the effects on the flux from cycle-to-cycle variations, flickering, and observational errors.
 |
Fig. 2 25 × 25 pix colormaps of four flux ratios defined by Eq. (2) for the same object are aligned from top to bottom. The two plots of Apri for TW Vir and WD 1144+011 lie alongside at the bottom, since Apri is the only available parameter for both CVs. The gray scale denotes the number of the flux ratios falling into each grid. The blue solid lines refer to the best-fitting curves, and the average and the corresponding coefficients of flux ratios are listed in Table 2. The arrow shown in Rdip plot of J0632+2536 indicates the transient event of J0632+2536 around BJD 2 456 790. The time pointed by the arrow in Apri plot of TW Vir is the same as that in panel a of Fig. 8. |
For visualization, each flux ratio was plotted into a 25 × 25 pix colormap (i.e., a diagram of flux ratio versus BJD). The K2 data were separated into 25 sections and all flux ratios were calculated for each section. The maximum and minimum flux ratio for all 25 sections were then set to be the upper and lower border of the diagrams. Between the two borders, the flux ratio was separated into 25 uniform sections. The number of calculated flux ratios falling into each grid was then counted. The resulting colormaps are shown in Fig. 2. Note that large, detectable amplitudes in the primary or secondary hump lead to Apri and Asec < 1, respectively. Also, unchanged flux ratios over the course of the observations indicate a stable modulation. Table 2 lists the averages of the four flux ratios for all 5 targets and the corresponding coefficients of the fits.
The four flux ratios.
4. Results
4.1. KZ Gem
4.1.1. Period analysis
KZ Gem is a poorly understood variable star first discovered by Hoffmeister (1966) and Kukarkin et al. (1968). Although it has been classified as a U Gem type dwarf nova (DN) in all versions of the CV catalogues (e.g. Downes & Shara 1993; Downes et al. 1997, 2001; Ritter & Kolb 2003), there was not any formal report or literature supporting its DN subtype identification until a recent DN outburst occurred in 2015 January (Lange 2016), which confirms its DN classification. The K2 variable catalogue1 classified KZ Gem as “OTHPER”, i.e., other periodic and quasi-periodic variables, via a quick and automated period search (Armstrong et al. 2015, 2016). Ritter & Kolb (2003) reported a period of 0.11122 day as the orbital period. This orbital period has not been confirmed with spectra.
In order to further test the period listed in the catalogs, the SFF corrected data of KZ Gem (Fig. 1) was analyzed by using the LSP, the same method used in Armstrong et al. (2015), and the PDM method. The strongest peak at a period of 0.1112 day (2.67 h) is consistent with the orbital period listed in the updated CV catalogue (RKcat Edition 7.24 seen in Ritter & Kolb 2003). Note that there is also a peak with less power at the period of 0.2225 day (5.34 h), which is exactly twice of the period of 2.67 h. The phased light curves of KZ Gem shown in the panels a and b of Fig. 3 correspond to the periods of 2.67 h and 5.34 h, respectively. The phased light curve using a period of 2.67 h shows a single minimum per orbit. However, despite the large scatter of the raw data, the binned data using a period of 5.34 h shows two distinct minima in a single orbit. This means that the phased light curve with the period of 2.67 h actually overlaps the two different minima, and the data scatter blurs them into the apparent single minimum, which can be proved by the larger scatter in the panel a than that in the panel b of Fig. 3. Thus, like 1RXS J0632+2536 (J0632+2536) and RZ Leo (Dai et al. 2016), the orbital period of KZ Gem is likely 5.34 h and the 2.67 h peak is a harmonic. This newly determined period indicates that KZ Gem is a normal long-period DN rather than one of the CVs in the period gap. This light curve resembles the light curve caused by ellipsoidal modulation (e.g Bochkarev et al. 1979).
A higher precision orbital period can be obtained by using our phase-correcting method. The K2 time series of KZ Gem spanning over 30 days was separated into 14 sections, using the period of 5.34 h and setting Ns as 10 (as the data is in LC model). Using Eq. (1), the final orbital period of KZ Gem is calculated to be 0.22242(1) day based on the shift rate Sphase = −0.002(5) derived from the 14 shifting phases shown in the upper panel of Fig. 4. The precision of the orbital period is an order of magnitude higher than that of the starting period obtained from the LSP and the PDM methods. In order to find further evidence that this is the orbital period of KZ Gem, the SFF corrected data of KZ Gem were first converted into K2 magnitude Kp2 using the conversion in Dai et al. (2016), and then all the 14 phased light curves folded on the improved orbital period of 0.22242(1) day, with an average amplitude of 0.0025 mag, were stacked (Fig. 5). These light curves indicate that the orbital modulation of KZ Gem is basically stable except for the two sections around BJD 2 456 784.35 and BJD 2 456 795.46. Obviously, all of the stable light curves with the smaller scatter show detailed features of the modulation including two different minima and similar maxima in one orbit, which is the typical ellipsoidal modulation light curve found in other binary systems, such as Nova A0620-00 (McClintock et al. 1983) and TT Crt (Szkody et al. 1992).
 |
Fig. 3 Phased and binned light curves of KZ Gem are plotted by the scatter dots and solid lines, respectively. The K2 light curves folded on the period of 0.1112 day (2.67 h) and of 0.2225 day (5.34 h) were shown in panels a and b, respectively. |
 |
Fig. 4 Shifting phases calculated in each section of KZ Gem and TW Vir are plotted in the upper and lower panels, respectively. The solid lines denote the linear fit to the data. |
4.1.2. Light-curve morphology
The stability of the orbital modulation of KZ Gem is also evident from the flux ratios (Fig. 2). All four diagrams in Fig. 2 are not only very close to the dashed line of 1, but also show considerably flat patterns with slopes around 10-5, which means that this low-amplitude modulation is stable. In spite of the scatter, the linear fit shown in the plot of Rpeak is closer to the line of 1 than that in the plot of Rdip. This may provide support that the orbital period of KZ Gem is 0.22242(1) day and the corresponding orbital modulation has two minima per orbital cycle rather than a single sinusoidal-like oscillation (as shown in panels a and b of Fig. 3).
In order to determine whether the stability of the orbital modulations of KZ Gem is unusual, we also investigated the stability of three other low-inclination CV type light curves: J0632+2536 observed in K2-C0, and RZ Leo and the pre-CV WD 1144+011 observed in K2-C1. Note that these CVs never show any superoutburst during the K2 observations. By using the four flux ratios defined in Sect. 3.2, their flat patterns like KZ Gem shown in Fig. 2 illustrate that all three CV light curves with the distinct orbital modulations derived by Dai et al. (2016) are basically stable throughout the K2 observations. Although J0632+2536 shows negative slopes in Rpeak and Apri and a quadratic-like pattern in Rdip, there is only a small distortion of the double-hump orbital modulation as the K2-C0 observation progresses. In addition, the sharp decrease of system light of J0632+2536 occurring around BJD 2 456 790 shown in the top panel of Fig. 1 of Dai et al. (2016) is coincident with the change in Rdip, as pointed out by the arrow in the Rdip plot. For RZ Leo, the fairly constant orbital modulation is in contrast to a model of a shifting hot spot proposed by Mennickent & Tappert (2001). And the “anti-humps” claimed by Mennickent et al. (1999) were undetected in the K2-C1 SC data. Since the average error of RZ Leo is from 0.04 mag to 0.07 mag and the maximal error bar is <0.1 mag (Fig. 6), the uncertainties of the data points are not enough to explain the large amplitude dispersion ~0.43 mag shown in the phased light curve of RZ Leo. Therefore, the flat patterns of RZ Leo imply that this scatter amplitude results from a uniform drift of the system light on a short timescale, rather than from any variations in the disk or hot spot.
 |
Fig. 5 Based on the 14 sections separated from the K2-C0 data of KZ Gem, all 14 phased light curves folded on the same period of 0.22242(1) day are stacked in chronological order from top to bottom. The labels of Y axis refer to the median times of the sections. The two blue sections indicate the unstable modulations. |
4.2. TW Vir
4.2.1. Period analysis
Although Shafter (1983) has published a spectroscopic orbital period of 4.38 h for TW Vir and there were 7872 photometric observations from 1955 to 1997 (Ak et al. 2002), the existence of a photometric orbital modulation is still unknown. The recent period analysis during the plateau of a superoutburst in TW Vir (Dai et al. 2016) only showed the well-known 6 h period due to the K2 satellite pointing drift, and some ambiguous peaks smaller than 4.38 h, which could be harmonics of this pseudo 6-hr period. The online K2 variable catalogue1 classified TW Vir as “RRab” (i.e., RRab lyrae star) without any available phase-folded light curve.
A 2D power spectrum analysis with a moving window of 1.6 day was applied to the whole K2 SC light curve of TW Vir. Inspection of Fig. 7 illustrates two significant and coherent black bars around the periods of 0.183(4) day (4.4 h) and 0.092(4) day (2.2 h), respectively. The latter period with less power is the second harmonic of the former one. This 2D power spectrum diagram supports the previous orbital period derived by Shafter (1983), and shows that the orbital modulation of TW Vir found in quiescence disappears during outburst (a result similar to that found for UV Gem, Dai et al. 2015). Thus, we focused on the quiescent light curve to improve the precision of the orbital period. Based on the times of appearance and disappearance of the orbital modulation, the light curve when Kp2 was fainter than 15.3 mag was defined to be the quiescent light curve. This light curve covers a total of 25 days, separated into three quiescent sections by one superoutburst and two normal outbursts (Fig. 7). The latter two quiescent sections completely cover the intervals between the three outbursts. The orbital modulation in quiescence between the superoutburst and the following normal outburst is remarkably stronger than that between the two normal outbursts. The maximal powers and the corresponding periods tracking along the black bar of the 2D power spectrum are plotted in the upper and lower panels of Fig. 8, respectively.
Considering the width of the black bar shown in Fig. 7 and the dispersion of the orbital period around 0.008 day (~0.2 h) denoted by the irregular variation shown in panel c of Fig. 8, we needed a detailed period analysis to improve the precision of the orbital period of TW Vir. We accomplished this by using the previously described phase-correcting method. An initial period was intentionally set to be 0.185 day (4.44 h) with a small deviation ~4 min away from the average period 4.38 h shown in the panel c of Fig. 8. Based on this initial period and the preset Ns = 5, the SC light curve of TW Vir observed in K2-C1 was separated into 80 sections. After subtracting the sections during the outbursts, the resulting 60 sections in quiescence were stacked in Figs. 9 and 10 illustrating the quiescent light curves around the superoutbust and between the two normal outbursts, respectively. The quiescent orbital modulations of TW Vir around the superoutburst are more stable despite the apparent differences in the modulation profiles before and after superoutburst (Fig. 11). We found that a stable orbital modulation was not established until BJD 2 456 829.26. There are 24 sections from BJD 2 456 825.56 to BJD 2 456 846.84 that were analyzed by our phase-correcting method. The orbital period of TW Vir was improved to 0.182682(3) day based on the linear shift phases shown in the lower panel of Fig. 4. The precision of the derived orbital period is an order magnitude higher than that obtained by Shafter (1983) and three orders of magnitude higher than that derived from the 2D power spectrum analysis. The 20 sections from BJD 2 456 829.26 to BJD 2 456 846.84 were folded on this period, and the resulting phased light curves are shown in Fig. 12. These phased light curves show clear orbital modulations. However, an accurate ephemeris for TW Vir cannot be derived from the K2 data since the cycle-to-cycle scatter makes a precise epoch difficult to determine.
 |
Fig. 7 Two-dimensional power spectrum of TW Vir calculated from a moving window 1.6 day is overplotted with its K2 light curve in magnitudes. A horizontal dash line at Kp2 = 15.3 mag is arbitrarily used to distinguish the two luminosity states: outburst and quiescence. The light curve between the two vertical dash lines lasting ~3.7 days may denote the rebuilding process of the orbital modulation that was interrupted by the superoutburst. |
 |
Fig. 8 Maximal power extracted from the 2D power spectrum of TW Vir shown in Fig. 7 and the corresponding periods were plotted in the left-side panels a and c, respectively. Similarly, the two diagrams on the right-side are for UV Gem. The solid and open circles in the plots of UV Gem refer to the orbital and possibly remaining superhump periods after an unrecorded superoutburst (Dai et al. 2015), respectively. The arrow shown in panel a denotes the changing point of the orbital modulation from strong to weak around BJD 2 456 839.9. |
 |
Fig. 9 29 phased light curves of TW Vir in quiescence around superoutburst folded on the initial period of 0.185 day and stacked in time order. Like Fig. 5, the median time of each section is labeled on the Y-axis. The blue and black light curves indicate the light curves before and after superoutburst, respectively. The red light curves are derived from the part of light curve between the two vertical dash lines shown in Fig. 7. According to our phase-correcting method, the 20 black light curves with the distinct double-hump modulation and the 4 red light curves were used to improve the orbital period of TW Vir. |
 |
Fig. 10 31 phased light curves of TW Vir folded on the initial period of 0.185 day between the two normal outburst are stacked in time order. |
 |
Fig. 11 Based on the light curves before and after superoutburst, the phased light curves of TW Vir with the corrected orbital period of 0.182682(3) day show the single-hump and double-hump modulation shown in panels a and b, respectively. The blue solid lines are the binned light curves. |
 |
Fig. 12 20 new phased light curves of TW Vir with the corrected period of 0.182682(3) day are stacked in time order. All light curves are the same as those listed in the right-side panel of Fig. 9. The significant and stable primary hump is set to be zero phase. |
4.2.2. Light-curve morphology
The phased light curves before and after superoutburst show different shapes (Fig. 12). During most quiescence times, a double hump orbital modulation (panel b) is apparent. However, the orbital modulation before the superoutburst appears to gradually mimic the shape of a typical superhump profile with a single maximum and minimum per cycle, similar to many other SU UMa type DNe (e.g. Patterson et al. 2003; Kato & Osaki 2013; Kato et al. 2013). Panel a of Fig. 11 illustrates this superhump-like modulation profile. Since TW Vir is classified as a UG Gem-type DN (O’Connell 1932) and its orbital period is far longer than the typical period of the SU UMa type DN, this single-peak modulation may represent the accretion pattern caused by an increased hot spot area before the upcoming superoutburst. The short time base of the K2 data before superoutburst cannot totally rule out the other possibility that the second hump may be overwhelmed by the large scatter. Post superoutburst, an orbital modulation began to form after BJD 2 456 825.56, which is close to the half time of the decay section of the outburst light curve. This part of the light curve from BJD 2 456 825.56 to BJD 2 456 846.84, lasting ~3.7 days at the end of the decay from superoutburst (Fig. 7), was divided into 4 sections shown in the bottom left plots of Fig. 9. These sections clearly indicate that the orbital modulation is becoming stronger, implying a reconstruction stage of the orbital modulation that was disrupted by the superoutburst. Panel a of Fig. 8 shows that the amplitude of the orbital modulation after the superoutburst first experiences a fast strengthening stage lasting about 10 days and then continuously weakens. This behavior is compared to that of UV Gem in Fig. 8b.
Since the quiescence following the next normal outburst seems to give rise to a chaotic orbital modulation, it is pointless to phase the entire K2-C1 quiescent dataset using this orbital period. Instead, we restrict our analysis to data taken between the superoutburst and following normal outburst(BJD 2 456 829−2 456 847). The relative high stability and the long time base of the light curve between the superoutburst and the following normal outburst (i.e., from BJD 2 456 829 to BJD 2 456 847), allowed this section to be used for further analysis. Since the indistinct second humps shown in panel b of Fig. 11 are highly variable, Apri is the only reliable parameter that could be used. The plot of Apri in Fig. 2 for TW Vir indicates a quadratic-like variation in primary amplitude.
The turning point of Apri is basically in accord with the strongest orbital modulation shown in panel a of Fig. 8. Combined with the variations in the amplitude of the spectrum power, the quadratic-like variation in Apri implies a scenario where the orbital modulation of TW Vir is quickly strengthened after superoutburst, lasts about 10 days, and then turns to a decay stage before the next normal outburst. Based on the quadratic fit to the curve shown in the Apri plot of Fig. 2, the spread of primary amplitude during this part of quiescence from superoutburst to normal outburst is about 4%. Since the enhancement of the primary amplitude is accompanied by the appearance of the orbital modulation before BJD 2 456 839.9, the enlarged amplitude may imply an adjustment of the accretion disk structure after superoutburst. Nevertheless, this recovered orbital modulation generally becomes unstable after BJD 2 456 839.9, and then almost falls into chaos after the following normal outburst, which can be clearly seen in Fig. 10. The transformation of the orbital modulation in a low inclination CV from stable to unstable has not been reported in the past. Since the turning point appears in the middle of the outburst interval, it is apparent that a stable orbital modulation, based on a typical CV accretion model (Warner 2003), is not maintained. Changes in accretion can definitely give rise to variations in orbital modulation, e.g., as recently reported in the eclipsing SU UMa type DN V1239 Her (Golysheva et al. 2015). Thus, the observed decrease of the amplitude of the orbital modulation suggests changes in the accretion disk structure of TW Vir around BJD 2 456 839.9. The high instability of the orbital modulation after the normal outburst may naturally explain why the optical orbital modulation of TW Vir was not observed in the 7872 observations of Ak et al. (2002).
5. Conclusions
The long datasets of K2-C0 and K2-C1 have allowed refined orbital periods for KZ Gem and TW Vir as well as a study of the stability of their photometric orbital variations. A phase-correcting method was successfully used to improve the orbital period of KZ Gem to 0.22242(1) day. This period confirms that KZ Gem is not a CV in the period gap, but a long-period DN. Our phased light curve folded on this period shows typical ellipsoidal modulations. Radial velocity measurements can provide further confirmation. By analyzing four defined flux ratios: Rpeak, Rdip, Apri and Asec and creating colormaps, KZ Gem, J0632+2536, RZ Leo and WD 1144+011 are shown to have flat or sloping patterns that indicate stable orbital modulations during quiescence. Despite the large scatter and variability of CV light curves, the orbital modulation is commonly stable for these low inclination CVs. However, TW Vir with a superoutburst and two normal outbursts shows unstable orbital modulation hidden in quiescence. Removing the outburst times from the K2-C1 SC data reveals its variable orbital modulation. By applying a phase-correcting method to 24 sections of data with the highest stability spanning over 17 days, the orbital period of TW Vir is improved to 0.182682(3) day. Two types of orbital modulation with signal-hump and double-hump profiles are derived before and after superoutburst, respectively. The amplitude of the orbital modulations are much stronger after a superoutburst than after the following normal outburst. These data may be the first visible detection of the rebuilding process of the accretion disk structure following a superoutburst. The reconstruction period of the orbital modulation is estimated as ~3.7 day. Based on a part of the quiescent light curve of TW Vir with a stable double-hump modulation, a nonlinear variation exists in the plot of Apri for TW Vir, corresponding to the time when the orbital modulation amplitude changes from strong to weak, rather than to any detectable transient event. The changing amplitudes are indicative of a changing accretion disk structure from superoutburst to quiescence.
Acknowledgments
This work was partly supported by CAS Light of West China Program and the Science Foundation of Yunnan Province (No. 2016FB007). P.S. acknowledges support from NSF grant AST-1514737. M.R.K. and P.G. acknowledge support from the Naughton Foundation and the UCC Strategic Research Fund.
References
- Ak, T., Ozkan, M. T., & Mattei, J. A. 2002, A&A, 389, 478 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armstrong, D. J., Kirk, J., Lam, K. W. F., et al. 2015, A&A, 579, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Armstrong, D. J., Kirk, J., Lam, K. W. F., et al. 2016, MNRAS, 456, 2260 [NASA ADS] [CrossRef] [Google Scholar]
- Bochkarev, N. G., Karitskaya, E. A., & Shakura, N. I. 1979, Pisma v Astronomicheskii Zhurnal, 23, 8 [Google Scholar]
- Bruch, A. 1991, A&A, 251, 59 [NASA ADS] [Google Scholar]
- Bruch, A. 1992, A&A 266, 237 [NASA ADS] [Google Scholar]
- Dai, Z. B., Szkody, P., Garnavich, P. M., & Kennedy, M. R. 2016, AJ, 152, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Dai, Z. B., Szkody, P., Garnavich, P. M., & Kennedy, M. R. 2015, Proc. The Golden Age of Cataclysmic Variables and Related Objects III, PoS, 28 [Google Scholar]
- Downes, R. A., & Shara, M. M. 1993, PASP 105, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, R. A., Webbink, R. F., & Shara, M. M. 1997, PASP, 109, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, R. A., Shara, M. M., Ritter, H., Kolb, U., et al. 2001, PASP, 113, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Golysheva, P., Shugarov, S., Katysheva, N., & Khruzina, T. 2015, ASPC, 496, 231 [NASA ADS] [Google Scholar]
- Howell, S. B., Sobeck, C., Haas, M., et al. 2014, PASP, 126, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffmeister, C. 1966, Astron. Nachr, 289, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, T., & Osaki, Y. 2013, PASJ, 65, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, T., Hambsch, Franz-Josef, Maehara, H., Masi, G., & Miller, I. 2013, PASJ, 65, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, M. R., Callanan, P., Garnavich, P. M., et al. 2016, MNRAS, 459, 3622 [NASA ADS] [CrossRef] [Google Scholar]
- Kukarkin, B. V., Kholopov, P. N., Efremov, Y. N., et al. 1968, IBVS, 311, 1 [NASA ADS] [Google Scholar]
- Lange, T. 2016, BAVSR, 65, 45. [NASA ADS] [Google Scholar]
- Lomb, N. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., Petro, L. D., Remillard, R. A., & Ricker, G. R. 1983, ApJ, 266, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Mennickent, R. E., & Tappert, C. 2001, A&A, 372, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennickent, R. E., Sterken, C., Gieren, W., & Unda, E. 1999, A&A, 352, 239 [NASA ADS] [Google Scholar]
- O’Connell, D J. K. 1932, Harvard College Observatory Bulletin, 890, 18 [NASA ADS] [Google Scholar]
- Patterson, J., Thorstensen, J. R., & Kemp, J., et al. 2003, PASP, 115, 1308 [NASA ADS] [CrossRef] [Google Scholar]
- Ritter, H., & Kolb, U. 2003, A&A, 404, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Shafter, A. W. 1983, IBVS, 2377 [Google Scholar]
- Stellingwerf, R. F. 1978, ApJ, 224, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Still, M., & Barclay, T. 2012, Astrophysics Source Code Library [records ascl:1208.004] [Google Scholar]
- Szkody, P., Williams, R. E., Margon, B., Howell, S. B., & Mateo, M. 1992, ApJ, 387, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Szkody, P., Mukadam, A. S., Gänsicke, B. T., et al. 2016, AJ, submitted [Google Scholar]
- Taylor, C. J., Thorstensen, J. R., & Patterson, J. 1999, PASP, 111, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderburg, A. 2014, ArXiv e-prints [arXiv:1412.1827] [Google Scholar]
- Vanderburg, A., & Johnson, J. A. 2014, PASP, 126, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Warner, B. 1995, Cataclysmic Variable Stars (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Warner, B. 2003, Cataclysmic Variable Stars (Cambridge: Cambridge Univ. Press) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SFF corrected light curve of KZ Gem observed in K2-C0. |
| In the text | |
 |
Fig. 2 25 × 25 pix colormaps of four flux ratios defined by Eq. (2) for the same object are aligned from top to bottom. The two plots of Apri for TW Vir and WD 1144+011 lie alongside at the bottom, since Apri is the only available parameter for both CVs. The gray scale denotes the number of the flux ratios falling into each grid. The blue solid lines refer to the best-fitting curves, and the average and the corresponding coefficients of flux ratios are listed in Table 2. The arrow shown in Rdip plot of J0632+2536 indicates the transient event of J0632+2536 around BJD 2 456 790. The time pointed by the arrow in Apri plot of TW Vir is the same as that in panel a of Fig. 8. |
| In the text | |
 |
Fig. 3 Phased and binned light curves of KZ Gem are plotted by the scatter dots and solid lines, respectively. The K2 light curves folded on the period of 0.1112 day (2.67 h) and of 0.2225 day (5.34 h) were shown in panels a and b, respectively. |
| In the text | |
 |
Fig. 4 Shifting phases calculated in each section of KZ Gem and TW Vir are plotted in the upper and lower panels, respectively. The solid lines denote the linear fit to the data. |
| In the text | |
 |
Fig. 5 Based on the 14 sections separated from the K2-C0 data of KZ Gem, all 14 phased light curves folded on the same period of 0.22242(1) day are stacked in chronological order from top to bottom. The labels of Y axis refer to the median times of the sections. The two blue sections indicate the unstable modulations. |
| In the text | |
 |
Fig. 6 Histogram of error distribution of the K2-C1 SC data for RZ Leo. |
| In the text | |
 |
Fig. 7 Two-dimensional power spectrum of TW Vir calculated from a moving window 1.6 day is overplotted with its K2 light curve in magnitudes. A horizontal dash line at Kp2 = 15.3 mag is arbitrarily used to distinguish the two luminosity states: outburst and quiescence. The light curve between the two vertical dash lines lasting ~3.7 days may denote the rebuilding process of the orbital modulation that was interrupted by the superoutburst. |
| In the text | |
 |
Fig. 8 Maximal power extracted from the 2D power spectrum of TW Vir shown in Fig. 7 and the corresponding periods were plotted in the left-side panels a and c, respectively. Similarly, the two diagrams on the right-side are for UV Gem. The solid and open circles in the plots of UV Gem refer to the orbital and possibly remaining superhump periods after an unrecorded superoutburst (Dai et al. 2015), respectively. The arrow shown in panel a denotes the changing point of the orbital modulation from strong to weak around BJD 2 456 839.9. |
| In the text | |
 |
Fig. 9 29 phased light curves of TW Vir in quiescence around superoutburst folded on the initial period of 0.185 day and stacked in time order. Like Fig. 5, the median time of each section is labeled on the Y-axis. The blue and black light curves indicate the light curves before and after superoutburst, respectively. The red light curves are derived from the part of light curve between the two vertical dash lines shown in Fig. 7. According to our phase-correcting method, the 20 black light curves with the distinct double-hump modulation and the 4 red light curves were used to improve the orbital period of TW Vir. |
| In the text | |
 |
Fig. 10 31 phased light curves of TW Vir folded on the initial period of 0.185 day between the two normal outburst are stacked in time order. |
| In the text | |
 |
Fig. 11 Based on the light curves before and after superoutburst, the phased light curves of TW Vir with the corrected orbital period of 0.182682(3) day show the single-hump and double-hump modulation shown in panels a and b, respectively. The blue solid lines are the binned light curves. |
| In the text | |
 |
Fig. 12 20 new phased light curves of TW Vir with the corrected period of 0.182682(3) day are stacked in time order. All light curves are the same as those listed in the right-side panel of Fig. 9. The significant and stable primary hump is set to be zero phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


