| Issue |
A&A
Volume 602, June 2017
|
|
|---|---|---|
| Article Number | A48 | |
| Number of page(s) | 8 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201628827 | |
| Published online | 07 June 2017 | |
Calculations of periodicity from Hα profiles of Proxima Centauri
1 University of Hertfordshire, College Lane, Hatfield, Herts, AL10 9AB, UK
e-mail: jmc@toad.me.uk
2 Department of Physical Sciences, The Open University, Walton Hall, Milton Keynes, MK7 6AA, UK
Received: 29 April 2016
Accepted: 2 February 2017
We investigate retrieval of the stellar rotation signal for Proxima Centauri. We make use of high-resolution spectra taken with UVES and HARPS of Proxima Centauri over a 13-yr period as well as photometric observations of Proxima Centauri from ASAS and HST. We measure the Hα equivalent width and Hα index, skewness and kurtosis and introduce a method that investigates the symmetry of the line, the peak ratio, which appears to return better results than the other measurements. Our investigations return a most significant period of 82.6 ± 0.1 days, confirming earlier photometric results and ruling out a more recent result of 116.6 days which we conclude to be an alias induced by the specific HARPS observation times. We conclude that whilst spectroscopic Hα measurements can be used for period recovery, in the case of Proxima Centauri the available photometric measurements are more reliable. We make 2D models of Proxima Centauri to generate simulated Hα, finding that reasonable distributions of plage and chromospheric features are able to reproduce the equivalent width variations in observed data and recover the rotation period, including after the addition of simulated noise and flares. However the 2D models used fail to generate the observed variety of line shapes measured by the peak ratio. We conclude that only 3D models which incorporate vertical motions in the chromosphere can achieve this.
Key words: methods: miscellaneous / line: profiles / stars: late-type / techniques: spectroscopic
© ESO, 2017
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0),
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0),
which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
M-dwarf stars account for over 75% of the stars within 25 pc of the Sun (Winters et al. 2015); and indeed, our nearest neighbour, Proxima Centauri, is an M5.5V star. Despite the prevalence of M-dwarfs, many aspects of their activity have remained less well characterised than more massive stars, mainly because of their inherent faintness. Since stars become fully convective at around M4V, the nature of magnetic activity and the relationship to the rotation period in the later M-dwarfs has been of particular interest, for example in Mohanty & Basri (2003) and Reiners & Basri (2008).
An understanding of the origin of periodic signals arising in a stellar system is important in the identification of exoplanets. For example, differing conclusions as to whether reported planets have been validly detected by their period have been offered, for example for GJ581 (Robertson et al. 2014; Robertson & Mahadevan 2014; Tuomi & Anglada-Escudé 2013; Hatzes 2016). The behaviour of the Hα line is a potentially important diagnostic because it is sensitive to magnetic activity and is a strong line usually seen in emission in later M-dwarf stars.
At a distance of only 1.3 pc, Proxima Centauri is a bright M5.5V star with a magnitude of 11.13 in the V-band. The rotation period of Proxima is nevertheless uncertain. The rotation period is of interest for various studies, including flare cycles (Davenport et al. 2016) and for the correct identification of radial velocity signals from orbiting planets (Anglada-Escudé et al. 2016) and subsequent work (Ribas et al. 2016). Previous studies have reported periods ranging from 31.5 ± 1.5 days (Guinan & Morgan 1996), through 41.3 days (Benedict et al. 1993) to between 82 and 84 days (Benedict et al. 1992, 1998). Kürster et al. (1999) found that the period is not less than 50 days (Kürster et al. 1999), while a more recent value of 82.5 days (Kiraga & Stepien 2007) has confirmed earlier estimates. All those measurements were obtained by photometry. An alternative method for establishing periodicity is the use of Hα, e.g., Feinstein (1976). An even longer rotation period of 116.6 days (Suárez Mascareño et al. 2015) has been suggested from spectroscopy, in particular via a study of the Hα line as the Hα index measure and Log(R′HK) from the HARPS data used in this paper. Cincunegui et al. (2007) reported a 442-day activity cycle, by consideration of the FWHM1 of the Hα line taken from observations using the 2.15 m telescope of CASLEO.
Here we investigate whether periodicity can be identified in the morphology of the Hα line in high-resolution spectra such as those obtained from the Ultraviolet and Visual Echelle Spectrograph (UVES) at the 8.2 m Very Large Telescope (VLT, UT 2) and the High Accuracy Radial velocity Planet Searcher (HARPS) at the ESO La Silla 3.6 m telescope. Proxima Centauri also shows frequent flaring activity and the presence of these flares is useful for determination of whether, and to what extent, they affect estimates of the rotation period.
2. Periodicity of Proxima Centauri from photometric measurements
To process the data for all the periodicity studies in this paper, we used a variety of Lomb-Scargle routines. This was necessary as different implementations return different periods, especially when peak significance is low. The Lomb-Scargle routine in Numerical Recipes2, modified to return false alarm probability (FAP) values for all peaks, is valuable for the periodograms where there are comparatively clear-cut peaks, however for many of the spectroscopic results it is unable to return any clear periods. For these cases software was written in Python using alternative Lomb-Scargle routines provided by SCIPY library (Jones et al. 2001), the ASTROML library, (Vanderplas et al. 2012) and the GATSPY library, (VanderPlas & Ivezić 2015), comparing the results. We did this because in some cases the results widely differed and it gave an assessment of the stability of the calculations. The GATSPY routine is the most recent and advanced algorithm by the same author as ASTROML, whilst the SCIPY routine is a recently-added part of a more general open-source package of software which often failed during execution, reporting faults such as “division-by-zero”, “singular matrix” and similar errors, not producing a result. More consistent results were obtained from GATSPY than the other two packages. However when the SCIPY routine returned results, they were more akin to those from GATSPY than ASTROML. This is generally consistent with the study by Jake Vanderplas3. Hence in cases where the Numerical Recipes routine failed to find the periods sought, the GATSPY routine was used. In some cases, such as with the comparison of spectroscopic methods discussed in Sect. 3.4, it was useful to tabulate and compare sets of results from all these methods.
As nearly all previous measurements of periodicity in Proxima Centauri were made using photometric observations, in this paper, we first present results obtained from the photometric observations for Proxima Centauri taken from the V-band (there were no data for the I-band) of the All Sky Automated Survey (ASAS; Pojmanski 1997), which contains data between the periods December 2000 to September 2009. This was done to experiment with the binning and also for the evaluation of the FAP and error bars from the HARPS data, as described in Sect. 3.5.
As indicated by the ASAS guidelines4, with Proxima Centauri set out in the ASAS data as having magnitude 11 in the V-band, we took the data from the second aperture. We are only considering the “best” (grade A) data from this aperture, which has 970 points. As some of the observations were overlapping in time, we binned these to 1 day, which reduced the number of points to 624. We then obtained the periodogram shown in the upper panel of Fig. 1. Periods between 20 and 160 days were taken in this case. It is noticeable that there only two significant peaks, at 82.6 and 106.8 days, with negligible FAPs.
We also obtained a periodogram from the HST data discussed in Benedict et al. (1992, 1998) consisting of 171 points obtained between July 1995 and January 1998, later enhanced so the last 18 points extended to January 2001, obtaining the lower panel of Fig. 1, again taking between 20 and 160 days. The observation times were either on separate days, or spaced out evenly throughout a single day with the result that binning this data would have reduced the data unacceptably, so we did not bin the HST data.
 |
Fig. 1 Upper panel: periodogram derived from the ASAS database for Proxima Centauri second aperture, binned to 1 day. Lower panel: periodogram derived from the HST data discussed in Benedict et al. (1998). FAP values for the strongest peaks were calculated and are shown as the dotted lines. Both periodograms are computed using the using the Numerical Recipes Lomb-Scargle routine. |
It is clear that there is consistent agreement between these results with a strong period of 82.6 ± 0.1 days and in agreement with the rotation period given in Benedict et al. (1998) and confirmed in Kiraga & Stepien (2007). The ASAS data also includes a reasonably strong additional signal of 106.5 ± 0.2 days. Taking account of the possibility of this being associated with some interaction between the main period and some other period, we considered whether this might be a “beat” period between the observation years and the rotational period, as we noticed the relationship 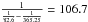 and we also noticed that
and we also noticed that 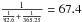 , which appears as the third peak observed in some of the periodograms obtained from all the ASAS apertures. We considered the window functions of the ASAS and HST data but were unable to find any significant periods around those values. We applied the method described in Dawson & Fabrycky (2010) to the ASAS and HST data and verified our our initial finding that the 82.6-day period was a genuine period and 106.7-day period of ASAS and the 77.8-day period of the HST data were aliases.
, which appears as the third peak observed in some of the periodograms obtained from all the ASAS apertures. We considered the window functions of the ASAS and HST data but were unable to find any significant periods around those values. We applied the method described in Dawson & Fabrycky (2010) to the ASAS and HST data and verified our our initial finding that the 82.6-day period was a genuine period and 106.7-day period of ASAS and the 77.8-day period of the HST data were aliases.
We also searched for very long periods up to the period spanned by the data in each case, however we did not find any strong periods, in particular nothing close to the 442 days reported in Cincunegui et al. (2007) based upon FWHM of Hα peaks from observations using CASLEO.
In any event the ASAS and HST provides a convenient benchmark for assessing the accuracy and reliability of the other methods based on the Hα line.
3. Spectra of Proxima Centauri
We looked at two sources of spectra for Proxima Centauri, the UVES spectra taken between 10th and 14th March 2009 studied in Fuhrmeister et al. (2011) and the HARPS spectra, with 260 data points between May 2004 and January 2014 from the ESO archive. The UVES data were obtained with a 0.8/1.10′′ slit, yielding a resolution of approximately 60 000, while the resolution of HARPS is approximately 120 000. The spectral range of UVES used for the observations is 6380 to 10 250 Å while the fixed format of HARPS gives wavelength coverage from 3780 to 6910 Å. We also studied the X-ray data from XMM-Newton used in the Fuhrmeister et al. (2011) paper (Provided by Fuhrmeister, priv. comm.) to identify any association between strong X-ray values and possible corresponding changes to the Hα profile. All the observation times of individual spectra were adjusted to take into account the appropriate barycentric correction and all the wavelengths in the spectra were adjusted to take account of the corresponding radial velocity corrections.
 |
Fig. 2 The Hα region of example spectra of Proxima Centauri taken from HARPS on 27 May 2004 02:10:14 UTC (black) and 15 March 2006 09:16:35 (brown). The region delineated with the dark red solid vertical lines shows the region used for calculation of the Hα equivalent width in this paper. The regions shaded in red and blue respectively show the regions used for calculation of the sizes of the two sub-peaks. The vertical purple lines mark the region chosen for calculation of the equivalent width and the vertical green lines mark the region chosen in Suárez Mascareño et al. (2015) for calculation of the Hα index. |
3.1. HARPS and UVES spectra of Proxima Centauri
As mentioned in Mohanty & Basri (2003) and subsequent papers such as Jenkins et al. (2009) and Barnes et al. (2014) the spectra of the later of late M-dwarfs from approximately M5 onward, usually show Hα in emission, Several of the M-dwarfs illustrated in Barnes et al. (2014, Fig. 6) additionally show a distinct “horned” appearance, due to a certain amount of self-absorption affecting the centre of the Hα peak. Proxima Centauri consistently shows this pattern, which is displayed in Fuhrmeister et al. (2011, Fig. 14). The two sub-peaks surround a local minimum. As well as the equivalent width of the entire Hα peak, the two sub-peaks vary in relative size over time on either side of the local minimum, which does not greatly change in morphology over time. This would appear to be because a more symmetrically-distributed spectral line from the photosphere is overlaid with plage and chromospheric effects which are asymmetric or localised to regions. In this paper we seek to study the variations in the line and sub-peaks to see if periodicity may be reliably recovered.
3.2. Hα line measurements
In Fig. 2, we show two example spectra, in this case from HARPS nearly 2 yr apart, clearly showing the changes in the amplitude and shape of the Hα line. Figure 2 also illustrates the regions used to investigate periodic variability. We used the HARPS data referred to in Suárez Mascareño et al. (2015, Table 3), which consists of 260 spectra taken between 27 May 2004 and 14 Jan. 2014. To calculate the equivalent width, the spectra were normalised by iteratively fitting a cubic polynomial to all the points in all the spectra, apart from the Hα region, then excluding points outside 2 standard deviations above or below the fitted polynomial to eliminate both emission and absorption lines. With the normalised spectra, we computed the equivalent widths and what we called the “peak ratio”, defined as the ratio of the mean values of the two sub-peaks. The ratio calculated is the mean value of the “red” sub-peak, i.e. that for the longer wavelength, divided by the mean value of the “blue” sub-peak (i.e. the ratio of the longer wavelength to the shorter wavelength peak). For calculation of the equivalent width, since pixel-wavelength scales are not identical, values of the flux are interpolated up to the boundaries of the regions chosen, to minimise integer pixel noise effects.
We restricted the Hα region for calculation of the equivalent width to the minima on either side of the peak to that from 6561.917 Å to 6563.839 Å) as delineated by the dark red vertical lines. The regions selected for the blue and red sub-peaks are shaded in blue and red and run from 6562.072 Å to 6562.613 Å and 6563.000 Å to 6563.517 Å respectively. These regions were chosen to optimise variability in the line profiles to give the highest degree of variability with the smallest amount of noise.
Note that the regions selected for calculation of the peak ratios are not quite the same width, the “blue” sub-peak region having a width of 0.541 Å and the “red” sub-peak region a width of 0.517 Å. This is because in the observed data the “red” sub-peak tends to be higher but narrower than the “blue” sub-peak. As the peak ratio is the ratio of the mean value in the two areas, this should not be of significance.
At the top of Fig. 2 is displayed the telluric line spectrum for an air mass of 1.4, to which 2.5 has been added for clarity of display. As demonstrated in Reiners et al. (2016, Fig. 1), the telluric effects are negligible in this region. (The Gaussian used to simulate Hα in that paper is considerably broader than that observed in Proxima Centauri, so the telluric line at 6564.2 Å can impinge on the former.) All the spectral lines identifiable from the Vienna Atomic Line Database (VALD) are TiO transitions, with the exception of a MgH line at 6564.29 Å.
In Suárez Mascareño et al. (2015), the authors use an Hα index, based in turn upon the work in Gomes da Silva et al. (2011), computed by the formula 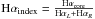 in which Hαcore is defined as the bandpass of width 1.6 Å centred on 6562.808 Å and HαL and HαR are defined respectively as continuum bands of widths 10.75 Å and 8.75 Å centred on 6550.87 Å and 6580.31 Å. An important difference between this and calculation of the equivalent widths and peak ratios is that the spectra do not have to be normalised prior to the Hα index calculation.
in which Hαcore is defined as the bandpass of width 1.6 Å centred on 6562.808 Å and HαL and HαR are defined respectively as continuum bands of widths 10.75 Å and 8.75 Å centred on 6550.87 Å and 6580.31 Å. An important difference between this and calculation of the equivalent widths and peak ratios is that the spectra do not have to be normalised prior to the Hα index calculation.
The region chosen for calculation of the Hα equivalent width in this paper is slightly wider than that chosen for the Hα index in the Suárez Mascareño et al. (2015). This was chosen as in our view it on average encompassed the base of the Hα peak more accurately. In practice there was negligible difference between the calculated results for either method using the two pairs of limits or adjusting the continuum regions.
Histograms of the equivalent widths are shown in Fig. 3. Note that all the equivalent widths from the UVES data are displayed, but the four very highest from the HARPS data are omitted, which have equivalent widths of over 6, listed in the caption to Fig. 3.
 |
Fig. 3 Histograms of equivalent widths for UVES in blue and HARPS in green, expressed as percentages with the same X axis scale. All the UVES spectra results are shown apart from those for one which appeared to be just noise (12 March 2009 UTC 02:31:11). HARPS spectra are omitted for four outlying cases which appeared to be dominated by flares at 16 July 2004 UTC 01:52:40, 27 March 2011 UTC 05:20:09, 05 May 2013 UTC 03:31:16 and 5 May 2013 UTC 03:41:47 with values of 21.69, 18.12, 6.76 and 6.19 respectively. |
We calculated the equivalent widths, Hα index, peak ratios, skewness, kurtosis5 and also Log(R′HK), as calculated by Suárez Mascareño et al. (2015) from the HARPS data for Proxima Centauri. Also calculated were equivalent widths and peak ratios from and residual Hα lines, created by division of each spectrum by the mean of the 5 spectra with the lowest equivalent widths. The median value and standard deviation of the HARPS equivalent width was 2.0 ± 1.8 and these values are used the our calculation of periodicity in Sect. 3.4. Hα index values were very similar to the equivalent widths in all cases.
3.3. Flares on UVES data and X-ray values
In Fuhrmeister et al. (2011, Figs. 1 to 3) the measured flux for various wavelengths for each of the three observation nights are presented. It should be noted that the X-ray flux is much greater on the third day and the scale is much smaller in the third figure of that paper. The UVES data showed a large flare during the third of the observation periods starting at approximately 06:15 on 14th March 2009. Both the equivalent width and X-ray counts rapidly reached a peak, with the equivalent width peaking approximately a minute before the X-ray count peaked. The equivalent width reached a similar level at the end of the first observation period to that which it reached during the flare in the third, albeit much more slowly, but with only very slight evidence of a corresponding increase in the X-ray count. However there was an increase in the UVES optical “blue” flux on the first day, as shown in Fuhrmeister et al. (2011, Fig. 1) corresponding to the higher equivalent widths suggestive of a flare.
There is no corresponding X-ray data available for the HARPS data, but the UVES data suggests that Hα equivalent width increases with flares. We thus selected the higher values of equivalent width in the HARPS data as indicative of flares. After some experimentation with investigation of periodicity, the effects of possible flares seemed to be minimised without losing too much data if the proportion of data with the lower 90% of equivalent widths were selected. In both UVES and HARPS this was approximately one standard deviation from the median, 3.8 in the case of HARPS.
 |
Fig. 4 Sample periodograms from the Hα peak of the HARPS data, for the range between 40 days and 130 days in steps of 0.01 days. Top panel: periodogram derived from the equivalent widths (EW) and the bottom panels ones derived from the peak ratios (PR). None have any clipping or binning of the data. The strongest five peaks are marked on the vertical black lines. |
3.4. Recovery of periods from HARPS data
We computed periodograms for periods between 40 days and 130 days, in steps of 0.01 days (14 min, 20 s) taking into account the minimum period of 50 days given by Kürster et al. (1999) and the 82 days of Benedict et al. 1992, 1993, 1998; Kiraga & Stepien 2007 and the 116.6 days of Suárez Mascareño et al. (2015, Table 3). Two sample periodograms are exhibited in Fig. 4. We tried all the methods described above in Sect. 3 and various combinations thereof. All the results were obtained using all three Python Lomb-Scargle routines as it was discovered that the results from these varied widely. It was difficult to identify any of these periods using the Numerical Recipes Lomb-Scargle routine, it either failed to find them, or it reported an FAP at or close to 1.0 if it did.
Results from equivalent width calculations and Hα index calculations were almost completely identical in all cases. We were able to reproduce, not necessarily as the strongest peak in the periodograms, the 116.6 days of Suárez Mascareño et al. (2015), although a period of 116.3 days was obtained, using equivalent width, Hα index, skewness and kurtosis measurements on untransformed data. A period of 115.9 days was also recovered from the Log(R′HK) measure. However the periods of this order disappeared as soon as any clipping or binning of the data was performed. In the window function of the observation times we note a small peak at 116.5 days. We did not think that the method described in Dawson & Fabrycky (2010) was applicable to the HARPS data as neither the 82.6-day period nor any other period reliably appeared as the strongest peak in any of the periodograms. We quantify the relative occurrence of periodogram peaks at the end of this section and refer further to it in Sect. 3.5.
There did not appear to be any consistent way of improving the performance of the various methods of measurement by treatments of the data. Treatments which were tried included:
-
Clipping data with extremes of equivalent width.
-
Binning to various periods ranging from 30 min through to 7 days.
-
Restricting the dataset to subsets within periods from 6 months through to 2 yr, in case differing activity levels over the period of the whole set were affecting the results.
-
Taking of residual spectra by dividing each spectrum by the mean of various-sized selections of the spectra with lowest equivalent widths6.
This yielded approximately 100 different treatments of the data. Each of these were processed with each Lomb-Scargle routine available.
For each measurement technique, we assessed the performance by considering how approximately how often it delivered:
-
The period of 82.6 days as the highest peak in theperiodogram.
-
The period of 82.6 days or the obvious sub-harmonic of half this period of 41.3 days as the highest peak.
-
The period of 82.6 days as one of the top 5 peaks in the periodogram.
-
The period of 82.6 days or 41.3 days as one of the top 5 peaks in the periodogram.
For equivalent widths the period of 82.6 days never appeared as the strongest peak, in 14% of the results as one of the top five peaks and 82.6 days or 41.3 days as one of the top five peaks in 43% of the results.
For peak ratios the period of 82.6 days appeared in 29% of the results as the strongest peak, in 48% of the results as one of the top five peaks and 82.6 days or 41.3 days as one of the top five peaks in 62% of the results.
Skewness and kurtosis measurements were intermediate in performance between these extremes but were much less affected by variations in the treatments of the data such as clipping, binning or restriction to subsets by date.
Again as with the ASAS and HST data, we checked for other periodic signals of up to the span of the data, but were unable to discern any strong period and in particular no sign of the 442-day period reported in Cincunegui et al. (2007; using measurements of the FWHM of the Hα line).
3.5. Comparison of ASAS and HARPS for period recovery
We chose to look in more detail at the ASAS data which offers similar sampling to the HARPS data discussed in Sect. 3.4 above. Of particular importance is the FAP of periods recovered from the spectroscopic data as well as the error bar from the calculated periods. None of the three Python routines directly return a FAP and the Numerical Recipes routine always returned an FAP of 1 if the periods were found at all, so we devised a Monte Carlo method of estimating this and at the same time estimating the uncertainty on the period recovered from the ASAS results.
The ASAS data has many more observation times than the spectroscopic data, with 970 points for each aperture, which even after binning to one day, reduces to 624 points. In contrast to this, the HARPS data studied in Sect. 3.4 has 260 spectra, which after clipping to less than 1 standard deviation above the median and binning as described in Sect. 3.3 reduces to 55 points.
 |
Fig. 5 Illustration of the effects of randomly selecting a given proportion of the ASAS data in terms of whether the same period of 82.6 days is recovered and the error in this result. The black vertical line represents the proportion of the ASAS data which corresponds to the number of spectra in the clipped and binned to one day HARPS data so that the relative performances of the spectroscopic results can be compared. |
To study how the performance of the recovery of the period is affected by the reduction in the data, we assumed for our purposes that the 82.6 day period is correct and tested how the recovery of this period is affected by random selection of subsets. First we took the ASAS data after binning to one day and then took various percentage-sized randomly-selected subsets of this data, recalculating the periods, noting whether a value close to the correct period was returned as the strongest peak, within the 5 strongest peaks, or not at all. If the period was recovered, we recorded the root mean square (rms) error, i.e. difference from 82.6 days. We took sizes of subset between 5% and 95% in steps of 5%. For each percentage sized subset, the process was repeated 2 000 times. The results are illustrated in Fig. 5.
In Fig. 5 are shown 4 results. On the X-axis is shown the percentage sized subset of the binned ASAS data which was used. On the left Y-axis is shown the percentage of recovery (i.e. 100% minus the FAP) of the correct period. On the right Y-axis is shown the rms error in the correctly-recovered period. The blue line shows the percentage recovery of the correct period as the strongest peak with various percentage sized subsets of the data. The green line shows the percentage recovery of the correct period as one of the five strongest peaks, not necessarily the strongest peak. It can be seen that the former reaches 100% recovery at about 70% and the latter at about 45%. The other two lines show the rms error in the correctly-returned results as various sized subsets of the data are selected. The purple line shows the rms error in the results corresponding to the case where only the strongest peak is selected and the red line that where the correct result is found in one of the top five peaks. It is noticeable that this reaches less than 0.1 days in both cases, lending weight to the conclusion that the uncertainty in the 82.6 day peak found by ASAS and HST is of the order of 0.1 days.
Finally we marked in, as the vertical black line in Fig. 5, the percentage sized subset of the data which corresponds to the number in the clipped and binned HARPS data (the binning was to one day also) so that a comparison can be made with the performance that against the ASAS data reduced to the same number of results. It can be seen that this intersects the blue line, representing the period found as the strongest peak, at just under 40% and the green line, where the period is found as one of the top five peaks, at just under 70%. As seen in Sect. 3.4 the corresponding figures for peak ratios on HARPS are 29% and 48% respectively and for equivalent widths 0% and 14%. With the same number of data points, therefore, the results from Hα peak ratios are roughly half as good as the photometric results and the equivalent width results are roughly a quarter as good as those for the peak ratios.
4. Modelling of Proxima Centauri spectra
In order to develop and refine the methods for evaluation of the periodicity of the sub-peaks in the Proxima Centauri spectra, we used a version of the “Doppler Tomography of Stars” (DoTS) modelling software (Collier-Cameron 2001). Although DoTS was written to recover surface imhomogeneities from time series spectra, here we use the forward modelling routines to generate synthetic spectra, with some modifications. Specifically, we construct a 3D model of the star, covered in a finite number of pixels. The intensity of each pixel can vary from a photospheric value to a value appropriate for plage. In order to obtain the appropriate photospheric intensity for each pixel at a given rotation phase of the 3D stellar model, we used the 4-parameter limb darkening law introduced by Claret from Phoenix model atmospheres (Claret 2000) for an effective temperature of 3000 K. The plage intensities were calculated according to Unruh et al. (1999, Sect. 4.1), who identified the centre to limb variability from plage regions relative to the photospheric (quiet) intensity for the Sun. Since no such observations exist for other stars, we adopted the same law with appropriate facular contrasts for Hα wavelengths (see Unruh et al. 1999, Figs. 3 and 4).
Since we wish to simulate the Hα line profile, a local intensity profile is assumed for the photosphere and the plage. For inactive photospheres of M-dwarfs of a similar spectral type to Proxima Centauri, Hα is not visible (e.g. see Hα profile in Barnes et al. 2014, Fig. 6, for GJ1061). Hence for the quiet photosphere, we assume a flat continuum. For active stars, Hα possesses a characteristic emission profile with self-absorption, resulting in a double-peaked profile. Since the v sin iis probably less than 0.1 km s-1 for Proxima Centauri, we based the local line profile shape for Hα on the observed Proxima Centauri line profile since it is unlikely to show rotational broadening. This profile was tuned to resemble the average Hα profile shown in the UVES data analysed in Fuhrmeister et al. (2011), but symmetric about the central wavelength. Specifically, we used a Gaussian profile to generate the emission peak and a second Gaussian with narrow width to represent the central self-absorption.
With our two-temperature model, in subsequent simulations, we assign either photospheric intensity or a plage intensity to each pixel. For a pixel containing plage, we thus scale the synthetic Hα profile and for the photosphere with no visible profile (as note above), we use the continuum level. The line profile is shifted appropriately for the Doppler shift of each pixel in our model. The model enables us to place circular spots of specified radii anywhere on the star. For each viewing angle (or equivalently observation phase), we calculate the appropriate intensity profiles of all visible pixels (according to position on the line and centre-to-limb variation) and sum them to obtain our simulated line profile.
A model star with plage regions that rotate into and out of view can thus potentially exhibit variability in the line shape since the pixels on different parts of the star possess different Doppler velocities. For stars such as Proxima Centauri, which possess a v sin imuch less than the instrumental resolution, any distortions in the line profile due to spots rotating into and out of view may be insignificant or very small. A plage region that rotates into view may nevertheless have a significant effect on the equivalent width of the simulated line since our local intensity profile for Hα possesses a normalised peak intensity of N times the continuum. For stars with rotational velocity much greater than the instrument resolution, line asymmetries are likely to be much more reliable.
4.1. Plage distribution and results
During the course of experimentation with models, we tried a selection of plage distributions, ranging from a single large spot on one face to randomly-placed spots of random sizes. However we found that the variation in equivalent widths from a low spot coverage bore no possible resemblance to that from observational data, in that just exhibited two extremes of equivalent widths and no intermediate values. On the other hand a coverage of more than about 30% provided very limited swings in the equivalent width compared those observed from HARPS and UVES. After some experimentation, we settled for randomly distributed plage of random sizes which filled up to 2.5% of the surface, towards the high end of the coverage of up to 2.7% reported in Guttenbrunner et al. (2014) in relation to the Sun. Equivalent widths were calculated for a variety of inclinations and starting periods. Peak ratios were evaluated, but the variations were too small to recover input periods. This was also the case for skewness and kurtosis measurements.
4.2. Adding in noise and flares
Despite the limitations of the simplistic model, it is clear that a good estimate of periodicity, to within ±0.1 days, may be obtained from the equivalent width method, although the peak ratio variations could not be reproduced and that method reliably applied. These results are for a noiseless set of models and to compare with reality the performance of the modelling results and the analysis methods in the presence of observational noise and also the influence of simulated flare events has to be considered.
As a first step in moving to something like actual observational data, we tried adding noise of a given signal to noise ratio over the whole of the simulated spectra and observed the effect on the accuracy of the periodicity measurements for various levels and inclinations. We tried adding Gaussian noise with signal-to-noise ratios (S/Ns) from 40 down to 1 in steps of 0.1. We tried this with all the combinations of inclinations and starting periods tried before.
It was noticeable that doing this only started to have any significant effect with S/N below 20. Below this level, two things started to happen, increasingly as the S/N was reduced. Either the error in the recovered period increased, although not by very much, up to ±0.5 days, alternatively the recovered period was manifestly incorrect, giving a clear False Positive such as returning a period of 50 days from a starting period of 80 days.
It was easy to discriminate between these two cases by setting a threshold of 5% for the difference between the recovered period and the starting period. If the difference exceeded this, then the period was regarded as incorrectly recovered, otherwise it was regarded as correctly recovered but with the given error. However in all the cases the difference was either substantially greater or substantially less than this. It was noticeable that in quite a number of cases a period close to 116 days was returned as a False Positive.
We also examined the possible effect of flares. We simulated the effect of flares by taking the spectra which were clipped as having excessive equivalent width in Sect. 3.3 and adding in the same proportionate excess over the median equivalent width to the model as was found in the observed data. The result was a poorer performance than with noise alone, but not by much. With just noise, the performance became markedly low with a S/N of 15 or below but adding flares as described significantly reduced the performance with a S/N of 20 or below. These values of S/N are much lower than the published values for UVES and HARPS, which are in both cases well over 100.
5. Discussion and conclusions
It is clear that the period of 82.6 ± 0.1 days given by the photometric results for ASAS and confirmed by HST must be the rotation period of Proxima Centauri, in line with Benedict et al. (1998) and confirmed by Kiraga & Stepien (2007). There is a near-zero FAP value and all the routines tried gave exactly the same result. We were not able to obtain as clear-cut results from spectroscopic methods involving analysis of the Hα peak of the Proxima Centauri spectra. The equivalent width and Hα index methods return very similar results but only return the 82.6 day period about 14% of the time, never as the strongest period. The peak ratio is about four times better.
There is also a strong peak of 106.3 ± 0.1 days on the ASAS results and in some of the spectroscopic results and the modelling, but not seen on the HST results. This period would appear to be a “beat” between the rotation period and an Earth year, which would not affect the HST results, which are far less constrained by the time of year.
It has proved possible to reproduce the 116.6 days of Suárez Mascareño et al. (2015, Table 3) in both the treatments of equivalent width and Hα index and in some of the other variants of the handling of those, together with periodograms taken from the skewness and kurtosis measurements, although not often as the strongest peak in the periodogram. Any kind of selection or binning of the data makes the 116.6-day figure disappear, as does adding in additional HARPS data subsequent to 2014. In addition, it was noticed that some of the modelling results which failed to give the expected period (see Sect. 4.2) also gave periods close to 116.6 days from the same observation times as in the HARPS data. From this analysis, we would have to discount this as a false positive, most probably an artefact of these observation times. As mentioned in Sect. 3.4, the window function of these observation times showed a small but distinct peak at 116.5 days which is further evidence of a false positive. This confirms the care which needs to be given where even with relatively extensive data, the two well-established activity indicators of Log(R′HK) and Hα can given the same period which is different from the correct period albeit with rather low significance.
Limiting the portion of the spectrum to just the Hα line of Proxima Centauri, even with the instrumental stability of HARPS, was proven to be less useful than ASAS ground-based photometry for the recovery of period. A future line of investigation which might be worth considering is that of combining fluxes from various magnetic/activity sensitive lines in various spectral orders to re-evaluate the composite spectral index referred to in Hall & Lockwood (1999, 2000).
We were able to reproduce the variations in equivalent width seen in Proxima Centauri using the DoTS model and show that the recovery of the rotation period has validity. However, even with extensive experimentation, including relatively extreme values for the various parameters for limb-darkening and contrast or extreme distributions of plage, we could not model the observed variations in peak ratio found either in the HARPS or UVES data. It is clear that the variations in the two sub-peaks that are purely due to Doppler shift from the rotational velocity are not large; with a radius of 0.141 Solar (Demory et al. 2009) and assuming a period of the order of 80 days the rotational velocity is at most 90 m s-1 yielding a Doppler shift of at most 0.003 Å in the Hα line between the extremes of the disk and the centre, far too low to reproduce the variations in the sub-peaks in the Hα line profile as illustrated in Fig. 2, for which the peak ratios were calculated in Sect. 3.2 as 0.994 ± 0.017, whereas the best standard deviation on a peak ratio close to 1.0 which could be obtained from the models was 2 × 10-5 or 2 × 10-4 for very extreme plage distributions. This was not surprising due to the lack of Doppler broadening of the line profile.
It is clear that the 2D model of static plage and spots supported by DoTS cannot reproduce the observed variations in the peak ratios. Likewise it cannot reproduce the range of phenomena which adversely affects obtaining periodicity from the equivalent widths. We did consider the possibility of differential rotation affecting the spectroscopic results, but discounted this in the light of finding no evidence in the available datasets and Barnes et al. (2005), which argues that differential rotation decreases with decreasing stellar mass.
This points to the need for a 3D model including vertical processes to properly understand the behaviour of Proxima Centauri. In Mohanty et al. (2002) and Mohanty & Basri (2003), where the activity of late M-dwarfs is found to be less closely tied to the rotation period than for earlier type stars, the authors propose a “turbulent dynamo” as the source of the activity, for which a 3D model is required. In consideration of this, we note the success of 3D magnetohydrodynamic simulation for the Sun in Leenaarts et al. (2012) and also the work on seismic shock waves such as in Donea et al. (2006). Similar conclusions are reached by Rauscher & Marcy (2006) as an explanation for H, K and Ca line asymmetry, where-the authors suggest that this is caused by slowly-decelerating motion toward the observer which does not fall back ballistically.
This can be obtained from http://numerical.recipes/
Acknowledgments
The HARPS data was obtained from HARPS public database at the European Southern Observatory (ESO), programs 072.C-0488(E), 082.C-0718(B), 183.C-0437(A) and 191.C-0505(A). We also wish to thank Birgit Fuhrmeister and Lalitha Sairam for providing us with some additional data referred to in Fuhrmeister et al. (2011). We acknowledge the value of the Vienna Atomic Line Database (VALD) for spectral line data and the ASAS for additional observations of Proxima Centauri. All the figures were produced via Python programs developed by the authors using the MATPLOTLIB libary, which is associated with the SCIPY library (Jones et al. 2001). We are grateful to the anonymous referee for his or her kind assistance in recommending significant improvements to prepare this paper for publication. Hugh R. A. Jones and John R. Barnes were supported by the Science and Technology Facilities Council grants ST/M001008/1 and ST/L000776/1 and Hugh R. A. Jones also by Leverhulme Trust grant, RPG- 2014-281.
References
- Anglada-Escudé, G., Amado, P. J., Barnes, J., et al. 2016, Nature, 536, 437 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Barnes, J. R., Collier Cameron, A., Donati, J.-F., et al. 2005, in 13th Cambridge Workshop on Cool Stars, Stellar Systems and the Sun, eds. F. Favata, G. A. J. Hussain, & B. Battrick, ESA SP, 560, 95 [Google Scholar]
- Barnes, J. R., Jenkins, J. S., Jones, H. R. A., et al. 2014, MNRAS, 439, 3094 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B., Nelan, E., et al. 1992, in BAAS, AAS Meeting Abstracts, 24, 1230 [Google Scholar]
- Benedict, G. F., Nelan, E., McArthur, B., et al. 1993, PASP, 105, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Benedict, G. F., McArthur, B., Nelan, E., et al. 1998, AJ, 116, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Cincunegui, C., Díaz, R. F., & Mauas, P. J. D. 2007, A&A, 461, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2000, A&A, 363, 1081 [NASA ADS] [Google Scholar]
- Collier-Cameron, A. 2001, Astrotomography, Lect. Notes Phys. (Springer) [Google Scholar]
- Davenport, J. R. A., Kipping, D. M., Sasselov, D., Matthews, J. M., & Cameron, C. 2016, ApJ, 829, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, R. I., & Fabrycky, D. C. 2010, ApJ, 722, 937 [NASA ADS] [CrossRef] [Google Scholar]
- Demory, B.-O., Ségransan, D., Forveille, T., et al. 2009, A&A, 505, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donea, A.-C., Besliu-Ionescu, D., Cally, P. S., Lindsey, C., & Zharkova, V. V. 2006, Sol. Phys., 239, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Feinstein, A. 1976, in Be and Shell Stars, ed. A. Slettebak, IAU Symp., 70, 149 [Google Scholar]
- Fuhrmeister, B., Lalitha, S., Poppenhaeger, K., et al. 2011, A&A, 534, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., & Bonfils, X. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 1117 [Google Scholar]
- Guinan, E. F., & Morgan, N. D. 1996, in BAAS, 28, 942 [Google Scholar]
- Guttenbrunner, S., Hanslmeier, A., Utz, D., et al. 2014, Central European Astrophysical Bulletin, 38, 81 [NASA ADS] [Google Scholar]
- Hall, J. C., & Lockwood, G. W. 1999, in BAAS, AAS Meeting Abstracts, 1531, 31 [Google Scholar]
- Hall, J. C., & Lockwood, G. W. 2000, ApJ, 541, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Hatzes, A. P. 2016, A&A, 585, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenkins, J. S., Ramsey, L. W., Jones, H. R. A., et al. 2009, ApJ, 704, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python [Google Scholar]
- Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
- Kürster, M., Hatzes, A. P., Cochran, W. D., et al. 1999, A&A, 344, L5 [NASA ADS] [Google Scholar]
- Leenaarts, J., Carlsson, M., & Rouppe van der Voort, L. 2012, ApJ, 749, 136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mohanty, S., & Basri, G. 2003, ApJ, 583, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Basri, G., Shu, F., Allard, F., & Chabrier, G. 2002, ApJ, 571, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Pojmanski, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
- Rauscher, E., & Marcy, G. W. 2006, PASP, 118, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2008, ApJ, 684, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Mrotzek, N., Lemke, U., Hinrichs, J., & Reinsch, K. 2016, A&A, 587, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribas, I., Bolmont, E., Selsis, F., et al. 2016, A&A, 596, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robertson, P., & Mahadevan, S. 2014, ApJ, 793, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., & Anglada-Escudé, G. 2013, A&A, 556, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unruh, Y. C., Solanki, S. K., & Fligge, M. 1999, A&A, 345, 635 [NASA ADS] [Google Scholar]
- Vanderplas, J., Connolly, A., Ivezić, Ž., & Gray, A. 2012, in Conference on Intelligent Data Understanding (CIDU), 47 [Google Scholar]
- VanderPlas, J. T., & Ivezić, Ž. 2015, ApJ, 812, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Winters, J. G., Henry, T. J., Lurie, J. C., et al. 2015, AJ, 149, 5 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Upper panel: periodogram derived from the ASAS database for Proxima Centauri second aperture, binned to 1 day. Lower panel: periodogram derived from the HST data discussed in Benedict et al. (1998). FAP values for the strongest peaks were calculated and are shown as the dotted lines. Both periodograms are computed using the using the Numerical Recipes Lomb-Scargle routine. |
| In the text | |
 |
Fig. 2 The Hα region of example spectra of Proxima Centauri taken from HARPS on 27 May 2004 02:10:14 UTC (black) and 15 March 2006 09:16:35 (brown). The region delineated with the dark red solid vertical lines shows the region used for calculation of the Hα equivalent width in this paper. The regions shaded in red and blue respectively show the regions used for calculation of the sizes of the two sub-peaks. The vertical purple lines mark the region chosen for calculation of the equivalent width and the vertical green lines mark the region chosen in Suárez Mascareño et al. (2015) for calculation of the Hα index. |
| In the text | |
 |
Fig. 3 Histograms of equivalent widths for UVES in blue and HARPS in green, expressed as percentages with the same X axis scale. All the UVES spectra results are shown apart from those for one which appeared to be just noise (12 March 2009 UTC 02:31:11). HARPS spectra are omitted for four outlying cases which appeared to be dominated by flares at 16 July 2004 UTC 01:52:40, 27 March 2011 UTC 05:20:09, 05 May 2013 UTC 03:31:16 and 5 May 2013 UTC 03:41:47 with values of 21.69, 18.12, 6.76 and 6.19 respectively. |
| In the text | |
 |
Fig. 4 Sample periodograms from the Hα peak of the HARPS data, for the range between 40 days and 130 days in steps of 0.01 days. Top panel: periodogram derived from the equivalent widths (EW) and the bottom panels ones derived from the peak ratios (PR). None have any clipping or binning of the data. The strongest five peaks are marked on the vertical black lines. |
| In the text | |
 |
Fig. 5 Illustration of the effects of randomly selecting a given proportion of the ASAS data in terms of whether the same period of 82.6 days is recovered and the error in this result. The black vertical line represents the proportion of the ASAS data which corresponds to the number of spectra in the clipped and binned to one day HARPS data so that the relative performances of the spectroscopic results can be compared. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


