| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 22 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629702 | |
| Published online | 04 April 2017 | |
Coronal loop seismology using damping of standing kink oscillations by mode coupling
II. additional physical effects and Bayesian analysis
Centre for Fusion, Space and Astrophysics, Department of Physics, University of Warwick, CV4 7AL, UK
e-mail: D.J.Pascoe@warwick.ac.uk
Received: 12 September 2016
Accepted: 18 January 2017
Context. The strong damping of kink oscillations of coronal loops can be explained by mode coupling. The damping envelope depends on the transverse density profile of the loop. Observational measurements of the damping envelope have been used to determine the transverse loop structure which is important for understanding other physical processes such as heating.
Aims. The general damping envelope describing the mode coupling of kink waves consists of a Gaussian damping regime followed by an exponential damping regime. Recent observational detection of these damping regimes has been employed as a seismological tool. We extend the description of the damping behaviour to account for additional physical effects, namely a time-dependent period of oscillation, the presence of additional longitudinal harmonics, and the decayless regime of standing kink oscillations.
Methods. We examine four examples of standing kink oscillations observed by the Atmospheric Imaging Assembly (AIA) onboard the Solar Dynamics Observatory (SDO). We use forward modelling of the loop position and investigate the dependence on the model parameters using Bayesian inference and Markov chain Monte Carlo (MCMC) sampling.
Results. Our improvements to the physical model combined with the use of Bayesian inference and MCMC produce improved estimates of model parameters and their uncertainties. Calculation of the Bayes factor also allows us to compare the suitability of different physical models. We also use a new method based on spline interpolation of the zeroes of the oscillation to accurately describe the background trend of the oscillating loop.
Conclusions. This powerful and robust method allows for accurate seismology of coronal loops, in particular the transverse density profile, and potentially reveals additional physical effects.
Key words: magnetohydrodynamics (MHD) / Sun: atmosphere / Sun: corona / Sun: magnetic fields / Sun: oscillations / waves
© ESO, 2017
1. Introduction
Standing kink oscillations of coronal loops were first observed using the Transition Region And Coronal Explorer (TRACE; Aschwanden et al. 1999, 2002; Nakariakov et al. 1999). Modern instruments such as the Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) of the Solar Dynamics Observatory (SDO) have made their detection routine (e.g., Zimovets & Nakariakov 2015; Goddard et al. 2016). Coronal seismology uses observations of various magnetohydrodynamic (MHD) waves in the solar atmosphere to reveal fundamental plasma parameters (e.g., reviews by Stepanov et al. 2012; De Moortel & Nakariakov 2012; Pascoe 2014; De Moortel et al. 2016). In particular, standing kink oscillations are commonly used to estimate the magnetic field strength (e.g., Nakariakov et al. 1999; Nakariakov & Ofman 2001; Van Doorsselaere et al. 2008; White & Verwichte 2012; Verwichte et al. 2013). MHD waves also attract interest because of their possible role in coronal heating and solar wind acceleration (e.g., reviews by Ofman 2010; Parnell & De Moortel 2012; Arregui 2015).
Another seismological application of kink modes is based on their strong damping after impulsive excitation. This damping is attributed to resonant absorption which is a form of mode coupling that occurs in coronal loops with a smooth transition between the high density plasma in their core and the background plasma. Inside this inhomogeneous layer there is a continuous range of Alfvén speeds and energy is transferred from the collective kink oscillation to a local, observationally unresolved Alfvén mode where the local Alfvén speed matches the kink speed Ck. This is a robust mechanism first discussed by Sedláček (1971) and also proposed as a plasma heating mechanism (Chen & Hasegawa 1974; Ionson 1978). Hollweg & Yang (1988) estimated that for coronal conditions the oscillations would be strongly damped. After the discovery of standing kink oscillations by TRACE it was revisited by Ruderman & Roberts (2002) and Goossens et al. (2002) to account for the damping which was indeed strong. Ruderman & Roberts (2002) calculated the inhomogeneous layer width for the oscillating loop observed by Nakariakov et al. (1999), and Goossens et al. (2002) calculated the layer width for 11 loop oscillations reported in Ofman & Aschwanden (2002), with both studies assuming the loops to be 10 times denser than the surrounding plasma. Aschwanden et al. (2003) extended these studies with independent estimates for the loop density contrast ratios based on TRACE 171 Å cross-sectional flux profiles. The density contrast ratios differing by a factor ~ 2 from those predicted using the oscillation damping time was attributed to the presence of hotter plasma not detected by TRACE 171 Å. Arregui et al. (2007) and Goossens et al. (2008) considered more general sesimological inversion strategies which include the Alfvén transit time in addition to the loop density profile parameters.
Initial application of mode coupling to account for the damping of kink modes of coronal loops produced analytical descriptions in the form of an exponential envelope (Ruderman & Roberts 2002; Goossens et al. 2002). On the other hand, numerical simulations by Pascoe et al. (2010, 2012) demonstrated that the predicted exponential envelope did not fully describe the damping behaviour and that a Gaussian envelope could be more suitable. This apparent contradiction was resolved by Hood et al. (2013) who produced an analytical description for the damping envelope for all times rather than just the asymptotic state. Accordingly, it can be seen that the Gaussian and exponential damping envelopes are approximations for the non-linear damping envelope which are applicable for early and late times, respectively. Pascoe et al. (2013) produced a general approximation for the damping envelope which consists of these two (Gaussian and exponential) approximations combined together and operating in different stages of the oscillation damping. Numerical simulations performed by Ruderman & Terradas (2013) also demonstrated the Gaussian and exponential regimes. Observational evidence for the Gaussian damping regime was found in TRACE data by De Moortel et al. (2002) and Ireland & De Moortel (2002), and in SDO data by Pascoe et al. (2016c), and supported by the statistical analysis of Morton & Mooroogen (2016). Pascoe et al. (2016b; Paper I hereafter) produced the first seismological inversions of the transverse density profile using the general damping envelope.
In this paper we extend the seismological analysis of standing kink oscillations in Paper I to include additional physical effects. In Sect. 2 we describe the seismological method used, in particular the modifications to describe the time-dependent period of oscillation, additional longitudinal harmonics, and the decayless regime of kink oscillations. We also describe our novel procedure for describing the background trend and the Bayesian inference method used in our analysis. Our results are presented in Sect. 3 where we apply several different models to four observations of oscillating loops. Discussion and conclusions are in Sect. 4.
2. Damping of kink oscillations by mode coupling
 |
Fig. 1 Illustration of the principle of seismological inversion based on kink damping envelope. The two density profiles (left panels) produce the same overall damping rate for their corresponding kink oscillations (right panels). However, they can be distinguished based on the shape of the damping envelope, characterised by the switch time ts (vertical dashed lines). |
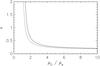 |
Fig. 2 The inverse relationship between the density contrast ratio and the inhomogeneous layer width ϵ. The curves in parameter space correspond to the same kink oscillation damping rate due to mode coupling (Fig. 1 shows two particular density profiles). The solid curve corresponds to the damping rate calculated using the general damping profile (Eq. (1)) while the dashed curve is for the exponential damping regime alone. |
The damping behaviour of kink oscillations depends on the transverse structure of the oscillating loop. The transverse density profile can be characterised by the ratio of the internal plasma density ρ0 to the external density ρe, and by the width of the inhomogeneous layer l within which mode coupling takes place. For a loop with (minor) radius R, the normalised inhomogeneous layer width is ϵ = l/R. It is also convenient to introduce the parameter κ = (ρ0−ρe)/(ρ0 + ρe) as a ratio of the plasma densities. The general damping profile (Pascoe et al. 2013, 2016b) for standing kink waves is then 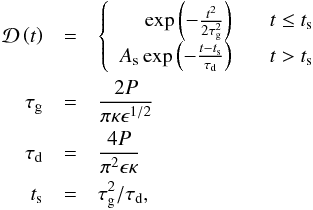 (1)where
(1)where 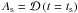 is the amplitude at the time ts when the switch between Gaussian and exponential damping profiles occurs. Here it is assumed that the oscillation is excited at time t = 0. Figure 1 shows two examples of the density profiles (left panels) and the corresponding damping envelopes (right panels). The two loop density profiles have been chosen to give the same overall damping rate, taken to be 90% attenuation after six cycles (t = 6P). The top panels represent the case of a loop with a low density contrast and a large inhomogeneous layer while the bottom panels are the case of a loop with a larger density contrast ratio and thinner inhomogeneous layer. There is an infinite number of such solutions which reproduce the observed behaviour if only the damping rate is considered and not also the shape of the damping profile, represented by the solid curve in parameter space shown in Fig. 2. This curve is based on the general damping profile Eq. (1) and is qualitatively the same as that for the exponential damping regime (dashed curve) alone which has been discussed by previous authors (e.g., Goossens et al. 2008; Arregui & Asensio Ramos 2014). A seismological inversion for the density profile parameters (ρ0/ρe, ϵ) based only on the overall damping rate produces a 1D curve in the 2D parameter space due to the problem being ill-posed. However, the inclusion of the additional information from the shape of the damping envelope, characterised by the parameter ts, makes the problem well-posed. For example, in Fig. 1, the loop with the lower density contrast and larger ϵ (top panel) is distinguished from the loop with the larger density contrast and smaller ϵ (bottom panel) by its later switch time ts, even though both loops have the same overall damping rate. However, the extent to which the structuring parameters may be constrained will still be affected by the inverse relationship shown in Fig. 2 (in addition to observational uncertainties). The parametric curve is asymptotic in the limits ρ0/ρe → 1 and ρ0/ρe → ∞. Consequently, when the observational data (damping envelope) implies a loop with a small density contrast ρ0/ρe ≳ 1, then ϵ will be less well constrained than for a large contrast ρ0/ρe ≳ 5 for which ϵ is almost independent of density contrast.
is the amplitude at the time ts when the switch between Gaussian and exponential damping profiles occurs. Here it is assumed that the oscillation is excited at time t = 0. Figure 1 shows two examples of the density profiles (left panels) and the corresponding damping envelopes (right panels). The two loop density profiles have been chosen to give the same overall damping rate, taken to be 90% attenuation after six cycles (t = 6P). The top panels represent the case of a loop with a low density contrast and a large inhomogeneous layer while the bottom panels are the case of a loop with a larger density contrast ratio and thinner inhomogeneous layer. There is an infinite number of such solutions which reproduce the observed behaviour if only the damping rate is considered and not also the shape of the damping profile, represented by the solid curve in parameter space shown in Fig. 2. This curve is based on the general damping profile Eq. (1) and is qualitatively the same as that for the exponential damping regime (dashed curve) alone which has been discussed by previous authors (e.g., Goossens et al. 2008; Arregui & Asensio Ramos 2014). A seismological inversion for the density profile parameters (ρ0/ρe, ϵ) based only on the overall damping rate produces a 1D curve in the 2D parameter space due to the problem being ill-posed. However, the inclusion of the additional information from the shape of the damping envelope, characterised by the parameter ts, makes the problem well-posed. For example, in Fig. 1, the loop with the lower density contrast and larger ϵ (top panel) is distinguished from the loop with the larger density contrast and smaller ϵ (bottom panel) by its later switch time ts, even though both loops have the same overall damping rate. However, the extent to which the structuring parameters may be constrained will still be affected by the inverse relationship shown in Fig. 2 (in addition to observational uncertainties). The parametric curve is asymptotic in the limits ρ0/ρe → 1 and ρ0/ρe → ∞. Consequently, when the observational data (damping envelope) implies a loop with a small density contrast ρ0/ρe ≳ 1, then ϵ will be less well constrained than for a large contrast ρ0/ρe ≳ 5 for which ϵ is almost independent of density contrast.
The model discussed so far is based on the presence of a single standing kink mode (the fundamental mode) with a constant period of oscillation. For the analysis in this paper, we extend this model to include a number of additional physical effects, namely a time-dependent period of oscillation, the presence of additional longitudinal harmonics (with and without longitudinal structuring), and the decayless regime of kink oscillations. Each of these are discussed below, as are the methods of Bayesian inference and Markov chain Monte Carlo (MCMC) sampling we use to test our models against the observational data, and our procedure for the background trend which describes an evolving equilibrium position about which the loop oscillates.
2.1. Time-dependent period of oscillation
The data analysed by Pascoe et al. (2016c,b) was limited by the demand that the period of oscillation remained constant. This is evident in, for example, Fig. 2 of Pascoe et al. (2016c), which shows the fitted oscillations stopping before the end of the data. Beyond these times, the loops continue to oscillate but if the fitted oscillation (with constant period) were extended it would move out of phase with the observational data and so would no longer represent a meaningful comparison. In the present paper, we relax the requirement of oscillations having a constant period and so allow longer time series to be considered. If we consider the period of oscillation of the fundamental standing kink mode as Pk = 2L/Ck then the period of oscillation may vary in time either due to changes in the loop length L and/or the kink speed Ck. The kink speed depends on the Alfvén speeds inside and outside the loop, which also determine the damping rate of kink oscillations by mode coupling. Furthermore, these are parameters we are typically interested in using our seismological method to determine and so independent observational evidence for their variation in time is unlikely. We therefore choose to consider the case of variations in period arising due to changes in loop length alone, i.e. we use the approximation that the transverse density profile remains unchanged during the oscillation. Since we intend the period of oscillation to be weakly varying we consider a low-order polynomial to describe its evolution; 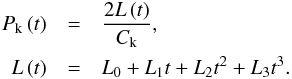 (2)Our use of a polynomial (rather than a linear trend) allows us to consider the general case of the period of oscillation increasing and/or decreasing during the oscillation, and for the rate of change to vary in time.
(2)Our use of a polynomial (rather than a linear trend) allows us to consider the general case of the period of oscillation increasing and/or decreasing during the oscillation, and for the rate of change to vary in time.
We note that although we consider the transverse loop structure to be constant, our time-dependent period of oscillation requires that the Gaussian and exponential damping times are also time-dependent since τg,d ∝ P. In this way our model differs from that of Morton & Mooroogen (2016) who consider the Gaussian damping regime with a time-dependent period of oscillation but a constant damping time characterised by the constant a4 in their Eq. (5). Their model therefore corresponds to changes in period being accompanied by changes in the transverse density profile such that τg remains constant. Changes in the period of oscillation of kink modes have been investigated using wavelet analysis by De Moortel et al. (2002) and Ireland & De Moortel (2002, these two studies also include the shape of the damping profile as a fitted parameter). White et al. (2013) and Morton & Mooroogen (2016) fit loop oscillations using a period of oscillation that varies linearly in time (and all were found to increase). Nisticò et al. (2013) related the (linear) increase of the decayless kink oscillation period to the observed expansion of the loop. Russell et al. (2015) examined the relationship between loop contraction and oscillation to changes in the magnetic environment produced by flares, while Hayes et al. (2016) have recently measured an increase in loop length during the decay phase of a flare.
For the purpose of analysing the loop oscillations we rewrite Eq. (2) since the loop length itself is not a parameter in our model (though it may be estimated separately as in Table 3). Instead we consider the Alfvén transit time TA = L/vA and then obtain 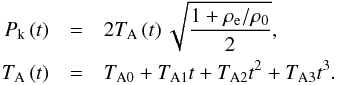 (3)Since we assume for simplicity there are no changes in density, the time-dependence of TA is most simply associated with changes in loop length as discussed above.
(3)Since we assume for simplicity there are no changes in density, the time-dependence of TA is most simply associated with changes in loop length as discussed above.
2.2. Longitudinal harmonics
 |
Fig. 3 Dependence of period ratios P1/ 2P2 (solid lines) and P1/ 3P3 (dashed lines) on the density scale height H (top panel) and loop expansion factor Γ (bottom panel). |
Several observations of standing kink waves in coronal loops suggest the presence of longitudinal harmonics other than, or in addition to, the fundamental mode (e.g., Verwichte et al. 2004; De Moortel & Brady 2007; Van Doorsselaere et al. 2007; Zaqarashvili et al. 2013; Kupriyanova et al. 2013; Kolotkov et al. 2015; Pascoe et al. 2016a).
White et al. (2012) interpret their observation as either a second or third longitudinal harmonic with vertical polarisation, while Yuan & Van Doorsselaere (2016) favour the third harmonic with a horizontal polarisation for this oscillation. Van Doorsselaere et al. (2009) demonstrate that horizontally and vertically polarised kink waves have effectively the same period of oscillation and so the polarisation is not important in terms of the damping behaviour, although it may provide information about the excitation mechanism.
For each of the loops in this paper we consider a single time series i.e. without spatial information. Furthermore, the loops were initially selected on the basis of exhibiting a clear (single) period of oscillation. However, it is also evident that the loops have an aharmonic shape to the oscillation at the beginning. Our primary motivation for considering additional harmonics in this paper is therefore to account for this aharmonic shape. We therefore expect the amplitudes of the higher harmonics to be small in comparison to the fundamental mode. However, they may also have important consequences for seismology since observations of higher harmonics can also provide additional information about the longitudinal structuring of the loop (e.g., review by Andries et al. 2009).
We limit our model to the first, second, and third harmonic standing modes. Each harmonic is a sinusoidal oscillation with the damping profile given in Eq. (1). We distinguish the parameters of the different harmonics with the addition of a subscript corresponding to the order n, e.g., the periods of oscillation for the fundamental, second, and third harmonic are P1, P2, and P3, respectively.
The damping behaviour due to mode coupling is based on the long wavelength approximation for which the kink mode experiences no geometrical dispersion and so the phase speed is the kink speed Ck (Edwin & Roberts 1983). The period of oscillation for the nth harmonic is then 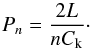 (4)The dispersionless and longitudinally uniform model therefore corresponds to the harmonics having frequencies that are integer multiples of the fundamental mode, i.e. P2 = P1/ 2 and P3 = P1/ 3.
(4)The dispersionless and longitudinally uniform model therefore corresponds to the harmonics having frequencies that are integer multiples of the fundamental mode, i.e. P2 = P1/ 2 and P3 = P1/ 3.
However, there have been numerous studies of the effect of longitudinal structuring on the period of standing kink modes. Variation of plasma parameters along the loop can modify the period of oscillation of different harmonics by different amounts such that P1/nPn ≠ 1. We consider two such models in this paper; longitudinal structuring due to density stratification, and longitudinal structuring due to loop expansion.
The effect of longitudinal stratification on period ratio has been considered by several authors (e.g., Andries et al. 2005; Safari et al. 2007; McEwan et al. 2008) and the period ratio of the fundamental and second harmonic has been used to estimate the coronal density scale height (e.g., Andries et al. 2005; Van Doorsselaere et al. 2007). For the modification of the periods of the longitudinal harmonics by density stratification we use the model considered by Andries et al. (2005) and Safari et al. (2007) which gives ![\begin{eqnarray} P_\textrm{1} &=& P_\textrm{k}/\left( 1 + L/3 \pi^2 H \right), \nonumber \\[1mm] P_\textrm{2} &=& P_\textrm{k}/2 \left( 1 + L/15 \pi^2 H \right), \nonumber \\[1mm] P_\textrm{3} &=& P_\textrm{k}/3 \left( 1 + L/35 \pi^2 H \right), \label{eq:stratified} \end{eqnarray}](/articles/aa/full_html/2017/04/aa29702-16/aa29702-16-eq44.png) (5)where H is the density scale height and the density decreases with height z as ∝exp(−L/πHsinπz/L). We consider Pk to be a function of time as given by Eq. (3).
(5)where H is the density scale height and the density decreases with height z as ∝exp(−L/πHsinπz/L). We consider Pk to be a function of time as given by Eq. (3).
Verth & Erdélyi (2008) studied the effect of longitudinal magnetic and density inhomogeneities on kink oscillations. In particular we consider their model for flux tube expansion with constant density which gives the periods of the longitudinal harmonics as ![\begin{eqnarray} \gamma &=& \arctan^{2} \left( \sqrt{\Gamma^2 - 1} \right), \nonumber \\[1mm] P_\textrm{1} &=& P_\textrm{k}, \nonumber \\[1mm] P_\textrm{2} &=& P_\textrm{k} \sqrt{\left( \pi^2/4 - \gamma \right)/\left(\pi^2 - \gamma \right)}, \nonumber \\[1mm] P_\textrm{3} &=& P_\textrm{k} \sqrt{\left( \pi^2/4 - \gamma \right)/\left(9 \pi^2/4 - \gamma \right)}, \label{eq:expanding} \end{eqnarray}](/articles/aa/full_html/2017/04/aa29702-16/aa29702-16-eq49.png) (6)where Γ is the loop expansion factor, defined as the ratio of the loop radius at the apex to the radius at the footpoints.
(6)where Γ is the loop expansion factor, defined as the ratio of the loop radius at the apex to the radius at the footpoints.
These two longitudinally structured models describe loops with a constant loop density contrast. We further assume that ϵ is constant and so the structuring modifies the period ratios P1/nPn with constant signal qualities τg,d/P for each harmonic as given in Eq. (1). These models provide analytical relationships for the periods of oscillation in terms of a single additional parameter with a physical meaning, i.e. the density scale height H for a stratified loop, and the expansion factor Γ for an expanding loop, rather than a more general approach where each Pn is considered independently and with no physical constraint. Figure 3 shows the dependence of the period ratios on the structuring parameters H and Γ. The loop expansion model describes period ratios P1/nPn greater than unity, while stratification can account for ratios both greater and less than unity. A period ratio greater than unity is therefore consistent with either an expanding loop, or a negative scale height (i.e. denser at the apex than at the footpoints) which has been considered for coronal loops (Andries et al. 2005; Pascoe et al. 2016a) and prominence threads (Soler et al. 2015; Arregui & Soler 2015).
2.3. Decayless component
The high-resolution imaging data provided by SDO led to the discovery of the low-amplitude decayless regime of coronal loop kink oscillations (Nisticò et al. 2013; Anfinogentov et al. 2013). High-amplitude decaying kink oscillations were initially suggested to be excited by blast-waves launched by flares (e.g., McLaughlin & Ofman 2008; Pascoe et al. 2009; De Moortel & Pascoe 2009; Pascoe & De Moortel 2014). A statistical study by Zimovets & Nakariakov (2015) shows that the majority of cases (but not all of them) are associated with low-coronal eruptions. In comparison, the decayless oscillations appear to be ubiquitous in active regions (Anfinogentov et al. 2015). Their excitation mechanism is not fully understood but has been modelled as a self-oscillatory process (Nakariakov et al. 2016). The driving mechanism for decayless standing modes might also be connected to the ubiquitous propagating kink waves discovered by Tomczyk et al. (2007). The transverse velocity perturbations have a broadband spectrum with a period of about 5 min and are strongly damped in coronal loops (Tomczyk & McIntosh 2009) which has also been explained in terms of mode coupling (e.g., Pascoe et al. 2010, 2011, 2015; Terradas et al. 2010; Verth et al. 2010; Goossens et al. 2012).
Loop #3 considered below has been studied by Nisticò et al. (2013) for exhibiting decayless oscillations before and after a large amplitude decaying oscillation associated with a flare. In our model, the decayless component is assumed to be a low amplitude and undamped fundamental standing mode with a period of oscillation P1 and amplitude A0. We may consider the decayless component as having a phase difference φ0 relative to the decaying components before the large amplitude perturbations are generated, although after this time it is required to be in phase with the decaying fundamental mode. However, here we only consider the oscillation after the impulsive excitation and so this parameter is not required in our modelling.
The models we consider therefore consist of up to four oscillatory components, in addition to the background trend (discussed in Sect. 2.5). The transverse displacement of the loop 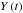 measured at a certain location (see slits in Fig. 5) is
measured at a certain location (see slits in Fig. 5) is ![\begin{eqnarray} Y \left( t \right) &=& \left[ A_\textrm{0} + A_\textrm{1} \mathcal{D}_\textrm{1} \left( \tilde{t} \right) \right] \sin \left( \frac{2 \pi \tilde{t}}{P_\textrm{1}} \right) \nonumber \\ &&+ A_\textrm{2} \mathcal{D}_\textrm{2} \left( \tilde{t} \right) \sin \left( \frac{2 \pi \tilde{t}}{P_\textrm{2}} + \phi_\textrm{2} \right) \nonumber \\ &&+ A_\textrm{3} \mathcal{D}_\textrm{3} \left( \tilde{t} \right) \sin \left( \frac{2 \pi \tilde{t}}{P_\textrm{3}} + \phi_\textrm{3} \right), \label{eq:model} \end{eqnarray}](/articles/aa/full_html/2017/04/aa29702-16/aa29702-16-eq56.png) (7)where
(7)where 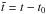 is the time after the start of the oscillation t0 and
is the time after the start of the oscillation t0 and 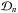 is the damping envelope for the nth harmonic given by Eq. (1) with
is the damping envelope for the nth harmonic given by Eq. (1) with 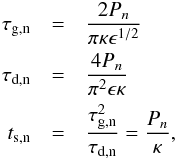 (8)where Pn is determined either by the dispersionless condition P1/nPn = 1 or by one of the longitudinally structured models given by Eqs. (5) or (6) and described in Sect. 2.2. We note that we assume all harmonics are damped by the same mechanism of resonant absorption.
(8)where Pn is determined either by the dispersionless condition P1/nPn = 1 or by one of the longitudinally structured models given by Eqs. (5) or (6) and described in Sect. 2.2. We note that we assume all harmonics are damped by the same mechanism of resonant absorption.
2.4. Bayesian inference
In Paper I, model parameters were determined by a Levenberg-Marquardt least-squares fit to the data using MPFIT (Markwardt 2009), with each point weighted according to its error (as estimated by the GAUSSFIT model of the transverse intensity profile using IDL). In this paper we instead use a method based on Bayesian inference. Bayesian analysis allows for robust estimation of the dependence of the model output on the input parameters. It has been successfully applied to the seismological inference of coronal loop parameters from the observations of damped kink oscillations (e.g., Arregui et al. 2013a, 2015; Arregui & Asensio Ramos 2011). Arregui et al. (2013b) describe a version of the seismological inversion technique using the Gaussian and exponential damping regimes based on Bayesian analysis, while Arregui & Asensio Ramos (2014) consider Bayesian analysis of the ill-posed case i.e. the exponential damping regime only.
In general, a parameter inference problem implies that the observed data D can be explained in terms of a model M having parameter set θ = [ θ1,θ2,...,θN ]. Thus, the aim is to find the value of parameters θ that gives the best possible agreement with the observed data D. The formulation of Bayesian parameter inference relies on three main definitions:
-
1.
The prior probability density function (PDF) P(θ) represents our knowledge about the model parameters θ before considering the observational data D. For example, this could be knowledge from previous measurements or a requirement that the particular model parameter lies inside a certain range.
-
2.
The sampling PDF P(D | θ) describes the conditional probability to obtain the observed data D for a fixed value θ of the model parameters. The likelihood function is P(D | θ) considered as a function of θ with fixed D. We note that the likelihood is not a PDF. In particular, its integral over θ is not equal to unity.
-
3.
The posterior PDF P(θ | D) describes the conditional probability that the model parameters are equal to θ under condition of observed data being equal to D. This function represents our knowledge about the model parameters θ after the observation, when the observed data D is known and fixed.
The Bayes theorem connects prior and posterior probability density functions and describes how the observational data D affects our knowledge about model parameters θ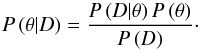 (9)The normalisation constant
(9)The normalisation constant 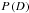 in denominator is the Bayesian evidence or marginal likelihood
in denominator is the Bayesian evidence or marginal likelihood 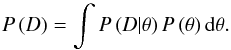 (10)For our prescribed prior probability
(10)For our prescribed prior probability 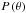 and likelihood P(D | θ) functions, the posterior probability distribution P(θ | D) can be readily computed for any value of the parameter set θ using the Bayes theorem in Eq. (9). However, in practical applications, we are interested to find most probable value and corresponding uncertainties for each parameter θi. For this purpose, we need to calculate the marginalised (integrated) posteriors
and likelihood P(D | θ) functions, the posterior probability distribution P(θ | D) can be readily computed for any value of the parameter set θ using the Bayes theorem in Eq. (9). However, in practical applications, we are interested to find most probable value and corresponding uncertainties for each parameter θi. For this purpose, we need to calculate the marginalised (integrated) posteriors 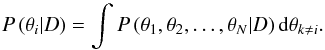 (11)For a simple low-parametric model (2–3 parameters), the integrals in Eq. (11) can be directly calculated using standard numerical methods. Unfortunately, it is practically impossible to use direct numerical integration for complicated models with a large set of parameters. Indeed, every additional parameter increases the computation time by several orders of magnitude. Therefore, sampling methods based on MCMC are preferable for complex models. MCMC allows us to obtain samples from the posterior probability distribution P(θ | D). When enough samples are obtained (our results are based on 106 samples for each model), the marginalised posterior (Eq. (11)) can be approximated by a histogram of the corresponding model parameter θi. In this paper, we use our own IDL code implementing the standard Metropolis-Hastings MCMC sampler (Metropolis et al. 1953; Hastings 1970).
(11)For a simple low-parametric model (2–3 parameters), the integrals in Eq. (11) can be directly calculated using standard numerical methods. Unfortunately, it is practically impossible to use direct numerical integration for complicated models with a large set of parameters. Indeed, every additional parameter increases the computation time by several orders of magnitude. Therefore, sampling methods based on MCMC are preferable for complex models. MCMC allows us to obtain samples from the posterior probability distribution P(θ | D). When enough samples are obtained (our results are based on 106 samples for each model), the marginalised posterior (Eq. (11)) can be approximated by a histogram of the corresponding model parameter θi. In this paper, we use our own IDL code implementing the standard Metropolis-Hastings MCMC sampler (Metropolis et al. 1953; Hastings 1970).
In many previous applications of Bayesian analysis to transverse coronal loop oscillations (e.g., Arregui et al. 2013a,b, 2015; Arregui & Asensio Ramos 2011, 2014) coronal loop parameters were derived from measured oscillation periods, decay times, and the corresponding uncertainties. On the other hand, Asensio Ramos & Arregui (2013) apply Bayesian analysis directly to the time series of a transverse oscillation, including a fixed background trend (described by a polynomial with coefficients taken from the analysis by Aschwanden et al. 2002). In our study, we use a more general approach by also applying Bayesian analysis to the measured loop positions (Yi, measured at times ti) but including the background trend as parameters varied during sampling. Asensio Ramos & Arregui (2013) note that no physical information is extracted from the coefficients of the polynomial describing the background trend, which also applies to the parameters describing our spline-based background trend (see Sect. 2.5). However, including the trend as a varied component of our model potentially allows for a more accurate description of the data and investigation of additional effects, such as the correlation of the trend with the period of oscillation (Sect. 3.2). We assume that the error corresponding to Yi measurements is normally distributed with a standard deviation of σY. Thus, the likelihood function is the product of Nd Gaussians ![\begin{equation} P \left( D|\theta \right) = \frac{1}{\left( 2\pi\sigma_Y^2 \right)^{\frac{N_{\rm d}}{2}}}\prod_{i=1}^{N_{\rm d}} \exp \left\lbrace - \frac{[Y_i - Y_\textrm{model}(t_i,\theta)]^2}{2\sigma_Y^2} \right\rbrace, \end{equation}](/articles/aa/full_html/2017/04/aa29702-16/aa29702-16-eq82.png) (12)where Nd is the number of data points and
(12)where Nd is the number of data points and 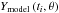 is the model function that describes the theoretical oscillation profile, and depends on the instance of time ti and model parameters θ. The measurement error σY is an unknown parameter. We assume it is the same for all data points and infer it during the MCMC sampling together with the other model parameters.
is the model function that describes the theoretical oscillation profile, and depends on the instance of time ti and model parameters θ. The measurement error σY is an unknown parameter. We assume it is the same for all data points and infer it during the MCMC sampling together with the other model parameters.
As an a priori knowledge, we assume the model parameters θ = [θ1,θ2,...,θN] to be equally probable inside the predefined ranges
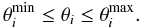 Thus, our prior probability distribution can be expressed as
Thus, our prior probability distribution can be expressed as 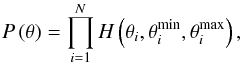 (13)where H(x,a,b) is a uniform probability density function defined as
(13)where H(x,a,b) is a uniform probability density function defined as 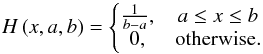 (14)The particular values of
(14)The particular values of 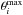 and
and 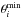 are determined by theoretical and/or practical considerations. For example, 0 ≤ ϵ ≤ 2 according to the definition of our density profile. For our model based on overdense loops, the density contrast has a defined lower limit of 1. The upper limit is taken to be 20, which is an arbitrary value aside from being significantly larger than what we expect for the typical EUV loops we observe. We find the following ranges to be suitable for our data
are determined by theoretical and/or practical considerations. For example, 0 ≤ ϵ ≤ 2 according to the definition of our density profile. For our model based on overdense loops, the density contrast has a defined lower limit of 1. The upper limit is taken to be 20, which is an arbitrary value aside from being significantly larger than what we expect for the typical EUV loops we observe. We find the following ranges to be suitable for our data ![\begin{eqnarray} t_\textrm{0} &\in& \left[ -5,5 \right] \textrm{min}, \nonumber \\ T_\textrm{A0} &\in& \left[ 0.1,10 \right] \textrm{min}, \nonumber \\ \rho_\textrm{0}/\rho_\textrm{e} &\in& \left[ 1,20 \right], \nonumber \\ \epsilon &\in& \left[ 0,2 \right], \nonumber \\ A_\textrm{0,1} &\in& \left[ -10,10 \right] \textrm{Mm}, \nonumber \\ A_\textrm{2,3} &\in& \left[ 0,10 \right] \textrm{Mm}, \nonumber \\ \phi_\textrm{2,3} &\in& \left[ -\pi,\pi \right], \nonumber \\ L/H &\in& \left[ -20,20 \right], \nonumber \\ \Gamma &\in& \left[ 1,2 \right], \nonumber \\ T_\textrm{A1,2,3} &\in& \left[ -1,1 \right], \nonumber \\ \sigma_Y &\in& \left[ 0,\mathrm{max}(Y)-\mathrm{min}(Y) \right], \label{eq:limits} \end{eqnarray}](/articles/aa/full_html/2017/04/aa29702-16/aa29702-16-eq94.png) (15)where TA1,2,3 are the polynomial coefficients for the time-dependent period of oscillation described by Eq. (3). We note that the decayless and fundamental harmonic amplitudes may be negative to accommodate the initial direction of the oscillation and since they are defined to have a phase shift of zero. In contrast, the amplitude of the second and third harmonics are restricted to positive values only since those components also allow for a phase shift φ2,3. Our choice of uniform priors is made as the simplest option, and is similar to maximum likelihood estimation. Our choice of prior ranges allows us to exclude unphysical values and improves the efficiency of sampling by restricting the parameter space. Limits are chosen to be broad enough to include all reasonable values and so the inference results are not sensitive to the selection, as demonstrated by inferred values of parameters being localised within their prior range. Occasional exceptions to this are for the prescribed limits ϵ → 2 and Γ → 1, which correspond to the physically allowed cases of fully inhomogeneous and non-expanding loops, respectively. On the other hand, the limits ρ0/ρe → 1 and ϵ → 0 should strictly be excluded since they correspond to no waveguide and no inhomogeneous layer, respectively, for which our model of damping due to mode coupling of kink waves is inapplicable. However, they also correspond to the limit of undamped oscillations, whereas our observations are of strongly damped oscillations, and so we are always far from these limits anyway.
(15)where TA1,2,3 are the polynomial coefficients for the time-dependent period of oscillation described by Eq. (3). We note that the decayless and fundamental harmonic amplitudes may be negative to accommodate the initial direction of the oscillation and since they are defined to have a phase shift of zero. In contrast, the amplitude of the second and third harmonics are restricted to positive values only since those components also allow for a phase shift φ2,3. Our choice of uniform priors is made as the simplest option, and is similar to maximum likelihood estimation. Our choice of prior ranges allows us to exclude unphysical values and improves the efficiency of sampling by restricting the parameter space. Limits are chosen to be broad enough to include all reasonable values and so the inference results are not sensitive to the selection, as demonstrated by inferred values of parameters being localised within their prior range. Occasional exceptions to this are for the prescribed limits ϵ → 2 and Γ → 1, which correspond to the physically allowed cases of fully inhomogeneous and non-expanding loops, respectively. On the other hand, the limits ρ0/ρe → 1 and ϵ → 0 should strictly be excluded since they correspond to no waveguide and no inhomogeneous layer, respectively, for which our model of damping due to mode coupling of kink waves is inapplicable. However, they also correspond to the limit of undamped oscillations, whereas our observations are of strongly damped oscillations, and so we are always far from these limits anyway.
 |
Fig. 4 Examples of oscillation fits (green lines) which include a background trend (blue lines) given by a 4th order polynomial (top panels) and our spline procedure (bottom panels) described in Sect. 2.5. The left panels show an example of a localised perturbation in the background (at around 35 min), the middle panels are an example of piecewise linear behaviour, and the right panels show an oscillating background. The spline procedure accurately recovers the actual trend (dashed lines), whereas the low-order polynomial trend can both introduce artifical modulation and fail to account for modulation that is present. |
The use of Bayesian analysis to discriminate between models of stratified and expanding loops was previously investigated by Arregui et al. (2013a) for the case of the fundamental and second harmonic kink modes. In principle, the use of the third (or other additional) harmonic could allow for both stratification and expansion to be considered simultaneously, though the required accuracy of the data to allow this is unlikely to be satisfied. Models Mi and Mj can be quantitatively compared using the Bayes factor (Jeffreys 1961), defined as 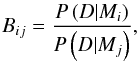 (16)where the evidences are calculated according to Eq. (10) using a Monte Carlo method with importance sampling (e.g., Chen et al. 2001; Hammersley 2013). The evidence for each model considered is calculated independently and then any two models may be compared by calculating the Bayes factor as the ratio of the evidences as given by Eq. (16). As proposed by Kass & Raftery (1995) and also used by Arregui et al. (2013a), it is convenient to consider twice the natural logarithm of this factor, i.e.
(16)where the evidences are calculated according to Eq. (10) using a Monte Carlo method with importance sampling (e.g., Chen et al. 2001; Hammersley 2013). The evidence for each model considered is calculated independently and then any two models may be compared by calculating the Bayes factor as the ratio of the evidences as given by Eq. (16). As proposed by Kass & Raftery (1995) and also used by Arregui et al. (2013a), it is convenient to consider twice the natural logarithm of this factor, i.e. 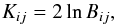 (17)where values of Kij greater than 2, 6 and 10 correspond to “positive”, “strong”, and “very strong” evidence for model Mi over model Mj, respectively. For example, Arregui et al. (2013a) demonstrate that for their level of uncertainty a period ratio P1/ 2P2< 0.71 would indicate very strong evidence for a stratified loop rather than a uniform loop, while P1/ 2P2> 1.28 indicates very strong evidence for an expanding loop over a uniform loop (the case of negative scale heights was not considered).
(17)where values of Kij greater than 2, 6 and 10 correspond to “positive”, “strong”, and “very strong” evidence for model Mi over model Mj, respectively. For example, Arregui et al. (2013a) demonstrate that for their level of uncertainty a period ratio P1/ 2P2< 0.71 would indicate very strong evidence for a stratified loop rather than a uniform loop, while P1/ 2P2> 1.28 indicates very strong evidence for an expanding loop over a uniform loop (the case of negative scale heights was not considered).
 |
Fig. 5 SDO/AIA 171 Å images of the four loops we analyse in this paper. The axis of the chosen loop is indicated by a dashed red line, which is either an elliptical or a linear fit depending on the loop orientation. The solid blue line shows the location of the slit used to generate the time series. |
2.5. Background trend
In Paper I, the loop oscillations were interpreted in terms of a single harmonic component and so it was convenient to detrend the loop displacement time series before fitting. The background trend was determined by spline interpolation of the maxima and minima to accurately calculate the equilibrium position of the oscillation. In Pascoe et al. (2016a), observations of a fundamental and second harmonic kink mode were analysed. To avoid the detrending procedure influencing the two fitted harmonic components, the background trend was described by a polynomial and was fitted simultaneously with the harmonic components. A polynomial trend was sufficient in that case because typically a low number of cycles of the oscillation were analysed. For the same reason, only the Gaussian damping regime was considered.
In this paper we wish to consider long time series which demonstrate significant dynamical behaviour for the loop equilibrium position. On the other hand, the trend should be included in the model to ensure it is does not have an unwanted influence on the other model parameters. In contrast with the spline trend used in Paper I which was based on locating the maxima and minima, the trend used in this paper is based on the zeroes of the oscillation. Each sampling of our model includes estimates for t0 and P1. We use these parameters to define a series of interpolation points approximately corresponding to zeroes of the oscillation 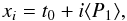 where we use the mean value of P1 for our case of a weakly varying period of oscillation. Some other characteristic timescale could be used to separate modelled oscillations from the background behaviour, where generally we wish to consider variations in the trend which have a longer timescale than the longest timescale described by our physical model. Two additional points for interpolation are defined by the start and end of the time series. The corresponding values of the background equilibrium position yi at these times xi are taken as additional model parameters to be varied. The background trend is then defined by spline interpolation of the points (xi,yi) (e.g., see bottom panel of Fig. 10) using the spline function in IDL (with tension parameter being its default value Sigma = 1.0).
where we use the mean value of P1 for our case of a weakly varying period of oscillation. Some other characteristic timescale could be used to separate modelled oscillations from the background behaviour, where generally we wish to consider variations in the trend which have a longer timescale than the longest timescale described by our physical model. Two additional points for interpolation are defined by the start and end of the time series. The corresponding values of the background equilibrium position yi at these times xi are taken as additional model parameters to be varied. The background trend is then defined by spline interpolation of the points (xi,yi) (e.g., see bottom panel of Fig. 10) using the spline function in IDL (with tension parameter being its default value Sigma = 1.0).
The background trend for coronal loop oscillations is frequently modelled using a low-order polynomial function. We note there is no theoretical justification for this choice, or the order of the polynomial, and no physical interpretation associated with polynomial coefficients. For example, Aschwanden et al. (2002) contains examples of polynomial trends with order 1–6, White & Verwichte (2012) use a 3rd order polynomial for the background, and Morton & Mooroogen (2016) compare results using 3rd and 4th order polynomials.
Figure 4 demonstrates examples of fitting oscillation data with a model using a background trend given by a polynomial function (4th order with constant coefficients; top panels) or our spline procedure described above (bottom panels). The time series of the oscillation (circles) are calculated as a harmonic oscillation (with constant period and amplitude) about the equilibrium position given by the dashed lines. The left panels show an example of a localised perturbation in the background and the middle panels are an example of piecewise linear behaviour. These trends are approximately based on the behaviour seen in Loops #3 and #4. The polynomial trend is particularly poor at describing localised changes in the background such as that around 35 min (left panels). The use of a low-order polynomial trend has the effect of smoothing out the background behaviour and introduces artificial modulation of the amplitude of the oscillation. Since our seismological method is based on measuring the amplitude modulation (damping) of the loop oscillation we wish to avoid introducing this artificial modulation. The top panels also show how the polynomial trend can erroneously suggest the background trend is oscillatory. Conversely, when the background trend is actually oscillatory (right panels), the low-order polynomial describes an approximately linear trend through the centre of the background oscillation.
Since a polynomial function describes a background trend with a fixed amount of information (d + 1 coefficients for a polynomial of degree d), then as the time series considered becomes longer, the polynomial trend becomes less sensitive to localised changes, i.e. the background trend and hence oscillation depend on the particular number of cycles chosen for analysis, and the trend becomes less accurate as more data is considered. Our spline trend is designed to avoid this limitation. By defining the interpolation points in terms of P1 (the longest period of oscillation in our physical model) each component of the spline is a low-order polynomial over this timescale and describes the local equilibrium of the oscillation. However, since the number of interpolation points depends on the number of cycles within the time series, trends for longer time series remain as well-resolved as those for shorter time series.
For our spline procedure, the varied parameters for the trend correspond to a series of points within the range of the oscillation signal. The prior ranges for our Bayesian analysis are therefore taken to be ![\hbox{$y_i \in \left[ \min\left(Y\right),\max\left(Y\right) \right]$}](/articles/aa/full_html/2017/04/aa29702-16/aa29702-16-eq119.png) . For our models which use a polynomial background trend (e.g., Sect. 4), the same prior range is used for the constant term for the polynomial. The prior ranges for the coefficients of the higher order terms are [− 1,1], which are found to be sufficient for our data.
. For our models which use a polynomial background trend (e.g., Sect. 4), the same prior range is used for the constant term for the polynomial. The prior ranges for the coefficients of the higher order terms are [− 1,1], which are found to be sufficient for our data.
3. Analysis of loop oscillations
SDO/AIA observations of standing kink modes analysed in this paper.
Parameters for Loops #1–#4 for different models.
The loop oscillations we analyse were selected from the catalogue of kink oscillations compiled by Zimovets & Nakariakov (2015) and are shown in Fig. 5. Table 1 records the designation (loop No.) by which they will be referred to in this paper, the designation used in Goddard et al. (2016), and the date and time of the event. Loops #1–#3 are the same as those considered in Paper I. Loop #4 was identified by Pascoe et al. (2016c) as having a Gaussian damping profile, however a full seismological inversion could not be performed since the exponential regime was not initially detected. We analyse the loop oscillations according to the general approach described in Sect. 2. We consider each event in detail in the subsections below.
Even without the presence of a decayless oscillation we do not typically observe a kink oscillation decay to an amplitude of zero since we restrict the analysed signal to a time at which the model oscillation remains consistent with the data. Therefore we do not consider the presence of a decayless component of the oscillation except where it can be justified by a plateau in the damping rate and a continuation of the oscillation for several cycles. This condition is satisfied for Loop #3 alone, which demonstrates approximately four cycles without significant attenuation at the end of the signal and was also previously analysed by Nisticò et al. (2013) as an example of a decayless oscillation.
Pascoe et al. (2016a) report the observation of a spatially resolved second harmonic kink mode with an amplitude comparable to that of the fundamental kink mode. However, more typically higher harmonics are excited less efficiently than the fundamental mode. Additionally, they are damped more efficiently by mode coupling since τg,d ∝ P from Eq. (1). The combination of these two effects means that the presence of additional harmonics in the signal may not be readily revealed by methods such as periodogram or wavelet analysis (see Fig. 18). A possible indicator that the oscillation is not composed of a single mode is an aharmonic shape to the signal. However, in the absence of additional evidence, we must also consider alternative possibilities. An aharmonic signal might arise instead as a consequence of non-linear effects rather than additional longitudinal harmonics. This would also account for the aharmonic shape being more prominent at the start of the oscillation (when the amplitude is greatest) and becoming less prominent as the oscillation decays. Goddard & Nakariakov (2016) also report statistical evidence for the dependence of kink oscillation damping time on the amplitude of oscillation which may be indicative of non-linear effects. Since the aharmonic shape exists for a significant time t ≳ P1 we do not consider it to be a transient feature, such as the impulsive leaky phase which exists for t ≪ P1 (e.g., Terradas et al. 2006).
The results of the analysis for Loops #1–#4 for different models are summarised in Table 2 and described in detail below. For comparison with Paper I we include results for a model including the fundamental kink mode only (i.e. no additional harmonics or decayless component). This also serves as a basis to test our more sophisticated models against using Bayesian model comparison.
In general the main parameters do not change much for our different models, which indicates the robustness of the seismological method, i.e. the density contrast and ϵ depend on the damping behaviour which is weakly dependent on the additional harmonics. This is not necessarily always the case since the additional harmonics having a low amplitude in our chosen data was part of our initial selection process. On the other hand, the large differences between models indicated by the Bayes factors is related to how well the entire oscillation (i.e. not just the damping envelope) is described by the model, specifically how the inclusion of additional harmonics accurately accounts for the aharmonic shape of the oscillation.
3.1. Loop #1
 |
Fig. 6 Analysis for Loop #1 using the dispersionless model. Top left: loop position (symbols) as a function of time is described by our model (green line) which includes a background trend (blue line) described by our spline procedure. The red shaded region represents the 99% credible intervals for the loop position predicted by the model, including an estimated noise σY. The dotted and dashed lines denote t0 and ts1, respectively. Top right: wavelet analysis of the loop position with colours representing the normalised spectral amplitude. The dashed lines show the time-dependent periods of oscillation described by our model. The hatched region denotes the cone of influence. Middle left: detrended loop position (symbols) with the first (green), second (blue), and third (red) longitudinal harmonics. Times ts1, ts2, and ts3 are denoted by the dashed lines in the corresponding colour. Middle right: density profile parameters determined by the oscillation damping envelope. The red bars are based on the median values and the 95% credible intervals, indicated by the dotted and dashed lines, respectively, in the histograms (bottom panels). The solid curves are fits to the histogram data using the exponentially modified Gaussian function. |
 |
Fig. 7 Histograms of the longitudinal structuring parameters for the stratified (left panels) and expanding (right panels) models for Loops #1–#4. |
Figure 6 summarises the results of our analysis for the oscillation of Loop #1. The top left panel shows the position of the loop centre as a function of time (symbols). We use Bayesian analysis (Sect. 2.4) to calculate how our oscillation model describes the observational data. Our Bayesian analysis returns the posterior PDF for each of the model parameters. These may be plotted as histograms, such as those for ρ0/ρe and ϵ in Fig. 6, or summarised by quoting the median and 95% credible intervals as in Table 2. The red shaded region represents the 99% credible interval for the loop position described by our model, including the estimated noise σY. The parameters (e.g., vertical dotted line denoting t0) or model components (e.g., background trend shown by blue line in top left panel) plotted in figures correspond to the median values of the relevant parameters. For comparison, the results for analysing Loop #1 with a model including the fundamental kink mode only is shown in Fig. 16.
The top right panel shows the wavelet analysis of the signal. The colour contours represent the spectral amplitude (square root of the spectral power). The dashed lines show the time-dependent periods of oscillation Pn, which demonstrate a gradual increase during the course of the oscillation of approximately 20%.
The middle right panel shows a 2D histogram of the seismologically determined transverse density profile parameters based on our 106 MCMC model samplings (with intensity normalised to unity). The red bars correspond to the median values and 95% credible intervals based on the individual 1D histograms (bottom panels) and quoted in Table 2. They give a convenient summmary of the localisation of the parameters by our model fit, though we note that they do not reflect the strong inverse relationship between ρ0/ρe and ϵ in determing the damping rate (see Fig. 2). Consequently, the 2D contour (likely density profile parameters) is significantly more localised than considering the posterior credible intervals independently would suggest. It is necessary to appreciate this inverse relationship when considering the quality of the constraint on density profile indicated by the data. For example, ϵ is generally less well constrained for lower density contrasts than for larger density contrasts, as discussed in Sect. 2.
We note that the 95th percentiles quoted in this paper correspond to a 2σ confidence interval, in contrast to Paper I where the errors were estimated values of 1σ. For example, Paper I gives the density contrast for Loop #1 as 1.69 ± 0.56, and here (Table 2) it is 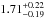 , which corresponds to a σ that is approximately five times smaller. On the other hand, the σ for the ϵ here is comparable to that in Paper I. The solid curves in the histogram plots are fits to the data using the exponentially modified Gaussian function of the form
, which corresponds to a σ that is approximately five times smaller. On the other hand, the σ for the ϵ here is comparable to that in Paper I. The solid curves in the histogram plots are fits to the data using the exponentially modified Gaussian function of the form 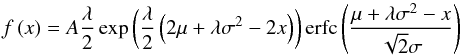 (18)where
(18)where 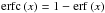 is the complementary error function, A is a constant determining the amplitude, μ and σ are the mean and standard deviation of the Gaussian component, respectively, and λ is the rate of the exponential component. Equation (18) is found to describe the histogram profiles well, in particular when the distribution is asymmetric such as for ϵ which has a strong inverse relationship with ρ0/ρe.
is the complementary error function, A is a constant determining the amplitude, μ and σ are the mean and standard deviation of the Gaussian component, respectively, and λ is the rate of the exponential component. Equation (18) is found to describe the histogram profiles well, in particular when the distribution is asymmetric such as for ϵ which has a strong inverse relationship with ρ0/ρe.
The large range of ϵ returned by the seismological inference is a consequence of this inverse relationship to the density contrast (see Fig. 2). When the estimated density contrast is low, as for this loop, ϵ is very sensitive to the particular value of ρ0/ρe. Conversely, when the estimated density contrast is large (e.g., ρ0/ρe ≳ 6 in Fig. 2), ϵ is practically independent of ρ0/ρe. The range of ϵ calculated for this loop effectively extends up to 2, which is the maximum value consistent with the definition of the transverse density profile. Corrections to the model for the effects of large ϵ (e.g., Van Doorsselaere et al. 2004; Arregui et al. 2005) would also be required before this limit is reached. The inversions for Loops #2 and #3 are much more strongly localised with respect to ϵ due to their larger values of ρ0/ρe (Figs. 9 and 11), while for Loop #4 the estimated density contrast is again very low and the corresponding range of ϵ is large (Fig. 15).
Table 2 also shows results for analysis using the stratified and expanding loop models. The histograms for the longitudinal structuring parameters, i.e. L/H for the stratified model and Γ for the expanding model, are shown in Fig. 7. For Loop #1, the period ratios are greater than unity which can be accounted for either by a negative density scale height 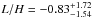 or a loop expansion of
or a loop expansion of 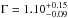 , with other varied parameters being consistent between models. We note that the uniform limit for both models (L/H → 0 and Γ → 1) lies within the 95% credible intervals for each longitudinal structuring parameter. Additionally, the clear influence of the lower limit of 1 (by definition) for the prior for Γ means we can effectively only derive an upper limit from the posterior distribution. In Table 2, Ki0 represents the Bayes factor Eq. (17) calculated for each of the models in comparison to a model based on the fundamental kink mode only. For Loop #1, each value is greater than 10, corresponding to very strong evidence in favour of the models with additional harmonics, reflecting the significantly improved account of the observational data provided by these models. On the other hand, the Bayes factors do not imply there is positive evidence to prefer either of the longitudinally structured models over the dispersionless model. This, combined with the large credible intervals for the structuring parameters, advises caution for the interpretation of the results of the longitudinally structured models for this loop.
, with other varied parameters being consistent between models. We note that the uniform limit for both models (L/H → 0 and Γ → 1) lies within the 95% credible intervals for each longitudinal structuring parameter. Additionally, the clear influence of the lower limit of 1 (by definition) for the prior for Γ means we can effectively only derive an upper limit from the posterior distribution. In Table 2, Ki0 represents the Bayes factor Eq. (17) calculated for each of the models in comparison to a model based on the fundamental kink mode only. For Loop #1, each value is greater than 10, corresponding to very strong evidence in favour of the models with additional harmonics, reflecting the significantly improved account of the observational data provided by these models. On the other hand, the Bayes factors do not imply there is positive evidence to prefer either of the longitudinally structured models over the dispersionless model. This, combined with the large credible intervals for the structuring parameters, advises caution for the interpretation of the results of the longitudinally structured models for this loop.
 |
Fig. 8 Wavelet analysis for Loop #1 background trend. |
The background trend for Loop #1 exhibits oscillatory behaviour. The spectral analysis of the trend component of the model is shown in Fig. 8 and exhibits a periodicity of approximately 10–11 min. Pascoe & De Moortel (2014) performed numerical simulations of standing kink modes in curved coronal loops. Owing to the symmetry of the initial condition the loop is embedded in a magnetic arcade and consequently the applied perturbation excites not only the fundamental kink mode of the loop with period Pk = 2L/Ck but also an oscillation of the external medium with period PA = 2L/CAe determined by the external Alfvén speed CAe. Since the external Alfvén speed is higher than the kink speed PA<Pk. (The presence of this additional oscillation accounts for the period of oscillation of the kink mode appearing shorter than Pk in Pascoe et al. 2009; De Moortel & Pascoe 2009). In the numerical simulations of Pascoe & De Moortel (2014), the perturbation of the external medium had the same spatial scale as the embedded loop by definition. However, we can consider a generalised version of this where the external medium oscillation is determined by a characteristic length scale that is not necessarily the length of a particular loop but related to the size of the perturbed region, i.e. PA = 2l/CAe. If we consider the seismologically estimated external Alfvén speed CAe ≈ 1.8 Mm/s then the characteristic length scale that corresponds to the oscillation period of 10.5 min is l ≈ 570 Mm which is comparable to the size of the active region. SDO images for the oscillation show that Loop #1 appears to be embedded in a larger magnetic structure containing other loops which also oscillate in response to two CMEs which take place within several hours. In fact, there are two such larger regions of loops and the eruptions are located in between them such that they oscillate in anti-phase with each other. This event was also investigated Harra et al. (2014) using the Interface Region Imaging Spectrograph (IRIS) in addition to SDO. Analysis of the spectral lines measured with IRIS demonstrated the existence of flows in the loops before the eruption which were affected by the subsequent impact of the filament and indicate plasma motions parallel to the line of sight preceding the transverse oscillations.
3.2. Loop #2
Figure 9 summarises the results of our analysis of the oscillation of Loop #2. The oscillation of Loop #2 exhibits a more aharmonic shape than Loop #1, with a slightly triangular appearance that is also seen for Loops #3 and #4. The aharmonic shape of the signal for the first couple of cycles is well-described by the presence of small amplitude second and third longitudinal harmonics. These harmonics have damped significantly by t ≳ 10 min, after which the signal appears more harmonic. Figure 7 shows the histograms for the longitudinal structuring parameters for the stratified and expanding loop models. The Bayes factors for the longitudinally structured models do not indicate any evidence to prefer them over the dispersionless model.
There is a high correlation (0.89) between the background trend and the time-dependent period of oscillation for this loop, which are shown in more detail in Fig. 10. Both begin at a higher value at the start then decrease until t ≈ 25 min, after which they remain roughly constant. The position along our observational slit is measured from the inside of the loop to the outside, and so an increase in the value of the background trend would generally correspond to loop expansion, and a decrease to loop contraction. However, additional effects such as distortion of the loop shape can complicate this dependence since we only consider the oscillation at a single point along the loop. For comparison, Loop #1 has a correlation between the trend and period of oscillation of 0.77, while Loops #3 and #4 do not show any significant correlation (in the case of Loop #3 this is expected based on the orientation of the slit shown in Fig. 5).
3.3. Loop #3
Figure 11 summarises the results of our analysis of the oscillation of Loop #3. As with Loop #2, the aharmonic shape of the signal for the first couple of cycles is reproduced by small amplitude second and third longitudinal harmonics, which have damped significantly by t ≳ 10 min, after which the signal appears more harmonic. The main difference compared with Loop #2 is that Loop #3 contains a decayless component, represented by the yellow line in the oscillation components panel of Fig. 11. The presence of the decayless component is also confirmed by | A0 | being significantly greater than zero, shown in Fig. 12. For t ≳ 25 min, the fundamental kink oscillation has damped below the amplitude of the decayless component.
For comparison, Fig. 13 shows the results of the MCMC inversion without including the decayless component. The switch time ts occurs sooner and consequently the inferred density contrast is larger than when the decayless component is included. The estimated value of σY is larger for this model, indicating a poorer description of the data by this model, most evident towards the end of the signal when the modelled oscillation continues to decay while the observational signal remains constant. The presence of the decayless component of oscillation makes the overall damping rate appear lower than that for the decaying component alone. For damping by mode coupling, a lower damping rate is associated with either a smaller density contrast or layer width. We might therefore expect an unaccounted decayless component would lead to an underestimate of the density contrast. However, it also has the effect of decreasing the damping rate during the exponential damping regime. This lower damping rate corresponds to a smaller switch time ts, which corresponds to a higher density contrast ratio. This accounts for the higher estimation of the density contrast in Paper I. We note that the density contrast credible interval is significantly higher for the model using the fundamental mode alone in this paper than in Paper I. This is due to the time series being restricted in Paper I to reduce the influence of the decayless regime. Including the decayless regime reduces the value of the inferred density contrast and the estimated range. For a lower density contrast, the credible interval for the inhomogeneous layer width increases. However, we note that for the larger density contrast estimate ϵ was being constrained by the inverse relationship with ρ0/ρe, i.e. ϵ is approximately constant for large contrasts (e.g., Fig. 2).
The background trend for Loop #3 exhibits an oscillation at the start which quickly damps by about 15 min, by which time the trend is mainly a gradual decrease. Loop #3 is located at the end of an arcade of loops and so this damped oscillation in the background may be associated with interaction with the arcade. For example, Verwichte et al. (2004) measured the oscillations of 9 loops within a coronal arcade and found evidence of multiple oscillation modes and a wide range of periods (240–450 s). The oscillation in the background trend may therefore represent the influence of a nearby oscillating loop with a longer period of oscillation, although a detailed analysis is beyond the scope of the present paper. There is another perturbation in the background trend at around 30 min, which is indicative of the dynamical nature of the corona that must be taken into account in detailed analysis. This kind of feature is not accounted for when modelling the background with a low-order polynomial (see Sect. 2.5 and Figs. 4 and 17).
 |
Fig. 10 Time-dependent period of oscillation (top) and background trend (bottom) for Loop #2. The blue circles represent the interpolation points (xi,yi). |
Comparison of the seismologically estimated density scale height H with the hydrostatic scale height Hs implied by the loop temperature T estimated using DEM analysis.
Loop #3 demonstrates the strongest Bayes factors for the models with additional harmonics in comparison to the model based on a fundamental kink mode only. This can be attributed to the additional effect from including the decayless regime in the multi-harmonic models. There is also very strong evidence for the stratified model over the dispersionless model KHD = 12.6, and strong evidence for the dispersionless model over the expanding model KDΓ = 6.1. The stratified model gives mean period ratios P1/ 2P2 = 0.82, P1/ 3P3 = 0.79. These period ratios are significantly less than unity, making the stratified model preferable to the dispersionless one. On the other hand, since the expanding model can only account for period ratios greater than unity it is less preferable than the dispersionless model, i.e. Γ → 1 and so the inclusion of the additional parameter Γ does not improve how well the model describes the observational data.
Taking into account the uncertainties for the estimated loop length of L = 234 ± 31 Mm and the credible interval for L/H, the range of scale heights is H = 18–42 Mm. Figure 14 shows the results of differential emission measure (DEM) analysis to estimate the loop temperature. The panels show the DEM for several temperature intervals calculated using the regularization method of Hannah & Kontar (2012). Obtaining a precise estimate of the loop temperature is complicated due to loops being multi-thermal (e.g., Nisticò et al. 2014) and the effects of line-of-sight integration (e.g., Cooper et al. 2003; De Moortel & Pascoe 2012; Viall & Klimchuk 2013) in the optically thin corona which can include contributions from high temperature background structures. We estimate the temperature range by considering the intervals for which the oscillating loop (dashed white lines) can be clearly identified against the background emission, which is typically 0.75–1.25 MK. For these temperatures, the hydrostatic density scale height Hs ≈ 50T gives 37.5–62.5 Mm. The seismologically determined density scale height is therefore not consistent with the hydrostatic approximation, as also reported by previous authors, although for this observation the result is sub-hydrostatic rather than super-hydrostatic (e.g., Van Doorsselaere et al. 2007; Verwichte et al. 2013). Table 3 shows these estimates for all four loops. For Loops #1, #2, and #4 the seismologically estimated scale heights are super-hydrostatic and consistent with the longitudinally uniform limit H → ∞.
3.4. Loop #4
Figure 15 summarises the results of our analysis for Loop #4. The oscillation features are qualitatively similar to those of Loop #1; the loop has a low density contrast with ts1 being towards the end of the signal and consequently producing a low estimate for the density contrast and hence a wide credible interval for ϵ, and the additional longitudinal harmonics exhibit weak departure from the dispersionless model (Fig. 7). Similar to Loop #2, the aharmonic shape of the oscillation is mainly accounted for by a third harmonic component with approximately 20% of the amplitude of the fundamental kink mode.
The calculated Bayes factors support there being very strong evidence for the dispersionless model over the model with no harmonics. However, this evidence drops to only “strong” for the longitudinally structured (stratified and expanding) models. This weaker evidence can be attributed to the fact that the longitudinally structured models tend to their uniform limits anyway, and so the inclusion of these effects does not improve the description of the data by the model. This differs from Loops #1–#3 for which all models with additional harmonics were “very strong” in comparison to the model without harmonics.
4. Discussion and conclusions
 |
Fig. 11 Analysis for Loop #3 using the dispersionless model including the decayless regime. Panels as in Fig. 6 except the components panel also includes the decayless oscillation (yellow line). |
Comparison of results for Loops #1–#4 when using a spline or polynomial background trend.
We have extended the analysis of Paper I for the seismology of coronal loops using damped kink oscillations. This paper represents the extension and combination of many aspects of theoretical modelling and analytical methods developed over almost two decades of observations of coronal loop oscillations. The features of the method used in this paper are summarised below.
-
The start time of the oscillation t0 is a varied parameter in the model since it influences the additional harmonics and the damping profile. Also, where data allows, we generally want to model the evolution of the background trend before the oscillation begins.
-
The period of oscillation is considered to be time-dependent (e.g., the linear variations modelled in Nisticò et al. 2013; White et al. 2013; Morton & Mooroogen 2016). In this paper we use a polynomial (3rd order) to allow increases and/or decreases during the oscillation and to test the correlation with the background trend, which may represent changes in loop length (when the loop has an appropriate orientation).
-
The damping of the kink oscillations is explained in terms of mode coupling and modelled using the general damping profile (Pascoe et al. 2013, 2016b) which includes both the Gaussian (e.g., Pascoe et al. 2012; Hood et al. 2013; Ruderman & Terradas 2013) and exponential (e.g., Ruderman & Roberts 2002; Goossens et al. 2002) damping regimes.
-
The presence of additional longitudinal harmonics (second and third) is considered, including longitudinal structuring due to density stratification (e.g., Andries et al. 2005; Safari et al. 2007; McEwan et al. 2008) or loop expansion (Verth & Erdélyi 2008) and their potential seismological application (e.g., Andries et al. 2005; Van Doorsselaere et al. 2007; Arregui et al. 2013a). The frequency-dependent damping due to mode coupling (e.g., Pascoe et al. 2010; Verth et al. 2010; Pascoe et al. 2015) is accounted for in the model.
-
The decayless regime of standing kink oscillations (Nisticò et al. 2013; Anfinogentov et al. 2013, 2015) is included (for Loop #3) and its influence on the seismologically determined loop parameters is investigated.
-
Bayesian analysis and MCMC sampling are used to investigate the dependence of results on model parameters and perform quantitative model comparison (e.g., Arregui et al. 2013a,b, 2015; Arregui & Asensio Ramos 2011, 2014). The Bayes factor compares how well a particular model describes the data (relative to another model), whereas a goodness of fit test, for example χ2, compares only the best fits. Morton & Mooroogen (2016) apply an alternative approach to loop oscillation model comparison using the Kolmogorov-Smirnoff test.
-
The dynamical background behaviour is accurately described using a spline-based trend.
However, a number of effects still have not been incorporated, such as flows (e.g., Soler et al. 2011); changes in density (e.g., Cargill et al. 2016); the effects of instabilities such as magnetic reconnection, the Kelvin-Helmholtz instability (e.g., Soler et al. 2010; Zaqarashvili et al. 2015; Okamoto et al. 2015; Antolin et al. 2015; Mishin & Tomozov 2016), or MHD avalanches (Hood et al. 2016). Also, the theoretical model we apply does not include non-linear effects or modifications for a wide inhomogeneous layer (e.g., Van Doorsselaere et al. 2004; Arregui et al. 2005), or the effects of alternate profiles for the density inside the inhomogeneous layer (e.g., Goossens et al. 2002; Roberts 2008; Arregui et al. 2015; Yu et al. 2015).
By allowing the period of oscillation to vary in time we have been able to extend the time series used for analysis in comparison with Paper I. The loops we analyse were initially selected on the basis of a stable period of oscillation and so these variations in the period of oscillation are typically small. For Loops #1 and #2, the correlation of the period of oscillation with the background trend supports the interpretation of the time-dependence being related to changes in loop length.
 |
Fig. 12 Histogram for A0 for Loop #3 for the dispersionless model with the decayless regime shown in Fig. 11. |
 |
Fig. 13 Analysis for Loop #3 using the dispersionless model without including the decayless regime. Panels as in Fig. 6. |
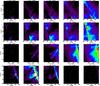 |
Fig. 14 DEM analysis for Loops #1 (top) to #4 (bottom) used to estimate the temperature (Table 3) of the oscillating loop (dashed white lines). Each panel corresponds to a particular temperature interval. |
 |
Fig. 16 Analysis for Loops #1–#4 using a model including the fundamental kink mode only. Panels as in Fig. 6. |
 |
Fig. 17 Summary of results using a polynomial (4th order) trend. Panels are comparable to those in Figs. 6, 9, 11, and 15 which show the same models with a background trend using our spline procedure described in Sect. 2.5. |
 |
Fig. 18 Demonstration of spectral analysis for damped kink oscillations. Test data (left panel) contains second and third harmonics with 20% amplitude of the fundamental mode. Owing to the frequency-dependent damping by mode coupling, these components have negligible signatures in periodogram (middle panel) and wavelet (right panel) analysis. |
We have also used a new method for describing the background trend. The method is based on spline interpolation and so is better capable of describing the dynamical background behaviour exhibited in the solar corona. The new method is simple to implement and is built directly into the model function, whereas in Paper I the time series was detrended before fitting, using the assumption that the signal contained a single mode of oscillation. The new trend method does not require us to make this assumption about the signal and allows the trend to adapt according to the values of other parameters (most importantly the additional longitudinal harmonics) in the model to provide the most accurate account of the observational data. An important feature of our procedure is that the number of points used to describe the trend scales with the number of cycles of oscillation analysed, ensuring signals with higher quality factors are as well-resolved as those with smaller quality factors. The effect of using a polynomial background trend is shown in Fig. 17 and summarised in Table 4 (the results are given for the dispersionless model, including the decayless component in the case of Loop #3). The Bayes factor KSP compares the model with the spline background trend to that with the polynomial trend (with all other model features identical). For all loops the value indicates very strong evidence for the spline-based models over the polynomial ones. The improvement to the models provided by the spline-based trend is also reflected in the lower estimates of the loop position noise σY. In terms of the seismologically determined density profile parameters, the results for Loops #1, #2, and #4 are similar, with the credible intervals being only marginally greater when using the polynomial trend, i.e. the spline and polynomial trend models produce the same seismological results when the background trend can be well-described using a low-order polynomial. The largest difference is for Loop #3, for which the spline and polynomial trends lead to significantly different density profile parameters. The evidence in favour of the spline-based model is also greatest for Loop #3. This is not surprising given that Loop #3 has the greatest signal quality and a number of localised perturbations in the trend, which a low-order polynomial trend is least able to describe, and which our spline procedure is specifically designed to accommodate (Sect. 2.5).
Another benefit of the more accurate background trend produced by our spline procedure is the opportunity to detect additional physical effects. Loop #1 demonstrates evidence of a persistent long period oscillation which may be associated with oscillations in the larger magnetic structure of the surrounding active region. For Loop #2 the background trend is strongly correlated with the period of oscillation, consistent with the period changing due to changes in loop length (the polynomial trend is a good approximation for this loop and also gives the same correlation). The trend for Loop #3 exhibits a damped oscillation near the start which might also be associated with the surrounding environment, in this case an arcade of oscillating loops. The spline-based background trends for Loops #3 and #4 also reflect the dynamical nature of the corona with a number of localised perturbations. In contrast, for a dynamical background a low-order polynomial may not provide an accurate description of either the oscillation or the background trend (e.g., Figs. 4 and 17).
Figure 18 demonstrates the potential limitations of spectral analysis for damped kink oscillations. Test data (left panel) contains second and third harmonics with 20% amplitude of the fundamental mode. Owing to their initial low amplitude and the frequency-dependent damping by mode coupling, these components have a negligible signatures in periodogram (middle panel) and wavelet analysis (right panel). Our method based on forward modelling of the oscillation signal benefits from having this damping behaviour built directly into the model. Furthermore, since the damping rates in Eq. (1) are also informed by the relationships for the periods Pn (dispersionless or with longitudinal structuring), we are not required to calculate the damping rates of the harmonics independently, which would be subject to large uncertainties, but instead determine all parameters simultaneously as part of a self-consistent physical model.
Our consideration of additional longitudinal harmonics is mainly intended to account for the aharmonic shapes of the oscillations, which it does successfully, but can also potentially provide additional seismological information using the ratios of the periods of oscillation. In this paper we considered the effects of density stratification and loop expansion. The additional harmonics are low amplitude in comparison to the fundamental mode, which is partly a selection effect when we chose our events to consider. However, this interpretation of the aharmonic shape requires further evidence. Furthermore, the results of our Bayesian model comparison suggests caution in interpreting these period ratios except for the case of Loop #3, for which there is very strong evidence for the stratified model (or another model which describes P1/nPn< 1). It is unclear why this loop differs from the others, and the method applied in this paper may produce more conclusive results for other data (particularly oscillations with additional harmonics having amplitudes more comparable with that of the fundamental mode). On the other hand, the seismological estimates for the transverse loop density profile parameters evidently remain robust despite these additional questions regarding the longitudinal structuring.
The method combining forward modelling, Bayesian inference, MCMC sampling, and spline interpolation of the background trend we use in this paper is powerful and robust, and could be applied to other data. For example, Pugh et al. (2016) recently studied the properties of quasi-periodic pulsations in white-light flares observed with Kepler, and discovered evidence of both Gaussian and exponential damping profiles. The oscillations with a Gaussian damping profile also exhibit a decay time that is proportional to the period of oscillation, consistent with mode coupling of kink waves.
Acknowledgments
This work is supported by the European Research Council under the SeismoSun Research Project No. 321141 (D.J.P., S.A., C.R.G., V.M.N.) and the STFC consolidated grant ST/L000733/1 (G.N., V.M.N.). The data is used courtesy of the SDO/AIA team. D.J.P. thanks C. Carbaugh and B. Clark who were supported by Nuffield Research Placements.
References
- Andries, J., Arregui, I., & Goossens, M. 2005, ApJ, 624, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Andries, J., van Doorsselaere, T., Roberts, B., et al. 2009, Space Sci. Rev., 149, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Anfinogentov, S., Nisticò, G., & Nakariakov, V. M. 2013, A&A, 560, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anfinogentov, S. A., Nakariakov, V. M., & Nisticò, G. 2015, A&A, 583, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antolin, P., Okamoto, T. J., De Pontieu, B., et al. 2015, ApJ, 809, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I. 2015, Philos. Trans. Roy. Soc. London Ser. A, 373, 20140261 [Google Scholar]
- Arregui, I., & Asensio Ramos, A. 2011, ApJ, 740, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., & Asensio Ramos, A. 2014, A&A, 565, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., & Soler, R. 2015, A&A, 578, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Van Doorsselaere, T., Andries, J., Goossens, M., & Kimpe, D. 2005, A&A, 441, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Andries, J., Van Doorsselaere, T., Goossens, M., & Poedts, S. 2007, A&A, 463, 333 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arregui, I., Asensio Ramos, A., & Díaz, A. J. 2013a, ApJ, 765, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Asensio Ramos, A., & Pascoe, D. J. 2013b, ApJ, 769, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Arregui, I., Soler, R., & Asensio Ramos, A. 2015, ApJ, 811, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., de Pontieu, B., Schrijver, C. J., & Title, A. M. 2002, Sol. Phys., 206, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Nightingale, R. W., Andries, J., Goossens, M., & Van Doorsselaere, T. 2003, ApJ, 598, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Asensio Ramos, A., & Arregui, I. 2013, A&A, 554, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cargill, P. J., De Moortel, I., & Kiddie, G. 2016, ApJ, 823, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, L., & Hasegawa, A. 1974, Phys. Fluids, 17, 1399 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, M., Shao, Q., & Ibrahim, J. 2001, Monte Carlo Methods in Bayesian Computation, Springer Series in Statistics (New York: Springer) [Google Scholar]
- Cooper, F. C., Nakariakov, V. M., & Tsiklauri, D. 2003, A&A, 397, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., & Brady, C. S. 2007, ApJ, 664, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Nakariakov, V. M. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3193 [Google Scholar]
- De Moortel, I., & Pascoe, D. J. 2009, ApJ, 699, L72 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., & Pascoe, D. J. 2012, ApJ, 746, 31 [NASA ADS] [CrossRef] [Google Scholar]
- De Moortel, I., Hood, A. W., & Ireland, J. 2002, A&A, 381, 311 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Moortel, I., Pascoe, D. J., Wright, A. N., & Hood, A. W. 2016, Plasma Physics and Controlled Fusion, 58, 014001 [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, C. R., & Nakariakov, V. M. 2016, A&A, 590, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddard, C. R., Nisticò, G., Nakariakov, V. M., & Zimovets, I. V. 2016, A&A, 585, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goossens, M., Andries, J., & Aschwanden, M. J. 2002, A&A, 394, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goossens, M., Arregui, I., Ballester, J. L., & Wang, T. J. 2008, A&A, 484, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goossens, M., Soler, R., Arregui, I., & Terradas, J. 2012, ApJ, 760, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Hammersley, J. 2013, Monte Carlo Methods, Monographs on Statistics and Applied Probability (Netherlands: Springer) [Google Scholar]
- Hannah, I. G., & Kontar, E. P. 2012, A&A, 539, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harra, L. K., Matthews, S. A., Long, D. M., Doschek, G. A., & De Pontieu, B. 2014, ApJ, 792, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Hayes, L. A., Gallagher, P. T., Dennis, B. R., et al. 2016, ApJ, 827, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Hollweg, J. V., & Yang, G. 1988, J. Geophys. Res., 93, 5423 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., Ruderman, M., Pascoe, D. J., et al. 2013, A&A, 551, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hood, A. W., Cargill, P. J., Browning, P. K., & Tam, K. V. 2016, ApJ, 817, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Ionson, J. A. 1978, ApJ, 226, 650 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, J., & De Moortel, I. 2002, A&A, 391, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability, 3rd edn. (Oxford) [Google Scholar]
- Kass, R. E., & Raftery, A. E. 1995, J. Am. Stat. Assoc., 90, 773 [Google Scholar]
- Kolotkov, D. Y., Nakariakov, V. M., Kupriyanova, E. G., Ratcliffe, H., & Shibasaki, K. 2015, A&A, 574, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kupriyanova, E. G., Melnikov, V. F., & Shibasaki, K. 2013, Sol. Phys., 284, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- McEwan, M. P., Díaz, A. J., & Roberts, B. 2008, A&A, 481, 819 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., & Ofman, L. 2008, ApJ, 682, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Mishin, V. V., & Tomozov, V. M. 2016, Sol. Phys., 291, 3165 [NASA ADS] [CrossRef] [Google Scholar]
- Morton, R. J., & Mooroogen, K. 2016, A&A, 593, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., & Ofman, L. 2001, A&A, 372, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakariakov, V. M., Ofman, L., Deluca, E. E., Roberts, B., & Davila, J. M. 1999, Science, 285, 862 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Nakariakov, V. M., Anfinogentov, S. A., Nisticò, G., & Lee, D.-H. 2016, A&A, 591, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Nakariakov, V. M., & Verwichte, E. 2013, A&A, 552, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2014, A&A, 570, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L. 2010, Liv. Rev. Sol. Phys., 7 [Google Scholar]
- Ofman, L., & Aschwanden, M. J. 2002, ApJ, 576, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T. J., Antolin, P., De Pontieu, B., et al. 2015, ApJ, 809, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Parnell, C. E., & De Moortel, I. 2012, Roy. Soc. London Philos. Trans. Ser. A, 370, 3217 [Google Scholar]
- Pascoe, D. J. 2014, Res. Astron. Astrophys., 14, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., & De Moortel, I. 2014, ApJ, 784, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., de Moortel, I., & McLaughlin, J. A. 2009, A&A, 505, 319 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Wright, A. N., & De Moortel, I. 2010, ApJ, 711, 990 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Wright, A. N., & De Moortel, I. 2011, ApJ, 731, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D. J., Hood, A. W., de Moortel, I., & Wright, A. N. 2012, A&A, 539, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Hood, A. W., De Moortel, I., & Wright, A. N. 2013, A&A, 551, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Wright, A. N., De Moortel, I., & Hood, A. W. 2015, A&A, 578, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., & Nakariakov, V. M. 2016a, A&A, 593, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016b, A&A, 589, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascoe, D. J., Goddard, C. R., Nisticò, G., Anfinogentov, S., & Nakariakov, V. M. 2016c, A&A, 585, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pugh, C. E., Armstrong, D. J., Nakariakov, V. M., & Broomhall, A.-M. 2016, MNRAS, 459, 3659 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B. 2008, in IAU Symp., 247, eds. R. Erdélyi, & C. A. Mendoza-Briceno, 3 [Google Scholar]
- Ruderman, M. S., & Roberts, B. 2002, ApJ, 577, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Terradas, J. 2013, A&A, 555, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russell, A. J. B., Simões, P. J. A., & Fletcher, L. 2015, A&A, 581, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safari, H., Nasiri, S., & Sobouti, Y. 2007, A&A, 470, 1111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sedláček, Z. 1971, J. Plasma Phys., 5, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Terradas, J., Oliver, R., Ballester, J. L., & Goossens, M. 2010, ApJ, 712, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Terradas, J., & Goossens, M. 2011, ApJ, 734, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Goossens, M., & Ballester, J. L. 2015, A&A, 575, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stepanov, A. V., Zaitsev, V. V., & Nakariakov, V. M. 2012, Coronal Seismology: Waves and Oscillations in Stellar Coronae (Wiley-VCH Verlag GmbH & Co) [Google Scholar]
- Terradas, J., Oliver, R., & Ballester, J. L. 2006, Philos. Trans. Roy. Soc. London Ser. A, 364, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Goossens, M., & Verth, G. 2010, A&A, 524, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tomczyk, S., & McIntosh, S. W. 2009, ApJ, 697, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Tomczyk, S., McIntosh, S. W., Keil, S. L., et al. 2007, Science, 317, 1192 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Van Doorsselaere, T., Andries, J., Poedts, S., & Goossens, M. 2004, ApJ, 606, 1223 [NASA ADS] [CrossRef] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., & Verwichte, E. 2007, A&A, 473, 959 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., Young, P. R., & Verwichte, E. 2008, A&A, 487, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Doorsselaere, T., Verwichte, E., & Terradas, J. 2009, Space Sci. Rev., 149, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Verth, G., & Erdélyi, R. 2008, A&A, 486, 1015 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verth, G., Terradas, J., & Goossens, M. 2010, ApJ, 718, L102 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Nakariakov, V. M., Ofman, L., & Deluca, E. E. 2004, Sol. Phys., 223, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Verwichte, E., Van Doorsselaere, T., Foullon, C., & White, R. S. 2013, ApJ, 767, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2013, ApJ, 771, 115 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. S., & Verwichte, E. 2012, A&A, 537, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., Verwichte, E., & Foullon, C. 2012, A&A, 545, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. S., Verwichte, E., & Foullon, C. 2013, ApJ, 774, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H., Li, B., Chen, S.-X., & Guo, M.-Z. 2015, ApJ, 814, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, D., & Van Doorsselaere, T. 2016, ApJS, 223, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Melnik, V. N., Brazhenko, A. I., et al. 2013, A&A, 555, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Zhelyazkov, I., & Ofman, L. 2015, ApJ, 813, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Zimovets, I. V., & Nakariakov, V. M. 2015, A&A, 577, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional fitted parameters
Figure A.1 shows histograms for additional model parameters fitted for Loop #1.
All Tables
Comparison of the seismologically estimated density scale height H with the hydrostatic scale height Hs implied by the loop temperature T estimated using DEM analysis.
Comparison of results for Loops #1–#4 when using a spline or polynomial background trend.
All Figures
 |
Fig. 1 Illustration of the principle of seismological inversion based on kink damping envelope. The two density profiles (left panels) produce the same overall damping rate for their corresponding kink oscillations (right panels). However, they can be distinguished based on the shape of the damping envelope, characterised by the switch time ts (vertical dashed lines). |
| In the text | |
 |
Fig. 2 The inverse relationship between the density contrast ratio and the inhomogeneous layer width ϵ. The curves in parameter space correspond to the same kink oscillation damping rate due to mode coupling (Fig. 1 shows two particular density profiles). The solid curve corresponds to the damping rate calculated using the general damping profile (Eq. (1)) while the dashed curve is for the exponential damping regime alone. |
| In the text | |
 |
Fig. 3 Dependence of period ratios P1/ 2P2 (solid lines) and P1/ 3P3 (dashed lines) on the density scale height H (top panel) and loop expansion factor Γ (bottom panel). |
| In the text | |
 |
Fig. 4 Examples of oscillation fits (green lines) which include a background trend (blue lines) given by a 4th order polynomial (top panels) and our spline procedure (bottom panels) described in Sect. 2.5. The left panels show an example of a localised perturbation in the background (at around 35 min), the middle panels are an example of piecewise linear behaviour, and the right panels show an oscillating background. The spline procedure accurately recovers the actual trend (dashed lines), whereas the low-order polynomial trend can both introduce artifical modulation and fail to account for modulation that is present. |
| In the text | |
 |
Fig. 5 SDO/AIA 171 Å images of the four loops we analyse in this paper. The axis of the chosen loop is indicated by a dashed red line, which is either an elliptical or a linear fit depending on the loop orientation. The solid blue line shows the location of the slit used to generate the time series. |
| In the text | |
 |
Fig. 6 Analysis for Loop #1 using the dispersionless model. Top left: loop position (symbols) as a function of time is described by our model (green line) which includes a background trend (blue line) described by our spline procedure. The red shaded region represents the 99% credible intervals for the loop position predicted by the model, including an estimated noise σY. The dotted and dashed lines denote t0 and ts1, respectively. Top right: wavelet analysis of the loop position with colours representing the normalised spectral amplitude. The dashed lines show the time-dependent periods of oscillation described by our model. The hatched region denotes the cone of influence. Middle left: detrended loop position (symbols) with the first (green), second (blue), and third (red) longitudinal harmonics. Times ts1, ts2, and ts3 are denoted by the dashed lines in the corresponding colour. Middle right: density profile parameters determined by the oscillation damping envelope. The red bars are based on the median values and the 95% credible intervals, indicated by the dotted and dashed lines, respectively, in the histograms (bottom panels). The solid curves are fits to the histogram data using the exponentially modified Gaussian function. |
| In the text | |
 |
Fig. 7 Histograms of the longitudinal structuring parameters for the stratified (left panels) and expanding (right panels) models for Loops #1–#4. |
| In the text | |
 |
Fig. 8 Wavelet analysis for Loop #1 background trend. |
| In the text | |
 |
Fig. 9 Analysis for Loop #2 using the dispersionless model. Panels as in Fig. 6. |
| In the text | |
 |
Fig. 10 Time-dependent period of oscillation (top) and background trend (bottom) for Loop #2. The blue circles represent the interpolation points (xi,yi). |
| In the text | |
 |
Fig. 11 Analysis for Loop #3 using the dispersionless model including the decayless regime. Panels as in Fig. 6 except the components panel also includes the decayless oscillation (yellow line). |
| In the text | |
 |
Fig. 12 Histogram for A0 for Loop #3 for the dispersionless model with the decayless regime shown in Fig. 11. |
| In the text | |
 |
Fig. 13 Analysis for Loop #3 using the dispersionless model without including the decayless regime. Panels as in Fig. 6. |
| In the text | |
 |
Fig. 14 DEM analysis for Loops #1 (top) to #4 (bottom) used to estimate the temperature (Table 3) of the oscillating loop (dashed white lines). Each panel corresponds to a particular temperature interval. |
| In the text | |
 |
Fig. 15 Analysis for Loop #4 using the dispersionless model. Panels as in Fig. 6. |
| In the text | |
 |
Fig. 16 Analysis for Loops #1–#4 using a model including the fundamental kink mode only. Panels as in Fig. 6. |
| In the text | |
 |
Fig. 17 Summary of results using a polynomial (4th order) trend. Panels are comparable to those in Figs. 6, 9, 11, and 15 which show the same models with a background trend using our spline procedure described in Sect. 2.5. |
| In the text | |
 |
Fig. 18 Demonstration of spectral analysis for damped kink oscillations. Test data (left panel) contains second and third harmonics with 20% amplitude of the fundamental mode. Owing to the frequency-dependent damping by mode coupling, these components have negligible signatures in periodogram (middle panel) and wavelet (right panel) analysis. |
| In the text | |
 |
Fig. A.1 Histograms for additional model parameters for Loop #1 for the model shown in Fig. 6. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


