| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A86 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629344 | |
| Published online | 05 April 2017 | |
Mysterious eclipses in the light curve of KIC8462852: a possible explanation
Astronomical Institute, Slovak Academy of Sciences, 05960 Tatranská Lomnica, Slovak Republic
e-mail: ne@ta3.sk; budaj@ta3.sk
Received: 20 July 2016
Accepted: 9 December 2016
Context. Apart from thousands of “regular” exoplanet candidates, Kepler satellite has discovered a small number of stars exhibiting peculiar eclipse-like events. They are most probably caused by disintegrating bodies transiting in front of the star. However, the nature of the bodies and obscuration events, such as those observed in KIC 8462852, remain mysterious. A swarm of comets or artificial alien mega-structures have been proposed as an explanation for the latter object.
Aims. We explore the possibility that such eclipses are caused by the dust clouds associated with massive parent bodies orbiting the host star.
Methods. We assumed a massive object and a simple model of the dust cloud surrounding the object. Then, we used the numerical integration to simulate the evolution of the cloud, its parent body, and resulting light-curves as they orbit and transit the star.
Results. We found that it is possible to reproduce the basic features in the light-curve of KIC 8462852 with only four objects enshrouded in dust clouds. The fact that they are all on similar orbits and that such models require only a handful of free parameters provides additional support for this hypothesis.
Conclusions. This model provides an alternative to the comet scenario. With such physical models at hand, at present, there is no need to invoke alien mega-structures for an explanation of these light-curves.
Key words: radiation: dynamics / minor planets, asteroids: general / planets and satellites: general / planet-star interactions / binaries: eclipsing
© ESO, 2017
1. Introduction
Kepler satellite marks a revolution in the field of extra-solar planet study (Borucki et al. 2010). Apart from thousands of “normal” transiting exoplanet candidates showing periodic, non-variable, and symmetric dips, a small number of exceptional transit-like signals were detected. Using data from this satellite, Rappaport et al. (2012) discovered a transiting disintegrating exoplanet KIC12557548b (KIC1255). Unlike all other exoplanets, it exhibits a strong variability in the transit depth. On average, transits are approximately 0.6% deep but they may exceed 1% or disappear for some period of time. The shape of the transit is highly asymmetric with a significant brightening immediately before the eclipse with a sharp ingress followed by a smooth egress. The planet also has an extremely short orbital period of approximately 16 hours.
The interpretation of the light-curve is that the planet is in a stage of catastrophic evaporation (Perez-Becker & Chiang 2013). This creates a comet-like dusty tail extending well beyond the planet’s Hill radius that is responsible for the observed variable transits. The planet itself is too small to be seen in transit. The mass of the planet must be relatively small too, less than that of Mars, otherwise the material would not be able to escape from its deep gravitational well. This is supported by Garai et al. (2014) who found no evidence for the dusty tails in other more massive close-in exoplanets observed by Kepler. The planet’s tail is dominated by radiative and gravitational forces as well as an interplay between the grain condensation and evaporation. There are also indications that stellar activity may affect the behavior of the dusty tail since a quasi-periodic long term variability in the tail (Budaj 2013) as well as a correlation of the transit depth with the rotation period of the star (Kawahara et al. 2013) were detected. Croll et al. (2015) argue that the modulation of the transit with the rotation period may also occur as a result of the star spot occultations. Pre-transit brightening as well as the color dependence of the transit depth can constrain the particle size of dust grains in the comet-like tail, which was found to be of the order of 1 micron (Brogi et al. 2012; Budaj 2013; Croll et al. 2014; van Werkhoven et al. 2014; Bochinski et al. 2015; Schlawin et al. 2016).
Two other objects of this kind (KOI-2700b, K2-22b) were discovered already by Rappaport et al. (2014) and Sanchis-Ojeda et al. (2015). Their orbital periods are less than one day. The average transit depth of KOI-2700b is approximately 0.04% and decreases with time. Transits of K2-22b (EPIC201637175B) are 0−1.3% deep. The observed tail lengths in these objects are consistent with corundum dust grains (van Lieshout et al. 2014, 2016). It has been argued and demonstrated that dust clouds associated with such exoplanets may not be uniform and may consist of several structures that may differ in dust properties and chemical composition. For example, KIC 1255 may have an “inner tail” (coma) and an “extended trailing tail’ (tail) (Budaj 2013; van Werkhoven et al. 2014). A leading tail may also occur, for example, in K2-22b, if the star is cool and the radiative acceleration on dust is negligible compared to gravity (Sanchis-Ojeda et al. 2015).
Another exotic object with similar dips in the light-curve is a white dwarf, WD 1145+017 (Vanderburg et al. 2015; Croll et al. 2017; Xu et al. 2016). It features semi-periodic eclipses with periods of approximately 4.5 h, which are as deep as 40%. A probable explanation is that these dips are caused by disintegrating planetesimals or asteroids transiting the star. They gradually fall onto the white dwarf contaminating its atmosphere with heavy elements. The transits are highly variable, with timescales of days. The light-curve contains many sharp features that drift if phased with the dominant period (Gänsicke et al. 2016; Rappaport et al. 2016). Zhou et al. (2016) carried out simultaneous optical and near infrared observations and placed the lower limit of 0.8 micron on the particle size of dust grains.
Recently, an even more peculiar object was discovered in the Kepler data by Boyajian et al. (2016) named KIC8462852 (KIC8462). KIC8462 is a 12 mag main sequence F3V/IV star with mass of approximately M⋆ = 1.43 M⊙, radius R⋆ = 1.58 R⊙, effective temperature Teff = 6 750 K, and luminosity L⋆ = 4.7 L⊙. It exhibits the asymmetric variable dips in the brightness similar to the above mentioned objects. However, here the dips have irregular shapes with a tendency towards a smooth long ingress and sharp egress. Moreover, the dips are much deeper, sometimes eating up more than 20% of the flux, and do not show any obvious periodicity. There is no simple explanation of such behavior. A first view with Gaia also indicates that it is a normal F3V star at a distance of 390 pc (Hippke & Angerhausen 2016).
Based on the analogy with the above mentioned objects, and the strong extinction properties of dust, one can assume that eclipses are due to large and opaque dust clouds passing in front of the star. Such dust clouds may be associated with various objects and/or events. Boyajian et al. (2016) have considered several scenarios; a collision within an asteroid belt or planet impact; dust enshrouded planetesimals; and the passage of a family of exocomet fragments, all of which are associated with a single previous breakup event. The latter scenario seems to be the most consistent with the data. However, it falls short of explaining the shape of the dips.
Infrared observations using WISE, Spitzer, and NASA/IRTF 3 m (Boyajian et al. 2016; Marengo et al. 2015; Lisse et al. 2015) have not detected any significant infrared excess emission, which puts strong constraints on the presence and amount of hot dust in the vicinity of the star. Aside from this non-detection, no significant emission from cold dust was detected at millimeter and sub-millimeter wavelengths by Thompson et al. (2016), which limits the amount of dust within 200 au from the star to less than 7.7 M⊕ and amount of dust actually occulting the star to less than approximately 10-3M⊕.
Bodman & Quillen (2016) investigated the possible comet scenario and found that it is possible to fit most of the features in the Kepler light-curve with several clusters of comets containing 70−700 comets. However, it was not possible to reproduce a large dip at day 800 due to its smooth shape and gradual ingress followed by a sharp egress.
It was pointed out by Wright et al. (2016) that the above mentioned kind of variability might be consistent with a “swarm” of artificial mega-structures produced by an extraterrestrial civilization. Harp et al. (2016) and Schuetz et al. (2016) searched for the presence of radio and optical signals from extraterrestrial intelligence in the direction of the star and found no narrow band or wide band radio signals or periodic optical signal. Abeysekara et al. (2016) also searched for brief optical flashes towards the target and found no evidence of pulsed optical beacons above a pulse intensity at the Earth of approximately 1 photon per m2.
The recent discovery of a long-term fading of the star by 0.16 mag over the last century makes the situation even more complicated and also poses a problem for the comet scenario (Schaefer 2016). “Fortunately”, as pointed out by Hippke et al. (2016a, 2017) and Lund et al. (2017), this long-term trend is most likely a data artifact, and it is probably not of astrophysical origin. Nevertheless, Montet & Simon (2016) found convincing evidence from the Kepler data that the star had dimmed by approximately 3% during the duration of the Kepler mission. In connection with this, it was suggested that the variability may be due to free-travelling interstellar material in the form of either a dark cloud (Bok globule), a disk around a stellar remnant, a swarm of comet-like objects, or planetesimals crossing the line of sight (Wright & Sigurdsson 2016; Makarov & Goldin 2016; Lacki 2016). Lisse et al. (2016) suggest a parallel between KIC8463 and the observations of a late, heavy bombardment of η Corvi.
The aim of the present study is to explore the shapes of the eclipse events observed in KIC8462 and investigate whether or not it is possible to comprehend their basic features in terms of eclipses of only a small number of massive bodies and associated dust clouds (hence a small number of free parameters). We do not aim to determine the parameters of the dust and parent bodies unambiguously but rather provide hints for future more detail investigations.
2. Observations, motivation, and aims
We use the data for KIC8462852 obtained by the Kepler satellite (Borucki et al. 2010). These are 18 quarters of long cadence observations in the form of PDCSAP flux as a function of Kepler barycentric Julian day (BKJD). The exposure time of long-cadence observations was approximately 30 min. There are significant offsets between the data from different quarters, and for this reason, each quarter was normalized separately. Normalization was very simple; PDCSAP flux from each quarter was divided by a single constant. The advantage of such a simple normalization is that it does not introduce any artificial trend to the data. Four main events can be observed in this light-curve around BKJD of 800, 1520, 1540, and 1570, respectively. They are shown in Fig. 1. Aside from that, there are other relatively small transit events, for example, at 140 and 260 days with a depth of approximately 0.6%. These are not the subject of this study but this information is used later in the discussion.
 |
Fig. 1 Four main eclipse events in the light-curve of KIC8462 observed with Kepler (Boyajian et al. 2016) and also analyzed in this study. |
As already mentioned above, even the most promising comet scenario (Bodman & Quillen 2016) fails to explain all of the recorded observations. Most of the observed dips (see Fig. 1) tend to have a slow ingress followed by a sharp egress. This is in contrast with a typical transit of a comet-like body, which would show a steep ingress followed by a slow egress (Lecavelier Des Etangs et al. 1999). The observed light-curves, if explained by comets, would require comets in large numbers, larger than 102, and consequently many free parameters. Furthermore, it is difficult to reproduce, for example, the egress part of light-curves. Some features cannot be represented at all, such as a smooth feature at 800 days. Some others, such as a symmetric triple feature at 1540 days, might suggest the presence of a ring-like structure that would imply an object with a non-negligible gravity. This motivates our search for an alternative explanation of the phenomenon. Our goal is to investigate whether or not it is possible to reproduce the observed features with only a small number of eclipsing objects, based on first principles and simple assumptions. Of course one cannot expect a perfect fit with only a handful of free parameters.
The transit of a dark spherical opaque body can cause a relative drop in the light-curve as deep as 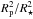 where Rp and R⋆ are radii of the body and star, respectively. No single planet or brown dwarf could cause an asymmetric 20% dip in the light-curve of a solar type main-sequence star. That is why we will assume a massive object (MO) surrounded by a dust cloud. It would be this dust cloud that would cause the eclipse events. We refer to a “massive object” as an object with a non-negligible gravity (heavier than a large comet in the solar system) so that it has to be taken into account.
where Rp and R⋆ are radii of the body and star, respectively. No single planet or brown dwarf could cause an asymmetric 20% dip in the light-curve of a solar type main-sequence star. That is why we will assume a massive object (MO) surrounded by a dust cloud. It would be this dust cloud that would cause the eclipse events. We refer to a “massive object” as an object with a non-negligible gravity (heavier than a large comet in the solar system) so that it has to be taken into account.
Here, “dust cloud” refers to a cloud containing numerous individual massless dust particles (DPs), which initially reside within the gravity well of the parent body. This helps to keep the DPs together to form a cloud associated with the parent body. One could argue that (A) the probability of a transit rapidly decreases with the distance of the cloud from the star indicating that the star-cloud distance during the transit may be rather small. On the other hand, (B) the dust cloud will radiate in the optical region (scattered light) as well as in the infrared and mm region (thermal radiation). This radiation diminishes with approximately the square of the star-cloud distance, and, as mentioned in the Sect. 1, observations of the thermal radiation exclude large amounts of the dust located close to the star at the time of observations. It is possible to adhere to both constraints (A) and (B) if a dust cloud is located on a highly eccentric orbit. The same idea and arguments are used in the comet scenario and are therefore also acceptable in this scenario.
Ultimately, a small number of massive objects with dust clouds would be needed to describe the small number of complex features seen in the light-curve. The orbits of these objects should be situated in the same plane and have similar trajectories. Notice that although we go on to assume approximately four massive objects on almost identical orbits, these objects are not ‘statistically’ independent. They are apparently of a common origin, that is, the result of a break-up process. Thus, the statistical probability of our model is reduced to the existence of a single massive body on an eccentric orbit and a break-up process.
The origin of the dust clouds and their parent bodies is not the subject of this study and their presence and initial structure are both assumed for the purpose of this study. Nevertheless, one can speculate that they might be the result of an impact, collision, or break-up event facilitated by the rotation, tides, or heating from the star. For example, a recent study of catastrophic disruption of asteroids in the solar system by Granvik et al. (2016) shows that asteroids break up at much larger distances from the Sun than previously thought; approximately 0.094 au. If this value were scaled by 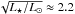 , asteroids around KIC8462 would break up at a distance of 0.20 au, which is considerably larger than its Roche limit, which is approximately 2.44 R⋆ or 0.018 au (assuming that the density of the star and that of the asteroid are approximately the same). The low-albedo asteroids break up more easily and at larger distances than high-albedo asteroids. Another possibility is that rocks break into small grains by thermal cracking, or the YORP effect causes the asteroids to spin faster, to the point when gravity and cohesive forces can no longer keep them intact (Vokrouhlický et al. 2015). A third possibility is that all asteroids contain volatile elements that, when sublimating at moderate temperatures, exert enough pressure on the body to cause it to explode.
, asteroids around KIC8462 would break up at a distance of 0.20 au, which is considerably larger than its Roche limit, which is approximately 2.44 R⋆ or 0.018 au (assuming that the density of the star and that of the asteroid are approximately the same). The low-albedo asteroids break up more easily and at larger distances than high-albedo asteroids. Another possibility is that rocks break into small grains by thermal cracking, or the YORP effect causes the asteroids to spin faster, to the point when gravity and cohesive forces can no longer keep them intact (Vokrouhlický et al. 2015). A third possibility is that all asteroids contain volatile elements that, when sublimating at moderate temperatures, exert enough pressure on the body to cause it to explode.
 |
Fig. 2 Left: total opacity of various dust species at 0.6 microns as a function of particle size. Right: radiative to gravity acceleration ratio (β parameter) of various dust species for KIC8462 as a function of the particle size. Olmg50 refers to olivine (50% iron), pyrmg40 refers to pyroxene (60% iron), and carbon is at 1000 °C. |
Discovery of KIC8462 in the Kepler data may be used to estimate the frequency f of such systems under the assumption that they are associated with a massive body on a highly eccentric orbit, such as the one used in our calculations, for example, with a periastron of approximately 0.1 au and an apastron of approximately 50 au. The number of such events, Nobs, observed during the duration of the Kepler mission is: 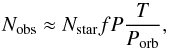 (1)where Nobs = 1 is the number of such events discovered with Kepler. Nstar is the number of stars monitored with Kepler (approximately 105) (main sequence stars brighter than approximately mV = 14 mag.). P is the probability that the body has a proper inclination and argument of periastron to detect the transit, which is approximately 0.01−0.1 for the assumed body. T/Porb is the probability of catching the transit. T = 4 yr is the duration of the Kepler mission and Porb ≈ 102yr is the orbital period of the assumed body. From the above equation, the probability that a star currently hosts pieces of such a broken body with dust clouds that are capable of producing such events is f ≈ 10-2.
(1)where Nobs = 1 is the number of such events discovered with Kepler. Nstar is the number of stars monitored with Kepler (approximately 105) (main sequence stars brighter than approximately mV = 14 mag.). P is the probability that the body has a proper inclination and argument of periastron to detect the transit, which is approximately 0.01−0.1 for the assumed body. T/Porb is the probability of catching the transit. T = 4 yr is the duration of the Kepler mission and Porb ≈ 102yr is the orbital period of the assumed body. From the above equation, the probability that a star currently hosts pieces of such a broken body with dust clouds that are capable of producing such events is f ≈ 10-2.
The existence of a massive body on a highly eccentric orbit may not be highly unusual. In our own solar system, some comets from the Oort cloud (e.g., Duncan et al. 1987; Neslušan & Jakubík 2005) as well as trans-Neptunian objects (Emel’yanenko et al. 2007) have been found to migrate down to the region of terrestrial planets. Their perihelion can be reduced to a few astronomical units or even closer. The aphelion of such an object can remain beyond the orbit of the outermost planet. According to Bailey et al. (1992), if the orbital inclination of the objects entering the inner solar system is high, the perihelion distance of many of them is further reduced due to the long-term secular resonances and the objects become sun-grazing at intervals of approximately 103 revolutions. The authors introduced five representative comets currently evolving to become the sun-grazers: 96P/Machholz, 161P/Hartley-IRAS, C/1846 B1, C/1989 A3, and C/1932 G1.
Close to the periastron located in close vicinity to the central star, the object can be destroyed by the tidal action of the star. A remnant of such destruction in the solar system can still be detected in the form of small sun-grazing comets orbiting the Sun along similar orbits. Specifically, four such groups of sun-grazing comets are observed in our solar system at present; Kreutz, Meyer, Marsden, and Kracht group (Biesecker et al. 2002; Knight et al. 2010). Each group is believed to originate from a single, more massive progenitor. The most highly populated is the Kreutz group. Besides the small cometary nuclei, bright comets have also been observed within this group, providing evidence that some large fragments still exist in it (e.g., Sekanina & Kracht 2015). Consequently, the occurrence of a massive body on such an eccentric orbit at any time is not rare. If there are groups of comets, each group moving in similar orbits and originating from a single progenitor in our own solar system, there could also be a group of objects in almost identical orbits at the KIC8462.
Perhaps it is worth noting that the similarity of the orbits of group members (orbits of the MOs) occurs due to the small velocity of the separation of the members from their progenitor at its break-up in comparison to the orbital velocity of the progenitor itself.
Minimum dust mass in M⊕ for different dust compositions.
3. Dust properties
The shape and depth of obscuration events will depend on certain properties of dust grains. It is mainly the number of dust particles along the line of sight and their size that determines the opacity and optical depth along the line of sight. This is illustrated in Fig. 2 for a number of refractory dust species and for a wavelength of approximately 0.6 microns corresponding to the Kepler spectral window. The opacities include both absorption and scattering opacity and are in cm2g-1 , which means that they are per gram of the dust material. One can see that the opacity of most species has a pronounced maximum at approximately 0.1 microns.
 |
Fig. 3 Illustration of the behavior of a dust cloud projected into the orbital plane of the MO for different β values. Plot a): β = 0.007 – particles tend to stay on the elliptical orbit and follow the parent body, the trajectory of which is shown with the red solid curve. Plot b): β = 0.7 – the cloud of particles soon separates from the parent body and the particles move in their own elliptical trajectories. Plot c): β = 1 – the P-R drag balances the gravity and therefore the particles move uniformly along a straight line. Plot d): β = 1.4 – particles easily decouple from the parent body and settle onto hyperbolic orbits. Positions of the MO (crosses) are shown at the same moments as the positions of the individual DPs (dots). Different colors are used for different times, separated by 25-day intervals. The position of KIC8462, in the origin of coordinate x−y plane, is drawn with the violet full circle. Calculated for model A of a cloud with a body mass of m = 10-10M⋆. |
It takes much more dust at low opacity to produce the same dip in the light-curve compared to dust at high opacity. Table 1 lists the minimum amount of dust required to produce a 20% deep eclipse of KIC8462 at 0.6 microns as a function of the particle size for iron, forsterite (an iron free silicate of the olivine family), and liquid water, assuming an optically thin dusty environment. No other assumption is involved in this estimate. The amount of dust required in the form of even larger particles is linearly proportional to the size of particles and can be easily extrapolated.
Another important property of dust grains is that apart from gravity of the MO and the star, they may experience significant acceleration due to the radiation of the host star. This radiative acceleration is also controlled by the absorption and scattering opacities of the grain, angular distribution of the light scattered by the grain, and spectral energy distribution, size, and distance of the star. This is also illustrated in Fig. 2 as a function of particle size in the form of the β parameter, which is the radiative to gravity acceleration ratio. Since the mass of KIC8462 and, hence, its gravity is larger than that of the Sun, one must remember that the same value of β means a larger radiation pressure at KIC8462 than at the Sun.
The β parameter also shows a maximum at approximately 0.1 microns, which reflects the peak in opacity. Because the radiative acceleration upon a grain is proportional to its cross-section while gravity is proportional to its volume, very large and heavy grains have β ≪ 1. In such a case, the radiative pressure can be neglected and, in the absence of other massive objects, grains remain on an elliptical orbit around the star. For grains with β = 1, gravity from the star will be balanced by the radiation pressure and, once the grain escapes the gravity of the MO, it follows an almost straight line. Grains with β> 1 and “out of reach” of the MO will follow a hyperbolic orbit around the star forbidding them from passing close to the star or revolving around it; such grains are expelled from the system. Consequently, the chance of causing an occultation event is significantly lower for these grains unless they are constantly replenished. This is the case for dust grains with a size of approximately 0.1 microns as well as smaller carbon, iron, or iron-rich grains. This is shown in Fig. 3 assuming a model A of the cloud (see Sect. 4 below) around the MO with the mass m = 10-10M⋆. The plots (a), (b), (c), and (d) illustrate the motion of the DPs calculated for β = 0.007, 0.7, 1, and 1.4, respectively.
Given the above mentioned accounts, opaque grains with β< 1 values are the best candidates for causing such obscuration events. This is fulfilled for grains with 0.1 <β< 1, which translates to particle sizes of approximately 0.3−10 microns for most of the dust species. Based on Table 1 it would require at least 10-10 Earth masses of dust. The above mentioned calculations made use of the on-line tables of dust properties calculated by Budaj et al. (2015). They assume homogeneous spherical grains with a relatively narrow Deirmendjian particle-size distribution. Particle size of such a distribution refers to its modal particle size. Radiative accelerations assume non-black body radiation from the star1 with effective temperature, mass, and radius of Teff = 6750 K, M = 1.43 M⊙, and R = 1.58 R⊙, respectively (Boyajian et al. 2016). Table 2 lists the sources of the refractive index used in the calculations.
Reference list for the refraction index used in this work.
4. Calculations of the obscuration events
4.1. Model of the dust cloud
Light-curves of the obscuration events depend on the properties, position(s), and velocity(ies) of the parent massive body and the individual dust grains, as well as the position of the observer. These are all unknown quantities. Furthermore, there is an infinite number of possible models of a dust cloud to be envisaged and it is impossible to study all of them in detail. That is why, in this primary study, we restrict our efforts to a few simple models that can be described by a relatively small number of free parameters. At the same time we use only a small number of the more important and/or probable values of these free parameters.
For example, in line with what was argued in the Sect. 2, we assume a massive object analogous to a destabilized trans-Neptunian object, orbiting KIC8462 at a highly eccentric orbit. More specifically, we often consider a “standard orbit” with the apastron equal to 50 au. The periastron is assumed to equal 0.1 au, which fits well with individual features and is still inside the 0.2 au destruction zone mentioned in Sect. 2. For simplicity, an edge-on inclination of i = 90° is assumed. We consider a range of masses from that of a giant cometary nucleus (≈ 10-6M⊕) to approximately four Moon masses (≈ 5 × 10-2M⊕). Detailed information about the input parameters in all considered models is given in Tables A.1 to A.5.
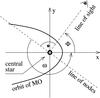 |
Fig. 4 Coordinate system in respect to the MO orbit and direction towards the observer. |
Further, we assume a cloud of massless dust particles orbiting the MO. Their initial locations and velocities are defined at the moment when the MO is situated at a distance ro from the star, well before the periastron. The vast majority of models assume ro = 5 au. This choice was motivated by the comet activity in our solar system due to sublimation of water ice at a distance of approximately 2−3 au from the Sun (Delsemme & Miller 1971). Scaling this distance by a factor of 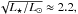 one could expect an onset of similar activity of KIC8462 at a distance of approximately 4−7 au. In a number of test models (see tables in Appendix), the cloud was also created in the periastron or immediately before it, when the MO reached a distance critical for its splitting. However, the light-curves from these models did not match, even approximately, their observed counterparts. This is because DPs did not have enough time to be dispersed.
one could expect an onset of similar activity of KIC8462 at a distance of approximately 4−7 au. In a number of test models (see tables in Appendix), the cloud was also created in the periastron or immediately before it, when the MO reached a distance critical for its splitting. However, the light-curves from these models did not match, even approximately, their observed counterparts. This is because DPs did not have enough time to be dispersed.
A 3D Cartesian coordinate system O(xyz) is used to describe the orientation of the MO and DPs, and for the calculations. x−y is the MO’s orbital plane, x axis points towards the MO periastron, y axis is oriented in the sense of motion of the MO at the periastron, and the z axis is such that one would see an anti-clockwise orbit from the positive z-values − see the scheme in Fig. 4. The angle measured from the x-axis to the line of sight is denoted by Φ. The following three models for the dust clouds, specified by the initial conditions of DPs, were considered.
-
Model (A): all DPs are placed on initially eccentric orbits aroundMO. We assume several specific values of their (unique)pericenters and initial pericenter velocities (seeTables A.1−A.3). The pericenter (qtp) and apocenter (Qtp) distances of the DPs with respect to the MO were mostly assumed to equal 103 and 105km, respectively. The orientation of the orbits is random, as is the line of apsides. All DPs are simultaneously released from their pericenters with similar velocities, meaning similar apocenters. This might be interpreted as a spherical shell occurring after a sudden release of dust, outburst, eruption, or explosion on the object. The sudden outburst may be common, especially on smaller objects, such as comets (a good example is the well-known frequently outbursting comet 29P/Schwassmann-Wachmann 1) or some asteroids, such as (596) Scheila (Warner 2006; Husárik 2012) or P/2010 A2 (Jewitt 2009; Birtwhistle et al. 2010, and many others). However, notice that since all the particles are initially located at their pericenters and are released simultaneously on elliptical orbits with similar pericenters and apocenters, this may trigger an oscillation of the cloud. The oscillation period equals the orbital period of DPs, which depends on their semi-major axes and the mass of MO. For example, assuming the masses of the MO equal 10-8, 10-10, and 10-12M⋆, and a DP semi-major axis of 50 000 km, a given particle would reach its apocenter on Keplerian orbit after 9.5, 95, and 950 days, respectively. We were originally skeptical about such a simple type of model but, to our surprise, we found a number of light-curves which resemble the observed ones.
-
Model (B): similar to model (A) except that the particles are not released simultaneously from the pericenter. They initially have a random distribution of their mean anomalies. At the same time, they have a random distribution of their initial velocities (corresponding to the apocenter distances typically in a range from 10 000 to 100 000 km; some other intervals of the apocenters were also considered, however, (see Table A.4). The value of the pericenter distance is still chosen to be the same for all DPs. The random mean anomaly and initial velocity places them on different orbits around MO with different orbital periods. The model might resemble a dusty envelope or a huge spherical atmosphere of the MO. It would appear that this model best fits the 800-day feature.
-
Model (C): this is an initially planar, ring-like structure around the MO. Even a small amount of angular momentum present in the dust cloud often tends to form such a structure. We inspected a few different values of the inner as well as the outer radius of the ring − see Table A.5. The minimum inner radius was assumed to be comparable with the physical radius of the MO depending on its mass and density. In the rectangular coordinate frame O(xyz) with the x axis aligned to the MO’s line of apsides and the x−y plane to be the orbital plane of the MO, we situated the ring in the following way: firstly, the frame was rotated clockwise around the coordinate z-axis by the angle ϑ. This new frame O(x′y′z′) was then rotated, clockwise again, around the x′-axis by the angle σ. (A small number of values for these angles were inspected but mostly ϑ = 30° and σ = 45° were used – see Table A.5.) We obtained frame O(x′′y′′z′′). The new plane x′′−z′′ was chosen to be the plane of the ring. Initial results with the disks spanning the range from 5000 to 10 000 km were encouraging. Therefore, we tried to improve these models assuming a non-uniform radial distribution of the DPs in the ring. A peak in this distribution centered on the MO-centric distance of 7500 km was assumed, whereby the MO-centric distance of the jth particle, rj, in kilometers was calculated according to the relation rj = 7500 ± 2 500ηs, where the sign in pair ± was randomly generated and η was a random number from the interval (0, 1). Three values for the s index were considered: 1, 3/2, and 2. In constructing the C-type model, we kept in the mind the idea that the ring could persist more than a single orbital revolution of MO around the central star. This could be possible if the ring consisted of larger particles, which would have been a source of smaller particles causing the occultation. The ring could survive the periastron passage if it were situated within the corresponding Hill’s radius. Therefore, the extent of the ring in a majority of models satisfies this demand. The ring in models C20 to C34 spans from the physical surface of a (spherical) MO to the Hill radius. The radius of the physical surface is calculated assuming a mean density equal to 2 000 kg m-3. One exception to the stipulation that the whole ring be situated within the MO’s Hill radius is model C13, where the outer radius of the ring is equal to approximately two MO Hill radii.
In each type of model, we varied the P-R drag parameter β. We also created a small number of models to investigate the effect of changing the standard orbit of a MO and/or the effect of starting a dust cloud model at distances other than ro = 5 au.
4.2. Evolution of the cloud and light-curves
Next, we followed the evolution of the dust cloud and MO during one periastron passage and back to a distance ro. Integrator RA15 (Everhart 1985) within the MERCURY package, version 6, created by Chambers (1999) was used for this purpose. The MERCURY integrator defines “big” and “small” objects. It calculates for the mutual gravitational interaction of all big objects (i.e., star with planets and multiple massive bodies) as well as for their effects upon the small objects (massless particles). On the contrary, small massless DPs do not affect the motion of massive bodies or that of one another.
Besides the gravity of the central star and the MO, the motion of the DPs is obviously influenced by the radiation of the central star. This action is known as the Poynting-Robertson (P-R) effect. We consider the basic components of acceleration due to the P-R drag: radial given by ar = β(GM⋆/r2)(1−2vr/c) and transverse given by at = −β(GM⋆/r2)(vt/c), where β is the ratio of the P-R drag and gravitational accelerations of the central star, G is the gravitational constant, vr is the radial component of the star-centric velocity of the DP, vt is its transverse component laying in the orbital plane of the DP and oriented in the sense of its motion, and c is the speed of light. The third, perpendicular component of the P-R drag acceleration is assumed to be zero. The subroutine calculating the P-R drag acceleration was added into MERCURY version 6.2.
We assume that all individual DPs are identical and characterized by the same value of β. We concentrate on dust grains with 0.1 <β< 1 but have also carried out dozens of models beyond this range (see the tables in Appendix). We neglect other potential non-gravitational effects.
Once we have the location of each individual DP as a function of time, we can calculate the number of DPs transiting KIC8462 from the point of view of the observer as a function of time. DPs in transit are simply those that happen to project onto the stellar disk at a particular time, that is, their distance from the line of sight towards the exact center of the stellar disk is smaller than the radius of this star, R⋆. We consider the coordinate frame having the reference plane parallel to the sky and with the axis perpendicular to this plane oriented outward from the position of the observer. In this coordinate frame, the inclination of the orbital plane, i, of MO is i = 90° (observer is sitting in the orbital plane of MO). We denote the angle between the line of apsides and observer’s line of sight to KIC8462, measured in the direction of the MO’s motion, by Φ as shown in Fig. 4. In this figure, the crossing of the reference plane and orbital plane of MO is shown with the dashed line. Angle Φ is related to the argument of periastron of MO, ω, via Φ + ω = 270°.
We assume the set of values of angle Φ ranging from 0° to 360° with increments of 1° but we exclude the interval 170°−190°, which is near the apastron. We consider a cloud of 1 000 DPs in a broad parameter space but use 10 000 particles when zooming into a few specific locations in the grid of our A-models (see Tables A.1−A.3). Finally, we convert the number of particles in transit, n(t), into a synthetic light-curve, f(t), for comparison with the observations, by shifting it to the proper BKJD values and scaling its intensity as follows: 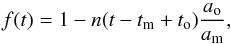 (2)where tm,am are the time and amplitude of the model (n(t) function) while to and ao are the time and depth of the observed feature. This simple and fast procedure is equivalent to the assumption that the dust is optically thin and that it only absorbs and scatters the radiation out of the beam while the scattering emission into the line of sight is ignored. The limb darkening is not taken into account.
(2)where tm,am are the time and amplitude of the model (n(t) function) while to and ao are the time and depth of the observed feature. This simple and fast procedure is equivalent to the assumption that the dust is optically thin and that it only absorbs and scatters the radiation out of the beam while the scattering emission into the line of sight is ignored. The limb darkening is not taken into account.
5. Results
We calculated the synthetic light-curves in 187 models of type A, 27 models of type B, and 39 models of type C. The initial parameters of all models are given in Tables A.1 through A.5. Although a quantitative match between the model and theory with only a small number of free parameters is very hard to achieve, a surprising qualitative, morphological similarity appeared for several models, the best of which we describe in the following.
To evaluate the match between the observed event and corresponding model, we attempted to find some automatic minimization technique that would pick the best matching models from the set of created models but were not successful. This is most probably due to the fact that the observed features are too complicated (often with multiple peaks), the range of free parameters is too large (many orders of magnitude), while our coverage of the parameter space is very limited (with large steps). For, this reason, we manually reviewed all the synthetic light-curves. In spite of such a subjective method, however, we hope to demonstrate that almost all observed features can be understood within an appropriate simple model.
5.1. Feature at 800 days
This feature is a single minimum with a smooth decline and a sharper egress. It was not explained in terms of the comet scenario. This kind of shape is produced naturally in our models since as the dust cloud approaches the periastron, it shrinks and creates a sort of leading tail. Figure 5 displays one of them and how it compares to the observations. This particular model was type (A) and was obtained assuming mass, periastron, and apastron of the MO: 10-11M⋆, 0.1 au, and 50 au, respectively (model A39 in Table A.1). The spherical dust cloud was composed of DPs having the properties corresponding to β = 0.629, which were initially placed on elliptical orbits around MO with pericenters and apocenters of 75 km and 75 000 km. Start/end of integration was at the pre-periastron star-centric distance of MO equal to 5 au and the line of sight had Φ = 29°.
However, it appears that the models of type (B) can reproduce this kind of shape even better. Two of them are depicted in Fig. 6 and their parameters are listed in Table A.4 − models B18 and B5. The periastron and apastron of the MO are the same as in the A39 model. The dotted blue line is for the MO mass of 10-10M⋆ (B18). The DPs constituting the spherical dust cloud move in orbits with pericenters equal to 1000 km. The interval of the randomly distributed initial velocities in the pericenter corresponds to the interval of apocenters randomly distributed from 10 to 100 times of the pericenter distance. The same good fit can be obtained for the same value of angle Φ = 29°.
The dashed green line corresponds to the MO mass of 10-8M⋆ (B5). The DPs constituting the spherical dust cloud initially move in orbits with pericenters equal to 1000 km. The interval of the randomly distributed initial velocities in the pericenter corresponds to the interval of apocenters randomly distributed from 30 to 300 times the pericenter distance in this case. The good fits are observed also at the pre-periastron part of the orbit and this particular one is for angle Φ = −24°. The properties of the DPs were identical to those in model (A), that is, β = 0.629.
 |
Fig. 5 Comparison of observations with model (A). Each row corresponds to one of the 800-, 1520-, 1540-, and 1570-day features. Left column: the observations (red/solid line) and model (A) (green/dashed). The fits may not be perfect but the main morphological features are represented. Right column: the cloud of particles (dots) and its parent body (solid line) orbiting the star. Different colors are used to plot particles at different times separated by 25-day intervals. A small number of particles may suffer from close encounters and were thrown into chaotic orbits. |
 |
Fig. 6 Comparison of observations with model (B). Left column: the observations (solid line), two models (green-dashed and blue-dashed; see the text for a description). Right column: the cloud of particles and its parent body corresponding to the green-dashed model orbiting the star at 25-day intervals distinguished by different colors. |
 |
Fig. 7 Comparison of observations with model (C). Left column: the observations (solid line), model (dashed). Right column: the cloud of particles and their parent body orbiting the star at 25-day intervals. |
5.2. Feature at 1520 days
This is the deepest feature and is very complex. It contains several peaks, which gradually increase in depth before the global minimum is reached, and there is one further bump on the egress. The feature may be analogous to that at 800 days in the sense that if it were smoothed by some effect, the two would resemble one another. Again, we were surprised to see a number of models, with only one MO and a simple dust cloud, which were able to reproduce the essence of this complicated morphology. One of them is illustrated in Fig. 5 in the second row from the top. This particular model is also A-type (A4) and was obtained with the following assumptions, which are very similar to the previous model. Mass, periastron, and apastron of the MO: 10-10M⋆, 0.1 au and 50 au, respectively. The spherical dust cloud composed of DPs with β = 0.629 placed initially on elliptical orbits around MO with pericenters and apocenters of 1000 km and 100 000 km. Start/end of integration was at a distance of MO equal to 5 au and the line of sight had Φ = 29°. The model fits the location of almost all bumps and, qualitatively, also agrees with their strengths.
Notice that there is a shallow and smooth bump at BKJD 1511, which was not reproduced with such a model. One could speculate that an additional body/cloud is required to bring about the above observations or that they could be caused by, for example, a population of particles on slightly different orbits with slightly lower values of β ≈ 0.559, which would allow them to move slightly faster on the pre-periastron part of the orbit. The same values of periastron, apastron, and angle Φ implies that both objects and associated dust clouds responsible for the 800- and 1520-day features, moved in very similar orbits, with the same orientation in space and also suggests that the two objects might have a common progenitor.
5.3. Feature at 1540 days
This feature has three main peaks, the middle one being the strongest. The feature differs from the others since it appears symmetrical, thus invoking ideas of a body with a ring structure transiting the star. Also, this structure is in agreement with our calculations. We observed numerous instances of triple-peak structures with peaks moving in time and intensity for model (A). The third pair of panels in Fig. 5 shows one example of the A-model (A27) applied to this feature. We were not able to fit the width of the main peak completely, but nevertheless, from rather high angles (e.g., Φ = 94°), the calculations grasp the main morphological structure. The following parameters were used: mass, periastron, and apastron of the MO: 10-10M⋆, 0.1 au, and 50 au, respectively. The spherical dust cloud composed of DPs with β = 0.629 initially placed on elliptical orbits around MO with pericenters and apocenters of 100 km and 100 000 km, respectively. Start/end of integration was at a distance of MO equal to 5 au and the line of sight had Φ = 94°. Thus, this might be a considerable smaller body compared to the two MOs mentioned above, but on almost the same orbit, only its argument of periastron would have to be tilted to account for different line of sight angle.
We also found that some models of type (C) fit the feature quite well even if we assume an initially uniform distribution of the DPs in the ring. A significantly better match was obtained, however, when we considered the ring of the DPs with the distribution peaked in the middle. The best model for the 1540-day structure is illustrated in Fig. 7 and its parameters are given in Table A.5, model C37. The position and width of the three peaks fit very well and only the intensity of the central peak is stronger. The observed feature also exhibits broader outer wings. This fit was obtained with the following parameters. It is an inclined ring with ϑ = 30° and σ = 45°, inner and outer radius of 5000 and 10 000 km, respectively. The initial distribution of the DPs in the ring was generated using the formula for the calculation of MO-centric distance of jth particle rj = 7500 ± 2500η3/2. The mass of the central body was 10-8M⋆, and its orbit was the same as before. The line of sight had Φ = 29°. Notice, that the ring breaks and decouples from the object after passing the periastron.
The radiative acceleration causes periodic ripples in the cloud, which in 3D resemble a sort of squeezed spiral, and are the reason for the observed light-curve structure. This is illustrated in Fig. 8, which displays the individual DPs passing in front of the star at a moment during the eclipse. So, in this model, the three main peaks in the light-curve are not due to a ring passing in front of a star, although there was a ring structure before. It is very encouraging that this parent body has the same orbit as the two bodies before and even the line of sight is the same. For this reason we prefer the model (C) rather than the model (A) for this object.
 |
Fig. 8 Dust cloud with individual particles (dots) corresponding to the C-model (C37) passing in front of the star (ellipse) during the eclipse causing the observed 1540-day feature. |
5.4. Feature at 1 570 days
This feature exhibits three dips increasing in depth, which resembles the feature at 1520 days or the gradual ingress of the feature at 800 days. Our model is displayed in Fig. 5 in the bottom part. It fits very well the position of all peaks but the strongest one is more shallow and wider than expected. It was obtained using the following parameters (model A124 in Table A.3). Mass, periastron, and apastron of the MO: 10-10M⋆, 0.1 au, and 50 au, respectively. Spherical dust cloud is composed of DPs with β = 0.629 initially placed on elliptical orbits around MO with pericenters and apocenters of 1000 km and 10 000 km, respectively. This time, start/end of integration were at a distance of MO equal to 10 au and the line of sight had Φ = 0°. This body and orbit are also very similar to those responsible for other features and only the line of sight (i.e., the argument of periastron) is shifted.
6. Discussion, comments, and speculations
As we have already stated, the question of the origin or the long-term stability of dust clouds we modeled are beyond the scope of the present paper. Nevertheless, these are important questions that can significantly affect the probability of observing the studied events. That is why we present a number of tests, comments and/or speculations to address this issue.
Clouds composed of particles with high β values are extremely vulnerable and easily decouple from the parent massive body and will not be observed during multiple transits. This means that the chance of observing such events is rare compared to low-β particles. On the other hand, large particles with low β values might stay within a Hill radius of the parent body and return back to cause new eclipses provided that they are not perturbed by other MOs. It might be that they serve as a dust reservoir and, upon their return, collide and produce new smaller and more opaque debris particles that can obscure the star more easily.
The Hill radius RH for an MO on a highly eccentric orbit with eccentricity e and semi-major axis a is based on the calculations of Hamilton & Burns (1992) and is analogous to the common Hill radius for a circular orbit, however it assumes the pericenter distance rather than the radius, that is, 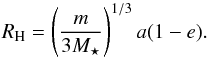 (3)
(3)
6.1. Perturbation of the dust cloud near the periastron
A scenario that we have not addressed so far is a possible interaction between the massive objects and their dust clouds. In this work, the clouds were studied during only a fraction of their orbit in the star-centric distance typically equal to or less than 5 au. Although they were modeled independently, their parent MOs may have a common origin, they may be in relatively close proximity to one another, and may therefore affect each other as well as their dust clouds. A feature observed at 800 days is separated by 730 days from the other three features and by approximately 530 days from the two very small features observed in the light-curve earlier (they are too small and are not modeled in this paper). However, the latter three objects (features) are separated only by Δt ≈ 20 days in the time domain. Assuming that they follow one another on the same orbit, this time lag can be translated into their physical separation Δl, which will decrease with their distance from the star as, approximately, 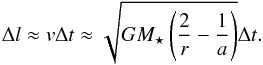 (4)To investigate a mutual influence of the two MOs on one another as well as an influence of the second MO on the dust cloud of the first MO, we carried out the following simulation. We assumed a MO orbiting a star with the same orbit as before, that is, mass, periastron, and apastron 10-8M⋆, 0.1, and 50 au, respectively. Further, we assumed the dust cloud of type (A) of massless particles placed initially on orbits around the MO as before. The orbits of the DPs were oriented randomly and were all given pericenters and apocenters equal to 1000 km and 100 000 km, respectively. Since we intend to test the stability of the cloud in respect to the gravitational perturbations, no P-R drag was considered. The motion of the MO and its cloud was integrated during a fraction of the orbital period at star-centric of less than 5 au.
(4)To investigate a mutual influence of the two MOs on one another as well as an influence of the second MO on the dust cloud of the first MO, we carried out the following simulation. We assumed a MO orbiting a star with the same orbit as before, that is, mass, periastron, and apastron 10-8M⋆, 0.1, and 50 au, respectively. Further, we assumed the dust cloud of type (A) of massless particles placed initially on orbits around the MO as before. The orbits of the DPs were oriented randomly and were all given pericenters and apocenters equal to 1000 km and 100 000 km, respectively. Since we intend to test the stability of the cloud in respect to the gravitational perturbations, no P-R drag was considered. The motion of the MO and its cloud was integrated during a fraction of the orbital period at star-centric of less than 5 au.
In the following step, we repeated the same integration but with another MO added to the system. The latter was placed in an identical orbit to the first MO but with a time lag of 20 days as indicated by the observations. The mass of the second MO was chosen to be 10-8M⋆ to maximize its perturbation effect. Then we compared the results of the calculations with and without the second MO. Even in this extreme case, the change of the orbit of the first MOs as well as the structure of its dust cloud was negligible. We conclude that our MOs and their dust clouds can be regarded as independent entities during the fraction of their orbit within the star-centric distance of 5 au considered in this paper and where the obscuration events have happened. This a posteriori justifies our presumption in the calculations and choice to model only one MO and one dust cloud at a time.
6.2. Perturbations between the massive bodies
After the two MOs, following each other with a time lag of 20 days on the same orbit passed the periastron, the physical distance between them becomes shorter according to Eq. (4), implying that the first MO moves slower than the second. At some point, they may become too close and their mutual gravity might kick in. This would shrink the distance between them even closer and a strong mutual interaction might occur affecting their dust clouds. To investigate what might happen beyond that part of the orbit considered in our previous calculations, we explored in the following scenario.
We assumed a MO orbiting the KIC8462 with the same orbit as before, that is, periastron and apastron of 0.1 and 50 au, respectively, and a mass of 10-8M⋆. In the beginning of our simulation, this MO was situated in the pre-periastron arc at a star-centric distance of 5 au. Another MO in the same orbit with the same mass followed the first MO with a time lag Δt = 20 days. We integrated this system over a single orbital period of the MOs on their initial Keplerian orbit (104 yr). It indeed appears that both MOs influence each other during a short period of mutual close approach, which occurred ~7530 days after the first MO passed the periastron. In the post-periastron arc of orbit, the second MO approaches the first MO since its star-centric speed is larger. Its distance to the first MO is also reduced by the mutual gravity of the MOs.
After 7530 days from the moment when the first MO passed the periastron, the MOs are separated by only approximately 0.00082 au and a strong perturbation occurs. The change of periastron distance and semi-major axis of both MOs is shown in Figs. 9a,b. Specifically, the orbits of the MOs change significantly for a short period of time. The distance between both MOs suddenly increases and the mutual perturbation becomes insignificant. Then the original orbits are almost restored.
 |
Fig. 9 Evolution of periastron distance (plots a) and c)) and semi-major axis (plots b) and d)) of two mutually perturbing MOs moving around the KIC8462 in orbits described in Sect. 6. In the first case (plots a) and b)), the masses of both MOs are the same and equal to 10-8M⋆. In the second case (plots c) and d)), the mass of the first (second) MO is 10-14M⋆ (10-8M⋆). |
In addition, we also investigated the perturbation effect of the second MO with mass 10-8M⋆ on the first MO, when the mass of the latter is negligible, only 10-14M⋆. In this case, the orbit of the second MO remained practically the same. As expected, the orbit of the lighter MO changed more than in the case of two equal-mass MOs. The change happened at the close approach of both MOs, to a distance of only 0.00019 au, which occured ~8850 days after the first-MO periastron passage, in this case. The change of the periastron distance and semi-major axis of this MO is shown in Figs. 9c,d. Again, the orbital elements change their values for only a short part of the duration of strong perturbation. Then the original values are almost restored. Hence, our assumption of a series of MOs moving in identical orbits is reasonable. We note, a new cloud can be formed due to the tidal action of the perturbing MO at the close approach, if the parent MO contains some volatile material.
6.3. Perturbation on a tight dust cloud
In Sect. 6.1, we considered the gravitational perturbation caused by a second MO on the cloud of model (A) around the first MO. This cloud appeared to be almost unaffected during the investigated period. The DPs in this cloud are at relatively large distances from their parent MO. Hence, the close approach of the second MO to the first MO does not mean the close approach of the former to the DPs. This is, however, no longer true if we consider a tight dust cloud, at a relatively short distances from its parent MO. The DPs in the tight cloud can be expected to be perturbed with almost the same strength as the parent MO alone.
To see the effect of the perturbation on the tight cloud we performed the following two calculations. Firstly, we assumed a MO with mass of 10-8M⋆ on the same orbit as in the first simulation described in Sect. 6.2 and a tight dust cloud of type (A) around it. The DPs in the cloud have β = 0 and pericenters and apocenters of 1894 km (radius of the MO) and 15 000 km, respectively, This is within the Hill radius of the MO, which is approximately 22 000 km. Integration started at ro = 5 au. In the other simulation, we added a second MO with the same mass as the first. This MO was released into the same orbit following the first MO after a time delay of 20 days.
The results of both simulations were compared. In the first simulation, the cloud remains almost untouched after the single orbital revolution. If the second MO is considered, the cloud survives until the close mutual approach of both MOs. Then the pericenters of 16.6% of the DPs are reduced and these DPs end up on the MO’s surface. The other DPs are detached from their parent MO and follow their own trajectory around the central star. One might anticipate that during such a bombardment of the first MO’s surface, a sub-surface layer of volatile material would be exposed, which could trigger an enhanced activity upon the next approach to the star, in analogy to the activity of Main Belt Comets (Haghighipour et al. 2016).
6.4. Differences in the argument of periastron
Another problem to discuss is the difference in the angle Φ for various features. The features at 800, 1520, and 1540 days could all be fitted by models when value Φ = 29° is considered. The last feature, at 1570 days, can be fitted with a significantly lower value of Φ = 0°. Nevertheless, even such a relatively large difference in the argument of periastron ~30° in ω might still allow a common progenitor. We can look for an explanation in our own solar system again, with the groups of sun-grazing comets representing one particular inspiration. Namely, Ohtsuka et al. (2003) and Sekanina & Chodas (2005) argued for a common origin, in the same progenitor, of all Marsden and Kracht groups of sun-grazing comets, comet 96P/Machholz, and the daytime Arietid meteoroid stream. Sekanina and Chodas found the difference between the mean ω of Marsden and Kracht groups to be 36.7°. Ohtsuka et al. (2003) presented the orbits of these groups with an even larger maximum ω-difference, equal to approximately 47°.
6.5. Feature at 1210 days and miscellaneous comments
We would like to point out that in this paper, we modeled only the four strongest features observed in the Kepler light curve of this object. Aside from these, there are several other, considerably fainter features. One of them is found at approximately 1210 days and deserves further attention. It is illustrated in Fig. 10. This is a symmetric triple peak structure with the central peak being the strongest, and closely resembles the feature seen at 1540 days investigated as part of this study. The ratio of the central to side peaks is almost the same but is, in fact, slightly narrower. This similarity allows us to argue that it is also caused by a similar object with a dusty ring, model (C).
While this feature does not pose a significant problem for our model (it takes only one additional massive object with a dusty cloud on the same orbit), its existence renders many other theories much less plausible. For example, the comet scenario (Bodman & Quillen 2016) would require the comets to gather by chance into the same constellation as during the 1540 feature. Within the interstellar cloud, ISM structure, and a dark disk with a black hole scenario (Wright & Sigurdsson 2016) an accidental repetition of the same structure within the cloud would also be required.
There are other tiny features observed at 140 and 260 days. These features may show a “pre-transit” and “post-transit” brightening. Such a brightening is most probably caused by the forward scattering of light from the host star by the dust cloud. This would require that the cloud be close to the star, that is, of circumstellar origin, and would rule out all theories in which the eclipsing object is in the interstellar medium or solar system.
An increasing fading of the star by approximately 3% during the Kepler mission may not be a problem for our model. Dust clouds or debris associated with four massive objects may naturally extend and spread along their orbit. The highest concentration should be near the objects which is where it is observed.
 |
Fig. 10 Tiny eclipse event observed near to day 1210, which is very similar to the one observed at 1540 days, may have important consequences for the different scenarios. |
7. Conclusions
Our main findings and arguments are briefly summarized below.
-
1.
We demonstrate that it is possible to explain the complexmorphology of the Kepler light-curve of KIC8462852 with a verysimple model. Only four massive objects, each surrounded by adust cloud, can account for most of the observed features. Theobjects are apparently of a common origin, that is, the result of abreak-up process of a single progenitor.
-
2.
Most of the features may be represented by a simple, initially spherical dust cloud. Such clouds in eccentric orbits are observed to naturally vertically shrink and develop a leading tail as they approach periastron. The feature at 1540 days seems to be special since it is best reproduced by an initially ring-like structure.
-
3.
This scenario of four massive objects with clouds is further supported by the following arguments: the smooth shape of the 800-day feature, which is difficult to assemble from a number of smaller objects such as comets; a tendency towards shallower ingress and steeper egress of the 800-day feature, which is exactly the opposite of what is expected for the less massive objects such as comets; the 1520 and 1570-day features also show a gradual increase in strengths of individual “sub-features” and fast recovery, resembling the 800-day feature; the symmetric “ring-like” structure of the 1540-day feature, which would presume a non-negligible gravity of the object; the existence of another symmetric structure at 1210 days, which is very similar to the above mentioned feature and is difficult to understand within a comet scenario or other models; the clustering of the obscuration features into four main events, which naturally leads to the association with four objects; as well as by the fact that our solution indicates that all four bodies are on very similar eccentric orbits. Further, all best fits were for the P-R drag parameter β = 0.629, which indicates that also the dust particles may be similar in size and chemical composition.
-
4.
It is not claimed that we found the only/best solution within this concept of four massive bodies. We rather state that we found a possible solution.
-
5.
Iron or carbon grains smaller than approximately 0.1 microns experience a very strong radiative push, which quickly disconnects them from the parent body and places them on hyperbolic orbits. Thus, it is unlikely that such grains contribute significantly to the observed features.
-
6.
Grains larger than approximately 100 microns experience small radiative accelerations and may remain bound to the massive object. Their opacity is small, therefore they are not likely to contribute significantly to the obscuration events. However, they may act as a reservoir and produce smaller dust grains.
-
7.
It is argued that 0.3−10 micron-sized dust grains are the best candidates for explaining the obscuration events. Smaller grains, unless they were being replenished, would be easily expelled from the system while larger grains would have a relatively small opacity.
-
8.
It was shown that the mutual interaction between the massive objects and their dust clouds within few astronomical units from the periastron can be neglected and that they can be treated independently of each other in this region.
-
9.
If the two massive objects follow each other on identical eccentric orbits with a short enough time lag, a strong interaction between them and their dust clouds may happen at larger distances from the star, which might disperse the clouds but, at the same time, also expose sub-surface volatile material, trigger outbursts, and produce debris.
The outlined concept provides an alternative explanation of the observed light-curve of KIC8462852. It is a simple model with only a small number of free parameters. Although the similarity between the observed and simulated light-curves is striking, the fits can certainly be improved; motivation for further research in this direction. There is a plethora of possibilities of how to improve, modify, or advance such models. Especially, more extensive calculations with more realistic dust clouds with sublimation combined with some minimization techniques might shed more light onto what has happened around this interesting star. On the other hand, at the moment, there is no need to invoke alien mega-structures to explain the above mentioned light-curves.
BT-Settl models (Allard et al. 2003; Baraffe et al. 2015).
Acknowledgments
We thank David Vokrouhlický and Oleksandra Ivanova for stimulating discussion and an anonymous referee for careful reading of the manuscript and comments that helped to improve the paper considerably. This work was supported by VEGA – the Slovak Grant Agency for Science, grants Nos. 2/0143/14 and 2/0031/14 as well as by the APVV 15-0458 project. This article was also created by the realization of the project ITMS No. 26220120029, based on the supporting operational Research and development program financed by the European Regional Development Fund.
References
- Abeysekara, A. U., Archambault, S., Archer, A., et al. 2016, ApJ, 818, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Guillot, T., Ludwig, H.-G., et al. 2003, in Brown Dwarfs, ed. E. Martín, IAU Symp., 211, 325 [Google Scholar]
- Bailey, M. E., Chambers, J. E., & Hahn, G. 1992, A&A, 257, 315 [NASA ADS] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biesecker, D. A., Lamy, P., St. Cyr, O. C., Llebaria, A., & Howard, R. A. 2002, Icarus, 157, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Birtwhistle, P., Ryan, W. H., Sato, H., Beshore, E. C., & Kadota, K. 2010, Central Bureau Electronic Telegrams, 2114 [Google Scholar]
- Bochinski, J. J., Haswell, C. A., Marsh, T. R., Dhillon, V. S., & Littlefair, S. P. 2015, ApJ, 800, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Bodman, E. H. L., & Quillen, A. 2016, ApJ, 819, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Boyajian, T. S., LaCourse, D. M., Rappaport, S. A., et al. 2016, MNRAS, 457, 3988 [NASA ADS] [CrossRef] [Google Scholar]
- Brogi, M., Keller, C. U., de Juan Ovelar, M., et al. 2012, A&A, 545, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Budaj, J. 2013, A&A, 557, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Budaj, J., Kocifaj, M., Salmeron, R., & Hubeny, I. 2015, MNRAS, 454, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Croll, B., Rappaport, S., DeVore, J., et al. 2014, ApJ, 786, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Rappaport, S., & Levine, A. M. 2015, MNRAS, 449, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Dalba, P. A., Vanderburg, A., et al. 2017, ApJ, 836, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Delsemme, A. H., & Miller, D. C. 1971, Planet. Space Sci., 19, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Duncan, M., Quinn, T., & Tremaine, S. 1987, AJ, 94, 1330 [NASA ADS] [CrossRef] [Google Scholar]
- Emel’yanenko, V. V., Asher, D. J., & Bailey, M. E. 2007, MNRAS, 381, 779 [NASA ADS] [CrossRef] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proceedings of IAU Colloq. 83, held in Rome, Italy, June 11−15, 1984 eds. A. Carusi, & G. B. Valsecchi (Dordrecht: Reidel), 185 [Google Scholar]
- Gänsicke, B. T., Aungwerojwit, A., Marsh, T. R., et al. 2016, ApJ, 818, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Garai, Z., Zhou, G., Budaj, J., & Stellingwerf, R. F. 2014, Astron. Nachr., 335, 1018 [NASA ADS] [CrossRef] [Google Scholar]
- Granvik, M., Morbidelli, A., Jedicke, R., et al. 2016, ApJ, 830, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Haghighipour, N., Maindl, T., Schaefer, C., Speith, R., & Dvorak, R. 2016, ApJ, 830, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Hamilton, D. P., & Burns, J. A. 1992, Icarus, 96, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Harp, G. R., Richards, J., Shostak, S., et al. 2016, ApJ, 825, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Hippke, M., & Angerhausen, D. 2016, arXiv e-prints [arXiv:1609.05492] [Google Scholar]
- Hippke, M., Angerhausen, D., Lund, M. B., Pepper, J., & Stassun, K. G. 2016a, ApJ, 825, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hippke, M., Kroll, P., Matthei, F., et al. 2017, ApJ, 837, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Husárik, M. 2012, Contributions of the Astronomical Observatory Skalnate Pleso, 42, 15 [NASA ADS] [Google Scholar]
- Jäger, C., Dorschner, J., Mutschke, H., Posch, T., & Henning, T. 2003, A&A, 408, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jager, C., Mutschke, H., & Henning, T. 1998, A&A, 332, 291 [NASA ADS] [Google Scholar]
- Jewitt, D. 2009, Hubble Investigation of the Unusual Object P/2010 A2, HST Proposal 12053, 17 [Google Scholar]
- Johnson, P. B., & Christy, R. W. 1974, Phys. Rev. B, 9, 5056 [NASA ADS] [CrossRef] [Google Scholar]
- Kawahara, H., Hirano, T., Kurosaki, K., Ito, Y., & Ikoma, M. 2013, ApJ, 776, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Knight, M. M., A’Hearn, M. F., Biesecker, D. A., et al. 2010, AJ, 139, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Koike, C., Kaito, C., Yamamoto, T., et al. 1995, Icarus, 114, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Lacki, B. C. 2016, ArXiv e-prints [arXiv:1610.03219] [Google Scholar]
- Lecavelier Des Etangs, A., Vidal-Madjar, A., & Ferlet, R. 1999, A&A, 343, 916 [NASA ADS] [Google Scholar]
- Lisse, C. M., Sitko, M. L., & Marengo, M. 2015, ApJ, 815, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Lisse, C. M., Sitko, M. L., & Marengo, M. 2016, in Lun. Planet. Sci. Conf., 47, 2965 [Google Scholar]
- Lund, M. B., Pepper, J., Stassun, K. G., Hippke, M., & Angerhausen, D. 2017, ApJ, submitted [arXiv:1605.02760] [Google Scholar]
- Makarov, V. V., & Goldin, A. 2016, ApJ, 833, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Marengo, M., Hulsebus, A., & Willis, S. 2015, ApJ, 814, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Montet, B. T., & Simon, J. D. 2016, ApJ, 830, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Neslušan, L., & Jakubík, M. 2005, A&A, 437, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ohtsuka, K., Nakano, S., & Yoshikawa, M. 2003, PASJ, 55, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Ordal, M. A., Bell, R. J., Alexander, Jr., R. W., Newquist, L. A., & Querry, M. R. 1988, Appl. Opt., 27, 1203 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Perez-Becker, D., & Chiang, E. 2013, MNRAS, 433, 2294 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Levine, A., Chiang, E., et al. 2012, ApJ, 752, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Barclay, T., DeVore, J., et al. 2014, ApJ, 784, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, S., Gary, B. L., Kaye, T., et al. 2016, MNRAS, 458, 3904 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Rappaport, S., Pallé, E., et al. 2015, ApJ, 812, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E. 2016, ApJ, 822, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Schlawin, E., Herter, T., Zhao, M., Teske, J. K., & Chen, H. 2016, ApJ, 826, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Schuetz, M., Vakoch, D. A., Shostak, S., & Richards, J. 2016, ApJ, 825, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z., & Chodas, P. W. 2005, ApJS, 161, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Sekanina, Z., & Kracht, R. 2015, ApJ, 801, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, M. A., Scicluna, P., Kemper, F., et al. 2016, MNRAS, 458, L39 [NASA ADS] [CrossRef] [Google Scholar]
- van Lieshout, R., Min, M., & Dominik, C. 2014, A&A, 572, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Lieshout, R., Min, M., Dominik, C., et al. 2016, A&A, 596, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Werkhoven, T. I. M., Brogi, M., Snellen, I. A. G., & Keller, C. U. 2014, A&A, 561, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderburg, A., Johnson, J. A., Rappaport, S., et al. 2015, Nature, 526, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Bottke, W. F., Chesley, S. R., Scheeres, D. J., & Statler, T. S. 2015, in Asteroids IV, eds. P. Michel, F. E. DeMeo, & W. F. Bottke, 509 [Google Scholar]
- Warner, B. D. 2006, Minor Planet Bulletin, 33, 58 [NASA ADS] [Google Scholar]
- Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res. (Atmospheres), 113, 14220 [Google Scholar]
- Wright, J. T., & Sigurdsson, S. 2016, ApJ, 829, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Cartier, K. M. S., Zhao, M., Jontof-Hutter, D., & Ford, E. B. 2016, ApJ, 816, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, S., Jura, M., Dufour, P., & Zuckerman, B. 2016, ApJ, 816, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, G., Kedziora-Chudczer, L., Bailey, J., et al. 2016, MNRAS, 463, 4422 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Characteristics of all models
Initial characteristics of A-type models with 1000 test particles and the massive object in “standard orbit” (periastron distance of 0.1 au; apastron distance of 50 au) as well as in the standard initial star-centric distance (5 au).
Initial characteristics of A-type models with the number of test particles, N, other than 1000 and the massive object in “standard orbit” (periastron distance of 0.1 au; apastron distance of 50 au) as well as in the standard initial star-centric distance (5 au).
Initial characteristics of A-type models with the massive object in orbits other than the “standard orbit” (periastron distance of 0.1 au; apastron distance of 50 au) and/or at distances other than the standard initial star-centric distance (5 au).
Initial characteristics of B-type models.
Initial characteristics of C-type models.
All Tables
Initial characteristics of A-type models with 1000 test particles and the massive object in “standard orbit” (periastron distance of 0.1 au; apastron distance of 50 au) as well as in the standard initial star-centric distance (5 au).
Initial characteristics of A-type models with the number of test particles, N, other than 1000 and the massive object in “standard orbit” (periastron distance of 0.1 au; apastron distance of 50 au) as well as in the standard initial star-centric distance (5 au).
Initial characteristics of A-type models with the massive object in orbits other than the “standard orbit” (periastron distance of 0.1 au; apastron distance of 50 au) and/or at distances other than the standard initial star-centric distance (5 au).
All Figures
 |
Fig. 1 Four main eclipse events in the light-curve of KIC8462 observed with Kepler (Boyajian et al. 2016) and also analyzed in this study. |
| In the text | |
 |
Fig. 2 Left: total opacity of various dust species at 0.6 microns as a function of particle size. Right: radiative to gravity acceleration ratio (β parameter) of various dust species for KIC8462 as a function of the particle size. Olmg50 refers to olivine (50% iron), pyrmg40 refers to pyroxene (60% iron), and carbon is at 1000 °C. |
| In the text | |
 |
Fig. 3 Illustration of the behavior of a dust cloud projected into the orbital plane of the MO for different β values. Plot a): β = 0.007 – particles tend to stay on the elliptical orbit and follow the parent body, the trajectory of which is shown with the red solid curve. Plot b): β = 0.7 – the cloud of particles soon separates from the parent body and the particles move in their own elliptical trajectories. Plot c): β = 1 – the P-R drag balances the gravity and therefore the particles move uniformly along a straight line. Plot d): β = 1.4 – particles easily decouple from the parent body and settle onto hyperbolic orbits. Positions of the MO (crosses) are shown at the same moments as the positions of the individual DPs (dots). Different colors are used for different times, separated by 25-day intervals. The position of KIC8462, in the origin of coordinate x−y plane, is drawn with the violet full circle. Calculated for model A of a cloud with a body mass of m = 10-10M⋆. |
| In the text | |
 |
Fig. 4 Coordinate system in respect to the MO orbit and direction towards the observer. |
| In the text | |
 |
Fig. 5 Comparison of observations with model (A). Each row corresponds to one of the 800-, 1520-, 1540-, and 1570-day features. Left column: the observations (red/solid line) and model (A) (green/dashed). The fits may not be perfect but the main morphological features are represented. Right column: the cloud of particles (dots) and its parent body (solid line) orbiting the star. Different colors are used to plot particles at different times separated by 25-day intervals. A small number of particles may suffer from close encounters and were thrown into chaotic orbits. |
| In the text | |
 |
Fig. 6 Comparison of observations with model (B). Left column: the observations (solid line), two models (green-dashed and blue-dashed; see the text for a description). Right column: the cloud of particles and its parent body corresponding to the green-dashed model orbiting the star at 25-day intervals distinguished by different colors. |
| In the text | |
 |
Fig. 7 Comparison of observations with model (C). Left column: the observations (solid line), model (dashed). Right column: the cloud of particles and their parent body orbiting the star at 25-day intervals. |
| In the text | |
 |
Fig. 8 Dust cloud with individual particles (dots) corresponding to the C-model (C37) passing in front of the star (ellipse) during the eclipse causing the observed 1540-day feature. |
| In the text | |
 |
Fig. 9 Evolution of periastron distance (plots a) and c)) and semi-major axis (plots b) and d)) of two mutually perturbing MOs moving around the KIC8462 in orbits described in Sect. 6. In the first case (plots a) and b)), the masses of both MOs are the same and equal to 10-8M⋆. In the second case (plots c) and d)), the mass of the first (second) MO is 10-14M⋆ (10-8M⋆). |
| In the text | |
 |
Fig. 10 Tiny eclipse event observed near to day 1210, which is very similar to the one observed at 1540 days, may have important consequences for the different scenarios. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


