| Issue |
A&A
Volume 599, March 2017
|
|
|---|---|---|
| Article Number | A24 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629228 | |
| Published online | 21 February 2017 | |
Evolution of the dust-to-metals ratio in high-redshift galaxies probed by GRB-DLAs⋆
1 Max-Planck-Institute für Extraterrestrische Physik (MPE), Giessenbachstrasse 1, 85748 Garching, Germany
e-mail: wiseman@mpe.mpg.de
2 Dark Cosmology Centre, Niels Bohr Institute, University of Copenhagen, Juliane Maries Vej 30, 2100 Copenhagen, Denmark
Received: 1 July 2016
Accepted: 26 October 2016
Context. Several issues regarding the nature of dust at high redshift remain unresolved: its composition, its production and growth mechanisms, and its effect on background sources.
Aims. We provide a more accurate relation between dust depletion levels and dust-to-metals ratio (DTM), and to use the DTM to investigate the origin and evolution of dust in the high-redshift Universe via gamma-ray burst damped Lyman-alpha absorbers (GRB-DLAs).
Methods. We use absorption-line measured metal column densities for a total of 19 GRB-DLAs, including five new GRB afterglow spectra from VLT/X-Shooter. We use the latest linear models to calculate the dust depletion strength factor in each DLA. Using these values we calculate total dust and metal column densities to determine a DTM. We explore the evolution of DTM with metallicity, and compare it to previous trends in DTM measured with different methods.
Results. We find significant dust depletion in 16 of our 19 GRB-DLAs, yet 18 of the 19 have a DTM significantly lower than the Milky Way. We find that DTM is positively correlated with metallicity, which supports a dominant ISM grain-growth mode of dust formation. We find a substantial discrepancy between the dust content measured from depletion and that derived from the total V-band extinction, AV, measured by fitting the afterglow SED. We advise against using a measurement from one method to estimate that from the other until the discrepancy can be resolved.
Key words: galaxies: evolution / dust, extinction / ISM: abundances / gamma-ray burst: general
© ESO, 2017
1. Introduction
The abundances and compositions of the dust and metals in the interstellar medium (ISM) can reveal important information about local environmental conditions. Despite the wealth of information on our doorstep regarding the ISM of the Milky Way (MW) and Local Group galaxies, it is also necessary to investigate the ISM in the distant Universe in order to trace its properties in very different environments, as well as its evolution over cosmic history.
One of the key constituents of the ISM is dust. Dust is produced in a range of environments, from the stellar sources of outer envelopes of post-aysmptotic giant branch (AGB) stars and the expanding and cooling ejecta of supernova to grain growth and accretion in the ISM. It reveals itself via emission in the far-infrared and sub-mm wavelength range and through absorption and scattering of visible and ultraviolet (UV) light from background sources, and its effect must be corrected for when studying sources that shine through it. For example, everything outside the Galaxy must be observed through the dust of the MW, which has a complex topography (Schlafly & Finkbeiner 2011). It is estimated that up to 30% of all light in the Universe has been reprocessed by dust grains (Bernstein et al. 2002). Dust is also necessary for, and traces, star formation across the Universe (Sanders & Mirabel 1996; Genzel et al. 1998; Peeters et al. 2004; Mckee & Ostriker 2007). Conversely, star formation also destroys dust at differing rates (Draine & Salpeter 1979a,b; McKee 1989; Jones et al. 1996; Dwek 1998; Bianchi & Ferrara 2005; Yamasawa et al. 2011). Along with the ISM, dust is present in substantial quantities alongside gas and metals in the circum-galactic medium (CGM; Bouche et al. 2007; Peeples et al. 2014; Peek et al. 2015.) It is therefore of fundamental importance to the theory of star formation and thus galaxy evolution to understand the nature of all dust processes, such as formation, composition, evolution, and destruction, as well as its observational characteristics, both in the local and distant Universe. Since dust is intimately connected to the conditions of the ISM and the properties of gas (Draine 2003), the dust-to-gas ratio (DTG; Bohlin et al. 1978) is a good indicator of the dust content of a galaxy or gas cloud. The dust-to-metals ratio (DTM; Predehl & Schmitt 1995; Güver & Özel 2009; Watson 2011), which is the DTG corrected for the metallicity of the gas, thus describing the fraction of the total metals that are in the solid dust phase, can reveal more about the nature of the dust itself, its production mechanisms, and the processes by which it evolves.
The evolution of the DTM over cosmic time is a tracer of the history of the interplay between gas and dust in the ISM of galaxies, and its distribution in comparison to metallicity can be used to infer clues about the origin of interstellar dust. If all dust and metals were to be produced in and ejected from stars, one would expect the DTM to remain constant in both time and metallicity (e.g. Franco & Cox 1986). In models, this is often assumed (e.g. Edmunds & Eales 1998), especially in the local Universe (Inoue 2003), and a fairly constant dust-to-metals ratio is indeed observed (Issa et al. 1990; Watson 2011). At higher redshift, Zafar & Watson (2013) found that the DTM in a sample of foreground absorbers to gamma-ray bursts (GRBs) and quasars tends not to vary significantly over a wide range of redshifts, metallicities, and hydrogen column densities, proposing a universally constant DTM. Chen et al. (2013) find a slow redshift evolution of DTM in lensed galaxies. These findings suggest that most of the dust is produced “instantaneously” in the ejecta of core-collapse supernova (CCSNe), a result supported by recent models by McKinnon et al. (2016), who find that roughly two-thirds of the dust in MW-like galaxies at z = 0 is produced in Type II SNe. These authors all use the traditional method of measuring DTM: the extinction, AV, is compared to the equivalent metal column density, log N(H) + [M/H], where [M/H] is the logged metallicity of the gas (see Eq. (2)).
Other studies use a different definition of DTM, namely by determining the dust fraction ℱd from the dust depletion (Sect. 2) of metals observed in damped Lyman-α absorbers (DLAs) on sight lines to quasars (Vladilo 2004) and GRBs (De Cia et al. 2013). These studies, unlike those using AV as their dust quantifier, claim detections of increasing evolution of the DTM with metallicity. This would suggest that the majority of the dust is formed by growth onto grains in the ISM (Draine 2009) rather than simultaneously together with the metals formed in CCSNe and post-AGB star envelopes. Tchernyshyov et al. (2015) use depletion observations in the Small Magellanic Cloud (SMC) to suggest the trend between DTM and metallicity only occurs below a certain metallicity threshold that depends on gas density. Mattsson et al. (2014) provide a comprehensive discussion on the debate from a theoretical standpoint, suggesting that selection effects or statistical fluctuations could explain the differing observed trends, and Feldmann (2015) attempts to model the observed evolution of dust and metal parameters via production, accretion, destruction, as well as gas infall and outflow from the galaxy, and also reproduce an evolution of the DTM at low metallicities. McKinnon et al. (2016) include stellar production and accretion along with destruction by SN shocks and winds driven by star formation in models that predict the DTM of MW-like galaxies.
GRBs are useful tools with which to study trends in the DTM in the distant Universe. They are extremely bright, allowing their detection even at very high redshift (Tanvir et al. 2009), and occur in galaxies with a wide range of dust content and metallicities (e.g. Fynbo et al. 2008; Mannucci et al. 2011; Krühler et al. 2015; Cucchiara et al. 2015). GRBs are massive stellar explosions (e.g. Galama et al. 1998), the afterglows of which are observed to have featureless synchrotron spectra (Meszaros & Rees 1997). This means that any absorption lines or changes to the shape of the spectrum must originate from an absorbing medium between the explosion site and the observer. Typically they manifest themselves in the form of DLAs in the host galaxy of the GRB. A DLA is defined as an absorbing system with log (N(H i)) > 20.3 (Wolfe et al. 2005), and it has been found that a large proportion of GRB afterglow spectra that lie in the redshift range for the Ly-α transition to fall into the atmospheric transmission window (z> ~ 1.7) do indeed fulfil this criterion (e.g. Krühler et al. 2013; Sparre et al. 2014; Friis et al. 2015). With such a large pool of neutral gas, the ionization fraction is so small that the dominant state of the elements used in this analysis is the singly ionized one (Wolfe et al. 2005; Viegas 1995; Peroux et al. 2007), and the measurements of singly ionized metal species are taken to be representative of the total gas phase abundance of these metals in the DLA. We do commonly detect highly ionized species such as C iv and Si iv, both often saturated, which might call the above assumption into question, and Fox et al. (2004) do indeed use the ratio [C iv/ O vi] as proportional to the total [C/O]. However, these lines often show broader velocity structure and/or offsets in central velocity than the low-ionization lines (e.g. Fox et al. 2007), suggesting that the gas with a higher ionization state does not trace the same structure as the low-ionization lines. This issue is also addressed in Ellison et al. (2010), and while they suggest that there may be some ionization corrections below log (N(H i)) < 21, they are still low, and only two of the objects in our sample have a neutral hydrogen column density below this value. We thus make no ionization corrections throughout the paper, and take the low-ionization abundances to be representative.
In this paper, we present spectral analysis of five previously unpublished GRBs, and we combine them with 14 more GRB-DLAs from the literature, all but three of which have mid- to high-resolution spectroscopy. We compute dust depletion curves using all of the available metals, which we then use to calculate average DTM values, and investigate their relation with metallicity and redshift in order to investigate the evolution of DTM.
The structure of this paper is as follows. In Sect. 2 we describe the background and updated methods available to parameterize dust-depletion. The initial sample is presented in Sect. 3. In Sect. 4 we introduce our method of fitting for depletions in GRB-DLAs, and in Sect. 5 we present the results; we discuss the results in Sect. 6 and conclude in Sect. 7. Throughout the paper we assume the solar abundances from Asplund et al. (2009).
2. Dust depletion
Using spectroscopy, it is possible to measure the column density of ISM constituents through absorption lines. However, what is achieved here is a measure of the gas phase abundance of that element, as any metal atoms in the dust grains do not contribute to the observed absorption. The difference between the observed column and intrinsic, total column density of metal X is referred to as dust depletion ![\begin{equation} \label{eq:delta_def} \delta_{X} = [X/\mathrm{H}]_{\mathrm{obs}} - [X/\mathrm{H}]_{\mathrm{in}} , \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq14.png) (1)where a greater amount of element X is expected to be depleted onto dust grains with increasing negative values of δX. We use the standard relative abundance notation,
(1)where a greater amount of element X is expected to be depleted onto dust grains with increasing negative values of δX. We use the standard relative abundance notation, ![\begin{equation} \label{eq:relative} [X/Y]= \frac{\log{N(X)}}{\log{N(Y)}} - \frac{\log{N(X)}_{\mathrm{ref}}}{\log{N(Y)}_{\mathrm{ref}}} \cdot \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq16.png) (2)To calculate the amount of depletion, we need to know two things: the observed gas-phase abundance of each element, and the total intrinsic (gas + dust) abundance. The observed column densities are obtained from the GRB afterglow spectrum, but the intrinsic values are harder to come by, as we do not know a priori the total column density of a metal in both the gas and solid phase (i.e. dust). It was shown by Savage & Sembach (1996) that different elements deplete onto dust at different rates. Some elements, such as Fe and Ni, deplete rapidly and are known as refractory elements. Others, such as Zn, P, S, and Si, are almost always entirely in the gas phase and are denoted as volatile. The measured abundance of these volatile elements in this formulation are taken to be a good indicator of the metallicity of the system, and the difference in the relative abundances of a volatile and a refractory element, such as the ratio [Zn/Fe], is thus a basic quantifier of depletion.
(2)To calculate the amount of depletion, we need to know two things: the observed gas-phase abundance of each element, and the total intrinsic (gas + dust) abundance. The observed column densities are obtained from the GRB afterglow spectrum, but the intrinsic values are harder to come by, as we do not know a priori the total column density of a metal in both the gas and solid phase (i.e. dust). It was shown by Savage & Sembach (1996) that different elements deplete onto dust at different rates. Some elements, such as Fe and Ni, deplete rapidly and are known as refractory elements. Others, such as Zn, P, S, and Si, are almost always entirely in the gas phase and are denoted as volatile. The measured abundance of these volatile elements in this formulation are taken to be a good indicator of the metallicity of the system, and the difference in the relative abundances of a volatile and a refractory element, such as the ratio [Zn/Fe], is thus a basic quantifier of depletion.
Savage & Sembach (1996) measured the depletions of several elements towards a set of different sight lines in the MW, from the dust-poor warm halo (WH) clouds, increasing in dust content to warm disk+ halo (WDH), warm disk (WD), and finally heavily dusty cold disk (CD) clouds. They reported typical depletion levels of each element for each cloud (Fig. 5 and Table 6 in Savage & Sembach 1996). When investigating depletion in a DLA, fitting each of the MW depletion patterns to the observed relative abundances can be attempted. Since the metallicity and dust-to-metals ratio in the DLA are likely to be different to the MW, they are left as free parameters; the relative abundances expected from the model are adjusted until they best match those of the observed abundances, a method described by Savaglio (2001) and Savaglio et al. (2003). Although these methods provide a basis for depletion studies, it is often found that GRB-DLAs tend not to follow any Local Group depletion patterns particularly well (e.g. D’Elia et al. 2014; Friis et al. 2015).
Based on the concept of Savage & Sembach (1996), a more continuous determination of depletion was introduced by Jenkins (2009), based on depletions observed in 17 elements towards stars along 243 MW sight lines. It was found that all elements deplete in a linear fashion, such that the rate of depletion of an element X, δX, can be given as  (3)where AX is the depletion slope, and BX and zX are constant offsets. This formulation implies that the difference between the depletion of any two elements should depend only on the value F∗, the depletion strength factor of the environment. That is, the relative abundances between any set of two or more elements in a single sight line can only be described by one unique value of F∗, which is then a powerful tool that can be used to calculate an overall, average DTM using multiple elements. In the Jenkins (2009) formulation, F∗ = 0 is given to those sight lines where the least depletion was observed, with F∗ = 1 the value for the most depleted MW systems. The F∗ method is also applied to the abundances in the Savage & Sembach (1996) models, with the WH clouds having F∗ = −0.28, whereas F∗ = 0.90 in the dusty CD environment.
(3)where AX is the depletion slope, and BX and zX are constant offsets. This formulation implies that the difference between the depletion of any two elements should depend only on the value F∗, the depletion strength factor of the environment. That is, the relative abundances between any set of two or more elements in a single sight line can only be described by one unique value of F∗, which is then a powerful tool that can be used to calculate an overall, average DTM using multiple elements. In the Jenkins (2009) formulation, F∗ = 0 is given to those sight lines where the least depletion was observed, with F∗ = 1 the value for the most depleted MW systems. The F∗ method is also applied to the abundances in the Savage & Sembach (1996) models, with the WH clouds having F∗ = −0.28, whereas F∗ = 0.90 in the dusty CD environment.
A study of the Magellanic Clouds (MCs) was presented by Tchernyshyov et al. (2015) who used the F∗ method to ascertain whether depletion slopes and offsets followed the MW trends from Jenkins (2009). Here they combined the offsets AX and zX into one offset, δ0, which simply describes the level of depletion at F∗ = 0. Compared to the MW, they found differences in the offsets for the elements P, Zn, Si, Cr, and Fe, and that δ0 decreases with metallicity of the sight line. Depletion slope AX, however, tends to stay constant. The main interpretation of this is that at lower metallicities, a higher F∗ is needed before metals begin to form dust, although this is based on a fairly small sample covering only the metallicities of the Small and Large Magellanic Clouds.
 |
Fig. 1 Depletion δX as a function of F∗. The slope is defined by the parameter B, and the point of zero-depletion by A. The elements are listed in order of depletion strength. |
Recently, the most comprehensive study yet of depletion patterns down to low metallicity and dust content has been conducted by De Cia et al. (2016), detailing depletion sequences of nine elements (P, O, Zn, S, Si, Mg, Mn, Cr, Fe) in 70 QSO-DLAs at redshifts of 1.7–4, and metallicities from the solar value down to 1/100 Z⊙. They use a very similar method to Jenkins (2009): the depletion of each element in each DLA is plotted against [Zn/Fe], used here as the dust quantifier instead of Jenkins’ F∗, although the two parameters are directly and linearly linked. The Zn is used as a proxy for an undepleted element, but in reality this is not the case. It is corrected for its own depletion by comparing the [Zn/H] and [Zn/Fe] values in the MW. For a measured [Zn/Fe] in a QSO sightline, De Cia et al. (2016) interpolate the MW [Zn/Fe] – [Zn/H] relation to find the corresponding Zn depletion. This missing Zn is then added to give a corrected [Zn/Fe] to be used as the final depletion strength indicator for that sight line. To add continuity to the depletion sequences, these QSO data are supplemented with Jenkins’ data from the MW, and it can be seen that the high-z data show the same behaviour as – and are a simple continuation of – those from the MW. For each element, De Cia et al. (2016) then use linear regression techniques to fit the depletion sequences and calculate two parameters: A, the depletion at [Zn/Fe] = 0, and B, the depletion slope. These depletion sequences are shown in Fig. 1. There are distinct clusters of elements: P, O, Zn, and S, which are volatile elements; Cr, Ni, and Fe, which are refractory elements; Si, Mg, and Mn, which lie between the volatile and refractory elements; and Ti, which seems to lie distinctly below all of the others.
From Fig. 1 it can be seen that at F∗ = 0 there is still significant depletion (~1 dex), especially in the refractory elements, which shows that even the least depleted MW clouds are more dusty than those in low-metallicity QSO-DLAs. The parameter A can best be seen as the offset in the relative abundance of the element at the point of no iron depletion, [Zn/Fe] = 0. Since they are all very small, the point at which the depletion starts (i.e. δX = 0) is very similar for each element, suggesting that all elements begin forming dust at some distinct threshold in temperature or density.
The analysis from De Cia et al. (2016) shows that the slopes are linear and well determined in the whole range from low metallicity and low dust content right through to the dustiest MW clouds, which we believe is strong evidence that the depletion mechanism works in the same way in all environments, and can indeed always be quantified by a single depletion strength factor. For this reason, we use the slopes from De Cia et al. (2016) for our depletion analysis of the typically low-dust, low-metal GRB-DLA environments in order to calculate DTMs and metallicities, which we describe in Sect. 4.
3. Sample and data reduction
In order to select our sample, we require GRBs with mid- to high-resolution spectroscopy as this allows us to resolve relatively well the velocity structure of the absorber, thus limiting the effect of unidentified saturation in the lines. The spectrum must also cover the Ly-α line, such that we can verify that it is a DLA, and thus regard any ionization correction as negligible. Finally, we require that the spectrum includes unsaturated detections of at least four singly ionized metals in order to increase the precision on a measurement of F∗1.
A state-of-the-art example of an instrument that produces such spectra is X-Shooter (Vernet et al. 2011), mounted at ESO’s VLT at Cerro Paranal, Chile. X-Shooter operates simultaneously in three spectral arms, namely the bands UVB (3000–5500 Å), VIS (5500–10 000 Å), and NIR (10 000–25 000 Å), thus allowing absorption line metallicity measurements from redshifts ≳1.8, and providing a wide spectral range. It operates at a resolving power of around R = 8000, depending on the arm, slit used, and atmospheric conditions. Twelve GRBs observed with X-Shooter pass our selection criteria. Seven of these, GRBs 090809, 090926A, 100219A, 111008A, 120327A, 120815A, and 121024A (references in Table 1), have already been published in the literature, and we include them in the sample. In this paper we present the analysis for the remaining five2: 120119A, 120716A, 120909A, 130408A, and 141028A (see Sect. 3.1). A further two GRBs observed with UVES pass the selection criteria (050730 and 081008, both taken from the literature), and an additional two GRBs observed with Keck HIRES and ESI have data published and are therefore also included in sample (050820A and 000926, respectively). Unpublished GRBs with Keck high-resolution spectral data cannot be included in the sample since data are not public. In order to help populate the sample with dust-rich sight lines, we add three low-resolution (VLT/FORS) spectra of GRBs 050401, 070802, and 090323, which have high N(H), high AV, and high metallicity, respectively. However, given the uncertainty in the derived column densities for these GRBs, we distinguish them from the rest of the sample when presenting our results. The final sample of 19 GRBs along with references is presented in Table 1; the H i measurements are given in Table 2.
Hydrogen and metal abundances in our sample of GRB afterglows.
Results of the fitting of the F∗ depletion model to metal column densities from 19 GRB-DLAs.
3.1. New GRB spectra
For the spectra of GRBs 120119A, 120716A, 120909A, 130408A, and 141028A we perform our own analysis on the spectra obtained from X-Shooter. The general method used to reduce the raw spectra is based on the standard X-Shooter pipeline (Goldoni et al. 2006; Modigliani et al. 2010), which we modify in accordance with the procedures outlined in Krühler et al. (2015), including a correction for telluric absorption using the Molecfit software (Smette et al. 2015). To normalize, we select points on the continuum unaffected by absorption lines, and fit a spline function. Owing to good seeing, the measured resolving power is often larger than the value determined from arc lamp exposures (see e.g. Krühler et al. 2013). We therefore follow the standard procedure, which is to measure the velocity resolution from unsaturated, single telluric lines. Since there are no telluric lines in the UVB, we use the resolution of those measured in the other two arms, calculating the resolution in the UVB using known conversion factors in line with Fynbo et al. (2011). We perform Voigt-profile fits on the absorption lines using the line-fitting software VPFit v.10.23. At resolutions typically around 30 km s-1, we often resolve multiple velocity components, each with distinct b-parameters. We determine the nature of any such components by fitting singly ionized, unsaturated, and unblended transitions; e.g. Fe iiλ1611, Ni iiλλ1751, 1741, Si iiλ1808, and Mn iiλ2606 are often useful transitions. We then fix redshift, z, and broadening parameter, b km s-1, for each velocity component across all species, leaving column density N cm-2 as the free parameter. We present the resulting column densities in Table 1, and present a selection of line fits for each GRB in Appendix A.
3.1.1. Hidden saturation
An issue that commonly plagues absorption line astronomy, particularly at mid to low resolution and poor signal-to-noise ratio (S/N), is that of hidden saturation. This occurs when a line that is in reality marginally saturated is smoothed out by the instrument resolution and noise to appear unsaturated in the actual observed spectrum. The pitfalls of this have been well documented by e.g. Prochaska (2006), Rafelski et al. (2012), Jorgenson et al. (2013) and Cucchiara et al. (2015), who typically ignore any lines that show any sign that they could be saturated. However, because the basis of our analysis is the use of multiple species to constrain the metallicity and dust depletion, we require measurements of as many lines as possible in the often low S/N GRB spectra.
To investigate and quantify the effect this has on our results we run a set of simulations, similar to those of Jorgenson et al. (2013) who used the apparent optical depth method (AODM). Initially we take the worst-case scenario, and assume the lowest S/N and highest resolution in our GRB sample spectra, which corresponds to 7.5 and 35.0 km s-1, respectively, in the case of GRB 120716A. We then simulate a set of absorption lines of one transition, namely Si iiλ1526, at a common b-parameter but with increasing column density so as to straddle the theoretical point at which that line saturates. We choose a b-parameter of 10 km s-1 as this represents the smallest value typically seen with higher resolution instruments, with smaller components typically blended (Jorgenson et al. 2013). We create lines starting from unsaturated column densities of 1014.4 cm-2 up to heavily saturated column densities of 1018.4 cm-2, and convolve with the X-Shooter resolution measured in GRB 120716A. We add Gaussian noise at a S/N of 7.5 and use VPFit to fit a Voigt profile and measure the column density. The results for 100 trials, with different noise added each time, are plotted in Fig. 2. The thick black curve shows that on average the measured column densities are always within 0.2 dex of the true value, with a standard deviation around 0.4 dex. Above 1016.6 cm-2 there is on average no deviation, and above 1014.4 cm-2 the data points have a standard deviation lower than 0.1 dex, reflecting the fitting of the damping wings.
 |
Fig. 2 Difference between the measured column density of Si iiλ1526 after convolving with the X-Shooter resolution and adding noise at S/N = 7.5, similar to the lowest quality of our data. The thick black line shows the mean residual, while the dashed curves show the 1σ level. The vertical dashed line marks the point at which this line saturates in the original spectrum. |
From these simulations, we find that there is only a small loss of accuracy of our column density measurements when lines are saturated, although we do continue to avoid using strongly saturated lines, especially when several components are evident. We also find that the uncertainty on the column densities provided by VPFit is often an underestimate compared to that from our simulations. To find the uncertainty for all of our measurements, including those on lines with potential hidden saturation, or evident but mild saturation, we thus conduct a second round of simulations. For each GRB, we take the S/N and resolution measured from the spectrum and simulate the line with the above method 100 times, but this time for only one unsaturated column density of 1015.8 cm-2. We take the standard deviation of our measurements as the error on a single line measurement for that GRB. For species with multiple lines used, we add the errors from each line in quadrature.
4. Method
4.1. Depletion model fitting
Using the concept of linear depletion sequences and F∗ from Jenkins (2009), De Cia et al. (2016) use the observable [Zn/Fe] as their dust indicator. It is possible to directly translate between the two with the relation F∗ = 1.48 × [Zn/Fe] −1.50. To avoid confusion between [Fe/Zn] as an intrinsic measured value, and “adjusted” [Fe/Zn] as a dust indicator, we use F∗ as our depletion strength factor. For a given metallicity and dust depletion strength, the relative abundance in element X that we expect to measure according to the model is thus ![\begin{equation} [X/\mathrm{H}]_{\mathrm{exp}} = \delta_X + [\mathrm{M/H}] = A + B \frac{\left(F_*-1.50\right)}{1.48} + [\mathrm{M/H}] , \label{xhmod} \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq284.png) (4)where [M/H] is the metallicity of the system, and A and B are the updated linear depletion parameters from De Cia et al. (2016). In a similar way to Savaglio et al. (2003), we vary F∗ and [M/H] to minimize the χ2 parameter between the observed abundances and those expected from the model, thus achieving a best fit depletion strength and metallicity. The 1σ errors on the parameters are calculated for a single parameter of freedom. Typically, volatile elements such as Zn, P, S, and Si are used as metallicity tracers, often left uncorrected for dust (e.g. Cucchiara et al. 2015). Our method goes one step further: with the large spectral range of X-Shooter, we use the information from all of the possible species to fit for dust depletion and thus retrieve a metallicity. We are therefore less sensitive to the pitfalls of only using a particular metallicity tracer.
(4)where [M/H] is the metallicity of the system, and A and B are the updated linear depletion parameters from De Cia et al. (2016). In a similar way to Savaglio et al. (2003), we vary F∗ and [M/H] to minimize the χ2 parameter between the observed abundances and those expected from the model, thus achieving a best fit depletion strength and metallicity. The 1σ errors on the parameters are calculated for a single parameter of freedom. Typically, volatile elements such as Zn, P, S, and Si are used as metallicity tracers, often left uncorrected for dust (e.g. Cucchiara et al. 2015). Our method goes one step further: with the large spectral range of X-Shooter, we use the information from all of the possible species to fit for dust depletion and thus retrieve a metallicity. We are therefore less sensitive to the pitfalls of only using a particular metallicity tracer.
The errors on F∗ and [M/H] are dependent on the errors on the column densities of H i, each individual element, and on the number of elements included in the dust depletion curve fits. Therefore, when only four elements are available or when the column density measurements are not tightly constrained, the uncertainty on the metallicity and F∗ can be quite large. The 2D chi-squared contour plots are provided in Appendix B. The shape of these plots show elongated confidence regions, which can be seen as a degeneracy between the two parameters. In most cases F∗ and [M/H] are still well constrained, and when this is not the case it is reflected in large errors, for example in GRB 050401.
Unfortunately, De Cia et al. (2016) did not publish measurements for Ni or Ti. Nickel in particular is measured in the majority of our spectra; it is a strongly refractory element with depletion properties similar to Fe, and provides valuable information on the dust content of the DLA. To calculate Zn depletion, De Cia et al. (2016) use the Jenkins (2009) MW data and a least-squares method to fit the slope between [Zn/Fe] and [Zn/H]. We use the same technique with Ni and Ti, using column densities from Jenkins (2009) and orthogonal distance regression to linearly fit the data and retrieve A and B parameters. We have seen that the slopes measured down to low dust content are compatible with those measured only in the Galaxy to within the uncertainties, and as such we trust that our Ni and Ti A and B values also follow this trend, and provide model values consistent with those for the other elements.
4.1.1. Nucleosynthesis
Dust depletion analysis relies on the difference between an observed and an expected, intrinsic abundance for each metal. We use the solar abundances from Asplund et al. (2009) as our reference. This could, however, lead to errors in the depletion calculation. Similar to the composition of dust grains, it is perfectly logical to assume that intrinsic abundances in a qqq high-redshift DLA are somewhat different to those observed in the Sun.
One of the most common nucleosynthetic effects at high redshift and low metallicity is an overabundance of α-elements such as O, Si, S and Mg, in comparison to Fe, often denoted by the factor [α/Fe.] The De Cia et al. (2016) depletion patterns have been corrected for these effects, and we adopt their method of applying corrections in our work. In short, this involves applying the observed trend between [Zn/Fe] and [Zn/H] to use [Zn/Fe] as a basic proxy to estimate metallicity. We then use conversions provided by De Cia et al. (2016) which show the nucleosynthetic correction to the abundances at that [Zn/Fe], based upon their observations alongside those by Lambert (1987), McWilliam (1997), Wheeler et al. (1989), for α-enhancement, and Wheeler et al. (1989), Mishenina et al. (2015), Battistini & Bensby (2015) for Mn.
Vladilo et al. (2011) calculate the reference abundances in a more theoretical way, using galaxy evolution models to predict metal abundances. It would be interesting to see how such an approach affected our results, but such an analysis is beyond the scope of this paper.
 |
Fig. 3 Dust depletion fits for the nine lowest metallicity GRB-DLAs in our sample. The diamond points are the observed relative abundances, the dot-dashed line follows the expected depletion at a strength of the best fit F∗, and the dashed line represents the best fit metallicity. Unfilled markers represent low-resolution spectral data (we continue this in all following plots), and squares with up (down) arrows represent lower (upper) limits. |
4.2. Dust-to-metals ratio
Rather than comparing dust and metal quantities measured by different means (e.g. Zafar & Watson 2013), or by using only one refractory element to trace the dust, we use the depletion strength factor F∗ along with our best fit [M/H] and measured N(H) to calculate the total column densities in dust phase for all 11 elements, including those not measured in the spectrum: ![\begin{equation} \label{eq:X_dust_col} N\left(\mathrm{X}\right)_{\mathrm{dust}} \approx N\left(\mathrm{H}\right) 10^{[X/\mathrm{H}]_{\sun}} 10^{[\mathrm{M/H}]}\left(1-10^{\delta_X}\right) \mathrm{cm}^{-2}, \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq287.png) (5)where δX is the depletion in element X as calculated from the best fit F∗. We can then sum over the elements to find the total dust column density in terms of atoms in the dust phase per cm2.
(5)where δX is the depletion in element X as calculated from the best fit F∗. We can then sum over the elements to find the total dust column density in terms of atoms in the dust phase per cm2.![\begin{equation} N\left(\mathrm{dust}\right) \approx N\left(\mathrm{H}\right) \frac{Z}{Z_{\sun}} \sum\limits_X 10^{[X/\mathrm{H}]_{\sun}}\left(1-10^{\delta_X}\right) \mathrm{cm}^{-2},\label{eq:dust_col} \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq289.png) (6)and similarly for the total metal column:
(6)and similarly for the total metal column: ![\begin{equation} \label{eq:met_col} N\left(\mathrm{metals}\right) \approx N\left(\mathrm{H}\right) \frac{Z}{Z_{\sun}} \sum\limits_X 10^{[X/\mathrm{H}]_{\sun}} ~\mathrm{cm}^{-2}, \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq290.png) (7)with Z/Z⊙ = 10[M/H]. We then take the ratio between the dust and total metal column densities, to find a dust-to-metals ratio for the DLA. We can see that metallicity and N(H) cancel out, such that the DTM calculation is independent of the best fit metallicity and hydrogen column density.
(7)with Z/Z⊙ = 10[M/H]. We then take the ratio between the dust and total metal column densities, to find a dust-to-metals ratio for the DLA. We can see that metallicity and N(H) cancel out, such that the DTM calculation is independent of the best fit metallicity and hydrogen column density. ![\begin{equation} \label{eq:dtm} \mathrm{DTM} = \frac {N\left(\mathrm{dust}\right)}{N\left(\mathrm{metals}\right)} = \frac{\sum\limits_X 10^{[X/\mathrm{H}]_{\sun}}\left(1-10^{\delta_X}\right)}{\sum\limits_X 10^{[X/\mathrm{H}]_{\sun}}} \cdot \end{equation}](/articles/aa/full_html/2017/03/aa29228-16/aa29228-16-eq292.png) (8)As is customary in DTM analysis, we normalize our values to that of the MW. We comput a Galactic DTM using the same procedure as outlined above, assuming an F∗ of 0.5, as this is the average found in the 243 J09 lines of sight. We denote the MW-normalized value as
(8)As is customary in DTM analysis, we normalize our values to that of the MW. We comput a Galactic DTM using the same procedure as outlined above, assuming an F∗ of 0.5, as this is the average found in the 243 J09 lines of sight. We denote the MW-normalized value as  .
.
We calculate the error on  by propagating those from the best fit depletion through Eq. (8). In particular, the error on the metal fraction, 10δX, is 10δXln10 αδX, where αδX is the error on the depletion in X. This is then propagated in quadrature with those from the reference abundances.
by propagating those from the best fit depletion through Eq. (8). In particular, the error on the metal fraction, 10δX, is 10δXln10 αδX, where αδX is the error on the depletion in X. This is then propagated in quadrature with those from the reference abundances.
5. Results
The depletion curves for each GRB-DLA are shown in Figs. 3 and 4, the results of which are presented in Table 2, including output values for F∗, metallicity, and dust-to-metals ratio.
5.1. Metallicity
We present dust-corrected metallicities for the 19 GRB-DLAs, including 5 previously unpublished objects. The metallicities range from the very metal-poor [M/H] = –2.37 in GRB 090926A to the supersolar [M/H] = 0.41 in GRB 090323, with a median of [M/H] = –0.63, which is equal to 0.25 Z⊙, similar to the SMC. The metallicities for all of the GRBs in this sample were presented by Cucchiara et al. (2015) using the apparent optical depth (AOD) method to measure column density. Our metallicities tend to agree with those from that work, although they are typically slightly higher, due to the fact that we make a correction for dust depletion. They find a weak decrease in metallicity with redshift. The metallicity as a function of redshift for our sample is shown in Fig. 5. There is no significant trend, although we do note that excluding the low-resolution, supersolar data point at redshift 3.6, there could be a slight decrease in metallicity with redshift, as one would expect given the evolution of galaxies over cosmic time.
The metallicities we derive tend to have a larger uncertainty than those often quoted for GRB-DLAs. Most published metallicities do not account for dust depletion, assuming that volatile elements are good metallicity tracers as they do not deplete strongly into dust. We quote our metallicities with the knowledge that even the most volatile elements deplete to some degree, and in a linear fashion with F∗, thus giving rise to a larger uncertainty due to a degeneracy between [M/H] and F∗. We note that GRBs with detections of numerous species tend to produce a smaller uncertainty on the metallicity than those with only four, since the degeneracy can better be disentangled.
5.2. Dust-to-metals ratio
The F∗ values have a mean of –0.52, which equates to a [Zn/Fe] of 0.66, 0.6 dex lower than the mean Galactic value of 1.22. This is reflected in a mean  of 0.62, while the median is 0.74. The standard deviation of
of 0.62, while the median is 0.74. The standard deviation of  is 0.27, such that the mean differs from the Galactic DTM by nearly 2σ while the median is lower at just below 1σ significance. This result is similar to the QSO-DLA results from De Cia et al. (2016), whose mean and standard deviation are 0.70 and 0.26 respectively. GRB 090926A is the only DLA which shows no dust depletion with F∗ = −1.7, which lies to the left of the point where all the depletion slopes cross the axis of zero depletion in Fig. 1.
is 0.27, such that the mean differs from the Galactic DTM by nearly 2σ while the median is lower at just below 1σ significance. This result is similar to the QSO-DLA results from De Cia et al. (2016), whose mean and standard deviation are 0.70 and 0.26 respectively. GRB 090926A is the only DLA which shows no dust depletion with F∗ = −1.7, which lies to the left of the point where all the depletion slopes cross the axis of zero depletion in Fig. 1.
Figure 6 shows the  plotted against redshift. From this small sample, we don’t see any significant trend with redshift. This result is consistent with the hydrodynamical simulations of McKinnon et al. (2016), who find no evolution in the DTM at redshifts z ≥ 1. In Fig. 7, we plot our
plotted against redshift. From this small sample, we don’t see any significant trend with redshift. This result is consistent with the hydrodynamical simulations of McKinnon et al. (2016), who find no evolution in the DTM at redshifts z ≥ 1. In Fig. 7, we plot our  against metallicity, and find a positive correlation between the two with a Spearman’s Rank of ρ = 0.63, which with 19 data pairs leads to a false-correlation probability of 0.004. There is a potential flattening of the relation, such that above [M/H] = −1 there is no real correlation. The potential reasons for this are discussed in the following section.
against metallicity, and find a positive correlation between the two with a Spearman’s Rank of ρ = 0.63, which with 19 data pairs leads to a false-correlation probability of 0.004. There is a potential flattening of the relation, such that above [M/H] = −1 there is no real correlation. The potential reasons for this are discussed in the following section.
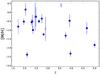 |
Fig. 5 Metallicity [M/H] as a function of redshift. Open symbols are those taken from low-resolution spectra. |
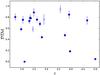 |
Fig. 6
|
 |
Fig. 7
|
6. Discussion
6.1. The origin of dust
Figure 7 shows that the dust-to-metals ratio increases with metallicity. Typically, this would support the view that the dust is formed by grain growth in the ISM (Draine 2009). Mattsson et al. (2014) can also explain this scenario in terms of dust created in stars and supernovae, and then kept in balance by ISM grain growth counteracting dust destruction mechanisms. We also notice a potential flattening of this trend above metallicities of 0.1 Z⊙. This flattening is the opposite to what is predicted in the models of Mattsson et al. (2014) and Mattsson (2016) where the DTM is fairly constant (and low) until a critical metallicity of 0.1 Z⊙ at which point dust production via grain growth is kick-started and the DTM grows towards the Galactic value at solar metallicity. Our observed trend can instead be explained by a higher rate of dust destruction at lower metallicities. As noted in De Cia et al. (2013), this could be due to the star forming environments that GRBs are known to trace (e.g. Savaglio et al. 2009), which are somewhat different to the solar-like environment of Mattsson (2016). The strong radiation fields in such environments produced by young OB stars and shocks from supernovae (SNe) may destroy dust faster than it can be created by grain growth when the metallicity is low. Another possibility is that the GRB-DLAs are actually tracing dust in the CGM rather than the ISM of their host galaxies where dust evolution is likely to be somewhat different to that in the ISM models referred to previously. Typically, however, the DLAs are located a few hundred parsecs from the GRB site itself (e.g. Hartoog et al. 2013; D’Elia et al. 2014; Friis et al. 2015), and thus located in the ISM of the GRB’s host galaxy.
The amount of dust along the line of sight can also be measured by the effect it has on the spectral energy distribution (SED) of a GRB afterglow. Specifically, the SED is “reddened”, and this reddening can be expressed as the total extinction in the V-band, AV. The values for AV;SED are found by fitting broadband SEDs from the optical to the X-ray regimes (see e.g. Greiner et al. 2011; Schady et al. 2012; Covino et al. 2013; and upcoming papers Bolmer et al. and Greiner et al., both in prep.). For all bursts from 2007 onwards, we use optical/NIR data from the seven-channel imager GROND (Greiner et al. 2008), and X-ray data from the X-ray Telescope (XRT; Burrows et al. 2005) on board Swift (Gehrels et al. 2004). For the pre-GROND bursts, see Schady et al. (2011). A simple power-law or broken power-law is fit to the observed data, and “missing” flux in the bluer visible bands is attributed to dust. This reddening is fit with one of three different exctintion laws, namely those from the SMC, LMC, and MW (Pei 1992), and is described by the colour excess, E(B−V). This is converted into AV;SED via the relation 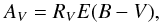 (9)where RV is the total-to-selective extinction, and is fairly well known for the Local Group extinction curves at an average of 3.08, 3.16, and 2.93 for the MW, LMC and SMC, respectively. It includes silicates and carbonaceous grains and depends largely on the grain-size distribution. Typically, these Local Group extinction laws produce a good fit to GRB SEDs (Schady et al. 2010; Kann et al. 2010; Greiner et al. 2011), although a more complex dust model might fit the extinction curves better. Although the best fit AV varies slightly depending on which curve is used, the use of NIR and X-ray data in the SED fit typically provides good constraints on AV;SED. The extinction law used for the final AV;SED measurement is that which results in the best
(9)where RV is the total-to-selective extinction, and is fairly well known for the Local Group extinction curves at an average of 3.08, 3.16, and 2.93 for the MW, LMC and SMC, respectively. It includes silicates and carbonaceous grains and depends largely on the grain-size distribution. Typically, these Local Group extinction laws produce a good fit to GRB SEDs (Schady et al. 2010; Kann et al. 2010; Greiner et al. 2011), although a more complex dust model might fit the extinction curves better. Although the best fit AV varies slightly depending on which curve is used, the use of NIR and X-ray data in the SED fit typically provides good constraints on AV;SED. The extinction law used for the final AV;SED measurement is that which results in the best  value.
value.
In Fig. 8, we plot the metals-to-dust ratio according to the definition of Zafar & Watson (2013), which uses the AV as a dust tracer. As in that work, we see no strong trend with metallicity, at odds with the result from Fig. 7. We note than our mean metals-to-dust of 21.65 cm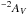 mag-1 is higher than that from their sample, and we see a higher spread of σ = 0.46 dex. A Spearman’s rank test gives ρ = 0.38 with a false positive probability of P = 0.11, suggesting that there is perhaps a slight positive correlation, and indeed in the opposite direction to that in our
mag-1 is higher than that from their sample, and we see a higher spread of σ = 0.46 dex. A Spearman’s rank test gives ρ = 0.38 with a false positive probability of P = 0.11, suggesting that there is perhaps a slight positive correlation, and indeed in the opposite direction to that in our  method. Given that the metal measurement comes from the same place in both methods, there must be a discrepancy between how the dust is measured, the reasons for which we explore in the following sections.
method. Given that the metal measurement comes from the same place in both methods, there must be a discrepancy between how the dust is measured, the reasons for which we explore in the following sections.
6.2. The AV;SED to AV;DTM discrepancy
We can see from Figs. 7 and 8 that depletion and extinction seem either to have different sensitivity, or not to trace the same dust along the line of sight, or properties thereof. To compare these values we look to the relation used to calculate a value of AV from a depletion-measured DTM, which we label AV;DTM. This is based on the average extinction for a given hydrogen column density in the MW, scaled for DTM and metallicity, as per Savaglio et al. (2003), and using the N(H) /AV from Watson (2011)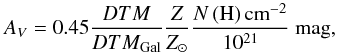 (10)with N(H) measured in cm-2. In the literature there are many cases of GRB afterglows where a direct AV measurement from the SED was possible, as well as spectra with measurable depletion, and there is often disagreement between the two values, with the depletion-inferred AV usually higher than the SED value (e.g. Watson et al. 2006; Savaglio et al. 2012; Friis et al. 2015). For our sample, we compare our independently measured AV;SED values to AV;DTM based upon the
(10)with N(H) measured in cm-2. In the literature there are many cases of GRB afterglows where a direct AV measurement from the SED was possible, as well as spectra with measurable depletion, and there is often disagreement between the two values, with the depletion-inferred AV usually higher than the SED value (e.g. Watson et al. 2006; Savaglio et al. 2012; Friis et al. 2015). For our sample, we compare our independently measured AV;SED values to AV;DTM based upon the  , N(H) and [M/H] from our fits, the result of which is shown in Fig. 9. There seem to be two distinct categories of objects: group (1) are found above the green 1:1 line and make up the majority of the sample and show the known overprediction of AV;DTM compared to AV;SED, which are best fit by the blue dashed line; group (2) are found below this line and are those whose AV;DTM prediction is lower than that measured from the SED. These objects include the known outlier GRB 070802 (Krühler et al. 2008; Elíasdóttir et al. 2009) at an AV;SED of 1.23 mag. This underprediction for GRB 070802 is also noted by De Cia et al. (2016), and could be a result of the uncertain column density measurements resulting from low-resolution spectral data.
, N(H) and [M/H] from our fits, the result of which is shown in Fig. 9. There seem to be two distinct categories of objects: group (1) are found above the green 1:1 line and make up the majority of the sample and show the known overprediction of AV;DTM compared to AV;SED, which are best fit by the blue dashed line; group (2) are found below this line and are those whose AV;DTM prediction is lower than that measured from the SED. These objects include the known outlier GRB 070802 (Krühler et al. 2008; Elíasdóttir et al. 2009) at an AV;SED of 1.23 mag. This underprediction for GRB 070802 is also noted by De Cia et al. (2016), and could be a result of the uncertain column density measurements resulting from low-resolution spectral data.
Including those GRBs with AV;SED upper limits, 11 are categorized as overpredictions in group (1), while 6 are definitely in group (2). Of these, one is GRB 070802. The others are GRBs 050820A, 100219A, 111008A, 130408A, and 141028A. GRB 090926A shows negligible dust in both depletion and extinction.
 |
Fig. 8 Metals-to-dust diagnostic used by Zafar & Watson (2013), as applied to our data along with the Local Group average and standard deviation that they quote (dashed line and shaded area). |
6.3. Accuracy of AV;DTM – depletion as a reliable tracer of dust
A potential reason for the discrepancy is touched upon in Zafar & Watson (2013), who mention that while depletion is often based upon Fe, the vast majority of dust mass is composed of O, C, Mg, and Si, arguing that Fe-based depletion measurements may not correctly trace most of the dust. Indeed, Dwek (2016) provide a compelling argument for Fe dust production being different to that of the bulk of the elements; specifically, it is formed by cold grain growth in the ISM rather than in CCSNe and post-AGB star envelopes. In this argument, depletion based upon iron measurements is therefore bound to trace different dust to extinction. However, the linear depletion sequences seen by Jenkins (2009) and De Cia et al. (2016) show that by calculating the F∗ for a particular line of sight, we can get a robust prediction for dust fractions and columns for all elements, including those not measured in the DLA, and thus we incorporate not only the dust compounds traced by iron, but the silicates and carbonaceous grains as well.
We have followed the procedure in De Cia et al. (2016; see Sect. 4.1.1) to correct relative abundances for nucleosynthetic effects, such that any discrepancies between our adopted intrinsic abundance and that true to the DLA are likely to be marginal, and certainly not large enough to cause the observed offset in the AV;DTM prediction.
6.4. Accuracy of AV;SED
Assuming that our depletion measure is indeed a solid representation of the total dust column, we look to AV;SED for the reason why there could be a discrepancy. The question is whether the Local Group extinction curves are a good fit for GRB-DLAs or whether something other than the MW, LMC, or SMC should be used as their model, such as grey dust (Perley et al. 2008). Indeed, Friis (2015) claim that grey dust extinction, so called because the extinction is weakly dependent on wavelength, could be prominent in up to 25% of GRB-DLAs, including GRB 121024A which is included in our sample. Their reasoning is that a top-heavy grain-size distribution would cause a very flat extinction curve. When fitting a broken power-law SED, there is then a degeneracy between the steepness of the extinction curve (i.e. the AV), and the position of the break between X-ray optical power-law slopes (Schady et al. 2012); one of the solutions is a large amount of grey dust, which corresponds to a large AV for a small E(B−V). If the extinction in our group (1) DLAs is caused by grey dust, then we may be able to reconcile the overpredicted AV;DTM with AV;SED. However, some of these DLAs show compelling evidence for the contrary: GRB 120327A is best fit by a simple power law and an SMC-like extinction of AV;SED = 0.05 mag, with AV;DTM = 0.18 mag. The power law removes any degeneracy in the slope of the dust extinction law, and thus excludes the possibility of significant grey dust. Another example is GRB 120815A, whose SED is fit by a power law and SMC-like extinction to give an AV;SED value of 0.08 mag, which is significantly smaller than the AV;DTM of 0.44 mag. We find that GRB 121024A is also best fit with a power law. Indeed, Fig. 9 shows that only one object that has an overpredicted AV was fit with a broken power law.
Although there is strong evidence for dust destruction caused by the GRB itself (Morgan et al. 2014), this would not cause a discrepancy between AV;SED and AV;DTM. Any dust that extinguishes the GRB would also be visible in depletion, so if that dust is destroyed it is no longer visible in depletion or extinction.
 |
Fig. 9 AV as measured directly from the SED against that calculated from the DTM. The green line indicates a 1:1 conversion between the two. Blue circles represent SEDs best fit with a simple power-law, whereas red triangles are used for broken power-law fits. Empty points refer to depletion measured from low-resolution spectra. Large error bars are due to significant errors in several measured parameters being combined in quadrature. |
Intervening systems such as Mg ii absorbers are known to contain similar quantities of dust as galaxies (e.g. Ménard & Fukugita 2012), although QSO-DLAs tend to show very little reddening (Krogager et al. 2016; De Cia et al. 2016). For the group (2) objects, we notice that 050820A, 100219A, 111008A, and 130408A all have intervening absorbing systems. Should these objects have a high dust content, they could significantly affect the SED of the GRB afterglow, such that the reddening caused by dust in the host galaxy itself is indeed smaller, and thus pushes these objects towards the 1:1 line. However, for these intervening systems to be the reason for a much higher AV;SED than from DTM, they would need to contribute around 80% of the extinction along the line of sight, whereas the systems in our sample are much weaker in metal line absorption than the host DLA (e.g. in GRB 100219A, Thöne et al. 2013). We therefore find it unlikely that a significant amount of the extra extinction is caused by intervening systems.
6.5. Equivalent dust column density
Having established that depletion is a good tracer of the dust, and with AV;SED being accurate and reliable, we look to the relation used to calculate AV;DTM, Eq. (10). This is based upon the relation between hydrogen and dust in the Galaxy, where a column of N(H) = 1021 cm-2 results in an AV of 0.45. We note that the value of the Galactic gas-to-dust ratio varies depending on the sample and technique used to measure it. We use the result of Watson (2011). Measurements of this value have been consistent over the past few decades, and include those by Bohlin et al. (1978), Predehl & Schmitt (1995), and Güver & Özel (2009). The value used does not alter the fact that a significant discrepancy is observed. In DLAs, the hydrogen column density is scaled for dust-to-metals ratio and metallicity to take into account the differing dust-to-gas ratios in such environments. However, the discrepancies in Fig. 9 show that the scaling between this equivalent dust column density and the AV may well be incorrect. That is to say that in DLAs, such a column of dust does not have as much of a reddening effect as in the MW (see e.g. Campana et al. 2009.) This would indeed be solved by the make-up of the dust being different, but this is hard to explain given the well-determined extinction laws that are observed in GRB afterglows, which are consistent with the Local Group extinction laws (Schady et al. 2011; Greiner et al. 2011; Covino et al. 2013). One could argue that the problem arises from using a MW scaling relation with AV;SED measurements based upon mostly SMC-like extinction laws, but both Magellanic Clouds have similar a AV/NH to that in the MW (Zafar & Watson 2013; Watson 2011).
The reason for the scatter thus remains unclear, and we therefore advise significant caution against basing AV predictions on the AV-to-N(H) ratio of the MW and Local Group. We also suggest that the discrepancy between the different methods of quantifying dust is the reason for the disagreement between the trend, or non-trend, seen in DTM with metallicity.
7. Conclusion
Gamma-ray bursts are a unique if somewhat biased probe of the dust-to-metals ratio in the high-redshift Universe. GRBs occur only within certain types of galaxies (Krühler et al. 2015; Perley et al. 2015a,b), and thus are not totally unbiased probes, although this effect is reduced as redshifts greater than around 2 are reached (Perley et al. 2013; Greiner et al. 2015; Schulze et al. 2015). They are also complementary to QSO-DLAs, and this work expands our observational knowledge of the DTM into the inner regions of galaxies in the distant Universe. We have used optical/NIR spectroscopy from a sample of 19 GRB afterglows in order to measure the metal and dust content of the DLAs in their host galaxies, including previously un-published metal column densities and metallicities for five objects. By using dust depletion models based on the MW, as well as QSO-DLAs, we have used a thorough method to determine the column densities of dust and of metals in order to calculate a dust-to-metals ratio. We find that the DTM follows a positive trend with metallicity, supporting the theory that a significant amount of dust is formed in situ in the ISM. We have investigated the discrepancy between the results of De Cia et al. (2013) and Zafar & Watson (2013), concluding that AV;SED and depletion are not analogous measurements of dust. We see the common trend that AV;DTM is often higher than AV;SED, which we tentatively suggest could be due to the scaling between depletion-measured DTM and AV being different in GRB host galaxies to the MW. We also note a significant number of objects whose AV;DTM values are underpredictions compared to AV;SED, and despite seeing what looks like two distinct populations, we are unable to satisfactorily reconcile the two using theories such as grey dust or intervening systems. We thus suggest that, given the large scatter between the two, DTM measured from depletion should not be used as a proxy for AV, and encourage further work with larger samples to investigate the problem further.
Spectra of GRBs 120716A, 120909A, and 130408A have been analysed by Cucchiara et al. (2015), but that work presents column density measurements for only Ly-α and one other element, and does not show line fits and velocity components, as we do here.
Acknowledgments
We thank the anonymous referee for the thorough feedback and detailed comments which have significantly enhanced the strength of this paper. We are grateful for the support of the GROND GRB team. We thank Annalisa De Cia and Darach Watson for interesting and useful discussions. We thank C. Ledoux and P. Vreeswijk for providing a compilation of oscillator strengths. P.W, P.S, and R.M.Y acknowledge support through the Sofja Kovalevskaja Award to P.S from the Alexander von Humboldt Foundation of Germany. Part of the funding for GROND (both hardware and personnel) was generously granted from the Leibniz-Prize to Prof. G. Hasinger (DFG grant HA 1850/28-1).
References
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, Astrophys. Space Sci., 47, 481 [Google Scholar]
- Battistini, C., & Bensby, T. 2015, A&A, 577, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernstein, R. A., Freedman, W. L., & Madore, B. F. 2002, ApJ, 571, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, S., & Ferrara, A. 2005, MNRAS, 358, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bouche, N., Lehnert, M. D., Aguirre, A., Peroux, C., & Bergeron, J. 2007, MNRAS, 378, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, D. N., Hill, J. E., Nousek, J. A., et al. 2005, Space Sci. Rev., 120, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Thone, C. C., Postigo, A. D. U., et al. 2009, MNRAS, 402, 2429 [Google Scholar]
- Chen, B., Dai, X., Kochanek, C. S., & Chartas, G. 2013, ArXiv [arXiv:1306.0008] [Google Scholar]
- Covino, S., Melandri, A., Salvaterra, R., et al. 2013, MNRAS, 432, 1231 [NASA ADS] [CrossRef] [Google Scholar]
- Cucchiara, A., Fumagalli, M., Rafelski, M., et al. 2015, ApJ, 804, 51 [NASA ADS] [CrossRef] [Google Scholar]
- De Cia, A., Ledoux, C., Savaglio, S., Schady, P., & Vreeswijk, P. M. 2013, A&A, 560, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cia, A., Ledoux, C., Mattsson, L., et al. 2016, A&A, 596, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Elia, V. 2010, A&A, 523, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Elia, V., Campana, S., Covino, S., et al. 2011, MNRAS, 418, 680 [NASA ADS] [CrossRef] [Google Scholar]
- D’Elia, V., Fynbo, J. P. U., Goldoni, P., et al. 2014, A&A, 564, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. 2009, in Cosm. Dust – Near Far, eds. T. Henning, E. Grün, & J. Steinacker, 414, 453 [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979a, ApJ, 231, 438 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979b, ApJ, 231, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E. 1998, ApJ, 501, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E. 2016, ApJ, 825, 136, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Edmunds, M. G., & Eales, S. A. 1998, MNRAS, 299, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Elíasdóttir, Á., Fynbo, J. P. U., Hjorth, J., et al. 2009, ApJ, 697, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Prochaska, J. X., Hennawi, J., et al. 2010, MNRAS, 406, 1435 [NASA ADS] [Google Scholar]
- Feldmann, R. 2015, MNRAS, 449, 3274 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, A. J., Savage, B. D., Wakker, B. P., et al. 2004, ApJ, 602, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, A. J., Ledoux, C., Petitjean, P., & Srianand, R. 2007, A&A, 473, 791 [Google Scholar]
- Franco, J., & Cox, D. P. 1986, PASP, 98, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Friis, M. 2015, Ph.D dissertation, University of Iceland, Reykjavik, ArXiv, e-prints [arXiv:1512.03205] [Google Scholar]
- Friis, M., De Cia, A., Krühler, T., et al. 2015, MNRAS, 451, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Prochaska, J. X., Sommer-Larsen, J., Dessauges-Zavadsky, M., & Moller, P. 2008, ApJ, 683, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Ledoux, C., Noterdaeme, P., et al. 2011, MNRAS, 413, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Gehrels, N., Chincarini, G., Giommi, P., et al. 2004, ApJ, 611, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Lutz, D., Sturm, E., et al. 1998, ApJ, 498, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Goldoni, P., Royer, F., François, P., et al. 2006, Ground-based Airborne Instrum. Astron., ed. McLean, 6269, 80 [Google Scholar]
- Greiner, J., Bornemann, W., Clemens, C., et al. 2008, PASP, 120, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Greiner, J., Krühler, T., Klose, S., et al. 2011, A&A, 526, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greiner, J., Fox, D. B., Schady, P., et al. 2015, ApJ, 809, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Hartoog, O. E., Wiersema, K., Vreeswijk, P. M., et al. 2013, MNRAS, 430, 2739 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A. K. 2003, PASJ, 55, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Issa, M. R., MacLaren, I., & Wolfendale, A. W. 1990, A&A, 236, 237 [NASA ADS] [Google Scholar]
- Jenkins, E. B. 2009, ApJ, 700, 1299 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, A. P., Tielens, A. G. G. M., & Hollenbach, D. J. 1996, ApJ, 469, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Jorgenson, R. A., Murphy, M. T., & Thompson, R. 2013, MNRAS, 435, 482 [NASA ADS] [CrossRef] [Google Scholar]
- Kann, D. A., Klose, S., Zhang, B., et al. 2010, ApJ, 720, 1513 [NASA ADS] [CrossRef] [Google Scholar]
- Krogager, J. K., Fynbo, J. P. U., Heintz, K. E., et al. 2016, ApJS, 832, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Küpcü Yoldaş, A., Greiner, J., et al. 2008, ApJ, 685, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Krühler, T., Ledoux, C., Fynbo, J. P. U., et al. 2013, A&A, 557, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krühler, T., Malesani, D., Fynbo, J. P. U., et al. 2015, A&A, 581, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, D. L. 1987, J. Astrophys. Astron., 8, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, C., Vreeswijk, P. M., Smette, A., et al. 2009, A&A, 506, 661 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Salvaterra, R., & Campisi, M. A. 2011, MNRAS, 414, 1263 [NASA ADS] [CrossRef] [Google Scholar]
- Mattsson, L. 2016, Planetary and Space Science, 133, 107 [Google Scholar]
- Mattsson, L., De Cia, A., Andersen, A. C., & Zafar, T. 2014, MNRAS, 440, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F. 1989, ApJ, 345, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Mckee, C. C. F., & Ostriker, E. C. E. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- McKinnon, R., Torrey, P., & Vogelsberger, M. 2016, MNRAS, 457, 3775 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A. 1997, Annu. Rev. Astron. Astrophys., 35, 503 [Google Scholar]
- Ménard, B., & Fukugita, M. 2012, ApJ, 754, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Meszaros, P., & Rees, M. J. 1997, ApJ, 476, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Mishenina, T., Gorbaneva, T., Pignatari, M., Thielemann, F. K., & Korotin, S. A. 2015, MNRAS, 454, 1585 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, Obs. Oper. Strateg., 7737, 56 [Google Scholar]
- Morgan, A. N., Perley, D. A., Cenko, S. B., et al. 2014, MNRAS, 440, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Peek, J. E. G., Ménard, B., & Corrales, L. 2015, ApJ, 813, 7 [Google Scholar]
- Peeples, M. S., Werk, J. K., Tumlinson, J., et al. 2014, ApJ, 786, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Peeters, E., Spoon, H. W. W., & Tielens, A. G. G. M. 2004, ApJ, 613, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Pei, Y. C. 1992, ApJ, 395, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Bloom, J. S., Butler, N. R., et al. 2008, ApJ, 672, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Levan, A. J., Tanvir, N. R., et al. 2013, ApJ, 778, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, D. A., Krühler, T., Schulze, S., et al. 2015a, ApJ, 817, 7 [Google Scholar]
- Perley, D. A., Tanvir, N. R., Hjorth, J., et al. 2015b, ApJ, 817, 8 [Google Scholar]
- Peroux, C., Dessauges-Zavadsky, M., D’Odorico, S., Kim, T.-S., & McMahon, R. G. 2007, MNRAS, 382, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Predehl, P., & Schmitt, J. H. M. M. 1995, A&A, 293, 889 [NASA ADS] [Google Scholar]
- Prochaska, J. X. 2006, ApJ, 650, 272 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Prochaska, J. X., Chen, H. W., Bloom, J. S., et al. 2007, ApJ, 168, 231 [Google Scholar]
- Rafelski, M., Wolfe, A. M., Prochaska, J. X., Neeleman, M., & Mendez, A. J. 2012, ApJ, 755, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, A., Savaglio, S., Krühler, T., et al. 2010, ApJ, 720, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D. B., & Sembach, K. R. K. 1996, ARA&A, 34, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Savaglio, S. 2001, in Extragalactic Infrared Backgr. its Cosmol. Implic., IAU Symp., 204, 307 [NASA ADS] [Google Scholar]
- Savaglio, S., Fall, S. M., & Fiore, F. 2003, ApJ, 585, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Savaglio, S., Glazebrook, K., & Le Borgne, D. 2009, ApJ, 691, 182 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Savaglio, S., Rau, A., Greiner, J., et al. 2012, MNRAS, 420, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P., Dwelly, T., Page, M. J., et al. 2012, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schady, P., Page, M. J., Oates, S. R., et al. 2010, MNRAS, 401, 2773 [NASA ADS] [CrossRef] [Google Scholar]
- Schady, P., Savaglio, S., Krühler, T., Greiner, J., & Rau, A. 2011, A&A, 525, 1 [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, S., Chapman, R., Hjorth, J., et al. 2015, ApJ, 808, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Skúladóttir, Á. 2010, Master Thesis, Univ. Copenhagen [Google Scholar]
- Smette, A., Sana, H., Noll, S., et al. 2015, A&A, 576, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sparre, M., Hartoog, O. E., Krühler, T., et al. 2014, ApJ, 785, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Starling, R. L. C., Wijers, R. A. M. J., Wiersema, K., et al. 2007, ApJ, 661, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Tanvir, N. R., Fox, D. B., Levan, A. J., et al. 2009, Nature, 461, 1254 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tchernyshyov, K., Meixner, M., Seale, J., et al. 2015, ApJ, 811, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Thöne, C. C., Fynbo, J. P. U., Goldoni, P., et al. 2013, MNRAS, 428, 3590 [NASA ADS] [CrossRef] [Google Scholar]
- Viegas, S. M. 1995, MNRAS, 276, 268 [NASA ADS] [Google Scholar]
- Vladilo, G. 2004, A&A, 421, 479 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vladilo, G., Abate, C., Yin, J., Cescutti, G., & Matteucci, F. 2011, A&A, 530, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, D. 2011, A&A, 533, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Watson, D. J., Fynbo, J. P. U., Ledoux, C., et al. 2006, ApJ, 652, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, J. C., Sneden, C., & Truran, J. W. J. 1989, ARA&A, 27, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, A. M., Gawiser, E., & Prochaska, J. X. 2005, ARA&A, 43, 861 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Yamasawa, D., Habe, A., Kozasa, T., et al. 2011, ApJ, 735, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Zafar, T., & Watson, D. 2013, A&A, 560, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1 Metal absorption lines in the X-shooter spectrum of GRB 120119A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 31.4 km s-1. |
 |
Fig. A.2 Metal absorption lines in the X-shooter spectrum of GRB 120716A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 35.0 km s-1. |
 |
Fig. A.3 Metal absorption lines in the X-shooter spectrum of GRB 120909A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 30.1 km s-1. The continuum in Mg ii 1239/1240 and S ii 1250 is affected by the Lyman-α red damping wing. The extra absorption apparent in Fe ii 1611 is from the excited state transition Fe ii 5s 1612. |
 |
Fig. A.4 Metal absorption lines in the X-shooter spectrum of GRB 130408A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 20.0 km s-1. The continuum in S ii 1250/1253/1259 is affected by the Lyman-α red damping wing. |
 |
Fig. A.5 Metal absorption lines in the X-shooter spectrum of GRB 130408A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 20.0 km s-1. The absorption to the right of the Mn ii 2606 line is due to telluric absorption. |
 |
Fig. A.6 Metal absorption lines in the X-shooter spectrum of GRB 141028A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 25.0 km s-1. The narrow saturated lines in the Mg ii 2796/2803 and Mg i 2852 are due to telluric absorption. |
Appendix B: Additional figures
 |
Fig. B.1 Confidence regions for F∗ and [M/H] for GRB 000926. |
 |
Fig. B.2 Confidence regions for F∗ and [M/H] for GRB 050401. |
 |
Fig. B.3 Confidence regions for F∗ and [M/H] for GRB 050730. |
 |
Fig. B.4 Confidence regions for F∗ and [M/H] for GRB 050820A. |
 |
Fig. B.5 Confidence regions for F∗ and [M/H] for GRB 070802. |
 |
Fig. B.6 Confidence regions for F∗ and [M/H] for GRB 081008. |
 |
Fig. B.7 Confidence regions for F∗ and [M/H] for GRB 090323. |
 |
Fig. B.8 Confidence regions for F∗ and [M/H] for GRB 090809F. |
 |
Fig. B.9 Confidence regions for F∗ and [M/H]. for GRB 090926A |
 |
Fig. B.10 Confidence regions for F∗ and [M/H] for GRB 100219A. |
 |
Fig. B.11 Confidence regions for F∗ and [M/H] for GRB 111008A. |
 |
Fig. B.12 Confidence regions for F∗ and [M/H] for GRB 120119A. |
 |
Fig. B.13 Confidence regions for F∗ and [M/H] for GRB 120327A. |
 |
Fig. B.14 Confidence regions for F∗ and [M/H] for GRB 120716A. |
 |
Fig. B.15 Confidence regions for F∗ and [M/H] for GRB 120815A. |
 |
Fig. B.16 Confidence regions for F∗ and [M/H] for GRB 120909A. |
 |
Fig. B.17 Confidence regions for F∗ and [M/H] for GRB 121024A. |
 |
Fig. B.18 Confidence regions for F∗ and [M/H] for GRB 130408A. |
 |
Fig. B.19 Confidence regions for F∗ and [M/H] for GRB 141028A. |
All Tables
Results of the fitting of the F∗ depletion model to metal column densities from 19 GRB-DLAs.
All Figures
 |
Fig. 1 Depletion δX as a function of F∗. The slope is defined by the parameter B, and the point of zero-depletion by A. The elements are listed in order of depletion strength. |
| In the text | |
 |
Fig. 2 Difference between the measured column density of Si iiλ1526 after convolving with the X-Shooter resolution and adding noise at S/N = 7.5, similar to the lowest quality of our data. The thick black line shows the mean residual, while the dashed curves show the 1σ level. The vertical dashed line marks the point at which this line saturates in the original spectrum. |
| In the text | |
 |
Fig. 3 Dust depletion fits for the nine lowest metallicity GRB-DLAs in our sample. The diamond points are the observed relative abundances, the dot-dashed line follows the expected depletion at a strength of the best fit F∗, and the dashed line represents the best fit metallicity. Unfilled markers represent low-resolution spectral data (we continue this in all following plots), and squares with up (down) arrows represent lower (upper) limits. |
| In the text | |
 |
Fig. 4 A continuation of Fig. 3 for the ten GRB-DLAs with highest metallicity. |
| In the text | |
 |
Fig. 5 Metallicity [M/H] as a function of redshift. Open symbols are those taken from low-resolution spectra. |
| In the text | |
 |
Fig. 6
|
| In the text | |
 |
Fig. 7
|
| In the text | |
 |
Fig. 8 Metals-to-dust diagnostic used by Zafar & Watson (2013), as applied to our data along with the Local Group average and standard deviation that they quote (dashed line and shaded area). |
| In the text | |
 |
Fig. 9 AV as measured directly from the SED against that calculated from the DTM. The green line indicates a 1:1 conversion between the two. Blue circles represent SEDs best fit with a simple power-law, whereas red triangles are used for broken power-law fits. Empty points refer to depletion measured from low-resolution spectra. Large error bars are due to significant errors in several measured parameters being combined in quadrature. |
| In the text | |
 |
Fig. A.1 Metal absorption lines in the X-shooter spectrum of GRB 120119A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 31.4 km s-1. |
| In the text | |
 |
Fig. A.2 Metal absorption lines in the X-shooter spectrum of GRB 120716A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 35.0 km s-1. |
| In the text | |
 |
Fig. A.3 Metal absorption lines in the X-shooter spectrum of GRB 120909A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 30.1 km s-1. The continuum in Mg ii 1239/1240 and S ii 1250 is affected by the Lyman-α red damping wing. The extra absorption apparent in Fe ii 1611 is from the excited state transition Fe ii 5s 1612. |
| In the text | |
 |
Fig. A.4 Metal absorption lines in the X-shooter spectrum of GRB 130408A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 20.0 km s-1. The continuum in S ii 1250/1253/1259 is affected by the Lyman-α red damping wing. |
| In the text | |
 |
Fig. A.5 Metal absorption lines in the X-shooter spectrum of GRB 130408A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 20.0 km s-1. The absorption to the right of the Mn ii 2606 line is due to telluric absorption. |
| In the text | |
 |
Fig. A.6 Metal absorption lines in the X-shooter spectrum of GRB 141028A. Red dashed lines indicate velocity components. Resolution in VIS arm: v = 25.0 km s-1. The narrow saturated lines in the Mg ii 2796/2803 and Mg i 2852 are due to telluric absorption. |
| In the text | |
 |
Fig. B.1 Confidence regions for F∗ and [M/H] for GRB 000926. |
| In the text | |
 |
Fig. B.2 Confidence regions for F∗ and [M/H] for GRB 050401. |
| In the text | |
 |
Fig. B.3 Confidence regions for F∗ and [M/H] for GRB 050730. |
| In the text | |
 |
Fig. B.4 Confidence regions for F∗ and [M/H] for GRB 050820A. |
| In the text | |
 |
Fig. B.5 Confidence regions for F∗ and [M/H] for GRB 070802. |
| In the text | |
 |
Fig. B.6 Confidence regions for F∗ and [M/H] for GRB 081008. |
| In the text | |
 |
Fig. B.7 Confidence regions for F∗ and [M/H] for GRB 090323. |
| In the text | |
 |
Fig. B.8 Confidence regions for F∗ and [M/H] for GRB 090809F. |
| In the text | |
 |
Fig. B.9 Confidence regions for F∗ and [M/H]. for GRB 090926A |
| In the text | |
 |
Fig. B.10 Confidence regions for F∗ and [M/H] for GRB 100219A. |
| In the text | |
 |
Fig. B.11 Confidence regions for F∗ and [M/H] for GRB 111008A. |
| In the text | |
 |
Fig. B.12 Confidence regions for F∗ and [M/H] for GRB 120119A. |
| In the text | |
 |
Fig. B.13 Confidence regions for F∗ and [M/H] for GRB 120327A. |
| In the text | |
 |
Fig. B.14 Confidence regions for F∗ and [M/H] for GRB 120716A. |
| In the text | |
 |
Fig. B.15 Confidence regions for F∗ and [M/H] for GRB 120815A. |
| In the text | |
 |
Fig. B.16 Confidence regions for F∗ and [M/H] for GRB 120909A. |
| In the text | |
 |
Fig. B.17 Confidence regions for F∗ and [M/H] for GRB 121024A. |
| In the text | |
 |
Fig. B.18 Confidence regions for F∗ and [M/H] for GRB 130408A. |
| In the text | |
 |
Fig. B.19 Confidence regions for F∗ and [M/H] for GRB 141028A. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


