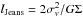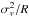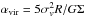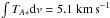| Issue |
A&A
Volume 598, February 2017
|
|
|---|---|---|
| Article Number | A96 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628251 | |
| Published online | 07 February 2017 | |
Revealing a spiral-shaped molecular cloud in our galaxy: Cloud fragmentation under rotation and gravity
1 University Observatory Munich, Scheinerstr. 1, 81679 München, Germany
e-mail: gxli@usm.lmu.de
2 Max-Planck-Institut für Radioastronomie, Auf dem Hügel, 69, 53121 Bonn, Germany
Received: 4 February 2016
Accepted: 23 September 2016
The dynamical processes that control star formation in molecular clouds are not well understood, and in particular, it is unclear if rotation plays a major role in cloud evolution. We investigate the importance of rotation in cloud evolution by studying the kinematic structure of a spiral-shaped Galactic molecular cloud G052.24+00.74. The cloud belongs to a large filament, and is stretching over ~100 pc above the Galactic disk midplane. The spiral-shaped morphology of the cloud suggests that the cloud is rotating. We have analysed the kinematic structure of the cloud, and study the fragmentation and star formation. We find that the cloud exhibits a regular velocity pattern along west-east direction – a velocity shift of ~10km s-1 at a scale of ~30 pc. The kinematic structure of the cloud can be reasonably explained by a model that assumes rotational support. Similarly to our Galaxy, the cloud rotates with a prograde motion. We use the formalism of Toomre (1964) to study the cloud’s stability, and find that it is unstable and should fragment. The separation of clumps can be consistently reproduced assuming gravitational instability, suggesting that fragmentation is determined by the interplay between rotation and gravity. Star formation occurs in massive, gravitational bound clumps. Our analysis provides a first example in which the fragmentation of a cloud is regulated by the interplay between rotation and gravity.
Key words: ISM: clouds / ISM: bubbles / ISM: kinematics and dynamics / stars: formation / galaxies: star formation / galaxies: star clusters: individual: G052.24+00.74
© ESO, 2017
1. Introduction
Star formation takes place in the dense and shielded parts of the molecular interstellar medium. An increasingly dynamical picture of cloud evolution has been revealed by recent observations and simulations (Dobbs et al. 2014; Heyer & Dame 2015, and references therein). Star formation may be determined by a combination of turbulence (Mac Low & Klessen 2004; Hennebelle & Falgarone 2012), gravity (Heyer et al. 2009; Ballesteros-Paredes et al. 2011, 2012), magnetic field (Li et al. 2014) and ionisation radiation (Whitworth et al. 1994; Dale et al. 2009).
The hierarchical structures of molecular clouds are produced by a series of fragmentation processes. In the theory of turbulence-regulated star formation (Ballesteros-Paredes et al. 1999; Padoan & Nordlund 1999; Mac Low & Klessen 2004; Krumholz & McKee 2005), supersonic turbulence creates a set of density fluctuations, and it is the high-density parts that undergo gravitational collapse. It has also been alternatively proposed that the evolution of molecular clouds is governed by gravity, and gravitational collapse creates a hierarchy of structures which then form stars (Hoyle 1953; Larson 1973; Zinnecker 1984; Heitsch & Hartmann 2008; Ballesteros-Paredes et al. 2011). It is unclear what dominates the evolution of molecular clouds.
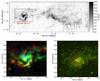 |
Fig. 1 Upper panel: 13CO(1–0) emission integrated from −4.5 to 15.0 kms-1 from the GRS (Jackson et al. 2006). The cloud G052.24+00.74 is on the left side. This cloud is connected with the neighbouring cloud G051.69+00.74 by some filamentary gas wisps. Channel maps of the region can be found in Appendix A. Lower left panel: composite three-color image of the 13CO(1–0) emission from the Spiral Cloud G052.24+00.74. Red: 6.52 <vlsr< 15.0kms-1; green: 3.12 <vlsr< 6.10kms-1; blue: −4.53 <vlsr< 2.7kms-1. The velocity centroid map and velocity FWHM map can be found in Appendix D. Lower right panel: Spitzer GLIMPSE (Benjamin et al. 2003) and MPISGAL three-color image of the Spiral Cloud G052.24+00.74. Red: 24 μm; green: 8 μm; blue: 3.6 μm. Overlaid contours are the velocity-integrated 13CO(1–0) emission (integrated from −4.5 km s-1<vlsr< 11.5km s-1). Contours correspond to 5.1, 10.2, 15.3 Kkms-1. The white diamond at the centre stands for a star cluster discovered in the GLIMPSE survey (Mercer et al. 2005), and the green stars stand for H ii regions collected from the literature (Lockman 1989; Urquhart et al. 2009). |
In recent years, the importance of environment on cloud evolution has been addressed. It is now relatively well-recognised that molecular clouds are not isolated objects. They can belong to large-scale structures (Ragan et al. 2014; Wang et al. 2015; Zucker et al. 2015; Li et al. 2016; Abreu-Vicente et al. 2016; Li et al. 2013), suggesting a connection between Galactic shear and cloud evolution. A connection between cloud evolution and large-scale magnetic field has also been suggested (Li et al. 2015). Moreover, cloud evolution can be significantly influenced by stellar feedback (Elmegreen & Lada 1977; Whitworth et al. 1994; Whitworth & Francis 2002). All these effects have been proven to be important at least in some cases. Nevertheless, the role of angular momentum in molecular clouds is still unclear.
In this work, we present a study of a spiral-shaped molecular cloud G052.24+00.74. The cloud is identified from the Galactic Ring Survey (GRS; Jackson et al. 2006). It belongs to a large (~500 pc) gas filament (filamentary gas wisp) discussed in an earlier work (Li et al. 2013). The molecular gas of the cloud is distributed in spiral-arm-like features, and we have named it “Spiral Cloud”. The whole cloud exhibits a regular velocity pattern and clear signs of fragmentation on the “spiral arm” part of the cloud. A star cluster has already formed in one of the clumps. In this paper we focus on the global kinematic structure of the cloud, and addresses its connection with the ongoing star formation activities.
2. Archival data
We used 13CO(1–0) molecular line data (ν0 = 110.2GHz) from the GRS (Jackson et al. 2006), which is a survey of the Milky Way disk with the SEQUOIA multipixel array on the Five College Radio Astronomy Observatory 14 m telescope, and covers a longitude range of 18°<l< 55.7° and a latitude range of | b | < 1° with a spatial resolution of 46″. The beam efficiency is ηmb = 0.48 (Ridge et al. 2006). At a distance of 9.8 kpc (Li et al. 2013), the spatial resolution is around 2.2 pc. The velocity resolution is 0.22km s-1. For our region, the rms sensitivity is σ(TA∗) ≈ 0.24 K. These observations are velocity-resolved which allowed us to trace and analyse the cloud’s kinematic structure in detail.
We have made use of 3.6 μm and 8 μm data from the GLIMPSE project (Benjamin et al. 2003), which is a fully sampled, confusion-limited, four-band near-to-mid infrared survey of the inner Galactic disk. We use 24 μm data from the MIPSGAL project (Carey et al. 2009), which is a survey of the Galactic disk with the MIPS instrument on Spitzerat 24 μm and 70 μm. The 3.6 μm emission is sensitive to the presence of YSOs, and the 8 μm emission typically traces polycyclic aromatic hydrocarbon (PAHs). Star formation can be traced by the 24 μm emission, which originates from the dust heated by newly-born stars.
3. Results
3.1. Multi-scale structure
From the 13CO data of the GRS (Fig. 1) we found that the cloud belongs to a larger system of two clouds (the Spiral Cloud, G025.24+00.74 and G051.69+00.74). This double cloud system has a total mass of 1.2 × 105M⊙ (Roman-Duval et al. 2010) and a total physical extent of ~140pc. Wisps of molecular gas connect the cloud with another cloud at l ~ 51° (G051.69+00.74). The lower boundary of the two clouds is arc-like, and is associated with the G52L nebula in Bania et al. (2012).
 |
Fig. 2 An illustration of the geometry of the Spiral Cloud. The left panel is a 3-colour rendering of the spiral cloud. Red colour stand for redshifted gas, and blue colour stand for blueshifted gas. On top of the image, we overlay the suggested rotational axis. In the right panel, we present a 3D ellipsoid, with two longer axes and one shorter axis. The orientation mimic the suggested orientation of the spiral cloud. The ellipsoid (representing the Spiral Cloud) is rotating with respect to its shorter axis, which we have indicated in the plot. The western side of the Spiral Cloud is rotating toward the observer. The angle between the rotational axis of the Spiral Cloud and the rotational axis of the Milky Way disk is estimated to be 22.5°, and the cloud inclination is estimated to be 45°. |
This large double cloud system stretches to a ~500pc filamentary gas wisp (Li et al. 2013). Recently, such filamentary structures have been found to be relatively common throughout the Galaxy (Ragan et al. 2014; Wang et al. 2015; Zucker et al. 2015; Li et al. 2016; Abreu-Vicente et al. 2016) and are predicted by theory and simulations (Smith et al. 2014; Dobbs 2015; Pringle et al. 2001).
3.2. Structure of the cloud
The whole Spiral Cloud has a mass of 2.72 × 104M⊙ and a radius of ~12pc (Roman-Duval et al. 2010). It has a centrally-condensed morphology, and exhibits a regular velocity pattern (Figs. 1 and D.1) where the south-eastern part of the cloud is red-shifted and the north-western part of the cloud is blue-shifted. The spiral-shaped structure lead us to assume that the velocity difference originates from rotation. The inferred cloud rotation is similar to the Milky Way rotation, and the projected angle between the cloud rotational axis and the rotation axis of the Galactic disk is estimated to be 22.5° (measured directly from the map). The rotation is also visible in channel maps (Fig. A.1). Velocity centroid map and velocity FWHM map can be found in Appendix D.
Because of the observed rotational pattern, we assume that in 3D the cloud can be approximated as an ellipsoid characterised by two longer axis and one shorter axis, and is rotating with respect to its shorter axis. A prior, the cloud’s inclination is unknown 1, and from the map we estimate an inclination of 45°. Because of projection, one can not readily tell which part of the cloud is closer to us in 3D. However, we can still infer the 3D geometry by assuming that the spiral arms are trailing, and thus we infer the orientation of the cloud as illustrated in Fig. 2.
To better analyse the cloud structure from the centre to the outside, we divided the 13CO(1–0) map into rings. Ideally, each of the ring corresponds to a circle were the cloud is viewed face-on. We measured the longer and shorter axes manually from the map. Based on this, we divided the cloud into different rings. The semi-major axes of the rings (which correspond to the radii of the circles in 3D when de-projected) are called cloud radii. The widths of the rings were chosen to be 2.7 pc, which is larger and still comparable to the resolution derived from the beam size (2.2 pc).The structure of the individual rings can be found in Appendix C. The velocity structure of the cloud can be well seen in each ring.
For each ring, we measured the mean column density. The velocity range was chosen to be −4.5 km s-1<vlsr< 11.5km s-1 to cover the whole cloud. To focus on the spiral structure, we only analysed regions that have 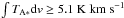 . This corresponds to 3.5 times the rms noise level. The corresponding region is indicated in Fig. C.1.
. This corresponds to 3.5 times the rms noise level. The corresponding region is indicated in Fig. C.1.
We estimated the H2 column density using NH2 = 5 × 1020Tmb dv/ (Kkms-1) (Simon et al. 2001). Tmb = TA ∗/ηmb, where TA ∗ is the antenna temperature and ηmb is the beam efficiency, v is the velocity.This conversion has been derived assuming an excitation temperature Tex = 10 K, and a 13CO abundance R(13CO/H2) = 1.7 × 10-6. Figure 3 shows the mean surface density as a function of the sizes of the rings (which we named Cloud Radius rcloud). From Fig. 3, we found that mean column density measured in H2 can be expressed as a function of cloud radius rcloud: 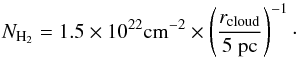 (1)The surface density of the cloud can be estimated as Σ = NH2 × mH2 × 1.36 where mH2 is the mass of H2 and 1.36 is the correction for helium and other heavy elements. At the outer regions, Eq. (1) captures the structure of the cloud quite well, but at the inner ~3 pc region, there are some noticeable differences between the column density in the analytical model and the observational data. However, this discrepancy is not severe since this is also the region where the 13CO is likely to be optically thick and the observations are underestimating the column density.
(1)The surface density of the cloud can be estimated as Σ = NH2 × mH2 × 1.36 where mH2 is the mass of H2 and 1.36 is the correction for helium and other heavy elements. At the outer regions, Eq. (1) captures the structure of the cloud quite well, but at the inner ~3 pc region, there are some noticeable differences between the column density in the analytical model and the observational data. However, this discrepancy is not severe since this is also the region where the 13CO is likely to be optically thick and the observations are underestimating the column density.
 |
Fig. 3 Column density structure of the Spiral Cloud. The figure presents ring-averaged column density as a function of cloud radius. The blue line stands for the data and the red line stands for the analytical model (Eq. (1)). The telescope resolution is ~2.2pc at a distance of 9.8kpc. The resolution of the plot (2.7 pc, limited by the widths of the rings) is indicated as the blue horizontal bar. See Sect. 3.2 for details. |
Assuming that the gas in the cloud stays in a flattened disk, by taking advantage of the fact that the column density scales as 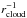 , one can analytically evaluate the expected rotation profile following Mestel (1963). Disks that share this kind of density profiles are called “Mestel disks”. The rotation velocity profiles can be determined from the balance between centrifugal force and gravitational force, they are flat, characterised by constant circular velocities. In the case of our disk, the model is accurate only at rcloud ≳ 5pc where the model does capture the density structure to a reasonable accuracy. The theoretical circular velocity can be computed as
, one can analytically evaluate the expected rotation profile following Mestel (1963). Disks that share this kind of density profiles are called “Mestel disks”. The rotation velocity profiles can be determined from the balance between centrifugal force and gravitational force, they are flat, characterised by constant circular velocities. In the case of our disk, the model is accurate only at rcloud ≳ 5pc where the model does capture the density structure to a reasonable accuracy. The theoretical circular velocity can be computed as 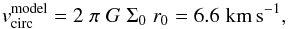 (2)where Σ0r0 can be found in Eq. (1), r0 = 5pc and Σ0 can be evaluated from Eq. (1). Assuming that the cloud is rotationally supported, the absolute velocity difference between the left and right side of the disc is thus of 2 vcir (i.e. 13.2 km s-1).
(2)where Σ0r0 can be found in Eq. (1), r0 = 5pc and Σ0 can be evaluated from Eq. (1). Assuming that the cloud is rotationally supported, the absolute velocity difference between the left and right side of the disc is thus of 2 vcir (i.e. 13.2 km s-1).
Assuming an inclination of 45°, the predicted velocity shift of either side of the disk is 4.68 km s-1 with respect to the systemic velocity. This is the theoretically-expected velocity shift if we assume that the cloud is gravitationally bound and has a disk-like geometry. In Appendix C we compare the velocity structure of the cloud with the expected velocity structure derived from the Mestel (1963) model. In general, the agreement is better at rcloud ≳ 15pc. Inside the inner 15 pc, the velocity difference is not always obvious. However, in this region, the model is not so accurate because of the deviation of the real density profile from the density profile of the Mestel (1963) model, and the data are not accurate either, because of the observed line widths are typically large (around a few km s-1).
The agreement between the model and the data leads us to conclude that the cloud is probably rotationally-supported. We note, however, that there are still structures that do not follow this regular rotation pattern. A few explanations are possible: first, the cloud is already fragmented, and for each ring, only a small portion is sampled by the molecular gas. Thus this incomplete sampling introduces some irregularities to our data. Second, for each line of sight, a typical line width of ~1km s-1 is common (see e.g. Table B.1). Third, the cloud is already fragmented, and the very process of gravitational instability can introduce significant deviations from regular circular rotation. The gas motion would also be influenced by the expansion of the embedded HII regions. These observational and theoretical uncertainties can potentially account for the observed velocity irregularities.
3.3. Fragmentation
We used the Dendrogram program (Rosolowsky et al. 2008; Goodman et al. 2009)2 to quantify the clumpy structure of the cloud. The Dendrograms are representations of how the isosurfaces in a 3D PPV data cube nest inside one another. The “Leaves” of a Dendrogram correspond to the regions that have emission enhancements in the 3D PPV data cube, and they correspond to the “clumps” found by the well-known clumpfind algorithm (Williams et al. 1994). One advantage of using Dendrogram is that its results are less dependent on technical parameters (for instance, the brightness temperature difference between contours). In this work, the term cloud is used to refer to the whole cloud G052.24+00.74, and the term clump is used to refer to the sub-structures of the cloud identified by the Dendrogram algorithm.
In this work, we smoothed the data in the velocity direction. The smoothed data cube has a velocity resolution of 0.4 km s-1 and a rms noise level of 0.17 K. Then we identify clumps from the data using the Dendrogram program. The program requires three inputs, the minimum value to consider in the dataset (min_value), and minimum difference for a structure to be considered as independent (min_delta), as well as the minimum number of pixels in a given structure (min_npix). We use min_value = 0.67 K, min_delta = 0.33 K and min_npix = 16. This choice of the parameters is relatively conservative, which ensures that only highly significant structures are considered independent. A change of these thresholds to lower values produces a larger number of smaller clumps, but the significant (e.g. these marked red in Fig. 6) structures remain unchanged3.
One should also note that the velocity dispersions of the extracted structures are dependent on the choice of the parameters. Structures identified with a relatively high threshold are more compact in 3D PPV space, and thus have smaller velocity dispersions. This may be part of the reason why the total velocity dispersions (e.g. as in Fig. D.1) estimated on lines of sights are larger than the velocity dispersion of the clumps.
In Fig. 5 we plot the leaves of the Dendrogram. IDs of the leaves are also plotted. A detailed catalogue can be found in Appendix B.
Toomre (1964) developed a theory for the stability of a disk of stars. The formalism is general and has been applied to various systems that are rotationally supported, such as disk galaxies and protostellar disks. In this formalism, the stability of a disk is characterised by the Toomre Q parameter 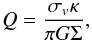 (3)where κ is the epicyclic frequency, σv represents “internal” supports such as thermal support and turbulence, and Σ is the surface density. If Q> 1 the disk is stable, and if Q< 1 the disk is unstable against perturbations and would fragment. We choose σv = 1km s-1, which is the typical velocity dispersion to expect for clumps (Wienen et al. 2015)4. In Fig. 4 plot the Toomre Q as a function of disk radius. Except the central region, the disk is unstable with Q< 1. This is consistent with the fact that the disk fragments into clumps due to gravitational instability.
(3)where κ is the epicyclic frequency, σv represents “internal” supports such as thermal support and turbulence, and Σ is the surface density. If Q> 1 the disk is stable, and if Q< 1 the disk is unstable against perturbations and would fragment. We choose σv = 1km s-1, which is the typical velocity dispersion to expect for clumps (Wienen et al. 2015)4. In Fig. 4 plot the Toomre Q as a function of disk radius. Except the central region, the disk is unstable with Q< 1. This is consistent with the fact that the disk fragments into clumps due to gravitational instability.
 |
Fig. 4 Toomre Q parameter as a function of cloud radius (rcloud). The Toomre Q is defined as Q = σvκ/πGΣ where σv = 1km s-1, Σ is the ring-averaged column density and κ is the epicyclic frequency. The resolution of the plot is 2.7 pc (limited by the size of the rings). It is indicated as the blue horizontal bar. The central 5 pc is dominated by the central clump. This is indicated by the vertical red dashed line. |
 |
Fig. 5 Clumps (leaves) identified by the Dendrogram method. Here we use different colours to indicate different leaves for clarity. Each leaf has a unique ID. We divide the leaves into three groups, one group contains clumps that belong to the “spiral arm” of the cloud (red numbers), and the other group contain clumps that are outside the “spiral arm” (blue numbers). The third group contains clumps 2, 4 and 7, which exhibit clear evidences of ongoing star formation (red stars). |
 |
Fig. 6 Physical scales involved in the fragmentation process. The x-axis is the cloud radius, and the y-axis denotes the critical length scales involved in the fragmentation process. The blue dashed line stands for the Toomre length lToomre = 2πGΣ /κ2. In the blue shaded region fragmentation is suppressed due to shear. The red solid line stands for the Jeans length |
In the formalism of Toomre (1964; see also Binney & Tremaine Binney & Tremaine 2008; Elmegreen & Elmegreen 1983), the fragmentation is determined by two length scales: the Toomre length and the Jeans length. The Toomre length is defined as 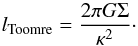 (4)For disks with flat rotational profiles,
(4)For disks with flat rotational profiles, 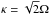 where Ω is the angular velocity, and Ω = vcirc/r = 6.6km s-1/rcloud in our case. This sets an upper limit to the fragmentation length scale, and the growth of perturbations with l>lToomre are suppressed due to shear. The Jeans length is defined as
where Ω is the angular velocity, and Ω = vcirc/r = 6.6km s-1/rcloud in our case. This sets an upper limit to the fragmentation length scale, and the growth of perturbations with l>lToomre are suppressed due to shear. The Jeans length is defined as 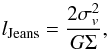 (5)where σv is the velocity dispersion, and it includes thermal and non-thermal (e.g. turbulent) contributions. The Jeans length is a lower limit to the fragmentation length, and growth of perturbations with l<lJeans are suppressed due to thermal and non-thermal (e.g. turbulent) supports. Only perturbations with lJeans<l<lToomre can be amplified.
(5)where σv is the velocity dispersion, and it includes thermal and non-thermal (e.g. turbulent) contributions. The Jeans length is a lower limit to the fragmentation length, and growth of perturbations with l<lJeans are suppressed due to thermal and non-thermal (e.g. turbulent) supports. Only perturbations with lJeans<l<lToomre can be amplified.
The fragmentation length scale can be probed by studying the separations of the neighbouring clumps. In Fig. 6 we plot these two length scales as a function of cloud radius (defined in Sect. 3.2). From the cloud, we identify a pair of clumps (4–7, see Fig. 5). Excluding the clump at the very centre, this is the only pair of clumps that are significant on the ATLASGAL (Schuller et al. 2009) tile andthus covered in subsequent studies (Wienen et al. 2015). The clump pair 4–7 share a cloud radius of 14 parsec and are separated by ~10 parsec. They are well separated and both exhibit signs of star formation. Since we did not deproject the separation into 3D, we estimate an uncertainty of 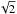 of the clump separation estimate (because the cloud inclination is 45°).In Fig. 6, this pair occupies a position where the growth of perturbations is allowed. The predicted length scale of the fragmentation process using the formalism of Toomre (1964) matches well with the observed clump separation. Interestingly, this pair also stays at a radius where the fragmentation is most likely to occur (measured by the difference between lJeans and lToomre). This supports our hypothesis that the Spiral Cloud fragments due to gravitational instability.
of the clump separation estimate (because the cloud inclination is 45°).In Fig. 6, this pair occupies a position where the growth of perturbations is allowed. The predicted length scale of the fragmentation process using the formalism of Toomre (1964) matches well with the observed clump separation. Interestingly, this pair also stays at a radius where the fragmentation is most likely to occur (measured by the difference between lJeans and lToomre). This supports our hypothesis that the Spiral Cloud fragments due to gravitational instability.
3.4. Star formation in the clumps
To further study the fragmentation process, we divide the leaves (clumps) into different groups. First, we make a distinction between the clumps inside the spiral arm and the clumps outside the spiral arm. Second, since three of the clumps (clump 2, 4 and 7) show evidences of star formation (inside clump 2, a star cluster has already formed, and massive stars inside this star cluster are probably triggering the formation of a next generation of stars. A bubble is found in clump 7. RMS YSOs are found in clump 4, Thompson et al. 2012), we separate them from the rest of the clumps. Finally, we have three groups of clumps. The first group include the clumps that exhibit obvious star formation activities (clump 2, 4 and 7), the second group include the other clumps that are inside the spiral arm, and the third group consists of the rest of the clumps.
 |
Fig. 7 Ratio of |
 |
Fig. 8 Clump mass versus clump radius for all the clumps. We divide the clumps into three groups, one group contains the clumps that belong to the spiral arm of the cloud (red crosses), and the other group contain the clouds that are outside the “spiral arm” (blue crosses). The third group contains clumps 2, 4 and 7, which exhibit clear evidences of ongoing star formation (red stars with numbers). IDs of the clumps are indicated. Lines of different free-fall time tff ~ ρ− 1/2 are included. The red solid line corresponds to the threshold of massive star formation M = 870 M⊙(r/ pc)1.33 derived in Kauffmann et al. (2010). |
We analyse the physical properties of the three different groups of clumps. In deriving the properties, we use the same formalism as used in Goodman et al. (2009). The detailed properties of the clumps can be found in Appendix B. In Fig. 7, we plot 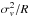 versus Σ for all the clumps (Simon et al. 2001, where Σ ≡ M/πR2). Lines of different virial parameters are derived from (Bertoldi & McKee 1992)
versus Σ for all the clumps (Simon et al. 2001, where Σ ≡ M/πR2). Lines of different virial parameters are derived from (Bertoldi & McKee 1992) 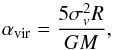 (6)where αvir is the viral parameter, σv is the velocity dispersion of the clumps, R is the radii of the clumps, G is gravitational constant, and M is the mass clump. The clumps that belong to the spiral arm are close to gravitationally bound (0.5 <αvir< 1), while the other clumps are not. Interestingly, all the three clumps that show star formation activities are gravitationally bound.
(6)where αvir is the viral parameter, σv is the velocity dispersion of the clumps, R is the radii of the clumps, G is gravitational constant, and M is the mass clump. The clumps that belong to the spiral arm are close to gravitationally bound (0.5 <αvir< 1), while the other clumps are not. Interestingly, all the three clumps that show star formation activities are gravitationally bound.
The correspondence of a small viral parameter and active star formation leads us to suggest that the star formation inside the clumps is controlled largely by self-gravity. Another way to look at the problem is to consider the free-fall timescale. This is a characteristic timescale that governs the gravitational collapse. It is defined as tff ~ (Gρ)− 1/2, ρ ≡ M/R3. In Fig. 8 we plot the masses of the clumps against the radii of the clumps. Lines that correspond to different free-fall timescales tff are added. The clumps that belong to the spiral arm have significantly shorter free-fall timescales, and the three clumps that are forming stars have not only short free-fall timescales but also higher masses.
A star cluster has formed at the centre of clump 2 (Mercer et al. 2005). This clump is distinguished in two ways. First, it is the clump that resides right at the centre of the spiral structure. Second, compared to all the other clumps, it has the smallest viral parameter and the shortest free-fall timescale. The connection between star formation and indicators of the importance of self-gravity suggests that gravity is playing a determining role in the evolution of the clumps. Kauffmann et al. (2010) derived an empirical threshold M = 870 M⊙(r/ pc)1.33 for the formation of massive stars in the mass-size plane, e.g. clumps that are above this line are active in massive star formation. The results have been confirmed by studies of larger samples, e.g. ATLASGAL clumps (Urquhart et al. 2013). This threshold is also indicated in Fig. 8. Only clumps 2, 4 and 7 host H ii regions5, and clumps 2 and 4 are above this threshold. However, we note that the result is true for these clump-like objects only in a statistical sense.
4. Rotating molecular clouds in observations and simulations
How do molecular clouds evolve? It is widely recognised that cloud evolution is governed by the combined effects of (ordered or disordered) kinematic motion, turbulence, gravity and magnetic field. However, the relative importance of these factors is not known. The importance of rotation in cloud evolution has long been recognised (Phillips 1999) but remains poorly-constrained.
In the case of the Spiral Cloud, rotation seems to play an important role. The dynamics of the cloud can be reasonably described as a balance between rotation and gravity, the interplay of which regulates the fragmentation process.
Is rotation playing a role in molecular clouds in general? The idea of rotating clouds is not new (Bastien 1983; Zinnecker 1984; Bodenheimer 1978; Phillips 1999). However, from the current literature it is still unclear if rotation is playing a role in the Milky Way molecular clouds. Interestingly, the possibility of rotating molecular clouds has been suggested by several groups from observations of different galaxies (Rosolowsky 2007; Imara et al. 2011). Recently, Utomo et al. (2015) reported CARMA observations of the lenticular galaxy NGC4526 in 12CO line where the authors found the angular momentum vectors of the molecular clouds tend to align with the minor axis of the galaxy.This leads the authors to conclude that the clouds are rotating. Our Spiral Cloud could be representative of a population of rotating molecular clouds in our galaxy.
Rotation can be important also at clump and core scales (Goodman et al. 1993). In our case, it is possible that a significant amount of angular momentum of the cloud will be transferred to the clumps (Zinnecker 1984). The 13CO emission is optically thick at these scales and we are not able to test this hypothesis. However, recent results do indicate that rotation can become dominant at ~sub-pc scale (Liu et al. 2015; Liu 2017).
Even though turbulence does not seem to be dominant in shaping the structure of the cloud on the large scale, it may play important roles in controlling the fragmentation of the individual clumps. Indeed, all the clumps that belong to the spiral arm exhibit supersonic line widths. It is possible that these clumps are supported by turbulent motion, and turbulence in the clumps can be generated during the fragmentation process (Klessen & Hennebelle 2010). Further observations with higher angular resolutions are needed, in order to disentangle the roles of turbulence and rotation on the subsequent fragmentation of the clumps.
5. Conclusions
We report the study of a spiral-shaped molecular cloud in our Galaxy.
The cloud belongs to a large 500 pc gas filament (Li et al. 2013), which is stretching over ~100pc above the Galactic disk midplane.The cloud exhibits a spiral-shaped morphology. It shows a velocity shift of ~10km s-1 at a scale of ~30pc. The observed kinematic structure can be reproduced if the cloud is rotationally supported. This lead us to conclude that on the cloud scale, rotation is important in balancing against gravity. The cloud is rotating in prograde direction with respect to the bulk of the Milky Way.
We analysed the dynamics and the fragmentation process under the framework of gravitational instability of Toomre (1964). We found that our cloud is unstable against gravitational collapse. By analysing the cloud structure in detail we found that the separation between the clumps can be consistently reproduced assuming gravitational instability.
We studied the physical properties of the fragments, and found that the clumps on the spiral arm part of the cloud are close to gravitationally bound. Star formation occurs in the clumps that are gravitationally bound with short free-fall times. All the facts seem to indicate that gravitational instability is crucial for the fragmentation of the cloud and self-gravity is driving the subsequent star formation. When viewed against observations of cloud rotation in other Galaxies, we speculate that our cloud could represent a category of rotationally-supported clouds for which the interplay between gravity and rotation plays a determining role in their evolution.
Available at http://www.Dendrograms.org/en/latest/
One can find in Li (2014) results from a different combination of parameters. The clumps identified with these different parameter combinations are sometimes different, but the most significant clumps can always be robustly identified.
Which is consistent with the velocity dispersions of the clumps presented in Table B.1.
Results from the Simbad database http://simbad.u-strasbg.fr/simbad/
Acknowledgments
Guang-Xing Li received support for this research through a stipend from the International Max Planck Research School (IMPRS) for Astronomy and Astrophysics at the Universities of Bonn and Cologne and is currently supported by the Priority Program 1573 ISM-SPP from the DFG (Deutsche Forschungsgemeinschaft). Guang-Xing Li would like to thank ISIMA (International Summer Institute for Modelling in Astrophysics, now Kavli Summer Program in Astrophysics) for facilitating collaborations, and would like to thank Nicolas Peretto and Patrick Hennebelle for discussions. Lee Hartman is acknowledged for giving a nice lecture in ISIMA, which motivates the thinking of gravity, and Di Li is acknowledged for providing references on angular momentum. Guang-Xing Li thanks Alexei Kritsuk for discussions and for his final push towards the publication of the results. Guang-Xing Li thanks Manuel Behrendt for discussions of gravitational instabilities and clumps in disk galaxies. This publication makes use of molecular line data from the Boston University-FCRAO Galactic Ring Survey (GRS). The GRS is a joint project of Boston University and Five College Radio Astronomy Observatory, funded by the National Science Foundation under grants AST-9800334, AST-0098562, and AST-0100793. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. We also would like to thank Thomas Robitaille for making his code publicly available. The research made use of the astropy package. The referee has to be acknowledged, whose comments have lead to very significant improvements in our paper.
References
- Abreu-Vicente, J., Ragan, S., Kainulainen, J., et al. 2016, A&A, 590, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Hartmann, L., & Vázquez-Semadeni, E. 1999, ApJ, 527, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Hartmann, L. W., Vázquez-Semadeni, E., Heitsch, F., & Zamora-Avilés, M. A. 2011, MNRAS, 411, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., D’Alessio, P., & Hartmann, L. 2012, MNRAS, 427, 2562 [NASA ADS] [CrossRef] [Google Scholar]
- Bania, T. M., Anderson, L. D., & Balser, D. S. 2012, ApJ, 759, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Bastien, P. 1983, A&A, 119, 109 [NASA ADS] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Bertoldi, F., & McKee, C. F. 1992, ApJ, 395, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, in Galactic Dynamics, 2nd edn. (Princeton University Press) [Google Scholar]
- Bodenheimer, P. 1978, ApJ, 224, 488 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Noriega-Crespo, A., Mizuno, D. R., et al. 2009, PASP, 121, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Wünsch, R., Whitworth, A., & Palouš, J. 2009, MNRAS, 398, 1537 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L. 2015, MNRAS, 447, 3390 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., Krumholz, M. R., Ballesteros-Paredes, J., et al. 2014, Protostars and Planets VI, 3 [Google Scholar]
- Elmegreen, B. G., & Elmegreen, D. M. 1983, MNRAS, 203, 31 [NASA ADS] [Google Scholar]
- Elmegreen, B. G., & Lada, C. J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Rosolowsky, E. W., Borkin, M. A., et al. 2009, Nature, 457, 63 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Heitsch, F., & Hartmann, L. 2008, ApJ, 689, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., & Dame, T. M. 2015, ARA&A, 53, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F. 1953, ApJ, 118, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Imara, N., Bigiel, F., & Blitz, L. 2011, ApJ, 732, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, J., Pillai, T., Shetty, R., Myers, P. C., & Goodman, A. A. 2010, ApJ, 716, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1973, ARA&A, 11, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Li, G.-X. 2014, Ph.D. Thesis, Rheinische Friedrich-Wilhelms-Universität Bonn [Google Scholar]
- Li, G.-X., Wyrowski, F., Menten, K., & Belloche, A. 2013, A&A, 559, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, H.-B., Goodman, A., Sridharan, T. K., et al. 2014, Protostars and Planets VI, 101 [Google Scholar]
- Li, H.-B., Yuen, K. H., Otto, F., et al. 2015, Nature, 520, 518 [CrossRef] [Google Scholar]
- Li, G.-X., Urquhart, J. S., Leurini, S., et al. 2016, A&A, 591, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, H. B. 2017, A&A, 597, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, H. B., Galván-Madrid, R., Jiménez-Serra, I., et al. 2015, ApJ, 804, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J. 1989, ApJS, 71, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Mercer, E. P., Clemens, D. P., Meade, M. R., et al. 2005, ApJ, 635, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Mestel, L. 1963, MNRAS, 126, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., & Nordlund, Å. 1999, ApJ, 526, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. P. 1999, A&AS, 134, 241 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pringle, J. E., Allen, R. J., & Lubow, S. H. 2001, MNRAS, 327, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Ragan, S. E., Henning, T., Tackenberg, J., et al. 2014, A&A, 568, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ridge, N. A., Di Francesco, J., Kirk, H., et al. 2006, AJ, 131, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Jackson, J. M., Heyer, M., Rathborne, J., & Simon, R. 2010, ApJ, 723, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. 2007, ApJ, 654, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E. W., Pineda, J. E., Kauffmann, J., & Goodman, A. A. 2008, ApJ, 679, 1338 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, R., Jackson, J. M., Clemens, D. P., Bania, T. M., & Heyer, M. H. 2001, ApJ, 551, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Glover, S. C. O., Clark, P. C., Klessen, R. S., & Springel, V. 2014, MNRAS, 441, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, M. A., Urquhart, J. S., Moore, T. J. T., & Morgan, L. K. 2012, MNRAS, 421, 408 [NASA ADS] [Google Scholar]
- Toomre, A. 1964, ApJ, 139, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Urquhart, J. S., Hoare, M. G., Purcell, C. R., et al. 2009, A&A, 501, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, J. S., Thompson, M. A., Moore, T. J. T., et al. 2013, MNRAS, 435, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Utomo, D., Blitz, L., Davis, T., et al. 2015, ApJ, 803, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, K., Testi, L., Ginsburg, A., et al. 2015, MNRAS, 450, 4043 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Whitworth, A. P., & Francis, N. 2002, MNRAS, 329, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Whitworth, A. P., Bhattal, A. S., Chapman, S. J., Disney, M. J., & Turner, J. A. 1994, A&A, 290, 421 [NASA ADS] [Google Scholar]
- Wienen, M., Wyrowski, F., Menten, K. M., et al. 2015, A&A, 579, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Zinnecker, H. 1984, MNRAS, 210, 43 [Google Scholar]
- Zucker, C., Battersby, C., & Goodman, A. 2015, ApJ, 815, 23 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Channel maps of the molecular complex at l ~ 52
In Fig. A.1 we present the 13CO(1–0) channel maps of the molecular cloud complex from the GRS (Jackson et al. 2006).
 |
Fig. A.1 13CO(1–0) channel maps of the cloud complex. The red “+” marker indicate the centre of the Spiral Cloud. The cloud complex belongs to a 500-pc filamentary gas wisp, which has been reported in Li et al. (2013). |
Appendix B: Physical properties of the clumps
The physical properties of the clumps are evaluated using the formalism outlined in Goodman et al. (2009). The radii of the clumps are evaluated as 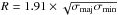 where σmaj and σmin are the major and minor axis dispersion (Solomon et al. 1987). The velocity dispersions of the clumps are evaluated
where σmaj and σmin are the major and minor axis dispersion (Solomon et al. 1987). The velocity dispersions of the clumps are evaluated
using the intensity-weighted standard deviation of velocities of all vorxels that belong to the clumps. The column densities of the clumps are evaluated as Σ = M/πR2. The physical properties of the clumps are listed in Table B.1.
Properties of the 13CO Clumps.
Appendix C: Analysis of the structure
To analyse its structure we divide the cloud into different rings. The positions of the rings are presented in Figs. C.1, and C.2 we present the velocity structure of the cloud inside these rings.
We adopt a systemic velocity of 5 km s-1 for the Spiral Cloud. For each position, the FHWMs of the emission lines are determined by FWHM ≈ 0.93I/Tpeak where I is the integrated intensity, and Tpeak is the peak the emission line.
We also compare the observational data with a model of a flat rotating disk model (Mestel 1963), described in detail in Sect. 3.2. The model has a constant circular velocity (flat rotation profile), characterised by vcirc, which is 6.6 km s-1 (Eq. (2)). Assuming an inclination of 45°, we derive the observed velocity signature of such a model.
At the very inner regions (up to rcloud = 7.48pc), the observed lines are sometimes not purely Gaussian. This might lead to some underestimates of the column density, and might make the velocity centroid estimates inaccurate. Indeed, the line profiles are more irregular at the region l ≈ 52.26°, b ≈ 0.76° where the line widths are much higher (Fig. D.1). A few causes for the irregular line profiles are possible, such as line of sight superposition and opacity broadening. If the latter is dominating, the deviation of our model from the model of Mestel (1963) would be smaller than Fig. 3 suggests.
Another uncertainty in our modelling is the distance. The expected rotational velocity is linked to r0 by Eq. (2), and r0 is proportional to the distance. Since the distance used in our analysis is the kinematic distance, whose uncertainty is typically 20%, we expect a similar uncertainty to exist in the expected rotational velocity. The expected velocity shift is also dependent on the assumed inclination of the cloud.
 |
Fig. C.1 A demonstration of our ring-based analysis of the cloud. The spacing of the rings are 2.7 pc, which is comparable to the beam size (which is 2.2 pc). The blue solid lines stand for the region within which the emission is analysed. The cut was made at |
 |
Fig. C.2 Structure of the cloud viewed within rings. On the left panels, we present the distributions of estimated H2 column densities of the pixels. The mean radii of the rings (rcloud) are indicated at the upper left corners of each panel. In the middle panels, we plot the boundaries of the rings. The proposed rotational axis is represented by the red lines. The red solid lines represent parts of the rotational axes that are in front of the cloud, and the red dashed lines represent parts of the rotational axes that are at the back of the cloud. The right panels present the velocity centroids of the emission in the position-velocity space. Here, we have projected individual line of sight observations onto the major axis of ellipsoid representing the cloud, and the x-axes are the projected offests from the centres. The horizontal lines in the right panels denote the range of velocities within which the gas is gravitationally bound to the cloud. For each line of sight, we plot the velocity centroids and the FWHMs. The centroids of the emission lines are represented as the red symbols, and the FWHMs of the of the emission lines are represented as the errorbars. The horizontal red lines represent the systemic velocity of the cloud, which is 5km s-1. The blue curve is the expected rotational signature assuming the balance between rotation and gravity (Sect. 3.2). The vertical blue lines in the middle and right panels indicate the centre of the cloud. This figure is to be continued in the next page. |
 |
Fig. C.2 continued. |
 |
Fig. C.2 continued. |
Appendix D: Detailed velocity structure of the spiral cloud
In Fig. D.1 we present the velocity centroid map and the velocity FWHM map of the cloud.
 |
Fig. D.1 Detailed velocity structure of the spiral cloud. The left panel shows the velocity centroid map, and the right panel shows the velocity FWHM map. Overlaid contours are velocity-integrated 13CO(1–0) emission, and the levels correspond to 5.1, 10.2, 15.3 Kkms-1. In producing these maps, we have excluded vorxels where the emission is below 0.43 K, which corresponds to three times the rms noise level of the data cube. |
All Tables
All Figures
 |
Fig. 1 Upper panel: 13CO(1–0) emission integrated from −4.5 to 15.0 kms-1 from the GRS (Jackson et al. 2006). The cloud G052.24+00.74 is on the left side. This cloud is connected with the neighbouring cloud G051.69+00.74 by some filamentary gas wisps. Channel maps of the region can be found in Appendix A. Lower left panel: composite three-color image of the 13CO(1–0) emission from the Spiral Cloud G052.24+00.74. Red: 6.52 <vlsr< 15.0kms-1; green: 3.12 <vlsr< 6.10kms-1; blue: −4.53 <vlsr< 2.7kms-1. The velocity centroid map and velocity FWHM map can be found in Appendix D. Lower right panel: Spitzer GLIMPSE (Benjamin et al. 2003) and MPISGAL three-color image of the Spiral Cloud G052.24+00.74. Red: 24 μm; green: 8 μm; blue: 3.6 μm. Overlaid contours are the velocity-integrated 13CO(1–0) emission (integrated from −4.5 km s-1<vlsr< 11.5km s-1). Contours correspond to 5.1, 10.2, 15.3 Kkms-1. The white diamond at the centre stands for a star cluster discovered in the GLIMPSE survey (Mercer et al. 2005), and the green stars stand for H ii regions collected from the literature (Lockman 1989; Urquhart et al. 2009). |
| In the text | |
 |
Fig. 2 An illustration of the geometry of the Spiral Cloud. The left panel is a 3-colour rendering of the spiral cloud. Red colour stand for redshifted gas, and blue colour stand for blueshifted gas. On top of the image, we overlay the suggested rotational axis. In the right panel, we present a 3D ellipsoid, with two longer axes and one shorter axis. The orientation mimic the suggested orientation of the spiral cloud. The ellipsoid (representing the Spiral Cloud) is rotating with respect to its shorter axis, which we have indicated in the plot. The western side of the Spiral Cloud is rotating toward the observer. The angle between the rotational axis of the Spiral Cloud and the rotational axis of the Milky Way disk is estimated to be 22.5°, and the cloud inclination is estimated to be 45°. |
| In the text | |
 |
Fig. 3 Column density structure of the Spiral Cloud. The figure presents ring-averaged column density as a function of cloud radius. The blue line stands for the data and the red line stands for the analytical model (Eq. (1)). The telescope resolution is ~2.2pc at a distance of 9.8kpc. The resolution of the plot (2.7 pc, limited by the widths of the rings) is indicated as the blue horizontal bar. See Sect. 3.2 for details. |
| In the text | |
 |
Fig. 4 Toomre Q parameter as a function of cloud radius (rcloud). The Toomre Q is defined as Q = σvκ/πGΣ where σv = 1km s-1, Σ is the ring-averaged column density and κ is the epicyclic frequency. The resolution of the plot is 2.7 pc (limited by the size of the rings). It is indicated as the blue horizontal bar. The central 5 pc is dominated by the central clump. This is indicated by the vertical red dashed line. |
| In the text | |
 |
Fig. 5 Clumps (leaves) identified by the Dendrogram method. Here we use different colours to indicate different leaves for clarity. Each leaf has a unique ID. We divide the leaves into three groups, one group contains clumps that belong to the “spiral arm” of the cloud (red numbers), and the other group contain clumps that are outside the “spiral arm” (blue numbers). The third group contains clumps 2, 4 and 7, which exhibit clear evidences of ongoing star formation (red stars). |
| In the text | |
 |
Fig. 6 Physical scales involved in the fragmentation process. The x-axis is the cloud radius, and the y-axis denotes the critical length scales involved in the fragmentation process. The blue dashed line stands for the Toomre length lToomre = 2πGΣ /κ2. In the blue shaded region fragmentation is suppressed due to shear. The red solid line stands for the Jeans length |
| In the text | |
 |
Fig. 7 Ratio of |
| In the text | |
 |
Fig. 8 Clump mass versus clump radius for all the clumps. We divide the clumps into three groups, one group contains the clumps that belong to the spiral arm of the cloud (red crosses), and the other group contain the clouds that are outside the “spiral arm” (blue crosses). The third group contains clumps 2, 4 and 7, which exhibit clear evidences of ongoing star formation (red stars with numbers). IDs of the clumps are indicated. Lines of different free-fall time tff ~ ρ− 1/2 are included. The red solid line corresponds to the threshold of massive star formation M = 870 M⊙(r/ pc)1.33 derived in Kauffmann et al. (2010). |
| In the text | |
 |
Fig. A.1 13CO(1–0) channel maps of the cloud complex. The red “+” marker indicate the centre of the Spiral Cloud. The cloud complex belongs to a 500-pc filamentary gas wisp, which has been reported in Li et al. (2013). |
| In the text | |
 |
Fig. C.1 A demonstration of our ring-based analysis of the cloud. The spacing of the rings are 2.7 pc, which is comparable to the beam size (which is 2.2 pc). The blue solid lines stand for the region within which the emission is analysed. The cut was made at |
| In the text | |
 |
Fig. C.2 Structure of the cloud viewed within rings. On the left panels, we present the distributions of estimated H2 column densities of the pixels. The mean radii of the rings (rcloud) are indicated at the upper left corners of each panel. In the middle panels, we plot the boundaries of the rings. The proposed rotational axis is represented by the red lines. The red solid lines represent parts of the rotational axes that are in front of the cloud, and the red dashed lines represent parts of the rotational axes that are at the back of the cloud. The right panels present the velocity centroids of the emission in the position-velocity space. Here, we have projected individual line of sight observations onto the major axis of ellipsoid representing the cloud, and the x-axes are the projected offests from the centres. The horizontal lines in the right panels denote the range of velocities within which the gas is gravitationally bound to the cloud. For each line of sight, we plot the velocity centroids and the FWHMs. The centroids of the emission lines are represented as the red symbols, and the FWHMs of the of the emission lines are represented as the errorbars. The horizontal red lines represent the systemic velocity of the cloud, which is 5km s-1. The blue curve is the expected rotational signature assuming the balance between rotation and gravity (Sect. 3.2). The vertical blue lines in the middle and right panels indicate the centre of the cloud. This figure is to be continued in the next page. |
| In the text | |
 |
Fig. C.2 continued. |
| In the text | |
 |
Fig. C.2 continued. |
| In the text | |
 |
Fig. D.1 Detailed velocity structure of the spiral cloud. The left panel shows the velocity centroid map, and the right panel shows the velocity FWHM map. Overlaid contours are velocity-integrated 13CO(1–0) emission, and the levels correspond to 5.1, 10.2, 15.3 Kkms-1. In producing these maps, we have excluded vorxels where the emission is below 0.43 K, which corresponds to three times the rms noise level of the data cube. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.