| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 10 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201629282 | |
| Published online | 11 January 2017 | |
Successive injection of opposite magnetic helicity in solar active region NOAA 11928
1 Indian Institute of Astrophysics, II Block, Koramangala, 560 034 Bangalore, India
e-mail: vemareddy@iiap.res.in
2 Observatoire de Paris, LESIA, UMR 8109 (CNRS), 92195 Meudon, France
e-mail: Pascal.Demoulin@obspm.fr
Received: 11 July 2016
Accepted: 1 November 2016
Aims. Understanding the nature and evolution of the photospheric helicity flux transfer is crucial to revealing the role of magnetic helicity in coronal dynamics of solar active regions.
Methods. We computed the boundary-driven helicity flux with a 12-min cadence during the emergence of the AR 11928 using SDO/HMI photospheric vector magnetograms and the derived flow velocity field. Accounting for the footpoint connectivity defined by nonlinear, force-free magnetic extrapolations, we derived and analyzed the corrected distribution of helicity flux maps.
Results. The photospheric helicity flux injection is found to change sign during the steady emergence of the AR. This reversal is confirmed with the evolution of the photospheric electric currents and with the coronal connectivity as observed in EUV wavelengths with SDO/AIA. During approximately the three first days of emergence, the AR coronal helicity is positive while later on the field configuration is close to a potential field. As theoretically expected, the magnetic helicity cancellation is associated with enhanced coronal activity.
Conclusions. The study suggests a boundary driven transformation of the chirality in the global AR magnetic structure. This may be the result of the emergence of a flux rope with positive twist around its apex while it has negative twist in its legs. The origin of such mixed helicity flux rope in the convective zone is challenging for models.
Key words: Sun: magnetic fields / Sun: flares / Sun: activity / Sun: photosphere / Sun: corona
© ESO, 2017
1. Introduction
The magnetic energy and helicity in the solar active regions (ARs) are two important parameters for a quantitative study of magnetic origins of solar eruptions. The field lines in a closed magnetic structure of the corona have footpoints that are rooted in the photospheric boundary. During the emergence of AR and its evolution, the lower boundary acts as a driver of the evolution in the structure either via boundary flows or the injection of an additional structure in the AR.
Magnetic helicity is a metric describing the volumetric complexity such as the twist and shear magnetic field of the AR. It is a well-conserved quantity even in nonideal cases and its injection, under ideal conditions, through boundary-like photosphere, S, is derived (Berger & Field 1984; Finn & Antonsen 1985) as 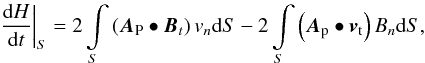 (1)where Ap is the vector potential of the potential field Bp, which is computed from the photospheric Bn distribution; Bt and Bn are the tangential and normal magnetic fields; and vt and vn are the tangential and normal components of the plasma velocity v. This relation identifies that the magnetic helicity in the corona primarily originates from the twisted magnetic flux tubes emerging from the solar interior into the corona (first term; vn term hereafter), and is further generated by shearing and braiding the field lines by the tangential motions on the solar surface (second term; vt term). While flux is emerging, using a geometrical relation of the apparent horizontal footpoint velocity of field lines (u; flux transport velocity) with the plasma velocity (v) implies the relation
(1)where Ap is the vector potential of the potential field Bp, which is computed from the photospheric Bn distribution; Bt and Bn are the tangential and normal magnetic fields; and vt and vn are the tangential and normal components of the plasma velocity v. This relation identifies that the magnetic helicity in the corona primarily originates from the twisted magnetic flux tubes emerging from the solar interior into the corona (first term; vn term hereafter), and is further generated by shearing and braiding the field lines by the tangential motions on the solar surface (second term; vt term). While flux is emerging, using a geometrical relation of the apparent horizontal footpoint velocity of field lines (u; flux transport velocity) with the plasma velocity (v) implies the relation 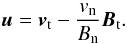 (2)With this equation Démoulin & Berger (2003) combined the two terms in Eq. (1) to measure helicity flux using the observations of line-of-sight magnetic fields at the photosphere with only the knowledge of Bn and u.
(2)With this equation Démoulin & Berger (2003) combined the two terms in Eq. (1) to measure helicity flux using the observations of line-of-sight magnetic fields at the photosphere with only the knowledge of Bn and u.
Equation (1) with the help of Eq. (2) can be written as (Berger 1988; Pariat et al. 2005) 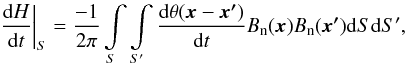 (3)where
(3)where ![\begin{equation} \frac{{\rm d}\theta (\boldsymbol{x}-\boldsymbol{{x}'})}{{\rm d}t}=\frac{{{\left. \left[ \left( \boldsymbol{x}-\boldsymbol{{x}'} \right)\times \left( \boldsymbol{u}-\boldsymbol{{u}'} \right) \right] \right|}_{n}}}{{{\left| \boldsymbol{x}-\boldsymbol{{x}'} \right|}^{2}}} \label{eq4} \end{equation}](/articles/aa/full_html/2017/01/aa29282-16/aa29282-16-eq15.png) (4)is the relative angular velocity between field line footpoints located at x and x′. Here the helicity flux dH/ dt is the summation over all the photospheric elementary flux pairs of their net angular rotation around each other weighted by
(4)is the relative angular velocity between field line footpoints located at x and x′. Here the helicity flux dH/ dt is the summation over all the photospheric elementary flux pairs of their net angular rotation around each other weighted by 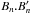 . For example, if two positive (negative) end points rotate counter clockwise (dθ/ dt> 0) then their net contribution to dH/dt is negative and consequently the field lines above them become twisted in a left-handed sense.
. For example, if two positive (negative) end points rotate counter clockwise (dθ/ dt> 0) then their net contribution to dH/dt is negative and consequently the field lines above them become twisted in a left-handed sense.
Employing a technique for deriving flow velocity, the differential affine velocity estimator for vector magnetograms (DAVE4VM; Schuck 2008), Liu & Schuck (2012) recently found that Eqs. (1) and (3) are not yielding identical results when applied to photospheric observations. Then, these authors suggested calculating individual terms in Eq. (1). With that, on re-expansion of Eq. (3) with Eq. (2) yields ![\begin{eqnarray} \left. \frac{\text{d}H}{\text{d}t} \right| _{S} & =& \frac{1}{2\pi } \int\limits_{S} \int\limits_{S'} \boldsymbol{\hat{n}} \bullet \frac{\boldsymbol{x}-\boldsymbol{{x}'}} {\left| \boldsymbol{x}-\boldsymbol{{x}'} \right|^2} \times \, \boldsymbol{bv}_n ~{\rm d}S\,{\rm d}{S}' \nonumber \\ && \quad - \frac{1}{2\pi }\int\limits_{S}\int\limits_{S'} \boldsymbol{\hat{n}} \bullet \frac{\boldsymbol{x}-\boldsymbol{{x}'}} {\left| \boldsymbol{x}-\boldsymbol{{x}'} \right|^2} \times \, \boldsymbol{bv}_t ~{\rm d}S\,{\rm d{}S}' \nonumber \\ &=& \int\limits_{S} \left[ G_{\theta ,~v_{\rm n}} (\boldsymbol{x}) + G_{\theta ,~v_{\rm t}} (\boldsymbol{x}) \right] \, {\rm d}S \nonumber \\ &=& \int\limits_{S} G_{\theta } (\boldsymbol{x}) ~{\rm d}S \label{eq5} \end{eqnarray}](/articles/aa/full_html/2017/01/aa29282-16/aa29282-16-eq23.png) (5)with
(5)with ![\begin{eqnarray} \boldsymbol{bv}_n &=& \boldsymbol{B}_{\rm t}(\boldsymbol{x}) ~ {v}_{n}(\boldsymbol{x}) ~{B}_{\rm n}(\boldsymbol{{x}'}) - \boldsymbol{B}_{\rm t}(\boldsymbol{{x}'}) ~{v}_{\rm n}(\boldsymbol{{x}'}) ~{B}_{\rm n}(\boldsymbol{x}) \nonumber \\ \boldsymbol{bv}_{\rm t} &=& \left[ \boldsymbol{v}_{\rm t} (\boldsymbol{x}) - \boldsymbol{v}_{\rm t} (\boldsymbol{{x}'}) \right] ~{B}_{\rm n} (\boldsymbol{x}) ~{B}_{\rm n} (\boldsymbol{{x}'}), \nonumber \end{eqnarray}](/articles/aa/full_html/2017/01/aa29282-16/aa29282-16-eq24.png) where Gθ,vn and Gθ,vt denote helicity flux distribution due to vn and vt terms as in Eq. (1). The above equation includes helicity injection due to the apparent relative rotation of elementary polarity with regard to surrounding polarities and also due to the inherent twist while flux emerges from the subphotosphere.
where Gθ,vn and Gθ,vt denote helicity flux distribution due to vn and vt terms as in Eq. (1). The above equation includes helicity injection due to the apparent relative rotation of elementary polarity with regard to surrounding polarities and also due to the inherent twist while flux emerges from the subphotosphere.
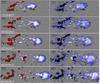 |
Fig. 1 HMI magnetic and deduced velocity fields of AR 11928 at different times. In all the panels, the gray levels show the vertical component, Bz, of the magnetic field and contours of Bz( ± 120 G) and the magnitude of the transverse vectors is indicated by the light blue segment located in the top left of each panel. Left panels: vector magnetic field observations indicate blue/red arrows above positive/negative Bz values. Vectors point to horizontal field direction and their length corresponds to the horizontal field magnitude (a zoom on a computer screen is needed to better view these arrows). Right panels: the horizontal velocity vectors (Vh) are shown with blue arrows. The velocity pattern in the leading polarity indicates the presence of a counter-clockwise rotating motion of the magnetic elements on 19 and 20 December 2013. The field of view is a portion of the actual observation indicated with white rectangular box in Fig. 2a. |
 |
Fig. 2 Top view of the magnetic structure of AR 11928 at four different times of the evolution. Color scale along each field line represents the horizontal field strength. The lower boundary (z = 0) shows the vertical component Bz at the photospheric level with gray levels in the range [−100, 100] G. The white rectangular box in panel a) refers to the field of view of panels in Fig. 1 and the black dashed rectangular box indicates the field of view of observations as plotted in Fig. 6. |
Observational studies on quantitative estimates of dH/dt from Eq. (3), or equivalent formula, were carried out to reveal the role of helicity in the eruptive nature of ARs (Chae 2001; Démoulin et al. 2002; Kusano et al. 2002; Moon et al. 2002; Chae et al. 2004; LaBonte et al. 2007). Few studies claim that the monotonous accumulation of helicity in the corona comes from magnetic domains with uniform signed distribution of helicity flux and therefore are prone to launch coronal mass ejections (Pariat et al. 2006; Vemareddy et al. 2012a,b). On the other hand, domains with opposite signed distribution of helicity flux were speculated to be related to more energetic events, as these events can liberate more free energy because the system can relax to a potential field state (Chandra et al. 2010; Romano et al. 2011; Vemareddy et al. 2012b).
Since the magnetic helicity is not a local quantity, the helicity flux distribution is only meaningful when one considers a whole elementary flux tube rather than its individual footpoints (Pariat et al. 2005). As a consequence, the earlier interpretations of observed activity based on computed helicity flux distribution remains speculative.
Considering the whole elementary flux tube, Pariat et al. (2005) defined an improved helicity flux distribution assuming information of coronal connectivity (inferred from a model). The new flux density of helicity is written as 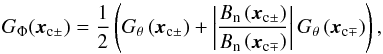 (6)where c denotes a closed elementary flux tube with footpoints at xc ± in the photosphere. The factor 1/2 present in the above equation assumes that the helicity is injected equally between the two footpoints of each field line (see Pariat et al. 2005,for a more general case). Recently, this helicity flux proxy was tested using analytical case studies and numerical simulations by Dalmasse et al. (2014), and these authors observationally found evidence for the existence of opposite signed helicity flux distribution in the flaring AR 11158 (Dalmasse et al. 2013).
(6)where c denotes a closed elementary flux tube with footpoints at xc ± in the photosphere. The factor 1/2 present in the above equation assumes that the helicity is injected equally between the two footpoints of each field line (see Pariat et al. 2005,for a more general case). Recently, this helicity flux proxy was tested using analytical case studies and numerical simulations by Dalmasse et al. (2014), and these authors observationally found evidence for the existence of opposite signed helicity flux distribution in the flaring AR 11158 (Dalmasse et al. 2013).
The present study is an attempt to further understand the distribution of the helicity injection flux in an emerging AR. In an extensive study of three emerging ARs Vemareddy (2015) found corresponding signatures of helicity flux distribution Gθ with the observed activity. We consider here one of their cases, AR 11928, and computed the connectivity-based helicity flux distribution (GΦ) at successive stages of evolution to explore its nature and a possible physical significance. Data sets and methodology are given in Sect. 2, and results are presented in Sect. 3. A discussion of the results is made in Sect. 4.
2. Observations and employed procedure
The studied AR 11928 appeared on 16 December 2013 at a location of E40°S15° on the solar disk. It emerged progressively and evolved to a leading major positive polarity sunspot and following plage group regions of negative polarity. We covered this AR evolution with 12-min cadence magnetograms for four days since its emergence.
The required photospheric vector magnetic field observations (B, at a resolution of 0.5′′per pixel) are obtained from Helioseismic and Magnetic Imager (HMI; Schou et al. 2012) on board the Solar Dynamic Observatory. The HMI science team had pipelined the process of retrieving vector field information from filtergrams (Hoeksema et al. 2014, and references therein) and made the direct usable vector products (hmi.sharp.cea.720s) available to the solar community. The pipeline procedure involves inversion of stokes vectors using the very fast inversion of the Stokes vector algorithm (Borrero et al. 2011; Centeno et al. 2014) based on the Milne-Eddington atmospheric model and removing 180° azimuthal ambiguity using the minimum energy method (Metcalf et al. 1995; Leka et al. 2009). The projection effects in the field components in the cutout area are corrected by transforming them into the disk center using the cylindrical equal area projection method (Calabretta & Greisen 2002; Bobra et al. 2014). Detailed documentation on the pipeline processing of HMI magnetic field data, including various data artifacts, is available in Hoeksema et al. (2014).
From these vector magnetic field observations, we first derived the flow velocity (v) by employing the DAVE4VM technique, then the flux transport velocity (u) with the DAVE technique. Then, we calculated Gθ(x) (Pariat et al. 2006; Liu & Schuck 2012; Vemareddy 2015). For connectivity information of footpoints, we performed nonlinear force-free field (NLFFF) extrapolation via an optimization procedure involving the minimization of Lorentz force and divergence conditions (Wiegelmann 2004; Wiegelmann & Inhester 2010; and also see Vemareddy & Wiegelmann 2014). The photospheric boundary conditions are derived from the vector magnetic field observations after preprocessing to satisfy force-free conditions as best possible (Wiegelmann et al. 2006). We embedded the lower boundary field in a large null array to minimize effect of lateral boundaries. We then rebinned the data by a factor two to have a reasonable computation time. Having carried out these systematic procedures, we obtained 3D magnetic field in a uniform spacing Cartesian grid of 400 × 400 × 256 corresponding to physical dimensions of 292 × 292 × 187 Mm3 encompassing the AR. Given well-known difficulty in constructing 3D fields from boundary field observations (e.g., De Rosa et al. 2009), we regard these NLFFF extrapolations as an approximation to the coronal magnetic fields of this AR.
We adopted the procedure detailed in Dalmasse et al. (2013) to compute GΦ from Eq. (6). First we traced field lines having one footpoint in a polarity region (xc +/xc −) and found the corresponding conjugate footpoint (xc −/xc +) after landing at the boundary at z = 0. Having footpoint coordinates of all field lines in a magnetic structure of AR, we implement Eq. (6) by using a bi-linear interpolation. Traced field lines that touch the lateral boundaries are considered open-like. In all our magnetogram sequence, the fraction of open-like field lines found is up to 10% and the redistribution of helicity density, Eq. (6), is not applied as connectivity is undefined for those lines.
3. Results
3.1. Global evolution
AR 11928 initially emerges with a bipolar field distribution and evolves to a large leading positive polarity sunspot and a more dispersed following negative polarity. In Fig. 1, we plot the vector magnetograms at different times in the local solar frame (local horizontal and vertical directions) after the transformation from the observed frame. For both velocity and magnetic fields, the horizontal field component is plotted with arrows indicating the direction and magnitude. The background is the map of the vertical magnetic field component (Bz). These panels show the emergence of small bipoles, which are the consequence of the development of the undulatory instability or of the upward convective motions, creating a sea-serpent configuration with magnetic dips (e.g., Pariat et al. 2004; Valori et al. 2012). Polarities with opposite sign diverge and like polarities coalesce to form strong concentrated spots of opposite magnetic polarity that separate as the AR evolves in time. This evolution is typical for AR emergence (van Driel-Gesztelyi & Green 2015). While these prominent polarities are in separating motion, a reverse orientation bipole, which is larger than others, forms and develops in the middle of the AR (panel at 19/12:00 UT in Fig. 1). This creates a complex magnetic topology for the AR coronal configuration (Fig. 2c). This bipole progressively disappears with time (e.g., the bottom panel at 20/06:00 UT in Fig. 1).
In order to compare the NLFF model for the coronal field, we plot the field lines on AIA 171 Å observations in Fig. 3. Field lines in the core of the AR globally resemble the coronal loops. However, a closer look shows also some deviations; for example, the computed field lines are more symmetric in the east-west direction than the observed loops, as some field lines show a sharp bend near the leading polarity. Such deviations could have several origins. This could be due to the missing electric currents in the magnetograms from a spatial resolution that is too coarse and not able to resolve their magnetic structures. This effect is further increased by the rebinning procedure applied to the magnetograms to achieve feasible computing times; that is, the magnetograms are not in a fully force-free region in contrast to the equations solved in the coronal volume (e.g., De Rosa et al. 2015). Moreover, convergence to a NLFF field with a small divergence for the magnetic field is another issue (e.g., Wiegelmann et al. 2012). Finally, the involved assumptions with the boundary observations are not yet settled (e.g., De Rosa et al. 2009). All these issues contribute to the deviations of the model field lines with the actual observations. Despite all these limitations we obtained a coherent global resemblance between modeled field lines and the coronal loops over the entire AR evolution.
 |
Fig. 3 Field lines, computed from the magnetic extrapolation, plotted on co-aligned AIA 171 Å images. In the core of the AR, there is a relatively good global correspondence between field lines and loops. The field-of-view is same as Fig. 2. |
In order to examine the magnetic helicity flux, we derived the photospheric velocity field by employing DAVE4VM method on the time sequences of vector magnetic field observations. The horizontal velocity field at different stages is plotted on the Bz map in the right panels of Fig. 1. The velocities are typically up to 0.9 km s-1 and earlier on they are dominantly translational in the leading polarity. However, by December 18 onward, the velocity vectors in the leading positive polarity indicate the presence of an anticlockwise rotating motion, especially in the southern portion of the leading polarity. This motion becomes prominent later in time while separation motion continues (see the three right bottom panels of Fig. 1).
 |
Fig. 4 Evolution of magnetic flux and electric current in AR 11928. a) Net magnetic flux (Φ) from north (N, Bz> 0) and south (S, Bz< 0) polarity as a function of time. b) Total net vertical current (I) and net currents from north (IN) and south (IS) magnetic polarity as a function of time. The vertical line at 18T22:00 UT indicates the sign reversal of net current in each magnetic polarity. Panels c) and d) separate the absolute value of positive and negative currents (+ ve and −ve) from north and south polarities, respectively. |
In Fig. 2, we plot the extrapolated magnetic structure of AR 11928 at different stages of evolution. The field lines are represented with a color scale of horizontal field strength. The magnetic structure is nonpotential in the early emergence phase and becomes more relaxed as AR evolves. The field structure appears close to potential field from December 18 onward, globally connecting the leading and following polarities. Because of the formation of a reverse orientation bipolar region in between the separating leading and following polarity, a low-lying bipolar structure exists in the December 19 frames.
We derived the net vertical magnetic flux Φ = ∑ i = 1,N(Bz)i ΔxΔy) in both AR magnetic polarities (Fig. 4a). The flux of both polarities predominantly increases in time owing to the emergence of these flux regions. This AR has an almost constant rate of flux emergence which is not so frequent (e.g., see examples in Poisson et al. 2015). The observed activity is limited to GOES class C without coronal mass ejections (CMEs). However, jet like ejections often occurred during the AR evolution.
3.2. Electric current evolution
We also computed net vertical electric current (I = ∑ i = 1,N(Jz)i ΔxΔy) in each AR magnetic polarity and plot their time evolution in Fig. 4b. Here Jz in the local frame is derived with the horizontal field components 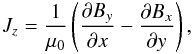 where μ0 = 4π × 10-7 H m-1. Partial derivatives are approximated by a three-point Lagrangian interpolation procedure. The net current in each polarity is much more time varying both in magnitude and sign than the magnetic flux (Figs. 4a,b). The current profiles show prominent variations with a timescale of around 12 h, while they are small in the magnetic flux profiles. These variations are due to the orbital rotation of the SDO spacecraft and are also seen in other active region studies (Hoeksema et al. 2014). There is also a longer timescale variation at the scale of a day, which is comparable in the north and south polarities (as expected if the field is force-free). The absolute value of both currents first reach maximum at 02:00 UT on December 18 (2 × 1012A in the north polarity and −1.8 × 1012A in south polarity). Later on the net currents exhibit a counter evolution, then they both change in sign at 22:00 UT on December 18 and with again a reversal in sign around the end of December 19.
where μ0 = 4π × 10-7 H m-1. Partial derivatives are approximated by a three-point Lagrangian interpolation procedure. The net current in each polarity is much more time varying both in magnitude and sign than the magnetic flux (Figs. 4a,b). The current profiles show prominent variations with a timescale of around 12 h, while they are small in the magnetic flux profiles. These variations are due to the orbital rotation of the SDO spacecraft and are also seen in other active region studies (Hoeksema et al. 2014). There is also a longer timescale variation at the scale of a day, which is comparable in the north and south polarities (as expected if the field is force-free). The absolute value of both currents first reach maximum at 02:00 UT on December 18 (2 × 1012A in the north polarity and −1.8 × 1012A in south polarity). Later on the net currents exhibit a counter evolution, then they both change in sign at 22:00 UT on December 18 and with again a reversal in sign around the end of December 19.
Since the positive/negative magnetic polarity is predominantly from leader/follower polarity, we can also interpret the current evolution in terms of unbalanced current in the leader/following polarity. For that, we separately compute the positive (I+) and negative currents (I−) in each polarity and compared their absolute values in Figs. 4c,d. Those currents are about a factor 10 larger in magnitude than those described before (Fig. 4b). The ratio of positive and negative current varies within 0.82−1.33 in the leader polarity and within 0.83−1.18 in the follower polarity, and then the currents in each magnetic polarity nearly neutralizes. This is because of a small magnetic shear along the main AR inversion line (Fig. 1, left panels) as shown by Dalmasse et al. (2015).
 |
Fig. 5 Time evolution of αav (defined by Eq. (7)) in the entire AR 11928. The error bars are obtained from a least squares regression procedure in the plot of Jz and Bz (see Eq. (8)). The value αav changes sign several times at the beginning of the emergence, as well as later on when the AR is well developed at 18T22:00 UT (vertical line). |
We next investigate the mean evolution of α = Jz/Bz called αav. It is a proxy for the average twist of the AR field lines (Hagino & Sakurai 2004). Using the three components of vector magnetic field, we compute this parameter as ![\begin{equation} {\alpha }_{av}=\frac{\sum{{J_{z}}(x,y)\text{sign}[{B_{z}}(x,y)]}}{\sum{|{B_{z}}|}} \cdot \label{eq7} \end{equation}](/articles/aa/full_html/2017/01/aa29282-16/aa29282-16-eq70.png) (7)If the positive and negative magnetic fluxes are in balance, the above equation is equivalent to
(7)If the positive and negative magnetic fluxes are in balance, the above equation is equivalent to ![\begin{eqnarray*} \alpha_{\rm av}=\frac{1}{2}\left[\frac{\sum\limits_{B_z>0}J_z(x,y)}{\sum\limits_{B_z<0}B_z(x,y)}+\frac{\sum\limits_{B_z>0}J_z(x,y)}{\sum\limits_{B_z<0}B_z(x,y)}\right], \end{eqnarray*}](/articles/aa/full_html/2017/01/aa29282-16/aa29282-16-eq71.png) which is the mean of
which is the mean of 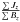 over the two polarities. This equation is an estimation of how twisted is the magnetic configuration. Since Eq. (7) corresponds to the usual least-squares fit assuming a linear regression Jz = αavBz, the error in αav is estimated by
over the two polarities. This equation is an estimation of how twisted is the magnetic configuration. Since Eq. (7) corresponds to the usual least-squares fit assuming a linear regression Jz = αavBz, the error in αav is estimated by ![\begin{equation} \delta \alpha _{\rm av}^{2}=\frac{{{\sum{\left[ {{J}_{z}}(x,y)-{{\alpha }_{\rm av}}{B_{z}}(x,y) \right]}}^{2}}/|{B_{z}}(x,y)|}{(N-1)\sum{|{B_{z}}(x,y)}|} \label{eq8} , \end{equation}](/articles/aa/full_html/2017/01/aa29282-16/aa29282-16-eq74.png) (8)where N is the number of pixels with | Bt | > 150 G.
(8)where N is the number of pixels with | Bt | > 150 G.
The time variation of αav is shown in Fig. 5 with the error bars indicating ± δαav. Just like the net current in the early emergence phase (Fig. 4b), αav changes sign four times. This is likely due to the limited spatial resolution since the AR has a low spatial extension at these times. After 04:00 UT on December 17, αav remains positive with significant variations till 22:00 UT on December 18 (vertical line), from which time it turns negative, reversing of sign again by the end of December 19. The value αav is indeed related to the current distribution in the AR but with a different weighting in the summation than for the net currents.
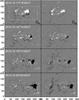 |
Fig. 6 Snapshots of helicity flux distributions with Gθ maps (left column) and GΦ maps (right column) at four different times of the evolution of AR 11928. GΦ is derived from Gθ taking into account the connectivity of the field line footpoints (Eq. (6)). Intense positive helicity flux in Gθ maps is associated with the leading major sunspot polarity, which becomes negative over the time. This flux is redistributed to the following polarity flux by closed field lines in GΦ maps. In all panels, contours of Bz at ± 120 G (black/white) are overplotted. All maps were scaled with gray levels within ± 1 × 10-19 Mx2 cm-2 s-1. Axes units are in arcseconds and the field of view is same as indicated by the black dashed rectangle in Fig. 2a. The rectangular white box in the top left panel refers to the field of view of the panels in Fig. 1. |
3.3. Helicity flux
The flux density of magnetic helicity is computed with the method recalled in Sect. 1. Figure 6 shows the helicity flux distribution at four times of Fig. 1. The Gθ distribution (left column panels) shows both positive and negative values. The distribution has a range of flux exceeding ± 1 × 1019 Mx2 cm-2 s-1, but we scaled the maps within these values. A dominant positive signal is persistent mostly within the leading positive sunspot till 06:00 UT on December 18, by which time the sunspot got well separated from the following polarity. In the later stages, strong negative signal with the leading sunspot kept increasing in magnitude.
On December 17 and 18, the magnetic polarities are elongated and are globally resembling a yin and yang pattern. These observed features, called magnetic tongues, are produced by the azimuthal field component of the emerging flux rope projected on the vertical direction (see, e.g., Poisson et al. 2015). These features are present when the magnetic flux is growing as long as the top horizontal portion of the twisted flux tube is crossing the photosphere. The magnetic flux distribution due to the magnetic tongues is directly related to the sign of the twist in the emerging AR (see Fig. 1 in Luoni et al. 2011). In AR 11928 magnetic tongues on December 17 and 18 indicates a positive twist in agreement with the positive helicity flux. In contrast, the negative helicity flux observed next has no trace on the distribution of the vertical field component.
Having defined connectivity from NLFFF extrapolation (Sect. 2, Fig. 2), the computed GΦ distribution is shown in the right column of Fig. 6. This distribution is computed with Eq. (6) when the field line is closed within the computation box, otherwise the local value Gθ is kept. Since field lines from the leader sunspot connect to the following polarity, the dominant helicity flux from the leading sunspot redistributes to the following polarity regions by means of Eq. (6). Since the helicity flux is larger in absolute value in the leading polarity than the following polarities, the GΦ distribution is also negative in the following polarity on 19 December and later on.
 |
Fig. 7 a) Time evolution of the net helicity flux in AR 11928, which turns from positive to negative at 20T00:20 UT (black vertical line). Earlier on the net magnetic helicity flux computed with GΦ have well-correlated profiles in both north (orange) and south (green) polarities. This indicates a proper redistribution at footpoints of closed field lines (reaching the computation box boundary). Later on, after 18:00 UT December 18, unequal net values in north and south polarities are present owing to undefined connectivity for open field lines. b) Evolution of the signed net helicity flux in positive and negative magnetic polarities. |
In Fig. 7a, we plot the summation of Gθ and GΦ over the entire AR with respect to time. Both Gθ and GΦ profiles have undergone a smoothing window of seven successive data points. The time profiles of Gθ and GΦ fluxes are correlated to a high accuracy (Fig. 7a) as expected from the redistribution, which theoretically preserves the total helicity flux (Pariat et al. 2005). The net helicity flux increases from zero to a maximum value of 8.5 × 10-37 Mx2 cm-2 s-1 at 18:00 UT on December 17. Owing to the change in sign of Gθ and GΦ (Fig. 6), the helicity flux then decreases toward near zero values. Next, it turns to negative value at 00:20 UT on December 20. This helicity time profile has similar variations as the net current profiles in both polarities (Fig. 4b, taking into account that the current sign is reversed in the following negative polarity) and as αav (Fig. 5), except with different relative amplitudes and a time delay of between 2.5 and 7 h, depending on whether the reversal or extremums are taken into account.
The net Gθ flux is dominated by the vt term (Eq. (5)) over vn by a factor of about six, so the helicity flux evolution is mostly related to horizontal boundary motions (see Fig. 6 of Vemareddy 2015). Still, we observe similar flux profiles for the vt and vn terms. Moreover, while this separation in vn and vt terms was studied in many previous publications, its physical relevance is doubtful since each term is not separately gauge invariant in Eq. (1) and a particular gauge was used to derive Eq. (5) (Pariat et al. 2015).
 |
Fig. 8 a) Comparison of helicity flux calculated from DAVE4VM (estimating v, Eq. (1)) and DAVE (estimating u, Eq. (3)). The general behavior and the sign reversal at 19T22:00 UT found with DAVE is similar to that found with DAVE4VM. b) Comparison of the accumulated helicity in the AR coronal part since the middle of 16 Dec. as computed with Eq. (9) and normalized by Φ2, which has the same units as helicity, where Φ is the mean of positive and negative magnetic fluxes. |
Furthermore, we separately computed the net helicity flux of GΦ from north (GΦ,N) and south (GΦ,S) polarity regions. The underlying assumption here is that the net GΦ,N and GΦ,S fluxes should be equal provided exact connectivity for every polarity pixel, i.e., closed flux system in the AR. From the yellow and green curves of Fig. 7a, their time profiles have approximately equal trends until 18:00 UT on December 18, 2013. After that they exhibit noticeable deviations with their dominant helicity fluxes coming from north (leading) polarity. With increasingly separation, the open field lines (those reaching top/lateral boundaries) from the leading polarity increases, and then a full redistribution is not applicable and, therefore, there is a dominant negative helicity flux from N polarity after 19 December.
Next, we separately computed the net GΦ flux from north, GΦ, N, and south, GΦ, S, polarity regions separating the positive and negative contributions (Fig. 7b). This shows that the helicity flux is a mix of positive and negative contributions with two main phases: a positive injection followed, about two days later, by a negative injection from both polarities.
We also computed Gθ from the horizontal velocity field, u, derived from DAVE (Schuck 2005) using line-of-sight magnetograms. We obtained LOS magnetic field observations from HMI and we aligned them to the time of the central meridian passage by removing the differential rotation. The helicity flux is computed with Eqs. (3), (4). Its time profile (dH/ dt)DAVE is shown in Fig. 8 in a comparison to (dH/ dt)DAVE4VM. Both profiles are well correlated in time. However, they differ significantly in magnitude at most times. Despite that, the sign reversal time of net helicity flux in both methods agree within 2.3 h; for DAVE4VM the reversal is at 19T00:20 UT, while for DAVE it is at 18T22:00 UT.
The accumulated helicity in the corona over time is given by 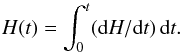 (9)Since the magnitude of magnetic helicity is proportional to square of the magnetic flux (Berger & Field 1984), in Fig. 8b we plotted the normalized helicity (H(t)/Φ2), where Φ is the average AR flux between polarities (Φ = ( | ΦS | + | ΦN | )/2), to compare magnetic helicity with other ARs. This normalized quantity indicates how much the magnetic configuration is twisted/sheared because for a uniformly twisted flux tube with n turns, the helicity H is equal to n Φ2, where Φ is its axial flux. In our case, the absolute value of the normalized helicity is less than 0.07 turns before and after H reversal. These values are in comparison with previous AR studies having a minimum of 0.01 to a maximum of 0.2 (see for a review Démoulin & Pariat 2009). The sign reversal of this quantity, for both DAVE and DAVE4VM procedures, is well after the reversal of dH/dt (19T18:00UT) because it requires time to cancel preaccumulated positive helicity by pumping negative quantity. Since the positive and negative H injections are realized in almost the same magnetic structures (Fig. 6), helicity cancellation can occur while the negative injection is occurring without the need of magnetic reconnection (between independent flux tubes).
(9)Since the magnitude of magnetic helicity is proportional to square of the magnetic flux (Berger & Field 1984), in Fig. 8b we plotted the normalized helicity (H(t)/Φ2), where Φ is the average AR flux between polarities (Φ = ( | ΦS | + | ΦN | )/2), to compare magnetic helicity with other ARs. This normalized quantity indicates how much the magnetic configuration is twisted/sheared because for a uniformly twisted flux tube with n turns, the helicity H is equal to n Φ2, where Φ is its axial flux. In our case, the absolute value of the normalized helicity is less than 0.07 turns before and after H reversal. These values are in comparison with previous AR studies having a minimum of 0.01 to a maximum of 0.2 (see for a review Démoulin & Pariat 2009). The sign reversal of this quantity, for both DAVE and DAVE4VM procedures, is well after the reversal of dH/dt (19T18:00UT) because it requires time to cancel preaccumulated positive helicity by pumping negative quantity. Since the positive and negative H injections are realized in almost the same magnetic structures (Fig. 6), helicity cancellation can occur while the negative injection is occurring without the need of magnetic reconnection (between independent flux tubes).
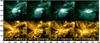 |
Fig. 9 AIA coronal observations of AR 11928 in 94 Å (top row) and 171 Å (bottom row) wavelengths. Plasma loops represent the magnetic structure in the AR connecting the magnetic regions at the photosphere. A prominent loop and its shape transformation is shown with a dotted white line. The field of view is same as Fig. 2 with axis units in arc seconds and origin set at the left bottom corner. |
4. Discussion
Solar magnetic fields, upon their emergence, are driven by photospheric plasma motions governed by the induction equation. Consequently the coronal magnetic helicity, which plays a prime role in most of the activity, is generated by these photospheric motions. In the present work, we studied the time evolution of connectivity based helicity flux of an emerging AR associated with weak flaring activity.
Reconstructing the coronal magnetic field every 12 min using the observed field is a computationally expensive task. Moreover, several issues of the NLFFF modeling of the coronal field with observed photospheric boundary data are still not fully solved (see Sect. 3.1). The implications of these issues for helicity studies can be checked by comparing the helicity flux maps and the helicity fluxes derived with and without involving the computed coronal connectivities. Finally, the derived results are useful for studying helicity flux maps in relation to coronal activity as the studied AR shows.
The helicity flux derived from the photospheric velocities, which are in turn derived from DAVE4VM, changes from positive to negative sign around the end of December 18. Helicity flux derived from DAVE method also exhibits a similar evolution profile. The evolution of average twist (αav) has a comparable evolution but is delayed in time by few hours (up to 7), which is a delay needed to accumulate enough coronal magnetic helicity. At the photosphere, plasma motions drive magnetic fields, so the observed evolution of αav is most likely caused by these boundary evolution. Recent reports (e.g., Vemareddy et al. 2012a,and references therein) also delineate such a relation of sunspot rotation with the nature of helicity of magnetic fields. The coronal consequences of the change of helicity flux sign is present in the observed coronal loops that are tracing part of the magnetic structure. We examined the AIA coronal observations obtained in 94 and 171 Å wavelengths. In Fig. 9, we plot them at four different time instances. During the evolution until the end of 18 December, the coronal loops exhibit a S-shape morphology (e.g., the dotted line in Fig. 9 frames). This is also well present when comparing the observed coronal loops to a potential field extrapolation represented with the same viewing point. This indicates a positive magnetic helicity in agreement with the mild clockwise motions that are detected in leading polarity and the positively oriented magnetic tongues observed with the vertical field component (Fig. 1). Next, from 19 December onward, the magnetic elements within the leading sunspot present counter-clockwise motions. In response, the coronal structure becomes more potential-like. The profile of normalized helicity H/ Φ2 is also in line with these coronal observations. Its maximum value is 0.07 turns so it is equivalent in terms of magnetic helicity to a weakly twisted flux tube. The injection of opposite helicity in the same magnetic structures in the GΦ maps is an indication of the cancellation of coronal helicity by the negative injection later on. In fact the coronal loops are not far from potential field at 19T18:00UT.
 |
Fig. 10 Time evolution of EUV flux of AIA 171 and 94 Å passbands. These fluxes are normalized by the mean magnetic flux (Φ) of photospheric polarities to suppress enhanced trend due to the emerging magnetic flux and by a constant scaling factor (arbitary units). Vertical dotted line indicates the time when the AR is positioned at the central meridian and the solid vertical line refers to the sign reversal time of the photospheric helicity flux (Fig. 7a). |
A further clue comes from the observed activity. Rather than helicity injection of an opposite sign, if the helicity injection had continued to be positive, its storage in the corona would have built an increasingly stressed magnetic field, which makes it a good candidate to become unstable and launch a CME. However, the observed activity is limited to C-class flares and jets so that the energy is released in many small events, as well as in coronal heating, rather than building a flux rope that is expected to erupt as a CME at some point of the evolution.
In order to follow the coronal flaring activity we computed EUV 94 and 171 Å fluxes integrated within the AR with 3-min cadence. These fluxes (F94, F171) are normalized by mean magnetic line-of-sight fluxes to suppress the increased EUV fluxes due to magnetic fluxes becoming larger (e.g., see Démoulin 2004,and references therein). Next, we scaled the fluxes by an appropriate constant value to plot them on the same graph because the evolution trend is the only required observable for the following analysis. Time profiles of these fluxes are plotted in Fig. 10. Enhanced emissions in both F94 and F171 are present after the sign reversal of the magnetic helicity flux (indicated by a vertical solid black line). The short time peaks of F94 are due to C-class flares (C1.8 at 19/09:03, C1.6 at 19/10:14, C2.2 at 19/15:26, C1.4 at 19/19:39, C5.4 at 20/16:23, C8.5 at 20/15:26, C3.2 at 20/14:52, C2.7 at 20/21:08, and C2.3 at 20/17:11UT) because the AIA 94 Å passband detects hot emission (≈ 6 MK) near soft X-ray range (1−100 Å). The F171 enhancement is more continuous, without peaks, indicating less hot emission over the entire AR (Fig. 9). The coronal helicity cancellation is realized progressively by the continuous injection of opposite helicity flux (Fig. 8a). Therefore the enhancement of F94 and F171 fluxes is continuing well after the middle of 19 Dec.
In summary, the evolution of AR 11928 is peculiar compared to most of ARs studied previously since the positive H injection is followed by a larger negative injection in the same emerging magnetic structure. The initial positive injection is supported by DAVE, DAVE4VM, αav, the magnetic tongues, and the shape of coronal loops. The negative injection is supported by DAVE, DAVE4VM, αav, and the shape of coronal loops, which become more potential-like. This AR provides an example of magnetic energy release because of the cancellation of magnetic helicities of the opposite sign. Of course the maximum value of H/ Φ2 is modest in present AR, so the amount of available magnetic energy is also modest.
Finally, these results suggest a scenario of an emerging flux tube with the helicity distribution changing sign over its length. This could have been created in the convective zone by a vortex locally rotating the magnetic flux tube which, by conservation of H, creates both H> 0 and H< 0 on the sides of the rotated region. In order to answer whether this is an isolated case or whether it reveals a relatively common convective zone process, the study of a much broader sample of emerging ARs is needed.
Acknowledgments
The data used here are courtesy of the NASA/SDO and the HMI science team. This work used the DAVE and DAVE4VM codes, written and developed by P. W. Schuck at the Naval Research Laboratory. We thank T. Wiegelmann for providing NLFFF code. P.V. is supported by an INSPIRE grant under the AORC scheme of the Department of Science and Technology. This work acknowledges an extensive usage of the multi-node, multi-processor high performance computing facility at IIA. We thank the anonymous referee for critical comments and suggestions.
References
- Berger, M. A. 1988, A&A, 201, 355 [NASA ADS] [Google Scholar]
- Berger, M. A., & Field, G. B. 1984, J. Fluid Mech., 147, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Bobra, M. G., Sun, X., Hoeksema, J. T., et al. 2014, Sol. Phys., 289, 3549 [NASA ADS] [CrossRef] [Google Scholar]
- Borrero, J. M., Tomczyk, S., Kubo, M., et al. 2011, Sol. Phys., 273, 267 [Google Scholar]
- Calabretta, M. R., & Greisen, E. W. 2002, A&A, 395, 1077 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centeno, R., Schou, J., Hayashi, K., et al. 2014, Sol. Phys., 289, 3531 [Google Scholar]
- Chae, J. 2001, ApJ, 560, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Chae, J., Moon, Y.-J., & Park, Y.-D. 2004, Sol. Phys., 223, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Chandra, R., Pariat, E., Schmieder, B., Mandrini, C. H., & Uddin, W. 2010, Sol. Phys., 261, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Dalmasse, K., Pariat, E., Valori, G., Démoulin, P., & Green, L. M. 2013, A&A, 555, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalmasse, K., Pariat, E., Démoulin, P., & Aulanier, G. 2014, Sol. Phys., 289, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Dalmasse, K., Aulanier, G., Démoulin, P., et al. 2015, ApJ, 810, 17 [Google Scholar]
- De Rosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
- DeRosa, M. L., Wheatland, M. S., Leka, K. D., et al. 2015, ApJ, 811, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P. 2004, Multi-Wavelength Investigations of Solar Activity, eds. A. V. Stepanov, E. E. Benevolenskaya, & A. G. Kosovichev, IAU Symp. 223, 13 [Google Scholar]
- Démoulin, P., & Berger, M. A. 2003, Sol. Phys., 215, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., & Pariat, E. 2009, Adv. Space Res., 43, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., Mandrini, C. H., van Driel-Gesztelyi, L., et al. 2002, A&A, 382, 650 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finn, J. M., & Antonsen, T. M. 1985, Comments Plasma Phys. Controlled Fusion, 9, 111 [Google Scholar]
- Hagino, M., & Sakurai, T. 2004, PASJ, 56, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeksema, J. T., Liu, Y., Hayashi, K., et al. 2014, Sol. Phys., 289, 3483 [Google Scholar]
- Kusano, K., Maeshiro, T., Yokoyama, T., & Sakurai, T. 2002, ApJ, 577, 501 [NASA ADS] [CrossRef] [Google Scholar]
- LaBonte, B. J., Georgoulis, M. K., & Rust, D. M. 2007, ApJ, 671, 955 [CrossRef] [Google Scholar]
- Leka, K. D., Barnes, G., Crouch, A. D., et al. 2009, Sol. Phys., 260, 83 [Google Scholar]
- Liu, Y., & Schuck, P. W. 2012, ApJ, 761, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Luoni, M. L., Démoulin, P., Mandrini, C. H., & van Driel-Gesztelyi, L. 2011, Sol. Phys., 270, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalf, T. R., Jiao, L., McClymont, A. N., Canfield, R. C., & Uitenbroek, H. 1995, ApJ, 439, 474 [NASA ADS] [CrossRef] [Google Scholar]
- Moon, Y. J., Chae, J., Wang, H., Choe, G. S., & Park, Y. D. 2002, ApJ, 580, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Aulanier, G., Schmieder, B., et al. 2004, ApJ, 614, 1099 [Google Scholar]
- Pariat, E., Démoulin, P., & Berger, M. A. 2005, A&A, 439, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Nindos, A., Démoulin, P., & Berger, M. A. 2006, A&A, 452, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Valori, G., Démoulin, P., & Dalmasse, K. 2015, A&A, 580, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poisson, M., Mandrini, C. H., Démoulin, P., & López Fuentes, M. 2015, Sol. Phys., 290, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, P., Pariat, E., Sicari, M., & Zuccarello, F. 2011, A&A, 525, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., & et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Schuck, P. W. 2005, ApJ, 632, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Schuck, P. W. 2008, ApJ, 683, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Valori, G., Green, L. M., Démoulin, P., et al. 2012, Sol. Phys., 278, 73 [NASA ADS] [CrossRef] [Google Scholar]
- van Driel-Gesztelyi, L., & Green, L. M. 2015, Liv. Rev. Sol. Phys., 12 [Google Scholar]
- Vemareddy, P. 2015, ApJ, 806, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Vemareddy, P., & Wiegelmann, T. 2014, ApJ, 792, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Vemareddy, P., Ambastha, A., & Maurya, R. A. 2012a, ApJ, 761, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Vemareddy, P., Ambastha, A., Maurya, R. A., & Chae, J. 2012b, ApJ, 761, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., & Inhester, B. 2010, A&A, 516, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiegelmann, T., Inhester, B., & Sakurai, T. 2006, Sol. Phys., 233, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T., Thalmann, J. K., Inhester, B., et al. 2012, Sol. Phys., 281, 37 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 HMI magnetic and deduced velocity fields of AR 11928 at different times. In all the panels, the gray levels show the vertical component, Bz, of the magnetic field and contours of Bz( ± 120 G) and the magnitude of the transverse vectors is indicated by the light blue segment located in the top left of each panel. Left panels: vector magnetic field observations indicate blue/red arrows above positive/negative Bz values. Vectors point to horizontal field direction and their length corresponds to the horizontal field magnitude (a zoom on a computer screen is needed to better view these arrows). Right panels: the horizontal velocity vectors (Vh) are shown with blue arrows. The velocity pattern in the leading polarity indicates the presence of a counter-clockwise rotating motion of the magnetic elements on 19 and 20 December 2013. The field of view is a portion of the actual observation indicated with white rectangular box in Fig. 2a. |
| In the text | |
 |
Fig. 2 Top view of the magnetic structure of AR 11928 at four different times of the evolution. Color scale along each field line represents the horizontal field strength. The lower boundary (z = 0) shows the vertical component Bz at the photospheric level with gray levels in the range [−100, 100] G. The white rectangular box in panel a) refers to the field of view of panels in Fig. 1 and the black dashed rectangular box indicates the field of view of observations as plotted in Fig. 6. |
| In the text | |
 |
Fig. 3 Field lines, computed from the magnetic extrapolation, plotted on co-aligned AIA 171 Å images. In the core of the AR, there is a relatively good global correspondence between field lines and loops. The field-of-view is same as Fig. 2. |
| In the text | |
 |
Fig. 4 Evolution of magnetic flux and electric current in AR 11928. a) Net magnetic flux (Φ) from north (N, Bz> 0) and south (S, Bz< 0) polarity as a function of time. b) Total net vertical current (I) and net currents from north (IN) and south (IS) magnetic polarity as a function of time. The vertical line at 18T22:00 UT indicates the sign reversal of net current in each magnetic polarity. Panels c) and d) separate the absolute value of positive and negative currents (+ ve and −ve) from north and south polarities, respectively. |
| In the text | |
 |
Fig. 5 Time evolution of αav (defined by Eq. (7)) in the entire AR 11928. The error bars are obtained from a least squares regression procedure in the plot of Jz and Bz (see Eq. (8)). The value αav changes sign several times at the beginning of the emergence, as well as later on when the AR is well developed at 18T22:00 UT (vertical line). |
| In the text | |
 |
Fig. 6 Snapshots of helicity flux distributions with Gθ maps (left column) and GΦ maps (right column) at four different times of the evolution of AR 11928. GΦ is derived from Gθ taking into account the connectivity of the field line footpoints (Eq. (6)). Intense positive helicity flux in Gθ maps is associated with the leading major sunspot polarity, which becomes negative over the time. This flux is redistributed to the following polarity flux by closed field lines in GΦ maps. In all panels, contours of Bz at ± 120 G (black/white) are overplotted. All maps were scaled with gray levels within ± 1 × 10-19 Mx2 cm-2 s-1. Axes units are in arcseconds and the field of view is same as indicated by the black dashed rectangle in Fig. 2a. The rectangular white box in the top left panel refers to the field of view of the panels in Fig. 1. |
| In the text | |
 |
Fig. 7 a) Time evolution of the net helicity flux in AR 11928, which turns from positive to negative at 20T00:20 UT (black vertical line). Earlier on the net magnetic helicity flux computed with GΦ have well-correlated profiles in both north (orange) and south (green) polarities. This indicates a proper redistribution at footpoints of closed field lines (reaching the computation box boundary). Later on, after 18:00 UT December 18, unequal net values in north and south polarities are present owing to undefined connectivity for open field lines. b) Evolution of the signed net helicity flux in positive and negative magnetic polarities. |
| In the text | |
 |
Fig. 8 a) Comparison of helicity flux calculated from DAVE4VM (estimating v, Eq. (1)) and DAVE (estimating u, Eq. (3)). The general behavior and the sign reversal at 19T22:00 UT found with DAVE is similar to that found with DAVE4VM. b) Comparison of the accumulated helicity in the AR coronal part since the middle of 16 Dec. as computed with Eq. (9) and normalized by Φ2, which has the same units as helicity, where Φ is the mean of positive and negative magnetic fluxes. |
| In the text | |
 |
Fig. 9 AIA coronal observations of AR 11928 in 94 Å (top row) and 171 Å (bottom row) wavelengths. Plasma loops represent the magnetic structure in the AR connecting the magnetic regions at the photosphere. A prominent loop and its shape transformation is shown with a dotted white line. The field of view is same as Fig. 2 with axis units in arc seconds and origin set at the left bottom corner. |
| In the text | |
 |
Fig. 10 Time evolution of EUV flux of AIA 171 and 94 Å passbands. These fluxes are normalized by the mean magnetic flux (Φ) of photospheric polarities to suppress enhanced trend due to the emerging magnetic flux and by a constant scaling factor (arbitary units). Vertical dotted line indicates the time when the AR is positioned at the central meridian and the solid vertical line refers to the sign reversal time of the photospheric helicity flux (Fig. 7a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


