| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A25 | |
| Number of page(s) | 46 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628776 | |
| Published online | 19 December 2016 | |
The millimeter IRAM-30 m line survey toward IK Tauri⋆,⋆⋆
1 Instituto de Ciencia de Materiales de Madrid, CSIC, c/ Sor Juana Inés de la Cruz 3, 28049 Cantoblanco, Madrid, Spain
e-mail: lvelilla@icmm.csic.es
2 Centro de Astrobiología, INTA-CSIC, 28691 Villanueva de la Cañada, Madrid, Spain
3 Observatorio Astronómico Nacional (IGN), Ap 112, 28803 Alcalá de Henares, Madrid, Spain
4 Observatorio Astronómico Nacional (IGN), Alfonso XII No 3, 28014 Madrid, Spain
5 LERMA, Observatoire de Paris, Sorbonne Université, UPMC, UMR 8112, 92195 Meudon, France
6 Université de Bordeaux, LAB, UMR 5804, 33270 Floirac, France
7 CNRS, LAB, UMR 5804, 33270 Floirac, France
8 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received: 22 April 2016
Accepted: 24 August 2016
Aims. We aim to investigate the physical and chemical properties of the molecular envelope of the oxygen-rich AGB star IK Tau.
Methods. We carried out a millimeter wavelength line survey between ~79 and 356 GHz with the IRAM-30 m telescope. We analysed the molecular lines detected in IK Tau using the population diagram technique to derive rotational temperatures and column densities. We conducted a radiative transfer analysis of the SO2 lines, which also helped us to verify the validity of the approximated method of the population diagram for the rest of the molecules.
Results. For the first time in this source we detected rotational lines in the ground vibrational state of HCO+, NS, NO, and H2CO, as well as several isotopologues of molecules previously identified, namely, C18O, Si17O, Si18O, 29SiS, 30SiS, Si34S, H13CN, 13CS, C34S, H234S, 34SO, and 34SO2. We also detected several rotational lines in vibrationally excited states of SiS and SiO isotopologues, as well as rotational lines of H2O in the vibrationally excited state ν2 = 2. We have also increased the number of rotational lines detected of molecules that were previously identified toward IK Tau, including vibrationally excited states, enabling a detailed study of the molecular abundances and excitation temperatures. In particular, we highlight the detection of NS and H2CO with fractional abundances of f(NS)~10-8 and f(H2CO) ~ [10-7–10-8]. Most of the molecules display rotational temperatures between 15 and 40 K. NaCl and SiS isotopologues display rotational temperatures higher than the average (~65 K). In the case of SO2 a warm component with Trot~ 290 K is also detected.
Conclusions. With a total of ~350 lines detected of 34 different molecular species (including different isotopologues), IK Tau displays a rich chemistry for an oxygen-rich circumstellar envelope. The detection of carbon bearing molecules like H2CO, as well as the discrepancies found between our derived abundances and the predictions from chemical models for some molecules, highlight the need for a revision of standard chemical models. We were able to identify at least two different emission components in terms of rotational temperatures. The warm component, which is mainly traced out by SO2, is probably arising from the inner regions of the envelope (at ≲8 R∗) where SO2 has a fractional abundance of f(SO2) ~ 10-6. This result should be considered for future investigation of the main formation channels of this, and other, parent species in the inner winds of O-rich AGB stars, which at present are not well reproduced by current chemistry models.
Key words: astrochemistry / line: identification / stars: abundances / stars: AGB and post-AGB / circumstellar matter
Based on observations carried out with the IRAM-30 m Telescope. The Institut de Radioastronomie Millimétrique (IRAM) is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).
Full Tables E.1 and E.2 and the reduced spectrum (FITS file) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/597/A25
© ESO, 2016
1. Introduction
Asymptotic giant branch (AGB) stars are the main contributors to the interstellar medium (ISM) chemical enrichment. The physical conditions, that is, the high densities (≳1012 cm-3) and temperatures (~2000–3000 K), in their atmospheres allow the formation of stable molecules. All this molecular material is driven by the slow AGB wind creating a circumstellar envelope (CSE) that surrounds the star, up to regions where the interstellar UV field photodissociates the molecules. Carbon and oxygen are the two most abundant and reactive elements in the atmospheres and winds of AGB stars, after hydrogen. All the possible carbon monoxide, which is a very stable molecule, is formed and then depending on which element (carbon or oxygen) is in excess, other molecules will be formed. Hence, the chemistry in these objects mainly depends on the elemental carbon to oxygen ratio, being O-rich ([C]/[O] < 1), C-rich ([C]/[O] > 1) or S-type stars ([C]/[O] ~ 1) (e.g. Olofsson 1996).
Since the first detection of CO in the millimeter wavelength range toward the CSE of an AGB star (Solomon et al. 1971), the observations of the molecular emission of CSEs in that wavelength domain have increased (e.g. Morris et al. 1975; Bujarrabal & Alcolea 1991; Cernicharo et al. 2015). These studies have been mostly focused on C-rich CSEs given that carbon is more chemically active than oxygen and, therefore, C-rich envelopes are expected and observed to display a large variety of different molecular species (e.g. Cernicharo et al. 2000; Smith et al. 2015). However, the number of studies in the millimeter wavelength range has increased in the last years, and these studies have evidenced that O-rich CSEs do also host a rich variety of molecules (Ziurys et al. 2007; Kim et al. 2010; De Beck et al. 2013; Sánchez Contreras et al. 2015, and references therein).
Our motivation is to observe and to study the molecular content of the oxygen-rich CSE IK Tauri which is one of the most studied O-rich CSEs, and is considered a reference of its class.
1.1. IK Tauri
IK Tauri (hereafter IK Tau), also known as NML Tau, is a Mira-type variable star with a period of 470 days and a spectral type ~M9 (Pesch 1967; Wing & Lockwood 1973; Alcolea et al. 1999). This star was discovered by Neugebauer et al. (1965) and it is located at α(J2000) = 3h53m28.s87 and δ(J2000) = 11°24′21.′′7 (Cutri et al. 2003). The distance to IK Tau was estimated to be 250–265 pc (Hale et al. 1997; Olofsson et al. 1998). The systemic velocity of the star with respect to the local standard of rest is 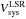 ~ 34 km s-1 (Kim et al. 2010, and references therein). Its effective temperature is Teff ~ 2200 K and the stellar radius is R∗~2.5 × 1013 cm (Decin et al. 2010a).
~ 34 km s-1 (Kim et al. 2010, and references therein). Its effective temperature is Teff ~ 2200 K and the stellar radius is R∗~2.5 × 1013 cm (Decin et al. 2010a).
The star is surrounded by a an O-rich CSE, composed of dust and gas, which is the result of mass loss at a rate that has been estimated by different methods. Neri et al. (1998) estimated Ṁ~ 3.8 × 10-6 M⊙ yr-1 from the model of 12CO J = 1–0 and J = 2–1 lines. González Delgado et al. (2003) estimated Ṁ~ 3.0 × 10-5 M⊙ yr-1 from the model of 12CO J = 1–0, J = 2–1, J = 3–2, and J = 4–3 lines. Recent modelling of the J = 3–2, J = 4–3, and J = 7–6 lines of 12CO yielded Ṁ~ 4.7 × 10-6 M⊙ yr-1 (Kim et al. 2010). The terminal expansion velocity of the CSE is ν∞~ 18.5 km s-1 as measured from De Beck et al. (2013) and references therein. The size of the CSE depends on the molecule used to trace it out. Bujarrabal & Alcolea (1991) gave a half-intensity diameter of θ1/2 ~ 16–17′′ measured for 12CO J = 1–0 and 12CO J = 2–1 emission detected with the IRAM-30 m telescope. Kim et al. (2010) measured a θ1/2 ~ 20′′ for 12CO J = 3–2 with the Atacama Pathfinder EXperiment (APEX) telescope. Recent observations with the Plateau de Bure Interferometer (PdBI), showed that 12CO (J = 1–0) displays a θ1/2~ 18′′ (Castro-Carrizo et al. 2010). Also, HCN J = 1−0 was observed with the Owens Valley millimeter-array by Marvel (2005), displaying a size of θ1/2~ 3.′′85. The size of the SiO v = 0J = 2−1 emission is θ1/2 = 2.′′2 ± 0.′′1 as determined with PdBI (Lucas et al. 1992). Finally, the emission of several lines of PN and PO has been mapped with the SubMillimeter Array (SMA), with θ1/2≲ 0.′′65 (De Beck et al. 2013).
The O-rich CSE around IK Tau displays maser emission of OH, H2O, and SiO (Lane et al. 1987; Bowers et al. 1989; Alcolea & Bujarrabal 1992; Kim et al. 2010, and references therein). It also shows thermal molecular emission of 12CO, 13CO, SiO, 29SiO, 30SiO, OH, SiS, HCN, HC3N, H2S, SO, SO2, NaCl, H2O, H217O, H218O, NH3, CS, CN, PO, PN, AlO, and tentatively, HNC (Lindqvist et al. 1988; Omont et al. 1993; Bujarrabal et al. 1994; Milam et al. 2007; Kim et al. 2010; Decin et al. 2010b; Menten et al. 2010; Justtanont et al. 2012; De Beck et al. 2013, 2015, and references therein). Some of the molecules observed up to date in IK Tau have been compared with chemical models and their line emission analysed with radiative transfer models (Willacy & Millar 1997; Duari et al. 1999; Cherchneff 2006; Kim et al. 2010; Decin et al. 2010a; Danilovich et al. 2016; Gobrecht et al. 2016; Li et al. 2016). Nevertheless, most of the reported abundances in previous studies were derived from the analysis of a moderated number of lines (e.g. Milam et al. 2007; De Beck et al. 2013). Additionally, discrepancies remain between the predicted abundances and the observations, for example for SO2 (Decin et al. 2010a; Gobrecht et al. 2016).
1.2. This paper
In this article we report the millimeter wavelength survey between ~79 and ~356 GHz carried out with the IRAM-30 m telescope toward IK Tau, which allowed us to detect rotational lines of 34 different species (including isotopologues). We detected for the first time in this source HCO+, NS, H2CO, and NO, as well as several isotopologues of previously identified molecules, such as C18O, Si17O, Si18O, 29SiS, 30SiS, Si34S, H13CN, 13CS, C34S, H234S, 34SO, and 34SO2. For molecules with previous detections reported in the literature, we increased significantly the number of transitions observed, which is needed for a robust estimate of the excitation conditions and molecular abundances. We report the results of our analysis based on population diagrams, used to derive rotational temperatures and column densities. We also estimated fractional abundances which have been compared with values derived from previous observations and with predictions by chemical models. In the particular case of SO2, we performed a radiative transfer calculation to study the excitation conditions of the ~90 lines detected with more detail. This suggests that this molecule is rather abundant not only in the intermediate and outer envelope but also in the inner, hotter and more dense regions of the CSE, where we estimate an average fractional abundance of ~10-6 (with respect to H2). This radiative transfer model also allowed us to verify the validity of the population diagram analysis for the rest of the species detected.
2. Observations
The observations presented in this paper correspond to a sensitive millimeter-wavelength (~79–356 GHz) survey carried out with the IRAM-30 m telescope toward the CSEs of two O-rich evolved stars, IK Tau and OH231.8+4.2, during several observing runs from 2009 to 2014. Partial results from the survey toward OH 231.8+4.2 are reported in Sánchez Contreras et al. (2014, 2015) and Velilla Prieto et al. (2013, 2015).
We used the heterodyne Eight MIxer Receiver (EMIR) working at four different wavelengths bands: E090 = 3 mm, E150 = 2 mm, E230 = 1.3 mm, and E330 = 0.9 mm (Carter et al. 2012). This receiver system was operated in single-sideband (SSB) mode for the E150 band and in dual sideband (2SB) mode for bands E090, E230, and E330. Two polarizations – horizontal and vertical – were available per sideband. The typical EMIR value image band rejection is approximately −14 dB or better, this implies that the peak intensity of a line entering through the image band is only ≲4% of its real value. We verified this value for the image band rejection measuring the relative intensities of strong lines that appear both in the signal and image bands.
Four different backends or spectrometers were connected to each receiver depending on their availability: the WIde Lineband Multiple Autocorrelator (WILMA), the fast Fourier Transform Spectrometer (FTS), the VErsatile SPectrometer Array (VESPA) and the 4 MHz spectrometer. The capabilities of these spectrometers and their usage are summarised in Table 1.
Specifications for the spectrometers used.
The observational technique used was the wobbler switching with a single pointing toward the position of the source (see Sect. 1.1) and a wobbler throw of 120′′ in azimuth. We configured different setups (tuning steps) to observe both polarizations simultaneously until we covered the total frequency range available for each EMIR band. We selected a small overlap between adjacent setups to ensure a uniform calibration across the bands. During the observations we checked regularly the pointing and focus of the antenna every ~1.5 and ~4 h, respectively, on strong nearby sources. On-source integration times per setup were ~1 h. Calibration scans on the standard two loads + sky system were taken every ~18 min using the atmospheric transmission model (ATM) adopted by IRAM-30 m (Cernicharo et al. 1985; Pardo et al. 2001). Errors in the absolute flux calibration are expected to be ≲25%.
The data reduction, analysis and also most of the graphic representation were done using the GILDAS1 software package. The standard procedure followed to reduce the data and obtain the final spectra consists of the flagging of bad channels, the flagging of low-quality scans, the baseline substracting, and finally, the averaging of individual scans.
The output spectra obtained from the antenna are calibrated in antenna temperature (TA∗), which can be converted to main beam temperature (Tmb) and brightness temperature (TB) according to:  where η is the main beam efficiency, bff is the beam-filling factor, Beff is the main-beam efficiency of the antenna, Feff is the forward efficiency of the antenna, θs is the size (diameter) of the emitting region of the source, and θb is the half power beamwidth (HPBW) of the main beam of the antenna. See Table 2 for a summary of the relevant telescope parameters.
where η is the main beam efficiency, bff is the beam-filling factor, Beff is the main-beam efficiency of the antenna, Feff is the forward efficiency of the antenna, θs is the size (diameter) of the emitting region of the source, and θb is the half power beamwidth (HPBW) of the main beam of the antenna. See Table 2 for a summary of the relevant telescope parameters.
Main parameters of the IRAM-30 m antenna measured with EMIR between 2009 and 2013 at representative frequencies.
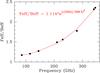 |
Fig. 1 Fit of the inverse of the main beam efficiency for the IRAM-30 m with EMIR. |
The half power width of the main beam can be approximated, using the values in Table 2, to a good accuracy by the expression: 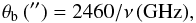 (4)and the inverse of the main beam efficiency can be fitted (see Fig. 1) using the parameters in Table 2, to obtain:
(4)and the inverse of the main beam efficiency can be fitted (see Fig. 1) using the parameters in Table 2, to obtain: 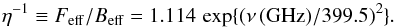 (5)
(5)
 |
Fig. 2 Overall view of the survey observed with WILMA (top) and FTS (bottom). The spectral resolution is Δν = 2 MHz. |
2.1. Observational results
Our results are based mainly on the spectra obtained with WILMA and FTS given their better spectral resolution and bandwidth. The data obtained with the 4 MHz spectrometer were used to check the edges of the setups that were only observed with WILMA, given that the 4 MHz bandwidth is slightly larger than the bandwidth of WILMA, but it has the same bandwidth than that of the FTS (see Table 1). VESPA data were used only to check certain line profiles. However, only WILMA was available to cover the full EMIR wavelength range. For example, FTS was not avaliable in the E150 band at the epoch of the observations and also some technical issues prevented us from use the FTS with the E090 band.
The spectra of the full mm-wavelength survey carried out with IRAM-30 m toward IK Tau with the WILMA and the FTS spectrometers can be seen in Fig. 2 and also in more detail in Fig. C.1. The 12CO, 13CO, and C18O line profiles are shown in Fig. 3. In Table 3 we show a summary of the observational results.
Summary of the observational results.
 |
Fig. 3 12CO, 13CO, and C18O lines detected with our millimeter wavelength survey with a spectral resolution of Δν = 2 MHz. The fit of each line to a function of the type given by Eq. (6) is shown in blue. |
3. Line identification
For the line identification, we used the public line catalogues from the Cologne Database for Molecular Spectroscopy (CDMS, Müller et al. 2005) and the Jet Propulsion Laboratory (JPL, Pickett et al. 1998), together with a private spectroscopic catalogue that assembles information for more than five thousand spectral entries (atoms and molecules, including vibrationally excited states), compiled from extensive laboratory and theoretical works (the MADEX code, Cernicharo 2012).
Given the wavelength range covered in our observations, we detected, mainly, rotational transitions in the ground vibrational state, but also, rotational transitions in higher vibrational states (i.e. SiO v = 1, SiO v = 2, SiO v = 3, 29SiO v = 1, 29SiO v = 2, 29SiO v = 3, 30SiO v = 1, 30SiO v = 2, H2O ν2 = 1, and H2O ν2 = 2). We established the detection limit at ≥5σ with respect to the integrated intensity for well detected features, and between 3σ and 5σ for tentative detections, although, these tentative detections may be more reliable when they belong to well-known species that have been identified through other stronger lines.
We detected ~450 spectral features in the spectra of IK Tau, ~90 % of which are lines in the signal side band of the receivers. Of the ~400 signal band features, ~350 lines have been unambiguously identified with rotational transitions of 34 different species (including vibrationally excited states), which are reported in Tables A.1 and A.2, along with some of their spectroscopic parameters and their fitted parameters. The rest of the lines (~35) remain unidentified, although, we proposed a tentative identification for some of them (see Table B.1).
There were several lines that we assigned to spurious features produced in the receivers in the range 167 475–174 800 MHz (Table B.2). These spurious features are symmetrical replicas at both sides of certain strong real emission lines, with the intensities of the replicas decreasing with the frequency distance to the real feature. We show in Fig. B.1 an example of this problem. The features of the image band and the spurious features were blanked in the final data.
We identified for the first time toward IK Tau, rotational lines of: HCO+, NO, H2CO, NS, C18O, SiO v = 2, 29SiO v = 2, 29SiO v = 3, 30SiO v = 2, Si17O, Si18O, 29SiS, 30SiS, Si34S, SiS v = 1, H13CN, 13CS, C34S, H234S, 34SO, 34SO2, and H2O ν2 = 2. We also detected rotational lines of: 12CO, 13CO, SiO, SiO v = 1, SiO v = 3, 29SiO, 29SiO v = 1, 30SiO v = 1, SiS, HCN, HNC, CS, NaCl, H2S, SO, SO2, PN, PO, CN, H2O, and H2O ν2 = 1. The result of the identification can be seen in Fig. C.1.
4. Data analysis
4.1. Line profiles
Most of the lines show profiles that can be reasonably well fitted with the so-called shell profile provided by the software CLASS2: ![\begin{equation} \label{eq:shell} f(\nu)=\frac{A}{\Delta\nu}\frac{1+4H[(\nu - \nu_{\rm o})/\Delta\nu]^{2}}{1+H/3}, \end{equation}](/articles/aa/full_html/2017/01/aa28776-16/aa28776-16-eq83.png) (6)where A is the area under the profile, νo is the central frequency, Δν is the full width at zero intensity, and H is the horn to centre ratio. The expansion velocity (νexp) can be related to the Δν of a line through the expression:
(6)where A is the area under the profile, νo is the central frequency, Δν is the full width at zero intensity, and H is the horn to centre ratio. The expansion velocity (νexp) can be related to the Δν of a line through the expression: 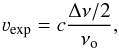 (7)where c is the speed of light.
(7)where c is the speed of light.
In the case of a spherical CSE, there are several typical line profiles which are commonly found: U-shaped, parabolic, flat-topped, Gaussian-like or triangular. Each type of profile has a particular interpretation in terms of the size of the emitting region compared to the θb of the telescope, the optical thickness of the line, and the kinematical properties of the gas responsible of the spectroscopic feature (e.g. Zuckerman 1987; Habing & Olofsson 2004). All these profiles are described to a good accuracy by the shell function described before in Eq. (6).
 |
Fig. 4 Representative profiles of the lines observed. From top-left to bottom-right: U-shaped, Gaussian-like, triangular, flat-topped, parabolic, complex, flat-topped, and a narrow maser-like line. The spectral resolution is Δν = 2 MHz. The fit of each line to a function of the type given by Eq. (6) is shown in blue. |
In Fig. 4 we show a sample of the line profiles observed. Most of the lines display profiles that match one of the types mentioned before, although, some profiles are complex and have to be considered carefully in the analysis. We also observed lines that are significatively narrower and more intense than the average, that is, they show maser like spectral profiles (see Fig. 4 bottom-right panel). For the sake of consistency we used the shell profile described in Eq. (6) to fit all the lines detected, even for the narrow lines since that should give us an approximated idea of the characteristic velocity in the regions of the wind acceleration. The aim of the fit is to estimate the centroids and linewidths, however, the velocity integrated intensities given in Tables A.1, A.2, and B.1 were obtained integrating the whole line profiles. The line profiles observed are discussed in detail for each detected molecule in Sect. 6.
4.2. Population diagrams and fractional abundances
Using the population diagram technique (Goldsmith & Langer 1999), we derived rotational temperatures and column densities averaged in the emitting region of the molecules detected. These values were derived using the following equation: 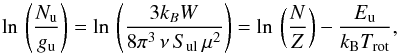 (8)where Nu is the column density of the upper level, gu is the degeneracy of the upper level, W is the velocity-integrated intensity of the line, kB is the Boltzmann constant, ν is the rest frequency of the transition, Sul is the line strength, μ is the dipole moment of the molecule, N is the total column density, Z is the partition function, Eu is the upper level energy of the transition, and Trot is the rotational temperature. The results of the populations diagrams are reported in Sect. 5.2 and Appendix D.
(8)where Nu is the column density of the upper level, gu is the degeneracy of the upper level, W is the velocity-integrated intensity of the line, kB is the Boltzmann constant, ν is the rest frequency of the transition, Sul is the line strength, μ is the dipole moment of the molecule, N is the total column density, Z is the partition function, Eu is the upper level energy of the transition, and Trot is the rotational temperature. The results of the populations diagrams are reported in Sect. 5.2 and Appendix D.
This method relies on local thermodynamical equilibrium (LTE), optically thin emission, as well as an uniform rotational temperature for the gas shell, and it permits the analysis of all the molecules using a homogeneus criteria. Also, the size of the emitting region for each molecule has to be known to account for the proper dilution of the emission. We have adopted approximate sizes of the emitting regions of θs(12CO,13CO) = 18′′ which is a representative value for the sizes measured in Bujarrabal & Alcolea (1991), Castro-Carrizo et al. (2010), and Kim et al. (2010). We also adopted the sizes θs(HCN, H13CN) = 4′′ (Marvel 2005), θs = 2′′ for SiO isotopologues (Lucas et al. 1992), and θs≲ 0.′′7 for PO and PN (De Beck et al. 2013). Similar values have been also used for these molecules by Kim et al. (2010). For the rest of the molecules, which have not been mapped, we assumed emitting region sizes according to observational constraints, previous estimations, or predictions by radiative transfer and chemical models. These values are given in Table 5 and discussed in Sect. 6. We note that the adopted sizes are uncertain for some molecules and also that the emitting region size may vary for each transition of a given molecule. In general, an underestimation of the size of any emitting region will cause an underestimation of the beam filling factor (see Eq. (3)) and, thus, an overestimation of the abundance, and vice versa.
There are additional sources of uncertainty in the values derived from the population diagrams. In particular, the kinetic temperature (Tkin) throughout the CSE is not expected to be constant. This effect is less important for the molecules whose emission arises from regions with very uniform physical conditions (inner layers, photodissociation layers, etc.), and it must be more important for species whose emission extends through the whole envelope, such as probably SO2, for which we did a more detailed radiative transfer analysis (see Sect. 4.3).
In the population diagrams, we have included lines (unambigously identified and unblended) with fluxes above 5σ. For those molecules well known to be present in the envelope of IK Tau, we have also included lines with 3–5σ detections. In the case of molecules with a hyperfine structure that cannot be spectrally resolved with the spectral resolution achieved, that is, CN, NS, and NO, we measured the total integrated intensity of the blend of the hyperfine components and we calculated the sum of the strength of the hyperfine components to compute their population diagrams. In the case of H2S we fitted together the lines of the ortho and para species due to the scarce number of lines detected for each species individually.
We have not calculated population diagrams for the molecules SiO v = 1, SiO v = 2, SiO v = 3, 29SiO v = 1, 29SiO v = 2, 29SiO v = 3, 30SiO v = 1, 30SiO v = 2, H2O, H2O ν2 = 1 or H2O ν2 = 2. Some of these lines are masers and their populations are expected to strongly deviate from a Boltzmann distribution. Also, the intensity of the lines of these molecules may vary with the stellar pulsation phase and, given that the observations spread over a period of time of approximately five years, the excitation conditions may have changed along the observational runs (see Sect. 6.1).
The fractional abundances averaged in the emitting region for the molecules detected are calculated using the following equation: 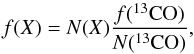 (9)where f(X) and N(X) represent the fractional abundance (with respect to H2) and column density of the molecule analysed, respectively. N(13CO) is the column density that we derived from the 13CO population diagram, and f(13CO) = 1.4 × 10-5 (Decin et al. 2010a).
(9)where f(X) and N(X) represent the fractional abundance (with respect to H2) and column density of the molecule analysed, respectively. N(13CO) is the column density that we derived from the 13CO population diagram, and f(13CO) = 1.4 × 10-5 (Decin et al. 2010a).
4.3. Radiative transfer model: MADEX
MADEX (Cernicharo 2012) is a radiative transfer code which is able to operate under LTE and large velocity gradient (LVG) approximation (Goldreich & Kwan 1974). It solves the radiative transfer problem coupled with statistical equilibrium equations to derive the radiation field and populations of the levels on each point of a gas cloud. Then, the emergent profile of the lines is obtained through ray-tracing.
We used MADEX to calculate line opacities, excitation temperatures, and critical densities for the physical conditions expected at a given distance from the star, that is, n(r) and Tkin(r) (see Table 4), along with the column densities derived from the population diagrams (given in Table 5), and the νexp derived from the line fitting (given in Table A.1) for all the molecules detected. We systematically used this procedure to compare the line opacities obtained from the interpretation of the line profiles and to verify if a given molecule could be sub-thermally excited or not. These calculations are detailed in each subsection of the Sect 6. The sets of the collisional coefficients used for these calculations (when available) are: CO (Yang et al. 2010), SiO (Dayou & Balança 2006), H2O (Daniel et al. 2011), HCN (Ben Abdallah et al. 2012), CS (Lique & Spielfiedel 2007), SiS (Toboła et al. 2008), NaCl (Quintana-Lacaci et al. 2016), SO (Lique et al. 2007), PN (Toboła et al. 2007), CN (Lique & Kłos 2011), HCO+ (Flower 1999), and H2CO (Schöier et al. 2005, and references therein). We also obtained synthetic spectra that helped us to correctly identify the spectral features.
As it is shown in Sect 5.2, the detected SO2 transitions have a large span in energies (i.e. from 7.7 up to 733.4 K). The population diagram analysis of this molecule indicates that it is possibly tracing out an inner region of the CSE, with a Tkin≳ 290 K which is not observed for other molecules, and also a more external region with Trot~ 40 K from where most of the emission of the rest of the molecules arises. To investigate more precisely the excitation conditions of SO2 and to confirm or not the temperature stratification inferred from the population diagrams, we have performed a detailed radiative transfer calculation for SO2. Our main goal is to investigate the presence of SO2 in the innermost regions of the CSE.
Results from the population diagrams, sorted according to the molecular fractional abundance (relative to H2) in descending order.
The physical model consists on a spherical expanding envelope of dust and gas with a constant mass loss rate, similar to the model presented in Agúndez et al. (2012) but corrected for IK Tau (see Table 4). The radius of the star is 2.5 × 1013 cm (Decin et al. 2010a). The density of particles is calculated with the law of conservation of mass, that is, n ∝ r-2 (valid for a CSE expanding at constant velocity). In terms of νexp, the envelope is divided in three regions: (i) from 1 to 5 R∗ where νexp = 5 km s-1 as an average value in this region (Decin et al. 2010b), (ii) from 5 to 8 R∗ where νexp = 10 km s-1 according to the dust condensation radius (Gobrecht et al. 2016), and (iii) from 8 R∗ to the end of the CSE where νexp = 18.5 km s-1(see Sect. 5.1). Concerning dust, we adopted a dust-to-gas ratio of 1.3 × 10-4 for the region (i), a value of 1.2 × 10-3 for region (ii) and a value of 2.3 × 10-3 for the region (iii), according to the values given by Gobrecht et al. (2016) for silicates. The dust temperature has been taken from Decin et al. (2006; see Table 4). The optical properties of the silicate dust and the size of the grains (0.1 μm) have been adopted from Suh (1999). For the microturbulence velocity we adopted the values given in Agúndez et al. (2012) for the C-rich CSE IRC+10216. We used different SO2 abundance profiles (see Fig. 5) in order to investigate the presence of warm SO2 in the inner regions of the CSE. For the calculations we used a set of collisional coefficients which are described in Appendix E. The results of the radiative transfer model are shown in Fig. 11 and discussed in Sect. 6.5.1.
 |
Fig. 5 Radial profiles of the abundance adopted for the radiative transfer model of the lines of SO2. We tested three different radial profiles: (i) an inner distribution of SO2 with f(SO2) = 3 × 10-6 between 1–8 R∗ (red line); (ii) a constant radial profile with f(SO2) = 2 × 10-6 between 8–640 R∗ (blue line); and (iii) a two component profile (green line) which includes an inner warm component plus an extended component of SO2. The results of the different models are shown in Fig. 11. |
 |
Fig. 6 Graph of the rotational temperatures (orange bars) and column densities (blue bars), with their formal uncertainties (black lines), derived from the population diagrams. Vertical blue arrows are plotted to indicate column density lower limits over each corresponding molecule. The temperature scale is represented on the left vertical axis, and the column density logarithmic scale is represented on the right vertical axis. The limits of the temperature scale are different in both boxes to improve the visual aspect of the figures. The values represented are tabulated in Table 5. |
5. Results
Here we present the general results from the analysis, which are summarised in Table 5 and Fig. 6.
5.1. Expansion velocity
The terminal expansion velocity of the CSE (ν∞) can be estimated from the linewidths of the spectral features that arise from the outer (r> 8R∗, Gobrecht et al. 2016) envelope regions where the gas has been fully accelerated to this maximal velocity. We estimated the ν∞ from the 13CO linewidths (see Table A.1) given that 13CO emission certainly extends beyond the wind acceleration region, and the line profiles display a clear U-shaped profile (see Fig. 3) and, thus, no significant opacity broadening is expected (Phillips et al. 1979). Assuming a mean density of n(H2) = 105 cm-3, and the temperature and column density given in Table 5, the highest opacity measured with MADEX is τ = 0.13 for the 13CO J = 3–2 line. We derived ν∞ = 18.6±1.2 km s-1 which is in good agreement with previous measurements (e.g. De Beck et al. 2013).
Most of the rest of the lines detected display linewidths consistent with ν∞ like for example SiS (see Tables A.1, A.2 and Fig. 7). In the particular case of H2CO, we stacked the lines with K = 0, K = 1, and K = 2 to confirm that H2CO linewidths are consistent with νexp = ν∞ (Fig. 8). There are also several lines with linewidths larger than ν∞, due to a blend of several hyperfine components (as occurs for NO and NS), or a poor fitting for lines detected below 5σ.
Additionally, the lines with Eu≳ 160 K, that is, the lines of vibrationally excited states (Table A.2), H2O, PO, NaCl, and several high-Eu SO2lines, have line profiles indicative of νexp≲ 10 km s-1, consistent with emission from the inner regions of the CSE where the gas is still being accelerated (r< 8R∗, i.e. ~2 × 1014 cm-2, Decin et al. 2010b; Gobrecht et al. 2016). In order to obtain a more reliable estimate of the NaCl linewidths, we stacked the lines with Eu = [22.5–56.9] K (group 1), Eu = [85.0–118.7] K (group 2), and Eu = [131.2–187.4] K (group 3) (see Fig. 8). The linewidths measured are consistent with νexp = 14.8±2.2 km s-1 (group 1), νexp = 20.1 ± 1.1 km s-1 (group 2), and νexp = 11.8 ± 1.1 km s-1 (group 3). Therefore, it seems that νexp<ν∞ at least for the lines of the group 3, that is to say, the high-Eu lines.
There are also some lines with low Eu (<200 K) which appear to have expansion velocities of ~10 km s-1 (e.g. SO2, see Fig. 7). Such low values of the νexp were measured for weak SO2 lines with low S/N, thus, the linewidths observed in their profiles are uncertain.
 |
Fig. 7 Plot of the νexp derived from the fit of the lines as a function of the Eu of the corresponding transition for several molecules. In the top, we did not represent each error bar to improve the visualization of the figure. A typical error bar of 4 km s-1 is plotted in the top left corner of the box. The values and uncertainties of the bottom correspond to the values given in Table A.2. For those lines that were observed in different epochs, we adopted an average value of the different measurements for the νexp and its uncertainty. |
 |
Fig. 8 Line stacking of the H2CO (left) and the NaCl (right) lines detected, with a spectral resolution of 2 MHz. Black spectrum correspond to the H2CO Ka = 0 lines and the NaCl lines with Eu = [22.5–56.9] K, pink spectrum correspond to the H2CO Ka = 1 lines and the NaCl lines with Eu = [85.0–118.7] K, and blue spectrum correspond to the H2CO Ka = 2 lines and the NaCl lines with Eu = [131.2–187.4] K. |
5.2. Rotational temperatures, column densities and fractional abundances
The population diagrams for all the molecules detected are shown in Appendix D, in Figs. D.1–D.13. Most diagrams display a linear trend, however, the population diagrams of, for example, SiO, 29SiO, or SO, display departures from a linear behaviour, which are more notable for low J transitions (see e.g. Fig. D.2). These departures are discussed in detail in Sect. 6 and they reflect the effect of optically thick emission and/or sub-thermal excitation. For SO2 we see two different trends for lines below and above Eu = 160 K. We fitted both separately and their implications are explained in Sect. 6.5.1.
The rotational temperatures derived range from 9 K (for CN) to 290 K (for the warm component of SO2), with most of the molecules displaying rotational temperatures between 15 K and 40 K (see Fig. 6). The column densities range from ≳1.3 × 1017 cm-2 for 12CO, down to 2.6 × 1013 cm-2 for NS. We obtained averaged fractional abundances using the Eq. (9), which range between >1.1 × 10-4 for 12CO, down to 2.3 × 10-8 for NS. We calculated the isotopic ratios of the molecules for which several isotopologues were detected. Results are presented in Table 6 and discussed in Sect. 6.10.
Isotopic ratios obtained from the abundances derived with the population diagrams.
 |
Fig. 9 Variability of some of the lines observed. The observation dates which correspond to the spectra are shown in the top right corner of each box with its corresponding colour. The spectral resolution is 2 MHz. As discussed in Sect. 6.1, variations of up to a 25% are within the uncertainties of the calibration, pointing and baseline substraction (i.e. left boxes). Variations of intensity higher than a 25% are observed in vibrationally excited lines or masers (i.e. right boxes). |
6. Discussion: an overall picture of the whole envelope
6.1. Variability
The excitation mechanisms of the lines are a mix of collisional and radiative procceses, where the radiation emitted by the central star has an impact on the population of the rotational levels (e.g. H2O Agúndez & Cernicharo 2006). Since AGB stars are variable with periods of one to two years, the net excitation mechanism for those molecules is variable and the results obtained from the analysis of the molecular lines of AGB CSEs could be affected by this variability. In the case of O-rich stars, the impact of radiative pumping effects on masers is well-known (e.g. Nakashima & Deguchi 2007). Thermal line observations of CSEs have also to be considered carefully in the sub-millimeter and far-IR domain, while for the millimeter wavelength range, specially for low-J lines, the variation of the stellar light has not a major impact (Cernicharo et al. 2014). Given that our observations spread over a period of approximately five years, we observed a few spectral ranges at different epochs and here we discuss the results observed.
For the spectra observed at different epochs we observed intensity variations of less than 25% for the rotational lines of the ground vibrational levels. This value (i.e. 25%) was taken as the calibration uncertainty (see Sect. 2), and considered in the results presented throughout this work (Fig. 9 left). However, we observed strong intensity variations (>25%) for several lines, like for example the SiO v = 1J = 7–6, (see Table A.2 and Fig. 9). These strongly variable lines correspond to rotational transitions of vibrationally excited states with νexp≲ 10 km s-1, which arise from very inner regions of the CSE. The excitation mechanism of these lines may be correlated with the stellar phase, thus, it is not possible to extract any information of their abundances. In Table A.2 we present the fit parameters for these vibrationally excited and maser lines, where we included the mean Julian date of the observation and, in case that the feature was observed in different epochs, multiple measurements of that spectral feature.
6.2. O-bearing molecules
CO is the most abundant molecule in IK Tau (after H2). It is distributed along the whole CSE with a size of ~[7–8] × 1016 cm (see Sect. 1.1). The 12CO J = 2–1 and 12CO J = 3–2 lines display parabolic profiles typical of optically thick lines, while the 12CO J = 1–0 line, all the 13CO lines, and the C18O lines show U-shaped profiles typical of optically thin lines (Fig. 3). The emission of all the CO isotopologues is probably spatially resolved considering the typical beam size (Table 2) and the shape of the line profiles. The population diagrams of 12CO and 13CO hint small departures from a linear trend, owing to high optical depth and/or sub-thermal excitation (Fig. D.1). The results can be seen in Table 5 and Fig. 6. We derived a fractional abundance f(12CO)≳ 1.1 × 10-4 (with respect to H2) in agreement with previous estimates. For C18O, we estimated f(C18O)~ 4 × 10-8, assuming the same excitation temperature (20 K) and emitting size as for 13CO.
We used MADEX to estimate the opacities of the CO lines (using the Tkin, the νexp derived from the linewidhts, the column density derived from the population diagram, and the n(H2) density at the outer radius of the shell according to the equation given in Table 4). With these input parameters, MADEX predicts that the 12CO J = 2–1 and the J = 3–2 lines are moderately thick (τ ≲ 1.4), while the J = 1–0 line is optically thin (τ ~ 0.2). This is consistent with CO tracing the coolest, outermost layers of the CSE and 13CO probing also regions deeper inside.
For SiO isotopologues we have adopted an emitting size equivalent to 7.9 × 1015 cm (2′′) at a distance of 265 pc (Sect. 1.1). All the line profiles of the different SiO isotopologues are parabolic, consistent with optically thick emission. The rotational diagrams of all the SiO isotopologues display small departures from a linear trend, except perhaps for Si17O (Fig. D.2). We found similar Trot for all the isotopologues, that is, Trot~ 20 K, which are much lower than the Tkin expected at a distance of 1′′ from the star (i.e. Tkin~ 105 K). Hence, sub-thermal excitation may have an impact on the values derived from the population diagrams of SiO isotopologues.
MADEX (see Sect. 4.3) predicted τ>1 for all of the SiO, 29SiO and 30SiO lines (except for the J = 2–1 lines of 29SiO and 30SiO, for which MADEX predicted τ ≲ 0.6.) These values are consistent with the observed line profiles. For Si18O and Si17O lines, MADEX predicted τ< 0.5. Therefore, except for Si18O and Si17O, the column densities and the abundances derived for the SiO isotopologues, given in Table 5, should be considered lower limits. The lower limit obtained, f(SiO)> 8.0 × 10-6, is in good agreement with previous measures (Decin et al. 2010a, and references therein), and, in principle, is also consistent with the low SiO abundances predicted by the model by Gobrecht et al. (2016) that proposes the formation of SiO in abundance under thermodynamical equilibrium (TE) in the stellar photosphere, and a significant abundace decay (to 1.5 × 10-5) already at 6 R∗ mainly due to dust condensation.
6.3. C-bearing molecules
We detected emission of molecules, like CS, HCN and HNC, that are typically found in C-rich CSEs (e.g. Bujarrabal et al. 1994; Cernicharo et al. 2000; Zhang et al. 2009).
According to Marvel (2005), the HCN emission arises from a compact region with θs ~ 4′′, which we adopted in this work. For CS, there are no observational constraints on the size of the emission, therefore, we adopted a size of θs = 2′′ which is the same size used for SiO and it is consistent with the extent of the CSE emission predicted by chemical models (Li et al. 2016). Adopting these sizes we obtained Trot(HCN) ~ 10 K and Trot(CS) ~ 25 K, and Ntot(HCN)≳ 8 × 1014 cm-2 and Ntot(CS)~ 9 × 1014 cm-2 (Figs. D.3 and D.4).
Using MADEX, we found optically thick lines (τ ≳ 1.5) for HCN, and moderately thick lines (τ ≲ 1.2) for H13CN. Therefore, the column density and the abundance of HCN should be considered as lower limits. In the case of CS isotopologues, with the physical conditions expected at r ~ 1′′, MADEX predicted optically thin lines (τ ≲ 1.0). Finally, given that Tkin(r ≲ 1′′) ≳ 100 K, the lines of HCN and CS isotopologues are most likely sub-thermally excited.
The rotational temperatures and abundances derived for HCN and CS isotopologues (see Table 5) are consistent with previous measurements in IK Tau (Lindqvist et al. 1988; Kim et al. 2010). The HCN abundance is in the high end of the abundance range deduced by Schöier et al. (2013) in a sample of M-type AGB stars. The TE models for O-rich CSEs do not account for the HCN and CS abundances observed in O-rich CSEs, predicting values of f(HCN)~ 10-11 and f(CS)~ 10-10 (Duari et al. 1999; Gobrecht et al. 2016). The inclusion of shocks can contribute to enhance the formation of HCN in O-rich stars (Duari et al. 1999; Cherchneff 2006; Gobrecht et al. 2016), but it also brings up a theoretical homogeinity on the expected HCN abundances among different chemical types of stars that it is not observed, as noted by Schöier et al. (2013). Other authors invoked the photochemistry to try to explain the abundances of C-bearing molecules observed in O-rich CSEs (Nercessian et al. 1989; Ziurys et al. 2009). In particular, the chemical model of Willacy & Millar (1997) predicts peak abundances of f(HCN)~ 1 × 10-7 and f(CS)~ 3 × 10-7, although the carbon source proposed by these authors is CH4 which has been later on refuted (Marvel 2005). Additionally, it has been also proposed that CSEs could be clumpy, hence, photochemistry could be important also in the inner layers of the envelopes (Agúndez et al. 2010). Our results do not conclude clearly which is the most likely scenario, although, our derived abundances are more similar to those predicted by the models of Gobrecht et al. (2016).
Finally, we detected two HNC lines, in particular, the J = 1–0, and the J = 3–2 line, which is blended with the image of the SiO J = 6–5 line. We estimated f ~ 8 × 10-9, assuming an excitation temperature of ~30 K and a size of 2′′ for the emitting region, which are average values for these parameters.
6.4. Refractory species
We confirmed the presence of two important refractory molecules which are mainly found in C-rich envelopes: SiS and NaCl. The emission of these molecules has not been mapped in previous studies and, therefore, the size of the emitting region is unknown. The NaCl line profiles, with νexp~ 14 km s-1, are narrower than those of SiS, consistent with νexp~ 18.5 km s-1, which suggests a more inner distribution of NaCl around the star (see Fig. 7). This molecule may condense onto the dust grains beyond the dust condensation radius, as proposed by Milam et al. (2007). The profiles of the lines of NaCl and SiS isotopologues indicate spatially unresolved emission, which is compatible with the Gaussian-like profiles observed in the case of NaCl, and the triangular or parabolic profiles observed for the SiS isotopologues. Moreover, the Gaussian-like profiles observed for NaCl may support that the emission of this molecule arises from the innermost regions of the CSE, where the gas has not been fully accelerated.
We adopted a size of θs = 2′′ for SiS isotopologues, as a first guess considering the emission size of SiO (θs = 2′′). This size is also consistent with the size predicted by recent chemical model of IK Tau (Li et al. 2016). For NaCl we adopted a size of θs(NaCl) = 0.′′3 (Milam et al. 2007). We derived similar rotational temperatures for SiS and NaCl (i.e. Trot~ 65 K) even higher for 29SiS, 30SiS, and Si34S (see Figs. D.5 and D.6). According to the size adopted for SiS (i.e. r ≲ 4 × 1015 cm), we estimated Tkin≳ 105 K, and n(H2) ≳ 3.5 × 105 cm-3. For the size adopted for NaCl (i.e. r ≲ 6 × 1014 cm), we estimated Tkin≳ 330 K. Hence, SiS and NaCl are most likely sub-thermally excited. We estimated critical densities for the SiS lines of ncrit ~ [ 104–106] cm-3 for a temperature of ~105 K, therefore, n ≲ ncrit for several lines of SiS confirming sub-thermal excitation. For NaCl the critical densities expected are even higher, ncrit ≳ 5 × 107 cm-3, due to the high dipole moment of NaCl. MADEX predicted optically thin lines for both SiS (τ< 0.6) and NaCl (τ< 0.3).
We derived f(SiS) ~ 5 × 10-6. This value is in good agreement with the estimations by Kim et al. (2010). The chemical model by Gobrecht et al. (2016) predicts a SiS abundance of 4 × 10-8 under TE and up to ~3 × 10-7 including dust condensation and shocks due to the pulsation of the star, which is at least one order of magnitude lower than our results. Willacy & Millar (1997) used SiS in their chemical models as a parent molecule with an abundance consistent with our observations (see Table 5).
Concerning NaCl, Milam et al. (2007) derived a rotational temperature and a column density consistent with our results. However, Milam et al. (2007) derived a fractional abundance ~80 times lower than ours, through the population diagram of two low S/N NaCl emission lines, and also a radiative transfer calculation using the code by Bieging & Tafalla (1993), with a set of SiO-corrected collisional coefficients. We detected 13 NaCl lines which cover a wide range in Eu and have better S/N, from which we derived an average fractional abundance of f(NaCl) = 3 × 10-7 (see Table 5 and Fig. D.6). We cannot rule out uncertainties in our estimation due to the emitting size, and the 13CO column density adopted, which could not be representative in the region of NaCl emission. Moreover, NaCl line profiles are not incompatible with θs(NaCl) ≳ 0.′′3, in particular, if θs(NaCl) = 1′′ we would derive f(NaCl) = 3 × 10-8. TE calculations predict abundances of 10-11 up to 10-7 (Tsuji 1973; Milam et al. 2007), while Gobrecht et al. (2016) models (TE and shocks) predicts NaCl abundances between 4 × 10-12 up to 1 × 10-8. It would be necessary to obtain maps of the NaCl spatial distribution in order to clarify these discrepancies.
6.5. S-bearing molecules
Here we discuss the detected emission of H2S, SO, and SO2. The first detection of these molecules toward IK Tau and their chemistry in O-rich CSEs was presented in Omont et al. (1993) and references therein. Omont et al. (1993) only detected one line of H2S, and they were not able to estimate its abundance toward IK Tau. The emission of SO and SO2 molecules in O-rich CSEs, including IK Tau, has been recently reviewed and modelled by Danilovich et al. (2016).
We detected three ortho and one para lines of H2S as well as one line of o-H234S, which point out νexp~ν∞. The profiles of the lines indicate spatially unresolved emission. Since there are not maps of the H2S emission, we adopted a size of θs(H2S) = 2′′ which is consistent with the size predicted by chemical models (Li et al. 2016). Given that we only detected two lines of o-H2S with S/N> 5, we calculated the population diagram (Fig. D.7) of ortho and para species together adopting an ortho-to-para ratio of 3:1 which is the value that could be expected from the formation processes of H2S. We derived Trot~ 40 K and f(H2S)~ 1 × 10-6. This value is consistent with the chemical models presented by Gobrecht et al. (2016) at a few stellar radii. We found that the lines of H2S are likely to be sub-thermally excited at the distances adopted for the H2S emission (r ≲ 1′′). However, we did not made further non-LTE calculations due to the lack of a set of collisional coefficients for H2S. Under LTE conditions, MADEX predicts optically thin lines (τ< 0.6).
 |
Fig. 10 Line profiles of some of the SO lines identified. The quantum numbers of each transition are plotted in red in each box.The spectral resolution is 2 MHz for all the spectra shown. |
The profiles of the SO lines observed are varied (see Fig. 10). Most of them are flat-topped (optically thin and spatially unresolved emission), some of them display parabolic profiles (optically thick or moderately thick emission) and a few SO lines display profiles which seem to be composed of two components, at least: one dominant flat-topped or parabolic component with linewidths consistent with ν∞, and an additional narrow feature which may indicate SO gas inside the gas acceleration region. These two components are more clearly seen in several SO2 lines (Fig. 11) which display a broad component plus a bulge-like centred narrow component, which we interpreted as SO2 emission arising from r< 8R∗ (see Sect. 6.5.1). Nevertheless, we have not detected high-Eu SO narrow lines or two different trends in the SO population diagram (see below) which could prove a very inner component of warm SO gas (contrary to SO2 as discussed in Sect. 6.5.1). Thus we have no firm evidence that could prove the presence of warm SO gas in the innermost regions of the CSE with a noticeable abundance. Finally, the 34SO flat-topped (optically thin emission) profiles yield also νexp~ν∞.
The brightness distribution of SO has not been mapped before, thus, we adopted a size of θs(SO) = 2′′ as well as for 34SO, according to the models by Li et al. (2016). The population diagrams (Fig. D.8) display departures from a linear trend for SO. We obtained Trot(SO) ~Trot(34SO) ~ 15 K, Ntot(SO)≳ 9 × 1015 cm-2 and Ntot(34SO)~ 9 × 1014 cm-2. We verified with MADEX (see Sect. 4.3) that SO lines would be moderatelly thick (τ ≲ 1.5) with a Tkin = 105 K and n ~ 4 × 105 cm-3 at r = 1′′. MADEX predicted optically thin lines for 34SO (τ ≲ 0.2). Furthermore, we estimated ncrit(SO)~ [ 105–107] cm-3 and similar values for 34SO, which suggests sub-thermal excitation of several transitions.
We derived abundances of f(SO)≳ 8 × 10-6 and f(34SO)~ 8 × 10-7. The abundance measured of SO is at least a factor three higher compared to previous observational works toward IK Tau (Omont et al. 1993; Bujarrabal et al. 1994; Kim et al. 2010). On the other hand, TE models predict abundances of f(SO)~ [2–4] × 10-8 (Duari et al. 1999; Gobrecht et al. 2016). Willacy & Millar (1997) derived peak abundances up to f(SO)~ 9 × 10-7 with a chemical model for an O-rich CSE that used only H2S and SiS as parent S-bearing molecules. Compared to these models, our derived abundance is at least nine times higher than the highest value obtained from the models. Our analysis seems to overestimate the SO abundance compared to previous measurements and chemical models. These dicrepancies may be explained given the uncertainty on the size of the SO emitting region adopted, and the f(13CO) adopted (see Eq. (9)). In particular, a size of θs(SO)~ 5′′ would fix this discrepancy.
 |
Fig. 11 Results of the radiative transfer models of SO2 explained in Sects. 4.3 and 6.5.1. The coloured curves correspond to the models adopting the abundance profiles shown in Fig. 5. The spectral resolution is 2 MHz. The temperature scale is in main beam temperature. |
6.5.1. SO2 and 34SO2
We detected ~90 lines of SO2 displaying complex profiles which can be grouped according to their νexp: (i) ~60 lines with νexp~ 18 km s-1 consistent with the ν∞ of the CSE; and (ii) ~30 lines with νexp<ν∞, with velocities as low as ~5 km s-1 (see Fig. 7). The lines of SO2 display parabolic profiles, flat-topped profiles, and complex profiles. Several lines display a self-absorption in the blue side of the line (see Fig. 11). This self-absorption may be explained considering that part of the SO2 emission arising from the inner and warm shells of the CSE, is absorbed by the external and cold shells of the CSE, which are located (within the line of sight) between us and the warm gas. The narrow lines seem to be spatially unresolved, although, for the lines that have νexp~ν∞ it is not clear whether they are spatially resolved or not. Most of the 34SO2 lines show flat-topped profiles with indicative of spatially unresolved emission.
The rotational diagram of SO2 was done adopting an emission size of θs(SO2) = 2′′, which should be considered as an educated guess derived from the chemical models by Li et al. (2016). From the population diagram of SO2 (Fig. D.9) we observed also two components, a cold component with Trot~ 40 K traced out by ~60 lines with Eu ≲ 160 K and a warm component with Trot~ 290 K traced out by ~30 lines with Eu> 160 K. The cold component displays a slight change in the trend for the lines with Eu ≲ 50 K which may be explained as a result of moderate optically thick emission for those lines and/or sub-thermal excitation. Using Eq. (9) we derived f(SO2, cold) ≳9.6 × 10-6 and f(SO2, warm) ≳ 2.7 × 10-6. For 34SO2 we derived a Trot~ 35 K and f(34SO2) ~ 9.6 × 10-7.
As we said in Sect. 4.3, the SO2 lines detected span over a wide range of energies, thus, the parameters derived from the population diagram may be unreliable given that the homogenous temperature assumption may turn out to be a very crude approximation. We carried out several LVG models adopting different radial abundance profiles (see Sect. 4.3 and Fig. 5). As it is discussed below, the different abundance profiles were adopted mainly to illustrate the need of the presence of warm SO2 at r< 8R∗ in order to reproduce the profiles of the high-Eu lines. The results of the radiative transfer models are shown in Fig. 11 for several lines of SO2.
The first model (red line in Figs. 5 and 11) reproduces to a good accuracy the profiles of the narrow high-Eu (i.e. Eu> 160 K) lines observed. However, it is unable to reproduce the line profiles of the low-Eu (i.e. Eu< 160 K) lines, underestimating their emission completely. We created a second model (blue line in Figs. 5 and 11) which reproduces, within a factor two in intensity, most of the low-Eu SO2 lines observed. However, this model is unable to explain the narrow profiles of the high-Eu SO2 lines, predicting wide flat-topped lines or even no emission for these high energy lines. We may note, that the fractional abundance adopted for this second model is approximately a factor five lower than the abundance derived from the population diagram of the SO2 cold component. If the abundance is increased up to a value consistent with the population diagram results for the cold component (i.e. f(SO2) = 9.6 × 10-6), the model highly overestimates the line profiles observed. This discrepancy may arise from the lack of precise information about the spatial distribution of SO2 toward the CSE.
Finally, we tested the possibility of SO2 being distributed as a sum of two components, in particular, the sum of a compact inner component plus an extended component with a shell-like enhancement in the outermost part of the CSE, in order to reproduce the whole set of SO2 lines observed with a single radial abundance profile. This last model (green line in Figs. 5 and 11) is able to approximately reproduce both the low- and high-Eu SO2 lines observed, although, it does not reproduces perfectly all the line profiles. The discrepancies found between this best model and the observations are within a factor two or three in intensity for most of the lines observed. This disagreement emerges probably from the lack of precise information about the spatial distribution of SO2. The radial abundance profile adopted for the model is consistent, within a factor two or three in intensity, with the results obtained from the population diagram for the SO2 warm and cold components. Additionally, the best model predicts both optically thin and optically thick lines which is consistent with the variety of profiles observed.
Hence, we can conclude that SO2 is distributed along the CSE with an average fractional abundance of f(SO2) ~ 10-6. Our models evidenced the presence of an inner (1–8 R∗) warm (≳290 K) component of SO2 with fractional abundances ~10-6, which produces most of the emission from SO2 lines with Eu≳ 160 K. This is also consistent with the narrow profiles of the high-Eu SO2 lines. Nevertheless, our model is not able to reproduce the complexity observed in the profiles, which probably indicates the simplicity of the approximated physical model. In particular, the outer radius of the SO2 cold component is critical to control the expected intensities of the low-Eu lines, which we adopted from the chemical model by Li et al. (2016). Therefore, it would be necessary to map the brightness distribution of this molecule in order to constrain the outer radius of SO2 emission. High angular resolution observations are also required to map the innermost regions of the CSE, since the distribution of SO2 in the region between 1–20 R∗ would improve the results obtained not only for the high-Eu lines but also for those lines that display a narrow core component (e.g. SO2 73,5–72,6 in Fig. 11).
Previous works toward IK Tau pointed out SO2 abundances in the intermediate and outer envelope consistent with our results (Omont et al. 1993; Kim et al. 2010; Decin et al. 2010a). Decin et al. (2010a) hinted the presence of SO2 in the inner wind, since they were not able to reproduce with their radiative transfer model simultaneously the emission of a few lines with Eu~ 140 K detected with APEX and the low-Eu transitions observed with the IRAM-30 m telescope. Given the limited number of high-Eu lines detected by Decin et al. (2010a), these authors were unable to reach conclusive results on the presence of SO2 in the inner wind of IK Tau and its abundance. Recent research was conducted to investigate one SO2 line with Eu~ 600 K detected with Herschel/HIFI as well as other SO2 lines reported in the literature toward IK Tau with a radiative transfer model by Danilovich et al. (2016). Their best-fit model has a peak abundance of f(SO2) = 2 × 10-6 and an e-folding radius Re = 1016 cm, although, it is unable to reproduce all the SO2 observed line profiles as indicated by these authors.
TE models predict the formation of SO2 in the photosphere of the star with abundances of f(SO2) ~ 10-11 (Tsuji 1973; Gobrecht et al. 2016), which is approximately five orders of magnitude lower than our results. Willacy & Millar (1997) predicted a peak abundance of f(SO2) ~ 2 × 10-7 in the intermediate and outer parts of the CSE, at r ~ 1016 cm (i.e. ~500 R∗), and f(r ≲ 3 × 1015 cm) ≲ 10-10, where they used H2S and SiS as the S-bearing parent molecules of the model. This chemical model is also inconsistent with our results given that they do not predict the formation of SO2 in the inner parts of the CSE and the abundance in the intermediate and outer parts is aprroximately two orders of magnitude lower than our measures. In the recent chemical model presented by Li et al. (2016), the authors explore the effect of including SO2 as a parent molecule. In the absence of a reliable observational estimate of the SO2 abundance in the inner envelope, these authors adopt f(SO2) = 2 × 10-6, which is the value estimated from low-Eu SO2 transitions arising in the outer envelope regions (Decin et al. 2010a). In the innermost parts of the envelope (r< 8R∗) the SO2 abundance can be enhanced up to f(SO2) = 4 × 10-9 including the effect of shocks and dust grains (Gobrecht et al. 2016). These authors suggest that the production of SO triggers the formation of SO2 at ~4 R∗ in the gas phase through the reaction with OH. Although, the SO2 abundance obtained with the inclussion of shocks is approximately two or three orders of magnitude lower than our estimates. Photochemistry may also enhance the formation of SO2 in the inner layers of the CSE, which would require an additional source of UV radiation to dissociate H2O providing OH to react with the SO formed leading to the enhancement of SO2. This could be plausible if the envelope of IK Tau is clumpy, as proposed for other objects (Agúndez et al. 2010).
6.6. N-bearing molecules
Besides HCN, HNC and PN, which are discussed in other sections, we detected CN, NS, and NO. The CN lines with unblended hyperfine components have widths consistent with νexp = ν∞ within errors. The spatial distribution of CN in IK Tau is unknown. CN has been observed in the outer shells of the C-rich CSE IRC+10216 (Lucas et al. 1995), and chemical models predict that it is formed as a result of the photodissociation of HCN and HNC in these outer shells (e.g. Nejad & Millar 1988). Given that the HCN size is θs(HCN) = 3.′′85, CN would be expected to be in a shell external to the HCN. According to the chemical model by Li et al. (2016), the CN peak abundance occurs at r ~ 1.5 × 1016 cm. We converted the area between the HCN outer shell and the CN abundance peak to an equivalent emitting size, obtaining θs(CN)~ 6′′. With this size, we calculated the population diagram of CN (Fig. D.10). We estimated Trot = 9 ± 2 and Ntot ~ 1 × 1014 cm-2. At r ~ 1.5 × 1016 cm, Tkin is ~50 K and n(H2) ~ 2 × 104 cm-3, thus, CN lines are probably sub-thermally excited (ncrit ≳ 106 cm-3). With these physical conditions MADEX predicted optically thin lines. We estimated f(CN)~ 1 × 10-7 which is consistent with previous estimations (Kim et al. 2010). Chemical models predict abundances up to 3 × 10-7 (Willacy & Millar 1997; Li et al. 2016), which are also in good agreement with our observations.
As far as we know, our discovery of NS emission toward IK Tau is the first detection of this molecule in this source. Given that we did not resolve its hyperfine structure we cannot extract information on the line profiles observed. There are not observational constraints on the emission size of this molecule. According to the chemical model by Li et al. (2016), which predicts that NS would be formed through the neutral-neutral reaction of NH and S in an external shell of the envelope, similar to the CN shell, we adopted a θs(NS)~ 6′′. With this size, from its population diagram (Fig. D.11), we derive a Trot = 18 ± 2 K and a column density of (2.6 ± 0.5) × 1013 cm. As for CN, the lines of NS may be sub-thermally excited. Since, we have not a set of collisional coefficients for NS we could neither estimate the opacities of the lines nor their critical densities. A rough estimation under LTE conditions with MADEX yields optically thin lines (τ< 0.1). We derived an abundance of f(NS)~ 2 × 10-8. The chemistry of NS in O-rich CSEs was discussed in Willacy & Millar (1997), although, these authors did not give a value for the predicted NS abundance. Recently, chemical models by Li et al. (2016) predicted f(NS)~ 8 × 10-9, which is (within uncertainties) consistent with our results.
For NO, we only detected two lines with low S/N. One of them is a blend of several hyperfine components. For the NO hyperfine component spectrally resolved we derived νexp = ν∞. We estimated a rough value of the NO abundance adopting θs ~ 6′′ (like for CN and NS), and an excitation temperature of 30 K, which is representative of the Tkin in the outer shells of the CSE (r ~ [2–5] × 1016 cm). With these considerations, we obtained f(NO)~ 2 × 10-6, in agreement with the predictions of the chemical model by Li et al. (2016).
6.7. P-bearing molecules
PN and PO were detected for the first time toward IK Tau by De Beck et al. (2013), and we detected one additional line of PN, and seven additional lines of PO. Concerning PO, which has hyperfine structure, we observed several spectrally resolved (as well as unresolved) lines with linewidths consistent with νexp~ 9 km s-1. This suggests that PO emission lines arise from r< 8R∗. De Beck et al. (2013) mapped the brightness distribution of both PN and PO toward IK Tau, and found θs ≲ 0.′′7. With this size we calculated the rotational diagram of both molecules (Fig. D.12), and we derived low rotational temperatures (Trot~ 20 K), Ntot(PN)~ 8 × 1014 cm-2 and Ntot(PO)~ 2 × 1015 cm-2. The low Trot deduced for PN and PO is probably indicative of sub-thermal excitation since at the inner wind layers (<0.7′′) where the emission is produced, the gas kinetic temperature is expected to be well above 200 K. We used our radiative transfer code (see Sect. 4.3) to confirm our results. MADEX predicted optically thin (τ ≲ 0.4) and sub-thermally excited lines for PN. In the case of PO, MADEX predicted optically thin (τ< 0.1) PO lines, under LTE approximation given that there is not a set of PO collisional coefficients available. We derived f(PN)~ 7 × 10-7 and f(PO)~ 2 × 10-6, which are consistent with previous estimates considering uncertainties (De Beck et al. 2013).
Concerning chemical models, these P-bearing molecules are adopted as parent molecules and their abundances are assumed from observations of the inner region of the CSE (De Beck et al. 2013; Li et al. 2016). TE calculations predict abundances for PN compatible with our results, and one order of magnitude lower than our measurements for PO (Tsuji 1973; Agúndez et al. 2007; Milam et al. 2008).
6.8. HCO+
We detected the J = 1–0 line of the HCO+ ion. The J = 3–2 line was not detected probably due to an unsufficient sensitivity. The J = 2–1 and the J = 4–3 lines lie in wavelength ranges that were not observed. The flat-topped profile of the HCO+J = 1–0 line indicates νexp~ν∞, optically thin, and spatially unresolved emission. We estimated a very rough value of the f(HCO+) adopting an emission region and an excitation temperature equal to those adopted for NO (see Sect. 6.6) since both molecules are expected to be formed in the outer shells of the CSE. With these values, we obtained f(HCO+) ~ 10-8.
According to chemical models, this molecule is formed efficiently in the outer layers of O-rich CSEs as a result of reactions that involve CO, H2O, and their photodissociation products, with abundances consistent with our results (Willacy & Millar 1997; Sánchez Contreras et al. 2015, and references therein).
6.9. The organic precursor missing link to carbon chemistry: H2CO
This is the first detection of the organic precursor molecule H2CO toward IK Tau. We detected ortho and para lines with flat-topped profiles, indicating optically thin and spatially unresolved emission, even for the lines at high frequencies with θb ~ 8′′ (see Eq. (4)). We adopted a size of θs(H2CO)= 2′′, which is an educated guess, taking into account that most of the molecules detected are expected to emit in that region of the CSE.
In the population diagram of H2CO (see Fig. D.13), the Ka = 0, Ka = 1, and Ka = 2 ladders were fitted separately. For Ka = 2 only two data were collected. The average rotational temperature indicated by the fits of the different Ka ladders is ~10 K. For the Ka = 3 ladder we only detected two lines with the same upper energy level, therefore, we adopted an average excitation temperature of ~10 K to derive a rough value of the Ka = 3 column density. Formaldehyde is an asymmetric rotor with its dipolar moment oriented along the a axis. Therefore, transitions between different Ka levels are weakly connected through radiative processes. This explains why each of the Ka ladders appears as separated lines in the rotational diagram. The column densities derived result in an ortho-to-para ratio of ~3:1, which has been computed dividing the sum of the Ka = 1 and 3 (ortho transitions) by the sum of the Ka = 0 and 2 (para transitions) column densities (see Fig. D.13). The total column density is Ntot(H2CO)~ 3 × 1014 cm-2. Adding both o-H2CO and p-H2CO, we obtained a fractional abundance of f(H2CO)~ 2 × 10-7. In this case, MADEX predicted optically thin lines (τ< 0.3) and sub-thermal excitation which is consistent with Tkin(r = 1″) >Trot.
The origin of formaldehyde, as well as other C-bearing species, in O-rich envelopes has puzzled the scientific community since H2CO was first detected in the O-rich CSE OH231.8+4.2, with a fractional abundance of 4 × 10-8 (Lindqvist et al. 1992; Charnley et al. 1995). Millar & Olofsson (1993) proposed a formation route which requires methane to produce formaldehyde in the external envelope with abundances up to 10-7 depending on the mass loss rate of the star. Methane is a highly symmetric molecule with no permanent dipole, thus, indirect evidence for the presence of methane can be provided by the search of expected products of CH4 chemistry, such as C2H and CH3OH. A previous search for these molecules toward IK Tau and other O-rich CSEs has resulted in non-detections of C2H (f(C2H)< 9.7 × 10-9) and methanol (f(CH3OH)< 3.2 × 10-8; Charnley & Latter 1997; Marvel 2005). We also did not detect emission of these molecules consistent with the upper limits provided by Marvel (2005). If the correct scenario were that H2CO is formed in the outer envelope, the size adopted for the calculation of the population diagram would result in an abundance overestimate. In that case, assuming θs = 6′′, like for CN, NS, or NO, we derive an abundance of f(H2CO)~ 2 × 10-8. Furthermore, a clumpy envelope may lead to an enhanced photochemistry in the inner layers of the CSE, which result in the formation of carbon molecules in the inner and intermediate layers of O-rich CSEs, and in particular formaldehyde with f(H2CO)~ 10-9 (Agúndez et al. 2010).
6.10. Isotopic ratios
Isotopic ratios of different species can be measured from the column densities derived in the rotational diagrams (see Table 6). However, these ratios have to be considered as lower limits when the molecule used to calculate the ratio has optically thick lines. In case that the opacities are moderately high, the isotopic ratio can be corrected using the approach by Goldsmith & Langer (1999).
For 12C/13C ratio, we measured values of eight to ten depending on the molecule used (i.e. CO, CS or HCN). The opacity correction yielded a 12C/13C ratio of ~10 from CO. This value is in good agreement with that obtained by Ramstedt & Olofsson (2014) from their radiative transfer model of the 12CO and 13CO emission in IK Tau. This ratio is also compatible with other estimates in M-type stars like TX Cam or W Hya, consistent with a standard evolution for an M-type star (Ramstedt & Olofsson 2014, and references therein).
For the 16O/17O and 16O/18O ratios, we estimated lower limits of 90 and 60, respectively. MADEX predicted opacities as high as τ ~ 10 for a few SiO lines that would result in opacity corrected values of one order of magnitude higher, in agreement with previous estimates (Decin et al. 2010b).
The opacity corrected isotopic ratios of 28Si/29Si and 28Si/30Si are ~18 and ~34, respectively. Both isotopic ratios are (within uncertainties) in reasonable agreement with previous estimations toward IK Tau (Decin et al. 2010a), and also with the solar ratios ([28Si/29Si] ~ 20 and [28Si/30Si] ~ 30, Asplund et al. 2009). Therefore, it seems that in the case of IK Tau, Si isotopic ratios do not indicate significant alterations in the post-main sequence evolution.
Finally, we measured the isotopic ratio of 32S/34S using SO, SiS, SO2, and CS obtaining values between 10 and 13. We corrected the effect of optically thick emission and we estimated a 32S/34S ratio of ~15. As far as we know, there are no previous observational constraints to this isotopic ratio toward IK Tau. The solar 32S/34S ratio is ~22 (Asplund et al. 2009). Recently, Danilovich et al. (2016) reported [32S/34S] ~ 32 toward the O-rich CSE of R Dor. Both, Sun and R Dor isotopic ratios are, within uncertainties, compatible with our estimations.
6.11. Qualitative comparison with other O-rich objects
The molecular content of only a few O-rich CSEs has been studied so far. In particular, the best studied objects are the AGB CSE IK Tau, the CSE of the hypergiant VY CMa and the peculiar object OH231.8+4.2 (Alcolea et al. 2013; De Beck et al. 2013; Matsuura et al. 2014; Sánchez Contreras et al. 2015; Ziurys et al. 2007, and references therein).
IK Tau has, in terms of chemical composition, more similarities with VY CMa. AlOH and H3O+ are the only molecules present in the CSE of VY CMa that are not found in the CSE of IK Tau. Formaldehyde is found in the CSE of IK Tau but it is not found in the CSE of VY CMa. Regardless of the possible chemical processes at work in the CSE of IK Tau, the presence of CO, CN, CS, HCN, HNC, HCO+, and H2CO in IK Tau indicates that the emission of C-bearing molecules in VY CMa is not so unique (Ziurys et al. 2009).
OH231.8+4.2 displays emission of several molecules that are not found toward IK Tau: HNCO, HNCS, OCS, H13CO+, SO+, N2H+, and H3O+. The remarkable chemistry of OH231.8+4.2 probably reflects the molecular regeneration process within its envelope after the passage of fast (~100 km s-1) shocks that accelerated and dissociated molecules in the AGB wind ~800 yr ago (Sánchez Contreras et al. 2015). In IK Tau there is no evidence of a similar molecular destruction process by fast (~100 km s-1) velocity shocks. Instead, slower shocks due to stellar pulsation may have an impact on the chemistry of AGB CSEs (Gobrecht et al. 2016). However, the fact that these molecules are not observed toward IK Tau point out that slow shocks are not able to enhance the formation of these particular species, which are unexpectedly abundant in OH231.8+4.2 (Velilla Prieto et al. 2015). Nevertheless, slow shocks could enhance the formation of molecules like HCN or CS (see Sect. 6.3). Another difference with respect to OH231.8+4.2 is that IK Tau displays emission of NaCl and more intense lines of vibrationally excited SiO (Velilla Prieto et al., in prep.). The emission of these lines arises from very warm and inner regions of the CSE. The absence of NaCl and the weakness of the vibrationally excited SiO lines toward OH231.8+4.2, probably indicates that the mass loss rate of OH231.8+4.2 is decreasing at present (as suggested by Sánchez Contreras et al. 2002), which results in the progressive growth of a central cavity around the star.
7. Conclusion
In this work we present the detection toward IK Tau of ~350 rotational lines corresponding to a list of H-, O-, C-, N-, S-, Si- and P-bearing molecules, which evidences an active chemistry for an O-rich AGB CSE.
We detected for first time in this source emission of HCO+, NO, H2CO, and NS. We also detected for the first time toward IK Tau rotational lines of C18O, Si17O, Si18O, 29SiS, 30SiS, Si34S, H13CN, 13CS, C34S, H234S, 34SO, 34SO2, and H2O ν2 = 2, as well as several rotational lines of SiO isotopologues in vibrationally excited states. In addition, we significantly increased the number of lines detected for those molecules that were previously identified toward IK Tau. This has allowed us to deduce characteristic values of the rotational temperatures, column densities, and ultimately fractional abundances of the molecules present in its envelope. From our work we extract the following conclusions:
-
The intensity of the rotational lines of molecules in the groundvibrational state do not show a significant variability as a functionof time, for the spectral ranges that we could observe in differentepochs. The small variations found for these lines can beexplained owing to calibration or pointing uncertainties within aa 25%. We confirmed the time variability of the intensity of thelines of molecules in vibrationally excited states (e.g. SiO v = 1) by anaverage factor of 60%.
-
Most of the molecules display rotational temperatures between 15 and 40 K. NaCl and SiS isotopologues display rotational temperatures of ~65 K.
-
We detected a warm component of SO2 traced out by lines with upper energy levels between 160 and 730 K which display νexp<ν∞. This points out that SO2 is present close to the stellar surface (≲8 R∗) with an abundance of f(SO2) ~ 10-6.
-
Among the species detected, we highlight the detection of H2CO and NS for the first time in this source with abundances of f(H2CO)~ [ 10-7–10-8] and f(NS)~ 10-8. We also estimated fractional abundances for the first time detected (toward IK Tau) molecules HCO+ and NO obtaining f(HCO+) ~ 10-8 and f(NO) ~ 10-6.
-
The detection of several C-bearing species like HCN, CS, H2CO or CN with abundances of ~10-7 indicates an active carbon chemistry which is not expected given that most of the available carbon should be locked up into CO.
-
The greatest discrepancies between our results and previous chemical models are found for PO, NaCl, and SO2.
It would be necessary to obtain very high angular resolution observations to characterise the molecular emission in the inner parts of the CSE and the abundances and distribution of the molecules formed in this region. Further investigation is required to understand the nature of the discrepancies found between our derived values and chemical models, in particular, the discrepancies for S-bearing molecules and C-bearing molecules. The inclusion of photo-induced or shock-induced chemistry or maybe other processes is necessary to enhance the formation of these molecules up to values comparable to the abundances observed. Additionally, there are ~40 lines that still remain unidentified. We expect that future observations, supported by improvements in the molecular catalogues and chemical models, lead to fully understand the envelope of IK Tau and, more generally, in O-rich AGB envelopes.
GILDAS is a world-wide software to process, reduce and analyse astronomical single-dish and interferometric observations mainly. It is maintained by the Institut de Radioastronomie Millimétrique (IRAM). See http://www.iram.fr/IRAMFR/GILDAS
Acknowledgments
We acknowledge the IRAM staff for the support and help offered during all the observational runs. We acknowledge the Spanish MICINN/MINECO for funding support through grants AYA2009-07304, AYA2012-32032, the ASTROMOL Consolider project CSD2009-00038 and also the European Research Council funding support (ERC grant 610256: NANOCOSMOS). L.V.P. also acknowledges the support of the Universidad Complutense de Madrid Ph.D. programme. This research has made use of the The JPL Molecular Spectroscopy catalog, The Cologne Database for Molecular Spectroscopy, the SIMBAD database operated at CDS (Strasbourg, France), the NASA’s Astrophysics Data System, the IRAM GILDAS software, and Aladin.
References
- Alcolea, J., & Bujarrabal, V. 1992, A&A, 253, 475 [NASA ADS] [Google Scholar]
- Alcolea, J., Pardo, J. R., Bujarrabal, V., et al. 1999, A&AS, 139, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcolea, J., Bujarrabal, V., Planesas, P., et al. 2013, A&A, 559, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., & Cernicharo, J. 2006, ApJ, 650, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2007, ApJ, 662, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Guélin, M. 2010, ApJ, 724, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Fonfría, J. P., Cernicharo, J., et al. 2012, A&A, 543, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ben Abdallah, D., Najar, F., Jaidane, N., Dumouchel, F., & Lique, F. 2012, MNRAS, 419, 2441 [NASA ADS] [CrossRef] [Google Scholar]
- Bieging, J. H., & Tafalla, M. 1993, AJ, 105, 576 [NASA ADS] [CrossRef] [Google Scholar]
- Bowers, P. F., Johnston, K. J., & de Vegt, C. 1989, ApJ, 340, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bujarrabal, V., & Alcolea, J. 1991, A&A, 251, 536 [NASA ADS] [Google Scholar]
- Bujarrabal, V., Fuente, A., & Omont, A. 1994, A&A, 285, 247 [NASA ADS] [Google Scholar]
- Carter, M., Lazareff, B., Maier, D., et al. 2012, A&A, 538, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Castro-Carrizo, A., Quintana-Lacaci, G., Neri, R., et al. 2010, A&A, 523, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J. 1985, Internal IRAM report (Granada: IRAM) [Google Scholar]
- Cernicharo, J. 2012, EAS Pub. Ser., 58, 251 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Spielfiedel, A., Balança, C., et al. 2011, A&A, 531, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Teyssier, D., Quintana-Lacaci, G., et al. 2014, ApJ, 796, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., McCarthy, M. C., Gottlieb, C. A., et al. 2015, ApJ, 806, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., & Latter, W. B. 1997, MNRAS, 287, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Kress, M. E. 1995, MNRAS, 274, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Cherchneff, I. 2006, A&A, 456, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Daniel, F., Dubernet, M.-L., & Grosjean, A. 2011, A&A, 536, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., De Beck, E., Black, J. H., Olofsson, H., & Justtanont, K. 2016, A&A, 588, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dayou, F., & Balança, C. 2006, A&A, 459, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Beck, E., Kamiński, T., Patel, N. A., et al. 2013, A&A, 558, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Beck, E., Kamiński, T., Menten, K. M., et al. 2015, Why Galaxies Care about AGB Stars III: A Closer Look in Space and Time, 497, 73 [Google Scholar]
- Decin, L., Hony, S., de Koter, A., et al. 2006, A&A, 456, 549 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., De Beck, E., Brünken, S., et al. 2010a, A&A, 516, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Justtanont, K., De Beck, E., et al. 2010b, A&A, 521, L4 [Google Scholar]
- Duari, D., Cherchneff, I., & Willacy, K. 1999, A&A, 341, L47 [NASA ADS] [Google Scholar]
- Flower, D. R. 1999, MNRAS, 305, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M. C., & Bromley, S. T. 2016, A&A, 585, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., & Langer, W. D. 1999, ApJ, 517, 209 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, D., Olofsson, H., Kerschbaum, F., et al. 2003, A&A, 411, 123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, S. 1976, J. Chem. Phys., 64, 3463 [NASA ADS] [CrossRef] [Google Scholar]
- Green, S. 1979, J. Chem. Phys., 70, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H.J., & Olofsson, H. 2004, AGB Stars, A&A Library (Berlin: Springer) [Google Scholar]
- Hale, D. D. S., Bester, M., Danchi, W. C., et al. 1997, ApJ, 490, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Justtanont, K., Khouri, T., Maercker, M., et al. 2012, A&A, 537, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, H., Wyrowski, F., Menten, K. M., & Decin, L. 2010, A&A, 516, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lane, A. P., Johnston, K. J., Bowers, P. F., Spencer, J. H., & Diamond, P. J. 1987, ApJ, 323, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Li, X., Millar, T. J., Heays, A. N., et al. 2016, A&A, 588, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lindqvist, M., Nyman, L.-A., Olofsson, H., & Winnberg, A. 1988, A&A, 205, L15 [NASA ADS] [Google Scholar]
- Lindqvist, M., Olofsson, H., Winnberg, A., & Nyman, L. A. 1992, A&A, 263, 183 [NASA ADS] [Google Scholar]
- Lique, F., & Kłos, J. 2011, MNRAS, 413, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lique, F., & Spielfiedel, A. 2007, A&A, 462, 1179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lique, F., Senent, M.-L., Spielfiedel, A., & Feautrier, N. 2007, J. Chem. Phys., 126, 164312 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lucas, R., Bujarrabal, V., Guilloteau, S., et al. 1992, A&A, 262, 491 [NASA ADS] [Google Scholar]
- Lucas, R., Guélin, M., Kahane, C., Audinos, P., & Cernicharo, J. 1995, Ap&SS, 224, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Marvel, K. B. 2005, AJ, 130,261 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuura, M., Yates, J. A., Barlow, M. J., et al. 2014, MNRAS, 437, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Menten, K. M., Wyrowski, F., Alcolea, J., et al. 2010, A&A, 521, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milam, S. N., Apponi, A. J., Woolf, N. J., & Ziurys, L. M. 2007, ApJ, 668, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Halfen, D. T., Tenenbaum, E. D., et al. 2008, ApJ, 684, 618-625 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., & Olofsson, H. 1993, MNRAS, 262, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Morris, M., Gilmore, W., Palmer, P., Turner, B. E., & Zuckerman, B. 1975, ApJ, 199, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Nakashima, J.-I., & Deguchi, S. 2007, ApJ, 669, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Nejad, L. A. M., & Millar, T. J. 1988, MNRAS, 230, 79 [NASA ADS] [Google Scholar]
- Nercessian, E., Omont, A., Benayoun, J. J., & Guilloteau, S. 1989, A&A, 210, 225 [NASA ADS] [Google Scholar]
- Neri, R., Kahane, C., Lucas, R., Bujarrabal, V., & Loup, C. 1998, A&AS, 130, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neugebauer, G., Martz, D. E., & Leighton, R. B. 1965, ApJ, 142, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H. 1996, Ap&SS, 245, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H., Lindqvist, M., Nyman, L.-A., & Winnberg, A. 1998, A&A, 329, 1059 [NASA ADS] [Google Scholar]
- Omont, A., Lucas, R., Morris, M., & Guilloteau, S. 1993, A&A, 267, 490 [NASA ADS] [Google Scholar]
- Pardo, J. R., Cernicharo, J., & Serabyn, E. 2001, IEEE Trans. Antennas and Propagation, 49, 1683 [Google Scholar]
- Pesch, P. 1967, ApJ, 147, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, T. G., Huggins, P. J., Wannier, P. G., & Scoville, N. Z. 1979, ApJ, 231, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Trans. 60, 883 [Google Scholar]
- Quintana-Lacaci, G., Cernicharo, J., Agúndez, M., et al. 2016, ApJ, 818, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Ramstedt, S., & Olofsson, H. 2014, A&A, 566, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Contreras, C., Desmurs, J. F., Bujarrabal, V., Alcolea, J., & Colomer, F. 2002, A&A, 385, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez Contreras, C., Velilla, L., Alcolea, J., et al. 2014, Asymmetrical Planetary Nebulae VI Conference, 88 [Google Scholar]
- Sánchez Contreras, C., Velilla Prieto, L., Agúndez, M., et al. 2015, A&A, 577, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., Ramstedt, S., Olofsson, H., et al. 2013, A&A, 550, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, C. L., Zijlstra, A. A., & Fuller, G. A. 2015, MNRAS, 454, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P., Jefferts, K. B., Penzias, A. A., & Wilson, R. W. 1971, ApJ, 163, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Spielfiedel, A., Senent, M.-L., Dayou, F., et al. 2009, J. Chem. Phys., 131, 014305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Suh, K.-W. 1999, MNRAS, 304, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Toboła, R., Kłos, J., Lique, F., Chałasiński, G., & Alexander, M. H. 2007, A&A, 468, 1123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Toboła, R., Lique, F., Kłos, J., & Chałasiński, G. 2008, J. Phys. B At. Mol. Phys., 41, 155702 [CrossRef] [Google Scholar]
- Tsuji, T. 1973, A&A, 23, 411 [NASA ADS] [Google Scholar]
- Velilla Prieto, L., Sánchez Contreras, C., Cernicharo, J., et al. 2013, Highlights of Spanish Astrophysics VII, 676 [Google Scholar]
- Velilla Prieto, L., Sánchez Contreras, C., Cernicharo, J., et al. 2015, A&A, 575, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willacy, K., & Millar, T. J. 1997, A&A, 324, 237 [NASA ADS] [Google Scholar]
- Wing, R. F., & Lockwood, G. W. 1973, ApJ, 184, 873 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Kwok, S., & Nakashima, J.-I. 2009, ApJ, 700, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Ziurys, L. M., Milam, S. N., Apponi, A. J., & Woolf, N. J. 2007, Nature, 447, 1094 [Google Scholar]
- Ziurys, L. M., Tenenbaum, E. D., Pulliam, R. L., Woolf, N. J., & Milam, S. N. 2009, ApJ, 695, 1604 [NASA ADS] [CrossRef] [Google Scholar]
- Zuckerman, B. 1987, Astrochemistry, 120, 345 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Table of measured lines
Measured and spectroscopic parameters of the detected lines.
Line parameters for transitions that may present variability.
Appendix B: Unidentified lines
Unidentified features and, in some cases, tentative line identification.
Artifacts identified in the spectra between 167 475–174 800 MHz.
 |
Fig. B.1 Example of the artifacts (R) produced by the receivers (see Table B.2). Several symmetrical spurious replicas of the real SiO J = 4–3 line appear at both sides of it (equidistant). The intensities of the replicas decrease with the frequency distance to the real feature. |
Appendix C: IRAM-30 m survey of IK Tau
 |
Fig. C.1 Line identification of the IRAM-30 m line survey of IK Tau. We marked in red the unidentified lines (UIs) with the central frequency of the line. The lines which display time variability of their intensity are marked in blue. Image band and spurious feaures/artifacts have been blanked off (see Table B.2 and Fig. B.1) |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
 |
Fig. C.1 continued. |
Appendix D: Population diagrams
 |
Fig. D.1 Population diagrams for CO and 13CO. The results from the fit (red dashed line) are shown in each box. The emission size adopted and the dipole moment of the molecule are shown in the bottom-left corner of each box. Error bars include the formal uncertainty of the measurement and a 25% uncertainty due to flux calibration or poor baseline substraction. |
 |
Fig. D.7 As in Fig. D.1 but for H2S. We fitted simultaneously the ortho and para species adopting an ortho-to-para ratio of 3:1 (Decin et al. 2010a). The line o-H2S J,Ka, k = 41,4–32,1 significantly outlies the fit probably owing to its low S/N, therefore, it has been excluded from the diagram. |
 |
Fig. D.9 As in Fig. D.1 but for SO2 isotopologues. The rotational diagram of SO2 was separated in two different trends (see Sect. 5.2). |
 |
Fig. D.12 As in Fig. D.1 but for P-bearing molecules. The PO line Ω = 1/2, e, J,F = (11/2, 5)–(9/2, 5) significantly outlies the fit probably owing to its low S/N, therefore, it has been excluded from the diagram. |
 |
Fig. D.13 Population diagram for H2CO. We show the results from the fits of the rotational ladders Ka = 0 (red), Ka = 1 (blue), and Ka = 2 (green). For the Ka = 3 (pink) we adopted as rotational temperature the average of the rotational temperatures of the Ka = 0, 1, and 2 ladders to estimate a rough value for the Ka = 3 column density. |
Appendix E: SO2 IOS calculations
Close coupling (CC) calculations based on a state-of-the-art potential-energy surface (PES) (Spielfiedel et al. 2009) have provided collisional para- and ortho-H2 rate coefficients for temperatures ranging from 5 to 30 K for the 31 lowest SO2 rotational levels (Cernicharo et al. 2011). However, an extension of these full CC calculations to a large number of SO2 rotational levels and high temperatures would be prohibitive in terms of memory and CPU time, so the use of different approximate methods (coupled states (CS) and infinite order sudden (IOS)) is needed (Green 1976, 1979). Considering the high-J SO2 levels observed in the present work, we used the IOS approximation which is expected to give reliable estimates of rate coefficients, except for low energies. State-to-state de-excitation rate coefficients between the 410 lowest levels (with energy up to 743.9 K) were calculated for energies up to 9000 cm-1 (value limited by the validity domain of the PES) giving data for temperatures up to 1000 K Balança et al. (in prep.). The SO2 energy levels and wave functions were obtained from spectroscopic constants describing the SO2 Hamiltonian up to the fourth order and provided by the MADEX code (Cernicharo 2012). The results show a relatively flat temperature variation of the rates.
The accuracy of these data was studied by comparing the resulting rate coefficients with CC and CS values obtained for collisions with para and ortho-H2 and all transitions involving the 31 lowest levels. Compared to CC and CS data, it is found that the IOS approach leads a systematic underestimation of para-H2 rates, within a factor better than 50% in average, the agreement being better at high temperatures. However, the situation is not as good for collisions with ortho-H2 as the IOS approximation describes collisions with para-H2 (jH2 = 0) and does take into account all the angular couplings involved in collisions with ortho-H2. The comparison between ortho- and para-H2 CS rate coefficients shows that ortho-H2 rates are systematically larger than para-H2 rates by a factor two in average, with larger differences (up to a factor eight) for a number of transitions mainly identified as ΔKa = 1 transitions.
The rate coefficients were implemented in MADEX fitting the logarithm of the rate coefficients to a sixth order polynomial as: 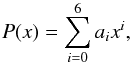 (E.1)where
(E.1)where 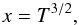 (E.2)which reproduces practically all the rates with a relative error below 30% for temperatures between 20 and 1000 K, 410 energy levels and a maximum Eu = 744 K. We provide the energy levels involved in the calculations in Table E.1, as well as the polynomial coefficients of the fit in Table E.2. The level identifier used in Table E.2 can be consulted in Table E.1 to find the corresponding level.
(E.2)which reproduces practically all the rates with a relative error below 30% for temperatures between 20 and 1000 K, 410 energy levels and a maximum Eu = 744 K. We provide the energy levels involved in the calculations in Table E.1, as well as the polynomial coefficients of the fit in Table E.2. The level identifier used in Table E.2 can be consulted in Table E.1 to find the corresponding level.
Parameters of the energy levels used for SO2 modelling.
Polynomial coefficients of the fit to the rate coefficients.
All Tables
Main parameters of the IRAM-30 m antenna measured with EMIR between 2009 and 2013 at representative frequencies.
Results from the population diagrams, sorted according to the molecular fractional abundance (relative to H2) in descending order.
Isotopic ratios obtained from the abundances derived with the population diagrams.
All Figures
 |
Fig. 1 Fit of the inverse of the main beam efficiency for the IRAM-30 m with EMIR. |
| In the text | |
 |
Fig. 2 Overall view of the survey observed with WILMA (top) and FTS (bottom). The spectral resolution is Δν = 2 MHz. |
| In the text | |
 |
Fig. 3 12CO, 13CO, and C18O lines detected with our millimeter wavelength survey with a spectral resolution of Δν = 2 MHz. The fit of each line to a function of the type given by Eq. (6) is shown in blue. |
| In the text | |
 |
Fig. 4 Representative profiles of the lines observed. From top-left to bottom-right: U-shaped, Gaussian-like, triangular, flat-topped, parabolic, complex, flat-topped, and a narrow maser-like line. The spectral resolution is Δν = 2 MHz. The fit of each line to a function of the type given by Eq. (6) is shown in blue. |
| In the text | |
 |
Fig. 5 Radial profiles of the abundance adopted for the radiative transfer model of the lines of SO2. We tested three different radial profiles: (i) an inner distribution of SO2 with f(SO2) = 3 × 10-6 between 1–8 R∗ (red line); (ii) a constant radial profile with f(SO2) = 2 × 10-6 between 8–640 R∗ (blue line); and (iii) a two component profile (green line) which includes an inner warm component plus an extended component of SO2. The results of the different models are shown in Fig. 11. |
| In the text | |
 |
Fig. 6 Graph of the rotational temperatures (orange bars) and column densities (blue bars), with their formal uncertainties (black lines), derived from the population diagrams. Vertical blue arrows are plotted to indicate column density lower limits over each corresponding molecule. The temperature scale is represented on the left vertical axis, and the column density logarithmic scale is represented on the right vertical axis. The limits of the temperature scale are different in both boxes to improve the visual aspect of the figures. The values represented are tabulated in Table 5. |
| In the text | |
 |
Fig. 7 Plot of the νexp derived from the fit of the lines as a function of the Eu of the corresponding transition for several molecules. In the top, we did not represent each error bar to improve the visualization of the figure. A typical error bar of 4 km s-1 is plotted in the top left corner of the box. The values and uncertainties of the bottom correspond to the values given in Table A.2. For those lines that were observed in different epochs, we adopted an average value of the different measurements for the νexp and its uncertainty. |
| In the text | |
 |
Fig. 8 Line stacking of the H2CO (left) and the NaCl (right) lines detected, with a spectral resolution of 2 MHz. Black spectrum correspond to the H2CO Ka = 0 lines and the NaCl lines with Eu = [22.5–56.9] K, pink spectrum correspond to the H2CO Ka = 1 lines and the NaCl lines with Eu = [85.0–118.7] K, and blue spectrum correspond to the H2CO Ka = 2 lines and the NaCl lines with Eu = [131.2–187.4] K. |
| In the text | |
 |
Fig. 9 Variability of some of the lines observed. The observation dates which correspond to the spectra are shown in the top right corner of each box with its corresponding colour. The spectral resolution is 2 MHz. As discussed in Sect. 6.1, variations of up to a 25% are within the uncertainties of the calibration, pointing and baseline substraction (i.e. left boxes). Variations of intensity higher than a 25% are observed in vibrationally excited lines or masers (i.e. right boxes). |
| In the text | |
 |
Fig. 10 Line profiles of some of the SO lines identified. The quantum numbers of each transition are plotted in red in each box.The spectral resolution is 2 MHz for all the spectra shown. |
| In the text | |
 |
Fig. 11 Results of the radiative transfer models of SO2 explained in Sects. 4.3 and 6.5.1. The coloured curves correspond to the models adopting the abundance profiles shown in Fig. 5. The spectral resolution is 2 MHz. The temperature scale is in main beam temperature. |
| In the text | |
 |
Fig. B.1 Example of the artifacts (R) produced by the receivers (see Table B.2). Several symmetrical spurious replicas of the real SiO J = 4–3 line appear at both sides of it (equidistant). The intensities of the replicas decrease with the frequency distance to the real feature. |
| In the text | |
 |
Fig. C.1 Line identification of the IRAM-30 m line survey of IK Tau. We marked in red the unidentified lines (UIs) with the central frequency of the line. The lines which display time variability of their intensity are marked in blue. Image band and spurious feaures/artifacts have been blanked off (see Table B.2 and Fig. B.1) |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. C.1 continued. |
| In the text | |
 |
Fig. D.1 Population diagrams for CO and 13CO. The results from the fit (red dashed line) are shown in each box. The emission size adopted and the dipole moment of the molecule are shown in the bottom-left corner of each box. Error bars include the formal uncertainty of the measurement and a 25% uncertainty due to flux calibration or poor baseline substraction. |
| In the text | |
 |
Fig. D.2 As in Fig. D.1 but for SiO isotopologues. |
| In the text | |
 |
Fig. D.3 As in Fig. D.1 but for HCN isotopologues. |
| In the text | |
 |
Fig. D.4 As in Fig. D.1 but for CS isotopologues. |
| In the text | |
 |
Fig. D.5 As in Fig. D.1 but for SiS isotopologues. |
| In the text | |
 |
Fig. D.6 As in Fig. D.1 but for NaCl. |
| In the text | |
 |
Fig. D.7 As in Fig. D.1 but for H2S. We fitted simultaneously the ortho and para species adopting an ortho-to-para ratio of 3:1 (Decin et al. 2010a). The line o-H2S J,Ka, k = 41,4–32,1 significantly outlies the fit probably owing to its low S/N, therefore, it has been excluded from the diagram. |
| In the text | |
 |
Fig. D.8 As in Fig. D.1 but for SO isotopologues. |
| In the text | |
 |
Fig. D.9 As in Fig. D.1 but for SO2 isotopologues. The rotational diagram of SO2 was separated in two different trends (see Sect. 5.2). |
| In the text | |
 |
Fig. D.10 As in Fig. D.1 but for CN. |
| In the text | |
 |
Fig. D.11 As in Fig. D.1 but for NS. |
| In the text | |
 |
Fig. D.12 As in Fig. D.1 but for P-bearing molecules. The PO line Ω = 1/2, e, J,F = (11/2, 5)–(9/2, 5) significantly outlies the fit probably owing to its low S/N, therefore, it has been excluded from the diagram. |
| In the text | |
 |
Fig. D.13 Population diagram for H2CO. We show the results from the fits of the rotational ladders Ka = 0 (red), Ka = 1 (blue), and Ka = 2 (green). For the Ka = 3 (pink) we adopted as rotational temperature the average of the rotational temperatures of the Ka = 0, 1, and 2 ladders to estimate a rough value for the Ka = 3 column density. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


