| Issue |
A&A
Volume 597, January 2017
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425342 | |
| Published online | 09 January 2017 | |
VIMOS Ultra-Deep Survey (VUDS): IGM transmission towards galaxies with 2.5 < z < 5.5 and the colour selection of high-redshift galaxies ⋆
1 Aix Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique de Marseille) UMR 7326, 13388 Marseille, France
e-mail: romain.thomas@lam.fr
2 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 INAF–IASF, via Bassini 15, 20133 Milano, Italy
4 INAF–Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
5 University of Bologna, Department of Physics and Astronomy (DIFA), V. le Berti Pichat 6/2, 40127 Bologna, Italy
6 INAF–IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
7 Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université Pierre et Marie Curie, 98bis boulevard Arago, 75014 Paris, France
8 Institut de Recherche en Astrophysique et Planétologie – IRAP, CNRS, Université de Toulouse, UPS-OMP, 14, avenue É. Belin, 31400 Toulouse, France
9 Department of Astronomy, University of Geneva ch. d’cogia 16, 1290 Versoix, Switzerland
10 Geneva Observatory, University of Geneva, ch. des Maillettes 51, 1290 Versoix, Switzerland
11 Centro de Estudios de Física del Cosmos de Aragón, 44001 Teruel, Spain
12 Department of Astronomy, California Institute of Technology, 1200 E. California Blvd., MC 249–17, Pasadena, CA 91125, USA
13 Astronomy Department, University of Massachusetts, Amherst, MA 01003, USA
14 Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching bei München, Germany
15 Research Center for Space and Cosmic Evolution, Ehime University, Bunkyo-cho 2-5, 790-8577 Matsuyama, Japan
16 SUPA, Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
17 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
18 Instituto de Fisica y Astronomía, Facultad de Ciencias, Universidad de Valparaíso, Gran Bretaña 1111, Playa Ancha, Valparaíso, Chile
Received: 14 November 2014
Accepted: 28 June 2016
The observed UV rest-frame spectra of distant galaxies are the result of their intrinsic emission combined with absorption along the line of sight produced by the inter-galactic medium (IGM). Here we analyse the evolution of the mean IGM transmission Tr(Lyα) and its dispersion along the line of sight for 2127 galaxies with 2.5 < z < 5.5 in the VIMOS Ultra Deep Survey (VUDS). We fitted model spectra combined with a range of IGM transmission to the galaxy spectra using the spectral fitting algorithm GOSSIP+. We used these fits to derive the mean IGM transmission towards each galaxy for several redshift slices from z = 2.5 to z = 5.5. We found that the mean IGM transmission defined as Tr(Lyα) = e− τ (with τ as the HI optical depth) is 79%, 69%, 59%, 55%, and 46% at redshifts 2.75, 3.22, 3.70, 4.23, and 4.77, respectively. We compared these results to measurements obtained from quasar lines of sight and found that the IGM transmission towards galaxies is in excellent agreement with quasar values up to redshift z ~ 4. We found tentative evidence for a higher IGM transmission at z ≥ 4 compared to results from QSOs, but a degeneracy between dust extinction and IGM prevents us from firmly concluding whether the internal dust extinction for star-forming galaxies at z > 4 takes a mean value significantly in excess of E(B−V) > 0.15. Most importantly, we found a large dispersion of IGM transmission along the lines of sight towards distant galaxies with 68% of the distribution within 10 to 17% of the median value in δz = 0.5 bins, similar to what is found on the lines of sight towards QSOs. We demonstrate that taking this broad range of IGM transmission into account is important when selecting high-redshift galaxies based on their colour properties (e.g. LBG or photometric redshiftselection) because failing to do so causes a significant incompleteness in selecting high-redshift galaxy populations. We finally discuss the observed IGM properties and speculate that the broad range of observed transmissions might be the result of cosmic variance and clustering along lines of sight. This clearly shows that the sources that cause this extinction need to be more completely modelled.
Key words: Galaxy: evolution / Galaxy: formation / galaxies: high-redshift / cosmology: observations / large-scale structure of Universe
© ESO, 2017
1. Introduction
The light coming from distant sources in the Universe is subject to increasingly higher absorption from gas clouds along the line of sight (LOS) as redshift increases. Photons from a distant source with a wavelength corresponding to the Lyman series of hydrogen at the redshift of the gas cloud are partially or totally absorbed. With many clouds along the LOS, the resulting absorption pattern is known as the Lyman-α forest. As the distance to the source is increasing, the number of gas clouds may become so high that all photons below the Lymanα-1216 Å line (hereafter, Lyα) at the source are entirely absorbed. The Lyα forest is thought to be the natural result of hierarchical structure formation within cold dark matter models (e.g. Cen et al. 1994), and is therefore a powerful probe of matter distribution in the Universe.
With a hypothesis on the distribution of gas clouds along the LOS, such as their numbers and redshift distribution N(z), it is possible to model the average transmission towards distant sources. The result is quite striking: as shown in models by Madau (1995, hereafter M95), the average transmission strongly decreases with increasing redshift and has a characteristic pattern, with several steps corresponding to the Lyman series of hydrogen, most prominently the Lyα, Lyβ, and Lyγ transitions. In his models, M95 noted the possibly wide spread in the average transmission by computing 1σ variations from the mean. At λ = 1100 Å (rest-frame), the average transmission at z = 3.5 is predicted to vary from 20% to 70% around a mean of 40%. Using simulations, Moller & Jakobsen (1990, hereafter MJ90) pointed out that the statistical dispersion on the inter-galactic medium (IGM) transmission could be very large. At z = 3.2, their simulation showed that the IGM transmission could be between 50% and 100%. The range of LOS absorption was further explored by Bershady et al. (1999) using Monte Carlo simulations of the IGM absorbers. They found that the range of possible IGM transmission was narrower than in the model of M95. Meiksin (2006, hereafter M06) produced updated IGM models using the ΛCDM model of Meiksin & White (2004) and found higher IGM transmission than M95, identified as the result of differences in the estimates of the contributions of resonant absorption. This has recently been confirmed in a model by Inoue et al. (2014).
The average IGM transmission Tr(z) has been directly estimated from Lyα forest measurements on the LOS of QSOs. The IGM transmission can be related to τeff, the HI effective optical depth, as Tr(Lyα) = e− τeff to constrain the intensity of the ionizing background (Haardt & Madau 1996; Rauch et al. 1997; Bolton et al. 2005), and is therefore used to investigate the sources responsible for this ionizing background. Songaila (2004) measured the average IGM transmission and dispersion on the LOS of 50 QSOs in 2004, and the data showed a range of transmission values around the mean. Dall’Aglio et al. (2008) used 40 bright quasars to determine the redshift evolution of the HI effective optical depth in the Lyα forest between 2.2 <z< 5 and found a good agreement with measurements based on smaller samples. Faucher-Giguère et al. (2008a) reported on the mean transmission using 86 QSOs with 2.2 <z< 4.6 and claimed to identify a departure from a power-law evolution τeff = 0.0018(1 + z)3.92 at around z ~ 3.2, which they tentatively identified as the signature of the reionization of HeII. Using 6065 QSOs from the Sloan Digital Sky Survey (SDSS), Becker et al. (2013) reported on the mean τeff over 2.2 <z< 5.5, finding no sign of a departure from a smooth evolution with redshift. Their best measurements indicate an error on the mean transmission of about ~ 1% in δz = 0.1 bins.
While the mean value of the IGM transmission is important, the dispersion around the mean is a key information as well because the properties of the IGM transmission are extensively used to pre-select galaxies and QSOs in the distant Universe. In a seminal work, Steidel and collaborators (Steidel et al. 1996) presented the Lyman-break selection method based on the Lyman-break produced by the Lyman-limit at 912 Å and its position in a three-band filter set, producing a colour difference that can easily be identified from deep photometric observations. This galaxy selection has become a standard to find large samples of galaxies, called Lyman break galaxies (LBG), from a wide range of redshifts. In addition to the 912 Å Lyman limit, this technique relies on the average IGM transmission, as the observed flux between the Lyman limit and Lyα is strongly affected by the IGM. At increasing redshifts and with increasing IGM extinction, a strong apparent continuum break builds up as the flux blueward of Lyα at the source is increasingly suppressed. This property is extensively used to identify dropout galaxies up to the highest possible redshifts (e.g. Bouwens et al. 2015, and references therein). A good knowledge of the average IGM transmission and the dispersion around the mean is then not only crucial for understanding the properties of the IGM itself, with the distribution and content of the gas clouds, but also for understanding how high-redshift galaxies are selected and how they may be missed.
Today, the knowledge of the IGM transmission is mostly provided by QSOs studies (Becker et al. 2013, and references therein) with the measurement of the optical depth τeff, and it can be predicted from simulations (MJ90, M95, M06, Inoue et al. 2014). Surprisingly, only few reports have been published on the observed dispersion in Tr(Lyα) as a function of redshift. Faucher-Giguère et al. (2008b) used 86 high-resolution quasar spectra with a high signal-to-noise ratio to provide reference measurements of the dispersion in Tr(Lyα) over 2.2 <z< 4.6. Cutting the IGM along the LOS into segments of 3 Mpc, they presented the observed Tr(Lyα) for these individual measurements, with a standard deviation of the individual 3 Mpc segments of σ(Tr(Lyα))i = 0.1−0.15. The individual Tr(Lyα) reported in Dall’Aglio et al. (2008) indicate a similar dispersion.
No observational study has been made of the evolution of the IGM transmission from galaxy samples mainly because we lack large spectroscopic samples with high signal-to-noise ratios that would probe significantly bluer than Lyα. Hence the comparison of IGM transmission towards extended galaxies with point-like QSOs has not yet been performed. In this paper we use 2127 galaxies that include the galaxies with the highest signal-to-noise ratio in the VIMOS Ultra Deep Survey (VUDS; Le Fèvre et al. 2015) to compute the mean IGM transmission and the distribution around the mean in the range 2.5 < z < 5.5. This large sample enables us to probe many different lines of sight and to characterize the statistical properties of the IGM transmission towards galaxies. We describe the VUDS galaxy sample in Sect. 2. The GOSSIP+ spectral fitting algorithm and the range of IGM templates used in the spectral fitting is described in Sect. 3. The results of the spectral fitting of the IGM transmission and dispersion are described in Sect. 4. The evolution of the Lyα effective optical depth is presented in Sect. 5. We discuss the uncertainties in measurements and models in Sect. 6. The effect of the IGM transmission dispersion on the selection of high-redshift galaxies is analysed in Sect. 7. Our results are summarized in Sect. 8.
All magnitudes are given in the AB system unless specified otherwise, and we use a cosmology with ΩM = 0.3, ΩΛ = 0.7 and h = 0.7. QSO studies often consider the redshift zα defined by 1 + zα = λ0(1 + zs) /λLyα where zs is the emission redshift of the source (e.g. Becker et al. 2013; Inoue et al. 2014). All the redshifts in our paper are given as zs and have been transformed from zα when necessary.
2. Data: the VUDS survey
The VUDS survey is described in detail in Le Fèvre et al. (2015); we provide a summary in this section. The main target selection of the survey is based on photometric redshifts with zphot + 1σ ≥ 2.4 and iAB ≤ 25, and it also includes objects whose secondary peak in the photometric redshift probability distribution function is zphot + 1σ ≥ 2.4 even if the primary peak might be very different. This primary target selection is supplemented by colour−colour selection (BzK, LBG), adding those objects that failed to satisfy the zphot criterion, but which satisfy the colour−colour selection at the corresponding redshift; this adds about 10% of the objects. Observations are performed with the VIMOS multi-slit spectrograph on the ESO-VLT (Le Fèvre et al. 2003), using the LRBLUE and LRRED grisms with a spectral resolution R ≃ 230, and integration times of ~14 h for each grism, covering a wavelength range 3650 ≤ λ ≤ 9350 Å.
Data were processed within the VIPGI environment (Scodeggio et al. 2005), and redshifts were measured with the EZ code (Garilli et al. 2010) based on cross-correlation with reference templates. The redshift measurement process includes visual inspection of all spectra by two independent observers, each making their best redshift measurement running EZ manually if necessary. These two measurements are compared in a personal meeting of the researchers to produce the final redshift measurement and associated reliability flag. All VUDS galaxies are matched to deep photometric samples existing in each of the three VUDS fields: COSMOS, ECDFS, and VVDS-02h, as described in Le Fèvre et al. (2015).
To study the absolute amount of IGM transmission in observed spectra, the UV flux has to be calibrated to better than 10% over the observed wavelength range, particularly for all wavelengths below Lyα. The relative spectrophotometry over the entire VIMOS wavelength range calibrated on reference stars is accurate to better than a few percent (Le Fèvre et al. 2003) when observations are taken at the zenith on point sources. However, by comparing the observed photometry to the photometry computed from the spectra and normalized in the i band, we observed that the spectroscopic photometry was lacking ~ 40% of the flux in the u band. This apparent lack of flux was traced back to three different processes: extinction from the Milky Way galaxy, atmospheric absorption, and atmospheric refraction. The galactic extinction is due to the presence of dust in the Milky Way. This was corrected by applying the E(B−V) maps of Schlegel et al. (1998). This correction is small (~ 7% at 4000 Å) but necessary because we compare the spectrophotometry of VIMOS spectra with broad-band photometry corrected for the Milky Way extinction. The atmospheric absorption depends on the quantity of airmass on the light path. To correct for this effect, we used the prescription of Patat et al. (2011), which is defined for the Paranal observatory. Finally, the atmosphere is equivalent to a small-angle prism before entering the telescope, and this leads to a spread of the incoming light into a small spectrum whose length depends on the airmass and parallactic angle, which is the angle of the slit to the zenithal angle. As this small pseudo-spectrum is produced before entering the spectrograph slit, a significant fraction of the flux may be lost when entering the 1 arcsec slits used for the VUDS observations. The effect is negligible beyond ~ 4500 Å observed wavelength and becomes increasingly stronger farther down in wavelength towards the UV domain. This loss was estimated and then corrected for using a geometrical model for each source based on its light moments (size, ellipticity) to compute which fraction of the flux was out of the VIMOS slit. With these corrections implemented, the magnitudes measured from the u band imaging agree to within 0.02 ± 0.3 mag with the u band magnitudes as derived from the spectra, the standard deviation being dominated by u-band photometric errors for u band magnitudes ranging up to u ~ 27.
We used the VUDS sample with redshift reliability flags 2, 3, and 4 (primary and secondary objects), the highest reliability flags as defined in Le Fèvre et al. (2015) with a confidence level of ~ 75%, 95%, and 100% for the spectroscopic redshift measurements for these three flags, respectively (see Le Fèvre et al. 2005a; 2013a, and 2015, for more details about the redshift flag system). In addition, we selected only objects whose spectra had the highest signal-to-noise ratio (S/N). We computed the S/N from the mean and 1σ standard deviation of the spectral continuum in two regions, 1345−1395 Å and 1415−1515 Å rest-frame, which were chosen to avoid emission or absorption features. We only considered galaxies whose spectra have a S/N ratio higher than 5 per pixel at z < 4 (S/N > 12 per resolution element) and higher than 3.5 at z > 4 (> 8.5 per resolution element).
The sample we used in this study contains 2127 galaxies with 2.5 <z< 5.5. This is the largest sample of galaxies with high S/N spectra covering this redshift range.
3. Measuring the IGM transmission with spectral fitting
3.1. IGM transmission measurements
Several methods have been used to measure the IGM transmission using the mean transmitted flux F(z) from quasar spectra. The measurement of F(z) can be performed by fitting a power law representative of a quasar spectrum on regions redward of the Lyα emission and free of emission or absorption features, as applied at the highest redshifts z> 5 (Songaila 2004; Fan et al. 2006; Becker et al. 2007). The power law is then extrapolated blueward of the Lyα line, and the transmission is the result of the ratio between the power law and the QSO spectrum in the region 1070−1170 Å . With medium-resolution spectroscopy, several methods have been applied, including the fit of individual quasars using principal component analysis (PCA; e.g. Pâris et al. 2011) or with bias corrections estimated from model spectra (Dall’Aglio et al. 2008). At high spectral resolution R ~ 30 000−40 000, the IGM transmission is expected to reach 100% for a sufficient number of spectral resolution elements so that the quasar continuum can be estimated (e.g. Faucher-Giguère et al. 2008a,b; Dall’Aglio et al. 2008; Becker et al. 2011). Faucher-Giguère et al. (2008a,b) applied statistical corrections to the continua as a function of redshift based on artificial spectra drawn from hydrodynamic simulations. Another powerful method is to use composite quasar spectra to directly estimate the IGM transmission with continuum measurements; this was applied by Becker et al. (2013).
Working with a faint galaxy sample observed at low spectral resolution, we have opted to measure the Lyα transmission from a model fit of the observed spectra. Figure 1 presents the method we adopted. The best-fit spectrum is produced from a χ2 minimisation on models built from combining stellar population synthesis models, dust extinction, and IGM transmission spectrum templates. The IGM transmission is then measured directly on the IGM template that has been selected for the best fit (as described in the next section). The transmission is computed shortward of the Lyα line in the wavelength range 1070 ≤ λ ≤ 1170 Å as measured on the IGM template. This wavelength range avoids immediate proximity effects of the circum-galactic medium (CGM) in the vicinity of the galaxy itself.
 |
Fig. 1 Method adopted for the IGM transmission measurement when fitting VUDS galaxy spectra. The observed spectrum (here a stack with a high signal-to-noise ratio from VUDS galaxies at z ~ 3.4) is presented in black. The best-fit model (see Sect. 3.2) resulting from the combination of a stellar population synthesis model, dust extinction, and IGM transmission is plotted in red. The same stellar population synthesis model with dust but without the IGM transmission applied is shown in blue. The IGM template selected for the best fit is presented in green (the value of the transmission is given on the right y-axis). The IGM transmission is then the average transmission in the wavelength range 1070 ≤ λ ≤ 1170 Å (vertical dashed lines) as measured directly on the IGM template selected in the best fit. |
3.2. Spectral fitting software: GOSSIP+
The galaxy observed-simulated SED interactive program (GOSSIP, Franzetti et al. 2008) is a software created to fit the spectrophotometric flux of galaxies, including spectra, against a set of synthetic models, and was born in the framework of previous large galaxy surveys such as the VVDS (Le Fèvre et al. 2005a). The aim is to find the model galaxy that best reproduces the observed data, using spectra, photometric magnitudes, or both together, making it a unique tool. The result of the fit can be used to estimate a number of physical parameters such as the star formation rate (SFR), age, or stellar mass of the observed galaxy by computing their probability distribution function (PDF). GOSSIP correlates spectra and spectral energy distributions (SED) with model spectra covering ranges of ages, metallicities, dust extinctions E(B−V), and star formation histories (SFH). The range of models used in this study is presented in Table 1 and is discussed in Sect. 4. The model spectra are computed from current galaxy population synthesis models: BC03 (Bruzual & Charlot 2003) and M05 (Maraston 2005). An object SED and/or spectrum is cross-correlated against all model spectra, and the best model is identified by means of the best reduced χ2. The new upgraded version of the software, GOSSIP+ that we used in this paper has been developed with new functionalities and will be described in detail in a forthcoming paper (Thomas et al., in prep). For the purpose of the present paper, the main improvement included in GOSSIP is related to the treatment of the IGM. While most of the SED-fitting programs use the M95 prescription, which gives a single IGM transmission curve as a function of wavelength for a given redshift, GOSSIP can choose at each redshift among seven different IGM curves with different IGM transmission, as presented in the next section. This allows us to choose among different possible transmission curves, and hence enables identifying IGM values that deviate from the mean transmission when the IGM transmission indeed varies.
3.3. IGM transmission templates
The flux we observe from distant galaxies is the result of two distinct sets of processes: emission and absorption from the galaxy itself and its immediate surroundings in the CGM, and absorption from H i clouds located between the observer and the galaxy. The latter is the result of gas clouds along the LOS that absorb the light blueward of the Lyα line at 1216 Å. The models used to reproduce this effect exhibit several differences: M95 is based on an empirical model that uses a Poissonian distribution for the Lyα forest (with a fixed Doppler parameter). M06 is based on ΛCDM cosmological simulations from which the Lyα forest number density as well as the Doppler parameter are derived (Meiksin & White 2004). Comparing these models to observations along the LOS of QSOs, M95 predicted a transmission too low to reproduce the observed IGM attenuation, while M06 agreed better with observations (e.g. Inoue et al. 2014). In this paper, we base our spectral fitting on M06, augmented by the possibility of using a range of seven different transmission templates at any given redshift, and we refer to M06 for a detailed comparison between the models of M06 and M95.
M95 and M06 both produce a single attenuation curve for a given redshift. This is equivalent to saying that at a given redshift all LOS towards distant objects are populated by the same number of gaseous clouds with similar properties, producing the same transmission independently of the position of the observed galaxy or QSO in the sky. As quoted by M95, this is not expected to be the case because of the way absorbing clouds are distributed along the LOS, but experimental measurements of the transmission dispersion are scarce in the literature, and this point remains open. It is also unclear whether the covering factor of clouds along the LOS would affect the flux transmission in the same way for a point-source QSO or for an extended galaxy. Because of these uncertainties, we allowed the IGM to vary in our SED/spectra fitting prescription to enable measuring the transmission scatter. This adds an extra free parameter in the SED or spectral fitting.
To test variations in the IGM transmission, we constructed IGM templates probing a range of transmissions around the mean IGM of M06. The range of possible transmission was set using the ± 1σ range of IGM transmission from M95 (see their Fig. 3a at z = 3.5). To better probe this range, we added transmission templates computed from the ± 0.5σ and the ± 1.5σ around the mean. It is important to note that our IGM templates are defined to probe a wide range of IGM transmission, independently of whether the ± 1σ model values of M95 are correct. Our logic was to use templates that reproduce the wavelength dependence of the IGM transmission reasonably well, whether the transmission is high or low (even if some of our templates might be unphysical when saturating to a transmission of one at z ~ 3). The fitting process is then free to choose which of the IGM templates best reproduces each observed galaxy spectrum, in combination with all other model parameters. We note that at the spectral resolution R ~ 230 of our observations we can measure the IGM transmission averaged in 1070−1170 Å, but not the transmission from individual cloud absorption lines. This average transmission is then best reproduced by models like those of M95 or M06, which are in effect an average over many lines of sight, and extending the IGM templates with a range of transmissions around the mean models.
GOSSIP+ calculated the seven IGM templates using the transformation described above for each galaxy depending on its redshift, and these templates were then used in the fitting process for that galaxy. The sets of templates allowed in our study at z = 3.0, z = 4.0 and z = 5.0 (based on M06 models) are shown in Fig. 2. Each template is identified by an identification number (hereafter id) 0, ± 1, ± 2, and ± 3 (middle panel). The id = 0 (red curve) is the M06 mean IGM transmission curve. The id ranges from −3 (smallest transmission; −1.5σ) to + 3 (highest transmission; + 1.5σ). The range of IGM transmission is broad at any redshift and allowed us to explore the dispersion around the mean. With our adopted templates the IGM transmission at 1100 Å may vary from 19% to 100% at z = 3.0 and from 5% to 50% at z = 5.0.
In summary, the spectral fitting procedure with GOSSIP+ allowed us to consider very different average IGM transmissions along the lines of sight from one spectrum to another, as the fitting algorithm tested each galaxy model with all of the seven IGM transmission templates.
 |
Fig. 2 Seven IGM transmission templates used in this work at z = 3.0, z = 4.0, and z = 5.0. The mean M06 IGM transmission is represented by the dashed red line. The ± 0.5σ, ± 1.0σ, and ± 1.5σ curves are the six black curves of different thickness. The thicker lines represent ± 1.5σ. |
3.4. Simulation of spectra: ability of recovering the line-of-sight integrated IGM transmission
We performed extensive spectral fit simulations to test the ability of GOSSIP+ to retrieve the IGM transmission. To be representative of our galaxies, we simulated 50 times each 3-tuple (redshift, iAB, S/N) that we have in our sample of 2127 galaxies. In our data the redshift ranges from 2.5 to 5.5, the S/N per resolution element ranges from 5 to 25 (at z< 4) and from 3.5 to 10 (at z> 4), the magnitude iAB varies from 22 to 25. The final sample of mock galaxies was then populated by almost 108 000 objects. Each mock galaxy was based on a galaxy model randomly chosen from a BC03 model library composed of a wide range of model parameters. The E(B−V) extinction ranged from 0 to 0.5. The metallicity was chosen in the range Z = [0.004,0.05]. The star formation history was a delayed exponential (see Sect. 4) with a timescale that ranged from 0.1 to 1.0 Gyr. Ages were limited by the age of the Universe at the given redshift and for the selected cosmology. We randomly used an IGM transmission spectrum chosen among 30 different IGM transmission templates at a given redshift built from the average transmission in M06, as presented in Fig. 3. Each model spectrum was multiplied by one of these 30 IGM templates, selected randomly. The Poisson noise was then added to the data as the square root of the simulated flux.
 |
Fig. 3 Thirty IGM transmission templates available to make the mock galaxies at z = 3.5 (as an example of the simulation process). At this redshift, one of these template is chosen randomly and applied to the galaxy template. In red we plot the seven IGM templates used in GOSSIP+ to perform the fit and verify whether the simulated IGM can be recovered. |
The synthetic galaxies were then fitted with GOSSIP+, using the seven IGM templates as defined in Sect. 3.3. As for the data, we ignored emission line regions for the fit (Lyα). Since we created those mock galaxies with BC03 templates, we chose to fit the model spectra using a library computed from the M05 synthesis models (the results still hold when fitting with BC03). This library was computed with an exponentially delayed SFH with a timescale that ranges from 0.1 to 1.0 Gyr (with a step of 0.1 Gyr), E(B−V) can take values in [0.0, 0.05, 0.1, 0.2, 0.3, 0.4, 0.5], and the metallicity ranges from Z = 0.001 to Z = 0.04. This library was computed with a Chabrier initial mass function (IMF, Chabrier 2003).
The relation between the simulated transmission and the transmission obtained by the fitting process is given by ΔTr(Lyα)/Tr(Lyα)input defined as 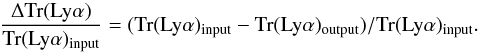 (1)The results of the simulation on this quantity is presented in Fig. 4, representing the accuracy of GOSSIP+ in retrieving the correct Tr(Lyα) as a function of redshift for galaxies with a similar range of properties as in the VUDS sample. For the whole simulated sample ΔTr(Lyα)/Tr(Lyα)input = −0.01 ± 0.09. The ΔTr(Lyα)/Tr(Lyα)input ranges from −0.08 ± 0.11 at z = 2.75 to −0.07 ± 0.05 at z = 4.8. There is therefore very little deviation from the mean, and this shows that GOSSIP+ can retrieve the correct Lyα transmission at all redshifts and over the spectral S/N considered in this study. Additionally, we note that the dispersion on the quantity ΔTr(Lyα) = Tr(Lyα)input−Tr(Lyα)output decreases with redshift, most likely the result of a larger Lyα dropout break at the higher redshifts and stronger IGM features, which results in easier retrieval in the fitting process. The influence of this IGM prescription on other physical parameters when fitting spectra/SED will be fully discussed in a forthcoming paper (Thomas et al., in prep.).
(1)The results of the simulation on this quantity is presented in Fig. 4, representing the accuracy of GOSSIP+ in retrieving the correct Tr(Lyα) as a function of redshift for galaxies with a similar range of properties as in the VUDS sample. For the whole simulated sample ΔTr(Lyα)/Tr(Lyα)input = −0.01 ± 0.09. The ΔTr(Lyα)/Tr(Lyα)input ranges from −0.08 ± 0.11 at z = 2.75 to −0.07 ± 0.05 at z = 4.8. There is therefore very little deviation from the mean, and this shows that GOSSIP+ can retrieve the correct Lyα transmission at all redshifts and over the spectral S/N considered in this study. Additionally, we note that the dispersion on the quantity ΔTr(Lyα) = Tr(Lyα)input−Tr(Lyα)output decreases with redshift, most likely the result of a larger Lyα dropout break at the higher redshifts and stronger IGM features, which results in easier retrieval in the fitting process. The influence of this IGM prescription on other physical parameters when fitting spectra/SED will be fully discussed in a forthcoming paper (Thomas et al., in prep.).
 |
Fig. 4 Evolution of the difference in transmission ΔTr(Lyα)/Tr(Lyα) with redshift between the input simulated spectra and the result of the fit with GOSSIP+. |
3.5. Lyα forest simulation vs. IGM templates
In addition to the simulation we ran in the previous section, we ran a simulation where the input Lyα transmission was different from the IGM transmission templates used in the GOSSIP+ fit, therefore testing possible circular arguments.
We used mock cosmological simulations of the Lyα forest with known line-of-sight integrated IGM transmission to test the ability of our method to recover the IGM transmission of realistic spectra. The mock IGM transmission skewers were taken from the BOSS DR11 public mock catalogue simulating the Lymanα forest (Font-Ribera et al. 2011; Bautista et al. 2015). We created 5025 mock galaxies, following the same method as described in the previous section, but randomly drawing IGM transmissions from this mock set. The redshifts of simulated galaxies are distributed between z = 2.8 and z = 3.5, the latter being the high-redshift limit of the mock catalogue.
 |
Fig. 5 Three examples of Lyα skewers at z = 2.936, z = 3.287, and z = 3.49. In each plot, the black spectrum represents the high spectral resolution BOSS DR11 mock IGM transmission, while the same spectrum in red is degraded to the VUDS lower resolution. The blue lines in each panel represent the wavelength interval where the Lyα transmission is estimated (1070−1170 Å). |
We used the same library for stellar emission and dust extinction as for the simulation in Sect. 3.4, but the IGM transmission was now one of the BOSS DR11 Lyα transmission skewers, Gaussian smoothed to the lower resolution of VUDS. Three examples of such skewers are presented in Fig. 5. Each skewer in our Lyα Forest sample includes a large number of absorbing clouds, including high-column density absorbers, which become hard to identify individually at the VUDS resolution. The simulated spectra were then fitted with GOSSIP+ to identify which of the seven reference IGM templates defined in Sect. 3.3 best reproduces the integrated line-of-sight IGM transmission.
The comparison of the Lyα transmission from the input simulated Lyα forest transmission and the transmission recovered from the GOSSIP+ fit with the seven IGM templates is presented in Fig. 6. This figure shows that our galaxy template fitting is able to provide an excellent estimate of the Lyα transmission, even when the input IGM is a realistic Lyα forest simulation. The difference between the input Lyα transmission, Tr(Lyα)Forest, and the transmission as recovered by the GOSSIP+ method, Tr(Lyα)fit, has a mean value of 0.013 (and a median of 0.002), while the standard deviation is of 0.13 (and the error on the mean is ~ 10-4).
Based on this realistic simulation, we conclude that the method developed in this paper is able to estimate the LOS integrated Lyα transmission towards distant faint galaxies very reliably.
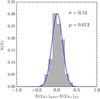 |
Fig. 6 Comparison of the Lyα transmission from the input mock Lyα forest and the output IGM template selected by GOSSIP+. In red we plot the distribution of the difference Tr(Lyα)Forest-Tr(Lyα)fit. The blue line is a Gaussian fit of the red histogram where μ = 0.013 and σ = 0.13. |
4. Evolution of the mean IGM transmission and its dispersion as a function of redshift
Here we present the IGM transmission obtained from the fit of VUDS galaxy spectra with redshifts between z = 2.5 and z = 5.5, with the selection as described in Sect. 2 and using GOSSIP+ as discussed in Sect. 3.2. Since we combined the IGM transmission templates with different galaxy models, we expect the results to be as independent of stellar population synthesis models as possible. We ran GOSSIP+ twice, using both a BC03 model library and a library computed with M05 models. The large parameter space explored during the fitting process is summarized in Table 1.
Parameter space used for the spectral fitting, using existing BC03 and M05 stellar population models.
The star formation history used in this study is a delayed exponential. It is defined as 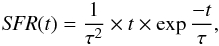 (2)where τ is the SFH timescale. It corresponds to the time after which the SFR is highest. A range of τ from 0.1 to 1.0 Gyr allows us to produce very different SFHs, from a fast-rising star formation rate to an early peak in star formation followed by a rapid decrease, to a more extended period of almost continuous star formation. We used the initial mass function (IMF) of Chabrier (2003). The dust extinction was applied through the value of E(B−V) using the Calzetti et al. (2000) law. As our model spectra did not include emission lines, the wavelength domain around known emission lines in the observed spectra were ignored in the fitting process.
(2)where τ is the SFH timescale. It corresponds to the time after which the SFR is highest. A range of τ from 0.1 to 1.0 Gyr allows us to produce very different SFHs, from a fast-rising star formation rate to an early peak in star formation followed by a rapid decrease, to a more extended period of almost continuous star formation. We used the initial mass function (IMF) of Chabrier (2003). The dust extinction was applied through the value of E(B−V) using the Calzetti et al. (2000) law. As our model spectra did not include emission lines, the wavelength domain around known emission lines in the observed spectra were ignored in the fitting process.
Figure 7 presents the results of spectral fitting for ten representative objects at different redshifts between z = 2.5 and z = 5.5. For four of them, the fit locks on an IGM identical to the mean IGM. For the other six, GOSSIP+ identifies an IGM transmission different from the mean.
 |
Fig. 7 Example of spectral fitting for ten representative galaxies in the VUDS sample, using the BC03 model spectra. The IGM “id” (cf. Sect. 2) and the redshift of the galaxy are indicated for each fit. The best fit obtained with our prescription of varying the IGM transmission is shown in red, while the best fit with the IGM transmission set to the mean M06 value is shown in blue for comparison (the E(B−V) dust extinction is reported for both). For four objects the best fit finds an IGM equal to the mean, while for the six others GOSSIP+ selects an IGM template different from the mean. |
We performed the fit with GOSSIP+ for all 2127 galaxies in the VUDS sample described in Sect. 2. Measurements of the median IGM transmission are presented in Table 2 and in Figs. 8 and 9. The dispersion around the median is computed as the value including 68% of the full sample in each redshift bin. Figure 8 shows the distribution of Tr(Lyα) in five redshift bins from z = 2.5 to z = 5.5. Tr(Lyα) is computed on the IGM templates obtained from the GOSSIP+ fit for each VUDS galaxy. As shown in Fig. 8, there are no significant differences between the distribution of transmission observed for the most reliable flags 3 and 4 in our sample compared to flag 2 with its lower reliability. We note that the use of BC03 or M05 templates in the fitting process provides indistinguishable results on measured IGM properties at any redshift. This effect is expected because the main difference between BC03 and M05 is the treatment of TP-AGB stars that influence the red part of the model spectra. The median and mean transmission values are nearly identical in our sample. In the following we use mean transmission or median transmission to mean the same. A wide range of IGM transmission is observed at all redshifts.
Median IGM transmission and dispersion around the median as observed from the VUDS spectra fitting.
As expected, the mean IGM transmission decreases with redshift (Fig. 9). This is the first time this is clearly demonstrated from galaxy spectra. The IGM transmission derived from VUDS galaxy spectra agrees remarkably well with the mean transmission in the IGM model of M06 up to z = 4. At a redshift z > 4 we find tentative evidence that the median IGM transmission is slightly higher than expected from the M06 model. The difference in transmission between the observed and theoretical model is ΔTr(Lyα) = 0.03 at 4.0 < z < 4.5 and reaches ΔTr(Lyα) = 0.09 at 4.5 < z < 5.5 (corresponding to ~18% of the theoretical value). Whether this is a real physical result or the result of a degeneracy between IGM transmission and dust internal to the galaxies is further discussed in Sect. 6.2. We report in Fig. 9 IGM transmission values obtained for two different dust extinction conditions with dust extinction limited to E(B−V) ≤ 0.15 and E(B−V) ≤ 0.05 in the fitting process.
The other important result from our study is the high dispersion of Tr(Lyα) observed for all redshifts in the range we explored. To compute the dispersion in IGM transmission, we corrected the observed dispersion in quadrature for the dispersion resulting from our fitting method. The latter was derived from the simulations presented in Sect. 3.4 for spectra with a S/N in the range of the VUDS spectra. The resulting transmission dispersion is found to be high, with a slow decrease with increasing redshift. It ranges from σ ~ 0.18 at redshift 2.8 to σ ~ 0.10 at redshift 4.8. We stress that these are effective 1σ values, and we observe that all seven IGM templates covering the range ± 1.5σ allowed in the fitting were used at any redshift. We find that in 72% (fitting with BC03 templates) and 75% (with M05) of the cases GOSSIP+ choose one of the six additional transmission curves. The observed variation in Tr(Lyα) is large enough to require a wide range of IGM variation when fitting the spectra or SED of galaxies as well as in colour−colour selection of galaxies (see Sect. 7).
 |
Fig. 8 IGM transmission Tr(Lyα) measured from 2127 VUDS galaxies in increasing redshift bins from z = 2.5 to z = 5.5. The black vertical lines represent the median of the distributions in each redshift bin. A wide spread in transmission is observed at all redshifts. The red shaded histograms include all galaxies with flags 2, 3, and 4, while the white striped histograms only represent flag 2. No significant difference is found between the IGM properties of flags 3 and 4 and flag 2. The distribution of IGM transmission is somewhat discretized because of the seven IGM templates used in the spectral fitting. The median and dispersion values measured by Faucher-Giguère et al. (2008b) using QSOs are represented by the blue distribution in each redshift bin. The median values from VUDS galaxies are in excellent agreement with Faucher-Giguère et al. (2008b) for z < 4, while the VUDS results seem to show higher transmission at z > 4 (see text for a discussion). The dispersion values are also in excellent agreement at all redshifts. |
 |
Fig. 9 Median IGM transmission Tr(Lyα) derived from the LOS towards 2127 VUDS galaxies (full red circles). IGM transmission values are computed from the distribution of IGM transmission measurements resulting from the fit with GOSSIP+, in redshift bins δz = 0.5 at a mean redshifts 2.75, 3.25, 3.75, and 4.25 and in a redshift bin δz = 0.8 at z = 4.8, and using a dust extinction limit E(B−V) ≤ 0.15. The error bars represent the 68% interval in the distribution of IGM transmission values as measured from the 2127 LOS probed by the VUDS galaxies. The empty red circles at z > 4 represent the measurements obtained when setting the dust extinction limit to E(B−V) ≤ 0.05. The blue triangles and associated error bars are median transmission and 1σ dispersion values taken from Faucher-Giguère et al. (2008b). At z > 4, points have been artificially shifted in redshift for clarity. |
IGM transmission studies from QSOs often quote the error on the mean 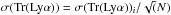 where N is the number of independent measurements. Faucher-Giguère et al. (2008a) found σ(Tr(Lyα)) ~ 0.008% at z = 3 and ~ 1% at z = 4 in redshift bins δz = 0.2, while Becker et al. (2013) quoted about 1% in δz = 0.1 bins. Only a few studies have reported the dispersion around the mean IGM transmission. Faucher-Giguère et al. (2008b) presented the distribution in transmission from z = 2.2 to z = 4.6 and derived a dispersion ranging from σ = 0.11 to 0.15 in δz = 0.2 bins. Songaila (2004) measured the IGM transmission from 50 high-redshift quasars and its evolution with redshift. They stated a transmitted fraction ranging from 46% to 90% between z = 2.5 and z = 3.5, and from 20% to 80% between z = 3.5 and z = 4.5, a range similar to Faucher-Giguère et al. (2008b) and our VUDS measurements.
where N is the number of independent measurements. Faucher-Giguère et al. (2008a) found σ(Tr(Lyα)) ~ 0.008% at z = 3 and ~ 1% at z = 4 in redshift bins δz = 0.2, while Becker et al. (2013) quoted about 1% in δz = 0.1 bins. Only a few studies have reported the dispersion around the mean IGM transmission. Faucher-Giguère et al. (2008b) presented the distribution in transmission from z = 2.2 to z = 4.6 and derived a dispersion ranging from σ = 0.11 to 0.15 in δz = 0.2 bins. Songaila (2004) measured the IGM transmission from 50 high-redshift quasars and its evolution with redshift. They stated a transmitted fraction ranging from 46% to 90% between z = 2.5 and z = 3.5, and from 20% to 80% between z = 3.5 and z = 4.5, a range similar to Faucher-Giguère et al. (2008b) and our VUDS measurements.
The dispersion derived by Faucher-Giguère et al. (2008b) was based on breaking up the part of the same QSO spectrum affected by the IGM into segments of 3 h-1 Mpc along the LOS and measuring the dispersion among these from different LOS to emulate a large number of independent measurements. The dispersion measurements on VUDS galaxies were made in the wavelength domain 1070−1170 Å, corresponding to a scale of about 70 h-1 Mpc at z ~ 3.5. As the sizes of IGM absorbers are thought to have remained roughly constant with time and smaller than 100 h-1 kpc (Cen 2012), much smaller than 3 h-1 Mpc, our measurements should be directly comparable to those of Faucher-Giguère et al. (2008b). To compare dispersion values, we also need to use the same redshift bins because part of the dispersion stems from the evolution in the transmission itself, changing by 5−10% over δz = 0.5 for the redshift range considered. Using the δz = 0.2 values from Faucher-Giguère et al. (2008b), we find that the dispersion from their data in δz = 0.5 is increased by about 20%, resulting in even better agreement of our dispersion measurements. Although working with smaller samples, the reverse is also verified when computing the dispersion in δz = 0.2 bins: we find a dispersion similar to that of Faucher-Giguère et al. (2008b). We therefore conclude that the dispersion observed in our data on galaxies is in excellent agreement with the dispersion found along the LOS of QSOs and reflects the intrinsic properties of the IGM.
We plot in Fig. 10 the average of 60 spectra with the highest IGM transmission (Tr(Lyα) ≥ Tr(Lyα)mean + 1σ) and 53 spectra with the lowest IGM transmission (Tr(Lyα) ≤ Tr(Lyα)mean−1σ), compared to the mean spectrum, for galaxies with 3.2 ≤ z ≤ 3.8 (and with the highest reliability flags 3 and 4). The spectra are normalized to the same continuum value redward of Lyα (in the range free of strong lines between 1345–1395 and 1415−1515 Å). The difference observed between galaxies with IGM transmission measured at ± 1σ from the mean and the mean spectrum of the full sample is quite striking and provides further support to the observed range in IGM transmission reported above. The stacked spectrum of the full sample and spectra at ± 1σ from the mean agree within errors in slope or in absorption lines strengths. This shows that stellar populations at the source emission are very similar, lending additional support that the IGM and not the source properties are responsible for the observed spectral differences below Lyα. The only notable difference is the strength of the Lyα emission line, with equivalent width EW(Lyα) = 16 Å for high IGM transmission spectra and EW(Lyα) = 10 Å for low-transmission spectra. This difference might further indicate that Lyα photons are more absorbed by the CGM of the galaxy in the latter case.
 |
Fig. 10 Average (stacked) spectra for VUDS galaxies with 3.2 ≤ z ≤ 3.8 (zmed = 3.4) for which GOSSIP+ identifies an IGM transmission ≥ 1σ above (golden spectrum) and below (green spectrum) the mean IGM transmission of M06. The average VUDS spectrum over all galaxies in the sample is shown as the black shaded-grey spectrum. All three spectra are normalized in the range 1400 <λ< 1510 Å. |
5. Evolution of the Lyα effective optical depth
The mean IGM transmission is related to the HI effective optical depth, τeff(z), by 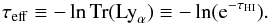 (3)We obtained the evolution of τeff with redshift (Fig. 11). This was compared with τeff derived from QSO spectra as there is no measurement derived from galaxy spectra in the literature. Our measurements from z = 2.5 to z = 4 are in excellent agreement with the mean τeff reported in the literature for samples with large numbers of QSOs (left panel of Fig. 11, e.g. Becker et al. 2013; Faucher-Giguère et al. 2008a; Dall’Aglio et al. ( 2008). This agreement is quite remarkable, considering that we used a sample of faint galaxies to derive the optical depth. This result therefore further validates our method of treating the IGM as a free parameter in the fitting.
(3)We obtained the evolution of τeff with redshift (Fig. 11). This was compared with τeff derived from QSO spectra as there is no measurement derived from galaxy spectra in the literature. Our measurements from z = 2.5 to z = 4 are in excellent agreement with the mean τeff reported in the literature for samples with large numbers of QSOs (left panel of Fig. 11, e.g. Becker et al. 2013; Faucher-Giguère et al. 2008a; Dall’Aglio et al. ( 2008). This agreement is quite remarkable, considering that we used a sample of faint galaxies to derive the optical depth. This result therefore further validates our method of treating the IGM as a free parameter in the fitting.
Our highest redshift measurements at z = 4.2 and z = 4.75 present a lower optical depth than those of M06. This is due to the high IGM transmission reported in Sect. 4. At these redshifts the IGM transmission values are somewhat degenerate with the dust extinction in galaxies as discussed in Sect. 6.2. Therefore, we present the IGM transmission values obtained in the case when the E(B−V) extinction at the source is let free to vary up to E(B−V) = 0.15, as well as transmission values obtained for E(B−V) ≤ 0.05. In this latter case, the IGM transmission is significantly lower and becomes compatible with QSO measurements and models within measurement errors as shown in Fig. 11. This is further discussed in Sect. 6.2.
We fit our data with a power law of the form τeff = C × (1 + z)γ , which is generally used in the literature to reproduce the evolution of τeff. The fit is presented in the right panel of Fig. 11. Our mean optical depth increases, following a power law with 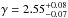 and
and 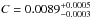 . We also display as comparison the models from M06, M95, and Inoue et al. (2014).
. We also display as comparison the models from M06, M95, and Inoue et al. (2014).
 |
Fig. 11 Left panel: the HI optical depth τeff as computed from the measured IGM transmission in the VUDS galaxy data (red filled circles for E(B−V) ≤ 0.15 and empty red circles for E(B−V) ≤ 0.05). The error bars on τeff represent the error on the mean (defined as |
6. Uncertainties in observations and models
6.1. Possible observational biases at z > 4
While the IGM transmission that we find in 2.5 <z< 4.0 is in excellent agreement with QSO measurements and the latest models from M06 and Inoue et al. (2014), we need to understand whether the higher transmission values we find at z> 4 are physical measurements or the result of some uncertainty or bias in our data or methods.
As presented in Sect. 2, VUDS galaxies were selected mainly using their photometric redshift. Photometric redshifts were computed with the code LePhare (Ilbert et al. 2006; 2009), which uses the M95 prescription with a single mean IGM transmission at a given redshift. Therefore this selection is expected to preferably select galaxies with the M95 IGM transmission. As the M95 transmission is somewhat lower than is observed from QSOs or the more recent simulations of M06 and Inoue et al. (2014), the photometric selection with Le Phare and the M95 IGM transmission would result in a sample bias, if any, towards galaxies with a lower transmission on their LOS than observed from QSOs. Our highest redshift data points at z = 4.2 and z = 4.8 seem to indicate a higher transmission, a trend opposite to what would be expected from our photometric redshift selection. If any such bias existed, correcting it would further increase the difference between the observed mean and the model M06 mean. Therefore, it is likely that our data are not affected by this type of bias.
As described in Sect. 2, the VIMOS spectra are corrected for atmospheric extinction and refraction (in addition to galactic extinction, which is negligible for the effects discussed here). The highest flux correction applied to spectra is ~60% at 3800 Å, while it is lower than 25% at 4500 Å and lower than 10% at 5500 Å. The mean distribution of the corrected spectroscopic fluxes agrees with the fluxes obtained from the multi-band photometry within 2% (Sect. 2), with a 1σ standard deviation lower than 5% in the u band when corrected with the magnitude errors for faint magnitudes u< 25 in this band. This is further confirmed with the brighter g-band magnitudes where 1σ < 2%. These values are significantly lower than the IGM transmission dispersion of ~ 15% observed in our data. Furthermore, spectral flux calibration corrections mainly affect the u-band and would therefore affect the IGM transmission measurements for a redshift z ~ 2.5, while residual errors in g-band corrections would affect measurements for z < 3.0. These small residual instrumental calibration errors are unlikely to have an effect on the measured IGM transmission dispersion.
Another possible observational bias is that the spectra of galaxies with the lowest IGM transmission are most likely in our high S/N sample because the break produced in the spectrum is easier to identify when measuring the spectroscopic redshifts of these distant galaxies. This would create a distribution skewed towards low-transmission systems, which is again the opposite to what is observed in our data at z > 4. We note that we used the LOS towards 43 high S/N galaxies at z ~ 4.8, therefore the sample is still small and subject to cosmic variance. More LOS will need to be observed to confirm the trend for observed higher transmission compared to models at z > 4.
It is also important to note that the IGM transmission in our sample is computed from extended galaxies and not from point-like QSOs. This is further discussed in Sect. 6.3.
6.2. Dust versus IGM at z > 4
The other main parameter that affects the fit in the UV part of the spectra in addition to IGM transmission is dust extinction internal to the galaxies. A possible way to compensate for a change in the IGM transmission is to change the dust content of the galaxy: if the IGM transmission is higher (lower), then the dust extinction would need to be higher (lower) in the best fit.
At z < 4 we computed the E(B−V) values from the spectral fitting using a limit of E(B−V) = 0.5 and obtained a mean value of E(B−V) = 0.12 at z ~ 3. This is in agreement with Cucciati et al. (2012), who found E(B−V) = 0.14 at z = 3.0, and Shapley et al. (2003), who reported E(B−V) in the range 0−0.2. At z> 4, we computed our E(B−V) with a limit of E(B−V) = 0.15, as presented in Sect. 4. We found a mean E(B−V) of 0.12 for these galaxies. At z ~ 4 Tresse et al. (2007) and Cucciati et al. (2012) reported a mean E(B−V) ~ 0.05−0.1, somewhat lower than Ouchi et al. (2004), who computed E(B−V) ~ 0.15 at z = 4.7. At even higher redshifts, Bouwens et al. (2013) reported E(B−V) < 0.02−0.03. The E(B−V) is poorly constrained from the fit of a UV-rest spectrum, therefore we used the E(B−V) computed from the full SED fitting of all photometric data points and found that the mean E(B−V) at z > 4 is E(B−V) = 0.03.
To study the dependence of dust extinction on our results, we ran GOSSIP+ again for z > 4 galaxies with three different limits: E(B−V)max = 0.05, E(B−V)max = 0.15 and E(B−V)max = 0.5. When the fit was able to explore a wider range of E(B−V), the mean E(B−V) increased. This results in a higher IGM transmission and therefore a lower optical depth. At z = 4.2, the IGM transmission ranges from 49% when E(B−V) ≤ 0.05 to 65% when E(B−V) ≤ 0.5. At z = 4.8 the change is less pronounced and the IGM transmission varies from 42% for E(B−V) ≤ 0.05 to 51% for E(B−V) ≤ 0.53. We also computed the mean E(B−V) values obtained when changing the high limit of E(B−V) at z > 4. For E(B−V)max = 0.5 the mean E(B−V) is 0.12, while it decreases to 0.03 when E(B−V)max = 0.05.
Consequently, setting a high dust extinction limit of E(B−V) = 0.5 drives τeff away from the simulation of M06 and also from the measurements derived from QSOs, while lowering the highest E(B−V) allowed in the fit brings it closer. This is indirect evidence that the measured dust extinction in our galaxies might be lower than a fit without E(B−V) constraints would indicate. Therefore, we provide as our best measurement at z > 4 the IGM transmission obtained for a dust content of galaxies up to E(B−V) = 0.15, and we also report the IGM transmission for a dust content limited to E(B−V) = 0.05 (Table 2).
Another a priori hypothesis in our analysis is the dust extinction law. While we used the law of Calzetti et al. (2000), the use of a different extinction law like that of the SMC (Prévot et al. 1984) has been advocated for galaxies with lower metallicity at high redshifts (e.g. Speagle et al. 2014). In a preliminary analysis we used the SMC extinction law for the fit of our z > 4 galaxies for E(B−V)max = 0.15. We found that the IGM transmission is even more different from the mean transmission from QSOs or models. Since the extinction law of the SMC has a steeper slope than the Calzetti (2000) law, the same E(B−V) value leads to a more pronounced extinction with the SMC extinction law. Thus, to compensate for this effect, the IGM transmission must be higher.
 |
Fig. 12 Effect of dust extinction on optical depth measurements at z > 4. The optical depth τeff is shown for different limits in E(B−V): E(B−V)max = 0.05 (in green), E(B−V)max = 0.15 (in red) and E(B−V)max = 0.5 (in black). The blue points are the measurement from Faucher-Giguère (2008b), and the brown line is from Becker et al. (2013). |
6.3. Uncertainties in IGM transmission models and angular projection effects
One important aspect to consider in comparing to models is that the dominant contribution to the continuum opacity arises from a small number of absorbers at the highest column densities in a given LOS (Madau et al. 1996). As pointed out by Bershady et al. (1999), small number statistics on those absorbers may cause strong variations in the observed colours of high-redshift galaxies of the same intrinsic spectral type. Moreover, there are still uncertainties in the distribution of column densities and Doppler b parameters of intervening absorbers, which are fundamental ingredients in the simulations. One connected aspect that also might affect the dispersion in IGM transmission is that the sources responsible for IGM absorption are expected to be clustered in space. Gas clouds producing the absorption are connected to large-scale structures and follow the general clustering of matter (Prochaska et al. 2014). This aspect remains to be fully treated in IGM simulations at z > 2.5 and could affect both the mean transmission and its dispersion (Bershady et al. 1999; Inoue et al. 2014; Prochaska et al. 2014). These effects might lead to significant cosmic variance around the mean IGM extinction in models, and modelling them would need to be fully tested from a number of independent LOS in large cosmological simulations.
An effect that can additionally complicate the computation of the mean IGM transmission and its dispersion in models is the covering factor of IGM clouds on an extended galaxy compared to a point-source QSO. The smaller the clouds, the more likely that the IGM clouds would block only part of an extended source. We simulated this effect by taking a distribution of clouds along the LOS of an extended galaxy with increasing size. This is shown in Fig. 13. The top panel represents the influence of the galaxy size (0.5′′ and 1.5′′) on the IGM transmission for a maximum cloud size of 50 kpc. We find that when the size of the galaxy increases, the transmission increases for a fixed maximum cloud size. This agrees with what we expect because only a part of the galaxy light is attenuated by the clouds along the LOS. In this model the mean transmission is equal to that of QSOs for galaxy sizes that become point-like (like QSOs). The bottom panel presents the same study performed with different maximum cloud sizes (25 and 100 kpc). The larger the clouds, the smaller the difference between M06 and our simulation. The reason is that when the size of the clouds increases, the light of the galaxy is more likely to be absorbed and the difference between QSOs and galaxies tends to disappear.
 |
Fig. 13 Simulation of the IGM transmission expected when the source is an extended galaxy and not a point-like QSO. Top panel: simulation for different galaxy sizes from 0.5′′ to 1.5′′ and a maximum cloud size of 50 kpc. Bottom panel: simulation for a galaxy of 0.5′′ and different maximum cloud size of 25 and 100 kpc. The IGM transmission increases with decreasing size of the clouds or increasing size of the source. |
7. Consequences for the selection of high-redshift galaxies
The observed range of IGM transmission at a fixed redshift may have a significant effect on selecting galaxies at z > 2.5. The classical way to select galaxies at these redshifts is to use the Lyman break galaxy (LBG) selection technique. The LBG selection criteria rely on the a priori knowledge of the average properties of the IGM coupled to the 912 Å Lyman continuum limit (break) intrinsic to a galaxy (Steidel et al. 1996) as well as to the dust content and Lyman continuum escape fraction (Cooke et al. 2014). These components are responsible for the drop-out in flux and the resulting strong change in colours with redshift when the break in the continuum produced by the combination of the Lyman break and the IGM goes through a set of filters. These properties are used to infer the locus of galaxies with different redshifts in colour−colour diagrams and to identify large samples of LBGs for analysis of the galaxy population or for follow-up spectroscopic surveys (e.g. Steidel et al. 2003) at increasingly high redshifts. The technique of deriving photometric redshifts from SED fitting also assumes average IGM properties (most often M95 in existing codes), and therefore is also expected to be dependent on the exact IGM transmission and its dispersion. As LBG and photometric redshift techniques have become the main way to identify large samples of candidate high-redshift galaxies to study galaxy evolution, it is very important to ensure that the assumed IGM properties are validated by observational data and that no major population is missed when using modelled average IGM properties a priori.
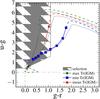 |
Fig. 14 Effect of the change in IGM transmission on the colour−colour (u−g,g−r) tracks of a galaxy with 2.5 < z < 3.5 and its selection. As an example we use a template galaxy with average properties at this redshift: 0.4 Gyr old, with E(B−V) = 0.1, a metallicity of Z⊙/ 2.5, and an SFH timescale of 0.3 Gyr. The blue curve represents the (u−g,g−r) track for a low IGM transmission (mean −1.0σ), while the green curve represents the track computed with a high IGM transmission (mean +1.0σ). The red track is computed with the mean IGM transmission from M06. The grey dashed box corresponds to the LBG selection for this filter set (from Le Fèvre et al. 2013b). For each of the high- or low-transmission tracks the full line with squares (displayed at steps of Δz = 0.1) ranges from z = 2.7 to z = 3.5, while the dashed line is for z < 2.7 and z > 3.5. We use an apparent (observed) flux below the Lyman limit of 3% of the flux at 1500 Å as measured by Le Fèvre et al (2014) in the VUDS survey (see also Cooke et al. 2014). The black lines are the corresponding tracks computed with the M95 models. |
 |
Fig. 15 (u−g,g−r) colour−colour diagrams for galaxies simulated with BC03 synthetic galaxy spectra. Left: simulation using a fixed IGM value at a given redshift following the mean value of the M06 model. Right: simulation using a varying IGM transmission following the observed dispersion from QSOs of the VUDS sample presented here. |
We have modelled how galaxy tracks in colour−colour space are modified when the IGM departs from the mean values of M06 and M95. In Fig. 14 we present the tracks as a function of redshift for a galaxy in the (u−g, g−r) colour−colour diagram classically used as a basis for LBG galaxy selection at z ~ 3. When the IGM transmission is low, the magnitude difference in bands straddling the continuum in the IGM-affected wavelength domain blueward of Lyα and redward of the Lyman limit is more pronounced than when the transmission is high. This has a strong effect on the (g−r) colour such that it reddens with decreasing IGM transmission, while the (u−g) colour changes less drastically because it is dominated by the Lyman-limit continuum break. The net effect is that galaxies will leave the LBG box at lower redshifts when the IGM transmission decreases. For the simulated galaxy in Fig. 14 the tracks leave the selection box at z ≥ 3.2 instead of z ≥ 3.5 for our IGM model −1σ below the mean. Interestingly, this mean−1σ track enters the LBG selection box at z = 2.1, earlier than z = 2.7, as expected from the mean transmission. This then implies that galaxies would be selected at lower redshifts than the anticipated z = 2.7 limit. These effects are further compounded with the effect of a varying Lyman continuum escape fraction (Cooke et al. 2014). Significant flux is observed below the Lyman limit for high-redshift galaxies, as discussed in Cooke et al. (2014) and observed in the VUDS sample discussed here with a flux ~ 3% of the flux at 1500 Å (Le Fèvre et al. 2015). This observed flux below 912 Å could either be escaping Lyman continuum photons from the galaxy or be artificially produced by contamination along the LOS, but either of these effects will affect the strength of the observed Lyman-limit break. In addition, photometric errors on the (u−g) and (g−r) colours range from about 0.2 to 0.5 mag and will further scatter objects outside of the selection box, especially for objects near the boundaries of the box, and therefore concerns objects for which IGM transmission along the LOS is low.
We estimated the efficiency of the colour−colour selection in the presence of variable IGM transmission by producing two large simulations of galaxies with 2.7 < z < 3.5. We used the BC03 stellar population models and a range of E(B−V), SFH, ages, and metallicities as defined in Table 1. The first simulation was based on a fixed M06 IGM transmission, while the second simulation randomly added a variable IGM transmission with the seven templates defined in Sect. 3.3 following the observed dispersion. We derived the (u−g) and (g−r) colours for each simulated galaxy for the two simulations. The resulting (u−g,g−r) colour−colour plots are shown in Fig. 15. When the IGM is in the range reported in Sect. 4, a number of galaxies are no longer inside the LBG selection box. We computed the relative fraction of galaxies included in and excluded from the LBG selection box for this redshift range. We found that the fraction of objects outside the LBG box increases to 16% when the IGM is let to vary. This effect is more pronounced in the high-redshift part of the selection. Between z = 3.2 and z = 3.5 the proportion of selected/unselected galaxies changes from 6% to 23%, just by making the IGM a free parameter.
To check whether the observed sample agrees with the simulations, we plot the individual galaxies in the (u−g, g−r) diagram coded as a function of the IGM transmission measured from the spectral fitting in Fig. 16. The galaxies outside the selection area for redshifts 2.7 < z < 3.5 are predominantly galaxies for which the IGM transmission is lower than the mean, in agreement with simulations. Finding galaxies in the correct redshift range but outside the LBG selection area has been reported before (e.g. Le Fèvre et al. 2005b, 2013b); this paper shows that the wide range in IGM transmission is one possible explanation for these observations.
 |
Fig. 16 (u−g,g−r) colour−colour diagram for VUDS galaxies used in this study. The points are colour-coded based on the IGM transmission measured from the spectral fitting for each of them. The red points are the galaxies for which GOSSIP+ identified an IGM equal to the mean M06 model. The blue points are the objects for which the IGM transmission is −0.5, −1.0, or −1.5σ below the mean, and green points are for +0.5, +1.0, or +1.5σ above the mean. The galaxies outside the box have an IGM transmission below the mean M06 IGM transmission. Black points represent the whole VUDS sample at 2.7 < z < 3.5. |
Figure 17 shows the same analysis for (g−r, r−i) colour−colour selection used to select galaxies between z = 3.5 and z = 4.5. The discussion for ugr selection also applies at these redshifts. The lowest IGM transmission allows us to select galaxies as early as z = 3.1 but limits the selection of the highest redshift galaxies to z ≤ 4.3 when the IGM transmission is lower than the mean transmission.
From this analysis we conclude that it is advisable to allow for a range of IGM transmission when defining the locus of galaxies in a colour−colour diagram for LBG selection or when performing SED fitting to derive a photometric redshift (and associated physical parameters) before defining large complete galaxy samples. This will be studied in more detail in a forthcoming paper (Thomas et al., in prep.).
8. Summary
This paper presented a study of the transmission of the inter-galactic medium using galaxy spectra over the redshift range 2.5 < z < 5.5. We computed the IGM transmission from the highest S/N UV rest-frame spectra of 2127 galaxies with iAB ≤ 25 in the Vimos Ultra Deep Survey (VUDS, Le Fèvre et al. 2015), which uses integration times of ~ 14 h on VLT-VIMOS.
To study the IGM transmission on the LOS of these galaxies, we used the GOSSIP+ software to perform spectral fitting of the VUDS VIMOS spectra. A new IGM prescription that treats the IGM as a free parameter was presented and implemented in the spectral fitting process. The IGM transmission can be any of seven IGM templates at any redshift defined from the mean M06 transmission and ranging up to ± 1.5σ as defined in the M95 models. We simulated mock galaxies to test the reliability of GOSSIP+ to retrieve the right IGM transmission for spectra with the same S/N as our observed sample and measured the success rate to be ~ 74%. We then measured the IGM transmission by fitting our VUDS spectra and estimated this transmission directly from the IGM template selected from the best fit.
The mean IGM transmission is found to be in remarkable agreement with the M06 theoretical model and measurements using QSOs up to z = 4. We transformed our transmissions into HI effective optical depths τeff and found that the mean values also agree very well with the optical depths measured from the LOS towards QSOs as reported in the literature (e.g. Becker et al. 2013). The fact that the IGM transmissions derived from galaxies and from QSOs agree so well in this redshift range seems to indicate that the source properties and the properties of the CGM in the immediate surroundings on these objects have little effect on the integrated IGM transmission properties, as would be generally expected.
We reported tentative evidence that at z> 4 the mean IGM transmission is higher than expected from the IGM model of M06, reaching a difference of ~9% at z = 4.75. We discussed possible observational biases that might produce this difference and concluded that these would not affect the sample in a way to produce a transmission observed to be higher than the mean M06 or than the values from QSOs, but instead would produce the opposite. We found that, not surprisingly, at z> 4 the dust extinction at the source is somewhat degenerate with the IGM transmission. The IGM is able to compensate for a change in the E(B−V) value when performing the spectral fitting: the higher the dust content, the higher the IGM transmission has to be. When the E(B−V) was free to take values up to E(B−V) = 0.5, we found a higher transmission than observed from QSOs, but when we restricted the dust extinction to E(B−V) ≤ 0.05, we found a mean IGM transmission compatible with the observed values from QSOs and simulations within measurement errors.
Most importantly, we found that the dispersion of IGM transmission around the mean is high, ranging from 1σ = 0.15 at redshift 2.8 to 1σ = 0.10 at redshift 4.8. Our transmission values show a range and dispersion very similar to that reported by Faucher-Giguères et al. (2008b) from QSOs, confirming that our measurements are a true indication that the IGM dispersion is high at any of the observed redshifts. We discuss the possibility that the high dispersion found in our sample may be the result of incomplete treatment of the clustering of IGM clouds in models, which results in large cosmic variance. We also discussed the possibility that the IGM transmission may be different when observing extended galaxies instead of point-like QSOs and presented a simple model supporting this view.
The high dispersion in observed IGM transmission in our study has important consequences. We explored the effect of this high dispersion on the selection of high-redshift galaxies z > 2.5 when using photometric techniques such as LBG or photometric redshifts. We showed that when the IGM is allowed to vary, the range of redshifts satisfying colour−colour (LBG) selection changes and that part of the galaxy population in the range expected from the LBG selection technique can easily escape photometric selection. This was further compounded when IGM properties were combined to observed non-zero flux below the Lyman limit, either from Lyman continuum escape fraction or from contamination along the LOS (see e.g. Cooke et al. 2014). We used large simulations to compare the colour−colour distribution when the IGM has a fixed value and when the IGM transmission varies. We found that the fraction of galaxies that can escape detection in the LBG box may reach up to 16% (23% at 3.2 < z < 3.5) as a result of the IGM dispersion alone. This fraction can further increase when a wide range of IGM transmission is combined with a significant continuum level below 912 Å produced either by high Lyman continuum escape or by contaminating objects on the LOS. This will be explored with more extensive simulations (Thomas et al., in prep.).
We have presented the first comprehensive study of the IGM transmission properties using a galaxy sample up to z ~ 5. The average IGM transmission found in this work is in excellent agreement with QSO studies and models at z < 4 and validates the IGM transmission properties independent of QSO samples. Our results demonstrate that the spectral fitting method we developed including varying the IGM transmission is fully able to recover the mean IGM transmission in the Universe from a faint galaxy sample. While quasar studies will remain the most powerful probe of the IGM properties, applying this powerful method to even larger galaxy samples will complement the knowledge of the IGM recovered from QSO spectra analysis and opens a new window of investigation for the IGM. The large distribution of IGM transmission observed in our sample and a possible higher transmission at z > 4 calls for more investigations, both from the observational and model perspectives, to better understand the IGM transmission properties. We stress the importance to take large IGM transmission variations into account when searching for distant galaxies and fitting their spectral energy distribution.
Acknowledgments
We thank G. Becker, J. M. Deharveng, A. Inoue, C. Péroux, and M. Pieri for useful discussions. This work is supported by funding from the European Research Council Advanced Grant ERC-2010-AdG-268107-EARLY and by INAF Grants PRIN 2010, PRIN 2012 and PICS 2013. A.C., O.C., M.T. and V.S. acknowledge the grant MIUR PRIN 2010–2011. This work is based on data products made available at the CESAM data center, Laboratoire d’Astrophysique de Marseille, France.
References
- Bautista, J. E., Bailey, S., Font-Ribera, A., et al. 2015, J. Cosmol. Astropart. Phys., 05, 60 [Google Scholar]
- Becker, G. D., Rauch, M., & Sargent, W. L. W. 2007, ApJ, 662, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, G., Hewett, P. C., Worseck, G., et al. 2013, MNRAS, 430, 2067 [NASA ADS] [CrossRef] [Google Scholar]
- Bershady, M. A., Carlton, J. C., & Geoffroy, J. M. 1999, ApJ, 518, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Bolton, J. S., Haehnelt, M. G., Viel, M., & Springel, V. 2005, MNRAS, 357, 1178 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R., Illingworth, G. D., Oesch, P. A., et al. 2013, ApJ, 793, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Bouwens, R., Illingworth, G. D., Oesch, P. A., et al. 2015, ApJ, 803, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, H. W. 2012, MNRAS, 427, 1238 [NASA ADS] [CrossRef] [Google Scholar]
- Cen, R., Miralda-Escudé, J., Ostriker, J. P., et al. 1994, ApJ, 437, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Cooke, J., Ryan-Weber, E. V., Garel, T., & Dáz, C. G. 2014, MNRAS, 441, 837 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Tresse, L., Ilbert, O., et al. 2012, A&A, 539, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dall’Aglio, A., Wisotzki, L., & Worseck, G. 2008, A&A, 491, 465 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fan, X., Strauss, M. A., Becker, R. H., et al. 2006, AJ, 132, 117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faucher-Giguère, C. A., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008a, ApJ, 688, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Faucher-Giguère, C. A., Prochaska, J. X., Lidz, A., Hernquist, L., & Zaldarriaga, M. 2008b, ApJ, 681, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Franzetti, P., Scodeggio, M., Garilli, B., Fumana, M., & Paioro, L. 2008, ASP Conf. Ser., 394, 642 [Google Scholar]
- Garilli, B., Fumana, M., Franzetti, P., et al. 2010, PASP, 122, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, A., Shimizu, I., Iwata, I., & Tanaka, M., et al. 2014, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, SPIE, 4841, 1670 [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005a, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Paltani, S., Arnouts, S., et al. 2005b, Nature, 437, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013a, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013b, ArXiv e-prints [arXiv:1307.6518] [Google Scholar]
- Le Fèvre, O., Tasca, L. A. M., Cassata, P., et al. 2015, A&A, 576, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Madau, P. 1995, ApJ, 441, 18 (M95) [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., Ferguson, H. C., Dickinson, M., et al. 1996, MNRAS, 283, 1388 [NASA ADS] [CrossRef] [Google Scholar]
- Maraston, C. 2005, MNRAS, 362, 799 (M05) [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A. 2006, MNRAS, 365, 807 (M06) [NASA ADS] [CrossRef] [Google Scholar]
- Meiksin, A., & White, M. 2004, MNRAS, 350, 1107 [NASA ADS] [CrossRef] [Google Scholar]
- Moller, P., & Jakobsen, P. 1990, A&A, 228, 299 [Google Scholar]
- Ouchi, M., himasaku, K., Okamura, S., et al. 2004, ApJ, 611, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Pâris, I., Petitjean, P., Rollinde, E., et al. 2011, A&A, 530, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patat, N., Moehler, S., O’Brien, K., et al. 2011, A&A, 527, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prévot, M. L., Lequeux, J., Prevot, L., et al. 1984, A&A, 132, 389 [Google Scholar]
- Prochaska, J., Madau, P., O’Meara, J. M., et al., MNRAS, 438, 476 [Google Scholar]
- Rauch, M., Miralda-Escudé, J., Sargent, W. L. W., et al. 1997, ApJ, 489, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A. 2004, AJ, 127, 2598 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Steidel, C. C., Giavalisco, M., Pettini, M., Dickinson, M., & Adelberger, K. L. 1996, ApJ, 462, 17 [Google Scholar]
- Steidel, C. C., Adelberger, K. L., Shapley, A. E., et al. 2003, ApJ, 592, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Tresse, L., Ilbert, O., Zucca, E., et al. 2007, A&A, 472, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Parameter space used for the spectral fitting, using existing BC03 and M05 stellar population models.
Median IGM transmission and dispersion around the median as observed from the VUDS spectra fitting.
All Figures
 |
Fig. 1 Method adopted for the IGM transmission measurement when fitting VUDS galaxy spectra. The observed spectrum (here a stack with a high signal-to-noise ratio from VUDS galaxies at z ~ 3.4) is presented in black. The best-fit model (see Sect. 3.2) resulting from the combination of a stellar population synthesis model, dust extinction, and IGM transmission is plotted in red. The same stellar population synthesis model with dust but without the IGM transmission applied is shown in blue. The IGM template selected for the best fit is presented in green (the value of the transmission is given on the right y-axis). The IGM transmission is then the average transmission in the wavelength range 1070 ≤ λ ≤ 1170 Å (vertical dashed lines) as measured directly on the IGM template selected in the best fit. |
| In the text | |
 |
Fig. 2 Seven IGM transmission templates used in this work at z = 3.0, z = 4.0, and z = 5.0. The mean M06 IGM transmission is represented by the dashed red line. The ± 0.5σ, ± 1.0σ, and ± 1.5σ curves are the six black curves of different thickness. The thicker lines represent ± 1.5σ. |
| In the text | |
 |
Fig. 3 Thirty IGM transmission templates available to make the mock galaxies at z = 3.5 (as an example of the simulation process). At this redshift, one of these template is chosen randomly and applied to the galaxy template. In red we plot the seven IGM templates used in GOSSIP+ to perform the fit and verify whether the simulated IGM can be recovered. |
| In the text | |
 |
Fig. 4 Evolution of the difference in transmission ΔTr(Lyα)/Tr(Lyα) with redshift between the input simulated spectra and the result of the fit with GOSSIP+. |
| In the text | |
 |
Fig. 5 Three examples of Lyα skewers at z = 2.936, z = 3.287, and z = 3.49. In each plot, the black spectrum represents the high spectral resolution BOSS DR11 mock IGM transmission, while the same spectrum in red is degraded to the VUDS lower resolution. The blue lines in each panel represent the wavelength interval where the Lyα transmission is estimated (1070−1170 Å). |
| In the text | |
 |
Fig. 6 Comparison of the Lyα transmission from the input mock Lyα forest and the output IGM template selected by GOSSIP+. In red we plot the distribution of the difference Tr(Lyα)Forest-Tr(Lyα)fit. The blue line is a Gaussian fit of the red histogram where μ = 0.013 and σ = 0.13. |
| In the text | |
 |
Fig. 7 Example of spectral fitting for ten representative galaxies in the VUDS sample, using the BC03 model spectra. The IGM “id” (cf. Sect. 2) and the redshift of the galaxy are indicated for each fit. The best fit obtained with our prescription of varying the IGM transmission is shown in red, while the best fit with the IGM transmission set to the mean M06 value is shown in blue for comparison (the E(B−V) dust extinction is reported for both). For four objects the best fit finds an IGM equal to the mean, while for the six others GOSSIP+ selects an IGM template different from the mean. |
| In the text | |
 |
Fig. 8 IGM transmission Tr(Lyα) measured from 2127 VUDS galaxies in increasing redshift bins from z = 2.5 to z = 5.5. The black vertical lines represent the median of the distributions in each redshift bin. A wide spread in transmission is observed at all redshifts. The red shaded histograms include all galaxies with flags 2, 3, and 4, while the white striped histograms only represent flag 2. No significant difference is found between the IGM properties of flags 3 and 4 and flag 2. The distribution of IGM transmission is somewhat discretized because of the seven IGM templates used in the spectral fitting. The median and dispersion values measured by Faucher-Giguère et al. (2008b) using QSOs are represented by the blue distribution in each redshift bin. The median values from VUDS galaxies are in excellent agreement with Faucher-Giguère et al. (2008b) for z < 4, while the VUDS results seem to show higher transmission at z > 4 (see text for a discussion). The dispersion values are also in excellent agreement at all redshifts. |
| In the text | |
 |
Fig. 9 Median IGM transmission Tr(Lyα) derived from the LOS towards 2127 VUDS galaxies (full red circles). IGM transmission values are computed from the distribution of IGM transmission measurements resulting from the fit with GOSSIP+, in redshift bins δz = 0.5 at a mean redshifts 2.75, 3.25, 3.75, and 4.25 and in a redshift bin δz = 0.8 at z = 4.8, and using a dust extinction limit E(B−V) ≤ 0.15. The error bars represent the 68% interval in the distribution of IGM transmission values as measured from the 2127 LOS probed by the VUDS galaxies. The empty red circles at z > 4 represent the measurements obtained when setting the dust extinction limit to E(B−V) ≤ 0.05. The blue triangles and associated error bars are median transmission and 1σ dispersion values taken from Faucher-Giguère et al. (2008b). At z > 4, points have been artificially shifted in redshift for clarity. |
| In the text | |
 |
Fig. 10 Average (stacked) spectra for VUDS galaxies with 3.2 ≤ z ≤ 3.8 (zmed = 3.4) for which GOSSIP+ identifies an IGM transmission ≥ 1σ above (golden spectrum) and below (green spectrum) the mean IGM transmission of M06. The average VUDS spectrum over all galaxies in the sample is shown as the black shaded-grey spectrum. All three spectra are normalized in the range 1400 <λ< 1510 Å. |
| In the text | |
 |
Fig. 11 Left panel: the HI optical depth τeff as computed from the measured IGM transmission in the VUDS galaxy data (red filled circles for E(B−V) ≤ 0.15 and empty red circles for E(B−V) ≤ 0.05). The error bars on τeff represent the error on the mean (defined as |
| In the text | |
 |
Fig. 12 Effect of dust extinction on optical depth measurements at z > 4. The optical depth τeff is shown for different limits in E(B−V): E(B−V)max = 0.05 (in green), E(B−V)max = 0.15 (in red) and E(B−V)max = 0.5 (in black). The blue points are the measurement from Faucher-Giguère (2008b), and the brown line is from Becker et al. (2013). |
| In the text | |
 |
Fig. 13 Simulation of the IGM transmission expected when the source is an extended galaxy and not a point-like QSO. Top panel: simulation for different galaxy sizes from 0.5′′ to 1.5′′ and a maximum cloud size of 50 kpc. Bottom panel: simulation for a galaxy of 0.5′′ and different maximum cloud size of 25 and 100 kpc. The IGM transmission increases with decreasing size of the clouds or increasing size of the source. |
| In the text | |
 |
Fig. 14 Effect of the change in IGM transmission on the colour−colour (u−g,g−r) tracks of a galaxy with 2.5 < z < 3.5 and its selection. As an example we use a template galaxy with average properties at this redshift: 0.4 Gyr old, with E(B−V) = 0.1, a metallicity of Z⊙/ 2.5, and an SFH timescale of 0.3 Gyr. The blue curve represents the (u−g,g−r) track for a low IGM transmission (mean −1.0σ), while the green curve represents the track computed with a high IGM transmission (mean +1.0σ). The red track is computed with the mean IGM transmission from M06. The grey dashed box corresponds to the LBG selection for this filter set (from Le Fèvre et al. 2013b). For each of the high- or low-transmission tracks the full line with squares (displayed at steps of Δz = 0.1) ranges from z = 2.7 to z = 3.5, while the dashed line is for z < 2.7 and z > 3.5. We use an apparent (observed) flux below the Lyman limit of 3% of the flux at 1500 Å as measured by Le Fèvre et al (2014) in the VUDS survey (see also Cooke et al. 2014). The black lines are the corresponding tracks computed with the M95 models. |
| In the text | |
 |
Fig. 15 (u−g,g−r) colour−colour diagrams for galaxies simulated with BC03 synthetic galaxy spectra. Left: simulation using a fixed IGM value at a given redshift following the mean value of the M06 model. Right: simulation using a varying IGM transmission following the observed dispersion from QSOs of the VUDS sample presented here. |
| In the text | |
 |
Fig. 16 (u−g,g−r) colour−colour diagram for VUDS galaxies used in this study. The points are colour-coded based on the IGM transmission measured from the spectral fitting for each of them. The red points are the galaxies for which GOSSIP+ identified an IGM equal to the mean M06 model. The blue points are the objects for which the IGM transmission is −0.5, −1.0, or −1.5σ below the mean, and green points are for +0.5, +1.0, or +1.5σ above the mean. The galaxies outside the box have an IGM transmission below the mean M06 IGM transmission. Black points represent the whole VUDS sample at 2.7 < z < 3.5. |
| In the text | |
 |
Fig. 17 Same as Fig. 14 but for a (g−r,r−i) colour−colour selection at 3.7 <z< 4.5. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.