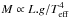| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 26 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201628760 | |
| Published online | 21 November 2016 | |
Critical study of the distribution of rotational velocities of Be stars
I. Deconvolution methods, effects due to gravity darkening, macroturbulence, and binarity⋆
1 Sorbonne Universités, UPMC Université
Paris 6 et CNRS UMR 7095, Institut d’Astrophysique de
Paris 75014 Paris France
e-mail: zorec@iap.fr
2 CNRS UMR 7095, Institut
d’Astrophysique de Paris, 98bis bd
Arago, 75014
Paris,
France
3 Royal Observatory of Belgium,
3 avenue
Circulaire, 1180
Bruxelles,
Belgium
4 Université Côte d’Azur, Observatoire
de la Côte d’Azur, CNRS UMR 7293, Lagrange, 28 avenue Valrose, 06108
Nice Cedex 2,
France
5 GEPI, Observatoire de Paris, PSL
Research University, CNRS UMR 8111, Université Paris Diderot,
Sorbonne Paris Cité, 5 place Jules
Janssen, 92190
Meudon,
France
6 Facultad de Ciencias Astronómicas y
Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque S/N, 1900
La Plata,
Argentina
7 Instituto de Astrofísica La Plata,
CONICET,
1900
La Plata,
Argentina
8 Geneva Observatory, University of
Geneva, chemin des Maillettes
51, 1290
Sauverny,
Switzerland
9 European Organization for
Astronomical Research in the Southern Hemisphere, Alonso de Cordova 3107, Vitacura,
Santiago de Chile,
Chile
Received:
21
April
2016
Accepted:
8
June
2016
Context. Among intermediate-mass and massive stars, Be stars are the fastest rotators in the main sequence (MS) and, as such, these stars are a cornerstone to validate models of structure and evolution of rotating stars. Several phenomena, however, induce under- or overestimations either of their apparent Vsini, or true velocity V.
Aims. In the present contribution we aim at obtaining distributions of true rotational velocities corrected for systematic effects induced by the rapid rotation itself, macroturbulent velocities, and binarity.
Methods. We study a set of 233 Be stars by assuming they have inclination angles distributed at random. We critically discuss the methods of Cranmer and Lucy-Richardson, which enable us to transform a distribution of projected velocities into another distribution of true rotational velocities, where the gravitational darkening effect on the Vsini parameter is considered in different ways. We conclude that iterative algorithm by Lucy-Richardson responds at best to the purposes of the present work, but it requires a thorough determination of the stellar fundamental parameters.
Results. We conclude that once the mode of ratios of the true velocities of Be stars attains the value V/Vc ≃ 0.77 in the main-sequence (MS) evolutionary phase, it remains unchanged up to the end of the MS lifespan. The statistical corrections found on the distribution of ratios V/Vc for overestimations of Vsini, due to macroturbulent motions and binarity, produce a shift of this distribution toward lower values of V/Vc when Be stars in all MS evolutionary stages are considered together. The mode of the final distribution obtained is at V/Vc ≃ 0.65. This distribution has a nearly symmetric distribution and shows that the Be phenomenon is characterized by a wide range of true velocity ratios 0.3 ≲ V/Vc ≲ 0.95. It thus suggests that the probability that Be stars are critical rotators is extremely low.
Conclusions. The corrections attempted in the present work represent an initial step to infer indications about the nature of the Be-star surface rotation that will be studied in the second paper of this series.
Key words: stars: emission-line, Be / stars: rotation
Full Tables 1 and 4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/595/A132
© ESO, 2016
1. Introduction
A classical Be star is a non-supergiant B-type star whose spectrum has, or had shown at some time one or more Balmer lines in emission (Jaschek et al. 1981; Collins 1987). This definition selects objects in the main-sequence evolutionary phase (MS) underscoring thus the “active” character of the Be phenomenon. These stars have the faculty of creating their own circumstellar environment in which emission lines are produced. This is in contrast to early-type supergiants in which emission in the Balmer lines is a “passive” consequence of their extended atmosphere. Even when some classic Be stars are believed to survive as such in the bright giant phase (Negueruela 2004), this definition excludes the heterogeneous group of objects presenting the B[e] phenomenon, which likely manifests at different states of stellar evolution (Lamers et al. 1998). Be stars have long been known as rapid rotators (Struve 1931) and, accordingly, these stars are assumed to create their circumstellar disk or envelope thanks mainly to this rapid rotation. General properties of Be stars and mechanisms to build up their circumstellar envelopes (hereafter CE) or disks are reviewed by Rivinius et al. (2013).
The rapid decrease of the source function of Balmer lines in two domains of effective temperatures, those larger than Teff ≈ 27 000 K, and lower than Teff ≈ 12 000 K, makes the corresponding emission signatures produced by CE or disks too weak to be detected in the respective spectral type domains (Zorec et al. 2007). Adding to this the steep drop of the IMF for masses M ≳ 15 M⊙, the observed frequency of Be stars displays two maxima and becomes significant only in a limited range of stellar masses, i.e., 3 ≲ M/M⊙ ≲ 30. Nothing precludes, however, that continuous and variable winds implying mass-loss rates Ṁ ~ 10-11−10-9M⊙/yr (Snow 1981) and episodic mass ejections up to Ṁ ~ 10-7M⊙/yr that are typical in Be stars (Brown & Wood 1992; Hanuscihk et al. 1993; Floquet et al. 2000; Hubert et al. 2000; Keller et al. 2002; Mennickent et al. 2002; de Wit et al. 2006; Meilland et al. 2006) be present in more- and less-massive rapidly rotating stars than in those of B spectral type considered in the present paper. The conclusions drawn in this work may also concern stars in these two mass extremes.
Regarding the critical rotation, statistical analyses (Cranmer 2005; Frémat et al. 2005) conclude that Be stars are under-critical rotators. Studies of individual stars, based on nonradial pulsation modes (Cameron et al. 2008; Saio 2013) and rotational rates inferred from interferometric data (Meilland et al. 2012; Domiciano de Souza et al. 2014), produce estimates of Ω / Ωc ranging from 0.60 to 0.98, which correspond to linear velocities ratios 0.44 ≲ V/Vc ≲ 0.88 (Vc is the critical equatorial linear velocity) or to ratios of centrifugal to gravity accelerations 0.14 ≲ ac/ag ≲ 0.70. These rates suggest that the surface rotational velocities of Be stars are undoubtedly very high, but they are not necessarily critical. It is then important to inquire how rapid the rotation of Be stars actually is and how much complementary energy is then necessary to release the mass required to build up CEs or disks. On the other hand, these stars represent a paradigm for rapid rotators and, as such, they are the cornerstone to validate the physical input in models of the structure and evolution of rotating stars.
In most cases, the stellar rotation is apprehended through the Vsini parameter. Nevertheless, a number of phenomena act either to underestimate or increase the Vsini of Be stars systematically. In the present paper we only pay attention to the following phenomena: (1) the gravity darkening effect (hereafter GD), which may carry a systematic underestimation of the Vsini (Stoeckley 1968; Townsend et al. 2004; Cranmer 2005; Frémat et al. 2005); (2) more or less chaotic macroscopic velocity fields present in atmospheres of active stars, called macroturbulence, and since Unsöld & Struve (1949) and Huang & Struve (1953) are known to contribute a nonrotational broadening component of spectral lines; (3) under certain conditions, the orbital motion increases the apparent value of Vsini because this phenomenon can concern a large fraction of Be stars that are members of binary systems (Kriz & Harmanec 1975; Harmanec 1987; Gies 2000; Chini et al. 2012; Nasseri et al. 2013; Oudmaijer & Parr 2010).
The final distribution Φ(u) of velocity ratios u = V/Vc obtained in the present work will be analyzed in the following paper (Paper II, Zorec et al. 2016) to determine the degree of surface differential rotation that may affect the Vsini parameters and is consistent with the function Φ(u) derived here.
The present work (Paper I) is organized as follows. In Sect. 2 presents the stellar sample and the data used in the paper. The Sect. 3 is devoted to the discussion of pros and cons of the most commonly used methods to derive the distribution of rotational velocities corrected for the inclination angle factor sini. The effect of the macroturbulence and the presence of binary components on the distribution of velocity ratios are studied in Sects. 4 and 5, respectively. A discussion and comments on the results obtained are summarized in Sect. 6.
2. Data
2.1. The studied stellar sample
The stellar sample used in this work has 233 Galactic classical Be stars, which have been previously studied by Chauville et al. (2001), Frémat et al. (2005), Zorec et al. (2005), Frémat et al. (2006) and Levenhagen & Leister (2006). They are listed in Table 1. This sample was chosen not only because the Vsini parameters were determined using very similar methods, but also because the spectra were corrected for CE emission perturbations.
As the discussion in Sect. 3 requires that all stars had fundamental parameters determined, a significant part of this section is dedicated to their estimation. Details concerning the acquisition and reduction of data proper are found in the papes cited above.
2.2. Fundamental parameters
Rapidly rotating stars undergo geometrical deformations and the concomitant GD. They can then be characterized with two types of fundamental parameters:
-
Apparent fundamental parameters. Following Frémat et al. (2005), the directly observed parameters are called apparent fundamental parameters, which describe only the average properties of the photosphere in the hemisphere projected toward the observer. In the present work we deal with four independent observed apparent quantities:
- (i)
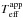 , is the apparent effective temperature,
which corresponds to the effective temperature of a classical nonrotating,
plane-parallel model of stellar atmospheres without GD that describes the
observed spectrum in a limited wavelength domain.
, is the apparent effective temperature,
which corresponds to the effective temperature of a classical nonrotating,
plane-parallel model of stellar atmospheres without GD that describes the
observed spectrum in a limited wavelength domain. - (ii)
As for the effective temperature,
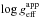 is the apparent effective surface gravity
of the observed stellar hemisphere determined with classical plane-parallel
model atmospheres.
is the apparent effective surface gravity
of the observed stellar hemisphere determined with classical plane-parallel
model atmospheres. - (iii)
Lapp, is the apparent bolometric luminosity emitted by the aspect-angle dependent stellar hemisphere.
- (iv)
Vsini, is the apparent rotational velocity of a rigidly rotating star that accounts for the observed spectral line broadening in the visual spectral range when GD is not taken into account.
- (i)
-
Parent nonrotating counterpart parameters. To make the calculation of quantities, such as the stellar mass, stellar age, or the inclination angle i, easier, in Sect. 3.5.1 we determine the stellar parent nonrotating counterpart parameters. These are called, in short, the pnrc fundamental parameters that correspond to the associated nonrotating stars having the same mass as the studied objects (Frémat et al. 2005).
Although the parameters (Teff, log g, log L/L⊙,Vsini) of our stellar sample were discussed several times (see Chauville et al. 2001; Frémat et al. 2005, 2006; Zorec et al. 2005), since then new data have been obtained for some of them. These data enabled us to redetermine their bolometric luminosities. We briefly detail the characteristics of the apparent parameters adopted in the present work.
2.2.1. The apparent effective temperature and surface gravity
The apparent effective temperature 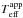 and surface gravity
and surface gravity 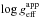 of stars employed in this work were determined in two different ways: (a) from spectrophotometric observations in the 3500 ≤ λ ≤ 4600 Å wavelength interval; and (b) using high resolution spectra in the blue spectral range. In Table 1 gives the sources of the observed parameters, wavelength intervals observed, characteristics of the spectra, and instruments used.
of stars employed in this work were determined in two different ways: (a) from spectrophotometric observations in the 3500 ≤ λ ≤ 4600 Å wavelength interval; and (b) using high resolution spectra in the blue spectral range. In Table 1 gives the sources of the observed parameters, wavelength intervals observed, characteristics of the spectra, and instruments used.
- a)
The stars in Chauville et al. (2001), Frémat et al. (2005) and Zorec et al. (2005) have apparent effective temperatures and gravities determined from the (λ1,D) parameters defined in the BCD (Barbier, Chalonge, Divan) spectrophotometric system (Chalonge & Divan 1952). For a number of these stars, we added new BCD observations obtained by Cochetti (2014), which are indicated with “4” in Table 1. We redetermined the
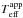 for these Be stars using the calibrations given
in Zorec et al. (2009), while for
for these Be stars using the calibrations given
in Zorec et al. (2009), while for 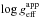 we used those listed in Zorec (1986) and Divan &
Zorec (1982a).The (λ1,D)
parameters describe the energy distribution around the Balmer discontinuity
(hereafter BD), which is roughly from λ 3500 Å to λ 4500 Å.
Explanations on the characteristics, use and advantages of the BCD (λ1,D) parameters
to determine
we used those listed in Zorec (1986) and Divan &
Zorec (1982a).The (λ1,D)
parameters describe the energy distribution around the Balmer discontinuity
(hereafter BD), which is roughly from λ 3500 Å to λ 4500 Å.
Explanations on the characteristics, use and advantages of the BCD (λ1,D) parameters
to determine 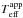 and
and 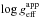 of Be stars can be found in Zorec & Briot (1991), Cidale et al. (2001) and Gkouvelis et al. (2016). To indicate average MK spectral types,
we employ the S70 parameter (Zorec et al. 1983) that in the BCD
(λ1,D)-classification
diagram (Chalonge & Divan 1952)
corresponds to the value of the BD determined by the intersection of the
λ1 − 3700
= 70 Å line with the curve of intrinsic color gradient
Φrb
passing through the stellar (λ1,D) point in
the BCD (λ1,D)-classification
diagram (Chalonge & Divan 1952). The
S70 identifies curves of constant
effective temperatures (Zorec et al. 2009)
and nicely correlates with the spectral classification parameter “s” defined by de Jager & Nieuwenhuijzen (1987).
of Be stars can be found in Zorec & Briot (1991), Cidale et al. (2001) and Gkouvelis et al. (2016). To indicate average MK spectral types,
we employ the S70 parameter (Zorec et al. 1983) that in the BCD
(λ1,D)-classification
diagram (Chalonge & Divan 1952)
corresponds to the value of the BD determined by the intersection of the
λ1 − 3700
= 70 Å line with the curve of intrinsic color gradient
Φrb
passing through the stellar (λ1,D) point in
the BCD (λ1,D)-classification
diagram (Chalonge & Divan 1952). The
S70 identifies curves of constant
effective temperatures (Zorec et al. 2009)
and nicely correlates with the spectral classification parameter “s” defined by de Jager & Nieuwenhuijzen (1987). -
b)
The
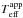 and
and 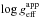 from Frémat et
al. (2006) and Levenhagen & Leister
(2006) were determined by fitting spectra in the blue spectral range
and/or ratios of H , He , Si, and N lines in the
3900 ≤ λ ≤
5000 Å spectral range. Depending on the intensity of the
emission in the Balmer lines, corrections to the spectra were carried out for
veiling effect. Details on this technique can be found in Ballereau et al. (1995) and Semaan et al. (2013). For those stars where effective temperatures and
gravities were determined using both spectrophotometric and spectroscopic data, we
adopted the weighted averages, where the weights were assigned using the
individual uncertainties of parameters determined in both methods.
from Frémat et
al. (2006) and Levenhagen & Leister
(2006) were determined by fitting spectra in the blue spectral range
and/or ratios of H , He , Si, and N lines in the
3900 ≤ λ ≤
5000 Å spectral range. Depending on the intensity of the
emission in the Balmer lines, corrections to the spectra were carried out for
veiling effect. Details on this technique can be found in Ballereau et al. (1995) and Semaan et al. (2013). For those stars where effective temperatures and
gravities were determined using both spectrophotometric and spectroscopic data, we
adopted the weighted averages, where the weights were assigned using the
individual uncertainties of parameters determined in both methods.
A statement detailing the uncertainties of the fundamental parameters introduced by the use of the BCD quantities (λ1,D) can be found in Zorec & Briot (1991) and Zorec et al. (2009). A comparison of effective temperatures determined with the BCD (λ1,D) parameters for B stars without emission with those obtained in the literature using other methods is shown in Appendix A.1.
2.2.2. The apparent bolometric luminosity
We call Lλ(η,i) the monochromatic luminosity emitted at the wavelength λ by the hemisphere seen under the inclination angle i of a star rotating at a velocity characterized by the ratio η defined as ![\begin{equation} \eta = \frac{a_{\rm c}}{a_{\rm g}} = \left(\frac{\Omega_{\rm e}}{\Omega_{\rm c}}\right)^2\left[\frac{R_{\rm e}(\eta)}{R_{\rm c}}\right]^3 \label{eq_4_1_1} , \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq43.png) (1)where ac is the centrifugal acceleration and ag the gravitational acceleration at the equator; Ωe and Ωc are the actual and critical stellar angular velocities at the equator, respectively; and Re(η) and Rc are the rotationally modified stellar equatorial and critical radii, respectively.
(1)where ac is the centrifugal acceleration and ag the gravitational acceleration at the equator; Ωe and Ωc are the actual and critical stellar angular velocities at the equator, respectively; and Re(η) and Rc are the rotationally modified stellar equatorial and critical radii, respectively.
According to the data we have at our disposal, we write the apparent bolometric luminosity Lapp as 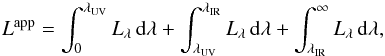 (2)where λUV is the shortest wavelength at which was observed the energy distribution of a star in the far-UV; λIR is the longest wavelength observed in the far-infrared (IR). The parameters λUV and λIR are different from star to star, according to the satellites or instruments that recorded the data. To make easier the estimate of Lapp, Eq. (2) is rewritten as
(2)where λUV is the shortest wavelength at which was observed the energy distribution of a star in the far-UV; λIR is the longest wavelength observed in the far-infrared (IR). The parameters λUV and λIR are different from star to star, according to the satellites or instruments that recorded the data. To make easier the estimate of Lapp, Eq. (2) is rewritten as
![\begin{equation} \begin{array}{rcl} &&L^{\rm app} = \left[1+\Delta_{\rm L}(\eta,i,M,t)\right]\int_{\lambda_{\rm UV}}^{\lambda_{\rm IR}}L_{\lambda}\,{\rm d}\lambda \\ &&\Delta_{\rm L}(\eta,i,M,t) = \Sigma_i\int_{\Delta\lambda_i}F_{\lambda}\,{\rm d}\lambda/\int_{\lambda_{\rm UV}}^{\lambda_{\rm IR}}F_{\lambda}\,{\rm d}\lambda, \\ \end{array} \label{eq_4_1_3} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq54.png) (3)where M is the stellar mass and t its age. The spectral regions that are not attainable by direct observation are completed with ΔL(η,i,M,t); these are determined with model-atmosphere fluxes Fλ of rotating stars calculated with FASTROT (Frémat et al. 2005). The completion factor ΔL in Eq. (3) is adjusted consistently, according to the iterated parameters (η,i,M,t), as explained in Sect. 3.5.1.
(3)where M is the stellar mass and t its age. The spectral regions that are not attainable by direct observation are completed with ΔL(η,i,M,t); these are determined with model-atmosphere fluxes Fλ of rotating stars calculated with FASTROT (Frémat et al. 2005). The completion factor ΔL in Eq. (3) is adjusted consistently, according to the iterated parameters (η,i,M,t), as explained in Sect. 3.5.1.
In Lapp, only the factor 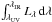 is a genuine observed quantity, which was determined following the same procedure as described in detail by Zorec et al. (2009). Although the use of this method is only justified for rotating stars without emission, it can also be applied to objects with emission lines, such as Be stars, provided that some modifications are introduced that take the characteristics of their energy distributions into account.
is a genuine observed quantity, which was determined following the same procedure as described in detail by Zorec et al. (2009). Although the use of this method is only justified for rotating stars without emission, it can also be applied to objects with emission lines, such as Be stars, provided that some modifications are introduced that take the characteristics of their energy distributions into account.
Studied sample of Be stars and their apparent fundamental parameters.
The energy distribution in the visual spectral range of Be stars is variable, displaying flux excesses or deficiencies according to the sub-wavelength domain and/or emission phase B normal, Be proper, or Be shell (Divan et al. 1982, 1983; Divan & Zorec 1982b; Zorec & Briot 1991; Moujtahid et al. 1998, 1999). To extract the nonvariable photospheric component 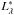 from the luminosity Lλ emitted by the star+CE system, we have written
from the luminosity Lλ emitted by the star+CE system, we have written 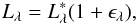 (4)where ϵλ represents the contribution from the CE, so that the apparent luminosity Lapp becomes
(4)where ϵλ represents the contribution from the CE, so that the apparent luminosity Lapp becomes ![\begin{equation} L^{\rm app} = \left[1+\Delta_{\rm L}(\eta,i,M,t)\right]\int_{\lambda_{\rm UV}}^{\lambda_{\rm IR}}\frac{L_{\lambda}}{1+\epsilon_{\lambda}}\,{\rm d}\lambda. \label{eq_4_1_5} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq94.png) (5)For ϵλ we used the expression obtained in Moujtahid (1998) (Moujtahid et al. 1999, 2000a,b), which accounts for the energy distribution of Be stars from λ ~ 3000 Å to the near-IR and is a function of the following parameters: r = R∗/Renv is the inverse of the radius of the effective layer representing the circumstellar environment; Bλ(Tenv) is the source function of this layer given by the Planck function at a temperature Tenv; τλ = τe + τV(λ/λV)3 (Moujtahid et al. 1999) is the optical depth at λ of the equivalent layer, where τe is the electron scattering component, and τV accounts for the bf+ff opacity at λV ≃ 5500 Å. These quantities are only used as fitting parameters so that they are not a specific physical interpretation in any case. For those stars for which we had enough data, the CE parameters were determined in the same way as described in Moujtahid et al. (2000a,b) using the Moujtahid et al. (1998) catalog that lists changes with time of: (a) the total BD D = D∗ + d of Be stars, where D∗ is the photospheric BD and d ⋛ 0 is the second BD due to the CE; and (b) the flux and color excess at λV ≃ 5500 Å. The explicit form of ϵλ used and the parameters (r,Tenv,τe,τV) obtained for the ten program Be stars with rather strong emission characteristics are given in Appendix B.
(5)For ϵλ we used the expression obtained in Moujtahid (1998) (Moujtahid et al. 1999, 2000a,b), which accounts for the energy distribution of Be stars from λ ~ 3000 Å to the near-IR and is a function of the following parameters: r = R∗/Renv is the inverse of the radius of the effective layer representing the circumstellar environment; Bλ(Tenv) is the source function of this layer given by the Planck function at a temperature Tenv; τλ = τe + τV(λ/λV)3 (Moujtahid et al. 1999) is the optical depth at λ of the equivalent layer, where τe is the electron scattering component, and τV accounts for the bf+ff opacity at λV ≃ 5500 Å. These quantities are only used as fitting parameters so that they are not a specific physical interpretation in any case. For those stars for which we had enough data, the CE parameters were determined in the same way as described in Moujtahid et al. (2000a,b) using the Moujtahid et al. (1998) catalog that lists changes with time of: (a) the total BD D = D∗ + d of Be stars, where D∗ is the photospheric BD and d ⋛ 0 is the second BD due to the CE; and (b) the flux and color excess at λV ≃ 5500 Å. The explicit form of ϵλ used and the parameters (r,Tenv,τe,τV) obtained for the ten program Be stars with rather strong emission characteristics are given in Appendix B.
The monochromatic fluxes used to determine Lλ and calculate the integral in Eq. (5) are from the spectrophotometric data obtained in the far-UV by the TD1, ANS satellites (Jamar et al. 1976; Macau-Hercot et al. 1978; Wesselius et al. 1982) and from the IUE satellite low resolution spectra (CDS compilation). In the visible and near-IR domains the data are from the BCD spectrophotometric data collection, the 13-color photometry (Johnson & Mitchell 1975) and various UBV, uvby, UBVRIJHK, or JHK photometric catalogs (CDS database). The far-IR data are from the ISO infrared sources (CDS). In Table 1 we identified with “f” those stars where log Lapp/L⊙ was estimated by integrating the fluxes from λUV to λIR.
For some program stars, we did not find the required far-UV and/or far-IR spectrophotometry. In these cases we could not do better than conform with the apparent bolometric luminosity estimated from the bolometric absolute magnitude Mbol =MV + BC(Teff) with 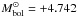 mag, where MV is the visual absolute magnitude and BC(Teff) the bolometric correction (Flower 1996; Torres 2010; Nieva 2013). The magnitude MV was determined using the apparent magnitude V of an emissionless phase.
mag, where MV is the visual absolute magnitude and BC(Teff) the bolometric correction (Flower 1996; Torres 2010; Nieva 2013). The magnitude MV was determined using the apparent magnitude V of an emissionless phase.
No matter which method is used, to estimate log Lapp/L⊙ we need to know the ISM extinction Aλ = kλE(B − V), where kλ is the ISM extinction law given by Cardelli et al. (1988, 1989) and E(B − V) is the ISM determined in several ways: a) from a smoothed distributions of the absorption E(B − V) against the distance of stars without emission located in as narrow as possible intervals of equatorial spherical coordinates (Δα,Δδ ≲ 1°) around each studied Be star [see examples of its use in Aidelman et al. (2012)]; (b) by rectifying the energy distributions near the λ 2200 Å absorption bump (Beeckmans & Hubert-Delplace 1980; Briot & Zorec 1987) using TD1, ANS far-UV spectrophotometric observations, and/or IUE low resolution spectra, or through the fitting parameters of the 2200 UV bump given by Guertler et al. (1982), Friedemann et al. (1983), Friedemann & Roeder (1987) as used in Zorec & Briot (1991). Table 1 lists the adopted average values of all independent determinations of E(B − V) for each program Be star and their respective 1σ dispersion.
The transformation from the apparent bolometric fluxes to bolometric luminosities is finally realized using Hipparcos parallaxes (van Leeuwen 2007). For stars where the trigonometric parallaxes are negative or nonexistent, we had to estimate spectroscopic distances. To this end, we used the diagrams of the long-term variability of the apparent magnitude V made by Moujtahid et al. (1998), which enabled us to seize the value corresponding to Be star emissionless-like phase. The stars with spectroscopic distances are identified with “d” in Table 1.
Appendix A.2 gives a short statement on the systematic deviations that may characterize our estimates of bolometric luminosities. We use for this average MK spectral-luminosity classes of emissionless B-type stars.
2.2.3. The apparent rotational velocity
A projected rotational velocity Vsini determined as detailed below is considered here as an apparent quantity because it can be more or less underestimated due to the GD (Stoeckley 1968; Townsend et al. 2004; Frémat et al. 2005).
For those program stars where 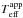 and
and 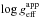 were redetermined, as mentioned in Sect. 2.2.1, we estimated the Vsini parameter using the robust CERN-MINUIT algorithm to fit the spectra (minimization package available at CERN1). Otherwise, the Vsini parameters were determined by Chauville et al. (2001), Frémat et al. (2006), and Levenhagen & Leister (2006), who took similar precautions and approaches to determine these parameters. The main characteristics of the adopted Vsini parameters
were redetermined, as mentioned in Sect. 2.2.1, we estimated the Vsini parameter using the robust CERN-MINUIT algorithm to fit the spectra (minimization package available at CERN1). Otherwise, the Vsini parameters were determined by Chauville et al. (2001), Frémat et al. (2006), and Levenhagen & Leister (2006), who took similar precautions and approaches to determine these parameters. The main characteristics of the adopted Vsini parameters
-
a)
are based on the interpretation of He i 4 471 and Mg ii 4 481 lines corrected for veiling effect;
-
b)
give a measurement of the line broadening as produced by rigidly rotating atmospheres without GD;
-
c)
are determined by comparing the observed line profiles with synthetic spectra to avoid uncertainties produced by the use of a unique limb darkening coefficient over the wavelengths inside the spectral lines (Collins & Truax 1995).
When several determinations existed for a given star, we adopted the weighted average. These averages and their 1σ deviations are given in Table 1.
2.3. The critical linear velocity
Gathering Be stars, and rapid rotators in general, into spectral type groups and luminosity classes makes little sense because both characteristics are aspect-angle dependent and do not clearly reflect either the true stellar mass or its evolutionary stage. In order to keep a statistically reliable set of stars and minimize the bf uncertainties introduced by differences in masses and/or evolutionary stages on the studied velocity distributions, the calculations performed in this work use the Vsini parameters normalized to the critical linear rotational velocity Vc. We adopted the following definition for the critical linear rotational velocity Vc: ![\begin{equation} V_{\rm c} = 436.7\left[\frac{M/M_{\odot}}{R_{\rm c}(M,t)/R_{\odot}}\right]^{1/2}\ \ \ {\rm km~s^{-1}}, \label{vc} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq122.png) (6)whose use for the studied Be stars is justified in Appendix C. The stellar masses needed to estimate Vc were interpolated in the evolutionary tracks calculated by Ekström et al. (2012) with metallicity Z = 0.014 suited for the solar environment (Asplund et al. 2009). The entries to these models are the pnrc effective temperatures and bolometric luminosities defined in Sects. 2.2.1 and 2.2.2. They also determine the pnrc stellar radius Ro(M,t) /R⊙ used to obtain Rc(M,t) /R⊙, where the ratio Rc(M,t) /Ro(M,t) comes from two-dimensional (2D) models of rotating stars (Zorec et al. 2011; Zorec & Royer 2012).
(6)whose use for the studied Be stars is justified in Appendix C. The stellar masses needed to estimate Vc were interpolated in the evolutionary tracks calculated by Ekström et al. (2012) with metallicity Z = 0.014 suited for the solar environment (Asplund et al. 2009). The entries to these models are the pnrc effective temperatures and bolometric luminosities defined in Sects. 2.2.1 and 2.2.2. They also determine the pnrc stellar radius Ro(M,t) /R⊙ used to obtain Rc(M,t) /R⊙, where the ratio Rc(M,t) /Ro(M,t) comes from two-dimensional (2D) models of rotating stars (Zorec et al. 2011; Zorec & Royer 2012).
The mass and radius of the parent nonrotating object needed to estimate Vc cannot be estimated in a simple way from the apparent effective temperature and apparent bolometric luminosity because in rapidly rotating stars both are deeply marred by rotational effects. Moreover, they are both more or less aspect-angle dependent. On the other hand, the apparent Vsini parameters have to be corrected for underestimation induced by the rapid rotation of stars. Since this correction, as well as its use to pass from a distribution of apparent Vsini to the corresponding one of true velocities V, both depend on the pnrc parameters, we first define in Sect. 3 these corrections and the required deconvolution methods. We postpone the formal determination of the pnrc quantities to Sect. 3.5.1 where, in particular, we consistently obtain the mass and radius of the parent nonrotating object needed to estimate Vc.
We can wonder whether systematic differences exist between our estimates of Vc and those derived from the fundamental parameters adopted in the literature for the spectral types studied in the present work (cf. Collins et al. 1991; Lang 1992; Townsend et al. 2004; Frémat et al. 2005; Huang & Gies 2006). Such a comparison is attempted in Fig. 1, where the Vc parameters were calculated for masses and radii corresponding to the average MS spectral type-luminosity classes according to the different calibrations. Filled symbols and the respective 1σVc dispersion bars represent the Vc obtained from fundamental parameters given in the literature for the average MK spectral types (see Appendix A.2), while the open symbols correspond to our estimates of Vc. Figure 1 shows that, depending on the spectral type and luminosity class, our Vc estimates can differ at most by 10 to 20 km s-1 with those given by other authors.
Since in the BCD spectral classification system a given MK spectral type-luminosity class covers a curvilinear quadrilateral in the (λ1,D) diagram, our estimates of Vc shown in Fig. 1, and given in Table 2, correspond to the centroids of these quadrilaterals, which do not necessarily coincide with those implied by the average MK spectral types defined by the stellar samples studied by other authors. In this table, and in Fig. 1, the spectral types are represented with the BCD index S70 given in dex.
 |
Fig. 1 Filled symbols: average critical velocities Vc and the related dispersions against the MK spectral type for luminosity classes V, IV, and III. These Vc were calculated using the effective temperatures and bolometric luminosities from calibrations carried out by various authors. Open symbols: critical velocities for the average MK spectral types and luminosity classes that conform with the method used in this work to obtain the Vc for individual stars. The MK spectral types are represented with the BCD parameter S70 dex. |
Critical velocities Vc derived in this work for average MK spectral types and luminosity classes.
3. Distribution of “true” rotational velocities
In this section we determine the distribution of ratios Vsini/Vc, where the Vsini are corrected only for measurement uncertainties. This distribution is used in the rest of this work as the reference distribution of the data relative to rotational velocities. In a second step, we transform the distribution of projected ratios Vsini/Vc into a distribution of ratios V/Vc of true rotational velocities. For this transformation we discuss two methods in which Stoeckley’s corrections (Stoeckley 1968) of the observed Vsini parameters are considered in different ways.
Since we shall deal with distributions corrected successively for a series of different effects, we adopt the notations v and Ψ(v) for velocity ratios and the corresponding distribution function as they are “before correction for some geometrical or physical effect”. The notations u and Φ(u) are used for velocity ratios and their distribution “after correction”, respectively. These notations can concern either the projected velocity ratios Vsini/Vc or the true ratios V/Vc. We may then speak of v = Vsini/Vc and Ψ(v) before correction for measurement uncertainties of the v values, which after correction become u = Vsini/Vc and Φ(u), respectively. In the same way we have v = V/Vc and Ψ(v) before correcting the v ratios, for example for binary effects, which convert into u = V/Vc and Φ(u) once the correction is applied.
 |
Fig. 2 a) Histogram giving the number N(Vsini/Vc) of observed ratios v = Vsini/Vc per class Δv studied in this work; b) smoothed density distribution Ψ(u) of projected velocity ratios u = Vsini/Vc, where measurement uncertainties on u = Vsini were taken into account. The error bars indicate the statistical uncertainty affecting the smoothed Ψ(u) distribution. |
3.1. Distribution of rotational velocities corrected for measurement uncertainties
To obtain a first glance on the aspect of the distribution of apparent ratios v = Vsini/Vc, we show in Fig. 2 the histogram constructed using the whole stellar sample regardless of the evolutionary state of the individual stars. The effect of the stellar evolution is minimized by considering Vsini/Vc velocity ratios, where Vc is calculated consistently with the mass and evolutionary state of each object. Nonetheless, we discuss the possible evolutionary effects on the V/Vc ratios in Sect. 3.6. The class-steps of the histogram were established according to the bin-width optimization method by Shimazaki & Shinomoto (2007). We then obtained a smoothed version of the frequency density distribution of ratios Vsini/Vc corrected for measurement uncertainties, which represents the reference distribution of the observed projected rotational velocities for the present work. This distribution was established using kernel estimators (Bowman & Azzalini 1997), where each observed parameter v = Vsini/Vc was represented by a Gaussian distribution, whose dispersion is given by the standard deviation of individual estimates. The distribution Ψ(u) thus obtained of ratios 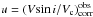 , i.e., observed ratios v corrected for measurement uncertainties, is represented with a blue curve in Fig. 2. The error bars indicate the statistical uncertainty affecting the determination of the so-called smoothed distribution Ψ(u).
, i.e., observed ratios v corrected for measurement uncertainties, is represented with a blue curve in Fig. 2. The error bars indicate the statistical uncertainty affecting the determination of the so-called smoothed distribution Ψ(u).
3.2. The Stoeckley effect
In rapid rotators, the emitted bolometric flux weakens from the pole to the equator as a function of the surface effective gravity (von Zeipel 1924; Lucy 1967; Espinosa Lara & Rieutord 2011). The contribution of the radiation to the total λ-dependent flux in a spectral line broadened by the rotation is thus less effective from the equatorial regions, which consequently translates into an underestimation of the Vsini parameter. As this effect was first studied by Stoeckley (1968), in what follows we refer to it as the Stoeckley effect. The expected value of (Vsini)Σ corrected from the Stoeckley effect can be written as 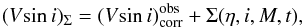 (7)where
(7)where  is the observed projected rotational velocity corrected for measurement uncertainties; Σ is the correction for the rotationally induced underestimation that hereafter, and depending on the circumstances, we call Stoeckley’s correction or Stoeckley’s underestimation. A schematic representation of the relation between the true Vsini and the observed one is shown in Fig. 3.
is the observed projected rotational velocity corrected for measurement uncertainties; Σ is the correction for the rotationally induced underestimation that hereafter, and depending on the circumstances, we call Stoeckley’s correction or Stoeckley’s underestimation. A schematic representation of the relation between the true Vsini and the observed one is shown in Fig. 3.
 |
Fig. 3 Blue line: relation between the observed |
After Stoeckley (1968), a number of authors have calculated Σ, in particular Townsend et al. (2004), Cranmer (2005), and Frémat et al. (2005), who calculated this correction strictly in the frame of rigid rotation with the classical formulation of the GD effect by von Zeipel (1924). Frémat et al. (2005) calculated spectral lines in the visible spectral range in great detail using non-LTE model atmospheres of massive and intermediate-mass stars, mainly for He i 4471 and Mg ii 4481 lines.
It is worth mentioning, however, that in spite of the colatitude θ-dependent GD exponent β1 (Espinosa Lara & Rieutord 2011; Rieutord 2016; Zorec et al. 2016), the effective temperature is still written as (von Zeipel 1924; Tassoul 1978) 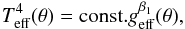 (8)
(8)
with β1 = 1. Other formulations of this relation for conservative and nonconservative rotation laws, produce β1< 1 (e.g., von Zeipel 1924; Lucy 1967; Smith & Worley 1974; Kippenhahn 1977; Hadrava 1992; Maeder 1999, 2009; Lovekin et al. 2006; Gillich et al. 2008; Dall & Sbordone 2011; Espinosa Lara & Rieutord 2011; Claret 2012). Moreover, because of the simple fact that β1 is colatitude θ-dependent, an observed β1 is necessarily a function of the aspect angle (Domiciano de Souza et al. 2014; Rieutord 2016; Zorec et al. 2016). Holding forcibly β1 = const. over the stellar surface, form Eqs. (4), (27), and (28) in Espinosa Lara & Rieutord (2011) and the condition that for rigid rotation the ratio between the equatorial and polar radii is Re/Rp = 1 + η/ 2, readily yields ![\begin{equation} \beta_1=1-\frac{2}{3}\left[\frac{\ln(1-\eta)+\eta(1+\eta/2)^{-3}}{\ln(1-\eta)-2\ln(1-\eta/2)}\right] \label{eq_beta1} , \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq159.png) (9)
(9)
which shows that this exponent varies from β1 = 1 at η = 0 to β1 = 1 / 3 when η = 1. The function β = β1/ 4 against the stellar flattening ε = 1 − Rp/Re = η/ (2 + η) is shown in Espinosa Lara & Rieutord (2011) and Domiciano de Souza et al. (2014). According to this dependence of β1 with η, the contrast between the emitted polar and equatorial radiative fluxes reduces significantly when η → 1 as compared to predictions obtained with β1 = 1. We adopted β1 = 1 on purpose, however, to produce the highest possible contrasts of effective temperatures in the stellar surface and maximize in this way the correction Σ(η,i,M,t). This favors artificially inferring the highest possible values of V in the Vsini parameter. Following these assumptions, we recalculated Σ with FASTROT (Frémat et al. 2005) imposing rigid rotation and, for angular velocity, ratios ranging from Ω / Ωc = 0.0 to Ω / Ωc = 0.9999 (0 ≤ η ≤ 0.985).
3.3. Deconvolution methods
When the inclination angle of the stellar rotational axis is assumed to be distributed at random, the probability of occurrence of the inclination angle between i and i + di is given by P(i)di = sini di. To derive the distribution Φ(u) of ratios of true velocities u = V/Vc from the distribution Ψ(v) of ratios of apparent velocities v = Vsini/Vc, we can adapt the rules given in Appendix D by writing v = usini. The variables (x,y,z) in Appendix D then translate into (u,i,v) and the functions Z(z) and X(x) into Ψ(v) and Φ(u), respectively. Accordingly, dz/ (∂z/∂y) becomes di = dv/ (ucosi) and Eq. (D.3) transforms into the known Abel-like integral equation, first discussed by Kuiper (1935) and Chandrasekhar & Münch (1950)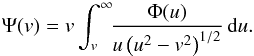 (10)Cranmer (2005) notes that when we have to deal with the corrected velocity ratio v = usini + Σ(η,i), Eq. (10) does not take into consideration the effect of the term Σ, and the correspondence between Φ(u) and Ψ(v) is no longer unique.
(10)Cranmer (2005) notes that when we have to deal with the corrected velocity ratio v = usini + Σ(η,i), Eq. (10) does not take into consideration the effect of the term Σ, and the correspondence between Φ(u) and Ψ(v) is no longer unique.
So, if we take this observation by Cranmer into account, we guess that at least two different ways can be envisioned to derive Φ(u) from Ψ(v): a) using the method introduced by Cranmer (2005), where Φ(u) is given a generic analytic form and each ratio v is corrected for the corresponding GD effect according to all possible values of u and i to form the same v; b) using the Lucy-Richardson method (Lucy 1974; Richardson 1972) to solve Eq. (10), where v of each star is corrected in advance for Stoeckley’s underestimation.
In Sects. 3.4 and 3.5 we apply both methods in turn and discuss the pros and cons of their use.
3.4. Cranmer method
In the method originally introduced by Cranmer (2005), the function Φ(u)2 is represented by a truncated linear function (trapezoid), 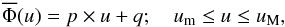 (11)
(11)
where four parameters have to be determined: the constants p and q, and the two extreme values [um,uM] over which is defined 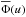 , so that
, so that 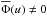 when um ≤ u ≤ uM, and
when um ≤ u ≤ uM, and 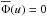 outside the interval. Actually, only three of them are iterated, since q is determined automatically through the normalization condition
outside the interval. Actually, only three of them are iterated, since q is determined automatically through the normalization condition  . These parameters are inferred by fitting the function Ψ(v) with a series of Monte Carlo trials using N = 105 model stars. In this method, the basic requirement of Cranmer is solved by assigning Stoeckley’s correction to each built projected velocity ratio v = usini, where the quantity u belongs to a defined basis function and i is assigned at random. The ratios v are treated with an imposed uncertainty.
. These parameters are inferred by fitting the function Ψ(v) with a series of Monte Carlo trials using N = 105 model stars. In this method, the basic requirement of Cranmer is solved by assigning Stoeckley’s correction to each built projected velocity ratio v = usini, where the quantity u belongs to a defined basis function and i is assigned at random. The ratios v are treated with an imposed uncertainty.
We tested the Cranmer method, but introduce small formal changes as follows:
-
(1)
The simulations were tested using the distribution of projected rotational velocities corrected in advance for measurement uncertainties, for example, the distribution obtained in Sect. 3.1. According to this, the ratios v = usini simulated in the Monte Carlo trials are considered free from measurement uncertainties.
- (2)
In Appendix F it is shown that within some limiting conditions we can choose many different analytical expressions for Φ(u), which all can be considered statistically equivalent. We then replaced the above trapezoidal form by the following function,
![\begin{equation} \displaystyle \overline{\Phi}(u) = Au^a\exp\left[-b(u-c)^2\right], \label{eq_4} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq192.png) (12)which also depends on four free parameters: A, a, b, and c, where A is fixed by the normalization condition
(12)which also depends on four free parameters: A, a, b, and c, where A is fixed by the normalization condition 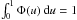 . This analytical form was chosen because it resembles the Φ(u) function determined by the Lucy-Richardson deconvolution method of data analyzed in the present work (see Sect. 3.5).
. This analytical form was chosen because it resembles the Φ(u) function determined by the Lucy-Richardson deconvolution method of data analyzed in the present work (see Sect. 3.5). -
(3)
Stoeckley’s correction were assigned to the v parameters not only as a function of the u- and i-Monte Carlo simulated parameters, but also depending on (Teff,log g). The effective temperatures and gravities used are the average Teff and log g values calculated from the apparent parameters of the studied stellar sample distributed in 16 equidistant groups. For each tested triplet (a,b,c), the fraction of model stars with the same (Teff,log g) is determined by the fraction of real stars in the corresponding (Teff,log g) group.
-
(4)
The method was applied twice: (i) using a predefined basis u −function; (ii) with a Monte Carlo sorting of the u parameters, using the probability function Φ(u) defined by the ongoing tested a, b, and c parameters. We noted that both methods lead to the same result.
-
(5)
The N simulated v = usini parameters were gathered into an histogram whose class width, determined as in Sect. 3.1, was adopted as the dispersion of the Gaussian kernels needed to obtain a smoothed version of the predicted frequency density distribution of apparent velocity ratios. As in Cranmer’s method, the quality of the fit of the predicted frequency with the reference distribution Ψ(v) was controlled with the χ2 test.
Curiously, two sets of parameters (a,b,c) for 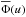 given by Eq. (12) were obtained that produce the same ‘best’ fit of Ψ(v) according to the χ2 test. We call these solutions
given by Eq. (12) were obtained that produce the same ‘best’ fit of Ψ(v) according to the χ2 test. We call these solutions 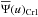 and
and 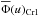 , respectively. They are shown in Fig. 4 and the parameters characterizing them are given in Table 3. For comparison sake, Fig. 4 also shows the reference distribution Ψ(v) obtained in Sect. 3.1 (see Fig. 2 curve b). Nevertheless, both solutions
, respectively. They are shown in Fig. 4 and the parameters characterizing them are given in Table 3. For comparison sake, Fig. 4 also shows the reference distribution Ψ(v) obtained in Sect. 3.1 (see Fig. 2 curve b). Nevertheless, both solutions 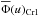 and
and 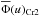 are probably equivalent within the uncertainties that affect Ψ(v) shown in Fig. 2 (curve b).
are probably equivalent within the uncertainties that affect Ψ(v) shown in Fig. 2 (curve b).
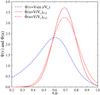 |
Fig. 4 Diagram showing the two functions |
3.5. Lucy-Richardson deconvolution method
In the original Lucy-Richardson deconvolution method, the solution for Φ(u) is obtained from Eq. (10) with a subsidiary equation constructed using a Bayesian equivalence principle. According to this principle the probability of occurrence of u and v can be written either as Φ(u)P(u | v) or Ψ(v)P(v | u), where for a value v the probability of the occurrence of u is represented with P(u | v), presently given by the factor multiplying Φ(u) in the integrand of Eq. (12). This equivalence translates into ![\begin{equation} \Phi^{r+1}(u) = \Phi^{r}(u)\int_{\mathscr{V}(u)}\left[\frac{\Psi(v)} {\Psi^{r}(v)}\right]P(v|u)\,{\rm d}v, \label{eq_6} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq216.png) (13)
(13)
which together with Eq. (10) enables iteration of Φ(u) and Ψ(v). In Eq. (13), Φr(u) and Ψr(v) are the r-iterated estimates of the respective distributions, and V(u) represents the integration interval dependent on u. The optimal number of required iterations was controlled through the Kolmogorov-Smirnov test over Φ(u) and on the recalculated Ψ(v) compared with the original or input apparent distribution.
To account for the main Cranmer demand, i.e., to consider Stoeckley’s correction consistently, the application of the Lucy-Richardson method becomes possible when each apparent ratio v is corrected for Stoeckley’s underestimation in advance of the iteration process. In the next section we detail our procedure to estimate Σ(η,i,M,t) and derive v = Vsini/Vc corrected for Stoeckley’s underestimation.
 |
Fig. 5 a) Function CT(M,t,η,i); b) function CL(M,t,η,i); c) function CG(M,t,η,i). The pnrc parameters used here are |
3.5.1. Correction Σ(η,i,M,t) as a function of pnrc parameters
To estimate Σ(η,i,M.t) we assume that stars are rigid rotators and use Eq. (8) with β1 = 1. Stoeckley’s correction is then a function of the stellar mass M/M⊙, stellar age t/tMS (tMS is the time a rotating star spends in the main-sequence phase), the ratio of the centrifugal to gravitational acceleration at the equator η (see Eq. (1)), and inclination i of the rotation axis. To determine these quantities, the following form is given to the stellar apparent fundamental parameters:
where Re(M,t,η) and Rc(M,t) are the actual and critical stellar equatorial radii, which are determined using our 2D models of rigidly rotating stars (Zorec et al. 2011; Zorec & Royer 2012). The left side of Eq. (3) is associated with the observed (apparent) fundamental parameters determined in Sect. 2.2. On the right side of Eq. (3), 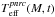 ,
, 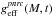 , Lpnrc(M,t) are the pnrc effective temperature, surface gravity and bolometric luminosity introduced in Sect. 2.2. The functions CT(M,t,η,i), CG(M,t,η,i), and CL(M,t,η,i) carry all the information relative to the geometrical deformation of the rotating star and of its GD over the observed hemisphere.
, Lpnrc(M,t) are the pnrc effective temperature, surface gravity and bolometric luminosity introduced in Sect. 2.2. The functions CT(M,t,η,i), CG(M,t,η,i), and CL(M,t,η,i) carry all the information relative to the geometrical deformation of the rotating star and of its GD over the observed hemisphere.
To determine CT(M,t,η,i) and CG(M,t,η,i), we calculated synthetic spectra in the λλ 4000−4500 Å wavelength interval as emitted by our 2D models of rigid rotators seen at several aspect angles i. The effective temperature and surface gravity of the rotationless counterparts of these models define the respective 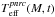 and
and 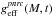 parameters. The effective temperatures and surface gravities of classic nonrotating, plane-parallel model atmospheres, which fit the above synthetic spectra of rotating stars, define the theoretical
parameters. The effective temperatures and surface gravities of classic nonrotating, plane-parallel model atmospheres, which fit the above synthetic spectra of rotating stars, define the theoretical 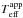 and
and 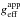 parameters; this enables us to calculate the functions
parameters; this enables us to calculate the functions 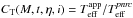 and
and 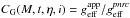 . The fit of spectra was performed with the CERN-MINUIT minimization package.
. The fit of spectra was performed with the CERN-MINUIT minimization package.
The function CL(M,t,η,i) was determined employing a similar formulation as in Georgy et al. (2014), except that in Eq. (8) we maintained β1 = 1 on purpose for all values of η to produce the largest possible Stoeckley’s corrections Σ(M,t,η,i). Figure 5 shows the functions CT(M,t,η,i), CL(M,t,η,i) and CG(M,t,η,i) calculated for an object with mass M/M⊙ = 8.2 and age t/tMS = 0.9, i.e., pnrc parameters 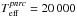 K and log gpnrc = 3.8.
K and log gpnrc = 3.8.
As a result of the known “mass-lowering effect” induced by the rotation (Milne 1923; Sackmann 1970; Bodenheimer 1971; Tuominen 1972; Clement 1979), according to which a rotating star behaves as another object with lower mass and, thus, its bolometric luminosity is lower the higher its rotation, these functions depend sensitively on the stellar mass and age. Hence, the coefficients CT, CL, and CG calculated for the present work do not exactly reproduce the behavior of the absolute magnitude MV against the color (B − V) as a function of η and the inclination i obtained by Collins et al. (1991). In fact, the magnitude MV determined by Collins et al. (1991) remains brighter than that of a nonrotating counterpart even at i ≳ 60° as η → 1 for spectral types hotter than B3. This is because of two important simplifications introduced in their calculations: (1) the “mass-lowering effect” was neglected; and (2) the polar radius Rp is maintained unchanged, even though its variation with η introduces non-negligible effects on the magnitudes as i ≳ 50°. The changes of the bolometric luminosity used in the present work are detailed in Frémat et al. (2005), while the variation of the Re and Rp radii are given in Zorec et al. (2011) and Zorec & Royer (2012). We recall that for M/M⊙ = 3 the lowering in the bolometric magnitude ranges from ΔMbol = + 0.12 to + 0.22 mag as η changes from 0.3 to 1.0, while for M/M⊙ = 20 we have ΔMbol = + 0.08 mag at η = 0.3 and ΔMbol = + 0.12 mag at η = 1.0. The respective changes ΔMV are slightly smaller because of the additional bolometric corrections. In any case, the aspect-angle dependence of MV with i ≳ 50° and η are much larger than those predicted by Collins et al. (1991).
The solution of Eq. (3) automatically determines the Σ(M,t,η,i) that corrects the apparent Vsini of each star for the GD effect in a consistent way with the stellar fundamental parameters M/M⊙, t/tMS, η and i. Details on the method used to solve the system of equations in Eq. (3) are given in Sect. E. The pnrc effective temperatures, gravities, bolometric luminosities, ratios η, and inclinations i obtained for the program Be stars are listed in Table 4. We did not considered the stars HD 49131, HD 50737, HD 112091, HD 166566, HD 171054, and HD 330950 in this work because we obtained uncertain pnrc fundamental parameters, which situate then far below the ZAMS.
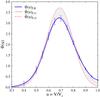 |
Fig. 6 Distribution function Φ(u)LR obtained with the Lucy-Richardson method (blue curve) with the corresponding statistical uncertainties. Both distributions |
pnrc fundamental parameters of the studied Be stars.
We then determined the smoothed distribution of projected velocity ratios v = [Vsini + Σ(M,t,η,i)] /Vc corrected for measurement uncertainties of Vsin, using the same procedure as in Sect. 3.1 that by iteration of Eqs. (10) and (13) enabled us to derive the distribution Φ(u)LR of ratios u = V/Vc, which is shown in Fig. 6 (blue curve). This figure shows the statistical uncertainties of Φ(u)LR and, for comparison, the two distributions Φ(u)Cr1,2 derived with Cranmer’s method (red curves).
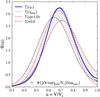 |
Fig. 7 Distributions Φ(u)LR obtained with Stoeckley’s corrections Σ(η,β1 = 1) calculated for different values of η: η = η∗ (derived in Sect. 3.5.1); η = ηmin; η = 1.0 and η = 0.0. For comparison the smoothed distribution of ratios of pnrc velocities Vsini/Vcsini (crosses) is also shown. |
Since Φ(u)LR depends on Stoeckley’s corrections Σ obtained by solving Eq. (3), it is worth asking what uncertainties affect its determination that rely on the estimate of η. To this end we have tested three extreme cases: (a) all stars have the lower possible rotational parameter ηmin, i.e., the value derived when we consider that V(ηmin) = Vsini; (b) Stoeckley’s corrections estimated for η = 1, i.e., V(η = 1) = Vc; (c) neglecting Stoeckley’s correction, i.e., Σ(M,t,η = 0,i) = 0 in all stars. The distribution functions Φ(u)LR thus obtained are shown in Fig. 7. Also, the solution that comes from η = η∗ derived with Eq. (3) (blue full line) is also shown in this section. As expected, approximation (a) produces a slight excess of low rotators (dashed red line); solution (b) is characterized by an excess of rapid rotators (red full line); (c) the distribution is shifted to smaller values of u = V/Vc (blue long-dashed line).
Another test of consistency of both the pnrc parameters used to infer Stoeckley’s correction and of Φ(u)LR can be performed by calculating just the smoothed distribution Φ(upnrc) of the true velocity ratios defined as upnrc = [(Vsini)pnrc/Vc] / sinipnrc, and thus obtained independently of the Lucy-Richardson method. The smoothed distribution is established using the kernel-estimator method (Bowman & Azzalini 1997) employed in Sect. 3.1. Figure 7 shows this function as a black cross-marked curve. This function, despite the errors that may affect the solutions issued from Eq. (3), in particular the inclination angles, adjusts the distribution Φ(u)LR, which is obtained in Sect. 3.5 with Eqs. (10) and (13), and is widely within the statistical uncertainty limits.
As noted above, we used Eq. (8) with β1 = 1 to simulate the GD effect with the purpose of having the largest possible mode of the Φ(V/Vc) distribution. Nonetheless, because in real stars not only β1< 1, but also β1 = β1(θ) (Espinosa Lara & Rieutord 2011; Zorec et al. 2016), it is expected that the actual mode of Φ(V/Vc) be displaced to a even lower value that found here, i.e., (V/Vc)mode< 0.7.
If the inclination angles were not distributed at random, Φ(u)LR could suffer from an additional skewness, which is a function of that particular distribution of inclination angles. This issue is briefly discussed in Sect. 3.7.
3.5.2. Comments on the obtained distributions Φ(u) and adopted deconvolution method
Having obtained the distribution Φ(u) using two different methods, where both enforce the basic requirements for Stoeckley’s correction of the apparent ratio v = Vsini/Vc, we would like to know whether they can be considered equivalent to each other.
We can notice that the Lucy-Richardson method does not impose any restriction to the functional aspect of Φ(u), although it requires that Stoeckley’s correction be applied before the iteration procedure, which is not a straightforward task.
The Cranmer method imposes the use of an analytical expression 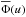 meant to represent the actual function Φ(u), which necessarily depends on a limited number of free parameters. In this way, only a limited number of moments of the actual distribution Φ(u) can be accounted for. Moreover, when a deconvolution has to be carried out with kernels determined by complicated probability distributions, doubts may arise as to whether the chosen analytical function
meant to represent the actual function Φ(u), which necessarily depends on a limited number of free parameters. In this way, only a limited number of moments of the actual distribution Φ(u) can be accounted for. Moreover, when a deconvolution has to be carried out with kernels determined by complicated probability distributions, doubts may arise as to whether the chosen analytical function 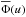 may correctly account for the physical phenomena that shape the actual Φ(u) distribution.
may correctly account for the physical phenomena that shape the actual Φ(u) distribution.
Nonetheless, the application of the Cranmer method is simple and the Monte Carlo simulation can be significantly shortened when an approximation of the free parameters defining 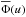 is known in advance. In Appendix F we develop a simple analytical way to calculate these quantities for trapezoidal and triangular distributions
is known in advance. In Appendix F we develop a simple analytical way to calculate these quantities for trapezoidal and triangular distributions 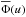 . If the apparent variable v is corrected in advance for Stoeckley’s underestimation, the analytical method produces the final values of the sought free parameters.
. If the apparent variable v is corrected in advance for Stoeckley’s underestimation, the analytical method produces the final values of the sought free parameters.
We compared the Cranmer and Lucy-Richardson methods using quantitative procedures. To this end, we have applied Cranmer’s algorithm in full to our stellar sample using Eq. (12), trapezoidal, and triangular functions to represent 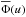 . The free parameters thus obtained are given in Table 5, and the respective functions are shown in Fig. 8a. We then applied two different tests: (i) comparison of the first four moments of distributions and (ii) the Kolmogorov-Smirnov test.
. The free parameters thus obtained are given in Table 5, and the respective functions are shown in Fig. 8a. We then applied two different tests: (i) comparison of the first four moments of distributions and (ii) the Kolmogorov-Smirnov test.
- (i)
Moments of distributions The first four moments are usually employed to control four basic characteristics of distributions: the average value of the studied random variable; the variance, or dispersion of the studied random variable; the skewness, or symmetry of distributions; and the kurtosis, or flattening of distributions. In Table 6 are given the moments ⟨ un ⟩, with n =1,...,4, of functions Φ(u)LR, Φ(u)Cr1,2, Φ(u)trapezoid, and Φ(u)triangle, as well as their respective modes (umax).
Table 5Parameters defining trapezoidal and triangular
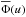 derived according to the Cranmer
method.
derived according to the Cranmer
method.
Fig. 8 a) Distribution function ΦLR(u) and the associated auxiliary trapezoidal and triangular distributions
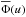 . b) Cumulative distributions
. b) Cumulative distributions ![\hbox{$C[\Phi(u)]\equiv\int_0^1\Phi(u){\rm d}u$}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq313.png) of the density distributions shown in
a).
of the density distributions shown in
a).From Fig. 6 and the quantities given in Tables 5 and 6 we can then conclude:
- (1)
The distributions, Φ(u)Cr1,2 and Φ(u)LR are defined over the same interval of u ratios and their modes are fairly similar.
- (2)
The Cranmer solution Φ(u)Cr2 is closer to Φ(u)LR. The approach Φ(u)Cr1 suggests a relative lower number of rotators with V/Vc ≳ 0.8 and a relative higher number of rotators, but it has nearly the same mode of velocities. This may be due to a compensation effect related to the use of an imposed analytical form for Φ(u).
- (3)
The first three moments produced by the trapezoidal and triangular auxiliary distributions using the Cranmer algorithm in full are closer to those of Φ(u)LR than those due to pseudo-Maxwellian auxiliary distributions.
- (4)
Different analytical forms of
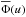 are in principle able to reproduce
distributions that reassemble the observed Φ(v) ,
i.e., having nearly the same first four moments, even though the same
probability P(u |
v) was employed in all cases.
are in principle able to reproduce
distributions that reassemble the observed Φ(v) ,
i.e., having nearly the same first four moments, even though the same
probability P(u |
v) was employed in all cases.
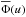 may reliably describe the properties of the actual and sought distribution Φ(u).
may reliably describe the properties of the actual and sought distribution Φ(u).
- (1)
- (ii)
The Kolmogorov-Smirnov test
To simplify the comparisons, we compared the distributions Φ(u)Cr1,2 and
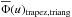 with Φ(u)LR. The cumulative distributions C [Φ(u)Cr1,2],
with Φ(u)LR. The cumulative distributions C [Φ(u)Cr1,2], ![\hbox{$C[\overline{\Phi}(u)_{\rm trapezoid}]$}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq320.png) and
and ![\hbox{$C[\overline{\Phi}(u)_{\rm triangle}]$}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq321.png) are shown in Fig. 8b; the notation means
are shown in Fig. 8b; the notation means 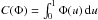 . The last column of Table 6 gives the probability at which the analytical functions
. The last column of Table 6 gives the probability at which the analytical functions 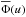 imposed here can be considered parent to Φ(u)LR. Table 6
imposed here can be considered parent to Φ(u)LR. Table 6First four moments of the function Φ(u) derived according to different approaches used: Lucy-Richardson; Cranmer with pseudo-Maxwellian, trapezoidal and triangular functions.
According to the Kolmogorov-Smirnov test, we see that the Cranmer solutions Φ(u)Cr1,2 with pseudo-Maxwellian functions can be considered parent distributions of Φ(u)LR, respectively, within 60.0% and 99.9% levels of confidence, while
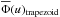 and
and 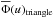 are at 20.5% and 99.4% confidence levels, respectively. Also, the use of trapezoidal distributions to discuss the velocity distributions of Be stars is less appropriate.
are at 20.5% and 99.4% confidence levels, respectively. Also, the use of trapezoidal distributions to discuss the velocity distributions of Be stars is less appropriate. So, according to tests (i) and (ii), it seems sensible to use the Lucy-Richardson deconvolution method because it avoids imposing analytical behaviors for Φ(u). Moreover, the complexity of some corrections applied in the next sections, makes the use of analytical auxiliary functions to account for the inherent subtleties that may characterize Φ(u) rather uncertain and complicated.
3.6. Effects of stellar evolution on the distribution of V/Vc ratios
In general, a stellar sample can be considered statistically reliable if it is formed by a rather large number of objects, which all have roughly the same masses and ages. When this is not so, however, the effects assumed by the differences in masses can be somewhat suppressed using normalized apparent rotational velocities Vsini/Vc. Nevertheless, the ratio V/Vc depends on stellar evolutionary effects, which are controlled by the rotation itself (cf. Maeder 2009). It is then difficult to establish a statistically sample of Be stars where the effects of the evolution are entirely obliterated.
In this study we considered all Be stars forming a unique group, although they are in different MS evolutionary phases. It is however important to inquire which statistical tendencies can be brought out from rotation-velocity distributions of stars in different evolutionary time intervals, in particular on the evolution of the ratio V/Vc. For early-type stars, few studies have attempted to tackle this issue by putting stars into luminosity-class groups (Balona 1975; Zorec 1986; Zorec et al. 1988, 1990, 2004; Yudin 2001; Cranmer 2005). When dealing with rapid rotators, however, the MK luminosity classes are apparent stellar properties whose relation with the actual evolutionary characteristics is not straightforward. We then divided our Be-star sample into three groups of different fractional age t/tMS −intervals: early MS period, intermediate MS period, and late MS period, using the t/tMS determined in Sect. 3.5.1. This division is marred by uncertainties. Adopting equal t/tMS −intervals, the number of stars in each of these groups is very different; in particular, there are some which can be considered statistically ‘underpopulated’ groups. On the contrary, if the same number of stars is demanded for each group, the t/tMS −intervals become very unequal. Some of them are quite large in duration, which cannot then single out characteristics proper to a given short evolutionary period. Table 7 gives the characteristics of some Be-star groups we could form. As a number of stars have t/tMS ≳ 1, we also established a group with objects in 0.66 ≤ t/tMS ≤ 1.00.
Main-sequence evolutionary subphases, number of program stars in each group, the corresponding average fractional times ⟨t/tMS⟩ with their dispersions, modes (V/Vc)mode of the distributions, and the respective characteristic dispersions.
 |
Fig. 9 a) Distributions of velocity ratios u = V/Vc of the program Be stars corresponding to three MS evolutionary subphases, which are indicated in the inlay. Each group has roughly the same number of stars. b) Distributions of velocity ratios u = V/Vc corresponding to three MS evolutionary subphases of the same duration, which are indicated in the inlay. In each block, the normalization is made by adding the area of all three distributions. |
The distributions of Φ(u) velocity ratios u = V/Vc obtained for these stellar groups are shown in Fig. 9, where the area under each curve is proportional to the number of stars in the group. It is thus clear that a significantly larger number of objects would be necessary to draw more precise results on the evolution of the ratio V/Vc. However, these distributions confirm the known fact that V/Vc becomes globally larger as stars evolve from early MS evolutionary phases to later evolutionary phases, whether or not they are rapid rotators (Yudin 2001; Zorec et al. 2004; Cranmer 2005). Nevertheless, Fig. 9 uncovers another property that becomes evident when we compare the V/Vc-distributions of intermediate and late MS evolutionary periods, which is probably specific to Be stars: once the mode (V/Vc)mode ≃ 0.77 is attained at some intermediate evolutionary phase in the MS, it will stay unchanged up to the end of the MS evolutionary lifespan (see rows 2, 3, 6 and 7 in Table 7).
Studies of other effects that change the V/Vc-distributions of Be stars would certainly benefit from sample divisions by shorter evolutionary intervals than those that we outlined here. Nevertheless, on account of the statistical uncertainties just mentioned above, in the remainder of this work and in Paper II of this series (Zorec et al. 2016), we continue to treat the entire stellar sample forming a unique, single group.
The discussion of the variation of the ratio V/Vc with the age can be extended a little by studying its dependence with the stellar mass. We distributed our stellar sample in age-mass groups with the goal of having the same average masses in the different age intervals. Unfortunately, this attempt ends up with groups where the number of objects are not the same and some of them are rather under-represented to the detriment of the quality of statistics. These groups and the corresponding average values of the pnrc velocity ratios Vsini/Vc and V/Vc are given in Table 8.
From Table 8 we can conclude that in each studied age interval, the dependence of the average of true velocity ratios with the stellar mass is marginal, if there is any. There is, however, a dependence with age in the sense that V/Vc is higher as the age ratio t/tMS → 1 in all mass groups. Thus, this result does not confirm the claim by Cranmer (2005), which states that the lower limit of V/Vc to form circumstellar disks in the hottest (more massive) Be stars is “well below 1”, while the lower limit approaches 1 in the less massive Be stars.
Average pnrc velocity ratios ⟨Vsini/Vc⟩ and ⟨V/Vc⟩ for mass-age groups of the studied Be star sample.
3.7. Effects on the distribution of ratios V/Vc due to nonrandomly distributed inclinations
In Sects. 3.3−3.5 we assumed that the inclination angles are distributed at random, however, the studied sample may not agree with this hypothesis. To complete the discussion on the characteristics of distributions of true rotational velocities, we simulate cases where the inclination angle i of the stellar rotational axis is not distributed at random and observe the induced effects on the distributions of ratios of true rotational velocities. Because there is not a unique way to formulate the lack of randomness, we assume the density probability of the occurrence of an inclination between i and i + di is given by 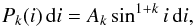 (15)
(15)
where k is a free parameter, while Ak is the normalization constant. With k> 0, there are simulated frequencies favoring high inclinations, while k< 0 produces an excess of low inclination angles as compared to those predicted by randomly distributed inclined axes (k = 0). Figure 10a shows some functions Pk(i), while Fig. 10b shows the histograms calculated for the same number of objects as in our stellar sample. The observed distribution Ψ(v) of apparent ratios v = Vsini/Vc and the distribution Φ(u) of true ratios u = V/Vc is now written as 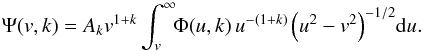 (16)
(16)
Using the Lucy-Richardson algorithm, we obtain the distributions shown in Fig. 10c. In these calculations we used Stoeckley’s corrections derived in Sect. 3.5.1. Although it is not shown explicitly, we note that the statistical uncertainty affecting the correction of distributions for measurement uncertainties is smaller than the spread of distributions Φ(u,k) obtained with −0.5 ≲ k ≲ 0.5. The modes and dispersions of functions Φ(u,k) due to Pk(i) given in Eq. (15) are almost the same. On the contrary, their skewness and kurtosis are sensitive to k.
 |
Fig. 10 a) Density probability distributions Pk(i) against sini for k = −0.5, 0.0 and + 0.5. b) Frequency histograms of inclinations i against sini for k = −0.5, 0.0 and + 0.5. c) Distributions Φ(u,k) of ratios u = V/Vc assuming that the distributions of inclinations angles is given by Pk(i) in Eq. (15). The tested cases are for k = 0 (random) and nonrandom distributions with k = + 0.5 and k = −0.5. |
One might be tempted to inquire how the distribution of the inclination angles determined in this work compares with the random distribution. Using the derived inclinations and their uncertainties, we obtained the histogram shown in Fig. 11 (blue), which is compared with the histogram obtained for randomly distributed inclinations (white). In both cases the respective sampling uncertainties are shown. The student test performed on the individual classes in the interval 0 < sini ≲ 0.5 shows that both distributions are the same to better than 99% confidence level, while they are definitely different in 0.5 ≲ sini ≲ 1.0. In this last interval of inclinations, a function given by Eq. (15) with k< 0 might fit the distribution.
Before concluding anything about the actual distribution of the inferred angles i, it is important to note the following: (1) the CT, CL, and CG functions entering Eq. (3) do not vary strongly in the interval 0.7 ≲ η ≲ 1.0, which according to the algorithm used to solve this system of equations, the propagation of the uncertainties affecting the observed parameters produces sightly overestimated values of η and, thus, the number of stars with inclinations in the interval 35° ≲ i ≲ 70° is increased; (2) for some unknown reason, the stellar data used here do not frequently produce sini ≳ 0.95, a high value indeed, but low enough to underestimate the number of stars with i ≳ 75°; (3) in spite of the care we payed to estimate the bolometric luminosity of stars, Lapp, this parameter is probably the main source of uncertainties because we can never be absolutely sure that the effects due to the variable circumstellar envelope of Be stars have been correctly or entirely accounted for; and (4) all stars were assumed to be rigid rotators. Nevertheless, they can have some degree of differential rotation, which would then require that the line broadening be reinterpreted and given the right meaning to the Vsini parameter (see Paper II).
Thus, because of the difficulties listed above in determining the absolute inclination angles, it is not possible to figure out the actual distribution of inclinations of the studied Be stars. On the other hand, in Fig. 7 we have shown that the distribution of the velocity ratios (V/Vc)pnrc = [(Vsini)pnrc/Vc] / sinipnrc (crosses), which depends on the derived inclination angles i, fits very closely the distribution of ratios V/Vc obtained assuming that the inclination angles are distributed at random. We can then conclude that even if the individual inclinations are still rough estimates, they are precise enough to warrant that the conclusions drawn from the statistical distribution of V/Vc obtained in Sect. 3.5 is reliable.
 |
Fig. 11 Comparison of the distribution of inferred inclination angles for the program stars (cyan histogram) with the histogram for randomly distributed inclinations (white histogram). The error bars correspond to sampling uncertainties. |
4. Effect carried by the macroturbulence
4.1. Preliminary comments
Since the early fifties it has been recognized that spectral lines may undergo broadening due to random motions of eddies in the stellar atmospheres (Unsöld & Struve 1949; Huang & Struve 1953). When these movements are characterized by distance scales on the order or lower than the mean free-path of photons, they are called microturbulence. These movements affect the line absorption coefficient and produce the so-called “second-class” line broadening. Movements of eddies implying distance scales that are larger that photon mean free-paths are called macroturbulence and they do not change the effective mean atomic-line absorption coefficient. The line broadening is then produced by the Doppler effect associated with the macroscopic motion of eddies and is called first class. Howarth et al. (1997) claim that macroturbulence can be an important line broadening mechanism in O- and early B-type supergiants that adds to rotation. Nevertheless, its determination is not unique, since the same broadening can be produced by combining large ranges of macroturbulent velocities vmt and Vsini values (Ryans et al. 2002).
Like microturbulence, macroturbulence hides in principle a series of motions due to physical nature that is not yet well identified. Cantiello et al. (2009) evoke the subphotospheric convection to account for the microturbulent motions, while Aerts et al. (2009, 2014) suggest that macro-turbulence could be ascribed to low-amplitude gravity modes of nonradial pulsations. Similar conclusions are also put forward by Simón-Díaz (2015).
Two models are currently used to describe the line broadening carried by macroturbulent motions: isotropic Gaussian and anisotropic with radial and tangential components, which each have a Gaussian-dependent velocity distribution (Gray 1975, 1992). Although the anisotropic model depends on at least three free parameters, these authors assume that both models are characterized by a unique dispersion of macroturbulent velocities σmt, which is somewhat correlated with the stellar effective temperature. Generally, more effective fits of spectral line profiles are obtained using the anisotropic model, which requires slightly larger values of vmt than the isotropic model (Simón-Díaz & Herrero 2007, 2014; Dufton et al. 2006a). Both models are, however, nothing but spectral line fitting procedures that mask unidentified line broadening phenomena.
Up to now, macroturbulence was mostly explored in early-type stars of several luminosity classes, mainly supergiants, but all they have low values of Vsini (cf. Howarth et al. 1997; Ryans et al. 2002; Dufton et al. 2006a; Simón-Díaz & Herrero 2007; Fraser et al. 2010; Sundqvist et al. 2013). The existence of macroturbulence was also noticed in later B-type supergiants (Dufton et al. 2006a). According to Simón-Díaz & Herrero (2014) and Sundqvist et al. (2013) macroturbulence should not be entirely negligible in early-type dwarfs to giants. We can then expect that macroturbulent-like movements also exist in the atmospheres from B-type dwarfs to giants of lower effective temperatures than those explored in the above cited works. This can be the case of all those stars that undergo nonradial pulsations and/or a wide funnel of instabilities induced by the rotation. We assume then that the photospheric spectral lines currently used to determine the Vsini parameters of Be stars are affected by macroturbulence. It is worth noting that the macroturbulent motions are detected on average only when apparent rotational velocities are low, i.e., Vsini ≤ 150 km s-1. Spectral lines broadened by Vsini ≳ 150 km-1 remain fairly insensitive to broadening induced by macroturbulent motions. Although in these cases we are not able to detect such motions, we should not conclude that they are not present, regardless of their physical origin. This is particularly valid in Be stars, where atmospheres can undergo significant upheavals maintained by nonradial pulsations, a large spectrum of instabilities induced by the rapid rotation, and possible disordered magnetic fields generated by underphotospheric convection (Clement 1979; Maeder et al. 2008; Cantiello et al. 2009; Cantiello & Braithwaite 2011).
4.2. Formulation
Following the composition rules of probabilities given in Appendix D, the relation between the frequency Ψ(v) of velocity ratios v = (Vsini)mt/Vc, where the (Vsini)mt is the projected rotational velocity affected by macroturbulence, and the frequency Φ(u) of ratios u =Vsini/Vc corrected for macroturbulence, is given by ![\begin{equation} \Psi(v) = \int_0^v\!\!\Phi[v-\epsilon(v_{\rm mt},u)]\left\{\frac{\phi(v_{\rm mt},u)}{ \partial\epsilon/\partial v_{\rm mt}}\right\}\,{\rm d}u \label{eq_10} , \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq384.png) (17)where we have written
(17)where we have written 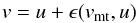 (18)
(18)
with ϵ(vmt,u) representing the overestimation of the actual apparent rotation velocity assumed by the macroturbulence. In Eq. (17), φ(vmt) is the occurrence probability of the macroturbulent velocity vmt. We assume that this distribution is the same for all B-type stars from dwarfs to giants.
The definition of ϵ(vmt,u) given in Eq. (18) is the same as used by Simón-Díaz & Herrero (2007, see their Fig. 10), and it is adapted to account for the effect introduced by macroturbulence on the distribution function of rotational velocities. Its formal aspect can make us believe that a single scalar can also accurately account for the effects of macroturbulence on line profiles. In fact, the effects on a line profile depend on several parameters, depending on the approximation used to describe the macroturbulent motions: isotropic or anisotropic (Gray 1975, 1992). In any case, all these parameters are free without clear physical meaning and their values are not unique, as shown by Ryans et al. (2002). The parameter ϵ(vmt,u) simply accounts for the difference between the Vsini parameters determined with the FT method, once from rotationally broadened spectral lines convolved and then from not convolved line profiles for macroturbulence effects. We used the anisotropic approach to represent macroturbulence in the currently used monoparametric version (see Simón-Díaz & Herrero 2007). Other details for its use in Eq. (18) are given in Sect. 4.3.
 |
Fig. 12 Normalized distributions Φ(vmt,u) against the macroturbulent velocity vmt given by Eq. (19) for some u = Vsini/Vc values that are identified in the figure. |
To carry out the deconvolution of Φ(u) in Eq. (17) we need to specify φ(vmt). To this end we used the compilation of vmt values presented by Simón-Díaz (2015), which encompass 100 O- and 200 B-type stars of different spectral types and luminosity classes. This compilation is presented in Fig. 1 of Simón-Díaz (2015) as a two-dimensional distribution φ(vmt,u) of discrete macroturbulent velocity vmt determinations as a function of Vsini. Making cuts in this diagram by intervals of Vsini against vmt, and cuts by intervals of vmt against the Vsini, we produced least-squares fits of the resulting one-dimensional distributions of points with the following system of functions;
![\begin{equation} \begin{array}{lcl} &&\displaystyle \phi(v_{\rm mt},u) = \displaystyle [1-\gamma(u)]\phi_{\rm G}(v_{\rm mt})+\gamma(u)\phi_{\rm F}(v_{\rm mt}) \\[2mm] &&\displaystyle \phi_{\rm G}(v_{\rm mt},u) = \displaystyle c_{\rm g}\exp\left\{-\frac{1}{2\sigma^2}\left[v_{\rm mt}-v_{\rm M}(u)\right]^2\right\} \\[2mm] &&\displaystyle \phi_{\rm F}(v_{\rm mt},u) = \displaystyle c_{\rm f}\left\{1-\exp\left[\frac{A(u)}{v_{\rm mt}}\right]^{b(u)}\right\} \\[2mm] &&\displaystyle A(u) = \displaystyle \left[\frac{b(u)}{b(u)-1}\right]v_{\rm M}(u), \label{eq_12} \end{array} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq390.png) (19)which we adopted as the analytical translation of the φ(vmt,u) distribution of points in Simón-Díaz (2015). This density of points increases as a function of vmt and attains a maximum at vmt = vM, which in turn is an increasing function of Vsini. For Vsini ≳ 80 km s-1 the points acquire a rather uniform distribution in the (Vsini,vmt) diagram. In Eq. (19), cg and cf are normalization constants. γ(u) is a linear function of u = Vsini/Vc that varies from 0 to 1 as Vsini goes from 0 to 80 km s-1. The exponent b(u) accounts for the density of points, whose value ranges from b = 12 in the interval 0 ≲ u ≲ 0.2 (0 ≲ Vsini ≲ 80 km s-1) to about b = 100 as Vsini → 200 km s-1. The dispersion σ = 17.5 km s-1 as well as the functions vM(u), γ(u), and b(u) are determined in the fitting procedure of the mentioned diagram in Simón-Díaz (2015). The obtained analytical distribution φ(vmt,u) against vmt for some values 0.0 ≤ u = Vsini/Vc ≤ 0.4 is shown in Fig. 12.
(19)which we adopted as the analytical translation of the φ(vmt,u) distribution of points in Simón-Díaz (2015). This density of points increases as a function of vmt and attains a maximum at vmt = vM, which in turn is an increasing function of Vsini. For Vsini ≳ 80 km s-1 the points acquire a rather uniform distribution in the (Vsini,vmt) diagram. In Eq. (19), cg and cf are normalization constants. γ(u) is a linear function of u = Vsini/Vc that varies from 0 to 1 as Vsini goes from 0 to 80 km s-1. The exponent b(u) accounts for the density of points, whose value ranges from b = 12 in the interval 0 ≲ u ≲ 0.2 (0 ≲ Vsini ≲ 80 km s-1) to about b = 100 as Vsini → 200 km s-1. The dispersion σ = 17.5 km s-1 as well as the functions vM(u), γ(u), and b(u) are determined in the fitting procedure of the mentioned diagram in Simón-Díaz (2015). The obtained analytical distribution φ(vmt,u) against vmt for some values 0.0 ≤ u = Vsini/Vc ≤ 0.4 is shown in Fig. 12.
 |
Fig. 13 Macroturbulent broadening ϵ(vmt,u) for 10 values of the macroturbulent velocity vmt scaled by steps of 10 km s-1, as a function of the ratio u = Vsini/Vc. |
4.3. Distribution of true velocities corrected from macroturbulent broadening
We calculated a great number of He i 4471 and Mg ii 4481 line profiles for many effective temperatures and log g = 3.8 to sketch an average MS evolutionary phase. They were all broadened assuming that stars were gravity-darkened rigid rotators (Frémat et al. 2005). The obtained line profiles were then broadened for macroturbulence with the currently used simplified anisotropic model. For each adopted macroturbulent velocity vmt, we calculated the weighted average of the broadening differences ϵ(vmt,u). The weights are the fractions of sample stars that enter per interval of effective temperatures. Figure 13 shows the deviations ϵ(vmt,u) obtained for several values of vmt against u = Vsini/Vc.
To obtain Φ(u) in Eq. (17), we used the Lucy-Richardson algorithm (Lucy 1974; Richardson 1972) and the probability distribution φ(vmt,u) given by Eq. (19). The results thus obtained are shown in Fig. 14. The blue line represents the normalized distribution of parameters Vsini/Vc corrected for both, measurement uncertainties and Stoeckley’s effect (cf. Fig. 2). The red curve represents the normalized distribution Φ(u) of u = Vsini/Vc statistically corrected for macroturbulent line broadening obtained with b = 12 in 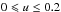 . As expected, the distribution is slightly affected in the interval 0.0 ≲ u = Vsini/Vc ≲ 0.4, and suggests a modest increase of genuine low rotators, while the mode of the distribution is slightly reduced. We do not have a reliable explanation for the bump-shaped excess at u = Vsini/Vc ~ 0.10−0.15. If there were a higher number of points in 0 ≲ u ≲ 0.2 than actually displayed by Simón-Díaz (2015), we should need b< 12. Figure 14 show the effect produced by a hypothetical exponent b = 6 (black dashed curve).
. As expected, the distribution is slightly affected in the interval 0.0 ≲ u = Vsini/Vc ≲ 0.4, and suggests a modest increase of genuine low rotators, while the mode of the distribution is slightly reduced. We do not have a reliable explanation for the bump-shaped excess at u = Vsini/Vc ~ 0.10−0.15. If there were a higher number of points in 0 ≲ u ≲ 0.2 than actually displayed by Simón-Díaz (2015), we should need b< 12. Figure 14 show the effect produced by a hypothetical exponent b = 6 (black dashed curve).
In conclusion, owing to the correction for macroturbulent line broadening, the number of low rotators is slightly increased to the detriment of rotators with velocity ratios near the mode of the distribution, but the mode itself is almost preserved.
 |
Fig. 14 Distribution Φ(u) after correction for macroturbulence. The blue line represents the normalized distribution Ψ(v) of parameters v = Vsini/Vc corrected for both, measurement uncertainties and Stoeckley’s effect. The red and dashed black curves represent the normalized distribution Φ(u) of ratios u = Vsini/Vc corrected for macroturbulent motions using different values of b (see text). |
5. Effect carried by the presence of a binary component
In Be stars, binarity not only helps to form a circumstellar disk during a mass-transfer episode (Kriz & Harmanec 1975; Harmanec 1987), but also to spin up one of the components owing to the angular momentum gained during a mass transfer event (Packet 1981; Gies 2000; Harmanec et al. 2002; de Mink et al. 2013). In the context of our subject, it has long been accepted that binarity can alter the Vsini parameters of the individual components.
As in other stellar classes, a rather large fraction fbin of Be stars studied in this work can be binaries. Recent statistics show that among massive stars this frequency can be as high as 70% (de Mink et al. 2013), while it climbs to nearly 100% (Sana et al. 2012, 2014) for O-type stars. Chini et al. (2012) report that the frequency of binaries is higher than 80% for masses M> 16 M⊙, and it steadily decreases to 20% for masses M ~ 3 M⊙. Oudmaijer & Parr (2010) find that the frequency of binaries among B stars without emission is 30% and it is the same for Be stars. In the past there have been several surveys of B star binarity: Abt et al. (1990) obtain 74% binaries among B2-B5-type stars, considering both spectroscopic and visual; Kouwenhoven et al. (2007) infer that in the Sco OB2 association there must be 70% binaries among intermediate-mass stars (B- to A-type); and Mason et al. (2009) find 64% binaries in a speckle interferometry survey of Galactic B stars.
Beyond the low-mass extreme of B-type stars, Fuhrmann & Chini (2012) report that the percentage of binary stars may probably increase to 100% from F to late A-type stars, although these last are considered with all their aspects of multiplicity. Recent studies based on adaptive optics surveys (De Rosa et al. 2014), and VLTI/PIONIER interferometry (Marion et al. 2014) note an increase of 13% A-type stars among objects considered single object up to now.
Since the frequency of binary systems for O-type stars approaches 100% and the multiplicity of all kinds among late A-type stars attains similar percentages, we can ask whether the above noted low frequency of binary systems of B spectral type is biased in some way.
According to environments, authors and methods used to detect binaries, the frequency for B-type binaries ranges from 30% to 70%. Frequently, the search of binaries among them is limited to the use of Balmer lines, whose large broadening easily hides the existence of components leading thus to underestimate the frequency of binaries. On the other hand, the occurrence of the Be phenomenon is the largest among stars of apparent B2 spectral type. These stars have masses of apparent O9-B1 spectral types (Zorec & Briot 1997; Zorec et al. 2007), implying M ≳ 12 M⊙, which enters the domain of massive stars, where binarity is frequent. As a consequence of these uncertainties, the curious lack of binaries among B-type stars appears rather doubtful. Thus, we proceed by making the ansatz that at least 70% of Be stars are binaries.
5.1. Formulation
We assume that the measured Vsini parameter of an object in a binary system mainly reflects the rotation of the primary. This value can then be affected by the orbital angular velocity, but the effect depends on the mass ratio and the separation of components.
The radial velocity of a point 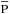 located on the observed hemisphere of the tested primary component, whose rotation axis is for simplicity taken parallel to that of the orbital rotation, is given by (Limber 1963; Moreno & Koenigsberger 1999; Moreno et al. 2005)
located on the observed hemisphere of the tested primary component, whose rotation axis is for simplicity taken parallel to that of the orbital rotation, is given by (Limber 1963; Moreno & Koenigsberger 1999; Moreno et al. 2005) ![\begin{equation} \begin{array}{rcl} \displaystyle V_{\rm x} & = & \displaystyle \left\{\!\frac{q}{1+q}r(\theta)\omega(t)\!\left[r(\theta)\frac{e}{p}r(\theta)\sin^2\theta+\cos\theta\!\right]\right. \\ & & \displaystyle \left.-\left[\Omega_{\rm p}+\omega(t)\right]x_1\!\phantom{\frac{q}{1+q}}\hspace*{-0.8cm}\right\}\sin i, \\ \end{array} \label{eq_13} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq418.png) (20)
(20)
where q = Ms/Mp is the mass ratio of the secondary to the primary; ω(t) is the time dependent orbital angular velocity; e is the eccentricity of the orbit; p = a(1 − e2) is the conic parameter with a = ap + as the semimajor axis of the relative orbit, with ap and as being those of the components; θ is the polar azimuthal coordinate; Ωp is the value of the nonsynchronous angular velocity of the primary; r(θ) is the time-dependent separation of the components; x1 is the coordinate of the test point  measured positively from the center of the primary toward the secondary on the axis that joins both components; and sini accounts for the inclination between the rotation axis and the direction toward the observer. Because of several other uncertainties that we may deal with in the present discussion, we assume that all binaries have circular orbits (e = 0), so that ω(t) = ω = constant. We also do not take into account the periodical apparent changes of Vsini due to spectral effects produced by mutual reflection effects. The determination of Vsini requires that all spectral lines are reduced to a common radial velocity. This means that the first term in Eq. (20), which represents the orbital motion, is removed. According to these simplifications, the effective velocity that broadens the spectra lines reduces to (cf. Eq. (20))
measured positively from the center of the primary toward the secondary on the axis that joins both components; and sini accounts for the inclination between the rotation axis and the direction toward the observer. Because of several other uncertainties that we may deal with in the present discussion, we assume that all binaries have circular orbits (e = 0), so that ω(t) = ω = constant. We also do not take into account the periodical apparent changes of Vsini due to spectral effects produced by mutual reflection effects. The determination of Vsini requires that all spectral lines are reduced to a common radial velocity. This means that the first term in Eq. (20), which represents the orbital motion, is removed. According to these simplifications, the effective velocity that broadens the spectra lines reduces to (cf. Eq. (20)) ![\begin{equation} \displaystyle V_{\rm x} = \displaystyle \left[\Omega_{\rm p}+\omega\right]x_1\!\sin i, \label{eq_13b} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq431.png) (21)which means that V in the measured Vsini is
(21)which means that V in the measured Vsini is 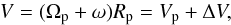 (22)where Rp is the radius of the primary. Using the third law of Kepler, we readily obtain the expression for the normalized perturbation component Δv = ΔV/Vc,
(22)where Rp is the radius of the primary. Using the third law of Kepler, we readily obtain the expression for the normalized perturbation component Δv = ΔV/Vc, ![\begin{equation} \Delta v = \left[(1+q)\delta^{-3}\right]^{1/2}, \label{eq_15} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq434.png) (23)where we have written δ = a/Rp. It is easy to see that the range of variation of Δv is limited to 0 ≤ Δv ≤ 0.5, where Δv = 0.5 corresponds to the extreme configuration given by q = 1 and δmin = 2.
(23)where we have written δ = a/Rp. It is easy to see that the range of variation of Δv is limited to 0 ≤ Δv ≤ 0.5, where Δv = 0.5 corresponds to the extreme configuration given by q = 1 and δmin = 2.
 |
Fig. 15 Curves log f(Δv). All 9 solutions obtained with −0.6 ≤ α ≤ 0.3 and −0.5 ≤ β ≤ 0.5 in Eq. (26) for f(Δv) are comprised in the gray-shaded region. The red line represents the average of the 9 tested solutions and the blue line corresponds to the solution for α = β = 0. |
The calculation of the effect carried by Δv on the observed distribution of V/Vc depends on the occurrence probability f(Δv) of Δv. Following the definition of probability and the relations presented in Appendix D, the frequency function f(Δv) can be obtained with the surface integral 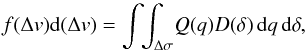 (24)
(24)
which is calculated over the area Δσ and limited by the curves Δv = Δv(q,δ) and Δv + d(Δv) = Δv(q,δ). In Eq. (24), Q(q) is the probability distribution of the binary mass-ratios q, while D(δ) represents the probability of the occurrence of the orbital separation δ. We adopt for Q(q) and D(δ) the following expressions frequently used in the literature (Kobulnicky & Fryer 2007; Reggiani & Meyer 2013; de Mink et al. 2013), 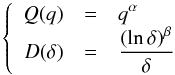 (25)
(25)
Introducing these definitions into Eq. (24) and knowing that for each δ = const. it is dq = d(Δv) / | ∂v/∂q |, where 1 / (∂v/∂q) = 2Δvδ3, the integration of Eq. (24) over δ from Δv− 2 / 3 to (2Δv2)1 / 2 (see Eq. (23)), we obtain ![\begin{equation} f(\Delta v) = \frac{f_{\rm o}}{\Delta v}\int_{0}^{1}\!q^{\alpha}\left[\ln\left(\frac{1+q}{\Delta v^2}\right)\right]^{\beta}\,{\rm d}q \label{eq_18} , \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq458.png) (26)
(26)
where fo stands for a normalization constant. Since the exponents α and β are highly uncertain (Shatsky & Tokovinin 2002; Kobulnicky & Fryer 2007; Reggiani & Meyer 2013; de Mink et al. 2013, and references therein) to account for the large range of their possible values, we calculated Eq. (26) using nine pairs (α,β) with α = −0.6, −0.15, 0.3 and β = −0.5, 0.0, 0.5. The nine functions f(Δv) thus obtained are all comprised in the shaded region shown in Fig.15. Because the higher frequencies f(Δv) are for 0 ≤ Δv ≲ 0.2, we can safely adopt a unique average relation, which nearly coincides with the expected canonical solution for α = β = 0 (blue curve in Fig.15) adopted by de Mink et al. (2013), which can be nicely represented by the following simple interpolation expression: 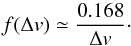 (27)
(27)
Since Q(q) and D(δ) are given by power laws, the normalization of f(Δv) must be carried out with limited values of Δv. Apart from Δvmax = 0.5, the other limiting value Δv → 0 was here assumed to be provided by Δvmin = 10-4, which implies a negligible effect on V and roughly corresponds to an orbital separation δmax = 600.
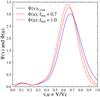 |
Fig. 16 Distribution functions of true velocity ratios V/Vc. Ψ(v)Σ + mt is the distribution of v = V/Vc corrected for measurement uncertainties, Stoeckley’s effect (Σ), macroturbulent velocities (mt) with b = 12 and projection factor sini. It distinguish thus from Φ(u)b = 12 shown in Fig. 14, which is not corrected for effects owing to sini. Full red line corresponds to the distribution of u = V/Vc corrected for Σ + mt and binarity with fbin = 0.7. Dashed red line corresponds to the distribution corrected for Σ + mt and binarity assuming fbin = 1.0. |
5.2. Distribution velocities corrected for effects due to binarity
Assuming that the same fraction fbin of binaries occurs in all spectral types and luminosity classes, the relation between the observed frequency function Ψ(v) of ratios v = V/Vc perturbed by the presence of binaries and the “actual” frequency Φ(u) of “unperturbed” ratios u = v − Δv is given by  (28)
(28)
which is solved with the Lucy-Richardson deconvolution algorithm (Richardson 1972; Lucy 1974). Figure 16 shows the results obtained for fbin = 0.7 and fbin = 1.0. In this figure, Ψ(v)Σ + mt stands for the input distribution of velocity ratios V/Vc corrected for Stoeckley’s effect and macroturbulent velocities. Apart from the modes, which are systematically shifted to lower values the higher is the fraction fbin, there is a small secondary bump at V/Vc ~ 0.1 that appears due to the correction for macroturbulent velocities. Perhaps, according to speculations in Fig. 14, instead of a “bump” at V/Vc ~ 0.1, there is a “depression” in 0.15 ≲ V/Vc ≲ 0.35, which reveals a possible insufficient correction for macroturbulence or even other perturbations that we are not able to detect at such rotational velocity ratios.
6. Comments and conclusions
The main purpose of this work is to obtain the distribution Φ(u) of rotational velocity ratios u = V/Vc (Vc is the critical velocity at the equator) of a sample of Galactic classical Be stars. The distributions of ratios V/Vc were corrected statistically for a number of phenomena affecting the value of the Vsini that blurs the information on the stellar rotation contained in the factor V. The function Φ(u) obtained in the present work is used in the second paper of this series (Zorec et al. 2016) to inquire about the average properties of the surface rotation in Be stars.
Because the parameter Vsini of Be stars suffers from effects of gravitational darkening (GD), we discussed two statistical deconvolution procedures that take “Stoeckley’s underestimation” in different ways and produce distributions of ratios V/Vc from the observed distributions of projected velocity ratios Vsini/Vc. The results obtained using these methods can be summarized as follows:
-
We adopted a sample of 233 classic Be stars that was previously studied in Chauville et al. (2001), Frémat et al. (2005), Zorec et al. (2005), Frémat et al. (2006) and Levenhagen & Leister (2006), whose apparent (viewing angle dependent) fundamental parameters were rediscussed. The selection of this stellar sample is justified by the similarity in the approaches and in precautions taken to determine the Vsini (Sect. 2.1).
-
The translation of the distribution of Vsini/Vc into another one corrected for the i-viewing angle effect proceeds by assuming that i is distributed at random and considering that the parameters Vsini are systematically underestimated because of GD (Sect. 3).As it is still rather widely presumed in the literature that Be stars are critical rotators, we used the original von Zeipel formulation to determine the distribution Φ(V/Vc) characterized by the largest possible mode to calculate the GD effect, i.e., the larger value of the ratio V/Vc at which Φ takes its maximum.
-
We discussed two deconvolution methods:
- (a)
The Cranmer (2005) method (see Sect. 3.4) uses a Monte Carlo simulation based on a mathematical stellar sample, where each parameter Vsini is corrected for the GD effect, and sampled statistically according to the quantities V and i. This method also uses an imposed analytical expression for
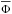 to represent the actual distribution
Φ whose defining
free parameters are selected by searching the best fit of the observed
distribution Ψ of
Vsini. We have shown
that even when the set of moments that characterizes each function
to represent the actual distribution
Φ whose defining
free parameters are selected by searching the best fit of the observed
distribution Ψ of
Vsini. We have shown
that even when the set of moments that characterizes each function 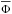 is similar to that of the actual
distribution Φ,
the Kolmogorov-Smirnov test indicates that not all analytical functions
is similar to that of the actual
distribution Φ,
the Kolmogorov-Smirnov test indicates that not all analytical functions 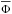 defined with the same number of free
parameters can be used to represent the sought function Φ reliably. In this context, the
trapezoidal function
defined with the same number of free
parameters can be used to represent the sought function Φ reliably. In this context, the
trapezoidal function 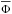 is less appropriate. From this study it
also emerges that there can be analytical expressions for
is less appropriate. From this study it
also emerges that there can be analytical expressions for 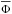 where the characterizing free parameters
can have different values, but they lead to equally “well satisfying fits” of
the observed distribution Ψ.
where the characterizing free parameters
can have different values, but they lead to equally “well satisfying fits” of
the observed distribution Ψ. - (b)
The Lucy-Richardson (1972, 1974) method (see Sect. 3.5) is based on the iteration of the distribution Φ(u) of ratios u = V/Vc and the distribution Ψ(v) of ratios v = Vsini/Vc. This method is free from any imposed analytical expression of Φ, but requires that the ratios Vsini/Vc be corrected for Stoeckley’s underestimation in advance. Such a correction requires a thorough determination of the fundamental parameters of each studied object. To this end, we ntroduced a method to determine the stellar mass, age, rotational ratio η (ratio of centrifugal to the gravitational acceleration at the equator), and approximate inclination angle i of each star in the studied sample (Sect. 3.5.1). The distribution Φ(u) of ratios u = V/Vc corrected for GD effect finally adopted here is that obtained with the Lucy-Richardson method.
- (a)
-
We separated the stars into three MS evolutionary groups, early, intermediate, and late, to provide an idea on the evolution effect on the distribution of ratios V/Vc (Sect. 3.6). In spite of the uncertainties related to the definition of reliable statistical samples, we found that once the mode
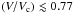 is attained by Be stars at some intermediate evolutionary phase in the MS, it will stay unchanged up to the end of the MS evolutionary lifespan. This behavior may represent a property that can be specific to Be stars.
is attained by Be stars at some intermediate evolutionary phase in the MS, it will stay unchanged up to the end of the MS evolutionary lifespan. This behavior may represent a property that can be specific to Be stars. -
We attempted a discussion of the effect introduced on Φ(V/Vc) by a nonrandom distribution of the inclination angle i of the stellar rotation axis (Sect. 3.7). According to the assumed function that gives the probability of occurrence of inclination angles, the mode of Φ does not change heavily but its skewness and kurtosis depend on the parameter that represents the deviation to the randomness.
The Lucy-Richardson iteration method was then used to introduce two different corrections to the distributions of velocity ratios to account for phenomena that carry systematic overestimations of parameters Vsini:
-
I.
We have taken into account the effects on the distribution Ψ(Vsini/Vc) due to the macroturbulent motions in the stellar atmospheres (Sect. 4). This correction slightly increases the frequency Φ(V/Vc) in the interval of velocity ratios 0 ≲ V/Vc ≲ 0.3, but does not significantly change the mode of Φ(V/Vc) .
-
II.
As there can be an additional component in the Vsini owing to the orbital motion of objects in a binary system (Sect. 5), we formulated the correction for this effect and considered that there must be at least fbin = 70% binary stars among Be stars. This fbin is because there are no clear reasons that among B-type stars the frequency of binaries is significantly smaller than in both B-type spectral extremes, i.e., more and less massive objects than those assigned to B-type objects. The effect for binarity is the last correction introduced here on the distribution of velocity ratios V/Vc.
Thus, according to the corrections taken into account thus far, we conclude the following:
-
(i)
The mode of Φ(V/Vc) depends on the frequency fbin of binaries: for fbin = 0.7 the mode is at (V/Vc)mode = 0.663, while for fbin = 1.0 it becomes (V/Vc)mode = 0.644. If we had admitted that fbin = 0.3, the mode would be at (V/Vc)mode = 0.680, while for fbin = 0.0 it is at (V/Vc)mode = 0.681. At fractions fbin ≳ 0.7 the number of rotators with 0.75 ≲ V/Vc ≲ 1.0 reduces significantly.
-
(ii)
In Fig. 16 we can see that for fbin = 0.7 the most frequent rotation of classic Be stars is characterized by (V/Vc)mode = 0.663, which implies η = 0.35 or Ω / Ωc = 0.84. From Φ(u)Σ + mt + bin0.7 we can show that 90% of program stars, i.e., 210 objects, rotate with 0.44 ≲ V/Vc ≲ 0.89, which means 0.61 ≲ Ω / Ωc = 0.98 or 0.14 ≲ η ≲ 0.73. Accordingly, 7% of them (16 stars) have V/Vc ≲ 0.4 and barely 3% of them (7 stars) have V/Vc ≳ 0.9. Since half of the Be stars in the whole sample rotate roughly with V/Vc ≲ 0.65, saying that Be stars are critical rotators sounds excessive.
-
(iii)
According to Fig. 9, the larger fraction of Be stars with 0.44 ≲ V/Vc ≲ 0.89 is in the second half of the MS evolutionary phase (t/tMS ≳ 0.5).
-
(iv)
From Fig. 16 we can see that the difference in velocities owing to the presence of binary components represent ΔV ≃ 14 km s-1 at V/Vc = 0.4 and ΔV ≃ 38 km s-1 at V/Vc = 0.9, which are measurable.
We note that Eq. (8) is not appropriate even for rigid rotators because β1 is a function of the stellar colatitude θ and its value decreases as η → 1 (Espinosa Lara & Rieutord 2011; Zorec et al. 2016). However, in the present contribution Stoeckley’s correction Σ(η,i,M,t) given in Eq. (7) was calculated imposing β1 = 1, so as to overestimate the GD effect on purpose. This means that the correction for GD used in this work is the highest we could apply to an observed Vsini parameter and that the characteristic V/Vc ratios of Be stars must actually be lower than inferred in this work.
Finally, if critical rotation is a transient phenomenon that helps the star to eject the matter needed to form its CE, the transition from some V/Vc = 0.9 to V/Vc = 1.0 would require that during a short time a sufficient amount of energy be provided to photospheric layers to let them at critical rotation. Critical rotation maintains, however, the surface layers bound to the star, which can be freed only if the rotation rate attains the escape velocity, 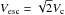 .
.
Assuming that the excess of energy necessary to attain the critical rotation is supplied by a magnetic field, in a star with an equatorial rotation velocity V, the strength of this field must obey B2/ 2μo ~ ρphot [1 − (V/Vc)2] / 2, where ρphot is an average density of photospheric layers of dwarf B-type stars. In a typical Be star Vc = 480 km s-1 and ρphot ~ 6 × 10-10 g cm-3. The above mentioned change of surface rotational velocities would then imply B ≳ 2 × 103 G. Such magnetic fields could certainly be detected if they existed and were global. As they are not detected, magnetic fields of such intensities could nonetheless exist, but must be concentrated in small areas, and maintained perhaps by a dynamo process hosted in the rotationally enlarged subsurface convection zones, such as those suggested by Clement (1979) and Maeder et al. (2008). Under such cases it would also be possible to think of activities that evoke flares with huge mass-ejection episodes through magnetic recombination phenomena. For example, emerging magnetic fields from the surface of some 102 G by magnetic buoyancy in massive stars that originate in the thin “iron convection zone” were already foreseen by Cantiello & Braithwaite (2011).
In Paper II we complete the discussion started in the present work. To this end we assume that stars undergo surface differential rotation and derive: (1) the distribution function Φ(u) corrected for differential rotation; (2) the density probability function for the occurrence of a gradient of the angular velocity in the stellar surface that is consistent with the predicted line broadening and with the distribution Φ(u) of ratios u = V/Vc obtained in Sect. 5.1. In Paper II we also discuss a number of measurement and conceptual uncertainties affecting the Vsini determination of Be stars. These include the effects due to surface differential rotation, bivalued relations between line broadening and the Vsini, expansion velocities in atmospheres of active stars, and effects on spectral lines due to tides in binaries.
Acknowledgments
This research has widely made use of the SIMBAD database, operated at CDS, Strasbourg, France. We are grateful to an anonymous referee for his(her) detailed reading of our manuscript and for his(her) helpful comments and suggestions.
References
- Abt, H. A., Gomez, A. E., & Levy, S. G. 1990, ApJS, 74, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Adelman, S. J., Pintado, O. I., Nieva, M. F., Rayle, K. E., & Sanders, Jr., S. E. 2002, A&A, 392, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C., Puls, J., Godart, M., & Dupret, M.-A. 2009, A&A, 508, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aerts, C., Simón-Díaz, S., Groot, P. J., & Degroote, P. 2014, A&A, 569, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aidelman, Y., Cidale, L. S., Zorec, J., & Arias, M. L. 2012, A&A, 544, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aller, L. H., Appenzeller, I., Baschek, B., et al. 1982, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology − New Series, Gruppe/Group 6 Astronomy and Astrophysics, Vol. 2 Schaifers/Voigt: Astronomy and Astrophysics, Stars and Star Clusters [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Ballereau, D., Chauville, J., & Zorec, J. 1995, A&AS, 111, 423 [NASA ADS] [Google Scholar]
- Balona, L. A. 1975, MNRAS, 173, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Beeckmans, F., & Hubert-Delplace, A. M. 1980, A&A, 86, 72 [NASA ADS] [Google Scholar]
- Bodenheimer, P. 1971, ApJ, 167, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Bowman, A. W., & Azzalini, A. 1997, Applied smoothing techniques for data analysis: the kernel approach with S-plus illustrations, Oxford Stat. Sci. Ser. 18 (Clarendon Press) [Google Scholar]
- Briot, D., & Zorec, J. 1987, in Physics of Be Stars, eds. A. Slettebak, & T. P. Snow, IAU Colloq., 92, 214 [Google Scholar]
- Brown, J. C., & Wood, K. 1992, A&A, 265, 663 [NASA ADS] [Google Scholar]
- Cameron, C., Saio, H., Kuschnig, R., et al. 2008, ApJ, 685, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Cantiello, M., & Braithwaite, J. 2011, A&A, 534, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cantiello, M., Langer, N., Brott, I., et al. 2009, A&A, 499, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1988, ApJ, 329, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chalonge, D., & Divan, L. 1952, Ann. Astrophys., 15, 201 [NASA ADS] [Google Scholar]
- Chandrasekhar, S., & Münch, G. 1950, ApJ, 111, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chauville, J., Zorec, J., Ballereau, D., et al. 2001, A&A, 378, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chini, R., Hoffmeister, V. H., Nasseri, A., Stahl, O., & Zinnecker, H. 2012, MNRAS, 424, 1925 [NASA ADS] [CrossRef] [Google Scholar]
- Cidale, L., Zorec, J., & Tringaniello, L. 2001, A&A, 368, 160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A. 2012, A&A, 538, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clement, M. J. 1979, ApJ, 230, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Cochetti, Y. R. 2014, Tésis de Licenciatura, Universidad Nacional de La Plata, Argentina [Google Scholar]
- Collins, II, G. W. 1987, in Physics of Be Stars, eds. A. Slettebak, & T. P. Snow, IAU Colloq., 92, 3 [Google Scholar]
- Collins, II, G. W., & Truax, R. J. 1995, ApJ, 439, 860 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, II, G. W., Truax, R. J., & Cranmer, S. R. 1991, ApJS, 77, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R. 2005, ApJ, 634, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Dall, T. H., & Sbordone, L. 2011, J. Phys. Conf. Ser., 328, 012016 [NASA ADS] [CrossRef] [Google Scholar]
- de Jager, C., & Nieuwenhuijzen, H. 1987, A&A, 177, 217 [NASA ADS] [Google Scholar]
- de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [NASA ADS] [CrossRef] [Google Scholar]
- De Rosa, R. J., Patience, J., Wilson, P. A., et al. 2014, MNRAS, 437, 1216 [NASA ADS] [CrossRef] [Google Scholar]
- de Wit, W. J., Lamers, H. J. G. L. M., Marquette, J. B., & Beaulieu, J. P. 2006, A&A, 456, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deutschman, W. A., Davis, R. J., & Schild, R. E. 1976, ApJS, 30, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Divan, L., & Zorec, J. 1982a, in The Scientific Aspects of the Hipparcos Space Astrometry Mission, eds. M. A. C. Perryman, & T. D. Guyenne, ESA SP, 177, 101 [Google Scholar]
- Divan, L., & Zorec, J. 1982b, in Be Stars, eds. M. Jaschek, & H.-G. Groth, IAU Symp., 98, 61 [Google Scholar]
- Divan, L., Zorec, J., & Briot, D. 1982, in IAU Symp. 98, Be Stars, eds. M. Jaschek, & H.-G. Groth, 53 [Google Scholar]
- Divan, L., Zorec, J., & Andrillat, Y. 1983, A&A, 126, L8 [NASA ADS] [Google Scholar]
- Domiciano de Souza, A., Kervella, P., Moser Faes, D., et al. 2014, A&A, 569, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dufton, P. L., Ryans, R. S. I., Simón-Díaz, S., Trundle, C., & Lennon, D. J. 2006a, A&A, 451, 603 [Google Scholar]
- Dufton, P. L., Smartt, S. J., Lee, J. K., et al. 2006b, A&A, 457, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2005, AJ, 129, 1642 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Floquet, M., Hubert, A. M., Hirata, R., et al. 2000, A&A, 362, 1020 [NASA ADS] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Fraser, M., Dufton, P. L., Hunter, I., & Ryans, R. S. I. 2010, MNRAS, 404, 1306 [NASA ADS] [Google Scholar]
- Frémat, Y., Zorec, J., Hubert, A.-M., & Floquet, M. 2005, A&A, 440, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frémat, Y., Neiner, C., Hubert, A.-M., et al. 2006, A&A, 451, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedemann, C., & Roeder, U.-K. 1987, Astron. Nachr., 308, 41 [Google Scholar]
- Friedemann, C., Guertler, J., Schielicke, R., & Dorschner, J. 1983, Astron. Nachr., 304, 237 [Google Scholar]
- Fuhrmann, K., & Chini, R. 2012, ApJS, 203, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Georgy, C., Granada, A., Ekström, S., et al. 2014, A&A, 566, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gies, D. R. 2000, in The Be Phenomenon in Early-Type Stars, eds. M. A. Smith, H. F. Henrichs, & J. Fabregat, IAU Colloq., 175, ASP Conf. Ser., 214, 668 [Google Scholar]
- Gillich, A., Deupree, R. G., Lovekin, C. C., Short, C. I., & Toqué, N. 2008, ApJ, 683, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Gkouvelis, L., Fabregat, J., Zorec, J., et al. 2016, A&A, 591, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 1975, ApJ, 202, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, D. F. 1992, The observation and analysis of stellar photospheres Camb. Astrophys. Ser. (Cambridge University Press) [Google Scholar]
- Guertler, J., Schielicke, R., Dorschner, J., & Friedemann, C. 1982, Astron. Nachr., 303, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Hadrava, P. 1992, A&A, 256, 519 [NASA ADS] [Google Scholar]
- Hanuscihk, R. W., Dachs, J., Baudzus, M., & Thimm, G. 1993, A&A, 274, 356 [NASA ADS] [Google Scholar]
- Harmanec, P. 1987, in Physics of Be Stars, eds. A. Slettebak, & T. P. Snow, IAU Colloq. 92, 339 [Google Scholar]
- Harmanec, P., Bisikalo, D. V., Boyarchuk, A. A., & Kuznetsov, O. A. 2002, A&A, 396, 937 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S.-S., & Struve, O. 1953, ApJ, 118, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, W., & Gies, D. R. 2006, ApJ, 648, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Hubert, A. M., Floquet, M., & Zorec, J. 2000, in The Be Phenomenon in Early-Type Stars, eds. M. A. Smith, H. F. Henrichs, & J. Fabregat, IAU Colloq., 175, ASP Conf. Ser., 214, 348 [Google Scholar]
- Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jamar, C., Macau-Hercot, D., Monfils, A., et al. 1976, Ultraviolet bright-star spectrophotometric catalogue, A compilation of absolute spectrophotometric data obtained with the Sky Survey Telescope (S2/68) on the European Astronomical Satellite TD-1 (Paris: European Space Agency) [Google Scholar]
- Jaschek, M., Slettebak, A., & Jaschek, C. 1981, Be Star Newsletter, 4, 9 [NASA ADS] [Google Scholar]
- Johnson, H. L., & Mitchell, R. I. 1975, Rev. Mex. Astron. Astrofis., 1, 299 [Google Scholar]
- Keller, S. C., Bessell, M. S., Cook, K. H., Geha, M., & Syphers, D. 2002, AJ, 124, 2039 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R. 1977, A&A, 58, 267 [NASA ADS] [Google Scholar]
- Kobulnicky, H. A., & Fryer, C. L. 2007, ApJ, 670, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Kouwenhoven, M. B. N., Brown, A. G. A., Portegies Zwart, S. F., & Kaper, L. 2007, A&A, 474, 77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kriz, S., & Harmanec, P. 1975, Bull. Astron. Inst. Czechoslovakia, 26, 65 [Google Scholar]
- Kuiper, G. P. 1935, PASP, 47, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. 1993, Opacities for Stellar Atmospheres: [+0.0], [+0.5], [+1.0]. Kurucz CD-ROM No. 2 (Cambridge, Mass.: Smithsonian Astrophysical Observatory), 2 [Google Scholar]
- Lamers, H. J. G. L. M., Zickgraf, F.-J., de Winter, D., Houziaux, L., & Zorec, J. 1998, A&A, 340, 117 [NASA ADS] [Google Scholar]
- Lang, K. R. 1992, Astrophysical Data I. Planets and Stars (Springer-Verlag) [Google Scholar]
- Levenhagen, R. S., & Leister, N. V. 2006, MNRAS, 371, 252 [NASA ADS] [CrossRef] [Google Scholar]
- Limber, D. N. 1963, ApJ, 138, 1112 [NASA ADS] [CrossRef] [Google Scholar]
- Lovekin, C. C., Deupree, R. G., & Short, C. I. 2006, ApJ, 643, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Lucy, L. B. 1967, Z. Astrophys., 65, 89 [Google Scholar]
- Lucy, L. B. 1974, AJ, 79, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Macau-Hercot, D., Jamar, C., Monfils, A., et al. 1978, Supplement to the ultraviolet bright-star spectrophotometric catalogue, A compilation of absolute spectrophotometric data obtained with the sky survey telescope (S2/68) on the European Astronomical Satellite TD-1 (Paris: European Space Agency), ESASR [Google Scholar]
- Maeder, A. 1999, A&A, 347, 185 [NASA ADS] [Google Scholar]
- Maeder, A. 2009, Phys., Formation and Evolution of Rotating Stars (Springer) [Google Scholar]
- Maeder, A., Georgy, C., & Meynet, G. 2008, A&A, 479, L37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marion, L., Absil, O., Ertel, S., et al. 2014, A&A, 570, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mason, B. D., Hartkopf, W. I., Gies, D. R., Henry, T. J., & Helsel, J. W. 2009, AJ, 137, 3358 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meilland, A., Stee, P., Zorec, J., & Kanaan, S. 2006, A&A, 455, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meilland, A., Millour, F., Kanaan, S., et al. 2012, A&A, 538, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennickent, R. E., Pietrzyński, G., Gieren, W., & Szewczyk, O. 2002, A&A, 393, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milne, E. A. 1923, MNRAS, 83, 118 [NASA ADS] [Google Scholar]
- Mokiem, M. R., de Koter, A., Evans, C. J., et al. 2006, A&A, 456, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moon, T. T., & Dworetsky, M. M. 1985, MNRAS, 217, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, E., & Koenigsberger, G. 1999, Rev. Mexicana Astron. Astrofis., 35, 157 [Google Scholar]
- Moreno, E., Koenigsberger, G., & Toledano, O. 2005, A&A, 437, 641 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moujtahid, A. 1998, Ph.D. Thesis, Université Pierre & Marie Curie, Paris [Google Scholar]
- Moujtahid, A., Zorec, J., & Hubert, A. M. 1999, A&A, 349, 151 [NASA ADS] [Google Scholar]
- Moujtahid, A., Zorec, J., Hubert, A. M., Garcia, A., & Burki, G. 1998, A&AS, 129, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moujtahid, A., Zorec, J., & Hubert, A. M. 2000a, in The Be Phenomenon in Early-Type Stars, eds. M. A. Smith, H. F. Henrichs, & J. Fabregat, IAU Colloq. 175, ASP Conf. Ser., 214, 506 [Google Scholar]
- Moujtahid, A., Zorec, J., & Hubert, A. M. 2000b, in I 175: The Be Phenomenon in Early-Type Stars, eds. M. A. Smith, H. F. Henrichs, & J. Fabregat, IAU Colloq. 175, ASP Conf. Ser., 214, 510 [Google Scholar]
- Napiwotzki, R., Schoenberner, D., & Wenske, V. 1993, A&A, 268, 653 [Google Scholar]
- Nasseri, A., Dembsky, T., Drass, H., Hoffmeister V. H., & Chini R. 2013, Central European Astrophysical Bulletin, 37, 51 [NASA ADS] [Google Scholar]
- Negueruela, I. 2004, Astron. Nachr., 325, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Nieva, M.-F. 2013, A&A, 550, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oudmaijer, R. D., & Parr, A. M. 2010, MNRAS, 405, 2439 [NASA ADS] [Google Scholar]
- Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
- Reggiani, M., & Meyer, M. R. 2013, A&A, 553, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richardson, W. H. 1972, J. Opt. Soc. Am., 62, 55 [Google Scholar]
- Rieutord, M. 2016, in Lect. Notes Phys. (Springer Int. Publ.), 914, 101 [Google Scholar]
- Rivinius, T., Carciofi, A. C., & Martayan, C. 2013, A&ARv, 21, 69 [Google Scholar]
- Ryans, R. S. I., Dufton, P. L., Rolleston, W. R. J., et al. 2002, MNRAS, 336, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Sackmann, I. J. 1970, A&A, 8, 76 [NASA ADS] [Google Scholar]
- Saio, H. 2013, in Lect. Not. Phys. 865, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer Verlag), 159 [Google Scholar]
- Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Semaan, T., Hubert, A. M., Zorec, J., et al. 2013, A&A, 551, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shatsky, N., & Tokovinin, A. 2002, A&A, 382, 92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimazaki, H., & Shinomoto, S. 2007, Neural Computation, 19, 1503 [Google Scholar]
- Simón-Díaz, S. 2015, in IAU Symp., 307, eds. G. Meynet, C. Georgy, J. Groh, & P. Stee, 194 [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2007, A&A, 468, 1063 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simón-Díaz, S., & Herrero, A. 2014, A&A, 562, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, R. C., & Worley, R. 1974, MNRAS, 167, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, Jr., T. P. 1981, ApJ, 251, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Stoeckley, T. R. 1968, MNRAS, 140, 141 [NASA ADS] [Google Scholar]
- Struve, O. 1931, ApJ, 73, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., Simón-Díaz, S., Puls, J., & Markova, N. 2013, A&A, 559, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassoul, J.-L. 1978, Theory of rotating stars (Princeton: University Press) [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Townsend, R. H. D., Owocki, S. P., & Howarth, I. D. 2004, MNRAS, 350, 189 [Google Scholar]
- Tuominen, I. V. 1972, Ann. Acad. Sci. Fennicae, 392 [Google Scholar]
- Unsöld, A., & Struve, O. 1949, ApJ, 110, 455 [NASA ADS] [CrossRef] [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Wegner, W. 2006, MNRAS, 371, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Wesselius, P. R., van Duinen, R. J., de Jonge, A. R. W., et al. 1982, A&AS, 49, 427 [NASA ADS] [Google Scholar]
- Yudin, R. V. 2001, A&A, 368, 912 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J. 1986, Ph.D. Thesis, Université Paris VII, Paris [Google Scholar]
- Zorec, J., & Briot, D. 1991, A&A, 245, 150 [NASA ADS] [Google Scholar]
- Zorec, J., & Briot, D. 1997, A&A, 318, 443 [NASA ADS] [Google Scholar]
- Zorec, J., & Royer, F. 2012, A&A, 537, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Divan, L., & Briot, D. 1983, A&A, 126, 205 [NASA ADS] [Google Scholar]
- Zorec, J., Mochkovitch, R., & Divan, L. 1988, C. R. Acad. Sci. Paris, Ser. Sci. Phys., 306, 1265 [Google Scholar]
- Zorec, J., Mochkovitch, R. A., & Garcia, A. 1990, in Angular Momentum and Mass Loss for Hot Stars, eds. L. A. Willson, & R. Stalio, NATO ASIC Proc. 316, 239 [Google Scholar]
- Zorec, J., Domiciano de Souza, A., & Frémat, Y. 2004, in Stellar Rotation, eds. A. Maeder & P. Eenens, IAU Symp., 215, 21 [Google Scholar]
- Zorec, J., Frémat, Y., & Cidale, L. 2005, A&A, 441, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Frémat, Y., Martayan, C., Cidale, L. S., & Torres, A. F. 2007, in Active OB-Stars: Laboratories for Stellar and Circumstellar Physics, eds. A. T. Okazaki, S. P. Owocki, & S. Stefl, ASP Conf. Ser., 361, 539 [Google Scholar]
- Zorec, J., Cidale, L., Arias, M. L., et al. 2009, A&A, 501, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Frémat, Y., Domiciano de Souza, A., et al. 2011, A&A, 526, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorec, J., Frémat, Y., Domiciano de Souza, A., et al. 2016, A&A, submitted (Paper II) [Google Scholar]
Appendix A: Fundamental parameters
Appendix A.1: The effective temperature
 |
Fig. A.1 a) Effective temperatures for MK luminosity classes V, IV, and III determined by de Jager & Nieuwenhuijzen (1987) against those extracted from the BCD calibration; b) effective temperatures determined from the uvby photometry using the calibration by Napiwotzki et al. (1993) against those obtained in the BCD system; and c) average effective temperatures determined by Adelman et al. (2002), Nieva (2013), and Fitzpatrick & Massa (2005) against those obtained in the BCD system for a number of common OB stars without emission. The red dashed lines correspond to x = y diagonal. |
 |
Fig. A.2 Comparison of bolometric luminosities derived using different calibrations of MV with those derived for the same discrete MK spectral types and luminosity classes using integrated fluxes that are identified here with log L(λ1,D) /L⊙ (red lines). The identifications are dJM (de Jager & Nieuwenhuijzen 1987), DDS (Deutschman et al. 1976), SK (Aller et al. 1982), and W (Wegner 2006). The blocks a), b), and c) are for average MK luminosity classes V, IV, and III, respectively. |
There are many independent calibrations of effective temperatures given in the literature, which are useful to estimate stellar radii and masses and could be used as references to inquire whether our apparent Teff(λ1,D) (Zorec et al. 2009) and the critical velocities Vc related to it are affected by systematic deviations. We have chosen: (1) de Jager & Nieuwenhuijzen (1987) because it was used by Cranmer (2005) to discuss the distribution of rotational velocities of Be stars; (2) the calibration of the ubvy −Strömgren photometric indices given by Moon & Dworetsky (1985) and revisited by Napiwotzki et al. (1993); and (3) the effective temperatures derived from fitted visible spectral energy distributions by Adelman et al. (2002), Fitzpatrick & Massa (2005), and Nieva (2013). In Fig. A.1a the effective temperatures by de Jager & Nieuwenhuijzen (1987) are compared with the Teff(λ1,D) for the average luminosity classes V, IV, and III in the stars studied in the present paper. The effective temperatures determined with the ubvy indices obtained with the relation given by Napiwotzki et al. (1993) for OBA starswithout emission are compared in Fig. A.1b with Teff(λ1,D) given in Zorec et al. (2009). Figure A.1c compares the effective temperatures obtained by Adelman et al. (2002) and Nieva (2013) (indicated with AN) with those from Fitzpatrick & Massa (2005) (FM). From these figures we can then conclude that there are no significant systematic deviations between Teff(λ1,D), Teff(AN) and Teff(FM) for stars in the interval of spectral types studied in the present work.
Appendix A.2: The bolometric luminosity
The bolometric luminosities of the program Be stars were determined from integrated monochromatic fluxes. Even though these fluxes were corrected for the presence of circumstellar envelopes/disks, the calculation followed the same rules and data gathered from the same sources as those used in Zorec et al. (2009) for OB stars without emission. Then, we can use the bolometric luminosities for average MK spectral types and luminosity classes that can be determined from this paper to test whether our estimates of bolometric luminosities suffer from some systematic deviations. To this end, we compare our mean log Lapp/L⊙ with those given by de Jager & Nieuwenhuijzen (1987) and with the bolometric luminosities derived indirectly using calibrations of visual absolute magnitudes MV. In this last case, MV is transformed into absolute bolometric magnitude using the Teff(λ1,D) and bolometric corrections (Flower 1996; Torres 2010; Nieva 2013) with 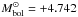 mag. The calibrations of MV against the spectral classes used are from Wegner (2006), Deutschman et al. (1976), and Aller et al. (1982). The log L/L⊙ against the average MK spectral type determined for the average luminosity classes V, IV, and III with the cited methods are shown in Figs. A.2a−c. We can then conclude that our bolometric luminosity estimates are consistent with those determined by other methods. In Fig. A.2, however, there can be a systematic deviation between the BCD luminosities of the average spectral-luminosity classes with those of other authors that stem from the BCD definition of average spectral-luminosity classes. The average log Lapp/L⊙ of the BCD system correspond to the barycenter of the curvilinear quadrilaterals in the (λ1,D)-diagram assigned to the average MK spectral types and luminosity classes, while in other calibrations these averages are defined by the specific stellar sample used to carry out the calibrations, which do not necessarily characterize the same centroids as in the BCD system.
mag. The calibrations of MV against the spectral classes used are from Wegner (2006), Deutschman et al. (1976), and Aller et al. (1982). The log L/L⊙ against the average MK spectral type determined for the average luminosity classes V, IV, and III with the cited methods are shown in Figs. A.2a−c. We can then conclude that our bolometric luminosity estimates are consistent with those determined by other methods. In Fig. A.2, however, there can be a systematic deviation between the BCD luminosities of the average spectral-luminosity classes with those of other authors that stem from the BCD definition of average spectral-luminosity classes. The average log Lapp/L⊙ of the BCD system correspond to the barycenter of the curvilinear quadrilaterals in the (λ1,D)-diagram assigned to the average MK spectral types and luminosity classes, while in other calibrations these averages are defined by the specific stellar sample used to carry out the calibrations, which do not necessarily characterize the same centroids as in the BCD system.
Appendix B: The energy emitted by the star-CE system
The energy emitted by the star-CE system mentioned in Sect. 2.2.2 has been written as (Moujtahid 1998; Moujtahid et al. 2000a) ![\appendix \setcounter{section}{2} \begin{equation} 1+\epsilon_{\lambda} = \alpha_{\lambda}(r,\tau_{\lambda}) + r^{-2}\beta_{\lambda}(r,\tau_{\lambda})[S_{\lambda}(T_{\rm env})/F_{\lambda}^*] \label{eq1} , \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq532.png) (B.1)where r = R∗/Renv; Renv is an equivalent mean extent of the circumstellar region analyzed, R∗ is the stellar radius,
(B.1)where r = R∗/Renv; Renv is an equivalent mean extent of the circumstellar region analyzed, R∗ is the stellar radius, 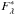 is the stellar flux, τλ is the total continuum opacity of the region, and Sλ is its source function for continuum radiation given here simply by the Planck function in terms of the CE temperature Tenv: Sλ = Bλ(Tenv). The functions αλ and βλ are given by
is the stellar flux, τλ is the total continuum opacity of the region, and Sλ is its source function for continuum radiation given here simply by the Planck function in terms of the CE temperature Tenv: Sλ = Bλ(Tenv). The functions αλ and βλ are given by
![\appendix \setcounter{section}{2} \begin{eqnarray} && \alpha_{\lambda}(r,\tau_{\lambda}) = r^{-2}\left[E_3(\tau_{\lambda}) + \mu_o^2E_3\left({\tau_{\lambda}\over\mu}\right)\right] \nonumber \\ && \beta_{\lambda}(r,\tau_{\lambda}) = 1 - r^{-2}\alpha(r,\tau_{\lambda}) - 2\mu^2E_3\left({2\tau_{\lambda}\over\mu}\right) , \label{eq2} \end{eqnarray}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq541.png) (B.2)where E3 is the exponential integral or order 3 and μo = [1 − r2] 1 / 2. In the limits for r → 0 and r → 1, the expression in Eq. (B.1) recovers the forms commonly used in the literature
(B.2)where E3 is the exponential integral or order 3 and μo = [1 − r2] 1 / 2. In the limits for r → 0 and r → 1, the expression in Eq. (B.1) recovers the forms commonly used in the literature ![\appendix \setcounter{section}{2} \begin{eqnarray} && 1+\epsilon_{\lambda} = {\rm e}^{-\tau_{\lambda}} + r^{-2}S_{\lambda}[1-2E_3(2\tau_{\lambda})]\quad \quad \quad \, {\rm for}\ r\to0 \nonumber\\ && 1+\epsilon_{\lambda} = 2E_3(\tau_{\lambda})F_{\lambda} + r^{-2}S_{\lambda}[1-2E_3(\tau_{\lambda})] \quad {\rm for}\ r\to1 . \label{eq3} \end{eqnarray}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq546.png) (B.3)
(B.3)
CE parameters derived for 10 Be stars studied here with the stronger emission in the Hα line.
Appendix C: The equatorial critical linear velocity
In principle, the radiation pressure in the hottest Be stars may produce a significant compensation of the stellar-inside directed effective gravity, so that two critical rotational velocities can be defined (Maeder 2009). Writing the total surface gravity as ![\appendix \setcounter{section}{3} \begin{equation} g_{\rm tot}=g_{\rm eff}[1-\Gamma(\Omega,\theta)], \label{gtot1} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq587.png) (C.1)
(C.1)
for which the following definitions hold:
where geff is the colatitude-angle dependent surface effective gravity; R(θ) is the stellar surface radius vector; κ(θ) is the Rosseland mean total opacity for the atmospheric optical depth τ = 2 / 3; L(Ω) is the bolometric luminosity changed by the rotational effects, and 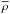 is the stellar density averaged over its entire volume. For Γ(Ω,θ) < 1, the critical velocity is determined by geff = 0, which for a surface rigid rotation occurs at the equator (θ = π/ 2) and corresponds to η(θ = π/ 2) = 1.0 that translates into the well-known expression for the equatorial critical linear velocity
is the stellar density averaged over its entire volume. For Γ(Ω,θ) < 1, the critical velocity is determined by geff = 0, which for a surface rigid rotation occurs at the equator (θ = π/ 2) and corresponds to η(θ = π/ 2) = 1.0 that translates into the well-known expression for the equatorial critical linear velocity ![\appendix \setcounter{section}{3} \begin{equation} V_{\rm c} = 436.7\left[\frac{M/M_{\odot}}{R_{\rm c}(M,t)/R_{\odot}}\right]^{1/2}\ \ \ {\rm km~s^{-1}}. \label{vc1} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq599.png) (C.3)In very massive Be stars, i.e., Oe stars with M ≲ 40 M⊙, we could have Γ(Ω,θ) = 1 at some colatitude θ where η(θ = π/ 2) < 1.0. Nevertheless, using the von Zeipel relation to describe the latitudinal variation of the effective temperature, the absorption coefficients calculated for the corresponding gravity and temperature (Kurucz 1993), and knowing that m(Ω) ≤ 0.361 (Maeder 2009), the condition Γ(Ω,θ) = 1 can be translated into To/T⊙ ≳ 12.5(go/g⊙)1 / 4 (To and T⊙ are the effective temperatures of a parent nonrotating star and solar, respectively, while go and g⊙ are the respective surface gravities). Since of the Be stars in our sample most have M ≲ 25 M⊙ (only 16 of then seem to have M ≳ 25 M⊙) for which it is To/T⊙ ≲ 12.5(go/g⊙)1 / 4, in our calculation we used the equatorial critical velocity given by Eq. (6).
(C.3)In very massive Be stars, i.e., Oe stars with M ≲ 40 M⊙, we could have Γ(Ω,θ) = 1 at some colatitude θ where η(θ = π/ 2) < 1.0. Nevertheless, using the von Zeipel relation to describe the latitudinal variation of the effective temperature, the absorption coefficients calculated for the corresponding gravity and temperature (Kurucz 1993), and knowing that m(Ω) ≤ 0.361 (Maeder 2009), the condition Γ(Ω,θ) = 1 can be translated into To/T⊙ ≳ 12.5(go/g⊙)1 / 4 (To and T⊙ are the effective temperatures of a parent nonrotating star and solar, respectively, while go and g⊙ are the respective surface gravities). Since of the Be stars in our sample most have M ≲ 25 M⊙ (only 16 of then seem to have M ≳ 25 M⊙) for which it is To/T⊙ ≲ 12.5(go/g⊙)1 / 4, in our calculation we used the equatorial critical velocity given by Eq. (6).
Appendix D: Integral equation of probability density distributions
In several sections of this paper we construct integral equations that relate the distributions (frequency of probability densities) of the respective, either true and apparent parameters, or parameters corrected statistically from some physical effect. To avoid repetitions, we summarize below the basics of the formulation followed in each particular application of the method.
We consider an observed parameter z, whose observed distribution is Z(z) and where z is function of parameters x and y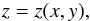 (D.1)with probability densities distributions of X(x) and Y(y), respectively. According to the definition of probability, Z(z) dz must be the surface integral of X(x)Y(y) over the area Δσ between the curves z = constant and z + dz = constant
(D.1)with probability densities distributions of X(x) and Y(y), respectively. According to the definition of probability, Z(z) dz must be the surface integral of X(x)Y(y) over the area Δσ between the curves z = constant and z + dz = constant  (D.2)For some explicit value of x in Eq. (D.2), the width of the strip Δσ is obviously dy = dz/ [∂z/∂y] that introduced into Eq. (D.2) leads to
(D.2)For some explicit value of x in Eq. (D.2), the width of the strip Δσ is obviously dy = dz/ [∂z/∂y] that introduced into Eq. (D.2) leads to ![\appendix \setcounter{section}{4} \begin{equation} Z(z) = \int\limits_{x\,=\,x_z(y)}\!\!\!\!X(x)\frac{Y[y(x,z)]}{\partial{z}/\partial{y}}\,{\rm d}x, \label{eq_l3} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq623.png) (D.3)which has to be integrated over the curve x = x(y) given by Eq. (D.1) for the required value of z and within the limits of x established by the specific physical phenomenon analyzed. In the same way, we can obtain and equivalent expression to Eq. (D.3) given by
(D.3)which has to be integrated over the curve x = x(y) given by Eq. (D.1) for the required value of z and within the limits of x established by the specific physical phenomenon analyzed. In the same way, we can obtain and equivalent expression to Eq. (D.3) given by ![\appendix \setcounter{section}{4} \begin{equation} Z(z) = \int\limits_{y\,=\,y_z(x)}\!\!\!\!Y(y)\frac{X[x(y,z)]}{\partial{z}/\partial{x}}\,{\rm d}y. \label{eq_l4} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq625.png) (D.4)In this paper, we derive the distributions X(x) or Y(y) as counterparts of Z(z) or simply Z(z) once X(x) and Y(y) are defined.
(D.4)In this paper, we derive the distributions X(x) or Y(y) as counterparts of Z(z) or simply Z(z) once X(x) and Y(y) are defined.
Appendix E: Determination of pnrc parameters
Appendix E.1: Two-fold iterations
The calculation of parameters M/M⊙, t/tMS, η and i with Eq. (3) requires two iteration “series” or “stages”. In the first stage, we derive M/M⊙ and t/tMS, while in the second stage, we refine the estimates of η and i.
Test pnrc solutions parameters.
 |
Fig. E.1 a) Determination of the pnrc mass M/M⊙ interpolated in stellar evolution models with rotation (black and red lines) and from the relation |
The models of stellar evolution with rotation used to interpolate masses and ages (Ekström et al. 2012) require the use of fundamental parameters averaged over the rotationally deformed stellar surface. At each n −iteration step of (M/M⊙,t/tMS) quantities we establish a list of m −pairs (ηk,ik), k = 1,...,m (m ≃ 100), so that ηmin(M,t) ≤ ηk ≤ 1 and the respective inclinations range in the interval π/ 2 ≥ ik ≥ imin. From Eq. (3) we draw m-triplets (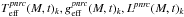 ) calculated as
) calculated as 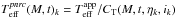 ,
, 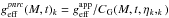 and Lpnrc(M,t)k = Lapp/CL(M,t,ηk,ik), which are then used to determine the m-surface-averaged values ⟨Teff(M,t,η)⟩ k, ⟨g(M,t,η)⟩ k, ⟨L(M,t,η)⟩ k. Taken by pairs [⟨Teff(M,t,η)⟩ k, ⟨g(M,t,η)⟩ k] and [⟨Teff(M,t,η)⟩ k, ⟨g(M,t,η)⟩ k] as entry parameters to the models of stellar evolution, we determine two independent series of mass and age estimates [ Mk/M⊙,ηk], [tk/tMS,ηk]. A third series of mass estimates comes from the definition
and Lpnrc(M,t)k = Lapp/CL(M,t,ηk,ik), which are then used to determine the m-surface-averaged values ⟨Teff(M,t,η)⟩ k, ⟨g(M,t,η)⟩ k, ⟨L(M,t,η)⟩ k. Taken by pairs [⟨Teff(M,t,η)⟩ k, ⟨g(M,t,η)⟩ k] and [⟨Teff(M,t,η)⟩ k, ⟨g(M,t,η)⟩ k] as entry parameters to the models of stellar evolution, we determine two independent series of mass and age estimates [ Mk/M⊙,ηk], [tk/tMS,ηk]. A third series of mass estimates comes from the definition 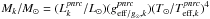 . The interpolation of masses and ages is made on the evolutionary models with rotation, labeled with ZAMS rotational velocity previously determined with curves giving the variation of Ω / Ωc with time calculated by Ekström et al. (2012), so that at the iterated stellar age tk/tMS we recover the Ωk/ Ωc for the given ratio ηk.
. The interpolation of masses and ages is made on the evolutionary models with rotation, labeled with ZAMS rotational velocity previously determined with curves giving the variation of Ω / Ωc with time calculated by Ekström et al. (2012), so that at the iterated stellar age tk/tMS we recover the Ωk/ Ωc for the given ratio ηk.
The intersection of the three series of curves [Mk/M⊙,ηk], [t/tMS,ηk] determine the n −estimate of the stellar mass Mn/M⊙ and age tn/tMS as shown in Fig. E.1a, which corresponds to the iteration step n = 1. These three mass/age curves are only coincident for nonrotating stars. Depending on the star, we need from 5 to 50 iterations to obtain that all three curves in Fig. E.1a determine a unique crossing point.
In the second iteration series, we take advantage of the above estimated Mn/M⊙ and tn/tMS to establish five relations between sini and η, whose common intersection is considered the refined estimate of η and i. These curves are the solutions of Eq. (3) written as sini = sini(η) for the given values of Mn/M⊙ and tn/tMS, respectively. A fifth curve is also obtained from the combination 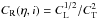 , which may seem redundant, but it is sometimes useful to disentangle the right solution when the intersection of other curves is not unique. Figure E.1b shows the behavior of these relations obtained at the very end of the iteration procedure. This iteration requires another 3 to 15 iteration steps.
, which may seem redundant, but it is sometimes useful to disentangle the right solution when the intersection of other curves is not unique. Figure E.1b shows the behavior of these relations obtained at the very end of the iteration procedure. This iteration requires another 3 to 15 iteration steps.
The observed parameters [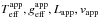 ] of each program star are considered with their respective uncertainties. So, an observed quantity X is assigned 11 different values within the interval [Xo − 2.5σx,Xo + 2.5σx] using random numbers, which means that for a given star we get 14 641 quartets (
] of each program star are considered with their respective uncertainties. So, an observed quantity X is assigned 11 different values within the interval [Xo − 2.5σx,Xo + 2.5σx] using random numbers, which means that for a given star we get 14 641 quartets ( ). Obviously, a certain number of such combinations do not produce any viable solution, however, for most stars we obtain more than Nsol ≃ 104 solutions for [ M/M⊙,t/tMS,η,i]. In most cases these solutions have asymmetric distributions, which are used as weighting functions to produce weighted averages and their respective equivalent 1σ dispersions.
). Obviously, a certain number of such combinations do not produce any viable solution, however, for most stars we obtain more than Nsol ≃ 104 solutions for [ M/M⊙,t/tMS,η,i]. In most cases these solutions have asymmetric distributions, which are used as weighting functions to produce weighted averages and their respective equivalent 1σ dispersions.
This procedure enables us to obtain Stoeckley’s correction Σ(M,t,η,i), which is consistent with the stellar fundamental parameters.
Appendix E.2: Reliability of the inferred pnrc parameters
We tested the procedure described in Sects. 3.5.1 and E.1 using several model stars, where the apparent parameters were simulated with FASTROT using model atmospheres with solar metallicity as required for the program stars. We performed many tests, in particular for a typical model star characterized by 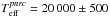 K,
K, 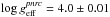 , log Lpnrc/L⊙ = 3.461 ± 0.025, so that M/M⊙ = 7.31 ± 0.08, t/tMS = 0.710 ± 0.016 and
, log Lpnrc/L⊙ = 3.461 ± 0.025, so that M/M⊙ = 7.31 ± 0.08, t/tMS = 0.710 ± 0.016 and 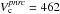 km s-1. This mathematical object was assumed to rotate successively at η = 0.2, 0.5 and 0.75, and each time seen at inclinations i = 20°, 50° and 80°. The results obtained for this model object are given in Table E.1, where we can see that the algorithm recovers the right pnrc parameters if they are treated without uncertainties. However, when the input parameters are taken with their uncertainties, as occurs with the observed stars, unavoidable deviations appear because the error propagation is asymmetric. Nevertheless, in Table E.1 we see that the error bars of the recovered pnrc quantities are not larger than the input uncertainties quoted above in this paragraph, which warrants that the algorithm is consistent.
km s-1. This mathematical object was assumed to rotate successively at η = 0.2, 0.5 and 0.75, and each time seen at inclinations i = 20°, 50° and 80°. The results obtained for this model object are given in Table E.1, where we can see that the algorithm recovers the right pnrc parameters if they are treated without uncertainties. However, when the input parameters are taken with their uncertainties, as occurs with the observed stars, unavoidable deviations appear because the error propagation is asymmetric. Nevertheless, in Table E.1 we see that the error bars of the recovered pnrc quantities are not larger than the input uncertainties quoted above in this paragraph, which warrants that the algorithm is consistent.
Appendix F: Approximate or auxiliary distributions
Let x be a random variable defined in the interval 0 ≤ x ≤ 1, whose probability density distribution is Π(x). When the moments of Π(x) are known up to degree n = 3, it is possible to derive simplified analytical expressions  that can be considered statistically quasi-equivalent to Π(x) because they reproduce the same average value of x, the same variance (or dispersion), and the same skewness (or symmetry) of the Π(x). The degree n can be higher than 3, so that moments of higher order can accounted for. We limit our discussion to n = 3 because we compare the Lucy-Richardson deconvolution method to the Cranmer method, where n = 3 was used. Thus, we develop here simple rules to derive trapezoidal or truncated linear functions, and triangular quasi-equivalent distribution functions
that can be considered statistically quasi-equivalent to Π(x) because they reproduce the same average value of x, the same variance (or dispersion), and the same skewness (or symmetry) of the Π(x). The degree n can be higher than 3, so that moments of higher order can accounted for. We limit our discussion to n = 3 because we compare the Lucy-Richardson deconvolution method to the Cranmer method, where n = 3 was used. Thus, we develop here simple rules to derive trapezoidal or truncated linear functions, and triangular quasi-equivalent distribution functions  .
.
First four moments of the function Π(x) and the parameters of its quasi-equivalent trapezoidal and triangular functions  .
.
Appendix F.1: Trapezoidal functions
We assume that 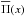 is given by
is given by
![\appendix \setcounter{section}{6} \begin{equation} \overline{\Pi}(x) = \left\{ \begin{array}{rl} px+q & x \in [a,b] \\ 0 & x \notin [a,b], \end{array} \right. \label{eq_trapz_1} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq756.png) (F.1)where p and q, as well as the boundaries a and b are parameters that we need to determine. We then ask that the moments are conserved, i.e.,
(F.1)where p and q, as well as the boundaries a and b are parameters that we need to determine. We then ask that the moments are conserved, i.e., 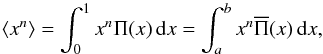 (F.2)where n = 0 indicates the normalization condition for both Π(x) and
(F.2)where n = 0 indicates the normalization condition for both Π(x) and 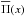 . Calling ζ = a + b and ξ = a − b, the normalization of
. Calling ζ = a + b and ξ = a − b, the normalization of 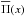 and its moment of first order requires that
and its moment of first order requires that
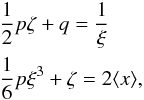 (F.3)while the moments of order n = 2 and 3 lead to
(F.3)while the moments of order n = 2 and 3 lead to 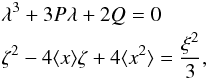 (F.4)where the following definitions hold:
(F.4)where the following definitions hold:
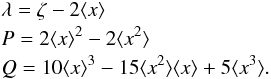 (F.5)Solving in Eq. (F.4) the algebraic equation of 3rd order for λ, we derive an expression for ζ, which in turn determines ξ using the 2nd relation in Eq. (F.4). The constants a and b are then obtained from Eq. (F.3), which lead to p and q.
(F.5)Solving in Eq. (F.4) the algebraic equation of 3rd order for λ, we derive an expression for ζ, which in turn determines ξ using the 2nd relation in Eq. (F.4). The constants a and b are then obtained from Eq. (F.3), which lead to p and q.
Appendix F.2: Triangular functions
We assume that  is defined as
is defined as
![\appendix \setcounter{section}{6} \begin{eqnarray*} \overline{\Pi}(x) = \left\{ \begin{array}{rl} \overline{\Pi}_1(x)=p_1x+q_1 \,\,& x \in [a,c] \\ \overline{\Pi}_2(x)=p_2x+q_2\, \,& x \in [c,b], \end{array} \right. \end{eqnarray*}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq767.png) where the constants to be determined are p1, p2, q1, and q2. The conditions
where the constants to be determined are p1, p2, q1, and q2. The conditions 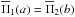 and
and 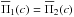 produce
produce
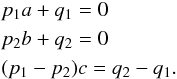 (F.6)The normalization of
(F.6)The normalization of 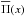 imposes
imposes
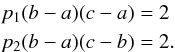 (F.7)We then impose that the moments ⟨xn⟩ (n = 1 to 3) are conserved as in Eq. (F.2), so that
(F.7)We then impose that the moments ⟨xn⟩ (n = 1 to 3) are conserved as in Eq. (F.2), so that
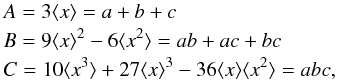 which lead to the following 3rd order equation that enables us to calculate the boundary a
which lead to the following 3rd order equation that enables us to calculate the boundary a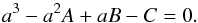 (F.8)Defining α = b + c = A − a and β = bc = C/a, we obtain the 2nd order algebraic equation for the boundary b,
(F.8)Defining α = b + c = A − a and β = bc = C/a, we obtain the 2nd order algebraic equation for the boundary b,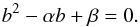 (F.9)Once a and b are known, we get c = α − b. Then, from Eq. (F.7) we readily obtain p1 and p2, so that q1 and q2 can be drawn from Eq. (F.6).
(F.9)Once a and b are known, we get c = α − b. Then, from Eq. (F.7) we readily obtain p1 and p2, so that q1 and q2 can be drawn from Eq. (F.6).
For the sake of an exercise, we adopt the following distribution function3: ![\appendix \setcounter{section}{6} \begin{eqnarray*} \begin{array}{rcl} \Pi(x) & = & \left\{0.3183\left[1-(2x-1)^2\right]^{1/2}\right. \\ & & \left.+~ 0.375\left[1-(2x-1)^2\right]\right\}\times[1+\gamma(2x-1)], \end{array} \end{eqnarray*}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq779.png) defined for 0 ≤ x ≤ 1, which is shown in Fig. F.1, for γ = −0.75, 0.0 and 0.75. From the relations obtained in Sects. F.1 and F.2 we derive the parameters of the quasi-equivalent trapezoidal and triangular distributions
defined for 0 ≤ x ≤ 1, which is shown in Fig. F.1, for γ = −0.75, 0.0 and 0.75. From the relations obtained in Sects. F.1 and F.2 we derive the parameters of the quasi-equivalent trapezoidal and triangular distributions 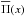 given in Table F.1, and the respective functions
given in Table F.1, and the respective functions 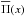 are shown in Fig. F.1 (blue and red curves). In this figure the respective cumulative distributions
are shown in Fig. F.1 (blue and red curves). In this figure the respective cumulative distributions 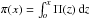 (right side blocks) are also shown.
(right side blocks) are also shown.
 |
Fig. F.1 Left side: distribution functions Π(x) (thick black curves) and their quasi-equivalent trapezoidal (blue curves) and triangular (red curves) |
For the approximations 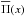 obtained here, where by definition only the first three moments are conserved, the most important question to solve is, which of these moments should be considered the closer parent distribution to the actual Π(x) one? To this end we added in Table F.1 the moments of order four ⟨x4⟩ issued from the respective simplified functions
obtained here, where by definition only the first three moments are conserved, the most important question to solve is, which of these moments should be considered the closer parent distribution to the actual Π(x) one? To this end we added in Table F.1 the moments of order four ⟨x4⟩ issued from the respective simplified functions 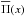 and the probabilities p% that, according to the Kolmogorov-Smirnov test, can be considered parent with Π(x). We thus immediately note that in Cranmer’s attempts the triangular would clearly be a better choice than the trapezoidal. Nevertheless, depending on the statistical problem, the suited simplified functional form
and the probabilities p% that, according to the Kolmogorov-Smirnov test, can be considered parent with Π(x). We thus immediately note that in Cranmer’s attempts the triangular would clearly be a better choice than the trapezoidal. Nevertheless, depending on the statistical problem, the suited simplified functional form 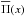 is probably different. Moreover, this leads us to conclude that it is not enough to claim that Gaussian or Maxwellian distributions are consistent with the observed distributions simply because the first two moments (average and dispersion) coincide, as the literature sometimes concludes (e.g., Mokiem et al. 2006; Dufton et al. 2006b; Hunter et al. 2008).
is probably different. Moreover, this leads us to conclude that it is not enough to claim that Gaussian or Maxwellian distributions are consistent with the observed distributions simply because the first two moments (average and dispersion) coincide, as the literature sometimes concludes (e.g., Mokiem et al. 2006; Dufton et al. 2006b; Hunter et al. 2008).
The approximate distributions are useful when Stoeckley’scorrection can be neglected. Nevertheless, using the relations between moments of apparent and true distributions, Ψ(v) and Φ(u) given by Chandrasekhar & Münch (1950), provide a first good guess for the searched parameters defining the functions 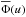 that are supposed to represent Φ(u). Trapezoidal and triangular distributions
that are supposed to represent Φ(u). Trapezoidal and triangular distributions 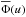 are dependent on four independent parameters, which means that apart from the normalization condition, they can reproduce only the first three moments of the actual distribution Φ(u).
are dependent on four independent parameters, which means that apart from the normalization condition, they can reproduce only the first three moments of the actual distribution Φ(u).
All Tables
Critical velocities Vc derived in this work for average MK spectral types and luminosity classes.
Parameters defining trapezoidal and triangular 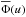 derived according to the Cranmer
method.
derived according to the Cranmer
method.
First four moments of the function Φ(u) derived according to different approaches used: Lucy-Richardson; Cranmer with pseudo-Maxwellian, trapezoidal and triangular functions.
Main-sequence evolutionary subphases, number of program stars in each group, the corresponding average fractional times ⟨t/tMS⟩ with their dispersions, modes (V/Vc)mode of the distributions, and the respective characteristic dispersions.
Average pnrc velocity ratios ⟨Vsini/Vc⟩ and ⟨V/Vc⟩ for mass-age groups of the studied Be star sample.
CE parameters derived for 10 Be stars studied here with the stronger emission in the Hα line.
First four moments of the function Π(x) and the parameters of its quasi-equivalent trapezoidal and triangular functions 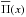 .
.
All Figures
 |
Fig. 1 Filled symbols: average critical velocities Vc and the related dispersions against the MK spectral type for luminosity classes V, IV, and III. These Vc were calculated using the effective temperatures and bolometric luminosities from calibrations carried out by various authors. Open symbols: critical velocities for the average MK spectral types and luminosity classes that conform with the method used in this work to obtain the Vc for individual stars. The MK spectral types are represented with the BCD parameter S70 dex. |
| In the text | |
 |
Fig. 2 a) Histogram giving the number N(Vsini/Vc) of observed ratios v = Vsini/Vc per class Δv studied in this work; b) smoothed density distribution Ψ(u) of projected velocity ratios u = Vsini/Vc, where measurement uncertainties on u = Vsini were taken into account. The error bars indicate the statistical uncertainty affecting the smoothed Ψ(u) distribution. |
| In the text | |
 |
Fig. 3 Blue line: relation between the observed |
| In the text | |
 |
Fig. 4 Diagram showing the two functions |
| In the text | |
 |
Fig. 5 a) Function CT(M,t,η,i); b) function CL(M,t,η,i); c) function CG(M,t,η,i). The pnrc parameters used here are |
| In the text | |
 |
Fig. 6 Distribution function Φ(u)LR obtained with the Lucy-Richardson method (blue curve) with the corresponding statistical uncertainties. Both distributions |
| In the text | |
 |
Fig. 7 Distributions Φ(u)LR obtained with Stoeckley’s corrections Σ(η,β1 = 1) calculated for different values of η: η = η∗ (derived in Sect. 3.5.1); η = ηmin; η = 1.0 and η = 0.0. For comparison the smoothed distribution of ratios of pnrc velocities Vsini/Vcsini (crosses) is also shown. |
| In the text | |
 |
Fig. 8 a) Distribution function ΦLR(u) and the associated
auxiliary trapezoidal and triangular distributions |
| In the text | |
 |
Fig. 9 a) Distributions of velocity ratios u = V/Vc of the program Be stars corresponding to three MS evolutionary subphases, which are indicated in the inlay. Each group has roughly the same number of stars. b) Distributions of velocity ratios u = V/Vc corresponding to three MS evolutionary subphases of the same duration, which are indicated in the inlay. In each block, the normalization is made by adding the area of all three distributions. |
| In the text | |
 |
Fig. 10 a) Density probability distributions Pk(i) against sini for k = −0.5, 0.0 and + 0.5. b) Frequency histograms of inclinations i against sini for k = −0.5, 0.0 and + 0.5. c) Distributions Φ(u,k) of ratios u = V/Vc assuming that the distributions of inclinations angles is given by Pk(i) in Eq. (15). The tested cases are for k = 0 (random) and nonrandom distributions with k = + 0.5 and k = −0.5. |
| In the text | |
 |
Fig. 11 Comparison of the distribution of inferred inclination angles for the program stars (cyan histogram) with the histogram for randomly distributed inclinations (white histogram). The error bars correspond to sampling uncertainties. |
| In the text | |
 |
Fig. 12 Normalized distributions Φ(vmt,u) against the macroturbulent velocity vmt given by Eq. (19) for some u = Vsini/Vc values that are identified in the figure. |
| In the text | |
 |
Fig. 13 Macroturbulent broadening ϵ(vmt,u) for 10 values of the macroturbulent velocity vmt scaled by steps of 10 km s-1, as a function of the ratio u = Vsini/Vc. |
| In the text | |
 |
Fig. 14 Distribution Φ(u) after correction for macroturbulence. The blue line represents the normalized distribution Ψ(v) of parameters v = Vsini/Vc corrected for both, measurement uncertainties and Stoeckley’s effect. The red and dashed black curves represent the normalized distribution Φ(u) of ratios u = Vsini/Vc corrected for macroturbulent motions using different values of b (see text). |
| In the text | |
 |
Fig. 15 Curves log f(Δv). All 9 solutions obtained with −0.6 ≤ α ≤ 0.3 and −0.5 ≤ β ≤ 0.5 in Eq. (26) for f(Δv) are comprised in the gray-shaded region. The red line represents the average of the 9 tested solutions and the blue line corresponds to the solution for α = β = 0. |
| In the text | |
 |
Fig. 16 Distribution functions of true velocity ratios V/Vc. Ψ(v)Σ + mt is the distribution of v = V/Vc corrected for measurement uncertainties, Stoeckley’s effect (Σ), macroturbulent velocities (mt) with b = 12 and projection factor sini. It distinguish thus from Φ(u)b = 12 shown in Fig. 14, which is not corrected for effects owing to sini. Full red line corresponds to the distribution of u = V/Vc corrected for Σ + mt and binarity with fbin = 0.7. Dashed red line corresponds to the distribution corrected for Σ + mt and binarity assuming fbin = 1.0. |
| In the text | |
 |
Fig. A.1 a) Effective temperatures for MK luminosity classes V, IV, and III determined by de Jager & Nieuwenhuijzen (1987) against those extracted from the BCD calibration; b) effective temperatures determined from the uvby photometry using the calibration by Napiwotzki et al. (1993) against those obtained in the BCD system; and c) average effective temperatures determined by Adelman et al. (2002), Nieva (2013), and Fitzpatrick & Massa (2005) against those obtained in the BCD system for a number of common OB stars without emission. The red dashed lines correspond to x = y diagonal. |
| In the text | |
 |
Fig. A.2 Comparison of bolometric luminosities derived using different calibrations of MV with those derived for the same discrete MK spectral types and luminosity classes using integrated fluxes that are identified here with log L(λ1,D) /L⊙ (red lines). The identifications are dJM (de Jager & Nieuwenhuijzen 1987), DDS (Deutschman et al. 1976), SK (Aller et al. 1982), and W (Wegner 2006). The blocks a), b), and c) are for average MK luminosity classes V, IV, and III, respectively. |
| In the text | |
 |
Fig. E.1 a) Determination of the pnrc mass M/M⊙ interpolated in stellar evolution models with rotation (black and red lines) and from the relation |
| In the text | |
 |
Fig. F.1 Left side: distribution functions Π(x) (thick black curves) and their quasi-equivalent trapezoidal (blue curves) and triangular (red curves) |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



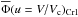
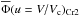
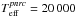
![\begin{equation} \label{eq_8} \begin{array}{rcl} &&\displaystyle T_{\rm eff}^{\rm app} = \displaystyle T_{\rm eff}^{{\it pnrc}}(M,t)\ C_{\rm T}(M,t,\eta,i) \\[0.8mm] &&\displaystyle g_{\rm eff}^{\rm app} = \displaystyle g_{\rm eff}^{{\it pnrc}}(M,t)\ C_{\rm G}(M,t,\eta,i) \\[0.8mm] &&\displaystyle L^{\rm app} = \displaystyle L^{{\it pnrc}}(M,t)\ C_{\rm L}(M,t,\eta,i) \\[0.8mm] &&\displaystyle \frac{(V\!\sin i)_{\rm app}}{V_{\rm c}(M,t)} = \displaystyle \left[\frac{\eta}{R_{\rm e}(M,t,\eta)/R_{\rm c}(M,t)}\right]^{1/2}\!\!\!\!\sin i-\frac{\Sigma(M,t,\eta,i)}{V_{\rm c}(M,t)}, \\ \end{array} \end{equation}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq233.png)
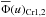
![\appendix \setcounter{section}{3} \begin{eqnarray} &&g_{\rm eff} = \frac{GM}{R(\theta)}\{[1-\eta(\theta)\sin^2\theta]^2+\eta^2(\theta)\sin^2\theta\cos^2\theta\}, \nonumber \\ &&\eta(\theta) = \frac{\Omega^2R^3(\theta)}{GM}, \nonumber \\ &&\Gamma(\Omega,\theta) = \frac{\kappa(\theta)L(\Omega)}{4\pi c\,GM[1-m(\Omega)]},\nonumber \\ &&m(\Omega) = \left(\frac{\Omega^2}{2\pi\,G\,\overline{\rho}}\right), \label{gtot2} \end{eqnarray}](/articles/aa/full_html/2016/11/aa28760-16/aa28760-16-eq588.png)