| Issue |
A&A
Volume 595, November 2016
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628338 | |
| Published online | 15 November 2016 | |
Where does the gas fueling star formation in brightest cluster galaxies originate?
1 INAF–IASF Milano, via E. Bassini 15, 20133 Milano, Italy
e-mail: silvano@iasf-milano.inaf.it
2 INAF–Osservatorio Astrofisico di Firenze, Largo Enrico Fermi 5, 50125 Firenze, Italy
3 Department of Astrophysical Sciences, Princeton University, Princeton, NJ 08544, USA
4 INAF–Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate, Italy
5 Department of Physics and Astronomy, University of California at Irvine, 4129 Frederick Reines Hall, Irvine, CA 92697-4575, USA
6 Dipartimento di Fisica dell’Università degli Studi di Milano, via Celoria 16, 20133 Milan, Italy
Received: 18 February 2016
Accepted: 21 June 2016
Aims. We investigate the relationship between X-ray cooling and star formation in brightest cluster galaxies (BCGs).
Methods. We present an X-ray spectral analysis of the inner regions, 10−40 kpc, of six nearby cool core clusters (z < 0.35) observed with Chandra ACIS. This sample is selected on the basis of the high star formation rate (SFR) observed in the BCGs. We restrict our search for cooling gas to regions that are roughly cospatial with the starburst. We fit single- and multi-temperature mkcflow models to constrain the amount of isobarically cooling intracluster medium.
Results. We find that in all clusters, below a threshold temperature ranging between 0.9 and 3 keV, only upper limits can be obtained. In four out of six objects, the upper limits are significantly below the SFR and in two, namely A1835 and A1068, they are less than a tenth of the SFR.
Conclusions. Our results suggests that a number of mechanisms conspire to hide the cooling signature in our spectra. In a few systems the lack of a cooling signature may be attributed to a relatively long delay time between the X-ray cooling and the star burst. However, for A1835 and A1068, where the X-ray cooling time is shorter than the timescale of the starburst, a possible explanation is that the region where gas cools out of the X-ray phase extends to very large radii, likely beyond the core of these systems.
Key words: galaxies: clusters: intracluster medium / X-rays: galaxies: clusters
© ESO, 2016
1. Introduction
Most of the baryonic matter in galaxy clusters resides in the form of virialized hot gas (Lin et al. 2003; Gonzalez et al. 2013) that emits in the X-ray band via thermal bremsstrahlung. The short cooling time associated with the high-density regions in cluster cores, immediately led to the conclusion that a massive cooling flow was developing in the intracluster medium (ICM) of most clusters (Silk 1976; Cowie & Binney 1977; Fabian & Nulsen 1977; Mathews & Bregman 1978). On the basis of the isobaric cooling flow model (Fabian & Nulsen 1977; Fabian 1994), it was estimated that typical cooling flows could develop mass cooling rates in the range 100−1000 M⊙ yr-1. However, the lack of massive star formation events and of large reservoirs of cold gas at the center of galaxy clusters has cast some doubts on the hypothesis of a complete cooling of the ICM in cluster cores. Indeed, if a significant fraction of the ICM is deposited, it should cool through all the phases and, in a quasi-stationary scenario, a noticeable amount of cooling gas should be observed at all temperatures in the X-ray range, from the ambient temperature down to the lowest detectable temperature (about 0.15 keV).
The perspective changed radically fifteen years ago when XMM-Newton observations, carried out with EPIC and with RGS, revealed a lack of cool gas at temperatures lower than about one-third of the cluster virial temperature (Molendi & Pizzolato 2001; Tamura et al. 2001; Peterson et al. 2003). As a consequence, the mass cooling rates have been revised towards values more than one order of magnitude lower (see Peterson & Fabian 2006). These observations necessarily imply the existence of some process that heats the gas and suppresses its cooling. Among the many mechanisms investigated so far, active galactic nucleus (AGN) feedback is considered the most plausible (see Fabian 2012). Although the detailed underlying physics is not fully understood, AGN outbursts can inject sufficient amounts of energy into the ICM to offset cooling (e.g., McNamara et al. 2005; Gaspari 2015). The relativistic electrons in jets associated with the central cluster galaxy are able to carve large cavities into the ICM. The free energy associated with these “bubbles„ is plausibly transferred into the ICM and thermalized through turbulence (see McNamara & Nulsen 2012). This feedback mechanism has been observed in its full complexity in a few nearby clusters like Perseus (Fabian et al. 2003, 2006, 2011), Hydra A (McNamara et al. 2000), and a few others at large distances (see Blanton et al. 2011).
In addition, some of the large elliptical galaxies often found at the minimum of the cluster potential well (brightest cluster galaxy − BCG) contain significant amounts of cold gas (among the most recent results, see McNamara et al. 2014) and exhibit signs of ongoing star formation at a level of 10−100 M⊙ yr-1 (Hoffer et al. 2012). The star formation rate (SFR) of BCGs has been found to be generally consistent with the mass cooling rate Ṁ measured with X-ray spectroscopy in cool cores (Rafferty et al. 2006); we note, however, that O’Dea et al. (2008) have found that cooling rates are in excess of SFRs by a factor of a few. A correlation between cool cluster cores and IR measured SFR in BCGs has recently been confirmed (Rawle et al. 2012). These results have generally been interpreted as evidence that star formation is driven and fueled by the cooling of the ICM.
Galaxy clusters selected in our sample, ranked from the highest to the lowest measured SFR in the BCG.
In this paper we revisit this relation by improving the measurement of the mass cooling rates in cool cores. We start from the fact that the emission measure of the coldest gas (< 1 keV) in cooling flow models is a few percent of the total X-ray emission in the core region, so that the measurement of mass cooling rate based on X-ray spectroscopy is dominated by the emission of gas at relatively high temperatures (about 2 keV). The presence of gas in the range 0.5−1 keV is mostly associated with the Fe XVII emission lines, which is the most reliable diagnostic for gas in this temperature range. Although Fe XVII emission lines have been detected in some cases, the amount of cold gas associated with that emission is still quite uncertain owing to the strong continuum produced by much hotter gas which unavoidably overwhelms the line emission.
In this paper we address a specific issue: is the amount of gas cooling in the region where star formation is occurring sufficient to fuel this process? Within this framework, angular resolution becomes a critical factor in order to ascertain the presence of the coldest components of a cooling flow; in several cases it is more relevant than spectral resolution, and CCD data can be as effective as grating data despite its modest spectral resolution.
In this work we exploit the angular resolution of Chandra ACIS-S and ACIS-I to avoid as much as possible the hot gas surrounding the core region. We consider six nearby (z< 0.35) cool core clusters observed with Chandra, whose BCG exhibit the highest SFR. For all these clusters, the mass cooling rates have been previously estimated from X-ray spectral analysis, but in all cases within regions much larger than those considered here (10−40 kpc centered on the BCG). Our goal is to robustly estimate the mass cooling rate Ṁ or, alternatively, to put a robust upper limit to Ṁ, and finally to compare this to the observed SFR in the same region.
The paper is organized as follows. In Sect. 2 we describe the sample selection. In Sect. 3 we describe the data reduction and analysis, and in Sect. 4 we provide the measurements of the mass cooling rate in each cluster of our sample. In Sect. 5 we go through a detailed evaluation of possible systematic effects that can potentially hide the presence of cooling gas or interfere with its measurement. The final result is a robust evaluation of mass cooling rates Ṁ which includes systematic effects. In Sect. 6 we discuss our results, and finally, in Sect. 7 we summarize our conclusions. Throughout the paper, we adopt a ΛCDM cosmology with Ω0 = 0.3,ΩΛ = 0.7, and H0 = 70. Quoted errors always correspond to a 1σ confidence level.
2. Sample selection
Our goal is to investigate the relation between the mass cooling rate and SFR in cool core (CC) clusters. We selected those CC clusters with high-quality X-ray data and the highest measured SFR. This choice allows us to investigate the relation between BCG SFR and Ṁ starting from the clusters where the expected Ṁ should be highest1.
We search in the Chandra archive as of June 2014 for clusters with ACIS-I or ACIS-S observations longer than 9 ks. We then select those clusters that have published SFR in excess of 30 M⊙ yr-1. When there is more than one measurement of the SFR, we prefer measurements that are based on infrared data, whenever available, since UV and optical measures can significantly underestimate obscured star formation (see Rawle et al. 2012). We also favor estimates based on infrared spectral energy distribution (IR SED) fitting, rather than on single-band measurements, as they can properly account for the contribution from the central AGN which, in many cases, can be relevant. For systems where this method has been used, the uncertainties on the SFRs are expected to be modest, below ~ 20% (see Rawle et al. 2012). We finally apply a cut in redshift, choosing systems with z< 0.35. The upper limit is chosen in order to avoid clusters where a large part of the cold gas emission is redshifted out of the Chandra energy range used for this analysis (0.5−8 keV). We note that one of the strongest candidates that harbors a massive cooling flow, SPT-CL J2344-4243 (the Phoenix cluster, see McDonald et al. 2012), is excluded from this sample owing to its high redshift z ~ 0.6. A dedicated paper, based on a deep XMM-Newton observation, has recently been published by our group (Tozzi et al. 2015).
Our final sample is rather small, and consists of six systems, most of which are well known. In Table 1 we list our objects and include redshift, measured SFR in the BCG, the method used to measure the SFR, and measured cold molecular gas, when available. This sample is not meant to be complete or representative, but simply satisfies the requirements needed to perform our analysis: Chandra ACIS data, presence of a cool core, and a reliable measurement of SFR in the BCG larger than 30 M⊙ yr-1.
Summary of Chandra observations used in this work.
3. Data reduction and analysis
3.1. Data reduction
We performed a standard data reduction starting from the level 1 event files, using the CIAO 4.6 software package, with version (CALDB 4.6.3) of the Chandra Calibration Database. All the observation ID numbers (Obsid) and with the corresponding instruments, effective exposure times after data reduction, and the data acquisition modes are listed in Table 2. When observations are taken in the VFAINT mode, we run the task acis_process_events to flag background events that are most likely associated with cosmic rays and remove them. With this procedure, the ACIS particle background can be significantly reduced compared to the standard grade selection. The data is filtered to include only the standard event grades 0, 2, 3, 4, and 6. We checked visually for hot columns left after the standard reduction. For exposures taken in VFAINT mode, there are practically no hot columns or flickering pixels left after filtering out bad events. We also apply CTI correction to the ACIS-I data. We finally filter time intervals with high background by performing a 3σ clipping of the background level using the script analyze_ltcrv. The final effective exposure times are generally very close to the original observing time. We note that our data reduction is not affected by possible undetected flare since we are able to compute the background in the same observation from a large source-free region around the cluster, thus taking into account any possible spectral distortion of the background itself induced by the flares. However, given the small source extraction regions and the high surface brightness of the core, the background correction is always negligible.
We select regions from which X-ray spectra are extracted in such a way to include the entire star forming region. Indeed, choosing regions that do not fully encompass the SF region may introduce a bias and lower the cooling rate, while in the opposite case the sensitivity to the cooler X-ray emitting gas will be significantly reduced owing to the presence of larger amounts of ambient gas. However, in several cases the star forming region is not precisely identified. Therefore, to show that our results are not sensitive to the size of the extraction regions, we always analyze the X-ray emission within two different regions selected from a suite of four circles with radii of 10, 20, 30, and 40 kpc. All the circular regions are centered on the position of the BCG or of the main starburst, when not coincident with the BCG, as obtained from optical data. Details on the specific selections are provided in the subsections describing the analysis of individual systems. We exclude the inner 2 arcsec when an unresolved X-ray AGN is found in the BCG. When a merged spectrum from multiple exposures is extracted, the response matrix files and ancillary response files are computed for each Obsid and then added together weighted by the corresponding exposure time. However, three of our clusters are observed in single exposures. Finally, the results for ZW 3146 and RXC J1504 are obtained by performing the combined fit of the spectra from two different Obsid without merging them due to the different observing modes (FAINT and VFAINT).
3.2. Fitting method
Our goal is to constrain the mass cooling rate in the projected regions 10−40 kpc in size centered on the BCG or on the star forming regions. We use the model mkcflow (Mushotzky & Szymkowiak 1988), which is based on a combination of single-temperature mekal models (Mewe et al. 1985, 1986; Kaastra 1992; Liedahl et al. 1995) according to the expectation of the isobaric cooling flow model. This model assumes a unique mass cooling rate throughout the entire temperature range probed by the data. The actual situation may be more complex; some of the gas above a given temperature threshold may cool at a relatively high rate, consistent with the isobaric cooling assumption. Instead, mass cooling associated with colder gas may be much lower. Indeed, grating spectra of cool cores are traditionally fitted with an isobaric cooling flow model with a cutoff temperature below which there is no gas (Peterson & Fabian 2006). Therefore, to explore more complex scenarios, we also measure the cooling rate in several temperature intervals by using a set of mkcflow models in contiguous temperature bins.
In practice, we measure the spectral mass deposition rate in two different ways:
-
a cooling flow model mkcflow coupled to onesingle-temperature mekal component. The upper temperatureof the mkcflow component is frozen to 3 keV, while the temperature of the mekal component is left free. The lowest temperature of the mkcflow component it frozen to 0.15 keV. By setting the minimum temperature to 0.15 keV, we can interpret the normalization of the mkcflow model as the maximum cooling rate allowed for an isobaric cooling flow across the entire temperature range (from 3 to 0.15 keV). By setting the maximum temperature of the mkcflow model to 3 keV, we include in this component all the phases that contribute significantly to the Fe-Lshell emission. A minimum temperature of 4 keV is set for the mekal component to avoid superposition with the mkcflow component. The metal abundance of the mkcflow and mekal models are tied together.
-
A set of mkcflow models whose lower and upper temperatures are tied together in order to avoid overlap. Here the normalization of each component provides the mass cooling rate of the gas in the corresponding temperature interval. The upper and lower temperatures are frozen to the following values: 0.15−0.25, 0.25−0.45, 0.45−0.9, 0.9−1.8, and 1.8−3.0. As for the single mkcflow model, by setting the maximum temperature to 3 keV we include in the mkcflow components all the phases that contribute significantly to the Fe-Lshell emission. A mekal component accounts for the hotter gas; a minimum temperature of 4 keV is set to avoid superposition with the mkcflow components. The metal abundance values of the various mkcflow components are tied to one another, while the metal abundance of the mekal component is left free.
It is worth noting that above 3 keV, a single mekal model can account for the presence of several hot components since it is not possible to identify them in the spectral analysis (see Mazzotta et al. 2004). Another possible approach would be to link the highest temperature of the last mkcflow model to that of the mekal model. However, whenever we repeat our fits linking the highest mkcflow temperature to the mekal component, we find only negligible changes in the best-fit values of the mass cooling rate.
The Galactic absorption, NH, is frozen to the value obtained from the radio map of Kalberla et al. (2005) at the position of the cluster. We will discuss in Sect. 5 the effect of leaving the NH value free to vary under reasonable assumptions. Finally, the redshift is frozen to the best-fit value obtained by fitting the Kα line emission complex from H-like and He-like Fe after checking that this value is in agreement with the optical value.
Typically, in the soft energy range (0.5−2 keV), the fraction of the signal associated with the cold (kT< 3 keV) components in our models is below 10%, and in several instances below 1%. Clearly at these very low levels systematic effects associated with our limited knowledge of the Chandra effective areas can play an important role. In Sect. 5 we will present a simple method to derive estimates of the systematic uncertainties on mass cooling rates. The use of the mkcflow model allows us to directly obtain the best-fit mass cooling rate Ṁ. Finally, the quoted error bars correspond to a 1σ confidence level.
4. Measurement of mass cooling rate in individual systems
In this section we describe the analysis of the cool core regions at different radii in each cluster. We provide full details for A1835, and refer to this analysis for the remaining clusters.
4.1. Abell 1835
 |
Fig. 1 Measured cooling rate as a function of temperature range. Left: red circles show the values of Ṁ measured in different temperature bins in the inner 10 kpc of A1835. Error bars correspond to 1σ, arrows indicate 95% confidence upper limits. The shaded area is the 1σ uncertainty or the 95% upper limit interval of the global mass cooling rate obtained with a single mkcflow model in the temperature range 0.15−3.0 keV. Right: same as left panel for the inner 20 kpc. |
Best-fit values for Ṁ obtained from single and multi mkcflow models.
A1835 is one of the first clusters in which the lack of cold gas below ~1 keV was unambiguously observed thanks to CCD (Molendi & Pizzolato 2001) and grating (Peterson et al. 2001) spectroscopy with XMM-Newton. In the latter work, an upper limit of 200 M⊙ yr-1 at the 90% confidence level was obtained. A1835 also harbors a radio AGN, which is responsible for cavities clearly seen in the X-ray surface brightness near the center. For these reasons, A1835 is considered an archetypical cool core cluster regulated by radio-mode feedback (McNamara et al. 2014).
Abell 1835 was observed with ACIS-S for a total of 30 ks of effective exposure in 1999/2000, and with ACIS-I for a total of 193 ks in 2005/2006. The ACIS-S data were taken in the FAINT mode, and date back to the early epochs of Chandra operation. Here we focus only on the deeper ACIS-I exposures taken in the VFAINT mode, and which contain most of the information. The redshift of the cluster is measured with the X-ray spectral analysis of the global emission, and is found to be 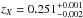 . This value is in good agreement with the optical value zopt = 0.2523 (Crawford et al. 1999). At this redshift the angular diameter scale corresponds to 3.91 kpc/arcsec. Therefore, 10 kpc corresponds to 5.2 physical pixels on ACIS-I (one pixel corresponds to 0.492 arcsec) and 20 kpc to 10.4 pixels. Given the exquisite resolution of Chandra at the aimpoint, we neglect effects due to the point spread function. We choose the center to be on the optical position of the BCG, which is RABCG = 14:01:02.0, DecBCG = + 2:52:43.0. The position of the BCG nucleus appears to be ~ 2′′ away from the peak in the X-ray surface brightness, corresponding to one of the two bright spots in the cluster core (see Fig. 9 in McNamara et al. 2006).
. This value is in good agreement with the optical value zopt = 0.2523 (Crawford et al. 1999). At this redshift the angular diameter scale corresponds to 3.91 kpc/arcsec. Therefore, 10 kpc corresponds to 5.2 physical pixels on ACIS-I (one pixel corresponds to 0.492 arcsec) and 20 kpc to 10.4 pixels. Given the exquisite resolution of Chandra at the aimpoint, we neglect effects due to the point spread function. We choose the center to be on the optical position of the BCG, which is RABCG = 14:01:02.0, DecBCG = + 2:52:43.0. The position of the BCG nucleus appears to be ~ 2′′ away from the peak in the X-ray surface brightness, corresponding to one of the two bright spots in the cluster core (see Fig. 9 in McNamara et al. 2006).
 |
Fig. 2 Measured cooling rate in RXC J1504 in the inner 20 kpc (left panel) and 40 kpc (right panel). Symbols as in Fig. 1. |
According to Fig. 2 in McNamara et al. (2006), the bulk of the star formation, as measured from optical colours, occurs within ≃10 kpc. In particular, the central blue colors associated with the starburst are found at radii smaller than 7′′ (corresponding to ~ 27 kpc) from the BCG center (see also their Fig. 3). Furthermore, recent ALMA observations (McNamara et al. 2014) provide evidence of large amounts of molecular gas at the level of ≃ 5 × 1010M⊙ within a few kpc of the center. However, the position of the molecular gas does not overlap with the position of the two X-ray bright regions, where the gas is expected to cool most rapidly. These two regions are partially included in the 10 kpc circle, and fully included in the 20 kpc circle. Therefore, our choice of extracting two spectra in the inner 10 and 20 kpc nicely matches the central starburst region and the maximum region encompassing all possible star formation events.
We find about 7500 and 26400 net counts (0.5−7 keV band) in the inner 10 and 20 kpc, respectively. The background is sampled from the ACIS-I CCD3 in a region far from the cluster. Given the extent of this massive cluster, the background may be contaminated by some emission from the cluster itself. However, given the small size of the regions under investigation, the background contribution is minimal and always below 0.1% of the total emission. We fit each region with our two methods (see Sect. 3.2 for details). The redshift parameter is frozen; however, we verified that leaving it free does not have any noticeable effect on the fit. The Galactic hydrogen column density is frozen to the value NH = 2.04 × 1020 cm-2, derived by Kalberla et al. (2005) through radio observations.
With our first model (mkcflow + mekal) we measure a 95% one-sided confidence level, i.e., upper limits (corresponding to ΔCstat = 2.71), of Ṁ = 23 M⊙ yr-1 in the inner 10 kpc and 22 M⊙ yr-1 for 20 kpc (see Fig. 1 and Table 3). The temperature of the mekal component is rather stable, with best-fit values of 4.4 ± 0.2 and 4.3 ± 0.1 keV for the 10 and 20 kpc, respectively. We find that in the 0.5−2 keV band, the contribution to the signal from gas below 3 keV is 6% and 2% within 10 and 20 kpc, respectively. This will be relevant in Sect. 5 when discussing possible systematics associated with a global ~ 3% uncertainty in the effective area of Chandra. We also postpone to Sect. 5 the discussion on the effects of a larger NH.
Next we fit our spectra with composite models consisting of five mkcflow components in fixed temperature bins and a mekal component with free temperature (see Sect. 3.2 for details). Our results for the two regions are summarized in the two panels of Fig. 1, where the 95% confidence level upper limit range from the single mkcflow model is shown by the shaded area (see also Table 3). As we can see, irrespective of the extraction radius, emission from gas below 1.8 keV is not detected. The lowest temperature range we investigate, here and in other clusters, is characterized by a significantly less constraining upper limit for the simple reason that emission from gas in this temperature range contributes only in a modest way to the spectrum above 0.5 keV where we perform our measurements. Above 1.8 keV, the gas seems to cool at a rate of ~ 200−300 M⊙ yr-1. Our analysis suggests that the ICM in A1835 cools down to a temperature that is approximately 2.4 keV, which is roughly 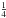 of the ambient temperature, 9.7 ± 0.14 keV, measured from the circular ring defined by 40 kpc <r<400 kpc. Below this temperature, there is no clear evidence of significant cooling. If we require the four mkcflow components covering the 0.15−1.8 keV range to have the same mass deposition rate, we find that
of the ambient temperature, 9.7 ± 0.14 keV, measured from the circular ring defined by 40 kpc <r<400 kpc. Below this temperature, there is no clear evidence of significant cooling. If we require the four mkcflow components covering the 0.15−1.8 keV range to have the same mass deposition rate, we find that 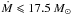 yr-1 and 10 M⊙ yr-1 at a 95% confidence level (corresponding to ΔCstat = 2.71) for the 10 and 20 kpc regions, respectively. We conclude that the spectral mass cooling rate Ṁ in the starburst region is lower by about one order of magnitude than the SFR in the BCG (see Table 1).
yr-1 and 10 M⊙ yr-1 at a 95% confidence level (corresponding to ΔCstat = 2.71) for the 10 and 20 kpc regions, respectively. We conclude that the spectral mass cooling rate Ṁ in the starburst region is lower by about one order of magnitude than the SFR in the BCG (see Table 1).
 |
Fig. 3 Measured cooling rate in RXC J1532 in the inner 10 kpc (left panel) and 20 kpc (right panel). Symbols as in Fig. 1. |
Finally, we compare our results based on low-resolution spectra with previous results based on grating spectra and published in the literature (Peterson et al. 2003; Sanders et al. 2010). The advantage of RGS spectra over CCD spectra is that it affords direct detection of emission lines associated with plasma of different temperatures. As pointed out by Sanders et al. (2010), the RGS spectrum of A1835 shows no evidence of emission lines from plasma with temperatures below ~ 3 keV. Under these circumstances, the breakup of the spectrum in different components relies mostly on its overall shape, and RGS data is no better suited for this purpose than CCD data. Actually, under the assumption that the mass cooling occurs in the same region where the star formation is taking place, i.e., roughly within 20 kpc of the center (McNamara et al. 2006), the limited spatial resolution of the RGS, ~ 30 arcsec corresponding to ~ 120 kpc, results in a significant disadvantage as any emission from cool thermal components coming from within ~ 30 kpc will be swamped by the emission from the much larger RGS extraction region. This is likely the reason for the order of magnitude large upper limit to the mass cooling rate, Ṁ < 200 M⊙ yr-1 (Sanders et al. 2010) and Ṁ < 140 M⊙ yr-1 (Peterson et al. 2003), both at a 90% confidence level, found in A1835 with XMM-Newton gratings data.
4.2. RXC J1504
RXC J1504 was observed with ACIS-I for a total of 13.2 ks of effective exposure in the FAINT mode and for 39 ks in the VFAINT mode. We measure the redshift of the cluster from the global X-ray spectrum finding 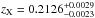 , in agreement, within 1σ, with the optical value zopt = 0.2153 (Ogrean et al. 2010). We prefer to use the value of zX which makes the fit more sensitive to the presence of line blends from cool gas. At this redshift the angular diameter scale is 3.45 kpc/arcsec. Therefore 20 kpc corresponds to 11.6 physical pixels and 40 kpc to 23.2 pixels. We choose the center to be on the center of the BCG galaxy, RABCG = 15:04:07.490, DecBCG = −2:48:15.97, which is within ~ 5 kpc from the peak in the X-ray surface brightness. Most star formation occurs in the core of the BCG and in a 42-kpc-long filament of blue continuum, line emission and X-ray emission, that extends southwest of the galaxy and that is entirely included in a circle with a 40 kpc radius centered on the BCG (see Fig. 9 in Ogrean et al. 2010). Therefore, for this cluster we perform our analysis in two circles with radii of 20 and 40 kpc.
, in agreement, within 1σ, with the optical value zopt = 0.2153 (Ogrean et al. 2010). We prefer to use the value of zX which makes the fit more sensitive to the presence of line blends from cool gas. At this redshift the angular diameter scale is 3.45 kpc/arcsec. Therefore 20 kpc corresponds to 11.6 physical pixels and 40 kpc to 23.2 pixels. We choose the center to be on the center of the BCG galaxy, RABCG = 15:04:07.490, DecBCG = −2:48:15.97, which is within ~ 5 kpc from the peak in the X-ray surface brightness. Most star formation occurs in the core of the BCG and in a 42-kpc-long filament of blue continuum, line emission and X-ray emission, that extends southwest of the galaxy and that is entirely included in a circle with a 40 kpc radius centered on the BCG (see Fig. 9 in Ogrean et al. 2010). Therefore, for this cluster we perform our analysis in two circles with radii of 20 and 40 kpc.
We find ~16 600 (5700) and 39 400 (13 600) net counts (0.5−7 keV band) within 20 and 40 kpc of the center of the BCG, respectively, in the ACIS-I VFAINT (FAINT) observation. The background is sampled from the ACIS-I CCD3, in a region far from the cluster. Also in this case, given the extent of this nearby massive cluster, the background is contaminated by some emission from the cluster itself. However, given the small size of the region we are investigating, the background contribution is minimal and always below 0.2% of the total emission. The value of the Galactic hydrogen column density is NH = 5.94 × 1020 cm-2 according to Kalberla et al. (2005).
With the single mkcflow model in the 0.15−3.0 keV temperature range, we find very low 95% confidence level upper limits on the order of 10 M⊙ yr-1 irrespective of the extraction radius (see Fig. 2 and Table 3). The results from the multi-component models, show that the two lowest temperature bins (energies below 0.5 keV) are almost unconstrained owing to the large Galactic absorption, which removes a large part of the signal at the lowest energies. As shown in Fig. 2 (see also Table 3) the 95% upper limit on Ṁ in the range 0.5−1.8 keV is ~ 30 M⊙ yr-1, irrespective of the extraction radius. It grows to ~ 180 M⊙ yr-1 in the temperature range 1.8−3.0 keV. If we require the four mkcflow components covering the 0.15−1.8 keV range to have the same mass deposition rate, we find that 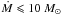 yr-1 and
yr-1 and 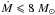 yr-1 at a 95% confidence level (corresponding to ΔCstat = 2.71) for the 20 and 40 kpc regions, respectively, which are, within the errors, consistent with those from the single mkcflow model. These values are more than an order of magnitude smaller than the SFR in the BCG. Our results can be compared to those reported by Ogrean et al. (2010), who find 3σ upper limits of 156 M⊙ yr-1 and 239 M⊙ yr-1 from the analysis of EPIC and RGS spectra respectively. As in the case of A1835 the far less constraining XMM-Newton limits likely follow from the much larger extraction regions chosen by these authors: namely 0.67 arcmin (140 kpc) for EPIC and 2 arcmin (414 kpc) for RGS.
yr-1 at a 95% confidence level (corresponding to ΔCstat = 2.71) for the 20 and 40 kpc regions, respectively, which are, within the errors, consistent with those from the single mkcflow model. These values are more than an order of magnitude smaller than the SFR in the BCG. Our results can be compared to those reported by Ogrean et al. (2010), who find 3σ upper limits of 156 M⊙ yr-1 and 239 M⊙ yr-1 from the analysis of EPIC and RGS spectra respectively. As in the case of A1835 the far less constraining XMM-Newton limits likely follow from the much larger extraction regions chosen by these authors: namely 0.67 arcmin (140 kpc) for EPIC and 2 arcmin (414 kpc) for RGS.
4.3. RX J1532
RX J1532 was observed with ACIS-I and ACIS-S in 2001 for about 10 ks for both exposures. However, in 2011, a much deeper exposure of 88 effective ks with ACIS-S, VFAINT mode, has been acquired. Therefore, we use this last ACIS-S observation for our analysis. We measure the redshift of the cluster from the global X-ray spectrum finding 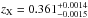 , this is the value that will be used in the X-ray analysis. We verified that when the redshift is left free during the fits, its best-fit value does not change significantly. The star formation observed in the BCG has been measured to be 110 M⊙ yr-1 by Hoffer et al. (2012). Recently, Hlavacek-Larrondo et al. (2013), using HST data, has derived the total SFR associated with the BCG within a circular region centered on the galaxy with a radius of 3.5 arcsec (~ 18 kpc), while beyond this region they detected no significant UV emission2. Therefore, we choose to extract spectra from two circular regions of 10 and 20 kpc in radius centered on the BCG at RABCG = 15:32:53.796, DecBCG = + 30:20:58.97.
, this is the value that will be used in the X-ray analysis. We verified that when the redshift is left free during the fits, its best-fit value does not change significantly. The star formation observed in the BCG has been measured to be 110 M⊙ yr-1 by Hoffer et al. (2012). Recently, Hlavacek-Larrondo et al. (2013), using HST data, has derived the total SFR associated with the BCG within a circular region centered on the galaxy with a radius of 3.5 arcsec (~ 18 kpc), while beyond this region they detected no significant UV emission2. Therefore, we choose to extract spectra from two circular regions of 10 and 20 kpc in radius centered on the BCG at RABCG = 15:32:53.796, DecBCG = + 30:20:58.97.
The angular diameter scale for RX J1532 is 5.04 kpc/arcsec, 10 kpc corresponds to 4 physical pixels on ACIS-S and 20 kpc to 8 pixels. We find 2500, 7900 net counts (0.5−7 keV band) within 10 and 20 kpc of the center, respectively. The background is sampled from the ACIS-S CCD7, and as for our other systems, the background contribution is low, always below 0.2% of the total emission.
The value of the Galactic hydrogen column density is NH = 2.3 × 1020 cm-2 according to Kalberla et al. (2005). For the single mkcflow model we have a marginal detection (about 2σ) of a non-negligible mass cooling rate within 10 kpc, 38 ± 20 M⊙ yr-1, while for 20 kpc we derive an upper limit of about 100 M⊙ yr-1 (see Fig. 3 and Table 3). The temperature of the mekal component is kT = 4.5 ± 0.4 and 4.2 ± 0.2 keV for 10 and 20 kpc, respectively. The multi-component analysis shows, as for A1835, no evidence of emission below 1.8 keV (see Fig. 3 and Table 3). If we require the four mkcflow components covering the 0.15−1.8 keV range to have the same mass deposition rate, we find that 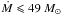 yr-1 at a 95% confidence level, corresponding to ΔCstat = 2.71, for the 10 kpc region. A somewhat less constraining upper limit,
yr-1 at a 95% confidence level, corresponding to ΔCstat = 2.71, for the 10 kpc region. A somewhat less constraining upper limit, 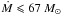 yr-1, is found for the 20 kpc region that presumably encompasses the entire star formation region. We conclude that the currently available data is of insufficient statistical quality to provide constraints for a useful comparison with the SFR.
yr-1, is found for the 20 kpc region that presumably encompasses the entire star formation region. We conclude that the currently available data is of insufficient statistical quality to provide constraints for a useful comparison with the SFR.
4.4. Abell 1068
 |
Fig. 4 Measured cooling rate in A1068 in the inner 20 kpc (left panel) and 40 kpc (right panel). Symbols as in Fig. 1. |
The Chandra data on A1068 consist of 30 ks with ACIS-S in the FAINT mode. The total exposure time amounts to 26.6 ks after the standard data reduction procedure. A1068 is also observed in other ACIS-I and ACIS-S pointings, but always at large off-axis angles, therefore we do not consider further data for our analysis. The spectral analysis of the ACIS-S data published in Wise et al. (2004) found a total mass cooling rate of ~150 M⊙ yr-1 from the total emission, while only ~ 40 M⊙ yr-1 within the inner 30 kpc. In the same paper the authors discuss the possibility that the observed starburst may also be triggered by interactions between the BCG and a group of companion galaxies rather than by a cooling flow. According to Wise et al. (2004, see their Fig. 2) the bulk of the starburst is contained within ≃ 4′′ (~10 kpc) of the center and is fully contained within ≃ 6′′ (15 kpc). A secondary starburst is located approximately 15′′ (35 kpc) SE of the core, and one anomalous blue region is seen up to 35′′ from the optical center (see their Fig. 3). Finally, according to Fig. 1 in Wise et al. (2004), the optical peak is offset west with respect to the X-ray peak by about 3′′. Conversely, according to Edge et al. (2010) the IR emission is on scales <5′′. To include all possible cooling sites, we center our extraction regions on the optical position of the BCG (RABCG = 0:40:44.508; DecBCG = + 39:57:11.23) and consider extraction radii of 20 and 40 kpc.
At the cluster redshift the angular diameter scale is 2.44 kpc/arcsec. Therefore, on ACIS-S, 20 kpc corresponds to 16.7 physical pixels and 40 kpc to 33.3 pixels. We fix the redshift to the value obtained from the best fit to the total spectrum 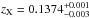 . We identify the presence of a weak AGN in the hard 2−7 keV image, and therefore remove the inner 2.2 kpc to exclude its emission. We find 9160 and 17500 net counts (0.5−7 keV band) within 20 and 40 kpc, respectively. The background is sampled from the ACIS-S CCD7 as in the previous cases, and the background contribution is always below 0.2% of the total emission. The value of the Galactic hydrogen column density is NH = 1.69 × 1020 cm-2 according to Kalberla et al. (2005).
. We identify the presence of a weak AGN in the hard 2−7 keV image, and therefore remove the inner 2.2 kpc to exclude its emission. We find 9160 and 17500 net counts (0.5−7 keV band) within 20 and 40 kpc, respectively. The background is sampled from the ACIS-S CCD7 as in the previous cases, and the background contribution is always below 0.2% of the total emission. The value of the Galactic hydrogen column density is NH = 1.69 × 1020 cm-2 according to Kalberla et al. (2005).
For the single mkcflow model we obtain Ṁ< 15M⊙ yr-1 and Ṁ< 13M⊙ yr-1 for 20 and 40 kpc, respectively (see Fig. 4 and Table 3). The multi-component mkcflow model highlights tight upper limits on emission from gas with temperature in the range 0.25−0.9 keV (see Fig. 4 and Table 3). Emission could be present in the energy range 0.9 to 1.8 keV, albeit at a low statistical significance of ~ 2σ. If we require the four mkcflow components covering the 0.15−1.8 keV range to have the same mass deposition rate, we find that 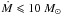 yr-1 and
yr-1 and 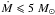 yr-1 at a 95% confidence level, corresponding to ΔCstat = 2.71 for the 20 and 40 kpc region, respectively. Thus, for A1068, our upper limit is lower by an order of magnitude or more with respect to the SFR reported by Rawle et al. (2012).
yr-1 at a 95% confidence level, corresponding to ΔCstat = 2.71 for the 20 and 40 kpc region, respectively. Thus, for A1068, our upper limit is lower by an order of magnitude or more with respect to the SFR reported by Rawle et al. (2012).
4.5. ZW 3146
 |
Fig. 5 Measured cooling rate in ZW 3146 in the inner 20 kpc (left panel) and 30 kpc (right panel). Symbols as in Fig. 1. |
ZW 3146 was observed with ACIS-I for a total of 45.6 ks of effective exposure in the FAINT mode and for 40 ks in the VFAINT mode. We measure the redshift of the cluster from the global X-ray spectrum finding 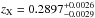 , and we keep this value frozen in the spectral fits. At this redshift the angular diameter scale is 4.36 kpc/arcsec. Therefore, 20 kpc corresponds to 9.3 physical pixels on ACIS-I and 30 kpc to 14 pixels. ZW 3146 hosts a significant amount of star formation in the BCG. According to Table 4 in Crawford et al. (1999) the Hα flux comes from a slit with a size of ~ 6′′ corresponding to a width of 26 kpc. Moreover, according to Edge et al. (2010), the dust emission has an extent comparable to the bulk of the CO emitting gas and optical emission lines (less than 5′′). Finally, the X-ray center is offset from the peak of UV starburst (see O’Dea et al. 2010). Therefore, we choose the center to be on the center of the BCG galaxy, RABCG = 10:23:39.6, DecBCG = + 04:11:10.8, which is within ~ 10 kpc of the centroid of the X-ray surface brightness. We perform extractions within 20 and 30 kpc radii to encompass any possible region with significant star formation.
, and we keep this value frozen in the spectral fits. At this redshift the angular diameter scale is 4.36 kpc/arcsec. Therefore, 20 kpc corresponds to 9.3 physical pixels on ACIS-I and 30 kpc to 14 pixels. ZW 3146 hosts a significant amount of star formation in the BCG. According to Table 4 in Crawford et al. (1999) the Hα flux comes from a slit with a size of ~ 6′′ corresponding to a width of 26 kpc. Moreover, according to Edge et al. (2010), the dust emission has an extent comparable to the bulk of the CO emitting gas and optical emission lines (less than 5′′). Finally, the X-ray center is offset from the peak of UV starburst (see O’Dea et al. 2010). Therefore, we choose the center to be on the center of the BCG galaxy, RABCG = 10:23:39.6, DecBCG = + 04:11:10.8, which is within ~ 10 kpc of the centroid of the X-ray surface brightness. We perform extractions within 20 and 30 kpc radii to encompass any possible region with significant star formation.
We find ~ 4140 (4650) and 6820 (7800) net counts (0.5−7 keV band) within 20 and 30 kpc, respectively, in the ACIS-I VFAINT (FAINT) observation. The background is sampled from the ACIS-I CCD3 in a region far from the cluster core. Also in this case, given the extent of this nearby and massive system, the background is contaminated by some outer emission of the cluster itself. However, given the small size of the region we investigate, the background contribution is minimal and always below 0.1% of the total emission. The value of the Galactic hydrogen column density is NH = 2.46 × 1020 cm-2 according to Kalberla et al. (2005).
With the single mkcflow model in the 0.15−3.0 keV temperature range, we find Ṁ< 94 M⊙ yr-1 and Ṁ< 56 M⊙ yr-1 for 20 and 30 kpc, respectively (see Fig. 5 and Table 3). The temperature of the mekal component is around 4 keV ( 4.1 ± 0.2 and 4.2 ± 0.1 keV for 20 and 30 kpc, respectively). From the results obtained with the multi-component mkcflow models, shown in Fig. 5 and Table 3, we find that the tightest constraints on emission come from the 0.45−0.9 keV temperature interval. If we link the four mkcflow components covering the range 0.15−1.8 keV we find an upper limit of 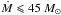 yr-1 and
yr-1 and 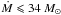 yr-1 at a 95% confidence level, corresponding to ΔCstat = 2.71 for the 20 and 30 kpc region, respectively. Despite these rather loose constraints, the cooling rates are a factor of 2−3 smaller than the measured SFR (see Table 1).
yr-1 at a 95% confidence level, corresponding to ΔCstat = 2.71 for the 20 and 30 kpc region, respectively. Despite these rather loose constraints, the cooling rates are a factor of 2−3 smaller than the measured SFR (see Table 1).
A previous estimate of the spectroscopic mass cooling rate was performed in Rafferty et al. (2006), using Chandra ACIS spectra; however, the extraction region was significantly larger, namely 186 kpc. These authors found a cooling rate of 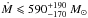 yr-1.
yr-1.
4.6. Z0348
 |
Fig. 6 Measured cooling rate in Z0348 in the inner 10 kpc (left panel) and 20 kpc (right panel). Symbols as in Fig. 1. |
The Chandra data on Z0348 consist of 47.8 ks, after the standard data reduction procedure, with ACIS-S in the VFAINT mode. We detect an AGN in the center of the cluster, and we remove it for the sake of our spectral analysis. As in the case of the Phoenix cluster (McDonald et al. 2012) the X-ray emission of this active nucleus in the middle of a bright cool core appears to be strongly absorbed. We fix the redshift to the value obtained from the best fit to the total spectrum, which gives zX = 0.256 ± 0.002, in very good agreement with the optical value z = 0.254. At the cluster redshift the angular diameter scale is 3.97 kpc/arcsec. Therefore, 10 kpc corresponds to 5.1 physical pixels and 20 kpc to 10.2 pixels. We choose the center to be on the X-ray peak, which coincides with the position of the AGN and with the center of the BCG at RABCG = 1:06:49.410, DecBCG = + 1:03:22.55 (see O’Dea et al. 2010). The BCG in Z0348 features diffuse Lyα emission extending out to some 5′′ (20 kpc) from the position of the unresolved VLA radio source, coincident with the X-ray AGN. Beyond this value, the Lyα emission is negligible (O’Dea et al. 2010). We extract spectra from two regions with bounding radii of 10 kpc and 20 kpc, encompassing all star forming sites.
We measure 1100 and 4150 net counts (0.5−7 keV band) within 10 and 20 kpc, respectively, after removing the inner 2′′, contaminated by the AGN. The background is sampled from the ACIS-S CCD7, as it was in previous cases, and the background correction is always below 0.1% of the total emission. The value of the Galactic hydrogen column density is NH = 2.5 × 1020 cm-2 according to Kalberla et al. (2005).
For the single mkcflow model we obtain an upper limit of Ṁ< 26.4M⊙ yr-1 and Ṁ< 56.1M⊙ yr-1 for 10 and 20 kpc, respectively (see Fig. 6 and Table 3). We note that for Z0348 the ambient temperature is rather low, leaving little room to constrain the mass cooling rate.
The analysis with the multi-component models shown in Fig. 6 and Table 3 confirms that the upper limits allow for a significant cooling rate. If we consider the 0.45−0.95 keV range where constraints are tightest, we find upper limits of 38 M⊙ yr-1 and 72 M⊙ yr-1 at a 95% confidence level for 10 and 20 kpc, respectively. By linking the four mkcflow components covering the range 0.15−1.8 keV, we find upper limits of 21.3 M⊙ yr-1 and 47.9 M⊙ yr-1 for 10 and 20 kpc, respectively. These values are broadly consistent with the SFR in the BCG. We conclude that in Z0348 there is no substantial disagreement between star formation and mass cooling rate. A deeper exposure on this cluster should allow us to put stronger constraints on the mass cooling rate.
4.7. Summary of measures on individual systems
For all our systems, once emission above a given threshold is excluded, we find no significant evidence of cooling gas. The threshold is found to be 1.8 keV for all systems but A1068 and RX J1504, whose emission is detected down to 0.9 keV and 3.0 keV, respectively. In Table 4 we report, for all our systems, the 95% upper limit on the mass cooling rate obtained by linking all cooling components below the threshold value.
5. Systematics
Best-fit upper limits at the 95% confidence level for Ṁ obtained from a modified multi mkcflow model (see text for details) compared to estimates of systematic effects on Ṁ.
Even in presence of a significant mass cooling rate of several tens M⊙ yr-1, the emission associated with the cold gas contributes about 10−20% of the total emission in the soft band. Clearly, our measurements are critically dependent on any effect that may alter the signal in this energy range. In this section we discuss several aspects that may affect our results, showing in detail how our estimates or upper limits on the mass cooling rates change with relevant parameters.
5.1. Statistical uncertainties in the Galactic absorption
The first parameter that can affect the soft emission is the Galactic absorption NH. In our fitting method we keep NH frozen to the value found in Kalberla et al. (2005) at the position of the cluster. To investigate the effect of a different value of NH on our results, we repeat some of our fits with a varying Galactic absorption. This is motivated by the possible presence of unnoticed fluctuations in the Galactic neutral hydrogen column densities on scales smaller than the resolution of Kalberla et al. (2005). The typical fluctuations expected on scales of ~1 arcmin are on the order of 10−40% (Barnes & Nulsen 2003). Clearly, the absorption is too weak to be measured independently during the fit. Generally, the effect of leaving the Galactic absorption free to vary is that of pushing NH towards high values to accommodate more soft emission. Therefore, the best-fit values or the upper limits on Ṁ will generally increase whenever NH is a free parameter. In order to achieve a very conservative upper limit to the amount of cold gas, we assume a maximum positive variation of 40% in NH.
In Table 4 we list the Ṁ values obtained in each cluster with a multi mkcflow model where all components up to a threshold value of Ethr, also reported in the table, are linked. For comparison we also report values of Ṁ obtained by performing the same fit with NH fixed to the value found in Kalberla et al. (2005).
For A1835 the largest admissible value for the Galactic absorption is NH = 2.86 × 1020 cm-2. The new upper limits are somewhat higher reaching Ṁ ~ 23 M⊙ yr-1 and Ṁ ~ 16 M⊙ yr-1 respectively for the 10 kpc and 20 kpc regions. Even in this case, the upper limits on the mass cooling rate are almost an order of magnitude lower than the SFR in the BCG. For RXC J1504, the maximum value of NH = 8.3 × 1020 cm-2 provides mass cooling rates twice as large as in the case with NH frozen to its nominal values. As for A1835, this upper limit is about an order of magnitude lower than the SFR in the BCG. For RX J1532, allowing NH to vary leads to a mass cooling rate of about 100 M⊙ yr-1, which is comparable to the SFR. For A1068, NH is allowed to range up to 2.35 × 1020 cm-2, and in this case the mass cooling rates increase by less than a factor of 2, leaving the upper limit to less than a tenth of the SFR. For ZW 3146, the values of Ṁ are roughly twice as large as when NH is fixed, and the discrepancy with the SFR is relatively modest. Finally, in the case of Z0348, NH is allowed to range up to 3.5 × 1020 cm-2, bringing the new Ṁ upper limits in agreement with the SFR.
Therefore, while the value of NH clearly affects the measurement of Ṁ, our results change only moderately if we allow NH to increase up to a maximum of 40% of its value measured by Kalberla et al. (2005). In addition, it is clearly very unlikely that all the measurements of NH for our clusters are systematically underestimated by this amount. We conclude that our results are not significantly affected by uncertainties in NH.
5.2. Systematic uncertainties in the effective areas
A robust characterization of weak and cool components in a hot environment requires that systematic effects on the effective areas be properly taken into account. Indeed, these components emerge only in a restricted low-energy range, below 1 keV, where their contribution to the total flux may be quite small. Clearly, when the relative intensity of the component becomes comparable to the systematic uncertainties in the effective areas, any detection based on our maximum-likelihood analysis of the data is not reliable. Since a fully self-consistent treatment of systematic uncertainties in the analysis of X-ray spectra has yet to be devised (see however the relevant work by Drake et al. 2006), we resort to a rather crude but effective ad hoc technique. For each spectrum we take as a systematic uncertainty in the reconstruction of the spectral shape in the 0.5−0.9 keV band, a value of 3% of the total count rate in that band. Thus, the systematic error on Ṁ is defined as the value that the normalization of the mkcflow model assumes when its 0.5−0.9 keV count rate equals 3% of the total count rate. We apply this only to the single mkcflow model since it would be unrealistic to apply the entire 3% uncertainty to a limited temperature range, and leave the other components unaffected.
We report the Ṁ associated with a 3% uncertainty in the normalization of the mkcflow model in Table 4. Clearly the effect rises rapidly with the size of the extraction region, since it is proportional to the absolute emission in the 0.5−0.9 energy range. This is found to be lower than our upper limits in most cases, the exceptions are the 20 and 40 kpc regions of RX J1504 and the 40 kpc region of A1068. We also note that if we include the systematics on NH in our comparison, the only region to be dominated by the effective area systematics is the 40 kpc region of RX J1504. In this case the difference between a cooling rate upper limit and SFR is reduced to a factor of roughly 5. We conclude that systematic effects on the effective area (1) do not affect the main conclusion of this work and (2) are in most instances subdominant, implying that further accumulation of data will lead to stronger constraints on the mass cooling rate.
5.3. Best estimates and comparison with SFR
Having evaluated what we consider to be the most relevant systematics, we are now in a position to provide a final estimate on mass cooling rates for our systems. We do this by considering for each system the cooling rate coming from the larger of the two regions we have considered, these have been chosen to include all known star formation regions and, in general, to provide more conservative upper limits. A statistics only estimate is provided by the values reported in the fourth column of Table 4. An estimate including systematic effects is obtained by taking the largest between the values reported in Cols. 5 and 6. We note that in only one instance, namely RXC J1504.1, is the dominant systematic associated with the effective area. Finally, a comparison of both estimates (i.e., excluding and including systematic effects) with SFR measures is provided in Fig. 7. As shown, in some cases, the upper limits are comparable with the SFR; however, in two instances, the mass cooling rate is well below the SFR. Indeed, in the case of A1835 and A1068, the upper limits, even allowing for systematic uncertainties, are a factor of ten lower than the SFR. If we consider only statistical uncertainties the number of such systems goes up to 3 (i.e., half of our sample). It is also worth bearing in mind that we do not have a cooling rate detection for any of the systems in our sample, all well-known extreme star forming objects.
 |
Fig. 7 Mass cooling rate vs. SFR. Filled red circles refer to the statistical 95% confidence upper limits on mass cooling rates. Empty blue circles refer to upper limits on cooling rates that include systematic errors. Dashed and solid lines show the relations Ṁ = SFR and Ṁ = 0.1 SFR, respectively. |
6. Discussion
Over the past decade, a widely accepted picture has emerged where the cooling of the bulk of the gas in cores is prevented by some form of heating related to feedback from the massive black hole residing at the center of these systems. The general idea is that small amounts of gas do manage to cool down; one part of this gas ends up forming stars, while the other part accretes onto the black hole, thereby producing feedback effects. In this scenario when, occasionally, feedback effects completely shut down accretion onto the black hole, the hot gas experiences a rapid cooling, a sort of short-lived cooling flow phase, which is immediately followed by vigorous star formation and refueling of the black hole, thereby restarting the cycle. We note that the cooling flow phase must be short-lived, otherwise the spectroscopic signature of the cooling gas would have been detected in some of the many systems where it has been searched.
In this framework, the systems we have selected, i.e., those experiencing the most significant star formation events, should also be those undergoing the most intense cooling in soft X-rays. Regrettably, this is not what we find: none of our systems show evidence of gas cooling below a threshold temperature. Moreover, in several instances – four or five out of six, depending on whether we include systematic effects in our estimates – our upper limits are significantly below the SFRs. In two or three cases – depending on whether we include systematic effects in our estimates – we have upper limits on cooling rates that are an order of magnitude below the SFR.
Two kinds of solutions to this problem can be considered. In the first, the gas is provided by some source which is not the ICM. Voit & Donahue (2011), for instance, proposed stellar mass-loss from the old stellar population; however, in this case the expected rate is only on the order of 10 M⊙ yr-1 (see also criticism in Rawle et al. 2012), which is significantly smaller than the SFR in all the systems we are considering here.
In the second class of solutions it is postulated that the gas is supplied from the hot phase. In this context, one way to explain the mismatch, is to assume there is a delay between the cooling and the star formation. If this is the case, the systems we have chosen may have already concluded their most significant cooling phase. We now investigate this possibility in some detail. The hot X-ray gas must first cool down to ~ 104 K, which is the first thermally stable region. This takes ~ tcool, which is several 100 Myr for the X-ray gas. Second, the warm gas must condense to 10−20 K, i.e., the molecular cloud regime. This is relatively fast (<1 Myr) if there are some significant perturbations. Third, at the molecular stage, the gas will start forming stars at a given rate that depends on the dynamical timescale, tdyn = (3π/ 32Gρ)1 / 2, which, in our case, should be on the order of 10−50 Myr. It is true that tdyn is quite short; however, in many astrophysical environments, the efficiency with which stars are formed is observed to be quite small, i.e., only a few percent of what might be expected if tdyn were the relevant timescale (e.g., Federrath 2015, and references therein). If these small efficiencies apply to the core regions of BCGs, there might be a latency time of roughly 1 Gyr and objects with very high SFRs, such as the ones considered in this paper, may not be the ones currently undergoing the most intense cooling in X-rays. To address this issue, we estimate directly from existing data the depletion timescale, tdep, i.e., the timescale over which the molecular gas is turned into stars. We define tdep ≡ Mmol/SFR, where Mmol is the mass of molecular gas and SFR is the star formation rate. We have measures of the molecular gas for a few of our systems (A1835, RX J1532, A1068, and ZW 3146; see Table 1 for details) and for one system that has purposely been left out of our study: the Phoenix Cluster (Tozzi et al. 2015). For the four systems in our study we find depletion timescales of roughly 350 Myr for A1835 and A1068 and 1 Gyr for ZW 3146 and RX J1532, showing that the latency time for at least two of these systems is relatively short. Interestingly, for the Phoenix Cluster, the depletion timescale is only 30 Myr, i.e., about a factor of 10 smaller than for A1835 and A1068. The reason for much of this difference lies in the different CO to H2 conversion factor adopted by different authors. As pointed out in McDonald et al. (2014), all these systems harbor similar amounts of molecular gas. If the CO measurements of A1835 and A1068 are converted into H2 mass estimates using the same conversion factor adopted for the Phoenix Cluster, the depletion timescales drops below 100 Myr, leaving essentially no latency time between X-ray cooling and star formation. While a detailed discussion on what conversion factor should be adopted for our systems is beyond the scope of this paper, we do wish to note that according to several recent works (see Bolatto et al. 2013, for a review), the conversion factor anti-correlates with the surface density of gas and stars. In general in BCGs the surface density is high; for instance, in the case of A1835, in the innermost kpcs, it is on the order of 2000 M⊙ pc-2 (McNamara et al. 2014). This suggest that, for our systems, a low conversion factor, such as the one adopted for the Phoenix Cluster, may indeed be appropriate. It therefore seems that the two systems for which the upper limit on the cooling rate is a factor of 10 smaller than the star formation, namely A1068 and A1835, are also those for which the delay time argument does not provide an adequate explanation for this discrepancy. Of course, although it is unlikely, we might be observing A1835 and A1068 in the short time interval between the shutting off of the cooling and the consequent depletion of the molecular gas.
Another possibility is that the gas that is forming stars in our systems originates in a significantly larger volume than the one where it currently resides. If we assume that within a region where the cooling time is relatively short, e.g., several Gyr, corresponding to scales of several tens of kpc, and some of the gas does indeed manage to cool down to a cold phase, it will increase its density significantly as it contracts and, in the absence of countering forces, fall towards the center of the cluster under its own weight. Over the last few years, several high-resolution 3D simulations have been carried out to study in detail the multi-phase condensation mechanism we have sketched here (e.g., Gaspari et al. 2012, 2013, 2015) which is known as chaotic cold accretion (CCA). Such a precipitation mechanism has been corroborated by independent observational evidence (e.g., Voit et al. 2015, and references therein). Within this scenario, our X-ray cooling rates might be reconciled with SFRs if we increase the size of the regions over which we search for the cooling gas. We have tested this possibility on the two systems where the upper limits on the cooling rates are most constraining, namely A1835 and A1068 (see Table 4). We extended our spectral analysis for both to 100 kpc, where the cooling time is roughly 5 Gyr. In neither case did we find evidence of emission of gas cooling below 1.8 keV. We estimated upper limits of roughly 60 M⊙ yr-1 for A1835 and 40 M⊙ yr-1 for A1068; in both cases a dominant contribution to the upper limit comes from systematic errors (see Sect. 5), more specifically the error associated with the effective area for A1835 and a combination of effective area and galactic absorption for A1068. These limits are still a factor of 2 below the SFRs. Thus, extending our search out to large radii alleviates the tension between cooling and SFRs, but does not dissolve it entirely. A further possibility, along these lines, is that gas with very short cooling time, <1 Gyr, exist out to significantly larger radii or perhaps throughout the cluster. Indeed, given the limited efficiency of mechanism such as thermal conduction and mixing, a moderate degree of multi-phaseness or “clumping” as it is sometimes called, cannot be ruled out in the ICM at large (e.g., Molendi et al. 2016, and references therein). We also note that emission from the infalling cold gas may well be below the detection threshold of available instrumentation.
Finally, we should not dismiss the possibility that, for some unknown reason, the cooling through the soft X-ray band is either hidden from us or simply does not occur. Solutions along these lines were proposed more than a decade ago (Fabian et al. 2001). More recently (Fabian 2012) has pointed out that cold gas could be rapidly growing by mixing with the hot gas.
7. Summary
We computed the isobaric mass cooling rate for a small sample of X-ray clusters observed with Chandra, whose BCGs are observed to host among the most significant episodes of star formation with SFR in the range 30−150 M⊙ yr-1. To this end, at variance with several previous studies, we considered primarily regions close to where star formation is known to occur. Our results are summarized as follows.
All our measurements are upper limits: in no instance do we detect gas cooling all through the soft X-ray band. In two cases, the upper limit on the cooling rates are comparable to the SFR; in two more they are significantly below. In the last two cases, namely A1835 and A1068, even allowing for systematic uncertainties, they are a factor of ten lower than the SFR.
Possible systematic effects related to poor knowledge of the Galactic column density or to uncertainties in the Chandra calibration may affect our measurement of Ṁ by about a factor of 2. However, in most of our systems, their magnitude is too modest to reconcile the discrepancy between the upper limit on the mass cooling rate and the SFR.
We have examined several possible solutions to the cooling vs. SFR discrepancy.
-
An origin of the gas other than the ICM appears implausible asthere is no obvious source.
-
In two of our systems a delay between cooling and star formation could explain the mismatch between rates; however, for the two systems showing an order of magnitude discrepancy between star formation and cooling rates, namely A1835 and A1068, this seems unlikely.
-
A solution can be found for A1835 and A1068, if we accept that gas is cooling out of the X-ray phase in regions that are much larger than those on which we observe the starburst. These regions need to extend beyond the cores of our clusters possibly encompassing significant fractions of these systems.
Finally we would like to point out that since systematics affecting many of our measurements are not severe, a wider investigation on a larger sample of clusters, possibly with deeper data, could provide further insight into the relation between cooling flows and star formation events in the BCGs.
See Sect. 6 for a discussion of possible delays between X-ray cooling and star formation events.
The UV SFR measured by Hlavacek-Larrondo et al. (2013) is 76 ± 38 M⊙ yr-1, consistent with the IR measure by Hoffer et al. (2012).
Acknowledgments
We acknowledge financial contribution from contract PRIN INAF 2012 (“A unique dataset to address the most compelling open questions about X-ray galaxy clusters”). M.G. is supported by NASA through Einstein Postdoctoral Fellowship Award Number PF-160137 issued by the Chandra X-ray Observatory Center, which is operated by the SAO for and on behalf of NASA under contract NAS8-03060.
References
- Barnes, D. G., & Nulsen, P. E. J. 2003, MNRAS, 343, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, E. L., Randall, S. W., Clarke, T. E., et al. 2011, ApJ, 737, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Cowie, L. L., & Binney, J. 1977, ApJ, 215, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Crawford, C. S., Allen, S. W., Ebeling, H., Edge, A. C., & Fabian, A. C. 1999, MNRAS, 306, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Drake, J. J., Ratzlaff, P., Kashyap, V., et al. 2006, in SPIE Conf. Ser., 6270, 1 [Google Scholar]
- Edge, A. C. 2001, MNRAS, 328, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Edge, A. C., Oonk, J. B. R., Mittal, R., et al. 2010, A&A, 518, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C. 1994, ARA&A, 32, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C. 2012, ARA&A, 50, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., & Nulsen, P. E. J. 1977, MNRAS, 180, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Mushotzky, R. F., Nulsen, P. E. J., & Peterson, J. R. 2001, MNRAS, 321, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Allen, S. W., et al. 2003, MNRAS, 344, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Fabian, A. C., Sanders, J. S., Taylor, G. B., et al. 2006, MNRAS, 366, 417 [Google Scholar]
- Fabian, A. C., Sanders, J. S., Allen, S. W., et al. 2011, MNRAS, 418, 2154 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C. 2015, MNRAS, 450, 4035 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M. 2015, MNRAS, 451, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Ruszkowski, M., & Sharma, P. 2012, ApJ, 746, 94 [Google Scholar]
- Gaspari, M., Ruszkowski, M., & Oh, S. P. 2013, MNRAS, 432, 3401 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Brighenti, F., & Temi, P. 2015, A&A, 579, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, A. H., Sivanandam, S., Zabludoff, A. I., & Zaritsky, D. 2013, ApJ, 778, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Hlavacek-Larrondo, J., Allen, S. W., Taylor, G. B., et al. 2013, ApJ, 777, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Hoffer, A. S., Donahue, M., Hicks, A., & Barthelemy, R. S. 2012, ApJS, 199, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. 1992, An X-Ray Spectral Code for Optically Thin Plasmas (Internal SRONLeiden Report, updated version 2.0) [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, Y.-T., Mohr, J. J., & Stanford, S. A. 2003, ApJ, 591, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, W. G., & Bregman, J. N. 1978, ApJ, 224, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., Rasia, E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Bayliss, M., Benson, B. A., et al. 2012, Nature, 488, 349 [NASA ADS] [CrossRef] [Google Scholar]
- McDonald, M., Swinbank, M., Edge, A. C., et al. 2014, ApJ, 784, 18 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., Wise, M., Nulsen, P. E. J., et al. 2000, ApJ, 534, L135 [CrossRef] [Google Scholar]
- McNamara, B. R., Nulsen, P. E. J., Wise, M. W., et al. 2005, Nature, 433, 45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- McNamara, B. R., Rafferty, D. A., Bîrzan, L., et al. 2006, ApJ, 648, 164 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. R., Russell, H. R., Nulsen, P. E. J., et al. 2014, ApJ, 785, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511 [NASA ADS] [Google Scholar]
- Molendi, S., & Pizzolato, F. 2001, ApJ, 560, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Molendi, S., Eckert, D., De Grandi, S., et al. 2016, A&A, 586, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mushotzky, R. F., & Szymkowiak, A. E. 1988, in NATO ASIC Proc. 229: Cooling Flows in Clusters and Galaxies, ed. A. C. Fabian, 53 [Google Scholar]
- O’Dea, C. P., Baum, S. A., Privon, G., et al. 2008, ApJ, 681, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- O’Dea, K. P., Quillen, A. C., O’Dea, C. P., et al. 2010, ApJ, 719, 1619 [NASA ADS] [CrossRef] [Google Scholar]
- Ogrean, G. A., Hatch, N. A., Simionescu, A., et al. 2010, MNRAS, 406, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, J. R., & Fabian, A. C. 2006, Phys. Rep., 427, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, J. R., Paerels, F. B. S., Kaastra, J. S., et al. 2001, A&A, 365, L104 [Google Scholar]
- Peterson, J. R., Kahn, S. M., Paerels, F. B. S., et al. 2003, ApJ, 590, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Rawle, T. D., Edge, A. C., Egami, E., et al. 2012, ApJ, 747, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Salomé, P., & Combes, F. 2003, A&A, 412, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanders, J. S., Fabian, A. C., Smith, R. K., & Peterson, J. R. 2010, MNRAS, 402, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1976, ApJ, 208, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Tamura, T., Kaastra, J. S., Peterson, J. R., et al. 2001, A&A, 365, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tozzi, P., Gastaldello, F., Molendi, S., et al. 2015, A&A, 580, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voit, G. M., & Donahue, M. 2011, ApJ, 738, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M., Donahue, M., Bryan, G. L., & McDonald, M. 2015, Nature, 519, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wise, M. W., McNamara, B. R., & Murray, S. S. 2004, ApJ, 601, 184 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Galaxy clusters selected in our sample, ranked from the highest to the lowest measured SFR in the BCG.
Best-fit upper limits at the 95% confidence level for Ṁ obtained from a modified multi mkcflow model (see text for details) compared to estimates of systematic effects on Ṁ.
All Figures
 |
Fig. 1 Measured cooling rate as a function of temperature range. Left: red circles show the values of Ṁ measured in different temperature bins in the inner 10 kpc of A1835. Error bars correspond to 1σ, arrows indicate 95% confidence upper limits. The shaded area is the 1σ uncertainty or the 95% upper limit interval of the global mass cooling rate obtained with a single mkcflow model in the temperature range 0.15−3.0 keV. Right: same as left panel for the inner 20 kpc. |
| In the text | |
 |
Fig. 2 Measured cooling rate in RXC J1504 in the inner 20 kpc (left panel) and 40 kpc (right panel). Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 3 Measured cooling rate in RXC J1532 in the inner 10 kpc (left panel) and 20 kpc (right panel). Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 4 Measured cooling rate in A1068 in the inner 20 kpc (left panel) and 40 kpc (right panel). Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 5 Measured cooling rate in ZW 3146 in the inner 20 kpc (left panel) and 30 kpc (right panel). Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 6 Measured cooling rate in Z0348 in the inner 10 kpc (left panel) and 20 kpc (right panel). Symbols as in Fig. 1. |
| In the text | |
 |
Fig. 7 Mass cooling rate vs. SFR. Filled red circles refer to the statistical 95% confidence upper limits on mass cooling rates. Empty blue circles refer to upper limits on cooling rates that include systematic errors. Dashed and solid lines show the relations Ṁ = SFR and Ṁ = 0.1 SFR, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


