| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 13 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201628571 | |
| Published online | 09 August 2016 | |
Superposed epoch study of ICME sub-structures near Earth and their effects on Galactic cosmic rays
1 Departamento de Física − IFIBA, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
e-mail: masiasmj@df.uba.ar
2 Instituto de Astronomía y Física del Espacio, UBA-CONICET, CC. 67, Suc. 28, 1428 Buenos Aires, Argentina
3 Departamento de Ciencias de la Atmósfera y los Océanos and Departamento de Física, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, 1428 Buenos Aires, Argentina
4 Observatoire de Paris, LESIA, UMR 8109 (CNRS), 92195 Meudon Principal Cedex, France
5 Solar–Terrestrial Center of Excellence – SIDC, Royal Observatory of Belgium, Av. Circulaire 3, 1180 Brussels, Belgium
6 Institut d’Astrophysique Spatiale, UMR8617, Université Paris-Sud-CNRS, Université Paris-Saclay, Bâtiment 121, 91405 Orsay Cedex, France
Received: 21 March 2016
Accepted: 12 May 2016
Context. Interplanetary coronal mass ejections (ICMEs) are the interplanetary manifestations of solar eruptions. The overtaken solar wind forms a sheath of compressed plasma at the front of ICMEs. Magnetic clouds (MCs) are a subset of ICMEs with specific properties (e.g. the presence of a flux rope). When ICMEs pass near Earth, ground observations indicate that the flux of Galactic cosmic rays (GCRs) decreases.
Aims. The main aims of this paper are to find common plasma and magnetic properties of different ICME sub-structures and which ICME properties affect the flux of GCRs near Earth.
Methods. We used a superposed epoch method applied to a large set of ICMEs observed in situ by the spacecraft ACE, between 1998 and 2006. We also applied a superposed epoch analysis on GCRs time series observed with the McMurdo neutron monitors.
Results. We find that slow MCs at 1 AU have on average more massive sheaths. We conclude that this is because they are more effectively slowed down by drag during their travel from the Sun. Slow MCs also have a more symmetric magnetic field and sheaths expanding similarly as their following MC, while in contrast, fast MCs have an asymmetric magnetic profile and a sheath in compression. In all types of MCs, we find that the proton density and the temperature and the magnetic fluctuations can diffuse within the front of the MC due to 3D reconnection. Finally, we derive a quantitative model that describes the decrease in cosmic rays as a function of the amount of magnetic fluctuations and field strength.
Conclusions. The obtained typical profiles of sheath, MC and GCR properties corresponding to slow, middle, and fast ICMEs, can be used for forecasting or modelling these events, and to better understand the transport of energetic particles in ICMEs. They are also useful for improving future operative space weather activities.
Key words: cosmic rays / solar-terrestrial relations / Sun: magnetic fields / Sun: coronal mass ejections / Sun: heliosphere / solar wind
© ESO, 2016
1. Introduction
Coronal mass ejections (CMEs) are associated with magnetic instabilities occurring in the solar corona, and they are expelled during solar eruptive flare events. As a consequence of these instabilities, large quantities of plasma and magnetic fields are expelled into the interplanetary space (IP), which can be observed by coronagraphs as CMEs. When their interplanetary manifestations (interplanetary CMEs or ICMEs) arrive at Earth, the observed intensity of energetic particles (e.g. Galactic cosmic rays, GCR) is modified. When they arrive at other planets (e.g. Mars) energetic particle fluxes can also be modified. Interplanetary CMEs can also produce perturbations in the magnetosphere, triggering geomagnetic storms. A subset of ICMEs include magnetic clouds, (MC) which are characterised by a low proton temperature and an enhanced magnetic field intensity | B | with a smooth rotation of its vector components, resembling that of a flux rope (Burlaga et al. 1981). The solar wind following an MC is expected to be perturbed, with characteristics similar to a wake.
Typically, MCs travel faster than the local Alfvén waves in the solar wind reference frame, producing a fast MHD shock ahead of them. This shock produces an intermediate region of compressed plasma between the shock interface and the MC leading edge. This region is characterised by high temperatures produced by the conversion of macroscopic to thermal energy at the shock, and therefore it generally presents high plasma β values. Typically, sheath regions also present large magnetic intensity and a high level of magnetic fluctuations.
Fluctuations around the shocks in the solar wind are observed after the shock (downstream) as typically observed in fluids, but also upstream (before the arrival of the shock). This last case is mainly due to beam instabilities that are induced by shock-accelerated particles. These instabilities can generate waves in the upstream region (e.g. Blanco-Cano et al. 2011; Wang et al. 2015; Strumik et al. 2015), so that an increased level of fluctuations is expected before and after the shocks associated with ICMEs.
During their propagation away from the Sun, MCs interact with the plasma and magnetic field encountered in the interplanetary medium. This interaction can induce reconnection between the sheath and the MC magnetic fields. This implies changes of the magnetic connectivity of the flux rope (McComas et al. 1988), and a consequent peel off (erosion) of magnetic flux from the leading edge of the MC. This also implies the formation of a back region that involves field lines that were part of the MC before the erosion (Dasso et al. 2006; Ruffenach et al. 2015). The back region is located in the MC wake and it typically has mixed plasma and magnetic field properties of ambient solar wind and MC.
Sheaths in front of MCs significantly differ from planetary magneto-sheaths mainly because ICMEs not only propagate but also expand into the IP medium (e.g. Démoulin & Dasso 2009; Gulisano et al. 2010). In particular, the lateral deflection of the solar wind away from the nose of an MC is reduced owing to the expansion, and the solar wind tends to pile up in front of an MC instead of flowing around it (Siscoe & Odstrcil 2008). This effect is more important near the corona, where the expansion is stronger, than in the interplanetary medium (Das et al. 2011). Moreover, the drainage towards the sides can be enhanced because of the magnetic reconnection between the magnetic field of the sheath and flux rope.
Summarising, a typical ICME is expected to be formed by the following sub-structures: slightly enhanced level of fluctuations (upstream waves turbulence), shock (driven by the MC), sheath (shocked, compressed, heated, and turbulent material), MC (flux rope), back (mixed flux rope and solar wind plasma when erosion has occurred), and wake (perturbed solar wind after the back region of the flux rope).
Transient structures in the heliosphere affect the transport of energetic particles in the solar wind (e.g. Masson et al. 2012, and references therein). On the one hand, acceleration at shocks driven by ICMEs is the main mechanism involved in the production of gradual energetic particle events in the inner heliosphere (e.g. Vainio et al. 2009). On the other hand, the decrease in the flux of energetic particles over a huge range of energies is associated with shocks and ICMEs. At lower energy, this is observed in situ. For higher energies (e.g. galactic cosmic rays; GCRs) this is observed at ground level by neutron monitors (e.g. Simpson 1954), by muon telescopes (e.g. Arunbabu et al. 2015), or by water-Cherenkov detectors (Abreu et al. 2011; Dasso et al. 2012; Asorey et al. 2016).
In particular, the passage of ICMEs and their associated shocks have important effects on GCRs. Indeed, a Forbush decrease (FD) of galactic particles is typically observed during several days and in association with the passage of an ICME (e.g. see the review, Cane et al. 2000). Additionally, a smaller amplitude and a higher frequency variability in the GCR intensity compared with classical FDs can also be observed in situ near Earth (e.g. Mulligan et al. 2009). Furthermore, a decrease in the abundance of energetic particles associated with FD has also been in situ observed by the Mars Science Laboratory’s rover Curiosity, during its cruise phase from Earth to Mars (Guo et al. 2015).
The full structure of ICMEs can perturb the transport of GCRs and has important effects both locally and globally on the density of GCRs. These effects are associated respectively with (1) strong changes of the local properties of the solar wind turbulence (mainly in the sheath) which consequently affect the diffusion coefficients of these energetic particles and (2) the presence of structures with smooth closed B field lines with typically high | B | values inside MCs, which hardly allow diffusion transport across B (e.g. Krittinatham & Ruffolo 2009).
From a statistical study of interplanetary properties of ICMEs and muon data for cut-off rigidities between 14 and 24 GV (using the GRAPES-3 muon telescope), Arunbabu et al. (2015) found that the enhancement of the interplanetary magnetic field inside the sheath regions is strongly associated with the observed FD profile. They concluded that FDs are mainly caused by the cumulative diffusion of protons across B in the sheath. However, it remains quantitatively unclear how FDs can be modelled, and in particular how one can quantify the importance of | B | and the level of turbulent fluctuations.
In this paper we characterise the mean properties of MCs at 1 AU and their relation to GCR transport. We apply the superposed epoch analysis method on in situ solar wind data and ground-based neutron monitor observations. This method is powerful because it emphasises the common properties and removes peculiarities of some events. It is similar to the superposed epoch developed by Lepping et al. (2003), where they studied 19 MCs from 1995 to 1998 and created a profile of magnetic field and plasma parameters of MCs. Our method is also similar to the method recently developed in Rodriguez et al. (2016), to analyse plasma, magnetic, and composition properties, focussing on the physical mechanisms for the formation of structures inside and at the rear of MCs. It is also close to the method used by Badruddin & Kumar (2016), where the response of GCRs to corotating interaction regions and ICMEs was studied with a focus on their interfaces with the ambient solar wind.
Finally, our study is related to that of Belov et al. (2015) since they model the response of GCRs inside MCs as a function of the interplanetary conditions (plasma speed and magnetic field), and geomagnetic properties (Dst index). In particular, they report the presence of a local minimum of GCR inside MCs for strong-field events.
In Sect. 2 we present the ICMEs studied and the data used to analyse them. In Sect. 3 the superposed epoch method, applied to our sample, provides the typical profiles of magnetic field and plasma parameters in ICMEs containing an MC. In Sect. 4 we further investigate how these profiles depend on the strength of the MC, in particular its mean velocity. For that we split our sample in slow, middle and fast events. The association of the event properties with the observed flux of GCRs is presented in Sect. 5. These results allow us to propose a novel quantitative model to describe the temporal evolution of GCR flux using parameters observed in the solar wind. Finally, in Sect. 6, we present our conclusions.
2. Data and events selection
 |
Fig. 1 Time profiles for different observables, from top to bottom: magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, normalised magnetic-fluctuation density rmsBoB (Eq. (1)), and absolute magnetic fluctuation rmsB (Eq. (2)). We show three different events; one per column. Each of these events belongs to each of the groups analysed in Sect. 4; from left to right, the events belong to the slow, intermediate, and fast groups. The date of the shock arrival is shown at the top of each column in UT. The passage of the sheath is indicated in orange, and the passage of the MC in blue. The fastest event shows stronger compression at the MC front, with respect to the others. The slowest event presents higher density values within the sheath. See Sect. 2.2 for a description of the main important features shown in each panel. |
In this section we present the data used for the analysis, the sample of studied events, and the observed physical quantities we explore.
2.1. Events selection
We use data of interplanetary magnetic field and plasma from the MAG and SWEPAM experiments on board the ACE spacecraft (Smith et al. 1998; McComas et al. 1998), using a 64 s time cadence1. The intensity of GCRs is analysed using data from McMurdo neutron monitors with one hour time cadence2.
We studied events taken from the list of Richardson & Cane (2010), including only ICMEs flagged as MCs from 1998 to 20063. Specifically, we use only those events satisfying the following conditions: (a) ICMEs with flag 2 in the list, which means that they are included in the WIND MC list compiled by R.P. Lepping4; (b) no multiple MCs, to avoid complex structures involving interactions of different events; and (c) MCs with a sheath and with an associated shock.
We selected the shock events from the shock list of Wang et al. (2010). We intersect both ICME and shock catalogues, only selecting ICMEs for which associated shocks are less than 3 h before the ICME starting time. The above procedure defines 44 events, and we summarise their main characteristics in Table A.1.
Because the times listed in the table of Richardson & Cane (2010) are referenced at Earth and our data are referenced at L1, we shift these listed times at L1, where the ACE data are observed. We use a global time shift as defined by the time difference of the shock observed at L1 and at Earth. We made this shift for each ICME by identifying the shock discontinuity in the time series of the magnetic field and plasma parameters. The time shifts are written in Col. 5, shown in Table A.1.
2.2. Analysed physical quantities
In this section we describe some characteristics of three individual events as a context for further discussions of our results on average profiles. In Fig. 1 we show three MCs: one with a slow bulk velocity, one with a middle velocity value, and a fast one (shown in the left, central, and right columns, respectively).
The upper panels show that the magnetic field strength has a comparable magnitude for the three selected MCs (Bmax ≈ 20 nT). The compression of the magnetic field (enhanced intensity) is present in the MC sheath, especially for the middle and fast MCs. The faster MC also presents the most asymmetric B profile while the slow MC present a very symmetric B profile.
The second row of panels shows a gradient in the velocity profile. This typical velocity profile is associated with the MC expansion as it moves away from the Sun. The slow and fast events present a very different change in the velocity during the MC passage (so that ΔV = Vend−Vstart is larger for the fast event compared to the slow event, a result that is consistent with the results of Gulisano et al. (2010) for MCs observed in the inner heliosphere). Finally, we note that the event chosen with intermediate speed looks perturbed with a break in the velocity profile around the half time of the MC.
In the third and fourth rows, we see enhanced proton density np and temperature Tp inside the sheaths, as expected because these regions are formed of compressed and heated plasma behind the shock.
In the fifth row, we show the plasma β. Its value is estimated with the same method as in the OMNI database, i.e. by assuming that the temperature of alpha particles, Tα, is proportional to the proton temperature with Tα = 4Tp, and that the electron temperature is constant Te = 1.4 × 105 K5. These examples show that β can be greater than 10 inside the sheath, while inside the MC, β ≪ 1 as expected (e.g. Dasso et al. 2005).
We also present the fluctuations of the unit vector of the magnetic field B, which we call the normalised magnetic fluctuations (i.e., rms of B over its magnitude B) and write it as rmsBoB hereon. We define it with: 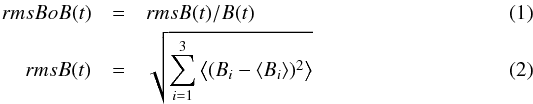 where rmsB is computed in time windows of 16 seconds, using a high time cadence of 3 vectors per second, and the mean value of each component ⟨ Bi ⟩ is computed inside this time window (as provided by the ACE webpage). The value rmsBoB is much lower inside MCs, than outside (sixth row of Fig. 1). In the next section, we see that this magnitude is a very robust quantity within MCs.
where rmsB is computed in time windows of 16 seconds, using a high time cadence of 3 vectors per second, and the mean value of each component ⟨ Bi ⟩ is computed inside this time window (as provided by the ACE webpage). The value rmsBoB is much lower inside MCs, than outside (sixth row of Fig. 1). In the next section, we see that this magnitude is a very robust quantity within MCs.
The magnetic fluctuations rmsB are shown in the seventh (bottom) row. They have maximum values within the sheath, while inside MCs it is roughly similar to the values observed before the shock arrival.
Besides these expected features in these three cases, we obtain below typical profiles of ICME events, and quantify them. This is the motivation to implement a superposed epoch analysis in the next section.
 |
Fig. 2 Superposed epoch for different quantities derived with the method described in Sect. 3.1. The sheath is shown with an orange background colour (time range 0 <t< 1) and the MC with a blue background colour (1 <t< 4). The time t is normalised with the sheath duration for t< 1 and with the MC duration for t> 1 (the MC duration is three times longer than the sheath duration as observed in average). The black dots, connected with a line, are averaged values for each bin on the time axis, the grey band represents the error of the mean and the red line represents the median values in each time bin. The average profiles were computed filtering those events that had less than 20% of data gaps in the transient structure (MC or sheath). The number of events after filtering is shown in each panel. The panels represent: magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, normalised magnetic-fluctuation density rmsBoB (Eq. (1)), GCR intensity normalised to the pre-ICME level nGCR and absolute magnetic fluctuation rmsB, Eq. (2). A clear discontinuity of the magnetic fluctuation intensity, rmsB, is present at the shock position (front of the sheath). The normalised magnetic fluctuations, rmsBoB, inside the MC are significantly lower than in the ambient solar wind (by a factor of ≃3). |
3. Superposed epoch for the sheath and MC structures
3.1. Method
The main aim of the superposed epoch is to obtain an average profile by taking a sample of individual profiles. Each individual profile must have the same number of data points or bins in the time dimension to obtain this average. The primitive data have different durations for different events, however, so we implement a re-binning such that within each MC we end up with 50 time bins. Then, the data within each bin are averaged to a single value per bin. In the case in which a primitive time series has a data gap in more than 20% of the MC structure, we discard it from the average profile. We also re-bin the data obtained after the MC, over the same time interval and with the same number of bins. Next, we average the data associated with the different events, by averaging each quantity (B, V, β, etc.) bin by bin, which finally builds the average profiles.
We repeat this procedure to obtain average profiles of the sheath structure. Again, we resample all the time series to 50 bins inside each sheath. Since the number of events that have more than 20% of gaps are not necessarily the same for the sheath analysis as for the MC analysis, we have indicated in each graph the total number of cases taken for both the sheath and the MC. The same time normalisation as for the sheath is used to resample the data before the shock, over twice the time interval of each sheath.
We next build a combined profile that shows an average profile for the background solar wind, the sheath, the MC, and the MC wake. We select the time origin at the shock. Finally, we set the temporal lengths of the MC to sheath to a ratio 3:1 to better represent the typical relative durations of each structure.
In Fig. 2, we show the average profiles (black lines) with the associated errors of the means (grey bands), and the median values (red lines). The difference between the median and the mean profiles is a proxy of how non-symmetric the distributions of the quantities are. Indeed, in the central part of MCs, the observables are distributed in a log-normal manner (Rodriguez et al. 2016). Similar log-normal distributions also have been found for ICME observables in Guo et al. (2010) and Mitsakou & Moussas (2014).
Mean values of all quantities (Col. 1) for all events (Cols. 2 and 3), and for each group of events associated with MCs with low, middle, and high velocities (Cols. 4 to 9).
3.2. Results for the average profiles
From the mean profiles in Fig. 2, we can clearly see sharp jumps at the arrival of the fast shock. B, V, Np, and T jump by factors of ~100%, ~30 %, ~150%, and ~300%, respectively. Then, all quantities behave differently whether in sheath or in the MC. We describe briefly below the main results for each of the panels of Fig. 2 (except the bottom left panel, which is described in Sect. 5.2). Some results in this subsection closely agree with those found in the sample of MCs studied in Rodriguez et al. (2016).
The upper left panel of Fig. 2 shows the piled-up magnetic field B in the sheath. The field B is enhanced by more than a factor 2 with respect to the pre-shock value. Next, the B profile inside the MC is strongly asymmetric, with its maximum strongly shifted to the front of the MC. Indeed, because of the flux rope expansion, a stronger B is expected at the front compared to the rear since the spacecraft crosses the front earlier during the propagation of the MC than the rear (e.g. see Figs. 3 and 4, and associated explanation in the main text of Démoulin et al. 2008). This is the so-called aging effect, however, it was previously shown that expansion is typically not sufficient to explain such a B asymmetry (see the upper panel of Fig. 6 and associated main text of Démoulin et al. 2008).
The speed profile (upper right panel of Fig. 2) shows that across the shock there is a jump from 420−440 km s-1 to 520−540 km s-1. The first part of the sheath shows a fast compressing profile, while it later stabilises to be at a roughly constant speed up to the boundary with the flux rope. Inside the MC, the speed is a decreasing time function, in agreement with the expected typical expansion. The linear decrease ends before the MC rear boundary. This characteristic is present both in individual profiles and in other superposed epoch studies (e.g. Lepping et al. 2003; Rodriguez et al. 2016). A peak of V is also present after the MC.
 |
Fig. 3 Normalised values of average parameters corresponding to each subgroup (split according to the ordering parameter Vmc): low Vmc (blue triangle down), middle Vmc (green circle), and high Vmc (red triangle up). Empty symbols are for sheaths and filled symbols for MCs. For each quantity, we use the mean values of all events for the normalisation of each parameter (grey horizontal line). From left to right, the parameters are the means of magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, normalised magnetic-fluctuation density rmsBoB (Eq. (1)), absolute magnetic fluctuation rmsB (Eq. (2)), and GCR intensity normalised to the pre-ICME level nGCR. |
In the second left panel of Fig. 2 the high proton density, np, in the sheath contrasts with its lower value in the sheath surroundings. However, np has no discontinuity at the interface between the sheath and the MC. On the contrary, np starts to decrease from the sheath-MC interface to inside the MC, up to around 15−20% of the MC size where its value becomes constant. This is not an effect of smearing the MC boundary in the averaging since this effect is also present in some individual MCs (e.g. Fig. 1). Finally, a clear density peak is present just after the rear boundary. Its physical origin was investigated in Rodriguez et al. (2016), where it was shown that several possible mechanisms, such as compression from a fast overtaking stream, or intrinsic mechanisms, such as the eruption conditions at the Sun, could account for this density peak.
While in the sheath, the magnetic field, velocity and density are roughly constant (besides fluctuations), the proton temperature Tp (right second panel of Fig. 2) has a steep maximum near the shock. This is a consequence of the macroscopic to thermal energy conversion produced at the shock. Later on Tp progressively decreases towards the MC. As observed for np the temperature profile is continuous around the sheath-MC interface without a clear break, up to a ~15−20% of the mean MC size. Later on, Tp stabilises to a roughly constant value up to almost the end of the MC.
In the density and temperature profiles (Fig. 2), the transition between the sheath region and the MC is not as abrupt as expected, considering that the MC environment is much different from the sheath region. This transition can be explained as follows. Gosling et al. (1995) discuss a mechanism in which part of the field lines at the MC periphery are magnetically connected to the outer heliosphere after reconnection occurred. Case studies (Dasso et al. 2006, 2007; Feng & Wang 2013) and a statistical analysis of a large sample of events (Ruffenach et al. 2015) indicate that an MC can suffer magnetic erosion at its front during its travel in the heliosphere, forming a back region with mixed properties of both MC and ambient solar wind (Dasso et al. 2006; Ruffenach et al. 2012). Thus, because MCs are 3D structures, it is possible that this erosion only happens at various specific locations along the flux rope. Then, the transition region between the sheath and the MC, explored by the spacecraft, can be magnetically connected to another region where erosion has already occurred. This gives a possibility for solar wind material and heat to diffuse along the reconnected field lines, which leads to a smoother profile at the interface between those sub-structures. In this paper we refer to this mechanism as “3D reconnection”.
 |
Fig. 4 Average profiles (black lines) distributed in three columns for the three subsets of events. Left: slow (V< 450 km s-1), middle: medium (450 km s-1<V< 550 km s-1), and right: fast MCs (V> 550 km s-1). The black line represents the average value, the grey band represents the error of the mean and the red line represents the median values in each time bin. As in Fig. 2, for t< 1, time is normalised with the sheath average radial duration and for t> 1, time is normalised with the average MC radial duration. Orange delimits the sheath region (0 <t< 1), and blue the MC region (1 <t< 4). See the caption of Fig. 2 for more information. From top to bottom the parameters are the means of magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, and normalised magnetic-fluctuation density rmsBoB, Eq. (1). |
The plasma β and the normalised magnetic fluctuations rmsBoB (left/right third panels of Fig. 2) are the quantities that most clearly mark the MC boundaries. Both are roughly symmetric around the MC centre with a flat minimum, as rmsBoB is even more symmetric than β; rmsBoB shows a maximum at the shock, and then a smooth decrease towards almost one-third of the MC size.
The level of absolute fluctuations rmsB (right bottom panel of Fig. 2) shows a sharp jump with a maximum at shock arrival, while it later continuously decreases to almost one-third of the MC. After the MC, it recovers towards typical solar wind values, but with slightly higher values.
To summarise this section, we describe the differences between mean values inside sheaths and MCs (Cols. 2 and 3 of Table 1). All the quantities are higher in sheaths than in MCs, by 7% for V, 8% for B, ~twice for np, ~3.5 times for Tp, ~4 times for β, ~2.5 times for rmsBoB, and ~2.6 times for rmsB.
4. Sheath and MC properties for slow and fast events
4.1. Criterion to define an ordering parameter
The mean velocity inside the ICME at 1 AU, its mean magnetic field intensity, and its time duration could be considered as different proxies for the strength of the event. Moreover, these values can be computed with a time window inside an ICME sub-structure such as the sheath or the MC; namely Vsh, Bsh, Δtsh, Vmc, Bmc, Δtmc, where the suffixes “sh” and “mc” are associated with the sheath and the MC, respectively.
Which is the most relevant parameter to order the events? To answer this question, we first preliminarily consider one of the possible strength ordering parameters, Vmc. We then split our sample of 44 events into 3 subgroups with roughly the same number of events: weak (slow), middle, and strong (fast). We produce separate superposed epoch profiles for every physical quantity analysed (similar to those shown in Fig. 2), and for each subgroup. Finally, we repeat this procedure for all the possible ordering parameters: Bmc, Δtmc, Vsh, Bsh, and Δtsh.
The criterion to select the best ordering parameter is as follows. For every ordering parameter we construct a plot as that shown in Fig. 3 (where Vmc was used in this case). This figure shows normalised average values of all observables for each subgroup. These values are derived from Table 1. The average value of each subgroup is shown with red triangle up (events with large velocities: Vmc> 550 km s-1), green circle (middle velocities events: 450 km s-1 < Vmc< 550 km s-1), and blue triangle down (events with weak velocities: Vmc< 450 km s-1). These values are normalised with the global average using all events. The criterion to select which strength parameter is the best is to observe i) the largest separation between mean values of the three subgroups and ii) a coherent ordering between these values.
Among all the plots (not shown here) that we looked at, we realised that the best parameter to order the MCs is the mean MC speed Vmc, which happened to be better for splitting our sample into three groups. As is seen in Fig. 3, most of the parameters are well ordered (red, green, and blue in succession for each parameter). The same quality of ordering and spacing as Fig. 3 was not found for any of the other explored ordering parameters, for example Bmc.
The parameters with largest spread are the proton density np, proton temperature Tp, plasma β, and GCR percentage of depression nGCR (see Sect. 5). On the other hand, the parameter showing less split and no coherent order is rmsBoB. This implies that the normalised magnetic fluctuations are very similar in all groups within a ~20% factor from the global mean. Next, we observe that when the splitting is large between the groups, the relative order and spread for the sheaths are typically the same as for the MCs (e.g. see V, np, and Tp in Fig. 3). Finally, the fastest MCs (red triangle up) have the largest B intensity, lowest proton density, hottest temperature, lowest plasma beta, strongest magnetic fluctuations rmsB, and deepest associated GCR depression.
4.2. Superposed epoch for each MC subset
We analyse below the averaged profiles of the three subsets. In the upper row of Fig. 4 we find large differences in the B profiles: for faster/stronger events, B is more peaked towards the start of the MC, while for slower/weaker events, it is more peaked towards the MC centre. Also, B jumps at the shock with ΔB = 7, 8, and 13 nT, for slow, middle, and fast events, respectively.
In the second row of Fig. 4, the ambient solar wind before the front of the sheaths is slower for weaker/slower events compared with stronger/faster events, then they are not propagating in the same mean solar wind. Next, the speed profiles in the three groups all have a linear profile within the MCs, which indicates a common expansion process. For sheaths, we also see expansion in slow events, but for fast events the sheaths have profiles showing compression. This bimodal feature of the sheath, with an expansion and a compression, has not been reported before as far as we know, and it is shown pretty clearly in these superposed profiles with both processes having a comparable effect for MCs with middle velocities. The fact that fast events are related to compressing sheaths is the result of the fast overtaking MC behind. For the slow events, the magnetic field and plasma had the time to reach a quasi-pressure balance. This implies an expansion similar to that of the flux rope (as modelled by Démoulin & Dasso 2009).
In the third row of Fig. 4, slower events have higher proton density in all the sub-structures: sheath, MC, and its wake. By contrast, the ambient solar wind at the front does not show systematic changes along the three groups. We interpret the higher density in the sheath of slow events as a selection effect due to the drag force as follows. The CMEs that are fast near the Sun and that later on encounter slow solar wind ahead, which is typically denser in the inner heliosphere (e.g. see Wolfe 1972), accumulate more mass with a low velocity, resulting in a denser sheath and a slower MC by conservation of mechanic momentum. Studies in this direction have been made in Feng et al. (2015), where they find that the SW pile-up of mass during the CME expulsion can be an important contribution to the mass increase determined by coronagraph observations. We explore this observed feature in more detail in Sect. 4.3. Next, the low np values observed in the wake of fast cases (right column of Fig. 4) can be due to the sweeping of ambient solar wind plasma made by faster MCs (which are also typically larger, e.g., Janvier et al. 2014) combined with the difficulty in re-filling this space with new solar wind material just after the passage of the flux rope.
In the fourth row of Fig. 4 the proton temperature in the ambient solar wind is lower for slow events, which are also traveling in a slower solar wind. These results are consistent because of the known direct correlation of speed and proton temperature in the quiet solar wind (e.g. Lopez & Freeman 1986; Démoulin 2009). Next, the faster MCs present much hotter sheaths than slower MCs; this is a consequence of the local heating near the shock. The temperature in slow MCs is lower. This is consistent with a relaxed flux rope, which had time to adapt to the ambient solar wind pressure, to fully expand and, accordingly, to cool.
 |
Fig. 5 Left panel: average proton surface densities of sheaths σsh, Eq. (3), as a function of the average MC speeds (Vmc) of all events. The vertical dashed lines indicate the thresholds between the three groups shown in Figs. 4 and 6. The quantity σsh is a proxy of the accumulated material ahead of MCs, within the sheaths. On average, slower MCs drag more material. Right panel: histogram of σsh for the 44 events. |
In the fifth row of Fig. 4 the average plasma β values are higher for slower events, for all ICME sub-structures. Even in the ambient solar wind we note a tendency for slow events to travel in a less magnetised plasma (higher β). Within the sheaths, β is more constant and inside the MC the β profile is more symmetric for slow events. For faster events β has a more asymmetric profile, according to the asymmetry of B (first row of Fig. 4).
In the last row of Fig. 4 we observe big differences between the rmsBoB fluctuation profiles of slow and fast events. For instance, the fluctuation intensity is much higher near the shock for fast events. Also, these fluctuations start even before the shock arrival and with a clearer effect for faster events. This can be related to foreshock waves excited by energetic particles near interplanetary shocks (e.g. see, Blanco-Cano et al. 2011). Next, the magnetic fluctuations have a steeper drop in the sheath-MC interface for the slow events. In contrast, the fluctuations are roughly the same inside the MC for the three groups. Finally, the extension of low rmsBoB values in the back suggests the presence of remnant MC-like structure due to magnetic reconnection at the front, as summarised in Sect. 3.2.
4.3. Surface density of protons in the sheath
To further explore the drag as the physical reason for finding some slow events, we estimate the accumulated material inside the sheath for every event by defining the “surface density” σsh, 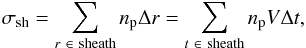 (3)where Δt is the time resolution of the data, and the sum approximates an integral along the radial direction in the ecliptic plane within the sheath boundaries. The parameter σsh characterises the total amount of material per unit surface (perpendicular to the radial from the Sun) and σsh is associated with the material that has not escaped perpendicularly to the spacecraft crossing. The right panel of Fig. 5 shows an asymmetric distribution of σsh that has more cases with σsh≲ 3 × 1014 cm-2.
(3)where Δt is the time resolution of the data, and the sum approximates an integral along the radial direction in the ecliptic plane within the sheath boundaries. The parameter σsh characterises the total amount of material per unit surface (perpendicular to the radial from the Sun) and σsh is associated with the material that has not escaped perpendicularly to the spacecraft crossing. The right panel of Fig. 5 shows an asymmetric distribution of σsh that has more cases with σsh≲ 3 × 1014 cm-2.
On the left side of Fig. 5 we show a scatter plot of σsh versus the average MC speeds for all the studied events. Faster MCs tend to have less material ahead of them. This result may seem surprising at first, since faster MCs are expected to overtake more solar wind and moreover the plasma has more difficulty escaping from the sides (faster and larger MCs). However, this is consistent again with the drag scenario in which the MCs are slowed down when they are ejected with a high speed in the corona and encounter a slow and dense solar wind. In contrast, high speed MCs encountering a fast solar wind ahead are less slowed down (lower mass pile-up with faster velocity). These cases correspond to the lower right region of the scatter plot. Finally, the lower left part of the plot would correspond to MCs with a slow speed encountering a low solar wind density along their travel to 1 AU.
5. Analysis of associated Forbush events
5.1. Superposed epoch analysis
We analyse below the cosmic rays observed with ground-based detectors. We use data from McMurdo neutron monitors because they are close enough to one geomagnetic pole, and then they can measure particles with low energies. In particular, they can observe primary protons with energies as low as ~500 MeV (e.g. Jordan et al. 2011). The Larmor radius for these particles is ~5 × 10-3 AU, when they are embedded in an interplanetary magnetic field of ~5 nT. For normal conditions, particles observed by these detectors are mainly of galactic origin.
An additional treatment with respect to the previous quantities (Sects. 3 and 4) is that we use the average GCR intensity before the MC sheath arrival as a reference level. In essence, we take the data from two days prior to the sheath arrival. If a ground level enhancement (GLE) is present, we only take data from six hours prior to the sheath arrival (we verify for each event that during this time interval there is no GLE or intense noises). Then, we normalise the GCR flux of each event with this level taken before the MC sheath defining the percentage of variation nGCR. Next, we continue with the same treatment as in Sect. 3.1.
The superposed epoch of all events is shown in the bottom left panel of Fig. 2. There is a strong decrease in nGCR in the sheath followed by a progressive recovery phase during and after the MC. The importance of these effects depends on the MC speed as shown in the second row of Fig. 6. The recovery time (τFD) and the amplitude (AFD) of the GCR depressions are larger for the faster events; this result is consistent with the following previous studies: Penna & Quillen (2005) and Richardson & Cane (2011). A minimum of nGCR is present near the rear of the sheath for the three subsets. For fast events, another minimum can be observed within the fluctuations, inside the MC window and near the MC center. This second minimum is associated with the shielding of a strong magnetic field within the flux rope configuration (with closed field lines still connected to the Sun). This result is consistent with Belov et al. (2015), in which they report that for a strong-field (>18 nT), there is a local minimum of nGCR inside MCs.
5.2. Model for the nGCR typical profiles
 |
Fig. 6 Superposed epoch for the three subsets of events. Left: slow (V< 450 km s-1); middle: medium (450 km s-1<V< 550 km s-1); and right: fast MCs (V> 550 km s-1). First row: mean profiles of magnetic fluctuations rmsB, Eq. (2). Typically, inside the MCs, the fluctuations are the same as in the ambient solar wind. For slow and middle groups, rmsB has higher values in the rear with respect to the ambient solar wind. Second row: mean profiles of GCR intensity nGCR. Before averaging events, the intensity was normalised by the pre-shock level. In the first and second rows the black line represents the average value, the grey band represents the error of the mean, and the red line represents the median values in each time bin. Third row: fitted model (red lines) to the observed average profiles (see Sect. 5.2). See the caption of Fig. 2 for more information. |
A theoretical model to describe the profile of FD was developed by Wibberenz et al. (1998). They did not explicitly include small-scale interplanetary magnetic fluctuations, while it was shown that these can contribute to the variety of FD profiles (e.g. Jordan et al. 2011).
To quantitatively analyse the processes involved in the GCR shielding produced by ICMEs, we construct a mathematical model to reproduce the GCR profiles. In particular, we use B to account for the strong closed field lines of the MC, and rmsB to account for the scattering turbulence.
From the superposed epoch profiles, we learned the following contributions (second row of Fig. 6):
-
i)
Inside the sheath region, nGCR can be thought to bedetermined by an accumulation of interactions between the highenergy particles and scattering centres. The efficiency of thescattering is related to the level of turbulent fluctuations rmsB.
-
ii)
The decrease in nGCR is larger for a stronger magnetic field inside the MC.
-
iii)
The recovery mechanism is effective after the passage of the scattering turbulence region.
-
iv)
There is a jump in nGCR at the interface between the sheath and the MC; this can also be seen in the individual profiles. This feature can be related to the change of the cross diffusion coefficients associated with the plasma properties in these two different structures.
By representing each of these mechanisms with a contributing term for the temporal evolution of the GCRs flux at Earth position, we propose the following model: ![\begin{eqnarray} \begin{array}{lll} \dfrac{{\rm d} n_{\rm GCR}(t)}{{\rm d} t} = q_{\xi} \, \xi(t) &\rm (i) \\[2mm] \qquad \,\,\, \qquad + q_{\rm b} \, b(t) & \rm (ii) \\[2mm] \qquad \,\,\, \qquad + \frac{-1}{\tau_{\rm FD}} n_{\rm GCR}(t) \, \Theta(t-1) & \rm (iii) \\[2mm] \qquad\,\,\, \qquad + \Delta_{\rm o} \, \delta (t-1) & {\rm (iv)} & \forall t>0 \label{eq_FD_model} \end{array} \end{eqnarray}](/articles/aa/full_html/2016/08/aa28571-16/aa28571-16-eq67.png) (4)with,
(4)with, 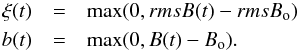 (5)The parameter ξ(t) is the rmsB(t) value above its value in the quiet solar wind, rmsBo, when rmsB(t) is larger than rmsBo; b is the magnetic field above a reference value Bo when B>Bo; and Θ is the Heaviside function indicating that the recovery mechanism starts at the beginning of the MC. This simplification facilitates the mathematical fit and we checked that the recovery is negligible during the passage of the sheath. The parameter δ is the Dirac delta function (more precisely distribution), which accounts for the observed jump of nGCR at the sheath-MC interface. There are five free parameters to fit: qξ, qb, Bo, τFD, and Δo. This model does not explicitly include the larger expansion of faster events nor a non-local effect due to the sheath and MC spatial extension. The expansion rate is correlated to the field strength, so it is implicitly included, while we cannot include the effect of the global extension from local measurements.
(5)The parameter ξ(t) is the rmsB(t) value above its value in the quiet solar wind, rmsBo, when rmsB(t) is larger than rmsBo; b is the magnetic field above a reference value Bo when B>Bo; and Θ is the Heaviside function indicating that the recovery mechanism starts at the beginning of the MC. This simplification facilitates the mathematical fit and we checked that the recovery is negligible during the passage of the sheath. The parameter δ is the Dirac delta function (more precisely distribution), which accounts for the observed jump of nGCR at the sheath-MC interface. There are five free parameters to fit: qξ, qb, Bo, τFD, and Δo. This model does not explicitly include the larger expansion of faster events nor a non-local effect due to the sheath and MC spatial extension. The expansion rate is correlated to the field strength, so it is implicitly included, while we cannot include the effect of the global extension from local measurements.
In order to perform the non-linear fit of the time integral of Eq. (4) to the data, we employ the L-BFGS-B algorithm (Zhu et al. 1997; Byrd et al. 1995). This algorithm is suitable when working with a large number of fitting variables, and it uses the gradient information of a multiple variable function to be minimised within given bounds. Mainly, we use this method instead of other alternatives because we observe a better convergence for our problem.
The third row of Fig. 6 shows the fitted models to each of the average nGCR profiles, where the detailed reproduction of the observations is notable. The inclusion of the magnetic fluctuations allows the reproduction of the observed mean decrease in nGCR within the sheath with only one adjusted parameter qξ. Moreover, for the slow Vmc group, we see a small decrease in nGCR right after the MC passage, which according to our model, is due to the enhancement of rmsB in the wake of the flux rope (see the left column of Fig. 6). This behaviour is also present, but weaker, for the middle velocity group. This result at the MC rear provides a further confirmation that magnetic fluctuations are locally affecting GCRs. It is also in agreement with Badruddin & Kumar (2016, see their Fig. 7), where they find a GCR decrease around the ICME trailing edge, and simultaneously find enhanced magnetic fluctuations. Finally, | qξ | is decreasing from the low to the fast velocity group (Table 2), which may be due to non-linearities in the diffusion process that are not taken into account in our model.
The contribution of the magnetic field B is only important for the group of fast Vmc, where nGCR has a local minimum inside the MC. As mentioned before, this can also be related to the larger expansion of the flux rope compared to the surrounding solar wind. This leads to a decrease in the local density of the high energetic particles (e.g. Munakata et al. 2006).
Next, the normalised time τFD, as well as the time τFD in hours (taking into account the mean MC duration of each group) are both increasing by more than a factor 2 from the slow to the fast velocity group (Table 2). Finally, it is worth mentioning that without the inclusion of the jump parameter Δo, it is not possible to reproduce the recovery profile for the slow and fast Vmc groups that clearly show this discontinuity.
Fitted values of the Forbush decrease model (see Eq. (4)), for the three subset of events.
6. Summary and conclusions
We obtained superposed epoch profiles during the passage of MCs and their sheaths at 1 AU for different physical quantities observed in situ. This technique allows us to identify several phenomena that are common to most of the events. First, the magnetic field strength and plasma velocity in the MC sheath are typically close to the values found at the beginning of the MC. Second, the MC has a similar density as the background solar wind, while the sheath is a factor ≈2.5 denser.
We next explored how the sheath and MC properties could be best differentiated according to the importance of the event. We found that the mean MC velocity is the best parameter to order the sheath and MC properties. This provides a measure of the strength of the events. Then, we separated our sample into three groups: slow/intermediate/fast events and compared their superposed epoch profiles.
We found that the slowest MCs have a larger proton density in their sheaths than faster events. We next computed the density of protons per unit of surface along the sunwards direction to better characterise the accumulated material that does not escape from the MC front to the sides. We found that on average, slow events have more massive sheaths than fast events. We attribute this result to a selection effect: a part of the slow MCs at 1 AU were initially fast events close to the Sun but they were slowed down as they encountered slow and dense plasma on their path to 1 AU. Then, such decelerated MCs have more massive sheaths at 1 AU.
The comparison of the three groups shows that the slow MCs have properties that are compatible with a more relaxed configuration. First, they have an expanding sheath with a very similar expansion rate as in the following MC. Then, the accumulated magnetic field in the sheath has the time to reach a quasi-equilibrium with the surrounding solar wind, which implies that the sheath expands with a similar rate as the driving flux rope. Second, the slow MCs have a nearly symmetric magnetic profile around their centre. Finally, they have a lower proton temperature (as they have the time to expand enough to be in quasi-equilibrium with the surrounding solar wind). All these characteristics together indicate that the slower MCs are expected to be in a more relaxed force-free state than faster MCs.
The proton density and temperature are significantly larger in sheaths than in MCs. Still, there is no sharp transition but a progressive sheath-MC transition that extends up to 20% of the MC duration. A very similar transition is also present for the amplitude of the magnetic fluctuations. These results are present for all three groups of events as well as in individual events, so they are not from a smearing of sheath properties inside the MC due to inappropriate boundary definition. We interpret these results as the consequence of magnetic reconnection at various locations along the flux rope between sheath and flux-rope magnetic fields. Then, while along the spacecraft trajectory the crossed magnetic field appears as belonging to the flux rope, some parts of the crossing can belong to a magnetic field region that has reconnected with the sheath magnetic field further away from the local spacecraft trajectory. This allows plasma, heat, and magnetic fluctuations to enter in this reconnected field implying, on average, sheath properties “diffusing” within the front of the MC.
We next studied the typical effects that these sheaths and MCs have on the cosmic ray transport by studying the associated Forbush decrease profiles. For all MCs a local minimum of the GCR flux is present inside the sheaths, while for fast MCs another minimum is also present within the MCs. In the superposed epoch profiles of Forbush events, we found a discontinuity of the GCR flux at the sheath-MC interface, probably owing to the change of properties in the cross magnetic-field diffusion coefficients in these two structures. Indeed, GCRs encounter a structure with closed and intense magnetic field lines, where the high energy particles have difficulty penetrating.
We finally derive a new semi-empirical model for the Earth observations of the Forbush profile that takes into account the former process as a simple superposition of (1) the enhancement of magnetic fluctuations over a threshold; (2) the intensity of the magnetic field over a threshold; (3) a jump at the time of the sheath-MC interface to consider the change of the magnetic connectivity; and (4) a recovery phase for times after the sheath-MC interface. This model has five free parameters. We fit the model to each of the groups of events. Besides reproducing the first steep decrease in GCRs after the shock time and the recovery phase, we can reproduce a second decrease in GCRs in the wake of the slow MCs. This second fall is due to the presence of scattering centres, which we associate with the amplitude of the magnetic fluctuations. This last result is in agreement with the recent study of Badruddin & Kumar (2016).
Furthermore, our model also reproduces a local nGCR minima inside the MC for the sub-group of fast events. This feature is consistent with Belov et al. (2015), in which they find that strong field (>18 nT) is associated with local minima of nGCR within MCs.
Finally, we find that the recovery time τFD is increasing by a factor a bit larger than two from the slow to fast events.
The results presented here improve the knowledge of MCs and their sheaths, their evolution in the solar wind, and also the relationship between MCs and their GCR shielding. In particular, the semi-empirical model for the FD profile we presented will help to improve the understanding of energetic particle transport in the heliosphere, and can be used to put constraints on theoretical models that consider (1) global macro-scale magnetic configurations for MCs and (2) turbulent properties of the solar wind.
Available at http://www.srl.caltech.edu/ACE/ASC/level2/
These data are available at http://neutronm.bartol.udel.edu/~pyle/bri_table.html
Acknowledgments
Thanks to the public service of NASA Space Physics Data Facility (SPDF) for the observations. We thank Roger Clay and the anonymous referee for careful reading of the manuscript, and for their valuable comments. This work was partially supported by the Argentine grants UBACyT 20020120100220 (UBA), PICT-2013-1462 (FONCyT-ANPCyT), PIP-11220130100439CO (CONICET) and PIDDEF 2014-2017 nro. 8 (Ministerio de Defensa, Argentina), and by a one month invitation of SD by Paris Observatory. J.J.M.M., S.D., and L.R. acknowledge the cooperation project BE/13/07 (F.R.S.-FNRS/MinCyT) between Belgium and Argentina. S.D. is member of the Carrera del Investigador Científico, CONICET. J.J. Masías-Meza is a fellow of CONICET. L.R. acknowledges support from the Belgian Federal Science Policy Office through the ESA-PRODEX programme. This research has been partially funded by the Interuniversity Attraction Poles Programme initiated by the Belgian Science Policy Office (IAP P7/08 CHARM).
References
- Abreu, P., Aglietta, M., The Pierre Auger Collaboration, et al. 2011, J. Inst., 6, 1003 [NASA ADS] [Google Scholar]
- Arunbabu, K. P., Antia, H. M., Dugad, S. R., et al. 2015, A&A, 580, A41 [Google Scholar]
- Asorey, H., Dasso, S., Nunez, L., et al. 2016, PoS(ICRC2015)142 [Google Scholar]
- Badruddin, K. A. 2016, Sol. Phys., 291, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Belov, A., Abunin, A., Abunina, M., et al. 2015, Sol. Phys., 290, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco-Cano, X., Kajdič, P., Omidi, N., & Russell, C. T. 2011, J. Geophys. Res., 116, 9101 [CrossRef] [Google Scholar]
- Burlaga, L., Sittler, E., Mariani, F., & Schwenn, R. 1981, J. Geophys. Res., 86, 6673 [Google Scholar]
- Byrd, R. H., Lu, P., Nocedal, J., & Zhu, C. 1995, SIAM J. Sci. Comput., 16, 1190 [Google Scholar]
- Cane, H. V., Richardson, I. G., & Cyr, O. C. S. 2000, Geophys. Res. Lett., 27, 3591 [Google Scholar]
- Das, I., Opher, M., Evans, R., Loesch, C., & Gombosi, T. I. 2011, ApJ, 729, 112 [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., Luoni, M. L., & Gulisano, A. M. 2005, Adv. Space Res., 35, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Mandrini, C. H., Démoulin, P., & Luoni, M. L. 2006, A&A, 455, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dasso, S., Nakwacki, M. S., Démoulin, P., & Mandrini, C. H. 2007, Sol. Phys., 244, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Dasso, S., Asorey, H., & Pierre Auger Collaboration 2012, Adv. Space Res., 49, 1563 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P. 2009, Sol. Phys., 257, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Démoulin, P., & Dasso, S. 2009, A&A, 498, 551 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Démoulin, P., Nakwacki, M. S., Dasso, S., & Mandrini, C. H. 2008, Sol. Phys., 250, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, H., & Wang, J. 2013, A&A, 559, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feng, L., Wang, Y., Shen, F., et al. 2015, ApJ, 812, 70 [Google Scholar]
- Gosling, J. T., Birn, J., & Hesse, M. 1995, Geophys. Res. Lett., 22, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Gulisano, A. M., Démoulin, P., Dasso, S., Ruiz, M. E., & Marsch, E. 2010, A&A, 509, A39 [Google Scholar]
- Guo, J., Feng, X., Zhang, J., Zuo, P., & Xiang, C. 2010, J. Geophys. Res., 115, 9107 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, J., Zeitlin, C., Wimmer-Schweingruber, R. F., et al. 2015, A&A, 577, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janvier, M., Démoulin, P., & Dasso, S. 2014, J. Geophys. Res., 119, 7088 [Google Scholar]
- Jordan, A. P., Spence, H. E., Blake, J. B., & Shaul, D. N. A. 2011, J. Geophys. Res., 116, 11103 [NASA ADS] [CrossRef] [Google Scholar]
- Krittinatham, W., & Ruffolo, D. 2009, ApJ, 704, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Lepping, R. P., Berdichevsky, D. B., Szabo, A., Arqueros, C., & Lazarus, A. J. 2003, Sol. Phys., 212 [Google Scholar]
- Lopez, R. E., & Freeman, J. W. 1986, J. Geophys. Res., 91, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Démoulin, P., Dasso, S., & Klein, K.-L. 2012, A&A, 538, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McComas, D. J., Gosling, J. T., Winterhalter, D., & Smith, E. J. 1988, J. Geophys. Res., 93, 2519 [Google Scholar]
- McComas, D. J., Bame, S. J., Barker, P., et al. 1998, Space Sci. Rev., 86, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsakou, E., & Moussas, X. 2014, Sol. Phys., 289, 3137 [Google Scholar]
- Mulligan, T., Blake, J. B., Shaul, D., et al. 2009, J. Geophys. Res., 114, 07105 [CrossRef] [Google Scholar]
- Munakata, K., Yasue, S., Kato, C., et al. 2006, Adv. Geosci., 2, 115 [CrossRef] [Google Scholar]
- Penna, R. F., & Quillen, A. C. 2005, J. Geophys. Res., 110, 09S05 [CrossRef] [Google Scholar]
- Richardson, I. G., & Cane, H. V. 2010, Sol. Phys., 264, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Richardson, I., & Cane, H. 2011, Sol. Phys., 270, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez, L., Masías-Meza, J., Dasso, S., et al. 2016, Sol. Phys., in press [Google Scholar]
- Ruffenach, A., Lavraud, B., Owens, M. J., et al. 2012, J. Geophys. Res., 117, A09101 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffenach, A., Lavraud, B., Farrugia, C. J., et al. 2015, J. Geophys. Res., 120, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. A. 1954, Phys. Rev., 94, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Siscoe, G., & Odstrcil, D. 2008, J. Geophys. Res., 113, 00B07 [Google Scholar]
- Smith, C. W., J. L’Heureux, N. F., Ness, M. H., et al. 1998, Space Sci. Rev., 86, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Strumik, M., Roytershteyn, V., Karimabadi, H., et al. 2015, Geophys. Res. Lett., 42, 5109 [NASA ADS] [CrossRef] [Google Scholar]
- Vainio, R., Desorgher, L., Heynderickx, D., et al. 2009, Space Sci. Rev., 147, 187 [Google Scholar]
- Wang, C., Li, H., Richardson, J. D., & Kan, J. R. 2010, J. Geophys. Res., 115, 9215 [CrossRef] [Google Scholar]
- Wang, X., Tu, C., Wang, L., He, J., & Marsch, E. 2015, Geophys. Res. Lett., 42, 3654 [NASA ADS] [CrossRef] [Google Scholar]
- Wibberenz, G., Le Roux, J. A., Potgieter, M., & Bieber, J. 1998, Space Sci. Rev., 83, 317 [Google Scholar]
- Wolfe, J. H. 1972, NASA Sp. Publ., 308, 170 [NASA ADS] [Google Scholar]
- Zhu, C., Byrd, R. H., Lu, P., & Nocedal, J. 1997, ACM Trans. Math. Softw., 23, 550 [CrossRef] [MathSciNet] [Google Scholar]
Appendix A: Additional table
List of the 44 events studied.
All Tables
Mean values of all quantities (Col. 1) for all events (Cols. 2 and 3), and for each group of events associated with MCs with low, middle, and high velocities (Cols. 4 to 9).
Fitted values of the Forbush decrease model (see Eq. (4)), for the three subset of events.
All Figures
 |
Fig. 1 Time profiles for different observables, from top to bottom: magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, normalised magnetic-fluctuation density rmsBoB (Eq. (1)), and absolute magnetic fluctuation rmsB (Eq. (2)). We show three different events; one per column. Each of these events belongs to each of the groups analysed in Sect. 4; from left to right, the events belong to the slow, intermediate, and fast groups. The date of the shock arrival is shown at the top of each column in UT. The passage of the sheath is indicated in orange, and the passage of the MC in blue. The fastest event shows stronger compression at the MC front, with respect to the others. The slowest event presents higher density values within the sheath. See Sect. 2.2 for a description of the main important features shown in each panel. |
| In the text | |
 |
Fig. 2 Superposed epoch for different quantities derived with the method described in Sect. 3.1. The sheath is shown with an orange background colour (time range 0 <t< 1) and the MC with a blue background colour (1 <t< 4). The time t is normalised with the sheath duration for t< 1 and with the MC duration for t> 1 (the MC duration is three times longer than the sheath duration as observed in average). The black dots, connected with a line, are averaged values for each bin on the time axis, the grey band represents the error of the mean and the red line represents the median values in each time bin. The average profiles were computed filtering those events that had less than 20% of data gaps in the transient structure (MC or sheath). The number of events after filtering is shown in each panel. The panels represent: magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, normalised magnetic-fluctuation density rmsBoB (Eq. (1)), GCR intensity normalised to the pre-ICME level nGCR and absolute magnetic fluctuation rmsB, Eq. (2). A clear discontinuity of the magnetic fluctuation intensity, rmsB, is present at the shock position (front of the sheath). The normalised magnetic fluctuations, rmsBoB, inside the MC are significantly lower than in the ambient solar wind (by a factor of ≃3). |
| In the text | |
 |
Fig. 3 Normalised values of average parameters corresponding to each subgroup (split according to the ordering parameter Vmc): low Vmc (blue triangle down), middle Vmc (green circle), and high Vmc (red triangle up). Empty symbols are for sheaths and filled symbols for MCs. For each quantity, we use the mean values of all events for the normalisation of each parameter (grey horizontal line). From left to right, the parameters are the means of magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, normalised magnetic-fluctuation density rmsBoB (Eq. (1)), absolute magnetic fluctuation rmsB (Eq. (2)), and GCR intensity normalised to the pre-ICME level nGCR. |
| In the text | |
 |
Fig. 4 Average profiles (black lines) distributed in three columns for the three subsets of events. Left: slow (V< 450 km s-1), middle: medium (450 km s-1<V< 550 km s-1), and right: fast MCs (V> 550 km s-1). The black line represents the average value, the grey band represents the error of the mean and the red line represents the median values in each time bin. As in Fig. 2, for t< 1, time is normalised with the sheath average radial duration and for t> 1, time is normalised with the average MC radial duration. Orange delimits the sheath region (0 <t< 1), and blue the MC region (1 <t< 4). See the caption of Fig. 2 for more information. From top to bottom the parameters are the means of magnetic field B, bulk velocity V, proton density np, proton temperature Tp, plasma beta β, and normalised magnetic-fluctuation density rmsBoB, Eq. (1). |
| In the text | |
 |
Fig. 5 Left panel: average proton surface densities of sheaths σsh, Eq. (3), as a function of the average MC speeds (Vmc) of all events. The vertical dashed lines indicate the thresholds between the three groups shown in Figs. 4 and 6. The quantity σsh is a proxy of the accumulated material ahead of MCs, within the sheaths. On average, slower MCs drag more material. Right panel: histogram of σsh for the 44 events. |
| In the text | |
 |
Fig. 6 Superposed epoch for the three subsets of events. Left: slow (V< 450 km s-1); middle: medium (450 km s-1<V< 550 km s-1); and right: fast MCs (V> 550 km s-1). First row: mean profiles of magnetic fluctuations rmsB, Eq. (2). Typically, inside the MCs, the fluctuations are the same as in the ambient solar wind. For slow and middle groups, rmsB has higher values in the rear with respect to the ambient solar wind. Second row: mean profiles of GCR intensity nGCR. Before averaging events, the intensity was normalised by the pre-shock level. In the first and second rows the black line represents the average value, the grey band represents the error of the mean, and the red line represents the median values in each time bin. Third row: fitted model (red lines) to the observed average profiles (see Sect. 5.2). See the caption of Fig. 2 for more information. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


