| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 7 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201628379 | |
| Published online | 19 July 2016 | |
Millimeter wave spectra of carbonyl cyanide⋆,⋆⋆
1 Laboratoire de Physique des Lasers, Atomes et Molécules, UMR CNRS 8523, Université de Lille 1, 59655 Villeneuve d’Ascq Cedex, France
e-mail: roman.motienko@univ-lille1.fr
2 Grupo de Astrofísica Molecular, Instituto de Ciencias de Materiales de Madrid (ICMM-CSIC), C/ Sor Juana Inés de la Cruz, 3, Cantoblanco, 28049 Madrid, Spain
3 Institut des Sciences Chimiques de Rennes, École Nationale Supérieure de Chimie de Rennes, CNRS, UMR 6226, 11 allée de Beaulieu, CS 50837, 35708 Rennes Cedex 7, France
Received: 25 February 2016
Accepted: 9 May 2016
Context. More than 30 cyanide derivatives of simple organic molecules have been detected in the interstellar medium, but only one dicarbonitrile has been found and that very recently. There is still a lack of high-resolution spectroscopic data particularly for dinitriles derivatives. The carbonyl cyanide molecule is a new and interesting candidate for astrophysical detection. It could be formed by the reaction of CO and CN radicals, or by substitution of the hydrogen atom by a cyano group in cyanoformaldehyde, HC(=O)CN, that has already been detected in the interstellar medium.
Aims. The available data on the rotational spectrum of carbonyl cyanide is limited in terms of quantum number values and frequency range, and does not allow accurate extrapolation of the spectrum into the millimeter-wave range. To provide a firm basis for astrophysical detection of carbonyl cyanide we studied its millimeter-wave spectrum.
Methods. The rotational spectrum of carbonyl cyanide was measured in the frequency range 152−308 GHz and analyzed using Watson’s A- and S-reduction Hamiltonians.
Results. The ground and first excited state of v5 vibrational mode were assigned and analyzed. More than 1100 distinct frequency lines of the ground state were fitted to produce an accurate set of rotational and centrifugal distortion constants up to the eighth order. The frequency predictions based on these constants should be accurate enough for astrophysical searches in the frequency range up to 500 GHz and for transition involving energy levels with J ≤ 100 and Ka ≤ 42. Based on the results we searched for interstellar carbonyl cyanide in available observational data without success. Thus, we derived upper limits to its column density in different sources.
Key words: ISM: molecules / ISM: abundances / submillimeter: ISM / molecular data / methods: laboratory: molecular / line: identification
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2011.0.00009.SV. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan) with NRC (Canada), NSC, and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. This work was also based on observations carried out with the IRAM 30-m telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
The full Tables 3 and 4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/592/A43
© ESO, 2016
1. Introduction
The choice of new target compounds as candidates for the interstellar medium (ISM) is never easy but often follows some rules: compounds recently observed in this medium can be considered as a starting material, the abundance of some functional group can indicate a higher probability of finding one more components with this substituent, the knowledge of a possible chemistry of these media can allow to deduce the possible presence of derivatives formed starting from the detected species. The cyanide derivatives are the most abundant family of compounds detected in the ISM with more than 30 molecules. The recent discovery of protonated cyanogen (NCCNH+) in the ISM (Agúndez et al. 2015a) pushes us to imagine the presence of other dinitrile derivatives. However the fact that compounds should possess a permanent dipolar moment to be detectable by microwave spectroscopy limits the choice of candidates. On the basis of the substitution of a hydrogen by a cyano group (and without consideration of chemical reactions) many compounds can be correlated two-by-two such as CH4 and CH3CN, C2H2 and HC3N, CH3C2H and CH3C3N, C2H4 and H2C=CHCN, NH3 and NH2CN, H2CO and HC(O)CN, H2O and HOCN, H2S and HSCN, NH2CH3 and NH2CH2CN, HN=CH2 and HN=CHCN, amongst others. Taking into consideration such analogies, we started the study of the microwave spectrum of 2-oxopropanedinitrile (carbonyl cyanide) (NC-C(=O)-CN) since HC(=O)CN is present in the ISM (Remijan et al. 2008). It could be formed from CO and CN radicals, two molecules in abundance in the ISM.
The carbonyl cyanide, belonging to the family of cyanides, is a simple molecule composed of six atoms with molar mass equal to 80 g mol-1 and a dipole moment μb = 0.704 ± 0.007D (Lees 1971). This molecule is characterized by its strong reaction with water, producing CO2 and HCN. Similarly, it may decompose into CO and C2N2 (intermolecular decomposition) (Glemser & Häusser 1948). Lees (1971) was the first to study this molecule in the microwave range between 8 and 40 GHz. Several studies have since been interested by the chemical reactivity of this molecule. The interest for the chemical reactivity of this molecule lies in the fact that the carbonyl cyanide possesses 2 cyanogen groups attached symmetrically to a carbonyl group. The single bonds C−C are located between a double bond C=O and a triple bond C≡N. These bonds cause significant effects of electron delocalization. We note that no experiment was able to validate the actual geometry of the carbonyl cyanide because in the spectroscopic studies of Lees (1971) only parent isotopic species were considered. To have the most reliable structural parameters, Typke et al. (1980) determined the lengths of the bonds of this molecule by means of gas phase electron diffraction, by combining experimental data of electron diffraction and microwave spectroscopy, obtained from the study of Lees (1971). Bates & Smith (1970) measured the infrared and Raman spectra of C3N2O in different phases (vapor, liquid and solid phase) from 10 to 2500 cm-1. This study led to the identification of twelve fundamental frequencies and determination of intramolecular harmonic force field. The Raman and infrared absorption spectra also showed that carbonyl cyanide is planar and its normal state belongs to a symmetry group C2v.
The information on the rotational spectrum of carbonyl cyanide available from the only study by Lees (1971) is limited in terms of frequency range and quantum numbers. The frequency predictions on the basis of the study by Lees (1971) are accurate enough only in the frequency range up to 50 GHz, and for the rotational transitions involving quantum numbers J ≤ 12. Whereas the absorption maximum for rotational spectrum of carbonyl cyanide under conditions of hot interstellar clouds lies in millimeter-wave range above 200 GHz. The main goal of this study is to extend the measurements and analysis of the rotational spectrum of carbonyl cyanide in order to provide a reliable database of rotational transitions. On the basis of the results obtained, we searched for carbonyl cyanide in different star-forming regions.
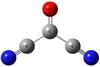 |
Fig. 1 Structure of the carbonyl cyanide molecule. |
2. Experiments
The 2-oxopropanedinitrile was synthesized as previously reported (Linn 1969; Martin 1971). The 13C NMR spectroscopy results are: (CDCl3, 100 MHz, − 30 °C) 110.7 (s, CN); 140.4 (s, CO).
The rotational spectrum of carbonyl cyanide was measured in the frequency range between 152 and 308 GHz using the terahertz absorption spectrometer based on frequency multiplication chain in Lille (Zakharenko et al. 2015). Due to the rapid decomposition of the sample the experiments were carried out in the so-called flow mode, that is the sample of carbonyl cyanide was evaporated outside the cell and injected into it through a side opening at one end of the cell and continuously pumped out through another side opening at the other end. The optimal pressure in the absorption cell used during measurements was 12 μbar. The measurement uncertainty for a strong isolated line is estimated to be 0.03 MHz. The frequencies of the lines with poor signal-to-noise ratio or the lines with distorted lineshape were measured with 0.05 MHz or 0.1 MHz accuracy.
3. Assignments and fit
Values of s111 for different combinations between reductions and coordinate representations.
Rotational constants of carbonyl cyanide in the ground and v5 = 1 excited vibrational states.
The spectral analysis was preceded by ab initio calculations performed using Gaussian 09 suite of programs (Frisch et al. 2009). Calculations were performed at MP2 level of theory using correlation-consistent triple-ζ wave function basis set augmented with diffuse functions (aug-cc-pVTZ). The results of calculations include structural optimization with tight convergence criteria, and harmonic force field parameters in order to provide the information on rotational and quartic centrifugal distortion constants as well as on low frequency vibrational modes.
The Ray’s asymmetric parameter of carbonyl cyanide κ = (2B−A−C) / (A−C) = −0.624 is relatively far from prolate symmetric top limit of − 1. The choice of an appropriate model for the spectral analysis is particularly important in molecular spectral predictions. To get the most compatible form of Watson’s Hamiltonian (Watson 1977) for the molecule, one must make the choice of suitable coordinate representation and reduction (A or S). This implies a calculation of the s111 parameter for various possible cases (Margulès et al. 2010). Table 1 shows the different values of the parameter s111 calculated. The coordinate representation IIIr is a choice to avoid, bearing in mind that s111 must be set to the smallest possible value. However, for the representation Ir, for both reductions of the Hamiltonian, the values of s111 are relatively close. That makes it impossible to choose between A- and S-reduction, based solely on this criteria. For this reason, the spectrum was analyzed using both reductions of the Hamiltonian. The best configuration should be chosen based on other criteria obtained from the fit (residuals of the fit, its standard deviation, the number of fitted parameters, etc.) The adjustment of the spectral data was made first with the Z. Kisiel’s ASFIT program (Kisiel 2001). The final spectral predictions were made with CALPGM (Pickett 1991) program suite most commonly used by astrophysicists (Pearson et al. 2010).
In the previous study (Lees 1971) for the frequency range 8−40 GHz, on the basis of 49 measured rotational transitions, three rotational constants A, B and C and four of six non-reduced centrifugal distortion constants τ for the ground state were determined. In our investigation, first we fitted these transitions using a set of rotational constants varied, and quartic centrifugal distortion parameters fixed to the values available from quantum chemical calculations. The results of this fit were used to obtain the initial predictions of the rotational spectrum in the millimeter-wave range. The spectral assignment began with the R branch (ΔJ = 1) for transitions with Ka = 0, 1 being the most intense lines. They were found relatively close to the position predicted. The assigned transitions were added to existent dataset and fitted to improve the values of rotational and centrifugal distortion parameters. The following assignment was performed in the same manner, when new assigned transitions were fitted, and new set parameters was used to calculate frequency predictions and to search for new lines. In total, for the ground state and for the frequency range 152−308 GHz, the number of assigned rotational lines is 1165 with maximum values of J and Ka90 and 37 respectively. All the assigned transitions satisfy b-type selection rules, as it is the only non-zero dipole moment component in the molecule.
Assigned rotational transitions of the ground state and the first excited vibrational state (v5 = 1) of carbonyl cyanide.
Predicted transitions of the ground vibrational state of carbonyl cyanide.
In addition to the ground state, we treated the first excited vibrational state, v5 = 1, that corresponds to the symmetric C−C≡N bending in the molecular plane. Based on quantum chemical calculations, this state is located 124.7 cm-1 above the ground state, and its Boltzmann factor is 0.415 at room temperature. In the low-resolution infrared spectrum from the study of Bates & Smith (1970) this band was observed at 127 cm-1. The initial frequency predictions for v5 = 1 state were calculated on the basis of the fit of ten transitions measured by Lees (1971). These transitions were fitted with a set of rotational constants that varied, and quartic centrifugal distortion parameters fixed to the values of the corresponding ground state parameters, as in this case, the vibrational excitation should not vary too much the centrifugal distortion. We applied the same assignment algorithm as for the ground state. In total, we assigned 866 rotational lines of v5 = 1 state of carbonyl cyanide with the highest quantum number values J and Ka respectively 84 and 33.
The results of the least squares fits of the ground and v5 = 1 excited vibrational states using A- and S-reductions of the Watson’s Hamiltonian in Ir coordinate representation are presented in Table 2. The complete list of measured rotational transitions of the ground and v5 = 1 states is presented in Table 3 available at the CDS. Here, only part of Table 3 is shown as example. As follows from the comparison of the results in Table 2, both Hamiltonian models give similar results in terms of rms, weighted rms deviation, number of parameters used, and condition number. The rms and wrms deviations of the ground state fit using the A-reduction are slightly better, for the same number of fitted parameters as in the S-reduction. For the v5 = 1 state, better results using the A-reduction are achieved with one parameter less, than in the case of the S-reduction. In all the fits, the parameters listed in Table 3 are the only parameters determined better than 10σp, where σp is the parameter uncertainty. The inclusion of others parameters of 8th or even 10th order only slightly improves the rms and weighted rms of the fit, but also leads to bad conditioning of the system of normal equations, and correlation problems. As a conclusion, despite rather asymmetric character of the molecule (κ = −0.624), both A- and S-reduction Hamiltonians in the Ir coordinate representation may be equivalently used for fitting within experimental accuracy and predicting the rotational spectra of carbonyl cyanide.
The intensities of the rotational transitions of carbonyl cyanide depend strongly on the spin statistics. The molecule of carbonyl cyanide belongs to the symmetry point group C2v. The symmetry operation C2b that corresponds to the rotation about b axis by π radians exchanges the positions of two nitrogen nuclei that have the integer spin I = 1. Because carbon and oxygen nuclei have zero spin the resultant statistics is Bose-Einstein, and the complete wave function Ψtot = ψeψvψrψn must be symmetric with respect to the C2b operation. The electronic and vibrational wave functions of the fundamental state, ψe and ψv, are symmetric. The parity of the rotational wave function depends on the value of the sum of Ka and Kc quantum numbers. For Ka + Kc = even, ψr is symmetric; for Ka + Kc = odd, ψr is asymmetric. Thus, a symmetric complete wave function may be obtained by either of two combinations: 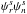 or
or 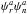 . The total number of nuclear spin functions is (2IN + 1)2 = 9, six of them should be symmetric and three should be asymmetric, in order to satisfy Bose-Einstein statistics. The nuclear statistical weight is six for the rotational levels with Ka + Kc = even, and three for the rotational levels with Ka + Kc = odd. The same is valid for v5 = 1 excited vibrational state, as v5 vibrational mode belongs to A1 irreducible representation of C2v point group. The influence of nuclear spin statistics on the distribution of intensities is shown in Fig. 2. The nuclear spin weight factors were also taken into account in fitting the frequencies of blended lines (see Table 3). Such an approach is important to get better accuracy of the fit, because the calculated intensity weighted mean frequency of blended transitions depends on the intensity weight factors.
. The total number of nuclear spin functions is (2IN + 1)2 = 9, six of them should be symmetric and three should be asymmetric, in order to satisfy Bose-Einstein statistics. The nuclear statistical weight is six for the rotational levels with Ka + Kc = even, and three for the rotational levels with Ka + Kc = odd. The same is valid for v5 = 1 excited vibrational state, as v5 vibrational mode belongs to A1 irreducible representation of C2v point group. The influence of nuclear spin statistics on the distribution of intensities is shown in Fig. 2. The nuclear spin weight factors were also taken into account in fitting the frequencies of blended lines (see Table 3). Such an approach is important to get better accuracy of the fit, because the calculated intensity weighted mean frequency of blended transitions depends on the intensity weight factors.
 |
Fig. 2 A portion of the rotational spectrum of carbonyl cyanide in the ground state illustrating the influence of nuclear spin statistics on transition intensities. In red we show experimental spectrum, in blue two theoretical spectra assuming equivalent statistical weights and even/odd = 6 / 3. |
 |
Fig. 3 ALMA SV data of three different positions at selected frequencies together with the synthetic spectra of NCCOCN obtained using the column densities given as upper limits (see Table 6). A vLSR of +9.0 km s-1 is assumed. |
The predictions of the ground state rotational spectrum of carbonyl cyanide up to 500 GHz are given in Table 4. The table provides quantum numbers, followed by calculated transition frequencies and their uncertainties, the product μ2S (where μ is the dipole moment of the molecule and S is transition linestrength), the nuclear spin statistical weight, and the energy of the lower state. Owing to its significant size the complete version of the Table 4 is available at the CDS. In Table 4 we included only the transitions whose predicted uncertainties are less than 1 MHz, which is a typical limitation for astronomical observations. These uncertainties are based on a propagation of errors estimated from a least-squares fit of the observed frequencies to a model Hamiltonian, and do not account for the lack of higher-order centrifugal distortion parameters (Pickett 1991). In terms of quantum number values, on the basis of the existing dataset for the ground vibrational state of carbonyl cyanide, the limitations for the calculated predictions are: J ≤ 100, and Ka ≤ 40. In the present case, the extrapolation of the predictions for J quantum number up to 100 is plausible for relatively low Ka transitions. As one may see from Table 4 the uncertainly for J = 95 ← 95 transition is less than 40 kHz. The extrapolation for Ka quantum number may be much more sensitive to the lack of higher-order centrifugal distortion terms, and therefore we limited our predictions by the maximum Ka value of the observed transitions. In addition, in Table 5, we provide the full partition function Qtot(T) = Qv(T) × Qr(T) for various characteristic temperatures. The Qr(T) and Qv(T) values were calculated using approximate formulae that may be found elsewhere (see, for example Haykal et al. 2013). The values of Qr(T) take the nuclear spin statistics into account.
Rotation Qr(T) and vibration Qv(T) part of the total internal partition function Q(T) = Qv(T) × Qr(T) for carbonyl cyanide.
Physical parameters of the considered cloud cores.
4. Searching for NCCOCN in space
Thanks to these new spectroscopic results, a rigorous search for carbonyl cyanide in space can be carried out. Only one species in the ISM has been detected that harbours a ketone functional group, namely acetone (CH3COCH3), in objects related to high- and intermediate-mass star formation (Combes et al. 1987; Snyder et al. 2002; Friedel et al. 2005; Palau et al. 2011; Codella et al. 2013; Fuente et al. 2014; Rong et al. 2016) and in comets (Goesmann et al. 2015). In addition, a molecule containing the N≡C−C=O bounds, cyanoformaldehyde (CNCHO), has been detected towards the Sagittarius (Sgr) clouds (Remijan et al. 2008). These identifications, together with the high abundance of −CN species in several astrophysical environments (see, e.g. Mauersberger et al. 1991; Liszt & Lucas 2001; Cazaux et al. 2003; Remijan et al. 2004; López et al. 2014; Bell et al. 2014; Agúndez et al. 2015b), could suggest the presence of NCCOCN in space.
We searched for NCCOCN in different star-forming regions. First, we used the millimeter IRAM 30 m survey of Orion KL (Tercero et al. 2010) and the ALMA Science Verification (SV) data of the same source to check a wide frequency band and different positions (hot core, compact ridge, and MM4, see e.g. Wu et al. 2014; Gong et al. 2015) of the nearest high-mass star-forming region (see e.g. Menten et al. 2007). No NCCOCN has been identified above the detection limit of these data. Table 6 shows the derived upper limits to the column density using the MADEX code (Cernicharo 2012), together with the adopted physical parameters for each dataset and/or position (see, e.g. Cernicharo et al. 2016; Tercero et al. 2015). In Fig. 3 we depicted the derived model assuming the column densities of Table 6 and the ALMA SV data at selected frequencies and positions. Above the limit established by these models, we see that many NCCOCN lines are missing or produce a poor fit to the data.
To search for NCCOCN in other sources, we explored public data of Sgr B2. We found no evidence of the presence of NCCOCN in the PRIMOS survey (Neill et al. 2012) nor in the IRAM 30 m survey of Sgr B2(N) at 3 mm (Belloche et al. 2013). In Table 6, upper limits to the NCCOCN column density are provided for different cloud components of Sgr B2 (see e.g. Belloche et al. 2013; Brünken et al. 2010).
Finally, we used the IRAM 30 m data presented by Cernicharo et al. (2012) to attempt the identification of this species in dark clouds. Once again, we only derived upper limits to its column density in B1-b (Barnard 1-b) and TMC-1 (Taurus Molecular Cloud 1; see Table 6).
5. Conclusions
In this study, the spectral information obtained has a sufficiently precise basis for the detection of carbonyl cyanide in the ISM. More than 1100 distinct frequency lines of the ground vibrational state were fitted within experimental accuracy. Using different theoretical approaches accurate rotational parameters up to the eighth order were determined. We also showed the influence of spin statistics on the rotational line intensities of carbonyl cyanide. The analysis covers a large part of the range of frequencies of the most intense transitions at the typical temperatures of the hot areas of the ISM (150 K). It allows the calculation of frequency predictions within 1 MHz precision for transitions with J ≤ 100 and Ka ≤ 40, and in the frequency range up to 500 GHz. On the basis of spectroscopic results obtained in this study, we attempted to detect carbonyl cyanide towards different star-forming regions using different surveys, but none of these searches was successful. Thus, only upper limits to NCCOCN column density were estimated.
Acknowledgments
B.T. and J.C. thank MINECO for funding support from the CONSOLIDER-Ingenio program “ASTROMOL” CSD 2009-00038, AYA2012-32032, CTQ 2013-40717 P, CTQ 2010-19008, and the ERC synergy grant ERC-2013-Syg-610256-NANOCOSMOS. J.-C.G., L.M. and R.M. thank the Centre National d’Etudes Spatiales (CNES) and the Program Physique et Chimie du Milieu Interstellaire (PCMI) (INSU-CNRS) for grants.
References
- Agúndez, M., Cernicharo, J., de Vicente, P., et al. 2015a, A&A, 579, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Cernicharo, J., Quintana-Lacaci, G., et al. 2015b, ApJ, 814, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, J. B., & Smith, W. 1970, Spectrochimica Acta A: Molecular Spectroscopy, 26, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T., Cernicharo, J., Viti, S., et al. 2014, A&A, 564, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Müller, H. S., Menten, K. M., Schilke, P., & Comito, C. 2013, A&A, 559, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brünken, S., Belloche, A., Martín, S., Verheyen, L., & Menten, K. 2010, A&A, 516, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazaux, S., Tielens, A., Ceccarelli, C., et al. 2003, ApJ, 593, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J. 2012, EAS Pub. Ser., 58, 251 [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Marcelino, N., Roueff, E., et al. 2012, ApJ, 759, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Kisiel, Z., Tercero, B., et al. 2016, A&A, 587, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Codella, C., Beltrán, M., Cesaroni, R., et al. 2013, A&A, 550, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Combes, F., Gerin, M., Wootten, A., et al. 1987, A&A, 180, L13 [NASA ADS] [Google Scholar]
- Friedel, D., Snyder, L., Remijan, A. J., & Turner, B. 2005, ApJ, 632, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2009, Gaussian 09 Revision E.01, Gaussian Inc. Wallingford CT [Google Scholar]
- Fuente, A., Cernicharo, J., Caselli, P., et al. 2014, A&A, 568, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glemser, O., & Häusser, V. 1948, Z. Naturforsch. B, 3, 159 [Google Scholar]
- Goesmann, F., Rosenbauer, H., Bredehöft, J. H., et al. 2015, Science, 349, aab0689 [Google Scholar]
- Gong, Y., Henkel, C., Thorwirth, S., et al. 2015, A&A, 581, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haykal, I., Motiyenko, R., Margulès, L., & Huet, T. 2013, A&A, 549, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kisiel, Z. 2001, in Spectroscopy from Space (Springer), 91 [Google Scholar]
- Lees, R. 1971, Can. J. Phys., 49, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Linn, W. J. 1969, Org. Synth., 49, 103 [CrossRef] [Google Scholar]
- Liszt, H., & Lucas, R. 2001, A&A, 370, 576 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López, A., Tercero, B., Kisiel, Z., et al. 2014, A&A, 572, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Margulès, L., Motiyenko, R., Alekseev, E., & Demaison, J. 2010, J. Mol. Spec., 260, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, E. L. 1971, Org. Synth., 51, 70 [CrossRef] [Google Scholar]
- Mauersberger, R., Henkel, C., Walmsley, C., Sage, L., & Wiklind, T. 1991, A&A, 247, 307 [NASA ADS] [Google Scholar]
- Menten, K., Reid, M., Forbrich, J., & Brunthaler, A. 2007, A&A, 474, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neill, J. L., Muckle, M. T., Zaleski, D. P., et al. 2012, ApJ, 755, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Palau, A., Fuente, A., Girart, J. M., et al. 2011, ApJ, 743, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J., Müller, H., Pickett, H., Cohen, E., & Drouin, B. 2010, J. Quant. Spec. Rad. Trans., 111, 1614 [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spec., 148, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A., Sutton, E., Snyder, L., et al. 2004, ApJ, 606, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Remijan, A. J., Hollis, J., Lovas, F., et al. 2008, ApJ, 675, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Rong, J., Qin, S.-L., Zapata, L. A., et al. 2016, MNRAS, 455, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Snyder, L. E., Lovas, F. J., Mehringer, D. M., et al. 2002, ApJ, 578, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Tercero, B., Cernicharo, J., Pardo, J., & Goicoechea, J. 2010, A&A, 517, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tercero, B., Cernicharo, J., López, A., et al. 2015, A&A, 582, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Typke, V., Dakkouri, M., & Schlumberger, F. 1980, J. Mol. Struct., 62, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Watson, J. K. 1977, Vibrational spectra and structure, 6, 1 [Google Scholar]
- Wu, Y., Liu, T., & Qin, S.-L. 2014, ApJ, 791, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharenko, O., Motiyenko, R. A., Margulès, L., & Huet, T. R. 2015, J. Mol. Spec., 317, 41 [Google Scholar]
All Tables
Values of s111 for different combinations between reductions and coordinate representations.
Rotational constants of carbonyl cyanide in the ground and v5 = 1 excited vibrational states.
Assigned rotational transitions of the ground state and the first excited vibrational state (v5 = 1) of carbonyl cyanide.
Rotation Qr(T) and vibration Qv(T) part of the total internal partition function Q(T) = Qv(T) × Qr(T) for carbonyl cyanide.
All Figures
 |
Fig. 1 Structure of the carbonyl cyanide molecule. |
| In the text | |
 |
Fig. 2 A portion of the rotational spectrum of carbonyl cyanide in the ground state illustrating the influence of nuclear spin statistics on transition intensities. In red we show experimental spectrum, in blue two theoretical spectra assuming equivalent statistical weights and even/odd = 6 / 3. |
| In the text | |
 |
Fig. 3 ALMA SV data of three different positions at selected frequencies together with the synthetic spectra of NCCOCN obtained using the column densities given as upper limits (see Table 6). A vLSR of +9.0 km s-1 is assumed. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


