| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A55 | |
| Number of page(s) | 17 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201628292 | |
| Published online | 25 July 2016 | |
The kinematics of globular clusters systems in the outer halos of the Aquarius simulations
Kapteyn Astronomical Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
e-mail: jovan@astro.rug.nl
Received: 10 February 2016
Accepted: 27 April 2016
Stellar halos and globular cluster (GC) systems contain valuable information regarding the assembly history of their host galaxies. Motivated by the detection of a significant rotation signal in the outer halo GC system of M 31, we investigate the likelihood of detecting such a rotation signal in projection, using cosmological simulations. To this end we select subsets of tagged particles in the halos of the Aquarius simulations to represent mock GC systems, and analyse their kinematics. We find that GC systems can exhibit a non-negligible rotation signal provided the associated stellar halo also has a net angular momentum. The ability to detect this rotation signal is highly dependent on the viewing perspective, and the probability of seeing a signal larger than that measured in M 31 ranges from 10% to 90% for the different halos in the Aquarius suite. High values are found from a perspective such that the projected angular momentum of the GC system is within ≲40 deg of the rotation axis determined via the projected positions and line-of-sight velocities of the GCs. Furthermore, the true 3D angular momentum of the outer stellar halo is relatively well aligned, within 35 deg, with that of the mock GC systems. We argue that the net angular momentum in the mock GC systems arises naturally when the majority of the material is accreted from a preferred direction, namely along the dominant dark matter filament of the large-scale structure that the halos are embedded in. This, together with the favourable edge-on view of M 31’s disk suggests that it is not a coincidence that a large rotation signal has been measured for its outer halo GC system.
Key words: Galaxy: kinematics and dynamics / globular clusters: general / Galaxy: halo
© ESO, 2016
1. Introduction
According to the currently preferred Λ cold dark matter (ΛCDM) cosmological model of galaxy formation, massive galaxies are at least partly built by hierarchical coalescence of smaller subgalactic components (e.g. Helmi & White 1999; Abadi et al. 2003a,b; Bullock & Johnston 2005). The by-product of such stochastic accumulation of matter are the diffuse stellar halos surrounding massive galaxies. Even though they contain only a small fraction of the total galaxy mass, the far outer halos of galaxies are the most likely places in which we are able to directly observe the remnants of past accretion events, which – owing to the long dynamical timescales in these regions – have the form of spatially coherent stellar streams. Consequently, the characteristics of these regions provide valuable information regarding how galaxies form and evolve through time. Studying the stellar populations residing in the outskirts of galaxies, their structure and kinematics, is a powerful way to test the predictions of the ΛCDM paradigm in detail, and to gain insight into how galaxies assemble.
Naturally, the most detailed, complete studies of stellar halos to date have been conducted in the Local Group using resolved stellar photometry. These studies have uncovered a number of stellar streams in the Milky Way (e.g. Belokurov et al. 2006; Grillmair & Dionatos 2006; Grillmair 2006; Martin et al. 2014; Bernard et al. 2014), which are thought to be tidally disrupted dwarf galaxies or star clusters. Observations of the Sagittarius dwarf galaxy, which is currently being accreted onto our Galaxy, directly shows that the Milky Way’s stellar halo is still actively evolving (e.g. Ibata et al. 1994; Majewski et al. 2003; Koposov et al. 2012; Slater et al. 2013). The Gaia mission will probe further into the Milky Way halo and provide deeper insight into its properties. Similarly, wide-field observations of our closest neighbour, M 31, have revealed a highly complex halo dominated by various stellar streams and overdensities, extending at least out to 150 kpc in projection (e.g. McConnachie et al. 2009; Ibata et al. 2014). In addition, integrated photometric surveys have been able to uncover structure in the extended halos of other nearby galaxies outside the Local Group (e.g. Martínez-Delgado et al. 2008, 2010). Furthermore, numerical simulations have also been able to create lumpy stellar halos resembling those around Milky Way-sized galaxies that arise as a result of their hierarchical formation history (e.g. Cooper et al. 2010; Helmi et al. 2011).
The detection of stellar halos is, however, a major observational challenge owing to the low surface brightness (~30 mag arcsec-2) of the stellar populations that inhabit these regions. An alternative way to study galaxy halos is through their globular cluster (GC) systems. Because of their high luminosities, GCs are much easier to observe compared to the underlying stellar field component. Since GC systems frequently extend to large radii, knowledge of their kinematics is of a particular importance. Globular cluster motions can provide information on the assembly history of the host galaxy, the mass enclosed by the system, the dark matter distribution and the shape of the gravitational potential (e.g. Schuberth et al. 2010, 2012; Strader et al. 2011). By searching for spatial and dynamical correlations amongst GCs, these objects can also be used as tracers of past accretion events (e.g. Perrett et al. 2003; Romanowsky et al. 2012).
The first indication that the Milky Way’s halo was at least partly formed through the amalgamation of smaller components came from exploring the properties of the Galactic GCs (Searle & Zinn 1978). The direct evidence for the globular cluster population came from exploring the accreting Sagittarius dwarf galaxy, which is currently found to be donating at least 5 GCs to the Galactic GC system (e.g. Da Costa & Armandroff 1995; Ibata et al. 1995). Further supporting evidence for the external origin of the halo GCs in the Milky Way is found by analysing their ages, metallicities, kinematics, horizontal branch morphologies, luminosities, and sizes; they are all consistent with the predictions of hierarchical formation models (e.g. Mackey & Gilmore 2004; Mackey & van den Bergh 2005; Marín-Franch et al. 2009; Forbes et al. 2010; Dotter et al. 2011; Keller et al. 2012).
Our closest massive neighbour, M 31, at a distance of only ~780 kpc, hosts a rich GC system comprising over 500 confirmed members (Galleti et al. 2004). Recent wide-field surveys showed that this system is quite extended in nature, with ~90 GCs having projected radii larger than 30 kpc, thus probing the outer halo of this galaxy (e.g. Huxor et al. 2005, 2008, 2014; di Tullio Zinn & Zinn 2013). Indeed, analysis of the M 31’s outer halo GC system yielded particularly interesting results. Mackey et al. (2010) found ~80% of the GCs to preferentially project onto the various stellar overdensities, suggesting that these objects were brought into the M 31 system by accreted dwarf galaxies, an observation which supports hierarchical formation models. Recent kinematic studies of the M 31 outer halo GC system (Veljanoski et al. 2013, 2014) have found various velocity correlations or clustering exhibited by GCs that project along particular stellar debris features. This not only supports the accretion hypothesis but also highlights the power of using GCs as tracers of accretion events.
Even more intriguing is the discovery of a high degree of rotation exhibited by the outer halo GCs out to a radius of ~150 kpc in projection, which shares the same direction and rotation axis, and save for the smaller amplitude, as the GCs that reside in the inner regions of M 31 (Veljanoski et al. 2014). While it has been known for quite some time that the clusters dwelling in the disk of this galaxy rotate quite rapidly (e.g. Perrett et al. 2002), such coherent motion is unexpected for the halo population. For comparison, the halo GCs in the Milky Way appear to be fully pressure supported (e.g. Harris 2001).
Given the compelling evidence that a high fraction of its members have an accretion origin, it is of interest for galaxy formation studies to explain what caused the rotation in the M 31’s halo GC population. One idea that could explain this observation suggests that dwarf galaxies fell into the potential of M 31 from few preferred directions on the sky, possibly in groups (e.g. Li & Helmi 2008; Libeskind et al. 2011; Lovell et al. 2011). Having support from cosmological simulations, this idea is particularly attractive because it is also used to explain the planar structures formed by satellite galaxies around the Milky Way, M 31 and more recently NGC 5128 (Metz et al. 2007; Ibata et al. 2013; Tully 2013; Tully et al. 2015). Interestingly, the plane of satellites uncovered by Ibata et al. (2013), which contains nearly half of all known satellites around M 31, is found to rotate in the same direction as the halo GC population, although their rotation axes are offset by ~45° on the sky. Even though Veljanoski et al. (2014) found no correlation between the dwarf galaxies that are members of the rotating plane and the outer halo GCs, the parent galaxies of the latter could have had a similar configuration with correlated angular momenta, much like the satellites comprising the rotating plane observed today.
Apart from M 31, to date only a few attempts have been made to explore the kinematics of GC systems in spiral galaxies. Olsen et al. (2004) studied the GC kinematics hosted by six spiral galaxies in the nearby Sculptor group. For two of them, they found the GCs to exhibit significant rotation in the same sense as the HI gas. For the remaining four, the authors found tentative rotation signals, which may be influenced by the very low number of clusters. Nantais & Huchra (2010) analysed the GC system of nearby spiral M 81, and found it to be highly rotating with an amplitude of 108 ± 22 km s-1. Their GC sample only extends to ~10 kpc in projection, however.
On the other hand, there are numerous studies targeting elliptical galaxies with varied results. While it is not uncommon to find rotating GC populations in elliptical galaxies, it is rare to detect such a phenomenon beyond a few tens of kpc in projection. Schuberth et al. (2010) found the blue GC population around NGC 1399 to show notable rotation out to ~60 kpc in projection, while the red GCs are consistent with being fully pressure supported. On the other hand, in NGC 4636 it is the red GCs that exhibit a rotation signal out to ~40 kpc in projection, while the blue populations show only marginal evidence for such a coherent motion (Schuberth et al. 2012). Strader et al. (2011) detected significant rotation of the GCs around M 87 out to at least 55 kpc in projection, while Blom et al. (2012) found evidence for rotation in each of the distinct three subpopulations of GCs around NGC 4365, all located within 60 kpc in projection. Pota et al. (2013) analysed the kinematics of GCs hosted by 13 early-type galaxies, and found varying results. Typically, the red GCs were found to exhibit a higher rotation amplitude than their blue counterparts. These authors also detected a significant rotation signal out to ~90 kpc in projection for NGC 1407 and M 87.
To gain further physical insight regarding the possible origin of a rotation signal in galaxy halos, and in particular of M 31’s halo, we turn to numerical simulations and explore the kinematics of mock GC systems in galactic halos created in the Aquarius project (Springel et al. 2008; Cooper et al. 2010). The aim is to constrain how likely it is for a rotational signal to be detected from a halo GC population that has an accreted origin, and to what extent one can constrain the direction of the angular momentum of a stellar halo using the GCs as tracer objects. The Aquarius galactic halos are excellent study cases because they share many key properties observed in M 31 (see Sect. 2.1). This paper is organized as follows: in Sect. 2 we describe the Aquarius simulations, how we create mock GC systems around each primary halo, and how we determine their kinematic properties. In Sect. 3 we describe the kinematics of the generated GC systems in a statistical sense, discussing each Aquarius system individually. Finally, the results of this study are summarized and discussed in Sect. 4.
2. Methodology
2.1. The Aquarius simulations
The Aquarius project is a suite of high resolution simulations that follow the formation and growth of 6 dark matter halos in a hierarchical ΛCDM universe (Springel et al. 2008). These halos, dubbed Aq-A to Aq-F, were selected from the Millenium-II cosmological simulation, and were individually re-simulated using the parallel Tree-PM GADGET-3 code, an updated version of GADGET-2 (Springel 2005). Each halo comprises more than 108 individual dark matter particles, and has a total mass of 1–2 × 1012M⊙. Mass values in this range are typically estimated for the Milky Way and M 31. In this paper, we use the “level 2” simulations, the highest resolution available for all six halos1.
 |
Fig. 1 Left panel: metal-poor ([Fe/H] ≲−1.4) stellar density map of M 31 in standard tangential coordinates. Right panel: equivalent stellar halo of the simulated Aq-C, seen from 1 Mpc away. The displayed region is 300 × 300 kpc wide. To give a better sense of scale, a dashed purple circle with a radius of 100 kpc is drawn in both panels. Similar debris resulting from accretion events are easily seen in the halos of both M 31 and Aq-C. In the real and the simulated galaxy, the accreting substructures have anisotropic distributions on the sky. We note that the entire Aq-C stellar halo is built from accreted material since the simulations contain no in situ components. |
By coupling the dynamical information of the dark matter particles to galform, the Durham semi-analytic galaxy formation model (Bower et al. 2006), Cooper et al. (2010) was able to imprint baryonic content into the Aquarius halos. To do this, at each output of the dark matter simulation, Cooper et al. (2010) assigns stellar properties such as ages, luminosities, masses and metallicities to 1% of the most bound dark matter particles in those halos for which the semi-analytic model predicts that stars will be formed. The 1% fraction is chosen so that the models can reproduce the observed distributions of half-mass radii, as well as the observed profiles and velocity dispersions of the surviving satellites. This method, with which 4–6 × 105 particles are tagged, is very suitable for tracing the build-up and evolution of accreted stellar halos without needing to include gas physics. In addition, the post-processing done in this way is considerably less computationally expensive than running a hydrodynamical simulation on the same scale; the semi-analytic model takes short time to execute and it can be run multiple times in order to determine the most realistic values for the free parameters.
Given that the dynamics in these simulations are collisionless, it is important to note that these models do not track the formation and evolution of in situ stellar populations. For example, our sample of Aquarius halos are likely to host a massive disk, since no major merger has occurred in the past several Gyrs (see e.g. Scannapieco et al. 2009). The existence of such a disk does mean that a galaxy is likely to have a well-defined angular momentum, at least in the inner regions. However, the orientation of the angular momentum of the disk is often correlated with that of the dark matter halo (Bett et al. 2010). In addition, the existence of a massive disk is likely to influence the orbits and the disruption times of the infalling satellites. Nonetheless, we do not expect this to have any qualitative impact on our analysis.
The Aquarius simulations are thus well suited for achieving our goal, which is to study the kinematics of outer halo GC systems that primarily have an external origin, hosted by galaxies analogous to M 31. Figure 1 presents important similarities between M 31’s stellar halo, shown in the left panel, and that of Aq-C for instance, displayed in the right panel. Both halos are abundant in stellar substructures of various forms that are the indications of past accretion events. The disrupted substructures in these halos are not spherically distributed but lie along a particular direction, which is a very important property that has the power to potentially provide information regarding the origin of the progenitor satellites (Helmi et al. 2011). While this has not been strictly quantified in the case of M 31, looking at the left panel of Fig. 1 it can easily be seen that most of the stellar debris is indeed aligned along the south-east to north-west direction. Similar anisotropy is readily observed in the simulations as well. Finally, and most importantly, many of the satellites that contribute to the build-up of the Aquarius stellar halos are massive enough to be likely parents of GCs, and their accretion can result in a formation of a GC system akin to that observed in M 31 as we discuss below.
2.2. Creating mock globular cluster systems
We create mock GC systems of the final snapshot of the simulation around the main Aquarius halos using the dark matter particles tagged with stellar properties by Cooper et al. (2010). The resolution of these simulations does not allow for individual GCs to be resolved – however, these objects would undoubtedly exist – so we assume that certain tagged particles can also represent the position and velocity of a GC contained within them. We are unconcerned with the physical characteristics of the GCs (ages, metallicities, luminosities, sizes), but are only interested in their spatial and kinematic properties. By carefully selecting sets of these particles, we are effectively building mock GC systems around the Aquarius galaxies.
2.2.1. Galaxy scaling and placement of virtual observers
Of all the Aquarius holos, the Aq-A halo has a total mass most similar to M 31 (Fardal et al. 2013), and so we use it as a reference point. It also has the largest total mass and is the most radially extended in nature. In order to explore the kinematic properties of GC systems in galaxies that have equal total mass but different formation histories, we scale the positions and velocities of the remaining Aquarius halos to match the mass of Aq-A. This is done via the scaling 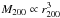 and
and 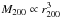 (Helmi et al. 2002).
(Helmi et al. 2002).
Prior to generating the mock GC systems, we “observe” each individual halo. This means that we reformat the simulated data in way to emulate it being obtained by a virtual observer placed 1000 kpc from the centre of the primary galaxy. The 3D position of each star particle is transformed to a set of pseudo-standard coordinates – the particles are projected onto a plane passing through the centre of mass of the primary halo and perpendicular to the line of sight of the virtual observer – while the 3D velocity is converted to a line-of-sight velocity according to the location of the observer. The right panel of Fig. 1 shows how Aq-C is seen from one such perspective.
We place 16 virtual observers around each Aquarius galaxy. Three are located along the principal axis of the dark matter halo. The remaining 13 are arranged in a regular pattern on a hemisphere centred on the target system. Of these 13, one observer is placed at the arbitrarily chosen “pole” with polar coordinates (θ,φ) = (0,0) in the reference frame of that hemisphere. The remaining 12 observers are grouped into three sets having polar angles θ = (45,90,135) deg, and the 4 observers in each such set are separated by 45 deg in azimuth, i.e. φ = (0,45,90,135) deg.
2.2.2. Build-up of a halo GC system
Given the design of the Aquarius simulations, our mock GC systems are fully populated by objects donated from the accreted dwarf galaxies, i.e. there is no in situ contribution. If such clusters exist, they are likely dominant in the central regions of the galaxy, which we do not consider in this work. Of course, it is possible that some of the in situ clusters might be “kicked” to a larger radius by the complex interactions between the primary galaxy and the accreting components, but such cases are expected to be rare. Accreted satellites are eligible to donate GCs to the primary halo only if they have a stellar mass higher than 106M⊙. The number of GCs donated by each stream is related to its stellar mass.
In their model, Cooper et al. (2010) chose to tag 1% of the most bound particles with stellar properties, successfully reproducing the structural properties and the luminosity function of the surviving satellites around the main halos. This choice, however, caused the luminosity of Aq-A to be ~100 times fainter than that of M 31 even though it has a similar total mass and its stellar halo is approximately as extended as that of our neighbour. This effectively implies a steeper M∗/Mhalo relation at the faint end than the values used by e.g. Starkenburg et al. (2013), who also use the Aquarius suite. Had the semi-analytic model been tuned in a way to make the halo of Aq-A have similar luminosity to that of M 31, the stellar streams around Aq-A would also be brighter and of higher mass. This would in turn imply that they are able to carry more GCs than their current mass ranges suggest particularly compared to the amount of GCs observed in dwarf galaxies (e.g. Miller & Lotz 2007; Peng et al. 2008; Georgiev et al. 2010; Veljanoski et al. 2014).
This is why we decided to populate mock GC systems according to the following rules: If the predicted stellar mass of the progenitor according to Cooper et al. (2010) is between 106 and 107M⊙, that progenitor will contribute between 7 and 19 GCs, a value chosen uniformly at random. If the accreted dwarf galaxy has a mass in the range of 107–108M⊙, it will donate between 15 and 35 GCs, and if its mass is larger than 108M⊙ the contribution will range from 35 to 55 GCs. Taking this into consideration, the number of GCs donated by each stream having a mass in the above ranges is carefully scaled in such a manner that on average a mock GC system created around Aq-A has as many members residing beyond 30 kpc in projection – seen from a randomly placed virtual observer around that galaxy – as found in the halo of M 31. It is worth nothing that these scalings are consistent with the recently measured correlations between the number and mass of globular cluster systems and the host halo total mass by Harris et al. (2015).
As we want to create halo GC systems, only particles residing at projected radii ≥30 kpc may be chosen to represent GCs. To create a spatially unbiased sample in the generation process, the number of GCs a stream can donate to the galaxy, chosen based on its mass, is further multiplied by the fraction of its particles that have projected radii ≥30 kpc. This choice is based on the assumption that GCs follow the light profile of their parent dwarf galaxies or stellar streams. The limit of 30 kpc, chosen semi-arbitrarily, marks the point where the stellar halo starts to dominate in the case of M 31, and is appropriate for our simulated galaxies given their mass and the radial range to which the star particles extend to. An additional motivation comes from observations of nearby galaxies, in which it is difficult to disentangle the in situ from the accreted stellar and GC populations within this radial limit.
2.2.3. Radial profile constraints, and GC selection algorithm
Because we are trying to create GC systems analogous to that of M 31, we require the clusters in our simulations to follow the projected radial number density profile of the star particles. In M 31, the metal-poor halo stars and halo GCs have similar radial number density profiles that have the same overall shape, and features of interest are found at the same projected distances (see Fig. 11 in Huxor et al. 2011). This is unsurprising given the likely common origin of a dominant fraction of GCs and halo stars in this galaxy. Therefore, we determine the projected radial number density profile for each of the primary Aquarius galaxies self consistently. Figure 2 displays the average of 16 different profiles as seen by the virtual observers placed around each simulated galaxy. For comparison, the figure also shows the radial number density profile of metal-poor stars in the outer halo of M 31, represented by an intrinsic (not projected) power law with index of − 3.34 (Ibata et al. 2014) and two generic power laws having indices of − 3 and − 4. From Fig. 2 it can easily be seen that the projected profiles of Aq-A, Aq-C, and Aq-D are similar to that of M 31, while Aq-B and Aq-E are considerably steeper and hence more compact in nature.
 |
Fig. 2 Coloured lines represent the average stellar radial number density profiles of each of the five Aquarius halos considered, as seen by 16 observers, 3 of whom are located along the principal axis of the respective dark matter halo, while the rest are arranged in a regular pattern spanning one hemisphere centred on the target galaxy (see text for details). The black line shows the stellar radial profile of metal-poor stars in the halo of M 31, represented by a power law with index of − 3.34 (Ibata et al. 2014). For reference, two generic power laws having indices of − 3 and − 4 are plotted with dashed lines. |
In summary, we generate a mock GC system following this algorithm: a stellar halo is observed from the point of view of each observer. Following this, the contribution of each stellar stream towards the build-up of the GC system is decided. The stellar halo is then divided into six equal projected radial bins between 30 and 150 kpc. The number of clusters in each radial bin is determined by the stellar radial number density profile, as measured by the respective observer. Stellar particles are then randomly chosen to represent the positions and velocities of GCs from the appropriate streams in a way to populate the radial bins following the conditions detailed above. Throughout the selection process, no restriction is put on how the GCs are selected in terms of their azimuthal distribution. However, since the azimuthal distribution of the accreted streams is not uniform, the GCs are also likely to depict some amount of anisotropy.
2.3. Kinematic modelling
The main goal of this paper is to determine the kinematic properties of the mock GC systems generated around the Aquarius galaxies. Following the example set by Veljanoski et al. (2014, 2015), we construct a kinematic model and then apply Bayesian tools to determine the most likely values for its free parameters. Our model features two main components, one that constrains the velocity dispersion of a GC system, while the other models the overall rotation of the system, if present.
For the overall rotation component, we adopt the model described in detail in Côté et al. (2001), which has the form: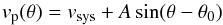 (1)where vp and θ are the radial velocities and position angles of the GCs, and θ0 the position angle of the rotation axis of the GC system respectively. The rotational amplitude is denoted A, while vsys represents the systemic radial motion of the GC system as a whole. For each halo, vsys is the mean velocity of all particles located within 30 kpc of the centre, as seen from each observer individually. This is equivalent to adopting the systemic motion of the host galaxy as the mean velocity of a GC system and is a common practice when determining the kinematic properties of real GC systems.
(1)where vp and θ are the radial velocities and position angles of the GCs, and θ0 the position angle of the rotation axis of the GC system respectively. The rotational amplitude is denoted A, while vsys represents the systemic radial motion of the GC system as a whole. For each halo, vsys is the mean velocity of all particles located within 30 kpc of the centre, as seen from each observer individually. This is equivalent to adopting the systemic motion of the host galaxy as the mean velocity of a GC system and is a common practice when determining the kinematic properties of real GC systems.
We assume that the velocity dispersion can be well represented by a Gaussian which does not vary as a function of projected distance from the centre of the galaxy. Mathematically, it can be expressed as: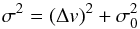 (2)where σ0 is the intrinsic velocity dispersion of the GC system around a particular galaxy and Δv are the uncertainties in the radial velocities of the GCs. In this work, we do not aim to simulate the observations and the data acquisition process; assign observation uncertainties to the radial velocities of the GC particles to be ±15 km s-1, a typical value expected when observing a cluster near the peak of the GC luminosity function observed with a 4-m ground-based facility, with a signal-to-noise ratio of 3 <S/N< 8.
(2)where σ0 is the intrinsic velocity dispersion of the GC system around a particular galaxy and Δv are the uncertainties in the radial velocities of the GCs. In this work, we do not aim to simulate the observations and the data acquisition process; assign observation uncertainties to the radial velocities of the GC particles to be ±15 km s-1, a typical value expected when observing a cluster near the peak of the GC luminosity function observed with a 4-m ground-based facility, with a signal-to-noise ratio of 3 <S/N< 8.
Putting together Eqs. (1) and (2), we are able to construct our kinematic model which has the form: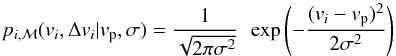 (3)where, as described earlier, vp and σ are the overall rotation and velocity dispersion of the GC system, and vi are the radial velocities of the GCs. The likelihood function for the above model is therefore:
(3)where, as described earlier, vp and σ are the overall rotation and velocity dispersion of the GC system, and vi are the radial velocities of the GCs. The likelihood function for the above model is therefore: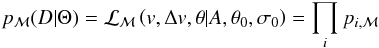 (4)in which v, Δv and θ are the observed properties of the GCs, while A, θ0, σ0 are the free parameters of the model. The index i loops over each GC. In the following analysis, we assume flat priors for all free parameters. One advantage of our approach is that we characterize the rotation (if present) and dispersion simultaneously, and thus avoid any biases that could be introduced when trying to model these properties in succession.
(4)in which v, Δv and θ are the observed properties of the GCs, while A, θ0, σ0 are the free parameters of the model. The index i loops over each GC. In the following analysis, we assume flat priors for all free parameters. One advantage of our approach is that we characterize the rotation (if present) and dispersion simultaneously, and thus avoid any biases that could be introduced when trying to model these properties in succession.
The likelihood function is computed via a brute-force method over a regular grid shaped by the free parameters of the kinematic model. In these computations, the rotation amplitude A and the velocity dispersion σ0 span the ranges from 0 to 150 km s-1and from 0 to 200 km s-1respectively, both with resolution of 3 km s-1. The rotation axis θ0 is searched in the interval between 0 and 2π rad with a step size of 0.15 rad. We carefully tested the choice of parameter ranges and the sampling, and find them to give excellent balance between computational speed and resolution of the likelihood function and the posterior probability distributions. Once the likelihood function is determined, we calculate the marginalized posterior probability distribution function for each free parameter.
3. Kinematic analysis
The purpose of this experiment is to study the kinematic properties of mock GC systems as if they were observed in the same fashion as the GC system of M 31. In order to get a statistically more robust estimate, and to reduce Poisson noise effects, we independently generate 100 mock GC systems for each of the 16 observers placed around the Aquarius halos via our prescription detailed in Sect. 2.2. The multiple observers ensure that we can analyse the halo from many different perspectives, since in reality galaxies have many different orientations that influence the measurements. Having observed the Aquarius galaxies from different perspectives allows us to compare the kinematic properties of the associated mock GC systems as a function of galaxy orientation. Iterating the procedure 100 times per observer helps to determine the representative properties of a typical GC system that could exist in that particular halo.
We apply our Bayesian methodology as described in Sect. 2.3 to each of these systems, and calculate the most likely values for the amplitude and axis of rotation and for the velocity dispersion. The degree of rotation in each GC system is typically classified by the ratio between the maximum rotation amplitude and the velocity dispersion 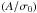 , also called the kinematic ratio. If (A/σ0) < 0.5, the system is deemed to be non-rotating (or slowly rotating); if 0.5 < (A/σ0) < 1.0, the system has a non-negligible rotation signature; if (A/σ0) > 1.0, the system is a fast rotator. For reference, the kinematic ratio of the halo GC system of M 31 is 0.67 (Veljanoski et al. 2014). In that study, the authors applied a similar but not identical kinematic model since they also considered how the velocity dispersion varies as a function of projected radius. Applying the exact model used in this study to the data presented in Veljanoski et al. (2014) we find the kinematic ratio of the M 31 outer halo GC system to be 0.93.
, also called the kinematic ratio. If (A/σ0) < 0.5, the system is deemed to be non-rotating (or slowly rotating); if 0.5 < (A/σ0) < 1.0, the system has a non-negligible rotation signature; if (A/σ0) > 1.0, the system is a fast rotator. For reference, the kinematic ratio of the halo GC system of M 31 is 0.67 (Veljanoski et al. 2014). In that study, the authors applied a similar but not identical kinematic model since they also considered how the velocity dispersion varies as a function of projected radius. Applying the exact model used in this study to the data presented in Veljanoski et al. (2014) we find the kinematic ratio of the M 31 outer halo GC system to be 0.93.
 |
Fig. 3 Top panel: highly rotating (A/σ0 = 1.38) mock GC system around Aq-A, observed from perspective (θ,φ) = (0,0). The colours of the points marking the positions of the GCs correspond to their radial velocity as seen by the virtual observer. The arrow in the bottom right corner of the map indicates the orientation of the angular momentum of the stellar halo as seen on the plane of the sky. Four diagnostic plots are displayed below each of the two maps. The top left shows the line-of-sight velocities of the GCs as a function of their position angle. The best fit rotation curve is fitted through the plots according to Eq. (1). The horizontal dashed line represents the systemic velocity of the halo. The remaining three plots (moving clockwise) display the posterior probability distribution functions for the amplitude, velocity dispersion, and rotation axis of the mock GC system as determined by our Bayesian machinery. The peak of each distribution and the 1−σ uncertainties are indicated by the dashed and solid vertical lines, respectively. |
 |
Fig. 4 Same as Fig. 3, but for a mock GC system observed from (θ,φ) = (135,0), which shows no rotation signal (A/σ0 ≈ 0). |
To illustrate how our cluster selection and kinematic analysis algorithms work in practice, we show two examples in Figs. 3 and 4. Figure 3 shows a mock GC system around Aq-A observed from the perspective (θ,φ) = (0,0), which exhibits a notable rotation signal (A/σ0 = 1.38). The system shown in Fig. 4, observed from the perspective (θ,φ) = (135,0), does not appear to be rotating (A/σ0 ≈ 0). In addition, four diagnostic plots are shown below each of the example maps. Three of these give the posterior probability distribution functions for the free parameters of our kinematic model, while one is a plot of the line-of-sight velocities of the GCs versus their position angles as seen on the sky. On these plots one can clearly see the presence, or absence, of a rotation signature.
In order to check whether the azimuthal distribution of the GCs around each Aquarius halo has any effect on the kinematic results we derive in our analysis, we select a subsample of our mock systems that have similar azimuthal distributions to the globulars around our neighbour. This is done in the following manner: we split the halo of M 31 into four equal quadrants, the borders of which are the natural major and minor axis of its disk, as seen on the sky. Counting the number of GCs in each region, we find that one quadrant has ~1σ more and one quadrant has ~1σ less than the average number of GCs contained in all four quadrants. We look for the same spatial property in our mock systems by separating the halos into four quadrants where the borders are marked by the lines due north-south and east-west, as seen on the arbitrarily oriented sky by each observer. We then select those systems which feature two quadrants that deviate from the mean by 1σ: one quadrant is required to be underpopulated and the other overpopulated with clusters. On average, nearly half of all generated GC systems around the five Aquarius halos satisfy this criteria. Although the orientation of the quadrants is chosen arbitrarily, we note that this particular choice has no effect on the results. Choosing a different, random orientation for the quadrants does not change the results that we discuss below.
Table 1 presents the main bulk kinematic properties of the five Aquarius galaxies that we consider in this work. The table shows that on average little rotation signal is detected when attempting to constrain the kinematics of a GC system by viewing it from a random direction. However, when looking from the “correct” point of view, one can indeed detect a significant degree of rotation. In what follows we describe the results for each halo individually. We focus on the bulk kinematic properties of the GC systems generated around each halo, while also investigating how well the true kinematic properties of the GC systems are recovered by our analysis, and to what degree we can constrain the direction of of the angular momentum vector of the stellar halos by studying the motions of the associated GCs.
Bulk kinematic properties of the mock GC systems in the Aquarius galaxies.
3.1. Aq-A
Aq-A has a virial mass of 1.84 × 1012M⊙, the highest of the Aquarius halos. Out of the seven streams that have stellar masses higher than 106M⊙ and abide in the outer regions of this halo, six donate at least 10 GCs, while two of them contribute more than 17 GCs on average. A typical mock GC system of Aq-A comprises 84 members. The mean uncertainty with which the rotation amplitude, rotation axis, and velocity dispersion are determined is 17 km s-1, 42 deg, and 7 km s-1 respectively2.
Figure 5 shows a histogram of the kinematic ratio for all mock GC systems generated in the halo of Aq-A, regardless of where the virtual observers are placed. It is clear that the mean kinematic ratio for all mock GC systems is only 0.3, as shown by the vertical solid line in the figure. In fact, the chance of observing a mock halo GC system that has a kinematic ratio as large as that observed in M 31 or larger when Aq-A is observed from a random perspective is, on average, lower than 0.1%.
This kinematic picture changes significantly once we look at each observer individually. Figure 6 displays in histogram format the kinematic ratio of the mock GC systems as measured by the 16 observers placed around Aq-A. The histogram clearly shows that the results are highly dependant on the location of the observer. For instance, the observer located at (θ,φ) = (0,0) in an arbitrary oriented reference frame centred on Aq-A, detects the highest rotation signal of all the observers, while the observer located at (θ,φ) = (135,0) measures no rotation signature. From the favourable perspective, (θ,φ) = (0,0), the probability of observing a GC system that has a A/σ at least as high as the halo GC system around M 31 is 30%. We note that when determining the kinematic parameters for the GC systems observed from this perspective, the corresponding uncertainties for the rotation amplitude, rotation axis, and velocity dispersion are 16 km s-1, 15 deg, and 6 km s-1, respectively.
The histograms drawn with dashed lines in Figs. 5 and 6 correspond to the subsamples of GC systems that have azimuthal distribution similar to the halo GC system of M 31. The figures show that this subsample of systems does not deviate from the trends set by the overall population. The same holds true for the other four halos we are exploring.
In Fig. 7 we investigate how well the true kinematic properties of the mock GC systems are recovered by our kinematic analysis. Here we plot the kinematic ratio of the mock GC systems around Aq-A versus the difference between the position angle of the true angular momentum of each system projected onto the plane of the sky, and the position angle of the axis of rotation as determined by our kinematic analysis. The top panel in this figure shows the systems observed from the perspective from which the detected rotation signal is highest (θ,φ) = (0,0), while the systems displayed in the middle panel are observed from a perspective with no such signal, (θ,φ) = (135,0). The bottom panel in this plot shows all mock GC systems, irrespective of the viewing perspective. The dotted horizontal line in these panels represents the kinematic ratio of M 31’s outer halo GC system. For the cases in which the determined kinematic ratio is at least as high as that of the outer halo GC system of M 31, the difference between the projected angular momentum and the measured rotation axis is less than 35 deg for 86% of the systems, i.e. for 35 of the 40 systems that have A/σ0 ≥ 0.93. Naturally, when the rotation signal is zero or spurious, as it is in the middle panel in Fig. 7, such a comparison cannot be made.
 |
Fig. 5 Kinematic ratio A/σ0 for all generated mock GC systems in the halo of Aq-A, regardless of viewing angle. The dashed histogram shows the subsample of systems that have similar azimuthal distributions to the halo GC system of M 31 (see text for details). The solid and dashed vertical lines represent the mean kinematic ratio measured for all systems and for the azimuthally selected subsample of systems, respectively. |
The idea that a GC system can be used to constrain the kinematics of the halo it is inhabiting is further supported by Fig. 8. Here we plot the kinematic ratio of all our mock GC systems, regardless of the viewing perspective, versus the angular difference between the true 3D angular momentum vector of those GC systems and the net angular momentum of all star particles located beyond 30 kpc, i.e. in the outer halo. We find that for 86% of the cases, the mock GC systems constrain the orientation of the angular momentum of the stellar halo within 65 deg of the true direction. This number is reduced to only 25 deg if we consider GC systems having A/σ0 ≥ 0.93.
 |
Fig. 6 Kinematic ratio of the generated GC systems around Aq-A for each of the 16 individual observers in histogram format. The dashed histograms show the subsample of systems that have similar azimuthal distributions to the GCs in the halo of M 31. The solid and dashed vertical lines represent the mean kinematic ratio measured for all systems and for the azimuthally selected subsample of systems, respectively. |
3.2. Aq-B
In contrast to Aq-A, Aq-B is the least massive Aquarius halo; it has a virial mass of 0.82 × 1012M⊙ prior to scaling. It is also the most compact of the halos we are considering. As a result, there are only four streams that can donate GCs to the halo of this galaxy. Two of these streams contribute ~10 while the other two supply ~6 members to the mock cluster systems. The ensembles have 30 members on average. The mean uncertainty when determining the rotation amplitude, axis, and velocity dispersion are 32 km s-1, 50 km s-1, and 12 km s-1, respectively.
The top left panel in Fig. 9 shows that on average the mock GC systems around this halo show little to no rotation signal, with the mean kinematic ratio being less than 0.1. Breaking down the analysis for each different viewing perspective (see Appendix A), we note that there is one observer located at (θ,φ) = (90,90) who would see a significant mean value of (A/σ) of 0.8. While this kinematic ratio is similar to the one around Aq-A when viewed from the favourable perspective, the circumstances that give rise to it are different. Closer inspection reveals that when observed from perspective (θ,φ) = (90,90), the halo Aq-B is dominated by one of the two streams contributing ~10 clusters to its halo. This stream passes through the centre of Aq-B, and the GCs that it donates make up at least 50% of the total number in a typical system. Thus, the entire rotation signal we are detecting, if present, is due to the GCs associated with this stream. The other and usually dominant stellar stream – when viewed from this perspective – projects on the sky in such a way that it contributes ~5 GCs to the halo, but they have little effect on the net rotation signal we are measuring.
The middle panel of the top row in Fig. 9 shows the difference in angle between the orientation of the angular momentum, projected on the plane of the sky, and the rotation axis determined through our kinematic analysis as a function of A/σ0. Even for the systems that exhibit a significant rotation signal, there is no consistent agreement between the true and the derived orientation of the angular momentum. This is primarily due to the low number of clusters available for the analysis. The low number statistics is also the primary contributor toward the large uncertainty in determining the kinematic parameters for the systems around this halo. This also makes it impossible to constrain the direction of the angular momentum of the outer stellar halo around Aq-B using the GCs as tracers, as shown in the third panel of the first row in Fig. 9.
 |
Fig. 7 Kinematic ratio of the mock GC systems in the outer halo of Aq-A versus the difference between the position angle of their angular momentum projected on the plane of the sky and the position angle of the rotation axis as determined by our kinematic analysis. The top panel shows the systems seen from an observer located at (θ,φ) = (0,0) who detects the maximum rotation signal, and the middle panel shows the systems seen by an observer located at (θ,φ) = (135,0) who detects no such structured motion. The bottom panel displays all systems regardless of the viewing perspective. We note that the projected angular momentum and rotation axis agree well for systems that exhibit a high degree of rotation. |
 |
Fig. 8 Kinematic ratio of the mock GC systems around Aq-A versus the difference in angle between their true 3D angular momentum vector and the 3D angular momentum vector of the outer halo star particles, regardless of the viewing perspective. The misalignment between the GC and halo angular momentum is relatively small, especially for high kinematic ratios. |
3.3. Aq-C
Even prior to the scaling, Aq-C had a similar virial mass to Aq-A. Aq-C has the brightest stellar halo beyond 30 kpc amongst the galaxies comprising the Aquarius suite of simulations. There are nine streams in its outer halo that are eligible to carry GCs, with five streams donating on average more than 10 clusters. Of these five streams, two typically donate over 20 clusters, while one stream donates over 30 members to the GC ensembles generated around Aq-C. A typical mock GC system in the outer halo this galaxy contains 106 members. The mean uncertainty of the kinematic parameters is 15 km s-1, 31 deg, and 7 km s-1 for the amplitude, rotation axis, and velocity dispersion, respectively.
On average, the mock GC systems generated around Aq-C show a weak rotation signal when observed from a random location, as shown in Fig. 9. With a A/σ0 = 0.4, the GC systems around this galaxy have the highest mean kinematic ratio when the observing perspective is not taken into account, save for Aq-E. Even so, the probability of observing a GC system that has a kinematic ratio at least as high as the one seen for the outer halo cluster system of M 31 is only 0.1.
Examining the distributions of A/σ0 for the mock cluster systems from each of the 16 different viewing perspectives, we can single out one such view point, (θ,φ) = (90,45), from which the observer detects a significant degree of rotation. In fact, when the halo is viewed from this perspective, the A/σ0 ~ 1. In addition, the probability of observing a GC system with the same or larger kinematic ratio compared to M 31 is 0.6.
Figure 9 also shows the comparison between the orientation of the recovered rotation axis and the angular momentum of the GC systems projected on the plane of the sky as a function of A/σ0. These quantities agree to within ~65 deg for 86% of the mock GC systems generated around Aq-C. It is interesting to see that in systems having (A/σ0 ≥ 0.93), we observe a relatively high misalignment of ~40 deg between these two quantities. Even though this misalignment is not significant considering the uncertainty with which the rotation axis is determined, it is higher than naively expected. By carefully examining the stellar streams around Aq-C, we found this effect to be largely caused by the most massive, dominant constituent of this halo. This stream loops a few times around the centre of Aq-C, its shape resembling an incomplete Rosetta pattern. While this object is the primary driver of the rotation signal, it only contributes ~25% of the total number of clusters in a typical system when the halo is observed from this perspective. The scatter in position and velocity of the remaining GCs is the cause, since their parent streams are not aligned with the dominant stream.
The direction of the 3D angular momentum of the entire stellar halo, on the other hand, can be quite well constrained considering the angular momentum of the mock GC system. The last panel of the second row in Fig. 9 shows that these quantities agree with each other to within 15 deg for 86% of the generated GC systems, regardless of the kinematic ratio.
3.4. Aq-D
At first glance, Aq-D looks quite similar to Aq-C: they both have luminous extended stellar outer halos, and nearly identical virial masses. The outer halo of Aq-D comprises 10 streams with stellar masses larger than 106M⊙. Four of these streams contribute more than 10 systems, while one stream contributes more than 25 GCs to the generated mock GC systems on average. A typical ensemble around Aq-D contains 94 clusters. The mean errors of the rotation amplitude, axis, and the velocity dispersion are 13 km s-1, 47 deg, and 5 km s-1, respectively.
Figure 9 shows that mock GC systems generated around Aq-D, much like those around the other Aquarius halos, exhibit very weak signs of coherent rotation. The mean kinematic ratio of all mock GC systems populating the outer halo of Aq-D is ~0.2. The chance of observing a GC system that has similar kinematic properties to that inhabiting the outer halo of M 31 is <1%. Unlike the other cases we have considered so far, the GC systems around Aq-D show no notable rotation signal even when we consider the 16 viewing perspectives separately; no viewing angle shows a significant average kinematic ratio.
To understand the reason behind this, we need to consider the assembly history of the structure around Aq-D. Vera-Ciro et al. (2011) studied in detail the evolution of the dark matter halo surrounding the Aquarius galaxies. In the case of Aq-D, they found that until redshift of z ≈ 0.75, most of the material infall occurred along the primary filament this halo was situated on. After this time, material was fed into the halo of Aq-D mainly via a secondary filament, oriented nearly perpendicular to the primary filament that dominates the local large-scale structure. Vera-Ciro et al. (2011) find that the dark matter halo of Aq-D changes its orientation owing to the change in infall direction. This change in infall direction is likely the main reason why no rotation signal is detected in the mock GC systems around this halo.
Since we are unable to detect any significant net rotation signal, the determined rotation axis is very uncertain. As a result, it is not possible to constrain the direction of the projected angular momentum of the GC systems in the halo of this galaxy, regardless of the direction they are observed from, as seen in the middle panel of the third row in Fig. 9. Conversely, by knowing the true 3D angular momentum of the GCs it is possible to put reasonable constraints on the direction on the entire outer stellar halo surrounding Aq-D. By looking at the right panel of the third row in Fig. 9, we find that the 3D angular momentum of the GC systems and that of the stellar halo agree within ~40 deg 86% of the time.
3.5. Aq-E
Aq-E is a quite compact object, similar to Aq-B. It contains the faintest stellar halo beyond 30 kpc of all the Aquarius galaxies. The outer halo of Aq-E comprises only five stellar streams eligible to donate GCs to the main potential. One of these streams dominates the halo structure and contributes on average 10 GCs. Thus there are, on average, only 20 clusters in a typical outer halo of Aq-E. The typical uncertainties of the derived kinematic parameters are 32 km s-1, 40 deg, and 15 km s-1 for the rotation amplitude, rotation axis, and the velocity dispersion, respectively.
 |
Fig. 9 Bulk kinematic properties of the mock GC systems generated in the halos around Aq-B through Aq-E. Each row corresponds to the same Aquarius galaxy. The first column shows the distribution of kinematic ratios for all GC systems, regardless of the viewing angle. The second column shows the difference in the position angle between the angular momentum of the GC systems projected on the plane of the sky and the rotation axis determined via our analysis as a function of A/σ0. The third column shows the angular difference between the orientation of the 3D angular momenta of the mock GC systems and the angular momentum of the entire stellar halo located beyond 30 kpc in projection. |
As Fig. 9 shows, the cluster systems around Aq-E have the highest kinematic ratio of the five Aquarius objects. The probability of observing a GC in the outskirts of Aq-E having the same A/σ0 as the halo clusters of M 31 is 0.7, significantly higher than for the previous cases we examined. The cause behind this observation is a combination of low number statistics in the number of contributing streams, and the dominating effect that the most extended stream has on the kinematics of the mock GC systems. This is seen more clearly when examining the distributions of A/σ0 as a function of viewing perspective. The kinematic ratio is the highest for perspective (θ,φ) = (105,−80) for which an observer can see the dominating stream extending almost perpendicularly to the line of sight (see Appendix A).
The GCs associated with the most extended stream in the Aq-E halo are the main drivers behind the rotation signal, which is due to how they sample the orbit of their parent object. These clusters alone are not sufficient to constrain the direction of the projected angular momentum of the full halo cluster system, however, mainly due to poor sampling of the streams, as seen in the bottom middle panel in Fig. 9. Even so, by knowing the 3D angular momentum of the GC system around this halo, it is possible to put broad constraints on the direction of the 3D angular momentum of the stellar halo. As the bottom right panel in Fig. 9 shows, these quantities agree within ~60 deg for 86% of the mock GC systems around this halo.
4. Conclusions
In this study we attempted to constrain the probability of finding a rotation signal exhibited by GC systems residing in the outer halos of Milky Way-sized galaxies, assembled in a cosmological setting. Using the Aquarius stellar halos from Cooper et al. (2010), we carefully selected tagged particles to mark the positions and velocities of GCs. This way we generated numerous sets of mock halo GC systems, which were observed from various viewing angles. Our comprehensive kinematic analysis yielded the following results:
-
If a stellar halo possesses net angular momentum, it will bereflected in the halo GC population as well, and can be detected as arotation signal exhibited by those clusters;
-
The amplitude of this rotation signal is highly dependent upon the viewing angle. The rotation amplitude is significant when the halo is observed from a perspective such that the true angular momentum vector of the GC system is aligned by ≲40 deg from the rotation axis determined via the projected positions and line-of-sight velocities of the GCs;
-
The orientation of the true, 3D angular momentum vector of a halo GC system is in very good agreement with that of the stellar halo, with the angular difference between the two being ~40 deg on average. This is the case provided the main streams in the halos considered are well sampled with enough GCs located beyond 30 kpc in projection.
Considering these points, we can attempt to understand the origin of the rotation signal exhibited by the halo GC systems, or more generally, the origin of the common orientation of the angular momenta amongst the substructures that comprise stellar halos, which then gives rise to the rotation signal of the associated GC systems. The Aquarius simulations were done in a cosmological setting, and their assembly process can be followed through time. In the final snapshot, it is readily seen that the distribution of stellar streams around each Aquarius halo is anisotropic (Helmi et al. 2011). Looking back through the earlier snapshots of the simulations, we note that most of the matter flows into the Aquarius halos along the dominant filaments (Vera-Ciro et al. 2011), which produces the anisotropic spatial distribution of the building blocks and satellites. Hence, provided that most of the material needed to assemble the primary halo was indeed accreted from a preferred direction, namely along the dominant filament, a rotation signal of that stellar halo is naturally expected to arise because the infalling components transfer their angular momentum to their new host. This picture is consistent with the simulations of (e.g. Li & Helmi 2008, Libeskind et al. 2011, Lovell et al. 2011) and Deason et al. (2011) also regarding the satellite population. Hence, finding stellar halos, and associated GC systems – to have a non-negligible net angular momentum is not surprising in a ΛCDM universe (Libeskind et al. 2015).
Another interesting question to consider is how the net angular momentum of the stellar halo is related to the disk of a galaxy. While the Aquarius simulations do not contain a disk component, they clearly show that there is a preferential infall along filaments, implying that the satellites, their debris, and the gas that is accreted onto the primary system have similar angular momentum orientation. Thus, it is not unreasonable to expect that, once settled, the gas to have the same rotation sense as that of the stellar halo, albeit with a much higher amplitude since it will have collapsed to the centre. This picture also explains why the rotation axis of the outer halo GCs is virtually indistinguishable from that of the GCs located in the disk of M 31. Therefore, the detection of the high rotation signal exhibited by the outer halo GC system around M 31 is not so surprising, especially since we are observing this galaxy almost edge-on.
Acknowledgments
We thank the anonymous referee for the useful comments that improved the manuscript. The authors acknowledge financial support from the European Research Council under ERC–StG grant GALACTICA–240271, NOVA, and NWO in the form of a Vici grant to A.H.. We are also grateful to the VIRGO consortium including Andrew Cooper, for collaborations carried out in the context of the Aquarius project.
References
- Abadi, M. G., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003a, ApJ, 591, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Abadi, M. G., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003b, ApJ, 597, 21 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Belokurov, V., Zucker, D. B., Evans, N. W., et al. 2006, ApJ, 642, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Schlafly, E. F., et al. 2014, MNRAS, 443, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Bett, P., Eke, V., Frenk, C. S., Jenkins, A., & Okamoto, T. 2010, MNRAS, 404, 1137 [NASA ADS] [Google Scholar]
- Blom, C., Forbes, D. A., Brodie, J. P., et al. 2012, MNRAS, 426, 1959 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Bullock, J. S., & Johnston, K. V. 2005, ApJ, 635, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, A. P., Cole, S., Frenk, C. S., et al. 2010, MNRAS, 406, 744 [NASA ADS] [CrossRef] [Google Scholar]
- Côté, P., McLaughlin, D. E., Hanes, D. A., et al. 2001, ApJ, 559, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Da Costa, G. S., & Armandroff, T. E. 1995, AJ, 109, 2533 [NASA ADS] [CrossRef] [Google Scholar]
- Deason, A. J., McCarthy, I. G., Font, A. S., et al. 2011, MNRAS, 415, 2607 [NASA ADS] [CrossRef] [Google Scholar]
- di Tullio Zinn, G., & Zinn, R. 2013, AJ, 145, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Dotter, A., Sarajedini, A., & Anderson, J. 2011, ApJ, 738, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Fardal, M. A., Weinberg, M. D., Babul, A., et al. 2013, MNRAS, 434, 2779 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Spitler, L. R., Harris, W. E., et al. 2010, MNRAS, 403, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Galleti, S., Federici, L., Bellazzini, M., Fusi Pecci, F., & Macrina, S. 2004, A&A, 416, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Georgiev, I. Y., Puzia, T. H., Goudfrooij, P., & Hilker, M. 2010, MNRAS, 406, 1967 [NASA ADS] [Google Scholar]
- Grillmair, C. J. 2006, ApJ, 645, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Grillmair, C. J., & Dionatos, O. 2006, ApJ, 643, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 2001, in Saas-Fee Advanced Course 28: Star Clusters, eds. L. Labhardt, & B. Binggeli, 223 [Google Scholar]
- Harris, W. E., Harris, G. L., & Hudson, M. J. 2015, ApJ, 806, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., & White, S. D. M. 1999, MNRAS, 307, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., White, S. D., & Springel, V. 2002, Phys. Rev. D, 66, 063502 [NASA ADS] [CrossRef] [Google Scholar]
- Helmi, A., Cooper, A. P., White, S. D. M., et al. 2011, ApJ, 733, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Huxor, A. P., Tanvir, N. R., Irwin, M. J., et al. 2005, MNRAS, 360, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Huxor, A. P., Tanvir, N. R., Ferguson, A. M. N., et al. 2008, MNRAS, 385, 1989 [NASA ADS] [CrossRef] [Google Scholar]
- Huxor, A. P., Ferguson, A. M. N., Tanvir, N. R., et al. 2011, MNRAS, 414, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Huxor, A. P., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2165 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1994, Nature, 370, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Gilmore, G., & Irwin, M. J. 1995, MNRAS, 277, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., Conn, A. R., et al. 2013, Nature, 493, 62 [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., McConnachie, A. W., et al. 2014, ApJ, 780, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Keller, S. C., Mackey, D., & Da Costa, G. S. 2012, ApJ, 744, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Koposov, S. E., Belokurov, V., Evans, N. W., et al. 2012, ApJ, 750, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y.-S., & Helmi, A. 2008, MNRAS, 385, 1365 [NASA ADS] [CrossRef] [Google Scholar]
- Libeskind, N. I., Knebe, A., Hoffman, Y., et al. 2011, MNRAS, 411, 1525 [NASA ADS] [CrossRef] [Google Scholar]
- Libeskind, N. I., Hoffman, Y., Tully, R. B., et al. 2015, MNRAS, 452, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Lovell, M. R., Eke, V. R., Frenk, C. S., & Jenkins, A. 2011, MNRAS, 413, 3013 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., & Gilmore, G. F. 2004, MNRAS, 355, 504 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mackey, A. D., & van den Bergh, S. 2005, MNRAS, 360, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Mackey, A. D., Huxor, A. P., Ferguson, A. M. N., et al. 2010, ApJ, 717, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Skrutskie, M. F., Weinberg, M. D., & Ostheimer, J. C. 2003, ApJ, 599, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Marín-Franch, A., Aparicio, A., Piotto, G., et al. 2009, ApJ, 694, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, N. F., Ibata, R. A., Rich, R. M., et al. 2014, ApJ, 787, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Peñarrubia, J., Gabany, R. J., et al. 2008, ApJ, 689, 184 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Delgado, D., Gabany, R. J., Crawford, K., et al. 2010, AJ, 140, 962 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Metz, M., Kroupa, P., & Jerjen, H. 2007, MNRAS, 374, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, B. W., & Lotz, J. M. 2007, ApJ, 670, 1074 [NASA ADS] [CrossRef] [Google Scholar]
- Nantais, J. B., & Huchra, J. P. 2010, AJ, 139, 2620 [NASA ADS] [CrossRef] [Google Scholar]
- Olsen, K. A. G., Miller, B. W., Suntzeff, N. B., Schommer, R. A., & Bright, J. 2004, AJ, 127, 2674 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, E. W., Jordán, A., Côté, P., et al. 2008, ApJ, 681, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K. M., Bridges, T. J., Hanes, D. A., et al. 2002, AJ, 123, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K. M., Stiff, D. A., Hanes, D. A., & Bridges, T. J. 2003, ApJ, 589, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Pota, V., Forbes, D. A., Romanowsky, A. J., et al. 2013, MNRAS, 428, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Romanowsky, A. J., Strader, J., Brodie, J. P., et al. 2012, ApJ, 748, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, C., White, S. D. M., Springel, V., & Tissera, P. B. 2009, MNRAS, 396, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2010, A&A, 513, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuberth, Y., Richtler, T., Hilker, M., et al. 2012, A&A, 544, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Slater, C. T., Bell, E. F., Schlafly, E. F., et al. 2013, ApJ, 762, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Wang, J., Vogelsberger, M., et al. 2008, MNRAS, 391, 1685 [NASA ADS] [CrossRef] [Google Scholar]
- Starkenburg, E., Helmi, A., De Lucia, G., et al. 2013, MNRAS, 429, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Strader, J., Romanowsky, A. J., Brodie, J. P., et al. 2011, ApJS, 197, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tully, R. B. 2013, Nature, 493, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Tully, R. B., Libeskind, N. I., Karachentsev, I. D., et al. 2015, ApJ, 802, L25 [Google Scholar]
- Veljanoski, J., Ferguson, A. M. N., Mackey, A. D., et al. 2013, ApJ, 768, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Veljanoski, J., Mackey, A. D., Ferguson, A. M. N., et al. 2014, MNRAS, 442, 2929 [NASA ADS] [CrossRef] [Google Scholar]
- Veljanoski, J., Ferguson, A. M. N., Mackey, A. D., et al. 2015, MNRAS, 452, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Vera-Ciro, C. A., Sales, L. V., Helmi, A., et al. 2011, MNRAS, 416, 1377 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The GC systems of all Aq halos
Here we show the distributions of kinematic ratios for different observing perspective for halos Aq-B through Aq-E.
 |
Fig. A.1 Same as Fig. 6 in the case of Aq-B. The GC systems viewed from perspective (θ,φ) = (90,90) show a significant mean A/σ. This is driven by GCs associated with a single dominant stream in the halo of Aq-B. See Sect. 3.2 for details. |
 |
Fig. A.2 Same as Fig. 6 in the case of Aq-C. The rotation and velocity dispersion have, on average, equal share in the kinematics of the GCs that were observed from (θ,φ) = (90,45). |
 |
Fig. A.3 Same as Fig. 6 in the case of Aq-D. Unlike the other cases we consider, the mock GCs generated around Aq-D show very weak or no rotational signal regardless of the perspective they are observed from. This is most likely related to the evolutionary history of the dark matter halo of Aq-D. See Sect. 3.4 for details. |
All Tables
All Figures
 |
Fig. 1 Left panel: metal-poor ([Fe/H] ≲−1.4) stellar density map of M 31 in standard tangential coordinates. Right panel: equivalent stellar halo of the simulated Aq-C, seen from 1 Mpc away. The displayed region is 300 × 300 kpc wide. To give a better sense of scale, a dashed purple circle with a radius of 100 kpc is drawn in both panels. Similar debris resulting from accretion events are easily seen in the halos of both M 31 and Aq-C. In the real and the simulated galaxy, the accreting substructures have anisotropic distributions on the sky. We note that the entire Aq-C stellar halo is built from accreted material since the simulations contain no in situ components. |
| In the text | |
 |
Fig. 2 Coloured lines represent the average stellar radial number density profiles of each of the five Aquarius halos considered, as seen by 16 observers, 3 of whom are located along the principal axis of the respective dark matter halo, while the rest are arranged in a regular pattern spanning one hemisphere centred on the target galaxy (see text for details). The black line shows the stellar radial profile of metal-poor stars in the halo of M 31, represented by a power law with index of − 3.34 (Ibata et al. 2014). For reference, two generic power laws having indices of − 3 and − 4 are plotted with dashed lines. |
| In the text | |
 |
Fig. 3 Top panel: highly rotating (A/σ0 = 1.38) mock GC system around Aq-A, observed from perspective (θ,φ) = (0,0). The colours of the points marking the positions of the GCs correspond to their radial velocity as seen by the virtual observer. The arrow in the bottom right corner of the map indicates the orientation of the angular momentum of the stellar halo as seen on the plane of the sky. Four diagnostic plots are displayed below each of the two maps. The top left shows the line-of-sight velocities of the GCs as a function of their position angle. The best fit rotation curve is fitted through the plots according to Eq. (1). The horizontal dashed line represents the systemic velocity of the halo. The remaining three plots (moving clockwise) display the posterior probability distribution functions for the amplitude, velocity dispersion, and rotation axis of the mock GC system as determined by our Bayesian machinery. The peak of each distribution and the 1−σ uncertainties are indicated by the dashed and solid vertical lines, respectively. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for a mock GC system observed from (θ,φ) = (135,0), which shows no rotation signal (A/σ0 ≈ 0). |
| In the text | |
 |
Fig. 5 Kinematic ratio A/σ0 for all generated mock GC systems in the halo of Aq-A, regardless of viewing angle. The dashed histogram shows the subsample of systems that have similar azimuthal distributions to the halo GC system of M 31 (see text for details). The solid and dashed vertical lines represent the mean kinematic ratio measured for all systems and for the azimuthally selected subsample of systems, respectively. |
| In the text | |
 |
Fig. 6 Kinematic ratio of the generated GC systems around Aq-A for each of the 16 individual observers in histogram format. The dashed histograms show the subsample of systems that have similar azimuthal distributions to the GCs in the halo of M 31. The solid and dashed vertical lines represent the mean kinematic ratio measured for all systems and for the azimuthally selected subsample of systems, respectively. |
| In the text | |
 |
Fig. 7 Kinematic ratio of the mock GC systems in the outer halo of Aq-A versus the difference between the position angle of their angular momentum projected on the plane of the sky and the position angle of the rotation axis as determined by our kinematic analysis. The top panel shows the systems seen from an observer located at (θ,φ) = (0,0) who detects the maximum rotation signal, and the middle panel shows the systems seen by an observer located at (θ,φ) = (135,0) who detects no such structured motion. The bottom panel displays all systems regardless of the viewing perspective. We note that the projected angular momentum and rotation axis agree well for systems that exhibit a high degree of rotation. |
| In the text | |
 |
Fig. 8 Kinematic ratio of the mock GC systems around Aq-A versus the difference in angle between their true 3D angular momentum vector and the 3D angular momentum vector of the outer halo star particles, regardless of the viewing perspective. The misalignment between the GC and halo angular momentum is relatively small, especially for high kinematic ratios. |
| In the text | |
 |
Fig. 9 Bulk kinematic properties of the mock GC systems generated in the halos around Aq-B through Aq-E. Each row corresponds to the same Aquarius galaxy. The first column shows the distribution of kinematic ratios for all GC systems, regardless of the viewing angle. The second column shows the difference in the position angle between the angular momentum of the GC systems projected on the plane of the sky and the rotation axis determined via our analysis as a function of A/σ0. The third column shows the angular difference between the orientation of the 3D angular momenta of the mock GC systems and the angular momentum of the entire stellar halo located beyond 30 kpc in projection. |
| In the text | |
 |
Fig. A.1 Same as Fig. 6 in the case of Aq-B. The GC systems viewed from perspective (θ,φ) = (90,90) show a significant mean A/σ. This is driven by GCs associated with a single dominant stream in the halo of Aq-B. See Sect. 3.2 for details. |
| In the text | |
 |
Fig. A.2 Same as Fig. 6 in the case of Aq-C. The rotation and velocity dispersion have, on average, equal share in the kinematics of the GCs that were observed from (θ,φ) = (90,45). |
| In the text | |
 |
Fig. A.3 Same as Fig. 6 in the case of Aq-D. Unlike the other cases we consider, the mock GCs generated around Aq-D show very weak or no rotational signal regardless of the perspective they are observed from. This is most likely related to the evolutionary history of the dark matter halo of Aq-D. See Sect. 3.4 for details. |
| In the text | |
 |
Fig. A.4 Same as Fig. 6 in the case of Aq-E. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


