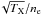| Issue |
A&A
Volume 592, August 2016
|
|
|---|---|---|
| Article Number | A157 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201527824 | |
| Published online | 24 August 2016 | |
Origin of central abundances in the hot intra-cluster medium
I. Individual and average abundance ratios from XMM-Newton EPIC
1 SRON Netherlands Institute for Space Research, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
e-mail: F.Mernier@sron.nl
2 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
3 Institute of Astronomy, Madingley Road, CB3 0 HA Cambridge, UK
4 Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
5 Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, 452 Lomita Mall, Stanford, CA 94305, USA
6 Department of Physics, Stanford University, 382 Via Pueblo Mall, Stanford, CA 94305-4060, USA
Received: 24 November 2015
Accepted: 3 June 2016
The hot intra-cluster medium (ICM) is rich in metals, which are synthesised by supernovae (SNe) explosions and accumulate over time into the deep gravitational potential well of clusters of galaxies. Since most of the elements visible in X-rays are formed by type Ia (SNIa) and/or core-collapse (SNcc) supernovae, measuring their abundances gives us direct information on the nucleosynthesis products of billions of SNe since the epoch of the star formation peak (z ~ 2−3). In this study, we use the EPIC and RGS instruments on board XMM-Newton to measure the abundances of nine elements (O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni) from a sample of 44 nearby cool-core galaxy clusters, groups, and elliptical galaxies. We find that the Fe abundance shows a large scatter (~20−40%) over the sample, within 0.2r500 and especially 0.05r500. Unlike the absolute Fe abundance, the abundance ratios (X/Fe) are uniform over the considered temperature range (~0.6−8 keV) and with a limited scatter. In addition to an unprecedented treatment of systematic uncertainties, we provide the most accurate abundance ratios measured so far in the ICM, including Cr/Fe and Mn/Fe which we firmly detected (>4σ with MOS and pn independently). We find that Cr/Fe, Mn/Fe, and Ni/Fe differ significantly from the proto-solar values. However, the large uncertainties in the proto-solar abundances prevent us from making a robust comparison between the local and the intra-cluster chemical enrichments. We also note that, interestingly, and despite the large net exposure time (~4.5 Ms) of our dataset, no line emission feature is seen around ~3.5 keV.
Key words: X-rays: galaxies: clusters / galaxies: clusters: general / galaxies: clusters: intracluster medium / galaxies: abundances / supernovae: general / dark matter
© ESO, 2016
1. Introduction
About 80−90% of the baryonic matter in the Universe is in the form of a hot and diffuse intergalactic gas, which has mostly a very low density and, therefore, is hard to observe. However, in the largest gravitationally bound regions of the Universe, which are clusters of galaxies, the density and temperature of this hot gas, or intra-cluster medium (ICM), becomes high enough for it to glow in X-rays. This ICM, which has been extensively studied by X-ray observatories over the past decades (for a review, see Böhringer & Werner 2010), is particularly rich in metals (e.g. Mitchell et al. 1976; Mushotzky et al. 1996). Since the baryonic content of the Universe just after the Big Bang consists exclusively of hydrogen and helium (and traces of lithium), these heavy elements − typically from oxygen to nickel − must have been synthesised by stars and supernovae (SNe) in the galaxy members and then ejected into the ICM (for a review, see Werner et al. 2008; de Plaa 2013).
Although the general picture of this chemical enrichment is now well established, many aspects are still poorly understood. In addition to the question of the transport mechanisms that drive the enrichment, a major uncertainty resides in the metal yields produced by type Ia (SNIa) and core-collapse (SNcc) supernovae. In fact, the nature of the SNIa progenitors and the SNIa explosion mechanisms are still under debate, while the global nucleosynthesis of SNcc highly depends on the initial mass function (IMF) and the initial metallicity of the considered stellar population. Moreover, in addition to SNe, AGB stars can also play a role in releasing lighter metals (e.g. nitrogen) or even heavy metals (via the s-process). Taken together, these unsolved questions lead to large uncertainties in predicting the global abundance ratios that are finally released by the SNe and AGB stars into the ICM.
In contrast to the remaining uncertainties in the theoretical yields from the SNe/AGB models, the current generation of X-ray observatories measures the chemical abundances in the ICM with remarkable accuracy since most transitions of H- and He-like elements from Z = 7 to Z = 28 fall within 0.2−12 keV. Thanks to the large effective area and the good spectral resolution of its European Photon Imaging Camera (EPIC, Strüder et al. 2001; Turner et al. 2001) and Reflection Grating Spectrometer (RGS, den Herder et al. 2001), XMM-Newton is particularly suitable for measuring abundances of elements like oxygen (O), neon (Ne), magnesium (Mg), silicon (S), sulfur (S), argon (Ar), calcium (Ca), iron (Fe), and nickel (Ni), especially in cool-core objects1 which exhibit a high surface brightness in X-ray and where the most prominent K-shell emission lines of these elements are clearly detected. Consequently, the accuracy of these measurements can, in principle, bring new constraints on the SNe (and AGB) models, and can lead to a deeper understanding of the chemical enrichment processes beyond galactic scales.
Several authors have reported such analyses by measuring the abundances in the ICM of nearby clusters and groups. For instance, de Plaa et al. (2007) has compiled a sample of 22 cool-core clusters and found that the standard SNIa models fail to reproduce the Ar/Ca and Ca/Fe abundance ratios. They also show that the number of SNIa over the total number of SNe highly depends on the considered models. De Grandi & Molendi (2009) have shown that Si/Fe abundance ratios are remarkably uniform over a sample of 26 cool-core clusters observed with XMM-Newton, arguing for a similar enrichment process within cluster cores. However they suggest that systematic uncertainties are too large to precisely estimate the relative contribution of SNIa and SNcc. Finally, many abundance studies have also been performed on individual objects (e.g. Werner et al. 2006; de Plaa et al. 2006; Sato et al. 2007a; Simionescu et al. 2009; Mernier et al. 2015). From these studies, and considering the actual instrumental performances of current X-ray observatories, it appears that higher quality data (i.e. with longer exposure time) spread over larger samples are needed to clarify the actual picture of the precise origin of metals in the ICM.
In this work (hereafter Paper I), we use new and archival XMM-Newton EPIC observations to measure the chemical abundances of nine elements (O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni) in the core of a sample of nearby cool-core galaxy clusters, groups, and elliptical galaxies. These EPIC observations are then combined with the RGS abundance measurements adapted from de Plaa et al. (2016) in order to derive average X/Fe abundance ratios representative of the nearby ICM. Taking into account as many systematic uncertainties as possible, we discuss the robustness of these measurements and compare them to the proto-solar abundances. In a second paper (Mernier et al. 2016, hereafter Paper II), we discuss in detail the astrophysical implications of our results, and compare our average abundance pattern presented here with predictions from theoretical SNIa and SNcc yield models.
This paper is structured as follows. In Sect. 2, we present the sample and the data reduction pipeline. In Sect. 3 we describe the spectral analysis procedure applied to our EPIC observations. Our results are presented in Sect. 4, briefly discussed in Sect. 5, and summarised in Sect. 6. Throughout this paper we assume cosmological parameters of H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7. All the error bars are given at a 68% confidence level.
XMM-Newton/EPIC observations used in this paper (see Pinto et al. 2015, for details on RGS observations).
2. Observations and data preparation
Our sample consists of the CHEERS2 catalogue (de Plaa et al. 2016), and is detailed in Table 1 (see also Pinto et al. 2015, and de Plaa et al. 2016). It includes 44 nearby (z< 0.1) cool-core clusters, groups, and elliptical galaxies for which the O viii 1s−2p line at 19 Å is detected by the RGS instrument with >5σ. More information on the intrinsic properties of these objects (e.g. fluxes) can be found in various available cluster catalogues, such as the HIGFLUGCS (Reiprich & Böhringer 2002), the REFLEX (Böhringer et al. 2004), and the ACCEPT (Cavagnolo et al. 2009) catalogues. In our sample, recent XMM-Newton observations (AO-12, PI: de Plaa) have been combined with archival data. We only select the pointings for which the combined EPIC observations (MOS 1, MOS 2, and pn) gather at least 15 ks of net exposure time. The observations that suffer from high soft flare events or calibration problems are also excluded.
2.1. Data reduction
All the data are reduced with the XMM-Newton Science Analysis System (SAS) v14.0.0 and by using the calibration files dated by March 2015. The RGS data are the same as used in Pinto et al. (2015, see their Table 1), and are reduced the same way. We reduce the EPIC data by using the standard pipeline command emproc and epproc, and, following the standard recommendations, we keep the single to quadruple pixel MOS events (PATTERN≤12), and only the single pixel pn events (PATTERN==0). Moreover, only the highest quality MOS and pn events (FLAG==0) are taken into account. We filter our observations from soft-proton flares by building good time interval (GTI) files following the method described in Mernier et al. (2015). We extract light curves within the 10−12 keV (MOS) and the 12−14 keV (pn) bands in 100 s bins, we calculate the mean count rate μ and the standard deviation σ, and we apply a threshold of μ ± 2σ to the fitted distribution. For safety (Lumb et al. 2002), we repeat the procedure for the 0.3−10 keV band in 10 s bins. The average fraction of “good” time accepted after such a filtering is ~77%, ~78%, and ~66% for MOS 1, MOS 2, and pn, respectively, although this fraction varies widely from pointing to pointing. For each object, the net exposure times of the EPIC instruments are indicated in Table 1. Combining our whole dataset, we obtain total EPIC and RGS net exposure times of ~4.5 Ms and ~5.1 Ms, respectively.
Finally, point-like sources might pollute our spectra; therefore, we need to discard all of them from the rest of our analysis. We first detect the point sources of every dataset within four spectral bands (0.3−2 keV, 2−4.5 keV, 4.5−7.5 keV, and 7.5−12 keV) using the SAS task edetect_chain. After a second check by eye, we excise circular regions with 10′′ of radius around the point sources (except in some specific situations where a larger excision radius is required to remove scattered photons from bright foreground sources). This radius size is estimated to be a good compromise between discarding the polluting flux of the point sources and keeping a maximum of cluster emission in their neighbourhood (Mernier et al. 2015). Depending on the target, the typical fraction of removed flux after discarding the point sources varies between ~0.3% and ~4%.
2.2. Spectra extraction
The sources of our sample span a wide range of sizes, masses, and temperatures, and studying their elemental abundances with EPIC over one common astrophysical scale rcore is difficult in practice. A definition of rcore as 0.2r5003 for the farther (and, by selection, hotter) clusters is commonly found in the literature (e.g. de Plaa et al. 2007); however, most of the nearest galaxy groups from our sample are seen at this radius with an angular size θ> 15 arcmin, i.e. beyond the EPIC field of view (FoV). Moreover, extracting spectra over a large θ for these cooler and more compact objects will include a lot of background, which may dominate beyond ~2−3 keV and entirely flood the K-shell lines of crucial elements such as S, Ar, Ca, or Ni. Therefore, we choose to split our sample into two subsamples:
- 1.
the “hot” galaxy clusters (kT ≥ 1.7 keV, 23 objects);
- 2.
the “cool” galaxy groups and ellipticals (kT< 1.7 keV, 21 objects).
Table 1 classifies each object in one of these two subsamples. Only M 87 deviates from the rule. Indeed, although its main central temperature is about ~2 keV (and is thus considered a hot object), its 0.2r500 limit is beyond the EPIC FoV, and only the spectra within 0.05r500 could be extracted.
We extract the RGS spectra as described in Pinto et al. (2015) and in de Plaa et al. (2016). Since the dispersion direction of RGS extends along the whole EPIC FoV, its extraction region will be always different from our circular EPIC extraction regions. Therefore, we extract all the RGS spectra using a cross-dispersion width of 0.8′ from the EPIC FoV, which still focuses on the ICM core. In Sect. 4.3 we show that this choice does not affect our results.
The redistribution matrix file (RMF), which gives the channel probability distribution for a photon of given energy, is built using the task rmfgen. The ancillary response file (ARF), which provides the effective area curve as a function of the energy and the position on the detectors, is built using the task arfgen. Both the RMF and the ARF contain all the information relative to the response of the instruments, and need to be further applied for each observation to the spectral modelling4.
3. EPIC spectral analysis
We use the SPEX fitting package (Kaastra et al. 1996) v2.05 to perform the spectral analysis of our sample. We fit all our spectra using the C-statistics (i.e. a modified Cash statistics; Cash 1979), which is appropriate for Poisson-noise dominated data (see the SPEX manual).
Making the reasonable assumption that the hot ICM is in a collisional ionisation equilibrium (CIE) state, throughout this paper we describe its emission using a cie model (based on an updated version of the MEKAL plasma code, Mewe et al. 1985). This model includes processes such as collisional ionisation and excitation-autoionisation, as well as radiative and dielectronic recombination (for further details, we refer the reader to the SPEX manual5). We adopt the updated ionisation balance calculations of Bryans et al. (2009). The abundances are calculated from all the transitions and ions of a given element, and are scaled to the proto-solar values6 of Lodders et al. (2009).
We fit the cluster emission component in EPIC with a multi-temperature cie model, the Gaussian Differential Emission Measure (gdem) model, which reproduces a Gaussian temperature distribution in the form 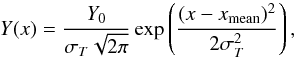 (1)where x = log (kT) and xmean = log (kTmean), kTmean is the peak temperature of the distribution, and σT is the full width at half maximum of the distribution (see de Plaa et al. 2006). By definition, σT=0 provides a single-temperature cie model (1T).
(1)where x = log (kT) and xmean = log (kTmean), kTmean is the peak temperature of the distribution, and σT is the full width at half maximum of the distribution (see de Plaa et al. 2006). By definition, σT=0 provides a single-temperature cie model (1T).
The use of a multi-temperature model for such a study is crucial since most of the clusters and groups have a complicated thermal structure in their cores where the cooling rate and temperature gradient are quite important. Therefore, assuming the plasma to be isothermal in general may lead to the so-called Fe bias, i.e. an underestimate of the Fe abundance (see e.g. Buote & Canizares 1994; Buote & Fabian 1998; Buote 2000). The effects of different thermal models on the abundances and a comparison between EPIC and RGS measurements are discussed below (Sect. 4.3).
For both EPIC and RGS abundances, we also correct the O and Ne estimates from updated calculations of the radiative recombination contribution to the cluster emission as a function of its mean temperature. We do so by multiplying the O and Ne best-fit measurements of each object by the factors of the corrected O viii and Ne x Lyman α fluxes, as described in Appendix B. On average, these corrections increase the O and Ne abundances by ~20% and ~6%, respectively.
The Galactic absorption that we apply to our fitted thermal models is modelled by the transmission of a neutral plasma (hot model, for which kT = 0.5 eV). In EPIC, the hydrogen column density NH has been estimated from a grid search of (fixed) values within 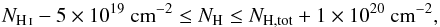 (2)where NH i and NH,tot are respectively the neutral (Kalberla et al. 2005) and total (neutral and molecular) hydrogen column densities estimated using the method of Willingale et al. (2013). More details on the reasons for this approach are given in Appendix A.
(2)where NH i and NH,tot are respectively the neutral (Kalberla et al. 2005) and total (neutral and molecular) hydrogen column densities estimated using the method of Willingale et al. (2013). More details on the reasons for this approach are given in Appendix A.
Details on the RGS spectral analysis (including models, free parameters, and background treatment) can be found in de Plaa et al. (2016), and in Pinto et al. (2015).
3.1. Background modelling
Although the clusters considered in this work are usually bright and display a high S/N within their core, in most of them the EPIC background can still play a significant role, especially in the hard spectral bands (i.e. ≳2 keV) where less thermal emission is expected. Because a slightly incorrect scaling in the subtraction of background data (taken from either filter closed wheel data or blank sky observations) can significantly affect the temperature estimates and thus bias the spectral analyses (de Plaa et al. 2006), we choose here to model the background directly in our spectra. The method we use is extensively described in Mernier et al. (2015). In summary, we model five separate background components:
-
the local hot bubble, modelled by a non-absorbed isothermal ciecomponent, whose abundances are kept proto-solar;
-
the galactic thermal emission, modelled by an absorbed isothermal cie component, whose abundances are also kept proto-solar;
-
the unresolved point sources, modelled by an absorbed power law with a photon index fixed to 1.41 (De Luca & Molendi 2004);
-
the hard particle background, modelled by a broken power law (unfolded by the effective area) and several instrumental Gaussian profiles. The parameters are taken from Mernier et al. (2015), except for all the normalisations, which are left free;
-
the soft-proton background, modelled by a power law (unfolded by the effective area). The parameters are estimated using EPIC spectra covering the total FoV (where the parameters of the gdem component from the ICM are also left free; see Sect. 3.2). From such spectra, the ICM emission can be easily constrained in the soft band (≲2 keV), while the particle backgrounds clearly dominate the harder bands, making the soft-proton background contribution easier to estimate.
The fluxes and the temperatures of the local hot bubble and galactic thermal emission components, as well as the flux of the unresolved point sources, are estimated from ROSAT PSPC spectra extracted from the region beyond r200 of each object (Zhang et al. 2009).
Finally, all these background components are fixed and rescaled to the sky area of our EPIC core spectra (except the normalisation of the hard particle background, which we always left free in order to avoid incorrect scalings and temperature biases, see above).
In addition to the background described above, M 87, M 89, NGC 4261, NGC 4636, and NGC 5813 host a powerful active galactic nucleus (AGN), which can generate cavities in the hot gas (e.g. Russell et al. 2013), but can also pollute the total X-ray emission. For each of these observations, we start by extracting a circular region of 30′′ centred on the AGN, and we fit its EPIC spectra with an absorbed power law (in addition to the cluster emission and the background components described above). We then extrapolate this additional component to the EPIC core spectra, fixing its column density and photon index values derived from the 30′′ aperture region, and rescaling its normalisation to the area ratio of these two extracted regions. We note that in the EPIC core spectra the 0.5−10 keV flux of the AGN component is never larger than ~15−20% of the cluster emission. This justifies a posteriori our choice of fitting the AGN contribution rather than excising the AGN, i.e. where the peak of the cluster emission is.
3.2. Global fits
In addition to the normalisation of the hard particle background, the only parameters that are left free when fitting our spectral components to the EPIC spectra of the core regions are the normalisation (or emission measure, 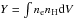 ) of the gdem model; its mean temperature (kTmean); σT; and the abundances of O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni. The other Z ≥ 6 abundance parameters are coupled to the value of the Fe abundance parameter, and are thus not free. The MOS and pn spectra of every pointing are fitted simultaneously. Since the large number of total parameters prevents us from fitting simultaneously three observations or more, for each object we5 form pairs of two pointings that we fit simultaneously. For objects including ≥3 pointings, we then combine the results of the fitted pairs using a weighting factor of
) of the gdem model; its mean temperature (kTmean); σT; and the abundances of O, Ne, Mg, Si, S, Ar, Ca, Fe, and Ni. The other Z ≥ 6 abundance parameters are coupled to the value of the Fe abundance parameter, and are thus not free. The MOS and pn spectra of every pointing are fitted simultaneously. Since the large number of total parameters prevents us from fitting simultaneously three observations or more, for each object we5 form pairs of two pointings that we fit simultaneously. For objects including ≥3 pointings, we then combine the results of the fitted pairs using a weighting factor of 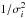 , where σi is the statistical error on the considered parameter.
, where σi is the statistical error on the considered parameter.
An important variable that might affect our EPIC results is the spectral ranges of our fits. In particular, significant cross-calibration issues between MOS and pn have been reported in the soft bands (Read et al. 2014; Schellenberger et al. 2015). Similarly, we observe a sharp and extremely variable soft tail in the EPIC filter wheel closed events7 that might considerably affect the spectra below 0.5 keV. On the other hand, we would like to keep our spectral range as large as possible, for instance to estimate the abundance measurements of O and the temperature structure in the Fe-L complex. A good compromise is found by using the 0.5−10 keV and 0.6−10 keV bands for MOS and pn, respectively.
3.3. Local fits
In the case of a plasma in CIE, the abundances of a given element showing prominent and well-resolved emission lines are easy to derive as they are proportional to the ratio between the line flux and the continuum flux, namely the equivalent width (EW). However, as a consequence of the imperfections of the EPIC instruments effective areas, when fitting the EPIC spectra over a large range (0.5/0.6−10 keV in the previous subsection, hereafter the “global” fits), the modelled continuum emission may be slightly over- or underestimated in some specific energy bands. Consequently, the modelled line fluxes tend to compensate the continuum discrepancies in the global fits, by, in turn, slightly under- or overestimating the value of the abundance parameters.
This effect, already discussed in Mernier et al. (2015), can be easily corrected by fitting the EPIC spectra locally, in order to allow the modelled continuum to be fitted to its correct (local) level. Therefore, we re-fit the EPIC spectra within local bands successively centred around the strongest K-shell lines of each element (except Ne, whose strongest lines reside in the Fe-L complex and are not resolved by the EPIC instruments). The temperature parameters kTmean and σT are frozen to their EPIC global best-fit values, in such a way that in every local fit, the free parameters are only the (local) normalisation Y and the abundance of the considered element. We compare these abundances estimated locally in MOS (MOS 1 and MOS 2 are fitted simultaneously) and in pn individually. If the MOS and pn abundances agree within 1σ, we combine the measurements using a weighting factor of 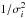 (see also Sect. 3.2). Otherwise, we compute the weighted average and artificially increase the combined uncertainties until they fully cover the extreme MOS and pn 1σ values. By applying such a conservative method to each object, we cover individual systematic uncertainties related to the EPIC cross-calibration issues (see also Sect. 4.3), and ensure getting fully reliable abundance measurements.
(see also Sect. 3.2). Otherwise, we compute the weighted average and artificially increase the combined uncertainties until they fully cover the extreme MOS and pn 1σ values. By applying such a conservative method to each object, we cover individual systematic uncertainties related to the EPIC cross-calibration issues (see also Sect. 4.3), and ensure getting fully reliable abundance measurements.
Hereafter, all the EPIC abundances are locally corrected, unless otherwise stated. We note, however, that the EPIC Fe abundances reported in this paper are obtained using global fits because they are more accurately determined using both the Fe-K and Fe-L complexes. Except A 3526 (for which we estimate Fe using local fits), all the other objects show (<2σ) consistent EPIC Fe abundances when using successively local and global fits, so this choice does not affect our results.
4. Results
The final abundance estimates for EPIC (within 0.2r500 and 0.05r500) and RGS of all the objects in the sample are presented in Fig. 1 (Fe abundance) and Fig. 2 (other relative-to-Fe abundance ratios), spread over their EPIC mean temperatures.
 |
Fig. 1 Mean temperature (EPIC) versus absolute Fe abundance for the full sample. The black squares and the red triangles show the EPIC measurements within 0.05r500 and 0.2r500, respectively. Each pair of measurements (0.05r500,0.2r500) that belong to the same hot cluster is connected by a grey dash-dotted line. The blue stars show the RGS measurements (adapted from de Plaa et al. 2016), scaled on their respective EPIC mean temperature within 0.2r500. The vertical black dotted line separates the cool groups/ellipticals from the hot clusters (see text). |
 |
Fig. 2 Same as Fig. 1 for the other (relative-to-Fe) abundance ratios. For clarity, the (0.05r500,0.2r500) pairs are not shown explicitly. |
As can be seen in Fig. 1, some sources show a significant discrepancy between their EPIC and RGS measured Fe abundances. This is not surprising, since the RGS extraction regions always have the same angular size (~30′ × 0.8′), while the radius of the circular EPIC extraction regions is different for each object (Sect. 2.2). Moreover, owing to its poorly constrained continuum level and its limited spectral range (in particular with no access to the Fe-K lines), RGS is not very suitable for deriving absolute Fe abundances. In the case of very extended sources, the instrumental line broadening makes Fe even more difficult to derive with RGS, leading to larger uncertainties. Nevertheless, the relative abundance ratios O/Fe, Ne/Fe, and Mg/Fe measured with RGS do not depend on the continuum and are easier to constrain (Sect. 4.1).
Within 0.2r500 (red triangles), the Fe abundance of the hot clusters are somewhat dispersed, with a mean value of 0.71. Within 0.05r500 (black squares), the mean Fe abundance in the cool groups/ellipticals is 0.64, while in the hot clusters it is 0.78 (see also Fig. 3). We estimate the intrinsic scatter in our subsamples, and its upper and lower 1σ limits by following the method described in de Plaa et al. (2007). Knowing the statistical errors σstat of our measurements, we determine the intrinsic scatter σint using fits to our data with a constant model and with total uncertainties 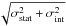 that have
that have 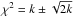 (where k is the number of degrees of freedom). For the hot clusters we find an intrinsic scatter of (21 ± 4)% within 0.2r500, and (33 ± 7)% within 0.05r500. The intrinsic scatter in the cool groups (0.05r500) is (31 ± 5)%, which is comparable to the value found in hot clusters within the same core radius. Finally, we note an interesting trend regarding the pair of measurements (0.05r500,0.2r500) for each hot cluster (blue dotted lines). When the cluster mean temperature increases, the temperature gradient seems to increase, while on the contrary, the Fe gradient seems to flatten.
(where k is the number of degrees of freedom). For the hot clusters we find an intrinsic scatter of (21 ± 4)% within 0.2r500, and (33 ± 7)% within 0.05r500. The intrinsic scatter in the cool groups (0.05r500) is (31 ± 5)%, which is comparable to the value found in hot clusters within the same core radius. Finally, we note an interesting trend regarding the pair of measurements (0.05r500,0.2r500) for each hot cluster (blue dotted lines). When the cluster mean temperature increases, the temperature gradient seems to increase, while on the contrary, the Fe gradient seems to flatten.
All the abundance ratios shown in Fig. 2 are consistent with being uniform over the considered temperatures range, even when considering the two different EPIC extraction regions. This is particularly striking for Si/Fe (although a slightly decreasing trend cannot be excluded) and S/Fe. This trend is investigated more quantitatively in Sect. 4.3 where we compare the average abundance ratios of the hot and the cool objects. Moreover, we note that both EPIC and RGS measurements are consistent; the exception is Ne/Fe, for which the RGS measurements remain uniform while the EPIC values suggest a decrease with temperature (see discussion in Sect. 4.1, and a further inspection in Sect. 4.3). Finally, although their uncertainties are large and deriving any trend is very difficult, we note that the Ni/Fe abundance ratios are all consistent with being larger than the proto-solar value.
 |
Fig. 3 Distributions of the EPIC absolute Fe abundances for all the objects in our sample. Three subsamples (hot clusters within 0.2r500 and 0.05r500, and cool groups within 0.05r500) are considered separately (see also Fig. 1). |
4.1. Estimating reliable average abundances
Assuming that all these relative-to-Fe abundance ratios are indeed uniform over clusters and do not depend (much) on their histories, we can combine our individual measurements and estimate for each element one average abundance ratio representative of the nearby cool-core ICM as a whole. We estimate the average relative-to-Fe abundance of a given element “X” by using the weighting factors 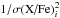 , where σ(X / Fe)i is the uncertainty on the X/Fe abundance in the ith observation. In the case of asymmetric X/Fe uncertainties in some observations, we systematically choose the larger one (in absolute value).
, where σ(X / Fe)i is the uncertainty on the X/Fe abundance in the ith observation. In the case of asymmetric X/Fe uncertainties in some observations, we systematically choose the larger one (in absolute value).
In addition to studying the subsamples of the hot clusters (within either 0.2r500 or 0.05r500), we can also combine the hot subsample (within 0.2r500) with the cool subsample (within 0.05r500), in order to get a “full” sample, named hereafter (0.05 + 0.2)r500, which contains the highest statistics. A complete comparison of this full sample with the three subsamples mentioned above is discussed in Sect. 4.3.
As mentioned earlier, RGS measures the absolute Fe abundance with a high degree of uncertainty. However, it is quite reliable in measuring the abundance ratios of O/Fe, Ne/Fe, and sometimes Mg/Fe (assuming a low redshift and a high S/N, which is the case for our sample). Unlike RGS, EPIC is not very suitable for measuring O/Fe abundance ratios (whose main emission lines reside at ~0.6 keV near the O absorption edge and where the calibration is somewhat uncertain) and Ne/Fe abundance ratios (whose K-shell transitions are within the Fe-L complex, which depends on the temperature structure and is not resolved by the EPIC instruments), but can in principle make reliable measurements of all the other considered ones. Moreover, EPIC observes both the Fe-L and Fe-K complexes, as well as the continuum emission, and thus provides more trustworthy absolute Fe abundances and temperatures. We note that we find large positive residuals around 1.2 keV in the EPIC spectra of NGC 5813 and NGC 5846, which prevents us from estimating reasonable Mg abundances, even by performing local fits. For these two groups, the Mg/Fe ratios inferred from RGS are undoubtedly more reliable.
Taking these instrumental characteristics into account, in the following we use the O/Fe and Ne/Fe abundances from RGS. We use EPIC for the Mg/Fe (except in NGC 5813 and NGC 5846), Si/Fe, S/Fe, Ar/Fe, Ca/Fe, Fe, and Ni/Fe abundances. We discuss more extensively the robustness of this choice in Sect. 4.3. Table D.1 shows the best estimated temperature and selected abundance measurements for all the objects in our samples. The average abundance ratios and their statistical uncertainties σstat are indicated in the second and third columns of Table 2. We note again that O/Fe and Ne/Fe have been corrected from updated radiative recombination calculations (Appendix B).
4.2. EPIC stacked residuals
The large net exposure time allows us to stack the residuals of the previously fitted global EPIC spectra. The residuals of each observation are obtained after fitting the three instruments simultaneously for each pointing (Sect. 3.2), and are corrected from their respective redshift before the stacking process. The residuals are summed over observations following 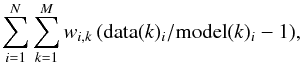 (3)where data(k)i and model(k)i are respectively the measured and modelled count rates of the ith observation at its kth spectral bin, N is the total number of observations, M is the number of spectral bins (in the considered spectrum), and wi,k is the weight used to stack the results. This weight, which depends on both the observation and the spectral bin considered, is the product of two values: the inverse square of the statistical error of data(k)i and a factor, between 0 and 1, corresponding to the overlapping fraction between a bin from a reference spectrum, and a bin from a spectrum to be stacked to the reference one (e.g. if the “reference spectrum” and “stacking spectrum” bins do not overlap, the overlapping fraction is 0, if they fully overlap, the fraction is 1; see also Leccardi & Molendi 2008). This second factor is necessary because the spectra (or spectral residuals) from different observations have different offsets in their rest frame binning owing to their different redshift corrections. Figure 4 (top three panels) shows the stacked MOS 1, MOS 2, and pn residuals.
(3)where data(k)i and model(k)i are respectively the measured and modelled count rates of the ith observation at its kth spectral bin, N is the total number of observations, M is the number of spectral bins (in the considered spectrum), and wi,k is the weight used to stack the results. This weight, which depends on both the observation and the spectral bin considered, is the product of two values: the inverse square of the statistical error of data(k)i and a factor, between 0 and 1, corresponding to the overlapping fraction between a bin from a reference spectrum, and a bin from a spectrum to be stacked to the reference one (e.g. if the “reference spectrum” and “stacking spectrum” bins do not overlap, the overlapping fraction is 0, if they fully overlap, the fraction is 1; see also Leccardi & Molendi 2008). This second factor is necessary because the spectra (or spectral residuals) from different observations have different offsets in their rest frame binning owing to their different redshift corrections. Figure 4 (top three panels) shows the stacked MOS 1, MOS 2, and pn residuals.
 |
Fig. 4 Top: EPIC MOS 1, MOS 2, and pn stacked and redshift-corrected residuals of the (0.05 + 0.2)r500 sample (using a gdem model). Before stacking, the MOS and pn spectra of every pointing were fitted simultaneously with coupled parameters. The vertical dotted lines indicate the position of the detected line emissions in the EPIC spectra (see lower panel). Bottom: EPIC stacked and redshift-corrected residuals of the (0.05 + 0.2)r500 sample (using a gdem model, all instruments combined). Before stacking, the MOS and pn spectra of every pointing were fitted independently and the line emission was set to zero in the model. The height of the peak of the Fe-K complex is ~1.95. |
Although the deviations are not larger than a few per cent, remaining cross-calibration issues between MOS and pn effective areas clearly appear, and positive residuals in one instrument are often compensated by negative residuals in the other, especially around the Fe-L complex (and more generally below 2 keV). In the 4−6 keV band, the model underestimates the spectra, while above 7 keV, the opposite situation occurs. It is also worth mentioning the apparent slightly overestimated broadening of the modelled Fe-K line complex, in particular in MOS (seen through the characteristic dips on both sides of the peak), which is likely due to imperfections of the RMF. The pn stacked residuals also suggest a small offset due to incorrect energy calibration. Although the last two points should not significantly affect our results, the overall shape of the stacked residuals clearly illustrates that, despite past and recent efforts to cross-calibrate the EPIC instruments, imperfections are still present and bring additional uncertainties in the parameter determination (see also Schellenberger et al. 2015). In particular, the biased determination of the continuum, especially beyond 4 keV, emphasises the importance of using a local fitting method to derive reliable abundances (Sect. 3.3).
We do the same exercise, this time by fitting the instruments independently (to minimise the cross-calibration residuals discussed above), and by setting all the line emission to zero in the gdem model after having fitted the spectra. We calculate the residuals relative to this “continuum only” model for each observation, and we sum the residuals as described above. The stacked result is shown in the lower panel of Fig. 4, and reveals all the emission lines/complexes that the EPIC instruments are able to resolve. The small stacked error bars on the residuals allow us to detect the main emission lines of chromium (Cr) and manganese (Mn) around ~5.7 keV and ~6.2 keV respectively. Following the Gauss method described in Mernier et al. (2015), we re-fit locally the EPIC spectra of every pointing with a local continuum and an additional Gaussian centred successively on these two energies. From this we get the EWs of the two lines, which we can convert into Cr and Mn abundances. After stacking these measurements over the whole sample, the MOS and pn instruments find a positive detection of Cr/Fe with >7σ and >4σ significances, respectively. For Mn/Fe, the positive detection is >5σ in both MOS and pn. Combining the MOS and pn instruments, we obtain average Cr/Fe and Mn/Fe abundances of 1.56 ± 0.19 and 1.70 ± 0.22, respectively. These abundances are not so different from the Fe values assumed for Cr and Mn in the previously discussed fits (Sect. 3.2), and consequently, their residuals did not bias our fits much, if at all. We also note that because the error bars of these abundances in individual pointings are often 1σ consistent with zero, we must ensure that negative abundances are allowed in order to avoid statistical biases when averaging over the whole sample (Leccardi & Molendi 2008).
 |
Fig. 5 Same as Fig. 4 (bottom), this time comparing the 0.05r500 cool (grey curve) and the 0.2r500 hot (black curve) subsamples. The height of the peak of the Fe-K complex in the 0.2r500 hot sample is ~2.23. |
The stacking process described above can also be performed separately in the hot and cool subsamples, respectively within 0.2r500 and 0.05r500. This comparison is shown in Fig. 5. Unsurprisingly, most of the emission lines, including the Fe-L complex, are clearly enhanced in the cool subsample (grey curve), while the Fe-K and Ni-K lines are more prominent in the hot subsample (black). Beyond ~6 keV, the overestimate of the continuum (discussed above and in Sect 3.3) also seems more important in the cool subsample.
4.3. Systematic uncertainties
A crucial point when averaging the abundances over a large sample is that the stacked statistical uncertainties become very small. Therefore, the systematic uncertainties may clearly dominate, and care must be taken to evaluate them properly. The average abundance ratios and all their uncertainties discussed below are summarised in Table 2.
First, because of their different chemical histories, it seems reasonable to assume that some clusters intrinsically deviate from the average estimated abundances. Such an intrinsic scatter σint has been already introduced, and has been estimated (as well as their 1σ uncertainties) for all the available abundance ratios (Table 2). Except for O/Fe (~16%) and Mg/Fe (~29%), the intrinsic scatter of the other elements are of the order of a few percent. In order to remain as conservative as possible in determining our final abundance ratios, we choose to consider the most extreme case where the true instrinsic scatters would actually correspond to the (1σ) upper limits of σint. In the following, the systematic uncertainties we associate with the instrinsic scatters are, therefore, σint + 1σ. Owing to their still large statistical error bars, no intrinsic scatter was needed for Ar/Fe, Cr/Fe, Mn/Fe, and Ni/Fe.
Second, we investigate whether the average abundance ratios change significantly when considering different EPIC extraction regions and/or subsamples. The comparison of these ratios over the four (sub-)samples described in Sect. 4.1 is shown in Fig. 6 (left panel). The abundance ratios of all the elements are consistent, except for S/Fe and Ar/Fe, which we discuss more extensively in Sect. 5.1. For these two elements, we determine the systematic uncertainty σregion by artificially increasing their combined uncertainties 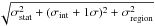 , until they cover the discrepancies between the (sub-)samples, and make them all ≤1σ consistent.
, until they cover the discrepancies between the (sub-)samples, and make them all ≤1σ consistent.
Third, after correction for σint and σregion, we look for possible cross-calibration biases by comparing the average abundances estimated from the separate XMM-Newton instruments (Fig. 6, right panel). Three elements have MOS and pn abundance ratios that differ with more than 1σ significance, and need an additional systematic uncertainty (σcross - cal, defined similarly to σregion): Si/Fe, Ar/Fe, and Ni/Fe. The last two are the most striking: pn estimates the Ar/Fe and Ni/Fe ratios on average respectively ~25% lower and ~52% higher than MOS. A further discussion on the discrepancies found in these two ratios will be addressed in Sect. 5.1.
Fourth, since the conversion from the EW of a considered line to the abundance of its element strongly depends on the plasma temperature, a multi-temperature structure deviating from the gdem distribution may affect the abundance ratios. We investigate this dependency for the best EPIC observations of Perseus and M 87 in Appendix C. Among the two continuous temperature distributions tested here (which are thought to be the most reasonable to describe the thermal structure of the ICM; e.g. de Plaa et al. 2006), we find that the deviations in the EPIC abundance ratios are marginal, well below the range of the other systematic uncertainties discussed above. Therefore, we do not consider this effect in the rest of this paper.
Assuming the systematic errors mentioned above to be roughly symmetric, we add them in quadrature to obtain the total uncertainties: 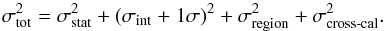 (4)Finally, we must note that further systematic uncertainties might still play a role. For example, we show in Appendix B that too simple approximations in the calculation of the emission processes might alter the line emissivities, and thus the abundances we measure. Therefore, we cannot exclude that future improvements in the currently used spectral fitting codes could still slightly affect the measurements we report here. Moreover, from some aspects (e.g. Fe xvii line ratios; see de Plaa et al. 2012), small deviations have been reported in the spectral modelling of CIE plasmas using either the SPEX code, or the APEC model (based on the AtomDB code). In terms of abundances, the discrepancies between the two codes may bring further uncertainties, at least for RGS measurements (de Plaa et al. 2016); however, APEC is a single-temperature model, which should be avoided in this kind of analysis (Sect. 3). Moreover, this lack of multi-temperature distribution for APEC makes a direct comparison between the two codes difficult.
(4)Finally, we must note that further systematic uncertainties might still play a role. For example, we show in Appendix B that too simple approximations in the calculation of the emission processes might alter the line emissivities, and thus the abundances we measure. Therefore, we cannot exclude that future improvements in the currently used spectral fitting codes could still slightly affect the measurements we report here. Moreover, from some aspects (e.g. Fe xvii line ratios; see de Plaa et al. 2012), small deviations have been reported in the spectral modelling of CIE plasmas using either the SPEX code, or the APEC model (based on the AtomDB code). In terms of abundances, the discrepancies between the two codes may bring further uncertainties, at least for RGS measurements (de Plaa et al. 2016); however, APEC is a single-temperature model, which should be avoided in this kind of analysis (Sect. 3). Moreover, this lack of multi-temperature distribution for APEC makes a direct comparison between the two codes difficult.
Average abundance ratios estimated from the (0.05 + 0.2)r500 sample, as well as their statistical, systematic, and total uncertainties.
 |
Fig. 6 Left: average abundance ratios considering different (sub-)samples and/or different EPIC extraction regions. The O/Fe and Ne/Fe ratios are measured using RGS (cross-dispersion width of 0.8′). For these two ratios there is thus no distinction between the two hot samples or between the two full samples. The error bars incorporate the statistical errors (σstat) and the intrinsic scatters (σint + 1σ). Right: average abundance ratios estimated from the (0.05 + 0.2)r500 sample, measured independently by different combinations of instruments. The error bars incorporate the statistical errors (σstat), the intrinsic scatters (σint + 1σ), and the uncertainties derived from the different EPIC extraction regions and/or subsamples (σregion, see left panel). |
5. Discussion
In this work, we have derived the abundances in the cores of 44 galaxy clusters, groups, and ellipticals (CHEERS), using both the EPIC and RGS instruments. We have shown (Fig. 2) that the abundance ratios of O/Fe, Ne/Fe, Mg/Fe, Si/Fe, S/Fe, Ar/Fe, Ca/Fe, and Ni/Fe are quite uniform over the considered ranges of temperatures in the sample (0.6−8 keV). These results corroborate the study of De Grandi & Molendi (2009), who also found flat trends for Si/Fe and Ni/Fe independently of the considered clusters. This strongly suggests that regardless of their precise nature and of their different spatial scales, the physical processes that are responsible for the enrichment of the ICM must be the same for ellipticals, galaxy groups, and galaxy clusters.
Unlike these ratios, the absolute Fe abundance is far from being uniform, and seems much more dependent on cluster history (Fig. 1). The scatter is more important in the inner regions (0.05r500) of the core. A less scattered Fe abundance within 0.2r500 could suggest a flatter abundance distribution as we look away from the centre with a similar level of enrichment outside the core of most objects. This is in agreement with the hypothesis of an early (pre-)enrichment, supported by recent Suzaku observations of outskirts of clusters/groups (Werner et al. 2013; Simionescu et al. 2015).
The cool groups/ellipticals appear on average to be less Fe-rich than the hot clusters. In particular, it is interesting to note that nine hot clusters have an Fe abundance that is higher than proto-solar within 0.05r500, while, at the same scale, no cool group/elliptical has a similar feature (Fig. 3). This trend has been already reported observationally (Rasmussen & Ponman 2009) and in simulations (Liang et al. 2016). It might be explained by several scenarios:
-
More massive objects are more efficient in retaining metalswithin their core (owing to their larger gravitational well or a lesspowerful AGN activity).
-
The more massive clusters are somewhat more efficient in injecting synthesised metals into the ICM.
-
The galaxies of the more massive clusters are somewhat more efficient in producing stars, and hence, SNe.
-
A more efficient cooling in group cores removes the enriched gas observed in X-ray.
While Liang et al. (2016) propose that the last scenario explains the lack of metal-rich gas in lower-mass (hence, lower-temperature) objects, Rasmussen & Ponman (2009) explored the four possibilities, and argue that the two first are the most likely. In particular, the galactic outflows could be less efficient in releasing metals in the ICM of cooler groups or, alternatively, the AGN activity of the BCG could have helped to remove metals from their core (see also Yates et al. 2016). However, we must emphasise that several of these mechanisms might co-exist, and that the list above is not necessarily exhaustive. For instance, Elkholy et al. (2015) recently found a hint of a positive correlation between the metallicity in low-mass clusters, and the morphological disturbance of their ICM (likely related to the dynamical activity of their galaxy members). Alternatively, cooler ICM might be more efficient in depleting ionic Fe (and probably other metals) into grains close to the brightest central galaxy, although Panagoulia et al. (2015) found hints of Fe depletion in the cores of more massive clusters as well.
We must warn, however, that the large intrinsic scatters mentioned above prevent us from claiming any clear and significant trend on the absolute Fe abundances. Moreover, a more complicated thermal structure in groups/ellipticals than in more massive clusters cannot be excluded, and could lead to a slight but significant Fe bias, which would affect in priority the cooler objects in our sample.
We have also found an apparent variation in the Fe abundance and temperature gradients (i.e. between 0.05r500 and 0.2r500) in the hot clusters. These differences could be related to the individual cluster enrichment histories or to other parameters, such as the cooling rate. Linking the history of each cluster/group to its Fe budget requires a more careful spatial study of the Fe distribution. Establishing radial profiles for the entire sample is beyond the scope of this work, but will be addressed in a separate paper.
From the stacked results of our (0.05 + 0.2)r500 sample, we have estimated the average abundance ratios and their respective total uncertainties (statistical and systematic). This also includes Cr/Fe and Mn/Fe, which we have detected within >4σ significance with MOS and pn independently. To our knowledge, this is the first time that Mn has been firmly detected in the ICM. For comparison, Werner et al. (2006) already detected Cr in 2A 0335+096 within 2σ (but were unable to detect Mn), while Cr and Mn have been detected in Perseus within 5σ and 1σ, respectively (Tamura et al. 2009). It is also striking to note that we do not see any emission line feature around ~3.5 keV in the stacked EPIC spectra (Fig. 4 bottom, Fig. 5) contrary to several claims from recent studies, in particular Bulbul et al. (2014) and Boyarsky et al. (2014), whose total EPIC net exposure times are ~3 Ms and ~1.5 Ms, respectively (i.e. less than in this work). Such an apparent non-detection is thus very interesting to report, since it might challenge the hypothesis of decaying sterile neutrinos, known as a dark matter candidate, being observed in the ICM. We note that the dark matter interpretation is far from being the only possible explanation of an emission line at ~3.5 keV (e.g. Gu et al. 2015), and our non-detection could also be explored in the context of these other possibilities. However, this question is not the initial purpose of this present study, and a more detailed investigation of our stacked spectra around ~3.5 keV, and consequent discussions, are left to a future paper.
5.1. Discrepancies in the S/Fe, Ar/Fe and Ni/Fe ratios
The average S/Fe ratio shows a slight but significant enhancement in the cool objects within 0.05r500 compared to the hot objects within 0.2r500 (Fig. 6). From Fig. 2 (left, third panel), it is clearly that M 49 (kTmean ~ 1.148 keV) and A 3581 (kTmean ~ 1.637 keV) largely contribute to this higher S/Fe ratio measured in the cool subsample because their statistical errors are small compared to the other cool objects. Moreover, the >1σ discrepancy between the cool and hot measured S/Fe ratios disappears when considering the same radius (0.05r500) for all the objects.
The Ar/Fe discrepancy observed in Fig. 6 (left) is more intriguing, since a larger aperture seems to lower its measurement. This trend is difficult to interpret. A change in the relative Ar to Fe radial distribution in the ICM cannot be excluded, although we would then expect it for other elements as well. A full study of the abundance radial profiles of the sample will be performed in a future paper. Furthermore, it also appears from Fig. 6 (right) that MOS and pn measure significantly different Ar/Fe values, even after taking account of the uncertainty described above (i.e. σregion). The reason for this second Ar/Fe discrepancy is again challenging to clearly identify, but it is very likely due to imperfections in the calibration of the EPIC instruments.
 |
Fig. 7 Average abundance ratios in our (0.05 + 0.2)r500 sample (black squares) versus proto-solar abundances (grey dashed line) and their 1σ uncertainties (red dash-dotted lines, adapted from Lodders et al. 2009). |
As seen in Fig. 6 (right), the large MOS-pn discrepancy in the Ni/Fe abundance ratio prevents us from deriving a precise measurement. This discrepancy is worrying, but can be explained by imperfections in the cross-calibration of the two instruments. Alternatively, and perhaps more likely, the high energy band around the Ni-K transitions is significanly affected by the instrumental background (as the flux of the cluster emission sharply decreases at high energies). This hard particle background (already mentioned in Sect. 3.1) has a different spectral shape in MOS and pn, which might even vary with time, thus between observations. In particular, an instrumental line (Cu Kα) is known to affect pn at a rest-frame energy of ~8 keV (Mernier et al. 2015). Despite our efforts to carefully estimate the background, that line might interfere with the Ni-K line in several observations, making a proper modelling of the Ni-K line impossible, and hence, boosting the Ni absolute abundance in pn. In this context, it can be instructive to compare our Ni/Fe measurements with those of Suzaku, which has a lower relative hard particle background. Sato et al. (2007b) (A 1060) and Tamura et al. (2009) (Perseus) reported ratios of ~1.3 ± 0.4 and ~1.11 ± 0.19, respectively (after rescaling to the proto-solar values). Although these measurements might be also be affected by further uncertainties (e.g. the choice of the spectral modelling, Sect. 4.3), they appear to be consistent with the Ni/Fe average ratio measured with MOS is this work, favouring our above supposition that MOS is more trustworthy than pn for measuring Ni/Fe. However, in order to be conservative, we prefer to retain the pn value as a possible result and, therefore, we keep large systematic uncertainties for Ni/Fe. We finally note that, unsurprisingly, Ni/Fe cannot be constrained in the cool objects (Fig. 6, left) because the gas temperature is too low to excite Ni-K transitions.
5.2. Comparison with the proto-solar abundance ratios
In Fig. 7 (black squares), we report our final X/Fe abundance pattern measured in the (0.05 + 0.2)r500 sample, accounting for all the systematic uncertainties discussed earlier in this paper. At first glance, most of the abundance ratios measured in the ICM look significantly different from the proto-solar abundance ratios. Indeed, if we fit a constant to our abundance pattern (dashed grey line), we obtain a χ2 of 43.1 for 10 degrees of freedom, in poor agreement with the abundance ratios in the ICM. However, as shown by the red dash-dotted lines (adapted from Lodders et al. 2009), the solar abundance ratios also suffer from large uncertainties, typically about 20−25%. When comparing the two sets of abundance ratios taken with their respective uncertainties, we find that the O/Fe, Ne/Fe, Mg/Fe, Si/Fe S/Fe, Ar/Fe, and Ca/Fe ratios measured in the ICM are consistent within 1σ with the proto-solar values (±1σ). The Cr/Fe abundance ratios measured in the ICM are consistent within 2σ with the proto-solar values (±1σ), and the Mn/Fe and Ni/Fe abundance ratios are consistent within 3σ.
Given these considerations, whether the chemical enrichment in the ICM is similar to the chemical enrichment of the solar neighbourhood is not a trivial question to solve. As mentioned above, while most of the relative abundances appear to be consistent with being proto-solar, Ni/Fe, Mn/Fe, and perhaps Cr/Fe seem to be significantly enhanced. This result might be of interest since significant different abundance ratios in the ICM means that the fraction of SNIa (or conversely SNcc) responsible for the ICM enrichment differs from that of the Galactic enrichment. We will address this discussion in greater detail in Paper II. We recall, however, that the abundances of interest in this context (Cr, Mn, and Ni) are not well constrained in X-ray, given the current instrument capabilities. Moreover, as specified in Sect. 4.3, we do not exclude that differences in current atomic codes might bring further systematic uncertainties to the measurements reported in this work. Therefore, whether our abundance ratios are significantly more accurate than the proto-solar estimates should still be considered an open question.
5.3. Current limitations and future prospects
As we have shown throughout this paper, our excellent data quality (~4.5 Ms and ~3.7 Ms of total net exposure time for EPIC MOS and pn, respectively) provides very accurate abundance measurements in the ICM of cool-core galaxy clusters and groups. Therefore, these data should be a legacy for any future work directly or indirectly related to the chemical enrichment in the ICM. However, our study clearly reveals that the abundance ratios of some elements of interest are still poorly constrained. In particular, the Cr/Fe, Mn/Fe, and Ni/Fe ratios in our study appear higher than the solar neighbourhood and are thus crucial to study in detail, which is currently challenging given the limited spectral resolution of CCDs and the large cross-calibration uncertainties (at least for Ni/Fe) that we emphasise here.
In this work we probably reach the instrumental limitations of XMM-Newton in terms of abundance determination, and thus stacking more data will have very little impact on the current accuracy of our already existing measurements. Indeed, in our sample, the statistical uncertainties are already marginal compared to the systematic ones. In addition to further efforts in calibrating the instruments and improving the atomic databases, it is clear that a sensibly higher X-ray spectral resolution is now needed.
Such an improvement can be reached with micro-calorimeter spectrometers, which should be on board the next generation of X-ray observatories. In particular, the Japanese X-ray observatory Hitomi (formerly named ASTRO-H; Takahashi et al. 2014) has been able to resolve, for instance, K-shell and also L-shell Ni lines with a limited instrumental background, and should thus reduce the Ni/Fe uncertainties to a few per cent. Unfortunately, owing to a loss of contact a few weeks after launch, the fate of the mission is now unclear. Alternatively, the X-IFU instrument, which will be on board the Athena observatory (Nandra et al. 2013), will greatly improve the spectral resolution currently achieved with XMM-Newton to ~2.5 eV. Undoubtedly, this upcoming mission will allow a significant step forward in such an analysis, especially if improvements in atomic data are also carried out.
6. Conclusions
In this paper, we have used the XMM-Newton EPIC and RGS instruments to investigate the Fe abundance and abundance ratios of O/Fe, Ne/Fe, Mg/Fe, Si/Fe, S/Fe, Ar/Fe, Ca/Fe, Cr/Fe, Mn/Fe, and Ni/Fe in the central regions of 44 cool-core galaxy clusters, groups, and elliptical galaxies (CHEERS). Our main results can be summarised as follows.
-
The X/Fe abundance ratios appear quite uniform over the mean temperature range of our sample. This confirms previous results, and indicates that no matter what the physical mechanisms responsible for the enrichment are, they must be very similar in enriching the ICM of ellipticals, groups, and clusters of galaxies.
-
By stacking all the EPIC spectra of our sample (within 0.2r500 when possible, within 0.05r500 otherwise), we were able to derive abundances of Cr/Fe and Mn/Fe independently with MOS and pn, with >4σ significance. While Cr had been already detected in the past, this is the first time that a firm detection of Mn in the hot ICM has been reported.
-
Contrary to recent claims, and despite the large net exposure time (~4.5 Ms) of our combined data, we do not see any emission line at ~3.5 keV. Although a deeper investigation will be addressed in a future paper, this might challenge the possibility of decaying sterile neutrinos, a dark matter candidate, being observed in the ICM.
-
The Fe abundance varies between 0.2−2 times the proto-solar values, and shows an important scatter, especially within a radius of 0.05r500 (~30−40%). Looking at smaller (0.05r500) and larger (0.2r500) central regions in a subsample of hot clusters, it appears that the Fe peak sharpens and the temperature drop flattens as the mean cluster temperature decreases. Clearly, these various Fe abundances must depend on individual clusters histories, and complete abundance radial profiles will be investigated in greater detail in a future work.
-
Having benefited from a large total net exposure time (~4.5 Ms) and having processed a very careful estimation of the systematic effects that could affect our measurements, we have shown that the systematic uncertainties clearly dominate over the statistical ones. Taking these systematic uncertainties into account, most of the ICM abundance ratios measured in this work are consistent with the proto-solar abundance ratios. Notable exceptions are Mn/Fe, Ni/Fe, and perhaps Cr/Fe, which are found to be significanly higher in the ICM than in the solar neighbourhood.
-
Overall, our careful analysis demonstrates that stacking more observations would not further improve the accuracy of our results, and, more generally, that we have probably reached the limits of the current X-ray capabilities (in particular XMM-Newton) for this science case. Therefore, our data constitute the most accurate abundance ratios ever measured in the ICM, and should be a legacy for future work. Using the results presented in this paper, a full discussion on the role of the SNIa and SNcc in the context of both the proto-solar and the ICM enrichments will be addressed in Paper II. However, a more accurate comparison between the local Galactic enrichment and the ICM enrichment in the local Universe will require improvements in atomic data, as well as better calibration of the instruments. In parallel to these needs for improvements, the upcoming X-ray observatories should further improve the accuracy of the abundance measurements, and thus help to solve the puzzle of the chemical enrichment in the hot ICM.
The proto-solar abundances used in this paper (Lodders et al. 2009) are the most up-to-date representative abundances of the solar system at its formation, as they are based on meteoritic compositions.
Acknowledgments
The authors would like to thank the referee Marten van Kerkwijk for his helpful comments and suggestions. This work is partly based on the XMM-Newton AO-12 proposal “The XMM-Newton view of chemical enrichment in bright galaxy clusters and groups” (PI: de Plaa), and is a part of the CHEERS (CHEmical Evolution Rgs cluster Sample) collaboration. The authors thank its members, as well as Liyi Gu and Craig Sarazin for helpful discussions. P.K. thanks Steve Allen and Ondrej Urban for support and hospitality at Stanford University. Y.Y.Z. acknowledges support by the German BMWI through the Verbundforschung under grant 50 OR 1506. This work is based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA member states and the USA (NASA). The SRON Netherlands Institute for Space Research is supported financially by NWO, the Netherlands Organisation for Space Research.
References
- Badnell, N. R. 2006, ApJS, 167, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., & Werner, N. 2010, A&ARv, 18, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyarsky, A., Ruchayskiy, O., Iakubovskyi, D., & Franse, J. 2014, Phys. Rev. Lett., 113, 251301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bryans, P., Landi, E., & Savin, D. W. 2009, ApJ, 691, 1540 [NASA ADS] [CrossRef] [Google Scholar]
- Bulbul, E., Markevitch, M., Foster, A., et al. 2014, ApJ, 789, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A. 2000, MNRAS, 311, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., & Canizares, C. R. 1994, ApJ, 427, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Buote, D. A., & Fabian, A. C. 1998, MNRAS, 296, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- De Grandi, S., & Molendi, S. 2009, A&A, 508, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J. 2013, Astron. Nachr., 334, 416 [NASA ADS] [CrossRef] [Google Scholar]
- de Plaa, J., Kaastra, J. S., Tamura, T., et al. 2004, A&A, 423, 49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Bykov, A. M., et al. 2006, A&A, 452, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Werner, N., Bleeker, J. A. M., et al. 2007, A&A, 465, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Plaa, J., Zhuravleva, I., Werner, N., et al. 2012, A&A, 539, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- den Herder, J. W., Brinkman, A. C., Kahn, S. M., et al. 2001, A&A, 365, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elkholy, T. Y., Bautz, M. W., & Canizares, C. R. 2015, ApJ, 805, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, L., Kaastra, J., Raassen, A. J. J., et al. 2015, A&A, 584, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hudson, M. J., Lucey, J. R., Smith, R. J., Schlegel, D. J., & Davies, R. L. 2001, MNRAS, 327, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Kaastra, J. S., Mewe, R., & Nieuwenhuijzen, H. 1996, in UV and X-ray Spectroscopy of Astrophysical and Laboratory Plasmas, eds. K. Yamashita, & T. Watanabe, 411 [Google Scholar]
- Kaastra, J. S., Tamura, T., Peterson, J. R., et al. 2004, A&A, 413, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 487, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, L., Durier, F., Babul, A., et al. 2016, MNRAS, 456, 4266 [NASA ADS] [CrossRef] [Google Scholar]
- Lodders, K., Palme, H., & Gail, H.-P. 2009, Landolt Börnstein (Springer), 44 [Google Scholar]
- Lumb, D. H., Warwick, R. S., Page, M., & De Luca, A. 2002, A&A, 389, 93 [Google Scholar]
- Mahdavi, A., & Geller, M. J. 2001, ApJ, 554, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, J., & Kaastra, J. 2016, A&A, 587, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mernier, F., de Plaa, J., Lovisari, L., et al. 2015, A&A, 575, A37 [Google Scholar]
- Mernier, F., de Plaa, J., Pinto, C., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201628765 (Paper II) [Google Scholar]
- Mewe, R., & Gronenschild, E. H. B. M. 1981, A&AS, 45, 11 [NASA ADS] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Mitchell, R. J., Culhane, J. L., Davison, P. J. N., & Ives, J. C. 1976, MNRAS, 175, 29P [NASA ADS] [CrossRef] [Google Scholar]
- Morris, R. A. H., Phillipps, S., Jones, J. B., et al. 2007, A&A, 476, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mushotzky, R., Loewenstein, M., Arnaud, K. A., et al. 1996, ApJ, 466, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Nandra, K., Barret, D., Barcons, X., et al. 2013, ArXiv e-prints [arXiv:1306.2307] [Google Scholar]
- Panagoulia, E. K., Sanders, J. S., & Fabian, A. C. 2015, MNRAS, 447, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, C., Fabian, A. C., Werner, N., et al. 2014, A&A, 572, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, C., Sanders, J. S., Werner, N., et al. 2015, A&A, 575, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasmussen, J., & Ponman, T. J. 2009, MNRAS, 399, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Read, A. M., Guainazzi, M., & Sembay, S. 2014, A&A, 564, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reiprich, T. H., & Böhringer, H. 2002, ApJ, 567, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, H. R., McNamara, B. R., Edge, A. C., et al. 2013, MNRAS, 432, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, K., Tokoi, K., Matsushita, K., et al. 2007a, ApJ, 667, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, K., Yamasaki, N. Y., Ishida, M., et al. 2007b, PASJ, 59, 299 [NASA ADS] [Google Scholar]
- Schellenberger, G., Reiprich, T. H., Lovisari, L., Nevalainen, J., & David, L. 2015, A&A, 575, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Simionescu, A., Werner, N., Böhringer, H., et al. 2009, A&A, 493, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simionescu, A., Werner, N., Urban, O., et al. 2015, ApJ, 811, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Lucey, J. R., Hudson, M. J., Schlegel, D. J., & Davies, R. L. 2000, MNRAS, 313, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Takahashi, T., Mitsuda, K., Kelley, R., et al. 2014, ArXiv e-prints [arXiv:1412.2351] [Google Scholar]
- Tamura, T., Maeda, Y., Mitsuda, K., et al. 2009, ApJ, 705, L62 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, N., de Plaa, J., Kaastra, J. S., et al. 2006, A&A, 449, 475 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Werner, N., Durret, F., Ohashi, T., Schindler, S., & Wiersma, R. P. C. 2008, Space Sci. Rev., 134, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, N., Urban, O., Simionescu, A., & Allen, S. W. 2013, Nature, 502, 656 [NASA ADS] [CrossRef] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Yates, R. M., Thomas, P. A., & Henriques, B. M. B. 2016, MNRAS, submitted [arXiv:1603.04858] [Google Scholar]
- Zhang, Y.-Y., Reiprich, T. H., Finoguenov, A., Hudson, D. S., & Sarazin, C. L. 2009, ApJ, 699, 1178 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: EPIC absorption column densities
In the hot model used in this work to mimic absorption of X-rays through interstellar material (Sect. 3), we initially fixed the hydrogen column density NH to the weighted value NH,tot of both the neutral (NH i, Kalberla et al. 2005) and the molecular (NH2, Schlegel et al. 1998) materials, calculated using the method of Willingale et al. (2013)8. However, this approach often gives poor fits in the soft band of our EPIC spectral modelling, by significantly under- or overestimating the flux of its continuum. In order to compensate this effect, the O abundance is often biased consequently by the fits. Figure A.1 (red data points) clearly illustrates that some objects have their EPIC O/Fe ratio significantly offset from the corresponding RGS values.
 |
Fig. A.1 Comparison between the EPIC and RGS measurements of the O/Fe abundance ratio in most objects of our (0.05 + 0.2)r500 sample. The blue dotted line shows the one-to-one EPIC-RGS correspondence. In our fits we alternatively fix the NH to the weighted neutral+molecular values calculated from Willingale et al. (2013), and leave it free within the ranges given by Eq. (A.1). The two approaches are shown in red and black, respectively. |
The EPIC-RGS correlation for the O/Fe ratio is clearly improved if we free the NH (Fig. A.1, black data points). Similarly, most of the fits are improved in terms of C-stat/d.o.f. However, keeping NH as a free parameter without any further constraint is quite dangerous, and might lead to unphysical results. In order to remain reasonably consistent with the estimated values of NH i and NH,tot mentioned above, we allow NH to take values within the following arbitrary limits: 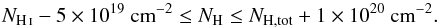 (A.1)These upper and lower ranges allow limited deviations also around NH i and NH,tot. Since constraining a free parameter within a narrow range can lead to problems in evaluating the statistical errors, we perform a grid search of fixed NH values (taken within the limits mentioned above), and select the one that gives the lowest C-stat/d.o.f. to the fits. Despite all these precautions, it should also be kept in mind that the O abundance measured in clusters with EPIC is also affected by the oxygen absorption in the interstellar medium, which in turn depends on NH (e.g. de Plaa et al. 2004). Similarly, the measured O abundance in the ICM may be also affected by the foreground thermal X-ray emission.
(A.1)These upper and lower ranges allow limited deviations also around NH i and NH,tot. Since constraining a free parameter within a narrow range can lead to problems in evaluating the statistical errors, we perform a grid search of fixed NH values (taken within the limits mentioned above), and select the one that gives the lowest C-stat/d.o.f. to the fits. Despite all these precautions, it should also be kept in mind that the O abundance measured in clusters with EPIC is also affected by the oxygen absorption in the interstellar medium, which in turn depends on NH (e.g. de Plaa et al. 2004). Similarly, the measured O abundance in the ICM may be also affected by the foreground thermal X-ray emission.
Appendix B: Radiative recombination corrections
The version of SPEX that is used in this work calculates the line emissivities assuming that the radiative recombination (RR) rates of the cluster emission can be expressed as a power law of the electron temperature (Mewe & Gronenschild 1981; Mewe et al. 1985). However, this approximation has turned out to be too simplified at high temperature. A more accurate calculation of the RR rate coefficients has been done by Badnell (2006), and parametrised by Mao & Kaastra (2016) as a function of the temperature T in the form 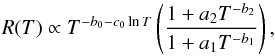 (B.1)where a0, b0, c0, a1, a2, b1, and b2 are constant (fitted) parameters.
(B.1)where a0, b0, c0, a1, a2, b1, and b2 are constant (fitted) parameters.
Since the RR rates directly affect the line emissivities, which in turn affect our estimated abundances, the RR updated model of Mao & Kaastra (2016) must be taken into account in our analysis, even though its implementation into SPEX is yet to come. Knowing that the O and Ne emission lines seen in clusters spectra are dominated by H-like Lyman α transitions, and that these two elements are the most affected by changing RR rates, we correct their abundances by computing the change in flux of their H-like Lyman α lines from the old RR calculations (i.e. used in the current SPEX version) to the new ones. This RR correction factor is shown (again, for O and Ne) in Fig. B.1 as a function of the plasma temperature, and is to be multiplied by the measured O and Ne abundances of each object in our sample.
 |
Fig. B.1 Calculated radiative recombination correction factors of H-like Lyman α lines of O and Ne as a function of the cluster (mean) temperature (adapted from the results of Mao & Kaastra 2016). |
Figure B.1 clearly shows that better calculations of the RR rates can lead to significant increases of the estimated O and Ne abundances in hot clusters. After applying this RR correction factor for each source, we find that, on average, the O/Fe and Ne/Fe abundance ratios increase by ~20% and ~9%, respectively. We note, however, that reprocessing the whole analysis presented in this paper by using the uncorrected O and Ne abundance values does not affect our main conclusions, since we keep large systematic uncertainties in the final abundance ratios.
Appendix C: Effects of the temperature distribution on the abundance ratios
As already specified in Sect. 3, the measured absolute abundances (in particular Fe) are in principle sensitive to the choice of the thermal model used in the fits (single- vs. multi-temperature). Among multi-temperature models, the assumed temperature distribution might also affect the measured (X/Fe) abundances. We explore this possibility by successively fitting the best-quality observations of Perseus and M 87 (which both have excellent statistics but rather different mean temperatures) with a 1T (i.e. cie), a 2T (i.e. cie+cie), and a power-law differential emission measure model9 (wdem; see e.g. Kaastra et al. 2004). The results are shown in Fig. C.1 and Table C.1. From Fig. C.1, it clearly appears that the abundance pattern depends on the considered thermal model. In particular, Ne/Fe varies a lot (i.e. by more than a factor of 6 for Perseus and by almost a factor of 3 for M 87) because the Ne abundance parameter from the models is used by the fits to compensate the EPIC residuals in the Fe-L complex (e.g. de Plaa et al. 2006). This illustrates that the EPIC estimate of Ne/Fe cannot be interpreted as a reliable Ne abundance (Sect. 4.1). Striking differences in the Ca/Fe and Ni/Fe ratios considering the four different models should also be noted; for instance, a considerably high Ca/Fe ratio is measured by the 1T and/or 2T model(s).
 |
Fig. C.1 EPIC abundance measurements in the two best-quality observations of our sample, based on global fittings (see also Table C.1). Four thermal models are successively considered: 1T (black empty squares), 2T (blue filled squares), wdem (orange filled squares), and gdem (red filled squares). The Fe abundance is given in absolute values, while the other abundances are given relative to Fe. Left: perseus (0.2r500). Right: M 87 (0.05r500). |
Comparison of the abundance results obtained by performing global fittings to the best-quality EPIC spectra of Perseus (0.2r500) and M 87 (0.05r500).
Despite these considerations, and the fact that the real temperature distributions in the ICM is unknown, considering a continuous distribution is clearly more realistic than only one or two unique temperatures. By comparing only the gdem and wdem models, we note that they give very similar abundance ratios for both Perseus and M 87. Except for Ne/Fe, the largest difference is found for Ni/Fe, and is clearly smaller than the range of systematic uncertainties affecting the measurements. Therefore, using a wdem model instead of a gdem model should have a limited impact on our EPIC final results. For comparison, de Plaa et al. (in prep.) find that such an effect on the O/Fe ratio derived from RGS is always smaller than 20%. Therefore, considering further uncertainties related to the thermal models is not necessary for the purpose of this work.
Appendix D: Best-fit temperature and abundances
In Table D.1 we present the full results of our best-fit parameters (kT, σT, the absolute Fe abundance, and the abundance ratios of O/Fe, Ne/Fe, Mg/Fe, Si/Fe, S/Fe, Ar/Fe, Ca/Fe, and Ni/Fe) for each object of CHEERS, within a radius of 0.05r500. When possible (hot clusters), we indicate the parameters extracted from 0.2r500 as well. The O/Fe and Ne/Fe abundances have been corrected from updated RR calculations, as described in Appendix B.
Summary of the best-fit temperatures, σT and abundances for all the clusters/groups/ellipticals of the CHEERS.
All Tables
XMM-Newton/EPIC observations used in this paper (see Pinto et al. 2015, for details on RGS observations).
Average abundance ratios estimated from the (0.05 + 0.2)r500 sample, as well as their statistical, systematic, and total uncertainties.
Comparison of the abundance results obtained by performing global fittings to the best-quality EPIC spectra of Perseus (0.2r500) and M 87 (0.05r500).
Summary of the best-fit temperatures, σT and abundances for all the clusters/groups/ellipticals of the CHEERS.
All Figures
 |
Fig. 1 Mean temperature (EPIC) versus absolute Fe abundance for the full sample. The black squares and the red triangles show the EPIC measurements within 0.05r500 and 0.2r500, respectively. Each pair of measurements (0.05r500,0.2r500) that belong to the same hot cluster is connected by a grey dash-dotted line. The blue stars show the RGS measurements (adapted from de Plaa et al. 2016), scaled on their respective EPIC mean temperature within 0.2r500. The vertical black dotted line separates the cool groups/ellipticals from the hot clusters (see text). |
| In the text | |
 |
Fig. 2 Same as Fig. 1 for the other (relative-to-Fe) abundance ratios. For clarity, the (0.05r500,0.2r500) pairs are not shown explicitly. |
| In the text | |
 |
Fig. 3 Distributions of the EPIC absolute Fe abundances for all the objects in our sample. Three subsamples (hot clusters within 0.2r500 and 0.05r500, and cool groups within 0.05r500) are considered separately (see also Fig. 1). |
| In the text | |
 |
Fig. 4 Top: EPIC MOS 1, MOS 2, and pn stacked and redshift-corrected residuals of the (0.05 + 0.2)r500 sample (using a gdem model). Before stacking, the MOS and pn spectra of every pointing were fitted simultaneously with coupled parameters. The vertical dotted lines indicate the position of the detected line emissions in the EPIC spectra (see lower panel). Bottom: EPIC stacked and redshift-corrected residuals of the (0.05 + 0.2)r500 sample (using a gdem model, all instruments combined). Before stacking, the MOS and pn spectra of every pointing were fitted independently and the line emission was set to zero in the model. The height of the peak of the Fe-K complex is ~1.95. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 (bottom), this time comparing the 0.05r500 cool (grey curve) and the 0.2r500 hot (black curve) subsamples. The height of the peak of the Fe-K complex in the 0.2r500 hot sample is ~2.23. |
| In the text | |
 |
Fig. 6 Left: average abundance ratios considering different (sub-)samples and/or different EPIC extraction regions. The O/Fe and Ne/Fe ratios are measured using RGS (cross-dispersion width of 0.8′). For these two ratios there is thus no distinction between the two hot samples or between the two full samples. The error bars incorporate the statistical errors (σstat) and the intrinsic scatters (σint + 1σ). Right: average abundance ratios estimated from the (0.05 + 0.2)r500 sample, measured independently by different combinations of instruments. The error bars incorporate the statistical errors (σstat), the intrinsic scatters (σint + 1σ), and the uncertainties derived from the different EPIC extraction regions and/or subsamples (σregion, see left panel). |
| In the text | |
 |
Fig. 7 Average abundance ratios in our (0.05 + 0.2)r500 sample (black squares) versus proto-solar abundances (grey dashed line) and their 1σ uncertainties (red dash-dotted lines, adapted from Lodders et al. 2009). |
| In the text | |
 |
Fig. A.1 Comparison between the EPIC and RGS measurements of the O/Fe abundance ratio in most objects of our (0.05 + 0.2)r500 sample. The blue dotted line shows the one-to-one EPIC-RGS correspondence. In our fits we alternatively fix the NH to the weighted neutral+molecular values calculated from Willingale et al. (2013), and leave it free within the ranges given by Eq. (A.1). The two approaches are shown in red and black, respectively. |
| In the text | |
 |
Fig. B.1 Calculated radiative recombination correction factors of H-like Lyman α lines of O and Ne as a function of the cluster (mean) temperature (adapted from the results of Mao & Kaastra 2016). |
| In the text | |
 |
Fig. C.1 EPIC abundance measurements in the two best-quality observations of our sample, based on global fittings (see also Table C.1). Four thermal models are successively considered: 1T (black empty squares), 2T (blue filled squares), wdem (orange filled squares), and gdem (red filled squares). The Fe abundance is given in absolute values, while the other abundances are given relative to Fe. Left: perseus (0.2r500). Right: M 87 (0.05r500). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.