| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A129 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628655 | |
| Published online | 28 June 2016 | |
V346 Centauri: Early-type eclipsing binary with apsidal motion and abrupt change of orbital period⋆,⋆⋆
1 Astronomical Institute of the Charles University, Faculty of Mathematics and Physics, V Holešovičkách 2, 180 00 Praha 8, Czech Republic
e-mail: mayer@cesnet.cz
2 Department of Astrophysics and Planetary Sciences, Villanova University, 800 East Lancaster Ave, Villanova, PA 19085, USA
3 Royal Observatory of Belgium, Ringlaan 3, 1180 Brussels, Belgium
4 Department of Theoretical Physics and Astrophysics, Masaryk University, Kotlářská 2, 611 37 Brno, Czech Republic
5 Institute of Physics, The Czech Academy of Sciences, Na Slovance 1999/2, 182 21 Praha 8, Czech Republic
6 Variable Star and Exoplanet Section of the Czech Astronomical Society, Vsetínská 941/78, 757 01 Valašské Meziříčí, Czech Republic
Received: 7 April 2016
Accepted: 2 May 2016
New physical elements of the early B-type eclipsing binary V346 Cen are derived using the HARPS spectra downloaded from the ESO archive and also numerous photometric observations from various sources. A model of the observed times of primary and secondary minima that fits them best is a combination of the apsidal motion and an abrupt decrease in the orbital period from 6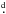 322123 to 6
322123 to 6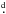 321843 (shortening by 24 s), which occurred somewhere around JD 2 439 000. Assumption of a secularly decreasing orbital period provides a significantly worse fit. Local times of minima and the final solution of the light curve were obtained with the program PHOEBE. Radial velocities of both binary components, free of line blending, were derived via 2D cross-correlation with a program built on the principles of the program TODCOR. The oxygen lines in the secondary spectra are weaker than those in the model spectra of solar chemical composition. Using the component spectra disentangled with the program KOREL, we find that both components rotate considerably faster than would correspond to the synchronization at periastron. The apside rotation known from earlier studies is confirmed and compared to the theoretical value.
321843 (shortening by 24 s), which occurred somewhere around JD 2 439 000. Assumption of a secularly decreasing orbital period provides a significantly worse fit. Local times of minima and the final solution of the light curve were obtained with the program PHOEBE. Radial velocities of both binary components, free of line blending, were derived via 2D cross-correlation with a program built on the principles of the program TODCOR. The oxygen lines in the secondary spectra are weaker than those in the model spectra of solar chemical composition. Using the component spectra disentangled with the program KOREL, we find that both components rotate considerably faster than would correspond to the synchronization at periastron. The apside rotation known from earlier studies is confirmed and compared to the theoretical value.
Key words: stars: early-type / binaries: close / stars: individual: V346 Cen
Based on observations made with the ESO telescopes at the La Silla Paranal Observatory under programmes ID 083.D-0040(A), 085.C-0614(A), and 178.D-0361(B).
Tables A.2–A.6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/591/A129
© ESO, 2016
1. Introduction
The eclipsing binary V346 Cen (HD 101837; 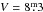 in maximum, with a period of 6
in maximum, with a period of 6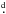 322) has an eccentric orbit with e = 0.29 and is one of the early-type binaries for which the apside line rotation has been found. Its variability was discovered by O’Leary & O’Connell (1936) and the presence of apsidal motion was first reported by Dugan & Wright (1939) and O’Connell (1939). Although the star was classified as B5 on a slit spectrogram by Popper (1966), the standard MK spectral type appears to be B0.5 IV according to Fitzgerald & Miller (1983). The binary is a member of the open cluster Stock 14.
322) has an eccentric orbit with e = 0.29 and is one of the early-type binaries for which the apside line rotation has been found. Its variability was discovered by O’Leary & O’Connell (1936) and the presence of apsidal motion was first reported by Dugan & Wright (1939) and O’Connell (1939). Although the star was classified as B5 on a slit spectrogram by Popper (1966), the standard MK spectral type appears to be B0.5 IV according to Fitzgerald & Miller (1983). The binary is a member of the open cluster Stock 14.
Journal of photometric observations of V346 Cen.
Several photometric and spectroscopic studies of V346 Cen have been carried out, the fundamental paper being by Giménez et al. (1986a, GCA). They obtained the apside line rotation period of 321 ± 16 years. An important contribution has also been presented by Drobek et al. (2013); they give the apsidal period as 306 ± 4 yr. New photometric and spectroscopic data have been published since then and we have secured several sets of new photometric observations.
2. Photometry
New photometric observations have been published by van Houten et al. (2009), by the ASAS 2 and ASAS 3 project teams (Pojmański 1998, 2002), and by Drobek et al. (2013). We used the photographic light curve of O’Connell (1939) and obtained new BVR, BVRI, and non-stardard green photometry at three different stations. The journal of photometric observations used here is in Table 11. Details on the individual data sets and tables with new observations can be found in the Appendix. We note that one of the comparison stars we used at the Mount John Observatory, and which was also used by O’Connell (1939) and van Houten et al. (2009), is an irregular B0.5 e variable V916 Cen that should be abandoned as a comparison in any future observations (see Fig. B.1). Pojmański (2000) and several other investigators reported that the star is an eclipsing binary with a period of 1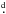 463, but we argue that it is a typical Be variable showing the variations on several time scales (see Appendix B for details). Obviously, the van Houten et al. (2009) and our Mt. John observations should be treated with some caution.
463, but we argue that it is a typical Be variable showing the variations on several time scales (see Appendix B for details). Obviously, the van Houten et al. (2009) and our Mt. John observations should be treated with some caution.
2.1. Times of minima
The first times of minima were published by the discoverers of the variability O’Leary & O’Connell (1936), O’Connell (1939), and Dugan & Wright (1939). When Hernandez & Sahade (1978) obtained the first radial-velocity (RV) curve of the primary component of V346 Cen, it turned out that Dugan & Wright (1939) had incorrectly identified the primary and secondary minima. Their identification is correct in O’Connell (1939). Van Houten (2009) obtained the light curve in four passbands of the Walraven system and also published a time of a primary minimum. The star was not observed by Hipparcos, and the TYCHO data are too noisy to be used to determine the times of minima. The time of the primary minimum RJD 50 554.442 was obtained from the ASAS 2 observations by Pojmański (1998) (although his period of 6.295 d is rather off). Ogloza & Zakrzewski (2004) have published several times of minima based on ASAS 2 photometry, but their primary and secondary minima are also reversed. Drobek et al. (2013) published several times of minima, based once more on the ASAS 2, on ASAS 3 (Pojmański 2002), van Houten et al. (2009), and their new observations.
Here, we adopt a different approach. Considering that the orbital period is rather long for an accurate determination of individual minima, and having all the light curves at our disposal, we fitted all individual local light curves in individual passbands, covering time segments not longer than 1500 d (and usually much shorter – see the time intervals specified in Table 1) using the PHOEBE program (Prša & Zwitter 2005, 2006) rel. 1.0 with several passbands added. In this way, we kept most of the elements fixed at the values of our final solution (see Sect. 4) and we only allowed convergency of the phase shift from a local mean epoch, local value of the longitude of periastron, and the light level. This way, we obtained the local epochs of the primary and secondary minima. A few examples of the light-curve fits can be found in Fig. A.1.
For completeness we mention that there is also a photographic light curve by Gaposchkin (1953) constructed from estimates on plates of the Harvard collection obtained in the years 1941–1950. The light curve is published only in the form of 28 normal points, which inevitably smears out the effects of the apsidal motion. For this reason, we have not considered this data in our analyses.
Dugan & Wright (1939) published only the times of minima, not the individual magnitude estimates. Since they mention that they applied the heliocentric corrections of time, we tried to reconstruct the accurate times of minima from their Table 3, using their epochs and the O–C tabulated separately in days, and in orbital phases. This gave HJDs, which never differed for more than 0.003 d and we adopted the mean of these two estimates. All these reconstructed Dugan & Wright (1939) minima are summarized in Table A.1. The minima based on local fits of the light curves are listed in Table 2. They are complemented by two estimates of local minima based on our RV solutions for the Hernandez & Sahade (1978), and our new RVs (see below).
Following the procedure already applied by Dugan & Wright (1939), we derived two straight lines via least-squares fits in the O–C residuals and taking the weights of individual minima into account. In doing so we omitted (as also advised by Dugan & Wright 1939) the first three primary minima, and the first secondary minimum. From the intersection of both straight lines thus constructed we estimated the instant when the longitude of periastron was ω = 270° as RJD 21 128. Dugan & Wright (1939) gives this time as RJD 21 963, Drobek et al. (2013) as 20 750. These numbers probably characterize the uncertainty of this determination.
The differences between the times of the primary and secondary minima at a given epoch depend on the rate of the apside rotation alone (see e.g. Giménez & Garcia-Pelayo 1983; Khaliullina et al. 1985; Giménez & Bastero 1995). When Drobek et al. (2013) carried out the analysis of the apsidal motion, they also found a clear deviations from a pure apsidal motion (cf. their Fig. 14). They tentatively suggested that these deviations could be due to the light-time effect caused by the presence of a third body in the system with an orbital period longer than 100 yr.
Because we had more observations than Drobek et al. (2013) at our disposal, we repeated their analysis, using the primary and secondary minima from Tables A.1 and 2; the result is shown in Fig. 1. A somewhat better fit than theirs was obtained when we used our value RJD = 21 128 for the epoch, when ω = 270°; the period of the apsidal advance of 306 years does not need any revision.
 |
Fig. 1 Differences of times of minima from Table A.1 (open circles) and Table 2 (filled circles; triangles when the time results from a RV curve) are shown. Some data, probably of low accuracy, differ from the dominant trend. The curve corresponds to the period of apsidal advance 306 years and parameters in Tables 3 and 5. |
 |
Fig. 2 Time plot of the O–C deviations from the fit of the apsidal-motion curves to the minima of V346 Cen. The asymmetry of the plot depends on Psider used; here it is 6 |
Our plot of O–C deviations from the model apsidal motion is in Fig. 2. It would be difficult to explain it as an effect of a third body since, for example, the shape of the plot of deviations is not that of a sine-type curve expected for the light-time effect. With the period about 200 years and semi-amplitude ≈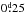 the minimum mass of the third body (for the masses of the eclipsing binary components according to Table 5) would have to be more than ≈10M⊙. No such body with the corresponding luminosity is detectable in either the light curves or the high signal-to-noise (S/N) spectra, as detailed below. Even if we assume that the third body is a binary, its light and spectral lines should be visible (and the body should be observable by speckle interferometry as the separation should be of the order of tens of mas).
the minimum mass of the third body (for the masses of the eclipsing binary components according to Table 5) would have to be more than ≈10M⊙. No such body with the corresponding luminosity is detectable in either the light curves or the high signal-to-noise (S/N) spectra, as detailed below. Even if we assume that the third body is a binary, its light and spectral lines should be visible (and the body should be observable by speckle interferometry as the separation should be of the order of tens of mas).
One possible explanation could be a continuous secular change in the period, shown in Fig. 2 by a parabola with 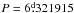 and with the second order term −3.22 × 10-8 × E2. This fit could be improved if a combination with the light-time effect by a third body were considered. The light-time effect amplitude might then be small and there would be no problem with the absence of the signatures of the third body in the spectra and photometric solutions.
and with the second order term −3.22 × 10-8 × E2. This fit could be improved if a combination with the light-time effect by a third body were considered. The light-time effect amplitude might then be small and there would be no problem with the absence of the signatures of the third body in the spectra and photometric solutions.
As Fig. 2 shows, the assumption of a sudden decrease in the sidereal period near RJD 39 000 fits the observations much better. If the decrease occurred, the sidereal period was 6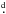 322123 prior to RJD 39 000 (similar to 6
322123 prior to RJD 39 000 (similar to 6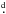 322070 advocated by O’Connell 1939) and 6
322070 advocated by O’Connell 1939) and 6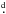 321843 after RJD 39 000. The change is 1:1.000044 (a decrease of 24 s) and it occurred during an interval of about a 30 yr for which no observations of eclipses are available. A similar period decrease happened in the V505 Sgr three-body system, and Brož et al. (2010) tentatively explained it by a close encounter with a body on hyperbolic orbit. A sudden period change was observed for several other binaries, e.g. TW Dra (Zejda et al. 2008) and UV Leo (Mikuz et al. 2002); in these cases, periods increased. Moreover, TW Dra is a semi-detached system, where an episode of more intense mass transfer would not be so surprising.
321843 after RJD 39 000. The change is 1:1.000044 (a decrease of 24 s) and it occurred during an interval of about a 30 yr for which no observations of eclipses are available. A similar period decrease happened in the V505 Sgr three-body system, and Brož et al. (2010) tentatively explained it by a close encounter with a body on hyperbolic orbit. A sudden period change was observed for several other binaries, e.g. TW Dra (Zejda et al. 2008) and UV Leo (Mikuz et al. 2002); in these cases, periods increased. Moreover, TW Dra is a semi-detached system, where an episode of more intense mass transfer would not be so surprising.
For the moment, we have no clear explanation for either the continuous or sudden period change of V346 Cen; judging by a normal appearance of the Hα line, without any detectable trace of emission indicative of the presence of some circumstellar matter in the system, we do not find the possibility of a transient mass transfer event very probable, though we admit that we do not have any spectra taken around RJD 39 000.
3. Spectroscopy
At present, there are 33 spectra in the ESO archive taken by the echelle spectrograph HARPS at the 3.6 m ESO telescope. These spectra were obtained during a 6-day interval in April 2009 and are available as a pipeline product. The list of spectra is in Table 4. The spectra cover the region from 378 to 691 nm and have the resolving power of 115 000; we binned the spectra to the resolution 0.06 Å, typically obtaining a S/N of ~250. Fringing is apparent at wavelengths longer than 450 nm. Examples of the He i 4922 Å line near two opposite elongations are in Fig. 3.
3.1. Radial velocities
As already mentioned, the first RV curve of the primary component V346 Cen was obtained by Hernandez & Sahade (1978), but it seems that this curve was affected by the line blending of the primary and secondary. The authors themselves noted that the high eccentricity of 0.40 ± 0.02 they obtained is suspect. Our experience from other similar systems is, however, that their RVs can still be used to determine local epochs of the primary and secondary minima if the correct value of eccentricity is fixed in the solution. Using the program FOTEL (Hadrava 2004a), we therefore derived a new solution for their primary RVs, keeping the sidereal period fixed at our value of 6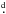 322123 and the eccentricity at a value of 0.287, which follows from new RVs and light curves (see below). The solution is given in Table 3.
322123 and the eccentricity at a value of 0.287, which follows from new RVs and light curves (see below). The solution is given in Table 3.
Two 20 Å mm-1 fine-grained photographic spectra at both elongations were obtained by GCA, who estimated K1 = 135 ± 5, and K2 = 190 ± 10 km s-1. Clearly, new and more complete RV curves of both components are desirable.
 |
Fig. 3 He i 4922 Å line in the spectra of extreme velocities (black line: RJD 54 928.50, grey line: RJD 54 930.81). The line is blended with O ii 4924.52 Å and is affected by the O ii 4906.82 Å line at the blue side. |
Orbital solutions for the RVs of the primary obtained by Hernandez & Sahade (1978), and for our new HARPS RVs derived with asTODCOR.
Determination of RVs by direct measurements of individual lines (e.g. using Gaussians) in the HARPS spectra is not a good method for V346 Cen. The lines are rotationally broadened and nearly all stronger lines (mainly He i) are accompanied by numerous blends, most often by O ii lines, which prevents reliable measurements. In another attempt, we tried to disentangle the spectra using the program KOREL (Hadrava 2004b) in several spectral regions. The spread of the results was larger than expected. Nevertheless, we formed a mean of the KOREL solutions from six spectral regions and used it as a starting solution for spectra disentangling. A relatively large spread in RVs was also found when we tried to obtain them from the comparison of individual spectra with two synthetic spectra.
Therefore, we finally used the program as TODCOR2 based on the principles of a 2D cross-correlation approach, first suggested by Zucker & Mazeh (1994) – see Desmet et al. (2010) for the details of program asTODCOR. Following Harmanec et al. (2015) we adopted the spectra disentangled by KOREL as the templates for the 2D cross-correlation. The spectral region 4460–4486 Å was used.
The orbital solution based on asTODCOR RVs had small rms errors, and actually agrees very well with the mean KOREL solution. The asTODCOR RVs are listed in Table 4, the RV curves are in Fig. 4, and the orbital solution for the fixed values of Psider. and e are also listed in Table 3.
3.2. A negative search for the tertiary
We carried out several experiments with KOREL to check whether a line spectrum of a putative tertiary could not be found in the high-quality HARPS spectra. Because all HARPS spectra were obtained within a short interval of 6 days, it is clear that the exact value of the long orbital period (more than some 100 yr, see Sect. 2.1) used for the disentangling is not important. We ran a number of trial solutions with KOREL, but in no case were any lines of a tertiary found.
 |
Fig. 4 Radial velocities of the primary and secondary components of V346 Cen as calculated by asTODCOR. |
HARPS spectra and RVs derived with asTODCOR.
3.3. Comparison with synthetic spectra
We tried to support the spectral classification of the binary components via a comparison of the disentangled and synthetic spectra. The spectra were disentangled by KOREL for the fixed orbital elements given by the HARPS solution of Table 3. We used a Python program PYTERPOL, which interpolates in a pre-calculated grid of synthetic spectra in order to estimate radiative properties of components of multiple systems3. We used it to fit the disentangled spectra with the synthetic BSTAR spectra (Lanz & Hubeny 2007). Solar metallicity and a microturbulence of 2 km s-1 were assumed; the log g values were fixed from the joint light-curve and RV curve solution (see Sect. 4). Formally, the best fit temperatures were Teff,1 = 27 141 ± 25 K and Teff,2 = 20 991 ± 190 K. The comparison also provided rotational velocities of both components (see Table 5). As already noted by GCA, who obtained values of 165 ± 15 and 140 ± 15 km s-1, these rotation velocities are considerably higher than those corresponding to (pseudo)synchronization (see Table 5).
The effective temperature of the secondary obtained this way is much lower than that derived from the light-curve solution (Sect. 4). It seems that the reason is the weakness of the O ii lines in the secondary spectrum. A part of the disentangled spectrum with several O ii lines is shown in Fig. 5. When we compared the disentangled spectra of the secondary with a synthetic spectrum for Teff = 25 000 K obtained from the light-curve solution for He i and some other lines, we found a very good agreement. Even a direct comparison of the 21 000 K and 25 000 K synthetic spectra for log g = 4.0 [cgs] rotated to 93 km s-1 shows their close similarity for the majority of spectral features in the optical part of the spectrum. We therefore believe that there is no real discrepancy, but only a mild underabundancy of O ii in the atmosphere of the secondary.
3.4. Spectral type of the secondary
The spectral type and luminosity class of the primary noted in the Introduction is accepted here; according to Schmidt-Kaler (in Aller et al. 1982), the temperature Teff,1 is then ≈27 000 K. The secondary can be classified using the criteria listed by Lesh (1968): as the line O ii 4072 Å is not present in the secondary spectrum, the type is B2; and since O ii 4121 Å is weaker than He i 4144 Å, the luminosity is V. We see that the mass and radius agree with expectations for such a classification.
4. Final light-curve and RV curve solution
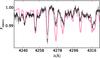 |
Fig. 5 Disentangled spectrum of the secondary in the wavelength region from 4230 to 4325 Å. The metallic lines seen in the observed spectrum are the O ii lines at 4253.9, 4254.1, 4276.8, 4283.0 and 4303.8 Å, N ii 4241.8 Å line and C ii 4267.1 Å line. The O ii lines in the disentangled spectrum of the secondary (black line) are weaker than suggested by the synthetic spectrum for the temperature of 25 500 K (violet/gray line). |
Combined radial-velocity curve and light-curve solution with PHOEBE.
 |
Fig. 6 Light curve of V346 Cen. Points correspond to the u measurements by GCHV, the solid line to the solution by PHOEBE with parameters from Table 5. We show the u data since their deviations from the model curve are the largest, as they are in GCA. |
The excellent uvby light curves published by Giménez et al. (1986b, GCHV) are still the best light curves available for V346 Cen. Each of them is formed by 1056 individual observations obtained in the years 1982 and 1983. As yet another check on the possible presence of a third light, we first run a PHOEBE solution in which third light was among the free parameters of the solution. It resulted in finding zero third light as the optimal result.
To derive the final solution we therefore used the uvby observations together with the asTORCOR RVs from the HARPS spectra and for the sidereal period derived in the previous section. We fixed the gravity darkening and albedos of both components at 1.0 and the limb-darkening coefficients were interpolated in the grid of pre-calculated model atmospheres. The effective temperature of the primary was kept fixed at Teff,1 = 27 141 K. The theoretical u light curve is compared with the measurements in Fig. 6.
The GCHV light curves were solved by GCA, who used the program WINK (Wood 1973), and noted the disagreement between the theoretical and observed curves around periastron. Even the inclusion of the reflection did not improve the fit. In a “Note added in proof” GCA remarked that a more advanced treatment of the gravity darkening – in addition to other program changes – removed most of the disagreement, but they gave no numerical details.
5. Absolute parameters and apside line rotation
The absolute parameters of the components are in Table 5. We compared these values with the evolutionary models by Claret (2004).
We followed the steps used by Claret & Giménez (2010) and calculated the coefficients c2i (respecting the fast rotation of both components) and the general relativity contribution (0.00130 deg/cycle). Then 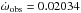 ,
, 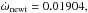 and log k2,newt = −2.428. To find the expected value of the apside line rotation, the tables published by Claret (2004) were considered. However, in this case the Claret models do not represent the primary component well. For the given mass and radius the model is too cold and old. From our parameters, the value of the primary k2 might be estimated as −2.36. The fast rotation probably means that the correct model value is smaller (Claret 1999), i.e. close to the observed value.
and log k2,newt = −2.428. To find the expected value of the apside line rotation, the tables published by Claret (2004) were considered. However, in this case the Claret models do not represent the primary component well. For the given mass and radius the model is too cold and old. From our parameters, the value of the primary k2 might be estimated as −2.36. The fast rotation probably means that the correct model value is smaller (Claret 1999), i.e. close to the observed value.
As the binary is a member of the open cluster Stock 14, it is possible to compare the distance obtained from the binary parameters with the distance determined for the cluster. Paunzen & Netopil (2006) give the cluster distance as 2439 ± 326 pc (according to Fitzgerald & Miller 1983, the distance is 2870 pc) and the age 10 Myr. The parameters of the binary components obtained by GCA are very similar to ours; therefore, their results – age 10 Myr and distance 2380 pc – are still valid. The good agreement with the cluster data supports the correctness of the binary solution.
The only remaining open problem is to confirm the abrupt change in the orbital period and to find its true cause.
A description of the program, developed by J.N., together with a tutorial is available at: https://github.com/chrysante87/pyterpol/wiki
Acknowledgments
The research of P.M., P.H., M.W., and J.N. was supported by the grants P209/10/0715 and GA15-02112S of the Czech Science Foundation. Mr. D. Drobek kindly informed us about details of Siding Springs CCD observations of V346 Cen. We gratefully acknowledge the use of the electronic databases: SIMBAD at CDS, Strasbourg, and NASA/ADS, USA, and the data archive of Acta Astronomica. The operation of the robotic telescope FRAM has been supported by the grants of the Ministry of Education of the Czech Republic (MSMT-CR LG13007 and LG15014) and by grant No. 14-175 of the Czech Science Foundation.
References
- Aller, L. H., Appenzeller, I., Baschek, B., et al. 1982, Landolt-Börnstein: Numerical Data and Functional Relationships in Science and Technology, New Series, Group 6 Astronomy and Astrophysics, Vol. 2 (Springer) [Google Scholar]
- Brož, M., Mayer, P., Pribulla, T., et al. 2010, AJ, 139, 2258 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A. 1999, A&A, 350, 56 [NASA ADS] [Google Scholar]
- Claret, A. 2004, A&A, 424, 919 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., & Giménez, A. 2010, A&A, 519, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Desmet, M., Frémat, Y., Baudin, F., et al. 2010, MNRAS, 401, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Drobek, D., Pigulski, A., Shobbrook, R. R., & Narwid, A. 2010, Astron. Nachr., 331, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Drobek, D., Pigulski, A., Shobbrook, R. R., & Narwid, A. 2013, Acta Astron., 63, 339 [NASA ADS] [Google Scholar]
- Dugan, R. S., & Wright, F. W. 1939, Contributions from the Princeton University Observatory, 19, 10 [Google Scholar]
- Ebr, J., Janeček, P., Prouza, M., et al. 2014, Rev. Mex. Astron. Astrofis. Conf. Ser., 45, 114 [NASA ADS] [Google Scholar]
- Fitzgerald, M. P., & Miller, M. L. 1983, PASP, 95, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Gaposchkin, S. 1953, Annals of Harvard College Observatory, 113, 67 [Google Scholar]
- Giménez, A., & Bastero, M. 1995, Ap&SS, 226, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., & Garcia-Pelayo, J. M. 1983, Ap&SS, 92, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Giménez, A., Clausen, J. V., & Andersen, J. 1986a, A&A, 160, 310 [NASA ADS] [Google Scholar]
- Giménez, A., Clausen, J. V., Helt, B. E., & Vaz, L. P. R. 1986b, A&AS, 66, 45 [NASA ADS] [Google Scholar]
- Hadrava, P. 2004a, Publ. Astron. Inst. Acad. Sci. Czech Rep., 92, 1 [Google Scholar]
- Hadrava, P. 2004b, Publ. Astron. Inst. Acad. Sci. Czech Rep., 92, 15 [Google Scholar]
- Harmanec, P. 1983, Hvar Observatory Bull., 7, 55 [Google Scholar]
- Harmanec, P. 1984, Bull. Astron. Inst. Czechoslovakia, 35, 193 [NASA ADS] [Google Scholar]
- Harmanec, P. 1998, A&A, 335, 173 [NASA ADS] [Google Scholar]
- Harmanec, P., Matthews, J. M., Bozic, H., et al. 1991, Bull. Astron. Inst. Czechoslovakia, 42, 1 [Google Scholar]
- Harmanec, P., Koubský, P., Nemravová, J. A., et al. 2015, A&A, 573, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernandez, C. A., & Sahade, J. 1978, PASP, 90, 728 [NASA ADS] [CrossRef] [Google Scholar]
- Hut, P. 1981, A&A, 99, 126 [NASA ADS] [Google Scholar]
- Khaliullina, A. I., Khaliullin, K. F., & Martynov, D. I. 1985, MNRAS, 216, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Lanz, T., & Hubeny, I. 2007, ApJS, 169, 83 [CrossRef] [Google Scholar]
- Lesh, J. R. 1968, ApJS, 17, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mermilliod, J.-C., Mermilliod, M., & Hauck, B. 1997, A&AS, 124, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mikuz, H., Dintinjana, B., Prsa, A., Munari, U., & Zwitter, T. 2002, IBVS, 5338, 1 [NASA ADS] [Google Scholar]
- O’Connell, D. 1939, Publ. Riverview College Observatory, 2, 5 [Google Scholar]
- Ogloza, W., & Zakrzewski, B. 2004, IBVS, 5507, 1 [NASA ADS] [Google Scholar]
- O’Leary, W., & O’Connell, D. 1936, Astron. Nachr., 259, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Paunzen, E., & Netopil, M. 2006, MNRAS, 371, 1641 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The Hipparcos and TYCHO catalogues, Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission (Noordwijk, The Netherlands: ESA Publ. Division) [Google Scholar]
- Pigulski, A., & Pojmański, G. 2008, A&A, 477, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pojmański, G. 1998, Acta Astron., 48, 35 [Google Scholar]
- Pojmański, G. 2000, Acta Astron., 50, 177 [NASA ADS] [Google Scholar]
- Pojmański, G. 2002, Acta Astron., 52, 397 [Google Scholar]
- Popper, D. M. 1966, AJ, 71, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., & Zwitter, T. 2005, ApJ, 628, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Prša, A., & Zwitter, T. 2006, Ap&SS, 36 [Google Scholar]
- van Houten, C. J., van Houten-Groeneveld, I., van Genderen, A. M., & Kwee, K. 2009, J. Astron. Data, 15, 2 [NASA ADS] [Google Scholar]
- Wood, D. B. 1973, PASP, 85, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Zejda, M., Mikulášek, Z., & Wolf, M. 2008, A&A, 489, 321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucker, S., & Mazeh, T. 1994, ApJ, 420, 806 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
Appendix A: Photometric data used
 |
Fig. A.1 Examples of local fits in PHOEBE for selected light curves. From top to bottom: (1) photographic light curve by O’Connell (1939); (2) ASAS2 I light curve (RJDs 51 200–51 403); (3) R light curve from FRAM automatic telescope. |
Since PHOEBE internally uses fluxes calculated from the observed magnitudes, normalized to some defined magnitude value, it is advisable to use observations converted at least approximately to magnitudes and not the magnitude differences alone, especially in situations when different comparison stars were used by different observers.
Times of the primary and secondary minima of V346 Cen estimated by us from Table 3 of Dugan & Wright (1939).
Here we provide some comments on individual data sets used for those who would like to carry out independent analyses. Unpublished individual magnitudes with their RJDs are available at CDS as Tables A.2 to A.6. The journal of all data sets is in Table 1. For illustration, we also show the quality of local fits for several different light curves in Fig. A.1.
-
Dugan & Wright (1939)Times of minima derivedby us are in Table A.1.
-
Riverview photographic magnitudes: these photographic observations were obtained by O’Connell (1939) and reduced from photographic plates relative to four comparison stars HD 101511, HD 101838, HD 101794, and HD 102053. We digitized the individual observations from both minima from their Table II. Unfortunately, observations outside minima were only published as normal points in Table III. For normal points outside minima we therefore reconstructed artificial RJDs, corresponding to the mean epoch of all observations, and assigned them weights proportional to the number of observations forming each normal point. This data set is also available at CDS as Table A.2.
-
Walraven VBUL observations: these differential observations were published by van Houten et al. (2009) in the form of magnitude differences (not as the usual log [flux] values) relative to the comparison star HD 101 794, for which we adopted V = 8m.684, B = 8m.733, and U = 7m.990 from the electronic catalogue maintained at the Geneva Observatory (see Mermilliod et al. 1997), and an artifically estimated value L = 8m.300, and added these values to the respective magnitude differences.
-
ESO La Sillauvby observations: these superb photometric observations were published by Giménez et al. (1986b) as magnitude differences relative to HD 101 466. We adopted the values derived by these authors for HD 101466 (y = 7m.322, b = 7m.367, v = 7m.535, and u = 8m.765) and added them to the magnitude differences. Since these observations are not available in digital form, we deposited them as Table A.3 at CDS.
-
ASAS 2 I all-sky photometry: these observations were divided into four shorter time intervals not only to monitor the changes due to apsidal motion, but also because these early observations exhibit a secular drift. Data from the first time interval are also notably less accurate. We omitted a number of observations with larger deviations from the phase curve.
-
ASAS 3 V all-sky photometry: these observations were divided into two shorter time intervals to monitor the changes due to apsidal motion. Data from diaphragm No. 3 were used because they have, on average, the smallest rms errors. We omitted a number of observations with larger deviations from the phase curve.
-
Mount John BVR photometry: these differential CCD observations were secured by MZ relative to the Be star HD 101794 = V916 Cen, but it seems that the irregular variability of the comparison had no adverse effects on the photometry of V346 Cen, which was secured only during three consecutive nights. For comparison, we adopted V = 8
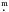 684 and B = 8
684 and B = 8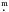 733 from the Geneva database (Mermilliod et al. 1997), and artificially set R = 9
733 from the Geneva database (Mermilliod et al. 1997), and artificially set R = 9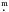 8. The RJDs and magnitude differences V346 Cen − V916 Cen are available as Table A.4 at CDS.
8. The RJDs and magnitude differences V346 Cen − V916 Cen are available as Table A.4 at CDS. -
Siding SpringsUBV photometry: these observations were secured by Drobek et al. (2013) and are available in electronic form as magnitude differences to the mean of several comparison stars in the field of the CCD camera, but no details are known. We added △V = 10m.66, △B = 10m.64, and △U = 10m.06 to the magnitude differences to reproduce the UBV magnitudes of V346 Cen.
-
Sutherland broad-band green CCD photometry: these observations were obtained by JL during his visit to the South African Astronomical Observatory and were reduced relative to the A0 star HD 102152 (V = 9m.15, and B = 9m.16 according to Mermilliod et al. 1997). We added 9m.15 to the magnitude differences. The RJDs and magnitude differences V346 Cen − HD 102152 are available as Table A.5 at CDS.
-
FRAM BVRI photometry: these CCD observations were secured by JJ, KH, and MM with the remotely controlled automatic photometric telescope located at the Pierre Auger Observatory in Argentina. They were reduced relative to CD−61°3157, for which we adopted V = 9m.4, B = 11m.2, and R = 9m.900 from the SIMBAD database. The RJDs and magnitude differences are in Table A.6 at CDS.
Appendix B: Nature of the light variations of V916 Cen
As already mentioned, the light variations of this object were discovered by Perryman & ESA (1997) and classified – correctly, in our opinion – as typical for Be stars (see Fig. B.1). Harmanec (1983) already pointed out that Be stars vary on at least three distinct time scales, combining long-term changes due to secular variations of their extended envelopes, medium time changes on a scale of week to months, and rapid cyclic or even periodic changes occurring on a time scale comparable to stellar rotational period. Pojmański (2000) analysed the ASAS2 photometry secured in the infrared I filter and reported that the star is an eclipsing binary with two similar eclipses, a period of 1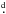 463279, and a full amplitude of 0m.1. Later Pigulski & Pojmański (2008) analysed the ASAS3 V photometry and concluded that the object is also a β Cep variable with a period of 0
463279, and a full amplitude of 0m.1. Later Pigulski & Pojmański (2008) analysed the ASAS3 V photometry and concluded that the object is also a β Cep variable with a period of 0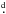 224648 and an amplitude of 0
224648 and an amplitude of 0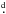 015, and a λ Eri variable with a period of 0
015, and a λ Eri variable with a period of 0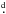 54362 and an amplitude of 0m.011. After removing the rapid changes and long-term variations, they were able to fold the residuals with a period of
54362 and an amplitude of 0m.011. After removing the rapid changes and long-term variations, they were able to fold the residuals with a period of
1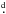 4632361, which they again interpreted as the light curve of a double-lined eclipsing binary. Drobek et al. (2010) analysed their V photometry from the Siding Springs Observatory and once more confirmed the 1
4632361, which they again interpreted as the light curve of a double-lined eclipsing binary. Drobek et al. (2010) analysed their V photometry from the Siding Springs Observatory and once more confirmed the 1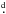 4632 period after removal of rapid changes for which they found a period of 0
4632 period after removal of rapid changes for which they found a period of 0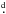 22481.
22481.
We inspected one HARPS ESO and two FEROS archival spectra of V916 Cen to find that they do not show evidence of large RV changes, expected for a short-period eclipsing binary. We estimated the projected rotational velocity as v sin i = 250 km s-1. We note that for a reasonable equatorial radius of the B0 star, e.g. 7 R⊙, the 1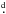 46 is a plausible value for the stellar rotational period.
46 is a plausible value for the stellar rotational period.
We therefore tentatively suggest that V916 Cen is not an eclipsing binary but a typical Be star also showing variations on the time scale of stellar rotation. Good examples of such light curves are EM Cep (see Harmanec 1984, P = 0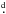 8) or LQ And (Harmanec et al. 1991, P = 0
8) or LQ And (Harmanec et al. 1991, P = 0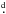 62). Particularly, EM Cep had long been considered to be an eclipsing binary, but no corresponding RV changes could be found for it or for LQ And. A dedicated spectral and photometric study of the object is undoubtedly still necessary.
62). Particularly, EM Cep had long been considered to be an eclipsing binary, but no corresponding RV changes could be found for it or for LQ And. A dedicated spectral and photometric study of the object is undoubtedly still necessary.
 |
Fig. B.1 Time plot of the V magnitude of V916 Cen = HD 101794 versus time. Blue dots are the Hipparcos Hp observations (Perryman & ESA 1997, flags 0 and 1 only) converted to the Johnson V magnitude after Harmanec (1998), red dots are the ASAS3 observations (Pojmański 2002), and green dots are observations published by Drobek et al. (2013). Long-term changes of this B0.5e star are obvious. |
All Tables
Orbital solutions for the RVs of the primary obtained by Hernandez & Sahade (1978), and for our new HARPS RVs derived with asTODCOR.
Times of the primary and secondary minima of V346 Cen estimated by us from Table 3 of Dugan & Wright (1939).
All Figures
 |
Fig. 1 Differences of times of minima from Table A.1 (open circles) and Table 2 (filled circles; triangles when the time results from a RV curve) are shown. Some data, probably of low accuracy, differ from the dominant trend. The curve corresponds to the period of apsidal advance 306 years and parameters in Tables 3 and 5. |
| In the text | |
 |
Fig. 2 Time plot of the O–C deviations from the fit of the apsidal-motion curves to the minima of V346 Cen. The asymmetry of the plot depends on Psider used; here it is 6 |
| In the text | |
 |
Fig. 3 He i 4922 Å line in the spectra of extreme velocities (black line: RJD 54 928.50, grey line: RJD 54 930.81). The line is blended with O ii 4924.52 Å and is affected by the O ii 4906.82 Å line at the blue side. |
| In the text | |
 |
Fig. 4 Radial velocities of the primary and secondary components of V346 Cen as calculated by asTODCOR. |
| In the text | |
 |
Fig. 5 Disentangled spectrum of the secondary in the wavelength region from 4230 to 4325 Å. The metallic lines seen in the observed spectrum are the O ii lines at 4253.9, 4254.1, 4276.8, 4283.0 and 4303.8 Å, N ii 4241.8 Å line and C ii 4267.1 Å line. The O ii lines in the disentangled spectrum of the secondary (black line) are weaker than suggested by the synthetic spectrum for the temperature of 25 500 K (violet/gray line). |
| In the text | |
 |
Fig. 6 Light curve of V346 Cen. Points correspond to the u measurements by GCHV, the solid line to the solution by PHOEBE with parameters from Table 5. We show the u data since their deviations from the model curve are the largest, as they are in GCA. |
| In the text | |
 |
Fig. A.1 Examples of local fits in PHOEBE for selected light curves. From top to bottom: (1) photographic light curve by O’Connell (1939); (2) ASAS2 I light curve (RJDs 51 200–51 403); (3) R light curve from FRAM automatic telescope. |
| In the text | |
 |
Fig. B.1 Time plot of the V magnitude of V916 Cen = HD 101794 versus time. Blue dots are the Hipparcos Hp observations (Perryman & ESA 1997, flags 0 and 1 only) converted to the Johnson V magnitude after Harmanec (1998), red dots are the ASAS3 observations (Pojmański 2002), and green dots are observations published by Drobek et al. (2013). Long-term changes of this B0.5e star are obvious. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


