© ESO, 2016

1. Introduction

Star formation is known to be a multiscale, multiphysics process. As pointed out by McKee & Ostriker (2007), star formation is a hierarchical process starting from giant molecular associations or HI superclouds in the diffuse interstellar medium (ISM), fragmenting into giant molecular clouds and the star-forming clumps therein. The sequential condensation from diffuse ISM to a newborn star includes a density change of orders of magnitude. Meanwhile, it is much more affordable and comprehensive if we can disentangle this complexity to some certain degree by studying this process step by step. As stars are often born in clusters (Lada & Lada 2003; Allen et al. 2007; McKee & Ostriker 2007), their properties are more likely determined by the cluster environment, rather than directly inherited from the parent molecular cloud. Understanding how the cluster forms out of a molecular cloud would thus provide us with useful information on the initial conditions of the star-forming environment, and would give important clues to the origin of the initial mass function (IMF). Pfalzner et al. (2016) recently pointed out that there is a tight correlation between the mass-size relations of star-forming clumps and stellar clusters, and suggested that cluster studies should be performed in conditions corresponding to the clumps.

Star-forming clumps that have been observed span a broad range of mass and radius. A cluster mass-size relation R ∝ M^0.38 has been inferred from observations by Fall et al. (2010) for clumps with masses from 10² to 10⁴ solar masses. A more complete data set from the ATLASGAL survey (Urquhart et al. 2014) shows the dependence R ∝ M^0.50. The dispersions in those data are compatible with a power-law exponent of between 0.4 and 0.6, leaving some uncertainties. Theoretical works have been peformed to better understand the gaseous protoclusters, the gas-dominated primary phase of cluster formation. Hennebelle (2012) previously derived the mass-size relation by balancing the gravitational energy, turbulent energy, and ram pressure of an accreting system. The relation R ∝ M^1/2 or R ∝ M^2/3 was found with different accretion schemes and successfully reproduced the observational results. He then applied the Hennebelle-Chabrier theory of star formation (Hennebelle & Chabrier 2008, 2009, 2013) to the gas inside the gaseous protocluster to obtain the cluster IMF. A similar analytical model by Matzner & Jumper (2015) also tried to characterize the steadily growing star-forming clump by balancing gravity and the turbulence driven by large-scale accretion and stellar outflow. These authors studied the effect of the star-forming environment on the protostellar population. On the other hand, Pfalzner (2011) regarded this mass-size relation as a growth sequence, and Parmentier & Pfalzner (2013) applied a star formation model that depends on local density to relate star-forming clumps to stellar clusters.

So far these models have ignored rotation. However rotation has been observed in several stellar clusters (Hénault-Brunet et al. 2012; Davies et al. 2011; Mackey et al. 2013), moreover it is not known to be a common feature that has been found in most, if not all, contracting systems (Longmore et al. 2014). Indeed structures forming from collapse usually exhibit important rotational motions due to angular momentum conservation (Lee & Hennebelle 2016, hereafter Paper I). We therefore follow a similar idea to Hennebelle (2012), while taking the rotation and turbulence into account to develop an analytical model to derive gaseous protocluster properties from those of the parent cloud out of which they form.

In the companion simulation paper (Paper I), we see a virialized structure forming at the center of a collapsing molecular cloud simulation. The goal of the present paper is to provide an analytical model that could be confronted with the numerical results. This gas-dominated structure, the protocluster, is the primary site of star formation and subsequently evolves into a stellar cluster. It is bound by its own gravitational potential and the ram pressure of the infalling flow, and is supported by supersonic turbulence that is nourished by the accretion. Observational analyses of the star-forming clump G28.34+0.06 P1 performed by Zhang et al. (2015) demonstrate that the 10³ M_⊙, 0.6 pc object is close to virial equilibrium, and that cores are forming from fragmentation while mass is being accreted from the filament in which it is embedded. In this paper, we introduce a simple analytical model that is very similar to this scenario to account for the formation of the gaseous protocluster and to predict its mass-size relation. Observationally, the infall motion is detected with a double-peaked, blue-skewed line profile, while complicated by density, molecular abundance, and excitation temperature. Nevertheless, clear global infall at clump scale is difficult to detect (López-Sepulcre et al. 2010; Reiter et al. 2011) since local star formation also creates infall and outflow signatures. Infall rates of star-forming clumps are observed to be small, about 10% of the free-fall velocity (Rolffs et al. 2011; Tan et al. 2014; Wyrowski et al. 2016), supporting a quasi-static picture. Rygl et al. (2013) suggested that the infall and outflow only become evident when the clump-cloud column density contrast exceeds 2 and, at more evolved stage, the infall is halted.

Given the small infall and the observed sequence (Fall et al. 2010; Urquhart et al. 2014), an equilibrium, at least not quickly and globally collapsing, assumption is highly plausible. Our model applies to low-mass clusters, and those with mass above 10⁴ are beyond the scope of our discussion since more massive clumps tend to evolve more quickly and form massive stars that, in turn, disrupt the cloud via feedback. In consequence, massive star-forming clumps do not live as long and possibly follow a different evolutionary track. One motivation to propose this quasi-static equilibrium model comes from the fact that we do see them forming in collapsing molecular cloud simulations (Paper I). On the other hand, the gaseous protocluster must live for long enough to be observed, and the tight correlation between their mass and size should be a consequence of certain self-regulation during the evolution. We should caution that although we refer to this gaseous protocluster as the first phase of stellar cluster formation, this is actually a continuous process; the stars start to form as the gas protocluster is still accreting and finally take over after the gas expulsion. In this picture, the gaseous protocluster is globally in equilibrium, while density fluctuations therein cause local infall to form stars. In this study, we restrict ourselves to the earliest stage where the effects of the stars are less important. In Sect. 2, we first describe how the virial theorem should be decomposed into two dimensions to account for a flattened rotating system. The influences of model parameters are discussed in Sect. 3. As sink particle are allowed to form in the simulation, we also adapt our analytical model to yield a comparison with the simulation results. These are followed by the conclusions in Sect. 4.

2. Two-dimensional model: modified virial theorem

In this section, we present a simple analytical model to describe the gaseous protocluster formation from the collapse of a molecular cloud: a virial model, adapted to the turbulent and rotational kinematics of the cluster under mass accretion. We propose that a gaseous protocluster is a structure in global virial equilibrium where the rotational and turbulent kinetic energy support against its self-gravity and ram pressure confinement. We stress that this global equilibrium does not preclude local infall and star formation. Indeed this is what we observe in the simulations. The important rotation results from the amplification due to angular momentum conservation under collapse, while the turbulence is sustained by the accreting gas and decays in one crossing time.

We start by deducing the two-dimensional virial theorem for an ellipsoidal structure with rotation and turbulence, and then discuss the energy balance from accretion and turbulent dissipation. The mass accretion rate and the specific angular momentum are evaluated as properties of the parent cloud. Finally, we present the mass-size relation predicted by the model.

2.1. Two-dimensional virial theorem of the gaseous protocluster

Since a cluster with rotational motion is indeed anisotropic, a spherically symmetric model could be too simplistic and may fail to capture all essential features. In this section, a two-dimensional model of an oblate ellipsoid is considered with its minor axis coinciding with the rotational axis. The three semiaxes are a = b = R>c = H. Virial theorem was discussed in tensor form by Parker (1954), showing how forces in different directions are balanced. We demonstrate how the virial integral of the system is calculated in two dimensions.

The thermal terms are neglected, for simplicity, because turbulence is generally supersonic as is the magnetic pressure since it is not very important at the cluster scale, as seen in the simulations (Fig. 11 of Paper I). The model is axisymmetric and we take the inner product of the momentum equation ρd_tv = −ρ∇φ with the r and z vectors in the cylindrical coordinate before integrating over the volume of the ellipsoid. We first consider the inner product with r as follows: $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}{v}\mathrm{·}{r}\mathrm{d}\mathit{V}\mathrm{=}& \underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{-}\mathit{\rho }\mathrm{\nabla }\mathit{\phi }\mathrm{·}{r}\mathrm{d}\mathit{V}\mathit{.}& \end{array}$(1)The integration gives (see Appendix A for detailed derivations) $\begin{array}{ccc}& & \frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}^{\mathrm{2}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{r}}^{\mathrm{2}}\mathrm{d}\mathit{V}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{S}}}\mathit{\rho }{\mathit{r}}^{\mathrm{2}}{v}\mathrm{·}\mathrm{d}{S}\mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{r}}\mathit{r\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V}\mathrm{=}\\ & & \end{array}$(2)where v_2d is the velocity in the x−y plane, and v_r is the velocity in the r direction; $\mathit{\eta }\mathrm{=}\frac{\mathit{H}}{\mathit{R}}$ represents the aspect ratio of the ellipsoid. In the z direction we obtain $\begin{array}{ccc}& & \underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}{v}\mathrm{·}{z}\mathrm{d}\mathit{V}\mathrm{=}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{-}\mathit{\rho }\mathrm{\nabla }\mathit{\phi }\mathrm{·}{z}\mathrm{d}\mathit{V}\\ & & \frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}^{\mathrm{2}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{z}}^{\mathrm{2}}\mathrm{d}\mathit{V}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{S}}}\mathit{\rho }{\mathit{z}}^{\mathrm{2}}{v}\mathrm{·}\mathrm{d}{S}\mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{z}}\mathit{z\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{1}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V}\mathrm{=}\\ & & \end{array}$where v_1d = v_z is the velocity in the z direction.

Virial equilibrium is reached when the time derivative terms are zero. The first term on the left-hand side of Eqs. (2) and (4) is analogous to the acceleration of inertia changing rate, and the second term corresponds to the change in mass accretion rate multiplied by the surface. As we describe later, the mass accretion rate can be roughly regarded as a constant of time and, therefore, these terms become less important and can be treated as zero in equilibrium at a later phase when the gaseous protocluster has gained sufficiently high mass. The third term on the left-hand side of both equations is the counterpart of the ram pressure term in the spherical model (Hennebelle 2012), while the geometry renders its interpretation less obvious since we are ignorant of the mass infall pattern. There exist solutions in two regimes: gravitation dominated and ram pressure dominated. While the ram pressure dominated solution has a radius that is too large and density that is too low, which does not correspond to the conditions discussed here, and the supersonic approximation probably is not valid, it is neglected for simplicity of the discussion. See Appendix C for further discussions on ram pressure and see that the effect on cluster size is indeed a small correction. Therefore we have the equations for virial equilibrium in two dimensions by simplifying Eqs. (2) and (4) as $\begin{array}{ccc}\mathit{M}{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}& \mathrm{=}& \\ \mathit{M}{\mathit{v}}_{\mathrm{1}\mathrm{d}}^{\mathrm{2}}& \mathrm{=}& \end{array}$

2.2. The energy equilibrium of an ellipsoidal cluster

In an accreting system, the turbulence is driven by the gravitational energy released from the accreted material (Klessen & Hennebelle 2010; Goldbaum et al. 2011), and it dissipates through the turbulent cascade on the timescale of the crossing time of the system. The turbulent energy is found by balancing the energy released from accretion and its dissipation. Studies such as that of Newton, Maclaurin, and Jacobi have been carried out to understand the force balancing in a homogeneous uniformly rotating body; these authors calculated the gravitational force for oblate ellipsoids (Chandrasekhar 1967; Binney & Tremaine 2008). Neutsch (1979) explored related functions for ellipsoidal bodies. He derived the gravitational potential energies for ellipsoids with uniform, Gaussian, and exponential density profiles, and found these to be different only by a factor of order unity. We consider a uniform ellipsoid with semiaxes a ≥ b ≥ c and we, therefore, have the gravitational potential energy given by the Legendre elliptical integral of the first kind $\mathit{F}\mathrm{\left(}\mathit{\varphi }\mathrm{\right|}\mathit{k}\mathrm{)}\mathrm{=}{{}^{\mathrm{\int }}}_{\mathrm{0}}^{\mathit{\varphi }}\frac{\mathrm{d}\mathit{\theta }}{\sqrt{\mathrm{1}\mathrm{-}{\mathit{k}}^{\mathrm{2}}\sin {\mathit{\theta }}^{\mathrm{2}}}}$. This is written as $\begin{array}{ccc}{\mathit{E}}_{\mathrm{grav}}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{10}}\mathit{G}{\mathit{M}}^{\mathrm{2}}\frac{\mathrm{2}}{\sqrt{{\mathit{a}}^{\mathrm{2}}\mathrm{-}{\mathit{c}}^{\mathrm{2}}}}\mathit{F}\left({\cos }^{-1}\left(\frac{\mathit{c}}{\mathit{a}}\right)\begin{array}{c}\mathrm{|}\\ \mathrm{|}\\ \mathrm{|}\\ \mathrm{|}\\ \mathrm{|}\\ \mathrm{|}\end{array}\frac{{\mathit{a}}^{\mathrm{2}}\mathrm{-}{\mathit{b}}^{\mathrm{2}}}{{\mathit{a}}^{\mathrm{2}}\mathrm{-}{\mathit{c}}^{\mathrm{2}}}\right)\\ & \mathrm{=}& \frac{\mathrm{3}}{\mathrm{10}}\mathit{G}{\mathit{M}}^{\mathrm{2}}\frac{\mathrm{2}}{\sqrt{{\mathit{R}}^{\mathrm{2}}\mathrm{-}{\mathit{H}}^{\mathrm{2}}}}{\cos }^{-1}\left(\frac{\mathit{H}}{\mathit{R}}\right)\\ & \mathrm{=}& \frac{\mathrm{3}}{\mathrm{5}}\frac{\mathit{G}{\mathit{M}}^{\mathrm{2}}}{\mathit{R}}\frac{{\cos }^{-1}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}}{\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}}\mathrm{=}\frac{\mathit{G}{\mathit{M}}^{\mathrm{2}}}{\mathit{R}}{\mathit{u}}_{\mathit{g}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathit{.}\end{array}$(7)If we assume that the density stays uniform, the released gravitational energy available to aliment the turbulence is $\begin{array}{ccc}\mathit{Ė}\mathrm{grav}\mathrm{=}\mathit{ϵ}\frac{\mathit{G}{\mathit{M}}^{\mathrm{2}}}{\mathit{R}}{\mathit{u}}_{\mathit{g}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\left(\frac{\mathrm{2}\mathit{Ṁ}}{\mathit{M}}\mathrm{-}\frac{\mathit{Ṙ}}{\mathit{R}}\mathrm{+}\frac{{\mathit{u}}_{\mathit{g}}^{\mathrm{\prime }}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathit{\eta ̇}}{{\mathit{u}}_{\mathit{g}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}}\right)\mathit{,}& & \end{array}$(8)where the unknown factor ϵ ≤ 1 stands for the transformation efficiency of gravitational energy into kinetic energy, while part of the energy is dissipated at the accretion shock. The change in η should be small compared to that in M. The change of radius is also small at the beginning of gaseous protocluster formation and thus is negligible. At a later time once the stationary regime is reached, it should follow a power-law dependence on the mass and therefore the second term is proportional to the first term. By absorbing the second and third terms in the parenthesis into the uncertainties of accretion driving efficiency, we obtain $\begin{array}{ccc}\mathit{Ė}\mathrm{grav}\mathrm{=}{\mathit{ϵ}}_{\mathrm{acc}}\frac{\mathrm{2}\mathit{GM}\mathit{Ṁ}}{\mathit{R}}{\mathit{u}}_{\mathit{g}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathit{.}& & \end{array}$(9)The turbulence dissipates via turbulent cascade on the crossing time of the system τ_diss, while the directional energy distribution and the relevant scale is less well understood in ellipsoidal geometry. We discuss two sets of assumptions. Firstly, we assume that the turbulence is anisotropic and that the turbulent energy follows the inertial regime of the Kolmogorov spectrum even though the structure is not spherically symmetric, that is, the energy cascades down length scales at the same rate and is eventually dissipated. This implies ${\mathit{\sigma }}_{\mathit{R}}^{\mathrm{3}}\mathit{/}\mathit{R}\mathrm{=}{\mathit{\sigma }}_{\mathit{H}}^{\mathrm{3}}\mathit{/}\mathit{H}$, where σ_R and σ_H are the rms velocity of vortices of size R and H, respectively. The velocity dispersion σ_x in the x direction has contributions from motions parallel to the x−y plane, where the limiting scale is R and those parallel to the x−z plane with scale H and likewise for σ_y. In the direction parallel to the short axis, σ_z is limited both in x−z and y−z planes by the semiminor axis H. We thus have $\begin{array}{ccc}{\mathit{\sigma }}_{\mathit{x}}^{\mathrm{2}}& \mathrm{=}& {\mathit{\sigma }}_{\mathit{y}}^{\mathrm{2}}\mathrm{=}\mathrm{(}\mathrm{1}\mathrm{+}{\mathit{\eta }}^{\frac{\mathrm{2}}{\mathrm{3}}}\mathrm{)}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{2}}\mathit{/}\mathrm{2}\\ {\mathit{\sigma }}_{\mathit{z}}^{\mathrm{2}}& \mathrm{=}& {\mathit{\eta }}^{\frac{\mathrm{2}}{\mathrm{3}}}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{2}}\\ \mathit{Ė}\mathrm{diss}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{2}}\mathit{M}{\mathit{\sigma }}_{\mathit{H}}^{\mathrm{2}}\mathit{/}{\mathit{\tau }}_{\mathrm{diss}}\mathrm{=}\frac{\mathrm{3}}{\mathrm{2}}\mathit{M}{\mathit{\sigma }}_{\mathit{H}}^{\mathrm{2}}\mathit{/}\frac{\mathrm{2}\mathit{H}}{{\mathit{\sigma }}_{\mathit{H}}}\mathrm{=}\frac{\mathrm{3}}{\mathrm{4}}\mathit{M}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{3}}\mathit{/}\mathit{R}\mathit{.}\end{array}$

On the other hand, if the inertial range at which the energy is dominating is reached at scales smaller than the cluster size, the turbulence should be isotropic. By assuming the dominating scale ϵ_dissH<H, we obtain $\begin{array}{ccc}{\mathit{\sigma }}_{\mathit{x}}^{\mathrm{2}}& \mathrm{=}& {\mathit{\sigma }}_{\mathit{y}}^{\mathrm{2}}\mathrm{=}{\mathit{\sigma }}_{\mathit{z}}^{\mathrm{2}}\mathrm{=}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{2}}\\ \mathit{Ė}\mathrm{diss}& \mathrm{=}& \frac{\mathrm{3}}{\mathrm{2}}\mathit{M}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{2}}\mathit{/}{\mathit{\tau }}_{\mathrm{diss}}\mathrm{=}\frac{\mathrm{3}}{\mathrm{2}}\mathit{M}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{2}}\mathit{/}\frac{\mathrm{2}{\mathit{ϵ}}_{\mathrm{diss}}\mathit{H}}{{\mathit{\sigma }}_{\mathit{R}}}\mathrm{=}\frac{\mathrm{3}}{\mathrm{4}}\mathit{M}{\mathit{\sigma }}_{\mathit{R}}^{\mathrm{3}}\mathit{/}{\mathit{ϵ}}_{\mathrm{diss}}\mathit{\eta R}\mathit{.}\end{array}$

This introduces two sets of equations with similar form but different coefficients when we proceed to solve for equilibrium solutions.

Fig. 1 Gravitational potential in blue curves (solid: complete potential ug, dashed: ur, dot-dashed: uz) and the ram pressure factors in cyan (dashed: pr, dot-dashed: pz; see Appendix C) as functions of the ellipsoid aspect ratio η.

The rotation provides support only in the directions perpendicular to the rotational axis. By using the averaged specific angular momentum j, the rotational energy of the cluster is $\mathrm{2}{\mathit{E}}_{\mathrm{rot}}\mathrm{=}\frac{\mathrm{5}}{\mathrm{2}}\mathit{M}{{}^{\mathrm{\right(}}\frac{\mathit{j}}{\mathit{R}}^{\mathrm{\left)}}}^{\mathrm{2}}$. The factor $\frac{\mathrm{5}}{\mathrm{2}}$ comes from uniform density and rigid body assumptions, which suffers from some uncertainty since we do not know the actual distribution of mass and angular momentum. A numerical evaluation from simulation results is performed by taking the ratio between JI^-1J and $\mathit{M}{{}^{\mathrm{\right(}}\frac{\mathit{j}}{\mathit{R}}^{\mathrm{\left)}}}^{\mathrm{2}}$, since the former is a good estimation of the rotational energy. J and I are the angular momentum and rotational inertia matrix of the cluster. This gives values ranging between 2 and 4, confirming that we are not too far from reality. Finally, using Eqs. (5), (6) and (9)–(9) while splitting the two-dimensional motion perpendicular to the short axis into rotation and turbulence, we obtain the equation set to be solved, i.e., $\begin{array}{ccc}\frac{\mathrm{5}}{\mathrm{2}}{\left(\frac{\mathit{j}}{\mathit{R}}\right)}^{\mathrm{2}}\mathrm{+}{\mathit{s}}_{\mathit{r}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}{\mathit{\sigma }}^{\mathrm{2}}& \mathrm{=}& \frac{\mathit{GM}}{\mathit{R}}{\mathit{u}}_{\mathit{r}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\\ {\mathit{s}}_{\mathit{z}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}{\mathit{\sigma }}^{\mathrm{2}}& \mathrm{=}& \frac{\mathit{GM}}{\mathit{R}}{\mathit{u}}_{\mathit{z}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\\ \mathit{Ė}\mathrm{diss}\mathit{/}\mathit{M}\mathrm{=}\mathit{d}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\frac{{\mathit{\sigma }}^{\mathrm{3}}}{\mathrm{4}\mathit{R}}& \mathrm{=}& \mathit{Ė}\mathrm{grav}\mathit{/}\mathit{M}\mathrm{=}{\mathit{ϵ}}_{\mathrm{acc}}\frac{\mathrm{2}\mathit{G}\mathit{Ṁ}}{\mathit{R}}{\mathit{u}}_{\mathit{g}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathit{,}\end{array}$where the geometrical factors s_r, s_z, and d are described in Eqs. (8) and (9) for two cases. The subscript of σ_R is omitted for simplicity. The factors u_r, u_z, and u_g are functions of the aspect ratio $\mathit{\eta }\mathrm{=}\frac{\mathit{H}}{\mathit{R}}$ of the ellipsoid, as shown in Fig. 1. The essential idea is to decompose the gravitational potential resulting from force in different directions. It could be readily verified that u_r(η) + u_z(η) = u_g(η) and that ${\mathit{u}}_{\mathit{g}}\mathrm{\left(}\mathrm{1}\mathrm{\right)}\mathrm{=}\frac{\mathrm{3}}{\mathrm{5}}$, which corresponds to the spherical case.

2.3. Accretion rate

The solutions of Eqs. (10) are set by the mass, accretion rate, and the specific angular momentum, The latter two are estimated as functions of the cluster mass, or more precisely, the cloud mass.

The accretion rate is estimated with the free-fall collapse of the parent cloud, while assuming that the accretion rate of a cluster inside a cloud is close to that of the cloud if the masses are comparable. We start by calculating the time of free fall into a finite volume, and show that the mass accretion rate reaches almost a constant when the central mass exceeds about a tenth of the cloud mass. The cloud density profile used in our simulations (see Paper I) and its mean density inside radius r are $\begin{array}{ccc}\mathit{\rho }\mathrm{\left(}\mathit{r}\mathrm{\right)}& \mathrm{=}& \\ \overline{\mathit{\rho }}\mathrm{\left(}\mathit{r}\mathrm{\right)}& \mathrm{=}& \frac{{\mathrm{\int }}_{\mathit{V}\mathrm{\left(}\mathit{r}\mathrm{\right)}}\mathit{\rho }\mathrm{\left(}{\mathit{r}}^{\mathrm{\prime }}\mathrm{\right)}\mathrm{d}\mathit{V}\mathrm{\left(}{\mathit{r}}^{\mathrm{\prime }}\mathrm{\right)}}{\mathit{V}\mathrm{\left(}\mathit{r}\mathrm{\right)}}\mathrm{=}\mathrm{3}{\mathit{\rho }}_{\mathrm{0}}\mathrm{(}\mathit{\xi }\mathrm{-}{\tan }^{-1}{\mathit{\xi }}^{\mathrm{)}}{\mathit{\xi }}^{-3}\mathit{,}\end{array}$where ξ_ext = r_ext/r₀ = 3 in our case, and we consider the free-fall time for a shell mass at r to arrive at the cluster radius r_f (see Appendix B for detailed derivation), $\begin{array}{ccc}{\mathit{t}}_{\mathrm{ff}}\mathrm{\left(}\mathit{r}\mathrm{\right)}& \mathrm{=}& \end{array}$(15)It could be alternatively written with the normalized parameters ξ and ξ_f = r_f/r₀ as follows: $\begin{array}{ccc}{\mathit{t}}_{\mathrm{ff}}\mathrm{\left(}\mathit{\xi }\mathrm{\right)}& \mathrm{=}& \sqrt{\frac{\mathrm{1}}{\mathrm{8}\mathit{\pi G}{\mathit{\rho }}_{\mathrm{0}}}}{\mathrm{(}\mathit{\xi }\mathrm{-}{\tan }^{-1}{\mathit{\xi }}^{\mathrm{)}}}^{\frac{-1}{\mathrm{2}}}{\mathit{\xi }}^{\frac{\mathrm{3}}{\mathrm{2}}}\\ & & \mathrm{\times }\left[{\cos }^{-1}\left(\sqrt{\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}}\right)\mathrm{+}\sqrt{\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}\left(\mathrm{1}\mathrm{-}\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}\right)}\right]\mathrm{·}\end{array}$(16)Consider a cloud that starts as static and collapses in free fall, the collapse proceeds as an outward expansion wave from the center. This equation signifies that at t_ff(r) all the mass originally inside radius r is accreted onto the cluster. Therefore the mass inside the cluster radius r_f at time t is expressed as $\begin{array}{ccc}\mathit{M}\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathrm{=}\mathit{M}\mathrm{\left(}{\mathit{t}}_{\mathrm{ff}}^{-1}\mathrm{\right(}\mathit{t}\mathrm{\left)}\mathrm{\right)}\mathrm{=}\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\mathrm{0}}{\mathit{r}}_{\mathrm{0}}^{\mathrm{3}}\mathrm{(}\mathit{\xi }\mathrm{-}{\tan }^{-1}{\left(\mathit{\xi }\right)}^{\mathrm{)}}\mathit{,}{\mathit{t}}_{\mathrm{ff}}\mathrm{\left(}\mathit{\xi }\mathrm{\right)}\mathrm{=}\mathit{t}\mathit{.}& & \end{array}$(17)The mass accretion, equivalent to the rate at which new mass shells are included, is expressed as $\begin{array}{ccc}\mathit{Ṁ}\mathrm{0}\mathrm{\left(}\mathit{t}\mathrm{\right)}& \mathrm{=}& \mathit{Ṁ}\mathrm{\left(}{\mathit{t}}_{\mathrm{ff}}^{-1}\mathrm{\right(}\mathit{t}\mathrm{\left)}\mathrm{\right)}\\ & \mathrm{=}& \mathrm{4}\mathit{\pi r}\mathrm{\left(}\mathit{t}{\mathrm{)}}^{\mathrm{2}}\mathit{\rho }\mathrm{\right(}\mathit{r}\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathrm{)}\frac{\mathrm{d}\mathit{r}\mathrm{\left(}\mathit{t}\mathrm{\right)}}{\mathrm{d}\mathit{t}}\\ & \mathrm{=}& \mathrm{4}\mathit{\pi r}\mathrm{\left(}\mathit{t}{\mathrm{)}}^{\mathrm{2}}\mathit{\rho }\mathrm{\right(}\mathit{r}\mathrm{\left(}\mathit{t}\mathrm{\right)}\mathrm{)}\mathit{/}\frac{\mathrm{d}{\mathit{t}}_{\mathrm{ff}}}{\mathrm{d}\mathit{r}}\\ & \mathrm{=}& \mathrm{4}\mathit{\pi }{\mathit{r}}_{\mathrm{0}}^{\mathrm{2}}{\mathit{\xi }}^{\mathrm{2}}\frac{{\mathit{\rho }}_{\mathrm{0}}}{\mathrm{1}\mathrm{+}{\mathit{\xi }}^{\mathrm{2}}}{\mathit{r}}_{\mathrm{0}}\mathit{/}\frac{\mathrm{d}{\mathit{t}}_{\mathrm{ff}}}{\mathrm{d}\mathit{\xi }}\\ & \mathrm{=}& \frac{{\mathit{M}}_{\mathrm{c}}\sqrt{\mathrm{8}\mathit{\pi G}{\mathit{\rho }}_{\mathrm{0}}}}{\left({\mathit{\xi }}_{\mathrm{ext}}\mathrm{-}{\tan }^{-1}\left({\mathit{\xi }}_{\mathrm{ext}}\right)\right)}\mathrm{\times }{\mathit{\xi }}^{\frac{\mathrm{3}}{\mathrm{2}}}{\mathrm{(}\mathit{\xi }\mathrm{-}{\tan }^{-1}{\left(\mathit{\xi }\right)}^{\mathrm{)}}}^{\frac{\mathrm{1}}{\mathrm{2}}}\\ & & \mathrm{\times }\{\left[\frac{\mathrm{-}{\mathit{\xi }}^{\mathrm{3}}\mathit{/}\mathrm{2}}{\mathit{\xi }\mathrm{-}{\tan }^{-1}\mathit{\xi }}\mathrm{+}\frac{\mathrm{3}}{\mathrm{2}}\mathrm{(}\mathrm{1}\mathrm{+}{\mathit{\xi }}^{\mathrm{2}}\mathrm{)}\right][{\cos }^{-1}\left(\sqrt{\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}}\right)\\ & & {\mathrm{+}\sqrt{\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}\left(\mathrm{1}\mathrm{-}\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}\right)}]}^{}{\mathrm{+}\mathrm{(}\mathrm{1}\mathrm{+}{\mathit{\xi }}^{\mathrm{2}}\mathrm{)}\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}\sqrt{\frac{\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}}{\mathrm{1}\mathrm{-}\frac{{\mathit{\xi }}_{\mathit{f}}}{\mathit{\xi }}}}\begin{array}{c}\mathrm{⎫}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎬}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎪}\\ \mathrm{⎭}\end{array}}^{-1}\mathrm{·}\end{array}$(18)For a given ξ_f, the mass M(r_f) and accretion rate Ṁ(r_f) of the gaseous protocluster could be calculated at the same time as functions of ξ. Figure 2 shows the gaseous protocluster mass accretion rate plotted against mass in a molecular cloud of 10⁴ solar mass at several final radii r_f, which correspond to the range of the protocluster radius in our simulations.

Fig. 2 Mass accretion rate plotted against mass for several final radius values rf/r0 inside a 104 M⊙ cloud, assuming the interior of the cloud collapses in free fall. The radius at which Ṁ is evaluated increases from the top to the bottom curve.

After the gaseous protocluster mass reaches over 10³ M_⊙, the accretion rate becomes weakly dependent on the cluster mass for any cluster radius and approaches a value that is characteristic of the cloud mass. It is therefore reasonable to estimate the cluster accretion rate with the cloud mass and from Eq. (18) we obtain $\begin{array}{ccc}\mathit{Ṁ}\mathrm{0}\mathrm{\propto }{\mathit{M}}_{\mathrm{c}}\sqrt{{\mathit{\rho }}_{\mathrm{c}}}\mathit{,}& & \end{array}$(19)where M_c and ρ_c are the cloud mass and density. Consider a molecular cloud following the Larson relations (Larson 1981; Falgarone et al. 2004, 2009; Hennebelle & Falgarone 2012; Lombardi et al. 2010) $\begin{array}{ccc}{\mathit{\rho }}_{\mathrm{c}}\mathrm{\propto }{\mathit{R}}_{\mathrm{c}}^{\mathrm{-}\mathit{\gamma }}\mathrm{and}{\mathit{\sigma }}_{\mathrm{c}}\mathrm{\propto }\sqrt{\frac{\mathit{M}}{\mathit{R}}}\mathrm{\propto }{\mathit{R}}_{\mathrm{c}}^{\mathrm{1}\mathrm{-}\frac{\mathit{\gamma }}{\mathrm{2}}}\mathit{,}& & \end{array}$(20)where different values of γ (typically around 0.7 or 1) are quoted in the literature. We obtain $\begin{array}{ccc}\mathit{Ṁ}\mathrm{0}\mathrm{\propto }{\mathit{M}}_{\mathrm{c}}\sqrt{{\mathit{\rho }}_{\mathrm{c}}}\mathrm{\propto }{\mathit{R}}_{\mathrm{c}}^{\mathrm{3}}{\mathit{\rho }}_{\mathrm{c}}^{\mathrm{1.5}}\mathrm{~}{\mathit{R}}_{\mathrm{c}}^{\mathrm{3}\mathrm{-}\mathrm{1.5}\mathit{\gamma }}\mathrm{\propto }{\mathit{M}}_{\mathrm{c}}^{\mathrm{(}\mathrm{6}\mathrm{-}\mathrm{3}\mathit{\gamma }\mathrm{)}\mathit{/}\mathrm{(}\mathrm{6}\mathrm{-}\mathrm{2}\mathit{\gamma }\mathrm{)}}\mathit{.}& & \end{array}$(21)With γ = 1 or 0.7, we get $\mathit{Ṁ}{}_{\mathrm{0}}\mathrm{\propto }{\mathit{M}}_{\mathrm{c}}^{{\mathit{\gamma }}_{\mathit{Ṁ}}}$, where γ_Ṁ = 0.75 or 0.85, respectively. While the accretion rate Ṁ₀ is estimated for a cloud without turbulent support, an empirical correction is made by multiplying the self-gravitating force by a dilution factor (1−κ), where κ = E_turb/E_grav is the ratio between turbulent kinetic energy and gravitational energy of the cloud. This intervenes in the accretion rate through Eq. (15) and lengthens the free-fall time by a factor $\mathrm{1}\mathit{/}\sqrt{\mathrm{1}\mathrm{-}\mathit{\kappa }}$. A numerical evaluation is made for the cloud of 10⁴ solar mass as that in our simulations, obtaining $\begin{array}{ccc}\mathit{Ṁ}& \mathrm{=}& \mathit{Ṁ}\mathrm{0}\sqrt{\mathrm{1}\mathrm{-}\mathit{\kappa }}\\ & \mathrm{=}& \mathrm{4.0}\mathrm{\times }{\mathrm{10}}^{-3}{\mathit{M}}_{\mathrm{\odot }}{\mathrm{yr}}^{-1}{\left(\frac{{\mathit{\alpha }}_{\mathrm{\ast }\mathit{,c}}{\mathit{M}}_{\mathrm{\ast }}}{{\mathrm{10}}^{\mathrm{4}}{\mathit{M}}_{\mathrm{\odot }}}\right)}^{{\mathit{\gamma }}_{\mathit{Ṁ}}}\sqrt{\mathrm{1}\mathrm{-}\mathrm{0.35}{\left(\frac{{\mathit{\sigma }}_{\mathrm{rms}}}{{\mathit{\sigma }}_{\mathrm{vir}}}\right)}^{\mathrm{2}}}\mathit{,}\end{array}$(22)where α_{∗ ,c} = M_c/M_∗ is the cloud-cluster mass ratio. The κ factor scales to the square of the ratio between the actual velocity dispersion and that of a virialized cloud. A geometrical factor 0.35 accounts for the centrally concentrated mass distribution and accords the estimations to the values in simulations. Simplifying by using the same accretion rate for a protocluster of any mass inside the cloud of same mass, the canonical value 4.0 × 10^-3 M_⊙ yr^-1, which corresponds to the accretion rate at M_∗ = 2 × 10³ M_⊙, is used as normalization reference. We stress that the parameter α_{∗ ,c} is setting the strength of the accretion rate. Lower values of α_{∗ ,c} simply correspond to lower accretion. An example of mass accretion rate evaluated at radius 1 pc, corresponding to r_f/r₀ = 0.13, is shown in Fig. 3 for four simulations with different levels of turbulent support. The mass accretion rate in the simulations is evaluated as follows: We first calculate the mass contained inside an ellipsoidal region (defined in Paper I), which has the same volume as that of a 1 pc radius sphere at several time steps. The mass is then fitted as a function of time and in turn gives its time derivative. The accretion rates evaluated from simulations are plotted with solid curves, and the modeled values are multiplied by the correction factors with dashed lines. The model value is taken at M_∗ = 2 × 10³ M_⊙ and the accretion rate is assumed to be constant for all cluster masses (only a function of cloud mass). This empirical correction for turbulent support is very simplistic. However, the error is within a factor 2 and the four turbulence levels cover a large range of accretion rates, which all give reasonable mass-size relations (see Sect. 3.3). Thus we conclude that this accretion rate approximation does not affect the results too much. Observations show that star-forming clumps accrete at about 10^-3 M_⊙ yr^-1 with an infall velocity of around 1 km s^-1 (Fuller et al. 2005; Peretto et al. 2006; López-Sepulcre et al. 2010; Rygl et al. 2013), which is consistent with our model estimation.

Fig. 3 Mass accretion rate plotted against mass at r = 1 pc. The solid curves represent values evaluated in simulations with different levels of turbulent support, where κ is the ratio of turbulent over gravitational energy. The dashed curve in magenta is the analytical solution for a 104 M⊙ cloud in free fall. The accretion rate with the empirical correction $\sqrt{\mathrm{1}\mathrm{-}\mathit{\kappa }}$ is plotted in dashed curves with corresponding colors. The accretion rate is approximated to be constant at its value at M∗ = 2 × 103 M⊙.

2.4. Angular momentum

The estimation of angular momentum is motivated by the simulation. In a large molecular cloud, there exists very often a residual rotation after cancellation of turbulent vortices, and this rotation becomes important as the cloud collapses due to angular momentum conservation, as demonstrated by the remarkable rotation of the gaseous protocluster (Paper I). For a simple analysis, we take a characteristic rotational velocity that is proportional to the turbulent velocity dispersion and follows the scaling law v_rot ∝ v_rms(r/r₀)^0.5 (Dib et al. 2010; Burkert & Bodenheimer 2000). By assuming random rotational axis in spherical shells, we have the averaged specific angular momentum inside a sphere of radius r with the density profile described in Eq. (13), $\begin{array}{ccc}\overline{\mathit{j}}\mathrm{\left(}\mathit{r}\mathrm{\right)}& \mathrm{=}& {\left[\frac{\underset{}{{\mathrm{\int }}^{\mathit{M}\mathrm{\left(}\mathit{r}\mathrm{\right)}}}\mathrm{(}{\mathit{v}}_{\mathrm{rot}}\mathit{r}{\mathrm{)}}^{\mathrm{2}}\mathrm{d}\mathit{m}}{\underset{}{{\mathrm{\int }}^{\mathit{M}\mathrm{\left(}\mathit{r}\mathrm{\right)}}}\mathrm{d}\mathit{m}}\right]}^{\frac{\mathrm{1}}{\mathrm{2}}}\\ & \mathrm{=}& \mathrm{0.22}{\mathit{v}}_{\mathrm{rms}}{\mathit{r}}_{\mathrm{0}}\frac{\mathrm{1}}{\mathrm{2}}{\left[\frac{{\mathit{\xi }}^{\mathrm{4}}\mathrm{-}\mathrm{2}{\mathit{\xi }}^{\mathrm{2}}\mathrm{+}\mathrm{2}\log \mathrm{(}\mathrm{1}\mathrm{+}{\mathit{\xi }}^{\mathrm{2}}\mathrm{)}}{\mathit{\xi }\mathrm{-}\arctan \left(\mathit{\xi }\right)}\right]}^{\frac{\mathrm{1}}{\mathrm{2}}}\mathit{,}\end{array}$(23)where ξ = r/r₀. The constant is measured from the simulations (Paper I). The average specific angular momentum plotted against mass at varying radius is plotted in Fig. 4 for the initial condition of four runs (solid curves) with varying levels of turbulent support, as well as the analytical solutions (dashed curves) with corresponding v_rms. The specific angular momentum roughly has the dependence $\overline{\mathit{j}}\mathrm{\left(}\mathit{r}\mathrm{\right)}\mathrm{\propto }\mathit{M}\mathrm{(}\mathit{r}{\mathrm{)}}^{\mathrm{0.59}}$ in the mass range of our interest (10³−10⁴ M_⊙).

Fig. 4 Specific angular momentum plotted against mass contained inside varying radius. Solid curves represent the values calculated in ellipsoidal regions (described in Paper I) inside the initial cloud. Dashed curves show the values estimated analytically. Values from four simulations with various initial turbulent supports are shown, and the specific angular momentum scales with the velocity dispersion.

As discussed in Paper I, regardless of the angular momentum loss of sink particles (protostars), the specific angular momentum of the gas component is more or less conserved at the protocluster scale during the collapse. We therefore do not consider its loss by angular momentum transport in our model.

The averaged specific angular momentum in the gaseous protocluster thus has the form,: $\begin{array}{ccc}{\mathit{j}}_{\mathrm{\ast }}& \mathrm{\propto }{\mathit{j}}_{\mathrm{c}}{\mathrm{(}{\frac{{\mathit{M}}_{\mathrm{\ast }}}{{\mathit{M}}_{\mathrm{c}}}}^{\mathrm{)}}}^{\mathrm{0.59}}\mathrm{\propto }{\mathit{\sigma }}_{\mathrm{c}}{\mathit{R}}_{\mathrm{c}}{\mathit{\alpha }}_{\mathrm{\ast }\mathit{,}\mathrm{c}}^{-0.59}\mathrm{\propto }{\mathit{M}}_{\mathrm{c}}^{\mathrm{(}\mathrm{4}\mathrm{-}\mathit{\gamma }\mathrm{)}\mathit{/}\mathrm{(}\mathrm{6}\mathrm{-}\mathrm{2}\mathit{\gamma }\mathrm{)}}{\mathit{\alpha }}_{\mathrm{\ast }\mathit{,}\mathrm{c}}^{-0.59}\mathit{.}& \end{array}$(24)As in the discussions of mass accretion, the quantities are estimated for the parent cloud and the mass ratio α_{∗ ,c} is used to map the cloud to the protocluster. The last approximation comes from the Larson relations (see Eqs. (20)). Applying physical values gives $\begin{array}{ccc}{\mathit{j}}_{\mathrm{\ast }}\mathrm{=}\mathrm{6.7}\mathrm{\times }{\mathrm{10}}^{\mathrm{19}}{\mathrm{m}}^{\mathrm{2}}\hspace{0.17em}{\mathrm{s}}^{-1}\frac{{\mathit{\sigma }}_{\mathrm{rms}}}{{\mathit{\sigma }}_{\mathrm{vir}}}{\left(\frac{{\mathit{\alpha }}_{\mathrm{\ast }\mathit{,}\mathrm{c}}{\mathit{M}}_{\mathrm{\ast }}}{{\mathrm{10}}^{\mathrm{4}}{\mathit{M}}_{\mathrm{\odot }}}\right)}^{{\mathit{\gamma }}_{\mathit{j}}}{\mathit{\alpha }}_{\mathrm{\ast }\mathit{,}\mathrm{c}}^{-0.59}\mathit{,}& & \end{array}$(25)where γ_j = 0.75 or 0.72 corresponding to γ = 1 or 0.7. This value is normalized with a 10⁴ M_⊙ cloud following Larson relations (which is close to virial equilibrium) and should be multiplied by a correction factor σ_rms/σ_vir if the turbulence is not following such relations.

2.5. Solving for the gaseous protocluster mass-size relation

We obtained Ṁ and j as functions of the gaseous protocluster mass M, and thereby we could solve Eqs. (10) to infer the three variables R, η, σ² for a given mass in equilibrium. This is equivalent to solving for η and R from equations $\begin{array}{ccc}\mathit{f}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}& \mathrm{=}& \frac{\mathrm{8}{\frac{\mathrm{5}}{\mathrm{2}}}^{\frac{\mathrm{3}}{\mathrm{2}}}{\mathit{j}}^{\mathrm{3}}\mathit{Ṁ}}{{\mathit{G}}^{\mathrm{2}}{\mathit{M}}^{\mathrm{3}}}\\ & \mathrm{=}& \{\begin{array}{c}\\ & \\ & \end{array}\\ \mathit{R}\mathrm{=}& \frac{\mathrm{5}{\mathit{j}}^{\mathrm{2}}}{\mathrm{2}\mathit{GM}}\mathit{r}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathrm{=}\{\begin{array}{c}\\ & \\ & \end{array}& \end{array}$The functions f(η) and r(η) are geometrical factors that depend on the aspect ratio η. They are shown in Fig. 5 in solid and dashed curves (r(η) is multiplied by 0.1 and indicated in the same figure), respectively. The anisotropic functions are plotted in yellow and the isotropic functions are plotted in red. We also plot in dotted curves, dlog r/ dlog f, the ratio between the relative growth rate of r and f, to highlight how the gaseous protocluster radius solution depends on the model parameters and, in turn, on f(η). This is further discussed in Sect. 3.1.

Fig. 5 Functions f(η) (solid curves) and r(η) (dashed curves, the value multiplied by 0.1 to be shown in the same figure) for both anisotropic (yellow) and isotropic (red) assumptions of the turbulence. Dotted curves indicate the ratio between the changing rates of r and f plotted in absolute value.

The solution occurs at the intersection of f(η) and a constant determined by M, and j as seen in Eq. (26). Since f(η) is first increasing and then decreasing in the interval η ∈ [0,1], two solutions coexist when there are solutions. The solution with a higher value of η is physical because it reduces to the spherical case when the angular momentum goes to zero. The recovered η value in turn gives the radius of the gaseous protocluster by Eq. (27). In this solution, turbulent energy dominates over rotational energy; the simulation results (see Paper I) also confirm that the rotational energy is small initially and accounts for 30−40% of the total kinetic energy of the gaseous protocluster by the end of the simulation.

The gaseous protocluster mass-size relation is governed by several parameters. We first apply some canonical values to illustrate the solution properties before confronting the model predictions with simulation results. Three cloud-cluster mass ratios α_{∗ ,c} = 1,2,3 are used for virialized molecular clouds, i.e., σ_rms/σ_vir = 1, in Eqs. (22) and (25). The canonical turbulence driving efficiency ε = 0.5 is used; see Eqs. (9), (10), and (26), ε = ϵ_acc and ε = ϵ_dissϵ_acc, respectively. The resulting mass-size relation is shown in Figs. 6 and 7 for two γ values, and the range of solutions with ε ∈ [0.2,0.7] is represented by the shadowed region to illustrate the dependence of the radius on ε. The radius of the cluster decreases with increasing ε. Nonetheless, the dispersion of observations is compatible with a large range of the model parameters, guaranteeing the robustness of our model prediction regardless of some poorly controlled factors. Solutions might not exist for large ε, large α_{∗ ,c}, or highly supervirial clouds.

This is reasonable since large α_{∗ ,c} is interpreted as the early stage of gaseous protocluster formation, i.e., a protocluster with high turbulence driving needs a larger mass to keep itself bound, and an originally more turbulent cloud feeds the protocluster with more angular momentum and kinetic energy.

Our two-dimensional virial model yields a R ∝ M^0.5 relation for γ = 1 and R ∝ M^0.42−0.44 for γ = 0.7, depending on the parameters used. These power-law exponents are compatible with those from Fall et al. (2010, 0.38) and Urquhart et al. (2014, 0.50). We overplot the model with their star-forming clumps. The trend is very closely reproduced, however, there exists a slight shift, which could depend on the observation sensitivity, the definition of radius, and the fact that we use a uniform density model. The underlying assumptions of turbulent energy distribution in anisotropic configuration does not change the resulting gaseous protocluster size too much, and its effect is rather pronounced in the aspect ratio of the gaseous protocluster. The mass-size relations that we obtained is thus robust despite our ignorance of the properties of the turbulence. The curves do not represent evolutionary sequences. After a gaseous protocluster reaches equilibrium, it evolves toward sequences with smaller α_{∗ ,c} presuming that the parent cloud is not accreting mass much faster than the gaseous protocluster. We trace in yellow the gaseous protocluster formed inside a 10⁴ M_⊙ cloud in Figs. 6 and 7, which is indicative as an evolutionary sequence following R ∝ M. A gaseous protocluster in equilibrium could not exist for a mass that is too small, and its maximum mass is limited by the parent cloud. Therefore, the clumps should not migrate too much on this equilibrium sequence during their lifespan, and the mass-size relation observed for star-forming clumps is rather a result of gaseous protoclusters forming from a range of different gas reservoir than an evolutionary track.

Fig. 6 Mass-size relation of ellipsoidal clusters, shown with cloud-cluster mass ratio α∗ ,c = 1,2,3, which are plotted with blue solid, green dashed, red dot-dashed lines, respectively, using anisotropic turbulence following Kolmogorov spectrum (upper panel) and isotropic turbulence (lower panel). The turbulence efficiency ε = 0.5 is used, and the shadowed region represents the range of solutions for ε ∈ [0.2,0.7]. The elliptical patches represent the form of the clusters. With the molecular cloud density-size relation ρ ∝ R-1, the clusters follow a R ∝ M0.5 trend for a given α∗ ,c. The gaseous protocluster corresponding to 104 M⊙ cloud is traced in yellow, which is indicative of an evolutionary sequence roughly following R ∝ M. The radius of the gaseous protocluster does not depend too much on the underlying assumption of the turbulent energy distribution, while the aspect ratio is smaller in the anisotropic case. The dots are the observed star-forming clumps from Fall et al. (2010) and Urquhart et al. (2014).

Fig. 7 Same as Fig 6 for gaseous protoclusters inside parent clouds following ρ ∝ R-0.7 relation. The mass-size relation follows R ∝ M0.42−0.44.

3. Discussion and comparison

Now that we obtained the two-dimensional virial theorem for the rotating and accreting gaseous protocluster, in this section we discuss how the parameters affect the model prediction. Most importantly, we yield a comparison with the gaseous protoclusters formed in simulations (Paper I). Care must be taken in this comparison when adapting a pure gas model to simulations with sink particle prescriptions.

3.1. Dependence of the equilibrium state on gaseous protocluster properties

As described by Eq. (26), the equilibrium solution is determined by the intersection of the function f(η) with a constant proportional to j³ṀM^-3, hence, the existence of solutions is dependent on these parameters. First we discuss how the parameters affect the form of the cluster. The gaseous protocluster parameters are scaled self-similarly in Figs. 6 and 7, while there can be deviations if they do not follow exactly the same relations. We consider the solution in the regime where f(η) is monotonically decreasing. We can see from Fig. 5 that the gaseous protocluster is flatter and more extended if rotational support is important. Higher accretion rate also results in flatter form probably because shorter crossing time is required to dissipate larger energy input. In terms of the mass, when a cluster is more massive, it tends to be more spherical. The yellow line in Figs. 6 and 7 roughly indicates a track where the mass is increasing, while the accretion rate stays almost the same and the specific angular momentum does not grow as rapidly as the mass (Eq. (25)). In this case the aspect ratio increases as expected from Eq. (26).

On the other hand, equilibrium cannot exist if the angular momentum is too high. This could partly be due to the simplifications of angular momentum conservation applied to the model. If the angular momentum of the system becomes high enough, its loss by angular momentum transport should no longer be neglected. The dissipative loss should be considered to give a lower angular momentum, therefore extending the range of equilibrium existence. High mass accretion rate could result in high velocity dispersion, which could no longer be balanced by gravity. In this case, the ram pressure also becomes important and should not be neglected. This results in a system that is predominantly equilibrated by the supporting turbulence and confining surface ram pressure. However, this is beyond the scope of our discussion since the gaseous protoclusters do not have such high accretion rate and its self-gravity dominates over the ram pressure. As for the mass of the gaseous protocluster, no equilibrium solution could exist for systems with a mass that is too low (for a given cloud mass), which is obvious since this corresponds to the early stage of gaseous protocluster formation and self-gravity is not yet important enough to confine the system.

The turbulence driving efficiency by accretion ϵ_acc is a poorly understood factor. Some energy is radiated away as heat at the accretion shock. An efficiency that is too high results in the nonexistence of equilibrium, while this problem is less constrained in the isotropic case where we have an extra factor of ϵ_diss< 1 and f_iso>f_aniso. On the other hand, efficiency that is too low would yield gaseous protoclusters that are too extended. This could be explained by Fig. 5, in which r(η) increases while f(η) deceases with η. In our parameter domain of clouds following Larson relations, the isotropic case can tolerate ε = ϵ_dissϵ_acc up to 1 while it is by definition less than 1. On the other hand, the anisotropic case has ε = ϵ_acc limited to about 0.7 for larger α_{∗ ,c}, that is to say, 3. This means that if the turbulence-driving efficiency is indeed high, the turbulence inside the gaseous protocluster would prevent equilibrium and cause expansion at the beginning of its formation, and the quasi-static equilibrium could only be reached after enough mass is accreted. As shown in Fig. 5, the radius is less dependent of ε at a larger driving efficiency and a lower limit is well defined, while it grows very fast toward high values at small ε. The model ceases to be valid when the gaseous protocluster radius comes close to that of the cloud, or equivalently, when ε ≲ 0.1. This should correspond to the condition in which a gaseous protocluster has not yet formed inside the cloud. The infall is small compared to turbulence, and the flow that is not oriented well is dominated by dissipation and thus has low driving efficiency.

Our model accounts for the gaseous protocluster that has reached quasi-static equilibrium, that is, a centrally concentrated mass is readily marked inside the molecular cloud. In this regime, the model is robust as long as the turbulence-driving efficiency is not too small (>0.1). Nonetheless, more care should be taken as we wish to understand the formation stage of the gaseous protocluster. One interesting thing to be noted is that at larger η, dlog r/ dlog f is close to −2/3, giving in turn r ∝ f^{− 2/3} and thus from Eq. (27) we derive R ∝ MṀ^{− 2/3} independent of the angular momentum. Using Eq. (21), we obtain R ∝ M^0.5 or R ∝ M^0.43 for γ = 1 or 0.7. This means that if we simply consider a turbulent spherical model without rotation (j → 0), a similar gaseous protocluster mass-size relation would be concluded and this goes back to the Hennebelle (2012) result while the general rotating motion and flattened geometry would be missed.

We discuss two possibilities of turbulent energy distribution in a nonspherically symmetric system: anisotropy and isotropy. In the isotropic case, f(η) is larger than that in the anisotropic case, meaning that the equilibrium solution exists for a larger range of model parameters. Nonetheless, the recovered mass-size relations are not significantly different, guaranteeing that our assumptions are robust. Last but not least, it is important to keep in mind that the analytical study is based on uniform density assumption of the gaseous protocluster; each term in the equations may differ from the actual value by a factor of order unity in consequence. However, our conclusions should stay valid qualitatively, and the energy analysis of simulated protoclusters (see Paper I) indeed coincides with this picture of two-dimensional global virial equilibrium.

3.2. Adapting the model parameters to simulations

So far the analytical model includes only the gaseous component, while in the simulations we performed (see Paper I) sink particles are used to follow the dense regions. The analytical model should be adapted to yield a better comparison with simulations and, therefore, we use the modified equation set for the 2D virial equilibrium: $\begin{array}{ccc}\frac{\mathrm{5}}{\mathrm{2}}{\mathit{M}}_{\mathrm{g}}{\left(\frac{\mathit{j}}{\mathit{R}}\right)}^{\mathrm{2}}\mathrm{+}{\mathit{M}}_{\mathrm{g}}{\mathit{s}}_{\mathit{r}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}{\mathit{\sigma }}^{\mathrm{2}}& \mathrm{=}& \frac{\mathit{G}{\mathit{M}}_{\mathrm{\ast }}{\mathit{M}}_{\mathrm{g}}}{\mathit{R}}{\mathit{u}}_{\mathit{r}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\\ {\mathit{M}}_{\mathrm{g}}{\mathit{s}}_{\mathit{z}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}{\mathit{\sigma }}^{\mathrm{2}}& \mathrm{=}& \frac{\mathit{G}{\mathit{M}}_{\mathrm{\ast }}{\mathit{M}}_{\mathrm{g}}}{\mathit{R}}{\mathit{u}}_{\mathit{z}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\\ {\mathit{M}}_{\mathrm{g}}\mathit{d}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\frac{{\mathit{\sigma }}^{\mathrm{3}}}{\mathrm{4}\mathit{R}}& \mathrm{=}& \end{array}$where M_g is the gas mass and M_∗ is the cluster mass with the sink mass included. The underlying assumption of this formalism is that both gas and sinks are uniformly distributed, thus we are allowed to integrate over mass M_g the gravitational force created by mass M_∗. As seen in the simulations that the gas mass inside the cluster stays relatively constant and most of the mass is accreted onto the sinks, we make the simplification Ṁ_g = 0 and the variable M_g could be eliminated from all the equations. The equation set remains almost unchanged with respect to the pure gas model (Eqs. (10)), except a factor 2 in the energy released from accretion. Feedback mechanisms are not taken into account in the simulations. In more realistic runs where accretion is partly prevented by feedback, we should have something between this setup and the pure gas description. This adaptation turns out not to influence the model predictions much, which should therefore be robust during the early protocluster evolution before stellar feedbacks (not treated in this study) significantly modify the cluster environment. The mass intervening in the model, from which the accretion rate and the angular momentum are also evaluated, is the total cluster mass instead of the gas mass.

3.3. The cluster mass-size relation compared to simulations

In Paper I, we evaluate the protocluster mass and size using gas kinematics and sink particle distributions. The gaseous protocluster mass-size relations determined with gas kinematics are overplotted with models with corresponding levels of turbulence for four simulations in Fig. 8. We do not discuss the sink cluster since our model only considers the gas component. Paper I provides a comparison between the gas and sink clusters. The level of turbulent support is represented by the viral parameter α_vir = 2E_kin/E_grav. The angular momentum in the model is multiplied by the ratio between the level of turbulence in each of the runs and the virialized value, the mass accretion rate is also calculated accordingly. We show models with values 1 and 0.7 for the molecular cloud Larson relation ρ ∝ R^{− γ}. Canonical values of cloud-cluster mass ratio α_{∗ ,c} = 3 and ε = 0.5 are used along with isotropic turbulence.

The earlier time steps (before 2 Myr) in simulations are shown with thinner lines. The results show that the protocluster could be identified at a relative early stage when the mass is still small, and that as the gaseous protocluster accretes mass, it arrives on the sequence where virial equilibrium is reached. The model does not explain the gaseous protocluster well at the early stage, possibly because the time dependent terms and ram pressure are still relatively important and should not be neglected, while we use quasi-stationary assumptions. Once the mass is large enough, the simulations are in good agreement with the model. The case with α_vir = 0.12 is probably too strongly accreting owing to the weak kinetic support, thus this case does not correspond well to the quasi-stationary model. Otherwise, though showing slightly different trends, the model with two γ values are both compatible with the simulation results.

Fig. 8 Mass-size relation of ellipsoidal clusters; the total mass inside the ellipsoidal region defined with gas kinematics overplotted with a model of the corresponding levels of turbulence with γ = 1 (upper panel) and 0.7 (lower panel). The velocity dispersion increases from the bottom to the top curve. Simulation results at time before 2 Myr are plotted with thin lines. The model is in good agreement with simulation only after the protocluster gains enough mass, possibly implying that the time dependent terms and ram pressure should not be neglected at early stage.

3.4. The IMF peak position

The theoretical prediction of the core mass function (CMF) peak position (Hennebelle & Chabrier 2013) depends on the Jeans mass and the Mach number of the star-forming gas. We calculate for our model the Jeans mass ${\mathit{M}}_{\mathrm{J}}\mathrm{=}{\mathit{\pi }}^{\mathrm{5}\mathit{/}\mathrm{2}}{\mathit{c}}_{\mathit{s}}^{\mathrm{3}}\mathit{/}\mathrm{6}\sqrt{{\mathit{G}}^{\mathrm{3}}\mathit{\rho }}$ (thin curves) and the predicted CMF peak mass M_peak = M_J/ (1 + b²ℳ²) (thick curves), which are shown in Fig. 9. A canonical value b = 0.5 is used (Federrath et al. 2010). We present the result with two γ values (see Eq. (20)). As for the sound speed, we consider either the isothermal case at 10 K or gas following polytropic relation P ∝ ρ^Γ, where Γ = 0.85 (Hennebelle 2012).

Fig. 9 Initial mass function peak prediction from protocluster model with isotropic turbulence for cloud-cluster mass ratio α∗ ,c = 1,2,3 plotted against protocluster mass. The values 1 and 0.7 are used for the Larson relation ρ ∝ R− γ. As for the polytropic index Γ of gas inside the protocluster, values 1 (isothermal) and 0.85 are considered. The Jeans mass is plotted with thin curves, and the IMF peak mass is plotted with thick curves. Color codings are same as those in Fig. 6.

The average density decreases with gaseous protocluster mass and the Jeans mass is thus increasing. On the other hand, the turbulence increases with gaseous protocluster mass and gives a reasonable IMF peak prediction assuming that CMF and IMF peaks coincide. In the mass range between 10² and 10⁴ solar mass, where most clusters are observed, the predicted IMF peak value is around 0.1−0.3 M_⊙ with less than 1 dex variation. The molecular clouds following ρ ∝ R^-1 give a flatter relation. It is probably too simplifying to assume the same temperature for all clusters, since higher mass clusters have lower densities and thus slightly higher temperatures. The theoretical peak position depends on the temperature as T^5/2, thus the variation could be further reduced if this effect is taken into account. With the polytropic index Γ = 0.85, the inferred peak mass is more uniform among clusters of different masses, suggesting that an isothermal approach might be too simplistic. The observed IMF peak is about 0.3 M_⊙ with some dispersions (e.g., Bastian et al. 2010), which is slightly higher than what we discover here. This is the case, in particular, if we would take into account the apparent shift that is observed between the CMF and IMF (e.g., André et al. 2010). However, the magnetic field, which provides additional support against self-gravity, is not considered and can shift the peak toward a higher value when incorporated in the model. Furthermore, when stars start forming, this environment may be self-regulated due to stellar feedback. Nonetheless, this simple prediction gives a general picture that is compatible with a universal IMF peak.

4. Conclusions

As it is known that a significant fraction of stars form in clusters, it is fundamental understanding how these latter form and what their physical characteristics are. We confronted observations and simulation results with a simple analytical model; we showed that before stars start forming, the molecular cloud gas is reprocessed and a gaseous protocluster environment in global energy equilibrium is established that is much more favorable for star formation than the more diffuse large-scale molecular clumps. This gaseous protocluster sets a more general condition for stellar cluster formation and to some extent decouples star formation from the large-scale molecular clump. This is compatible with the idea that stellar clusters form in similar environments and that the IMF is regulated by more local conditions.

We developed an analytical model to account for the gaseous protocluster in virial equilibrium. A two-dimensional model is derived for a system with rotation, turbulence, and accretion, which predicts the radius, aspect ratio, and velocity dispersion given the mass, angular momentum, and accretion rate of the system. The mass accretion rate is estimated using free-fall collapse of a molecular cloud in which resides the gaseous protocluster, while adding a correction for varying level of turbulent support. The angular momentum of the gaseous protocluster is estimated using residual turbulent vortices while assuming no loss by transport. Its absolute value is scaled to coincide with that in the simulations. Given these estimations, we obtained an ellipsoidal virialized structure that is supported by rotation and supersonic turbulence against self-gravity. We produced a mass-size relation for gaseous protoclusters that is in coherence with observational (Fall et al. 2010; Urquhart et al. 2014) and simulation results (Paper I). The model dependence of the parameters was also discussed and we found our model to be very robust in predicting the gaseous protocluster properties regardless of the turbulence nature, turbulence driving efficiency, and infalling flow pattern, which are not well known.

We conclude that the gaseous protoclusters lie on an equilibrium sequence that is governed by the interaction of gravity and turbulence. This yields a mass-size relation similar to the Larson relation, while a gaseous protocluster is roughly ten times more massive than a molecular cloud of the same size. Such a resemblance is seen in the two relations since both are outcomes of turbulence and gravity interaction. Notwithstanding, we emphasize that in the case of a gaseous protocluster, accretion is relatively important in concentrating mass and sustaining turbulence, thus creating an environment that is different from that of the molecular cloud. As most stars form in clusters, the gaseous protocluster properties should be indeed used for understanding star formation. Using a simple estimate for the peak position of the CMF, we show that because of various compensations, it depends only weakly on the cluster mass, which suggests that the physical conditions of gaseous protoclusters may be, at least in part, responsible for the apparent universality of the IMF.

Acknowledgments

This work was granted access to HPC resources of CINES under the allocation x2014047023 made by GENCI (Grand Equipement National de Calcul Intensif). This research has received funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007–2013 Grant Agreement no. 306483). The authors thank the anonymous referee for the careful reading and useful suggestions.

References

Appendix A: Two-dimensional virial integration

The virial theorem is conventionally used for uniform density spheres. Here we deduce a more general form for an oblate ellipsoidal cluster of uniform density. The gravitational potential inside a uniform density ellipsoid is given by (Neutsch 1979) $\begin{array}{ccc}\mathit{\phi }\mathrm{\left(}\mathit{x,y,z}\mathrm{\right)}& \mathrm{=}& \mathrm{-}\mathit{G\rho \pi abc}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{x}}^{\mathrm{2}}}{{\mathit{a}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}\mathrm{-}\frac{{\mathit{y}}^{\mathrm{2}}}{{\mathit{b}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{c}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}{\sqrt{\mathrm{(}{\mathit{a}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}\mathrm{(}{\mathit{b}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}\mathrm{(}{\mathit{c}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}}}\mathrm{d}\mathit{\lambda }\\ & \mathrm{=}& \end{array}$(A.1)where the general form of an ellipsoid with semiaxes a ≥ b ≥ c is applied to our oblate ellipsoid of semiaxes R and H. Cylindrical coordinate is used. This allows us to integrate the right-hand side of the virial equation in r-direction and gives a term analogous to gravitational potential energy, while it is the result of only two of the dimensions of the gravity. The same is the case for z-direction potential.

We first consider multiplying by the r vector in a plane, $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}{v}\mathrm{·}{r}\mathrm{d}\mathit{V}\mathrm{=}& \underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{-}\mathit{\rho }\mathrm{\nabla }\mathit{\phi }\mathrm{·}{r}\mathrm{d}\mathit{V}\mathit{.}& \end{array}$(A.2)The left-hand side becomes $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}{v}\mathrm{·}{r}\mathrm{d}\mathit{V}& \mathrm{=}& \underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}\mathrm{(}{v}\mathrm{·}{r}\mathrm{)}\mathrm{d}\mathit{V}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{v}\mathrm{·}{{v}}_{\mathrm{2}\mathrm{d}}\mathrm{d}\mathit{V}\\ & \mathrm{=}& \underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{\partial }}_{\mathit{t}}\mathrm{(}{v}\mathrm{·}{r}\mathrm{)}\mathrm{d}\mathit{V}\mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{v}\mathrm{·}\mathrm{\nabla }\mathrm{(}{v}\mathrm{·}{r}\mathrm{)}\mathrm{d}\mathit{V}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V}\\ & \mathrm{=}& {\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }\mathrm{(}{v}\mathrm{·}{r}\mathrm{)}\mathrm{d}\mathit{V}\mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{\nabla }\mathrm{·}\mathrm{(}{v}\mathrm{·}{r}\mathit{\rho }{v}\mathrm{)}\mathrm{d}\mathit{V}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V}\\ & \mathrm{=}& {\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}\left(\frac{{r}\mathrm{·}{r}}{\mathrm{2}}\right)\mathrm{d}\mathit{V}\mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{v}\mathrm{·}{r}\mathit{\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V}\\ & \mathrm{=}& {\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{\partial }}_{\mathit{t}}\left(\frac{{\mathit{r}}^{\mathrm{2}}}{\mathrm{2}}\right)\mathrm{d}\mathit{V}\mathrm{+}{\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{v}\mathrm{·}\mathrm{\nabla }\left(\frac{{\mathit{r}}^{\mathrm{2}}}{\mathrm{2}}\right)\mathrm{d}\mathit{V}\\ & & \mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{r}}\mathit{r\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V}\\ & \mathrm{=}& \frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}^{\mathrm{2}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{r}}^{\mathrm{2}}\mathrm{d}\mathit{V}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{S}}}\mathit{\rho }{\mathit{r}}^{\mathrm{2}}{v}\mathrm{·}\mathrm{d}{S}\\ & & \mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{r}}\mathit{r\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{2}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V,}\end{array}$(A.3)

where u_2d is the velocity in the x−y plane and u_r is the velocity in the r direction. The right-hand side becomes (while assuming uniform density) $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{-}\mathit{\rho }\mathrm{\nabla }\mathit{\phi }\mathrm{·}{r}\mathrm{d}\mathit{V}& \mathrm{=}& \mathrm{-}\mathit{\rho }”{\mathit{\partial }}_{\mathit{r}}\mathit{\phi r}\mathrm{2}\mathit{\pi r}\mathrm{d}\mathit{r}\mathrm{d}\mathit{z}\\ & \mathrm{=}& \mathrm{-}\mathit{\rho }\mathrm{\int }\mathrm{\left(}\mathit{\phi r}\mathrm{2}\mathit{\pi r}\mathrm{\right)}{\mathrm{|}}_{\mathit{r}\mathrm{=}\mathrm{0}}^{{\mathit{r}}_{\mathit{s}}\mathrm{\left(}\mathit{z}\mathrm{\right)}}\mathrm{d}\mathit{z}\mathrm{+}\mathit{\rho }”\mathrm{2}\mathit{\phi }\mathrm{2}\mathit{\pi r}\mathrm{d}\mathit{r}\mathrm{d}\mathit{z}\\ & \mathrm{=}& \mathrm{2}\mathit{\rho }\mathrm{\int }\left(\mathrm{\int }\mathit{\phi }\mathrm{2}\mathit{\pi r}\mathrm{d}\mathit{r}\mathrm{-}\mathit{\phi }\mathrm{\left(}{\mathit{r}}_{\mathit{s}}\mathrm{\right)}\mathit{\pi }{\mathit{r}}_{\mathit{s}}^{\mathrm{2}}\right)\mathrm{d}\mathit{z}\\ & \mathrm{=}& \mathrm{2}\mathit{\rho }\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{\left(}\mathit{\phi }\mathrm{\right(}\mathit{r,z}\mathrm{)}\mathrm{-}\mathit{\phi }\mathrm{(}{\mathit{r}}_{\mathit{s}}\mathit{,z}\mathrm{\left)}\mathrm{\right)}\mathrm{d}\mathit{V}\\ & \mathrm{=}& \mathrm{-}\mathrm{2}\mathit{G}{\mathit{\rho }}^{\mathrm{2}}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\mathit{H}\underset{}{{\mathrm{\int }}^{\mathit{V}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}\sqrt{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}\\ & & \mathrm{-}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{r}}_{\mathit{s}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}\sqrt{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}\mathrm{d}\mathit{\lambda }\mathrm{d}\mathit{V}\\ & \mathrm{=}& \mathrm{-}\mathrm{2}\mathit{G}{\mathit{\rho }}^{\mathrm{2}}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\mathit{H}\underset{}{{\mathrm{\int }}^{\mathit{V}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}{\mathit{R}}^{\mathrm{2}}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }{\mathrm{)}}^{\mathrm{2}}\sqrt{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}\mathrm{d}\mathit{\lambda }\mathrm{d}\mathit{V}\\ & \mathrm{=}& \mathrm{-}\mathrm{2}\mathit{G}{\mathit{\rho }}^{\mathrm{2}}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\mathit{H}\frac{{\mathit{R}}^{\mathrm{2}}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{-}{\mathit{H}}^{\mathrm{2}}{\mathrm{)}}^{\frac{\mathrm{3}}{\mathrm{2}}}}\left[{\cos }^{-1}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathrm{-}\mathit{\eta }\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}\right]\\ & & \mathrm{\times }\mathrm{\int }\left(\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}}\right)\mathrm{d}\mathit{V}\\ & \mathrm{=}& \end{array}$(A.4)

where $\mathit{\eta }\mathrm{=}\frac{\mathit{H}}{\mathit{R}}$ represents the aspect ratio of the ellipsoid and r_s(z) is the r value corresponding to a given z on the surface of the ellipsoid. The last integration could be carried out with simple geometrical argument by integrating inside a sphere and then rescaling with the aspect ratio $\begin{array}{ccc}{\mathrm{\int }}_{\mathrm{ellp}}\left(\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}}\right)\mathrm{d}\mathit{V}& \mathrm{=}& \\ \mathit{\eta }{\mathrm{\int }}_{\mathrm{sph}}\left(\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}}\right)\mathrm{d}\mathit{V}& \mathrm{=}& \mathit{\eta }\frac{\mathrm{2}}{\mathrm{5}}{\mathit{V}}_{\mathrm{sph}}\mathrm{=}\frac{\mathrm{2}}{\mathrm{5}}{\mathit{V}}_{\mathrm{ellp}}\mathit{.}\end{array}$(A.5)We note that r in the ellipsoid is the distance to the semiminor axis and that in the sphere is the distance to the center.

The virial equation in the z direction gives $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}{v}\mathrm{·}{z}\mathrm{d}\mathit{V}\mathrm{=}& \underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{-}\mathit{\rho }\mathrm{\nabla }\mathit{\phi }\mathrm{·}{z}\mathrm{d}\mathit{V}\mathit{.}& \end{array}$(A.6)Similarly, the left-hand side becomes $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{d}}_{\mathit{t}}{v}\mathrm{·}{z}\mathrm{d}\mathit{V}& \mathrm{=}& \hspace{0.17em}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}^{\mathrm{2}}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{z}}^{\mathrm{2}}\mathrm{d}\mathit{V}\\ & & \mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\partial }}_{\mathit{t}}\underset{}{{\mathrm{\int }}^{\mathit{S}}}\mathit{\rho }{\mathit{z}}^{\mathrm{2}}{v}\mathrm{·}\mathrm{d}{S}\mathrm{+}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{u}}_{\mathit{z}}\mathit{z\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{-}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathit{\rho }{\mathit{v}}_{\mathrm{1}\mathrm{d}}^{\mathrm{2}}\mathrm{d}\mathit{V,}\end{array}$(A.7)where u_1d is the velocity in the z direction, and is equivalent to u_z; and the right-hand side becomes $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{-}\mathit{\rho }\mathrm{\nabla }\mathit{\phi }\mathrm{·}{z}\mathrm{d}\mathit{V}& \mathrm{=}& \mathrm{-}\mathit{\rho }”{\mathit{\partial }}_{\mathit{z}}\mathit{\phi z}\mathrm{2}\mathit{\pi r}\mathrm{d}\mathit{z}\mathrm{d}\mathit{r}\\ & \mathrm{=}& \mathrm{-}\mathit{\rho }\mathrm{\int }\mathrm{\left(}\mathit{\phi z}\mathrm{2}\mathit{\pi r}\mathrm{\right)}{\mathrm{|}}_{\mathit{z}\mathrm{=}\mathrm{-}{\mathit{z}}_{\mathit{s}}\mathrm{\left(}\mathit{r}\mathrm{\right)}}^{{\mathit{z}}_{\mathit{s}}\mathrm{\left(}\mathit{r}\mathrm{\right)}}\mathrm{d}\mathit{r}\mathrm{+}\mathit{\rho }”\mathit{\phi }\mathrm{2}\mathit{\pi r}\mathrm{d}\mathit{z}\mathrm{d}\mathit{r}\\ & \mathrm{=}& \hspace{0.17em}\mathit{\rho }\mathrm{\int }\left(\mathrm{\int }\mathit{\phi }\mathrm{d}\mathit{z}\mathrm{2}\mathit{\pi r}\mathrm{-}\mathit{\phi }\mathrm{\left(}{\mathit{z}}_{\mathit{s}}\mathrm{\right)}\mathrm{2}{\mathit{z}}_{\mathit{s}}\mathrm{2}\mathit{\pi r}\right)\mathrm{d}\mathit{r}\\ & \mathrm{=}& \hspace{0.17em}\mathit{\rho }\underset{}{{\mathrm{\int }}^{\mathit{V}}}\mathrm{\left(}\mathit{\phi }\mathrm{\right(}\mathit{r,z}\mathrm{)}\mathrm{-}\mathit{\phi }\mathrm{(}\mathit{r,}{\mathit{z}}_{\mathit{s}}\mathrm{\left)}\mathrm{\right)}\mathrm{d}\mathit{V}\end{array}$(A.8)$\begin{array}{ccc}& & \mathrm{=}\mathrm{-}\mathit{G}{\mathit{\rho }}^{\mathrm{2}}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\mathit{H}\underset{}{{\mathrm{\int }}^{\mathit{V}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}\sqrt{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}\\ & & \mathrm{-}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}\mathrm{-}\frac{{\mathit{z}}_{\mathit{s}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}\sqrt{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}\mathrm{d}\mathit{\lambda }\mathrm{d}\mathit{V}\\ & & \mathrm{=}\mathrm{-}\mathit{G}{\mathit{\rho }}^{\mathrm{2}}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\mathit{H}\underset{}{{\mathrm{\int }}^{\mathit{V}}}{\mathrm{\int }}_{\mathrm{0}}^{\mathrm{\infty }}{\mathit{H}}^{\mathrm{2}}\frac{\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }\mathrm{)}{\sqrt{{\mathit{H}}^{\mathrm{2}}\mathrm{+}\mathit{\lambda }}}^{\mathrm{3}}}\mathrm{d}\mathit{\lambda }\mathrm{d}\mathit{V}\\ & & \mathrm{=}\mathrm{-}\mathit{G}{\mathit{\rho }}^{\mathrm{2}}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\mathit{H}\{\frac{\mathrm{2}\mathit{H}}{{\mathit{R}}^{\mathrm{2}}}\mathrm{-}\frac{\mathrm{2}{\mathit{H}}^{\mathrm{2}}}{\mathrm{(}{\mathit{R}}^{\mathrm{2}}\mathrm{-}{\mathit{H}}^{\mathrm{2}}{\mathrm{)}}^{\frac{\mathrm{3}}{\mathrm{2}}}}\\ & & \mathrm{\times }\left[{\cos }^{-1}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathrm{-}\mathit{\eta }\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}\right]\}\\ & & \mathrm{\times }\mathrm{\int }\left(\mathrm{1}\mathrm{-}\frac{{\mathit{r}}^{\mathrm{2}}}{{\mathit{R}}^{\mathrm{2}}}\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{H}}^{\mathrm{2}}}\right)\mathrm{d}\mathit{V}\\ & & \mathrm{=}\mathrm{-}\frac{\mathrm{3}}{\mathrm{5}}\frac{\mathit{G}{\mathit{M}}^{\mathrm{2}}}{\mathit{R}}\left[\frac{\mathit{\eta }}{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}\mathrm{-}\frac{{\mathit{\eta }}^{\mathrm{2}}{\cos }^{-1}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}}{\mathrm{(}\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}{\mathrm{)}}^{\frac{\mathrm{3}}{\mathrm{2}}}}\right]\mathit{,}\end{array}$

where z_s(r) is the z value corresponding to a given r on the surface of the ellipsoid. We therefore decompose the virial theorem into two equations for two directions that are balanced, respectively.

Appendix B: Free-fall time evaluated at gaseous protocluster radius

The free-fall time typically used represents the formation time of an infinitely small object by free collapse without any support. Here we make a correction for free-falling collapse onto the gaseous protocluster, which is comparable in size to its parent cloud. The mass in free fall follows the equation for any radius r within the cloud region, $\begin{array}{ccc}\begin{array}{c}\mathrm{¨}\\ \mathit{r}\end{array}\mathrm{=}\mathrm{-}\frac{\mathit{GM}\mathrm{\left(}\mathit{r}\mathrm{\right)}}{{\mathit{r}}^{\mathrm{2}}}\mathit{,}& & \end{array}$(B.1)where G and M(r) are the gravitational constant and the mass contained inside radius r. Multiplying by ṙ on both sides gives $\begin{array}{ccc}\frac{\mathrm{1}}{\mathrm{2}}{\mathit{d}}_{\mathit{t}}\mathit{ṙ}\mathrm{2}& \mathrm{=}& {\mathit{d}}_{\mathit{t}}\frac{\mathit{GM}\mathrm{\left(}\mathit{r}\mathrm{\right)}}{\mathit{r}}\\ {\left(\frac{\mathrm{d}\mathit{r}}{\mathrm{d}\mathit{t}}\right)}^{\mathrm{2}}& \mathrm{=}& \frac{\mathrm{2}\mathit{GM}}{\mathit{r}}\mathrm{-}\frac{\mathrm{2}\mathit{GM}}{{\mathit{r}}_{\mathit{i}}}\\ {\mathit{t}}_{\mathrm{ff}}\mathrm{\left(}{\mathit{r}}_{\mathit{i}}\mathrm{\right)}& \mathrm{=}& \int \begin{array}{c}{\mathit{t}}_{\mathrm{ff}}\\ \mathrm{0}\end{array}\mathrm{d}\mathit{t}\mathrm{=}{\mathrm{\int }}_{{\mathit{r}}_{\mathit{i}}}^{{\mathit{r}}_{\mathit{f}}}\mathrm{-}{\left(\frac{\mathrm{2}\mathit{GM}}{\mathit{r}}\mathrm{-}\frac{\mathrm{2}\mathit{GM}}{{\mathit{r}}_{\mathit{i}}}\right)}^{\mathrm{-}\frac{\mathrm{1}}{\mathrm{2}}}\mathrm{d}\mathit{r}\\ & \mathrm{=}& \sqrt{\frac{\mathrm{3}}{\mathrm{8}\mathit{\pi G}\overline{\mathit{\rho }}\mathrm{\left(}{\mathit{r}}_{\mathit{i}}\mathrm{\right)}}}{\mathrm{\int }}_{\mathrm{1}}^{\frac{{\mathit{r}}_{\mathit{f}}}{{\mathit{r}}_{\mathit{i}}}}\mathrm{-}\sqrt{\frac{\mathit{\xi }}{\mathrm{1}\mathrm{-}\mathit{\xi }}}\mathrm{d}\mathit{\xi }\\ & \mathrm{=}& \sqrt{\frac{\mathrm{3}}{\mathrm{8}\mathit{\pi G}\overline{\mathit{\rho }}\mathrm{\left(}{\mathit{r}}_{\mathit{i}}\mathrm{\right)}}}\left[{\cos }^{-1}\sqrt{\frac{{\mathit{r}}_{\mathit{f}}}{{\mathit{r}}_{\mathit{i}}}}\mathrm{+}\sqrt{\frac{{\mathit{r}}_{\mathit{f}}}{{\mathit{r}}_{\mathit{i}}}\left(\mathrm{1}\mathrm{-}\frac{{\mathit{r}}_{\mathit{f}}}{{\mathit{r}}_{\mathit{i}}}\right)}\right]\mathrm{·}\end{array}$We thus have the time that the mass originally situated at radius r_i takes to arrive at r_f, given $\overline{\mathit{\rho }}\mathrm{\left(}{\mathit{r}}_{\mathit{i}}\mathrm{\right)}$, the initial averaged density inside r_i. At r_f = 0, this converges to the conventional free-fall time $\sqrt{\frac{\mathrm{3}\mathit{\pi }}{\mathrm{32}\mathit{G}\overline{\mathit{\rho }}}}$.

Appendix C: The decomposed ram pressure

When integrating the virial equations, a term analogous to the ram pressure in the spherical model (Hennebelle 2012) appears, while the ellipsoidal geometry renders its interpretation less obvious since we are ignorant of the mass infall pattern. As long as we obtain Ṁ = −^∫Sρ_infv_inf·dS, the integrals could be expressed in the following form by assuming that the gas reaches free-fall velocity upon accretion, i.e., $\begin{array}{ccc}\underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{r}}\mathit{r\rho }{v}\mathrm{·}\mathrm{d}{S}& \mathrm{=}& \mathit{Ṁ}\sqrt{\mathrm{2}\mathit{GMR}}{\mathit{p}}_{\mathit{r}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\\ \underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{z}}\mathit{z\rho }{v}\mathrm{·}\mathrm{d}{S}& \mathrm{=}& \mathit{Ṁ}\sqrt{\mathrm{2}\mathit{GMR}}{\mathit{p}}_{\mathit{z}}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}\mathit{,}\end{array}$where p_r(η) and p_z(η) are dimensionless factors as functions of the ellipsoid aspect ratio.

Two extreme cases could be easily examined: the accretion coming entirely along the edge or the pole of the ellipsoid. In the first case, we have p_r = 1 and p_z = 0, and in the second we obtain p_r = 0 and ${\mathit{p}}_{\mathit{z}}\mathrm{=}\sqrt{\mathit{\eta }}$. A more sophisticated estimation is made by assuming that ρ_infv_inf is constant and in radial direction on the whole ellipsoid surface and that v_inf has constant value $\sqrt{\mathrm{2}\mathit{GM}\mathit{/}\mathit{R}}$. 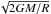This allows us to integrate the mass accretion rate, therefore, giving p_r(η) and p_z(η), i.e., $\begin{array}{ccc}& & \mathit{Ṁ}\mathrm{=}\mathrm{-}{\mathit{\rho }}_{\inf }{{v}}_{\inf }\mathrm{4}\mathit{\pi }{\mathit{R}}^{\mathrm{2}}\frac{\mathit{\eta }}{\mathrm{2}\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}}\left[\frac{\mathit{\pi }}{\mathrm{2}}\mathrm{-}\arctan \left(\frac{\mathrm{2}{\mathit{\eta }}^{\mathrm{2}}\mathrm{-}\mathrm{1}}{\mathrm{2}\mathit{\eta }\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}}\right)\right]\\ & & \underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{r}}\mathit{r\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{=}\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\inf }{\mathit{v}}_{\inf }^{\mathrm{2}}{\mathit{R}}^{\mathrm{3}}\frac{\mathit{\eta }}{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}\left[\mathrm{1}\mathrm{-}\frac{{\mathit{\eta }}^{\mathrm{2}}\mathrm{arcsech}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}}{\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}}\right]\\ & & \underset{}{{\mathrm{\int }}^{\mathit{S}}}{\mathit{v}}_{\mathit{z}}\mathit{z\rho }{v}\mathrm{·}\mathrm{d}{S}\mathrm{=}\mathrm{4}\mathit{\pi }{\mathit{\rho }}_{\inf }{\mathit{v}}_{\inf }^{\mathrm{2}}{\mathit{R}}^{\mathrm{3}}\frac{{\mathit{\eta }}^{\mathrm{3}}}{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}\left[\frac{\mathrm{arcsech}\mathrm{\left(}\mathit{\eta }\mathrm{\right)}}{\sqrt{\mathrm{1}\mathrm{-}{\mathit{\eta }}^{\mathrm{2}}}}\mathrm{-}\mathrm{1}\right]\mathit{.}\end{array}$These are presented in Fig. 1 with other coefficients.