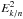| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 10 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201527852 | |
| Published online | 21 June 2016 | |
Non-parametric determination of H and He interstellar fluxes from cosmic-ray data
1
LPSC, Université Grenoble-Alpes, CNRS/IN2P3,
53 avenue des Martyrs,
38026
Grenoble,
France
e-mail:
alexandre.ghelfi@lpsc.in2p3.fr; david.maurin@lpsc.in2p3.fr
2
LIP, 1000
Lisboa,
Portugal
Received:
27
November
2015
Accepted:
26
March
2016
Context. Top-of-atmosphere (TOA) cosmic-ray (CR) fluxes from satellites and balloon-borne experiments are snapshots of the solar activity imprinted on the interstellar (IS) fluxes. Given a series of snapshots, the unknown IS flux shape and the level of modulation (for each snapshot) can be recovered.
Aims. We wish (i) to provide the most accurate determination of the IS H and He fluxes from TOA data alone; (ii) to obtain the associated modulation levels (and uncertainties) while fully accounting for the correlations with the IS flux uncertainties; and (iii) to inspect whether the minimal force-field approximation is sufficient to explain all the data at hand.
Methods. Using H and He TOA measurements, including the recent high-precision AMS, BESS-Polar, and PAMELA data, we performed a non-parametric fit of the IS fluxes JISH,~He and modulation level φi for each data-taking period. We relied on a Markov chain Monte Carlo (MCMC) engine to extract the probability density function and correlations (hence the credible intervals) of the sought parameters.
Results. Although H and He are the most abundant and best measured CR species, several datasets had to be excluded from the analysis because of inconsistencies with other measurements. From the subset of data passing our consistency cut, we provide ready-to-use best-fit and credible intervals for the H and He IS fluxes from MeV/n to PeV/n energy (with a relative precision in the range [ 2−10% ] at 1σ). Given the strong correlation between JIS and φi parameters, the uncertainties on JIS translate into Δφ ≈ ± 30 MV (at 1σ) for all experiments. We also find that the presence of 3He in He data biases φ towards higher φ values by ~30 MV. The force-field approximation, despite its limitation, gives an excellent (χ2/d.o.f. = 1.02) description of the recent high-precision TOA H and He fluxes.
Conclusions. The analysis must be extended to different charge species and more realistic modulation models. It would benefit from the AMS-02 unique capability of providing frequent high-precision snapshots of the TOA fluxes over a full solar cycle.
Key words: astroparticle physics / Sun: activity / cosmic rays
© ESO, 2016
1. Introduction
H and He interstellar (IS) fluxes are the most abundant species in the cosmic radiation. The low-energy part of their spectrum (MeV/n to GeV/n) is responsible for ionising the interstellar medium (ISM; Webber 1987; Nath & Biermann 1994; Webber 1998; Nath et al. 2012) and molecular clouds (e.g. Padovani et al. 2009). They also interact with the ISM to produce light LiBeB isotopes (Reeves 1970; Meneguzzi et al. 1971; Vangioni-Flam et al. 2000; Prantzos 2012) and nuclear γ-rays (Meneguzzi & Reeves 1975; Lingenfelter & Ramaty 1977; Ramaty et al. 1979; Kozlovsky et al. 2002; Tatischeff & Kiener 2004). Uncertainties on the low-energy IS flux shape affect all these quantities (Indriolo et al. 2009). The high-energy part of the IS flux (from GeV/n to PeV/n) is involved in the secondary production of γ-rays, neutrinos, antiprotons, and positrons (Strong et al. 2007). In particular, the hint at an energy break at hundreds of GeV energy (Ahn et al. 2010; Adriani et al. 2011; Ackermann et al. 2014), now confirmed by the AMS-02 collaboration (Aguilar et al. 2015a,b), must be accounted for as it affects the number of secondaries created (Donato & Serpico 2011; Lavalle 2011). All these observables underline the necessity of a description as accurate as possible of the H and He IS fluxes over a wide energy range.
A standard approach is to rely on top-of-atmosphere (TOA) data and simultaneously fit the IS flux parameters and solar modulation parameters (Garcia-Munoz et al. 1975; Casadei & Bindi 2004; O’Neill 2006; Shikaze et al. 2007)1. At the crossroad of cosmic-ray and solar physics, these data give a unique perspective on the IS fluxes and the 22-year modulation cycle related to solar activity. The difficulty is that we do not know which solar modulation model (and parameters) to apply, but these models can be tested with high-statistics TOA data. We restrict ourselves in the present work to the simple force-field approximation (Gleeson & Axford 1967, 1968; Perko 1987; Boella et al. 1998), which, despite some limitations (e.g. Caballero-Lopez & Moraal 2004), is still widely used in the literature owing to its simplicity; it depends on a single free parameter φ(t).
Uncertainties on the IS fluxes translate into uncertainties on the solar modulation parameters. For instance, dark matter interpretations of the antiprotons and positrons fluxes are sensitive to φ uncertainties (e.g. Lavalle et al. 2014; Giesen et al. 2015). In general, there is no consensus on the required modulation level for a given data set and no consistency (of method and assumptions) between the various evaluations of φ provided by different experimental teams (see the discussion in Maurin et al. 2014), which is problematic. Also directly related to the correlation between the IS flux and modulation level is the difficulty of establishing reliable and consistent modulation time-series from ground-based detector count rates (Usoskin et al. 2011) and/or from the concentration of cosmogenic radionuclides in ice cores (Webber & Higbie 2003; Herbst et al. 2010). As underlined in several studies, the use of several IS flux parametrisations (Garcia-Munoz et al. 1975; Burger et al. 2000; Langner et al. 2003; Webber & Higbie 2003, 2009; O’Neill 2006; Shikaze et al. 2007) leads to shifts of these time series up to Δφ ~ ± 200 MV (e.g. Maurin et al. 2015). This motivates us even more to find a better characterisation of the IS flux, modulation level, and of the correlations between these parameters. The recent publication of high-precision data from PAMELA (Adriani et al. 2014), BESS-Polar (Abe et al. 2016), and AMS-02 (Aguilar et al. 2015a,b) is also a strong incentive to repeat and improve on the procedure of extracting these quantities from TOA CR data.
In Sect. 2 we describe the use of spline fit functions (in lieu of less flexible parametrisations previously used in the literature) to achieve a non-parametric determination of the H and He fluxes2. A simple χ2 analysis is then used to select the subset of CR TOA data passing a consistency criterion. In Sect. 3 we replace the χ2 analysis by a Markov chain Monte Carlo (MCMC) exploration of the parameter space to obtain the credible intervals (CIs) and correlations between IS flux and modulation parameters. We also compare our results to the recent low-energy Voyager data, which are considered to be a direct probe of the local IS fluxes (Stone et al. 2013; Webber & Higbie 2013; Webber et al. 2013a,b), and to the indirect observation of IS fluxes in the direction of molecular complexes from Fermi-LAT γ-ray data (Neronov et al. 2012; Kachelrieß & Ostapchenko 2012; Yang et al. 2014; Strong 2015), before concluding in Sect. 4. The short Appendix A investigates possible systematic effects on the φ determination that are due to deuteron and 3He contamination in H and He fluxes (Appendix A.1), or when using TOA data obtained from long data-taking periods (Appendix A.2).
2. Methodology
To perform the analysis, the modulation model, the parametrisation of the IS flux, and the set of CR TOA data used for the minimisation must be specified. In this section, we present our setup, emphasising on the improvements made with respect to previous studies.
2.1. Modulation: force-field approximation
The simplest modulation model to link unmodulated (IS) to modulated (TOA) quantities is
the force-field approximation (Gleeson & Axford 1967, 1968): 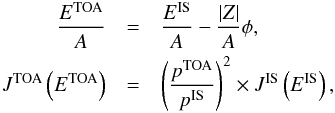 (1)where
E is the
total energy, p the momentum, and J ≡ dJ/
dEk/n
is the differential flux per kinetic energy per nucleon Ek/n.
This model has a single free parameter φ(t), whose dimension is rigidity.
(1)where
E is the
total energy, p the momentum, and J ≡ dJ/
dEk/n
is the differential flux per kinetic energy per nucleon Ek/n.
This model has a single free parameter φ(t), whose dimension is rigidity.
2.2. Analysis and χ2
The approach to break the degeneracy between JIS and φ is to simultaneously fit s different snapshots { t1...,ts } of the same CR species Nj and/or n different CR species { N1...,Nn } at the same ti. In the former approach, we benefit from sampling the same IS flux at the cost of one additional modulation parameter per snapshot: depending on the data precision and the periods used, ideally both high and low solar activity periods, the degeneracy is mostly lifted, although some significant uncertainties can remain (e.g. Maurin et al. 2015). In the second approach, the modulation level φ(ti) is now the quantity sampled several times by different species, each new species requiring several additional shape parameters: the benefit is that species with different Z/A (e.g. proton and helium) are differently modulated, even in the simple force-field approximation (see Eq. (1)). More generally, species with different charges (e.g. electrons and positrons) can probe different modulation models as a dependence on Z is expected for example in drift modulation models (see Potgieter 2013, for a review).
The χ2 for a simultaneous fit over the TOA
flux snapshots ti, with several
possibly measured species Nj(i)
at this ti, and over all
Ek(i,j)
energy bins measured, is given by 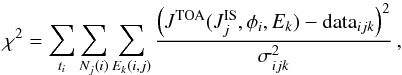 (2)where the free parameters
are the IS flux parameters for each species and the modulation parameters per TOA flux
snapshot. The three cases considered in this study all involve fits over different
snapshots {
t1...,ts
} for
(2)where the free parameters
are the IS flux parameters for each species and the modulation parameters per TOA flux
snapshot. The three cases considered in this study all involve fits over different
snapshots {
t1...,ts
} for
-
p data only,
-
He data only, and
-
p and He data simultaneously.
The last option enables checking the consistency of the modulation levels derived with the values obtained from the separate species analysis (see Sect. 3).
2.3. Non-parametric IS flux: splines
Fits of the IS fluxes in the literature are mostly based on simple power laws in total energy (e.g. O’Neill 2006; Yang et al. 2014) or rigidity (e.g. Shikaze et al. 2007; Maurin et al. 2014). Recently, to account for the high-energy break, broken power-laws were proposed (Donato & Serpico 2011; Lavalle 2011; Aguilar et al. 2015a). Whereas these parametrisations are flexible enough to describe the smooth behaviour above tens of GeV/n energies, the low-energy behaviour governed by a βa term (in front of the power-law) does not offer enough freedom to fit the log-parabola-shaped TOA flux. We find that pure and broken power laws in rigidity, kinetic energy, and total energy (i) give poor fits to the data for all parametrisations (χ2/d.o.f. ~ 1.6−1.8); (ii) do not allow assessing the relative merit of the different parametrisations, which complicates the task of providing a statistically meaningful description of the IS fluxes and their uncertainties.
To solve these problems, we used a spline function, which gives an excellent fit of the
TOA data (χ2/d.o.f. ≲ 1, see below) and also encompasses all the
above parametrisations. A spline is a piecewise function defined by polynomials connecting
at knots. The order of the spline is related to the highest order n of the polynomial used,
and smoothness is guaranteed by the fact that continuity of the spline and its
n − 1
derivatives are imposed. Here, we used a cubic spline (n = 3) in x =
log (R) and y = log (JIS), with
R =
pc/Ze the rigidity in GV. The
y-values
(flux) are the free parameters of the fit, while the number of knots N and their x-position (rigidity) have
to be set carefully to describe the shape of the data correctly. No structures are
expected at low energy in the IS fluxes, therefore a small number of knots is enough to
reproduce the smooth shape. Several knots are needed at and around the high-energy break
position (Aguilar et al.
2015a) to be able to match the structure. We find that at least six knots
from 1 GV to 800 GV are necessary to provide a good description of the IS fluxes. The
positions of the knots are the same for both H and He and are taken to be
 (3)As a sanity check, we
added at random x-positions additional knots and repeated the fitting
analysis (described below). No difference in the best-fit spectrum being observed, we
conclude that the six-knot third-order spline function provides a non-parametric
determination of the IS fluxes.
(3)As a sanity check, we
added at random x-positions additional knots and repeated the fitting
analysis (described below). No difference in the best-fit spectrum being observed, we
conclude that the six-knot third-order spline function provides a non-parametric
determination of the IS fluxes.
2.4. Data selection
We retrieved TOA CR data for H and He from the cosmic-ray data base CRDB3(Maurin et al.
2014). In principle, all the data should be used in the analysis. However,
inconsistencies between different measurements are common, especially for the oldest
datasets. To identify and then reject these inconsistent datasets, we performed a
χ2 minimisation on all p data, see Eq. (1), for which we relied on the Minuit
minimisation package (James 1994) from the
Root CERN libraries4(Brun
& Rademakers 1997). For each dataset, we then calculated an a
posteriori distance between the data and the globally determined best-fit TOA flux for
this set: 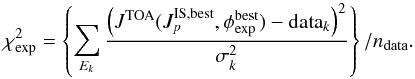 (4)We then excluded all data
with
(4)We then excluded all data
with 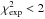 .
Strictly speaking, this quantity is just a distance and has no statistical bearing, but it
nevertheless gives a good estimate of the goodness of fit of each dataset (see the values
obtained in Table 1). This procedure accounts for
modulation effects, hence allows checking the TOA data consistency over their full energy
range.
.
Strictly speaking, this quantity is just a distance and has no statistical bearing, but it
nevertheless gives a good estimate of the goodness of fit of each dataset (see the values
obtained in Table 1). This procedure accounts for
modulation effects, hence allows checking the TOA data consistency over their full energy
range.
List of proton and helium data tested and rejected (italics) for the analysis.
In practice, the procedure must be repeated several times because
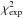 values are
modified each time non-compatible datasets are removed, as shown in Table 1. Surprisingly, the AMS-01 and PAMELA
(2006−2008) He data do not
pass the cut. This is illustrated in Fig. 1, which
represents (symbols) the ratio between the best-fit model
(
values are
modified each time non-compatible datasets are removed, as shown in Table 1. Surprisingly, the AMS-01 and PAMELA
(2006−2008) He data do not
pass the cut. This is illustrated in Fig. 1, which
represents (symbols) the ratio between the best-fit model
(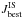 modulated by the
associated φbest) to TOA data. For good data, this
ratio is mostly contained in the data error bars (solid and dashed lines for
p and He,
respectively). AMS-01 He data (empty red circles in top-left panel) are an illustration of
rejected data. We note that inconsistencies in the data at low energy may be indicative of
a failure of the simple force-field approximation we used and not of underestimated
systematics in the data, for instance. More realistic modulation models will be
investigated in a forthcoming study. However, Fig. 1
shows for the very case of AMS-01 He data that the inconsistency with other datasets is
not related to solar modulation as differences are at high energy.
modulated by the
associated φbest) to TOA data. For good data, this
ratio is mostly contained in the data error bars (solid and dashed lines for
p and He,
respectively). AMS-01 He data (empty red circles in top-left panel) are an illustration of
rejected data. We note that inconsistencies in the data at low energy may be indicative of
a failure of the simple force-field approximation we used and not of underestimated
systematics in the data, for instance. More realistic modulation models will be
investigated in a forthcoming study. However, Fig. 1
shows for the very case of AMS-01 He data that the inconsistency with other datasets is
not related to solar modulation as differences are at high energy.
From comparing the results from one experiment to another, we see no clear trend for a systematic bias towards lower or higher values of the fluxes. The only case for which a pattern in the energy dependence is observed is for the various PAMELA data because they come from the same experimental setup and same analyses. This is not seen for BESS experiments, the configuration of which slightly changes between different flights.
 |
Fig. 1 Ratio of the best-fit model for p (filled black circles) and He (empty red circles) to data for the experiments passing our selection (see Table 1). The solid blue (dashed red) lines correspond to the uncertainties (statistical and systematics combined) on the p (He) measurements. We note that the AMS-01 (top left panel) and PAMELA (2006−2008) He data (red empty circles; left panel, third row) are excluded based on their χ2 value (see Table 1) and are shown for illustration only. |
We underline that neither Table 1 nor Fig. 1 show all the data rejected by the analysis. Moreover, some data were not considered for the MCMC analysis of Sect. 3 for the following reasons:
-
At low energy (≲GeV/n): several low-energy datasets passed the cut (several sets for ISEE-MEH, Kroeger 1986, and Voyager, Webber & Yushak 1983), but as they have no effect on the result (as checked from the χ2 minimisation analysis), we discarded them to avoid increasing the number of parameters (and runtime) in the MCMC analysis.
-
At intermediate energy: several datasets have a limited energy range with large error bars, hence no effect on the fit. For the same reason as above, they were not considered in the MCMC analysis.
-
At high energy (≳10 TeV/n): we recall that these data are not sensitive to solar modulation, but they determine the high-energy IS flux shape. We discarded them as the data are mostly inconsistent with one another (especially for He, see Fig. 5).
3. Markov chain Monte Carlo analysis
On these data we used a Markov chain Monte Carlo (MCMC) algorithm as implemented in the GreAT package (Putze & Derome 2014) to determine the probability density functions (PDF), correlations, and CIs for φ and IS flux parameters.
3.1. MCMC algorithm
The MCMC algorithm is based on the Bayes theorem that links the multidimensional PDF of
the parameters to the likelihood function of the model and the prior on each parameter:
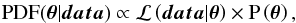 (5)with
θ corresponding to all IS flux and solar
modulation parameters, and data the selected subset of
experiments (see Sect. 2.4). In the Bayesian
interpretation of statistics, the function
(5)with
θ corresponding to all IS flux and solar
modulation parameters, and data the selected subset of
experiments (see Sect. 2.4). In the Bayesian
interpretation of statistics, the function 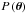 describes our prior knowledge on each parameter, and we took here a flat prior for all
parameters. For the likelihood, with χ2 defined in Eq. (2), we used
describes our prior knowledge on each parameter, and we took here a flat prior for all
parameters. For the likelihood, with χ2 defined in Eq. (2), we used
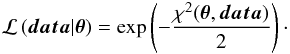
The algorithm, based on random numbers, generates a chain θi = 1...N of N elements based on the following iterative process (see e.g. Putze et al. 2009):
-
1.
Randomly pick θ0 in the parameter space as the starting point of the chain; the current point is defined as θcurrent = θ0.
-
2.
Propose a new point θproposed from a proposition function, here a multidimensional Gaussian, centred on θcurrent.
-
3.
Compute the probability of θproposed
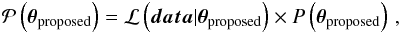 and
apply the Metropolis-Hastings criterion (Neal
1993; MacKay 2003): θproposed is added to
the chain and becomes the new current point θcurrent with a
probability
and
apply the Metropolis-Hastings criterion (Neal
1993; MacKay 2003): θproposed is added to
the chain and becomes the new current point θcurrent with a
probability 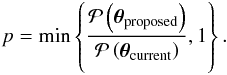 If
θproposed does not
pass this criterion, θcurrent is added
instead.
If
θproposed does not
pass this criterion, θcurrent is added
instead. -
4.
Repeat 2 until the chain has N elements.
The chain is Markovian, meaning that the sampling of θi + 1 only depends on the value θi. This implies a correlation between the consecutive values of θ in the chain. This correlation is corrected for by calculating the correlation length to select independent samples of θi. A burning length is computed to estimate the number of steps needed to forget about the starting point, and these points are removed; for more details, see Putze et al. (2009) and Putze & Derome (2014). This procedure ensures that the multidimensional PDF of the parameters is correctly sampled. The outputs of the MCMC algorithm are
-
a natural marginalisation of the multidimensional PDF PDF(θ | data) to access the 1D and 2D PDFs of the parameters, and
-
a vector of the model parameters that can be straightforwardly used to calculate CIs on quantities derived from the parameters (e.g. the IS fluxes for p and He).
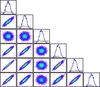 |
Fig. 2 PDF (diagonal) and 2D correlations (off-diagonal) plots for three selected knots y = log JIS(R) at position { R0,R1,R3 } = { 1 ,7 ,100 } GV and φ for three high-statistics datasets AMS-02, BESS-POLARII, and PAMELA (2006−2008): positive correlations are observed for all low-energy knots and datasets; knots above 100 GV show no correlation with any other parameter (the parameter distribution only depends then on the data uncertainties). |
3.2. Results of the MCMC analysis
The marginalised PDFs for a selected subset of the IS flux and modulation parameters are
presented in Fig. 2. The PDFs for
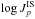 and
φ are close
to Gaussian. The 2D PDFs show strong and expected correlations between the low-energy
proton IS flux and the solar modulation levels: an increase of the IS flux must be
balanced by an increase of the modulation level to recover the same TOA flux. The typical
≲10% uncertainty on (or dispersion between)
the data at GeV/n energies (see Fig. 1) translates into a similar uncertainty on φ values (see Fig. 3) and on
and
φ are close
to Gaussian. The 2D PDFs show strong and expected correlations between the low-energy
proton IS flux and the solar modulation levels: an increase of the IS flux must be
balanced by an increase of the modulation level to recover the same TOA flux. The typical
≲10% uncertainty on (or dispersion between)
the data at GeV/n energies (see Fig. 1) translates into a similar uncertainty on φ values (see Fig. 3) and on 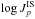 at GV
rigidities (see Fig. 4). At high enough energy, as
shown for the knot at R =
100 GV (third parameter in Fig. 2), the IS flux is no longer correlated to φ. This reflects that solar
modulation changes become irrelevant compared to data uncertainties (or dispersion between
datasets).
at GV
rigidities (see Fig. 4). At high enough energy, as
shown for the knot at R =
100 GV (third parameter in Fig. 2), the IS flux is no longer correlated to φ. This reflects that solar
modulation changes become irrelevant compared to data uncertainties (or dispersion between
datasets).
 |
Fig. 3 PDF of the solar modulation level φ for the three most recent datasets with the highest statistics. We show the results for a fit on all selected data from Table 1, for p data alone (blue solid line), He data alone (red dashed line), and p and He data simultaneously (black dash-dotted line). |
As underlined in Sect. 2.2, the analysis can be performed separatley for proton and helium data or for both simultaneously (to probe the consistency of the derived φ values). The TOA data uncertainties propagate to the IS flux parameters, and then to φ values because of the correlations seen in Fig. 2. Figure 3 shows the PDF of φAMS−02 (top), φBESS−POLARII (middle), and φPAMELA (bottom)5. The widths of the PDFs obtained in these three examples are representative of the width obtained for less accurate or lower-statistics experiments, indicating that the TOA data dispersion (between different experiments) dominates the TOA data uncertainties. We observe (at 1σ) typically Δφp ≈ ± 10 MV for the p-only analysis and ΔφHe ≈ ± 30 MV for both the He-only and p and He simultaneous analyses. The larger uncertainty for He is the result of a larger scatter in He data than in p data (He data uncertainties are similar to proton uncertainties, see in Fig. 1), which is explained by the fact that He is less abundant and more difficult to measure. The central value for the φp + He analysis is in between φp and φHe. We note that for the dataset where only p data are available (e.g. PAMELA, bottom panel), the PDF obtained for the p and He simultaneous analysis is also wider than for the p-only analysis because of the correlations between the parameters. Table 2 gathers the median and 68% CI on the modulation level φ for the experiments selected in this analysis.
More important from Fig. 3 is the fact that the
φp and φHe values are
not compatible at the 3σ level. This could be an indication that the
force-field approximation is rejected by the data. However, first, the best
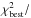 d.o.f. values for the
best-fit models found in the MCMC chains are 0.26 and 0.71 for these two analyses,
possibly indicating an underestimation of the data uncertainties. For comparison, the
p and He
simultaneous analysis gives a very good fit with
d.o.f. values for the
best-fit models found in the MCMC chains are 0.26 and 0.71 for these two analyses,
possibly indicating an underestimation of the data uncertainties. For comparison, the
p and He
simultaneous analysis gives a very good fit with 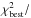 d.o.f. = 1.02. Second, as
shown in Appendix A.1 on simulated data, the
isotopic contamination of 2H and 3He leads to biased φ values, with an overshoot
larger by typically ~50 MV for φHe than for φp. This allows us to
reconcile the results of the p-only and He-only analyses. To reduce and eventually
eliminate this bias, high-precision data (e.g. from AMS-02) are desired.
d.o.f. = 1.02. Second, as
shown in Appendix A.1 on simulated data, the
isotopic contamination of 2H and 3He leads to biased φ values, with an overshoot
larger by typically ~50 MV for φHe than for φp. This allows us to
reconcile the results of the p-only and He-only analyses. To reduce and eventually
eliminate this bias, high-precision data (e.g. from AMS-02) are desired.
φ values obtained with the MCMC analysis for each experiment.
 |
Fig. 4 Proton (blue) and helium (red) IS fluxes obtained from the various MCMC analyses.
Top panel a): 68%, 95%, and 99% CIs (from darker to
lighter shade) from the p+He analysis. The fluxes are multiplied by
|
3.3. Credible intervals (CI) on JIS
For each point θ in the MCMC chain, we can compute the associated p and He IS fluxes at any energy. For each of these energies, we thus have a distribution of values from which we can calculate the PDF and CI; for rigidity values corresponding to the spline knots, the IS flux PDF at that point is directly the PDF from the MCMC analysis (see Fig. 2). In Fig. 4 the top panel shows in various shades of blue (p) and red (He) the 68%, 95%, and 99% CI on the IS flux (from the p+He simultaneous analysis). The middle panel shows the 68% contours divided by the median flux to emphasise the uncertainties: we have ΔJ/J ≲ 10% at GeV/n, ΔJ/J ≲ 5% above 1 TeV/n, and ΔJ/J ≲ 2% in between. The uncertainties for p and He are of the same order of magnitude. The bottom panel shows a comparison of the p-only and He-only analyses to the p+He simultaneous analysis (ratio of the median and 68% contour to the median p+He flux). The median flux for p is unchanged, and the p-only analysis leads to smaller uncertainties (compare the blue curves in panels b and c). The He fluxes are more sensitive to the analysis chosen, but they are compatible within their 95% CIs (not shown). This last panel illustrates the fact that the fit is driven by p data, so that the p+He combined analysis only affects He. As for the modulation parameters (see Sect. 3.2), it also illustrates the effect of correlations in the determination of the IS flux parameters because the p+He simultaneous analysis enlarges the uncertainties on the proton IS flux.
 |
Fig. 5 Same as Fig. 4, but compared to other direct or indirect IS flux determinations. Top panel a): green (Orion A) and grey (Perseus OB2) dashed areas are γ-ray derived limits from local giant molecular clouds using Fermi-LAT data (Yang et al. 2014); symbols are for low-energy Voyager 1 measurements (Stone et al. 2013) and high-energy data. Bottom panel b): thick lines are from the 68% CI of this analysis; shaded areas correspond to the 68%CI from a likelihood analysis of Fermi-LAT γ-ray emissivity, and PAMELA (2006−2008) plus AMS-01 (1998) p+He+e++e− analysis (Casandjian 2015); chained lines are from a χ2-minimisation analysis of BESS data (Shikaze et al. 2007). |
3.4. Comparison with other determinations
The top panel of Fig. 5 shows comparisons with
-
a proton flux estimate from nearby giant molecular clouds in the Gould Belt. These fluxes are derived from γ-ray data, assuming that the interactions of CR with the ambient gas are fully responsible for the Fermi-LAT-observed fluxes (Yang et al. 2014). We find a very good match for the highest-emitting clouds (Orion A and Perseus OB2). Yang and collaborators compared their fluxes to the modulated PAMELA data (their Figs. 5 and 6) and found an excess below 10 GeV/n, which might be interpreted as CR that are locally accelerated inside the cloud; when we compare this to our IS flux instead, this turns into a deficit for most of the clouds that might be explained by increased energy losses and destruction of CRs in the clouds.
-
For the sake of completeness, we also compared our high-energy extrapolation (above the vertical arrow) to high-energy data that were not included in the fit: ATIC (Panov et al. 2009), CREAM-I (Yoon et al. 2011), JACEE (Asakimori et al. 1998), MUBEE (Zatsepin et al. 1993), PAMELA-CALO (Adriani et al. 2013c), RICH-II (Diehl et al. 2003), RUNJOB (Derbina et al. 2005), and SOKOL (Ivanenko et al. 1993). Given the discrepancies between the datasets, our extrapolation is a fair estimate of the IS flux at these high energies.
The bottom panel of Fig. 5 shows the ratio of various parametrisations of IS fluxes to our best-fit result, compared to the 68% CIs on our IS fluxes (dashed and dash-dotted lines):
-
the best-fit and (shaded) contours of Casandjian (2015) were derived with a likelihood analysis based on PAMELA (2006−2008) and AMS-01 (1998) data (considering p, He, but also e+ and e−), plus the use of Fermi-LAT data on γ-ray emissivities. Overall, using more recent and more data yields smaller CIs. At high energies, the two results are not consistent within their 68% CIs. At low energy, our smaller error bars may result from the use of a more flexible parametrisation (spline) than is the pure power-law used in Casandjian (2015).
-
The best-fit fluxes (solid lines) of Shikaze et al. (2007) result from a fit to all BESS data in which the authors relied on a pure power-law. The high-energy feature is caused by the break in our parametrisation. In the energy range where both their fit and ours are not extrapolated, the largest difference between the two p parametrisations is ~30% at 100 GeV/n, with their He flux systematically lower than ours.
3.5. IS flux parametrisation with and without Voyager data
It is also interesting to compare our flux derived from TOA-only data to the Voyager 1 data (Stone et al. 2013). The latter are believed to provide a direct measurement of the local IS (LIS) flux outside the solar cavity. However, the possibility of a small radial gradient in the outer heliosheath over hundreds of AU remains (Scherer et al. 2011; Kóta & Jokipii 2014). This must be balanced by indirect arguments (Lallement et al. 2014) and simulation of this region (Guo & Florinski 2014; Luo et al. 2015; Zhang et al. 2015) that support the hypothesis that Voyager has indeed reached the LIS.
To test the consequences of the two above alternatives, we added Voyager data (open circles in Fig. 5) to the analysis. We then compared the results for the modulation values and IS fluxes obtained with and without Voyager data, either letting φVoyager be a free parameter or enforcing it to be zero. In the former case, the best-fit with Voyager data is φVoyager = 65 MV, without a modification of the IS fluxes. Conversely, if Voyager data are interstellar, we must enforce φVoyager = 0: in that case, we observe (i) a decrease of ~62 MV on φ values for all other experiments; (ii) a worsened χ2/d.o.f. = 1.27; and (iii) a lower best-fit IS flux at low energy (see long-dashed curves in Fig. 5). We did not repeat the MCMC analysis because the (very small) Voyager uncertainties (Stone et al. 2013) certainly do not include all the systematics.
Given the important role played by the H and He IS fluxes, we provide a simple
implementation of our IS fluxes as a mixture of a log-polynomial and power-law
extrapolation (spectral index 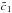 ):
):
![\begin{equation} \log_{10}(J_{\rm IS}) = \begin{cases} \sum_{i=0}^{12} c_{i}\times \left(\frac{\log_{10}(E_{k})}{\log_{10}(800~{{\rm GeV}/{\it n}})}\right)^{i} {\rm if}\quad E_{k/n} < 800~GeV/{\it n};\\[1mm] \tilde{c}_0 - \tilde{c}_1 \left(\frac{\log_{10}(E_{k/n})}{\log_{10}(800~{{\rm GeV}/n})}\right) \quad \textrm{otherwise}. \label{eq:fit-poly} \end{cases} \end{equation}](/articles/aa/full_html/2016/07/aa27852-15/aa27852-15-eq121.png) (6)Table
3 provides all theses coefficients for two cases
(both obtained from the p+He simultaneous analysis):
(6)Table
3 provides all theses coefficients for two cases
(both obtained from the p+He simultaneous analysis):
-
the first five columns provide coefficients for the median and CIsfrom the MCMC analysis (without Voyager data), to beconsidered as a high estimate of the H and He IS fluxes (not validbelow 400 MeV/n), and
-
the last column provides the best-fit including Voyager data (with φVoyager = 0), to be considered as a low estimate of the IS H and He fluxes.
Coefficients for H (top) and He (bottom) IS fluxes as parametrised by Eq. (6).
4. Conclusion
We have revisited the determination of IS fluxes and solar modulation parameters from TOA data alone. We took advantage of recent high-statistics experiments (AMS-02, BESS-Polar, PAMELA), we relied on a non-parametric fit of the IS fluxes (based on spline functions), and we used an MCMC to extract the PDF, CIs, and the correlation between the sought parameters. A preliminary step of the analysis was a consistency check that allowed rejecting some of the data. With the remaining data, we obtained reliable constraints on the p and He IS fluxes in the region of GeV/n to several hundreds of TeV/n. These fluxes are very important for many applications in the literature (ISM ionisation, CR secondary production, etc.), therefore we provide in Table 3 ready-to use parametrisations based on our best-fit and IS flux contours with and without Voyager data.
Correlations between IS flux parameters and solar modulation parameters were found to be important to estimate all the CIs properly. We studied p and He separately or simultaneously to check the consistency of the modulation (most experiments measured p and He data during the same period). Although the preferred φ values are slightly different in the separate analyses, the simultaneous p+He analysis gives a very good fit (χ2/d.o.f. =1.02) to all the data, with a 1σ uncertainty of 30 MV. As in many previous studies, H and He data are assimilated to pure 1H and 4He. However, we have shown that the presence of 2H and 3He leads to a ~30 MV positive bias in the p+He analysis, which is already similar to the systematic uncertainty. The bias is dominated by the presence of 3He in He (~50 MV bias in the He-only analysis), therefore this contamination needs to be accounted for in future studies.
From the data we conclude that the simple force-field approximation is effective in providing a good description (within the uncertainties) of the modulated p and He fluxes at Earth. The situation may change because AMS-02 data have the capability and the statistics to provide monthly, weekly, or even daily average fluxes. This could be used to check the limitation of the force-field (or more evolved models, e.g. Corti et al. 2015 and Cholis et al. 2016) over a full solar modulation cycle, in particular during a solar polarity change. Adding more species to the analysis, for example, e+ and e−(Casadei & Bindi 2004), or even antiprotons, is the obvious next step to proceed with characterising IS CR fluxes and the solar modulation.
Note added in proof. During the completion of this work, we became aware of a related study by Corti, Bindi, Consolandi and Whitman (Corti et al. 2015). It focuses on the IS proton flux and explores a modulation model beyond the force-field approximation. The data sets and methods both differ from those of our study, making the two analyses complementary. A comparison of their proton IS flux (obtained with the energy-dependent solar modulation parameter) and ours (obtained in the force-field approximation) shows a very good agreement in the range 4 GV−1 TeV, but with different uncertainties.
Variations on this approach are to use IS fluxes obtained from cosmic-ray propagation codes (e.g. Putze et al. 2011), and/or the sparser radial-dependent CR data (Burger et al. 2000; Langner et al. 2003; Webber & Higbie 2009) in the context of more realistic modulation models.
Throughout the paper, we refer indifferently to p or H to denote the proton flux; see discussion in Appendix A.1.
Acknowledgments
We thank J.-M. Casandjian for providing the values of his IS flux determination, and C. Combet for a careful reading of the manuscript. This work has been supported by the “Investissements d’avenir, Labex ENIGMASS” and by the French ANR, Project DMAstro-LHC, ANR-12-BS05-0006. This study used the CC-IN2P3 computation center of Lyon.
References
- Abe, K., Fuke, H., Haino, S., et al. 2016, ApJ, 822, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2014, Phys. Rev. Lett., 112, 151103 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2011, Science, 332, 69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2013a, ApJ, 765, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2013b, ApJ, 770, 2 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2013c, Adv. Space Res., 51, 219 [Google Scholar]
- Adriani, O., Barbarino, G. C., Bazilevskaya, G. A., et al. 2014, Phys. Rep., 544, 323 [Google Scholar]
- Aguilar, M., Alcaraz, J., AMS Collaboration, et al. 2002, Phys. Rep., 366, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Alcaraz, J., Allaby, J., AMS Collaboration, et al. 2011, ApJ, 736, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2015a, Phys. Rev. Lett., 114, 171103 [CrossRef] [PubMed] [Google Scholar]
- Aguilar, M., Aisa, D., Alpat, B., et al. 2015b, Phys. Rev. Lett., 115, 211101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ahn, H. S., Allison, P., Bagliesi, M. G., et al. 2010, ApJ, 714, L89 [Google Scholar]
- Alcaraz, J., Alpat, B., Ambrosi, G., et al. 2000, Phys. Lett. B, 490, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Asakimori, K., Burnett, T. H., Cherry, M. L., et al. 1998, ApJ, 502, 278 [Google Scholar]
- Boella, G., Gervasi, M., Potenza, M. A. C., Rancoita, P. G., & Usoskin, I. 1998, Astropart. Phys., 9, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Boezio, M., Carlson, P., Francke, T., et al. 1999, ApJ, 518, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Boezio, M., Bonvicini, V., Schiavon, P., et al. 2003, Astropart. Phys., 19, 583 [Google Scholar]
- Brun, R., & Rademakers, F. 1997, Nucl. Instr. Meth. Phys. Res. A, 389, 81 [Google Scholar]
- Burger, R. A., Potgieter, M. S., & Heber, B. 2000, J. Geophys. Res., 105, 27447 [Google Scholar]
- Caballero-Lopez, R. A., & Moraal, H. 2004, J. Geophys. Res., 109, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Casadei, D., & Bindi, V. 2004, ApJ, 612, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Casandjian, J.-M. 2015, ApJ, 806, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Cholis, I., Hooper, D., & Linden, T. 2016, Phys. Rev. D, 93, 043016 [NASA ADS] [CrossRef] [Google Scholar]
- Corti, C., Bindi, V., Consolandi, C., & Whitman, K. 2015, ArXiv e-prints [arXiv:1511.08790] [Google Scholar]
- Coste, B., Derome, L., Maurin, D., & Putze, A. 2012, A&A, 539, A88 [NASA ADS] [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- de Nolfo, G. A., Barbier, L. M., Christian, E. R., et al. 2000, in Acceleration and Transport of Energetic Particles Observed in the Heliosphere, eds. R. A. Mewaldt, J. R. Jokipii, M. A. Lee, E. Möbius, & T. H. Zurbuchen, AIP Conf. Ser., 528, 425 [Google Scholar]
- Derbina, V. A., Galkin, V. I., Hareyama, M., et al. 2005, ApJ, 628, L41 [Google Scholar]
- Diehl, E., Ellithorpe, D., Müller, D., & Swordy, S. P. 2003, Astropart. Phys., 18, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Donato, F., & Serpico, P. D. 2011, Phys. Rev. D, 83, 023014 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia-Munoz, M., Mason, G. M., & Simpson, J. A. 1975, ApJ, 202, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Giesen, G., Boudaud, M., Génolini, Y., et al. 2015, J. Cosmol. Astropart. Phys., 9, 23 [Google Scholar]
- Gleeson, L. J., & Axford, W. I. 1967, ApJ, 149, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Gleeson, L. J., & Axford, W. I. 1968, ApJ, 154, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, X., & Florinski, V. 2014, ApJ, 793, 18 [Google Scholar]
- Herbst, K., Kopp, A., Heber, B., et al. 2010, J. Geophys. Res., 115 [Google Scholar]
- Indriolo, N., Fields, B. D., & McCall, B. J. 2009, ApJ, 694, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanenko, I. P., Shestoperov, V. Y., Chikova, L. O., et al. 1993, in Int. Cosm. Ray Conf., 2, 17 [Google Scholar]
- James, F. 1994, CERN Program Library Writeup, 506 [Google Scholar]
- Kachelrieß, M., & Ostapchenko, S. 2012, Phys. Rev. D, 86, 043004 [NASA ADS] [CrossRef] [Google Scholar]
- Kóta, J., & Jokipii, J. R. 2014, ApJ, 782, 24 [Google Scholar]
- Kozlovsky, B., Murphy, R. J., & Ramaty, R. 2002, ApJS, 141, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Kroeger, R. 1986, ApJ, 303, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Bertaux, J. L., Quémerais, E., & Sandel, B. R. 2014, A&A, 563, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Langner, U. W., Potgieter, M. S., & Webber, W. R. 2003, J. Geophys. Res., 108, 8039 [CrossRef] [Google Scholar]
- Lavalle, J. 2011, MNRAS, 414, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Lavalle, J., Maurin, D., & Putze, A. 2014, Phys. Rev. D, 90, 081301 [NASA ADS] [CrossRef] [Google Scholar]
- Lingenfelter, R. E., & Ramaty, R. 1977, ApJ, 211, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, X., Zhang, M., Potgieter, M., Feng, X., & Pogorelov, N. V. 2015, ApJ, 808, 82 [NASA ADS] [CrossRef] [Google Scholar]
- MacKay, D. 2003, Information Theory, Inference, and Learning Algorithms (Cambridge University Press) [Google Scholar]
- Maurin, D., Melot, F., & Taillet, R. 2014, A&A, 569, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maurin, D., Cheminet, A., Derome, L., Ghelfi, A., & Hubert, G. 2015, Adv. Space Res., 55, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Meneguzzi, M., & Reeves, H. 1975, A&A, 40, 91 [NASA ADS] [Google Scholar]
- Meneguzzi, M., Audouze, J., & Reeves, H. 1971, A&A, 15, 337 [NASA ADS] [Google Scholar]
- Menn, W., Hof, M., Reimer, O., et al. 2000, ApJ, 533, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., & Biermann, P. L. 1994, MNRAS, 267, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., Gupta, N., & Biermann, P. L. 2012, MNRAS, 425, L86 [NASA ADS] [CrossRef] [Google Scholar]
- Neal, R. M. 1993, Probabilistic Inference Using Markov Chain Monte Carlo Methods, Technical Report CRG-TR-93-1, Department of Computer Science, University of Toronto [Google Scholar]
- Neronov, A., Semikoz, D. V., & Taylor, A. M. 2012, Phys. Rev. Lett., 108, 051105 [Google Scholar]
- O’Neill, P. M. 2006, Adv. Space Res., 37, 1727 [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Panov, A. D., Adams, J. H., Ahn, H. S., et al. 2009, Bull. Russian Academy of Science, Phys., 73, 564 [Google Scholar]
- Papini, P., Piccardi, S., Spillantini, P., et al. 2004, ApJ, 615, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Perko, J. S. 1987, A&A, 184, 119 [NASA ADS] [Google Scholar]
- Potgieter, M. 2013, Liv. Rev. Sol. Phys., 10, 3 [Google Scholar]
- Prantzos, N. 2012, A&A, 542, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Putze, A., & Derome, L. 2014, Phys. Dark Universe, 5, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Putze, A., Derome, L., Maurin, D., Perotto, L., & Taillet, R. 2009, A&A, 497, 991 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Putze, A., Maurin, D., & Donato, F. 2011, A&A, 526, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramaty, R., Kozlovsky, B., & Lingenfelter, R. E. 1979, ApJS, 40, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Reeves, H. 1970, Nature, 226, 727 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Scherer, K., Fichtner, H., Strauss, R. D., et al. 2011, ApJ, 735, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Shikaze, Y., Haino, S., Abe, K., et al. 2007, Astropart. Phys., 28, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, E. C., Cummings, A. C., McDonald, F. B., et al. 2013, Science, 341, 150 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strong, A. W. 2015, in 34th Int. Cosm. Ray Conf., July 30 to August 6, Hague, The Netherlands [arXiv:1507.05006] [Google Scholar]
- Strong, A. W., Moskalenko, I. V., & Ptuskin, V. S. 2007, Ann. Rev. Nucl. Part. Sci., 57, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Tatischeff, V., & Kiener, J. 2004, New A Rev., 48, 99 [Google Scholar]
- Usoskin, I. G., Bazilevskaya, G. A., & Kovaltsov, G. A. 2011, J. Geophys. Res., 116, 2104 [Google Scholar]
- Vangioni-Flam, E., Cassé, M., & Audouze, J. 2000, Phys. Rep., 333, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J. Z., Seo, E. S., Anraku, K., et al. 2002, ApJ, 564, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Webber, W. R. 1987, A&A, 179, 277 [NASA ADS] [Google Scholar]
- Webber, W. R. 1998, ApJ, 506, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Webber, W. R., & Higbie, P. R. 2003, J. Geophys. Res., 108, 1355 [Google Scholar]
- Webber, W. R., & Higbie, P. R. 2009, J. Geophys. Res., 114, 2103 [Google Scholar]
- Webber, W. R., & Higbie, P. R. 2013, ArXiv e-prints [arXiv:1308.6598] [Google Scholar]
- Webber, W. R., & Yushak, S. M. 1983, ApJ, 275, 391 [Google Scholar]
- Webber, W. R., Higbie, P. R., & McDonald, F. B. 2013a, ArXiv e-prints [arXiv:1308.4426] [Google Scholar]
- Webber, W. R., Higbie, P. R., & McDonald, F. B. 2013b, ArXiv e-prints [arXiv:1308.1895] [Google Scholar]
- Yang, R.-z., de Oña Wilhelmi, E., & Aharonian, F. 2014, A&A, 566, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yoon, Y. S., Ahn, H. S., Allison, P. S., et al. 2011, ApJ, 728, 122 [CrossRef] [Google Scholar]
- Zatsepin, V. I., Zamchalova, E. A., Varkovitskaya, A. Y., et al. 1993, in Int. Cosm. Ray Conf., 2, 13 [Google Scholar]
- Zhang, M., Luo, X., & Pogorelov, N. 2015, Phys. Plasmas, 22, 091501 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Systematics on φ determination
Appendix A.1: Effect of deuteron (3He) contamination of H (He) in φ determination
Cosmic-ray experiments rarely achieve isotopic separation, even at low energy. Because solar modulation affects isotopes differently, see Eq. (1), the deuteron contamination of a few percent in H or the ~20%3He contamination in He that peaks at GeV/n energy (e.g. Coste et al. 2012) must be accounted for.
To test the effect of isotopic contamination on the modulation levels, we proceeded in three steps:
-
We estimated the interstellar fluxes for 2H and 3He running the same analysis as for p and He data (see Sect. 2), that is:
-
we retrieved 2H and 3He TOA data from CRDB (Maurin et al. 2014),
-
for the IS flux determination, only three knots for deuterons at { 0.8, 3, 7 } GV and two knots for 3He at { 0.6, 2 } GV are necessary, and
-
the data passing the selection cut are ISEE (Kroeger 1986), CAPRICE (Boezio et al. 1999; Papini et al. 2004), IMAX (de Nolfo et al. 2000), AMS-01 (Aguilar et al. 2002, 2011), and PAMELA (Adriani et al. 2013b). The minimisation on these data provides the best-fit IS fluxes for 2H and 3He.
-
For each p and He TOA data set, we simulated data based on the IS fluxes obtained from our analysis. The data points of each data set reflect the uncertainties of the experiment they comes from. Assuming that the above 2H and 3He IS fluxes are perfectly known, we modulated JH − J2H and JHe − J3He with the corresponding solar modulation levels in Table 2.
We then repeated the fit and compared the obtained φ to those in Table 2. We observe a systematic deficit for all modulation levels at the level of Δφ ∈ [ 24−33 ] MV for the p +He simultaneous analysis, and Δφ ∈ [ 53−74 ] MV for the He-only analysis.
We conclude that the presence of 2H and 3He (in H and He data, respectively) induces a non-negligible bias of ~30 MV in the determination of φ, which is to be compared to the Δφ ~ ± 30 MV systematic uncertainty from the MCMC analysis (see Fig. 3). This bias is larger ~65 MV for the He-only analysis, but smaller for the p-only analysis, providing a way to reconcile the discrepant values obtained in Fig. 3.
Appendix A.2: Effect of TOA flux long-time average on ⟨ φ ⟩ determination
PAMELA (2006−2008) and AMS-02 data are time averages over three years of the TOA fluxes. Assuming that the IS flux is perfectly known (taken to be the best-fit flux obtained in this paper), we compared two different calculations of the modulation value (all brackets below correspond to time averages):
-
φ⟨ JTOA ⟩ calculated from the TOA flux ⟨ JTOA ⟩ obtained over a given data-taking period (e.g. the above-mentioned AMS-02 data), and
-
⟨ φJTOA ⟩ calculated from the average of all modulation levels associated with JTOA sampled over the whole data-taking period.
Solar modulation does not linearly transform IS fluxes, therefore there is no reason for these two quantities to be equal. To estimate the effect of using one or the other approach, we proceeded as follows:
-
1.
We used neutron monitor data to sample a realistic φi time series over the AMS-02 data-taking period,
-
2.
we calculated for each time of the series the associated
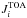 ,
, -
3.
we calculated ⟨ φ ⟩ = ∑ iφi/N and
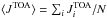 , and
, and -
4.
we calculated φ⟨ JTOA ⟩ fitting ⟨ JTOA ⟩ using AMS-02 errors.
We find that ⟨ JTOA(φi) ⟩ is within a few percent of JTOA( ⟨ φi ⟩), whereas ⟨ φ ⟩ and φ⟨ JTOA ⟩ differ by 5 MV. To generalise this result, different three-year time periods were tested to probe the effect of stronger or different solar activity levels; the ~5 MV difference remains. This is negligible compared to Δφ ~ ± 30 MV obtained in Fig. 3.
All Tables
All Figures
 |
Fig. 1 Ratio of the best-fit model for p (filled black circles) and He (empty red circles) to data for the experiments passing our selection (see Table 1). The solid blue (dashed red) lines correspond to the uncertainties (statistical and systematics combined) on the p (He) measurements. We note that the AMS-01 (top left panel) and PAMELA (2006−2008) He data (red empty circles; left panel, third row) are excluded based on their χ2 value (see Table 1) and are shown for illustration only. |
| In the text | |
 |
Fig. 2 PDF (diagonal) and 2D correlations (off-diagonal) plots for three selected knots y = log JIS(R) at position { R0,R1,R3 } = { 1 ,7 ,100 } GV and φ for three high-statistics datasets AMS-02, BESS-POLARII, and PAMELA (2006−2008): positive correlations are observed for all low-energy knots and datasets; knots above 100 GV show no correlation with any other parameter (the parameter distribution only depends then on the data uncertainties). |
| In the text | |
 |
Fig. 3 PDF of the solar modulation level φ for the three most recent datasets with the highest statistics. We show the results for a fit on all selected data from Table 1, for p data alone (blue solid line), He data alone (red dashed line), and p and He data simultaneously (black dash-dotted line). |
| In the text | |
 |
Fig. 4 Proton (blue) and helium (red) IS fluxes obtained from the various MCMC analyses.
Top panel a): 68%, 95%, and 99% CIs (from darker to
lighter shade) from the p+He analysis. The fluxes are multiplied by
|
| In the text | |
 |
Fig. 5 Same as Fig. 4, but compared to other direct or indirect IS flux determinations. Top panel a): green (Orion A) and grey (Perseus OB2) dashed areas are γ-ray derived limits from local giant molecular clouds using Fermi-LAT data (Yang et al. 2014); symbols are for low-energy Voyager 1 measurements (Stone et al. 2013) and high-energy data. Bottom panel b): thick lines are from the 68% CI of this analysis; shaded areas correspond to the 68%CI from a likelihood analysis of Fermi-LAT γ-ray emissivity, and PAMELA (2006−2008) plus AMS-01 (1998) p+He+e++e− analysis (Casandjian 2015); chained lines are from a χ2-minimisation analysis of BESS data (Shikaze et al. 2007). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.