| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A78 | |
| Number of page(s) | 9 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201628336 | |
| Published online | 16 May 2016 | |
The Gaia-ESO Survey: A lithium-rotation connection at 5 Myr? ⋆
1
Univ. Grenoble Alpes, IPAG,
38000
Grenoble,
France
e-mail:
Jerome.Bouvier@obs.ujf-grenoble.fr
2
CNRS, IPAG, 38000
Grenoble,
France
3
Università di Catania, Dipartimento di Fisica e
Astronomia, Sezione Astrofisica,
via S. Sofia 78, 95123
Catania,
Italy
e-mail:
Alessandro.Lanzafame@oact.inaf.it
4
INAF–Osservatorio Astrofisico di Catania, via S. Sofia
78, 95123
Catania,
Italy
5
INAF–Osservatorio Astronomico di Palermo G.S. Vaiana, Piazza del
Parlamento 1, 90134
Palermo,
Italy
6
Astrophysics Group, Keele University, Keele, Staffordshire, ST5
5BG, UK
7
INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi
5, 50125
Florence,
Italy
8
Spitzer Science Center, California Institute of
Technology, Pasadena,
CA
91125,
USA
9
NASA Ames Research Center, Kepler Science Office,
Mountain View, CA
94035,
USA
10
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
11 Instituto de Física y Astronomía, Universidad de
Valparaíso, Chile
12
Lund Observatory, Dept of Astronomy and Theoretical Physics, Box
43, 22100
Lund,
Sweden
13
INAF–Osservatorio Astronomico si Bologna, via Ranzani
1, 40127
Bologna,
Italy
14
European Southern Observatory, Alonso de Cordova 3107, Santiago, Chile
15
Instituto de Astrofisica de Andalucía – CSIC,
Apdo. 3004, 18008
Granada,
Spain
16
Instituto de Astrofísica e Ciências do Espaço, Universidade do
Porto, CAUP, Rua das
Estrelas, 4150-762
Porto,
Portugal
17
Astrophysics Research Institute, Liverpool John Moores
University, 146 Brownlow
Hill, Liverpool
L3 5RF,
UK
18
Universidad Andres Bello, Departamento de Ciencias Físicas,
Facultad de Ciencias Exactas, Fernandez Concha 700, Las Condes, Santiago, Chile
19
Millennium Institute of Astrophysics, Pontificia Universidad
Católica de Chile, Vicuña Mackenna
4860, Macul, Santiago, Chile
20
INAF–Osservatorio Astronomico di Padova, Vicolo Osservatorio
5, 35122
Padova,
Italy
21
University of Ljubljana, Faculty of Mathematics and
Physics, Jadranska
19, 1000
Ljubljana,
Slovenia
Received: 18 February 2016
Accepted: 25 April 2016
Context. The evolution of lithium abundance in cool dwarfs provides a unique probe of nonstandard processes in stellar evolution.
Aims. We investigate the lithium content of young low-mass stars in the 5 Myr old, star forming region NGC 2264 and its relationship with rotation.
Methods. We combine lithium equivalent width measurements (EW(Li)) from the Gaia-ESO Survey with the determination of rotational periods from the CSI 2264 survey. We only consider bona fide nonaccreting cluster members to minimize the uncertainties on EW(Li).
Results. We report the existence of a relationship between lithium content and rotation in NGC 2264 at an age of 5 Myr. The Li-rotation connection is seen over a restricted temperature range (Teff = 3800–4400 K), where fast rotators are Li-rich compared to slow rotators. This correlation is similar to, albeit of lower amplitude than, the Li-rotation connection previously reported for K dwarfs in the 125 Myr old Pleiades cluster. We investigate whether the nonstandard pre-main-sequence models developed so far to explain the Pleiades results, which are based on episodic accretion, pre-main-sequence, core-envelope decoupling, and/or radius inflation due to enhanced magnetic activity, can account for early development of the Li-rotation connection. While radius inflation appears to be the most promising possibility, each of these models has issues. We therefore also discuss external causes that might operate during the first few Myr of pre-main-sequence evolution, such as planet engulfment and/or steady disk accretion, as possible candidates for the common origin for Li excess and fast rotation in young low-mass pre-main-sequence stars.
Conclusions. The emergence of a connection between lithium content and rotation rate at such an early age as 5 Myr suggests a complex link between accretion processes, early angular momentum evolution, and possibly planet formation, which likely impacts early stellar evolution and has yet to be fully deciphered.
Key words: stars: abundances / stars: pre-main sequence / stars: rotation / open clusters and associations: individual: NGC 2264
Full Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/590/A78
© ESO, 2016
1. Introduction
Lithium is a sensitive probe of stellar evolution and most importantly of nonstandard transport processes occurring in the stellar interiors. Lithium, a fragile element, is burnt at a temperature of 2.5 MK, which corresponds to the temperature at the base of the convective zone of a solar-mass star on the zero-age main sequence (ZAMS; Siess et al. 2000). Hence, lithium is slowly depleted and its surface abundance steadily decreases over time in solar-type and lower mass stars (e.g., Basri et al. 1991; Martin et al. 1994; Sestito & Randich 2005; Randich 2010; Jeffries 2014). The rate of this secular evolution may be modified, either increased or reduced, by so-called nonstandard transport processes, such as rotational mixing, internal magnetic fields, gravity waves, or tidal interactions and by structural changes induced by, for instance, rotation, magnetic activity, metallicity, or accretion (e.g., Pinsonneault et al. 1990; Zahn 1992; Ventura et al. 1998; Piau & Turck-Chièze 2002; Talon & Charbonnel 2005; Denissenkov 2010; Eggenberger et al. 2012; Théado & Vauclair 2012). These additional processes may vary from star to star, depending on initial conditions and specific evolutionary paths and, thus, have the potential to produce an enhanced lithium spread in otherwise similar stars at the same age (e.g., Pasquini et al. 2008; Do Nascimento et al. 2010; Ramírez et al. 2012).
In an attempt to relate lithium scatter to other stellar properties, Soderblom et al. (1993) reported a clear connection between lithium abundance and rotation rate among the 125 Myr old Pleiades K dwarfs. The finding that fast rotators were systematically more Li rich than their slowly rotating counterparts was the first clear empirical evidence that rotation could indeed impact the lithium abundance of solar-type stars as early as the ZAMS stage. This result actually came as a surprise as rotational mixing from dynamical instabilities was thought to scale with surface rotation, which would predict fast rotators to be more lithium-depleted compared to slow rotators (e.g., Pinsonneault et al. 1989); this trend is opposite to that observed in the Pleiades. Since then, various ideas have been proposed that could potentially account for the Pleiades Li-rotation connection, including the impact of initial disk lifetimes on rotational mixing (Bouvier 2008; Eggenberger et al. 2012), and structural changes linked to magnetic activity (Ventura et al. 1998; Somers & Pinsonneault 2014, 2015) or episodic accretion (Baraffe & Chabrier 2010). Weaker evidence for a lithium-rotation connection has also been reported for ages slightly younger than the Pleiades, for example, for the 80 Myr old Alpha Per cluster (Randich et al. 1998; Balachandran et al. 2011) but it is unclear at what age it begins to develop.
Tracing the evolving pattern of lithium abundance and its spread as a function of age offers a unique opportunity to gain more insight into the fundamental processes occuring in stellar interiors. Our goal here is to investigate whether the link between lithium content and rotation may already be present at an age much earlier than the ZAMS (cf. Martin et al. 1994). We thus focus on the low-mass stellar population of the young open cluster NGC 2264 at an age of 3–6 Myr (Mayne & Naylor 2008; Gillen et al. 2014). In order to build a large and homogeneous sample of low-mass pre-main-sequence (PMS) stars in this cluster that allows us to investigate the lithium-rotation connection at very young ages, we combined two major surveys. We take advantage of: i) precise lithium measurements (cf. Lanzafame et al. 2015) obtained with VLT/FLAMES for the low-mass members of NGC 2264 in the framework of the Gaia-ESO Survey (GES; Gilmore et al. 2012; Randich et al. 2013); and ii) the derivation of accurate rotational periods (Venuti et al., in prep.; see also Affer et al. 2013) from the CoRoT light curves of the CSI 2264 campaign (Coordinated Synoptic Investigation of NGC 2264; Cody et al. 2014), which photometrically monitored the NGC 2264 star forming region over 40 days. In Sect. 2, we describe the sample we built from the combination of these two surveys. In Sect. 3, we investigate the connection between lithium and rotation in this sample and report a statistically significant relationship between lithium equivalent width (EW(Li)) and rotational period over a limited Teff range. In Sect. 4, we review how the various scenarios developed to reproduce the Pleiades lithium scatter may account for its emergence on a much shorter timescale during the early PMS and consider external factors such as disk accretion and/or planet engulfment as alternatives as well. The conclusions of this study are given in Sect. 5.
2. The sample
The sample we use in this study was built by cross-correlating the CSI 2264 database (Cody et al. 2014) with the fourth internal data release (iDR4) of the GES. From the former we extracted photometry, fundamental parameters (mass and radius), and rotational periods, and from the latter EW(Li), radial and rotational velocities, and effective temperatures. Specifically, we first selected all of the stars from CSI 2264 that were classified either as weak-line (WTTS) or classical T Tauri stars (CTTS) in Venuti et al. (2014) that also had a measured photometric (rotational) period; we chose most of these stars from Venuti et al. (in prep.) and some from the literature (Lamm et al. 2004; Affer et al. 2013). We then cross-correlated this subsample with the GES database, which yielded 295 objects with a Teff less than 6600 K, of which 217 are WTTS. Of the latter, 16 lacked an EW(Li) value in the GES iDR4, even though most exhibited a strong lithium absorption line in their spectrum. Appendix A provides details on EW(Li) measurements. As explained there, the lack of internal agreement between EW(Li) values reported for these stars, mostly due to difficulties in estimating the continuum level, prevented a recommended value to be defined. We note that 12 of these sources are M-type stars, and nine are fast rotators with vsini larger than 80 km s-1, which might account for the lack of consistent EW(Li) measurements. Only two of those stars lie in the 3800–4400 K Teff range, which we discuss in more detail in Sect. 3 below1, and are therefore unlikely to affect our results. We are thus left with 201 WTTS with known stellar parameters, rotational periods, and EW(Li), whose properties are listed in Table 12. While most of these stars have a strong membership likelihood, based on photometry, accretion diagnotics, and/or X-ray emission (see Venuti et al. 2014), upon further analysis a few were rejected as nonmembers (see Table 1 and next section).
3. Results
 |
Fig. 1 Lithium equivalent width is plotted as a function of effective temperature for weak-line T Tauri stars. The average rms error is 200 K on Teff and 10 mÅ on EW(Li). |
Figure 1 shows EW(Li) plotted as a function of effective temperature for the WTTS only. A strong dependency is observed between EW(Li) and Teff with EW(Li) rapidly increasing toward lower Teff, as previously reported for various young clusters (e.g., Bayo et al. 2011; Jeffries et al. 2014). This trend is also seen for CTTS (not shown) whose EW(Li) is, however, affected by veiling and, therefore, consistently lower at a given effective temperature than those of WTTS. The limited accuracy of veiling measurements makes the derivation of intrinsic, i.e., veiling-corrected, EW(Li) for CTTS more uncertain. We therefore elected to consider only WTTS for this study and thus concentrate on the 201 nonaccreting sources in the sample. As is apparent from Fig. 1, nine of these have a EW(Li) that is significantly smaller than expected for their Teff. Of these, eight also have discrepant radial velocities relative to the average3 (⟨ Vrad ⟩ = 19.8 ± 2.5 km s-1; Jackson et al. 2016) of the cluster. We rejected those nine sources as likely nonmembers4 and this leaves us with 192 WTTS to investigate further for their lithium content.
 |
Fig. 2 Lithium equivalent width is plotted as a function of effective temperature for weak-line T Tauri stars. The decreasing EW(Li) trend toward higher Teff continues up to 6600 K (cf. Fig. 1). The color scale is representative of the rotational period, and is limited up to eight days to maximize the contrast (see the scale on the right side of the panel in units of days). |
Figure 2 highlights the lower Teff range, from 3300 K to 5000 K, which is shown in Fig. 1. The color code scales with rotational period, which for stars in our sample ranges from less than 1 day up to more than 12 days. The figure reveals significant lithium scatter over some effective temperature ranges. This is most notably the case for Teff ≤ 3800 K, i.e., M-type stars. EW(Li) is notoriously difficult to measure in such cool stars, as the line is located in deep TiO absorption bands. We therefore cannot exclude that the lithium measurement error is underestimated for the very low-mass stars in our sample and could at least in part account for the enhanced Li scatter over this temperature range.
Such an explanation, however, cannot hold for K stars where the stellar continuum is relatively flat around the Li 6708 Å line. Its equivalent width can thus be easily and accurately measured at the spectral resolution of VLT/Flames (cf. Appendix A). Interestingly, over the temperature range from about 3800 K up to about 4400 K (SpT ~ K4–M0), Fig. 2 shows that fast rotators tend to lie on the upper part of the EW(Li)-Teff sequence, while many of the slow rotators lie on the lower part of it. This suggests that the lithium scatter seen over this temperature range could be linked with the rotational properties of the stars. In Appendices A and B we argue that this scatter does not result from a rotation-induced bias in the measurement of EW(Li) nor from intrinsic EW(Li) variability. We further note that this correlation is not seen at lower Teff, below 3800 K.
 |
Fig. 3 Lithium equivalent width is plotted as a function of effective temperature for weak-line T Tauri stars over the Teff range 3800–4400 K. The symbol size is proportional to the angular velocity (1 /Prot). |
In order to put the above statement on a firmer quantitative ground, we proceeded as follows. Figure 3 shows EW(Li) as a function of Teff over the 3800–4400 K range with a symbol size proportional to the angular velocity, Ω ∝ 1 /Prot. This subsample includes 62 WTTS with accurate EW(Li) measurements and robust period determinations5. A similar figure is obtained when the symbol size is taken to be proportional to Veq = 2πR⋆/Prot, where R⋆ is the stellar radius taken from Venuti et al. (2014). The trend of increasing EW(Li) toward lower Teff is clearly seen (cf. also Fig. 1) and we assume it is linear in the restricted Teff range considered here to obtain 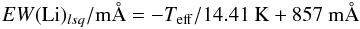 from a linear least-squares fit. We then compute the EW(Li) residuals relative to the fit as
from a linear least-squares fit. We then compute the EW(Li) residuals relative to the fit as 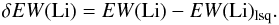 In the following, we refer to “Li excess” stars as those that have a positive δEW(Li), and to “Li deficient” stars as those with a negative δEW(Li).
In the following, we refer to “Li excess” stars as those that have a positive δEW(Li), and to “Li deficient” stars as those with a negative δEW(Li).
 |
Fig. 4 Top panel: EW(Li) residuals are plotted as a function of rotational period. The symbol size is proportional to Teff. Lower left panel: rotational period distribution of Li-excess (thick red) and Li-deficient (shaded black) stars. Lower right panel: cumulative distribution of rotational periods for Li-excess (thick red) and Li-deficient (thin black) stars. |
Figure 4 shows δEW(Li) plotted as a function of rotational period. An overall trend is seen for the Li excess to be preferentially associated with fast rotators (short rotational periods), while Li-deficient stars appear to be present at all but the shortest periods. Histograms of the rotational distributions of Li-excess and Li-deficient stars are also shown in Fig. 4. The Li-deficient stars exhibit a broad distribution over the 2–11 d period range, while the Li-excess stars appear to concentrate at periods shorter than 5 d. As a check, a two-sided Kolmogorov-Smirnov test was run on the rotational distributions of Li-excess and Li-deficient stars. The test returns a probabilty of 4 × 10-3 for the two samples to be drawn from the same parental population67.
4. Discussion
The results reported above suggest that a relationship exists between the lithium content and spin rate of young stars at an age as early as 5 Myr, where faster rotators are more lithium rich. The lithium-rotation connection is best seen for NGC 2264 members spanning the Teff range from about 3800 K to 4400 K, which corresponds to a mass range of 0.5–1.2 M⊙ at that age (Siess et al. 2000). This encompasses the mass range over which a similar lithium-rotation relationship has previously been reported for the 125 Myr old Pleiades dwarfs, as more rapidly rotating K stars are more lithium rich than slow rotating K stars (Soderblom et al. 1993). A variety of ideas have been put forward to account for the lithium-rotation connection at the age of the Pleiades on the ZAMS. In this section, we examine whether any of the proposed scenarios is consistent with the appearance of the Li-rotation relationship indeed occuring much earlier in time during the PMS, or whether there is a need to seek alternative explanations.
The lithium equivalent width of fast rotators in NGC 2264 is on the order of 600 mÅ over the Teff range from 4000 to 4400 K (cf. Fig. 3). According to the local thermodynamic equilibrium (LTE) curves of growth published by Soderblom et al. (1993), and in agreement with lithium abundances reported for these stars in the GES internal data release, this corresponds to a lithium abundance of A [ Li ] ≃ 3.0–3.2 dex8. This suggests that fast rotators have almost no lithium depletion at the age of NGC 2264 compared to the meteoritic abundance (Soderblom et al. 1999). The lower EW(Li) of slow rotators over the same temperature range, amounting to around 530 mÅ on average, translates to a lithium abundance of A [ Li ] = 2.8–3.0 dex, i.e., about 0.2 dex less than that of fast rotators. The models by Baraffe et al. (2015) indeed predict a 0.12–0.25 dex lithium depletion relative to initial abundances for stars over this Teff range at 5 Myr. Over the same Teff range, the models by Siess et al. (2000) also predict significant lithium burning with δ [ Li ] ~ 0.05–0.20 dex at this age. Assuming an age of 5 Myr for the cluster (Gillen et al. 2014), these models would then suggest that slow rotators behave as expected, while fast rotators have apparently been prevented from depleting lithium. However, assuming an age of 3 Myr for the cluster (Mayne & Naylor 2008), the same models would suggest instead that fast rotators are Li undepleted as expected for this younger age, while slow rotators have undergone enhanced lithium depletion. Moreover, PMS lithium depletion, as predicted by standard evolutionary models, is highly sensitive to the physics included in the model, most notably the treatment of convection (e.g., Jeffries 2014). Hence, any model-based prediction of lithium abundances as a function of mass and age in the PMS is subject to those uncertainties, and they are very sensitive to the assumed cluster age.
An immediate interpretation of the lithium scatter would be to assign it to a corresponding age spread among the stars in our subsample (e.g., Palla et al. 2005; Zwintz et al. 2014). According to the models by Baraffe et al. (2015), the required age spread would be of the order of 2–3 Myr, which is a significant fraction of the cluster age. It is notoriously difficult to measure individual ages for young stars (e.g., Soderblom et al. 2014). Nevertheless, following Venuti et al. (2014), we checked EW(Li) against the age values they report for our subsample and against the location of the same stars in the HR diagram and their spatial distribution over the star forming region. None of these checks provided any evidence for an age spread bearing responsibility for the observed Li scatter. In addition, it could be expected that the older WTTS have spun up to faster rates than the younger WTTS. This would then result in a lower lithium content in faster rotators with an age effect alone, which is a trend that is opposite to the lithium-rotation relationship reported here. Hence, a significant age spread among the cluster members would tend to minimize the observed lithium spread. Although larger samples and better individual age estimates are clearly needed to fully tackle this issue, we discuss alternative scenarios below.
Soderblom et al. (1993) reported lithium measurements for about 100 F, G, and K dwarfs in the Pleiades. They confirmed the large lithium abundance spread, most notably seen in K dwarfs where it amounts to 1–1.5 dex. Within this spread, they showed that the fastest rotators showed the largest lithium abundances (see also Butler et al. 1987). They investigated effects that could possibly impact on the lithium abundance determination, such as chromospheric activity and/or stellar spots, and concluded that they cannot account for their results (see also Favata et al. 1995; King et al. 2010). They thus claimed that the connection between excess Li and rapid rotation is real and clearly present among Pleiades low-mass stars on the ZAMS. While this early result raised fundamental issues regarding the PMS lithium depletion history of cool dwarfs and its relationship with angular momentum evolution, no satisfactory explanation could be offered at that time.
Since then, Baraffe & Chabrier (2010) revisited the issue of PMS lithium depletion in the framework of episodic accretion. They showed that repeated accretion bursts during the early PMS can modify the internal structure of young low-mass stars in such a way as to enhance their central temperature, hence increasing the lithium depletion rate. Indeed, their model predicts that episodic accretion onto an initial protostellar seed of 10 Jupiter masses, which eventually produces a solar-mass star, would fully deplete lithium in less than 1 Myr. In contrast, standard nonaccreting models would preserve most of the initial lithium content for several Myr (e.g., Siess et al. 2000). Hence, a coeval young stellar population may exhibit a significant dispersion in lithium content at a few Myr, depending on the specific accretion history of its members. As noted in Baraffe & Chabrier (2010), this model prediction heavily relies on the assumptions of a very low-mass protostellar seed combined with a low specific entropy for the accreted material. For a larger initial seed and/or a higher fraction of internal accretion energy that is absorbed by the protostar, the lithium depletion rate is similar to that of nonaccreting models. Indeed, these assumptions are challenged by the lack of a significant scatter observed in the lithium abundances of the accreting populations of the Orion Nebula Cluster and NGC 2264 (Sergison et al. 2013). We cannot totally exclude a different accretion history for the subsample of NGC 2264 low-mass members investigated here. However, the lithium-rotation link reported here would additionally call for a direct impact of episodic accretion onto angular momentum evolution. More specifically, to recover the enhanced lithium depletion rate in slowly rotating stars, one would have to assume that accretion bursts also yield lower spin rates at a few Myr. This is somewhat paradoxical, as violent accretion bursts are expected to spin the central star up, although it must be acknowledged that the spin evolution of young eruptive stars remains uncertain (e.g., Popham 1996).
A more direct link between PMS lithium depletion and angular momentum evolution has been suggested by Bouvier (2008). Recent models of PMS spin evolution indicate that the outer convective envelope of contracting young stars is held at nearly constant angular velocity for a few Myr through its magnetic coupling with the circumstellar disk (e.g., Gallet & Bouvier 2013). As the inner radiative core develops, unimpeded by external braking torques, differential rotational sets in between the fast radiative core and the slower outer convective envelope. In turn, the internal angular velocity gradient promotes increased rotational mixing, which results in an enhanced lithium depletion. The models predict that slow rotators remain coupled to their disk for a longer period of time and therefore experience a larger differential rotation than fast rotators (cf. Gallet & Bouvier 2015). The former are thus expected to reach the ZAMS with a lower lithium content than the latter, as observed in the Pleiades. Whether this process is able to account for the development of the lithium-rotation connection at an age as early as 5 Myr is, however, unclear. Nonaccreting stellar evolution models predict that a 0.8 M⊙ star starts to develop a radiative core at about 3 Myr (Siess et al. 2000; Baraffe et al. 2015). At 5 Myr, the models by Baraffe et al. (2015) predict that stars less massive than 0.6 M⊙ are still fully convective while stars in the mass range from 0.7 to 1.0 M⊙ have a radiative core whose mass increases from 5 to 30%, respectively, of the stellar mass, and whose radius extends from about 20 to 40% of the stellar radius9. Hence, over the Teff range investigated here, only the more massive WTTS may possess a significant radiative core at the assumed age of NGC 2264. It therefore remains to be seen whether a prolonged disk braking phase lasting a few Myr may effectively produce the level of lithium dispersion observed here for NGC 2264 low-mass members on a timescale as short as 5 Myr (see Eggenberger et al. 2012)10. Nevertheless, we note that the amplitude of the lithium scatter increases from a mere 20% in NGC 2264 (see Sect. 2) to a factor of 6 in the Pleiades (Soderblom et al. 1993). Hence, the long-lasting core-envelope decoupling process triggered by extended disk lifetime in the early PMS may still play a central role during the late PMS stage in widening the initially modest lithium dispersion up to the ZAMS.
A more subtle link between rotational evolution and lithium depletion during the PMS was recently advocated by Somers & Pinsonneault (2014), based on an earlier suggestion by King et al. (2010). Following models by, Chabrier et al. (2007) among others, Somers & Pisonneault argue that the strong magnetic fields of young stars partly inhibit the convective energy transport and therefore lead to inflated radii. In turn, an enhanced radius results in a lower temperature at the bottom of the convective zone and therefore reduces the rate of lithium burning. These authors further argue that, if magnetic field strength scales with rotation in young low-mass stars, fast rotators have the most inflated radius and therefore only experience reduced lithium burning. Hence, the Li excess observed in fast rotators by the Pleiades age would ultimately result from the impact of dynamo-generated magnetic fields scaling with rotation rate onto the PMS stellar structure. The models by Somers & Pinsonneault (2014) predict a slight depletion of lithium abundances already occurring at 6 Myr over the Teff range investigated here with a dispersion of about 0.4 dex, i.e., of similar magnitude as or even slightly larger than observed here for NGC 2264 (see their Fig. 18). We note, however, that the assumption of a magnetic field strength scaling with rotation rate might not hold during the PMS. While this relationship is well established for main-sequence dwarfs (e.g. Petit et al. 2008; Donati & Landstreet 2009), PMS stars, slow and fast rotators alike, appear to lie in a “saturated” magnetic activity regime at low Rossby numbers (Gregory et al. 2012; Donati et al. 2013). Hence, PMS low-mass stars may have an inflated radius due to enhanced magnetic activity compared to mature dwarfs (Jackson et al. 2016). However, the relationship between radius inflation, magnetic strength, and spin rate during the PMS, which is a central assumption indeed for this scenario to hold, is still a matter of debate (see Somers & Pinsonneault 2015). We empirically tested whether we could find any correlation between X-ray luminosity and rotation (E. Flaccomio, priv. comm.) or between the amplitude of variability and rotation (Venuti et al., in prep.) in our subsample of WTTS; we found no correlation that would support a clear relationship between rotation and either coronal emission or spottedness in this subsample (see also Messina et al. 2003; Argiroffi et al. 2016).
Finally, since none of the above scenarios is totally exempt from difficulties in explaining how a lithium-rotation connection may appear in low-mass PMS stars at an age of 5 Myr, we have to contemplate other possibilities and envision in particular factors extrinsic to the stars, such as accretion of fresh lithium from the circumstellar disk or through planet engulfment. The age of the NGC 2264 cluster is similar to the average lifetime of accretion disks around young low-mass stars (Bell et al. 2013). Hence, a fraction of stars in our sample must have lost their disk very recently. According to Vasconcelos & Bouvier (2015) Monte Carlo simulations, nonaccreting stars at 5 Myr span the whole range of rotational periods from less than 2 days up to 15 days. Slowly rotating nonaccreting stars lost their disks only recently and had no time to spin up yet, while fast rotating WTTS lost their disks earlier and have already had time to spin up under contraction. Fast rotating WTTS are thus more evolved than slow rotating WTTS, at least in terms of disk evolution. If fresh lithium could be provided to the star from the disk during the steady accretion phase while the star is still fully convective, one would then expect a slowly rotating WTTS that had a prolonged disk accretion phase to exhibit higher lithium content11. This is opposite from what is actually observed. Alternatively, if the disk dissipation is somehow linked to planet formation, young planetary systems around WTTS might already be in the process of early dynamical evolution (e.g., Albrecht et al. 2012). Random gravitational encounters may then promote dynamical ejections and, eventually, planet engulfment by the central star that would then gain angular momentum (Bolmont et al. 2012; Bouvier & Cébron 2015) and be replenished in lithium, albeit at a very modest rate for fully convective stars unless a significant amount of Li-rich planetary material is accreted. Admittedly, this interpretation is bound to remain speculative until we better understand how planetary systems form and evolve around young stars.
5. Conclusions
We report here a connection between lithium content and rotation rate for low-mass members of the 5 Myr old NGC 2264 cluster over a restricted Teff range from 3800 K to 4400 K. The amplitude of the EW(Li) scatter over this Teff range is about 20%, i.e., much smaller than the lithium dispersion reported for K-dwarfs in the 125 Myr old Pleiades cluster, which amounts to a factor of six. The relationship between lithium content and rotation nevertheless goes in the same direction, where fast rotators are more Li rich than slow rotators. This strongly suggests that a lithium-rotation connection is already established early on during PMS evolution and continues to grow further up to the ZAMS. Among the nonstandard evolutionary models developed so far to account for a lithium-rotation connection in low-mass dwarfs, those calling for a reduced lithium depletion rate during the PMS, as a result of radius inflation linked to fast rotation and magnetic activity, may prove the most able to account for the results reported here. Yet, the long-lasting impact of disk lifetime on the internal rotation profile of young solar-type stars may also contribute to the large lithium scatter observed on the ZAMS and beyond.
None of these models is without difficulties and external factors cannot be excluded at this point, such as the prompt injection of fresh lithium to the star by either disk accretion or planet engulfment. The evidence we report here for a rapidly increasing lithium scatter as a function of age, from the early PMS to the ZAMS, is very reminiscent of the observed widening of the angular momentum distribution of low-mass stars during this phase. Hence, the existence of a lithium-rotation connection in low-mass stars at 5 Myr may be indicative of an intimate link between accretion history, planet formation, and early angular momentum evolution, which is a complex interplay indeed whose breadth and underlying physics remain to be fully deciphered. As additional lithium measurements become available for other young clusters from the Gaia-ESO Survey and rotational period distributions are derived from continuous photometric monitoring, it will be most interesting to trace the origin and development of the lithium scatter and its relationship with rotation along PMS evolution from a few Myr up to the ZAMS.
Even though the GES iDR4 release provides Lithium abundances for this subsample, we prefer to use EW(Li) because uncertainties on the stellar parameters, mostly on Teff, do not propagate on EW(Li) (except for line blends, cf. Appendix A), while they do on abundances. Moreover, EW(Li) is directly measured on the spectra while abundances are model dependent.
The ninth source we reject is Mon 1115 (Teff = 4833 K) which, in spite of its low EW(Li) = 75 mÅ, has Vrad = 18.3 km s-1 that is consistent with the average of the cluster, as well as a high vsini = 30 km s-1 for its K6 spectral type, a sign of youth. It therefore deserves further membership analysis.
A Spearman rank test (Press et al. 1992) yields a correlation coefficient of ρ = −0.50 with a significance of level σ = 2.9 × 10-5, which indicates a highly significant correlation between δEW(Li) and Prot.
The outlier in Figs. 3 and 4 is Mon 910 (Teff = 3806 K, EW(Li) = 503.6 mÅ, Prot = 2.58 d). Its EW(Li) is lower than that of other cluster members of the same Teff, which might indicate that Mon 910 is a slightly older star unrelated to the cluster. Besides, it lies at the edge of the temperature domain considered here. We checked that excluding this object from the sample does not affect the significance results (the KS probability becomes 7 × 10-3), although it does change the EW(Li)–Teff least-squares fit and thus the actual δEW(Li) values.
Non-LTE corrections depend on the temperature, gravity, and Li abundance itself (see, e.g., Lind et al. 2009, and refs. therein), but, generally, for cool stars at solar metallicity the corrections are small (≤0.1 dex) and negative, i.e., non-LTE abundances are slightly lower than LTE abundances. Hence the maximum abundances measured in NGC 2264 would be consistent with the meteoritic abundance.
Similar figures arise from models by Siess et al. (2000).
P. Eggenberger kindly ran a 0.8 M⊙ rotating model with the same assumptions as the 1 M⊙ model published in Eggenberger et al. (2012) and obtained similar results, namely an insignificant impact of enhanced rotational mixing upon lithium depletion at an age of 5 Myr.
In contrast, when accretion of heavy material occurs once the star has settled on the ZAMS, it promotes lithium depletion (cf. Théado & Vauclair 2012).
These methods are the direct profile integration available in the IRAF-splot procedure (OACT node), DAOSPEC (Stetson & Pancino 2008, OAPA node), and a semiautomatic IDL procedure specifically developed for the Gaia-ESO by the Arcetri node.
In iDR4 at least two of the independent measurements must be available before combining the results into the final recommended value (A. C. Lanzafame, priv. comm.). When three measurements are available, the outlier-resistant mean procedure resistant_mean in the IDL Astronomy Library (http://idlastro.gsfc.nasa.gov) with 3σ outlier rejection is used. When two measurements are available, they are averaged only if they differ by less then 2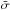 , where
, where 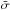 is the mean of the uncertainties of the individual measurements; otherwise no final recommended value is given.
is the mean of the uncertainties of the individual measurements; otherwise no final recommended value is given.
Acknowledgments
We would like to dedicate this paper to our friend and colleague Francesco Palla, a pioneer in the investigation of lithium in young stars. We thank Patrick Eggenberger for running additional models of PMS lithium depletion, and Silvano Desidera and Elvira Covino for sharing results on lithium rotational variability in advance of publication. J. Bouvier and E. Moraux thank the staff of the Osservatorio Astrofisico di Catania for their kind hospitality in the autumn of 2015. They acknowledge the Agence Nationale pour la Recherche program ANR 2010 JCJC 0501 1“DESC (Dynamical Evolution of Stellar Clusters)” for the funding of their stay at OACT during which this study was performed. This study was also supported by the Agence Nationale pour la Recherche program ANR 2011 Blanc SIMI 5-6 020 01 “Toupies (Towards understanding the spin evolution of stars)”. A. Bayo acknowledges financial support from the Proyecto Fondecyt Iniciación 11140572.
Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under program ID 188.B-3002. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and by the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. These data have been obtained from the Gaia-ESO Survey Data Archive, prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council. This work was partly supported by the European Union FP7 program through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’ Istruzione, dell’ Università’ e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012” and “The Chemical and Dynamical Evolution of the Milky Way and the Local Group Galaxies” (prot. 2010LY5N2T). The results presented here benefit from discussions held during the Gaia-ESO workshops and conferences supported by the ESF (European Science Foundation) through the GREAT Research Network Programme.
References
- Affer, L., Micela, G., Favata, F., Flaccomio, E., & Bouvier, J. 2013, MNRAS, 430, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Albrecht, S., Winn, J. N., Johnson, J. A., et al. 2012, ApJ, 757, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Argiroffi, C., Caramazza, M., Micela, G., et al. 2016, A&A, 589, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balachandran, S. C., Mallik, S. V., & Lambert, D. L. 2011, MNRAS, 410, 2526 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., & Chabrier, G. 2010, A&A, 521, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basri, G., Martin, E. L., & Bertout, C. 1991, A&A, 252, 625 [NASA ADS] [Google Scholar]
- Bayo, A., Barrado, D., Stauffer, J., et al. 2011, A&A, 536, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmont, E., Raymond, S. N., Leconte, J., & Matt, S. P. 2012, A&A, 544, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J. 2008, A&A, 489, L53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouvier, J., & Cébron, D. 2015, MNRAS, 453, 3720 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Marcy, G. W., Cohen, R. D., & Duncan, D. K. 1987, ApJ, 319, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Gallardo, J., & Baraffe, I. 2007, A&A, 472, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cody, A. M., Stauffer, J., Baglin, A., et al. 2014, AJ, 147, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Denissenkov, P. A. 2010, ApJ, 719, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Do Nascimento, J. D., da Costa, J. S., & de Medeiros, J. R. 2010, A&A, 519, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Donati, J.-F., & Landstreet, J. D. 2009, ARA&A, 47, 333 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Donati, J.-F., Gregory, S. G., Alencar, S. H. P., et al. 2013, MNRAS, 436, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Haemmerlé, L., Meynet, G., & Maeder, A. 2012, A&A, 539, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Favata, F., Barbera, M., Micela, G., & Sciortino, S. 1995, A&A, 295, 147 [NASA ADS] [Google Scholar]
- Fernandez, M., & Miranda, L. F. 1998, A&A, 332, 629 [NASA ADS] [Google Scholar]
- Gallet, F., & Bouvier, J. 2013, A&A, 556, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallet, F., & Bouvier, J. 2015, A&A, 577, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giampapa, M. S. 1984, ApJ, 277, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Gillen, E., Aigrain, S., McQuillan, A., et al. 2014, A&A, 562, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Gregory, S. G., Donati, J.-F., Morin, J., et al. 2012, ApJ, 755, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, R. J., Jeffries, R. D., Randich, S., et al. 2016, A&A, 586, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffries, R. D. 1999, MNRAS, 309, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D. 2014, in EAS Pub. Ser., 65, 289 [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Cottaar, M., et al. 2014, A&A, 563, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- King, J. R., Schuler, S. C., Hobbs, L. M., & Pinsonneault, M. H. 2010, ApJ, 710, 1610 [NASA ADS] [CrossRef] [Google Scholar]
- Lamm, M. H., Bailer-Jones, C. A. L., Mundt, R., Herbst, W., & Scholz, A. 2004, A&A, 417, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzafame, A. C., Frasca, A., Damiani, F., et al. 2015, A&A, 576, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lind, K., Asplund, M., & Barklem, P. S. 2009, A&A, 503, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Makidon, R. B., Rebull, L. M., Strom, S. E., Adams, M. T., & Patten, B. M. 2004, AJ, 127, 2228 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, E. L., Rebolo, R., Magazzu, A., & Pavlenko, Y. V. 1994, A&A, 282, 503 [NASA ADS] [Google Scholar]
- Mayne, N. J., & Naylor, T. 2008, MNRAS, 386, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Messina, S., Pizzolato, N., Guinan, E. F., & Rodonò, M. 2003, A&A, 410, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palla, F., Randich, S., Flaccomio, E., & Pallavicini, R. 2005, ApJ, 626, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Pallavicini, R., Cutispoto, G., Randich, S., & Gratton, R. 1993, A&A, 267, 145 [NASA ADS] [Google Scholar]
- Pasquini, L., Biazzo, K., Bonifacio, P., Randich, S., & Bedin, L. R. 2008, A&A, 489, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petit, P., Dintrans, B., Solanki, S. K., et al. 2008, MNRAS, 388, 80 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Piau, L., & Turck-Chièze, S. 2002, ApJ, 566, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., Sofia, S., & Demarque, P. 1989, ApJ, 338, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Pinsonneault, M. H., Kawaler, S. D., & Demarque, P. 1990, ApJS, 74, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Popham, R. 1996, ApJ, 467, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN. The art of scientific computing (Cambridge University Press) [Google Scholar]
- Ramírez, I., Fish, J. R., Lambert, D. L., & Allen de Prieto, C. 2012, ApJ, 756, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Randich, S. 2010, in IAU Symp. 268, eds. C. Charbonnel, M. Tosi, F. Primas, & C. Chiappini, 275 [Google Scholar]
- Randich, S., Martin, E. L., Garcia Lopez, R. J., & Pallavicini, R. 1998, A&A, 333, 591 [NASA ADS] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium. 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Robinson, R. D., Thompson, K., & Innis, J. L. 1986, PASA, 6, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Sergison, D. J., Mayne, N. J., Naylor, T., Jeffries, R. D., & Bell, C. P. M. 2013, MNRAS, 434, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Sestito, P., & Randich, S. 2005, A&A, 442, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [Google Scholar]
- Soderblom, D. R., Jones, B. F., Balachandran, S., et al. 1993, AJ, 106, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., King, J. R., Siess, L., Jones, B. F., & Fischer, D. 1999, AJ, 118, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Hillenbrand, L. A., Jeffries, R. D., Mamajek, E. E., & Naylor, T. 2014, Protostars and Planets VI, 219 [Google Scholar]
- Somers, G., & Pinsonneault, M. H. 2014, ApJ, 790, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Somers, G., & Pinsonneault, M. H. 2015, MNRAS, 449, 4131 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Théado, S., & Vauclair, S. 2012, ApJ, 744, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasconcelos, M. J., & Bouvier, J. 2015, A&A, 578, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ventura, P., Zeppieri, A., Mazzitelli, I., & D’Antona, F. 1998, A&A, 331, 1011 [NASA ADS] [Google Scholar]
- Venuti, L., Bouvier, J., Flaccomio, E., et al. 2014, A&A, 570, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
- Zwintz, K., Fossati, L., Ryabchikova, T., et al. 2014, Science, 345, 550 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Appendix A: Lithium equivalent width measurements in NGC 2264
As described in Lanzafame et al. (2015), the Gaia-ESO PMS analysis makes use of three independent methods to derive EW(Li) from the GIRAFFE spectra12. In order to improve further the reliability of the final recommended EW(Li), a robust average procedure was introduced in iDR4 for deriving the final recommended values from the independent measurements13. Hence, the final recommended EW(Li) for NGC 2264 have a median standard deviation of 10 mÅ, in which 99% of the values have an estimated precision better than 6%. We further checked this estimate by analyzing a subsample of 12 stars, over the Teff range 3800–4440 K, which were observed repeatedly on a timescale of several weeks. Each of these sources has at least 20 FLAMES spectra in the ESO archive and EW(Li) was measured on each spectrum. The results indicate an average rms dispersion around the mean of 5–6 mÅ, in agreement with the above estimate.
The contribution of lines blended with Li (6707.84 Å) in the GIRAFFE spectra is estimated by a spectral synthesis using Spectroscopy Made Easy (SME; Valenti & Piskunov 1996) with MARCS model atmospheres as input, taking the stellar Teff, log g, and [Fe/H] into account. Blends are estimated on a wavelength range of 1 Å centered on the Li (6707.84 Å) line, then subtracted from the raw EW(Li). Since vsini is not taken into account as of yet, further lines can in principle contribute to the measured EW(Li) for sufficiently fast rotating stars, which can introduce a bias. In order to estimate such a bias at increasing vsini, we have taken a dozen HR15N spectra of young stars with S/N ≈ 60, 400 ≤ EW(Li) ≤ 500 mÅ, 3800 ≤ Teff ≤ 4400 K, and vsini < 20 km s-1, convolved them with rotational broadening kernels to simulate the effect of increasing rotation velocity, measured EW(Li) in each of them, and compared the results with the original spectra. The results are summarized in Fig. A.1. Differences with the original spectrum, ΔEW(Li), remain less than the median standard deviation in NGC 2264 up to vsini ≈ 80 km s-1 and become increasingly significant only above this value, where we have only five NGC 2264 members in the sample considered here. Furthermore, we estimate that only the presence of a significant fraction of stars with vsini > 100 km s-1 would introduce a bias in the observed distribution of EW(Li) versus rotation, but indeed only one NGC 2264 member in our sample lies in this range. Figure A.1 also shows that, in some cases, for 20 < vsini < 50 km s-1 the EW(Li) measurement can actually be slightly less than the original measurement, but still within the typical standard deviation, since the merging of lines due to the rotational broadening can lead to a small underestimation of the local continuum.
We therefore conclude that the systematic differences in the rotation distribution of Li-excess and Li-deficient stars in NGC 2264 cannot be due to such a bias.
 |
Fig. A.1 Differences in EW(Li) measurements between artificially broadened spectra and the original spectra for a selected sample of stars (see text for details). The dotted line indicates the approximate distance between the Li-excess and Li-deficient distributions. |
Appendix B: Lithium equivalent width intrinsic variability
We investigate here how intrinsic EW(Li) variability could impact our results. The first evidence for the rotational modulation EW(Li) on spotted low-mass stars was reported by Robinson et al. (1986). They observed an increased EW(Li) when the star was fainter, i.e., at maximum spot visibility. The EW(Li) enhancement in spotted areas was already documented well in the case of the Sun (Giampapa 1984). However, there are also cases when the EW(Li) dependence on the spottedness level is observed only at some epochs, e.g., V410 Tau (Fernandez & Miranda 1998), but is absent at other epochs (see Basri et al. 1991). Also, spectroscopic monitoring of some active stars in the Pleiades revealed no significant Li variations (Pallavicini et al. 1993; Jeffries 1999). This nonunivocal behavior suggests that additional factors other than spots can play a role in the observed EW(Li) variations.
The amplitude of the EW(Li) rotational modulation is generally of a few percent. Messina et al. (in prep.) measured EW(Li) variations in a sample of 18 low-mass stars over the age range from 6 Myr to the Pleiades age. The EW(Li) variations were measured in all stars over up to three consecutive years. When present, EW(Li) variations were found to correlate with both photometric variations and chromospheric activity indices (e.g., Ca II H&K) with enhanced EW(Li) corresponding to light curve minimum and maximum chromospheric intensity. None of these EW(Li) variations exceeded 5%. We therefore conclude that, while the NGC 2264 low-mass members may well undergo intrinsic EW(Li) variations, the increased lithium scatter to be expected remains small compared to the amplitude of the lithium-rotation connection reported here. Hence, intrinsic EW(Li) variations are unlikely to affect our results.
NGC 2264 WTTS considered in this study.
All Tables
All Figures
 |
Fig. 1 Lithium equivalent width is plotted as a function of effective temperature for weak-line T Tauri stars. The average rms error is 200 K on Teff and 10 mÅ on EW(Li). |
| In the text | |
 |
Fig. 2 Lithium equivalent width is plotted as a function of effective temperature for weak-line T Tauri stars. The decreasing EW(Li) trend toward higher Teff continues up to 6600 K (cf. Fig. 1). The color scale is representative of the rotational period, and is limited up to eight days to maximize the contrast (see the scale on the right side of the panel in units of days). |
| In the text | |
 |
Fig. 3 Lithium equivalent width is plotted as a function of effective temperature for weak-line T Tauri stars over the Teff range 3800–4400 K. The symbol size is proportional to the angular velocity (1 /Prot). |
| In the text | |
 |
Fig. 4 Top panel: EW(Li) residuals are plotted as a function of rotational period. The symbol size is proportional to Teff. Lower left panel: rotational period distribution of Li-excess (thick red) and Li-deficient (shaded black) stars. Lower right panel: cumulative distribution of rotational periods for Li-excess (thick red) and Li-deficient (thin black) stars. |
| In the text | |
 |
Fig. A.1 Differences in EW(Li) measurements between artificially broadened spectra and the original spectra for a selected sample of stars (see text for details). The dotted line indicates the approximate distance between the Li-excess and Li-deficient distributions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


