| Issue |
A&A
Volume 588, April 2016
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201527879 | |
| Published online | 14 March 2016 | |
Efficient ortho-para conversion of H2 on interstellar grain surfaces
1 LERMA, Observatoire de Paris, PSL Research University, CNRS, Sorbonne Universités, UPMC Université Paris 06, 92190 Meudon, France
e-mail: emeric.bron@obspm.fr
2 Université Paris Diderot, Sorbonne Paris Cité, 75013 Paris, France
Received: 2 December 2015
Accepted: 16 January 2016
Context. Fast surface conversion between ortho- and para-H2 has been observed in laboratory studies, and it has been proposed that this mechanism plays a role in the control of the ortho-para ratio in the interstellar medium. Observations of rotational lines of H2 in photo-dissociation regions (PDRs) have indeed found significantly lower ortho-para ratios than expected at equilibrium. The mechanisms controlling the balance of the ortho-para ratio in the interstellar medium thus remain incompletely understood, while this ratio can affect the thermodynamical properties of the gas (equation of state, cooling function).
Aims. We aim to build an accurate model of ortho-para conversion on dust surfaces based on the most recent experimental and theoretical results, and to validate it by comparison to observations of H2 rotational lines in PDRs.
Methods. We propose a statistical model of ortho-para conversion on dust grains with fluctuating dust temperatures. It is based on a master equation approach. This computation is then coupled to full PDR models and compared to PDR observations.
Results. We show that the observations of rotational H2 lines indicate a high conversion efficiency on dust grains and that this high efficiency can be accounted for if taking dust temperature fluctuations into account with our statistical model of surface conversion. Simpler models that neglect the dust temperature fluctuations do not reach the high efficiency deduced from the observations. Moreover, this high efficiency induced by dust temperature fluctuations is very insensitive to the values of the model’s microphysical parameters.
Conclusions. Ortho-para conversion on grains is thus an efficient mechanism in most astrophysical conditions and can play a significant role in controlling the ortho-para ratio.
Key words: ISM: molecules / dust, extinction / photon-dominated region (PDR) / astrochemistry / molecular processes / methods: numerical
© ESO, 2016
1. Introduction
Molecular hydrogen is the main constituent of molecular clouds. It can be observed in absorption in diffuse gas and in emission in warm gas and/or high UV field conditions (mainly photodissociation regions, hereafter PDRs, and shocks). Its low rotational levels are collisionaly excited and trace the gas temperature in the emitting material, while its vibrational levels are either pumped by the UV radiation field or collisionaly excited in hot shocked material. Excitation at formation has also been proposed as a contributor to vibrational excitation.
In the diffuse interstellar medium (ISM), H2 has mainly been observed in absorption (Savage et al. 1977; Rachford et al. 2002, 2009; Tumlinson et al. 2002; Gry et al. 2002; Richter et al. 2003; Lacour et al. 2005; Gillmon et al. 2006), with the only observation in emission being Falgarone et al. (2005). The excitation temperature of the first two rotational levels (T01) is commonly used as a measure of the gas temperature in diffuse clouds, although it could stop being a meaningful measure at low N(H2) (Srianand et al. 2005; Roy et al. 2006). Higher rotational levels appear suprathermaly excited and could trace a small fraction of warm gas heated by the dissipation of interstellar turbulence in shocks or vortices (Gredel et al. 2002; Godard et al. 2014; Bron 2014).
Observed in emission in brighter PDRs (Fuente et al. 1999; Moutou et al. 1999; Habart et al. 2003, 2004; Allers et al. 2005; Thi et al. 2009; Fleming et al. 2010; Habart et al. 2011; Sheffer et al. 2011), it traces the surface layer of warm molecular gas close to the H/H2 transition and can be used as a diagnostics of the gas temperature and UV radiation field. It can also help in constraining processes such as H2 formation or photoelectric heating (Habart et al. 2004, 2011).
It has also been observed in extragalactic environments. Observations of rotational emission in other galaxies has shown that the overall H2 emission could be explained by PDRs (Naslim et al. 2015 in the LMC, Roussel et al. 2007 in the SINGS galaxy sample, Higdon et al. 2006 in ULIRGs) except in Seyfert galaxies where a significant shock contribution might be present (Rigopoulou et al. 2002; Pereira-Santaella et al. 2014). In addition, H2 has been detected in absorption in DLAs (Ledoux et al. 2003; Noterdaeme et al. 2007; Muzahid et al. 2015).
The hydrogen molecule exists as two spin isomers: para-H2 with the spins of its two nucleus in opposite directions, and ortho-H2 with parallel nuclear spins. In the ground electronic state, ortho-H2 can only have an odd rotational number J, while para-H2 only takes even rotational numbers. As conversion between the two spin isomers is forbidden for an isolated molecule (e.g., Pachucki & Komasa 2008: radiative transition rate of 6 × 10-14 yr-1) and only reactive collisions can induce conversion, the ortho-to-para ratio (OPR) can be out of local thermal equilibrium (LTE). At LTE, the OPR is close to 3 at high temperatures (> 200 K) and goes to zero at low temperatures. The ratio between the successive rotational lines of H2 can thus be affected by an out-of-equilibrium OPR, and interpretation of H2 emission requires a good understanding of the OPR. Moreover, the excitation temperature T01 used in absorption studies only traces the gas temperature if the OPR is thermalized.
Several observations have derived out-of-equilibrium OPR values from the pure rotational lines of H2 in PDRs (Fuente et al. 1999; Moutou et al. 1999; Habart et al. 2003, 2011; Fleming et al. 2010), with OPR values ~ 1, significantly lower than the value of ~ 3 expected from the excitation temperature of the low-J rotational lines. Out-of-equilibrium rotational OPR values have also been reported in the SINGS galaxy sample by Roussel et al. (2007). This is a different problem from the low values of the OPR derived from vibrational lines of H2. Low OPR values in the vibrational levels can be caused by preferential UV pumping of para-H2 due to preferential self-shielding of ortho-H2 even when the true OPR (dominated by the v = 0 levels) is 3, as described in great detail in Sternberg & Neufeld (1999).
In dark dense clouds, H2 cannot be directly observed, and the OPR can only be determined indirectly. For instance, Troscompt et al. (2009) deduce the OPR from the anomalous absorption of H2CO owing to the different collisional rates with ortho-H2 and para-H2. Maret & Bergin (2007) use DCO+, because the fractionation reaction 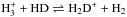 is very sensitive to the OPR of H2. Pagani et al. (2009) similarly use the influence of the OPR on the deuterium chemistry and deduce the OPR from observations of N2D+, N2H+, and H2D+. All find an OPR that is higher than the LTE value in cold gas. Non-dissociative shocks, in which the quickly heated gas makes H2 observable in emission but does not have time to significantly change its OPR, can also offer a way to estimate the OPR in the preshock dark molecular gas (Neufeld et al. 2006; Yuan & Neufeld 2011).
is very sensitive to the OPR of H2. Pagani et al. (2009) similarly use the influence of the OPR on the deuterium chemistry and deduce the OPR from observations of N2D+, N2H+, and H2D+. All find an OPR that is higher than the LTE value in cold gas. Non-dissociative shocks, in which the quickly heated gas makes H2 observable in emission but does not have time to significantly change its OPR, can also offer a way to estimate the OPR in the preshock dark molecular gas (Neufeld et al. 2006; Yuan & Neufeld 2011).
The OPR of H2 plays several important roles in the physico-chemistry of the ISM. First, it can significantly affect the dynamics of core formation through gravitational collapse in star-forming clouds by modifying the heat capacity and the equation of state of the gas, as was shown by Vaytet et al. (2014), who compared numerical simulations with different prescriptions corresponding to LTE OPR or fixed OPR of 3. Second, it controls large parts of the chemistry in dense clouds, such as the nitrogen chemistry (Dislaire et al. 2012; Faure et al. 2013) through the reaction N+ + H2 ⇌ NH+ + H, or the deuterium chemistry (Flower et al. 2006) through the fractionation reaction 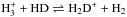 . Finally, the slow conversion process between the two spin isomers has been used as a tool to measure the age of molecular clouds (Pagani et al. 2011, 2013).
. Finally, the slow conversion process between the two spin isomers has been used as a tool to measure the age of molecular clouds (Pagani et al. 2011, 2013).
The OPR is controlled by several processes, as first investigated by Burton et al. (1992):
-
Formation is usually assumed to occur with an OPR of 3, but this value is uncertain (Takahashi 2001; Yabushita et al. 2008; Gavilan et al. 2012).
-
Photo-dissociation can sometimes destroy para-H2 because of the faster self-shielding of ortho-H2 when the OPR is > 1. This can lead to the OPR being > 3 locally (Abgrall et al. 1992; Sternberg & Neufeld 1999).
-
Reactive collisions can induce conversion between the two spin isomers. The main conversion reactions are proton exchange with H+ (Gerlich 1990; Honvault et al. 2011) and with H
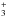 (Gómez-Carrasco et al. 2012) and hydrogen exchange with H (Schulz & Le Roy 1965; Truhlar 1976; Mandy & Martin 1992, 1993; Sun & Dalgarno 1994; Lique et al. 2012). This last reaction possesses an activation barrier (~ 5000 K) and is thus only efficient in warm gas. Reactive collisions with H2 have an even higher activation barrier (~ 60 000 K, Carmona-Novillo et al. 2007) and are usually neglected. These reactions tend to thermalize the OPR to the gas temperature.
(Gómez-Carrasco et al. 2012) and hydrogen exchange with H (Schulz & Le Roy 1965; Truhlar 1976; Mandy & Martin 1992, 1993; Sun & Dalgarno 1994; Lique et al. 2012). This last reaction possesses an activation barrier (~ 5000 K) and is thus only efficient in warm gas. Reactive collisions with H2 have an even higher activation barrier (~ 60 000 K, Carmona-Novillo et al. 2007) and are usually neglected. These reactions tend to thermalize the OPR to the gas temperature. -
H2 molecules that are adsorbed on the surface of dust grains can interact with the magnetic fields caused by impurities and surface defects and convert from one spin isomer to the other (Fukutani & Sugimoto 2013, and references therein). This process is the subject of the present article, and it tends to thermalize the OPR to the dust temperature, which is significantly lower than the gas temperature in PDRs.
An approximate treatment of ortho-para conversion on dust was used in Le Bourlot (2000) to investigate the effect of this process in PDRs. The process was found to only be efficient on cold dust grains. It was then shown that with a few hypotheses favoring high efficiency (high binding energy, low dust temperatures), the pure rotational lines of H2 were strongly affected. Sheffer et al. (2011) find that PDR models could successfully explain observed OPR values lower than LTE in the PDR NGC 2023 South when including this process with the high-efficiency hypothesis of Le Bourlot (2000).
In this article, we investigate the efficiency of this process using a detailed model based on the most recent experimental and theoretical results reviewed by Fukutani & Sugimoto (2013). Since the surface processes are highly sensitive to the dust temperature and small dust grains are known to have fluctuating temperatures that can significantly affect the efficiency of surface processes (e.g., Bron et al. 2014, for H2 formation), we have built a statistical model of ortho-para conversion on dust grains with temperature fluctuations, which we compare to a simpler rate equation model without fluctuations. We then investigate the effect of this process in PDR models and compare the predicted observable OPR values to PDR observations.
In Sect. 2, we present the physical processes at play and define their rates. We also present a simple rate equation model that neglects the temperature fluctuations for comparison with the more sophisticated model that we present in the following sections. In Sect. 3, we present the statistical method that we employed to compute the effect of dust temperature fluctuations on ortho-para conversion on grains. Section 4 presents the results of this statistical computation and discusses the importance of the various microphysical parameters. In Sect. 5, we couple this statistical computation of the ortho-para conversion rate to the Meudon PDR code to study the impact of this new computation on full PDR models and compare their results to observations of the ortho-para ratio in PDRs. Finally we give our conclusions in Sect. 6.
2. Processes and rate equation model
We consider dust grains of sizes above 1 nm. Ortho-para conversion on polycyclic aromatic hydrocarbons (PAHs) is probably much less efficient owing to the lack of surface defects and impurity sites that are thought to allow ortho-para conversion on graphite surfaces.
We have adopted a simple spherical grain model. We denote a as the grain radius and assume uniformly distributed adsorption sites on the surface, characterized equivalently by the surface density of sites ns, the typical distance between sites ds, or the total number of sites Ns. Those quantities are related by 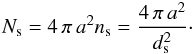 In addition, we denote Td as the grain temperature, Tgas the gas temperature, no and np respectively as the number of ortho-H2 and para-H2 molecules physisorbed on the grain surface, and
In addition, we denote Td as the grain temperature, Tgas the gas temperature, no and np respectively as the number of ortho-H2 and para-H2 molecules physisorbed on the grain surface, and 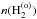 and
and 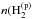 ) as the gas phase densities of ortho- and para-H2, respectively.
) as the gas phase densities of ortho- and para-H2, respectively.
We now go on to describe the different processes affecting the adsorbed H2 molecules that we include in our model.
2.1. Adsorption of molecular hydrogen
The first step in the ortho-para conversion of an H2 molecule is physisorption on the grain surface, in which the molecule binds to the grain through van der Waals interactions. A gas H2 molecule hitting the grain on an empty site becomes physisorbed with a probability S(Tgas) called the sticking probability. We discuss the choice of this sticking function below. We assume rejection if the molecule hits an occupied site. The rates of adsorption of ortho-H2 and para-H2 molecules on the grain (in s-1) are thus 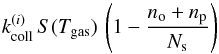 (1)with
(1)with 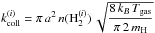 , where i = o for ortho-H2 and i = p for para-H2. In the following, we define
, where i = o for ortho-H2 and i = p for para-H2. In the following, we define 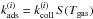 to simplify the notations.
to simplify the notations.
Few measurements of the sticking function for H2 on dust surfaces have ever been made. The only full measurement as a function of the gas temperature is given by Matar et al. (2010), who measured the sticking function on amorphous water ice in the temperature range 30−350 K. They give the prescription 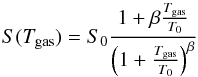 (2)with S0 = 0.76, T0 = 87 K, and β = 5/2. This formula is derived from a statistical model of sticking on amorphous surfaces, which is fitted to the experimental results.
(2)with S0 = 0.76, T0 = 87 K, and β = 5/2. This formula is derived from a statistical model of sticking on amorphous surfaces, which is fitted to the experimental results.
 |
Fig. 1 Sticking coefficients of H2 on different grain surfaces from the literature. |
This sticking function is shown in Fig. 1 (blue curve). Theoretical calculation have also been presented in Leitch-Devlin & Williams (1985) and are also shown on the graph: 0.4 for graphite and 0.05 for silicates at ~ 100 K. In the present paper, our comparison to observations will focus on rotational H2 emission in PDRs. In the regions of interest, ice mantles are thus not present yet, and we need sticking functions on bare carbonaceous and silicate surfaces. Since we lack precise determinations of these sticking functions, and because the Matar et al. (2010) sticking function is compatible with the value for graphite from Leitch-Devlin & Williams (1985), we use this sticking function (Eq. (2)) for all models in this article. The surface ortho-para conversion efficiency is directly proportional to the sticking coefficient, so that a lower sticking coefficient would proportionally reduce the importance of surface conversion.
In comparison, Acharyya (2014) determined lower limits to the sticking coefficient of H2 on olivine as a function of temperature for a very limited range of gas temperatures (7−14 K). These lower limits are also presented in Fig. 1 and seem to indicate a steeper decrease with temperature, but the limited range of temperatures and that they are only lower limits make conclusions difficult to draw.
2.2. Ortho-para conversion
Once physisorbed, an ortho-H2 molecule can convert to a para-H2 molecule with rate ko → p(Td), and vice versa with rate kp → o(Td). Conversion occurs because of electro-magnetic interactions with the surface allowing spin-transfer through various processes, and often involves impurity sites or surface defects (see Fukutani & Sugimoto 2013; and Ilisca & Ghiglieno 2014 for recent overviews of these processes).
Those two rates are related because for an adsorbed population of H2 without desorption or arrival, the populations of ortho-H2 and para-H2 at equilibrium must yield an equilibrium ortho-para ratio. We thus have 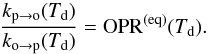 (3)We neglect here the fact that the energy levels of physisorbed H2 are slightly modified compared to the gas phase values and take the gas phase equilibrium OPR function.
(3)We neglect here the fact that the energy levels of physisorbed H2 are slightly modified compared to the gas phase values and take the gas phase equilibrium OPR function.
Several experiments, which we discuss below, have measured a conversion timescale τconv to pure para-H2 on a cold surface. In such experiments, H2 is first adsorbed on the surface with some initial OPR. Since the temperature of the surface is very low, it then progressively converts to para-H2. Desorption is negligible. In this case, the evolution matrix is 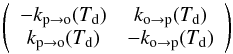 (4)with eigenvalues kp → o(Td) + ko → p(Td) and 0. The measured characteristic time is thus
(4)with eigenvalues kp → o(Td) + ko → p(Td) and 0. The measured characteristic time is thus 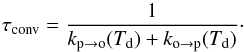 (5)We note that this characteristic time scale is related to the half life that is often used by thalf−life ≃ 0.69 τconv.
(5)We note that this characteristic time scale is related to the half life that is often used by thalf−life ≃ 0.69 τconv.
From Eqs. (3) and (5), we can deduce expressions for the conversion rate coefficients: 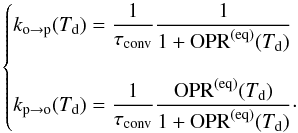 (6)Because we lack experimental determinations of the temperature dependance of τconv, we take it as a constant.
(6)Because we lack experimental determinations of the temperature dependance of τconv, we take it as a constant.
Experimental measurements of the ortho-para conversion timescale on different surfaces.
Several experiments have measured the ortho-para conversion timescale. A few experiments have measured the conversion timescale on graphite. The first measurement was done by Kubik et al. (1985), who measured conversion rates of 0.40 %/h (characteristic time τconv ~ 104 s) for H2 ortho-para conversion and of 0.069 %/h (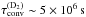 ) for D2 para-ortho conversion. Another measurement was performed by Palmer & Willis (1987) at a surface temperature of 10 K, finding full conversion for H2 in less than 1 min (τconv< 20 s). Finally, Yucel et al. (1990) measured the para-ortho conversion of D2 and found a conversion time of 20 min at 10 K. Assuming the same ratio between the H2 ortho-para conversion rate and the D2 para-ortho conversion rate as found in Kubik et al. (1985), this would lead to a conversion timescale of 2.5 s for H2, in agreement with Palmer & Willis (1987). Yucel et al. (1990) also showed that the conversion timescale increases with the surface coverage and that it is roughly constant with temperature in the range 10−25 K, increasing sharply to ~ 70 min at 8−10 K.
) for D2 para-ortho conversion. Another measurement was performed by Palmer & Willis (1987) at a surface temperature of 10 K, finding full conversion for H2 in less than 1 min (τconv< 20 s). Finally, Yucel et al. (1990) measured the para-ortho conversion of D2 and found a conversion time of 20 min at 10 K. Assuming the same ratio between the H2 ortho-para conversion rate and the D2 para-ortho conversion rate as found in Kubik et al. (1985), this would lead to a conversion timescale of 2.5 s for H2, in agreement with Palmer & Willis (1987). Yucel et al. (1990) also showed that the conversion timescale increases with the surface coverage and that it is roughly constant with temperature in the range 10−25 K, increasing sharply to ~ 70 min at 8−10 K.
Several measurements have been made on amorphous water ice. The oldest estimation is Sandler (1954), giving a conversion half life of ~ 10 h (τconv ~ 5 × 104 s) on solid D2O at 90 K. Hixson et al. (1992) then measured a half time of ~ 40 min (τconv ~ 3.6 × 103 s) on solid D2O at 12 K. They proposed that there are different kinds of sites, some of which having enhanced conversion. They also suspect a low level of oxygen contamination. Amiaud et al. (2008) find no detectable para-ortho conversion of D2 at 10 K in a time of ~ 103 s (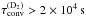 ). Watanabe et al. (2010) experimental results seem to indicate a conversion of about 10%−20% in 20 min at 15 K (τH2 = 5 × 103−1 × 104 s). Chehrouri et al. (2011) find that the conversion is helped by co-adsorbed O2. In the presence of O2, they find a conversion time of ~ 220 s, while in the absence of O2, they find a rate less than 15%/h (τH2> 2 × 104 s). In contrast, Sugimoto & Fukutani (2011) measure a conversion timescale in the range 230−710 s on clean ice at 10 K and propose a theoretical model predicting a timescale of ~ 102 s.
). Watanabe et al. (2010) experimental results seem to indicate a conversion of about 10%−20% in 20 min at 15 K (τH2 = 5 × 103−1 × 104 s). Chehrouri et al. (2011) find that the conversion is helped by co-adsorbed O2. In the presence of O2, they find a conversion time of ~ 220 s, while in the absence of O2, they find a rate less than 15%/h (τH2> 2 × 104 s). In contrast, Sugimoto & Fukutani (2011) measure a conversion timescale in the range 230−710 s on clean ice at 10 K and propose a theoretical model predicting a timescale of ~ 102 s.
These values are gathered in Table 1. The results are thus quite contradictory, so we have to explore values of the conversion timescale in the range 1−104 s. The most likely value seems to be 1−10 s on graphite, and 102−104 s on ices.
2.3. Thermal desorption
Experimental and theoretical determinations of the binding energy of H2 on different surfaces.
In competition with the conversion process, the H2 molecule can also desorb thermally from the surface. The thermal desorption rate of ortho- and para-H2 is determined by their physisorption energies. Several studies have measured the adsorption energy of H2 on various surfaces, most of which do not distinguish between ortho- and para-H2. As para-H2 is insensitive to the anisotropic part of the adsorption potential while ortho-H2 is not, ortho-H2 tends to have a higher binding energy than para-H2 (Fukutani & Sugimoto 2013).
For crystalline silicates, Katz et al. (1999) give an adsorption energy of 27.1 meV (314.5 K). For amorphous silicates, Vidali et al. (2007) and Perets et al. (2007) find that the distribution of binding energies can be described with two values: 35 meV (406 K) and 53 meV (615 K). Vidali & Li (2010) determine the full distribution of binding energies and find a distribution with a peak at 57 meV (662 K) that extends from 45 meV (522 K) to 90 meV (1044 K). For amorphous carbon, Katz et al. (1999) give 46.7 meV (542 K). For amorphous water ice (ASW), Manicò et al. (2001) find 63 meV (731 K). Roser et al. (2002) study the binding energy distribution for various types of ices, describing the distribution by two energy values. They find 45 meV (522 K) and 68 meV (789 K) for heat-treated low-density ASW, 39 meV (453 K) and 67 meV (778 K) for vapor-deposited low-density ASW, and 53 meV (615 K) and 69 meV (801 K) for high-density ice. Finally, Buch et al. (1993) give the only measurement of the binding energy difference between ortho- and para-H2 on an astrophysically relevant surface: amorphous water ice. Experimentally, they find a lower limit on the adsorbed OPR of 9 at 12 K before conversion has time to take place, which corresponds to a difference between ortho- and para-binding energies of ΔTphys ≥ 13 K. They also study the distribution of binding energies numerically for both ortho- and para-H2 on amorphous water ice, and find for para-H2 a binding energy of 646 ± 177 K and a difference between the ortho- and para- binding energies of 30 ± 16 K.
These values of the binding energy are summarized in Table 2. Overall, a value of 500−600 K seems reasonable for both amorphous carbons and amorphous silicates, a value of 315 K for crystalline silicates and a value in the range 500−800 K for amorphous water ices. We therefore explore a range of binding energies between 300 and 800 K. In addition, we investigate the effect of an ortho/para difference in binding energies by testing both without difference and with a difference of 30 K.
The desorption rates of ortho- and para-H2 (for one molecule) are then 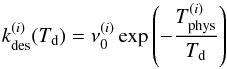 (7)with i = o for ortho-H2 and i = p for para-H2, and where the ν0 are typical vibration frequencies given by (Hasegawa et al. 1992)
(7)with i = o for ortho-H2 and i = p for para-H2, and where the ν0 are typical vibration frequencies given by (Hasegawa et al. 1992) 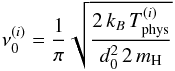 (8)with d0 = 0.1 nm the typical width of the potential well.
(8)with d0 = 0.1 nm the typical width of the potential well.
2.4. Photon emission and absorption
These surface processes are sensitive to the grain temperature. This temperature is controlled by the absorption and emission of photons by the grain, which we model as in Bron et al. (2014).
The power received by the grain at a photon energy U is Pabs(U) = 4π2a2Qabs(U) IU(U), where Qabs(U) is the absorption efficiency coefficient of the grain at photon energy U, and IU(U) the radiation field intensity at photon energy U (in units of W m-2 J-1 sr-1). Later, we need transition rates between thermal energy states of the grain. The rate of photon absorptions at this energy U is 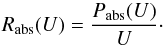 (9)We approximate the grain emission by a modified black body law with a specific intensity Qabs(U) BU(U,Td), where BU(U,T) is the usual black body specific intensity. The power emitted at photon energy U is then Pem(U,Td) = 4π2a2Qabs(U) BU(U,Td), and the photon emission rate is
(9)We approximate the grain emission by a modified black body law with a specific intensity Qabs(U) BU(U,Td), where BU(U,T) is the usual black body specific intensity. The power emitted at photon energy U is then Pem(U,Td) = 4π2a2Qabs(U) BU(U,Td), and the photon emission rate is 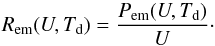 (10)These events occur randomly as Poisson processes and cause fluctuations of the grain temperature. The impact of these fluctuations on the efficiency of ortho-para conversion on dust grains is investigated in detail in the following sections. In the simpler rate equation treatment that we use for comparison, we neglect these fluctuations and use the usual equilibrium temperature Teq of the grain, defined by the balance between the instantaneous emitted and absorbed powers:
(10)These events occur randomly as Poisson processes and cause fluctuations of the grain temperature. The impact of these fluctuations on the efficiency of ortho-para conversion on dust grains is investigated in detail in the following sections. In the simpler rate equation treatment that we use for comparison, we neglect these fluctuations and use the usual equilibrium temperature Teq of the grain, defined by the balance between the instantaneous emitted and absorbed powers: 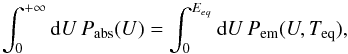 (11)where the upper bound on the righthand side accounts for the finite total energy of the grain (Eeq is the thermal energy of the grain at the equilibrium temperature, related to Teq by
(11)where the upper bound on the righthand side accounts for the finite total energy of the grain (Eeq is the thermal energy of the grain at the equilibrium temperature, related to Teq by 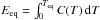 , with C(T) the heat capacity of the grain).
, with C(T) the heat capacity of the grain).
In the following, we use a standard interstellar radiation field (Mathis et al. 1983) and apply a scaling factor χ to the UV component of the field. We measure the UV intensity of those fields using the usual 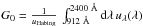 , where uHabing = 5.3 × 10-15 J m-3, and G0 is related to χ as G0 ≃ 0.65 χ.
, where uHabing = 5.3 × 10-15 J m-3, and G0 is related to χ as G0 ≃ 0.65 χ.
The dust properties (C(Td), Qabs(U), and ρ) are taken from Compiègne et al. (2011) and the DustEM code1. We consider amorphous carbon and silicate dust populations and use the properties used in this reference (see references therein, in their Appendix A).
2.5. Rate equation model at constant temperature
We compare the results of our statistical treatment presented in the next section to a simpler rate equation model that neglects dust temperature fluctuations and that we present in this section. In this simple model, the grain is thus supposed to be at a constant temperature Td, for which we take the equilibrium temperature defined by Eq. (11).
Using the rates of the different processes defined above, we can thus write a system of rate equations: 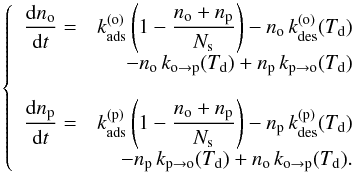 (12)At equilibrium, we find
(12)At equilibrium, we find 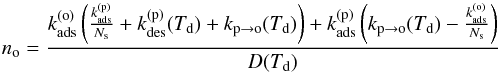 (13)and
(13)and 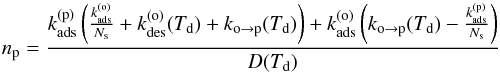 (14)with
(14)with 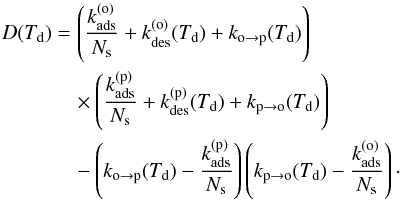 (15)To evaluate the efficiency of the ortho-para conversion process, we first define the net ortho-para conversion rate (in s-1) on the grain surface as
(15)To evaluate the efficiency of the ortho-para conversion process, we first define the net ortho-para conversion rate (in s-1) on the grain surface as 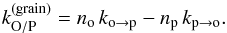 (16)The net conversion rate is positive when conversion occurs in the usual ortho-to-para direction and negative if para-to-ortho conversion occurs. The latter case could happen if the grains are warmer than the gas.
(16)The net conversion rate is positive when conversion occurs in the usual ortho-to-para direction and negative if para-to-ortho conversion occurs. The latter case could happen if the grains are warmer than the gas.
We then define the ortho-para conversion efficiency as 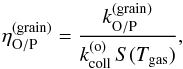 (17)which represents the fraction of the ortho-H2 molecules sticking to the grain that are converted to para-H2 (in a stationary situation). We took the parts that depend on the gas conditions (density, temperature) out of our definition of the conversion efficiency, in order to separate the effects of the sticking coefficient from the surface conversion process. We also note that this definition is only meaningful if conversion occurs in the ortho-to-para direction, which will be the case in our applications.
(17)which represents the fraction of the ortho-H2 molecules sticking to the grain that are converted to para-H2 (in a stationary situation). We took the parts that depend on the gas conditions (density, temperature) out of our definition of the conversion efficiency, in order to separate the effects of the sticking coefficient from the surface conversion process. We also note that this definition is only meaningful if conversion occurs in the ortho-to-para direction, which will be the case in our applications.
In this constant temperature rate equation model, the results are not directly affected by the grain size, except through the equilibrium temperature, which depends on size. We thus show a few results here as a function of dust temperature.
Since the conversion efficiency is controlled by the competition between conversion and desorption (an ortho-H2 molecule needs to have time to convert before desorbing), the two main parameters affecting this efficiency are the binding energy Tphys, which controls the desorption rate, and the conversion timescale τconv.
 |
Fig. 2 Conversion efficiency as a function of the grain temperature for different para-H2 binding energies in the constant temperature rate equation model. The gas ortho-para ratio is taken as 3, and the conversion timescale at 10 s. |
Figure 2 shows the impact of the binding energy on the conversion efficiency. In all cases, the efficiency curves are bell-shaped, with a flat top at full efficiency. At high temperature, desorption is too fast, and the adsorbed H2 molecules do not have time to convert from ortho to para. At low temperatures, H2 molecules cover all the surface because desorption is very slow, and most molecules coming from the gas are rejected. The range of temperature where conversion is efficient is thus very limited.
The width and position of the efficiency window is strongly affected by the binding energy, going from 7−10 K for Tphys = 300 K to 17−26 K for Tphys = 800 K. Consequently, this model predicts that in PDR conditions where the grains are exposed to a strong UV field and are thus warmer than this efficiency window (typically 30−50 K for small grains), ortho-para conversion on dust grain should be inefficient. We see in Sect. 4 that taking the dust temperature fluctuations into account changes this picture significantly.
Figure 3 shows the influence of the conversion timescale. It only affects the upper limit of the efficiency window because the lower limit is due to rejection and controlled by the competition between adsorption and desorption. Its impact is less than that of the binding energy because the conversion rate is inversely proportional to this timescale, while the desorption rate depends exponentially on the binding energy. It can still double the width of the efficiency window over the range of relevant values.
 |
Fig. 3 Conversion efficiency as a function of the grain temperature for different conversion timescales in the constant temperature rate equation model. The gas ortho-para ratio is taken as 3, and the binding energy at 650 K. |
 |
Fig. 4 Ortho-para ratio of the adsorbed molecules with and without a difference of binding energy ΔTphys between ortho-H2 and para-H2. This computation was done with a gas ortho-para ratio of 3, a binding energy for para-H2 of 500 K, and a conversion timescale of 10 s. |
Finally, Fig. 4 shows how a difference in binding energy ΔTphys between ortho-H2 and para-H2 affects the OPR of the adsorbed molecules. At low temperature, conversion is much faster than desorption and the OPR on the surface is very low. When desorption starts to become significant, para-H2 desorbs faster than ortho-H2, and the surface population is enriched in ortho-H2, leading to a surface OPR significantly higher than 3. This enrichment could play a role in further surface reactions leading to more complex molecules. A higher binding energy for ortho-H2 than for para-H2 also makes the high efficiency window slightly larger, but the effect is small compared to the effects of the other parameters described above.
3. Method for a stochastic model
We now take the dust temperature fluctuations into account. We are interested in the average conversion efficiency under the effect of these fluctuations in a statistically stationary situation. It is thus sufficient to compute the stationary probability density function (PDF) of the state of the grain, f(Td,no,np), and from this all average quantities of interest can be deduced. In the following, we denote T as the instantaneous temperature of the grain to simplify the notations. Moreover, we work with the thermal energy of the grain E rather than its temperature T. The two are related by 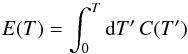 (18)where C(T) is the heat capacity of the grain. Conversely, we also denote T(E) as the temperature corresponding to thermal energy E.
(18)where C(T) is the heat capacity of the grain. Conversely, we also denote T(E) as the temperature corresponding to thermal energy E.
3.1. General master equation
Since the state of the system evolves in time by discrete events (photon absorption or emission, adsorption, desorption or conversion of a molecule), the evolution of its PDF is governed by a master equation of the form 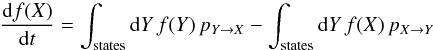 (19)where X generically describes the state of the system, and pX → Y are the transition rates from state X to state Y. The integrals are to be interpreted as integrals over the continuous state variables (e.g., the thermal energy E of the grain) and sums over the discrete state variables (e.g., the number no of ortho-H2 molecules on the surface).
(19)where X generically describes the state of the system, and pX → Y are the transition rates from state X to state Y. The integrals are to be interpreted as integrals over the continuous state variables (e.g., the thermal energy E of the grain) and sums over the discrete state variables (e.g., the number no of ortho-H2 molecules on the surface).
The transition rates of the possible events are 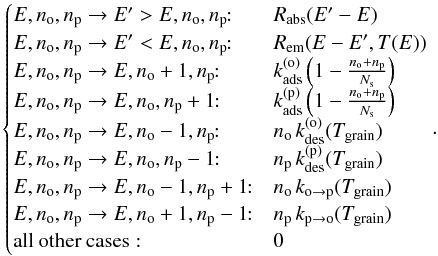 (20)Explicitly writing the terms corresponding to the different processes in Eq. 19 and considering statistical equilibrium, we get the stationary master equation governing f(E,no,np):
(20)Explicitly writing the terms corresponding to the different processes in Eq. 19 and considering statistical equilibrium, we get the stationary master equation governing f(E,no,np): 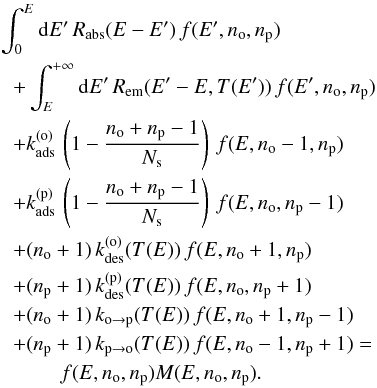 (21)where
(21)where 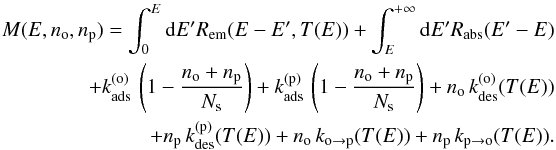 (22)As boundary conditions, f(E,no,np) = 0 if no< 0, np< 0, E< 0 or no + np>Ns.
(22)As boundary conditions, f(E,no,np) = 0 if no< 0, np< 0, E< 0 or no + np>Ns.
Directly solving this equation numerically would be extremely time-consuming because the unknown is a function of three variables. We can, however, simplify the problem by noting that all the average quantities of interest can be expressed in terms of the marginal thermal energy PDF, 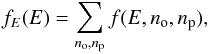 (23)and of the conditional expectation for the ortho and para populations at a given instantaneous thermal energy
(23)and of the conditional expectation for the ortho and para populations at a given instantaneous thermal energy 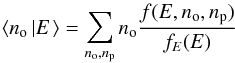 (24)and
(24)and 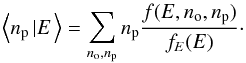 (25)For instance, the average conversion efficiency (using the definition by Eq. (17))
(25)For instance, the average conversion efficiency (using the definition by Eq. (17)) 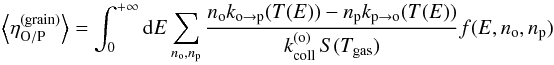 (26)can also be expressed as
(26)can also be expressed as 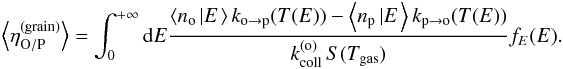 (27)We thus compute three single-variable functions rather than one three-variable function. We now deduce the equations governing these three functions.
(27)We thus compute three single-variable functions rather than one three-variable function. We now deduce the equations governing these three functions.
3.2. Marginal temperature equation
We start by deriving the equation governing the marginal thermal energy PDF. This equation can be deduced from the main master equation Eq. (19). By applying 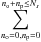 to Eq. (19), we get
to Eq. (19), we get 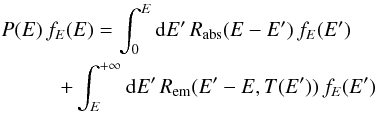 (28)with
(28)with 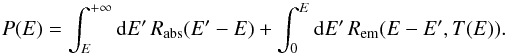 (29)This equation governs the marginal PDF fE(E) of the thermal energy of the grain, which describes the stationary statistics of the temperature fluctuations. It was already encountered in Bron et al. (2014) when studying the impact of dust temperature fluctuations on H2 formation on grain surfaces. We use the same numerical resolution method here, which consists in iteratively applying the operator
(29)This equation governs the marginal PDF fE(E) of the thermal energy of the grain, which describes the stationary statistics of the temperature fluctuations. It was already encountered in Bron et al. (2014) when studying the impact of dust temperature fluctuations on H2 formation on grain surfaces. We use the same numerical resolution method here, which consists in iteratively applying the operator = \frac{\int_{0}^{E}{\rm d}E'\,R_{\mathrm{abs}}(E\!-\!E')\,f_{E}(E')\!+\!\int_{E}^{+\infty}{\rm d}E'\,R_{\mathrm{em}}(E'\!-\!E,T(E'))\,f_{E}(E')}{P(E)} \end{eqnarray}](/articles/aa/full_html/2016/04/aa27879-15/aa27879-15-eq227.png) (30)to an initial guess until some convergence criterium is met.
(30)to an initial guess until some convergence criterium is met.
The thermal energy PDF fE can be converted into the temperature PDF fT using the usual variable change rule for PDFs: 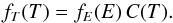 (31)
(31)
3.3. Marginal population equations
We now deduce the equations governing the conditional expectation of the ortho and para populations. Applying the operators 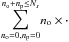 and
and 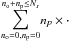 to Eq. (19) yields the system of equations governing ⟨no|E⟩ and
to Eq. (19) yields the system of equations governing ⟨no|E⟩ and 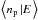 :
: 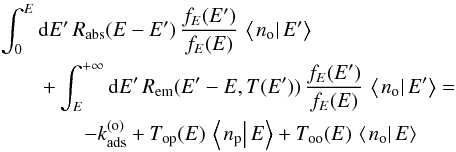 (32)and
(32)and 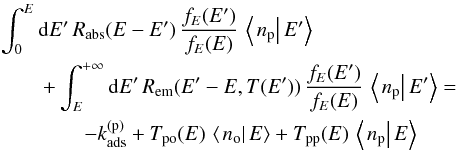 (33)where
(33)where 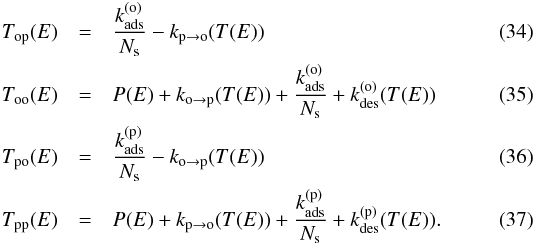 This is a system of coupled inhomogeneous second-kind Fredholm equations. Similar to the situation encountered in Bron et al. (2014) with a similar equation, the discretized version of this system gives a linear system that converges exponentially fast toward a singular system when the grain size a grows. To avoid numerical problems, we use the same trick as in Bron et al. (2014) and eliminate the constant terms
This is a system of coupled inhomogeneous second-kind Fredholm equations. Similar to the situation encountered in Bron et al. (2014) with a similar equation, the discretized version of this system gives a linear system that converges exponentially fast toward a singular system when the grain size a grows. To avoid numerical problems, we use the same trick as in Bron et al. (2014) and eliminate the constant terms 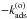 and
and 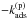 to get a system of homogeneous second-kind Fredholm equation that can be solved by the same iterative method as the marginal temperature equation in the previous section.
to get a system of homogeneous second-kind Fredholm equation that can be solved by the same iterative method as the marginal temperature equation in the previous section.
By multiplying Eqs. (32) and (33) by fE(E) and integrating over E, we obtain 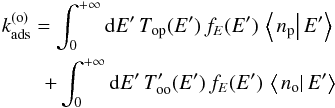 (38)and
(38)and 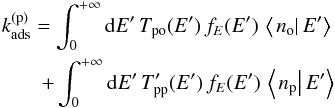 (39)with
(39)with 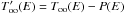 and
and 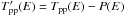 .
.
Injecting Eqs. (38) and (39) into Eqs. (32) and (33), we get ![\begin{eqnarray} \int_{0}^{+\infty}{\rm d}E'\left[\frac{G(E,E')}{f(E)}+T_{\mathrm{oo}}'(E')\right]f_{E}(E')\,\left\langle \left.n_{\mathrm{o}}\right|E'\right\rangle \nonumber\\ +\int_{0}^{+\infty}{\rm d}E'\,T_{\mathrm{op}}(E')\,f_{E}(E')\,\left\langle \left.n_{\mathrm{p}}\right|E'\right\rangle =\nonumber\\ T_{\mathrm{op}}(E)\,\left\langle \left.n_{\mathrm{p}}\right|E\right\rangle +T_{\mathrm{oo}}(E)\,\left\langle \left.n_{\mathrm{o}}\right|E\right\rangle \label{eq:pop_equations_interm_o} \end{eqnarray}](/articles/aa/full_html/2016/04/aa27879-15/aa27879-15-eq244.png) (40)and
(40)and ![\begin{eqnarray} \int_{0}^{+\infty}{\rm d}E'\left[\frac{G(E,E')}{f_{E}(E)}+T_{\mathrm{pp}}'(E')\right]f_{E}(E')\,\left\langle \left.n_{\mathrm{p}}\right|E'\right\rangle\nonumber \\ +\int_{0}^{+\infty}{\rm d}E'\,T_{\mathrm{po}}(E')\,f_{E}(E')\,\left\langle \left.n_{\mathrm{o}}\right|E'\right\rangle =\nonumber\\ T_{\mathrm{po}}(E)\,\left\langle \left.n_{\mathrm{o}}\right|E\right\rangle +T_{\mathrm{pp}}(E)\,\left\langle \left.n_{\mathrm{p}}\right|E\right\rangle \label{eq:pop_equation_interm_p} \end{eqnarray}](/articles/aa/full_html/2016/04/aa27879-15/aa27879-15-eq245.png) (41)with
(41)with 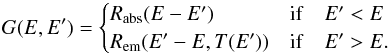 (42)Equations (40) and (41) are now homogeneous.
(42)Equations (40) and (41) are now homogeneous.
Finally, we can rewrite this system in vector form as![\begin{eqnarray} &&\left(\begin{array}{cc} T_{\mathrm{oo}}(E) & T_{\mathrm{op}}(E)\\ T_{\mathrm{po}}(E) & T_{\mathrm{pp}}(E) \end{array}\right)^{-1}\times\int_{0}^{+\infty}{\rm d}E'\nonumber\\ &&\left[ \left(\begin{array}{cc} \left[\frac{G(E,E')}{f(E)}+T_{\mathrm{oo}}'(E')\right]f_{E}(E') & T_{\mathrm{op}}(E')\,f_{E}(E')\\ T_{\mathrm{po}}(E')\,f_{E}(E') & \left[\frac{G(E,E')}{f(E)}+T_{\mathrm{pp}}'(E')\right]f_{E}(E') \end{array}\right)\left(\begin{array}{c} \left\langle \left.n_{\mathrm{o}}\right|E'\right\rangle \\ \left\langle \left.n_{\mathrm{p}}\right|E'\right\rangle \end{array}\right) \right]\nonumber\\ &&=\left(\begin{array}{c} \left\langle \left.n_{\mathrm{o}}\right|E\right\rangle \\ \left\langle \left.n_{\mathrm{p}}\right|E\right\rangle \end{array}\right),\label{eq:population_marginal_equation_vector_form_final} \end{eqnarray}](/articles/aa/full_html/2016/04/aa27879-15/aa27879-15-eq247.png) (43)where the integral sign is to be applied to each component of the vector. The first matrix is always invertible, as can be easily verified by expressing its determinant.
(43)where the integral sign is to be applied to each component of the vector. The first matrix is always invertible, as can be easily verified by expressing its determinant.
This equation shows that the solution is an eigenvector associated with eigenvalue 1 for the linear integral operator defined by the lefthand side. After discretization of the problem, we numerically compute such an eigenvector, and we then normalize it using Eqs. 38 and 39. Once fE(E), ⟨no|E⟩ and 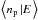 are computed, we can compute all the average quantities of interest.
are computed, we can compute all the average quantities of interest.
4. Results
We now present the results of this computation of the ortho-para conversion efficiency that takes the dust temperature fluctuations into account. We first discuss how the temperature fluctuations change the efficiency in PDR-like conditions significantly, before investigating the influence of the microphysical parameters of the model. When not specified otherwise, our standard model consists of amorphous carbon grains with a binding energy of H2Tphys = 550 K and a conversion timescale τconv = 10 s.
4.1. Efficiency of the conversion process in PDR-like conditions
 |
Fig. 5 Conversion efficiency on one grain as a function of grain size for different radiation field intensities G0. Solid lines: full statistical model; dashed lines: rate equation model without dust temperature fluctuations. |
We present the results in terms of the average conversion efficiency defined by Eq. (27). Figure 5 shows this average conversion efficiency for a single grain as a function of grain size and for different ambient UV radiation field intensities G0. The results of the full statistical computation (solid lines) are compared to those of the simpler rate equation model that neglects the dust temperature fluctuations (dashed lines).
In the rate equation model, the grains are assumed to be at a constant temperature at their equilibrium temperature. As discussed in Sect. 2.5, the ortho-para conversion process is then only efficient when the grains are sufficiently cold. The rate equation model thus only approaches full efficiency for the largest grains, and gives efficiencies that decrease sharply with the radiation field intensities for all sizes. Under G0 = 1, the efficiency is a few percent for most sizes.
The full statistical model gives significantly different results. For large grains, UV photons (limited to the Lyman limit in PDRs) do not have enough energy to cause significant fluctuations in the dust temperature. The full model and the rate equation model thus give the same efficiencies for large grains. For small grains, the full model finds efficiencies that are orders of magnitude higher than the rate equation model. There seems to be a critical size below which conversion occurs at almost full efficiency. This critical size distinguishes small grains for which the temperature PDF is wide enough to overlap with the high efficiency window found in Sect. 2.5 from large grains whose narrow temperature PDF falls entirely outside this window. Small grains thus spend a very large portion of their time at low temperatures, where conversion is efficient, between very short high temperature spikes during which desorption becomes dominant.
 |
Fig. 6 Temperature PDF of amorphous carbon grains of various sizes under an external UV field with G0 = 100. |
These temperature PDFs can be seen in Fig. 6 in the case of an external radiation field with G0 = 100 (corresponding to the red curve in Fig. 5). Grains of size 1 nm and 3 nm have very wide temperature PDFs with a high probability around 10−20 K, corresponding to the cold state of grains between the high-temperature spikes caused by UV-photon absorption. (The high-temperature spikes correspond here to the long low-probability high-temperature tails for these sizes.) This temperature range also corresponds to the high conversion efficiency window found in Sect. 2.5, which explains why we find high conversion efficiency for these grain sizes in Fig. 5. In comparison, the temperature PDFs for sizes of 10, 30, and 100 nm are not wide enough to cover the high efficiency window, so these grain sizes have much lower conversion efficiencies.
To evaluate the resulting overall efficiency, we can then integrate the average net conversion rate 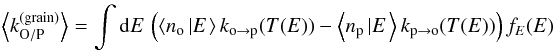 (44)over the full dust size distribution to obtain the overall net conversion rate
(44)over the full dust size distribution to obtain the overall net conversion rate 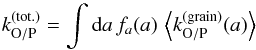 (45)where fa(a) is the dust size distribution. We then define the overall conversion efficiency as
(45)where fa(a) is the dust size distribution. We then define the overall conversion efficiency as 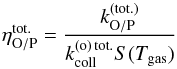 (46)where
(46)where 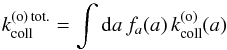 (47)is the total collision rate of ortho-H2 on grains.
(47)is the total collision rate of ortho-H2 on grains.
In this section, we use a simplified dust population comprising only amorphous carbon grains from 1 nm to 0.3 μm with a MRN-like (Mathis et al. 1977) power-law size distribution with exponent −3.5. Since we assume that conversion is inefficient on PAHs, not including them in our dust population does not affect the results.
 |
Fig. 7 Overall conversion efficiency for a full dust size distribution as a function of the UV intensity G0. |
Figure 7 shows the resulting total conversion efficiency for the full dust distribution as a function of UV intensity G0. The results of the full statistical computation (solid line) are again compared to those of the rate equation model without fluctuations (dashed lines). In the rate equation model, we saw in Fig. 5 that all sizes exceping the largest had low efficiencies that were sharply decreasing when increasing the UV intensity. Since small grains represent most of the dust surface in our dust population, the overall conversion efficiency in the rate equation model is never higher than a few percent, and it decreases quickly when G0 is increased. In the full model, the efficiencies of the smallest grains were almost unaffected by the UV intensity. Because they dominate the total dust surface available for conversion, the overall conversion efficiency is much less affected by G0 and remains above 10% up to G0 = 1000.
Dust temperature fluctuations thus make ortho-para conversion on grains efficient in most PDR conditions, because small grains, which dominate the total surface and undergo large temperature fluctuations, spend a large portion of their time at low temperature between the temperature spikes caused by photon absorption events. This efficiency does not include the sticking efficiency.
4.2. Influence of the microphysical parameters
We now investigate the impact of the uncertainties on the microphysical parameters. The two most important parameters are the binding energy Tphys, which controls the desorption rate, and the conversion timescale τconv, which controls the conversion rate.
 |
Fig. 8 Overall conversion efficiency as a function G0 for different values of the binding energy of H2, Tphys. |
Figure 8 shows the effect of the binding energy Tphys on both the rate equation model (dashed lines) and the full statistical model. While the rate equation model is highly sensitive to the value of the binding energy (seven order-of-magnitude difference at low G0 between Tphys = 300 K and 800 K), the effect on the full statistical model is much less. As Tphys is decreased, the high efficiency window described in Sect. 2.5 is shifted to a lower temperature. In the rate equation model where a grain has a single constant temperature, this temperature will at some point fall out of the efficiency window, resulting in a sharply decreasing efficiency. In contrast, small grains in the full statistical model have a wide temperature PDF. As the efficiency window is shifted, it will still be covered by the tails of the PDF, resulting in a much smoother decrease in the efficiency. The uncertainties on the binding energies thus only cause uncertainties on the efficiency of at most slightly more than one order of magnitude, instead of the seven orders of magnitude of uncertainty when neglecting the fluctuations.
 |
Fig. 9 Overall conversion efficiency as a function G0 for different values of the conversion timescale τconv. |
Figure 9 similarly shows the impact of the uncertainties on τconv. A similar effect is observed, although less dramatic. While in the rate equation models, the uncertainties on τconv cause a four order-of-magnitude difference in the efficiency, the full model is almost unaffected up to G0 ≃ 100, and it leads to differences of slightly more than two orders of magnitude at most for the strongest UV fields.
The dust temperature fluctuations thus significantly reduce the impact of the uncertainties about the microphysical parameters. Uncertainties of typically one or two orders of magnitude still remain on the final conversion efficiency.
5. PDR models and PDR observations
We now investigate the effects of this new computation of the ortho-para conversion rate on grains in full PDR models. The code developed here to perform the statistical calculation of the conversion rate has been coupled to the Meudon PDR code (Le Petit et al. 2006; Goicoechea & Le Bourlot 2007; Gonzalez Garcia et al. 2008; Le Bourlot et al. 2012).
This code2 solves the stationary state of a one-dimensional PDR by self-consistently computing the chemical balance (147 species and 2835 reactions here), the thermal balance between heating (photoelectric effect, cosmic rays, exothermic reactions, as well as H2 collisional de-excitation and dust-gas collisions that can act as heating or cooling terms), cooling (by the lines of 28 species for which level populations are computed from statistical balance), and the radiative transfer in the continuum (from radio to UV wavelength, taking dust absorption and scattering into account, as well as continuum absorption by the ionization of species such as C and S) and in the lines of the species for which the level populations are computed.
At each position in the cloud, the local radiation field, gas density, gas-phase H2 density, and OPR computed by the Meudon PDR Code are used for the statistical computation of the ortho-para conversion rate, which is sent back to the Meudon PDR Code for a new iteration. The dust population comprises a mixture of carbonaceous and silicate grains following a power-law size distribution with exponent −3.5 (Mathis et al. 1977) from 1 nm to 0.3 μm.
In addition, the Meudon PDR code includes the other processes affecting the ortho-para ratio: formation on grains is assumed to occur with an OPR of 3, photodissociation and shielding are computed level by level and thus naturally include preferential shielding of ortho-H2, and gas-phase ortho-para conversion includes reactive collisions with H (Le Bourlot et al. 1999, and references therein), H+ (Gerlich 1990), and H3+ (assuming identical rates as with H+).
In this section, we first present a detailed study of an example PDR model, discuss the local OPR in the regions emitting the rotational lines of H2, and show the impact of the conversion process on grains on the local OPR and on the intensities of the rotational lines. For a full grid of models, we then compare the OPR values that can be deduced from the predicted line intensities to actual PDR observations. Finally, we discuss the influence of the microphysical parameters τconv and Tphys on these results.
5.1. A typical PDR
As a typical PDR example, we consider here an isobaric model with P = 107 K cm-3 illuminated by the standard ISRF scaled by a factor χ = 103. In such a PDR, the first rotational lines of H2 are mainly emitted in the warm molecular layer that follows the H/H2 transitions and will thus provide information about the local OPR in this region.
 |
Fig. 10 Upper panel: density profiles of H (blue) and H2 (green) and gas temperature profile (red) in the PDR (P = 107 K cm-3, χ = 103). Lower panel: local emissivity profiles (color lines) of the first rotational lines of H2 (solid lines for para transitions and dashed lines for ortho transitions) compared to the local OPR profile (black). Local emissivities are multiplied by d so that the contribution of a given region to the total intensity is proportional to its area under the curve despite the logarithmic axis. Each emissivity curve has been scaled so that its maximum is 1 for ease of comparison. |
Because of the large energy differences between the first rotational levels and the temperature gradient present in this layer, the successive lines are emitted in overlapping but relatively separated layers, as can be seen in Fig. 10. This figure shows the local emissivity profiles as a function of position, compared to the local OPR (lower panel), for a model that includes our treatment of surface conversion. We multiply the local emissivity ϵ by the distance from the edge so that the contribution of a given region to the total line intensity can be evaluated visually as the area under the curve in this region despite the logarithmic scale used for the distance axis. The emissivity profile of each line has also been scaled so that its maximum is 1. For reference, the density profiles of H and H2 and the temperature profile are shown in the upper panel.
The local OPR shows a bump above 3 just before the H/H2 transition, owing to preferential self-shielding of ortho-H2 compared to para-H2 as H2 is assumed to form with an OPR of 3 (as discussed in Abgrall et al. 1992; Sternberg & Neufeld 1999). The OPR is then at 3 immediately after the H/H2 transition before decreasing sharply between 8 × 10-3 and 10-2 pc. The position of this sharp decrease is controlled by the efficiency of the ortho-para conversion process on grains, as we show later.
We see that the emission regions of the H2 lines, starting at the H/H2 transition for the higher lines, extend farther than the OPR drop for the lower lines. The first five rotational lines usually observed in PDR are thus emitted in a region with a strongly varying OPR. We can thus expect that the OPR values deduced from the line intensities will vary from 3 for the highest lines to a significantly lower value for the lowest lines. As described in the next section, we have thus computed observational OPR values based on each successive triplet of lines for our comparison between models and observations.
We can also note that the sharp decrease in the OPR causes an increase in the para lines relative to the ortho lines, resulting in an inversion of the emission peaks of the S(1) and S(2) lines, the S(1) emission peak occurring before (and thus in warmer gas than) the S(2) peak, which in turn occurs after the OPR drop. This inversion is highly dependent on the efficiency of ortho-para conversion on grains. Resolving this inversion at the distance of a PDR such as NGC 7023 would, for instance, require a ~ 1″ spatial resolution for the rotational lines of H2, and will become possible with the James Webb Space Telescope.
 |
Fig. 11 Comparison of the local OPR profiles in the PDR in models with P = 107 K cm-3 and χ = 103 for the four prescriptions for ortho-para conversion on grains: no conversion (purple), rate equation approach neglecting the fluctuations (green), statistical approach taking the fluctuations into account (blue), and full conversion for H2 molecules sticking to grains (red). The temperature profile of the PDR is also shown for reference (dotted black line), along with the corresponding LTE OPR profile (solid black line). |
Figure 11 shows the influence of the surface conversion efficiency on the position of the OPR drop. We compare the OPR profile corresponding to LTE with the local temperature (black) to the OPR profiles obtained in PDR models implementing four different prescriptions for ortho-para conversion on grains: no surface conversion (purple); the rate equation treatment presented in Sect. 2.5, which neglects dust temperature fluctuations (green); the full statistical treatment described in Sect. 3, which takes fluctuations into account (blue); and a model assuming that all H2 molecules sticking to grains are converted (red). As expected, the more efficient surface conversion, the closer to the H/H2 transition the OPR drop occurs. We also see that the results of the statistical computation are distinctly different from those of the simpler approximations and cannot be approximated by a simpler formalism. In the absence of surface conversion, the OPR drop starts when the temperature falls below 200 K as expected for a LTE OPR. Just before the drop in the case without surface conversion, the OPR peaks at ~ 3.7 because photodissociation-formation cycling becomes the dominant mechanism again, since reactive collisions with H collapse proportionally to the H density after the H/H2 transition. This only affects the local OPR in the absence of efficient surface conversion, and no such effect is present in our model that includes the statistical treatment of surface conversion.
 |
Fig. 12 Conversion rates by the different processes: gas-phase reactive collisions (magenta), destruction-formation cycling (green), and dust surface conversion (blue). |
These OPR profiles can be better understood by considering the rates of the different conversion processes that control the local OPR. Figure 12 shows the conversion rates per H2 molecules by gas-phase reactive collisions (magenta), by destruction-formation cycling (green), and by dust surface conversion (blue), for a model that includes our statistical treatment of surface conversion. Both ortho-para (solid lines) and para-ortho (dashed lines) rates are shown. In this representation (assuming chemical balance), the local OPR is equal to the ratio of total para-ortho conversion rate to total ortho-para conversion. Before the H/H2 transition, conversion is mainly due to reactive collisions (with H), but photodissociation is non-negligible and causes the OPR bump (OPR > 3) due to preferential shielding of ortho-H2. After the transition, reactive collisions dominate until conversion on grain surface becomes comparable, at which point the local OPR decreases sharply to low values. This transition of the local OPR from 3 to very low values is thus due to surface conversion becoming dominant over reactive collisions. This explains why the position of this transition appeared to be controlled by the efficiency of surface conversion on Fig. 11.
Previous studies of the OPR in PDR observations (e.g., Fleming et al. 2010) have advocated advection flows that bring cold (low-OPR) gas from the molecular cloud through the PDR front to explain the low OPR values that are observed. We see in the next section that the observed values can be explained by our model without advection flows. We can, however, estimate the minimum velocity required for an advection flow to affect H2 rotational lines intensities. Such a flow would need to bring cold (low-OPR) gas into the region where we predict an OPR of three. The OPR transition occurs on a width of ~ 3 × 10-3 pc, and the para-ortho conversion rate at the start of this transition is on the order of 10-11 s-1. A minimum advection velocity of ~ 1 km s-1 would thus be required to affect the observable OPR in rotational intensities. This value corresponds to the maximum advection velocity through the dissociation front computed by Störzer & Hollenbach (1998) for PDRs with an advancing photo-ionization front. We thus estimate that advection could only affect the observable OPR of the rotational lines in the most dynamical PDRs with fast photo-ionization fronts.
 |
Fig. 13 Intensities of the first rotational lines of H2 predicted by the same PDR model (P = 107 K cm-3 and χ = 103) for the four prescriptions for ortho-para conversion on grains: no conversion (purple), rate equation approach neglecting the fluctuations (green), statistical approach taking the fluctuations into account (blue), and full conversion for H2 molecules sticking to grains (red). |
Finally, we show the impact of these differences on the line intensities of the rotational lines of H2 in Fig. 13. The lines S(3), S(4), and S(5), which are mainly emitted before the OPR drop in all cases, are almost unaffected. The lines S(0), S(1), and S(2) are strongly affected with a S(1)/S(2) ratio varying by a factor of 4, and a S(3)/S(2) ratio varying by a factor of almost 3. The impact tends to be stronger for lower pressure models, as seen in the next section.
5.2. Comparison of a grid of models to PDR observations
Sample of PDR observations of lines S(0) to S(3) with the derived values of T24, OPR234, T35, and OPR345.
As discussed in the previous section, the different rotational lines are emitted in regions with large differences in local OPR values. Interpreting observed rotational diagrams with a single OPR value is thus insufficient. We try here to measure the OPR as locally as possible by computing separate OPR values for each triplet of successive lines. We note OPRj−1,j,j+1 the OPR computed from the column densities of levels J = j−1, j and j + 1 (derived from the line intensities of lines S(j−3), S(j−2), and S(j−1)). This OPR value is computed from the misalignment of level j with respect to the line defined by levels j−1 and j + 1 in the rotational diagram as 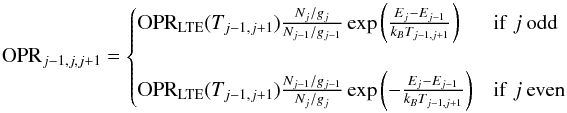 (48)where Nj is the column density of level j (deduced from the intensity of line S(j−2)), gj and Ej the degeneracies and energies of level j, and Tj−1,j + 1 is the excitation temperature computed from levels j−1 and j + 1 (thus unaffected by OPR effects),
(48)where Nj is the column density of level j (deduced from the intensity of line S(j−2)), gj and Ej the degeneracies and energies of level j, and Tj−1,j + 1 is the excitation temperature computed from levels j−1 and j + 1 (thus unaffected by OPR effects), 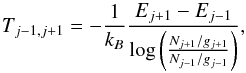 (49)and OPRLTE(T) is the thermal equilibrium value of the OPR at temperature T.
(49)and OPRLTE(T) is the thermal equilibrium value of the OPR at temperature T.
This measure of the OPR can be affected by the presence of a curvature in the excitation diagram, corresponding for instance to a strong temperature gradient in the region of emission. A positive curvature will lead to an overestimation of OPRj−1,j,j+1 for even values of j and an underestimation for odd values of j, as it will create a misalignment caused not by an actual out-of-equilibrium OPR value but by a varying excitation temperature for increasing values of J. We therefore compare the OPR values derived from the observations to OPR values similarly derived from the line intensities predicted by the models rather than to the actual local OPR value. However, lower-than-three OPR values are found for both odd and even values of j in the observations, indicating a physical OPR lower than three.
We will focus on the lines that are the most affected by surface conversion on grains, the lines S(0) to S(3), which are also observed in a larger sample of PDR observations. The observation sample gathered from the literature is presented in Table 3, with the values of T24, OPR234, T35, and OPR345 derived from the observed line intensities.
As shown by Joblin et al. (in prep.), the pressure in the dense structures of PDRs seems to be related to the intensity of the UV radiation field, with a roughly constant P/G0 ratio. The typical value for the ratio P/G0 in PDRs appears to be ~ 2 × 104 with a scatter of a factor of 2−3 above and below. In our PDR models, we recall that G0 is related to the scaling factor χ by the relation G0 ~ 0.65χ. The observed P−G0 relation thus corresponds to P/χ ~ 104. We thus use a grid of models covering a range of P/χ from 2 × 103 to 5 × 104 (a factor 5 above and below the observed value), and a range of pressures from P = 105 to 109 K cm-3.
In the region where lines S(0) to S(3) are emitted, the local OPR is controlled by the balance between gas phase reactive collisions, which tends to thermalize the OPR to 3 and whose efficiency depends on the gas temperature, and surface conversion, which tends to thermalize the OPR to a lower value corresponding to dust temperature. The resulting observable OPR thus depends both on the surface conversion efficiency (which we wish to constrain) and on the gas temperature (which is controlled by the photoelectric efficiency in this region). Rather than simply comparing the measured OPR values, we thus investigate the OPR-Tgas relation in both observations and model. When considering OPRj−1,j,j+1, we therefore estimate the gas temperature of the corresponding layer of the PDR through the excitation temperature Tj−1,j + 1.
 |
Fig. 14 OPR computed from levels J = 2, 3,and4 as a function of the excitation temperature T24, comparing PDR observations (symbols) to PDR models (lines). PDR models implement four prescriptions for ortho-para conversion on grains: no conversion (purple), rate equation approach without fluctuations (green), statistical approach with fluctuations (blue), and full conversion (red). Solid lines correspond to models with P/χ = 104, while models with P/χ a factor of 5 above and below this value are shown as dotted lines. |
 |
Fig. 15 Same as Fig. 14 for the OPR computed from levels J = 3, 4, and 5, shown as a function of the excitation temperature T35. |
We present our comparison between models and observations in two figures that present the OPR234-T24 relationship (Fig. 14) and the OPR345-T35 relationship (Fig. 15). In both figures, we compare the observed values (symbols with error bars) to model results. As previously, we compare models with four different prescriptions for ortho-para conversion on grains: no surface conversion (purple), the rate equation treatment presented in Sect. 2.5 that neglects dust temperature fluctuations (green), the full statistical treatment described in Sect. 3 that takes fluctuations into account (blue), and a model assuming that all H2 molecules sticking to grains are converted (red). The solid lines show the results of models with P/χ = 104, while the dotted lines correspond to models with P/χ ratios a factor of 5 above and below this value. Finally, the LTE value of the OPR as a function of the local temperature is shown as a black line.
In Fig. 14, which corresponds to lines S(0), S(1), and S(2), we see a clear separation between high efficiency models (statistical approach and full efficiency hypothesis) and the models without conversion on dust. The observational data points all fall close to the curve of these high efficiency models and are clearly incompatible with the no-conversion models. The observations thus indicate that high-efficiency conversion on grains is indeed occurring in PDRs. We also see that the models with the rate equation treatment of surface conversion, which neglects dust temperature fluctuations, give results that are close to models with no conversion. The statistical effect of fluctuations is thus necessary to explain the high conversion efficiency that the observations seem to indicate. Finally, the observations seem to favor the full statistical treatment over a simpler full efficiency hypothesis, but the difference is smaller, and other uncertainties (for instance on the total dust surface available) could induce similar differences. However, the statistical treatment of fluctuations is again the only way to physically explain a high conversion efficiency.
In Fig. 15, which corresponds to lines S(1), S(2), and S(3), the observations are more scattered, but most datapoints again fall close to the results of models with the statistical treatment of fluctuations. The two outliers are the California PDR, whose large error bars still make it compatible with the models, and the Orion Bar PDR which seems to have a clearly different behavior from all other PDRs. Again, the observations indicate a high conversion efficiency on grains, which cannot be explained when neglecting the fluctuations and which slightly favor our statistical model over a full efficiency hypothesis.
In both figures, higher excitation temperatures correspond to higher pressure models. We see that the low-conversion-efficiency models (no conversion and rate equations neglecting the fluctuations) sometimes exhibit OPR values higher than 3. For OPR345, this is due to the strong curvature of the rotational diagram for low pressure models. For OPR234, curvature effects play in the opposite direction and only explain the drop in the OPR at the lowest temperature. The values above 3 are actually caused by the local peak of the OPR, seen in Fig. 11 after the H/H2 transition for models without efficient surface conversion. It is due to preferential photodissociation of para-H2 in a fully molecular region where reactive collisions with H are very rare. Moderate curvature effects are also seen in how the OPR values of models at high temperatures seem to converge towards a value lower than 3 for OPR234 and higher than 3 for OPR345. These measures of the OPR are thus slightly biased owing to the curvature of the rotational diagrams. Observations and models are, however, similarly biased, and these figures present equivalent information to S(1) /S(0) vs. S(2) /S(0) and S(2) /S(1) vs. S(3) /S(1) graphs, in a more physically meaningful form.
Finally, we note that the range in excitation temperatures found by the models is significantly more extended than the range of observed excitation temperatures, even though the observed objects cover a wide range of conditions. This probably indicates that the temperature profile (and possibly the density profile) in the region that emits H2 rotational lines is not adequate in the models. It could come from incorrectly estimating photoelectric heating or from the dynamics of the photodissociation front affecting the density profile of the PDR. The observations seem to indicate that PDRs with very different excitation conditions still have relatively similar temperatures (200−300 K) in the region where the first rotational lines of H2 (S(0) to S(2)) are emitted.
5.3. Influence of the microphysical parameters
Our microphysical model of ortho-para conversion on dust grains depends on two poorly constrained parameters: the surface conversion timescale τconv and the physisorption binding energy Tphys (cf. Sects. 2.2 and 2.3). We now investigate the impact of these uncertainties on the previously presented results.
We first study the impact of the conversion timescale τconv. We took τconv = 10 s as our standard value, while the possible values found in the literature range from 1 s to 104 s. Figures 16 and 17 therefore compare the results of PDR models using these three values of τconv. Only the models with the statistical treatment of fluctuations (solid lines) and with the rate equation treatment without fluctuations (dashed lines) are shown, in comparison to the observations. In both figures, the impact of the variations in τconv on the models with the statistical treatment is limited, and the model results remain compatible with the observations. Models implementing the rate equation treatment are more strongly affected (for OPR234) but remain incompatible with the observations.
 |
Fig. 16 Influence of the surface conversion timescale τconv on the observable OPR234 as a function of T24. We compare model results for three values of τconv (1 s in red, 10 s in blue, and 104 s in green) and for two different prescriptions of the ortho-para conversion on grains (rate equation neglecting fluctuations in dashed lines, full statistical treatment of fluctuations in solid lines) to the PDR observations. |
For the physisorption binding energy Tphys, we took a standard value of 550 K. The values found in the literature range from 300 K to 800 K. Figures 18 and 19 show the model results for these three values. Again only the rate equation treatment (dashed lines) and the statistical treatment (solid lines) are shown. The binding energy Tphys has a dramatic impact on the results when neglecting fluctuations, while its impact is small when taking the fluctuations into account. At Tphys = 800 K, the rate equation results start to approach the observations as desorption becomes slower and efficient conversion can happen, but the results remain less fitting than the results of the statistical treatment.
 |
Fig. 18 Influence of the physisorption binding energy Tphys on the observable OPR234 as a function of T24. We compare models results for three values of Tphys (300 K in red, 550 K in blue, and 800 K in green) and for two different prescriptions of the ortho-para conversion on grains (rate equation neglecting fluctuations in dashed lines, full statistical treatment of fluctuations in solid lines) to the PDR observations. |
The conclusions of the previous section are thus unaffected by the uncertainties on the microphysical parameters. The dust temperature fluctuations make the conversion rate much less dependent on the detail of the microphysics. Dust temperature indeed explore a wide range of temperatures during the fluctuations, and the average efficiency is thus controlled by the fraction of the grains whose temperature fall in the range where the instantaneous rate is high (in other terms, the portion of the temperature PDF that falls in this range). Varying the microphysical parameters, and thus the extent of the temperature range where the instantaneous rate is high only changes this fraction slowly while it can change the instantaneous rate at a given temperature dramatically (for instance the equilibrium temperature used when neglecting fluctuations). A similar effect of the dust temperature fluctuations was found in Bron et al. (2014) for H2 formation.
There is, however, one source of uncertainties that is not reduced by the effects of temperature fluctuations: as discussed in Sect. 2.1 the sticking function on bare grains is not well known and the conversion efficiency is directly proportional to the sticking probability. In the region where surface conversion affects the local OPR and H2 rotational emission lines, the gas temperature is in the range 100−400 K. The sticking function that we used (Matar et al. 2010) gives sticking probabilities in the range 0.1−0.4 for this temperature range. A sticking function significantly lower than these values would thus reduce the impact of surface conversion on H2 emission. Finally, the total available dust surface and especially the dust surface corresponding to small grains would also affect the total surface conversion rate. The PDR observations to which we compared our results seem to agree with the prescriptions used for the sticking function and the dust population.
6. Conclusions
We have built a model of ortho-para conversion of H2 on dust grains based on the latest experimental and theoretical results. When neglecting dust temperature fluctuations, conversion is found to be strongly suppressed by the presence of a UV radiation field.
We developed a statistical calculation of the conversion rate, based on a master equation approach (similar to the method used in Bron et al. 2014 for H2 formation), that takes the statistical effect of dust temperature fluctuations into account. Conversion on grains is found to stay efficient under much higher UV radiation fields when fluctuations are considered. Despite being too warm on average, small grains spend a sufficiently large portion of their time between temperature spikes at colder temperatures where conversion is efficient.
This conversion process on grains is found to play an important role in PDRs, affecting the rotational lines intensities. The local OPR falls from 3 to a low value inside the region where H2 rotational lines are emitted, and the position of this transition is controlled by the conversion efficiency on dust grains. As a result, the OPR determined from the line intensities of the first few rotational lines is a signature of the efficiency of this process.
The comparison of our models to a sample of PDR observations of rotational H2 lines indicates a high conversion efficiency on dust grains. Models implementing the exact statistical treatment with dust temperature fluctuations give results that are consistent with the observations. Models that neglect the fluctuations cannot account for the high conversion efficiency indicated by the observations. Ortho-para conversion on dust grains is thus an efficient and important process in PDRs, which can only be accurately described by a statistical treatment of the impact of dust temperature fluctuations. This process is responsible for the OPR values lower than 3 derived from rotational lines observations of PDRs.
We also found that this efficiency induced by temperature fluctuations is much less sensitive to the microphysical parameters of the model (binding energy, surface conversion timescale) than the efficiency at a single fixed temperature (e.g., the equilibrium temperature). As a consequence, the results obtained here are robust despite large uncertainties on the microphysical parameters (binding energy in the range 300−800 K, conversion timescale in the range 1−104 s). A similar effect was found in Bron et al. (2014) for H2 formation on grains, and it seems to be a general consequence of having a distribution of dust temperatures rather than a single dust temperature.
In this study, the statistical formalism used to take temperature fluctuations into account, which was developed in the case of a single chemical variable for H2 formation in Bron et al. (2014), was extended to a case with two chemical variables, demonstrating that this method could be generalized to larger chemical networks. For instance, it could be used to study the impact of cosmic-ray-induced fluctuations on ice chemistry.
Available at http://www.ias.u-psud.fr/DUSTEM/
The Meudon PDR code can be downloaded by following the instructions given at http://ism.obspm.fr
Acknowledgments
This work was supported by the French CNRS national program PCMI. We thank Evelyne Roueff and the anonymous referee for their comments on the paper.
References
- Abgrall, H., Le Bourlot, J., Pineau Des Forets, G., et al. 1992, A&A, 253, 525 [NASA ADS] [Google Scholar]
- Acharyya, K. 2014, MNRAS, 443, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- Allers, K. N., Jaffe, D. T., Lacy, J. H., Draine, B. T., & Richter, M. J. 2005, ApJ, 630, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Amiaud, L., Momeni, A., Dulieu, F., et al. 2008, Phys. Rev. Lett., 100, 056101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bron, E. 2014, Ph.D. Thesis, Université Paris Diderot, France [Google Scholar]
- Bron, E., Le Bourlot, J., & Le Petit, F. 2014, A&A, 569, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buch, V., Silva, S. C., & Devlin, J. P. 1993, J. Chem. Phys., 99, 2265 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, M. G., Hollenbach, D. J., & Tielens, A. G. G. 1992, ApJ, 399, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Carmona-Novillo, E., Bartolomei, M., Hernández, M. I., & Campos-Martínez, J. 2007, J. Chem. Phys., 126, 124315 [NASA ADS] [CrossRef] [Google Scholar]
- Chehrouri, M., Fillion, J.-H., Chaabouni, H., et al. 2011, Phys. Chem. Chem. Phys., 13, 2172 [NASA ADS] [CrossRef] [Google Scholar]
- Compiègne, M., Verstraete, L., Jones, A., et al. 2011, A&A, 525, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dislaire, V., Hily-Blant, P., Faure, A., et al. 2012, A&A, 537, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Verstraete, L., Pineau Des Forêts, G., & Hily-Blant, P. 2005, A&A, 433, 997 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faure, A., Hily-Blant, P., Le Gal, R., Rist, C., & Pineau des Forêts, G. 2013, ApJ, 770, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, B., France, K., Lupu, R. E., & McCandliss, S. R. 2010, ApJ, 725, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau Des Forêts, G., & Walmsley, C. M. 2006, A&A, 449, 621 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuente, A., Martín-Pintado, J., Rodríguez-Fernández, N. J., et al. 1999, ApJ, 518, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Fuente, A., Martin-Pintado, J., Rodriguez-Fernández, N. J., Cernicharo, J., & Gerin, M. 2000, A&A, 354, 1053 [NASA ADS] [Google Scholar]
- Fukutani, K., & Sugimoto, T. 2013, Prog. Surface Sci., 88, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Gavilan, L., Vidali, G., Lemaire, J. L., et al. 2012, ApJ, 760, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gerlich, D. 1990, J. Chem. Phys., 92, 2377 [NASA ADS] [CrossRef] [Google Scholar]
- Gillmon, K., Shull, J. M., Tumlinson, J., & Danforth, C. 2006, ApJ, 636, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, B., Falgarone, E., & Pineau des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goicoechea, J. R., & Le Bourlot, J. 2007, A&A, 467, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gómez-Carrasco, S., González-Sánchez, L., Aguado, A., et al. 2012, J. Chem. Phys., 137, 094303 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez Garcia, M., Le Bourlot, J., Le Petit, F., & Roueff, E. 2008, A&A, 485, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gredel, R., Pineau des Forêts, G., & Federman, S. R. 2002, A&A, 389, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gry, C., Boulanger, F., Nehmé, C., et al. 2002, A&A, 391, 675 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., et al. 2003, A&A, 397, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Boulanger, F., Verstraete, L., Walmsley, C. M., & Pineau des Forêts, G. 2004, A&A, 414, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habart, E., Abergel, A., Boulanger, F., et al. 2011, A&A, 527, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hasegawa, T. I., Herbst, E., & Leung, C. M. 1992, ApJS, 82, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Higdon, S. J. U., Armus, L., Higdon, J. L., Soifer, B. T., & Spoon, H. W. W. 2006, ApJ, 648, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Hixson, H. G., Wojcik, M. J., Devlin, M. S., Devlin, J. P., & Buch, V. 1992, J. Chem. Phys., 97, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Honvault, P., Jorfi, M., González-Lezana, T., Faure, A., & Pagani, L. 2011, Phys. Rev. Lett., 107, 023201 [NASA ADS] [CrossRef] [Google Scholar]
- Ilisca, E., & Ghiglieno, F. 2014, Eur. Phys. J. B, 87, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Katz, N., Furman, I., Biham, O., Pirronello, V., & Vidali, G. 1999, ApJ, 522, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kubik, P. R., Hardy, W. N., & Glattli, H. 1985, Canad. J. Phys., 63, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Lacour, S., Ziskin, V., Hébrard, G., et al. 2005, ApJ, 627, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J. 2000, A&A, 360, 656 [Google Scholar]
- Le Bourlot, J., Pineau des Forêts, G., & Flower, D. R. 1999, MNRAS, 305, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Le Bourlot, J., Le Petit, F., Pinto, C., Roueff, E., & Roy, F. 2012, A&A, 541, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ledoux, C., Petitjean, P., & Srianand, R. 2003, MNRAS, 346, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Leitch-Devlin, M. A., & Williams, D. A. 1985, MNRAS, 213, 295 [NASA ADS] [Google Scholar]
- Lique, F., Honvault, P., & Faure, A. 2012, J. Chem. Phys., 137, 154303 [NASA ADS] [CrossRef] [Google Scholar]
- Mandy, M. E., & Martin, P. G. 1992, J. Chem. Phys., 97, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Mandy, M. E., & Martin, P. G. 1993, ApJS, 86, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Manicò, G., Ragunì, G., Pirronello, V., Roser, J. E., & Vidali, G. 2001, ApJ, 548, L253 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., & Bergin, E. A. 2007, ApJ, 664, 956 [NASA ADS] [CrossRef] [Google Scholar]
- Matar, E., Bergeron, H., Dulieu, F., et al. 2010, J. Chem. Phys., 133, 104507 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Moutou, C., Verstraete, L., Sellgren, K., & Leger, A. 1999, in The Universe as Seen by ISO, eds. P. Cox, & M. Kessler, ESA SP, 427, 727 [Google Scholar]
- Muzahid, S., Srianand, R., & Charlton, J. 2015, MNRAS, 448, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Naslim, N., Kemper, F., Madden, S. C., et al. 2015, MNRAS, 446, 2490 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Melnick, G. J., Sonnentrucker, P., et al. 2006, ApJ, 649, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Ledoux, C., Petitjean, P., et al. 2007, A&A, 474, 393 [Google Scholar]
- Pachucki, K., & Komasa, J. 2008, Phys. Rev. A, 77, 030501 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Vastel, C., Hugo, E., et al. 2009, A&A, 494, 623 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pagani, L., Roueff, E., & Lesaffre, P. 2011, ApJ, 739, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Pagani, L., Lesaffre, P., Jorfi, M., et al. 2013, A&A, 551, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Palmer, R. E., & Willis, R. F. 1987, Surf. Science, 179, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Spinoglio, L., van der Werf, P. P., & Piqueras López, J. 2014, A&A, 566, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perets, H. B., Lederhendler, A., Biham, O., et al. 2007, ApJ, 661, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Rachford, B. L., Snow, T. P., Tumlinson, J., et al. 2002, ApJ, 577, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Rachford, B. L., Snow, T. P., Destree, J. D., et al. 2009, ApJS, 180, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Richter, P., Wakker, B. P., Savage, B. D., & Sembach, K. R. 2003, ApJ, 586, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Rigopoulou, D., Kunze, D., Lutz, D., Genzel, R., & Moorwood, A. F. M. 2002, A&A, 389, 374 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roser, J. E., Manicò, G., Pirronello, V., & Vidali, G. 2002, ApJ, 581, 276 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H., Helou, G., Hollenbach, D. J., et al. 2007, ApJ, 669, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Roy, N., Chengalur, J. N., & Srianand, R. 2006, MNRAS, 365, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Sandler, Y. L. 1954, J. Phys. Chem., 58, 54 [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, W. R., & Le Roy, D. J. 1965, J. Chem. Phys., 42, 3869 [NASA ADS] [CrossRef] [Google Scholar]
- Sheffer, Y., Wolfire, M. G., Hollenbach, D. J., Kaufman, M. J., & Cordier, M. 2011, ApJ, 741, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Srianand, R., Petitjean, P., Ledoux, C., Ferland, G., & Shaw, G. 2005, MNRAS, 362, 549 [Google Scholar]
- Sternberg, A., & Neufeld, D. A. 1999, ApJ, 516, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Störzer, H., & Hollenbach, D. 1998, ApJ, 495, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Sugimoto, T., & Fukutani, K. 2011, Nat. Phys., 7, 307 [CrossRef] [Google Scholar]
- Sun, Y., & Dalgarno, A. 1994, ApJ, 427, 1053 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, J. 2001, ApJ, 561, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Thi, W.-F., van Dishoeck, E. F., Bell, T., Viti, S., & Black, J. 2009, MNRAS, 400, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Timmermann, R., Bertoldi, F., Wright, C. M., et al. 1996, A&A, 315, L281 [NASA ADS] [Google Scholar]
- Troscompt, N., Faure, A., Maret, S., et al. 2009, A&A, 506, 1243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Truhlar, D. G. 1976, J. Chem. Phys., 65, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Shull, J. M., Rachford, B. L., et al. 2002, ApJ, 566, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Vaytet, N., Tomida, K., & Chabrier, G. 2014, A&A, 563, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vidali, G., & Li, L. 2010, J. Phys. Condens. Matter, 22, D4012 [Google Scholar]
- Vidali, G., Pirronello, V., Li, L., et al. 2007, J. Phys. Chem. A, 111, 12611 [CrossRef] [Google Scholar]
- Watanabe, N., Kimura, Y., Kouchi, A., et al. 2010, ApJ, 714, L233 [NASA ADS] [CrossRef] [Google Scholar]
- Yabushita, A., Hama, T., Iida, D., et al. 2008, ApJ, 682, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, Y., & Neufeld, D. A. 2011, ApJ, 726, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Yucel, S., Alexander, N., & Honig, A. 1990, Phys. Rev. B, 42, 820 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Experimental measurements of the ortho-para conversion timescale on different surfaces.
Experimental and theoretical determinations of the binding energy of H2 on different surfaces.
Sample of PDR observations of lines S(0) to S(3) with the derived values of T24, OPR234, T35, and OPR345.
All Figures
 |
Fig. 1 Sticking coefficients of H2 on different grain surfaces from the literature. |
| In the text | |
 |
Fig. 2 Conversion efficiency as a function of the grain temperature for different para-H2 binding energies in the constant temperature rate equation model. The gas ortho-para ratio is taken as 3, and the conversion timescale at 10 s. |
| In the text | |
 |
Fig. 3 Conversion efficiency as a function of the grain temperature for different conversion timescales in the constant temperature rate equation model. The gas ortho-para ratio is taken as 3, and the binding energy at 650 K. |
| In the text | |
 |
Fig. 4 Ortho-para ratio of the adsorbed molecules with and without a difference of binding energy ΔTphys between ortho-H2 and para-H2. This computation was done with a gas ortho-para ratio of 3, a binding energy for para-H2 of 500 K, and a conversion timescale of 10 s. |
| In the text | |
 |
Fig. 5 Conversion efficiency on one grain as a function of grain size for different radiation field intensities G0. Solid lines: full statistical model; dashed lines: rate equation model without dust temperature fluctuations. |
| In the text | |
 |
Fig. 6 Temperature PDF of amorphous carbon grains of various sizes under an external UV field with G0 = 100. |
| In the text | |
 |
Fig. 7 Overall conversion efficiency for a full dust size distribution as a function of the UV intensity G0. |
| In the text | |
 |
Fig. 8 Overall conversion efficiency as a function G0 for different values of the binding energy of H2, Tphys. |
| In the text | |
 |
Fig. 9 Overall conversion efficiency as a function G0 for different values of the conversion timescale τconv. |
| In the text | |
 |
Fig. 10 Upper panel: density profiles of H (blue) and H2 (green) and gas temperature profile (red) in the PDR (P = 107 K cm-3, χ = 103). Lower panel: local emissivity profiles (color lines) of the first rotational lines of H2 (solid lines for para transitions and dashed lines for ortho transitions) compared to the local OPR profile (black). Local emissivities are multiplied by d so that the contribution of a given region to the total intensity is proportional to its area under the curve despite the logarithmic axis. Each emissivity curve has been scaled so that its maximum is 1 for ease of comparison. |
| In the text | |
 |
Fig. 11 Comparison of the local OPR profiles in the PDR in models with P = 107 K cm-3 and χ = 103 for the four prescriptions for ortho-para conversion on grains: no conversion (purple), rate equation approach neglecting the fluctuations (green), statistical approach taking the fluctuations into account (blue), and full conversion for H2 molecules sticking to grains (red). The temperature profile of the PDR is also shown for reference (dotted black line), along with the corresponding LTE OPR profile (solid black line). |
| In the text | |
 |
Fig. 12 Conversion rates by the different processes: gas-phase reactive collisions (magenta), destruction-formation cycling (green), and dust surface conversion (blue). |
| In the text | |
 |
Fig. 13 Intensities of the first rotational lines of H2 predicted by the same PDR model (P = 107 K cm-3 and χ = 103) for the four prescriptions for ortho-para conversion on grains: no conversion (purple), rate equation approach neglecting the fluctuations (green), statistical approach taking the fluctuations into account (blue), and full conversion for H2 molecules sticking to grains (red). |
| In the text | |
 |
Fig. 14 OPR computed from levels J = 2, 3,and4 as a function of the excitation temperature T24, comparing PDR observations (symbols) to PDR models (lines). PDR models implement four prescriptions for ortho-para conversion on grains: no conversion (purple), rate equation approach without fluctuations (green), statistical approach with fluctuations (blue), and full conversion (red). Solid lines correspond to models with P/χ = 104, while models with P/χ a factor of 5 above and below this value are shown as dotted lines. |
| In the text | |
 |
Fig. 15 Same as Fig. 14 for the OPR computed from levels J = 3, 4, and 5, shown as a function of the excitation temperature T35. |
| In the text | |
 |
Fig. 16 Influence of the surface conversion timescale τconv on the observable OPR234 as a function of T24. We compare model results for three values of τconv (1 s in red, 10 s in blue, and 104 s in green) and for two different prescriptions of the ortho-para conversion on grains (rate equation neglecting fluctuations in dashed lines, full statistical treatment of fluctuations in solid lines) to the PDR observations. |
| In the text | |
 |
Fig. 17 Same as Fig. 16 for OPR345 as a function of T35. |
| In the text | |
 |
Fig. 18 Influence of the physisorption binding energy Tphys on the observable OPR234 as a function of T24. We compare models results for three values of Tphys (300 K in red, 550 K in blue, and 800 K in green) and for two different prescriptions of the ortho-para conversion on grains (rate equation neglecting fluctuations in dashed lines, full statistical treatment of fluctuations in solid lines) to the PDR observations. |
| In the text | |
 |
Fig. 19 Same as Fig. 18 for OPR345 as a function of T35. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


