| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 8 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526918 | |
| Published online | 10 February 2016 | |
Microlensing constraints on the size of the gamma-ray emission region in blazar B0218+357
1 Max-Planck Institut für Physik, Föhringer ring 6, 80805 Munich, Germany
e-mail: Ievgen.Vovk@mpp.mpg.de
2 ISDC, Astronomy Department, University of Geneva, Ch. d’Ecogia 16, 1290 Versoix, Switzerland
Received: 8 July 2015
Accepted: 19 October 2015
Context. Observations of the effect of microlensing in gravitationally lensed quasars could potentially be used to study the structure of the source on very small distance scales – down to the size of the supermassive black hole, that powers the quasar activity.
Aims. We search for the microlensing effect in the γ-ray band using the signal from a gravitationally lensed blazar, B0218+357.
Methods. We develop a method to deconvolve the contributions from the two images of the source, which allows us to reconstruct the flaring light curve in the γ-ray band. We use this method to study the evolution of the magnification factor ratio between the two images throughout the flaring episodes. We interpret the time variability of the ratio as a signature of the microlensing effect and derive constraints on the physical parameters of the γ-ray source by comparing the observed variability properties of the magnification factor ratio with those derived from numerical simulations of the microlensing caustics networks.
Results. We find that the magnification factor ratio experienced a change characteristic for a caustic-crossing microlensing event that occurred during a 100 d flaring period in 2012. It changed again between 2012 and a recent flaring episode in 2014. We use the measurement of the maximal magnification and duration of the caustic-crossing event to derive an estimate of the projected size of the γ-ray emission region in B0218+357, Rγ ~ 1014−1015 cm. This estimate is compatible with a complementary estimate found from the minimal variability time scale. The microlensing/minimal variability time scale measurements of the source size suggest that the γ-ray emission is produced at the base of the blazar jet, in the direct vicinity of the central supermassive black hole.
Key words: gravitational lensing: micro / gamma rays: galaxies / galaxies: active
© ESO, 2016
1. Introduction
Almost 100 years after the discovery of the first large scale jet in an active galactic nucleus (AGN; Curtis 1918), the origin of the jets and the details of the mechanism for their production and high-energy activity remain uncertain.
Radio observations are now beginning to reach the angular resolution that is sufficient to resolve the details of the region of the jet formation in the direct vicinity of the supermassive black hole in nearby AGN (Doeleman et al. 2012). The angular resolution of γ-ray telescopes will not be comparably high in this foreseeable future. This precludes the possibility of getting the necessary imaging data which would provide answers to the most basic questions, such as the location of the site of the γ-ray emission region in blazars (AGNs with jets aligned along the line of sight, Urry & Padovani 1995).
The only possibility of overcoming the limitations created by the limited angular resolution of γ-ray telescopes is provided by the effect of the gravitational microlensing, observable in the blazars/AGN that are parts of strong gravitational lens systems (Chang & Refsdal 1979). In such systems, the flux from small-scale substructures in the lensed source is selectively magnified by the effect of microlensing by individual stars in the lensing galaxy. The microlensing magnification factor scales inversely proportional to the size of the source. Consequently, it affects mostly the flux from the smallest structures inside the source. The study of time and energy/wavelength dependence of the microlensing effect enables the study of the details of the source structure on the distance scales R ≪ 1016 cm (or micro-arcseconds), comparable to the size of the supermassive black hole powering the AGN activity (Torres et al. 2003; Kochanek 2004). The microlensing data in the optical and X-ray continuum and line emission allow the structure of the accretion flow to be probed from its outer to inner regions (even close to the black hole; Eigenbrod et al. 2008; Dai et al. 2010; Blackburne et al. 2011; Chartas et al. 2012), locate the line-emission regions within the AGN central engine (Abajas et al. 2002; Guerras et al. 2013) and/or the properties of the lensing galaxy (Mediavilla et al. 2015) to be probed.
Only two strongly lensed blazars are detected in the GeV energy band by the Fermi Large Area Telescope (LAT; Abdo et al. 2015; Cheung et al. 2014). The microlensing effect has already been discussed in the literature for one of the two sources, PKS 1830-211 (Donnarumma et al. 2011; Abdo et al. 2015), and was recently detected (Neronov et al. 2015), limiting the source size to being not larger than 10−100 Schwarzschild radii of the supermassive black hole that is powering the source.
The other γ-ray-loud blazar which is a part of the strong gravitational lens is B0218+357 (Cheung et al. 2014), which has also been detected in the sub-TeV band by the MAGIC telescopes (Mirzoyan 2014). The system includes the lensing galaxy at the redshift z ≈ 0.68 (Browne et al. 1993) and a more distant blazar at z ≈ 0.94 (Cohen et al. 2003). The gravitational time delay between the two images of the source is determined in the radio, τrad = 10.5 ± 0.2 d (Biggs et al. 1999), τrad = 10.1 ± 0.8 d (Cohen et al. 2000; see also Eulaers & Magain 2011) and in the γ-ray band – τγ ≈ 11.46 ± 0.16 days (Cheung et al. 2014) (all uncertainties correspond to 68% confidence interval). The flux ratio between the two images changes from ≃2 at 1.65 GHz frequency up to ≃4 at 15 GHz, presumably because of the free-free absorption in a giant molecular cloud (GMC), which is located in the lensing galaxy in front of the image A (Mittal et al. 2007).
In the γ-ray band, the two images of the source, separated by only 0.3′′, are not resolved. Measuring the magnification factor ratio is based on the fitting of the γ-ray light curve of the source, which is composed of the contributions from the two sources. This gives the result μγ ≈ 1 (Cheung et al. 2014), which is different from the free-free absorption corrected magnification factor ratio in the radio band (Mittal et al. 2007).
The difference in the magnification factor ratios between the radio and γ-ray bands could be a signature of the microlensing (Torres et al. 2003; Abdo et al. 2015; Cheung et al. 2014; Neronov et al. 2015). This information could be interesting when constraining the size of the γ-ray source. However, the chromatic behaviour of the radio magnification factor makes a straightforward interpretation of the magnification factor difference difficult.
In what follows we notice that the microlensing does affect the magnification factor ratio in the γ-ray band. We deduce this from the time variability of the γ-ray magnification factor ratio, both on yearly (Cheung et al. 2014; Buson et al. 2015) and – through a decomposition/modeling of the light curves of the two images – weekly time scales. The detection of the microlensing of the γ-ray flux of the source enables us to derive a constraint on the size of the γ-ray source. As in the case of PKS 1830-211 (Neronov et al. 2015), the source size is found to be compact, with an order of magnitude size estimate of ~1014−1015 cm. The compact size of the γ-ray source indicates that the γ-ray emission is produced at the base of the jet, close to the supermassive black hole.
2. Fermi/LAT data analysis
In this work we use the publicly available Fermi/LAT Pass 7 reprocessed photon data set1. The data were analysed using the Fermi Science Tools package2 v9r33p0, using the Source (P7REP_SOURCE) event class. The photons were selected from the region of 20° in radius around the position of B0218+357. The fluxes of all sources in the selected region were estimated from the unbinned likelihood fit, which included all the sources from the 2FGL (Nolan et al. 2012) catalogue within 28 deg from B0218+357. For the fit we used the spectral models given in 2FGL. The source spectral shapes were frozen to those suggested in the catalogue and only normalizations were allowed to vary; for the sources outside of the region of region of interest (in the 20°−28° range) we also fixed the normalizations to the catalogue values. However, during the 2014 flare, a harder spectral index of Γ = 1.4 was used for B0218+357, as revealed by a dedicated analysis of this particular period (Buson et al. 2015). Throughout the fit we used the gll_iem_v05_rev1 Galactic diffuse emission model and the iso_source_v05_rev1 model to account for the isotropic diffuse γ-ray background.
The likelihood fitting procedure was repeated for each of the time bins of the source light curve. To ensure convergence of the fit, we only allowed the normalizations to vary for the brightest sources in the B0218+357 region. To select these, we visually examined the 0.1−510 GeV sky map of the region during the weaker 2014 flare and selected only the sources with more than half of B0218+357 counts in the same map. We checked that the inclusion of a larger number of sources to the fit did not significantly affect the derived light curve, resulting only in minor changes of the flux estimates. In this way, we extracted the source fluxes in the 0.1−510 GeV energy band (the maximal energy is set by the maximal energy considered in the Pass 7 Instrument Response Functions, Ackermann et al. 2012). We estimated the significance of detection in each time bin using the test statistic value (TS, Mattox et al. 1996), obtained from the fit. Whenever the TS values dropped below ten (which roughly corresponds to 3σ significance), the source detection was considered to be non-significant.
2.1. Timing analysis
 |
Fig. 1 Light curves of the B0218+357 in 0.1−510 GeV band over its 2012 (top) and 2014 (bottom) flaring episodes. The bin size is 0.5 days for the 2012 and 1 day for 2014 light curve. Blue and grey data points indicate the significant and non-significant detections, respectively. |
 |
Fig. 2 Arrival times and energies of photons above 1 GeV during the 2014 flare (bottom panel) and during the period after the gravitational time delay (top panel). Grey vertical bands mark the intervals of time, when Fermi/LAT pointing was not farther away than 60° from the source position. Photons were selected within the circle of 0.5° in radius. |
During the Fermi/LAT observations, B0218+357 experienced two pronounced flaring periods (Cheung et al. 2014; Buson et al. 2015). A close-up on these periods is shown in Fig. 1. The light curve of the source during the 2012 flare reveals strongly variable behaviour on different time scales, from the intraday to ~100 d (Cheung et al. 2014). The gravitational delay time scale is in between these minimal/maximal scales, so that a straightforward decomposition of the source flux onto the two separate contributions from the two images is not possible. However, the gravitational time delay could be reliably estimated using the fast variability episodes that occur on the time scale that is much shorter than τγ = 11.46 ± 0.16 d (Cheung et al. 2014).
The gravitationally delayed flare expected 11.5 d after the 2014 episode is not detected. This is also clear from a detailed pattern of photon arrival times in the energy band above 1 GeV, shown in Fig. 2. Here, 30 photons are detected within a short 15 h period of the main flare. The rise time of the flare is comparable to the time interval between subsequent exposures of the source by the LAT, ≃3 h. Detection of the delayed flare with comparable flux and a comparably sharp rising front would provide a precision measurement of the gravitational time delay with the minimal possible error bar of 3 h. However, no delayed flare is detected, as one can see in the upper panel of Fig. 2, limiting the flux of the delayed component down to the level, which is an order of magnitude lower than the flux of the main flare.
We note that Buson et al. (2015) claim the detection of the expected delayed component in the 2014 flaring episode. This was based on both the detection of the emission during the expected time delay and the harder then usual spectrum for both the initial flare and the delayed emission. To compare this conclusion with our findings, we ran a dedicated analysis of the emission in the interflare interval MJD 56 853−56 862 and in both the leading (MJD 56 851−56 853) and delayed flares (MJD 56 862−56 866), using the same setup as described above, but leaving the spectral index of B0218+357 free. The resulting spectral index in the interflare period Γ = 2.08 ± 0.14 is consistent, though a bit softer, with Γ = 1.9 ± 0.1 found for the delayed component (a similar spectral index was already identified by Buson et al. 2015). The TS of these detections is, respectively, TS = 100 and TS = 198. In addition, the mean flux during this period F = (1.8 ± 0.4) × 10-7 ph / (cm2 s) is consistent with the flux during the putative delayed echo F = (2.0 ± 0.3) × 10-7 ph / (cm2 s) (these values are different from those in Fig. 1 since there we used the fixed spectral index of Γ = 1.4, corresponding to the leading flare). The significant detection of the source on a daily basis during the expected echo in this case is explained by the TOO observations that were performed by Fermi/LAT3, which resulted in higher exposure of the Fermi/LAT towards the source around that time.
2.2. Gamma ray magnification factor ratio
Estimating the magnification factor ratio between the two lensed images of the source is difficult in the γ-ray band because the images are not resolved. As a result, the light curve of the γ-ray source has contributions from both images: 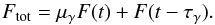 (1)Here F(t) represents the observed flux of the second (delayed) image, μγ denotes the magnification factor ratio between the leading and delayed images, and τγ is the gravitational time delay.
(1)Here F(t) represents the observed flux of the second (delayed) image, μγ denotes the magnification factor ratio between the leading and delayed images, and τγ is the gravitational time delay.
In real γ-ray data analysis, the continuous function F(t) is replaced with a set of measurements of the source flux at discrete moments of time Fi = F(ti) and Eq. (1) becomes 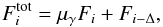 (2)where Δ denotes the shift τγ in terms of the light curve bins size. This equation can be rewritten in the matrix form:
(2)where Δ denotes the shift τγ in terms of the light curve bins size. This equation can be rewritten in the matrix form:  (3)The source flux at the start of the observations (tstart) is composed of the total flux of the two images in the time interval preceding the tstart. In this way the system in Eq. (3) can only be solved if the boundary condition for the moments of time t<tstart is provided. In the case of isolated flares, one can assume that the source flux before the moment tstart is equal to a constant quiescent flux Fbase, as it is done in Eq. (3). One should note that Fbase in Eq. (3) does not represent the “pedestal” flux, on top of which the solution for F(t) is found. It only sets the initial condition for the system in Eq. (3) and the obtained solution F(t) can, in principle, be smaller than Fbase for t>tstart.
(3)The source flux at the start of the observations (tstart) is composed of the total flux of the two images in the time interval preceding the tstart. In this way the system in Eq. (3) can only be solved if the boundary condition for the moments of time t<tstart is provided. In the case of isolated flares, one can assume that the source flux before the moment tstart is equal to a constant quiescent flux Fbase, as it is done in Eq. (3). One should note that Fbase in Eq. (3) does not represent the “pedestal” flux, on top of which the solution for F(t) is found. It only sets the initial condition for the system in Eq. (3) and the obtained solution F(t) can, in principle, be smaller than Fbase for t>tstart.
If τγ and μγ are known, an approximate solution of Eq. (3) can be found from the least-square minimization under the condition Fi> 0. The uncertainties of the flux estimates can be propagated to this system by simply dividing each value of  and ith row of the matrix by the corresponding uncertainty σi. This transforms the least-square solution of the system in Eq. (3) to the minimum-χ2 one.
and ith row of the matrix by the corresponding uncertainty σi. This transforms the least-square solution of the system in Eq. (3) to the minimum-χ2 one.
The value of the time delay τγ can be found from the combined source light curve using, e.g. the autocorrelation function analysis, which results in τγ ≈ 11.5 days (Cheung et al. 2014). The magnification factor ratio μγ is more difficult to assess because of the large number of unknowns Fi in the system (3), equal to the number of equations. To assist the situation, an additional constraint on the solution Fi can be imposed.
In the absence of accidental fine-tuning of parameters, the true solution F(t) of Eq. (1) (or Eq. (2)) should not contain an autocorrelation at the time scale of the gravitational delay. In this way the best solution of the system in Eq. (3) can be found by minimizing the residuals between the autocorrelation value of F(t) around the position of expected time delay τγ and its local approximation, e.g. by a power law.
In a particular case of B0218+357, the major source flare in 2012 was preceded by the period of a relatively constant flux (Cheung et al. 2014). This enables the estimation of the initial flux Fbase, which is needed to solve the system (3).
Solving the system (3) using the procedure described above and assuming μγ constant in time, we find no acceptable solution. To get an acceptable solution, the assumption on the constancy of μγ has to be relaxed. In principle, the time scale of variability of μγ is not known a priori. However, general considerations of microlensing suggest that, even if the source size is as small as the size of the supermassive black hole, the variability time scale of the magnification factor ratio is in the months-to-years range.
The 2012 major flare can be split into several shorter flaring episodes, identified by Cheung et al. (2014). To study the variability of μγ, we modify our procedure for solving the system (3) by allowing μγ to change from sub-flare to sub-flare (in a stepwise manner). We search for a solution to the system (3) by performing a scan over the magnification factor ratios for each flaring episode. This results in an acceptable solution F(t) shown in Fig. 3.
 |
Fig. 3 Top left: decomposition of the different flaring episodes of the B0218+357 major flare in 2012. The original Fermi/LAT light curve is shown in blue, the reconstructed light curve of the leading image μγF(t) is shown in red, and the total reconstructed light curve Ftot(t) is shown with a green line. Top right: derived magnification factor ratio for each of the flaring episodes. Black dashed line indicates the approximate value of the magnification factor ratio in radio band μrad ≈ 4. The red line depicts the variation of the magnification factor ratio during one of the caustic-crossing events in our simulations, which can be tentatively associated with the observed behaviour. It was computed for Rsource ≈ 1014 cm. This event is shown in lower panels. Bottom: microlensing caustic-magnification patterns that can be associated with the detected variability of magnification factor during the 2012 and 2014 flares. The colour bars represent the microlensing magnification (or demagnification if the value is <1). Distances are given in the source plane. The patterns are shown separately for the leading (left) and delayed images (right). Solid white lines indicate the putative trajectories of the images during the 2012 flare, dashed lines depict the displacement of the images over the 2012−2014 period. |
To estimate the uncertainties in the derived best-fit μγ for each flaring episode, as well as on the intrinsic light curve F(t), we have simulated a number of artificial light curves Ftot(t) in which the flux values in each time bin are randomly scattered within the error bars of the original flux measurement. These light curves were substituted into Eq. (3), which was solved as described above. The distributions of the best-fit μγ for each flaring episode is shown in Fig. 4. To quantify the scatter of the derived values of the magnification factor, we fitted these distributions with a Gaussian profile. The width of the profiles is shown as the errorbars on the measurements of μγ in each episode in the right panel of Fig. 3.
 |
Fig. 4 Distributions of the best-fit values of the magnification factor ratio μ for the three brightest flaring episodes in 2012 (3 central panels in Fig. 3), derived through the Monte Carlo simulations. |
We note that a similar behaviour of the magnification factor during the 2012 flare can be also seen in the analysis of Cheung et al. (2014), although the superposition of the leading and delayed flaring components do not allow them to draw firm conclusions (Cheung et al. 2014, see Fig. 4 therein).
Contrary to Cheung et al. (2014), we do not find evidence for the “orphan” sub-flares, with no associated delayed emission found in their analysis in shorter, 6-h time bins. The solution to Eq. (3), obtained here, reproduces all the variations in the 12-h light curve of B0218+357 in the present analysis, including those that were suggested to have no counterparts (Cheung et al. 2014). This can be seen in Fig. 3, where the total light curve Ftot(t) is plotted with the green line. Detection of these sub-flares would imply a very rapid variation of the magnification factor, which would be interesting when searching for microlensing. However, we find that the data are consistent with relatively slow modulation of the magnification factor ratio over the entire 2012 flare.
The magnification factor ratio, measured during the second flare of the source in 2014, shown in Fig. 1, can not be directly established because the source flux at the moment Tflare + τγ is consistent with the flux inbetween the putative flares, i.e. the delayed emission was not detected by Fermi/LAT. The rising part of the flare in the energy band above 1 GeV is very sharp, with the overall duration of several hours, see Fig. 2. During the 15-h flaring time, 30 photons with >1 GeV energies were detected within the circle of the radius 0.5° around the source. At the same time, only four photons were detected during the 15-h time window of the delayed flare (compare the lower and upper panels of Fig. 2). It is not clear to which of the two images these four photons belong. The ratio of the photon counts of the “prompt” and “delayed” 2014 flares provides a lower bound on the magnification factor ratio μγ> 5 during this flare.
3. Discussion
The analysis of the previous section shows that the magnification factor ratio μγ varied during the 2012 flaring period and has changed further from 2012 to 2014. An immediate consequence of the detection of time variability of μγ is the conclusion in the detection of the microlensing effect in the γ-ray band. An alternative possibility for the variations of the magnification factor ratio (as discussed by Barnacka et al. 2015 in the case of PKS 1830-211) would be the different locations of the 2012 and 2014 flaring regions inside the source. This, however, would require the displacements of the order of the Einstein radius of the (macro)lens, ~1 kpc, even during the same flaring period. The scale of displacements is much larger than the typical estimates of the sizes of the γ-ray emission regions in blazars/quasars and radio galaxies and, moreover, in the case of the 2012 flaring episode in B0218+357, it is unlikely that two distant flaring regions would flare simultaneously within a 100-day period.
On the other hand, the assumption of microlensing provides a natural explanation for the detected magnification factor ratio behaviour. Using the simulated microlensing caustic-pattern maps described in Sect. 3.2, we were able to tentatively associate the variation of μγ over the 2012−2014 flares with the events of caustic crossing. Crossing of the delayed source image by a microlensing caustic can explain the detected variations of the magnification factor ratio in 2012, while the movement over a larger scale pattern of lensing caustics can account for the change in magnification of the leading image between 2012 and 2014. This tentative association is illustrated in the lower panels of Fig. 3 and provides a reasonable description of the observed behaviour.
3.1. Qualitative estimates of the microlensing constraint on the source size
The microlensing magnifies the flux of the source if it is smaller or comparable in size to the lens Einstein radius ![\begin{equation} R_{\rm E}(M) = \sqrt{ \frac{4GM}{c^2} \frac{D_{\rm L} D_{\rm LS}}{D_{\rm S}} } \approx 3 \times 10^{16} \left[\frac{M}{M_\odot}\right]^{1/2} ~ \mathrm{cm} \label{eq::R_E} , \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq59.png) (4)where DS,DL,DLS are the angular diameter distances to the source, the lens and between the source and the lens, and M is the mass of the lens.
(4)where DS,DL,DLS are the angular diameter distances to the source, the lens and between the source and the lens, and M is the mass of the lens.
If the lensing centres in the lens galaxy are stars, only a source of the projected size less than RE, which corresponds to the lenses of the masses ~M⊙, is subject to the microlensing. In particular, the radio source, which is known to be large (it is resolved in the radio band) Rradio ~ 10 pc (Mittal et al. 2007), is not influenced by the microlensing by stars.
The fact that the microlensing effect is detected in the γ-ray band immediately implies a constraint on the size of the γ-ray source projected on the plane of the sky: 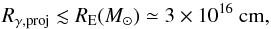 (5)under the “default” assumption M ~ M⊙.
(5)under the “default” assumption M ~ M⊙.
The microlensing magnification factor is variable in time as a result of the relative motion of the source, the lensing centres, and the observer. Maximal magnification is achieved at the moments of crossing of the microlensing caustics in front of one of the two images of the source. At these moments, an order of magnitude estimate for the magnification factor is (Chang 1984) ![\begin{equation} \mu^{\rm micro} \simeq \sqrt{R_{\rm E}/R_{\gamma,\rm proj}} \simeq 10 \left[\frac{R_{\gamma,\rm proj}}{3\times 10^{14}\mbox{ cm}}\right]^{-1/2} \label{eq::microlensing_magnification}\cdot \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq67.png) (6)Assuming that the high-frequency (15 GHz) radio observations provide a fair estimate of the macro-lensing magnification factor ratio, μradio ≃ 3.7, the overall magnification factor ratio is expected to vary in the range μradio/μmicro<μγ<μradioμmicro, where we have made a simplifying assumption that both images of the source are affected by the microlensing in a similar way.
(6)Assuming that the high-frequency (15 GHz) radio observations provide a fair estimate of the macro-lensing magnification factor ratio, μradio ≃ 3.7, the overall magnification factor ratio is expected to vary in the range μradio/μmicro<μγ<μradioμmicro, where we have made a simplifying assumption that both images of the source are affected by the microlensing in a similar way.
Measurement of the variability of the magnification factor ratio from μγ ≲ 0.4 ± 0.1 to μγ ≳ 5 allows us to make an estimate of μmicro ~ 10. This gives an order of magnitude estimate of the source size: ![\begin{equation} \label{eq:estimate} R_{\gamma,\rm proj}\sim 3\times 10^{14}\left[\frac{\mu^{\rm micro}}{10}\right]^{-2}\mbox{ cm} . \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq73.png) (7)An additional constraint on the projected size of the source stems from the measurement of the time scale of the variability of μγ. The variability shown in the right panel of Fig. 3 is characteristic for a caustic-crossing episode during which μmicro reaches a maximum/minimum. The typical time scale of caustic-crossing events is determined by the relative velocity v of the source with respect to the caustic’s pattern and the observer (Kayser et al. 1986). Assuming that the velocities of the source and the lens are of the same order as the velocity of the Sun with regard to the cosmic microwave background reference frame v ≃ 300 km s-1 (Kogut et al. 1993), one could find that the strong magnification events that are related to the crossing of the source by the microlensing caustics last for
(7)An additional constraint on the projected size of the source stems from the measurement of the time scale of the variability of μγ. The variability shown in the right panel of Fig. 3 is characteristic for a caustic-crossing episode during which μmicro reaches a maximum/minimum. The typical time scale of caustic-crossing events is determined by the relative velocity v of the source with respect to the caustic’s pattern and the observer (Kayser et al. 1986). Assuming that the velocities of the source and the lens are of the same order as the velocity of the Sun with regard to the cosmic microwave background reference frame v ≃ 300 km s-1 (Kogut et al. 1993), one could find that the strong magnification events that are related to the crossing of the source by the microlensing caustics last for ![\begin{equation} \Delta t_\gamma = R_{\rm \gamma,proj} / v_{\rm rel} \simeq 100\left[\frac{R_{\rm \gamma,proj}}{3\times 10^{14}~\mathrm{cm}} \right] \left[\frac{v_{\rm rel}}{300~\mathrm{km\,s^{-1}}} \right]^{-1} ~\mathrm{d} \label{eq::microlensing_duration} , \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq78.png) (8)which is consistent with the data of the 2012 flaring episode.
(8)which is consistent with the data of the 2012 flaring episode.
The caustic crossing also provides a natural explanation for the exceptional brightness of the 2012 flaring episode. In the absence of the microlensing, the flux from the dimmer image of the blazar is lower than the flux of the brighter component by a factor of four. A moderate flaring activity typically produces the flux at the level F ~ 10-6 ph/(cm2 s) in the brighter image of the source and just at the level F ~ 3 × 10-7 ph/(cm2 s) in the dimmer image. An order of magnitude change in the magnification factor of the dimmer image, caused by the caustic crossing, resulted in a boost of the dimmer image flux up to F ~ 3 × 10-6 ph/(cm2 s), so that the overall source flux has increased to Ftot ~ 4 × 10-6 ph/(cm2 s) during the flaring period.
 |
Fig. 5 Top: distribution of the average durations of the microlensing magnification episodes obtained from the simulations for Σ = 0.5 and v = 300 km s-1. Horizontal shaded region depicts the range 60−120 days of the apparent variability time scales of the magnification factor ratio in B0218+357, and the vertical one depicts the microlensing magnification ratio range, suggested by the observations. Bottom: cumulative probability of observing microlensing magnification factor ratio >μ for different source sizes, estimated from the simulations. The vertical shaded region is the same as in the upper panel. |
3.2. Numerical modelling of the microlensing magnification factor statistics
Qualitative estimates presented above are uncertain because of the low statistics of the microlensing events (caustic crossings) in the Fermi/LAT data. Only one such event is detected after six years of Fermi/LAT exposure. The maximal magnification factor and the time scale of the caustic-crossing events fluctuate because of the complex shapes of the caustic patterns. These fluctuations introduce an uncertainty into the estimates of the source size, based on the microlensing data.
This uncertainty is illustrated in Fig. 5, where the expected statistics of the magnification factor ratio, which takes into account the microlensing effect, is calculated for different γ-ray source sizes. The calculation presented in this figure was performed via the simulation of the microlensing magnification maps that use the inverse ray shooting method (Kayser et al. 1986; Schneider & Weiss 1986, 1987). The simulated region of space encompasses 0.2 × 0.2 pc in the source plane and contains 300−1700 star lenses, depending on the assumed optical depth Σ with respect to microlensing. This optical depth represents the average amount of stars per 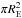 , which was scanned in range Σ = [0.2,1.0]. The mass distribution of the lenses was chosen to follow the Chabrier (2003) initial mass function with the cut-off at 10 M⊙. For each simulation run we randomly selected ten trajectories for each of the two lensed images of the source. The “magnification light curves”, computed along these trajectories, represent the magnification of each of the images during the source movement with respect to the lens. To compare with the detected magnification factor ratio, we computed the ratio of the trajectories for both images. Using these simulated magnification ratio curves, we then calculated the average durations of the episodes of high magnification μmicro>μ.
, which was scanned in range Σ = [0.2,1.0]. The mass distribution of the lenses was chosen to follow the Chabrier (2003) initial mass function with the cut-off at 10 M⊙. For each simulation run we randomly selected ten trajectories for each of the two lensed images of the source. The “magnification light curves”, computed along these trajectories, represent the magnification of each of the images during the source movement with respect to the lens. To compare with the detected magnification factor ratio, we computed the ratio of the trajectories for both images. Using these simulated magnification ratio curves, we then calculated the average durations of the episodes of high magnification μmicro>μ.
Figure 5 shows the dependence of the variability time scale of the microlensing on the source size, as obtained from the simulations. It can be seen that a source larger than 3 × 1015 cm is typically not expected to change the magnification factor ratio on a time scale shorter than two years, as observed in B0218+357 system. At the same time, a source that measures 3 × 1014 cm would exhibit variations of the magnification factor ratio seen already on the time scale of the 2012 flare. Thus, the detection of the microlensing implies an estimate of the source size Rγ ≲ 3 × 1014(v/ 300 km s-1) cm.
The largest uncertainty of the estimate stems from the unknown projected velocity of the source. In principle, this velocity could be up to v ~ c, because the flaring source could be a relativistically moving blob inside the jet. The apparent velocity of this kind of blob βapp with respect to the line of sight is βapp = βsinα/ (1−βcosα), where β is the true velocity of the blob in units of c. Assuming that the blob is moving with the Lorentz factor Γ ≳ 10 close to the line of sight, we can write βapp ≈ 3(α/ 1°)(Γ / 10)2. This expression is valid only for the relatively small angles α below αmax ≃ 1 / Γ, which maximizes the apparent velocity βapp (see also Ghisellini et al. 1993). Even so, the beamed radiation of blazars is emitted within the cone with the same opening angle ~1 / Γ, so this expression provides a reasonable description of the situation. In addition, the observed superluminal motions in AGNs from the MOJAVE sample also typically lie in the range βapp ≃ 5−10 (Lister et al. 2009). This kind of fast motion of the flaring blob would explain the “orphan” high magnification sub-flares that are tentatively found in the analysis of Cheung et al. (2014). At the same time, this would imply a significantly larger source size Rγ ≈ 3 × 1017(v/c)(Δtγ/ 100 days) cm to account for the detected duration Δtγ ~ 100 days of the high magnification event during the 2012 flaring episode. The possible apparent superluminal motion vapp>c of the highly relativistic blobs would make this estimate even larger. This source size is much larger than the size of the Einstein ring of the micro-lens in B0218+357. In this situation, the microlensing would not be able to significantly affect the source flux, as can be seen from the upper panel of Fig. 5. Still, a mildly relativistic source with v ~ 0.1c of the size ≲1016 cm would already occasionally produce high-magnification events with μmicro ~ 10.
The cases of large, fast-moving source and smaller slow-moving source could be distinguished, based on the expected statistics of the high-magnification events. After more than six years of Fermi/LAT observations, only one caustic crossing/high magnification event was detected. This fact provides a rough estimate of the probability of finding the value μmicro ≳ 10 in the microlensing light curve, p(μmicro ≳ 10) ≃ (60d / (6·365d) ≃ 3%. The lower panel of Fig. 5 shows that this estimate favours the compact source of the size ≲3 × 1014 cm. If the source size is larger, the fraction of caustic-crossing events with sufficiently high magnification decreases. Of course, with only one detected caustic-crossing event, the estimate of p(μmicro ≳ 10) ≃ 3% is not very precise. Further monitoring of the source is needed to confirm the hypothesis of the small source size.
3.3. Comparison of the microlensing constraint with the constraint from the minimal variability time scale
The microlensing constraint on the source size is consistent with the constraint stemming from the minimal variability time scale. The 2014 flare was particularly sharp in time, with the overall duration τflare ≲ 15 h in the energy band above 1 GeV (see Fig. 2). The rise time of the flare is comparable with the interval between the subsequent Fermi/LAT exposures of the source spaced by the τrise ≃ TLAT = 3.2 h period. This variability is much shorter than the microlensing caustic-crossing time scale, considered here (see Sect. 2.2), and can thus be attributed to the intrinsic variability in the leading image of B0218+357. A similar variability time scale was also found during the 2012 flaring episode by Cheung et al. (2014). This fast variability constrains the linear source size to (Celotti et al. 1998; Neronov et al. 2008) ![\begin{equation} R_\gamma\lesssim c\tau_{\rm rise}\Gamma^2 / (1+z) \simeq 2\times 10^{14}\Gamma^2\left[\frac{\tau_{\rm rise}}{10^4\mbox{ s}}\right]\mbox{ cm} , \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq120.png) (9)where Γ is the bulk Lorentz factor of the jet. If the jet is aligned along the line of sight within a viewing angle θ ~ Γ-1, the size of the emission region projected on the plane of the sky is limited to
(9)where Γ is the bulk Lorentz factor of the jet. If the jet is aligned along the line of sight within a viewing angle θ ~ Γ-1, the size of the emission region projected on the plane of the sky is limited to ![\begin{equation} R_{\rm \gamma,proj}=R_\gamma\theta\lesssim c\tau_{\rm rise}\Gamma / (1+z) \simeq 2\times 10^{15}\left[\frac{\Gamma}{10}\right]\left[\frac{\tau_{\rm rise}}{10^4\mbox{ s}}\right]\mbox{ cm} . \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq123.png) (10)Assuming the jet bulk Lorentz factor Γ ~ 1−10, the projected size of the γ-ray emission region derived from the variability analysis could to be comparable to the estimate of the size of the γ-ray emission region from the microlensing analysis.
(10)Assuming the jet bulk Lorentz factor Γ ~ 1−10, the projected size of the γ-ray emission region derived from the variability analysis could to be comparable to the estimate of the size of the γ-ray emission region from the microlensing analysis.
3.4. The problem of very-high-energy γ-rays escaping from the source
The compactness of the γ-ray emission region in B0218+357 might pose a problem for the escape of very-high-energy γ-rays, which have recently been detected by MAGIC telescopes in the 100−200 GeV band (Mirzoyan 2014). Gamma rays with energies above 100 GeV produce e+e− pairs in interactions with optical-UV photons of energies about ϵ ≳ 1 eV and, thus, might be significantly absorbed if the optical photon density is sufficiently high.
Luminosity of the source in this energy range is about LV ~ 1044 erg/s (Abdo et al. 2010; Ghisellini et al. 2010). If this luminosity stems from the accretion flow (as in the modelling of Ghisellini et al. 2010), the soft photon distribution is isotropic in the black hole reference frame. If the soft photon source size is RV, the number density of the photons is about ![\begin{equation} n_{\rm ph} = \frac {L_{V}} {4\pi R_{V}^2 c \epsilon} \simeq 10^{11} \left[\frac {R_{V}} {10^{16}\mbox{ cm}} \right]^{-2} \left[\frac {L_{V}} {10^{44}\mbox{ erg/s}} \right] \mbox{ cm}^{-3} . \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq129.png) (11)
The mean free path of the 100–200 GeV γ-rays is limited to
(11)
The mean free path of the 100–200 GeV γ-rays is limited to ![\begin{equation} \lambda_{\gamma\gamma}=\frac{1}{\sigma_{\gamma\gamma}n_{\rm ph}} \sim 10^{14} \left[\frac {R_{V}} {10^{16}\mbox{ cm}} \right]^{2} \left[\frac {L_{V}} {10^{44}\mbox{ erg/s}} \right]^{-1}\mbox{ cm} , \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq130.png) (12)(we have used an estimate σγγ ≃ 10-25 cm2 for the maximal value pair production cross-section at the centre-of-mass energy several times higher than the threshold, see Neronov & Aharonian 2007) and the optical depth of the source with respect to the pair production is
(12)(we have used an estimate σγγ ≃ 10-25 cm2 for the maximal value pair production cross-section at the centre-of-mass energy several times higher than the threshold, see Neronov & Aharonian 2007) and the optical depth of the source with respect to the pair production is ![\begin{equation} \tau_{\gamma\gamma} = \frac {R_{V}} {\lambda_{\gamma\gamma}} \simeq 10^2 \left[\frac {R_{V}} {10^{16}\mbox{ cm}} \right]^{-1} \left[\frac {L_{V}} {10^{44}\mbox{ erg/s}} \right]\cdot \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq132.png) (13)Thus, if the low-energy photon source is as compact as the γ-ray source, RV ≲ 1015 cm, the highest energy (100 GeV) photons could not escape from the source. The detection of this type of photon by MAGIC telescope (Mirzoyan 2014) implies that in the visible to UV band source is large,
(13)Thus, if the low-energy photon source is as compact as the γ-ray source, RV ≲ 1015 cm, the highest energy (100 GeV) photons could not escape from the source. The detection of this type of photon by MAGIC telescope (Mirzoyan 2014) implies that in the visible to UV band source is large, ![\begin{equation} R_{V} \gtrsim 10^{18}\tau_{\gamma\gamma}^{-1} \left[\frac {L_{V}} {10^{44}~\mbox{erg/s}} \right] \mbox{ cm.} \end{equation}](/articles/aa/full_html/2016/02/aa26918-15/aa26918-15-eq135.png) (14)The origin of the source flux in the visible to UV band is uncertain. If the emission is dominated by the jet, the bulk of the visible/UV flux is most probably produced via inverse Compton scattering by relatively low energy electrons, so that the large size of the visible/UV source does not appear surprising. Otherwise, if the accession flow onto the black hole in B0218+357 is radiatively inefficient, the optical emission is produced by the inverse Compton scattering by the non-relativistic electrons at large distances from the black hole. In this case, it is natural to expect the large size of the source.
(14)The origin of the source flux in the visible to UV band is uncertain. If the emission is dominated by the jet, the bulk of the visible/UV flux is most probably produced via inverse Compton scattering by relatively low energy electrons, so that the large size of the visible/UV source does not appear surprising. Otherwise, if the accession flow onto the black hole in B0218+357 is radiatively inefficient, the optical emission is produced by the inverse Compton scattering by the non-relativistic electrons at large distances from the black hole. In this case, it is natural to expect the large size of the source.
The constraint on the optical source size could be directly verified via the (non)-observation of the effect of the microlensing in the optical band. Indeed, a source of the size RV ≳ RE(M⊙) should almost not be affected by the microlensing. Simultaneous γ-ray and optical observations of the source could be used to measure the time variability of the magnification factor in the optical band (or the absence of it). Variations of the magnification factor ratio comparable to those observed in the γ-ray band should produce an order of magnitude variations of the optical flux. Tracing the variations of the magnification factor ratio via γ-ray observations and comparing them with the variations of the optical flux should provide a test of the presence/absence of the microlensing effect in the optical band.
3.5. Location of the emission region
The detection of microlensing, reported here, constrains the size of the γ-ray emission in B0218+357 – but does not constrain its location within the source. Though there is no central supermassive black hole mass estimate for this source in the literature, the similarity of the microlensing constraint with the plausible supermassive black hole size RBH ≃ 3 × 1014(M/ 109M⊙) cm suggests the connection between the two, though other possibilities also exist.
The derived extremely compact emission region size is in contradiction with the possibility that the γ-ray emission is coming from large-scale “knots”, commonly found in the AGN jets. Indeed the transverse size of the jet – and the corresponding knot – scales with the distance from the SMHB as RjetΘjet, reaching parsec scales (~1018 cm) at 10−100 pc distances, typical for the knots. This is thousands of times larger than the derived size.
Much more compact emission regions are suggested under the framework of the so-called jet-in-jet models (Ghisellini & Tavecchio 2008; Ghisellini et al. 2009; Giannios et al. 2009; Narayan & Piran 2012). They attribute the observed γ-ray emission to the ~1014 cm blobs, moving relativistically with respect to the jet. The Lorentz factor of these blobs with respect to the observer is 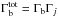 , with Γj being the Lorentz factor of the jet and Γb is a Lorentz factor of the blob relative to the jet. To account for the observed γ-ray emission, these blobs are assumed to move with
, with Γj being the Lorentz factor of the jet and Γb is a Lorentz factor of the blob relative to the jet. To account for the observed γ-ray emission, these blobs are assumed to move with 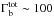 . In the absence of fine tuning, such high Lorentz factors suggest the apparent velocities of the blobs to be vapp ≫ c, which, given the observed duration of the microlensing event in B0218+357, leads to an emission region size Rγ ~ 1017(vapp/c) cm (see Sect. 3.2 for a detailed calculation). As this size of emission region is much larger than the Einstein radius of the solar-mass microlenses RE ≃ 3 × 1016 cm, its significant magnification is unlikely, as demonstrated in Sect. 3.2.
. In the absence of fine tuning, such high Lorentz factors suggest the apparent velocities of the blobs to be vapp ≫ c, which, given the observed duration of the microlensing event in B0218+357, leads to an emission region size Rγ ~ 1017(vapp/c) cm (see Sect. 3.2 for a detailed calculation). As this size of emission region is much larger than the Einstein radius of the solar-mass microlenses RE ≃ 3 × 1016 cm, its significant magnification is unlikely, as demonstrated in Sect. 3.2.
As a result, the detection of microlensing suggests that the emission region is Rγ ~ 1−100RBH in size and non-relativistic, which strongly favours its association with the central supermassive black hole.
4. Conclusions
We have demonstrated that the γ-ray signal from the gravitationally lensed blazar B0218+357 is affected by microlensing. Our conclusion is based on the detection of variability of the magnification factor ratio in the range μγ ≃ 0.4 to μγ ≳ 5, both on short (≲100 days) and long (~600 days) time scales.
Using the data on the time variability of the magnification factor ratio, we have derived a constraint on the projected size and location of the γ-ray emission region. The order of magnitude estimate of the size is Rγ ~ 1014−1015 cm. The microlensing estimate of the source size is consistent with an estimate stemming from the minimal variability time scale of the source. The γ-ray emission region is not moving with relativistic speed so that its most probable location is close to the blazar central engine, at the base of the jet.
Constraints on the size and location of the γ-ray emission region in B0218+357 are similar to those derived from the detection of microlensing in the other strongly lensed blazar PKS 1830-211 (Neronov et al. 2015). This demonstrates that the small size and location close to the supermassive black hole are generic features of γ-ray emission from blazars.
Acknowledgments
The work of I.V. is supported by the Swiss National Science Foundation grant P2GEP2_151815.
References
- Abajas, C., Mediavilla, E., Muñoz, J. A., Popović, L. Č., & Oscoz, A. 2002, ApJ, 576, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Agudo, I., et al. 2010, ApJ, 716, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2015, ApJ, 799, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Ackermann, M., Ajello, M., Albert, A., et al. 2012, ApJS, 203, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Barnacka, A., Geller, M. J., Dell’Antonio, I. P., & Benbow, W. 2015, ApJ, 809, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Biggs, A. D., Browne, I. W. A., Helbig, P., et al. 1999, MNRAS, 304, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Blackburne, J. A., Pooley, D., Rappaport, S., & Schechter, P. L. 2011, ApJ, 729, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Browne, I. W. A., Patnaik, A. R., Walsh, D., & Wilkinson, P. N. 1993, MNRAS, 263, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Buson, S., Cheung, C. C., Larsson, S., & Scargle, J. D. 2015, 2014 Fermi Symp. Proc., eConf C14102.1 [arXiv:1502.03134] [Google Scholar]
- Celotti, A., Fabian, A. C., & Rees, M. J. 1998, MNRAS, 293, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, K. 1984, A&A, 130, 157 [NASA ADS] [Google Scholar]
- Chang, K., & Refsdal, S. 1979, Nature, 282, 561 [Google Scholar]
- Chartas, G., Kochanek, C. S., Dai, X., et al. 2012, ApJ, 757, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, C. C., Larsson, S., Scargle, J. D., et al. 2014, ApJ, 782, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, A. S., Hewitt, J. N., Moore, C. B., & Haarsma, D. B. 2000, ApJ, 545, 578 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, J. G., Lawrence, C. R., & Blandford, R. D. 2003, ApJ, 583, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Curtis, H. 1918, Pub. Lick Obs., 13, 31 [Google Scholar]
- Dai, X., Kochanek, C. S., Chartas, G., et al. 2010, ApJ, 709, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Doeleman, S. S., Fish, V. L., Schenck, D. E., et al. 2012, Science, 338, 355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Donnarumma, I., De Rosa, A., Vittorini, V., et al. 2011, ApJ, 736, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Eigenbrod, A., Courbin, F., Meylan, G., et al. 2008, A&A, 490, 933 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eulaers, E., & Magain, P. 2011, A&A, 536, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ghisellini, G., & Tavecchio, F. 2008, MNRAS, 386, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Padovani, P., Celotti, A., & Maraschi, L. 1993, ApJ, 407, 65 [Google Scholar]
- Ghisellini, G., Tavecchio, F., Bodo, G., & Celotti, A. 2009, MNRAS, 393, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2010, MNRAS, 402, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Giannios, D., Uzdensky, D. A., & Begelman, M. C. 2009, MNRAS, 395, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Guerras, E., Mediavilla, E., Jimenez-Vicente, J., et al. 2013, ApJ, 778, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Kayser, R., Refsdal, S., & Stabell, R. 1986, A&A, 166, 36 [NASA ADS] [Google Scholar]
- Kochanek, C. S. 2004, ApJ, 605, 58 [Google Scholar]
- Kogut, A., Lineweaver, C., Smoot, G. F., et al. 1993, ApJ, 419, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lister, M. L., Cohen, M. H., Homan, D. C., et al. 2009, AJ, 138, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Mattox, J. R., Bertsch, D. L., Chiang, J., et al. 1996, ApJ, 461, 396 [NASA ADS] [CrossRef] [Google Scholar]
- Mediavilla, E., Jimenez-Vicente, J., Muñoz, J. A., Mediavilla, T., & Ariza, O. 2015, ApJ, 798, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Mirzoyan, R. 2014, ATel, 6349, 1 [NASA ADS] [Google Scholar]
- Mittal, R., Porcas, R., & Wucknitz, O. 2007, A&A, 465, 405 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., & Piran, T. 2012, MNRAS, 420, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., & Aharonian, F. A. 2007, ApJ, 671, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., Semikoz, D., & Sibiryakov, S. 2008, MNRAS, 391, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Neronov, A., Vovk, I., & Malyshev, D. 2015, Nature Physics, 11, 664 [Google Scholar]
- Nolan, P. L., Abdo, A. A., Ackermann, M., et al. 2012, ApJS, 199, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Weiss, A. 1986, A&A, 164, 237 [NASA ADS] [Google Scholar]
- Schneider, P., & Weiss, A. 1987, A&A, 171, 49 [NASA ADS] [Google Scholar]
- Torres, D. F., Romero, G. E., Eiroa, E. F., Wambsganss, J., & Pessah, M. E. 2003, MNRAS, 339, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Light curves of the B0218+357 in 0.1−510 GeV band over its 2012 (top) and 2014 (bottom) flaring episodes. The bin size is 0.5 days for the 2012 and 1 day for 2014 light curve. Blue and grey data points indicate the significant and non-significant detections, respectively. |
| In the text | |
 |
Fig. 2 Arrival times and energies of photons above 1 GeV during the 2014 flare (bottom panel) and during the period after the gravitational time delay (top panel). Grey vertical bands mark the intervals of time, when Fermi/LAT pointing was not farther away than 60° from the source position. Photons were selected within the circle of 0.5° in radius. |
| In the text | |
 |
Fig. 3 Top left: decomposition of the different flaring episodes of the B0218+357 major flare in 2012. The original Fermi/LAT light curve is shown in blue, the reconstructed light curve of the leading image μγF(t) is shown in red, and the total reconstructed light curve Ftot(t) is shown with a green line. Top right: derived magnification factor ratio for each of the flaring episodes. Black dashed line indicates the approximate value of the magnification factor ratio in radio band μrad ≈ 4. The red line depicts the variation of the magnification factor ratio during one of the caustic-crossing events in our simulations, which can be tentatively associated with the observed behaviour. It was computed for Rsource ≈ 1014 cm. This event is shown in lower panels. Bottom: microlensing caustic-magnification patterns that can be associated with the detected variability of magnification factor during the 2012 and 2014 flares. The colour bars represent the microlensing magnification (or demagnification if the value is <1). Distances are given in the source plane. The patterns are shown separately for the leading (left) and delayed images (right). Solid white lines indicate the putative trajectories of the images during the 2012 flare, dashed lines depict the displacement of the images over the 2012−2014 period. |
| In the text | |
 |
Fig. 4 Distributions of the best-fit values of the magnification factor ratio μ for the three brightest flaring episodes in 2012 (3 central panels in Fig. 3), derived through the Monte Carlo simulations. |
| In the text | |
 |
Fig. 5 Top: distribution of the average durations of the microlensing magnification episodes obtained from the simulations for Σ = 0.5 and v = 300 km s-1. Horizontal shaded region depicts the range 60−120 days of the apparent variability time scales of the magnification factor ratio in B0218+357, and the vertical one depicts the microlensing magnification ratio range, suggested by the observations. Bottom: cumulative probability of observing microlensing magnification factor ratio >μ for different source sizes, estimated from the simulations. The vertical shaded region is the same as in the upper panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


