| Issue |
A&A
Volume 586, February 2016
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526470 | |
| Published online | 02 February 2016 | |
The imprint of satellite accretion on the chemical and dynamical properties of disc galaxies
1 Departamento de Física Teórica y del Cosmos, Universidad de Granada, Campus de Fuentenueva, 18071 Granada, Spain
e-mail: ruizlara@ugr.es
2 Instituto Carlos I de Física Teórica y computacional, Universidad de Granada, 18071 Granada, Spain
3 School of Physics, University of Exeter, Stocker Road, Exeter EX4 4QL, UK
4 E.A. Milne Centre for Astrophysics, Department of Physics & Mathematics, University of Hull, Hull, HU6 7RX, UK
5 Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
6 Departamento de Física Teórica, Universidad Autónoma de Madrid, 28049 Cantoblanco, Spain
Received: 5 May 2015
Accepted: 1 December 2015
Aims. We study the effects of the cosmological assembly history on the chemical and dynamical properties of the discs of spiral galaxies as a function of radius.
Methods. We made use of the simulated Milky Way mass, fully-cosmological discs from Ramses Disc Environment Study (RaDES). We analysed their assembly history by examining the proximity of satellites to the galactic disc, instead of their merger trees, to better gauge which satellites impact the disc. We presented stellar age and metallicity profiles, age-metallicity relation (AMR), age-velocity dispersion relation (AVR), and stellar age distribution (SAD) in several radial bins for the simulated galaxies.
Results. Assembly histories can be divided into three different stages: i) a merger dominated phase, when a large number of mergers with mass ratios of ~1:1 take place (lasting ~3.2 ± 0.4 Gyr on average); ii) a quieter phase, when ~1:10 mergers take place (lasting ~4.4 ± 2.0 Gyr); and iii) a secular phase where the few mergers that take place have mass ratios below 1:100, which do not affect the disc properties (lasting ~5.5 ± 2.0 Gyr). The first two phases are able to kinematically heat the disc and produce a disc that is chemically mixed over its entire radial extension. Phase 2 ends with a final merger event (at time tjump) marking the onset of important radial differences in the AMR, AVR, and SAD.
Conclusions. Inverted AMR trends in the outer parts of discs, for stars younger than tjump, are found as the combined effect of radial motions and star formation in satellites temporarily located in these outer parts. U-shaped stellar age profiles change to an old plateau (~10 Gyr) in the outer discs for the entire RaDES sample. This shape is a consequence of inside-out growth of the disc, radial motions of disc stars (inwards and outwards), and the accretion of old stars from satellites. We see comparable age profiles even when ignoring the influence of stellar migration due to the presence of early in situ star formation in the outer regions of the galaxy.
Key words: galaxies: stellar content / galaxies: spiral / galaxies: evolution / galaxies: formation / galaxies: structure / methods: numerical
© ESO, 2016
1. Introduction
The accepted scenario of galaxy formation involves an extended process of hierarchical merging of structures until systems settle into the entities we observe today (e.g. White & Rees 1978; Lacey & Cole 1993). During these mergers, satellites are thought to leave a signature of their impact upon the host. Whether these signatures are major, minor, long-, or short-lived, remains an intense topic of debate; however, it is clear that the interplay between such merger/interaction-driven processes and later, internal, secular evolution, all combine to shape the galaxies we see now (e.g. Dressler 1980; Donzelli & Pastoriza 2000; Márquez et al. 2002; Lambas et al. 2003; Kewley et al. 2006; Michel-Dansac et al. 2008).
While idealised galaxy simulations are important to understand secular processes (e.g. Athanassoula 2005; Debattista et al. 2006; Roškar et al. 2008a, 2012; Athanassoula et al. 2009a,b, 2010), simulations run in a cosmological context allow us to study the environmental effects of evolution, including the impact of satellite-host interactions through to the quiescent, settled, disc phase (e.g. Katz & Gunn 1991; Navarro & Benz 1991; Katz et al. 1992; Navarro & White 1994; Steinmetz & Muller 1995; Steinmetz & Navarro 2002; Abadi et al. 2003). These simulations are a critical tool for understanding the effect of accretion and interactions in the build-up of disc galaxies (e.g. Abadi et al. 2003; Governato et al. 2004; Kazantzidis et al. 2008).
However, early cosmological simulations failed to replicate late-type massive spiral galaxies because of the so-called “angular momentum problem” (e.g. Steinmetz & Navarro 2002). This problem consists of the over-production of the spheroid component of simulated galaxies due to enhanced star formation at early epochs. Currently, by modifying numerical and physical parameters in the simulations, more realistic galaxies have been reproduced (see Hummels & Bryan 2012, for a study about the effect on the angular momentum of numerical parameters such as supernova (SN) feedback, spatial resolution, and star formation efficiency, amongst many others). State-of-the-art numerical simulations have overcome this “angular momentum problem” and are able to reproduce the scaling relations and galaxy properties found in nature (e.g. Robertson et al. 2004; Governato et al. 2007; Scannapieco et al. 2009; Sánchez-Blázquez et al. 2009; Stinson et al. 2010; Rahimi et al. 2010; Brooks et al. 2011; Brook et al. 2012; Stinson et al. 2012; Calura et al. 2012; Gibson et al. 2013; Obreja et al. 2014; Few et al. 2014, amongst others).
Most of the successful cosmological simulations have been focused on reproducing Milky Way-type galaxies (e.g. House et al. 2011; Macciò et al. 2012; Calura et al. 2012; Gibson et al. 2013; Walker et al. 2014; Marinacci et al. 2014). Our privileged position inside the Milky Way allows us to take high quality spatial and spectroscopic data against which to confront simulations. A number of contemporary observational studies are exploring the solar neighbourhood with unprecedented quality, providing astronomers with a vast amount of information, including Gaia (Perryman et al. 2001), RAVE (Steinmetz et al. 2006; Zwitter et al. 2008; Siebert et al. 2011; Kordopatis et al. 2013), and SEGUE (Yanny et al. 2009). Simulations play a pivotal role in interpreting the physical mechanisms that shape these datasets.
One of the most striking observations that needs a theoretical counterpart to be understood is the age-metallicity relation (AMR) in the solar neighbourhood (e.g. Powell 1972; Hearnshaw 1972; Twarog 1980). Stars are born from the collapse of molecular clouds that imprint their chemical composition upon newly formed stars. Those stars undergo nuclear fusion reactions in their cores, thereby, changing their chemical composition. According to stellar evolution and galactic chemical evolution models (e.g. Prantzos & Aubert 1995; Fenner & Gibson 2003; Romano et al. 2005), once these stars reach the end of their lives they form new elements and expel part of their mass to the interstellar medium, increasing the interstellar medium’s metal content. As a direct consequence, the subsequent generation of stars is more metal rich than the former1, resulting in a tightly correlated AMR in which younger stars are more metal rich and older stars are more metal poor. However, studies of the AMR in the solar neighbourhood have found an almost flat AMR for thin disc stars with significant dispersion in metallicity at a given age (e.g. Carlberg et al. 1985; Edvardsson et al. 1993; Feltzing et al. 2001; Nordström et al. 2004; Bergemann et al. 2014), while thick disc stars seem to show a steep AMR (Haywood et al. 2013).
Different theoretical works have been able to reproduce aspects of the observed AMR of the solar neighbourhood, bulge, and nearby dwarf discs, by allowing for stellar radial motions in their models that contaminate the expected relation for stars born in the solar neighbourhood (e.g. Roškar et al. 2008a; Sánchez-Blázquez et al. 2009; Schönrich & Binney 2009; Pilkington et al. 2012b). Radial motions (especially of older stars) can mix stars with different enrichment histories and different chemical composition (i.e. formed from different molecular clouds at different galaxy evolutionary stages). This effect can lead to flattening and greater dispersion in the AMR. Several authors have tried to explain what stimulates stars to move radially. Some of the proposed causes are i) the exchange of angular momentum at the corotation resonance of transient spiral arms (e.g. Sellwood & Binney 2002; Roškar et al. 2008b); ii) non-linear coupling between the bar and the spiral waves (e.g. Minchev & Famaey 2010; Minchev et al. 2012a,b); and iii) the influence of satellites (e.g. Younger et al. 2007; Quillen et al. 2009; Bird et al. 2012). These theoretical works have eased the debate about the observed AMR in the solar neighbourhood. However, there are some observational works still claiming that, although some changes to the AMR can be attributed to stellar migration, a large part of the observed scatter is intrinsic to the star formation processes or related to contamination of the solar neighbourhood by stars on apo- and pericentres (Feltzing et al. 2001; Haywood et al. 2013).
Despite the high quality, spatial resolution, and details of the data that we can acquire for stars in the Milky Way, the study of our Galaxy presents a number of significant disadvantages: i) the Milky Way is just one galaxy amongst the myriad different types of galaxies in the Universe; ii) our inside view restricts our observations to the solar neighbourhood because the observable region is obscured by dust, preventing a global view of the Milky Way. To achieve a wider understanding of galaxies in the Universe, we need to study external systems (e.g. MacArthur et al. 2009; Yoachim et al. 2012; Pérez & Sánchez-Blázquez 2011; Sánchez-Blázquez et al. 2011, 2014; Peletier et al. 2012; Catinella et al. 2013; Ahn et al. 2014). Those studies provide us with statistical information about integrated properties such as age and metallicity gradients (mass- and light-weighted), star formation histories (SFHs), light and mass distributions, or age-metallicity relations. The new full spectrum fitting techniques used on these unresolved systems have been proved reliable when compared with the analysis of resolved stellar populations (Ruiz-Lara et al. 2015)2.
The joint study of observations and realistic simulations can expand our knowledge about galaxy formation and evolution (e.g. Bakos et al. 2008; Sánchez-Blázquez et al. 2009; Martínez-Serrano et al. 2009; Pilkington et al. 2012a; Yoachim et al. 2012). Simulations allow one to isolate the primary impact of satellite merging in different environments, including, for example the formation of thick discs (e.g. Quinn et al. 1993; Brook et al. 2004; Villalobos & Helmi 2008), inflows of external material (e.g. Kereš et al. 2005; Dekel & Birnboim 2006), or radial mixing (e.g. Quillen et al. 2009; Bird et al. 2012). The establishment of testable predictions through simulations can be a powerful tool in designing future observational campaigns.
In this paper, we make use of the cosmological hydrodynamical simulations of Milky Way-mass galaxies presented in Few et al. (2012; RaDES: Ramses Disc Environment Study). We study those simulated galaxies to search for signatures of their assembly processes in the age-metallicity-radius relationship. Although the outer parts of the disc represent a small fraction of a galaxy’s total mass, the study of the assembly of these outer regions is especially important because these regions are very sensitive to satellite accretion or external mass perturbations and provide a guide to galaxy formation and evolution.
In Sect. 2, we present the sample of galaxies, the simulations, and their assembly histories. Section 3 presents the main observational characteristics of each simulation. The primary results are shown in Sect. 4 where we discuss the impact of the assembly history on both the AMR and spatially-resolved SFH of the disc. The discussion and main conclusions are provided in Sect. 5.
2. Sample of galaxies
In this work, we use the RaDES (Few et al. 2012) galaxies. The RaDES set of galaxies was created to study differences between galaxies in loose group and field environments through cosmological simulations. The RaDES galaxies are comprised of 19 galaxies with masses similar to the Milky Way and disc characteristics similar to other observed disc galaxies (Few et al. 2012; Pilkington et al. 2012a). While each system has similar properties in relation to their matter content (total, dark, stellar, baryonic, and gaseous mass), they also show important differences concerning their kinematic heating profiles (see Fig. 9 of Few et al. 2012), star formation histories (see Fig. A.1 of Few et al. 2012), disc fractions, and assembly histories.
For brevity, we focus on the analysis of three discs from the RaDES sample. These three span the range of assembly histories of the full sample, from intensive to quiescent; our conclusions are robust against the specific choice of systems.
2.1. Simulations
The RaDES galaxies are simulated with the adaptive mesh refinement code ramses (Teyssier 2002). The simulations track dark matter, stars, and gas on cosmological scales. The hydrodynamical evolution of gas uses a refining grid such that the resolution of the grid evolves to follow over-densities reaching a peak resolution of 436 pc (16 levels of refinement). The ramses code includes gas cooling/heating and a polytropic equation of state is used for dense gas to prevent numerical fragmentation.
Star formation occurs in gas that is more dense than ρ0 = 0.1 nH cm-3 at a rate of 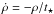 , where t⋆ = t0(ρ/ρ0)−1/2 with t0 = 8 Gyr. Stellar feedback is delayed by 107 years and imparts kinetic energy, mass, and metals to the gas within a two-cell radius sphere. The mass fraction of stellar particles that explode as SN is 10% and each SN provides 1051 erg; 10% of non-metals are converted to metals by each star particle.
, where t⋆ = t0(ρ/ρ0)−1/2 with t0 = 8 Gyr. Stellar feedback is delayed by 107 years and imparts kinetic energy, mass, and metals to the gas within a two-cell radius sphere. The mass fraction of stellar particles that explode as SN is 10% and each SN provides 1051 erg; 10% of non-metals are converted to metals by each star particle.
The galaxies were simulated with cosmological parameters as follows: H0 = 70 km s-1 Mpc-1, Ωm = 0.28, ΩΛ = 0.72, Ωb = 0.045, and σ8 = 0.83. Two volumes are used with a size of 20 h-1 Mpc and 24 h-1 Mpc. The mass resolution of dark matter particles is either 5.5 × 106 M⊙ or 9.5 × 106 M⊙, depending on which of two volumes the galaxy is drawn from. Details of the halo selection process and the simulation parameters may be found in Few et al. (2012) and in Sect. 2.2, below.
Characteristics of the last accretion episode.
2.2. RaDES assembly histories
The assembly histories of the RaDES galaxies have been obtained with a careful study of the merger trees discussed in Few et al. (2012). In short, we use the adaptahop algorithm (Aubert et al. 2004) to create a catalogue of haloes and sub-haloes in the simulation at each time step. We are able to identify, not only each halo, but also their progenitors, descendants, sub-haloes, etc. By linking all these catalogues, we can create merger trees for the different haloes following the “most massive substructure method” (Tweed et al. 2009). The analysis of those merger trees shows that all RaDES galaxies display, generally speaking, similar disc assembly histories in terms of phases or stages.
 |
Fig. 1 Schematic representation of the satellite orbits for Selene (left) and Oceanus (right). On the y-axis we plot the three-dimensional distance (R3D) from the satellite centre to the host galaxy centre. On the x-axis we plot the lookback time (13.5 Gyr being the beginning of the simulation). Each point represents one satellite at a given snapshot with points corresponding to the same satellite at different timesteps linked by a solid black line. In some cases, the halo tracking between snapshots fails, leading to missing connecting lines. We colour-code the points according to log10(Msat/Mhost) (the size of each point is also proportional to that value) as an indicator of the magnitude of the mergers. We have applied a cut in log10(Msat/Mhost) to clean the plot of the least massive satellites; satellites with (Msat/Mhost)t below 0.005 are ruled out in the plots. The dashed red line represents the time evolution of the host galaxy virial radius. Last merger times (tjump) are denoted via dashed cyan vertical lines. For Selene (left) the last merger happened 6.0 Gyr ago with Msat/Mhost ~ 0.089 when it enters the virial radius and ~0.0126 when the merger happens. The two merging events associated with the cessation of the two assembly phases in Oceanus (right), where (Msat/Mhost)v is ~0.056 (0.05) and (Msat/Mhost)t is ~0.006 (0.005) for the first (second) merging event finishing each epoch. |
In Fig. 1, we plot the distance between the centre of the host galaxy and its satellites for two RaDES galaxies as a function of lookback time (Selene, left panel; Oceanus, right panel). Each point in Fig. 1 represents one satellite at a given timestep with the points colour-coded on a logarithmic scale according to the virial mass of the satellite divided by the virial mass of the host halo (Msat/Mhost). All RaDES galaxies underwent three well-defined assembly phases: i) an initial phase of merger-dominated evolution lasting ~3.2 ± 0.4 Gyr on average, while mergers of systems with similar masses occur, Msat/Mhost (when the distance to the host galaxy is lower than 5 kpc) ranging from 0.1 (the majority) to 3 (several of them). This first period is followed by ii) a quieter phase where the number of mergers is minimised by a factor of two with respect to the previous stage. During this phase (lasting ~4.4 ± 2.0 Gyr) several major satellites with Msat/Mhost = 0.01 − 0.3, merge with the host galaxy. This epoch ends with a last merging event, occurring at different times depending on the galaxy in question. We refer to this stage in the galaxy’s evolution as tjump (see Table 1), defined as the time at which this last merger dissolves in the host galaxy. Finally, iii) the disc settles and evolves secularly with just minor satellite mergers (Msat/Mhost< 0.01) disturbing the host disc (lasting ~5.5 ± 2.0 Gyr).
This last accreted satellite is characterised by a value of Msat/Mhost~0.12 ± 0.09 at the time it enters the virial radius ((Msat/Mhost)v) and Msat/Mhost~0.013 ± 0.006 (averaged values) when it merges at tjump ((Msat/Mhost)t). All the characteristics of these latest mergers are shown in Table 1.
While most of the galaxies exhibit just one merger epoch (Phases 1 and 2) followed by a quiescent phase (Phase 3), some others show two different merging events (two Phase 2 events) with the above outlined characteristics. After the first merger event (tjump − a), Phase 2 does not end, but continues until a second event takes place (tjump − b). Artemis and Oceanus are examples of this behaviour (see right panel of Fig. 1).
Figure 1 shows the satellites affecting the discs of Selene and Oceanus as two examples of the above outlined behaviour (one-merging-epoch and two-merging-epoch galaxies, respectively). For resolution/aesthetic purposes, we applied a cut in Fig. 1 to remove the more insignificant satellites, i.e. (Msat/Mhost)t below 0.005. We checked that those satellites not fulfilling our criterion have low masses, and thus, little influence in the disc evolution. For Selene, during the first 3.5 Gyr the evolution is characterised by an unsettled phase dominated by satellite accretion (Phases 1 and 2). The lack of important mergers is the main characteristic during the rest of the simulation, although some low-mass satellites do orbit the host. The last important merger that Selene underwent took place ~6.0 Gyr ago (tjump) with (Msat/Mhost)v ~ 0.089 and (Msat/Mhost)t ~ 0.0126. In the case of Oceanus (two-merging-epochs), the unsettled phase lasts for almost 6 Gyr, finishing with a satellite with (Msat/Mhost)v ~ 0.056 and (Msat/Mhost)t ~ 0.006 (at tjump − a ~ 7.5 Gyr). After that, a 6 Gyr quiescent phase follows with several low-mass satellites remaining isolated from the host disc, followed by another merging episode ~1.2 Gyr ago with (Msat/Mhost)v ~ 0.05 and (Msat/Mhost)t ~ 0.005 (tjump − b~ 1.2 Gyr).
In the next Sects. 3 and 4, we concentrate on the effect that these assembly histories produce on the RaDES galaxies.
3. Disc characteristics
3.1. Disc decomposition
One of the classic problems plaguing the simulation of disc galaxies in a cosmological context is the overproduction of stars associated with the spheroid (bulge and/or halo). Significant advances have been made over the past decade in ameliorating this problem, although this manifestation of the classical over-cooling and angular momentum catastrophe problems has not yet been fully eliminated. Instead, as is standard practice in the field, we post-process the simulations to mitigate the contamination of the disc by spheroid stars.
Definition of the four radial regions studied in this analysis.
To separate the disc from the spheroid component, we apply a kinematic selection criterion based upon the circularity (Jz/Jcirc) distribution (e.g. Scannapieco et al. 2009; Stinson et al. 2010). We have labelled disc stars as those with circularities ranging from 0.9 to 1.1; in this way, we ensure we are considering particles on circular orbits in the plane of the disc. Although different selection criteria can be found in the literature (e.g. Sánchez-Blázquez et al. 2009; Few et al. 2012; Pilkington et al. 2012a) ending with subtly different sub-sets of “disc” particles, we have checked that our results are robust to the specific selection criteria. While our chosen circularity criterion might appear restrictive, the characteristics of the discs so defined (mass, age, and metallicity profiles, etc.) are consistent with those of observed galaxy discs.
Figure 2 shows the spatial distribution of the stellar particles for Selene when our kinematic criterion is applied (right) compared to the distribution when all the particles are represented (left). A careful inspection of the edge-on views allows us to conclude that our criterion properly clean our discs from the spheroid component. The thick disc is not strictly spatially resolved in these simulations and our disc selection is an aggregate thick and thin disc. The face-on view of this particular galaxy highlights some disc characteristics, such as the spiral structure, and we conclude that our strict selection of disc particles allows us to perform our analysis without contamination by halo stars.
 |
Fig. 2 Face-on (top panels) and edge-on (bottom panels) surface density maps of Selene considering every particle in the simulation (left panels) or just disc particles (right panels). |
To spatially sample each disc’s characteristics from the inner to the outer disc, we scaled each one to the radius corresponding to a stellar mass surface density of 107 M⊙kpc-2 (hereafter R7); this “normalisation” corresponds to the typical “break radius” in the surface density profile of disc galaxies (e.g. Roškar et al. 2008b; Sánchez-Blázquez et al. 2009), and has been chosen as useful scaling, but does not impact the conclusions whatsoever. We study four radial regions (see Table 2 and Sects. 3.3, 3.4, and 4), defined as i) inner, this region accounts for the particles in the inner disc scale length (hin) obtained analysing the SDSS r-band mock images from SUNRISE (Jonsson 2006); the images generated by SUNRISE can be seen in Few et al. (2012) (see Appendix A for further information); ii) middle disc, this is a hin-width region around R7/ 2; iii) outer disc, hin-width region around R7; and iv) outskirts, 3hin-width region around R7 + 2 × hin. We apply these spatial cuts for every galaxy, avoiding overlap between regions. We followed the same approach for every RaDES galaxy with no assumptions regarding the surface brightness profile of the discs. Again, we tested various ways of radially scaling our discs and the results are not contingent upon this convenient normalisation.
3.2. Stellar age and metallicity distribution of disc stars
Different groups have tried to study, both observationally and theoretically, the properties of the stellar populations as a function of radius in spiral galaxies. In Roškar et al. (2008a), using N-body + SPH simulations of an isolated and idealised disc, the authors generated age profiles with a characteristic U-shape attributed to radial migration induced by transient spiral arms. On the other hand, Sánchez-Blázquez et al. (2009), using fully-cosmological hydrodynamical simulations, also found such an age profile in their simulations, but proposed a combination of two different processes to explain it: i) a radial change in the star formation history linked to a drop in the gas density (itself, due to a warp) as the main cause; and ii) a radial migration of stars towards larger radii; we emphasize, however, that the said U-shaped age gradient was found even in the absence of radial migration. Observationally, Bakos et al. (2008) stacked the SDSS data from Pohlen & Trujillo (2006), obtaining a clear U-shaped g − r colour profile for type II galaxies (those showing a down-bending surface brightness profile). However, this work has two main disadvantages: i) it is based on stacked profiles and a careful study of individual galaxies show that not all of them display this inversion in the age profile nor the minimum in age (colour) located at the break radius (Roediger et al. 2012); and ii) as they use colour profiles, it is highly affected by the age-metallicity degeneracy, so the g − r colour cannot be interpreted either as the age or metallicity of the stellar populations. The difficulty of obtaining good spectroscopic data in the outer parts of the spiral galaxies to minimise the age-metallicity degeneracy (e.g. Ganda et al. 2009) has hampered the study of reliable stellar age profiles reaching beyond the break radius. Yoachim et al. (2012) studied the stellar content of 12 spiral galaxies with Mitchell Spectrograph IFS data (Hill et al. 2008). They obtained U-shaped age profiles in three out of the six galaxies that they were able to study beyond their break radius. Currently, we are analysing the stellar content focused on the outer parts of the CALIFA galaxies (Sánchez et al. 2012) and obtaining no clear relation between the occurrence of U-shape age profiles and their surface brightness profiles (Ruiz-Lara et al. 2016).
A recent study has carefully analysed the stellar content in the outer parts of M31 by means of 14 resolved fields (Bernard et al. 2015). They find that the outermost fields show that a significant fraction of their mass had already formed by z ~ 1, while fields a bit closer to the centre are on average younger. They suggest this is the consequence of a complicated galaxy evolution due to mergers. The study of age and metallicity profiles in simulated galaxies as well as more observational effort helps us to better understand the behaviour of the stellar age in the outer parts of spiral galaxies.
 |
Fig. 3 Upper panel: Selene stellar disc age profile. Middle panel: Selene stellar disc metallicity profile. Bottom panel: Selene total velocity dispersion profile (disc stars). Red (blue) vertical dashed lines are located at the surface brightness break (minimum age) radius. The errorbars indicate the standard deviation of the values of every particle within each radial bin. hin is the inner disc scale length in SDSS r-band mock images from SUNRISE (Jonsson 2006). These mock images can be seen in Few et al. (2012). Vertical arrows are located at the beginning and the end of the four regions defined in Table 2. Blue, region 1; green, region 2; red, region 3; black, region 4. |
With this purpose, we have studied the age and metallicity distribution of the RaDES galaxies’ discs by means of one-dimensional profiles. We obtain those profiles by applying a mass-weighted average to all disc particles within 0.5 kpc-wide radial bins. Figure 3 shows the age, metallicity, and velocity dispersion profiles characterising the disc of one such galaxy, Selene. Each of the 19 analysed galaxies show similar profiles regardless their morphology and characteristics: i.e. negative mass-weighted metallicity gradients and U-shaped mass-weighted age profiles. The radius where the minimum in age is reached is roughly located in region 3 for all of them. The outermost parts of every galaxy show an extended, old plateau (older than 10 Gyr, beyond ~6.4 hr). The metallicity profiles show a flattening in the centre, mainly caused by the low metallicity of the older stars populating the inner region of our discs (see Figs. 5 and 7). These profiles are extensively analysed in Sect. 5.1.
In addition to the age and metallicity profiles, we obtained the velocity dispersion profiles (bottom panel of Fig. 3) for each of the above-defined RaDES discs. They also show a U-shaped form. In fact, there is a correlation in the shapes of the age and velocity dispersion profiles with the minimum of both distributions located roughly at the same radial position. This is related to the age-velocity dispersion relation expected for galactic discs (discussed in the following section) where, in general, younger stars have lower velocity dispersions. As stars age they are heated by the effect of the galaxy dynamics and/or satellites (see Fig. 4). This aspect might deepen the U-shape age profile as the stars that are being born at the minimum age radius have less time to move away and, on average, make other regions younger. Similar U-shapes in the velocity dispersion profiles have been found in the Villalobos & Helmi (2008) simulations as a consequence of the accretion of a discy satellite with an initial orbital inclination for the satellite with respect to the mid-plane of the host disc of 30° (they obtain similar results using spherical satellites and an orbital inclination of 60°).
3.3. Age-velocity dispersion relation
 |
Fig. 4 Radial velocity dispersion vs. age for Apollo (upper panel), Selene (middle panel), and Oceanus (bottom panel) disc stars, colour-coded according to their radial positions. Blue: region 1: inner region (one disc scale-length width, hin using the SDSS r-band mock images from SUNRISE Jonsson 2006; these mock images can be seen in Few et al. 2012). Red: region 2: a 1-hin width annulus between the centre and the 107 M⊙kpc-2 mass surface density. Green: region 3: a 1-hin width annulus centred at the 107 M⊙kpc-2 mass surface density. Black: A 3.5-hin width annulus further out (see text, Table 2, and Fig. 4 for further details). The parameter hin is 2.34, 5.67, and 8.07 kpc for Apollo, Selene, and Oceanus, respectively. The parameter tjump is denoted for each galaxy with dashed cyan vertical lines (the moment when the last main satellite is accreted). This plot is aimed at illustrating different epochs for different galaxies when the last major accretion event happened. Dashed lines show the AVR at intermediate simulation stages between the formation of the galaxy and the present day to address the effect of the last merger episode in the AVR (1.49 Gyr ago for Apollo, 4.34 for Selene, and 5.75 Gyr for Oceanus). |
In the solar neighbourhood of the Milky Way, the stellar velocity dispersion increases with the stellar age, however, the exact shape/behaviour of the relationship remains a matter of debate (e.g. Wielen 1977; Binney et al. 2000; Seabroke & Gilmore 2007). Nordström et al. (2004) made use of the Geneva–Copenhagen Survey to study the Age-Velocity dispersion Relation (AVR) in the solar neighbourhood. They studied each velocity component separately, finding that power laws can fit the relation found in every direction. They interpreted those results as evidence for a continuous heating of the disc. Conversely, several works have found some saturation in the V and W velocity dispersion components (Soubiran et al. 2008). Aumer & Binney (2009), using Hipparcos and Geneva-Copenhagen data, were not able to rule out such saturation for stars older than 4 Gyr, combined with an abrupt increase in velocity dispersion for the oldest stars. Martig et al. (2014), based on seven simulated galaxies, proposed that continuous heating takes place to explain the slope of the AVR for stars younger than 8−9 Gyr, but also found a step in the AVR for the oldest stellar population, related to an early merger phase. The authors showed that the maximum in σz is strongly decreased when age errors of 30% are implemented, suggesting that observations can easily miss such a jump with the current accuracy of age measurements. Although it is hard to distinguish among the different heating agents (e.g., bars, spirals, mergers, and stars born hot at high redshift), Martig et al. showed that radial migration does not heat the disc, in agreement with Minchev et al. (2012a) and Vera-Ciro et al. (2014).
In a comparison of our simulations with both the existing empirical and model AVRs in order to identify the heating mechanisms underpinning RaDES, in Fig. 4 we show how the stellar radial velocity dispersion varies as a function of stellar age for three of the RaDES galaxies (Apollo, Selene, and Oceanus). We study this relation in the four different regions outlined earlier (Sect. 3.1). The behaviour for the individual velocity components (R, φ, and z) parallels that of Fig. 9 of Few et al. (2012). The shape of the AVR is very similar across the four regions, suggesting that heating is consistent over the entire disc, albeit, there are qualitative differences in the strength of this heating as a function of radius.
The most remarkable feature we can find in these age-velocity diagrams is the presence of an increase in the velocity dispersion values around a given age (~tjump), which is a feature that is apparent throughout the entire disc (in the four radial regions). Although for some galaxies this jump in the AVR is smooth (as is the case for Apollo), other galaxies show a clear sudden jump (e.g. Selene and Oceanus, see Fig. 4). Stars older than tjump have a larger velocity dispersion than the stars with ages younger than tjump for all RaDES galaxies: this jump is clearly linked to their last important merger (happening at tjump with (Msat/Mhost)t ~ 0.0126; see Sect. 2.2). This jump is more evident for the outer parts and fades towards the centre; mergers affect the outer disc more strongly because of its lower surface density.
The dashed lines in Fig. 4 represent the AVR at different evolutionary stages, which allow us to appreciate how our galaxies have evolved since the last merger. We show the AVR from 1.49 and 4.34 Gyr ago for Apollo and Selene, respectively. We observe that the AVR taken in the present day and just after the mergers have similar shapes across the four regions, i.e. the disc kinematics respond qualitatively the same at all radii. Some differences exist in how the four regions evolve, however; in the case of Apollo (the galaxy with the smoothest jump of the three), the AVR was also smooth 1.49 Gyr ago, yet since that time, regions 2–4 have relaxed more than region 1. For Selene, the AVR 4.34 Gyr ago and the one found currently are similar in that the step in velocity dispersion exists immediately after the merger and persists to the present day. The difference between the AVR at intermediate evolutionary epochs and the AVR displayed at present time suggests that, apart from the effect caused by the mergers, secular evolution following the merger clearly affects the final AVR shape (a similar behaviour is displayed by Oceanus).
 |
Fig. 5 Age-metallicity relation for Selene disc stars, colour-coded according to their current radial positions (see text, Table 2, and Fig. 4 for more information). Blue crosses represent stars currently located in region 1. Green asterisks represent stars currently in region 2. Red dots represent stars currently in region 3. Black triangles represent stars currently in region 4. The two histograms on top of the AMR and on the right represent the age and metallicity distribution function, respectively (colour-coded in the same way). The parameter tjump is denoted by the dashed cyan vertical line. Solid lines correspond to the linear fits performed to the AMR of the stars in the four radial regions for epoch 2 (from tjump until 10 Gyr ago) and epoch 3 (from the present day until tjump). |
In the case of Oceanus (see Fig. 4), one of the galaxies where two merger episodes can be identified by its assembly history (see Fig. 1), we can also distinguish two jumps in the AVR. The more recent event presents a more prominent jump, while the earlier event is more subtle because it is swamped by the combination effect of the latest merger and secular heating. This swamping of the earlier jump might be caused by a differential heating between cold and hot stars minimising the extant jump, affecting cold stars more than hot stars. To check our hypothesis, in Fig. 4 we show the AVR displayed by Oceanus disc stars 5.75 Gyr ago, i.e. after the first merger event and prior to the second event; while at the end of the simulation, the jump at 7.5 Gyr is almost negligible, the AVR at 5.75 Gyr ago shows a more prominent jump for stars older than 7.5 Gyr, which is more evident for the inner region. This result favours our idea that the jump experienced by stars older than 7.5 Gyr was caused by a merger event 7.5 Gyr ago, but has been partially swamped by the last merger and the subsequent secular heating (especially true for region 1).
Major mergers are not the only source of kinematic heating affecting our discs: internal secular evolution processes and other minor mergers can also shape the AVR. These plots do, however, prove that satellite merging is an important heating mechanism affecting the kinematic state of the stars experiencing these events and, therefore, the AVR.
We also find another striking point shown by the AVRs in the values found for the velocity dispersion. Our velocity dispersions are higher than those observed in the solar vicinity (e.g. Holmberg et al. 2009). Old stars show values as high as twice the value for Milky Way old stars, and young stars show those values presented by solar neighbourhood old stars. It is expected that higher velocity dispersions are found within our simulated discs than for the Milky Way, as high velocity dispersions are endemic to almost all of the cosmological simulations of disc galaxies (see House et al. 2011). High velocity dispersions may also be due to contamination of the disc by spheroid stars, however, we have minimised that effect by applying our disc particle criterion. Furthermore, none of our galaxies are a perfect match to the Milky Way, so we do not expect the same behaviour as shown by the Milky Way, which has a different assembly histories than the simulated discs underwent.
3.4. Age-metallicity relation
We have analysed the AMR for the discs of the RaDES galaxies. In Figs. 5 and 7 we show, as two representative examples, the AMR for the Selene and Oceanus disc stars, colour-coded according to their radial location (see Table 2 for the definition of the extent of each region). In these figures, we also show the age and metallicity distribution functions for each region (top and right-hand panels, respectively). We split this figure into four different panels corresponding to the four radial regions under study (see Fig. 6) to properly appreciate the details of Fig. 5.
 |
Fig. 6 Age-metallicity relation for Selene disc stars, equivalent to Fig. 5, but split into four different panels; one per region. |
 |
Fig. 7 Age-metallicity relation for Oceanus disc stars; see Fig. 5 for more information. The parameters tjump − a and tjump − b are denoted by the dashed cyan vertical lines. |
The chemical properties of the stars show a different behaviour depending on the assembly history stage they were born in, which common to all the galaxies analysed. Figure 6 clearly shows well-differentiated epochs according to the dispersion of the AMR displayed by the stars corresponding to the three-phase assembly history described in Sect. 2.2: stars formed during epoch 1 (older than 10 Gyr) show very small dispersion, while stars born at epochs 2 and 3 display a larger dispersion at all ages. This tight AMR for old stars is a direct consequence of the origin of old stars, accreted from satellites or formed in the early host galaxy: these environments are spatially small and have comparatively homogeneous metal abundances and enrichment histories. Afterwards, when quiescent phases dominate the mass assembly, the diversity of satellite metallicity increases and the galaxy develops a metallicity gradient that enhances the dispersion of the AMR. The metallicity distribution is also broadened as late-forming satellites with lower metallicities are accreted by the enriched host galaxy. Radial stellar motions also increase the dispersion of each region as stars move from the metal-enhanced centre of the galaxy and the relatively metal-poor outskirts to other regions. These radial motions tend to affect older populations more strongly (as we show in Sect. 4.1), yet only broaden the dispersion of the AMR if stars exist with distinct metallicities in other regions of the galaxy. It is for this reason that radial motions broaden the AMR dispersion for a given region for the epoch 2 stars (because a metallicity gradient exists at this time) but does not broaden the AMR dispersion for epoch 1 (when the metallicity is very homogeneous) or epoch 3 stars (when less radial migration has taken place; see Sect. 4.1).
In addition, we have carefully analysed other aspects of the AMR such as: i) the metallicity distribution, suggesting different degrees of chemical mixing according to the age-metallicity plots; and ii) the slopes in the AMR; we compute these slopes in the AMR for epochs 2 and 3, avoiding the more turbulent epoch 1.
i) We have analysed the MDF (see Fig. 8) for stars in regions 1 to 4, distinguishing between young (younger than tjump, 1 to 2 Gyr) and old (older than tjump, 8 to 9 Gyr) stars (see left panel of Fig. 8 for Selene). For every galaxy, the metallicity dispersion is larger in the outer parts than in the inner parts (irrespective of age), ranging from 0.04 vs. 0.10 dex in region 1 to 0.07 vs. 0.13 dex in region 4 for the young vs. old components, respectively (averaged values for all 19 RaDES galaxies). This is consistent with Minchev et al. (2014), where the increase in the AMR scatter with radius was related to the expected increase in contamination from migration and heating with radius. The metallicity dispersion for old stars is also larger than for young stars. If we define the change in the metallicity dispersion between old and young component as 100 ∗ (σmet,old − σmet,young) /σmet,old, its radial evolution is 58.7% in region 1, 37.9% in region 2, 26.4% in region 3, and 21.6% in region 4, i.e. the differences are minimised at greater radii.
 |
Fig. 8 Metallicity distribution in the four different radial regions distinguishing between young (1−2 Gyr, upper panel) and old stars (8−9 Gyr, bottom panel) for Selene (left, current locations; middle, birth locations; right, current location not considering accreted stars). Blue, green, red, and black histograms represent particles in regions 1, 2, 3, and 4 respectively. The distributions are different for the young stars compared to the similar distributions in the case of the old component. |
If we do not focus on the radial evolution of the MDF for old or young stars, we can find interesting differences in the discrepancies between old and young populations. Young stars show very different MDFs for the different radial bins, while more similar distributions are shown by old stars in regions 1 to 4. We analysed the differences between the metallicity distributions of different radial regions for young and old stars (at their current positions), using Kolmogorov-Smirnov (KS) statistical tests, to quantify this statement. The KS test effectively determines whether two sets of data are drawn from the same statistical distribution and the differences between those distributions. For our purposes, larger KS values when comparing different radial regions would imply a greater degree of chemical mixing. According to these tests, young stars show distinct metallicity distributions between the different radial regions, while old stars in each region show similar metallicity distributions to one another. The average of the KS statistic values for all the galaxies comparing all the possibilities of pair or regions (i.e. 1−2, 1−3, 1−4, 2−3, 2−4, and 3−4) is 0.85 for young stars and 0.45 for old stars. These KS tests allow us to conclude that the degree of chemical mixing is greater for old stars than for young stars.
Figure 8 shows the MDF for young and old stars not only at the current position (left panel), but also at their birth location (middle panel) for Selene to properly assess the cause of different mixing degrees for old and young stars. If the well-mixed MDFs displayed by old stars were due to the merger event, we should observe that old stars, taken at their birth location, exhibit distinct MDFs. However, Fig. 8 (left and middle panels for old stars) reveals that while there is some degree of mixing of the MDFs after the formation of the stars, there is no clear separation as found in the younger populations and the majority of the similarity in the MDFs of old stars in different regions is imprinted at birth. This statement is backed by the mean and dispersion values displayed by these distributions. Although slightly lower dispersion values and larger mean metallicity ranges are found for stars at their birth position than at the current position, this is not enough as to suggest that the mixing was imprinted by merger events4.
To further quantify the importance of mixing induced by accretion (in contrast to mixing imprinted at birth, the right panel of Fig. 8 shows the MDF of the Selene stars of star particles at regions 1 to 4 (current position) excluding accreted stars (i.e. Rbirth> 20 kpc and | z | > 3 kpc). The mean metallicity values of those MDFs are −0.23, −0.39, −0.48, and −0.56, while their dispersions are 0.13, 0.12, 0.11, and 0.07 for old stars from regions 1 to 4. If we compare these values with those computed for the MDFs for old stars at their current positions (mean metallicities of −0.23, −0.38, −0.48, and −0.56 and dispersions of 0.13, 0.12, 0.12, and 0.11 for regions 1−4, respectively) and also compare the MDF shapes, we can conclude that the mixing is particularly important for region 4.
In Fig. 9 we show the MDFs of these stars at their current location (top panel) and at their birth location (bottom panel) to determine if the MDFs of epoch 1 stars (10 to 11.5 Gyr old) have changed during the evolution of the galaxy. The time evolution of these old stars is much weaker than for other age ranges because the MDFs of our four regions are mixed so well when the stars are born5. The MDFs of regions do change over time but there is no clear trend present in the MDFs taken at birth locations. Taken together with Fig. 8, this further demonstrates that the clearly separated MDFs seen in the youngest stars were never present in older populations that form with more homogeneous MDFs.
 |
Fig. 9 Metallicity distribution in the four different radial regions for very old stars (10.0−11.5 Gyr) for Selene. Coloured histograms follow the colour code explained in Fig. 8. |
 |
Fig. 10 Metallicity distribution in the four different radial regions distinguishing between young (0−0.5 Gyr, upper panel), intermediate (4−5 Gyr, middle panel) and old stars (8−9 Gyr, bottom panel) for Oceanus (current locations). Coloured histograms follow the colour code explained in Fig. 8. The distributions are different for young stars compared to the similar distributions in the case of the old component. Intermediate-aged stars show an intermediate behaviour. |
In summary, the well-mixed MDFs displayed by stars born during Phases 1 and 2 is not directly a result of a single satellite accretion event (although it also has an effect), but because of the collective activity in Phases 1 and 2 that homogenise the chemical characteristics of the gas from which stars are born.
ii) The slopes of the AMR for the four regions are always negative for the old stars (for every galaxy with just one tjump). These slopes are computed by means of a linear fit to the points in the AMR in the plane [M/H]-Age (thus in units of dex/Gyr). These old-star AMR slopes are roughly similar, as expected from stars born at a more chemically homogeneous time in the assembly history. The relative slope differences (00 × (slopei − slopej) /slopej, with i and j ranging from 1 to 4 accounting for all the possibilities) are under 40% for the entire sample of the RaDES galaxies (40% is reached just for the most extreme cases; the median is around 20%). When considering the younger part of the AMR (stars younger than tjump), the slopes range from negative (regions 1 and 2) to positive (region 4) in most of the galaxies. Region 3 is the region with the shallowest AMR slope. The average values considering the 19 RaDES galaxies are −0.031, −0.027, −0.004, and 0.008 dex/Gyr for regions 1 to 4, respectively. In the particular case of Selene the values are −0.016, −0.007, 0.002, and 0.06 dex/Gyr from region 1 to 4.
 |
Fig. 11 Age-metallicity relation for Selene applying different cuts in the Jz/Jcirc ratio. Upper left, particles with Jz/Jcirc between 0.5 and 0.7; upper right, particles with Jz/Jcirc between 0.7 and 0.9; lower left, particles with Jz/Jcirc between 0.9 and 1.1; lower right, particles with Jz/Jcirc between 1.1 and 1.3 |
The case of Oceanus (as well as Artemis, not shown here) is a special one that deserves to be analysed in further detail. As we have already commented, Oceanus shows two merger episodes during the simulation with similar characteristics to those described in Sect. 2.2. Both episodes imprint a jump in the AVR (see Sect. 3.3; the jump at 7.5 Gyr is later erased by the effect of the last merger event) and leave a signature in the AMR. In Fig. 7 we can clearly distinguish three main age regions, delimited by tjump − a ~ 7.5 and tjump − b ~ 1.2 Gyr. Figure 10 shows the metallicity distributions for three different age bins (young, intermediate, and old) for Oceanus. In this case the radial evolution of the MDF is weaker for the older age bins. The young component shows metallicity dispersions of 0.071, 0.036, 0.056, and 0.071 dex (regions 1 to 4). For the intermediate (old) component, we find a radial evolution of 0.132, 0.133, 0.111, and 0.125 dex (0.176, 0.170, 0.182, and 0.188 dex). However, it is still true (even for this two-event galaxy) that the metallicity dispersion is higher for older stars (those with ages in the range 7.5–10 Gyr), the metallicity dispersion has intermediate values for intermediate-aged stars, and lower values for young stars. As already outlined in the case of Selene, these well-mixed MDFs displayed by stars born during epochs 1 and 2 are mainly a consequence of gas mixing that is imprinted on the stars at birth. The radial evolution of the slope in the AMR from negative to positive is also found for the youngest stars (− 0.054, − 0.025, − 0.0018, and 0.022 dex/Gyr), while negative AMR slopes are obtained for the intermediate and old components (except for the slope of intermediate-aged stars in region 4, which is consistent with the increasingly positive slope as a function of radius). To assess the degree of chemical mixing we decided, as described above, to make use of KS tests. We can draw similar conclusions as before, i.e. the youngest component of the AMR has four different metallicity distributions (KS statistic of 0.96), the intermediate component shows a higher degree of mixing (KS statistic of 0.60), and the old component shows the most similar metallicity distributions (KS statistic of 0.24).
The negative-to-positive change (with decreasing age) in the slopes of the AMRs deserves a further explanation. Negative slopes in the AMR are a direct consequence of chemical enrichment due to stellar evolution. Positive slopes are difficult to produce (and indeed are not frequently found in nature) owing to chemical evolution alone, requiring efficient inflows of unenriched gas into the galaxy. Inversion of the AMR is more easily achieved through the dynamical effects of satellite accretion (metal-rich stars that are formed in the core of the satellites while passing through region 4), accretion of metal-poor gas (to form young, metal-poor stars), and radial migration. Further details can be found in Sect. 5.
In order to check the influence of our kinematic selection criterion for disc/non-disc particles on the AMR, we have repeated our analysis of the AMR for Selene considering four different Jz/Jcirc ranges (0.5−0.7, 0.7−0.9, 0.9−1.1, and 1.1−1.3, see Fig. 11). The main results outlined in this section remain true for each of the Jz/Jcirc selections, albeit with slight differences: there tend to be fewer stars forming post-tjump in the lower Jz/Jcirc cuts (particularly at larger radii) making the inverted portion of the AMR non-existent. Our disc star criterion (0.9 <Jz/Jcirc< 1.1) strengthens our results as this choice is the most representative of a disc population, though it should be clear from Fig. 11 that the inversion is present if stars with Jz/Jcirc in the range 0.5−1.3 were all included.
4. Chemo-dynamical imprints of satellite accretion: radial stellar motions
Sections 3.3 and 3.4 clearly point towards the effect of satellite accretion on observables such as the AVR or the AMR. We can, however, study galaxy properties other than those presently apparent, such as time evolution, stellar motions, and angular momentum, considering the richness of cosmological simulations. A careful inspection of these simulations can help us to understand the mechanisms responsible for the present-day observed properties.
In this section, we further investigate the effect of satellite accretion in the stellar age distribution at different radii (see Sect. 4.1) and the signatures that these events leave in the AMR (see Sect. 4.2).
4.1. Hints from the stellar age distribution
The study of stellar properties, such as the age or metallicity of stars currently located at specific regions, as well as their original positions, can provide us with keys to understanding galaxy evolution. Figure 12 shows the current stellar age distribution (SAD; normalised to the mass of the whole galaxy) for Selene’s disc stars in the four scaled regions (solid black line). At this stage we add two more regions from the outermost parts corresponding to the old plateau: region 5 at 4.4hin − 6.2hin and region 6 at 6.2hin − 7.9hin. We separate the components of this current SAD according to i) particles born in each region that have stayed there (in situ stars, solid red line); ii) born outwards then moved in (solid green line less than 5.0 kpc, solid cyan line more than 5.0 kpc); and iii) stars born inwards and moved out (solid blue line). In this third case, we also divide them depending on the birth region: iiia) born in region 1 (dotted blue line); iiib) born in region 2 (dotted-dashed blue line); and iiic) born in region 3 (dashed blue line). Our birth radius is very close to the instantaneous radius at the time of the birth of the stars. It is defined as the location of the star in the first snapshot.
 |
Fig. 12 Radially resolved, stellar age distribution for the Selene disc normalised to the total stellar mass. The different panels show the stellar age distribution of the stars currently located in regions 1 (upper left), 2 (upper right), 3 (middle left), and 4 (middle right); see Table 2 for more information. We added two more regions in the outer most part of the galaxy. Region 5 goes from 4.4hin to 6.2hin and region 6 goes from 6.2hin to 7.9hin. These two regions have been added to study the causes of the old plateau in the age distribution seen in the outermost disc. Black solid lines represent particles currently in that region; solid red line particles born and stayed there; solid blue line particles born inwards and moved outwards currently in that region; solid green line particles born outwards and moved in; solid cyan line particles born way out and moved in; dashed cyan line accreted particles (i.e. Rbirth> 20 kpc and | z | > 3 kpc); dotted blue line particles born in region 1 that end up there; dotted-dashed blue line particles born in region 2 that end up there; and dashed blue line particles born in region 3 that end up there. The definitions of the lines are described in full in the main text. |
As a general trend, radial region 1 is mainly populated by old stars (older than 10 Gyr whose distribution shows a peak at 12 Gyr) that were born and stayed in that region (red line, accounting for ~23% of the mass in region 1), with a non-negligible fraction of stars coming from the outer parts (~20% of the mass in region 1). The oldest stars (older than 10 Gyr) in radial region 2 were formed inside (~5% of the mass in region 2) or far outside (~7% of the mass in region 2), while the majority of the young stars (younger than 4 Gyr) formed in situ (~33% of the mass in region 2) with an important contribution of stars also born inside and outside that region (~6% of the mass in region 2). The same dichotomy is found in regions 3 and 4 where older stars were born inside or much further out while young stars mainly formed there or moved outwards from the inner regions with fewer in situ stars, especially for region 4, which is mainly dominated by migrated stars with a small percentage of in situ stars (~16% of the mass in region 4). Studying outwards travellers in region 4, we can see that the older the star is the more it has travelled outwards (from regions 1, 2, or 3). The radial evolution of the red lines reflects a clear inside-out growth of the disc, and we can analyse when star formation starts in each radial region: stars were formed in region 1 since the beginning of the simulation; region 2 started forming stars 10 Gyr ago; region 3, 6 Gyr ago; and region 4, 2 Gyr ago. The vast majority (~92%) of stars migrating more than 5 kpc (solid cyan lines in Fig. 12) are accreted from outside the galaxy, i.e. Rbirth> 20 kpc and | zbirth | > 3 kpc. The age distribution of these accreted stars is shown in Fig. 12 as a dashed cyan line.
Regions 5 and 6 are mainly populated by old stars on circular orbits coming from well outside the host galaxy (cyan lines in Fig. 12). Some stars from the inner parts are also found, however, the main cause of the old plateau observed in all the RaDES galaxy discs is the accretion of old stars from early satellites. This is in contrast to the interpretation by Roškar et al. (2008a), who suggested that the oldest stars in the outskirts have migrated from the inner disc. We find no stars that were born in the outer parts, are still in that region, and meet our criterion for disc stars.
4.2. Hints from the age-metallicity relation
In Sect. 3.4 we showed the radial evolution of the AMR in our disc galaxies and outlined the first signatures left by satellite accretion in this relation. Here, we study in more detail the AMR and expand the imprints of satellite accretion on the chemistry and dynamics of our galaxies.
Figure 13 shows the same AMR displayed in Fig. 5, but this time split into four different sub-panels (one for each radial region) and colour-coded according to the Rcurrent − Rbirth for each particle. We can draw similar conclusions to those outlined in the previous section: region 1 is mainly populated by in situ stars at all ages with a significant number of stars that have moved inwards, particularly from the last satellite (cyan line, stars born before tjump; see Fig. 12). As we compare the inner with the outer regions, more and more stars appear that are moving outwards (especially amongst older populations) and fewer stars move inwards, except for those stars moving inwards that were born at the furthest distances in satellites (dark blue points in Fig. 13). The extreme case is found in region 4 where the majority of particles have been formed at smaller radii, some old stars come from satellites, and just a few have been born in situ (stars younger than 2 Gyr, when the inside-out growth of the disc reached region 4). Every old particle now located in regions 3 or 4 is either coming from the inner parts or from satellites (consistent with Fig. 12).
The AMR of the last accreted satellite can be discerned from the older and dark blue points in regions 1 and 2 in Fig. 13 (for aesthetic reasons we restrict the colour bar range from −4 to 4 kpc, i.e. dark blue points mean Rcurrent − Rbirth ≤ − 4.0). The shape of this AMR mimics that of the host galaxy. There is a correlation between dips in the AMR envelope of the host disc stars and of the satellite. We can explain such a correlation as the consequence of repeated fly-bys that the satellite has experienced during its approach.
In Pilkington et al. (2012a), we studied the time evolution of one of the RaDES galaxy’s (Apollo) “instantaneous” or gas-phase metallicity gradient, finding a shallower profile presently than at early simulation stages, i.e. the metallicity gradient of the galaxy is flattening with time. According to that work, we would expect the mean metallicity of each region to be similar for young stars and more different for older stars. However, Fig. 5 shows the opposite behaviour, i.e. the difference in the mean metallicity at a given age between two adjacent regions is increasing as we are moving towards younger ages. However, this neglects the effect of stellar migration, which may flatten the metallicity profile. Radial motion causes this effect as stars from the metal-rich centre of the galaxy move to the outskirts. This pushes up the mean metallicity for intermediate-aged stars found at larger radii and inverts the expected trend of the AMR because the youngest stars are born from gas with a metallicity that is lower than the centre had in the past.
A striking segregation can be seen in the metallicity of stars depending upon how they have migrated. Stars that have moved outwards are systematically more metal rich than particles that have stayed in a region or moved inwards (see Fig. 13). This is a direct consequence of the negative metallicity gradients and stellar radial motions and consistent with Minchev et al. (2013). In fact, if we infer the metallicity gradients from these plots (~−0.071 dex/kpc), we obtain similar results to those presented in Few et al. (2012) (Table 2, ~−0.061 dex/kpc).
Satellite accretion not only produces a mixture in the spatial distribution of stars and an exchange of stars moving inwards/outwards, it also leaves a signature in the dynamics of the stars. In Fig. 14 we show the AMR split in four sub-panels, as in Fig. 13, but now colour-coding each stellar particle according to its circularity (Jz/Jcirc). Despite the narrow range of Jz/Jcirc we are considering in our discs (see Sect. 3.1) we find another interesting trend. Specifically, in every analysed region there is little or no correlation between the stellar metallicity and Jz/Jcirc prior to tjump. This might suggest that during the epoch of satellite accretion (phases 1 and 2 in Sect. 2.2), the disc was hot and mixed well, and those stars still preserve that state (as already shown and quantified in Sect. 3.4). If we consider the subsequent quiescent phase after satellite accretion, the stars born after tjump display a new segregation with the more metal-rich stars, which tend to be migrating outwards, with the least circular orbits and vice versa.
 |
Fig. 13 Age-metallicity relation for Selene disc particles in four radial bins (current positions); every point represents a stellar particle colour-coded according to its Rcurrent − Rbirth. Distribution of plots as in Fig. 12 (regions 1 to 4). Dashed cyan vertical lines are located at tjump. We must highlight that, although the colour-coded range goes from −4 to 4 kpc, we plot all the disc particles in that region, i.e. light green (dark blue) really means Rcurrent − Rbirth ≥ 4.0 (Rcurrent − Rbirth ≤ − 4.0). |
 |
Fig. 14 Age-metallicity relation for Selene disc particles in four radial bins (current positions); every point represents a stellar particle colour-coded according to its Jz/Jcirc. Distribution of plots as in Fig. 12 (regions 1 to 4). Dashed cyan vertical lines are located at tjump. |
We should emphasise that Fig. 1 shows (by means of tjump, dashed cyan vertical lines) the moment when the last satellite merges with the disc of the host galaxy. After this time the satellites do not dynamically affect the host disc any longer. We can conclude from the above outlined analysis that satellites affect the disc properties in a continuous way until the last one totally merges with the host galaxy (not when it enters the virial radius), after that our discs evolve mostly quiescently.
5. Discussion and conclusions
We have analysed the stellar content of the RaDES galaxies (Few et al. 2012) to study the effect of satellite accretion in shaping the chemo-dynamical properties of their discs. In this work, we concentrate on the characterisation of the assembly history of these galaxies and the influence of this assembly on stellar disc properties such as the age and metallicity profiles (Sect. 3.2); the age-velocity dispersion relation (AVR; see Sect. 3.3); the age-metallicity relation (AMR; see Sect. 3.4); and other dynamic and kinematic properties (see Sect. 4). We study the radial evolution of several of those properties by dividing our discs into four radial regions (see Table 2).
The assembly histories of the RaDES galaxies are characterised by three main epochs: i) A first merger-dominated epoch, when most of the mass of the galaxy is formed via accretion of massive satellites (Msat/Mhost ranging from 0.1 to 3). ii) During the second phase the host galaxy still suffers several mergers but decreases in number and mass ratio (Msat/Mhost ranging from 0.01 to 0.3, at a distance smaller than 5 kpc). iii) This second phase is followed by a quiescent period (with some sporadic satellite accretion with Msat/Mhost ~ 0.001) in which the disc has settled. We define tjump as the time boundary between Phases 2 and 3, at which time the last satellite merges with the host galaxy. This latest accretion event is characterised by its satellite having similar characteristics for all the RaDES galaxies (Msat/Mhost ~ 0.12 ± 0.09 when it enters the virial radius and Msat/Mhost ~ 0.013 ± 0.006 when the merger happens, averaged values; see Table 1). This event marks the end of the active merging period and the beginning of quiescent evolution.
This assembly history leaves an imprint on the chemical and dynamical properties of the stellar discs of our galaxies. The AVR shows a clear jump (sudden for some galaxies, smooth for others) at around tjump (see Fig. 4). This feature is a direct consequence of the heating produced by the satellite accretion. Those stars that underwent Phases 1 and 2 (older than tjump) are in a hotter state now (high velocity dispersion) than young stars that were born in the quiescent Phase 3. The smoothness of the jump depends on the “merging timescale” of the latest accretion event and subsequent internal evolution.
These differences in the velocity dispersion between old and young stars lead to differential chemical mixing in our discs. While different radial regions show different AMRs (with very different metallicity distributions) for young stars, Kolmogorov-Smirnov statistical tests show that the metallicity distributions of old stars display similar characteristics at different radii (see Figs. 5, 7, 8, and 10). Although the radial redistribution of stars due to satellite accretion and secular activity does take place, we find that the radial distribution of metals in the gas from which old stars were formed was homogeneous during Phases 1 and 2 compared with the Phase 3, and that this is the main cause of the similar MDFs displayed by old stars. Thus, radial redistribution of stars does little to change the MDFs of these older stars that are born with a flat metallicity gradient.
Most of the analysed galaxies show the above outlined assembly scenario leaving the same imprints in the AMR and MDFs. However, two of these galaxies show two different accretion events after the disc is settled (Artemis and Oceanus; see Figs. 4 and 7). Similar results and conclusions as those outlined before for the rest of galaxies apply to these two cases. The bottom panel of Fig. 4 shows how this second event is able to heat the stars of the entire disc, regardless of their ages. The fact that the jump in the AVR at 7.5 Gyr is smoother than that at 1.2 Gyr might be a consequence of such heating produced by this latest accretion event (at 1.2 Gyr). To test this hypothesis, we analysed the AVR at 5.75 Gyr ago (dashed lines in the bottom panel of Fig. 4). We can observe that the jump in velocity dispersion at 7.5 Gyr was more important in the past than it is currently. This confirms the suggestion that the merger event is able to heat the entire disc of the host galaxy, swamping previous jumps in the AVR, especially in the inner regions. Thus, old steps in the AVR can be erased by later mergers as heating produced by mergers is more efficient on kinematically cold stars than on hot stars. In the particular case of Oceanus, the latest merger event blurs the jump observed at 7.5 Gyr. Our KS tests comparing the radial metallicity distribution of three age bins according to these two merger events also show that old stars display higher mixing degree, while intermediate-aged and young stars show a lower mixing degree (with the youngest stars displaying the lowest mixing; see Fig. 10). Although part of the observed mixing might be induced by merging of structures, the greater mixing degree displayed by old stars was imprinted at birth (as for the case of galaxies with just one merger event). The activity in Phases 1 and 2 homogenises the chemical characteristics of the gas along the entire galaxy and, as a consequence, stars formed from this homogenised gas display similar MDFs regardless of their location.
Figures 5, 7, and 15 show dips in the maximum [M/H] of the central region (region 1) located at tjump as well as at other time steps (to a lesser degree). Those shallower dips are related to the galaxy accretion history as they correspond to close encounters between the host galaxy and minor satellites. The dips are caused by temporary dilution of the gas in the central region by the merger either bringing metal-poor gas from the halo of the galaxy or simply adding the metal-poor gas from the surroundings of the satellite. In both cases, this gas has a lower metallicity than the gas in the centre of the galaxy.
We observe two interesting segregations in our AMR plots (see Figs. 13 and 14). The innermost regions (regions 1 and 2) of our galaxies show that metal-rich stars have moved outwards, while metal-poorer stars have moved inwards. This behaviour can easily be explained by the observed negative metallicity profile (in fact, their gradients can be inferred from such plots; see Sect. 4.2). The outermost parts of the galaxies (regions 3 and 4) show such behaviour for the young stars (younger than tjump), while the old stars populating those regions have migrated from the inner parts or come from satellites, i.e. formed outside of the galaxy itself.
The segregation in circularity (Jz/Jcirc) deserves further explanation. Figure 14 shows that old stars display well-mixed values of their circularity regardless of their metallicity (a consequence of the heating mechanisms that they have undergone). However, in the case of the young stars (younger than tjump), the more metal rich the star is, the lower the circularity is. We can explain this by the expectation that stars with higher Jz/Jcirc and lower metallicities are born outside the studied annulus (as shown by Fig. 13). There are two ways in which these stars can appear in an annulus inwards of their birth places: i) Their angular momenta decreased (i.e. inwards migration) to the value of the stars born locally, in which case Jz/Jcirc is close to 1; or ii) they have reached the final annulus on their pericentres, but with angular momenta that is still larger than that appropriate for the annulus under consideration. It is the second case that causes the green outline at the lower metallicity range. Those stars have guiding radii outside the studied region. Similarly, lower angular momentum disc stars (dark-blue points) are accumulated at the upper metallicity edge.
In Sect. 3.4, we describe and quantify the main characteristics of the AMR in different radial bins for Selene. Apart from the differences in the chemical mixing between old and young stars, one of the most interesting aspects outlined is the progressive change in slope from regions 1 to 4. A negative slope in the AMR is easily explained by the fact that young stars (in a simple scenario) are born from enriched gas, and thus, are expected to be more metal rich than old stars populating the same region. The presence of radial motions (as those described in Fig. 13) combined with a negative metallicity profile can produce a higher dispersion in the AMR and a change in the AMR slope (Roškar et al. 2008a; Sánchez-Blázquez et al. 2009). Extreme radial motions can even cause the inversion that we observe: old stars migrate from the metal-rich centre of the galaxy to the outer parts, and stars from intermediate radii (less metal rich) move inwards. However, if we now recreate Fig. 5, this time colour-coding the point according to the region in which the stars were born instead of their present-day position, we still have some inversion (see Fig. 15). A careful analysis of the time evolution of the AMR at birth location for region 4 can explain this inverted AMR. Satellites orbiting around the host galaxy are forming stars in their inner parts with metallicities similar to those displayed by the centre of the host galaxy. Before merging with the host galaxy, the satellites pass through region 4 several times (the clusters of black triangles at ~6.5 and 8.0 Gyr in the case of the satellite responsible for the tjump) forming stars within region 4, particles that after the merger took place acquire a circular orbit (fulfilling our disc criterion). These particles are metal-rich stars. In addition, we find a low number of particles that are born in region 4 from metal-poor gas accreted from the halo or other satellite haloes with ages between 3.0 and 6.0 Gyr. As a consequence of the metal-poor gas accretion and the low star formation activity, gas in region 4 becomes progressively more metal poor. Finally, we find a group of newly born stars (younger than 2.0 Gyr) due to inside-out growth of the disc reaching region 4 (see red line in region 4, Fig. 12). Once true disc star formation is established the normal negative gradient to the AMR reappears (the last 2.0 Gyr). This scenario naturally leads to an inverted AMR in region 4 even when radial motions are not considered. The same reasoning can be applied to region 3 (outer parts in general), with the difference that inside-out growth reaches this region much sooner (6 Gyr ago; see Fig. 12).
 |
Fig. 15 Age-metallicity relation for Selene disc stars, colour-coded according to their birth radius. See Fig. 5 for further information. |
Positive slopes in the AMR of the outer parts of nearby galaxies have already been observed. Bernard et al. (2012) studied the SFH and AMR of two outer fields in M31 and another field in M33 using the data from Barker et al. (2011), both based on HST/ACS colour−magnitude diagrams (CMDs). The SFH and AMR found in both galaxies show enhanced SF at ~2 Gyr and an inverted AMR for stars younger than ~3 Gyr, similar to that in the outer parts of Oceanus in this work. They suggest that this SF enhancement and the inverted AMR is caused by a close encounter between M31 and M33 2−3 Gyr ago according to the N-body simulations by McConnachie et al. (2009). In addition, Bernard et al. (2012) find that the analysed outer fields in M31 and M33 are older than the inner parts, suggesting a U-shaped age profile in contrast to the purely negative profile found by Williams et al. (2009) in M33. To compare with our results we must keep in mind that, while they are observing the consequences of a close encounter between two massive spiral galaxies, we are considering the entire assembly history of the RaDES galaxies. Our work and these observational and theoretical works confirm that satellite merging or galaxy encounters leave a signature in observable quantities, such as the AMR or the age profile, especially in the outer parts.
In Bernard et al. (2015), the team expanded upon their previous analysis in M31 by analysing 14 outer fields located along the disc, the giant stellar stream (GSS, caused by satellite accretion), and in regions in between. They are able to confirm the inverted AMR already outlined in Barker et al. (2011) and Bernard et al. (2012) for all the analysed fields. In addition, they deduce that most of the mass in the disc regions was already formed by z ~ 1, while stream-like regions are on average older, as expected since the GSS origin is linked to satellite accretion. Joining the above result with our findings, we confirm that satellite merging or galaxy encounters leave a signature in observable quantities, such as the AMR or the age profile, especially in the entire outer disc.
In Villalobos & Helmi (2008, 2009), the authors study the effect that 1:5 mass-ratio (at virial radius) satellite mergers have upon the thick disc properties using N-body simulations of a satellite that is accreted by a pre-existing disc galaxy. They find that ~2 Gyr after the merger event occurs the properties of the heated discs have settled and stop evolving further (roughly consistent with our findings). They claim that the kinematic impact on their host (thin) discs is almost negligible in the case of the vertical and azimuthal components, while in the case of the radial velocity dispersions they usually increase their value by 5−10 km s-1 at all radii. We find increases from ~50% in the inner parts to ~100% in the velocity dispersion of the outer parts for Selene (latest satellite with a mass ratio of ~1:10). This suggests strong disc flaring, which is an important aspect of the formation of thick discs in a cosmological context (Minchev et al. 2015). However, although the effect we see in our simulations in the heating of the discs from satellite accretion is greater than in the case of Villalobos & Helmi (2008, 2009), we must take into account that the jump in the AVR is a consequence of Phases 1 and 2. While Villalobos & Helmi (2008, 2009) analyse controlled experiments in which one unique satellite merges with a host galaxy, our simulations are embedded in a cosmological context and, thus, this greater heating is not only caused by the latest merging event, but is a consequence of all previous mergers.
5.1. Revisiting the U-shape age profile
 |
Fig. 16 Selene age and metallicity profiles for all particles and for disc particles alone, either including or removing radial motions. Solid lines: we allow stars to move radially to compute the age and metallicity profiles. Dashed lines: stars born locally, not allowing radial motions. Black lines: all the particles in the simulation (disc+spheroid). Magenta lines: particles fulfilling our disc criterion. This plot is focused on understanding the effect of radial motions in the age and metallicity profiles. Red (blue) vertical dashed lines are located at the break (minimum age) radius. hin is the inner disc scale length in SDSS r-band mock images from SUNRISE (Jonsson 2006); these mock images can be seen in Few et al. (2012). |
Every age profile for the RaDES galaxies exhibits the same behaviour (see Sect. 3.2 and Fig. 3): a negative profile, followed by an upturn that ends up in an old plateau at large galactocentric radius. Recent simulations find these U-shape profiles in the stellar age distribution of their simulated discs (e.g. Roškar et al. 2008b,a; Sánchez-Blázquez et al. 2009; Martínez-Serrano et al. 2009). Different mechanisms have been proposed to explain these profiles, but there is still a lack of consensus (see Sect. 3.2).
The findings presented in this paper point to three main aspects responsible for shaping the disc age profiles:
-
a)
An inside-out growth of the disc: as discussed inSect. 4.1 and shown by Fig. 12 (redlines), our discs display a clear inside-out growth of the disc. Thismechanism can account for the inner part (negative gradient) ofthe age profile.
-
b)
Radial motions (inwards and outwards) of stars belonging to the disc: Fig. 12 (blue lines) also shows that the regions where the upturn in age appears are dominated by old stars that have move outwards (especially region 4) with the contribution of some young, in situ stars.
-
c)
Accreted, old stars from satellites: Phases 1 and 2 populate our discs with old stars coming from the accretion of satellites. Such accretion is also responsible for the U-shape in the age profile as part of the old stars in regions 3 and 4 come from satellites (cyan lines in Fig. 12). However, these old accreted stars are especially responsible for the old plateau observed at large galactocentric distances (see Fig. 3). Regions 5 and 6 are mainly populated by these old accreted stars.
However, although radial motions might play an important role in creating the U-shaped age profile (Roškar et al. 2008b,a), they are not necessarily needed to build up such a profile (Sánchez-Blázquez et al. 2009; Halle et al. 2015). In Fig. 16 we analyse the effect that radial motions and our disc-particle criterion (based on Jz/Jcirc) imprint in the shape of the age and metallicity profiles.
 |
Fig. 17 Radially resolved, stellar age distribution for Selene, normalised to the total stellar mass. In this plot we study all the particles in the simulation (in Fig. 12 we show only disc particles). The upper panel shows the stellar age distribution of the stars currently located in region 5 (from 4.4hin to 6.2hin), while the bottom panel shows stars currently located in region 6 (6.2hin to 7.9hin). Lines and colours represent the same as in Fig. 12. A low number of old, in situ stars are responsible for shaping the old outer plateau even in the absence of radial motions if we do not apply our disc criterion. |
Radial motions have their greatest effect on the age minimum, i.e. a younger minimum in the age profile is found when suppressing radial motions. This is because the minimum age is in a prime location to be migrated to (it can easily receive stars from larger and smaller radii) and because migrating stars tend to be older. However, U-shaped age profiles are found whether we allow stars to migrate or not, i.e. radial motions affect the shape of the age profile but are not in fact the origin of the U-shape.
To explain why the U-shaped age profile is still recovered after suppressing radial motions, we need to analyse the stellar content in the outer parts of our simulated galaxies (regions 4, 5, and 6, see Fig. 12). Region 4 shows some in situ star formation around 6, 7, and 11 Gyr ago, this star formation can easily explain the upturn in the age profile. However, the old plateau disappears if we suppress radial motions for disc stars (while still visible if we analyse all the particles; see Fig. 16). This old plateau disappears for disc particles because of the lack of in situ disc stars at large radii. However, if we study the entire sample of stellar particles (spheroid and disc component), we can find that an old, non-disc population exists in this outermost regions of the RaDES galaxies, suggesting early star formation in these outer parts (see Fig. 17).
In recent years, there is a growing body of work claiming that the formation of the outer disc of the Milky Way may have begun as early as 10 Gyr ago (e.g. see discussions in Haywood et al. 2013; Snaith et al. 2014; Halle et al. 2015). This suggests that, apart from radial migration, other mechanisms might be in place while shaping these outer regions. In particular, Nidever et al. (2014), analysing APOGEE data (Majewski et al. 2010), find a complex Milky Way formation from a well-mixed and turbulent interstellar medium with different SFHs for inner and outer discs. In addition, more studies are finding upturns in the age profiles in the outer parts of, not only spiral galaxies, but also dwarfs (Hidalgo et al. 2013).
Both radial motions and the application of less restrictive disc-particle criteria have a flattening effect on metallicity profiles. The reason for this is straightforward; particles that move radially inwards by the greatest distances are old, metal-poor stars that strongly affect the regions where the average metallicity is higher (lowering the average metallicity). In addition, particles moving outwards were formed in high-metallicity gas and move towards regions dominated by low-metallicity stars, thus, this outwards motion increases the mean stellar metallicity in the outer parts. The impact of relaxing our disc-particle criterion has the same effect. Relaxing the criteria allows more spheroid particles to be considered in the analysis, in particular particles that are characterised as old and metal poor, and thus reduces the mean metallicity in the metal-rich regions more strongly while making little difference to the metal-poor regions. In the case of Selene, the metallicity gradient evolves from −0.20, −0.19, −0.13, and −0.12 dex/hin from locally born disc stars, all locally born stars, disc stars with radial motions, and all stars with radial motions, respectively.
The assembly history of disc galaxies leaves important fingerprints in their chemical and dynamical properties. Based on this assembly history, we have been able to explain previously observed features, such as the dispersion in the AMR, inverted AMR gradients, and U-shaped age profiles. Satellites mainly affect the host disc when they completely merge with it, although some star formation and gas dilution can be observed during the different satellite fly-bys. These fingerprints should be easily observed in present and upcoming spectroscopic surveys, such as Gaia (Perryman et al. 2001), RAVE (Steinmetz et al. 2006; Zwitter et al. 2008; Siebert et al. 2011; Kordopatis et al. 2013), SEGUE (Yanny et al. 2009), APOGEE (Majewski et al. 2010), or 4MOST (de Jong et al. 2012) helping us to understand the physics shaping the present-day observable properties of the Milky Way.
Certain star formation and infall rate scenarios can lead, in some cases, to a subsequent decline in metalicity (e.g. Matteucci & Gibson 1995).
Conversely, comparing resolved stellar populations with only a restricted subset of line indices can prove problematic (e.g. Gibson et al. 1999).
The mean metallicities ([M/H]) for old stars at their current position are −0.23, −0.38, −0.48, and −0.56 from regions 1 to 4, with metallicity dispersion of 0.13, 0.12, 0.12, and 0.11, respectively. However, at their birth location those values change to −0.20, −0.44, −0.58, and −0.31 (mean metallicities) and 0.09, 0.07, 0.07, and 0.16 (metallicity dispersions) for the particular case of Selene.
Acknowledgments
We thank the anonymous referee for very useful comments. This research has been partly supported by the Spanish Ministry of Science and Innovation (MICINN) under grants AYA2011-24728 and AYA2014-53506-P, by the Junta de Andalucía (FQM-108), and the UK’s Science & Technology Facilities Council (ST/J001341/1: B.K.G., ST/F007701/1: C.G.F.). The generous allocation of resources from STFC’s DiRAC Facility (COSMOS: Galactic Archaeology), the DEISA consortium, co-funded through EU FP6 project RI-031513 and the FP7 project RI-222919 (through the DEISA Extreme Computing Initiative), and the PRACE-2IP Project (FP7 RI-283493), are gratefully acknowledged. T.R.L. thanks the support of the Spanish Ministerio de Educación, Cultura y Deporte by means of the FPU fellowship. C.G.F. acknowledges the support of the European Research Council for the FP7 ERC starting grant project LOCALSTAR. P.S.-B. acknowledges support from the Ramón y Cajal program and to the grant ATA2010-21322-C03-02 from the Spanish Ministry of Economy and Competitiveness (MINECO). This research made use of python (http://www.python.org), of Matplotlib (Hunter 2007), a suite of open-source python modules that provides a framework for creating scientific plots, and Astropy, a community-developed core Python package for Astronomy (Robitaille et al. 2013).
References
- Abadi, M. G., Navarro, J. F., Steinmetz, M., & Eke, V. R. 2003, ApJ, 597, 21 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E. 2005, MNRAS, 358, 1477 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Romero-Gómez, M., Bosma, A., & Masdemont, J. J. 2009a, MNRAS, 400, 1706 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Romero-Gómez, M., & Masdemont, J. J. 2009b, MNRAS, 394, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Athanassoula, E., Romero-Gómez, M., Bosma, A., & Masdemont, J. J. 2010, MNRAS, 407, 1433 [NASA ADS] [CrossRef] [Google Scholar]
- Aubert, D., Pichon, C., & Colombi, S. 2004, MNRAS, 352, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, J., Trujillo, I., & Pohlen, M. 2008, ApJ, 683, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, M. K., Ferguson, A. M. N., Cole, A. A., et al. 2011, MNRAS, 410, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Bergemann, M., Ruchti, G. R., Serenelli, A., et al. 2014, A&A, 565, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Barker, M. K., et al. 2012, MNRAS, 420, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Bernard, E. J., Ferguson, A. M. N., Richardson, J. C., et al. 2015, MNRAS, 446, 2789 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., Dehnen, W., & Bertelli, G. 2000, MNRAS, 318, 658 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, J. C., Kazantzidis, S., & Weinberg, D. H. 2012, MNRAS, 420, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Kawata, D., Gibson, B. K., & Freeman, K. C. 2004, ApJ, 612, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Brook, C. B., Stinson, G., Gibson, B. K., Wadsley, J., & Quinn, T. 2012, MNRAS, 424, 1275 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, A. M., Solomon, A. R., Governato, F., et al. 2011, ApJ, 728, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Calura, F., Gibson, B. K., Michel-Dansac, L., et al. 2012, MNRAS, 427, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Carlberg, R. G., Dawson, P. C., Hsu, T., & Vandenberg, D. A. 1985, ApJ, 294, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Schiminovich, D., Cortese, L., et al. 2013, MNRAS, 436, 34 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
- Debattista, V. P., Mayer, L., Carollo, C. M., et al. 2006, ApJ, 645, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birnboim, Y. 2006, MNRAS, 368, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Donzelli, C. J., & Pastoriza, M. G. 2000, AJ, 120, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Erwin, P., Pohlen, M., & Beckman, J. E. 2008, AJ, 135, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Feltzing, S., Holmberg, J., & Hurley, J. R. 2001, A&A, 377, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fenner, Y., & Gibson, B. K. 2003, PASA, 20, 189 [Google Scholar]
- Few, C. G., Gibson, B. K., Courty, S., et al. 2012, A&A, 547, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Few, C. G., Courty, S., Gibson, B. K., Michel-Dansac, L., & Calura, F. 2014, MNRAS, 444, 3845 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C. 1970, ApJ, 160, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Ganda, K., Peletier, R. F., Balcells, M., & Falcón-Barroso, J. 2009, MNRAS, 395, 1669 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K., Madgwick, D. S., Jones, L. A., Da Costa, G. S., & Norris, J. E. 1999, AJ, 118, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, B. K., Pilkington, K., Brook, C. B., Stinson, G. S., & Bailin, J. 2013, A&A, 554, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Governato, F., Mayer, L., Wadsley, J., et al. 2004, ApJ, 607, 688 [NASA ADS] [CrossRef] [Google Scholar]
- Governato, F., Willman, B., Mayer, L., et al. 2007, MNRAS, 374, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Gutiérrez, L., Erwin, P., Aladro, R., & Beckman, J. E. 2011, AJ, 142, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Halle, A., Di Matteo, P., Haywood, M., & Combes, F. 2015, A&A, 578, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haywood, M., Di Matteo, P., Lehnert, M. D., Katz, D., & Gómez, A. 2013, A&A, 560, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hearnshaw, J. B. 1972, MmRAS, 77, 55 [NASA ADS] [Google Scholar]
- Hidalgo, S. L., Monelli, M., Aparicio, A., et al. 2013, ApJ, 778, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, G. J., MacQueen, P. J., Smith, M. P., et al. 2008, in SPIE Conf. Ser., 7014 [Google Scholar]
- Holmberg, J., Nordström, B., & Andersen, J. 2009, A&A, 501, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- House, E. L., Brook, C. B., Gibson, B. K., et al. 2011, MNRAS, 415, 2652 [NASA ADS] [CrossRef] [Google Scholar]
- Hummels, C. B., & Bryan, G. L. 2012, ApJ, 749, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Jonsson, P. 2006, MNRAS, 372, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, N., & Gunn, J. E. 1991, ApJ, 377, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Katz, N., Hernquist, L., & Weinberg, D. H. 1992, ApJ, 399, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Kazantzidis, S., Bullock, J. S., Zentner, A. R., Kravtsov, A. V., & Moustakas, L. A. 2008, ApJ, 688, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Kereš, D., Katz, N., Weinberg, D. H., & Davé, R. 2005, MNRAS, 363, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Geller, M. J., & Barton, E. J. 2006, AJ, 131, 2004 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Gilmore, G., Steinmetz, M., et al. 2013, AJ, 146, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Lacey, C., & Cole, S. 1993, MNRAS, 262, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Lambas, D. G., Tissera, P. B., Alonso, M. S., & Coldwell, G. 2003, MNRAS, 346, 1189 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- MacArthur, L. A., González, J. J., & Courteau, S. 2009, MNRAS, 395, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Macciò, A. V., Stinson, G., Brook, C. B., et al. 2012, ApJ, 744, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Majewski, S. R., Wilson, J. C., Hearty, F., Schiavon, R. R., & Skrutskie, M. F. 2010, in IAU Symp. 265, eds. K. Cunha, M. Spite, & B. Barbuy, 480 [Google Scholar]
- Marinacci, F., Pakmor, R., & Springel, V. 2014, MNRAS, 437, 1750 [NASA ADS] [CrossRef] [Google Scholar]
- Márquez, I., Masegosa, J., Moles, M., et al. 2002, A&A, 393, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martig, M., Minchev, I., & Flynn, C. 2014, MNRAS, 443, 2452 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Serrano, F. J., Serna, A., Doménech-Moral, M., & Domínguez-Tenreiro, R. 2009, ApJ, 705, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F., & Gibson, B. K. 1995, A&A, 304, 11 [NASA ADS] [Google Scholar]
- McConnachie, A. W., Irwin, M. J., Ibata, R. A., et al. 2009, Nature, 461, 66 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Michel-Dansac, L., Lambas, D. G., Alonso, M. S., & Tissera, P. 2008, MNRAS, 386, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012a, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012b, A&A, 548, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2013, A&A, 558, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Chiappini, C., & Martig, M. 2014, A&A, 572, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Martig, M., Streich, D., et al. 2015, ApJ, 804, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., & Benz, W. 1991, ApJ, 380, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., & White, S. D. M. 1994, MNRAS, 267, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Nidever, D. L., Bovy, J., Bird, J. C., et al. 2014, ApJ, 796, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Obreja, A., Brook, C. B., Stinson, G., et al. 2014, MNRAS, 442, 1794 [NASA ADS] [CrossRef] [Google Scholar]
- Peletier, R. F., Kutdemir, E., van der Wolk, G., et al. 2012, MNRAS, 419, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, I., & Sánchez-Blázquez, P. 2011, A&A, 529, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilkington, K., Few, C. G., Gibson, B. K., et al. 2012a, A&A, 540, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilkington, K., Gibson, B. K., Brook, C. B., et al. 2012b, MNRAS, 425, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Powell, A. L. T. 1972, MNRAS, 155, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Prantzos, N., & Aubert, O. 1995, A&A, 302, 69 [NASA ADS] [Google Scholar]
- Quillen, A. C., Minchev, I., Bland-Hawthorn, J., & Haywood, M. 2009, MNRAS, 397, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Quinn, P. J., Hernquist, L., & Fullagar, D. P. 1993, ApJ, 403, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Rahimi, A., Kawata, D., Brook, C. B., & Gibson, B. K. 2010, MNRAS, 401, 1826 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, B., Yoshida, N., Springel, V., & Hernquist, L. 2004, ApJ, 606, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Tollerud, E. J., et al. Astropy Collaboration 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roediger, J. C., Courteau, S., Sánchez-Blázquez, P., & McDonald, M. 2012, ApJ, 758, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Chiappini, C., Matteucci, F., & Tosi, M. 2005, A&A, 430, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008a, ApJ, 684, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Stinson, G. S., et al. 2008b, ApJ, 675, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., & Wadsley, J. 2012, MNRAS, 426, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz-Lara, T., Pérez, I., Gallart, C., et al. 2015, A&A, 583, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruiz-Lara, T., Pérez, I., Florido, E., et al. 2016, MNRAS, 456, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Courty, S., Gibson, B. K., & Brook, C. B. 2009, MNRAS, 398, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Ocvirk, P., Gibson, B. K., Pérez, I., & Peletier, R. F. 2011, MNRAS, 415, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Rosales-Ortega, F. F., Méndez-Abreu, J., et al. 2014, A&A, 570, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scannapieco, C., White, S. D. M., Springel, V., & Tissera, P. B. 2009, MNRAS, 396, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Seabroke, G. M., & Gilmore, G. 2007, MNRAS, 380, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Williams, M. E. K., Siviero, A., et al. 2011, AJ, 141, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Snaith, O. N., Haywood, M., Di Matteo, P., et al. 2014, ApJ, 781, L31 [CrossRef] [Google Scholar]
- Soubiran, C., Bienaymé, O., Mishenina, T. V., & Kovtyukh, V. V. 2008, A&A, 480, 91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinmetz, M., & Muller, E. 1995, MNRAS, 276, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., & Navarro, J. F. 2002, New A, 7, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Stinson, G. S., Bailin, J., Couchman, H., et al. 2010, MNRAS, 408, 812 [NASA ADS] [CrossRef] [Google Scholar]
- Stinson, G. S., Brook, C., Prochaska, J. X., et al. 2012, MNRAS, 425, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Twarog, B. A. 1980, ApJ, 242, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Tweed, D., Devriendt, J., Blaizot, J., Colombi, S., & Slyz, A. 2009, A&A, 506, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vera-Ciro, C., D’Onghia, E., Navarro, J., & Abadi, M. 2014, ApJ, 794, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, Á., & Helmi, A. 2008, MNRAS, 391, 1806 [NASA ADS] [CrossRef] [Google Scholar]
- Villalobos, Á., & Helmi, A. 2009, MNRAS, 399, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, A. P., Gibson, B. K., Pilkington, K., et al. 2014, MNRAS, 441, 525 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Wielen, R. 1977, A&A, 60, 263 [NASA ADS] [Google Scholar]
- Williams, B. F., Dalcanton, J. J., Dolphin, A. E., Holtzman, J., & Sarajedini, A. 2009, ApJ, 695, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., Roškar, R., & Debattista, V. P. 2012, ApJ, 752, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Cox, T. J., Seth, A. C., & Hernquist, L. 2007, ApJ, 670, 269 [Google Scholar]
- Zwitter, T., Siebert, A., Munari, U., et al. 2008, AJ, 136, 421 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Surface brightness profiles
The study of the light distribution in observed spiral galaxies has recently led to a rapid evolution in our thinking regarding its structural characteristics. The wide variety of surface brightness (SB) profiles reported (e.g. Pohlen & Trujillo 2006; Erwin et al. 2008; Gutiérrez et al. 2011, amongst others) intimates that such profiles may hold a key piece of the puzzle towards understanding galaxy formation and evolution; the plethora of profiles now found in the literature are a contrast to the canonical wisdom that discs were single exponentials (Freeman 1970). For completeness, we show here the light distribution of the RaDES sample, derived from one-dimensional SB profiles of the mock images presented in (Few et al. 2012); these images were produced using SUNRISE (Jonsson 2006). SUNRISE uses the stellar and gaseous distributions, as well as spectral energy distributions (SEDs) for each composite stellar particle, drawn from the Starburst99 stellar population models (Leitherer et al. 1999) to generate bandpass-dependent mock images. One-dimensional profiles were then fitted with the function presented in (Erwin et al. 2008, Eqs. (5) and (6)) with a broken exponential profile implemented. This way, we can distinguish between galaxies with exponential, up-bending, or down-bending profiles and characterise the light distribution of the inner and outer discs. Figure A.1 shows those profiles. Table A.1 summarises the light distribution information for the 19 simulated galaxies.
 |
Fig. A.1 Surface brightness profiles in SDSS r band for Apollo (top left), Artemis (top right), Atlas (middle left), Ben (middle right), Castor (bottom left), and Daphne (bottom right). Blue solid line: “observed” SB profile using the SUNRISE (Jonsson 2006) mock images; those images can be seen in Few et al. (2012). Red solid line: single/double disc fit. Green, vertical, solid lines: these lines delimit the extent where the fit has been performed. Black vertical solid line: Boundary between the spheroid component and the disc; it is computed as the point where the distance between red and blue solid lines is less than 0.1 mag arcsec-1. Red, vertical, dashed line: location of the break. |
 |
Fig. A.2 Same as Fig. A.1 but for Eos (top left), Helios (top right), Hyperion (middle left), Krios (middle right), Leia (bottom left), and Leto (bottom right). |
 |
Fig. A.3 Same as Fig. A.1 but for Luke (top left), Oceanus (top right), Pollux (middle left), Selene (middle right), Tethys (bottom left), and Tyndareus (bottom right). |
Main disc properties from the light distribution in the g, r, and i SDSS bands for the RaDES galaxies.
All Tables
Main disc properties from the light distribution in the g, r, and i SDSS bands for the RaDES galaxies.
All Figures
 |
Fig. 1 Schematic representation of the satellite orbits for Selene (left) and Oceanus (right). On the y-axis we plot the three-dimensional distance (R3D) from the satellite centre to the host galaxy centre. On the x-axis we plot the lookback time (13.5 Gyr being the beginning of the simulation). Each point represents one satellite at a given snapshot with points corresponding to the same satellite at different timesteps linked by a solid black line. In some cases, the halo tracking between snapshots fails, leading to missing connecting lines. We colour-code the points according to log10(Msat/Mhost) (the size of each point is also proportional to that value) as an indicator of the magnitude of the mergers. We have applied a cut in log10(Msat/Mhost) to clean the plot of the least massive satellites; satellites with (Msat/Mhost)t below 0.005 are ruled out in the plots. The dashed red line represents the time evolution of the host galaxy virial radius. Last merger times (tjump) are denoted via dashed cyan vertical lines. For Selene (left) the last merger happened 6.0 Gyr ago with Msat/Mhost ~ 0.089 when it enters the virial radius and ~0.0126 when the merger happens. The two merging events associated with the cessation of the two assembly phases in Oceanus (right), where (Msat/Mhost)v is ~0.056 (0.05) and (Msat/Mhost)t is ~0.006 (0.005) for the first (second) merging event finishing each epoch. |
| In the text | |
 |
Fig. 2 Face-on (top panels) and edge-on (bottom panels) surface density maps of Selene considering every particle in the simulation (left panels) or just disc particles (right panels). |
| In the text | |
 |
Fig. 3 Upper panel: Selene stellar disc age profile. Middle panel: Selene stellar disc metallicity profile. Bottom panel: Selene total velocity dispersion profile (disc stars). Red (blue) vertical dashed lines are located at the surface brightness break (minimum age) radius. The errorbars indicate the standard deviation of the values of every particle within each radial bin. hin is the inner disc scale length in SDSS r-band mock images from SUNRISE (Jonsson 2006). These mock images can be seen in Few et al. (2012). Vertical arrows are located at the beginning and the end of the four regions defined in Table 2. Blue, region 1; green, region 2; red, region 3; black, region 4. |
| In the text | |
 |
Fig. 4 Radial velocity dispersion vs. age for Apollo (upper panel), Selene (middle panel), and Oceanus (bottom panel) disc stars, colour-coded according to their radial positions. Blue: region 1: inner region (one disc scale-length width, hin using the SDSS r-band mock images from SUNRISE Jonsson 2006; these mock images can be seen in Few et al. 2012). Red: region 2: a 1-hin width annulus between the centre and the 107 M⊙kpc-2 mass surface density. Green: region 3: a 1-hin width annulus centred at the 107 M⊙kpc-2 mass surface density. Black: A 3.5-hin width annulus further out (see text, Table 2, and Fig. 4 for further details). The parameter hin is 2.34, 5.67, and 8.07 kpc for Apollo, Selene, and Oceanus, respectively. The parameter tjump is denoted for each galaxy with dashed cyan vertical lines (the moment when the last main satellite is accreted). This plot is aimed at illustrating different epochs for different galaxies when the last major accretion event happened. Dashed lines show the AVR at intermediate simulation stages between the formation of the galaxy and the present day to address the effect of the last merger episode in the AVR (1.49 Gyr ago for Apollo, 4.34 for Selene, and 5.75 Gyr for Oceanus). |
| In the text | |
 |
Fig. 5 Age-metallicity relation for Selene disc stars, colour-coded according to their current radial positions (see text, Table 2, and Fig. 4 for more information). Blue crosses represent stars currently located in region 1. Green asterisks represent stars currently in region 2. Red dots represent stars currently in region 3. Black triangles represent stars currently in region 4. The two histograms on top of the AMR and on the right represent the age and metallicity distribution function, respectively (colour-coded in the same way). The parameter tjump is denoted by the dashed cyan vertical line. Solid lines correspond to the linear fits performed to the AMR of the stars in the four radial regions for epoch 2 (from tjump until 10 Gyr ago) and epoch 3 (from the present day until tjump). |
| In the text | |
 |
Fig. 6 Age-metallicity relation for Selene disc stars, equivalent to Fig. 5, but split into four different panels; one per region. |
| In the text | |
 |
Fig. 7 Age-metallicity relation for Oceanus disc stars; see Fig. 5 for more information. The parameters tjump − a and tjump − b are denoted by the dashed cyan vertical lines. |
| In the text | |
 |
Fig. 8 Metallicity distribution in the four different radial regions distinguishing between young (1−2 Gyr, upper panel) and old stars (8−9 Gyr, bottom panel) for Selene (left, current locations; middle, birth locations; right, current location not considering accreted stars). Blue, green, red, and black histograms represent particles in regions 1, 2, 3, and 4 respectively. The distributions are different for the young stars compared to the similar distributions in the case of the old component. |
| In the text | |
 |
Fig. 9 Metallicity distribution in the four different radial regions for very old stars (10.0−11.5 Gyr) for Selene. Coloured histograms follow the colour code explained in Fig. 8. |
| In the text | |
 |
Fig. 10 Metallicity distribution in the four different radial regions distinguishing between young (0−0.5 Gyr, upper panel), intermediate (4−5 Gyr, middle panel) and old stars (8−9 Gyr, bottom panel) for Oceanus (current locations). Coloured histograms follow the colour code explained in Fig. 8. The distributions are different for young stars compared to the similar distributions in the case of the old component. Intermediate-aged stars show an intermediate behaviour. |
| In the text | |
 |
Fig. 11 Age-metallicity relation for Selene applying different cuts in the Jz/Jcirc ratio. Upper left, particles with Jz/Jcirc between 0.5 and 0.7; upper right, particles with Jz/Jcirc between 0.7 and 0.9; lower left, particles with Jz/Jcirc between 0.9 and 1.1; lower right, particles with Jz/Jcirc between 1.1 and 1.3 |
| In the text | |
 |
Fig. 12 Radially resolved, stellar age distribution for the Selene disc normalised to the total stellar mass. The different panels show the stellar age distribution of the stars currently located in regions 1 (upper left), 2 (upper right), 3 (middle left), and 4 (middle right); see Table 2 for more information. We added two more regions in the outer most part of the galaxy. Region 5 goes from 4.4hin to 6.2hin and region 6 goes from 6.2hin to 7.9hin. These two regions have been added to study the causes of the old plateau in the age distribution seen in the outermost disc. Black solid lines represent particles currently in that region; solid red line particles born and stayed there; solid blue line particles born inwards and moved outwards currently in that region; solid green line particles born outwards and moved in; solid cyan line particles born way out and moved in; dashed cyan line accreted particles (i.e. Rbirth> 20 kpc and | z | > 3 kpc); dotted blue line particles born in region 1 that end up there; dotted-dashed blue line particles born in region 2 that end up there; and dashed blue line particles born in region 3 that end up there. The definitions of the lines are described in full in the main text. |
| In the text | |
 |
Fig. 13 Age-metallicity relation for Selene disc particles in four radial bins (current positions); every point represents a stellar particle colour-coded according to its Rcurrent − Rbirth. Distribution of plots as in Fig. 12 (regions 1 to 4). Dashed cyan vertical lines are located at tjump. We must highlight that, although the colour-coded range goes from −4 to 4 kpc, we plot all the disc particles in that region, i.e. light green (dark blue) really means Rcurrent − Rbirth ≥ 4.0 (Rcurrent − Rbirth ≤ − 4.0). |
| In the text | |
 |
Fig. 14 Age-metallicity relation for Selene disc particles in four radial bins (current positions); every point represents a stellar particle colour-coded according to its Jz/Jcirc. Distribution of plots as in Fig. 12 (regions 1 to 4). Dashed cyan vertical lines are located at tjump. |
| In the text | |
 |
Fig. 15 Age-metallicity relation for Selene disc stars, colour-coded according to their birth radius. See Fig. 5 for further information. |
| In the text | |
 |
Fig. 16 Selene age and metallicity profiles for all particles and for disc particles alone, either including or removing radial motions. Solid lines: we allow stars to move radially to compute the age and metallicity profiles. Dashed lines: stars born locally, not allowing radial motions. Black lines: all the particles in the simulation (disc+spheroid). Magenta lines: particles fulfilling our disc criterion. This plot is focused on understanding the effect of radial motions in the age and metallicity profiles. Red (blue) vertical dashed lines are located at the break (minimum age) radius. hin is the inner disc scale length in SDSS r-band mock images from SUNRISE (Jonsson 2006); these mock images can be seen in Few et al. (2012). |
| In the text | |
 |
Fig. 17 Radially resolved, stellar age distribution for Selene, normalised to the total stellar mass. In this plot we study all the particles in the simulation (in Fig. 12 we show only disc particles). The upper panel shows the stellar age distribution of the stars currently located in region 5 (from 4.4hin to 6.2hin), while the bottom panel shows stars currently located in region 6 (6.2hin to 7.9hin). Lines and colours represent the same as in Fig. 12. A low number of old, in situ stars are responsible for shaping the old outer plateau even in the absence of radial motions if we do not apply our disc criterion. |
| In the text | |
 |
Fig. A.1 Surface brightness profiles in SDSS r band for Apollo (top left), Artemis (top right), Atlas (middle left), Ben (middle right), Castor (bottom left), and Daphne (bottom right). Blue solid line: “observed” SB profile using the SUNRISE (Jonsson 2006) mock images; those images can be seen in Few et al. (2012). Red solid line: single/double disc fit. Green, vertical, solid lines: these lines delimit the extent where the fit has been performed. Black vertical solid line: Boundary between the spheroid component and the disc; it is computed as the point where the distance between red and blue solid lines is less than 0.1 mag arcsec-1. Red, vertical, dashed line: location of the break. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but for Eos (top left), Helios (top right), Hyperion (middle left), Krios (middle right), Leia (bottom left), and Leto (bottom right). |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 but for Luke (top left), Oceanus (top right), Pollux (middle left), Selene (middle right), Tethys (bottom left), and Tyndareus (bottom right). |
| In the text | |
 |
Fig. A.4 Same as Fig. A.1 but for Zeus. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


