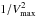| Issue |
A&A
Volume 585, January 2016
|
|
|---|---|---|
| Article Number | A116 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201526718 | |
| Published online | 05 January 2016 | |
Reconstructing the galaxy density field with photometric redshifts
I. Methodology and validation on stellar mass functions
1
University of Bologna, Department of Physics and Astronomy
(DIFA), v.le Berti Pichat
6/2, 40127
Bologna,
Italy
e-mail:
nicola.malavasi@unibo.it
2
INAF–Osservatorio Astronomico di Bologna, via Ranzani
1, 40127
Bologna,
Italy
Received: 10 June 2015
Accepted: 29 September 2015
Context. Measuring environment for large numbers of galaxies in the distant Universe is an open problem in astrophysics, as environment is important in determining many properties of galaxies during their formation and evolution. In order to measure galaxy environments, we need galaxy positions and redshifts. Photometric redshifts are more easily available for large numbers of galaxies, but at the price of larger uncertainties than spectroscopic redshifts.
Aims. We study how photometric redshifts affect the measurement of galaxy environment and how the reconstruction of the density field may limit an analysis of the galaxy stellar mass function (GSMF) in different environments.
Methods. Through the use of mock galaxy catalogues, we measured galaxy environment with a fixed aperture method, using each galaxy’s true and photometric redshifts. We varied the parameters defining the fixed aperture volume and explored different configurations. We also used photometric redshifts with different uncertainties to simulate the case of various surveys. We then computed GSMF of the mock galaxy catalogues as a function of redshift and environment to see how the environmental estimate based on photometric redshifts affects their analysis.
Results. We found that the most extreme environments can be reconstructed in a fairly accurate way only when using high-precision photometric redshifts with σΔz/ (1 + z) ≲ 0.01, with a fraction ≥ 60 ÷ 80% of galaxies placed in the correct density quartile and a contamination of ≤10% by opposite quartile interlopers. A length of the volume in the radial direction comparable to the ±1.5σ error of photometric redshifts and a fixed aperture radius of a size similar to the physical scale of the studied environment grant a better reconstruction than other volume configurations. When using this kind of an estimate of the density field, we found that any difference between the starting GSMF (divided accordingly to the true galaxy environment) is damped on average by ~0.3 dex with photometric redshifts, but is still resolvable. Although derived with mock galaxy catalogues, these results may be used to interpret real data, as we obtained them by comparing results between the true redshift and photometric redshift case, therefore, in a way that does not completely depend on how well the mock catalogues reproduce the real galaxy distribution.
Conclusions. This work allows us several useful considerations on how to interpret results of an analysis of the GSMF in different environments when the density field is measured with photometric redshifts and represents a preparatory study for future wide area photometric redshift surveys, such as the Euclid Survey. We plan to apply the result of this work to an environmental analysis of the GSMF in the UltraVISTA Survey in future work.
Key words: methods: data analysis / galaxies: luminosity function, mass function / galaxies: statistics / galaxies: clusters: general / galaxies: distances and redshifts
© ESO, 2016
1. Introduction
It is a current view in modern astrophysics that the formation and evolution of galaxies are influenced by the environment in which they reside. Although the actual specific effects of the environment on galaxy properties are still largely debated, it is not possible to neglect the importance that the density field has in determining many galaxy parameters. Star formation quenching is thought to be deeply related to environment (see e.g. Peng et al. 2010; Ilbert et al. 2013) through a variety of physical processes (see e.g. Fig. 10 of Treu et al. 2003). As a full understanding of the role of the environment is still missing, a detailed study of the density field is vital for creating a consistent picture of galaxy evolution.
Much observational evidence has been gathered (both at low and high redshift) of the effect of environment on all the main observables, including galaxy colours (see e.g. Dressler 1980; Balogh et al. 2004; Baldry et al. 2006; Cucciati et al. 2006, 2010; Cooper et al. 2006, 2007; Sobral et al. 2011; Muzzin et al. 2012; Scoville et al. 2013), galaxy scaling relations (see e.g. Focardi & Malavasi 2012, and references therein), radio AGN presence (see e.g. Bardelli et al. 2010; Hatch et al. 2014; Malavasi et al. 2015), galaxy masses, and star formation activity. These two last properties are better analysed through the use of the galaxy stellar mass function (GSMF). A key feature of environmental processes is that their effect is visible in the GSMF. A differential analysis based on environmental density of the galaxy stellar mass function may thus help to unveil the physical processes that lead galaxies to form and evolve.
For this reason, many studies have focused on the relation between GSMF and environment, analysing this problem both at z ≲ 1.5 (see e.g. Balogh et al. 2001; Kodama & Bower 2003; Bundy et al. 2006; Cooper et al. 2010; Bolzonella et al. 2010; Davidzon et al. 2016) and higher (e.g. Mortlock et al. 2015; Darvish et al. 2015). Although qualitatively in agreement among them, these works rely on different methods to estimate environments, with various degrees of accuracy. This is not surprising, as a universal definition of environment is still missing and different methods probe different spatial scales through the use of different tracers (for brief reviews of the various adopted methods in the literature, see e.g. Cucciati et al. 2010; Kovač et al. 2010; Muldrew et al. 2012; Darvish et al. 2015 and references therein).
The first studies of the GSMF in different environments (e.g. Balogh et al. 2001; Kodama & Bower 2003; Bundy et al. 2006; Cooper et al. 2010; Bolzonella et al. 2010; Davidzon et al. 2016) all relied on spectroscopic redshifts to determine the density field and are all limited to z ≤ 1.5. Indeed, spectroscopic redshifts grant small errors and high accuracy in the estimate of galaxy positions, but are not available for faint sources and have a limited redshift range (usually not larger than 0 <z< 1.5; spectroscopic redshifts may be available at higher redshifts for very small sky areas). Moreover, given the flux limit and small sky coverage, the sampling rate for spectroscopic redshifts is typically low.
In recent years, large and new data sets have become available as wide-area and high-redshift sky surveys have been undertaken and many more have been planned (e.g. COSMOS, Scoville et al. 2007; Ilbert et al. 2009, UltraVISTA, McCracken et al. 2012; Ilbert et al. 2013; UKIDSS Lawrence et al. 2007, among those for which photometric redshifts are available, and J-PAS, ALHAMBRA, DES, and Euclid, among those ongoing or planned). This great availability of data has been made possible through the use of photometric redshifts, which provide the opportunity to probe the galaxy population in wider areas and at higher redshifts compared to spectroscopic redshifts. Recent studies have increasingly relied on photometric redshifts to study the GSMF in different environments (see e.g. Mortlock et al. 2015; Darvish et al. 2015).
Unfortunately, photometric redshifts lack the precision offered by spectroscopic samples and this limits their potential. Therefore, the issue of using photometric redshifts to estimate galaxy environments needs to be carefully investigated, as a high uncertainty in the redshift measurement may lead to an inaccurate environmental estimate, biasing an interpretation of the GSMF in relation to environment. This has already been studied at low redshifts by Cooper et al. (2005); Etherington & Thomas (2015) and has been also marginally investigated in Muldrew et al. (2012) and Fossati et al. (2015). There are also some works where photometric redshifts are used in synergy with spectroscopic redshifts for environmental studies (see e.g. Kovač et al. 2010; Cucciati et al. 2014; Strazzullo et al. 2015).
We explore how the reconstruction of the environment is affected by the use of photometric redshifts, pushing the analysis to z ~ 3 and studying in detail the effect on the GSMF. We compare the density field, using simulated data, as obtained with each galaxy’s true redshift and photometric redshift. We then apply our analysis to GSMF as a function of redshift and galaxy environment.
We describe the galaxy mock catalogue used in this work in Sect. 2, and we explain the method used to measure galaxy environments in Sect. 3. We discuss results on the environmental reconstruction for the best-case photometric redshift errors in Sect. 4, and we study the impact of varying the photometric redshift uncertainty in Sect. 5. We finally investigate the dependence of the GSMF on the accuracy of the environmental reconstruction for the best-case photometric redshift error in Sect. 6. We summarize our conclusions in Sect. 7. Throughout this work, we assume the standard cosmology (Ωm = 0.3, ΩΛ = 0.7, H0 = 70 km s-1 Mpc-1).
2. Mock data
We aim to determine the effect of photometric redshifts on the study of galaxy stellar mass functions in different environments. A possible way to achieve this would be to compare the measurement of the density field for a sample of galaxies with both measured spectroscopic redshifts and measured or simulated photometric redshifts, taking the environmental estimate in the case when spectroscopic redshifts are used as a reference. This has been done for example by Etherington & Thomas (2015) using SDSS galaxies. We chose a different approach, relying on mock galaxy catalogues. With this approach, we extended our analysis to redshifts higher than z> 1.5, while considering a large sky area to increase sample statistic. Moreover, by comparing the density field and GSMF when using each galaxy’s true and photometric redshifts, we were able to derive results that do not completely depend on how well the mock galaxy catalogues reproduce the spatial distribution of real galaxies. As such, the results of this work can also be applied to real data, as we plan to do in future work.
The data set that we used is composed of the mock galaxy catalogues of Merson et al. (2013)1. These were created for the Euclid Survey, cover an area of 100deg2 in the redshift range z ∈ [ 0,3 ], and are limited to a maximum magnitude of H ≤ 27. They were constructed using the Millennium Run dark matter simulation (Springel et al. 2005) and the galform semi-analytic model of galaxy formation (Cole et al. 2000; Bower et al. 2006; Lagos et al. 2012). A complete description of the mock lightcones can be found in Merson et al. (2013). A summary of the lightcone geometry and physical parameters can be found in Table 1.
Lightcone geometry and cosmology.
For our purposes, we did not use the whole lightcone, but rather we extracted a smaller square area of 8deg2 from the whole 100deg2. We tuned several lightcone parameters to match at best the UltraVISTA Survey (see McCracken et al. 2012 for the survey overview and data reduction process, and Ilbert et al. 2013 for the photometric redshift calculation). We kept the redshift range unaltered, but we introduced a further cut in K-band magnitude to K ≤ 24 to be consistent with the UltraVISTA data magnitude limit and with that expected for the Euclid Survey. The final sample is composed of 1 054 752 galaxies.
For each galaxy, several parameters were available, but in particular we used two redshifts values in the estimate of the density field. One is the true (cosmological) redshift of each galaxy (ztrue) and the other is the same redshift to which the peculiar motion of each galaxy was added (zobs). In order to create a photometric redshift measure for each source, we randomly extracted values from a Gaussian distribution with dispersion σΔz/ (1 + z) × (1 + zobs) and we added them to each galaxy’s zobs. In the following, we refer to these constructed photometric redshifts as zphot.
3. The measurement of the density field
 |
Fig. 1 Lightcones. In each panel, left plot shows the lightcone obtained using the ztrue of galaxies, middle plot using zobs and right plot using zphot with σΔz/ (1 + z) = 0.01. For the sake of clarity, the lightcones have been limited in declination to the central 1.2deg. z ∈ [ 0,1 ]. |
 |
Fig. 1 continued, z ∈ [ 1,2 ]. |
 |
Fig. 1 continued, z ∈ [ 2,3 ]. |
Although several ways of estimating the local environment around a given source are available (see e.g. Cucciati et al. 2010; Kovač et al. 2010; Muldrew et al. 2012; Darvish et al. 2015), we only applied a fixed aperture method, as this approach allows us to choose a scale for the environment parametrization that is independent of redshift. In the following, we refer to the true environment (ϱtrue) when the ztrue of each galaxy is used for the environmental estimate, while we refer to the reconstructed environment (ϱrec) in case the zphot of each galaxy is used. We regard to the true environment as the reference environment and we estimate how much photometric redshifts impact the density field reconstruction by comparing it to the reconstructed environment. It is important to keep in mind that even the definition of the true environment is not unambiguous, as different scales and different definitions probe different physical processes.
We estimated galaxy environments as the volume density of objects inside a cylinder with base radius R and height h, centred on each galaxy of the sample, using all other galaxies as tracers. We adopted several values of R and h, so as to have an exploration of the dependence of the environment reconstruction precision on these two parameters. In particular, we varied the base radius of the cylinder between R = 0.3 Mpc and R = 2 Mpc comoving. We chose the height of the cylinder (i.e. its length on the radial direction) proportional to redshift in two different ways, according to whether we performed the environmental estimate via the ztrue or zphot of galaxies. In particular, h is defined as 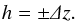 (1)When using ztrue, we adopted a Δz corresponding to a dv = 1000 km s-1, through the formula
(1)When using ztrue, we adopted a Δz corresponding to a dv = 1000 km s-1, through the formula 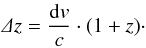 (2)We chose this cylinder length to be consistent with other definitions of local environment from the literature, as this is the value that is generally adopted to estimate the density field when using spectroscopic redshifts.
(2)We chose this cylinder length to be consistent with other definitions of local environment from the literature, as this is the value that is generally adopted to estimate the density field when using spectroscopic redshifts.
In the zphot case, this small height for the cylinder is useless as the errors on the redshift are much larger than that. An environmental estimate with photometric redshifts and Δz from Eq. (2)has been performed as well, but it is only used as a reference for what happens when the cylinder length is very small compared to the photometric redshift uncertainty. Therefore, in the zphot case, we chose Δz proportional to the error on the photometric redshift 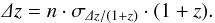 (3)We varied the parameter n as n = 0.5,1.5,3 to have a total length of the cylinder h, ranging from ±0.5σ to ±1.5σ and ±3σ photometric redshift error. To mimic with our analysis the UltraVISTA data (McCracken et al. 2012), we adopted a value for the photometric redshift error of σΔz/ (1 + z) = 0.01, according to the value reported in Fig. 1 of Ilbert et al. (2013). This figure shows a comparison between the photometric redshifts and a sample of spectroscopic redshifts at KS ≤ 24. We also chose this value because it is in agreement with the mean of the error values reported in Table 1 of Ilbert et al. (2013), weighted by the number of sources in each spectroscopic sample used to determine the error. This takes into account the fact that the spectroscopic samples used to derive the values of Table 1 of Ilbert et al. (2013) are sometimes small, composed of a few tens of galaxies, and therefore the errors reported may not be representative of the whole spectroscopic sample at KS ≤ 24. We use the value of σΔz/ (1 + z) = 0.01 to expose our main results, although we also performed several tests choosing different values for σΔz/ (1 + z), which we discuss in Sect. 5.
(3)We varied the parameter n as n = 0.5,1.5,3 to have a total length of the cylinder h, ranging from ±0.5σ to ±1.5σ and ±3σ photometric redshift error. To mimic with our analysis the UltraVISTA data (McCracken et al. 2012), we adopted a value for the photometric redshift error of σΔz/ (1 + z) = 0.01, according to the value reported in Fig. 1 of Ilbert et al. (2013). This figure shows a comparison between the photometric redshifts and a sample of spectroscopic redshifts at KS ≤ 24. We also chose this value because it is in agreement with the mean of the error values reported in Table 1 of Ilbert et al. (2013), weighted by the number of sources in each spectroscopic sample used to determine the error. This takes into account the fact that the spectroscopic samples used to derive the values of Table 1 of Ilbert et al. (2013) are sometimes small, composed of a few tens of galaxies, and therefore the errors reported may not be representative of the whole spectroscopic sample at KS ≤ 24. We use the value of σΔz/ (1 + z) = 0.01 to expose our main results, although we also performed several tests choosing different values for σΔz/ (1 + z), which we discuss in Sect. 5.
Environmental reconstruction.
 |
Fig. 2 Environment comparison. Comparison between ϱtrue and ϱrec (black points) in four representative redshift bins, labelled on top of each plot. Cyan horizontal lines represent the quartiles of the ϱrec distribution, while yellow vertical lines are the quartiles of the ϱtrue distribution. The 1:1 relation is reported as a red dashed line for reference. Parameters used in the environmental estimate are R = 1 Mpc, n = 1.5 and σΔz/ (1 + z) = 0.01. |
We calculated volume densities by dividing the number counts of objects inside each cylinder by the cylinder volume. Many studies rely on surface densities of galaxies inside a redshift bin to define environments instead of volume densities. We also calculated surface densities as the number counts inside each fixed aperture volume divided by the aperture base area. Nevertheless, in the following we use volume densities to derive our results as they allow us to homogenize results inside each redshift bin. In fact, our redshift bins are large enough for galaxies to have a redshift distribution inside each redshift bin. As the fixed aperture volume depends on the redshift of each galaxy, because we chose a length proportional to the photometric redshift uncertainty, galaxies closer to the lower bound of each redshift bin have environments measured using smaller volumes compared to galaxies closer to the upper bound of each redshift bin. Therefore, even inside each redshift bin, galaxies at different redshifts have environments measured with different volume sizes and this may bias the results, preventing a consistent comparison of environmental densities. Surface densities do not take this problem into account, because the area of each cylinder remains the same, once the aperture radius is fixed. Defining environments through the use of volume densities, instead, allows us to take the cylinder dimensions into account on a galaxy by galaxy basis, in a more consistent fashion, even if it has the effect of smoothing out extreme over- and under-densities. As a test, we have also derived our results through the use of surface densities and we discuss these results in Sect. 4.2.
We defined high-density and low-density environments with the percentiles of the volume density distributions calculated in redshift bins of width dz = 0.25, ranging from z = 0 to z = 3. We defined galaxies residing in environments denser than the 75th percentile of the distribution of volume densities as belonging to high-density environments, and, conversely, we defined galaxies whose environment is less dense than the 25th percentile as belonging to low-density environments. In the following, we also refer to these environments as D75 and D25 for high-density and low-density environments, respectively. We also performed our analysis by choosing more extreme environments, using the 10% and 90% of the distribution. Nevertheless, the results found with quartiles are more stable and more significant because of the larger statistics of the samples of galaxies constituting the various environments. Therefore, we focus our analysis on high-density and low-density environments derived using the quartile distinction. At high redshift (generally at z> 2.5) it may become difficult to define the 25th percentile of the volume density distribution, as the reduced statistical sample of the highest redshift bins leads the smallest volume density recovered to be shared by more than 25% of galaxies. For this reason, we decided to limit our analysis at redshifts lower than z ≤ 2.5 in order to not introduce a bias in our results. A summary of the various environmental reconstructions can be found in Table 2.
3.1. An overview of the mock data
Before performing an accurate and quantitative analysis of the results, it is useful to have a qualitative look at the differences between the various environmental reconstructions to have an overall view of how the estimate is dependent on the redshift accuracy.
The three panels of Fig. 1 each show three slices of the analysed sky field, with RA on the abscissas and redshift on the ordinate. In each panel, from left to right, the redshift on the vertical axis changes from ztrue to zobs and zphot. The three panels correspond to three large redshift ranges, namely z ∈ [ 0,1 ], z ∈ [ 1,2 ], and z ∈ [ 2,3 ]. For the sake of clarity, the slices have been limited in declination to the central 1.2deg (−0.6 < dec < 0.6).
It can be easily seen how the overdense regions that are so sharply defined in the ztrue case become more elongated when we use zobs and blurred when relying on the zphot. Nevertheless, it can be seen how high-density regions are still recognisable as distinct from the mean density field and low-density areas, in the case of zphot with σΔz/ (1 + z) = 0.01 also. Therefore, we can still make a precise quantitative estimate of the accuracy that can be attained in reconstructing the environment for different purposes.
We show a first analysis of the various environmental estimates in Fig. 2. This figure shows the comparison between the reconstructed (with n = 1.5) environment and the true environment on a scale of R = 1 Mpc. We find correlation between the two environments is present, although the scatter is large and the points result tilted and displaced from the 1:1 relation. In fact, in each panel (which correspond to four representative redshift bins), ϱtrue spans a wider range of volume densities (going from 0.005 ÷ 5 Mpc-3 at z ~ 0 to 0.001 ÷ 0.1 Mpc-3 at z ~ 2) compared to ϱrec (which ranges from 0.005 ÷ 1 Mpc-3 at z ~ 0 to 0.002 ÷ 0.02 Mpc-3 at z ~ 2). As mentioned in Sect. 3, the tilt occurs because volume densities tend to dilute environmental variations inside each redshift bin, therefore, bringing the whole environmental measurement closer to the mean value of the density field and flattening the correlation between ϱrec and ϱtrue. We derived these same plots with surface densities instead of volume densities and found a smaller tilt with the points closer to the 1:1 relation. Nevertheless, we used volume densities, as they allow us to take into account the fact that, even inside the same redshift bin, galaxies at different redshifts have environments measured with volumes of different lengths. This allows for a more self-consistent study of the density field (see also Fig. 8 for a more quantitative example of the effect of surface densities on D75 and D25 definition).
At very low densities the distribution of the points begins to show vertical and horizontal bands, with points clustering at precise density values. This is due to the process of environmental estimate: as we count galaxies inside each cylinder and then we divide by the cylinder volume, volume densities can only assume discrete values. At high densities, where the dynamic range is large, discretization effects are less visible and the volume density distribution becomes more continuous. At very low densities, the effect of discretization is more visible as there is only a small and finite amount of galaxies inside each volume. This results in a loss of continuity in the density values in low-density environments, which become progressively less discrete going towards high-densities. This discretization effect is also visible at higher density values moving at high redshifts. It seems plausible, though, that at least the most extreme environments (such as those set by the quartiles of the distributions) could be well recovered. Comparisons like that shown in Fig. 2 have been studied for all the samples described later in the text (not shown).
The two main problems that affect environment parametrization, when passing from the true to the reconstructed estimate, are shown in Fig. 3. This figure shows ϱtrue as a function of redshift. Objects that are placed in high-density reconstructed environments, for the parameter combination n = 1.5, R = 1 Mpc and σΔz/ (1 + z) = 0.01 are highlighted. High-density reconstructed environments are contaminated by many galaxies coming from low-density true environments, and D75 environments are not fully recovered. This figure also shows the effects of discretization at low densities as a lack of continuous density values, which progressively disappears moving at high-density values. We study all these effects in detail in the following sections.
 |
Fig. 3 Density-redshift relation. ϱtrue as a function of redshift (black points). Cyan points highlight galaxies in high-density regions (according to ϱrec). The parameters used for the environmental reconstruction are R = 1 Mpc, n = 1.5 and σΔz/ (1 + z) = 0.01. The yellow and magenta lines refer to true environment D75 and D25, respectively, while the red and purple lines refer to the reconstructed D75 and D25, respectively. |
3.2. The definition of recovery and contamination fractions
The assessment of how close ϱrec is to ϱtrue is no simple matter. Several parameters play a role in determining the accuracy of the density field reconstruction. An exploration of the parameter space is needed to study the degeneracies between R and Δz of the cylinders and the effect induced by choosing redshifts with worsening precision. In particular, in the following analysis we look for two distinct effects in the environmental reconstruction, which we call recovery and contamination.
With recovery (fRec), we indicate the fraction of galaxies that are correctly placed in either high-density or low-density regions according both to ϱtrue and ϱrec. In particular, 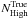 and
and 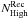 are the number of galaxies in high-density environments according to ϱtrue and ϱrec, respectively (and, correspondingly,
are the number of galaxies in high-density environments according to ϱtrue and ϱrec, respectively (and, correspondingly, 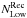 and
and 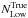 for low-density environments). So, if NHH is the number of galaxies that are placed in a high-density environment according both to ϱtrue and ϱrec, and, correspondingly, NLL for low-density environments, then the recovery fraction is defined as
for low-density environments). So, if NHH is the number of galaxies that are placed in a high-density environment according both to ϱtrue and ϱrec, and, correspondingly, NLL for low-density environments, then the recovery fraction is defined as 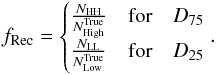 (4)Therefore, a fRec of 1 means that all the galaxies that are in the high-density (or low-density) reconstructed environments are placed in the correct true density quartile.
(4)Therefore, a fRec of 1 means that all the galaxies that are in the high-density (or low-density) reconstructed environments are placed in the correct true density quartile.
It is then useful to calculate the contamination fraction, fCon. This quantity is the fraction of galaxies that are placed in a density quartile according to ϱrec, which actually come from the opposite quartile according to ϱtrue. If NHL is the number of galaxies that are placed in a high-density environment when relying on ϱrec, but that actually come from a low-density environment when relying on ϱtrue (and, conversely, NLH is the number of galaxies that are placed in a low-density environment when relying on ϱrec, but that actually come from a high-density environment when relying on ϱtrue), then the contamination fraction (fCon) is expressed as 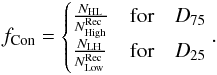 (5)We expect both these quantities to vary with redshift as the reconstruction of the environment is more difficult for high-redshift galaxies because of the lower accuracy of the photometric redshift estimate. A good way to visualize these quantities is shown in Fig. 4. We only report four redshift bins for reference.
(5)We expect both these quantities to vary with redshift as the reconstruction of the environment is more difficult for high-redshift galaxies because of the lower accuracy of the photometric redshift estimate. A good way to visualize these quantities is shown in Fig. 4. We only report four redshift bins for reference.
In this figure we show how the high-density sample (objects above the 75th percentile) and low-density sample (objects below the 25th percentile), which are identified using ϱrec, with n = 1.5, R = 1 Mpc and σΔz/ (1 + z) = 0.01, are distributed according to ϱtrue. The distribution of ϱtrue is also reported for reference, together with vertical dashed lines corresponding to 25% and 75% of the ϱtrue distribution. At very high densities and very low densities, the D75 and D25ϱrec distributions closely follow the corresponding parts of the ϱtrue distribution. The better a reconstructed distribution follows the true distribution, the higher its recovery fraction fRec. The ideal case of perfect reconstruction would imply that the reconstructed distribution of the high-density environments followed the ϱtrue distribution down to the line of the 75th percentile and then dropped to zero, or that the low-density reconstructed distribution rose following the ϱtrue distribution up to the 25th percentile line and then dropped to zero as well.
However, it can be seen how the distributions of the ϱrecD25 and D75 environments have tails extending to ϱtrue values of the opposite quartile. This means that a fraction of objects identified as high- or low-density objects according to ϱrec actually comes from low- or high-density regions according to ϱtrue. This fraction contributes to the contamination fraction of the sample (fCon).
4. Results for the best case of σΔz/(1 + z) = 0.01
As different physical processes operate on different scales, it is of great importance to determine which environmental scale can be better reconstructed with a fixed aperture volume of given R and Δz. We propose a solution to this problem by investigating which is the best combination of R and Δz to optimize the fixed aperture volume for reconstructing a given physical scale. This way of analysing the problem also accounts for different issues in the creation of the reconstructed environment that can potentially lead to biases in the conclusions.
First of all, even when relying on mock catalogues, there is no unambiguous way to define a reference true environment. There is no reason for which the environment estimated with a fixed aperture (or even a nearest-neighbour) method should completely describe the true spatial distribution of galaxies, even when relying on ztrue with no intrinsic error.
Secondly, different spatial scales traced by different fixed aperture radii probe different physical mechanisms (see e.g. Fig. 10 of Treu et al. 2003): smaller apertures (in our case R = 0.3 ÷ 0.6 Mpc) more likely trace interacting pairs, very small groups or the very centre of bound structures, whereas greater spatial scales (as in this work the R = 2 Mpc case) are more sensitive to larger structures and clusters. Therefore, finding the best way to study environments on various scales helps to create a better consistent picture of the role of the environment in galaxy evolution.
4.1. The differential effect of n and R on environmental reconstruction
We performed several tests on the data in order to explore how the R and n parameters used in the fixed aperture volume definition affect the reconstruction of the density field. Figure 5 shows the effect of varying the n value on the environmental reconstruction. For all values of n the reconstruction of high-density environments is fairly accurate and, in any case, better than that of low-density environments. The recovery fraction in the high-density case is above 55% up to z ~ 2, and above 60% at z< 1. Contamination fractions are always below 10% at all redshifts, although we do not extend our analysis farther than z ~ 2.5, as the reduced sample size in the farthest redshift bins may have a predominant role in creating the trends observed in the data.
 |
Fig. 4 Distributions comparison. Distribution in terms of ϱtrue of the high-density and low-density samples, identified using ϱrec in four representative redshift bins (labelled on top of each plot). In particular, the black histogram is the ϱtrue distribution shown as a reference, the cyan histogram refers to D75ϱrec, while the red histogram refers to D25ϱrec. The environmental estimate has been performed with n = 1.5, R = 1 Mpc and σΔz/ (1 + z) = 0.01. The two vertical dashed lines are the values of environmental density corresponding to the 25th and 75th percentile of the ϱtrue distribution. |
 |
Fig. 5 Recovery and contamination fractions – varying n. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of n (yellow: dv = 1000 km s-1; red: n = 0.5; cyan: n = 1.5; and green: n = 3). The radius has been fixed to RT = RR = 1 Mpc and the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01. There is a different scale on the ordinate axis between high-density and low-density environments. |
The situation is slightly worse for low-density environments, which are reconstructed in a less precise way, because low number counts have a higher error. Contamination from high-density interlopers is low, but fRec is never above 60%.
The most important feature that can be observed in this figure is, nevertheless, the fact that the length of the cylinder used for environmental reconstruction has indeed an effect on how accurately the environment is recovered. In fact, both volume heights that are too small (such as n = 0.5 or dv = 1000 km s-1) or too large (such as n = 3) compared to the 3σ error of the photometric redshifts have the effect of worsening the reconstruction of the environment, increasing fCon and decreasing fRec. To summarize, we found that when dealing with high-precision photometric redshifts (σΔz/ (1 + z) = 0.01) a fixed aperture volume with a length roughly of the scale of ±1.5σ error around zphot grants the best environmental reconstruction.
We then fixed the height of the volume used to check the effect that a varying fixed aperture radius from R = 0.3 Mpc to R = 2 Mpc may have on the process. For clarity, in the following we distinguish between RT, when we refer to the radius used to estimate ϱtrue, and RR, when we refer to the radius used to estimate ϱrec. Results are shown in Fig. 6. Again it can be seen that the reconstructed environment is not too different from the true environment, with fRec always above 55% up to redshift z ~ 2 (above 60% at redshift z ≲ 1) and fCon always below 10% at all redshifts. Again, the environmental reconstruction is better for high-density environments than for low-density environments.
 |
Fig. 6 Recovery and contamination fractions – varying RR. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of RR (blue: RR = 0.3 Mpc; green: RR = 0.6 Mpc; cyan: RR = 1 Mpc; and purple: RR = 2 Mpc). The volume height has been fixed to n = 1.5, the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01 and the true environment has been estimated on a scale RT = 1 Mpc. There is a different scale on the ordinate axis between high-density and low-density environments. |
Figure 6 shows that also the aperture radius has an effect on the environmental reconstruction when dealing with high-precision photometric redshifts (σΔz/ (1 + z) = 0.01). In particular, both radii that are too large (e.g. RR = 2 Mpc) and radii that are too small (e.g. RR = 0.3 Mpc), compared to RT (in this case RT = 1 Mpc), have the effect of lowering the accuracy of the reconstructed environment, increasing fCon and decreasing fRec. Thus, it is possible to conclude that increasing or decreasing the fixed aperture size too much has the effect of worsening the precision of the environmental reconstruction. To summarize, we found that when dealing with high-precision photometric redshifts (σΔz/ (1 + z) = 0.01) a value of RR ≃ RT optimizes the environmental reconstruction. These results are generalized for all aperture radii and various values of σΔz/ (1 + z) in Sect. 5.
4.2. Additional tests on the survey magnitude limit and on the use of surface densities
We also performed additional tests on the samples to assess the effect of other issues on the environmental reconstruction. In particular, in this section we discuss the effect of restricting the sample used in the environmental definition to only bright objects at K ≤ 22, and we propose an example of the effect introduced by relying on surface densities for the definition of high- and low-density environments.
We performed the analysis explained so far using only the brightest galaxies, both as targets for the estimate of the environment and as tracers of the density field. This is a preliminary step to simulate the case of shallower surveys, as many large-area photometric redshift sky surveys are not able to reach K-band magnitude values as deep as K = 24. We therefore reduced the sample to 230 050 objects, through a cut to magnitude K ≤ 22 and we used this sample to estimate both ϱtrue and ϱrec. We found that all the results exposed so far are maintained, both as a function of n and R only out to z ~ 1.5.
We show an example of this in Fig. 7, where we report fRec and fCon for both D75 and D25 as a function of redshift. Recovery and contamination fractions from the K ≤ 24 case of Fig. 5 are reported for reference. The fraction values in the case of K ≤ 22 follow closely those of the K ≤ 24, which are between 60% ÷ 80% (recovery) and lower than 10% (contamination) out to z ~ 1.5. We could not perform this analysis up to redshifts higher than z = 1.5 as the statistics in each redshift bin becomes too small to correctly define high- and low-density environments. At these redshifts (not shown here) a comparison therefore becomes impossible between the K ≤ 24 and the K ≤ 22 case.
 |
Fig. 7 Recovery and contamination fractions – K ≤ 22. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Solid and dotted lines are for high-density environments, while dashed and dot-dashed lines are for low-density environments. Red curves are for K ≤ 22 objects, while cyan curves are for K ≤ 24 objects. The volume height has been fixed to n = 1.5, the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01 and both ϱtrue and ϱrec have been estimated on a scale RT = RR = 1 Mpc. |
It can be concluded that an estimate of the density field only based on the brightest objects is accurate enough to reproduce the trends observed for fainter K-band magnitude values, but in a narrower redshift range. This test shows how an environmental estimate performed with only a population of easily-observable bright K ≤ 22 objects is accurate, but needs either a large survey area or an extension to fainter magnitudes (such as K ≤ 24) to increase the sample statistics enough to draw conclusions for high-redshift objects. Nevertheless, this analysis shows that the fixed aperture method that we adopted is robust enough not to depend too much on the magnitude cut of the sample. The limitation in this kind of approach is, nevertheless, the fact that the luminous K ≤ 22 tracers are too few to extend the analysis beyond z = 1.5.
Figure 8, instead, shows fRec and fCon for high-density and low-density environments, when volume densities and surface densities are used for the environmental definition. It can be seen that, although in the high-density case the agreement between volume and surface densities is remarkable, in low-density environments recovery fractions defined through the use of surface densities are more noisy and tend to oscillate around the values set by recovery fractions in the volume density case. The peaks in the fRec values of the D25 galaxies are caused by the discretization effect already described in Sect. 3, which is enhanced by the use of surface densities compared to the volume density case for the true environment. This represents a problem in the definition of the low-density environments, as even for low redshifts the value of the surface density distribution corresponding to the 25th percentile is shared by more than 25% of galaxies. Therefore, as the discretization effect is lower for the reconstructed environment case, the recovery fraction is higher. Nevertheless, this must be regarded as a spurious effect and as a signal that volume densities are preferrable for the definition of high-density and low-density environments. Contamination fractions show the same effect and are slightly larger than in the volume density case, as they are around 15% at z> 1. As stated in the previous sections, volume densities grant a more accurate environmental reconstruction as they allow us to account for differences in the cylinder length used for environmental definition on a galaxy by galaxy basis.
 |
Fig. 8 Recovery and contamination fractions – surface densities. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Solid and dotted lines are for high-density environments, while dashed and dot-dashed lines are for low-density environments. Magenta curves are for environments defined through the use of surface densities, while blue curves are for environments defined through the use of volume densities. The volume height has been fixed to n = 1.5, the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01 and both ϱtrue and ϱrec have been estimated on a scale RT = RR = 1 Mpc. |
5. The importance of σΔz/(1 + z)
So far, we have chosen a value of σΔz/ (1 + z) = 0.01 (see Sect. 3). In the overview of the photometric redshift surveys, this is a fairly optimistic value, as very few surveys can reach this kind of precision (e.g. the expected value of the photometric redshift precision for the Euclid survey is σΔz/ (1 + z) = 0.03 ÷ 0.05). Our choice for such a small value has been determined by the fact that this is the value of the uncertainty of photometric redshifts in the COSMOS-UltraVISTA Survey sample (see McCracken et al. 2012; Ilbert et al. 2013) to which we plan to apply our results. Nevertheless, many other surveys show a variety of photometric redshift errors and it is possible that the results exposed in the previous sections do not hold when the photometric redshift error is larger.
To test this possibility we have redone the analysis, exploring several values for the photometric redshift error. In particular, we have chosen to vary σΔz/ (1 + z) from σΔz/ (1 + z) = 0.003 to σΔz/ (1 + z) = 0.03,0.06. We chose these values as representative of various future and ongoing surveys, in particular, σΔz/ (1 + z) = 0.003 is the value expected for the Javalambre Physics of the accelerating universe Astronomical Survey2 (J-PAS; PI: see Benitez et al. 2015), σΔz/ (1 + z) = 0.03 is the minimum error expected for the Euclid Survey3 (PI: Mellier, see Laureijs et al. 2011), σΔz/ (1 + z) = 0.06 is the error on photometric redshifts derived for the sources in previous releases of the COSMOS Survey4 (PI: Scoville, see Scoville et al. 2007; Capak et al. 2007; Ilbert et al. 2009) and used for example in Malavasi et al. (2015).
A first, expected result is that the environmental reconstruction is more difficult when using photometric redshifts with large uncertainties. Figure 9 shows how both in the high-density and low-density situations fRec decreases and fCon increases with increasing σΔz/ (1 + z).
 |
Fig. 9 Recovery and contamination fractions – varying σΔz/ (1 + z). fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). The volume parameters for environmental reconstruction have been kept fixed to RR = RT = 1 Mpc and n = 1.5. |
In particular, for high-density environments fRec is always above 75% (and close to 90% at z ~ 0) in the high-accuracy σΔz/ (1 + z) = 0.003 case, and progressively decreases to values slightly above 40% at all redshifts in the low-accuracy σΔz/ (1 + z) = 0.06 one. Contamination fractions, instead, range from below 5% (σΔz/ (1 + z) = 0.003,0.01) to between 10% and 20% (σΔz/ (1 + z) = 0.03,0.06). For low-density environments, fRec is lower, ranging from around 75% at all redshifts for σΔz/ (1 + z) = 0.003 and progressively decreasing to slightly above 35% with increasing photometric redshift uncertainty. Contamination fractions are also lower, but show the same trend in σΔz/ (1 + z) as for high-density environments, which are below 5% for σΔz/ (1 + z) = 0.003,0.01 and progressively reaching 10–15% for σΔz/ (1 + z) = 0.03,0.06.
5.1. The impact of n in the case of varying σΔz/ (1 + z)
As done before for the best-case photometric redshift uncertainty of σΔz/ (1 + z) = 0.01, we also investigated the dependence of the accuracy in reconstructing the environment on the parameters of the volume for the various photometric redshift errors. We found that the R and n parameters have a great impact on the measurement of the density field also in the case of large σΔz/ (1 + z) values.
Figure 10 shows fRec and fCon for only three redshift bins (namely 1.50 ≤ z ≤ 1.75, 2.00 ≤ z ≤ 2.25 and 2.50 ≤ z ≤ 2.75) as a function of the n parameter for various values of σΔz/ (1 + z). In the high-density case, fRec is generally higher for a value of n = 1.5, a trend shared by all redshift bins. Only for really large values of the photometric redshift uncertainty (σΔz/ (1 + z) = 0.06) is n = 0.5 a viable solution too, but the difference in fRec between this value and the one obtained with n = 1.5 is negligible. Instead, fCon is always lower in the case of n = 1.5 independent of redshift and photometric redshift uncertainty.
 |
Fig. 10 Varying σΔz/ (1 + z) – effect of n. fRec and fCon as a function of the n parameter in three redshift bins, namely 1.50 <z< 1.75 (solid lines), 2.00 <z< 2.25 (dashed lines), and 2.50 <z< 2.75 (dotted lines). Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). The aperture radius has been kept fixed to RR = RT = 1 Mpc. |
In the low-density case, shown in the bottom panel of the same figure, it is shown that fRec is always higher and fCon is lower when a value of n = 1.5 is adopted. This generalizes the result obtained previously in the case of σΔz/ (1 + z) = 0.01 (see Fig. 5) showing that environmental reconstruction is better performed when it is chosen a value of the cylinder length of a similar size as the ±1.5σ error on the photometric redshifts.
5.2. The effect of the fixed aperture radius R
Figures 11 and 12 show fRec and fCon for only one redshift bin (1.50 ≤ z ≤ 1.75) as a function of the ratio RR/RT, for various values of σΔz/ (1 + z). We normalized all values of fRec and fCon to their value at RR/RT = 1, separately for every case of σΔz/ (1 + z) considered to better visualize the trend in the fractions with RR/RT. With this approach, the intrinsic dispersion in the data because smaller scales are better reconstructed than large scales has been reduced for the sake of clarity. We show residual scatter as shaded regions for each curve. The points at RR/RT< 1 are given by apertures whose ratio is lower than 1, for example, RR = 1 Mpc and RT = 2 Mpc, which yield RR/RT = 0.5 and so on. Moreover a fixed value of RR/RT could be given by more than one combination of RR and RT, for example, RR/RT = 0.5 could be given by RR = 0.3 Mpc and RT = 0.6 Mpc or by RR = 1 Mpc and RT = 2 Mpc. For this reason at a given value of RR/RT more than one point may be visible. The only exception is the point at RR/RT = 1 where all the curves have been normalized to unity.
Hence, the normalization of each curve corresponding to each value of σΔz/ (1 + z) is lost, but the shapes and the trends in RR/RT can be better studied.
Recovery fractions (Fig. 11) clearly show a steep decrease for RR/RT> 1 for every value of σΔz/ (1 + z). This decrease is similar for all values of photometric redshift uncertainty in the D75 case and it is shallower for larger values of σΔz/ (1 + z) in the D25 case. For values of RR/RT< 1, instead, an increase in the fraction values is present for values of σΔz/ (1 + z)< 0.06 in the D25 case, and for values of σΔz/ (1 + z) ≤ 0.01 in the D75 case. For these values of σΔz/ (1 + z), a maximum in the recovery fraction can be clearly individuated at RR/RT = 1, which translates in the best value for the fixed aperture radius to obtain an accurate environmental reconstruction. For larger σΔz/ (1 + z) values, instead, smaller apertures than the physical scale that is to be investigated should be considered.
 |
Fig. 11 Varying σΔz/ (1 + z) – effect of RR/RT, recovery. fRec (normalized to the value of fRec at RR/RT = 1 separately for each value of σΔz/ (1 + z)) as a function of RR/RT in the redshift bin 1.50 <z< 1.75. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). Shaded regions show the dispersion in the fraction values at fixed RR/RT given by different RT because smaller RT are reconstructed better than larger RT. The length of the volume has been kept fixed, with n = 1.5. |
Contamination fractions (Fig. 12) show a minimum in RR/RT = 1 for all values of σΔz/ (1 + z) only in the D25 case, while the minimum is clearly recognizable in the D75 case only for values of σΔz/ (1 + z) ≤ 0.01. For larger values of the photometric redshift uncertainty, the curves corresponding to the contamination fractions in the high-density case are rather flat or slightly increasing. Again, for small values of σΔz/ (1 + z) the trend is confirmed of RR/RT = 1 as the best choice for the environmental reconstruction, while for larger values, an aperture radius smaller than the physical scale that is to be investigated is probably preferable. This generalizes the result obtained previously in the case of σΔz/ (1 + z) = 0.01 (see Fig. 6).
 |
Fig. 12 Varying σΔz/ (1 + z) – effect of RR/RT, contamination. fCon (normalized to the value of fCon at RR/RT = 1 separately for each value of σΔz/ (1 + z)) as a function of RR/RT in the redshift bin 1.50 <z< 1.75. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). Shaded regions show the dispersion in the fraction values at fixed RR/RT given by different RT because smaller RT are reconstructed better than larger RT. The length of the volume has been kept fixed, with n = 1.5. |
The fact that the best environmental reconstruction is obtained for RR ≃ RT is not an obvious result, as for large photometric redshift uncertainties fixed aperture radii smaller than the physical scale of the studied environment may be the best option to limit the number of contaminating interlopers. Here we showed that this is indeed the case for σΔz/ (1 + z) = 0.03,0.06, while for lower values of σΔz/ (1 + z) the situation where RR/RT = 1 optimizes the environmental reconstruction. For all curves, shaded regions show the residual dispersion (after normalization) in the fraction values at fixed RR/RT. This dispersion occurs because smaller scales (RR = RT = 0.3 Mpc) are reconstructed better than large scales (RR = RT = 2 Mpc). Therefore, even at fixed RR/RT smaller scales have higher fRec and lower fCon compared to larger scales, as already found for the σΔz/ (1 + z) = 0.01 case.
To summarize, we can conclude that it is possible to reconstruct the environment in an accurate way only if the photometric redshift uncertainty is small (σΔz/ (1 + z) ≤ 0.01), otherwise the environment is not sufficiently recovered (fRec< 50% ÷ 60%) and it becomes too contamined (fCon> 10%). Moreover, for uncertainty values σΔz/ (1 + z) ≤ 0.01, the best environmental reconstruction is obtained for n = 1.5 and for RR/RT = 1. This also remains generally true for values of σΔz/ (1 + z) = 0.03, although the recovery fraction is lower and the contamination fraction is higher. For values of σΔz/ (1 + z)> 0.03, the recovery and contamination fractions do not allow us to reconstruct the environment in an accurate fashion and volume parameters n = 0.5 and RR/RT< 1 optimize the measurement of the density field as they limit the number of contaminating interlopers.
6. The reconstruction of the galaxy stellar mass function for the best-case σΔz/(1 + z) = 0.01
On the basis of this analysis we now investigate whether the accuracy of the environmental reconstruction with photometric redshifts has consequences for the differential study of galaxy stellar mass functions in different environments. In fact, it is known from spectroscopic surveys that mass functions of galaxies in different environments have a different shape at least up to z ≤ 1 (Bolzonella et al. 2010). This is caused by the different formation and evolution scenarios of galaxies within clusters and in the field. For this reason, the contamination of interlopers from different environments (the fCon defined above) along with the dilution of the signal of environmental segregation (due to values of fRec< 100%) might have the effect of changing the shape of the mass function, by mixing together galaxies with different properties. In the following, we attempt an investigation to quantify the degree of accuracy with which an analysis of the GSMF in different environments is possible if the density field is reconstructed using photometric redshifts with an error of σΔz/ (1 + z) = 0.01. We chose this value of photometric redshift uncertainty, as for higher values it is not possible to reliably reconstruct galaxy environments as described in Sect. 5. Moreover, this value has been derived for the photometric redshifts of the UltraVISTA survey, to which we plan to apply our results. We chose this value, as it is in agreement with that reported in Fig. 1 of Ilbert et al. (2013), which shows a comparison between the photometric redshifts and a sample of spectroscopic redshifts at KS ≤ 24. It is also in agreement with the mean of the error values reported in Table 1 of Ilbert et al. (2013), weighted by the number of sources in each spectroscopic sample used to determine the error. This takes into account the fact that the spectroscopic samples used to derive the values of Table 1 of Ilbert et al. (2013) are sometimes small, composed of a few tens of galaxies, and therefore the errors reported may not be representative of the whole spectroscopic sample at KS ≤ 24.
6.1. The lightcone mock catalogue GSMF
We compare the mass functions for the galaxies of the mock catalogue used for the environmental analysis. In particular, we derived the mass functions of high-density and low-density environments based on ϱrec with n = 1.5, σΔz/ (1 + z) = 0.01 and RT = RR = 0.3 and RT = RR = 2 Mpc. We only considered the smallest and largest radii since they grant the best and worst environmental reconstruction. All other values of R grant intermediate fRec and fCon. The mass functions of the mock catalogues are shown in Fig. 13 for the RR = RT = 0.3 Mpc case and in Fig. 15 for the RR = RT = 2 Mpc case.
 |
Fig. 13 Mock catalogues mass functions – RR = RT = 0.3 Mpc. The dark green and light green curves refer to the total GSMF, respectively, using ztrue and zphot for the calculation of the mass function. Dark red and light red curves refer to high-density environments, respectively, using ϱtrue, dark red, and using ϱrec, light red. Dark blue and light blue curves refer to low-density environments, respectively, using ϱtrue, dark blue, and using ϱrec, light blue. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 0.3 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
We derived mass functions using the non-parametric 1 /Vmax estimator (see Avni & Bahcall 1980; Bolzonella et al. 2002 and references therein for further information), considering all the galaxies down to K ≤ 24. As the zmax information was not available, we used the total volume in the considered redshift range. In particular, not taking the zmax into account mainly affects the low-mass end of the mass function, where the volume occupied by each source is more likely to be overestimated. For this reason, we also derived mass completeness limits as in Pozzetti et al. (2010), but at the upper boundary of each redshift bin (instead of at the lower boundary, which is the case when zmax values are available).
The error bars shown in the plots represent only the Poissonian errors. As the UltraVISTA Survey field is smaller compared to the area of the mock catalogues that we considered (1.48deg2 for UltraVISTA compared to the 8deg2 used in this work), we also calculated the GSMF for galaxies in five independent areas of 1.48deg2 to simulate the real UltraVISTA data. We extracted five independent areas and have redone the GSMF calculation in each of them in order to not be biased by cosmic variance. We found that, despite the larger error bars due to the lower number of galaxies present in the smaller fields, the results found with the larger area, and detailed below, hold up to z ~ 2. At higher redshifts, massive galaxies of M∗ ≳ 1011 M⊙ (which carry most of the signal of environmental difference) are too few in every redshift bin, because of the smaller area, in the true environment case already; therefore no environmental difference is recoverable. Nevertheless this may not be a limit in the analysis of the UltraVISTA data, as different mass or redshift bins may be applied to increase statistics, and because mock galaxy catalogues may underestimate the number of massive galaxies in comparison to reality (see Figs. 14 and 15 of Ilbert et al. 2013). For these reasons, we show here GSMF calculated with an area of 8deg2.
It is known that galaxies in high-density environments occupy a smaller volume than galaxies in low-density environments. To account for this fact and to be able to compare GSMF in different environments, we normalized GSMF in high-density and low-density environments to 1/4 of the value that the total GSMF has at the mass limit, both in the true and reconstructed environments. Hence, although the information on the GSMF normalization is lost, it is still possible to compare their shapes.
From Fig. 13 it is possible to see how the mass functions of true D75 and D25 environments are intrinsically different in the RR = RT = 0.3 Mpc case. This difference is a function of mass and redshift and for masses M ≳ 1011 M⊙ ranges between ≳ 1 dex at z< 0.5 and ~0.3 dex at z ~ 2.5. At higher redshifts the two mass functions become undistinguishable. This trend with mass and redshift of the differences between true environment GSMF can be better appreciated in the ratio between D75 and D25 GSMF, shown in Fig. 14.
 |
Fig. 14 Ratio of high-density and low-density mass functions – RR = RT = 0.3 Mpc. Ratio of the high-density mass function and the low-density mass function (ΦD75/ ΦD25) in the true (light green curve) and reconstructed (purple curve) environments. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 0.3 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
The situation is worse when considering RR = RT = 2 Mpc (Figs. 15 and 16). At low redshifts the difference between the true D75 and D25 GSMF is already ≲0.5 dex for masses below 1011 M⊙. This difference is of ~0.1 dex at z ~ 2.5 for M ~ 1011 M⊙. The ratio of the two mass functions is significantly different from one below z ~ 2 and only for masses above 1011 M⊙.
 |
Fig. 15 Mock catalogues mass functions – RR = RT = 2 Mpc. The dark green and light green curves refer to the total GSMF, respectively, using ztrue and zphot for the calculation of the mass function. Dark red and light red curves refer to high-density environments, respectively, using ϱtrue, dark red, and using ϱrec, light red. Dark blue and light blue curves refer to low-density environments, respectively, using ϱtrue, dark blue, and using ϱrec, light blue. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 2 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
 |
Fig. 16 Ratio of high-density and low-density mass functions – RR = RT = 2 Mpc. Ratio of the high-density mass function and the low-density mass function (ΦD75/ ΦD25) in the true (light green curve) and reconstructed (purple curve) environments. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 2 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
In the same four figures we also report GSMF in different reconstructed environments together with their ratios. In the RR = RT = 0.3 Mpc case (Fig. 13), it is possible to see how the reconstructed environment GSMF closely follows the true environment, since D75 is well distinguishable from the D25 at low redshifts and shows the same trends in mass and redshift. Also, the ratio of D75 to D25 GSMF (Fig. 14) follows the true case, although it is possible to see that resulting differences are somewhat damped when passing from ϱtrue to ϱrec. To quantify this decrease of the difference between high-density and low-density environments, we report in Table 3 the maximum decrease of the ratio of the mass functions in extreme environments between the ϱtrue and the ϱrec case, defined as ![\begin{eqnarray} \label{xi} \xi = \max \left[\log\left(\frac{\Phi(D75)}{\Phi(D25)}\right)\Bigg|_{\rm true} - \log\left(\frac{\Phi(D75)}{\Phi(D25)}\right)\Bigg|_{\rm Rec} \right]. \end{eqnarray}](/articles/aa/full_html/2016/01/aa26718-15/aa26718-15-eq158.png) (6)
(6)
Maximum decrease between ϱrec and ϱtrue, D75 and D25 GSMF.
The reduction in the differences is always below ~0.7 dex. This value is obtained at high masses (M ~ 1011 M⊙) where the starting (true environment) GSMF are intrinsically different. Table 4 shows that this is true also for the RR = RT = 2 Mpc case. Although, from Figs. 15 and 16 it is possible to see that already the starting true environment GSMF are less different between high- and low-density than in the RR = RT = 0.3 Mpc case.
Maximum decrease between ϱrec and ϱtrue, D75 and D25 GSMF.
Thus, we showed that if differences are present they are recovered (although somewhat reduced), while if there are no differences in the true environment GSMF then no spurious differences are introduced when using reconstructed environments. We can then conclude that an analysis of the GSMF in different environments is possible, even when relying on photometric redshifts for the environmental reconstruction. This result is encouraging, as when using real data the risk will be of missing or underestimating differences in the GSMF of different environments, rather than detecting differences that are not real. This is generally true at all redshifts (up to z ~ 2.5), at all masses, and for both large and small scales.
These results allow us to draw important conclusions on what to expect from real data. In particular, when investigating the differences between GSMF calculated for galaxies in high-density and low-density environments with high-precision photometric redshifts, all differences found may be considered as lower limits of the true differences in galaxy properties. In fact, our analysis shows that the effect of the error of photometric redshifts on the GSMFs of galaxies in different environments is to damp differences between high-density and low-density regions, while nevertheless not deleting them completely. Any environmental effect recovered would be greater if a measure of the true density field were available.
7. Conclusions and summary
The GSMF and its relation to different environments are of vital importance for understanding how galaxies have formed and evolved. Galaxy stellar mass functions in different environments have been studied at z ≤ 1 through the use of spectroscopic redshifts and now need to be investigated at higher redshifts. As spectroscopic redshifts are not available for large samples of galaxies, to high redshifts, and on wide sky areas, it is often necessary to rely on photometric redshifts. Photometric redshifts are more easily available for large statistical samples on wide sky areas and in a large resdshift range, but are characterized by a high uncertainty, which may limit their use for deriving GSMF in different environments.
In this work, we made use of the validated mock galaxy catalogues by Merson et al. (2013) to investigate how the galaxy environment can be reconstructed based on high-precision photometric redshifts (with σΔz/ (1 + z) = 0.01). We selected the mock galaxy sample to have K ≤ 24 and we extracted an area of 8deg2 from the original 100deg2 of the catalogue. We used each galaxy’s cosmological redshift (ztrue) and we simulated a set of photometric redshifts (zphot) with varying precision by adding a Gaussian error to each galaxy’s observed redshift (i.e. the cosmological redshift to which the contribution of the galaxy peculiar velocity has been added). We chose an error on the photometric redshifts of σΔz/ (1 + z) = 0.01 as a reference error because it is in agreement with the value reported in Fig. 1 of Ilbert et al. 2013 (which shows a comparison between photometric and spectroscopic redshifts at KS ≤ 24), and with the mean of the errors reported in Table 1 of Ilbert et al. (2013) weighted by the number of sources in each spectroscopic sample used for the calculation (which, because they are rather small, may not be representative of the whole spectroscopic sample at KS ≤ 24).
We estimated galaxy environments through the use of a fixed aperture method, by counting objects inside a cylinder of base radius R and length h proportional to the photometric redshift uncertainty through the parameter n as h = ± n·σΔz/ (1 + z)·(1 + z). We defined high-density (D75) and low-density (D25) environments using the 75th and 25th percentiles of the volume density distribution. For each galaxy, we derived both a true environment estimate (ϱtrue, using each galaxy’s ztrue) and a reconstructed estimate (ϱrec using each galaxy’s zphot). We studied several combinations of both the fixed aperture volume parameters n and R and of the photometric redshift uncertainty σΔz/ (1 + z). We then compared the derived ϱtrue and ϱrec to study how the density field can be reconstructed with photometric redshifts. We also applied our results to the study of the GSMF in different environments for the best-case photometric redshift uncertainty σΔz/ (1 + z) = 0.01. What we found can be summarized as follows:
-
1.
It is only still possible to reconstruct galaxyenvironments in an accurate way with theuse of high-precision photometric redshifts(σΔz/ (1 + z) = 0.01). In particular, to well recover high- and low-density environments (with fRec ≥ 60% ÷ 80%) with a low level of contaminating interlopers (fCon ≤ 10%), it is necessary to carefully tune the parameters of the volume used for the estimate of the density field. In our case, the best environmental reconstruction is obtained considering a cylinder with length ∝±1.5σ error on the photometric redshift and a radius RR = RT. A volume with a length too large or too small compared to the ±1.5σ error and with a base area too large or too small compared to the size of the physical scale of the studied environment leads to an inaccurate environmental reconstruction, with lower fRec and higher fCon.
-
2.
Even if all the volume parameters are tuned to have the best case of environmental reconstruction, recovery fractions are still higher (fRec ≥ 70%) and contamination fractions are lower fCon ≤ 5% for smaller physical scales (RR = RT = 0.3 ÷ 0.6 Mpc) compared to larger scales (RR = RT = 1 ÷ 2 Mpc).
-
3.
The above results only hold well for high-precision photometric redshifts with σΔz/ (1 + z) ≤ 0.01, where recovery fractions are between 60 ÷ 80% and contamination fractions below ≤10%. For higher uncertainty values (σΔz/ (1 + z) ≥ 0.03) recovery fractions lower rapidly to fRec< 50% and contamination fractions increase up to fCon ~ 20%. This result is reasonable if we consider that the typical velocity dispersion inside the richest galaxy clusters is on the order of
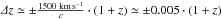 , which is comparable to our best-case photometric redshift uncertainty. Moreover, for photometric redshift errors on the order of σΔz/ (1 + z) ≤ 0.01 recovery fractions are still higher and contamination fractions lower for n = 1.5 and RR/RT = 1, while for higher values of σΔz/ (1 + z) values of RR/RT< 1 are preferable.
, which is comparable to our best-case photometric redshift uncertainty. Moreover, for photometric redshift errors on the order of σΔz/ (1 + z) ≤ 0.01 recovery fractions are still higher and contamination fractions lower for n = 1.5 and RR/RT = 1, while for higher values of σΔz/ (1 + z) values of RR/RT< 1 are preferable. -
4.
The use of only brightest objects (K ≤ 22) as both targets and tracers of the density field to simulate the case of surveys shallower than the UltraVISTA Survey, has the effect of reducing the maximum redshift to which our analysis can be extended, from z ≤ 2.5 to z ≤ 1.5. Nevertheless, in this redshift range our method is robust enough to reproduce the same results as in the case of K ≤ 24.
-
5.
When applying these results to the GSMF (in the best-case of σΔz/ (1 + z) = 0.01) it is found that differences (if present) can be recovered accurately, although some reduction (which reaches at most ~0.7 dex, with an average of ~0.3 dex) is inevitable. Nevertheless, fictitious differences do not seem to be created, therefore any environmental segregation found in real data may be regarded as a lower limit of what would be found if a measure of the intrinsic density field were available.
With this study, we found that an analysis of the GSMF in different environments is only possible with high-precision σΔz/ (1 + z) ≤ 0.01 photometric redshifts, provided that the fixed aperture lenght and radius are optimized to give the best measurement of the density field. Galaxy stellar mass functions in different environments can be studied while keeping in mind that photometric redshifts, even high-precision redshifts, reduce differences between high-density and low-density environments by as much as ~0.7 dex. Further investigation of these issues is strongly needed as the availability of large area, deep photometric redshift surveys is increasing. Photometric redshifts enable the measurement of galaxy properties on large sky areas and in a large redshift range, but it is necessary to carefully check for the effects that their uncertainty has on the analysis that is going to be performed. This work constitutes a preliminary study to better understand results found investigating real data. As an application of this method, we plan an analysis of the GSMF of the UltraVISTA Survey (McCracken et al. 2012) in different environments and for this reason all the possible parameters of this study have been tuned so as to match those of the sample that will be used (Ilbert et al. 2013). The final aim of this work is to try to better understand the systematic effects in the reconstruction of the density field, as this may help to improve the comprehension of the physical processes behind the formation and evolution of galaxies.
The mock catalogues are freely available for download at http://astro.dur.ac.uk/~d40qra/lightcones/EUCLID/
Acknowledgments
We acknowledge the financial contributions by grants ASI/INAF I/023/12/0 and PRIN MIUR 2010-2011 “The dark Universe and the cosmic evolution of baryons: from current surveys to Euclid”. We thank the anonymous referee for helpful comments.
References
- Avni, Y., & Bahcall, J. N. 1980, ApJ, 235, 694 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Balogh, M. L., Bower, R. G., et al. 2006, MNRAS, 373, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Christlein, D., Zabludoff, A. I., & Zaritsky, D. 2001, ApJ, 557, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Baldry, I. K., Nichol, R., et al. 2004, ApJ, 615, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bardelli, S., Schinnerer, E., Smolčic, V., et al. 2010, A&A, 511, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2015, Highlights of Spanich Astrophysics VIII, 148 [Google Scholar]
- Bolzonella, M., Pelló, R., & Maccagni, D. 2002, A&A, 395, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolzonella, M., Kovač, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Ellis, R. S., Conselice, C. J., et al. 2006, ApJ, 651, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Cole, S., Lacey, C. G., Baugh, C. M., & Frenk, C. S. 2000, MNRAS, 319, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Madgwick, D. S., et al. 2005, ApJ, 634, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Croton, D. J., et al. 2006, MNRAS, 370, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Newman, J. A., Coil, A. L., et al. 2007, MNRAS, 376, 1445 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Coil, A. L., Gerke, B. F., et al. 2010, MNRAS, 409, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Iovino, A., Marinoni, C., et al. 2006, A&A, 458, 39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Iovino, A., Kovač, K., et al. 2010, A&A, 524, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Granett, B. R., Branchini, E., et al. 2014, A&A, 565, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Darvish, B., Mobasher, B., Sobral, D., Scoville, N., & Aragon-Calvo, M. 2015, ApJ, 805, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Cucciati, O., Bolzonella, M., et al. 2016, A&A, in press, DOI: 10.1051/0004-6361/201527129 [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Etherington, J., & Thomas, D. 2015, MNRAS, 451, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Focardi, P., & Malavasi, N. 2012, ApJ, 756, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Fossati, M., Wilman, D. J., Fontanot, F., et al. 2015, MNRAS, 446, 2582 [NASA ADS] [CrossRef] [Google Scholar]
- Hatch, N. A., Wylezalek, D., Kurk, J. D., et al. 2014, MNRAS, 445, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kodama, T., & Bower, R. 2003, MNRAS, 346, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Lilly, S. J., Cucciati, O., et al. 2010, ApJ, 708, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. d. P., Bayet, E., Baugh, C. M., et al. 2012, MNRAS, 426, 2142 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lawrence, A., Warren, S. J., Almaini, O., et al. 2007, MNRAS, 379, 1599 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Malavasi, N., Bardelli, S., Ciliegi, P., et al. 2015, A&A, 576, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merson, A. I., Baugh, C. M., Helly, J. C., et al. 2013, MNRAS, 429, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Mortlock, A., Conselice, C. J., Hartley, W. G., et al. 2015, MNRAS, 447, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Muldrew, S. I., Croton, D. J., Skibba, R. A., et al. 2012, MNRAS, 419, 2670 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Wilson, G., Yee, H. K. C., et al. 2012, ApJ, 746, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-j., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Arnouts, S., Aussel, H., et al. 2013, ApJS, 206, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Smail, I., et al. 2011, MNRAS, 411, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Strazzullo, V., Daddi, E., Gobat, R., et al. 2015, A&A, 576, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Treu, T., Ellis, R. S., Kneib, J.-P., et al. 2003, ApJ, 591, 53 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Lightcones. In each panel, left plot shows the lightcone obtained using the ztrue of galaxies, middle plot using zobs and right plot using zphot with σΔz/ (1 + z) = 0.01. For the sake of clarity, the lightcones have been limited in declination to the central 1.2deg. z ∈ [ 0,1 ]. |
| In the text | |
 |
Fig. 1 continued, z ∈ [ 1,2 ]. |
| In the text | |
 |
Fig. 1 continued, z ∈ [ 2,3 ]. |
| In the text | |
 |
Fig. 2 Environment comparison. Comparison between ϱtrue and ϱrec (black points) in four representative redshift bins, labelled on top of each plot. Cyan horizontal lines represent the quartiles of the ϱrec distribution, while yellow vertical lines are the quartiles of the ϱtrue distribution. The 1:1 relation is reported as a red dashed line for reference. Parameters used in the environmental estimate are R = 1 Mpc, n = 1.5 and σΔz/ (1 + z) = 0.01. |
| In the text | |
 |
Fig. 3 Density-redshift relation. ϱtrue as a function of redshift (black points). Cyan points highlight galaxies in high-density regions (according to ϱrec). The parameters used for the environmental reconstruction are R = 1 Mpc, n = 1.5 and σΔz/ (1 + z) = 0.01. The yellow and magenta lines refer to true environment D75 and D25, respectively, while the red and purple lines refer to the reconstructed D75 and D25, respectively. |
| In the text | |
 |
Fig. 4 Distributions comparison. Distribution in terms of ϱtrue of the high-density and low-density samples, identified using ϱrec in four representative redshift bins (labelled on top of each plot). In particular, the black histogram is the ϱtrue distribution shown as a reference, the cyan histogram refers to D75ϱrec, while the red histogram refers to D25ϱrec. The environmental estimate has been performed with n = 1.5, R = 1 Mpc and σΔz/ (1 + z) = 0.01. The two vertical dashed lines are the values of environmental density corresponding to the 25th and 75th percentile of the ϱtrue distribution. |
| In the text | |
 |
Fig. 5 Recovery and contamination fractions – varying n. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of n (yellow: dv = 1000 km s-1; red: n = 0.5; cyan: n = 1.5; and green: n = 3). The radius has been fixed to RT = RR = 1 Mpc and the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01. There is a different scale on the ordinate axis between high-density and low-density environments. |
| In the text | |
 |
Fig. 6 Recovery and contamination fractions – varying RR. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of RR (blue: RR = 0.3 Mpc; green: RR = 0.6 Mpc; cyan: RR = 1 Mpc; and purple: RR = 2 Mpc). The volume height has been fixed to n = 1.5, the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01 and the true environment has been estimated on a scale RT = 1 Mpc. There is a different scale on the ordinate axis between high-density and low-density environments. |
| In the text | |
 |
Fig. 7 Recovery and contamination fractions – K ≤ 22. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Solid and dotted lines are for high-density environments, while dashed and dot-dashed lines are for low-density environments. Red curves are for K ≤ 22 objects, while cyan curves are for K ≤ 24 objects. The volume height has been fixed to n = 1.5, the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01 and both ϱtrue and ϱrec have been estimated on a scale RT = RR = 1 Mpc. |
| In the text | |
 |
Fig. 8 Recovery and contamination fractions – surface densities. fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Solid and dotted lines are for high-density environments, while dashed and dot-dashed lines are for low-density environments. Magenta curves are for environments defined through the use of surface densities, while blue curves are for environments defined through the use of volume densities. The volume height has been fixed to n = 1.5, the uncertainty in the photometric redshift is σΔz/ (1 + z) = 0.01 and both ϱtrue and ϱrec have been estimated on a scale RT = RR = 1 Mpc. |
| In the text | |
 |
Fig. 9 Recovery and contamination fractions – varying σΔz/ (1 + z). fRec (solid and dashed lines) and fCon (dotted and dot-dashed lines) as a function of redshift. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). The volume parameters for environmental reconstruction have been kept fixed to RR = RT = 1 Mpc and n = 1.5. |
| In the text | |
 |
Fig. 10 Varying σΔz/ (1 + z) – effect of n. fRec and fCon as a function of the n parameter in three redshift bins, namely 1.50 <z< 1.75 (solid lines), 2.00 <z< 2.25 (dashed lines), and 2.50 <z< 2.75 (dotted lines). Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). The aperture radius has been kept fixed to RR = RT = 1 Mpc. |
| In the text | |
 |
Fig. 11 Varying σΔz/ (1 + z) – effect of RR/RT, recovery. fRec (normalized to the value of fRec at RR/RT = 1 separately for each value of σΔz/ (1 + z)) as a function of RR/RT in the redshift bin 1.50 <z< 1.75. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). Shaded regions show the dispersion in the fraction values at fixed RR/RT given by different RT because smaller RT are reconstructed better than larger RT. The length of the volume has been kept fixed, with n = 1.5. |
| In the text | |
 |
Fig. 12 Varying σΔz/ (1 + z) – effect of RR/RT, contamination. fCon (normalized to the value of fCon at RR/RT = 1 separately for each value of σΔz/ (1 + z)) as a function of RR/RT in the redshift bin 1.50 <z< 1.75. Bottom panel refers to low-density environments, while top panel refers to high-density environments. The various curves are colour-coded according to the various values of σΔz/ (1 + z) (purple: σΔz/ (1 + z) = 0.003; blue: σΔz/ (1 + z) = 0.01; green: σΔz/ (1 + z) = 0.03; and red: σΔz/ (1 + z) = 0.06). Shaded regions show the dispersion in the fraction values at fixed RR/RT given by different RT because smaller RT are reconstructed better than larger RT. The length of the volume has been kept fixed, with n = 1.5. |
| In the text | |
 |
Fig. 13 Mock catalogues mass functions – RR = RT = 0.3 Mpc. The dark green and light green curves refer to the total GSMF, respectively, using ztrue and zphot for the calculation of the mass function. Dark red and light red curves refer to high-density environments, respectively, using ϱtrue, dark red, and using ϱrec, light red. Dark blue and light blue curves refer to low-density environments, respectively, using ϱtrue, dark blue, and using ϱrec, light blue. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 0.3 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
| In the text | |
 |
Fig. 14 Ratio of high-density and low-density mass functions – RR = RT = 0.3 Mpc. Ratio of the high-density mass function and the low-density mass function (ΦD75/ ΦD25) in the true (light green curve) and reconstructed (purple curve) environments. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 0.3 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
| In the text | |
 |
Fig. 15 Mock catalogues mass functions – RR = RT = 2 Mpc. The dark green and light green curves refer to the total GSMF, respectively, using ztrue and zphot for the calculation of the mass function. Dark red and light red curves refer to high-density environments, respectively, using ϱtrue, dark red, and using ϱrec, light red. Dark blue and light blue curves refer to low-density environments, respectively, using ϱtrue, dark blue, and using ϱrec, light blue. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 2 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
| In the text | |
 |
Fig. 16 Ratio of high-density and low-density mass functions – RR = RT = 2 Mpc. Ratio of the high-density mass function and the low-density mass function (ΦD75/ ΦD25) in the true (light green curve) and reconstructed (purple curve) environments. The black dashed lines are the mass completeness limits described in the text. The parameter values for the aperture are set to RR = RT = 2 Mpc and n = 1.5, with σΔz/ (1 + z) = 0.01. Error bars refer to |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.