| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A46 | |
| Number of page(s) | 11 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201526737 | |
| Published online | 18 November 2015 | |
The GIRAFFE Inner Bulge Survey (GIBS)
II. Metallicity distributions and alpha element abundances at fixed Galactic latitude ⋆,⋆⋆
1 European Southern Observatory, A. de Cordova 3107, 19001 Casilla Santiago 19, Chile
e-mail: ogonzale@eso.org
2 Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, 4860 Av. Vicuña Mackenna, Santiago, Chile
3 Millennium Institute of Astrophysics, Av. Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
4 Laboratoire Lagrange UMR 7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, CS 34229, 06304 Nice Cedex 04, France
5 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
6 Excellence Cluster Universe, Boltzmannstr. 2, 85748 Garching, Germany
7 INAF–Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
8 GEPI, Observatoire de Paris, CNRS UMR 8111, Université Paris Diderot, 92125 Meudon Cedex, France
9 Departamento de Ciencias Físicas, Universidad Andrés Bello, 220 República, Santiago, Chile
10 Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD 21218, USA
11 Vatican Observatory, V 00120 Vatican City State, Italy
Received: 14 June 2015
Accepted: 3 August 2015
Aims. We investigate metallicity and α-element abundance gradients along a Galactic longitude strip, at latitude b ~ −4°, with the aim of providing observational constraints for the structure and origin of the Milky Way bulge.
Methods. High-resolution (R ~ 22 500) spectra for 400 K giants, in four fields within −4.8° ≲ b ≲ −3.4° and −10° ≲ l ≲ +10°, were obtained within the GIRAFFE Inner Bulge Survey (GIBS) project. To this sample we added another ~400 stars in Baade’s Window at (l,b) = (1°,−4°), observed with the identical instrumental configuration: FLAMES GIRAFFE in Medusa mode with HR13 setup. All target stars lie within the red clump of the bulge colour−magnitude diagram, thus minimising contamination from the disc or halo stars. The spectroscopic stellar surface parameters were derived with an automatic method based on the GALA code, while the [Ca/Fe] and [Mg/Fe] abundances as a function of [Fe/H] were derived through a comparison with the synthetic spectra using MOOG. We constructed the metallicity distributions for the entire sample, and for each field individually, in order to investigate the presence of gradients or field-to-field variations in the shape of the distributions.
Results. The metallicity distributions in the five fields are consistent with being drawn from a single parent population, indicating the absence of a gradient along the major axis of the Galactic bar. The global metallicity distribution is nicely fitted by two Gaussians. The metal-poor component is rather broad, with a mean at ⟨ [Fe/H] ⟩ = −0.31 dex and σ = 0.31 dex. The metal-rich component is narrower, with mean ⟨ [Fe/H] ⟩ = + 0.26 and σ = 0.2 dex. The [Mg/Fe] ratio follows a tight trend with [Fe/H], with enhancement with respect to solar in the metal-poor regime similar to the value observed for giant stars in the local thick disc. [Ca/Fe] abundances follow a similar trend, but with a considerably larger scatter than [Mg/Fe]. A decrease in [Mg/Fe] is observed at [Fe/H] = −0.44 dex. This knee is in agreement with our previous bulge study of K-giants along the minor axis, but is 0.1 dex lower in metallicity than the value reported for the microlensed dwarf and subgiant stars in the bulge. We found no variation in α-element abundance distributions between different fields.
Key words: Galaxy: bulge / Galaxy: abundances / Galaxy: formation / Galaxy: evolution
Based on observations taken with ESO telescopes at the La Silla Paranal Observatory under programme IDs 187.B-909(A) and 71.B-0196.
Full Table 3 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A46
© ESO, 2015
1. Introduction
In the last few years we have witnessed important progress towards the understanding of the Milky Way bulge. The availability of large photometric and spectroscopic datasets from ongoing surveys are finally allowing us to obtain a wider view of the bulge properties, even expanding our knowledge to the innermost regions not previously accessible.
The bar in the inner regions of the Galaxy was first suggested by de Vaucouleurs (1964) and its main structural properties have been investigated in detail since then (Blitz & Spergel 1991; Stanek et al. 1994; Dwek et al. 1995; Babusiaux & Gilmore 2005; Rattenbury et al. 2007; Gonzalez et al. 2011,and references therein). The use of red clump (RC) giant stars as a distance indicator has been a fundamental tool for bulge morphology studies (Stanek et al. 1994). Based on this technique the axial ratios of the bar have been currently constrained to be about 1:0.4:0.3 with a bar size of about 3.1−3.5 kpc major-axis length. The position angle of the bar has been historically measured to range between ~20−40 deg with respect to the Sun-centre line of sight with its near end towards positive Galactic longitudes (Blitz & Spergel 1991; Stanek et al. 1994; Dwek et al. 1995; Binney et al. 1997; Bissantz & Gerhard 2002; Benjamin et al. 2005; Babusiaux & Gilmore 2005; Rattenbury et al. 2007; Cao et al. 2013). Recently, detailed comparisons of RC stellar counts to N-body models (e.g. Wegg & Gerhard 2013) have allowed the bar position angle to be constrained to 27−33°. The RC technique used to measure distances towards the bulge led to the discovery of a split RC at l = 0° and | b | > 5° by Nataf et al. (2010) and McWilliam & Zoccali (2010). This discovery was quickly followed by the construction of wider, more detailed 3D maps that revealed the X-shaped structure of the Bulge (Saito et al. 2011; Wegg & Gerhard 2013) as first suggested by McWilliam & Zoccali (2010). This X-shape structure is often seen in external galaxies and is accurately reproduced by dynamical models of disc galaxies (e.g. Li & Shen 2012; Gardner et al. 2014). They correspond to an extreme case of the boxy/peanut (B/P) structures observed in several external disc galaxies formed as the consequence of buckling instabilities of galaxy bars. The buckling process of the bar causes the stellar orbits to heat up in the vertical direction (e.g., Combes et al. 1990; Athanassoula 2005; Martinez-Valpuesta et al. 2006; Debattista et al. 2005). Because of the absence of an external influence in this process, a reference of these structures as so-called pseudo-bulges (see Kormendy & Kennicutt 2004, for a detail definition of such structures) is often found in the literature. However, we refrain from using this definition to differentiate them from the young stellar disc-like structures formed in the inner part of bars due to the continuous in-fall of gas. We refer to this structure simply as the B/P bulge of the Milky Way.
The Bulge Radial Velocity Assay survey (BRAVA; Howard et al. 2009; Kunder et al. 2012), measured radial velocities for ~10 000 bulge M giants at latitudes b = −4°,−6°,−8° and longitudes −10°< l < 10°. The BRAVA survey provided strong evidence for the cylindrical rotation of the bulge, concluding that a B/P bulge would be enough to reproduce the rotation curve of the bulge without the need of a classical component formed via mergers in the early evolution of the Galaxy (Howard et al. 2009; Shen et al. 2010). The cylindrical rotation was also confirmed recently by the GIBS survey in Zoccali et al. (2014, hereafter Paper I) where it was extended to latitudes (b ~ −2°).
While the B/P bulge has been shown to rotate cylindrically, the bulk of its stellar population is over ~10 Gyr old (e.g. Zoccali et al. 2003; Clarkson et al. 2011; Valenti et al. 2013). A ~10 Gyr look-back time brings us to redshift z ~ 2, where galaxies are radically different from local ones and live at the epoch when the overall star formation rate (SFR) in the Universe peaked. Massive galaxies with stellar masses comparable to those seen today (~1010−1011 M⊙) are forming stars at rates of ~20−200 M⊙/yr, some 20 times higher than in local galaxies of the same mass. These higher SFRs are a consequence of higher gas mass fractions in these systems, typically ~30−50% as revealed by CO observations (Tacconi et al. 2010, 2013; Daddi et al. 2010). Moreover, adaptive optics resolved Hα kinematic studies have revealed that most z ~ 2 main-sequence galaxies are large rotation-dominated discs, with a minor fraction of major mergers, and are characterised by very high-velocity dispersion (~50−100 km s-1) and by the presence of actively star-forming clumps at scales of several kpc, (e.g. Förster Schreiber et al. 2009; Genzel et al. 2011; Mancini et al. 2011; Newman et al. 2013). In parallel with these findings, a new paradigm has emerged in which bulges form by the migration and coalescence to the centre of massive star-forming clumps (Immeli et al. 2004; Bournaud et al. 2007, 2009; Elmegreen et al. 2008), a situation which may even develop into a global violent disc instability, leading to a dissipational formation of compact bulges (Dekel & Burkert 2014). Considering all the processes that can be involved in the formation of bulges, it becomes clear that kinematics alone would not be sufficient to reconstruct the formation mechanism of the Galactic bulge. Indeed, the chemical abundance measurements of individual stars have been shown to provide a different perspective, especially when combined with the kinematics.
Several studies have investigated the metallicity distribution functions near to Baade’s Window at (l,b) = (0°,−4°) (e.g. Rich 1988; McWilliam & Rich 1994a; Minniti 1996; Sadler et al. 1996; Ramírez et al. 2000; Zoccali et al. 2003; Fulbright et al. 2006) deriving a wide distribution with metallicities ranging from −1.6 to 0.5 dex and a peak at solar metallicities. Zoccali et al. (2008), and Johnson et al. (2011, 2013) used high-resolution spectra to derive metallicity distributions in different bulge regions along the minor axis and have firmly established the presence of a vertical metallicity gradient with field stars closer to the Galactic centre being on average more metal rich. Furthermore, the general picture of these metallicity gradients in the bulge was presented in Gonzalez et al. (2013) who showed the global mean photometric metallicity map of the Galactic bulge based on the Vista Variables in the Via Lactea (VVV) ESO public survey data (Minniti et al. 2010).
By combining [Fe/H] and [Mg/Fe] abundances and kinematics, Hill et al. (2011) and Babusiaux et al. (2010) suggested the presence of two distinct components in the bulge: a metal-poor one (⟨ [Fe/H] ⟩ ~ −0.3) with kinematics typical of a classical spheroid, and a metal-rich one, (⟨ [Fe/H] ⟩ ~ + 0.3) concentrated towards the Galactic plane with a significant vertex deviation, suggestive of a bar-like component (see also Soto et al. 2007). The origin of the observed metallicity gradients would then be the natural consequence of the different contribution of each of these components as a function of Galactic latitude. A similar conclusion was reached by Rojas-Arriagada et al. (2014) based on the Gaia-ESO survey data.
A step further in the interpretation of the bulge metallicity distribution was taken using the Abundances and Radial velocity Galactic Origins Survey (ARGOS; Freeman et al. 2013). Ness et al. (2013a,b) measured radial velocities, [Fe/H], and [α/Fe] ratios for ~28 000 bulge stars at different regions well distributed across the bulge. They find the same cylindrical rotation found by the BRAVA and GIBS survey, but suggested the presence of five components in the metallicity distribution of the bulge. They suggested that the actual bulge component would be the metal-rich one ([Fe/H] ~ + 0.15), and perhaps the component at [Fe/H] ~ −0.25 dominating at high latitudes. Additional components would belong to the inner disc and halo.
On the other hand, α-element abundances in bulge stars provide us with with an additional constraint on the formation history of the stellar populations in the bulge: their formation timescale. As suggested by Tinsley (1979) the ratio of [α/Fe] compared to [Fe/H] is expected to be a function of the time delay between the production of both α- and iron-peak elements by SNe II (e.g. Woosley & Weaver 1995) and the yield of mostly iron-peak elements with little α-element production by SNe Ia (e.g. Nomoto et al. 1984). Clearly, a sufficient amount of time needs to be accounted for such that enough SNe Ia events occur for the [α/Fe] ratio to decline from the SNe II value. The α-element abundances of bulge stars with [Fe/H] <−0.3 have been historically found to be enhanced over iron by [α/Fe] ~ + 0.3 dex (McWilliam & Rich 1994b; Rich & Origlia 2005; Cunha & Smith 2006; Fulbright et al. 2007; Lecureur et al. 2007; Rich et al. 2007) thus suggesting a fast formation scenario. Metal-rich stars on the other hand show a decrease in [α/Fe] reaching [α/Fe] = 0 for metallicities above solar values. However, the SNe Ia delay time might vary depending on the different production channels that could be present, and therefore obtaining a direct translation of these trends to absolute timescales is not straightforward. As a consequence, the comparison of [α/Fe] values in bulge stars against those of other Galactic components has been proven to be a useful tool for investigating the bulge formation timescale with respect to the other components such as the disc and halo. Based on this relative measurement approach, Fulbright et al. (2007), Zoccali et al. (2006), and Lecureur et al. (2007) concluded that the [α/Fe] ratio was enhanced by nearly +0.1 dex with respect to the trends of both the local thin and the thick disc as traced by nearby dwarf stars. Therefore, these results implied a shorter formation timescale for the bulge than for both discs. However, Meléndez et al. (2008), Alves-Brito et al. (2010), Johnson et al. (2011, 2013), and Gonzalez et al. (2011) found a similarity between the [α/Fe] abundance ratio of bulge and thick disc giant stars. The origin of this discrepancy might be a systematic difference that occurs when analysing the abundances of dwarf stars from the disc and bulge giants (Meléndez et al. 2008). In support of this scenario, the microlensed dwarfs from the bulge have shown a similar α-element enhancement to dwarf stars from the thick disc (Bensby et al. 2011). Therefore, using well-calibrated measurements on homogeneous datasets is fundamental for these kinds of studies.
Some high-resolution studies have looked at a few fields located at relatively similar latitude (e.g. Johnson et al. 2013), but always at latitudes higher than | b | = 4° where the contribution of the metal-rich stars is known to decrease (Zoccali et al. 2008; Johnson et al. 2013; Ness et al. 2013a). The limited samples could therefore miss some subtle gradients. In this work we investigate ~100 stars per field in a region where the two populations are well represented. This study provides important constraints on the global view of the metallicity and α-element distribution of the bulge which are fundamental in order to reconstruct its formation scenario.
2. GIBS high-resolution spectra
The Giraffe Inner Bulge Survey (GIBS) is a survey of ~6500 RC stars in the Milky Way bulge observed with the GIRAFFE spectrograph on the FLAMES instrument (Pasquini et al. 2000) at the ESO Very Large Telescope (VLT). The aim of the GIBS survey is to investigate the metallicity and radial velocity distribution of bulge stars across different fields, spread over a large area of the inner Galactic bulge (−10° ≤ l ≤ + 10° and −10° ≤ b ≤ + 4°). A detailed description of the target selection and data products of the programme is given in Paper I. In this article, we focus on the analysis of the high-resolution spectra of 400 RC stars located in four fields at Galactic latitude b ~ −3.5° for which we provide a brief description summary.
 |
Fig. 1 The location of the fields analysed in the present study (red circles) overplotted on an optical image of the Milky Way bulge (© Serge Brunier). The location of the fields discussed in previous studies (Zoccali et al. 2008; Hill et al. 2011) are shown as Z08 and H11; the location of the Ness et al. (2013a), Johnson et al. (2011), and Johnson et al. (2013) fields are shown as ARGOS, J11 and J13, respectively. The lower panel shows the colour−magnitude diagram for field HRm5m3. Red filled circles show the corresponding target stars for this field. |
Target stars for the spectroscopic observations were selected from the VVV multi-band photometric catalogues (Gonzalez et al. 2012). The location of the fields was carefully selected in order to overlap with additional optical photometric observations from the OGLEII survey (Sumi et al. 2004). This allows us to add extra information on the target stars such as proper motions and a larger colour baseline (V−Ks) for deriving the initial values of the effective temperatures.
Observed fields and final number of stars analysed in this work.
Figure 1 shows the location of the four fields analysed in the present study overplotted on an optical image of the Milky Way bulge. The location of other fields with previous studies similar to the one presented here (Zoccali et al. 2008; Ness et al. 2013a; Johnson et al. 2011, 2013) are also shown. The colour−magnitude diagram for one of our observed fields (HRm5m3), where our selected targets are clearly highlighted, is shown as well. The selection box of targets in the colour−magnitude diagram can be clearly seen in Fig. 1 and it was designed to target RC stars while minimising the contamination for foreground disc stars.
A description of the observations is listed in Table 1. All spectra in the fields analysed in this study were observed using the high-resolution grating (R = 22 500) through setup HR13 centred at ~6300 Å in order to measure the chemical abundance of iron and α-elements similar to the procedure used in Gonzalez et al. (2011).
Reduction of the spectra was carried out using the ESO GIRAFFE pipeline. Bias and flat-field correction, individual spectral extraction, and wavelength calibration have been applied by using the ESO/GIRAFFE pipeline1. An adequate sky spectrum for each exposure was obtained by co-addition of sky spectra obtained from dedicated fibres in each GIRAFFE configuration. Sky subtraction was carried out on each spectrum using the skytweak task in IRAF as described in Paper I. Heliocentric radial velocities were measured using the IRAF fxcor task by cross–correlation against a synthetic spectra for a typical bulge K giant star (Teff = 4500 K, log g = 2.3 and [Fe/H] = −0.3), covering the corresponding wavelength range of the GIRAFFE HR13 setup from 6100 Å to 6400 Å. For each star, multiple exposures (~10) were individually corrected for radial velocity and individual products were mean combined to produce the final set of spectra for each field. The errors measured on radial velocities were typically ~1 km s-1.
3. Stellar parameters
Stellar parameters, namely effective temperature (Teff), surface gravity (log g), microturbulence velocity (ξ), and metallicity ([Fe/H]) were derived based on an iterative method similar to the one described in Zoccali et al. (2008) and Gonzalez et al. (2011). The method consists of the spectroscopic refinement of a set of the first guess photometric stellar surface parameters based on the measurement of the equivalent width (EW) of Fe lines. The objective was to find the best combination of parameters in order to impose an excitation equilibrium of Fe lines (zero slope of Fe abundance as a function of excitation potential of Fe lines) and to simultaneously measure the same Fe abundance for all lines independently of their EW (measuring a zero slope of Fe abundance as a function of log (EW/λ)). We note that we only used FeI lines for this procedure, as the resolution GIRAFFE spectra does not provide us with sufficient number of clean FeII lines across our analysed spectral region. In Zoccali et al. (2008) and Gonzalez et al. (2011) this process was done manually, in the sense that the parameters were modified by hand to minimise the corresponding slopes. This manual procedure was found to produce some systematics, particularly in the high metallicity regime (Hill et al. 2011). To correct for this issue and to bring our datasets into a common baseline, we have now changed our method into an automatic procedure, similar to the one used in Hill et al. (2011) but using the GALA code (Mucciarelli et al. 2013) to spectroscopically refine the first guess photometric parameters. We note that another difference with respect to the aforementioned studies is that for this work we have used ATLAS9 model atmospheres (Castelli & Kurucz 2004). We chose these models because GALA already includes a dynamic call to the ATLAS9 code so that whenever GALA needs to investigate a new set of atmospheric parameters, ATLAS9 is called and a new model atmosphere is computed.
As a first step, the photometric temperature is calculated for each star using the (V−Ks) colours from OGLEII (Udalski et al. 2002) and VVV survey catalogues (Gonzalez et al. 2012), dereddened based on the high-resolution extinction maps from Gonzalez et al. (2012), and applying the Ramírez & Meléndez (2005) calibration. Absolute V-band magnitudes, calculated from the measured distances to each specific field from Gonzalez et al. (2013) and bolometric corrections from Alonso et al. (1999), are then used to estimate photometric gravities based on the usual formula,
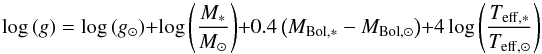 where MBol,⊙ = 4.72, Teff,⊙ = 5770 K, and log (g⊙) = 4.44 dex. A fixed value of M∗ = 0.8 M⊙ has been adopted similarly to Zoccali et al. (2008) and Hill et al. (2011). Microturbulence velocity and global metallicity are set to 1.5 and 0.0, respectively, as a first step. These values are used to obtain a first guess ATLAS9 stellar model atmosphere and are subsequently refined spectroscopically by GALA using the equivalent widths of isolated Fe lines obtained by means of DAOSPEC (Stetson & Pancino 2008).
where MBol,⊙ = 4.72, Teff,⊙ = 5770 K, and log (g⊙) = 4.44 dex. A fixed value of M∗ = 0.8 M⊙ has been adopted similarly to Zoccali et al. (2008) and Hill et al. (2011). Microturbulence velocity and global metallicity are set to 1.5 and 0.0, respectively, as a first step. These values are used to obtain a first guess ATLAS9 stellar model atmosphere and are subsequently refined spectroscopically by GALA using the equivalent widths of isolated Fe lines obtained by means of DAOSPEC (Stetson & Pancino 2008).
After feeding GALA with the photometric stellar surface parameters and the corresponding model atmosphere, the code iteratively searches for spectroscopic effective temperatures and microturbulence velocity by imposing excitation equilibrium and the null slope of iron abundance versus equivalent width of the Fe lines. During each iteration, a new model atmosphere is generated by GALA using the refined stellar parameters. Although available in GALA, we do not refine log g values by requiring ionisation equilibrium, but we rely on the values derived photometrically. As discussed in Zoccali et al. (2008), the resolution of GIRAFFE is not high enough to resolve a sufficient number of clean FeII lines in our spectra and thus using the few available lines would introduce more errors than just using the photometrically derived values for log g. Therefore, after a first set of best-fitting values for Teff, ξ, and [Fe/H] is found by GALA, we recalculate the log g value according to the new parameters and perform another set of GALA iterations to refine the stellar parameters with the new log g.
Atomic line list for Mg and Ca used in this work, excitation potential (χex), and oscillator strength (log gf) for each analysed line.
The list of FeI lines used for this method is the one used in Lecureur et al. (2007) following a careful cleaning of blended lines. The check for blends of the Fe lines was done using a spectrum of μ Leo obtained at the Canada-France-Hawaii Telescope with the ESPaDOnS spectro-polarimeter at a resolution R ~ 80 000 and high S/N per pixel (~500). As a first step, the resolution of the μ Leo spectrum was degraded to the resolution of the GIRAFFE HR13 setup of R ~ 22 500. This was followed by a line-by-line inspection performed over the wavelength range of our science data. Several blended Fe lines were removed from the list ending with a total of 27 non-blended Fe lines in the HR13 setup. The log gf values from the original line list from Lecureur et al. (2007) are calibrated so that each line provides an abundance of 0.30 dex from the EW measured in the spectrum of μ Leo while adopting Teff = 4540 K, log g = 2.30, and ξ = 1.30. Therefore, in order to further check our final Fe line list, we measured the EW of the corresponding line using DAOSPEC in the μ Leo spectrum (now at GIRAFFE resolution) and used GALA to derive the Fe abundance by fixing the model to those same stellar parameters from Lecureur et al. (2007). GALA retrieved an abundance of [Fe/H] = 0.32, in excellent agreement with the literature value of [Fe/H] = 0.34 (Gratton & Sneden 1990). On the other hand, by leaving the stellar parameters free with the exception of log g which was fixed to log g = 2.30, GALA retrieves Teff = 4490 K, ξ = 1.43, and [Fe/H] = 0.31 for μ Leo. These values are in good agreement with those reported in the literature (Smith & Ruck 2000; Gratton & Sneden 1990). The final list of FeI lines used in our analysis is provided in Table 2.
Particular care has been devoted to ensure that the adopted stellar parameters are i) sufficiently accurate to allow reliable abundance estimates; and ii) consistent with previous analyses to guarantee a homogeneous comparison across various samples. This provides us with a test for our stellar parameter measurements while at the same time it ensures that our newly derived abundances can be safely compared to our previous work. With this aim, we have rederived the abundances for the Baade’s Window sample of Red-Giant-Branch (RGB) stars from Zoccali et al. (2008) and for the RC sample from Hill et al. (2011) using the GALA-based procedure described above. Figure 2 shows the comparison between the stellar surface parameters and [Fe/H] for RC and RGB samples from Hill et al. (2011) and those derived with our method. This comparison involves only the calculation of stellar parameters, since the EW measurement is performed using DAOSPEC both in Hill et al. (2011) and in this work.
 |
Fig. 2 Differences between metallicity (upper panel), effective temperature (middle panel) and microturbulence velocity (lower panel) for a sample of RC (red filled circles) and RGB (black empty circles) derived in this work and as derived in Hill et al. (2011). Solid lines in each panel indicate the mean difference of each sample and the dashed lines shows the 1σ range around the mean. |
As shown in Fig. 2, there is a good agreement between the two methods with no significant differences for either of the two samples analysed (RGB and RC stars). In particular, for effective temperature we find a mean difference ΔTeff = 2 ± 199 K and −23 ± 185 K for RGB and RC, respectively. On the other hand, micro-turbulence velocities result in a mean difference of Δξ = −0.14 ± 0.19 km s-1 for RGB stars and Δξ = −0.12 ± 0.26 km s-1 for RC stars. These stellar parameters translate into a mean metallicity difference of [Fe/H] = −0.02 ± 0.19 and [Fe/H] = −0.01 ± 0.15 dex. The derived differences are negligible and the scatter between the two samples is in good agreement with the expected errors on the measurements of the surface stellar parameters as discussed in Hill et al. (2011). Furthermore, this confirms that our results and those from Hill et al. (2011) are in good agreement, with no systematic differences between metallicities obtained for RGB stars from Zoccali et al. (2008) and for RC stars as previously reported in Hill et al. (2011). Therefore, the measurements on the Baades Window samples (RC and RGB) can be compared in a consistent and homogenous way with the results from the GIBS survey discussed in the present study.
Finally, we investigated the dependence of the final [Fe/H] abundance on the initial photometric estimations of the stellar parameters. Reddening corrections and distance spread translate into uncertainties in the initial photometric parameters. Furthermore, adopting an effective temperature calibration different to that of Ramírez et al. (2000) would cause a different starting point for the first run of GALA. In order to evaluate the impact of these parameters in the final abundances, we have tested a run of the RC sample from Hill et al. (2011), but starting from the same set of stellar parameters for all the stars: Teff = 4500 K, ξ = 1.5 km s-1, log g = 1.9 dex, and [Fe/H] = 0.00. Figure 3 shows the comparison between the original [Fe/H] for this sample and the value resulting from the same stellar parameters. Because the mean difference in the [Fe/H] estimates is Δ [Fe/H] = 0.02 dex, no significant systematic offsets are expected in the final set of [Fe/H] abundances due to the adopted set of initial stellar parameters, no matter how far they are from the correct values. On the other hand, the dispersion between the [Fe/H] is found to be σ[Fe/H] = 0.13 dex, which is not negligible. Differences of up to 0.3 dex can be found among the most metal-rich stars as a result of using an incorrect set of initial parameters. It is worth mentioning that GALA has an optional initial stage, called the guess working block, where the stellar parameter space is explored in a coarse grid in order to verify and refine poorly known initial parameters. However, in our case concerning bulge giant stars, the reddening and distance spread uncertainties are always propagated into the calculation of the photometric surface gravity. The non-variation of this value against the procedure of GALA makes the guess working block redundant and an error similar to the Δ [Fe/H] = 0.13 dex observed in this test is expected within the uncertainty of this particular parameter. Most likely, the observed uncertainty associated with the initial stellar parameters is not caused by GALA itself, but by the inability to optimise the entire grid of parameters simultaneously in the bulge. Were a larger number of FeI and Fe II lines available in our spectra, the final scatter on stellar parameters would converge to less than 50 K in Teff and 0.09 in log g as described in Mucciarelli et al. (2013) thus decreasing the relatively large scatter in [Fe/H] observed in Fig. 3.
 |
Fig. 3 Difference between the [Fe/H] abundances obtained with the adopted GALA procedure using the correct set of initial stellar surface parameters and using fixed values (Teff = 4500 K, ξ = 1.5 km s-1, log g = 1.9, and [Fe/H] = 0.00) for the RC sample from Hill et al. (2011) |
The uncertainties in the stellar parameters are derived internally by GALA. As pointed out in Mucciarelli et al. (2013), the errors on the stellar parameters are dominated by the number of FeI lines used and their distribution in both χex range and transition values. For each stellar parameter, an optimisation parameter is calculated by applying a jackknife bootstrapping technique. This means that if the optimisation is computed using a set of N spectral lines, the parameters will then be recalculated N times, but using N−1 lines each time. This calculation is then related to a parametrisation factor that measures the way each parameter affects the slopes and iron abundance differences within the GALA procedure. This parametrisation value is calculated by GALA by varying the best value found around the local minimum. This method and their respective equations are described in detail in Mucciarelli et al. (2013). In our sample, the resulting errors are found to be σTeff = 245 ± 99 K and σξ = 0.29 ± 0.11 km s-1. Each parameter is then varied by its corresponding uncertainty while keeping the others unchanged, and the abundances are rederived. The individual effects in abundance from the variations of each parameter are added in quadrature to obtain the final error in metallicity. In our sample, this computation results in a mean metallicity error of σ[Fe/H] = 0.20 ± 0.07 dex. However, we note that the errors on [Fe/H] can reach up to 0.4 dex for the most metal-rich stars, but can be lower than 0.1 dex for metal-poor stars, and are mostly driven by Teff uncertainties. These errors are consistent with those reported in Hill et al. (2011) and Zoccali et al. (2008) for similar datasets and are also in agreement with the differences seen in Fig. 2. Furthermore, the larger errors on stellar parameters towards the high metallicity regime are expected. Extensive analysis of errors on derivation of stellar parameters was presented in Smiljanic et al. (2014) in the context of the Gaia-ESO survey and showed how the errors become larger at high metallicities due to the increase of line blends.
4. α element abundances
In order to measure α-element abundances for all the target stars we adopt the same procedure and line lists used in Gonzalez et al. (2011). As a first step, the corresponding ATLAS9 model atmosphere (Castelli & Kurucz 2004) is generated using the stellar parameters found by GALA for each star. This model is then fed to MOOG (v. Feb2013, Sneden 1973) in order to generate a synthetic spectrum. The synthetic spectrum is iteratively compared with the observed one after a local normalisation of the continuum, by varying only the elemental abundance of interest in each iteration until the best-fitting abundance if found.
Stellar parameters, [Fe/H], [Mg/Fe], and [Ca/Fe] abundance ratios for stars in the four high-resolution GIBS fields.
Based on a similar dataset – the same setup, resolution, and similar signal-to-noise – Gonzalez et al. (2011) showed that among all the α-elements measurable in the observed spectral range Mg has the smallest scatter. Therefore, we consider Mg to be the key element that allows a precise comparison between the abundance trend observed in different bulge and disc star samples. However, in order to obtain precise abundances of Mg we need to first calculate Ca abundances. Indeed, as discussed in detail in Lecureur et al. (2007), Hill et al. (2011), and Gonzalez et al. (2011) the continuum around the Mg triplet at 6319 Å is severely affected by the 6318.1 Å Ca I autoionisation line. The large broadening of this Ca line causes a drop in the Mg triplet region that can result in an incorrect abundance measurement for Mg. For this reason, we first measured Ca abundances using two lines at 6162.1 and 6166.43 Å (see Fig. 4, lower panel and Table 2). Once the Ca abundances have been measured we provide this value as an additional input for MOOG to be included in the synthesis used for the calculation of Mg abundances. The local normalisation of the continuum is then manually improved as an additional way to account for any failure to reproduce the underlying Ca autoionisation line. An example of this fit is shown in Fig. 4. This procedure was applied to all the analysed stars, obtaining Ca and Mg abundances for a total of 400 stars spread over our four fields. Figure 4 also shows an example of the sensitivity of the lines to the variations in [Mg/H] and [Ca/H]. For a variation of ± 0.1 dex, the effect in the fit region of Mg is clearly seen, while the Ca lines appear to be less sensitive to such variations. Both of the Ca lines that are used in this work show a similar behaviour. The difference in [Ca/Fe] abundances measured from each of the lines has a σ of 0.05 dex, which is negligible compared to the errors involved in our analysis owing to the stellar parameter uncertainties.
 |
Fig. 4 Observed (black circles) and synthetic spectra for a star (OGLE26-415574) in the field HRm5m3 zoomed into the region used to derive Ca (upper panel) and Mg (lower panel) abundances. The synthetic spectra created with the best-fitting Ca ([Ca/Fe] = 0.06) and Mg ([Mg/Fe] = 0.05) abundances are shown in solid red lines. The elements producing the strongest absorption lines are marked in each panel. For each spectral region we show a zoomed-in section around the Ca line at 6166.4 Å and the Mg triplet that includes the synthesis produced using the best-fitting abundance as red solid lines. In blue and green we show the synthetic spectra using a 0.1 dex abundance variation around the best-fitting value. The Y-axis of both zoomed-in regions have the same scale with normalised fluxes that range from 0.8–0.5 for Ca and 1.0–0.7 for Mg lines. |
The uncertainties on the measured [Mg/H] and [Ca/H] abundances were calculated in the same way as in Gonzalez et al. (2011) by varying the stellar parameters by their corresponding uncertainties and recalculating the best-fitting abundances. These errors are then added in quadrature together with the error from our spectral synthesis fitting procedure of 0.1 dex derived in Gonzalez et al. (2011). The errors are individually listed in Table 3 and are found to be of the order of 0.14 dex for [Mg/H] and 0.21 dex for [Ca/H]. Figure 5 shows the error estimation for Ca and Mg abundances as a function of the estimated uncertainties for the stellar parameters of each star. It can be clearly seen that Ca abundances are much more sensitive to any variations on stellar parameters than Mg abundances. Furthermore, the larger sensitivity of Ca abundances to stellar parameters is seen at all metallicities, but is even larger in the metal-rich regime.
 |
Fig. 5 Abundance measurement errors as a function of errors on the stellar parameters: [Fe/H] (upper left panel), microturbulence velocity (upper right panel) and effective temperature (lower left panel). Errors as a function of the corresponding [Fe/H] value are also displayed (lower right panel). In all panels errors for [Ca/H] abundances are shown as red empty circles and errors for [Mg/H] as red filled circles. |
 |
Fig. 6 Overall metallicity distribution obtained from the combination of the four GIBS high-resolution fields and the RC sample of Hill et al. (2011). The probability density distribution is overplotted in the upper panel as a dashed line. The corresponding variance on the calculated probability densities is shown in blue. The lower panel shows the two best Gaussian fits to the upper panel distribution. The resulting distribution from the two Gaussians is shown as a solid line. |
5. Results
Stellar parameters, [Fe/H], [Ca/Fe], and [Mg/Fe] values measured for a total of 400 stars in the GIBS sample are listed in Table 3 and discussed in detail in this section.
5.1. Bulge metallicity distributions at constant latitude
The derived metallicity distribution of the five fields located at latitude b ~ −3.5° (i.e. the four GIBS fields and the Baade’s window RC sample from Hill et al. 2011) are very similar to each other (see Fig. 7). Therefore, in order to increase the number statistics, we initially construct the global metallicity distribution from all the stars in the five fields together. Figure 6 shows the resulting global metallicity distribution. In order to avoid binning effects when looking at the shape of the distribution, we have estimated the probability density underlying in the global sample by using the kernel density estimator method (Silverman et al. 1998). We have adopted a Gaussian kernel and the optimal smoothing parameter as defined in Silverman et al. (1998).
The good number statistics of the total sample allows us to investigate in detail the metallicity distribution. In particular, we are interested in evaluating the decomposition of the distribution in two populations, as suggested in previous studies (Hill et al. 2011; Rojas-Arriagada et al. 2014). We note that Ness et al. (2013a) suggested that the bulge metallicity distribution can be decomposed into five Gaussian components, each of them corresponding to different populations from the bulge and foreground disc. Here, we limit this decomposition to only two Gaussian components. The main reason for setting this limit is that studies based on both bulge kinematics and morphology have found evidence for only two main components: a metal-poor spheroid-like component and a metal-rich bar-like component. Also, in this study we are restricted to inner bulge fields in which we have a narrow target selection box in the colour−magnitude diagram. For this reason, the contamination by the thin/thick disc and halo is negligible here (components D, F, and E in Ness et al. 2013a). It is worth emphasising that here the use of two Gaussian distributions is not necessarily meant to describe the actual shape of the metallicity distribution of each of the two components. It represents the attempt to perform the best possible parametrisation of the observed global metallicity distribution, so we can therefore investigate how its shape changes across the fields.
We perform a least-squares Gaussian fit to the global metallicity distribution using the IDL routine XGAUSSFIT (Lindler 2001). The code automatically fits the main Gaussian component, and additional components can then be included by specifying an initial guess for the mean, peak, and sigma values. The code then refines the fit for both Gaussian functions simultaneously. The best-fit Gaussian distributions and the global metallicity distribution are shown in Fig. 6. The resulting parameters for the best-fit metal-poor Gaussian component are ⟨ [Fe/H] ⟩ = −0.31 and σ [Fe/H] = + 0.31. On the other hand, the metal-rich Gaussian component has a mean ⟨ [Fe/H] ⟩ = + 0.26 and σ [Fe/H] = + 0.20. The two Gaussian fits to our global metallicity distribution are in good agreement with those of Hill et al. (2011) who find a metal-poor component with mean of [Fe/H] = −0.27 and a metal-rich one of [Fe/H] = + 0.29. The sigma of the metal-poor component is in good agreement with that of Hill et al. (2011), who find a broad metal-poor component with σ [Fe/H] = 0.31. On the other hand, Hill et al. (2011) find a metal-rich component slightly narrower than ours with σ [Fe/H] = 0.12. Nevertheless, the results are fully compatible. The observed differences in the widths of the metal-rich components originate from the increase of the [Fe/H] errors towards the metal-rich regime and the respective error deconvolution that was applied in the Hill et al. (2011) analysis.
 |
Fig. 7 Metallicity distributions for the four GIBS high-resolution fields. Additionally, the metallicity distribution for Baade’s window from Hill et al. (2011) is shown in red in the middle panel. For each of the metallicity distributions we overplot the probability density distribution for the entire sample of metallicities shown in Fig. 6. |
The individual metallicity distributions for all the fields presented in this work are shown in Fig. 7. From the measured mean metallicity in each field we see no evidence of a gradient such as the one seen along the minor axis (Zoccali et al. 2008; Ness et al. 2013a). The observed mean [Fe/H] values of the fields studied in this work are in the range [Fe/H] = 0.10−0.20, consistent with what is shown in the mean photometric metallicity map from Gonzalez et al. (2013). We do not attempt a multi-Gaussian fit to the individual field metallicity distributions because we do not have enough statistics in each field, which therefore prevents us from deriving a statistically robust conclusion. However, we use the probability density distribution that was obtained from the global metallicity distribution as a reference in order to evaluate field-to-field variations. In Fig. 7 we can see that the metallicity distribution of individual fields span the same range: −1 ≤ [Fe/H] ≤ + 1. The general shape of the distributions is nicely represented by the probability density distribution constructed over the global metallicity distribution. A more noticeable difference can be observed in field m5m3 where the metal-rich side of the distribution shows a strong peak near solar metallicity that is not seen in the other fields.
In order to evaluate whether the metallicity distributions for each field originate from different populations or not, we performed a two-sample Kolmogorov-Smirnov (K-S) test and compared the metallicity distribution found in Baade’s window with the individual GIBS field distributions. The K-S test returns p-values (i.e. the probability that two functions belong to the same distribution) of 0.22 for p8m3, 0.48 for p4m3, 0.03 for m5m3, and 0.16 for m7m3. With the exception of field m5m3, the K-S test confirms that our samples are most likely drawn from the same parent population. For field m5m3, the result is not conclusive. From the visual inspection of the metallicity distribution we notice that the main difference with respect to the other fields comes from a concentration of stars at [Fe/H] ~ + 0.1.
We conclude in favour of a null mean metallicity gradient along the bulge major axis, as previously suggested in Johnson et al. (2013) at higher latitudes (but see Rangwala & Williams 2009 and Babusiaux et al. 2014). Furthermore, we conclude that the metallicity distributions presented in this work for fields along the longitude strip at b = −4° originate from the same parent population. Based on these conclusions, we suggest that the relative contribution of the two different Bulge components (spheroid-like and bar) does not change along the major axis, providing that this is indeed the origin of the metallicity gradient found along the minor axis.
 |
Fig. 8 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] used as a diagnostic of the formation timescale of the bulge. Shown as red circles are the [Mg/Fe] and [Ca/Fe] values obtained from the HR13 spectra of 400 stars in the four GIBS fields presented in this work compared to those for RGB stars from the Baade’s window sample of Gonzalez et al. (2011) which are shown as black empty circles. Measurements for the local thin (black squares) and thick (blue triangles) disc stars from the sample from Gonzalez et al. (2011) are also shown in both panels. The uncertainties for [Ca/Fe] and [Mg/Fe] abundances are shown as a light blue contour in both panels according to the individual uncertainties reported in Table 3. |
 |
Fig. 9 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] as in Fig. 11. Here we colour-coded the abundances of [Ca/Fe] and [Mg/Fe] according to the estimated uncertainty value. The colour-coding was fixed in both panels to the range of [Mg/Fe] uncertainties between 0.07−0.20 dex from black to red. The uncertainty contour of [Mg/Fe] is also shown in the background of both panels as a reference. |
 |
Fig. 10 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] for the GIBS high-resolution fields studied in this work and for the measurements from Johnson et al. (2014) for giant stars (black squares) and microlensed dwarfs from Bensby et al. (2013; blue triangles). In the upper panel, the solid lines show the best-fit relation between [Mg/Fe] and [Fe/H] for the metal-poor and metal-rich regime. The intersection point is shown and represents the position of the knee. The uncertainties for [Ca/Fe] and [Mg/Fe] abundances of this work are shown as a light blue contour in both panels. |
5.2. Bulge α-element abundances at constant latitude
We now present the results for [Ca/Fe] and [Mg/Fe] abundances for all our target stars, obtained by comparison to synthetic spectra created using the corresponding stellar surface parameters and [Fe/H] discussed in previous sections. A total sample of 400 stars have been analysed and their [Ca/Fe] and [Mg/Fe] over [Fe/H] trends are shown in Fig. 8. Also in Fig. 8 we show a comparison of our results with respect to those derived from a similar sample in Baade’s window measured in Gonzalez et al. (2011).
While the scatter of the measurements in [Ca/Fe] are comparable in both samples, the [Mg/Fe] trend shows a remarkable reduction of the scatter with respect to the previous measurement from Gonzalez et al. (2011). This is most likely a consequence of our improved calculation of stellar parameters as discussed in Sect. 3. The larger dispersion in Ca abundances with respect to Mg can be clearly seen in Fig. 8. This spread in [Ca/Fe] is most likely caused by the larger dependence of Ca abundance on stellar parameter uncertainties. In Fig. 9 we show that when only the stars with small uncertainties are considered, the sequence of [Ca/Fe] becomes tighter, with much less scatter at all metallicities. It can be seen that stars with high [Ca/Fe] found at high metallicities [Fe/H] > 0 are restricted to those measurements with large uncertainties. In our measurements any error in Ca abundances should in principle translate into an incorrect Mg abundances due to the underlying auto-ionisation Ca line that strongly affects the continuum around the Mg triplet (Hill et al. 2011). Therefore, the adoption of an incorrect [Ca/Fe] abundance could result in a larger scatter for [Mg/Fe] abundances due to a poorer quality fit in the respective region. We do not see this wide spread in Mg abundances, most likely because this is partially solved by the local normalisation of the continuum. The resulting [Mg/Fe] trend for the bulge actually be traced with a great level of detail.
We compare the trends of [Ca/Fe] and [Mg/Fe] as a function of [Fe/H] for our entire sample with those from giant stars of the local thin and thick disc published in Gonzalez et al. (2011). As seen in both Ca and Mg abundances in Fig. 8, the α-element enhancement of the bulge with respect to the thin disc is found at all metallicities. The thick disc on the other hand appears to be as enhanced in α-element abundances as the metal-poor bulge giants, though covering a much smaller range in [Fe/H]. These patterns in the α-element abundances of bulge stars with respect to the disc abundances has already been observed in several studies, based on different samples and measurement techniques (Meléndez et al. 2008; Alves-Brito et al. 2010; Gonzalez et al. 2011; Bensby et al. 2010, 2011; Ryde et al. 2010; Hill et al. 2011; Johnson et al. 2011, 2013, 2014). In addition, we have calculated the metallicity at which the [Mg/Fe] abundance starts to decrease (the so-called knee) as it does in Gonzalez et al. (2011), by producing a linear fit to the metal-poor ([Fe/H] =−1.6 to −0.6) and metal-rich ([Fe/H] =−0.3 to + 0.3) stars. The intersection between both linear fits corresponds to the α-element knee located at [Fe/H] =−0.44, in good agreement with the values found in Gonzalez et al. (2011) in a field located at the same latitude b = −4°.
Bensby et al. (2013) suggested that the position of the knee in the [α/Fe] plot is found at 0.1–0.2 dex higher metallicities in the bulge than in the thick disc. A similar result was proposed by Johnson et al. (2014) who added the analysis of Fe-peak elements finding in particular that Co, Ni, and Cu appear enhanced compared to the disc. We note that the results presented in Johnson et al. (2014) have been obtained by comparing bulge giants to dwarf stars from the disc. This technique might suffer from systematic offsets (Meléndez et al. 2008) and it thus needs to be investigated further. The results from Bensby et al. (2013) do not suffer from these systematics, as the comparison involves only dwarf and subgiant stars for both disc and bulge; however, because the microlensed dwarf sample is still relatively small, for the time being the derived result is far from being statistically robust. Unfortunately, in our work we do not have measured abundances for a sufficiently large number of thick disc giant stars to calculate the position of the corresponding [α/Fe] knee with enough accuracy to compare it with the value ([Fe/H] =−0.44 dex) measured in the GIBS fields. However, we note that for the bulge we find a [α/Fe] knee ~ 0.1 dex more metal-poor than the value presented in Bensby et al. (2013). This means that, assuming that our study is on the same scale as the Bensby et al. (2013) study, our abundances would not favour a more metal-rich knee for the bulge than the local thick disc.
 |
Fig. 11 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] using different symbols for the four GIBS high-resolution fields studied in this work. The solid lines show the best-fit relation between [Mg/Fe] and [Fe/H] for the metal-poor and metal-rich regimes obtained using the entire sample. The uncertainties for [Ca/Fe] and [Mg/Fe] abundances are shown as a light blue contour in both panels. |
In Fig. 10 we show a comparison between the [Mg/Fe] and [Ca/Fe] trends between GIBS giants, the giants analysed in Johnson et al. (2014), and the microlensed dwarfs from Bensby et al. (2013). The trends are very similar for [Mg/Fe] abundances while for [Ca/Fe] there is a clear systematic offset of the Bensby et al. (2013) abundances with respect to both GIBS and Johnson et al. (2014). The fact that the offset is not seen in [Mg/Fe] indicates that most likely it is not due to a different method of spectral analysis, but it emphasises the risk of comparing abundances for stars in very different temperature and/or gravity regimes (giants versus dwarfs, in this case) because the abundances of some elements may be affected by different systematic errors.
Finally, in Fig. 11 we show the individual trends of [Mg/Fe] and [Ca/Fe] abundances as a function of [Fe/H] for the four fields presented in this work, compared to the [Mg/Fe] abundances for the local thick and thin disc. No evident field-to-field variations can be seen and the same similarity between the metal-poor bulge (i.e. [Fe/H] ≤−0.5) and the local thick disc is found in all fields. This result for a strip at constant Galactic latitude is in agreement with the conclusions of Gonzalez et al. (2011) for the minor axis.
6. Conclusions
In this work we presented the surface stellar parameters, and the [Fe/H], [Ca/Fe], and [Mg/Fe] element ratios for 400 RC stars in four fields of the GIBS survey, corresponding to the high-resolution sample at b = −4° observed with the GIRAFFE HR13 setup. Spectroscopic stellar surface parameters were obtained with an automatic method using the GALA code. These parameters were used to obtain [Ca/Fe] and [Mg/Fe] abundances for each star based on the fitting of synthetic spectra. The global and individual field metallicity distributions were constructed in order to investigate the presence of gradients and field-to-field changes in the shape of the distributions. We also investigated the [Ca/Fe] and [Mg/Fe] abundances as a function of [Fe/H] as a constraint for the timescale of formation for the bulge.
The results can be summarised as follows:
-
A null metallicity gradient was found along Galactic longitude for a constant Galactic latitude. The metallicity distributions of all the fields presented here are consistent with an origin from the same parent population.
-
A two-Gaussian component provides a good fit to the global metallicity distribution at b = −4° with a narrow metal-rich ([Fe/H] ~+0.26) population of stars and a broad metal-poor ([Fe/H] ~−0.31) component. This is in agreement with previous studies suggesting a bimodal population for the bulge. This exercise has been carried out because several independent observations, including stellar kinematics and distance distribution, suggest the presence of two stellar populations in the Galactic bulge. Whether the two components indeed have indeed a different formation history needs to be seen by model comparisons to observations like the ones presented here.
-
A very close relation was found between [Mg/Fe] and [Fe/H], showing enhancement with respect to the solar ratio in the metal-poor regime, similar to the one seen in the local thick disc, and a decrease in [Mg/Fe] starting at [Fe/H] ~−0.44. All studied fields share these properties, with no appreciable differences. The observed position of the so-called knee is in agreement with our previous results but it occurs at ~0.1 dex lower metallicity than what is observed in the bulge microlensed dwarfs and subgiants.
-
The [Mg/Fe] and [Ca/Fe] results presented here are fully compatible with previous results based on giant stars; however, we see a systematic offset in [Ca/Fe] with respect to the abundances from the microlensed dwarf stars in Bensby et al. (2013). This difference is not seen in [Mg/Fe]. This offset is most likely due to different systematics affecting stars in different temperature and gravity regimes.
Acknowledgments
We are grateful for the useful comments received from an anonymous referee. We warmly thank the ESO Paranal Observatory staff for performing the observations for this programme. M.Z. and D.M. acknowledge funding from the BASAL CATA through grant PFB-06, and the Chilean Ministry of Economy through ICM grant to the Millennium Instritute of Astrophysics. M.Z. acknowledges support by Proyecto Fondecyt Regular 1150345. D.M. acknowledges support by FONDECYT No. 1130196.
References
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 140, 261 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves-Brito, A., Meléndez, J., Asplund, M., Ramírez, I., & Yong, D. 2010, A&A, 513, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Athanassoula, E. 2005, Celes. Mech. Dyn. Astron., 91, 9 [Google Scholar]
- Babusiaux, C., & Gilmore, G. 2005, MNRAS, 358, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Babusiaux, C., Gómez, A., Hill, V., et al. 2010, A&A, 519, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Babusiaux, C., Katz, D., Hill, V., et al. 2014, A&A, 563, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2005, ApJ, 630, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., Johnson, J. A., et al. 2010, A&A, 512, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Adén, D., Meléndez, J., et al. 2011, A&A, 533, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensby, T., Yee, J. C., Feltzing, S., et al. 2013, A&A, 549, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binney, J., Gerhard, O., & Spergel, D. 1997, MNRAS, 288, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Bissantz, N., & Gerhard, O. 2002, MNRAS, 330, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Spergel, D. N. 1991, ApJ, 379, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Elmegreen, D. M. 2007, ApJ, 670, 237 [Google Scholar]
- Bournaud, F., Elmegreen, B. G., & Martig, M. 2009, ApJ, 707, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, L., Mao, S., Nataf, D., Rattenbury, N. J., & Gould, A. 2013, MNRAS, 434, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, W. I., Sahu, K. C., Anderson, J., et al. 2011, ApJ, 735, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., Debbasch, F., Friedli, D., & Pfenniger, D. 1990, A&A, 233, 82 [NASA ADS] [Google Scholar]
- Cunha, K., & Smith, V. V. 2006, ApJ, 651, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
- de Vaucouleurs, G. 1964, in The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, IAU Symp., 20, 195 [NASA ADS] [Google Scholar]
- Debattista, V. P., Carollo, C. M., Mayer, L., & Moore, B. 2005, ApJ, 628, 678 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Burkert, A. 2014, MNRAS, 438, 1870 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E., Arendt, R. G., Hauser, M. G., et al. 1995, ApJ, 445, 716 [CrossRef] [Google Scholar]
- Elmegreen, B. G., Bournaud, F., & Elmegreen, D. M. 2008, ApJ, 688, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., Ness, M., Wylie-de-Boer, E., et al. 2013, MNRAS, 428, 3660 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2007, ApJ, 661, 1152 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, E., Debattista, V. P., Robin, A. C., Vásquez, S., & Zoccali, M. 2014, MNRAS, 438, 3275 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Newman, S., Jones, T., et al. 2011, ApJ, 733, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2011, A&A, 530, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2012, A&A, 543, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzalez, O. A., Rejkuba, M., Zoccali, M., et al. 2013, A&A, 552, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gratton, R. G., & Sneden, C. 1990, A&A, 234, 366 [NASA ADS] [Google Scholar]
- Hill, V., Lecureur, A., Gómez, A., et al. 2011, A&A, 534, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howard, C. D., Rich, R. M., Clarkson, W., et al. 2009, ApJ, 702, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Immeli, A., Samland, M., Gerhard, O., & Westera, P. 2004, A&A, 413, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johnson, C. I., Rich, R. M., Fulbright, J. P., Valenti, E., & McWilliam, A. 2011, ApJ, 732, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., et al. 2013, ApJ, 765, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, C. I., Rich, R. M., Kobayashi, C., Kunder, A., & Koch, A. 2014, AJ, 148, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Kunder, A., Koch, A., Rich, R. M., et al. 2012, AJ, 143, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Lecureur, A., Hill, V., Zoccali, M., et al. 2007, A&A, 465, 799 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, Z.-Y., & Shen, J. 2012, ApJ, 757, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Lindler, D. 2001, FUSE IDL Tools Reference Handbook, in Users Guide, Far Ultraviolet Spectroscopic Explorer (Baltimore, MD: Johns Hopkins University) [Google Scholar]
- Mancini, C., Förster Schreiber, N. M., Renzini, A., et al. 2011, ApJ, 743, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Martinez-Valpuesta, I., Shlosman, I., & Heller, C. 2006, ApJ, 637, 214 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994a, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Rich, R. M. 1994b, ApJS, 91, 749 [NASA ADS] [CrossRef] [Google Scholar]
- McWilliam, A., & Zoccali, M. 2010, ApJ, 724, 1491 [NASA ADS] [CrossRef] [Google Scholar]
- Meléndez, J., Asplund, M., Alves-Brito, A., et al. 2008, A&A, 484, L21 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Minniti, D. 1996, ApJ, 459, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Minniti, D., Lucas, P. W., Emerson, J. P., et al. 2010, New A, 15, 433 [Google Scholar]
- Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Nataf, D. M., Udalski, A., Gould, A., Fouqué, P., & Stanek, K. Z. 2010, ApJ, 721, L28 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013a, MNRAS, 430, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Freeman, K., Athanassoula, E., et al. 2013b, MNRAS, 432, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, S. F., Genzel, R., Förster Schreiber, N. M., et al. 2013, ApJ, 767, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Thielemann, F.-K., & Wheeler, J. C. 1984, ApJ, 279, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquini, L., Avila, G., Allaert, E., et al. 2000, in Optical and IR Telescope Instrumentation and Detectors, eds. M. Iye, & A. F. Moorwood, SPIE Conf. Ser., 4008, 129 [Google Scholar]
- Ramírez, I., & Meléndez, J. 2005, ApJ, 626, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, S. V., Stephens, A. W., Frogel, J. A., & DePoy, D. L. 2000, AJ, 120, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Rangwala, N., & Williams, T. B. 2009, ApJ, 702, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Rattenbury, N. J., Mao, S., Sumi, T., & Smith, M. C. 2007, MNRAS, 378, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M. 1988, AJ, 95, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Rich, R. M., & Origlia, L. 2005, ApJ, 634, 1293 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Rich, R. M., Origlia, L., & Valenti, E. 2007, ApJ, 665, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Rojas-Arriagada, A., Recio-Blanco, A., Hill, V., et al. 2014, A&A, 569, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ryde, N., Gustafsson, B., Edvardsson, B., et al. 2010, A&A, 509, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadler, E. M., Rich, R. M., & Terndrup, D. M. 1996, AJ, 112, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Saito, R. K., Zoccali, M., McWilliam, A., et al. 2011, AJ, 142, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, J., Rich, R. M., Kormendy, J., et al. 2010, ApJ, 720, L72 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, G., & Ruck, M. J. 2000, A&A, 356, 570 [NASA ADS] [Google Scholar]
- Sneden, C. 1973, ApJ, 184, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Soto, M., Rich, R. M., & Kuijken, K. 2007, ApJ, 665, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Stanek, K. Z., Mateo, M., Udalski, A., et al. 1994, ApJ, 429, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Stetson, P. B., & Pancino, E. 2008, PASP, 120, 1332 [Google Scholar]
- Sumi, T., Wu, X., Udalski, A., et al. 2004, MNRAS, 348, 1439 [NASA ADS] [CrossRef] [Google Scholar]
- Tacconi, L. J., Genzel, R., Neri, R., et al. 2010, Nature, 463, 781 [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- Tinsley, B. M. 1979, ApJ, 229, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Kubiak, M., et al. 2002, Acta Astron., 52, 217 [NASA ADS] [Google Scholar]
- Valenti, E., Zoccali, M., Renzini, A., et al. 2013, A&A, 559, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wegg, C., & Gerhard, O. 2013, MNRAS, 435, 1874 [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Zoccali, M., Renzini, A., Ortolani, S., et al. 2003, A&A, 399, 931 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Lecureur, A., Barbuy, B., et al. 2006, A&A, 457, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Hill, V., Lecureur, A., et al. 2008, A&A, 486, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zoccali, M., Gonzalez, O. A., Vasquez, S., et al. 2014, A&A, 562, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Atomic line list for Mg and Ca used in this work, excitation potential (χex), and oscillator strength (log gf) for each analysed line.
Stellar parameters, [Fe/H], [Mg/Fe], and [Ca/Fe] abundance ratios for stars in the four high-resolution GIBS fields.
All Figures
 |
Fig. 1 The location of the fields analysed in the present study (red circles) overplotted on an optical image of the Milky Way bulge (© Serge Brunier). The location of the fields discussed in previous studies (Zoccali et al. 2008; Hill et al. 2011) are shown as Z08 and H11; the location of the Ness et al. (2013a), Johnson et al. (2011), and Johnson et al. (2013) fields are shown as ARGOS, J11 and J13, respectively. The lower panel shows the colour−magnitude diagram for field HRm5m3. Red filled circles show the corresponding target stars for this field. |
| In the text | |
 |
Fig. 2 Differences between metallicity (upper panel), effective temperature (middle panel) and microturbulence velocity (lower panel) for a sample of RC (red filled circles) and RGB (black empty circles) derived in this work and as derived in Hill et al. (2011). Solid lines in each panel indicate the mean difference of each sample and the dashed lines shows the 1σ range around the mean. |
| In the text | |
 |
Fig. 3 Difference between the [Fe/H] abundances obtained with the adopted GALA procedure using the correct set of initial stellar surface parameters and using fixed values (Teff = 4500 K, ξ = 1.5 km s-1, log g = 1.9, and [Fe/H] = 0.00) for the RC sample from Hill et al. (2011) |
| In the text | |
 |
Fig. 4 Observed (black circles) and synthetic spectra for a star (OGLE26-415574) in the field HRm5m3 zoomed into the region used to derive Ca (upper panel) and Mg (lower panel) abundances. The synthetic spectra created with the best-fitting Ca ([Ca/Fe] = 0.06) and Mg ([Mg/Fe] = 0.05) abundances are shown in solid red lines. The elements producing the strongest absorption lines are marked in each panel. For each spectral region we show a zoomed-in section around the Ca line at 6166.4 Å and the Mg triplet that includes the synthesis produced using the best-fitting abundance as red solid lines. In blue and green we show the synthetic spectra using a 0.1 dex abundance variation around the best-fitting value. The Y-axis of both zoomed-in regions have the same scale with normalised fluxes that range from 0.8–0.5 for Ca and 1.0–0.7 for Mg lines. |
| In the text | |
 |
Fig. 5 Abundance measurement errors as a function of errors on the stellar parameters: [Fe/H] (upper left panel), microturbulence velocity (upper right panel) and effective temperature (lower left panel). Errors as a function of the corresponding [Fe/H] value are also displayed (lower right panel). In all panels errors for [Ca/H] abundances are shown as red empty circles and errors for [Mg/H] as red filled circles. |
| In the text | |
 |
Fig. 6 Overall metallicity distribution obtained from the combination of the four GIBS high-resolution fields and the RC sample of Hill et al. (2011). The probability density distribution is overplotted in the upper panel as a dashed line. The corresponding variance on the calculated probability densities is shown in blue. The lower panel shows the two best Gaussian fits to the upper panel distribution. The resulting distribution from the two Gaussians is shown as a solid line. |
| In the text | |
 |
Fig. 7 Metallicity distributions for the four GIBS high-resolution fields. Additionally, the metallicity distribution for Baade’s window from Hill et al. (2011) is shown in red in the middle panel. For each of the metallicity distributions we overplot the probability density distribution for the entire sample of metallicities shown in Fig. 6. |
| In the text | |
 |
Fig. 8 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] used as a diagnostic of the formation timescale of the bulge. Shown as red circles are the [Mg/Fe] and [Ca/Fe] values obtained from the HR13 spectra of 400 stars in the four GIBS fields presented in this work compared to those for RGB stars from the Baade’s window sample of Gonzalez et al. (2011) which are shown as black empty circles. Measurements for the local thin (black squares) and thick (blue triangles) disc stars from the sample from Gonzalez et al. (2011) are also shown in both panels. The uncertainties for [Ca/Fe] and [Mg/Fe] abundances are shown as a light blue contour in both panels according to the individual uncertainties reported in Table 3. |
| In the text | |
 |
Fig. 9 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] as in Fig. 11. Here we colour-coded the abundances of [Ca/Fe] and [Mg/Fe] according to the estimated uncertainty value. The colour-coding was fixed in both panels to the range of [Mg/Fe] uncertainties between 0.07−0.20 dex from black to red. The uncertainty contour of [Mg/Fe] is also shown in the background of both panels as a reference. |
| In the text | |
 |
Fig. 10 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] for the GIBS high-resolution fields studied in this work and for the measurements from Johnson et al. (2014) for giant stars (black squares) and microlensed dwarfs from Bensby et al. (2013; blue triangles). In the upper panel, the solid lines show the best-fit relation between [Mg/Fe] and [Fe/H] for the metal-poor and metal-rich regime. The intersection point is shown and represents the position of the knee. The uncertainties for [Ca/Fe] and [Mg/Fe] abundances of this work are shown as a light blue contour in both panels. |
| In the text | |
 |
Fig. 11 Distribution of [Mg/Fe] (upper panel) and [Ca/Fe] (lower panel) as a function of [Fe/H] using different symbols for the four GIBS high-resolution fields studied in this work. The solid lines show the best-fit relation between [Mg/Fe] and [Fe/H] for the metal-poor and metal-rich regimes obtained using the entire sample. The uncertainties for [Ca/Fe] and [Mg/Fe] abundances are shown as a light blue contour in both panels. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


