| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A47 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201526367 | |
| Published online | 18 November 2015 | |
Terrestrial-type planet formation
Comparing different types of initial conditions
Facultad de Ciencias Astronómicas y Geofísicas, Universidad Nacional de La Plata and Instituto de Astrofísica de La Plata, CCT La Plata-CONICET-UNLP, Paseo del Bosque S/N (1900), La Plata, Argentina
e-mail: mpronco@fcaglp.unlp.edu.ar
Received: 20 April 2015
Accepted: 8 September 2015
Context. The initial distributions of planetary embryos and planetesimals used in N-body simulations play an important role for studies of the terrestrial-type planet formation during the post oligarchic growth. In general, most of these studies typically use ad hoc initial distributions based primarily on theoretical and numerical studies.
Aims. We analyze the formation of planetary systems without gas giants around solar-type stars by focusing on the sensitivity of the results to the particular initial distributions used for planetesimals and planetary embryos at the end of the gas phase of the protoplanetary disk. The formation process of terrestrial planets in the habitable zone (HZ) and their final water contents are also topics of special interest in this work.
Methods. We developed two different sets of N-body simulations starting with the same protoplanetary disk. The first set assumes typical ad hoc initial distributions for embryos and planetesimals, and the second set obtains these initial distributions from the results of a semi-analytical model that simulates the evolution of the protoplanetary disk during the gaseous phase.
Results. The two sets of simulations form planets within the HZ. Using ad hoc initial conditions, the masses of the planets that remain in the HZ range from 0.66 M⊕ to 2.27 M⊕. Using more realistic initial conditions obtained from a semi-analytical model, we found that the masses of the planets range from 1.18 M⊕ to 2.21 M⊕. Both sets of simulations form planets in the HZ with water contents ranging between 4.5% and 39.48% by mass. The planets that have the highest water contents with respect to those with the lowest water contents present differences regarding the sources of water supply.
Conclusions. From comparing the two sets of simulations, we suggest that the number of planets that remain in the HZ is not sensitive to the particular initial distribution of embryos and planetesimals, and therefore the results are globally similar between them. However, the main differences observed between the two sets are associated with the accretion history of the planets in the HZ. These discrepancies have a direct impact on the accretion of water-rich material and the physical characteristics of the resulting planets.
Key words: planets and satellites: formation / planets and satellites: terrestrial planets / protoplanetary disks
© ESO, 2015
1. Introduction
The formation process of terrestrial-type planets passes through different stages. In the classical core-accretion model (Lissauer & Stevenson 2007), the first step in the planet formation process is the sedimentation onto the mid-plane of the dust of the disk and the formation of planetesimals. The mechanisms that lead to the formation of planetesimals are still under debate. However, in the past few years, three main scenarios for the formation of planetesimals have emerged: formation through coagulation-fragmentation cycles and mass transfer from small to large aggregates, growth of fluffy particles and subsequent compaction by self-gravity, and concentration of small particles (often called pebbles) in the turbulent gas, and gravitational fragmentation of over dense filaments (see Johansen et al. 2014 for a detailed discussion and references therein). After the formation of the first population of planetesimals, these bodies grow quickly by mutual accretion until some of them (often called embryos) start to separate from the population of planetesimals. This process is known as planetesimal runaway growth. When embryos begin to gravitationally dominate the dynamic of the population of planetesimals, the runaway growth regime switches to the oligarchic growth regime. In this regime, the gravitational excitation of the embryos over the planetesimals limits their growth, and embryos are the only population that continue growing by accretion of planetesimals (Kokubo & Ida 1998).
The interaction of the embryos with the gaseous disk could lead to the migration of these bodies along the disk, a phenomenon known as type I migration. In idealized isothermal disks, type I migration always moves inward and at high migration rates (Tanaka et al. 2002). However, if more realistic disks are considered (Paardekooper et al. 2010, 2011), type I migration could be moving outward. This outward migration can also occur when the planet achieves a significant mass (~10 M⊕) and corotation torques become not negligible (Masset et al. 2006). But even in isothermal disks, type I migration could be outward directed if full magnetohydrodynamic (MHD) disk turbulence is considered (Guilet et al. 2013). More recently, Benítez-Llambay et al. (2015) found that if the energy released by the planet as a result of accretion of solid material is taken into account, this phenomenon generates a heating torque that could significantly slow down, cancel, or even reverse inward type I migration for planets with masses ≲5 M⊕. Embryos continue growing by accretion of planetesimals and other embryos when the distance between them becomes smaller than three to four mutual Hill radii (Agnor & Asphaug 2004) because the damping generated by the gas causes the embryos to remain in nearly circular and coplanar orbits.
A new alternative model was recently proposed for the formation of giant planet cores and terrestrial planets. This model proposes that the core of giant planets and terrestrial planets could be formed as seeds that accrete small particles, often called pebbles. Ormel & Klahr (2010), Lambrechts & Johansen (2012), and Guillot et al. (2014) showed that pebbles that are strongly coupled to the gas could be accreted very efficiently to form planetary bodies.
More recently, Johansen et al. (2015) showed that other structures of our solar system, such as the asteroid and transneptunian belt, could also be explained by the pebble accretion mechanism.
When the gas has dissipated from the system and some giant planets may have formed, the terrestrial planet region contains a great number of planetary embryos that still evolve embedded in a remnant swarm of planetesimals. Embryos continue growing by accreting planetesimals and by stochastic collisions with other embryos in a regime known as post-oligarchic growth. Finally, the terrestrial-type planets form and settle onto stable orbits on timescales on the order of 108 yr.
In general terms, the numerical simulations that analyze the late-stage planetary accretion after the gas disk dissipation require physical and orbital initial conditions for planetesimals and planetary embryos as well as for the gas giants of the system. These initial conditions are typically selected ad hoc by many works that investigate the process of planetary formation (O’Brien et al. 2006; Raymond et al. 2009; Morishima et al. 2010; Walsh et al. 2011).
Studying planetary systems without gas giants is very interesting. Several observational studies (Cumming et al. 2008; Mayor et al. 2011) and theoretical works (Mordasini et al. 2009; Miguel et al. 2011) have suggested that planetary systems consisting only of rocky planets would seem to be the most common in the Universe. Recently, Ronco & de Elía (2014) have analyzed the terrestrial-type planet formation and water delivery in systems without gas giants around Sun-like stars. In particular, the authors focused on low-mass protoplanetary disks for a wide range of surface density profiles. Ronco & de Elía (2014) assumed ad hoc initial conditions for the distributions of planetesimals and planetary embryos after the gas dissipation.
Here, we present results of N-body simulations aimed at analyzing the process of planetary formation around Sun-like stars without gas giants. In particular, we focus on the sensitivity of the results to the particular initial distribution adopted for planetesimals and planetary embryos after the gas dissipation. To do this, we decided to carry out two different sets of numerical simulations that start with the same initial protoplanetary disk, and we then modified the particular initial distribution for planetesimals and planetary embryos. The first set of numerical simulations assumes ad hoc initial conditions for planetesimals and embryos like in Ronco & de Elía (2014), while the second set of numerical simulations obtains initial conditions from a semi-analytical model that is able to analyze the evolution of a system of planetesimals and embryos during the gaseous phase. A comparative analysis between these two sets of numerical simulations then allows us to enrich our knowledge concerning the process of planetary formation. Moreover, we consider that the present work allows us to clarify our understanding about the correct selection of initial conditions for numerical simulations of the formation and evolution of planetary systems.
This paper is therefore structured as follows. In Sect. 2, we present the main properties of the protoplanetary disk used in our simulations. Then, we outline our choice of initial conditions in Sect. 3 and discuss the main characteristics of the N-body code in Sect. 4. In Sect. 5, we present the results of all our simulations. We discuss these results within the framework of the current knowledge of planetary systems in Sect. 6 and present our conclusions in Sect. 7.
2. Protoplanetary disk: Properties
The properties of the protoplanetary disk considered here are the same as in Ronco & de Elía (2014). The gas surface density profile that represents the structure of the protoplanetary disk is given by 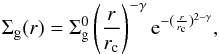 (1)where
(1)where 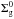 is a normalization constant, rc a characteristic radius, and γ the exponent that represents the surface density gradient.
is a normalization constant, rc a characteristic radius, and γ the exponent that represents the surface density gradient. 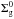 can be found by integrating Eq. (1) over the total area of the disk and is a function of γ, rc, and the mass of the disk Md.
can be found by integrating Eq. (1) over the total area of the disk and is a function of γ, rc, and the mass of the disk Md.
Analogously, the solid surface density profile Σs(r) is represented by 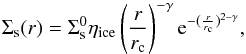 (2)where ηice represents an increase of a factor of 4 in the amount of solid material that is due to the condensation of water beyond the snow line, which is located at 2.7 au (Hayashi 1981). Although other authors found a much lower value for this increase of solids (Lodders 2003), we used the same factor as Ronco & de Elía (2014) to be consistent with the comparisons.
(2)where ηice represents an increase of a factor of 4 in the amount of solid material that is due to the condensation of water beyond the snow line, which is located at 2.7 au (Hayashi 1981). Although other authors found a much lower value for this increase of solids (Lodders 2003), we used the same factor as Ronco & de Elía (2014) to be consistent with the comparisons.
The relation between the two profiles is given by ![\begin{eqnarray} \left(\dfrac{\Sigma^{0}_{\text{s}}}{\Sigma^{0}_{\text{g}}}\right)_{\star} = \left(\dfrac{\Sigma^{0}_{\text{s}}}{\Sigma^{0}_{\text{g}}}\right)_{\odot}10^{[\text{Fe}/\text{H}]} = z_{0}10^{[\text{Fe}/\text{H}]}, \end{eqnarray}](/articles/aa/full_html/2015/12/aa26367-15/aa26367-15-eq19.png) (3)where z0 is the primordial abundance of heavy elements in the Sun and [Fe/H] is the metallicity.
(3)where z0 is the primordial abundance of heavy elements in the Sun and [Fe/H] is the metallicity.
The central star is assumed to have the same mass as our Sun and is a star of solar metallicity, so that [Fe/H] = 0. Then, 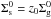 where z0 = 0.0149 (Lodders 2003). We considered a low-mass disk with Md = 0.03 M⊙ to guarantee that no giant planets are formed (Miguel et al. 2011). For the characteristic radius rc we adopted a value of 50 au, which agrees with the different disk observations studied by Andrews et al. (2010), and for the exponent γ we adopted a value of 1.5 according to other planetary formation works (Raymond et al. 2005; Miguel et al. 2011). The gas surface density profile of this disk is a factor of 1−1.7 higher than that proposed by the minimun mass solar nebula (MMSN) between 0 and 15 au. It is worth noting that the simulations developed by Ronco & de Elía (2014) using density profiles with γ = 1.5 show distinctive results since true water worlds are formed in the habitable zone1 (HZ) of the system.
where z0 = 0.0149 (Lodders 2003). We considered a low-mass disk with Md = 0.03 M⊙ to guarantee that no giant planets are formed (Miguel et al. 2011). For the characteristic radius rc we adopted a value of 50 au, which agrees with the different disk observations studied by Andrews et al. (2010), and for the exponent γ we adopted a value of 1.5 according to other planetary formation works (Raymond et al. 2005; Miguel et al. 2011). The gas surface density profile of this disk is a factor of 1−1.7 higher than that proposed by the minimun mass solar nebula (MMSN) between 0 and 15 au. It is worth noting that the simulations developed by Ronco & de Elía (2014) using density profiles with γ = 1.5 show distinctive results since true water worlds are formed in the habitable zone1 (HZ) of the system.
Finally, we assumed that the protoplanetary disk presents a radial compositional gradient. Thus, the water content by mass W(r) assumed as a function of the radial distance r is described as follows. Embryos and planetesimals contain 0.001% water inside 2 au, contain 0.1% water between 2 au and 2.5 au, contain 5% water between 2.5 au and 2.7 au, and 50% water past 2.7 au. This water distribution is the same as was used by Ronco & de Elía (2014) and is based on the distribution proposed by Raymond et al. (2004). This distribution is assigned to each body in the N-body simulations, based on its starting location. Our model does not consider water loss during impacts, thus, the final water contents of the resulting planets represent upper limits.
3. Initial conditions
As mentioned in Sect. 1, the process of planetary formation has often been considered with ad hoc initial conditions, particularly equally dividing the solid mass of the disk between the planetesimal and embryo components. Moreover, some works (Chambers 2001; O’Brien et al. 2006) assumed that the individual mass of the planetary embryos has a constant value throughout the portion of the disk under consideration. However, it is worth emphasizing that these conditions represent a particular state of the disk. To consider that the solid mass in the inner region of the disk is equally distributed between embryos and planetesimals could be a reasonable assumption because this depends on the evolution of the system. However, considering that the population of planetesimals is homogeneously distributed throughout the inner region of the disk could not be a reasonable assumption. Planetesimal accretion rates are proportional to the surface density of solids and to the Keplerian frequency. These two quantities increase closer to the star. Thus, it is expected that inner embryos grow quickly by accreting all the available planetesimals. Because embryos can only accrete planetesimals from their feeding zones, which are very narrow closer to the central star, we expect a considerable number of small embryos, and practically no planetesimals in the inner region at the moment of the dissipation of the disk.
Another consideration that could be not realistic is that all the embryos have the same mass in the inner region of the disk. Basically, the final mass of an embryo (during the gaseous phase) is a function of the distance to the star and of the timescale dissipation of the disk. Brunini & Benvenuto (2008) showed that this functional dependence is maximized near the snow line. Thus, it is expected that the most massive embryos of the distribution are located near the snow line.
To test the sensitivity of the results to the initial distributions of planetary embryos and planetesimals, we constructed two different sets of simulations from the same protoplanetary disk. The first one uses ad hoc initial conditions for planetesimals and embryos like in Ronco & de Elía (2014), while the second set assumes initial conditions derived from a semi-analytical model that analyzes the evolution of embryos and planetesimals in detail during the gaseous phase.
Since our main goal is to analyze the formation process of terrestrial planets and to focus on those of the HZ, the region we studied lies between 0.5 au and 5 au. Our model assumes an inner zone in the disk between 0.5 au and the snow line and an outer zone that lies between the snow line and 5 au.
In the following, we describe the generation of initial conditions for the two sets of numerical simulations.
3.1. First set: ad hoc initial conditions
In this first set of simulations, we assumed the ad hoc initial conditions used by Ronco & de Elía (2014). Considering a protoplanetary disk of 0.03 M⊙ and an exponent γ = 1.5 associated with the surface density profile, the total mass of solids in the region of study is 13.66 M⊕. In agreement with various planetary accretion studies such as that of Kokubo & Ida (1998), this mass of solids is divided equally between the planetesimal and embryo components. On the one hand, 45 planetary embryos are distributed in the studied region, 35 of which are in the inner zone with masses of 0.06 M⊕, and 10 in the outer zone with masses of 0.47 M⊕. On the other hand, 1000 planetesimals are distributed in the disk with masses of 2.68 × 10-3 M⊕ and 0.021 M⊕ in the inner and outer zone, respectively.
3.2. Second set: initial conditions from a semi-analytical model
In this second set of simulations, we generate initial conditions for embryos and planetesimals using a semi-analytical model based on Brunini & Benvenuto (2008) and Guilera et al. (2010) with the inclusion of some minor improvements. This model analyzes the evolution of a protoplanetary disk during the gaseous phase, which enables obtaining more realistic initial conditions to be used in an N-body code. A detailed description of this model can be found in de Elía et al. (2013).
In this semi-analytical model, the embryos are separated by 10 mutual Hill radii, and the mass of each embryo corresponds to the transition mass between runaway and oligarchic growth (Ida & Makino 1993). At the beginning there are 223 embryos in the studied region, between 0.5 au and 5 au with a density of 3 gr cm-3, while the planetesimals have a density of 1.5 gr cm-3 and radii of 10 km. The population of planetesimals is represented by the density profile of the planetesimals. In this model, the initial planetesimal size distribution evolves in time through planetesimal migration and accretion by embryos. Embryos then grow by accretion of planetesimals and also by collisions between them. We did not include type I migration in our model. The main reason for neglecting this effect is that many quantitative aspects of the type I migration are still uncertain, as we have already mentioned in Sect. 1. In addition, although planetesimals are affected by the gas drag because they are so large (10 km), this migration is not strong enough to produce significant changes in the final amounts of water on embryos and in the distribution of water along the planetesimal population. We consider that when the distance between two embryos becomes smaller than 3.5 mutual Hill radii, they merge into one object. We assume perfect inelastic collisions. For mergers between embryos, we neglected the presence of embryo gaseous envelopes because the masses of the embryos are small enough not to produce major differences.
 |
Fig. 1 Initial and final distributions of embryos and planetesimals generated by the semi-analytical model. Panels a) and b) represent the initial and final mass distribution of embryos. At the beginning a) there were 223 embryos between 0.5 au and 5 au, and after 3 Myr of evolution b) there only remain 57 embryos. Panels c) and d) represent the initial and final density profile of planetesimals. Panels b) and d) then represent the final results obtained with the semi-analytical model after 3 Myr of evolution and the initial conditions for the N-body simulations. The vertical lines in gray represent the position of the snow line at 2.7 au. A color figure is available in the electronic version. |
The final configuration obtained after the gas is completely dissipated in 3 Myr also agrees with that used ad hoc in several works, as mentioned in Sect. 3.1: we found the same proportion for both populations, half the mass in embryos and half the mass in planetesimals. Figure 1 shows the results of our semi-analytical model for the distribution of embryos and planetesimals for a disk of 0.03 M⊙ at the end of the gas phase. In particular, the top left panel represents the mass distribution of planetary embryos as a function of the distance from the central star that was used to initiate the evolution of the gas phase with the semi-analytical model, while the left bottom panel shows the surface density profile of planetesimals used to do the same. The top right panel represents the final distribution of embryos obtained with the semi-analytical model after 3 Myr of evolution until the gas is already gone, and the bottom right panel represents the final surface density profile of planetesimals. These (right panels) final distributions of embryos and planetesimals represent the initial conditions to be used in our N-body simulations. In this case, 57 planetary embryos are distributed between 0.5 au and 5 au and 1000 planetesimals with individual masses of 7.24 × 10-3 M⊕ are generated using the distribution shown in Fig. 1d.
 |
Fig. 2 a) Distributions of embryos used to start the N-body simulations. The squares represent the distribution of embryos obtained with the first set of simulations. The circles represent the final results obtained with the semi-analytical model (the second set of simulations). b) Surface density profiles used to distribute 1000 planetesimals to start the N-body simulations. The dashed line represents the surface density for the first set, the solid line the surface density for the second set obtained with the semi-analytical model. A color figure is available in the electronic version. |
4. N-body simulations: characteristics
Our N-body simulations begin when the gas of the disk has already dissipated. The numerical code used in our N-body simulations is the MERCURY code developed by Chambers (1999). We particularly adopted the hybrid integrator, which uses a second-order mixed variable simplectic algorithm to treat the interaction between objects with separations greater than 3 Hill radii, and a Burlisch-Stoer method for resolving closer encounters.
In both sets of simulations, all collisions were treated as inelastic mergers that conserve mass and water content. Given that the N-body simulations are numerically very costly, we decided to reduce the CPU time by only considering gravitational interactions between embryos and planetesimals (Raymond et al. 2006). Thus, planetesimals do not gravitationally interact or collide with each other. These N-body high-resolution simulations allowed us to describe the dynamical processes in detail that are involved during the formation and post evolution stages.
Since terrestrial planets in our solar system may have formed in 100–200 Myr (Touboul et al. 2007; Dauphas & Pourmand 2011), we integrated each simulation for 200 Myr. To compute the inner orbit with enough precision, we used a six-day time step. Moreover, the solar radius was artificially increased to 0.1 au to avoid numerical errors for small-perihelion orbits.
The orbital parameters, such as initial eccentricities and inclinations, were taken randomly considering values lower than 0.02 and 0.5° for embryos and planetesimals. In the same way, we adopted random values for the argument of pericenter ω, longitude of ascending node Ω, and the mean anomaly M between 0° and 360°.
Because of the stochastic nature of the accretion process, we performed three simulations, S1–S3, with different random number seeds for every set of initial conditions. Each simulation conserved energy to at least one part in 103.
5. Results
5.1. General comparative analysis
The initial distributions associated with planetary embryos and planetesimals for the two sets of simulations that were used as initial conditions for the N-body simulations are shown in Fig. 2. The blue distributions correspond to the simulations performed by Ronco & de Elía (2014), the red distributions to the new set of simulations performed from a semi-analytical model. Panel a) presents the initial distributions of embryos corresponding to the end of the gas phase, panel b) the surface density profiles used to distribute 1000 planetesimals in the studied region, also when the gas is already dissipated.
 |
Fig. 3 Evolution in time of the S2 simulation of the first set. The blue and light-blue shaded areas represent the conservative and the optimistic HZ, and the blue and light-blue curves show curves of constant perihelion and aphelion, both for the conservative and the optimistic HZ. Planetary embryos are plotted as colored circles and planetesimals with black dots. The color scale represents the fraction of water of the embryos with respect to their total masses. In this case, there are two planets within the optimistic HZ with masses of 1.19 M⊕ and 1.65 M⊕. They present 4.51% and 39.48% of water content by mass, which represents 192 and 2326 Earth oceans, respectively. A color figure is available in the electronic version. |
 |
Fig. 4 Evolution in time of the S3 simulation of the second set. The blue and light-blue shaded areas represent the conservative and the optimistic HZ, and the blue and light-blue curves show curves of constant perihelion and aphelion, both for the conservative and the optimistic HZ. Planetary embryos are plotted as colored circles and planetesimals with black dots. The color scale represents the fraction of water of the embryos with respect to their total masses. Two planets remain within the optimistic HZ with masses of 1.37 M⊕ and 1.65 M⊕. They present 7.49% and 24.38% of water content by mass, which represents 366 and 1437 Earth oceans, respectively. A color figure is available in the electronic version. |
The embryos inside the snow line of the second set of simulations present masses that range from once to twice the masses of the embryos inside the snow line of the first set. Something similar happens with the embryos beyond the snow line. The masses of the outermost embryos of the first set of simulations are at most five times greater than those of the second set. Another difference shown in panel b) is that the surface densities of the planetesimals in both sets are quite different in the region inside the snow line since the surface density profile of planetesimals for the second set of simulations is almost zero between 0.5 au and 2.7 au. This is because the planetesimals in this region were accreted by the embryos during the gaseous phase. Could these differences lead to significant changes in the final results of our simulations or not? We discuss this question in Sect. 6.
General characteristics of the most distinctive planets formed in the S1–S3 simulations of the first set, using ad hoc initial conditions.
Figures 3 and 4 show six snapshots in time on the semi-major axis eccentricity plane of the evolution of the S2 and S3 simulations of the first and the second set, respectively. In general terms, the overall progression of the two sets of simulations can be described as follows. From the beginning, the planetary embryos are quickly excited by their own mutual gravitational perturbations. At the same time, the planetesimals, which are not self-interacting bodies, significantly increase their eccentricities due to perturbations from embryos. In time, the eccentricities of embryos and planetesimals increase until their orbits cross and accretion collisions occur. Then, planetary embryos grow by accretion of other embryos and planetesimals, and the total number of bodies decreases. Finally, at the end of the simulations, the entire study region from 0.5 au and 5 au contains between four and seven planets with separations ranging from 18 to 53 mutual hill radii and a total mass that represents between 55% and 56% of the initial mass of solids in the disk, which is 13.66 M⊕.
Three classes of special interest can be distinguished among the resulting planets of each simulation: 1) the innermost planet of the system; 2) the planet (or planets) in the HZ; and 3) the most massive planet of the system. Tables 1 and 2 show the general characteristics of these three distinctive planets resulting from S1–S3 simulations for the first and the second set of initial conditions, and Fig. 5 shows the final configuration of all the simulations performed. The main similarities and differences obtained in these simulations for the resulting planets as well as the remaining planetesimal population are discussed in the following subsections.
General characteristics of the most distinctive planets formed in the S1–S3 simulations of the second set, using initial conditions from a semi-analytical model.
 |
Fig. 5 Final configuration of the first and second set of simulations. The color scale represents the water content and the shaded regions, the optimistic and the conservative HZ. The eccentricity of each planet is shown above it, by its radial movement over an orbit. A color figure is available in the electronic version. |
5.2. Removal of embryos and planetesimals
While the total mass of the planetesimal population starting the N-body simulations is almost the same for the two sets of initial conditions (~6.9 M⊕ for the first and 7.2 M⊕ for the second set), the initial surface density profile of planetesimals is very different in both cases (see Fig. 2b). For the first set of simulations, 31% of the mass of the planetesimal population is located inside the snow line, while the remaining 69% is distributed beyond 2.7 au. On the other hand, for the second set of initial conditions, only 10% of the mass of the planetesimal population is distributed inside the snow line, while the remaining 90% is located beyond 2.7 au. Thus, some differences should be observed in the evolution of the planetesimal population between both sets of initial conditions.
After 200 Myr of evolution, many embryos and planetesimals were removed from the disks of the two sets of simulations. In the S2 simulation of the first set of initial conditions, the mass that still remains in the studied region, between 0.5 au and 5 au, is ~7 M⊕ for planetary embryos and 0.43 M⊕ for planetesimals. We consider that this remaining planetesimal mass, which represents 6.3% of the initial planetesimal mass, is not significant enough to produce important changes in the orbital and physical characteristics of the resulting planets. Similar results were found in the other simulations of this set.
In the S3 simulation of the second set of initial conditions, the mass that still survives after 200 Myr is 7.49 M⊕ in embryos and 1.08 M⊕ in planetesimals. Thus, the remaining mass of planetary embryos in the studied region is similar in the two sets of initial conditions. However, the mass of remaining planetesimals associated with the second set of simulations, which represents 15% of the initial planetesimal mass, is a factor of ~2.4 greater than that obtained from the first set of initial conditions. This situation is repeated in the remaining simulations of this set.
From a quantitative point of view, the populations of embryos at the end of a simulation obtained from the two sets of initial conditions are similar, while the remaining populations of planetesimals show major discrepancies. To understand these differences, it is very important to analyze the main mechanisms by which planetesimals are removed in our simulations. On the one hand, in the S2 simulation of the first set, 3.78 M⊕ in planetesimals, which represents 55% of the initial mass in planetesimals, collides with the central star, remains outside the studied region (beyond 5 au), or is ejected from the disk. On the other hand, in the S3 simulation of the second set 3.83 M⊕, which represents 53% of the initial mass in planetesimals, collides with the central star, remains outside the studied region, or is ejected from the disk. Then, the removed mass in planetesimals is also similar in the two sets of simulations. However, the accreted mass in planetesimals (by embryos) represents 37.9% of the initial mass in planetesimals for the S2 simulation of the first set and represents 32.3% of the initial mass in planetesimals for the S3 simulation of the second set. Similar results were found for the remaining simulations. While the removed mass in planetesimals is similar in both sets and ranges between ~53% and 55% of the initial planetesimal mass for the second and the first set, the percentage of the accreted mass in planetesimals ranges between 37.9% and 41% for the first set and between 31.7% and 32.3% for the second set. This difference in the accreted mass in planetesimals between the two sets of simulations reveals different accretion histories of the final planets. The accretion history of the planets is of great interest because the final characteristics and properties of the planets depend on it. Thus, initial conditions obtained from more realistic models allow us to obtain more reliable physical properties of the resulting planets, such as a more reliable final water distribution.
5.3. Dynamical friction
From the beginning, the dynamical friction seems to be a significant phenomenon in the two sets of simulations. This dissipative force dampens the eccentricities and inclinations of the large bodies embedded in a swarm of smaller bodies represented by planetesimals. Figure 6 shows the evolution of the eccentricities and inclinations of the innermost planet and the most massive planet in S3 of the first set and in S3 of the second set. The masses of the innermost planets are similar, and the same occurs with the most massive planets (see Tables 1 and 2). Thus, we find similar results for both of them.
 |
Fig. 6 Evolutions of eccentricities, a), b), and inclinations, c), d), as a function of time for the innermost planet (black curve) and the most massive planet (red curve) of the S3 simulations and S3 simulations in the first and in the second set. The dynamical friction effects prevail over the larger bodies, which evolve in both sets of simulations in regions of the disk that are embedded in a swarm of planetesimals. A color figure is available in the electronic version. |
On the one hand, the innermost planets of 1.13 M⊕ and 1.18 M⊕ show mean values of the eccentricity of 0.08 and 0.06 for the first and the second set, respectively, while the mean values for the inclinations are 4.04° and 2.47°. On the other hand, the most massive planets of 3.08 M⊕ and 2.36 M⊕ present mean values of the eccentricity of 0.04 for the first and 0.03 for the second set, while the mean values for the inclinations are 1.47° and 1.55°. This means that for both simulations, the effects of dynamical friction still prevail over larger bodies. It is worth noting that both planets are initially located in regions embedded in planetesimals, therefore, it is expected to see the same effects in both of them.
Similar results are obtained with the comparison between S2 of the first set and S1 of the second set. In this particular scenario, it is worth noting that the most massive planet in S1 of the second set is not located in a region embedded in planetesimals at the beginning of the integration. However, this planet has about 5 × 105 close encounters with planetesimals during its evolution, which allow keeping the low values associated with its eccentricity and inclination. Therefore, the fact that the planet is located at the beginning in a region without planetesimals does not imply that the effect of dynamic friction is absent throughout its evolution.
It is interesting to analyze the scenario represented for the S2 simulation of the second set. In this particular case, the innermost and the most massive planets started the simulation in a region of the disk that is not embedded in planetesimals at the beginning of the integration. It is important to note that the final masses of such planets have similar values. However, the mean values of the eccentricity and inclination of the innermost planet are a factor of ~2 greater than those associated with the most massive planet. This difference arises because the most massive planet suffered one order of magnitude more close encounters with planetesimals than the innermost planet throughout the evolution. Thus, the results of our simulations suggest that the dynamical friction is an inefficient mechanism for the innermost planets.
5.4. Planets in the habitable zone
The formation of terrestrial planets in the HZ of the system and the analysis of their water contents are topics of special interest in our work. The HZ is defined as the range of heliocentric distances at which a planet can retain liquid water on its surface (Kasting et al. 1993). For the solar system, Kopparapu et al. (2013a,b) proposed that an optimistic HZ is between 0.75 au and 1.77 au and a conservative HZ is defined to lie between 0.99 au and 1.67 au. However, even when a planet is located in the HZ, this does not guarantee that there may be developed life. Planets with very eccentric orbits may pass most of their periods outside the HZ, not allowing long times of permanent liquid water on their surfaces. To avoid this problem, we considered that a planet is in the optimistic HZ if it has a perihelion q ≥ 0.75 au and a aphelion Q ≤ 1.77 au and is in the conservative HZ if it has a perihelion q ≥ 0.99 au and a aphelion Q ≤ 1.67 au. In this work, we considered it is sufficient that a planet is in the optimistic HZ to be potentially habitable. On the other hand, we considered the water contents to be significant when they are similar to that of the Earth. The mass of water on the Earth surface is 2.8 × 10-4 M⊕, which is defined as 1 Earth ocean. Taking into account the water content in the Earth mantle, several studies (Lécuyer & Gillet 1998; Marty 2012) suggested that the present-day water content on Earth should be ~0.1% to 0.2% by mass, which represents between ~3.6 to 7.1 Earth oceans. Moreover, some works suggest that the primitive mantle of the Earth could have contained between 10 and 50 Earth oceans (Abe et al. 2000; Righter & Drake 1999), although this is still under debate.
We developed three different N-body simulations for each of the two sets of initial conditions. All of them form planets within the optimistic HZ. For the first set of initial conditions, our simulations produce a total of five planets in the HZ with masses from 0.66 M⊕ to 2.27 M⊕ and final water contents ranging from 4.5% to 39.48% of the total mass, which represents from 192 to 2326 Earth oceans. For the second set, our simulations form a total number of six planets in the HZ with masses ranging from 1.18 M⊕ to 2.21 M⊕ and final water contents from 7.5% to 33.63% of the total mass, which represents from 427 to 2006 Earth oceans.
 |
Fig. 7 Evolution in time of the semi-major axis (black), the perihelion (red), and the aphelion (orange) of the planets that remain within the HZ of each simulation in both the first (left panel) and the second set (right panel) of simulations. The blue and light-blue shaded areas represent the conservative and the optimistic HZ, and the dashed gray line represents the position of the snow line. A color figure is available in the electronic version. |
Figure 7 shows the evolution of the semi-major axis, the perihelion and the aphelion of the planets that remain in the HZ at the end of the simulation for both sets of initial conditions. Most of the planets are kept within the conservative HZ almost throughout the whole integration, and their semi-major axes do not change significantly in the last 100 Myr of evolution. Planet b (S2 simulation) in the first set of initial conditions as well as planets a (S1 simulation) and e (S3 simulation) in the second set remain within the limits of the optimistic HZ, with perihelions entering and leaving it as a result of oscillations in the eccentricity of their orbits. Since the definition of HZ is not accurate, we consider these planets targets of potential interest. Planet d (S2 simulation) in the second set of initial conditions reaches highest eccentricity values of ~0.15. This planet shows changes in its aphelion, which carry it in and out of the HZ at the end of the simulation. The incident stellar flux on such a planet may considerably vary between perihelion and aphelion. Williams & Pollard (2002) showed that provided that an ocean is present to act as a heat capacitor, the time-averaged flux is the main effect on the habitability over an eccentric orbit. Given that planets on eccentric orbits have higher average orbital flux, planet d (S2 simulation) in the second set may maintain habitable conditions.
5.4.1. Highly water-rich planets
Tables 1 and 2 show that simulations developed from the two sets of initial conditions form planets in the HZ with a wide range of final water contents. In particular, some of them show very high water contents. Planets a, c, and e in the first set of simulations show water contents of 32.6%, 39.5% and, 32.5% by mass, respectively, while planets b, d and f in the second set present 24.3%, 33.6%, and 24.4% water by mass, respectively. The evolution of such water-rich planets has different characteristics for the two sets of simulations. Tables 1 and 2 and Fig. 7 highlight this point. Table 1 and Fig. 7 (left panel) show that potentially habitable planets a, c, and e of the first set of simulations come from beyond the snow line. The migration suffered by these planets is due to the strong gravitational interaction between planetary embryos and planetesimals in the outer disk. Given their initial locations, it is worth noting that a high percentage (31–36%) of the very high final water contents of these planets is primordial. Moreover, our simulations indicate that the remaining water content of these planets is acquired by impacts of planetesimals and planetary embryos in equal parts. Thus, taking into account the primordial and acquired water contents, we infer that the embryos play the most important role in providing water to the potentially habitable planets a, c, and e of the first set of simulations.
 |
Fig. 8 Feeding zones of the planets that remain in the HZ of S1, S2, and S3 simulations of the first (top panel) and the second set of simulations (bottom panel). The y axis represents the fraction of each planet’s final mass after 200 Myr of evolution. A color figure is available in the electronic version. |
Table 2 and Fig. 7 (right panel) show that potentially habitable planets b, d, and f of the second set of simulations present different characteristics. On the one hand, planet d starts the simulation beyond the snow line, like the potentially habitable planets a, c, and e of the first set. In the same way, 41.4% of the high final water content of this planet is primordial, which is a consequence of its initial location. Moreover, the remaining water content is provided equally by impacts of embryos and planetesimals associated with the outer disk. Thus, taking into account the primordial water content, we find that the embryos are mainly responsible for providing water to planet d of the second set of simulations. On the other hand, planets b and f present a semi-major axis that does not change significantly from the beginning of the integration. This means that these planets grow near their initial positions and do not suffer significant migration. Given their initial locations, the primordial water content of planets b and f is negligible. For both planets, the final water content is fully acquired throughout the evolution by impacts of planetesimals and planetary embryos associated with the outer disk. This is shown in the bottom panel of Fig. 8, where the feeding zones of the planets are represented. In particular, planets b and f accreted two and one embryos from beyond the snow line, respectively, which significantly increased their final water contents. However, planetesimals provide 53% and 44% of the final water contents of planet b and f. In these cases, both embryos and planetesimals are therefore equally responsible for providing the final water contents of these planets.
Although these highly water-rich planets remain within the optimistic habitable zone, their potential habitability is still under debate (Abbot et al. 2012; Alibert 2014; Kitzmann et al. 2015), and this analysis is beyond the scope of this work. However, we consider water worlds as a particular and very interesting kind of exoplanets.
5.4.2. Earth-like planets
General characteristics of the Earth-like planets formed within the HZ in the two sets of simulations.
Our simulations also form Earth-like or terrestrial-type planets within the optimistic HZ. We consider that Earth is comparable to these planets not only because they present masses similar to that of the Earth, but also because of the features that are connected with the dynamics of their formation. These Earth-like planets in our simulations form in situ. There is no significant migration of the accretion seeds that finally form these planets. Moreover, their feeding zones, unlike what occurs with highly water-rich planets, are restricted to the inner region of the disk (see Fig. 8). This type of exoplanets is the most interesting one from an astrobiological point of view since, as they present similarities in terms of the dynamics of the formation of the Earth, they are more likely to develop life. These Earth-like planets formed in our simulations present several times the Earth’s water content. This is directly related to two important facts: on the one hand, as we mentioned before, our model does not consider water loss during impacts, thus, the final water contents represent upper limits. On the other hand, our formation scenario without gas giants is particularly conducive to a more efficient water delivery from external planetesimals. Giant planets could act as a barrier preventing that many of the external planetesimals, which are now accreted by the planets in the HZ, reach the inner zone of the disk (Raymond et al. 2009).
Two of the five planets formed within the optimistic HZ in the first set and three of the six planets that remain in the HZ of the second set are Earth-like planets. The Earth-like planets in the first set (see Table 1: planet b in S2 and planet d in S3) present masses of 1.19 M⊕ and 0.66 M⊕ and water contents of 4.51% and 8.10% by mass, respectively, which represent 192 and 190 Earth oceans. The Earth-like planets in the second set (see Table 2: planet a in S1, planet c in S2 and planet e in S3) present masses of 2.21 M⊕, 2 M⊕ and 1.37 M⊕, and water contents of 8.75%, 10.76% and 7.49% by mass, respectively, which represent 692, 768 and 366 Earth oceans.
The evolution of these Earth-like planets shows similar characteristics in both sets of simulations, unlike what occurs with the water worlds described before. Figure 7 shows that planets b and d in the first set and planets a, c, and e in the second set start their formation in the inner zone of the disk, particularly inside 1.5 au, and they evolve without exceeding this limit. This means that the percentage of water that they have acquired during their evolution is not primordial. A detailed analysis of their collisional histories reveals that planetesimals are the only population responsible for their final amounts of water. Moreover, none of them accreted embryos from beyond the snow line. However, there is a difference in the class of planetesimals these planets have accreted. We distinguish planetesimals of class D, which are those planetesimals that were originally located inside the snow line and are dry, and planetesimals of class W, which are those planetesimals that were originally located beyond the snow line and present half of their mass in water. Planets b and d of the first set accreted 185 and 100 planetesimals of the total of planetesimals, of which only 5 were class W. This represents only 2.7% and 5% of the total amount of accreted planetesimals. In contrast, planets a, c, and e of the second set accreted 65, 69, and 41 planetesimals of the total accreted planetesimals, of which 53, 59, and 28 were class W planetesimals. This represents 81.5%, 85.5%, and 68% of the total amount of accreted planetesimals for planets a, c, and e, respectively. Thus, the class W planetesimals accreted for the two sets of simulations is quite different. Nevertheless, we recall that the masses of the class W planetesimals are different in the two sets of simulations. The mass of water accreted by the Earth-like planets considering only class W planetesimals in the second set is between 1.9 and 4 times the mass of water accreted by the planets of the first set.
An important topic to consider is the comparison between the timescale for an Earth-like planet to accrete half of the class W population of planetesimals (t50.class - W), the timescale to accrete half of the class D planetesimals (t50.class - D), and the timescale for the same planet to acquire at least 50% of its final mass (T50%). Table 3 shows the main characteristics of the Earth-like planets formed within the HZ in the two sets of simulations and shows that for all of them, t50.class - W is greater than t50.class - D, greater than T50% and even more, is greater than T75%. This means that class W population of planetesimals was accreted significantly later than class D planetesimals during the formation process and after the planet acquired half of its final mass. Moreover, class W planetesimals were accreted after the planet acquired 75% of its final mass. This late arrival of the class W planetesimals during the formation of terrestrial planets may favor water retention on the surface of the planet brought by these planetesimals. O’Brien et al. (2014) studied the water delivery and giant impacts on terrestrial planets in the Grand Tack scenario. Particularly, O’Brien et al. (2014) analyzed the water delivery of primitive planetesimals (the C-type planetesimals in Walsh et al. 2011), which were initially located between the orbits of Jupiter and Saturn, or beyond. Although the Grand Tack scenario is quite different from the one we proposed since our planetary systems do not include giant planets, we find similar results for the timescales of primitive planetesimal accretion.
Moreover, we find that the Earth-like planets of the first and the second set are still accreting water due to class W planetesimals after ~90 Myr of evolution. Although planets b and d of the first set only accreted 5 class W planetesimals, 3 of them were accreted after 90 Myr, particularly between 110 and 170 Myr. These planetesimals provided 58.7% and 39.3% of the total accreted water by planets b and d, respectively, which represent 2.64% and 3.2% of their final masses. For the second set, planet a accreted 10 class W planetesimals between 93 and 191 Myr, which provided 18.7% of the total accreted water and represents 1.64% of its final mass. Planet c accreted 20 class W planetesimals between 91 and 199 Myr, which provided 33.6% of the total accreted water and represent s3.62% of its final mass, and finally, planet e accreted 11 class W planetesimals between 92 and 192 Myr, which provided 38.8% of the total accreted water and represents 2.91% of its final mass. This analysis may be of particular interest for the habitable-zone planets formed around M dwarfs regarding the work of Tian & Ida (2015). Although the Earth-mass planets found by Tian & Ida (2015) in M dwarf habitable zones may have lost their water content through dissociation and hydrodynamic scape during the first ~ 90 Myr of evolution, they could still accrete ice planetesimals and retain significant amounts of water on their surfaces.
6. Discussion
 |
Fig. 9 Timescales for planets in the HZ to reach a given fraction (50%, 75%, or 90%) of their final masses for the set of simulations with ad hoc initial conditions and for the set of simulations with initial conditions from a semi-analytical model. These values are averaged for all the HZ planets in each simulation. |
We found that at the end of the evolution of our simulations, five and six planets are produced in the HZ of the system from the first and second set of initial conditions, respectively. For the first set, planets of the HZ present masses ranging from 0.66 M⊕ to 2.27 M⊕, with a median value of 1.65 M⊕. For the second set, the mass of the planets formed in the HZ ranges from 1.18 M⊕ to 2.21 M⊕, with a median value of 1.66 M⊕. The timescales associated with the last giant impact received for the planets of the HZ are quite similar for both sets of simulations, with mean values of 35 Myr and 40 Myr for the first and second set, respectively. However, the last giant impact does not always mean that the planet presents the majority of its final mass. Figure 9 shows the mean time values that the planets in the HZ need to reach 50%, 75%, and 90% of their final mass for the two sets. The values are averages for all planets in the HZ, and the results are also evidently quite similar for both sets.
A simple analysis of the feeding zones of the HZ planets (Fig. 8) reveals that the planets in the first set of simulations accrete a higher percentage of material from the outer disk than the potentially habitable planets produced in the second set. In fact, for the first set, the final water contents range from 4.5% to 39.5% by mass, with a median value of 32.5%. For the second set, planets in the HZ have final water contents ranging from 7.5% to 33.6% by mass, with a median value of 17.5%.
Our simulations form Earth-like planets and highly water-rich planets or water worlds in the HZ. All the Earth-like planets, in both sets, grow in situ and their feeding zones are restricted to the inner disk. Thus, their final water contents are not primordial, and a detailed analysis shows that planetesimals are the only population responsible for their final amounts of water. In addition, an analysis of the accretion timescales shows that all these planets accreted half of the class W planetesimals after they had acquired 75% of their final masses. Moreover, they continue accreting class W planetesimals after 90 Myr of evolution. On the other hand, the Earth-like planets in the two sets of simulations accreted different ammounts of class W planetesimals. Particularly the mass of water accreted by the Earth-like planets of the second set is greater than the one accreted by the first set, by a factor of 1.9–4. The highly water-rich planets are planets whose accretion seeds come from the outer zone of the disk (planets a, c, and e of the first set and planet d of the second set) or grow near their initial positions, but have accreted embryos from beyond the snow line. The sources of water supply are also different in the two sets. Planetary embryos are mainly responsible for the final water contents of the water worlds of the first set, but for two of the three planets of the second set, the final water contents are provided by embryos and planetesimals in equal parts.
However, it is worth mentioning that embryos and planetesimals might not be the only source of water. Izidoro et al. (2013) suggested that a compound model that considers water accretion through collisions of protoplanetary bodies and the contribution of the water locally adsorbed from the nebula is more efficient in the amount and time of the delivery of water to Earth-like planets.
More realistic initial conditions need to be included in the N-body simulations to obtain a more realistic accretion history of the final planets. However, the semi-analytical model used to generate these initial conditions contains several simplifications that might affect the results and could lead to different final configurations for the distribution of embryos and planetesimals. Our model in particular neglects the presence of embryo gaseous envelopes because the masses of the embryos are small enough not to produce major differences. Moreover, the semi-analytical model does not include the effects of planetesimal fragmentation or pebble accretion. On the other hand, we did not include type I migration in our model because many aspects of this phenomenon are still under debate. Computing the N-body interactions for the embryos during the gaseous phase could also change their spacial distribution. Regarding the planetesimal distribution, different sizes of planetesimals could lead to different final planetesimal surface densities.
A detailed knowledge about the accretion history of the planets of a given system is very important for analyzing several physical characteristics. In particular, all our simulations are developed assuming perfectly inelastic collisions that conserve mass and water content. However, a more realistic treatment of the collisions can lead to a better understanding of the differentiation of a planet, composition, formation of structures such as a core and a mantle, and help quantify its abundance of water (Marcus et al. 2010; Chambers 2013; Bonsor et al. 2015). In the same way, a better knowledge of the accretion history of a planet allows us to understand the evolution of its atmosphere (Schlichting et al. 2015). Impacts that are due to planetary embryos and planetesimals can generate a relevant atmospheric mass loss during the formation and evolution process.
7. Conclusions
We carried out N-body simulations aimed at studying the planetary formation process and water delivery around Sun-like stars in low-mass disks and in absence of gas giants. The main goal of our investigation was to study the sensitivity of the results to the particular initial distribution adopted for planetesimals and planetary embryos after the gas dissipation. The first set of simulations was based on results reported by Ronco & de Elía (2014) and assumed ad hoc initial conditions, while the second set of simulations derived initial conditions from a semi-analytical model that is capable of analyzing the evolution of a planetary system during the gas phase. Our main results suggest the following.
The number of planets formed in the HZ of the system is not sensitive to the initial conditions proposed in the two sets of simulations. Moreover, the masses of the planets of the HZ do not show significant differences in either of the sets.
The main differences observed between the two sets of simulations are associated with the accretion history of the planets of the HZ. These discrepancies are primarily related to the accretion of water-rich material.
Earth-like planets form in situ and their feeding zones are restricted to the inner region of the disk, and these Earth-like planets present several Earth water contents.
Highly water-rich planets present different characteristics in the two sets: these are planets whose accretion seeds come from the outer zone of the disk or planets that grow near their initial positions, but have accreted embryos from beyond the snow line, meaning that their feeding zones extend to the outer region of the disk.
Our simulations indicate that planetary embryos are mainly responsible for the final water contents of the water worlds in the HZ of the first set, while planetesimals play a secondary role. Of the three water worlds formed in the HZ from the second set of initial conditions, only one shows a similar behavior to that previously described. However, the primordial water content of two of these planets is negligible, and their final water contents are provided by impacts of embryos and planetesimals in equal parts.
Almost all the simulations formed Earth-like planets within the HZ. As they grow in situ, their final water contents are not primordial, and planetesimals are the only population responsible for their final amounts of water. In addition, all these planets accreted half of the class W planetesimals after they had acquired 75% of their final masses. Moreover, they continued accreting class W planetesimals after 90 Myr of evolution. These results show that the water delivery is a late process in the evolution of an Earth-like planet, and this is of great interest because it can facilitate the retention of water and other volatiles on the surface.
Finally, we conclude that including more realistic initial conditions in N-body simulations of terrestrial-type planet formation is crucial for a more realistic analysis of the accretion history of the planets resulting from the formation of a planetary system.
The definition of the habitable zone is given in Sect. 5 but we note here that we consider a conservative and an optimistic habitable zone as in Kopparapu et al. (2013a,b).
Acknowledgments
We thank the anonymous referee for constructive comments that helped us to improved the manuscript. This work was funded with grants from Consejo Nacional de Investigaciones Científicas y Técnicas de la República Argentina and the Universidad Nacional de La Plata (Argentina).
References
- Abbot, D. S., Cowan, N. B., & Ciesla, F. J. 2012, ApJ, 756, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Abe, Y., Ohtani, E., Okuchi, T., Righter, K., & Drake, M. 2000, Water in the Early Earth, eds. R. M. Canup, K. Righter, et al., 413 [Google Scholar]
- Agnor, C., & Asphaug, E. 2004, ApJ, 613, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Alibert, Y. 2014, A&A, 561, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Hughes, A. M., Qi, C., & Dullemond, C. P. 2010, ApJ, 723, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., Masset, F., Koenigsberger, G., & Szulágyi, J. 2015, Nature, 520, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Bonsor, A., Leinhardt, Z. M., Carter, P. J., et al. 2015, Icarus, 247, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Brunini, A., & Benvenuto, O. G. 2008, Icarus, 194, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 1999, MNRAS, 304, 793 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Chambers, J. E. 2001, Icarus, 152, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Chambers, J. E. 2013, Icarus, 224, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Butler, R. P., Marcy, G. W., et al. 2008, PASP, 120, 531 [CrossRef] [Google Scholar]
- Dauphas, N., & Pourmand, A. 2011, Nature, 473, 489 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Elía, G. C., Guilera, O. M., & Brunini, A. 2013, A&A, 557, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilera, O. M., Brunini, A., & Benvenuto, O. G. 2010, A&A, 521, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilet, J., Baruteau, C., & Papaloizou, J. C. B. 2013, MNRAS, 430, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hayashi, C. 1981, Progr. Theor. Phys. Suppl., 70, 35 [Google Scholar]
- Ida, S., & Makino, J. 1993, Icarus, 106, 210 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Izidoro, A., de Souza Torres, K., Winter, O. C., & Haghighipour, N. 2013, ApJ, 767, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Blum, J., Tanaka, H., et al. 2014, Protostars and Planets VI, 547 [Google Scholar]
- Johansen, A., Mac Low, M.-M., Lacerda, P., & Bizzarro, M. 2015, Sci. Adv., 1, 15109 [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kitzmann, D., Alibert, Y., Godolt, M., et al. 2015, MNRAS, 452, 3752 [NASA ADS] [CrossRef] [Google Scholar]
- Kokubo, E., & Ida, S. 1998, Icarus, 131, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013a, ApJ, 770, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Kopparapu, R. K., Ramirez, R., Kasting, J. F., et al. 2013b, ApJ, 765, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lécuyer, C., & Gillet, P., Robert, F. 1998, Chem. Geol., 145, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., & Stevenson, D. J. 2007, Protostars and Planets V, 591 [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [NASA ADS] [CrossRef] [Google Scholar]
- Marcus, R. A., Sasselov, D., Stewart, S. T., & Hernquist, L. 2010, ApJ, 719, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Marty, B. 2012, Earth Planet. Sci. Lett., 313, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., D’Angelo, G., & Kley, W. 2006, ApJ, 652, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Miguel, Y., Guilera, O. M., & Brunini, A. 2011, MNRAS, 417, 314 [CrossRef] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., & Naef, D. 2009, A&A, 501, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morishima, R., Stadel, J., & Moore, B. 2010, Icarus, 207, 517 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, D. P., Morbidelli, A., & Levison, H. F. 2006, Icarus, 184, 39 [NASA ADS] [CrossRef] [Google Scholar]
- O’Brien, D. P., Walsh, K. J., Morbidelli, A., Raymond, S. N., & Mandell, A. M. 2014, Icarus, 239, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., Crida, A., & Kley, W. 2010, MNRAS, 401, 1950 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2004, Icarus, 168, 1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2005, ApJ, 632, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., Quinn, T., & Lunine, J. I. 2006, Icarus, 183, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Raymond, S. N., O’Brien, D. P., Morbidelli, A., & Kaib, N. A. 2009, Icarus, 203, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Righter, K., & Drake, M. J. 1999, Earth Planet. Sci. Lett., 171, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Ronco, M. P., & de Elía, G. C. 2014, A&A, 567, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlichting, H. E., Sari, R., & Yalinewich, A. 2015, Icarus, 247, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Tian, F., & Ida, S. 2015, Nature Geosci, 8, 177 [Google Scholar]
- Touboul, M., Kleine, T., Bourdon, B., Palme, H., & Wieler, R. 2007, Nature, 450, 1206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Williams, D. M., & Pollard, D. 2002, in The Evolving Sun and its Influence on Planetary Environments, eds. B. Montesinos, A. Gimenez, & E. F. Guinan, ASP Conf. Ser., 269, 201 [Google Scholar]
All Tables
General characteristics of the most distinctive planets formed in the S1–S3 simulations of the first set, using ad hoc initial conditions.
General characteristics of the most distinctive planets formed in the S1–S3 simulations of the second set, using initial conditions from a semi-analytical model.
General characteristics of the Earth-like planets formed within the HZ in the two sets of simulations.
All Figures
 |
Fig. 1 Initial and final distributions of embryos and planetesimals generated by the semi-analytical model. Panels a) and b) represent the initial and final mass distribution of embryos. At the beginning a) there were 223 embryos between 0.5 au and 5 au, and after 3 Myr of evolution b) there only remain 57 embryos. Panels c) and d) represent the initial and final density profile of planetesimals. Panels b) and d) then represent the final results obtained with the semi-analytical model after 3 Myr of evolution and the initial conditions for the N-body simulations. The vertical lines in gray represent the position of the snow line at 2.7 au. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 2 a) Distributions of embryos used to start the N-body simulations. The squares represent the distribution of embryos obtained with the first set of simulations. The circles represent the final results obtained with the semi-analytical model (the second set of simulations). b) Surface density profiles used to distribute 1000 planetesimals to start the N-body simulations. The dashed line represents the surface density for the first set, the solid line the surface density for the second set obtained with the semi-analytical model. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 3 Evolution in time of the S2 simulation of the first set. The blue and light-blue shaded areas represent the conservative and the optimistic HZ, and the blue and light-blue curves show curves of constant perihelion and aphelion, both for the conservative and the optimistic HZ. Planetary embryos are plotted as colored circles and planetesimals with black dots. The color scale represents the fraction of water of the embryos with respect to their total masses. In this case, there are two planets within the optimistic HZ with masses of 1.19 M⊕ and 1.65 M⊕. They present 4.51% and 39.48% of water content by mass, which represents 192 and 2326 Earth oceans, respectively. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 4 Evolution in time of the S3 simulation of the second set. The blue and light-blue shaded areas represent the conservative and the optimistic HZ, and the blue and light-blue curves show curves of constant perihelion and aphelion, both for the conservative and the optimistic HZ. Planetary embryos are plotted as colored circles and planetesimals with black dots. The color scale represents the fraction of water of the embryos with respect to their total masses. Two planets remain within the optimistic HZ with masses of 1.37 M⊕ and 1.65 M⊕. They present 7.49% and 24.38% of water content by mass, which represents 366 and 1437 Earth oceans, respectively. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 5 Final configuration of the first and second set of simulations. The color scale represents the water content and the shaded regions, the optimistic and the conservative HZ. The eccentricity of each planet is shown above it, by its radial movement over an orbit. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 6 Evolutions of eccentricities, a), b), and inclinations, c), d), as a function of time for the innermost planet (black curve) and the most massive planet (red curve) of the S3 simulations and S3 simulations in the first and in the second set. The dynamical friction effects prevail over the larger bodies, which evolve in both sets of simulations in regions of the disk that are embedded in a swarm of planetesimals. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 7 Evolution in time of the semi-major axis (black), the perihelion (red), and the aphelion (orange) of the planets that remain within the HZ of each simulation in both the first (left panel) and the second set (right panel) of simulations. The blue and light-blue shaded areas represent the conservative and the optimistic HZ, and the dashed gray line represents the position of the snow line. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 8 Feeding zones of the planets that remain in the HZ of S1, S2, and S3 simulations of the first (top panel) and the second set of simulations (bottom panel). The y axis represents the fraction of each planet’s final mass after 200 Myr of evolution. A color figure is available in the electronic version. |
| In the text | |
 |
Fig. 9 Timescales for planets in the HZ to reach a given fraction (50%, 75%, or 90%) of their final masses for the set of simulations with ad hoc initial conditions and for the set of simulations with initial conditions from a semi-analytical model. These values are averaged for all the HZ planets in each simulation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


