| Issue |
A&A
Volume 583, November 2015
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201527120 | |
| Published online | 02 November 2015 | |
Research Note
Identifying the best iron-peak and α-capture elements for chemical tagging: The impact of the number of lines on measured scatter⋆
1 Instituto de Astrofísica e Ciências do Espaço, Universidade do Porto, CAUP, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: Vardan.Adibekyan@astro.up.pt
2 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
3 Byurakan Astrophysical Observatory, 0213 Byurakan, Aragatsotn province, Armenia
4 Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
5 Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
Received: 4 August 2015
Accepted: 8 September 2015
Aims. The main goal of this work is to explore which elements carry the most information about the birth origin of stars and, as such, which are best suited for chemical tagging.
Methods. We explored different techniques to minimize the effect of outlier value lines in the abundances by using Ni abundances derived for 1111 FGK-type stars. We evaluate how the limited number of spectral lines can affect the final chemical abundance. Then we make an efficient even footing comparison of the [X/Fe] scatter between the elements that have a different number of observable spectral lines in the studied spectra.
Results. When several spectral lines are available, we find that the most efficient way of calculating the average abundance of elements is to use a weighted mean (WM), whereby we consider the distance from the median abundance as a weight. This method can be used effectively without removing suspected outlier lines. When the same number of lines are used to determine chemical abundances, we show that the [X/Fe] star-to-star scatter for iron group and α-capture elements is almost the same. The largest scatter among the studied elements, was observed for Al and the smallest for Cr and Ni.
Conclusions. We recommend caution when comparing [X/Fe] scatters among elements where a different number of spectral lines are available. A meaningful comparison is necessary to identify elements that show the largest intrinsic scatter, which can then be used for chemical tagging.
Key words: stars: abundances / stars: general / stars: fundamental parameters
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Studies of large samples of stars are very important for understanding the Galactic and stellar chemical evolution. Understanding the effects of these two mechanisms is, in turn, crucial for studying the chemical properties of individual stars. A representative example is the so-called Tc-trend – a trend of chemical abundance with the condensation temperature of the elements – the real nature of which is still being debated (e.g., Meléndez et al. 2009; Ramírez et al. 2009; González Hernández et al. 2010, 2013; Schuler et al. 2011; Adibekyan et al. 2014; Önehag et al. 2014; Maldonado et al. 2015; Nissen 2015).
Precise and detailed chemical composition studies of large samples of stars are also of great importance for different areas of Galactic astronomy. For the development of many of these areas, the so-called chemical tagging technique, i.e., the identification of stars by their chemical properties, had an important role. This technique was introduced by Freeman & Bland-Hawthorn (2002) and then explored and developed by many other authors (e.g., De Silva et al. 2006; Tabernero et al. 2012, 2015; Mitschang et al. 2013, 2014; Blanco-Cuaresma et al. 2015). Chemical tagging is a very powerful tool for identifying stellar groups and clusters (e.g., Tabernero et al. 2015; De Silva et al. 2013; Spina et al. 2014a,b; Quillen et al. 2015) and is even used to identify solar siblings (e.g., Batista et al. 2014; Ramírez et al. 2014; Liu et al. 2015).
In all likelihood, not all elements are equally useful for chemical tagging. One way of selecting the elements that can be used to tag stars is to look at the star-to-star [X/Fe] abundance ratio scatter at solar metallicities, where the Galactic chemical evolution does not have a very strong effect. Elements that show the largest star-to-star scatter are more informative, because of their physical origin.
The works of De Silva et al. (2006, 2007, 2009) on open clusters, and those of Ramírez et al. (2009) and González Hernández et al. (2010) for solar twins and analogs, clearly reveal that most of the elements show very small star-to-star [X/Fe] scatter. These authors performed a fully differential chemical abundance analysis on a line-by-line basis relative to a solar spectrum reference, as well as to a star that is expected to belong to a given open cluster or kinematical group. In particular, in the recent work of Ramírez et al. (2014), a higher weight were given to Na, Al, V, Y, and Ba for chemical tagging. However, when the star-to-star [X/Fe] scatters were compared for different elements in all the above-mentioned studies, an important parameter was not taken into account: the number of spectral lines that were used to derive abundances for each element.
In this work, we study the dependence of [X/Fe] scatter on the number of spectral lines by using a large amount of high-quality data of solar-type stars. This allows us to make a comparison on the same basis as the [X/Fe] scatter for different elements by using the same number of lines. Our sample comes from Adibekyan et al. (2012) and consists of 1111 FGK-type dwarfs observed with the high-resolution HARPS spectrograph. The stellar parameters and abundances of the stars were derived from the high signal-to-noise ratio (S/N) spectra with a median S/N of 235 (only 15% of the spectra have S/N< 100).
We organize our paper as follows. In Appendix A, we quantify the precision in the abundance value as a function of number of spectral lines and summarize the results in Sect. 2. The discussion on the [X/Fe] star-to-star abundance scatter and conclusions are presented in Sects. 3 and 4.
2. Reducing the impact of outlier lines
The data used in this work is taken from Adibekyan et al. (2012), which provides chemical abundances for 12 iron-peak and α-capture elements (15 ionized or neutral species). In the present paper we did not use the final (average) abundances of different elements, but instead we use the abundances derived from individual lines of each element. As stated previously, this is because we aim to study the dependence of precision in abundances on the number of lines.
A standard and widely used technique for calculating chemical abundances that are derived from several spectral lines is to apply an outlier-removal criterion and to then calculate the arithmetic mean (AM) of the abundances from the remaining lines. However, detecting of outliers is not an easy task. There are several outlier removal methods discussed in the literature, for example σ-clipping (e.g. Shiffler 1988), modified Z-score (Iglewicz & Hoaglin 1993), Tukey’s (boxplot) method (Tukey 1977), and median-rule (Carling 1998). However, most of them are model-dependent as well as being dependent on the applied threshold for which there is no clear prescription or theoretical basis. We note that outlier removal is not the only method used to characterize an underlying distribution in a data set. A representative example is the weighted least-squares regression to minimize the effects of outlier data (Rousseeuw & Leroy 1987).
In Appendix A, we present a comprehensive discussion about different outlier methods and a new weighted mean (WM) method where we use (inverse) distance from the median value (measured in units of standard deviations (SD)) as weight. We made several tests to evaluate the impact of outliers on the chemical abundances (using Ni for our tests) and the dependence of the precision of the abundances on the number of lines.
When the number of lines is large, our tests show that different outlier removal techniques and criteria provide similar final abundances. However, the line-to-line dispersion, which is usually used to estimate the error on abundances, strongly depends on the criteria and can be artificially (unrealistically) reduced, depending on the outlier removal method and threshold. We conclude and recommend using the WM (instead of any outlier removal technique) when several lines are available.
Even for solar-type stars, for which high-quality data is available, we find that significant deviations in abundances from the real value are possible when the number of lines is small. For details of the tests and a discussion we refer to Appendix A .
 |
Fig. 1 [X/Fe] star-to-star scatter for solar analogs with solar metallicity. The dashed lines, which represent [X/Fe] = 0.03 and 0.06 dex, show the comparison of the [X/Fe] scatters between the elements more clearly. |
 |
Fig. 2 [X/Fe] star-to-star scatter for solar analogs with solar metallicity. The [X/Fe] scatter is derived by using 2, 6, 13, and 20 lines. The error bars show the standard deviation of the scatter calculated using different combinations of lines. The dashed lines, which represent [X/Fe] = 0.03 and 0.06 dex, show the comparison of the [X/Fe] scatters between the elements more clearly. |
3. [X/Fe] star-to-star scatter
Recently, several works on solar analogs (e.g., Ramírez et al. 2009; González Hernández et al. 2010, 2013) show that the [X/Fe] versus [Fe/H] trends show very little star-to-star scatter at the solar metallicities for most of the elements. In Fig. 1, we plot [X/Fe] scatter (rms) for dwarf stars (log g ≥ 4 dex) that have effective temperatures within 300 K of that of the Sun (Teff ≤ 5777 ± 300 K) and have metallicities in the range of [Fe/H] = 0.0 ± 0.05, [Fe/H] = 0.0 ± 0.10, and [Fe/H] = 0.0 ± 0.20 dex, respectively. The abundances of all the elements were derived using all the available lines by applying the WM technique. We only selected stars with solar metallicities to minimize the effect of Galactic chemical evolution and the thin/thick disk dichotomy (see, however, the discussion in Adibekyan et al. (2011) and Adibekyan et al. (2013) about thin/thick disk separation at solar and super-solar metallicities). The constraint on Teff serves to select the stars with the highest precision of the stellar parameters and chemical abundances (Sousa et al. 2008; Adibekyan et al. 2012; Tsantaki et al. 2013). We note that the sample size is large enough to minimize the errors related to the sampling of the population. For example, if the scatter (standard deviation) is of about 0.05 dex (which is the case for most of the elements), the 95% confidence interval of this value would be from 0.045 to 0.056 for the sample size of 152 (the number of stars in the metallicity range of 0.0 ± 0.10 dex)1.
Figure 1 shows that among the studied elements, the highest [X/Fe] scatter is observed for Na and Al, and the lowest scatter is for Si, Ca, Cr, and Ni. The number of available lines that were used to derive abundances of Na and Al is the lowest, i.e., only two lines, while elements that show the smallest scatter usually have more than ten lines. From the figure, it is apparent that the scatter does not change much when different metallicity intervals are used. The only exception is Mn, where scatter increases with the width of the metallicity interval. We note that, for the derivation of Mn abundances we did not consider hyperfine structure (hfs), which is important for odd-Z elements and, if not considered, might overestimate the Mn abundances deduced from a given EW. This can be one of the reasons for the observed increase in [Mn/Fe] scatter with metallicity. Another reason for the observed high scatter at larger range of [Fe/H] could be the strong Galactic evolution trend in the [Mn/Fe]–[Fe/H] plane at solar metallicities (e.g., Adibekyan et al. 2012; Battistini & Bensby 2015). We note that the trend is strong even if the hfs effect, but not a non local thermodynamic equilibrium (non-LTE) effect, is taken into account (e.g., Battistini & Bensby 2015).
To evaluate the impact of the number of lines (e.g., precision) on the [X/Fe] scatter, we did a test similar to that presented in the previous section (see Appendix A for details). For each element, we randomly drew N number of lines (where N is from one to the maximum number of lines) and calculated the [X/Fe] scatter for solar analogs in the metallicity range of 0.0 ± 0.10 dex. If the number of possible combinations of the lines is less than 1000 we considered all of them, otherwise we limited ourselves to a fixed number of 1000 random but different, i.e., without replacement, combinations.
In Fig. B.1, we plot the dependence of [X/Fe] star-to-star scatter as a function of the number of lines that were used for [X/H] abundance derivations. The plot clearly shows that the average scatter decreases with the number of lines. The plot also shows that the WM always gives smaller scatter than the AM (when the number of lines is greater than two, of course). This fact can be considered as an independent confirmation of the better “precision” of the abundances calculated using WM technique.
It is also interesting to note that some individual lines can introduce a very large scatter while others provide a very small one. The results of this test can be used to rank the spectral lines according to the [X/Fe] scatter they provide. This can be used as an independent method to eliminate outliers and select the best possible lines. For example, there is one Ca line (λ5261.71) that clearly shows a very large scatter (0.16 dex) compared to the rest of the 12 lines (on average ~0.06 dex). It is interesting and important to note that the average difference of the [Ca/H] abundance that is derived by using this line from the mean abundance is very small, but again with a large dispersion ⟨ Δ [Ca/H] ⟩ = 0.05 ± 0.15 dex. This means that the line does not systematically show higher or lower abundance when compared to the abundance that is derived with the remaining lines. If all the 1111 stars were to be considered, then this difference grows smaller and negative, ⟨ Δ [Ca/H] ⟩ = −0.02 ± 0.15 dex. Our analysis of the [Ca/Fe] versus Teff for this line shows a very weak trend (0.05 dex/1000 K) and particularly large scatter at low temperatures. However, we find that the deviation of the Ca abundance of this line from the mean Ca abundance depends on the EW. The average EW of this line is 104 ± 23 and 116 ± 45 mÅ for the solar analogs and for all the stars, respectively. When the EW is greater than 100 mÅ, the deviation increases significantly.
Similar to the Ca line mentioned above, we found that some lines show distinguishably large dispersion for the other elements. We provide a ranked list of all the lines in order of scatter size2.
Using the [X/Fe] scatter for all the elements and for different number of lines, we compare the [X/Fe] star-to-star scatter for different elements, using the same number of lines in Fig. 2. We plot the scatter that is derived using 2, 6, 13, and 20 lines because these numbers better match the number of lines available, thus maximizing the number of lines and elements in the panels. For example, all the elements have at least two lines and there is only one element that has between six and 13 lines.
The top lefthand panel of Fig. 2 shows that, when only two lines are used for all the elements to calculate [X/Fe], almost all the elements show a similar scatter of about 0.06 dex. Aluminum shows the largest while Cr and Ni show the smallest scatters. However, one can also see that, depending on the combinations of lines, the [X/Fe] scatter can be different for the same element (the error bar in the plot). The three other panels, which provide information that is more statistically significant (since this is based on larger number of lines), show that Ti, V, ScII, and Co have the largest scatter, among the elements that have at least six lines. Again, Cr and Ni show the smallest scatter. Although the obtained differences in [X/Fe] scatter between elements are not large, we note that they are based on a large sample and can thus be considered statistically significant.
The decrease in the [X/Fe] scatter with the number of lines means that a fraction of the observed scatter does not have an astrophysical origin. Table 3 of Adibekyan et al. (2012) provides the average error of the [X/Fe] ratios for the same sample of stars. The table shows that the average error varies from 0.01 to 0.03 dex. For the elements that have at least 13 lines (SiI, CaI, TiI, CrI, and NiI) the average error on [X/Fe] is 0.01 dex.
Our results show the importance of the initial selection of the lines, especially when the number of lines is small. By carefully selecting lines for individual stars with a given set of stellar parameters and a given quality of the spectra, one can derive precise chemical abundances even when the number of lines is small and have small [X/Fe] scatter. This has already been demonstrated for solar analog stars by, for example, Ramírez et al. (2009) and González Hernández et al. (2010). However, when dealing with a large number of stars with different combinations of stellar parameters and quality of the spectra, it is not realistic to control abundances of each individual line in each individual star.
4. Summary and conclusion
In this paper, we used a large sample of FGK stars (Adibekyan et al. 2012) to study the dependence of precision of chemical abundances on the number of lines and how this affects the [X/Fe] star-to-star scatter at solar metallicities. We have explored different techniques to calculate the mean abundance and minimize the effect of possible outliers when several spectral lines are available for an element.
Based on our tests, we conclude and recommend the use of a WM (instead of any outlier removal technique) when several lines are available. The distance from the median abundance can be used effectively as a weight, as demonstrated.
By selecting only solar analogs with metallicities similar to that of the Sun by 0.10 dex, we show that [X/Fe] scatter strongly depends on the number of lines. This suggests that one should be cautious when comparing star-to-star abundance dispersion of elements where the abundances were derived using a different number of lines. The decrease in scatter with the number of lines suggests that some fraction of the observed scatter has a non-astrophysical nature. A large number of lines is needed to reduce the precision-induced scatter.
The comparison of the [X/Fe] scatter for different elements using the same number of lines show that most elements display a very similar dispersion. The largest scatter among the elements studied in this work was found for Na, Al, Ti, V, ScII, and Co, while Cr and Ni show the smallest scatter. The similarity and differences in [X/Fe] scatter between the elements have different/similar nucleosynthesis production sites (see, e.g., Nomoto et al. 2013).
Our group is currently working on the derivation of abundances of volatile (C and N) and r- and s-process elements (Suárez-Andrés et al., in prep.; Delgado-Mena et al, in prep.). When the data is ready, a similar analysis will be done for these elements to select the elements that are the most informative for chemical tagging.
Online material
Appendix A: Dependence of abundances on the number of lines: the case of Ni
The data used in this work was taken from Adibekyan et al. (2012), which provides chemical abundances for 12 iron-peak and α-capture elements (15 ionized or neutral species).
The lines used are based on the line list of Neves et al. (2009). From the VALD3 online database, 180 lines were carefully selected in the solar spectrum to be: not-blended, have equivalent widths (EW) above 5 mÅ and below 200 mÅ, and be located outside of the wings of very strong lines. Later on, the semi-empirical oscillator strengths for the lines were calculated by calibrating the log gf values to the solar reference of Anders & Grevesse (1989). Moreover, only “stable” lines, which do not show high abundances dispersion (i.e., 1.5 times the rms) from the mean abundance for each element, were selected. In this later test, 451 stars with a wide range of stellar parameters and S/N were used. The selected 180 lines were re-checked in Adibekyan et al. (2012), where several lines were excluded because of the observed abundance trend [X/Fe] with the effective temperature. For more details about the selection of the lines, see Neves et al. (2009) and Adibekyan et al. (2012). Our final line-list consists of 164 lines4.
We stress that the main goal of this work is not to re-check the quality of the lines, nor to provide a range of parameter space (stellar parameters and S/N) where each individual line can be used safely and reliably. Since different authors use different sets of spectral lines and different atomic data for the lines, for us it is more straightforward and scientifically interesting to discuss methods that can, in principle, work effectively for different line lists and be applied to large data sets, as is often the case.
Appendix A.1: Comparing methods
In Adibekyan et al. (2012) the final abundance for each star and element was calculated as the arithmetic mean (AM) of the abundances given by all lines detected in a given star and element after a two-sigma clipping was applied. This is a standard and widely used technique that avoids the errors caused by bad pixels, bad measurements, cosmic rays, and other unknown localized effects. However, this type of outlier removal technique depends on the threshold (2σ in our case) that is applied. There is no clear prescription or theoretical ground for this and the choice ends up being very subjective. The choice of threshold should also depend on the sample size. A simple demonstration of this dependence on sample size is presented by Shiffler (1988), who showed that the possible maximum Z-score (the number of SD a data-point is far from the mean) depends (only) on the sample size and is computed as (n−1)/![\hbox{$\sqrt[]{n}$}](/articles/aa/full_html/2015/11/aa27120-15/aa27120-15-eq18.png) . From this formula we understand that the maximum deviation that one can obtain in a sample of five points (lines) is 1.79σ, i.e., no outliers can be identified in the data if 2σ-clipping is applied. One can alternatively use median and median absolute deviation (MAD), which is expected to be less sensitive to outliers, or one can apply other outlier removal methods (e.g., Hodge & Austin 2004; Iglewicz & Hoaglin 1993). However, it is very difficult to choose a single method and a criterion that will work efficiently for samples of different sizes. Moreover, when a certain criterion is applied to remove possible outliers, some valid lines from the real distribution may be removed as well. Finally, one should also bear in mind that most of the outlier removal methods are model-dependent, assuming some distributions for the real and outlier data.
. From this formula we understand that the maximum deviation that one can obtain in a sample of five points (lines) is 1.79σ, i.e., no outliers can be identified in the data if 2σ-clipping is applied. One can alternatively use median and median absolute deviation (MAD), which is expected to be less sensitive to outliers, or one can apply other outlier removal methods (e.g., Hodge & Austin 2004; Iglewicz & Hoaglin 1993). However, it is very difficult to choose a single method and a criterion that will work efficiently for samples of different sizes. Moreover, when a certain criterion is applied to remove possible outliers, some valid lines from the real distribution may be removed as well. Finally, one should also bear in mind that most of the outlier removal methods are model-dependent, assuming some distributions for the real and outlier data.
To explore and choose the method that allows a derivation of the most precise final abundances of the elements, we selected Ni for our analysis because it has the largest line list (43 lines). By plotting the individual Ni abundances in the full sample of 1111 stars, we noticed that many of the stars have Ni lines that show deviation from the average value by more than 3σ. To understand if these lines are outliers or just extremes of the distribution (a normal distribution is assumed here) we performed some simple calculations. If one assumes a normal distribution, then a 3σ corresponds to P = 0.003 probability. Since on average we derive Ni abundance from 43 lines, then the probability that we will have at least one “outlier” is of 43 × 0.003 = 0.129. This means that among the 1111 stars, we expect to have about 0.129 × 1111 = 143 stars with one “outlier” line. However, the number of stars that have at least one “outlier” is 626. To estimate the probability of having that many stars with at least one “outlier” we used binomial probability distribution. The probability that more than 200 stars (any number above 200) can have an “outlier” is already 8×10-7. This means that, under our assumption of Gaussian distribution of the abundances derived from different lines, some of the lines which show large dispersion (>3σ) can be real outliers of different origin and are not just coming from the wings of the Gaussian distribution. We note, that the results of this test do not depend on the applied threshold (3σ in this case).
Fortunately, if the line list is large, the possible outliers do not greatly affect the final (mean) abundance. We first tested three different outlier removal methods, namely σ-clipping (e.g., Shiffler 1988), modified Z-score (Iglewicz & Hoaglin 1993), and median-rule (Carling 1998) on our data. The modified Z-score method is similar to n × σ-clipping, but instead of mean and SD, the median and MADe5 are used. Median-rule is a modification of Tukey’s (boxplot) method (Tukey 1977), and defines outliers as points that lie further than median ± k × IQR, where IQR is the interquartile range. We varied the k to { 2,2.5,3 } for the σ-clipping and median-rule, and k = { 2.5,3,3.5 } for the modified Z-score. The selected values of k are within the intervals suggested in the above-cited references.
A potential difficulty that one faces when trying to remove outliers is the so-called masking and swamping effects. Removal of one outlier changes the “status” of the other data points (Acuna & Rodriguez 2004). This means that it is advisable to remove one outlier at a time and apply the criteria recursively. However, it is not obvious when the outlier removal criteria should be stopped (the problem also exists when all the outliers are removed at once). Two approaches were considered in our tests when modified Z-score method was used: i) remove all the outliers at once (referred to as MADe technique in the remainder of the paper) and ii) remove one outlier at a time and then apply the criterion again iteratively (hereafter referred to as MAD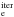 technique). For the second approach we allowed a maximum number of ten iterations, although in most cases, a lower number of iterations were needed (depending, of course, on the threshold accepted).
technique). For the second approach we allowed a maximum number of ten iterations, although in most cases, a lower number of iterations were needed (depending, of course, on the threshold accepted).
 |
Fig. A.1 Difference in [Ni/H] and σ[Ni/H] when WM and AM without outlier removal methods are applied (left). The same as in the left panel, but the parameters are derived using WM and MAD |
Outlier removal is not the only method used to characterize an underlying distribution in a data set. An example is the weighted least-squares regression to minimize the effects of outlier data (Rousseeuw & Leroy 1987). The last method that we use to calculate the final abundance and its line-to-line scatter is the WM and weighted SD. As a weight we used the (inverse) distance from the median value in terms of SD and then binned it. Using MAD and SD in the calculations of the weight on the average give very similar results, but if the values of more than the half of the points (lines) are the same (which can happen when the number of lines is small) then MAD is by definition zero and cannot be used to calculate the weight. Since the distance of the median point from the median is zero, the weight of that line would be infinite. To avoid giving a very high weight to the points that are initially close to the median (the final value would, by construction, be very close to the median), we decided to bin the distances with an interval of 0.5SD. For example, a 0.5 × SD weight was given to the lines that are 0 to 0.5 SD away from the median. Similarly, a 1 × SD weight was given to the lines lying at distances of 0.5 to 1 × SD, and so on.
Difference in Ni abundances when WM method and other methods are applied for the derivation of Ni.
The results of our tests are summarized in Table A.1. The test showed that all the outlier removal methods give a mean, final abundance similar to that of the WM. Since the number of lines is relatively large, the impact of possible outliers is small, and all the values were also similar to the abundance calculated by the AM of all the points. However, we note that, when the lowest thresholds were set to remove outliers, some stars showed deviations in the final abundance from the mean abundance derived from different methods. This was because of the large number of removed “outliers”. Another important point to stress is that, when outlier removal methods were applied with low thresholds, the line-to-line scatter (which is usually used as an error estimate of the final abundance) was usually small, which was expected.
 |
Fig. A.2 Difference between original Ni abundance and Ni abundances derived with only 2, 10, and 30 Ni lines. |
 |
Fig. A.3 Average deviation from the original Ni abundance for 1111 stars versus number of lines that were used for the abundance derivations. The right panel is the zoom of the left plot, limited to only six lines. Different techniques that were used in the calculations are mentioned in the plots. |
 |
Fig. A.4 Dependence of the average deviation from the original Ni abundance for 1111 stars versus stellar parameters and S/N. The abundance deviation represents the difference between original Ni abundance and Ni abundance derived with only 2 lines. |
From these tests (and further tests presented next in this work), we conclude that the best way to calculate the final abundance and its error is to use the WM. In this case, the weight of real outliers (extremes) is low, and the final abundance is not affected. With this approach, we also do not reduce the scatter by artificially removing points from the distribution. In Fig. A.1, we plot the distribution of the Ni abundance and its error (line-to-line dispersion) differences when WM and AM method is applied (left plot), and when WM and MAD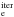 (median ± 3MAD) criteria are applied (right plot). From the plot and table, it is very clear that, when the number of lines is large, different methods for outlier removal (or not) provide very similar results for Ni abundances, however the error associated with these values depends on the method. In particular, Fig. A.1 (left plot) shows that line-to-line scatter of [Ni/H] is always larger when the Ni abundance is calculated by the AM than when the WM method is used (the difference in σ[Ni/H] is always positive). The righthand panel of the same figure shows that the difference in σ[Ni/H] is usually small and can be both positive and negative when Ni abundance is calculated by WM and MAD
(median ± 3MAD) criteria are applied (right plot). From the plot and table, it is very clear that, when the number of lines is large, different methods for outlier removal (or not) provide very similar results for Ni abundances, however the error associated with these values depends on the method. In particular, Fig. A.1 (left plot) shows that line-to-line scatter of [Ni/H] is always larger when the Ni abundance is calculated by the AM than when the WM method is used (the difference in σ[Ni/H] is always positive). The righthand panel of the same figure shows that the difference in σ[Ni/H] is usually small and can be both positive and negative when Ni abundance is calculated by WM and MAD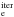 .
.
A word of caution should be added at this point. In the methods that we tested to remove “outliers”, as well as in the WM technique we assume that the distribution of the abundances (or the distribution of the errors on abundances) is symmetric6. However, as was shown in Bertran de Lis et al. (2015), for very weak lines with an assumption of local thermodynamic equilibrium (LTE), the distribution of uncertainties of abundances is asymmetric. The authors also showed that this effect depends on the S/N and is negligible for lines with EW greater than 8 mÅ, regardless of S/N. However, since in all the methods are based on the same hypothesis, the WM technique remains favorable for us.
Appendix A.2: Abundance precision dependence on the number of lines
To evaluate the impact of the number of lines (used for abundance derivations) on the abundances, we did the following simple tests. For each star in the sample, we randomly drew N Ni lines (N = 2, 3, ..., 42) and calculated the Ni abundance. We used the above-mentioned WM technique for the calculation of the abundances. Then we compared the resulting abundances with the supposed Ni abundance value (derived by using all 43 available lines and the WM technique). If the number of possible combinations is less than 1000, we considered all the possible combinations of lines, otherwise we drew N = 1000 random, but different, combinations of lines7.
In Fig. A.2, we plot an example (for two stars) of the distribution of the differences in Ni abundances (Δ[Ni/H]) when three different number of Ni lines (2, 10, and 30 lines) and all the available lines are used. The stars have different stellar parameters and different S/N in the spectra. The plot shows that, when the number of lines is increased, the abundance difference decreases. It also shows that, while the Δ[Ni/H] is close to zero in most of cases/trials, it is possible to obtain very large differences when only two lines are used (even for very high S/N data).
We did the aforementioned computations for all the 1111 stars and for each number of lines we calculated the standard deviation of Δ[Ni/H] distribution – σdev. In Fig. A.3, we plot the dependence of the average of the σdev for all 1111 stars as a function of the number of lines. In the plot, we limited ourselves only to examples of four techniques with different thresholds so as not to overload the figure, while applying all the techniques and thresholds presented in Table A.1. Moreover, since the size of the sample (lines) varies in these tests, we also decided to test lower outlier removal thresholds: k = 1.5 for σ-clipping and median-rule methods, and k = 2 for modified Z-score methods.
Figure A.3 shows the range of possible deviations (1σ deviation if the distribution was a Gaussian) from the original value for a given random star, when randomly draw N lines are used. It clearly shows that the deviation decreases very steeply with the number of lines and becomes less than 0.01 dex when more than 15 lines are used.
In the righthand panel of Fig. A.3, we show that there is a subtle difference between different outlier removal techniques for a number of lines less than or equal to six. It clearly shows that the smallest average deviation is obtained when the WM is used. We note that other tests show similar results with different thresholds. The low thresholds for outlier removal techniques give results closer to those obtained by using WM for a small number of lines. However, when low thresholds are considered for a large number of lines, the final results deviate from the abundances obtained by using the WM method. This is because of the high number of excluded lines. For the remainder of the paper we use abundances calculated by the WM method if another method is not specified. Here we should stress again that we plot the possible deviations of Ni abundances that were averaged for 1111 stars. While these average values are low, the deviations for individual stars can be very significant (as demonstrated in Fig. A.2).
It is natural to expect that the observed deviations should depend chiefly on the quality of the data (e.g., S/N) and also on the atmospheric parameters of the stars. This is because, for example, spectral lines in cooler stars’ spectra are usually more blended, and also because, for example, different lines form at different layers of the atmospheres and have different sensitivities to the non-LTE effects. In Fig. A.4, we plot the dependence of the average σdev on the stellar atmospheric parameters and on the S/N, when only two lines were used to derive the abundances. The plot shows that there is only a strong and clear dependence on Teff. This result is to be expected since, at low temperatures, the spectra of cool stars are crowded and line-blending plays a stronger role. Lowest metallicity stars and stars with the lowest S/N also show somewhat larger deviations. It is interesting to note that, even if the S/N is very high, it is possible to obtain a Ni abundance of up to 0.1 dex different from the original abundance, depending on stellar parameters, when only two Ni lines are used.
Appendix B: [X/Fe] star-to-star scatter: dependence on the number of lines
 |
Fig. B.1 Dependence of [X/Fe] star-to-star scatter for solar analogs with [Fe/H] = 0.0 ± 0.10 dex on the number of lines. Red triangles show the scatter when the individual abundances are calculated as an AM and the blue squares indicate the scatter in [X/Fe] when the WM method was used for the abundance derivation. The black dots show the [X/Fe] scatter for each individual line that was used to derive [X/H]. The error bars indicate the dispersion of possible combinations of the lines. |
The confidence interval of SD can be calculated as presented in Sheskin (2007).
This line list was subsequently analyzed in Adibekyan et al. (2015) to select a sub-list of lines suitable for the derivation of abundances for cool, evolved stars.
Acknowledgments
This work was supported by Fundação para a Ciência e a Tecnologia (FCT) through the research grant UID/FIS/04434/2013. P.F., N.C.S., and S.G.S. also acknowledge the support from FCT through Investigador FCT contracts of reference IF/01037/2013, IF/00169/2012, and IF/00028/2014, respectively, and POPH/FSE (EC) by FEDER funding through the program “Programa Operacional de Factores de Competitividade – COMPETE”. P.F. further acknowledges support from Fundação para a Ciência e a Tecnologia (FCT) in the form of an exploratory project of reference IF/01037/2013CP1191/CT0001. V.A. and E.D.M. acknowledge the support from the FCT (Portugal) in the form of the grants SFRH/BPD/70574/2010 and SFRH/BPD/76606/2011, respectively. J.P.F. acknowledges the support from FCT through the grant reference SFRH/BD/93848/2013. M.O. acknowledges support by Centro de Astrofísica da Universidade do Porto through a grant, reference CAUP-15/2014-BDP. J.I.G.H. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness (MINECO) under the 2011 Severo Ochoa Program MINECO SEV-2011-0187. We acknowledge the support from FCT, in the form of grant, reference PTDC/FIS-AST/1526/2014.
References
- Acuna, E., & Rodriguez, C. 2004, Classification, Clustering and Data Mining Applications (Heidelberg: Springer Verlag), 639 [Google Scholar]
- Adibekyan, V. Z., Santos, N. C., Sousa, S. G., & Israelian, G. 2011, A&A, 535, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 554, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., González Hernández, J. I., Delgado Mena, E., et al. 2014, A&A, 564, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Benamati, L., Santos, N. C., et al. 2015, MNRAS, 450, 1900 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Batista, S. F. A., Adibekyan, V. Z., Sousa, S. G., et al. 2014, A&A, 564, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battistini, C., & Bensby, T. 2015, A&A, 577, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertran de Lis, S., Delgado Mena, E., Adibekyan, V. Z., Santos, N. C., & Sousa, S. G. 2015, A&A, 576, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Heiter, U., et al. 2015, A&A, 577, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carling, K. 1998, Resistant outlier rules and the non-Gaussian case, Working Paper Series 2001:7, IFAU – Institute for Evaluation of Labour Market and Education Policy [Google Scholar]
- De Silva, G. M., Sneden, C., Paulson, D. B., et al. 2006, AJ, 131, 455 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., Freeman, K. C., Asplund, M., et al. 2007, AJ, 133, 1161 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., Freeman, K. C., & Bland-Hawthorn, J. 2009, PASA, 26, 11 [NASA ADS] [CrossRef] [Google Scholar]
- De Silva, G. M., D’Orazi, V., Melo, C., et al. 2013, MNRAS, 431, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K., & Bland-Hawthorn, J. 2002, ARA&A, 40, 487 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Israelian, G., Santos, N. C., et al. 2010, ApJ, 720, 1592 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Delgado-Mena, E., Sousa, S. G., et al. 2013, A&A, 552, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hodge, V., & Austin, J. 2004, in Artificial Intelligence Review, 22, 85 (the Netherlands: Kluwer Academic Publishers) [Google Scholar]
- Iglewicz, B., & Hoaglin, D. 1993, How to Detect and Handle Outliers, ASQC basic references in quality control (Milwaukee, WI: ASQC Quality Press) [Google Scholar]
- Liu, C., Ruchti, G., Feltzing, S., et al. 2015, A&A, 575, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Eiroa, C., Villaver, E., Montesinos, B., & Mora, A. 2015, A&A, 579, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meléndez, J., Asplund, M., Gustafsson, B., & Yong, D. 2009, ApJ, 704, L66 [NASA ADS] [CrossRef] [Google Scholar]
- Mitschang, A. W., De Silva, G., Sharma, S., & Zucker, D. B. 2013, MNRAS, 428, 2321 [NASA ADS] [CrossRef] [Google Scholar]
- Mitschang, A. W., De Silva, G., Zucker, D. B., et al. 2014, MNRAS, 438, 2753 [NASA ADS] [CrossRef] [Google Scholar]
- Neves, V., Santos, N. C., Sousa, S. G., Correia, A. C. M., & Israelian, G. 2009, A&A, 497, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nissen, P. E. 2015, A&A, 579, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., Kobayashi, C., & Tominaga, N. 2013, ARA&A, 51, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Önehag, A., Gustafsson, B., & Korn, A. 2014, A&A, 562, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quillen, A. C., Anguiano, B., De Silva, G., et al. 2015, MNRAS, 450, 2354 [NASA ADS] [CrossRef] [Google Scholar]
- Ramírez, I., Meléndez, J., & Asplund, M. 2009, A&A, 508, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramírez, I., Bajkova, A. T., Bobylev, V. V., et al. 2014, ApJ, 787, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Rousseeuw, P. J., & Leroy, A. M. 1987, Robust Regression and Outlier Detection (New York: John Wiley & Sons, Inc.) [Google Scholar]
- Schuler, S. C., Flateau, D., Cunha, K., et al. 2011, ApJ, 732, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Sheskin, D. J. 2007, Handbook of Parametric and Nonparametric Statistical Procedures, 4th edn. (Chapman & Hall/CRC) [Google Scholar]
- Shiffler, R. E. 1988, The American Statistician, 42, 79 [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014a, A&A, 568, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014b, A&A, 567, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabernero, H. M., Montes, D., & González Hernández, J. I. 2012, A&A, 547, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabernero, H. M., Montes, D., Gonzalez Hernandez, J. I., & Ammler-von Eiff, M. 2015, A&A, in press [Google Scholar]
- Tsantaki, M., Sousa, S. G., Adibekyan, V. Z., et al. 2013, A&A, 555, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tukey, J. W. 1977, Exploratory Data Analysis (Addison-Wesley) [Google Scholar]
All Tables
Difference in Ni abundances when WM method and other methods are applied for the derivation of Ni.
All Figures
 |
Fig. 1 [X/Fe] star-to-star scatter for solar analogs with solar metallicity. The dashed lines, which represent [X/Fe] = 0.03 and 0.06 dex, show the comparison of the [X/Fe] scatters between the elements more clearly. |
| In the text | |
 |
Fig. 2 [X/Fe] star-to-star scatter for solar analogs with solar metallicity. The [X/Fe] scatter is derived by using 2, 6, 13, and 20 lines. The error bars show the standard deviation of the scatter calculated using different combinations of lines. The dashed lines, which represent [X/Fe] = 0.03 and 0.06 dex, show the comparison of the [X/Fe] scatters between the elements more clearly. |
| In the text | |
 |
Fig. A.1 Difference in [Ni/H] and σ[Ni/H] when WM and AM without outlier removal methods are applied (left). The same as in the left panel, but the parameters are derived using WM and MAD |
| In the text | |
 |
Fig. A.2 Difference between original Ni abundance and Ni abundances derived with only 2, 10, and 30 Ni lines. |
| In the text | |
 |
Fig. A.3 Average deviation from the original Ni abundance for 1111 stars versus number of lines that were used for the abundance derivations. The right panel is the zoom of the left plot, limited to only six lines. Different techniques that were used in the calculations are mentioned in the plots. |
| In the text | |
 |
Fig. A.4 Dependence of the average deviation from the original Ni abundance for 1111 stars versus stellar parameters and S/N. The abundance deviation represents the difference between original Ni abundance and Ni abundance derived with only 2 lines. |
| In the text | |
 |
Fig. B.1 Dependence of [X/Fe] star-to-star scatter for solar analogs with [Fe/H] = 0.0 ± 0.10 dex on the number of lines. Red triangles show the scatter when the individual abundances are calculated as an AM and the blue squares indicate the scatter in [X/Fe] when the WM method was used for the abundance derivation. The black dots show the [X/Fe] scatter for each individual line that was used to derive [X/H]. The error bars indicate the dispersion of possible combinations of the lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


