| Issue |
A&A
Volume 582, October 2015
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 20 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526153 | |
| Published online | 30 September 2015 | |
A homogeneous analysis of disks around brown dwarfs⋆,⋆⋆
1 Purple Mountain Observatory, Chinese Academy of Sciences, 210008 Nanjing, PR China
e-mail: yliu@pmo.ac.cn
2 Key Laboratory for Radio Astronomy, Chinese Academy of Sciences, 2 West Beijing Road, 210008 Nanjing, PR China
3 Max-Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
4 Universität Heidelberg, Zentrum für Astronomie, Inst. für Theor. Astrophysik, Albert-Ueberle-Str. 2, 69120 Heidelberg, Germany
5 Departamento de Física y Astronomía, Facultad de Ciencias, Universidad de Valparaíso, Av. Gran Bretaña 1111, 5030 Casilla, Valparaíso, Chile
Received: 22 March 2015
Accepted: 13 July 2015
We re-analyzed the Herschel/PACS data of a sample of 55 brown dwarfs (BDs) and very low mass stars with spectral types ranging from M5.5 to L0. We investigated the dependence of disk structure on the mass of the central object in the substellar regime based on a homogeneous analysis of Herschel data from flux density measurements to spectral energy distribution (SED) modeling. The broadband SEDs were compiled by adding previous photometry at shorter wavelengths and (sub-)millimeter data. We performed detailed SED analysis for the 46 targets that show infrared (IR) excess emission using radiative transfer models and evaluated the constraints on the disk parameters through Bayesian inference. A systematic comparison between the derived disk properties and those of sun-like stars shows that the disk flaring of BDs and very low mass stars is generally smaller than that of their higher mass counterparts, the disk mass is orders of magnitude lower than the typical value found in T Tauri stars, and the disk scale heights are comparable in both sun-like stars and BDs. We further divided our sample into an early-type brown dwarf (ETBD) group and a late-type brown dwarf (LTBD) group by using spectral type (=M8) as the border criterion. We systematically compared the modeling results from Bayesian analysis between these two groups, and found the trends of flaring index as a function of spectral type also present in the substellar regime. The spectral type independence of the scale height is also seen between high-mass and very low-mass BDs. However, both the ETBD and LTBD groups feature a similar median disk mass of 1 × 10-5 M⊙ and no clear trend is visible in the distribution, probably due to the uncertainty in translating the far-IR photometry into disk mass, the detection bias and the age difference among the sample. Unlike previous studies, our analysis is completely homogeneous in Herschel/PACS data reduction and modeling with a statistically significant sample. Therefore, we present evidence of stellar-mass-dependent disk structure down to the substellar mass regime, which is important for planet formation models.
Key words: stars: low-mass / circumstellar matter / brown dwarfs / protoplanetary disks
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
How brown dwarfs (BDs) form is one of the main open questions in the field of star formation and remains a subject of debate. Several scenarios have been proposed: for instance, a scaled down version of star formation processes, gravitational instabilities in disks and ejection of the stellar embryo (e.g., Reipurth & Clarke 2001; Bate et al. 2003; Stamatellos & Whitworth 2011; Chabrier et al. 2014). Similar to their higher mass counterparts, such as T Tauri stars, young BDs are shown to have circumstellar disks, producing substantial excess emission at wavelengths ranging from infrared (IR) to (sub)millimeter (e.g., Liu et al. 2003, 2015; Scholz et al. 2006; Bayo et al. 2012; Harvey et al. 2012a, 2014; Ricci et al. 2014). Disks are also found around very faint objects with masses down to the planetary regime, for example Cha 110913 − 773444 (~ 8 MJup, Luhman et al. 2005a), LOri 156 (~ 23 MJup, Bayo et al. 2012), and OTS 44 (~ 12 MJup, Luhman et al. 2005b; Joergens et al. 2013). The phenomena of mass accretion and outflow, which are common by-products of the star formation process (e.g., Audard et al. 2014; Frank et al. 2014, for reviews), have also been detected in young BDs (e.g, Mohanty et al. 2005; Phan-Bao et al. 2008; Rigliaco et al. 2012; Joergens et al. 2012) even down to the planetary mass regime (e.g., Bayo et al. 2012; Joergens et al. 2013). The dust evolution in BD disks appears to follow a similar manner (i.e., grain growth, settling and crystallization) of that in T Tauri disks, although observations suggest different timescales of dust processing in disks around different stellar mass hosts (e.g., Apai et al. 2005; Bouy et al. 2008; Pascucci et al. 2009; Riaz et al. 2012). These observations show that BDs resemble hydrogen-burning stars in many aspects during their early evolution, implying that they may form through the canonical star formation processes.
Characterizing the physical properties of disks plays a crucial role in understanding the formation mechanisms of BDs (e.g., Reipurth & Clarke 2001; Bate et al. 2003) and planets. In addition, thorough comparisons between disk properties, such as the mass, flaring, and scale height in different stellar mass regimes, are very useful and important. So far, there have been many works in this direction. Early disk studies in substellar regime are mainly based on Spitzer data. For instance, Szűcs et al. (2010) investigated the IRAC and MIPS 24 μm photometry of ~ 200 stars in the Chamaeleon I star formation region and found that disks around cooler objects are generally flatter than the case of earlier type stars. The Herschel space telescope has unprecedented sensitivity and angular resolution in the far-IR, enabling the detection of many faint disks at this wavelength domain for the first time. The Herschel data, on the one hand, improve the determination of disk properties, and, on the other hand, provide an alternative way to estimate the disk mass of BDs. Harvey et al. (2012a) observed a large sample of low-mass stars and BDs with Herschel/PACS and found that the disk masses of low-mass stars and BDs extend to well below typical values found in T Tauri stars. The lower disk mass around cooler stars as revealed by far-IR measurements is consistent with the strong correlation between the stellar and disk masses given by Andrews et al. (2013) from a millimeter survey of Class II sources in the Taurus molecular cloud. Several recent works obtained similar results, although the sample size and assumptions used to analyze the Herschel data differ (e.g., Alves de Oliveira et al. 2013; Spezzi et al. 2013; Olofsson et al. 2013; Liu et al. 2015). Note that the above disk comparisons were mostly conducted between two stellar mass bins, i.e., the sun-like stars and the BDs including very low-mass stars. These works have yielded some evidence of spectral-type-dependent disk structure in the low stellar mass regime.
Source summary.
To date, however, there are seldom studies that investigate the dependency of disk properties on the spectral type (or the mass) of the central object within the substellar regime. It is quite unclear as to whether the observed trend of disk properties as a function of spectral type is also valid down to very low-mass BDs and even toward planetary mass objects. This kind of study needs great care because the disk parameters are not direct observables and determining them requires additional assumptions, such as the disk model and dust opacity used in the spectral energy distribution (SED) analysis. Moreover, the Herschel data is currently better understood, and this knowledge leads to a difference with reported fluxes and uncertainties published at the early stages of the mission (Balog et al. 2014), which in turn induces discrepancy in the value of parameters used to describe the disk structure. Considering these factors, it is not appropriate to analyze the results collected from the literature, which reduce and model the Herschel data in different ways. This may be another reason why Olofsson et al. (2013) did not find a correlation between the stellar and disk masses in the substellar mass regime from a comparison between their results and those in the literature.
In this work, we reanalyzed the Herschel/PACS data of a sample of 55 BDs and very low-mass stars, and fit their broadband SEDs, using self-consistent radiative transfer models with as few free parameters as possible. We estimated the constraints on key disk parameters (i.e., flaring index, scale height and disk mass) through Bayesian analysis. We extensively discussed the trends of these parameters as a function of spectral type. Since our analysis is homogeneous from data reduction to modeling, within a statistically significant sample, we present the first comprehensive study of stellar-mass-dependent disk structure down to the planetary mass regime.
The structure of this paper is as follows: we describe our sample in the following section. In Sect. 3, we delineate the observations and data reduction. A detailed description of the modeling is presented in Sect. 4. We discuss our results in Sect. 5, followed by a brief summary in Sect. 6.
2. Sample
Our sample consists of 55 spectroscopically confirmed targets in nearby star formation regions. The spectral types (SpTs) of the sample are in the range from M5.5 to L0. Thus most of the sources have substellar masses according to theoretical evolutionary models (e.g., Baraffe et al. 2003). We do not include any BD candidate lacking spectroscopic confirmation to avoid identification work and ambiguity of the results. Evidence for circumstellar dust emission as revealed by thermal IR measurements is a crucial criterion of our sample selection.
The sample of this paper was selected based on a study by Harvey et al. (2012a), on the one hand, and a search for the lowest mass objects in the Herschel/PACS archive, on the other hand. Harvey et al. (2012a) conducted the first comprehensive Herschel/PACS program to measure far-IR emission from young BDs. We reperform the analysis for the objects in their survey that satisfy the above criteria. For each of these targets, we provide the modeling results that were not reported in their work. In addition, we include the lowest-mass BDs (with SpT M8 and later) observed with PACS from the Herschel archive to probe differences in disk properties between high-mass and low-mass BDs. Furthermore, we also add several targets without clear excess at near- and mid-IR, which are thought to have experienced significantly inside-out disk evolution, but the cool and outer regions of the disk, if survived, are sensitive to Herschel observations. We note that including all substellar objects from the Herschel/PACS archive in our analysis, although desirable, was not possible due to limited computational power. The sample presented here is therefore biased toward very low-mass substellar objects.
Since the SpT is a good proxy for stellar mass in the low stellar mass regime, our sample can be generally divided into two groups: (1) a group of 30 early-type brown dwarfs (ETBDs) with spetral type earlier than M8; and (2) a group of 25 late-type brown dwarfs (LTBDs) with spectral type M8 and later. With this kind of division, we can investigate the dependence of the disk structure on the mass of the central object in the substellar mass regime, which yields important clues to understand the formation mechanism of BDs and planets.
Table 1 summarizes the properties of our sample, including target name, coordinates and SpT. Our targets are located in eight different star formation regions with ages ranging from ~ 1 − 3 Myr (e.g., Taurus and Ophiuchus) to ~ 10 Myr (e.g., TW Hydrae association and Upper Scorpius), see Table 2 for a summary of the cloud ages and distances. The effects of a mixed sample age on the results are discussed in detail in Sect. 5. For our sample, we cannot evaluate the disk frequency of BDs at far-IR because of the incompleteness of the sample selection and the detection bias in various clouds at different distances to the Earth.
Cloud age and distance assumed in this work.
3. Observations and data reduction
All the targets have been observed by the Photodetector Array Camera and Spectrograph (PACS; Poglitsch et al. 2010) on board Herschel with various programs (André et al. 2010; Harvey et al. 2012a; Alves de Oliveira et al. 2013; Bulger et al. 2014). The ObsIDs for all the observations are listed in Table 1. The majority of the observations were performed in the mini-scan map mode. The only exceptions are those for GY92 3, GY92 264, GY92 310 and J125758.7-770120. They were observed in the standard PACS scan map mode. Parallel mode observations were not considered. We took the data from the Herschel Science Archive at the processing stage of Level 1, Version 12.1 of the standard pipeline (SPG = Standard Product Generation) and further processed the data by producing maps and by conducting photometry.
3.1. Mapping
The Level 1 data from the archive are fully calibrated (Balog et al. 2014). We are only missing the last steps to Level 2 and 2.5, which consist of deglitching, signal drift suppression and mapping to convert the detector data into a map that superimposes the detector signals for any given position on the sky covered during the observation.
Since we are only interested in the point sources, the highpass filtering algorithm was applied to get rid of the background and detector signal drifts. This approach only conserves the source flux, if an object mask indicates those parts of the data that are not considered as background. For very faint objects like BDs, the mask produced by the SPG is insufficient. Therefore, we produced new and adequate source masks from Level 2.5 SPG maps (scan and cross-scan pairs are coadded) based on a signal-to-noise criterion.
After deglitching the data as done by the SPG, we produced maps using the photProject task. It converts the flux distribution as measured by the fixed detector pixel grid into a rebinned map, where the flux is redistributed on a freely selectable and virtual pixel grid. Since the map pixels are usually smaller, distorted and rotated relative to the detector pixels, the flux distribution must and can be done with great care. There is a “drizzling” algorithm, originally invented for the HST, which facilitates modifying crucial parameters when reconstructing the map (Fruchter & Hook 2002).
The SPG uses a so-called drop size that is relatively large. This is a scaling factor of the detector pixel sizes, which is applied before projecting them on the final map grid. This leads to a redistribution of the source flux on larger areas of the final map. This produces prettier, i.e., smoother images, due to the convolution of neighboring detector pixel signals. This also averages out noise, which leads to an underestimate of the real detector noise. Reducing the drop size can minimize this effect. The images look sharper, but also noisier. However, the resulting noise properties are much closer to the reality than what one gets with large drop sizes. Therefore, the subsequent photometry is also more accurate. We adopted 0.1 as the drop size for all maps. The pixel sizes were chosen to be 1′′ at 70 μm and 2′′ at 160 μm.
Finally, we combine the map pairs of a so-called scan and a cross-scan, corresponding to the Level 2.5 stage of the SPG.
3.2. Photometry
Since the sources are very faint and the vicinities around the targets of interest are full of other and brighter sources, a simple aperture photometry procedure is not sufficient. Therefore, we applied a HIPE built-in source extraction and photometry tool called Sussextractor. It is based on Bayesian statistics and delivers the most likely result for the target position and the integrated source flux by fitting 2D Gaussians to the detected sources (Savage & Oliver 2007).
A Gaussian source model is not adequate for the more complicated PSF shape of Herschel/PACS point sources. Only the core of the PACS PSF is close to Gaussian, but it also contains a trilobal shape at a level of a few percent of the peak intensity superimposed by an extended and slowly declining halo. Therefore, a correction factor has to be applied to the photometry derived by Sussextractor.
For this purpose, we reprocessed standard star data of alpha Boo (a PACS prime standard) in the same way as the BDs and then applied the Sussextractor algorithm and compared the results with those derived from a standardized aperture photometry procedure, including an aperture correction that was derived during the PACS flux calibration program. The multiplicative correction factors turned out to be 1.513 at 70 μm and 1.427 at 160 μm. The photometry errors given by the Sussextractor tool were corrected in the same way and regarded as the photometric errors. Additional systematic uncertainties were not considered. For non-detections, upper limits have been obtained by a statistical analysis of a series of aperture photometry measurements on the background as explained in Balog et al. (2014). This approach avoids underestimating the noise obtained from the map pixel statistics that is affected by correlation artefacts introduced by the drizzling algorithm.
 |
Fig. 1 Our Herschel/PACS flux densities at 70 μm (upper panel) and 160 μm (lower panel) as compared to previous results. The red dots depict real detections identified by both our work and previous works, whereas green marks consisting of leftward and downward arrows symbolize the upper limits. The black squares with downward arrows and blue squares with leftward arrows show detections by our study and previous works, respectively. |
 |
Fig. 2 Cumulative distribution of the 70 μm flux density for early-type brown dwarfs (ETBDs, blue) and late-type brown dwarfs (LTBDs, red). All flux densities are scaled assuming a distance of 100 pc. The median values are indicated as vertical dashed lines. |
3.3. General trends of the observational data
The measured flux densities at PACS bands are summarized in Table 1, whereas Fig. 1 shows a comparison between our results and previously published photometry. It is clear that most detections at 70 μm by other studies are confirmed with our reanalysis of the data. In particular, our flux measurements of the detected sources are in agreement with previous results (see the red dots in the upper panel of Fig. 1). However, we obtained less than one half of 160 μm detections that were reported before. This is probably because Herschel 160 μm images of faint disks are easily contaminated with the extended emission from the background, and the effects of using different data reduction algorithms on the results are significant in this case. In Table 1, we mark two kinds of objects for which the reanalyzed PACS photometry are significantly different from the literature values: (1) the difference in the flux density between our results and previous results is larger than 3σ, where σ refers to the root-mean-square level for each object given here; (2) firm detections reported before, with upper limits deduced by us, and vice versa. Since the constraints on the disk structure, especially the structure of the outer and cool regions of the disk, are sensitive to far-IR data points (e.g., Harvey et al. 2012a,b; Olofsson et al. 2013), the discrepancies in the PACS photometry between our results and previous results lead to different model explanations of the data. Therefore, our homogeneous analysis of the Herschel data and subsequent self-consistent modeling have the potential to retrieve the hidden statistical trends of disk properties in the substellar mass regime.
We generated the cumulative distributions f( ≥ Fν) of PACS photometry, using the Kaplan-Meier product-limit estimator to properly account for censored data sets, i.e., upper limits on Fν (Feigelson & Nelson 1985). This was done to examine any statistical difference in the far-IR emission between the two groups differing in terms of SpT. All flux densities are scaled by assuming a distance of 100 pc. The results are shown in Fig. 2. The LTBD sample (red line) has systematically lower flux densities than those of the ETBD group (blue line), which is consistent with the finding by Liu et al. (2015) that the amount of Herschel far-IR emission correlates well with the SpTs of the host BDs. From the distribution, the median flux densities are estimated, which we show as the vertical dashed lines. The median 70 μm flux density of the ETBD group is F70 = 22 mJy, which is at least three times larger than that of the LTBDs, i.e., F70< 7 mJy. We consider the latter case as an upper limit because more than half of the sources are undetected at this wavelength (Mathews et al. 2013). For the same reason, we do not perform the Kaplan-Meier product-limit estimation for the 160 μm data.
From a theoretical point of view, disks with a larger flaring index intercept a larger portion of the central star’s radiation because of a larger flaring angle and consequently re-emit more IR flux (e.g., Chiang & Goldreich 1997). The systematically lower flux density at far-IR wavelengths of the LTBDs implies that disks around lower mass stars are generally less flared. Bulger et al. (2014) investigated the effect of individual disk parameter on the appearance of the SED, and their results indicate that the flaring index and scale height work together to determine the emission level at Herschel/PACS bands. Moreover, the observational trends of far-IR flux densities may also help us to consider whether there is any evidence for differences in disk mass with different stellar masses, since the Herschel/PACS photometry can provide a rough mass estimation of BD disks (e.g., Harvey et al. 2012a; Spezzi et al. 2013; Liu et al. 2015). Nevertheless, interpreting the observational trends presented here needs detailed SED analysis in which efforts of reducing model degeneracy should be made as far as possible given that the data available are limited.
4. SED Modeling
All the targets have been observed over a broad range of wavelengths. We constructed the broadband SEDs of our sources by using our Herschel/PACS flux measurements and adding ancillary data at optical and mid-IR wavelengths, from the SDSS catalog (Ahn et al. 2012), DENIS survey (DENIS Consortium 2005), 2MASS (Cutri et al. 2003), Spitzer, and WISE catalogs (e.g., Cutri et al. 2012). We also took into account the upper limits of flux measurements in the (sub)millimeter regime available for a few of our sources (e.g., Mohanty et al. 2013; Broekhoven-Fiene et al. 2014). We derived the (sub)stellar properties of each target from thoroughly modeling the photosphere. For the 46 targets that show IR excess produced by circumstellar dust, we conducted detailed SED analysis using the radiative transfer code MC3D developed by Wolf (2003) to characterize the structure of their surrounding disks.
4.1. Determination of the (sub)stellar properties
We performed a thorough modeling of the photosphere of each object by fitting the BT-Settl models (Allard et al. 2012) with a χ2 minimization as well as Bayesian statistics (Bayo et al. 2008, 2014). The BT-Settl models incorporate a sophisticated treatment of photospheric dust, which is likely to affect the atmospheres and correspondingly the radiation field of cool objects like BDs in our sample. The broadband photometry for the photospheric part of the SED are taken into account in the fitting procedure. A similar analysis was done by Joergens et al. (2013) for their case study of OTS 44, a BD at the planetary mass border.
For objects in star-forming regions, we use the standard distances with errors to the cloud as given by the Handbook of Star formation (Reipurth 2008b,a), while the kinematic distances for objects in loose associations are adopted (e.g., Ducourant et al. 2014). The extinction is treated as a free parameter. For objects in star-forming regions, we use as starting point upper limits for the extinction based on extinction maps from Kainulainen et al. (2009) and Cambresy et al. (1997). For objects in loose associations, we consider an upper limit of 0.1 mag, and for σ Ori, we convert the standard E(B − V) value to extinction AV, assuming RV = 3.1 since this is the basic assumption for the extinction law used in VOSA (Bayo et al. 2008).
The derived best-fit (χ2) and most probable values for the effective temperatures, luminosities, and extinctions are in good agreement with each other for ~ 90% of the objects. For a few cases, we only get moderate fitting results: (i) for object 21 (J04274538+2357243), the extinction AV is loosely constrained, and we therefore took the value that minimizes the χ2. (ii) For object 34 (2MJ110703), there is no data point bluer than 2MASS/J band. In this case, we fixed AV to 15 mag, which is lower than the value of 16.5 mag estimated in Furlan et al. (2009), but is in agreement with that derived by Luhman et al. (2008). (iii) Object 36 (ISO 252), for which the best and second best fits are indistinguishable in terms of χ2 and the Bayesian analysis shows that it is hard to break the degeneracy between Teff and AV. We took the best-fit parameter set for this object. The derived effective temperatures, luminosities and extinctions are summarized in Table 3.
Photospheric and best-fit/most-probable disk parameters from this work.
4.2. Disk model
Dust distribution:We employed the standard flared disk model with well-mixed gas and dust, which has been successfully used to explain the observed SEDs of a large sample of young stellar objects and BDs (e.g., Wolf et al. 2003; Sauter et al. 2009; Harvey et al. 2012a; Joergens et al. 2013; Liu et al. 2015). The structure of the dust density is assumed with a Gaussian vertical profile ![\begin{equation} \rho_{\rm{dust}}=\rho_{0}\left(\frac{R_{*}}{\varpi}\right)^{\alpha}\exp\left[-\frac{1}{2}\left(\frac{z}{h(\varpi)}\right)^2\right], \label{dust_density} \end{equation}](/articles/aa/full_html/2015/10/aa26153-15/aa26153-15-eq66.png) (1)and the surface density is described as a power-law function
(1)and the surface density is described as a power-law function 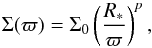 (2)where ϖ is the radial distance from the central star measured in the disk midplane, and h(ϖ) is the scale height of the disk. The disk extends from an inner radius Rin to an outer radius Rout. To the best of our knowledge, among our sample, there are five objects that have been identified as binary systems so far. They are 2M1207 (a~55 AU, Chauvin et al. 2004), J04221332+1934392 (a~7 AU, Todorov et al. 2014), J04414489+2301513 (a~15 AU, Todorov et al. 2014), USD161833 (a~134 AU, Bouy et al. 2006), and USD161939 (a ~ 26 AU, Bouy et al. 2006), where a refers to the separation within the system. The disks around individual components in binary systems are expected to have truncation radii of the order of (0.3 − 0.5)a (Papaloizou & Pringle 1977). We adopted 0.5 a as the disk outer radii for 2M1207, USD161833, and USD161939. For the close pairs (a ≲ 15 AU, J04221332+1934392 and J04414489+2301513), dynamical simulations of star-disk interactions suggest that individual disks are unlikely to survive (e.g., Artymowicz & Lubow 1994). Disk modeling is complicated in those close multiple systems. For simplicity, we assume that the emission is associated with circumbinary disks of 100 AU in size. For other objects, we fix Rout = 100 AU in the modeling because the choice of this parameter value makes essentially no difference to the synthetic SEDs in the simulated wavelength range (Harvey et al. 2012a). The scale height follows the power-law distribution
(2)where ϖ is the radial distance from the central star measured in the disk midplane, and h(ϖ) is the scale height of the disk. The disk extends from an inner radius Rin to an outer radius Rout. To the best of our knowledge, among our sample, there are five objects that have been identified as binary systems so far. They are 2M1207 (a~55 AU, Chauvin et al. 2004), J04221332+1934392 (a~7 AU, Todorov et al. 2014), J04414489+2301513 (a~15 AU, Todorov et al. 2014), USD161833 (a~134 AU, Bouy et al. 2006), and USD161939 (a ~ 26 AU, Bouy et al. 2006), where a refers to the separation within the system. The disks around individual components in binary systems are expected to have truncation radii of the order of (0.3 − 0.5)a (Papaloizou & Pringle 1977). We adopted 0.5 a as the disk outer radii for 2M1207, USD161833, and USD161939. For the close pairs (a ≲ 15 AU, J04221332+1934392 and J04414489+2301513), dynamical simulations of star-disk interactions suggest that individual disks are unlikely to survive (e.g., Artymowicz & Lubow 1994). Disk modeling is complicated in those close multiple systems. For simplicity, we assume that the emission is associated with circumbinary disks of 100 AU in size. For other objects, we fix Rout = 100 AU in the modeling because the choice of this parameter value makes essentially no difference to the synthetic SEDs in the simulated wavelength range (Harvey et al. 2012a). The scale height follows the power-law distribution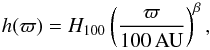 (3)with the exponent β characterizing the degree of flaring and H100 representing the scale height at a distance of 100 AU from the central star. The indices α, p, and β are codependent through p = α − β. We fix p = 1, which is the typical value found for T Tauri disks in the sub-millimeter (e.g., Isella et al. 2009; Guilloteau et al. 2011), since only spatially resolved data can place constraints on this parameter (e.g., Ricci et al. 2013, 2014). Dust properties:We assume the dust grains to be a homogeneous mixture of 75% amorphous silicate and 25% carbon with a mean density of ρgrain = 2.5 g cm-3 and the complex refractive indices given by Jäger et al. (1994, 1998), and Dorschner et al. (1995). Porous grains are not considered because the fluxes at wavelengths beyond ~ 2 μm are almost independent of the degree of grain porosity in low-mass disks, as shown by Kirchschlager & Wolf (2014). The grain size distribution is given by the standard power law dn(a) ∝ a-3.5da with minimum and maximum grain sizes amin = 0.1 μm and amax = 100 μm, respectively. The choice of the minimum value for the grain size, amin, ensures that its exact value has a negligible impact on the synthetic SEDs. Since there is no information about the maximum grain sizes of our target disks, as provided, e.g., by the (sub)millimeter spectral index, we adopt amax = 100 μm. The Herschel/PACS far-IR observations are sensitive to dust grains with this assumed sizes. Strong grain growth up to millimeter sizes as detected in some BD disks (e.g., Ricci et al. 2012, 2013, 2014; Broekhoven-Fiene et al. 2014) would remain undetected in our data and could affect the disk mass. Our prescription for the dust properties is identical to those used in Liu et al. (2015).
(3)with the exponent β characterizing the degree of flaring and H100 representing the scale height at a distance of 100 AU from the central star. The indices α, p, and β are codependent through p = α − β. We fix p = 1, which is the typical value found for T Tauri disks in the sub-millimeter (e.g., Isella et al. 2009; Guilloteau et al. 2011), since only spatially resolved data can place constraints on this parameter (e.g., Ricci et al. 2013, 2014). Dust properties:We assume the dust grains to be a homogeneous mixture of 75% amorphous silicate and 25% carbon with a mean density of ρgrain = 2.5 g cm-3 and the complex refractive indices given by Jäger et al. (1994, 1998), and Dorschner et al. (1995). Porous grains are not considered because the fluxes at wavelengths beyond ~ 2 μm are almost independent of the degree of grain porosity in low-mass disks, as shown by Kirchschlager & Wolf (2014). The grain size distribution is given by the standard power law dn(a) ∝ a-3.5da with minimum and maximum grain sizes amin = 0.1 μm and amax = 100 μm, respectively. The choice of the minimum value for the grain size, amin, ensures that its exact value has a negligible impact on the synthetic SEDs. Since there is no information about the maximum grain sizes of our target disks, as provided, e.g., by the (sub)millimeter spectral index, we adopt amax = 100 μm. The Herschel/PACS far-IR observations are sensitive to dust grains with this assumed sizes. Strong grain growth up to millimeter sizes as detected in some BD disks (e.g., Ricci et al. 2012, 2013, 2014; Broekhoven-Fiene et al. 2014) would remain undetected in our data and could affect the disk mass. Our prescription for the dust properties is identical to those used in Liu et al. (2015).
Heating sources:The disk is assumed to be passively heated by stellar irradiation (e.g., Chiang & Goldreich 1997; Dullemond et al. 2001). Other heating sources, such as the viscous accretion, are not taken into account as this would only introduce further free parameters without any qualitative constraints from the modeling. We use the BT-Settl atmosphere models (Allard et al. 2012) as incident flux with parameters as constrained in Sect. 4.1. The radiative transfer problem is solved self-consistently considering 100 wavelengths, which are logarithmically distributed in the range of [0.05 μm, 2000 μm].
 |
Fig. 3 Spectral energy distributions of the target disks. The dots depict the photometry at various wavelengths. Spitzer/IRS spectra are indicated with red lines. The upside down triangles show the 3σ upper limits of the flux density. The best-fit models are indicated with black solid lines, whereas the dashed lines represent the photospheric emission levels. The gray lines denote all probable model fits that are derived by Bayesian analysis, showing the strength of constraints of the best-fit models for each object, see Sect. 4.3. |
 |
Fig. 3 continued. |
 |
Fig. 3 continued. |
4.3. Fitting method
The task of SED fitting was conducted with a grid of precalculated models for each target. The model grids can give us an overview of the fitting quality in different parameter domains and clues to improve the quality of the fit with further attempts if necessary. Table 4 summarizes the explored ranges of each parameter considered here. The grid adds up to a total number of 37 440 models for each source. We tried to achieve a better explanation of the observations, on one hand, by reducing the dimensionality of the parameter space as far as possible and, on the other hand, by using a denser grid of models as compared to previous studies on Herschel/PACS data of BD disks (e.g., Harvey et al. 2012a,b; Alves de Oliveira et al. 2013; Olofsson et al. 2013; Spezzi et al. 2013). For objects for which we could not obtain good results from the grid, a simulated annealing approach was additionally invoked to improve the solution by taking the best model in the grid as the starting point of the Markov chain. Generally, ~ 1000 steps for the local fit with simulated annealing are enough (Liu et al. 2013). This kind of methodology makes use of the advantages of both database method and simulated annealing algorithm and has already been demonstrated to be successful for SED analysis (Liu et al. 2012; Madlener et al. 2012).
Parameter range of the model grids computed in this work.
The fitting results are shown in Fig. 3. The best-fit models are indicated as black solid lines, whereas the dashed lines represent the photospheric emission level. The corresponding disk parameter sets are listed in Table 3. The Spitzer/IRS spectra, when available, are taken into account by fitting the subjacent continuum. Since our goal is to characterize the overall structure of the disks, we therefore did not attempt to reproduce the exact shape of the silicate feature, which is mainly related to silicate mineralogy of the dust in the disk atmosphere (e.g., Bouwman et al. 2008; Olofsson et al. 2010). We emphasize that the best fits presented here cannot be considered as a unique solution because of the degeneracy of SED models. Despite this, previous studies have shown that modeling SEDs with broad wavelength coverage can constrain the mass and geometry of disks around BDs (e.g., Harvey et al. 2012a,b; Olofsson et al. 2013; Spezzi et al. 2013). In particular, the Bayesian inference can analyze the potential correlations and interplay between different parameters in a statistical way (e.g., Pinte et al. 2008). We derived the Bayesian probability distributions of the disk parameters, from which we calculated the most probable values and estimated the validity ranges for each parameter, corresponding to regions where P> 0.5 × PMax (e.g., Liu et al. 2015). The gray lines in Fig. 3 denote all the models that are within the validity ranges.
5. Discussion
We reanalyzed the Herschel/PACS data of a sample of 55 BDs and very low-mass stars in a homogeneous way and constructed their observed SEDs by complementing our Herschel photometry with previous flux measurements available at wavelengths ranging from optical to (sub)millimeter. For the 46 targets that show IR excess emission, we characterized the properties of their surrounding disks using radiative transfer technique under identical assumptions for the modeling setup. Moreover, we evaluated the constraints on different disk parameters through Bayesian analysis.
Despite the good wavelength coverage of observations and efforts to reduce the degree of freedom, the degeneracy of SED models still exists. Therefore, we statistically analyzed the most probable results from Bayesian statistics, other than the best-fit models because the former case is likely more representative of the overall fitting quality. The most probable parameter sets for each target are identified as the peak of Bayesian probability distribution. The derived values are summarized in Table 3.
5.1. Overview of modeling results
We characterized the studied disks by determining their inner radii Rin, flaring indices β, scale heights H100, disk masses Mdisk, and inclinations i. The results are listed in Table 3. We give an overview of the statistical behavior of these properties in the following.
The disk inner radius can be well constrained for all objects because the observed SEDs are well sampled in the near- and mid-IR domains. The inner radii of the disks are likely close to the dust sublimation radii rsub, which are of the order of [0.005−0.05 AU] from the faintest to the brightest targets in our sample. We found four candidates of BD transition disks with Rin> 20 rsub, i.e., source 22 (J04302365+2359129), source 24 (KPNO 9), source 25 (J04361030+2159364), and source 29 (J04221332+1934392). Current data indicate no detectable excess shortward of 12 μm accompanying with a steep slope in the mid-IR of these four objects. However, none of them is detected at Herschel/PACS bands. Follow-up observations, in particular spatially resolved millimeter images, are required to clarify their evolutionary stages (e.g., Williams & Cieza 2011; Andrews et al. 2011). The inclination of the disk cannot be constrained very well with the available SED data as shown by the flat probability distribution of this parameter nearly for all targets. Accurate determination of disk inclinations requires spatially resolved observations (e.g., Chiang & Goldreich 1999; Robitaille et al. 2007).
The geometric structure of the disk is described by the flaring index β and scale height H100 according to the model ansatz, see Sect. 4.2. Our detailed SED analysis places tight constraints on the disk geometry because the best-fit β and H100 are in good agreement with the most probable values (see Table 3) and the probability distribution functions are clearly nonflat for most objects (see the Appendix). We observed a preferential values of β in the range 1.05 − 1.20, while the majority of the target disks are best modeled with H100 of the order of 5 − 20 AU. As shown by Harvey et al. (2012a) and Liu et al. (2015), most parts (except for the inner region) of typical BD disks produce optically thin emission at far-IR wavelengths, demonstrating the applicability of PACS photometry as a diagnosis for the disk mass of BDs. Objects with detections at 70 and/or 160 μm enable reasonable determination of their disk masses, as demonstrated by clear peaks in the Bayesian probability distributions of Mdisk in these cases. For the remaining targets, the disk mass is not well constrained, typically showing two or three indistinguishable peaks in the probability distributions. Overall, the likely disk masses feature a wide range of [10-6,10-4 M⊙] with a median value of the order of 10-5 M⊙, where we assume the dust properties as described in Sect. 4.2 and a gas-to-dust mass ratio of 100. Our statistical results on the disk parameters of substellar hosts are widely in agreement with previous findings from case studies and surveys, however, for individual sources presented here our measured PACS flux densities and correspondingly the model solutions differ from those of previous works (e.g., Harvey et al. 2012a,b; Riaz & Gizis 2012; Alves de Oliveira et al. 2013; Joergens et al. 2012, 2013; Spezzi et al. 2013). A few BDs detected at (sub)millimeter to date and their model explanations also support our results on the typical structural properties, especially the mass of BD disks (e.g., Klein et al. 2003; Scholz et al. 2006; Mohanty et al. 2013; Ricci et al. 2012, 2013, 2014; Broekhoven-Fiene et al. 2014).
5.2. Comparison with disks around young stellar objects
Comparing the derived disk properties with those of their higher mass counterparts, such as T Tauri disks, can provide important insights into understanding the formation of BDs and very low-mass stars. Several attempts have been made in this direction (e.g., Pascucci et al. 2009; Szűcs et al. 2010). Plenty of multiwavelength data, including spatially resolved data, exist for young stellar objects, leading to robust constraints on the structure and mass of their disks. In particular, coherent multiwavelength modeling suggests a typical flaring index β ~ 1.25 and a favorable range 5 − 20 AU of H100 for T Tauri disks (e.g., Wolf et al. 2003; Walker et al. 2004; Sauter et al. 2009; Madlener et al. 2012; Gräfe et al. 2013; Garufi et al. 2014). Based on (sub)millimeter measurements of a large sample of young stellar objects in various star formation regions, the disk masses of T Tauri stars are found in the range of [10-3,10-1 M⊙] (e.g., Andrews & Williams 2007; Lee et al. 2011; Sicilia-Aguilar et al. 2011; Andrews et al. 2013; Carpenter et al. 2014).
We found significant evidence for different properties of disks between sun-like and cool stars, showing that disks around BDs and very low-mass stars are generally flatter and orders of magnitude less massive than T Tauri disks. Although similar conclusions were drawn by previous studies (Pascucci et al. 2009; Szűcs et al. 2010; Olofsson et al. 2013), the evidence we found should be more significant because our results are based for the first time on a homogenous analysis from Herschel data reduction and flux density measurement, to SED modeling, and interpretation. Theoretical models predict that disks around cooler stars should be more extended in the vertical direction (Walker et al. 2004). However, our results, together with previous studies (e.g., Harvey et al. 2012a; Alves de Oliveira et al. 2013; Olofsson et al. 2013), indicate that the disk scale height is independent of the host stellar mass. Dust growth and settling are the two pivotal physical processes simultaneously shaping the disk structure, for instance, reducing the disk scale height (D’Alessio et al. 2006). Mid-IR observations have shown that these processes probably occur in early stages of the disk evolution (e.g., Furlan et al. 2006; McClure et al. 2010). Given the broad age spread, our targets may be at different evolutionary stages during which the degrees of dust growth and settling are not at the same level. This will probably weaken any relation, if present, between the scale height and the (sub)stellar mass. Nevertheless, analyses of coeval samples, for example in Cha I (Olofsson et al. 2013) and ρ Oph (Alves de Oliveira et al. 2013), also indicate that disk scale heights are comparable in both sun-like stars and BDs. Future high-resolution (sub)millimeter observations are indispensable to quantify the degree of dust settling and better constrain the disk scale height (e.g., Sauter et al. 2009; Boehler et al. 2013).
5.3. Dependence of disk parameters on the mass of substellar hosts
There is growing observational evidence that disk evolution depends on the mass of the central object. For example, the primordial dust disks are believed to live longer for cool stars, because the observed disk frequency of cool stars and BDs is higher in comparison with sun-like stars (e.g., Carpenter et al. 2006; Scholz et al. 2007; Riaz & Gizis 2008; Bayo et al. 2012; Ribas et al. 2015). The observed trend of small disk accretion rates of BDs indicates that the scaling between the accretion rate and stellar mass (i.e., 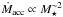 ), deduced mainly from low- and intermediate-mass stars extends to the substellar mass spectrum (e.g., Muzerolle et al. 2005; Mohanty et al. 2005; Herczeg et al. 2009; Bayo et al. 2012). Analysis of Spitzer/IRS spectra demonstrates that the dust processing, such as grain growth and crystallization, in the mid-IR emitting regions of BDs and very low-mass stars appears to be more advanced than in disks around sun-like stars with similar age (e.g., Apai et al. 2005; Pascucci et al. 2009; Riaz 2009). Moreover, Pascucci et al. (2013) also found stellar-mass-dependencies in the atomic and molecular content of disk atmospheres.
), deduced mainly from low- and intermediate-mass stars extends to the substellar mass spectrum (e.g., Muzerolle et al. 2005; Mohanty et al. 2005; Herczeg et al. 2009; Bayo et al. 2012). Analysis of Spitzer/IRS spectra demonstrates that the dust processing, such as grain growth and crystallization, in the mid-IR emitting regions of BDs and very low-mass stars appears to be more advanced than in disks around sun-like stars with similar age (e.g., Apai et al. 2005; Pascucci et al. 2009; Riaz 2009). Moreover, Pascucci et al. (2013) also found stellar-mass-dependencies in the atomic and molecular content of disk atmospheres.
Searching for evidence of stellar-mass-dependent disk properties is very common and interesting, because it has important implications for planet formation theories. Szűcs et al. (2010) divided ~ 200 young stellar objects and BDs in the Chamaeleon I star-forming region into two groups with SpTs earlier or later than ~M4.5. Through modeling the median SEDs (longward of MIPS 24 μm) of these two groups, they found that the disk is on average flatter in the lower stellar mass group than in the group with higher stellar masses. Based on Spitzer data, several other works hinted at similar results (e.g., Riaz et al. 2012). As laid out in Sect. 5.2, our results derived by including the Herschel far-IR observations evince the same tendency. Note that this is a statistical behavior shown from the ensemble of the 46 modeled very low-mass stars and BDs.
 |
Fig. 4 Flaring index β (top) and scale height H100 (bottom) as a function of SpT. We found that β decreases clearly from early-type BDs to late-type BDs (top), while H100 appears independent of the spectral type in the BD regime. The inserted diagrams in each panel show the histograms of these two parameters calculated for targets that belong to the ETBD and LTBD groups, respectively. The vertical dashed lines symbolize the criterion (i.e., M8) used to divide the targets, see Sect. 2. Blue dots represent objects located in clusters with ages < 5 Myr, whereas the red dots refer to older (≳ 5 Myr) targets. The blue square in the upper panel points to the obvious outlier target (OTS 44) of the observed relation. For better representation, slight changes in either the SpT or disk parameters are made for objects with a pair of identical values. |
As a further step toward examining whether the trends of disk properties extend to the low end of the substellar mass regime, we performed a detailed comparison of the fitted disk geometry parameters between the ETBD and LTBD groups, as introduced in Sect. 2. These results are illustrated in Fig. 4, in which the upper panel shows a clear decrease of disk flaring from early- to late-type BDs, with a typical dispersion of the order of ~ 0.1. The histogram inside the figure confirms the relationship between the flaring index β and SpT. In particular, the median value of β is 1.10 in the LTBD group, while the ETBD group features a higher median value of 1.175. The mean value of β is also found to be smaller in the LTBD group, i.e., βmean = 1.10, as compared to βmean = 1.16 for the ETBD group. The difference in the median/mean disk flaring between the two groups is Δ β ~ 0.07, which is about three times the step size for this dimension used to build the model grid. The lower β of cooler BDs suggests that disk flaring is very sensitive to far-IR photometry because the LTBD group is generally fainter at 70 μm, see Sect. 3.3. OTS 44, an M9.5 BD with an estimated mass of ~ 12 MJup in the Cha I star-forming region (Bonnefoy et al. 2014), is an obvious outlier of the observed relation; see the blue square in the upper panel of Fig. 4. The significant IR excess, together with a rising SED from 24 to 70 μm, require a highly flared disk to reproduce the data (Joergens et al. 2013, 2015, this work). We note that our remeasurement of the Herschel/PACS flux densities of OTS 44 leads to a slightly smaller disk mass of 3.2 × 10-5 M⊙ (~ 10 M⊕; Joergens et al. 2015, this work) compared to a previous estimate (~ 30 M⊕; Joergens et al. 2013) based on the photometry given by Harvey et al. (2012a). VLT/SINFONI spectra revealed active mass accretion for this extremely low-mass object (Joergens et al. 2013), suggesting that OTS 44’s disk is probably at its early stage of evolution, during which dust settling (a key role of reducing β) has not yet proceeded very far. The observed SpT − β dependency is unlikely a bias of the mixed ages and evolutionary stages of the sample, since both the young (<5 Myr, blue points) and old (≳5 Myr, red points) subgroups show the same tendency, see Fig. 4.
As shown in the lower panel of Fig. 4, there is no clear trend visible in the distribution of scale height. The median or mean values of H100 are close to each other for both the ETBD and LTBD groups, i.e., H100 ~ 14 AU. This means that the independency of H100 on SpT is also found in the low-mass substellar regime. The disk scale height varies like H ∝ ( ⟨ Td ⟩ /M⋆)0.5 if the hydrostatic equilibrium between the dust and gas phases is assumed, where ⟨ Td ⟩ is the density weighted mean dust temperature. Andrews et al. (2013) found that ⟨ Td ⟩ scales with the host stellar luminosity basically according to ⟨ Td ⟩ ≈ 25(L⋆/L⊙)1 / 4 K. The stellar luminosities 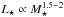 in their sample covers the substellar regime. This suggests that the correlation between the scale height and M⋆ may not be intrinsically tight. The scaling between the scale height and M⋆ highly depends on the detailed coupling (i.e., dust settling) between the gas and small dust grains, which is very complicated and has to be investigated with future high-resolution (sub-)millimeter observations (e.g., Sauter et al. 2009; Boehler et al. 2013).
in their sample covers the substellar regime. This suggests that the correlation between the scale height and M⋆ may not be intrinsically tight. The scaling between the scale height and M⋆ highly depends on the detailed coupling (i.e., dust settling) between the gas and small dust grains, which is very complicated and has to be investigated with future high-resolution (sub-)millimeter observations (e.g., Sauter et al. 2009; Boehler et al. 2013).
The median disk masses for both the ETBD and LTBD groups are Mdisk = 10-5 M⊙, a value essentially consistent with that given by Harvey et al. (2012a). As shown in Fig. 5, we did not find an obvious correlation between the disk mass and SpT (as a proxy for the mass of the central object) in the BD mass regime, which seems to deviate from the speculation from the tight correlation between the PACS 70 μm flux density and SpT shown by Liu et al. (2015). This is probably due to one or more of the following reasons: (1) the constraints on the disk mass are mostly from the 70 μm photometry in our study. However, only 52% (i.e., 11/21) of the modeled LTBD objects are detected at 70 μm, whereas the detection rate is 88% (i.e., 22/25) for the ETBD group, see Table 1. The (most probable) disk masses of the undetected sources are very uncertain, potentially preventing the underlying correlation, if present, from showing up. (2) The conversion from PACS 70 μm flux density to disk mass is not straightforward. On the one hand, the target disks are not completely optically thin at PACS wavelengths (Harvey et al. 2012a), and on the other hand, 70 μm is not in the clear Rayleigh-Jeans tail of the SED. (3) Our correlation analysis is based on a sample of targets that span a wide range of ages. Therefore, the targets are probably at different evolutionary stages, which may weaken any relation between the (sub)stellar and disk masses. Beside the issue of incompleteness of our sample selection in each cloud, the detection bias can also affect the correlation because more distant clouds have a worse sensitivity to disk mass compared to closer siblings.
 |
Fig. 6 Left panels: median SEDs of Class II ETBDs (upper) and LTBDs (lower) in the Taurus molecular cloud. The dots depict the median flux densities at various bands. The upside down triangles show that the median flux densities at the corresponding wavelengths are treated as upper limits. The best-fit models are indicated with solid lines, whereas the dashed lines mark the photospheric emission levels. In the fitting procedure, the disk scale height H100 and inclination i are fixed to 14 AU and 45°, respectively. The parameter set of the best model in the upper panel: Rin = 0.09 AU, Mdisk = 3 × 10-5 M⊙, β = 1.16. The parameter values of the best model in the lower panel: Rin = 0.03 AU, Mdisk = 5 × 10-6 M⊙, β = 1.14. Right panels: 2D contour plots of the χ2 function projected over disk mass Mdisk and flaring index β. Contours with different shades of red are drawn at the 68%, 90%, 95% 2D confidence intervals. The blue stars represent the best-fit disk models. The hashed regions correspond to models that overpredict the upper limits of the median flux density. |
To further investigate the Mdisk − SpT relation in the substellar mass regime, we compile the median SEDs of Class II Taurus sources with SpTs lying in the same range defined in our sample selection. Our compilation is entirely based on the catalog as reported by Bulger et al. (2014). We only consider sources that have flux density measurements including upper limits available at all the 2MASS J/H/K bands, four IRAC and WISE bands, MIPS 24 μm, and PACS 70 and 160 μm. With this criterion, there are in total 32 targets entering in the analysis. Twenty-five sources are ETBDs, whereas seven targets are LTBDs. The Kaplan-Meier product-limit estimator is used to properly account for upper limits, if encountered, in the estimation of median flux density. All the PACS flux densities are taken from Bulger et al. (2014) for homogeneity, although we reperformed photometry for some Taurus targets. The median SEDs of Taurus ETBDs and LTBDs are shown as blue dots in Fig. 6. An important result is that the median F70 = 36 mJy of Taurus ETBD group is at least 12 times larger than that of the Taurus LTBDs, i.e., F70< 3 mJy. The difference in 70 μm flux density between early- and late-type targets becomes significantly larger in coeval planet-forming disks as compared to the result from our sample of objects with different ages; see Sect. 3.3. We fit the median SEDs using the disk and dust models, as described in Sect. 4.2. As we discussed above, the disk scale height H100 is independent on SpT. Hence, we fixed H100 to 14 AU, i.e., the aforementioned median value of H100 of our sample. The disk inclination i was set to 45° because SED modeling cannot provide tight constraints on this parameter. These assumptions were made to further reduce the model degeneracy, and therefore to focus on the parameter study between β, Mdisk and SpT. Figure 6 shows the fitting results and 2D contour plots of the χ2 function projected over Mdisk and β. The flaring index β is not well constrained in Taurus LTBD group, with probable values extending to a lower level than in the case of Taurus ETBDs. This may be an indicator that disks around lower mass objects are indeed less flared in general. The best-fit value together with the confidence intervals clearly indicate that Taurus ETBDs are very likely more massive than Taurus LTBDs, which appears discrepant with the theoretical predictions of disk fragmentation models (Stamatellos & Herczeg 2015). However, further efforts are highly desired to clarify this issue given the fact that the disk mass presented here is roughly estimated with far-IR data. With its unprecedented performance, ALMA can observe very faint disks at longer wavelength and provide robust measurement of disk mass (e.g., Ricci et al. 2014), so as to testify whether the BD disks obey the same Mdisk − SpT scaling law to the corresponding relations established for higher mass stars.
6. Summary
We reprocessed the Herschel/PACS data and measured the 70 and 160 μm flux density for a sample of 55 BDs and very low-mass stars with SpT ranging from M5.5 to L0. Supplemented with previous observations at shorter and (sub-)millimeter wavelengths, we constructed their broadband SEDs with extended wavelength coverage, providing a valuable opportunity to characterize the disk properties in the substellar mass regime. We divided our sample into two groups, i.e., an ETBD and LTBD group that consists of targets with SpT earlier or later than M8. We found significant differences in the cumulative distributions of the flux densities between these two groups. In particular, the ETBD group features a median 70 μm flux density at 100 pc, which is at least three times higher than that of the other group. We studied the dependence of disk properties on the SpT (as a proxy for the mass) of the central object down to the low-mass BD regime and even entering the planetary regime. This knowledge is important for us to understand the formation mechanism of BDs and to improve the planet formation models. Unlike previous studies, our analysis is homogeneous all the way from Herschel/PACS data reduction and flux density measurement to SED modeling within the substellar regime.
For the 46 objects that show IR excess above the photospheric emission, we performed detailed SED analysis using self-consistent radiative transfer models. We introduced as few free parameters as possible in the fitting procedure to reduce the model degeneracy. The statistics based on the entire sample shows that the disk flaring of BDs and very low-mass stars is indeed smaller than that of their higher mass counterparts like T Tauri disks, the disk mass is orders of magnitude lower than the typical value found in T Tauri stars, and the scale height is independent on the mass of the central object. Moreover, we systematically compared the modeling results from Bayesian analysis between the ETBD and LTBD groups and found similar trends of flaring index as a function of SpT. The disk scale heights are comparable in both the high-mass and very low-mass BDs. Both groups feature a similar median disk mass and no clear trend is visible in the distribution, probably because of the uncertainty in translating the PACS photometry into disk mass, the detection bias, and the difference in evolutionary stage among the targets. Future deeper far-IR surveys and ALMA observations are required to improve constraints on the underlying morphology of the relationship between the stellar and disk properties in the low-end stellar mass regime.
Online material
Appendix A: Bayesian probability distributions of selected disk parameters for each modeled object
 |
Fig. A.1 Bayesian probability distributions of β, H100 and Mdisk for each object. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
Acknowledgments
We acknowlegde helpful discussions about Herschel/PACS observations with Ulrich Klaas and Hendrik Linz. Y.L. acknowledges the support by the Natural Science Foundation of Jiangsu Province (Grant No. BK20141046). This work is supported by the Strategic Priority Research Program “The Emergence of Cosmological Structures” of the Chinese Academy of Sciences, Grant No. XDB09000000. A.B. acknowledges financial support from the Proyecto Fondecyt de Iniciación 11140572. M.N. is funded by the Deutsches Zentrum für Luft- und Raumfahrt (DLR). This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. PACS was developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/ OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain).
References
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2012, ApJS, 203, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, F., Homeier, D., Freytag, B., & Sharp, C. M. 2012, in EAS PS 57, eds. C. Reylé, C. Charbonnel, & M. Schultheis, 3 [Google Scholar]
- Allen, P. R., Luhman, K. L., Myers, P. C., et al. 2007, ApJ, 655, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Alves de Oliveira, C., Moraux, E., Bouvier, J., et al. 2010, A&A, 515, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves de Oliveira, C., Ábrahám, P., Marton, G., et al. 2013, A&A, 559, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., & Williams, J. P. 2007, ApJ, 671, 1800 [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Apai, D., Pascucci, I., Bouwman, J., et al. 2005, Science, 310, 834 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Ardila, D., Martín, E., & Basri, G. 2000, AJ, 120, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Artymowicz, P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Audard, M., Ábrahám, P., Dunham, M. M., et al. 2014, Protostars and Planets VI, 387 [Google Scholar]
- Balog, Z., Müller, T., Nielbock, M., et al. 2014, Exp. Astron., 37, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baraffe, I., Chabrier, G., Barman, T. S., Allard, F., & Hauschildt, P. H. 2003, A&A, 402, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrado Y Navascués, D. 2006, A&A, 459, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Bromm, V. 2003, MNRAS, 339, 577 [NASA ADS] [CrossRef] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado Y Navascués, D., et al. 2008, A&A, 492, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Barrado, D., Huélamo, N., et al. 2012, A&A, 547, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bayo, A., Rodrigo, C., Barrado, D., et al. 2014, in ASI Conf. Ser., 11, 93 [Google Scholar]
- Boehler, Y., Dutrey, A., Guilloteau, S., & Piétu, V. 2013, MNRAS, 431, 1573 [NASA ADS] [CrossRef] [Google Scholar]
- Bonnefoy, M., Chauvin, G., Lagrange, A.-M., et al. 2014, A&A, 562, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwman, J., Henning, T., Hillenbrand, L. A., et al. 2008, ApJ, 683, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Bouy, H., Martín, E. L., Brandner, W., et al. 2006, A&A, 451, 177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouy, H., Huélamo, N., Pinte, C., et al. 2008, A&A, 486, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Briceño, C., Luhman, K. L., Hartmann, L., Stauffer, J. R., & Kirkpatrick, J. D. 2002, ApJ, 580, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Broekhoven-Fiene, H., Matthews, B., Duchêne, G., et al. 2014, ApJ, 789, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Bulger, J., Patience, J., Ward-Duong, K., et al. 2014, A&A, 570, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cambresy, L., Epchtein, N., Copet, E., et al. 1997, A&A, 324, L5 [NASA ADS] [Google Scholar]
- Canty, J. I., Lucas, P. W., Roche, P. F., & Pinfield, D. J. 2013, MNRAS, 435, 2650 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Mamajek, E. E., Hillenbrand, L. A., & Meyer, M. R. 2006, ApJ, 651, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M., Ricci, L., & Isella, A. 2014, ApJ, 787, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., Johansen, A., Janson, M., & Rafikov, R. 2014, Protostars and Planets VI, 619 [Google Scholar]
- Chauvin, G., Lagrange, A.-M., Dumas, C., et al. 2004, A&A, 425, L29 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1999, ApJ, 519, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, F., Spezzi, L., & López Martí, B. 2009, A&A, 500, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Cutri et al., R. M. 2012, VizieR Online Data Catalog: II/311 [Google Scholar]
- D’Alessio, P., Calvet, N., Hartmann, L., Franco-Hernández, R., & Servín, H. 2006, ApJ, 638, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Damjanov, I., Jayawardhana, R., Scholz, A., et al. 2007, ApJ, 670, 1337 [NASA ADS] [CrossRef] [Google Scholar]
- DENIS Consortium 2005, VizieR Online Data Catalog: II/263 [Google Scholar]
- Dorschner, J., Begemann, B., Henning, T., Jaeger, C., & Mutschke, H. 1995, A&A, 300, 503 [NASA ADS] [Google Scholar]
- Ducourant, C., Teixeira, R., Galli, P. A. B., et al. 2014, A&A, 563, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Feigelson, E. D., & Nelson, P. I. 1985, ApJ, 293, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, A., Ray, T. P., Cabrit, S., et al. 2014, Protostars and Planets VI, 451 [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Furlan, E., Hartmann, L., Calvet, N., et al. 2006, ApJS, 165, 568 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Furlan, E., Watson, D. M., McClure, M. K., et al. 2009, ApJ, 703, 1964 [NASA ADS] [CrossRef] [Google Scholar]
- Garufi, A., Podio, L., Kamp, I., et al. 2014, A&A, 567, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gizis, J. E. 2002, ApJ, 575, 484 [NASA ADS] [CrossRef] [Google Scholar]
- Gräfe, C., Wolf, S., Guilloteau, S., et al. 2013, A&A, 553, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guieu, S., Pinte, C., Monin, J.-L., et al. 2007, A&A, 465, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guilloteau, S., Dutrey, A., Piétu, V., & Boehler, Y. 2011, A&A, 529, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gully-Santiago, M. A., Allers, K. N., & Jaffe, D. T. 2011, in 16th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. C. Johns-Krull, M. K. Browning, & A. A. West, ASP Conf. Ser., 448, 633 [Google Scholar]
- Harvey, P. M., Henning, T., Liu, Y., et al. 2012a, ApJ, 755, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Henning, T., Ménard, F., et al. 2012b, ApJ, 744, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Henning, T., Liu, Y., & Wolf, S. 2014, ApJ, 795, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., Cruz, K. L., & Hillenbrand, L. A. 2009, ApJ, 696, 1589 [Google Scholar]
- Isella, A., Carpenter, J. M., & Sargent, A. I. 2009, ApJ, 701, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Jäger, C., Mutschke, H., Begemann, B., Dorschner, J., & Henning, T. 1994, A&A, 292, 641 [NASA ADS] [Google Scholar]
- Jäger, C., Mutschke, H., & Henning, T. 1998, A&A, 332, 291 [NASA ADS] [Google Scholar]
- Joergens, V., Pohl, A., Sicilia-Aguilar, A., & Henning, T. 2012, A&A, 543, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joergens, V., Bonnefoy, M., Liu, Y., et al. 2013, A&A, 558, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joergens, V., Bonnefoy, M., Liu, Y., Bayo, A., & Wolf, S. 2015, in Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun 18, eds. G. T. van Belle, & H. C. Harris, Proc. of Lowell Observatory, 1019 [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirchschlager, F., & Wolf, S. 2014, A&A, 568, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klein, R., Apai, D., Pascucci, I., Henning, T., & Waters, L. B. F. M. 2003, ApJ, 593, L57 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, N., Williams, J. P., & Cieza, L. A. 2011, ApJ, 736, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, M. C., Najita, J., & Tokunaga, A. T. 2003, ApJ, 585, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Madlener, D., Wolf, S., Wang, H., & Ruge, J. P. 2012, A&A, 546, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Y., Madlener, D., Wolf, S., & Wang, H.-C. 2013, Res. Astronom. Astrophys., 13, 420 [Google Scholar]
- Liu, Y., Herczeg, G. J., Gong, M., et al. 2015, A&A, 573, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L. 2004, ApJ, 602, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L. 2006, ApJ, 645, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L. 2007, ApJS, 173, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Peterson, D. E., & Megeath, S. T. 2004, ApJ, 617, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Adame, L., D’Alessio, P., et al. 2005a, ApJ, 635, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., D’ Alessio, P., Calvet, N., et al. 2005b, ApJ, 620, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Whitney, B. A., Meade, M. R., et al. 2006, ApJ, 647, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Allen, L. E., Allen, P. R., et al. 2008, ApJ, 675, 1375 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., Mamajek, E. E., Allen, P. R., & Cruz, K. L. 2009, ApJ, 703, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Madlener, D., Wolf, S., Dutrey, A., & Guilloteau, S. 2012, A&A, 543, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martín, E. L., Delfosse, X., & Guieu, S. 2004, AJ, 127, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, G. S., Pinte, C., Duchêne, G., Williams, J. P., & Ménard, F. 2013, A&A, 558, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClure, M. K., Furlan, E., Manoj, P., et al. 2010, ApJS, 188, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Jayawardhana, R., & Basri, G. 2005, ApJ, 626, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., Greaves, J., Mortlock, D., et al. 2013, ApJ, 773, 168 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Luhman, K. L., Briceño, C., Hartmann, L., & Calvet, N. 2005, ApJ, 625, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, J., Augereau, J.-C., van Dishoeck, E. F., et al. 2010, A&A, 520, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Olofsson, J., Szűcs, L., Henning, T., et al. 2013, A&A, 560, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Papaloizou, J., & Pringle, J. E. 1977, MNRAS, 181, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Apai, D., Luhman, K., et al. 2009, ApJ, 696, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Pascucci, I., Herczeg, G., Carr, J. S., & Bruderer, S. 2013, ApJ, 779, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Pecaut, M. J., Mamajek, E. E., & Bubar, E. J. 2012, ApJ, 746, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Phan-Bao, N., Riaz, B., Lee, C.-F., et al. 2008, ApJ, 689, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Pinte, C., Padgett, D. L., Ménard, F., et al. 2008, A&A, 489, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reipurth, B. 2008a, Handbook of Star Forming Regions, Volume I: The Northern Sky (Astronomical Society of the Pacific) [Google Scholar]
- Reipurth, B. 2008b, Handbook of Star Forming Regions, Volume II: The Southern Sky (Astronomical Society of the Pacific) [Google Scholar]
- Reipurth, B., & Clarke, C. 2001, AJ, 122, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Riaz, B. 2009, ApJ, 701, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Riaz, B., & Gizis, J. E. 2008, ApJ, 681, 1584 [NASA ADS] [CrossRef] [Google Scholar]
- Riaz, B., & Gizis, J. E. 2012, A&A, 548, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riaz, B., Honda, M., Campins, H., et al. 2012, MNRAS, 420, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, Á., Bouy, H., & Merín, B. 2015, A&A, 576, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., Scholz, A., & de Gregorio-Monsalvo, I. 2012, ApJ, 761, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Isella, A., Carpenter, J. M., & Testi, L. 2013, ApJ, 764, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2014, ApJ, 791, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Rigliaco, E., Natta, A., Randich, S., et al. 2011, A&A, 526, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigliaco, E., Natta, A., Testi, L., et al. 2012, A&A, 548, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJS, 169, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Sauter, J., Wolf, S., Launhardt, R., et al. 2009, A&A, 505, 1167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, R. S., & Oliver, S. 2007, ApJ, 661, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, R.-D., McCaughrean, M. J., Zinnecker, H., & Lodieu, N. 2005, A&A, 430, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scholz, A., Jayawardhana, R., & Wood, K. 2006, ApJ, 645, 1498 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, A., Jayawardhana, R., Wood, K., et al. 2007, ApJ, 660, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Sherry, W. H., Walter, F. M., & Wolk, S. J. 2004, AJ, 128, 2316 [NASA ADS] [CrossRef] [Google Scholar]
- Sicilia-Aguilar, A., Henning, T., Dullemond, C. P., et al. 2011, ApJ, 742, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Slesnick, C. L., Carpenter, J. M., Hillenbrand, L. A., & Mamajek, E. E. 2006, AJ, 132, 2665 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzi, L., Alcalá, J. M., Covino, E., et al. 2008, ApJ, 680, 1295 [NASA ADS] [CrossRef] [Google Scholar]
- Spezzi, L., Cox, N. L. J., Prusti, T., et al. 2013, A&A, 555, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stamatellos, D., & Herczeg, G. J. 2015, MNRAS, 449, 3432 [NASA ADS] [CrossRef] [Google Scholar]
- Stamatellos, D., & Whitworth, A. 2011, in Computational Star Formation, eds. J. Alves, B. G. Elmegreen, J. M. Girart, & V. Trimble, IAU Symp., 270, 223 [Google Scholar]
- Szűcs, L., Apai, D., Pascucci, I., & Dullemond, C. P. 2010, ApJ, 720, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Todorov, K. O., Luhman, K. L., Konopacky, Q. M., et al. 2014, ApJ, 788, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, C., Wood, K., Lada, C. J., et al. 2004, MNRAS, 351, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Wilking, B. A., Greene, T. P., & Meyer, M. R. 1999, AJ, 117, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Wilking, B. A., Meyer, M. R., Robinson, J. G., & Greene, T. P. 2005, AJ, 130, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S. 2003, Comput. Phys. Comm., 150, 99 [Google Scholar]
- Wolf, S., Padgett, D. L., & Stapelfeldt, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Our Herschel/PACS flux densities at 70 μm (upper panel) and 160 μm (lower panel) as compared to previous results. The red dots depict real detections identified by both our work and previous works, whereas green marks consisting of leftward and downward arrows symbolize the upper limits. The black squares with downward arrows and blue squares with leftward arrows show detections by our study and previous works, respectively. |
| In the text | |
 |
Fig. 2 Cumulative distribution of the 70 μm flux density for early-type brown dwarfs (ETBDs, blue) and late-type brown dwarfs (LTBDs, red). All flux densities are scaled assuming a distance of 100 pc. The median values are indicated as vertical dashed lines. |
| In the text | |
 |
Fig. 3 Spectral energy distributions of the target disks. The dots depict the photometry at various wavelengths. Spitzer/IRS spectra are indicated with red lines. The upside down triangles show the 3σ upper limits of the flux density. The best-fit models are indicated with black solid lines, whereas the dashed lines represent the photospheric emission levels. The gray lines denote all probable model fits that are derived by Bayesian analysis, showing the strength of constraints of the best-fit models for each object, see Sect. 4.3. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 3 continued. |
| In the text | |
 |
Fig. 4 Flaring index β (top) and scale height H100 (bottom) as a function of SpT. We found that β decreases clearly from early-type BDs to late-type BDs (top), while H100 appears independent of the spectral type in the BD regime. The inserted diagrams in each panel show the histograms of these two parameters calculated for targets that belong to the ETBD and LTBD groups, respectively. The vertical dashed lines symbolize the criterion (i.e., M8) used to divide the targets, see Sect. 2. Blue dots represent objects located in clusters with ages < 5 Myr, whereas the red dots refer to older (≳ 5 Myr) targets. The blue square in the upper panel points to the obvious outlier target (OTS 44) of the observed relation. For better representation, slight changes in either the SpT or disk parameters are made for objects with a pair of identical values. |
| In the text | |
 |
Fig. 5 Disk mass Mdisk as a function of SpT. The symbols are the same as in Fig. 4. |
| In the text | |
 |
Fig. 6 Left panels: median SEDs of Class II ETBDs (upper) and LTBDs (lower) in the Taurus molecular cloud. The dots depict the median flux densities at various bands. The upside down triangles show that the median flux densities at the corresponding wavelengths are treated as upper limits. The best-fit models are indicated with solid lines, whereas the dashed lines mark the photospheric emission levels. In the fitting procedure, the disk scale height H100 and inclination i are fixed to 14 AU and 45°, respectively. The parameter set of the best model in the upper panel: Rin = 0.09 AU, Mdisk = 3 × 10-5 M⊙, β = 1.16. The parameter values of the best model in the lower panel: Rin = 0.03 AU, Mdisk = 5 × 10-6 M⊙, β = 1.14. Right panels: 2D contour plots of the χ2 function projected over disk mass Mdisk and flaring index β. Contours with different shades of red are drawn at the 68%, 90%, 95% 2D confidence intervals. The blue stars represent the best-fit disk models. The hashed regions correspond to models that overpredict the upper limits of the median flux density. |
| In the text | |
 |
Fig. A.1 Bayesian probability distributions of β, H100 and Mdisk for each object. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


