| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 15 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425405 | |
| Published online | 20 July 2015 | |
Infrared-faint radio sources remain undetected at far-infrared wavelengths
Deep photometric observations using the Herschel Space Observatory⋆
1 Astronomisches Institut, Ruhr-Universität Bochum, Universitätsstr. 150, 44801 Bochum, Germany
e-mail: herzog@astro.rub.de
2 Macquarie University, Sydney, NSW 2109, Australia
3 CSIRO Astronomy and Space Science, Marsfield, PO Box 76, Epping, NSW 1710, Australia
4 Australian Astronomical Observatory, PO Box 915, North Ryde, NSW 1670, Australia
5 Max-Planck-Institut für Astronomie, Königsstuhl 17, 69117 Heidelberg, Germany
6 Department of Physics, Chong Yeut Ming Physics Building, The University of Hong Kong, Pokfulam Road , Hong Kong
Received: 26 November 2014
Accepted: 27 May 2015
Context. Showing 1.4 GHz flux densities in the range of a few to a few tens of mJy, infrared-faint radio sources (IFRS) are a type of galaxy characterised by faint or absent near-infrared counterparts and consequently extreme radio-to-infrared flux density ratios up to several thousand. Recent studies showed that IFRS are radio-loud active galactic nuclei (AGNs) at redshifts ≳2, potentially linked to high-redshift radio galaxies (HzRGs).
Aims. This work explores the far-infrared emission of IFRS, providing crucial information on the star forming and AGN activity of IFRS. Furthermore, the data enable examining the putative relationship between IFRS and HzRGs and testing whether IFRS are more distant or fainter siblings of these massive galaxies.
Methods. A sample of six IFRS was observed with the Herschel Space Observatory between 100 μm and 500 μm. Using these results, we constrained the nature of IFRS by modelling their broad-band spectral energy distribution (SED). Furthermore, we set an upper limit on their infrared SED and decomposed their emission into contributions from an AGN and from star forming activity.
Results. All six observed IFRS were undetected in all five Herschel far-infrared channels (stacking limits: σ = 0.74 mJy at 100 μm, σ = 3.45 mJy at 500 μm). Based on our SED modelling, we ruled out the following objects to explain the photometric characteristics of IFRS: (a) known radio-loud quasars and compact steep-spectrum sources at any redshift; (b) starburst galaxies with and without an AGN and Seyfert galaxies at any redshift, even if the templates were modified; and (c) known HzRGs at z ≲ 10.5. We find that the IFRS analysed in this work can only be explained by objects that fulfil the selection criteria of HzRGs. More precisely, IFRS could be (a) known HzRGs at very high redshifts (z ≳ 10.5); (b) low-luminosity siblings of HzRGs with additional dust obscuration at lower redshifts; (c) scaled or unscaled versions of Cygnus A at any redshift; and (d) scaled and dust-obscured radio-loud quasars or compact steep spectrum sources. We estimated upper limits on the infrared luminosity, the black hole accretion rate, and the star formation rate of IFRS, which all agreed with corresponding numbers of HzRGs.
Key words: techniques: photometric / galaxies: active / galaxies: high-redshift / galaxies: star formation / infrared: galaxies
© ESO, 2015
1. Introduction
A new class of extreme radio galaxies, which are characterised by their infrared (IR) faintness and their enormous radio-to-IR flux density ratios, has recently been found in deep surveys: the class of infrared-faint radio sources (IFRS; Norris et al. 2006). While various suggestions had been presented to explain the extreme characteristics of these objects, recent observations clearly indicate that IFRS are radio-loud (RL) active galactic nuclei (AGNs) at high redshifts.
Infrared-faint radio sources were first discovered in the Chandra Deep Field South (CDFS) and the European Large Area Infrared space observatory Survey South 1 (ELAIS-S1) field of the Australia Telescope Large Area Survey (ATLAS) by Norris et al. (2006) and Middelberg et al. (2008a), respectively. The radio maps at 1.4 GHz provided detections with flux densities in the order of tenths to tens of mJy, whilst the co-located Spitzer Wide-area Infrared Extragalactic Survey (SWIRE; Lonsdale et al. 2003) showed only a faint or, in most cases, no IR counterpart at 3.6 μm with a noise σ = 1 μJy. Later, Zinn et al. (2011) defined the class of IFRS by two selection criteria:
-
(i)
radio-to-IR flux density ratioS1.4 GHz/S3.6 μm > 500; and
-
(ii)
3.6 μm flux density S3.6 μm < 30 μJy.
The enormous radio-to-IR flux density ratios imply that IFRS are clear outliers from the radio-IR correlation. The second criterion implicates a distance selection, preventing ordinary objects of redshift ≲1.4 from being included in the class of IFRS. In addition to the detections by Norris et al. (2006) and Middelberg et al. (2008a), IFRS were later found in the Spitzer extragalactic First Look Survey (xFLS) field by Garn & Alexander (2008), in the Cosmological Evolution Survey (COSMOS) by Zinn et al. (2011), in the European Large Area IR space observatory Survey North 1 (ELAIS-N1) by Banfield et al. (2011), and in the Lockman Hole field by Maini et al. (2015). In total, around 100 IFRS have been found in these deep fields at a sky density of a few per square degree.
Recently, Collier et al. (2014) found 1317 IFRS in shallow all-sky catalogues, that satisfied both selection criteria given above. They used the Unified Radio Catalog (URC; Kimball & Ivezić 2008) based on the NRAO VLA Sky Suvey (NVSS; Condon et al. 1998) and data from the all-sky Wide-Field Infrared Survey Explorer (WISE; Wright et al. 2010). Collier et al. replaced S3.6 μm by S3.4 μm. All IFRS in that sample provide an IR counterpart at 3.4 μm and have radio flux densities above 7.5 mJy at 1.4 GHz, some of them exceeding 100 mJy. By this, the IFRS in this sample are on average radio-brighter than the IFRS found in the deep fields by around one order of magnitude. Since the WISE sensitivity is non-uniform, Collier et al. could only set a lower limit on the sky density of IFRS with a radio flux density above 7.5 mJy of ~0.1 deg-2.
First attempts to explain the existence of IFRS included lobes or hotspots of radio galaxies, obscured star forming galaxies (SFGs), pulsars or high-redshift RL galaxies. Later results (for an overview, see Collier et al. 2014 and references therein) provided evidence that IFRS are indeed RL AGN at high redshifts.
Norris et al. (2007) and Middelberg et al. (2008b) used very long baseline interferometry (VLBI) to confirm the presence of active nuclei in two IFRS. Recently, Herzog et al. (2015) detected 35 out of 57 IFRS in VLBI observations, unquestionably confirming that at least a significant fraction of all IFRS contains AGN.
Garn & Alexander (2008) and Huynh et al. (2010) present the first spectral energy distribution (SED) modelling of IFRS and find that 3C sources (for example 3C 273) can reproduce the observational data when redshifted to z ≳ 2. Furthermore, Garn & Alexander and Huynh et al. conclude that obscured SFGs cannot explain the characteristics of IFRS since the radio-to-IR flux density ratios of IFRS significantly exceed those of SFGs. This finding suggests the presence of an AGN in IFRS, too.
Recently, the first spectroscopic redshifts of IFRS were found, confirming the suggested high-redshift character of this class of objects. Collier et al. (2014) find 19 redshifts for their all-sky sample of IFRS, all but one in the range 2 <z< 3. The outlier is expected to be a misidentification or an SFG with an AGN in its centre. Herzog et al. (2014) measured redshifts of three IFRS in the deep ATLAS fields based on optical spectroscopy from the Very Large Telescope (VLT) and found them to be in the range 1.8 <z< 2.8. The IFRS with spectroscopic redshifts, both from Collier et al. and Herzog et al., lie at the IR-bright boundary of this class of objects with IR flux densities between 14 μJy and 30 μJy at 3.6 μm or 3.4 μm. Both Collier et al. and Herzog et al. suggest that the IFRS with measured spectroscopic redshifts are the closest ones and that IR-fainter IFRS are at even higher redshifts.
Additionally, the results by Collier et al. (2014) and Herzog et al. (2014) finally disposed of the alternative hypothesis that IFRS are hotspots of spatially separated radio galaxies. If the IR detections were real counterparts of the radio detections, the redshift distribution of these objects would be expected to follow that of Fanaroff Riley type 2 (FRII) galaxies which peaks at z ~ 1. In contrast, if the IR detections were spurious associations to the radio emission, their redshift distribution would be expected to follow that of star forming galaxies, peaking at z ~ 0. Both cases are in clear disagreement with the observed redshift distribution of IFRS, providing redshifts only in the regime 1.8 ≲ z ≲ 3.0.
Based on the redshifts measured in their work, Herzog et al. (2014) present the first redshift-based SED modelling of IFRS. They find the templates of an RL AGN (3C 273) and a compact-steep spectrum (CSS) source (3C 48) in agreement with all available photometric data, while an ultraluminous IR galaxy (ULIRG, Arp 220) or a Seyfert galaxy (Mrk 231) are clearly ruled out.
Huynh et al. (2010) and Middelberg et al. (2011) first pointed out a potential similarity between IFRS and high-redshift radio galaxies (HzRGs). HzRGs are a class of powerful radio galaxies (L3 GHz> 1026 W Hz-1) at high redshifts (z ≥ 1). They are amongst the most massive and most luminous galaxies in the early universe and are expected to be the progenitors of the most massive galaxies in the local universe (e.g. Seymour et al. 2007; De Breuck et al. 2010). Moreover, HzRGs are known to host powerful AGNs and to show high star formation rates (SFRs). Therefore, they are an important tool to study galaxy evolution and the interplay between AGNs and star forming activity. However, HzRGs are rare objects; only around 100 of these objects are known in the entire sky, located at redshifts 1 ≤ z ≲ 5.
Huynh et al. note that IFRS have similar mid-IR to radio flux density ratios to those of HzRGs. Middelberg et al. studied the radio properties of IFRS in the ELAIS-S1 field and find steep radio spectra between 2.3 GHz and 8.4 GHz with a median of α = −1.41 and no index larger than −0.7. This is steeper than the general radio souce population (α = −0.86) and the AGN source population (α = −0.82) in that field. Middelberg et al. find that the radio spectra are even steeper than those of the sample of HzRGs by Seymour et al. (2007), showing a median radio spectral index α = −1.02. HzRGs are the only objects known at significant redshifts sharing the extreme radio-to-IR flux densities of IFRS in the order of thousands as shown by Norris et al. (2011). Furthermore, Norris et al. suggest that IFRS might follow the correlation between 3.6 μm flux density and redshift found for the sample of HzRGs by Seymour et al., similar to the K−z relation for other radio galaxies (Willott et al. 2003).
Collier et al. (2014) and Herzog et al. (2014) tested this hypothesis in the reachable redshift range between 2 and 3 and find IFRS follow this correlation. This adds evidence to the suggestion that IR-fainter IFRS are located at even higher redshift, potentially reaching z ≈ 5 or 6. Furthermore, Herzog et al. show that the radio luminosities of IFRS are in the same range as for HzRGs, although IFRS lie at the lower bound of the radio luminosity distribution of HzRGs.
Besides these similarities between IFRS and HzRGs, there is one significant difference. While HzRGs are rare objects of which only around 100 are known in the entire sky, IFRS are much more abundant. The observed sky density of IFRS in the ATLAS fields is around 5 deg-2; Zinn et al. (2011) estimate a survey-independent sky density of (30.8 ± 15.0) deg-2.
Summarising, there is growing evidence that IFRS are related to HzRGs in the sense that IFRS are fainter, but much more abundant siblings of HzRGs, potentially at even higher redshifts. HzRGs are known to be vigorously forming stars while harbouring AGNs in their centres. Both components dominate the emission of galaxies in the IR regime. Observations at far-infrared (FIR) wavelengths are a key test for the hypothesis that IFRS are related to HzRGs.
Here, we analyse the IR and particularly the FIR regime of IFRS based on Herschel observations. Results in this wavelength range will enable us to further study the suggested link between IFRS and HzRGs.
This paper is organised as follows. In Sect. 2, we describe the sample selection of the observed IFRS and the observations with Herschel. The calibration of the resulting data and the mapping is presented in Sect. 3. In Sect. 4, we describe the photometry and the consequent stacking analysis. We use the resulting flux density upper limits in Sect. 5 for two different modelling approaches. First, we model the broad-band SED of IFRS based on SED templates of known galaxies (Sect. 5.1). In a second approach, we set an upper limit on the IR SED of IFRS in order to constrain their IR emission (Sect. 5.2). Based on the latter fitting, we estimate the black hole accretion rate and upper limits for the star formation rate. Finally, in Sect. 6, we present our conclusion. In this paper, we use flat ΛCDM cosmological parameters ΩΛ = 0.7, ΩM = 0.3, H0 = 70 km s-1 Mpc-1 and the calculator by Wright (2006).
2. Sample and observations
Six IFRS from the sample compiled by Zinn et al. (2011) were photometrically observed with the ESA Herschel Space Observatory (Pilbratt et al. 2010), using the instruments PACS (Photodetecting Array Camera and Spectrometer; Griffin et al. 2010) and SPIRE (Spectral and Photometric Imaging Receiver; Poglitsch et al. 2010). The sources were selected to be comparatively bright in the radio regime, showing 1.4 GHz flux densities between 7 mJy and 26 mJy, and to provide high radio-to-IR flux density ratios (see Table 1 also in the following). Since all observed sources are undetected in the SWIRE data between 3.6 μm and 24 μm, their S1.4 GHz/S3.6 μm lower limits based on SWIRE range between 2300 and 8700. Five observed IFRS are located in the field of ELAIS-S1 and one in the CDFS. No IFRS located in the ELAIS-S1 field has been detected in the X-ray XMM-Newton survey (flux limit of ~5.5 × 10-16 erg cm-2 s-1 in the 0.5–2 keV band; Puccetti et al. 2006) as mentioned by Zinn et al. (2011). IFRS S703, located in the CDFS field, has not been covered by the CDFS Chandra 4 Ms survey (Xue et al. 2011). No optical counterpart is known for the six observed IFRS (Norris et al. 2006; Middelberg et al. 2008a). By these characteristics, the six observed sources are prototypical for the class of IFRS. We note that Maini et al. (2015) find a 3σ counterpart at 3.6 μm based in the Spitzer Extragalactic Representative Volume Survey (SERVS; Mauduit et al. 2012) for IFRS S427 after the observations with Herschel were carried out.
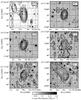 |
Fig. 1 SWIRE 3.6 μm maps (greyscale; Lonsdale et al. 2003) of all six IFRS observed with Herschel overlaid by the 1.4 GHz radio contours (ATLAS data release 3; σ ≈ 20 μJy beam-1; Franzen et al. 2015). Shown are the contours at 2σ, 4σ, 8σ, 16σ, etc. Top down and from left to right: S703, S427, S509, S749, S798, and S973. |
Figure 1 shows the SWIRE 3.6 μm maps of all IFRS observed with Herschel, overlaid by the 1.4 GHz radio contours. IFRS S427, S509, and S798 are point-like sources and show almost no extended structure. For S703, in contrast, it might be suggested because of the additional radio component at around RA 03h35m33.5s Dec −27°26′40′′ and the bridge to the IFRS itself that the IFRS is part of a double lobe radio source with the IFRS and the additional component as radio lobes and the host galaxy in between those two components. However, the additional radio component shows a weak 3.6 μm counterpart, excluding this component as a radio lobe. Therefore, S703 can be considered as a proper IFRS.
Sample of IFRS observed with Herschel.
Infrared-faint radio source S973 shows an extended structure and has been listed as two components (RA 00h38m44.723m Dec −43°19′14.58′′ and RA 00h38m43.489s Dec −43°19′26.94′′) by Middelberg et al. (2008a), with the source position in between the two components. Here, however, we considered the position of the second, radio-brighter component to be the centre of the host with the weaker component more likely to be a jet. However, the choice of host position does not affect our overall conclusion. The position of the brighter component is listed in Table 1.
Infrared-faint radio source S749 shows an extended structure in the radio map, too. However, this source is located close to the edge of the ATLAS ELAIS-S1 field and, therefore, the noise is higher than for the other IFRS discussed in this work. In the scheduling of the Herschel observations, a slightly wrong position of IFRS S749 had been used. Thus, this source is not located in the centre of the Herschel maps but closer to the edge, resulting in a higher noise compared to the other sources, particularly at shorter wavelengths. Therefore, we exclude this source from our stacking analysis in Sect. 4.
The PACS observations of these six objects were carried out in July and December 2011 (observation IDs 1342224373, 1342224374, 1342233615, 1342233616, 1342233617, 1342233618, 1342233619, 1342233620, 1342233621, 1342233622, 1342233623, 1342233624). Using the mode mini-scan map, each observation was divided into two parts, arising from two different scan angles. Both scanning parts were centred on the source, observing simultaneously at 100 μm and 160 μm with a total on-source time of 22.5 min for each source.
The SPIRE observations were carried out in December 2011 and January 2012 (observation IDs 1342234729, 1342234730, 1342234731, 1342234732, 1342234733, 1342238290). Using the observing mode SpirePhotoSmallScan, the sources were observed simultaneously at 250 μm, 350 μm and 500 μm for 12 min each.
We recognise that, since these observations were made and this analysis was performed, additional Herschel data on IFRS have been released into the public domain by the Herschel Multi-Tiered Extragalactic Survey (HerMES; Oliver et al. 2012), the PACS Evolutionary Probe (PEP; Lutz et al. 2011), and the Cosmic Assembly Near-infrared Deep Extragalactic Legacy Survey (CANDELS; Grogin et al. 2011). These data have not been used for the study presented in this work, but will be discussed in a future paper.
3. Data calibration and mapping
The data sets were calibrated using the Herschel Interactive Processing Environment (HIPE; Ott 2010, version 12.1.0). We followed the steps presented in the PACS photometer pipeline for deep survey maps provided within HIPE to process the PACS data sets from level 0 to level 2. During the processing to level 1, a mask was created and applied in the task highpass filter to prevent artefacts in this median-subtraction process arising from nearby bright sources. The position of the IFRS has also been masked. We obtained the best results using a highpass filter radius of 15″. The final maps were built using the task photProject, setting the parameter pixfrac to 0.5, both for 100 μm and 160 μm. Output pixel sizes of 1.5′′ (for 100 μm) and 2.1′′ (for 160 μm), respectively, were found to provide the best maps. Both quantities are parameters of the task photProject which is based on the Drizzle method (Fruchter & Hook 2002). Finally, we matched the two maps of each object, obtained from the two different scan angles, using the task mosaic. The final PACS maps have a size of around 3.5′ × 6.5′. The central region with a diameter of around 50′′ provides the highest and an almost uniform sensitivity. Figure 2 (upper subplots) shows the final PACS maps of IFRS S509.
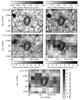 |
Fig. 2 Final Herschel maps (greyscale) of IFRS S509 overlaid by the 1.4 GHz radio contours (ATLAS data release 3; σ ≈ 20 μJy beam-1; Franzen et al. 2015). Shown are the contours at 2σ, 4σ, 8σ, 16σ, etc. Top down and from left to right: 100 μm, 160 μm (both PACS), 250 μm, 350 μm, and 500 μm (SPIRE) maps. None of the five maps provides a detection of S509. |
Characteristics of the instruments and parameters of the data reduction and photometry, used in HIPE for the different channels.
Correspondingly, for the SPIRE data sets, we followed the steps in the appropriate HIPE standard pipeline – the “Photometer Small Map user pipeline” – to calibrate the data. The maps were built using the task Destriper, an iterative algorithm to remove the baseline signal in the timeline data. In this task, the implemented deglitcher was used. We used the algorithm naive mapping implemented in HIPE to build the final maps, projecting the full power seen by each bolometer timeline step to the closest sky map pixel with the pixel sizes given in Table 2. The usable area of the final SPIRE maps is around 8′ × 10′. Figure 2 (lower three subplots) shows the resulting SPIRE maps of IFRS S509.
4. Photometry and stacking
4.1. Photometry
We used the HIPE task AnnularSkyAperturePhotometry for photometry on the PACS maps, performing aperture photometry on a chosen target based on a circular aperture. The related task PhotApertureCorrectionPointSource corrected the measured flux density for the finite size of the applied aperture, yielding the requested flux density of the nominal source. We used aperture radii of 5.6′′ and 10.5′′ for the PACS maps at 100 μm and 160 μm, respectively. The background was estimated und subtracted based on a ring between 20′′ and 25′′, and 24′′ and 28′′, respectively. The flux density uncertainties were obtained from 100 similar apertures randomly placed on the map where the coverage was at least 75% of the maximum coverage. We fit a Gaussian to the histogram of these background flux densities, providing the Gaussian width σ. We repeated this procedure ten times and took the median of these Gaussian widths as the uncertainty of the measured flux density. For S749, where the IFRS was not in the centre of the Herschel maps as discussed in Sect. 2, we placed 100 similar apertures in a field with a maximum distance to the source of five times the full width at half maximum (FWHM) of a point source to estimate the flux uncertainty.
Our six nominal objects were not detected at 100 μm or at 160 μm. Table 3 summarises the resulting point source flux density uncertainties σ for the six observed IFRS.
Photometry on the SPIRE maps was carried out using the HIPE task sourceExtractorSussextractor based on the SUSSEXtractor algorithm (Savage & Oliver 2007). Adapting this task to the maps, sources were extracted, providing data about brightnesses, positions, and related errors of the sources as well as a cleaned map. The extracted sources were checked for their angular distance to the known position of IFRS (<0.5 FWHM). We repeated this procedure as a second level source extraction on the cleaned map. Again, we checked the extracted sources for their distance to the IFRS′ positions. By this, we were able to extract sources which had been overseen in the first extraction step because of bright and close by sources in the map. These sources had been eliminated in the cleaned map.
For five out of the six IFRS, the source extraction did not provide any FIR component in any SPIRE channel, neither by the source extraction performed on the map itself nor on the cleaned map. For S973, we found 3σ detections in the cleaned maps at 350 μm and 500 μm. The positions of these two FIR counterparts were in agreement with each other and were 12′′ distant from the IFRS radio position, which is only slightly below our distance criterion. However, we found that these FIR detections were very close to one source which was detected with a flux density of 6.1 μJy at 3.6 μm in the SERVS survey. Because of those three reasons – weak flux, relatively large distance to the IFRS position, and overlap with a SERVS source – we suggest that these FIR counterparts are associated with the SERVS source and not with our SERVS-undetected IFRS.
We summarise that none of the six observed IFRS was detected in any SPIRE channel. The flux density uncertainties were obtained from the cleaned map by fitting a Gaussian to the pixel values within a square of the size of eight times the FWHM of a point source (see numbers in Table 2). The SPIRE flux density uncertainties at the positions of the IFRS are summarised in Table 3. Our mean noise is lower than the overall confusion noise of 5.8 mJy, 6.3 mJy, and 6.8 mJy at 250 μm, 350 μm, and 500 μm, respectively (Nguyen et al. 2010). However, Nguyen et al. also showed that the residual confusion noise after removing bright sources is lower. Our noises are in agreement with these numbers.
Resulting point source flux density uncertainties for the six IFRS at the five observed wavelengths.
4.2. Stacking of Herschel maps
Since no counterpart of an IFRS was detected in the Herschel maps, we performed a stacking analysis to search for a potentially weak counterpart slightly below the detection limit. The positional uncertainties for our sources are at least one order of magnitude lower than the pixel size of the Herschel maps (see Tables 1 and 2). For each observed wavelength, we stacked the maps centred on the known position of the IFRS. However, we excluded IFRS S749 from the stacking analysis because of the higher noise in the FIR maps (see discussion in Sect. 2). The stacking maps are the results of median stacking the Herschel maps for all the five sources with proper centring and signal-to-noise ratio at each wavelength. In case of SPIRE maps, we stacked the cleaned maps, resulting from the first iteration of source extraction described above. The stacking map at 100 μm is shown in Fig. 3 and did not provide a detection. Corresponding stacking maps at 160 μm, 250 μm, 350 μm, and 500 μm, respectively, were similar and did not provide a detection either. We performed photometry on the stacked maps in the same way as described in Sect. 4.1 for the individual maps. The resulting flux density uncertainties are summarised in the last column in Table 3.
4.3. Stacking in the near- and mid-infrared regime
Since the six observed IFRS were also undetected in the SWIRE maps at 3.6 μm and 24 μm, we performed a stacking analysis at these wavelengths to obtain mean properties of our IFRS population in the following analysis.
At 3.6 μm, all six IFRS were covered by SWIRE, but only four by the deeper SERVS survey. We median stacked the 3.6 μm maps at the positions of the six sources. We carried out aperture photometry using an annulus of 1.9′′ in radius and a background ring between 3.8′′ and 7.6′′ and applied aperture corrections. No source was found in the stacked map. The uncertainty was obtained based on 225 randomly placed apertures and background rings of same size and iteratively removing those apertures resulting in flux densities exceeding 3σ. We found an uncertainty of σ3.6 μm = 0.397 μJy in the stacked map.
At 24 μm, all six IFRS were covered by SWIRE. We median stacked the six individual maps and carried out aperture photometry using an annulus of 3.5′′ in radius and a background ring between 6.0′′ and 8.0′′and applying aperture corrections. No source was found in the stacked map either. We obtained the uncertainty in the same was as described for the stacked map at 3.6 μm and found it to be σ24 μm = 31.3 μJy.
5. Modelling and analysis
The Herschel observations between 100 μm and 500 μm of the six IFRS presented in this work did not provide a detection. A stacking analysis did not show an FIR counterpart below the detection limit either. However, the flux density upper limits measured in Sect. 4 put constraints on the SED of IFRS.
The six IFRS observed with Herschel were selected to show high radio-to-IR flux density ratios (>2000; see Sect. 2). Five of these IFRS are undetected in the near-IR regime while SERVS provides a 3.2σ couterpart at 3.6 μm for one IFRS as reported by Maini et al. (2015). This counterpart was unknown at the time when the observations with Herschel were carried out. Except for this single near-IR detection, these six IFRS are solely detected in the radio regime. Thus, no redshift is known for these sources. By these characteristics, the six IFRS observed with Herschel are among the most extreme objects in the class of IFRS.
All IFRS with known spectroscopic redshifts, presented by Collier et al. (2014) and Herzog et al. (2014), are faintly detected in the near-IR regime. Their redshifts, 1.8 ≲ z ≲ 3, are in agreement with the suggestion by Norris et al. (2011) that IFRS follow the correlation between 3.6 μm flux density and redshift found for HzRGs by Seymour et al. (2007). Assuming that this correlation holds at lower IR flux densities, as it does for HzRGs, the IFRS observed with Herschel would be placed at redshifts of z ≳ 4 or higher because of their 3.6 μm faintness.
We emphasise that no redshift above z ≳ 3 has been measured for an IFRS, presumably because those are too faint for spectroscopic observations. Although we speculate that the IFRS discussed here are at z ≳ 4, we consider the broad redshift range 1 ≤ z ≤ 12.
In the following, we tried to limit possible explanations for the phenomenon of IFRS, performing a broad-band SED modelling based on SED templates of known galaxies (Sect. 5.1). We started with the simplest approach and shifted these templates in a broad redshift range, testing them against the photometric data of IFRS (Sect. 5.1.1). Subsequently, we broadened the parameter space by modifying our broad-band SED templates. We scaled the templates in luminosity (Sect. 5.1.2), added extinction (Sect. 5.1.3), and finally modified them simultaneously in luminosity and extinction (Sect. 5.1.4). In each approach, we tested their compatibility with the photometric constraints of IFRS. Finally, we constrained the IR SED of IFRS based on decomposing their IR SED into an AGN and a starburst (SB) component (Sect. 5.2), both putatively contributing to the total emission of this peculiar class of objects.
 |
Fig. 3 Resulting stacking map obtained from a median stack of the five IFRS at 100 μm. IFRS S749 was excluded because of the higher noise as discussed in Sect. 2. The individual maps were centred on the position of the IFRS which is marked by a cross in the centre of the map. No detection has been found in the stacking map. |
5.1. Broad-band SED modelling
 |
Fig. 4 Broad-band SED modelling for IFRS, using the FIR flux density upper limits measured in this work (red arrows), SERVS/SWIRE near- and mid-IR flux density upper limits (black arrows), and the detections at 1.4 GHz (black bar). The template SEDs were shifted to redshifts between z = 1 and z = 12. Shown are the results at z = 1 (upper left subplot), z = 4 (upper right), z = 8 (lower left), and z = 10 (lower right), respectively. The legend shown in the upper left subplot is valid for all four subplots. At redshifts z ≲ 5, no template is in agreement with the photometric constraints of IFRS. However, if shifted to the redshift regime 5 ≲ z ≲ 8.5, Cygnus A (orange solid line) is in agreement with all constraints. The spiderweb galaxy (black dashed line) provides an appropriate template if shifted to very high redshifts z ≳ 10.5. The CSS source 3C 48 (blue dotted line) and the RL quasar 3C 273 (magenta dashed-dotted line) fulfil the constraint in the radio regime at redshifts 6 ≲ z ≲ 9 and 8 ≲ z ≲ 12, respectively, but disagree with the 3.6 μm flux density upper limits at these redshifts. |
In order to model the broad-band SED of IFRS, we used photometric data of our objects in all available wavelength regimes. The IFRS observed with Herschel provided 1.4 GHz flux densities between 7 mJy and 26 mJy. In the modelling, we used a median 1.4 GHz flux density of 15 mJy, but also discuss the outcome for higher and lower radio flux densities. Furthermore, we used available constraints at 3.6 μm and 24 μm. At 3.6 μm, we used a median 3σ flux density upper limit of 1.19 μJy as discussed in Sect. 4.3. In the mid-IR at 24 μm, we used a 3σ flux density upper limit of 94 μJy based on the stacking described in Sect. 4.3. Furthermore, we made use of the FIR flux density upper limits at five wavelengths between 100 μm and 500 μm measured in this work. More precisely, we used 3σ flux density upper limits based on the uncertainties in the median stacked maps presented in Sect. 4.2 and summarised in the last column in Table 3.
Based on photometric data and redshifts from the NASA/IPAC Extragalactic Database (NED), we built SED templates for different objects by connecting the data points and smoothing the template where appropriate. We used templates of the spiderweb galaxy (an HzRG, also known as MRC 1138-262), the local radio galaxy Cygnus A (also known as 3C 405), the CSS source 3C 48, the RL quasar 3C 273, the local ULIRG Arp 220, the Seyfert galaxy Mrk 231, the local SB galaxy M82, an RL hyper-luminous infrared galaxy (HyLIRG; IRAS F15307+3252), IRAS F00183-7111 (referred to as F00183; this object is a ULIRG, showing contribution of an RL AGN combined with significant SB activity), and the quiescent elliptical brightest cluster galaxy NGC 1316. We added photometric IR data between 100 μm and 870 μm from Seymour et al. (2012) to the template of the spiderweb galaxy since the IR coverage of this template is poor in NED and this wavelength regime is crucial for our analysis. All photometric data points from Seymour et al. are at least 4σ detections.
5.1.1. Shifting broad-band SED templates to various redshifts
 |
Fig. 5 Score for different SED templates as a function of redshift, measured in our broad-band SED modelling. A score of 1 implies that the SED is in agreement with all photometric constraints of the IFRS discussed in this work. Shown is the score resulting from modelling without scaling and without additional extinction (upper left), with scaling and without additional extinction (upper right), without scaling and with additional extinction (lower left), and with scaling and with additional extinction (lower right subplot), respectively. In both plots on the right hand side, the templates were scaled to a 1.4 GHz flux density of 15 mJy. The legend shown in the upper left subplot is valid for all four subplots. |
As a simplest approach, we tested whether any SED template of a known galaxy is in agreement with the available photometric data of IFRS when these templates were shifted to different redshifts, keeping constant rest-frame luminosity and scaling flux densities using a flat ΛCDM cosmology (ΩΛ = 0.7, ΩM = 0.3, H0 = 70 km s-1 Mpc-1). The resulting plots for redshifts of 1, 4, 8, and 10, respectively, are shown in Fig. 4.
In the redshift regime 1 ≲ z ≲ 5, no template fulfils all available photometric constraints, i.e. none of these objects would produce the observational characteristics of IFRS if placed at redshifts z ≲ 5. However, for redshifts in the range 5 ≲ z ≲ 8.5, Cygnus A provided an appropriate template to fulfil the photometric constraints of IFRS. The spiderweb galaxy SED was in agreement with all available photometric data of IFRS when shifted to z ≳ 10.5. At lower redshifts, the radio and the near-, mid-, and FIR flux densities of the spiderweb galaxy exceeded the measured fluxes of IFRS. We also tried templates of other HzRGs (e.g. 3C 470, 4C 23.56) and found the same qualitative result.
The CSS source 3C 48 and the RL quasar 3C 273 matched the measured radio flux density of IFRS if shifted to the redshift regimes 6 ≲ z ≲ 9 and 8 ≲ z ≲ 12, respectively. However, at these redshifts, their 3.6 μm flux densities exceeded the related measured flux density upper limits of IFRS up to a factor of ten, ruling out these templates. All other templates were found to be in strong disagreement with the IFRS data at all redshifts between 1 and 12. Either the radio flux densities of the templates exceeded the measured flux density of IFRS or the templates disagreed with the near-, mid-, and FIR flux density upper limits of IFRS by several orders of magnitude.
We also estimated a score for each SED template at each redshift. For this purpose, we derived the score s based on a modified L1 norm (e.g. Horn & Johnson 1985) given by ![\begin{eqnarray} s = 10^{-\sum \limits_{i} \big| \log_{10} \frac{y_i}{m_i} \big| ~-~ \sum \limits_{j} H[m_j - 3\sigma_j] ~ \big| \log_{10} \frac{3\sigma_j}{m_j} \big| }. \label{eq:score} \end{eqnarray}](/articles/aa/full_html/2015/08/aa25405-14/aa25405-14-eq102.png) (1)The first sum in the exponent runs over the wavelengths i at which our sample of IFRS is detected, where y denotes the flux density of IFRS and m the flux density of the respective SED model. The second sum accounts for deviations of the SED model from the flux density upper limits of IFRS and sums over the wavelengths j at which the IFRS are undetected with an rms σ, using a Heaviside step function H. In order to avoid an overweighting of the FIR regime when deriving a score due to the five independent flux density measurements in this regime, we only used one out of the five Herschel wavelengths. Thus, the wavelength resulting in the highest addend | log 10(3σj/mj) | was used for this purpose.
(1)The first sum in the exponent runs over the wavelengths i at which our sample of IFRS is detected, where y denotes the flux density of IFRS and m the flux density of the respective SED model. The second sum accounts for deviations of the SED model from the flux density upper limits of IFRS and sums over the wavelengths j at which the IFRS are undetected with an rms σ, using a Heaviside step function H. In order to avoid an overweighting of the FIR regime when deriving a score due to the five independent flux density measurements in this regime, we only used one out of the five Herschel wavelengths. Thus, the wavelength resulting in the highest addend | log 10(3σj/mj) | was used for this purpose.
This implies that a score of 1 is obtained by an SED which is in agreement with all eight photometric constraints of the IFRS considered in this work. We emphasise that a score of 1 does not imply that the SED of IFRS necessarily follows the respective template. However, the score provides useful insights how well a template agrees with the data of IFRS at a respective redshift. The upper left subplot in Fig. 5 shows the score as a function of redshift for different templates.
We found only the spiderweb galaxy and Cygnus A are consistent with the photometric data of IFRS when shifted to appropriate redshifts. If IFRS have the SED of a known galaxy, IFRS have to be at redshifts z ≳ 5. This is consistent with the suggestion by Norris et al. (2011), Collier et al. (2014), and Herzog et al. (2014) that the IFRS observed with Herschel are at redshifts z ≳ 4 because of their faintness at 3.6 μm as discussed above.
5.1.2. Modifying broad-band SED templates in redshift and luminosity
In the broad-band SED modelling presented in Sect. 5.1.1, redshift was the only free parameter. We found that only HzRGs (e.g. the spiderweb galaxy) and Cygnus A provide appropriate templates to explain the emission characteristics of IFRS, and only if shifted to redshifts z ≳ 5. In the following, however, we aimed at testing whether the SED characteristics of IFRS can be reproduced by objects at lower redshifts. For this purpose, we broadened the parameter space and used templates modified by varying their luminosity.
In this approach, we included a wavelength-independent luminosity scaling factor as an additional parameter. This allowed the templates to be scaled to match the mean radio flux density of the IFRS observed with Herschel (S1.4 GHz ≈ 15 mJy), since these sources are solely detected in the radio regime apart from the weak 3.6 μm counterpart of S427.
The upper right subplot in Fig. 5 shows the score versus redshift for the different templates when they were scaled in luminosity to match the median radio flux density of the IFRS discussed in this work. In this approach, we found the spiderweb galaxy is in agreement with the available photometric constraints at redshifts in the range 4 ≲ z ≲ 6.5 when scaled in luminosity by factors between 0.08 and 0.4. At higher redshifts, the scaled template SED exceeded the 24 μm flux density upper limits and therefore resulted in a score below 1. The SED template of Cygnus A was also found to be in agreement with the data at z ~ 1 and in the redshift range 4 ≲ z ≲ 10 when scaled in luminosity by factors between 0.007 and 2. In the redshift range 1.5 ≲ z ≲ 4, the scaled template disagreed with the 3.6 μm flux density upper limit. All other templates were in disagreement with at least one upper limit at any redshift.
When scaling the templates to match the faint end of the observed radio flux density range of IFRS of 7 mJy, the spiderweb galaxy template was in agreement with all constraints when shifted to the redshift range z ≳ 3.5, and Cygnus A if shifted to the range z ≲ 2 or 3 ≲ z ≲ 10.5. None of the other templates agreed with all photometric constraints. In contrast, if the templates were scaled to the radio flux density of the radio-brightest IFRS in our sample (26 mJy), only the template of Cygnus A was in agreement with the IR flux density upper limits (4.5 ≲ z ≲ 10). However, at z ~ 4, the template of the spiderweb galaxy only slighly violated the 24 μm flux density upper limit.
5.1.3. Modifying broad-band SED templates in redshift and extinction
We found in Sect. 5.1.1 that the redshifted SED templates of 3C 48, and 3C 273 were in agreement with the radio flux density range and the FIR flux density upper limits of IFRS, however exceeding the near- or mid-IR flux density upper limits. Therefore, here, we tested whether some of our templates could be squeezed below these IR flux density upper limits when additional extinction was added to the templates.
For this purpose, we added extinction in the rest-frame optical and near-IR regime of the template SEDs if required. We used the Calzetti et al. (2000) reddening law which reduces emission at rest-frame wavelengths between 0.12 μm and 2.2 μm. We limited the additional extinction to an arbitrary number of 500 mag. In our modelling, we applied energy conservation by calculating the power hidden by the additional amount of dust in the rest-frame optical and near-IR regime and re-radiating this power at mid- and FIR wavelengths. We implemented this power conservation in our modelling by adding a dust emission component of the same power as hidden by the additional extinction in the optical and near-IR regime.
The emission of dust is usually described by a modified black-body spectrum, i.e. Sν ∝ Bν(T)ϵν, where Bν(T) is the black-body emission given by the temperature T and ϵν is the emissivity function at a frequency ν. We followed simple approaches, using only one dust temperature T = 70 K and assuming ϵ ∝ νβ with β = 1.5. The emissivity spectral index β depends on dust grain properties as size and composition and usually ranges between 1 and 2. We note that the choice of this spectral index in the given range did not qualitatively change our results; neither did changing the dust peak temperature between 30 K and 100 K.
The plot of the scores resulting from this modelling approach – adding extinction to the redshifted SED templates – is shown in the lower left subplot in Fig. 5. It should be noted that no scaling in luminosity as presented in Sect. 5.1.2 had been applied in this approach. We found the spiderweb galaxy template in agreement with the data at redshifts z ≳ 9.5. At z ~ 10, 5.6 mag of additional extinction brought this SED template in agreement with the data. At higher redshifts, no additional extinction was required. Cygnus A was in agreement with all flux density upper limits in the redshift range 5 ≲ z ≲ 9 without adding extinction as shown in Sect. 5.1.1. 3C 273 matched the data at redshifts z ≳ 7.5 if between 8.6 mag and 1.4 mag of extinction were added. 3C 48 was in agreement with all IR flux density upper limits at z ≳ 7 if between 1.4 mag and 0.2 mag of extinction were added. However, the radio flux density of 3C 48 deceeded the minimum flux density of 7 mJy at high redshifts z ≳ 9.5. All other SED templates were found to be in disagreement with the data at any redshift.
Even enormous and unphysically high amounts of extinction of 500 mag were insufficient to squeeze the near-IR emission of some templates below the flux density upper limit at the observed wavelength of 3.6 μm. In that case, we did not add extinction to the templates, resulting in the appropriately low score at the respective redshift. This happened for all radio-quiet templates like Arp220, Mrk231, or M82 at redshifts z ≲ 5. However, at higher redshifts, when additional extinction was able to squeeze the templates below the IR flux density upper limits, the templates were by far too faint in the radio regime to explain the emission features of IFRS.
5.1.4. Modifying broad-band SED templates in redshift, luminosity, and extinction
Finally, in the last step of our broad-band SED modelling, we combined the approaches presented in Sects. 5.1.2 and 5.1.3. Here, we modified the SED templates by shifting them in the redshift range 1 ≤ z ≤ 12, scaling them in luminosity to match the observed radio flux density, and adding extinction – if required – to squeeze the SED templates below the near- and mid-IR flux density upper limits. IR re-radiation was implemented as described in Sect. 5.1.3.
The resulting plot of the score as a function of redshift is shown in the lower right subplot in Fig. 5. We note that each template at each redshift had been modified by an individual scaling factor and – if necessary – an individual amount of extinction had been added.
Similar to the approaches presented before, we only found the spiderweb galaxy, Cygnus A, the CSS source 3C 48, and the RL quasar 3C 273 to provide suitable templates to explain the observational data of IFRS. The spiderweb galaxy was in agreement with the data at all redshifts except for the range 6.5 ≲ z ≲ 9.5. In this redshift range, the template exceeded the 24 μm flux density upper limit despite adding additional extinction. The template of Cygnus A matched all constraints at z ≲ 10 and 3C 273 at redshifts z ≳ 2.5. 3C 48 was in agreement with the data at any redshift except for very low redshifts z ≲ 1.5 and except for the range 2.5 ≲ z ≲ 7.
In the respective redshift ranges, an appropriate scaling factor and an appropriate amount of extinction was found for the spiderweb galaxy, Cygnus A, 3C 48, and 3C 273 to match all photometric constraints known for these IFRS. For example at z = 4, the spiderweb galaxy and Cygnus A needed to be scaled down in luminosity by a factor of 10 and 3, respectively, to match the radio flux density of 15 mJy. No extinction was needed in these cases. In contrast, 3C 273 required 3.2 mag of extinction when scaled down by a factor of 5 to match the radio data point, while 3C 48 could not be modified at this redshift to match all constraints.
Matching the radio flux densities of the radio-brightest IFRS in our sample (26 mJy at 1.4 GHz), again in case of a shift to z = 4, an additional extinction of 1.3 mag was required in case of Cygnus A, whereas no reasonable amount of extinction could be added to the templates of the spiderweb galaxy, 3C 48, and 3C 273, to match the near- and mid-IR flux density upper limits. Considering the radio-brightest IFRS in our sample, at z ≲ 4.5, only the Cygnus A SED template could be brought in agreement with the constraints of these most extreme – i.e. with the highest radio-to-IR flux density ratios – IFRS, if up to 4.1 mag of extinction were added. At higher redshifts z ≳ 10, 3C 48 and the spiderweb galaxy provided appropriate templates, too. 3C 273 was in agreement with the data at 4.5 ≲ z ≲ 5.5 and 7.5 ≲ z ≤ 12. In contrast, if the templates were scaled to a 1.4 GHz flux density of 7 mJy, the spiderweb galaxy, Cygnus A, 3C 273, and 3C 48 could be modified to be in agreement with all photometric constraints at any redshift, except for Cygnus A at very high redshifts z ≳ 10.
All other templates used in this broad-band SED modelling disagreed with the observational data when shifted to the redshift range 1 ≤ z ≤ 12, scaled in luminosity, and extinction was added. These templates were clearly ruled out by their disagreement with the flux density upper limits of IFRS in the FIR regime measured in this work. Particularly, the templates of an RL HyLIRG or F00183, representing common classes of luminous objects at z ≳ 2, were found to be inappropriate to reproduce the SED constraints of IFRS at any redshift.
5.1.5. Summary of broad-band SED modelling
We summarise our findings from the broad-band SED modelling as follows. When using templates of existing galaxies (Sect. 5.1.1), the SED characteristics of IFRS can only be explained by the SEDs of Cygnus A and HzRGs, however only at high redshifts 5 ≲ z ≲ 8.5 and z ≳ 10.5, respectively. If IFRS are at lower redshifts (z ≲ 5), their SED constraints can be fulfilled by fainter versions of an HzRG or Cygnus A (Sects. 5.1.2 and 5.1.4), by a dust-obscured CSS source, or by a dust-obscured RL quasar (Sects. 5.1.3 and 5.1.4).
If IFRS are linked to HzRGs as suggested by Middelberg et al. (2011), Norris et al. (2011), Collier et al. (2014), and Herzog et al. (2014), there are two different suggested options: (a) IFRS are very similar to HzRGs – i.e. with similar luminosities – however at higher redshifts (z ≳ 5); or (b) IFRS are fainter siblings of HzRGs at similar redshifts (1 ≤ z ≲ 5). Based on the template of the spiderweb galaxy, we found that both options are consistent with the FIR flux density upper limits of IFRS measured in this work and the related broad-band SED modelling. If IFRS have the same intrinsic properties as HzRGs, represented by no scaling and no adding of extinction in our modelling, they have to be located at very high redshifts z ≳ 10.5 (Fig. 5, upper left subplot). Alternatively, if IFRS are fainter siblings of HzRGs, i.e. they are scaled down in luminosity and potentially more dusty, they could be located at lower redshifts z ≥ 1 (Fig. 5, lower right subplot). It should be noted that extinctions between 14 mag and 5 mag had to be added to the scaled spiderweb galaxy SED template at redshifts z ≤ 2 to match the IR flux density upper limits.
Two of the templates, 3C 48 and 3C 273, were found to be in agreement with the data of IFRS only if additional extinction in the order of up to several magnitudes was added to the templates as discussed in Sect. 5.1.4. Particularly, these modified templates did not exceed the FIR flux density upper limits of IFRS measured in this work. This implies that a significant dust obscuration in IFRS, explaining the optical and near-IR faintness of these objects, cannot be ruled out. In fact, if the IFRS observed here are similar to 3C 48 or 3C 273, these sources have to be dust obscured to produce the photometric constraints of IFRS.
The results of this broad-band SED modelling are generally in agreement with the findings by Herzog et al. (2014). Herzog et al. measured spectroscopic redshifts of three IFRS detected in the optical and near- and mid-IR regime and did the first redshift-based SED modelling for the class of IFRS. They find the modified templates of 3C 48 and 3C 273 in agreement with all available photometric data of these three IFRS, whereas the templates of star forming galaxies and Seyfert galaxies were clearly ruled out. We also agree with the finding that only RL objects can explain the photometric constraints of IFRS. However, Herzog et al. find that no additional extinction is required for 3C 48 and 3C 273 in their SED modelling. Here, in contrast, we found that IFRS might be dust obscured RL quasars with spectra similar to 3C 48 or 3C 273. However, Herzog et al. studied the IR-brightest IFRS, whereas the IR-faintest IFRS are studied in the current work, providing a valid reason for the discrepancy. Huynh et al. (2010) modelled the SED of individual IFRS and find that the scaled SED template of 3C 273 is in agreement with their data if around one magnitude of extinction was added. This is in agreement with our modelling, considering that the IFRS from Huynh et al. are more than ten times fainter in the radio compared to the IFRS discussed in the present work. We found that IFRS have to be dust obscured, too, if IFRS are similar to HzRGs at z ≲ 3.5. However, if the spectral shape of IFRS is related to that of HzRGs, no extinction is required to explain the SED characteristics of IFRS if these templates are shifted to higher redshifts.
Our broad-band SED modelling showed that the SED templates of the spiderweb galaxy and of Cygnus A can be shifted to 1 ≤ z ≤ 2 and modified to agree with the photometric observations of IFRS. However, in contrast, all 21 spectroscopic redshifts of IFRS are in the range 1.8 <z< 3, i.e. no IFRS has been found at lower redshifts z ~ 1. There are two potential reasons for this discrepancy. (a) Our modelling – by shifting the templates in redshift, scaling them in luminosity, and adding extinction – is not physically realistic for galaxies at z ~ 1. At these low redshifts, all appropriate templates needed to be scaled down in luminosity up to factors of 500. Presumably, the black hole mass needs to be scaled down by a similar factor. However, RL AGN with lower-mass black holes are very rare (Rees et al. 2015). If the galaxy loses its radio excess by scaling down the black hole mass, the characteristically high radio-to-IR flux density ratio of IFRS would not be reached and the galaxy would not be considered as an IFRS. Furthermore, in case of the spiderweb galaxy template, the required high amounts of additional extinction of around 10 mag at low redshifts are very rare and decrease the possibility to observe such extreme objects. (b) The IFRS discussed in this work are intrinsically different to the IFRS with known spectroscopic redshifts. Cygnus A provided the only template which can reproduce the characteristics of IFRS at z ~ 1 without additional dust obscuration. However, it is known that Cygnus A contains a hidden quasar (Antonucci et al. 1994), resulting in narrow emission lines, whereas IFRS were found to show broad emission lines in their optical spectra (Collier et al. 2014; Herzog et al. 2014). If the IFRS discussed in this work are indeed fainter versions of Cygnus A at redshifts z ~ 1, these IFRS would have different properties than the IR-detected IFRS presented by Collier et al. and Herzog et al.. They would form a separate subclass with different redshift and emission line properties. However, so far, no evidence has been found that the population of IFRS might be divided into two sub-classes.
We note that the modified templates of Cygnus A, 3C 48, and 3C 273 – found to match all photometric constraints of IFRS – can be considered as HzRGs in our modelling at z ≥ 1. At these redshifts, they fulfil both selection criteria of HzRGs: z> 1 and L3 GHz> 1026 W Hz-1. Although we scaled down the templates in luminosity at lower redshifts, they were radio-luminous enough to be considered as HzRGs. We can therefore conclude that only HzRGs can explain the photometric characteristics of IFRS.
Our broad-band SED modelling showed several templates that contain a significant SB contribution in disagreement with the available photometric data (Arp220, M82, RL HyLIRG, F00183). In contrast, the highly star forming spiderweb galaxy fulfilled the photometric data constraints of IFRS. Therefore, in the following, we analysed a potential star forming contribution to the SED of IFRS, instead or in addition to an RL AGN.
5.2. IR SED modelling
One of the crucial questions in revealing the nature of IFRS consists in unmasking the star forming activity and its contribution to the energy output in contrast to the activity of the galactic nucleus. In the IR regime, the emission of galaxies is mainly given by these two components, i.e. AGN and SB. The AGN emission comes from dust, reprocessing far-UV through optical light, and peaks at around 10 μm, corresponding to a dust temperature of 300 K. In contrast, the stellar component is strongest in the FIR and arises from stellar emission reprocessed to the FIR regime by dust grains with a maximum at a wavelength around 100 μm, corresponding to 30 K.
5.2.1. IR SED fitting based on IR flux density upper limits
In order to decompose the IR emission of HzRGs, Drouart et al. (2014) fit the IR SED of HzRGs constrained by Herschel and ancillary IR data. They used an IR SED model based on the assumption that the IR emission comes from dust heated by star forming activity and an AGN. They built template SEDs, adding an empirical AGN template and one SB template out of a set of empirical SB templates.
Here, we followed this approach, aiming at setting upper limits on the IR SED of IFRS based on the available FIR flux density upper limits measured in Sect. 4. We used templates derived by Mullaney et al. (2011), covering the rest-frame wavelength range between 6 μm and 1090 μm. Mullaney et al. empirically built five different SB templates, differing in their peaking temperature as well as in the strength of the emission of the polycyclic aromatic hydrocarbon (PAH) molecules. These templates cover the entire range of host galaxies (see Mullaney et al. 2011 for a detailed description of the SEDs). Based on these SB templates, they derived one AGN template as the residual SED after removing the SB contribution.
We used these templates and built the total IR SED by multiplying the AGN template by a wavelength-independent luminosity scaling factor and adding one SB template which was also multiplied by a wavelength-independent luminosity scaling factor. We set an upper limit on the IR emission by modelling the SED in order to minimise the deviation between the total SED, i.e. the sum of SB and AGN template, and the available observed 3σ FIR flux density upper limits from the stacked maps (see last column in Table 3). It was required that the available flux density upper limits were fulfilled in the modelling. In this procedure, the most appropriate SB template out of the five available templates was determined based on the lowest deviation. At redshifts z ≤ 3, the observed 24 μm emission fell into the templates’ wavelength coverage. At these redshifts, we used the 3σ flux density upper limit at 24 μm – measured in Sect. 4.3 from the stacked map – in addition to the FIR flux density upper limits measured in the present work.
 |
Fig. 6 IR SED modelling for IFRS at redshift z = 4, using the FIR flux density upper limits (red arrows) measured in this work. The total (black solid line) IR emission is composed of an AGN component (red dotted line) and a SB component (blue dashed line). The maximum model represents an upper limit on the IR emission of IFRS and is defined by the highest IR flux which is in agreement with all available flux density upper limits. |
By this approach, we determined exactly that total IR SED – consisting of the AGN template and one SB template – which has maximum IR flux but is still in agreement with all available flux density upper limits. Figure 6 shows the resulting IR SED modelling for z = 4. We emphasise that our modelling represents an upper limit on the total IR emission of IFRS.
This approach implies that the true AGN contribution to the emission of the IFRS could be higher than the contribution calculated from the maximum total model described above, though accompanied by a lower SB contribution, and the other way around. However, the difference to the highest possible contribution of each component is generally rather low.
By this modelling, aiming at setting upper limits on the IR emission and referred to as “maximum model”, we decomposed the maximum IR SED into an AGN component and an SB component. Based on this decomposition, we were able to derive IR luminosities of both components by integrating the flux density in the rest-frame wavelength range between 8 μm and 1000 μm. Figure 7 shows the IR luminosities versus redshift for both components and the total IR luminosity of the maximum model. Furthermore, the figure shows the absolute upper limit for both the SB and the AGN IR luminosity, assuming that the other IR emitting process does not contribute at each time. For both components, the luminosities of the maximum model are generally only slightly lower than the absolute upper limit luminosities, except for the SB component at very high redshifts. We note that the jump in the maximum IR luminosity of the AGN and of the SB component at z = 3 is related to the flux density upper limit at 24 μm which only coincides with the template’s wavelength range at redshifts z ≤ 3.
 |
Fig. 7 Infrared luminosity versus redshift for the SB (blue) and AGN (red) component as well as for the total IR luminosity (black). The dashed lines show the data of the maximum IR SED model, combining the AGN and the most appropriate SB template. The solid lines show the IR luminosity upper limits for both components, assuming that the other component does not contribute to the IR emission at each time. |
We emphasise that almost any decomposition of the IR SED into SB and AGN component is possible for IFRS since this wavelength regime is only constrained by upper limits. Therefore, we are only able to set upper limits on the luminosity. Particularly, we note that the maximum model shown in Figs. 6 and 7 is not more likely than any other combination of SB and AGN components which is in agreement with the flux density upper limits. However, the maximum model represents exactly that combination of SB and AGN components which results in the highest total flux but is still in agreement with all flux density upper limits. Therefore, this maximum model sets the upper limit on the total IR luminosity.
We found that the FIR flux density upper limits measured in this work constrain IFRS to have total IR luminosities of <1012L⊙ at redshifts z ≲ 1.5. At z ≲ 2.5, IFRS can have a maximum IR luminosity between 1012L⊙ and 1013L⊙. Such sources are labelled as ULIRGs. At redshifts z ≲ 6, the IR luminosity of IFRS can be at most 1014L⊙ which allows IFRS to be HyLIRGs.
Drouart et al. (2014) find absolute numbers and upper limits for the total IR luminosity of HzRGs in the range of a few to a few tens of 1012L⊙. Our redshift-dependent IR luminosity upper limits of IFRS are in agreement with these numbers of HzRGs.
We note that the maximum model shown in Fig. 7 (dashed lines) is unphysical for redshifts z ≲ 2.5. For these redshifts, the AGN contribution to the maximum model is very low, corresponding to a very low AGN activity or even an absent AGN. Instead, according to that model, the IR emission is mainly or even completely produced by SB activity. In case of a purely star forming galaxy, a direct connection between the radio and the IR emission was found (i.e. Yun et al. 2001), known as radio-IR correlation. Using the outcome of the maximum model that the emission of IFRS is dominated by the SB component for redshifts z ≲ 2.5, we could estimate the radio luminosity from the IR luminosity. Using our FIR luminosity upper limits, we found that this radio luminosity is at least two orders of magnitude lower than the radio luminosity calculated from the measured 1.4 GHz flux density of IFRS. This discrepancy clearly showed that the existence of an AGN in the IFRS is essential to explain their radio flux densities. Modelling their IR SED by only an SB template is inappropriate. The existence of an AGN in IFRS is also in agreement with VLBI observations by Norris et al. (2007), Middelberg et al. (2008b), and Herzog et al. (2015).
5.2.2. Including the radio data point into the IR SED modelling
The IR SED modelling presented above, aiming at setting upper limits on the total IR flux of IFRS, led to unphysical results because it neglected the measured radio flux density of IFRS. In this section, we attempted to address this issue by expanding our modelling to the radio regime based on an RL AGN template.
In Sect. 5.1, we showed that all SEDs in agreement with the photometric characteristics of IFRS were HzRGs and that the spiderweb galaxy provided an appropriate SED template in the broad-band SED modelling. It is known that both star forming activity and an AGN contribute to the emission of this powerful galaxy. Therefore, in the following, we used the broad-band SED of the spiderweb galaxy, built from NED and the additional IR data from Seymour et al. (2012) as described in Sect. 5.1, as a basic template, modified by a wavelength-independent luminosity scaling factor. Beyond that, to account for an SB component independent of the component already present in the spiderweb galaxy template, we added the most appropriate SB template from the sample by Mullaney et al. (2011). Similar to our approach in Sect. 5.2.1, we modified this SB template by a wavelength-independent luminosity scaling factor. However, here, we also used the radio-IR correlation (Yun et al. 2001) to estimate the radio luminosity of the star formation component, in addition to that from the RL AGN.
Recapitulating, similar to the approach presented in Sect. 5.2.1, we composed our total SED of two different components. The spiderweb galaxy contributed SB and AGN emission, while the additional SB component contributed additional SB emission. Based on the two independent scaling factors, both the AGN contribution and the SB contribution could be varied independently. We note that the scaling factor of the additional SB component could also be negative, i.e. representing a lower star forming activity than that in the spiderweb galaxy.
Similar to our approach in Sect. 5.2.1, we modelled the maximum IR SED by maximising the flux of the total template – i.e. composite from the spiderweb galaxy template and one additional SB template – however, requesting the template to be in agreement with all available flux density upper limits. Furthermore, here, we required the total template to match the median measured 1.4 GHz flux density of the observed IFRS of 15 mJy. Figure 8 shows the resulting maximum model for z = 4.
 |
Fig. 8 IR SED modelling for IFRS at redshift z = 4, using the FIR flux density upper limits (red arrows) measured in this work, the SERVS/SWIRE flux density upper limits (black arrows), and the measured radio flux density of 15 mJy at 1.4 GHz. The total (solid line) emission is composed of the scaled spiderweb galaxy template (dotted line) and one scaled SB component (dashed line). Note that the limited wavelength coverage of the SB template caused the leaps at 30 μm and 5450 μm. The fit represents an upper limit on the IR emission of IFRS and is defined by matching the radio flux density of 15 mJy at 1.4 GHz and providing the lowest deviation between all available flux density upper limits and the total SED. Note that the dash at 21 cm (flux density of ≈20 μJy) is the contribution of the additional SB component to the 1.4 GHz flux density. |
We found that the contribution of the additional SB component to the radio emission, calculated based on the radio-IR correlation, is negligible compared to the radio emission of the spiderweb galaxy template. In case of z = 4, this SB contribution is around 20 μJy at 1.4 GHz which is more than two orders of magnitude lower than the contribution of the spiderweb galaxy template at this frequency.
Based on the results of this modelling, we calculated the maximum total IR luminosity by integrating the flux density of the total SED template between 8 μm and 1000 μm in the rest frame. Furthermore, we decomposed the maximum IR luminosity in the SB contribution and the AGN contribution. Seymour et al. (2012) studied the IR properties of the spiderweb galaxy and find that 59% of its IR luminosity is contributed from the AGN and 41% from the star forming activity. We used these fractional numbers and decomposed the contribution of the spiderweb galaxy template correspondingly. The maximum total IR luminosity and its decomposition in AGN and SB contribution as a function of redshift are shown in Fig. 9. We found that, based on this modelling, IFRS are constrained to IR luminosities below 1012L⊙ at redshifts z ≲ 2. At z ≲ 5, IFRS can have a maximum luminosity of 1013L⊙. At higher redshifts, we cannot exclude IFRS to be HyLIRGs which are defined by IR luminosities above 1013L⊙.
 |
Fig. 9 Maximum infrared luminosity versus redshift for the AGN (red dotted line) component, the SB (blue dashed line) component, and for the total IR luminosity (black solid line). The underlying model (see Fig. 8 for an example) matched the measured radio flux density of 15 mJy at 1.4 GHz. We note that the total IR luminosity and the SB IR luminosity are upper limits. |
We note that the luminosity upper limits obtained in this approach are up to one order of magnitude lower than those inferred in Sect. 5.2.1 and presented in Fig. 7. This shows that it is crucial to include the measured radio flux density in the IR SED modelling. A modelling just based on the IR flux density upper limits is physically inappropriate and results in excessive IR luminosities.
The numbers of the maximum total IR luminosity and the SB contribution are upper limits since they were obtained by a model aiming at the lowest deviation to the available IR flux density upper limits. In contrast, the IR luminosities of the AGN component can be considered to be rough estimates because of their direct link to the measured radio flux density. However, we point out that the IR emission of AGNs at high redshifts is known to spread by more than one order of magnitude (Drouart et al. 2014). It should be emphasised that we assumed IFRS to be similar to HzRGs in this approach. Although several indications for this similarity have been found so far, it is not proven yet. While the luminosities shown in Fig. 9 can be considered to be more realistic numbers, the IR luminosity upper limits presented in Fig. 7 are absolute upper limits which should not be exceeded, independent of the nature of IFRS.
In our broad-band SED modelling described in Sect. 5.1, we found that the local radio galaxy Cygnus A, the local CSS source 3C 48 and the RL quasar 3C 273 provide appropriate templates to explain the SED characteristics of IFRS, too. As mentioned above, these modified templates shifted to z ≥ 1 fulfil the selection criteria of HzRGs. Therefore, we also used the SEDs of these galaxies as basic templates, i.e. containing an AGN and potentially a certain contribution from star forming activity, instead of the spiderweb galaxy. We performed the modelling in the same way as described above, i.e. using the scaled SED of Cygnus A, 3C 48 and 3C 273, respectively, as basic template and adding the most appropriate and scaled SB template, matching all available flux density upper limits and the measured 1.4 GHz flux density. However, in case of Cygnus A, 3C 48 and 3C 273, we did not find appropriate numbers in the literature to convert the IR emission of these objects into an AGN and an SB contribution as we did for the spiderweb galaxy based on the results from Seymour et al. (2012). Therefore, we could only compare the total IR luminosity upper limits. We found that these numbers derived based on Cygnus A, 3C 48 and 3C 273 as basic templates are very similar to the numbers based on the spiderweb galaxy template shown in Fig. 9, differing by not more than a factor of two. This finding provides evidence that the total IR luminosity upper limits presented in Fig. 9 are indeed general upper limits, independent on the assumed nature of IFRS.
5.2.3. Estimates of star formation and black hole accretion rate upper limits
Based on the maximum IR luminosities measured in Sect. 5.2.2, we derived upper limit estimates of the star formation rate (SFR), causing the IR emission given by the SB component, and estimates of the black hole accretion rate, generating the AGN contribution to the IR flux. Since these numbers can only be considered as rough estimates, we used very general and simple approaches. We calculated the SFR based on the IR luminosity 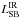 integrated between 8 μm and 1000 μm,
integrated between 8 μm and 1000 μm, ![\begin{eqnarray} {\it SFR}\,[{M}_\odot\,\mathrm{yr}^{-1}]=1.72\times 10^{-10}\times L_\mathrm{SB}^\mathrm{IR}\,[L_\odot], \end{eqnarray}](/articles/aa/full_html/2015/08/aa25405-14/aa25405-14-eq168.png) (2)following the relation for local galaxies from Kennicutt (1998).
(2)following the relation for local galaxies from Kennicutt (1998).
We estimated the black hole accretion rate (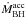 ) from the equation
) from the equation 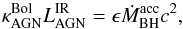 (3)based on the IR luminosity
(3)based on the IR luminosity 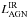 of the AGN. This relation assumes that a fraction of the rest-frame energy of the matter accreting onto the black hole is converted into radiation over the whole electromagnetic spectrum. The conversion is given by the efficiency factor ϵ, only slightly constrained by empirical studies. While for example Shankar et al. (2010) suggest ϵ> 0.2 based on quasar clustering, others like Davis & Laor (2011) find 0.06 <ϵ< 0.4, depending on the mass. Here, we used a conservative number ϵ = 0.1 since we were interested in upper limits for the black hole accretion rate. Furthermore, we needed to make an assumption for the factor κ, converting the IR AGN luminosity to the bolometric luminosity. This factor is uncertain and can vary between 1.4 and 15. We adopted the number from Drouart et al. (2014), κ = 6, assuming an RL AGN template.
of the AGN. This relation assumes that a fraction of the rest-frame energy of the matter accreting onto the black hole is converted into radiation over the whole electromagnetic spectrum. The conversion is given by the efficiency factor ϵ, only slightly constrained by empirical studies. While for example Shankar et al. (2010) suggest ϵ> 0.2 based on quasar clustering, others like Davis & Laor (2011) find 0.06 <ϵ< 0.4, depending on the mass. Here, we used a conservative number ϵ = 0.1 since we were interested in upper limits for the black hole accretion rate. Furthermore, we needed to make an assumption for the factor κ, converting the IR AGN luminosity to the bolometric luminosity. This factor is uncertain and can vary between 1.4 and 15. We adopted the number from Drouart et al. (2014), κ = 6, assuming an RL AGN template.
 |
Fig. 10 Star formation rate (blue line) and accretion rate (red line) versus redshift. The calculation of both rates is based on the modelling described in Sect. 5.2.2, matching the measured 1.4 GHz flux density of 15 mJy and providing the lowest deviation to all available flux density upper limits. The red shaded area represents the uncertainty in the determination of the BH accretion rate, based on varied numbers for the efficiency factor ϵ and the conversion factor κ. We note that the SFR is meant to be an upper limit since the SB contribution is only constrained by upper limits. |
Figure 10 shows the estimated upper limit of the SFR and an estimate of the black hole accretion rate versus redshift based on the maximum IR luminosities derived in Sect. 5.2.2. For the accretion rate, we also showed the related uncertainty, arising from the assumptions made for the efficiency factor ϵ and the conversion factor κ as discussed above. Varying ϵ between 0.06 and 0.4, and κ between 1.4 and 15, representing the range of reasonable numbers, results in the uncertainties shown by the red shaded area in Fig. 10.
We found that IFRS at z ≲ 4.5 are constrained by SFRs of a few hundred solar masses per year. The SFR upper limit increases with redshift and exceeds 104M⊙ yr-1 at z ≈ 11. Drouart et al. (2014) find SFRs for their HzRGs in the range of 100 M⊙ yr-1 to 5000 M⊙ yr-1. These numbers are in agreement with our results, considering that the SFRs calculated here are meant to be upper limits.
The estimates of the black hole accretion rate are below 1 M⊙ yr-1 at z ≲ 3 and below 10 M⊙ yr-1 at z ≈ 6. At redshifts z ≥ 10, the accretion rate is below a few tens of solar masses per year. Drouart et al. (2014) find accretion rates between 1 M⊙ yr-1 and 100 M⊙ yr-1 for their sample of HzRGs. Again, our results are in agreement with the numbers presented by Drouart et al.. Considering that the HzRGs in the sample of Drouart et al. are at z ≲ 5, IFRS seem to show lower accretion rates if they are located at similar redshifts. In contrast to the SFR estimated in this work, which are meant to be upper limits as discussed above, the black hole accretion rates are considered to be rough estimates under the assumption that the SEDs of IFRS are similar to those of HzRGs. However, the assumption for the conversion factor κ and the efficiency factor ϵ and the scattering of the IR luminosity of AGNs (Drouart et al. 2014) add significant uncertainties.
All our findings in this IR SED modelling are in agreement with the results by Drouart et al. (2014) for HzRGs. The redshift-dependent IR luminosity upper limits and the directly related SFRs and black hole accretion rates derived in this work agree with the numbers calculated by Drouart et al. for their sources which, in contrast to IFRS, partially provide FIR detections. In our IR SED modelling, we did not find any evidence disproving the hypothesis that IFRS are similar to HzRGs.
6. Conclusion
In this work, we presented the first FIR data of IFRS. Six IFRS have been observed between 100 μm and 500 μm with the instruments PACS and SPIRE on board the Herschel Space Observatory. None of the observed IFRS has been detected at any of the five FIR wavelengths down to median 3σ levels between 4.4 mJy at 100 μm and 17.6 mJy at 500 μm. Even the stacking of the five maps of five IFRS at each wavelength did not provide a detection.
We used the FIR flux density upper limits combined with the radio detections and the SERVS/SWIRE flux density upper limits to model the broad-band SED of IFRS. The characteristics of IFRS can only be explained by known SEDs of HzRGs (e.g. the spiderweb galaxy) if these templates are shifted to z ≳ 10.5 or by the SED of Cygnus A at 5 ≲ z ≲ 8.5. All other templates, for example RL HyLIRGs, ULIRGs with an AGN in their centre, or RL quasars fail to reproduce the SED constraints of IFRS. We also tested whether modified templates of known galaxies can explain the characteristics of IFRS at lower redshifts z ≲ 5. In this approach, we scaled the templates in luminosity to match the measured flux densities at 1.4 GHz or added extinction in the rest-frame optical and near-IR regime if required. We found that the templates of the spiderweb galaxy, Cygnus A, the CSS source 3C 48, and the RL quasar 3C 273 can be modified to match all photometric constraints of IFRS. However, at low redshifts, additional obscuration by dust was needed for most SED templates to match the near-IR faintness of IFRS.
Although no IFRS has been found at low redshifts z ~ 1, our modelling provided appropriate modified templates for this scenario. This implies that our modelling is physically unrealistic at low redshifts, potentially because of scaling down the luminosity and – by this – the supermassive black hole (SMBH) mass which might prevent the object to be an RL AGN. On the other hand, if the IFRS analysed in this work are indeed at z ~ 1, they would form a new subclass of IFRS with different characteristics than the IFRS with known spectroscopic redshifts. Particularly, we showed that SED templates of star forming galaxies, Seyfert galaxies, ULIRGs, and HyLIRGs are inappropriate to reproduce the photometric constraints of IFRS.
We modelled the maximum IR SED of IFRS based on a set of SB templates and an AGN contribution and using all available flux density upper limits, aiming at measuring the maximum IR flux of IFRS. We found that this model is unphysical at lower redshifts because of its disagreement with the radio-IR correlation. We found that the IFRS could also be modelled by the spiderweb galaxy template, together with an additional SB component. The related IR luminosity upper limits are in agreement with those of HzRGs. Using these maximum IR luminosities, we estimated black hole accretion rates and upper limits for the SFR. These numbers agree with the numbers of HzRGs, too.
In summary, the IFRS discussed here might be (a) objects identical to known HzRGs, but at high redshifts (z ≳ 10.5); (b) objects similar to Cygnus A, but at high redshifts 5 ≲ z ≲ 8.5; (c) objects similar to known HzRGs or Cygnus A, but scaled down in luminosity; or (d) objects similar to CSS sources or RL quasars, but modified by significant additional extinction and scaled in luminosity which makes these templates to HzRGs, too. In any case, objects which reproduce the characteristics of IFRS fulfil the selection criteria of HzRGs. We estimated that IFRS contain SMBHs accreting at the rate of 1 M⊙ yr-1 to 50 M⊙ yr-1, together with star formation at a rate of up to several thousand solar masses per year in case of an additional SB component.
Acknowledgments
We thank the anonymous referee who has helped to improve this paper significantly. We also thank Nick Seymour for valuable discussions about the IR SED modelling and Elaine Sadler for suggestions about SED templates. A.H. acknowledges funding from Bundesministerium für Wirtschaft und Technologie under the label 50 OR 1202. The author is responsible for the content of this publication. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). SPIRE has been developed by a consortium of institutes led by Cardiff University (UK) and including Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA). HIPE is a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Antonucci, R., Hurt, T., & Kinney, A. 1994, Nature, 371, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Banfield, J. K., George, S. J., Taylor, A. R., et al. 2011, ApJ, 733, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Collier, J. D., Banfield, J. K., Norris, R. P., et al. 2014, MNRAS, 439, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., & Laor, A. 2011, ApJ, 728, 98 [CrossRef] [Google Scholar]
- De Breuck, C., Seymour, N., Stern, D., et al. 2010, ApJ, 725, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Drouart, G., De Breuck, C., Vernet, J., et al. 2014, A&A, 566, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franzen, T. M. O., Banfield, J. K. Hales, C. A., et al. 2015, MNRAS, submitted [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Garn, T., & Alexander, P. 2008, MNRAS, 391, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Grogin, N. A., Kocevski, D. D., Faber, S. M., et al. 2011, ApJS, 197, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Herzog, A., Middelberg, E., Norris, R. P., et al. 2014, A&A, 567, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herzog, A., Middelberg, E., Norris, R. P., et al. 2015, A&A, 578, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Horn, R. A., & Johnson, C. R. 1985, Matrix Analysis (New York, NY, USA: Cambridge University Press) [Google Scholar]
- Huynh, M. T., Norris, R. P., Siana, B., & Middelberg, E. 2010, ApJ, 710, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kimball, A. E., & Ivezić, Ž. 2008, AJ, 136, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Lonsdale, C. J., Smith, H. E., Rowan-Robinson, M., et al. 2003, PASP, 115, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Poglitsch, A., Altieri, B., et al. 2011, A&A, 532, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maini, A., Prandoni, I., Norris, R. P., et al. 2015, A&A, 578, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mauduit, J.-C., Lacy, M., Farrah, D., et al. 2012, PASP, 124, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Norris, R. P., Cornwell, T. J., et al. 2008a, AJ, 135, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Middelberg, E., Norris, R. P., Tingay, S., et al. 2008b, A&A, 491, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middelberg, E., Norris, R. P., Hales, C. A., et al. 2011, A&A, 526, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Goulding, A. D., & Hickox, R. C. 2011, MNRAS, 414, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Nguyen, H. T., Schulz, B., Levenson, L., et al. 2010, A&A, 518, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, R. P., Afonso, J., Appleton, P. N., et al. 2006, AJ, 132, 2409 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Tingay, S., Phillips, C., et al. 2007, MNRAS, 378, 1434 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Afonso, J., Cava, A., et al. 2011, ApJ, 736, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puccetti, S., Fiore, F., D’Elia, V., et al. 2006, A&A, 457, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rees, G. A., Spitler, L. R., Norris, R. P., et al. 2015, MNRAS, submitted [Google Scholar]
- Savage, R. S., & Oliver, S. 2007, ApJ, 661, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Seymour, N., Stern, D., De Breuck, C., et al. 2007, ApJS, 171, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Seymour, N., Altieri, B., De Breuck, C., et al. 2012, ApJ, 755, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Shankar, F., Weinberg, D. H., & Shen, Y. 2010, MNRAS, 406, 1959 [NASA ADS] [Google Scholar]
- Willott, C. J., Rawlings, S., Jarvis, M. J., & Blundell, K. M. 2003, MNRAS, 339, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L. 2006, PASP, 118, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, Y. Q., Luo, B., Brandt, W. N., et al. 2011, ApJS, 195, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Yun, M. S., Reddy, N. A., & Condon, J. J. 2001, ApJ, 554, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Zinn, P.-C., Middelberg, E., & Ibar, E. 2011, A&A, 531, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Characteristics of the instruments and parameters of the data reduction and photometry, used in HIPE for the different channels.
Resulting point source flux density uncertainties for the six IFRS at the five observed wavelengths.
All Figures
 |
Fig. 1 SWIRE 3.6 μm maps (greyscale; Lonsdale et al. 2003) of all six IFRS observed with Herschel overlaid by the 1.4 GHz radio contours (ATLAS data release 3; σ ≈ 20 μJy beam-1; Franzen et al. 2015). Shown are the contours at 2σ, 4σ, 8σ, 16σ, etc. Top down and from left to right: S703, S427, S509, S749, S798, and S973. |
| In the text | |
 |
Fig. 2 Final Herschel maps (greyscale) of IFRS S509 overlaid by the 1.4 GHz radio contours (ATLAS data release 3; σ ≈ 20 μJy beam-1; Franzen et al. 2015). Shown are the contours at 2σ, 4σ, 8σ, 16σ, etc. Top down and from left to right: 100 μm, 160 μm (both PACS), 250 μm, 350 μm, and 500 μm (SPIRE) maps. None of the five maps provides a detection of S509. |
| In the text | |
 |
Fig. 3 Resulting stacking map obtained from a median stack of the five IFRS at 100 μm. IFRS S749 was excluded because of the higher noise as discussed in Sect. 2. The individual maps were centred on the position of the IFRS which is marked by a cross in the centre of the map. No detection has been found in the stacking map. |
| In the text | |
 |
Fig. 4 Broad-band SED modelling for IFRS, using the FIR flux density upper limits measured in this work (red arrows), SERVS/SWIRE near- and mid-IR flux density upper limits (black arrows), and the detections at 1.4 GHz (black bar). The template SEDs were shifted to redshifts between z = 1 and z = 12. Shown are the results at z = 1 (upper left subplot), z = 4 (upper right), z = 8 (lower left), and z = 10 (lower right), respectively. The legend shown in the upper left subplot is valid for all four subplots. At redshifts z ≲ 5, no template is in agreement with the photometric constraints of IFRS. However, if shifted to the redshift regime 5 ≲ z ≲ 8.5, Cygnus A (orange solid line) is in agreement with all constraints. The spiderweb galaxy (black dashed line) provides an appropriate template if shifted to very high redshifts z ≳ 10.5. The CSS source 3C 48 (blue dotted line) and the RL quasar 3C 273 (magenta dashed-dotted line) fulfil the constraint in the radio regime at redshifts 6 ≲ z ≲ 9 and 8 ≲ z ≲ 12, respectively, but disagree with the 3.6 μm flux density upper limits at these redshifts. |
| In the text | |
 |
Fig. 5 Score for different SED templates as a function of redshift, measured in our broad-band SED modelling. A score of 1 implies that the SED is in agreement with all photometric constraints of the IFRS discussed in this work. Shown is the score resulting from modelling without scaling and without additional extinction (upper left), with scaling and without additional extinction (upper right), without scaling and with additional extinction (lower left), and with scaling and with additional extinction (lower right subplot), respectively. In both plots on the right hand side, the templates were scaled to a 1.4 GHz flux density of 15 mJy. The legend shown in the upper left subplot is valid for all four subplots. |
| In the text | |
 |
Fig. 6 IR SED modelling for IFRS at redshift z = 4, using the FIR flux density upper limits (red arrows) measured in this work. The total (black solid line) IR emission is composed of an AGN component (red dotted line) and a SB component (blue dashed line). The maximum model represents an upper limit on the IR emission of IFRS and is defined by the highest IR flux which is in agreement with all available flux density upper limits. |
| In the text | |
 |
Fig. 7 Infrared luminosity versus redshift for the SB (blue) and AGN (red) component as well as for the total IR luminosity (black). The dashed lines show the data of the maximum IR SED model, combining the AGN and the most appropriate SB template. The solid lines show the IR luminosity upper limits for both components, assuming that the other component does not contribute to the IR emission at each time. |
| In the text | |
 |
Fig. 8 IR SED modelling for IFRS at redshift z = 4, using the FIR flux density upper limits (red arrows) measured in this work, the SERVS/SWIRE flux density upper limits (black arrows), and the measured radio flux density of 15 mJy at 1.4 GHz. The total (solid line) emission is composed of the scaled spiderweb galaxy template (dotted line) and one scaled SB component (dashed line). Note that the limited wavelength coverage of the SB template caused the leaps at 30 μm and 5450 μm. The fit represents an upper limit on the IR emission of IFRS and is defined by matching the radio flux density of 15 mJy at 1.4 GHz and providing the lowest deviation between all available flux density upper limits and the total SED. Note that the dash at 21 cm (flux density of ≈20 μJy) is the contribution of the additional SB component to the 1.4 GHz flux density. |
| In the text | |
 |
Fig. 9 Maximum infrared luminosity versus redshift for the AGN (red dotted line) component, the SB (blue dashed line) component, and for the total IR luminosity (black solid line). The underlying model (see Fig. 8 for an example) matched the measured radio flux density of 15 mJy at 1.4 GHz. We note that the total IR luminosity and the SB IR luminosity are upper limits. |
| In the text | |
 |
Fig. 10 Star formation rate (blue line) and accretion rate (red line) versus redshift. The calculation of both rates is based on the modelling described in Sect. 5.2.2, matching the measured 1.4 GHz flux density of 15 mJy and providing the lowest deviation to all available flux density upper limits. The red shaded area represents the uncertainty in the determination of the BH accretion rate, based on varied numbers for the efficiency factor ϵ and the conversion factor κ. We note that the SFR is meant to be an upper limit since the SB contribution is only constrained by upper limits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


