Chaotic cold accretion on to black holes in rotating atmospheres

M. Gaspari; F. Brighenti; P. Temi

doi:10.1051/0004-6361/201526151

Home

All issues

Volume 579 (July 2015)

A&A, 579 (2015) A62

Full HTML

Free Access

Issue		A&A Volume 579, July 2015


Article Number		A62
Number of page(s)		18
Section		Extragalactic astronomy
DOI		https://doi.org/10.1051/0004-6361/201526151
Published online		29 June 2015

A&A 579, A62 (2015)

Chaotic cold accretion on to black holes in rotating atmospheres

M. Gaspari¹, F. Brighenti² and P. Temi³

¹ Max Planck Institute for Astrophysics, Karl-Schwarzschild-Strasse 1, 85741 Garching, Germany
e-mail: mgaspari@mpa-garching.mpg.de
² Astronomy Department, University of Bologna, via Ranzani 1, 40127 Bologna, Italy
³ Astrophysics Branch, NASA/Ames Research Center, MS 245-6, Moffett Field, CA 94035, USA

Received: 21 March 2015
Accepted: 4 May 2015

Abstract

The fueling of black holes is one key problem in the evolution of baryons in the universe. Chaotic cold accretion (CCA) profoundly differs from classic accretion models, as Bondi and thin disc theories. Using 3D high-resolution hydrodynamic simulations, we now probe the impact of rotation on the hot and cold accretion flow in a typical massive galaxy. In the hot mode, with or without turbulence, the pressure-dominated flow forms a geometrically thick rotational barrier, suppressing the black hole accretion rate to ~1/3 of the spherical case value. When radiative cooling is dominant, the gas loses pressure support and quickly circularizes in a cold thin disk; the accretion rate is decoupled from the cooling rate, although it is higher than that of the hot mode. In the more common state of a turbulent and heated atmosphere, CCA drives the dynamics if the gas velocity dispersion exceeds the rotational velocity, i.e., turbulent Taylor number Ta_t< 1. Extended multiphase filaments condense out of the hot phase via thermal instability (TI) and rain toward the black hole, boosting the accretion rate up to 100 times the Bondi rate (Ṁ_• ~ Ṁ_cool). Initially, turbulence broadens the angular momentum distribution of the hot gas, allowing the cold phase to condense with prograde or retrograde motion. Subsequent chaotic collisions between the cold filaments, clouds, and a clumpy variable torus promote the cancellation of angular momentum, leading to high accretion rates. As turbulence weakens (Ta_t > 1), the broadening of the distribution and the efficiency of collisions diminish, damping the accretion rate ∝ Ta_t^-1, until the cold disk drives the dynamics. This is exacerbated by the increased difficulty to grow TI in a rotating halo. The simulated sub-Eddington accretion rates cover the range inferred from AGN cavity observations. CCA predicts inner flat X-ray temperature and r^-1 density profiles, as recently discovered in M 87 and NGC 3115. The synthetic Hα images reproduce the main features of cold gas observations in massive ellipticals, as the line fluxes and the filaments versus disk morphology. Such dichotomy is key for the long-term AGN feedback cycle. As gas cools, filamentary CCA develops and boosts AGN heating; the cold mode is thus reduced and the rotating disk remains the sole cold structure. Its consumption leaves the atmosphere in hot mode with suppressed accretion and feedback, reloading the cycle.

Key words: accretion, accretion disks / black hole physics / hydrodynamics / galaxies: ISM / instabilities / turbulence

© ESO, 2015

1. Introduction and observations

In current astrophysics, a marked disconnection exists between theoretical works focusing on the vicinity of supermassive black holes (SMBHs) and those studying the large-scale properties of the host (a massive elliptical, galaxy group or cluster). The former often employ idealized, constant boundary conditions, while the latter are forced to rely on semianalytic subgrid models. The intermediate zone, between a few 10 kpc of the host galaxy and the sub-pc core, is however a crucial region that often determines the fueling and feeding of the black hole.

Gaspari et al. (2013; hereafter G13) aimed to fill this gap, showing that realistic turbulence, cooling, and heating affecting the hot gaseous halo, can dramatically change the accretion flow on to black holes, departing from the idealized picture of Bondi (1952) formula. As the cooling time becomes relatively low compared with the dynamical time (t_cool ≲ 10 t_ff), cold clouds and filaments condense out of the hot phase via nonlinear thermal instability (TI). Chaotic collisions promote the funneling of the cold phase toward the BH, leading to episodic spikes in the accretion rate up to ~100 × the Bondi rate. For the more poetic minds, chaotic cold accretion (CCA) can be viewed as raining on to black holes.

Because of the simplicity of the Bondi formula, it is tempting to exploit it in theoretical and observational studies (e.g., Reynolds et al. 1996; Loewenstein et al. 2001; Churazov et al. 2002; Baganoff et al. 2003; Di Matteo et al. 2003, 2005; Springel et al. 2005; Allen et al. 2006; Croton et al. 2006; Hopkins et al. 2006; Rafferty et al. 2006; Cattaneo & Teyssier 2007; Sijacki et al. 2007; Hardcastle et al. 2007; Booth & Schaye 2009; Cattaneo et al. 2009; Barai et al. 2014; Nemmen & Tchekhovskoy 2015). Knowing the black hole mass M_• and the gas entropy at large radii (K ∝ T/ρ^{γ − 1}, where γ is the adiabatic index, ρ the gas density, and T the gas temperature) allows us to immediately retrieve the accretion rate via 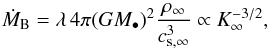$Ṁ B = λ 4 π (G M_{•})^{2} \frac{ρ_{\infty}}{c_{s, \infty}^{3}} \propto K_{\infty}^{- 3 / 2},$ $\begin{equation} \label{e:MdotB} \dot M_{\rm B} = \lambda\, 4\pi (GM_\bullet)^2\frac{\rho_{\infty}}{c^3_{{\rm s}, \infty}} \propto K_\infty^{-3/2}, \end{equation}$ (1)where λ is a factor of order unity (varying as a function of γ and the accretor radius; cf. G13, Sect. 1). However, Eq. (1) can only be used if the hydrodynamic flow is adiabatic (no heating or cooling), unperturbed, spherically symmetric, with steady boundary conditions at infinity. If one of these conditions is violated, then Bondi derivation and formula cannot be applied. Bondi himself warns in the first line of his 1952 abstract that he is investigating a special accretion problem. In the last decade, observations and simulations of gas in galaxies, groups, and clusters have proven that atmospheres are turbulent (e.g., Norman & Bryan 1999; Schuecker et al. 2004; Dolag et al. 2005; Kim & Ryu 2005; Nagai et al. 2007; Lau et al. 2009; Vazza et al. 2009; Borgani & Kravtsov 2011; de Plaa et al. 2012; Sanders & Fabian 2013; Gaspari & Churazov 2013; Banerjee & Sharma 2014; Gaspari et al. 2014b; see also interstellar medium studies, Elmegreen & Scalo 2004), while continuously shaped by the competition of cooling and heating processes (e.g., Vikhlinin et al. 2006; McNamara & Nulsen 2007, 2012; Diehl & Statler 2008; Rasmussen & Ponman 2009; Sun et al. 2009; Gaspari et al. 2014a).

Tracking the realistic accretion rate and dominant mode of SMBH fueling is fundamental to understand and model the impact of active galactic nucleus (AGN) feedback. The energy released by a SMBH can reach 10⁶² erg, which is able to affect the host galaxy and the surrounding group or cluster gaseous halo (e.g., Gaspari et al. 2011a,b, 2012a,b). The AGN feedback can address many astrophysical problems, such as heating cooling flows, quenching star formation, forming buoyant bubbles and shocks, or ejecting metals and low-entropy gas at large radii (Gaspari et al. 2013a, for a brief review). Overall, SMBHs can be seen as the thermostats regulating the baryonic structures throughout the cosmic evolution.

In recent times, it has become clear that most, if not all, massive galaxies retain a hot, X-ray emitting atmosphere down to galaxies with stellar masses (Anderson et al. 2015; see also Planck Collaboration Int. XI 2013, Fig. 4), including spirals (e.g., Anderson & Bregman 2011; Dai et al. 2012). Therefore, cold gas condensation and accretion is expected to play central role in the evolution of SMBHs and their host galaxies, as supported by other works (e.g., Pizzolato & Soker 2005; Soker 2006; Soker et al. 2009; Barai et al. 2012). Although we focus in this study on a massive early-type galaxy (with inefficient star formation), CCA is also expected to be relevant in high-redshift and disk galaxies. These systems host large reservoir of cold gas and thus do not necessitate TI condensation from a hot halo to ignite CCA. On top of that, cold accretion can be augmented via cosmic-web inflows, and the related large-scale disk instabilities or tidal torques (e.g., Dekel et al. 2009; Hopkins & Quataert 2010). Chaotic collisions via minor mergers can also boost cold accretion (e.g., King & Pringle 2006).

Observations of multiphase gas (T< 10⁶ K) embedded in the hot, X-ray emitting plasma of massive halos have exponentially grown over the last decade. These observations detect extended ionized gas in optical Hα+[NII] (Heckman et al. 1989; Macchetto et al. 1996; Crawford et al. 1999; McDonald & Veilleux 2009; McDonald et al. 2010, 2011, 2012; Werner et al. 2014; Sect. 8), which is typically cospatial with infrared H₂ (e.g., Jaffe et al. 2005; Hatch et al. 2005; Wilman et al. 2009, 2011; Oonk et al. 2010), molecular gas traced by CO (Lim et al. 2000; Edge 2001; Salomé & Combes 2003; Combes et al. 2007; Salomé et al. 2008; Hamer et al. 2014), far-infrared [CII], [OI] (Mittal et al. 2012; Werner et al. 2013), and far-ultraviolet CIV (Sparks et al. 2012). These data strongly favor the scenario of in-situ condensation via TI, as opposed to gas stripping from infalling galaxies. Recently, the unprecedented resolution and sensitivity of ALMA has further proven the central role of condensed cold gas in the form of clouds, turbulent disks, and outflows (Combes et al. 2013, 2014; David et al. 2014; McNamara et al. 2014; Russell et al. 2014). Remarkably, most cool-core systems with t_cool< 1 Gyr contain filamentary multiphase gas (Cavagnolo et al. 2008; Rafferty et al. 2008) and central radio sources (Mittal et al. 2009), indicating that the cooling gas is the main driver of AGN feedback. The increase of radio-loud AGN with more massive halos (Best et al. 2007), which have higher cooling rates (Shabala et al. 2008) and slower rotation, further supports the fueling via CCA. It shall be noted that molecular gas does not need to be strictly correlated with AGN bubbles, jets, or outflows (e.g., Werner et al. 2014), since CCA quickly consumes the infalling cold gas. Powerful AGN feedback can also drag it out of the galaxy (e.g., Canning et al. 2013).

After the initial study by G13, many features of the newly proposed CCA remain to be tackled, in this and future investigations. One important open question concerns the role of rotation in being able to suppress accretion, in combination with cooling, heating, and turbulence (see also Proga & Begelman 2003; Krumholz et al. 2005, 2006; Pizzolato & Soker 2010; Hobbs et al. 2011; Narayan & Fabian 2011; Li et al. 2013). Current surveys using integral-field spectroscopy (Emsellem et al. 2007, 2011) show that early-type galaxies display slow or fast rotating stellar kinematics, likely reflecting separate formation and evolution histories. While low-luminosity galaxies are typically fast rotators, massive galaxies (as brightest cluster or group galaxies), the focus of the present work, belong to the “slow” rotator family (e.g., Jimmy et al. 2013; Kormendy et al. 2009 for a review). Recurrent gas-poor (dry) mergers (e.g., Bois et al. 2011) or AGN outflows (e.g., Gaspari et al. 2012b) can both contribute in reducing angular momentum. Slow rotators or massive ellipticals have angular momentum parameter λ_{R_e} ~ 0.1–0.3 (Emsellem et al. 2007), corresponding to stellar rotational velocities v_{∗, rot} ~ 0.1–0.3σ_∗ (Binney et al. 1990; Caon et al. 2000; Pinkney et al. 2003; Jimmy et al. 2013). A notable example with significant rotation is NGC 4649.

Compared with the stellar kinematics, the rotation of the gas in observed massive ellipticals is more uncertain. Roughly 70% of the hot gas within the effective radius likely comes from stellar mass loss (e.g., Brighenti & Mathews 1999), thereby gas rotation is expected to share similar specific angular momentum as the local stars, v_rot ~ 0.1–0.3σ_∗ (e.g., Caon et al. 2000). Evidence for gas rotation in the inner part of the galaxy is given by the X-ray ellipticity, typically ≲0.2, which steadily declines below that of the stars at r ≳ 1 kpc (Diehl & Statler 2007; Brighenti et al. 2009). The negative slope of the X-ray ellipticity is typically moderate (Diehl & Statler 2007), suggesting that transport processes, such as turbulence, are required to circularize the isophotes and to prevent the rapid spin-up of the gas due to cooling flows (e.g., Brighenti & Mathews 1996, 2000). Nonzero gas angular momentum can also be associated with subsonic sloshing motions and cold fronts due to infalling substructures (Markevitch & Vikhlinin 2007; ZuHone et al. 2013) or with galaxy peculiar velocity (e.g., Zabludoff et al. 1993).

In this study, we perform astrophysical experiments, dissecting each physics in a methodical way to disentangle its impact on the hot and cold accretion flow affected by rotation in a massive early-type galaxy. The key objective is to further unveil and understand CCA, rather than covering any possible accretion scenario. In Sect. 2, we review the physical and numerical ingredients of the simulations. In Sect. 3, we study the rotating flow in the adiabatic galactic atmosphere. In Sect. 4, we analyze pure cooling and the related cold thin disk. Section 5 shows the impact of realistic turbulence in the rotating hot flow. In Sect. 6, we combine cooling and stirring, while in Sect. 7 we present the complete CCA evolution in a rotating halo, including heating and varying levels of turbulence. In Sect. 8, we compute synthetic Hα images and compare them with the most recent observations obtained with the SOAR telescope (Werner et al. 2014). In Sect. 9, we summarize and discuss our findings in the context of the long-term AGN feedback loop. Remarkably, CCA is unhindered as long as a key dimensionless quantity, which we define as “turbulent Taylor”¹ number, remains below unity, i.e., 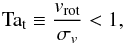$T a_{t} \equiv \frac{v_{rot}}{σ_{v}} < 1,$ $\begin{equation} \label{e:Tt} {\rm Ta_t} \equiv \frac{v_{\rm rot}}{\sigma_v} < 1, \end{equation}$ (2)where v_rot and σ_v are the rotational velocity and turbulent velocity dispersion of the gas, respectively.

2. Physics and numerics

The implemented physics and numerics are described in depth in G13 (Sect. 2). Here we summarize the essential features and new ingredients, such as rotation (Sect. 2.1).

2.1. Initial conditions and rotation

We study the accretion flow in a typical massive elliptical galaxy (NGC 5044) embedded in the gaseous intragroup medium. The initial temperature and gravitational potential profiles are unchanged compared with our previous work. The T profile is directly derived from Chandra and XMM observations (Gaspari et al. 2011b). Since we focus on a virialized galaxy, we use a static potential φ, which is given by the central SMBH (), the galactic stellar component (, with effective radius ≃10 kpc), and a dark matter Navarro-Frenk-White (1996) halo with virial mass and concentration ≃ 9.5. The Schwarzschild and Bondi radii are R_S ≡ 2GM_•/c² ≃ 3 × 10^-4 pc and 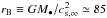$r_{B} \equiv G M_{•} / c_{s, \infty}^{2} ≃ 85$ $\hbox{$r_{\rm B}\equiv GM_\bullet/c_{\rm s, \infty}^2 \simeq 85$}$ pc, respectively (the sound speed is c_s,∞ ≃ 390 km s^-1 near 1 kpc). We integrate the system for a long-term evolution, ~200 t_B, where t_B ≡ r_B/c_s,∞ ≃ 210 kyr.

The density profile is retrieved from hydrostatic equilibrium (neglecting the black hole). We test the gas rotation, which induces a centrifugal force, effectively lowering the gravitational acceleration g along R ≡ (x² + y²)^1/2. This partially changes the stratification of the hot gaseous halo. The new hydrostatic equilibrium can be better visualized and set up separating the two main directions, R and z, as follows: 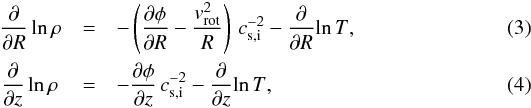$\begin{matrix} \frac{\partial}{∂R} \ln ρ & = & - (\frac{∂φ}{∂R} - \frac{v_{rot}^{2}}{R}) c_{s, i}^{-2} - \frac{\partial}{∂R} \ln T, \\ \frac{\partial}{∂z} \ln ρ & = & - \frac{∂φ}{∂z} c_{s, i}^{-2} - \frac{\partial}{∂z} \ln T, \end{matrix}$ $\begin{eqnarray} \label{e:HSER} \frac{\partial}{\partial R}\ln\rho &=& - \left(\frac{\partial\phi}{\partial R} - \frac{v^2_{\rm rot}}{R} \right)\,c^{-2}_{\rm s,i} - \frac{\partial}{\partial R}{\ln T}, \\ \label{e:HSEz} \frac{\partial}{\partial z}\ln\rho \, &=& - \frac{\partial\phi}{\partial z}\,c^{-2}_{\rm s,i} - \frac{\partial}{\partial z}{\ln T}, \end{eqnarray}$ where $c_{s, i}^{2} = k_{b} T / μ m_{p}$ $\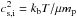hbox{$c_{\rm s,i}^2=k_{\rm b} T/\mu m_{\rm p}$}$ is the isothermal sound speed (the mean particle weight is μ ≃ 0.62). As is customary (e.g., Strickland & Stevens 2000), the rotational velocity of the gas is parametrized as a fraction of the circular velocity, 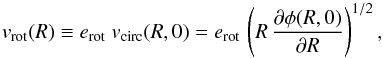$v_{rot} (R) \equiv e_{rot} v_{circ} (R, 0) = e_{rot} {(R \frac{∂φ (R, 0)}{∂R})}^{1 / 2},$ $\begin{equation} \label{e:vrot} v_{\rm rot}(R) \equiv e_{\rm rot}\;v_{\rm circ} (R,0) = e_{\rm rot}\,\left(R\,\frac{\partial\phi(R,0)}{\partial R}\right)^{1/2}, \end{equation}$ (5)where e_rot is a free parameter ranging between 0 and 1, the latter corresponding to full rotational support. We first integrate the hydrostatic equilibrium along R (Eq. (3)), then along the z direction (Eq. (4)), linearly interpolating the retrieved 2D matrix in the discretized 3D domain. The central density normalization is the same as in G13. The initial profiles are shown in Fig. 3. As suggested by observations, the resultant rotational velocity is fairly constant with R (outside the Keplerian influence region of the SMBH); at 26 kpc v_rot is just ~30% higher than at 1 kpc. Using constant specific angular momentum at large radii (v_rot ∝ R^-1) should be thus avoided as an initial condition.

We discuss now the reference e_rot. The Jeans equation for a spherically symmetric, isotropic stellar system in equilibrium can be written as 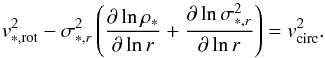$v_{*, rot}^{2} - σ_{*,r}^{2} (\frac{\partial \ln ρ_{*}}{\partial \ln r} + \frac{\partial \ln σ_{*,r}^{2}}{\partial \ln r}) = v_{circ}^{2} .$ $\begin{equation} \label{e:jeans} v^2_{\ast,\rm rot}-\sigma_{\ast,r}^2 \left(\frac{\partial\ln\rho_\ast}{\partial\ln r} + \frac{\partial\ln\sigma^2_{\ast, r}}{\partial \ln r}\right) = v^2_{\rm circ}. \end{equation}$ (6)Neglecting rotation, the radial stellar velocity dispersion for our simulated galaxy peaks at σ_{∗ ,r} ≃ 230 km s^-1 (the 3D velocity dispersion is 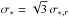$σ_{*} = \sqrt{3} σ_{*,r}$ $\hbox{$\sigma_\ast=\sqrt{3}\,\sigma_{\ast, r}$}$ ). For weak rotation, the stellar velocity dispersion is a good proxy for the circular velocity. Massive elliptical galaxies are known to have irregular velocity profiles, at best with mild coherent rotation, in particular for the gas component (e.g., Caon et al. 2000). As discussed in Sect. 1, gas rotation can typically reach v_rot ≲ 0.3 σ_∗. To maximize the impact of rotation, we thus adopt e_rot = 0.3 as reference, leading to an average gas rotational velocity v_rot ≈ 100 km s^-1 (r ~ 1–13 kpc). Adopting slower rotation has negligible impact on the CCA dynamics, resembling G13 models, since v_rot ≪ σ_v. As faster rotation flattens the density profile and isophotes too much (Sect. 1), it is better to compare models with fixed e_rot and varying σ_v (the cooling rate also remains the same), albeit Ta_t defines the self-similar dynamics in both cases (Sect. 7).

2.2. Hydrodynamics and source terms

We use a modified version of the adaptive-mesh-refinement code FLASH4 (Fryxell et al. 2000) to integrate the well-known equations of hydrodynamics (e.g., Gaspari et al. 2011b), adopting a very large dynamical range. The maximum resolution is ≃0.8 pc, with radially concentric fixed meshes in cartesian coordinates (G13, Sect. 2.1). The box width reaches 52 kpc (~600 r_B), an extension of almost a factor 10⁵ (see G13, for further details on resolution and convergence). Notice that using e_rot = 0.3 implies that the circularization radius is r_circ = (v_rot/v_circ) r_init = 0.3 r_init. Even considering the steepening of v_circ due to the SMBH potential (~4000 km s^-1 at 1 pc), we can resolve circular motions down to a few 10 pc. Thermal instabilities form up to several kpc, hence we can clearly assess whether the cold gas is accreted or circularizes (see the thin disk evolution in Sect. 4).

In addition to hydrodynamics, we add the source terms related to the black hole sink, turbulence driving, radiative cooling, and distributed heating, testing step by step the contribution of each physics to the accretion process. Using the pseudo-relativistic Paczyński & Wiita (1980) BH potential, the sonic point (for adiabatic index γ = 5/3) is not located at r = 0, but at a finite distance near the pc scale. This justifies the use of a central gas sink or void region (ρ ≃ 10^-35 g cm^-3 and v = 0) with ≈3 cells radius (which avoids artificial overpressure bounces), since the internal region is causally disconnected (G13, Sect. 2.2). Self-gravity is here not included; the cold clouds are not massive enough to overcome the external potential (see G13, end of Sect. 7.3 for an extended discussion).

Turbulence is implemented via a spectral forcing scheme, based on an Ornstein-Uhlenbeck random process, which drives a time-correlated and zero-mean acceleration field, reproducing experimental high-order structure functions (Fisher et al. 2008). The source of turbulence can be galaxy motions, substructure mergers, supernovae, or AGN feedback (e.g., Norman & Bryan 1999; Lau et al. 2009; Vazza et al. 2009; Gaspari et al. 2012b). We keep the subsonic turbulent velocity used in G13 as reference, σ_v ~ 150 km s^-1 (3D Mach number Ma ~ 0.35), stirring the gas at injection scales L ≳ 4 kpc, and allowing the gas to naturally develop a Kolmogorov-like cascade. Long-term AGN feedback simulations typically retrieve such turbulence characteristics (e.g., Gaspari et al. 2012b; Vazza et al. 2012). Mergers inject higher kinetic energy at 100 s kpc; however, velocities decay through the Kolmogorov cascade and, below 10 kpc, σ_v reaches again a few 100 km s^-1 (Gaspari et al. 2014b). The reference turbulence model has Taylor number Ta_t ~ 0.7, as we use e_rot = 0.3. In Sects. 5–7, we test weaker turbulence, i.e., Ta_t = 1.5 and 3. Turbulent heating (with timescale ∝Ma^-2) is subdominant during our entire evolution.

The hot plasma cools via X-ray radiation mainly because of Bremsstrahlung at T ≳ 10⁷ K and line emission at lower temperature. The radiative emissivity is ℒ = n_en_i Λ, where n_e and n_i are the electron and ion number density, respectively. The cooling function Λ(T) is modeled following Sutherland & Dopita (1993), adopting solar metallicity. As is customary, the cold phase has temperature floor at 10⁴ K where the abrupt recombination of hydrogen and the steepening of Λ (with slope ≫ 2) induces a thermally stable region (Field 1965). The initial ratio of the cooling time, t_cool ≡ 1.5 nk_BT/n_en_iΛ, and free-fall time, t_ff ≡ (2r/g)^1/2 has a minimum ~4–5 near 250 pc. As t_cool/t_ff< 10 TI can grow nonlinearly (Gaspari et al. 2012a; McCourt et al. 2012; Sharma et al. 2012; for classic studies on TI see Field 1965; Krolik & London 1983; Balbus & Soker 1989; Pizzolato & Soker 2005).

AGN feedback, in conjunction with stellar heating and mergers (e.g., Brighenti & Mathews 2003; Gaspari et al. 2011a,b; Barai et al. 2014), acts to maintain the cool core of galaxies, groups, and clusters in global thermal quasiequilibrium (≲10 percent), preserving core temperatures at ~1/3 of the virial temperature (e.g., Vikhlinin et al. 2006; Diehl & Statler 2008; Rasmussen & Ponman 2009; Sun et al. 2009). We do not model AGN outflows or jets as in Gaspari et al. (2012a,b), since this is computationally unfeasible. In the final models (Sect. 7), we inject distributed heating, mimicking a post-outburst phase, when the feedback heating has been properly deposited (Gaspari et al. 2012a, Fig. 9). Computationally, we set the heating rate (per unit volume) to be equal to the average radiative emissivity in finite radial shells at each timestep, ℋ ≈ ⟨ ℒ ⟩.

3. Adiabatic accretion

Fig. 1

Adiabatic rotating accretion: evolution of the accretion rate (1 Myr average). Top: accretion rate in yr^-1 units, for the rotating (e_rot = 0.3; solid) and nonrotating atmosphere (dot-dashed; see G13). Bottom: accretion rate normalized to the runtime Bondi rate (averaged over r ≈ 1–2 kpc as in large-scale simulations) for the reference rotation e_rot = 0.3 (solid) and e_rot = 0.15 (dotted). The central rotational barrier forming within r_B suppresses accretion by a factor ~3 compared with the spherically symmetric accretion flow.

Following the procedure presented in G13, we test step by step the impact of each physical process. We begin analyzing the model purely based on classic hydrodynamics. No cooling, heating, or turbulence is affecting the accretion flow. The adiabatic flow shares tight connection with Bondi (1952) accretion, albeit the spherical symmetry is broken by the initial gas rotation (e_rot = 0.3, i.e., v_rot ≈ 100 km s^-1; see Sect. 2.1).

3.1. Accretion rate

In Fig. 1, we show the main diagnostic plot: the temporal evolution of the accretion rate during 40 Myr (~200t_B). The impact of rotation (solid line; top) is to suppress the accretion rate by a factor ~3 compared with the nonrotating atmosphere (dashed line; Sect. 3.1 in G13), reaching yr^-1. The average rate is slightly decreasing due to the presence of the galactic gradients, progressively altering the ‘boundary’ conditions at a few r_B (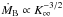 $Ṁ_{B} \propto K_{\infty}^{- 3 / 2}$ $\hbox{$\dot M_{\rm B}\propto K_\infty^{-3/2}$}$ ; the Bondi boundary conditions at infinity have no meaning in stratified atmospheres). Beside such minor trend, the accretion rate is solely stifled by the central rotationally-supported barrier, reaching statistical steady state in a few 10 t_B.

In the bottom panel (Fig. 1), the accretion rate is normalized to the Bondi rate (Eq. (1)), averaged over r ≈1–2 kpc, as customarily employed in large-scale or cosmological simulations. Comparing the reference run with e_rot = 0.3 (solid) and the model with e_rot = 0.15 (dotted) indicates that the final accretion rate is weakly lowered with increasing rotation. Interestingly, adopting the Bondi formula at large radii predicts a fairly realistic accretion rate, within a factor ≲2. Therefore, boosting the Bondi accretion rate by a large factor (~100; e.g., Di Matteo et al. 2005; Booth & Schaye 2009) is not required, even if r_B is under-resolved, at least in the regime of a hot and rotating atmosphere (a similar conclusion applies in the presence of turbulence, but not if cooling is dominant).

3.2. Dynamics

Fig. 2

Adiabatic accretion with e_rot = 0.3: x-y rotational plane cross-section (2 kpc²) of the mass-weighted temperature at final time; the normalization of the velocity field is 2000 km s^-1 (such unit arrow is 1/8 of the image width). The gas progressively circularizes toward the equatorial plane, stifling accretion. Within the Bondi radius, the pressure-supported toroidal structure is variable, experiencing recurrent mild expansions and contractions, thus forming the pinwheel configuration.

Fig. 3

Adiabatic accretion with e_rot = 0.3: evolution of the mass-weighted electron density (top; n_e ≃ ρ/ 1.93 × 10^-24 cm^-3) and temperature (bottom) radial profiles, sampled every 1 Myr (from dark blue to cyan). The cuspy profiles are similar to the classic Bondi solution (G13), smoothly joining the galactic gradients at large r.

Fig. 4

Adiabatic accretion with e_rot = 0.3: mass “probability” distribution function (PDF) per bin of specific angular momentum along the rotation axis z (M_⊙ per kpc km s^-1), for the gas within r< 8 kpc. The color coding is the same as for the radial profiles (Fig. 3), covering 40 Myr. With no additional physics, the system overall preserves the initial angular momentum distribution (coherent counter-clockwise rotation).

The suppression of accretion is related to the formation of a central toroidal structure, where gas with relatively high angular momentum circularizes, further blocking part of the inflow solid angle. The hot gas can only accrete along the polar funnel perpendicular to the equatorial (x-y) plane. The circulation within the toroidal region is variable, as reflected by the mild oscillations in Ṁ_•. The configuration is partially unstable: the polar flow is inflowing, while the equatorial region is partially outflowing or circulating, leading to recurrent expansions and contractions (Fig. 2).

The “pinwheel” and toroidal configuration, as well as the suppression of the accretion rate, are consistent with the results of Proga & Begelman (2003) and Krumholz et al. (2005), although our flow is embedded in galactic gradients. For low or moderate vorticity as in our typical system (hot plasma in most galaxies has subsonic and sub-Keplerian velocities²), the accretion rate is weakly dependent on the initial angular momentum (Fig. 1, bottom), since the suppression in the final stage is related to the geometrically thick toroidal structure, which eventually builds up with similar shape. Its typical radius is the BH influence radius ~r_B with height H ~ r_B – for a Keplerian disk H = c_s/ω = (r³/r_B)^1/2. The polar funnel can be thus approximated as a cone with half-opening angle θ ~ π/ 4, allowing gas accretion within a solid angle Ω = 2π(1 − cosθ) ≃ 1.84. Considering the two cones, the funnel has Ω ~ 1/3 of the spherical solid angle, broadly consistent with the simulated Ṁ_• suppression (Fig. 1, top).

3.3. Radial profiles and l_z distribution

In Fig. 3, we show the mass-weighted radial profiles of electron gas density n_e (top) and temperature T_m (bottom), sampled every 1 Myr (dark blue to cyan color). The cuspy profiles are similar to the classic Bondi solution (e.g., T ∝ r^-1; G13), smoothly joining the galactic gradients at large radii. The slight central n_e decrease partly occurs due to the variable boundary conditions near r_B, and partly due to rotation. Since the hot flow is mainly dominated by pressure, the toroidal region has large height (H = c_s/ω) and is smooth, without a net demarcation line as in the radiative run forming a cold thin disk (Sect. 4). The X-ray emission-weighted profiles (not shown) are not dissimilar because of the absence of the cold phase. Therefore, X-ray observations would see peaked gas temperature in the nucleus of the galaxy, if the hot mode is the currently dominant regime of accretion (typically occurring after AGN feedback has overheated the system; see Sect. 9).

In Fig. 4, we present another important diagnostic tool: the mass distribution function (PDF) of specific angular momentum along the rotation axis l_z, during the 40 Myr evolution. Since the model has no heating, cooling, or turbulence, and the accretion is substantially inhibited, the system overall conserves the angular momentum distribution. Notice that the PDF of l_z has only positive values, the mark of coherent counter-clockwise rotation (the right tail is decreasing since we consider the gas within r< 8 kpc). Reshaping the angular momentum distribution via other physical processes is crucial to trigger boosted accretion.

4. Accretion with cooling

In the next model, the reference rotating accretion flow experiences cooling due to radiation (mainly Bremsstrahlung in the X-ray band and line cooling below 1 keV) with emissivity ℒ = n_en_i Λ(T). No source of heating or turbulence affects the dynamics.

4.1. Accretion rate

The central result is the decoupling between the accretion rate and the cooling rate (Fig. 5, top), no more closely tracking each other as in the spherically symmetric cooling flow (G13; Sect. 4). The dense gas quickly loses pressure support via radiative emission (initial minimum t_cool is ≈8 Myr) and forms a rotationally-supported thin disk. The fast condensation affects first the inner and denser gas with lower angular momentum, which can be quickly accreted (). After 10 Myr, the cold phase arises from the hot gas with high angular momentum. Falling from r >r_B toward the center, this cooling gas rapidly increases the rotational velocity and circularizes, damping the accretion rate. At final time, (blue) and the cooling rate³ is (dashed), a difference of two orders of magnitude. The normalized accretion rate is also low, roughly four times the Bondi rate at the kpc scale.

Compared with the adiabatic run (solid black), the accretion rate is about 6 × higher, since the weakened pressure support increases the effective inflow, in particular along the polar region. The presence of a condensing hot halo thus alters the classic thin disk picture, where the cold gas is the only entity.

Fig. 5

Accretion with cooling and e_rot = 0.3 (blue): evolution of the accretion rate (physical and normalized to the kpc-scale, runtime Bondi rate – top and bottom panel, respectively). The dashed line is the average cooling rate (related to the gas with T< 10⁵ K). Solid black line is the adiabatic rotating model (Sect. 3). Despite the substantial cooling rates, yr^-1, the final accretion rate is two orders of magnitude lower because of the formation of a rotationally-supported thin disk.

Fig. 6

Accretion with cooling and e_rot = 0.3: temperature cross-sections (2 × 2 kpc²) through z = 0 (top) and x = 0 (bottom), after 2 and 4 t_cool, respectively. The velocity field normalization is 6000 km s^-1 (unit arrow is 1/8 of the image width). The maps show the formation of a symmetric cold thin disk, which quickly condenses out of the hot phase and inhibits accretion.

Fig. 7

Accretion with cooling and e_rot = 0.3: 3D mass- and emission-weighted radial profiles of density and temperature (cf. Fig. 3). The T_ew profile has X-ray threshold of 0.3 keV and is computed in larger radial bins (emulating a Chandra observation). The cold thin disk keeps growing via condensation. The X-ray temperature is overall insensitive to the presence of the cold disk.

Fig. 8

Accretion with cooling and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the cold phase (full evolution from blue to cyan lines). Cold gas is related to T< 10⁵ K. The PDF of the hot phase (not shown) is analogous to that in Fig. 4, albeit shifting by ~15 percent to higher normalization and l_z. The cold phase emerges out of this distribution, adding during time higher l_z gas, and thus widening the PDF.

4.2. Dynamics

Figure 6 shows the formation of the symmetric thin disk in more detail. The hot gas loses internal energy and thus pressure, but it is still balanced by rotation along R, leading to the infall toward the direction perpendicular to the x-y plane, where the low-entropy gas finds a new rotational equilibrium. Because of the multiphase stratification and transonic inflow, the disk experiences shocks (see, e.g., Tejeda et al. 2012) and hydrodynamical instabilities, such as Kelvin-Helmoltz and Rayleigh-Taylor. The overall picture is very different from a spherically symmetric cooling flow (G13), since Ṁ_• ≪ Ṁ_cool. Along the polar funnel, the transonic flow is not inhibited by rotation and gas can quickly accrete.

Massive galaxies which are dominated by cooling (due to weak or no heating) are thus expected to show a rotationally supported cold disk, arising from the fast spin-up of the gas. The X-ray ellipticity greater than that of the stellar component in the inner 1 kpc may be a sign of this phenomenon (e.g., NGC 4649), albeit moderate turbulence is still required to avoid markedly flat isophotes inconsistent with observations (Diehl & Statler 2007; see also Brighenti & Mathews 2000).

4.3. Radial profiles and l_z distribution

The mass-weighted radial profiles in Fig. 7 reveal the presence of the highly dense (10³ cm^-3) and cold thin disk, which has condensed out of the hot atmosphere. At variance with T_m, the X-ray temperature (T weighted by X-ray emissivity using Chandra sensitivity; bottom panel) only has a mild decline from large to 1 kpc radius, where it starts to stabilize around 10⁷ K. The cold disk keeps growing through time because of the continuous condensation of higher angular momentum gas. The rotating structure is thin, with slightly expanding dense lobes where the warm gas is still condensing (H = c_s/ω; Fig. 6), which can be tracked in the radial profiles.

The disk extends to ~1 kpc after 40 Myr of evolution. Its growth diminishes as the cooling rate saturates (Fig. 5). During periods of weak heating and turbulence, this could be a common regime, facilitating the development of the rotating cold disks observed in many massive elliptical galaxies (e.g., NGC 6868, NGC 7049, and NGC 4261 – Werner et al. 2014; see also Mathews & Brighenti 2003; Young et al. 2011; Alatalo et al. 2013). The retrieved size of the disk (e.g., via ALMA or Herschel) may point out how long the cooling-dominated phase has lasted, setting constraints on the AGN feedback duty cycle (albeit we note that a clumpy rotational structure can be present during CCA and significant feedback; Sect. 7).

Figure 8 shows the l_z distribution of the cold phase. The PDF of the hot phase is analogous to that in Fig. 4, shifting by ~15 percent to higher normalization and l_z due to the large-scale inflow of gas losing pressure. The cold phase emerges out of the hot gas distribution, progressively accumulating higher l_z gas coming from larger radii, and thus widening the PDF while the disk grows (blue to cyan). As in the previous adiabatic run, l_z is only positive, the mark of coherent rotation, albeit now in the form of a cold thin disk. Again, such a distribution of angular momentum implies substantially suppressed Ṁ_•.

5. Adiabatic accretion with turbulence

Fig. 9

Adiabatic accretion with subsonic turbulence and e_rot = 0.3 (brown: Ma ~ 0.35, i.e., Ta_t ~ 0.75; orange: 1/4 lower Mach number, i.e., Ta_t ~ 3): evolution of the accretion rate. The accretion rate is suppressed by a factor ~3 compared with the nonrotating model (dot-dashed), as in the purely rotating run (solid black; Sect. 3), since turbulence still induces local (but not global) vorticity. The chaotic eddies generate however higher variability, as long as Ta_t< 1. In the opposite regime, rotation drives the dynamics.

Fig. 10

Adiabatic accretion with subsonic turbulence (reference Ma ~ 0.35) and e_rot = 0.3: mid-plane temperature cut (cf. Fig. 2). The equatorial plane does not display coherent rotation, since the gas cannot properly circularize in the presence of significant turbulence (σ_v >v_rot). The central vortical motions stifle again accretion.

Cosmic systems are rarely (if ever) in perfect hydrostatic equilibrium. The hot gas in galaxies, groups, and clusters is continuously stirred by the action of AGN, supernovae feedback, galaxy motions, and mergers. We thus probe the effect of turbulence on the rotating and adiabatic flow, testing intrinsic⁴ velocity dispersion in the range of σ_v ~ 40–150 km s^-1.

5.1. Accretion rate and dynamics

Figure 9 shows the evolution of the accretion rate for the reference Ma ~ 0.35 (brown) and for 1/4 lower Mach number (Ta_t ~ 3; orange). In both runs, the suppression of Ṁ_• is ~1/3 compared with the nonrotating Bondi flow (dashed line; see also G13). Remarkably, the suppression is analogous to that retrieved in the purely rotating run (black; Sect. 3). While turbulence with σ_v >v_rot is able to disrupt the coherent rotation and to prevent the full circularization, its basic action is to transport momentum. No total angular momentum is created, however, turbulence induces prograde or retrograde vorticity locally (Fig. 11) via eddies generated during the Kolmogorov cascade. The (subsonic) turbulent accretion flow is thus analogous to a gradually varying rotating flow near the accretor (Fig. 10). As discussed in Sect. 3, for a pressure-supported and slowly rotating flow, the geometric funnel in which the gas can accrete is roughly invariant, linked to a suppression ~1/3. The central spiraling motion is enhanced by the baroclinic instability because of the atmosphere stratification (Krumholz et al. 2006). For subsonic turbulence, local vorticity is more relevant than the gas bulk motion relative to the accretor. For reference Ma ~ 0.35, the Ṁ_• suppression related to the bulk motion (Bondi & Hoyle 1944) is just ∝ (1 + M²)^{− 3/2} ≃ 0.84.

A difference between the turbulent run and the purely rotating, adiabatic flow is the increased Ṁ_• variability. The turbulent eddies randomly have low or high angular momentum, generating the peaks and valleys observed in the accretion rate, which oscillate by a factor of ~2. The key role of the local eddy is remarked by the turbulent run with no rotation presented in G13 (Sect. 6), showing similarly suppressed Ṁ_•. As Ta_t > 1 (Fig. 9; orange), the flow is driven by coherent rotation, with only minor turbulent perturbations, thereby reverting to the evolution described in Sect. 3.

Fig. 11

Adiabatic accretion with subsonic turbulence (top: Ma ~ 0.35; bottom: 1/4 lower Mach number, i.e., Ta_t ~ 3) and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the gas within r< 8 kpc (cf. Fig. 4). If Ta_t< 1, turbulence widens the PDF, inducing both retrograde and prograde motions. In the opposite regime, Ta_t > 1, turbulence is too weak to induce retrograde motions: the underlying counter-clockwise rotation remains intact overall, with minor fluctuations superimposed.

Fig. 12

Adiabatic accretion with subsonic turbulence (Ma ~ 0.35) and e_rot = 0.3: mass-weighted profiles of density and temperature (cf. Fig. 3). The profiles are cuspy, as in the classic Bondi flow, albeit becoming progressively shallower because of turbulent diffusion (dissipational heating is negligible, as indicated by the large-scale T profile).

Fig. 13

Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mid-plane T_m cross-section through z = 0 (final time). Without heating, the system experiences a massive CCA flow. Extended cold filaments and clouds condense out of the hot phase via TI, and through recurrent chaotic collisions are quickly accreted by the BH. No steady thin disk can be formed.

5.2. Distribution of l_z and radial profiles

The importance of the threshold Ta_t ≡ v_rot/σ_v ~ 1 can be better appreciated in the distribution of angular momentum (Fig. 11). If Ta_t< 1 (top), stirring can substantially reshape PDF(l_z). Turbulence can be approximated as a diffusion process (with diffusivity ~σ_vL; Gaspari & Churazov 2013), spreading linear and thus⁵ angular momentum (an effective viscosity). The initially peaked and solely positive l_z distribution is progressively morphed into a broader PDF including negative values, with variance ∝σ_v. The PDF is skewed toward the right tail because of the initial rotation. In the σ_v ≫ v_rot regime, the PDF would be symmetric around zero.

The end product of real viscosity is homogeneous velocity (Dirac delta PDF), while the steady state of turbulence is always local perturbations (∝σ_v). Turbulent diffusion not only acts on momentum, but also on K, ρ, T, as shown by the gradually shallower radial profiles (Fig. 12), and by the power spectrum analysis presented in Gaspari et al. (2014b). The fact that turbulence mimics a transport mechanism, while inducing significant local fluctuations, is a key element to develop CCA (Sect. 7). The broadening of the angular momentum distribution alone does not stimulate boosted accretion. In contrast to the cold clouds experiencing major inelastic collisions, the hot diffuse halo is in global hydrostatic equilibrium because of the pressure support, thereby the subsonic eddies do not mostly cancel angular momentum.

In the opposite regime Ta_t > 1 (Fig. 11, bottom), turbulence is too weak to induce retrograde motions: the underlying counter-clockwise l_z distribution overall remains intact and the coherent rotation drives the dynamics. The reduced effective diffusivity is also evident in the radial profiles (not shown), where the central density decreases only to n_e ≃ 1.5 cm^-3.

6. Accretion with cooling and turbulence

In the next model, we turn on radiative cooling, while the reference subsonic turbulence (Ma ~ 0.35) stirs the hot atmosphere. The development of a clumpy multiphase medium completely changes the behavior of accretion. This simulation also warns how mild chaotic motions can profoundly modify the picture presented by analytic models (e.g., the classic thin disk).

6.1. Dynamics

In Fig. 13, the temperature map reveals the absence of major coherent motions. No source of heating is present, nevertheless the perturbations seeded by subsonic turbulence grow nonlinear via TI and produce extended multiphase structures (see G13 and McCourt et al. 2012 for further discussions on the formed TI). The dynamics of the gas is chaotic because of high sensitivity of the long-term dynamics on local TI. The recurrent chaotic collisions between the condensed clouds, filaments, and a clumpy torus in the inner region promote the cancellation of angular momentum (see also Nayakshin & King 2007; Pizzolato & Soker 2010) boosting the accretion rate. On top of turbulent diffusion, collisions promote further disruption of coherent motions and rotating structures. No steady thin disk can be formed (compare the evolution with that in Sect. 4), although at later times a volatile and clumpy cold torus emerges out of the residual gas with large l_z due to incomplete cancellation (Sect. 6.3). The multiphase gas halo in galaxies should be thus treated as a collisional, hydrodynamical system. The cold phase is not well described by ballistic orbits. The collisions are frequent in the inner 1 kpc core (with Myr variability), as major filaments have lengths comparable to this radius, initiating further interactions between cold elements.

6.2. Accretion rate

Chaotic cold accretion drives the dynamics, in a similar manner as found in G13 (as long as Ta_t< 1; see next Sect. 7). The cold clouds condense out of the stirred hot phase, thereby experiencing chaotic streamlines. The rapid prograde versus retrograde collisions cancel angular momentum, and consequently boost the accretion rate up to two orders of magnitude with respect to the kpc-scale Bondi rate (Fig. 14, bottom). Compared with the adiabatic run (either turbulent or rotating; solid black, top), the increase is almost a factor 10³. At variance with the thin disk evolution (Sect. 4), the accretion rate is linearly tied to Ṁ_cool (dashed), albeit experiencing substantial chaotic variability up to ~1 dex. The cooling rate saturates slightly faster around yr^-1 because of the turbulent mixing of entropy. At t > 25 Myr (top), the residual cold gas with high l_z > 0 induces deeper Ṁ_• valleys (via a clumpy torus).

Fig. 14

Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3 (green): evolution of the physical and normalized accretion rate (cf. Fig. 5; the average of Ṁ_• in the top panel has 0.1 Myr step). The dashed line is the average cooling rate (1 Myr step). The solid black line is the adiabatic rotating model (Sect. 3). Chaotic cold accretion drives the dynamics as long as Ta < 1. Recurrent collisions in the cold phase cancel angular momentum and boost the accretion rate up to two orders of magnitude with respect to the Bondi rate. The accretion rate is linearly tied to Ṁ_cool again.

This regime with no heating produces unrealistically high cooling rates and condensation. The X-ray spectra indicate Ṁ_cool lower by at least an order of magnitude (e.g., Tamura et al. 2003; Peterson & Fabian 2006, for a review). Nevertheless, it is instructive to understand CCA embedded in a pure cooling flow. Some systems may experience a delayed AGN feedback (in particular at high redshift), enabling a massive CCA for a transient time (e.g., Phoenix cluster; McDonald et al. 2013).

6.3. Distribution of l_z and radial profiles

At variance with the purely radiative run, the cold phase randomly condenses out of the l_z distribution shown in Fig. 11 (top), i.e., the cold clouds and filaments can be generated with both prograde and retrograde motions. Initially, the inner gas with lower l_z cools faster, growing a modest PDF (dark blue line). After 10 Myr, the wings of the broader PDF start to experience significant recurrent narrowing, as a result of violent collisions canceling angular momentum (occurring in a period of a few Myr). However, the mass of unaccreted cold gas tends to substantially rise with time (leading to a PDF with larger width and normalization), progressively obfuscating the previous effect. In the subsequent heated run (Fig. 19), it will be easier to isolate the action of collisions, lacking the formation of a massive cooling flow.

An unbalance toward the right wing (l_z > 200 kpc km s^-1) persists because of the initial halo rotation, implying that a prograde (though clumpy) torus-like structure is a recurrent phenomenon. As Ta_t ≪ 1, the role of rotation becomes negligible and the prograde bias disappears (G13). Conversely, as Ta_t > 3, the cold phase can only be generated with positive l_z (Fig. 11, bottom) and the accretion follows that of the coherent thin disk (Sect. 4).

Fig. 15

Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the cold phase (the hot phase has PDF analogous to Fig. 11, top). At variance with the purely radiative run, the cold phase randomly condenses out of a broad l_z distribution, including both prograde and retrograde motions. This permits frequent major collisions, canceling angular momentum. The mass of unaccreted cold gas tends to significantly rise with time due to the unheated cooling flow.

In Fig. 16, the radial profiles are analogous to that found in G13, showing the massive condensation of warm or cold gas out of the hot phase via TI, and the fluctuations imparted by turbulence. After full condensation, the cold gas typically populates the region within 3 kpc. Maximum density is slightly higher compared with G13 (n_e ~ 10⁴ cm^-3), since the initial hydrostatic atmosphere has slightly shallower density gradient. The core X-ray temperature is flat, a characteristic mark of cold accretion dominating over the hot mode.

Fig. 16

Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mass– and emission–weighted radial profiles of density and temperature (cf. Fig. 7). The profiles show the condensation of warm gas out of the hot phase via TI up to several kpc. The X-ray temperature is flat, with no cuspy core, which is a characteristic mark of cold accretion.

7. Accretion with heating, cooling, and turbulence: chaotic cold accretion

In the last set of models, we focus on the typical state of the hot plasma in a massive galaxy, group, or cluster. The cooling flow is now quenched via heating (Sect. 2.2) by 10–20 fold, in agreement with XMM-Newton spectral data (Tamura et al. 2003; Peterson & Fabian 2006). The source of heating is mainly attributed to AGN feedback, albeit supernovae, thermal conduction, and mergers can possibly contribute.

7.1. Accretion rate

The major result is that, even in the presence of significant rotation (v_rot ≈ 100 km s^-1), the accretion rate is boosted up to 100 × the Bondi rate (Fig. 17, red), which is consistent with the e_rot = 0 model presented in G13 (Sect. 7). The peaks in the accretion rate are comparable to the quenched cooling rate, (dashed)⁶. Adopting Ṁ_• ~ Ṁ_cool is an effective subgrid accretion model for large-scale simulations and analytic calculations. Initially, accretion is driven by the rotating hot flow. After 10 Myr, CCA drives the dynamics. At variance with the runs in Sect. 6, the presence of heating prevents the formation of a catastrophic cooling flow: the average Ṁ_• and Ṁ_cool do not increase with time. In the regions where t_cool/t_ff< 10 (between r ~ 100 pc and several kpc), TI grows nonlinearly (see also Gaspari et al. 2012a), the cold gas condenses out of the hot phase, and the chaotic collisions promote cancellation of angular momentum (Sect. 7.2). Multiwavelength observations support the TI and CCA scenario, detecting extended multiphase gas in the core of many massive galaxies which is cospatial in X-ray, FUV, Hα, and molecular band (McDonald et al. 2010, 2011; Werner et al. 2013, 2014; Sect. 8).

CCA dominates as long as the following criterium is met: 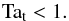$T a_{t} < 1.$ $\begin{equation} {\rm Ta_t} < 1. \end{equation}$ (7)In Fig. 17, we show the models with 1/2 and 1/4 lower turbulence with respect to the reference Ma ~ 0.35, which correspond to Ta_t ~ 1.5 (magenta) and 3 (orange), respectively. As the rotational velocity exceeds the turbulent velocity dispersion, the accretion rate is progressively suppressed by a factor ∝ Ta_t. The accretion flow shifts from turbulence-driven, with chaotic filaments and boosted Ṁ_•, to rotationally-driven, displaying a coherent disk and reduced Ṁ_•. In the regime Ta_t ≫ 1, Ṁ_• saturates around ~ yr^-1, as perturbations induced by turbulence are not influencing the evolution of the thin disk.

In a complementary run (not shown), we doubled the rotational velocity (≈200 km s^-1) while fixing the reference Ma ~ 0.35 (again Ta_t ~ 1.5). The results are analogous to the previous models after comparing identical cooling rate (a stronger flattening implies higher ρ at large r, thus larger cooling rates).

Comparing to observations, accretion rates can be estimated from the jet or cavity power, which for common massive ellipticals spans P_cav ≈ 10⁴²–10⁴⁴ erg s^-1 (Allen et al. 2006). From the quiescent to strong feedback state Ṁ_• = P_cav/ (εc²) ≈ 2 × 10^-2–, where ε ~ 10^-3 is the typical mechanical efficiency for massive ellipticals (Gaspari et al. 2012b). The simulated models cover this range (Fig. 17), with CCA representing the strong impulsive feedback stage, while the disk-dominated phase is associated with the more quiescent galaxies. We notice that the accretion rates are sub-Eddington, Ṁ_•/Ṁ_Edd ≈ 3×10^-4–3 × 10^-2 (where ), i.e., the common regime where AGN are observed to be radiatively inefficient and dominated by mechanical energy input (Russell et al. 2013).

Fig. 17

Accretion with heating, cooling, e_rot = 0.3, and varying levels of turbulence: evolution of the accretion rate (the Ṁ_• average in the top panel has 0.1 Myr step). The Mach number varies from the reference Ma ~ 0.35 (red) to 1/2 (magenta) and 1/4 (orange) of this value, i.e., Ta_t ≃ 0.7,1.5,3, respectively. The dashed line is the average net cooling rate (1 Myr step). As before, the solid black line is the adiabatic rotating model, and the runtime Bondi rate for the normalized plot is computed at r ≈ 1–2 kpc (Sect. 3). In the atmosphere with Ta_t< 1, CCA drives the dynamics, boosting the accretion rate up to 100 × the Bondi rate, which is consistent with the nonrotating CCA evolution shown in G13. As Ta_t > 1, the accretion flow shifts from turbulence-driven (linked to extended filaments and boosted accretion) to rotationally-driven (tied to a coherent disk and suppressed accretion).

Fig. 18

Accretion with heating, cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: temperature cross-section, with the velocity field overlaid. Full circularization is not possible in a turbulent environment characterized by Ta_t< 1. The recurrent chaotic collisions between the cold filaments, clouds, and the clumpy torus, cancel the angular momentum of the cold gas, leading to the rapid peaks in the accretion rate, Ṁ_• ~ Ṁ_cool.

Fig. 19

Accretion with heating, cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the cold phase (the hot phase has PDF analogous to Fig. 11, top). After three rapid Ṁ_• bursts, the PDF narrows on average from 20 Myr (solid) to 27 Myr (dashed) due to major collisions canceling positive and negative l_z. The action of collisions is periodically contrasted by fresh condensation, favoring a broader distribution.

7.2. CCA dynamics and l_z distribution

CCA is driven by the following processes. First, turbulence broadens the distribution of angular momentum related to the hot atmosphere, as shown in Fig. 11 (top; see discussion in Sect. 5.2). The broadening is ∝σ_v and induces both prograde and retrograde chaotic motions. The broadening of the PDF(l_z) alone does not imply boosted accretion, since the hot gas is supported by pressure. The second step is the condensation of cold gas. The cooling gas retains the imprint of the hot phase, emerging out of the broad l_z distribution with both positive and negative values. During infall⁷, the clouds start to significantly collide, mainly in the inner 1 kpc (Fig. 18), inducing major angular momentum cancellation (see also Pizzolato & Soker 2010). In Fig. 19, we focus on the PDF(l_z) evolution between 20 and 27 Myr, as three major Ṁ_• bursts and collisions occur in rapid succession. Despite the continuous cold gas condensation, a rapid narrowing of the l_z distribution occurs, leading to the Ṁ_• bursts seen in Fig. 17. At other times (not shown), gas condensation can regenerate one or both tails. Since the cooling rate and cold mass is quenched by more than an order of magnitude compared with the pure cooling flow (consistently with observations; Tamura et al. 2003), collisional effects are not as overwhelmed by condensation through time as in the nonheated run (Sect. 6). The residual cold phase achieves statistical steady state after ~2 t_cool, while being shaped by the recurrent broadening and narrowing of the angular momentum distribution with Myr variability (a prograde bias is still present after 40 Myr).

Both turbulence and collisions characterize CCA. Without turbulence the angular momentum of the newborn cold phase would only have positive l_z (cf. Fig. 11, bottom), leading to a coherent disk. Without collisions, the cold phase might not strongly boost accretion (no rapid l_z cancellation). Both processes are tightly related to σ_v. If Ta_t< 1, as in the reference run, turbulent diffusion dominates over the advection because of coherent rotation, leading to substantial PDF broadening and head-on cloud collisions.

However, if Ta_t > 1, the broadening is too weak and collisions cannot cancel angular momentum. The suppression in the accretion rate is relatively smooth, Ṁ_• ∝ Ta_t^-1 (Fig. 17), until the thin disk evolution dominates for Ta_t > 3 (i.e., at least an order of magnitude in classic Taylor number; Sect. 1).

The linear transition can be crudely understood in terms of mixing length approximation. Accretion in a rotating atmosphere is ultimately limited by the diffusion time related to collisions (the PDF broadening, albeit directly tied to Ta_t, is a necessary, but not sufficient, condition). Using as effective collisional viscosity⁸ν ~ σ_vλ, with λ the collisional mean free path, we can write the following scaling: 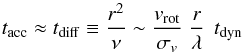$t_{acc} \approx t_{diff} \equiv \frac{r^{2}}{ν} ~ \frac{v_{rot}}{σ_{v}} \frac{r}{λ} t_{dyn}$ $\begin{equation} \label{e:diff} t_{\rm acc}\approx t_{\rm diff} \equiv\frac{r^2}{\nu} \sim \frac{v_{\rm rot}}{\sigma_ v}\; \frac{r}{\lambda}\; \,t_{\rm dyn} \end{equation}$ (8)where we assumed the gas dynamical timescale is mainly associated with rotation. The smaller the velocity dispersion, the longer the diffusion and hence accretion timescale. The clouds and filaments must travel into the inner 1 kpc region to experience major collisions. Here, the mean free path is typically comparable to the radius (yet smaller than the global system), yielding the scaling t_acc ~ Ta_tt_dyn, in agreement with our findings (Fig. 17). In general, λ varies depending on the size of the condensing clouds, which can be smaller than r. This slows the accretion time, creating the valleys in Ṁ_•. While the accretion peaks are provided by major collisions, the average accretion rate is ∝Ta_t^-1. As Ta_t< 1, turbulent diffusion overcomes rotation (Eq. (8) is no longer accurate) and the sinking of cold clouds, after condensation in a cooling time, occurs in a radial free-fall timescale, returning to the pure CCA evolution shown in G13.

We note that the ram pressure drag is here subdominant. The density contrast between the cold and hot phase is ρ_c/ρ_h ~ 10³. 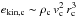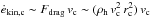The cloud halting distance to lose all the kinetic energy can be estimated as d_halt ~ (e_kin,c/ė_kin,c) v_c ~ (ρ_c/ρ_h) r_c, using $e_{kin, c} ~ ρ_{c} v_{c}^{2} r_{c}^{3}$ $\hbox{$e_{\rm kin,c}\sim \rho_{\rm c}\,v_{\rm c}^2\,r_{\rm c}^3$}$ and $ė_{kin, c} ~ F_{drag} v_{c} ~ (ρ_{h} v_{c}^{2} r_{c}^{2}) v_{c}$ $\hbox{$\dot{e}_{\rm kin,c}\sim F_{\rm drag}\,v_{\rm c} \sim (\rho_{\rm h}\,v_{\rm c}^2\,r_{\rm c}^2)\,v_{\rm c}$}$ . Therefore, even small clouds of 50 pc size would require distances larger than the box to lose most of the energy due to drag, while collisions occur in just a small fraction of the system size, mostly within r< 1 kpc.

Fig. 20

Accretion with heating, cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: 3D mass- (top) and X-ray emission-weighted (∝ ℒ; bottom) radial profiles of density and temperature (cf. Fig. 7). The profiles show the extended multiphase structure, which is largely concealed in the X-ray band. The X-ray temperature profile is remarkably flat, in contrast to the hot-mode accretion, which has a peaked temperature profile. This is a key observable, which can be thoroughly tested (Wong et al. 2014; Russell et al. 2015), to unveil the evolutionary stage in which the galaxy is residing.

The reference v_rot ≈ 100 km s^-1 is near the high end of the realistic range (as we want to clearly understand the impact of rotation). For e_rot > 0.3, the galaxy is substantially flattened and the gas v_rot would inconsistently exceed the stellar rotational velocity, which is commonly ~100 km s^-1 (Davies et al. 1983). Therefore, many massive elliptical galaxies should reside in the pure CCA regime (Ta_t ≪ 1), in particular after strong injection of turbulence, e.g., via AGN outbursts and merger events. On the other hand, a fraction of elliptical galaxies are observed to host central cold disks (Young et al. 2011; Alatalo et al. 2013), which is a by-product of incomplete angular momentum cancellation. This is associated with Ta_t ≳ 3 as turbulence and heating start to decrease, in agreement with the observational findings presented by Werner et al. (2014; Table 1). In the disk stage, AGN feedback can still be active (Hamer et al. 2014; McNamara et al. 2014), albeit being less episodic; the accretion rates and feedback are dramatically suppressed only in the hot mode (Sect. 5).

7.3. Radial profiles

The evolution of the t_cool/t_ff (TI-ratio) profiles is analogous to those presented in G13 (their Fig. 15). The threshold t_cool/t_ff ≲ 10 indicates where the nonlinear condensation of extended multiphase gas develops (Gaspari et al. 2012a; McCourt et al. 2012; Sharma et al. 2012). Within the Bondi radius and above ~7 kpc TI cannot grow nonlinearly, as buoyancy dominates. Most cold clouds and filaments fill the region 200 pc–1 kpc, where the TI-ratio has a minimum around 4 and the initial gas density is above 0.1 cm^-3, leading to more rapid condensation. The cloud funneling toward the BH allows more frequent interactions within such region. The dropout of cold gas results in a gradual increase of the average entropy and thus TI-ratio, as the plasma becomes more tenuous (in a later stage, feedback self-regulation prevents overheating; Gaspari et al. 2012a).

For systems with Ta_t > 1, the gas is mainly supported by coherent rotation during the condensation process, implying that radial compression is less relevant for TI growth. With no radially compressive term, it has been shown that the TI-ratio threshold is lower by an order of magnitude, t_cool/t_ff ≲ 1 (McCourt et al. 2012). The free-fall time does not increase: the effective gravity is lower along R, but the cold gas tends to fall along the z direction and settle on the equatorial plane; hence t_ff(z) = (2z/g(z))^1/2, which is identical to t_ff(r). In other words, nonlinear TI and fragmented clouds are more difficult to form in a cooling gas shaped by the centrifugal force. This is confirmed by the Ta_t > 1 runs, having a rather stable Ṁ_• evolution. Notice that t_cool/t_ff > 1 does not imply the cold phase will not form, but that the condensation is monolithic, leading to a disk structure instead of filaments (e.g., NGC 6868 and NGC 7049; Werner et al. 2014). The reduced fragmentation also affects the Ta_t = 0.7 run, favoring filaments instead of spherical clouds. The major cold phase interactions can be thus more prolonged inducing broader Ṁ_• peaks compared with G13 model.

The mass-weighted radial profiles (Fig. 20, top panels) highlight the extended multiphase structure and Myr variability of the accretion flow. The extension of multiphase filaments up to a few kpc is consistent with Hα observations (Fig. 1 in Werner et al. 2014; Sect. 8). Performing an X-ray observation (bottom) instead conceals them, allowing the hot component to emerge (T > 0.3 keV). As in G13, the X-ray emission-weighted temperature profile is flat, in contrast to the peaked profile of the adiabatic flow (Fig. 12). This is a key observable and prediction, which can be tested, in particular, with future X-ray missions (e.g., Athena). Recently, the Megasecond Chandra observation of NGC 3115 (Wong et al. 2014) discovered a flat temperature core with multiphase structure within the Bondi radius. Their retrieved density profile within 200 pc has moderate slope ∝r^-1, which is consistent with our findings (Fig. 20, bottom left). Russell et al. (2015) also discovered a flat X-ray temperature and r^-1 density profile within the Bondi radius of M 87 with deep Chandra data. Both observations remarkably corroborate the CCA predictions.

Fig. 21

Top: synthetic Hα surface brightness image along an arbitrary line of sight during the two characteristic late stages: the filamentary phase (left; run with Ta_t ≃ 0.7) and the disk-dominated phase (right; Ta_t ≃ 3). The resolution mimics that of SOAR, ~0.2 arcsec. Bottom: observed SOAR Hα+[NII] images from Werner et al. (2014) showing the two analogous stages in two real massive elliptical galaxies: CCA (left; NGC 5044) and the rotating disk (right; NGC 6868).

The mass-weighted density profiles show that an inner (~100 pc) clumpy torus is relatively common, though continuously formed and dismantled by the chaotic dynamics. In fact, even in CCA a prograde bias is still present in the long term (Sect. 6.3), as turbulence generates vorticity locally but not globally. The presence of an inner obscuring torus is supported by extensive AGN observations literature (Bianchi et al. 2012, for a review). The central volatile structure derives from the accumulation of multiple filaments, which have not yet completely canceled angular momentum. On the other hand, its rising cross-section increases the collisional rate with the incoming clouds, promoting efficient angular momentum cancellation. The PDF(l_z) of the cold gas within 100 pc is self-similar to Fig. 19, continuously broadening and narrowing through time, albeit in a smaller range, | l_z | < 40 kpc km s^-1 (i.e., below circular angular momentum at 100 pc). As Ta_t > 1, collisions become less efficient (Eq. (8)), and the torus can stabilize in a more coherent and extended disk.

The cold phase temperature can fluctuate between 10⁴–10⁵ K, implying that, in a heated and turbulent environment, the cooling gas does not have to necessarily collapse to the floor temperature, but it can remain relatively warm. Multiwavelength data similarly show cold filaments with a complex multitemperature transition layer (McDonald & Veilleux 2009; McDonald et al. 2010, 2011). Subsonic turbulence in the hot phase becomes supersonic through the cold medium, thus increasing the efficiency of both turbulent mixing and dissipation, consequently reheating the filaments. The observed filamentary warm gas frequently shows significant velocity dispersions (~100 km s^-1; e.g., Canning et al. 2014; Werner et al. 2014) corroborating the importance of turbulent motions.

8. Comparison with Hα observations

As reviewed in Sect. 1, massive elliptical galaxies have been observed to host a significant reservoir of cold gas within the central few kpc. In the CCA mechanism, the extended multiphase gas is a natural outcome of the TI condensation. A key observable of the condensed medium is Hα emission, which is mostly associated with gas at 10⁴ K. We thus compute synthetic surface brightness maps of Hα line from the last runs (Sect. 7) and compare them with the latest observations (Fig. 21).

The Hα emission (6564.6 Å; n = 3 → 2 hydrogen transition) is dominated by the recombination of ionized hydrogen H⁺ (Dong & Draine 2011; Draine 2011). The recombination luminosity is 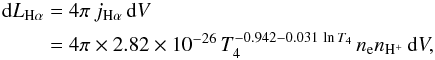$\begin{matrix} d L_{H α} & = & 4 π j_{H α} d V \\ = & 4 π \times 2.82 \times 10^{-26} T_{4}^{- 0.942 - 0.031 \ln T_{4}} n_{e} n_{H^{+}} d V, \end{matrix}$ $\begin{eqnarray} \label{e:Halpha} {\rm d}L_{\rm H\alpha} &=& 4\pi\,j_{\rm H\alpha}\,{\rm d}V \notag\\ &=&4\pi\times 2.82 \times 10^{-26}\,T_4^{-0.942-0.031\,\ln T_4} \,n_{\rm e} n_{\rm H^+}\,{\rm d}V, \end{eqnarray}$ (9)where T₄ ≡ T/ 10⁴ K. The 10⁴ K gas is optically thick to radiation above 13.6 eV, i.e., Lyman photons are quickly re-absorbed. The recombination rate j_Hα includes such absorption (the so-called “case B” recombination; see Draine 2011). The ionization fraction f ≡ n_H⁺/n_H is typically low at 10⁴ K. In abundance equilibrium, the recombination and collisional ionization rates (see Katz et al. 1996) determine f, such that n_H⁺/n_H = 1 + α_{R, H⁺}/ (α_R,H⁺ + Γ_C,H⁰). At T = 10⁴ K the ionization fraction is f ≃ 10^-3. Photoionization driven by OB and pAGB stars can increase this level. As adopted in reference literature studies (e.g., Joung & Mac Low 2006), we use f ~ 10^-2 (see also Dale et al. 2015). In a subsequent series of papers, we will retrieve and study the ionization fraction in a more realistic way with the inclusion of chemical reaction networks and stellar heating.

In Fig. 21 (top), we present the synthetic Hα maps at two characteristic moments, the filamentary and disk-dominated phase. The synthetic maps are created by summing the contribution from gas in each cell using Eq. (9); the latter equation naturally selects gas with T ≲ 10⁴ K. The resolution mimics that of SOAR, ~0.2 arcsec. In the bottom panels, we show for qualitative comparison the observed maps retrieved with the 4.1 m SOAR telescope (from Werner et al. 2014). In the top left image (Ta_t ≃ 0.7 run), a complex network of cold filaments and clouds has condensed out of the hot halo, reaching r ≃ 3.3 kpc. The system is in full CCA mode. Within 1 kpc, the frequent interactions between the filaments and clouds make the Hα distribution approach spherical symmetry. The observed Hα emission (bottom left) shows similar filamentary and core morphology. The real emission appears more extended, albeit the synthetic maps are not contaminated by the stellar and [NII] contribution. At a distance d_L ≃ 40.3 Mpc, the total synthetic Hα flux is F_Hα ≃ 4.0 × 10^-13 erg s^-1 cm^-2 (L_Hα ≃ 7.8 × 10⁴⁰ erg s^-1), which is comparable to the real NGC 5044 flux, F_{Hα + [ NII ]} ≃ 7.6 × 10^-13 erg s^-1 cm^-2 (Werner et al. 2014). It is worth noting that NGC 5044 Hα luminosity marks the upper envelope of observed values; several elliptical galaxies have ~1 dex lower luminosity⁹.

In the top right panel, the Ta_t ≃ 3 run displays a different behavior. The system is no longer in filamentary CCA mode; the rotating disk drives the dynamics. The disk is contained within 500 pc and is slightly perturbed by the relatively weak turbulence. The observed Hα image of the massive elliptical NGC 6868 (bottom right) shows a very similar smooth pattern associated with a rotating structure (which has been confirmed through the [CII] velocity distribution; Werner et al. 2014). Remarkably, NGC 6868 does not show major signs of AGN feedback, as radio jets or outflows, while NGC 5044 which resides in filamentary CCA mode is strongly perturbed by AGN activity (Gastaldello et al. 2009). Considering the disk size, this quiescent phase could last since ≳50 Myr. The NGC 6868 cooling time is indeed relatively long, t_cool ≈ 78 Myr. At a distance of 41.2 Mpc, the synthetic flux is F_Hα ≃ 1.1 × 10^-13 erg s^-1 cm^-2, which is consistent with the observed flux F_{Hα + [ NII ]} ≃ 2.7 × 10^-13 erg s^-1 cm^-2 (Macchetto et al. 1996).

To conclude, despite the fact that it is not our goal to match one-to-one the observed image of a single galaxy, as this would require artificial fine-turning of run parameters and initial conditions, the simulated models capture the essential features of real elliptical galaxies showing a dual morphology of filamentary and rotating multiphase nebulae within the core.

9. Summary and conclusions

We carried out 3D high-resolution simulations to perform controlled astrophysical experiments of the accretion flow on to a SMBH, resolving the galactic 50 kpc scale down to the inner sub-pc scale. We gradually increased the realistic complexity of the hydrodynamic flow, including cooling, turbulence, and heating. We focused on the role of rotation (reference e_rot = 0.3, i.e., v_rot ≈ 100 km s^-1) in altering accretion rates, in comparison with the nonrotating models presented in Gaspari et al. 2013b (G13). The main features of each accretion flow can be summarized as follows.

Adiabatic rotating flow. The hot pressure-dominated flow forms a central rotational barrier (≲r_B), with a thick toroidal geometry and mild variability. The gas can only accrete along a polar funnel with half-opening angle ~π/ 4. Compared with the spherically symmetric model, the accretion rate is suppressed by a characteristic factor of ~3. The accretion rate is comparable to the reference Ṁ_Bondi computed at r ~ 1–2 kpc. The stratification of the atmosphere slightly decreases the central density and accretion through time. The characteristic mark of the hot flow is the cuspy (X-ray or mass-weighted) temperature profile. The coherent prograde rotation preserves the initial positive angular momentum distribution.
Radiative rotating flow. The radiatively cooling gas loses pressure support in a cooling time and circularizes on the equatorial plane, forming a cold thin disk. At variance with the classic cooling flow, the accretion rate is suppressed and decoupled from the cooling rate, Ṁ_• ≲ 10^-2Ṁ_cool. However, Ṁ_• is still a decade higher compared with the adiabatic flow due to the halo condensation. The cold phase progressively accumulates higher positive l_z, as the kpc-size disk grows through time via condensation.
Adiabatic rotating flow stirred by turbulence. From the perspective of the accretion rate and ρ, T radial profiles, the stirred hot flow is analogous to the unperturbed adiabatic evolution, with increased variability (factor of 2). The similar ~1/3 suppression of Ṁ_• is because subsonic turbulence generates local, though not global, vorticity (which is further enhanced by the baroclinic instability in a stratified medium). As Ta_t ≡ v_rot/σ_v< 1, the l_z distribution is reshaped and substantially broadened via turbulent diffusion, generating both prograde and retrograde eddies. If Ta_t > 1, the initial PDF is only slightly modified: the flow is again driven and suppressed by coherent rotation (l_z > 0) and not by turbulent eddies.
CCA (cooling, heating, turbulence). As long as Ta_t< 1, CCA drives the dynamics, as found in G13. Within several kpc, TI can grow nonlinearly (t_cool/t_ff< 10), extended multi-temperature filaments condense out of the hot phase and rain toward the BH. The collisions (r< 1 kpc) between the cold clouds, filaments, and central clumpy torus enable to efficiently cancel angular momentum, boosting the accretion rate, with impulsive peaks up to the cooling rate or 100 × the Bondi rate. Using Ṁ_• ~ Ṁ_cool is thus a realistic (subgrid) model for large-scale simulations and analytic studies. Without heating, the CCA evolution is analogous, albeit the cold phase properties (cold mass, collisions, and PDF) are magnified by an order of magnitude. The condensed cold phase retains the imprint of the stirred hot phase, emerging out of the broadened l_z distribution. The presence of both prograde and retrograde motions permits the cancellation of angular momentum. After major collisions the PDF narrows (Ṁ_• peaks), while condensation broadens it again. Transient incomplete cancellation (Ṁ_• valleys) creates a clumpy, highly variable torus, later favoring the interactions with incoming clouds. In the regime Ta_t > 1, turbulent diffusion becomes weaker than advection due to rotation, reducing the relative PDF broadening and the efficiency of collisions. The accretion rate thus decreases as Ta_t^-1 until the cold disk drives the evolution again. This is aggravated by the increased difficulty of TI and fragmented clouds to form under coherent rotation, as the TI threshold is lowered because of the reduced influence of radial compression. The synthetic Hα maps trace the morphology of the condensed multiphase gas, reproducing the main features of observations (e.g., SOAR and Magellan), such as line fluxes, kpc-scale filaments, or the central rotating disk.

The present work, together with G13, emphasizes the central role of CCA in the evolution of (supermassive) black holes, even in the presence of rotation. The high and variable accretion rates, Ṁ_• ~ Ṁ_cool, can trigger the required level and self-regulation of the AGN feedback to quench cooling flows, star formation and to shape the observed thermodynamic properties of massive galaxies, groups, and clusters (Gaspari et al. 2011a,b, 2012a,b; Sect. 1).

The results obtained in recent years corroborate the following cosmic accretion and feedback cycle shaping gaseous halos. As gas cooling starts to overcome heating (t_cool/t_ff< 10 or central entropy K₀ ≲ 20 keV cm²), CCA is triggered¹⁰, boosting the accretion rate (Ṁ_• ≫ Ṁ_Bondi) and consequently the feedback injection via AGN outflows and/or jets (Ta_t< 1). This phase can be observationally probed via the extended Hα filaments (e.g., NGC 5044; McDonald et al. 2010, 2011; Werner et al. 2013) or inner flat temperature and r^-1 density profiles in X-ray, as recently discovered in NGC 3115 (Wong et al. 2014) and M 87 (Russell et al. 2015). As the core entropy rises and turbulence diminishes (Ta_t > 1), nonlinear TI weakens and the rotating disk is left as the sole cold structure (e.g., NGC 6868 or NGC 7049 in Werner et al. 2014; see also Mathews & Brighenti 2003; Young et al. 2011; Alatalo et al. 2013). The transition is associated with a gradual decrease in the accretion rate ∝Ta_t^-1 (feedback can still be active; e.g., NGC 4261). Waiting longer times, as the disk is consumed (e.g., via accretion and star formation) and the halo has been overheated by feedback, the hot gas is the only resource available to poorly fuel the SMBH (t_cool/t_ff ≫ 10). The main diagnostic of this hot-mode regime is the cuspy X-ray temperature profile, typically associated with more quiescent systems (e.g., NGC 4649, NGC 1332; Humphrey et al. 2008, 2009). Transitioning from the fully cold mode to hot mode, the accretion rate experiences a strong suppression, from 100 × to a small fraction of the Bondi rate. Feedback heating becomes negligible, entropy starts to decrease, and the gaseous halo is allowed to cool again, restarting a new cycle defined by CCA and boosted feedback to the rotating disk to the hot mode and suppressed feedback, and so on. The simulated accretion rates cover the realistic range based on the cavity power observed in massive ellipticals (Allen et al. 2006), Ṁ_• = P_cav/ (εc²) ≈ 2 × 10^-2–.

In the subsequent series of works, we will continue to investigate the role of additional physics (see Sect. 9.1 in G13 for a discussion) to further understand CCA and to better interpret new data. For instance, a rapidly varying potential (e.g., mergers) could facilitate TI and chaotic collisions, thereby promoting CCA via tidal torques (Sect. 1). Although star formation is observed to be inefficient in elliptical galaxies and in turbulent molecular clouds (≲1% efficiency; Federrath 2015), it can partially reduce the fueling of the SMBH. Stellar feedback, on the other hand, may reheat the cold gas, promoting additional turbulence and TI. Forthcoming observations of cold gas, which combine several wavelengths, e.g., via Herschel, HST, SOAR, CARMA, SKA, and the newly expanding ALMA observatory, will be instrumental in probing CCA and the related predictions with high accuracy. Besides improving the sample size, the new data should be able to shed light on key astrophysical questions, such as the amount of cold gas “raining” on to the black hole, the kinematics of the cold phase (filaments, clouds, and rotating disk), and its tight coupling with AGN feedback.

¹

This quantity shares similarities with the classic Taylor number, which characterizes the importance of centrifugal forces relative to viscous forces, i.e., Ta = ω²R⁴/ν², where ω is the angular velocity, R is the cylindrical radius, and ν is the kinematic viscosity. Notice that Ta ∝ Ta_t².

²

If the gas velocities are super Keplerian near r_B, accretion is driven by the action of shock dissipation allowing the gas to become bound; in this regime, the higher the vorticity, the lower Ṁ_•, typically with a very small and stable torus (cf. Krumholz et al. 2005).

³

The cooling rate is computed as ΔM_cold/ Δt, where M_cold is the cold gas mass in the box related to gas with T< 10⁵ K, not yet sinked by the BH.

⁴

The rotational velocity can be cleanly removed calculating the mean in cylindrical coordinates, v_rot = −v_xy/R + v_yx/R.

⁵

The radial displacement has uniformly random distribution.

⁶

Star formation is observed to be inefficient in massive elliptical galaxies, ≲1 percent of the pure cooling rate (McDonald et al. 2014).

⁷

Nonlinear condensation is too fast and clouds are too massive to be directly affected by the driving, which is slowly injected at large scale.

⁸

Notice that CCA diffusivity, based on collisions and l cancellation, is different from the shear viscosity and associated steady inward or outward transport of l_z postulated in Keplerian thin disks (Shakura & Sunyaev 1973). In the latter model, the velocity is either prograde or retrograde only, and the cold rings experience friction due to internal micro-turbulence (e.g., driven by the magnetorotational instability; Balbus & Hawley 1998).

⁹

Dust, which we do not model, can in part absorb Hα emission.

¹⁰

A nonzero level of subsonic turbulence is always present in real systems (Sect. 2.2), e.g., because of galaxy motions, mergers, stellar evolution. The initial AGN outburst generates further turbulence.

Acknowledgments

The FLASH code was in part developed by the DOE NNSA-ASC OASCR Flash center at the University of Chicago. M.G. is grateful for the financial support provided by the Max Planck Fellowship. F.B. is in part supported by the Prin MIUR grant 2010LY5N2T. HPC resources were provided by the NASA/Ames HEC Program (SMD-13-4373, SMD-13-4377, SMD-14-4819; Pleiades) and CLS center. The post-processing analysis was in part performed with YT (Turk et al. 2011). We thank R. Sunyaev, N. Werner, M. Anderson, R. Khatri, P. Girichidis, and A. Gatto for helpful discussions. We are grateful to N. Werner, who allowed us to reproduce the Hα SOAR images. We thank the anonymous referee who helped to improve the manuscript.

References

Alatalo, K., Davis, T. A., Bureau, M., et al. 2013, MNRAS, 432, 1796 [NASA ADS] [CrossRef] [Google Scholar]
Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21 [NASA ADS] [CrossRef] [Google Scholar]
Anderson, M. E., & Bregman, J. N. 2011, ApJ, 737, 22 [NASA ADS] [CrossRef] [Google Scholar]
Anderson, M. E., Gaspari, M., White, S. D. M., Wang, W., & Dai, X. 2015, MNRAS, 449, 3806 [NASA ADS] [CrossRef] [Google Scholar]
Baganoff, F. K., Maeda, Y., Morris, M., et al. 2003, ApJ, 591, 891 [NASA ADS] [CrossRef] [Google Scholar]
Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
Balbus, S. A., & Soker, N. 1989, ApJ, 341, 611 [NASA ADS] [CrossRef] [Google Scholar]
Banerjee, N., & Sharma, P. 2014, MNRAS, 443, 687 [NASA ADS] [CrossRef] [Google Scholar]
Barai, P., Proga, D., & Nagamine, K. 2012, MNRAS, 424, 728 [NASA ADS] [CrossRef] [Google Scholar]
Barai, P., Viel, M., Murante, G., Gaspari, M., & Borgani, S. 2014, MNRAS, 437, 1456 [NASA ADS] [CrossRef] [Google Scholar]
Best, P. N., von der Linden, A., Kauffmann, G., Heckman, T. M., & Kaiser, C. R. 2007, MNRAS, 379, 894 [NASA ADS] [CrossRef] [Google Scholar]
Bianchi, S., Maiolino, R., & Risaliti, G. 2012, Adv. Astron., 2012, 782030 [NASA ADS] [CrossRef] [Google Scholar]
Binney, J. J., Davies, R. L., & Illingworth, G. D. 1990, ApJ, 361, 78 [NASA ADS] [CrossRef] [Google Scholar]
Bois, M., Emsellem, E., Bournaud, F., et al. 2011, MNRAS, 416, 1654 [NASA ADS] [CrossRef] [Google Scholar]
Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
Booth, C. M., & Schaye, J. 2009, MNRAS, 398, 53 [NASA ADS] [CrossRef] [Google Scholar]
Borgani, S., & Kravtsov, A. 2011, Adv. Sci. Lett., 4, 204 [CrossRef] [Google Scholar]
Brighenti, F., & Mathews, W. G. 1996, ApJ, 470, 747 [NASA ADS] [CrossRef] [Google Scholar]
Brighenti, F., & Mathews, W. G. 1999, ApJ, 512, 65 [NASA ADS] [CrossRef] [Google Scholar]
Brighenti, F., & Mathews, W. G. 2000, ApJ, 539, 675 [NASA ADS] [CrossRef] [Google Scholar]
Brighenti, F., & Mathews, W. G. 2003, ApJ, 587, 580 [NASA ADS] [CrossRef] [Google Scholar]
Brighenti, F., Mathews, W. G., Humphrey, P. J., & Buote, D. A. 2009, ApJ, 705, 1672 [NASA ADS] [CrossRef] [Google Scholar]
Canning, R. E. A., Sun, M., Sanders, J. S., et al. 2013, MNRAS, 435, 1108 [NASA ADS] [CrossRef] [Google Scholar]
Canning, R. E. A., Ryon, J. E., Gallagher, J. S., et al. 2014, MNRAS, 444, 336 [NASA ADS] [CrossRef] [Google Scholar]
Caon, N., Macchetto, D., & Pastoriza, M. 2000, ApJS, 127, 39 [NASA ADS] [CrossRef] [Google Scholar]
Cattaneo, A., & Teyssier, R. 2007, MNRAS, 376, 1547 [NASA ADS] [CrossRef] [Google Scholar]
Cattaneo, A., Faber, S. M., Binney, J., et al. 2009, Nature, 460, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2008, ApJ, 683, L107 [NASA ADS] [CrossRef] [Google Scholar]
Churazov, E., Sunyaev, R., Forman, W., & Böhringer, H. 2002, MNRAS, 332, 729 [NASA ADS] [CrossRef] [Google Scholar]
Combes, F., Young, L. M., & Bureau, M. 2007, MNRAS, 377, 1795 [NASA ADS] [CrossRef] [Google Scholar]
Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Crawford, C. S., Allen, S. W., Ebeling, H., Edge, A. C., & Fabian, A. C. 1999, MNRAS, 306, 857 [NASA ADS] [CrossRef] [Google Scholar]
Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
Dai, X., Anderson, M. E., Bregman, J. N., & Miller, J. M. 2012, ApJ, 755, 107 [NASA ADS] [CrossRef] [Google Scholar]
Dale, J. E., Ercolano, B., & Bonnell, I. A. 2015, MNRAS, submitted [arXiv:1504.05896] [Google Scholar]
Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41 [NASA ADS] [CrossRef] [Google Scholar]
David, L. P., Lim, J., Forman, W., et al. 2014, ApJ, 792, 94 [NASA ADS] [CrossRef] [Google Scholar]
de Plaa, J., Zhuravleva, I., Werner, N., et al. 2012, A&A, 539, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Di Matteo, T., Allen, S. W., Fabian, A. C., Wilson, A. S., & Young, A. J. 2003, ApJ, 582, 133 [NASA ADS] [CrossRef] [Google Scholar]
Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Diehl, S., & Statler, T. S. 2007, ApJ, 668, 150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Diehl, S., & Statler, T. S. 2008, ApJ, 687, 986 [NASA ADS] [CrossRef] [Google Scholar]
Dolag, K., Vazza, F., Brunetti, G., & Tormen, G. 2005, MNRAS, 364, 753 [NASA ADS] [CrossRef] [Google Scholar]
Dong, R., & Draine, B. T. 2011, ApJ, 727, 35 [NASA ADS] [CrossRef] [Google Scholar]
Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
Edge, A. C. 2001, MNRAS, 328, 762 [NASA ADS] [CrossRef] [Google Scholar]
Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]
Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
Federrath, C. 2015, MNRAS, 450, 4035 [NASA ADS] [CrossRef] [Google Scholar]
Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]
Fisher, R. T., Kadanoff, L. P., Lamb, D. Q., et al. 2008, IBM J. Res., & Dev., 52, 127 [Google Scholar]
Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]
Gaspari, M., & Churazov, E. 2013, A&A, 559, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gaspari, M., Melioli, C., Brighenti, F., & D’Ercole, A. 2011a, MNRAS, 411, 349 [NASA ADS] [CrossRef] [Google Scholar]
Gaspari, M., Brighenti, F., D’Ercole, A., & Melioli, C. 2011b, MNRAS, 415, 1549 [NASA ADS] [CrossRef] [Google Scholar]
Gaspari, M., Ruszkowski, M., & Sharma, P. 2012a, ApJ, 746, 94 [Google Scholar]
Gaspari, M., Brighenti, F., & Temi, P. 2012b, MNRAS, 424, 190 [NASA ADS] [CrossRef] [Google Scholar]
Gaspari, M., Brighenti, F., & Ruszkowski, M. 2013a, Astron. Nachr., 334, 394 [NASA ADS] [Google Scholar]
Gaspari, M., Ruszkowski, M., & Oh, S. P. 2013b, MNRAS, 432, 3401 [NASA ADS] [CrossRef] [Google Scholar]
Gaspari, M., Brighenti, F., Temi, P., & Ettori, S. 2014a, ApJ, 783, L10 [NASA ADS] [CrossRef] [Google Scholar]
Gaspari, M., Churazov, E., Nagai, D., Lau, E. T., & Zhuravleva, I. 2014b, A&A, 569, A67 [Google Scholar]
Gastaldello, F., Buote, D. A., Temi, P., et al. 2009, ApJ, 693, 43 [NASA ADS] [CrossRef] [Google Scholar]
Hamer, S. L., Edge, A. C., Swinbank, A. M., et al. 2014, MNRAS, 437, 862 [NASA ADS] [CrossRef] [Google Scholar]
Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]
Hatch, N. A., Crawford, C. S., Fabian, A. C., & Johnstone, R. M. 2005, MNRAS, 358, 765 [NASA ADS] [CrossRef] [Google Scholar]
Heckman, T. M., Baum, S. A., van Breugel, W. J. M., & McCarthy, P. 1989, ApJ, 338, 48 [NASA ADS] [CrossRef] [Google Scholar]
Hobbs, A., Nayakshin, S., Power, C., & King, A. 2011, MNRAS, 413, 2633 [NASA ADS] [CrossRef] [Google Scholar]
Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [NASA ADS] [CrossRef] [Google Scholar]
Hopkins, P. F., Narayan, R., & Hernquist, L. 2006, ApJ, 643, 641 [NASA ADS] [CrossRef] [Google Scholar]
Humphrey, P. J., Buote, D. A., Brighenti, F., Gebhardt, K., & Mathews, W. G. 2008, ApJ, 683, 161 [NASA ADS] [CrossRef] [Google Scholar]
Humphrey, P. J., Buote, D. A., Brighenti, F., Gebhardt, K., & Mathews, W. G. 2009, ApJ, 703, 1257 [NASA ADS] [CrossRef] [Google Scholar]
Jaffe, W., Bremer, M. N., & Baker, K. 2005, MNRAS, 360, 748 [NASA ADS] [CrossRef] [Google Scholar]
Jimmy, Tran, K.-V., Brough, S., et al. 2013, ApJ, 778, 171 [NASA ADS] [CrossRef] [Google Scholar]
Joung, M. K. R., & Mac Low, M.-M. 2006, ApJ, 653, 1266 [NASA ADS] [CrossRef] [Google Scholar]
Katz, N., Weinberg, D. H., & Hernquist, L. 1996, ApJS, 105, 19 [NASA ADS] [CrossRef] [Google Scholar]
Kim, J., & Ryu, D. 2005, ApJ, 630, L45 [NASA ADS] [CrossRef] [Google Scholar]
King, A. R., & Pringle, J. E. 2006, MNRAS, 373, L90 [NASA ADS] [CrossRef] [Google Scholar]
Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]
Krolik, J. H., & London, R. A. 1983, ApJ, 267, 18 [Google Scholar]
Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005, ApJ, 618, 757 [NASA ADS] [CrossRef] [Google Scholar]
Krumholz, M. R., McKee, C. F., & Klein, R. I. 2006, ApJ, 638, 369 [NASA ADS] [CrossRef] [Google Scholar]
Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
Li, J., Ostriker, J., & Sunyaev, R. 2013, ApJ, 767, 105 [NASA ADS] [CrossRef] [Google Scholar]
Lim, J., Leon, S., Combes, F., & Dinh-V-Trung. 2000, ApJ, 545, L93 [NASA ADS] [CrossRef] [Google Scholar]
Loewenstein, M., Mushotzky, R. F., Angelini, L., Arnaud, K. A., & Quataert, E. 2001, ApJ, 555, L21 [NASA ADS] [CrossRef] [Google Scholar]
Macchetto, F., Pastoriza, M., Caon, N., et al. 1996, A&AS, 120, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mathews, W. G., & Brighenti, F. 2003, ARA&A, 41, 191 [NASA ADS] [CrossRef] [Google Scholar]
McCourt, M., Sharma, P., Quataert, E., & Parrish, I. J. 2012, MNRAS, 419, 3319 [NASA ADS] [CrossRef] [Google Scholar]
McDonald, M., & Veilleux, S. 2009, ApJ, 703, L172 [NASA ADS] [CrossRef] [Google Scholar]
McDonald, M., Veilleux, S., Rupke, D. S. N., & Mushotzky, R. 2010, ApJ, 721, 1262 [NASA ADS] [CrossRef] [Google Scholar]
McDonald, M., Veilleux, S., & Mushotzky, R. 2011, ApJ, 731, 33 [NASA ADS] [CrossRef] [Google Scholar]
McDonald, M., Veilleux, S., & Rupke, D. S. N. 2012, ApJ, 746, 153 [NASA ADS] [CrossRef] [Google Scholar]
McDonald, M., Benson, B., Veilleux, S., Bautz, M. W., & Reichardt, C. L. 2013, ApJ, 765, L37 [NASA ADS] [CrossRef] [Google Scholar]
McDonald, M., Roediger, J., Veilleux, S., & Ehlert, S. 2014, ApJ, 791, L30 [NASA ADS] [CrossRef] [Google Scholar]
McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]
McNamara, B. R., Russell, H. R., Nulsen, P. E. J., et al. 2014, ApJ, 785, 44 [NASA ADS] [CrossRef] [Google Scholar]
Mittal, R., Hudson, D. S., Reiprich, T. H., & Clarke, T. 2009, A&A, 501, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mittal, R., Oonk, J. B. R., Ferland, G. J., et al. 2012, MNRAS, 426, 2957 [NASA ADS] [CrossRef] [Google Scholar]
Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
Narayan, R., & Fabian, A. C. 2011, MNRAS, 415, 3721 [NASA ADS] [CrossRef] [Google Scholar]
Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
Nayakshin, S., & King, A. 2007, unpublished, ArXiv e-prints, [arXiv:0705.1686] [Google Scholar]
Nemmen, R. S., & Tchekhovskoy, A. 2015, MNRAS, 449, 316 [NASA ADS] [CrossRef] [Google Scholar]
Norman, M. L., & Bryan, G. L. 1999, in The Radio Galaxy Messier 87, eds. H.-J. Röser, & K. Meisenheimer (Berlin: Springer Verlag), Lect. Notes Phys., 530, 106 [Google Scholar]
Oonk, J. B. R., Jaffe, W., Bremer, M. N., & van Weeren, R. J. 2010, MNRAS, 405, 898 [NASA ADS] [Google Scholar]
Paczyński, B., & Wiita, P. J. 1980, A&A, 88, 23 [NASA ADS] [Google Scholar]
Peterson, J. R., & Fabian, A. C. 2006, Phys. Rep., 427, 1 [NASA ADS] [CrossRef] [Google Scholar]
Pinkney, J., Gebhardt, K., Bender, R., et al. 2003, ApJ, 596, 903 [NASA ADS] [CrossRef] [Google Scholar]
Pizzolato, F., & Soker, N. 2005, ApJ, 632, 821 [NASA ADS] [CrossRef] [Google Scholar]
Pizzolato, F., & Soker, N. 2010, MNRAS, 408, 961 [NASA ADS] [CrossRef] [Google Scholar]
Planck Collaboration Int. XI. 2013, A&A, 557, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Proga, D., & Begelman, M. C. 2003, ApJ, 582, 69 [NASA ADS] [CrossRef] [Google Scholar]
Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216 [NASA ADS] [CrossRef] [Google Scholar]
Rafferty, D. A., McNamara, B. R., & Nulsen, P. E. J. 2008, ApJ, 687, 899 [NASA ADS] [CrossRef] [Google Scholar]
Rasmussen, J., & Ponman, T. J. 2009, MNRAS, 399, 239 [NASA ADS] [CrossRef] [Google Scholar]
Reynolds, C. S., Di Matteo, T., Fabian, A. C., Hwang, U., & Canizares, C. R. 1996, MNRAS, 283, L111 [NASA ADS] [CrossRef] [Google Scholar]
Russell, H. R., McNamara, B. R., Edge, A. C., et al. 2013, MNRAS, 432, 530 [NASA ADS] [CrossRef] [Google Scholar]
Russell, H. R., McNamara, B. R., Edge, A. C., et al. 2014, ApJ, 784, 78 [NASA ADS] [CrossRef] [Google Scholar]
Russell, H. R., Fabian, A. C., McNamara, B. R., & Broderick, A. E. 2015, MNRAS, submitted [arXiv:1504.07633] [Google Scholar]
Salomé, P., & Combes, F. 2003, A&A, 412, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Salomé, P., Combes, F., Revaz, Y., et al. 2008, A&A, 484, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Sanders, J. S., & Fabian, A. C. 2013, MNRAS, 429, 2727 [NASA ADS] [CrossRef] [Google Scholar]
Schuecker, P., Finoguenov, A., Miniati, F., Böhringer, H., & Briel, U. G. 2004, A&A, 426, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Shabala, S. S., Ash, S., Alexander, P., & Riley, J. M. 2008, MNRAS, 388, 625 [NASA ADS] [CrossRef] [Google Scholar]
Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
Sharma, P., McCourt, M., Quataert, E., & Parrish, I. J. 2012, MNRAS, 420, 3174 [NASA ADS] [CrossRef] [Google Scholar]
Sijacki, D., Springel, V., Di Matteo, T., & Hernquist, L. 2007, MNRAS, 380, 877 [NASA ADS] [CrossRef] [Google Scholar]
Soker, N. 2006, New Astron., 12, 38 [NASA ADS] [CrossRef] [Google Scholar]
Soker, N., Sternberg, A., & Pizzolato, F. 2009, in AIP Conf. Ser. 1201, eds. S. Heinz, & E. Wilcots, 321 [Google Scholar]
Sparks, W. B., Pringle, J. E., Carswell, R. F., et al. 2012, ApJ, 750, L5 [NASA ADS] [CrossRef] [Google Scholar]
Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [NASA ADS] [CrossRef] [Google Scholar]
Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] [Google Scholar]
Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]
Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
Tamura, T., Kaastra, J. S., Makishima, K., & Takahashi, I. 2003, A&A, 399, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Tejeda, E., Mendoza, S., & Miller, J. C. 2012, MNRAS, 419, 1431 [NASA ADS] [CrossRef] [Google Scholar]
Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]
Vazza, F., Brunetti, G., Kritsuk, A., et al. 2009, A&A, 504, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vazza, F., Roediger, E., & Brüggen, M. 2012, A&A, 544, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
Werner, N., Oonk, J. B. R., Canning, R. E. A., et al. 2013, ApJ, 767, 153 [NASA ADS] [CrossRef] [Google Scholar]
Werner, N., Oonk, J. B. R., Sun, M., et al. 2014, MNRAS, 439, 2291 [NASA ADS] [CrossRef] [Google Scholar]
Wilman, R. J., Edge, A. C., & Swinbank, A. M. 2009, MNRAS, 395, 1355 [NASA ADS] [CrossRef] [Google Scholar]
Wilman, R. J., Edge, A. C., McGregor, P. J., & McNamara, B. R. 2011, MNRAS, 416, 2060 [NASA ADS] [CrossRef] [Google Scholar]
Wong, K.-W., Irwin, J. A., Shcherbakov, R. V., et al. 2014, ApJ, 780, 9 [Google Scholar]
Young, L. M., Bureau, M., Davis, T. A., et al. 2011, MNRAS, 414, 940 [NASA ADS] [CrossRef] [Google Scholar]
Zabludoff, A. I., Geller, M. J., Huchra, J. P., & Ramella, M. 1993, AJ, 106, 1301 [NASA ADS] [CrossRef] [Google Scholar]
ZuHone, J. A., Markevitch, M., Ruszkowski, M., & Lee, D. 2013, ApJ, 762, 69 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

Fig. 1

Adiabatic rotating accretion: evolution of the accretion rate (1 Myr average). Top: accretion rate in yr^-1 units, for the rotating (e_rot = 0.3; solid) and nonrotating atmosphere (dot-dashed; see G13). Bottom: accretion rate normalized to the runtime Bondi rate (averaged over r ≈ 1–2 kpc as in large-scale simulations) for the reference rotation e_rot = 0.3 (solid) and e_rot = 0.15 (dotted). The central rotational barrier forming within r_B suppresses accretion by a factor ~3 compared with the spherically symmetric accretion flow.

In the text

Fig. 2

Adiabatic accretion with e_rot = 0.3: x-y rotational plane cross-section (2 kpc²) of the mass-weighted temperature at final time; the normalization of the velocity field is 2000 km s^-1 (such unit arrow is 1/8 of the image width). The gas progressively circularizes toward the equatorial plane, stifling accretion. Within the Bondi radius, the pressure-supported toroidal structure is variable, experiencing recurrent mild expansions and contractions, thus forming the pinwheel configuration.

In the text

	Fig. 3 Adiabatic accretion with e_rot = 0.3: evolution of the mass-weighted electron density (top; n_e ≃ ρ/ 1.93 × 10^-24 cm^-3) and temperature (bottom) radial profiles, sampled every 1 Myr (from dark blue to cyan). The cuspy profiles are similar to the classic Bondi solution (G13), smoothly joining the galactic gradients at large r.
In the text

Fig. 4

Adiabatic accretion with e_rot = 0.3: mass “probability” distribution function (PDF) per bin of specific angular momentum along the rotation axis z (M_⊙ per kpc km s^-1), for the gas within r< 8 kpc. The color coding is the same as for the radial profiles (Fig. 3), covering 40 Myr. With no additional physics, the system overall preserves the initial angular momentum distribution (coherent counter-clockwise rotation).

In the text

Fig. 5

Accretion with cooling and e_rot = 0.3 (blue): evolution of the accretion rate (physical and normalized to the kpc-scale, runtime Bondi rate – top and bottom panel, respectively). The dashed line is the average cooling rate (related to the gas with T< 10⁵ K). Solid black line is the adiabatic rotating model (Sect. 3). Despite the substantial cooling rates, yr^-1, the final accretion rate is two orders of magnitude lower because of the formation of a rotationally-supported thin disk.

In the text

	Fig. 6 Accretion with cooling and e_rot = 0.3: temperature cross-sections (2 × 2 kpc²) through z = 0 (top) and x = 0 (bottom), after 2 and 4 t_cool, respectively. The velocity field normalization is 6000 km s^-1 (unit arrow is 1/8 of the image width). The maps show the formation of a symmetric cold thin disk, which quickly condenses out of the hot phase and inhibits accretion.
In the text

	Fig. 7 Accretion with cooling and e_rot = 0.3: 3D mass- and emission-weighted radial profiles of density and temperature (cf. Fig. 3). The T_ew profile has X-ray threshold of 0.3 keV and is computed in larger radial bins (emulating a Chandra observation). The cold thin disk keeps growing via condensation. The X-ray temperature is overall insensitive to the presence of the cold disk.
In the text

Fig. 8

Accretion with cooling and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the cold phase (full evolution from blue to cyan lines). Cold gas is related to T< 10⁵ K. The PDF of the hot phase (not shown) is analogous to that in Fig. 4, albeit shifting by ~15 percent to higher normalization and l_z. The cold phase emerges out of this distribution, adding during time higher l_z gas, and thus widening the PDF.

In the text

Fig. 9

Adiabatic accretion with subsonic turbulence and e_rot = 0.3 (brown: Ma ~ 0.35, i.e., Ta_t ~ 0.75; orange: 1/4 lower Mach number, i.e., Ta_t ~ 3): evolution of the accretion rate. The accretion rate is suppressed by a factor ~3 compared with the nonrotating model (dot-dashed), as in the purely rotating run (solid black; Sect. 3), since turbulence still induces local (but not global) vorticity. The chaotic eddies generate however higher variability, as long as Ta_t< 1. In the opposite regime, rotation drives the dynamics.

In the text

	Fig. 10 Adiabatic accretion with subsonic turbulence (reference Ma ~ 0.35) and e_rot = 0.3: mid-plane temperature cut (cf. Fig. 2). The equatorial plane does not display coherent rotation, since the gas cannot properly circularize in the presence of significant turbulence (σ_v >v_rot). The central vortical motions stifle again accretion.
In the text

Fig. 11

Adiabatic accretion with subsonic turbulence (top: Ma ~ 0.35; bottom: 1/4 lower Mach number, i.e., Ta_t ~ 3) and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the gas within r< 8 kpc (cf. Fig. 4). If Ta_t< 1, turbulence widens the PDF, inducing both retrograde and prograde motions. In the opposite regime, Ta_t > 1, turbulence is too weak to induce retrograde motions: the underlying counter-clockwise rotation remains intact overall, with minor fluctuations superimposed.

In the text

	Fig. 12 Adiabatic accretion with subsonic turbulence (Ma ~ 0.35) and e_rot = 0.3: mass-weighted profiles of density and temperature (cf. Fig. 3). The profiles are cuspy, as in the classic Bondi flow, albeit becoming progressively shallower because of turbulent diffusion (dissipational heating is negligible, as indicated by the large-scale T profile).
In the text

	Fig. 13 Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mid-plane T_m cross-section through z = 0 (final time). Without heating, the system experiences a massive CCA flow. Extended cold filaments and clouds condense out of the hot phase via TI, and through recurrent chaotic collisions are quickly accreted by the BH. No steady thin disk can be formed.
In the text

Fig. 14

Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3 (green): evolution of the physical and normalized accretion rate (cf. Fig. 5; the average of Ṁ_• in the top panel has 0.1 Myr step). The dashed line is the average cooling rate (1 Myr step). The solid black line is the adiabatic rotating model (Sect. 3). Chaotic cold accretion drives the dynamics as long as Ta < 1. Recurrent collisions in the cold phase cancel angular momentum and boost the accretion rate up to two orders of magnitude with respect to the Bondi rate. The accretion rate is linearly tied to Ṁ_cool again.

In the text

Fig. 15

Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the cold phase (the hot phase has PDF analogous to Fig. 11, top). At variance with the purely radiative run, the cold phase randomly condenses out of a broad l_z distribution, including both prograde and retrograde motions. This permits frequent major collisions, canceling angular momentum. The mass of unaccreted cold gas tends to significantly rise with time due to the unheated cooling flow.

In the text

	Fig. 16 Accretion with cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mass– and emission–weighted radial profiles of density and temperature (cf. Fig. 7). The profiles show the condensation of warm gas out of the hot phase via TI up to several kpc. The X-ray temperature is flat, with no cuspy core, which is a characteristic mark of cold accretion.
In the text

Fig. 17

Accretion with heating, cooling, e_rot = 0.3, and varying levels of turbulence: evolution of the accretion rate (the Ṁ_• average in the top panel has 0.1 Myr step). The Mach number varies from the reference Ma ~ 0.35 (red) to 1/2 (magenta) and 1/4 (orange) of this value, i.e., Ta_t ≃ 0.7,1.5,3, respectively. The dashed line is the average net cooling rate (1 Myr step). As before, the solid black line is the adiabatic rotating model, and the runtime Bondi rate for the normalized plot is computed at r ≈ 1–2 kpc (Sect. 3). In the atmosphere with Ta_t< 1, CCA drives the dynamics, boosting the accretion rate up to 100 × the Bondi rate, which is consistent with the nonrotating CCA evolution shown in G13. As Ta_t > 1, the accretion flow shifts from turbulence-driven (linked to extended filaments and boosted accretion) to rotationally-driven (tied to a coherent disk and suppressed accretion).

In the text

Fig. 18

Accretion with heating, cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: temperature cross-section, with the velocity field overlaid. Full circularization is not possible in a turbulent environment characterized by Ta_t< 1. The recurrent chaotic collisions between the cold filaments, clouds, and the clumpy torus, cancel the angular momentum of the cold gas, leading to the rapid peaks in the accretion rate, Ṁ_• ~ Ṁ_cool.

In the text

Fig. 19

Accretion with heating, cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: mass PDF per bin of specific angular momentum l_z, for the cold phase (the hot phase has PDF analogous to Fig. 11, top). After three rapid Ṁ_• bursts, the PDF narrows on average from 20 Myr (solid) to 27 Myr (dashed) due to major collisions canceling positive and negative l_z. The action of collisions is periodically contrasted by fresh condensation, favoring a broader distribution.

In the text

Fig. 20

Accretion with heating, cooling, turbulence (Ma ~ 0.35), and e_rot = 0.3: 3D mass- (top) and X-ray emission-weighted (∝ ℒ; bottom) radial profiles of density and temperature (cf. Fig. 7). The profiles show the extended multiphase structure, which is largely concealed in the X-ray band. The X-ray temperature profile is remarkably flat, in contrast to the hot-mode accretion, which has a peaked temperature profile. This is a key observable, which can be thoroughly tested (Wong et al. 2014; Russell et al. 2015), to unveil the evolutionary stage in which the galaxy is residing.

In the text

Fig. 21

Top: synthetic Hα surface brightness image along an arbitrary line of sight during the two characteristic late stages: the filamentary phase (left; run with Ta_t ≃ 0.7) and the disk-dominated phase (right; Ta_t ≃ 3). The resolution mimics that of SOAR, ~0.2 arcsec. Bottom: observed SOAR Hα+[NII] images from Werner et al. (2014) showing the two analogous stages in two real massive elliptical galaxies: CCA (left; NGC 5044) and the rotating disk (right; NGC 6868).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Alatalo, K., Davis, T. A., Bureau, M., et al. 2013, MNRAS, 432, 1796 [NASA ADS] [CrossRef] [Google Scholar]

[2] Allen, S. W., Dunn, R. J. H., Fabian, A. C., Taylor, G. B., & Reynolds, C. S. 2006, MNRAS, 372, 21 [NASA ADS] [CrossRef] [Google Scholar]

[3] Anderson, M. E., & Bregman, J. N. 2011, ApJ, 737, 22 [NASA ADS] [CrossRef] [Google Scholar]

[4] Anderson, M. E., Gaspari, M., White, S. D. M., Wang, W., & Dai, X. 2015, MNRAS, 449, 3806 [NASA ADS] [CrossRef] [Google Scholar]

[5] Baganoff, F. K., Maeda, Y., Morris, M., et al. 2003, ApJ, 591, 891 [NASA ADS] [CrossRef] [Google Scholar]

[6] Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]

[7] Balbus, S. A., & Soker, N. 1989, ApJ, 341, 611 [NASA ADS] [CrossRef] [Google Scholar]

[8] Banerjee, N., & Sharma, P. 2014, MNRAS, 443, 687 [NASA ADS] [CrossRef] [Google Scholar]

[9] Barai, P., Proga, D., & Nagamine, K. 2012, MNRAS, 424, 728 [NASA ADS] [CrossRef] [Google Scholar]

[10] Barai, P., Viel, M., Murante, G., Gaspari, M., & Borgani, S. 2014, MNRAS, 437, 1456 [NASA ADS] [CrossRef] [Google Scholar]

[11] Best, P. N., von der Linden, A., Kauffmann, G., Heckman, T. M., & Kaiser, C. R. 2007, MNRAS, 379, 894 [NASA ADS] [CrossRef] [Google Scholar]

[12] Bianchi, S., Maiolino, R., & Risaliti, G. 2012, Adv. Astron., 2012, 782030 [NASA ADS] [CrossRef] [Google Scholar]

[13] Binney, J. J., Davies, R. L., & Illingworth, G. D. 1990, ApJ, 361, 78 [NASA ADS] [CrossRef] [Google Scholar]

[14] Bois, M., Emsellem, E., Bournaud, F., et al. 2011, MNRAS, 416, 1654 [NASA ADS] [CrossRef] [Google Scholar]

[15] Bondi, H. 1952, MNRAS, 112, 195 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[16] Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]

[17] Booth, C. M., & Schaye, J. 2009, MNRAS, 398, 53 [NASA ADS] [CrossRef] [Google Scholar]

[18] Borgani, S., & Kravtsov, A. 2011, Adv. Sci. Lett., 4, 204 [CrossRef] [Google Scholar]

[19] Brighenti, F., & Mathews, W. G. 1996, ApJ, 470, 747 [NASA ADS] [CrossRef] [Google Scholar]

[20] Brighenti, F., & Mathews, W. G. 1999, ApJ, 512, 65 [NASA ADS] [CrossRef] [Google Scholar]

[21] Brighenti, F., & Mathews, W. G. 2000, ApJ, 539, 675 [NASA ADS] [CrossRef] [Google Scholar]

[22] Brighenti, F., & Mathews, W. G. 2003, ApJ, 587, 580 [NASA ADS] [CrossRef] [Google Scholar]

[23] Brighenti, F., Mathews, W. G., Humphrey, P. J., & Buote, D. A. 2009, ApJ, 705, 1672 [NASA ADS] [CrossRef] [Google Scholar]

[24] Canning, R. E. A., Sun, M., Sanders, J. S., et al. 2013, MNRAS, 435, 1108 [NASA ADS] [CrossRef] [Google Scholar]

[25] Canning, R. E. A., Ryon, J. E., Gallagher, J. S., et al. 2014, MNRAS, 444, 336 [NASA ADS] [CrossRef] [Google Scholar]

[26] Caon, N., Macchetto, D., & Pastoriza, M. 2000, ApJS, 127, 39 [NASA ADS] [CrossRef] [Google Scholar]

[27] Cattaneo, A., & Teyssier, R. 2007, MNRAS, 376, 1547 [NASA ADS] [CrossRef] [Google Scholar]

[28] Cattaneo, A., Faber, S. M., Binney, J., et al. 2009, Nature, 460, 213 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[29] Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2008, ApJ, 683, L107 [NASA ADS] [CrossRef] [Google Scholar]

[30] Churazov, E., Sunyaev, R., Forman, W., & Böhringer, H. 2002, MNRAS, 332, 729 [NASA ADS] [CrossRef] [Google Scholar]

[31] Combes, F., Young, L. M., & Bureau, M. 2007, MNRAS, 377, 1795 [NASA ADS] [CrossRef] [Google Scholar]

[32] Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[33] Combes, F., García-Burillo, S., Casasola, V., et al. 2014, A&A, 565, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[34] Crawford, C. S., Allen, S. W., Ebeling, H., Edge, A. C., & Fabian, A. C. 1999, MNRAS, 306, 857 [NASA ADS] [CrossRef] [Google Scholar]

[35] Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]

[36] Dai, X., Anderson, M. E., Bregman, J. N., & Miller, J. M. 2012, ApJ, 755, 107 [NASA ADS] [CrossRef] [Google Scholar]

[37] Dale, J. E., Ercolano, B., & Bonnell, I. A. 2015, MNRAS, submitted [arXiv:1504.05896] [Google Scholar]

[38] Davies, R. L., Efstathiou, G., Fall, S. M., Illingworth, G., & Schechter, P. L. 1983, ApJ, 266, 41 [NASA ADS] [CrossRef] [Google Scholar]

[39] David, L. P., Lim, J., Forman, W., et al. 2014, ApJ, 792, 94 [NASA ADS] [CrossRef] [Google Scholar]

[40] de Plaa, J., Zhuravleva, I., Werner, N., et al. 2012, A&A, 539, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[41] Dekel, A., Birnboim, Y., Engel, G., et al. 2009, Nature, 457, 451 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[42] Di Matteo, T., Allen, S. W., Fabian, A. C., Wilson, A. S., & Young, A. J. 2003, ApJ, 582, 133 [NASA ADS] [CrossRef] [Google Scholar]

[43] Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[44] Diehl, S., & Statler, T. S. 2007, ApJ, 668, 150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[45] Diehl, S., & Statler, T. S. 2008, ApJ, 687, 986 [NASA ADS] [CrossRef] [Google Scholar]

[46] Dolag, K., Vazza, F., Brunetti, G., & Tormen, G. 2005, MNRAS, 364, 753 [NASA ADS] [CrossRef] [Google Scholar]

[47] Dong, R., & Draine, B. T. 2011, ApJ, 727, 35 [NASA ADS] [CrossRef] [Google Scholar]

[48] Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]

[49] Edge, A. C. 2001, MNRAS, 328, 762 [NASA ADS] [CrossRef] [Google Scholar]

[50] Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]

[51] Emsellem, E., Cappellari, M., Krajnović, D., et al. 2007, MNRAS, 379, 401 [NASA ADS] [CrossRef] [Google Scholar]

[52] Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]

[53] Federrath, C. 2015, MNRAS, 450, 4035 [NASA ADS] [CrossRef] [Google Scholar]

[54] Field, G. B. 1965, ApJ, 142, 531 [NASA ADS] [CrossRef] [Google Scholar]

[55] Fisher, R. T., Kadanoff, L. P., Lamb, D. Q., et al. 2008, IBM J. Res., & Dev., 52, 127 [Google Scholar]

[56] Fryxell, B., Olson, K., Ricker, P., et al. 2000, ApJS, 131, 273 [NASA ADS] [CrossRef] [Google Scholar]

[57] Gaspari, M., & Churazov, E. 2013, A&A, 559, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[58] Gaspari, M., Melioli, C., Brighenti, F., & D’Ercole, A. 2011a, MNRAS, 411, 349 [NASA ADS] [CrossRef] [Google Scholar]

[59] Gaspari, M., Brighenti, F., D’Ercole, A., & Melioli, C. 2011b, MNRAS, 415, 1549 [NASA ADS] [CrossRef] [Google Scholar]

[60] Gaspari, M., Ruszkowski, M., & Sharma, P. 2012a, ApJ, 746, 94 [Google Scholar]

[61] Gaspari, M., Brighenti, F., & Temi, P. 2012b, MNRAS, 424, 190 [NASA ADS] [CrossRef] [Google Scholar]

[62] Gaspari, M., Brighenti, F., & Ruszkowski, M. 2013a, Astron. Nachr., 334, 394 [NASA ADS] [Google Scholar]

[63] Gaspari, M., Ruszkowski, M., & Oh, S. P. 2013b, MNRAS, 432, 3401 [NASA ADS] [CrossRef] [Google Scholar]

[64] Gaspari, M., Brighenti, F., Temi, P., & Ettori, S. 2014a, ApJ, 783, L10 [NASA ADS] [CrossRef] [Google Scholar]

[65] Gaspari, M., Churazov, E., Nagai, D., Lau, E. T., & Zhuravleva, I. 2014b, A&A, 569, A67 [Google Scholar]

[66] Gastaldello, F., Buote, D. A., Temi, P., et al. 2009, ApJ, 693, 43 [NASA ADS] [CrossRef] [Google Scholar]

[67] Hamer, S. L., Edge, A. C., Swinbank, A. M., et al. 2014, MNRAS, 437, 862 [NASA ADS] [CrossRef] [Google Scholar]

[68] Hardcastle, M. J., Evans, D. A., & Croston, J. H. 2007, MNRAS, 376, 1849 [NASA ADS] [CrossRef] [Google Scholar]

[69] Hatch, N. A., Crawford, C. S., Fabian, A. C., & Johnstone, R. M. 2005, MNRAS, 358, 765 [NASA ADS] [CrossRef] [Google Scholar]

[70] Heckman, T. M., Baum, S. A., van Breugel, W. J. M., & McCarthy, P. 1989, ApJ, 338, 48 [NASA ADS] [CrossRef] [Google Scholar]

[71] Hobbs, A., Nayakshin, S., Power, C., & King, A. 2011, MNRAS, 413, 2633 [NASA ADS] [CrossRef] [Google Scholar]

[72] Hopkins, P. F., & Quataert, E. 2010, MNRAS, 407, 1529 [NASA ADS] [CrossRef] [Google Scholar]

[73] Hopkins, P. F., Narayan, R., & Hernquist, L. 2006, ApJ, 643, 641 [NASA ADS] [CrossRef] [Google Scholar]

[74] Humphrey, P. J., Buote, D. A., Brighenti, F., Gebhardt, K., & Mathews, W. G. 2008, ApJ, 683, 161 [NASA ADS] [CrossRef] [Google Scholar]

[75] Humphrey, P. J., Buote, D. A., Brighenti, F., Gebhardt, K., & Mathews, W. G. 2009, ApJ, 703, 1257 [NASA ADS] [CrossRef] [Google Scholar]

[76] Jaffe, W., Bremer, M. N., & Baker, K. 2005, MNRAS, 360, 748 [NASA ADS] [CrossRef] [Google Scholar]

[77] Jimmy, Tran, K.-V., Brough, S., et al. 2013, ApJ, 778, 171 [NASA ADS] [CrossRef] [Google Scholar]

[78] Joung, M. K. R., & Mac Low, M.-M. 2006, ApJ, 653, 1266 [NASA ADS] [CrossRef] [Google Scholar]

[79] Katz, N., Weinberg, D. H., & Hernquist, L. 1996, ApJS, 105, 19 [NASA ADS] [CrossRef] [Google Scholar]

[80] Kim, J., & Ryu, D. 2005, ApJ, 630, L45 [NASA ADS] [CrossRef] [Google Scholar]

[81] King, A. R., & Pringle, J. E. 2006, MNRAS, 373, L90 [NASA ADS] [CrossRef] [Google Scholar]

[82] Kormendy, J., Fisher, D. B., Cornell, M. E., & Bender, R. 2009, ApJS, 182, 216 [NASA ADS] [CrossRef] [Google Scholar]

[83] Krolik, J. H., & London, R. A. 1983, ApJ, 267, 18 [Google Scholar]

[84] Krumholz, M. R., McKee, C. F., & Klein, R. I. 2005, ApJ, 618, 757 [NASA ADS] [CrossRef] [Google Scholar]

[85] Krumholz, M. R., McKee, C. F., & Klein, R. I. 2006, ApJ, 638, 369 [NASA ADS] [CrossRef] [Google Scholar]

[86] Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]

[87] Li, J., Ostriker, J., & Sunyaev, R. 2013, ApJ, 767, 105 [NASA ADS] [CrossRef] [Google Scholar]

[88] Lim, J., Leon, S., Combes, F., & Dinh-V-Trung. 2000, ApJ, 545, L93 [NASA ADS] [CrossRef] [Google Scholar]

[89] Loewenstein, M., Mushotzky, R. F., Angelini, L., Arnaud, K. A., & Quataert, E. 2001, ApJ, 555, L21 [NASA ADS] [CrossRef] [Google Scholar]

[90] Macchetto, F., Pastoriza, M., Caon, N., et al. 1996, A&AS, 120, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[91] Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[92] Mathews, W. G., & Brighenti, F. 2003, ARA&A, 41, 191 [NASA ADS] [CrossRef] [Google Scholar]

[93] McCourt, M., Sharma, P., Quataert, E., & Parrish, I. J. 2012, MNRAS, 419, 3319 [NASA ADS] [CrossRef] [Google Scholar]

[94] McDonald, M., & Veilleux, S. 2009, ApJ, 703, L172 [NASA ADS] [CrossRef] [Google Scholar]

[95] McDonald, M., Veilleux, S., Rupke, D. S. N., & Mushotzky, R. 2010, ApJ, 721, 1262 [NASA ADS] [CrossRef] [Google Scholar]

[96] McDonald, M., Veilleux, S., & Mushotzky, R. 2011, ApJ, 731, 33 [NASA ADS] [CrossRef] [Google Scholar]

[97] McDonald, M., Veilleux, S., & Rupke, D. S. N. 2012, ApJ, 746, 153 [NASA ADS] [CrossRef] [Google Scholar]

[98] McDonald, M., Benson, B., Veilleux, S., Bautz, M. W., & Reichardt, C. L. 2013, ApJ, 765, L37 [NASA ADS] [CrossRef] [Google Scholar]

[99] McDonald, M., Roediger, J., Veilleux, S., & Ehlert, S. 2014, ApJ, 791, L30 [NASA ADS] [CrossRef] [Google Scholar]

[100] McNamara, B. R., & Nulsen, P. E. J. 2007, ARA&A, 45, 117 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]

[101] McNamara, B. R., & Nulsen, P. E. J. 2012, New J. Phys., 14, 055023 [NASA ADS] [CrossRef] [Google Scholar]

[102] McNamara, B. R., Russell, H. R., Nulsen, P. E. J., et al. 2014, ApJ, 785, 44 [NASA ADS] [CrossRef] [Google Scholar]

[103] Mittal, R., Hudson, D. S., Reiprich, T. H., & Clarke, T. 2009, A&A, 501, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[104] Mittal, R., Oonk, J. B. R., Ferland, G. J., et al. 2012, MNRAS, 426, 2957 [NASA ADS] [CrossRef] [Google Scholar]

[105] Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]

[106] Narayan, R., & Fabian, A. C. 2011, MNRAS, 415, 3721 [NASA ADS] [CrossRef] [Google Scholar]

[107] Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]

[108] Nayakshin, S., & King, A. 2007, unpublished, ArXiv e-prints, [arXiv:0705.1686] [Google Scholar]

[109] Nemmen, R. S., & Tchekhovskoy, A. 2015, MNRAS, 449, 316 [NASA ADS] [CrossRef] [Google Scholar]

[110] Norman, M. L., & Bryan, G. L. 1999, in The Radio Galaxy Messier 87, eds. H.-J. Röser, & K. Meisenheimer (Berlin: Springer Verlag), Lect. Notes Phys., 530, 106 [Google Scholar]

[111] Oonk, J. B. R., Jaffe, W., Bremer, M. N., & van Weeren, R. J. 2010, MNRAS, 405, 898 [NASA ADS] [Google Scholar]

[112] Paczyński, B., & Wiita, P. J. 1980, A&A, 88, 23 [NASA ADS] [Google Scholar]

[113] Peterson, J. R., & Fabian, A. C. 2006, Phys. Rep., 427, 1 [NASA ADS] [CrossRef] [Google Scholar]

[114] Pinkney, J., Gebhardt, K., Bender, R., et al. 2003, ApJ, 596, 903 [NASA ADS] [CrossRef] [Google Scholar]

[115] Pizzolato, F., & Soker, N. 2005, ApJ, 632, 821 [NASA ADS] [CrossRef] [Google Scholar]

[116] Pizzolato, F., & Soker, N. 2010, MNRAS, 408, 961 [NASA ADS] [CrossRef] [Google Scholar]

[117] Planck Collaboration Int. XI. 2013, A&A, 557, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[118] Proga, D., & Begelman, M. C. 2003, ApJ, 582, 69 [NASA ADS] [CrossRef] [Google Scholar]

[119] Rafferty, D. A., McNamara, B. R., Nulsen, P. E. J., & Wise, M. W. 2006, ApJ, 652, 216 [NASA ADS] [CrossRef] [Google Scholar]

[120] Rafferty, D. A., McNamara, B. R., & Nulsen, P. E. J. 2008, ApJ, 687, 899 [NASA ADS] [CrossRef] [Google Scholar]

[121] Rasmussen, J., & Ponman, T. J. 2009, MNRAS, 399, 239 [NASA ADS] [CrossRef] [Google Scholar]

[122] Reynolds, C. S., Di Matteo, T., Fabian, A. C., Hwang, U., & Canizares, C. R. 1996, MNRAS, 283, L111 [NASA ADS] [CrossRef] [Google Scholar]

[123] Russell, H. R., McNamara, B. R., Edge, A. C., et al. 2013, MNRAS, 432, 530 [NASA ADS] [CrossRef] [Google Scholar]

[124] Russell, H. R., McNamara, B. R., Edge, A. C., et al. 2014, ApJ, 784, 78 [NASA ADS] [CrossRef] [Google Scholar]

[125] Russell, H. R., Fabian, A. C., McNamara, B. R., & Broderick, A. E. 2015, MNRAS, submitted [arXiv:1504.07633] [Google Scholar]

[126] Salomé, P., & Combes, F. 2003, A&A, 412, 657 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[127] Salomé, P., Combes, F., Revaz, Y., et al. 2008, A&A, 484, 317 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[128] Sanders, J. S., & Fabian, A. C. 2013, MNRAS, 429, 2727 [NASA ADS] [CrossRef] [Google Scholar]

[129] Schuecker, P., Finoguenov, A., Miniati, F., Böhringer, H., & Briel, U. G. 2004, A&A, 426, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[130] Shabala, S. S., Ash, S., Alexander, P., & Riley, J. M. 2008, MNRAS, 388, 625 [NASA ADS] [CrossRef] [Google Scholar]

[131] Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]

[132] Sharma, P., McCourt, M., Quataert, E., & Parrish, I. J. 2012, MNRAS, 420, 3174 [NASA ADS] [CrossRef] [Google Scholar]

[133] Sijacki, D., Springel, V., Di Matteo, T., & Hernquist, L. 2007, MNRAS, 380, 877 [NASA ADS] [CrossRef] [Google Scholar]

[134] Soker, N. 2006, New Astron., 12, 38 [NASA ADS] [CrossRef] [Google Scholar]

[135] Soker, N., Sternberg, A., & Pizzolato, F. 2009, in AIP Conf. Ser. 1201, eds. S. Heinz, & E. Wilcots, 321 [Google Scholar]

[136] Sparks, W. B., Pringle, J. E., Carswell, R. F., et al. 2012, ApJ, 750, L5 [NASA ADS] [CrossRef] [Google Scholar]

[137] Springel, V., Di Matteo, T., & Hernquist, L. 2005, MNRAS, 361, 776 [NASA ADS] [CrossRef] [Google Scholar]

[138] Strickland, D. K., & Stevens, I. R. 2000, MNRAS, 314, 511 [NASA ADS] [CrossRef] [Google Scholar]

[139] Sun, M., Voit, G. M., Donahue, M., et al. 2009, ApJ, 693, 1142 [NASA ADS] [CrossRef] [Google Scholar]

[140] Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]

[141] Tamura, T., Kaastra, J. S., Makishima, K., & Takahashi, I. 2003, A&A, 399, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[142] Tejeda, E., Mendoza, S., & Miller, J. C. 2012, MNRAS, 419, 1431 [NASA ADS] [CrossRef] [Google Scholar]

[143] Turk, M. J., Smith, B. D., Oishi, J. S., et al. 2011, ApJS, 192, 9 [NASA ADS] [CrossRef] [Google Scholar]

[144] Vazza, F., Brunetti, G., Kritsuk, A., et al. 2009, A&A, 504, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[145] Vazza, F., Roediger, E., & Brüggen, M. 2012, A&A, 544, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[146] Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]

[147] Werner, N., Oonk, J. B. R., Canning, R. E. A., et al. 2013, ApJ, 767, 153 [NASA ADS] [CrossRef] [Google Scholar]

[148] Werner, N., Oonk, J. B. R., Sun, M., et al. 2014, MNRAS, 439, 2291 [NASA ADS] [CrossRef] [Google Scholar]

[149] Wilman, R. J., Edge, A. C., & Swinbank, A. M. 2009, MNRAS, 395, 1355 [NASA ADS] [CrossRef] [Google Scholar]

[150] Wilman, R. J., Edge, A. C., McGregor, P. J., & McNamara, B. R. 2011, MNRAS, 416, 2060 [NASA ADS] [CrossRef] [Google Scholar]

[151] Wong, K.-W., Irwin, J. A., Shcherbakov, R. V., et al. 2014, ApJ, 780, 9 [Google Scholar]

[152] Young, L. M., Bureau, M., Davis, T. A., et al. 2011, MNRAS, 414, 940 [NASA ADS] [CrossRef] [Google Scholar]

[153] Zabludoff, A. I., Geller, M. J., Huchra, J. P., & Ramella, M. 1993, AJ, 106, 1301 [NASA ADS] [CrossRef] [Google Scholar]

[154] ZuHone, J. A., Markevitch, M., Ruszkowski, M., & Lee, D. 2013, ApJ, 762, 69 [NASA ADS] [CrossRef] [Google Scholar]

Chaotic cold accretion on to black holes in rotating atmospheres

1. Introduction and observations

2. Physics and numerics

2.1. Initial conditions and rotation

2.2. Hydrodynamics and source terms

3. Adiabatic accretion

3.1. Accretion rate

3.2. Dynamics

3.3. Radial profiles and lz distribution

4. Accretion with cooling

4.1. Accretion rate

4.2. Dynamics

4.3. Radial profiles and lz distribution

5. Adiabatic accretion with turbulence

5.1. Accretion rate and dynamics

5.2. Distribution of lz and radial profiles

6. Accretion with cooling and turbulence

6.1. Dynamics

6.2. Accretion rate

6.3. Distribution of lz and radial profiles

7. Accretion with heating, cooling, and turbulence: chaotic cold accretion

7.1. Accretion rate

7.2. CCA dynamics and lz distribution

7.3. Radial profiles

8. Comparison with Hα observations

9. Summary and conclusions

Acknowledgments

References

All Figures

3.3. Radial profiles and l_z distribution

4.3. Radial profiles and l_z distribution

5.2. Distribution of l_z and radial profiles

6.3. Distribution of l_z and radial profiles

7.2. CCA dynamics and l_z distribution