| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 18 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201525727 | |
| Published online | 30 June 2015 | |
The VIMOS Public Extragalactic Redshift Survey (VIPERS)
Hierarchical scaling and biasing⋆
1
INAF–Osservatorio Astronomico di Bologna, via Ranzani 1,
40127
Bologna,
Italy
e-mail:
alberto.cappi@oabo.inaf.it
2
Laboratoire Lagrange, UMR 7293, Université de Nice-Sophia
Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300
Nice,
France
3
Dipartimento di Fisica e Astronomia – Alma Mater Studiorum
Università di Bologna, viale Berti
Pichat 6/2, 40127
Bologna,
Italy
4
INFN, Sezione di Bologna, viale Berti Pichat 6/2,
40127
Bologna,
Italy
5
Centre de Physique Théorique, UMR 6207 CNRS-Université de
Provence, Case 907,
13288
Marseille,
France
6
Dipartimento di Matematica e Fisica, Università degli Studi Roma
Tre, via della Vasca Navale
84, 00146
Roma,
Italy
7
INFN, Sezione di Roma Tre, via della Vasca Navale
84, 00146
Roma,
Italy
8
INAF–Osservatorio Astronomico di Roma,
via Frascati 33, 00040 Monte
Porzio Catone ( RM), Italy
9
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
10
INAF–Osservatorio Astronomico di Brera, via Brera 28, 20122
Milano, via E. Bianchi 46, 23807
Merate,
Italy
11
Dipartimento di Fisica, Università di
Milano-Bicocca, P.zza della Scienza
3, 20126
Milano,
Italy
12
INAF – Osservatorio Astronomico di Torino,
10025
Pino Torinese,
Italy
13
Canada-France-Hawaii Telescope, 65–1238 Mamalahoa
Highway, Kamuela,
HI
96743,
USA
14
INAF–Istituto di Astrofisica Spaziale e Fisica Cosmica Milano, via
Bassini 15, 20133
Milano,
Italy
15
Astronomical Observatory of the University of
Geneva, Ch. d’Écogia
16, 1290
Versoix,
Switzerland
16
INAF–Osservatorio Astronomico di Trieste, via G. B. Tiepolo
11, 34143
Trieste,
Italy
17
Institute ofPhysics, Jan Kochanowski University,
ul. Swietokrzyska 15,
25-406
Kielce,
Poland
18
Department of Particle and Astrophysical Science, Nagoya
University, Furo-cho, Chikusa-ku,
464-8602
Nagoya,
Japan
19
National Centre for Nuclear Research, ul. Hoza 69,
00-681
Warszawa,
Poland
20
Institut d’Astrophysique de Paris, UMR 7095 CNRS, Université
Pierre et Marie Curie, 98bis
boulevard Arago, 75014
Paris,
France
21
Astronomical Observatory of the Jagiellonian
University, Orla
171, 30-001
Cracow,
Poland
22
Institute of Cosmology and Gravitation, Dennis Sciama Building,
University of Portsmouth, Burnaby
Road, Portsmouth,
PO1 3FX,
UK
23
INAF–Istituto di Astrofisica Spaziale e Fisica Cosmica Bologna,
via Gobetti 101, 40129
Bologna,
Italy
24
INAF–Istituto di Radioastronomia, via Gobetti 101,
40129
Bologna,
Italy
25
Università degli Studi di Milano, via G. Celoria 16, 20130
Milano,
Italy
26
SUPA, Institute for Astronomy, University of Edinburgh, Royal
Observatory, Blackford
Hill, Edinburgh
EH9 3HJ,
UK
27
Max-Planck-Institut für Extraterrestrische Physik,
84571
Garching b. München,
Germany
28
Universitätssternwarte München, Ludwig-Maximillians
Universität, Scheinerstr.
1, 81679
München,
Germany
Received: 23 January 2015
Accepted: 5 May 2015
Aims. Building on the two-point correlation function analyses of the VIMOS Public Extragalactic Redshift Survey (VIPERS), we investigate the higher-order correlation properties of the same galaxy samples to test the hierarchical scaling hypothesis at z ~ 1 and the dependence on galaxy luminosity, stellar mass, and redshift. With this work we also aim to assess possible deviations from the linearity of galaxy bias independently from a previously performed analysis of our survey.
Methods. We have measured the count probability distribution function in spherical cells of varying radii (3 ≤ R ≤ 10 h-1 Mpc), deriving σ8g (the galaxy rms at 8 h-1 Mpc), the volume-averaged two-, three-, and four-point correlation functions and the normalized skewness S3g and kurtosis S4g for different volume-limited subsamples, covering the following ranges: −19.5 ≤ MB(z = 1.1) − 5log (h) ≤ −21.0 in absolute magnitude, 9.0 ≤ log (M∗/M⊙h-2) ≤ 11.0 in stellar mass, and 0.5 ≤ z< 1.1 in redshift.
Results. We have performed the first measurement of high-order correlation functions at z ~ 1 in a spectroscopic redshift survey. Our main results are the following. 1) The hierarchical scaling between the volume-averaged two- and three-point and two- and four-point correlation functions holds throughout the whole range of scale and redshift we could test. 2) We do not find a significant dependence of S3g on luminosity (below z = 0.9 the value of S3g decreases with luminosity, but only at 1σ-level). 3) We do not detect a significant dependence of S3g and S4g on scale, except beyond z ~ 0.9, where S3g and S4g have higher values on large scales (R ≥ 10 h-1 Mpc): this increase is mainly due to one of the two CFHTLS Wide Fields observed by VIPERS and can be explained as a consequence of sample variance, consistently with our analysis of mock catalogs. 4) We do not detect a significant evolution of S3g and S4g with redshift (apart from the increase of their values with scale in the last redshift bin). 5) σ8g increases with luminosity, but does not show significant evolution with redshift. As a consequence, the linear bias factor b = σ8g/σ8m, where σ8m is the rms of matter at a scale of 8 h-1 Mpc, increases with redshift, in agreement with the independent analysis of VIPERS and of other surveys such as the VIMOS-VLT Deep Survey (VVDS). We measure the lowest bias b = 1.47 ± 0.18 for galaxies with MB(z = 1.1) − 5log (h) ≤ −19.5 in the first redshift bin (0.5 ≤ z< 0.7) and the highest bias b = 2.12 ± 0.28 for galaxies with MB(z = 1.1) − 5log (h) ≤ −21.0 in the last redshift bin (0.9 ≤ z< 1.1). 6) We quantify deviations from the linear bias by means of the Taylor expansion parameter b2. We obtain b2 = −0.20 ± 0.49 for 0.5 ≤ z< 0.7 and b2 = −0.24 ± 0.35 for 0.7 ≤ z< 0.9, while for the redshift range 0.9 ≤ z< 1.1 we find b2 = + 0.78 ± 0.82. These results are compatible with a null non-linear bias term, but taking into account another analysis for VIPERS and the analysis of other surveys, we argue that there is evidence for a small but non-zero non-linear bias term.
Key words: large-scale structure of Universe / cosmology: observations / dark matter / galaxies: statistics
Based on observations collected at the European Southern Observatory, Cerro Paranal, Chile, using the Very Large Telescope under programs 182.A-0886 and partly 070.A-9007. Also based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The VIPERS web site is http://www.vipers.inaf.it
© ESO, 2015
1. Introduction
In the standard model of structure formation, the growth of density fluctuations from a primordial Gaussian density field is driven by gravity; it is possible to follow the evolution of these fluctuations through analytical and numerical approaches and predict the statistical properties for the dark matter field and dark matter haloes. Galaxies form in a complex process following the baryonic infall into dark matter halos: this means that the comparison between theory and observations is not straightforward, but it also implies that the spatial distribution of galaxies contains a wealth of information relevant for both cosmology and the physics of galaxy formation.
Extracting and exploiting this information from the data requires a number of different and complementary statistical approaches. For example, while the two-point correlation function ξ2(r) is the simplest and most widely used statistical indicator of galaxy clustering, a complete description of a distribution is only given by the full J-point correlation functions ξJ, or equivalently, by the volume-averaged correlation functions  , which are related to the J-order moments of the count probability distribution function (PDF)1. The count PDF gives the probability of counting N objects as a function of volume V. High-order correlations are particularly interesting because perturbation theory and numerical simulations can describe their behaviour for the gravitational evolution of matter density fluctuations.
, which are related to the J-order moments of the count probability distribution function (PDF)1. The count PDF gives the probability of counting N objects as a function of volume V. High-order correlations are particularly interesting because perturbation theory and numerical simulations can describe their behaviour for the gravitational evolution of matter density fluctuations.
The first estimates of the two- and three -point galaxy correlations functions on angular catalogues of galaxies were made by Groth & Peebles (1977), who found that these estimates were well described by the hierarchical relation ξ3(r12,r13,r23) = Q [ ξ2(r12)ξ2(r13) + ξ2(r13)ξ2(r23) + ξ2(r12)ξ2(r23) ]. The three-point correlation function has subsequently become a standard statistical tool for the analysis of clustering and has been applied to simulations and recent surveys of galaxies (see e.g. Marín et al. 2008; Moresco et al. 2014), while its Fourier transform, the bispectrum, has also been applied to the analysis of the Lyα forest (Mandelbaum et al. 2003; Viel et al. 2004) and of the cosmic microwave background (CMB; Planck Collaboration XXIV 2014).
The scaling relation between the two- and three -point correlation functions was soon generalized to higher orders (Fry & Peebles 1978 up to J = 4; Sharp et al. 1984 up to J = 5) and was mathematically described by the so-called hierarchical models, where the J-point correlation functions are expressed as a function of products of the two-point correlation function. Different versions of these models were suggested, but Balian & Schaeffer (1989) showed that all of them belong to the general class of scale-invariant models, which are defined by the scaling property:  (1)From a physical point of view, the hierarchical scaling of the correlation functions is expected in the highly non-linear regime (the BBGKY hierarchy, see Davis & Peebles 1977; Fry 1984a; Hamilton 1988) and in the quasi-linear regime (from perturbation theory, see Peebles 1980; Fry 1984b; Bernardeau 1992; Bernardeau et al. 2002 and references therein).
(1)From a physical point of view, the hierarchical scaling of the correlation functions is expected in the highly non-linear regime (the BBGKY hierarchy, see Davis & Peebles 1977; Fry 1984a; Hamilton 1988) and in the quasi-linear regime (from perturbation theory, see Peebles 1980; Fry 1984b; Bernardeau 1992; Bernardeau et al. 2002 and references therein).
Another prediction of the hierarchical models is that the normalized high-order reduced moments  should be constant. In the present paper we focus on the normalized skewness S3 and kurtosis S4. Peebles (1980) showed that in second-order perturbation theory, assuming Gaussian primordial density fluctuations and an Einstein-de Sitter model, S3m, the normalized skewness of matter fluctuations assumes the value 34/7. Subsequent works have shown that the smoothed S3m depends on the slope of the power spectrum and has a very weak dependence on the cosmological model (see Bernardeau et al. 2002).
should be constant. In the present paper we focus on the normalized skewness S3 and kurtosis S4. Peebles (1980) showed that in second-order perturbation theory, assuming Gaussian primordial density fluctuations and an Einstein-de Sitter model, S3m, the normalized skewness of matter fluctuations assumes the value 34/7. Subsequent works have shown that the smoothed S3m depends on the slope of the power spectrum and has a very weak dependence on the cosmological model (see Bernardeau et al. 2002).
While in standard models with Gaussian primordial fluctuations the skewness and higher-order moments assume non-zero values as a consequence of gravitational clustering, scenarios with non-Gaussian primordial perturbations also predict a primordial non-zero skewness, particularly at large scales (≥10 h-1 Mpc; Luo & Schramm 1993; Fry & Scherrer 1994; Gaztañaga & Maehoenen 1996; Gaztañaga & Fosalba 1998; Durrer et al. 2000); therefore these scenarios can in principle be constrained by measuring the high-order moments (Mao et al. 2014).
Moreover, it has been shown that the hierarchy of the J-point functions and the measurement of S3 and S4 can be used as a cosmological test to distinguish between the standard Λ cold dark matter (ΛCDM) and models including long-range scalar interaction between dark matter particles (“fifth force” dark matter models), as shown by Hellwing et al. (2010), who found the largest deviations in the redshift range 0.5 <z< 2.
However, the comparison between the theoretical predictions for the matter distribution and the observed galaxy distribution is not trivial, as a consequence of bias. One of the first results derived from the analysis of the first redshift surveys was that the amplitude of the two-point correlation function depends on galaxy luminosity and galaxy colour (see Marulli et al. 2013, and references therein); therefore, the galaxy distribution must generally differ from the underlying matter distribution. A common assumption is that the galaxy and matter density fields are related by a linear relation, δg = bδm, where δg ≡ Δρg/ρg and δm ≡ Δρm/ρm are the galaxy and matter density contrast, respectively. This relation is a consequence of the scenario of biased galaxy formation, where galaxies form above a given threshold of the linear density field, in the limit of high threshold and low variance. Of course, this relation cannot have general validity: when b> 1 and δm< 0, the linear relation gives an unphysical value δg< −1.
A simple prediction of linear biasing is that the two-point correlation function is amplified by a factor b2, while S3 is inversely proportional to b. The analysis of the first redshift surveys revealed instead that different classes of galaxies selected in the optical and infrared bands, while differing in the amplitude of the two-point correlation function, have similar values of S3 (Gaztañaga 1992; Bouchet et al. 1993; Benoist et al. 1999); the same also holds for galaxy clusters (Cappi & Maurogordato 1995). In particular, Benoist et al. (1999) analysed volume-limited samples of the Southern Sky Redshift Survey 2 (SSRS2, da Costa et al. 1994) and found that, while the two-point correlation amplitude increases significantly with galaxy luminosity when L>L∗ (Benoist et al. 1996), the value of S3 does not scale with the inverse of the bias parameter b and is independent of luminosity and scale within the errors: this implies that the bias is non-linear. Similar results were obtained in the Durham/UKST and Stromlo-APM redshift surveys (Hoyle et al. 2000) and in the larger and deeper 2dF Galaxy Redshift Survey (2dFGRS, Baugh et al. 2004; Croton et al. 2004a), which enabled a more detailed analysis: for example, Croton et al. (2004b) found evidence for a weak dependence of S3 on luminosity, while according to Croton et al. (2007) the SJ of red galaxies depends on luminosity, while blue galaxies do not show any dependence. In an analysis of the Sloan Digital Sky Survey (SDSS) Ross et al. (2006) found that the values of SJ are lower for late-type than for early-types galaxies.
In more recent years, deeper surveys enabled exploring the effects of the evolution of gravitational clustering and bias, thus placing stronger constraints on models of galaxy formation and evolution.
Wolk et al. (2013) measured the hierarchical clustering of the CFHTLS-Wide from photometric redshifts. They found an indication that at small scales the hierarchical moments increase with redshift, while at large scales their results are still consistent with perturbation theory for ΛCDM cosmology with a linear bias, but suggest the presence of a small non-linear term.
From the analysis of the VIMOS-VLT Deep Survey, based on spectroscopic redshifts, Marinoni et al. (2005; see also Marinoni et al. 2008) found that the value of S3 for luminous (MB< −21) galaxies is consistent with the local value at z< 1 while decreasing beyond z ~ 1, and that the bias is non-linear.
In this paper we analyse the high-order correlations and moments of the first release of the VIMOS Public Extragalactic Redshift Survey (VIPERS2) in the redshift range 0.5 <z ≤ 1.1 as a function of luminosity and stellar mass. We also derive an estimate of the non-linear bias. Our analysis extends those presented in a number of recent works that have investigated various aspects of galaxy clustering in the VIPERS sample. Some works have focused on two-point statistics, like the standard galaxy-galaxy two-point correlation function to estimate redshift space distortions (de la Torre et al. 2013) and its evolution and dependence on galaxy properties (Marulli et al. 2013). A different type of two-point statistics, the clustering ratio, has been introduced by Bel & Marinoni (2014) and applied to VIPERS galaxies (Bel et al. 2014) to estimate the mass density parameter ΩM. Micheletti et al. (2014) have searched the VIPERS survey for galaxy voids and characterized their properties by means of the galaxy-void cross-correlation. Bel et al. (in prep.) have proposed a method to infer the one-point galaxy probability function from counts in cells that Di Porto et al. (2014) have exploited to search for and detect deviations from linear bias; a result that we directly compare our results with. Finally, Cucciati et al. (2014) studied different methods for accounting for gaps in the VIPERS survey and assessing their impact on galaxy counts.
As cosmological parameters we have adopted H0 = 70 km s-1 Mpc-1, ΩM = 0.25, ΩΛ = 0.75, but all cosmology-dependent quantities are given in H0 = 100 km s-1 Mpc-1 units associated with the corresponding power of h = H0/ 100.
2. High-order statistics
In this section we resume the formalism and define the statistical quantities measured in our work.
The volume-averaged J-point correlation functions are given by  (2)where for spherical cells (used in this work)
(2)where for spherical cells (used in this work)  is a function of the cell radius R and V = 4πR3/ 3.
is a function of the cell radius R and V = 4πR3/ 3.
The volume-averaged two-point correlation function gives the variance of the density contrast:  (3)The volume-averaged J-point correlation functions can be easily derived from the moments of the count PDF P(N,R), that is, the probability of counting N objects in a randomly chosen spherical volume of radius R (see Peebles 1980). For simplicity, in the following we omit the dependence on R. At a fixed scale R, the centred moments of order J are
(3)The volume-averaged J-point correlation functions can be easily derived from the moments of the count PDF P(N,R), that is, the probability of counting N objects in a randomly chosen spherical volume of radius R (see Peebles 1980). For simplicity, in the following we omit the dependence on R. At a fixed scale R, the centred moments of order J are  (4)where
(4)where  is the mean number of objects in a cell of radius R.
is the mean number of objects in a cell of radius R.
The volume-averaged correlation functions correspond to the reduced moments and up to the fourth order are given by the following relations:  (5)An alternative way to estimate the high-order correlations is through the factorial moments mk:
(5)An alternative way to estimate the high-order correlations is through the factorial moments mk:  (6)where
(6)where  (7)is the falling factorial power of order k (see e.g. Graham et al. 1994).
(7)is the falling factorial power of order k (see e.g. Graham et al. 1994).
In fact, for a local Poisson process the moments about the origin of a stochastic field are given by the factorial moments of N; as our variable is the number density contrast  , we have to convert the factorial moments mk into the moments about the mean (central moments)
, we have to convert the factorial moments mk into the moments about the mean (central moments)  through the standard relations
through the standard relations  (8)We can finally derive the volume-averaged J-point correlation functions
(8)We can finally derive the volume-averaged J-point correlation functions  (9)and the normalized moments SJ
(9)and the normalized moments SJ (10)The normalized moments can also be obtained through a recursive formula (Szapudi & Szalay 1993; Colombi et al. 2000):
(10)The normalized moments can also be obtained through a recursive formula (Szapudi & Szalay 1993; Colombi et al. 2000):  (11)where
(11)where  (12)The values given in this paper were calculated using factorial moments.
(12)The values given in this paper were calculated using factorial moments.
At a fixed scale R, the deterministic bias parameter b can be directly measured through the square root of the ratio of the galaxy variance  to the matter variance
to the matter variance  :
:  (13)In the case of linear biasing, the galaxy density contrast δg is proportional to the matter density contrast δm by a constant factor b, δg = bδm: there is no dependence on scale, and b is the only parameter that completely defines the relation between the galaxy and matter distribution.
(13)In the case of linear biasing, the galaxy density contrast δg is proportional to the matter density contrast δm by a constant factor b, δg = bδm: there is no dependence on scale, and b is the only parameter that completely defines the relation between the galaxy and matter distribution.
As we have noted in the introduction, the linear biasing cannot have a general validity. It is more general and realistic to assume a local, deterministic non-linear bias b(z,δm,R), which can be written as a Taylor expansion (Fry & Gaztanaga 1993):  (14)where b1 ≡ b. Fry & Gaztanaga (1993) have shown that such a local bias transformation preserves the hierarchical properties of the underlying matter distribution in the limit of small fluctuations (large scales).
(14)where b1 ≡ b. Fry & Gaztanaga (1993) have shown that such a local bias transformation preserves the hierarchical properties of the underlying matter distribution in the limit of small fluctuations (large scales).
In the case of linear bias, bk = 0 for k> 1, and the galaxy and matter normalized moments are then related by the following equation:  (15)In general, the deviation from linear biasing is measured by taking the second order of the expansion. In this case, the galaxy normalized skewness is given by the following relation:
(15)In general, the deviation from linear biasing is measured by taking the second order of the expansion. In this case, the galaxy normalized skewness is given by the following relation:  (16)
(16)
3. VIPERS survey
Definition of the samples.
The VIMOS Public Extragalactic Redshift Survey (VIPERS) is an ongoing ESO Large Programme aimed at determining redshifts for ~105 galaxies in the redshift range 0.5 <z< 1.2, to accurately and robustly measure clustering, the growth of structure (through redshift-space distortions) and galaxy properties at an epoch when the Universe was about half its current age (Guzzo & The Vipers Team 2013; Guzzo et al. 2014). The survey is divided into two separate areas and will cover ~24 deg2 when completed. The two areas are the so-called W1 and W4 fields of the Canada-France-Hawaii Telescope Legacy Survey Wide (CFHTLS-Wide); the CFHTLS optical photometric catalogues3 constitute the parent catalogue from which VIPERS spectroscopic targets were selected. The VIPERS survey strategy is optimized to achieve a good completeness in the largest possible area (Scodeggio et al. 2009). Galaxies are selected to a limit of iAB< 22.5, further applying a simple and robust gri colour pre-selection to effectively remove galaxies at z< 0.5. In this way, only one pass per field is required, allowing us to double the galaxy sampling rate in the redshift range of interest with respect to a pure magnitude-limited sample (~40%). The final volume of the survey will be 5 × 107h-3 Mpc3, comparable to that of the 2dFGRS at z ~ 0.1.
VIPERS spectra are obtained using the VLT Visible Multi-Object Spectrograph (VIMOS, Le Fèvre et al. 2002, 2003) at moderate resolution (R = 210), with the LR Red grism at R = 210 and a wavelength coverage of 5500–9500 Å. The typical radial velocity error is 140(1 + z) km s-1. A discussion of the survey data reduction and the first management infrastructure were presented in Garilli et al. (2012) and the detailed description of the survey was given by Guzzo et al. (2014).
The data set used in this and the other published papers is the VIPERS Public data release 1 (PDR-1) catalogue, made available to the public in 2013 (Garilli et al. 2014). It includes about 47 000 reliable spectroscopic redshifts of galaxies and active galactic nuclei (AGNs). We here only selected galaxies with reliable redshift, that is, with spectroscopic quality flags 2,3,4, or 9 (see Garilli et al. 2014 for the definition).
To avoid regions dominated by large gaps, we here selected a subset of the total area covered by VIPERS: our limits are 02h01m00s ≤ RA ≤ 02h34m50s, −5.08° ≤ Dec ≤ −4.17° (7.67 square degrees) in W1 and 22h01m12s ≤ RA ≤ 22h18m00s, 0.865° ≤ Dec ≤ 2.20° (5.60 square degrees) in W4.
We defined volume-limited subsamples with different absolute magnitude and stellar mass limits, following the same criteria as in Marulli et al. (2013). The choice of these particular samples is discussed in detail in that paper; here we recall their main properties.
The rest-frame B-band absolute magnitude and the stellar mass were estimated through the HYPERZMASS program (Bolzonella et al. 2000, 2010), which applies a spectral energy distribution (SED) fitting technique. To take into account luminosity evolution, we fixed as a reference limit the luminosity at our maximum redshift (z = 1.1) and assumed an evolution M(z) = M(0) − z (see Meneux et al. 2009 and also Ilbert et al. 2005; Zucca et al. 2009).
We did not correct the mass limit of the stellar-mass-limited subsamples; this limit was therefore kept fixed within each redshift bin because the evolution of M∗ is negligible in our redshift range (Pozzetti et al. 2007, 2010; Davidzon et al. 2013).
The respective numbers of galaxies for the different subsamples are given in Table 1. We note that these numbers are slightly different from those in Marulli et al. (2013) because we applied more stringent angular limits to avoid regions nearby prominent gaps that might affect the counts in spherical cells (while the direct estimate of the two-point correlation function through counts of galaxy pairs can be easily corrected for by using a random catalogue with the same survey geometry).
4. Analysis of mock catalogues
We used mock catalogues derived from cosmological simulations to estimate not only the statistical errors and the uncertainty related to cosmic variance, but also the systematic errors that are due to the inhomogeneous spectroscopic completeness and the specific geometry of the two fields. A detailed description of the way these mocks were built was given by de la Torre et al. (2013).
We analysed a set of 26 independent mock catalogues based on the dark matter halo catalogue of the MultiDark simulation (Prada et al. 2012), which assumes a flat ΛCDM cosmology with (ΩM, ΩΛ, Ωb, h, n, σ8m) = (0.27, 0.73, 0.0469, 0.7, 0.95, 0.82). This catalogue was populated with galaxies using halo occupation distribution prescriptions, as described in de la Torre et al. (2013). In particular, the original halo catalogue was repopulated with halos below the resolution limit with the new technique of de la Torre & Peacock (2013), which enables reproducing the range in stellar mass and luminosity probed by VIPERS data. For luminosity-limited subsamples, galaxy luminosities were calibrated using VIPERS data, while for stellar mass-limited subsamples masses were assigned to galaxies using the stellar-to-halo mass relation (SHMR) of Moster et al. (2013). From the parent mock catalogues, a set of spectroscopic catalogues was derived by applying the same angular, photometric, and spectroscopic selection functions as were applied to the real data. For a more detailed and complete description of the mock catalogues see de la Torre et al. (2013).
From the mock spectroscopic catalogues we derived volume-limited subsamples with cuts in blue absolute magnitude and stellar mass corresponding to the observed ones. First of all, these mocks were used to test the effect of the gaps in the survey. As VIMOS is made of four quadrants 7 × 8 separated by 2 arcmin, characteristic cross-shaped gaps are left in the survey; a further gap is present between the rows of pointings at different declination; finally, there are a few missing quadrants due to failed pointings. Cells whose projection on the sky includes a gap can potentially miss some galaxies, which affects final counts.
These gaps might be avoided by conservatively only counting galaxies in the cells that are completely included in one single quadrant, but in this way, only small scales would be sampled (the exact value obviously depends on the cell distance but it is generally lower than R ~ 5 h-1 Mpc). Alternatively, the counts in each cell might be associated with the effective volume of the cell, subtracting the volume falling into the gaps; but this less drastic choice, which would slightly alter the shape of the cells, would still limit the range of the sampled scales.
Another option would be filling the gaps. Cucciati et al. (2014) applied two algorithms that use the photometric redshift information and assign redshifts to galaxies based upon the spectroscopic redshifts of the nearest neighbours. In this way, it is also possible to take into account the varying completeness from field to field. Tests on mocks have shown that these algorithms are successful in reconstructing the lowest and highest density environments at a scale of 5 h-1 Mpc, but not in recovering the count PDF and its moments due to systematic biases.
 |
Fig. 1 Comparison between mock catalogues with a sampling rate of 100% and without gaps (red triangles), and with a sampling rate and gaps as in VIPERS (blue triangles). The subsamples are limited at MB(z = 1.1) − 5log (h) ≤ −20.5. From top to bottom: volume-averaged two-, three-, and four-point correlation functions, normalized skewness S3 and kurtosis S4 in redshift space. First column: 0.5 ≤ z< 0.7; second column: 0.7 ≤ z< 0.9; third column: 0.9 ≤ z< 1.1. |
We therefore here adopted another solution. The tests on mocks have shown that when cells are not allowed to cross the gaps by more than 40% of their volume, the non-observed regions and the varying sampling rate can be approximated by a random Poisson sampling, and the original count PDF can be recovered with good precision (Bel et al., in prep.). This means that to obtain good estimates of the quantities we discuss here (J-point correlations and normalized moments), which depend on the density contrast Δρ/ρ, it is sufficient to implement the restriction on the volume of the cells falling into the gaps.
In our analysis, we conservatively only considered spherical cells for which no more than 30% of the volume falls in a gap. Moreover, to improve the statistics, we combined the counts of the W1 and W4 fields.
In Fig. 1 we show the results obtained from the analysis of mock subsamples limited at MB(z = 1.1) − 5log (h) ≤ −20.5 in the three redshift bins [0.5, 0.7], [0.7, 0.9], [0.9, 1.1]. We compare the ideal case with 100% completeness and no gaps to the more realistic case with gaps and the same spectroscopic incompleteness as in our observed catalogue, that is, including the effects of the target sampling rate, TSR(Q), and the spectroscopic sampling rate, SSR(Q), where Q indicates the quadrant dependence.
Two other selection effects were not taken into account: the colour sampling rate, CSR(z), and the small-scale bias due to the constraints in the spectroscopic target selection (slits cannot overlap). The first effect depends on redshift but it is weak in our redshift range (see Fig. 5 of Guzzo et al. 2014), while the second effect is negligible because the angular radii of our cells are generally larger than the size of one quadrant.
We note that other sources of systematic errors, as discussed by Hui & Gaztañaga (1999), are the integral constraint bias, affecting the J-point correlation functions, and the ratio bias, affecting the estimate of SJ. Given the large size of our volumes, such systematic effects are weaker than the other errors, however, and can be neglected.
Figure 1 shows that the original values are recovered with good precision (within 1σ error), particularly in the scale range between 4 and 10 h-1 Mpc.
 |
Fig. 2 Fractional difference of the average |
A more detailed analysis of the differences is possible with Fig. 2, which gives the fractional difference for  ,
,  ,
,  , S3, and S4 as a function of scale for the same mock subsamples as in Fig. 1: it shows that in most cases we can retrieve the J-point correlation functions and SJ with only a small systematic difference. In the first redshift bin (0.5 ≤ z< 0.7) at a radius R = 8 h-1 Mpc,
, S3, and S4 as a function of scale for the same mock subsamples as in Fig. 1: it shows that in most cases we can retrieve the J-point correlation functions and SJ with only a small systematic difference. In the first redshift bin (0.5 ≤ z< 0.7) at a radius R = 8 h-1 Mpc,  is overestimated by 8%, while
is overestimated by 8%, while  is underestimated by 3% and
is underestimated by 3% and  by 6%: this translates into an underestimate of S3 by 16% and of S4 by 26%. We have similar values in the second redshift bin (0.7 ≤ z< 0.9). In the last redshift bin (0.9 ≤ z< 1.1) the J-point correlation functions show the largest difference, increasing with order J: but these deviations at different orders are correlated, so that finally the value of S3 at 8 h-1 Mpc is underestimated by only 10% and of S4 by 20%, which is comparable to what is found for the other two redshift bins. The cause of the larger deviations in the last redshift bin is the lower density of the subsample; we take these systematics into account in the discussion of our results.
by 6%: this translates into an underestimate of S3 by 16% and of S4 by 26%. We have similar values in the second redshift bin (0.7 ≤ z< 0.9). In the last redshift bin (0.9 ≤ z< 1.1) the J-point correlation functions show the largest difference, increasing with order J: but these deviations at different orders are correlated, so that finally the value of S3 at 8 h-1 Mpc is underestimated by only 10% and of S4 by 20%, which is comparable to what is found for the other two redshift bins. The cause of the larger deviations in the last redshift bin is the lower density of the subsample; we take these systematics into account in the discussion of our results.
It is interesting to point out that we find values between 1.8 and 2.1 for S3 and between 8 and 10 for S4 for mocks; as an example, the analysis of the mock subsamples limited at MB(z = 1.1) − 5log (h) ≤ −20.5 in the redshift bin [0.7, 0.9] gives S3 ~ 2.13 ± 0.16 and S4 ~ 9.8 ± 1.6 at R = 8 h-1 Mpc. S3 and S4 show no significant redshift evolution, and their values are also comparable within the errors to the value measured in local redshift surveys for galaxies in a similar luminosity range.
Because we know both the cosmological and the “observed” redshift for galaxies in the mock samples, including the peculiar velocity and measurement error, we can estimate the conversion factor from redshift to real space from the mock samples. We need this factor to compare our results with second-order perturbation theory predictions. Figure 3 shows the difference between the estimates in real and redshift space for the subsamples limited at MB(z = 1.1) − 5log (h) ≤ −20.5 in the three redshift ranges. The redshift space correlation functions show the expected loss of power at small scales and the reverse trend at large scales. The estimate of the volume-averaged two-point correlation function in redshift space is flatter than the corresponding estimate in real space; the difference becomes significant on scales smaller than ~4 h-1 Mpc. While the real space values of S3 and S4 increase at smaller scales, the increase is suppressed in redshift space; the difference becomes small beyond ~4 h-1 Mpc. However, at small scales we have large errors due to the small number of objects in the cells. For these reasons we focus our analysis on the 4–10 h-1 Mpc range, and particularly at 8 h-1 Mpc, where we expect to be in the quasi-linear regime and predictions of second-order perturbation theory should hold.
We recall here another bias affecting mass-selected galaxy samples, which has been discussed and tested with mock catalogues by Marulli et al. (2013). The lowest stellar mass subsamples suffer from incompleteness because VIPERS is magnitude limited (iAB< 22.5); as a consequence, we can miss high mass-to-light ratio galaxies. From the analysis of mocks, Marulli et al. (2013) found that these galaxies are faint and red and that the clustering amplitude can be suppressed up to 50% on scales below 1 h-1 Mpc. However, as discussed by Marulli et al. (2013), the abundance of red and faint galaxies is overpredicted by the semi-analytic model used for the tests, and the clustering of red galaxies appears to be overestimated with respect to real data (de la Torre et al. 2011; Cucciati et al. 2012), so that the amplitude of the effect might be overestimated. As we have previously noted, we did not analyse small scales and did not correct for stellar mass incompleteness.
 |
Fig. 3 Comparison between mock catalogues with 100% sampling rate and without gaps in real space (red squares) and redshift space (blue triangles). The subsamples are limited at MB(z = 1.1) − 5log (h) ≤ −20.5. First column: 0.5 ≤ z< 0.7; second column: 0.7 ≤ z< 0.9; third column: 0.9 ≤ z< 1.1. |
5. Results
5.1. Volume-averaged correlation functions
In this section we present the results of our statistical analysis on the combined W1 and W4 samples.
 |
Fig. 4 Volume-averaged two-point correlation functions |
Figure 4 shows the volume-averaged two-point correlation function obtained from counts in cells for luminosity- and stellar mass-limited subsamples in the three different redshift bins.
In the same figure, as a reference for comparing the results in the different redshift bins, we plot the expected real space power-law  in the redshift bin [0.5, 0.7] for the MB(z = 1.1) − 5log (h) ≤ −20.5 subsamples (top panels) and M∗ ≥ 10.0 M⊙ (bottom panels), derived from the ξ2 estimate of Marulli et al. (2013); we converted their two-point correlation function to the volume-averaged correlation function through the formula (Peebles & Groth 1976):
in the redshift bin [0.5, 0.7] for the MB(z = 1.1) − 5log (h) ≤ −20.5 subsamples (top panels) and M∗ ≥ 10.0 M⊙ (bottom panels), derived from the ξ2 estimate of Marulli et al. (2013); we converted their two-point correlation function to the volume-averaged correlation function through the formula (Peebles & Groth 1976):  (17)The line shows the effects of redshift space distortions, which lower the value of
(17)The line shows the effects of redshift space distortions, which lower the value of  on small scales and increase it on large scales.
on small scales and increase it on large scales.
It is clear that the amplitude of  increases with both luminosity and stellar mass at all redshifts.
increases with both luminosity and stellar mass at all redshifts.  appears to have a stronger dependence on stellar mass than on luminosity, in agreement with the results of Marulli et al. (2013): see their Fig. 3 for the redshift space two-point correlation functions.
appears to have a stronger dependence on stellar mass than on luminosity, in agreement with the results of Marulli et al. (2013): see their Fig. 3 for the redshift space two-point correlation functions.
There are some fluctuations: for example, the dependence on luminosity appears to be sligthly weaker in the intermediate and distant redshift bins. However, these variations are consistent when taking into account statistical errors and sample variance, which are included in error bars. We conclude that the dependence of the two-point correlation function on luminosity and stellar mass does not evolve significantly up to z ~ 1.
 |
Fig. 5 Volume-averaged three-point correlation functions as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). |
 |
Fig. 6 Volume-averaged four-point correlation functions as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). |
In Figs. 5 and 6 we show the volume-averaged three- and four-point correlation functions. Their behaviour reflects the two-point correlation functions, showing a stronger dependence of the correlation amplitude on stellar mass than on luminosity.
 |
Fig. 7 Scaling relation of the volume-averaged two- and three-point correlations as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). The dashed line represents the scaling relation |
 |
Fig. 8 Scaling relation of the volume-averaged two and four-point correlations as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). The dashed line represents the scaling relation |
The specific signature of the hierarchical scaling is the power-law relation between high-order correlation functions (Eq. (10)). In Figs. 7 and 8 we show the three- and four-point volume-averaged correlation functions as a function of the two-point volume-averaged correlation functions. The data clearly follow the hierarchical scaling relations  and
and  . These relations appear to hold at all luminosities and masses in the the first two redshift bins, but some systematic differences appear in the last redshift bin, particularly for the stellar-mass limited subsamples, where points are systematically higher than the reference scaling law, but in this case the values are also consistent with the same scaling relation observed at lower redshifts.
. These relations appear to hold at all luminosities and masses in the the first two redshift bins, but some systematic differences appear in the last redshift bin, particularly for the stellar-mass limited subsamples, where points are systematically higher than the reference scaling law, but in this case the values are also consistent with the same scaling relation observed at lower redshifts.
As we have previously discussed, the existence of these scaling relations has been verified in the local Universe: they are expected for the matter distribution in the quasi-linear regime, as a consequence of gravitational clustering. In this case, it is natural that they do not evolve with redshift: however, it is not an obvious result to observe the same hierarchical behaviour for the galaxy distribution at all redshifts, given the evolution of bias.
5.2. Skewness and kurtosis
From the counts in cells we derived the rms σ (Eq. (3)), the normalized skewness S3 and kurtosis S4 (Eq. (11)) for the different VIPERS subsamples. Their values at R = 8 h-1 Mpc are given in Cols. 4–6 of Table 1. The R = 8 h-1 Mpc reference radius is nearly optimal because it is large enough to enter into the quasi-linear regime, and at the same time it is in the scale range for which we have a good sampling.
In Figs. 9 and 10 we show S3 and S4 as a function of luminosity and stellar mass in the three redshift bins. We also show the predictions of second-order perturbation theory in real space for the matter distribution and the corresponding predictions for galaxies, derived from the matter value assuming the linear bias estimated from  , and corrected for redshift space distortion using the factors obtained from mocks. This derivation is described in the next subsection. The theoretical curves for S3 and S4 are shown for radii larger than ~6 h-1 Mpc, as they are calculated in the quasi-linear regime.
, and corrected for redshift space distortion using the factors obtained from mocks. This derivation is described in the next subsection. The theoretical curves for S3 and S4 are shown for radii larger than ~6 h-1 Mpc, as they are calculated in the quasi-linear regime.
 |
Fig. 9 Normalized skewness S3 as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). We note that black points corresponding to galaxies with M< −19.50 or M∗ ≥ 9.0 M⊙ are only plotted for the first redshift bin ([0.5, 0.7]), but most of them are not visible as they lie below the points of the other samples. The dashed line corresponds to S3 = 2. In the top panels, the dotted line is the prediction from second-order perturbation theory for the matter distribution in real space; the solid line is the prediction of S3 for galaxies with MB(z = 1.1) − 5log (h) ≤ −20.5 (to be compared to blue pentagons): it was obtained from the matter values, converted to redshift space and divided by the corresponding linear bias factor. |
 |
Fig. 10 Normalized skewness S4 as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). We note that black points corresponding to galaxies with M< −19.50 or M∗ ≥ 9.0 M⊙ are only plotted for the first redshift bin ([0.5, 0.7]), but most of them are not visible as they lie below the points of the other samples. The dashed line corresponds to S4 = 8. In the top panels, the dotted line is the prediction from second-order perturbation theory for the matter distribution in real space; the solid line is the prediction of S4 for galaxies with MB(z = 1.1) − 5log (h) ≤ −20.5 (to be compared to blue pentagons): it was obtained from the matter values, converted to redshift space and divided by the corresponding linear bias factor. |
In the first redshift bin, both for luminosity and stellar mass limited samples, the value of S3 is constant and around 2 at small and intermediate scales, but it starts decreasing beyond R ~ 8 h-1 Mpc. In principle, variations of S3 with scale can be due to changes in the slope of the power spectrum or to a scale-dependent bias. However, such a systematic effect can be ascribed to the small number of independent cells at large scales, as shown by mocks and reflected in the large error bars. In the same redshift bin, S4 shows a small decrease at large scales and is consistent with a constant value of ~7.3 between 4 and 10 h-1 Mpc. In the range 6–8 h-1 Mpc, the best scales to compare with perturbation theory (on larger scales the errors increase significantly), the theoretical predictions for S3 and S4 are slightly higher than the observed values corresponding to the MB(z = 1.1) − 5log (h) ≤ −20.5 subsample, but only at 1σ level.
In the second redshift bin the value of S3 for luminosity-limited subsamples is around 1.8, sligthly lower than in the first bin, but still consistent within the errors; moreover, it is consistent with a constant value in the whole range of scales. The value of S3 for mass-limited subsamples is also constant in the whole range of scales and is consistent with the value in the first redshift bin. S4 has an analogous behaviour: while showing a systematic decrease, particularly in luminosity-limited subsamples, it is still consistent with a constant value in the range 4–16 h-1 Mpc. As in the case of the first redshift bin, in the range 6–8 h-1 Mpc the theoretical predictions for S3 and S4 are slightly higher than the corresponding observed values.
In the third redshift bin the values of S3 and S4 for luminosity- and stellar-mass-limited subsamples increase systematically with scale. Moreover, in contrast with the two previous redshift bins, in the range 6–8 h-1 Mpc, the theoretical predictions for S3 and S4 are lower than the observed values.
To better appreciate the significance of these deviations, we note that of 26 mocks, 3 show an increase of the values of S3 and S4 similar to what we find in the last redshift bin.
In fact, higher-order statistics are very sensitive to large-scale structure, and the correlated variations in the measured values of S3 and S4 probably indicate genuine fluctuations in the galaxy distribution (see e.g. the discussion in Croton et al. 2004b).
In our case, this interpretation is suggested by checking the W1 and W4 fields separately: we find that in the outermost redshift shell, both S3 and S4 are larger in W1 than in W4. For example, for the MB(z = 1.1) − 5log (h) ≤ −21.0 subsample, at R = 8 h-1 Mpc, we find S3 = 2.7 ± 0.5 in W1 and S3 = 1.6 ± 0.3 in W4. Analogously, for the log (M/M⊙h-2) ≥ 10.5 subsample at R = 8 h-1 Mpc, we find S3 = 3.4 ± 0.5 in the W1 field and S3 = 2.0 ± 0.3 in the W4 field. This difference might be regarded as the imprint of spatially coherent structures more prominent in W1.
In conclusion, the values of S3 and S4 do not show any significant dependence on luminosity or on stellar mass: the points corresponding to different subsamples are consistent within the error bars (we discuss a possible weak dependence on luminosity in the next subsection). There is no evidence of evolution in redshift either, apart from the systematic increase of S3 and S4 with scale in the last redshift bin.
Taking into account the behaviour of mocks, the observed systematic variations in the values of high-order moments are consistent with the fluctuations expected for comparable volumes randomly extracted from a ΛCDM universe.
It is possible to compare our results on S3 and S4 with those obtained by Wolk et al. (2013) for the four CFHTLS-Wide fields. They have divided the galaxies in the photometric catalogue into four redshift bins through the estimated photometric redshifts; for galaxies with Mg< −20.7, they have estimated SJ as a function of angular scale and the corresponding 3D values through deprojection, which, as they discussed, rely on some approximations. Their work is therefore complementary to ours: they have a larger area and number of objects, but we can directly estimate the 3D (redshift space) SJ; they can sample smaller, highly non-linear scales where we do not have enough statistics, but we can better sample the quasi-linear scales; finally, we can also test the dependence of S3 on luminosity and stellar mass.
A comparison with their Fig. 12 shows that, as expected (see our Fig. 3), their deprojected values for S3 and S4 on small scales (R< 5 h-1 Mpc) are higher than our redshift space values. On larger scales, the redshift space effect on S3 and S4 becomes negligible, and their estimate is consistent with ours.
We note that Wolk et al. (2013) found significant deviations in the results for the W3 field, while we have found differences between W1 and W4 in our last redshift bin: this shows that sample variance is still significant for high-order statistics on the scale of CFHTLS Wide Fields.
5.3. Implications for biasing
We now discuss the implications of our analysis for biasing. We concentrate on the reference scale R = 8 h-1 Mpc, where second-order perturbation theory predictions can be applied and results are still reliable (errors and systematic deviations increase on larger scales). Because we aim to compare our results with the matter density field, statistical quantities referring to galaxies are indicated with a subscript g and those relative to matter with a subscript m.
Figure 11 shows the values of σ8g (top panel) and S3g (bottom panel) at R = 8 h-1 Mpc for the VIPERS volume-limited subsamples with different limiting absolute magnitudes and in the different redshift bins. In the same figure we also show the corresponding VVDS estimates (Marinoni et al. 2005) and the 2dFGRS estimates for the local Universe (Croton et al. 2004b) for galaxies with a similar luminosity as ours.
At a given redshift, VIPERS subsamples with a brighter absolute magnitude limit have higher values of σ8g, but there is no significant evolution of σ8g with redshift. The same holds when combining our results with those of the 2dFGRS in the local Universe and those of the VVDS at higher redshift: σ8g shows no significant evolution from z = 0 to z = 1.4 (VVDS points are systematically lower but at the 1σ level). This implies (see e.g. the discussion in Marinoni et al. 2005) a strong evolution of the linear bias b with redshift because σ8m increases with time (see Eq. (13)). There are various models that describe the evolution of b(z) and explain its decrease with time (see e.g. Blanton et al. 2000); from an empirical point of view, we note that the available data can be fitted by the simple relation b(z) ∝ 1/σ8m.
The skewness S3g of the VIPERS subsamples measured at 8 h-1 Mpc and plotted as a function of redshift has more fluctuations than σ8g, with a minimum value in the redshift bin [0.7,0.9], but it does not show a significant dependence on luminosity and is still consistent with a constant value independent of redshift. The values of S3g in the VVDS below z = 1.2 are lower than VIPERS values, but are consistent within the errors, while they start to decrease beyond z ~ 1.1.
The absence of a significant evolution of S3g with redshift is not limited to our redshift range: the values of S3g measured in VIPERS are similar to those measured in the 2dFGRS, that is, S3 ~ 2.0 ± 0.2, where depending on the subsample S3g varies from 1.95 to 2.58 (while not shown in the figure, the values of S4 are also consistent with the 2dFGRS ones). Therefore, taking into account all data points, starting from the local value for the 2dFGRS up to z = 1.1 (VIPERS and VVDS data), S3g is consistent with a constant value ~2: in VIPERS the strongest but marginal deviations of the S3g value are for MB(z = 1.1) − 5log (h) ≤ −20.0 galaxies in the nearest redshift range [0.5, 0.7] and for MB(z = 1.1) − 5log (h) ≤ −21.0 galaxies in the most distant redshift interval [0.9, 1.1], both giving a value of S3g that is 15% higher.
 |
Fig. 11 σ8g(upper panel) and S3g (lower panel) as a function of redshift. Colours represent the different absolute magnitude limits as in previous figures. The open hexagon represents the corresponding value for 2dFGRS galaxies in the absolute magnitude MbJ range [–21, –20] (Croton et al. 2004b). Black open squares are the values for VVDS galaxies brighter than MB = −21 (Marinoni et al. 2005). For better visibility, points corresponding to different redshifts are slightly shifted in magnitude. |
Figure 12 shows σ8g (top panel) and S3g at 8 h-1 Mpc (bottom panel) as a function of absolute magnitude for the three redshift bins. σ8g shows a systematic increase with luminosity (reflecting the dependence of the correlation amplitude on luminosity), but at a given absolute luminosity its value is similar in the three redshift bins.
S3g appears to be independent of absolute magnitude, with fluctuations from sample to sample. However, if we exclude the points relative to the last redshift bin, where S3g has a higher value, the data might suggest a small decrease of S3g with increasing luminosity, reminiscent of the results of Croton et al. (2004b) for the 2dFGRS.
A trend of S3g with luminosity is interesting because in the hypothesis of linear biasing, S3g is inversely proportional to the bias factor b: knowing from the two-point correlation function of our samples that b increases with luminosity, we expect a corresponding decrease of S3g.
 |
Fig. 12 σ8g (upper panel) and S3g at R = 8 h-1 Mpc (lower panel) as a function of galaxy luminosity for the three redshift bins. Red triangles: 0.5 ≤ z< 0.7; blue squares: 0.7 ≤ z< 0.9; green hexagons: 0.9 ≤ z< 1.1. For better visibility, points corresponding to different redshifts are slightly shifted in magnitude. |
To test whether our results are consistent with the linearity of bias, we therefore estimated the bias of galaxies with respect to the underlying matter density field at R = 8 h-1 Mpc, using the observed σ8g and S3g of the galaxy distribution and estimating σm and S3m of the matter distribution through perturbation theory.
Juszkiewicz et al. (1993) and Bernardeau (1994a, 1994b; see also Bernardeau et al. 2002, and references therein) have shown that for a smoothed density field with primordial Gaussian fluctuations, Peebles’ unsmoothed value of S3m = 34/7 (Peebles 1980) has to be corrected according to the expression 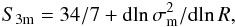 (18)where d
(18)where d is the logarithmic slope of the linear variance of the matter density field smoothed with a spherical top-hat function of radius R,
is the logarithmic slope of the linear variance of the matter density field smoothed with a spherical top-hat function of radius R,  (19)For a power-law spectrum P(k) ∝ kn, Eq. (18) becomes S3m = 34/7 − (n + 3).
(19)For a power-law spectrum P(k) ∝ kn, Eq. (18) becomes S3m = 34/7 − (n + 3).
Similar relations hold for higher orders, involving higher-order derivatives.
The values obtained from perturbation theory have been tested with numerical simulations, and it has been shown that in the range we are studying, that is, at R = 8 h-1 Mpc and for σ8m ~ 1, they are very accurate: for example, the difference in the S3 values is smaller than a few percent (Baugh et al. 1995; Fosalba & Gaztanaga 1998; Bernardeau et al. 2002).
Applying Eqs. (18) and (19) and using the software CAMB (Lewis & Bridle 2002), we have computed the values of σ8m and S3m for a power spectrum with the new cosmological parameters derived from the Planck mission (Planck Collaboration XVI 2014) and with the old Millennium parameters (first year WMAP data and 2dFGRS, with ΩM = 0,25, ΩΛ = 075, n = 1 and σ8m = 0.9).
We here assumed that the standard ΛCDM model is correct. With other assumptions, such as a dark energy component with an evolving equation of state or modified gravity, the clustering and bias evolution would be affected (see e.g. Munshi et al. 2004), as would the redshift distortions (Hellwing et al. 2013). This dependence on cosmology will be studied in a future work.
We also converted the observed σ8g and S3g to real space values by applying correction factors directly derived from the mocks.
For the subsample limited at MB(z = 1.1) − 5log (h) ≤ −20.50, we give in Table 2 the redshift range (Col. 1), the values of σ8g (Col. 2), σ8m (Col. 3), b = σ8g/σ8M (Col. 4), S3g (Col. 5), S3m (Col. 6), all measured at a scale of R = 8 h-1 Mpc.
In Fig. 13 we plot our estimates for the linear bias term b as a function of redshift, with the correponding estimates for VIPERS of Marulli et al. (2013) and Di Porto et al. (2014). As expected, the estimates are fully consistent, with b increasing with luminosity and redshift. As discussed by Di Porto et al. (2014), there is only a difference in the last redshift bin where the estimate of Marulli et al. is lower than that of Di Porto et al. (2014). The difference is probably due to the way b is estimated (counts in cells in our case and in Di Porto et al. 2014, pair counts in Marulli et al. 2013). Our estimate is consistent with both the other two estimates at the 1σ level, however.
In Fig. 14 we compare the linear bias directly measured from the ratio of the galaxy and matter rms, b = σ8g/σ8m, with the ratio of the galaxy and matter skewness, S3m/S3g. Under the hypothesis of linear biasing, the two ratios should have the same value. For the first two redshift bins we find slightly different values: the skewness ratio is systematically higher than the bias directly computed from the variance. The third redshift bin shows the largest discrepancy, but with the opposite behaviour, that is, the skewness ratio is lower than the bias directly computed from the variance. This different behaviour is a consequence of the fact that the value of S3g in the last redshift bin increases with scale and becomes higher than at lower redshifts.
We can quantify the degree of non-linearity by directly estimating the second-order term b2 from Eq. (16):  (20)where we used the real space values S3g and b obtained from the redshift space values by using the conversion factor calculated from the mocks. We note that this correction is small (a few percent) at our scale of R = 8 h-1 Mpc, because this scale is at the transition from the regime of small-scale velocity dispersion (where redshift space correlation functions are lower than real space ones) to the regime of infall where redshift space correlations are higher than real space ones (see Fig. 3).
(20)where we used the real space values S3g and b obtained from the redshift space values by using the conversion factor calculated from the mocks. We note that this correction is small (a few percent) at our scale of R = 8 h-1 Mpc, because this scale is at the transition from the regime of small-scale velocity dispersion (where redshift space correlation functions are lower than real space ones) to the regime of infall where redshift space correlations are higher than real space ones (see Fig. 3).
In this formalism, if b> 0, b2 is negative when σ8g/σ8m<S3m/S3g. This is what happens in the first two redshift bins, where at nearly all magnitudes b2 is negative: for example, for the subsample limited at M ≤ −20.5(z = 1.1) − 5log (h), we find b2 = −0.20 ± 0.49 in the first redshift bin and b2 = −0.24 ± 0.35, in the second redshift bin. In contrast, we find a positive b2 in the third bin, with b2 = + 0.78 ± 0.82.
As we have noted above when discussing the results of our tests on mocks, the assumption that masked regions and inhomogeneities can be described as a Poissonian random sampling gives a small bias with an overestimate of b of a few percent and an underestimate of S3 around 10–15%. Using the correction factors derived from the average of the mocks, we find for the subsample limited at M ≤ −20.5(z = 1.1) − 5log (h)b2 = −0.03 ± 0.49 in the first redshift, b2 = −0.25 ± 0.35 in the second redshift bin, and b2 = + 0.72 ± 0.82 in the third bin. The differences are well within 1σ error.
It would be tempting to interpret these results as suggesting a possible evolution of the non-linear bias b2 with redshift, with a similar trend, for example, as for the model of Sefusatti & Komatsu (2007). Unfortunately, the problem is the extreme sensitivity of b2 to the errors on b and S3g, amplified by a factor b2, and we have seen that subsamples in the last redshift bin are affected by larger errors and systematic trends.
Real space values of σ8 and S3 of galaxies with MB(z = 1.1) − 5log (h) ≤ −20.50 vs. those expected from second-order perturbation theory (with Millennium and Planck cosmological parameters).
 |
Fig. 13 Linear bias b as a function of redshift. Top panel: MB ≤ −20.0(z = 1.1) + 5log (h); middle panel: MB ≤ −20.5(z = 1.1) + 5log (h); bottom panel: MB ≤ −21.0(z = 1.1) + 5log (h). Red hexagons: our estimates of b = σ8g/σ8m. Blue squares: estimates of Marulli et al. (2013). Magenta triangles: Di Porto et al. (2014). |
 |
Fig. 14 Estimates of b = σ8g/σ8m (solid lines, filled symbols) and b′ ≡ S3m/S3g (dotted lines, open symbols); b′ = b under the assumption of linear bias. Red lines with triangles: 0.5 ≤ z< 0.7; blue lines with squares: 0.7 ≤ z< 0.9; green lines with hexagons: 0.9 ≤ z< 1.1. |
With these caveats, we can check the consistency of our results with other works in the same redshift and luminosity ranges. In this comparison, one has to take into account the sensitivity of b2 to the different methods and, as pointed out by Kovač et al. (2011), to sample variance. In fact, even local measurements of the non-linear term have given different values (see e.g. Verde et al. 2002 and Pan & Szapudi 2005, and the discussion in Gaztañaga et al. 2005 and Marinoni et al. 2008).
First of all, Di Porto et al. (2014) have analysed the VIPERS data reconstructing the bias relation from the estimate of the probability distribution function: they found a small (<3%) but significant deviation from linear bias.
In their analysis of the four CFHTLS Wide fields, Wolk et al. (2013) have found that perturbation theory predictions agree well with their measurements when taking into account the linear bias, but note that there is still a small discrepancy that can be explained by the presence of a non-linear bias term. This is also consistent with what we found.
Marinoni et al. (2005) have analysed VVDS volume-limited samples limited at MB< −20 + 5log (h) (this limit was fixed and did not take into account luminosity evolution) in the redshift bins 0.7 <z< 0.9 and 0.9 <z< 1.1, finding b2 = −0.20 ± 0.08 and b2 = −0.12 ± 0.08 (here the errors do not include sample variance): these values are consistent with ours below z = 1.
Kovač et al. (2011) analysed the zCOSMOS galaxy overdensity field and estimated the mean biasing function between the galaxy and matter density fields and its second moment, finding a small non-linearity, with the non-linearity parameter  (defined in the formalism of Dekel & Lahav 1999) at most 2% with an uncertainty of the same order.
(defined in the formalism of Dekel & Lahav 1999) at most 2% with an uncertainty of the same order.
Gaztañaga et al. (2005) have found  and
and  from the measurement of the Q3 parameter in the three-point correlation function of the 2dFGRS for the local Universe.
from the measurement of the Q3 parameter in the three-point correlation function of the 2dFGRS for the local Universe.
The non-linear term we have measured in the redshift interval between z = 0.5 and z = 0.9 is therefore similar to what has been measured in the above surveys. We conclude that there is general evidence for a small but non-zero non-linear b2 term. It is also clear that no evolution of b2 with redshift can be detected in the available data, in contrast to the linear bias term.
6. Conclusions
We have analysed the high-order clustering of galaxies in the first release of VIPERS, using counts in cells to derive the volume-averaged correlation functions and normalized skewness S3g and kurtosis S4g. We have analysed volume-limited subsamples with different cuts in absolute magnitude and stellar mass in three redshift bins; these subsamples are the same as in Marulli et al. (2013).
Errors were estimated through a set of mock catalogues, derived from dark matter halo catalogues repopulated with the method of de la Torre & Peacock (2013). The mocks were built to reproduce the properties of VIPERS, including masks and selection effects. Our analysis has shown that the high-order statistical properties of these mocks are consistent with observations.
We also studied the dependence of the second- and third-order statistics of galaxy counts on the bias, deriving the linear bias term b and the first non-linear term b2, and comparing our results with predictions from perturbation theory and with other works in the literature.
Here are our main conclusions.
-
We showed that the hierarchical scaling relations
 and
and  hold in the range of scales and redshifts we could sample, that is, 3 ≤ R ≤ 10 h-1 Mpc and 0.5 ≤ z< 1.1. These relations are consistent with predictions from gravitational clustering and with the scaling observed in local surveys.
hold in the range of scales and redshifts we could sample, that is, 3 ≤ R ≤ 10 h-1 Mpc and 0.5 ≤ z< 1.1. These relations are consistent with predictions from gravitational clustering and with the scaling observed in local surveys. -
S3g and S4g appear to be independent of luminosity; however, if we do not not take the last redshift bin into account, there is a slight decrease of S3g with increasing luminosity, an effect previously detected locally in the 2dFGRS by Croton et al. (2004b).
-
The values of S3g and S4g are scale-independent within the errors and do not evolve significantly at least up to z = 0.9. We detected a systematic increase with scale in the last redshift bin (beyond ~10 h-1 Mpc), mainly due to one of the two CFHTLS fields (W1); this deviation is consistent with what can be expected from the sample variance shown by mock catalogues.
-
The observed values of S3g ~ 2 ± 0.2 and S4g ~ 8 ± 0.4 are similar to those measured in local surveys for galaxies in the same luminosity range. This confirms the substantial absence of evolution of S3g in the redshift range 0 <z< 1 at the level of ~10%. This result is expected for S3m, but is not trivial for S3g, given the evolution of bias.
-
At second order, galaxies with higher luminosity or stellar mass have a larger amplitude (greater linear bias parameter) of the volume-averaged two-point correlation function, consistently with the direct analysis of the two-point correlation function by Marulli et al. (2013). We showed that our estimate of the linear bias parameter b = σ8g/σ8m is consistent within 1σ with those of Marulli et al. (2013) and Di Porto et al. (2014). The linear bias increases both with luminosity and with redshift: in our redshift range, we measured the lowest bias b = 1.47 ± 0.18 for galaxies with MB(z = 1.1) − 5log (h) ≤ −19.5 in the redshift bin 0.5 ≤ z< 0.7 and the largest bias b = 2.12 ± 0.28 for galaxies with MB(z = 1.1) − 5log (h) ≤ −21.0 in the redshift bin 0.9 ≤ z< 1.1.
-
For a given luminosity class, σ8g does not evolve with redshift. For example, comparing our values for MB(z = 1.1) − 5log (h) ≤ −20.5 to the corresponding value measured in the 2dFGRS, we found that σ8g is consistent with a constant value 1.0 (our 1σ error is 10%), from z = 0 to z ~ 1. Given that σ8m increases with time, we have the empirical relation b(z) ∝ 1 /σ8m(z).
-
The value of the non-linear bias parameter b2 measured below z ~ 1 at the scale R = 8 h-1 Mpc, that is, in the quasi-linear regime, is negative but not statistically different from zero when taking into account the error; however, taking into account the ensemble of results coming from this and other surveys in the redshift range 0.5 ≤ z< 1 (Marinoni et al. 2005; Kovač et al. 2011; Wolk et al. 2013; Di Porto et al. 2014), there is evidence for a small but non-zero non-linear term. Including the results from local surveys as well, no evolution of b2 with redshift can be detected in the available data.
-
The comparison with the properties of mocks and with the predictions of perturbation theory shows that our results are consistent with the general scenario of biased galaxy formation and gravitational clustering evolution in a standard ΛCDM cosmology.
In conclusion, we have provided an independent check on the second-order statistical studies of the galaxy distribution through our analysis; we explored the galaxy bias with an independent technique; finally, we determined the higher-order statistical properties of the galaxy distribution in the redshift range between 0.5 and 1.1, thanks to the combination of volume and density of galaxies in the VIPERS survey. When VIPERS is complete, it will be possible to perform a more general analysis, which will allow us not only to decrease error bars, but also to include the dependence of high-order statistics on galaxy colour, to apply other high-order statistical tools such as the void probability function, and to give better constraints on the non-linear bias.
However, there is the important exception of the lognormal distribution, see Coles & Jones (1991) and Carron (2011).
Mellier et al. (2008), http://terapix.iap.fr/cplt/oldSite/Descart/CFHTLS-T0005-Release.pdf
Acknowledgments
This work is based on observations collected at the European Southern Observatory, Cerro Paranal, Chile, using the Very Large Telescope under programs 182.A-0886 and partly 070.A-9007. Also based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The VIPERS web site is http://www.vipers.inaf.it/. We acknowledge the crucial contribution of the ESO staff for the management of service observations. In particular, we are deeply grateful to M. Hilker for his constant help and support of this program. Italian participation to VIPERS has been funded by INAF through PRIN 2008 and 2010 programs. D.M. gratefully acknowledges financial support of INAF-OABrera. L.G., A.J.H., and B.R.G. acknowledge support of the European Research Council through the Darklight ERC Advanced Research Grant (#291521). A.P., K.M., and J.K. have been supported by the National Science Centre (grants UMO-2012/07/B/ST9/04425 and UMO-2013/09/D/ST9/04030), the Polish-Swiss Astro Project (co-financed by a grant from Switzerland, through the Swiss Contribution to the enlarged European Union), and the European Associated Laboratory Astrophysics Poland-France HECOLS. K.M. was supported by the Strategic Young Researcher Overseas Visits Program for Accelerating Brain Circulation (#R2405). O.L.F. acknowledges support of the European Research Council through the EARLY ERC Advanced Research Grant (#268107). G.D.L. acknowledges financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement # 202781. W.J.P. and R.T. acknowledge financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement #202686. W.J.P. is also grateful for support from the UK Science and Technology Facilities Council through the grant ST/I001204/1. E.B., F.M. and L.M. acknowledge the support from grants ASI-INAF I/023/12/0 and PRIN MIUR 2010-2011. L.M. also acknowledges financial support from PRIN INAF 2012. Y.M. acknowledges support from CNRS/INSU (Institut National des Sciences de l’Univers) and the Programme National Galaxies et Cosmologie (PNCG). C.M. is grateful for support from specific project funding of the Institut Universitaire de France and the LABEX OCEVU. SdlT acknowledges the support of the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government program managed by the ANR.
References
- Balian, R., & Schaeffer, R. 1989, A&A, 220, 1 [NASA ADS] [Google Scholar]
- Baugh, C. M., Gaztanaga, E., & Efstathiou, G. 1995, MNRAS, 274, 1049 [NASA ADS] [Google Scholar]
- Baugh, C. M., Croton, D. J., Gaztañaga, E., et al. 2004, MNRAS, 351, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, J., & Marinoni, C. 2014, A&A, 563, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bel, J., Marinoni, C., Granett, B. R., et al. 2014, A&A, 563, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benoist, C., Maurogordato, S., da Costa, L. N., Cappi, A., & Schaeffer, R. 1996, ApJ, 472, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Benoist, C., Cappi, A., da Costa, L. N., et al. 1999, ApJ, 514, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F. 1992, ApJ, 392, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F. 1994a, ApJ, 433, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F. 1994b, A&A, 291, 697 [NASA ADS] [Google Scholar]
- Bernardeau, F., Colombi, S., Gaztañaga, E., & Scoccimarro, R. 2002, Phys. Rep., 367, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Blanton, M., Cen, R., Ostriker, J. P., Strauss, M. A., & Tegmark, M. 2000, ApJ, 531, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Bolzonella, M., Kovač, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchet, F. R., Strauss, M. A., Davis, M., et al. 1993, ApJ, 417, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Cappi, A., & Maurogordato, S. 1995, ApJ, 438, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Carron, J. 2011, ApJ, 738, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Coles, P., & Jones, B. 1991, MNRAS, 248, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S., Szapudi, I., Jenkins, A., & Colberg, J. 2000, MNRAS, 313, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Colless, M., Gaztañaga, E., et al. 2004a, MNRAS, 352, 828 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Gaztañaga, E., Baugh, C. M., et al. 2004b, MNRAS, 352, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Croton, D. J., Norberg, P., Gaztañaga, E., & Baugh, C. M. 2007, MNRAS, 379, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., De Lucia, G., Zucca, E., et al. 2012, A&A, 548, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cucciati, O., Granett, B. R., Branchini, E., et al. 2014, A&A, 565, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- da Costa, L. N., Geller, M. J., Pellegrini, P. S., et al. 1994, ApJ, 424, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Bolzonella, M., Coupon, J., et al. 2013, A&A, 558, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, M., & Peebles, P. J. E. 1977, ApJS, 34, 425 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., & Peacock, J. A. 2013, MNRAS, 435, 743 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Meneux, B., De Lucia, G., et al. 2011, A&A, 525, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dekel, A., & Lahav, O. 1999, ApJ, 520, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Di Porto, C., Branchini, E., Bel, J., et al. 2014, A&A, submitted [arXiv:1406.6692] [Google Scholar]
- Durrer, R., Juszkiewicz, R., Kunz, M., & Uzan, J.-P. 2000, Phys. Rev. D, 62, 021301 [NASA ADS] [CrossRef] [Google Scholar]
- Fosalba, P., & Gaztanaga, E. 1998, MNRAS, 301, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Fry, J. N. 1984a, ApJ, 277, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Fry, J. N. 1984b, ApJ, 279, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Fry, J. N., & Gaztanaga, E. 1993, ApJ, 413, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Fry, J. N., & Peebles, P. J. E. 1978, ApJ, 221, 19 [Google Scholar]
- Fry, J. N., & Scherrer, R. J. 1994, ApJ, 429, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Paioro, L., Scodeggio, M., et al. 2012, PASP, 124, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaztañaga, E. 1992, ApJ, 398, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Gaztañaga, E., & Fosalba, P. 1998, MNRAS, 301, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Gaztañaga, E., & Maehoenen, P. 1996, ApJ, 462, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Gaztañaga, E., Norberg, P., Baugh, C. M., & Croton, D. J. 2005, MNRAS, 364, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Graham, R., Knuth, D., & Patashnik, O. 1994, Concrete Mathematics (Addison Wesley) [Google Scholar]
- Groth, E. J., & Peebles, P. J. E. 1977, ApJ, 217, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Guzzo, L., & The Vipers Team 2013, The Messenger, 151, 41 [NASA ADS] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2014, A&A, 566, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamilton, A. J. S. 1988, ApJ, 332, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Hellwing, W. A., Juszkiewicz, R., & van de Weygaert, R. 2010, Phys. Rev. D, 82, 103536 [NASA ADS] [CrossRef] [Google Scholar]
- Hellwing, W. A., Li, B., Frenk, C. S., & Cole, S. 2013, MNRAS, 435, 2806 [NASA ADS] [CrossRef] [Google Scholar]
- Hoyle, F., Szapudi, I., & Baugh, C. M. 2000, MNRAS, 317, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, L., & Gaztañaga, E. 1999, ApJ, 519, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juszkiewicz, R., Bouchet, F. R., & Colombi, S. 1993, ApJ, 412, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Kovač, K., Porciani, C., Lilly, S. J., et al. 2011, ApJ, 731, 102 [NASA ADS] [CrossRef] [Google Scholar]
- LeFèvre, O., Mancini, D., Saisse, M., et al. 2002, The Messenger, 109, 21 [NASA ADS] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1670 [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, X., & Schramm, D. N. 1993, ApJ, 408, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., McDonald, P., Seljak, U., & Cen, R. 2003, MNRAS, 344, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Marín, F. A., Wechsler, R. H., Frieman, J. A., & Nichol, R. C. 2008, ApJ, 672, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Mao, Q., Berlind, A. A., McBride, C. K., et al. 2014, MNRAS, 443, 1402 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C., Le Fèvre, O., Meneux, B., et al. 2005, A&A, 442, 801 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marinoni, C., Guzzo, L., Cappi, A., et al. 2008, A&A, 487, 7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marulli, F., Bolzonella, M., Branchini, E., et al. 2013, A&A, 557, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneux, B., Guzzo, L., de la Torre, S., et al. 2009, A&A, 505, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micheletti, D., Iovino, A., Hawken, A. J., et al. 2014, A&A, 570, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moresco, M., Marulli, F., Baldi, M., Moscardini, L., & Cimatti, A. 2014, MNRAS, 443, 2874 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Naab, T., & White, S. D. M. 2013, MNRAS, 428, 3121 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., Porciani, C., & Wang, Y. 2004, MNRAS, 349, 281 [Google Scholar]
- Pan, J., & Szapudi, I. 2005, MNRAS, 362, 1363 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The large-scale structure of the universe (Princeton University Press) [Google Scholar]
- Peebles, P. J. E., & Groth, E. J. 1976, A&A, 53, 131 [NASA ADS] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2014, A&A, 571, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Lamareille, F., et al. 2007, A&A, 474, 443 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prada, F., Klypin, A. A., Cuesta, A. J., Betancort-Rijo, J. E., & Primack, J. 2012, MNRAS, 423, 3018 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Brunner, R. J., & Myers, A. D. 2006, ApJ, 649, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., Le Fèvre, O., & Guzzo, L. 2009, The Messenger, 135, 13 [NASA ADS] [Google Scholar]
- Sefusatti, E., & Komatsu, E. 2007, Phys. Rev. D, 76, 083004 [NASA ADS] [CrossRef] [Google Scholar]
- Sharp, N. A., Bonometto, S. A., & Lucchin, F. 1984, A&A, 130, 79 [NASA ADS] [Google Scholar]
- Szapudi, I., & Szalay, S. 1993, ApJ, 408, 43 [Google Scholar]
- Verde, L., Heavens, A. F., Percival, W. J., et al. 2002, MNRAS, 335, 432 [Google Scholar]
- Viel, M., Matarrese, S., Heavens, A., et al. 2004, MNRAS, 347, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Wolk, M., McCracken, H. J., Colombi, S., et al. 2013, MNRAS, 435, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, A&A, 508, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Real space values of σ8 and S3 of galaxies with MB(z = 1.1) − 5log (h) ≤ −20.50 vs. those expected from second-order perturbation theory (with Millennium and Planck cosmological parameters).
All Figures
 |
Fig. 1 Comparison between mock catalogues with a sampling rate of 100% and without gaps (red triangles), and with a sampling rate and gaps as in VIPERS (blue triangles). The subsamples are limited at MB(z = 1.1) − 5log (h) ≤ −20.5. From top to bottom: volume-averaged two-, three-, and four-point correlation functions, normalized skewness S3 and kurtosis S4 in redshift space. First column: 0.5 ≤ z< 0.7; second column: 0.7 ≤ z< 0.9; third column: 0.9 ≤ z< 1.1. |
| In the text | |
 |
Fig. 2 Fractional difference of the average |
| In the text | |
 |
Fig. 3 Comparison between mock catalogues with 100% sampling rate and without gaps in real space (red squares) and redshift space (blue triangles). The subsamples are limited at MB(z = 1.1) − 5log (h) ≤ −20.5. First column: 0.5 ≤ z< 0.7; second column: 0.7 ≤ z< 0.9; third column: 0.9 ≤ z< 1.1. |
| In the text | |
 |
Fig. 4 Volume-averaged two-point correlation functions |
| In the text | |
 |
Fig. 5 Volume-averaged three-point correlation functions as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). |
| In the text | |
 |
Fig. 6 Volume-averaged four-point correlation functions as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). |
| In the text | |
 |
Fig. 7 Scaling relation of the volume-averaged two- and three-point correlations as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). The dashed line represents the scaling relation |
| In the text | |
 |
Fig. 8 Scaling relation of the volume-averaged two and four-point correlations as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). The dashed line represents the scaling relation |
| In the text | |
 |
Fig. 9 Normalized skewness S3 as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). We note that black points corresponding to galaxies with M< −19.50 or M∗ ≥ 9.0 M⊙ are only plotted for the first redshift bin ([0.5, 0.7]), but most of them are not visible as they lie below the points of the other samples. The dashed line corresponds to S3 = 2. In the top panels, the dotted line is the prediction from second-order perturbation theory for the matter distribution in real space; the solid line is the prediction of S3 for galaxies with MB(z = 1.1) − 5log (h) ≤ −20.5 (to be compared to blue pentagons): it was obtained from the matter values, converted to redshift space and divided by the corresponding linear bias factor. |
| In the text | |
 |
Fig. 10 Normalized skewness S4 as a function of the B absolute luminosity (upper panels) and stellar mass (lower panels). The limits of the subsamples in absolute magnitude and stellar mass are shown in the left upper and lower panels (symbols and colours are the same as in Fig. 4). We note that black points corresponding to galaxies with M< −19.50 or M∗ ≥ 9.0 M⊙ are only plotted for the first redshift bin ([0.5, 0.7]), but most of them are not visible as they lie below the points of the other samples. The dashed line corresponds to S4 = 8. In the top panels, the dotted line is the prediction from second-order perturbation theory for the matter distribution in real space; the solid line is the prediction of S4 for galaxies with MB(z = 1.1) − 5log (h) ≤ −20.5 (to be compared to blue pentagons): it was obtained from the matter values, converted to redshift space and divided by the corresponding linear bias factor. |
| In the text | |
 |
Fig. 11 σ8g(upper panel) and S3g (lower panel) as a function of redshift. Colours represent the different absolute magnitude limits as in previous figures. The open hexagon represents the corresponding value for 2dFGRS galaxies in the absolute magnitude MbJ range [–21, –20] (Croton et al. 2004b). Black open squares are the values for VVDS galaxies brighter than MB = −21 (Marinoni et al. 2005). For better visibility, points corresponding to different redshifts are slightly shifted in magnitude. |
| In the text | |
 |
Fig. 12 σ8g (upper panel) and S3g at R = 8 h-1 Mpc (lower panel) as a function of galaxy luminosity for the three redshift bins. Red triangles: 0.5 ≤ z< 0.7; blue squares: 0.7 ≤ z< 0.9; green hexagons: 0.9 ≤ z< 1.1. For better visibility, points corresponding to different redshifts are slightly shifted in magnitude. |
| In the text | |
 |
Fig. 13 Linear bias b as a function of redshift. Top panel: MB ≤ −20.0(z = 1.1) + 5log (h); middle panel: MB ≤ −20.5(z = 1.1) + 5log (h); bottom panel: MB ≤ −21.0(z = 1.1) + 5log (h). Red hexagons: our estimates of b = σ8g/σ8m. Blue squares: estimates of Marulli et al. (2013). Magenta triangles: Di Porto et al. (2014). |
| In the text | |
 |
Fig. 14 Estimates of b = σ8g/σ8m (solid lines, filled symbols) and b′ ≡ S3m/S3g (dotted lines, open symbols); b′ = b under the assumption of linear bias. Red lines with triangles: 0.5 ≤ z< 0.7; blue lines with squares: 0.7 ≤ z< 0.9; green lines with hexagons: 0.9 ≤ z< 1.1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




