| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A106 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201525658 | |
| Published online | 08 July 2015 | |
Gas density drops inside dust cavities of transitional disks around young stars observed with ALMA⋆
1 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: nmarel@strw.leidenuniv.nl
2 Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
3 National Radio Astronomy Observatory, PO Box O, Socorro, NM 87801, USA
4 Rice University, 6100 Main Street, Houston, TX 77005, USA
Received: 13 January 2015
Accepted: 9 April 2015
Context. Transitional disks with large dust cavities are important laboratories in which to study planet formation and disk evolution. Cold gas may still be present inside these cavities, but quantying this gas is challenging. The gas content is important for constraining the origin of the dust cavity.
Aims. We use Atacama Large Millimeter/submillimeter Array (ALMA) observations of 12CO 6–5 and 690 GHz (Band 9) continuum of five well-studied transitional disks. In addition, we analyze previously published Band 7 observations of a disk in the 12CO 3–2 line and 345 GHz continuum. The observations are used to set constraints on the gas and dust surface density profiles, in particular, the drop δgas of the gas density inside the dust cavity.
Methods. The physical-chemical modeling code DALI was used to simultaneously analyze the gas and dust images. We modeled SR21, HD 135344B, LkCa15, SR24S, and RX J1615-3255 (Band 9) and J1604-2130 (Band 7). The spectral energy distribution and continuum visibility curve constrain the dust surface density. Then we used the same model to calculate the 12CO emission, which we compared with the observations through spectra and intensity cuts. The amount of gas inside the cavity was quantified by varying the δgas parameter.
Results. Model fits to the dust and gas indicate that gas is still present inside the dust cavity for all disks, but at a reduced level. The gas surface density drops inside the cavity by at least a factor 10, while the dust density drops by at least a factor 1000. Disk masses are comparable with previous estimates from the literature, cavity radii are found to be smaller than in the data obtained with the 345 GHz SubMillimeter Array.
Conclusions. The derived gas surface density profiles suggest that the cavity was cleared by one or more companions in all cases, which trapped the millimeter-sized dust at the edge of the cavity.
Key words: astrochemistry / protoplanetary disks / planet-disk interactions / ISM: molecules / stars: formation
Appendix is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Planets are formed in disks of dust and gas that surround young stars (e.g., Williams & Cieza 2011). Of particular interest are the so-called transitional disks with cleared-out cavities in the inner part of the dust disk. These disks are expected to be in the middle of active evolution and possibly planet formation. Transitional disks were originally identified through a dip in the mid-infrared part of the spectral energy distribution (SED), indicating a lack of small micron-sized dust grains close to the star. They were modeled as axisymmetric dust disks with inner cavities (e.g., Strom et al. 1989; Brown et al. 2007; Espaillat et al. 2014), which was subsequently confirmed by millimeter interferometry (e.g., Dutrey et al. 2008; Brown et al. 2009; Andrews et al. 2011; Isella et al. 2012). In recent years it has become clear that the gas and dust do not necessarily follow the same radial distribution in transition disks (e.g., Pontoppidan et al. 2008). High accretion rates (~ 10-8M⊙ yr-1, e.g., Calvet et al. 2005; Najita et al. 2007) indicate that the dust cavities are not empty, but gas is still flowing through the gap. Near-infrared observations of CO rovibrational lines indicate the presence of warm gas inside the dust cavity (Salyk et al. 2007, 2009; Pontoppidan et al. 2008; Brittain et al. 2009; Brown et al. 2012). However, these data do not trace the bulk of the molecular gas. Atacama Large Millimeter/submillimeter Array (ALMA) CO pure rotational line observations directly reveal the presence of gas inside the dust cavity (van der Marel et al. 2013; Bruderer et al. 2014; Pérez et al. 2014; Casassus et al. 2013; Zhang et al. 2014). In addition, the size distribution of the dust is possibly not uniform throughout the disk: micron- and millimeter-sized grains may have different distributions (Garufi et al. 2013; van der Marel et al. 2013) and millimeter- and centimeter-sized grains can show radial variations (Pérez et al. 2012).
Quantifying the density structure of the gas inside the dust hole is essential for distinguishing between the possible clearing mechanisms of the dust in the inner part of disk: photoevaporation (Clarke et al. 2001), grain growth (Dullemond & Dominik 2005), or clearing by (sub)stellar or planetary companions (e.g., Lin & Papaloizou 1979). Instabilities at the edges of dead zones have also been suggested to explain millimeter-dust rings and asymmetries (e.g., Regály et al. 2012). Planet candidates have been found in cavities of the transition disks T Cha (Huélamo et al. 2011), LkCa 15 (Kraus & Ireland 2012), and HD 100546 (Quanz et al. 2014), indicating planet clearing as a possible scenario.
Because detecting planets in disks is challenging, an indicator of the clearing by a (planetary) companion can be inferred from the difference in the structure of the gas compared to the dust in several of the observed disks, as shown by planet-disk interaction models in combination with dust evolution models (e.g., Pinilla et al. 2012). Companion clearing changes the gas surface density profile from that of a full disk: the density at and around the orbital radius of the planet is decreased, while at the outer edge of this gas gap the density slightly increases. As a result of the induced pressure gradients along the sides of this pressure bump, dust particles will drift toward the edge of the gap, become trapped, and grow efficiently to larger sizes. This results in a dust ring of millimeter-sized dust, or radial dust trap (Pinilla et al. 2012). The decrease in gas density due to companion clearing depends on the mass of the companion and other parameters such as the viscosity (Zhu et al. 2011; Dodson-Robinson & Salyk 2011; Pinilla et al. 2012; Mulders et al. 2013; Fung et al. 2014). Other effects that play a role in dynamic clearing are for example migration and planet accretion luminosity (e.g., Kley & Nelson 2012). Therefore, the amount of gas inside a cavity can help to constrain the mass of the companion in the planet disk-clearing and dust-trapping scenario if the viscosity is known. In comparison, the surface density of the millimeter-sized dust drops significantly deeper inside the cavity than the drop in gas surface density, due to the trapping of millimeter-sized dust (Pinilla et al. 2012). Therefore, the quantification of gas and dust inside the cavity indicates whether the trapping mechanism is due to a planet. Dust trapping at the edges of dead zones will also result in millimeter-sized dust rings, but in that scenario the gas surface density remains the same as for a full disk, apart from a minor density increase (lower than 50%) at the edge (Lyra et al. 2015).
The rovibrational lines used in previous work of transitional disks can indicate the presence of CO inside the dust cavity and the inner radius, but are unsuitable for quantifying the total gas density. The emission is very sensitive to the gas temperature, which is high but uncertain in the models in this regime. The dust opacity of the inner disk, which provides shielding, is likewise uncertain. The pure rotational CO lines provide better constraints on the gas surface density inside the cavity. The brightest molecular lines in the submillimeter regime are the rotational 12CO lines. Before ALMA, interferometric data generally did not have the sensitivity and spatial resolution to detect rotational 12CO emission inside the cavity. However, even if CO line emission is detected, this emission cannot be directly translated into densities, especially inside the dust cavity: the CO abundance is not constant throughout the disk with respect to molecular hydrogen because of the photodissociation by the UV radiation from the star and freeze-out onto dust grains in colder regions close to the midplane (van Zadelhoff et al. 2001; Aikawa et al. 2002). Furthermore, the gas temperature is decoupled from the dust temperature in the surface of the disk, particularly at the cavity wall that is directly heated and inside the dust-depleted cavity (e.g., Kamp & Dullemond 2004; Jonkheid et al. 2004; Gorti & Hollenbach 2008).
To determine the amount of gas that is present inside a dust cavity, the physical and chemical structure of the gas needs to be modeled. For this we make use of the physical-chemical modeling tool DALI (Bruderer et al. 2012; Bruderer 2013), which solves the heating-cooling balance of the gas and chemistry simultaneously to determine the gas temperature, molecular abundances, and molecular excitation for a given density structure. As a result of the disk Keplerian rotation and gas thermal and turbulent motions, the 12CO emission along any line of sight that intercepts the disk is a spectral line comprising an optically thick central part and potentially optically thin wings. With spatially resolved CO observations it is possible to infer emission from different lines of sight, which was not possible with previous single-dish spectral analysis. Bruderer et al. (2014) demonstrated for 12CO 6–5 lines in Oph IRS 48 that the emission in the optically thin wings can be used to constrain the gas density. In this case, the observations are found to be consistent with a physical disk model with two gas density drops inside the millimeter dust cavity. However, Oph IRS 48 has a very low disk mass (constrained by C17O observations), which means that even the 12CO line is close to optically thin. For more massive disks, the bulk of the 12CO emission may remain optically thick even if the gas density inside the dust-depleted cavities drops by one or two orders of magnitude. In that case, the 12CO emission originates from deeper in the disk (closer to the disk midplane) where the gas is colder than in the surface, causing a drop in the optically thick line intensity (Bruderer 2013).
Stellar properties.
To date, a total of nine transitional disks with large resolved millimeter dust cavities has been observed in ALMA Cycle 0 in dust continuum and 12CO. In this paper, we present observations of the disks SR21, HD 135344B, RX J1615-3255, LkCa15, and SR24S through 12CO 6–5 observations (Pérez et al. 2014) and J1604-2130 through 12CO 3–2 observations (Carpenter et al. 2014; Zhang et al. 2014). With DALI we determine the density structure of the gas and dust that is consistent with the SED, dust continuum interferometry, and the 12CO observations. If available, information on the hot gas and dust from the literature is included. The goals of this study are to determine the amount of the gas and dust inside the dust hole and the implications for potentially embedded planets, assuming that the millimeter dust rings are indeed dust traps. The derived physical models in this study can be used as a starting point for future ALMA observations of CO isotopologs, whose emission is optically thin and which therefore directly trace the density structure. Our analysis of the gas density structure is similar to that used for Oph IRS 48 through 12CO 6–5 and C17O 6–5 line observations as presented in Bruderer et al. (2014). The analysis of HD 142527, which has been observed in 12CO, 13CO and C18O 6–5, 3–2 and 2–1, is left for future studies. Perez et al. (2015) have modeled the J = 2–1 CO isotopologs and determined the gas mass remaining inside the cavity of that disk. Other transition disks that have been observed in ALMA Cycle 0 are HD 100546 (Walsh et al. 2014), TW Hya (Rosenfeld et al. 2014), Sz 91 (Canovas et al. 2015), and MWC 758 (not yet published), but since their dust holes remain unresolved in the current data, they are not considered in this study.
The paper is structured as follows. In Sect. 2.1 we describe the details of the ALMA observations. In Sect. 2.2 we present moment maps of the 12CO observations and the derived stellar position and orientation. The modeling approach and constraints from the literature are presented in Sect. 3. Section 4 presents the modeling results. Section 5 discusses the implications for embedded planets in the disk.
2. Data
Properties of the ALMA observations.
The continuum and 12CO line observations were obtained during ALMA Cycle 0 between June 2012 and January 2013, with baselines ranging from 20 to 500 m, probing scales from 0.2 to 4 arcsec. The sources and their properties are summarized in Table 2.
2.1. Observational details
Five transitional disks were observed in ALMA program 2011.0.00724.S (PI Pérez), two of these disks were presented in Pérez et al. (2014). The disks were observed in Band 9 (690 GHz, 440 μm), with four adjacent spectral windows of 1875 MHz, each with 3840 channels of 488 kHz (0.2 km s-1) width, for a total continuum bandwidth of 7.5 GHz. One spectral window was centered on the 12CO 6–5 line (691.47308 GHz). The bandpass was calibrated using 3C279, Titan was used as flux calibrator, and the phase and amplitude were calibrated using J1427-4206 (HD 135344B), J1625-2527 (SR21, SR24S and RX J1615-3255) and J0510+180 (LkCa15). Each target was observed for ~25 min on source. Given the high signal-to-noise ratio (S/N) of the continuum, amplitude and phase self-calibration were performed on all data and applied afterward to the 12CO data as well.
Disk J1604-2130 was observed as part of ALMA program 2011.0.00526.S (PI Carpenter) in Band 7 (345 GHz, 880 μm), with one spectral window centered on the 12CO 3–2 line (345.79599 GHz) with 488 kHz (0.42 km s-1) channel width. The data and observational details are presented in Zhang et al. (2014). Because of the longer wavelength, the beam size of these data is considerably larger than that of the Band 9 data.
The data were imaged using CASA v4.2, adopting the Briggs weighting scheme with a robust parameter of 0.5. The resulting rms and beam sizes of the line data are given in Table 2. During the cleaning process of the SR24S data, it became clear that there is extended emission that could not be recovered by the shortest baselines of these ALMA observations (50 kλ, or 4” scales).
2.2. Continuum and line maps
 |
Fig. 1 ALMA observations of the continuum and 12CO line. The first five disks show the 690 GHz (440 μm) continuum and the 12CO J = 6–5 line, the sixth is the 345 GHz (880 μm) continuum and 12CO J = 3–2 line. Left: continuum image. The stellar position is indicated by a white star, the white bar in the upper right corner indicates the 30 AU scale, and the yellow contour gives the 3σ detection limit. The colorbar units are given in Jy beam-1. Center: zero-moment 12CO map. The colorbar units are given in Jy beam-1 km s-1. Right: 12CO spectrum integrated over the entire disk. The dashed line indicates the zero flux level, and the gray areas indicate the parts of the spectrum affected by foreground absorption (seen in SR21 and SR24S). The beam is indicated in each map by a white ellipse in the lower left corner. |
Figure 1 shows the ALMA continuum image, zero-moment 12CO map, and 12CO spectrum of each of our targets. The spectrum was extracted from the region of the zero-moment map size. The contours indicate the 3σ detection limit in each image. The continuum images reveal ring-like structures for all targets except RX J1615-3255, even though its SED and the 345 GHz visibility curve show signs of a dust cavity (Andrews et al. 2011). The rings clearly show azimuthal asymmetries, which have been confirmed to be real intensity asymmetries for SR21 and HD 135344B (Pérez et al. 2014). For SR24S and LkCa15 the asymmetries are most likely caused by the geometry of the disk (i ~ 45°) and the dust continuum becoming optically thick at this wavelength (0.45 mm). The S/N on the continuum varies between ~65 and 400, which is much higher than previous SubMillimeter Array (SMA) observations.
The zero-moment 12CO maps reveal gas inside the dust hole for all targets, demonstrating different distributions of gas and dust. This does not mean that there can be no decrease in the gas density compared to a full disk density profile, because the 12CO emission is expected to be optically thick. The maps of HD 135344B and J1604-2130 show a decrement of emission around the stellar position, directly indicating a strong decrease of gas density. The size of this gas hole is much smaller than the dust hole and similar to the beam size. For LkCa15 there appears to be a slight offset between the continuum and integrated CO emission peaks; the maps are currently aligned to the same central position. This may be related to the proposed eccentric inner disk (Thalmann et al. 2014), which casts a more pronounced shadow on one side of the disk. However, considering the limited significance of this shift, modeling this asymmetry is beyond the scope of this paper.
All 12CO spectra are consistent with a rotating disk at an inclination >15°, revealing a double-peaked velocity profile, except for J1604-2130, which is known to be viewed almost face-on (Mathews et al. 2012; Zhang et al. 2014). The spectra of SR21 and SR24S are probably affected by foreground absorption, which is commonly observed in the Ophiuchus star-forming region (e.g. van Kempen et al. 2009), although no single-dish spectra of these targets are available to confirm this. The SR21 spectrum is somewhat asymmetric: the red side is narrower than the blue side. Furthermore, the data of SR24S are affected by extended emission outside the field of view of the ALMA observations. This may be related to the suggested circumbinary disk around SR24N, which is located 5′′ north, and SR24S (Mayama et al. 2010), but this cannot be confirmed with the available data. The apparent double peak in the spectrum is caused by foreground absorption: the bulk of this emission does not originate from the disk. Therefore, we did not aim to model the gas surface density of this target and only modeled the dust continuum structure.
The 12CO channel maps (binned to 1 km s-1) and first moment maps are presented in Fig. A.1. We derive the stellar position, inclination, position angle, and source velocity from the channel maps and first-moment map and overlay the corresponding Keplerian velocity pattern in white contours. The derived parameters are consistent within 5° with values from the literature for resolved gas and dust, where available (e.g., Pontoppidan et al. 2008; Andrews et al. 2011). For the stellar mass, we used values from the literature (see Table 1). The derived parameters are given in Table 2. The peak S/N of the channel maps is at least 10.
The channel maps confirm the presence of gas inside the dust cavities. The velocity range that falls within the derived dust cavity radius rcav is given in Table A.1. The velocity is calculated using 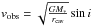 with G the gravitational constant. The channel maps also reveal that the detected CO emission is more extended in the outer disk than the dust continuum for all sources except SR21, although the S/N and image quality are low in the outer parts of the disks. The emission is probably not affected by spatial filtering, as shown in the visibilities (Fig. 4): the emission is well covered down to ~40kλ, corresponding to 5′′ (>600 AU) diameter scales. Whether or not the difference in extent is significant needs to be quantified with a physical model, because the dust emission may simply be too weak in the outer disk to be detected, while 12CO remains detectable because it is optically thick. The redshifted side of both SR21 and HD 135344B is somewhat weaker than the blueshifted side, as also seen in the spectrum (Fig. 1). The location of the decrease is cospatial with the peak of the asymmetry in the continuum map. This is possibly related to a higher continuum optical depth or lower temperature at the location of the asymmetry, as was also seen for H2CO emission of Oph IRS 48 (van der Marel et al. 2014).
with G the gravitational constant. The channel maps also reveal that the detected CO emission is more extended in the outer disk than the dust continuum for all sources except SR21, although the S/N and image quality are low in the outer parts of the disks. The emission is probably not affected by spatial filtering, as shown in the visibilities (Fig. 4): the emission is well covered down to ~40kλ, corresponding to 5′′ (>600 AU) diameter scales. Whether or not the difference in extent is significant needs to be quantified with a physical model, because the dust emission may simply be too weak in the outer disk to be detected, while 12CO remains detectable because it is optically thick. The redshifted side of both SR21 and HD 135344B is somewhat weaker than the blueshifted side, as also seen in the spectrum (Fig. 1). The location of the decrease is cospatial with the peak of the asymmetry in the continuum map. This is possibly related to a higher continuum optical depth or lower temperature at the location of the asymmetry, as was also seen for H2CO emission of Oph IRS 48 (van der Marel et al. 2014).
3. Method
3.1. Modeling
Our aim is to constrain a physical disk model that describes both the dust and gas structure of each disk. The main goal is to determine the drop in gas surface density δgas inside the dust hole, within the constraints of a model that fits the gas and dust in the outer disk (Fig. 2). Therefore the other disk parameters need to be constrained first, as they have a significant influence on the strength of the CO emission inside the cavity: the disk mass relates to the optical depth of the 12CO lines; the vertical structure affects the temperature by shadowing and the amount of exposed disk surface atmosphere by stellar light; the amount of dust inside the cavity, including the inner disk, shields the CO from photodissociation but also provides cooling; and the location of the cavity wall determines the temperature of the wall, where the bulk of the 12CO emission is expected to originate (see Sect. 3.3.3 for details). To this end, information was combined from the SED, the ALMA continuum and integrated CO visibilities, and the CO disk-integrated spectrum and zero-moment map.
 |
Fig. 2 Generic surface density profile for the gas and dust. |
Although the model is not expected to be unique, it sets a structure for the disk that can be tested with future ALMA observations of CO isotopologs. The main goal of this study is to compare the strongest possible decrease of the gas surface density with the minimum required decrease of the dust density inside the cavity. If the drop in gas density is less deep than for the millimeter-sized dust, this is direct evidence for the trapping scenario.
The axisymmetric physical-chemical model DALI was used for the analysis (Bruderer 2013, details next section), thus any azimuthal asymmetries were ignored. The most prominent asymmetries are seen in the millimeter-sized dust continuum in SR21 and HD 135344B (Pérez et al. 2014), but the influence of the millimeter dust on the gas temperature and UV shielding is negligible, therefore axisymmetry can be safely assumed. The small dust grains are the main heating agents of the gas. In the visibilities we therefore used the amplitude (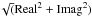 ), because the asymmetries and thus the variations in the imaginary part are small. The visibilities constrain the radial structure of the emission. Because of the limited u,v-coverage in these Cycle 0 data, the visibilities provide better constraints on the structure than the images alone, especially on the cavity radius through the location of the first null.
), because the asymmetries and thus the variations in the imaginary part are small. The visibilities constrain the radial structure of the emission. Because of the limited u,v-coverage in these Cycle 0 data, the visibilities provide better constraints on the structure than the images alone, especially on the cavity radius through the location of the first null.
3.2. DALI
The determination of the gas disk from the 12CO emission requires a thermo-chemical disk model, in which the heating-cooling balance of the gas and chemistry are solved simultaneously to determine the gas temperature and molecular abundances at each position in the disk. Moreover, even though the densities in disks are high, the excitation of the rotational levels may not be in local thermodynamic equilibrium (LTE), and the gas and dust temperature are decoupled, especially inside and at the cavity edge. The DALI model (Bruderer et al. 2012; Bruderer 2013) uses a combination of a stellar radiation field with a disk density distribution as input. DALI solves for the dust temperatures through continuum radiative transfer from UV to millimeter wavelengths and calculates the chemical abundances, the molecular excitation, and the thermal balance of the gas. It was developed for the analysis of gas emission structures in protoplanetary disks including transitional disks with varying gas-to-dust ratios (GDR; Bruderer 2013).
DALI uses a reaction network described in detail in Bruderer et al. (2012) and Bruderer (2013). It is based on a subset of the UMIST 2006 gas-phase network (Woodall et al. 2007). About 110 species and 1500 reactions are included. In addition to the gas-phase reactions, some basic grain-surface reactions (freeze-out, thermal and nonthermal sublimation and hydrogenation such as g:O → g:OH → g:H2O and H2/CH+ formation on polycyclic aromatic hydrocarbons (PAHs; Jonkheid et al. 2006) are included. The g:X notation refers to atoms and molecules on the grain surface. The photodissociation rates are obtained from the wavelength-dependent cross-sections by van Dishoeck et al. (2006). The adopted cosmic-ray ionization rate is ζH2 = 5 × 10-17 s-1. X-ray ionization (X-ray luminosity of 1030 erg s-1) and the effect of vibrationally exited H2 are also included in the network. Elemental abundances are taken from Jonkheid et al. (2006).
3.3. Approach
3.3.1. Physical model
As a starting point for our models we adopted the physical structure suggested by Andrews et al. (2011), as implemented by Bruderer (2013) and applied for a similar analysis of Oph IRS 48 (Bruderer et al. 2014). The gas surface density was assumed to be an exponential power-law following the time-dependent viscosity disk model ν ~ rγ (Lynden-Bell & Pringle 1974; Hartmann et al. 1998) 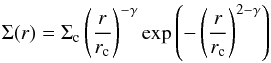 (1)and is defined by surface density Σc at critical radius rc. The power-law index γ was taken as 1, in line with the results for normal disks with continuous dust distributions and other transition disk studies (Andrews et al. 2011). The previous gas study of 12CO observations in IRS 48 (Bruderer et al. 2014) demonstrated that the slope of the surface density profile could not be determined with their data; the data in this new study have an even lower S/N, therefore we did not vary γ. The outer radius is set to rout. The dust density was taken to be Σ(r)/GDR, with the GDR set to 100 initially. The inner dust disk was defined by the Σ(r) profile, starting from the sublimation radius rsub = 0.07(L∗/L⊙)1/2 (assuming Tsub = 1500 K) out to rgap = 1 AU, scaled down by a factor δdust to fit the near-infrared part of the SED. The size of the inner disk is arbitrary as it does not have a significant effect on the near infrared excess. Between rgap and rcav, the cavity radius, the dust density was scaled down by a factor δdustcav (the drop in dust density inside the cavity), while the gas density Σ(r) was scaled down by a factor δgas. Figure 2 shows the generic density structure, and Table 3 explains each parameter.
(1)and is defined by surface density Σc at critical radius rc. The power-law index γ was taken as 1, in line with the results for normal disks with continuous dust distributions and other transition disk studies (Andrews et al. 2011). The previous gas study of 12CO observations in IRS 48 (Bruderer et al. 2014) demonstrated that the slope of the surface density profile could not be determined with their data; the data in this new study have an even lower S/N, therefore we did not vary γ. The outer radius is set to rout. The dust density was taken to be Σ(r)/GDR, with the GDR set to 100 initially. The inner dust disk was defined by the Σ(r) profile, starting from the sublimation radius rsub = 0.07(L∗/L⊙)1/2 (assuming Tsub = 1500 K) out to rgap = 1 AU, scaled down by a factor δdust to fit the near-infrared part of the SED. The size of the inner disk is arbitrary as it does not have a significant effect on the near infrared excess. Between rgap and rcav, the cavity radius, the dust density was scaled down by a factor δdustcav (the drop in dust density inside the cavity), while the gas density Σ(r) was scaled down by a factor δgas. Figure 2 shows the generic density structure, and Table 3 explains each parameter.
Parameter-fitting procedure.
For the stellar photosphere we generated a blackbody with the luminosity and temperature as in Table 1. Additional UV excess from accretion was added through a Tacc = 10 000 K blackbody for the Lacc corresponding to the measured accretion rate (Table 1), using 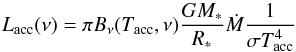 (2)with Bν(Tacc,ν) the Planck blackbody function, G the gravitational constant, M∗ and R∗ the mass and radius of the star, Ṁ the mass accretion rate, and σ the Stefan-Boltzmann constant. For SR21, no accretion luminosity was added since only an upper limit for the accretion is measured. Note that observed values of Ṁ are uncertain up to an order of magnitude and are often variable with time (e.g., Salyk et al. 2013). The interstellar radiation field incident on the disk surface was also included, but it does not affect the results presented here.
(2)with Bν(Tacc,ν) the Planck blackbody function, G the gravitational constant, M∗ and R∗ the mass and radius of the star, Ṁ the mass accretion rate, and σ the Stefan-Boltzmann constant. For SR21, no accretion luminosity was added since only an upper limit for the accretion is measured. Note that observed values of Ṁ are uncertain up to an order of magnitude and are often variable with time (e.g., Salyk et al. 2013). The interstellar radiation field incident on the disk surface was also included, but it does not affect the results presented here.
The vertical structure follows a Gaussian distribution, defined by a scale height angle 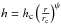 . A disk in hydrostatic equilibrium will have ψ = 0.25, while a flat (h/r = const.) disk will have ψ = 0. The near- and far-infrared excess in the SED relate directly to the resulting scale height h(r) at rsub and rcav, respectively. Our vertical structure is a simplification and does not account for hydrostatic equilibrium of gas or dust temperature. One of the main effects of the hydrostatic equilibrium is a puffed-up inner rim. Previous studies (e.g., Andrews et al. 2011) often used a parametrized puffed-up inner rim to fit the near- and far-infrared excess by adding a narrow scale height peak, but during our fitting procedure it became clear that a parametrized optically thick inner disk rim blocks a large amount of the UV irradiation and lowers the gas temperature significantly, as was also demonstrated in Woitke et al. (2009).
. A disk in hydrostatic equilibrium will have ψ = 0.25, while a flat (h/r = const.) disk will have ψ = 0. The near- and far-infrared excess in the SED relate directly to the resulting scale height h(r) at rsub and rcav, respectively. Our vertical structure is a simplification and does not account for hydrostatic equilibrium of gas or dust temperature. One of the main effects of the hydrostatic equilibrium is a puffed-up inner rim. Previous studies (e.g., Andrews et al. 2011) often used a parametrized puffed-up inner rim to fit the near- and far-infrared excess by adding a narrow scale height peak, but during our fitting procedure it became clear that a parametrized optically thick inner disk rim blocks a large amount of the UV irradiation and lowers the gas temperature significantly, as was also demonstrated in Woitke et al. (2009).
For the dust opacities we used the same approach as Andrews et al. (2011): a small (0.005–1 μm) and large (0.005 μm–1 mm) population of dust with a mass fraction fls in large grains. Settling was parametrized by defining the scale-height of the large grains as χh, that is, h is reduced by a factor χ (see Andrews et al. 2011 for definitions). We initially fixed fls and χ to 0.85 and 0.2, respectively, as adopted by Andrews et al. (2011). We included PAHs since many of our observed sources show PAH features (Brown et al. 2007; Geers et al. 2006), but at a low abundance of 0.1% of the ISM abundance. The turbulent width was set to 0.2 km s-1. Stellar parameters taken from the literature are given in Table 1.
3.3.2. Model-fitting approach
In the fitting procedure, we used an approach of manual fitting by eye and varied the parameters in a logical order so that they converged to a model that fits the data, similar to the approach in Bruderer et al. (2014). We did not use a χ2 or Markov chain Monte Carlo (MCMC) method because the computational time of the models is too long and the number of parameters too large. Although this approach reduces computational time, it means that it is not possible to derive uncertainties of model parameters, verify the uniqueness of the fit, and estimate the correlation between parameters. The fitting parameters are defined in Table 3.
-
1.
Fit Σc and δdust roughly through the SED and continuum image, using the rcav value from Andrews et al. (2011).
-
2.
Adjust rsub, rgap and δdust if necessary for the NIR excess.
-
3.
Vary the scale-height angle to fit the NIR and/or FIR excess in the SED by changing hc and ψ.
-
4.
Vary rcav and rc to match the null and slope of the submillimeter-dust visibility curve.
-
5.
If the MIR/FIR excess is too high, adjust the size distribution by increasing fls and χ.
-
6.
Find the highest possible value for δdustcav (drop of dust density inside the cavity) that is still consistent with the dust continuum.
-
7.
Check the fit to the CO intensity map, spectrum, and visibilities assuming the GDR to be 100 in the outer disk. If necessary, truncate the outer radius to fit the spectrum.
-
8.
Explore small variations in the vertical parameters to change the temperature structure; this is required to fit the optically thick 12CO emission.
-
9.
Finally, keep all other parameters constant while varying δgas to find the lowest possible value for δgas that is still consistent with the CO data.
We stress that this approach does not result in a unique model because of the degeneracies in parameter choices and because 12CO is optically thick. However, this approach seemed reasonable considering the different data sets taken into account, of which ALMA is the crucial one. Carmona et al. (2014) also demonstrated a modeling procedure that combines different datasets. The submillimeter continuum sets firm constraints on the total flux, the cavity size (the null in the visibility) and the dust extent (through rc) of the disk, as also shown in Andrews et al. (2011). The mid-infrared part of the SED and the 12CO are both sensitive to the combination of temperature and density structure of the disk, not only to the density, as both of these emission regimes are mostly optically thick. The temperature is controlled by the adopted vertical structure in the disk, as this determines the direct irradiation by the star, especially at the cavity wall. Therefore, several iterations were required to find a compromise for a decent fit of both the SED and 12CO.
 |
Fig. 3 Modeling results and observations of the dust surface density, comparing δdustcav ranging between 10-2 and 10-8 as indicated in the right panel. The observations are plotted in black. Left: spectral energy distribution. Middle left: amplitude of the 690 GHz continuum visibility for the deprojected baselines. The null line is indicated with a dashed line. Middle right: normalized intensity cuts through the major (bottom) and minor (top) axis of the 690 GHz continuum image. The model images are convolved with the same beam as the ALMA observations. Right: dust surface density profile. Indicated are the δdust, the drop in density to fit the inner disk through the near-infrared emission, and δdustcav, the minimum drop in dust density inside the cavity to fit the observations. In SR21 (top panel) the region inside 7 AU is assumed to be empty because of additional constraints (see main text). In all other disks δdustcav is found to be at most 10-4. All other disk parameters are as listed in Table 4. |
 |
Fig. 4 Modeling results and observations of the 12CO emission for the best-fitting physical model derived from the dust (see Fig. 3 and Table 4), with δgas = 1 (no drop in gas surface density inside the cavity). The observations are plotted in black, the models in purple. Left: 12CO spectrum integrated over the entire disk. Center: intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero moment map. The noise level is indicated by the gray zone. The model images are convolved with the same beam as the ALMA observations. Right: amplitude of the integrated 12CO visibility for the deprojected baselines. The null line is indicated with a dashed line, and error bars indicate the noise. |
3.3.3. CO emission inside the cavity
As the CO emission inside the cavity only partly depends on density, the derived δgas parameter is merely a constraint within the derived physical model. As discussed above, there are several effects that influence the strength of the emission: most important are gas temperature and CO abundance, which are very sensitive to the small dust grains inside the cavity. Different effects can play a role, as discussed extensively in Bruderer (2013).
-
Although the bulk of the 12CO emission is optically thick, the drop in gas surface density can still be constrained to within an order of magnitude with spatially resolved observations. Optically thick emission will slightly drop with decreasing δgas because the τ = 1 surface moves deeper into the disk, so the emission traces colder regions in the disk, as demonstrated in Sect. 5.2 and Figs. 9, 10 in Bruderer (2013).
-
An inner disk will cast a shadow on the gas inside the cavity, depending on the amount of dust and scale height. This will lower the gas temperature inside the cavity. On the other hand, the inner disk shields the stellar UV radiation that would photodissociate CO, so the CO abundance is increased. The structure of the inner disk is only poorly constrained from the available data, while it may have significant effects on the heating of the outer disk.
-
The presence of small dust grains and PAHs inside the cavity shields stellar UV radiation and decreases the photodissociation, thus increasing the CO abundance. The dust contributes to the heating and cooling of the gas, depending on the density. For high gas density, the gas temperature decreases when dust is added as a result of cooling by gas-grain collisions. For low gas density, the gas temperature decouples and becomes higher than the dust temperature as a result of photoelectric heating on grains and PAHs.
-
The increase of the gas temperature (increase of small dust grains) or an increase of the UV radiation (decrease of small dust grains) will also lead to an increase of vibrationally pumped H2, again increasing the formation of CO.
-
The presence of small dust grains and PAHs increases the formation of CH+ on the grain surfaces, which leads to increased formation of CO.
The consequences for the CO emission of adding small dust, either inside the entire cavity or just in the inner disk, strongly depends on the details of the structure of the disk. This is the reason why the SED and submillimeter visibilities are also included in the modeling procedure, and why a full physical-chemical model is required to analyze the CO emission.
 |
Fig. 5 Modeling results and observations of the 12CO emission for the best-fitting physical model for gas and dust (Fig. 4) comparing δgas (gas density drop inside the dust cavity). δgas is varied as 100, 10-1, ..., 10-4 as blue, light blue, green, yellow, and red in the left and middle plots, while the observational data are plotted in black. Left: the 12CO spectrum integrated over the disk area. Middle: the intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero-moment map for different δgas. The noise level is indicated by the gray area. The model images are convolved with the same beam as the ALMA observations. Right: the best-fitting result for possible values of δgas and δdustcav in red and blue. |
4. Results
Our best-fitting results for the dust and gas density structure are presented in Figs. 3 to 5 and Table 4. In Fig. 3 the output of the physical model is compared to the SED, the 690 GHz continuum visibility curve, and the normalized major/minor axis cuts of the 690 GHz continuum image (left panel of Fig. 1). Data points of the SED were dereddened using the extinction law by Weingartner & Draine (2001) with RV = 5.5. The SED constrains the vertical structure of the disk, while the visibility curve determines the cavity size and extent through the location of the null. The image cuts show the direct comparison of the image with model. Within each figure, the δdustcav value (drop of dust density inside the cavity) is varied with values between 10-2 and 10-6, to constrain the minimum drop in dust density inside the cavity. In the rightmost panel we present the density structure of the model.
Results of the fitting procedure for the gas density profile of each transition disk.
Reasonable fits are found for the continuum visibilities and SED within the constraints of our physical model for all targets. The inferred disk masses are similar to previous findings within a factor of a few, for instance, to those of Andrews et al. (2011). The models with δdustcav = 10-2 overproduce the emission inside the cavity in all cases, as seen both in the mid-infrared part of the SED and in the dust continuum image. Therefore, δdustcav is constrained to be at most a factor of 10-4, and even as low as 10-6 for J1604-2130. In the modeling of the gas, we set δdustcav to zero, except for SR21, where δdustcav is constrained by the visibilities. For the gas modeling of HD 135344B and J1604-2130, we included some additional dust between rcav and 30 AU as shown in the dust density profile in Fig. 5.
To analyze the gas density, we compared the result of the adopted disk model to the 12CO spectrum, the intensity cuts through the zero moment map, and the 12CO visibility curve in Fig. 4. SR24S was not included in this part of the analysis because the CO emission is too heavily confused by large-scale emission (Fig. A.1). The models were calculated assuming δgas = 1, that is, no drop in the gas surface density inside the dust cavity, except for J1604-2130, which shows a resolved drop in the CO emission inside 30 AU, which is adopted already. Because the CO visibilities do not show a clear null and the disks are not fully symmetric in the gas, the visibility curve was not used to fit our data exactly: it is merely included here to show that the emission from the moment map is well retrieved from the visibilities.
The models reproduce the CO emission well in the outer part of the disk (r>rcav). There was no need to change the GDR of 100 in any of the cases in the outer disk. This conclusion needs to be confirmed by optically thin CO isotopolog observations. The images and visibilities show that the outer extent of the dust and CO emission can indeed be fit with the same physical model, although observations with a better S/N are required to confirm this.
For SR21, HD 135344B, and LkCa15, the initial model overproduces the central part of the intensity cut by a factor 1.5–2, suggesting a decrease of gas surface density inside the dust cavity. In Fig. 5 we present the same physical model with δgas varying from 100 to 10-4 in steps of 10 to compare with the observations. The emission drops by less than a factor of 2 in each of these steps, which is due to the optical depth of the 12CO line, but within the noise level of the moment map this is sufficient to constrain δgas to within an order of magnitude because of the different gas temperatures at the τ = 1 surface in the disk. This result is different from Oph IRS 48, where the 12CO line wings were found to be optically thin (Bruderer et al. 2014). Only the emission in J1604-2130 inside 30 AU radius becomes optically thin. The range of δgas is indicated in the right panel of Fig. 5 and in Table 4.
In the following section we discuss the properties of each disk in more detail.
4.1. Results of individual targets
SR21
It is possible to fit the SED and amplitudes of the continuum visibilities simultaneously at least up to baselines of 600 kλ. The small inconsistency at longer baselines is possibly related to the dust asymmetry (Pérez et al. 2014), which is not taken into account. To fit the SED, we used for this disk an alternative dust opacity table for the small grains, without small silicates, because the normal dust table results in a strong silicate feature that is not seen in the data. We find a cavity size of at most 25 AU, which is significantly lower than the value of 36 AU previously found in the SMA data at 345 GHz (Brown et al. 2009; Andrews et al. 2011). It remains unclear whether this is due to differences in the modeling approach or a physical effect, since the 345 GHz emission traces somewhat larger dust grains (see also Sect. 5.2). Similar to Andrews et al. (2011), we find that this disk has a remarkably small radius: rc is only 15 AU, resulting in no detectable emission outside a radius of 75 AU.
Both hot CO line emission (Pontoppidan et al. 2008) and mid-infrared interferometry (Benisty, priv. comm.) suggest a hot ring at 7 AU and no material inside. Scattered light also shows that there is small dust down to <14 AU (Follette et al. 2013). Therefore, we assume that there is no gas between the star and 7 AU for SR21 (but still an inner dust disk due to the NIR excess), and dust with only a small grain population between 7 AU and rcav. The dust between 7 AU and the dust hole cavity of 25 AU is partly constrained by the visibility curve: without the additional dust, the second null is much farther out, although this may also be due to the asymmetry. In constraining δdustcav, this drop is assumed to start from 7 AU rather than from rgap (taken as 1 AU).
The central 12CO emission in the intensity cut is overproduced by about a factor of 2 in the initial model, especially inside the cavity region (Fig. 4). Only a deep drop in δgas of 2 orders of magnitude can match the peak of the zero-moment map, although the intensity cut is somewhat wider than the data. A minor dip of the 7 AU gap is seen in the intensity cut of the model-integrated 12CO emission: the gap is marginally resolved, but the dip is within the error bars of the observations, which means that it cannot be confirmed with these data.
HD 135344B
The continuum visibility is reasonably well fitted with a model with a cavity of 40 AU, slightly smaller than the 45 AU cavity found in previous work with 345 GHz SMA data (Brown et al. 2009; Andrews et al. 2011; Carmona et al. 2014). An increase of the large-grain fraction and large-grain scale height (χ = 0.8) is needed to fit the peak of the far-infrared part of the SED.
We find a smaller critical radius of only 25 AU and thus smaller extent of the disk than was reported by Andrews et al. (2011, who found rc = 55 AU), but the ALMA data quality is much better than the quality of the SMA data. Another main difference in the modeling procedure is the different vertical structure of this disk in our parametrization (no puffed-up inner rims), although this is not expected to change the emission in the outer disk. Scattered-light images show that there is small dust inside the millimeter-dust cavity down to 30 AU for HD 135344B (millimeter-dust cavity is ~46 AU; Garufi et al. 2013). Therefore we assume a finite drop in dust density between rcav and 30 AU. The scattered-light images, SED, and visibilities do not constrain the amount of dust: we chose a drop of 10-3. Garufi et al. (2013) and Muto et al. (2012) show signatures of spiral arms in the scattered-light images. The ALMA data resolution is too low to detect these arms if they were visible at millimeter wavelengths.
The initial model for this disk overproduces the CO emission inside the cavity. A δgas of 10-1 − 10-2 is sufficient to fit the peak in the moment map. A decrease in gas density inside the cavity was previously inferred from SMA CO line observations (Lyo et al. 2011). Carmona et al. (2014) required a surface density that increases with radius inside the cavity to fit the rovibrational CO lines in this disk. Fitting these lines is beyond the scope of this paper, but the drop in surface density may be similar to this increasing density profile, as discussed in Sect. 5.1. Motivated by the dust structure, we also tried to fit a gas model with a cavity size of 30 AU instead of 40 AU. There is no significant difference in the outcome for a gas cavity radius of 30 AU or 40 AU, however. As Fig. 6 shows, δgas = 10-1 − 10-2 also fits best for a gap of 30 AU.
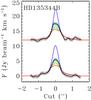 |
Fig. 6 Modeling results and observations of the 12CO emission for the best-fitting physical model for HD 135344B for a cavity of 30 AU instead of 40 AU for gas and dust (Fig. 4) for different values of δgas (gas density drop inside the dust cavity). δgas is varied as 100, 10-1, ..., 10-4 as blue, light blue, green, yellow, and red. The observations are plotted in black. The panel shows the intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero-moment map. |
LkCa15
LkCa15 is a well-studied transition disk with a large cavity of 50 AU (Isella et al. 2012). We modeled LkCa15 with a rather flat but massive disk structure. Our derived disk dust mass is three times higher than typically found in the literature, and the 690 GHz continuum is indeed optically thick, which explains the apparent asymmetry in the continuum image: the northwest side of the disk is brighter than the southeast side because of the geometry.
Just like HD 135344B, the initial model for this disk overproduces the CO emission inside the cavity, indicating a δgas of at least 10-1.
RX J1615-3255
RX J1615-3255 does not reveal a cavity in the continuum image, and the visibilities only show a hint of a null at the longer baselines (>500 kλ). Our best-fitting model has a cavity of 20 AU, somewhat smaller than the best-fit cavity in Andrews et al. (2011) of 30 AU. A model without cavity cannot fit the SED, which clearly indicates a deficit of dust close to the star. This indicates that the Band 9 continuum might be optically thick. An interesting aspect of this target is the outer part of the disk: a narrow radial dip is seen in the image at 0.6′′ from the center (corresponding to 110 AU at the distance of this disk). Figure 7 shows a zoomed-in image of the intensity cut from Fig. 3. This hints at the presence of a dust gap in the outer part of the disk between 110 and 130 AU, or an additional outer ring of dust, as seen in recent ALMA data of HD 100546 (Walsh et al. 2014).
The model with δgas = 1 does not reproduce the high velocity emission seen in the CO spectrum, but the S/N is low, which means that the significance of this remains debatable. The intensity cuts show that the gas density inside the dust hole can be up to four orders of magnitude lower before the CO becomes optically thin.
SR24S
SR24S is an inclined disk with a barely resolved cavity of about 30 AU. The long-wavelength part of the Spitzer IRS spectrum and the MIPS-24 flux are known to be confused by emission from its nearby companion SR24N (see, e.g., Andrews et al. 2011), thus these points were only used as upper limits in our fit. The visibility curve becomes inconsistent with our model for baselines >350 kλ, hinting at substructure inside the cavity. As we do not have any additional information on dust inside the cavity of this disk, we did not explore this further.
J1604
J1604-2130 is a transition disk at 345 GHz that was frequently studied with both SMA (Mathews et al. 2012) and ALMA (Zhang et al. 2014). Mathews and Zhang and collaborators both provided physical models for the dust and the gas. Zhang et al. (2014) used the same ALMA dataset as discussed here, but did not use a full physical-chemical model for the gas analysis. In neither of the two studies the near infrared excess was taken into account. The problem is the apparent variability: whereas the Spitzer IRAC photometry (taken in 2006 and used by Mathews) shows no near-infrared excess, the Spitzer IRS and WISE photometry (taken in 2007 and 2012, respectively) do reveal the excess. Zhang et al. noted this discrepancy and stated that the near-infrared excess can be fit with an optically thick inner disk ring, but did not include this in their model. Since the inner disk has a strong influence on the CO emission inside the cavity (and on the shadowing of the dust cavity wall), we chose to include the more recent photometry with near-infrared excess in our SED and fit the models accordingly.
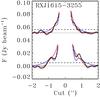 |
Fig. 7 Modeling results and observations of the 690 GHz continuum of RX J1615-3255. The panel shows the intensity cuts through the major (bottom) and minor (top) axis of the continuum image, zoomed in on the lowest flux levels (<20σ). The observations are plotted in black with the 1σ errors in gray. In red and blue we present the models with and without a dust gap between 110 and 130 AU. The dotted and dashed lines indicate the zero flux and 3σ limits, respectively. |
Mathews et al. (2012) introduced a two-drop dust density model to fit their SMA data, which was also adopted by Zhang et al. (2014) in the analysis of the ALMA data: one drop at 75 and one at 20 AU. We found that such a two-step decrease is indeed required to fit the continuum visibilities and adopted the same structure, although we set the inner drop radius at 30 AU to be consistent with the gas cavity. On the other hand, we required a much larger critical radius of 60 AU instead of the 10–20 AU used by Mathews and Zhang. This is most likely the result of shadowing by an inner disk. Our disk dust mass of 0.1 MJup is similar to their estimates.
In the gas a clear signature for a drop at 30 AU is seen in the CO moment map, which was modeled by Zhang et al. (2014) in a parametrized gas model of a power-law temperature profile with an empty gap. Their result is consistent with that of our full physical-chemical model, and the derived surface density profile is similar (right panel of Fig. 8). We can constrain the inner density drop to δgas2 = 10-5 (see Fig. 8), although this depends on the inner cavity size: a smaller cavity size would require an even deeper drop, a larger size a less deep drop. On the other hand, δgas (the drop inside the dust cavity radius) is 1, there is no visible drop in density between 30 and 70 AU.
 |
Fig. 8 Left: modeling results and observations of the 12CO emission for the best-fitting physical gas model for J1604-2130 for the inner 30 AU cavity comparing δgas2 (gas density drop inside the 30 AU dust cavity). δgas2 is varied as 100, 10-1, ..., 10-6 as blue, light blue, cyan, green, yellow, orange, and red (δgas is taken as 1). The observations are plotted in black. The panel shows the intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero-moment map. Right: comparison between the density profile derived in this study and the profile used in Zhang et al. (2014). |
5. Discussion
5.1. Implications of gas density drop
The key parameter in our analysis is δgas, the drop in gas density inside the dust hole, in comparison with δdustcav. For each target, the minimum required drop in dust density δdustcav is significantly lower than the possible values of δgas. Figure 5 and Table 4 show the range of possible values for these parameters for each target.
The significantly larger drop in dust density compared with the gas is consistent with the dust-trapping scenario by a companion, with gas present inside the millimeter-sized dust cavity (Pinilla et al. 2012). For the sources studied here, photoevaporation by itself is unlikely based on just the large cavity sizes and high accretion rates (Owen et al. 2011; Rosotti et al. 2013), and our results further strengthen this hypothesis. Especially SR21, HD 135344B, and LkCa15 require a minimum drop of a factor 10–100 within the gap in the gas surface density and are thus promising candidates for disks with embedded planets. The drop is deep enough to rule out the dead-zone scenario, which has a drop that is much smaller than an order of magnitude (Lyra et al. 2015). On the other hand, one has to be careful to avoid an overinterpretation at this point: the CO emission inside the gap is sensitive to the amount of small dust inside the cavity due to its shielding effect, which can also explain the apparent drop in CO emission. We have explored this within the constraints of our physical model, but any addition of dust or PAHs inside the cavity that is sufficient to lower the CO emission at the same time increases the mid-infared continuum emission in the SED to levels that are inconsistent with the data. The combination of SED modeling and spatially resolved 12CO emission thus provides unique constraints on the temperature and small dust grain composition. On the other hand, the vertical structure also influences the temperature structure and thus the 12CO emission and mid-infrared continuum emission, and this degeneracy remains uncertain.
The depth of the gas density drops at the cavity radius is still modest, only a factor δgas ~ 10-1 − 10-2. Comparison with the planet-disk interaction models of Jupiter-mass planets in Fig. 1 in Pinilla et al. (2012) indicates that any embedded planets responsible for this drop are unlikely to be more massive than 1–2 Jupiter masses, and even then only with high viscosity (α ~ 10-2). A high viscosity is inconsistent with the presence of long-lived vortices (e.g., Ataiee et al. 2013). Pérez et al. (2014) interpreted the asymmetries of SR21 and HD 135344B as possible vortices by comparing their analytic solution for the asymmetric dust structures with the vortex prescription of Lyra & Lin (2013). The lack of a deep gap in the CO argues against this interpretation. Pinilla et al. (2015) also concluded that for SR 21 the vortex scenario is unlikely by analyzing the observed dust distribution at different wavelengths with hydrodynamic and dust evolution models. However, a smaller gas cavity size with a deeper density drop would also fit our observations and be consistent with low viscosities. More high spatial resolution observations of CO isotopologs are needed to clearly distinguish cavity size and gas density drop.
The planet-disk interaction models predict rounded-off gradients rather than steep vertical drops such as parametrized in our model. A rounded-off dust wall was indeed inferred from mid-infrared interferometry data of HD 100546 (Mulders et al. 2013) by fitting the visibility curve, but the S/N of our data is insufficient to test this. One important conclusion of Pinilla et al. (2012) is that the gas cavity radius (location of the planet) is expected to be up to a factor of 2 smaller than the dust cavity radius (location of the radial pressure bump where the dust is trapped). This was indeed observed for J1604-2130 (Zhang et al. 2014; this study), Oph IRS 48 (Bruderer et al. 2014), and HD 142527 (Perez et al. 2015). As stated above, our estimates of the drop in gas density inside the cavity would probably increase if we were to assume a smaller gas cavity size, but the spatial resolution of our data is insufficient to constrain this. For HD 135344B we show the outcome for a gas cavity of 30 instead of 40 AU (Fig. 6), but for this radius the δgas is still limited to 10-1 − 10-2. For J1604-2130, we find clear evidence for an inner drop at 30 AU and no additional drop between 30 and 70 AU of 10-1, as found for Oph IRS 48 (Bruderer et al. 2014). A structure with a double drop or smaller gas cavity size hints at the possibility that there is more than one companion, or alternatively a shallow increasing slope such as seen in Pinilla et al. (2012, 2015). This possibility cannot be excluded for any of the other sources in this study with the available observations. Carmona et al. (2014) suggested a gas surface profile that increases with radius inside the cavity to match the gas and dust density distribution of HD 135344B, although this is only constrained by observations for the inner few AU. Modeling the shape of the gap is beyond the scope of this paper. Spatially resolved observations of CO isotopologs will provide better constraints on the density profile.
5.2. Cavity size and dust distribution
Another interesting aspect of our results is that all disks have significantly smaller cavity sizes (by 5–10 AU) in the 690 GHz continuum data than those derived by Andrews et al. (2011) based on the 345 GHz continuum observations taken with the SMA. The cavity size as derived with the ALMA continuum visibilities (location of the null) is constrained to better than ±5 AU. The S/N of the SMA data is much lower, so the cavity size is less precisely constrained, but the systematic trend is significant. For comparison, we list the location of the first null for both the 690 GHz and 345 GHz continuum of our adopted model in Table 5 and compare them with the null in Andrews et al. (2011).
Location of the null in the visibilities of models and SMA observations at various frequencies (Andrews et al. 2011).
Note that the null as derived from the models can shift slightly for the two frequencies as a result of the difference in dust opacity at the observed wavelengths. The null in the observed 345 GHz continuum is significantly smaller for SR21, HD 135344B, and RX J1615-3255 than that at 690 GHz, indicating a larger cavity size at this longer wavelength. This indicates a radial variation of the dust size distribution, as the continuum emission is sensitive to larger grains at longer wavelengths. A more concentrated dust ring (i.e., a narrower ring and thus a larger dust cavity size) is consistent with the dust-trapping scenario, because larger dust grains are further decoupled from the gas and thus more affected by radial drift and trapping (Brauer et al. 2008). Higher S/N ALMA Band 7 observations are required to confirm this.
6. Conclusions
We have analyzed high spatial resolution ALMA submillimeter observations of 12CO line emission from six transitional disks using a physical-chemical model. By comparing the SED, the 690 GHz continuum visibilities and the 12CO emission simultaneously, we derived a physical model of the gas and dust. With the model we set constraints on the surface density profile of the dust and gas and specifically, the amount of dust and gas in the cavity.
-
1.
All disks show clear evidence for gas inside the dust cavity.
-
2.
The gas and dust observations can be fit with a surface density profile with a steep density drop at the cavity radius, taking a gas-to-dust ratio of 100 in the outer disk.
-
3.
The combination of SED and spatially resolved 12CO intensity fitting sets constraints on the vertical and thus on the temperature structure of each disk.
-
4.
All disks except SR24S have a potential drop of 1 or 2 orders of magnitude in the gas surface density inside the mm-sized dust cavity, while the minimum required drop in dust surface density inside the cavity is at least 3 orders of magnitude.
-
5.
J1604-2130 has a deep resolved gas cavity that is smaller than the dust cavity. For the other disks it is possible that the gas cavity radius is smaller than the dust cavity radius, in which case the density drop will be deeper, but this cannot be constrained with the available data.
-
6.
The derived density profiles suggest the clearing of the cavity by one or more companions, as a result of which, the millimeter dust is trapped at the edge of the cavity.
-
7.
Our model for J1604-2130 is mostly consistent with the proposed physical structure by Zhang et al. (2014), derived using a parametrized temperature model.
-
8.
The continuum of RX J1615-3255 shows an additional dust ring around 120 AU.
-
9.
The derived cavity sizes of the millimeter dust (and location of the null in the visibilities) are consistently smaller for the 690 GHz/0.44 mm continuum than for the 345 GHz/0.88 mm continuum. This is consistent with the dust-trapping scenario, because trapping is more efficient for larger dust grains probed at longer wavelengths.
The derived physical model can be used as a start for the analysis of CO isotopolog observations, placing better constraints on the gas density inside and outside the cavity. We have recently obtained CO isotopolog ALMA observations for two disks of the sample in this study (van der Marel et al., in prep.).
Online material
Appendix A: Channel maps
Velocity range within the cavity radius.
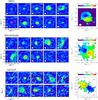 |
Fig. A.1 12CO channel maps for each observed target. Overlaid in white contours are the Keplerian velocity profiles for the derived inclination and given stellar mass. The yellow ellipse indicates the dust hole radius and the yellow contours the 5σ outer radius of the dust continuum. |
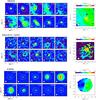 |
Fig. A.1 continued. |
Acknowledgments
The authors would like to thank P. Pinilla, A. Juhasz, and C. Walsh for useful discussions and the referee for the constructive comments. N.M. is supported by the Netherlands Research School for Astronomy (NOVA), S.B. acknowledges a stipend by the Max Planck Society. Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA), by a Royal Netherlands Academy of Arts and Sciences (KNAW) professor prize, and by the European Union A-ERC grant 291141 CHEMPLAN. This paper makes use of the following ALMA data: ADS/JAO.ALMA/2011.0.00724.S, 2011.0.00526.S and 2011.0.00733.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Aikawa, Y., van Zadelhoff, G. J., van Dishoeck, E. F., & Herbst, E. 2002, A&A, 386, 622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Ataiee, S., Pinilla, P., Zsom, A., et al. 2013, A&A, 553, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brittain, S. D., Najita, J. R., & Carr, J. S. 2009, ApJ, 702, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Dullemond, C. P., et al. 2007, ApJ, 664, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Blake, G. A., Qi, C., et al. 2009, ApJ, 704, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., Herczeg, G. J., Pontoppidan, K. M., & van Dishoeck, E. F. 2012, ApJ, 744, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S. 2013, A&A, 559, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A&A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., van der Marel, N., van Dishoeck, E. F., & van Kempen, T. A. 2014, A&A, 562, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N., D’Alessio, P., Watson, D. M., et al. 2005, ApJ, 630, L185 [NASA ADS] [CrossRef] [Google Scholar]
- Canovas, H., Schreiber, M. R., Cáceres, C., et al. 2015, ApJ, 805, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Carmona, A., Pinte, C., Thi, W. F., et al. 2014, A&A, 567, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carpenter, J. M., Ricci, L., & Isella, A. 2014, ApJ, 787, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Casassus, S., van der Plas, G., M, S. P., et al. 2013, Nature, 493, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Clarke, C. J., Gendrin, A., & Sotomayor, M. 2001, MNRAS, 328, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Dahm, S. E. 2008, AJ, 136, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson-Robinson, S. E., & Salyk, C. 2011, ApJ, 738, 131 [CrossRef] [Google Scholar]
- Dullemond, C. P., & Dominik, C. 2005, A&A, 434, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunkin, S. K., Barlow, M. J., & Ryan, S. G. 1997, MNRAS, 290, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Dutrey, A., Guilloteau, S., Piétu, V., et al. 2008, A&A, 490, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & Th. Henning (Tucson: University of Arizona Press), 497 [Google Scholar]
- Follette, K. B., Tamura, M., Hashimoto, J., et al. 2013, ApJ, 767, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fung, J., Shi, J.-M., & Chiang, E. 2014, ApJ, 782, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Garufi, A., Quanz, S. P., Avenhaus, H., et al. 2013, A&A, 560, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geers, V. C., Augereau, J.-C., Pontoppidan, K. M., et al. 2006, A&A, 459, 545 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gorti, U., & Hollenbach, D. 2008, ApJ, 683, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Grady, C. A., Schneider, G., Sitko, M. L., et al. 2009, ApJ, 699, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Huélamo, N., Lacour, S., Tuthill, P., et al. 2011, A&A, 528, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ingleby, L., Calvet, N., Bergin, E., et al. 2009, ApJ, 703, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Pérez, L. M., & Carpenter, J. M. 2012, ApJ, 747, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Jonkheid, B., Faas, F. G. A., van Zadelhoff, G.-J., & van Dishoeck, E. F. 2004, A&A, 428, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jonkheid, B., Kamp, I., Augereau, J.-C., & van Dishoeck, E. F. 2006, A&A, 453, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., & Dullemond, C. P. 2004, ApJ, 615, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kraus, A. L., & Ireland, M. J. 2012, ApJ, 745, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1979, MNRAS, 188, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Luhman, K. L., & Rieke, G. H. 1999, ApJ, 525, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Lyo, A.-R., Ohashi, N., Qi, C., Wilner, D. J., & Su, Y.-N. 2011, AJ, 142, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., & Lin, M.-K. 2013, ApJ, 775, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., Turner, N. J., & McNally, C. P. 2015, A&A, 574, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathews, G. S., Williams, J. P., & Ménard, F. 2012, ApJ, 753, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Mayama, S., Tamura, M., Hanawa, T., et al. 2010, Science, 327, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Mulders, G. D., Paardekooper, S.-J., Panić, O., et al. 2013, A&A, 557, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Strom, S. E., & Muzerolle, J. 2007, MNRAS, 378, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., & Randich, S. 2006, A&A, 452, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., Ercolano, B., & Clarke, C. J. 2011, MNRAS, 412, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Carpenter, J. M., Chandler, C. J., et al. 2012, ApJ, 760, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, L. M., Isella, A., Carpenter, J. M., & Chandler, C. J. 2014, ApJ, 783, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Perez, S., Casassus, S., Ménard, F., et al. 2015, ApJ, 798, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Piétu, V., Dutrey, A., & Guilloteau, S. 2007, A&A, 467, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., Benisty, M., & Birnstiel, T. 2012, A&A, 545, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinilla, P., de Juan Ovelar, M., Ataiee, S., et al. 2015, A&A, 573, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontoppidan, K. M., Blake, G. A., van Dishoeck, E. F., et al. 2008, ApJ, 684, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Prato, L., Greene, T. P., & Simon, M. 2003, ApJ, 584, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Amara, A., Meyer, M. R., et al. 2014, ApJ, submitted [arXiv:1412.5173] [Google Scholar]
- Regály, Z., Juhász, A., Sándor, Z., & Dullemond, C. P. 2012, MNRAS, 419, 1701 [NASA ADS] [CrossRef] [Google Scholar]
- Rosenfeld, K. A., Chiang, E., & Andrews, S. M. 2014, ApJ, 782, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rosotti, G. P., Ercolano, B., Owen, J. E., & Armitage, P. J. 2013, MNRAS, 430, 1392 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2007, ApJ, 655, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Blake, G. A., Boogert, A. C. A., & Brown, J. M. 2009, ApJ, 699, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Herczeg, G. J., Brown, J. M., et al. 2013, ApJ, 769, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Strom, K. M., Strom, S. E., Edwards, S., Cabrit, S., & Skrutskie, M. F. 1989, AJ, 97, 1451 [NASA ADS] [CrossRef] [Google Scholar]
- Thalmann, C., Mulders, G. D., Hodapp, K., et al. 2014, A&A, 566, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., & van Kempen, T. A. 2014, A&A, 563, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discussions, 133, 231 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Kempen, T. A., van Dishoeck, E. F., Salter, D. M., et al. 2009, A&A, 498, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Zadelhoff, G.-J., van Dishoeck, E. F., Thi, W.-F., & Blake, G. A. 2001, A&A, 377, 566 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, C., Juhász, A., Pinilla, P., et al. 2014, ApJ, 791, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Wichmann, R., Krautter, J., Covino, E., et al. 1997, A&A, 320, 185 [NASA ADS] [Google Scholar]
- Williams, J. P., & Cieza, L. A. 2011, ARA&A, 49, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W.-F. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, K., Isella, A., Carpenter, J. M., & Blake, G. A. 2014, ApJ, 791, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Nelson, R. P., Hartmann, L., Espaillat, C., & Calvet, N. 2011, ApJ, 729, 47 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Results of the fitting procedure for the gas density profile of each transition disk.
Location of the null in the visibilities of models and SMA observations at various frequencies (Andrews et al. 2011).
All Figures
 |
Fig. 1 ALMA observations of the continuum and 12CO line. The first five disks show the 690 GHz (440 μm) continuum and the 12CO J = 6–5 line, the sixth is the 345 GHz (880 μm) continuum and 12CO J = 3–2 line. Left: continuum image. The stellar position is indicated by a white star, the white bar in the upper right corner indicates the 30 AU scale, and the yellow contour gives the 3σ detection limit. The colorbar units are given in Jy beam-1. Center: zero-moment 12CO map. The colorbar units are given in Jy beam-1 km s-1. Right: 12CO spectrum integrated over the entire disk. The dashed line indicates the zero flux level, and the gray areas indicate the parts of the spectrum affected by foreground absorption (seen in SR21 and SR24S). The beam is indicated in each map by a white ellipse in the lower left corner. |
| In the text | |
 |
Fig. 2 Generic surface density profile for the gas and dust. |
| In the text | |
 |
Fig. 3 Modeling results and observations of the dust surface density, comparing δdustcav ranging between 10-2 and 10-8 as indicated in the right panel. The observations are plotted in black. Left: spectral energy distribution. Middle left: amplitude of the 690 GHz continuum visibility for the deprojected baselines. The null line is indicated with a dashed line. Middle right: normalized intensity cuts through the major (bottom) and minor (top) axis of the 690 GHz continuum image. The model images are convolved with the same beam as the ALMA observations. Right: dust surface density profile. Indicated are the δdust, the drop in density to fit the inner disk through the near-infrared emission, and δdustcav, the minimum drop in dust density inside the cavity to fit the observations. In SR21 (top panel) the region inside 7 AU is assumed to be empty because of additional constraints (see main text). In all other disks δdustcav is found to be at most 10-4. All other disk parameters are as listed in Table 4. |
| In the text | |
 |
Fig. 4 Modeling results and observations of the 12CO emission for the best-fitting physical model derived from the dust (see Fig. 3 and Table 4), with δgas = 1 (no drop in gas surface density inside the cavity). The observations are plotted in black, the models in purple. Left: 12CO spectrum integrated over the entire disk. Center: intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero moment map. The noise level is indicated by the gray zone. The model images are convolved with the same beam as the ALMA observations. Right: amplitude of the integrated 12CO visibility for the deprojected baselines. The null line is indicated with a dashed line, and error bars indicate the noise. |
| In the text | |
 |
Fig. 5 Modeling results and observations of the 12CO emission for the best-fitting physical model for gas and dust (Fig. 4) comparing δgas (gas density drop inside the dust cavity). δgas is varied as 100, 10-1, ..., 10-4 as blue, light blue, green, yellow, and red in the left and middle plots, while the observational data are plotted in black. Left: the 12CO spectrum integrated over the disk area. Middle: the intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero-moment map for different δgas. The noise level is indicated by the gray area. The model images are convolved with the same beam as the ALMA observations. Right: the best-fitting result for possible values of δgas and δdustcav in red and blue. |
| In the text | |
 |
Fig. 6 Modeling results and observations of the 12CO emission for the best-fitting physical model for HD 135344B for a cavity of 30 AU instead of 40 AU for gas and dust (Fig. 4) for different values of δgas (gas density drop inside the dust cavity). δgas is varied as 100, 10-1, ..., 10-4 as blue, light blue, green, yellow, and red. The observations are plotted in black. The panel shows the intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero-moment map. |
| In the text | |
 |
Fig. 7 Modeling results and observations of the 690 GHz continuum of RX J1615-3255. The panel shows the intensity cuts through the major (bottom) and minor (top) axis of the continuum image, zoomed in on the lowest flux levels (<20σ). The observations are plotted in black with the 1σ errors in gray. In red and blue we present the models with and without a dust gap between 110 and 130 AU. The dotted and dashed lines indicate the zero flux and 3σ limits, respectively. |
| In the text | |
 |
Fig. 8 Left: modeling results and observations of the 12CO emission for the best-fitting physical gas model for J1604-2130 for the inner 30 AU cavity comparing δgas2 (gas density drop inside the 30 AU dust cavity). δgas2 is varied as 100, 10-1, ..., 10-6 as blue, light blue, cyan, green, yellow, orange, and red (δgas is taken as 1). The observations are plotted in black. The panel shows the intensity cuts through the major (bottom) and minor (top) axis of the 12CO zero-moment map. Right: comparison between the density profile derived in this study and the profile used in Zhang et al. (2014). |
| In the text | |
 |
Fig. A.1 12CO channel maps for each observed target. Overlaid in white contours are the Keplerian velocity profiles for the derived inclination and given stellar mass. The yellow ellipse indicates the dust hole radius and the yellow contours the 5σ outer radius of the dust continuum. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


