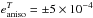| Issue |
A&A
Volume 579, July 2015
|
|
|---|---|---|
| Article Number | A7 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425600 | |
| Published online | 19 June 2015 | |
A weak lensing analysis of the PLCK G100.2-30.4 cluster ⋆
1 INAF–Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
e-mail: mario.radovich@oapd.inaf.it
2 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
3 Dipartimento di Fisica, Università Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
4 Institute of Theoretical Astrophysics, University of Oslo, Blindern, Oslo, Norway
5 Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université Paris-Sud 11, Bât. 121, 91405 Orsay, France
6 CNRS, IRAP, 9 avenue du colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
7 Laboratoire AIM, IRFU/Service d’Astrophysique, CEA/DSM, CNRS, Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
8 INAF–Osservatorio Astronomico di Capodimonte, Salita Moiariello 16, 80131 Napoli, Italy
9 Dipartimento di Fisica e Astronomia Alma Mater Studiorum – Universitá di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
10 INFN–Sezione di Bologna, viale Berti-Pichat 6/2, 40127 Bologna, Italy
11 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
Received: 30 December 2014
Accepted: 5 May 2015
We present a mass estimate of the Planck-discovered cluster PLCK G100.2-30.4, derived from a weak lensing analysis of deep Subaru griz images. We perform a careful selection of the background galaxies using the multi-band imaging data, and undertake the weak lensing analysis on the deep (1 h) r −band image. The shape measurement is based on the Kaiser-Squires-Broadhurst algorithm; we adopt the PSFex software to model the point spread function (PSF) across the field and correct for this in the shape measurement. The weak lensing analysis is validated through extensive image simulations. We compare the resulting weak lensing mass profile and total mass estimate to those obtained from our re-analysis of XMM-Newton observations, derived under the hypothesis of hydrostatic equilibrium. The total integrated mass profiles agree remarkably well, within 1σ across their common radial range. A mass M500 ~ 7 × 1014M⊙ is derived for the cluster from our weak lensing analysis. Comparing this value to that obtained from our reanalysis of XMM-Newton data, we obtain a bias factor of (1−b) = 0.8 ± 0.1. This is compatible within 1σ with the value of (1-b) obtained in Planck 2015 from the calibration of the bias factor using newly available weak lensing reconstructed masses.
Key words: galaxies: clusters: individual: PLCK G100.2-30.4 / gravitational lensing: weak / X-rays: galaxies: clusters / dark matter
© ESO, 2015
1. Introduction
Clusters of galaxies are a crucial probe for a variety of key cosmological topics. Among their many applications, knowledge of the mass function and its redshift evolution allows constraints to be put on the matter power spectrum and limits to be set on several cosmological parameters. The construction of the cluster mass function generally involves the following steps: 1) clusters should be identified in large surveys; 2) mass proxies should be used to estimate their masses; and 3) the mass function should be constructed by counting clusters in given mass and redshift bins. This process relies on the fundamental assumption that the scaling relations between the mass and its proxies are well calibrated and unaffected by selection biases (or that the biases have been accounted for). It has been successfully implemented both by using X-rays surveys such as the ROSAT All-Sky Survey, where proxies like the gas mass, the temperature, or the X-ray luminosity have been used to estimate the masses (e.g. Vikhlinin et al. 2009; Mantz et al. 2010), and in optical photometric optical surveys, for example the SDSS, where the masses are usually derived from the cluster richness (e.g. Rozo et al. 2009). More recently, searches for galaxy clusters have been started via the detection of the Sunyaev-Zel’dovich (SZ) effect on the photons of the cosmic microwave background. The newly established millimetric observatories, both ground-based (South Pole Telescope and Atacama Cosmology Telescope) and space-based (Planck), have provided catalogues of hundreds to thousands of clusters. The first cluster detections from the Planck all-sky survey were released in the Planck Early SZ sample (Planck Collaboration VIII 2011). A crucial part of the validation process involved the use of snapshot XMM-Newton observations; in the first two campaigns, 21 out of 25 newly identified cluster candidates were confirmed to be real (Planck Collaboration IX 2011).
 |
Fig. 1 Composite gri image of the inner 400″ × 400″ region of the PLCKG100 field. |
The XMM-Newton snapshot observations appeared to reveal a class of massive clusters with low X-ray luminosity and disturbed morphology, which may indicate a population of massive clusters that are under-represented in X-ray surveys. Since the cluster masses in SZ surveys are estimated from the integrated Compton Y parameter via scaling relations calibrated with optical or X-ray observations, this may have an effect on the estimate of the mass function, and thus our understanding of cluster growth and evolution. It is therefore of fundamental importance to study these systems in more detail.
Lensing is a powerful method for recovering the surface density field of clusters, thus allowing the spatial distribution of dark matter to be traced. Simulations have shown that provided wide-field observations of excellent quality are available, lensing allows an accurate measurement of the mass profile of clusters (Meneghetti et al. 2010), and hence the radial mass/luminosity (M/L) profile (Medezinski et al. 2010), and its dependence on early-type and late-type galaxies in the cluster. Combined with X-ray observations, lensing can help to characterize the dynamical state of the clusters, and probe deviations from hydrostatic equilibrium which may bias the X-ray masses (Mahdavi et al. 2008; Zhang et al. 2010).
In this paper we describe the first weak lensing analysis of the cluster PLCK G100.2-30.4 (hereafter PLCKG100), based on deep Subaru SuprimeCam images. PLCKG100 was detected via the SZ effect in the first ten months of the Planck survey and was confirmed by XMM-Newton X-ray observations (Planck Collaboration IX 2011). The cluster redshift was estimated by optical griz observations performed with the 0.80 m IAC80 telescope, and through X-ray spectroscopic observations of the Fe K line, giving zphot = 0.38 ± 0.04 and zFe = 0.31 ± 0.04, respectively (Planck Collaboration IX 2011). The cluster mass estimate, derived from XMM-Newton X-ray observations via iteration about the M500−YX relation of Arnaud et al. (2010), is M500 = (5.60 ± 0.22) × 1014M⊙, and the [0.1−2.4] keV X-ray luminosity was L500 = (3.36 ± 0.08) × 1044 erg s-1.
 |
Fig. 2 Zoom of the inner 100″ × 100″ region of the PLCKG100 field. Labels mark the ten brightest galaxies. Several strong lensing gravitational arcs are visible. |
Here we use deep (1 h) r-band and shallower (~30 min) giz images obtained with SuprimeCam at the Subaru telescope to derive the mass of the cluster by weak lensing. The paper is organized as follows. A summary of the observations and data reduction strategy is presented in Sect. 2. Techniques adopted for star/galaxy separation are described in Sect. 3. A comparison with cluster properties derived by optical photometry is given in Sect. 4. The weak lensing analysis is discussed in Sect. 5. We attempt to refine the hydrostatic mass estimate from XMM-Newton data in Sect. 6. Summary and conclusions are given in Sect. 7.
A standard concordance cosmology was adopted: ΩΛ = 0.7, ΩM = 0.3, H0 = 70 km s-1 Mpc-1, giving a scale of 4.7 kpc/arcsec at the redshift of PLCK G100.2-30.4 (z = 0.36, as derived in Sect. 4).
Summary of the observations.
2. Observations and data reduction
PLCKG100 (Fig. 1, Fig. 2) was observed in the second part of the night on July 23, 2012, in the griz bands, with the wide-field Suprime-Cam camera (Miyazaki et al. 2002) mounted at the 8 m Subaru telescope. The camera is composed of 10 CCDs, each with 2048 × 4096 pixels and pixel scale 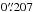 , allowing coverage of a field of 34′ × 27′. A sequence of 180 s exposures was obtained following the dithering pattern recommended for SuprimeCam. The deepest (1 h) image was taken in the r-band, to be used for the lensing analysis, with optimal seeing conditions (
, allowing coverage of a field of 34′ × 27′. A sequence of 180 s exposures was obtained following the dithering pattern recommended for SuprimeCam. The deepest (1 h) image was taken in the r-band, to be used for the lensing analysis, with optimal seeing conditions (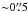 ). Images in g and i were obtained with a total exposure time of 1800 s as planned, while due to technical reasons only 8 out of the 10 planned exposures could be done in z, for a total exposure of 1440 s. Details of the observations are reported in Table 1.
). Images in g and i were obtained with a total exposure time of 1800 s as planned, while due to technical reasons only 8 out of the 10 planned exposures could be done in z, for a total exposure of 1440 s. Details of the observations are reported in Table 1.
The prereduction (overscan correction, bias, flat-fielding and masking of bad columns and autoguider) was based on the SDFRED2 (Yagi et al. 2002; Ouchi et al. 2004) pipeline developed for Suprime–Cam.
The tool AstromC (Romano et al. 2010) was then used to compute the astrometric solution describing the deformations in the field of view of individual exposures. For each filter, the astrometric solution was computed taking the NOMAD catalogue as reference, and at the same time minimizing the differences in the position of the same sources measured in different exposures; this allowed us to obtain an internal accuracy of ~ 0.01 arcsec, better than the accuracy of the NOMAD catalogue (rms ~ 0.2 arcsec). Images were then resampled and finally coadded using the SWarp software1 (Bertin 2010).
Photometric calibration was done by observing a field selected from the Stripe 82 area, and using the SDSS Stripe 82 Standard Star Catalog (Ivezić et al. 2007) to derive photometric zero points and SuprimeCam vs. SDSS colour terms. Limiting magnitudes for point–like sources at signal-to-noise levels of S/N = 5, 10 were computed as in Radovich et al. (2004): simulated images with the same depth and background rms as each science image were produced using SkyMaker2 software, and stars were added at random positions; errors on magnitudes were computed from the difference between input and measured magnitudes, and were used to derive the median magnitude for each value of S/N.
In addition to the stacked image obtained as described above, we also produced a set of stacks where the point spread function (PSF) was homogenized to the same Gaussian shape for all filters. This was done as follows:
-
1.
For each exposure, all CCD images were first regridded andcombined in one image using SWarp, adopting the same centre,pixel scale, and size as the coadded r-band stack derived above.
-
2.
For each image, stars were identified and the PSF fitted as a function of pixel coordinates using the PSFex software3 (Bertin 2011) as described later in Sect. 3.
-
3.
The psfmatch task in iraf was used to compute the kernel that transforms the PSF into a Gaussian with the target FWHM, chosen to be 0.9 arcsec, the worst seeing value measured in all exposures and bands; since the PSF changes across the field, we divided each image into sections of 100 × 100 pixels, and computed the kernel in each of them.
-
4.
For each filter, all convolved exposures were finally summed together.
These PSF-homogenized stacks were used for the photometric measurements only, not for shape measurements, for which we used the unconvolved r-band image. A multi-band photometric catalogue was extracted by running SExtractor4 (Bertin & Arnouts 1996) in dual mode, taking the r–band as the detection image, and measuring the photometry on the convolved stacks.
The Galactic dust extinction in the field covered by Suprime-Cam was computed using the Schlegel maps (Schlegel et al. 1998), obtaining an average value and rms: EB−V = 0.12 ± 0.01. For each galaxy, observed magnitudes were corrected in each filter by adopting the dust extinction computed at its position.
3. Star-galaxy classification
The selection of non-saturated stars and galaxies was undertaken in the magnitude (MAG_AUTO) vs. size (δ = MU_MAX-MAG_AUTO) space (Huang et al. 2011). MU_MAX is the peak surface brightness above background, which is constant for saturated stars. As in Huang et al. (2011), we rejected those sources with δ lower than for stars as spurious detections.
As a test of both the photometric accuracies and of the star-galaxy classification, we compared the g−r and i−z observed colours of stars with those derived at the Galactic plane position of PLCKG100 by the trilegal code (Girardi et al. 2005, 2012). trilegal allows the simulation of broad-band photometry of stars in any Galaxy field. The effect of the Galaxy dust extinction on stellar colours was also included in the models, starting from the average and rms E(B−V) values derived from the Schlegel maps, and assigning to each simulated star a random value within this distribution. The transmission curves obtained by the combination of Subaru/SuprimeCam CCD, telescope, atmosphere, and filter contributions were adopted. Model and observed stellar colours are shown in Fig. 3. The zero point offsets required to optimize the overlap of observed and model colours are +0.038 mag (g), −0.030 mag (r), −0.023 mag (i), and −0.016 mag (z).
Stars with S/N> 100 were extracted and used in the PSFex software, designed to model the PSF variations in astronomical images. The code allows the pixel-by-pixel PSF intensity to be modelled by a polynomial in a stamp of a given size as a function of the position in the field of view. Starting from this model, we can build a PSF stamp at each galaxy position, and derive the terms needed for the PSF correction of ellipticities, as described in Sect. 5.1. Different combinations of polynomial orders and stamp sizes were tried; based on the analysis of the residuals of the correction of the anisotropic PSF component (see Sect. 5.1), we selected a polynomial of order 6 and stamps with a size of 20 × 20 pixels (~ 5 × FWHM).
 |
Fig. 3 Stellar colours (top: i−z vs. g−r; bottom: r−i vs. g−r): measured data (red dots) are compared to the values obtained by TRILEGAL (green dots). |
4. Cluster photometric properties
Figure 2 shows the composite gri image of the cluster field: the ten brightest galaxies within 1 arcmin from the X-ray peak (Planck Collaboration IX 2011) are marked. Two galaxies of similar brightness (r ~ 18.20 mag) are present in this region. We select as the centre of the cluster the galaxy that lies closest to the X-ray peak, and identify it as the brightest cluster galaxy (BCG). Several strong–lensing gravitational arcs are also visible, the brightest of which lies at ~40 arcsec from the BCG. Another lies at ~60 arcsec from the BCG.
 |
Fig. 4 r vs. g−r colour plot of galaxies in the field. Galaxies classified as likely cluster members from their colours are plotted as green dots; the red dot is the BCG galaxy. The best fitting red sequence line is overplotted. |
4.1. Red sequence
We selected the galaxies located in the inner 5 arcmin around the BCG that were classified as cluster members according to their colours, as described in Sect. 5.2. The red sequence, g−r = a + br, was fitted by a biweight algorithm, giving a = 2.6, b = −0.05 (Fig. 4). Early-type galaxies were selected as those lying within 2σ from the best fitting line. Photometric redshifts were computed using the Zebra code (Feldmann et al. 2006): the cluster redshift, derived from the average photo-z of r< 22 mag cluster members, is z = 0.36 ± 0.08. For comparison, we obtain z = 0.41 ± 0.10 from the Sloan Digital Sky Survey (SDSS) photometric redshifts (DR9).
4.2. Richness
The parameter N200, i.e. the richness of the cluster within r200, was derived both from the selection of red-sequence cluster galaxies, and by making a statistical background subtraction. We used the r200 derived from the weak lensing analysis detailed in Sect. 5: r200 ~ 6 arcmin. Absolute r −band magnitudes and k-corrections were computed for all galaxies with the cluster redshift, z = 0.36, and to a magnitude limit of Mabs = −20 mag. The richness derived from the selection of red sequence galaxies produces N200 = 150. The richness estimate based on statistical background subtraction was done following Popesso et al. (2005); the density of background and foreground galaxies was then computed in each of the 20 sectors in an annulus with thickness 0.1 deg, starting at r200+0.1 deg. Sectors with too few galaxies were rejected, and the average density was finally computed, giving the number of background/foreground galaxies in the r200 area of the cluster. In this way, we derived a richness N200 ~ 135.
The richness can be translated to a mass estimate using e.g. Eq. (16) in Andreon & Hurn (2010): log M200 = (0.96 ± 0.15)(log N200−1.5) + 14.36 ± 0.04. From these two consistent values of the richness, a mass log M200 ~ (15.0 ± 0.1)M⊙ is derived.
5. Weak lensing analysis
5.1. Shape measurement
The derivation of the shear, and the correction of the effect of the PSF on galaxy shapes, is based on the Kaiser, Squires, and Broadhurst approach (Kaiser et al. 1995, hereafter KSB). In the last decade there has been a dedicated effort to develop new algorithms to improve the accuracy in shape measurement (see Kitching et al. 2012, for a comprehensive review), which is crucial in particular in order to derive cosmological parameters from weak gravitational lensing (cosmic shear). However, KSB is still widely used in the case of the analysis of massive structures such as galaxy clusters (see e.g. Okabe et al. 2010; Hoekstra et al. 2012; Umetsu et al. 2014; Applegate et al. 2014). Our implementation follows that described in Huang et al. (2011) with some differences, which are outlined below.
The KSB algorithm is based on the measurement of the following quantities for each galaxy, derived from the source brightness moments: the source ellipticity vector5eobs, and the smear polarizability (Psm) and shear polarizability (Psh) tensors.
The source ellipticity corrected for the anisotropic component of the PSF, eaniso , is first derived as  where starred terms indicate that they are derived from the measurement of stars. This is then related to the unknown intrinsic ellipticity e of the source and to the reduced shear, g = γ/ (1−κ), by
where starred terms indicate that they are derived from the measurement of stars. This is then related to the unknown intrinsic ellipticity e of the source and to the reduced shear, g = γ/ (1−κ), by 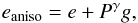 (3)where the effect of the (isotropic) seeing is corrected by the term Pγ, dubbed by Luppino & Kaiser (1997) as the pre-seeing shear polarizability:
(3)where the effect of the (isotropic) seeing is corrected by the term Pγ, dubbed by Luppino & Kaiser (1997) as the pre-seeing shear polarizability: 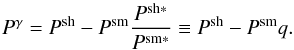 (4)The tangential and cross components of the reduced shear, gt and gx, are defined as
(4)The tangential and cross components of the reduced shear, gt and gx, are defined as  (5)ϕ being the position angle of the galaxy with respect to the assumed cluster centre.
(5)ϕ being the position angle of the galaxy with respect to the assumed cluster centre.
The source brightness moments are weighted by a window function to suppress the outer parts of the galaxies, which are noise dominated. As in Huang et al. (2011), the window function size was set to the value that maximizes the ellipticity signal-to-noise ratio SNe, defined as 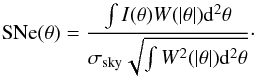 (6)Sources with SNe< 5 were rejected from the analysis. We further excluded those galaxies with Pγ< 0.1, for which the PSF correction of the ellipticity is less reliable.
(6)Sources with SNe< 5 were rejected from the analysis. We further excluded those galaxies with Pγ< 0.1, for which the PSF correction of the ellipticity is less reliable.
The final output of the pipeline is the vector eiso = eaniso/Pγ. Provided that the average intrinsic ellipticity vanishes, ⟨e⟩ = 0, the average reduced shear is ⟨g⟩ = ⟨eiso⟩; it is therefore common to set g = eiso.
As first pointed out by Hoekstra et al. (1998), it is important to adopt the same size of the window function to compute the galaxy ellipticities and the stellar correction terms used for the PSF correction. In Huang et al. (2011) we computed the stellar terms in bins with θ varying between the minimum and maximum values allowed for the size of the galaxies (2 and 10 pixels, respectively), with a step of 0.5 pixels. For each bin, they were then fitted by a polynomial, as a function of pixel coordinates, so that they could be derived at the position of each galaxy. This approach presents some disadvantages: (i) it is necessary to make a polynomial fit for each PSF correction term and for each window function size; (ii) large window sizes increase the amount of noise in the measurement of moments, even if we are using bright stars, which may contribute to different biases as a function of galaxy size. A more recent approach consists of modelling the PSF (Bergé et al. 2012), enabling us to reproduce the PSF at each galaxy’s position; this is now feasible with accuracies (Kitching et al. 2013) σ(e) < 10-3. To this end, here we used the PSFex 6 software, which allows modelling of the PSF as a linear combination of basis vectors and fits their coefficients with a polynomial as a function of the pixel position. For each galaxy position, PSF correction terms are then derived using exactly the same window function adopted for that galaxy. A similar approach was adopted in Gruen et al. (2013), who showed that using PSFex to model the PSF provides the accuracy required for weak lensing analysis of galaxy clusters. The accuracy of the PSF fitting was checked by deriving the anisotropy corrected ellipticities for stars, and verifying the absence of systematic effects in the residuals across the field of view (see Fig. 5). Using a polynomial of order 6 as described above, we obtained ⟨ e1aniso ⟩ = (−6 ± 2) × 10-4, ⟨ e2aniso ⟩ = (2 ± 1) × 10-4. Figure 6 shows the tangential component of the average stellar ellipticity before and after the anisotropic correction (< 6 × 10-4), at different distances from the cluster centre. All of the steps outlined above are implemented in the lensR pipeline introduced in Huang et al. (2011).
For each galaxy, we adopted the same weight definition as in Huang et al. (2011), 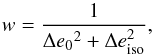 (7)where Δe0 ~ 0.3 is the typical intrinsic rms of galaxy ellipticities. The uncertainty on the corrected ellipticities, Δeiso, was computed following a numeric approach. For each star used in the PSF fitting, we compute the difference between the correction terms measured on the real stars and on the PSF model derived by PSFex, and fit them as a function of the position. This allows the estimation of an uncertainty on the stellar correction terms at each galaxy’s position. N values of eiso were then computed (e.g. N = 100), randomly drawing both the observed source ellipticity and the stellar correction terms from a Gaussian distribution built from their errors. The error on eiso used to compute the weight was taken to be the rms of these values.
(7)where Δe0 ~ 0.3 is the typical intrinsic rms of galaxy ellipticities. The uncertainty on the corrected ellipticities, Δeiso, was computed following a numeric approach. For each star used in the PSF fitting, we compute the difference between the correction terms measured on the real stars and on the PSF model derived by PSFex, and fit them as a function of the position. This allows the estimation of an uncertainty on the stellar correction terms at each galaxy’s position. N values of eiso were then computed (e.g. N = 100), randomly drawing both the observed source ellipticity and the stellar correction terms from a Gaussian distribution built from their errors. The error on eiso used to compute the weight was taken to be the rms of these values.
 |
Fig. 5 PSF anisotropy correction: the first three panels show the ellipticity pattern (measured, derived from the PSFex model, and corrected (eaniso); X and Y are in pixels). The scale is given by the arrows in the middle (e = 0.1). In the last panel, blue and red dots are the values of eaniso derived from real stars and from the PSFex model, respectively; green dots are the values after the correction. |
 |
Fig. 6 Average tangential PSF ellipticity at different distances from the cluster centre, before (black triangles) and after (red circles) the anisotropy correction. The shaded area is plotted at |
5.2. The background sample
The dilution bias introduced by unlensed galaxies in the sample used for the shape measurement can adversely affect the cluster mass estimate. To minimize the contamination of this sample by unlensed sources, we followed the approach described in Formicola et al. (2014). Using the galaxy catalogue with photometry in griz bands, we identified background populations, cluster members, and foreground populations in a colour-colour diagram derived by choosing the appropriate combination of colours to be investigated.
Our selection in the colour-colour (CC) space was based on the simultaneous analysis of galaxy colours and of the shear signal of the galaxies selected as background sources. We used the photometric data from the Cosmic Evolution Survey (COSMOS; Ilbert et al. 2009) to train the colour selection. The accurate photometric redshifts of the sample allow a careful characterization of the distribution of the galaxies belonging to different redshift ranges in CC space. At the same time, we tuned the colour cuts to maximize the amplitude of the tangential shear component (Eq. (5)) measured from the background sources.
Starting from the i−z vs. g−r CC plot of the COSMOS galaxies, we defined criteria based on colour and magnitude cuts allowing each galaxy population in the PLCKG100 images to be identified. To this end, we computed the distance d of each galaxy in the i−z vs. g−r diagram from the line represented in Fig. 7 (upper panel). This line (derived as described in Formicola et al. 2014) separates the overdense region mainly populated by sources at low redshift, from the overdense region mainly populated by sources at redshift higher than that of the cluster.
 |
Fig. 7 Selection in CC space. Upper panel: CC diagram for PLCK G100 galaxies. Cluster members are shown with orange dots, and foreground and background galaxies with green and magenta dots, respectively. Unclassified sources are plotted with black dots. Bottom panel: radial number density profiles of galaxies. The background density profile (magenta squares) shows a decrease in the central region; overplotted is the magnification effect expected for a NFW profile. |
The background population was selected according to the following criteria:
-
galaxies with: 24.5 <r< 26.5 mag;
-
or: d< 0, 21.8 <r< 24.5 mag, i−z> 0.1;
-
or: d ≥ 0, 21.5 <r< 24.5 mag, i−z< −0.3.
The foreground and the cluster member populations were identified according to these criteria:
-
foreground galaxies:d ≥ 0, 21.0 <r< 24.5 mag, −0.1 <i−z< 0.1;
-
cluster member galaxies: d ≥ 0, r< 23.5 mag, 0.65 <g−r< 2.0, 0.1 <i−z< 0.5.
The total sample of background galaxies is represented with magenta dots in Fig. 7 (upper panel), while foreground and cluster galaxies are marked with green and orange dots, respectively. Radial number density profiles for each identified population are shown in Fig. 7 (bottom panel). The radial number density profiles for cluster member sources (orange triangles) indicate a clear identification of the cluster member population as shown by the high clustering at small radii. As expected, the foreground population (green diamonds) appears uniformly distributed. The background sample (magenta squares) shows a drop in number counts towards the cluster centre, which is expected owing to the so-called magnification bias (Broadhurst et al. 2008). Also displayed in Fig. 7 is the depletion in counts expected for a Navarro-Frenk-White profile (Navarro et al. 1996, hereafter NFW) with the parameters derived by the weak lensing analysis in Sect. 5.4, showing good consistency with the observations.
Using the photo-z derived by Ilbert et al. (2009), we extracted the redshift distribution of the COSMOS galaxies with colour and magnitude cuts describing the background population needed for the evaluation of the critical density in the weak lensing analysis as described in Sect. 5.4.
 |
Fig. 8 r-band luminosity-weighted map in the PLCKG100 field. The overplotted contour lines are the weak lensing S-map showing the mass distribution derived by weak lensing, at levels σ = 3, 4.5, 6, 8.5. The cross marks the position of the BCG assumed as the centre of the halo. |
5.3. Simulations
The ellipticities derived from most of the available shape measurement algorithms are affected (see Heymans et al. 2006, and references therein) by a multiplicative (m) and an additive (c) bias defined as eobs−etrue = metrue + c. The value of m depends on the PSF type, as well as on the brightness and size of the galaxies, and in the case of KSB it is typically around 10−20% (Heymans et al. 2006).
To investigate this, we produced simulations using the GalSim7 software (Rowe et al. 2015), which was specifically designed to simulate sheared galaxies within the GREAT effort (see Mandelbaum et al. 2014, and references therein). GalSim offers the possibility of using both analytic models for the galaxies, and/or a sample of 260 000 real galaxies from Hubble Space Telescope COSMOS data. In addition, it can take as input the model produced by PSFex, and hence can produce an image with the same PSF shape and spatial variations as the real image. We built our simulations so that ellipticities were measured on individual stamps of sheared galaxies in order to avoid the effect of blending from neighbour sources.
To evaluate the bias, we first produced images with constant shear values, g = 0.01,0.05,0.1,0.15,0.2, for each ellipticity component. We randomly drew 10 000 galaxies from the full sample, and repeated the simulation ten times. For each shear value, we then verified that the expected input value could be recovered, and we evaluated the bias as a function of signal-to-noise ratio, as well as at different positions in the image to check for systematics related to a poor PSF correction. From these tests, we derived a multiplicative bias m = 10%, and no significant additive bias; we were not able to detect a significant dependence on the signal-to-noise ratio.
Secondly, we used GalSim to simulate the shear signal produced by a cluster having a NFW profile with redshift, virial mass (M ~ 1015h-1M⊙), and concentration parameter (c200 = 4) similar to the values we find here for PLCK-G100. We made ten such simulations and fitted the results in the same way as in Sect. 5.4, where the only free parameter was the mass, and the concentration parameter was set to the input value of the simulation. The mass obtained applying the multiplicative bias was M200 = (1.0 ± 0.2) × 1015h-1M⊙.
 |
Fig. 9 Shear profile detected for PLCKG100 (tangential and cross components, where the latter is expected to be null), and for comparison the values derived adopting the best-fit models. We indicate with mnfw the model obtained using the Duffy et al. (2008) relation and with nfw the model obtained keeping both Mvir and cvir as free parameters. |
5.4. Mass estimate
For the weak lensing analysis we used the sources in the catalogue satisfying the following criteria: (i) classified as extended (Sect. 3); (ii) with Pγ> 0.1, SNe > 10; e1iso, e2iso < 1; and (iii) outside regions masked by bad columns, haloes, or spikes near bright saturated stars. We further considered only those sources classified as background galaxies in Sect. 5.2. This produced a catalogue of 17 000 sources in a 0.227 sq. deg area, corresponding to a density of 21 gals arcmin-2.
Best-fit NFW parameters, at different overdensities, derived taking the two brightest galaxies as centre (n = 1,2).
We first extracted (Fig. 8) the S-map (see Huang et al. 2011, and references therein), showing the spatial distribution of the weak lensing signal. The peak is consistent with the position of the galaxy that we identified as the BCG of the cluster in Sect. 4. We therefore took this position as the centre of the cluster, and used it to compute the cross and tangential components of the ellipticities whose profiles are displayed in Fig. 9.
Computing the mass from the shear requires an estimate of the critical surface density, 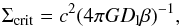 (8)where β = Dls/Ds; Dls, Ds, and Dl are the angular distances between lens and source, observer and source, and observer and lens, respectively. Since we have no spectroscopic training set, we are not able to judge the reliability of our photometric redshifts for the lensed background galaxies. We therefore adopted the approximation of a constant β for all galaxies. This introduces an overestimate of the average shear by a factor
(8)where β = Dls/Ds; Dls, Ds, and Dl are the angular distances between lens and source, observer and source, and observer and lens, respectively. Since we have no spectroscopic training set, we are not able to judge the reliability of our photometric redshifts for the lensed background galaxies. We therefore adopted the approximation of a constant β for all galaxies. This introduces an overestimate of the average shear by a factor 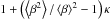 ~ 1 + 0.2κ at z = 0.36, as discussed in Hoekstra et al. (2000). The correction of this bias is included in our mass estimate. As described in Sect. 5.2, the value of ⟨β⟩ was computed using the photometric redshifts from the COSMOS sample, applying the colour and magnitude cuts adopted for the selection of background galaxies. We find ⟨β⟩ = 0.54, equivalent to assuming that all galaxies lie at the same redshift zs = 1.04.
~ 1 + 0.2κ at z = 0.36, as discussed in Hoekstra et al. (2000). The correction of this bias is included in our mass estimate. As described in Sect. 5.2, the value of ⟨β⟩ was computed using the photometric redshifts from the COSMOS sample, applying the colour and magnitude cuts adopted for the selection of background galaxies. We find ⟨β⟩ = 0.54, equivalent to assuming that all galaxies lie at the same redshift zs = 1.04.
The shear profile was first fitted assuming a NFW halo and using the analytical expression for the shear given by Wright & Brainerd (2000): a maximum likelihood fitting approach was adopted (Radovich et al. 2008; Huang et al. 2011). In order to see how the mass estimate is affected by the assumption on the cluster centre and on the model fitting parameters, we performed different tests: (a) selecting both of the two brightest galaxies as the cluster centre (n = 1,2), and (b) trying both a two-parameter fit (virial mass Mvir and concentration cvir), and by assuming a relation between Mvir, cvir and the cluster redshift zcl. In the latter case, we first used the relation in Duffy et al. (2008), 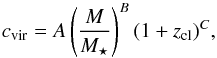 (9)with M⋆ = 2. × 1012/hM⊙, A = 7.85, B = −0.081, and C = −0.71. Then, we adopted the c−M−z relations discussed in Meneghetti et al. (2014, see their Table 2). These were based on numerical simulations of halos at different redshifts and halo relaxation states, undertaken for the analysis of the CLASH cluster sample. We used their 2D relations derived for NFW models for all halos, relaxed halos, and super-relaxed halos. The results are given in Table 2. The differences in the fitted parameters are within the uncertainties, with a slightly higher mass derived for n = 1.
(9)with M⋆ = 2. × 1012/hM⊙, A = 7.85, B = −0.081, and C = −0.71. Then, we adopted the c−M−z relations discussed in Meneghetti et al. (2014, see their Table 2). These were based on numerical simulations of halos at different redshifts and halo relaxation states, undertaken for the analysis of the CLASH cluster sample. We used their 2D relations derived for NFW models for all halos, relaxed halos, and super-relaxed halos. The results are given in Table 2. The differences in the fitted parameters are within the uncertainties, with a slightly higher mass derived for n = 1.
 |
Fig. 10 Wavelet reconstructed X-ray image in the [0.5−2.5] keV energy band, obtained from the combination of the three XMM EPIC camera images. The contours show the weak lensing S-map (see Fig. 8), at levels σ = 3.5,5,7,9. The circle denotes the cluster centroid derived by the XMM analysis. The cross and square mark the position of the two brightest cluster galaxies (1 and 2, respectively, in the text). |
 |
Fig. 11 Radial profiles of the X-ray properties are displayed as follows. Top, left: surface brightness in the [0.5–2.5] keV range. Points and the solid line represent the measured data and the best–fit modified beta profile, respectively. Top, right: electron density. Solid line and grey area represent the best-fit model and the relative error, respectively. Bottom, left: measured temperature profile. Points and solid line represent measured data and the temperature profile, respectively. Bottom, right: 3D temperature profile. Solid line and grey area represent the best-fit model and the error, respectively. |
A model-independent estimate of the mass was then derived using the aperture densitometry method (see Huang et al. 2011, and references therein). This method provides an estimate of the projected 2D mass within a radius θm, M2D( ≤ θm). As discussed e.g. in Okabe et al. (2010), before comparing the aperture (2D) and the NFW (3D) mass we first need to evaluate the correction factor f(θm) = M2D( ≤ θm) /M3D( ≤ θm) > 1. To this end, we used again the analytical expression given by Wright & Brainerd (2000) to compute f(θm) for an NFW halo with the best–fit values of cvir, Mvir found above (first row in Table 2). We obtained f = 1.39 at r500 and f = 1.31 at rvir. The deprojected mass values are 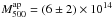 M⊙ and
M⊙ and 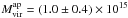 M⊙.
M⊙.
The mass derived by weak lensing can be affected by the presence of large-scale structures along the line of sight (Hoekstra 2003; Hoekstra et al. 2011). According to Figs. 6 and 7 in Hoekstra (2003), this uncertainty is of the order of ~ 2 × 1014h-1M⊙ for a cluster with M = 1015M⊙ at z ~ 0.4, θmax = 15 arcmin, which is comparable to the uncertainties derived in the fitting listed in Table 2.
 |
Fig. 12 Radial mass profile derived from the X-ray data, where the hydrostatic mass profile and uncertainties are shown by the solid line and the grey area. Error bars represent the 1σ uncertainties described in the text. Also shown are the mass profiles derived from the WL analysis (dashed line: NFW fit; points with error bars: aperture densitometry after deprojection). The inset shows M2500, M1000, M500, and Mvir derived from our XMM analysis (blue squares); the Planck analysis (green squares); WL NFW, first row in Table 2 (red triangles); WL, aperture densitometry (black circles): a small offset in radius is applied here for display purposes. |
6. X-ray analysis
PLCK G100.230.4 was observed for with the XMM-Newton (obs-ID 0656202301) European Photon Imaging Cameras (EPIC) during the follow-up campaign of Planck newly detected clusters. This dataset was re-processed using the XMM-Newton Science Analysis System (SAS) version 14.0.0 in order to select the relevant calibration files. To remove any flare contamination, i.e. observation periods with an unusual count rate, we applied a 3σ clipping and a temporal wavelet filter to the histogram of the photon arrival times, with a bin size of , in the energy band [1−5] and . After the flare removal procedure we find a useful exposure time of and for the two EPIC-MOS and the EPIC-PN datasets, respectively. To prepare the following imaging and spectroscopy analyses, we rebinned the flare-cleaned list of photon events in sky coordinates and energy, and associated both a 3D effective exposure and a background noise model to this data cube (see details in Bourdin & Mazzotta 2008).
The background noise was modelled after subtraction of all detected point-like sources using two components: the instrumental noise caused by high-energy particles interacting with the detectors, and several astrophysical components, namely the cosmic X-ray background (CXB) (e.g. Giacconi et al. 2001) plus a diffuse emission of Galactic origin (e.g. Snowden et al. 1995). For the instrumental component we used an analytical model inspired by the works of Kuntz & Snowden (2008) and Leccardi & Molendi (2008), which holds for each EPIC camera a continuum plus several fluorescence lines (see details in Bourdin et al. 2013). As proposed by Kuntz & Snowden (2000), the Galactic foreground was modelled using two absorbed APEC (Smith et al. 2001) spectra, with temperatures of and , respectively. The unresolved CXB spectrum follows a power law with Γ = 1.42 (Lumb et al. 2002). The particle background was normalized in order to match the count rates of each camera outside the target region and in the hard energy band of . The normalization of each astrophysical component was determined using a joint spectral fit outside any cluster emission in the same region where the particle background was normalized.
From the cleaned data we produced an image in the , which is background subtracted and corrected for any spatial variation of the effective area. From this image we determined the X-ray peak at (RA = 350.56228, Dec = 28.52041). Figure 10 shows a wavelet denoising of this image. As we can see from this figure, the X-ray peak (circle) lies within 5″ of the galaxy that we assumed to be the BCG (cross), whereas the second brightest galaxy is 18″ away. It is worth noting that there is also a good agreement between the direction of the elongation of the cluster, going from NE to SW, as seen by the X-ray image and the isocontours from the lensing analysis.
From the photon image we then extracted a point-source excised surface brightness profile, centred on the cluster X-ray peak. In Fig. 11, top left panel, we show this surface brightness profile, which we found to reach the background level at . The temperature profile, shown in Fig. 11, bottom left panel, was extracted in four bins from the same circular region as the surface brightness. The temperature was measured in each bin by fitting the spectrum in the energy band using an absorbed APEC thermal model with three parameters, namely the normalization, temperature, and metallicity. The thermal models were convolved by the instrument response, as described in detail in Bourdin & Mazzotta (2008). The atomic hydrogen column density was fixed to its Galactic value (Dickey & Lockman 1990).
To measure the X-ray mass we followed the “forward” procedure described in Meneghetti et al. (2010) and Rasia et al. (2012). In short, analytic profiles of the gas density and temperature Vikhlinin et al. (2006) were projected using the spectroscopic-like temperature Mazzotta et al. (2004) and fitted to the observed surface brightness and projected temperature. The 3D information were then folded into the hydrostatic mass equation (e.g. Sarazin 1988 or Ettori et al. 2013). The confidence envelopes of the 3D profiles in Fig. 12 were computed following a Monte Carlo procedure. More specifically, we generated several realizations of both a Poisson distributed surface brightness profile and a Gaussian distributed temperature profile, which hold the mean values and variances of the derived data quantities. For each of these realizations we fitted a new set of density and 3D temperature profiles, and stored these models when they obeyed the physical prior that the underlying hydrostatic mass profile is increasing and positive. From N = 500 remaining hydrostatic density, 3D temperature, and mass models, we drew the confidence envelopes that encompass 68% of the realizations with minimal distance to their relative best fit. The envelope of the mass profile allowed us to derive a cluster mass of 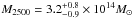 ,
, 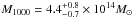 , and
, and 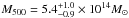 , which corresponds to , , and , respectively. The latter mass value is in excellent agreement with the mass derived from the iteration of the M500 - YX relation, M500 = (5.60 ± 0.22) × 1014M⊙ (Planck Collaboration IX 2011).
, which corresponds to , , and , respectively. The latter mass value is in excellent agreement with the mass derived from the iteration of the M500 - YX relation, M500 = (5.60 ± 0.22) × 1014M⊙ (Planck Collaboration IX 2011).
Figure 12 also shows a comparison of the X-ray total mass profile with those obtained from WL aperture mass densitometry and WL NFW model fitting (obtained with two free parameters). The inset shows the various mass estimates at density contrasts of 2500, 1000, and 500. The agreement between the different mass measurements is remarkably good at all density contrasts.
Planck Collaboration XX (2014) parameterized the difference between their mass estimate and the true mass by the factor (1−b), where b contains all possible sources of bias: neglect of the non-thermal pressure support in the hydrostatic assumption, multi-temperature structure in the ICM, instrumental calibration uncertainties, etc. Assuming a weak lensing reconstructed mass of M500,WL ~ (7 ± 1) × 1014M⊙ and comparing this to the mass estimate obtained by Planck Collaboration IX (2011), we obtain (1-b) = 0.8 ± 0.1 from the present observations.
Planck Collaboration XX (2014) obtained a bias factor of (1−b) = 0.8 from their calibration of b using numerical simulations, and used this value, with a flat prior of [0.7,1.0], as the baseline for their cosmological analysis. Planck Collaboration XXIV (2015) have updated this analysis to include a calibration of (1−b) using weak lensing mass measurements, taking into account sources of scatter such as triaxiality, the presence of subtructures, and systematic errors in the weak lensing measurement itself. Assuming the weak lensing mass to be the true mass, their analysis yields (1−b)WtG = 0.69 ± 0.07 and (1−b)CCCP = 0.78 ± 0.09 for the samples of von der Linden et al. (2014, Weighing the Giants) and Hoekstra et al. (2015, Canadian Cluster Cosmology Project), respectively. Under the same assumption, the value we obtain from PLCKG100 is compatible within 1σ with the bias factor derived from these updated measurements.
7. Summary and conclusions
We presented here the first weak lensing analysis of the PLCK G100.2-30.4 cluster. The analysis confirmed that this is a massive cluster (Mvir> 1015M⊙), in agreement with the value expected from the richness estimate.
At a density contrast of 500 with respect to the critical density of the Universe at the cluster redshift, the weak lensing mass from aperture densitometry is 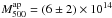 M⊙ after deprojection. An NFW fit in the radial range 1−15 arcmin, shown by the dotted line in Fig. 12, yields a mass M500 ~ (7 ± 1) × 1014M⊙. We checked the robustness of the weak lensing mass estimates by repeating the analysis with different choices of the cluster centre and of the NFW model fitting. In particular, we compared the results obtained by leaving both cvir and Mvir as free parameters, and using different (c,M,z) relations. These yield results consistent with those given above.
M⊙ after deprojection. An NFW fit in the radial range 1−15 arcmin, shown by the dotted line in Fig. 12, yields a mass M500 ~ (7 ± 1) × 1014M⊙. We checked the robustness of the weak lensing mass estimates by repeating the analysis with different choices of the cluster centre and of the NFW model fitting. In particular, we compared the results obtained by leaving both cvir and Mvir as free parameters, and using different (c,M,z) relations. These yield results consistent with those given above.
Comparing the mass derived by weak lensing with the value obtained by the reanalysis of XMM data, we obtain a bias factor of (1−b) = 0.8 ± 0.1. This is compatible within 1σ with the bias factor obtained by Planck Collaboration XXIV (2015) from their calibration of (1−b) using newly available weak lensing samples from von der Linden et al. (2014) and Hoekstra et al. (2015). The present results illustrate the importance of high-quality data and the need for larger samples in such cluster mass studies.
Acknowledgments
We thank the referee for the helpful comments that improved the paper. We acknowledge financial contributions from: contract ASI/INAF I/023/12/0 (L.M., M.R., M.M.); PRIN INAF 2009 “Weighing galaxy clusters with strong and weak lensing” (M.R., M.M.); PRIN MIUR 2010-2011 “The dark Universe and the cosmic evolution of baryons: from current surveys to Euclid” (LM, MR,MM); PRIN INAF 2012 “The Universe in the box: multiscale simulations of cosmic structure” (L.M.); contracts ASI-INAF I/009/10/0 and PRIN-INAF 2012 “A unique dataset to address the most compelling open questions about X-Ray Galaxy Clusters” (S.E.). M.R. also acknowledges Prof. P. Benvenuti (Department of Physics and Astronomy, University of Padova), for having made available his computing facilities.
References
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Applegate, D. E., von der Linden, A., Kelly, P. L., et al. 2014, MNRAS, 439, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergé, J., Price, S., Amara, A., & Rhodes, J. 2012, MNRAS, 419, 2356 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E. 2010, Astrophysics Source Code Library [record ascl : 1010.068] [Google Scholar]
- Bertin, E. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 435 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourdin, H., & Mazzotta, P. 2008, A&A, 479, 307 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourdin, H., Mazzotta, P., Markevitch, M., Giacintucci, S., & Brunetti, G. 2013, ApJ, 764, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T., Umetsu, K., Medezinski, E., Oguri, M., & Rephaeli, Y. 2008, ApJ, 685, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Ettori, S., Donnarumma, A., Pointecouteau, E., et al. 2013, Space Sci. Rev., 177, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmann, R., Carollo, C. M., Porciani, C., et al. 2006, MNRAS, 372, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Formicola, I., Radovich, M., Meneghetti, M., et al. 2014, MNRAS, submitted [Google Scholar]
- Girardi, L., Groenewegen, M. A. T., Hatziminaoglou, E., & da Costa, L. 2005, A&A, 436, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, L., Barbieri, M., Groenewegen, M. A. T., et al. 2012, in Astrophys. Space Sci. Proc., eds. A. Miglio, J. Montalbán, & A. Noels, 165 [Google Scholar]
- Giacconi, R., Rosati, P., Tozzi, P., et al. 2001, ApJ, 551, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Gruen, D., Brimioulle, F., Seitz, S., et al. 2013, MNRAS, 432, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Van Waerbeke, L., Bacon, D., et al. 2006, MNRAS, 368, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H. 2003, MNRAS, 339, 1155 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Franx, M., Kuijken, K., & Squires, G. 1998, ApJ, 504, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Franx, M., & Kuijken, K. 2000, ApJ, 532, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Hartlap, J., Hilbert, S., & van Uitert, E. 2011, MNRAS, 412, 2095 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z., Radovich, M., Grado, A., et al. 2011, A&A, 529, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Capak, P., Salvato, M., et al. 2009, ApJ, 690, 1236 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Smith, J. A., Miknaitis, G., et al. 2007, AJ, 134, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Kitching, T. D., Balan, S. T., Bridle, S., et al. 2012, MNRAS, 423, 3163 [NASA ADS] [CrossRef] [Google Scholar]
- Kitching, T. D., Rowe, B., Gill, M., et al. 2013, ApJS, 205, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntz, K. D., & Snowden, S. L. 2000, ApJ, 543, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Kuntz, K. D., & Snowden, S. L. 2008, A&A, 478, 575 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lumb, D. H., Warwick, R. S., Page, M., & De Luca, A. 2002, A&A, 389, 93 [Google Scholar]
- Luppino, G., & Kaiser, N. 1997, ApJ, 475, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Mahdavi, A., Hoekstra, H., Babul, A., & Henry, J. P. 2008, MNRAS, 384, 1567 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Rowe, B., Bosch, J., et al. 2014, ApJS, 212, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2010, MNRAS, 406, 1759 [NASA ADS] [Google Scholar]
- Mazzotta, P., Rasia, E., Moscardini, L., & Tormen, G. 2004, MNRAS, 354, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Medezinski, E., Broadhurst, T., Umetsu, K., et al. 2010, MNRAS, 405, 257 [NASA ADS] [Google Scholar]
- Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meneghetti, M., Rasia, E., Vega, J., et al. 2014, ApJ, 797, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, S., Komiyama, Y., Sekiguchi, M., et al. 2002, PASJ, 54, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Takada, M., Umetsu, K., Futamase, T., & Smith, G. P. 2010, PASJ, 62, 811 [NASA ADS] [Google Scholar]
- Ouchi, M., Shimasaku, K., Okamura, S., et al. 2004, ApJ, 611, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2011, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2015, A&A, submitted [arXiv:1502.01597] [Google Scholar]
- Popesso, P., Böringher, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radovich, M., Arnaboldi, M., Ripepi, V., et al. 2004, A&A, 417, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radovich, M., Puddu, E., Romano, A., Grado, A., & Getman, F. 2008, A&A, 487, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rasia, E., Meneghetti, M., Martino, R., et al. 2012, New J. Phys., 14, 055018 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, A., Fu, L., Giordano, F., et al. 2010, A&A, 514, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowe, B., Jarvis, M., Mandelbaum, R., et al. 2015, Astron. Comput., 10, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Rozo, E., Rykoff, E. S., Koester, B. P., et al. 2009, ApJ, 703, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Sarazin, C. L. 1988, X-ray emission from clusters of galaxies (Cambridge: Cambridge University Press) [Google Scholar]
- Schlegel, D., Finkbeiner, D., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. K., Brickhouse, N. S., Liedahl, D. A., & Raymond, J. C. 2001, ApJ, 556, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Freyberg, M. J., Plucinsky, P. P., et al. 1995, ApJ, 454, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2014, ApJ, 795, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A., Forman, W., et al. 2006, ApJ, 640, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Vikhlinin, A., Kravtsov, A. V., Burenin, R. A., et al. 2009, ApJ, 692, 1060 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, C. O., & Brainerd, T. G. 2000, ApJ, 534, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Yagi, M., Kashikawa, N., Sekiguchi, M., et al. 2002, AJ, 123, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y.-Y., Okabe, N., Finoguenov, A., et al. 2010, ApJ, 711, 1033 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Best-fit NFW parameters, at different overdensities, derived taking the two brightest galaxies as centre (n = 1,2).
All Figures
 |
Fig. 1 Composite gri image of the inner 400″ × 400″ region of the PLCKG100 field. |
| In the text | |
 |
Fig. 2 Zoom of the inner 100″ × 100″ region of the PLCKG100 field. Labels mark the ten brightest galaxies. Several strong lensing gravitational arcs are visible. |
| In the text | |
 |
Fig. 3 Stellar colours (top: i−z vs. g−r; bottom: r−i vs. g−r): measured data (red dots) are compared to the values obtained by TRILEGAL (green dots). |
| In the text | |
 |
Fig. 4 r vs. g−r colour plot of galaxies in the field. Galaxies classified as likely cluster members from their colours are plotted as green dots; the red dot is the BCG galaxy. The best fitting red sequence line is overplotted. |
| In the text | |
 |
Fig. 5 PSF anisotropy correction: the first three panels show the ellipticity pattern (measured, derived from the PSFex model, and corrected (eaniso); X and Y are in pixels). The scale is given by the arrows in the middle (e = 0.1). In the last panel, blue and red dots are the values of eaniso derived from real stars and from the PSFex model, respectively; green dots are the values after the correction. |
| In the text | |
 |
Fig. 6 Average tangential PSF ellipticity at different distances from the cluster centre, before (black triangles) and after (red circles) the anisotropy correction. The shaded area is plotted at |
| In the text | |
 |
Fig. 7 Selection in CC space. Upper panel: CC diagram for PLCK G100 galaxies. Cluster members are shown with orange dots, and foreground and background galaxies with green and magenta dots, respectively. Unclassified sources are plotted with black dots. Bottom panel: radial number density profiles of galaxies. The background density profile (magenta squares) shows a decrease in the central region; overplotted is the magnification effect expected for a NFW profile. |
| In the text | |
 |
Fig. 8 r-band luminosity-weighted map in the PLCKG100 field. The overplotted contour lines are the weak lensing S-map showing the mass distribution derived by weak lensing, at levels σ = 3, 4.5, 6, 8.5. The cross marks the position of the BCG assumed as the centre of the halo. |
| In the text | |
 |
Fig. 9 Shear profile detected for PLCKG100 (tangential and cross components, where the latter is expected to be null), and for comparison the values derived adopting the best-fit models. We indicate with mnfw the model obtained using the Duffy et al. (2008) relation and with nfw the model obtained keeping both Mvir and cvir as free parameters. |
| In the text | |
 |
Fig. 10 Wavelet reconstructed X-ray image in the [0.5−2.5] keV energy band, obtained from the combination of the three XMM EPIC camera images. The contours show the weak lensing S-map (see Fig. 8), at levels σ = 3.5,5,7,9. The circle denotes the cluster centroid derived by the XMM analysis. The cross and square mark the position of the two brightest cluster galaxies (1 and 2, respectively, in the text). |
| In the text | |
 |
Fig. 11 Radial profiles of the X-ray properties are displayed as follows. Top, left: surface brightness in the [0.5–2.5] keV range. Points and the solid line represent the measured data and the best–fit modified beta profile, respectively. Top, right: electron density. Solid line and grey area represent the best-fit model and the relative error, respectively. Bottom, left: measured temperature profile. Points and solid line represent measured data and the temperature profile, respectively. Bottom, right: 3D temperature profile. Solid line and grey area represent the best-fit model and the error, respectively. |
| In the text | |
 |
Fig. 12 Radial mass profile derived from the X-ray data, where the hydrostatic mass profile and uncertainties are shown by the solid line and the grey area. Error bars represent the 1σ uncertainties described in the text. Also shown are the mass profiles derived from the WL analysis (dashed line: NFW fit; points with error bars: aperture densitometry after deprojection). The inset shows M2500, M1000, M500, and Mvir derived from our XMM analysis (blue squares); the Planck analysis (green squares); WL NFW, first row in Table 2 (red triangles); WL, aperture densitometry (black circles): a small offset in radius is applied here for display purposes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.