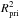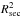| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 26 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201526229 | |
| Published online | 16 June 2015 | |
Search with UVES and X-Shooter for signatures of the low-mass secondary in the post common-envelope binary AA Doradus⋆,⋆⋆,⋆⋆⋆
1 Institute for Astronomy and Astrophysics, Kepler Center for Astro and Particle Physics, Eberhard Karls University, Sand 1, 72076 Tübingen, Germany
e-mail: rauch@astro.uni-tuebingen.de
2 Hamburger Sternwarte, Gojenbergsweg 112, 21029 Hamburg, Germany
3 NASA Goddard Space Flight Center, Greenbelt, MD 20771, USA
Received: 31 March 2015
Accepted: 25 April 2015
Context. AA Dor is a close, totally eclipsing, post common-envelope binary with an sdOB-type primary star and an extremely low-mass secondary star, located close to the mass limit of stable central hydrogen burning. Within error limits, it may either be a brown dwarf or a late M-type dwarf.
Aims. We aim to extract the secondary’s contribution to the phase-dependent composite spectra. The spectrum and identified lines of the secondary decide on its nature.
Methods. In January 2014, we measured the phase-dependent spectrum of AA Dor with X-Shooter over one complete orbital period. Since the secondary’s rotation is presumable synchronized with the orbital period, its surface strictly divides into a day and night side. Therefore, we may obtain the spectrum of its cool side during its transit and of its hot, irradiated side close to its occultation. We developed the Virtual Observatory (VO) tool TLISA to search for weak lines of a faint companion in a binary system. We successfully applied it to the observations of AA Dor.
Results. We identified 53 spectral lines of the secondary in the ultraviolet-blue, visual, and near-infrared X-Shooter spectra that are strongest close to its occultation. We identified 57 (20 additional) lines in available Ultraviolet and Visual Echelle Spectrograph (UVES) spectra from 2001. The lines are mostly from C ii-iii and O ii, typical for a low-mass star that is irradiated and heated by the primary. We verified the orbital period of P = 22 597.033201 ± 0.00007 s and determined the orbital velocity 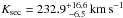 of the secondary. The mass of the secondary is
of the secondary. The mass of the secondary is 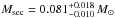 and, hence, it is not possible to reliably determine a brown dwarf or an M-type dwarf nature.
and, hence, it is not possible to reliably determine a brown dwarf or an M-type dwarf nature.
Conclusions. Although we identified many emission lines of the secondary’s irradiated surface, the resolution and signal-to-noise ratio of our UVES and X-Shooter spectra are not good enough to extract a good spectrum of the secondary’s nonirradiated hemisphere.
Key words: stars: abundances / binaries: eclipsing / stars: low-mass / stars: individual: AA Dor / virtual observatory tools
Based on observations collected at the European Southern Observatory, Chile, programs 066.D-1800 and 092.C-0692.
Figures 2–5, 9, and Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
AA Dor (CPD−69°389, HD 269696, LB 3459) was discovered to be a close, short-period, totally eclipsing binary (Kilkenny et al. 1978) with an inclination of 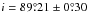 (Hilditch et al. 2003). It is a post common-envelope system (Schreiber & Gänsicke 2003) with a sdOB-type primary star and a low-mass companion (Rauch 2004). Its orbital period P = 0.261 539 7363(4) d (constant at a level of about 10-14 d per orbit) was determined by Kilkenny (2011) with high accuracy from the light curve, using eclipses from 1977 to 2010.
(Hilditch et al. 2003). It is a post common-envelope system (Schreiber & Gänsicke 2003) with a sdOB-type primary star and a low-mass companion (Rauch 2004). Its orbital period P = 0.261 539 7363(4) d (constant at a level of about 10-14 d per orbit) was determined by Kilkenny (2011) with high accuracy from the light curve, using eclipses from 1977 to 2010.
AA Dor belongs to the class of HW Vir-type variables. These are eclipsing binaries consisting of a B-type subdwarf star and a late M-type star. They experienced a common-envelope phase when the primary star evolved through a red-giant phase. Their orbital periods are generally short (P ≈ 0.1 d, Heber 2009). They are of great importance because eclipsing binaries allow precise mass determinations. Presently, we know more than 15 of these systems (Ritter & Kolb 2003; Almeida et al. 2012; Barlow et al. 2013; Schaffenroth et al. 2013, 2014, 2015). Yet another sdOB-type member was discovered (NSVS 14256825, Almeida et al. 2012). AA Dor is of special importance because it is one of the hottest members with one of the longest periods. It is one of the brightest (mV = 11.138) and, hence, best-studied HW Vir-type binaries.
AA Dor is a precataclysmic variable (Ritter 1986) and, thus, stringent constraints for the mass of the low-mass secondary, just at the limit of the hydrogen-burning mass, and its angular momentum are a prerequisite for reliable common-envelope modeling, especially the ejection mechanism (Livio & Soker 1984) and predictions of the evolution of AA Dor. Therefore, it is a key object for understanding common-envelope evolution.
Several spectral analyses by means of nonlocal thermodynamic equilibrium (NLTE) model atmospheres were performed, and the primary star of AA Dor (LB 3459) turned out to be one of the hottest sdOB stars (, Rauch 2000; Fleig et al. 2008). These analyses showed a discrepancy in the surface gravity that was derived by radial-velocity and light-curve analyses (Hilditch et al. 2003), log (g/ cm/s2) = 5.30 ± 0.1 and log g = 5.53 ± 0.03, respectively.
Since Vučković et al. (2008) for the first time identified spectral lines of the secondary in spectra obtained with the Ultraviolet and Visual Echelle Spectrograph (UVES1) at the European Southern Observatory (ESO) and determined a lower limit (Ksec ≥ 230 ± 10 km s-1) of its radial velocity amplitude, both components’ masses are known (Mpri = 0.45 M⊙, Msec = 0.076 M⊙), however, with rather large error bars. Müller et al. (2010) considered that, because of the refection effect, this measured Ksec comes from the outer edge of the stellar disk. They applied the stellar radius from Rauch (2000, Rsec = 0.135 R⊙ to shift the determined emission radius to the stellar center and used Ksec = 240 ± 20 km s-1 to calculate the stellar masses. With Kpri = 40.15 ± 0.11 km s-1, they derived 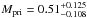 M⊙ and
M⊙ and 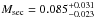 M⊙.
M⊙.
We recently performed an NLTE spectral analysis of the primary (Klepp & Rauch 2011), where we used a lower rotational velocity of vrot = 30 km s-1 (Müller et al. 2010; Geier et al. 2010) than before (35 km s-1, Fleig et al. 2008). With improved model atmospheres and improved Stark line-broadening tables for H i lines (Tremblay & Bergeron 2009), we determined Teff = 42 000 ± 1000 K and log g = 5.46 ± 0.05. Thus, the gravity problem is solved. From our mass determination of Mpri = 0.4714 ± 0.0050 M⊙, in comparison with evolutionary tracks of post-extended horizontal branch (post-EHB) stars (Dorman et al. 1993), we calculated (MpriKpri = MsecKsec) the secondary’s mass to be Msec = 0.0725−0.0863 M⊙. Since the hydrogen-burning mass limit is about 0.075 M⊙ (Chabrier & Baraffe 1997; Chabrier et al. 2000), the secondary may be either a brown dwarf or a late M-type dwarf.
To make progress in our understanding of common-envelope evolution in general and to further constrain the secondary’s nature, we measure the secondary’s contribution to the composite spectrum of AA Dor, especially in the infrared and follow its spectral evolution during one complete orbital period. We therefore performed phase-dependent spectroscopy with X-Shooter2 (Vernet et al. 2011) since this contribution is of the order of a few percent (Fleig et al. 2008) and, thus, a very high signal-to-noise ratio (S/N) of the observed spectra is required for its detection.
In Sect. 2, we briefly describe our new X-Shooter observations and the UVES data used by Rauch & Werner (2003). We determine the orbital period in Sect. 3. We then revisit the sdOB primary (Sect. 4) and demonstrate how the recently determined surface gravity of Klepp & Rauch (2011) impacts the element abundance determination of Fleig et al. (2008). In Sect. 5, we turn to the secondary star of AA Dor and introduce the newly developed, registered Virtual Observatory (VO) tool Tübingen Line Identification and Spectrum Analyzer (TLISA), which is part of the Tübingen German Astrophysical Virtual Observatory (GAVO3) project. Its application to the X-Shooter and UVES spectra of AA Dor is described. In Sect. 6, we present our results for the orbit dimensions of AA Dor, as well as the masses and radii of its components. We summarize and conclude in Sect. 7.
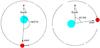 |
Fig. 1 Orbital location of the primary (light blue in the online version) and secondary (red) at the UVES (left) and X-Shooter (right) observation times. The start times of the two observation campaigns are indicated (HJD 2 451 917.5191833 and 2 456 665.5858551, respectively). The stars move counterclockwise. Dots mark the locations of the secondary at the start times of the individual observations. |
2. Observations
We took 105 UVES spectra (individual exposure times 180 s, 3743−4986 Å), which cover a complete orbital period (P = 0.26 d), on Jan. 8, 2001 (program 066.D-1800) at the Very Large Telescope/Unit Telescope 2 (VLT/UT2, Kueyen). The spectra were subject to the standard reduction provided by ESO. With a slit width of 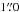 projected at the sky, a resolving power R ≈ 48 000 was achieved. The S/N of the single spectra is about 20−30. See Rauch & Werner (2003) for details.
projected at the sky, a resolving power R ≈ 48 000 was achieved. The S/N of the single spectra is about 20−30. See Rauch & Werner (2003) for details.
We obtained 300 X-Shooter spectra (in its three arms, UVB4, VIS5, and NIR6, each with 100 exposures of 160 s, 170 s, and 34 s, respectively) exactly 13 years later on Jan. 8, 2014 (program 092.C-0692) at the VLT/UT3 (Melipal). The observations of AA Dor started at 02:03 UT (air mass 1.4) and ended at 08:31 UT (air mass 2.3), just before morning twilight. The seeing7 was around 1′′ for much of the night but deteriorated greatly during the last two observation blocks (OBs), reaching almost 3′′ for the final OB (Roger Wesson, priv. comm.). We reduced this data with ESO’s Reflex Environment8 (version 2.6, downloaded Feb. 13, 2015, X-Shooter pipeline identifier 2.5.2). The S/N of the spectra is about 30−50.
Figure 1 displays the binary phases at the start times of the individual UVES and X-Shooter observations. Figures 2–5 show each individual spectrum of the UVES and X-Shooter observation campaigns. The X-Shooter spectra are compared with our best model for the primary (see Sect. 4). The synthetic spectrum is normalized to match the 2MASS Ks = 12.046 brightness. A reddening with EB−V = 0.08 is applied following the law of Fitzpatrick (1999, with RV = 3.1. The synthetic spectrum is convolved with a Gaussian to match the X-Shooter resolution.
3. Orbital period
Rauch & Werner (2003) determined an orbital period of P = 0.261 582 199(58) d from the He iiλ 4686 Å radial-velocity curve. This deviates (≈+ 0.016 %) from that of Kilkenny (2011, P = 0.261 539 7363(4) d measured from the light curve. Our X-Shooter data extended the timebase of the radial-velocity curve from 2535 days to 7283 days (including the measurements of Hilditch et al. 1996; Rauch & Werner 2003, and of FUSE observations in 2003 and 2004). We employed the Interactive Data Language (IDL9) to measure the Doppler shifts of He iiλ 4686 Å in the optical and determined those of C iii, O vi, Si iv, and P v lines in the far-ultraviolet (FUSE).
We used the TRIPP software package (Schuh et al. 2003; Geckeler et al. 2014) to determine the period (with T0 = 2 451 917.15269, the time of mid-transit, Rauch & Werner 2003). We confirmed Kilkenny’s light-curve solution (Fig. 6, P = 22 597.03320768 ± 0.0000691 s, Sect. 1).
We note that Fig. 4 of Rauch & Werner (2003) is incorrect. In its top panel, the data of Hilditch et al. (1996) is erroneously shown with an offset of +0.5 d, and the vrad values in the bottom panel have an incorrect sign. This explains the period deviation that was previously found (Sect. 1).
 |
Fig. 6 Comparison of radial-velocity measurements of AA Dor with a sine curve calculated with the period of P = 0.261 539 7363 d from the light-curve solution of Kilkenny (2011). Kpri = 40.15 km s-1 and T0 = 51917.15269 are from Müller et al. (2010) and Rauch & Werner (2003), respectively. From top to bottom, the panels show data from Hilditch et al. (1996), Rauch & Werner (2003, UVES), FUSE 2003, FUSE 2004, and our X-Shooter spectra. The measurements cover the time from Jan. 29, 1994, to Jan. 8, 2014. |
4. The primary
To disentangle the composite AA Dor spectra and to extract the secondary’s spectrum, we must subtract the primary’s contribution, considering its orbital motion, from all spectra. Therefore, we shifted all spectra to rest wavelengths, i.e., we applied a phase-dependent radial-velocity correction for the primary. Then, we coadded the spectra with the best S/N to achieve a master spectrum. The expected weak lines of the secondary smear out in this procedure and leave no detectable marks.
Since the primary’s master spectra (separately for UVES and X-Shooter) allowed us to verify the result of Klepp & Rauch (2011) for the surface gravity (log g = 5.46 ± 0.05), we decided to calculate a new grid of NLTE atmosphere models with our Tübingen NLTE Model-Atmosphere Package (TMAP10; Werner et al. 2003, 2012a; Rauch & Deetjen 2003) to investigate the impact of the higher log g on the photospheric abundances that were determined by Fleig et al. (2008), who used log g = 5.3. An indication that these abundances may be slightly different is the prominent Balmer-line problem (Napiwotzki & Rauch 1994; Rauch 2000, 2012) due to the underestimation of metal opacities (Bergeron et al. 1993; Werner 1996). The effect is apparently stronger at the higher log g (Klepp & Rauch 2011, their Fig. 5). Therefore the abundance determination was repeated. The H, He, C, N, O, Mg, Si, P, S, Fe, and Ni abundances were determined by spectral fits to ultraviolet observations obtained with the International Ultraviolet Explorer (IUE, cf. Rauch 2000) and the Far Ultraviolet Spectroscopic Explorer (FUSE, cf. Fleig et al. 2008) and to our UVES and X-Shooter spectra. Table 1 shows the adjusted abundance values. The errors are typically ± 0.2 dex. Significant deviations were found for Mg, Si, P, and Ni. They are not due to the higher log g but to an improved spectral fitting.
 |
Fig. 7 Comparison of synthetic profiles of H and He lines calculated from our models (, log g = 5.46) with our UVES observation (for clarity smoothed with a low-pass filter, Savitzky & Golay 1964). Left panel: abundances from Table 1, and Sc, Ti, V, Cr, Mn, and Co with solar abundances (Scott et al. 2015a). Right panel: similar model in the left panel, except the Sc, Ti, V, Cr, Mn, and Co abundances are artifically increased by a factor of 700. The vertical bar indicates 10% of the continuum flux. |
Photospheric abundances (mass fractions) of the primary of AA Dor, determined by Fleig et al. (2008, , log g = 5.30, denoted F and in this work (H, , log g = 5.46).
The Balmer-line problem, however, is still present at the same strength with the new, fine-tuned abundances. An additional model-atmosphere calculation with artificially increased (to 700 times solar, Scott et al. 2015a,b) iron-group (here Ca − Ni) abundances shows that the Balmer-line problem almost vanishes (Fig. 7). This corroborates the suggestion that missing metal opacities and, hence, cooling of the outer atmosphere are in general responsible for the Balmer-line problem. The real opacity source in AA Dor, however, is not known yet. On the one hand, the rotation of its primary (vrot = 30 km s-1, cf. Klepp & Rauch 2011) prohibits the detection of weak metal lines, and on the other hand, trans-iron-group elements (e.g., Werner et al. 2012b; Rauch et al. 2012, 2014a,b, 2015) have been totally neglected so far.
5. The secondary
Binary systems often reveal themselves by the sinusoidal movement of their components’ lines in trailed spectra (e.g., Maxted et al. 2000). Figure 8 shows a comparison of a synthetic and an observed “s-curve”. To search for lines of the AA Dor secondary, the primary’s master spectra (Sect. 4) are subtracted from the UVES and X-Shooter observations with a respective phase-dependent radial-velocity correction.
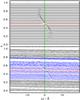 |
Fig. 8 Top: C iiλ 4267.09 Å line in a simulation (with an assumed Ksec = 230 km s-1). φ is the orbital phase. The transit (φ = 0.0) and the occultation (φ = 0.5) of the secondary are simulated. Bottom: same line in our X-Shooter observations. In the online version, the red spectra show the occultation of the secondary. In the blue spectra, C iiλ 4267.09 Å is prominent. The vertical (green) bar indicates the rest wavelength of the line. |
To make the application of the s-curve method easier, we have created a tool (Sect. 5.1) that even detects weak s-curves and that measures the orbital period and velocity amplitude via this sensitive visual method.
5.1. The new GAVO tool TLISA
In the framework of the Tübingen GAVO project, we developed the Tübingen Line Identification and Spectrum Analyzer (TLISA) tool that evaluates spectra and visualizes them. The first module, SEarch for Faint Objects in Binary Systems (SEFOBS), allows us to correct for orbital phase and velocity amplitude. Its sensitivity, i.e., the detection limit for lines is demonstrated in Fig. 9.
TLISA is a java11 tool that can be retrieved freely in its desktop version12. Our X-Shooter UVB spectra are provided there as a test data package. A brief description of TLISA is given in Appendix A. Screenshots of the TLISA SEFOBS input and analyzer windows are shown in Figs. A.1–A.3.
5.2. Search for spectral signatures
We applied TLISA to our UVES and X-Shooter data. Two representative examples for a successful search of a relatively strong and comparatively weak lines in the UVES data are shown in Figs. 10 and 11, respectively. In total, we identified 73 spectral lines that stem from the secondary. For their unambiguous assignment, we calculated TMAP models (, log g = 5.0), which included H and one metal (C, N, or O) at solar abundance (Asplund et al. 2009), with atomic data from the Tübingen Model-Atom database (TMAD13). Although the parameters do not represent the secondary, they are well suited for identification purposes. In particular, we modeled the multiplet line patterns precisely. Table 3 shows the identified lines. We indicate lines that we did not include in our models due to limited model atoms, but are found in the National Institute of Standards and Technology (Kramida et al. 2014) atomic spectra database. The identification plots for the UVES and X-Shooter UVB, VIS, and NIR spectra are visible in Appendices B, C, D, and E, respectively.
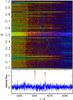 |
Fig. 10 Top: section of the secondary’s phase-dependent UVES spectra (4245 Å ≤ λ ≤ 4285 Å). Bottom: single spectrum (2001-01-08T00-53-54.965 UT) in the secondary’s rest frame in the respective wavelength interval; “unid.” denotes unidentified lines. |
Radial-velocity amplitudes for selected lines of the secondary.
It is worthwhile to note that neither Rauch & Werner (2003) nor Rucinski (2009, and priv. comm.) succeeded in a search for lines of the secondary. Vučković et al. (2008) identified more than 20 narrow emission lines, mainly of C ii and O ii and broad Balmer emission lines with core absorption (Table 3 indicates those explicitly mentioned by the authors). All these groups had the same UVES data at their disposal.
We used TLISA to determine the radial-velocity amplitude of the secondary and arrived at an average of 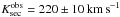 . To control the quality of this graphical method, we used the image reduction and analysis facility (IRAF14) to measure the wavelengths shifts for selected lines in all spectra (Table 2). We measured instrument-average values of
. To control the quality of this graphical method, we used the image reduction and analysis facility (IRAF14) to measure the wavelengths shifts for selected lines in all spectra (Table 2). We measured instrument-average values of 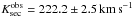 and
and 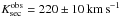 (1σ errors) from the UVES and X-Shooter UVB data. In the X-Shooter VIS data, only one line could be used from which we determined
(1σ errors) from the UVES and X-Shooter UVB data. In the X-Shooter VIS data, only one line could be used from which we determined 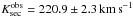 . Weighted by the number of individual results and the 13 times better spectral resolution of UVES, we calculate an average value of
. Weighted by the number of individual results and the 13 times better spectral resolution of UVES, we calculate an average value of 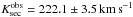 . This value is almost equal to the TLISA value (above) and demonstrates well that TLISA is a quite powerful tool.
. This value is almost equal to the TLISA value (above) and demonstrates well that TLISA is a quite powerful tool.
 |
Fig. 13 Extracted X-Shooter UVB spectra of the secondary with the primary master spectrum (Sect. 4) subtracted. The spectra are processed with a Savitzky-Golay low-pass filter (Savitzky & Golay 1964). Red: five spectra coadded just before occultation; blue: five spectra coadded just before transit. The identified lines (Table 3) are marked. |
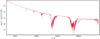 |
Fig. 14 X-Shooter spectra (smoothed with a Gaussian with a FWHM of 10 Å for clarity) during transit of the secondary (red, ten individual spectra next to T0 coadded) and during its occultation (blue, three spectra coadded). |
Figure 12 illustrates the dimensions and velocities of AA Dor. All rotations and orbital motions are counterclockwise. The parameter 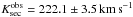 is measured.
is measured.
Our spectra show clearly that a day and a night side exist (Fig. 8). Neither an efficient horizontal energy flow nor a significantly unsynchronized rotation of the secondary15 yield an isothermal surface structure.
The assumption of a synchronized rotation of the secondary and of a strict separation of an irradiated day side and a nonirradiated night side is a simplification (cf., Barman et al. 2004). In reality, horizontal energy flows (heat conduction or winds) couples the two sides. Improved 1.5 dimensional (1.5 D) modeling of irradiated planets (Barman et al. 2005) have shown that the temperature and mean-intensity distribution at a planet’s surface resemble a horseshoe shape (Hauschildt et al. 2008). Better spectra with much higher S/N and resolution would allow us to investigate this effect and crucially constrain future (3D) modeling.
However, asec calculated from 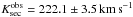 would be too small. Since no detailed model for the surface structure or phase-dependent spectra of the secondary of AA Dor exist, we estimate that the center of gravity of the measured emission lines is dominated by a region that lies toward the irradiating primary star, but not very much off the secondary’s orbital path. The maximum error is
would be too small. Since no detailed model for the surface structure or phase-dependent spectra of the secondary of AA Dor exist, we estimate that the center of gravity of the measured emission lines is dominated by a region that lies toward the irradiating primary star, but not very much off the secondary’s orbital path. The maximum error is 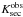 (emission region lies closest to the primary). We assume a quarter of that value with respective error range (
(emission region lies closest to the primary). We assume a quarter of that value with respective error range (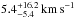 , with Rsec = 0.1112 R⊙, Sect. 6). In addition, the secondary is assumed to perform a synchronous rotation with
, with Rsec = 0.1112 R⊙, Sect. 6). In addition, the secondary is assumed to perform a synchronous rotation with 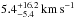 . Projected at our assumed main emission region, we use
. Projected at our assumed main emission region, we use 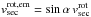 (with α = 15°). Thus, the real orbital velocity of the secondary is
(with α = 15°). Thus, the real orbital velocity of the secondary is 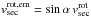 In the case of AA Dor, we calculate
In the case of AA Dor, we calculate 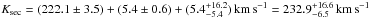 . This is, within its error limits, well in agreement with the previously determined value of Ksec ≥ 230 ± 10 km s-1 given by Vučković et al. (2008) and the estimate of Ksec = 240 ± 20 km s-1 by Müller et al. (2010).
. This is, within its error limits, well in agreement with the previously determined value of Ksec ≥ 230 ± 10 km s-1 given by Vučković et al. (2008) and the estimate of Ksec = 240 ± 20 km s-1 by Müller et al. (2010).
5.3. Spectrum of the secondary
We successfully extracted the spectrum of the secondary’s irradiated side (Fig. 13) from those X-Shooter UVB spectra where C iiλ 4267.09 Å (Fig. 8) is prominent. Although we observed spectrophotometric standard stars at the beginning and the end of the night, the observing conditions that were widely varying on short timescales during our X-Shooter night16 hampered the flux calibration and, thus, our ability to achieve the predicted, better quality even in the coadded spectrum.
In the X-Shooter UVB, VIS, and NIR spectra (Fig. 14), we did not find any significant, unambiguous spectral features of a (nonirradiated) low-mass dwarf star (e.g., Li et al. 2014; Littlefair et al. 2014; Manjavacas et al. 2014). In this phase, the expected secondary’s contribution to the composite spectrum of AA Dor is of the order of 0.1% in the NIR. Our UVES and X-Shooter spectra are not good enough to measure this. The small deviations between the individual observations stem most likely from variations of the telluric absorption during the night.
5.4. Inspection of the FUSE observations
The PHOENIX17 (Hauschildt & Baron 2009, 2010; Baron et al. 2010) model-atmosphere calculations for the irradiated secondary by Barman et al. (2004) show that its strongest lines are located in the ultraviolet (Fig. 15), especially in the FUSE wavelength range (910 Å ≲ λ ≲ 1188 Å).
To calculate the composite spectrum of AA Dor, the synthetic spectra of the primary (Klepp & Rauch 2011) and the secondary (Barman et al. 2004) were scaled with 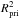 and
and 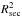 (Sect. 6), respectively. The contribution of the secondary to the composite spectrum is shown in Fig. 16.
(Sect. 6), respectively. The contribution of the secondary to the composite spectrum is shown in Fig. 16.
Therefore, we analyzed the 12 individual spectra (planned exposure time of 200 s each) that we obtained with FUSE (ObsId D0250101000, 2003-08-29, four observations, total exposure time of 731 s, D0250102000, 2004-06-22, eight observations, 1623 s). They cover about an eighth of the orbit of AA Dor (Fig. 17).
The procedure for analyzing the FUSE data was similar to that described above for the UVES and X-Shooter spectra. First, we measured the velocity offsets from one exposure to the next from the ISM features and coaligned the exposures on these. Then, we measured velocity offsets of the photospheric features (C iii, Si iv, and P v) relative to the ISM lines for each exposure and shifted the exposures in velocity space to coalign on the photospheric features. The phase coverage, while not complete, adequately determined the orbital phase for each exposure and confirms the phase predicted from the measured period. The phase-aligned spectra were then combined to produce a template of the primary star. As described above, any features of the secondary star spectrum should be widely dispersed in velocity space and should leave no imprint on this template. This template was shifted to match the velocity of the primary star in each exposure and then subtracted. We computed the velocity offset for the secondary star relative to the primary, based on our orbital solution (Sect. 3) and orbital velocity (Sect. 5.2). We then shifted each template-subtracted spectrum in velocity space by the predicted velocity offset of the secondary star, and combined the resulting spectra. Unfortunately, no features obviously appear to increase in significance in the coadded FUSE spectrum. Even an individual search for C ii-iii and O ii-iii lines remains entirely negative, although the spectra were taken in both years directly after the secondary’s occultation (Fig. 17) where the emission lines are strongest. This nondetection is unexplained. It appears possible that the contribution of the secondary to the composite spectrum of AA Dor in the FUSE wavelength range is overestimated by the current model (Fig. 16). A more thorough exploration of these models is beyond the scope of the present paper and will be the subject of a future study.
 |
Fig. 16 Top panel: contributions of the primary and the secondary to the composite flux of AA Dor in the FUSE wavelength range, convolved with rotational profiles using |
 |
Fig. 17 Same as Fig. 1, for our FUSE observations (2003: four big, green dots, 2008: eight small, blue dots). |
6. Orbit dimensions, masses, and radii
With both radial-velocity amplitudes known, Kpri = 40.15 ± 0.11 km s-1 (Müller et al. 2010) and 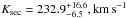 , we determined the dimensions, masses, and radii of the components of AA Dor. Their orbital radii and the distance of the stars were calculated with
, we determined the dimensions, masses, and radii of the components of AA Dor. Their orbital radii and the distance of the stars were calculated with
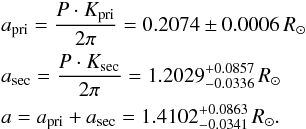 The total mass of the system is
The total mass of the system is 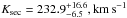 (with the gravitational constant G). With KpriMpri = KsecMsec, the components’ masses are
(with the gravitational constant G). With KpriMpri = KsecMsec, the components’ masses are 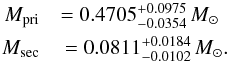 The radius of the primary is
The radius of the primary is 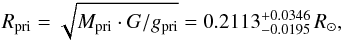 where gpri is its surface gravity. Kilkenny et al. (1979) determined Rpri/Rsec = 1.9. Therefore the secondary’s radius is
where gpri is its surface gravity. Kilkenny et al. (1979) determined Rpri/Rsec = 1.9. Therefore the secondary’s radius is 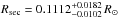 .
.
7. Results and conclusions
The extracted secondary’s spectrum allows us to investigate its nature. A cool brown dwarf shows, for Teff ≲ 1200 K, a typical spectrum that is dominated by NH3 and CH4 bands (see, for example, Burningham et al. 2008). In contrast, a late M-type dwarf exhibits, e.g., TiO bands (Kirkpatrick et al. 1993). We did not succeed in extracting the spectrum of the cool side of the secondary. However, both types exhibit emission lines of C ii and O ii (as already identified by Vučković et al. 2008) only due to irradiation of the primary and thus, the heating of one hemisphere.
We have identified 73 lines of the secondary (Table 3), i.e., the number of identified lines was increased by about a factor of three. This was possible because of the consequent implementation of the s-curve method in the VO tool TLISA, which allows us to search even for very weak lines. The identified lines stem mainly from C ii-iii and O ii.
To make progress on the understanding of the nature of the secondary and, hence, the whole system AA Dor, further UVES observations in its red arm (4200 Å ≥ λ ≥ 11 000 Å) on a dark night with superb seeing conditions are highly desirable.
We improved the period measurement of Rauch & Werner (2003) because of the extended time interval and verified the period of P = 22 597.03320768 ± 0.0000691 s, which was determined from the light curve of AA Dor by Kilkenny (2011). We measured an orbital velocity of 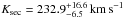 for the secondary. We determined masses of
for the secondary. We determined masses of 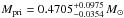 for the primary star and of
for the primary star and of 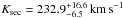 for the secondary star. The secondary’s mass is fully overlapping (Fig. 18) with the hydrogen-burning mass limit (0.075−0.085 M⊙, Chabrier & Baraffe 1997) and, thus, it is still not possible to decide about the nature of the object.
for the secondary star. The secondary’s mass is fully overlapping (Fig. 18) with the hydrogen-burning mass limit (0.075−0.085 M⊙, Chabrier & Baraffe 1997) and, thus, it is still not possible to decide about the nature of the object.
 |
Fig. 18 Top: dependency of the components’ masses (red: primary dashed lines show the error range, blue: secondary) on the orbital velocity of the secondary (for Kpri = 40.15 km s-1, Müller et al. 2010). The light blue horizontal region indicates the hydrogen-burning mass limit (Chabrier & Baraffe 1997). The green thick line shows our determination of Ksec = 232.9 km s-1. The error range is indicated by the green dashed lines. |
Our primary and secondary masses agree perfectly with those of Klepp & Rauch (2011, Mpri = 0.4714 ± 0.0050 M⊙, 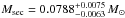 . They assumed a solar He abundance (Y = 0.288) on the horizontal branch (HB) and determined Mpri by a comparison with respective post-EHB evolutionary tracks (Fig. 19) of Dorman et al. (1993). Since AA Dor had experienced a common-envelope event and its present abundance pattern (Table 1) exhibits the interplay of gravitational settling and radiative levitation (cf. Rauch 2000), any information about its former photospheric abundances is lost. However, the assumption of solar abundances for AA Dor on the HB appears reasonable.
. They assumed a solar He abundance (Y = 0.288) on the horizontal branch (HB) and determined Mpri by a comparison with respective post-EHB evolutionary tracks (Fig. 19) of Dorman et al. (1993). Since AA Dor had experienced a common-envelope event and its present abundance pattern (Table 1) exhibits the interplay of gravitational settling and radiative levitation (cf. Rauch 2000), any information about its former photospheric abundances is lost. However, the assumption of solar abundances for AA Dor on the HB appears reasonable.
Our masses also agree well with those of Hilditch et al. (2003, 0.33 M⊙ ≤ Mpri ≤ 0.47 M⊙ and 0.064 M⊙ ≤ Msec ≤ 0.082 M⊙. The values of Müller et al. (2010, 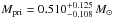 ,
, 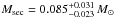 agree with ours within error limits.
agree with ours within error limits.
 |
Fig. 19 Location of the primary of AA Dor in the Teff−log g plane (the ellipse indicates the error limits given by Klepp & Rauch 2011) compared to sdBs and sdOBs from Edelmann (2003). Post-EHB tracks from Dorman et al. (1993, full black lines, labeled with the respective stellar masses in M⊙ are also shown for comparison. |
Detailed 3D modeling of the phase-dependent spectrum of the irradiated secondary of AA Dor that considers horizontal energy flows is highly desirable to verify our assumptions for the correction of the observed 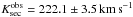 in Sect. 5.2. Our primary mass Mpri = 0.47 M⊙, which was calculated with Ksec = 232.9 km s-1, agrees with the mass interval of 0.33 M⊙ ≤ Mpri ≤ 0.47 M⊙ (Hilditch et al. 2003, from light-curve analysis). Higher values of Ksec yield higher values of Mpri (Fig. 18). E.g., Ksec = 240 km s-1 results in
in Sect. 5.2. Our primary mass Mpri = 0.47 M⊙, which was calculated with Ksec = 232.9 km s-1, agrees with the mass interval of 0.33 M⊙ ≤ Mpri ≤ 0.47 M⊙ (Hilditch et al. 2003, from light-curve analysis). Higher values of Ksec yield higher values of Mpri (Fig. 18). E.g., Ksec = 240 km s-1 results in 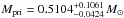 which is, even within error limits, outside the mass interval (see above).
which is, even within error limits, outside the mass interval (see above).
Online material
 |
Fig. 2 UVES spectrum (blue, start time 2001-01-08T00-27-37.434 UT). Identified lines of the primary are marked. ISM denotes interstellar lines. |
 |
Fig. 3 X-Shooter spectrum (blue, start time 2014-01-08T02-03-37.877 UT) taken in the UVB arm compared with our final model of the primary (red). Identified lines of the primary are marked. ISM denotes interstellar lines. |
 |
Fig. 4 X-Shooter spectrum (blue, start time 2014-01-08T02-03-43.068 UT) taken in the VIS arm compared with our final model of the primary (red). Identified lines of the primary are marked. |
 |
Fig. 5 X-Shooter spectrum (blue, start time 2014-01-08T02-03-45.7348) UT) taken in the NIR arm compared with our final model of the primary (red). Identified lines of the primary are marked. |
 |
Fig. 9 Detection limit for s-curves. A synthetic line profile (phase-dependently shifted with Ksec = 230 km s-1) at three strengths (equivalent widths of Wλ = 122,15,and 3 mÅ, from left to right) is shown for S/N = 50, 25 (approximately our UVES data value), and 10 (top to bottom). All panels show the same wavelength and phase intervals. |
Appendix A: TLISA
As a part of the Tübingen contribution to the GAVO project, the TLISA tool is generally designed in VO-compliant form. In particular, its menu navigation is fully intuitive, i.e., no profound knowledge of the background software by a VO user is necessary for an astronomically worthwhile usage. The TLISA tool is provided as a registered GAVO tool.
The TLISA tool is a module-based analyzer (like a Content-Management-System for websites), written in the programming language Java, which allows the user to develop a lot of modules and tools to analyze and modify spectra. For this purpose, the program provides many methods and classes (like a data container for FITS files).
The first module, which was developed for TLISA, is SEFOBS (SEarch for Faint Objects in Binary Systems). The module is divided into three parts. The data provider and the data analyzers for the primary and the secondary. The data provider allows the user to choose data and save path. The data can be a single FITS file, several FITS files or a directory, but can only contain files of the same object and the same wavelength interval.
The SEFOBS reads the data and saves it into the internally used variables. It arranges the data by its observation time and indicates the most important information.
In the second part, the user has the option to either calculate the system parameters of the primary by SEFOBS or to enter individual parameters (Fig. A.1).
The analyzer windows (Figs. A.2, A.3) are divided into two panels. The left panel with the spectrum and the right panel with the s-curve plot.
The s-curve plot has a width of 500 pixels. Every other pixel is a data point, i.e., we have 250 data points. With a wavelength step of 0.2 Å, we cover an interval of 50 Å. Thus, the spectrum is divided into 50 Å-wide intervals. With the two buttons at the bottom on the right panel and also with the input field, the user can navigate through the spectrum.
With the slider at the right panel, the user can choose an individual spectrum at a specific observation time. It is not possible to switch between MJD and phase because SEFOBS needs the system parameters to calculate the phase from MJD.
The SEFOBS assigns each flux value an equivalent color value. The SEFOBS contains a lot more options to manipulate the s-curve plot. The first option is the selection of the background color, that is given every other pixel. This is very important because it is a graphical analysis where we need high contrast between background and spectrum. For example, the wings of an absorption line have a higher flux value compared to the line core. A higher flux value means a brighter color (default: from black to white), i.e., the line core is black and the line wings may be very diffuse. A black background will therefore sharpen the line. Vice versa, this works for an emission line.
 |
Fig. A.1 TLISA. SEFOBS input window. |
 |
Fig. A.2 TLISA. SEFOBS analyzer window for the primary. |
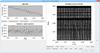 |
Fig. A.3 TLISA. SEFOBS analyzer window for the secondary. |
Appendix B: TLISA s-curve plots and secondary spectra from UVES data
Appendix C: TLISA s-curve plots and secondary spectra from X-Shooter UVB data
 |
Fig. C.1 Top: section of the phase-dependent X-Shooter UVB spectra (3780 Å ≤ λ ≤ 3820 Å). Bottom: |
 |
Fig. C.16 Same as Fig. C.1, for 4840 Å ≤ λ ≤ 4880 Å. Bottom spectrum taken at 2014-01-08T07-00-19.465 UT. |
Appendix D: TLISA s-curve plots and secondary spectra from X-Shooter VIS data
 |
Fig. D.1 Top: section of the phase-dependent X-Shooter VIS spectra (5855 Å ≤ λ ≤ 5895 Å). Bottom: |
Appendix E: TLISA s-curve plots and secondary spectra from X-Shooter NIR data
 |
Fig. E.1 Top: section of the phase-dependent X-Shooter VIS spectra (17590 Å ≤ λ ≤ 17710 Å). Bottom: |
http://iraf.noao.edu, IRAF is distributed by the National Optical Astronomy Observatory, which is operated by the Associated Universities for Research in Astronomy, Inc., under cooperative agreement with the National Science Foundation.
The rotation of the primary is not synchronized yet (Müller et al. 2010).
See http://astro.uni-tuebingen.de/~rauch/ESO_092.C-0692.gif for an impression.
Acknowledgments
D.H. and T.R. are supported by the German Aerospace Center (DLR, grants 50 OR 1501 and 05 OR 1402, respectively). The GAVO project at Tübingen was supported by the Federal Ministry of Education and Research (BMBF, grants 05 AC 6 VTB, 05 AC 11 VTB). The TLISA tool (http://astro.uni-tuebingen.de/~TLISA) used for this paper was constructed as part of the activities of the German Astrophysical Virtual Observatory. The UVES and X-Shooter spectra used in this analysis were obtained as parts of ESO Service Mode runs, programs 066.D-1800 and 092.C-0692, respectively. We thank David Kilkenny for his help in determining the exact time of the secondary’s occultation during our X-Shooter observations, Roger Wesson who had performed these observations and successfully covered this critical time, and Travis Barman who put the irradiated spectrum of the secondary at our disposal. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts. This research has made use of NASA’s Astrophysics Data System and the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Almeida, L. A., Jablonski, F., Tello, J., & Rodrigues, C. V. 2012, MNRAS, 423, 478 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, B. N., Kilkenny, D., Drechsel, H., et al. 2013, MNRAS, 430, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Hauschildt, P. H., & Allard, F. 2004, ApJ, 614, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Barman, T. S., Hauschildt, P. H., & Allard, F. 2005, ApJ, 632, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Baron, E., Chen, B., & Hauschildt, P. H. 2010, PHOENIX: A General-purpose State-of-the-art Stellar and Planetary Atmosphere Code, Astrophysics Source Code Library [record ascl: 1010.056] [Google Scholar]
- Bergeron, P., Wesemael, F., Lamontagne, R., & Chayer, P. 1993, ApJ, 407, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Burningham, B., Pinfield, D. J., Leggett, S. K., et al. 2008, MNRAS, 391, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 1997, A&A, 327, 1039 [NASA ADS] [Google Scholar]
- Chabrier, G., Baraffe, I., Allard, F., & Hauschildt, P. 2000, ApJ, 542, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Dorman, B., Rood, R. T., & O’Connell, R. W. 1993, ApJ, 419, 596 [CrossRef] [Google Scholar]
- Edelmann, H. 2003, Dissertation, University of Erlangen-Nuremberg [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fleig, J., Rauch, T., Werner, K., & Kruk, J. W. 2008, A&A, 492, 565 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geckeler, R. D., Schuh, S., Dreizler, S., et al. 2014, TRIPP: Time Resolved Imaging Photometry Package, Astrophysics Source Code Library [record ascl: 1405.008] [Google Scholar]
- Geier, S., Heber, U., Podsiadlowski, P., et al. 2010, A&A, 519, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2009, A&A, 498, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., & Baron, E. 2010, A&A, 509, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., Barman, T., & Baron, E. 2008, Phys. Scr. T, 130, 014033 [NASA ADS] [CrossRef] [Google Scholar]
- Heber, U. 2009, ARA&A, 47, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Hilditch, R. W., Harries, T. J., & Hill, G. 1996, MNRAS, 279, 1380 [NASA ADS] [Google Scholar]
- Hilditch, R. W., Kilkenny, D., Lynas-Gray, A. E., & Hill, G. 2003, MNRAS, 344, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D. 2011, MNRAS, 412, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1978, MNRAS, 183, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Kilkenny, D., Hilditch, R. W., & Penfold, J. E. 1979, MNRAS, 187, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Kelly, D. M., Rieke, G. H., et al. 1993, ApJ, 402, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Klepp, S., & Rauch, T. 2011, A&A, 531, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Yu. Ralchenko, Reader, J., & NIST ASD Team, 2014, NIST Atomic Spectra Database (ver. 5.2) http://physics.nist.gov/asd [Google Scholar]
- Li, L., Zhang, F., Han, Q., Kong, X., & Gong, X. 2014, MNRAS, 445, 1331 [NASA ADS] [CrossRef] [Google Scholar]
- Littlefair, S. P., Casewell, S. L., Parsons, S. G., et al. 2014, MNRAS, 445, 2106 [NASA ADS] [CrossRef] [Google Scholar]
- Livio, M., & Soker, N. 1984, MNRAS, 208, 783 [NASA ADS] [Google Scholar]
- Manjavacas, E., Bonnefoy, M., Schlieder, J. E., et al. 2014, A&A, 564, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maxted, P. F. L., North, R. C., & Marsh, T. R. 2000, The Newsletter of the Isaac Newton Group of Telescopes, 3, 7 [NASA ADS] [Google Scholar]
- Müller, S., Geier, S., & Heber, U. 2010, Ap&SS, 329, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Napiwotzki, R., & Rauch, T. 1994, A&A, 285, 603 [NASA ADS] [Google Scholar]
- Rauch, T. 2000, A&A, 356, 665 [NASA ADS] [Google Scholar]
- Rauch, T. 2004, Ap&SS, 291, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Rauch, T. 2012, in Fifth Meeting on Hot Subdwarf Stars and Related Objects, eds. D. Kilkenny, C. S. Jeffery, & C. Koen, ASP Conf. Ser., 452, 111 [Google Scholar]
- Rauch, T., & Deetjen, J. L. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 103 [Google Scholar]
- Rauch, T., & Werner, K. 2003, A&A, 400, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Biémont, É., Quinet, P., & Kruk, J. W. 2012, A&A, 546, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2014a, A&A, 564, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2014b, A&A, 566, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauch, T., Werner, K., Quinet, P., & Kruk, J. W. 2015, A&A, 577, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ritter, H. 1986, A&A, 169, 139 [NASA ADS] [Google Scholar]
- Ritter, H., & Kolb, U. 2003, A&A, 404, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rucinski, S. M. 2009, MNRAS, 395, 2299 [NASA ADS] [CrossRef] [Google Scholar]
- Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Schaffenroth, V., Geier, S., Drechsel, H., et al. 2013, A&A, 553, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Geier, S., Heber, U., et al. 2014, A&A, 564, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Barlow, B. N., Drechsel, H., & Dunlap, B. H. 2015, A&A, 576, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schreiber, M. R., & Gänsicke, B. T. 2003, A&A, 406, 305 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuh, S. L., Dreizler, S., Deetjen, J. L., & Göhler, E. 2003, Balt. Astron., 12, 167 [Google Scholar]
- Scott, P., Asplund, M., Grevesse, N., Bergemann, M., & Sauval, A. J. 2015a, A&A, 573, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scott, P., Grevesse, N., Asplund, M., et al. 2015b, A&A, 573, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblay, P.-E., & Bergeron, P. 2009, ApJ, 696, 1755 [NASA ADS] [CrossRef] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vučković, M., Østensen, R., Bloemen, S., Decoster, I., & Aerts, C. 2008, in Hot Subdwarf Stars and Related Objects, eds. U. Heber, C. S. Jeffery, & R. Napiwotzki, ASP Conf. Ser., 392, 199 [Google Scholar]
- Werner, K. 1996, ApJ, 457, L39 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, K., Deetjen, J. L., Dreizler, S., et al. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 31 [Google Scholar]
- Werner, K., Dreizler, S., & Rauch, T. 2012a, TMAP: Tübingen NLTE Model-Atmosphere Package, Astrophysics Source Code Library [record ascl: 1212.015] [Google Scholar]
- Werner, K., Rauch, T., Ringat, E., & Kruk, J. W. 2012b, ApJ, 753, L7 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Photospheric abundances (mass fractions) of the primary of AA Dor, determined by Fleig et al. (2008, , log g = 5.30, denoted F and in this work (H, , log g = 5.46).
All Figures
 |
Fig. 1 Orbital location of the primary (light blue in the online version) and secondary (red) at the UVES (left) and X-Shooter (right) observation times. The start times of the two observation campaigns are indicated (HJD 2 451 917.5191833 and 2 456 665.5858551, respectively). The stars move counterclockwise. Dots mark the locations of the secondary at the start times of the individual observations. |
| In the text | |
 |
Fig. 6 Comparison of radial-velocity measurements of AA Dor with a sine curve calculated with the period of P = 0.261 539 7363 d from the light-curve solution of Kilkenny (2011). Kpri = 40.15 km s-1 and T0 = 51917.15269 are from Müller et al. (2010) and Rauch & Werner (2003), respectively. From top to bottom, the panels show data from Hilditch et al. (1996), Rauch & Werner (2003, UVES), FUSE 2003, FUSE 2004, and our X-Shooter spectra. The measurements cover the time from Jan. 29, 1994, to Jan. 8, 2014. |
| In the text | |
 |
Fig. 7 Comparison of synthetic profiles of H and He lines calculated from our models (, log g = 5.46) with our UVES observation (for clarity smoothed with a low-pass filter, Savitzky & Golay 1964). Left panel: abundances from Table 1, and Sc, Ti, V, Cr, Mn, and Co with solar abundances (Scott et al. 2015a). Right panel: similar model in the left panel, except the Sc, Ti, V, Cr, Mn, and Co abundances are artifically increased by a factor of 700. The vertical bar indicates 10% of the continuum flux. |
| In the text | |
 |
Fig. 8 Top: C iiλ 4267.09 Å line in a simulation (with an assumed Ksec = 230 km s-1). φ is the orbital phase. The transit (φ = 0.0) and the occultation (φ = 0.5) of the secondary are simulated. Bottom: same line in our X-Shooter observations. In the online version, the red spectra show the occultation of the secondary. In the blue spectra, C iiλ 4267.09 Å is prominent. The vertical (green) bar indicates the rest wavelength of the line. |
| In the text | |
 |
Fig. 10 Top: section of the secondary’s phase-dependent UVES spectra (4245 Å ≤ λ ≤ 4285 Å). Bottom: single spectrum (2001-01-08T00-53-54.965 UT) in the secondary’s rest frame in the respective wavelength interval; “unid.” denotes unidentified lines. |
| In the text | |
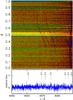 |
Fig. 11 Same as Fig. 10 for 4050 Å ≤ λ ≤ 4090 Å. |
| In the text | |
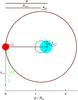 |
Fig. 12 Dimensions (drawn to scale), orbits, and velocities of AA Dor. |
| In the text | |
 |
Fig. 13 Extracted X-Shooter UVB spectra of the secondary with the primary master spectrum (Sect. 4) subtracted. The spectra are processed with a Savitzky-Golay low-pass filter (Savitzky & Golay 1964). Red: five spectra coadded just before occultation; blue: five spectra coadded just before transit. The identified lines (Table 3) are marked. |
| In the text | |
 |
Fig. 14 X-Shooter spectra (smoothed with a Gaussian with a FWHM of 10 Å for clarity) during transit of the secondary (red, ten individual spectra next to T0 coadded) and during its occultation (blue, three spectra coadded). |
| In the text | |
 |
Fig. 15 Synthetic spectrum of the irradiated hemisphere of the secondary of AA Dor. |
| In the text | |
 |
Fig. 16 Top panel: contributions of the primary and the secondary to the composite flux of AA Dor in the FUSE wavelength range, convolved with rotational profiles using |
| In the text | |
 |
Fig. 17 Same as Fig. 1, for our FUSE observations (2003: four big, green dots, 2008: eight small, blue dots). |
| In the text | |
 |
Fig. 18 Top: dependency of the components’ masses (red: primary dashed lines show the error range, blue: secondary) on the orbital velocity of the secondary (for Kpri = 40.15 km s-1, Müller et al. 2010). The light blue horizontal region indicates the hydrogen-burning mass limit (Chabrier & Baraffe 1997). The green thick line shows our determination of Ksec = 232.9 km s-1. The error range is indicated by the green dashed lines. |
| In the text | |
 |
Fig. 19 Location of the primary of AA Dor in the Teff−log g plane (the ellipse indicates the error limits given by Klepp & Rauch 2011) compared to sdBs and sdOBs from Edelmann (2003). Post-EHB tracks from Dorman et al. (1993, full black lines, labeled with the respective stellar masses in M⊙ are also shown for comparison. |
| In the text | |
 |
Fig. 2 UVES spectrum (blue, start time 2001-01-08T00-27-37.434 UT). Identified lines of the primary are marked. ISM denotes interstellar lines. |
| In the text | |
 |
Fig. 3 X-Shooter spectrum (blue, start time 2014-01-08T02-03-37.877 UT) taken in the UVB arm compared with our final model of the primary (red). Identified lines of the primary are marked. ISM denotes interstellar lines. |
| In the text | |
 |
Fig. 4 X-Shooter spectrum (blue, start time 2014-01-08T02-03-43.068 UT) taken in the VIS arm compared with our final model of the primary (red). Identified lines of the primary are marked. |
| In the text | |
 |
Fig. 5 X-Shooter spectrum (blue, start time 2014-01-08T02-03-45.7348) UT) taken in the NIR arm compared with our final model of the primary (red). Identified lines of the primary are marked. |
| In the text | |
 |
Fig. 9 Detection limit for s-curves. A synthetic line profile (phase-dependently shifted with Ksec = 230 km s-1) at three strengths (equivalent widths of Wλ = 122,15,and 3 mÅ, from left to right) is shown for S/N = 50, 25 (approximately our UVES data value), and 10 (top to bottom). All panels show the same wavelength and phase intervals. |
| In the text | |
 |
Fig. A.1 TLISA. SEFOBS input window. |
| In the text | |
 |
Fig. A.2 TLISA. SEFOBS analyzer window for the primary. |
| In the text | |
 |
Fig. A.3 TLISA. SEFOBS analyzer window for the secondary. |
| In the text | |
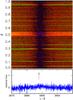 |
Fig. B.1 Same as Fig. 10, for 3870 Å ≤ λ ≤ 3910 Å. |
| In the text | |
 |
Fig. B.2 Same as Fig. 10, for 3900 Å ≤ λ ≤ 3940 Å. |
| In the text | |
 |
Fig. B.3 Same as Fig. 10, for 3935 Å ≤ λ ≤ 3975 Å. |
| In the text | |
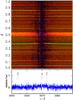 |
Fig. B.4 Same as Fig. 10, for 3950 Å ≤ λ ≤ 3990 Å. |
| In the text | |
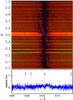 |
Fig. B.5 Same as Fig. 10, for 4080 Å ≤ λ ≤ 4120 Å. |
| In the text | |
 |
Fig. B.6 Same as Fig. 10, for 4105 Å ≤ λ ≤ 4145 Å. |
| In the text | |
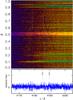 |
Fig. B.7 Same as Fig. 10, for 4165 Å ≤ λ ≤ 4205 Å. |
| In the text | |
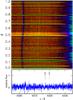 |
Fig. B.8 Same as Fig. 10, for 4295 Å ≤ λ ≤ 4335 Å. |
| In the text | |
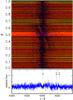 |
Fig. B.9 Same as Fig. 10, for 4320 Å ≤ λ ≤ 4360 Å. |
| In the text | |
 |
Fig. B.10 Same as Fig. 10, for 4395 Å ≤ λ ≤ 4435 Å. |
| In the text | |
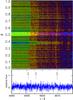 |
Fig. B.11 Same as Fig. 10, for 4580 Å ≤ λ ≤ 4620 Å. |
| In the text | |
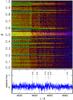 |
Fig. B.12 Same as Fig. 10, for 4625 Å ≤ λ ≤ 4665 Å. |
| In the text | |
 |
Fig. B.13 Same as Fig. 10, for 4650 Å ≤ λ ≤ 4690 Å. |
| In the text | |
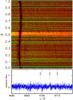 |
Fig. B.14 Same as Fig. 10, for 4680 Å ≤ λ ≤ 4720 Å. |
| In the text | |
 |
Fig. B.15 Same as Fig. 10, for 4840 Å ≤ λ ≤ 4880 Å. |
| In the text | |
 |
Fig. C.1 Top: section of the phase-dependent X-Shooter UVB spectra (3780 Å ≤ λ ≤ 3820 Å). Bottom: |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1, for 3815 Å ≤ λ ≤ 3855 Å. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.1, for 3870 Å ≤ λ ≤ 3910 Å. |
| In the text | |
 |
Fig. C.4 Same as Fig. C.1, for 3900 Å ≤ λ ≤ 3940 Å. |
| In the text | |
 |
Fig. C.5 Same as Fig. C.1, for 3950 Å ≤ λ ≤ 3990 Å. |
| In the text | |
 |
Fig. C.6 Same as Fig. C.1, for 4010 Å ≤ λ ≤ 4050 Å. |
| In the text | |
 |
Fig. C.7 Same as Fig. C.1, for 4050 Å ≤ λ ≤ 4090 Å. |
| In the text | |
 |
Fig. C.8 Same as Fig. C.1, for 4080 Å ≤ λ ≤ 4120 Å. |
| In the text | |
 |
Fig. C.9 Same as Fig. C.1, for 4130 Å ≤ λ ≤ 4170 Å. |
| In the text | |
 |
Fig. C.10 Same as Fig. C.1, for 4245 Å ≤ λ ≤ 4285 Å. |
| In the text | |
 |
Fig. C.11 Same as Fig. C.1, for 4300 Å ≤ λ ≤ 4340 Å. |
| In the text | |
 |
Fig. C.12 Same as Fig. C.1, for 4320 Å ≤ λ ≤ 4360 Å. |
| In the text | |
 |
Fig. C.13 Same as Fig. C.1, for 4395 Å ≤ λ ≤ 4435 Å. |
| In the text | |
 |
Fig. C.14 Same as Fig. C.1, for 4580 Å ≤ λ ≤ 4620 Å. |
| In the text | |
 |
Fig. C.15 Same as Fig. C.1, for 4625 Å ≤ λ ≤ 4665 Å. |
| In the text | |
 |
Fig. C.16 Same as Fig. C.1, for 4840 Å ≤ λ ≤ 4880 Å. Bottom spectrum taken at 2014-01-08T07-00-19.465 UT. |
| In the text | |
 |
Fig. C.17 Same as Fig. C.1, for 4905 Å ≤ λ ≤ 4945 Å. |
| In the text | |
 |
Fig. C.18 Same as Fig. C.1, for 4920 Å ≤ λ ≤ 4960 Å. |
| In the text | |
 |
Fig. D.1 Top: section of the phase-dependent X-Shooter VIS spectra (5855 Å ≤ λ ≤ 5895 Å). Bottom: |
| In the text | |
 |
Fig. D.2 Same as Fig. D.1, for 6130 Å ≤ λ ≤ 6170 Å. |
| In the text | |
 |
Fig. D.3 Same as Fig. D.1, for 6545 Å ≤ λ ≤ 6585 Å. |
| In the text | |
 |
Fig. D.4 Same as Fig. D.1, for 6560 Å ≤ λ ≤ 6600 Å. |
| In the text | |
 |
Fig. D.5 Same as Fig. D.1, for 6770 Å ≤ λ ≤ 6810 Å. |
| In the text | |
 |
Fig. D.6 Same as Fig. D.1, for 7045 Å ≤ λ ≤ 7085 Å. |
| In the text | |
 |
Fig. D.7 Same as Fig. D.1, for 8540 Å ≤ λ ≤ 8580 Å. |
| In the text | |
 |
Fig. E.1 Top: section of the phase-dependent X-Shooter VIS spectra (17590 Å ≤ λ ≤ 17710 Å). Bottom: |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.