| Issue |
A&A
Volume 578, June 2015
|
|
|---|---|---|
| Article Number | A137 | |
| Number of page(s) | 12 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201425236 | |
| Published online | 17 June 2015 | |
Seismic sensitivity to sub-surface solar activity from 18 yr of GOLF/SoHO observations⋆,⋆⋆
Laboratoire AIM, CEA/DSM-CNRS, Université Paris 7 Diderot, IRFU/SAp, Centre de Saclay, 91191 Gif-sur-Yvette, France
e-mail: david.salabert@cea.fr
Received: 28 October 2014
Accepted: 26 February 2015
Solar activity has significantly changed over the last two Schwabe cycles. After a long and deep minimum at the end of Cycle 23, the weaker activity of Cycle 24 contrasts with the previous cycles. In this work, the response of the solar acoustic oscillations to solar activity is used in order to provide insights into the structural and magnetic changes in the sub-surface layers of the Sun during this on-going unusual period of low activity. We analyze 18 yr of continuous observations of the solar acoustic oscillations collected by the Sun-as-a-star GOLF instrument on board the SoHO spacecraft. From the fitted mode frequencies, the temporal variability of the frequency shifts of the radial, dipolar, and quadrupolar modes are studied for different frequency ranges that are sensitive to different layers in the solar sub-surface interior. The low-frequency modes show nearly unchanged frequency shifts between Cycles 23 and 24, with a time evolving signature of the quasi-biennial oscillation, which is particularly visible for the quadrupole component revealing the presence of a complex magnetic structure. The modes at higher frequencies show frequency shifts that are 30% smaller during Cycle 24, which is in agreement with the decrease observed in the surface activity between Cycles 23 and 24. The analysis of 18 yr of GOLF oscillations indicates that the structural and magnetic changes responsible for the frequency shifts remained comparable between Cycle 23 and Cycle 24 in the deeper sub-surface layers below 1400 km as revealed by the low-frequency modes. The frequency shifts of the higher-frequency modes, sensitive to shallower regions, show that Cycle 24 is magnetically weaker in the upper layers of Sun.
Key words: methods: data analysis / Sun: helioseismology / Sun: activity
Appendices are available in electronic form at http://www.aanda.org
The following 68 GOLF frequency tables are available and Table A.1 is also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/578/A137
© ESO, 2015
1. Introduction
The unexpected extended minimum of the solar surface activity Cycle 23 in 2007–2008 puzzled over the complexity and the variability of the emerging solar magnetic fields generated in the convective zone. It revealed even more the difficulty of performing reliable predictions of the 11-yr solar cycle. The current cycle, Cycle 24, is showing one of the weakest levels of activity in the last century, with a surface activity that is about 30% lower than during Cycle 23. Moreover, Livingston et al. (2012) observed a continuous drop in sunspot magnetic field strength over the last 30 yr, arguing that sunspots could disappear from the Sun’s surface during Cycle 25 because the 1500 G threshold to form dark sunspots would be reached. Deeper inside the Sun, Howe et al. (2013) have used helioseismic data to follow the zonal flow pattern, called torsional oscillation, during Cycles 23 and 24. They showed in particular that the high-latitudinal pattern, one of the signatures of a new Cycle, has actually been absent since the beginning of Cycle 24, probably because of the lower polar magnetic field strength.
The solar acoustic (p) oscillation frequencies were revealed to respond to changes in the surface activit y, and to vary in correlation with solar proxies such as the sunspot number or the 10.7 cm radio emission. The temporal variations of the solar p-mode frequencies with solar activity were first reported by Woodard & Noyes (1985), and were confirmed by Fossat et al. (1987) and Libbrecht & Woodard (1990). They were attributed to changes taking place in the sub-surface layers. It has also been known for more than a decade that the extraction of the sound-speed profile in the core must be done carefully. It is the reason why this information was obtained using only low-degree modes with frequencies smaller than 2.4 mHz (Turck-Chièze et al. 2001; Turck-Chièze & Lopes 2012).
Today, solar frequencies are identified as a unique proxy of solar activity, as they might reveal inferences on sub-surface changes with solar activity not visible at the surface. They can also contribute to building varying topologies of magnetic fields below the surface. As longer and higher-quality helioseismic observations became available, the temporal variability of the p-mode frequencies were studied in greater detail. These frequency shifts were actually observed to be frequency dependent, the shifts being larger at higher frequencies, and to be angular-degree (l) dependent, i.e., mode-inertia dependent, although the l dependence is small for low-degree modes (see, e.g., Gelly et al. 2002; Howe et al. 2002; Jiménez-Reyes et al. 2004; Salabert et al. 2004). The shifts can be then interpreted as arising from structural changes in the sub-surface layers, such as changes in temperature (Kuhn 1988) or in the size of the acoustic cavity (Dziembowski & Goode 2005). Moreover, Howe et al. (2002) showed that the temporal and latitudinal distribution of the frequency shifts is correlated with the spatial distribution of the surface magnetic field. Thus, the frequency shifts cannot only be explained by structural changes and the determination of the dipolar and the toroidal magnetic fields of the sub-surface layers appear as one of the important outputs from these observables (Baldner et al. 2009).
However, while the frequency shifts varied closely to solar surface activity with very high levels of correlation over the last three complete solar Cycles (21, 22, and 23) spanning thirty years of solar activity (Chaplin et al. 2007), significant differences were observed between acoustic frequencies and solar activity during the unusual minimum of Cycle 23 as reported in Salabert et al. (2009), Broomhall et al. (2009), and Tripathy et al. (2010). Moreover, Basu et al. (2012) showed that the structure of the solar sub-surface layers was very different between Cycle 22 and Cycle 23, with deeper changes during Cycle 22 than during Cycle 23.
In this study we investigate in more detail the differences in the variability of the radial, dipolar, and quadrupolar low-degree modes. We show how the temporal evolution of the magnetic configuration imprints differently these modes during Cycle 23 and the weak on-going Cycle 24 by analyzing the low-degree oscillation frequencies extracted from the observations collected by the space-based, Sun-as-a-star Global Oscillations at Low Frequency instrument (GOLF; Gabriel et al. 1995) on board the Solar and Heliospheric Observatory (SoHO; Domingo et al. 1995) spacecraft. SoHO was launched on 1995 December 2, and since then has been collecting continuous data from a stable orbit around the L1 Lagrangian point. With more than 18 yr of space observations available today, free from any perturbations related to the Earth atmosphere as occurs from ground-based observations, the GOLF/SoHO observations provide an exquisite and unique dataset for global helioseismic studies of the low-degree oscillation modes. In Sect. 2, we describe the data used in this paper and how the seismic parameters were extracted. The frequency shifts thus estimated are presented and discussed in Sect. 3. In Sect. 4, we provide possible explanations and interpretations of the related structural and magnetic changes of the sub-surface layers during Cycle 24. The main results are summarized in Sect. 5. The tables containing the oscillation frequencies of the GOLF low-degree modes extracted from the 365-day spectra analyzed in this study are made available electronically as described in Appendix A. In Appendix B, 18 yr of frequency shifts at individual angular degree l are presented in more detail.
2. Data and analysis
2.1. Data sets
We analyzed 18 yr of continuous observations collected by the GOLF instrument, a resonant scattering spectrophotometer measuring the Doppler wavelength shift – integrated over the solar surface – in the D1 and D2 Fraunhofer sodium lines at 589.6 and 589.0 nm, respectively. It was designed to measure the Doppler shift by switching from one side of the wing to the other side, an additional coil allowing two near point measurements along each side of the wings in the more stable part of the lines (Gabriel et al. 1995). However, the GOLF instrument has not been used in its nominal configuration owing to a malfunction in its polarization switching mechanism identified shortly after the launch (García et al. 2004). As a consequence, observations from only one side of the sodium doublet have been collected, from which a proxy for the Doppler velocity signal is formed. Moreover, observations have been collected from each side of the doublet as follows: in the blue-wing configuration from 1996 April 11 until 1998 June 26, and later on from 2002 November 19 up to the present time (the so-called blue periods); and in the red-wing configuration of the sodium doublet between 1998 October 30 until 2002 November 18 (the so-called red period). These two configurations imply different spatial weightings of the solar disk (Garcia et al. 1998).
In addition, two extended gaps are present in the analyzed time series because of the temporary loss of the SoHO spacecraft. The first gap of about 100 days happened during the summer of 1998 after a bad maneuver of the SoHO rotation spacecraft. The second gap of a period around 1 month in January 1999 occurred while new software was being uploaded to the spacecraft and was caused by a failure in the SoHO gyroscopes.
The observational blue-wing configuration of the GOLF instrument has not been modified since November 2002, except for readjusting the photomultiplier high voltages in order to compensate for its aging. It corresponds today to almost 12 yr of continuous measurements, with a duty cycle close to 100%. The response function of the GOLF sodium Fraunhofer line is different between the blue- and the red-wing configurations (Lefebvre et al. 2008), with averaged heights in the solar atmosphere of 322 km and 480 km, respectively (Jiménez-Reyes et al. 2007). The measurements obtained in the red-wing configuration originate higher up in the solar atmosphere with larger contributions from the chromosphere.
A total of 6538 days of GOLF observations with a duty cycle of 96.0% covering 18 yr between 1996 April 11, and 2014 March 5, were analyzed. The GOLF velocity time series were obtained following García et al. (2005) and the amplitudes of the blue- and red-wing signals normalized as in Jiménez-Reyes et al. (2003). To obtain relations between mode frequencies and solar activity, this dataset was split into 69 contiguous 365-day subseries, with a four-time overlap of 91.25 days.
2.2. Extraction of the p-mode parameters
The power spectrum of each time series was fitted to estimate the mode parameters of the l = 0, 1, 2, and 3 modes as described in Salabert et al. (2007). Each mode component of radial order n, angular degree l, and azimuthal order m was parameterized with an asymmetric Lorentzian profile (Nigam & Kosovichev 1998), as 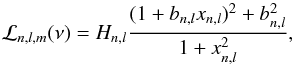 (1)where xn,l = 2(ν−νn,l)/Γn,l, and νn,l, Γn,l, and Hn,l represent the mode frequency, linewidth, and height of the spectral density, respectively. The peak asymmetry is described by the parameter bn,l. Because of their close proximity in frequency, modes are fitted in pairs (i.e., l = 2 with 0, and l = 3 with 1). While each mode parameter within a pair of modes is free, the peak asymmetry is set to be the same within pairs of modes. When present inside the fitting window, the l = 4 and 5 modes were included in the fitted model. An additive value B is added to the fitted profile representing a constant background noise in the fitted window. Since SoHO observes the Sun towards the equator, only the l + | m | even components are visible in the Sun-as-a-star observations from the GOLF instrument. The amplitude ratios between the l = 0,1,2, and 3 modes and the m-height ratios of the l = 2 and 3 multiplets calculated in Salabert et al. (2011) for the GOLF measurements were used. Finally, the mode parameters were extracted by maximizing the likelihood function, the power spectrum statistics being described by a χ2 with two degrees of freedom distribution. The natural logarithms of the mode height, linewidth, and background noise were varied resulting in normal distributions. The formal uncertainties in each parameter were then derived from the inverse Hessian matrix.
(1)where xn,l = 2(ν−νn,l)/Γn,l, and νn,l, Γn,l, and Hn,l represent the mode frequency, linewidth, and height of the spectral density, respectively. The peak asymmetry is described by the parameter bn,l. Because of their close proximity in frequency, modes are fitted in pairs (i.e., l = 2 with 0, and l = 3 with 1). While each mode parameter within a pair of modes is free, the peak asymmetry is set to be the same within pairs of modes. When present inside the fitting window, the l = 4 and 5 modes were included in the fitted model. An additive value B is added to the fitted profile representing a constant background noise in the fitted window. Since SoHO observes the Sun towards the equator, only the l + | m | even components are visible in the Sun-as-a-star observations from the GOLF instrument. The amplitude ratios between the l = 0,1,2, and 3 modes and the m-height ratios of the l = 2 and 3 multiplets calculated in Salabert et al. (2011) for the GOLF measurements were used. Finally, the mode parameters were extracted by maximizing the likelihood function, the power spectrum statistics being described by a χ2 with two degrees of freedom distribution. The natural logarithms of the mode height, linewidth, and background noise were varied resulting in normal distributions. The formal uncertainties in each parameter were then derived from the inverse Hessian matrix.
3. Results
The temporal variations of the mode frequencies, ⟨ Δνn,l ⟩, were defined as the differences between the frequencies observed at different dates and reference values of the corresponding modes. The set of reference frequencies was taken as the average over the years 1996–1997, corresponding to the minimum of activity Cycle 22. The formal uncertainties resulting from the peak-fitting analysis were used as weights in the average computation. The frequency shifts thus obtained were then weighted averaged over 15 consecutive radial orders between 1800 μHz and 3790 μHz. The lower frequency was defined by the lowest modes, which are accurately fitted in all the analyzed 365-day spectra, i.e., n = 12 for l = 0 and 1, and n = 11 for l = 2. We note that we did not use the l = 3 mode in the following analysis because of its lower signal-to-noise ratio. In addition, mean values of daily measurements of the 10.7 cm radio flux, F10.7, were used as a proxy of the solar surface activity1.
3.1. At different depths below the surface
As demonstrated, for example, by Chaplin et al. (1998), Howe et al. (1999), Jiménez-Reyes et al. (2001), and Salabert et al. (2004) for both low- and medium-angular degrees, the frequency shifts associated with the solar Schwabe cycle present a strong frequency dependence, going from small shifts at low frequency to much larger shifts at high frequency. As modes with different frequencies are sensitive to different layers in the sub-surface outer parts of the Sun, this information can be used to examine differences between solar Cycles 23 and 24 at different depths.
We thus defined three distinct frequency ranges each containing five consecutive radial orders covering different reflecting points in the solar atmosphere. The three frequency ranges were defined as follows: (1) the low-frequency range where 1800 μHz ≤ ν< 2450 μHz; (2) the medium-frequency range where 2450 μHz ≤ ν< 3110 μHz; and (3) the high-frequency range where 3110 μHz ≤ ν< 3790 μHz. These three frequency ranges allow us to study the response of the p-mode oscillations to solar activity at different depths below the surface, and thus to infer localizations of the layers where the magnetic fields affect the oscillation frequencies. Indeed, Basu et al. (2012) calculated that the averaged kernels of the mid- and the high-frequency ranges have their largest sensitivities at 0.9981 R⊙ (i.e., 1300 km) and 0.9989 R⊙ (i.e., 760 km), respectively, while the low-frequency modes peak deeper in the solar interior at 0.9965 R⊙ (i.e., 2400 km). Nevertheless, while the mid- and the high-frequency modes correspond to a thin layer below the Sun’s surface, the averaged kernel of the low-frequency modes covers a much wider region ranging from 1400 km down to 4000 km. Finally, four frequency ranges were thus used to calculate the frequency shifts; we include the one between 1800 μHz and 3790 μHz.
 |
Fig. 1 Temporal variations of the frequency shifts in μHz averaged over the modes l = 0,1, and 2, ⟨ Δνn,l = 0, 1, 2 ⟩, and calculated for four different frequency ranges (black dots). From left to right, the frequency ranges are the following: a) 1800 μHz ≤ ν< 3790 μHz; b) 1800 μHz ≤ ν< 2450 μHz; c) 2450 μHz ≤ ν< 3110 μHz; and d) 3110 μHz ≤ ν< 3790 μHz. The 10.7 cm radio flux, F10.7, averaged over the same 365-day timespan and scaled to match the rising phase and maximum of Cycle 23 is shown as a proxy of the solar surface activity (solid line). |
 |
Fig. 2 Same as Fig. 1 but after removing the QBO signature from the temporal variations of the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩ (black dots). The 10.7 cm radio flux, F10.7, was smoothed in the same way and scaled to match the rising phase and maximum of Cycle 23 (solid line). |
 |
Fig. 3 Left panel: frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, in μHz averaged over 15 radial orders over 1800 μHz ≤ ν< 3790 μHz as a function of the corresponding 10.7 cm radio flux, F10.7, once the QBO signature was removed. The rising (black dots) and declining (blue dots) phases of Cycle 23, and the rising phase (red dots) of Cycle 24 are indicated by different colors. Middle panel: same as left panel, but for the low-frequency modes averaged between 1800 μHz ≤ ν< 2450 μHz. Right panel: same as the left and middle panels, but for the high-frequency modes between 3110 μHz ≤ ν< 3790 μHz. |
Figure 1 shows the temporal variations of the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, averaged over the modes l = 0,1, and 2 and calculated over the four defined frequency ranges. The corresponding 10.7 cm radio flux averaged over the same 365-day subseries is also shown for comparison. It was scaled to match the rising phase and the maximum of solar Cycle 23, by performing a linear least-square regression with the frequency shifts. In Table 1, we present the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, calculated per unit of change in the 10.7 cm radio flux obtained by minimizing weighted linear regressions between these two quantities, as well as the associated linear correlation coefficients, derived for the different frequency ranges. We also note that the values given in Table 1 correspond to one set of independent spectra for every four points and that they are consistent within 1σ with any other of the chosen sets. As already widely established (see, e.g., the references given in Sect. 1), the temporal variabilities of the p-mode oscillation frequencies extracted from 18 yr of GOLF data are observed to be closely correlated with surface activity following the 11-yr periodicity of the solar cycle. The correlation coefficients are over 0.95 for the mid- and the high-frequency ranges, but the low-frequency modes show a smaller correlation with surface activity of about 0.5. While the higher frequency modes show the largest variations along the solar cycle with frequency shifts being more than 10 times larger than the ones at low frequency, the low-frequency p modes still show significant variations between periods of low and high surface activity (Fig. 1). Moreover, the minimum of Cycle 23 in the frequency shifts of the mid- and high-frequency modes is observed to be lower than the minimum of Cycle 22 in May–June 1996, which is in agreement with the weaker surface activity since the long and deep minimum of Cycle 23 compared to Cycle 22. The quasi-biennial oscillation (QBO; Fletcher et al. 2010) with an amplitude modulated by the 11-yr solar cycle is also visible in Fig. 1 in all the frequency ranges.
3.2. At different periods of the cycles
Significant differences in the relationship between acoustic oscillation frequencies and activity proxies were observed during the unusual extended minimum of Cycle 23 compared to other phases of activity (Salabert et al. 2009; Broomhall et al. 2009; Tripathy et al. 2010). For these reasons, we examined three separate periods: a) the rising phase of Cycle 23 going from April 1996 to October 2001 with a mean 10.7 cm radio flux of 129 RF2; b) the declining phase of Cycle 23 going from October 2001 to January 2009 with a mean 10.7 cm radio flux of 114 RF; and c) the rising phase of Cycle 24 going from January 2009 to April 2014 with a mean 10.7 cm radio flux of 99 RF. The starting and ending dates of each of the three activity phases were defined using the 10.7 cm radio flux properly smoothed to remove the signature of the QBO as described in Fletcher et al. (2010). Table 1 gives the gradients and the correlation coefficients between frequency shifts and radio flux during the three phases of activity for the four frequency ranges. It shows that the frequency shifts averaged over 1800 μHz ≤ ν< 3790 μHz are observed to be about 50% larger per unit of change in radio flux during the rise of Cycle 24 than during the rise of Cycle 23, whereas the radio emission decreased by about 30% over the same period of time. In addition, during the declining phase of Cycle 23, the gradients are observed to be about 15% larger than during the rising phase of Cycle 23. Moreover, the discrepancy in the relationship between frequencies and radio flux is more important for the low-frequency modes, i.e., for the modes going into deeper layers of the Sun than for the higher-frequency modes confined in shallower layers, and it is accentuated during the rise of Cycle 24 (Table 1). The correlation coefficients with solar activity also indicate a decrease of almost 40% between Cycle 23 and Cycle 24 for the low-frequency modes, while for the mid- and the high-frequency modes they remained similar.
Frequency shifts per unit of change in the 10.7 cm solar radio flux and linear correlations extracted from the analysis of independent 365-day GOLF spectra for different phases of solar Cycles 23 and 24.
 |
Fig. 4 Same as Fig. 1, but for the temporal variations in μHz of the frequency shifts (from top to bottom) ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l = 0, 1, and 2 (black dots). The associated 10.7 cm radio flux, F10.7, scaled to match the rising phase and the maximum of Cycle 23 is shown as a proxy of the solar surface activity (solid line). |
Figure 2 shows the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, averaged over the modes l = 0,1, and 2 once the QBO signature was removed by applying a proper smoothing of 2.5 yr as prescribed in Fletcher et al. (2010) for the four frequency ranges previously defined. The solid line in each panel corresponds to the scaled 10.7 cm radio flux, smoothed in the same manner. We note that in order to avoid misinterpretation caused by possible border effects introduced by the smoothing, we do not consider the extreme points corresponding to the first three and the last three points of the smoothed data. The larger frequency shifts compared to the surface activity proxy is clearly seen in Fig. 2 during the rise of Cycle 24 from 2008. The low-frequency modes show the largest deviation with the 10.7 cm radio flux, with much larger frequency shifts than would be expected based on the surface activity proxy. The declining phase associated with Cycle 23 is also much steeper than the activity proxy, unlike what is observed for the mid- and high-frequency p modes. Moreover, while the mid- and high-frequency ranges show temporal variations cleaned from the QBO, a longer period seems to appear in the low-frequency modes starting from 2006. Although this needs further observations in order to be confirmed, it could indicate changes related to the QBO deeper than 1400 km in the Sun’s sub-surface layers. See Appendix B for additional figures based on the analysis of the frequency shifts at individual angular degree.
The left panel of Fig. 3 shows the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, averaged over the 15 radial orders between 1800 μHz and 3790 μHz as a function of the associated 10.7 cm radio flux for the three phases of solar activity defined above, both quantities being properly smoothed as in Fletcher et al. (2010). A clear magnetic hysteresis appears between oscillation frequencies and radio flux over Cycle 23, but the pattern has changed since the minimum of Cycle 23 with larger frequency shifts for a given level of radio flux during the rising phase of Cycle 24. The middle and right panels of Fig. 3 show respectively the low- and the high-frequency shifts as a function of the corresponding radio flux. The different behavior between the lower and the higher frequency modes indicates differences in the structural and magnetic changes as a function of depth in the sub-surface layers of the Sun between Cycle 23 and Cycle 24 (see also the discussion in Sect. 4 and Appendix B for additional figures of hysteresis at each l). The frequency shifts are actually measured to be ahead of the radio flux by about 60 days in the velocity GOLF data, while a longer delay of about 90 days is observed with the data from the three solar photometers composing the Variability of Solar Irradiance and Gravity Oscillations (VIRGO; Fröhlich et al. 1995) instrument on board SoHO (Salabert et al. 2013).
Table 2 gives the differences in the frequency shifts averaged over l = 0, 1, and 2 modes between the maximum and minimum of each solar cycle for the different frequency ranges as illustrated in Fig. 2. The periods of minimum and maximum activity were defined by selecting the data points included within 15% of the minimum (or the maximum) of the radio flux. The mean values of the frequency shifts over these selected periods were obtained before calculating the differences. The last column in Table 2 shows the ratio of amplitudes between Cycle 24 and Cycle 23, in the sense (Max24 −Min23) − (Max23 −Min22). This indicates how the frequency shifts respond to the weaker Cycle 24 compared to Cycle 23. The low-frequency modes have comparable shifts between Cycle 23 and Cycle 24, while the mid- and the high-frequency modes are about 30% smaller during Cycle 24, which is comparable to the decrease observed in radio flux emission between Cycles 23 and 24. The differences between different frequency ranges thus suggest that the changes associated with the weaker Cycle 24 occur in shallower layers of the Sun, while the structure and the magnetic field deeper than 1400 km must have remained unchanged between Cycle 23 and Cycle 24, as inferred from the low-frequency modes.
Peak-to-peak variations of the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, averaged over the modes l = 0, 1, and 2 (in nHz) calculated between different activity phases of Cycles 23 and 24 over four different frequency ranges.
3.3. At individual angular degrees
Oscillation modes with different angular degrees l respond differently to the solar cycle (Salabert et al. 2009) in relation to the spatial distribution of the surface magnetic field (Howe et al. 2002; Jiménez-Reyes et al. 2004). Studying them individually can provide insights into the differences observed between activity cycles (see also Appendix B).
The twelve panels of Fig. 4 show the temporal variations of the frequency shifts extracted from the GOLF data at each individual l and calculated over the four frequency ranges. The individual l = 0, 1, and 2 modes are represented from top to bottom, while the different frequency ranges are shown from left to right as illustrated in Fig. 1. The 10.7 cm radio flux is also represented, scaled to match the rising phase and the maximum of Cycle 23 as was done previously. The corresponding gradients and the correlation coefficients between frequency shifts at each l and radio flux are also given in Table 1. Each individual l modes show different responses depending on the frequency range, indicating different temporal and latitudinal sensitivities to the structural and magnetic sub-surface changes with solar activity. The gradients between each l are of the same order of magnitude over a given frequency range. Nevertheless, the detailed temporal evolution of the individual frequency shifts is different from one degree to the other, and from one frequency range to the other, providing precious insights into the structural and magnetic changes as a function of latitude and depth that could be related to the dipole and the quadrupole components of the magnetic field, as discussed in the next section.
 |
Fig. 5 Differences in μHz between observed GOLF frequencies used for sound speed inversion (Turck-Chièze & Lopes 2012) and theoretical frequencies of the SSM scaled by the inertia ratio Qn,l using MLT convection (diamonds); the Canuto prescription of convection (triangles; Canuto & Mazzitelli 1991); the mean thermal description (crosses); and 3D simulations from (Nordlund & Stein 1998; squares). See also Piau et al. (2014) for the results obtained with the MDI data. |
4. Discussion
The temporal variability of the solar oscillation frequencies with solar activity results from the combination of structural changes in the sub-surface layers of the Sun, associated with other changes resulting from the topology of the magnetic field. In fact, the internal magnetic field does not act directly on the structure as the magnetic pressure is very low compared to the gas pressure in the solar interior, so it does not perturb it directly. This is the reason why the 1D modeling of the Sun through the standard solar model (SSM) or the seismic solar model (SeSM) does not contain any equations including the magnetic field (e.g., Turck-Chièze & Couvidat 2011; Basu et al. 2014).
It is now well established that the variability of the acoustic modes reveals a very small but important zone of the Sun located just below the surface called the superadiabatic region; see Fig. 1 of Lefebvre et al. (2009) illustrating the stratification of the upper layers of the Sun. The 3D simulations performed with STAGGER (Nordlund & Stein 1998) is one of the best ways to study the action of the magnetic field in this region as these simulations correspond to layers located between −2000 km and +900 km around the surface. STAGGER properly describes the turbulent pressure and the motions that act below the solar surface, and it reproduces remarkably well the convective motions at the surface. The addition of a magnetic field has two effects in that region of the Sun: it partly inhibits the turbulent pressure which cannot be properly described in a 1D solar model, and it directly acts on the gas pressure when the magnetic pressure is relatively non-negligible around the solar surface. The advantage of combining a real 3D turbulent structure with a 1D model was demonstrated by Piau et al. (2014); it improves the prediction of the absolute values of the acoustic frequencies and helps to interpret the observations of the sub-surface regions. The introduction of an accurate turbulent pressure modifies the absolute value of the theoretical acoustic mode frequencies. While the SSM or SeSM leads to theoretical frequencies greater than the observed ones by up to 10 μHz, a hydrodynamical model reduces the differences with the seismic values within 3 μHz because these layers are better described. Figure 5 shows this result compared to different ways of treating the convection in 1D.
The introduction of a magnetic field strength of 1200 G at the bottom of the simulation compatible with the strength of the toroidal field at 0.996 R⊙ extracted by Baldner et al. (2009) from the seismic observations collected by the Michelson Doppler Imager (MDI; Scherrer et al. 1995) on board SoHO, slightly reduces the turbulence and leads to a small decrease in the solar radius of dozens of kilometers at the surface (Piau et al. 2011). The l = 0 radial differences at the high-frequency range extracted from the GOLF observations (Fig. 4) of about 1.3 × 10-4 between minimum and maximum of activity could be attributed to pure structural changes. If we follow the relation 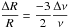 , which would correspond to an upper limit for a change in solar radius of about 50 km at maximum of Cycle 23 and of about 30 km during Cycle 24. Bush et al. (2015) extracted a radius change of 4 × 10-5 over the last four years using the observations from the Helioseismic and Magnetic Imager (HMI; Scherrer et al. 2012) instrument on board the Solar Dynamics Observatory spacecraft, which is compatible with the estimate extracted from the radial mode observed by the GOLF instrument. The l = 1 dipole and l = 2 quadrupole temporal variations shown in Fig. 4 at the high-frequency range, show reasonably well the same order of changes combined with a clear increase of the quasi-biennal component which probably translates the beating of the dipolar and quadrupolar components of the magnetic field just below the surface (Tobias 1996; Simoniello et al. 2013; Tobias & Cattaneo 2013).
, which would correspond to an upper limit for a change in solar radius of about 50 km at maximum of Cycle 23 and of about 30 km during Cycle 24. Bush et al. (2015) extracted a radius change of 4 × 10-5 over the last four years using the observations from the Helioseismic and Magnetic Imager (HMI; Scherrer et al. 2012) instrument on board the Solar Dynamics Observatory spacecraft, which is compatible with the estimate extracted from the radial mode observed by the GOLF instrument. The l = 1 dipole and l = 2 quadrupole temporal variations shown in Fig. 4 at the high-frequency range, show reasonably well the same order of changes combined with a clear increase of the quasi-biennal component which probably translates the beating of the dipolar and quadrupolar components of the magnetic field just below the surface (Tobias 1996; Simoniello et al. 2013; Tobias & Cattaneo 2013).
The temporal variations of the medium-frequency modes are clearly less sensitive to radius changes (0.15 μHz instead 0.4 μHz for the l = 0 modes). Lefebvre et al. (2009) demonstrated that a change in radius of 2 × 10-4 perturbs the internal structure down to 0.99 R⊙ through opacity and equation of state variations that could induce pulsations of these layers by kappa mechanisms. The differences observed here cannot then be interpreted as a pure structural change when the magnetic field in the sub-surface layers changes slightly. In order to better understand the situation, we also need to consider the observations of the emerging solar magnetic field. Three distinct results are useful in that respect: 1) the observation of the solar wind collected by the Ulysses mission has shown very different minima for Cycles 22 and 23, the minimum of Cycle 23 having a rather opened field near the equator, which shows the increasing importance of the toroidal component (McComas et al. 2008); 2) the dipolar and the radial magnetic fields observed at the Wilcox Solar Observatory (WSO; Hoeksema 2009) since 1978; and 3) the measurements of the sunspot magnetic field strength which has been decreasing since Cycle 22 and the measurement of the 1500 G threshold needed in order for dark sunspots to form (Livingston et al. 2012). The variability of the l = 1 and l = 2 modes is practically two times larger than the l = 0 mode variability, with a more perturbed temporal evolution than the one observed in the 10.7 cm radio flux and the l = 0 modes. This is particularly true for the l = 2 modes. This is in agreement with the observations of the magnetic field performed at WSO, which indicate that even if both dipolar and quadrupolar components of the external fields have been decreasing since at least 1985, the ratio between quadrupolar and dipolar components of the radial field shows a constant increase (Inceoglu et al. 2015).
The low-frequency range is the most interesting region to consider. Even if the effects are very small and the maximum of Cycle 23 is visible, we observe very perturbed signals for the low-degree modes mainly for the l = 2 modes. Table 1 shows low levels of correlation with the 10.7 cm radio flux since the maximum of Cycle 23, and Table 2 indicates that the ratio of the peak-to-peak variations of the frequency shifts between Cycle 24 and Cycle 23, (Max24 −Min23) − (Max23 −Min22), is larger for the low-frequency modes than for the medium- and high-frequency modes. Moreover, the toroidal field, responsible for the local partial inhibition of the turbulence and associated consequences, was observed to increase by about a factor of 3 during the maximum of Cycle 23 toward the solar interior between 0.999 R⊙ and 0.996 R⊙ (Baldner et al. 2009). What is unclear is whether the observed variability of the acoustic low-frequency modes comes from oscillations due to a kappa mechanism or from a beating between the poloidal and toroidal components of the magnetic field. The first assumption implies that the QBO signature should decrease as a function of time, which is not the case. We can then speculate about an amplification of the variations of the low-frequency shifts to an increase of the ratio between components of the magnetic field from Cycle 22 to Cycle 24. Nevertheless, the sudden increase in the l = 1 shifts at low frequency is unexpected in this context and justifies more investigations (see Appendix B). In addition, as observed in sunspot number, the last solar cycles present clear hemispheric asymmetries3, with successive dominant north and south hemispheres during the maximum of activity.
The study presented here indicates that the deeper toroidal magnetic field seems quite stable along Cycle 23 and 24, while the magnetic field at the surface is decreasing. As a consequence, a relative disconnection between acoustic frequencies and surface proxy, such as the 10.7 cm radio flux, is observed to be more and more visible in the deeper sub-surface layers of the Sun below 1400 km. The physical reason for this is not yet understood. One possibility is the existence of two dynamos, a deep one and a shallow one. Another possibility, among others, is that some variability, larger than the 11-yr timescale, exists in the tachocline and produces the emergence at the surface of varying flux tubes in addition to the small-scale convection present in the sub-surface layers. Moreover, the chaotically modulated solar dynamo, proposed by Tobias et al. (1995), does not appear to be in contradiction with the present observations. Any progress supposes a good knowledge of the deep magnetic field in the quiet and active Sun. More realistic 3D spherical simulations of the global dynamo coupled to superficial cartesian 3D simulations with different topologies of the magnetic field could provide invaluable understanding of the internal dynamical Sun.
5. Conclusions
We analyzed 18 yr of the Sun-as-a-star, space-based radial velocity helioseismic GOLF observations spanning the entire Cycle 23 and the rising phase of the weak Cycle 24. We studied the temporal variations of the low-degree oscillation frequencies along this 18-yr dataset in order to propose inferences on the structural and magnetic changes in the sub-surface layers of the Sun that could explain the progression of Cycle 24. Indeed, the averaged kernels of the acoustic modes at different frequency ranges have their largest sensitivities at different depths. While the sensitivity of the low-degree, high-frequency modes (between 3110 μHz ≤ ν< 3790 μHz) peaks at 0.9989 R⊙ (i.e., 760 km) from the Sun’s surface, the low-degree, low-frequency modes (1800 μHz ≤ ν< 2450 μHz) are mostly sensitive to deeper layers at 0.9965 R⊙ (i.e., 2400 km).
We showed that while the frequency shifts associated with layers above 1400 km have been following the decrease of surface activity during Cycle 24 compared to Cycle 23, the frequency shifts associated with layers below 1400 km remained similar between Cycle 23 and Cycle 24 for the extrema of the Schwabe cycle. The study of the temporal variations of the individual mode oscillation frequencies observed by GOLF thus suggests that while Cycle 24 is clearly magnetically weaker in the shallower parts of the Sun, solar Cycle 23 and 24 are magnetically and structurally similar below 1400 km, except for the quasi-biennial oscillation for the radial and quadrupole modes which is observed to be slightly amplified and which might have a longer temporal period in these deeper-lying parts during the rising phase of Cycle 24. However, the dipole modes show a specific and as yet unexplained behavior. Inversions combining low- and high-degree modes would provide a more precise localization of the evolution of the magnetic field from the surface to deeper parts of the Sun.
Online material
Appendix A: GOLF/SoHO low-degree acoustic oscillation frequencies
Table A.1 illustrates the content of the frequency tables made available electronically through this work. They contain the central frequencies of the low-degree acoustic modes of oscillations of the Sun extracted from 365-day subseries of 18 yr of GOLF/SoHO observations between 1996 April 11, and 2014 March 5. As a four-time overlap of 91.25 days was used, a total of 69 frequency tables are provided. We note that one of every four frequency tables contains frequencies extracted from independent subseries; see Sect. 2 for a detailed description of the methodology used to extract the mode frequencies. Quality criteria were defined based on the fitted mode parameters and their associated uncertainties in order to remove outliers: 1) the error of the mode frequency must be less than its mode width; 2) the signal-to-noise ratio must be larger than 1; and 3) the mode width must be larger than the frequency resolution. The entire set of tables containing the GOLF l = 0, 1, 2, and 3 p-mode frequencies between 1500 μHz and 4000 μHz and their associated formal 1σ uncertainties are available in a machine readable format at CDS. The GOLF velocity time series used in this work and the extracted frequency tables are directly available on the GOLF website at CEA4 and through the SoHO data archive at NASA and ESA.
Acoustic oscillation frequencies of the l = 0, 1, 2, and 3 modes extracted from the 365-day GOLF/SoHO spectrum calculated between 1996 April 11, and 1997 April 10.
 |
Fig. B.1 Temporal variations in μHz of the frequency shifts, ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l (from top to bottom), and calculated for four different frequency ranges with the QBO signature removed (black dots). From left to right, the frequency ranges are the following: a) 1800 μHz ≤ ν< 3790μHz; b) 1800 μHz ≤ ν< 2450μHz; c) 2450 μHz ≤ ν< 3110μHz; and d) 3110 μHz ≤ ν< 3790μHz. The 10.7 cm radio flux, F10.7, smoothed in the same way and scaled to match the rising phase and maximum of Cycle 23, is shown as a proxy of the solar surface activity (solid line). |
 |
Fig. B.2 Frequency shifts, ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l = 0, 1, and 2 (from left to right), as a function of the corresponding 10.7 cm radio flux, F10.7, and calculated for three different frequency ranges once the QBO signature was removed. From top to bottom, the frequency ranges are the following: a) 1800 μHz ≤ ν< 3790μHz; b) 1800 μHz ≤ ν< 2450μHz (low-frequency range); and c) 3110 μHz ≤ ν< 3790μHz (high-frequency range). The rising (black dots) and declining (blue dots) phases of Cycle 23, and the rising phase (red dots) of Cycle 24 are indicated by different colors. |
Appendix B: Frequency shifts at individual angular degree
Figure B.1 shows the temporal variations of the frequency shifts, ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, and ⟨ Δνn,l = 2 ⟩, at each individual angular degree l. The shifts were calculated over four frequency ranges: 1800 μHz ≤ ν< 3790μHz; 1800 μHz ≤ ν< 2450μHz (the low-frequency range); 2450 μHz ≤ ν< 3110μHz (the mid-frequency range); and 3110 μHz ≤ ν< 3790μHz (the high-frequency range). The QBO signature was removed by applying a proper smoothing of 2.5 yr as prescribed in Fletcher et al. (2010) for the four frequency ranges and for the 10.7 cm radio flux. We note that in order to avoid misinterpretation due to possible border effects introduced by the smoothing, we do not consider the extreme points corresponding to the first three and the last three points of the smoothed data. Each frequency range is sensitive to different depths in the sub-surface layers of the Sun, as calculated by Basu et al. (2012). The averaged kernels of the mid- and high-frequency ranges have their largest sensitivities at 0.9981 R⊙ (i.e., 1300 km) and 0.9989 R⊙ (i.e., 760 km), respectively, while the low-frequency modes peak deeper in the solar interior at 0.9965 R⊙ (i.e., 2400 km); see Sect. 3 for results of the frequency shifts averaged over the modes l = 0, 1, and 2, ⟨ Δνn,l = 0, 1, 2 ⟩.
While the temporal variations of the frequency shifts at l = 0, 1, and 2 show a good agreement with the 10.7 cm radio flux for the mid- and high-frequency modes, clear differences between the two quantities can be seen for the low-frequency modes. A residual after removing the QBO is still present in the l = 0 and l = 2 modes. The longer period observed in the low-frequency modes starting around 2006 and mentioned in Sect. 3 appears in the l = 0 and l = 2 modes only. On the other hand, the low-frequency l = 1 has a very different behavior. After a long period between 2004 and 2010 of practically no changes, a sharp increase of the l = 1 frequency shifts is measured starting from 2011, which is actually not present in the other angular degrees.
Figure B.2 shows the same frequency shifts, ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l, but as a function of the corresponding 10.7 cm radio flux, F10.7. Both quantities were properly smoothed as in Fletcher et al. (2010). The shifts obtained over three frequency ranges are represented: 1800 μHz ≤ ν< 3790μHz; 1800 μHz ≤ ν< 2450μHz (the low-frequency range); and c) 3110 μHz ≤ ν< 3790μHz (the high-frequency range). Different colors are used for the three different phases of solar activity: a) the rising phase of Cycle 23 going from 1996 April to 2001 October; b) the declining phase of Cycle 23 going from 2001 October to 2009 January; and c) the rising phase of Cycle 24 going from 2009 January to 2014 April (see Sect. 3 for more details). Again, the low-frequency
modes show a very different behavior from the higher-frequency modes. Moreover, a longer period than the quasi-biennial oscillation is observed for the radial and quadrupole modes during the rise of Cycle 24, while the dipole modes show a very distinct behavior.
The 10.7 cm radio flux data are available from the National Geophysical Data Center at http://www.ngdc.noaa.gov/stp/solar/solardataservices.html
Hemispheric sunspot numbers are provided by SILSO, Royal Observatory of Belgium, Brussels, at http://sidc.oma.be/silso/datafiles
The GOLF website at CEA is also mirrored through the SpaceInn website http://www.spaceinn.eu
Acknowledgments
The GOLF instrument on board SoHO is a cooperative effort of scientists, engineers, and technicians, to whom we are indebted. SoHO is a project of international collaboration between ESA and NASA. The authors strongly acknowledge the French space agency, CNES, for its support to GOLF since the launch of SoHO. We are also particularly grateful to Catherine Renaud for her daily check of the GOLF data. D.S. acknowledges the financial support from CNES. The research leading to these results has also received funding from the European Community’s Seventh Framework Programme ([FP7/2007-2013]) under grant agreement No. 312844 (SpaceInn). The 10.7 cm solar radio flux data were obtained from the National Geophysical Data Center. The authors acknowledge J. Ballot for useful discussions.
References
- Baldner, C. S., Antia, H. M., Basu, S., & Larson, T. P. 2009, ApJ, 705, 1704 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., Broomhall, A.-M., Chaplin, W. J., & Elsworth, Y. 2012, ApJ, 758, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Basu, S., Grevesse, N., Mathis, S., & Turck-Chièze, S. 2014, Space Sci. Rev., 3 [Google Scholar]
- Broomhall, A.-M., Chaplin, W. J., Elsworth, Y., Fletcher, S. T., & New, R. 2009, ApJ, 700, L162 [NASA ADS] [CrossRef] [Google Scholar]
- Bush, R. I., Emilio, M., Kuhn, J. R., & Scholl, I. 2015, Sol. Phys., in press [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Elsworth, Y., Isaak, G. R., et al. 1998, MNRAS, 300, 1077 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Elsworth, Y., Miller, B. A., Verner, G. A., & New, R. 2007, ApJ, 659, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Domingo, V., Fleck, B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Dziembowski, W. A., & Goode, P. R. 2005, ApJ, 625, 548 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, S. T., Broomhall, A.-M., Salabert, D., et al. 2010, ApJ, 718, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Fossat, E., Gelly, B., Grec, G., & Pomerantz, M. 1987, A&A, 177, L47 [NASA ADS] [Google Scholar]
- Fröhlich, C., Romero, J., Roth, H., et al. 1995, Sol. Phys., 162, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, A. H., Grec, G., Charra, J., et al. 1995, Sol. Phys., 162, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Garcia, R. A., Roca Cortes, T., & Regulo, C. 1998, A&AS, 128, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García, R. A., Jiménez-Reyes, S. J., Turck-Chièze, S., & Mathur, S. 2004, SOHO 14 Helio- and Asteroseismology: Towards a Golden Future, 559, 432 [NASA ADS] [Google Scholar]
- García, R. A., Turck-Chièze, S., Boumier, P., et al. 2005, A&A, 442, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gelly, B., Lazrek, M., Grec, G., et al. 2002, A&A, 394, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Howe, R., Komm, R., & Hill, F. 1999, ApJ, 524, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Komm, R. W., & Hill, F. 2002, ApJ, 580, 1172 [NASA ADS] [CrossRef] [Google Scholar]
- Howe, R., Christensen-Dalsgaard, J., Hill, F., et al. 2013, ApJ, 767, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeksema, J. T. 2009, in Solar and stellar variability: impact on earth and planets, eds. A. G. Kosovichev, A. H. Andrei, & J. P. Rozelot, IAU symp., 264, 222 [Google Scholar]
- Inceoglu, F., Simoniello, R., Knudsen, M. F., et al. 2015, MNRAS, submitted [Google Scholar]
- Jiménez-Reyes, S. J., Corbard, T., Pallé, P. L., Roca Cortés, T., & Tomczyk, S. 2001, A&A, 379, 622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez-Reyes, S. J., García, R. A., Jiménez, A., et al. 2003, ApJ, 595, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Reyes, S. J., García, R. A., Chaplin, W. J., & Korzennik, S. G. 2004, ApJ, 610, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Reyes, S. J., Chaplin, W. J., Elsworth, Y., et al. 2007, ApJ, 654, 1135 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, J. R. 1988, ApJ, 331, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Lefebvre, S., García, R. A., Jiménez-Reyes, S. J., Turck-Chièze, S., & Mathur, S. 2008, A&A, 490, 1143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lefebvre, S., Nghiem, P. A. P., & Turck-Chièze, S. 2009, ApJ, 690, 1272 [NASA ADS] [CrossRef] [Google Scholar]
- Libbrecht, K. G., & Woodard, M. F. 1990, Nature, 345, 779 [Google Scholar]
- Livingston, W., Penn, M. J., & Svalgaard, L. 2012, ApJ, 757, L8 [Google Scholar]
- McComas, D. J., Ebert, R. W., Elliott, H. A., et al. 2008, Geophys. Rev. Lett., 35, L18103 [NASA ADS] [CrossRef] [Google Scholar]
- Nigam, R., & Kosovichev, A. G. 1998, ApJ, 505, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, A., & Stein, R. F. 1998, New Eyes to See Inside the Sun and Stars, 185, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Piau, L., Stein, R. F., Melo, S., et al. 2011, SF2A-2011: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, 407 [Google Scholar]
- Piau, L., Collet, R., Stein, R. F., et al. 2014, MNRAS, 437, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Salabert, D., Fossat, E., Gelly, B., et al. 2004, A&A, 413, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Chaplin, W. J., Elsworth, Y., New, R., & Verner, G. A. 2007, A&A, 463, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., García, R. A., Pallé, P. L., & Jiménez-Reyes, S. J. 2009, A&A, 504, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salabert, D., Ballot, J., & García, R. A. 2011, A&A, 528, A25 [Google Scholar]
- Salabert, D., García, R. A., & Jiménez, A. 2013, ASP Conf. Ser., 478, 145 [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Simoniello, R., Jain, K., Tripathy, S. C., et al. 2013, ApJ, 765, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. M. 1996, ApJ, 467, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. M., & Cattaneo, F. 2013, Nature, 497, 463 [NASA ADS] [CrossRef] [Google Scholar]
- Tobias, S. M., Weiss, N. O., & Kirk, V. 1995, MNRAS, 273, 1150 [NASA ADS] [Google Scholar]
- Tripathy, S. C., Jain, K., Hill, F., & Leibacher, J. W. 2010, ApJ, 711, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Turck-Chièze, S., & Couvidat, S. 2011, Rep. Prog. Phys., 74, 086901 [NASA ADS] [CrossRef] [Google Scholar]
- Turck-Chièze, S., & Lopes, I. 2012, RA&A, 12, 1107 [Google Scholar]
- Turck-Chièze, S., Couvidat, S., Kosovichev, A. G., et al. 2001, ApJ, 555, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Woodard, M. F., & Noyes, R. W. 1985, Nature, 318, 449 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Frequency shifts per unit of change in the 10.7 cm solar radio flux and linear correlations extracted from the analysis of independent 365-day GOLF spectra for different phases of solar Cycles 23 and 24.
Peak-to-peak variations of the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, averaged over the modes l = 0, 1, and 2 (in nHz) calculated between different activity phases of Cycles 23 and 24 over four different frequency ranges.
Acoustic oscillation frequencies of the l = 0, 1, 2, and 3 modes extracted from the 365-day GOLF/SoHO spectrum calculated between 1996 April 11, and 1997 April 10.
All Figures
 |
Fig. 1 Temporal variations of the frequency shifts in μHz averaged over the modes l = 0,1, and 2, ⟨ Δνn,l = 0, 1, 2 ⟩, and calculated for four different frequency ranges (black dots). From left to right, the frequency ranges are the following: a) 1800 μHz ≤ ν< 3790 μHz; b) 1800 μHz ≤ ν< 2450 μHz; c) 2450 μHz ≤ ν< 3110 μHz; and d) 3110 μHz ≤ ν< 3790 μHz. The 10.7 cm radio flux, F10.7, averaged over the same 365-day timespan and scaled to match the rising phase and maximum of Cycle 23 is shown as a proxy of the solar surface activity (solid line). |
| In the text | |
 |
Fig. 2 Same as Fig. 1 but after removing the QBO signature from the temporal variations of the frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩ (black dots). The 10.7 cm radio flux, F10.7, was smoothed in the same way and scaled to match the rising phase and maximum of Cycle 23 (solid line). |
| In the text | |
 |
Fig. 3 Left panel: frequency shifts, ⟨ Δνn,l = 0, 1, 2 ⟩, in μHz averaged over 15 radial orders over 1800 μHz ≤ ν< 3790 μHz as a function of the corresponding 10.7 cm radio flux, F10.7, once the QBO signature was removed. The rising (black dots) and declining (blue dots) phases of Cycle 23, and the rising phase (red dots) of Cycle 24 are indicated by different colors. Middle panel: same as left panel, but for the low-frequency modes averaged between 1800 μHz ≤ ν< 2450 μHz. Right panel: same as the left and middle panels, but for the high-frequency modes between 3110 μHz ≤ ν< 3790 μHz. |
| In the text | |
 |
Fig. 4 Same as Fig. 1, but for the temporal variations in μHz of the frequency shifts (from top to bottom) ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l = 0, 1, and 2 (black dots). The associated 10.7 cm radio flux, F10.7, scaled to match the rising phase and the maximum of Cycle 23 is shown as a proxy of the solar surface activity (solid line). |
| In the text | |
 |
Fig. 5 Differences in μHz between observed GOLF frequencies used for sound speed inversion (Turck-Chièze & Lopes 2012) and theoretical frequencies of the SSM scaled by the inertia ratio Qn,l using MLT convection (diamonds); the Canuto prescription of convection (triangles; Canuto & Mazzitelli 1991); the mean thermal description (crosses); and 3D simulations from (Nordlund & Stein 1998; squares). See also Piau et al. (2014) for the results obtained with the MDI data. |
| In the text | |
 |
Fig. B.1 Temporal variations in μHz of the frequency shifts, ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l (from top to bottom), and calculated for four different frequency ranges with the QBO signature removed (black dots). From left to right, the frequency ranges are the following: a) 1800 μHz ≤ ν< 3790μHz; b) 1800 μHz ≤ ν< 2450μHz; c) 2450 μHz ≤ ν< 3110μHz; and d) 3110 μHz ≤ ν< 3790μHz. The 10.7 cm radio flux, F10.7, smoothed in the same way and scaled to match the rising phase and maximum of Cycle 23, is shown as a proxy of the solar surface activity (solid line). |
| In the text | |
 |
Fig. B.2 Frequency shifts, ⟨ Δνn,l = 0 ⟩, ⟨ Δνn,l = 1 ⟩, ⟨ Δνn,l = 2 ⟩, at each individual angular degree l = 0, 1, and 2 (from left to right), as a function of the corresponding 10.7 cm radio flux, F10.7, and calculated for three different frequency ranges once the QBO signature was removed. From top to bottom, the frequency ranges are the following: a) 1800 μHz ≤ ν< 3790μHz; b) 1800 μHz ≤ ν< 2450μHz (low-frequency range); and c) 3110 μHz ≤ ν< 3790μHz (high-frequency range). The rising (black dots) and declining (blue dots) phases of Cycle 23, and the rising phase (red dots) of Cycle 24 are indicated by different colors. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


