© ESO, 2015

1. Introduction

Coronal seismology as a tool for the remote diagnostic of fundamental plasma parameters is based on the modelling and observation of magnetohydrodynamic (MHD) waves in the solar atmosphere (e.g. reviews by Nakariakov & Verwichte 2005; Andries et al. 2009; De Moortel & Nakariakov 2012; Pascoe 2014). For example, standing kink oscillations of coronal loops have been used to infer the coronal magnetic field strength (e.g. Nakariakov et al. 1999; Nakariakov & Ofman 2001; White & Verwichte 2012) and it has been demonstrated that seismological inversions are consistent with values obtained by magnetic extrapolation and spectral observations (Verwichte et al. 2013a). Magnetohydrodynamic waves might also have a significant role in the processes of coronal heating and solar wind acceleration (e.g. review by Parnell & De Moortel 2012).

Resonant absorption was first suggested by Sedláček (1971) and discussed as a plasma heating mechanism by Chen & Hasegawa (1974) and Ionson (1978). There have subsequently been many numerical studies of the process. For example, Steinolfson & Davila (1993) investigated the importance of the global mode and scaling laws for coronal heating by resonant absorption. Poedts & Goedbloed (1994) performed 3D numerical simulations of non-linear wave heating with a varying background. Non-linear resonant absorption and heating was also studied numerically in a 3D slab model for a monochromatic driver by Ofman & Davila (1995) and for a broadband driver by Ofman & Davila (1996). Wright & Rickard (1995) performed a numerical study of resonant absorption in a magnetohydrodynamic cavity driven by a broadband spectrum. Wave heating of coronal loops driven by azimuthally polarised footpoint motions was studied by Berghmans & Tirry (1997) for dissipative MHD and by Tirry & Berghmans (1997) for ideal MHD. Excitation by radially polarised footpoint motions was considered for a slab in ideal MHD by Tirry et al. (1997) and De Groof & Goossens (2000). Ofman et al. (1998) studied the effects of coupling with the chromosphere on the resonant heating of coronal loops by a broadband wave source. Fast and Alfvén waves driven by azimuthal footpoint motions have been investigated for periodic (De Groof et al. 2002) and random (De Groof & Goossens 2002) drivers. Terradas et al. (2006) simulated the resonant damping of externally excited transverse coronal loop oscillations using a 1D model of a line-tied cylindrical loop while Terradas et al. (2008) considered the damping of oscillations in a 2D multi-stranded model. Russell & Wright (2010) studied resonant wave coupling in equilibria with a 2D structure perpendicular to the background magnetic field. Pascoe et al. (2011) considered mode coupling for propagating wavepackets in asymmetric loops and multi-stranded inhomogeneous media.

The transfer of energy from standing kink waves to azimuthal oscillations inside an inhomogeneous layer was used by Ruderman & Roberts (2002) and Goossens et al. (2002) to account for the strong damping of standing kink modes. Similarly, Pascoe et al. (2010) applied the model to propagating kink waves, which were observed to be spatially and temporally ubiquitous in the solar corona by Tomczyk et al. (2007) and to undergo rapid damping as they propagate along loop structures (Tomczyk & McIntosh 2009). Terradas et al. (2010) discussed the frequency dependence of the damping rate which may act as a low-pass filter for observations of broadband oscillations (Verth et al. 2010). Soler et al. (2011a,b, 2012) extended these studies to consider the effects of longitudinal background flows, stratification, and partial ionisation, respectively. Gravitational stratification causes an increase in amplitude of the velocity component (e.g. De Moortel et al. 1999; De Moortel & Hood 2004) of outwardly propagating waves and so can act to oppose the attenuation due to mode coupling.

Pascoe et al. (2012) considered strongly damped propagating kink waves and found that the damping behaviour for early times can be described by a Gaussian profile. Subsequently Hood et al. (2013) derived expressions for the damping behaviour for all times. The integro-differential equation for the continuous variation in amplitude with height z can be approximated by Gaussian and exponential functions at small and large z, respectively. This was employed by Pascoe et al. (2013) who produced a simpler, piecewise spatial damping profile suitable for use for seismological inversions. The initial stage of the damping envelope is described by a Gaussian function, $\mathit{A}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{=}\frac{{\mathit{A}}_{\mathrm{0}}}{\mathrm{2}}\left[\mathrm{1}\mathrm{+}\exp \left(\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}\right)\right]\mathit{,}$(1)where A₀ is the initial amplitude of the oscillation; L_g is the Gaussian damping length scale which depends on the loop parameters as ${\mathit{L}}_{\mathrm{g}}\mathrm{=}\frac{\mathrm{2}\mathit{\lambda }}{\mathit{\pi \kappa }{\mathit{ϵ}}^{\mathrm{1}\mathit{/}\mathrm{2}}}\mathit{,}$(2)where ϵ = l/R is the (normalised) inhomogeneous layer width, κ = (ρ₀ − ρ_e) / (ρ₀ + ρ_e) is a ratio of densities, and λ is the wavelength. Under the thin tube approximation, λ = C_kP, where C_k is the kink speed and P is the period of oscillation. The constant of proportionality is determined by the particular density profile in the inhomogeneous layer and the values used in this paper correspond to a linear profile.

The later stage of the damping envelope is described by an exponential function (e.g. Ruderman & Roberts 2002; Goossens et al. 2002; Terradas et al. 2010) of the form $\mathit{A}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{=}{\mathit{A}}_{\mathrm{0}}\exp \mathrm{(}\mathrm{-}\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}\mathrm{)}\mathit{,}$(3)where L_d is the exponential damping length scale given by ${\mathit{L}}_{\mathrm{d}}\mathrm{=}\frac{\mathrm{4}\mathit{\lambda }}{{\mathit{\pi }}^{\mathrm{2}}\mathit{\kappa ϵ}}\mathrm{·}$(4)Hence, the general spatial damping profile is $\mathit{A}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{=}\{\begin{array}{c}\\ \frac{{\mathit{A}}_{\mathrm{0}}}{\mathrm{2}}\left[\mathrm{1}\mathrm{+}\exp \left(\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}\right)\right]\mathit{,}& \mathit{z}\mathrm{\le }\mathit{h}\\ {\mathit{A}}_{\mathit{h}}\exp \mathrm{(}\mathrm{-}{\frac{\mathit{z}\mathrm{-}\mathit{h}}{{\mathit{L}}_{\mathrm{d}}}}^{\mathrm{)}}\mathit{,}& \mathit{z}\mathit{>}\mathit{h}\end{array}$(5)where A_h is the amplitude at the height h of the switch in profiles, given by $\mathit{h}\mathrm{=}\frac{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}{{\mathit{L}}_{\mathrm{d}}}\mathrm{=}\frac{\mathit{\lambda }}{\mathit{\kappa }}\mathrm{·}$(6)This profile can also be applied to standing waves with the appropriate change in variable (Pascoe et al. 2013; Ruderman & Terradas 2013). The Gaussian function in Eq. (1) gives an excellent fit to the integro-differential equation providing the damping is not too strong and so the constant term A₀ is smaller than the exponential term $\exp \mathrm{(}\mathrm{-}{\mathit{z}}^{\mathrm{2}}\mathit{/}{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}\mathrm{)}$. An alternative Gaussian function without this constant term is $\mathit{A}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{=}{\mathit{A}}_{\mathrm{0}}\exp \left(\mathrm{-}\frac{{\mathit{z}}^{\mathrm{2}}}{\mathrm{2}{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}\right)\mathrm{·}$(7)This Gaussian function may be used in place of Eq. (1) in the general spatial damping profile (Eq. (5)) when the damping is strong.

In Sect. 2 we apply the Gaussian spatial damping profile to the broadband oscillations observed by CoMP. In Sect. 3 we develop a new method for analysing broadband kink oscillations which, unlike Sect. 2, does not rely on the assumption of a particular damping profile. In Sect. 4 we demonstrate the application of this method using data from numerical simulations. In Sect. 5 we consider the effect of the spatial form of the driver on the observed oscillations. Conclusions are presented in Sect. 6.

2. Least squares fit to CoMP data

In this section we reconsider the analysis of CoMP data performed by Verth et al. (2010) using a Gaussian damping profile instead of the exponential profile used by those authors. The ratio of outward and inward power was calculated as a function of frequency and integrated over half a semi-circular loop. Their resulting expression (their Eq. (7)) is $\mathrm{⟨}\mathit{P}\left(\mathit{f}\right){\mathrm{⟩}}_{\mathrm{ratio}}\mathrm{=}\frac{{\mathit{P}}_{\mathrm{out}}\left(\mathit{f}\right)}{{\mathit{P}}_{\mathrm{in}}\left(\mathit{f}\right)}\exp \left(\frac{\mathrm{2}\mathit{L}}{{\mathit{v}}_{\mathrm{ph}}{\mathit{\xi }}_{\mathrm{E}}}\mathit{f}\right)\mathit{,}$(8)where L = 250 Mm is half the loop length, f is the frequency, and ξ_E = 2 /πκϵ. Assuming instead a Gaussian spatial damping profile of the form given by Eq. (7) we obtain $\mathrm{⟨}\mathit{P}\left(\mathit{f}\right){\mathrm{⟩}}_{\mathrm{out}}\mathrm{=}\frac{\mathrm{1}}{\mathit{L}}{\mathrm{\int }}_{\mathrm{0}}^{\mathit{L}}{\mathit{P}}_{\mathrm{out}}\left(\mathit{f}\right)\exp \mathrm{(}\mathrm{-}{\mathit{s}}^{\mathrm{2}}\mathit{/}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}^{\mathrm{)}}\mathrm{d}\mathit{s,}$(9)for the outward power, where s is the distance along the loop, and $\mathrm{⟨}\mathit{P}\left(\mathit{f}\right){\mathrm{⟩}}_{\mathrm{in}}\mathrm{=}\frac{\mathrm{1}}{\mathit{L}}{\mathrm{\int }}_{\mathit{L}}^{\mathrm{2}\mathit{L}}{\mathit{P}}_{\mathrm{in}}\left(\mathit{f}\right)\exp \mathrm{(}\mathrm{-}{\mathit{s}}^{\mathrm{2}}\mathit{/}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}^{\mathrm{)}}\mathrm{d}\mathit{s,}$(10)for the inward power. For the ratio we obtain $\mathrm{⟨}\mathit{P}\left(\mathit{f}\right){\mathrm{⟩}}_{\mathrm{ratio}}\mathrm{=}\frac{{\mathit{P}}_{\mathrm{out}}\left(\mathit{f}\right)}{{\mathit{P}}_{\mathrm{in}}\left(\mathit{f}\right)}\frac{\mathrm{erf}\mathrm{(}{\mathrm{\Lambda }}^{\mathrm{)}}}{\mathrm{erf}\mathrm{(}\mathrm{2}{\mathrm{\Lambda }}^{\mathrm{)}}\mathrm{-}\mathrm{erf}\mathrm{(}{\mathrm{\Lambda }}^{\mathrm{)}}}\mathit{,}$(11)where Λ = L/L_g and erf is the Error function. Whereas integrating the exponential spatial damping function over a loop element produces another exponential function (Eq. (8)), here the integration of the Gaussian damping profile produces a result in the form of Error functions. We can perform a least squares fit of Eq. (11) to observational data in the same way as for Eq. (8).

Fig. 1 Power ratio as a function of frequency for CoMP data. The dashed line represents the fit for an exponential spatial damping profile (Verth et al. 2010). The solid (red) line represents a fit for a Gaussian spatial damping profile.

Figure 1 shows the spectral power ratio as a function of frequency for the CoMP data presented in Verth et al. (2010). The dashed line represents the original fit found by those authors for an exponential spatial damping profile (Eq. (8)) i.e. P_out/P_in = 0.91 and ξ_E = 2.69. The solid (red) line represents a fit for a Gaussian spatial damping profile (Eq. (11)) with P_out/P_in = 1.19 and α = 0.76. (We note that the ratio P_out/P_in being greater or less than unity only refers to which of the two footpoints is driven more strongly. Alternatively, for an asymmetric loop the damping could be stronger on one side than the other.) It is clear that the noise in the data is too large to allow us to distinguish between the two fitted spatial damping profiles. We note that these two curves consider the limiting cases of entirely exponential and entirely Gaussian damping, whereas the most general behaviour would include both damping regimes as described by Eq. (5) and discussed in Sect. 4.2.

Although the CoMP data is too noisy to distinguish whether the damping profile is exponential or Gaussian, it is still instructive to develop analysis tools that will allow us to discriminate between the two profiles in the future. To test our proposed analysis technique we use numerical data since this has no noise. The spread in the observational data might also be a result of averaging along multiple loops along the line of sight, as considered by Verwichte et al. (2013b) who used a statistical approach to produce distributions for the values of loop parameters. We shall see in the following sections that it is indeed possible to identify the damping profile from broadband signals when the data is sufficiently clean and a single loop can be considered.

3. Analysis method for broadband kink oscillations

In the previous section we saw how integrating inward and outward power over the loop lost a lot of information and made it impossible to distinguish between the Gaussian and exponential wave profiles. In this section we present a new analysis method that does not integrate over the loop in such a straightforward fashion. The method we present facilitates the identification of the damping profile and is tested against numerical data for different coronal loop parameters and photospheric driving conditions.

First we examine the method used in the previous section in more detail. Taking $\mathit{P}{}^{\mathrm{\right(}}\mathit{z}^{\mathrm{\left)}}$ as the spectral power for, say, a transverse velocity signal, at some height z, then for an exponential spatial damping profile, Verth et al. (2010) obtain $\mathit{P}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{\propto }{\mathit{A}}^{\mathrm{2}}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{\propto }\exp \mathrm{(}\mathrm{-}\mathrm{2}\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}\mathrm{)}\mathit{,}$(12)where L_d = v_phξ_E/f and so the frequency dependence of the power at some height is given by $\mathit{P}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{\propto }\exp \left(\mathrm{-}\mathrm{2}\frac{\mathit{z}}{{\mathit{v}}_{\mathrm{ph}}{\mathit{\xi }}_{\mathrm{E}}}\mathit{f}\right)\mathrm{·}$(13)If we consider the ratio of spectral power at some height z to the spectral power at the source of the driver we obtain $\frac{\mathit{P}\mathrm{(}{\mathit{z}}^{\mathrm{)}}}{\mathit{P}\mathrm{(}\mathit{z}\mathrm{=}{\mathrm{0}}^{\mathrm{)}}}\mathrm{=}\frac{\exp \mathrm{(}\mathrm{-}\mathrm{2}\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}\mathrm{)}}{\exp \mathrm{\left(}\mathrm{0}\mathrm{\right)}}\mathit{,}$(14)and hence the ratio depends on z. Instead we now compare the ratio of P(z₀ + Δz) to $\mathit{P}{}^{\mathrm{(}}\mathit{z}_{\mathrm{0}}{}^{\mathrm{)}}$, where Δz is a fixed separation distance $\begin{array}{ccc}\frac{\mathit{P}\left({\mathit{z}}_{\mathrm{0}}\mathrm{+}\mathrm{\Delta }\mathit{z}\right)}{\mathit{P}\mathrm{(}{\mathit{z}}_{\mathrm{0}}\mathrm{)}}& \mathrm{=}& \frac{\exp \mathrm{(}\mathrm{-}\mathrm{2}\left({\mathit{z}}_{\mathrm{0}}\mathrm{+}\mathrm{\Delta }\mathit{z}\right)\mathit{/}{\mathit{L}}_{\mathrm{d}}\mathrm{)}}{\exp \mathrm{(}\mathrm{-}\mathrm{2}{\mathit{z}}_{\mathrm{0}}\mathit{/}{\mathit{L}}_{\mathrm{d}}\mathrm{)}}\\ & \mathrm{=}& \exp \left(\mathrm{-}\mathrm{2}\mathrm{\Delta }\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}\right)\\ & \mathrm{=}& \end{array}$(15)For an exponential spatial damping profile, the power ratio depends on the chosen Δz but is independent of z₀. Calculating the ratio for all available z₀ should give the same value. In practice the ratio will vary owing to errors and so an average ratio (for a given Δz) can be calculated, thus improving the statistical accuracy of the result compared with a single measurement.

We now consider a Gaussian spatial damping profile, again having the form given by Eq. (7), which is more convenient than Eq. (1) since the absence of the constant term A₀/ 2 makes taking ratios of functions much simpler. The spectral power is given by $\mathit{P}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{\propto }{\mathit{A}}^{\mathrm{2}}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{\propto }\exp \mathrm{(}\mathrm{-}{\mathit{z}}^{\mathrm{2}}\mathit{/}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}^{\mathrm{)}}\mathit{,}$(16)and for convenience we can introduce L_g = 1 /αf with α = πκϵ^{1 / 2}/ 2C_k. The frequency dependence of the power at some height is then given by $\mathit{P}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{\propto }\exp \mathrm{(}\mathrm{-}{\mathit{z}}^{\mathrm{2}}{\mathit{\alpha }}^{\mathrm{2}}{\mathit{f}}^{\mathrm{2}}\mathrm{)}\mathit{.}$(17)Considering a spectral power ratio as in Eq. (15), with z₁ = z₀ + Δz, now gives $\begin{array}{ccc}\frac{\mathit{P}\mathrm{(}{\mathit{z}}_{\mathrm{1}}\mathrm{)}}{\mathit{P}\mathrm{(}{\mathit{z}}_{\mathrm{0}}\mathrm{)}}& \mathrm{=}& \frac{\exp \mathrm{(}\mathrm{-}{\left({\mathit{z}}_{\mathrm{0}}\mathrm{+}\mathrm{\Delta }\mathit{z}\right)}^{\mathrm{2}}{\mathit{\alpha }}^{\mathrm{2}}{\mathit{f}}^{\mathrm{2}}\mathrm{)}}{\exp \mathrm{(}\mathrm{-}{\mathit{z}}_{\mathrm{0}}^{\mathrm{2}}{\mathit{\alpha }}^{\mathrm{2}}{\mathit{f}}^{\mathrm{2}}\mathrm{)}}\\ & \mathrm{=}& \end{array}$(18)Unlike the case of the exponential spatial damping profile, the power ratio now depends on the choice of z₀ and so an average value cannot be calculated using different values of z₀. Instead, if z₀ ranges from 0 to some maximum value z_m, there will be two bounding curves for the ratio. The upper bounding curve will correspond to z₀ = 0 and hence give a spectral power ratio $\frac{\mathit{P}\left({\mathit{z}}_{\mathrm{1}}\mathrm{=}\mathrm{\Delta }\mathit{z}\right)}{\mathit{P}\mathrm{(}{\mathit{z}}_{\mathrm{0}}\mathrm{=}{\mathrm{0}}^{\mathrm{)}}}\mathrm{=}\exp \mathrm{(}\mathrm{-}{\mathrm{\Delta }\mathit{z}}^{\mathrm{2}}{\mathit{\alpha }}^{\mathrm{2}}{\mathit{f}}^{\mathrm{2}}\mathrm{)}\mathit{,}$(19)while the lower bounding curve will correspond to z₀ = z_m and is given by $\frac{\mathit{P}\left({\mathit{z}}_{\mathrm{1}}\mathrm{=}{\mathit{z}}_{\mathrm{m}}\mathrm{+}\mathrm{\Delta }\mathit{z}\right)}{\mathit{P}\mathrm{(}{\mathit{z}}_{\mathrm{0}}\mathrm{=}{\mathit{z}}_{\mathrm{m}}\mathrm{)}}\mathrm{=}\exp \mathrm{(}\mathrm{-}\mathrm{(}\mathrm{2}{\mathit{z}}_{\mathrm{m}}\mathrm{\Delta }\mathit{z}\mathrm{+}{\mathrm{\Delta }\mathit{z}}^{\mathrm{2}}\mathrm{)}{\mathit{\alpha }}^{\mathrm{2}}{\mathit{f}}^{\mathrm{2}}\mathrm{)}\mathit{.}$(20)These two curves will converge in the limits f → 0 and f → ∞ but will otherwise be distinct. Increasing the separation distance Δz brings the curves closer together.

Fig. 2 Sketch of our method for calculating the spectral power ratio (e.g. Fig. 5). The spectral power of the transverse velocity signal at z1 is compared to that at z0 where Δz is a fixed separation distance. The colour represents the value of z0 from 0 (blue) to zm (red).

Figure 2 demonstrates this method of calculating the spectral power ratio for a chosen Δz and z_m. For each value of z₀, a section of the transverse velocity signal is selected and the corresponding spectral power profile is calculated. This can be compared to the spectral power profile for the signal at z₁. We note that all spectral power profiles are calculated for the same section of the signal, i.e. the finite propagation time must be accounted for (e.g. Fig. 4). For application to data from simulations, the choice of z_m is therefore restricted not only by the condition that z_m + Δz is within the numerical domain, but also by requiring that the simulation runs for sufficient time that the section of the signal analysed at z = 0 can also be analysed at z_m; i.e. for a signal of duration δt the simulation must run for a time of at least z_m/C_k + δt (assuming the kink waves satisfy the long wavelength approximation).

We note that in contrast to the integration-based analysis used in Sect. 2, the method of calculating $\mathit{P}{}^{\mathrm{(}}\mathit{z}_{\mathrm{1}}{}^{\mathrm{)}}\mathit{/}\mathit{P}{}^{\mathrm{(}}\mathit{z}_{\mathrm{0}}{}^{\mathrm{)}}$ does not assume a particular damping regime to begin with. However, it will give different results depending on the spatial damping profile/s present in the data. In the next section the method will be applied to numerical data demonstrating the results from the new analysis method for different damping regimes.

4. Numerical simulations of broadband oscillations

In this section we consider the propagation and damping due to mode coupling of kink waves excited by broadband footpoint motions. The initial equilibrium we consider is a straight and uniform magnetic field in the z direction with a field-aligned, cylindrical density structure. We use a density profile that varies linearly from ρ₀ at r ≤ ⁽R − l/ 2⁾ to ρ_e at r>⁽R + l/ 2⁾.

4.1. Power ratio in Gaussian damping regime

Here we first consider the case of the damping being dominated by the Gaussian spatial damping profile. The Gaussian damping profile applies for a greater number of oscillations when the density contrast is low (e.g. Eq. (6) and Pascoe et al. 2013). On the other hand, we want the damping rate to be sufficient to be readily measurable. Accordingly, we choose a low density contrast ρ₀/ρ_e = 2 and wide inhomogeneous layer thickness ϵ = 2 / 3.

The driver is chosen to simulate continuous random footpoint motions. For convenience the direction of oscillation of the loop axis is kept fixed along the x axis. The driving condition is applied to the lower z boundary and prescribes the x and y components of velocity, 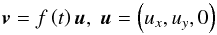${v}\mathrm{=}\mathit{f}\mathrm{(}{\mathit{t}}^{\mathrm{)}}{u}\mathit{,}{u}\mathrm{=}\mathrm{(}{\mathit{u}}_{\mathit{x}}\mathit{,}{\mathit{u}}_{\mathit{y}}\mathit{,}{\mathrm{0}}^{\mathrm{)}}$(21)where u has the same dipole form as in Pascoe et al. (2010; see their Eq. (4)) which is an efficient way of exciting the kink mode (m = 1). The time-dependence of our driver $\mathit{f}{}^{\mathrm{\right(}}\mathit{t}^{\mathrm{\left)}}$ is intended to simulate the broadband footpoint displacements of the loop axis. We generate our displacements using a method similar to Wright & Rickard (1995). A random number generator is used to produce a random amplitude ξ_i at a random time t_i, based on some characteristic frequency. A cubic spline is fitted to produce a piecewise continuous expression for the displacement so that the displacement at each numerical time step can be calculated. The time-dependence of the velocity driver is given by the time-derivative of the displacement. A set of such splines (each having a different timescale) is constructed and these are then summed to give a broadband signal. We choose the maximum value of the velocity perturbation u/C_Ae = 0.003 to be small in order to minimise non-linear effects. For the CoMP observations, the amplitude is reported to be ~0.3 km s^-1 (Tomczyk et al. 2007). For a background Alfvén speed C_Ae ~ 1 Mm/s this corresponds to u/C_Ae = 0.0003, so the linear regime is appropriate.

The simulation is performed using the MHD code Lare3D, which solves the 3D MHD equations by taking a Lagrangian predictor-corrector time step, after which all variables are conservatively re-mapped back onto the original Eulerian grid (Arber et al. 2001). The numerical domain is much larger in the z direction than in x or y in order to accommodate the continuously driven propagating wavepacket. However, the resolution is higher in the x and y directions in order to resolve the activity in the inhomogeneous layer for as long as possible. This is particularly important since phase mixing of Alfvén waves in the inhomogeneous layer takes place as a result of the continuously varying Alfvén speed. Values used are 300 × 300 × 1400 grid points for a numerical domain of 6 × 6 × 400 Mm (R = 0.75 Mm). The boundaries are periodic in the x and y directions, and are placed sufficiently far from the flux tube to not affect the results. The plasma β = 0.001 is chosen to be small, appropriate for the solar corona.

The transverse velocity perturbations excited at the lower boundary propagate along the magnetic field. The simulation ends before perturbations reach the upper boundary, to avoid unwanted reflections. As the kink wavepacket propagates along the tube, mode coupling leads to a transfer of energy to Alfvén waves in the inhomogeneous layer which then propagate at the local Alfvén speed and phase-mix (e.g. Heyvaerts & Priest 1983).

Fig. 3 Transverse velocity signal vx at the loop axis (x = y = 0) as a function of time. The signals at different heights are stacked along the y-axis by adding an appropriate constant. The lowest and highest signals correspond to heights of 0 and 86 Mm, respectively.

Fig. 4 Time-dependence of vx at the loop axis (top) and the corresponding power spectra (bottom). The dotted, dashed and solid lines represent the signals at heights at z = 0 (driver), 20 and 55 Mm, respectively. The driver approximates a broadband signal centred at ω ≈ 0.45s-1.

Figure 3 shows the transverse velocity signal v_x at the loop axis (x = y = 0) as a function of time. For an observer with a line of sight parallel (or nearly so) to the x-axis, this signal would be seen as oscillating Doppler shifts corresponding to a propagating kink mode. The signals at different heights are stacked along the y-axis by adding a constant proportional to the height. The lowest and highest signals correspond to heights of 0 and 86 Mm, respectively. The signal takes a finite time t₀ to reach a particular height z₀, where t₀ = z₀/C_k. Features of the initial signal can therefore be traced by eye by following a diagonal line. The two effects of mode coupling are readily apparent; the signal is increasingly attenuated with height as energy is transferred from transverse to azimuthal oscillations, and the higher frequency components are attenuated most rapidly. This is due to their shorter damping length scales given by Eqs. (2) and (4).

Figure 4 shows the transverse velocity signal at the loop axis at several heights. The dotted line denotes the driver at z = 0. The dashed and solid lines are the signals at heights of 20 and 55 Mm, respectively. Since the transverse velocity perturbations require a time t₀ to reach a height z₀, the time axis is shifted by Δt = t − t₀ so that we are considering the same part of the signal at later times. There is noticeable attenuation of the signal and loss of higher frequency components at larger heights. The bottom panel shows the spectral power for the transverse velocity signals. The driver signal is shown by the dotted line and approximates a broadband signal centred at ω ≈ 0.45s^-1. The decrease in spectral power for all frequencies at larger heights occurs as energy is transferred from the transverse kink mode to the azimuthal oscillations.

Fig. 5 Spectral power ratio for separation distances of Δz = 20 (top), 40 (middle) and 60 Mm (bottom). The colours represent the actual height of the normalising signals. The dashed and solid curves represent analytical expressions for the exponential and Gaussian spatial damping profiles, respectively.

Figure 5 shows the spectral power ratio calculated using the method described in Sect. 3 for separation distances of Δz = 20 (top), 40 (middle) and 60 Mm (bottom). This is done for each point along the loop axis up to z_m = 86 Mm, with the colour indicating data points taken lower down (blue) or higher up (red) along the axis (see Fig. 2). Points which have a low (less than 5% of the maximum value) spectral power at z₀ have been excluded to avoid large errors in calculating the ratio. The dashed curve represents the ratio calculated for an exponential spatial damping profile (Eq. (15)). The solid curves represent the bounding curves (Eqs. (19) and (20)) for a Gaussian spatial damping profile. We note that gaps in the data occur since the spectral profile of the driver (Fig. 4) does not contain significant power at all frequencies.

All of the features of Fig. 5 are consistent with the behaviour expected for mode coupling with a Gaussian spatial damping profile. Each of the data points, within reasonable error, falls within the two predicted bounding curves. The colour banding indicates how data points for lower values of z₀ have a higher power ratio (corresponding to less attenuation by mode coupling) than for higher values of z₀. As the separation distance is increased, the bounding curves move closer together and there is less scatter in the data points. While the analytical expression for an exponential damping profile shows the same effect of mode coupling acting as a low pass filter for a broadband signal, it does not account for these additional details.

4.2. Power ratio for general spatial damping profile

In Sect. 4.1 we considered the case of strongly damped kink oscillations dominated by a Gaussian damping profile. In this section we now consider weaker damping provided by a thinner inhomogeneous layer for which both the Gaussian and exponential damping regimes affect the damping rate of broadband kink oscillations.

We generate our data by performing 2D numerical simulations of propagating kink waves excited by a broadband driver using a Lax-Wendroff code to solve the linear MHD equations in cylindrical coordinates. The greater numerical efficiency afforded by a 2D (cylindrical) rather than 3D (Cartesian) code allows us to consider a thinner inhomogeneous layer. The footpoint driver is composed of several prescribed frequencies so that their sum is a broadband signal, i.e. the applied velocity perturbations are calculated as $\begin{array}{ccc}\mathit{A}\mathrm{(}{\mathit{t}}^{\mathrm{)}}& \mathrm{=}& \sum _{\mathit{i}}\sin \left(\frac{\mathrm{2}\mathit{\pi }}{{\mathit{P}}_{\mathit{i}}}\mathit{t}\mathrm{+}{\mathit{\phi }}_{\mathit{i}}\right)\mathit{,}\\ {\mathit{v}}_{\mathit{r}}& \mathrm{=}& \mathit{A}\mathrm{(}{\mathit{t}}^{\mathrm{)}}{\mathit{\xi }}_{\mathit{r}}\mathrm{(}{\mathit{r}}^{\mathrm{)}}\cos \mathrm{(}{\mathit{\theta }}^{\mathrm{)}}\mathit{,}\\ {\mathit{v}}_{\mathit{\theta }}& \mathrm{=}& \end{array}$(22)where P_i = [30,40,50,60,70,80,100,120] s and φ_i = [ 0,π/ 2,π, − π/ 2,0,π/ 2,π, − π/ 2 ]. We note that the radial profiles ξ_r and ξ_θ are discussed in detail in Sect. 5.1 and shown in Fig. 11, while the θ-dependence corresponds to the kink mode.

The density profile in the inhomogeneous layer is again linear, with ρ₀/ρ_e = 2 and ϵ = 0.2. The general spatial damping profile (Eq. (5)) envelopes for each of the eight components of the broadband signal are shown in Fig. 6. The lower curve corresponds to the shortest period of 30 s while the upper curve corresponds to the longest period of 120 s. For each envelope, the transition from the Gaussian to the exponential component (indicated by dashed lines) occurs within the numerical domain and while the oscillation still has a significant amplitude.

The spatial profile of the driver corresponds to a dipolar flow centred on the loop footpoint, describing the displacement of the footpoint back and forth which efficiently generates upward propagating kink waves, as in Sect. 4.1. Different spatial profiles for the driver will be considered in Sect. 5.

Fig. 6 Damping envelopes (Eq. (5)) for each of the eight components of the broadband signal. The lower curve corresponds to the shortest period of 30 s while the upper curve corresponds to the longest period of 120 s. The dashed lines indicate the locations of the switch from Gaussian to exponential damping profiles.

Fig. 7 Transverse velocity signal at the lower boundary z = 0 for a 2D numerical simulation. The thick dashed line is the analytically calculated signal. Lower panel: spectral profile of the signal.

Fig. 8 Same as Fig. 7 but for a height of z = 432 Mm.

Figure 7 shows the transverse velocity signal at the lower boundary z = 0. The solid line represents the numerical data while the thick dashed line is the analytical expression (Eq. (22)), which are identical for the driver. The lower panel shows the spectral profile of the signal. The vertical dashed lines show the frequencies chosen to make up the signal. The finite widths of the spectral peaks and their variation in amplitude arise since we consider a signal of finite duration.

Figure 8 is the same as Fig. 7 except the signal is now taken at a height of z = 432 Mm. The signal has been shifted to take into account the finite time for the wavetrain to propagate to this height. The effect of mode coupling acting as a low pass filter is again readily seen; the overall amplitude of the signal has reduced, and the spectral profile shows that the higher frequency components have been damped more strongly. The thick dashed line is again the analytically calculated signal, based on the input signal (Eq. (22)) and with each component damping as given by the general spatial damping profile (Eq. (5)). The two curves have excellent agreement, demonstrating that the general spatial damping profile provides an accurate account of each individual component of the signal (Pascoe et al. 2013) and so summing these components also provides an accurate account of the broadband signal.

Fig. 9 Spectral power ratio for separation distances of Δz = 40 (top), 120 (middle) and 240 Mm (bottom) for a 2D numerical simulation with ρ0/ρe = 2 and ϵ = 0.2. The dashed and solid curves represent analytical expressions for the exponential and Gaussian spatial damping profiles, respectively.

The damping envelopes (Fig. 6) demonstrate that this numerical simulation considers the most general case of spatial damping profile described by Hood et al. (2013) and Pascoe et al. (2013) in which both the initial Gaussian stage (z ≤ h) and the exponential damping profile (z>h) appear. We now calculate the spectral power ratio as in Sect. 3 and describe the influence of having both regimes on the results. Figure 9 shows the power ratio for separation distances of Δz = 40 (top), 120 (middle) and 240 Mm (bottom), with z_m = 980 Mm. In contrast with Fig. 5, we see that for these loop parameters the exponential damping ratio (dashed line) now falls between the upper and lower bounding curves for the Gaussian damping ratio (solid lines). The exponential damping ratio now becomes the lower bounding curve, as the exponential damping profile now determines the behaviour at large heights whereas in Sect. 4.1 the signal was strongly damped by the wider inhomogeneous layer within the first few wavelengths (and hence the exponential damping regime did not become relevant). The colour bands evident in Fig. 5 are no longer as prominent since the power ratio tends to a constant for large heights where the exponential damping profile applies. The corresponding points (coloured green to red) are therefore plotted on top of each other (on the dashed lines).

4.3. Power ratio in exponential damping regime

Finally we demonstrate the recovery of the power ratio (Eq. (15)) calculated by Verth et al. (2010) for a purely exponential damping profile. The height h at which the switch from Gaussian to exponential damping profiles occurs is inversely proportional to the density contrast of the loop. For the previous simulations with ρ₀/ρ_e = 2, the switch occurs at h/λ = 1 /κ = 3 (Eq. (6)). If we now consider ρ₀/ρ_e = 10, the switch occurs at h ≈ 1.2λ. The driver used is composed of periods in the range 30–120 s as in Sect. 4.2. The largest height at which the Gaussian damping profile remains is therefore h_max = λ_max/κ = C_kP_max/κ ≈ 63 Mm. If we calculate the spectral power ratio only using points above this height we expect to see the influence of the exponential damping profile alone. Such results are shown in Fig. 10 for an analytically calculated signal, having a single value for the power ratio at each frequency, consistent with an exponential damping profile.

Fig. 10 Spectral power ratio for separation distances of Δz = 40 (top), 80 (middle) and 160 Mm (bottom) for ρ0/ρe = 10 and ϵ = 0.1. The dashed and solid curves represent analytical expressions for the exponential and Gaussian spatial damping profiles, respectively. The exponential damping ratio is recovered by only considering points at a sufficiently large height z>h.

4.4. Limits for Gaussian and exponential damping regimes

We have demonstrated in previous sections how the spectral power ratio can be understood in terms of Gaussian and exponential damping profiles. We now note the different parametric regimes in which it is necessary to consider the Gaussian damping profile, exponential damping profile, or both profiles, in order to interpret broadband oscillations.

In Sect. 4.1, the damping behaviour was dominated by the Gaussian profile. This corresponds to the exponential power ratio (Eq. (15)) being less than the lower bounding curve for the Gaussian power ratio (Eq. (20)) as shown by the dashed and solid curves in the lower panel of Fig. 5. We therefore consider $\begin{array}{ccc}\exp \left(\mathrm{-}\mathrm{2}\mathrm{\Delta }\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}\right)& & \mathit{<}\exp \mathrm{(}\mathrm{-}\mathrm{(}\mathrm{2}{\mathit{z}}_{\mathrm{m}}\mathrm{\Delta }\mathit{z}\mathrm{+}{\mathrm{\Delta }\mathit{z}}^{\mathrm{2}}\mathrm{)}\mathit{/}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}^{\mathrm{)}}\\ \mathrm{-}\mathrm{2}\mathrm{\Delta }\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}& & \mathit{<}\mathrm{-}\mathrm{(}\mathrm{2}{\mathit{z}}_{\mathrm{m}}\mathrm{\Delta }\mathit{z}\mathrm{+}{\mathrm{\Delta }\mathit{z}}^{\mathrm{2}}\mathrm{)}\mathit{/}{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}\\ \mathrm{2}{\mathit{z}}_{\mathrm{m}}\mathrm{+}\mathrm{\Delta }\mathit{z}& & \mathit{<}\mathrm{2}{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}\mathit{/}{\mathit{L}}_{\mathrm{d}}\\ & & \mathit{<}\mathrm{2}\mathit{h}\mathit{.}\end{array}$(23)The Gaussian damping profile therefore determines the spectral power ratio when Δz and z_m are both smaller than h. 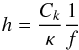We note that we may write $\mathit{h}\mathrm{=}\frac{{\mathit{C}}_{\mathit{k}}}{\mathit{\kappa }}\frac{\mathrm{1}}{\mathit{f}}$(24)using Eq. (6) and the thin tube approximation λ = C_kP in order to demonstrate the dependence on frequency and density contrast ratio.

The exponential power ratio applies when it is greater than the upper bounding curve for the Gaussian power ratio (e.g. lower panel of Fig. 10); $\begin{array}{ccc}\exp \left(\mathrm{-}\mathrm{2}\mathrm{\Delta }\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}\right)& & \mathit{>}\exp \mathrm{(}\mathrm{-}{\mathrm{\Delta }\mathit{z}}^{\mathrm{2}}\mathit{/}{{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}}^{\mathrm{)}}\\ \mathrm{-}\mathrm{2}\mathrm{\Delta }\mathit{z}\mathit{/}{\mathit{L}}_{\mathrm{d}}& & \mathit{>}\mathrm{-}{\mathrm{\Delta }\mathit{z}}^{\mathrm{2}}\mathit{/}{\mathit{L}}_{\mathrm{g}}^{\mathrm{2}}\\ \mathrm{\Delta }\mathit{z}& & \mathit{>}\mathrm{2}\mathit{h}\\ & & \mathit{>}\frac{\mathrm{2}{\mathit{C}}_{\mathit{k}}}{\mathit{\kappa }}\frac{\mathrm{1}}{\mathit{f}}\mathit{,}\end{array}$(25)i.e. when Δz is larger than h. Alternatively, for a given Δz the frequency at which the exponential behaviour applies may be calculated.

Aside from the above limiting cases, it is most appropriate to consider both the Gaussian and exponential damping behaviour of the general spatial damping profile. This corresponds to the exponential power ratio falling between the upper and lower bounding curves for the Gaussian power ratio, as in Sect. 4.2 and Fig. 9. From Eqs. (23) and (25), this occurs for $\mathrm{2}\mathrm{(}\mathit{h}\mathrm{-}{\mathit{z}}_{\mathrm{m}}\mathrm{)}\mathit{<}\mathrm{\Delta }\mathit{z}\mathit{<}\mathrm{2}\mathit{h}\mathit{.}$(26)We have therefore demonstrated that using the spectral power ratio to interpret broadband oscillations damped by mode coupling depends not only on the loop parameters and the frequency of oscillation, but also on the particular length scales (Δz, z_m) over which the analysis is performed.

5. Dependence of excitation and damping on the spatial profile of the driver

We now turn our attention to the effect of the spatial profile of the driver on the observed damping behaviour of propagating transverse waves. Previously the footpoint driver has described a lateral displacement of the loop footpoint (along a single axis) about its initial equilibrium position. In the case of this axis being perpendicular to an observer’s line of sight the kink waves excited may be seen as a transverse displacement e.g. in EUV imaging observations. In the case of this axis being parallel to the line of sight, the kink waves may appear as Doppler shifts. It has been shown that the damping behaviour arising as a result of this lateral displacement driver is well-described by the general spatial damping profile (Eq. (5)). In order to support the assumption of this driver in our work, here we consider alternative spatial profiles for the driver and investigate their effects on kink waves with respect to the efficiency of excitation and damping behaviour. This complements Pascoe et al. (2011) who considered the same dipolar driver used here but in the case of an inhomogeneous medium consisting of distorted or multiple loop structures. The mode coupling process was found to be weakly affected by the presence of fine structuring. Similar results were also found by Terradas et al. (2008) for the case of standing kink modes of a multi-stranded loop excited by an external perturbation.

Fig. 11 Radial dependence of the radial (top) and azimuthal (bottom) velocity components for a dipolar driver which dispaces the loop footpoint. The vertical dotted lines denote the edges of the inhomogeneous layer.

Fig. 12 Radial dependence of the radial (top) and azimuthal (bottom) velocity components for a driver describing a coupled kink and Alfvén eigenmode. The vertical dotted lines denote the edges of the inhomogeneous layer.

Fig. 13 Radial dependence of the amplitude (solid lines) and phase difference (dashed lines) for the radial (top) and azimuthal (bottom) velocity components for the driver in Fig. 12. The vertical dotted lines denote the edges of the inhomogeneous layer.

5.1. Excitation of kink modes by a highly structured driver

The spatial profile of the driver in our previous simulations corresponds to a 2D dipole circulation around the displaced flux tube in the photosphere. Figure 11 shows the radial dependence of the radial and azimuthal velocity components as applied at the loop footpoint z = 0. The radial velocity is constant within the loop up to r ≤ R and then decreases as r^-2. We note that the full velocity components are defined by multiplying the time-dependence $\mathit{f}{}^{\mathrm{\right(}}\mathit{t}^{\mathrm{\left)}}$ and the azimuthal dependence of the spatial profile assuming m = 1 symmetry, i.e. $\begin{array}{ccc}{\mathit{v}}_{\mathit{r}}& \mathrm{=}& {\mathit{\xi }}_{\mathit{r}}\mathrm{(}{\mathit{r}}^{\mathrm{)}}\sin \mathrm{(}\mathit{\omega }{\mathit{t}}^{\mathrm{)}}\cos \mathrm{(}{\mathit{\theta }}^{\mathrm{)}}\mathit{,}\\ {\mathit{v}}_{\mathit{\theta }}& \mathrm{=}& \end{array}$(27)Figure 12 shows the velocity components of a new driver that is intended to set up a kink normal mode with an exponential spatial damping profile. In such a mode we would expect there to be a significant amount of energy in azimuthal fields, and a radial displacement such that there is no compression of the magnetic field to leading order (Hood et al. 2013). The profiles in Fig. 12 match these requirements, although we do not suggest that realistic photospheric driving is likely to produce such a highly structured and tuned driver. Nevertheless, it is instructive to see how sensitive our simulation results are to the driver. We note that Fig. 12 is only a snapshot in time. Previously (Eq. (27)) the spatial and temporal components of the driver could be separated. In order to describe the phase-mixed Alfvén wave component of the eigenmode driver we now consider (Fig. 13) the spatial dependence of the amplitude (solid lines) and the phase (dashed lines, in radians) as $\begin{array}{ccc}{\mathit{v}}_{\mathit{r}}& \mathrm{=}& {\mathit{\xi }}_{\mathit{r}}\mathrm{(}{\mathit{r}}^{\mathrm{)}}\sin \left(\mathit{\omega t}\mathrm{+}{\mathit{\phi }}_{\mathit{r}}\mathrm{(}{\mathit{r}}^{\mathrm{)}}\right)\cos \mathrm{(}{\mathit{\theta }}^{\mathrm{)}}\mathit{,}\\ {\mathit{v}}_{\mathit{\theta }}& \mathrm{=}& \end{array}$(28)The oscillations are in phase near the centre of the loop for the (collective) kink mode but vary significantly within the inhomogeneous layer which describes phase-mixing. Hence this driver corresponds to an eigenmode comprised of coupled kink and Alfvén waves and tuned to the parameters of the coronal loop used in this particular simulation.

Fig. 14 Spatial damping profiles for the dipolar (top) and eigenmode (bottom) drivers. The dashed line shows the height h at which the envelope changes from Gaussian to exponential in the top panel, whereas the envelope is exponential for all heights in the bottom panel.

Figure 14 shows the spatial damping profiles produced by the dipolar (top) and eigenmode (bottom) drivers. The top panel demonstrates the general spatial damping profile (Eq. (5)) i.e. Gaussian up to a the height h (dashed line) where the envelope becomes exponential. In the bottom panel, the driver based on Eq. (28) instead produces an exponential damping profile for all heights.

In this section we have therefore demonstrated that the spatial damping profile of propagating kink waves depends on the spatial profile of the driver. An exponential damping profile for the kink mode can be obtained for all heights in the case of a driver with a finely tuned spatial profile. On the other hand, since such a driver has a significantly more complex form, and one which depends on the parameters of the particular overlying loop, it is unlikely to be generated in nature. In contrast, the dipolar driver of Fig. 11 corresponds to a simple lateral displacement of the loop which may be readily produced by photospheric convection.

Fig. 15 Spatial profile for dipolar (top) and turbulent (bottom) drivers. The contours represent the absolute velocity and the arrows show the velocity vectors. The line contours outline the edges of the inhomogeneous layer.

5.2. Excitation of kink modes by photospheric eddies

In this section we consider the generation of propagating kink modes by means of small scale motions at the loop footpoint, designed to approximate the effect of convective or turbulent motions at the photosphere. Since we no longer assume the driver is aligned with the coronal loop structure, we return to the 3D Cartesian setup for our simulations, as used in Sect. 4.1. Our footpoint driver is comprised of ten individual eddies and is applied to the lower boundary as u = (u_x,u_y,0) where ${\mathit{u}}_{\mathit{x}}\mathrm{=}\sum _{\mathit{i}}{\mathit{u}}_{\mathit{xi}}\mathit{,}{\mathit{u}}_{\mathit{y}}\mathrm{=}\sum _{\mathit{i}}{\mathit{u}}_{\mathit{yi}}\mathit{.}$(29)Each eddy is centred on (x_i,y_i) and has a radius R_i. The spatial profile of each eddy is defined as $\begin{array}{ccc}{\mathit{u}}_{\mathit{xi}}& \mathrm{=}& \mathrm{-}{\mathit{u}}_{\mathit{i}}\mathrm{(}{\mathit{r}}_{\mathit{i}}\mathrm{)}\sin \mathrm{(}{\mathit{\theta }}_{\mathit{i}}\mathrm{)}\mathit{,}\\ {\mathit{u}}_{\mathit{yi}}& \mathrm{=}& {\mathit{u}}_{\mathit{i}}\mathrm{(}{\mathit{r}}_{\mathit{i}}\mathrm{)}\cos \mathrm{(}{\mathit{\theta }}_{\mathit{i}}\mathrm{)}\mathit{,}\end{array}$(30)where $\begin{array}{ccc}{\mathit{r}}_{\mathit{i}}& \mathrm{=}& \sqrt{{\mathrm{(}\mathit{x}\mathrm{-}{\mathit{x}}_{\mathit{i}}\mathrm{)}}^{\mathrm{2}}\mathrm{+}{\left(\mathit{y}\mathrm{-}{\mathit{y}}_{\mathit{i}}\right)}^{\mathrm{2}}}\mathit{,}\\ {\mathit{\theta }}_{\mathit{i}}& \mathrm{=}& \arctan \left(\frac{\mathit{y}\mathrm{-}{\mathit{y}}_{\mathit{i}}}{\mathit{x}\mathrm{-}{\mathit{x}}_{\mathit{i}}}\right)\mathit{,}\end{array}$(31)and ${\mathit{u}}_{\mathit{i}}\mathrm{\left(}{\mathit{r}}_{\mathit{i}}\mathrm{\right)}\mathrm{=}\{\begin{array}{c}\\ \mathrm{0}\mathit{,}& {\mathit{r}}_{\mathit{i}}\mathit{>}{\mathit{R}}_{\mathit{i}}\\ \mathrm{4}{\mathit{f}}_{\mathit{i}}\mathrm{(}{\mathit{t}}^{\mathrm{)}}{\mathit{u}}_{\mathit{i}\mathrm{0}}{\mathit{r}}_{\mathit{i}}\mathrm{(}{\mathit{R}}_{\mathit{i}}\mathrm{-}{\mathit{r}}_{\mathit{i}}\mathrm{)}\mathit{,}& {\mathit{r}}_{\mathit{i}}\mathrm{\le }{\mathit{R}}_{\mathit{i}}\end{array}$(32)where u_i0 is chosen to be small to avoid non-linear effects. The time dependence ${\mathit{f}}_{\mathit{i}}{}^{\mathrm{\right(}}\mathit{t}^{\mathrm{\left)}}$ is taken to be the same broadband signal for all eddies. For comparison, we also perform a simulation with the same broadband time dependence but a dipolar driver. Other chosen parameters are R_i = 0.2 Mm, ρ₀/ρ_e = 2, R = 0.75 Mm, and l = 0.5 Mm.

Figure 15 shows the spatial profile for dipolar (top) and turbulent (bottom) drivers. The contours represent the absolute velocity and the arrows show the velocity vectors. The line contours outline the edges of the inhomogeneous layer. The eddies are randomly distributed about the loop with no particular symmetry, but we do not allow an eddy to cross the loop axis to avoid setting up an Alfvén wave there. In this way the velocity signal at the loop axis remains a signature of the kink mode alone. The (m = 1) kink mode is the only one that displaces the loop axis i.e. at r = 0. Modes with m> 1 (fluting modes) have nodes at r = 0. Therefore, having already excluded the possibility of generating a decoupled Alfvén wave at r = 0 by our choice of driver positions, no mode other than the m = 1 kink mode is present at r = 0. The broadband time dependence $\mathit{f}{}^{\mathrm{\right(}}\mathit{t}^{\mathrm{\left)}}$ is shown in Fig. 16.

Figure 17 shows the transverse velocity component v_x as a function of height taken at the loop axis. The solid line is for the dipolar driver while the dashed blue line is for the turbulent driver. We can consider the root mean square of the dipolar and turbulent drivers at the loop footpoint as ${\mathit{v}}_{\mathrm{rms}}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{1}}{\mathit{\pi }}{\mathrm{\int }}_{\mathit{r}\mathrm{=}\mathrm{0}}^{\mathrm{1}}{\mathit{v}}^{\mathrm{2}}\left(\mathit{x,y,}\mathrm{0}\right)\mathrm{d}\mathit{x}\mathrm{d}\mathit{y,}$(33)which gives the v_rms for the turbulent driver as ≈24 times larger than for the dipolar driver. On the other hand, in Fig. 17 the two drivers produce signals that are roughly the same amplitude, indicating that the turbulent driver is far less efficient at exciting kink oscillations than the dipolar driver, as expected.

Whilst v_x on the tube axis is a good proxy for the observable transverse motion of the whole interior of the tube (in the case of the dipolar driver), this will not be the case for the turbulent driver. We therefore consider the velocity signal averaged over different sized regions of the loop. We define the averaged transverse velocity as $\mathit{v̅}\mathit{x}\mathrm{(}{\mathit{z}}^{\mathrm{)}}\mathrm{=}\frac{\mathrm{1}}{\mathit{\pi }{\mathit{r}}_{\mathit{a}}^{\mathrm{2}}}{\mathrm{\int }}_{\mathit{r}\mathrm{=}\mathrm{0}}^{{\mathit{r}}_{\mathit{a}}}{\mathit{v}}_{\mathit{x}}\left(\mathit{x,y,z}\right)\mathrm{d}\mathit{x}\mathrm{d}\mathit{y}\mathit{.}$(34)Figure 18 shows the transverse velocity signals v_x at the loop axis (solid lines) compared with spatially averaged signals (red dashed lines). The left column corresponds to the dipolar driver and the right column the turbulent driver. The top panels are for averaging over r_a = 0.2 Mm, the middle panels for r_a = 0.5 Mm, and the bottom panels for r_a = 1 Mm. We note that this averaging still excludes modes with m> 1 since they contribute no net velocity as a result of their symmetry. In the case of the dipolar driver, the signal at the axis and the spatially averaged signal are show good agreement for averaging over the core region r ≤ 0.5 Mm. For larger integration areas differences arise because of the inclusion of azimuthal velocities from the (m = 1) Alfvén mode generated by mode coupling, which act to reduce the averaged transverse velocity component. For the turbulent driver, the differences between the signal at the axis and the spatially averaged signal are typically larger since the eddies themselves also contribute to the signal, being asymmetrically positioned about the loop by design. For r_a = 0.2 Mm, corresponding to the inner region of the loop core where eddies are excluded, the signals correspond to the induced kink motions alone (there is no turbulent driver wave energy) and so are identical except for early times, which reflects the finite time taken for the turbulent driver to excite the kink mode. In this section we have therefore demonstrated that it is possible to excite kink oscillations by small scale turbulent motions, although such a driver is very inefficient in terms of the amplitude of the kink mode excited. In addition, the observable amplitude of the kink oscillation can also be reduced further by spatial integration of the velocity (Doppler) signal in the optically thin corona (see also De Moortel & Pascoe 2012).

Fig. 16 Time dependence $\mathit{f}{}^{\mathrm{\right(}}\mathit{t}^{\mathrm{\left)}}$ of the drivers shown in Fig. 15.

Fig. 17 Transverse velocity component vx as a function of height taken at the loop axis. The solid line is for the dipolar driver while the dashed blue line is for the turbulent driver.

Fig. 18 Transverse velocity signals vx at the loop axis (solid lines) compared with spatially averaged signals (red dashed lines) given by Eq. (34). Left column: dipolar driver and right column: turbulent driver. The top panels are for averaging over ra = 0.2 Mm, the middle panels for ra = 0.5 Mm, and the bottom panels for ra = 1 Mm.

6. Conclusions

In this paper we have considered the excitation, propagation, and damping of kink oscillations generated by a broadband driver. When propagating through an inhomogeneous medium, such as the cylindrical density structure used here, mode coupling leads to the transfer of energy from transverse to azimuthal motions, which is observed as the decay of the initial kink disturbance. Mode coupling is expected to act as a low-pass filter for broadband oscillations in both the exponential (Terradas et al. 2010; Verth et al. 2010) and Gaussian (Pascoe et al. 2012; Hood et al. 2013) damping regimes. This effect is confirmed by our numerical simulations and we have developed a method for data analysis designed to more accurately describe the appearance of mode coupling when either or both damping regimes are present.

In the case of damping dominated by the Gaussian profile, e.g. strongly damped oscillations in a low density contrast loop, we have derived expressions for the spectral power ratio (Eqs. (19) and (20)) and power ratio integrated along a loop segment (Eq. (11)). We applied these results to observational data from CoMP. We demonstrated that this dataset is too noisy to distinguish between the Gaussian and exponential spatial damping profiles. Since the general spatial damping profile consists of both Gaussian and exponential stages, fits to data based on a single profile represent limiting cases. If the density contrast can be reliably estimated then it is possible to calculate which damping profile is most appropriate using Eqs. (5) and (6) (see also Pascoe et al. 2013).

The period of the propagating waves observed by CoMP is broadband and centred on 5 min (Tomczyk et al. 2007). The phase speed is reported as approximately 0.6 Mm/s (Tomczyk & McIntosh 2009), so we can consider a wavelength of λ = C_kP ≈ 180 Mm. (This is also consistent with the correlation length of 45 Mm reported by Tomczyk et al. (2007) which corresponds to ≈λ/ 4). For the loops considered in Sect. 2, the waves will have travelled approximately three wavelengths from one side of the loop to the other. The change from Gaussian to exponential damping profiles occurs at a height of h = 3λ for a density contrast of ρ₀/ρ_e = 2. The Gaussian damping profile would therefore be a more accurate basis for seismological inversions if the density contrast is ρ₀/ρ_e ≤ 2. For larger density contrasts the general spatial damping profile should be used, though the exponential damping profile would be a good approximation for ρ₀/ρ_e ≫ 2.

In Sect. 4.3 we demonstrated that the exponential damping regime can also be recovered by considering data only from points with a sufficiently large height to exclude the Gaussian damping regime. In Sect. 5.1 we considered a highly structured driver which can exhibit the exponential damping profile for all heights. However, since this required a finely structured driver tuned to the particular parameters of the coronal loop it is unlikely to represent a driving mechanism found in nature. The most general scenario therefore requires that the Gaussian damping regime must be considered in the analysis of propagating kink waves. Indeed the presence of the Gaussian damping regime offers an interpretation of a spread in damping rates for broadband waves instead of or in addition to observational errors or the integration of multiple signals along the line of sight.

Section 5 also considered excitation of kink waves by small-scale turbulent motions i.e. eddies with a spatial scale smaller than the loop width. It was demonstrated that such a driver can excite propagating kink waves but is much less efficient at doing so. This suggests that broadband kink waves observed in coronal loops will have properties determined by plasma motions at the footpoints which have a spatial scale comparable to the loop width or larger.

Acknowledgments

D.J.P. acknowledges financial support from STFC. I.D.M. acknowledges support of a Royal Society University Research Fellowship. The computational work for this paper was carried out on the STFC (DIRAC) funded cluster at the University of St Andrews (Scotland, UK). CoMP data provided courtesy of Scott W. McIntosh and Steven Tomczyk. The research leading to these results has also received funding from the European Commission Seventh Framework Programme (FP7/ 2007−2013) under the grant agreement SOLSPANET (project No. 269299, www.solspanet.eu/solspanet).

References

All Figures

	Fig. 1 Power ratio as a function of frequency for CoMP data. The dashed line represents the fit for an exponential spatial damping profile (Verth et al. 2010). The solid (red) line represents a fit for a Gaussian spatial damping profile.
In the text

	Fig. 2 Sketch of our method for calculating the spectral power ratio (e.g. Fig. 5). The spectral power of the transverse velocity signal at z1 is compared to that at z0 where Δz is a fixed separation distance. The colour represents the value of z0 from 0 (blue) to zm (red).
In the text

	Fig. 3 Transverse velocity signal vx at the loop axis (x = y = 0) as a function of time. The signals at different heights are stacked along the y-axis by adding an appropriate constant. The lowest and highest signals correspond to heights of 0 and 86 Mm, respectively.
In the text

	Fig. 4 Time-dependence of vx at the loop axis (top) and the corresponding power spectra (bottom). The dotted, dashed and solid lines represent the signals at heights at z = 0 (driver), 20 and 55 Mm, respectively. The driver approximates a broadband signal centred at ω ≈ 0.45s-1.
In the text

	Fig. 5 Spectral power ratio for separation distances of Δz = 20 (top), 40 (middle) and 60 Mm (bottom). The colours represent the actual height of the normalising signals. The dashed and solid curves represent analytical expressions for the exponential and Gaussian spatial damping profiles, respectively.
In the text

	Fig. 6 Damping envelopes (Eq. (5)) for each of the eight components of the broadband signal. The lower curve corresponds to the shortest period of 30 s while the upper curve corresponds to the longest period of 120 s. The dashed lines indicate the locations of the switch from Gaussian to exponential damping profiles.
In the text

	Fig. 7 Transverse velocity signal at the lower boundary z = 0 for a 2D numerical simulation. The thick dashed line is the analytically calculated signal. Lower panel: spectral profile of the signal.
In the text

	Fig. 8 Same as Fig. 7 but for a height of z = 432 Mm.
In the text

	Fig. 9 Spectral power ratio for separation distances of Δz = 40 (top), 120 (middle) and 240 Mm (bottom) for a 2D numerical simulation with ρ0/ρe = 2 and ϵ = 0.2. The dashed and solid curves represent analytical expressions for the exponential and Gaussian spatial damping profiles, respectively.
In the text

	Fig. 10 Spectral power ratio for separation distances of Δz = 40 (top), 80 (middle) and 160 Mm (bottom) for ρ0/ρe = 10 and ϵ = 0.1. The dashed and solid curves represent analytical expressions for the exponential and Gaussian spatial damping profiles, respectively. The exponential damping ratio is recovered by only considering points at a sufficiently large height z>h.
In the text

	Fig. 11 Radial dependence of the radial (top) and azimuthal (bottom) velocity components for a dipolar driver which dispaces the loop footpoint. The vertical dotted lines denote the edges of the inhomogeneous layer.
In the text

	Fig. 12 Radial dependence of the radial (top) and azimuthal (bottom) velocity components for a driver describing a coupled kink and Alfvén eigenmode. The vertical dotted lines denote the edges of the inhomogeneous layer.
In the text

	Fig. 13 Radial dependence of the amplitude (solid lines) and phase difference (dashed lines) for the radial (top) and azimuthal (bottom) velocity components for the driver in Fig. 12. The vertical dotted lines denote the edges of the inhomogeneous layer.
In the text

	Fig. 14 Spatial damping profiles for the dipolar (top) and eigenmode (bottom) drivers. The dashed line shows the height h at which the envelope changes from Gaussian to exponential in the top panel, whereas the envelope is exponential for all heights in the bottom panel.
In the text

	Fig. 15 Spatial profile for dipolar (top) and turbulent (bottom) drivers. The contours represent the absolute velocity and the arrows show the velocity vectors. The line contours outline the edges of the inhomogeneous layer.
In the text

	Fig. 16 Time dependence $\mathit{f}{}^{\mathrm{\right(}}\mathit{t}^{\mathrm{\left)}}$ of the drivers shown in Fig. 15.
In the text

	Fig. 17 Transverse velocity component vx as a function of height taken at the loop axis. The solid line is for the dipolar driver while the dashed blue line is for the turbulent driver.
In the text

	Fig. 18 Transverse velocity signals vx at the loop axis (solid lines) compared with spatially averaged signals (red dashed lines) given by Eq. (34). Left column: dipolar driver and right column: turbulent driver. The top panels are for averaging over ra = 0.2 Mm, the middle panels for ra = 0.5 Mm, and the bottom panels for ra = 1 Mm.
In the text