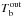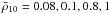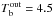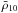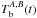| Issue |
A&A
Volume 577, May 2015
|
|
|---|---|---|
| Article Number | A5 | |
| Number of page(s) | 17 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201322690 | |
| Published online | 22 April 2015 | |
Quiescent thermal emission from neutron stars in low-mass X-ray binaries
1
Laboratorio TandarCNEA-CONICET,
Av. Gral Paz 1499, 1430 San Martín,
Buenos Aires,
Argentina
2
Deutsches Zentrum für Luft-und Raumfahrt, DLR-RY, Robert-Hooke
Str. 7, 28359
Bremen,
Germany
e-mail:
deborah.aguilera@dlr.de
3
Departament de Física Aplicada, Universitat
d’Alacant, Ap. Correus
99, 03080
Alacant,
Spain
Received: 16 September 2013
Accepted: 20 December 2014
Context. We monitored the quiescent thermal emission from neutron stars in low-mass X-ray binaries after active periods of intense activity in X-rays (outbursts).
Aims. The theoretical modeling of the thermal relaxation of the neutron star crust may be used to establish constraints on the crust composition and transport properties, depending on the astrophysical scenarios assumed.
Methods. We numerically simulated the thermal evolution of the neutron star crust and compared them with inferred surface temperatures for five sources: MXB 1659−29, KS 1731−260, XTE J1701−462, EXO 0748−676 and IGR J17480−2446.
Results. We find that the evolution of MXB 1659−29, KS 1731−260 and EXO 0748−676 can be well described within a deep crustal cooling scenario. Conversely, we find that the other two sources can only be explained with models beyond crustal cooling. For the peculiar emission of XTE J1701−462 we propose alternative scenarios such as residual accretion during quiescence, additional heat sources in the outer crust, and/or thermal isolation of the inner crust due to a buried magnetic field. We also explain the very recent reported temperature of IGR J17480−2446 with an additional heat deposition in the outer crust from shallow sources.
Key words: stars: neutron / binaries: general / X-rays: binaries / dense matter
© ESO, 2015
1. Introduction
Neutron star low-mass X-ray binaries (LMXBs) are systems formed by a neutron star (NS) that accretes matter from a low-mass companion star. These systems are most of the time in a quiescent state where little accretion occurs with an X-ray luminosity < 1034 erg s-1. Periodically, the compact object undergoes an accretion episode with a corresponding increase in luminosity of ~1036–1039 erg s-1. The accreted hydrogen- and helium-rich material at rates ~1015–1018 g s-1 undergoes thermonuclear fusion within hours to days of reaching the NS surface, releasing ~5 MeV per accreted nucleon (see, e.g., Bildsten 1998; Schatz et al. 1999 for a seminal work). The nuclear burning is thermally unstable on weakly magnetized NSs (B ≪ 1011 G) accreting at Ṁ< 1018 g s-1 and produces energetic (~1039 erg) Type I X-ray bursts when Ṁ< 1017 g s-1.
At the end of an active period, the emission shows a decreasing X-ray activity (quiescent phase) until a new accretion cycle begins. Most of the sources accrete for days or weeks, but there are only few of them that show unusually long active phases that last for years or decades. Recently, five so-called quasi-persistent sources have been monitored for about 103 days after the end of the outburst: MXB 1659−29 (Wijnands et al. 2003; Cackett et al. 2008), KS 1731−260 (Wijnands et al. 2001; Cackett et al. 2010a), EXO 0748−676 (Wolff et al. 2008; Degenaar et al. 2011b, 2014; Díaz Trigo et al. 2011), XTE J1701−462 (Fridriksson et al. 2010, 2011), and IGR J17480−2446 (Degenaar & Wijnands 2011a). All these sources have been accreting at rates ≃ 0.01 − 1 times the Eddington mass accretion rate, Ṁ ≃ 1018 g s-1 (Galloway et al. 2008; Degenaar et al. 2011b). The thermal component of the spectra is consistent with an overall decrease in the surface temperature of the NS; only for one source, MXB 1659−29, last measurements indicate that the star has reached an equilibrium temperature1, but for the others there is evidence for continued cooling (Fridriksson et al. 2011; Degenaar et al. 2014).
Theoretical explanations of the origin of the quiescent X-ray emission point to the thermal relaxation of the crust. Before the active phase it is assumed that the NS is old enough to have an isothermal interior and its surface temperature reflects the core temperature. During outbursts, the crust is heated up beyond thermal equilibrium by the accretion of matter that compresses the crust and triggers nuclear reactions. Once accretion falls to quiescent levels, it cools down by thermal radiation from the surface (mainly in the X-ray band), by heat conduction toward the core and consequent neutrino emission as the outer layers return to equilibrium with the interior; see the pioneering work by Brown et al. (1998) and Colpi et al. (2001). In quasi-persistent sources the crust is the region that is heated up because the outburst duration (~yr) is about as long as the crustal diffusion timescale. Nevertheless, observations of one source show that shorter accretion periods of a few months are thought to be responsible for the heating of the crust (see Degenaar et al. 2011a and analysis on EXO 0748−676 below). Typically, sources accrete for much shorter time, and the heat is generated mostly by thermonuclear reactions in the envelope that rapidly diffuses (~s, min) and does not affect the interior thermal state.
As a result of this long-term accretion phase, the cooling is modified not only by the energy released in the envelope (at densities 104–107 g cm-3) by thermonuclear reactions, but also by the energy generated in the inner crust (at 1011–1013 g cm-3) by electron captures, neutron emission, and density-driven nuclear fusion reactions (pycnonuclear reactions). Then, the so-called deep crustal heating controls the NS cooling in the quiescence phase. The rates of these processes have huge uncertainties: which particular reaction is taking place and at which density is still unknown. Fortunately, this uncertainty does not significantly affect the value of the total heat released Qtot ≃ 1.9 MeV (Haensel & Zdunik 2008, hereafter HZ08; Gupta et al. 2007), although the spatial distribution of heat sources in the inner crust is uncertain.
In the past decade, the comparison of observational data with cooling models including deep crustal heating allowed investigating crust properties and ultra-dense matter processes that influence the cooling curves (Rutledge et al. 2002). Simulations of the crust relaxation after outbursts for KS 1731−260 and MXB 1659−29 (Shternin et al. 2007 and Brown & Cumming 2009; hereafter Sht07 and BC09) suggested a rather high thermal conductivity in the outer crust (which requires a low impurity content), in agreement with recent molecular dynamics calculations (Horowitz et al. 2009) but in contrast with the inefficient crust conductivity necessary for carbon ignition in superbursts (Cooper & Narayan 2005; Cumming et al. 2006). A recent interpretation confirms the role of the crustal cooling as responsible for the quiescent emission for MXB 1659−29, KS 1731−260 and XTE J1701−462 and highlights the importance of the outburst duration in the subsequent cooling evolution (Page & Reddy 2013).
Many other open questions as well as new observational data challenge these models in several fronts. First some of the sources might still be cooling, as indicated by the last observation of KS 1731−260 (Fridriksson et al. 2011) and the high temperatures exhibit in XTE J1701−462. If these sources indeed continue to cool, models should account for longer relaxation times for the crust. This opens the possibility of revisiting the analysis of BC09, who assumed that the quiescent emission of the crust levels off with the core. Second, some sources might show variability in the thermal component: XTE J1701−462 has shown relatively short periods of increased temperatures during an overall cooling evolution. The origin of this variation is not clear, and one possible explanation is low-level accretion onto the NS surface during quiescence due to the correlated variability observed in the power-law spectral component (Fridriksson et al. 2011). Third, the candidate for crustal cooling recently detected in the globurar cluster Terzan 5, IGR J17480−2446, exhibits a higher temperature than the quiescent base level in 2009 (Degenaar et al. 2011b). More recently, five new observations have been reported (Degenaar et al. 2013), making its overall cooling even more puzzling. BC09-type cooling models can only account for these inferred temperatures if there is an additional heat generation in the outer crust (Degenaar et al. 2011a) whose location and origin is unknown2. Other recent theoretical speculations in the outer crust that may affect the crustal cooling (for instance, EXO 0748−676) include heat convection due to the chemical separation of light and heavy nuclei (Medin & Cumming 2014) or a shell with rapid neutrino cooling, which might have more dramatic consequences (Schatz et al. 2014).
In this paper, we aim at revisiting the problem by performing time-dependent simulations of the thermal evolution of the NS crust with deep crustal heating. The main purpose is to use our models to constrain the general properties of the NS crust (e.g. the crust thermal conductivity or impurities) by comparing our results with observational data of all available sources. We also discuss alternative scenarios for the sources that cannot be completely explained only by means of deep crustal heating.
The paper is organized as follows: in Sect. 2 we describe the five sources KS 1731−260, MXB 1659−29, EXO 0748−676, XTE J1701−462, and IGR J17480−2446 and briefly compare their remarkable characteristics. In Sect. 3 we describe the microphysics of the underlying neutron star model and the details for the numerical code. In Sects. 4−7 we test our cooling simulations in detail for the five sources. We summarize in Sect. 8.
2. Sources
The main observational facts of the five NSs in LMXBs detected in quiescence presented below are summarized in Fig. 1 and Table 1.
 |
Fig. 1 Observational data and corresponding fits taken from the literature. a) MXB 1659−29, data and fits from Cackett et al. (2008; 2013; open symbols). b) KS 1731−260, data and fits from Cackett et al. (2010a). c) EXO 0748−676, data and fits from Díaz Trigo et al. (2011) and Degenaar et al. (2011b). d) XTE J1701−462, data and fits from Fridriksson et al. (2011). Data with open symbols (XMM-3 and CXO-4) were not considered in fits. e) IGR J17480−2446, data and fits from Degenaar et al. (2013). Data from Chandra (circles), XMM-Newton (squares) and Swift (triangles) for all the sources. Exponential decay kBTs = a e− (t − t0) /τ + b (solid lines), and (broken) power-laws kBTs = α(t − t0)β (dashed lines) fits. |
Sources, average accretion rate Ṁobs,18 and accretion period tacc inferred from observations.
2.1. MXB 1659−29
This source was detected in outburst first in 1976–1979 and again in 1999–2001. Both outbursts lasted about 2.5 years (Lewin et al. 1976). Its quiescence was monitored by Chandra and XMM-Newton telescopes, the last observation was made by Chandra 11 years after the end of the last outburst (Fig. 1a). Assuming an accretion-power luminosity L = ϵṀc, with ϵ = 0.2, it is possible to estimate a mean value for the mass-accretion rate Ṁobs,18 ≃ 0.07–0.18, where Ṁobs,18 is in units of 1018 g s-1 (Galloway et al. 2008).
The first six observations of this source can be interpreted as the crust cooling down to equilibrium with the core. The evolution of the surface temperature can be well fit with an exponential function (Cackett et al. 2008), which shows that the flux and temperature of the last observation remained consistent with the previous two Chandra observations performed 1000 days before.
Recently, a new Chandra observation (Cackett et al. 2013) showed an unexpected drop in count rate and a change in the spectral shape that cannot be explained by continued cooling. Two possible scenarios are discussed in that work: i) it is assumed that the NS temperature remained unchanged and there was an increase in the column density; ii) alternatively, the NS surface temperature dropped and the spectrum is now dominated by a power-law component. Future observations of this source are necessary to distinguish between these two possibilities (corresponding temperatures are shown as open symbols in Fig. 1a).
2.2. KS 1731−260
First detected in 1989 (Sunyaev & Kwant Team 1989), the presence of Type I X-ray bursts identified this compact object as a NS. The source was actively accreting for 12.5 yr and the last detection in outburst was in January 2001 with a luminosity of 1036 erg s-1 (Wijnands et al. 2001) with an inferred Ṁobs,18 ~ 0.1 (Galloway et al. 2008).
Its first four years in quiescence were studied by Cackett et al. (2006); they analyzed XMM-Newton (XMM) and Chandra (CXO) observations and fit the data spectrum with an absorbed neutron star atmosphere (see Fig. 1b). In that work it was not clear whether the source had reached thermal equilibrium with the core or if it was still cooling, but the last observation seemed to indicate the first. Then, the data were well fit in a first moment by an exponential decay to a constant offset (see Table 1).
Years later, Cackett et al. (2010a) presented a new Chandra observation that shows a decrease in temperature that is inconsistent with the previous fit. From revising all the Chandra and XMM-Newton data, the authors concluded that the source was still cooling with the temperature following a power-law decay (see Table 1). However, one problem in this analysis is that the spectrum may not be purely thermal and some nonthermal contribution may not have been detected because of the low number of counts. Observations are consistent with a simple NS atmosphere model, but a low-level (lower than 10%) contribution from a power-law cannot be excluded.
We remark that first observations for KS 1731−260 and MXB 1659−29 were performed only 25 days after the end of the outburst (similarly as for EXO 0748−676 and IGR J17480−2446, as described below). Thus, important information about the first stage of cooling and the physics of the outermost layers is lacking.
2.3. EXO 0748−676
This source was first detected in 1980 (Parmar et al. 1986) at luminosities of ~1036 − 37 erg s-1; it remained active for more than 24 years. Short X-ray bursts were observed, and their rise time and duration suggested pure helium ignition. The transition from outburst to quiescence occurred during 2008 and was monitored by Degenaar et al. (2009, 2011b) and Díaz Trigo et al. (2011). They found an uncertain date for the end of the outburst phase, which was poorly constrainted in a period of seven weeks. The mass-accretion rate inferred is Ṁobs,18 ~ 0.03, but recent analysis pointed out the possibility of this being underestimated by a factor of 5 because of the high inclination of the binary system with respect to our line of sight (Degenaar et al. 2014).
The quiescent spectrum of EXO 0748−676 monitored by Chandra and Swift in the 19 months after outburst was described by assuming a combination of a NS atmosphere model plus a nonthermal power-law tail (see Fig. 1c and Table 1). The resulting gradual decrease in the NS effective temperature (from ~124 eV to 109 eV) was interpreted as crustal cooling by Degenaar et al. (2009). They also observed that quiescent light curves present a shift between data thermal fluxes (of ~6%) coming from the two satellites, apparently due to cross-calibration problems. Díaz Trigo et al. (2011) revisited the problem and analyzed XMM-Newton data, which are the most sensitive observations of the source. They found that XMM-Newton fluxes are compatible with Swift, which reaffirms the hypothesis of an offset in the calibration between Chandra and Swift.
The unabsorbed flux (7.7 × 10-13 erg cm-2 s-1) detected in April 2010 by Chandra is close to the flux measured by the Einstein observatory before the last outburst of the source (8.4 × 10-13 erg cm-2 s-1), supporting the idea that the crust has reached thermal equilibrium (Degenaar et al. 2011b). Nevertheless, Parmar et al. (1986) reported that EXO 0748−676 might undergo periods when it is a much fainter X-ray source because the accretion disk may completely hide the central emission. It is remarkable that there is much less cooling after the end of the outburst than in the other sources. Recently, a new observation of EXO 0748−676 was reported (Degenaar et al. 2014), showing a lower temperature ≃110 eV in 2013 and suggesting that the crust has not fully cooled yet. This last observation is consistent with the predictions of our simulations (see Sect. 6), and we will include these data in our fits in a future work.
2.4. XTE J1701−462
The neutron star transient XTE J1701−462 was discovered in 2006 (Remillard et al. 2006) and remained in an exceptional luminous outburst for about 19 months. The transition from outburst to quiescent emission and the first 800 days of the quiescent phase were first monitored by Fridriksson et al. (2010). During most of the quiescent period, the source was followed by Chandra in a campaign consisting of ten observations made between August 2007 and October 2009, and, lately, one more in October 2011. It was also observed three times with XMM-Newton in August 2007, September 2007, and March 2009, and last data came from April 2011 taken from Swift (Fridriksson et al. 2010, 2011) (see Fig. 1d). Here the luminosity was measured very early in the quiescent phase: three data points in the first twenty days. This gives valuable information about the physics of the outer layers of the NS that are directly involved in the cooling after outbursts. These early data are a qualitative difference to all other known sources. The inferred value for the mass-accretion rate for XTE J1701−462 is close to the Eddington rate, Ṁobs,18 = 1.1 (Cackett et al. 2010b).
Spectra of XTE J1701−462 show thermal and nonthermal components which latter is well fit by a power-law of index 1−2. The origin of the nonthermal emission is poorly understood, but it probably originates in magnetospheric activity (Campana et al. 1998). The thermal emission in quiescence (see Fig. 1d) shows a temperature decrease that is interpreted as the cooling of the NS crust that was heated up in the accretion phase. Nevertheless, some features in the observed luminosity indicate that the crustal cooling may be affected by other processes.
First, we note that the effective surface temperature decreases from approximately 160 eV to 120 eV, significantly higher temperatures than those inferred for MXB 1659−29 and KS 1731−260 (approx. from 120 eV to 60 eV). The relatively warm surface of XTE J1701−462 may be a result of the high (close to Eddington) accretion rate at which this source has been accumulating matter during most of its active phase. Alternatively, it might be due to a higher core temperature (maybe it is a young star?).
Second, the overall cooling rate seems to be explained by crustal heating, as analyzed in Fridriksson et al. (2011) from data from XMM-Newton and Chandra where they found good fits from considering exponential and broken power-law functions with χ2 = 1.07 and χ2 = 0.88, respectively. However, these fits do not include the third XMM-Newton (XMM-3) and the fourth Chandra (CXO-4) observations between ~200–300 days, which show a considerable increment in thermal and nonthermal spectral components (Fridriksson et al. 2011, see Table 1).
One more drawback is that it was unclear in Fridriksson et al. (2010) whether the XTE J1701−462 crust had already reached a thermal equilibrium with the core. The last Chandra observation indicated with 80% confidence that the surface temperature has decreased, implying that the source is still cooling (Fridriksson et al. 2011), which is inconsistent with previous fits.
Another challenge for crustal cooling models is that the temperatures registered at early times drop on a relatively short timescale with an e-folding time for the exponential fit of ~120 days (compared with ~300 days for MXB 1659−29 and ~460 days for KS 1731−260 Cackett et al. 2010a), which argues in favor of a highly conductive crust. Moreover, the temperature evolution shows a change in the slope at early times of about 80 − 100 days (Fridriksson et al. 2011 obtained even 25−80 days). This break in the evolution makes it difficult to reconcile the initial rapid cooling shown by early observations and the much slower decrease from the last data in the same cooling model.
2.5. IGR J17480−2446
The transient IGR J17480−2446 was found in the globular cluster TERZAN by Chandra telescope in 2003 (Heinke et al. 2006). In October 2010 it suddenly entered into an outburst period, increasing its intensity by approximately one order of magnitude (Bordas et al. 2010; Pooley et al. 2010). The source returned to quiescence after about ten weeks (Degenaar & Wijnands 2011a). A Chandra observation 50 days after the end of the outburst showed that the surface temperature was higher by a factor 4 than the base level observed in 2003 and 2009 (Degenaar & Wijnands 2011b).
More recently, Degenaar et al. (2013) reported new Chandra/ACIS observations on IGR J17480−2446 that extend the monitoring to 2.2 years into quiescence. They found that even when the thermal flux and NS temperature have decreased, their values still remain well above those measured in the previous accretion phase. They fit these last observations with exponential decays and found that when the quiescence base level is fixed to the temperature inferred from the 2003/2009 data, the fit results are poor (χ2 ~ 3). However, this is considerably improved (χ2 ~ 1.84) when this parameter varies freely, in which case the base level is b = (84.3 ± 1.4) eV, considerably higher than the quiescent level. Because this value is close to the obtained from the previous observation in 2013 February, this predicts that the NS crust has nearly leveled off (see solid curve in Fig. 1e). Nevertheless, the best fit corresponds to a power-law decay with a free base level for which b = (77.3 ± 1.0) eV, which is significantly lower than the most recent observation (see dashed curve Fig. 1e), which indicates a continued cooling of the crust.
2.6. Brief comparison of the sources
We can group MXB 1659−29 and KS 1731−260 together since they have similar accretion rates (~0.1 Mobs,18), evolve in a similar temperature range (~120–60 eV), and are (nearly) leveled off with the core on comparable timescales (~2000 days). Their data spectra are well fit with an absorbed NS atmosphere, and their exponential fits show similar e-folding times (~500–400 days). Although the data are sparse in time, their error bars are relatively low.
In contrast, EXO 0748−676 and XTE J1701−462 (and partially IGR J17480−2446) present peculiar characteristics. They are warmer than the sources in the first group and the data points show larger error bars (like EXO 0748−676) or exhibit a much higher variability (as in XTE J1701−462). Their temperatures evolve on a higher range (~125–110 eV for EXO 0748−676, ~170–120 eV for XTE J1701−462) than the first two, and the e-folding times are considerably shorter (~130 days for XTE J1701−462 and ~220 days for EXO 0748−676). EXO 0748−676 has the lowest accretion rate (~0.01M18) but the longest accretion time (~24 yr), which can be the origin of its high surface temperature. More puzzling is the small amount of cooling that it shows, its temperature decreases by only ~15 eV from the initial to the last observation. XTE J1701−462 instead has the highest accretion rate, at least ten times higher than the other sources. The pronounced break between the early and latest observations slope is not evident in the other sources. Finally, IGR J17480−2446 shows similarities to the first group, for instance, an accretion rate of the same order, but has a considerably shorter outburst time (the shortest among all sources). Like the second group, it exhibits a short e-folding time of ~60 days and a temperature drop in the overall cooling of only ~20 eV.
3. Baseline model and thermal evolution
3.1. Equation of state
At low density we used the BBP Baym et al. (1971) equation of state. The crust-envelope interface is placed at (5 − 6) × 108 g cm3 and we continued using the BBP EoS to describe the crust up to a density of 1.49 × 109 g cm-3. To take into account the effects of the accretion in the crust composition, we used the EoS presented in HZ08 in the range ρ = (1.49 × 109 − 3.5 × 1013) g cm-3. This is a BBP-like EoS, but modified by nonequilibrium nuclear reactions in the crust (see Sect. 3.3). The very high-density region in the inner crust and the core is described by a Skyrme-type EoS that considers a nucleon-nucleon SLy effective interaction Douchin & Haensel (2001). For this chosen EoS the crust-core interface is at 0.5ρ0, where ρ0 is the nuclear saturation density.
Throughout this paper we use two different NS models with masses M = 1.4M⊙ and 1.6 M⊙. Their properties are listed in Table 2: as the NS mass increases, the crust width decreases, which reduces the crustal relaxation time as  .
.
NS configurations: mass M, central density ρ0, stellar radius R, surface gravity g, and crust width ΔRc.
3.2. Superfluidity
Nucleon pairing does not affect the EoS, but it can play an important role in NS cooling since it strongly modifies the specific heat and neutrino emissivities of dense matter. Following Kaminker et al. (2001) and Andersson et al. (2005), we used a phenomenological formula for the momentum dependence of the neutron energy gap at zero temperature given by 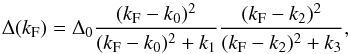 (1)where kF = (3π2n)1/3 is the Fermi momentum of neutrons and the parameters Δ0 and ki, i = 1...4 are values fit to microphysical calculations listed in Table 3. This expression is valid for k0<kF<k2, with vanishing Δ outside this range. In Fig. 2 we show three different functional forms for the density dependence of the neutron superfluidity energy gaps in the NS crust we used throughout: Sch03 gap (from Schwenk et al. 2003), deep gap, and small gap.
(1)where kF = (3π2n)1/3 is the Fermi momentum of neutrons and the parameters Δ0 and ki, i = 1...4 are values fit to microphysical calculations listed in Table 3. This expression is valid for k0<kF<k2, with vanishing Δ outside this range. In Fig. 2 we show three different functional forms for the density dependence of the neutron superfluidity energy gaps in the NS crust we used throughout: Sch03 gap (from Schwenk et al. 2003), deep gap, and small gap.
 |
Fig. 2 Energy gap models used as a function of density: Sch03 gap (solid line), deep gap (dashed dotted line), and small gap (dashed line). |
Parametrization of the energy gaps for neutron superfluidity.
The corresponding critical temperatures for the s-wave pairing can be approximately calculated as Tcrit = 0.56 Δ(T = 0). At the relevant densities, the crustal temperatures for the five sources are always lower than the corresponding Tcrit, and neutrons are already in a superfluid state in the inner crust. Unless otherwise stated, we considered Sch03 gap in our simulations.
3.3. Crust composition
The crust of an accreting NS can be partially replaced after an accretion period of several years. Thus, its composition can be significantly different from that of isolated NSs, see Fig. 3, in which the mass number A (circles) and the nuclear charge Z (stars) deviate from the non accreted composition (solid lines) along the NS crust. We refer to Sect. 2.1 of HZ08 for details about the capture rates in different regimes.
 |
Fig. 3 Accreted crust composition (stars, circles) for 56Fe burning ashes (HZ08) in comparison to the non-accreted crust (solid lines) (Douchin & Haensel 2001 above the neutron drip point and BPS, Baym et al. 1971 below that density). |
At densities above the neutron drip density, ρND ~ 3 × 1011 g cm-3, in the inner crust, there are neutron emissions triggered by electron captures that cause A to decrease. At higher densities (ρ> 1012 g cm-3) the mean distance between nuclei diminishes and quantum zero-point vibrations increase, which leads to pycnonuclear reactions that result in jumps in A. In Fig. 3 we can observe that the composition abruptly changes with depth, the jumps correspond to the location of thresholds for pycnonuclear reactions.
3.4. Transport properties and neutrino emission
The processes that dominate the crust thermal conductivity (strongly) depend on temperature and density. While electron-phonon scattering dominates at low densities in the outer crust, electron-impurity scattering is the most important process at higher densities in the inner crust. To calculate these processes, we used the public code of Potekhin3.
An important, but uncertain, parameter in calculating the thermal conductivity is the impurity parameter 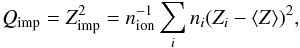 (2)which measures the quadratic charge deviation of lattice ions with ni ion density and charge number Zi with respect to the mean value ⟨ Z ⟩ and weighted to the mean ion density nion. High values of this parameter (Qimp ~ 100) correspond to an amorphous crust and a low thermal conductivity. Recent molecular dynamic calculations, however, predict a regular crystalline structure with a moderate value of Qimp on the order of unity (Horowitz et al. 2007, 2009) in the outer crust. BC09 estimated the value of Qimp by fitting the observational data of the sources KS 1731−260 and MXB 1659−29 and also found that Qimp ~ 1 − 5.
(2)which measures the quadratic charge deviation of lattice ions with ni ion density and charge number Zi with respect to the mean value ⟨ Z ⟩ and weighted to the mean ion density nion. High values of this parameter (Qimp ~ 100) correspond to an amorphous crust and a low thermal conductivity. Recent molecular dynamic calculations, however, predict a regular crystalline structure with a moderate value of Qimp on the order of unity (Horowitz et al. 2007, 2009) in the outer crust. BC09 estimated the value of Qimp by fitting the observational data of the sources KS 1731−260 and MXB 1659−29 and also found that Qimp ~ 1 − 5.
The crustal specific heat has contributions from the ion lattice, the degenerate electron gas, and the neutron gas in the inner crust that strongly depend on the temperature and density (see Aguilera et al. 2008 and references therein for the model used here; also Page & Reddy 2012 for a detailed discussion). Contributions from the neutron gas are suppressed by a Boltzmann-like factor, controlled by T/ Δ (see Levenfish & Yakovlev 1994) when the T falls below Tcrit for superfluidity. This means that if the neutrons are not superfluid, they control the specific heat in the inner crust at all T. If they were to become superfluid, then this probably is important only in a density region where the suppression is not effective. The other two crustal specific heat contributions also vary strongly with T and ρ: at T ≥ 108 K the ion lattice dominates in most of the crust (and is only overcome by unpaired neutrons). At lower T, the electron contribution is similar to the ionic at T ≃ 2 − 3 × 107 K and becomes dominating at T ≤ 107 K, again, at the layers without unpaired neutrons. Superfluid phonons (Aguilera et al. 2009) might have a negligible effect or only be relevant in a tinny region when T ≤ Tcrit and the superfluid phonons velocity approximates the transverse lattice phonon velocity (Page & Reddy 2012). We neglected the interaction between the ion lattice and the neutron gas (pioneering work Cirigliano et al. 2011; also more recently the entrainment studied in Chamel 2012), and this might be the main drawback of this approach since it may influence the thermal evolution of the crust, see Page & Reddy (2012). Nevertheless, the results are not conclusive about the strength of the coupling between superfluid neutrons and the lattice, and any type of disorder in the lattice might substantially reduce the effect (Chamel et al. 2013). We plan to investigate this problem in future works.
We included all relevant neutrino emission processes that influence the cooling of the crust (see Table 3 in Aguilera et al. 2008 for a list). At high temperatures (T ≃ 109 K) the dominant process is the plasmon decay. At intermediate values (T ≃ 5 × 108 K), the plasmon decay is only dominant in the outer crust, while electron-nuclei Bremsstrahlung becomes more efficient in a large part of the crust volume (Yakovlev et al. 2001). We also included the Cooper pair breaking and formation (CPBF) process, although it does not affect the thermal evolution of the inner crust.
3.5. Thermal evolution
After defining the baseline NS model, we followed its thermal evolution by solving the diffusion equation taking into account all energy gains and losses: 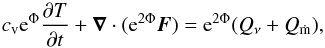 (3)where cv is the specific heat per unit volume, Qν denotes the energy loss by neutrino emissions and Qṁ considers energy gains as a consequence of the accretion of matter. As we mentioned in Sect. 3.1, the deep crustal heating considers that there are heat sources located in the inner crust as a result of pycnonuclear reactions and electron captures as well as other less intense sources in the outer crust (HZ08). The metric used is ds2 = − e2Φdt2 + e2Λdr2 + r2dΩ2 and in the diffusion limit the heat flux F is given by the following expression:
(3)where cv is the specific heat per unit volume, Qν denotes the energy loss by neutrino emissions and Qṁ considers energy gains as a consequence of the accretion of matter. As we mentioned in Sect. 3.1, the deep crustal heating considers that there are heat sources located in the inner crust as a result of pycnonuclear reactions and electron captures as well as other less intense sources in the outer crust (HZ08). The metric used is ds2 = − e2Φdt2 + e2Λdr2 + r2dΩ2 and in the diffusion limit the heat flux F is given by the following expression: 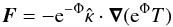 (4)where
(4)where 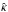 is the thermal conductivity tensor and eΦT is the redshifted temperature. In our one-dimensional treatment the flux is only radial and
is the thermal conductivity tensor and eΦT is the redshifted temperature. In our one-dimensional treatment the flux is only radial and 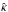 becomes a scalar k that includes contributions of electrons, neutrons, protons, and phonons:
becomes a scalar k that includes contributions of electrons, neutrons, protons, and phonons: 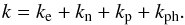 (5)The electronic term is dominant in the crust, while radiative transport is the most important process close to the surface.
(5)The electronic term is dominant in the crust, while radiative transport is the most important process close to the surface.
The temperature evolution is followed in the region that extends from the crust-core interface (ρcc = 1.3 × 1014 g cm-3) down to the base of the envelope (crust-envelope interface at ρb = 5.6 × 108 g cm-3).
3.6. Crustal heating during outbursts: generating the initial thermal profile
To simulate the accretion phase, we considered the heat released per nucleon as a function of the density (as in HZ08, Sect. 3.3). The integration in Eq. (3) was iterated until the temporal variable equaled the outburst duration. At this time, the NS crust has reached a thermal profile that depends on the local energy release per nucleon, the local accretion rate ṁ, the duration of the outburst tacc, and the crust microphysics as cv. Then, the quiescent phase begins and the NS crust starts to cool down from this initial thermal profile, which corresponds to the conditions at the end of the outburst.
3.7. Inner boundary: the core
The equilibrium temperature of the system is set by the core temperature, Tc, which mainly depends on the long-term averaged accretion rate. We assumed that the recurrence time, that is, the time between two accretion events, is shorter than the relaxation time of the core (~103 yr) and the source has gone through several accretion-quiescence cycles, therefore the core has reached thermal equilibrium and its temperature remains roughly constant. Thus, as an inner boundary condition, we fixed Tc to a constant value taken as a free parameter to fit the observations. If the NS has reached the thermal equilibrium with the core, Tc is determined by the last observations. Otherwise, if the source is still cooling, Tc is difficult to infer.
We checked that assuming a constant Tc is a good approximation for quasi-persistent sources unless accretion lasts for much longer than ~10 yr. In that case, the core could be heated up by an inward flux generated by the strong heat deposition over the extended period (e.g., for EXO 0748−676 if tacc ~ 100 yr).
3.8. Outer boundary: the envelope
To study the thermal evolution of the crust, the outer boundary condition presents numerical difficulties since the external layers have a thermal relaxation time (~1–100 s) much shorter than the crustal cooling timescale (~1000 days). Therefore we assumed that the crust is surrounded by a fully relaxed envelope and treated the two regions separately. The outer integration limit for the crustal cooling is then the bottom of the envelope placed at ρb, with a temperature Tb, which is influenced by thermonuclear reactions during outburst. In this sense, the initial value of this temperature at the beginning of the quiescence phase, 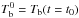 contains relevant information about the heating of the envelope during the active phase. In our approach (as in BC09), we set Tb to fit the cooling curves to the observational data and leave the envelope model and determining Tb for a future work.
contains relevant information about the heating of the envelope during the active phase. In our approach (as in BC09), we set Tb to fit the cooling curves to the observational data and leave the envelope model and determining Tb for a future work.
The boundary condition for our crustal cooling is the Tb − Ts relation shown in Fig. 4. At low Tb our partially accreted model (PA) converges to a fully accreted model (FA) composed mainly by H and He, as for example in (Potekhin et al. 1997; hereafter PCY97). For high Tb, however, it resembles the canonical relation for the non-accreted case (Gudmundsson et al. 1983, hereafter GPE83) in a Fe envelope. There is an overall agreement between our approach and the relation used in BC09 (stars), which facilitates the comparison of the cooling curves below.
 |
Fig. 4 Tb − Ts relation used in this work: the partial accreted model (PA, dashed-dotted line) and comparison with the non-accreted Fe envelope (NA, solid line) as in GPE83 (crosses) and the fully accreted (FA, dashed line) in an envelope composed mostly of light elements H and He, as in PCY97. The relation used in BC09 is shown with stars. |
Linearizing the Tb − Ts relations in a log-log plot for subsequent cooling simulations we obtained 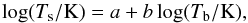 (6)with slight variations in the coefficients (a,b) = (2.15,0.49) and (a,b) = (2.20,0.49) for a (1.4, 1.6) M⊙ NS model, respectively.
(6)with slight variations in the coefficients (a,b) = (2.15,0.49) and (a,b) = (2.20,0.49) for a (1.4, 1.6) M⊙ NS model, respectively.
4. Revisiting crustal cooling
We now discuss our results, which we previously compare with existing works (see details in Appendix A) for testing purposes.
4.1. Deep crustal cooling model: testing MXB 1659−29
We begin with MXB 1659−29, which is considered the most standard case. We used a NS with a mass of 1.6 M⊙ and radius R = 11.79 km (Table 2), taking the impurity parameter Qimp, the accretion rate Ṁ18, and core temperature Tc,8 as free parameters. The temperature evolution at the outer boundary, Tb, during outburst and quiescence, the corresponding initial thermal profiles, and the cooling curve are plotted in Figs. 5a, b, and c, respectively.
 |
Fig. 5 Thermal evolution considering fixed (solid lines) or free (dashed lines) temperature during outburst |
First, we assumed that the temperature at the base of the envelope during outburst, 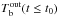 , is fixed to
, is fixed to 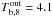 (Fig. 5, solid lines) while at the inner boundary the core temperature is kept fixed to Tc,8 = 0.29, both values chosen to fit the first and last observations, respectively. We set Ṁ18 = 0.1, Qimp = 4 and M = 1.6 M⊙, similar to those used in BC09, see Appendix A for a detailed comparison. Note that the initial thermal profile suitable to explain the data (brown ellipses in Fig. 5c) has an inverted temperature gradient and hence an inward-directed heat flux. As was pointed out before (BC09, Sht07), the (arbitrary) value of
(Fig. 5, solid lines) while at the inner boundary the core temperature is kept fixed to Tc,8 = 0.29, both values chosen to fit the first and last observations, respectively. We set Ṁ18 = 0.1, Qimp = 4 and M = 1.6 M⊙, similar to those used in BC09, see Appendix A for a detailed comparison. Note that the initial thermal profile suitable to explain the data (brown ellipses in Fig. 5c) has an inverted temperature gradient and hence an inward-directed heat flux. As was pointed out before (BC09, Sht07), the (arbitrary) value of  is crucial to explain the early decay. To illustrate this point, we plot the case when
is crucial to explain the early decay. To illustrate this point, we plot the case when 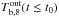 is not held fixed, but instead evolves freely (dashed curves), controlled only by deep crustal heating (HZ08). These curves fail to explain observations in the early cooling, and a higher value of
is not held fixed, but instead evolves freely (dashed curves), controlled only by deep crustal heating (HZ08). These curves fail to explain observations in the early cooling, and a higher value of 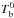 is necessary, as we can see from the cooling curves (Fig. 5c).
is necessary, as we can see from the cooling curves (Fig. 5c).
At each time, the surface temperature reflects the initial conditions at a particular depth. Deeper down, the crust did not have time to relax, and it exhibits roughly the initial thermal profile. Thus, each depth (or density) corresponds to an evolutionary time. The early cooling (first ~300 days) is controlled by the physics of the outer crust and the initial thermal profile, which depend strongly on Ṁ and on tacc. The following epoch corresponds to the inner crust thermal relaxation, (approx. ~(300–1000) days) and is determined by electron-impurity scattering. After ~400 days the imprint of the superfluid neutron gas is clear: the temperature fall and the subsequent slope is mostly controlled by the strength of the pairing energy gap (Page 2013) and the possible interaction of the free neutrons with the ion lattice, for example, as a result of entrainment effects (Chamel et al. 2013).
The cooling curve tail reflects the core thermal state (at 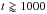 days) whose temperature remains nearly constant. We checked that the core temperature is not modified unless the accretion period lasts for much longer than ≃10 yr.
days) whose temperature remains nearly constant. We checked that the core temperature is not modified unless the accretion period lasts for much longer than ≃10 yr.
4.2. Heated-up envelope or incorrect accretion rate?
To show how critical the value of 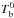 is for the early decay, we also explored the case where
is for the early decay, we also explored the case where 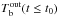 evolves freely. BC09 estimated that its value cannot rise to 108 K solely by means of deep crustal heating (HZ08 sources) and that the required energy release in the outer crust is ≃0.8 MeV nuc-1 for Ṁ18 = 0.1, well above that provided by electron captures (Gupta et al. 2007 and HZ08). Moreover, it must be released at a density ≲ 3 × 1010 gr cm-1, which is again below the density range of electron captures or other known reactions in the outer crust (like 24O burning, Horowitz et al. 2008).
evolves freely. BC09 estimated that its value cannot rise to 108 K solely by means of deep crustal heating (HZ08 sources) and that the required energy release in the outer crust is ≃0.8 MeV nuc-1 for Ṁ18 = 0.1, well above that provided by electron captures (Gupta et al. 2007 and HZ08). Moreover, it must be released at a density ≲ 3 × 1010 gr cm-1, which is again below the density range of electron captures or other known reactions in the outer crust (like 24O burning, Horowitz et al. 2008).
 |
Fig. 6 Additional heat or increased Ṁ? Left panels: dashed curves correspond to |
The steep fall in the inverted temperature gradient of the initial thermal profile is necessary to account for the relatively high temperature of the first observation (T ≃ 120 eV at 40 days) followed by the moderate value of the second one (T ≃ 90 eV at 300 days), see Fig. 6. Our results show that this profile is indeed difficult to achieve unless an additional heating source is assumed to be coming from a low-density layer. It originate either in the heated-up envelope during outburst (that modifies the boundary condition for the cooling through the value of 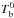 ) or in the outer crust at shallow depths. This fact was implicitly assumed in BC09 when
) or in the outer crust at shallow depths. This fact was implicitly assumed in BC09 when 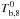 was fixed to a relatively high value ≃4. Alternatively, it has been proposed that MXB 1659−29 has been accreting at the Eddington rate Ṁ18 ~ 1, overestimating Ṁobs for MXB 1659−29 by about one order of magnitude (Sht07).
was fixed to a relatively high value ≃4. Alternatively, it has been proposed that MXB 1659−29 has been accreting at the Eddington rate Ṁ18 ~ 1, overestimating Ṁobs for MXB 1659−29 by about one order of magnitude (Sht07).
We simulated these two possibilities: additional shallow heat deposition and increased accretion rates. In the first case we considered the location of additional sources to vary in the range 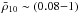 (where ρ10 is ρ in 1010 g cm-3) with radial width Δr = 5 m and a released energy of 1.6 MeV nuc-1 while keeping Ṁ18 = 0.1 (left panels of Fig. 6). We found that the modified Tb hardly reproduces the initial steep fall of
(where ρ10 is ρ in 1010 g cm-3) with radial width Δr = 5 m and a released energy of 1.6 MeV nuc-1 while keeping Ṁ18 = 0.1 (left panels of Fig. 6). We found that the modified Tb hardly reproduces the initial steep fall of 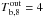 (solid lines) unless intense shallow additional sources are present (at ρ10 ≲ 0.08). If the heat originates in even more external layers, the energy deposited should be lower and the results are much similar to the case with fixed
(solid lines) unless intense shallow additional sources are present (at ρ10 ≲ 0.08). If the heat originates in even more external layers, the energy deposited should be lower and the results are much similar to the case with fixed 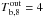 . This leads to the idea that the heat source is probably located at the top of the outer crust or even in the envelope.
. This leads to the idea that the heat source is probably located at the top of the outer crust or even in the envelope.
In the second case, we increased Ṁ18 = 0.1 − 1 (right panels of Fig. 6) without any additional heat source. We found that the resulting slope cannot explain the MXB 1659−29 early data (right panels of Fig. 6), which means that it is unlikely that Ṁobs has been underestimated.
We conclude that deep crustal heating by pycnonuclear reactions in the inner crust and e-captures in the outer crust is not enough to explain the early slope of MXB 1659−29 and additional energy from low density regions is needed either from the heated-up envelope during outburst or from additional shallow sources in the outer crust. Observations shortly after accretion stop are, therefore, crucial to clarify this point.
5. Influence of the thermal state of the envelope and core on the crustal cooling: limiting Tb and Tc
Next we assumed a starting model with fixed M = 1.6 M⊙, leaving Tc,8, and Tb as free parameters, usually set in each case to fit the first and the last observation of each source.
MXB 1659 − 29
We obtained a thermal evolution that is compatible with a low Qimp value in the crust and found that the source reaches thermal equilibrium in ~1000 days, which fully agrees with the simulations of BC09 and the exponential fits in Cackett et al. (2008). Cooling curves that fit the observations well (light regions with χ2< 2) are shown in Fig. 7. We found Tc,8 = 0.28 − 0.35 and Tb = 4.3 − 4.6, the solid curve is the best fit with Tc,8 = 0.315 and Tb = 4.39, as indicated as a cross in the inset.
 |
Fig. 7 Fits for MXB 1659−29. The light zone corresponds to cooling curves with χ2< 2, the solid line is our best fit with χ2 = 0.75. The inset shows the corresponding parameter space; the dark zone is for χ2< 1 and the cross the minimum. We fix M = 1.6 M⊙, Qimp = 3.5, and for the Sch03 gap and vary Ṁ18 = 0.11 − 0.16. |
EXO 0748 − 676
The quiescent luminosity for this source is higher than the prediction from standard cooling models (Degenaar et al. 2011b), and it has been suggested that residual accretion outside the main accretion period may be responsible for the high temperature (Brown et al. 1998; Rutledge et al. 2000; Colpi et al. 2001). Nevertheless, the XMM-Newton telescope (which has provided the most sensitive observations) has not shown features in the light curve that are associated with residual accretion (Díaz Trigo et al. 2011). Alternatively, it has been suggested that the core has reached a steady state in which the energy radiated during quiescence equals the heat released by the reactions taking place during outburst. Considering an accretion time of 24 yr and an accretion rate of Ṁ18 = 0.03, a steady state with such a high temperature would be compatible with a recurrence time of ~100 yr (Degenaar et al. 2011b), a scenario that cannot be ruled out.
 |
Fig. 8 Same as Fig. 7, but for EXO 0748−676 and only dark zones with χ2< 1 are shown. The minimum is at χ2 = 0.57. We fix M = 1.6 M⊙, Qimp = 1, and the Sch03 gap and vary Ṁ18 = 0.01 − 0.08. |
Another peculiarity of this source is the low temperature decrease after outburst: the surface temperature has decreased to a factor of ~0.9 in 650 days, in comparison to ~0.5 for MXB 1659−29 in the same time period. This is again compatible with a high core temperature and a low accretion rate. Another open question is the unknown origin of the power-law component in the spectra.
In spite of such peculiarities, the quiescent luminosity of EXO 0748−676 can also be very well reproduced by a crustal cooling model with a rather high core temperature Tc,8 ~ 1.25, approx. a factor 3 higher than that of MXB 1659−29 , which might indicate that EXO 0748−676 is a young NS whose core has not yet reached thermal equilibrium. The impurity parameter was fixed to Qimp = 1, but given that the source is hot, the results are quite insensitive to variations of Qimp. Free parameters varied in the ranges Tc,8 = 1.15 − 1.32 and Tb = 2.6 − 3.1. The dark regions in Fig. 8 indicate very good fits with χ2< 1; the best one corresponds to Tc,8 = 0.57 and Tb = 2.85.
Apparently, there is a shift between the Chandra and Swift observations that is maybe due to cross-calibration problems between the two satellites (Degenaar et al. 2011b). Even more, XMM-Newton and Swift fluxes are compatible, which also points to an offset in the calibration between Chandra and Swift (Díaz Trigo et al. 2011). Because of the small error bars, Chandra data allow for a better constraint of Tb, but these data do not provide information about early times. Conversely, Swift data allow for a better description of the early time, and XMM-Newton data are the most sensitive observations of this source in quiescence and, therefore, the most reliable (Díaz Trigo et al. 2011). We first fit XMM-Newton and Swift data together to find Tc,8 = 1.27, while Chandra data give Tc,8 = 1.24. Given this tiny difference, we included all the data in the present analysis4.
5.1. Summary of the crustal coolers
 |
Fig. 9 Contours for cooling curves for KS 1731−260, MXB 1659−29, and EXO 0748−676 with χ2< 1,2 (dark and light zones) by varying Tc and Tb for M = 1.6 M⊙. Contours with fixed Qimp are shown (values at their sides). |
In Fig. 9 we summarized contour plots for the three sources MXB 1659−29, KS 1731−260 and EXO 0748−676 in the Tc – Tb parameter space, defined by the conditions χ2< 1,2 (dark and light zones). We chose a 1.6 M⊙ NS star and a low value of Qimp(≲10) throughout. We show how the contours for fixed Qimp move in the parameter space.
6. Toward a model for crustal coolers: constraining the crust microphysics
This section is devoted to inferring some information about the crust microphysics, and therefore we mainly focus on the new constraints imposed by the last observation of KS 1731−260 and on exploring a model that could simultaneously fit the quiescence emission of MXB 1659−29, KS 1731−260, and EXO 0748−676.
6.1. Is KS 1731−260 still cooling? Constraints on neutron superfluidity energy gaps
The last observations of KS 1731−260 reported by Cackett et al. (2010a) seem to indicate that the source is still cooling, and if this is the case, previous models fail to explain the last temperature drop (Fig. 1b). Indeed, for our current set of microphysical inputs, none of the curves obtained by varying Qimp, Tc, or Tb succeed in explaining the last observation with χ2< 1 (no dark zones in Fig. 9); a longer relaxation time with a more effective storage of heat in the crust is needed. To achieve this, we explored a neutron energy gap for crust superfluidity with a relatively low maximum value, or, alternatively, an energy gap located at deep densities (near the crust-core interface) such that the resulting suppression of the neutron specific heat and the neutrino emissivity is less efficient.
In the results presented up to now we used the gap Sch03, which is similar to that used in BC09 or Sht07, which affects the range ρ ~ (1012 − 1014) g cm-3 with a maximum value of ≃1 MeV (Fig. 2) and results in a thermal evolution that levels off too fast with the core (dotted-dashed line in Fig. 10). The model we call deep gap (see Fig. 2) has a maximum located at ρ ~ 1014 g cm-3, with an accordingly longer thermal relaxation time for the crust. Cooling curves using this deep gap can fit the last data point substantially better (brown dark zones in Fig. 10). A similar effect can be obtained by considering a small gap with maximum value ≃0.1 MeV (dashed line in Fig. 2) or any gap contained within the colored regions in Fig. 2. With these new fits a lower Tc,8 ≃ 0.5 is reached; future observations are needed to confirm or refute the predicted core temperature.
 |
Fig. 10 Cooling curves for KS 1731−260 using a deep gap: the light (dark) brown zones correspond to χ2< 2( < 1), the solid curve is the best fit (χ2 = 0.69) with Tb,8 = 3.55. The dotted-dashed curve corresponds to the best fit (χ2 = 1.14) with the Sch03 gap and Tb,8 = 3.52. In all cases, M = 1.6 M⊙, Ṁ18 = 0.05, and Qimp ≃ 4 are fixed. |
6.2. Constraining the impurity parameter
In this subsection we explore the Qimp−Tc parameter space for the three sources MXB 1659−29, KS 1731−260, and EXO 0748−676.
 |
Fig. 11 Best-fit contours for KS 1731−260 comparing Sch03 gap (left panel) and deep gap (right panel). Colored regions satisfy χ2< 1,2 (dark and light) considering different Tb (Tb,8 values at the sides of the contours), accretion rates (dashed lines for Ṁ18 = 0.05, solid lines for Ṁ18 = 0.1) and NS masses (upper, purple contours for 1.4M⊙ and lower, green contours for 1.6 M⊙). |
 |
Fig. 12 Idem Fig. 11, but for MXB 1659−29 and corresponding accretion rates (dashed lines for Ṁ18 = 0.07, solid lines for Ṁ18 = 0.18). |
In the left panels of Figs. 11 and 12 we show contour levels corresponding to cooling curves that satisfy the conditions χ2< 2 (light regions) and χ2< 1 (dark regions) that were obtained for the Sch03 gap and two different masses, M = 1.4,1.6 M⊙. In right panels, we show the corresponding results for a deep gap. In the different panels we also vary the mass accretion rate Ṁ within the observational range as much as possible; the ellipses with solid (dashed) contours are calculated for the upper (lower) limit.
First we note some general trends in the figures:
-
i)
Qimp is correlated with Ṁ; as Ṁ is increased,the energy released in the inner crust by pycnonuclear reactions isincreased and overheats the deep layers. To balance this effect,Qimp must assume a lower value, which raises thethermal conductivity that favors heat transport to the core.
-
ii)
More massive NS has a thinner crust, which reduces the thermal relaxation time, and Qimp shows a shift toward higher values.
The comparison of these results with those for EXO 0748−676 is shown in Fig. 13. Since the last observation of this source was detected at ~600 days and the energy gap influences cooling curves only after ~500 days, data fits cannot help to distinguish between superfluid models. Remarkably, because at high temperatures (T ≳ 108 K) the contribution to the thermal conductivity due to e-impurities scattering is negligible, cooling curves are barely dependent on Qimp and the allowed range for it extends to much higher values than for the other two cases.
 |
Fig. 13 Constraints for MXB 1659−29, KS 1731−260, and EXO 0748−676 in the Tc-Qimp parameter space satisfying χ2< 1,2 (dark and light zones) by varying the accretion rate. Deep gap and 1.6M⊙ are assumed. |
6.3. General trends in the standard crustal coolers
When comparing results for MXB 1659−29, KS 1731−260 and EXO 0748−676 sources (summarized in Table 4), we note that while EXO 0748−676 shows a higher equilibrium core temperature, Tc,8 ~ 1, MXB 1659−29 and KS 1731−260 seem to level off at Tc,8 ~ 0.3 − 0.5. We stress that we obtained good fits (χ< 1) for the three sources with corresponding mass accretion rates compatible with those inferred from observations. Therefore, a model that fits the three sources simultaneously points to the an impurity parameter Qimp ≲ 5.
The trend in the fits points to an energy gap for neutron superfluidity with a relatively low maximum value (≃0.1 MeV) or peaked at deep densities close to the crust-core interface (ρ ~ 1014 g cm-3), but this is not conclusive; other processes influencing the contribution of the specific heat and/or the neutrino emissivity may explain the cooling as well.
A 1.6 M⊙ star indicates slightly lower values of Tc and Tb than for 1.4 M⊙. The value of Tb,8 ~ 2.8 − 4.5 is determined by the thermal state of the envelope bottom (at ρb,8 ~ 6) at the end of the outburst, and this will set some constraints on the outburst models.
Best fits for MXB 1659−29, KS 1731−260, and EXO 0748−676 with neutron star mass M, core temperature Tc and impurities Qimp, considering a deep gap.
Based on this analysis, we call these three sources standard crustal coolers; despite their differences, their quiescent emission can be explained by means of the heat released by pycnonuclear reactions deep in the inner crust, as long as the NS crust microphysics, models and boundary conditions (fixing the temperature at the envelope bottom and in the core) are adjusted. For the other two sources, XTE J1701−462 and IGR J17480−2446, these assumptions are not sufficient to account for their quiescent emission and additional heat sources in the outer crust/envelope, residual accretion or new processes affecting the thermal conductivity of the crust have to be assumed, as we discuss next.
7. Beyond crustal cooling
The peculiar observational data of XTE J1701−462 and IGR J17480−2446 require models that include additional considerations beyond the deep crustal cooling model controlled by pycnonuclear reactions and electron captures in the inner crust. In this section we investigate scenarios that could help to understand the quiescent emission for these warm sources: an additional heat deposition in the outer crust, a modified heat flow due to a buried magnetic field, or residual accretion responsible for the increment/variability in the temperature.
7.1. Additional heat in the outer crust?
Previous work on the heat released in the outer crust include the report of Gupta et al. (2007), who calculated the energy liberated by all thermonuclear reactions assuming a one-component plasma and found values ~0.2 MeV nuc-1. Later, Horowitz et al. (2008) calculated reaction rates of 24O and 28Ne for a multicomponent plasma and found that a composition in which (3 − 10)% of the ions are 24O causes reactions that release 0.52 MeV nuc-1 at ~1011 g cm-3. This energy could indeed influence the thermal state of the source going into quiescence.
An initial thermal profile that is peaked in the outer crust (typically 108 − 9 gr cm-3, see Fig. 14) influences the crustal thermal state and may be a plausible explanation for the break observed at ~20 − 150 days in XTE J1701−462 (Fig. 2d). Additional heat sources located in the outer crust that release high enough energy per nucleon could account for these kind of initial profiles (Fridriksson et al. 2010; BC09, Degenaar & Wijnands 2011a), as we show next for XTE J1701−462 and IGR J17480−2446.
 |
Fig. 14 Heat sources that affect the initial thermal profile: pycnonuclear reactions as in HZ08 (dashed line) and additional sources in the outer crust (solid lines). The cooling curves for these thermal profiles fitting XTE J1701−462 data are shown in Fig. 15. |
XTE J1701−462
This is the most peculiar source: in two observations, XMM-3 and CXO-4, it shows a sudden increase in temperature which so far lacks explanation. Without these two observations, the exponential fit gives the shortest e-folding time of ~100 days and the broken power-law fit predicts a break in the slope at about ~25–80 days (Fridriksson et al. 2011) (much earlier than the other sources). BC09 suggested that the break is due to the suppression of the specific heat in the transition from a classical to a quantum crystal. They estimated the time at which the break occurs (the diffusion time of the thermal flow from the density at which this transition occurs to the surface) and obtained ~300 days, much longer than expected from the data.
It is also difficult to reconcile the early temperature of XTE J1701−462 with the latest observations within a cooling model. More specifically, we can easily find a set of parameters for the thermal evolution that explains the first observation at the third day (COX-1) and the tail after ~400 days (COX-5 and subsequent), but the problem is to fit the data between ~10 and ~200 days with the same model.
An alternative explanation for the fast initial drop in temperature are additional heat sources in the outer crust that release energy close enough to the surface for the heat to be rapidly carried away. After this first stage, the temperature evolution should resemble the standard cooling model without additional heat sources. If this is the case, the early data of XTE J1701−462 are unique and offer valuable information about the depth of the layer where additional heat is released. The initial thermal profile is modified by the location of heat sources; if we consider shallow sources (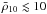 ), the heat accumulated during the accretion stage mostly diffuses to the surface, keeping the outer crust hot at early times. Instead, if we consider deep sources, the heat is carried toward the interior and is released by neutrino emission from the core, resulting in lower surface temperatures.
), the heat accumulated during the accretion stage mostly diffuses to the surface, keeping the outer crust hot at early times. Instead, if we consider deep sources, the heat is carried toward the interior and is released by neutrino emission from the core, resulting in lower surface temperatures.
We performed simulations considering that the additional heat is located in a shell characterized by the mean density, 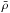 , at which the energy is deposited and its radial width, Δr. The results presented below are weakly sensitive to Δr in the range (1 − 50) m, therefore we kept Δr = 20 m fixed and chose a Tb value compatible with observations for an accretion rate of M18 = 1.1. By varying Tc,8 = 1.0 − 1.2 to adjust the first data (COX-1) and the tail (COX-5 and subsequents), we found that the best fit to the intermediate observations gives
, at which the energy is deposited and its radial width, Δr. The results presented below are weakly sensitive to Δr in the range (1 − 50) m, therefore we kept Δr = 20 m fixed and chose a Tb value compatible with observations for an accretion rate of M18 = 1.1. By varying Tc,8 = 1.0 − 1.2 to adjust the first data (COX-1) and the tail (COX-5 and subsequents), we found that the best fit to the intermediate observations gives 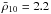 and q = 0.17 MeV nuc-1 (solid curve in Fig. 15).
and q = 0.17 MeV nuc-1 (solid curve in Fig. 15).
Compared with the calculations of Horowitz et al. (2008) for the 24O + 24O reaction5, our simulations predict a value of 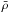 for the heat deposition one order of magnitude lower. This difference might be reduced if the effect of neutron skin dynamic is included in the approach, which may result in a significant enhancement of the reaction rate and, hence, a lowering of the corresponding density for the location of the sources.
for the heat deposition one order of magnitude lower. This difference might be reduced if the effect of neutron skin dynamic is included in the approach, which may result in a significant enhancement of the reaction rate and, hence, a lowering of the corresponding density for the location of the sources.
 |
Fig. 15 Cooling curves for XTE J1701−462 with additional heat sources; best fit with |
IGR J17480−2446
This is the first regular transient with a short active phase of ~weeks/months showing evidence of crustal cooling. It is remarkable that having been accreting for a much shorter period than the quasi-persistent sources, its thermal flux remains, after 2.2 years, still well above the quiescent emission value detected before outburst. For such a short active phase, it would be expected that the crust reaches a lower temperature.
The information on the previous quiescent equilibrium level imposes a constraint on Tc. If we leave Tc as a free parameter in our fits, we find that the NS crust levels off after ~2000 days at a temperature of Tc,8 = 0.75, which is far above than the quiescent level before outburst ~(0.44 − 0.55) × 108 K (see solid curve in Fig. 16), in agreement with the results of Degenaar et al. (2013).
 |
Fig. 16 Best cooling curves for IGR J17480−2446; the brown zone corresponds to χ2< 2, and the solid line is the best fit with χ2 = 1.18 (cross in the inset). We fix Ṁ18 = 0.2, Tb,8 = 4.06, and the Sch03 gap. |
Alternatively, if we fix Tc to the value in the previous quiescence period, all cooling curves underestimate the late-time temperatures (dashed curve in Fig. 17). One possible solution is again an additional heat source (Degenaar & Wijnands 2011a; Degenaar et al. 2011a); results are plotted in Fig. 17. Models satisfying the condition χ2< 2 are shown as light brown region, and the best fit corresponds to q = 3.8 MeV nuc-1 and 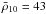 (solid curve). Comparing these results with those found previously for XTE J1701−462, we note that these heat sources are extremely intense and deeply located, and its origin can hardly be determined.
(solid curve). Comparing these results with those found previously for XTE J1701−462, we note that these heat sources are extremely intense and deeply located, and its origin can hardly be determined.
 |
Fig. 17 Idem Fig. 16, but with additional heat sources optimized with respect to |
We conclude that there are two different possibilities that can explain the observations of IGR J17480−2446. First, standard cooling (without additional heat sources) but with an equilibrium temperature well above the value measured in the previous quiescent phase. This can be a consequence of a change in the Tb − Ts relation with respect to the previous quiescent phase (because of a change in the envelope composition during the accretion phase), which could set a higher observed equilibrium level for the same interior temperature (Degenaar et al. 2013). Second, it is also possible to fit the data by fixing Tc in a value compatible with the quiescent band, but then it is necessary to consider very intense additional heat sources whose origin is unclear. Future monitoring of IGR J17480−2446 will determine if the source has leveled off, favoring the first scenario, or whether it is still cooling, which would indicate non-standard cooling.
 |
Fig. 18 Additional heat sources distribution and intensity for XTE J1701−462 (brown region), and IGR J17480−2446 (green region). Solid lines are HZ08 sources (inset). |
To summarize, in Fig. 18 we compare the additional heat sources needed to explain the quiescent emission of XTE J1701−462 and IGR J17480−2446 with the theoretical calculations of the heat deposited by crustal heating from HZ08. Colored bands illustrate how the source intensity is modified when they are located at different depths. The inset shows the HZ08 results in more detail.
7.2. Buried magnetic field
Another possibility that might explain a warmer outer crust at early times is a low conductivity layer between outer and inner crust. This can be the result of a buried magnetic field, as suggested by Payne & Melatos (2004), if the magnetic field lines are pushed into the crust and concentrate in a thin shell during the accretion period. The thermal conductivity would be highly reduced in the thin layer, and would act as a thermal insulator between outer and inner crust. The cooling curves will be affected by the suppressed thermal conduction, resulting in an accelerated cooling at early times (released of the heat deposited in the outer crust) followed by a slower temperature decrease.
To test this hypothesis, we suppressed the electronic thermal conductivity with a factor Rsup = 0.1 in a layer characterized by its radial width, Δr, and the mean density 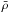 at which the suppression occurs, fixing the accretion rate to the observational value, Ṁ18 = 1.1 and Tb,8 = 4.05. Results show that the parameter range compatible with the observations is
at which the suppression occurs, fixing the accretion rate to the observational value, Ṁ18 = 1.1 and Tb,8 = 4.05. Results show that the parameter range compatible with the observations is 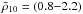 and Δr = (11.9 − 19.5) m (Fig. 19) and with a variation of Tc,8 = 1.35 − 1.40. The minimum is located at
and Δr = (11.9 − 19.5) m (Fig. 19) and with a variation of Tc,8 = 1.35 − 1.40. The minimum is located at 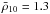 and Δr = 15.8 m (with χ2< 1). To analyze this more exhaustively it is necessary to study the influence of the magnetic field geometry on the results in a 2D model, which is far beyond the scope of this work.
and Δr = 15.8 m (with χ2< 1). To analyze this more exhaustively it is necessary to study the influence of the magnetic field geometry on the results in a 2D model, which is far beyond the scope of this work.
 |
Fig. 19 Cooling curves obtained by suppressing the electron thermal conductivity by Rsup = 0.1. The brown dark (light) regions correspond to χ2< 1( < 2), the solid line to χ2 = 0.61. We fix Tc,8 = 1.35 − 1.40, Ṁ = 1.1, Tb,8 = 4.05, Qimp = 1, and the Sch03 gap. The inset shows χ2< 2 contours in parameter space by varying Tc. |
7.3. Residual accretion in XTE J1701−462?
As an alternative scenario, we speculate that some data points in the emission of XTE J1701−462 may exhibit a higher temperature as a result of residual accretion episodes than a baseline standard cooling. Then we added two residual accretion periods: in the first ~150 days the period A coincident with CXO-2, XMM-1 and XMM2 and later, at about 200 days, with a duration of ~60 days, the period B in correlation with XMM-3 and CXO-4. We mimicked the change of the accretion mass rate with a variation of the temperature at the base of the envelope Tb for the periods A and B as shown in Fig. 20a. We took exponential decay functions 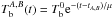 with
with 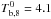 , μ = 475 days, tA = t0 and tB = 213 days for the accretion periods A and B (Fig. 20a). The corresponding cooling curves with residual accretion included are shown in Fig. 20b. A NS with M = 1.6 M⊙ was assumed. The brown region demarcates the curves that fit filled points with χ2< 1. The solid line is the best fit without accretion after t0; it predicts that the source is still cooling down. The dashed line is the temperature evolution including
, μ = 475 days, tA = t0 and tB = 213 days for the accretion periods A and B (Fig. 20a). The corresponding cooling curves with residual accretion included are shown in Fig. 20b. A NS with M = 1.6 M⊙ was assumed. The brown region demarcates the curves that fit filled points with χ2< 1. The solid line is the best fit without accretion after t0; it predicts that the source is still cooling down. The dashed line is the temperature evolution including 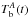 and fits the filled symbols plus CXO-2, XMM-1, and XMM2. The dotted line fits all the points, and also XMM-3 and CXO-4 assuming an accretion rate of
and fits the filled symbols plus CXO-2, XMM-1, and XMM2. The dotted line fits all the points, and also XMM-3 and CXO-4 assuming an accretion rate of 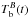 . Roughly estimated, we need a mean accretion rate of about 20% of the value of Ṁ during outburst to account for all observations.
. Roughly estimated, we need a mean accretion rate of about 20% of the value of Ṁ during outburst to account for all observations.
 |
Fig. 20 Residual accretion episodes during quiescence in XTE J1701−462. a) Evolution of Tb assumed during residual accretion episodes A and B (dashed and dotted lines, respectively). b) Cooling curves from fitting filled symbol data without residual accretion: solid line is the best fit with χ2 = 0.53 and brown band has χ2< 1 (with Ṁ18 = 0.7 − 1.3 and Tc,8 = 1.3 − 1.8). The dashed and dotted lines (χ2 = 0.55,0.63) include residual accretion through |
Even though our results show that residual accretion can explain the CXO-2, XMM-1, and XMM-2 observations, Fridriksson et al. (2011) stated that the thermal component outside flares (XMM-3 and CXO-4 observations) is probably not caused by ongoing low-level accretion. This is because the temperature evolution throughout quiescence (excluding flares) presents an smooth and monotonic decrease; if accretion contributed significantly to the thermal emission much more irregular variability would be observed in this component. Moreover, no correlation between thermal and non thermal fluxes outside flares has been observed, whereas both rise together during flares. Nevertheless, residual accretion outside flares is a possibility that cannot be conclusively ruled out.
8. Summary
We have presented detailed numerical models describing the thermal relaxation of the crust following long accretion periods. This was motivated by the increasing number of observations of MXB 1659−29, KS 1731−260, EXO 0748−676, XTE J1701−462, and IGR J17480−2446. Our main results are summarized as follows:
-
1.
First, we checked by fittingMXB 1659−29 observations thatthe energy released by pycnonuclear reactions (~0.05 MeV nuc-1) does not seem to be enough to explain the high initial temperature (~108 K), which confirms the results of BC09. Therefore, to explain the early slope of the cooling curves of MXB 1659−29, it its necessary to consider an additional inward-directed heat flux that originates in outer layers.
-
2.
We solved the thermal evolution of the neutron star crust as it cools down taking into account deep crustal heating and we successfully fit MXB 1659−29, KS 1731−260, and EXO 0748−676 observations by adjusting the neutron star microphysics. We also obtained, in agreement with previous works, that the impurity content Qimp has a low value (≲5).
-
3.
We also studied the influence of neutron superfluidity on the results. MXB 1659−29 and EXO 0748−676 can be modeled with the same microphysics as in BC09. However, KS 1731−260 imposes an additional constraint on the neutron energy gap. The last observation suggests a longer relaxation time, which is compatible with an energy gap for neutron superfluidity that has a low value (≲0.1 MeV) or is peaked at a relatively high density, deep in the inner crust (ρ ~ 1014 g cm-3), although this is not conclusive and other processes such as enhanced specific heat could result in the same effect.
-
4.
We found that XTE J1701−462 cannot be explained with a standard crustal cooling model. It requires additional heat sources located in the outer crust, at
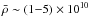 g cm-3, releasing q ~ (0.1 − 0.25) MeV nuc-1. In addition, we explored alternative scenarios, such as residual accretion during quiescence. Even though this model can explain data, the thermal component outside flares is probably not caused by ongoing low-level accretion (Fridriksson et al. 2011). We also probed the scenario of suppressed electronic thermal conductivity in a thin layer due to a buried magnetic field. We found that the layer must be thin, (Δr ~ (12 − 20) m), and located at ρ ~ 1010 g cm-3. For a better description it is necessary to solve a 2D problem considering the magnetic field geometry.
g cm-3, releasing q ~ (0.1 − 0.25) MeV nuc-1. In addition, we explored alternative scenarios, such as residual accretion during quiescence. Even though this model can explain data, the thermal component outside flares is probably not caused by ongoing low-level accretion (Fridriksson et al. 2011). We also probed the scenario of suppressed electronic thermal conductivity in a thin layer due to a buried magnetic field. We found that the layer must be thin, (Δr ~ (12 − 20) m), and located at ρ ~ 1010 g cm-3. For a better description it is necessary to solve a 2D problem considering the magnetic field geometry. 
Fig. 21 Cooling curve comparison of all the sources. In each case we show the best fit corresponding to the models: crustal cooling (MXB 1659−29), crustal cooling with small energy gap for neutron superfluidity (KS 1731−260), crustal cooling (all data fit, EXO 0748−676), crustal cooling with additional heat sources (XTE J1701−462), and crustal cooling with a high Tc (IGR J17480−2446).
-
5.
The quiescent emission of IGR J17480−2446 challenges our current understanding of crustal cooling since its thermal flux still remains above the value measured in the previous quiescent phase after spending 2.2 years in quiescence. This is difficult to reconcile with its short outburst (which lasted only two months). In agreement with Degenaar et al. (2013), we found that it is possible to explain the data if we consider that Tc is higher than the one measured in the last quiescent phase. Another possibility are, again, additional heat sources, but in this case, they must be considerably more intense (q ~ 3 MeV nuc-1) and must be located in deeper layers (
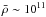 g cm-3) than for XTE J1701−462.
g cm-3) than for XTE J1701−462.
In Fig. 21 we summarize our results, showing the best fits obtained for all the sources. According to this, MXB 1659−29 and KS 1731−260 have already reached thermal equilibrium, with surface temperatures at kTeff ~ 55 eV and kTeff ~ 65 eV, respectively. EXO 0748−676 and IGR J17480−2446 seem likewise close to equilibrium levels, with temperatures of kTeff ~ 105 eV and kTeff ~ 83 eV, respectively. On the other hand, XTE J1701−462 is still far from thermal equilibrium, which we predict will be reached in several years at the value of kTeff ~ 107 eV. This high value is similar to that of EXO 0748−676, while the other sources level off at much lower temperatures. XTE J1701−462 has an early observation, which provides valuable information about the position and intensity of heat sources in the outer crust. Instead, we do not have information before ~30 days for the other sources. An open question is whether the other sources showed an early behavior similar to that of XTE J1701−462, for which observational data are lacking.
While this work was being written, a new observation of MXB 1659−29 was reported, the temperature of which has not been clearly determined yet (see discussion in Cackett et al. 2013); we did not include it in our analysis.
Another NSs went into quiescence in Terzan 5, EXO 1745−248 (Degenaar & Wijnands 2012), but it cannot be considered for crustal cooling since it lacks thermal emission; nevertheless it sets strong constraints on the properties of the NS core, which has efficiently cooled off.
The observation reported in Degenaar et al. (2014) is not included in this work, but we checked that our model can explain it successfully considering core temperatures of Tc,8 ≃ 1.4. We plan to publish the results in a future work.
Acknowledgments
This research was partially supported by CONICET, PIP-2011-00170 (DNA) and by the grant AYA 2010-21097-C03-02 (JAP). D.N.A. thanks Physics Dept. of Ohio University where part of this project started and Dept. of Applied Physics of Alicante University for warm hospitality.
References
- Aguilera, D. N., Pons, J. A., & Miralles, J. A. 2008, A&A, 486, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguilera, D. N., Cirigliano, V., Pons, J. A., Reddy, S., & Sharma, R. 2009, Phys. Rev. Lett., 102, 091101 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, N., Comer, G. L., & Glampedakis, K. 2005, Nucl. Phys. A, 763, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Baym, G., Bethe, H. A., & Pethick, C. J. 1971, Nucl. Phys. A, 175, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L. 1998, in The Many Faces of Neutron Stars, eds. R. Buccheri, J. van Paradijs, & M. A. Alpar (Dordrecht, Boston: Kluwer Academic Publishers), 419 [Google Scholar]
- Bordas, P., Kuulkers, E., Alfonso-Garzón, J., et al. 2010, ATel, 2919, 1 [NASA ADS] [Google Scholar]
- Brown, E. F., & Cumming, A. 2009, ApJ, 698, 1020 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, E. F., Bildsten, L., & Rutledge, R. E. 1998, ApJ, 504, L95 [Google Scholar]
- Cackett, E. M., Wijnands, R., Linares, M., et al. 2006, MNRAS, 372, 479 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Wijnands, R., Miller, J. M., Brown, E. F., & Degenaar, N. 2008, ApJ, 687, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Brown, E. F., Cumming, A., et al. 2010a, ApJ, 722, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Cackett, E. M., Brown, E. F., Miller, J. M., & Wijnands, R. 2010b, ApJ, 720, 1325 [Google Scholar]
- Cackett, E. M., Brown, E. F., Cumming, A., et al. 2013, ApJ, 774, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Campana, S., Colpi, M., Mereghetti, S., Stella, L., & Tavani, M. 1998, A&ARv, 8, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2012, Phys. Rev. C, 85, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Page, D., & Reddy, S. 2013, Phys. Rev. C, 87, 035803 [NASA ADS] [CrossRef] [Google Scholar]
- Cirigliano, V., Reddy, S., & Sharma, R. 2011, Phys. Rev. C, 84, 045809 [NASA ADS] [CrossRef] [Google Scholar]
- Colpi, M., Geppert, U., Page, D., & Possenti, A. 2001, ApJ, 548, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, R. L., & Narayan, R. 2005, ApJ, 629, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Cumming, A., Macbeth, J., in ’t Zand, J. J. M., & Page, D. 2006, ApJ, 646, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., & Wijnands, R. 2011a, MNRAS, 414, L50 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., & Wijnands, R. 2011b, MNRAS, 412, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., & Wijnands, R. 2012, MNRAS, 422, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Wijnands, R., Wolff, M. T., et al. 2009, MNRAS, 396, L26 [NASA ADS] [Google Scholar]
- Degenaar, N., Brown, E. F., & Wijnands, R. 2011a, MNRAS, 418, L152 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Wolff, M. T., Ray, P. S., et al. 2011b, MNRAS, 412, 1409 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Wijnands, R., Brown, E. F., et al. 2013, ApJ, 775, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Degenaar, N., Medin, Z., Cumming, A., et al. 2014, ApJ, 791, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz Trigo, M., Boirin, L., Costantini, E., Méndez, M., & Parmar, A. 2011, A&A, 528, A150 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douchin, F., & Haensel, P. 2001, A&A, 380, 151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fridriksson, J. K., Homan, J., Wijnands, R., et al. 2010, ApJ, 714, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Fridriksson, J. K., Homan, J., Wijnands, R., et al. 2011, ApJ, 736, 162 [Google Scholar]
- Galloway, D. K., Muno, M. P., Hartman, J. M., Psaltis, D., & Chakrabarty, D. 2008, ApJS, 179, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, S., Brown, E. F., Schatz, H., Möller, P., & Kratz, K. 2007, ApJ, 662, 1188 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., & Zdunik, J. L. 2008, A&A, 480, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinke, C. O., Wijnands, R., Cohn, H. N., et al. 2006, ApJ, 651, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Berry, D. K., & Brown, E. F. 2007, Phys. Rev. E, 75, 066101 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Dussan, H., & Berry, D. K. 2008, Phys. Rev. C, 77, 045807 [NASA ADS] [CrossRef] [Google Scholar]
- Horowitz, C. J., Caballero, O. L., & Berry, D. K. 2009, Phys. Rev. E, 79, 026103 [NASA ADS] [CrossRef] [Google Scholar]
- Kaminker, A. D., Haensel, P., & Yakovlev, D. G. 2001, A&A, 373, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levenfish, K. P., & Yakovlev, D. G. 1994, Astron. Rep., 38, 247 [NASA ADS] [Google Scholar]
- Lewin, W. H. G., Hoffman, J. A., Doty, J., & Liller, W. 1976, IAU Circ., 2994, 1 [NASA ADS] [Google Scholar]
- Medin, Z., & Cumming, A. 2014, ApJ, 783, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D. 2013, Fifty Years of Nuclear BCS: Pairing in Finite Systems, eds. R. A. Broglia et al. (World Scientific Publishing Co), 324 [Google Scholar]
- Page, D., & Reddy, S. 2012, ArXiv e-prints [arXiv:1201.5602] [Google Scholar]
- Page, D., & Reddy, S. 2013, Phys. Rev. Lett., 111, 241102 [NASA ADS] [CrossRef] [Google Scholar]
- Parmar, A. N., White, N. E., Giommi, P., & Gottwald, M. 1986, ApJ, 308, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Payne, D. J. B., & Melatos, A. 2004, MNRAS, 351, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Pooley, D., Homan, J., Heinke, C., et al. 2010, ATel, 2974, 1 [NASA ADS] [Google Scholar]
- Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
- Remillard, R. A., Lin, D., ASM Team at MIT, & NASA/GSFC 2006, ATel, 696, 1 [Google Scholar]
- Rutledge, R. E., Bildsten, L., Brown, E. F., Pavlov, G. G., & Zavlin, V. E. 2000, ApJ, 529, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Rutledge, R. E., Bildsten, L., Brown, E. F., et al. 2002, ApJ, 580, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., Bildsten, L., Cumming, A., & Wiescher, M. 1999, ApJ, 524, 1014 [NASA ADS] [CrossRef] [Google Scholar]
- Schatz, H., Gupta, S., Müller, P., et al. 2014, Nature, 505, 62 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schwenk, A., Friman, B., & Brown, G. E. 2003, Nucl. Phys. A, 713, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Shternin, P. S., Yakovlev, D. G., Haensel, P., & Potekhin, A. Y. 2007, MNRAS, 382, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R., & Kwant Team 1989, IAU Circ., 4839, 1 [NASA ADS] [Google Scholar]
- Wambach, J., Ainsworth, T. L., & Pines, D. 1993, Nucl. Phys. A, 555, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Miller, J. M., Markwardt, C., Lewin, W. H. G., & van der Klis, M. 2001, ApJ, 560, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Wijnands, R., Nowak, M., Miller, J. M., et al. 2003, ApJ, 594, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Wolff, M., Ray, P., Wood, K., & Wijnands, R. 2008, ATel, 1812, 1 [NASA ADS] [Google Scholar]
- Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., & Haensel, P. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Comparison with previous works
Appendix A.1: MXB 1659−29 results with BC09
To check our numerical approach and code, we first compared our results for MXB 1659−29 with BC09, in which Ṁ, Tc, Tb and Qimp are free parameters (Fig. A.1). Similarly as they did, we fixed M = 1.6 M⊙, Ṁ18 = 0.1 and Qimp = 4.0 and explored the behavior of the cooling curves against the variation of Tc and Tb. In Fig. A.1 the solid line corresponds to the best fit obtained with Tc,8 = 0.29 and Tb,8 = 4.1 (χ2 = 0.54). The brown zone is χ2< 2 with parameters in ranges of Tc,8 = (0.26 − 0.32) and Tb,8 = (3.9 − 4.4).
 |
Fig. A.1 Comparison of our cooling curves for MXB 1659−29 with BC09. The solid line is our best fit with χ2 = 0.54, the dashed line is the result of BC09. The brown region is our curves with χ2< 2 corresponding to Tc,8 = 0.26 − 0.32 and Tb,8 = 3.9 − 4.4. For all curves Ṁ18 = 0.1 is fixed. |
 |
Fig. A.2 Comparison of our results for KS 1731−260 with Sht07 (upper panel) and BC09 (bottom panel). Solid curves are our fits and dashed and dotted dashed curves are Sht07 and BC09 results, respectively. M = 1.6 M⊙ is fixed for all. The last observation (with a red square) was reported after the publication of those works. a) The solid line is our curve with Qimp = 2. The dashed curve is from Sht07. b) The solid curve is our best fit with χ2 = 0.5. Fixed parameters are Ṁ18 = 0.1 and Qimp = 1.5. The brown region corresponds to χ2< 2 with free parameters varying in ranges Tc,8 = (0.45 − 0.51) and Tb,8 = (2.5 − 3.4). |
We found that observations can be well described by our cooling curves, and they agree very well with BC09 results (dashed line).
Appendix A.2: KS 1731−260 results with BC09 and Sht07
We compare in Fig. A.2 our cooling curves for KS 1731−260 with previous results of Sht07 (top panel) and BC09 (bottom panel). The dashed line at the top panel is taken from from Sht07, the solid line is our result obtained by letting Tb evolve freely (as in Sect. 4). We considered Ṁ, Tc and Qimp as free parameters and found that the data can be explained with the values Ṁ18 = 0.28, Tc,8 = 0.46, and Qimp = 2. The NS mass is 1.6 M⊙ and the neutron superfluidity energy gap in the crust is that of Wambach et al. (1993) (moderate-superfluidity case in Sht07). For a better comparison of the results we show in addition to the data of Cackett et al. (2010a; considered so far) observations from Cackett et al. (2006; open circles) with 2σ error bars, which are the ones considered by Sht07.
In the bottom panel we compare our results with BC09. Now Tb is fixed during outburst to a constant value (as in Sect. 4), and we simulated with Tc, Tb and Qimp left free to vary. The dotted-dashed line was taken from BC09, the solid curve is our best fit with χ2 = 0.5. The brown region corresponds to Tc,8 = (4.5 − 5.0) and Tb,8 = (2.5 − 3.2) with χ2< 2; all these curves consider Qimp = 1.5 (the same value was used in BC09). The NS mass was fixed to 1.6 M⊙, and we considered the Sch03 energy gap for neutron superfluidity in the crust.
We conclude that our curves agree well with previous results, which make us confident in our work.
All Tables
Sources, average accretion rate Ṁobs,18 and accretion period tacc inferred from observations.
NS configurations: mass M, central density ρ0, stellar radius R, surface gravity g, and crust width ΔRc.
Best fits for MXB 1659−29, KS 1731−260, and EXO 0748−676 with neutron star mass M, core temperature Tc and impurities Qimp, considering a deep gap.
All Figures
 |
Fig. 1 Observational data and corresponding fits taken from the literature. a) MXB 1659−29, data and fits from Cackett et al. (2008; 2013; open symbols). b) KS 1731−260, data and fits from Cackett et al. (2010a). c) EXO 0748−676, data and fits from Díaz Trigo et al. (2011) and Degenaar et al. (2011b). d) XTE J1701−462, data and fits from Fridriksson et al. (2011). Data with open symbols (XMM-3 and CXO-4) were not considered in fits. e) IGR J17480−2446, data and fits from Degenaar et al. (2013). Data from Chandra (circles), XMM-Newton (squares) and Swift (triangles) for all the sources. Exponential decay kBTs = a e− (t − t0) /τ + b (solid lines), and (broken) power-laws kBTs = α(t − t0)β (dashed lines) fits. |
| In the text | |
 |
Fig. 2 Energy gap models used as a function of density: Sch03 gap (solid line), deep gap (dashed dotted line), and small gap (dashed line). |
| In the text | |
 |
Fig. 3 Accreted crust composition (stars, circles) for 56Fe burning ashes (HZ08) in comparison to the non-accreted crust (solid lines) (Douchin & Haensel 2001 above the neutron drip point and BPS, Baym et al. 1971 below that density). |
| In the text | |
 |
Fig. 4 Tb − Ts relation used in this work: the partial accreted model (PA, dashed-dotted line) and comparison with the non-accreted Fe envelope (NA, solid line) as in GPE83 (crosses) and the fully accreted (FA, dashed line) in an envelope composed mostly of light elements H and He, as in PCY97. The relation used in BC09 is shown with stars. |
| In the text | |
 |
Fig. 5 Thermal evolution considering fixed (solid lines) or free (dashed lines) temperature during outburst |
| In the text | |
 |
Fig. 6 Additional heat or increased Ṁ? Left panels: dashed curves correspond to |
| In the text | |
 |
Fig. 7 Fits for MXB 1659−29. The light zone corresponds to cooling curves with χ2< 2, the solid line is our best fit with χ2 = 0.75. The inset shows the corresponding parameter space; the dark zone is for χ2< 1 and the cross the minimum. We fix M = 1.6 M⊙, Qimp = 3.5, and for the Sch03 gap and vary Ṁ18 = 0.11 − 0.16. |
| In the text | |
 |
Fig. 8 Same as Fig. 7, but for EXO 0748−676 and only dark zones with χ2< 1 are shown. The minimum is at χ2 = 0.57. We fix M = 1.6 M⊙, Qimp = 1, and the Sch03 gap and vary Ṁ18 = 0.01 − 0.08. |
| In the text | |
 |
Fig. 9 Contours for cooling curves for KS 1731−260, MXB 1659−29, and EXO 0748−676 with χ2< 1,2 (dark and light zones) by varying Tc and Tb for M = 1.6 M⊙. Contours with fixed Qimp are shown (values at their sides). |
| In the text | |
 |
Fig. 10 Cooling curves for KS 1731−260 using a deep gap: the light (dark) brown zones correspond to χ2< 2( < 1), the solid curve is the best fit (χ2 = 0.69) with Tb,8 = 3.55. The dotted-dashed curve corresponds to the best fit (χ2 = 1.14) with the Sch03 gap and Tb,8 = 3.52. In all cases, M = 1.6 M⊙, Ṁ18 = 0.05, and Qimp ≃ 4 are fixed. |
| In the text | |
 |
Fig. 11 Best-fit contours for KS 1731−260 comparing Sch03 gap (left panel) and deep gap (right panel). Colored regions satisfy χ2< 1,2 (dark and light) considering different Tb (Tb,8 values at the sides of the contours), accretion rates (dashed lines for Ṁ18 = 0.05, solid lines for Ṁ18 = 0.1) and NS masses (upper, purple contours for 1.4M⊙ and lower, green contours for 1.6 M⊙). |
| In the text | |
 |
Fig. 12 Idem Fig. 11, but for MXB 1659−29 and corresponding accretion rates (dashed lines for Ṁ18 = 0.07, solid lines for Ṁ18 = 0.18). |
| In the text | |
 |
Fig. 13 Constraints for MXB 1659−29, KS 1731−260, and EXO 0748−676 in the Tc-Qimp parameter space satisfying χ2< 1,2 (dark and light zones) by varying the accretion rate. Deep gap and 1.6M⊙ are assumed. |
| In the text | |
 |
Fig. 14 Heat sources that affect the initial thermal profile: pycnonuclear reactions as in HZ08 (dashed line) and additional sources in the outer crust (solid lines). The cooling curves for these thermal profiles fitting XTE J1701−462 data are shown in Fig. 15. |
| In the text | |
 |
Fig. 15 Cooling curves for XTE J1701−462 with additional heat sources; best fit with |
| In the text | |
 |
Fig. 16 Best cooling curves for IGR J17480−2446; the brown zone corresponds to χ2< 2, and the solid line is the best fit with χ2 = 1.18 (cross in the inset). We fix Ṁ18 = 0.2, Tb,8 = 4.06, and the Sch03 gap. |
| In the text | |
 |
Fig. 17 Idem Fig. 16, but with additional heat sources optimized with respect to |
| In the text | |
 |
Fig. 18 Additional heat sources distribution and intensity for XTE J1701−462 (brown region), and IGR J17480−2446 (green region). Solid lines are HZ08 sources (inset). |
| In the text | |
 |
Fig. 19 Cooling curves obtained by suppressing the electron thermal conductivity by Rsup = 0.1. The brown dark (light) regions correspond to χ2< 1( < 2), the solid line to χ2 = 0.61. We fix Tc,8 = 1.35 − 1.40, Ṁ = 1.1, Tb,8 = 4.05, Qimp = 1, and the Sch03 gap. The inset shows χ2< 2 contours in parameter space by varying Tc. |
| In the text | |
 |
Fig. 20 Residual accretion episodes during quiescence in XTE J1701−462. a) Evolution of Tb assumed during residual accretion episodes A and B (dashed and dotted lines, respectively). b) Cooling curves from fitting filled symbol data without residual accretion: solid line is the best fit with χ2 = 0.53 and brown band has χ2< 1 (with Ṁ18 = 0.7 − 1.3 and Tc,8 = 1.3 − 1.8). The dashed and dotted lines (χ2 = 0.55,0.63) include residual accretion through |
| In the text | |
 |
Fig. 21 Cooling curve comparison of all the sources. In each case we show the best fit corresponding to the models: crustal cooling (MXB 1659−29), crustal cooling with small energy gap for neutron superfluidity (KS 1731−260), crustal cooling (all data fit, EXO 0748−676), crustal cooling with additional heat sources (XTE J1701−462), and crustal cooling with a high Tc (IGR J17480−2446). |
| In the text | |
 |
Fig. A.1 Comparison of our cooling curves for MXB 1659−29 with BC09. The solid line is our best fit with χ2 = 0.54, the dashed line is the result of BC09. The brown region is our curves with χ2< 2 corresponding to Tc,8 = 0.26 − 0.32 and Tb,8 = 3.9 − 4.4. For all curves Ṁ18 = 0.1 is fixed. |
| In the text | |
 |
Fig. A.2 Comparison of our results for KS 1731−260 with Sht07 (upper panel) and BC09 (bottom panel). Solid curves are our fits and dashed and dotted dashed curves are Sht07 and BC09 results, respectively. M = 1.6 M⊙ is fixed for all. The last observation (with a red square) was reported after the publication of those works. a) The solid line is our curve with Qimp = 2. The dashed curve is from Sht07. b) The solid curve is our best fit with χ2 = 0.5. Fixed parameters are Ṁ18 = 0.1 and Qimp = 1.5. The brown region corresponds to χ2< 2 with free parameters varying in ranges Tc,8 = (0.45 − 0.51) and Tb,8 = (2.5 − 3.4). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.