| Issue |
A&A
Volume 576, April 2015
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 16 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201425389 | |
| Published online | 02 April 2015 | |
Excitation properties of galaxies with the highest [O iii]/[O ii] ratios
No evidence for massive escape of ionizing photons⋆
1
LUTH, Observatoire de Meudon,
92195
Meudon Cedex,
France
e-mail:
grazyna.stasinska@obspm.fr
2
Main Astronomical Observatory, Ukrainian National Academy of
Sciences, Zabolotnoho
27, 03680
Kyiv,
Ukraine
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
4
Instituto de Astronomía, Universidad Nacional Autónoma de
México, Apdo. Postal 70264, Méx.
D.F., 04510
México,
Mexico
Received: 21 November 2014
Accepted: 3 February 2015
The possibility that star-forming galaxies may leak ionizing photons is at the heart of many present-day studies that investigate the reionization of the Universe. We test this hypothesis on local blue compact dwarf galaxies of very high excitation. We assembled a sample of such galaxies by examining the spectra from data releases 7 and 10 of the Sloan Digital Sky Survey. We argue that reliable conclusions cannot be based on strong lines alone, and adopt a strategy that includes important weak lines such as [O i] and the high-excitation He ii and [Ar iv] lines. Our analysis is based on purely observational diagrams and on a comparison of photoionization models with well-chosen emission-line ratio diagrams. We show that spectral energy distributions from current stellar population synthesis models cannot account for all the observational constraints, which led us to mimick several scenarios that could explain the data. These include the additional presence of hard X-rays or of shocks. We find that only ionization-bounded models (or models with an escape fraction of ionizing photons lower than 10%) are able to simultaneously explain all the observational constraints.
Key words: stars: atmospheres / galaxies: abundances / galaxies: starburst
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
By analyzing the entire Sloan Digital Sky Survey (SDSS-III) DR10 spectroscopic data base (Ahn et al. 2014), we found an appreciable number of compact star-forming galaxies with extremely high [O iii]/[O ii] ratios1, exceeding values of 10 and reaching up to 50. Hereafter these galaxies are called “extreme BCDs”, standing for “extreme blue compact dwarf galaxies”.
Atomic data used in our abundance determinations.
Extreme BCDs are local low-mass galaxies that are undergoing intense bursts of star formation. They represent a subset of Green Peas (Cardamone et al. 2009) when they are in the redshift range 0.1−0.3, or of luminous compact galaxies (Izotov et al. 2011) in a wider redshift range 0.0−0.6. Therefore, similar to Green Peas and luminous compact galaxies, extreme BCDs share some of the properties of Lyα emitting galaxies and Lyman break galaxies at high-z: they are compact, have low-mass (108–109 M⊙), low-metallicity (0.1−0.2 solar), and high specific star-formation rates (up to 10-7 yr-1; Cardamone et al. 2009; Izotov et al. 2011). Furthermore, unlike the typical local galaxies and like Lyα emitting galaxies and Lyman break galaxies (Nakajima et al. 2013; Shirazi et al. 2014; Shapley et al. 2015), extreme BCDs are characterized by high excitation, as measured by the [O iii]/[O ii] ratio. Thanks to these properties, extreme BCDs should be excellent local proxies for high-z Lyα emitting galaxies.
The high [O iii]/[O ii] ratios can be attributed to several possible factors (Overzier et al. 2009; Kewley et al. 2013; Nakajima & Ouchi 2014; Jaskot & Oey 2013): 1) a low metallicity; 2) a high ionization parameter; 3) a hard ionizing radiation field; 4) the presence of density-bounded H ii regions.
This last hypothesis, if proven true, may have important cosmological implications in studies of the secondary ionization of the Universe, because Lyman continuum (LyC) emission freely escapes the density-bounded H ii regions.
In this paper, we analyze the emission-line properties of local extreme BCDs with the aim of finding out whether these high ratios are due to significant leakage of ionizing photons.
To construct our extreme BCD sample, we have thus searched the SDSS-III DR10 spectroscopic data base for star-forming emission-line objects with the highest excitation, that is, those with the highest [O iii]/[O ii] ratios that show no sign of an active galactic nucleus (AGN). We have merged this sample with a sample of high-excitation galaxies from SDSS DR7. For these extreme BCDs, in contrast to high-redshift objects, SDSS spectra provide a lot of information in addition to the intensities of the strongest lines, some of it being crucial for a proper interpretation of the excitation conditions.
This paper is organized as follows: in Sect. 2 we present the observational database, in Sect. 3 we discuss some purely observational trends that lead to a zero-order interpretation, in Sect. 4 we present the policy we followed to interpret the observational data with the help of photoionization models, and in Sect. 5 we compare various possible scenarios with the observations. The conclusions are summarized in the last section.
2. The observational database
We (Y. I.) searched the SDSS/BOSS DR10 spectroscopic database by eye to find star-forming galaxies with high [O iii]/[O ii] ratios (≳5). Since we were interested in star-forming galaxies, we removed objects with AGN-like spectra (i.e., altogether strong [O ii] and [O iii], broad lines, strong [O i], [N ii], [S ii], strong He ii, in some cases, red continuum). We ended up with a sample of 149 objects. All of them except one have [O iii] λ4363 detected. In the following this sample is referred to as the DR10 sample.
To this sample we added the sample of star-forming galaxies selected from SDSS DR7 (Abazajian et al. 2009) by two of us (Y. I. and N. G.) and described in Vale Asari et al. (in prep.). This sample is composed of all the star-forming galaxies in the SDSS DR7 in which the [O iii] λ4363 line is seen and measured with an accuracy of at least 25%, and for which visual inspection of the spectra and images showed that they correspond to genuine star-forming galaxies (i.e., excluding giant H ii regions in spiral galaxies and active galactic nuclei). Furthermore, we considered only galaxies where [O ii]λ3727 is observed. With this criterion, all galaxies from the DR7 with z ≲ 0.02 are excluded. In the following this sample is referred to as the DR7 sample.
By combining our DR10 and DR7 samples, we obtained a sample of 778 objects, of which 268 have [O iii]/[O ii] ratios higher than 5, and 72 have [O iii]/[O ii] ratios higher than 10. The remaining objects are useful for the discussion because they allow us to consider a wider excitation sequence and ponder the parameters leading to the highest observed values of [O iii]/[O ii].
The spectra from DR10 were analyzed with the IRAF software package2 in exactly the same way as described in Vale Asari et al. (in prep.) for the DR7 spectra. In brief, the emission-line fluxes were measured “manually” using the IRAF SPLOT routine. Correction of hydrogen line fluxes for underlying absorption and reddening correction of all lines were performed as described in that paper.
In both the DR7 and DR10 samples, the abundances of N, O, Ne, S, Cl, Ar, and Fe were derived from the intensities of the lines [O ii] λ3727, [O iii] λ5007, [N ii] λ6584, [Ne iii] λ3869, [S ii] λ6716, λ6731, [S iii] λ9069, [Cl iii] λ5518+ 5538, [Ar iii] λ7135, [Ar iv] λ4740, and [Fe iii] λ4988 with respect to Hβ. We used the temperature from [O iii] λ4363/5007 for doubly and triply ionized species and a temperature derived from Eq. (14) of Izotov et al. (2006) for low-ionization species. The ionization correction factors used to obtain elemental abundances from ionic abundances were those described in Izotov et al. (2006). The atomic data involved in the computations are listed in Table 1.
The resulting abundance patterns for the DR10 and DR7 samples are presented in Appendix A. All the objects from our sample have low to moderate metallicities: 12 + log O/H in the range 7.5−8.5. This is a consequence of the fact that we imposed that the [O iii] λ4363 line be present, implying that the electron temperature be sufficiently high, and thus that the metallicity be sufficiently low.
 |
Fig. 1 BPT diagram for our DR10 objects (red circles) and those of DR7 (blue diamonds). The background gray scale map represents all the SDSS DR7 galaxies with a signal-to-noise ratio of at least 3 in the four diagnostic lines [O iii], Hβ, [N ii], and Hα. The gray scale is in logarithm of the number of objects per pixel, as indicated in the bar on the right. The blue curve represents the Kauffmann et al. (2003) line generally used to distinguish star-forming galaxies from AGN hosts. |
3. Clues from observational trends
In Fig. 1, we represent the position of the DR7 and DR10 samples in the classical emission-line ratio diagram [O iii]/Hβ vs. [N ii]/Hα (the famous BPT diagram from Baldwin et al. 1981). Throughout the paper, DR7 objects will be represented by blue symbols (diamonds in this figure) and DR10 objects by red symbols (circles in this figure). The background gray-scale plot is a 2D-histogram of all the galaxies in the 7th data release of the SDSS that have a signal-to-noise ratio larger than 3 for all the relevant lines. The gray scale at the right of the plot indicates the logarithm of the number of points in each pixel. We see that the number of points per gray pixel thus ranges from 1 to over 1000. The blue curve represents the empirical line drawn by Kauffmann et al. (2003) to distinguish star-forming galaxies from galaxies hosting an AGN. We see that our selection criteria for the DR7 and DR10 indeed sample selected star-forming galaxies, removing AGN hosts. We also see that they represent an extreme population of star-forming galaxies, with high values of [O iii]/Hβ, and [N ii]/Hα ratios that reach extremely low values.
In the following, we present purely observational diagrams to investigate the relations between [O iii]/[O ii] and characteristic parameters of the emitting nebulae. These are the metallicity, expressed in units of 12 + log O/H and the Hβ equivalent width, EW(Hβ), which measures the amount of ionizing photons produced by massive stars and absorbed by the gas with respect to the continuum at Hβ, which is mainly produced by the population of low-mass stars in the galaxy (which, in turn, is a proxy for the galaxy stellar mass).
Other parameters worthwhile considering are L(Hβ), the total Hβ luminosity corrected for extinction, and the density ne, which can be derived from the [S ii] λ6731/6717 line ratio.
As is well known, two important parameters in the study of emission-line nebulae are the mean ionization parameter 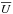 (defined in Sect. 4.1) and the mean effective temperature of the ionizing radiation field,
(defined in Sect. 4.1) and the mean effective temperature of the ionizing radiation field, 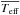 .
.
In a first approximation, the abundance ratio of two adjacent ions of the same element, for example Ar+++/Ar++, is given by the equation 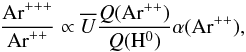 (1)where Q(Ar++) is the number of photons above the ionization threshold of Ar++, Q(H0) is the number of hydrogen ionizing photons, and α(Ar++) is the Ar++ recombination coefficient3. The Ar+++/Ar++ ratio is thus a function of both
(1)where Q(Ar++) is the number of photons above the ionization threshold of Ar++, Q(H0) is the number of hydrogen ionizing photons, and α(Ar++) is the Ar++ recombination coefficient3. The Ar+++/Ar++ ratio is thus a function of both 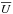 and of the mean effective temperature
and of the mean effective temperature 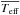 of the ionizing radiation, since Q(Ar++) /Q(H0) is an increasing function of
of the ionizing radiation, since Q(Ar++) /Q(H0) is an increasing function of 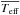 (see Fig. C.1).
(see Fig. C.1).
The ionization parameter 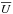 cannot be measured directly from observations, but, assuming a value for the volume-filling factor ϵ, it can be obtained from the product neL(Hβ) using Eq. (4) below, since L(Hβ) is a direct measure of the total number of hydrogen ionizing photons, Q(H0) (in the hypothesis of no leakage and minimal absorption of LyC photons by dust).
cannot be measured directly from observations, but, assuming a value for the volume-filling factor ϵ, it can be obtained from the product neL(Hβ) using Eq. (4) below, since L(Hβ) is a direct measure of the total number of hydrogen ionizing photons, Q(H0) (in the hypothesis of no leakage and minimal absorption of LyC photons by dust).
It has been proposed by Vílchez & Pagel (1988) that η, defined as (O+/O++)/(S+/S++) is a good indicator of 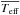 . We prefer to use a ratio based on line intensities rather than on ionic fractions, since it is readily obtained from observations. We also prefer to use a ratio that increases with
. We prefer to use a ratio based on line intensities rather than on ionic fractions, since it is readily obtained from observations. We also prefer to use a ratio that increases with 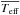 . Thus, rather than the η parameter, we use the ([O iii]/[O ii])/([S iii]/[S ii]) ratio. As shown in the bottom right panel of Fig. B.3, this ratio is far from being completely independent of
. Thus, rather than the η parameter, we use the ([O iii]/[O ii])/([S iii]/[S ii]) ratio. As shown in the bottom right panel of Fig. B.3, this ratio is far from being completely independent of 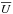 , and is sensitive to temperature especially at low values of Teff. A similar ratio is ([Ar iv]/[Ar iii])/([O iii]/[O ii]), which is much less sensitive to
, and is sensitive to temperature especially at low values of Teff. A similar ratio is ([Ar iv]/[Ar iii])/([O iii]/[O ii]), which is much less sensitive to 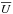 , but has a lower dynamic range as a function of Teff (see the bottom left panel of Fig. B.3).
, but has a lower dynamic range as a function of Teff (see the bottom left panel of Fig. B.3).
Finally, an important criterion to be considered when examining the question of LyC escape is the behavior of the [O i] line. In density-bounded objects, this line is the first to be suppressed, or, at least, weakened.
 |
Fig. 2 [O iii]/[O ii] ratio as a function of the oxygen abundance 12 + log O/H (left panel) and as a function of the equivalent width of the Hβ line (right panel). DR10 objects are represented in red and those of DR7 in blue. The total number of objects in each panel is indicated in the top right corner. |
Figure 2 shows the relation between [O iii]/[O ii] and the oxygen abundance (left) and EW(Hβ) (right) for the DR7 and DR10 samples. Clearly, the highest values of [O iii]/[O ii] correspond to the lowest metallicities and to the highest values of EW(Hβ). Note that in the range of metallicities covered by our DR7 and DR10 samples, a decrease in metallicity from 12 + log O/H = 8.5 to 7.4 produces an increase in [O iii]/[O ii] by about 0.3 dex if keeping the ionization parameter equal (see Fig. B.1), while the observed variation is of about 1.3 dex. Thus, there is something special about the objects with the highest [O iii]/[O ii], not only their low metallicity. The observed increase of [O iii]/[O ii] with EW(Hβ) suggests an increase with 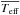 or perhaps an increase with L(Hβ), the total Hβ luminosity (since the continuum at Hβ is mainly due to low-mass stellar populations and not to the ionizing stellar populations). In any case, it argues against increasing LyC photon leakage, since the latter would produce a drop in EW(Hβ). It must be noted that at the highest metallicities encountered in the studied galaxies, dust absorption reduces the Hβ luminosities at the highest values of the ionization parameter (see Fig. B.2). But at the low metallicities where the highest [O iii]/[O ii] values are found, the effects of dust absorption on EW(Hβ) are not important.
or perhaps an increase with L(Hβ), the total Hβ luminosity (since the continuum at Hβ is mainly due to low-mass stellar populations and not to the ionizing stellar populations). In any case, it argues against increasing LyC photon leakage, since the latter would produce a drop in EW(Hβ). It must be noted that at the highest metallicities encountered in the studied galaxies, dust absorption reduces the Hβ luminosities at the highest values of the ionization parameter (see Fig. B.2). But at the low metallicities where the highest [O iii]/[O ii] values are found, the effects of dust absorption on EW(Hβ) are not important.
 |
Fig. 3 [O iii]/[O ii] ratio as a function of the electron density as derived from the [S ii] λ6731/6717 line ratio (left panel) and as a function of the total luminosity in the Hβ line, corrected for extinction. |
Figure 3 shows the relation between [O iii]/[O ii] and two other fundamental properties of the emitting regions: the electron density, ne, as derived from the [S ii] λ6731/6717 line ratio (left), and L(Hβ) (right). There is a slight tendency for high values of [O iii]/[O ii] to occur at higher values of ne (the Pearson correlation coefficient 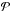 is 0.33). Note that the effect of collisional deexcitation at higher densities is only minor in this plot, since between log ne = 2 and 3.3, the emissivity ratio of [O iii] and [O ii] increases by only 0.1 dex. There is no significant correlation between [O iii]/[O ii] and L(Hβ) (
is 0.33). Note that the effect of collisional deexcitation at higher densities is only minor in this plot, since between log ne = 2 and 3.3, the emissivity ratio of [O iii] and [O ii] increases by only 0.1 dex. There is no significant correlation between [O iii]/[O ii] and L(Hβ) (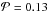 ).
).
 |
Fig. 4 [O iii]/[O ii] ratio vs. ([O iii]/[O ii])/([S iii]/[S ii]) (left panel) and vs. ([Ar iv]/[Ar iii])/([O iii]/[O ii]) (right panel). |
Figure 4 shows the relation between [O iii]/[O ii] and two parameters strongly related with the mean effective temperature of the ionizing radiation field, 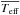 : ([O iii]/[O ii])/([S iii]/[S ii]) (left panel) and ([Ar iv]/[Ar iii])/([O iii]/[O ii]) (right panel). Both diagrams show a correlation, very strong for the first one (
: ([O iii]/[O ii])/([S iii]/[S ii]) (left panel) and ([Ar iv]/[Ar iii])/([O iii]/[O ii]) (right panel). Both diagrams show a correlation, very strong for the first one (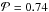 ), weak but still significant for the second one (
), weak but still significant for the second one (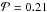 ). This suggests an increase of [O iii]/[O ii] with
). This suggests an increase of [O iii]/[O ii] with 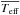 . Given that ([O iii]/[O ii])/([S iii]/[S ii]) is much more dependent on
. Given that ([O iii]/[O ii])/([S iii]/[S ii]) is much more dependent on 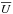 than ([Ar iv]/[Ar iii])/([O iii]/[O ii]) (see Fig. B.3), Fig. 4 suggests that the trend observed in [O iii]/[O ii] expresses a trend both with increasing
than ([Ar iv]/[Ar iii])/([O iii]/[O ii]) (see Fig. B.3), Fig. 4 suggests that the trend observed in [O iii]/[O ii] expresses a trend both with increasing 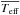 and increasing
and increasing 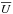 in our sample of galaxies. The increase in
in our sample of galaxies. The increase in 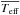 might actually be a mere metallicity effect, since ionizing spectra of more metal-poor stellar populations are harder (see Fig. C.2).
might actually be a mere metallicity effect, since ionizing spectra of more metal-poor stellar populations are harder (see Fig. C.2).
 |
Fig. 5 [O iii]/[O ii] ratio as a function of the product neL(Hβ) (left panel) and as a function of [O i]/[O ii] (right panel). |
Figure 5 (left) shows the relation between [O iii]/[O ii] and the product neL(Hβ), which as shown above, can be considered as a proxy for 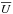 if the filling factor ϵ is constant. The fact that [O iii]/[O ii] is not seen to correlate with neL(Hβ) suggests that the variations in [O iii]/[O ii] are due to an intrinsic increase of
if the filling factor ϵ is constant. The fact that [O iii]/[O ii] is not seen to correlate with neL(Hβ) suggests that the variations in [O iii]/[O ii] are due to an intrinsic increase of 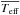 rather than of
rather than of 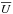 . Another option could be that ϵ varies systematically from lower to higher values as [O iii]/[O ii] increases. We have no way to check this directly with the data at hand, but this is a possibility. Figure 5 (right) shows the relation between [O iii]/[O ii] and [O i]/[O ii]. The first thing to note is that most objects do show [O i] emission, and that the [O i] emission is not limited to objects with the lowest values of [O iii]/[O ii]. Actually, most of the objects with the highest values of [O iii]/[O ii] show [O i]/[O ii] ratios higher than 1%. This suggests that the explanation for the highest values of [O iii]/[O ii] does not lie in LyC photon leakage. However, photoionization models are needed to confirm this interpretation. This is the subject of the next section.
. Another option could be that ϵ varies systematically from lower to higher values as [O iii]/[O ii] increases. We have no way to check this directly with the data at hand, but this is a possibility. Figure 5 (right) shows the relation between [O iii]/[O ii] and [O i]/[O ii]. The first thing to note is that most objects do show [O i] emission, and that the [O i] emission is not limited to objects with the lowest values of [O iii]/[O ii]. Actually, most of the objects with the highest values of [O iii]/[O ii] show [O i]/[O ii] ratios higher than 1%. This suggests that the explanation for the highest values of [O iii]/[O ii] does not lie in LyC photon leakage. However, photoionization models are needed to confirm this interpretation. This is the subject of the next section.
4. Photoionization model analysis
4.1. The photoionization model grid
The models were constructed with the photoionization code Cloudy version 13.03 (Ferland et al. 2013). The abundance ratios with respect to oxygen are defined as follows:
O:N:Ne:S:Cl:Ar:Fe = 1:0.0513:0.1854:0.0219:0.00029: 0.0048:0.0148, corresponding to the mean values of the logarithmic abundances derived for our merged DR7, DR10 sample (see Sect. 2 and Appendix A). Except for some of the models shown in Appendix B, which explore the effects of varying O/H, we adopted for all the models a value of 12 + log O/H = 8, equal to the average of the measured abundances in our merged sample. The adopted helium abundance by number relative to hydrogen is 0.086, that of Mg and Si is 0.0095.
The dust-to-gas abundance ratio is obtained by applying a factor 2 / 3 × 10(2.21 − y) to the default value in Cloudy when using the “ism” keyword. The expression for y is obtained from Table 1 (Broken law, MW case) of Rémy-Ruyer et al. (2014). The reduction factor of 2/3 is motivated by the study of Draine (2011).
For most models, the ionizing radiation field is given by the population synthesis code PopStar (Mollá et al. 2009) for a Chabrier (2003) stellar initial mass function and at the appropriate metallicity, obtained by interpolation. The reference case corresponds to an age of 1 Myr. Other ionizing radiation fields have also been considered, as described in the following sections. All the models assume a constant hydrogen density, but two geometries are considered. They are defined by two different values of fS = Rin/RS, where Rin is the model inner radius and RS is the Strömgren radius corresponding to Rin = 0. Models with fS = 0.03 are equivalent to a full sphere, models with fS = 3 correspond to a hollow spherical bubble. The models are computed until the ratio of ionized hydrogen to total hydrogen density falls below 0.02.
In addition to the spectral energy distribution (SED) of the ionizing radiation, the gas chemical composition and density, one needs to define the luminosity of the ionizing source. It is more convenient, actually, to fix the volume-averaged ionization parameter, 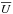 estimated in the following way. In a nebula, the ionization parameter U(R) at a distance R from the center is defined as
estimated in the following way. In a nebula, the ionization parameter U(R) at a distance R from the center is defined as 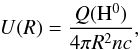 (2)where Q(H0) is the ionizing luminosity in photons s-1, n is the hydrogen density and c the speed of light. The volume averaged ionization parameter,
(2)where Q(H0) is the ionizing luminosity in photons s-1, n is the hydrogen density and c the speed of light. The volume averaged ionization parameter, 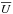 , is defined by
, is defined by 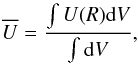 (3)where the integration is performed over the volume of the ionized nebula. The radius of the ionized nebula is obtained by equating Q(H0) with the total number of hydrogen recombinations to upper levels in the ionized volume. Assuming that the gas is uniformly distributed in the nebula with a constant density n and a volume filling factor ϵ, and assuming that the case B recombination coefficient, αB, is constant, we obtain
(3)where the integration is performed over the volume of the ionized nebula. The radius of the ionized nebula is obtained by equating Q(H0) with the total number of hydrogen recombinations to upper levels in the ionized volume. Assuming that the gas is uniformly distributed in the nebula with a constant density n and a volume filling factor ϵ, and assuming that the case B recombination coefficient, αB, is constant, we obtain 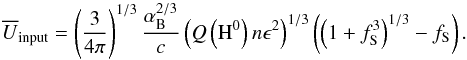 (4)Our series of models assume a density n = 100 cm-3 and take values of
(4)Our series of models assume a density n = 100 cm-3 and take values of 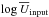 ranging from −4 to −1 by steps of 0.5 dex, which allows us to span the entire range of observed values of [O iii]/[O ii]4. As we show below, slight differences occur in the predicted line ratios with the same value of
ranging from −4 to −1 by steps of 0.5 dex, which allows us to span the entire range of observed values of [O iii]/[O ii]4. As we show below, slight differences occur in the predicted line ratios with the same value of 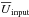 for the two geometries considered.
for the two geometries considered.
For each model, we created several density-bounded versions by trimming the outer parts and leaving only the inner parts corresponding to fHβ = 20, 40, 60, 80, and 100% of the value of the Hβ luminosity obtained for the radiation-bounded model.
4.2. How the models are used
In the present work we aim to determine the cause of the highest values of [O iii]/[O ii] observed and, in particular, whether they can be attributed to LyC photon leakage. One of the important lines to consider is therefore [O i] λ6300, which is produced in the warm transition region between fully ionized gas and neutral gas. The diagnostic diagram we chose to consider is [O iii]/[O ii] versus [O i]/[O iii]. In a first approximation, it is independent of O/H, which allows us to compare the models with 12 + log O/H = 8 with our entire observational sample.
Since we suspect that the highest [O iii]/[O ii] might be linked to high values of 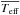 , it is of interest to use lines of ions with high ionization potentials as diagnostics. One such line is that of [Ar iv], since the ionization potential of Ar++ is 40.6 eV, significantly higher than the ionization potential of O+ (35.1 eV). Another option would be the [Ne iii] line, since the ionization potential of Ne+ is also 40.6 eV, and, in addition, there is no charge transfer between Ne++ and Ne+, in contrast to what occurs between Ar+++ and Ar++. The advantage of [Ar iv] is that it can be related to [Ar iii], and that the [Ar iv]/[Ar iii] ratio does not depend on abundances. The second diagnostic diagram we therefore chose to consider is [O iii]/[O ii] versus [Ar iv]/[Ar iii].
, it is of interest to use lines of ions with high ionization potentials as diagnostics. One such line is that of [Ar iv], since the ionization potential of Ar++ is 40.6 eV, significantly higher than the ionization potential of O+ (35.1 eV). Another option would be the [Ne iii] line, since the ionization potential of Ne+ is also 40.6 eV, and, in addition, there is no charge transfer between Ne++ and Ne+, in contrast to what occurs between Ar+++ and Ar++. The advantage of [Ar iv] is that it can be related to [Ar iii], and that the [Ar iv]/[Ar iii] ratio does not depend on abundances. The second diagnostic diagram we therefore chose to consider is [O iii]/[O ii] versus [Ar iv]/[Ar iii].
If we wish to understand the behavior of emission-line ratios in galaxies, we cannot put aside some lines, such as He ii, which, although weak, provide important diagnostics because they indicate a very hard ionizing radiation field (above 54.4 eV). Their systematic presence in H ii galaxies has first been noted and commented on by Garnett et al. (1991) and Stasińska & Izotov (2003), and was more thoroughly discussed by Shirazi & Brinchmann (2012) and Jaskot & Oey (2013). All the suggested explanations (Wolf-Rayet stars, shocks, X-ray binaries, stellar rotation effects on the effective temperature of massive stars, inaccurate predictions of stellar atmosphere models at high energies) can be disputed. In the present paper, our aim is not to propose an astrophysically valid explanation, so we consider different scenarios to explain the observed He ii/Hβ ratios and examine their effects on the remaining line ratios. We therefore choose as a third diagnostic diagram [O iii]/[O ii] versus He ii/Hβ, and retain photoionization models that predict He ii/Hβ≃ 0.01, which is representative of the bulk of the objects in our sample that show He ii emission (the He ii line is not detected in about one third of the objects of our sample, but in at least part of these cases this absence can be attributed to a too low signal-to-noise ratio).
 |
Fig. 6 [O iii]/[O ii] versus [Ar iv]/[Ar iii] (left), [O iii]/[O ii] versus [O i]/[O iii] (middle) and [O iii]/[O ii] versus He ii/Hβ (right) diagnostic diagrams. The red and blue points represent the DR10 and DR7 objects respectively. The curves represent our grid of models computed with the SED from PopStar models at an age of 1 Myr and with a metallicity 12 + log O/H = 8. The dashed lines link models with the same values of |
5. Comparing models with observations
5.1. Models using classical stellar population synthesis results
5.1.1. The reference model: PopStar with an age of 1 Myr
Figure 6 shows the distribution of the observational points in our three diagnostic diagrams: [O iii]/[O ii] versus [Ar iv]/[Ar iii] (left), [O iii]/[O ii] versus [O i]/[O iii] (middle), and [O iii]/[O ii] versus He ii/Hβ (right). Superimposed is our grid of photoionization models computed with the SED from PopStar models at an age of 1 Myr and with an oxygen abundance 12 + log O/H = 8. The dashed lines link models with the same values of 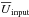 , while the continuous lines link models with the same value of the trimming parameter fHβ. The upper row of panels correspond to our filled sphere models (fS = 0.03), while the lower row corresponds to our bubble models (fS = 3). It can be seen that these models fall very short of reproducing the observed He ii/Hβ ratios, even if considering density-bounded models. The SED from the PopStar models at an age of 1 Myr simply does not provide enough He+ ionizing photons. The observational points fall well on the ionization-bounded models line in the [O iii]/[O ii] versus [O i]/[O iii] diagram5, both for the filled and hollow sphere models. However, this cannot be considered as proving that the objects are all ionization-bounded, since the models fail to reproduce the He ii/Hβ and the [Ar iv]/[Ar iii] line ratios (especially for the hollow sphere models). We note that the highest observed [O iii]/[O ii] ratios correspond to the highest values of
, while the continuous lines link models with the same value of the trimming parameter fHβ. The upper row of panels correspond to our filled sphere models (fS = 0.03), while the lower row corresponds to our bubble models (fS = 3). It can be seen that these models fall very short of reproducing the observed He ii/Hβ ratios, even if considering density-bounded models. The SED from the PopStar models at an age of 1 Myr simply does not provide enough He+ ionizing photons. The observational points fall well on the ionization-bounded models line in the [O iii]/[O ii] versus [O i]/[O iii] diagram5, both for the filled and hollow sphere models. However, this cannot be considered as proving that the objects are all ionization-bounded, since the models fail to reproduce the He ii/Hβ and the [Ar iv]/[Ar iii] line ratios (especially for the hollow sphere models). We note that the highest observed [O iii]/[O ii] ratios correspond to the highest values of 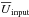 considered in our models. We also note that the hollow bubble models seem to provide a poorer fit to the observations in the [O iii]/[O ii] versus [Ar iv]/[Ar iii] diagram than the filled sphere models, but this question cannot be fully addressed until the SED problem is solved (see below).
considered in our models. We also note that the hollow bubble models seem to provide a poorer fit to the observations in the [O iii]/[O ii] versus [Ar iv]/[Ar iii] diagram than the filled sphere models, but this question cannot be fully addressed until the SED problem is solved (see below).
5.1.2. Other stellar populations
In Fig. C.3 we show the SEDs obtained at an age of 1 Myr with the same stellar initial mass function, but using the different assumptions for the stellar evolution models proposed by starburst99 (Leitherer et al. 1999): Geneva tracks with standard mass loss, Geneva tracks with high mass loss, original Padova tracks, and Padova tracks with AGB stars. All the SEDs have been obtained with the stellar atmosphere grid of Smith et al. (2002) based on atmosphere models of Pauldrach et al. (2001) and Hillier & Miller (1998), similarly to the PopStar models. From this figure, it is clear that at an age of 1 Myr, all these SEDs are equivalent and will lead to almost identical photoionization models.
Another question to consider is the age of the ionizing stellar populations. Figure C.4 shows the SEDs obtained by PopStar for several ages. We see that, for an age of 2 Myr, the SED is almost identical to that at 1 Myr, and that for 3 and 5 Myr, the SEDs are softer. This implies that they will lead to the same problems regarding [Ar iv]/[Ar iii] and He ii/Hβ. However, at an age of 4 Myr, which is when massive Wolf-Rayet stars begin to come into play, the SED is much harder.
Figure 7 shows the results of photoionization models computed with PopStar for an age of 4 Myr, using the same presentation as Fig. 6. We see that the [O iii]/[O ii] versus [O i]/[O iii] diagram is again compatible with ionization-bounded models, but that the SED at this age is even too hard to account for the bulk of the observed He ii/Hβ ratios. One then might think that the relevant ages for reproducing the He ii/Hβ ratios is larger than 3 Myr and somewhere in the vicinity of 4 Myr.
However, this cannot be the explanation for all the objects that show He ii emission. The He ii line has been observed in 488 objects out of the 778 objects in our sample. In a first approximation, in absence of leakage or dust absorption of ionizing photons, and assuming that all the photons with energies higher than 54.4 eV are absorbed by He+ (which is roughly correct except at low values of the ionization parameter, see Stasińska & Tylenda 1986), we have 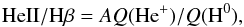 (5)where A is the ratio of emissivities of the He ii and Hβ lines divided by the ratio of the case B recombination coefficients αB(He+) /αB(H0). The coefficient A depends only weakly on the electron temperature and is equal to 1.74 at 20 000 K. The left panel of Fig. 8 shows the values of Q(He+) /Q(H0) predicted by PopStar models of metallicities Z = 0.004,0.008 and 0.02 (which correspond to 12 + log O/H = 7.7, 8 and 8.4) as a function of age. We see that Q(He+) /Q(H0) leads to a detectable He ii only during an age range of 3.9–4.25, 3.4–5.4, and 4.0–5.25 Myr, respectively, for the three metallicities considered, if we assume detectability at He ii/Hβ≥ 10-3. The right panel of Fig. 8 shows the values of He ii/Hβ as a function of EW(Hβ) for the same PopStar models, taking Eq. (5) to estimate He ii/Hβ. This figure can be directly compared to the observations, shown in the left panel of Fig. 9, having in mind the observed distribution of metallicities as a function of EW(Hβ), shown in the right panel of Fig. 9. We see that the models do not predict any He ii emission for EW(Hβ) above 200 Å, while many of our objects (and especially some of those with the highest values of [O iii]/[O ii] (see Fig. 2) show higher values of EW(Hβ). We must note, in addition, that the computed values of EW(Hβ) correspond to an instantaneous starburst, while in real objects, part of the continuum comes from old stellar populations that do not contribute to the ionization, so that the observed values of EW(Hβ) are lower than the theoretical values for the most recent starburst. This means that, even at values of EW(Hβ) lower than 200 Å, it is likely that in many of the objects the observed He ii line is not due to ionization by a simple stellar population. Considering the possibility of extended starbursts rather than instantaneous ones does not help since it dilutes the He ii emission simultaneously with the Hβ emission. A similar discussion can be found in Shirazi & Brinchman (2012) who, in addition, found that 40 per cent of the galaxies in their sample do not have Wolf-Rayet features in their spectra despite showing strong nebular He ii emission.
(5)where A is the ratio of emissivities of the He ii and Hβ lines divided by the ratio of the case B recombination coefficients αB(He+) /αB(H0). The coefficient A depends only weakly on the electron temperature and is equal to 1.74 at 20 000 K. The left panel of Fig. 8 shows the values of Q(He+) /Q(H0) predicted by PopStar models of metallicities Z = 0.004,0.008 and 0.02 (which correspond to 12 + log O/H = 7.7, 8 and 8.4) as a function of age. We see that Q(He+) /Q(H0) leads to a detectable He ii only during an age range of 3.9–4.25, 3.4–5.4, and 4.0–5.25 Myr, respectively, for the three metallicities considered, if we assume detectability at He ii/Hβ≥ 10-3. The right panel of Fig. 8 shows the values of He ii/Hβ as a function of EW(Hβ) for the same PopStar models, taking Eq. (5) to estimate He ii/Hβ. This figure can be directly compared to the observations, shown in the left panel of Fig. 9, having in mind the observed distribution of metallicities as a function of EW(Hβ), shown in the right panel of Fig. 9. We see that the models do not predict any He ii emission for EW(Hβ) above 200 Å, while many of our objects (and especially some of those with the highest values of [O iii]/[O ii] (see Fig. 2) show higher values of EW(Hβ). We must note, in addition, that the computed values of EW(Hβ) correspond to an instantaneous starburst, while in real objects, part of the continuum comes from old stellar populations that do not contribute to the ionization, so that the observed values of EW(Hβ) are lower than the theoretical values for the most recent starburst. This means that, even at values of EW(Hβ) lower than 200 Å, it is likely that in many of the objects the observed He ii line is not due to ionization by a simple stellar population. Considering the possibility of extended starbursts rather than instantaneous ones does not help since it dilutes the He ii emission simultaneously with the Hβ emission. A similar discussion can be found in Shirazi & Brinchman (2012) who, in addition, found that 40 per cent of the galaxies in their sample do not have Wolf-Rayet features in their spectra despite showing strong nebular He ii emission.
 |
Fig. 8 Left: Q(He+) /Q(H0) as a function of age for PopStar SEDs with metallicities Z = 0.004, 0.008, and 0.02 as indicated in the inset. Right: log He ii/Hβ versus EW(Hβ), where He ii/Hβ is taken equal to 1.74Q(He+) /Q(H0), for the same PopStar models. |
 |
Fig. 9 Left: observed values of log He ii/Hβ versus EW(Hβ) (for objects with no He ii detection log He ii/Hβ has been set to −4); right: observed values of 12 + log O/H versus EW(Hβ). |
The above discussion of the production of nebular He ii emission by stellar populations of about 4 Myr relies on PopStar models. Figure C.6 shows the SEDs obtained at 4 Myr for the same stellar synthesis models as Fig. C.3. We see that, at this age, the SEDs differ significantly owing to the different stellar evolutionary tracks involved. However, it can be intuited that the above discussion remains qualitatively valid and that the He ii emission observed in the objects of our sample cannot be in majority caused by Wolf-Rayet stars.
In the next subsections, we explore various scenarios based on modified ionizing SEDs that might better explain the observed trends in our diagnostic diagrams.
 |
Fig. 10 Same as Fig. 6, but with models computed with a blackbody ionizing source at a temperature of 60 000 K. |
 |
Fig. 11 [O iii]/[O ii] vs. [Ar iv]/[Ar iii] diagram for ionization-bounded photoionization models with a blackbody ionization source (12 + log O/H = 8). Top panel: models for filled spheres; bottom panel: models for spherical bubbles. Continuous lines correspond to different values of the effective temperature, while dashed lines correspond to different values of the ionization parameter. The color coding is indicated in the plot. The positions of the observational points for our samples (red for DR10, blue for DR7) are shown for comparison. This diagram shows that for a given value of [O iii]/[O ii] the value of [Ar iv]/[Ar iii] increases with Teff. |
5.2. Models using blackbodies as proxies for a harder stellar radiation field
Here we consider simple blackbodies as proxies for the SEDs of the ionizing stellar populations. We find that a blackbody with Teff= 60 000 K leads to a value of ~0.01 for He ii/Hβ in ionization-bounded models. Figure 10 shows the results of models built with this ionizing radiation field for our three diagnostic diagrams (i.e., it is the analog of Fig. 6 for this SED). We see that the values of [O i]/[O iii] fall on the ionization-bounded line, but that, again, the predicted [Ar iv]/[Ar iii] line ratios are too low. Considering slightly cooler blackbodies and density-bounded models, while acceptable for the [O iii]/[O ii] vs. He ii/Hβ diagram would be incompatible with the [O iii]/[O ii] vs. [Ar iv]/[Ar iii] diagram, since for a given value of [O iii]/[O ii] the models lead to lower values of [Ar iv]/[Ar iii] as Teff decreases, as shown in Fig. 11.
We remark that the [O iii]/[O ii] vs. [Ar iv]/[Ar iii] diagram demands a harder SED than that of a blackbody at 60 000 K, especially at the highest values of [O iii]/[O ii]. From Fig. 11 one can estimate that the SED above 40.8 eV should provide roughly as many photons as a blackbody at 90 000 K or more. Current synthetic stellar population models do not consider stellar atmospheres with such a hard radiation field. However, it is to be noted that some of the models for very massive stars at low metallicities computed with an appropriate treatment of radiation-driven winds (Kudritzki 2002) do provide the amount of photons needed to reproduce both the [O iii]/[O ii] vs. [Ar iv]/[Ar iii] and the [O iii]/[O ii] vs. He ii/Hβ diagrams. Perhaps using more realistic model atmospheres to construct SEDs from stellar population models could help.
5.3. Models using classical stellar populations and an additional bremsstrahlung
Another possibility to explain the observed values of He ii/Hβ might be the presence of massive X-ray binaries (Van Bever & Vanbeveren 2007) or of shocks in the atmospheres of stars leading to production of X-rays (Pauldrach et al. 2001), or else X-ray emission from protostars (Bonito et al. 2010). We mimicked all these possible scenarios by adding a bremsstrahlung component with a temperature of 108 K to the PopStar models of Sect. 5.1.1. This temperature is typical of the values inferred from a detailed analysis of A 0535+26, one of the best-studied massive X-ray binary (Rothschild et al. 2013). We adjusted the contribution from the bremsstrahlung so as to obtain He ii/Hβ≃ 0.01 in the resulting photoionization models. This implies that 1% of the ionizing photons come from this bremsstrahlung component of the spectrum. The resulting SED is shown in Fig. C.5. The results of the photoionization models in our diagnostic diagrams are shown in Fig. 12 (to be compared to Fig. 6). We see that, at the highest values of 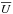 the ionization models slightly deviate from the observations in the [O iii]/[O ii] vs. [O i]/[O iii] plot, but that density-bounded models reproducing the observations have a LyC photon escape fraction of 10% or lower. We note, however, that in the [O iii]/[O ii] vs. [Ar iv]/[Ar iii] plot the observational points tend to lie below the models, meaning that the ionizing source does not provide enough photons at energies slightly above 40.6 eV.
the ionization models slightly deviate from the observations in the [O iii]/[O ii] vs. [O i]/[O iii] plot, but that density-bounded models reproducing the observations have a LyC photon escape fraction of 10% or lower. We note, however, that in the [O iii]/[O ii] vs. [Ar iv]/[Ar iii] plot the observational points tend to lie below the models, meaning that the ionizing source does not provide enough photons at energies slightly above 40.6 eV.
5.4. Models using classical stellar populations and adding the effects of shocks
Another option to consider is the effects of shocks either produced by supernovae from previous generations of stars or from random motions of interstellar clouds. Such shocks could easily produce He ii lines and were even advocated to explain the [Ne v] λ3426 emission observed in some star-forming galaxies (Izotov et al. 2012). We adopted the strategy of Izotov et al. (2012) and Jaskot & Oey (2013) to add the contribution of shocks to the emission-line properties of star-forming galaxies. We used the grid of radiative shock models from Allen et al. (2008) and extracted from it the models constructed with the SMC abundance set because this chemical composition is the most appropriate for our case among the available compositions.
Figure 13 shows the variations of [Ar iv]/Hβ, [O i]/Hβ, and He ii/Hβ as a function of the shock velocity for three different values of the magnetic field. The photoionization models and shock models are combined in the following way: 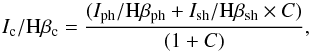 (6)where I/ Hβ stands for the intensity of a line relative to Hβ, the subscripts “c”, “ph”, and “sh” stand for “combined”, “photoionization”, and “shock”, respectively, and C is the adopted ratio of L(Hβ)sh/L(Hβ)ph.
(6)where I/ Hβ stands for the intensity of a line relative to Hβ, the subscripts “c”, “ph”, and “sh” stand for “combined”, “photoionization”, and “shock”, respectively, and C is the adopted ratio of L(Hβ)sh/L(Hβ)ph.
In Fig. 14 we show the combination of the models using PopStar with a shock model with a velocity of 300 km s-1 and a magnetic field strength of 0.5 μG. This value of the magnetic field minimizes the contribution to He ii/Hβ and maximizes the contribution of [O i]/Hβ. The value of C to obtain He ii/Hβ= 0.01 is 0.09. This figure shows that, at the highest values of [O iii]/[O ii] the combined models produce an [O i]/Hβ ratio significantly higher than observed, regardless of the value of the trimming parameter fHβ. The reason is that the [O i] emission in a combined model that explains the He ii/Hβ is completely dominated by the shocks. At low values of [O iii]/[O ii], on the other hand, the effect of the shocks on [O iii]/[O ii] is imperceptible.
 |
Fig. 12 Same as Fig. 6, but with models in which a bremsstrahlung at 108 K is added to the stellar ionizing radiation from the PopStar models corresponding to an age of 1 Myr, in such a proportion that 1% of the ionizing photons come from the bremsstrahlung. |
 |
Fig. 13 Line ratios He ii/Hβ (left panel), [O i]/Hβ (middle panel), and [Ar iv]/Hβ (right panel) as a function of shock velocity for the shock models from Allen et al. (2008; see text). The different curves correspond to different values of the magnetic field, with the color code indicated in the left panel. |
 |
Fig. 14 Same as Fig. 6, but with combined photoionization and shock models. The photoionization models use the energy distribution of PopStar at an age of 1 Myr. The shock models are extracted from the shock-model library of Allen et al. (2008) for a magnetic field of 0.5 μG and have a velocity of 300 km s-1. They are added in such a proportion to obtain He ii/Hβ= 0.01 for the combined model (see text for more details). |
In Fig. 15 we show the combination of the photoionization models using PopStar with a shock model with a velocity of 300 km s-1 and a magnetic field strength of 10 μG, this time maximizing the contribution to He ii/Hβ and minimizing the contribution to [O i]/Hβ. The value of C to obtain He ii/Hβ= 0.01 is 0.055. In this case, the grid of models follows the observational points in the [O iii]/[O ii] versus [O i]/[O iii] plot rather well, with however a slight deviation from the observed trend at the highest values of [O iii]/[O ii].
We thus find that for some combinations, a fraction of the observations are in fact compatible with density-bounded models, implying a leakage of ionizing photons in these cases (but the [Ar iv]/[Ar iii] ratio remains unsatisfactory). Note that at the highest values of [O iii]/[O ii] the [O i]/[O iii] ratio is entirely determined by the shock and that the curves corresponding to different values of fHβ merge. Estimating the amount of LyC photon leakage would at least require a simultaneous fitting of all the relevant line ratios for each object and an independent estimate of the ionization parameter. This procedure would involve many unconstrained parameters, such as the shock velocities or the strength of the magnetic field.
If, however, unlike what is assumed in our combined models, the shocks occur in the ionized region, the [O i] emission would be different. From basic knowledge of the physics of ionized nebulae, one can intuit that the extreme UV and X-ray photons produced by the shock would travel until the outskirts of the H ii region and produce an [O i] emission similar to that of our PopStar + bremsstrahlung models.
From these considerations, we conclude that the presence of shocks can enhance the He ii/Hβ ratio and cause it to agree with the observations and, at the same time, enhance the [O i]/[O iii] ratio, especially for the objects of highest excitation. In these circumstances, an analysis based only on emission-line ratios cannot determine the existence or importance of LyC photon leakage.
We note, however, that in the case of the objects with highest excitation the [O i]/[O iii] ratio is essentially determined by the shock. If the ionized nebulae in these objects were density-bounded, the tight correlation observed between [O iii]/[O ii] and [O i]/[O iii] would imply a very strong dependence of the shock properties on the characteristics of the photoionized nebula, in particular its ionization parameter. This is not impossible but is an additional requirement for the hypothesis of LyC photons leakage to be the correct interpretation.
 |
Fig. 16 Same as Fig. 6, but with models where a AGN-type ionizing spectrum is added to the stellar ionizing radiation from the PopStar models corresponding to an age of 1 Myr. The contribution of the AGN radiation is chosen to produce a resulting He ii/Hβ of ≃0.01. |
5.5. Models including the effect of an active nucleus
The final scenario we consider is that of an AGN embedded in a star-forming region. Again, the SED of the stellar population is provided by the PopStar models at an age of 1 Myr. For the AGN we took the standard AGN SED provided by Cloudy. This AGN spectrum was combined with the PopStar spectrum so as to obtain He ii/Hβ≃ 0.01. The contribution of the AGN to the total number of ionizing photons must be quite small otherwise the He ii/Hβ ratio is boosted toward values much higher than observed (this contribution is about 3% to obtain He ii/Hβ= 0.01). The combined SED is shown in Fig. C.5. The results of the photoionization models are shown in Fig. 16. Here, the models clearly indicate that the observed nebulae would be ionization-bounded. As in Figs. 6 and 12, the models give [Ar iv]/[Ar iii] ratios somewhat lower than observed.
6. Summary and discussion
We have tested the hypothesis of LyC photon leakage from local extreme BCDs by assembling a sample of high-excitation galaxies from the SDSS DR 10 and DR7 and by examining their spectroscopic properties in the light of photoionization models. We have argued that a proper diagnostic cannot rely on strong lines alone: some weak lines are of prime importance to provide an unambiguous answer. Such are the [O i] line, emitted in the warm transition region between ionized and neutral gas, and the [Ar iv] and He ii lines, which are indicative of the presence of photons at high energies (40.8 and 54.4 eV, respectively) that might blur the information from the [O i] lines.
After showing that photoionization models using SEDs from currently available stellar population synthesis models – even at ages when Wolf-Rayet stars are present – cannot account for all the observational constraints for the entire sample, we considered several scenarios that could explain the data. These include the additional presence of a hard X-ray spectrum that might be produced by massive X-ray binaries or shocks in the atmospheres of stars or protostars or by an active galactic nucleus. Another option would be shocks that might be produced by supernovae or cloud-cloud collisions. It turns out that only ionization-bounded models (or models with an escape fraction of Lyc photons lower than 10%) are able to explain all the observational constraints at the same time.
We also found that the current stellar population synthesis models provide too soft ionizing radiation fields to explain the observed [Ar iv]/[Ar iii] ratios. This is probably because the stellar atmosphere models incorporated in the codes underpredict the number of photons emitted between 40.8 and 54.4 eV, and perhaps even at higher energies.
Our study also showed that the extreme BCDs have higher ionization parameters (reaching log 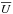 = −1.5 or even −1 depending on the nebular geometry) than galaxies with lower values of [O iii]/[O ii] ratios. Such high values of the ionization parameters are probably produced by a more compact distribution of the gas around the ionizing stars.
= −1.5 or even −1 depending on the nebular geometry) than galaxies with lower values of [O iii]/[O ii] ratios. Such high values of the ionization parameters are probably produced by a more compact distribution of the gas around the ionizing stars.
The question of the possible leakage of LyC photons in high-redshift galaxies should be examined with methods similar to tthose presented in this paper, and not relying on strong line ratios alone. This will be possible with future deep surveys such as the Keck Baryonic Structure Survey (Steidel et al. 2014).
We must acknowledge, however, that our study is based on idealized photoionization models. Perhaps some leakage might occur because of a nebular covering factor smaller than one and not because the nebulae are density-bounded? Perhaps the [O i] emission actually comes from optically thick clumps embedded in a density-bounded medium? Such hypotheses need to be tested by taking into account additional considerations (for example, imaging studies of nearby galaxies). In the meantime, our Occam’s razor approach of photoionization modeling, the fact that [O i]/[O iii] correlates so strongly with [O iii]/[O ii], and the fact that the highest [O iii]/[O ii] ratios correlate with the highest Hβ equivalent widths argue against strong LyC photon leakage from the galaxies with the highest observed [O iii]/[O ii] ratios.
Online material
Appendix A: Chemical abundances
Figure A.1 shows the abundance ratios N/O, Ne/O, S/O, Ar/O, Cl/O, Fe/O as a function of O/H for both our DR10 and DR7 samples (red and blue points, respectively). Note that we measured the S abundance only for objects from our DR10 sample since in the DR7 sample, the [S iii] λ9069 line for all the objects with measured [O ii] λ3727 lies beyond the spectroscopic range. The slight observed tendency between S/O and O/H might be due to inaccurate ionization correction factors. An improvement of the ionization correction factors presented in Izotov et al. (2006) would require a dedicated study that is beyond the scope of the present paper. The large dispersion in the computed Cl/O abundance ratios is essentially due to the extreme weakness of the lines and the large associated error bars. The dispersion in the N/O ratios is real and discussed in detail in Vale Asari et al. (in prep.). The trend of Fe/O decreasing with increasing O/H, already noted by Izotov et al. (2006) using galaxies from SDSS DR3, is an indication that more Fe is depleted into dust grains as metallicity increases.
For the photoionization modeling described in Sect. 4 we took a chemical composition defined by the mean abundances of our DR7-DR10 sample.
 |
Fig. A.1 Abundance ratios in our galaxy sample. DR10 objects are plotted in red, DR7 objects are in blue. The total number of objects included in each panel is indicated in the upper right corner. |
Appendix B: Didactic diagrams
 |
Fig. B.1 Effect of metallicity on the [O iii]/[O ii] ratio obtained from photoionization models. The models are computed for a PopStar ionizing radiation field (age 1 Myr) and are ionization-bounded. Continuous lines join models of same metallicity, while dashed lines join models with same ionization parameter. The color code is given in the plot. The positions of the observational points for our samples (red for DR10, blue for DR7) are shown for comparison. |
 |
Fig. B.2 Values of L(Hβ) /Q(H0) as a function of |
 |
Fig. B.3 Variations of several line ratios with blackbody temperature for different values of the ionization parameter (ionization-bounded models with 12 + log O/H = 8). Continuous lines join models of same effective temperature, while dashed lines join models with same ionization parameter. The color coding is the same as in Fig. 11. |
Appendix C: Spectral energy distributions
 |
Fig. C.1 Log of Q(E), the number of photons emitted above the energy threshold E as a function of E, for different spectral energy distributions (SEDs). The ionization thresholds of important ions are indicated by the vertical dashed lines. The different curves correspond to blackbodies at different temperatures, as indicated in the inset. The PopStar model at an age of 1 Myr of Fig. C.4 is shown for comparison. |
 |
Fig. C.2 Same as Fig. C.1 for SEDs obtained by PopStar at an age of 1 Myr for a Chabrier (2003) stellar initial mass and different metallicities Z as indicated by the color code in the inset. |
 |
Fig. C.3 Same as Fig. C.1 for several SEDs obtained with starburst99 with a Kroupa (2001) stellar initial mass function for a metallicity Z = 0.004 at an age of 1 Myr. The color coding indicates the different cases proposed by starburst99: Geneva tracks with standard mass loss, Geneva tracks with high mass loss, original Padova tracks, and Padova tracks with AGB stars. The PopStar model at an age of 1 Myr is shown for reference. We see that, at this age, all the SEDs are exactly sumperimposed. |
 |
Fig. C.4 Same as Fig. C.1, but with SEDs corresponding to PopStar models at a metallicity Z = 0.004 for different ages (1, 2, 3, 4, and 5 Myr). |
 |
Fig. C.5 Same as Fig. C.4 for SEDs corresponding to AGN spectral energy distribution, combined PopStar at an age of 1 Myr and AGN (Sect. 5.5), and combined PopStar at an age of 1 Myr and bremsstrahlung (Sect. 5.3). The pure PopStar model at an age of 1 Myr of Fig. C.4 is shown for comparison. |
 |
Fig. C.6 Same as Fig. C.3, but for an age of 4 Myr. Here, all the SEDs are harder than in the 1 Myr case, because of Wolf-Rayet stars. We also note a substantial difference between the various SEDs. |
It is interesting to note that, in the [O iii]/[O ii] versus [O i]/[O iii] plot, the curves for fHβ< 1 almost overlap, with only the fHβ = 1 curve standing out. This is because in that case the [O i] emission is dominated by the ionization front, while in the density-bounded cases it is produced by the traces of neutral hydrogen in the whole H ii region.
Acknowledgments
We thank the referee for the interesting questions raised in his/her report, which prompted a deeper analysis on several points. G.S. gratefully acknowledges financial support from the project UNAM PAPIIT IN109614 and the hospitality of the Instituto de Astronomia of the UNAM (Mexico), where part of this work was conducted. Yu.I. is grateful to the Observatoire de Paris for financial help and hospitality during the first stages of this work. C.M. acknowledges financial aid from CONACyT project CB-2010/153985. N.G. acknowledges financial support by the Max Planck Institute for Radioastronomy in Bonn (MPIfR). All the authors wish to thank the team of the Sloan Digital Sky Survey (SDSS) for their dedication to a project that has made the present work possible. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III Web site is http://www.sdss3.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A. et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Aggarwal, K. M., & Keenan, F. P. 1999, ApJS, 123, 311 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, M. G., Groves, B. A., Dopita, M. A., Sutherland, R. S., & Kewley, L. J. 2008, ApJS, 178, 20 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonito, R., Orlando, S., Miceli, M., et al. 2010, A&A, 517, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardamone, C., Schawinski, K., Sarzi, M., et al. 2009, MNRAS, 399, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, ApJ, 732, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Porter, R. L., van Hoof, P. A. M., et al. 2013, Rev. Mex. Astron. Astrophys., 49, 137 [Google Scholar]
- FroeseFischer, C., Tachiev, G., & Irimia, A. 2006, Atom. Data Nucl. Data Tables, 92, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Galavis, M. E., Mendoza, C., & Zeippen, C. J. 1997, A&AS, 123, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garnett, D. R., Kennicutt, R. C., Jr., Chu, Y.-H., & Skillman, E. D. 1991, ApJ, 373, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Hillier, D. J., & Miller, D. L. 1998, ApJ, 496, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Stasińska, G., Meynet, G., Guseva, N. G., & Thuan, T. X. 2006, A&A, 448, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izotov, Y. I., Guseva, N. G., & Thuan, T. X. 2011, ApJ, 728, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Privon, G. 2012, MNRAS, 427, 1229 [NASA ADS] [CrossRef] [Google Scholar]
- Jaskot, A. E., & Oey, M. S. 2013, ApJ, 766, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kewley, L. J., Maier, C., Yabe, K., et al. 2013, ApJ, 774, L10 [Google Scholar]
- Kisielius, R., Storey, P. J., Ferland, G. J., & Keenan, F. P. 2009, MNRAS, 397, 903 [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R. P. 2002, ApJ, 577, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Leitherer, C., Schaerer, D., Goldader, J. D., et al. 1999, ApJS, 123, 3 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, B. M., & Bell, K. L. 2000, J. Phys. B, 33, 597 [Google Scholar]
- Mendoza, C. 1983, IAUS, 103, 143 [Google Scholar]
- Mendoza, C., & Zeippen, C. J. 1983, MNRAS, 202, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Mollá, M., García-Vargas, M. L., & Bressan, A. 2009, MNRAS, 398, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Munoz Burgos, J. M., Loch, S. D., Ballance, C. P., & Boivin, R. F. 2009, A&A, 500, 1253 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakajima, K., & Ouchi, M. 2014, MNRAS, 442, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Nakajima, K., Ouchi, M., Shimasaku, K., et al. 2013, ApJ, 769, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Overzier, R. A., Heckman, T. M., Tremonti, C., et al. 2009, ApJ, 706, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Pauldrach, A. W. A., Hoffmann, T. L., & Lennon, M. 2001, A&A, 375, 161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramsbottom, C. A., Bell, K. L., & Keenan, F. P. 1997, MNRAS, 284, 754 [NASA ADS] [Google Scholar]
- Ramsbottom, C. A., Bell, K. L., & Keenan, F. P. 2001, Atom. Data Nucl. Data Tables, 77, 57 [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothschild, R., Markowitz, A., Hemphill, P., et al. 2013, ApJ, 770, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Reddy, N. A., Kriek, M., et al. 2015, ApJ, 801, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Shirazi, M., & Brinchmann, J. 2012, MNRAS, 421, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Shirazi, M., Brinchmann, J., & Rahmati, A. 2014, ApJ, 787, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, L. J., Norris, R. P. F., & Crowther, P. A. 2002, MNRAS, 337, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Stasińska, G., & Izotov, Y. 2003, A&A, 397, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., & Tylenda, R. 1986, A&A, 155, 137 [NASA ADS] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Tayal, S. S. 2011, ApJS, 195, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Tayal, S. S., & Gupta, G. P. 1999, ApJ, 526, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Tayal, S. S., & Zatsarinny, O. 2010, ApJS, 188, 32 [NASA ADS] [CrossRef] [Google Scholar]
- van Bever, J., & Vanbeveren, D. 2007, ASP Conf. Ser., 367, 579 [NASA ADS] [Google Scholar]
- Vilchez, J. M., & Pagel, B. E. J. 1988, MNRAS, 231, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Zeippen, C. J. 1982, MNRAS, 198, 111 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 BPT diagram for our DR10 objects (red circles) and those of DR7 (blue diamonds). The background gray scale map represents all the SDSS DR7 galaxies with a signal-to-noise ratio of at least 3 in the four diagnostic lines [O iii], Hβ, [N ii], and Hα. The gray scale is in logarithm of the number of objects per pixel, as indicated in the bar on the right. The blue curve represents the Kauffmann et al. (2003) line generally used to distinguish star-forming galaxies from AGN hosts. |
| In the text | |
 |
Fig. 2 [O iii]/[O ii] ratio as a function of the oxygen abundance 12 + log O/H (left panel) and as a function of the equivalent width of the Hβ line (right panel). DR10 objects are represented in red and those of DR7 in blue. The total number of objects in each panel is indicated in the top right corner. |
| In the text | |
 |
Fig. 3 [O iii]/[O ii] ratio as a function of the electron density as derived from the [S ii] λ6731/6717 line ratio (left panel) and as a function of the total luminosity in the Hβ line, corrected for extinction. |
| In the text | |
 |
Fig. 4 [O iii]/[O ii] ratio vs. ([O iii]/[O ii])/([S iii]/[S ii]) (left panel) and vs. ([Ar iv]/[Ar iii])/([O iii]/[O ii]) (right panel). |
| In the text | |
 |
Fig. 5 [O iii]/[O ii] ratio as a function of the product neL(Hβ) (left panel) and as a function of [O i]/[O ii] (right panel). |
| In the text | |
 |
Fig. 6 [O iii]/[O ii] versus [Ar iv]/[Ar iii] (left), [O iii]/[O ii] versus [O i]/[O iii] (middle) and [O iii]/[O ii] versus He ii/Hβ (right) diagnostic diagrams. The red and blue points represent the DR10 and DR7 objects respectively. The curves represent our grid of models computed with the SED from PopStar models at an age of 1 Myr and with a metallicity 12 + log O/H = 8. The dashed lines link models with the same values of |
| In the text | |
 |
Fig. 7 Same as Fig. 6, but for models at an age of 4 Myr. |
| In the text | |
 |
Fig. 8 Left: Q(He+) /Q(H0) as a function of age for PopStar SEDs with metallicities Z = 0.004, 0.008, and 0.02 as indicated in the inset. Right: log He ii/Hβ versus EW(Hβ), where He ii/Hβ is taken equal to 1.74Q(He+) /Q(H0), for the same PopStar models. |
| In the text | |
 |
Fig. 9 Left: observed values of log He ii/Hβ versus EW(Hβ) (for objects with no He ii detection log He ii/Hβ has been set to −4); right: observed values of 12 + log O/H versus EW(Hβ). |
| In the text | |
 |
Fig. 10 Same as Fig. 6, but with models computed with a blackbody ionizing source at a temperature of 60 000 K. |
| In the text | |
 |
Fig. 11 [O iii]/[O ii] vs. [Ar iv]/[Ar iii] diagram for ionization-bounded photoionization models with a blackbody ionization source (12 + log O/H = 8). Top panel: models for filled spheres; bottom panel: models for spherical bubbles. Continuous lines correspond to different values of the effective temperature, while dashed lines correspond to different values of the ionization parameter. The color coding is indicated in the plot. The positions of the observational points for our samples (red for DR10, blue for DR7) are shown for comparison. This diagram shows that for a given value of [O iii]/[O ii] the value of [Ar iv]/[Ar iii] increases with Teff. |
| In the text | |
 |
Fig. 12 Same as Fig. 6, but with models in which a bremsstrahlung at 108 K is added to the stellar ionizing radiation from the PopStar models corresponding to an age of 1 Myr, in such a proportion that 1% of the ionizing photons come from the bremsstrahlung. |
| In the text | |
 |
Fig. 13 Line ratios He ii/Hβ (left panel), [O i]/Hβ (middle panel), and [Ar iv]/Hβ (right panel) as a function of shock velocity for the shock models from Allen et al. (2008; see text). The different curves correspond to different values of the magnetic field, with the color code indicated in the left panel. |
| In the text | |
 |
Fig. 14 Same as Fig. 6, but with combined photoionization and shock models. The photoionization models use the energy distribution of PopStar at an age of 1 Myr. The shock models are extracted from the shock-model library of Allen et al. (2008) for a magnetic field of 0.5 μG and have a velocity of 300 km s-1. They are added in such a proportion to obtain He ii/Hβ= 0.01 for the combined model (see text for more details). |
| In the text | |
 |
Fig. 15 Same as Fig. 14, but for shock models with a magnetic field of 10 μG. |
| In the text | |
 |
Fig. 16 Same as Fig. 6, but with models where a AGN-type ionizing spectrum is added to the stellar ionizing radiation from the PopStar models corresponding to an age of 1 Myr. The contribution of the AGN radiation is chosen to produce a resulting He ii/Hβ of ≃0.01. |
| In the text | |
 |
Fig. A.1 Abundance ratios in our galaxy sample. DR10 objects are plotted in red, DR7 objects are in blue. The total number of objects included in each panel is indicated in the upper right corner. |
| In the text | |
 |
Fig. B.1 Effect of metallicity on the [O iii]/[O ii] ratio obtained from photoionization models. The models are computed for a PopStar ionizing radiation field (age 1 Myr) and are ionization-bounded. Continuous lines join models of same metallicity, while dashed lines join models with same ionization parameter. The color code is given in the plot. The positions of the observational points for our samples (red for DR10, blue for DR7) are shown for comparison. |
| In the text | |
 |
Fig. B.2 Values of L(Hβ) /Q(H0) as a function of |
| In the text | |
 |
Fig. B.3 Variations of several line ratios with blackbody temperature for different values of the ionization parameter (ionization-bounded models with 12 + log O/H = 8). Continuous lines join models of same effective temperature, while dashed lines join models with same ionization parameter. The color coding is the same as in Fig. 11. |
| In the text | |
 |
Fig. C.1 Log of Q(E), the number of photons emitted above the energy threshold E as a function of E, for different spectral energy distributions (SEDs). The ionization thresholds of important ions are indicated by the vertical dashed lines. The different curves correspond to blackbodies at different temperatures, as indicated in the inset. The PopStar model at an age of 1 Myr of Fig. C.4 is shown for comparison. |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1 for SEDs obtained by PopStar at an age of 1 Myr for a Chabrier (2003) stellar initial mass and different metallicities Z as indicated by the color code in the inset. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.1 for several SEDs obtained with starburst99 with a Kroupa (2001) stellar initial mass function for a metallicity Z = 0.004 at an age of 1 Myr. The color coding indicates the different cases proposed by starburst99: Geneva tracks with standard mass loss, Geneva tracks with high mass loss, original Padova tracks, and Padova tracks with AGB stars. The PopStar model at an age of 1 Myr is shown for reference. We see that, at this age, all the SEDs are exactly sumperimposed. |
| In the text | |
 |
Fig. C.4 Same as Fig. C.1, but with SEDs corresponding to PopStar models at a metallicity Z = 0.004 for different ages (1, 2, 3, 4, and 5 Myr). |
| In the text | |
 |
Fig. C.5 Same as Fig. C.4 for SEDs corresponding to AGN spectral energy distribution, combined PopStar at an age of 1 Myr and AGN (Sect. 5.5), and combined PopStar at an age of 1 Myr and bremsstrahlung (Sect. 5.3). The pure PopStar model at an age of 1 Myr of Fig. C.4 is shown for comparison. |
| In the text | |
 |
Fig. C.6 Same as Fig. C.3, but for an age of 4 Myr. Here, all the SEDs are harder than in the 1 Myr case, because of Wolf-Rayet stars. We also note a substantial difference between the various SEDs. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


