| Issue |
A&A
Volume 575, March 2015
|
|
|---|---|---|
| Article Number | A108 | |
| Number of page(s) | 11 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201425122 | |
| Published online | 04 March 2015 | |
Relative distribution of dark matter and stellar mass in three massive galaxy clusters⋆
INAF–Osservatorio Astronomico di Brera, via Brera 28, 20121 Milano, Italy
e-mail:
stefano.andreon@brera.inaf.it
Received: 7 October 2014
Accepted: 29 December 2014
This work observationally addresses the relative distribution of total and optically luminous matter in galaxy clusters by computing the radial profile of the stellar-to-total mass ratio. We adopt state-of-the-art accurate lensing masses free from assumptions about the mass radial profile and we use extremely deep multicolor wide-field optical images to distinguish star formation from stellar mass, to properly calculate the mass in galaxies of low mass, those outside the red sequence, and to allow a contribution from galaxies of low mass that is clustercentric dependent. We pay special attention to issues and contributions that are usually underrated, yet are major sources of uncertainty, and we present an approach that allows us to account for all of them. Here we present the results for three very massive clusters at z ~ 0.45, MACSJ1206.2-0847, MACSJ0329.6-0211, and RXJ1347.5-1145. We find that stellar mass and total matter are closely distributed on scales from about 150 kpc to 2.5 Mpc: the stellar-to-total mass ratio is radially constant. We find that the characteristic mass stays constant across clustercentric radii and clusters, but that the less-massive end of the galaxy mass function is dependent on the environment.
Key words: galaxies: luminosity function, mass function / dark matter / methods: statistical / galaxies: clusters: general
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Clusters of galaxies are the largest dynamically bound systems and are effective laboratories for studying the relationship between the distribution of dark and luminous matter. Since the pioneering work of Zwicky (1933), many studies (e.g., Fabricant et al. 1986; Eyles et al. 1991; Smail et al. 1995; Kaiser et al. 1998; Kneib et al. 2003; Medezinski et al. 2010; Okabe et al. 2014; Grillo et al. 2015) have analyzed the relative distribution of luminous and dark matter mass using the mass-over-luminosity (M/L) or its reciprocal, light-over-mass (L/M) ratio. Zwicky (1933) provided the first evidence of the existence of dark matter. Most weak-lensing studies, and several X-ray studies, find that the dark-matter component is well traced by the total light distribution of the cluster (e.g., Fabricant et al. 1986; Smail et al. 1995; Kneib et al. 2003; Umetsu et al. 2010; Medezinski et al. 2013; Okabe et al. 2014; Grillo et al. 2015). We note, however, that some lensing studies assume that the above holds. In fact, they take the light distribution as prior of the mass distribution, for example, holding the center of the sub-halos tied on the galaxy centers and scaling their mass by the galaxy luminosity (e.g., Grillo et al. 2015; Kneib et al. 1996).
Quantitatively, we are far from a consensus. Smail et al. (1995) and Annunziatella et al. (2014) find some evidence for a greater concentration of total matter compared to galaxies. Medezinski et al. (2013) find a radially decreasing M/L outside the cluster core, as Rines et al. (2000) for Abell 576 using caustics. Rines et al. (2004) find a decrease by a factor of two outside the virial radius in a combined sample of nine clusters including Coma and Abell 576. Instead, Hoekstra et al. (1998), Kneib et al. (2003), and others, measure a constant M/L with radius. Similarly, Rines et al. (2001) find, using caustics to estimate mass (e.g., Diaferio & Geller 1997), that the Coma cluster has a flat M/L over all scales going from the cluster center to several virial radii. At the cluster’s very center, Newman et al. (2013) find that within the brightest cluster galaxy effective radius almost all of the matter is formed by stars, i.e., that the stellar fraction is close to one at r = 0. Instead, Grillo et al. (2015) found a vanishing amount of stellar mass at the cluster center for the single cluster they studied. We note, however, that while Newman et al. (2013) take the cluster center co-incident with the center of a galaxy (the brightest one), Grillo et al. (2015) adopt a cluster center away from any galaxy, making the variance between the two results somewhat expected. Finally, Andreon (2012) measured the stellar masses for 12 clusters within two radii, r500 and r200, finding 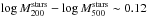 dex, close to the measured difference in mass between these radii. However, the masses at the largest radii are based on extrapolation because X-ray data do not reach that far.
dex, close to the measured difference in mass between these radii. However, the masses at the largest radii are based on extrapolation because X-ray data do not reach that far.
Recent hydrodynamical simulations (Battaglia et al. 2013; Planelles et al. 2013) implementing radiative cooling, star formation, and AGN feedback predict that stars in clusters mirror the dark matter distribution, i.e., that the stellar-to-total mass ratio is quite constant across most of the cluster radial range, with the possible exception of radii very close to the cluster center, where predictions are less accurate (see Newman et al. 2013). The constancy of the radial profile of the stellar-to-total-matter mass ratio agrees with qualitative expectations: stars are not expected to be stripped significantly because they are located deep in the galaxy potential, hence stellar mass should trace dark mass given that both are collisionless. However, from a theoretical and quantitative perspective, we are far from a satisfactory understanding because current numerical simulations grossly overpredict the total amount of stellar mass (e.g., Andreon 2010; Young et al. 2011; Planelles et al. 2013).
Impressive progress on the measurements of stellar mass and total cluster luminosity has occurred in recent years, overcoming limitations of past works, most of which, for example, did not consider galaxies outside the red sequence, or even in it, but in galaxies of low mass. These stellar masses are missed most of the time, or strong assumptions have been made about them, such as assuming a fixed proportion of massive and less massive galaxies. Some works assumed that the luminosity function is radial-independent, while luminosity segregation is known to exist in clusters (e.g., Andreon 2002b; Durret et al. 2002). Works using early releases of the Two Micron All Sky Survey (Skrutskie et al. 2006) photometry are missing light from outer regions of the detected galaxies and even whole galaxies of central surface brightness below average because of the shallow nature of the used data (e.g., Andreon 2002a; Kirby et al. 2008). In some rare cases, researchers were presented with data only allowing a coarse, or no, background subtraction.
There has also been impressive progress on the determination of the total matter radial profile, whose determination is hampered by substructure and deviations of clusters from equilibrium, which affect both X-ray observations and Jeans analyses (i.e., kinematics). Indeed, kinematic analysis assumes a) dynamical equilibrium; b) some dynamical modeling (on the distribution of orbits, for example); and c) knowledge of the velocity bias of the observed galaxy population. Stacking clusters erase the signature of the substructure on the combined sample, but the individual clusters in the sample are not for this reason closer to equilibrium. Removing galaxies in substructures from the stack is of no help in removing their effect on the other galaxies. X-ray estimates very rarely reach large cluster scales because the surface brightness emission falls precipitously with radius from the cluster center and spatially resolved temperature profiles at large clustercentric radii are therefore challenging. Progress has been made quite recently (e.g., Mamon et al. 2013, for kinematical estimates and Hoshino et al. 2010, for X-ray determinations), but early studies did not profit from this, of course.
Lensing (e.g., Mellier 1999) allows us to determine the projected mass profile free of assumption about (dynamical, hydrostatic, etc.) equilibrium. However, it is a new technique, which has impressively improved in various aspects over the years (modeling of PSF effects, estimate of the redshift distribution of the lensed sources, treatment of dilution effects, etc.), to such a degree that accurate mass radial profiles have only recently started to become available (Applegate et al. 2014; Umetsu et al. 2012, 2014). Furthermore, most of the mass profiles, including recent ones, are derived assuming a) azymuthal symmetry; b) a single or two parameters radial profile; and c) the assumption that the cluster is embedded in a smooth large-scale environment (e.g., Hoekstra et al. 2012; Merten et al. 2014; von der Linden et al. 2014). While numerical simulations predict a universal dark matter profile for the average halo close to a Navarro et al. (1997, hereafter NFW) profile, real massive clusters studied in weak-lensing works (and many of those studied using caustics or kinematics) are rarely that simple (e.g., Smail et al. 1995; Kneib et al. 2003; Umetsu 2013; Umetsu et al. 2014; Gruen et al. 2014; Klypin et al. 2014). Parametric estimates that assume a radial profile model that does not fit the data (e.g., because of cluster substructure) induce biases in the derived M/L (or stellar-to-total matter mass) ratio. In fact, deviations from the assumed radial model are not captured by the too simple model. Instead, a more flexible weak lensing model, such as the radial model-free modeling by Umetsu (2013) and Umetsu et al. (2014), does capture the complex morphology of the cluster in a far better way.
In this work we make use of the impressive progress in weak lensing and stellar mass measurements to present the first robust determination of the radial profile of the stellar-to-total matter mass ratio. In particular, we measure it for three massive clusters at intermediate redshift up to the virial radius, rvir, and beyond. We use up-to-date, robust, and radial-model free, weak lensing masses that are also free from assumptions about the cluster dynamical status. Thanks to Suprime-Cam multicolor wide-field optical images of exquisite depth and, unlike most previous works using the M/L ratio as proxy for the stellar-to-total matter ratio, we distinguish luminosity emitted by a recent minor (in mass) burst of star formation from the one emitted by a much larger amount of old stellar mass; we count the mass in galaxies outside the red sequence or in galaxies of low mass; and we allow (and we will indeed find) a cluster-centric dependent contribution from galaxies of low mass. Finally, we study the differential radial profile (i.e., f(r)) more sensitive to gradients than the integrated profiles (i.e., f( <r)) studied in past works. To achieve our aim, we are obliged to first derive (and use) the correct expression of the likelihood and to account for covariance across mass radial bins.
Throughout this paper, we assume ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s-1 Mpc-1. Magnitudes are in the AB system. We use the 2003 version of Bruzual & Charlot (2003, hereafter BC03) stellar population synthesis models with solar metallicity and a Salpeter initial mass function (IMF). We define stellar mass as the integral of the star formation rate, which includes the mass of gas processed by stars and returned to the interstellar medium. We allow both single stellar populations and exponential declining τ models. For star forming galaxies, we also include the stellar mass plausibly formed from the redshift of observation to z = 0 (i.e., we extend the integral of the star formation rate down to z = 0). Results of stochastic computations are given in the form x ± y, where x and y are the posterior mean and standard deviation. The latter also corresponds to 68 % intervals because we only summarized posteriors close to Gaussian in this way.
2. Samples and data
We study three clusters: MACSJ1206.2-0847 (z = 0.439), MACSJ0329.6-0211 (z = 0.450), and RXJ1347.5-1145 (z = 0.451), hereafter referred to as MACSJ1206, MACSJ0329, and RXJ1347, respectively. These are selected among CLASH clusters (Postman et al. 2012) with 1) state-of-the-art accurate weak lensing masses free from assumptions about the mass radial profile (taken from Umetsu et al. 2014); 2) with available Suprime-Cam images (Miyazaki et al. 2002); and 3) at z> 0.4 in order to probe ≫3 Mpc radii at the cluster redshift (needed to estimate the background inside the same Suprime-Cam pointing).
The basic data used in our analysis are V, R, and z′ photometry derived using the SExtractor code (Bertin & Arnouts 1996) on deep Subaru Suprime-Cam images delivered by the CLASH team1, described in Umetsu et al. (2014; see also Medezinski et al. 2013). Suprime-Cam images are ≈25′ × 25′ wide, have a pixel size of 0.2 arcsec, and are taken in sub-arcsec seeing conditions. We emphasize that the Suprime-Cam filters differ from the standard V, R, and z′ filters. We therefore compute the combined response of the filters, prime focus unit transmission, and CCD quantum efficiency2 and used these for the stellar population synthesis modeling. These filters, at z = 0.44, accurately sample the 4000 Å break, approximately corresponding to the u,B, and R filters. These are among the deepest cluster observations ever taken (e.g., Medezinski et al. 2010).
We conservatively consider galaxies brighter than z′ = 24 mag, which is much much brighter than the completeness limit of these images (e.g., by 2 mag in z′; see, e.g., Medezinski et al. 2010), to ignore incompleteness and its radial dependency (due to dithering, CCD gaps, variable source density or crowding, etc.). We adopt SExtractor’s magauto as total galaxy magnitudes, while colors are based on a fixed 2 arcsec aperture and are corrected for the color–magnitude slope. Since early-type galaxies have surface brightness profiles close enough to make global properties such as total luminosity independent of environment (e.g., Pahre et al. 1998), we do not expect that the precise definition of total mag affects the major conclusion of this work, namely a radially constant stellar-to-total mass ratio.
 |
Fig. 1 Mass function of red sequence (upper panels) and red galaxies plus BCG (lower panels) of MACSJ1206 in various clustercentric radial bins, as detailed in the panels. The arrow indicates the total mass inside the considered radial bin, disregarding the BCG, if any. The solid line is the mean model fitted to the individual galaxy data, while the shading indicates the 68% uncertainty (highest posterior density interval). Points and approximated error bars are derived by binning galaxies in magnitude bins, adopting approximated Poisson errors summed in quadrature, as commonly done in the literature. |
Two galaxy populations are of interest:
-
red sequence (RS) galaxies are defined as those within 0.1 mag redward and 0.2 mag blueward in V − z′ with respect to the red sequence;
-
red galaxies plus brightest cluster galaxies (R+BCGs). The former are defined as those redder than an exponential declining τ = 3.7 Gyr model, and bluer than 0.1 mag redward of the color–magnitude relation, as in several previous studies (e.g., Andreon et al. 2006; Raichoor & Andreon 2012a,b; Andreon 2012). These galaxies will be red at z = 0 according to the Butcher & Oemler (1984) definition. Of course, this sample includes RS galaxies. In the inner cluster radius a sizeable amount of stellar mass is missing for clusters with blue BCGs (one of the two BCGs of both MACSJ0329 and RXJ1347). Therefore, we add these two BCGs to the red galaxy population.
We also consider other, bluer, galaxy populations. However, we found that they are only minor populations for the three clusters studied and, as populations, marginally detected, if at all, in the background at most or all clustercentric radii, in agreement with the lack of a blue population in Andreon et al. (2006), De Propris et al. (2003), Haines et al. (2009), and Raichoor & Andreon (2012b). Given that in the studied clusters the population is small and of low mass for their luminosity -they are bright because they are strongly star forming, not because they are massive- we can safely neglect them in our stellar mass computation. Indeed, results for the R+BCG sample turns out not to depend on the details of the red definition (for example by adopting a τ = 5 model) because the adopted color boundaries fall (by design) in regions where no cluster galaxies (in an amount large enough to be detected in the background) are found. Using the large sample of spectroscopic redshift of MACS1206 (Biviano et al. 2013), which is biased against red galaxies, we found that less than 3% of the stellar mass is in bluer galaxies.
We estimate galaxy stellar masses from the z′ band luminosity and V − z′ color using the relation between M/L and galaxy color derived using the Bruzual & Charlot (2003) stellar population synthesis models (like that of Bell & de Jong 2001; and similarly to Kravtsov et al. 2014; Boselli et al. 2014; Fritz et al. 2014; Budzynski et al. 2014; Gladders et al. 2013; Oemler et al. 2013; and Dressler et al. 2013, to only mention cluster works that have appeared in the last year). This single-color estimate of stellar mass is found to give values consistent with full-SED fitting up to z ~ 2 (Koyama et al. 2013). In particular, the slope of M/L vs. V − z′ relation is derived by computing the color (in the observer frame for galaxies at the cluster redshift) of 0 <τ< 5 Gyr model galaxies.
To reduce the background contamination, we remove galaxies with V − z′> 2(V − R − 1) + 1.7 mag. As checked with CLASH HST 16-band photometric redshifts (these are available for galaxies in the inner arcmin only) these are in the cluster background with no exception and are recognized as such because they have the 4000 Å break in the R-band filter, not in the V band as do cluster members. Residual background galaxies are statistically accounted for, as mentioned below. Using MACS1206 spectroscopic redshifts (Biviano et al. 2013), we found that less than 0.5% of the mass is missed because of the color cut adopted.
We adopt radial bins equal to those adopted in Umetsu et al. (2014), after merging three Umetsu et al. (2014) bins into one, in order to have the same radial bins in the computation of the radial stellar-to-total matter ratio profile. Specifically, we adopt the following radii: 0,0.9,2.1,2.8,3.8,5.1,6.7, and, except for MACSJ1206, 9 arcmin as extremes of the considered coronae.
To correct for the missed flux (and hence mass) coming from the galaxy outer regions (e.g., Blanton et al. 2001; Andreon 2002a,b) and the intracluster light we increased the measured flux of all radial bins by 15% (Blanton et al. 2001; Andreon 2002a,b, 2010, 2012; Bahcall & Kulier 2014).
3. Characteristic mass, faint-end slope, and surface density stellar mass profile
3.1. Methods
To derive the galaxy mass function, we adopted a Bayesian approach, as has been done for the luminosity function of other clusters (e.g., Andreon 2006, 2010, 2012; Andreon et al. 2006, 2008; Meyers et al. 2012), and we account for the residual background (galaxies in the cluster line of sight not removed by the color cut), which is estimated outside a radius of 3 Mpc and inside the same Subaru pointing with the cluster, hence fully guaranteeing homogeneous data for cluster and control field. We adopted a Schechter (1976) mass function for cluster galaxies and we modeled the background counts with a power law of degree 3 (i.e., with four free parameters). We computed the total mass in stars from the integral, over all masses, of mass times the galaxy mass function.
The likelihood expression is derived and given in Andreon et al. (2005), which is an extension of the Sandage et al. (1979) likelihood expression for the case where a background is present. It allows signal fluctuations, i.e., it allows the model and observed number of galaxies to differ, accounting for fluctuations in the number of galaxies. Because of these number fluctuations, the stellar mass (and luminosity) inside a radial bin has a uncertainty larger than just the one induced by the finite number of collected photons even in ideal conditions, such as in the absence of a background and with perfect knowledge of the luminosity to mass conversion.
In the mass function computation, attention should be paid to the BCG, which might not be drawn from the Schechter (1976) function (e.g., Tremaine & Richstone 1977). This situation occurs for the inner corona of RXJ1347 and MACSJ0326, in which case we fit all galaxies excluding the two BCGs, and add their mass contribution separately.
We adopt weak, uniform priors on all parameters, thus allowing the cluster parameters to be radial-dependent (i.e., allowing mass segregation, a different contribution from low-mass galaxies, etc.) and we fit the individual galaxy data (i.e., we do not bin in mass). We checked convergence of the Markov chain Monte Carlo by running multiple chains, and by inspecting their traces, their autocorrelation functions, and how well the model fit the data. The Bayesian approach allows us to easily propagate uncertainties and their covariance into derived quantities, such as the surface stellar mass density. For example, we do not assume a perfect knowledge of the background contamination and instead marginalize over its uncertainty, allowing us to propagate this uncertainty into derived quantities. As a visual check and for illustration, we also computed the mass function by binning galaxies in mass bins, as is done for the luminosity functions by Zwicky (1957), Oemler (1974), and many papers since then.
Our analysis measures the projected stellar mass, i.e., within a cylinder of nonnegligible width in the line of sight. While our measurements are projected on the line of sight (i.e., 2D, not 3D) they are differential in the plane of the sky (i.e., we measure f(r), not f( <r)). Weak lensing masses measure projected masses including contamination by large-scale structures (LSS) located near the cluster redshift, as our stellar masses do. This is advantageous when we compute the stellar-to-total matter ratio profile because we are counting masses in similar volumes for both the numerator and denominator.
 |
Fig. 2 Radial profile of the characteristic stellar mass (upper panels), faint-end slope α (central panels) and projected surface stellar mass density (bottom panels) of the three clusters (MACSJ1206, MACSJ0329, and RXJ1347, from left to right). The central-left panel report the fitted linear trend. Arrows indicate rΔ values and are from Merten et al. (2014). The surface stellar mass density Σ is in M⊙/Mpc2 units. |
3.2. Results
In this section we present the mass function of the three clusters; we show that the characteristic mass M∗ is fairly constant as a function of clustercentric radius and across the three clusters, that the faint-end slope of the mass function shows a radial dependence indicating mass segregation, and we derive the surface stellar mass density profile of the three clusters.
Figure 1 shows the galaxy mass function of RS and R+BCG galaxies in MACSJ0216 with log M/M⊙> 9.7, our mass completeness limit, at various clustercentric radii. The very deep Suprime-Cam data very tightly constrain the cluster mass function. The three-parameter Schechter function accurately describes the behavior of the explored 2.5 dex in galaxy mass. Appendix A shows the mass function of the other two studied clusters.
The top and middle panels of Fig. 2 shows the radial trend of the derived characteristic mass M∗ and of the faint-end slope α of the Schechter (1976) mass function of the three studied clusters. There is no evidence for a radial-dependent characteristic mass, nor for a widely different value that depends on the considered galaxy population, nor for a difference from cluster to cluster: log M∗/M⊙ = 11.27 ± 0.04 (error on the mean) for red-sequence galaxies, and log M∗/M⊙ = 11.42 ± 0.03 for R+BCG galaxies. The radial independence of the massive end of the mass function suggests that environment plays a minor role in shaping the galaxy mass of the most massive galaxies. This interpretation, however, assumes that the current environment is still closely correlated to the environment where the galaxy mass was shaped, a correlation that we know is largely masked by the backsplash population (e.g., Gill et al. 2005).
The faint-end slope of MACSJ1206 steepens as we move toward larger radii. For R+BCG the slope of the α vs. r relation is −0.101 ± 0.028 (the slope is <0 with 99.97% probability). While for the R+BCG population the radial trend may be due to a change in the relative proportion of RS and non-RS galaxies, the effect is also significant for the RS population only, indicating a mass segregation. The radial trend of the faint-end slope of the mass function of the other clusters is less clear. Although there are various hints of possible cluster-center dependencies of the faint-end slope (perhaps easier to spot in the mass functions shown in Appendix A), none of them is, alone, overwhelmingly statistically significant.
The difference between the regular behavior of the α profile of MACSJ1206 and the apparently erratic behavior of the other two clusters is striking and suspicious. To investigate if the profiles were contaminated by another localized structure (a group, or another cluster, on a close line of sight) not recognized as such, we repeated the analysis but dividing the cluster area in octants and removing the two octants richer in galaxies (to remove the possible contaminating structure) and the two poorest ones (not to bias the average). We found indistinguishable profiles (apart for the reduced S/N), indicating that our profiles are robust to contaminating clusters/groups. Inspection of the 2D weak-lensing mass maps of Umetsu et al. (2014) shows substructures in the mass distribution of MACJ0329, which has an obvious secondary mass peak also pointed out by the shape of the gravitational arc and the distribution of galaxies. RXJ1347 also shows a secondary mass peak, also pointed out by the two similarly bright BCGs. MACSJ1206 instead shows a more regular mass map and therefore could be in a more evolved dynamical status of the other two clusters. It seems, therefore, that mass segregation (i.e., the regular steepening of the faint-end slope) is most obvious in the most evolved cluster, MACSJ1206. A larger sample of clusters is however needed to secure such an interpretation.
The bottom panel of Fig. 2 shows the projected surface mass density Σ (i.e., the mass included in the corona divided by its area) of both galaxy populations. These profiles are the main results of this section, and one of the two main ingredients of the computation of the stellar-to-total matter ratio described in the next section.
Fitting the stellar mass profiles with a NFW radial profile, for example to measure the relative distribution of stellar and total mass following previous works, is a risky operation because we known that the NFW profile is supposed to represent the mean, not every single, halo. Many clusters are known to possess total and stellar mass substructures and to live in complex environments. Because the model radial profile does not capture the complexity of the data being fitted, the best fit parameters depend, for example, on the fitted radial range. As mentioned, MACJ0329 and RXJ1347 both possess a secondary massive halo. Close inspection of the total surface mass density profile in Umetsu et al. (2014) shows deviations from a NFW radial profile, and indeed these are also present in our stellar mass density profiles. Therefore, we avoid fitting NFW radial profiles to stellar mass density profiles to measure the relative distribution of stellar and total mass.
To summarize, the characteristic mass is radial and cluster independent and shows minor differences depending on the considered population. The faint-end slope is, instead, radial dependent. In the more evolved cluster, MACSJ1206, the faint-end regularly steepens with increasing clustercentric radius. The other two clusters, both characterized by substructure, show more erratic faint-end slope radial profiles. Irrespective of the regular or erratic behavior of the radial profile of the faint-end slope, we surely cannot force the contribution of low-mass galaxies to be radial-independent, a modeling first enabled in this work.
4. Radial profile of the stellar-to-total matter ratio
In this section we investigate whether stellar mass and total mass are similarly spatially distributed by computing the radial profile of the stellar-to-total matter ratio. The two most important improvements of this work are the use of a radial-model-free estimate of the total and stellar mass, and the building of a framework able to properly use these data. We must avoid operating (rebinning or dividing) on the data, especially the weak lensing data, because this would destroy or distort the signal and noise there. In fact, there is an important covariance that naturally arises between weak lensing mass estimates in different coronae because they satisfy the observed cumulative mass constraint (Coe et al. 2010). One of the coronae in which stellar mass is measured consists of the union of three Umetsu et al. (2014) radial bins and weak lensing estimates extend to clustercentric radii larger than our stellar mass determination. Radial bins cannot be dropped or ignored (e.g., because they lack the corresponding stellar mass estimate) and we have to operate on the model, not on the data. The adoption of a Bayesian approach (Gelman et al. 2003) naturally solves all these problems.
4.1. Methods
Umetsu et al. (2014) give the posterior distribution of the surface total mass profile in 11 radial bins in the form of a maximum likelihood estimate si and its covariance matrix Cstat; this covariance matrix is a measure of the uncertainty, inclusive of the covariance across radial bins, of the mass estimate as derived from the joint likelihood analysis of shear and magnification data, 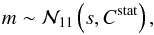 (1)where
(1)where 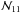 is the multinormal distribution in 11 dimensions (the 11 radial bins) and the symbol ~ reads “drawn from”.
is the multinormal distribution in 11 dimensions (the 11 radial bins) and the symbol ~ reads “drawn from”.
Projection noise (corresponding to Clss in Umetsu et al. 2014 notation) similarly affects both weak lensing and our stellar mass estimate and thus can be (and is) ignored. Systematics (corresponding to Csys in Umetsu et al. 2014 notation) are accounted for by allowing the mass, mt, to fluctuate around the true mass, m, by an amount given by Csys: 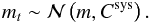 (2)As in Umetsu et al. (2014), a positively defined mass mt is enforced in all radial bins. We require that a >1012M⊙ mass be present in every radial bin and we checked that results do not depend on the minimal mass we assumed.
(2)As in Umetsu et al. (2014), a positively defined mass mt is enforced in all radial bins. We require that a >1012M⊙ mass be present in every radial bin and we checked that results do not depend on the minimal mass we assumed.
 |
Fig. 3 Radial profile of the stellar-to-total matter ratio of MACSJ1206 (left), MACSJ0329 (center), and RXJ1347 (right). The upper panels only consider red sequence galaxies, whereas lower panels consider red galaxies and BCGs. The multi-step function and the shading indicate soundly derived values (posterior mean) and 68 % errors (highest posterior interval), whereas points and error bars are approximate (see text). |
Coming to the surface stellar mass profile, the results of our analysis can be summarized as 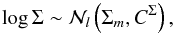 (3)where l is 6 or 7 (the number of stellar mass radial bins), Σm is the posterior mean (i.e., the point estimate in previous section), and the covariance vector CΣ is a diagonal matrix having as elements the square of the posterior standard deviation (errors of previous section). For our stellar masses there is almost no covariance across radial bins because the measurement is local, considering the luminosity of galaxies inside the corona. Instead, measurements are global in weak-lensing estimates. In the stellar mass measurements the only source of covariance comes from the uncertainty of the mean background stellar mass because it is inferred from a reference line of sight common to all radial bins. However, since the mean value is fairly well determined, the covariance induced by uncertainty on the mean value is negligible and neglected (while fluctuations around it are important and accounted for). In cases in which covariance is also present for stellar masses, Eq. (3) still holds, but the CΣ matrix is not diagonal.
(3)where l is 6 or 7 (the number of stellar mass radial bins), Σm is the posterior mean (i.e., the point estimate in previous section), and the covariance vector CΣ is a diagonal matrix having as elements the square of the posterior standard deviation (errors of previous section). For our stellar masses there is almost no covariance across radial bins because the measurement is local, considering the luminosity of galaxies inside the corona. Instead, measurements are global in weak-lensing estimates. In the stellar mass measurements the only source of covariance comes from the uncertainty of the mean background stellar mass because it is inferred from a reference line of sight common to all radial bins. However, since the mean value is fairly well determined, the covariance induced by uncertainty on the mean value is negligible and neglected (while fluctuations around it are important and accounted for). In cases in which covariance is also present for stellar masses, Eq. (3) still holds, but the CΣ matrix is not diagonal.
To deal with our second radial bin, formed by the union of the second to fourth Umetsu et al. (2014) bins, we only need to remember that the mean mass surface density inside any combination of bins is just the average over the concerned bins.
We assume a linear relation with slope γ and intercept β between the log of the stellar mass fraction and log of radius: 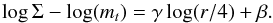 (4)As in Andreon et al. (2006, 2010), for example, we adopt a log scale because fractions are positively defined, while a linear scale would allow, at least in principle, unphysical (negative) values for the fraction. We zero-point radii at 4 arcmin in order to have intercepts (stellar mass fractions) at radii close to r500.
(4)As in Andreon et al. (2006, 2010), for example, we adopt a log scale because fractions are positively defined, while a linear scale would allow, at least in principle, unphysical (negative) values for the fraction. We zero-point radii at 4 arcmin in order to have intercepts (stellar mass fractions) at radii close to r500.
Finally, we adopt weak priors on the slope γ and intercept β, respectively a Student-t distribution (which is uniform on the angle), as in Andreon & Hurn (2010), and a Gaussian with large σ. These equations are solved by using a Marcov chain Monte Carlo sampler (JAGS, Plummer 2010). For drawing figures we instead operate on data and sum errors in quadrature and ignore covariance across radial bins.
The method detailed above, together with the methods described in Sect. 3.1, is the second result of this work, allowing us to confidently state the significance of found radial trends, or lack of them.
4.2. Results
Figure 3 shows the derived radial profiles of the stellar-to-total matter ratio.
RXJ1347 has a stellar fraction lower than the other two clusters, which is unsurprising because the stellar mass fraction decreases with cluster mass (Andreon 2010, 2012; Gonzalez et al. 2014), and this cluster has a much larger mass than the other two clusters (which are of comparable mass).
The radial profiles are very flat, especially the properly derived values (multistep function), with no evidence of gradients. Indeed, | γ | < 0.1 with error 0.33−0.50 (depending on the sample). This is one of the two main results of this work and shows that cold baryons (stars) are distributed as total mass over a wide range of clustercentric radii, 0.2 ≲ r/r200 ≲ 1.6.
From a galaxy evolution perspective, the flatness of the stellar-to-total matter ratio is hard to interpret. On the one hand, it is somewhat expected because galaxy harassment (Moore et al. 1996) and the cluster tidal field should not affect the stellar mass given that the latter is locked deep in the potential wells of galaxies. On the other hand, harassment and tidal field are able to strip part of the dark matter of both individual galaxies and infalling groups; i.e., they increase the stellar-to-total matter ratio. This infalling material, in turn, has a larger stellar-to-total matter ratio according to observations (e.g., Andreon 2010, which is also a consequence of the different shape of the luminosity and mass functions; Moster et al. 2010) and this, together with the stripping of part of the fragile dark halo, increases the contrast between the high ratio of infalling material and the low ratio of already fallen one. To keep the cluster (=fallen+infalling) profile flat, a redistribution of the dark matter component is therefore needed. Given that only a few crossing times have taken place in a Hubble time because of the large cluster size, the redistribution have not to take several crossing times to keep the cluster profile flat. Therefore, a mechanism much faster than the crossing time, and some fine-tuning, is needed to keep flat the ratio radial profile.
Neither a fast mechanism nor fine-tuning is needed if the infalling material includes not only halos with large values of stellar-to-total matter (i.e., groups and massive galaxies), but also halos of much lower mass (less massive galaxies and perhaps halos without any galaxy inside it), because the latter have a stellar content per unit mass comparable with, or lower than, the cluster composition (Hudson et al. 2015). A flat radial profile can be therefore naturally achieved if the stellar-to-total matter ratio of each infalling shell has a value for the ratio close to the already fallen material. Indeed, the M/L also seems nearly constant at the largest scales (Bahcall & Kulier 2014, and references therein), making fine-tuning and a fast mechanism unnecessary. However, the latter observations are measuring something conceptually different from a radial profile: measurements at different scales pertain to different objects, not to the same objects observed at larger radii. This means that our proposal still needs to be observationally confirmed.
It would be interesting to quantify these ideas using numerical simulations of the growth of clusters from their surrounding environments; however, this requires a numerical simulation of a quality higher than currently available. To test these ideas we need simulations with halos having a mass-dependent stellar-to-total matter ratio and current simulations fail to reproduce this feature (Andreon 2010; Young et al. 2011; Planelles et al. 2013; Battaglia et al. 2013).
From a cosmological perspective, the close resemblance of total and stellar matter profiles can be useful to improve lensing- and dynamical-based mass estimates by adopting the stellar matter profile as a prior for the total matter profile. The common flat M/L radial profiles found in the literature (see Introduction and next section) support our results obtained from a more detailed analysis (of only three clusters, however). This prior has already been exploited in some strong-lensing analyses such as Grillo et al. (2015) and Kneib et al. (1996), and our result of a flat radial profile supports their use. The similarity of total and stellar matter profiles is also cosmologically attractive for using the stellar matter profile as a mass proxy. This can be achieved either using the profile alone (i.e., only using the cluster size), or in combination with the stellar matter fraction. The simplest implementation of the former approach needs to assume a parametric form for the radial profile (e.g., a NFW profile), although nonparametric forms for the radial profiles are possible too, and have been used since Kneib et al. (1996). Instead, using the stellar matter profile together with the stellar matter fraction requires, at first sight, knowledge of mass (to compute the fraction). However, this dependency (degeneracy) may be broken as is done for the YX and YSZ proxies (which requires knowledge of rΔ, i.e., MΔ) by assuming the observed scaling relation (the mass-stellar fraction relation in our case). We leave this exploration to a later paper.
Finally, the flat stellar-to-total matter ratio profile is a technically important ingredient whose knowledge is needed for fitting the trend between stellar mass fraction and halo mass: if the radial profile is flat, the uncertainty on r500 induces a complete covariance between total and stellar masses.
4.2.1. Comparison with previous works
Before comparing our results to literature works, we emphasize differences between related, but distinct, concepts: light cannot be interpreted as stellar mass if the age of the stellar population is unconstrained, which makes the M/L different from the stellar-to-total matter ratio. Furthermore, as already mentioned, the radial profile of the stellar-to-total matter ratio is also conceptually different from the increase of the mass-to-light ratio with spatial scale (studied in, e.g., Bahcall et al. 1995 and references therein). Finally, one may have a constant stellar-to-total mass fraction and a luminosity segregation (brighter galaxies more concentrated in the cluster center, as in MACSJ1206 for example). Therefore the presence (or absence) of a luminosity segregation is not a measure of the stellar-to-total fraction profile, in particular of its radial trend.
Our flat radial profiles in stellar-to-total matter ratio confirm the many flat M/L profiles found in previous works and improve on them because they are based on state-of-the-art weak lensing. Unlike most previous works, our work offers a better sensitivity to radial gradients because it uses differential quantities (most previous works compute M/L( <r), not M/L(r)), does not assume a parametric form for the mass profile, does not miss stellar mass in non-RS galaxies or in galaxies of low-mass, discriminates star formation from stellar mass, does not assume a constant faint-end slope, and presents a sounder analysis accounting for error and covariance terms ignored in past works. Compared to analyses based on an “ensemble” cluster, such as the dynamical analysis by Carlberg et al. (1997), our result is independent of the assumption of the dynamical equilibrium and orbit distribution and, being derived on individual clusters, ensures that the found constancy of the stellar-to-total matter ratio is not an artifact of the scaling laws adopted to construct the ensemble.
Unlike a few literature findings, we do not find decreasing stellar-to-total matter ratio profiles. In particular, we do not confirm the tentative trend seen for RXJ1347 by Medezinski et al. (2010) which is remarkable because both weak lensing and stellar masses are based on non-independent data (Suprime-Cam images). We note, however, that Medezinski et al. (2010) use parametric weak-lensing mass estimates (from Broadhurst et al. 2008), not the radial nonparametric estimate we use (from Umetsu et al. 2014), and we have already remarked that individual clusters show deviation from the universal radial profile, including RXJ1347. We also warn that Medezinski et al. (2010) use very uncertain corrections for the background contamination, so uncertain that they are outside the physical range (0 to 100%) half of the time. We also do not confirm the main Annunziatella et al. (2014) conclusion on MACSJ1206, largely based on the same Subaru data used here, claiming a more concentrated dark matter distribution than stellar mass. Their conclusion, just as is the Medezinski et al. (2010) conclusion, is conditional upon the assumption that MACSJ1206 has a NFW profile. It is notable in this context that Young et al. (2014), having collected various evidence for the presence of a second component aligned in the cluster line of sight, fit a multi-halo NFW profile to weak lensing data of this cluster. When Annunziatella et al. (2014) get rid of this assumption (their Fig. 12) the ratio of the two mass profiles shows no trend with radius and is consistent with a single constant at all radii, precisely as our radial stellar-to-total matter ratio profile is. Finally, although our data are sensitive to gradients as large as those observed in Abell 576 by Rines et al. (2001), we do not observe them in the studied clusters. As remarked in Rines et al. (2001), the statistical significance of their found gradient is hard to establish because their analysis does not account for the mass covariance across radial bins; i.e., it lacks the necessary formalism introduced in our Sects. 3.1 and 4.1 several years after their paper. This shows, once more, that the significance of a claimed radial term, and the upper limit in case of a lack of detection, depends on which terms are included in the error budget, and, generally speaking, other works have smaller errors in spite of worse data because they include an inferior number of terms in the error budget (see Appendix B for details).
Finally, we conclude by pointing out the main limitation of our work. Since we use radial bins (largely fixed by weak-lensing measurements), we cannot explore the trend of the stellar-to-total matter ratio at scales lower than half the inner bin size, i.e., within the inner 150 kpc or 0.15r200. Measurements performed by Newman et al. (2013) nicely complement our work.
5. Summary
In this paper we used the extremely deep multicolor wide-field Suprime-Cam optical images and state-of-the-art accurate, yet projected, weak lensing masses to derive the relative distribution of stellar and total matter of three massive intermediate-redshift clusters. Weak lensing does not oblige us to make assumptions about the cluster dynamical (or hydrostatic) status, and our choice of using nonparametric estimates makes our derivation free from assumptions about the shape of the mass radial profile. Unlike most previous works, our analysis offers a better sensitivity to radial gradients because we use differential quantities (however projected along the line of sight). Our analysis pays special attention to items that are usually underrated: the stellar mass in galaxies outside the red sequence; those in galaxies of low mass, in particular below the observational limit (log M/M⊙ = 9.7 in our study); possible mass segregation and cluster substructure; uncertainty on the mean background value and background fluctuations (in number and in mass at a given total number); and discrimination of star formation from stellar mass. Given that we account for all source of errors (that we are aware of), and also mass covariance across radial bins, we can confidently state the significance of found radial trends, or lack of them. Building the statistical framework able to properly use the data is one of the two main results of this work.
The characteristic mass is radial and cluster independent and shows minimal differences depending on the considered population (log M∗/M⊙ = 11.27 ± 0.04 for red sequence galaxies and log M∗/M⊙ = 11.42 ± 0.03 for R+BCG galaxies). The faint-end slope is, instead, radial dependent, indicating mass segregation. In MACSJ1206, the cluster more regular and evolved and showing less substructure, the faint-end regularly steepens with increasing clustercentric radius. The other two clusters, both characterized by a second mass clump, show more erratic radial behaviors. Whether or not the radial profile of the faint-end slope is regular or erratic, the faint-end slope surely cannot be forced to be radial independent in the total luminosity computation.
The main result of this work is that the radial profile of the stellar-to-total mass is constant from about 150 kpc to the virial radius and beyond for the three studied clusters. Our sensitivity to gradients is a factor of two per decade in radius. The constant fraction is due to the remarkable similarly of the spatial distribution of stellar and dark (total) mass and implies that dark matter and cold baryons (stars) are very tightly coupled over a remarkable range of environmental densities going from the cluster core to its virial radius.
Online material
Appendix A: Other figures
This appendix presents the mass function of RS and of R+BCG galaxies in RXJ1347 and in MACJ0329 at various clustercentric radii.
 |
Fig. A.1 Mass function of red sequence (upper panels) and red galaxies plus BCG (lower panels) of RXJ1347 in various clustercentric radial bins, as detailed in the panels. Caption as in Fig. 1. |
 |
Fig. A.2 As previous figure, but for MACSJ0329. |
Appendix B: Fitting details and systematics
A proper estimation of the error is paramount to properly claim as significant a stellar-to-total matter (or M/L) ratio radial trend. In general, our stellar mass errors are much larger than those returned by procedures adopted in literature, sometime by a factor of 10 because these works chose not to include in the error budget terms that we instead consider important, for example Poisson fluctuations of the total number of background galaxies and of their number at a given mass. We see no reason why the background population in the cluster and control field lines of sight should be exactly average in number and total mass. We verified the existence of these well-known fluctuations by splitting the reference line of sight in parts. These number and mass fluctuations make the stellar mass in the background population subject to fluctuations much larger than those coming from photometric errors alone (i.e., the stochastic mass errors). This is a large source of uncertainty at all clustercentric radii except at the cluster center, where the background contamination is minimal. It is modeled in our work, but rarely included in previous works. Second, in addition to these Poisson fluctuations, the parameters that describe the mass distribution of background galaxies are measured with a finite precision, and we need to marginalize over this uncertainty too (i.e., over the uncertainty of the parameters describing the average expected background population). This marginalization is
naturally implemented in our Bayesian approach. This error term is minor for our own analysis because a large solid angle observed in fully homogeneous conditions is available for the mean background estimation, but is major, yet neglected, in some works. Third, given the extreme depth of our data, the stellar mass at masses lower than the mass completeness limit is negligible for whatever faint-end slope α> −2 for our study. Nevertheless, we account for it by marginalizion. Data of such depth are rare at best in the literature, yet we are aware of no previous work computing the stellar-to-total matter (or M/L) ratio profile that marginalizes over the faint-end slope uncertainty. Indeed, most studies do not even account for the possible different faint-end slope at different cluster-centric radii.
Some works use spectroscopic samples. Although the background contamination can be derived using spectroscopic redshifts, the sample with spectroscopic data is only a fraction of the whole sample needed to measure the total stellar mass, and the background contribution has to be inferred for the subsample without spectroscopic data. This is achieved by taking the estimate derived from the spectroscopic sample, assuming that there are no background fluctuations between the spectroscopic and photometric sample, and that the derived correction is perfectly known, none of which is true. Therefore, and for the same reasons just discussed, works using spectroscopic samples also have been too optimistic in their estimation of the stellar mass errors.
Acknowledgments
I acknowledge Keiichi Umetsu for giving me the mass profiles in tabular format and for useful discussion, the CLASH team for distributing the reduced Subaru images, Susan Planelles and Nick Battaglia for passing me in electronic form their stellar-to-total profiles, Elinor Medezinski and Andrea Biviano for useful discussion, and Kristin Riebe for help in using cosmological simulations. Annalisa Pillepich is thanked for an attentive reading of this paper.
References
- Andreon, S. 2002a, A&A, 382, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2002b, A&A, 382, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S. 2006, MNRAS, 369, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., 2008, MNRAS, 386, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2010, MNRAS, 407, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S. 2012, A&A, 548, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2010, MNRAS, 404, 1922 [NASA ADS] [Google Scholar]
- Andreon, S., & Hurn, M. A. 2013, Statistical Analysis and Data Mining, 6, 15 [Google Scholar]
- Andreon, S., Punzi, G., & Grado, A. 2005, MNRAS, 360, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Quintana, H., Tajer, M., Galaz, G., & Surdej, J. 2006, MNRAS, 365, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Puddu, E., de Propris, R., & Cuillandre, J.-C. 2008, MNRAS, 385, 979 [NASA ADS] [CrossRef] [Google Scholar]
- Andreon, S., Newman, A. B., Trinchieri, G., et al. 2014, A&A, 565, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Annunziatella, M., Biviano, A., Mercurio, A., et al. 2014, A&A, 571, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Applegate, D. E., von der Linden, A., Kelly, P. L., et al. 2014, MNRAS, 439, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & Kulier, A. 2014, MNRAS, 439, 2505 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., Lubin, L. M., & Dorman, V. 1995, ApJ, 447, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2013, ApJ, 777, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Rosati, P., Balestra, I., et al. 2013, A&A, 558, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Voyer, E., Boissier, S., et al. 2014, A&A, 570, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Butcher, H., & Oemler, A., Jr. 1984, ApJ, 285, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Budzynski, J. M., Koposov, S. E., McCarthy, I. G., & Belokurov, V. 2014, MNRAS, 437, 1362 [NASA ADS] [CrossRef] [Google Scholar]
- De Propris, R., Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 2003, ApJ, 598, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A., & Geller, M. J. 1997, ApJ, 481, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Oemler, A., Jr., Poggianti, B. M., et al. 2013, ApJ, 770, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Durret, F., Adami, C., & Lobo, C. 2002, A&A, 393, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evrard, A. E. 1987, ApJ, 316, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Eyles, C. J., Watt, M. P., Bertram, D., et al. 1991, ApJ, 376, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Fabricant, D., Beers, T. C., Geller, M. J., et al. 1986, ApJ, 308, 530 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, J., Poggianti, B. M., Cava, A., et al. 2014, A&A, 566, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gill, S. P. D., Knebe, A., & Gibson, B. K. 2005, MNRAS, 356, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., Oemler, A., Dressler, A., et al. 2013, ApJ, 770, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Grillo, C., Suyu, S. H., Rosati, P., et al. 2015, ApJ, 800, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Smith, G. P., Egami, E., et al. 2009, ApJ, 704, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Franx, M., Kuijken, K., & Squires, G. 1998, ApJ, 504, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., Mahdavi, A., Babul, A., & Bildfell, C. 2012, MNRAS, 427, 1298 [NASA ADS] [CrossRef] [Google Scholar]
- Hoshino, A., Henry, J. P., Sato, K., et al. 2010, PASJ, 62, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, M. J., Gillis, B. R., Coupon, J., et al. 2015, MNRAS, 447, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, E. M., Jerjen, H., Ryder, S. D., & Driver, S. P. 2008, AJ, 136, 1866 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Yepes, G., Gottlober, S., Prada, F., & Hess, S. 2014, MNRAS, submitted [arXiv:1411.4001] [Google Scholar]
- Kneib, J.-P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Kneib, J.-P., Hudelot, P., Ellis, R. S., et al. 2003, ApJ, 598, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, Y., Smail, I., Kurk, J., et al. 2013, MNRAS, 434, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A., Vikhlinin, A., & Meshscheryakov, A. 2014, ApJ, submitted [arXiv:1401.7329] [Google Scholar]
- Mamon, G. A., Biviano, A., & Boué, G. 2013, MNRAS, 429, 3079 [NASA ADS] [CrossRef] [Google Scholar]
- Medezinski, E., Broadhurst, T., Umetsu, K., et al. 2010, MNRAS, 405, 257 [NASA ADS] [Google Scholar]
- Medezinski, E., Umetsu, K., Nonino, M., et al. 2013, ApJ, 777, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Mellier, Y. 1999, ARA&A, 37, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Merten, J., Meneghetti, M., Postman, M., et al. 2014, ApJ, submitted [arXiv:1404.1376] [Google Scholar]
- Meyers, J., Aldering, G., Barbary, K., et al. 2012, ApJ, 750, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Miyazaki, S., Komiyama, Y., Sekiguchi, M., et al. 2002, PASJ, 54, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Newman, A. B., Treu, T., Ellis, R. S., & Sand, D. J. 2013, ApJ, 765, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Oemler, A., Jr., Dressler, A., Gladders, M. G., et al. 2013, ApJ, 770, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Pahre, M. A., de Carvalho, R. R., & Djorgovski, S. G. 1998, AJ, 116, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Planelles, S., Borgani, S., Dolag, K., et al. 2013, MNRAS, 431, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Plummer, M. 2010, JAGS Version 2.2.0 user manual [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Raichoor, A., & Andreon, S. 2012a, A&A, 537, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raichoor, A., & Andreon, S. 2012b, A&A, 543, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., Mohr, J. J., & Wegner, G. A. 2000, AJ, 120, 2338 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Kurtz, M. J., et al. 2001, ApJ, 561, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., Kurtz, M. J., & Jarrett, T. H. 2004, AJ, 128, 1078 [NASA ADS] [CrossRef] [Google Scholar]
- Sandage, A., Tammann, G. A., & Yahil, A. 1979, ApJ, 232, 352 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Smail, I., Ellis, R. S., Fitchett, M. J., & Edge, A. C. 1995, MNRAS, 273, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Broadhurst, T., et al. 2010, ApJ, 714, 1470 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2012, ApJ, 755, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Umetsu, K., Medezinski, E., Nonino, M., et al. 2014, ApJ, 795, 163 [NASA ADS] [CrossRef] [Google Scholar]
- von der Linden, A., Allen, M. T., Applegate, D. E., et al. 2014, MNRAS, 439, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, G., Kaiser, N., & Luppino, G. A. 2001, ApJ, 556, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Young, O. E., Thomas, P. A., Short, C. J., & Pearce, F. 2011, MNRAS, 413, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Young, A. H., Mroczkowski, T., Romero, C., et al. 2014 [arXiv:1411.0317] [Google Scholar]
- Zwicky, F. 1933, Helvetica Physica Acta, 6, 110 [Google Scholar]
All Figures
 |
Fig. 1 Mass function of red sequence (upper panels) and red galaxies plus BCG (lower panels) of MACSJ1206 in various clustercentric radial bins, as detailed in the panels. The arrow indicates the total mass inside the considered radial bin, disregarding the BCG, if any. The solid line is the mean model fitted to the individual galaxy data, while the shading indicates the 68% uncertainty (highest posterior density interval). Points and approximated error bars are derived by binning galaxies in magnitude bins, adopting approximated Poisson errors summed in quadrature, as commonly done in the literature. |
| In the text | |
 |
Fig. 2 Radial profile of the characteristic stellar mass (upper panels), faint-end slope α (central panels) and projected surface stellar mass density (bottom panels) of the three clusters (MACSJ1206, MACSJ0329, and RXJ1347, from left to right). The central-left panel report the fitted linear trend. Arrows indicate rΔ values and are from Merten et al. (2014). The surface stellar mass density Σ is in M⊙/Mpc2 units. |
| In the text | |
 |
Fig. 3 Radial profile of the stellar-to-total matter ratio of MACSJ1206 (left), MACSJ0329 (center), and RXJ1347 (right). The upper panels only consider red sequence galaxies, whereas lower panels consider red galaxies and BCGs. The multi-step function and the shading indicate soundly derived values (posterior mean) and 68 % errors (highest posterior interval), whereas points and error bars are approximate (see text). |
| In the text | |
 |
Fig. A.1 Mass function of red sequence (upper panels) and red galaxies plus BCG (lower panels) of RXJ1347 in various clustercentric radial bins, as detailed in the panels. Caption as in Fig. 1. |
| In the text | |
 |
Fig. A.2 As previous figure, but for MACSJ0329. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


