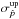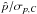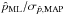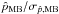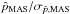| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 20 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201424451 | |
| Published online | 10 February 2015 | |
Polarization measurement analysis
II. Best estimators of polarization fraction and angle⋆
1
Université de Toulouse, UPS-OMP, IRAP,
31028
Toulouse Cedex 4,
France
e-mail:
ludovic.montier@irap.omp.eu
2
CNRS, IRAP, 9
Av. Colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
3
Laboratoire de l’Accélérateur Linéaire, Université Paris-Sud 11,
CNRS/IN2P3, Orsay,
France
4
LERMA/LRA–ENS Paris et Observatoire de Paris,
24 rue Lhormond, 75231
Paris Cedex 05,
France
5
Institut d’Astrophysique Spatiale, CNRS (UMR8617), Université
Paris-Sud 11, Bâtiment
121, Orsay,
France
Received: 23 June 2014
Accepted: 25 November 2014
With the forthcoming release of high precision polarization measurements, such as from the Planck satellite, it becomes critical to evaluate the performance of estimators for the polarization fraction and angle. These two physical quantities suffer from a well-known bias in the presence of measurement noise, as described in Part I of this series. In this paper, Part II of the series, we explore the extent to which various estimators may correct the bias. Traditional frequentist estimators of the polarization fraction are compared with two recent estimators: one inspired by a Bayesian analysis and a second following an asymptotic method. We investigate the sensitivity of these estimators to the asymmetry of the covariance matrix, which may vary over large datasets. We present for the first time a comparison among polarization angle estimators, and evaluate the statistical bias on the angle that appears when the covariance matrix exhibits effective ellipticity. We also address the question of the accuracy of the polarization fraction and angle uncertainty estimators. The methods linked to the credible intervals and to the variance estimates are tested against the robust confidence interval method. From this pool of polarization fraction and angle estimators, we build recipes adapted to different uses: the best estimators to build a mask, to compute large maps of the polarization fraction and angle, and to deal with low signal-to-noise data. More generally, we show that the traditional estimators suffer from discontinuous distributions at a low signal-to-noise ratio, while the asymptotic and Bayesian methods do not. Attention is given to the shape of the output distribution of the estimators, which is compared with a Gaussian distribution. In this regard, the new asymptotic method presents the best performance, while the Bayesian output distribution is shown to be strongly asymmetric with a sharp cut at a low signal-to-noise ratio. Finally, we present an optimization of the estimator derived from the Bayesian analysis using adapted priors.
Key words: polarization / methods: data analysis / methods: statistical
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The complexity of polarization measurement analysis has been described by Serkowski (1958) when discussing the presence of a systematic bias in optical measurements of linear polarization from stars, and then by Wardle & Kronberg (1974) when addressing the same issue in the field of radio astronomy. The bias of polarization measurements happens when one is interested in the polarization intensity 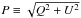 or in the polarization fraction p ≡ P/I and the polarization angle
or in the polarization fraction p ≡ P/I and the polarization angle 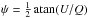 where I, Q, and U are the Stokes parameters, quantities that become systematically biased in the presence of noise. Working with the Stokes parameters Q and U as far as possible avoids this kind of bias.
where I, Q, and U are the Stokes parameters, quantities that become systematically biased in the presence of noise. Working with the Stokes parameters Q and U as far as possible avoids this kind of bias.
Once a physical modelling of p and ψ is available and can be translated into Q and U, a likelihood analysis can be performed directly on the Stokes parameters. For the other cases, where no modelling is available, Simmons & Stewart (1985) proposed the first compilation and comparison of methods to deal with the problem of getting unbiased polarization estimates of the polarization fraction and angle, with their associated uncertainties. Then Naghizadeh-Khouei & Clarke (1993) extended the work of Simmons & Stewart (1985) to the characterization of the polarization angle uncertainties, and Vaillancourt (2006) have proposed a method for building confidence limits on polarization fraction measurements.
More recently, Quinn (2012) has suggested using a Bayesian approach to get better polarization estimates. In all these studies, the authors have made strong assumptions: negligible or no noise on the intensity I and no correlation between the Q and U components, which were also assumed to have equal noise properties. Montier et al. (2015, hereafter PMA I) have quantified the impact of the asymmetry and the correlation between the Q and U noise components on the bias of the polarization fraction and angle measurements. They have shown that the asymmetry of the noise properties cannot be systematically neglected as is usually done and that the uncertainty of the intensity may significantly affect the polarization measurements in the low signal-to-noise (S/N) regime.
In the context of the new generation of polarization data, such as Planck1 (Planck Collaboration I 2011), Blast-Pol (The Balloon-borne Large Aperture Submillimeter Telescope for Polarimetry, Fissel et al. 2010), PILOT (Bernard et al. 2007), or ALMA (Pérez-Sánchez & Vlemmings 2013), which benefit from much better control of the noise properties, it is essential to take the full covariance matrix into account when deriving the polarization measurement estimates. In recent works no correction for the bias of the polarization fraction has been applied (e.g., Dotson et al. 2010), or only high S/N data were used for analysis (>3) to avoid these issues (e.g., Vaillancourt & Matthews 2012). Two issues are immediately apparent. First, this choice of the S/N threshold may not be relevant for all measurements, and the asymmetry between the orthogonal Stokes noise components could affect the threshold choice. Second, the question remains of how to deal with low S/N data. Using simply the measurements of the polarization parameters (we call them the “naïve” ones) as estimators of the true values leads to very poor performance, because they lack any information on the noise power. Instead, we would like to perform some transformation on the polarization parameters, in order to remove bias and improve the variance.
This work is the second in a series on “Polarization measurement analysis”. Its aim is to describe how to recover the true polarization fraction p0 and polarization angle ψ0 with their associated uncertainties from a measurement (p, ψ), taking the full covariance matrix Σ into account. We compare the performance of the various estimators that are available and study the impact of the correlation and ellipticity of the covariance matrix on these estimates. We stress that we adopt a frequentist approach to investigate the properties of these estimators, even when dealing with the method inspired by the Bayesian analysis. This means that the estimators are defined as single-value estimates, instead of considering the probability density function (PDF) as the proper estimate, as is usually done in Bayesian methods. The performance of these estimators will be evaluated using three main criteria: the minimum bias, the smallest risk function, and the shape of the distribution of the output estimates. The choice of the most appropriate estimator may vary with the application at hand, and a compromise among them may be chosen to achieve good overall performance. Throughout this work we make the following two assumptions: i) circular polarization is assumed to be negligible; and ii) the noise on Stokes parameters is assumed to be Gaussian. We also define four regimes of the covariance matrix to quantify its asymmetry in terms of effective ellipticity (εeff) as described in PMA I: the extreme (1 <εeff< 2), the low (1 <εeff< 1.1), the tiny (1 <εeff< 1.01), and the canonical (εeff = 1) regimes.
The paper is organized as follows. We first review in Sect. 2 the expression and the limitations of the polarization estimators, which are extended to take the full covariance matrix into account. In Sect. 3, we discuss the meaning of the polarization uncertainties and present the different uncertainty estimators. We then compare the performance of the estimators of the polarization fraction in Sect. 4 and of the polarization angle in Sect. 5. In Sect. 6, we discuss some aspects of the problem when the total intensity I is not perfectly known. We conclude with general recipes in Sect. 7.
2. Polarization estimators
Early work on polarization estimators was based on the Rice (1945) distribution, which provides the probability of finding a measurement p for a given true value p0 and the noise estimate σp of the Q and U Stokes parameters. The noise values of the Stokes parameters were assumed to be equal (σp = σQ/I0 = σU/I0), and the total intensity was assumed to be perfectly known, I = I0. Since we would like to include the full covariance matrix, we used the generalized expression of the PDF from PMA I, which provides the probability of getting the measurements (I, p, ψ), given the true values (I0, p0, ψ0) and the covariance matrix Σ. Following the notations of PMA I, the expression of the PDF in 3D, including the intensity terms, denoted f(I,p,ψ | I0,p0,ψ0,Σ), is given by Eq. (1), where Det(Σ) = σ6, and the PDF in 2D, f2D(p,ψ | I0,p0,ψ0,Σp), by Eq. (2) when the intensity I0 is assumed to be perfectly known. ![\begin{eqnarray} \label{eq:f_ipphi} f(I,p,\psi\, | \,I_0,p_0,\psi_0, \tens{\Sigma}) = \frac{2|p|\,I^2} {\sqrt{(2\pi)^3} \sigma^3} \, \mathrm{exp} \left \lgroup - \frac{1}{2} \left[ \begin{array}{c} I -I_0 \\ p \, I\, \cos2\psi-p_0\,I_0\cos2\psi_0 \\ p \, I\, \sin2\psi-p_0\,I_0\sin2\psi_0 \\\end{array} \right] ^{T} \tens{\Sigma}^{-1} \left[ \begin{array}{c} I-I_0 \\ p\,I\,\cos2\psi-p_0\,I_0\,\cos2\psi_0\\ p\,I\,\sin2\psi-p_0\,I_0\,\sin2\psi_0\\\end{array} \right] \right \rgroup , \end{eqnarray}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq26.png) (1)
(1)![\begin{eqnarray} \label{eq:f_2d_polar} f_{\rm 2D}(p,\psi\, | \, I_0\,p_0,\psi_0, \tens{\Sigma}_p) = \frac{p} {\pi \sigma_p^2} \, \mathrm{exp} \left \lgroup - \frac{1}{2} \left( p^2 \left[ \right] ^{T} \tens{\Sigma}_{p}^{-1} \left[ \right] - 2 pp_0 \left[ \right] ^{T} \tens{\tens{\Sigma}}_{p}^{-1} \left[ \right] +p_0^2 \left[ \right] ^{T} \tens{\Sigma}_{p}^{-1} \left[ \right] \right) \right \rgroup . \end{eqnarray}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq27.png) (2)We introduced the covariance matrix reduced in 2D,
(2)We introduced the covariance matrix reduced in 2D, 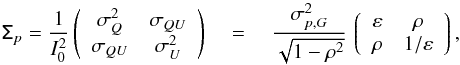 (3)where ε = σQ/σU is the ellipticity and ρ = σQU/σQσU is the correlation between the Q and U noise components, leading to an effective ellipticity given by
(3)where ε = σQ/σU is the ellipticity and ρ = σQU/σQσU is the correlation between the Q and U noise components, leading to an effective ellipticity given by 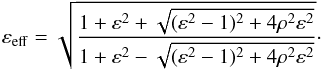 (4)With these notations, we have
(4)With these notations, we have 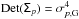 and
and 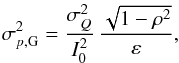 (5)which represents the equivalent radius of a circular Gaussian distribution with the same integrated area as the elliptical one. We also define σp = σQ/I0 = σU/I0 when εeff = 1. Finally the PDFs of p and ψ, fp, and fψ are obtained by marginalization of f2D over ψ and p, respectively. The expressions for the 1D PDFs fp and fψ depend on the full set of initial parameters (I0, p0, ψ0) in the general case, unlike the case under the canonical simplifications (see Appendix C of PMA I for fully developed analytical expressions).
(5)which represents the equivalent radius of a circular Gaussian distribution with the same integrated area as the elliptical one. We also define σp = σQ/I0 = σU/I0 when εeff = 1. Finally the PDFs of p and ψ, fp, and fψ are obtained by marginalization of f2D over ψ and p, respectively. The expressions for the 1D PDFs fp and fψ depend on the full set of initial parameters (I0, p0, ψ0) in the general case, unlike the case under the canonical simplifications (see Appendix C of PMA I for fully developed analytical expressions).
We describe below the various estimators of the polarization fraction and angle listed in Table 1. We stress that most of the expressions derived in this work have been obtained when restricting the analysis in the 2D case, assuming furthermore that the true intensity I0 is perfectly known, except for the Bayesian estimator where we present a 3D development (see Sect. 6).
List of the acronyms of the estimators used in this work.
2.1. Maximum likelihood estimators
The maximum likelihood (ML) estimators are defined as the values of p0 and ψ0 that maximize the PDF calculated at the polarization measurements p and ψ. When computed using the 2D PDF f2D to fit p0 and ψ0 simultaneously, this estimator gives back the measurements, regardless of the bias and the covariance matrix, and is inefficient at correcting the bias of the data.
After marginalization of the PDF f2D over ψ, the 1D ML estimator of p0,  , is now defined by
, is now defined by 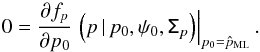 (6)The expression of fp is independent of the measurement ψ, but it still theoretically depends on the true value ψ0, which is unknown. In the canonical case (εeff = 1), ψ0 disappears from the expression, but it must be considered as a nuisance parameter in the general case. One way to proceed in such a case is to compute the mean of the solutions
(6)The expression of fp is independent of the measurement ψ, but it still theoretically depends on the true value ψ0, which is unknown. In the canonical case (εeff = 1), ψ0 disappears from the expression, but it must be considered as a nuisance parameter in the general case. One way to proceed in such a case is to compute the mean of the solutions 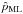 for ψ0 varying in the range − π/ 2 to π/ 2. As already stressed by Simmons & Stewart (1985), this estimator yields a zero estimate below a certain threshold of the measurement p, which implies a strong discontinuity in the resulting distribution of this p0 estimator. Nevertheless, unlike the 2D ML estimators, the p ML estimator does not give back the initial measurements, and is often used to build polarization estimates.
for ψ0 varying in the range − π/ 2 to π/ 2. As already stressed by Simmons & Stewart (1985), this estimator yields a zero estimate below a certain threshold of the measurement p, which implies a strong discontinuity in the resulting distribution of this p0 estimator. Nevertheless, unlike the 2D ML estimators, the p ML estimator does not give back the initial measurements, and is often used to build polarization estimates.
Similarly, the 1D ML estimator of ψ0, 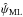 , is given after marginalization of f2D over p by
, is given after marginalization of f2D over p by 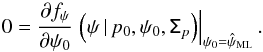 (7)As mentioned for the ML estimator
(7)As mentioned for the ML estimator 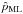 , the unknown parameter p0 in the above expression has to be considered as a nuisance parameter when solving Eq. (7). We stress that because the canonical simplifications have always been assumed in the literature, bias on the ψ measurements has not been previously considered, and the
, the unknown parameter p0 in the above expression has to be considered as a nuisance parameter when solving Eq. (7). We stress that because the canonical simplifications have always been assumed in the literature, bias on the ψ measurements has not been previously considered, and the 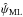 estimator has not yet been used and qualified to correct this kind of bias. This analysis is done in Sect. 5.
estimator has not yet been used and qualified to correct this kind of bias. This analysis is done in Sect. 5.
2.2. Most probable estimators
The most probable (MP) estimators of p0 and ψ0 are the values for which the PDF f2D reaches its maximum at the measurement values (p, ψ). The MP estimators ensure that the measurement values (p, ψ) are the most probable values of the PDF computed for this choice of p0 and ψ0; i.e., they take the maximum probability among all possible measurements with this set of p0 and ψ0. As a comparison, the ML estimators ensure that the measurement values (p, ψ) take the maximum probability for this choice of p0 and ψ0 compared to the probability of the same measurement values (p, ψ) for all other possible sets of p0 and ψ0.
The 2D MP estimators (MP2), 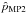 and
and 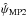 , are defined as the values of p0 and ψ0 simultaneously satisfying the two following relations:
, are defined as the values of p0 and ψ0 simultaneously satisfying the two following relations: 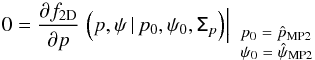 (8)and
(8)and 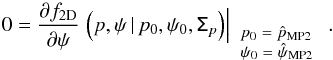 (9)These relations can be solved using the fully developed expression of f2D, including the terms of the inverse matrix
(9)These relations can be solved using the fully developed expression of f2D, including the terms of the inverse matrix 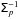 , as provided in Appendix A. When canonical simplifications are assumed, this yields
, as provided in Appendix A. When canonical simplifications are assumed, this yields 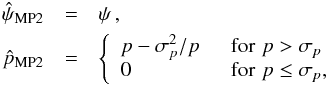 (10)as found in Wang et al. (1997) and Quinn (2012). We observe that the MP2 estimate of the polarization fraction is systematically lower than the measurements, so that this estimator tends to over-correct p, as shown in Sect. 4.
(10)as found in Wang et al. (1997) and Quinn (2012). We observe that the MP2 estimate of the polarization fraction is systematically lower than the measurements, so that this estimator tends to over-correct p, as shown in Sect. 4.
After marginalization over p or ψ, the 1D MP estimators, 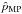 and
and 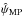 , are defined independently by
, are defined independently by 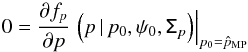 (11)and
(11)and 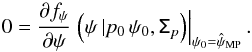 (12)The 1D and 2D estimators are not expected to provide the same estimates. Under the canonical assumptions, the MP estimator of p is commonly known as the Wardle & Kronberg (1974) estimator.
(12)The 1D and 2D estimators are not expected to provide the same estimates. Under the canonical assumptions, the MP estimator of p is commonly known as the Wardle & Kronberg (1974) estimator.
As mentioned earlier, the MP estimator yields a zero estimate below a certain threshold of p (Simmons & Stewart 1985), which implies a strong discontinuity in the resulting distribution of these estimators for low S/N measurements.
2.3. Asymptotic estimator
The asymptotic estimator (AS) of the polarization fraction p is usually defined in the canonical case by 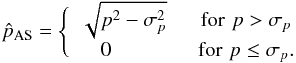 (13)The output distribution of the AS estimator appears as the asymptotic limit of the Rice (1945) distribution when p/σp tends to ∞, just as for the ML and MP estimators, and given by
(13)The output distribution of the AS estimator appears as the asymptotic limit of the Rice (1945) distribution when p/σp tends to ∞, just as for the ML and MP estimators, and given by 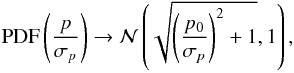 (14)where
(14)where 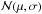 denotes the Gaussian distribution of mean μ and variance σ2. As with the previously presented estimators, this one suffers from a strong discontinuity at
denotes the Gaussian distribution of mean μ and variance σ2. As with the previously presented estimators, this one suffers from a strong discontinuity at 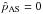 .
.
In the general case, when the canonical simplification is not assumed, it has been shown by Plaszczynski et al. (2014, hereafter P14) that the expression of the asymptotic estimator can be extended to a general expression by changing the term 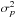 in Eq. (13) into a “noise-bias” parameter b2 defined by
in Eq. (13) into a “noise-bias” parameter b2 defined by 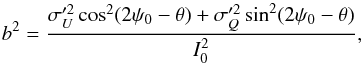 (15)where θ represents the position angle of the iso-probability bi-variate distribution, and
(15)where θ represents the position angle of the iso-probability bi-variate distribution, and 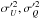 the rotated variances
the rotated variances
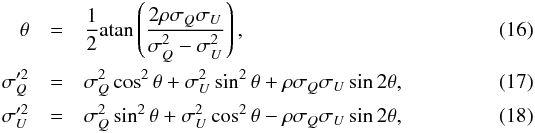 and ψ0 is the true polarization angle, which can be approximated asymptotically by the naïve measurement ψ or, even better, by the estimate
and ψ0 is the true polarization angle, which can be approximated asymptotically by the naïve measurement ψ or, even better, by the estimate 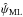 of Sect. 2.1. It has been shown that b2 ensures the minimal bias of
of Sect. 2.1. It has been shown that b2 ensures the minimal bias of 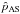 .
.
 |
Fig. 1 Distributions of |
2.4. Discontinuous estimators
The estimators of  introduced above (ML, MP, and AS) exhibit a common feature: below some cutoff value the estimator yields exactly zero. This means that the estimator distribution is discontinuous and is a mixture of a discrete one (at
introduced above (ML, MP, and AS) exhibit a common feature: below some cutoff value the estimator yields exactly zero. This means that the estimator distribution is discontinuous and is a mixture of a discrete one (at 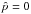 ) and a continuous one (for
) and a continuous one (for 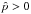 ). This type of distribution is illustrated in Fig. 1 for a S/N of p0/σp = 1 and a canonical covariance matrix. The distribution of the naïve measurements is built using 100 000 Monte-Carlo simulations, starting from true polarization parameters p0 and ψ0. The other three distributions of
). This type of distribution is illustrated in Fig. 1 for a S/N of p0/σp = 1 and a canonical covariance matrix. The distribution of the naïve measurements is built using 100 000 Monte-Carlo simulations, starting from true polarization parameters p0 and ψ0. The other three distributions of  are obtained after applying the ML, MP and AS estimators. A non-negligible fraction of the measurements provide null estimates of
are obtained after applying the ML, MP and AS estimators. A non-negligible fraction of the measurements provide null estimates of  . As shown in Fig. 2, this fraction of null estimates reaches 40% at low S/N with the MP and AS estimators, and more than 50% with the ML estimator for S/N< 1. It converges to 0% for S/N> 4.
. As shown in Fig. 2, this fraction of null estimates reaches 40% at low S/N with the MP and AS estimators, and more than 50% with the ML estimator for S/N< 1. It converges to 0% for S/N> 4.
If taken into account as a reliable estimate of  , null estimates will somewhat artificially lower the statistical bias of the
, null estimates will somewhat artificially lower the statistical bias of the  estimates compared to the true value p0, as explained in Sect. 4. A null value of these estimators should be understood as an indicator of the low S/N of this measurement, which actually has to be included in any further analysis as an upper limit value. In practice, the user seldom has various realizations at hand. Using these estimators then leads to a result with upper limits mixed with non-zero estimates in the analysis. Such complications may be especially hard to handle when studying polarized maps of the interstellar medium. On the other hand, it would be disastrous to omit those estimates in any statistical analysis, since weakly polarized points would be systematically rejected. To avoid such complications, we explore below other estimators that avoid this issue and lead to continuous distributions. This is especially important in the range of S/N between 2 and 3, where the discontinuous estimators still yield up to 20% of null estimates.
estimates compared to the true value p0, as explained in Sect. 4. A null value of these estimators should be understood as an indicator of the low S/N of this measurement, which actually has to be included in any further analysis as an upper limit value. In practice, the user seldom has various realizations at hand. Using these estimators then leads to a result with upper limits mixed with non-zero estimates in the analysis. Such complications may be especially hard to handle when studying polarized maps of the interstellar medium. On the other hand, it would be disastrous to omit those estimates in any statistical analysis, since weakly polarized points would be systematically rejected. To avoid such complications, we explore below other estimators that avoid this issue and lead to continuous distributions. This is especially important in the range of S/N between 2 and 3, where the discontinuous estimators still yield up to 20% of null estimates.
 |
Fig. 2 Statistical fraction of null estimates of |
2.5. Modified asymptotic estimator
A novel asymptotic estimator has been introduced by P14 to eliminate the discontinuous distribution of the standard estimators while still keeping the asymptotic properties. It has been derived from the first-order development of the asymptotic estimator, which has been modified to ensure positivity, smoothness, and asymptotical convergence at high S/N. The modified asymptotic (MAS) estimator is defined as 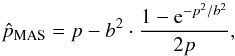 (19)where the “noise-bias” b2 is given by Eq. (15) and computed using a polarization angle assessed from each sample using the asymptotic estimator ψ.
(19)where the “noise-bias” b2 is given by Eq. (15) and computed using a polarization angle assessed from each sample using the asymptotic estimator ψ.
P14 also provides a sample estimate of the variance of the estimator that is shown to represent asymptotically the absolute risk function (defined in Sect. 3.1) of the estimator: 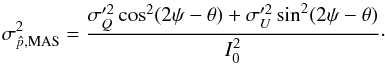 (20)This estimator focuses on getting a “good” distribution, which transforms smoothly from a Rayleigh-like to a Gaussian one, the latter being reached in the canonical case for a S/N of about 2.
(20)This estimator focuses on getting a “good” distribution, which transforms smoothly from a Rayleigh-like to a Gaussian one, the latter being reached in the canonical case for a S/N of about 2.
2.6. Bayesian estimators
The PDFs introduced in Sect. 2 provide the probability of observing a set of polarization measurements (I, p, ψ) given the true polarization parameters (I0, p0, ψ0) and the covariance matrix Σ. Because we are interested in the opposite, i.e., getting an estimate of the true polarization parameters given a measurement and knowledge of the noise properties, we use the Bayes theorem to build the posterior distribution. The posterior PDF B is given in the 3D case by 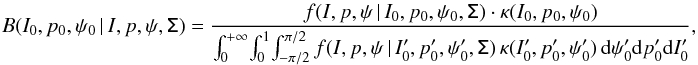 (21)where κ(I0,p0,ψ0) is the prior distribution, which represents the a priori knowledge of the true polarization parameters and has to be non-negative everywhere. When no a priori knowledge is provided, we have to properly define a non-informative prior, which encodes the ignorance of the prior. A class of non-informative priors is given by the Jeffreys’ prior (Jeffrey 1939) where the ignorance is defined under symmetry transformations that leave the prior invariant. As discussed by Quinn (2012) for the 2D case, this kind of prior can be built as a uniform prior in cartesian space (Q0,U0), but it will lead to an under-sampling of the low values of p in polar space (p0, ψ0). However, for the last reason, we prefer a uniform prior in polar space, which ensures uniform sampling even for low values of p0, but which can no longer be considered as a non-informative prior. While p0 and ψ0 are only defined on a finite range ([ 0,1 ] and [−π/ 2,π/ 2), respectively), the intensity I0 may be infinite in theory, which leads to a problem when defining the ignorance prior. In practice, an approximation of the ignorance prior for I0 will be chosen as a top hat centred on the measurement I and chosen to be wide enough to cover the wings of the distribution until it becomes negligible. Such uniform priors lead to the expression of B given in Eq. (22), where the normalization factor has been omitted. We emphasize that the definition of the ignorance prior introduced above becomes data-dependent, which does not strictly follow the Bayesian approach. Furthermore, the question of the definition range of the prior and the introduction of non-flat priors are discussed in Sect. 4.3 in the context of comparing the performance of the estimators inspired by the Bayesian approach.
(21)where κ(I0,p0,ψ0) is the prior distribution, which represents the a priori knowledge of the true polarization parameters and has to be non-negative everywhere. When no a priori knowledge is provided, we have to properly define a non-informative prior, which encodes the ignorance of the prior. A class of non-informative priors is given by the Jeffreys’ prior (Jeffrey 1939) where the ignorance is defined under symmetry transformations that leave the prior invariant. As discussed by Quinn (2012) for the 2D case, this kind of prior can be built as a uniform prior in cartesian space (Q0,U0), but it will lead to an under-sampling of the low values of p in polar space (p0, ψ0). However, for the last reason, we prefer a uniform prior in polar space, which ensures uniform sampling even for low values of p0, but which can no longer be considered as a non-informative prior. While p0 and ψ0 are only defined on a finite range ([ 0,1 ] and [−π/ 2,π/ 2), respectively), the intensity I0 may be infinite in theory, which leads to a problem when defining the ignorance prior. In practice, an approximation of the ignorance prior for I0 will be chosen as a top hat centred on the measurement I and chosen to be wide enough to cover the wings of the distribution until it becomes negligible. Such uniform priors lead to the expression of B given in Eq. (22), where the normalization factor has been omitted. We emphasize that the definition of the ignorance prior introduced above becomes data-dependent, which does not strictly follow the Bayesian approach. Furthermore, the question of the definition range of the prior and the introduction of non-flat priors are discussed in Sect. 4.3 in the context of comparing the performance of the estimators inspired by the Bayesian approach. ![\begin{eqnarray} \label{eq:B_ipphi} B(I_0,p_0,\psi_0\, | \,I,p,\psi, \tens{\Sigma}) \quad \propto \quad \sqrt{\frac{\rm{Det}(\tens{\Sigma}^{-1})}{2\pi^3}}\, \mathrm{exp} \left \lgroup - \frac{1}{2} \left[ \begin{array}{c} I -I_0 \\ p \, I\, \cos(2\psi)-p_0\,I_0\cos(2\psi_0) \\ p \, I\, \sin(2\psi)-p_0\,I_0\sin(2\psi_0) \\\end{array} \right] ^{T} \tens{\Sigma}^{-1} \left[ \begin{array}{c} I-I_0 \\ p\,I\,\cos(2\psi)-p_0\,I_0\,\cos(2\psi_0)\\ p\,I\,\sin(2\psi)-p_0\,I_0\,\sin(2\psi_0)\\\end{array} \right] \right \rgroup \! , \end{eqnarray}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq85.png) (22)Similarly, the posterior PDF in 2D (i.e., when the total intensity is perfectly known, I = I0) is defined by
(22)Similarly, the posterior PDF in 2D (i.e., when the total intensity is perfectly known, I = I0) is defined by 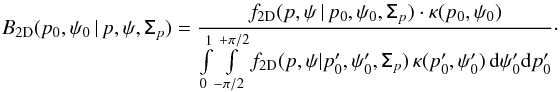 (23)The analytical expressions of the posterior PDF B2D with a flat prior is given in Eq. (24), where the normalization factors have been omitted, and the intensity has been assumed to be perfectly known. Illustrations of this posterior PDF are presented in Appendix B. We also introduce Bp and Bψ, the Bayesian posterior PDFs of p and ψ in 1D, respectively, and defined as the marginalization of B2D over ψ and p, respectively. We use the Bayesian posterior PDFs to build two frequentist estimators: the MAP and the MB.
(23)The analytical expressions of the posterior PDF B2D with a flat prior is given in Eq. (24), where the normalization factors have been omitted, and the intensity has been assumed to be perfectly known. Illustrations of this posterior PDF are presented in Appendix B. We also introduce Bp and Bψ, the Bayesian posterior PDFs of p and ψ in 1D, respectively, and defined as the marginalization of B2D over ψ and p, respectively. We use the Bayesian posterior PDFs to build two frequentist estimators: the MAP and the MB. ![\begin{eqnarray} \label{eq:B_2d_polar} B_{\rm 2D}(p_0,\psi_0\, | \,p,\psi, \tens{\Sigma}_p)\quad \propto \quad \frac{1}{\pi \sigma_{p,G}^2} \, \mathrm{exp} \left \lgroup - \frac{1}{2} \left[ \right] ^{T} \tens{\Sigma}_{p}^{-1} \left[ \right] \right \rgroup \!. \end{eqnarray}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq90.png) (24)The MAP2 and MAP estimators in 2D and 1D, respectively, are simply defined as the (p0, ψ0) values corresponding to the maximum of the posterior PDF, B2D, and Bp and Bψ, respectively. We recall that these estimators match the ML estimators of Sect. 2 in one and two dimensions exactly, respectively, when a uniform prior is assumed. As a result, the MAP2 estimators yield back the polarization measurements, whereas the MAP estimators provide a simple way to compute the ML estimates.
(24)The MAP2 and MAP estimators in 2D and 1D, respectively, are simply defined as the (p0, ψ0) values corresponding to the maximum of the posterior PDF, B2D, and Bp and Bψ, respectively. We recall that these estimators match the ML estimators of Sect. 2 in one and two dimensions exactly, respectively, when a uniform prior is assumed. As a result, the MAP2 estimators yield back the polarization measurements, whereas the MAP estimators provide a simple way to compute the ML estimates.
The mean Bayesian posterior (MB) estimators are defined as the first-order moments of the posterior PDF: 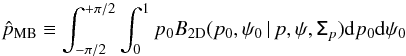 (25)and
(25)and 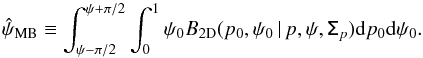 (26)In the definition of
(26)In the definition of 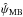 , the integral over ψ0 is performed over a range centred on the measurement ψ. This has to be done to take the circularity of the posterior PDF over the ψ0 dimension into account (see also Quinn 2012, when dealing with the circularity of the polarization angle). We note that B2D(p0,ψ0 | p,ψ,Σp) = B2D(p0,ψ0 + π | p,ψ,Σp).
, the integral over ψ0 is performed over a range centred on the measurement ψ. This has to be done to take the circularity of the posterior PDF over the ψ0 dimension into account (see also Quinn 2012, when dealing with the circularity of the polarization angle). We note that B2D(p0,ψ0 | p,ψ,Σp) = B2D(p0,ψ0 + π | p,ψ,Σp).
The frequentist estimators inspired by a Bayesian approach, 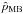 and
and 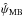 , introduced above in the 2D case can be easily extended to the 3D case by integrating the PDF B(I0,p0,ψ0 | I,p,ψ,Σ) of Eq. (21) over the I, p, and ψ dimensions. This is extremely powerful when the uncertainty of the intensity I has to be taken into account in the estimate of the polarization parameters, which is highly recommended in some circumstances, such as a low S/N on I (<5) or the presence of an unpolarized component on the line of sight (see Sect. 6 and PMA I for more details).
, introduced above in the 2D case can be easily extended to the 3D case by integrating the PDF B(I0,p0,ψ0 | I,p,ψ,Σ) of Eq. (21) over the I, p, and ψ dimensions. This is extremely powerful when the uncertainty of the intensity I has to be taken into account in the estimate of the polarization parameters, which is highly recommended in some circumstances, such as a low S/N on I (<5) or the presence of an unpolarized component on the line of sight (see Sect. 6 and PMA I for more details).
3. Uncertainties
We introduce here the various estimates of the uncertainty associated with a polarization measurement, making a clear distinction between the notions of variance and risk function. We emphasize the difference between two approaches: one based on the posterior uncertainties and the second based on confidence intervals.
3.1. Variance and risk function
It is important not to confuse the variance (noted V) of an estimator with its absolute risk function (noted R). For any distribution of the random variable X the definitions are
![\begin{eqnarray} \label{eq:var_risk} \mathsf{V}&\equiv&E\left[\left(X-E[X]\right)^2\right] \, \, \, \\ \mathsf{R}&\equiv& E\left[\left(X- X_0\right)^2\right] , \end{eqnarray}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq102.png) where E [ X ] is the expectation of the random variable X and X0 is the true value. Introducing the absolute bias, B, in E [ X ] = X0 + B and expanding both relations, the link between the variance and the absolute risk function is simply
where E [ X ] is the expectation of the random variable X and X0 is the true value. Introducing the absolute bias, B, in E [ X ] = X0 + B and expanding both relations, the link between the variance and the absolute risk function is simply 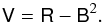 (29)Therefore, for a constant absolute risk function, the variance decreases with the absolute bias, and both are equal when the estimator is unbiased. The variance does not require knowing the true value of the random variable, which makes it useful to provide an uncertainty estimate, but it has to be used extremely carefully in the presence of bias. In such cases, the variance will always underestimate the uncertainty.
(29)Therefore, for a constant absolute risk function, the variance decreases with the absolute bias, and both are equal when the estimator is unbiased. The variance does not require knowing the true value of the random variable, which makes it useful to provide an uncertainty estimate, but it has to be used extremely carefully in the presence of bias. In such cases, the variance will always underestimate the uncertainty.
Furthermore, it is known that the variance is not appropriate for providing uncertainties with non-Gaussian distributions, which is the case for the polarization fraction and angle. In such circumstances, confidence intervals (see Sect. 3.3) are the preferred method for obtaining robust uncertainties. The variance, however, is often used as a proxy of the uncertainty in the high regime of the S/N. In Sects. 4.5 and 5.3, we detail the conditions under which this can still be applied.
3.2. Posterior uncertainties
One of the main benefits of the Bayesian approach is to provide simple estimates of the uncertainties associated with the polarization estimates. One option is to build credible intervals around the MAP estimates as it has been discussed by Vaillancourt (2006) or also Quinn (2012), and the other option is to use the variance of the PDF.
Given a polarization measurement (p, ψ) and the posterior PDF B2D(p0,ψ0 | p,ψ,Σp), the lower and upper limits of the λ% credible intervals are defined as the lower and upper limits of p0 and ψ0 for the iso-probability region Ω(λ,p,ψ) over which the integral of B equals λ%, so that 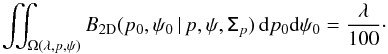 (30)These intervals,
(30)These intervals, ![\hbox{$[p^{\rm low}_{\text{MAP2}},p^{\rm up}_{\text{MAP2}}]$}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq112.png) and
and ![\hbox{$[\psi^{\rm low}_{\text{MAP2}},\psi^{\rm up}_{\text{MAP2}}]$}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq113.png) , estimated from the 2D expression of B2D, are defined around the MAP2 estimates
, estimated from the 2D expression of B2D, are defined around the MAP2 estimates 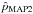 and
and 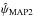 , which are equal to the measurements (p, ψ). It has to be noticed that, in general, 2D intervals are not uniquely defined (see Eq. (32) of PMA I).
, which are equal to the measurements (p, ψ). It has to be noticed that, in general, 2D intervals are not uniquely defined (see Eq. (32) of PMA I).
A similar definition can be given in the 1D case, which leads to different results. The lower and upper limits, 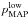 and
and 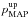 , around
, around 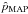 are defined as
are defined as 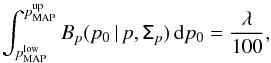 (31)with the constraint that the posterior probability function is identical for
(31)with the constraint that the posterior probability function is identical for 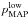 and
and 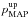 . Similarly, the lower and upper limits,
. Similarly, the lower and upper limits, 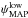 and
and 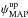 , around
, around 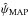 are given by
are given by 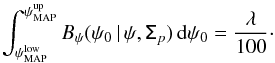 (32)We recall that this integral has to be computed around the measurement value
(32)We recall that this integral has to be computed around the measurement value 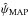 to take the circularity of the posterior PDF with the polarization angle into account. The credible intervals built in 1D or 2D are not supposed to be identical, because (
to take the circularity of the posterior PDF with the polarization angle into account. The credible intervals built in 1D or 2D are not supposed to be identical, because (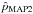 ,
, 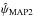 ) and (
) and (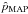 ,
, 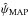 ) are not equal in the general case.
) are not equal in the general case.
The second definition of the uncertainty comes from the second moment of the 1D posterior probability density functions Bp and Bψ, as follows: 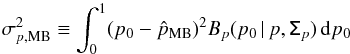 (33)and
(33)and 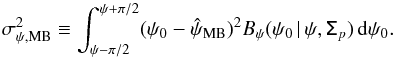 (34)The operation of subtraction between the two polarization angles must be done with care, restricting the maximum distance to π/ 2. At very low S/N, i.e., an almost flat uniform PDF, the uncertainty reaches the upper limit
(34)The operation of subtraction between the two polarization angles must be done with care, restricting the maximum distance to π/ 2. At very low S/N, i.e., an almost flat uniform PDF, the uncertainty reaches the upper limit 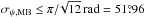 . We stress that these 1σ estimates may not be associated with the usual 68% confidence intervals of the normal distribution, because of the asymmetric shape of the posterior distribution and because of the circularity of the angular variable.
. We stress that these 1σ estimates may not be associated with the usual 68% confidence intervals of the normal distribution, because of the asymmetric shape of the posterior distribution and because of the circularity of the angular variable.
3.3. Confidence intervals
So far we have considered point estimation of the true p0 value which is somewhat tricky in the low S/N regime because of the non-Gaussian nature of the estimator distribution. A different approach that takes the entire shape of the distribution into account is to build confidence regions (or intervals), which allows bounds on the true value to be obtained at some significance level given an estimator value.
Simmons & Stewart (1985) have built the so-called Neyman “confidence belt” for the naïve estimator in the canonical case. PMA I proposed the construction of 2D (p0, ψ0) intervals, for the general covariance matrix case. The classical construction suffers from a standard problem: at very low S/N the confidence interval lies entirely in the unphysical p< 0 region, and both previous studies provide over-conservative regions.
P14 has implemented the Feldman-Cousins prescription (Feldman & Cousins 1998), which is based on using a likelihood ratio criterium in the Neyman construction. This allows building intervals that always lie in the physical region without ever being conservative. They provided these intervals for the MAS estimator, including analytical approximations to the upper and lower limits for 68%, 95%, and 99.5% significance levels.
4. 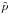 estimator performance
estimator performance
We investigate in this section the capability of providing polarization fraction estimates with low bias using the seven  estimators introduced in the previous sections: the naïve measurement p, the ML, the MP and MP2, the AS, the MAS, and the MB estimators. Their performance is first quantified in terms of relative bias and the risk function of the resulting estimates.
estimators introduced in the previous sections: the naïve measurement p, the ML, the MP and MP2, the AS, the MAS, and the MB estimators. Their performance is first quantified in terms of relative bias and the risk function of the resulting estimates.
4.1. Methodology
Given true polarization parameters (p0, ψ0) and a covariance matrix Σp, we build a sample of one million simulated measurements (p, ψ) by adding noise on the true Stokes parameters using the covariance matrix. We define the relative bias and risk function on p as 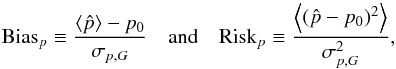 (35)where
(35)where  is the polarization fraction estimate computed on the simulated measurements p, p0 is the true polarization fraction, ⟨⟩ denotes the average computed over the simulated sample, and σp,G is the estimate of the noise of the polarization fraction. The choice of σp,G to scale the absolute bias and risk function, as a proxy of the
is the polarization fraction estimate computed on the simulated measurements p, p0 is the true polarization fraction, ⟨⟩ denotes the average computed over the simulated sample, and σp,G is the estimate of the noise of the polarization fraction. The choice of σp,G to scale the absolute bias and risk function, as a proxy of the  uncertainty, is motivated by the fact that it only depends on the effective ellipticity and not on ψ0. This choice can lead to a relative risk function falling below 1 at low S/N, because
uncertainty, is motivated by the fact that it only depends on the effective ellipticity and not on ψ0. This choice can lead to a relative risk function falling below 1 at low S/N, because 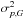 >V (variance, see Eq. (27)) in this regime. The accuracy of the p estimators is also quantified regarding the shape of their output distributions. We use the Jarque-Bera estimator (Jarque & Bera 1980) as a test of normality of the output distribution, and defined by
>V (variance, see Eq. (27)) in this regime. The accuracy of the p estimators is also quantified regarding the shape of their output distributions. We use the Jarque-Bera estimator (Jarque & Bera 1980) as a test of normality of the output distribution, and defined by 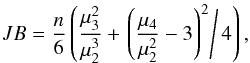 (36)where n is the number of samples and μi is the naïve estimate of the ith central moment of the distribution. This test is based on the joint hypothesis of the skewness and the excess kurtosis being zero simultaneously. A value JB = 0 means a perfect agreement with normality to fourth order, but does not prevent departure from normality at higher orders. This JB estimator tends to a χ2 test with two degrees of freedom when n becomes large enough. The JB therefore has to satisfy the condition
(36)where n is the number of samples and μi is the naïve estimate of the ith central moment of the distribution. This test is based on the joint hypothesis of the skewness and the excess kurtosis being zero simultaneously. A value JB = 0 means a perfect agreement with normality to fourth order, but does not prevent departure from normality at higher orders. This JB estimator tends to a χ2 test with two degrees of freedom when n becomes large enough. The JB therefore has to satisfy the condition 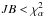 once a significance level α is chosen. For a significance level α = 5% and 1%, we get the conditions JB< 5.99 and JB< 9.21, respectively.
once a significance level α is chosen. For a significance level α = 5% and 1%, we get the conditions JB< 5.99 and JB< 9.21, respectively.
 |
Fig. 3 Comparison of the average relative bias (top), risk function (middle) and Jarque-Bera test (bottom) of the pure measurements (naïve, black), ML (dashed blue), MP (dashed light green), MP2 (dashed green), AS (dashed red), MAS (orange) and MB (pink) |
4.2. Canonical case
We first assume the canonical simplification of the covariance matrix (εeff = 1). The relative Biasp and Riskp quantities are shown in Fig. 3 for the seven  estimators and estimated using 100 000 Monte-Carlo simulations. We recall that the discontinuous estimators have an output distribution presenting a strong peak at zero, which artificially lowers the statistical relative Biasp when simply including null values instead of using upper limits, as discussed in Sect. 2.4. Actually, these estimators show the lowest relative biases (top panel of Fig. 3) compared to the MAS and MB estimators. The ML and MP2 estimators thus seem to statistically over-correct the data, below S/N = 3. Consequently, the ML, MP, and AS
estimators and estimated using 100 000 Monte-Carlo simulations. We recall that the discontinuous estimators have an output distribution presenting a strong peak at zero, which artificially lowers the statistical relative Biasp when simply including null values instead of using upper limits, as discussed in Sect. 2.4. Actually, these estimators show the lowest relative biases (top panel of Fig. 3) compared to the MAS and MB estimators. The ML and MP2 estimators thus seem to statistically over-correct the data, below S/N = 3. Consequently, the ML, MP, and AS  estimators have to be used with extreme care to deal with null estimates. We suggest focusing on the two continuous estimators, MAS and MB.
estimators have to be used with extreme care to deal with null estimates. We suggest focusing on the two continuous estimators, MAS and MB.
MAS provides the better performances in terms of relative bias over the whole range of S/N, while MB appears less and less efficient at correcting the bias when the S/N tends to zero. At higher S/N (>2), MB tends to slightly over-correct with a small negative relative bias (2% of σp) up to S/N ~ 5, while MAS converges quickly to a null relative bias for S/N> 3.
The MB estimator clearly minimizes the risk function in the range 0.7 <S/N< 3.2 (see middle panel of Fig. 3), as expected for this kind of posterior estimator. At higher S/N (>3.2), both MAS and MB have roughly the same behaviour, even if the risk function associated to MAS appears slightly lower.
 |
Fig. 4 Output distributions of the naïve (black), MAS (orange), and the MB (pink) |
The resulting 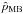 distribution is highly asymmetric at low S/N (see top panel of Fig. 4), with a sharp cutoff at 0.8σp. Moreover, we note that the output
distribution is highly asymmetric at low S/N (see top panel of Fig. 4), with a sharp cutoff at 0.8σp. Moreover, we note that the output 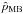 distribution depends not only on the S/N p0/σp, but also on the value of the true polarization fraction p0. We report two cases, p0 = 1% and 50% in Fig. 4. This comes from the prior of the Bayesian method, which bounds the estimate
distribution depends not only on the S/N p0/σp, but also on the value of the true polarization fraction p0. We report two cases, p0 = 1% and 50% in Fig. 4. This comes from the prior of the Bayesian method, which bounds the estimate 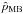 between 0 and 1. As a consequence, the normality of the Bayesian distribution is extremely poor, as pointed out in the bottom panel of Fig. 3, where we show that the JB test of the MB estimator is larger than 9.21 (consistent with a
between 0 and 1. As a consequence, the normality of the Bayesian distribution is extremely poor, as pointed out in the bottom panel of Fig. 3, where we show that the JB test of the MB estimator is larger than 9.21 (consistent with a 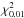 test) over the whole range of S/N explored here (up to S/N ~ 5). In contrast, the resulting
test) over the whole range of S/N explored here (up to S/N ~ 5). In contrast, the resulting 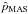 distribution of Fig. 4 looks much better, mimicking the Rayleigh distribution for low S/N and going neatly to the Gaussian regime, as pointed out by P14. The JB of the MAS estimator is the lowest for S/N> 3 (see bottom panel of Fig. 3), illustrating the consistency between the MAS distribution and the normal distribution. All distributions, naïve, MAS, and MB, converge to a Gaussian distribution at higher S/N.
distribution of Fig. 4 looks much better, mimicking the Rayleigh distribution for low S/N and going neatly to the Gaussian regime, as pointed out by P14. The JB of the MAS estimator is the lowest for S/N> 3 (see bottom panel of Fig. 3), illustrating the consistency between the MAS distribution and the normal distribution. All distributions, naïve, MAS, and MB, converge to a Gaussian distribution at higher S/N.
 |
Fig. 5 Impact of the flat prior interval upper limit (see Eq. (37)) on the relative Biasp performance of the MB estimator. |
4.3. Impact of the Bayesian prior
The choice of the prior is crucial in the Bayesian approach, and we have seen how it is hard to define a non-informative prior in Sect. 2.6. The MB estimator studied up to now assumes a flat prior in p0 between 0 and 1, which is already an informative prior (see Quinn 2012). In practice when dealing with astrophysical data, we can bound the expected true values of the polarization fraction between much tighter limits. We know, for example, that the polarization fraction of the synchrotron signal peaks at ~75%, but never reaches this maximum due to line of sight averaging. The maximum polarization fraction of the dust thermal emission is still a debated issue, but is unlikely to be greater than 20% to 30% (Benoît et al. 2004). Appropriate priors can then be introduced to take this a priori physical knowledge into account in the MB estimator.
We have already observed in Sect. 4.2 how the output distribution of the 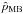 estimates is affected by the value of the true p0 (1% or 50%) due to the upper limit (p0< 1) of the prior, see Fig. 4. We explore here a family of simple priors defined by
estimates is affected by the value of the true p0 (1% or 50%) due to the upper limit (p0< 1) of the prior, see Fig. 4. We explore here a family of simple priors defined by ![\begin{equation} \label{eq:kappa} \kappa(p'_0) = \Bigg \{ \begin{array}{ll} 1/(kp_0) & \, \, \, \mathrm{for} \, \, p'_0 \in[0, kp_0] \\ \quad 0 & \, \, \, \mathrm{otherwise}, \end{array} \end{equation}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq164.png) (37)where we adjust the upper limit of the prior as a function of the expected true value. We performed Monte Carlo simulations in the canonical case by setting the true value at p0 = 1% and varying the upper limit of the prior (k = 2,3,5,10, and 100). The statistical relative Biasp of the MB estimators associated with each version of the priors is shown in Fig. 5. The lower the upper limit, the lower the relative Biasp, as expected. However, the upper limit of the prior has to be very constraining (k ≤ 3) to observe a decrease in the relative bias in the range of S/N between 1.5 and 3. This requires very good a priori knowledge. Using more relaxed priors (k ≥ 5) will significantly not improve the performances of the MB estimator at S/N> 1.
(37)where we adjust the upper limit of the prior as a function of the expected true value. We performed Monte Carlo simulations in the canonical case by setting the true value at p0 = 1% and varying the upper limit of the prior (k = 2,3,5,10, and 100). The statistical relative Biasp of the MB estimators associated with each version of the priors is shown in Fig. 5. The lower the upper limit, the lower the relative Biasp, as expected. However, the upper limit of the prior has to be very constraining (k ≤ 3) to observe a decrease in the relative bias in the range of S/N between 1.5 and 3. This requires very good a priori knowledge. Using more relaxed priors (k ≥ 5) will significantly not improve the performances of the MB estimator at S/N> 1.
When dealing with maps of polarized data, an interesting approach would be to start by estimating the histogram of p values in the map and use it as a prior in our MB estimators, even if this moves away from a strictly Bayesian approach again by introducing a data-dependent prior. As a first guess, the prior can be set to the histogram of the naïve estimates of  , but a more sophisticated prior would be an histogram of p deconvolved from the errors, using a maximum entropy method, for example.
, but a more sophisticated prior would be an histogram of p deconvolved from the errors, using a maximum entropy method, for example.
 |
Fig. 6 Illustration of the improvement in the MB estimator performances when using evolved priors. Starting from an input distribution of 10 000 simulated true values (p0,i), shown in Fig. 7, and the statistical relative bias is shown for four estimators: naïve, MAS, and MB with three different priors. |
 |
Fig. 7 Output distributions of the |
 |
Fig. 8 Same as Fig. 7 with a different initial distribution (p0,i) centred on a 20% polarization fraction. |
We illustrate the performance of the MB estimator with this kind of prior in Figs. 6 and 7. We start with a sample of 10 000 independent true values (p0,i) ranging between 0% and 20% polarization fractions, with a distribution shown in Fig. 7 on which a random realization of the noise is added with the same noise level over the whole sample, leading to varying S/Ns through the sample. We explore two extreme cases of the Bayesian prior, corresponding to i) an idealistic perfect knowledge of the input distribution and ii) its first guess provided by the naïve estimates. The prior is therefore chosen as the input distribution of the true p0,i values and the output distribution of the naïve estimates. We compare the performance of these two new versions of the MB estimators with the naïve, MAS, and flat prior MB estimators, in terms of relative bias in Fig. 6.
We stress that the relative bias values are not defined as previously done in Sect. 4.1, but refer now to the mean of the difference between each sample of true value p0,i and its associated estimate 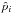 . The pink shaded region provides the domain of the possible improvement of the MB estimators, by setting an appropriate prior as close as possible to the true distribution. The improvements may seem spectacular, leading to a statistical relative bias close to zero at all S/Ns in the best configuration (dashed line). Caution is warranted, however, when looking at the output distributions associated with these new MB estimators in Fig. 7, shown for three levels of the noise chosen so that the mean S/N is
. The pink shaded region provides the domain of the possible improvement of the MB estimators, by setting an appropriate prior as close as possible to the true distribution. The improvements may seem spectacular, leading to a statistical relative bias close to zero at all S/Ns in the best configuration (dashed line). Caution is warranted, however, when looking at the output distributions associated with these new MB estimators in Fig. 7, shown for three levels of the noise chosen so that the mean S/N is 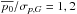 and 3. At low S/N (≃1), the output distribution of the MB estimator with a perfect prior (dashed line) is extremely peaked around the mean value of the sample
and 3. At low S/N (≃1), the output distribution of the MB estimator with a perfect prior (dashed line) is extremely peaked around the mean value of the sample 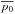 , but does not match the input distribution at all. Even at higher S/N (2−3), the three MB output distributions suffer from the same feature already mentioned in Sect. 4.2, a sharp cutoff at low values of p. Using a prior that is too constraining will yield dramatic cuts of the extremes values of the input distribution. By contrast, the naïve prior is quite effective in that it allows the MB estimator to recover the upper limit of the input distribution reasonably well at a S/N ≳ 2, while the other estimators fail to do so at such low S/N.
, but does not match the input distribution at all. Even at higher S/N (2−3), the three MB output distributions suffer from the same feature already mentioned in Sect. 4.2, a sharp cutoff at low values of p. Using a prior that is too constraining will yield dramatic cuts of the extremes values of the input distribution. By contrast, the naïve prior is quite effective in that it allows the MB estimator to recover the upper limit of the input distribution reasonably well at a S/N ≳ 2, while the other estimators fail to do so at such low S/N.
The performance of the MB estimator with an evolved prior will also strongly depend on the initial true distribution of the polarization fraction. For example we duplicated the analysis made above with a different initial distribution (p0,i) centred on 20% of polarization fraction instead of 10% (see Fig. 8). In this configuration, the output distributions of the Bayesian estimators are not as much affected by the cut-off at low p as observed in Fig. 7. The MB estimator with the naïve prior appears extremely effective, even at low S/N (~2).
4.4. Robustness to the covariance matrix
In PMA I we have extensively discussed the impact of the asymmetry of the covariance matrix on the measurements of the polarization fraction. In particular, we stressed that once the effective ellipticity departs from the canonical case, the bias on the polarization fraction depends on the true polarization angle ψ0, which remains unknown. We would like to explore in this section how the performance of the various  estimators are sensitive to the effective ellipticity of the covariance matrix.
estimators are sensitive to the effective ellipticity of the covariance matrix.
We illustrate the dependence of the  estimators on the true polarization angle ψ0 in Fig. 9. Given true polarization parameters (p0 = 0.1 and ψ0 ranging between − π/ 2 and π/ 2), a covariance matrix characterized by εeff = 2 and θ = 0 (left-hand panel), and a S/N p0/σp,G = 1, we first set the polarization measurements (p, ψ) to the maximum of the PDF f2D (left-hand panel). We apply then the six estimators on these measurements to get the
estimators on the true polarization angle ψ0 in Fig. 9. Given true polarization parameters (p0 = 0.1 and ψ0 ranging between − π/ 2 and π/ 2), a covariance matrix characterized by εeff = 2 and θ = 0 (left-hand panel), and a S/N p0/σp,G = 1, we first set the polarization measurements (p, ψ) to the maximum of the PDF f2D (left-hand panel). We apply then the six estimators on these measurements to get the  estimates for each ψ0 between − π/ 2 and π/ 2. With this particular setting, the MP2 (green) estimator gives back the true polarization fraction p0 whatever the polarization angle ψ0, by definition of this estimator and the choice of the measurement in this example. On the contrary, the MP (light green) and the ML (blue) estimators are extremely sensitive to the true polarization angle ψ0, yielding estimates spanning a large range between 0 and 2.2p0, while the AS (red) and MAS (orange) estimators yield results ranging between 1 to 1.8p0 when ψ0 varies. The MB (pink) estimator provides stable estimates in the range 1.4 to 1.5 p0, which is consistent with the fact that the posterior estimators minimize the risk function. This of course has a cost, and the MB estimator provides the largest averaged relative bias here compared to the other methods, with the exception of the naïve (black) one.
estimates for each ψ0 between − π/ 2 and π/ 2. With this particular setting, the MP2 (green) estimator gives back the true polarization fraction p0 whatever the polarization angle ψ0, by definition of this estimator and the choice of the measurement in this example. On the contrary, the MP (light green) and the ML (blue) estimators are extremely sensitive to the true polarization angle ψ0, yielding estimates spanning a large range between 0 and 2.2p0, while the AS (red) and MAS (orange) estimators yield results ranging between 1 to 1.8p0 when ψ0 varies. The MB (pink) estimator provides stable estimates in the range 1.4 to 1.5 p0, which is consistent with the fact that the posterior estimators minimize the risk function. This of course has a cost, and the MB estimator provides the largest averaged relative bias here compared to the other methods, with the exception of the naïve (black) one.
More generally, for each value of the true polarization angle ψ0 between − π/ 2 and π/ 2, we build a sample of 10 000 simulated measurements using the same setup of the covariance matrix as above. Then we compute the statistical average of the naïve, MAS, and MB estimates (black, orange, and pink lines, respectively) obtained on this simulated sample, with their associated 1σ dispersion (black, orange, and pink dot-dashed lines, respectively), as shown in the right-hand panel of Fig. 9. The averaged MB estimates present the same characteristic as shown in the left-hand panel. By contrast, the averaged MAS estimates are independent of the unknown ψ0 true polarization angle. The MAS 1σ dispersion is, however, slightly larger than the MB 1σ dispersion.
 |
Fig. 9 Illustration of the robustness of the |
 |
Fig. 10 Impact of the effective ellipticity of the covariance matrix on the statistical relative Biasp (left column) and Riskp (right column) quantities in the extreme (light shaded region) and low (dark shaded regions) regimes, for both MAS (orange, top) and MB (pink, bottom) |
The impact of the effective ellipticity of the covariance matrix is then analysed statistically for the MAS and MB estimators only in Fig. 10. Instead of looking at the accuracy of the  estimators around one particular measurement (the most probable one) as done in Fig. 9, for each set of true polarization parameters (p0 = 0.1, ψ0), with ψ0 ranging between − π/ 2 and π/ 2, we perform Monte Carlo simulations. For each set of true polarization parameters, we build a sample of 100 000 simulated measurements on which we apply the MAS and MB estimators to finally compute the statistical relative Biasp and Riskp, as defined in Sect. 4.1. This is done for various setups of the covariance matrix chosen to cover the whole range of the extreme and low regimes. The minimum and maximum relative Biasp and Riskp are then computed over the whole range of ψ0 and effective ellipticity εeff in each regime of the covariance matrix to build the shaded regions of Fig. 10 for the MAS (top panels) and MB (bottom panels)
estimators around one particular measurement (the most probable one) as done in Fig. 9, for each set of true polarization parameters (p0 = 0.1, ψ0), with ψ0 ranging between − π/ 2 and π/ 2, we perform Monte Carlo simulations. For each set of true polarization parameters, we build a sample of 100 000 simulated measurements on which we apply the MAS and MB estimators to finally compute the statistical relative Biasp and Riskp, as defined in Sect. 4.1. This is done for various setups of the covariance matrix chosen to cover the whole range of the extreme and low regimes. The minimum and maximum relative Biasp and Riskp are then computed over the whole range of ψ0 and effective ellipticity εeff in each regime of the covariance matrix to build the shaded regions of Fig. 10 for the MAS (top panels) and MB (bottom panels)  estimators. It appears that the relative Biasp of the MAS estimator is less affected by a change in ellipticity for S/N> 2 than the MB estimator, even in the extreme regime of the covariance matrix. The dependence of the risk function on the ellipticity is almost identical for the two estimators around their respective canonical curve. The thickness of the risk function region is slightly smaller for the MB estimator than for the MAS estimator at low S/N (<3), while it is the opposite for higher S/N (>3), as already observed in the canonical case.
estimators. It appears that the relative Biasp of the MAS estimator is less affected by a change in ellipticity for S/N> 2 than the MB estimator, even in the extreme regime of the covariance matrix. The dependence of the risk function on the ellipticity is almost identical for the two estimators around their respective canonical curve. The thickness of the risk function region is slightly smaller for the MB estimator than for the MAS estimator at low S/N (<3), while it is the opposite for higher S/N (>3), as already observed in the canonical case.
4.5. Polarization fraction uncertainty estimates
The questions of estimating the polarization uncertainties and how uncertainties are propagated are essential in reliable polarization analysis. The best approach consists of building the confidence intervals to retrieve robust estimates of the lower and upper limits of the 68%, 95%, or 99.5% intervals, which is valid even when the distribution is not Gaussian. As already mentioned in Sect. 3.3, building optimized confidence intervals including the full knowledge of the covariance matrix may represent a challenge for large samples of data. As a result, P14 provides analytic approximations of such confidence intervals for the MAS estimator, which can be extremely useful.
A commonly used approach, however, is to provide the 1σ dispersion, assuming the Gaussian distribution of the  estimates as a first approximation. We have already stressed the difference between the risk function and the variance, and the limitations of the latter to derive robust uncertainties in the presence of bias. We compare below the performance of the usual uncertainty estimates introduced in Sect. 3 to provide robust 68% tolerance intervals: MAS variance, credible intervals MAP, and 1σ a posteriori dispersion MB.
estimates as a first approximation. We have already stressed the difference between the risk function and the variance, and the limitations of the latter to derive robust uncertainties in the presence of bias. We compare below the performance of the usual uncertainty estimates introduced in Sect. 3 to provide robust 68% tolerance intervals: MAS variance, credible intervals MAP, and 1σ a posteriori dispersion MB.
Starting with a true p0 value, we performed Monte-Carlo simulations in the low regime of the covariance matrix, by exploring the whole range of the true polarization angle ψ0, with a S/N ranging from 0 to 30. For each simulated measurement (p, ψ), we compute the  estimates with their uncertainty estimators
estimates with their uncertainty estimators 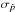 . We then compute the a posteriori probability to find the true p0 inside the interval
. We then compute the a posteriori probability to find the true p0 inside the interval ![\hbox{$[\hat{p}-\sigma^{\rm low}_{\hat{p}} , \hat{p}+\sigma^{\rm up}_{\hat{p}}]$}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq186.png) . In the case of the MAP estimator, the lower and upper limits of the interval,
. In the case of the MAP estimator, the lower and upper limits of the interval, 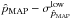 and
and 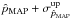 , are set to
, are set to 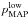 and
and 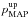 , respectively, (with λ = 68 as defined in Sect. 3.2), which can be asymmetric. We report the results compared to the expected 68% level in Fig. 11. We recall that this comparison approach is frequentist, while anything derived from the Bayesian PDF is used to build single estimates and to be compared with the confidence intervals.
, respectively, (with λ = 68 as defined in Sect. 3.2), which can be asymmetric. We report the results compared to the expected 68% level in Fig. 11. We recall that this comparison approach is frequentist, while anything derived from the Bayesian PDF is used to build single estimates and to be compared with the confidence intervals.
As pointed out in Sect. 3.1, the theoretical variance associated with the MAS estimator still tends to provide slightly lower probabilities than the expected 68% at low S/N, mainly due to the asymmetry of the distribution. The variance associated with the MB estimator, which is more biased at low S/N, gives extremely low probability of recovering the true p0 value at low S/N (<0.5). By contrast, it provides probabilities greater than 68% (as high as 90%) for S/N between 0.5 and 2. This comes from the fact that the MB variance statistically over-estimates, by a factor of 2, the exact variance of the a posteriori 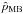 distribution at low S/N (<2). Thus the MB uncertainty estimator yields conservative estimates of the uncertainty for S/N> 0.5. At high S/N (>3), all these uncertainty estimators provide compatible estimates of the probability close to 68%.
distribution at low S/N (<2). Thus the MB uncertainty estimator yields conservative estimates of the uncertainty for S/N> 0.5. At high S/N (>3), all these uncertainty estimators provide compatible estimates of the probability close to 68%.
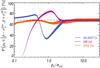 |
Fig. 11 Probability of finding the true polarization fraction p0 inside the interval |
 |
Fig. 13 Average measured S/N computed over 10 000 Monte-Carlo simualtions as a function of the true S/N for four methods: naïve |
Because the true S/N is always unknown (see Sect. 4.6), the probability of finding the true p0 value in the confidence interval is also shown as a function of the measured S/N in Fig. 12. This much more realistic picture shows that the variance estimates provide reliable probability for measured S/N greater than ~6.
4.6. Polarization signal-to-noise ratio
In any real measurement, the true S/N p0/σp,G remains unknown. From observations, we only have access to the measured S/N, which can be obtained by the ratio 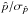 associated with each estimator or by a confidence interval approach (see P14), which is much more robust at a low true S/N. We show in Fig. 13 the accuracy of the measured S/N compared to the true S/N for the four following methods: the naïve estimate plus conventional estimate of the uncertainty, the MAS estimate with the associated variance, the MB estimate and its variance, and the ML estimate with the MAP credible intervals. We observe that all methods agree only for a true S/N over 3, giving back the true S/N in this regime. Below this true S/N, the measured S/N becomes extremely biased regardless of the method used, due to the bias of the measurement
associated with each estimator or by a confidence interval approach (see P14), which is much more robust at a low true S/N. We show in Fig. 13 the accuracy of the measured S/N compared to the true S/N for the four following methods: the naïve estimate plus conventional estimate of the uncertainty, the MAS estimate with the associated variance, the MB estimate and its variance, and the ML estimate with the MAP credible intervals. We observe that all methods agree only for a true S/N over 3, giving back the true S/N in this regime. Below this true S/N, the measured S/N becomes extremely biased regardless of the method used, due to the bias of the measurement  itself, but also due to the bias introduced by the variance as an estimate of the uncertainty when the output distribution departs from the Gaussian regime.
itself, but also due to the bias introduced by the variance as an estimate of the uncertainty when the output distribution departs from the Gaussian regime.
5. 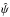 estimator performance
estimator performance
As pointed out by PMA I, once the covariance matrix is not canonical (εeff> 1), a bias of the polarization angle measurements ψ appears with respect to the true polarization angle ψ0. This bias may be positive or negative. We propose to compare the accuracy at correcting the bias of the polarization angle of the four following 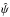 estimators: naïve measurements ψ, the ML
estimators: naïve measurements ψ, the ML 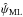 (which is equivalent to the MAP
(which is equivalent to the MAP 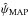 ), the MP2
), the MP2 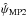 , and the MB
, and the MB 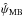 .
.
5.1. Methodology
Similarly to the  estimators, we define the relative bias and risk function on
estimators, we define the relative bias and risk function on 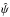 as
as 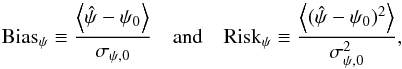 (38)where
(38)where 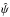 is the polarization angle estimate computed on the simulated measurements ψ, ψ0 is the true polarization angle, ⟨⟩ denotes the average computed over the simulated sample, and σψ,0 is the standard deviation of the simulated measurements.
is the polarization angle estimate computed on the simulated measurements ψ, ψ0 is the true polarization angle, ⟨⟩ denotes the average computed over the simulated sample, and σψ,0 is the standard deviation of the simulated measurements.
5.2. Performance comparison
We explore the performance of the four 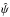 estimators at four S/N = 0.5,1,2, and 5 (from top to bottom) and a covariance matrix with an effective ellipticity εeff = 2, in Fig. 14. The relative Biasψ (left-hand panels) and Riskψ (right-hand panels) are plotted as a function of the true polarization angle ψ0. While the MB estimator seems to provide the least biased estimates with the lowest risk function at low S/N (<1), it becomes the least efficient at higher S/N. In contrast, the ML (or MAP too) presents poor performances at low S/N, but provides impressive results at high S/N, reducing the relative bias close to zero at a S/N of 5. The MP2 estimator does not present any satisfactory properties: strong relative bias and risk function in almost all cases. This
estimators at four S/N = 0.5,1,2, and 5 (from top to bottom) and a covariance matrix with an effective ellipticity εeff = 2, in Fig. 14. The relative Biasψ (left-hand panels) and Riskψ (right-hand panels) are plotted as a function of the true polarization angle ψ0. While the MB estimator seems to provide the least biased estimates with the lowest risk function at low S/N (<1), it becomes the least efficient at higher S/N. In contrast, the ML (or MAP too) presents poor performances at low S/N, but provides impressive results at high S/N, reducing the relative bias close to zero at a S/N of 5. The MP2 estimator does not present any satisfactory properties: strong relative bias and risk function in almost all cases. This 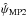 estimator can therefore be ruled out.
estimator can therefore be ruled out.
An overview of the performance of the four 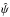 estimators as a function of the S/N is shown in Fig. 15 after marginalization over all the possible values of the ψ0 parameter. Since the relative Biasψ can be positive or negative depending on ψ0, we compute the average of the absolute value of the relative bias, ⟨ | Biasψ | ⟩ as an indicator of the statistical performance of the estimators regardless of the true polarization angle. We observe again in the left-hand panel of Fig. 15 that the MB estimator provides the lowest relative bias for S/N< 1.2, while the ML is especially powerful for S/N> 2. All estimators provide almost the same results for the average Riskψ (left-hand panel), even if MB appears slightly better than the others, including the naïve measurements.
estimators as a function of the S/N is shown in Fig. 15 after marginalization over all the possible values of the ψ0 parameter. Since the relative Biasψ can be positive or negative depending on ψ0, we compute the average of the absolute value of the relative bias, ⟨ | Biasψ | ⟩ as an indicator of the statistical performance of the estimators regardless of the true polarization angle. We observe again in the left-hand panel of Fig. 15 that the MB estimator provides the lowest relative bias for S/N< 1.2, while the ML is especially powerful for S/N> 2. All estimators provide almost the same results for the average Riskψ (left-hand panel), even if MB appears slightly better than the others, including the naïve measurements.
 |
Fig. 14 Comparison of the relative Biasψ (left) and Riskψ (right) quantities of the four |
 |
Fig. 15 Statistical relative | Biasψ | (left-hand panel) and Riskψ (right-hand panel) averaged over ψ0 between − π/ 2 and π/ 2, as a function of the S/N on p0/σp,G, for the four |
The examples provided above were computed with an extreme effective ellipticity (εeff = 2) to emphasize the observations, but the same conclusions can be reached for lower values of the ellipticity. See, for example, the case with εeff = 1.1 shown in Fig. 15. In the low regime of the covariance matrix, however, the statistical relative bias on ψ is very small, typically smaller than 5% of the dispersion, so that the need to correct the bias on ψ remains extremely limited.
5.3. Polarization angle uncertainty estimates
Once a reliable estimate of 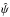 based on the MB and ML (MAP) estimators has been obtained, we would like to build a robust estimate of the associated uncertainties
based on the MB and ML (MAP) estimators has been obtained, we would like to build a robust estimate of the associated uncertainties 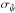 , which should be done by building confidence intervals. Because building confidence intervals may represent a hard task in some cases, for example when dealing with the full covariance matrix, we explain other methods below.
, which should be done by building confidence intervals. Because building confidence intervals may represent a hard task in some cases, for example when dealing with the full covariance matrix, we explain other methods below.
One option is to use the uncertainty associated with the MB estimator, 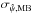 (see Eq. (34)). Another is to use the credible intervals built around the MAP estimates on the posterior PDF. We can keep the lower and upper limits,
(see Eq. (34)). Another is to use the credible intervals built around the MAP estimates on the posterior PDF. We can keep the lower and upper limits, 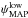 and
and 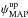 computed for a 68% credible interval or build a symmetrized uncertainty:
computed for a 68% credible interval or build a symmetrized uncertainty:  (39)A third option consists in taking the conventional uncertainty given in PMA I, derived from the derivatives of the polarization parameters. PMA I has already shown that this
(39)A third option consists in taking the conventional uncertainty given in PMA I, derived from the derivatives of the polarization parameters. PMA I has already shown that this 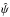 uncertainty estimator, associated with the naïve measurements, tends to systematically underestimate the true dispersion of the ψ distribution.
uncertainty estimator, associated with the naïve measurements, tends to systematically underestimate the true dispersion of the ψ distribution.
We first assume the canonical simplification of the covariance matrix, which implies that the ψ measurements are not statistically biased. We also recall that under such assumptions, the ML (MAP) and MB 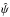 estimators will give back the measurements ψ. We study, however, how the uncertainties associated with these two estimators can be used to get a reliable estimate of the uncertainty
estimators will give back the measurements ψ. We study, however, how the uncertainties associated with these two estimators can be used to get a reliable estimate of the uncertainty 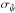 . Starting from a true point (p0, ψ0), we simulate a sample of 1000 simulated measurements p, ψ at a given S/N p0/σp, on which we apply the two ML (MAP) and MB
. Starting from a true point (p0, ψ0), we simulate a sample of 1000 simulated measurements p, ψ at a given S/N p0/σp, on which we apply the two ML (MAP) and MB 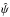 estimators and their associated uncertainty
estimators and their associated uncertainty  and
and 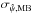 , respectively. From this simulated set, we can derive the averaged
, respectively. From this simulated set, we can derive the averaged 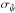 for both methods. Because all estimators give back the measurements in the canonical case, we compare the MAP and MB polarization angle uncertainties estimators directly to the true dispersion of the ψ measurements in Fig. 16. We also repeat the average of the conventional estimates of the polarization uncertainty estimate, which has been shown by PMA I (see their Fig. 7) to underestimate by a factor of two the true uncertainty at low S/N (<2). We observe that the MAP estimator
for both methods. Because all estimators give back the measurements in the canonical case, we compare the MAP and MB polarization angle uncertainties estimators directly to the true dispersion of the ψ measurements in Fig. 16. We also repeat the average of the conventional estimates of the polarization uncertainty estimate, which has been shown by PMA I (see their Fig. 7) to underestimate by a factor of two the true uncertainty at low S/N (<2). We observe that the MAP estimator  provides an extremely good estimate of the polarization angle uncertainty compared to the true one over the whole range of S/N, even if slightly conservative up to a S/N of 5. The MB estimator
provides an extremely good estimate of the polarization angle uncertainty compared to the true one over the whole range of S/N, even if slightly conservative up to a S/N of 5. The MB estimator 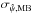 provides consistent estimates of the uncertainty from intermediate S/N ~ 1, but still underestimates at lower S/N (<1).
provides consistent estimates of the uncertainty from intermediate S/N ~ 1, but still underestimates at lower S/N (<1).
In the non-canonical case a statistical bias on ψ appears, which can be partially corrected using the appropriate 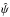 estimators (see Sect. 5.2), leading to an output distribution of the
estimators (see Sect. 5.2), leading to an output distribution of the 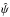 estimates. We quantify the performance of the ψ uncertainty estimators via Monte-Carlo simulations, as done for the
estimates. We quantify the performance of the ψ uncertainty estimators via Monte-Carlo simulations, as done for the  uncertainties. Starting from a set of polarization parameters (p0 = 0.1, − π/ 2 <ψ0<π/ 2), we build a sample of simulated measurements (p, ψ) using various setups of the covariance matrix in the low regime, and various S/Ns ranging from 0 to 30. We then compute the a posteriori probability to find the true polarization angle ψ0 in the interval
uncertainties. Starting from a set of polarization parameters (p0 = 0.1, − π/ 2 <ψ0<π/ 2), we build a sample of simulated measurements (p, ψ) using various setups of the covariance matrix in the low regime, and various S/Ns ranging from 0 to 30. We then compute the a posteriori probability to find the true polarization angle ψ0 in the interval ![\hbox{$[\hat{\psi}-\sigma^{\rm low}_{\hat{\psi}} , \hat{\psi}+\sigma^{\rm up}_{\hat{\psi}}]$}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq222.png) , where
, where 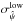 and
and 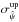 are symmetrized. The results are shown as a function of the true S/N p0/σp,G in Fig. 17 and of the measured S/N
are symmetrized. The results are shown as a function of the true S/N p0/σp,G in Fig. 17 and of the measured S/N 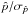 in Fig. 18. We observe that the MAP estimator provides slightly conservative probabilities over the whole range of S/N. The MB estimator gives low probabilities to recover the true polarization angle ψ0 for a true S/N< 1 and a measured S/N< 2.
in Fig. 18. We observe that the MAP estimator provides slightly conservative probabilities over the whole range of S/N. The MB estimator gives low probabilities to recover the true polarization angle ψ0 for a true S/N< 1 and a measured S/N< 2.
 |
Fig. 16 Average polarization angle uncertainty as a function of the S/N in the canonical case and computed over 1000 Monte-Carlo simulations for each value of the S/N: true uncertainty σψ,0 (black), conventional estimate σψ,C (C, dashed dark), ML |
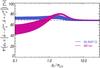 |
Fig. 17 Probability of finding the true polarization angle ψ0 inside the interval |
6. Three-dimensional case
In all of the preceding sections, the total intensity I was assumed to be perfectly known, I = I0. In some cases, however, this assumption is not valid as discussed by PMA I. For instance, one needs to subtract any unpolarized component from the observed intensity signal, leading to three main problems: i) the derived polarization fraction may be grossly underestimated if this is not done properly; ii) this subtraction may be subject to a relatively large uncertainty, larger than the noise on the total intensity, and could lead to diverging estimates of the polarization fraction when intensity crosses null values; iii) this uncertainty on this unpolarized component intensity level should be included in the 3D noise covariance matrix and propagated to the uncertainty estimates of the polarization fraction. This happens, for instance, when dealing with the polarization fraction of the Galactic dust component at high latitude, where the total intensity of the signal is strongly contaminated by the unpolarized signal of the cosmic infrared background (CIB).
The Bayesian approach has the definite advantage over other estimators discussed here in that it can deal fairly easily with 3D (I,Q,U) noise. However, an uncertain total intensity still poses problems, which are most acute in low brightness regions, since the noisy I may become zero or negative, leading to infinite or negative polarization fractions. With this in mind, it is possible that the choice of the prior in p0 and I0 may have a strong impact on the 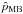 estimate. One may, for instance, choose to allow for negative I0 in low-brightness regions, which implies extending the definition range of the polarization fraction to the negative part, leading to a prior defined on [− 1,1]. Another possibility in this case, and a possible development of the present paper, is to extend the dimensionality of the problem to include the unpolarized intensity component Ioffset, e.g., with a flat prior between Ioffset,min and Ioffset,max, while still imposing I0> 0.
estimate. One may, for instance, choose to allow for negative I0 in low-brightness regions, which implies extending the definition range of the polarization fraction to the negative part, leading to a prior defined on [− 1,1]. Another possibility in this case, and a possible development of the present paper, is to extend the dimensionality of the problem to include the unpolarized intensity component Ioffset, e.g., with a flat prior between Ioffset,min and Ioffset,max, while still imposing I0> 0.
We stress that the Bayesian approach is also currently the only one that can deal with correlation between total intensity I to Stokes parameters Q and U. We note, however, (i) new and forthcoming polarization data sets have a much more control over these systematics; and (ii) the impact of these correlations between noise components on the polarization fraction and angle bias is quite limited, as shown by PMA I.
7. Conclusion
We have presented in this work an extensive comparison of the performance of polarization fraction and angle estimators. While Simmons & Stewart (1985) focused on the common estimators of the polarization fraction, such as the maximum likelihood (ML), the most probable (MP), and the asymptotic (AS), and Quinn (2012) suggested using a Bayesian approach to estimate the polarization fraction, we have generalized all these methods to consider the full covariance matrix of the Stokes parameters. We also included in this comparison a novel estimator of the polarization fraction, the modified asymptotic (MAS, Plaszczynski et al. 2014). In addition, we performed the first comparison of the performance of the polarization angle estimators, since a statistical bias of ψ is expected when the covariance matrix departs from its canonical form. We followed a frequentist methodology to investigate the properties of the polarization estimators, even when dealing with the frequentist estimators inspired by the Bayesian approach.
The question of the performance of a  or
or 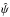 estimator depends intrinsically on the analysis we would like to carry out with these quantities. Whether one includes the full covariance matrix or not is one of the first questions that must be handled, but the more important aspect relies on the properties of the output distribution of each estimator. In practice, a compromise between three frequentist criteria has to be found: a minimum bias, a minimum risk function, and the shape of the output distribution, in terms of non-Gaussianity. We present below a few recipes associated to typical use cases:
estimator depends intrinsically on the analysis we would like to carry out with these quantities. Whether one includes the full covariance matrix or not is one of the first questions that must be handled, but the more important aspect relies on the properties of the output distribution of each estimator. In practice, a compromise between three frequentist criteria has to be found: a minimum bias, a minimum risk function, and the shape of the output distribution, in terms of non-Gaussianity. We present below a few recipes associated to typical use cases:
-
Build a mask. It is usually recommended to build a mask on the intensity map, instead of using the S/N of the polarization fraction, so that no values of the polarization fraction (especially low values of p ) are discarded in the further analysis. It can be useful, however, to build a mask based on the S/N of a polarization fraction map when we are interested in strong values of the polarization fraction only, and we try to reject p estimates artificially boosted by the noise. This is the case when we look for the maximum value of p , for example. In this context we suggest following the prescription of P14, using a combination of the MAS estimator with confidence intervals. This method allows building conservative domains where the S/N is ensured to be greater than a given threshold. P14 provide numerical approximations in the canonical case. If one wants to take the specificity of the noise properties in each pixel into account, confidence intervals can be built for any covariance matrix (including ellipticity and correlation), but it could require intensive computing. Another alternative in that case is to build credible intervals using the posterior distribution (MAP).
-
Large maps of the polarization fraction with high S/N on the intensity.Another typical use is to provide large maps of the polarization fraction with the associated uncertainty, when the intensity is assumed to be perfectly known. Because of their discontinuous distributions presenting a peak at
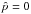 and their strong dependence on the unknown true polarization angle
ψ
0
, the common estimators of
p
(ML, MP, and AS) are not designed well for this purpose. These estimators could produce highly discontinuous patterns with zero values over the output
and their strong dependence on the unknown true polarization angle
ψ
0
, the common estimators of
p
(ML, MP, and AS) are not designed well for this purpose. These estimators could produce highly discontinuous patterns with zero values over the output
 map when the S/N goes below 4, which may imply complicated analysis that include upper limit values. To avoid these issues, we first suggest using the MAS estimator, which has been shown to produce the lowest relative bias, with a continuous output distribution that becomes close to a Gaussian for S/N greater than 2. Moreover, the relative risk function associated with the MAS estimator becomes competitive for
S/N> 3, while the MB estimator minimizes the relative risk function for an intermediate S/N between 1 and 3. The uncertainties can then be derived again from the confidence or credible intervals, depending on the ellipticity of the covariance matrix. A second option, especially suited to intermediate S/N (2
−
3), consists in performing a preliminary analysis on the data to build a prior from the
map when the S/N goes below 4, which may imply complicated analysis that include upper limit values. To avoid these issues, we first suggest using the MAS estimator, which has been shown to produce the lowest relative bias, with a continuous output distribution that becomes close to a Gaussian for S/N greater than 2. Moreover, the relative risk function associated with the MAS estimator becomes competitive for
S/N> 3, while the MB estimator minimizes the relative risk function for an intermediate S/N between 1 and 3. The uncertainties can then be derived again from the confidence or credible intervals, depending on the ellipticity of the covariance matrix. A second option, especially suited to intermediate S/N (2
−
3), consists in performing a preliminary analysis on the data to build a prior from the
 distribution, which can then be injected into the MB estimator. The performance of this method strongly relies on the properties of the initial true distribution. It is particularly efficient for true polarization fractions largely greater than zero, to avoid the major drawback of the MB estimator presenting a lower limit that is proportional to the noise level. The MB (with flat prior) estimator therefore presents a cut-off at 0.8
σ
p
, so that it can never provide null estimates of
distribution, which can then be injected into the MB estimator. The performance of this method strongly relies on the properties of the initial true distribution. It is particularly efficient for true polarization fractions largely greater than zero, to avoid the major drawback of the MB estimator presenting a lower limit that is proportional to the noise level. The MB (with flat prior) estimator therefore presents a cut-off at 0.8
σ
p
, so that it can never provide null estimates of
 . We stress that above a S/N of 4, all methods (except MP2) fall into agreement.
. We stress that above a S/N of 4, all methods (except MP2) fall into agreement.
-
Combined polarization fraction and angle analysis. The Bayesian estimators of
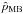 and
and
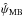 may be used to build estimates of the polarization fraction and angle simultaneously, by taking the full covariance matrix into account, including the ellipticity and correlation between
Q
and
U
, and the correlation between total and polarized intensity. This could be useful when performing an analysis over large areas with inhomogeneous noise properties, when the S/N on the intensity becomes problematic or when an important correlation between
I
and (
Q
,
U
) exists. Nevertheless, we stress that the output distributions of the MB estimates are strongly asymmetric at low S/N (
<
3) and that the Bayesian uncertainty estimates cannot be used as typical Gaussian 68% tolerance intervals.
may be used to build estimates of the polarization fraction and angle simultaneously, by taking the full covariance matrix into account, including the ellipticity and correlation between
Q
and
U
, and the correlation between total and polarized intensity. This could be useful when performing an analysis over large areas with inhomogeneous noise properties, when the S/N on the intensity becomes problematic or when an important correlation between
I
and (
Q
,
U
) exists. Nevertheless, we stress that the output distributions of the MB estimates are strongly asymmetric at low S/N (
<
3) and that the Bayesian uncertainty estimates cannot be used as typical Gaussian 68% tolerance intervals.
-
Low S/N on the intensity.We recommend in this case to use the Bayesian estimators that allow simultaneous estimates of the intensity and the polarization parameters, taking the full covariance matrix into account, and to include the impact of the uncertainty of the intensity on the polarization fraction estimate.
-
Very low S/N studies.Very low S/N s studies may require different approaches. We have seen that at low S/N, all estimators provide biased estimates of the polarization fraction, with highly asymmetric distributions. The more conservative option in this case is to use the confidence or credible intervals. Similarly the question of assessing the unpolarized level of a set of data (i.e., S/N ~ 0) has been first raised by Clarke et al. (1993) . They suggested using a Kolmogorov test to compare the measurement distributions with the expectation derived from the Rice distribution with p0 = 0. Another option is to build the likelihood in two dimensions ( Q,U ) to perform a χ 2 test with Q0 = U0 = 0. A last method could be to use the Bayesian posterior probability B(p0 | p,σp) to assess the probability of having p 0 within a specified interval of zero (or exactly p0 = 0 if delta functions are allowed in the prior) for a given measurement or a series of measurements by convolving all individual PDFs (see Quinn 2012 , for details about the complications that can arise in such an analysis).
-
Polarization angle. Concerning the polarization angle estimates
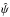 , we have shown that the ML provides the best performance in terms of relative bias and risk function for
S/N> 1. It corrects a potential bias of
ψ
when the covariance matrix is not in its canonical form. Because the ML and MAP estimators give equivalent results, the MAP can be used to efficiently build credible intervals and
symmetric
uncertainties, which have been shown to be in a very good agreement with the output distributions. Nevertheless, we stress that the level of the absolute bias of
ψ
remains
extremely
limited compared to the dispersion of the polarization angle in most cases (i.e., in the
low
and
tiny
regimes of the covariance matrix), so that it can usually be neglected.
, we have shown that the ML provides the best performance in terms of relative bias and risk function for
S/N> 1. It corrects a potential bias of
ψ
when the covariance matrix is not in its canonical form. Because the ML and MAP estimators give equivalent results, the MAP can be used to efficiently build credible intervals and
symmetric
uncertainties, which have been shown to be in a very good agreement with the output distributions. Nevertheless, we stress that the level of the absolute bias of
ψ
remains
extremely
limited compared to the dispersion of the polarization angle in most cases (i.e., in the
low
and
tiny
regimes of the covariance matrix), so that it can usually be neglected.
Online material
Appendix A: Most probable in general case
The MP2 estimators, 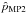 and
and 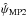 , have to satisfy Eqs. (8) and (9) simultaneously. These relations can be solved using the fully developed expression of f2D, including the terms of the inverse matrix
, have to satisfy Eqs. (8) and (9) simultaneously. These relations can be solved using the fully developed expression of f2D, including the terms of the inverse matrix 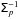 :
: 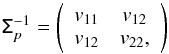 (A.1)leading to
(A.1)leading to 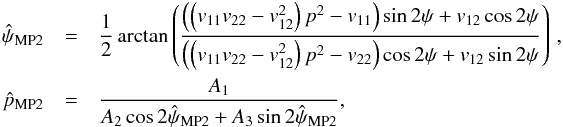 (A.2)with
(A.2)with 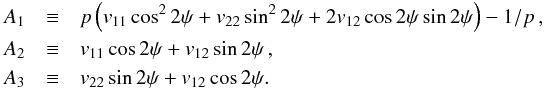 (A.3)This analytical solution only depends on the input measurements (p, ψ) and the covariance matrix Σp. Because the polarization fraction must be positive, there is a lower limit of the S/N so that
(A.3)This analytical solution only depends on the input measurements (p, ψ) and the covariance matrix Σp. Because the polarization fraction must be positive, there is a lower limit of the S/N so that 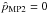 . In that case,
. In that case,  is not constrained anymore and can be chosen to be any possible value. We set it equal to
is not constrained anymore and can be chosen to be any possible value. We set it equal to
the measurement ψ. Moreover, this expression can be simplified when ρ = 0, which implies that v12 = 0, leading to 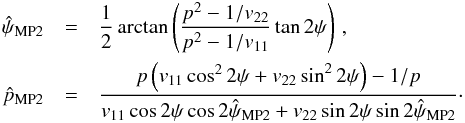 (A.4)In the canonical case (v12 = 0,
(A.4)In the canonical case (v12 = 0, 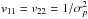 ), we recover the expression derived by Quinn (2012):
), we recover the expression derived by Quinn (2012): 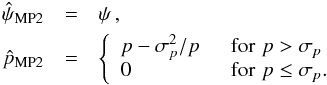 (A.5)
(A.5)
Appendix B: Bayesian posterior PDF
We illustrate the shape of the posterior PDF in Fig. B.1, where B2D(p0,ψ0 | p,ψ,Σp) is shown at four levels of the S/N and five couples of (ε, ρ). It is interesting to notice that the posterior PDF allows the polarization fraction to be zero at low S/N, when these values were rejected by the PDF (see Appendix B of PMA I). Moreover, the posterior PDF peaks at the location of the measurements used to compute it. As largely emphasized in PMA I, we also recall that once the effective ellipticity of the covariance matrix departs from the canonical simplification, the PDFs are sensitive to the initial true polarization angle ψ0.
 |
Fig. B.1 Posterior probability density functions B2D(p0,ψ0 | p,ψ,Σp) computed for the most probable measurements (p, ψ) of the f2D distribution (crosses), which were obtained for a given set of true polarization parameters ψ0 = 0° and p0 = 0.10 (dashed lines) and various configurations of the covariance matrix, at four levels of S/N p0/σp,G = 0.1,0.5,1, and 5 (top to bottom). The scales of the p0 and ψ0 axes may vary from one row to the next in order to focus on the interesting part of the PDF. The black contours provide the 90, 70, 50, 20, 10, 5, 1, and 0.1% levels. |
Appendix C: Mean Bayesian posterior analytical expression
In the canonical case, the MB estimator of the polarization fraction p takes a simple analytical expression. The Bayesian posterior on p is given in this case by 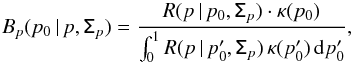 (C.1)where κ is the prior chosen equal to one over the definition range ([0,1]), and R denotes the Rice (1945) function which is defined by
(C.1)where κ is the prior chosen equal to one over the definition range ([0,1]), and R denotes the Rice (1945) function which is defined by 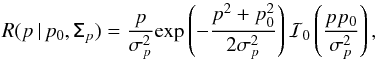 (C.2)where ℐ0(x) is the zeroth-order modified Bessel function of the first kind (Gradshteyn & Ryzhik 2007), and σp = σQ/I0 = σU/I0 is the characteristic noise level of the polarization fraction.
(C.2)where ℐ0(x) is the zeroth-order modified Bessel function of the first kind (Gradshteyn & Ryzhik 2007), and σp = σQ/I0 = σU/I0 is the characteristic noise level of the polarization fraction.
The MB estimator and the posterior variance take the following forms 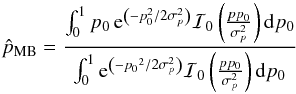 (C.3)and
(C.3)and 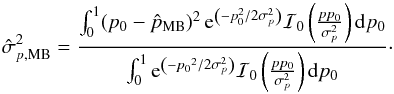 (C.4)If we assume in a first approximation that the integral of p0 over [ 0,1 ] can be taken over [ 0, + ∞) (which is fine at high S/N), and we use the formula of Prudnikov et al. (1986),
(C.4)If we assume in a first approximation that the integral of p0 over [ 0,1 ] can be taken over [ 0, + ∞) (which is fine at high S/N), and we use the formula of Prudnikov et al. (1986), 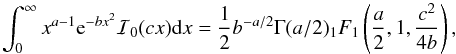 (C.5)where Γ is the Gamma function,
(C.5)where Γ is the Gamma function,  the confluent hypergeometric function of the first kind, and a, b, and c all positive reals, we can derive
the confluent hypergeometric function of the first kind, and a, b, and c all positive reals, we can derive ![\appendix \setcounter{section}{3} \begin{eqnarray} \int_0^{\infty} \!\! {\rm e}^{\left(-p_0^2/2\sigma_p^2\right)} \mathcal{I}_0\left(\frac{pp_0}{\sigma_p^2}\right){\rm d}p_0 \!& = & \! \frac{1}{2} \left(\frac{1}{2\sigma_p^2}\right)^{-\frac{1}{2}} \!\Gamma\left(\frac{1}{2}\right)_1\!F_1 \left( \frac{1}{2}, 1, \frac{p^2}{2\sigma_p^2} \right) \nonumber \\[1mm] \!& = &\! \sqrt{\pi/2} \, \sigma_p \, {\rm e}^{p^2 / 4\sigma_p^2} \mathcal{I}_0\left( p^2 / 4\sigma_p^2 \right) \nonumber \\ \end{eqnarray}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq274.png) (C.6)\pagebreak
(C.6)\pagebreak
and 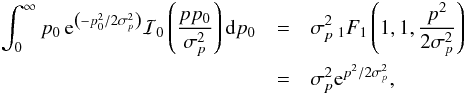 (C.7)and finally
(C.7)and finally 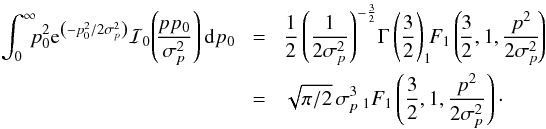 (C.8)We finally obtain the simple expression of the MB estimator and the associated Bayesian variance:
(C.8)We finally obtain the simple expression of the MB estimator and the associated Bayesian variance: 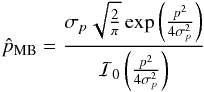 (C.9)and
(C.9)and 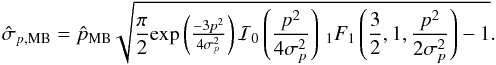 (C.10)As shown in Fig. C.1, this analytical approximation gives less than 0.15% of relative error at low S/N compared to the exact
(C.10)As shown in Fig. C.1, this analytical approximation gives less than 0.15% of relative error at low S/N compared to the exact 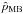 estimate and less than 0.05% for the associated uncertainty. This small departure quickly tends to 0 for a S/N> 4. Thus these expressions may be used to speed up the computing time when the canonical simplification may be assumed.
estimate and less than 0.05% for the associated uncertainty. This small departure quickly tends to 0 for a S/N> 4. Thus these expressions may be used to speed up the computing time when the canonical simplification may be assumed.
 |
Fig. C.1 Accuracy of the approximate analytical expression of the Bayesian estimates of the polarization fraction |
 |
Fig. C.2 Accuracy of the generalized approximate analytical expression of the Bayesian estimates |
We explore in Fig. C.2 to the extent at which the canonical simplification may be done in the presence of an effective ellipticity of the covariance matrix. In this more general case, we suggest changing σp into σp,G in the Eqs. (C.9) and (C.10). The relative error between the approximate estimate and the exact Bayesian estimate has been explored in two regimes of the covariance matrix, the low (1 <εeff< 1.1) and tiny (1 <εeff< 1.01) regimes. Three domains are observed in the top panel of Fig. C.2 dealing with the accuracy of the 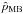 estimate: i) at low S/N (<1), the bias on p is so large that the presence of an effective ellipticity does not significantly affect the estimate in comparison; ii) for an intermediate range of the S/N (1 <S/N< 4), the effective ellipticity of the Σp significantly affects the Bayesian estimate so that the departure of the analytical approximation from the exact estimate becomes important; iii) at high S/N (>4), the noise is so low that the Bayesian estimate is not sensitive to the asymmetry of the covariance matrix anymore. Consequently, the approximate analytical expression provides very good estimates of
estimate: i) at low S/N (<1), the bias on p is so large that the presence of an effective ellipticity does not significantly affect the estimate in comparison; ii) for an intermediate range of the S/N (1 <S/N< 4), the effective ellipticity of the Σp significantly affects the Bayesian estimate so that the departure of the analytical approximation from the exact estimate becomes important; iii) at high S/N (>4), the noise is so low that the Bayesian estimate is not sensitive to the asymmetry of the covariance matrix anymore. Consequently, the approximate analytical expression provides very good estimates of 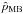 for S/N< 1 and S/N> 4, and 5% to 0.5% of relative error for intermediate 1 <S/N< 4 in the low and tiny regimes of the covariance matrix, respectively. In the extreme regime of the covariance matrix, the relative error increases up to 20%.
for S/N< 1 and S/N> 4, and 5% to 0.5% of relative error for intermediate 1 <S/N< 4 in the low and tiny regimes of the covariance matrix, respectively. In the extreme regime of the covariance matrix, the relative error increases up to 20%.
Concerning the accuracy of the Bayesian approximate estimate 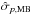 of the polarization fraction uncertainty (bottom panel), the agreement is better than 0.1% for S/N< 1, and about 8% S/N> 1 in the low regime, and 1% in the tiny regime. Because the uncertainty becomes small compared to the polarization fraction at high S/N, up to 8% of error in
of the polarization fraction uncertainty (bottom panel), the agreement is better than 0.1% for S/N< 1, and about 8% S/N> 1 in the low regime, and 1% in the tiny regime. Because the uncertainty becomes small compared to the polarization fraction at high S/N, up to 8% of error in 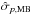 is still acceptable for this approximation.
is still acceptable for this approximation.
Planck (http://www.cosmos.esa.int/web/planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
Acknowledgments
This paper was developed to support the analysis of data from the Planck satellite. The development of Planck has been supported by: ESA; CNES, and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA, and RES (Spain); Tekes, AoF, and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.cosmos.esa.int/web/planck/planck-collaboration. We would also like to thank P. Leahy, S. Prunet, and M. Seiffert for their very useful comments, and J. Quinn for his efficient refereeing of this manuscript.
References
- Benoît, A., Ade, P., Amblard, A., et al. 2004, A&A, 424, 571 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bernard, J.-P., Ade, P., De Bernardis, P., et al. 2007, EAS Pub. Ser. 23, eds. M.-A. Miville-Deschênes, & F. Boulanger, 189 [Google Scholar]
- Clarke, D., Naghizadeh-Khouei, J., Simmons, J. F. L., & Stewart, B. G. 1993, A&A, 269, 617 [NASA ADS] [Google Scholar]
- Dotson, J. L., Vaillancourt, J. E., Kirby, L., et al. 2010, ApJS, 186, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, G. J., & Cousins, R. D. 1998, Phys. Rev. D, 57, 3873 [Google Scholar]
- Fissel, L. M., Ade, P. A. R., Angilè, F. E., et al. 2010, in SPIE Conf. Ser., 7741 [Google Scholar]
- Gradshteyn, I. S., & Ryzhik, I. M. 2007, Table of Integrals, Series, and Products (Elsevier) [Google Scholar]
- Jarque, C., & Bera, A. 1980, Economic Lett., 6, 255 [Google Scholar]
- Jeffrey, H. 1939, Theory of probability (Oxford University Press) [Google Scholar]
- Montier, L. A., Plaszczynski, S., Levrier, F., et al. 2015, A&A, 574, A135 [Google Scholar]
- Naghizadeh-Khouei, J., & Clarke, D. 1993, A&A, 274, 968 [NASA ADS] [Google Scholar]
- Pérez-Sánchez, A. F., & Vlemmings, W. H. T. 2013, A&A, 551, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2011, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plaszczynski, S., Montier, L., Levrier, F., & Tristram, M. 2014, MNRAS, 439, 4048 [NASA ADS] [CrossRef] [Google Scholar]
- Prudnikov, A. P., Brychkov, Yu. A., & Marichev, O. I. 1986, Integrals and Series: Elementary Functions, Vol. 1 (New York: Gordon & Breach Science Publishers), 798 [Google Scholar]
- Quinn, J. L. 2012, A&A, 538, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rice, S. O. 1945, Bell Systems Tech. J., 24, 46 [CrossRef] [Google Scholar]
- Serkowski, K. 1958, Acta Astron., 8, 135 [NASA ADS] [Google Scholar]
- Simmons, J. F. L., & Stewart, B. G. 1985, A&A, 142, 100 [NASA ADS] [Google Scholar]
- Vaillancourt, J. E. 2006, PASP, 118, 1340 [Google Scholar]
- Vaillancourt, J. E., & Matthews, B. C. 2012, ApJS, 201, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Wheeler, J. C., & Höflich, P. 1997, ApJ, 476, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, J. F. C., & Kronberg, P. P. 1974, ApJ, 194, 249 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Distributions of |
| In the text | |
 |
Fig. 2 Statistical fraction of null estimates of |
| In the text | |
 |
Fig. 3 Comparison of the average relative bias (top), risk function (middle) and Jarque-Bera test (bottom) of the pure measurements (naïve, black), ML (dashed blue), MP (dashed light green), MP2 (dashed green), AS (dashed red), MAS (orange) and MB (pink) |
| In the text | |
 |
Fig. 4 Output distributions of the naïve (black), MAS (orange), and the MB (pink) |
| In the text | |
 |
Fig. 5 Impact of the flat prior interval upper limit (see Eq. (37)) on the relative Biasp performance of the MB estimator. |
| In the text | |
 |
Fig. 6 Illustration of the improvement in the MB estimator performances when using evolved priors. Starting from an input distribution of 10 000 simulated true values (p0,i), shown in Fig. 7, and the statistical relative bias is shown for four estimators: naïve, MAS, and MB with three different priors. |
| In the text | |
 |
Fig. 7 Output distributions of the |
| In the text | |
 |
Fig. 8 Same as Fig. 7 with a different initial distribution (p0,i) centred on a 20% polarization fraction. |
| In the text | |
 |
Fig. 9 Illustration of the robustness of the |
| In the text | |
 |
Fig. 10 Impact of the effective ellipticity of the covariance matrix on the statistical relative Biasp (left column) and Riskp (right column) quantities in the extreme (light shaded region) and low (dark shaded regions) regimes, for both MAS (orange, top) and MB (pink, bottom) |
| In the text | |
 |
Fig. 11 Probability of finding the true polarization fraction p0 inside the interval |
| In the text | |
 |
Fig. 12 Same as Fig. 11 but plotted as a function of the measured S/N |
| In the text | |
 |
Fig. 13 Average measured S/N computed over 10 000 Monte-Carlo simualtions as a function of the true S/N for four methods: naïve |
| In the text | |
 |
Fig. 14 Comparison of the relative Biasψ (left) and Riskψ (right) quantities of the four |
| In the text | |
 |
Fig. 15 Statistical relative | Biasψ | (left-hand panel) and Riskψ (right-hand panel) averaged over ψ0 between − π/ 2 and π/ 2, as a function of the S/N on p0/σp,G, for the four |
| In the text | |
 |
Fig. 16 Average polarization angle uncertainty as a function of the S/N in the canonical case and computed over 1000 Monte-Carlo simulations for each value of the S/N: true uncertainty σψ,0 (black), conventional estimate σψ,C (C, dashed dark), ML |
| In the text | |
 |
Fig. 17 Probability of finding the true polarization angle ψ0 inside the interval |
| In the text | |
 |
Fig. 18 Same as Fig. 17, but plotted as a function of the measured S/N |
| In the text | |
 |
Fig. B.1 Posterior probability density functions B2D(p0,ψ0 | p,ψ,Σp) computed for the most probable measurements (p, ψ) of the f2D distribution (crosses), which were obtained for a given set of true polarization parameters ψ0 = 0° and p0 = 0.10 (dashed lines) and various configurations of the covariance matrix, at four levels of S/N p0/σp,G = 0.1,0.5,1, and 5 (top to bottom). The scales of the p0 and ψ0 axes may vary from one row to the next in order to focus on the interesting part of the PDF. The black contours provide the 90, 70, 50, 20, 10, 5, 1, and 0.1% levels. |
| In the text | |
 |
Fig. C.1 Accuracy of the approximate analytical expression of the Bayesian estimates of the polarization fraction |
| In the text | |
 |
Fig. C.2 Accuracy of the generalized approximate analytical expression of the Bayesian estimates |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



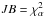
![\hbox{$\hat{p}_{\text{MB}} \in [0,1]$}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq158.png)
![\hbox{$\hat{p}_{\text{MB}}/p_0 \in [0,1/p_0]$}](/articles/aa/full_html/2015/02/aa24451-14/aa24451-14-eq159.png)