| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 13 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424950 | |
| Published online | 06 January 2015 | |
Census of H ii regions in NGC 6754 derived with MUSE: Constraints on the metal mixing scale
1 Instituto de Astronomía, Universidad Nacional Autonóma de México, A.P. 70-264, 04510 México, D.F., Mexico
e-mail: sfsanchez@astro.unam.mx
2 Millennium Institute of Astrophysics, Universidad de Chile, Casilla 36-D, Santiago, Chile
3 Departamento de Astronomía, Universidad de Chile, Casilla 36-D, Santiago, Chile
4 Instituto de Astrofísica de Andalucía (CSIC), Glorieta de la Astronomía s/n, Aptdo. 3004, 18080 Granada, Spain
5 Departamento de Física Teórica, Universidad Autónoma de Madrid, 28049 Madrid, Spain
6 Instituto de Astrofísica de Canarias (IAC), 38205 La Laguna, Tenerife, Spain
7 Depto. Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
8 Instituto Nacional de Astrofísica, Óptica y Electrónica, Luis E. Erro 1, 72840 Tonantzintla, Puebla, Mexico
9 Dpto. de Física Teórica y del Cosmos, University of Granada, Facultad de Ciencias (Edificio Mecenas), 18071 Granada, Spain
10 CEI Campus Moncloa, UCM-UPM, Departamento de Astrofísica y CC. de la Atmósfera, Facultad de CC. Físicas, Universidad Complutense de Madrid, Avda. Complutense s/n, 28040 Madrid, Spain
11 European Southern Observatory, Alonso de Cordova 3107, Casilla 19001, Vitacura, Santiago, Chile
Received: 10 September 2014
Accepted: 18 November 2014
We present a study of the H ii regions in the galaxy NGC 6754 from a two pointing mosaic comprising 197 637 individual spectra, using integral field spectroscopy recently acquired with the MUSE instrument during its Science Verification program. The data cover the entire galaxy out to ~2 effective radii (re), sampling its morphological structures with unprecedented spatial resolution for a wide-field Integral Field Unit. A complete census of the H ii regions limited by the atmospheric seeing conditions was derived, comprising 396 individual ionized sources. This is one of the largest and most complete catalogues of H ii regions with spectroscopic information in a single galaxy. We use this catalogue to derive the radial abundance gradient in this SBb galaxy, finding a negative gradient with a slope consistent with the characteristic value for disk galaxies recently reported. The large number of H ii regions allows us to estimate the typical mixing scale length (rmix ~ 0.4re), which sets strong constraints on the proposed mechanisms for metal mixing in disk galaxies, like radial movements associated with bars and spiral arms. We found evidence of an azimuthal variation in the oxygen abundance that may be connected with the radial migration. These results illustrate the unique capabilities of MUSE for the study of the enrichment mechanisms in Local Universe galaxies.
Key words: galaxies: individual: NGC 6754 / galaxies: ISM / galaxies: star formation / galaxies: abundances
© ESO, 2015
1. Introduction
Nebular emission lines have historically been the main tool at our disposal for direct measurement of the gas-phase abundance at discrete spatial positions in low-redshift galaxies (e.g., Alloin et al. 1979). They trace the young, massive star components in galaxies, illuminating and ionizing cubic kiloparsec-sized volumes of interstellar medium. Metals play a fundamental role in cooling mechanisms in the intergalactic and interstellar medium, and in processes of star formation, stellar physics, and planet formation.
Previous spectroscopic studies unveiled some aspects of the complex processes at play between the chemical abundances of galaxies and their physical properties. These studies were successful in determining important relationships, scaling laws, and systematic patterns (e.g., Lequeux et al. 1979; Diaz 1989; Zaritsky et al. 1994; Garnett 2002; Tremonti et al. 2004; Moustakas & Kennicutt 2006). However, these results are limited by statistics, either in the number of observed H ii regions or in the coverage of these regions across the galaxy surface.
The advent of multi-object spectrometers and integral field spectrocopy (IFS) instruments with large fields of view (FoV) now offers the opportunity to undertake a new generation of emission-line surveys based on samples of hundreds of H ii regions and full two-dimensional (2D) coverage of the disks of nearby spiral galaxies (e.g., Rosales-Ortega et al. 2010). One of the most interesting results recently derived using IFS data is that the oxygen abundance gradient seems to present a common slope ~−0.1 dex/re for non-interacting galaxies (Sánchez et al. 2012b, 2014b).
This result agrees with models based on the standard inside-out scenario of disk formation. This scenario predicts a relatively quick self-enrichment with oxygen and an almost universal negative metallicity gradient once it is normalized to the galaxy optical size (Boissier & Prantzos 1999, 2000). From the seminal works of Lacey & Fall (1985), Guesten & Mezger (1982), and Clayton (1987), most numerical models of chemical evolution explain the existence of the radial gradient of abundances by the combined effects of a star formation rate and an infall of gas, both varying with galactocentric radius (e.g., Mollá & Roy 1999).
Although there is a large number of studies focused on the analysis of the abundance gradient in galaxies, in contrast, little is known about the possible presence of azimuthal asymmetries in this distribution. Deviations from the radial abundance gradient are well-known features in the Milky Way, based on the study of Cepheids and open clusters (e.g., Chiappini et al. 2001; Lépine et al. 2011). However, the situation in other spiral galaxies is less clear, and suffers from poor statistics, either for the low number of H ii regions sampled per galaxy or for the large errors in the abundance estimation. Recently, using wide-field IFS Rosales-Ortega et al. (2011) showed that the radial metallicity gradient of NGC 628 varies slightly for different quadrants, although the differences are comparable to the uncertainties introduced by the adopted estimators of the oxygen abundances. More recently, Li et al. (2013) found marginal evidence of the existence of moderate deviations from chemical abundance homogeneity in the intestellar medium of M101, using a combination of strong-line abundance indicators and direct estimations based on the detection of the [O iii]λ4363 auroral line.
Despite the advances of recent IFS surveys in our understanding of the evolution of the chemical enrichment processes in galaxies, there are some limitations. The most important is the lack of the spatial resolution required to properly resolve individual small-scale morphological structures, in particular individual H ii regions. The IFS surveys with the best physical resolution, such as PINGS (Rosales-Ortega et al. 2010) or CALIFA (Sánchez et al. 2012a), have ~5 times lower spatial resolution than the typical ground-based imaging surveys. This results in a bias in the detection of H ii regions, which are aggregated based on their spatial vicinity (decreasing their number by a factor of three or more), and their spectra are polluted by diffuse gas emission (Mast et al. 2014).
 |
Fig. 1 RGB color image of NGC 6754 created using the line intensity maps of [O iii]λ5007 (blue), V-band (green), and Hα (red) extracted from the datacubes. Each large tick mark corresponds to 10″ (or 400 pc at the redshift of the galaxy). The green point-like sources are field stars. Each red structure corresponds to a single H ii region. |
In principle, the abundance scatter and azimuthal asymmetries of H ii regions around the average radial gradient can be used to constrain the spatial-scale of radial mixing (e.g., Scalo & Elmegreen 2004; Di Matteo et al. 2013). In the absence of radial mixing the only observed scatter around the abundance gradient should be produced by the errors in the individual measurements. Regardless of its origin (e.g., Athanassoula 1992), any radial mixing increases the scatter by moving regions of a certain abundance from one galactocentric distance to a different one. Therefore, the dispersion around the average slope is a constraint to the maximum radial mixing scale.
So far, for the reasons outlined above, the current IFS surveys have lacked the required resolution to address this important issue in the chemical evolution of galaxies. The Multi Unit Spectroscopic Explorer (MUSE, Bacon et al. 2010) has dramatically changed the perspective for these studies. This instrument is a unique tool for the spectroscopic analysis of resolved structures in galaxies, particularly in the Local Universe. The combination of a large FoV (~60″× 60″), unprecedented spatial sampling (0.2″/spaxel) for a wide-field integral field unit (IFU), which limits the spatial resolution to the atmospheric seeing, the spectral resolution and large wavelength coverage, and the large aperture of the VLT telescope, makes MUSE a well suited instrument to address these problems. Of course, there are other IFUs with similar or even larger FoVs, like PPAK (Kelz et al. 2006), VIMOS (Le Fèvre et al. 2003), or VIRUS-P (Hill et al. 2008), and other IFUs operating in the optical range have similar or better spatial sampling, like GMOS (Allington-Smith et al. 2002) or OASIS1. However, MUSE is the first one that combines the large FoV and the image-like spatial sampling.
In this work we study the oxygen abundance gradient of the spiral galaxy NGC 6754 using the data recently observed by MUSE as part of the Science Verification programs (SV). NGC 6754 is a barred Sb galaxy mildly inclined (i ~ 60°). Its brightness (B ~ 13 mag), projected size (r25 ~ 1′), and redshift (z = 0.0108), similar to the footprint of the CALIFA galaxies (e.g., Walcher et al. 2014), makes it suitable to perform a census of the H ii regions using MUSE to further understand the abundance distribution in this galaxy.
2. Data acquisition and reduction
NGC 6754 was observed on June 28 and 30, 2014, in the context of program 60.A-9329 (PI: Galbany) of the MUSE SV run. The observations were divided into two pointings covering the east and west parts of the galaxy. The final cube for each pointing is the result of three exposures of 900 s, where the second and third exposure were slightly shifted (2 arcsec NE and SW, respectively) and rotated 90° from the first exposure, in order to provide a uniform coverage of the field and to limit systematic errors in the reduction.
The reduction of the raw data was performed with Reflex (Freudling et al. 2013) using version 0.18.2 of the MUSE pipeline (Weilbacher et al. 2014), including the standard procedures of bias subtraction, flat fielding, wavelength calibration, flux calibration, and the final cube reconstruction by the spatial arrangement of the individual slits of the image slicers.
The final dataset comprises two cubes of ~100 k individual spectra, each covering a FoV slightly larger than ~1 arcmin2. Each spectrum covers the wavelength range 4800–9300 Å, with a typical spectral resolution between 1800 and 3600 (from blue to red). The cubes are aligned east-west, with an overlapping area of ~16″, where the galaxy center was sampled twice. The final mosaicked datacube comprises almost 200k individual spectra, covering the entire galaxy up to 2 effective radii, with a FoV of ~2′ × 1′. For practical reasons, we analyzed each cube separately and later combined the different data products.
Figure 1 illustrates the power of the combined large FoV and high spatial resolution of MUSE, and the quality of the data. It shows a true color image created using a combination of a V-band image and two continuum subtracted narrowband images of 30 Å width, centered in [O iii]λ5007 and Hα at the redshift of the galaxy. The three maps were synthetized from each datacube, and combined to create a single image for each band. For each of the narrowband images the continuum was estimated from the average of two additional narrowband images of similar width (i.e., 30 Å) extracted at a wavelength redshifted and blueshifted 100 Å from the nominal wavelength of the considered emission line at the redshift of the object. Finally, the V-band image was synthetized by convolving the spectra at each spaxel by the nominal response curve of the Johnson V-band filter. These images were used to illustrate the spatial resolution and image quality of the data. We note here than the V-band image does not include only continuum emission, since it is contaminated by both Hβ and [O iii]λ5007, and the Hα intensity map is contaminated by the adjacent [N ii] doublet. However, they clearly trace the continuum and emission line distribution across the galaxy. The spatial distribution of the individual ionized regions can be easily recognized by tracing the star forming regions along the spiral arms of the galaxy. Different seeing conditions for the east (~0.8″) and for the west (~1.8″) pointings are also clear.
3. Analysis
The main goals of this study are to characterize the abundance gradient in NGC 6754 and to estimate the dispersion of the abundances of the individual H ii regions around the average gradient. In this section we describe briefly how we select the H ii regions, extract and analyze their individual spectra, derive the corresponding oxygen abundance, and analyze their radial gradient. More details on the procedure are described in Sánchez et al. (2012b) and references therein.
3.1. Detection of the ionized regions
The segregation of H ii regions and the extraction of the corresponding spectra is performed using a semi-automatic procedure named HIIexplorer2. The details of this program are given in Sánchez et al. (2012b), and a detailed description of the overall detection process, Sánchez et al. (2014b). HIIexplorer requires as input a map of emission line intensities or equivalent widths, a minimum threshold above which the peak intensity of the H ii region is detected, and three different convergence criteria: (i) the maximum fractional difference between the peak intensity and the adjacent ones to be aggregated to a particular region; (ii) the minimum absolute intensity for a pixel to be aggregated; and (iii) the maximum distance between the pixel considered and the peak intensity. In this particular case we use the map of the equivalent width of Hα, EW(Hα), derived from the narrowband image described above. The use of the EW guarantees that the analysis is more homogeneous between the two pointings because this parameter is less affected by possible spectrophotometric differences and it is less sensitive to seeing variations. Whether the equivalent width is be contaminated or not by the adjacent [N ii] doublet is not relevant, since this map is only used to detect the emission line regions, and not in any further analysis throughout the article. Therefore, a possible contamination by [NII] may only affect the contrast, and only marginally, but not the detectability of the regions because the average contamination by this line is about a 30% of the total flux. The output of HIIexplorer is a segmentation map and the integrated spectrum for each of the H ii regions detected.
 |
Fig. 2 Color-coded map of the equivalent width of Hα in logarithmic scale. The areas with Hα density flux below 1.5 × 10-18 erg s-1 cm-2 spaxel-1 (~3σ detection limit) have been masked. The circles represent the detected H ii regions; the radius is proportional to the extraction aperture. |
We processed the two datacubes individually, fixing the input parameters to the optimal ones for the west-pointing, which was observed under the worst seeing conditions. We selected a threshold in the peak EW(Hα) = 20 Å, and minimum EW(Hα) = 8 Å, a minimum fractional peak of 1%, and a maximum distance of 2′′. Therefore, the convergence criteria restrict the detection of regions with at least EW(Hα) = 8 Å in every spaxel and a maximum diameter of 4′′. The selection of these parameters is based on our previous studies with other IFU data and different tests to optimize the results: (i) the minimum absolute EW(Hα) is selected to guarantee that all the pixels aggregated to a particular region are above the boundary between retired and star-forming regions proposed by Cid Fernandes et al. (2010) and discussed in Sánchez et al. (2014b), even if a very conservative error of 25% is assumed for this parameter, and/or taking into account the contamination by [N ii]; (ii) the threshold in the peak EW(Hα) is selected to be more than twice the minimum to guarantee that the region is actually clumpy or peaky, and not a diffuse ionized region; (iii) the maximum distance is fixed to the estimated size of an H ii region, that could have a diameter as large as ~1 kpc (e.g., NGC 5471, Oey et al. 2003; García-Benito et al. 2011), thus, ~4′′ at the redshift of the object. Using these parameters we detect a similar number of H ii regions in each pointing: 207 in the east pointing and 220 in the west.
 |
Fig. 3 Detail of the spectrum of a typical H ii region extracted from the galaxy. The black line shows the input spectrum in logarithmic scale, together with the best fitted stellar model in orange. The difference between the logarithms of the input spectrum and the model, shifted by 1, is shown as a blue line. The intensities of the emission lines are so high that the spectra are plotted in logarithmic scale to show them together with the detail of the underlying stellar population.The most prominent spectral features discussed throughout the article are marked. The spectral regions masked during the fitting of the underlying stellar population are not shown by the orange solid line. The two boxes show an expanded view around Hβ and Hα. |
The final catalogue was cleaned for double detections in the overlapping area by removing those H ii regions with coordinates that differ by less than 3″. A total of 396 individual clumpy ionized regions are detected, a factor of 5–10 times larger than the number found with lower spatial resolution IFU data (e.g., Sánchez et al. 2013), as predicted by the simulations presented by Mast et al. (2014). Figure 2 shows the EW(Hα) map illustrating the result of this procedure. The location and relative size of the H ii regions detected are indicated with black circles. We note here that the HIIexplorer provides us with a segmentation map, with not circular apertures. The current representation is therefore illusrative of the size of the H ii regions, but does not show the actual detailed shape of the associated segmented regions for which the spectra are extracted.
3.2. Measurement of the emission line intensities
In this analysis we follow the procedures described in Sánchez et al. (2014b), using the fitting package FIT3D3 (Sánchez et al. 2006, 2011). We perform a Monte Carlo fitting using two different single stellar population (SSP) libraries. In order to compare with previous results and provide useful information on the underlying stellar population, we first use a library that comprises 156 templates to model and remove the underlying stellar population. This library comprises 39 stellar ages from 1 Myr to 13 Gyr, and 4 metallicities (Z/Z⊙ = 0.2, 0.4, 1, and 1.5), and it is described in detail in Cid Fernandes et al. (2013). These templates were extracted from a combination of the synthetic stellar spectra from the GRANADA library Martins et al. (2005) and the SSP library provided by the MILES project (Sánchez-Blázquez et al. 2006; Vazdekis et al. 2010; Falcón-Barroso et al. 2011). They are restricted to a wavelength range lower than 7000 Å and so cannot be used to remove the underlying stellar population in the full spectral range covered by MUSE. To perform this step, we used a more restricted library extracted from the MIUSCAT models (Vazdekis et al. 2012). It comprises eight stellar ages, from 65 Myr to 17.7 Gyr, and three metallicities (Z/Z⊙ = 0.4, 1, and 1.5). Our previous experience indicates that to decouple the underlying stellar population from the emission lines a restricted library like this one is enough (e.g., Sánchez et al. 2014a). We do not find large differences between the residual spectra for the wavelength range in common, and therefore we adopted the results from the second library for the analysis of the emission lines.
Dust attenuation and stellar kinematics were taken into account as part of the fitting process. The stellar kinematics was derived as a first step, fitting the underlying stellar population with a subset of the full stellar library changing the systemic velocity and the velocity dispersion at random within the range of allowed values. Then a first model for the stellar population was derived. This model was used to obtain the dust attenuation, allowed to change randomly within a pre-defined range. The extinction law by Cardelli et al. (1989) was assumed, with a specific dust attenuation of RV = 3.1. For each iteration over the dust attenuation values a new model of the underlying stellar population was derived. The best combination of the stellar velocity, velocity dispersion and dust attenuation was recovered based on the lowest reduced χ2 provided. Finally, these parameters were fixed and the full stellar library was used to recover the underlying stellar population. Because of the Monte Carlo fitting adopted, the inaccuracies in the derivation of the underlying stellar population were propagated to the error budget in the emission line fitting, and therefore, into the errors estimated for the emission line fluxes.
Individual emission line fluxes were measured in the stellar-population subtracted spectra by fitting each of them with a single Gaussian function. For this particular dataset we extracted the flux intensity of the following emission lines: Hα, Hβ, [O iii] λ4959, [O iii] λ5007, [N ii] λ6548, [N ii] λ6583, [S ii] λ6717, [S ii] λ6731, [Ar iii] λ7135, and [S iii] λ9069. We notice here that many other relevant emission lines are detected within the wavelength range covered by the spectra. Figure 3 shows a detail of the spectrum of a typical H ii region within the sample, together with the best fitted stellar population model and the resulting emission-line spectrum. In addition to the emission lines measured, it is possible to identify weaker lines such as He i λ5876 and [O i] λ6300. The two components of the Na i absorption doublet at ~5892 Å are clearly resolved, with a contribution due to attenuation that cannot be reproduced by the stellar model, which was actually masked during the fitting process. The prominent CaTλ8542 Å stellar absorptions in the near-infrared is also clearly detected. In addition to the emission line fluxes, we derived the emission line equivalent widths. To do this, we divide the integrated flux of the line by the median flux density of the best fitted SSP model in a window of 100 Å centered in the wavelength of the emission line. Therefore, these equivalent widths are not contaminated by the contribution of any adjacent emission lines.
Two artifacts in the spectra are identified in Fig. 3, in particular in the residual emission line spectrum. They look like two bumps at ~4750 Å and ~6550 Å, just bluewards of Hβ and Hα. Although they have been masked during the fitting process we prefer to show them in the plot, since they seem to be present in all the MUSE spectra we have analyzed. We are not sure if they are a product of the reduction process or a feature in the raw data. In any case, they do not affect the measurements of the emission lines. Two additional spectral features that are not accurately reproduced by the SSP models correspond to the Na iλ5890, 5896 absorption feature at ~5950 Å at the redshift of the object, and the CaTλ8542 Å at ~8630 Å at the redshift of the object. The Na i mismatch is a well-known feature since this absorption line has two physical origins: (i) the absorption due to the presence of this element in the atmosphere of the stars, which is included in the SSP-templates; and (ii) the absorption due to the presence of this element in the inter-stellar medium, which produces an absorption proportional to the gas content (and dust attenuation). The CaTλ8542 Å is often problematic in the current SSP templates, which could be related to variations in the IMF, the abundance of Ca, or an incomplete understanding of this absorption feature (although this is not the case in the particular example shown in Fig. 3, for which we show the prediction from the fitted SSP model). Because of these well-known mismatches, both spectral regions were masked during the fitting process. Residuals from imperfect sky-subtraction of the strong OH-lines in the near-infrared are visible in the redder wavelength ranges, and a clear defect associated with telluric absoption is shown at λ ~ 7600 Å. None of the emission lines considered in this study are affected by this second effect.
 |
Fig. 4 [O iii] λ5007/Hβ vs. [N ii] λ6583/Hα diagnostic diagram for the 396 H ii ionized regions detected in NGC 6754, color-coded by the deprojected galactocentric distance (where bluer colors correspond to the central regions, and reddish-to-grey colors correspond to the outer regions). Solid and dashed lines represent, respectively, the Kauffmann et al. (2003) and Kewley et al. (2001) demarcation curves. They are usually invoked to distinguish between classical star-forming objects (below thesolid line), and AGN powered sources (above the dashed line). Regions between both lines are considered intermediate ones. The average error of the line ratios is represented by the error bar in the upper-right corner. |
3.3. Selection of H ii regions
Classical H ii regions are gas clouds ionized by short-lived hot OB stars, associated with ongoing star formation. They are frequently selected on the basis of demarcation lines defined in the so-called diagnostic diagrams (e.g., Baldwin et al. 1981; Veilleux & Osterbrock 1987), which compare different line ratios. Figure 4 shows the classical diagram using [O iii]/Hβ vs. [N ii]/Hα (Baldwin et al. 1981, hereafter BPT diagram), for the sample of H ii regions described above. This diagnostic diagram is frequently used since it uses very strong emission lines (e.g., Fig. 3), and it is less affected by dust attenuation and imperfections in the spectrophotometric calibration. The classical demarcation lines described by Kauffmann et al. (2003) and Kewley et al. (2001) have been included.
In this study we follow Sánchez et al. (2013) to select H ii regions as clumpy ionized regions with EW(Hα) > 6 Å and located below the Kewley et al. (2001) demarcation curve. This selection guarantees the exclusion of ionized regions possibly dominated by shocks that are not clumpy in general, regions whose ionization is dominated by post-AGB stars, and AGN-dominated regions (e.g., Cid Fernandes et al. 2010). Following these criteria all the ionized regions selected by HIIexplorer have been classified as H ii regions.
The distribution of H ii regions across the BPT diagram follows the characteristic pattern in Sa/Sb early-type spirals Sánchez et al. (2014a). They are mostly located at the bottom-right corner of the classical location of H ii regions in this diagram, with a tail towards the so-called intermediate region between the two demarcation lines described above. Kennicutt et al. (1989) first recognized that H ii regions in the center of galaxies are spectroscopically different from those in the disk in their stronger low-ionization forbidden emission, which places them in the so-called intermediate region. More recently Sánchez et al. (2014b) found a similar behavior for the H ii regions in early-type disk galaxies, like NGC 6754. The location of the H ii regions change across the BPT diagram with the galactocentric distance (Fig. 4), as a consequence of the change of the ionization conditions and in particular the radial gradient in the oxygen abundance (e.g., Evans & Dopita 1985; Dopita & Evans 1986).
3.4. Physical conditions in the H ii regions
The location in the BPT diagram for a classical H ii region ionized by young stars of a certain age is defined well by three main parameters: (a) the ionization parameter or fraction of Lyman continuum photons with respect to total amount of gas; (b) the electron density of the gas; and (c) the metallicity or chemical abundance of the ionized gas. We derive here the first two. In addition, we estimate the dust attenuation to correct the emission line fluxes when required.
The dust attenuation, AV, was derived for each H ii region based on the Hα/Hβ Balmer line ratio. The extinction law by Cardelli et al. (1989) was assumed, with a specific dust attenuation of RV = 3.1, and the theoretical value for the unobscured line ratio for case B recombination of Hα/Hβ = 2.86, for Te = 10 000 K and ne = 100 cm-3 (Osterbrock 1989). For this study we have assumed that the intrinsic Hα/Hβ line ratio does not vary significantly, although it is known that it presents a dependence on the electron density and the temperature (e.g., Osterbrock 1989). After deriving the dust attenuation, all the considered emission line fluxes were corrected adopting the same extinction law when needed.
The electron density, ne, was derived from the line ratio of the [S ii] doublet (e.g., Osterbrock 1989), by solving the equation ![\begin{eqnarray} \label{eq2} \frac{I({\rm [\ion{S}{ii}]\lambda6717})}{I({\rm [\ion{S}{ii}]\lambda6731})} &=& 1.49 \frac{1+3.77{x}}{1+12.8{x}}, \end{eqnarray}](/articles/aa/full_html/2015/01/aa24950-14/aa24950-14-eq37.png) (1)where x is the density parameter defined as x = 10-4net− 1/2, and t is the electron temperature in units of 104 K (McCall et al. 1985). For this calculation we assumed a typical electron temperature of T = 104 K, which is an average value that corresponds to the expected conditions in H ii regions (Osterbrock 1989). This equation reflects that the [S ii] doublet ratio is sensitive to changes in the electron density only for a limited range of values. For high and low values, it becomes asymptotic, and the value derived has to be treated with care and should not be used for quantitative statements. However, the value will still be valid to understand the possible dependences of the abundance gradient with this parameter.
(1)where x is the density parameter defined as x = 10-4net− 1/2, and t is the electron temperature in units of 104 K (McCall et al. 1985). For this calculation we assumed a typical electron temperature of T = 104 K, which is an average value that corresponds to the expected conditions in H ii regions (Osterbrock 1989). This equation reflects that the [S ii] doublet ratio is sensitive to changes in the electron density only for a limited range of values. For high and low values, it becomes asymptotic, and the value derived has to be treated with care and should not be used for quantitative statements. However, the value will still be valid to understand the possible dependences of the abundance gradient with this parameter.
For the ionization parameter, u, we adopted the [S iii]λ9069, 9532/[S ii]λ6717, 6731 calibrator described by Kewley & Dopita (2002). Since [S iii]λ9532 is not covered by our wavelength range, we adopted a theoretical ratio of [S iii]λ9532/ [S iii]λ9069 = 2.5 (Vilchez & Esteban 1996), fixed by atomic physics. Both emission lines were corrected for dust attenuation prior to deriving the ionization parameter.
3.5. Oxygen abundance of H ii regions
Accurate abundance measurements for the ionized gas in galaxies require the determination of the electron temperature (Te), usually obtained from the ratio of auroral to nebular line intensities (e.g., Osterbrock 1989). It is well known that this procedure is difficult to carry out for metal-rich galaxies, since as the metallicity increases the electron temperature decreases (because the cooling is via metal lines), and the auroral lines may become too faint to measure. Therefore, calibrators based on strong emission lines are used.
Strong-line indicators have the obvious advantage of using emission lines with higher signal-to-noise ratios, detected in mostly all H ii regions, and with wide dynamical ranges. However, they have the disadvantage that the line ratios considered do not trace the oxygen abundance only, but also depend on other properties of the ionized nebulae, like the electron density, and geometrical factors, and/or the shape of the ionizing radiation (normally parametrized by the ionization parameter, q, or u = q/c in its dimensionless form). It is well known that some of these parameters are correlated, like the trend between oxygen abundance and the ionization parameter, uncovered by the seminal studies by Evans & Dopita (1985), Dopita & Evans (1986), and recently revisited by Sánchez et al. (2014a).
There are two main schools in the derivation of oxygen abundance using strong-line indicators. One uses empirical calibrators based on the comparison of different of strong emission line ratios, with the corresponding abundance derived for a set of H ii regions for which Te is known. The line ratios in these methods are ![\begin{eqnarray} &&{\rm R23} = \frac{I([\ion{O}{iii}]~\lambda\lambda5007,4959)+I([\ion{O}{iii}]~\lambda3727)}{I({\rm H}\beta)} \\ && {\rm O3N2} = \frac{I([\ion{O}{iii}]~\lambda5007)/I({\rm H}\beta)}{I([\ion{N}{ii}]~\lambda6584)/I({\rm H}\alpha)} \\ && {\rm N2O2} = \frac{I([\ion{N}{ii}]~\lambda6584)}{I([\ion{O}{ii}]~\lambda3727)} \\ && {\rm N2} = \frac{I([\ion{N}{ii}]~\lambda6584)}{I(H\alpha)}\cdot \end{eqnarray}](/articles/aa/full_html/2015/01/aa24950-14/aa24950-14-eq47.png) This school of thought adopts in most cases emission line ratios that present little or no dependence on the dust attenuation (i.e., not far in wavelength), that uses the strongest available emission lines, and calibrators that present either a monotonic or even a linear dependence on the abundance, for example, the O3N2 and the N2 indicators (Alloin et al. 1979; Pettini & Pagel 2004; Stasińska et al. 2006; Marino et al. 2013). In some cases they use a combination of all the available emission lines, like the counterpart-method described by Pilyugin et al. (2012), or more complex combinations of non-linear equations to derive the abundances (e.g., Pilyugin et al. 2010; Pérez-Montero 2014). Since they adopted empirical correlations, the intrinsic dependences with other parameters, like u, are subsumed in the calibrator by construction.
This school of thought adopts in most cases emission line ratios that present little or no dependence on the dust attenuation (i.e., not far in wavelength), that uses the strongest available emission lines, and calibrators that present either a monotonic or even a linear dependence on the abundance, for example, the O3N2 and the N2 indicators (Alloin et al. 1979; Pettini & Pagel 2004; Stasińska et al. 2006; Marino et al. 2013). In some cases they use a combination of all the available emission lines, like the counterpart-method described by Pilyugin et al. (2012), or more complex combinations of non-linear equations to derive the abundances (e.g., Pilyugin et al. 2010; Pérez-Montero 2014). Since they adopted empirical correlations, the intrinsic dependences with other parameters, like u, are subsumed in the calibrator by construction.
A second school of thought prefers to use photoionization models to derive the dependence of the abundance and ionization strength with the different line ratios (e.g., Dopita et al. 2000; Kewley et al. 2001). A certain model for the ionizing stellar population is assumed, taking into account a certain burst of star formation, an initial mass function, a certain metallicity, and, in some cases, the age of the cluster. Under certain conditions for the ionized nebulae (e.g., geometry, electron density), it is possible to derive trends and correlations between the abundance and the line ratios considered. For this school, the preferred line ratios are those that depend on only one of the parameters, or for which the correction on the other is well understood. The procedure or prescriptions described by Kewley & Dopita (2002) or López-Sánchez et al. (2012) for how to derive the abundances is a good example of this approach.
The main difference between the two schools is that for the first the abundances derived are systematically lower. Dopita et al. (2014) studied a scenario in which the introduction of a κ distribution for the electron temperatures in the nebula allows us to reconcile both estimates of the oxygen abundance, based on the early studies by Binette et al. (2009). However, most of the followers of the first school still consider that the Te or direct method better represents the physical conditions in the nebulae, and requires fewer assumptions or dependences on still not well understood physical properties (like the amount of ionizing photons of young stars, which differs among the different stellar evolution models). Another criticism is that in many cases the calibrations based on photoionization models assume tight or fixed correlations between the abundances of different elements (like the N/O ratio), which may affect their derived values (e.g., Pérez-Montero 2014).
We adopted the indicator based on the O3N2 ratio described earlier in order to compare it with previous results in the same field. This line ratio involves the stronger emission lines in the wavelength range, as clearly seen in Fig. 3, and therefore minimize the errors due to the inaccuracies in the measurement of the involved line ratios. By construction, it presents a weak dependence on dust attenuation, already noticed by previous authors (e.g., Kewley & Dopita 2002). We adopted the recently updated calibration by Marino et al. (2013) that uses the largest sample of H ii regions with abundances derived using the direct, Te-based, method (hereafter M13). This calibration corrects the one proposed by Pettini & Pagel (2004), that (due to the lack of H ii regions in the upper abundance range) combined direct measurements for the lower abundance range and values derived from photoionization models for the more metal rich ones. As demonstrated by Marino et al. (2013), it produces abundance values very similar to the ones estimated based on the Pilyugin et al. (2012) method, with an accuracy better than ±0.08 dex.
The wavelength range covered by MUSE at the redshift of the galaxy does not include the [O ii]λ3727 emission line. Therefore, all indicators that include it, like R23, N2O2, or the combination of any of them, cannot be used. However, there are other less common abundance indicators covered in this wavelength range, such as ![\begin{eqnarray} && {\rm S23} = \frac{I([\ion{S}{iii}]~\lambda\lambda9069,9532)+I([\ion{S}{ii}]~\lambda6717,6731)}{I({\rm H}\beta)} \\ && {\rm S3O3} = \frac{I([\ion{S}{iii}]~\lambda\lambda9069)}{I([\ion{O}{iii}]~\lambda5007)}\\ && {\rm Ar3O3} = \frac{I([\ion{Ar}{iii}]~\lambda\lambda7135)}{I([\ion{O}{iii}]~\lambda5007)}\cdot \end{eqnarray}](/articles/aa/full_html/2015/01/aa24950-14/aa24950-14-eq50.png) The S23 indicator was first proposed by Díaz & Pérez-Montero (2000) as an alternative to the more widely used R23. Its main advantages are that the intensities of the lines are less affected by dust attenuation, that it presents a monotonic linear dependence with the abundance for a wide range of metallicities, and that it seems to be less dependent on the ionization parameter. This last statement was questioned by Kewley & Dopita (2002) on the basis of photoionization models. Oey & Shields (2000) already noticed that this indicator has a bi-valued behavior with respect to the abundance, similar to R23, and restricted the use of the calibrator proposed by Díaz & Pérez-Montero (2000) to subsolar metallicities (Z< 0.5Z·). This corresponds to an oxygen abundance of 12 + log (O/H) < 8.3, lower than the lowest abundances derived for the H ii regions discussed here based on the M13 calibrator.
The S23 indicator was first proposed by Díaz & Pérez-Montero (2000) as an alternative to the more widely used R23. Its main advantages are that the intensities of the lines are less affected by dust attenuation, that it presents a monotonic linear dependence with the abundance for a wide range of metallicities, and that it seems to be less dependent on the ionization parameter. This last statement was questioned by Kewley & Dopita (2002) on the basis of photoionization models. Oey & Shields (2000) already noticed that this indicator has a bi-valued behavior with respect to the abundance, similar to R23, and restricted the use of the calibrator proposed by Díaz & Pérez-Montero (2000) to subsolar metallicities (Z< 0.5Z·). This corresponds to an oxygen abundance of 12 + log (O/H) < 8.3, lower than the lowest abundances derived for the H ii regions discussed here based on the M13 calibrator.
There is no published calibration of the dependence of S23 with the oxygen abundance for the higher abundance branch. However, based on the photoionization models presented by Oey & Shields (2000), it is possible to derive an estimation of the abundance for that range: 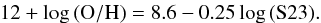 (9)The accuracy of this calibrator has to be tested extensively, but based on the range of values covered by the described models we estimate it to be not better than 0.15 dex.
(9)The accuracy of this calibrator has to be tested extensively, but based on the range of values covered by the described models we estimate it to be not better than 0.15 dex.
 |
Fig. 5 Comparison of the oxygen abundances derived using the different indicators described in the text: (i) S23 vs. O3N2 (top left panel); (ii) S3O3 vs. O3N2 (top right panel); (iii) ArO3 vs. O3N2 (bottom left panel); and (iv) ArO3 vs. S3O3 (bottom right panel). Each blue solid circle corresponds to an individual H ii region in the sample. The error bars represent half of the estimated error considering the propagation of the emission line errors and the uncertainty in the calibrator. The dashed line in each panel corresponds to the one-to-one relation. |
The S3O3 and Ar3O3 indicators were proposed by Stasińska (2006; hereafter S06). She derived a non-linear correlation for both indicators and the oxygen abundance that we adopt here. She estimated the accuracy of this calibrator to be on the order of ~0.09 dex.
In contrast with the O3N2 abundance indicator, which is basically independent of dust attenuation, all these indicators involve ratios of emission lines widely separated in wavelength, and therefore the line intensities must be corrected for dust attenuation prior to deriving the corresponding ratio and abundance. This introduces a new degree of uncertainty that we avoid by adopting the O3N2 calibrator.
Figure 5 shows the comparison among the different estimators for the oxygen abundance discussed. We consider only the emission lines and line ratios detected above a 5σ detection limit. Hence, each panel shows a different number of H ii regions, ranging between 210 (for the panels involving the ArO3 indicator) and 360 (for the panels involving the O3N2, S23, and S3O3 indicators), because the [Ar iii] emission line is fainter than any of the others (Fig. 3). There is very good agreement between the different estimators, despite the different ions involved in most of the calibrators, and the inhomogenous derivation of the calibrators. The largest differences are found in the calibrator involving the [Ar iii] emission line, for the reason indicated before: σ(XO3N2 − XAr3O3) = 0.08 and σ(XS3O3 − XAr3O3) = 0.07 dex, where σ is the standard deviation of the difference between the two estimations of the abundance, and X is the oxygen abundance, i.e., 12 + log (O/H). The smallest differences are found between the O3N2 and S23 indicators, with σ(XO3N2 − XS23) = 0.04 dex, a value smaller than the expected accuracies of both calibrators. In summary, this comparison shows that our estimation of the oxygen abundance does not depend strongly on the adopted indicator, and that on average the accuracy of our estimation is ~0.05 dex or better. This systematic error has been included in the error budget of the abundances derived for each individual H ii region.
3.6. Structural parameters of the galaxy
We derive the mean position angle, ellipticity, and effective radius of the disk by a surface brightness and morphological analysis performed on the MUSE data using a V-band image of NGC 6754 synthetized from the IFS cube. The procedure is extensively described in Sánchez et al. (2014b). In summary, an isophotal analysis is performed using the ellipse_isophot_seg.pl tool included in the HIIexplorer package4. Unlike other tools, like ellipse included in IRAF, this tool does not assume a priori a certain parametric shape for the isophotal distributions. The following procedures were followed for the V-band image: (i) the peak intensity emission within a certain distance of a user defined center of the galaxy was derived. Then, any region around a peak emission above a certain percentage of the galaxy intensity peak is masked, which effectively masks the brightest foreground stars; (ii) once the peak intensity is derived, the image is segmented in consecutive levels following a logarithmic scale from this peak value; (iii) once the image is segmented in nlevels isophotal regions, a set of structural parameters was derived for each of them, including the mean flux intensity and the corresponding standard deviation, the semi-major and semi-minor axis lengths, the ellipticity, the position-angle, and the barycenter coordinates. The median values of the derived position angles and ellipticities along the different isophotes are adopted as the position angle and ellipticity of the galaxy after excluding those affected by the seeing in the very central regions. Their standard deviations are considered as an estimation of the error in the derivation of these parameters. We derive an ellipticity of e = 0.88 ± 0.07 and a position angle of PA = 77 ± 9°. Assuming an intrinsic ellipticity for the galaxy of ~0.13 (Giovanelli et al. 1995, 1997), the inclination is estimated to be i = 64 ± 6°. Finally, we fit the surface brightness profile with a single exponential function to derive the disk scale length, and the correponding disk effective radius, as defined by Sánchez et al. (2014b). The effective radius derived at the distance of the galaxy was estimated as re = 10.7 ± 0.9 kpc.
4. Results
4.1. Oxygen abundance gradient
We deproject the position of each H ii region using the morphological parameters described in the previous section. Then, we derive the galactocentric radial distribution of the oxygen abundance for NGC 6754, based on the abundances measured for each individual H ii region. For the 396 H ii regions detected, Fig. 6 shows the abundance gradient derived out to ~2 re along the galactocentric distance normalized to the effective radius.
The shape of the abundance gradient shown in this figure is totally consistent with the pattern found in many previous studies. The gradient shows an almost linear decrease between ~0.3 and ~1.7 effective radius, with a drop in the central regions and a flattenning and/or up-turn in the outer regions. The linear regime has been interpreted as evidence of inside-out growth in spiral galaxies, with a metal enrichment dominated by local processes (e.g., Sánchez et al. 2014b, and references therein). The drop in the inner region is found in a fraction of the spiral galaxies. In some cases (e.g., NGC 628) it has been associated with a circumnuclear ring of star formation at the expected location of the inner Lindblad resonance radius, where the gas is expected to accumulate because of non-circular motions exerted by a bar or spiral arms (Sánchez et al. 2011; Rosales-Ortega et al. 2011). The nature of the flattening in the outer regions, which has also been observed in other galaxies (e.g., Marino et al. 2012), is still under debate. It could be an effect of the radial migration of stars that later pollute the surrounding gas, or a consequence of a change in the star formation efficiency.
 |
Fig. 6 Radial distribution for the oxygen abundance derived using the O3N2 indicator for the 396 H ii regions detected in NGC 6754, color-coded by the equivalent width of Hα. The small blue symbols correspond to H ii regions with an emission EW(Hα) lower than 20 Å, while the larger red and grey symbols correspond to regions with higher values. The error bars illustrate the individual errors of the abundance propagated from the estimated errors of the emission lines, not including the systematic error of the abundance calibrator. The dash-dotted black line shows the result of the best linear regression to all the points. The blue and red solid lines correspond to the results of the best linear regressions to the H ii regions of lower and higher values of EW(Hα). |
The dash-dotted black line in Fig. 6 shows the error-weighted linear fit to this radial distribution of the abundance. Following Sánchez et al. (2014b), the analysis is restricted to galactocentric distances 0.3 <r/re< 2.1. We find a slope in the abundance gradient of α = −0.10 ± 0.02 dex/re, which is similar to the common abundance slope reported by Sánchez et al. (2014b) of ~− 0.1 dex/re. If we used the same calibrator as the one adopted in that study, i.e., Pettini & Pagel (2004), instead of Marino et al. (2013), the slope would be slightly larger, α = −0.14 ± 0.02 dex/re. In both cases the slopes are totally compatible with the common gradient, since they are both within 1σ of the range of values described for this characteristic slope (Sánchez et al. 2014b).
The number of H ii regions detected for this galaxy is large enough to explore whether the abundance gradient depends on other properties of the nebular emission. The H ii regions in Fig. 6 have been color-coded according to the value of the EW(Hα). Adopting this scheme it is possible to distinguish between the regions with stronger specific star formation rates, which trace the spiral arms (Fig. 1), and those distributed more homogeneously across the entire disk. We repeat the fitting procedure splitting the sample in two, for H ii regions with equivalent width greater or smaller than 20 Å. We find that the H ii regions with lower equivalent widths present a somewhat shallower gradient (α = −0.09 ± 0.01) than those with higher equivalent widths (α = −0.12 ± 0.02). The two gradients are shown in Fig. 6. However, the difference is rather small, and may not be significant. In order to test it, we perform a Kolmogorov-Smirnov (KS) test to estimate how different the distributions of oxygen abundances in both cases are. We find that the probability that both distributions were not derived from the same sample is just 7.7%. Therefore, there is no significant difference between the abundance gradients for the regions with stronger or fainter specific star formation rates.
We explore possible differences in the abundance gradients based on other properties of the ionized nebulae. First, we considered the ionization parameter, splitting the sample into two subsamples with log (u) greater or smaller than − 3.6 (the median value for our sample). The differences in the slopes were even smaller (αhigh log (u) = −0.10 ± 0.02 dex and αlowlog (u) = −0.08 ± 0.03 dex). Then, we considered the electron density, splitting the sample in regions with ne greater or smaller than 75 cm-3 (the median value for our sample). In this case we find the same slope for both subsamples (αhigh ne = −0.10 ± 0.03 dex).
Finally, we explore whether the different spatial resolutions of the east and west pointings have an impact on the abundance distributions and gradients. We repeat the analysis restricting our sample to the regions detected in both pointings separately before joining them into a single catalogue. We find very similar slopes for both subsamples: αeast = −0.10 ± 0.02 dex and αwest = −0.12 ± 0.03 dex. Even more, a KS test indicates that the probability that both distributions were not derived from the sample sample is 0.02%.
4.2. Mixing scale length
This sample of H ii regions is large enough to derive an estimation of the mixing scale length. For this step we computed the dispersion of galactocentric distances with respect to the linear regression. The average of this relative distance is zero (by construction), and the standard deviation is the typical mixing scale, i.e., how far a certain H ii region has moved from its expected location based on a pure inside-out chemical enrichment without radial mixing. We find a mixing scale length rmix = 0.43 re, which corresponds to 4.6 kpc at the redshift of this galaxy.
We repeated the estimation for the different subsamples of H ii regions discussed earlier, and found similar dispersions, covering a range of values of rmix = 0.37 − 0.53 re. In particular, when taking into account the east and west pointing separately, we derive a very similar radial mixing scale length, slightly lower than the common one (rmix,east/west = 0.35 re). This indicates that (i) the different spatial resolution does not affect the result; and (ii) there seems to be an azimuthal variation of the oxygen abundances that increases the dispersion when not taken into account. Finally, we study if there is a dependence on galactocentric distance. We found that the mixing scale length is slightly lower in the inner regions rmix(r/re< 0.9) = 0.28 re than in the outer ones rmix(r/re> 0.9) = 0.67 re.
To know how sensitive this dispersion is to the errors and uncertainties in the derived parameter, we performed a simple Monte Carlo simulation, allowing each of the parameters (abundances, galactocentric distances, effective radius, and inclination) to vary within the estimated errors. The standard deviation between the different estimated radial mixing scales is ~0.15 re.
This parameter puts a strong constraint on the metal mixing scale length, independently of the mechanism required to produce the mixing. This is an upper limit to the mixing scale length, in particular if the abundance gradient depends on the equivalent width of Hα.
 |
Fig. 7 Azimuthal distribution of the residual of the oxygen abundance for the individual H ii regions after subtracting the average radial gradient. The colors and sizes indicate the galactocentric distance, with blue solid circles corresponding to H ii regions nearer to the center of the galaxy, and red or orange ones corresponding to those farther away. The solid line corresponds to the average value at each azimuthal angle for H ii regions within 25° of the considered angle. |
4.3. Azimuthal variations of the oxygen abundance
In a pure inside-out scenario where the metal enrichment is dominated by local processes (the metal pollution by stars that dies at a certain location), the abundance gradient should not present any azimuthal variation. Different mechanisms proposed for the radial mixing predict different characteristic patterns in the azimuthal distribution of the oxygen abundance. The sample of H ii regions provided by our MUSE data is large enough to explore whether there is an azimuthal variation in the distribution of oxygen abundances.
Figure 7 shows the azimuthal distribution of the oxygen abundances for the H ii regions of our catalogue, after the removal of the common radial gradient, for those regions within a ring of 0.3 <r/re< 2.1 (i.e., the linear regime of the abundance gradient). There is a clear pattern, even clearer when we derive the azimuthal average within a box of 25° around each value. Indeed, when removing this average pattern the dispersion around the mean value is reduced by 40%. The amplitude of the pattern does not follow a clear periodic sequence (like a sinusoidal structure), and there is no clear general dependence on the galactocentric distance.
However, in the strongest feature of this pattern, the wiggle between θ ~ 90° and θ ~ 160° with an amplitude of ~0.05 dex, there seems to be a trend with distance: the abundance decreases at intermediate distances and increases for both the inner and outer regions. This pattern corresponds to the spiral arm to the southeast of the center of the galaxy. If real, this could be a hint of radial mixing.
The radial mixing scale defined in the previous section is reduced to 0.39r/re, or 4.1 kpc, when the average azimuthal variation of the oxygen abundance is subtracted prior to derivng the dispersion around the radial abundance gradient.
5. Discussion and conclusions
In this study we analyze one of the first observations using MUSE on a spiral galaxy, NGC 6754. We detect and extract the spectroscopic information of a sample of 396 H ii regions, an order of magnitude larger than the average number observed in previous state-of-the-art IFU survey datasets (e.g., Sánchez et al. 2014b). This illustrates the capabilities of this unique instrument that are due to the combination of its large FoV and unprecedented spatial sampling and resolution.
The abundance distribution derived has a negative gradient, with a slope consistent with the characteristic value reported by previous studies (Sánchez et al. 2014b), in the linear regime between 0.3 and 1.7 re. The abundance decreases in the inner regions, and there is a hint of a flattening in the outer parts. Both features have been already observed in previous studies in individual galaxies (e.g., Bresolin et al. 2009; Yoachim et al. 2010; Rosales-Ortega et al. 2011; Marino et al. 2012; Bresolin et al. 2012). The central drop is in many cases associated with a circumnuclear star formation process (Sánchez et al. 2014b), and it could be related with the accumulation of gas due to non-circular motions exerted near the inner Lindblad resonance radius (e.g., Cepa & Beckman 1990).
The nature of the flattening is still not clear. A detailed discussion on the different scenarios proposed was presented by Sánchez et al. (2014b). In summary, under the usually observed star formation rates, the time required to enrich the ISM up to the observed abundances in these outer regions is on the order of the age of the Universe (Bresolin et al. 2012), and therefore it is unlikely that in situ star formation could have enriched the interstellar medium to the values observed. Among the main mechanisms proposed to explain the flattening we highlight the following: (i) angular momentum transport that produces a radial mixing (e.g., Lacey & Fall 1985; Goetz & Koeppen 1992; Portinari & Chiosi 2000; Schönrich & Binney 2009; Spitoni & Matteucci 2011); (ii) resonance scattering with transient spiral density waves (Sellwood & Binney 2002); (iii) the overlap of spiral and bar resonances (Minchev et al. 2011); (iv) stellar radial migration (e.g., Roškar et al. 2008b,a); and (v) minor mergers and captures of satellite galaxies (Quillen et al. 2009; Bird et al. 2012).
We explore the possible dependence of the slope of the abundance gradient on different properties of the ionized gas. Significant differences are not expected if the metal enrichment is dominated by the inside-out growth of the galaxy. However, local processes, like outflows or metal raining induced by enhanced star formation associated with the spiral arms may modify the chemical distribution locally. Under this assumption it would be expected that denser H ii regions in spiral arms, with greater EW(Hα), and ionization strengths present a different distribution of oxygen abundances than those H ii regions located in the inter-arm regions. Our results indicate that local processes do not seem to be relevant enough to modify the galactocentric abundance gradient in this particular galaxy.
We define a parameter to estimate the amount of the redistribution of metals within the galaxy that we call the mixing scale length, rmix. This parameter is defined as the dispersion around the abundance gradient along the galactocentric distance, and can be derived as the ratio between the dispersion in the abundance and the slope of the correlation. We estimate the typical rmix = 0.43 ± 0.15 re, i.e., ~4.6 kpc at the redshift of the galaxy. To our knowledge, this is the first time that this parameter has been defined in this way. However, it is possible to compare it with previous results if both the dispersion in abundance and the slope of the radial gradient are provided. The most recent exploration of the abundance gradient over a large sample of galaxies was published by Sánchez et al. (2012b, 2014b). They found that the common abundance gradient has a slope of α = −0.1 dex/re, with a dispersion of ~0.6 dex, for which an average mixing scale length of rmix ~ 0.6 re is derived. This value is slightly higher than the one we find for NGC 6754. However, we should note here that the estimation derived from the Sánchez et al. (2012b, 2014b) results is purely statistical, based on the average abundance gradient derived once the individual gradients for each galaxy are considered all together and normalized to the abundance at the effective radius. Measurements on individual galaxies have not been provided.
Bars have been proposed as an effective mechanism for radial migration (e.g., Athanassoula 1992; Sellwood & Binney 2002). Hydrodynamical simulations have shown that bars induce angular momentum transfer via gravitational torques, which result in radial flows and mixing of both stars and gas (e.g., Athanassoula 1992). These radial motions can produce a mixing and homogenization of the gas, which leads to a flattening of any abundance gradient (e.g., Friedli 1998). Resonances between the bar and the spiral pattern speeds can shift the orbits of stars, mostly towards the outer regions (Minchev & Famaey 2010), a mechanism that also affects the gas. Another process that produces a similar effect is the coupling between the pattern speed of the spiral arms and the bar, which induces angular momentum transfer at the corotation radius (e.g., Sellwood & Binney 2002). In a recent study Di Matteo et al. (2013) analyzed the signatures of radial migration in barred galaxies on the basis of simulations. They found that the slope of the abundance gradient does not change significantly up to ~1.5–2 re (when the scale length of their simulated disks are transformed to an effective radius), but a flattening is predicted beyond these galactocentric distances. This pattern is very similar to the one observed in our galaxy. However, as we discussed before, the flattening in the outer region seems to be present in spiral galaxies irrespective of the presence or absence of bars (Sánchez et al. 2014b).
Di Matteo et al. (2013) defined a parameter to quantify the amount of spatial redistribution of stars in a disk as the ratio between the maximum absolute variation of the metallicity with respect to the radial gradient compared to the slope of this gradient (δ[Fe/H]/ Δ[Fe/H]). With units of distance, this parameter is equivalent to our mixing scale length (rmix). They found that this parameter evolves with time and presents a weak radial dependence. At the peak of the radial migration it ranges between 1–1.5 kpc (0.17–0.26 re) for a galactocentric distance between 3 and 12 kpc (0.5–2 re). As time evolves it decreases, being slightly larger in the outer regions. Our derived rmix is larger, but certainly on the same order as that predicted by Di Matteo et al. (2013). It also presents a weak radial dependence, which may indicate that the peak of the migration has already past. This is a good agreement considering that we are not comparing with ad hoc simulations specifically done to reproduce our galaxy.
Another prediction from the simulations is that the radial mixing should not be homogeneous. These inhomogeneities are related to the way radial migration occurs in galaxies, following the arms pattern (e.g., Minchev et al. 2012): metal-rich stars that move to the outer disk are mostly from the region outside corotation (Brunetti et al. 2011) and migrate through spiral patterns to the outer parts of the disk. In other words, migration is not axisymmetric, but is associated to the distribution of arms and bars. In Sect. 4.3 we explored the possible azimuthal variations of the oxygen abundance, after subtracting the radial dependence, and we found evidence of an asymmetrical distribution. The strongest feature is associated with the spiral arms in the southeast of the galaxy. The amplitude seems to be smaller than that predicted by Di Matteo et al. (2013) for the epoch of the strongest migration: ~0.2 dex at ~7 kpc (1 re), at t = 1.1 Gyr in their simulations (see their Fig. 8, top panel). However, this effect is expected to become weaker with time (their Fig. 8, bottom panel), and our previous result indicates that this galaxy has already passed the peak of the strongest migration.
The proposed scenario assumes that the deviation of the abundances with respect to the radial gradient, due to the radial migration associated with arms and bars, should be stronger in barred galaxies. This is a consequence of the stronger radial movements expected to be induced by these morphological features. In this context it is interesting to note that recent results indicate that the stellar and gas kinematics of barred and un-barred galaxies seem to be very similar, without stronger distorsions induced by the presence of the bar, at least at large scales (Barrera-Ballesteros et al. 2014).
Despite this significant advance in our understanding of the possible effects of radial mixing, it is important to highlight that all these results were derived for a single galaxy. Larger samples of galaxies are needed to explorewhether the estimated mixing scale lengths and azimuthal variations depend on other properties of the galaxies, such as the presence or absence of bars, the strength of the bars, the interaction stage, the morphological type, and the stellar mass or luminosity. In particular, if the picture outlined by Di Matteo et al. (2013) is valid, we should find different strengths in both rmix and the intensity of the azimuthal variations depending on the timing of the evolution of the bars and whether or not there is coupling with the spiral arms. Another important caveat is that the results from the current simulations focus on the effects of the migration on old stars, and on their metallicities. As clearly illustrated by recent results in González Delgado et al. (2014), the gas-phase abundance is better correlated with the metallicity of young stars (t< 2 Gyr), with old stars being in general more metal poor. It is still unclear how these differences may affect the interpretation of our results on the basis of the simulations. However, there is a lack of similar simulations on the effects of radial migration for the gas-phase abundance.
The current results illustrate the ability of MUSE to accomplish this kind of study in a very efficient way, and demonstrate that it is possible to derive reliable dispersions around the mean abundance gradient. In future articles we will apply the methodology outlined here to a sample of galaxies with similar characteristics of cosmological distances and projected sizes, observed with this instrument, in order to explore the dependence of the results on galaxy type, as outlined before.
Acknowledgments
SFS thanks the director of CEFCA, M. Moles, for his sincere support. We thank the referee for his/her comments that have improved this manuscript. Based on observations made with ESO Telescopes at the Paranal Observatory under programme ID 60.A-9329. Support for L.G. and H.K. is provided by the Ministry of Economy, Development, and Tourism’s Millennium Science Initiative through grant IC12009, awarded to The Millennium Institute of Astrophysics, MAS. L.G. and H.K. acknowledge support by CONICYT through FONDECYT grants 3140566 and 3140563, respectively. S.F.S. acknowledges the Mexican National Council for Science and Technology (CONACYT) for financial support under the program Proyectos de Ciencia Basica. E.P. acknowledges funding from the Spanish MINECO grant AYA2010-15081. RA Marino was also funded by the Spanish programme of International Campus of Excellence Moncloa (CEI).
References
- Allington-Smith, J., Murray, G., Content, R., et al. 2002, PASP, 114, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Alloin, D., Collin-Souffrin, S., Joly, M., & Vigroux, L. 1979, A&A, 78, 200 [Google Scholar]
- Athanassoula, E. 1992, MNRAS, 259, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrera-Ballesteros, J. K., Falcón-Barroso, J., García-Lorenzo, B., et al. 2014, A&A, 568, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Binette, L., Flores-Fajardo, N., Raga, A. C., Drissen, L., & Morisset, C. 2009, ApJ, 695, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Bird, J. C., Kazantzidis, S., & Weinberg, D. H. 2012, MNRAS, 420, 913 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Ryan-Weber, E., Kennicutt, R. C., & Goddard, Q. 2009, ApJ, 695, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kennicutt, R. C., & Ryan-Weber, E. 2012, ApJ, 750, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Brunetti, M., Chiappini, C., & Pfenniger, D. 2011, A&A, 534, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cepa, J., & Beckman, J. E. 1990, ApJ, 349, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Schlickmann, M. S., et al. 2010, MNRAS, 403, 1036 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Pérez, E., García Benito, R., et al. 2013, A&A, 557, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clayton, D. D. 1987, ApJ, 315, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Haywood, M., Combes, F., Semelin, B., & Snaith, O. N. 2013, A&A, 553, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diaz, A. I. 1989, in Evolutionary Phenomena in Galaxies, eds. J. E. Beckman, & B. E. J. Pagel, 377 [Google Scholar]
- Díaz, A. I., & Pérez-Montero, E. 2000, MNRAS, 312, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., & Evans, I. N. 1986, ApJ, 307, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Kewley, L. J., Heisler, C. A., & Sutherland, R. S. 2000, ApJ, 542, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Rich, J., Vogt, F. P. A., et al. 2014, Ap&SS, 350, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, I. N., & Dopita, M. A. 1985, ApJS, 58, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Falcón-Barroso, J., Sánchez-Blázquez, P., Vazdekis, A., et al. 2011, A&A, 532, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedli, D. 1998, in Abundance Profiles: Diagnostic Tools for Galaxy History, eds. D. Friedli, M. Edmunds, C. Robert, & L. Drissen, ASP Conf. Ser., 147, 287 [Google Scholar]
- García-Benito, R., Pérez, E., Díaz, Á. I., Maíz Apellániz, J., & Cerviño, M. 2011, AJ, 141, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Salzer, J. J., et al. 1995, AJ, 110, 1059 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Herter, T., et al. 1997, AJ, 113, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Goetz, M., & Koeppen, J. 1992, A&A, 262, 455 [NASA ADS] [Google Scholar]
- González Delgado, R. M., Cid Fernandes, R., García-Benito, R., et al. 2014, ApJ, 791, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Guesten, R., & Mezger, P. G. 1982, Vistas in Astronomy, 26, 159 [Google Scholar]
- Hill, G. J., MacQueen, P. J., Smith, M. P., et al. 2008, in SPIE Conf. Ser., 7014, 70 [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kelz, A., Verheijen, M. A. W., Roth, M. M., et al. 2006, PASP, 118, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Keel, W. C., & Blaha, C. A. 1989, AJ, 97, 1022 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Lacey, C. G., & Fall, S. M. 1985, ApJ, 290, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1670 [Google Scholar]
- Lépine, J. R. D., Cruz, P., Scarano, Jr., S., et al. 2011, MNRAS, 417, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [NASA ADS] [Google Scholar]
- Li, Y., Bresolin, F., & Kennicutt, Jr., R. C. 2013, ApJ, 766, 17 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sánchez, Á. R., Dopita, M. A., Kewley, L. J., et al. 2012, MNRAS, 426, 2630 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, R. A., Gil de Paz, A., Castillo-Morales, A., et al. 2012, ApJ, 754, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Marino, R. A., Rosales-Ortega, F. F., Sánchez, S. F., et al. 2013, A&A, 559, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, L. P., González Delgado, R. M., Leitherer, C., Cerviño, M., & Hauschildt, P. 2005, MNRAS, 358, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Mast, D., Rosales-Ortega, F. F., Sánchez, S. F., et al. 2014, A&A, 561, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Combes, F., et al. 2011, A&A, 527, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollá, M., & Roy, J.-R. 1999, ApJ, 514, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., & Kennicutt, Jr., R. C. 2006, ApJS, 164, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., & Shields, J. C. 2000, ApJ, 539, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., Parker, J. S., Mikles, V. J., & Zhang, X. 2003, AJ, 126, 2317 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei (University Science Books) [Google Scholar]
- Pérez-Montero, E. 2014, MNRAS, 441, 2663 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Vílchez, J. M., & Thuan, T. X. 2010, ApJ, 720, 1738 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Mattsson, L. 2012, MNRAS, 424, 2316 [NASA ADS] [CrossRef] [Google Scholar]
- Portinari, L., & Chiosi, C. 2000, A&A, 355, 929 [NASA ADS] [Google Scholar]
- Quillen, A. C., Minchev, I., Bland-Hawthorn, J., & Haywood, M. 2009, MNRAS, 397, 1599 [NASA ADS] [CrossRef] [Google Scholar]
- Rosales-Ortega, F. F., Kennicutt, R. C., Sánchez, S. F., et al. 2010, MNRAS, 405, 735 [NASA ADS] [Google Scholar]
- Rosales-Ortega, F. F., Díaz, A. I., Kennicutt, R. C., & Sánchez, S. F. 2011, MNRAS, 415, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Quinn, T. R., Stinson, G. S., & Wadsley, J. 2008a, ApJ, 684, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Stinson, G. S., et al. 2008b, ApJ, 675, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., García-Lorenzo, B., Jahnke, K., et al. 2006, New A Rev., 49, 501 [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Kennicutt, R. C., et al. 2011, MNRAS, 410, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012a, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012b, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Pérez, E., Rosales-Ortega, F. F., et al. 2014a, A&A, in press, DOI: 10.1051/0004-6361/201424873 [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Iglesias-Páramo, J., et al. 2014b, A&A, 563, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J., & Elmegreen, B. G. 2004, ARA&A, 42, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Sellwood, J. A., & Binney, J. J. 2002, MNRAS, 336, 785 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., & Matteucci, F. 2011, A&A, 531, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G. 2006, A&A, 454, L127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stasińska, G., Cid Fernandes, R., Mateus, A., Sodré, L., & Asari, N. V. 2006, MNRAS, 371, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Sánchez-Blázquez, P., Falcón-Barroso, J., et al. 2010, MNRAS, 404, 1639 [NASA ADS] [Google Scholar]
- Vazdekis, A., Ricciardelli, E., Cenarro, A. J., et al. 2012, MNRAS, 424, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Vilchez, J. M., & Esteban, C. 1996, MNRAS, 280, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Walcher, C. J., Wisotzki, L., Bekeraité, S., et al. 2014, A&A, 569, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weilbacher, P. M., Streicher, O., Urrutia, T., et al. 2014, in ASP Conf. Ser. 485, eds. N. Manset, & P. Forshay, 451 [Google Scholar]
- Yoachim, P., Roškar, R., & Debattista, V. P. 2010, ApJ, 716, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Kennicutt, Jr., R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 RGB color image of NGC 6754 created using the line intensity maps of [O iii]λ5007 (blue), V-band (green), and Hα (red) extracted from the datacubes. Each large tick mark corresponds to 10″ (or 400 pc at the redshift of the galaxy). The green point-like sources are field stars. Each red structure corresponds to a single H ii region. |
| In the text | |
 |
Fig. 2 Color-coded map of the equivalent width of Hα in logarithmic scale. The areas with Hα density flux below 1.5 × 10-18 erg s-1 cm-2 spaxel-1 (~3σ detection limit) have been masked. The circles represent the detected H ii regions; the radius is proportional to the extraction aperture. |
| In the text | |
 |
Fig. 3 Detail of the spectrum of a typical H ii region extracted from the galaxy. The black line shows the input spectrum in logarithmic scale, together with the best fitted stellar model in orange. The difference between the logarithms of the input spectrum and the model, shifted by 1, is shown as a blue line. The intensities of the emission lines are so high that the spectra are plotted in logarithmic scale to show them together with the detail of the underlying stellar population.The most prominent spectral features discussed throughout the article are marked. The spectral regions masked during the fitting of the underlying stellar population are not shown by the orange solid line. The two boxes show an expanded view around Hβ and Hα. |
| In the text | |
 |
Fig. 4 [O iii] λ5007/Hβ vs. [N ii] λ6583/Hα diagnostic diagram for the 396 H ii ionized regions detected in NGC 6754, color-coded by the deprojected galactocentric distance (where bluer colors correspond to the central regions, and reddish-to-grey colors correspond to the outer regions). Solid and dashed lines represent, respectively, the Kauffmann et al. (2003) and Kewley et al. (2001) demarcation curves. They are usually invoked to distinguish between classical star-forming objects (below thesolid line), and AGN powered sources (above the dashed line). Regions between both lines are considered intermediate ones. The average error of the line ratios is represented by the error bar in the upper-right corner. |
| In the text | |
 |
Fig. 5 Comparison of the oxygen abundances derived using the different indicators described in the text: (i) S23 vs. O3N2 (top left panel); (ii) S3O3 vs. O3N2 (top right panel); (iii) ArO3 vs. O3N2 (bottom left panel); and (iv) ArO3 vs. S3O3 (bottom right panel). Each blue solid circle corresponds to an individual H ii region in the sample. The error bars represent half of the estimated error considering the propagation of the emission line errors and the uncertainty in the calibrator. The dashed line in each panel corresponds to the one-to-one relation. |
| In the text | |
 |
Fig. 6 Radial distribution for the oxygen abundance derived using the O3N2 indicator for the 396 H ii regions detected in NGC 6754, color-coded by the equivalent width of Hα. The small blue symbols correspond to H ii regions with an emission EW(Hα) lower than 20 Å, while the larger red and grey symbols correspond to regions with higher values. The error bars illustrate the individual errors of the abundance propagated from the estimated errors of the emission lines, not including the systematic error of the abundance calibrator. The dash-dotted black line shows the result of the best linear regression to all the points. The blue and red solid lines correspond to the results of the best linear regressions to the H ii regions of lower and higher values of EW(Hα). |
| In the text | |
 |
Fig. 7 Azimuthal distribution of the residual of the oxygen abundance for the individual H ii regions after subtracting the average radial gradient. The colors and sizes indicate the galactocentric distance, with blue solid circles corresponding to H ii regions nearer to the center of the galaxy, and red or orange ones corresponding to those farther away. The solid line corresponds to the average value at each azimuthal angle for H ii regions within 25° of the considered angle. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


