| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A130 | |
| Number of page(s) | 15 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201424209 | |
| Published online | 14 January 2015 | |
Model for straight and helical solar jets
I. Parametric studies of the magnetic field geometry
1
LESIA, Observatoire de Paris, CNRS, UPMC, Université Paris
Diderot,
92190
Meudon,
France
e-mail:
etienne.pariat@obspm.fr
2
Heliophysics Science Division, NASA Goddard Space Flight Center, Greenbelt, MD
20771,
USA
Received: 14 May 2014
Accepted: 27 November 2014
Context. Jets are dynamic, impulsive, well-collimated plasma events developing at many different scales and in different layers of the solar atmosphere.
Aims. Jets are believed to be induced by magnetic reconnection, a process central to many astrophysical phenomena. Studying their dynamics can help us to better understand the processes acting in larger eruptive events (e.g., flares and coronal mass ejections) as well as mass, magnetic helicity, and energy transfer at all scales in the solar atmosphere. The relative simplicity of their magnetic geometry and topology, compared with larger solar active events, makes jets ideal candidates for studying the fundamental role of reconnection in energetic events.
Methods. In this study, using our recently developed numerical solver ARMS, we present several parametric studies of a 3D numerical magneto-hydrodynamic model of solar-jet-like events. We studied the impact of the magnetic field inclination and photospheric field distribution on the generation and properties of two morphologically different types of solar jets, straight and helical, which can account for the observed so-called standard and blowout jets.
Results. Our parametric studies validate our model of jets for different geometric properties of the magnetic configuration. We find that a helical jet is always triggered for the range of parameters we tested. This demonstrates that the 3D magnetic null-point configuration is a very robust structure for the energy storage and impulsive release characteristic of helical jets. In certain regimes determined by magnetic geometry, a straight jet precedes the onset of a helical jet. We show that the reconnection occurring during the straight-jet phase influences the triggering of the helical jet.
Conclusions. Our results allow us to better understand the energization, triggering, and driving processes of straight and helical jets. Our model predicts the impulsiveness and energetics of jets in terms of the surrounding magnetic field configuration. Finally, we discuss the interpretation of the observationally defined standard and blowout jets in the context of our model, as well as the physical factors that determine which type of jet will occur.
Key words: Sun: corona / magnetic reconnection / magnetohydrodynamics (MHD) / Sun: flares / Sun: magnetic fields
© ESO, 2015
1. Introduction
In the solar atmosphere, jets are characterized by an impulsive evolution of a collimated plasma structure extending along a particular direction. Jet-like events occurs in a wide range of environments – active regions to coronal holes – on scales from the limit of instrumental resolution to hundreds of Mm, and in every layer of the atmosphere. Jet-like events have been detected in almost all wavelengths available to observers and have thus acquired a multitude of names: spicules (e.g., Beckers 1968; Sterling 2000), photospheric jets (e.g., Shibata et al. 2007; Nishizuka et al. 2011), chromospheric Hα surges (e.g., Schmahl 1981; Schmieder et al. 1995), chromospheric Ca II H jets (e.g., Nishizuka et al. 2008; Morita et al. 2010), coronal extreme-ultraviolet (EUV) jets and macrospicules (Yamauchi et al. 2004; Kamio et al. 2010), coronal X-ray jets (e.g., Shibata et al. 1992; Savcheva et al. 2007) and white-light polar jets (Wang et al. 1998; Wang & Sheeley 2002). However, jet-like events are typically visible in multiple domains of the electromagnetic spectrum and can be observed at different wavelengths. Multiwavelength observations show slightly different spatial, physical, and temporal properties in each observational bandwidth, revealing that each jet event is formed of multithermal and multivelocity plasmas (e.g., Canfield et al. 1996; Jiang et al. 2007; Chifor et al. 2008a; Liu et al. 2011b; Madjarska 2011; Chen et al. 2013).
Coronal jets, as impulsive events, exhibit many similarities with flares observed in active regions. As in flares and eruptions, magnetic reconnection is believed to be the central energy-release mechanism. A fundamental difference to flares is the inferred involvement of open magnetic field lines in jet-like events (Shibata et al. 1992, 1997, 2007; Schmieder et al. 1995; Shimojo & Shibata 2000a,b; Rachmeler et al. 2010). Jets are believed to involve interchange magnetic reconnection, that is, reconnection between closed and open flux. These configurations are very commonly observed in coronal holes (Shimojo et al. 1998; Savcheva et al. 2007; Shimojo & Tsuneta 2009), where the open field extends into the heliosphere. In active regions, the open field corresponds to field lines with one remote footpoint located very far from the locally closed domain (Shimojo & Shibata 2000a; Schmieder et al. 2013). The open magnetic field plays a key role in collimating jets (Wang & Pick 2006; Moreno-Insertis et al. 2008; Liu et al. 2009; Guo et al. 2013).
A typical magnetic topology associated with jets is the 3D null point associated with an embedded dipole, which has frequently been identified in magnetic extrapolations of the coronal field before jet-like events (Fletcher et al. 2001; Moreno-Insertis et al. 2008; Liu et al. 2011a; Zhang et al. 2012; Schmieder et al. 2013). This topology is also suggested by the anemone morphology (Shibata et al. 1992), the downflowing material after a jet (Liu et al. 2011b), and circular ribbons (Wang & Liu 2012). Three-dimensional null points are known to be preferred sites for the build-up of thin current sheets and the ensuing onset of magnetic reconnection (e.g., Lau & Finn 1990; Antiochos 1996; Masson et al. 2012; Pinto et al. 2011; Baumann et al. 2013a,b; Fuentes-Fernández & Parnell 2013; Pontin et al. 2013).
Magnetic reconnection accelerates the plasma in three ways (Shibata et al. 1997). With the tension-driven model, plasma is accelerated to Alfvénic velocities in the vicinity of the reconnection site by the retraction (slingshot effect) of the just-reconnected field lines. Tension-driven upflows have been commonly observed in 2.5D (e.g., Yokoyama & Shibata 1996; Nishizuka et al. 2008; Yang et al. 2013) and 3D (e.g., Galsgaard et al. 2007; Moreno-Insertis et al. 2008; Gontikakis et al. 2009) simulations. While reconnection is also necessary for the other jet acceleration mechanisms, the tension-driven model is the only one in which the plasma is directly accelerated by the magnetic tension of the newly reconnected field lines.
In the second reconnection-induced mechanism, the untwisting model (Shibata 1985, 1986; Schmieder et al. 1995; Canfield et al. 1996; Jibben & Canfield 2004), the closed magnetic field initially possesses some shear or twist. When the closed and twisted field lines reconnect with untwisted open field lines, the newly reconnected open field lines are sheared at their base while the top remains untwisted. This inevitably leads to the upward propagation of a nonlinear wave as the system untwists. The generation of an untwisting upflow therefore relies on the existence of pre-reconnection magnetic twist within the closed system. This differs from the magnetic geometry of the tension-driven model, for which the primary requirement is a local anti-parallel component (i.e., shear) in the vicinity of the reconnection current sheet. For the untwisting model, the compressive part of the induced nonlinear wave advects material and compresses the plasma as it propagates in the corona. In 2.5D, upflows are driven by a shear Alfvén wave (Karpen et al. 1995, 1998), while in 3D they are driven by torsional Alfvén waves (Patsourakos et al. 2008; Pariat et al. 2009, 2010; Török et al. 2009; Edmondson et al. 2009; Rachmeler et al. 2010; Dalmasse et al. 2012; Lynch et al. 2014). The untwisting model can explain the wave-like patterns and significant rotational motions observed in numerous coronal jets, in particular in cool emission lines (e.g., Canfield et al. 1996; Harrison et al. 2001; Patsourakos et al. 2008; Liu et al. 2009, 2011b; Kamio et al. 2010; Shen et al. 2011; Chen et al. 2012; Hong et al. 2013).
The evaporation model differs from the two models described above by producing a jet through secondary thermodynamic processes (Shibata et al. 1997; Shimojo & Shibata 2000b). Magnetic reconnection deposits energy in the plasma on reconnected field lines through a variety of mechanisms, including accelerated particles, Joule heating, shocks, and adiabatic compression. The plasma response to impulsive energy deposition in flares has been well studied, including the brightening of flare ribbons and the heating of post-flare loops (see review of Fletcher et al. 2011). In the evaporation model, the energy released by reconnection impulsively heats the plasma in both closed and open magnetic flux tubes formed by reconnection. On closed field lines, the resulting density increase produces enhanced EUV and soft X-ray emission, while on open flux tubes, the strong pressure and temperature gradients induce an evaporation upflow (e.g., Shimojo et al. 2001; Miyagoshi & Yokoyama 2003; Miyagoshi et al. 2006; Matsui et al. 2012). These pressure-driven upflows are much slower than those driven by tension or untwisting: evaporation is at most transonic, while tension and untwisting drive Alfvénic flows. Therefore, we focus on the physics of the tension-driven model and the untwisting model in the present study. While the evaporation model may explain some of the emission from coronal jets (Shimojo et al. 2001; Matsui et al. 2012), it is predominantly driven thermodynamically and not magnetically, and hence only indirectly relevant to our theme of reconnection-driven jets.
The dynamics and properties of the plasma in a real solar jet probably results from the action of one, or from the combination of two or more, of these processes: magnetic tension, untwisting, and evaporation or pressure gradients. Each driver has distinct observable signatures. Furthermore, the respective importance of each driver in a given event may depend on the ambient environmental conditions. Therefore, one goal of this study is to establish the characteristic effects of magnetic tension and untwisting on the initiation and subsequent physical properties of the jet. We accomplish this goal through 3D magneto-hydrodynamic (MHD) simulations, as in our earlier work on coronal jets.
Based on X-ray observational data, Moore et al. (2010, 2013) recently cataloged X-ray jets in two categories, standard and blowout jets, depending on their observed morphology and dynamic evolution. A standard jet has a relatively well-collimated spire and a point-like brightening at the base, while in a blowout jet the spire tends to be broader and more complex, with a larger volume of bright plasma within the domed base.
A blowout jet exhibits substantial emission in cooler EUV lines (particularly at 304 Å) indicating the ejection of T ~ 105 K plasma, while a standard jet emits much more weakly and less frequently in this cool line. In addition, a blowout jet exhibits strong rotation, while in a standard jet the spire does not present such systematic and significant rotation. In addition, as noted by Moore et al. (2010), the base arch of blowout jets is observed to erupt, unlike standard jets. These categories are now commonly used to characterize coronal jets (e.g., Liu et al. 2011a; Shen et al. 2011; Chen et al. 2013; Pucci et al. 2013), although it remains unclear whether these categories are truly distinct. For example, high-resolution observations of standard jets in different wavelengths possibly show evidence for small-scale rotations (Young & Muglach 2014a,b). In addition, the terms standard and blowout convolve observed properties with speculative interpretations, as described by Moore et al. (2010, 2013). Consequently, it is difficult to derive clear insight into the underlying physical mechanisms of observed jets classified in this manner by comparing them with jet models.
In this paper, we therefore use the terms straight and helical to describe the collimated upflows seen in our past and present numerical simulations. These structural descriptions are not mechanism dependent and are equally applicable to observations and simulations. In Sect. 2, we first discuss the results of our previous simulations within the framework of straight and helical jets. We show that our model intrinsically produces both types and that our system transitions from the former to the latter. The underlying difference between the two jet classes is in the triggering mechanism. The implications of our previous results for observed standard jets and blowout jets are discussed in Sect. 2.3. In Sect. 3 we describe the main setup of our numerical models. We performed two parametric studies designed to better reveal how energy is deposited in each mechanism, depending on two basic parameters that influence the magnetic system: the inclination of the background open field (Sect. 4), and the inhomogeneity of the distribution of open flux around the closed flux system (Sect. 5). The results of these studies illuminate how the straight jet phase modifies the onset of the helical jet phase and reveals how the inclination angle and photospheric flux distribution dictate the jet properties and onset. Section 6.1 summarizes our main results, and Sect. 6.2 discusses the implications of our results for understanding observed solar jets. Our conclusions regarding the standard jet and blowout jet classifications are presented in Sect. 7.
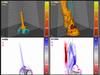 |
Fig. 1 Morphology of the straight jet (left panels, t = 580 nondimensional units) and the helical jet (right panels, t = 1000) in the θ = 10° run presented in Sect. 3. Top panels: isosurfaces of plasma density at ρ/ρ0 = 1.05 color-coded according to plasma temperature. The white field lines are plotted regularly along x = 0 and z = 0 from fixed footpoints in the initially open connectivity domain. The cyan field lines are plotted from fixed footpoints along a circle of radius r = 3 and are initially closed. Bottom left panel: 2D distribution of the z component of the velocity field in the x = 0 plane. Blue and red indicate upward and downward flows. Bottom right panel: 2D distribution of the x component of the velocity field in the x = 0 plane. Blue and red indicate flows toward and away from the observer. The black field lines are all initially closed and correspond to the cyan field lines of the upper panel. The magenta lines are isocontours of the electric current density magnitude in the plane. |
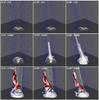 |
Fig. 2 Evolution of the system for θ = 3° (left column), 10° (central column), and 20° (right column). The bottom boundary displays the distribution of Bz. The top row shows the initial configuration. The blue field lines are plotted at fixed intervals along x = 0 and z = 0 from fixed footpoints in the initially open domain. The white field lines are plotted from fixed footpoints along a circle of radius r = 3 and are initially closed. The middle row displays the system at t = 600 during the straight jet phase. Isosurfaces of the plasma density at ρ/ρ0 = 1.05 are color shaded according to the vertical velocity vz, showing the acceleration of plasma in the straight jet. The bottom row presents the system during the helical jet phase. Isosurfaces of the plasma density at ρ/ρ0 = 1.2 are color shaded according to vx: red and blue indicate plasma flow away from and toward the observer (similar to Dopplergrams), highlighting the strong rotation in the helical jet. |
2. Our model for straight and helical jets
Our investigation builds upon our earlier numerical investigations of the embedded-bipole jet model (Patsourakos et al. 2008; Pariat et al. 2009, 2010; Rachmeler et al. 2010; Dalmasse et al. 2012). In Pariat et al. (2009, hereafter PAD09) we analyzed a helical jet released by interchange reconnection between open and closed magnetic fields, which generates a series of impulsive nonlinear Alfvénic or kink waves that propagate upward along reconnection-formed open field lines, ejecting most of the twist (magnetic helicity) stored in the closed domain. The main acceleration process is explained by the untwisting model, although a tension-driven flow is embedded within the structure of the helical jet (PAD09). Patsourakos et al. (2008) demonstrated the close correspondence between the geometry and dynamics of our modeled helical jet and those derived from stereoscopic jet observations by the STEREO mission (Kaiser et al. 2008). Rachmeler et al. (2010) carried out a comparative simulation using the purely ideal force-free magnetic solver FLUX (DeForest & Kankelborg 2007), in which the initial and boundary conditions were the same as in PAD09, but magnetic reconnection was prohibited. This study confirmed the central role played by magnetic reconnection in PAD09, because no helical jet was triggered without reconnection, and it highlighted the importance of the kink evolution that switched on the helical jet.
Pariat et al. (2010, hereafter PAD10), showed that quasi-homologous recurring jets can be triggered from the same magnetic system, as is commonly observed in the corona (e.g. Wang & Pick 2006; Chen et al. 2008; Chifor et al. 2008b,a; Kamio et al. 2010), by continuous driving motions at the photospheric boundary . Here the 3D null-point configuration acts as a topological capacitor for magnetic energy by enabling the system to store and periodically release the magnetic free energy that is injected continuously. PAD10 showed that the jet generation is divided into distinct energy-storage and energy-release phases. During the energy-storage phase, a current sheet develops along the fan surface and is most intense near the 3D null point, but this sheet evolves quasi-statically and is associated with a low reconnection rate. The resulting tension-driven upflows form a straight jet. This behavior was not observed in PAD09 because the strictly axisymmetric configuration inhibited the development of magnetic reconnection around the null in that case. In PAD10, on the other hand, the asymmetry of the initial magnetic configuration permitted reconnection to occur much earlier, driving a relatively gentle straight jet. Later, a far more explosive energy-release phase involves an extended thin 3D helical current sheet that rotates around the fan, across which magnetic flux reconnects rapidly over a very large surface area. This current-sheet rotation is essential for generating the helical jet. The impulsive and extremely dynamic mode of 3D reconnection that drives untwisting upflows differs substantially from the classical 2D reconnection that drives tension-driven upflows. These two regimes of reconnection in some coronal hole jets were suggested by Zhang et al. (2012).
The observed dichotomy denoted standard jets and blowout jets was established after our PAD09 and PAD10 studies. Therefore we reexamined our results to identify the correspondence between our simulated and helical jets and these observational categories. As discussed below, we find that the two regimes of reconnection can be generally linked to tour straight and helical jets. Furthermore, the quasi-steady straight jet created by tension release corresponds to a standard jet, while the impulsive helical jet created by untwisting corresponds to a blowout jet.
2.1. Straight jets
The upper left panel of Fig. 1 shows an isodensity surface of the straight jet from PAD10 during the quasi-steady phase; the bottom left panel shows the distribution of the vertical velocity. The straight jet is strongly collimated and possesses the classical inverse Y shape with a narrow spire, the main criterion defining standard jets (Moore et al. 2010, 2013). Unlike the helical jet, the straight jet presents little evidence of rotation and broadening of the spire. At this instant, the system is in many ways morphologically similar to the straight jets presented in Figs. 2 and 3 of Moreno-Insertis & Galsgaard (2013) and in the panels (a)–(e) of Fig. 1 of Archontis & Hood (2013; see also Galsgaard et al. 2007; Moreno-Insertis et al. 2008; Nishizuka et al. 2008), which have been identified with standard jets.
A stable current sheet around the 3D null point undergoes magnetic reconnection, yielding tension-driven upflows primarily along the outer spine of the embedded bipole and forming a straight jet. Hence the dynamics of the plasma during the quasi-steady phase possesses many properties that resemble those of a standard jet. In particular, the vz image (Fig. 1, lower left panel) shows that the flow is unidirectional and laminar; there is negligible rotation. We speculate that the plasma temperature in this collimated outflow would be hotter than the ambient corona as a result of magnetic reconnection, and thus might appear in the hotter EUV lines and soft X-rays. Below the main reconnection site, the hot dense region corresponding to closed post-reconnection loops would appear as the EUV/SXR bright point typically seen at the base of a standard jet. In the absence of a comprehensive energy equation in our computational model (Sect. 3), we cannot draw definitive conclusions about the thermal evolution of the plasma in either the closed or open flux systems.
We note, however, that the temperature increase in our straight jet is not as strong (only a factor of ~10%) as in Moreno-Insertis & Galsgaard (2013) and Archontis & Hood (2013) because the energy equation we solve is only adiabatic. The temperature increase is only created by the retraction of the reconnected flux and associated plasma compression; we do not capture any Ohmic heating because we do not prescribe an explicit resistivity (cf. Sect. 3). Hence we expect that the actual heating occurring in the quasi-steady phase is stronger in reality than predicted by our simulations. In contrast, Archontis & Hood (2013, and other works) used a conservative energy equation with explicit resistivity, which ensures that all of the magnetic energy dissipated in the reconnection current sheet is fully transferred to the system’s thermal energy. While numerically more consistent, this tend to overestimate the effect of the Joule heating. Energy budget of solar flares (Emslie et al. 2004, 2012; Fletcher et al. 2011) indeed show that a large part of the emitted energy is eventually carried by particles (either directly or later converted in electromagnetic emission). This energy sink was not treated in Archontis & Hood (2013), and therefore their temperature increase may be overestimated.
2.2. Helical jets
As discussed in Sect. 1, the blowout jet spire is much wider and more complex than the standard jet spire, with signs of strong helical rotation – a clear feature of the helical jets described in PAD09. The width of our model helical jet is similar to the scale of the photospheric magnetic polarity (Patsourakos et al. 2008), as observed with blowout jets. The upper right panel of Fig. 1 presents the isodensity surface of the plasma in a simulated helical jet. The initially closed cyan lines have been opened up by magnetic reconnection. The plasma in the helical jet rotates, as indicated by the synthetic Dopplergram map (bottom right panel, Fig. 1). As detailed in PAD09, the helical jet is driven mainly by untwisting, that is, by the nonlinear Alfvénic waves that are sequentially injected onto open lines formed through interchange reconnection. Because the helical jet is driven by a global train of waves, the phase speed differs from the plasma bulk speed. The energy is transferred to the plasma through the compressive part of the waves. Plasma is partly transported by the wave, and the plasma density partly increases through adiabatic compression induced by the wave train. This process is not as efficient as heating to increase the plasma temperature but can easily increase its local density. In addition, the pre-reconnection closed flux system probably contains higher density plasma than the surrounding open flux, as observed for the analogous structures in coronal holes, whereas our model imposes the same initial density everywhere. Therefore, on the Sun, newly formed (by interchange reconnection) open flux tubes would possess a significant pressure gradient around the former reconnection site that would inject denser material from the lower atmosphere. Hence the typical observable signature of the helical jet most probably corresponds to the structures observed for blowout jets in the EUV domain at 304 Å, even though some emission is also possible in warmer EUV lines. As a result, the untwisting model for the helical jet presented in PAD09 seems to fit the key observed properties of blowout jets very well (Moore et al. 2010, 2013; Liu et al. 2011a; Shen et al. 2011; Chen et al. 2012; Pucci et al. 2013): wide spires with multiple structures, intense emission at the footpoints, and strong rotation detected in cooler lines. More directly, the predicted density structure (line-of-sight integration of the square of the density) of our model matched the EUV observations of an example of a blowout jet very well (see Fig. 5 of Patsourakos et al. 2008).
 |
Fig. 3 Top panel: evolution of the free magnetic energy, Emag, for simulations with different values of the inclination angle θ. Bottom panel: time, Ttrig, of the onset of the helical jet (black stars) and accumulated free energy at Ttrig (Etrig = EM(Ttrig), red diamonds) as functions of θ. |
We conclude that the untwisting jet mechanism drives the helical jets seen in PAD09 and PAD10 and correspondingly explains the dynamics of the observed blowout jets. We believe that this mechanism also drives the helical jets described in the simulations of Archontis & Hood (2013) and Moreno-Insertis & Galsgaard (2013), which are generated following the reconnection of an emerging twisted flux rope with the overlying magnetic field. Magnetic reconnection is so efficient in these cases that the erupting flux rope eventually reconnects, and helicity is impulsively transferred to the overlying open magnetic-field lines.
Thus far, both the observations and modeling results summarized above indicate that the quasi-steady reconnection phase yields a straight jet, while the subsequent explosive reconnection phase drives a helical jet. As in PAD10, Edmondson et al. (2009) also simulated a straight-to-helical transition, although the embedded bipole in this case was initially located at the edge of a coronal hole, in closed flux, and not in fully open field. In that study, reconnection in a quasi-static current sheet eventually leads to untwisting, as indicated by the propagation of a low-frequency nonlinear wave in the open field (see also Lynch et al. 2014). It is interesting to note that the helical jet develops precisely when the reconnection site transitions into the open flux region. While not formally identified, the simulation of Török et al. (2009) also probably produces a straight jet before developing the helical jet. Observationally, such transitions have been described for several jet-like events (Liu et al. 2011a,b; Zhang et al. 2012). As found by PAD10, those observers note that the helical jet phase exhibits a much higher reconnection rate than the straight jet phase.
2.3. Triggering mechanisms
The simulation studies described above suggest that the straight and helical jets are triggered in fundamentally different ways. A straight jet can be triggered through either direct forcing of the current sheet or the onset of a local instability within the sheet that enhances the reconnection rate. Both flux emergence (e.g., Moreno-Insertis et al. 2008; Moreno-Insertis & Galsgaard 2013) and the expansion of the closed domain in response to added magnetic stress (e.g., PAD09; PAD10; Edmondson et al. 2009) drive flows that form and compress the current sheet. Unlike some other numerical experiments involving isolated 3D null points (e.g., Masson et al. 2009, 2012; Priest & Pontin 2009; Baumann et al. 2013a,b; Pontin et al. 2013), our line-tied forcing does not directly stress the separatrix surface (in this case, the fan). Instead, we inject energy into the system by footpoint motions in a band around the PIL, far from the separatrix surface. Because the system expands asymmetrically (cf. lower left panel, Fig. 1), the upper and lower spines become misaligned, deforming the null into a current sheet susceptible to reconnection.
A helical jet apparently results from a larger-scale instability that involves most, if not all, of the closed magnetic system. PAD09, PAD10, and Rachmeler et al. (2010) found that the helical jet is related to a global MHD kink-like instability that occurs when a threshold in energy or helicity or twist is exceeded. The instability leads to the global destabilization of the system, forcing reconnection through the separatrix surface and driving a helical jet. Similar kinking is also observed in laboratory experiments (Hsu & Bellan 2002, 2003; Bellan et al. 2007; Moser & Bellan 2012) driven there by non-neutralized electric currents.
The embedded-bipole configuration is not the only magnetic topology that can generate a helical jet. The primary requirement is that sufficient magnetic free energy can be stored and impulsively released. For example, Archontis & Hood (2013) and Moreno-Insertis & Galsgaard (2013) have shown that a helical jet can be produced by the emergence of a twisted flux rope into open field. In addition, many observations indicate that twisted flux exists and even kinks in some helical-jet sources (Raouafi et al. 2010; Liu et al. 2011b; Kayshap et al. 2013) and in the canonical blowout jets (Moore et al. 2010, 2013). It is important to keep in mind, however, that the presence of twisted flux is inferred from emitting plasmas assumed to trace the magnetic field, and not from direct magnetic measurements. The problem of the onset of a blowout jet seems thus to be equivalent to the trigger of eruptions. A fundamental difference with eruptions leading to CMEs is that the erupting helicity or current-carrying structure would be eventually completely destroyed in the case of blowout jets. Via reconnection with surrounding fields, the helicity-carrying structure fully transmits its twist to open field lines, inducing untwisting upflows.
While an emerging twisted flux rope superficially appears to be very different from a sheared embedded bipole, the final states achieved by these energy-injection mechanisms are topologically equivalent. In both cases, untwisting upflows result from driven interchange reconnection between a closed twisted magnetic structure and open untwisted flux. In the twisted flux-rope models the free energy enters the corona as flux emerges, while our previous and present simulations build up free energy through photospheric rotational motions; both processes are observed on the Sun. The pre-jet configuration in the emerging twisted flux-rope models also differs from that of PAD09 in the way magnetic twist is distributed in the closed domain. While in PAD09 (the axisymmetric case) the twist is evenly distributed around the inner spine, in the Archontis & Hood (2013) and Moreno-Insertis & Galsgaard (2013) simulations the twist is mostly concentrated in a substructure of the closed flux. The resulting helical jet properties are qualitatively equivalent, with some secondary differences in their development. We contend that while the distribution of twist in the closed flux can induce some different properties in the helical jet development, these differences are only secondary, as indicated by the qualitative comparison between our untwisting model and observations of blowout jets (e.g., see Fig. 5 of Patsourakos et al. 2008).
Therefore we contend that our energy-injection method contains all of the essential ingredients necessary to study the triggering of both straight and helical jets. While our model may not be able to reproduce the trigger of every observed blowout jets, it contains the key element to explain the generation of some of them. It is computationally straightforward and allows us to carry out efficient parametric studies of key factors in the onset and evolution of these jets. Whether a helical jet results from the eruption of a twisted flux rope or a sheared dipole, the morphology of the closed field region appears to be the most essential element of the triggering. Our earlier work indicated that axisymmetry inhibits the formation of a straight jet (PAD09), whereas modest departures from axisymmetry enable the generation of a mild straight jet followed by a stronger helical jet (Patsourakos et al. 2008; Pariat et al. 2010). Based on lessons learned from our earlier research, we designed the parametric studies discussed below to investigate the role of two geometric properties in depth. These calculations and their analysis have improved our understanding of the physics of straight and helical jets and shed light on their correspondence with standard and blowout jets.
3. Model description
The simulations presented here extend the work presented in PAD09 and PAD10 and use the same code, driving mechanism, and basic configuration. We used our adaptively refined magnetohydrodynamic solver (ARMS), whose flux-corrected transport algorithms are based on DeVore (1991). The time-dependent equations of ideal, single-fluid MHD, with the magnetic forces expressed in the Lorentz form, are solved on a dynamically adaptive grid managed by the toolkit PARAMESH (MacNeice et al. 2000). A Cartesian domain is assumed, with x and y the horizontal axes and z the vertical axis. The nonuniform initial grid is identical to that shown in Fig. 1 of PAD09. This grid refines and derefines adaptively during the simulation, as prescribed in the appendix of Karpen et al. (2012), to resolve the thin current layers that can undergo reconnection as finely as possible. No explicit resistive terms are included in the model. Numerical diffusion provides an effective resistivity where the spatial gradients of the magnetic field are strong, at the current sheets where the grid is most highly refined, which is sufficient to prevent unphysical oscillations in the solutions. In regions where the solutions are smooth, the resistivity is extremely low, as in most of the corona.
The domain is filled with a highly conducting low-pressure coronal plasma. For maximum generality, we use nondimensional units; a comparison with actual coronal scales can be found in Sect. 5.2 of PAD09. Our initial thermal pressure, P, and mass density, ρ, are uniform. We assume an ideal plasma equation of state, so the temperature T is initially uniform as well. The initial potential magnetic field is generated by a central vertical magnetic dipole placed under the photosphere (closed field), embedded in an inclined (with respect to the vertical direction) uniform open field. The central dipole is placed at (0, 0, zc = −1.5), and its magnetic moment mcez has μ0mc/ 4π = 25, with μ0 the vacuum magnetic permeability. The initial uniform open coronal magnetic field, Bv, is taken to be 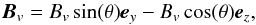 (1)with Bv = 1. The angle θ is the inclination of the open field with respect to the vertical direction z; θ = 0 corresponds to a vertical field. The initial vertical magnetic-field component in the baseline configuration, Bs,z, thus is given by the following equation:
(1)with Bv = 1. The angle θ is the inclination of the open field with respect to the vertical direction z; θ = 0 corresponds to a vertical field. The initial vertical magnetic-field component in the baseline configuration, Bs,z, thus is given by the following equation: 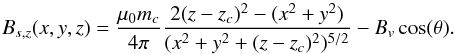 (2)In Sect. 4 we vary the inclination θ to determine its impact on the dynamic evolution of the straight and helical jets.
(2)In Sect. 4 we vary the inclination θ to determine its impact on the dynamic evolution of the straight and helical jets.
The resulting initial topological structure for three selected angles is shown in the top panels of Fig. 2. A 3D null point with its associated fan surface and two spine lines are present, with the outer spine following the general direction of the open field (thus inclined by θ). This embedded-bipole magnetic configuration is typical of observed jet-like events (cf. Sect. 1). The fan is a separatrix surface that divides the volume into two magnetic connectivity domains. Thus far, we have modeled a topology in which the initial fan surface is spherical (PAD09, PAD10) because the field distribution at the solar surface is quasi-axisymmetric (the symmetry is broken only by nonzero values of θ). In Sect. 5 we explore the influence of a more realistic geometry resulting from a nonuniform distribution of the surface magnetic field.
We assume the same boundary conditions as PAD09: closed on the four sides and open at the top. At the bottom boundary, line-tied conditions are used to emulate the high-β photosphere and chromosphere and forcing motions are imposed to drive the magnetic evolution. As in PAD09, the vertical field is driven by slow rotational motions restricted to the positive polarity for B>Bl = 0.4. The imposed tangential velocity v⊥(x,y,z = 0) is given by Eq. (7) of PAD09: 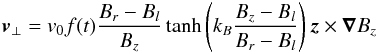 (3)
(3)![\begin{eqnarray} \text{with} \quad f(t)=\frac{1}{2}\left[1-\cos\left(2\pi\frac{t-t_l}{t_r-t_l} \right)\right] \quad \textrm{for} \quad t\in [t_l, t_r]. \end{eqnarray}](/articles/aa/full_html/2015/01/aa24209-14/aa24209-14-eq44.png) (4)In the present simulations v0 = 3 × 10-5, which is smaller than in PAD09 and thus injects twist into the closed domain more slowly. The prescribed velocity field imparts a clockwise rotation (seen from above) to the positive central polarity, injecting magnetic energy and positive helicity into the closed-field region and forming a clockwise whorl. The computed total helicity flux injected at the bottom boundary, using the method of Pariat et al. (2005), is 1050 helicity units. Given that the total closed magnetic flux is 30 units and assuming a uniformly twisted structure, the injected twist corresponds to 1.17 turns of the magnetic field lines around the central axis. Visual inspection of the field lines at the onset of the helical jet confirms this value.
(4)In the present simulations v0 = 3 × 10-5, which is smaller than in PAD09 and thus injects twist into the closed domain more slowly. The prescribed velocity field imparts a clockwise rotation (seen from above) to the positive central polarity, injecting magnetic energy and positive helicity into the closed-field region and forming a clockwise whorl. The computed total helicity flux injected at the bottom boundary, using the method of Pariat et al. (2005), is 1050 helicity units. Given that the total closed magnetic flux is 30 units and assuming a uniformly twisted structure, the injected twist corresponds to 1.17 turns of the magnetic field lines around the central axis. Visual inspection of the field lines at the onset of the helical jet confirms this value.
 |
Fig. 4 Top panel: evolution of the kinetic energy for simulations with different values of the inclination angle θ. Bottom panel: evolution of the normalized kinetic energy (see text), where Δt = 0 at the time of peak kinetic energy in each simulation. |
 |
Fig. 5 Left panels: top views of the bottom boundary distribution of the vertical magnetic-field component (Bz) coded in levels of gray for the different runs. The red field lines map the initial (t = 0) separatrices passing by the 3D null point, bounding the open and closed magnetic connectivity domains. Right panels: side views of the initial potential magnetic configuration (t = 0) for the different simulations. The red field lines are those shown in the left panels. The yellow field lines outline the connectivity in the closed domain and are plotted from footpoints distributed along a circle on the bottom boundary of radius r = 0.6 centered on the footpoint of the inner spine. |
As noted above, the fan is not directly stressed. The applied flow follows the contours of Bz, so as to leave its surface distribution unchanged in time. Therefore the potential field is constant in time, allowing us to follow the evolution of the free magnetic energy in the system, Emag, by calculating the difference between the total magnetic energy Em and its initial value Emag(t) = Em(t) − Em(t = 0).
4. Influence of the coronal field inclination
As discussed in Sect. 2.3, our previous simulations showed that the inclination is critical for the appearance of the straight jet phase. When the system is purely axisymmetric, no straight jet is observed. We performed a parametric study by varying the inclination of the coronal magnetic field to determine the conditions for the existence of the straight jet phase and its impact on the helical jet phase.
In all runs, the atmosphere is the same as in PAD09: P = 0.01, T = 1, and ρ = 1 in non-dimensional units. All parameters in the different runs are identical except for the inclination angle, which is in the interval θ = 0–20. This means that we test relatively small angular variations. For θ> 20°, the outer spine is no longer connected to the top boundary, but to a side boundary: this modifies the dynamics of the system when the jet hits the closed-side boundary. Since μ0m0/ 2π | zc | 3 ≫ Bv, the flux distribution in the central polarity is similar for all runs. Varying the angle barely modifies the initial magnetic energy; the largest relative difference is lower than 10-3.
Figure 2 shows the global evolution of the magnetic field and plasma density for selected simulations. The top panels of Figs. 3 and 4 plot the evolution of the free magnetic energy, Emag, and kinetic energy, Ekin, for the tested θ values. While there are distinctive differences between the runs, as shown by the energy curves, the system evolves similarly in the different simulations.
After a phase of relaxation, magnetic energy is injected in the closed domain by the line-tied twisting motions during the interval t ≈ 300–900 (cf. Fig. 3). The magnetic energy and pressure build-up causes the closed structure to expand (see also Hsu & Bellan 2002; Rachmeler et al. 2010). For all runs, a current sheet forms at the null point. For the runs with large θ, however, magnetic reconnection in this current sheet induces a straight jet (cf. Fig. 2), as reflected in the increased kinetic energy (cf. Fig. 4). The rate of free magnetic energy released by reconnection is lower than the rate of free energy injected, however, because magnetic energy and helicity continue to accumulate. At t ≈ 900, a helical jet is initiated, similar to the results of PAD09 and PAD10. The physical sequence leading to this untwisting upflow was described in Sect. 2.3. In all runs, the kinetic energy surges (Fig. 4) and the magnetic energy decreases significantly (Fig. 3, top panel), unlike the preceding straight jet phase.
4.1. Inclination angle and the helical jet
A significant result of our study is that all of the runs generate helical jets that are morphologically similar. The bottom panels of Fig. 2 show that for all values of θ, the plasma distributions exhibit the same shape and similar helical flows. The only noticeable difference is that the helical jet is more inclined when the initial configuration is more inclined. This is expected: in the untwisting model, the helical jet is driven by the nonlinear waves propagating along the inclined open field. This also agrees with the observed property that the jet spire tends to follow the magnetic field direction (e.g., Wang & Pick 2006; Moreno-Insertis et al. 2008; Liu et al. 2011b).
Nonetheless, we find significant differences in the time when the helical jet is triggered and the energy level at that moment. We define the time Ttrig as the moment when the free magnetic energy reaches its maximum, Etrig. That is, 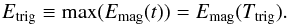 (5)Ttrig is a proxy for the trigger time of the helical jet, when the rate of energy injection by the boundary motions equals the rate of energy released by the reconnection that generates the nonlinear waves. At Ttrig, the system should already be unstable. Ttrig is thus an upper limit on the trigger time of the instability leading to the helical jet; Etrig is also an upper limit on the free magnetic energy.
(5)Ttrig is a proxy for the trigger time of the helical jet, when the rate of energy injection by the boundary motions equals the rate of energy released by the reconnection that generates the nonlinear waves. At Ttrig, the system should already be unstable. Ttrig is thus an upper limit on the trigger time of the instability leading to the helical jet; Etrig is also an upper limit on the free magnetic energy.
Because the driving motion is sinusoidal in time, peaking at t = 600 (cf. Eq. (3)), and the helical jets are triggered at different times depending on θ, the energy injection rate at Ttrig is not the same for every simulation. For low values of θ, Ttrig is close to 1100, when the driving motions are almost stopped and the energy injection is very weak; in this case, the precise jet onset time and Ttrig are very close. For the highest θ values, Ttrig ≈ 800–850 and the energy injection rate is higher by a factor of 6. In this case, the helical jet is very impulsive and the rate of energy release increases very rapidly, as shown in Fig. 4. From Fig. 4 of PAD10, we estimate that the exact trigger time of the helical jet is shorter than 50–100 time units earlier than Ttrig. Thus Ttrig remains a good proxy for comparing the onset times among the different simulations.
The lower panel of Fig. 3 shows the variation of Ttrig and Etrig as functions of the inclination angle. For low values of θ, Ttrig decreases rapidly as θ increases, reaching a minimum of Ttrig ≈ 800 for θ = 8°. Ttrig then increases slightly with higher θ values. The Etrig plot also decreases sharply for low θ values, then falls less steeply for θ> 10°. We tried to fit several simple functions (e.g., inverse, exponential) to these curves, but none fit satisfactorily (low χ2). Hence, the trigger time and energy do not follow simple rules, although the energy decreases monotonically with increasing angle θ.
This parametric study also reveals that less energy is needed to trigger the jet when θ is larger, when the system is more asymmetric. Quantitatively, roughly a third less energy is needed to trigger a helical jet for θ = 20° than for θ = 1°. The helical jet is triggered when the field lines attain a twist in the range 0.8–0.9 turns for θ> 8°, whereas in the θ = 1° run the critical number of turns is ~1.2. For comparison, the helical jet developed at 1.4 turns in the axisymmetric case (PAD09).
Our results imply that the instability leading to the generation of the helical jet is strongly influenced by the symmetry of the magnetic system. When the system is less symmetric, that is, at higher θ values, the instability is triggered more easily. The symmetry breaking associated with larger θ apparently lowers the energy and helicity threshold at which this kink-related instability develops. Note that this correlation does not necessarily mean that the inclination is directly responsible for modifying the energy threshold for the jet onset. As the parametric study discussed in Sect. 5 demonstrates, reconnection during the straight jet phase influences the subsequent catastrophic development of the helical jet.
We find that a lower amount of free magnetic energy available at the onset of the helical jet does not necessarily mean that the jet has less kinetic energy. The top panel of Fig. 4 clearly shows no correlation between the peak of the kinetic energy and θ. This absence of relation between kinetic energy and θ is probably due to the fact that the kinetic energy of the jet is always much lower than the magnetic energy released through reconnection (PAD09). At Ttrig, the system always has sufficient free energy and behaves in a similar way to generate a helical jet, regardless of θ. As implied by the plasma dynamics (Fig. 4, lower panel), the kinetic properties of the helical jet (speed, shape, morphology) are independent of θ. On the other hand, because the embedded-bipole configuration stores and releases more energy when the system is more symmetric, we expect that the observed emission properties of coronal jets will depend on their magnetic configuration. Observational tests of this prediction are discussed further in Sect. 6.2.
The Ttrig-θ relationship (Fig. 3, lower panel, black stars) is more complex to interpret. For small θ, the decrease in Ttrig is directly related to the lower energy needed to destabilize the system at the onset of the helical jet. Given that the energy injection is similar for all runs, the energy threshold to trigger the instability is reached and a helical jet occurs earlier as θ increases. For θ ≳ 8°, however, a new phenomenon – the straight jet phase – causes the helical jet trigger time to increase gradually.
4.2. Inclination angle and the straight jet
Unlike the helical jet, the very existence of the straight jet phase is directly controlled by θ. For low values of the inclination angle, the straight jet is barely present, as we found for the axisymmetric case of PAD09, while for θ larger than 8° a straight jet can be identified in the plasma flows (cf. Fig. 2, middle column).
The occurrence of the straight jet phase for θ above this critical value is highlighted by the kinetic-energy evolution. The bottom panel of Fig. 4 shows the variations of the normalized kinetic energy as a function of the time difference, ΔTmax: 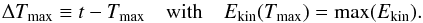 (6)Here Tmax is the time when the kinetic energy is highest. The kinetic energy curves are normalized by their highest values, so they all peak at 1 for ΔTmax = 0. In the bottom panel of Fig. 4 the curves are nearly identical for | ΔTmax | < 100, during the development of the helical jet. This confirms that the kinetic properties of the helical jet are uncorrelated with the inclination angle θ.
(6)Here Tmax is the time when the kinetic energy is highest. The kinetic energy curves are normalized by their highest values, so they all peak at 1 for ΔTmax = 0. In the bottom panel of Fig. 4 the curves are nearly identical for | ΔTmax | < 100, during the development of the helical jet. This confirms that the kinetic properties of the helical jet are uncorrelated with the inclination angle θ.
Well before the helical jet phase (ΔTmax< −200), however, the normalized kinetic energy curves differ significantly. For θ ≲ 8°, the normalized kinetic energy is negligible, and the curves are morphologically very similar to the θ = 1° case. For θ ≳ 8°, the kinetic energy is a significant fraction of its peak value, representing plasma accelerated by reconnection. In this early phase, the kinetic energy curves mark the activation of a tension-driven straight jet. Figure 4 quantitatively confirms that straight jets develop only for larger inclination angles, where the initial system is more asymmetric.
Overall, the larger the inclination, the earlier the kinetic energy begins to rise as the tension-driven upflows develop. We note that θ = 8° is not a strict transition between two regimes (with or without a straight jet). As the inclination angle increases, the system smoothly transitions from the 0–3° cases where reconnection is suppressed to the intermediate range (θ ≈ 4−8°) where some reconnection occurs but is indistinguishable from the beginning of the helical jet phase, to θ ≳ 8° where a straight jet is unambiguously observed. Figure 2 indeed shows that at t = 600, an increasingly potent straight jet occurs: the extent, volume, and mass of the upflowing plasma increase with θ for θ ≳ 8°. During the straight jet phase, as θ increases, a stronger current sheet forms at the null, yielding stronger reconnection. This reconnection is sufficiently intense and develops sufficiently early to drive a straight jet before the onset of a helical jet only for θ ≳ 8°.
The reconnection inducing the straight jet releases part of the free magnetic energy injected into the system and allows helicity to escape along open field lines. The larger the inclination angle, the earlier and the stronger the straight jet, the more injected energy is dissipated, and the lower the efficiency of free energy accumulation in the system. This is directly illustrated by the top panel of Fig. 3, where the slope of the magnetic energy curves becomes flatter as θ increases during the energy buildup phase (t ≈ 400–700).
Because the straight jet phase implies less efficient accumulation of energy, the time at which the helical jet threshold is reached should be delayed. Hence, when the straight jet is present and θ ≳ 8°, the following correlation applies: larger θ means more energy is released in the straight jet phase and the helical jet onset is later. This precisely describes the behavior of Ttrig at θ> 8° in Fig. 3 (lower panel, black stars). Therefore, the variation of Ttrig with θ is determined by two competing processes: the lowering of the energy or helicity threshold with increasing inclination (cf. Sect. 4.1) versus less efficient energy accumulation and more pronounced straight jets as θ increases. While the first process clearly dominates for θ< 8° when no straight jet is present, the second dominates for θ ≳ 8°. This behavior of Ttrig is further evidence for an energy or helicity threshold that must be exceeded to generate a helical jet.
Unlike the helical jet, the straight jet is not the consequence of an instability, but is the direct consequence of the applied driving (cf. Sect. 2.3). When the system is axisymmetric, reconnection is topologically inhibited (PAD09). As indicated by the stability experiments in PAD09, our present results demonstrate that this property applies not only to the θ = 0° case, but also to small inclination angles. For θ ≲ 8°, only a weak current sheet forms around the null-fan intersection during the energy-buildup (footprint driving) phase. For larger angles, the added magnetic stress yields a stronger current sheet. Open and closed flux on either side of this sheet reconnect through the null, yielding tension-driven flows as in the standard 2D reconnection scenario.
Our results generally indicate a close correlation between the intensity of the straight jet and the lower energy threshold of the helical jet. In this parametric study, the properties of the straight and helical jets both vary with increasing inclination angle. Consequently, we could not determine from this study alone whether the delay in helical jet onset is caused by a θ-dependent threshold for the kink-like instability or by the occurrence of the straight jet. In the following section, we describe a different set of parametric runs with θ held constant, which reveal that a lower energy threshold for the helical jet is most likely caused by stronger reconnection during the straight jet phase.
5. Influence of the magnetic field distribution
5.1. Setup
Our second parametric study was designed to determine whether the distribution of the coronal magnetic field affects the development of the jets. While our previous computations assumed a uniform distribution of the negative magnetic field in the closed domain, in the present section we describe a series of simulations where the negative magnetic field is more concentrated at several discrete locations. The resulting concentrations of negative polarity are distributed around the central positive polarity, still preserving the single 3D magnetic null point and its associated fan and spines. This is consistent with many observed jets, which emanate from magnetic-field configurations consisting of one or two central polarities surrounded by several concentrations of the opposite polarity (see, e.g., Figs. 3, 1, 4, and 1 in Krucker et al. 2011; Liu et al. 2011a; Zhang et al. 2012; Shen et al. 2012). For clarity, we have restricted our numerical investigation of this scenario to four different configurations formed by three negative polarities distributed around the central positive polarity. To limit the range of parameters, we only consider surrounding polarities of equal magnetic intensity, equidistant from the central polarity.
The surrounding magnetic polarities are created by embedding vertical magnetic dipoles, as for the central polarity. Each dipole is placed at a common depth zp = −0.6 and has a magnetic moment − mpez with μ0mp/ 4π = 1. Each polarity concentration is located on a circle of radius Rp = 1.8 centered on the central (positive) polarity of the jet. In the case of a uniform distribution (as in Sect. 4), the polarity inversion line is located at a radius of 1.6. The surrounding polarity concentrations therefore are located in the original negative field region and alter the field distribution of the central positive polarity only moderately. The initial vertical magnetic field, Bp,z, for this set of simulations is given by 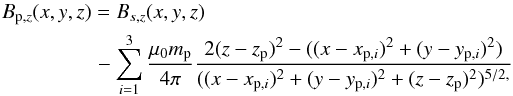 (7)where Bs,z is given by Eq. (2). The Cartesian coordinates of the center of each surrounding polarity are xp,i = Rpcosϕp,i and yp,i = Rpsinϕp,i, where ϕp,i is the azimuthal angle of the polarity on the circle with respect to ex. For all runs the inclination angle θ = 10°.
(7)where Bs,z is given by Eq. (2). The Cartesian coordinates of the center of each surrounding polarity are xp,i = Rpcosϕp,i and yp,i = Rpsinϕp,i, where ϕp,i is the azimuthal angle of the polarity on the circle with respect to ex. For all runs the inclination angle θ = 10°.
At the photospheric level, the maximum field strength in each of the surrounding negative polarities is max | Bp,z | ≃ 9, while max | Bc,z | ≃ 14 for the central positive polarity. Because the surrounding polarities are embedded closer to the surface and their magnetic moment is 25 times smaller relative to the central polarity, they are therefore more concentrated than the central polarity, occupying a smaller area and containing less magnetic flux. Despite the inhomogeneity of the negative polarity flux distribution, the overall magnetic topology is identical to the one used in our earlier models (PAD09, PAD10), as shown in Fig. 5. As in all our previous simulations, a 3D null point is present, dividing the domain in closed and open magnetic fields. In all the runs, the fan-spine topologies are completely equivalent morphologically (e.g., comparison of Figs. 5 and 1 of PAD09). Energy is injected in the closed domain in the same way as before.
In the baseline case with uniform distribution of the surrounding field (PAD09 and Sect. 4), the fan separatrix surface intersects the photosphere as a circle of radius 2.2. Therefore the negative polarity concentrations are mostly embedded within the closed domain. Another run performed with Rp = 2.1 (not shown here) showed few qualitative differences. Compared to the uniform distribution case, the surrounding polarities tend to concentrate the flux originating from the central positive polarity (cf. yellow field lines in the right panels of Fig. 5) nonuniformly within the closed domain. The fan surface is no longer a hemisphere and assumes different shapes and deformations depending on the relative positions of the negative polarities.
Azimuthal angles of the surrounding polarities (in degrees) for each simulation.
We have performed four runs with different values for ϕp,i, as given in Table 1. The corresponding initial potential magnetic configurations are depicted in Fig. 5. In both the SymOpp and Sym runs, the ey axis is an axis of symmetry for the magnetic configuration, and the polarities are equally spaced along the circle. In the SymOpp run, one polarity is located on the positive ey axis and, therefore, is located in the opposite direction to the open field inclination. (We recall that θ inclines the coronal field toward negative ey.) In the Sym run, one of the surrounding polarities is located on the negative ey axis, on the same side as the field inclination. In the Oneside run, the surrounding polarities are all located in the y> 0 domain, asymmetric relative to the ex axis. The MI08 run represents the largest asymmetry relative to the ey axis. Compared to the other runs, the MI08 configuration is morphologically closest to the observed magnetic configuration analyzed and simulated by Moreno-Insertis et al. (2008, cf. Fig. 2), although our simulations are not intended to reproduce this or any other observed event.
 |
Fig. 6 Top panel: evolution of the free magnetic energy, Emag for simulations with different bottom boundary distributions of the magnetic field, as shown in Fig. 5. Bottom panel: evolution of the kinetic energy Ekin for the simulations. |
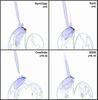 |
Fig. 7 Vertical velocity distribution in the y − z plane at the given values of x at t = 600, during the straight jet phase, for simulations with different photospheric field distributions. The velocity magnitude is color coded in blue (upflows) and red (downflows) similarly to the lower left panel of Fig. 1. The black lines are isocontours of the vertical velocity; the blue and green lines are isocontours of the electric current density. |
5.2. Dynamics of the straight and helical jets
The evolution of the magnetic and kinetic energy in each simulation is presented in Fig. 6. For comparison, the run Uni corresponds to a simulation with a uniform magnetic field distribution (as in Sect. 4, with θ = 10°). Note that the Uni curve cannot be directly compared to the other runs, however, because the integrated magnetic flux differs from that of the four other cases. All runs generate a helical jet, as implied by the drop in free magnetic energy and the rise in kinetic energy for t ≳ 800, and undergo a transition from a straight to a helical jet. The two jet phases produce two slopes in the rise of the kinetic energy: a slow increase during t ≈ 600–800 and a steeper increase for t ≳ 800. Both straight and helical phases are indeed observed in the dynamic evolution of the plasma.
This parametric study showed that the specific distribution of the magnetic field at the photosphere does not inhibit the generation of either the straight or the helical jets. This result strengthens and extends the validity of our model: as long as a 3D null point is present, the fundamental processes that generate a jet are inevitable. The closed flux is able to efficiently store free magnetic energy and helicity and release them impulsively through interchange reconnection. The sequential opening of the closed field lines and the propagation of twist along reconnected open field lines are consistent with the untwisting model as described in Sect. 2.
Some differences nonetheless appear between the runs. In all runs with surrounding polarity concentrations, more magnetic energy is stored and the helical jet occurs later than for the Uni simulation. Similar to the inclination-angle study (Sect. 4.2), the kinetic energy curves (Fig. 6, bottom panel) for t ≈ 600–800 provide clues about the strength of the straight jet. The kinetic energy is increasingly higher during the straight jet phase for the runs MI08, Oneside, Sym, SymOpp, and Uni (in this order). The development of the current sheet and the straight jet at t = 600 confirm this sequence. Figure 7 displays the distribution of the vertical velocity, vz, and outlines the location and shape of the electric current sheet for each simulation in the Oyz plane, where the straight jet is observed to be the strongest. For the Oneside and MI08 runs, the straight jet is not located strictly in the central x = 0 plane. We observe that at t = 600, the SymOpp & Sym runs form a longer and more intense current sheet than the other runs, yielding a straight jet with higher upward velocities distributed over a wider volume. For the Oneside and MI08 runs, the current sheet is smaller and the straight jet is less pronounced. This assessment is valid throughout the straight jet phase. Our visual inspection of the straight jet in the simulations confirms what we deduced from the kinetic energy curve: the respective runs MI08, Oneside, Sym, SymOpp, and Uni exhibit increasingly strong straight jets (i.e., MI08 displays the weakest straight jet and Uni the strongest).
The trigger time, Ttrig, and trigger energy, Etrig, given in Table 1 are determined from the peaks of the magnetic energy curves in Fig. 6 (top panel), following Eq. (5). Runs with shorterer Etrig also have earlier Ttrig. The helical jets in runs Uni, SymOpp , Sym, Oneside, and MI08 develop increasingly late (longest Etrig for MI08), with an increasing amount of free energy (longest Etrig for MI08). Later triggering of the helical jet is therefore anti-correlated with a stronger development of the straight jet. The runs creating a stronger straight jet (more kinetic energy, higher jet velocity, stronger and more extensive current sheet) also produce an earlier helical jet (earlier Ttrig) at a lower free energy level (shorter Etrig). This result is consistent with the results presented in Sect. 4, where we found that a strong straight jet was correlated with a helical jet triggered at a lower Etrig. As stated in Sect. 4.2, the straight jet partly inhibits the energy storage for θ ≳ 8°. Here, in contrast, the helical jet is triggered earlier for stronger straight jets: decreasing Etrig is correlated with decreasing Ttrig.
This parametric study allows us to refine the results reported in Sect. 4 regarding the link between the straight jet phase and the helical jet onset. For the uniform field distribution, we found that increasing the inclination of the coronal magnetic field yielded a stronger straight jet and a lower magnetic-energy threshold for triggering the helical jet. In this parametric study, we observe for a constant inclination that changing the photospheric flux distribution modifies the strength of the straight jet and the onset characteristics of the helical jet, as follows: the earlier the rise in kinetic energy appears, the stronger the quasi-steady reconnection and associated tension-driven upflows (the straight jet), the earlier is the helical jet triggered and the lower the energy accumulated at the helical jet onset (and, most likely, the associated threshold energy). The runs described here and in Sect. 4 jointly suggest that neither θ nor the field distribution alone determine the helical jet trigger. Instead, we conclude that the reconnection responsible for the straight jet phase strongly influences the timing and energetics of the helical jet phase. While the straight jet does not initiate the helical jet, as discussed in Sect. 2.3, the straight jet reconnection affects the helical jet onset mechanism. This important result is further confirmed by a parametric study of the effects of the plasma β on the same magnetic configuration, which will be discussed elsewhere (Pariat et al., in prep.).
It is unclear, however, why the straight jet phase is more intense for some field distributions than for others. We believe that the topological characteristics of the null, in particular the geometry of the fan surface, are fundamental for understanding the early development of the straight jet (as for example shown with the influence of the inclination angle). The four configurations studied here are too few and too diverse to provide much insight into the role of the flux distribution in generating a weaker or stronger straight jet. It is worth noting that a symmetric transformation relative to the (Ox) axis (SymOpp vs. Sym runs) leads to negligible differences. We also note that the configuration possessing the strongest asymmetry perpendicular to the inclination, MI08, yields the highest energy storage and the most impulsive and energetic helical jet. This configuration also most closely resembles the source region of an observed energetic X-ray jet (Moore et al. 2010, 2013).
6. Summary
6.1. Overview of the simulation results
We discussed two parametric studies of the generation of straight jets and helical jets: one varied the inclination angle of the coronal magnetic field, the other varied the photospheric distribution of the magnetic field while preserving the basic topology. We confirmed that the model of Pariat et al. (2009) is valid for a wide parameter range. Our study showed that helical jets are triggered for inclination angles in the range θ = 0−20° (cf. Sect. 4); a preliminary investigation indicated that the untwisting model also applies to larger angles, up to 40°. As long as a 3D magnetic null point is present, our model is also valid for different photospheric distributions of three negative flux concentrations surrounding the central embedded-bipole polarity, configurations that are frequently observed in the solar atmosphere (cf. Sect. 5).
While a helical jet was generated for all inclinations, our investigation revealed that this is not true for the straight jet (cf. Sect. 2.1). A straight jet was formed when the 3D null point was sufficiently stressed to form a current sheet, in our case, in response to boundary-driven motions. We found that straight jets appear only for inclination angles ≳8°. Larger inclinations produced closed flux systems that were more asymmetric, causing currents to build up earlier at the null and release energy through stronger reconnection. The resulting tension-driven flows were more energetic, corresponding to more potent straight jets. While a straight jet was observed only for sufficiently large inclinations, current sheets formed at the null even for very small angles. However, in the latter case the reconnection there was so slow that a straight jet was not unambiguously noted before the system reached the helical jet phase.
We found that diverse magnetic configurations strongly affect the generation of the straight jet (cf. Sect. 5). By varying the magnetic field distribution, we observed the formation of current sheets and the development of magnetic reconnection with different intensities. A stronger current sheet at the null and more intense reconnection during the straight jet phase triggered a helical jet at a lower energy level.
At the same time, the straight jet may inhibit the helical jet onset because it drains away free energy and twist. The reconnection driving the straight jet releases some of the free magnetic energy, which does not accumulate as fast as it would without the straight jet. Therefore the straight jet performs two competing functions: on one hand, it lowers the energy threshold for triggering the helical jet, but on the other hand, it inhibits the accumulation of the required energy. Thus, for a low-inclination angle, the helical jet was triggered earlier as the inclination increased, while for larger inclination angle the helical jet trigger was slightly delayed when the inclination increased even more (cf. Sect. 2.1). The transition occurred at an inclination angle around 8°, when a visible straight jet started to appear before helical jet onset. However, a helical jet was triggered in all of our runs.
Our results revealed key features of the instability that produces the helical jet. Our earlier explorations of the axisymmetric case (PAD09 and Rachmeler et al. 2010) identified kinking of the twisted, closed flux as the origin of highly dynamic jets. However, the ideal kink-like instability alone cannot generate the helical jet. Instead, magnetic reconnection most likely facilitates the development of a resistive kink instability, releasing a large portion of the stored free energy to power the jet. Our investigation also showed that a preceding reconnection-driven straight jet profoundly influences the onset of the following helical jet. Further theoretical and numerical research is needed to characterize this resistive instability and its nonlinear development. In this context, we note the intriguing parallel with our studies of coronal mass ejection initiation (Karpen et al. 2012), in which we found that the most explosive phase of energy release is enabled by a resistive instability.
6.2. Observational implications
The results of this investigation allow us to reproduce to some extent observable signatures (e.g., timing, speeds, and morphologies) of straight and helical jets. As stated in Sect. 2, standard jets are best described as straight jets, and blowout jets correspond most closely to helical jets. We found that when a straight jet occurs before a helical jet, the energy threshold for the helical jet onset is lowered. Less magnetic energy is therefore released during the development of the helical jet, which probably yields a weaker particle acceleration at the reconnection site. We found that the straight jet does not trigger the helical jet, but they are correlated in that the stronger the preceding straight jet, the weaker the helical jet. Therefore we predict that weaker radiative signatures would be observed for blowout jets that are preceded by strong standard jets.
A nearly axisymmetric configuration allows more free magnetic energy to be stored before the helical jet is triggered by inhibiting the formation of a substantial straight jet and setting a higher energy threshold for the helical jet onset. Because more magnetic energy and helicity are released during the development of the helical jet, the jet will be driven more strongly by nonlinear torsional waves transporting twist along the open field. Our earlier studies showed that in the untwisting model, most of the energy is carried by the Poynting flux, not by the kinetic energy flux (Pariat et al. 2009, 2010). Hence more energy can be transmitted to the plasma as the waves propagate upward, leading to even greater acceleration for nearly axisymmetric configurations. This could explain the nearly constant acceleration with height observed in some events (Patsourakos et al. 2008; Young & Muglach 2014b). Our model predicts that nearly axisymmetric systems will not generate a strong standard jet before initiating a blowout jet. Instead, these systems will produce more violent blowout jets, generating strongly blue- and redshifted and more intense emission-line profiles and ejecting more magnetic helicity (i.e., a brighter and more strongly twisted blowout jet). An observational study of jet characteristics as a function of inclination angle is needed to test these predictions.
While not seen in the present simulations, we expect that a strong standard jet may prevent the formation of a blowout jet if the rate of energy injected by footpoint motions is similar to the rate of energy released by the straight jet, or if the geometry of the system prevents the generation of a helical jet. For an untwisting upflows to develop, the reconnection site must be able to freely rotate along the fan surface to allow most of the twist accumulated in the closed field to be transferred efficiently to the open field. When the current sheet is extended primarily in one direction (as in the early emergence phase of Archontis & Hood 2013; and Moreno-Insertis & Galsgaard 2013), the freedom of motion of the current sheet is limited and only a straight jet is geometrically allowed. This may also explain why in the simulations of Edmondson et al. (2009) and Lynch et al. (2014) a helical jet was suddenly triggered as soon as the reconnection site moved into the open domain and was able to rotate. The observed transition from confined flares to jets (Wang & Liu 2012) might likewise be produced by similar evolution of the current sheet. On the other hand, our helical jet model releases a greater fraction of the free magnetic energy and twist than in our CME or eruptive flare simulations (e.g., Karpen et al. 2012).
In our helical jet model, the untwisting of newly reconnected open field lines drives most of the plasma flow. An essential point is that field lines are reconnected sequentially: the properties of the observed blowout jet result from these successive reconnections. The helical structure originates in the systematic nature of the reconnection, which progresses azimuthally around the fan surface. The untwisting produces two types of velocities: a wave that travels at a phase speed close to the Alfvén speed of the open field, and a bulk plasma flow traveling at only a fraction of the phase speed. The phase component might be responsible for the observed high speeds of blowout jets (as measured by, e.g., Savcheva et al. 2007). Spectroscopic imaging is necessary to measure the real bulk flow of the plasma (Harrison et al. 2001; Kamio et al. 2007, 2010; Madjarska 2011; Young & Muglach 2014b,a).
7. Conclusion
Although the correspondence between our model jets and the observed events denoted standard and blowout jets is not straightforward for all characteristics, our research leads to the following conclusions: the observed standard jets are associated with the straight jet phase of our simulations when only tension driving is active; the observed blowout jets are associated with the helical jet phase. The helical jet onset is apparently caused by a resistive kink-like instability because the reconnection occurring in our simulations strongly augments the minimal energy released by symmetry breaking in a purely ideal kink instability (Rachmeler et al. 2010). Because the untwisting mechanism is fully MHD, its evolution is adequately described by our model. Therefore the evolution of our model of a helical jet provides a basis for interpreting the dynamics of observed blowout jets.
The interpretation of the straight jet phase as a standard jet requires more caution, however. The tension-driven upflows critically depend on the kinetic-scale physics of reconnection, which is not reproduced by any MHD model. In addition, one should be careful in trying to compare simulation results too closely with observations when the computational approach lacks key thermodynamic terms. Evaporation flows, which require energy release by reconnection as well as heat conduction, probably plays a key role in producing the hot coronal emission observed at the base of many jets (see Sect. 1). The quasi-steady reconnection responsible for the straight jet may not be directly responsible for the observed evolution of the plasma emission. We critically point out that if the tension-driven mechanism alone were to directly explain the observed plasma acceleration, similar jet outflows would commonly be observed in flare and eruptions in which intense reconnection develops. However, such features are rarely observed in eruptive flares. Hence we expect that the tension-driven model is of secondary importance to explain the observed properties of jets.
In addition, the straight jet is not impulsively generated in our simulations; instead, it appears as a slow steady density increase in and around the fan and spine. To obtain an impulsive energy release, an instability in the current sheet would be needed. We did not observe any instability of this type in our 3D simulations, despite the deliberate placement of the smallest grid cells in the current sheets. On the other hand, triggering an impulsive straight jet may well rely on kinetic-scale processes that are beyond the scope of MHD simulations. In our view, it remains to be numerically demonstrated that a straight jet can be impulsively generated, leading us to speculate whether observed standard jets simply are unresolved blowout jets. More high spatial-resolution observations and numerical studies are needed to answer this question.
Acknowledgments
The authors thank the anonymous referee for his or her careful reading of the manuscript and remarks that helped to improve its readability. Authors C.R.D., S.K.A., and J.T.K. thank NASA’s Living With a Star program for supporting their participation in this work. The parametric studies presented in this work required a cumulated important amount of numerical resources over several years. We greatly appreciate the HPC resources of CINES, granted under the allocations 2010–046331, 2011–046331, 2012–046331, and 2013–046331 by GENCI (Grand Équipement National de Calcul Intensif), without which this work would have been impossible. Numerous test calculations were also performed on the quadric-core bi-Xeon computers of the Cluster of the Division Informatique de l’Observatoire de Paris. ISSI support for the workshops Understanding Solar Jets and their Role in Atmospheric Structure and Dynamics and the critical comments of the team members are gratefully acknowledged.
References
- Antiochos, S. K. 1996, Solar drivers of the interplanetary and terrestrial disturbances, ASP Conf. Ser., 95, 1 [NASA ADS] [Google Scholar]
- Archontis, V., & Hood, A. W. 2013, ApJ, 769, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, G., Galsgaard, K., & Nordlund, Å. 2013a, Sol. Phys., 284, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, G., Haugbølle, T., & Nordlund, Å. 2013b, ApJ, 771, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Beckers, J. M. 1968, Sol. Phys., 3, 367 [NASA ADS] [Google Scholar]
- Bellan, P. M., You, S., & Yun, G. S. 2007, J. Fusion Energy, 26, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Canfield, R. C., Leka, K. D., Shibata, K., Yokoyama, T., & Shimojo, M. 1996, ApJ, 464, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H. D., Jiang, Y. C., & Ma, S. L. 2008, A&A, 478, 907 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, H.-D., Zhang, J., & Ma, S.-L. 2012, Res. Astron. Astrophys., 12, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, N., Ip, W.-H., & Innes, D. 2013, ApJ, 769, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Chifor, C., Isobe, H., Mason, H. E., et al. 2008a, A&A, 491, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chifor, C., Young, P. R., Isobe, H., et al. 2008b, A&A, 481, L57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dalmasse, K., Pariat, E., Antiochos, S. K., & DeVore, C. R. 2012, EAS Pub. Ser., 55, 201 [CrossRef] [EDP Sciences] [Google Scholar]
- DeForest, C. E., & Kankelborg, C. C. 2007, J. Atmospheric and Solar-Terrestrial Physics, 69, 116 [NASA ADS] [CrossRef] [Google Scholar]
- DeVore, C. R. 1991, J. Comput. Phys., 92, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Edmondson, J. K., Lynch, B. J., Antiochos, S. K., De Vore, C. R., & Zurbuchen, T. H. 2009, ApJ, 707, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., Kucharek, H., Dennis, B. R., et al. 2004, J. Geophys. Res., 109, 10104 [NASA ADS] [CrossRef] [Google Scholar]
- Emslie, A. G., Dennis, B. R., Shih, A. Y., et al. 2012, ApJ, 759, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., Metcalf, T. R., Alexander, D., Brown, D. S., & Ryder, L. A. 2001, ApJ, 554, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., Dennis, B. R., Hudson, H. S., et al. 2011, Space Sci. Rev., 159, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Fuentes-Fernández, J., & Parnell, C. E. 2013, A&A, 554, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galsgaard, K., Archontis, V., Moreno-Insertis, F., & Hood, A. W. 2007, ApJ, 666, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Gontikakis, C., Archontis, V., & Tsinganos, K. 2009, A&A, 506, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guo, Y., Démoulin, P., Schmieder, B., et al. 2013, A&A, 555, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harrison, R. A., Bryans, P., & Bingham, R. 2001, A&A, 379, 324 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hong, J.-C., Jiang, Y.-C., Yang, J.-Y., et al. 2013, Res. Astron. Astrophys., 13, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, S. C., & Bellan, P. M. 2002, MNRAS, 334, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, S. C., & Bellan, P. M. 2003, Phys. Rev. Lett., 90, 215002 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Y. C., Chen, H. D., Li, K. J., Shen, Y. D., & Yang, L. H. 2007, A&A, 469, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jibben, P., & Canfield, R. C. 2004, ApJ, 610, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, M. L., Kucera, T. A., Davila, J. M., et al. 2008, Space Sci. Rev., 136, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Kamio, S., Curdt, W., Teriaca, L., Inhester, B., & Solanki, S. K. 2010, A&A, 510, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamio, S., Hara, H., Watanabe, T., et al. 2007, PASJ, 59, 757 [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & DeVore, C. R. 1995, ApJ, 450, 422 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., & DeVore, C. R. 2012, ApJ, 760, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Karpen, J. T., Antiochos, S. K., Richard DeVore, C., & Golub, L. 1998, ApJ, 495, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Kayshap, P., Srivastava, A. K., Murawski, K., & Tripathi, D. 2013, ApJ, 770, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Krucker, S., Kontar, E. P., Christe, S., Glesener, L., & Lin, R. P. 2011, ApJ, 742, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, Y.-T., & Finn, J. M. 1990, ApJ, 350, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., Title, A. M., & Tarbell, T. D. 2009, ApJ, 707, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Deng, N., Liu, R., et al. 2011a, ApJ, 735, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, W., Berger, T. E., Title, A. M., Tarbell, T. D., & Low, B. C. 2011b, ApJ, 728, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Lynch, B. J., Edmondson, J. K., & Li, Y. 2014, Sol. Phys., 289, 3043 [NASA ADS] [CrossRef] [Google Scholar]
- MacNeice, P., Olson, K. M., Mobarry, C., de Fainchtein, R., & Packer, C. 2000, Comp. Phys. Comm., 126, 330 [Google Scholar]
- Madjarska, M. S. 2011, A&A, 526, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masson, S., Pariat, E., Aulanier, G., & Schrijver, C. J. 2009, ApJ, 700, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Masson, S., Aulanier, G., Pariat, E., & Klein, K.-L. 2012, Sol. Phys., 276, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Matsui, Y., Yokoyama, T., Kitagawa, N., & Imada, S. 2012, ApJ, 759, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Miyagoshi, T., & Yokoyama, T. 2003, ApJ, 593, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Miyagoshi, T., Isobe, H., Yokoyama, T., & Shibata, K. 2006, A&A, 359, 164 [Google Scholar]
- Moore, R. L., Cirtain, J. W., Sterling, A. C., & Falconer, D. A. 2010, ApJ, 720, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, R. L., Sterling, A. C., Falconer, D. A., & Robe, D. 2013, ApJ, 769, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., & Galsgaard, K. 2013, ApJ, 771, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno-Insertis, F., Galsgaard, K., & Ugarte-Urra, I. 2008, ApJ, 673, L211 [Google Scholar]
- Morita, S., Shibata, K., Ueno, S., et al. 2010, PASJ, 62, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Moser, A. L., & Bellan, P. M. 2012, A&SS, 337, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Nishizuka, N., Shimizu, T., Nakamura, T., et al. 2008, ApJ, 683, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Nishizuka, N., Nakamura, T., Kawate, T., Singh, K. A. P., & Shibata, K. 2011, ApJ, 731, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Démoulin, P., & Berger, M. A. 2005, A&A, 439, 1191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2009, ApJ, 691, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Pariat, E., Antiochos, S. K., & DeVore, C. R. 2010, ApJ, 714, 1762 [NASA ADS] [CrossRef] [Google Scholar]
- Patsourakos, S., Pariat, E., Vourlidas, A., Antiochos, S. K., & Wuelser, J. P. 2008, ApJ, 680, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Pinto, R. F., Brun, A. S., Jouve, L., & Grappin, R. 2011, ApJ, 737, 72 [Google Scholar]
- Pontin, D. I., Priest, E. R., & Galsgaard, K. 2013, ApJ, 774, 154 [Google Scholar]
- Priest, E. R., & Pontin, D. I. 2009, Phys. Plasmas, 16, 2101 [Google Scholar]
- Pucci, S., Poletto, G., Sterling, A. C., & Romoli, M. 2013, ApJ, 776, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Rachmeler, L. A., Pariat, E., DeForest, C. E., Antiochos, S. K., & Török, T. 2010, ApJ, 715, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Raouafi, N. E., Georgoulis, M. K., Rust, D. M., & Bernasconi, P. N. 2010, ApJ, 718, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Savcheva, A., Cirtain, J. W., De Luca, E. E., et al. 2007, PAJS, 59, 771 [Google Scholar]
- Schmahl, E. J. 1981, Sol. Phys., 69, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Schmieder, B., Shibata, K., van Driel-Gesztelyi, L. L., & Freeland, J. M. 1995, Sol. Phys., 156, 245 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Schmieder, B., Guo, Y., Moreno-Insertis, F., et al. 2013, A&A, 559, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, Y., Liu, Y., Su, J., & Ibrahim, A. 2011, ApJ, 735, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, Y., Su, J., & Deng, Y. 2012, ApJ, 745, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K. 1985, Astrono. Soc. Japan, 37, 31 [Google Scholar]
- Shibata, K. 1986, Sol. Phys., 103, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K., Shimojo, M., Yokoyama, T., & Ohyama, M. 1997, Magnetic Reconnection in the Solar Atmosphere, eds. R. D. Bentley, & J. T. Mariska, ASP Conf. Ser., 111, 29 [Google Scholar]
- Shibata, K., Acton, L. W., Strong, K. T., et al. 1992, PASJ, 44, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K., Nakamura, T., Matsumoto, T., et al. 2007, Science, 318, 1591 [Google Scholar]
- Shimojo, M., & Shibata, K. 2000a, Adv. Space Res., 26, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Shimojo, M., & Shibata, K. 2000b, ApJ, 542, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Shimojo, M., & Tsuneta, S. 2009, ApJ, 706, L145 [NASA ADS] [CrossRef] [Google Scholar]
- Shimojo, M., Shibata, K., & Harvey, K. L. 1998, Sol. Phys., 178, 379 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Shimojo, M., Shibata, K., Yokoyama, T., & Hori, K. 2001, ApJ, 550, 1051 [NASA ADS] [CrossRef] [Google Scholar]
- Sterling, A. C. 2000, Sol. Phys., 196, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Török, T., Aulanier, G., Schmieder, B., Reeves, K. K., & Golub, L. 2009, ApJ, 704, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., & Liu, C. 2012, ApJ, 760, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., & Pick, M. 2006, ApJ, 639, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., & Sheeley, N. R. 2002, ApJ, 575, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y.-M., Sheeley, N. R., Howard, R. A., et al. 1998, ApJ, 508, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Yamauchi, Y., Moore, R. L., Tucker, S. T., Wang, H., & Sakurai, T. 2004, ApJ, 605, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, L., He, J., Peter, H., et al. 2013, ApJ, 777, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Yokoyama, T., & Shibata, K. 1996, PASJ, 48, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., & Muglach, K. 2014a, PASJ, in press http://pasj.oxfordjournals.org/contents/early/2014/11/20/pasj.psu088 [Google Scholar]
- Young, P. R., & Muglach, K. 2014b, Sol. Phys., 289, 3313 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Q. M., Chen, P.-F. F., Guo, Y., Fang, C., & Ding, M.-D. 2012, ApJ, 746, 19 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Morphology of the straight jet (left panels, t = 580 nondimensional units) and the helical jet (right panels, t = 1000) in the θ = 10° run presented in Sect. 3. Top panels: isosurfaces of plasma density at ρ/ρ0 = 1.05 color-coded according to plasma temperature. The white field lines are plotted regularly along x = 0 and z = 0 from fixed footpoints in the initially open connectivity domain. The cyan field lines are plotted from fixed footpoints along a circle of radius r = 3 and are initially closed. Bottom left panel: 2D distribution of the z component of the velocity field in the x = 0 plane. Blue and red indicate upward and downward flows. Bottom right panel: 2D distribution of the x component of the velocity field in the x = 0 plane. Blue and red indicate flows toward and away from the observer. The black field lines are all initially closed and correspond to the cyan field lines of the upper panel. The magenta lines are isocontours of the electric current density magnitude in the plane. |
| In the text | |
 |
Fig. 2 Evolution of the system for θ = 3° (left column), 10° (central column), and 20° (right column). The bottom boundary displays the distribution of Bz. The top row shows the initial configuration. The blue field lines are plotted at fixed intervals along x = 0 and z = 0 from fixed footpoints in the initially open domain. The white field lines are plotted from fixed footpoints along a circle of radius r = 3 and are initially closed. The middle row displays the system at t = 600 during the straight jet phase. Isosurfaces of the plasma density at ρ/ρ0 = 1.05 are color shaded according to the vertical velocity vz, showing the acceleration of plasma in the straight jet. The bottom row presents the system during the helical jet phase. Isosurfaces of the plasma density at ρ/ρ0 = 1.2 are color shaded according to vx: red and blue indicate plasma flow away from and toward the observer (similar to Dopplergrams), highlighting the strong rotation in the helical jet. |
| In the text | |
 |
Fig. 3 Top panel: evolution of the free magnetic energy, Emag, for simulations with different values of the inclination angle θ. Bottom panel: time, Ttrig, of the onset of the helical jet (black stars) and accumulated free energy at Ttrig (Etrig = EM(Ttrig), red diamonds) as functions of θ. |
| In the text | |
 |
Fig. 4 Top panel: evolution of the kinetic energy for simulations with different values of the inclination angle θ. Bottom panel: evolution of the normalized kinetic energy (see text), where Δt = 0 at the time of peak kinetic energy in each simulation. |
| In the text | |
 |
Fig. 5 Left panels: top views of the bottom boundary distribution of the vertical magnetic-field component (Bz) coded in levels of gray for the different runs. The red field lines map the initial (t = 0) separatrices passing by the 3D null point, bounding the open and closed magnetic connectivity domains. Right panels: side views of the initial potential magnetic configuration (t = 0) for the different simulations. The red field lines are those shown in the left panels. The yellow field lines outline the connectivity in the closed domain and are plotted from footpoints distributed along a circle on the bottom boundary of radius r = 0.6 centered on the footpoint of the inner spine. |
| In the text | |
 |
Fig. 6 Top panel: evolution of the free magnetic energy, Emag for simulations with different bottom boundary distributions of the magnetic field, as shown in Fig. 5. Bottom panel: evolution of the kinetic energy Ekin for the simulations. |
| In the text | |
 |
Fig. 7 Vertical velocity distribution in the y − z plane at the given values of x at t = 600, during the straight jet phase, for simulations with different photospheric field distributions. The velocity magnitude is color coded in blue (upflows) and red (downflows) similarly to the lower left panel of Fig. 1. The black lines are isocontours of the vertical velocity; the blue and green lines are isocontours of the electric current density. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


