| Issue |
A&A
Volume 572, December 2014
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201423814 | |
| Published online | 25 November 2014 | |
Separating gas-giant and ice-giant planets by halting pebble accretion
1 Lund ObservatoryDepartment of Astronomy and Theoretical Physics, Lund University, Box 43, 22100 Lund, Sweden
e-mail: michiel@astro.lu.se
2 Dep. Lagrange, UNSA, CNRS, OCA, Nice, France
Received: 15 March 2014
Accepted: 25 August 2014
In the solar system giant planets come in two flavours: gas giants (Jupiter and Saturn) with massive gas envelopes, and ice giants (Uranus and Neptune) with much thinner envelopes around their cores. It is poorly understood how these two classes of planets formed. High solid accretion rates, necessary to form the cores of giant planets within the life-time of protoplanetary discs, heat the envelope and prevent rapid gas contraction onto the core, unless accretion is halted. We find that, in fact, accretion of pebbles (~cm sized particles) is self-limiting: when a core becomes massive enough it carves a gap in the pebble disc. This halt in pebble accretion subsequently triggers the rapid collapse of the super-critical gas envelope. Unlike gas giants, ice giants do not reach this threshold mass and can only bind low-mass envelopes that are highly enriched by water vapour from sublimated icy pebbles. This offers an explanation for the compositional difference between gas giants and ice giants in the solar system. Furthermore, unlike planetesimal-driven accretion scenarios, our model allows core formation and envelope attraction within disc life-times, provided that solids in protoplanetary discs are predominantly made up of pebbles. Our results imply that the outer regions of planetary systems, where the mass required to halt pebble accretion is large, are dominated by ice giants and that gas-giant exoplanets in wide orbits are enriched by more than 50 Earth masses of solids.
Key words: planets and satellites: formation / planets and satellites: gaseous planets / planets and satellites: composition / planets and satellites: interiors / protoplanetary disks
© ESO, 2014
1. Introduction
In the core accretion scenario (Pollack et al. 1996), giant planets form by attracting a gaseous envelope onto a core of rock and ice. This theory is supported by the large amount of heavy elements – elements with atomic number above He – found in the giant planets in our solar system (Guillot 2005). Additional evidence is provided by the observed dependence of giant exoplanet occurrence on the host star metallicity, which is a proxy for the dust mass enrichment of the protoplanetary disc (Fischer & Valenti 2005; Buchhave et al. 2012).
However, from a theoretical perspective it is poorly understood how the core accretion scenario could have taken place, if the cores grew by accretion of km-sized planetesimals and their fragments. Protoplanetary disc life-times range from ~3 Myr (Haisch et al. 2001; Soderblom et al. 2013) to possibly as long as ~6 Myr (Bell et al. 2013). This is much shorter than the time needed to grow cores to completion in numerical simulations (Levison et al. 2010) of discs with solid surface densities comparable to the minimum mass solar nebula (MMSN, Hayashi 1981). Additionally, the gaseous envelope grows only slowly on Myr timescales, because of the continued heating by accretion of remnant planetesimals, even after clearing most of its feeding zone (Pollack et al. 1996; Ikoma et al. 2000). Therefore, planets with gaseous envelopes are difficult to form by planetesimal growth within ~10 Myr, especially outside the current orbit of Jupiter (5 AU), where core growth timescales rapidly increase (Dodson-Robinson et al. 2009).
As a result, protoplanetary discs with strongly enhanced solid surface densities in planetesimals (exceeding the MMSN by a factor of 10, Kobayashi et al. 2011) have been proposed in order to form the cores of the giant planets. For the gas giants, planetesimal accretion is then halted artificially, or the opacity in the envelope is lowered, in order to reduce the envelope attraction timescale (Hubickyj et al. 2005). The ice giants are envisioned to remain small, because the protoplanetary gas disc dissipates during slow envelope growth (Pollack et al. 1996; Dodson-Robinson & Bodenheimer 2010).
In this paper, we investigate the attraction of the gaseous envelope when growth occurs by the accretion of pebbles, as opposed to planetesimals. Pebble accretion rates are sufficiently high to form the cores of giant planets in less than 1 million years, even in wide orbits (Lambrechts & Johansen 2012). Previous studies (Johansen & Lacerda 2010; Ormel & Klahr 2010; Bromley & Kenyon 2011; Lambrechts & Johansen 2012; Morbidelli & Nesvorny 2012) demonstrate that this is the result of gas drag operating on pebbles, which dramatically increases the accretion cross section (Sect. 2). The rapid accretion of pebbles leads to high accretion luminosities that support a growing gaseous envelope around the core (Sect. 3). We proceed by calculating the critical core mass, the lowest mass for which a core can no longer sustain the hydrostatic balance of the proto-envelope. The critical core masses we find are of the order of ≈100 Earth masses (ME), too large compared to the inferred core masses of the gas giants in the solar system. Fortunately, we find that there is a threshold mass already around 20 ME, where the core perturbs the gas disc and halts the accretion of pebbles, which initiates the collapse of the envelope before the critical core mass is reached (Sect. 4). This threshold mass is reached by the cores of the gas giants, but not by the ice giants in wider orbits. By combining our calculations of the pebble isolation mass and the critical core mass as a function of the envelope enrichment, we can make estimates of the bulk heavy element content of the giant planets. We find a good agreement with the composition of the giant planets in the solar system (Sect. 5). We also discuss the implications of our model on the occurrence and composition of giant exoplanets (Sect. 6). Finally, we briefly summarize our work (Sect. 7).
2. Pebble accretion
The pebble accretion scenario, as outlined in Lambrechts & Johansen (2012), starts with the growth of pebbles from the initial grains embedded in the protoplanetary disc (with sizes ≈μm) by collisions (Birnstiel et al. 2012) or through sublimation and condensation cycles around ice lines (Ros & Johansen 2013). A fraction of the population of pebbles that drift towards the host star form dense swarms that subsequently collapse under self-gravity to create planetesimals 100−1000 km in size. Such concentrations can occur through the streaming instability, driven by the mutual drag between particles and gas (Youdin & Goodman 2005; Youdin & Johansen 2007; Johansen & Youdin 2007), or for example through the presence of vortices (Barge & Sommeria 1995) or pressure bumps (Whipple 1972). A more detailed discussion can be found in the reviews by Chiang & Youdin (2010) and Johansen et al. (2014). Finally, the largest planetesimals can act as the seeds of the planetary cores which grow by rapidly sweeping up the remaining pebbles (Lambrechts & Johansen 2012).
We consider here cores that grow predominantly by the accretion of particles with radii of approximately mm-cm. Particle sizes can be expressed as a function of the gas drag timescale (tf) and Keplerian frequency ΩK in terms of the Stokes number 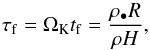 (1)where ρ• is the solid density, R the particle radius, ρ the midplane gas density, and H the local gas scale height of the disc. Small dust particles (τf ≪ 1) are thus strongly coupled and comoving with the gas, while much larger objects (τf ≫ 1) are only weakly affected by gas drag. In the outer parts of the MMSN, in the region with semi-major axis a between 5 and 30 AU, particle sizes between mm and cm correspond to τf ≈ 0.01 − 0.1.
(1)where ρ• is the solid density, R the particle radius, ρ the midplane gas density, and H the local gas scale height of the disc. Small dust particles (τf ≪ 1) are thus strongly coupled and comoving with the gas, while much larger objects (τf ≫ 1) are only weakly affected by gas drag. In the outer parts of the MMSN, in the region with semi-major axis a between 5 and 30 AU, particle sizes between mm and cm correspond to τf ≈ 0.01 − 0.1.
 |
Fig. 1 Pebble accretion rates (red), planetesimal accretion rates (grey), and minimal accretion rates required to sustain a stable gas envelope (black), as a function of the core mass. The curves for the minimal accretion rates are nearly independent of orbital radius between 5−30 AU, but depend strongly on the opacity (Appendix B.3) and on the level of envelope pollution by sublimation of icy pebbles. Labels at the top of the figure indicate H2O pollution of the atmosphere as a percentage with respect to pure H/He nebular gas, corresponding to the fraction 1 − β from Eq. (11). The critical core mass to collapse the gas envelope can be found at the intersection of an accretion curve with a critical curve. Accretion rate curves that fall in the yellow dashed region are too slow to form the cores of the giant planets before the dissipation of the gas disc (τacc = Mc/Ṁc>τdisc = 2 Myr). Red circles mark the mass above which pebble accretion is halted (Eq. (12)) and the gravitational collapse of the gas envelope is triggered. |
The seeds of the planetary cores accrete from the full scale height of pebbles at a rate 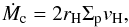 (2)(Ormel & Klahr 2010; Lambrechts & Johansen 2012). Here, Σp denotes for the surface density in pebbles and vH = rHΩK is the Hill velocity at the Hill radius
(2)(Ormel & Klahr 2010; Lambrechts & Johansen 2012). Here, Σp denotes for the surface density in pebbles and vH = rHΩK is the Hill velocity at the Hill radius ![\hbox{$r_{\rm H} = \left[GM_{\rm c}/(3\Omega_{\rm K}^2) \right]^{1/3}$}](/articles/aa/full_html/2014/12/aa23814-14/aa23814-14-eq31.png) , with G the gravitational constant. Particles entering the Hill sphere have a crossing time, τc ~ rH/vH, comparable to the orbital timescale. Gas drag operates on pebbles on similar timescales, leading to their accretion by the core. This accretion rate does not depend on the particle size between τf = 0.1 − 10, but moderately decreases ∝ (τf/ 0.1)2/3 for particles below τf = 0.1 (Lambrechts & Johansen 2012). We have assumed in Eq. (2) that the particle scale height is smaller than the Hill radius of the core, which is valid when core masses are larger than
, with G the gravitational constant. Particles entering the Hill sphere have a crossing time, τc ~ rH/vH, comparable to the orbital timescale. Gas drag operates on pebbles on similar timescales, leading to their accretion by the core. This accretion rate does not depend on the particle size between τf = 0.1 − 10, but moderately decreases ∝ (τf/ 0.1)2/3 for particles below τf = 0.1 (Lambrechts & Johansen 2012). We have assumed in Eq. (2) that the particle scale height is smaller than the Hill radius of the core, which is valid when core masses are larger than 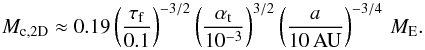 (3)Here we have taken for simplicity an MMSN model with a particle scale height given by
(3)Here we have taken for simplicity an MMSN model with a particle scale height given by 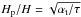 (Youdin & Lithwick 2007), where αt is the turbulent diffusion parameter. Low particle scale heights are expected in dead-zones and discs where angular momentum transport occurs primarily through disc winds (Turner et al. 2014). From particle stirring alone, scale heights of Hp/H ≈ 0.01 are expected (Bai & Stone 2010). In the MMSN, the accretion rate when Hp<rH translates into
(Youdin & Lithwick 2007), where αt is the turbulent diffusion parameter. Low particle scale heights are expected in dead-zones and discs where angular momentum transport occurs primarily through disc winds (Turner et al. 2014). From particle stirring alone, scale heights of Hp/H ≈ 0.01 are expected (Bai & Stone 2010). In the MMSN, the accretion rate when Hp<rH translates into 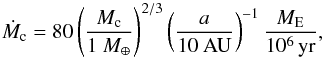 (4)which is illustrated in Fig. 1 (red curves).
(4)which is illustrated in Fig. 1 (red curves).
The growth of the core is driven by the radial drift of pebbles through the protoplanetary disc. Because of gas drag robbing pebbles of angular momentum, they spiral towards the star with a velocity 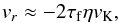 (5)for particles with τf< 1 (Weidenschilling 1977; Nakagawa et al. 1986). Here vK is the Keplerian velocity and
(5)for particles with τf< 1 (Weidenschilling 1977; Nakagawa et al. 1986). Here vK is the Keplerian velocity and 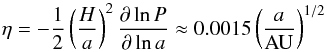 (6)is the fraction by which the gas orbits slower than pure Keplerian rotation, which is a function of the (local) gas scale height and pressure gradient ∂lnP/∂lna. Thus pebbles drift radially inwards within a short timescale,
(6)is the fraction by which the gas orbits slower than pure Keplerian rotation, which is a function of the (local) gas scale height and pressure gradient ∂lnP/∂lna. Thus pebbles drift radially inwards within a short timescale, 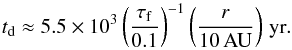 (7)A core embedded in the disc can accrete a sizable fraction of this radial pebble flux, f ≈ 30% (Morbidelli & Nesvorny 2012, see also Appendix A).
(7)A core embedded in the disc can accrete a sizable fraction of this radial pebble flux, f ≈ 30% (Morbidelli & Nesvorny 2012, see also Appendix A).
In this work, we use surface densities in pebbles comparable to MMSN estimates, unless mentioned otherwise. This approximation is supported by theoretical models of protoplanetary discs that include dust growth by coagulation and radial drift of particles (Brauer et al. 2008; Birnstiel et al. 2012). A more detailed discussion can be found in Appendix A. This approach can also be justified observationally: measurements of the spectral index of the dust opacity in protoplanetary discs reveal that a significant fraction of solids grow to mm and cm sizes early on and remain present over the life-time of the disc (Ricci et al. 2010). In an accompanying paper (Lambrechts & Johansen 2014) we study pebble accretion on global scales, including dust coagulation, pebble drift, and the growth of multiple cores. These results motivate the particle sizes and accretion rates used in this study.
To conclude this section, we briefly highlight the main differences between planetesimal and pebble accretion, which alter the accretion luminosity of the core and therefore the critical core mass. The pebble accretion rate given in Eq. (2) is the maximal possible one, because in this regime one accretes from the full Hill sphere, which is the largest possible gravitational reach of the core (Lambrechts & Johansen 2012). The accretion of planetesimals, on the other hand, is significantly less efficient compared to pebbles. The planetesimal accretion rate can be expressed as a fraction of the pebble accretion rate, 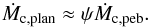 (8)The efficiency of accretion, ψ, is equal to the ratio of the core radius rc to Hill radius rH,
(8)The efficiency of accretion, ψ, is equal to the ratio of the core radius rc to Hill radius rH, 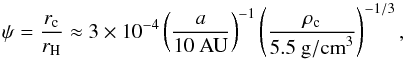 (9)where ρc is the material density of the core. The reduced accretion rates are indicated by the grey lines in Fig. 1. This result follows from the assumption that the planetesimal velocity dispersion is equal to the Hill speed (Dodson-Robinson et al. 2009; Dodson-Robinson & Bodenheimer 2010), vH = ΩrH, and gravitational focusing occurs from a radius (rc/rH)1/2rH, which is smaller than the planetesimal scale height Hplan = vH/ Ω = rH. This leads to planetesimal accretion rates
(9)where ρc is the material density of the core. The reduced accretion rates are indicated by the grey lines in Fig. 1. This result follows from the assumption that the planetesimal velocity dispersion is equal to the Hill speed (Dodson-Robinson et al. 2009; Dodson-Robinson & Bodenheimer 2010), vH = ΩrH, and gravitational focusing occurs from a radius (rc/rH)1/2rH, which is smaller than the planetesimal scale height Hplan = vH/ Ω = rH. This leads to planetesimal accretion rates 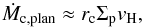 (10)with Σp now the surface density in planetesimals. Collisional fragments of planetesimals (0.1−1 km) have a reduced scale height and can be accreted more rapidly by a factor of 1/
(10)with Σp now the surface density in planetesimals. Collisional fragments of planetesimals (0.1−1 km) have a reduced scale height and can be accreted more rapidly by a factor of 1/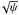 (Rafikov 2004).
(Rafikov 2004).
Planetesimals are dynamically heated by the cores, which triggers a fragmentation cascade. Because of efficient grinding of planetesimals to dust, the planetesimal mass reservoir is reduced with time (Kobayashi et al. 2010; Kenyon & Bromley 2008). Therefore, core formation at 5 AU requires massive planetesimal discs, at least 10 times as massive as expected from the MMSN (Kobayashi et al. 2011). At wider orbital radii no significant growth occurs, although pressure bumps caused by planet-triggered gap opening in the gas disc could increase the accretion efficiency of fragments (Kobayashi et al. 2012). Global simulations furthermore highlight that growth by fragments is inefficient, because they get trapped in mean motion resonances and push planetary cores towards the star (Levison et al. 2010). To overcome these issues, it has been proposed that fragmentation continues to mm-cm sizes (Ormel & Kobayashi 2012; Chambers 2014). Pebbles, because of gas drag, do not suffer from destructive excitations or resonant trapping.
3. The growth of the proto-envelope
3.1. Accretion luminosity
The attraction of the gaseous envelope is regulated by the growth of the solid core. Pebbles that rain down in the proto-atmosphere of the core deposit their potential energy close to the core surface which provides the heat necessary to support the envelope. The luminosity of the planet is thus a simple function of the accretion rate, 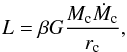 (11)where rc is the radius if the core (for an extended discussion see Appendix B). Depending on the composition of the accreted material, a fraction 1 − β of the mass attracted by the planet is lost by sublimation high up in the atmosphere and pollutes the envelope with material of high molecular weight (Hori & Ikoma 2011). For this study we assume the bulk of the pebbles to be of cometary composition, with a mass ratio of β = 0.5 of refractory elements to water ice. In Appendix B.3, we discuss in greater detail the influence of the composition of the accreted material. Knowing the luminosity of the planet, we can now proceed to calculate the structure of the hydrostatic envelope surrounding the core.
(11)where rc is the radius if the core (for an extended discussion see Appendix B). Depending on the composition of the accreted material, a fraction 1 − β of the mass attracted by the planet is lost by sublimation high up in the atmosphere and pollutes the envelope with material of high molecular weight (Hori & Ikoma 2011). For this study we assume the bulk of the pebbles to be of cometary composition, with a mass ratio of β = 0.5 of refractory elements to water ice. In Appendix B.3, we discuss in greater detail the influence of the composition of the accreted material. Knowing the luminosity of the planet, we can now proceed to calculate the structure of the hydrostatic envelope surrounding the core.
3.2. The critical core mass
There exists a critical core mass where the inwards gravitational pull of the core overcomes the pressure support by the released accretion heat and the envelope collapses. We numerically investigate the envelope mass as a function of the accretion luminosity by constructing spherically symmetric envelopes in hydrostatic equilibrium (Figs. B.1 and B.2, detailed description in Appendix B). We identify the critical core mass Mc,crit as the core mass for which we no longer find a hydrostatic solution (Mizuno 1980; Ikoma et al. 2000). This occurs in practice when the mass bound in the envelope is comparable to the mass of the core and the self-gravity of the gas atmosphere becomes important (Stevenson 1982). As a result the gas envelope falls onto the core on the Kelvin-Helmholtz timescale (Ikoma et al. 2000; Piso & Youdin 2014, see also Appendix C). Earlier investigations show that higher accretion rates increase Mc,crit (Ikoma et al. 2000; Rafikov 2006). In this study we have broadened the range of accretion rates studied to include those from pebbles. We also find that the critical core mass can be lowered significantly by increasing the mean molecular weight through sublimation of icy material in the deeper parts of the envelope where the temperature is above T ≈ 150 K, in agreement with previous studies (Stevenson 1982; Hori & Ikoma 2011). Figure 1 shows critical curves, in black, which connect the critical core mass to the accretion rate (for a standard opacity choice, see also Appendix B.3). We find that, unless accretion is interrupted, pebble accretion leads to critical core masses ≳ 100 ME between 5−30 AU, which is an order of magnitude larger than the cores in the solar system (Guillot 2005).
4. The pebble isolation mass
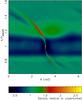 |
Fig. 2 Gravitational perturbation of the midplane gas density from a 50 ME-planet embedded in a protoplanetary disc. Displayed is a full annulus (θ = 2π-wide in azimuth) of the protoplanetary disc around the planet located at normalized radius r = 1. The resulting pressure perturbation halts the radial migration of pebbles and thus the solid accretion onto the core. The overdensities at radius r = 0.85 and r = 1.2 correspond to the regions with super-Keplerian rotation, that are highlighted in Fig. 3. A Rossby vortex, here centred at (θ = 3.8,r = 1.2) has formed outside the orbit of the planet. |
 |
Fig. 3 Deviation from the equilibrium sub-Keplerian velocity of the gas in the protoplanetary disc (vθ,gas/vK) due to the presence of a planetary core located at a normalized radius of r = 1 (here corresponding to an orbital radius of a = 5 AU). For cores with masses above 20ME (blue curve) and higher (red and black curves) the gas orbits faster than the Keplerian velocity (horizontal dashed line) in a region outside the orbit of the planet. This ring acts as a trap for pebbles drifting inwards and halts the accretion of pebbles onto the core. |
We now highlight the existence of a limiting mass for giant planets above which no additional pebbles are accreted. Detailed 3D numerical simulations of an annulus of the protoplanetary disc show that as the planet grows larger than the pebble isolation mass, 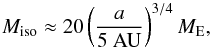 (12)local changes in the pressure gradient modify the rotation velocity of the gas, which halts the drift of pebbles to the core (Eqs. (5), (6) and Figs. 2, 3). The value of the pebble isolation mass depends dominantly on the orbital radius through the disc aspect ratio, Miso ∝ (H/a)3, see also Sect. 4.1. Therefore pebble isolation becomes harder to attain at wider orbital separations in flaring discs.
(12)local changes in the pressure gradient modify the rotation velocity of the gas, which halts the drift of pebbles to the core (Eqs. (5), (6) and Figs. 2, 3). The value of the pebble isolation mass depends dominantly on the orbital radius through the disc aspect ratio, Miso ∝ (H/a)3, see also Sect. 4.1. Therefore pebble isolation becomes harder to attain at wider orbital separations in flaring discs.
4.1. Calculation of the pebble isolation mass
We now determine at which mass a planet can isolate itself from the flux of pebbles, and the dependence of the result on the scale height of the disc and the planet’s location. A planet can perturb the gas-disc enough to make the gas velocity in a narrow ring just outside the orbit of the planet super-Keplerian (Paardekooper & Mellema 2006; Morbidelli & Nesvorny 2012). This happens when the planet is capable of perturbing significantly the density of the disc, changing locally the sign of the radial density gradient. In the ring where the gas is super-Keplerian, the action of gas-drag reverses. Pebbles are pushed outwards, instead of inwards. Thus, the pebbles have to accumulate at the outer edge of this ring, instead of migrating all the way through the orbit of the planet. The accretion of pebbles by the planet now suddenly stops. The enhancement in pebble density at the edge of the ring can possibly lead to the formation of new large planetesimals and even of new cores (Lyra et al. 2008; Kobayashi et al. 2012).
An isolation mass of about 50 ME, for a disc with a scale height of 5%, was previously suggested in Morbidelli & Nesvorny (2012). However, the authors used 2D simulations, which forced them to use a large smoothing parameter (equal to 60% of the planet’s Hill radius) in the planet’s gravitational potential. The use of a large smoothing parameter weakens the gravitational perturbations of the planet on the disc, so that their estimate is probably an overestimate.
To overcome this problem, we used here a new 3D version of the code FARGO (Masset 2000; Lega et al. 2013). The new code also handles the diffusion of energy and stellar irradiation, but we used here its isothermal version for simplicity. The 3D code adopts a cubic approximation for the gravitational potential of the planet (Kley et al. 2009), which is somewhat equivalent to assuming a very small smoothing parameter in a standard potential.
We modelled a disc from 0.625 to 1.62 in radius, the unit of distance being the radius of the planet’s orbit, with an aspect ratio of 5% and a viscosity given by an α prescription (Shakura & Sunyaev 1973) with αt = 6 × 10-3. The radial boundary conditions were evanescent, which prevented reflection of the spiral density wave. The boundary condition in co-latitude was instead reflecting. The resolution was 320 × 720 × 32 in the radial, azimuthal, and co-latitudinal directions, respectively. We did a simulation with a planet of 20, 30, and 50 ME. The simulations have been run for 60 orbits, when the disc seemed to have reached a stationary structure. For the purpose of identifying the pebble isolation mass, it is not necessary to explicitly model the trajectories of particles between τf = 0.001 − 1 (Morbidelli & Nesvorny 2012). We therefore limit ourselves to calculating the pressure perturbation able to halt the radial particle drift (Eq. (5)).
Figure 3 shows the ratio between the azimuthal velocity of the disc and the Keplerian velocity as a function of radius. For each radius, the azimuthal velocity has been computed on the mid-plane of the disc; its average over the azimuth has been mass-weighted. We also computed the vertically averaged azimuthal velocity (all averages were mass-weighted) and found essentially the same radial profile. As one can see in the figure, away from the planet, the disc is uniformly sub-Keplerian (the azimuthal velocity is 0.9962 times the Kepler velocity). Instead, the planet induces strong perturbations in the gas azimuthal velocity in its vicinity. In particular for the case of the 30 ME core, there are two strong signatures, associated with the edges of the shallow gap that the planet opens in the disc: a dip at r = 0.88 where the gas is strongly sub-Keplerian, and a peak at r = 1.11 where the gas exceeds the Keplerian velocity (the azimuthal velocity is 1.0025 times the Kepler velocity). In this situation, the pebbles are expected to stop drifting at r ≈ 1.15, where the gas turns from sub-Keplerian (beyond this distance) to super-Keplerian (inside this distance).
Performing a simulation with a 50 ME planet we checked that, as expected, the velocity perturbation is linear in the mass of the planet. Thus, the planet-mass threshold for turning the disc barely super-Keplerian is Miso ≈ 20 ME. We verified this result with a simulation with a planet of this mass.
We also checked, with a simulation with a 5 times smaller value of the turbulent αt parameter, that the azimuthal velocity has a negligible dependence on the viscosity of the disc. This was expected because for a disc undergoing perturbations by a small planet, the resulting disc structure is dominated by disc’s internal pressure and hence its aspect ratio (Crida et al. 2006). In completely inviscid discs, the estimate for the isolation mass is likely smaller by no more than a factor of ≈2 (Zhu et al. 2014).
The dependence of Miso on the aspect ratio can be estimated analytically. In fact, in the limit of negligible viscosity, scaling the disc’s aspect ratio H/a proportionally to the normalized Hill radius of the planet rH/a, and adopting rH as basic unit of length, the equations of motion for the fluid become independent of the planet mass (Korycansky & Papaloizou 1996). Given that the perturbation in azimuthal velocity is linear in the planet’s mass (Korycansky & Papaloizou 1996), the result implies that the perturbation in azimuthal velocity has to be proportional to (H/a)3. With this result, we can now conclude with the dependency of Miso on the location of the planet in a given disc. Assuming that a disc is flared like the MMSN, as H/a = 0.05(a/ 5 AU)1/4, we obtain the result expressed in Eq. (12). Alternatively, for discs irradiated by the star the gas scale height goes as H/a ∝ a2/7 (Chiang & Goldreich 1997). The exact value of H/a depends on the level of viscous heating in the inner disc (Bitsch et al. 2013), but for moderate disc accretion rates is similar to the MMSN estimate at 5 AU. Therefore, the scaling for the isolation mass in an irradiated disc takes the form Miso = 20 ME(a/ 5 AU)6/7, which is slightly steeper than the MMSN-estimate.
4.2. Implications of a pebble isolation mass
The existence of this pebble isolation mass has three major implications that show the advantage of pebble accretion over planetesimal accretion in setting the conditions for envelope collapse. Firstly, when a giant planet grows to a mass beyond the pebble isolation mass, solid accretion will be abruptly terminated. The accretion luminosity is quenched and the critical core mass drops to a value much smaller than the pebble isolation mass (Fig. 1), which triggers a phase of rapid gas accretion. This is in sharp contrast with core growth by planetesimal accretion, where the continuous delivery of solid material delays the gravitational collapse by millions of years (Pollack et al. 1996). Halting planetesimal accretion to overcome this difficulty has been previously proposed (Hubickyj et al. 2005), but the formation of a clean gap in a planetesimal disc demands small planetesimals with a low surface density (Shiraishi & Ida 2008), which is inconsistent with models of core growth with planetesimals (Levison et al. 2010; Kobayashi et al. 2011).
Secondly, the low value of the pebble isolation mass resolves an apparent paradox faced by any growth scenario for giant planets: the high accretion rates necessary to form cores before gas dissipation results in critical core masses that are too large by an order of magnitude (~ 100 ME, Fig. 1). Fortunately, the self-shielding nature of pebble accretion yields much lower core masses in 5−10 AU orbits.
Thirdly, the pebble isolation mass introduces a natural sharp divide of the giant planets into two classes: gas giants and ice giants. The latter category are those cores that did not reach the pebble isolation mass before disc dissipation. Therefore these planets never stopped accreting pebbles during the life-time of the gas disc and the resulting accretion heat prevents unpolluted H/He envelopes from becoming unstable and undergoing runaway gas accretion. As a result, low-mass cores only contract low-mass envelopes with increased mean molecular weight (Fig. 1), which occurs after pebbles sublimate below the ice line and the released water vapour is homogeneously distributed by convection. Formation of ice giants in this model is thus different from the classical core accretion scenario, where ice giants are giant planets that had their growth prematurely terminated by demanding gas dispersal during envelope contraction (Pollack et al. 1996; Dodson-Robinson & Bodenheimer 2010).
5. Pebble accretion in the solar system
 |
Fig. 4 Total heavy element mass fraction as a function of the total mass M of the giant planet, at different orbital radii (5, 10, 20, 30 AU). Planets that do not grow beyond the pebble isolation mass (red dots) remain core-dominated, while those that grow larger will have most of their mass in gas. Estimates of the composition of Uranus and Neptune (blue error bars, Helled et al. 2011) agree well with the prediction made in this paper for planets formed in the outer disc. Similarly, for the gas-giant planets Jupiter and Saturn we find a good agreement between the 5−10 AU curves and the total heavy element mass estimated by Guillot (2005), indicated by the orange error bars. In order to create this figure, we numerically calculated the composition of the planet when it becomes critical, taking into account the pollution of the envelope, for planet masses below the pebble isolation mass (light blue curves). When the planet reached a mass larger than the pebble isolation mass, only nebular gas was added to continue growth (black curves). Here we present results with refractory fraction β = 0.5, but results depend weakly on the choice of β between 0.1−1. |
The pebble isolation mass increases with orbital radius (Eq. (12), Fig. 1), so the ice giants cannot have formed too close to the host star (<5 AU) where they would have become gas giant planets. Such close formation distances for the ice giants are anyway not favoured in current models of the early migration history of the solar system (Walsh et al. 2011): following the gas giants, the ice giants migrated inwards, but remained outside 5 AU, and subsequently moved outwards to distances between 11–17 AU which are preferred to explain the late time orbital evolution after disc dissipation (Tsiganis et al. 2005). The formation of the ice giants in our model is therefore compatible with the understanding of planetary migration in the solar system. One intriguing option that was previously not possible, is the approximately in situ formation of ice giants beyond 20 AU, since pebble accretion is sufficiently fast.
5.1. Planetary composition
By combining our calculations of the pebble isolation mass and the critical core mass (including the effect of pebble sublimation) we can calculate the heavy element mass fraction as a function of the total planet mass (full description in Appendix B.2). We do not compare our results directly with the inferred core masses of the giant planets in the solar system, but instead with the total heavy element mass, as it is better constrained and transport could have occurred from core to envelope (Guillot 2005). We find good agreement for Jupiter and Saturn between 5−10 AU, while Uranus and Neptune could have formed at similar or wider orbits, as illustrated in Fig. 4.
In contrast, the composition of the giant planets is difficult to reproduce with planetesimal accretion. For ice giants, planetesimal accretion is too slow at wide orbits, which would make the critical core mass too low (Fig. 1). For gas giants, late-time planetesimal accretion after runaway gas accretion cannot add the significant mass fraction of heavy elements in their envelopes, because planetesimal capture rates are small (Guillot & Gladman 2000).
Our encouraging correspondence between the model and the composition of the giant planets does not depend strongly on the assumptions made on the composition or surface density of pebbles. For Fig. 5 we have repeated our analysis, but with a 10 times lower accretion luminosity, by introducing a fudge factor ϵ = 0.1 into Eq. (11). Such a reduced luminosity could for example be the result of the bulk composition of the pebbles to be largely in ice, reducing the refractory fraction β by a factor of ϵ. Or, alternatively, the consequence of a lower surface density in pebbles compared to an MMSN-estimate, which would lower the accretion rate and thus the luminosity by the same factor. These lower efficiencies do not change the fit for the solar system gas giants, while ice giants are in fact better matched, if they formed closer towards the star near the ice line, compared to their current orbits.
We briefly address two caveats concerning the measured heavy element masses of the gas giants. Recently, it has been suggested that layered convection is important for Saturn (Leconte & Chabrier 2013), which allows for a higher total heavy element mass (an upper limit on the heavy element content is indicated by the downwards arrow). Also it is possible that a fraction of the heavy elements gets delivered through gas accretion at a time close to the dissipation of the protoplanetary disc, which would explain the noble gas abundances of Jupiter. In Fig. 5, the red error bars are corrected for the heavy elements accreted in this stage after pebble accretion.
 |
Fig. 5 Similar to Fig. 4, but representing planetary compositions of planets located at 5 and 30 AU (full and dashed lines respectively) for different values of the accretion rate efficiency ϵ. The thick solid lines correspond to the case where the full pebble accretion luminosity is released (ϵ = 1) and the lower thin lines of the same colour to a 10 times smaller luminosity (ϵ = 0.1). The red error bars, slightly displaced to the left for readability, give the heavy element mass, without the contribution of heavy elements added by late time gas accretion in a disc with increased dust-to-gas ratio (Guillot & Hueso 2006), as suggested to explain the noble gas abundances in Jupiter. The orange downwards arrow is an upper limit on the heavy element content of Saturn if layered convection occurs in the envelope (Leconte & Chabrier 2013). |
6. Exoplanets
Our proposed formation model for giant planets is applicable to extrasolar planetary systems as well. If a core reaches the pebble isolation mass before disc dissipation, it becomes a gas giant. However, outside an orbital radius alim the growth of cores will be too slow and isolation masses too high for pebble isolation to occur within the disc life-time τdisc. Those cores end up as ice giants. In a disc with a solid surface density equal to the MMSN (ϵ = 1), we find the limiting semi-major axis for gas giants to be 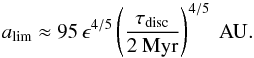 (13)In massive protoplanetary discs, ϵ is near unity or larger and alim is thus located far out in the disc. In such a case, wide-orbit gas giants, such as the four planets around the A star HR8799 located at a = 15 − 70 AU (Marois et al. 2010), can form in situ. We predict that their cores will be large (~ 50 − 100 ME), because of the high pebble isolation mass at large orbital distances (or from the similarly large critical core masses for pure H/He envelopes as seen in Fig. 1). Such solid-enriched compositions are supported by models of gas-giant exoplanets now in close orbits (but which likely formed at wider orbits) that show total heavy element masses ~ 100 ME, much larger than planetesimal isolation masses in classical core accretion (Pollack et al. 1996). For example, the gas giant CoRoT-10 b has a mass of 870ME, of which approximately 180 ME are in heavy elements (Bonomo et al. 2010). Similarly, Corot-13 b, 14 b, 17 b, 20 b, and 23 b all have ≳ 70 ME of heavy elements and are significantly enriched with respect to the host star metallicity (Moutou et al. 2013).
(13)In massive protoplanetary discs, ϵ is near unity or larger and alim is thus located far out in the disc. In such a case, wide-orbit gas giants, such as the four planets around the A star HR8799 located at a = 15 − 70 AU (Marois et al. 2010), can form in situ. We predict that their cores will be large (~ 50 − 100 ME), because of the high pebble isolation mass at large orbital distances (or from the similarly large critical core masses for pure H/He envelopes as seen in Fig. 1). Such solid-enriched compositions are supported by models of gas-giant exoplanets now in close orbits (but which likely formed at wider orbits) that show total heavy element masses ~ 100 ME, much larger than planetesimal isolation masses in classical core accretion (Pollack et al. 1996). For example, the gas giant CoRoT-10 b has a mass of 870ME, of which approximately 180 ME are in heavy elements (Bonomo et al. 2010). Similarly, Corot-13 b, 14 b, 17 b, 20 b, and 23 b all have ≳ 70 ME of heavy elements and are significantly enriched with respect to the host star metallicity (Moutou et al. 2013).
Nevertheless, giant planets at wide orbits will more commonly be ice giants. Indeed relaxing the efficiency somewhat results in, for example, alim = 15 AU for ϵ = 0.1 (in good agreement with the solar system). This seems also to be broadly consistent with the low occurrence of gas giants at very wide wide orbits inferred from direct imaging surveys (the fraction of FGKM stars with planetary companions ≳2 Jupiter masses beyond 25 AU is below 20%, Lafrenière et al. 2007). Altogether, pebble-driven envelope attraction predicts an orbital and compositional dichotomy, similar to the solar system, between gas giants and ice giants in extrasolar systems.
7. Summary
The model we propose can be summarized as follows. First, rocky/icy particles grow throughout the disc by sticking collisions and condensation around ice lines. When solids reach mm-cm sizes they start to decouple from the gas in the protoplanetary disc and drift towards the sun. Then, hydrodynamical concentration mechanisms of pebbles, such as the streaming instability or vortices, lead to the formation of a first generation of planetesimals. Subsequently, the largest of these planetesimals continue to grow by accreting from the flux of pebbles drifting through the disc. The high accretion rates result in core formation on a short timescale, within the disc life-time. Such fast growth implies that the atmospheres around the growing cores are strongly supported by the accretion heat.
We show that the evolution of the gas envelope is different depending on whether the core reaches the pebble isolation mass (or not), resulting in respectively gas giants or ice giants. When a core grows sufficiently large, around 20 ME at 5 AU, it can halt accretion of solids onto the core by gravitationally perturbing the surrounding gas disc. This creates a pressure bump that traps incoming pebbles. When the core gets isolated from pebbles, the envelope is no longer hydrostatically supported by accretion heat, and gas can be accreted in a runaway fashion. This leads to the formation of gas giants like Jupiter and Saturn.
Cores in wider orbits need to grow more massive than 20 ME to reach isolation, because of the steep increase in the gas scale height in flaring discs. Therefore, wide-orbit cores that do not grow larger than 50 − 100 ME during the gas disc phase remain supported by accretion heat and in hydrostatic balance. This offers an explanation for the occurrence of planets that only attract a thin envelope of hydrogen and helium, mixed with large amounts of water vapour released by sublimation of icy pebbles, such as the ice giants Uranus and Neptune in our solar system.
We demonstrate that this single model explains the bulk composition of all the giant planets in the solar system. Additionally, the pebble accretion scenario can be tested by studying exoplanet systems. We find that most exoplanets in wide orbits will be similar to ice giants. Only when cores grow very large (≳ 50 ME), within the disc life-time, can gas giants form in wide orbits. We therefore predict a high solid enrichment for gas-giant exoplanets in wide orbits, like those found in the HR8799 planetary system.
Acknowledgments
M.L. thanks K. Ros, B. Bitsch and T. Guillot for comments. The authors also wish to thank the referee for thoughtful feedback which helped improve the manuscript. A.J. and M.L. are grateful for the financial support from the Royal Swedish Academy of Sciences and the Knut and Alice Wallenberg Foundation. A.J. was also acknowledges funding from the Swedish Research Council (grant 2010-3710) and the European Research Council (ERC Starting Grant 278675-PEBBLE2PLANET). A.M. thanks the French ANR for support on the MOJO project.
References
- Andrews, S. M., Rosenfeld, K. A., Kraus, A. L., & Wilner, D. J. 2013, ApJ, 771, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Bai, X.-N., & Stone, J. M. 2010, ApJ, 722, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Barge, P., & Sommeria, J. 1995, A&A, 295, L1 [NASA ADS] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, C. P. M., Naylor, T., Mayne, N. J., Jeffries, R. D., & Littlefair, S. P. 2013, MNRAS, 434, 806 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Cleeves, L. I., Gorti, U., et al. 2013, Nature, 493, 644 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonomo, A. S., Santerne, A., Alonso, R., et al. 2010, A&A, 520, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bromley, B. C., & Kenyon, S. J. 2011, ApJ, 731, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Chambers, J. E. 2014, Icarus, 233, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, E., & Youdin, A. N. 2010, Ann. Rev. Earth Planetary Sci., 38, 493 [Google Scholar]
- Crida, A., Morbidelli, A., & Masset, F. 2006, Icarus, 181, 587 [Google Scholar]
- Dodson-Robinson, S. E., & Bodenheimer, P. 2010, Icarus, 207, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson-Robinson, S. E., Veras, D., Ford, E. B., & Beichman, C. A. 2009, ApJ, 707, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T. 2005, Ann. Rev. Earth Planetary Sci., 33, 493 [Google Scholar]
- Guillot, T., & Gladman, B. 2000, in Disks, Planetesimals, and Planets, eds. G. Garzón, C. Eiroa, D. de Winter, & T. J. Mahoney, ASP Conf. Ser., 219, 475 [Google Scholar]
- Guillot, T., & Hueso, R. 2006, MNRAS, 367, L47 [CrossRef] [Google Scholar]
- Haisch, Jr., K. E., Lada, E. A., & Lada, C. J. 2001, ApJ, 553, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, C. 1981, Prog. Theor. Phys. Suppl., 70, 35 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Helled, R., Anderson, J. D., Podolak, M., & Schubert, G. 2011, ApJ, 726, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Hori, Y., & Ikoma, M. 2011, MNRAS, 416, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Hubickyj, O., Bodenheimer, P., & Lissauer, J. J. 2005, Icarus, 179, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
- Johansen, A., & Youdin, A. 2007, ApJ, 662, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Blum, J., Tanaka, H., et al. 2014, in Protostars and Planets VI, in press [arXiv:1402.1344] [Google Scholar]
- Kenyon, S. J., & Bromley, B. C. 2008, ApJS, 179, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Springer) [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kobayashi, H., Tanaka, H., Krivov, A. V., & Inaba, S. 2010, Icarus, 209, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., Tanaka, H., & Krivov, A. V. 2011, ApJ, 738, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, H., Ormel, C. W., & Ida, S. 2012, ApJ, 756, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Korycansky, D. G., & Papaloizou, J. C. B. 1996, ApJS, 105, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Lafrenière, D., Doyon, R., Marois, C., et al. 2007, ApJ, 670, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, in press, DOI: 10.1051/0004-6361/201424343 [Google Scholar]
- Leconte, J., & Chabrier, G. 2013, Nature Geoscience, 6, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Lega, E., Morbidelli, A., & Nesvorný, D. 2013, MNRAS, 431, 3494 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Lyra, W., Johansen, A., Klahr, H., & Piskunov, N. 2008, A&A, 491, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marois, C., Zuckerman, B., Konopacky, Q. M., Macintosh, B., & Barman, T. 2010, Nature, 468, 1080 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mizuno, H. 1980, Prog. Theor. Phys., 64, 544 [Google Scholar]
- Morbidelli, A., & Nesvorny, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moutou, C., Deleuil, M., Guillot, T., et al. 2013, Icarus, 226, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Mumma, M. J., & Charnley, S. B. 2011, ARA&A, 49, 471 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ormel, C. W., & Kobayashi, H. 2012, ApJ, 747, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2006, A&A, 453, 1129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piso, A.-M. A., & Youdin, A. N. 2014, ApJ, 786, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hollenbach, D., Beckwith, S., et al. 1994, ApJ, 421, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Rafikov, R. R. 2006, ApJ, 648, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, L., Testi, L., Natta, A., et al. 2010, A&A, 512, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shiraishi, M., & Ida, S. 2008, ApJ, 684, 1416 [NASA ADS] [CrossRef] [Google Scholar]
- Soderblom, D. R., Hillenbrand, L. A., Jeffries, R. D., Mamajek, E. E., & Naylor, T. 2014, in Protostars and Planets VI, in press [arXiv:1311.7024] [Google Scholar]
- Stevenson, D. J. 1982, Planet. Space Sci., 30, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Supulver, K. D., & Lin, D. N. C. 2000, Icarus, 146, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Tsiganis, K., Gomes, R., Morbidelli, A., & Levison, H. F. 2005, Nature, 435, 459 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, in Protostars and Planets VI, in press [arXiv:1401.7306] [Google Scholar]
- Walsh, K. J., Morbidelli, A., Raymond, S. N., O’Brien, D. P., & Mandell, A. M. 2011, Nature, 475, 206 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Whipple, F. L. 1972, in From Plasma to Planet, ed. A. Elvius (New York: Wiley Interscience Division), 211 [Google Scholar]
- Youdin, A., & Johansen, A. 2007, ApJ, 662, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, Z., Stone, J. M., Rafikov, R. R., & Bai, X.-N. 2014, ApJ, 785, 122 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Pebble surface density and accretion efficiency
The pebble surface densities inferred from the minimum mass solar nebula, used throughout this paper, are broadly consistent with surface densities calculated in more detailed models of protoplanetary discs that combine dust growth and the drift of pebbles. The reconstruction of the MMSN is based on the questionable assumption that planets grow in situ out of all the material which is available locally. In contrast, observed protoplanetary discs are larger and show temporal evolution in both gas and dust components. This evolution is understood to be the consequence of a drift-limited dust growth by coagulation (Brauer et al. 2008). As demonstrated by Birnstiel et al. (2012), the dominant particle size is well characterized by an equilibrium between the local growth time scale and the drift timescale resulting in a narrow size range between τf = 0.01 − 0.1 at distances between 5−30 AU. The surface density of these pebbles also remains high during the disc life-time. During the first ≈1 Myr the initial dust-to-gas ratio of 0.01 is maintained, only to decay to ≈0.001 after ≈3 Myr. Therefore, the employed surface densities in the paper are adequate, certainly given the short timescales on which cores grow by pebble accretion. Furthermore, we also demonstrate our model holds for surface densities reduced by an order of magnitude (Fig. 5).
The total pebble mass in the disc needed for our model is also consistent with protoplanetary disc observations. Pebbles from the drift equilibrium model are efficiently accreted at a rate 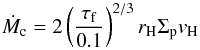 (A.1)as demonstrated by numerical simulations for particles in the τf = 0.01 − 0.1 range (Lambrechts & Johansen 2012). The radial flux of pebbles through the disc is given by
(A.1)as demonstrated by numerical simulations for particles in the τf = 0.01 − 0.1 range (Lambrechts & Johansen 2012). The radial flux of pebbles through the disc is given by 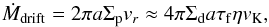 (A.2)where vK is the Keplerian velocity at orbital radius a and η is a dimensionless measure of radial gas pressure support (Eq. (6)). The embryo will accrete the fraction f = Ṁc/Ṁdrift of these solids,
(A.2)where vK is the Keplerian velocity at orbital radius a and η is a dimensionless measure of radial gas pressure support (Eq. (6)). The embryo will accrete the fraction f = Ṁc/Ṁdrift of these solids, 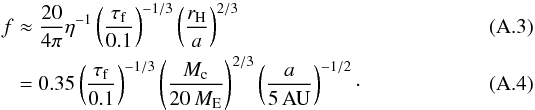 The filtering factor f itself does not explicitly depend on Σd, but does depend on η, thus in regions with reduced pressure support (pressure bumps) the efficiency could be higher. The necessary mass in pebbles in the disc can be estimated from dMp = f-1dMc,
The filtering factor f itself does not explicitly depend on Σd, but does depend on η, thus in regions with reduced pressure support (pressure bumps) the efficiency could be higher. The necessary mass in pebbles in the disc can be estimated from dMp = f-1dMc, 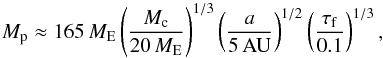 (A.5)in order to grow the core to 20ME (starting from 0.1 ME, but the integral only weakly depends on this choice). Therefore, the mass reservoir in the outer disc is on this order and the total disc mass should be about 0.05 solar mass (for a standard Z = 0.01 metallicity). Larger disc masses are not needed to form more planets in the disc, because of the low value of f for small core masses.
(A.5)in order to grow the core to 20ME (starting from 0.1 ME, but the integral only weakly depends on this choice). Therefore, the mass reservoir in the outer disc is on this order and the total disc mass should be about 0.05 solar mass (for a standard Z = 0.01 metallicity). Larger disc masses are not needed to form more planets in the disc, because of the low value of f for small core masses.
The disc masses needed for our model are consistent with observations. The best studied protoplanetary disc, the disc of the star TW Hydrae, has a gas mass of 0.05 M⊙ (Bergin et al. 2013) and the mm and gas distribution are well described by the model of Birnstiel et al. (2012). From mm-surveys it seems such disc masses for solar like stars show a large spread between 10-4–10-1M⊙ (Andrews et al. 2013) and therefore the disc mas in our model lies in the higher end of this distribution. However, disc mass estimates are based on an assumed ratio of gas to mm-sized dust of 100, and therefore these mass estimates may be lower limits.
The above analysis does not take into account the presence of ice lines. In these regions particle sizes and the local surface density are set by a condensation-sublimation cycle across the ice line, resembling hail formation (Ros & Johansen 2013). This is very different from the coagulation-drift equilibrium situation discussed above. Likely, around the various ice lines in protoplantary discs (H2O, CO2, CO) solid surface densities in pebbles of rather large size (τf ~ 0.1) greatly exceed MMSN estimates, promoting fast core growth. Furthermore, recondensation of sublimated pebbles onto particles exterior of the ice line reduces the loss of ices.
A more thorough discussion of core growth can be found in Lambrechts & Johansen (2014), where we investigate embryo growth in a global model that includes dust growth and the drift of pebbles.
Appendix B: Calculating the critical core mass
Appendix B.1: Structure of the proto-envelope
We numerically solve the standard equations for planetary atmospheres (Kippenhahn & Weigert 1990). The envelope is assumed to be spherically symmetric and in hydrostatic balance, 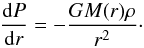 (B.1)Here G is the gravitational constant, P the pressure, and ρ the density at position r from the centre of the planet. The mass interior to a radius r is given by M(r). Mass continuity is guaranteed by
(B.1)Here G is the gravitational constant, P the pressure, and ρ the density at position r from the centre of the planet. The mass interior to a radius r is given by M(r). Mass continuity is guaranteed by 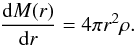 (B.2)Energy can be transported either by radiation diffusion or convection in optically thick regions. Convective heat transport is triggered when
(B.2)Energy can be transported either by radiation diffusion or convection in optically thick regions. Convective heat transport is triggered when 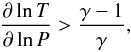 (B.3)where T is the local temperature and γ is the adiabatic index. Convective transport takes the form
(B.3)where T is the local temperature and γ is the adiabatic index. Convective transport takes the form 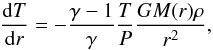 (B.4)while radiative transport depends on the opacity κ and the luminosity L,
(B.4)while radiative transport depends on the opacity κ and the luminosity L, 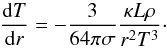 (B.5)The Stefan-Boltzmann constant is denoted by σ. The equation of state (EoS)
(B.5)The Stefan-Boltzmann constant is denoted by σ. The equation of state (EoS) 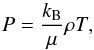 (B.6)with kB the Boltzmann constant and μ the mean molecular weight, relates the pressure to the density and closes the system of equations.
(B.6)with kB the Boltzmann constant and μ the mean molecular weight, relates the pressure to the density and closes the system of equations.
 |
Fig. B.1 Dependence of the hydrostatic envelope on orbital radius and envelope pollution. The left panels give the temperature (top) and density profile (bottom), for both a 50% polluted and unpolluted atmosphere (grey curve) of an 8 ME core accreting pebbles at 5 AU. Thick lines represent the regions where heat transport by convection dominates. The profile is given starting from the connection point to the Hill sphere. The yellow circle gives the photosphere of the envelope, while the black circle indicates the Bondi radius (the distance where the escape speed equals the local sound speed). The depth at which the envelope density is enhanced by water vapour is marked by the dashed blue lines in the lower panels. The dotted line represents the core radius (assuming ρc = 5.5 g/cm3). The right column is similar, but for a planet orbiting at 10 AU. |
 |
Fig. B.2 Comparison of the structure between the hydrostatic envelope enriched by H2O steam and a pure H/He atmospheres, around embryo cores of 8 ME located at 20 and 30 AU. Labels are similar to Fig. B.1. |
In principle, one could solve for an energy equation,  (B.7)where ϵ is the heat deposited at radius r. However, potential energy of accreted material is deposited deep in the convective interior close to the core surface, so we take a constant luminosity as a function of planetary radius L(r) = L. When pebbles settle with terminal velocity in the atmosphere, drag counterbalances gravity and locally deposits frictional heat per unit mass
(B.7)where ϵ is the heat deposited at radius r. However, potential energy of accreted material is deposited deep in the convective interior close to the core surface, so we take a constant luminosity as a function of planetary radius L(r) = L. When pebbles settle with terminal velocity in the atmosphere, drag counterbalances gravity and locally deposits frictional heat per unit mass 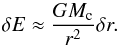 (B.8)Therefore, per unit length, the deposited energy is much larger close to the core surface than in the upper atmosphere, by a factor of 106 for the atmospheres studied here. The luminosity profile takes the form
(B.8)Therefore, per unit length, the deposited energy is much larger close to the core surface than in the upper atmosphere, by a factor of 106 for the atmospheres studied here. The luminosity profile takes the form 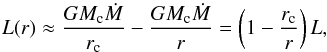 (B.9)revealing that the luminosity deviates from the constant value adopted here only near the core surface (Rafikov 2006). Additionally, we ignore the heat from the contraction of the envelope, the latent heat from evaporation, and nuclear heating by the core through the decay of 26Al, for the following reasons. The luminosity generated from binding the gas envelope to the growing core can be ignored when the core is subcritical (Rafikov 2006). We find that latent heat of water sublimation can only be important for small cores. For a certain accretion rate, we can assume that of the accreted material a fraction β of refractory grains settles to the core, while a remaining fraction 1 − β is water ice that sublimates. The latent heat per unit mass required for the sublimation of the water ice fraction is given by
(B.9)revealing that the luminosity deviates from the constant value adopted here only near the core surface (Rafikov 2006). Additionally, we ignore the heat from the contraction of the envelope, the latent heat from evaporation, and nuclear heating by the core through the decay of 26Al, for the following reasons. The luminosity generated from binding the gas envelope to the growing core can be ignored when the core is subcritical (Rafikov 2006). We find that latent heat of water sublimation can only be important for small cores. For a certain accretion rate, we can assume that of the accreted material a fraction β of refractory grains settles to the core, while a remaining fraction 1 − β is water ice that sublimates. The latent heat per unit mass required for the sublimation of the water ice fraction is given by 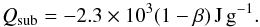 (B.10)The fraction that settles to the core gives
(B.10)The fraction that settles to the core gives 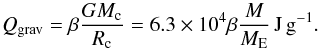 (B.11)So the latent heat becomes important for β = 0.1 and small cores (Mc ≲ 1 ME). Finally, radioactive decay of short-lived radio isotopes in chondritic material from the core releases a luminosity L = 1.5 × 1024(Mrock/ME)exp( − t/τ26Al) erg/s. Here, τ26Al = 1.01 Myr is the decay time of 26Al. The importance of this heat source depends on the time of giant planet formation after the formation of CAI, but remains about 4 orders of magnitude smaller that the heat released by the accretion of pebbles.
(B.11)So the latent heat becomes important for β = 0.1 and small cores (Mc ≲ 1 ME). Finally, radioactive decay of short-lived radio isotopes in chondritic material from the core releases a luminosity L = 1.5 × 1024(Mrock/ME)exp( − t/τ26Al) erg/s. Here, τ26Al = 1.01 Myr is the decay time of 26Al. The importance of this heat source depends on the time of giant planet formation after the formation of CAI, but remains about 4 orders of magnitude smaller that the heat released by the accretion of pebbles.
In practice we integrate stepwise from the Hill sphere, where we assume nebular conditions (T0,ρ0), to the core surface in order to calculate the envelope structure. We iterate this procedure to take the self-gravity of the envelope into account until we converge to a self-consistent solution. Additionally, we take into account the sublimation of ice from settling pebbles, by altering the mean molecular weight and the equation of state below the ice line, under the assumption that convection causes an approximately homogeneous mixture. There the molecular weight, 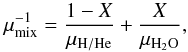 (B.12)depends on the mass fraction of water vapour with respect to the solar nebula H/He mixture X, with μH/He = 2.34 mH and μH2O = 18 mH (mH is the mass of the H atom). In the convective interior, the calculation of the temperature gradient relies on the specific heat capacity of the mixture cP,mix = (1 − X)cP,H/He + XcP,H2O, with cP,H/He = [γH/He/ (γH/He − 1)] kB/μH/He and cP,H2O = [γH2O/ (γH2O − 1)] kB/μH2O. We find that the critical core mass is very sensitive to the mean molecular weight, but less so to the adiabatic index, which we we have taken here to be γH/He = 1.4 (appropriate for a diatomic gas) and γH2O = 1.17 (for water steam at high T with all 12 degrees of freedom released). More detailed calculations of the adiabatic index would require solving for multiple chemical species in the envelope. Such calculations show that, in the limit of very polluted envelopes (~90%) from accreted material with a comet-like composition, changes in γ can lead to reduced critical core masses by at most a factor of 2 (Hori & Ikoma 2011), which is an effect also seen in our simplified model.
(B.12)depends on the mass fraction of water vapour with respect to the solar nebula H/He mixture X, with μH/He = 2.34 mH and μH2O = 18 mH (mH is the mass of the H atom). In the convective interior, the calculation of the temperature gradient relies on the specific heat capacity of the mixture cP,mix = (1 − X)cP,H/He + XcP,H2O, with cP,H/He = [γH/He/ (γH/He − 1)] kB/μH/He and cP,H2O = [γH2O/ (γH2O − 1)] kB/μH2O. We find that the critical core mass is very sensitive to the mean molecular weight, but less so to the adiabatic index, which we we have taken here to be γH/He = 1.4 (appropriate for a diatomic gas) and γH2O = 1.17 (for water steam at high T with all 12 degrees of freedom released). More detailed calculations of the adiabatic index would require solving for multiple chemical species in the envelope. Such calculations show that, in the limit of very polluted envelopes (~90%) from accreted material with a comet-like composition, changes in γ can lead to reduced critical core masses by at most a factor of 2 (Hori & Ikoma 2011), which is an effect also seen in our simplified model.
At wide orbital distances where the density is low, the photosphere is located below the Hill sphere and the region is nearly isothermal with 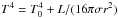 (Rafikov 2006). Examples of the envelope structure of planets located at various orbital distances can be inspected in Figs. B.1 and B.2. We discuss in greater detail the prescription of the opacity and the role of dust grains in Sect. B.3.
(Rafikov 2006). Examples of the envelope structure of planets located at various orbital distances can be inspected in Figs. B.1 and B.2. We discuss in greater detail the prescription of the opacity and the role of dust grains in Sect. B.3.
Appendix B.2: Determining the critical core mass
We find the critical core mass numerically by stepwise increasing the core mass. When we not longer find a hydrostatic solution for the envelope, we identify this core mass as the critical core mass, as is standardly done (Mizuno 1980). The precise value of the critical core mass depends on the assumed accretion rate, opacity, and composition of the envelope.
We have performed two classes of calculations of the critical core mass. In the first class, we have kept the accretion rate constant during the iteration over the core masses, in order to decouple the stability of an envelope from the assumed accretion rates by either planetesimals or pebbles onto cores. The results are the black curves in Fig. 1, where we explicitly showed the dependency on the assumed composition of the envelope. In the second class, we have self-consistently taken into account the dependency of the mass accretion rate of pebbles, and thus the luminosity, on the mass of the planet. This is important in obtaining the results displayed in Figs. 4 and 5, where we calculate the planetary composition as a function of mass. The curves in these figures are obtained by considering two regimes. In the first regime, the core has not reached isolation. Consequently, for a given mass, and thus accretion rate, we find by iteration the level of enrichment in heavy elements in the atmosphere required to collapse the envelope. The composition of the planet at this critical point is the one displayed by the ratio of the heavy elements, in the core plus envelope, to the total planet mass.
In the second regime, the planet has grown beyond the isolation mass. In this case, the mass of heavy elements is taken to be equal to that found in the previous regime for a planet mass equal to the pebble isolation mass. The remainder of the mass of the planet is H/He from the gas accretion phase. Formally, at isolation the envelope does not have to be polluted to start gas accretion, so one could also choose to include only the heavy elements from the core, but this would constitute only a minor correction to the composition compared to the total mass of the giant planets.
Appendix B.3: Dependence on the (bulk) composition of the accreted material and opacity
We assume the bulk composition of the material accreted by the planet to correspond to the bulk composition of cometary material (Mumma & Charnley 2011). The high fraction of water ice (≈50%) implies that the envelope gets efficiently polluted by water vapour. Already at temperatures higher than ≈100 K (Supulver & Lin 2000) ices sublimate, and this temperature depends only weakly on the pressure.
The composition of the accreted pebbles also influences the opacity of the envelope. Icy grains set the optical depth at temperatures below ~100 K and below the sublimation temperature of ~1000 K, opacity by silicate grains dominates (Pollack et al. 1994). It is however not known how many grains are continuously deposited in the planetary envelope after ice sublimation and through gas accretion from the disc. Similarly it is poorly understood how fast grains settle, which depends on their size, in turn set by the efficiency of grain growth and fragmentation.
Early core accretion studies (Mizuno 1980) already pointed out the large role the opacity of the envelope can play (Ikoma et al. 2000). We have adopted a modified version of the analytic expression for the Rosseland mean opacity by Bell & Lin (1994). Alternatively, one can approximate the opacity as a simple power law of both temperature and pressure (Rafikov 2006; Piso & Youdin 2014). The black curve in Fig. B.3 corresponds to the opacity used in this study, where we assume the dust opacity is reduced by a factor of 10 with respect to the disc (Rafikov 2006). This choice reproduces the critical core masses (within a factor of 2) found by Ikoma et al. (2000).
 |
Fig. B.3 Dependency of the critical core mass on the dust opacity in H/He envelopes. Grey curves correspond to factor of ten different dust opacities to the opacity used in this study (solid black line). The critical curves are here given at 5 AU, but have little dependency on orbital radius. |
Appendix C: Envelope contraction
Finally, we briefly discuss the Kelvin-Helmholtz timescale on which envelopes contract 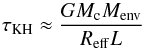 (C.1)with Reff some effective radius, typically taken to be the radius at the convective to radiative border (Ikoma et al. 2000; Pollack et al. 1996). After pebble isolation, the high luminosity from pebble accretion will almost instantaneously contract the core to a state where only luminosity caused from envelope contraction is important. Following numerical results by Ikoma et al. (2000) contraction occurs on a timescale
(C.1)with Reff some effective radius, typically taken to be the radius at the convective to radiative border (Ikoma et al. 2000; Pollack et al. 1996). After pebble isolation, the high luminosity from pebble accretion will almost instantaneously contract the core to a state where only luminosity caused from envelope contraction is important. Following numerical results by Ikoma et al. (2000) contraction occurs on a timescale 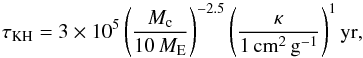 (C.2)for envelope masses comparable to core masses Mc. The dependency on the dust opacity κ means this is an upper limit in the case of pebble accretion, as after isolation few grains will be deposited in the envelope. Contraction could be delayed more by continued solid accretion from planetesimals (Pollack et al. 1996). However, this can be ignored in the scenario described in the main paper, as firstly we do not assume all solid density in planetesimals, and additionally we do not propose a significant enrichment of the planetesimal column density (larger than a factor of 5) as in Pollack et al. (1996). We emphasize that at the brink of collapse the Hill sphere of a gas giant is comparable to the gas disc scale height, which makes the spherical approximation invalid. Future studies will have to explore the effects of moving away from the standardly assumed spherical symmetry.
(C.2)for envelope masses comparable to core masses Mc. The dependency on the dust opacity κ means this is an upper limit in the case of pebble accretion, as after isolation few grains will be deposited in the envelope. Contraction could be delayed more by continued solid accretion from planetesimals (Pollack et al. 1996). However, this can be ignored in the scenario described in the main paper, as firstly we do not assume all solid density in planetesimals, and additionally we do not propose a significant enrichment of the planetesimal column density (larger than a factor of 5) as in Pollack et al. (1996). We emphasize that at the brink of collapse the Hill sphere of a gas giant is comparable to the gas disc scale height, which makes the spherical approximation invalid. Future studies will have to explore the effects of moving away from the standardly assumed spherical symmetry.
All Figures
 |
Fig. 1 Pebble accretion rates (red), planetesimal accretion rates (grey), and minimal accretion rates required to sustain a stable gas envelope (black), as a function of the core mass. The curves for the minimal accretion rates are nearly independent of orbital radius between 5−30 AU, but depend strongly on the opacity (Appendix B.3) and on the level of envelope pollution by sublimation of icy pebbles. Labels at the top of the figure indicate H2O pollution of the atmosphere as a percentage with respect to pure H/He nebular gas, corresponding to the fraction 1 − β from Eq. (11). The critical core mass to collapse the gas envelope can be found at the intersection of an accretion curve with a critical curve. Accretion rate curves that fall in the yellow dashed region are too slow to form the cores of the giant planets before the dissipation of the gas disc (τacc = Mc/Ṁc>τdisc = 2 Myr). Red circles mark the mass above which pebble accretion is halted (Eq. (12)) and the gravitational collapse of the gas envelope is triggered. |
| In the text | |
 |
Fig. 2 Gravitational perturbation of the midplane gas density from a 50 ME-planet embedded in a protoplanetary disc. Displayed is a full annulus (θ = 2π-wide in azimuth) of the protoplanetary disc around the planet located at normalized radius r = 1. The resulting pressure perturbation halts the radial migration of pebbles and thus the solid accretion onto the core. The overdensities at radius r = 0.85 and r = 1.2 correspond to the regions with super-Keplerian rotation, that are highlighted in Fig. 3. A Rossby vortex, here centred at (θ = 3.8,r = 1.2) has formed outside the orbit of the planet. |
| In the text | |
 |
Fig. 3 Deviation from the equilibrium sub-Keplerian velocity of the gas in the protoplanetary disc (vθ,gas/vK) due to the presence of a planetary core located at a normalized radius of r = 1 (here corresponding to an orbital radius of a = 5 AU). For cores with masses above 20ME (blue curve) and higher (red and black curves) the gas orbits faster than the Keplerian velocity (horizontal dashed line) in a region outside the orbit of the planet. This ring acts as a trap for pebbles drifting inwards and halts the accretion of pebbles onto the core. |
| In the text | |
 |
Fig. 4 Total heavy element mass fraction as a function of the total mass M of the giant planet, at different orbital radii (5, 10, 20, 30 AU). Planets that do not grow beyond the pebble isolation mass (red dots) remain core-dominated, while those that grow larger will have most of their mass in gas. Estimates of the composition of Uranus and Neptune (blue error bars, Helled et al. 2011) agree well with the prediction made in this paper for planets formed in the outer disc. Similarly, for the gas-giant planets Jupiter and Saturn we find a good agreement between the 5−10 AU curves and the total heavy element mass estimated by Guillot (2005), indicated by the orange error bars. In order to create this figure, we numerically calculated the composition of the planet when it becomes critical, taking into account the pollution of the envelope, for planet masses below the pebble isolation mass (light blue curves). When the planet reached a mass larger than the pebble isolation mass, only nebular gas was added to continue growth (black curves). Here we present results with refractory fraction β = 0.5, but results depend weakly on the choice of β between 0.1−1. |
| In the text | |
 |
Fig. 5 Similar to Fig. 4, but representing planetary compositions of planets located at 5 and 30 AU (full and dashed lines respectively) for different values of the accretion rate efficiency ϵ. The thick solid lines correspond to the case where the full pebble accretion luminosity is released (ϵ = 1) and the lower thin lines of the same colour to a 10 times smaller luminosity (ϵ = 0.1). The red error bars, slightly displaced to the left for readability, give the heavy element mass, without the contribution of heavy elements added by late time gas accretion in a disc with increased dust-to-gas ratio (Guillot & Hueso 2006), as suggested to explain the noble gas abundances in Jupiter. The orange downwards arrow is an upper limit on the heavy element content of Saturn if layered convection occurs in the envelope (Leconte & Chabrier 2013). |
| In the text | |
 |
Fig. B.1 Dependence of the hydrostatic envelope on orbital radius and envelope pollution. The left panels give the temperature (top) and density profile (bottom), for both a 50% polluted and unpolluted atmosphere (grey curve) of an 8 ME core accreting pebbles at 5 AU. Thick lines represent the regions where heat transport by convection dominates. The profile is given starting from the connection point to the Hill sphere. The yellow circle gives the photosphere of the envelope, while the black circle indicates the Bondi radius (the distance where the escape speed equals the local sound speed). The depth at which the envelope density is enhanced by water vapour is marked by the dashed blue lines in the lower panels. The dotted line represents the core radius (assuming ρc = 5.5 g/cm3). The right column is similar, but for a planet orbiting at 10 AU. |
| In the text | |
 |
Fig. B.2 Comparison of the structure between the hydrostatic envelope enriched by H2O steam and a pure H/He atmospheres, around embryo cores of 8 ME located at 20 and 30 AU. Labels are similar to Fig. B.1. |
| In the text | |
 |
Fig. B.3 Dependency of the critical core mass on the dust opacity in H/He envelopes. Grey curves correspond to factor of ten different dust opacities to the opacity used in this study (solid black line). The critical curves are here given at 5 AU, but have little dependency on orbital radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


