| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 17 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201423810 | |
| Published online | 03 September 2014 | |
A large sample of Kohonen-selected SDSS quasars with weak emission lines: selection effects and statistical properties⋆
1 Thüringer Landessternwarte Tautenburg, Sternwarte 5, 07778 Tautenburg, Germany
e-mail: meus@tls-tautenburg.de
2 Universität Leipzig, Faculty of Physics and Earth Sciences, Linnèstr. 5, 04103 Leipzig, Germany
e-mail: n.balafkan@studserv.uni-leipzig.de
Received: 14 March 2014
Accepted: 21 June 2014
Aims. A tiny fraction of the quasar population shows remarkably weak emission lines. Several hypotheses have been developed, but the weak line quasar (WLQ) phenomenon still remains puzzling. The aim of this study was to create a sizeable sample of WLQs and WLQ-like objects and to evaluate various properties of this sample.
Methods. We performed a search for WLQs in the spectroscopic data from the Sloan Digital Sky Survey Data Release 7 based on Kohonen self-organising maps for nearly 105 quasar spectra. The final sample consists of 365 quasars in the redshift range z = 0.6 − 4.2 (z̄ = 1.50 ± 0.45) and includes in particular a subsample of 46 WLQs with equivalent widths WMg ii< 11 Å and WC iv< 4.8 Å. We compared the luminosities, black hole masses, Eddington ratios, accretion rates, variability, spectral slopes, and radio properties of the WLQs with those of control samples of ordinary quasars. Particular attention was paid to selection effects.
Results. The WLQs have, on average, significantly higher luminosities, Eddington ratios, and accretion rates. About half of the excess comes from a selection bias, but an intrinsic excess remains probably caused primarily by higher accretion rates. The spectral energy distribution shows a bluer continuum at rest-frame wavelengths ≳1500 Å. The variability in the optical and UV is relatively low, even taking the variability-luminosity anti-correlation into account. The percentage of radio detected quasars and of core-dominant radio sources is significantly higher than for the control sample, whereas the mean radio-loudness is lower.
Conclusions. The properties of our WLQ sample can be consistently understood assuming that it consists of a mix of quasars at the beginning of a stage of increased accretion activity and of beamed radio-quiet quasars. The higher luminosities and Eddington ratios in combination with a bluer spectral energy distribution can be explained by hotter continua, i.e. higher accretion rates. If quasar activity consists of subphases with different accretion rates, a change towards a higher rate is probably accompanied by an only slow development of the broad line region. The composite WLQ spectrum can be reasonably matched by the ordinary quasar composite where the continuum has been replaced by that of a hotter disk. A similar effect can be achieved by an additional power-law component in relativistically boosted radio-quiet quasars, which may explain the high percentage of radio quasars.
Key words: quasars: general / quasars: emission lines
The full catalogue is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/568/A114
© ESO, 2014
1. Introduction
Broad emission lines (BELs) are a defining characteristic of type 1 active galactic nuclei (AGN). The weakness or even absence of BELs is the most remarkable feature of a class of high-luminosity AGNs called weak-line quasars (WLQs). The first discovered WLQ was the radio-quiet quasar PG 1407+265 at redshift z = 0.94 (McDowell et al. 1995) with undetectably weak Hβ and UV BELs although the continuum properties are similar to those of normal radio-quiet quasars. Fan et al. (1999) discovered the first high-z WLQ, SDSS J153259.96+003944.1 (z = 4.62) and suggested that it is either the most distant known BL Lac object with very weak radio emission or a new type of unbeamed quasars whose broad emission line region (BLR) is very weak or absent. Based on the multi-colour selection of the Sloan Digital Sky Survey (SDSS; York et al. 2000), about one hundred high-z WLQs have been found with Lyα-N v rest-frame equivalent width < 15 Å (Diamond-Stanic et al. 2009; Shemmer et al. 2010; Wu et al. 2012).
Low values of the equivalent widths of the BELs can be the result of abnormally low line fluxes or of an unusually strong continuum. Relativistic beaming provides an example for dilution of the line strength by a boosted continuum. However, such an interpretation of the WLQ phenomenon is widely considered unlikely because many properties of the WLQs (e.g. radio-loudness, variability, and polarisation) are different from those of BL Lac objects (McDowell et al. 1995; Shemmer et al. 2006; Diamond-Stanic et al. 2009; Plotkin et al. 2010; Lane et al. 2011; Wu et al. 2012). WLQs are also different from type 2 quasars where only the broad line components are missed in the unpolarised spectra, and the Eddington ratios ε = L/LEdd1 are usually lower (Tran et al. 2003; Shi et al. 2010; Shemmer et al. 2010). Factors that can mimic WLQ spectra are line absorption or a strong Fe ii pseudo-continuum (e.g. Lawrence et al. 1988). Such explanations may work for some objects but do not explain the WLQ phenomenon in general (McDowell et al. 1995). Any scenario based on dust absorption has to be able to explain the weakening of the BELs without any reddening of the continuum.
Though a number of ideas have been developed, the WLQ phenomenon remains puzzling. The hypotheses can be roughly grouped into two families based on either an extraordinary BLR or unusual properties of the central ionising source. The former includes, in particular, the ideas of generally abnormal properties of the BEL emitting clouds (Shemmer et al. 2010), a low covering factor of the BLR (i.e. a low fraction of the central source covered by BEL clouds, Nikołajuk et al. 2012), or a relative shortage of high-energy UV/X-ray photons due to a shielding gas with a high covering factor that prevents the X-ray photons from reaching the BLR (Lane et al. 2011; Wu et al. 2012). Abnormal properties of the continuum source may include a high Eddington ratio as in PHL 1811 (e.g. Leighly et al. 2007; but see Hryniewicz et al. 2010; Shemmer et al. 2010), a freshly launched wind from the accretion disk (Hryniewicz et al. 2010), an optically dull AGN (Comastri et al. 2002; Severgnini et al. 2003), or a cold accretion disk around a high-mass (M ≥ 3 × 109 M⊙) black hole (Laor & Davis 2011).
In a previous study (Meusinger et al. 2012, hereafter Paper I), we used the database of the 105 quasar spectra from the SDSS Seventh Data Release (DR7, Abazajian et al. 2009) to select the approximately one per cent of the quasars with the strongest deviations of their spectra from the ordinary quasar spectrum as represented by the SDSS quasar composite spectrum (Vanden Berk et al. 2001). About one fifth of this sample was classified as uncommon because of remarkably weak BELs. We found that these WLQs are, on average, more luminous, have a steeper composite spectrum (i.e. lower value of αλ,Fλ ∝ λαλ) at λ ≳ 2000 Å, and have a high percentage of radio-loud quasars (26%). In addition, in a study of the variability of the quasars in the SDSS stripe 82 revealed, it was found that WLQs tend to have lower variability amplitudes (Meusinger et al. 2011). No effort has been made to create complete WLQ samples in these previous studies.
 |
Fig. 1 Six examples of quasars with weak emission lines from the WLQ sample. For comparison the quasar composite spectrum from Vanden Berk et al. (2001; smooth red curve) is over-plotted, shifted to the redshift of the quasar and normalised to the total flux density between 3900 Å and 9000 Å (observer frame). At the top of each panel, the SDSS name, the redshift z, and the parameter FFT = first_fr_type (0 – not detected by FIRST; 1 – core-dominated radio source) from the Shen catalogue are given. The dotted vertical lines indicate the usually strong emission lines. |
The present paper is aimed at the construction and analysis of a more voluminous and more thoroughly selected sample of WLQs and WLQ-like objects by taking again advantage of the unprecedented spectroscopic data from the SDSS DR7. This study exploits the compilations of quasar properties by Schneider et al. (2010) and Shen et al. (2011) that are based on the SDSS DR7 and include data from the 1.4 GHz radio survey Faint Images of the Radio Sky at Twenty-Centimeters (FIRST; Becker et al. 1995). We apply essentially the same selection method as in Paper I. The selection and the construction of the WLQ sample is described in Sect. 2. Section 3 is considered with the UV composite spectrum, the luminosities, black hole masses, Eddington ratios, accretion rates, and variability, where particular attention is paid to the role of selection effects. The wide band spectral energy distribution (SED) and the radio properties are the subject of Sect. 4. The results are discussed in Sect. 5 and summarised in Sect. 6.
2. Selection of the WLQ sample
In Paper I, we have shown that the selection of unusual spectra from the huge database of the SDSS can be performed efficiently by the combination of the power of the Kohonen self-organising map (SOM) algorithm and the eyeball inspection of the resulting SOMs in the form of spectra icon maps. The Kohonen algorithm (Kohonen 2001), an unsupervised learning process based on an artificial neural network, generates a low-dimensional (typically two-dimensional) map of complex input data. The SOM algorithm and the software tool ASPECT2 used for the computation were described in detail in a separate paper (in der Au et al. 2012).
The present study is based on the 36 SOMs from Paper I for the nearly 105 objects classified as quasars with z = 0.6 − 4.2 by the spectroscopic pipeline of the SDSS DR7. Each SOM consists of the quasars within a z interval of the width Δz = 0.1, sorted (clustered) according to the relative similarity of their spectra. For each SOM, an icon map was created where each object is represented by its SDSS spectrum with largely reduced spectral resolution. Despite the loss of resolution, the icon maps are well suited to quickly localise objects with special broad spectral features, such as unusually red or reddened continua, broad absorption lines (BALs), and unusually strong or unusually weak BELs. In Paper I, we selected 103 unusual spectra of different types. This selection was not primarily aimed at high completeness, and particularly the subsample of quasars with weak BELs was supposed to be substantially incomplete. In the present study, we re-inspected all 36 spectra icon SOMs with the purpose to select solely spectra with relatively weak BELs. Unlike Paper I, the new selection includes only spectra with clearly recognised quasar-typical spectral features that allows us to estimate the redshift; i.e., featureless blue spectra were not included here. In the first step, a total number of nearly ~ 2500 candidates were selected as the initial sample of visually selected candidate WLQs, among them are 2249 quasars listed in the SDSS DR7 quasar catalogue (Schneider et al. 2010).
The selection procedure is of course subjective and the selected sample is contaminated by other types of objects such as quasars with line absorption (BALs or associated narrow absorption lines) reducing the BEL flux, some early-type stars, and also by different types of objects with noisy spectra where the signal-to-noise ratio (S/N) is too low for a certain classification. To purify the initial sample, the selected objects were inspected individually in more detail by fitting the de-redshifted and foreground extinction corrected SDSS spectra to the SDSS quasar composite spectrum from Vanden Berk et al. (2001). The fitting algorithm is aimed to match both the positions of the typical quasar emission lines and the shape of the pseudo-continuum. The z values derived in that way are generally in good agreement with those from the SDSS DR7 quasar catalogue, with only a few exceptions. Objects not identified in the quasar catalogue, as well as objects with discrepant z values, were simply rejected from the sample. The final WLQ sample consists of 365 quasars with counterparts in the SDSS DR7 quasar catalogue. The mean redshift is 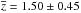 . Figure 1 displays six typical spectra.
. Figure 1 displays six typical spectra.
 |
Fig. 2 Equivalent width WC iv of the C iv λ1549 line versus equivalent width WMg ii of the Mg ii λ2798 line for the quasars from the WLQ sample with 1.50 ≤ z ≤ 2.22 (filled red squares) and for 35137 quasars in the same redshift range from the Shen catalogue (equally spaced logarithmic local point density contours estimated with a grid size of Δ = 2 Å on both axes). |
Relevant data for the WLQs were taken from Schneider et al. (2010) and Shen et al. (2011). From the catalogue of quasar properties from SDSS DR7 (Shen et al. 2011; hereafter Shen catalogue) we took in particular the equivalent widths (EWs) of the prominent BELs, the flux of the continuum close to these lines, the bolometric luminosity L, the fiducial virial black hole mass M from scaling relations, the Eddington ratio, and radio properties.
The line measurements in the Shen catalogue were made in the rest frame after removal of the Galactic foreground extinction. For each line, a local power law plus an iron template was fitted and then subtracted from the spectrum. The resulting line spectrum was modelled by various functions. Measurements of the EWs for both the Mg ii λ2798 line and the C iv λ1549 line are available for 136 of the selected WLQs with redshifts 1.50 ≤ z ≤ 2.22. Figure 2 shows the distribution of the WLQs on the WMg ii − WC iv plane in comparison with all SDSS DR7 quasars in the same redshift interval. The centroid of the WLQs at (WMg ii,WC iv) = (16.6 ± 6.5 Å, 14.2 ± 14.6 Å) is clearly distant from that of the ordinary quasars. On the other hand, our sample also contains quasars where obviously only one of the equivalent widths, WMg ii or WC iv, is low while the other is normal and even some quasars with normal values for both lines. We did not reject these quasars to clean the WLQ sample further because a wider span of properties allows us to study some trends of other properties with the EW.
32 objects rejected from the initial sample because of featureless spectra.
As mentioned above, the WLQ selection was confined to spectra with clearly recognisable quasar-typical features. The advantage of reliable redshifts is however at the expense of the completeness of such a sample at low EWs. In particular, we rejected 32 objects with blue spectra from our initial sample because the spectra appeared more or less featureless to us. To estimate how strongly our final sample may be biased against low-EW WLQs, we checked, a posteriori, several catalogues for additional information on these 32 rejected objects (Table 1). Altogether 18 objects were classified as white dwarfs (WDs) of spectral type DC or DQ, another one as a cataclysmic variable (CV). Ten sources are classified as high-confidence radio-loud BL Lacertae objects in the catalogue of optically selected BL Lac objects from the SDSS DR7 (Plotkin et al. 2010) and also in the Roma-BZCAT multifrequency catalogue of blazers (Massaro et al. 2009). One object, SDSS J160410.22+432614.6, is listed in the Plotkin et al. catalogue of weak-featured radio-quiet objects and may be a WLQ that is missed in the present sample. For the remaining two objects, the SDSS DR10 explorer tool gives high proper motions suggesting that they are nearby stars, most likely WDs.
Absolute proper motions are very helpful in distinguishing extragalactic objects from nearby white dwarfs. Table 1 lists the proper motions taken from the PPMXL catalogue (Röser et al. 2010). In addition, a proper motion index, Ipm is given that is defined as the pm in units of the pm error. For the 10 BL Lac objects, the mean pm index Ipm = 0.8 indicates zero proper motion. In contrast, the sample of the 18 WDs plus one CV has a mean pm of 79 mas/yr and a mean pm index Ipm = 12.9. The inspection of the individual sources yields that the pm index does not indicate significant proper motions for all BL Lac objects, the probably missed WLQ SDSS J160410.22+432614.6, and for two objects classified as stellar in the literature (SDSS J220911.31-003543.0 and SDSS J224303.81+221456.0). A low pm does not necessarily exclude that these objects are nearby stars. On the other hand, however, we cannot definitively exclude that they are WLQs.
Mean properties of the WLQ, rWLQ, WLQ-EWS, rWLQ-EWS, and comparison sample.
Only three objects from Table 1 are in the Shen catalogue: the probable WLQ SDSS J160410.22+432614.6 and the two BL Lac objects SDSS J113245.62+003427.7 and SDSS J170108.89+395443.0. The EWs of the Mg ii line are 1.0 Å, 5.8 Å, and 9.4 Å. The mean value of 5.4 Å is close to the 5 Å EW limit for the selection of BL Lac objects (e.g. Plotkin et al. 2008; Ghisellini et al. 2011). The EWs of the WLQ sample follow a log-normal distribution with the lower 3σ deviation from the mean value at 4.6 Å. There are only two WLQs (0.5%) with lower EWs in our sample. We assume therefore that the minimum Mg ii EW threshold of our selection is at about 5 Å. Given that this threshold is exceeded by SDSS J170108.89+395443.0 with WMg ii = 9.4 Å, we conclude that Table 1 may contain up to altogether four wrongly rejected WLQs.
For some purposes it is useful to restrict the quasar sample to the redshift interval 0.7 ≤ z ≤ 1.7 (Meusinger & Weiss 2013). First, the formal uncertainties of the catalogued bolometric luminosities and black hole masses are lowest for such redshifts. As pointed out by Shen et al. (2011), the mass uncertainty was propagated from the measurement uncertainties of the continuum luminosities and the line width, but does neither include systematic effects nor the statistical uncertainty from the calibration of the scaling relations. Secondly, in that z interval, the fiducial black hole masses from the Shen catalogue are uniformly derived from the scaling relation for the Mg ii line. Virial masses derived from the C iv line are considered to be less reliable than those from the Hβ or the Mg ii line (e.g. Shen & Liu 2012). Moreover, the estimation of the accretion rate (Sect. 3.2) requires the knowledge of the continuum slope αλ between 3000 and 4800 Å, which can be measured from the SDSS spectra only for not too high z. The restricted WLQ sample (hereafter: rWLQ sample) with 0.7 ≤ z ≤ 1.7 contains 261 quasars. It is particularly useful when luminosities, black hole masses, Eddington ratios, or accretion rates are considered.
Because it is difficult to compare the resulting WLQ sample with known WLQ samples defined by the measured EWs, it is helpful to consider a subsample that follows a statistically based selection. Following Diamond-Stanic et al. (2009), we assumed a log-normal EW distribution and defined WLQs as quasars having EWs below a 3σ threshold. For the quasars from the Shen catalogue in the redshift range of the rWLQ sample we obtain the mean EWs 34.1 Å, 38.7 Å and the WLQ selection thresholds 11 Å, 4.8 Å for the Mg ii line and the C iv line, respectively. The subsamples from the entire WLQ sample and the rWLQ sample, respectively, with EWs below these thresholds are hereafter indicated by the suffix EWS. The WLQ-EWS subsample consists of 46 quasars with a mean redshift 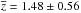 and mean EWs 8.8 ± 1.9 Å, 2.6 ± 1.2 Å. Assuming that Table 1 contains at most four wrongly rejected WLQs, the completeness of this sample, compared with other samples based on the SDSS DR7 spectroscopic quasar catalogue, is expected to be about 90%. It must be noted, however, that this catalogue itself is biased against quasars with very week emission lines. The rWLQ-EWS subsample consists of 33 quasars with
and mean EWs 8.8 ± 1.9 Å, 2.6 ± 1.2 Å. Assuming that Table 1 contains at most four wrongly rejected WLQs, the completeness of this sample, compared with other samples based on the SDSS DR7 spectroscopic quasar catalogue, is expected to be about 90%. It must be noted, however, that this catalogue itself is biased against quasars with very week emission lines. The rWLQ-EWS subsample consists of 33 quasars with 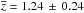 and 9.0 ± 1.8 Å, 2.5 ± 1.3 Å.
and 9.0 ± 1.8 Å, 2.5 ± 1.3 Å.
 |
Fig. 3 Arithmetic median composite spectrum (thick red curve) and standard deviation (green shaded area) for a) the WLQ-EWS sample; b) the entire WLQ sample; and c) the radio-loud subsample. For comparison, the SDSS quasar composite spectrum (thin blue curve) from Vanden Berk et al. (2001) is over-plotted, normalised to match the WLQ composites at the right hand side. |
3. UV/optical properties of the selected quasars
In this Section, we analyse mean properties of our WLQs where various subsamples are considered. Particular attention should be payed to the WLQ-EWS and rWLQ-EWS subsamples because they are closest to traditional WLQ samples. On the other hand, these subsamples are small and it thus makes sense to also consider the corresponding parent samples for comparison. In the context of the black hole mass, the Eddington ratio, and especially the accretion rate, the rWLQ-EWS and the rWLQ sample should be preferred (see above). For the comparison with normal quasars, the z dependence of quasar properties must be taken into consideration because the z distribution of the rWLQ sample is different from that of the entire Shen catalogue. Therefore, we created a comparison sample of ordinary quasars with the same z distribution following the procedure outlined in Paper I. The comparison sample is about ten times larger than the rWLQ sample. For the mean EW of the comparison quasars we find (WMg ii,WC iv) = (42 ± 22 Å, 51 ± 52 Å) compared with (17 ± 7 Å, 17 ± 18 Å) for the rWLQ sample (Table 2).
3.1. Composite spectra
The individual inspection of the SDSS spectra led to the impression that many WLQs show a steeper continuum than the SDSS quasar composite spectrum (see Fig. 1). This tendency was already reported in Paper I, but it appears even more pronounced in the present WLQ sample.
We computed composite spectra in the same way as in Paper I. The procedure is essentially based on the combining technique described by Vanden Berk et al. (2001). Figure 3 shows the resulting arithmetic median composite spectra for (a) the WLQ-EWS subsample and (b) the entire WLQ sample. For comparison, the SDSS quasar composite spectrum from Vanden Berk et al. (2001) is over-plotted, arbitrarily normalised at 3200 Å. The comparison clearly illustrates the weaker BELs and the steeper (i.e. less reddened) ultraviolet continuum for both (a) the WLQ-EWS subsample and (b) the entire WLQ sample.
We also confirm the finding from Paper I that the WLQ spectra flatten at short wavelengths, approximately below 2000 Å. We estimated the spectral slopes of the individual spectra by fitting the Fλ ∝ λαλ power law in pseudo-continuum windows (see Paper I) and found a mean value of 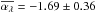 for the rWLQs compared to −1.53 ± 0.39 for the ordinary quasars from the comparison sample with S/N> 5 in both cases. For the 97 quasars with 1.7 <z< 3 in the full WLQ sample the mean slope is
for the rWLQs compared to −1.53 ± 0.39 for the ordinary quasars from the comparison sample with S/N> 5 in both cases. For the 97 quasars with 1.7 <z< 3 in the full WLQ sample the mean slope is 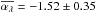 .
.
A possible explanation of the steeper continuum could be an additional non-thermal component in WLQ spectra. Therefore, we also computed the composite spectrum of the subsample of radio-loud WLQ. Usually, quasars are classified as radio-loud based on the radio-to-optical flux ratio. Kellermann et al. (1989) defined the radio-loudness parameter R = F5 GHz/F4400 Å, where F5 GHz and F4400 Å are the flux densities at rest-frame 5 GHz and 4400 Å, and called quasars with R greater than 10 as radio-loud. Since then, R = 10 is commonly used to distinguish radio-loud and radio-quiet quasars (e.g. Francis et al. 1993; Urry & Padovani 1995; Ivezić et al. 2002; McLure & Jarvis 2004; Richards et al. 2011), although this value is to some degree rather arbitrary (e.g. Falcke et al. 1996; Wang et al. 2006; Sect. 5 below). We took the radio-loudness parameter from the Shen catalogue. Shen et al. (2011) estimated the radio-loudness R = F6 cm/F2500 Å following Jiang et al. (2007), where F6 cm is the flux density at rest-frame 6 cm determined from the FIRST integrated flux density at 20 cm assuming a power law Fν ∝ λαν with αν = −0.5. The rest-frame 2500 Å flux density F2500Å is determined from the power-law continuum fit to the SDSS spectrum. Following Jiang et al. (2007), we use the criterion R> 10 to classify radio-loud quasars. Figure 3c shows the radio-loud WLQ composite spectrum. It is very similar to that of the entire WLQ sample, which is dominated by radio-quiet quasars. We conclude that there is no significant difference between the composites of radio-loud and of radio-quiet WLQs, in accordance with earlier findings for ordinary quasars (e.g. Francis et al. 1993).
 |
Fig. 4 Two interpretations of the steeper slope of the WLQ continuum. a) At the bottom of the panel, the WLQ composite spectrum (red) is compared with the slightly smoothed SDSS quasar composite spectrum (solid blue) fitted by a MTBB model with temperature parameter T∗ = 8 × 104 K (dotted blue). The thick black curve above is a modified version of the SDSS quasar composite with a hotter continuum fitted to the MTBB model for T∗ = 105 K and compared with the WLQ composite spectrum (red) that is normalised to match the former at the right hand side. b) as a), but the modification of the SDSS quasar composite spectrum consists of an additional power-law component instead of a hotter continuum. Vertical lines: continuum windows. |
It is known from both multi-epoch photometry and spectroscopy of SDSS quasars that the variability in the emission line flux is only ~ 10% of the variability in the underlying continuum (Wilhite et al. 2005; Meusinger et al. 2011). Let us assume that the WLQs represent a stage where the continuum is significantly enhanced but the lines are not. At the bottom of Fig. 4 a, the continuum of the SDSS composite spectrum between the Lyα and the Mg ii line is fitted by a simple multi-temperature black body (MTBB) model with a temperature parameter T∗ ≈ 8 × 104 K that provides a good fit to the observed quasar composite spectra over a much wider wavelength range (e.g. Meusinger & Weiss 2013). The steeper WLQ composite requires a higher temperature. Indeed, the fit is considerably improved when we subtract the continuum of the 8 × 104 K MTBB from the SDSS composite and add instead the continuum of the 105 K model. An alternative way to achieve a similar result is shown in Fig. 4b. We simply added a hypothetical further power-law component Fλ ∝ λ-1.7, i.e. αν = −0.3, of approximately the same level as the thermal continuum at 3000 Å. In both cases, the WLQ composite spectrum is well matched by the modified SDSS quasar composite spectrum. The enhancement of the continuum flux dilutes the line flux and reduces the EWs of the lines correspondingly.
3.2. Luminosity, black hole mass, Eddington ratio, and accretion rate
3.2.1. Mean properties and correlation diagrams
Table 2 lists the mean values of the bolometric luminosity L, the black hole mass M, the Eddington ratio ε, and the accretion rate Ṁ for the WLQ-EWS subsample, the rWLQ-EWS subsample, the corresponding parent samples, and the comparison sample. The rWLQ sample is subdivided into the subsamples of radio-loud and not radio-loud quasars, and the radio-loud subsample is subdivided into core-dominated and lobe-dominated radio sources. Quasars with R> 10 are classified as radio-loud (Sect. 3.1). The not radio-loud subsample includes both radio-quiet quasars, i.e. R< 10, and quasars outside the FIRST footprint area. With the exception of Ṁ, all data were taken from the Shen catalogue. The distinction of lobe-dominated and core-dominated radio sources is based on the parameter first_radio_flag.
We estimated the accretion rate in the same way as in Meusinger & Weiss (2013). This approach is based on the scaling relation for Ṁ derived by Davis & Laor (2011) from the standard accretion disk model. As was shown by Davis & Laor (2011), this relation can be used to compute Ṁ from the optical luminosity and is thus less affected by the uncertainties of the innermost part of the accretion disk. We slightly modified this relation to 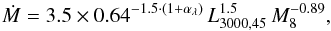 (1)by extrapolating the optical luminosity from the continuum luminosity L3000 at 3000 Å adopting a power law with the spectral index αλ where L3000,45 is L3000 in units of 1045 erg s-1 and M8 is the black hole mass in units of 108 M⊙. We derived the continuum spectral index αλ for each quasar individually by fitting a power law to the foreground extinction-corrected SDSS spectrum in the continuum windows. These individual slopes were used for all those quasars having spectra with S/N> 3 in at least three windows. For quasars with noisier spectra we simply adopted the mean slope αλ = −1.52 from the composite spectrum of the parent sample. The average accretion rate for the rWLQ-EWS sample is three times higher than for the comparison sample. The rWLQ sample shows a higher average accretion rate as well3.
(1)by extrapolating the optical luminosity from the continuum luminosity L3000 at 3000 Å adopting a power law with the spectral index αλ where L3000,45 is L3000 in units of 1045 erg s-1 and M8 is the black hole mass in units of 108 M⊙. We derived the continuum spectral index αλ for each quasar individually by fitting a power law to the foreground extinction-corrected SDSS spectrum in the continuum windows. These individual slopes were used for all those quasars having spectra with S/N> 3 in at least three windows. For quasars with noisier spectra we simply adopted the mean slope αλ = −1.52 from the composite spectrum of the parent sample. The average accretion rate for the rWLQ-EWS sample is three times higher than for the comparison sample. The rWLQ sample shows a higher average accretion rate as well3.
Table 2 suggests that our WLQs tend to have on average higher luminosities, black hole masses, Eddington ratios, and accretion rates compared to ordinary quasars. We tested the null hypothesis H0 that the WLQ samples and the comparison sample are drawn from the same population against the alternative hypothesis H1 that the values of the population from which the WLQs were drawn are statistically higher than the values of the population of ordinary quasars. We applied the one-tailed Kolmogorov-Smirnov two sample test (e.g. Siegel & Castellan 1988). H0 has to be rejected with an error probability α if the test statistic Dmax is larger than a critical value Dcrit,α(n1,n2), where α is the probability of rejecting H0 when it is in fact true, n1 and n2 are the numbers of quasars in the two samples. Table 3 lists the values for Dmax for the first seven samples from Table 2, the subsample of lobe-dominant radio-loud WLQ was omitted because of the small sample size. In the last two columns, the critical values Dcrit are listed for α = 0.01 and 0.001, respectively. With two exceptions, H0 has to be rejected in favour of H1 at α = 0.001. The null hypothesis cannot be rejected for the black hole masses of the EWS subsamples. There is no strong difference, on the other hand, between WLQs of different radio properties, although the radio-loud subsample is a little bit more extreme than the radio-quiet one.
Figure 5 displays the distributions in the L − M − ε − Ṁ parameter space. The top row shows the rWLQ-EWS sample and the rWLQ sample as symbols and the comparison sample by contours. The WLQ sample contains several extremely luminous quasars. The highest luminosity is measured for SDSS J152156.48+520238.5 with log L = 48.1, which is one of the four most luminous quasars in the SDSS DR7 quasar catalogue4. Also the black hole mass M = 1.3 × 1010 M⊙ and the Eddington ratio ε = 0.95 of SDSS J152156.48+520238.5 are very high, whereas the accretion rate Ṁ = 2.1 M⊙/yr is rather normal. However, these values should be interpreted with caution because the virial mass is derived from the C iv line (see Sect. 2). High-quality data provided by Wu et al. (2011), based on near-infrared spectroscopy, yield M = 6.2 × 109 M⊙ and ε = 0.81. With z = 2.238 (Wu et al. 2011), this quasar does not belong to the rWLQ sample, but there is also an overabundance of very luminous quasars in the rWLQ sample. On the other hand, the top left panel of Fig. 5 indicates a lower luminosity threshold for the rWLQs at log Llow ≈ 46.3, though there is some scatter. The higher mass of the rWLQs is probably the consequence of the correlation between L and M in the parent sample (see also Meusinger & Weiss 2013). There is no significant difference between the distributions of the radio-loud subsample and the rest, though radio-loud WLQs tend to be slightly more luminous.
 |
Fig. 5 Bolometric luminosity (left), Eddington ratio ε (middle), and accretion rate (right) as a function the black hole mass. Top: rWLQ sample (magenta frames: rWLQ-EWS subsample, filled red squares: FIRST-detected, open red squares: FIRST undetected) and comparison sample (CS; contours). Second row: high-luminosity subsample (blue symbols) from a simulated quasar sample (contours). Third row: The subsample of comparison quasars with WMg ii< 15 Å and WC iv< 7 Å (black symbols) compared with the entire comparison sample (contours). Bottom: quasars with high-S/N spectra (magenta symbols) from the comparison sample compared with the entire comparison sample (contours). |
Because the lower luminosity cut does obviously not significantly depend on M, it produces M-dependent lower limits of the Eddington ratio with log εlow ∝ − log M and of the accretion rate with log Ṁlow ∝ − 0.89log M that are clearly seen in the corresponding panels in the top row of Fig. 5. We demonstrate such an effect by a simple simulation. The approach is described in detail in Meusinger & Weiss (2013), here we only repeat the most important steps. We simulated a quasar sample with a z distribution similar to that of the rWLQ sample and with a reasonable mass distribution. Then we assigned a randomly chosen value of the radiative efficiency of the accretion process η = 0.057...0.321 for non-rotating to maximum spin black holes. With η = L/(Ṁc2) and the scaling relation for Ṁ, we get a relation between η,L, and M and can thus compute L for each quasar assuming, for simplicity, the same spectral slope αλ = −1.52 for all quasars. We applied a z-dependent lower L limit corresponding to the flux limit of the survey, an upper L limit corresponding to the luminosity distribution, and Gaussian distributed errors of the “observed” mass. This simulated “observed” quasar sample shows distributions on the L − M, ε − M, and Ṁ − M planes similar to those of our comparison sample of ordinary quasars. The differences may be due primarily to the very rough assumptions on the mass distribution and the η − M relation and are not relevant here. Next, we created a subsample of high-luminosity quasars simply by arbitrarily selecting a proportion (20%) of the quasars with log L> 46.3. The simulated sample and the high-L subsample are shown in the second row of Fig. 5. The distributions in the ε − M plane and in the Ṁ − M plane are very similar to the observed ones in the top row of Fig. 5. Such an agreement cannot be achieved for a subsample determined by a threshold of the Eddington ratio. Therefore, we conclude that the visually selected WLQ sample is better characterised by higher luminosities. The differences in ε and Ṁ are then at least partly a consequence of the higher L in combination with the intrinsic L − M relation of the parent SDSS quasar sample and the ε − L or Ṁ − M relation, respectively.
The third row of Fig. 5 shows a subsample of low-EW quasars drawn from the comparison sample of ordinary quasars by an EW threshold. There are too few quasars in the comparison sample that satisfy the selection criterion of the rWLQ-EWS subsample. Therefore, the constraint had to be relaxed to WMg ii< 15 Å and WC iv< 7 Å. The thus selected subsample appears to be characterised by higher Eddington ratios, accretion rates, and luminosities compared with the parent sample, but clearly not by higher masses.
Finally, the bottom row of Fig. 5 shows another subsample from the comparison sample. Here, only quasars with high S/N of their spectra, S/N> 9, were selected. The distributions are remarkably similar to those of the rWLQ sample in the top row.
3.2.2. S/N bias
Is the tendency of WLQs to be more luminous than ordinary quasars at the same z a selection effect? When measuring the spectral index αλ, the mean S/N in the pseudo continuum windows was estimated and quasars with a mean S/N< 2 were excluded. However, the number of the rejected quasars is very low and this explicit selection threshold is thus not very important. A much stronger bias towards higher S/N might be implicitly introduced by the visual selection from the icon maps. A certain classification as a WLQ candidate requires sufficient S/N and S/N is tightly correlated with the flux density.
 |
Fig. 6 Left: signal-to-noise ratio versus i band magnitude for the rWLQ sample (filled red squares; magenta frames: rWLQ-EWS subsample) and for the WLQ candidates that were rejected as noisy (black plus signs). For comparison, the contour curves show the distribution of the comparison sample (equally spaced logarithmic local point density contours estimated with a grid size of Δx,Δy = 0.1,0.05). Horizontal dashed line: explicit selection threshold S/N> 2, dotted line: 12th percentile of the rWLQ sample and 88th percentile of the unclassified noisy spectra at S/N = 9. Right: frequency distribution for the rWLQ sample (solid red), the rWLQ-EWS subsample (dashed magenta), and the WLQ candidates rejected as noisy (solid black). The histogram for the rWLQ-EWS subsample is stretched by a factor of two for better visibility. |
Figure 6 shows the measured S/N versus SDSS i band magnitude for both the rWLQ sample and the comparison sample. The distribution of the rWLQ-EWS subsample is similar to that of the rWLQ sample. The rWLQ sample only populates the upper part of the region populated by the comparison sample. There are two possible explanations for this difference: WLQs either have higher S/N due to a selection effect or are more luminous than normal quasars. In reality, both effects can be combined, of course. When we consider the distribution of those quasars that were rejected in the course of the classification procedure because the spectra appeared too noisy, we find a dichotomy. 88% of the rWLQ sample have S/N = 9, while about the same percentage of the objects with noisy spectra are below that value. Taking S/N = 9 as representative for the selection threshold and applying this threshold to the comparison sample, we find the mean luminosity of the high-S/N subsample to be about two times higher than that of the entire comparison sample. The quasars from the rWLQ sample are on average ~ 4 times brighter than normal (Table 2). About half of the luminosity excess is explained by the S/N selection bias.
To summarise, Figs. 5 and 6 along with Table 2 suggest that WLQs have higher luminosities, Eddington ratios, and accretion rates than normal quasars, although our basic sample is strongly affected by a selection bias. The relatively high masses of our WLQs are most likely a consequence of this selection effect.
 |
Fig. 7 Equivalent width of the Mg ii line versus a) bolometric luminosity; b) black hole mass; c) Eddington ratio; and d) accretion rate for the rWLQ sample. Filled red squares: FIRST detected WLQs, open red squares: FIRST undetected, magenta frames: rWLQ-EWS subsample. Straight lines: linear regression curves for the rWLQ sample. The distributions for the comparison sample are indicated by equally spaced logarithmic local point density contours estimated with a grid size of Δx,Δy = 0.1,0.05 dex. |
 |
Fig. 8 Variability index V in the u, g, r, and i band (left to right) versus luminosity for the 23 WLQs identified in the variability catalogue (filled red squares, magenta frames: WLQ-EWS subsample). For comparison, the entire sample from the variability catalogue is indicated by the median relation (thick blue curve) with standard deviation (shaded green area) and by the equally spaced logarithmic local point density contours (estimated with a grid size of Δx,Δy = 0.2,0.2). Open circle with error bars: mean value and 1σ deviations of the WLQs. |
3.2.3. Baldwin effect
The anti-correlation between the luminosity5 and the EW of the C iv line was first discovered by Baldwin (1977) and has become known as the Baldwin effect. A number of subsequent studies have confirmed this effect for the C iv line and for many other emission lines in the ultraviolet and optical (e.g. Green et al. 2001; Dietrich et al. 2002; Wu et al. 2009; Richards et al. 2011; Bian et al. 2012). Several interpretations about the origin of the Baldwin effect have been proposed, but there is currently no consensus about the fundamental mechanisms behind it. A promising explanation is that it is related to a luminosity-dependence of the SED shape (e.g. Netzer et al. 1992; Zheng & Malkan 1993; Dietrich et al. 2002; Wu et al. 2009). In the last decade, several studies proposed that the Baldwin effect may be driven by the Eddington ratio (Shang et al. 2003; Bachev et al. 2004; Baskin & Laor 2004; Dong et al. 2009; 2011; Bian et al. 2012).
In Fig. 7, the Mg ii equivalent width is plotted versus L,M,ε, and Ṁ, respectively. The Baldwin effect is clearly indicated for the comparison sample where we observe slightly stronger anti-correlations with ε and Ṁ than with L. The strongest effect is found for Ṁ probably indicationg that the accretion rate is the main driver. No significant correlation is indicated with the black hole mass M. As in Fig. 5, there is no significant difference between radio-loud and not radio-loud quasars. Similar to Fig. 5, the areas populated by the rWLQ sample in Fig. 7 are identical with the regions of low W and high L, ε, and Ṁ of normal quasars. The rWLQ-EWS sample is simply the low-EW part of the rWLQ sample. (Note that there are a few WLQs with WMg ii below but WC iv above the EWS threshold.) The high mean values of the luminosity, the Eddington ratios, and the accretion rate in Table 2 are thus partly a reflex of the Baldwin effect. The Baldwin effect is also present in the rWLQ sample (regression lines). Because of the inherent selection bias it is, however, not useful to compare the slopes with those from the literature
3.3. Variability
In a previous study (Meusinger et al. 2011), we exploited the Light-Motion Curve Catalogue (LMCC; Bramich et al. 2008) of 3.7 million objects with multi-epoch photometry from the S82 of the SDSS DR7 to analyse the light curves for about 9000 quasars in the five SDSS bands. We computed the rest-frame first-order structure function (SF) D(τrf) for each LMCC light curve in each band. The SF is a sort of running variance of the magnitudes as a function of the rest-frame time-lag τrf, i.e. the time difference between two arbitrary measurements. The arithmetic mean of all noise-corrected SF data points in the interval τrf,max ≈ 1 − 2 yr was taken as variability estimator. In other words, the quantity V used to describe the strength of the variability of a quasar is the variance of its magnitude differences from all those pairs of two measurements that have rest-frame time-lags between 1 and 2 yr. V was computed for each of the five SDSS bands.
The sample from our previous study included three quasars from the WLQ sample of Diamond-Stanic et al. (2009). Variability was found to be close to the median value for one of them but is remarkably lower for the other two. Also other quasars with relatively weak BELs selected from the same sample were found to vary by less than the general median dispersion. However, this previous WLQ sample was very low and the interpretation of some of these objects remains uncertain.
We identified 23 WLQs from our present sample with entries in the variability catalogue of S82 quasars. Using the variability estimators from this catalogue, we found again a tendency towards lower variability for the WLQs compared to the entire sample. Figure 8 shows the variability-luminosity diagrams using the variability indices V in the u, g, r, and i band, respectively.
It has been known for a long time that variability is anti-correlated with luminosity, in the sense that, at a given rest-frame wavelength, more luminous AGNs tend to vary with lower fractional amplitudes than less luminous AGNs (e.g. Pica & Smith 1983; Hook et al. 1994; Paltani & Courvoisier 1997; Vanden Berk et al. 2004; De Vries et al. 2005; Meusinger et al. 2011). The main driver behind the V − L relation may be the Eddington ratio or the accretion rate (e.g. Ai et al. 2010; Meusinger & Weiss 2013). A tendency towards lower variability indices of our WLQs is thus expected as a consequence of their higher luminosities. However, the mean values for the 23 WLQs are below the mean V − L relation in all SDSS bands. Figure 8 thus indicates that the continuum in WLQs is, on average, at least not more variable than in ordinary quasars. This conclusion is boosted by the fact that the variability of the line flux is weaker than the variability of the underlying continuum (Wilhite et al. 2005; Meusinger et al. 2011).
4. Wide band spectral energy distribution
 |
Fig. 9 SDSS and WISE colour-redshift diagrams for the WLQ sample (filled red squares; magenta frames: WLQ-EWS subsample). For comparison, the distributions of all quasars from the Shen catalogue are shown by contours (equally spaced logarithmic local point density contours estimated with a grid size of Δx,Δy = 0.1,0.1) and by the median colour redshift relation (thick blue curve) with standard deviation (shaded green area). |
4.1. From Lyα to the mid-infrared
Information on the SED of the quasars with a much wider wavelength coverage than the SDSS spectra is available particularly thanks to the sky surveys in the infrared. We used the photometric data for the J, H, and K band from the Two Micron All-Sky Survey (2MASS; Skrutskie et al. 2006) and for the w1 to w4 bands from the Wide-Field Infrared Survey Explorer (WISE; Wright et al. 2010) in combination with the u, g, r, i, and z magnitudes from the SDSS. The SDSS and 2MASS magnitudes were taken from the SDSS DR7 quasar catalogue (Schneider et al. 2010). We identified 95% of the SDSS DR7 quasars in the WISE All-Sky Source Catalog6 within a search radius of 6″. 99% of the identified quasars have SDSS-WISE position differences less than 3″. 2MASS J, H, and K band magnitudes are only available for 38, 28, and 28%, respectively.
The colour-redshift diagrams from the SDSS and WISE data are shown in Fig. 9. Although at first glance the mean colours of the WLQs are similar to those of the entire quasar population, the wavy structure is less pronounced for the WLQs and even less for the WLQ-EWS subsample. The features in the SDSS colour-z diagrams can be understood as being caused by the strong emission lines moving in and out of the filters with changing redshift (e.g. Richards et al. 2001). For example, normal quasars have a relatively blue r − i at z ≈ 1, where the Mg ii line dominates the r band, and a relatively red r − i at z ≈ 1.7 where it falls into the i band. The weaker Mg ii line of the WLQs results in a redder colour r − i at z ≈ 1 and a bluer at z ≈ 1.7 compared to the median colour redshift relation. There are no systematic differences in the WISE colour-z diagrams between the WLQs and the normal quasars. For the rWLQ sample, we derived mean colour indices w1 − w2 = 1.22 ± 0.25,w2 − w3 = 2.97 ± 0.33,w3 − w4 = 2.66 ± 0.52 compared to w1 − w2 = 1.28 ± 0.22,w2 − w3 = 2.97 ± 0.35,w3 − w4 = 2.71 ± 0.51 for the comparison samples. However, in a colour-z diagram for a combined SDSS-WISE colour, the WLQs appear to be significantly bluer on average, as shown for i − w1 in the Fig. 9e. For z = 0.7...2, this colour index reflects the slope of the SED between rest-frame near-ultraviolet and near-infrared.
After applying Galactic extinction corrections to the photometry in all 12 bands, the magnitudes were transformed into monochromatic fluxes per wavelength interval, Fλ, and the effective wavelengths of each filter were transformed into rest-frame wavelengths. We arbitrarily normalised the rest-frame SED of each quasar at 3000 Å. Therefore, the redshift range had to be restricted to 0.3 ≤ z ≤ 2. The sample contains 79 055 quasars. After normalisation, we computed the arithmetic median and standard deviation of all data points in narrow wavelength intervals.
 |
Fig. 10 Wide band (wb) SED. a) Shen catalogue with z< 2 (yellow solid curve: median, green shaded area: 1σ errors) and WLQ comparison sample (black dotted curve), normalised at 3000 Å. Over-plotted (blue): SDSS quasar composite spectrum from Vanden Berk et al. (2001). The horizontal lines indicate the wavelengths intervals covered by the different photometric bands. The inset shows the wb SED of all SDSS quasars (solid green) and of the comparison sample (black dotted) in the wavelength range 1300Å −3000 Å in linear scale, as well as the SDSS quasar composite spectrum smoothed with a 300 Å boxcar (blue dashed). b) WLQ-EWS sample (red solid curve) and comparison sample (black dotted curve and green shaded area). Over-plotted (blue): SDSS WLQ composite spectrum from Fig. 3. c) as b), but for the entire WLQ sample instead of the WLQ-EWS subsample. d) as b), but the comparison sample SED is boosted by a power-law component (plc) with αλ = −1.7 and re-normalised, the green shaded area indicates the 1σ errors of the WLQ sample, and the SDSS composite spectrum was omitted for the sake of clarity. |
In Fig. 10a, we plotted the arithmetic median wide band SED and the 1σ error interval for the entire quasar sample from the SDSS DR7 quasar catalogue. It is well matched by the SDSS composite spectrum from Vanden Berk et al. (2001). The de-redshifted wavelengths intervals covered by the various photometric bands are indicated by the vertical lines and labelled in the lower part. It is evident that the structures seen in the 1σ area are related to the edges of the bands in combination with the different photometric errors. In the near infrared, the strong incompleteness of the 2MASS photometry must be mentioned.
Quasar to quasar variations of the host galaxy fraction contribute to the increase of the scatter from UV to optical wavelengths. Because the host contamination depends on the quasar luminosity, the WLQ sample with its higher mean luminosity is expected to have a smaller host contribution compared to the entire quasar sample. We therefore have to compare the SED of the WLQs with that of a comparison sample with the same luminosity distribution. We constructed such a control sample in a similar way as mentioned in Sect. 2, but this time the two-dimensional distribution in the L − z space is required to match that of the WLQ sample. The size of this (L,z) comparison sample is again ten times that of the WLQ sample. The wide band SED of the (L,z) comparison sample, over-plotted in Fig. 10 a, indicates smaller host contributions compared to the parent SDSS quasar sample, as expected.
The wide band SED of the WLQ-EWS sample is shown in Fig. 10 b along with that of the (L,z) comparison sample. The agreement is relatively good, but the WLQ SED turns out to be slightly steeper over nearly the covered wavelength range. The same trend is seen for the wide band SED of the entire WLQ sample (Fig. 10c) that shows less fluctuations because of the larger sample size. Figure 10d shows that the agreement between the WLQ sample and the comparison sample is improved after adding a power-law component Fλ, add = cλαλ to the comparison sample SED. We checked various parameter combinations (c,αλ) and found a good match for αλ ≈ − 1.8... − 1.7, i.e. αν = −0.2... − 0.3, and an enhancement of the total flux density at 3000 Å by a factor ~ 2.
4.2. Radio emission
Table 2 indicates a relatively high percentage of radio-loud WLQs compared to the entire SDSS DR7 quasar sample. In general, the distribution of the radio-loudness of quasars appears to be bimodal with about 10% being radio-loud (Kellermann et al. 1989; White et al. 2000; Ivezić et al. 2002).
Radio properties of the WLQs and of the comparison samples.
Table 4 gives an overview of the radio properties of various samples. The proportion of radio-loud quasars, i.e. the ratio frl = Nrl/Nall of the number Nrl of radio-loud quasars to the number Nall of all WLQs in FIRST footprint amounts to 0.26 for the WLQ sample and 0.22 for the rWLQ sample. The radio-loudness proportion is even higher for the EWS subsamples (0.35 and 0.37). In the comparison sample, only 6% of the quasars are radio-loud, in good agreement with the value of 8% found for the SDSS quasar sample (Ivezić et al. 2002). A high amount of radio-loud quasars was also found for the WLQ sample from Paper I. In addition, we constructed a sample of 98 WLQs from the literature (Diamond-Stanic et al. 2009; Shemmer et al. 2010; Lane et al. 2011; Nikołajuk & Walter 2012; Wu et al. 2012). The percentage of radio-loud quasars is lower for that sample. However, the majority of these quasars have higher redshifts than ours and when we reject those with z> 3, the remaining subsample has a radio-loudness rate as high as in our WLQ sample. The lower radio-loudness percentage among the high redshift WLQs from the literature is mainly due to the fact that many of these sources were selected to be not radio-loud. Finally, we selected all quasars with Mg ii equivalent widths WMg ii< 15 Å from Shen et al. (2011). Again, the radio-loudness proportion (0.22) is much higher than typical for the parent quasar sample. On the other hand, though frl is high, the mean radio-loudness  for the WLQs is much lower than for the comparison sample.
for the WLQs is much lower than for the comparison sample.
 |
Fig. 11 Fraction of a) FIRST radio-detected quasars and b) radio-loud quasars in luminosity bins for the quasars from the Shen catalogue (blue asterisks), the subsample of Shen quasars with WMg ii< 11 Å and WC iv< 4.8 Å (open blue squares), our WLQ sample (filled red squares), and the WLQ-EWS subsample (magenta framed squares). All samples restricted to 0.6 ≤ z ≤ 2. |
 |
Fig. 12 Radio loudness and equivalent width of Mg ii (left) and C iv (right). Top: radio-loudness parameter R (filled red squares: rWLQ sample, magenta framed filled squares: rWLQ-EWS sample, large open red circle with error bars: mean value and 1σ error of rWLQs, blue plus signs: comparison sample, contours: all quasars from the Shen catalogue with bal_flag = 0). Middle: proportion fr of FIRST-detected quasars in EW bins (filled red squares: rWLQ sample, magenta framed filled square: mean value from the rWLQ-EWS sample, open blue squares: comparison sample, black lozenge: WLQ Lit (z< 3) sample, black asterisks: all quasars from the Shen catalogue with bal_flag = 0, horizontal bars: binning intervals, vertical bars: uncertainties from Poisson statistics and error propagation). Bottom: histogram distribution of the EW (solid red: rWLQ sample, dashed blue: comparison sample). |
The proportion fr ≡ Nr;R> 0/Nall of the radio-detected quasars in the FIRST survey area amounts to 0.34 for the entire WLQ sample, 0.33 for the rWLQ sample, but only 0.06 for the comparison sample. Again, the ratios are higher for the EWS subsamples (0.42 and 0.47). The radio proportion is also higher for the other WLQ samples in Table 4. It is qualitatively expected that the percentage of radio detections is higher for our WLQ sample than for the comparison sample because of the higher luminosity. As a consequence of the relatively narrow z range, the luminosity strongly correlates with the flux density and the WLQ sample is thus expected to also have a higher number of quasars with 1.4 GHz radio flux densities exceeding the FIRST detection limit, even if R is independent of L.
Figure 11 shows the proportion of (a) the radio-detected quasars and (b) the radio-loud quasars as functions of the luminosity for both WLQs and ordinary quasars from the Shen catalogue. Both samples were restricted to z = 0.6 − 2.0, where the overwhelming majority (93%) of the WLQs are found. For the Shen catalogue sample, the trend with L is only moderate for the proportion of radio-loud quasars but strong for the proportion of radio detections. On the other hand, Fig. 11 clearly shows that the luminosity dependence of the proportion of radio detections is by far not strong enough to explain the high rates of FIRST-detected WLQs. The WLQ-EWS subsample follows the same trend as our visually selected WLQ sample. We conclude that the high percentage of radio sources among our WLQs is not primarily a consequence of the higher luminosities, i.e. of the Baldwin effect in combination with the S/N selection bias discussed in Sect. 3.2.
In the top panels of Fig. 12, we plotted R as a function of WMg ii (left) and WC iv (right), respectively, for the rWLQ sample and the comparison sample of normal quasars. In addition, the distributions for all quasars from the Shen catalogue is shown by contour lines. There is a wide scatter, but the linear regressions for the comparison sample indicates an increase of R with increasing W. The centroid of the WLQ distribution is slightly below the regression line. The middle panels of Fig. 12 show the proportins fr(W) of radio-detected quasars in EW bins. There seems to be a negative correlation between fr and W for the WLQs.
The overwhelming majority of the FIRST-detected WLQs are core-dominant radio sources. The ratio rN,cl = Nc/Nl of the numbers of core-dominant to lobe-dominant sources is about three times higher than for the comparison sample. Again, high ratios rN,cl are also found for the other WLQ samples. On the other hand, the ratio  of the mean radio-loudness of the core-dominant to that of the lobe-dominant sources is about 2...3 times lower than usual. The very low value of rR,cl = 0.04 for the rWLQ-EWS subsample is likely an effect of the poor statistics with only two lobe-dominated quasars.
of the mean radio-loudness of the core-dominant to that of the lobe-dominant sources is about 2...3 times lower than usual. The very low value of rR,cl = 0.04 for the rWLQ-EWS subsample is likely an effect of the poor statistics with only two lobe-dominated quasars.
4.3. X-rays
Finally, we briefly consider the rate of X-ray sources. We use the column rass_offset from the Shen catalogue to select X-ray detections. For an offset less then 30 arcsec, we find a percentage of 6.5% for the rWLQ sample compared to 2.6% for the comparison sample. If we restrict the offset to less than 10 arcsec, the corresponding proportions are 1.8% and 0.6%, respectively. Therewith, the X-ray percentage appears to be three times higher for the WLQs than for the ordinary quasars, but this low-number statistics is very uncertain. The mean redshifts and RASS count rates are similar for both samples.
5. Discussion
We found that the continuum of the composite SED for the WLQ sample is steeper than for ordinary quasars. The WLQ composite spectrum is reasonably well matched by a modified composite of normal quasars where the BELs are normal but the continuum is hotter than usual. We also found that the WLQs have higher luminosities, Eddington ratios, and accretion rates, while the variability is lower. Finally, the WLQ sample is also significantly different from the comparison sample of ordinary quasars with respect to the radio properties. In this section, we try to give a consistent interpretation of these findings.
In the standard picture (Shakura & Sunyaev 1973; Frank et al. 2002), the temperature of the accretion disk around a black hole of given mass is determined by the accretion rate. Higher accretion rates lead to higher disk temperatures, luminosities, and Eddington ratios. The variability is known to anti-correlate with the Eddington ratio and the accretion rate (Wilhite et al. 2008; Bauer et al. 2009; Zuo et al. 2012; Meusinger & Weiss 2013). The accretion process in quasars is probably accompanied by strong local temperature fluctuations (Dexter & Agol 2011; Dexter et al. 2012; Ruan et al. 2014) and perhaps also by global fluctuations of the accretion rate (Pereyra et al. 2006; Li & Cao 2008; Zuo et al. 2012). The variability strength of the BEL flux is an order of magnitude less than for the underlying continuum (Wilhite et al. 2005; Meusinger et al. 2011). A change of the level of the continuum flux is not immediately accompanied by a change of the line flux on the same level. Hryniewicz et al. (2010) proposed a scenario where quasar activity has an intermittent character with several subphases. Each subphase starts with a slow development of the BLR. At least in a statistical sense, the WLQs in our sample can be consistently understood as AGNs in the beginning of a phase of stronger accretion, i.e. accretion rate and luminosity enhanced and variability thus reduced, whereas the BLR has not yet adapted to the level of the disk. In such a scenario, high ionisation BELs, like C iv and Lyα, are expected to be weaker than low ionisation BELs, like Mg ii, because they are formed at a higher distance from the disk. In fact, our WLQ sample indicates more weakening of the high ionisation compared to the low ionisation lines (Table 2; Fig. 4).
In order to account for the high amount of radio-detected quasars among our WLQs, we consider the viewing angle towards a radio jet as another possibly important aspect for the WLQ phenomenon. We found that our WLQs are, on average, less radio-loud than ordinary quasars but are much more likely to have FIRST counterparts. About one third of the WLQs in our sample are radio sources on the FIRST level.
First, however, we have to make sure that the high percentage of radio detections is not a selection effect. In Paper I, we found remarkably high radio detection rates for different types of unusual quasars, particularly for unusual BAL quasars. The radio detection rate was found there to positively correlate with the degree of the deviation from the SDSS quasar composite spectrum. The ratio, NF/NC, of the number of quasars with the FIRST target flag set to the number of quasars with their colour target flag set was found there significantly higher for the unusual quasars (0.33) than for the entire quasar catalogue (0.07). In addition, we considered the ratio NFs/NCs, where NFs is the number of quasars selected solely by the FIRST selection but not the colour selection and NCs is the number of quasars without FIRST counterparts but selected solely based on their colours. Again, we found a much higher value (0.22) for the unusual than for the entire quasar sample (0.01). For the WLQ sample of the present study, we have NF/NC = 0.33, reflecting once again the high proportion of radio detections, but NFs/NCs = 0.01, which is in accordance with the ordinary quasars. The latter is actually not surprising because the SDSS colour-z relations of the WLQs are not much different from the mean relations (Fig. 9). This indicates that, different from e.g. the unusual BAL quasars in Paper I, the high radio detection rate of the WLQs cannot be unambiguously attributed to a selection bias in the sense that a high number were only targeted by SDSS because they had been detected as radio sources. As a consequence, we have to assume that the high percentage of radio sources is an intrinsic property.
Our WLQ sample was visually selected from the Kohonen icon maps (Sect. 2). The basic criterion for the inclusion into the final sample was the presence of weak but clearly identifiable BELs. Moreover, we only accepted objects identified in the SDSS DR7 quasar catalogue (Schneider et al. 2010; Shen et al. 2011) where the presence of broad lines in the spectra is required to be included. The presence of BELs is usually considered as evidence that the continuum radiation is not dominated by a beamed synchrotron component. Therefore our sample is unlikely to be dominated by BL Lac objects where the beamed synchrotron emission strongly overpowers the thermal emission. The variability data (Sect. 3.3) are also inconsistent with a dominance of beamed non-thermal emission.
It has been suggested that the radio-to-optical flux ratio Rc from the radio core is a useful statistical measure of orientation (Baker & Hunstead 1995; Wills & Brotherton 1995; Kimball et al. 2011). In standard unification theory, orientation has an effect on the optical spectrum both via obscuration in the plane of the accretion flow and via relativistic boosting in the line of sight close to the relativistic outflow. High values of Rc are supposed to indicate a low angle to the jet axis. We did not explicitly separate the radio emission into core and extended components. However, because the majority (> 90%) of our radio-detected WLQs are core dominant, we simply identify R with Rc. Then, Fig. 12 would mean that our radio-detected WLQs have higher inclination angles to the jet. A similar trend of Rc with WMg ii and WC iv was reported by Kimball et al. (2011) who predicted that this correlation may be caused by anisotropic emission from the BLR. From the study of composite spectra of quasar samples grouped by the radio core-to-lobe ratio, Baker & Hunstead (1995) found stronger reddening in lobe-dominated quasars thought to be observed at higher inclination angles to the jet (i.e. edge-on). Because the core-to-lobe ratio is correlated with Rc (Kimball et al. 2011), we would expect that our WLQs exhibit stronger reddened spectra because of their lower mean R value. This, however, is clearly not the case. The median SED of the WLQs is steeper than that of the comparison sample. If this would be caused by reddening, the WLQ sample would be less reddened. We conclude that the WLQs in our sample are not seen preferentially edge on.
The majority (65%) of the WLQs with R> 10 have radio-loudness parameters in the range 25...250, sometimes called radio-intermediate. It was proposed that flat-spectrum radio-intermediate quasars are relativistically boosted radio-quiet quasars (Falcke et al. 1996; Wang et al. 2006). If this also applies to the radio-intermediate WLQs in our sample, we expect to view these quasars at low inclination angles to the jet. We argued (Fig. 10) that the difference between the slopes of the median wide band SEDs of the WLQ sample and the comparison sample can be explained by an additional power-law component, respectively a hotter continuum (Fig. 4), that does not dominate but makes a substantial contribution to the observed flux of the WLQs. An enhancement of the continuum by a factor of two caused by an additional component reduces the EW of the lines correspondingly (Fig. 4).
6. Summary and conclusions
We performed a new search for quasars with weak emission lines in the spectroscopic data from the SDSS DR7. We visually inspected the 36 self-organising maps (Kohonen maps) from Paper I for nearly 105 spectra classified as quasars by the SDSS spectroscopic pipeline and selected a sample of ~ 2500 WLQ candidates. After the thorough individual analysis of all selected spectra we created a final sample of 365 WLQs with mean redshift z = 1.50 ± 0.45. The mean equivalent widths are 17 ± 8 Å for Mg ii and 13 ± 14 Å for C iv. To avoid contamination, featureless spectra were not included. The corresponding incompleteness is estimated to about 10%. The sample includes a subsample of 46 WLQs with EWs below 3-sigma thresholds defined by the EW distribution of the ordinary quasars (EWS subsample). Especially for the analysis of the accretion rates, a subsample restricted to the redshift range 0.7 <z< 1.7 was considered (rWLQ sample).
The investigation of the properties of the WLQs (WLQ-EWS subsample, rWLQ-EWS subsample, and their parent samples) and their comparison with corresponding control samples yields the following results:
-
The SDSS composite spectrum for the WLQs showssignificantly weaker BELs and a bluer continuum compared tothe ordinary quasars. Therefore it can be excluded that WLQs arestronger affected by dust reddening than usual and it is unlikelythat WLQs are preferentially seen edge-on. No significantdifferences are found between the composites of the radio-loudand the not radio-loud WLQs. (Sect. 3.1)
-
The wide-band SED constructed from the SDSS, 2MASS, and WISE photometric data (Sect. 4.1) shows that the trend of a steeper continuum continues towards the mid infrared.
-
The WLQs have, on average, significantly higher luminosities, Eddington ratios, and accretion rates, but not significantly higher black hole masses (Sect. 3.2). About half of the luminosity excess is produced by a S/N bias in the selection process. The remaining intrinsic luminosity excess corresponds to the Baldwin effect and also manifests by higher accretion rates and Eddington ratios. The higher mean mass is simply a consequence of the higher mean luminosity in combination with the positive M − L correlation in the parent sample.
-
Indicators for the strength of the UV and optical variability are available for 23 WLQs from our sample. They show a wide scatter with a tendency towards lower variability than that of the ordinary quasars of comparable luminosities (Sect. 3.3).
-
The WLQ sample has remarkable radio properties (Sect. 4.2) that are probably not produced by selection effects. The percentage of radio-detected quasars is more than five times higher then for the control sample and the ratio of the number of core-dominant to the number of lobe-dominant radio sources is about three times higher. On the other hand, the mean radio-loudness of the radio-detected WLQs is much lower than for the ordinary quasars. The propotion of radio-sources increases towards lower equivalent widths while the mean radio loudness decreases.
The higher luminosities and Eddington ratios in combination with a bluer SED can be consistently explained by hotter accretion disks, i.e. by stronger accretion. According to the scenario proposed by Hryniewicz et al. (2010), a change towards a higher accretion rate is accompanied by an only slow development of the BLR. We have shown that the composite WLQ spectrum can be reasonably matched by the ordinary quasar composite where the continuum has been replaced by that of a hotter disk (Fig. 4). Therewith, at least a substantial percentage of the WLQs can be normal quasars in an early stage of increased accretion activity. On the other hand, a similar effect can be achieved by an additional power-law component, perhaps in relativistically boosted radio-quiet quasars viewed at low inclination angles to the jet.
Our WLQ sample is thus probably a mixture of quasars at the beginning of a stage of increased accretion activity on the one hand side and of beamed radio-quiet quasars on the other. There are hints on a close link between the accretion process and the relativistic jets (e.g. Falcke & Biermann 1995; Rawlings & Saunders 1991; Cao & Jiang 1999; Dexter et al. 2012) and one may expect that the two scenarios are closely linked to each other where an initially high or an enhanced accretion rate is the reason for the relatively high rate of radio detected quasars.
The accretion rates estimated for the WLQ-EWS sample and the entire WLQ sample, respectively, are even higher, but are not listed in Table 2 because of the anticipated higher uncertainties.
Acknowledgments
We thank the anonymous referee for suggestions that significantly improved our manuscript. We further thank Martin Haas for valuable comments and tips. This research has made use of data products from the Sloan Digital Sky Survey (SDSS), the Two Micron All-Sky Survey (2MASS), and the Wide-Field Infrared Survey (WISE). Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions (see below), the National Science Foundation, the National Aeronautics and Space Administration, the US Department of Energy, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are: the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge (Cambridge University), Case Western Reserve University, the University of Chicago, the Fermi National Accelerator Laboratory (Fermilab), the Institute for Advanced Study, the Japan Participation Group, the Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), the New Mexico State University, the Ohio State University, the University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. The Two Micron All Sky Survey is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. The Wide-field Infrared Survey Explorer is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Ai, Y., Yuan, W., Zhou, H., et al. 2010, ApJ, 716, 31 [Google Scholar]
- Baker, J. C., & Hunstead, R. W. 1995, ApJ, 286, 23 [Google Scholar]
- Bachev, R., Marziani, P., Sulentic, J. W., et al. 2004, ApJ, 617, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. 1977, ApJ, 214, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Baskin, A., & Laor, A. 2004, MNRAS, 350, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Bauer, A., Baltey, C., Coppi, P., et al. 2009, ApJ, 705, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Bian, W.-H., Fang, L.-L., Huang, K.-L., et al. 2012, MNRAS, 427, 2881 [NASA ADS] [CrossRef] [Google Scholar]
- Bramich, D. M., Vidrih, S., Wyrzykowski, L., et al. 2008, MNRAS, 386, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, X., & Jiang, D. R. 1999, MNRAS, 307, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Mignoli, M., Ciliegi, P., et al. 2002, ApJ, 571, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, S. W., & Laor, A. 2011, ApJ, 728, 98 [CrossRef] [Google Scholar]
- De Vries, W. H., Becker, R. H., White, R. L., & Loomis, C. 2005, AJ, 129, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, S. W., & Agol, E. 2011, ApJ, 727, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Dexter, J., McKinney, J. C., & Agol, E. 2012, MNRAS, 421, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond-Stanic, A. M., Fan, X., Brandt, W., et al. 2009, ApJ, 699, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Dietrich, M., Hamann, F., Shields, J. C., et al. 2002, ApJ, 581, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, X.-B., Wang, T.-G., Wang, J.-G., et al. 2009, ApJ, 703, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, X.-B., Wang, J.-G., Ho, L. C., et al. 2011, ApJ, 736, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., & Biermann, P. 1995, A&A, 293, 665 [NASA ADS] [Google Scholar]
- Falcke, H., Sherwood, W., & Patnaik, A. R. 1996, ApJ, 471, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Fan, X., Strauss, M. A., Gunn, J. E., et al. 1999, ApJ, 526, L57 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Francis, P. J., Hooper, E. J., & Impey, C. D. 1993, AJ, 106, 417 [NASA ADS] [CrossRef] [Google Scholar]
- Frank, J., King, A. R., & Raine, D. J. 2002, Accretion Power in Astrophysics, 3rd edn. (Cambridge University Press) [Google Scholar]
- Ghisellini, G., Tavecchio, F., Foschini, L., et al. 2012, MNRAS, 414, 2674 [Google Scholar]
- Girven, J., Gänsicke, B. T., Steeghs, D., & Koester, D. 2011, MNRAS, 417, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Green, P. J., Forster, K., & Kuraszkiewicz, J. 2001, ApJ, 556, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Hook, I. M., McMahon, R. G., Boyle, B. J., & Irwin, M. J. 1994, MNRAS, 268, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Hryniewicz, K., Czerny, B., Nikołajuk, M., & Kuraszkiewicz, J. 2010, MNRAS, 404, 2028 [NASA ADS] [Google Scholar]
- in der Au, A., Meusinger, H., Schalldach, P., & Newholm, M. 2012, A&A, 547, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezić, Ž., Menou, K., Knapp, G. R., et al. 2002, AJ, 124, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan, X., Ivezić, Ž., et al. 2007, ApJ, 656, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Kellermann, K. I., Sramek, R., Schmidt, M., et al. 1989, AJ, 98, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kimball, A. E., Ivezić, Ž., Wiita, P. J., & Schneider, D. P., 2011, AJ, 141, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Kleinman, S. J., Kepler, S. O., Koester, D., et al. 2013, ApJS, 204, 5 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Kohonen, T. 2001, Self-Organizing Maps, 3rd edn. (New York: Springer) [Google Scholar]
- Lane, R. A., Shemmer, O., Diamond-Stanic, A. M., et al. 2011, ApJ, 743, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., & Davis, S. W. 2010, MNRAS, 417, 681-688 [Google Scholar]
- Lawrence, A., Saunders, W., Rowan-Robinson, M., et al. 1988, MNRAS, 235, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Leighly, K. M., Halpern, J. P., Jenkins, E. B., et al. 2007, ApJS, 173, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Li, S.-L., & Cao, X. 2008, MNRAS, 387, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Giommi, P., Leto, C., et al. 2009, A&A, 495, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCook, G. P., & Sion, E. M. 1999, ApJS, 121, 1 [NASA ADS] [CrossRef] [Google Scholar]
- McDowell, J. C., Canizares, C., Elvis, M., et al. 1995, ApJ, 450, 585 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Jarvis, M. J. 2004, MNRAS, 353, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Meusinger, H., & Weiss, V. 2013, A&A, 560, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meusinger, H., Hinze, A., & de Hoon, A. 2011, A&A, 525, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meusinger, H., Schalldach, P., Scholz, R., et al. 2012, A&A, 541, A77 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H., Laor, A., & Gondhalekar, P. M. 1992, MNRAS, 254, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Nikołajuk, M., & Walter, R. 2012, MNRAS, 420, 2518 [NASA ADS] [CrossRef] [Google Scholar]
- Paltani, S., & Courvoisier, T. 1997, A&A, 291, 74 [Google Scholar]
- Pereyra, N. A., Van den Berk, D. E., Turnshek, D. A., et al. 2006, ApJ, 642, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Pica, A. J., & Smith, A. G. 1983, ApJ, 272, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Plotkin, R. M., Anderson, S. F., Hall, P. B., et al. 2008, AJ, 135, 2453 [NASA ADS] [CrossRef] [Google Scholar]
- Plotkin, R. M., Anderson, S. F., Brandt, W., et al. 2010, ApJ, 721, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Rawlings, S. G., & Saunders, R. D. 1991, Nature, 349, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Fan, X., Schneider, D. P., et al. 2001, AJ, 121, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Kruczek, N. E., Gallagher, S. C., et al. 2011, AJ, 141, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Röser, S., Demleitner, M., & Schilbach, E. 2010, AJ, 139, 2440 [NASA ADS] [CrossRef] [Google Scholar]
- Ruan, J. J., Anderson, S. F., Dexter, E., & Agol, E. 2014, ApJ, 783, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Severgnini, P., Caccianiga, A., Braito, V., et al. 2003, A&A, 406, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shang, Z., Wills, B. J., Robinson, E. L., et al. 2003, ApJ, 586, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Brandt, W., Netzer, H., et al. 2006, ApJ, 646, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Trakhtenbrot, B., Anderson, S. F., et al. 2010, ApJ, 722, L152 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Liu, X. 2012, ApJ, 753, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Rieke, G. H., Smith, P., et al. 2010, ApJ, 714, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Siegel, S., & Castellan, N. J. 1988, Nonparametric Statistics for the Behavioral Sciences (New York: McGraw-Hill, Inc.) [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Thostensen, J. R., & Skinner, J. N. 2012, AJ, 144, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Tran, H. D. 2003, ApJ, 583, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Van den Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Van den Berk, D. E., Wilhite, B. C., Kron, R. G., et al. 2004, ApJ, 601, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T.-G., Zhou, H.-Y., Wang, J.-X., et al. 2006, ApJ, 645, 856 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. L., Becker, R. H., Gregg, M. D., et al. 2000, ApJS, 126, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Wills, B. J., & Brotherton, M. S. 1995, ApJ, 448, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhite, B. C., Van den Berk, D. E., Kron, R. G., et al. 2005, ApJ, 633, 638 [NASA ADS] [CrossRef] [Google Scholar]
- Wilhite, B. C., Brunner, R. J., Grier, C. J., et al. 2008, MNRAS, 383, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., VandenBerk, D. E., Brandt, W. N., et al. 2009, ApJ, 702, 767 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Brandt, W., Hall, P. B., et al. 2011, ApJ, 736, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, J., Brandt, W., Anderson, S. F., et al. 2012, ApJ, 747, 10 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zheng, W., & Malkan, M. A. 1993, ApJ, 415, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Zuo, W., Wu, X.-B., Liu, Y.-Q., & Jiao, C.-L. 2012, ApJ, 758, 104 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Six examples of quasars with weak emission lines from the WLQ sample. For comparison the quasar composite spectrum from Vanden Berk et al. (2001; smooth red curve) is over-plotted, shifted to the redshift of the quasar and normalised to the total flux density between 3900 Å and 9000 Å (observer frame). At the top of each panel, the SDSS name, the redshift z, and the parameter FFT = first_fr_type (0 – not detected by FIRST; 1 – core-dominated radio source) from the Shen catalogue are given. The dotted vertical lines indicate the usually strong emission lines. |
| In the text | |
 |
Fig. 2 Equivalent width WC iv of the C iv λ1549 line versus equivalent width WMg ii of the Mg ii λ2798 line for the quasars from the WLQ sample with 1.50 ≤ z ≤ 2.22 (filled red squares) and for 35137 quasars in the same redshift range from the Shen catalogue (equally spaced logarithmic local point density contours estimated with a grid size of Δ = 2 Å on both axes). |
| In the text | |
 |
Fig. 3 Arithmetic median composite spectrum (thick red curve) and standard deviation (green shaded area) for a) the WLQ-EWS sample; b) the entire WLQ sample; and c) the radio-loud subsample. For comparison, the SDSS quasar composite spectrum (thin blue curve) from Vanden Berk et al. (2001) is over-plotted, normalised to match the WLQ composites at the right hand side. |
| In the text | |
 |
Fig. 4 Two interpretations of the steeper slope of the WLQ continuum. a) At the bottom of the panel, the WLQ composite spectrum (red) is compared with the slightly smoothed SDSS quasar composite spectrum (solid blue) fitted by a MTBB model with temperature parameter T∗ = 8 × 104 K (dotted blue). The thick black curve above is a modified version of the SDSS quasar composite with a hotter continuum fitted to the MTBB model for T∗ = 105 K and compared with the WLQ composite spectrum (red) that is normalised to match the former at the right hand side. b) as a), but the modification of the SDSS quasar composite spectrum consists of an additional power-law component instead of a hotter continuum. Vertical lines: continuum windows. |
| In the text | |
 |
Fig. 5 Bolometric luminosity (left), Eddington ratio ε (middle), and accretion rate (right) as a function the black hole mass. Top: rWLQ sample (magenta frames: rWLQ-EWS subsample, filled red squares: FIRST-detected, open red squares: FIRST undetected) and comparison sample (CS; contours). Second row: high-luminosity subsample (blue symbols) from a simulated quasar sample (contours). Third row: The subsample of comparison quasars with WMg ii< 15 Å and WC iv< 7 Å (black symbols) compared with the entire comparison sample (contours). Bottom: quasars with high-S/N spectra (magenta symbols) from the comparison sample compared with the entire comparison sample (contours). |
| In the text | |
 |
Fig. 6 Left: signal-to-noise ratio versus i band magnitude for the rWLQ sample (filled red squares; magenta frames: rWLQ-EWS subsample) and for the WLQ candidates that were rejected as noisy (black plus signs). For comparison, the contour curves show the distribution of the comparison sample (equally spaced logarithmic local point density contours estimated with a grid size of Δx,Δy = 0.1,0.05). Horizontal dashed line: explicit selection threshold S/N> 2, dotted line: 12th percentile of the rWLQ sample and 88th percentile of the unclassified noisy spectra at S/N = 9. Right: frequency distribution for the rWLQ sample (solid red), the rWLQ-EWS subsample (dashed magenta), and the WLQ candidates rejected as noisy (solid black). The histogram for the rWLQ-EWS subsample is stretched by a factor of two for better visibility. |
| In the text | |
 |
Fig. 7 Equivalent width of the Mg ii line versus a) bolometric luminosity; b) black hole mass; c) Eddington ratio; and d) accretion rate for the rWLQ sample. Filled red squares: FIRST detected WLQs, open red squares: FIRST undetected, magenta frames: rWLQ-EWS subsample. Straight lines: linear regression curves for the rWLQ sample. The distributions for the comparison sample are indicated by equally spaced logarithmic local point density contours estimated with a grid size of Δx,Δy = 0.1,0.05 dex. |
| In the text | |
 |
Fig. 8 Variability index V in the u, g, r, and i band (left to right) versus luminosity for the 23 WLQs identified in the variability catalogue (filled red squares, magenta frames: WLQ-EWS subsample). For comparison, the entire sample from the variability catalogue is indicated by the median relation (thick blue curve) with standard deviation (shaded green area) and by the equally spaced logarithmic local point density contours (estimated with a grid size of Δx,Δy = 0.2,0.2). Open circle with error bars: mean value and 1σ deviations of the WLQs. |
| In the text | |
 |
Fig. 9 SDSS and WISE colour-redshift diagrams for the WLQ sample (filled red squares; magenta frames: WLQ-EWS subsample). For comparison, the distributions of all quasars from the Shen catalogue are shown by contours (equally spaced logarithmic local point density contours estimated with a grid size of Δx,Δy = 0.1,0.1) and by the median colour redshift relation (thick blue curve) with standard deviation (shaded green area). |
| In the text | |
 |
Fig. 10 Wide band (wb) SED. a) Shen catalogue with z< 2 (yellow solid curve: median, green shaded area: 1σ errors) and WLQ comparison sample (black dotted curve), normalised at 3000 Å. Over-plotted (blue): SDSS quasar composite spectrum from Vanden Berk et al. (2001). The horizontal lines indicate the wavelengths intervals covered by the different photometric bands. The inset shows the wb SED of all SDSS quasars (solid green) and of the comparison sample (black dotted) in the wavelength range 1300Å −3000 Å in linear scale, as well as the SDSS quasar composite spectrum smoothed with a 300 Å boxcar (blue dashed). b) WLQ-EWS sample (red solid curve) and comparison sample (black dotted curve and green shaded area). Over-plotted (blue): SDSS WLQ composite spectrum from Fig. 3. c) as b), but for the entire WLQ sample instead of the WLQ-EWS subsample. d) as b), but the comparison sample SED is boosted by a power-law component (plc) with αλ = −1.7 and re-normalised, the green shaded area indicates the 1σ errors of the WLQ sample, and the SDSS composite spectrum was omitted for the sake of clarity. |
| In the text | |
 |
Fig. 11 Fraction of a) FIRST radio-detected quasars and b) radio-loud quasars in luminosity bins for the quasars from the Shen catalogue (blue asterisks), the subsample of Shen quasars with WMg ii< 11 Å and WC iv< 4.8 Å (open blue squares), our WLQ sample (filled red squares), and the WLQ-EWS subsample (magenta framed squares). All samples restricted to 0.6 ≤ z ≤ 2. |
| In the text | |
 |
Fig. 12 Radio loudness and equivalent width of Mg ii (left) and C iv (right). Top: radio-loudness parameter R (filled red squares: rWLQ sample, magenta framed filled squares: rWLQ-EWS sample, large open red circle with error bars: mean value and 1σ error of rWLQs, blue plus signs: comparison sample, contours: all quasars from the Shen catalogue with bal_flag = 0). Middle: proportion fr of FIRST-detected quasars in EW bins (filled red squares: rWLQ sample, magenta framed filled square: mean value from the rWLQ-EWS sample, open blue squares: comparison sample, black lozenge: WLQ Lit (z< 3) sample, black asterisks: all quasars from the Shen catalogue with bal_flag = 0, horizontal bars: binning intervals, vertical bars: uncertainties from Poisson statistics and error propagation). Bottom: histogram distribution of the EW (solid red: rWLQ sample, dashed blue: comparison sample). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


