| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 14 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201423808 | |
| Published online | 05 June 2014 | |
The HARPS search for southern extra-solar planets⋆,⋆⋆,⋆⋆⋆
XXXV. The interesting case of HD 41248: stellar activity, no planets?
1
Centro de Astrofísica, Universidade do Porto,
Rua das Estrelas,
4150-762
Porto,
Portugal
e-mail:
nuno@astro.up.pt
2
Departamento de Física e Astronomia, Faculdade de Ciências,
Universidade do Porto, Rua do Campo
Alegre, 4169-007
Porto,
Portugal
3
Observatoire de Genève, Université de Genève,
51 Ch. des
Maillettes, 1290
Sauverny,
Switzerland
4
Harvard-Smithsonian Center for Astrophysics, 60 Garden Street,
Cambridge,
MA
02138,
USA
5
European Southern Observatory, Casilla 19001
Santiago,
Chile
6
Instituto de Astrofísica de Canarias, 38200, La Laguna, Tenerife, Spain
7
INAF − Osservatorio Astrofisico di Torino, via Osservatorio 20, 10025
Pino Torinese,
Italy
8
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
9
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge, CB3 0HA, UK
Received: 14 March 2014
Accepted: 22 April 2014
Context. The search for planets orbiting metal-poor stars is of utmost importance for our understanding of planet formation models. However, no dedicated searches have been conducted so far for very low mass planets orbiting such objects. Only a few cases of low-mass planets orbiting metal-poor stars are thus known. Amongst these, HD 41248 is a metal-poor, solar-type star on the orbit of which a resonant pair of super-Earth-like planets has been announced. This detection was based on 62 radial velocity measurements obtained with the HARPS spectrograph (public data).
Aims. We present a new planet search program that is using the HARPS spectrograph to search for Neptunes and super-Earths that orbit a sample of metal-poor FGK dwarfs. We then present a detailed analysis of 162 additional radial velocity measurements of HD 41248, obtained within this program, with the goal of confirming the existence of the proposed planetary system.
Methods. We analysed the precise radial velocities, obtained with the HARPS spectrograph, together with several stellar activity diagnostics and line profile indicators.
Results. A careful analysis shows no evidence for the planetary system. One of the signals, with a period of ~25 days, is shown to be related to the rotational period of the star, and is clearly seen in some of the activity proxies. We were unable to convincingly retrieve the remaining signal (P ~ 18 days) in the new dataset.
Conclusions. We discuss possible causes for the complex (evolving) signals observed in the data of HD 41248, proposing that they might be explained by the appearance and disappearance of active regions on the surface of a star with strong differential rotation, or by a combination of the sparse data sampling and active region evolution.
Key words: planetary systems / stars: individual: HD 41248 / stars: solar-type / stars: activity / stars: abundances / surveys
Based on observations collected at ESO facilities under programs 082.C-0212, 085.C-0063, 086.C-0284, and 190.C-0027 (with the HARPS spectrograph at the ESO 3.6-m telescope, La Silla-Paranal Observatory).
Table 1 is available in electronic form at http://www.aanda.org
Radial velocity data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/566/A35
© ESO, 2014
1. Introduction
Precise spectroscopic studies of stars with giant planets show that their frequency is a strong function of the stellar metallicity. It is easier to find such a planet around a metal-rich star than around a metal-poor object (Gonzalez 1998; Santos et al. 2001, 2004b; Reid 2002; Fischer & Valenti 2005; Sousa et al. 2011b). Several studies on solar neighbourhood stars have shown that at least 25% of stars with [Fe/H] above +0.3 dex (twice the solar value) have an orbiting giant planet. This frequency decreases to about 5% for solar metallicity stars. This observational result is usually interpreted to be due to a higher probability of forming a giant-planet core before the dissipation of the proto-planetary disk in a metal-rich environment (e.g. Mordasini et al. 2009).
A number of questions are still open, however, whose answer may have strong implications for planet formation models, especially in the metal-poor regime. In the context of one of the HARPS surveys, a search for giant planets around a sample of ~100 metal-poor stars was conducted. Three new giant-planet candidates were discovered, and a fourth interesting candidate was announced (Santos et al. 2007, 2011). As expected, the results seem to confirm that metal-poor stars have a lower frequency of short-period giants (see also Sozzetti et al. 2009), and when these are found, they tend to have orbits with longer periods (Adibekyan et al. 2013). Curiously, however, the results also suggest that the frequency of giant planets that orbit metal-poor stars may be higher than previously thought, at least for values of [Fe/H] > −0.7 (Mortier et al. 2012).
Present numbers also indicate that the frequency of giant planets as a function of stellar metallicity may not be described by a simple power-law (as previously suggested for the metal-rich regime – Johnson et al. 2010), and may be flat for metallicities below −0.1 dex (e.g. Udry & Santos 2007; Mortier et al. 2013). A tentative lower limit of the stellar metallicity (~−0.7 dex) below which no giant planets can be formed was found as well (e.g. Mortier et al. 2013). In brief, the giant-planet formation efficiency in the metal-poor regime is still a matter of lively debate. Since the metallicity is one of the most important ingredients controlling planet formation (Ida & Lin 2004; Mordasini et al. 2009), answering these questions is mandatory if we wish to fully understand the process of planet formation and evolution.
Additional information about the frequency of other types of planets (Neptune- and super-Earth-like) as a function of stellar metallicity is key in this discussion. In fact, contrarily to what one might expect, the known correlation between the presence of planets and the stellar metallicity that exists for stars hosting giant planets does not seem to exist for stars hosting their lower mass planetary counterparts (Udry et al. 2006; Sousa et al. 2008). Recent results have shown that stars with Neptune-mass planets have a rather flat metallicity distribution. Moreover, considering systems with only hot Neptunes (without any other Jupiter-mass analogue), the metallicity distribution becomes slightly metal-poor, although few of these systems are detected as yet (e.g. Mayor et al. 2011; Sousa et al. 2011b; Buchhave et al. 2012).
These observational facts are supported by theoretical work (Ida & Lin 2004; Mordasini et al. 2009), showing that planets in the Neptune-mass regime are expected to be common around stars with a wide range of metallicities, while giant planets probably are more common only around metal-rich stars. This might be because high-metallicity proto-planetary disks are able to form rocky/icy cores fast enough for gas runaway accretion to lead to the formation of a giant planet before disk dissipation occurs. In turn, lower metallicity disks will imply longer planet formation timescales, leading to a lower fraction of giant planets: cores do not grow fast enough to accrete gas in large quantities before disk dissipation and thus remain Neptune- or super-Earth-like. However, given both the still relatively small number of discovered low-mass planets and of metal-poor stars surveyed (no specific survey for low-mass planets orbiting metal-poor stars has been carried out), it is still not possible to conclude on the frequency of low-mass planets as a function of stellar metallicity.
In this paper we present a new project that makes use of precise HARPS radial velocities to search for Neptunes and super-Earth planets that orbit a sample of metal-poor stars. The goals of the programme and the sample are presented. We then turn our attention to HD 41248, a metal-poor G dwarf from our sample that was recently announced to have a pair of resonant super-Earths or Neptunes (Jenkins et al. 2013). Using the set with more than 200 precise radial velocities measurements together with different stellar activity diagnostics, we explore the existence of the planets announced by Jenkins et al. (2013). The results of this analysis are presented and discussed.
2. Metal-poor survey
To our knowledge, no specific radial velocity survey for Neptunes and super-Earths that orbit a sample of low-metallicity stars has been carried out. To improve this situation, we started a dedicated programme in October 2008 using the HARPS spectrograph at the 3.6-m ESO telescope (La Silla Paranal-Observatory, Chile). The first set of observations, acquired in three different ESO periods between October 2008 and March 2011 (ESO programs 082.C-0212, 085.C-0063, and 086.C-0284) revealed several interesting candidates (see next section for the case presented here). However, despite the total granted 60 observing nights, the sparse time sampling of the observations did not allow us to conclude on the nature of any of the observed signals.
To address this problem, this initial observing programme was granted an extra 80 nights over three years (starting in October 2012) within an ESO Large Program (190.C-0027). The goals of this programme are twofold: first, to complete the search that had already begun, and second to confirm the very good candidates discovered in the previous runs. When this programme is completed, we expect to be able to derive the frequency of Neptunes and super-Earths in the metal-poor regime and compare it with the published results for solar metallicity stars and with the model predictions (e.g. Mayor et al. 2011). To achieve this goal, the idea is to obtain a number of points per star that is similar to the one obtained in the HARPS-Guarantee Time Observations (GTO) survey for very low mass planets around solar neighbourhood stars (e.g. Mayor et al. 2011), so that a similar detectability limit is reached.
The results of this survey will then allow us to compare the results and frequencies of Neptunes and super-Earths with those obtained in the HARPS-GTO program to search for very low mass planets orbiting a sample of solar-neighbourhood stars – centred on values close to solar metallicity. Together, the surveys will set important constraints for planet formation and evolution models (e.g. Mordasini et al. 2012). Addressing this problem will help us to provide a proper estimate of the frequency of planets (including Earth-like planets) in our Galaxy.
As is widely known, the search for low-mass planets is a difficult and time-consuming process because they induce only very low amplitude signals in radial velocities. This is very well illustrated by the huge number of data points that was recently required to detect the Earth-mass planet around α Cen B (Dumusque et al. 2012). In addition, analysing low-amplitude signals is very difficult. For instance, stellar activity may induce false-positive signals that can mimic the radial velocity signature of a low-mass planet (e.g. Forveille et al. 2009). Furthermore, recent results from radial velocity surveys have shown that many of the low-mass planets are located in systems where several planets produce overlapping signals in the data, which complicates the analysis even more (e.g. Lovis et al. 2011b). The ubiquity of multi-planet systems has also been demonstrated by the results of the Kepler mission (e.g. Batalha et al. 2013).
2.1. Target selection and stellar properties
The target list was chosen based on two sub-sets of the former HARPS-GTO planet search programme (completed in 2009). The first was a survey for giant planets orbiting metal-poor stars (Santos et al. 2007). The second was a programme to search for giant planets orbiting a volume-limited sample of FGK dwarfs (Naef et al. 2007). Both sets of stars were surveyed with a precision of ~2−3 m s-1, which is clearly insufficient to allow for the detection of Neptune-like planets (the observing strategy and frequency of measurements was inadequate for this goal as well).
Merging these two HARPS samples, we took all stars that met the following criteria:
-
not known to harbor low-mass planets;
-
metallicities below −0.4 dex (derived from HARPS CCF – see e.g. Santos et al. 2002);
-
chromospherically quiet (
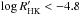 , as measured from HARPS spectra);
, as measured from HARPS spectra); -
present radial velocity variations with a dispersion below 10 m s-1 (higher dispersions may imply the presence of higher mass planets);
-
brighter than V = 9.5 (to allow a photon noise precision of 1 m s-1 after 900 s).
The previous information gathered in both surveys was thus sufficient to define a good sample of 109 metal-deficient stars (−1.5 < [Fe/H] < −0.4) that are suitable targets for detecting very low mass planets (Neptunes or super-Earths) – Table 1. To these we added the three long-period planet-hosting stars presented in Santos et al. (2011), whose planets were discovered in the context of the HARPS-GTO programme to search for giant planets that orbit metal-poor stars (HD 171028, HD 181720, and HD 190984), as well as a fourth long-period planet-hosting candidate (HD 107094). The goal is to search for very low mass planets that orbit these stars.
Stellar parameters for 106 out of the 109 targets were derived from a set of high-resolution HARPS spectra taken during the HARPS-GTO programme1. The values were presented in Sousa et al. (2011b,a). In Fig. 1 we present the distributions of [Fe/H] and effective temperature. All the stars in the sample have metallicities lower than solar, with an average [Fe/H] of −0.58. However, since these parameters were derived after the sample was defined2, not all stars have a metallicity below −0.4 dex: 21 stars have spectroscopic [Fe/H] values higher than this value, but lower than −0.22 dex. One single outlier was found to have almost solar metallicity (HD 144589, [Fe/H] = −0.05).
 |
Fig. 1 Distribution of metallicity (top) and effective temperature (bottom) for the stars in our sample. |
3. HD 41248
In a recent paper, Jenkins et al. (2013) used the first 62 (public) radial velocity measurements of the star HD 41248 to announce the detection of a system of two super-Earth or Neptune-mass planets with orbital periods of ~18.36 and 25.65 days. While the second of these signals was not very conspicuous, the first is clear on the dataset they analysed.
The 18-day-period signal had been spotted by us in 2010. However, since its value was close to the expected rotational period of the star as computed from the activity level (see Sect. 3.1 and Jenkins et al. 2013), and because a possible peak at the same period was also seen in the bisector inverse slope (BIS) of the HARPS cross-correlation function (CCF) – Fig. 5 – we decided that it would be wise to gather a new batch of observations before announcing the putative planet. In the following we present the results of the analysis of the whole dataset gathered in the programmes presented above.
3.1. Stellar properties
HD 41248 (HIP 28460) is a V = 8.82 magnitude G2 dwarf in the southern constellation Pictor. According to the new Hipparcos catalogue reduction (van Leeuwen 2007), it has a parallax of 19.22 ± 0.79 mas, which sets it at a distance of 52 ± 2 parsec from the Sun. Sousa et al. (2011b) derived precise stellar parameters for this star using a set of high-resolution and high S/N spectra obtained during the HARPS-GTO programme. The resulting values are Teff = 5713 ± 21 K, log g = 4.49 ± 0.05 dex, and [Fe/H] = −0.37 ± 0.01 dex3. These values are very similar to those listed by Jenkins et al. (2013): Teff = 5713 ± 50 K, log g = 4.48 ± 0.10 dex, and [Fe/H] = −0.43 ± 0.10 dex. Compatible values for the effective temperature are also listed in the PASTEL catalogue (Soubiran et al. 2010): Masana et al. (2006) derived Teff = 5827 K, while Casagrande et al. (2011) obtained Teff = 5927 K.
Stellar parameters for HD 41248.
An estimate for the mass and radius of HD 41248 can be obtained using the calibration in Torres et al. (2010). The value and its uncertainty were derived using a Monte Carlo approach, where random values of effective temperature, surface gravity, and metallicity as derived by Sousa et al. (2011b) were drawn taking into account the (Gaussian) uncertainties. Final values of 0.94 ± 0.02 M⊙ and 0.92 ± 0.06 R⊙ were derived for the mass and radius (Table 2). Using this value for the stellar mass, the effective temperature derived by Sousa et al., the parallax, the visual magnitude, and the bolometric correction of −0.09 as derived from the calibration of Flower (1996), we derive an astrometric surface gravity of 4.56 dex (see Eq. (1) in Santos et al. 2004b), very similar to the spectroscopic value. These are typical stellar parameters for a G2 moderately metal-poor dwarf.
The analysis of the HARPS spectra (see below) also allows us to derive the stellar activity level of the star, using the Ca ii H and K lines (Lovis et al. 2011a). The average value over the ~ten years of measurements is 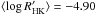 , with the values ranging from −5.20 to −4.79. These values are typical for a solar-like activity star in the low-activity part of the Vaughan-Preston gap (Vaughan & Preston 1980). The observed value can be used to derive an estimate for the rotational period of the star. Using the calibrations of Noyes et al. (1984) and Mamajek & Hillenbrand (2008), we obtain values for the rotational period of 19.8 ± 3.6 and 20.1 ± 3.0 days4, respectively. Finally, from the full width at half maximum (FWHM) of the HARPS cross-correlation function we estimate a value of 1.0 km s-1 for the projected rotational velocity of the star (see e.g. Santos et al. 2002), which is slightly lower than the 2.4 km s-1 listed by Jenkins et al. (2013).
, with the values ranging from −5.20 to −4.79. These values are typical for a solar-like activity star in the low-activity part of the Vaughan-Preston gap (Vaughan & Preston 1980). The observed value can be used to derive an estimate for the rotational period of the star. Using the calibrations of Noyes et al. (1984) and Mamajek & Hillenbrand (2008), we obtain values for the rotational period of 19.8 ± 3.6 and 20.1 ± 3.0 days4, respectively. Finally, from the full width at half maximum (FWHM) of the HARPS cross-correlation function we estimate a value of 1.0 km s-1 for the projected rotational velocity of the star (see e.g. Santos et al. 2002), which is slightly lower than the 2.4 km s-1 listed by Jenkins et al. (2013).
HD 41248 is a thin-disk star both in terms of kinematics and chemistry. With a value of [α/Fe] = 0.05 dex (Adibekyan et al. 2012b), the star does not show any α-element enhancement, a characteristic that is used to distinguish thin- and thick-disk stars at that metallicity (Fuhrmann et al. 1998; Bensby et al. 2003; Adibekyan et al. 2012b). Its oxygen-to-iron abundance ratio, derived using the OI 6300 Å line is [O/Fe] = 0.11 dex, which also agrees with the results for other α-elements. Note also that the α-enhancement has been shown to correlate with the presence of planets in the metal-poor regime (Haywood 2008; Adibekyan et al. 2012a).
The galactic space velocity components of the star (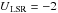 , VLSR = −6, and
, VLSR = −6, and 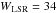 km s-1) also suggest a thin-disk origin with a probability of ~95% (Adibekyan et al. 2012b). HD 41248 has a low Galactic orbital eccentricity (0.04) and low Zmax5 of about 0.6 kpc (Casagrande et al. 2011). Finally, it shows a Li abundance of 1.56 ± 0.10 (Delgado Mena et al. 2014). This value is typical for a star of its effective temperature and does not reflect any particularly strong Li depletion, as is often found in planet-hosting stars of similar temperature (see e.g. Delgado Mena et al. 2014).
km s-1) also suggest a thin-disk origin with a probability of ~95% (Adibekyan et al. 2012b). HD 41248 has a low Galactic orbital eccentricity (0.04) and low Zmax5 of about 0.6 kpc (Casagrande et al. 2011). Finally, it shows a Li abundance of 1.56 ± 0.10 (Delgado Mena et al. 2014). This value is typical for a star of its effective temperature and does not reflect any particularly strong Li depletion, as is often found in planet-hosting stars of similar temperature (see e.g. Delgado Mena et al. 2014).
3.2. Radial velocities
Between October 2003 and December 2013, a total of 223 radial velocity measurements were obtained of HD 41248 using the HARPS spectrograph at the 3.6 m ESO telescope (La Silla-Paranal Observatory). The simultaneous calibration mode was used. Starting in March 2013, the simultaneous calibration was made using the available Fabry-Perot system, while before this date the ThAr lamp was used in this process. The average signal-to-noise ratio of the HARPS spectra in order 60 (~6200 Å) is 93, with values ranging from around 20 up to 150.
An analysis of the HARPS spectra allows us to exclude problematic measurements a priori (before the radial velocity analysis). This includes measurements with very low S/N or spectra with an abnormal blue-to-red flux ratio, for example. This occurred typically on nights when the transmissions was particularly bad (e.g. because of cirrus) or when observations were performed at high air-mass values. Two of the measurements in our dataset (JD = 55 304.518017 and 56 409.495511) were excluded based on these criteria. In the analysis presented here we used the remaining 221 data points.
The radial velocities (RVs) were derived using the HARPS pipeline (version 3.7) making use of the weighted cross-correlation technique, and using a cross-correlation mask optimised for a G2 dwarf (the same spectral type as HD 41248). The average error of the RVs is 1.4 m s-1. This value includes the photon noise, the calibration noise, and the uncertainty in the measurement of the instrumental drift. In the subsequent analysis, an error of 70 cm s-1 was added quadratically to this uncertainty, to take into account other possible sources of noise including instrumental, atmospheric, and stellar contaminants, as well as stellar jitter (see e.g. Pepe et al. 2011). The addition of this white noise will not introduce artificial signals in the data.
As presented in Sect. 2.1, the first set of RV data points obtained for this star was gathered in the context of a sub-survey of the HARPS-GTO programme. The goal of this sub-sample was to search for giant planets, and a corresponding strategy was adopted in terms of precision. As such, the error bars in a large part of the first dataset are significantly higher than those found in later measurements. After October 2008 (when the large programme began), the measurements were obtained with a completely different strategy. Exposure times were set at a minimum of 15 min to average-out the noise from stellar oscillations (e.g. Santos et al. 2004a). Starting in October 2012, we also decided to obtain whenever possible more than one spectrum of the star in a given night, separated by several hours. This strategy was used to minimise sources of stellar noise such as stellar oscillations and granulation and has proven to be very efficient when searching for extremely low amplitude RV signals (Pepe et al. 2010; Dumusque et al. 2010). Since the periodic signals we analyse here are much longer than one night, we used the nightly binned data in our analysis. This implies that “only” a total of 156 separate data points (in 156 different nights) were considered6.
 |
Fig. 2 Time series of the radial velocity, stellar activity, FWHM, and BIS. |
The HARPS pipeline also derives values for other parameters such as the bisector inverse slope (BIS – Queloz et al. 2001), the cross-correlation function (CCF) parameters FWHM and contrast, as well as the activity level of the star using the Ca ii K and K lines (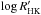 ). To these, we also separately computed (using the software described in Appendix A) a number of alternative line profile variation indicators as defined in Boisse et al. (2011, Vspan, Nardetto et al. (2006, biGauss), and Figueira et al. (2013, Vasy, BIS+, and BIS−. These indices were used to analyse and interpret the observed radial velocity signals.
). To these, we also separately computed (using the software described in Appendix A) a number of alternative line profile variation indicators as defined in Boisse et al. (2011, Vspan, Nardetto et al. (2006, biGauss), and Figueira et al. (2013, Vasy, BIS+, and BIS−. These indices were used to analyse and interpret the observed radial velocity signals.
In Fig. 2 we plot the radial velocity time series together with the derived values for the activity level and the CCF parameters FWHM and BIS. The plots show that the RV values slightly increase with time. No clear trend is seen for the 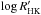 activity index, the FWHM, or the BIS, which suggests that this drift is not related to the variation of activity level along the magnetic cycle of the star (Santos et al. 2010; Lovis et al. 2011a; Dumusque et al. 2011).
activity index, the FWHM, or the BIS, which suggests that this drift is not related to the variation of activity level along the magnetic cycle of the star (Santos et al. 2010; Lovis et al. 2011a; Dumusque et al. 2011).
3.3. Keplerian fitting
To test whether the signals detected by Jenkins et al. (2013) are still present in the data after including the additional RVs, we decided as a first approach to use the yorbit algorithm (Ségransan et al., in prep.) to fit the whole dataset with a model composed of two Keplerian functions and one linear trend. Yorbit uses a hybrid method based on a fast linear algorithm (Levenberg-Marquardt) and genetic operators (breeding, mutations, cross-over), and has been optimised to explore the parameter space for Keplerian fitting of radial velocity datasets. Since the first goal was to explore the existence of the signals announced by Jenkins et al., we chose to explore only the solutions with periods between 16 and 20 days (for the first planet), and between 24 and 28 days (for the second planet).
 |
Fig. 3 Phase folded radial velocities of HD 41248 with the best fit Keplerian functions at ~18-days (top) and ~25 days (bottom). |
The phase-folded best-fit Keplerian solutions are presented in Fig. 3. The final solutions converged to orbital periods of 18.336 ± 0.006 and 25.623 ± 0.010 days, with eccentricities of 0.54 ± 0.09 and 0.36 ± 0.07 and semi-amplitudes of 2.46 ± 0.41 and 3.32 ± 0.26 m s-1, respectively. If caused by the presence of planets, and assuming a stellar mass of 0.94 M⊙, these solutions correspond to the signal induced by super-Earth or Neptune-like planets with masses of 8.2 and 13.7 M⊕, respectively. The residuals to the fit show an rms of 2.15 m s-1, clearly above the average error bar of the measurements (1.4 m s-1). Some structure is also present in the residuals: a generalised Lomb-Scargle periodogram (GLS, Zechmeister & Kürster 2009) shows some power at ~30 days, but this is not statistically significant (the computed false-alarm probability is around 5%). Given the complexity of the observed signals (see discussion below), we do not discuss the nature of this signal in detail7.
The 25-day-period fit presented in Fig. 3 looks perfectly reasonable. However, the 18-day signal is visually not convincing because it owes its shape mostly to a few points near phase 0 (or 1). But even if it were credible, the fact that visually these solutions might be acceptable does not, of course, confirm that there are planets that orbit HD 41248. For instance, several cases have shown that stable active regions can be present in the photospheres of solar-type stars (e.g. Queloz et al. 2001; Forveille et al. 2009; Figueira et al. 2010). These may produce RV signals that mimic those expected from real planetary systems.
A simple comparison of the fitted signals with those presented in Jenkins et al. (2013) shows that the periods we found are consistent with the earlier values. The eccentricities, however, are significantly higher than those (close to zero) presented by these authors. The amplitude of the 25-day-period signal is also significantly higher than the highest value listed by Jenkins et al. (2.97 m s-1). Imposing circular orbits decreases the amplitudes to 1.99 and 2.99 m s-1, respectively, but produces a slightly poorer fit with an rms of 2.26 m s-1. In any case, these values suggest that at least the 25-day-period signal has evolved in amplitude over time.
3.3.1. Bayesian analysis with Keplerian functions
In complement, we also performed a Bayesian analysis of the whole dataset following the methodology reported for example by Gregory (2011). In this process we used large and uninformative priors, except for the orbital eccentricity, for which we chose a beta distribution, as suggested by Kipping (2013). We also assumed here that the data can be modelled by a series of Keplerian orbits and a linear drift. We ran a large number of chains using the Markov chain Monte Carlo (MCMC) algorithm implemented in the PASTIS software (Díaz et al. 2014); we refer to this paper for more details. We then computed the Bayes factor of models with n + 1 Keplerian orbits against models with n Keplerian orbits by estimating the evidence of each model using the truncated posterior mixture as described by Tuomi & Jones (2012).
We found that the data can be modelled by up to five significant Keplerians with periods of P1 = 25.628 ± 0.011 days, P2 = 18.349 ± 0.012 days, P3 = 30.715 ± 0.031 days, P4 = 12.6291 ± 0.0034 days, and 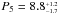 days. All these Keplerian orbits are found to have significant eccentricities, except for those at ~18 and ~8.8 days. The two first Keplerian orbits are compatible with those reported by Jenkins et al. (2013), while P4 and P5 are found to be really close to P1/ 2 and P1/ 3.
days. All these Keplerian orbits are found to have significant eccentricities, except for those at ~18 and ~8.8 days. The two first Keplerian orbits are compatible with those reported by Jenkins et al. (2013), while P4 and P5 are found to be really close to P1/ 2 and P1/ 3.
As we show below, we conclude that the P4 and P5 are the harmonic of the stellar activity signal that has a main period of P1 ≈ 25.6 days. We also found strong indications that the third Keplerian orbit, with P3 ≈ 30.7 days, is related to stellar activity.
3.4. Analysing the periodograms
To take the analysis of the data one step further, we defined three different sets: set #1, which corresponds to the data used by Jenkins et al. (JD up to 55 647), set #2 with JD between 55 904.8 and 56 414.5, and set #3 with JD between 56521.9 and 56 632.7. Sets #2 and #3 correspond to two different observing seasons and are separated by a temporal gap (caused by the passage of the star close to the Sun). There are 61, 50, and 45 data points in set #1, #2, and #3. In the following, and before dividing the data into the three different sets, we fitted and subtracted from the RVs a linear trend (Fig. 4) with a slope of 0.52 ± 0.14 m s-1/yr. Since the signals we explored here all have relatively short periods, this decision has no impact on the results.
 |
Fig. 4 Time series of the radial velocity and a linear fit to the data. The residuals are shown in the lower panel. |
In Figs. 5−8 we present from top to bottom the GLS of the RV, FWHM, BIS, 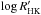 , BIS−, BIS+, biGauss, Vasy, and Vspan for the data in sets #1, #2, #3, as well as for all our data together. In all the plots, the horizontal line denotes the 1% false-alarm probability (which we considered as the significance limit). This value was computed using a permutation test; more details can be found in Mortier et al. (2012). The vertical dashed lines denote the locus of the 18- and 25-day periods.
, BIS−, BIS+, biGauss, Vasy, and Vspan for the data in sets #1, #2, #3, as well as for all our data together. In all the plots, the horizontal line denotes the 1% false-alarm probability (which we considered as the significance limit). This value was computed using a permutation test; more details can be found in Mortier et al. (2012). The vertical dashed lines denote the locus of the 18- and 25-day periods.
 |
Fig. 5 Periodograms of (from top to bottom) the RV, FWHM, BIS, |
In set #1 (Fig. 5), the highest and only significant peak in RV is at ~18 days, as already pointed out in Jenkins et al. (2013). This peak corresponds to the signal that these authors attributed to the presence of one of the planets. No similarly significant peak is seen in any of the other indices, although a clear peak near 18 days is also observed at least in the BIS and BIS+ line-profile indicators. The peak at ~25 days, which corresponds to the second candidate planet announced by Jenkins et al., also has some power in the FWHM and Vasy, but never at a significant level. A peak close to 25 days is also present in 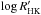 . Finally, a peak close to 30 days (one of the periods mentioned in Sect. 3.3.1) is also seen in FWHM, BIS−, and Vasy.
. Finally, a peak close to 30 days (one of the periods mentioned in Sect. 3.3.1) is also seen in FWHM, BIS−, and Vasy.
For dataset #2 alone, the periodograms in Fig. 6 show that no significant peaks are detected in any of the variables. In RV, a forest of peaks is present, the most conspicuous at ~35 days (with some power at a similar value in FWHM, BIS+, and Vasy), followed by one at ~25 days. This signal, at or close to 25 days, is also seen in all the remaining variables, with the exception of the Vspan. In RV, no peak is present at 18 days, although clear peaks close to that period are observed in BIS, BIS+, biGauss, and Vspan. Finally, a clear peak at ~60 days is seen in all the variables, with the exception of Vasy.
For dataset #3, Fig. 7 shows that for RV, FWHM, and 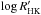 there is a clear signal at 25 days, as well as at its first harmonic (P/2 ~ 12.5). No clear signal is observed at 18.36 days, although a non-significant bump in the peridogram exists at ~19 days. A peak at ~19 days is also seen in the periodogram of the FWHM. Interestingly, the periodogram of BIS, BIS−, BIS+, biGauss, and Vspan shows a significant peak at ~4.5 days, which is 1/4th of 18 days. The cause for this peak is not discussed in more detail because we have no clear explanation for its existence.
there is a clear signal at 25 days, as well as at its first harmonic (P/2 ~ 12.5). No clear signal is observed at 18.36 days, although a non-significant bump in the peridogram exists at ~19 days. A peak at ~19 days is also seen in the periodogram of the FWHM. Interestingly, the periodogram of BIS, BIS−, BIS+, biGauss, and Vspan shows a significant peak at ~4.5 days, which is 1/4th of 18 days. The cause for this peak is not discussed in more detail because we have no clear explanation for its existence.
Finally, the periodograms of the whole dataset (Fig. 8) show, as already mentioned above, that the pattern observed in RV is also well reproduced in the FWHM, with the clear and significant 25-day-period signal present in both variables (the first and second harmonics, P/2 and P/3, are also visible at least in the RV). No peak at 18 days is seen in the periodograms, but a hint of power at ~19.5 days is seen in the FWHM. The GLS of BIS, BIS+, biGauss, and Vspan also show some power close to 18 days, but no significant peak is seen. A peak around 31 days is also observed in the FWHM and in Vasy.
Furthermore, the amplitude of the ~25-day-period signal seems to increase as we move from set #1 to set #3. The analysis of the RV and 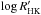 periodograms also shows that its phase did not significantly vary over time. In complement with the analysis presented below, this suggests that we may be detecting a signal produced by an evolving (growing) active longitude (Berdyugina & Usoskin 2003; Ivanov 2007) that remained relatively constant in position on the stellar disk over the past years.
periodograms also shows that its phase did not significantly vary over time. In complement with the analysis presented below, this suggests that we may be detecting a signal produced by an evolving (growing) active longitude (Berdyugina & Usoskin 2003; Ivanov 2007) that remained relatively constant in position on the stellar disk over the past years.
In brief, the periodogram of the RV shows a complex pattern that clearly evolves as a function of time, which complicates and hinders our analysis of the data. The same is true for the activity and line-profile indicators. The periods found by the Bayesian fitting procedure, for example, all correspond to peaks in stellar activity or line-profile indicators that vary over time.
When multiple signals (e.g. red noise or other Keplerians) with high enough significant amplitudes are present in the data, one coherent signal may in principle remain undetected by a periodogram analysis, even if it is still present in the data (since it might be diluted by the remaining signals). This problem exists for any analysis of data that is made without a full model. Several of the tests presented here and in the following sections are thus valid under the assumption that no additional sufficiently stronger signals exist that can (at least completely) hide the periodicities we tested. Note, however, that our whole analysis is based on several diagnostics, which makes it more reliable.
3.5. The 25-day period
As discussed in Sect. 3.4, from the analysis of the whole dataset there is no sign of the 18-day-period signal that was clearly observed in Jenkins et al. (2013). However, a distinctive peak at ~25 days dominates the GLS. A second and third peak, at about ~13 and ~8.5-days, are also observed. These two peaks are at the approximate position of the first and second harmonics of the ~25-day period.
The periodogram can be interpreted in the light of at least three distinct scenarios: i) the observed signal is caused by one eccentric planet (as fitted in Sect. 3.3) with a period of 25-days (whose Keplerian signal produced a periodogram showing the periods and its harmonics); ii) this is a system of several planets with periods that are in resonance with the 25-day-period signal (see Sect. 3.3.1); or iii) this signal is caused by stellar spots or other activity-related phenomena. The pattern observed is indeed very similar to the expected RV signal caused by a spotted star, as presented and discussed in Boisse et al. (2011).
In Fig. 9 we present the time series of the RV, 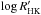 , FWHM, and BIS for the last series of RV data, obtained at the end of 2013 (corresponding to the last measurements of set #3). As we can see from the plot, there is a clear correlation between the RV and both the FWHM and the stellar activity index
, FWHM, and BIS for the last series of RV data, obtained at the end of 2013 (corresponding to the last measurements of set #3). As we can see from the plot, there is a clear correlation between the RV and both the FWHM and the stellar activity index 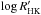 . With this information we conclude that the 25-day-period signal observed in RV (and its harmonics) most likely corresponds to the rotational period of the star and that the RV signal observed is caused by the rotational modulation of activity features on the stellar photosphere. The 25-day signal announced by Jenkins et al. (2013) is thus most likely better explained with stellar activity and not with a planet orbiting HD 41248.
. With this information we conclude that the 25-day-period signal observed in RV (and its harmonics) most likely corresponds to the rotational period of the star and that the RV signal observed is caused by the rotational modulation of activity features on the stellar photosphere. The 25-day signal announced by Jenkins et al. (2013) is thus most likely better explained with stellar activity and not with a planet orbiting HD 41248.
 |
Fig. 9 Time series of the radial velocity, stellar activity, FWHM, and BIS for the period between JD = 2 456 580 and 2 456 640. |
The analysis of the GLS periodograms shows that the phase of the RV signal plotted in Fig. 9 (and in particular the peak in its value) is about ~35 and ~15 degrees behind the one observed in FWHM and 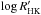 , respectively. This lag is expected if the RV signal is caused by stellar spots (see e.g. Forveille et al. 2009). Indeed, when the active regions appear and occupy the blueshifted side of the star, the RV will show an increasing value with time. Simulations with the SOAP code (Boisse et al. 2011)8 show that the maximum of this RV will occur when the spots are ~45 degrees from meridian (or close to disk center). Given the simple physics9 used in the model, we consider that this number is compatible with the observed value. The value will then decrease to zero when the spot is at meridian. This instant sets the highest activity level as the active region shows its maximum projected area10.
, respectively. This lag is expected if the RV signal is caused by stellar spots (see e.g. Forveille et al. 2009). Indeed, when the active regions appear and occupy the blueshifted side of the star, the RV will show an increasing value with time. Simulations with the SOAP code (Boisse et al. 2011)8 show that the maximum of this RV will occur when the spots are ~45 degrees from meridian (or close to disk center). Given the simple physics9 used in the model, we consider that this number is compatible with the observed value. The value will then decrease to zero when the spot is at meridian. This instant sets the highest activity level as the active region shows its maximum projected area10.
As a complementary test, we computed the Pearson correlation coefficient (ρ) between the RV and the different line-profile indicators for dataset #3. For the correlation with FWHM, a value of ρ = 0.52 was obtained. A Monte Carlo simulation was then made to calculate the probability of reaching this value by a chance alignment of the data points. This test was made by performing a Fisher-Yates shuffling of the values of RV and FWHM 100 000 times, computing the correlation coefficient for each simulated dataset, and deriving the distribution of the resulting ρ values. For details about the method and its background we point to Figueira et al. (2013). The test showed that the observed ρ is at 4.5 sigma from an uncorrelated (shuffled) distribution, meaning that it is very unlikely that it is caused by a chance event. Note that despite the significant correlation found, the value of ρ is not particularly high. This is because the RV and the different line-profile indicators are usually not correlated with a 1:1 relation, among other reasons (see e.g. Figueira et al. 2013). This point is also illustrated by the phase shift observed between the FWHM and RV as discussed above.
3.6. The 18-day period
The result presented above does not per se discard the presence of planets orbiting HD 41248 at other periods. In particular, they do not allow us to discard the existence of the 18-day-period signal that was present in the first batch of data and was interpreted by Jenkins et al. (2013) to be caused by a super-Earth-mass planet.
As discussed above, however, if we divide the whole dataset into three different groups, the GLS analysis suggests that the 18-day-period signal is only observed in the first dataset (set #1), which corresponds to the data used by Jenkins et al. No signature of the 18-day period is visible in the remaining data, even if the number of points in sets #2 and #3 are similar to those in set #1. The question then is whether the 18-day-period signal is still present in the data, meaning, whether it is constant over time, or alternatively if it was only present in the first dataset. To answer this question we ran a series of tests, as follows.
3.6.1. Subtracting the 25-day-period signal
Set #3 has by far the best time coverage of the data. That makes it particularly suitable to analyse the existing signals. We thus decided to analyse this set in detail to test whether the 18-day-period signal can be retrieved after removing the signal at 25 days.
To do this we used the approach of Boisse et al. (2011) to fit the rotational period and its harmonics, as was successfully done by Dumusque et al. (2012) for α Cen B. We applied two methods. In the first one, we fitted a P ~ 25 day sinusoidal together with the first harmonic (at P/2) to the RV time series. In the second case we decided to use the FWHM variation as a proxy for activity-induced RV variations, and fixed P using the analysis of the FWHM signal. This procedure allows us to guarantee that we did not absorb signals in the fitting process that are present in the RV, for example, but are not caused by activity-related phenomena (such as real planetary signals). The residuals of the fit using both methods were analysed.
 |
Fig. 10 Periodograms of the residuals of the harmonics fit described in Sect. 3.6.1, making use of the RV (top) and FWHM (bottom) to fix the period used to subtract the RV signal and its harmonics. The dashed line indicates the position of the 18.36 day period. The horizontal line represents the 1% FAP. |
The results of the two tests can be seen in Fig. 10, where we present the GLS of the residuals to both fits. In both panels, the dashed line indicates the 18.36-day period, while the horizontal line represents the 1% FAP. No significant peak exist at ~18 days. The highest peak in each plot is at 15.77 and 15.94 days, respectively. The second-highest signal in the top panel is at a period of 19.02 days.
Although not conclusive, this test does not support the planetary explanation for the 18.36-day signal presented in Jenkins et al. (2013). In fact, as we show in the next section, if that signal were present in dataset #3, it should have been easily spotted. We assume here that no significantly stronger signal at another period was present that would have masked it. The absence of any strong peak in the GLS of Fig. 10 at any other period supports this assumption.
3.6.2. Simulating the data
As a second test, we generated a set of full synthetic radial velocities for each of the three time series of data mentioned above. The data were generated considering the real observed dates to mimic the real time-sampling. The error bars for each RV point were also kept as in the original data. To each dataset, we first added a Keplerian signal of ~18.36-day period as observed by Jenkins et al. (2013). White noise was then added to each point in agreement with the error bars to simulate the different average measurement errors in each dataset.
 |
Fig. 11 Periodograms of the different datasets, both of the real (left) and simulated data (right). Vertical dashed lines represent the position of the 18- and 25-day signals presented in Jenkins et al. |
In addition, we injected a signal of 25 days into the data as fit to the last dataset where the time coverage of the data clearly allows us to model the 25-day signal. Again, the fit was made using the approach in Boisse et al. (2011), that is, fitting the rotational period and its first harmonic (P/2)11. In each of the three datasets (set #1, #2, and #3), however, the injected 25-day-period signal was varied in amplitude until the rms of the synthetic data was the same as measured in the real data.
Note again that we found evidence that the observed activity signature has been growing over time. Not only do the peridograms show that the 25-day peak increases in significance from set #1 to set #3, but the rms of the data also increased from 2.6 m s-1 in set #1 to 3.0 m s-1 in set #2, and finally to 3.2 m s-1 in set #3.
In Fig. 11 we present both the observed and simulated peridograms of the data for the whole dataset (set #123), as well as for set #1, set #2, set #3, and for sets #2 and #3 together (set #23). While in the simulated data the 18-day-period signal was always clear (even if often with an amplitude lower than the one seen for the 25-day-period signal), the situation in the real data is different: except for the first set of data (set #1), the 18-day-period signal is not observed in any other dataset. In other words, the simulations presented here suggest that the signal at 18 days should in principle have been clearly detected in sets #2 and #3 if it had the same amplitude and phase as found in set #1. Once again, this result does not support the scenario of the existence of an 18-day-period signal as reported in Jenkins et al. (2013).
3.6.3. Bayesian analysis including activity
To further test if the 18-day signal is supported by the new data, we performed a new Bayesian analysis following the same procedure as in Sect. 3.3.1 but using dataset #3 alone. This time, however, we modelled the 25-day-period activity signal as in Sect. 3.6.1, using two sines at Prot and Prot /2 (Boisse et al. 2011).
We then computed the Bayes factor between the following two models: an activity signal at ~25 d with a Keplerian at ~18 days and a ~25 d activity signal alone. The results indicate that, statistically, we cannot distinguish between the two models. This therefore strongly suggests that the 18-d planet, as found by Jenkins et al. (2013), is not confirmed (but not rejected either) by the new observations of dataset #3.
4. Analysing the residuals: planet detection limits
Assuming that the 18- and 25-day signals detected in set #1 are purely of stellar origin (induced by activity), we can test whether another signal exists in the data that can be attributed to a planet.
As a first note of caution, its important to note that at present we do not have the necessary tools to model the whole dataset in a correct, physical way. This is because the activity pattern in HD 41248 has been shown to be complex, inducing clear but variable signals in amplitude and (likely) in period as a function of time. No strictly periodic signal is thus valid when modelling the whole data, independently of the methodology used for the fit (e.g. frequentist analysis vs. Bayesian fittings). This implies that we cannot simply model the whole dataset with a series of Keplerian functions, for example.
To test the existence of additional signals, we then first removed the two signals in the first dataset by fitting a two-Keplerian function. The best fit found is similar to the one derived by Jenkins et al. (2013), but in our case we found an eccentricity of 0.38 for the 18-day-period Keplerian fit. Note that the 25-day-period signal is not statistically significant in dataset #1. However, since it has been shown to be coherent and has the same origin as the clear signal found in set #3, we decided to remove it.
For set #2, since no significant peaks appear in the RV periodogram, we did not remove any signal. For set #3 we again removed the 25-day signal and its first harmonic, as discussed in Sect. 3.6.1, while fixing P using the RV dataset itself.
After removing the different signals in the three different sets we analysed the joint data using the GLS. The results show that the highest peak appears at 193 days, but a permutation test shows that it is not significant (it has a false-alarm probability of 30%).
With this set of residuals we were also able to derive the detection limits of potential planets in the data. For this we used the same approach as in Mortier et al. (2012). The results of this analysis are presented in Fig. 12 and suggest that we can reasonably exclude planets with masses higher than 10 M⊕ in the period range up to ~100 days. This value decreases to ~4M⊕ if we restrict the period range to shorter than 10 days.
Note that the results do not significantly vary when the FWHM is used to fix P when removing the signal in set #3. In addition, no significant differences are observed when we only subtracted the 18-day-period signal in set #1.
5. Discussion and conclusions
In a recent paper, Jenkins et al. (2013) reported the existence of a system of two low-mass planets orbiting HD 41248 on almost circular orbits of periods ~18 and 25 days. In this paper we analysed this system after adding almost 160 new radial velocity points obtained with the HARPS spectrograph.
The results of this analysis do not allow us to confirm the planetary origin of the signals observed in the RV data of HD 41248 as previously suggested by Jenkins et al. (2013). The observed 25-day-period signal is almost exactly reproduced in the stellar activity index 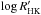 and in the FWHM of the HARPS CCF. This signal has a complex structure and varying amplitude with time, which make it difficult to model with present-day tools. This in turn renders the analysis of the putative 18-day periodicity difficult. However, although we cannot fully discard the existence of a stable, periodic signal at 18 days as expected from the presence of a planet, the different tests we conducted show that the current data (both the RV and activity/line-profile indicators) do not support its existence. In brief, the 25-day-period signal detected by Jenkins et al. (2013) is best explained as caused by stellar activity phenomena. Our analysis also suggests that the 18-day signal may have a similar origin.
and in the FWHM of the HARPS CCF. This signal has a complex structure and varying amplitude with time, which make it difficult to model with present-day tools. This in turn renders the analysis of the putative 18-day periodicity difficult. However, although we cannot fully discard the existence of a stable, periodic signal at 18 days as expected from the presence of a planet, the different tests we conducted show that the current data (both the RV and activity/line-profile indicators) do not support its existence. In brief, the 25-day-period signal detected by Jenkins et al. (2013) is best explained as caused by stellar activity phenomena. Our analysis also suggests that the 18-day signal may have a similar origin.
 |
Fig. 12 Minimum planetary mass against period. The solid line represents the detection limits. The dashed line indicates a circular planetary signal with an RV semi-amplitude of 1, 3, and 5 m s-1. |
We assume here that at a period of 25-days, a Neptune-like planet will not be able to enter into strong tidal or magnetic interactions with the star that might result in an activity signature with a period similar to the orbital period of the planet (Saar & Cuntz 2001; Shkolnik et al. 2003)12. We note that cases have been found where the orbital period seems to coincide, within the uncertainties, with the rotational period of the host star (Santos et al. 2003). If this is the case for HD 41248, the low amplitude of the signals and the complexity of the data will make it very difficult to confirm.
The complexity of the signals and the estimate for the rotational period of the star (~20 days – Table 2) led us to propose that the observed 18-day and 25-day signals may be caused by at least two different active regions/longitudes in a star presenting a strong differential rotation pattern. In this scenario, the 18- and 25-day-period signals would imply a differential rotation with an amplitude of about 25%. The Sun itself rotates at the equator with a rotational period of 26 days, while at the poles the value increases to ~35 days. Higher levels of differential rotation have been found in earlier-type stars (Barnes et al. 2005; Reiners 2006; Ammler-von Eiff & Reiners 2012; Reinhold et al. 2013)13. A difference in rotational period of 25% in the surface of HD 41248 seems thus perfectly plausible. This scenario would explain the existence of a growing 25-day period signal, caused by a growing active region that kept its phase throughout the entire period of our measurements, as well as the disappearance of the 18-day-period signal, if caused by an active region that disappeared (or became much weaker) and was positioned at a lower stellar latitude. It would also provide a simple explanation for the forest of peaks observed in dataset #2, if we assume that other active regions may have appeared and disappeared at other latitudes.
One alternative scenario to explain the observed complex pattern is related to the fact that the data have a very complex structure. It is clear from the plots that the activity patterns of this star present signatures of having evolved over the time span (more than ten years) of our measurements. An interesting hint may come, however, from the study of Lanza et al. (2003), where the authors analysed the rotational period of the Sun using the total solar irradiance (TSI) observed during the maximum of the eleven-year cycle. In the Sun, large spot groups have typical lifetimes of 10−15 days, while the rotational period is close to 25 days. The fact that the timescales for spot evolution are shorter than the rotational period, together with the appearance and disappearance of new spot groups in different rotational phases, renders the derivation of rotational periods (from the data) a complex task. As a result, Lanza et al. (2003) have found that during the 1999−2001 period when the Sun was close to solar maximum, it was impossible to properly retrieve the rotational period of the Sun using the TSI data, as the analysis yielded values from 24 up to 31 days. Given the complex pattern of data presented in the present paper for HD 41248, together with the uneven sampling, the presence of signals at 18 and 25 days may simply reflect a difficulty in fitting the data properly (at least using “simple” Keplerian functions).
This paper is a good example of how difficult the analysis of radial velocity data can be when searching for very low mass planets that induce low-amplitude signals that lie close to the measurement precision. The results also point out very clearly the importance of following a star for a sufficiently long period of time until one can confidently secure the characterisation of the whole system, including the effects of stellar activity. In this particular case, a proper sampling of the data (as in set #3) was fundamental to separate the sources of the radial velocity signals.
This study also showed that Bayesian analyses are not immune from false-positive detections, especially in the presence of stellar activity that might not be approximated by a series of Keplerian functions. The present case also demonstrated how important it is to use methodologies and tools to model and understand the signals produced by stellar activity. A complete characterisation of the data may need more detailed physical models of stellar activity and its impact on radial velocity measurements (e.g. Boisse et al. 2012), as well as of more sensitive diagnostic methods (e.g. Figueira et al. 2013). Without this, it will be very difficult to fully analyse these systems with any statistical/fitting procedure. The amplitudes of the RV signals caused by stellar activity are, even in a relatively inactive star such as HD 41248, often of the same order of magnitude as the expected signals from a low-mass planet. Alternatively, complementary spectroscopic measurements using other wavelengths (e.g. near-IR) may be useful to distinguish real planets from activity-induced signals (e.g. Huélamo et al. 2008; Prato et al. 2008; Figueira et al. 2010). A new generation of near-IR spectrographs is currently being developed (e.g. CARMENES and Spirou – Quirrenbach et al. 2014; Delfosse et al. 2013); they will open great perspectives in this domain.
Online material
List of stars in the sample, their V magnitudes, and coordinates (2000.0 equinox).
As we show below, a peak at this period is clearly seen in the FWHM, BIS−, and Vasy periodogram of set #1 as well (Fig. 5).
Gastine et al. (2014) suggested that the cooler stars may even present antisolar differential rotation, where the poles rotate faster than the equator.
Acknowledgments
We would like to thank N. Lanza for fruitful discussions. We acknowledge support from Fundação para a Ciência e a Tecnologia (FCT, Portugal) through FEDER funds in program COMPETE, as well as through national funds, in the form of grants reference PTDC/CTE-AST/120251/2010 (COMPETE reference FCOMP-01-0124-FEDER-019884), RECI/FIS-AST/0176/2012 (FCOMP-01-0124-FEDER-027493), and RECI/FIS-AST/0163/2012 (FCOMP-01-0124-FEDER-027492). This work was supported by the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953. N.C.S. and P.F. were supported by FCT through the Investigador FCT contract references IF/00169/2012 and IF/01037/2013 and POPH/FSE (EC) by FEDER funding through the program Programa Operacional de Factores de Competitividade − COMPETE. X. Dumusque was supported by the Swiss National Science Foundation. This work made use of the SIMBAD database.
References
- Adibekyan, V. Z., Delgado Mena, E., Sousa, S. G., et al. 2012a, A&A, 547, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Sousa, S. G., Santos, N. C., et al. 2012b, A&A, 545, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Adibekyan, V. Z., Figueira, P., Santos, N. C., et al. 2013, A&A, 560, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ammler-von Eiff, M., & Reiners, A. 2012, A&A, 542, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, J. R., Collier Cameron, A., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bensby, T., Feltzing, S., & Lundström, I. 2003, A&A, 410, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., & Usoskin, I. G. 2003, A&A, 405, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Pepe, F., Perrier, C., et al. 2012, A&A, 545, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Donati, J.-F., Kouach, D., et al. 2013, in SF2A-2013: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. L. Cambresy, F. Martins, E. Nuss, & A. Palacios, 497 [Google Scholar]
- Delgado Mena, E., Israelian, G., González Hernández, J. I., et al. 2014, A&A, 562, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz, R. F., Almenara, J. M., Santerne, A., et al. 2014, MNRAS, accepted [arXiv:1403.6725] [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N., & Monteiro, M. J. F. P. G. 2010, A&A, accepted [arXiv:1010.2616] [Google Scholar]
- Dumusque, X., Lovis, C., Ségransan, D., et al. 2011, A&A, 535, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Pepe, F., Lovis, C., et al. 2012, Nature, 491, 207 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Figueira, P., Marmier, M., Bonfils, X., et al. 2010, A&A, 513, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Figueira, P., Santos, N. C., Pepe, F., Lovis, C., & Nardetto, N. 2013, A&A, 557, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, D. A., & Valenti, J. 2005, ApJ, 622, 1102 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Forveille, T., Bonfils, X., Delfosse, X., et al. 2009, A&A, 493, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, K., Pfeiffer, M. J., & Bernkopf, J. 1998, A&A, 336, 942 [NASA ADS] [Google Scholar]
- Gastine, T., Yadav, R. K., Morin, J., Reiners, A., & Wicht, J. 2014, MNRAS, 438, L76 [NASA ADS] [CrossRef] [Google Scholar]
- Gonzalez, G. 1998, A&A, 334, 221 [NASA ADS] [Google Scholar]
- Gregory, P. C. 2011, MNRAS, 415, 2523 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, A&A, 482, 673 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huélamo, N., Figueira, P., Bonfils, X., et al. 2008, A&A, 489, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ida, S., & Lin, D. N. C. 2004, ApJ, 616, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Ivanov, E. V. 2007, Advances in Space Research, 40, 959 [Google Scholar]
- Jenkins, J. S., Tuomi, M., Brasser, R., Ivanyuk, O., & Murgas, F. 2013, ApJ, 771, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, J. A., Aller, K. M., Howard, A. W., & Crepp, J. R. 2010, PASP, 122, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2013, MNRAS, 434, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F., Rodonò, M., Pagano, I., Barge, P., & Llebaria, A. 2003, A&A, 403, 1135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011a, A&A, submitted [arXiv:1109.2497] [Google Scholar]
- Lovis, C., Ségransan, D., Mayor, M., et al. 2011b, A&A, 528, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Masana, E., Jordi, C., & Ribas, I. 2006, A&A, 450, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, A&A, accetped [arXiv:1109.2497] [Google Scholar]
- Mordasini, C., Alibert, Y., & Benz, W. 2009, A&A, 501, 1139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C., Alibert, Y., Benz, W., Klahr, H., & Henning, T. 2012, A&A, 541, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sozzetti, A., et al. 2012, A&A, 543, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mortier, A., Santos, N. C., Sousa, S., et al. 2013, A&A, 551, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Naef, D., Mayor, M., Benz, W., et al. 2007, A&A, 470, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nardetto, N., Mourard, D., Kervella, P., et al. 2006, A&A, 453, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F. A., Cristiani, S., Rebolo Lopez, R., et al. 2010, in SPIE Conf. Ser., 7735 [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prato, L., Huerta, M., Johns-Krull, C. M., et al. 2008, ApJ, 687, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Caballero, J. A., et al. 2014, in IAU Symp., 299, eds. M. Booth, B. C. Matthews, & J. R. Graham, 395 [Google Scholar]
- Reid, I. N. 2002, PASP, 114, 306 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A. 2006, A&A, 446, 267 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Cuntz, M. 2001, MNRAS, 325, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2001, A&A, 373, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2002, A&A, 392, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Udry, S., Mayor, M., et al. 2003, A&A, 406, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Bouchy, F., Mayor, M., et al. 2004a, A&A, 426, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Israelian, G., & Mayor, M. 2004b, A&A, 415, 1153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Bouchy, F., et al. 2007, A&A, 474, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Gomes da Silva, J., Lovis, C., & Melo, C. 2010, A&A, 511, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Bonfils, X., et al. 2011, A&A, 526, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shkolnik, E., Walker, G. A. H., & Bohlender, D. A. 2003, ApJ, 597, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Soubiran, C., Le Campion, J.-F., Cayrel de Strobel, G., & Caillo, A. 2010, A&A, 515, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., et al. 2011a, A&A, 526, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Udry, S. 2011b, A&A, 533, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sozzetti, A., Torres, G., Latham, D. W., et al. 2009, ApJ, 697, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Andersen, J., & Giménez, A. 2010, A&ARv, 18, 67 [Google Scholar]
- Tuomi, M., & Jones, H. R. A. 2012, A&A, 544, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., & Santos, N. 2007, ARAA, 45, 397 [Google Scholar]
- Udry, S., Mayor, M., Benz, W., et al. 2006, A&A, 447, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Lib. (Berlin: Springer) 350 [Google Scholar]
- Vaughan, A. H., & Preston, G. W. 1980, PASP, 92, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Line-profile analysis suite
In a recent paper, Figueira et al. (2013) analysed a series of line-profile indicators and discussed how these can help us pinpoint an RV signal created by stellar phenomena. These indicators and the associated statistical tests are now wrapped up in a simple code made available in the ExoEarths software webpage14. A living version of it can be accessed through a bitbucket repository15.
The program is run simply by calling it using python (i.e. python LineProf.py), with all the information being provided by an ASCII configuration file. No programming experience is thus required; we note, however, that the program was written in a modular way, so that it can be used as a building block for complex data analysis software.
The program automatically reads a list of FITS files (e.g. HARPS-N or HARPS-S), or ASCII data with the CCFs to analyse. It applies the indicators presented in Figueira et al. (2013), and evaluates the correlation between these indicators and RVs. Then 100 000 non-correlated datasets are obtained by performing a Fisher-Yates shuffle of the data pairs, and the correlation of the original set compared with the correlation of the shuffled set. The z-value is provided, along with the (Gaussian) probability that the correlation is drawn from an uncorrelated dataset. All these results are stored in ASCII files, and paper-quality plots for all the indicators selected are generated. The program can digest several dozens of files and do the complete analysis in a few minutes on a normal desktop/laptop.
All Tables
List of stars in the sample, their V magnitudes, and coordinates (2000.0 equinox).
All Figures
 |
Fig. 1 Distribution of metallicity (top) and effective temperature (bottom) for the stars in our sample. |
| In the text | |
 |
Fig. 2 Time series of the radial velocity, stellar activity, FWHM, and BIS. |
| In the text | |
 |
Fig. 3 Phase folded radial velocities of HD 41248 with the best fit Keplerian functions at ~18-days (top) and ~25 days (bottom). |
| In the text | |
 |
Fig. 4 Time series of the radial velocity and a linear fit to the data. The residuals are shown in the lower panel. |
| In the text | |
 |
Fig. 5 Periodograms of (from top to bottom) the RV, FWHM, BIS, |
| In the text | |
 |
Fig. 6 Same as Fig 5 for dataset #2. |
| In the text | |
 |
Fig. 7 Same as Fig 5 for dataset #3. |
| In the text | |
 |
Fig. 8 Same as Fig 5 for all the data. |
| In the text | |
 |
Fig. 9 Time series of the radial velocity, stellar activity, FWHM, and BIS for the period between JD = 2 456 580 and 2 456 640. |
| In the text | |
 |
Fig. 10 Periodograms of the residuals of the harmonics fit described in Sect. 3.6.1, making use of the RV (top) and FWHM (bottom) to fix the period used to subtract the RV signal and its harmonics. The dashed line indicates the position of the 18.36 day period. The horizontal line represents the 1% FAP. |
| In the text | |
 |
Fig. 11 Periodograms of the different datasets, both of the real (left) and simulated data (right). Vertical dashed lines represent the position of the 18- and 25-day signals presented in Jenkins et al. |
| In the text | |
 |
Fig. 12 Minimum planetary mass against period. The solid line represents the detection limits. The dashed line indicates a circular planetary signal with an RV semi-amplitude of 1, 3, and 5 m s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


