| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323116 | |
| Published online | 17 June 2014 | |
Tracing the ISM magnetic field morphology: the potential of multi-wavelength polarization measurements⋆
1
Institut für Theoretische Physik und Astrophysik,
Christian-Albrechts-Universität zu Kiel,
Leibnizstraße 15,
24098
Kiel,
Germany
e-mail: sreissl@astrophysik.uni-kiel.de; wolf@astrophysik.uni-kiel.de
2
Hamburger Sternwarte, Universität Hamburg,
Gojenbergsweg 112, 21029
Hamburg,
Germany
e-mail:
dseifried@hs.uni-hamburg.de
Received:
22
November
2013
Accepted:
25
March
2014
Aims. We present a case study to demonstrate the potential of multi-wavelength polarization measurements. The aim is to investigate the effects that dichroic polarization and thermal re-emission have on tracing the magnetic field in the interstellar medium (ISM). Furthermore, we analyze the crucial influence of imperfectly aligned compact dust grains on the resulting synthetic continuum polarization maps.
Methods. We developed an extended version of the well-known 3D Monte-Carlo radiation transport code MC3D for multi-wavelength polarization simulations running on an adaptive grid. We investigated the interplay between radiation, magnetic fields and dust grains. Our results were produced by post-processing both ideal density distributions and sophisticated magnetohydrodynamic (MHD) collapse simulations with radiative transfer simulations. We derived spatially resolved maps of intensity, optical depth, and linear and circular polarization at various inclination angles and scales in a wavelength range from 7 μm to 1 mm.
Results. We predict unique patterns in linear and circular polarization maps for different types of density distributions and magnetic field morphologies for test setups and sophisticated MHD collapse simulations. We show that alignment processes of interstellar dust grains can significantly influence the resulting synthetic polarization maps. Multi-wavelength polarization measurements allow one to predict the morphology of the magnetic field inside the ISM. The interpretation of polarization measurements of complex structures still remains ambiguous because of the large variety of the predominant parameters in the ISM.
Key words: techniques: polarimetric / methods: numerical / radiative transfer / dust, extinction / ISM: magnetic fields / ISM: structure
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Magnetic fields in the interstellar medium (ISM) affect astrophysical processes in various environments and scales in a crucial way. Especially the collapse of molecular clouds and the driving forces behind star formation are topics of ongoing research (Mouschovias & Ciolek 1999; Elmegreen 2000; McKee & Ostriker 2007). So far, vital questions about the role of magnetic fields remain unanswered.
The current paradigms of what drives star formation (magnetically supported (Mouschovias & Ciolek 1999) or turbulent models (Klessen et al. 2004) make different predictions of the magnetic field geometry. In models preferring magnetic support, gas falls parallel to the field lines. The magnetic field lines are frozen in to the matter, mass-dragged field lines form an hourglass morphology (Nakamura & Li 2005). In general, the magnetic field lines are expected to be smooth, with a regular structure.
The turbulent model, in turn, predicts a magnetic field that is too weak to resist the deformation by the local turbulent ISM environment. In this case, the magnetic field lines have an irregular and chaotic structure. Such irregularities should be easily recognizable in polarization measurements because of a correlation between polarization patterns and the density distribution.
To test the role of magnetic fields in the star formation process proper knowledge of the magnetic field strength and field morphology involved are required. Different methods are available for determining the magnetic field strength, such as the Chandrasekhar-Fermi method (Chandrasekhar & Fermi 1953; Crutcher et al. 2004), Zeeman measurements (e.g. Crutcher et al. 2008) and the field morphology by taking advantage of the polarization effects of non-spherical aligned dust particles inside the ISM (e.g. Girart et al. 1999; Lucas et al. 2004; Tang et al. 2010). However, from an observational point of view, the difficulty is that the reliability of polarization measurements and their interpretation depends on a wide range of physical parameters that are still discussed.
So far, knowledge about magnetic field morphologies in star formation regions has been accumulated by measurements of thermal dust re-emission by aligned dust grains at far-infrared (FIR) to sub-millimeter (sub-mm) wavelength (e.g. Frau et al. 2011). Although the polarization of light by interstellar dust was discovered in the middle of the last century (Hiltner 1949), its potential as a tool for tracing the magnetic field in the ISM is still high. Especially circular polarization is an often neglected source of additional information. In the mid-/far-infrared wavelength range where extinction is not dominated by scattering one can expect significant insights into the magnetic field structures by polarization measurements in combination with the ongoing research in grain alignment mechanisms. Existing theories of grain alignment (e.g. Davis & Greenstein 1951; Lazarian 2007) agree that rotating non-spherical dust grains align with their shorter axis parallel to the magnetic field direction. As a result, previously unpolarized light will be polarized by thermal dust remission and dichroic extinction perpendicular and parallel, respectively, to the magnetic field lines. This makes multi-wavelength observation on multiple scales a powerful tool completing our understanding of the fundamental physics of star formation processes.
The paper is arranged in the following order: in Sect. 2.1 in detail we present the theoretical basis for the considered mechanisms of dichroic polarization. In Sect. 2.2 the parameters of the applied dust grain model are described. We introduce the considered mechanisms of grain alignment in Sects. 2.3 and 2.4. To investigate the effects of polarization and alignment we apply these mechanisms in Sect. 3.1 to simple setups of various density and temperature distributions with analytically modeled field configurations. In Sect. 3.2 we extend the investigation to more realistic setups including sophisticated MHD collapse simulations. We discuss and summarize the effects observed in the resulting synthetic polarization maps in Sect. 4 and demonstrate that the magnetic field morphology can be traced from the complexity of the involved density distribution.
2. Basics
2.1. Dichroic polarization
As the source of polarization in the ISM we consider the effects of dichroic extinction
and re-emission of light by compact elongated dust grains aligned with the magnetic field
lines. Additional contributions to linear and circular polarization from scattering at
optical/near-infrared wavelengths are not considered. In the presence of magnetic fields
dust particles align with their minor axis parallel to the field direction. Previously
unpolarized light is polarized by passing non-spherical particles because of different
cross sections that are parallel and perpendicular to the particles alignment axis. This
results in linear and circular polarization. Our approach is to analyze the change in the
Stokes vector that is caused by aligned grains along the line of sight. The polarization
effects of extinction and re-emission are treated separately. By applying the Stokes
vector formalism to the radiative transfer equation we obtain a system of equations in
matrix form for the extinction: 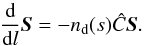 (1)The Stokes vector
S =
(I,Q,U,V)T changes along a distinct
pathway dl
that depends on the number density nd(s) of the dust
grains and their cross-section matrix Ĉ (see Appendix A). The parameter I corresponds to intensity, ± Q and ± U to a linear
polarization, and ±
V indicates counter-clockwise and clockwise circular
polarization, respectively. Here the +
Q – system is defined to be in the EW – direction on the plane
sky.
(1)The Stokes vector
S =
(I,Q,U,V)T changes along a distinct
pathway dl
that depends on the number density nd(s) of the dust
grains and their cross-section matrix Ĉ (see Appendix A). The parameter I corresponds to intensity, ± Q and ± U to a linear
polarization, and ±
V indicates counter-clockwise and clockwise circular
polarization, respectively. Here the +
Q – system is defined to be in the EW – direction on the plane
sky.
The temperature Td of the dust grains leads to an
additional contribution to intensity and linear polarization as a result of its thermal
re-emission. However, the characteristic of the re-emitted light depends on the magnetic
field direction, the absorption properties, and the geometry of the dust particle. The
angle of highest re-emission is perpendicular to the magnetic field. For the source term
of the radiative transfer equation we consider the dust grains to be perfect blackbody
radiators: 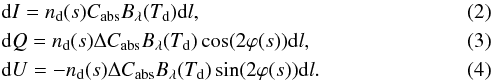 Here,
Bλ(Td)
is the Planck function and Cabs the cross section for absorption.
For the definition of the angle ϕ see Fig. 1.
The V
parameter remains unaffected by thermal re-emission. Here, the Stokes vector and the dust
grains are considered to be in the same frame of reference. Below we discuss the problems
of separate coordinate systems and their transformation in detail.
Here,
Bλ(Td)
is the Planck function and Cabs the cross section for absorption.
For the definition of the angle ϕ see Fig. 1.
The V
parameter remains unaffected by thermal re-emission. Here, the Stokes vector and the dust
grains are considered to be in the same frame of reference. Below we discuss the problems
of separate coordinate systems and their transformation in detail.
For non-spherical particles the cross sections for absorption, extinction, and birefringence vary with respect to the incident angle and polarization angle of the passing light rays. Subsequently, dichroic extinction and thermal re-emission mechanisms lead to linear as well as circular polarization, depending on the number density nd, the topology of the magnetic field B, and the dust temperature Td. Therefore, the polarized light carries with it the information of the projected configuration of the magnetic field and the local dust parameter along the line of sight.
 |
Fig. 1 Geometrical configuration for oblate dust grains with their shorter axis perfectly aligned (PA) with the direction of the magnetic field B. The angle ϕ is defined by the projection of B into the Q− coordinate system of the Stokes vector and the inclination angle ϑ is made by the direction of propagation k and the plane of rotation perpendicular to B. |
The degree of linear and circular polarization depends on optical depth and temperature. In low optical depth regions the dominating factor of linear polarization is the dust grain temperature because of thermal re-emission. In the intermediate region where the ISM starts to become optically thick, dichroic extinction can lead to high values of the Q, U and V parameter. However, with increasing optical depth, U and V fast approach zero and the light remains polarized in Q, while the intensity I decreases. The exact degree of polarization depends on the interplay of all the physical parameters inside the ISM along the line of sight.
2.2. Dust model
Interstellar dust grains are a composite of materials of distinct size distributions and complex shapes. The problem of modeling the cross-section behavior depends on the particle shape, size, material, wavelength, and the angles of incident radiation. The composition and computation of the optical properties of these dust grains are still a matter of debate.
We calculated the optical properties of the dust according to the dust model by Mathis et al. (1977). The MRN model, named after its authors, consists of a compositions of silicate and carbon distributed with a power-law distribution of n(a) ∝ a-3.5 in a range of effective radii ai with sharp cut-offs at amin = 5 nm and amax = 250 nm. However, the MRN model is missing the extinction features in the FUV and UV regions because of absent polycyclic aromatic hydrocarbons (PAHs) at the small-size end of the distribution.
Li & Greenberg (1997) proposed a dust model with a silicate – PAH mixture that satisfies the interstellar extinction, polarization, and abundance constraints. This model required hypothetical optical constants to fit the extinction in the far-UV and is of no practical use. Draine & Li (2001) and Li & Draine (2001) presented a model in agreement with observations by using optical properties of the PAHs based on laboratory data. But this model requires an unrealistic amount of certain elements inside the ISM, which is inconsistent with solar abundances.
Currently, there is no dust model available that simultaneously fits all extinction, re-emission and, abundance constraints. However, in the desired range of wavelengths from 7 μm to 1 mm, the MRN dust model still agrees with observations of the ISM extinction curve. Furthermore, because of its power law-size distribution, the MRN model predicts a larger amount of small and partly aligned dust species to dominate the extinction. The degree of polarization is determined by large and rare grains with a higher alignment efficiency. This is consistent with the findings of Davis & Greenstein (1951) and Hong & Greenberg (1980) which makes the MRN model an excellent candidate for our investigations. The application of different dust models would primarily only result in a shift in the characteristic features of graphite and silicate depending on composition or in additional absorption and emission lines if we were to choose a dust model with a PAH component.
For each wavelength we calculated 150 absorption and extinction efficiencies
logarithmically distributed over the range of effective radii. We uses a composition of
62.5% silicate and
37.5% graphite. The graphite
component is highly anisotropic in nature. Therefore, the refractive index depends on the
orientation of light relative to the symmetry axis of the graphite. To take into account
the anisotropic structure, we applied the  approximation as presented in Draine & Malhotra
(1993). We assumed both materials to have similar size distributions and
alignment behaviors.
approximation as presented in Draine & Malhotra
(1993). We assumed both materials to have similar size distributions and
alignment behaviors.
The corresponding cross sections are defined as the product of an efficiency factor and the geometric cross section Cλ = πa2Qλ, where a is the radius of a spherical grain of equivalent volume. The mass of the particles does therefore not depend on the particle shape.
We calculated the efficiencies for extinction of the grains using the discrete dipole approximation (DDA). The idea behind this approximation is to model the shape of the dust grains with a distinct number of dipoles and material parameter as it is implemented in the well-tested program DDSCAT 7.2 (Draine & Flatau 2012). We used the refraction indices of silicate and graphite as published in (Weingartner & Draine 2000).
We weighted the efficiencies for each wavelength according to the power-law distribution
to derive the average cross sections over all effective radii: 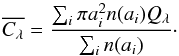 (5)We assumed a gas-to-dust
ratio of 100:1.
(5)We assumed a gas-to-dust
ratio of 100:1.
2.3. Perfect grain alignment
In the case of perfect grain alignment (PA) the cross sections are only dependent on the two angles defined by the direction of the incident light and the orientation of the coordinate system of the Stokes vector with respect to the direction of the magnetic field B.
In the general case, the aligned grain and the incident light are not in the same frame
of reference. To rotate the Stokes parameter relative to the coordinate system of the dust
grain, Q and
U of the
Stokes vector have to be adjusted. The I and V components remain invariant under rotation. We
defined the angle ϕ to be the one between the magnetic field vector
projected into the coordinate system of the Stokes vector and the −Q direction (see Fig.
1). To rotate the Stokes vector by an arbitrary
angle we applied the rotation matrix R and R-1: 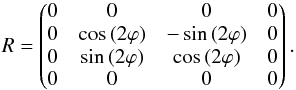 (6)The second angle,
Θ, is defined by the
direction of wave propagation k of the incident light and the
plane perpendicular to the magnetic field vector. To correct the cross-sections that
depend on the tilt one finds (Greenberg 1968)
(6)The second angle,
Θ, is defined by the
direction of wave propagation k of the incident light and the
plane perpendicular to the magnetic field vector. To correct the cross-sections that
depend on the tilt one finds (Greenberg 1968)
![\begin{eqnarray} \label{eq:Qsum} &&\overline{C_{\lambda}}(\Theta)= \frac{1}{2} \left[ \overline{C}_{\lambda,\bot}+\overline{C}_{\lambda,||}+ \left(\overline{C}_{\lambda,\bot}-\overline{C}_{\lambda,||}\right) \cos^2(\Theta) \right], \\ \label{eq:Qdiff} &&\Delta \overline{C_{\lambda}}(\Theta)= \frac{\overline{C}_{\lambda,\bot}-\overline{C}_{\lambda,||}}{2} \sin^2(\Theta). \end{eqnarray}](/articles/aa/full_html/2014/06/aa23116-13/aa23116-13-eq44.png) However,
perfect alignment of the dust grains does not take into consideration any deviation due to
the local physical conditions of the ISM and remains an ideal approximation.
However,
perfect alignment of the dust grains does not take into consideration any deviation due to
the local physical conditions of the ISM and remains an ideal approximation.
2.4. Imperfect grain alignment
The perfect alignment of dust grains is hindered by gas-grain collisions. Depending on the local conditions in the ISM, dust grains are partially misaligned. However, a consistent theory of grain alignment is still lacking. The proposed mechanism is based on alignment e.g. due to paramagnetic relaxation (Davis & Greenstein 1951) or radiative torques (RAT), the grain interaction with the radiation field Hoang et al. (2007). However, an analytical alignment distribution function for the RAT alignment of dust grains is still missing. The required magnetic field strength for the RAT alignment to be efficient is still debated as well (see Hughes et al. 2009).
Therefore, we implemented the classical imperfect Davis-Greenstein (IDG) mechanism to
model the impact of imperfectly aligned dust grains on our radiative transfer and
polarization simulations. We assumed silicate and graphite grains to be equally affected
by IDG. For imperfectly aligned dust grains the cross sections depend on the angular
distribution (Jones & Spitzer 1967)
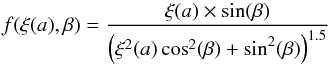 (9)of
the cone angle β between the angular momentum vector of the dust
grain and the magnetic field vector (see Fig. 2). The
angle between the direction of propagation and the magnetic field is Ω. The quantity Θ is no longer constant but depends on
β,
Ω and the precession angle
ω. The
angular distribution of β is determined by the grain alignment parameter:
(9)of
the cone angle β between the angular momentum vector of the dust
grain and the magnetic field vector (see Fig. 2). The
angle between the direction of propagation and the magnetic field is Ω. The quantity Θ is no longer constant but depends on
β,
Ω and the precession angle
ω. The
angular distribution of β is determined by the grain alignment parameter:
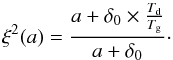 (10)Here, a is the effective radius,
Td the dust temperature, and
Tg the kinetic gas temperature. The grain
alignment parameter depends on the ratio Td/Tg
and δ0 and acts as a threshold between
perfectly aligned and imperfectly aligned dust grains. For grains with an effective radius
below this threshold δ0, the cone angle distribution
f(ξ(a),β)
behaves like a delta function and the shorter axis parallel to the particle is aligned to
the magnetic field direction. With decreasing δ0 more dust grain species become
disaligned and behave like spherical particles. Subsequently, if kinetic gas temperature
Tg and dust temperature Td have the same
value, no alignment can take place. With the dimensionless material constant
κ = 2.5 ×
10-12 (Davis &
Greenstein 1951), the magnetic field strength B, and the number density
of the gas nH, one can derive the parameter
(10)Here, a is the effective radius,
Td the dust temperature, and
Tg the kinetic gas temperature. The grain
alignment parameter depends on the ratio Td/Tg
and δ0 and acts as a threshold between
perfectly aligned and imperfectly aligned dust grains. For grains with an effective radius
below this threshold δ0, the cone angle distribution
f(ξ(a),β)
behaves like a delta function and the shorter axis parallel to the particle is aligned to
the magnetic field direction. With decreasing δ0 more dust grain species become
disaligned and behave like spherical particles. Subsequently, if kinetic gas temperature
Tg and dust temperature Td have the same
value, no alignment can take place. With the dimensionless material constant
κ = 2.5 ×
10-12 (Davis &
Greenstein 1951), the magnetic field strength B, and the number density
of the gas nH, one can derive the parameter
![\begin{equation} \delta_{\rm{0}} = 8.23\times 10^{31} \frac{\kappa B^2}{n_{\rm{g}} T_{\rm{d}} \sqrt{T_{\rm{g}}}} [\rm{m}]. \label{eq:delta} \end{equation}](/articles/aa/full_html/2014/06/aa23116-13/aa23116-13-eq57.png) (11)Values of
δ0 up to a factor of 100 higher can be
obtained by including superparamagnetic relaxation due to ferromagnetic inclusions or dust
grains surrounded by an ice mantle (Jones &
Spitzer 1967; Duley 1978; Sorrell 1994). With an increasing effective radius,
ξ2(a) approaches unity
for lower values of a. Thus, particles with an effective radius of
a>δ0
hardly contribute to the net polarization while their extinction remains unaffected.
(11)Values of
δ0 up to a factor of 100 higher can be
obtained by including superparamagnetic relaxation due to ferromagnetic inclusions or dust
grains surrounded by an ice mantle (Jones &
Spitzer 1967; Duley 1978; Sorrell 1994). With an increasing effective radius,
ξ2(a) approaches unity
for lower values of a. Thus, particles with an effective radius of
a>δ0
hardly contribute to the net polarization while their extinction remains unaffected.
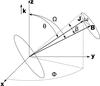 |
Fig. 2 Geometrical configuration of a rotating oblate dust grain with angular momentum J no longer in alignment with the magnetic field B. The precession of J around B is defined by the precession angle ω and the cone angle β. The direction of propagation k is parallel to the z-axis. The inclination angle θ is not constant but varies with ω, the angle Ω between k, and magnetic field, and β. |
The cross sections can be calculated by averaging over size distribution n(a),
precession angle ω, and cone angle distribution f(ξ(a),β).
For oblate dust particles one obtains 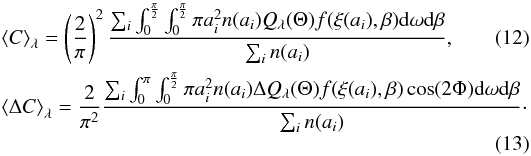 Since
polarization depends on the difference of cross sections for wobbling dust grains, certain
orientations cancel each other out. Therefore, ⟨ΔC⟩λ must be weighted
with cos(2Φ) where the factor
can be expressed as a function of β, Θ and ω (for details see Hong & Greenberg 1980; Das et al.
2010).
Since
polarization depends on the difference of cross sections for wobbling dust grains, certain
orientations cancel each other out. Therefore, ⟨ΔC⟩λ must be weighted
with cos(2Φ) where the factor
can be expressed as a function of β, Θ and ω (for details see Hong & Greenberg 1980; Das et al.
2010).
 |
Fig. 3 3D plots for the toroidal (panel a), Eq. (17)), hourglass (panel b), Eq. (18)), quadrupole (panel c), Eq. (19)), and helical (panel d), superposition of Eq. (17) and Eq. (18)) magnetic field morphologies. |
Physical parameters for the presented ideal Bonnor−Ebert sphere setups and MHD setups.
3. Applications
We aim to model the underlying processes that lead to linear and circular polarization of previously unpolarized light to reveal the morphology of the magnetic field in the ISM. We developed an extended version of the well-established 3D Monte Carlo radiative transfer code MC3D (Wolf 2003) and implement the equations of Sect. 2.1 for dichroic absorption and re-emission as well as the grain alignment mechanisms of Sects. 2.3 and 2.4 as an optional feature. To increase performance and reduce the amount of data, we applied an adaptive Cartesian grid with an octree-structure. The grid automatically refines the cell structure in regions with higher density distribution and optical depth, respectively, inside the model space. The dust temperature is predetermined by the model setup.
The probability for a scattering event is completely determined by the ratio of Csca/Cext. Since we operate in a regime of wavelengths of 7 μm−1 mm where this ratio strongly decreases from 1.3 × 10-3 to 7.9 × 10-9, the contribution of scattering is marginal even in optically thick regions. Hence, we applied an algorithm purely based on ray-tracing in contrast to a more time consuming Monte-Carlo – scattering algorithm to calculate the polarization maps. Each grid cell contains a unique set of parameters. As a first step the cross sections for all cells in the model space were re-calculated for all required angles and wavelength. Then the positive and negative intensity contributions were added up along given paths. The reference frame of the Stokes parameter is determined by the first point of interaction with the ISM inside the model space. Finally, all Stokes vectors were rotated into the coordinate system of the model space.
According to the Stokes formalism, linear polarization is determined by the degree of
linear polarization Pl and its position angle in the plane of
the sky:  The
degree of circular polarization Pc is defined to be
The
degree of circular polarization Pc is defined to be 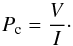 (16)The grain temperature
only weakly depends on the effective radius \citep{ 1980A&A....88..194H} and on
elongation for an aspect ratio of \begin{lxirformule}$s \leq 2$\end{lxirformule} (Voshchinnikov et al. 1999). Hence, we applied a constant
temperature to the entire ensemble of dust grains weighted over the effective radii. Since
our main focus is not on the grain parameter itself, we applied a fixed ratio of
s = 2 for the
oblate dust grains to all setups. Higher aspect ratios would result in higher peak values
and more contrast in the maps of linear and circular polarization.
(16)The grain temperature
only weakly depends on the effective radius \citep{ 1980A&A....88..194H} and on
elongation for an aspect ratio of \begin{lxirformule}$s \leq 2$\end{lxirformule} (Voshchinnikov et al. 1999). Hence, we applied a constant
temperature to the entire ensemble of dust grains weighted over the effective radii. Since
our main focus is not on the grain parameter itself, we applied a fixed ratio of
s = 2 for the
oblate dust grains to all setups. Higher aspect ratios would result in higher peak values
and more contrast in the maps of linear and circular polarization.
 |
Fig. 4 Linear polarization (left) and circular polarization (right) of ideal setup BEtoro with inclination angles of 3° (top), 45° (middle) and 87° (bottom), a constant dust temperature Td = 15 K, a characteristic radius Rc = 1100 AU and a density n0 = 1013 m-3 in the center. We added an offset angle of 90° to the vectors of linear polarization to match the projected magnetic toroidal field. The dust particles are perfectly aligned. |
3.1. Ideal test − setups
We began with analytical models assuming ideal conditions and included our dust model as presented in Sect. 2.2. The density profile is spherical and follows a Bonnor−Ebert profile (Bonnor 1956; Ebert 1955) with a characteristic radius of Rc = 1100 AU and a central number density of n0 = 1013 m-3 typical of protostellar cores (Launhardt & Henning 1997; Galli et al. 2002; Sipilä et al. 2011). The side length of the model space is 0.2 pc. All models and relevant physical parameter are listed in Table 1. A 3D plot of all considered magnetic field morphologies is provided in Fig. 3.
In the first setup (BEtoro) we assumed a constant temperature of
Td = 15
K for the dust component and applied a toroidal magnetic field
morphology 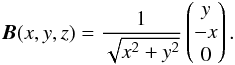 (17)The dust particles were
considered to be perfectly aligned (PA).
(17)The dust particles were
considered to be perfectly aligned (PA).
In the following, we include the effects of imperfectly aligned dust grains as described in Sect. 2.4. Here, the additional parameter of dust temperature Tg and field strength B0 are required. We chose the parameter B0 for a Bonnor−Ebert sphere with an average temperature of Tg = 20 K to keep the mass-to-flux ratio consistent with recent observations (Wolf et al. 2004; Falgarone et al. 2008; Girart et al. 2009; Beuther et al. 2010). We varied the temperature such that Tg was in the range 10 K−25 K and Td is in the range 5 K−15 K with the higher temperature in the center for later research on the impact of IDG grain alignment. This range of temperatures agrees well with theoretical models (e.g. Galli et al. 2002; Keto & Field 2005; Sipilä et al. 2011) and observational data (e.g. Launhardt & Henning 1997).
For the magnetically supported model of star formation a characteristic hourglass field is predicted by theory (e.g. Galli & Shu 1993) and MHD simulations (e.g. Banerjee et al. 2006). An originally parallel magnetic field morphology turns into an hourglass morphology since the tension of the bent magnetic field lines provides support. Therefore, a preserved orientation in the polarization maps on multiple scales should be a strong indication for a significant contribution of the magnetic field to the star formation process. Recent polarization measurements (Frau et al. 2011; Stephens et al. 2013) strongly indicate the existence of such hourglass structures. However, for a definitive conclusion measurements of such magnetic field structure are still too rare.
The problem may be resolved by exploring the influence of inclination angle and grain alignment on synthetic polarization maps for different field morphologies. In the next setups we compare the pattern of linear polarization and circular polarization for an hourglass and a quadrupole field morphology dependent on inclination angle.
In contrast to exact physical solutions (e.g. Galli
& Shu 1993; Li & Shu 1996)
for the models BEhour1 and BEhour2 we approximated the hourglass morphology of the
magnetic field by an analytical function (see Fig. 3b) 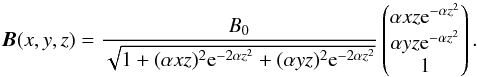 (18)The scaling parameter
B0 is for the field strength and is listed
in Table 1 for each model. Here, the quantity
α is a
shape parameter to adjust the field geometry. Higher values of α will lead to denser
magnetic field lines toward the center region. This geometry allows for an accurate and
expedient treatment of ambipolar diffusion to demonstrate the effects of different
inclination angles to the maps of linear and circular polarization. As shape parameter for
the magnetic field we used α =
10. The quadrupole field for the models BEquad1 and BEquad2 is defined as follows
(see Fig. 3c):
(18)The scaling parameter
B0 is for the field strength and is listed
in Table 1 for each model. Here, the quantity
α is a
shape parameter to adjust the field geometry. Higher values of α will lead to denser
magnetic field lines toward the center region. This geometry allows for an accurate and
expedient treatment of ambipolar diffusion to demonstrate the effects of different
inclination angles to the maps of linear and circular polarization. As shape parameter for
the magnetic field we used α =
10. The quadrupole field for the models BEquad1 and BEquad2 is defined as follows
(see Fig. 3c): 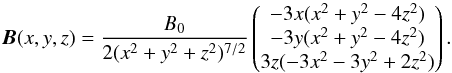 (19)Cloud cores are observed
to rotate (e.g. Goodman et al. 1993). It is
expected for a magnetic field in a rotating cloud to have a toroidal component as well. We
assumed the axis of rotation to be parallel to the predominant direction of the
hourglass-shaped magnetic field lines and modeled the morphology as a normalized
superposition of Eqs. (17) and (18). The resulting magnetic field morphology
for models BEhelic1
and BEhelic2 is
plotted in Fig. 3d.
(19)Cloud cores are observed
to rotate (e.g. Goodman et al. 1993). It is
expected for a magnetic field in a rotating cloud to have a toroidal component as well. We
assumed the axis of rotation to be parallel to the predominant direction of the
hourglass-shaped magnetic field lines and modeled the morphology as a normalized
superposition of Eqs. (17) and (18). The resulting magnetic field morphology
for models BEhelic1
and BEhelic2 is
plotted in Fig. 3d.
We calculated the inclination-angle-dependent polarization maps of linear and circular polarization resulting from thermal re-emission and dichroic extinction. Simultaneously, we obtained the corresponding intensity maps of the optical depth and net polarization.
3.2. MHD − setups
To test the results of our code against realistic scenarios we used our code to post-process an MHD simulation (MHDsim1 and MHDsim2) of a collapsing magnetized molecular cloud presented in Seifried et al. (2013). We took a snapshot of a run with a core mass of 300 M⊙ that has a diameter of 0.24 pc, and a magnetic field initially parallel to the z-axis (for more details we refer to Seifried et al. 2013). The snapshot is taken 11.8 kyr after the first protostar has formed. The magnetic field is in a range of B ∈ [8.8 × 10-10 T;9.4 × 10-5 T]. However, the dust temperature is not calculated from the radiation field of the newly born stars but is calculated in the MHD collapse simulation itself (for details about the heating and cooling processes see Banerjee et al. 2006). We just probed the inner core with our ray-tracing algorithm, leading to a side length of 7734 AU. The highest temperature in this area is below the sublimation temperature of the silicate grains and graphite grains, respectively, so that each cell contributes fully to the resulting maps of optical depth, intensity, linear polarization, and circular polarization. We adjusted the adaptive grid to maintain the original data structure of the simulation.
4. Discussion
4.1. Impact of different inclination angles
Figure 4 shows the degree of circular and linear polarization overlaid with the normalized orientation vectors for three different inclination angles for the model setup BEtoro. For inclination angles of 0° and 90°, respectively, the toroidal magnetic field has no crossing field-lines along the line of sight. The same holds for the hourglass and quadrupole morphology, respectively (see Figs. 3a−c). As expected, the resulting degree of circular polarization is zero (see Eq. (A.2)). For an inclination angle of 3° the toroidal magnetic field is still radially symmetric. However, we find a recognizable pattern of circular polarization. The underlying toroidal morphology is not yet apparent. In model setup BEtoro, the temperature is constant and the dust grains are perfectly aligned. For a low inclination angle near zero the angle of aligned dust grains with respect to the line of sight remains constant, leading to an expected pattern of almost homogenous linear polarization. In this case deviations in the pattern of linear polarization are just a result of the 3D density distribution and inclination angle. With increasing inclination angle, the angle of grain orientation with respect to the line of sight remains constant along the projected symmetry axis of the toroidal field, whereas in the outer regions, the dust grain orientation reaches 90° and ΔCabs decreases. As expected, this results in a low degree of linear polarization in the outer regions for an inclination angle of 87°, demonstrating the accuracy of the applied radiative transfer code. The behavior of the degree of linear and circular polarization dependent on grain alignment and inclination angle is presented in Fig. 8. This figure is below discussed in detail.
 |
Fig. 5 Same as in Fig. 4 for model BEhour2. The characteristic radii for the temperature distribution are adjusted to keep the gas temperature and dust temperature in a range of 10 K−25 K and 5 K−15 K, respectively. The dust particles are imperfectly aligned. |
 |
Fig. 7 Same as in Fig. 6 for model BEhelic2 with inclination angles of 0° (top), 45° (middle) and 90° (bottom). |
Figures 6 and 5 show the degrees of linear and circular polarization for three different inclination angles for the model setup BEquad2 and BEhour2. Here, the degree of polarization also depends on dust temperature Td, gas temperature Tg, and alignment mechanism, leading to an inhomogeneous polarization pattern. With increasing inclination angle the hourglass morphology and quadrupole morphology (see Figs. 3b and c), respectively, becomes apparent. However, for an inclination angle as low as 3°, the underlying field morphology remains ambiguous. In both configurations the vector field of linear polarization shows a similar radial symmetric pattern. Both setups BEhour2 and BEquad2 would be indistinguishable by measurements of linear polarization alone. Most important, the same pattern would be observable for a variety of field morphologies (e.g. a dipole field). In contrast to the ambiguities in the pattern of linear polarization, the maps of circular polarization remain unique for each field morphology, as we show in the right columns in Figs. 6 and 5. Here, we demonstrate that the hourglass and quadrupole fields are distinguishable even for observations with low inclination angels because of the unique symmetry axis of each morphology which results in the characteristic pattern of circular polarization.
In Fig. 7 we present the degree of circular polarization and degree of linear polarization overlaid with the normalized position vectors for the model setup BEhelic2. Since BEhelic2 has no rotation symmetry, crossing magnetic field lines along any line of sight and pattern of circular polarization are present even for inclination angles of 0° and 90°. Note that the presence of crossing field lines does not necessarily lead to a low degree of linear polarization. As long as the directions of the field lines are not perpendicular to each other, they can still contribute to the net polarization due to dichroic extinction. Furthermore, nearby hot but optically thin regions can also rapidly build up linear polarization because of thermal remission.
Because of its helical symmetry, the initial symmetric pattern of BEhelic2 in the synthetic linear and circular polarization maps becomes distorted while rotating the model space toward higher inclination angles. Here, we see toroidal patterns in the top rows of Fig. 4 similar to those in Fig. 7 for low inclination-angles. The same would be observable if the dust grains in model BEtoro were imperfectly aligned. A similar behavior can be found for high-inclination angles in the model setups BEhour2 and BEhelic2, as shown in the bottom rows of 7 and Fig. 5. Although the patterns of linear polarization deviate in both cases, the orientation vectors match quite well, which provide the possibility for misinterpretations under realistic observational conditions. Again, unique patterns in circular polarization measurements allow an unambiguous identification of the predicted magnetic field morphology independent of inclination angle.
4.2. Influence of alignment mechanism
In Fig. 8 we present plots of the degree of linear (top) and circular (bottom) polarization as a function of the inclination for models with perfect alignment (BEtoro, BEquad1, BEhour1, and BEhelic1 on the left) and imperfect alignment (BEquad2, BEhour2, and BEhelic2 on the right). In spherical models the degree of circular polarization is expected to be symmetrical with respect to the x-axis. But for the models BEhelic1 and BEhelic2 the inherent helical symmetry of the magnetic field morphology becomes apparent and the mirror symmetry in the plot is broken (see black lines and bottom row in Fig. 8). Perfectly aligned grains lead to an unrealistically high degree of linear polarization. One approach to solve this problem is provided in Fiege & Pudritz (2000) where the cross sections of the dust and the alignment efficiencies were modeled by a single parameter to adjust the degree of linear polarization to observational data. However, this is without any physical motivation. As we demonstrate here, lower degrees for the highest linear polarization of ≈15% as required by observational data (Girart et al. 1999; Gonçalves et al. 2005; Davidson et al. 2011) can be achieved by applying a realistic dust grain model and alignment mechanism to radiative transfer calculations. For the exemplary case with a wavelength of 811 μm, as we show in Fig. 8 on the right-hand side, the peak values and mean values of linear polarization behave very well in the observed limitations. So far, there is no observational data available for the limitations of circular polarization caused by dichroism.
Beside the reduction in the maximum degree of linear and circular polarization the usage of the IDG mechanism leads to some additional effects. Compared with Fig. 4, toward the center region in Figs. 6, 5 and 7, the IDG mechanism results in depolarization for the linear polarization. The same behavior can be found for the circular polarization because of the adjustment of the parameter δ0 with respect to the higher density and and temperatures (see Eq. (11)).
However, even with circular polarization measurements the interpretation of linear polarization data remains difficult in a complex environment because of other effects of ambiguity. In each cell of the model space the linear polarization is determined by dichroic extinction and thermal re-emission perpendicular to each other. Depending on the cross sections of extinction and absorption, the process of polarization can be dominated either by extinction or thermal re-emission (see Appendix B). Since the cross sections are functions of a distinct set of physical parameters (wavelength, alignment efficiency, orientation and strength of the magnetic field) in each region inside the ISM, this can lead to a flip of the orientation angle by 90°.
In Fig. 10 we compare the effects of grain alignment in a complex environment provided by MHD simulations (see Sect. 3.2) for an exemplarily chosen wavelength of λ = 248 μm. With perfectly aligned dust grains (MHDsim1) the resulting intensity and linear polarization pattern is completely dominated by the outer regions with a thin and hot gas phase. With the exception of the dense core in both cases (MHDsim1 and MHDsim2), the model space is almost completely optically thin at 248 μm. With the IDG mechanism, acting on the dust grains, a high number density nd and the resulting lower value of the parameter δ0 leads to a depolarization in the central region. Due to the averaging of the cross sections according to the IDG mechanism the cross sections decrease and the dust grains behave more like spherical particles independent of the angle with respect to the incident light-ray, and the degree of linear polarization is reduced. As a result of this, the intensity and optical depth is lower and the optical depth is smoother than for PA aligned grains (see Figs. 9 and 10). The effect of the 90° flip can be observed depending on grain alignment in the pattern of the linear polarization vectors. However, the density, temperature, and the magnetic field structure are far too complex in both cases to derive any meaningful interpretation about the underlying magnetic field morphology from the pattern of linear and circular polarization. We plan to investigate this problem in a forthcoming paper.
 |
Fig. 8 Resulting degrees of linear polarization Pl (top) and circular polarization Pc (bottom) for perfectly (left) and imperfectly (right) aligned dust grains depending on inclination angle at a wavelength of 811 μm for the ideal Bonnor−Ebert sphere setups as presented in Sect. 3.1. For the degree of linear polarization Pl the mean values are plotted as solid lines and the peak values are in dashed lines. For circular polarization Pc the lowest values are plotted as solid lines, the highest values as dashed lines. The details of all model setups are listed in Table 1. |
 |
Fig. 9 Resulting peak values (dashed lines) and mean values (solid lines) of intensity I, optical depth τ, and degree of linear polarization Pl for the MHD − simulation as presented in Sect. 3.2. For circular polarization polarization Pc the lowest values are plotted as solid lines and the highest values as dashed lines. The red lines correspond to the setup with perfectly aligned dust grains (MHDsim1) and the blue lines to the setup with imperfectly aligned grains (MHDsim2). |
4.3. Effect on multi-wavelength polarization maps
Figure 9 shows the intensity, optical depth, polarization, and circular polarization of the post-processed MHD collapse simulation (MHDsim2) as a function of wavelength for PA and IDG alignment. The intensity and optical depth (left panels) follow the dependence determined by the characteristic features of the applied silicate − graphite dust model. The characteristic mid-IR silicate bump at 10 μm leads to an increased optical depth and a diminished intensity due to extinction. This behavior is also recognizable in the curves of linear and circular polarization (right panels). The degree of circular polarization also depends on sin and cos terms (see Eq. (A.3)). This results in an oscillation in the minimum and maximum degree of circular polarization as a function of wavelength. As mentioned in the previous discussion, the degree of linear polarization in model MHDsim1 amounts to 100%, which is unrealistically high. In the case of IDG alignment (MHDsim2) the trend in the curves of intensity and optical depth remain unaffected. However, as demonstrated before, the IDG alignment mechanism changes the degree of linear and circular polarization dramatically. We did not smooth our synthetic data over beam size or angular resolution to mimic realistic observational conditions or existing equipment. Nevertheless, for the mean value, the degree of linear polarization corresponds very well to the limitations derived from observation (Girart et al. 1999; Gonçalves et al. 2005; Davidson et al. 2011).
In Fig. 11, we show maps of the optical depth overlaid with vectors of linear polarization for three distinct wavelengths with perfectly aligned grains (MHDsim1) in comparison with imperfectly aligned grains (MHDsim2). The border of optically thin and optically thick regions is indicated by contour lines. With increasingly longer wavelengths, the transition between the regimes of wavelength-dominated by dichroic extinction and thermal re-emission manifests itself in a flip of the orientation angles of 90°, as described before. However, a detailed comparison of maps at different wavelengths reveals several polarization vectors with a continuous rotation. The effect of thermal re-emission depends on both dust temperature and number density. Regions with different temperatures and densities can dominate the thermal re-emission at different wavelengths. A region with low density and hot dust becomes optically thick at shorter wavelength, blocking the contributions of colder and denser regions appearing first along the line of sight. For longer wavelengths, this region becomes optical thin and its contribution to thermal remission decreases because of the behavior of the Planck function. The thermal re-emission process is now dominated by the cold and dense regions. Since along the line of sight the magnetic field direction varies, a continuous rotation of the observed orientation vectors of linear polarization can occur. This is consistent with the effect of the 90° flip (see Appendix B) since the cross sections of extinction of absorption depend on wavelength and the applied alignment mechanism.
To demonstrate this effect, we calculateed additional linear polarization maps similar to
the parameter of setup BEhour2 for two different wavelengths. We lowered the
central density of the Bonnor−Ebert sphere to n0 = 1012 m-3. In
this case, the magnetic field strength scales with 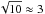 . The result is shown in Fig.
12. For the longer wavelength (left), the
hourglass-field morphology is apparent. However, for the shorter wavelength (right), the
effect of the 90°
flip dominates the central region. A careful comparison along the way from the center to
the outer regions also reveals polarization vector of angles between 0° and 90°.
. The result is shown in Fig.
12. For the longer wavelength (left), the
hourglass-field morphology is apparent. However, for the shorter wavelength (right), the
effect of the 90°
flip dominates the central region. A careful comparison along the way from the center to
the outer regions also reveals polarization vector of angles between 0° and 90°.
 |
Fig. 10 Resulting intensity maps (top row), optical depth maps (second top row), maps of linear (third top row) and circular (bottom row) polarization of setup MHDsim1 (left column) and MHDsim2 (right column) at a wavelength of λ = 248 μm. The intensity is in Wm-2 m-1 and the vectors of linear polarization have an offset angle of 90°. The color bar of the intensity map is on a logarithmic scale, and for the optical depth we apply an upper cut-off at 15% for illustrative purposes. The transition between optically thin and optically thick regions is indicated by the green contour lines and a marker in the color bar. |
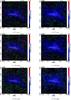 |
Fig. 11 Resulting optical depth maps of setup MHDsim1 (left column) in comparison with setup MHDsim2 (right column) at three distinct wavelengths. The vectors of linear polarization have an offset angle of 90° to match the projected magnetic field. We adjust the color bars of the optical depth with an upper cut-off at 15% for illustrative purposes. The transition between optically thin and optically thick regions is indicated by the green contour lines and a marker in the color bar. |
5. Summary and conclusions
We demonstrated the influence of grain alignment mechanisms and magnetic field configurations by a first case study of the potential of multi-wavelength polarization measurements. For this reason we developed an extended version of the radiative transfer code MC3D (Wolf 2003) and demonstrateed its accuracy. We included a dust grain model consistent with observations and studied the effects of non-spherical dust particles with perfect alignment and imperfect alignment with respect to the direction of the magnetic field. The effects of dichroic polarization and thermal re-emission allowed us to calculate synthetic polarization maps. To do this we used ideal Bonnor−Ebert sphere setups and a sophisticated MHD collapse simulation as test models (see Table 1). We showed that measurements of linear polarization in combination with measurements of circular polarization as an additional source of information allow one to reveal the underlying morphology of the magnetic field for different inclination angles. The limiting factors for interpreting continuum polarization measurements are the current uncertainty of different physical parameters concerning alignment theory and dust composition. We demonstrated that the influence of imperfect grain alignment changes the behavior for circular and linear polarization radically. We conclude that possible ambiguities in the interpretation of observational data can be resolved by including additional measurements of circular polarization in future observation missions. However, it remains unclear whether the low values of circular polarization in the order of 10-4−10-6 as predicted by our models are accessible to observational equipment in the near future.
An additional source of ambiguity is inherent in the dichroic polarization mechanism itself. We identified two effects of rotation in the orientation angles of the vectors of linear polarization projected on the plane sky. The orientation of linear polarization is determined by a critical value of the cross sections for absorption and extinction (see Appendix B). Since the cross sections depend on wavelength and alignment this effect leads to a flip in the orientation of linear polarization by 90°. Additionally, thermal re-emission depends on dust temperature and number density. This results in a continuous rotation of the orientation angle of linear polarization as a function of wavelength. This might easily veil the underlying field morphology even for a symmetrical density distribution and field morphology. Therefore, measurements for linear polarization at a distinct wavelength alone are insufficient to identify the underlying magnetic field morphology because of effects of the wavelength-dependent rotations on the polarization vectors.
Resolving complex density and magnetic field structures, however, is currently ambiguous because of open questions about interstellar dust composition and the absence of a consistent theory of grain alignment mechanisms (Hoang et al. 2007; Das et al. 2010). A reliable theory about the dominating grain alignment mechanisms inside the ISM (e.g. Lazarian & Hoang 2011) and a sophisticated understanding of the dust composition is essential to resolve these uncertainties.
 |
Fig. 12 Orientation vectors of linear polarization with an inclination angle of 75° for a wavelength of λ = 46 μm (left) and λ = 811 μm (right). The parameters are identical to those of BEhour2. However, the density is n0 = 1012 m-3 in the center and the field strength is 6.0 × 10-8T. The linear polarization vectors have an offset angle of 90° to match the projected magnetic hourglass field. The orientation angles of linear polarization in the center regions differ from each other because of the 90° flip (see Appendix B). |
Online material
Appendix A: Radiative transfer equation
Here, we provide a brief description of the equations we used to treat the radiative transfer and dichroic polarization in dusty environments. Under the assumption that no light is scattered into the line of sight, the radiative transfer equation can be written in the Stokes vector formalism as follows (Martin 1974):
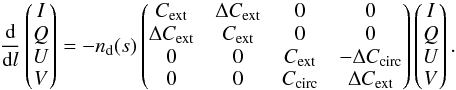 (A.1)The mechanisms of
dichroic polarization are straightforward to calculate by analytical functions since we
consider the number density \begin{lxirformule}$n_{\rm{d}}$\end{lxirformule} of the dust
to be constant in each cell. This condition is given since each cell in the model space
of MC3D operates with a set of constant physical parameter. The matrix elements
Cext and ΔCext are the
cross section for extinction and linear polarization, ΔCcirc for
circular polarization due to birefringence. With the constant number density of the dust
(nd) the system of equations decays into
two uncoupled systems (Whitney & Wolff
2002). The first system of equations solely describes the change of the
I and
Q
parameter due to dichroic extinction. It can be solved by simple substitution and
integration:
(A.1)The mechanisms of
dichroic polarization are straightforward to calculate by analytical functions since we
consider the number density \begin{lxirformule}$n_{\rm{d}}$\end{lxirformule} of the dust
to be constant in each cell. This condition is given since each cell in the model space
of MC3D operates with a set of constant physical parameter. The matrix elements
Cext and ΔCext are the
cross section for extinction and linear polarization, ΔCcirc for
circular polarization due to birefringence. With the constant number density of the dust
(nd) the system of equations decays into
two uncoupled systems (Whitney & Wolff
2002). The first system of equations solely describes the change of the
I and
Q
parameter due to dichroic extinction. It can be solved by simple substitution and
integration:
![\appendix \setcounter{section}{1} \begin{equation} \begin{pmatrix} I_{i+1}+Q_{i+1}\\ I_{i+1}-Q_{i+1} \end{pmatrix} = \begin{pmatrix} (I_i+Q_i) \times \exp\,(-n_i \times l_i\left[C_{\rm{ext},i}+\Delta C_{\rm{ext},i}\right]) \\ (I_i-Q_i) \times \exp\,(-n_i \times l_i\left[C_{\rm{ext},i}-\Delta C_{\rm{ext},i}\right]) \end{pmatrix}. \label{eq:sol1} \end{equation}](/articles/aa/full_html/2014/06/aa23116-13/aa23116-13-eq142.png) (A.2)The second system of
equations can be handled as a complex eigenvalue problem. This leads to additional
cosine and sine terms and a transfer between linear
and circular polarization
(A.2)The second system of
equations can be handled as a complex eigenvalue problem. This leads to additional
cosine and sine terms and a transfer between linear
and circular polarization 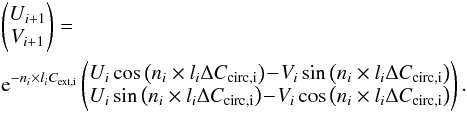 (A.3)Linear
polarization arises from linear dichroism alone, while circular polarization depends on
both a non-zero value in the U parameter and birefringence. Subsequently,
circular polarization can occur in the case of non-parallel magnetic field lines along
the line of sight.
(A.3)Linear
polarization arises from linear dichroism alone, while circular polarization depends on
both a non-zero value in the U parameter and birefringence. Subsequently,
circular polarization can occur in the case of non-parallel magnetic field lines along
the line of sight.
Appendix B: Orientation of polarization
It is possible to determine the exact conditions for the 90° flip in a single cell of the model space. In general, a threshold for
this effect does not exist along the entire line of sight. In each cell of our model
space we have the two opposing effects of dichroic extinction and thermal re-emission
adding to the linear polarization perpendicular to each other. In the reference frame of
the magnetic field the dichroic extinction provides a negative contribution to the
Q
parameter while thermal re-emission contributes positively to Q. In this orientation
the U and
V
parameter remain zero. If we solve Eq. (A.2) for the Qi + 1 parameter,
we can calculate the conditions when the two effects cancel each other out:
![\appendix \setcounter{section}{2} \begin{equation} Q_{i+1} = {\rm e}^{-n_i \times l_i C_{\rm{ext},i}}\left[ Q_i \cosh(n_i l_i \Delta C_{\rm{ext},i}) - I_i \sinh(n_i l_i \Delta C_{\rm{ext},i}) \right] = 0 \label{eq:Qnext}. \end{equation}](/articles/aa/full_html/2014/06/aa23116-13/aa23116-13-eq147.png) (B.1)The contribution of
thermal re-emission is determined by the temperature of the dust Td, the number
density nd, the cross sections for absorption
ΔCabs,Cabs
and the path length l. Inside each cell all the parameters and
functions nd, l, ΔCabs,
Cabs, Cext,
Bλ(T)
are positive and constant, so one can solve Eq. (B.1). As we can derive from Eqs. (2) and (3), the
contributions of Ii and
Qi in a single cell
are as follows:
(B.1)The contribution of
thermal re-emission is determined by the temperature of the dust Td, the number
density nd, the cross sections for absorption
ΔCabs,Cabs
and the path length l. Inside each cell all the parameters and
functions nd, l, ΔCabs,
Cabs, Cext,
Bλ(T)
are positive and constant, so one can solve Eq. (B.1). As we can derive from Eqs. (2) and (3), the
contributions of Ii and
Qi in a single cell
are as follows:  For
a wavelength of λ > 7 μm
one can approximate Cabs,i ≈
Cext,i. By
introducing the optical depths for extinction
For
a wavelength of λ > 7 μm
one can approximate Cabs,i ≈
Cext,i. By
introducing the optical depths for extinction
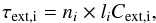 (B.4)and polarization
(B.4)and polarization
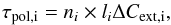 (B.5)we can derive an
inequality for the Q parameter to change its sign as a function of the
inverse hyperbolic tangent:
(B.5)we can derive an
inequality for the Q parameter to change its sign as a function of the
inverse hyperbolic tangent: 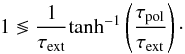 (B.6)If the right-hand side
is larger than 1, the polarization process is dominated by thermal re-emission and, in
the reverse case, by dichroic extinction. However, in the calculated synthetic
polarization maps the observed flip of 90° for the orientation of linear polarization depends
on all the physical quantities along the entire line of sight and cannot be determined
with this inequality.
(B.6)If the right-hand side
is larger than 1, the polarization process is dominated by thermal re-emission and, in
the reverse case, by dichroic extinction. However, in the calculated synthetic
polarization maps the observed flip of 90° for the orientation of linear polarization depends
on all the physical quantities along the entire line of sight and cannot be determined
with this inequality.
Acknowledgments
We wish to thank the referee for a careful review and for the comments that helped improve our paper. We also thank Robi Banerjee, Gesa Bertrang and Peter Scicluna for fruitful discussions and Florian Kirchschlager for the introduction into DDSCAT. For this project the authors S.R. and S.W. acknowledge the support of the DFG: WO 857/11-1. D.S. acknowledges funding by the Deutsche Forschungsgemeinschaft via grant BA 3706/3-1 within the SPP The interstellar medium.
References
- Banerjee, R., Pudritz, R. E., & Anderson, D. W. 2006, MNRAS, 373, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Beuther, H., Vlemmings, W. H. T., Rao, R., & van der Tak, F. F. S. 2010, ApJ, 724, L113 [Google Scholar]
- Bonnor, W. B. 1956, MNRAS, 116, 351 [CrossRef] [Google Scholar]
- Chandrasekhar, S., & Fermi, E. 1953, ApJ, 118, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Nutter, D. J., Ward-Thompson, D., & Kirk, J. M. 2004, ApJ, 600, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Hakobian, N., & Troland, T. H. 2008 [arXiv:0808.1150] [Google Scholar]
- Das, H. K., Voshchinnikov, N. V., & Il’in, V. B. 2010, MNRAS, 404, 265 [NASA ADS] [Google Scholar]
- Davidson, J. A., Novak, G., Matthews, T. G., et al. 2011, ApJ, 732, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, Jr., L., & Greenstein, J. L. 1951, ApJ, 114, 206 [Google Scholar]
- Draine, B. T., & Flatau, P. J. 2012 [arXiv:1202.3424] [Google Scholar]
- Draine, B. T., & Li, A. 2001, ApJ, 551, 807 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Malhotra, S. 1993, ApJ, 414, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Duley, W. W. 1978, ApJ, 219, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Ebert, R. 1955, ZAp, 37, 217 [Google Scholar]
- Elmegreen, B. G. 2000, ApJ, 530, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Troland, T. H., Crutcher, R. M., & Paubert, G. 2008, A&A, 487, 247 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiege, J. D., & Pudritz, R. E. 2000, ApJ, 544, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Frau, P., Galli, D., & Girart, J. M. 2011, A&A, 535, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, D., & Shu, F. H. 1993, ApJ, 417, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girart, J. M., Crutcher, R. M., & Rao, R. 1999, ApJ, 525, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., & Estalella, R. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gonçalves, J., Galli, D., & Walmsley, M. 2005, A&A, 430, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodman, A. A., Benson, P. J., Fuller, G. A., & Myers, P. C. 1993, ApJ, 406, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Greenberg, J. M. 1968, Interstellar Grains, eds. B. M. Middlehurst & L. H. Aller (The University of Chicago Press), 221 [Google Scholar]
- Hiltner, W. A. 1949, Nature, 163, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Hoang, T., Lazarian, A., & Yan, H. 2007, in AAS Meeting Abstracts, BAAS, 39, 984, 138.07 [NASA ADS] [Google Scholar]
- Hong, S. S., & Greenberg, J. M. 1980, A&A, 88, 194 [NASA ADS] [Google Scholar]
- Hughes, A. M., Wilner, D. J., Cho, J., et al. 2009, ApJ, 704, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, R. V., & Spitzer, Jr., L. 1967, ApJ, 147, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E., & Field, G. 2005, ApJ, 635, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Ballesteros-Paredes, J., Li, Y., & Mac Low, M.-M. 2004, in The Formation and Evolution of Massive Young Star Clusters, eds. H. J. G. L. M. Lamers, L. J. Smith, & A. Nota, ASP Conf. Ser., 322, 299 [Google Scholar]
- Launhardt, R., & Henning, T. 1997, A&A, 326, 329 [NASA ADS] [Google Scholar]
- Lazarian, A. 2007, J. Quant. Spectrosc. Rad. Transfer., 106, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Hoang, T. 2011, in ASP Conf. Ser. 449, eds. P. Bastien, N. Manset, D. P. Clemens, & N. St.-Louis, 116 [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Li, A., & Greenberg, J. M. 1997, A&A, 323, 566 [NASA ADS] [Google Scholar]
- Li, Z.-Y., & Shu, F. H. 1996, ApJ, 472, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, P. W., Fukagawa, M., Tamura, M., et al. 2004, MNRAS, 352, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G. 1974, ApJ, 187, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Mouschovias, T. C., & Ciolek, G. E. 1999, in NATO ASIC Proc. 540: The Origin of Stars and Planetary Systems, ed. C. J. Lada & N. D. Kylafis (Kluwer Academic Publishers), 305 [Google Scholar]
- Nakamura, F., & Li, Z.-Y. 2005, ApJ, 631, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Banerjee, R., Pudritz, R. E., & Klessen, R. S. 2013, MNRAS, 432, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Sipilä, O., Harju, J., & Juvela, M. 2011, A&A, 535, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sorrell, W. H. 1994, MNRAS, 268, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, I. W., Looney, L. W., Kwon, W., et al. 2013, ApJ, 769, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Tang, Y.-W., Ho, P. T. P., Koch, P. M., & Rao, R. 2010, ApJ, 717, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Voshchinnikov, N. V., Semenov, D. A., & Henning, T. 1999, A&A, 349, L25 [NASA ADS] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2000, in AAS Meeting Abstracts, BAAS, 32, 1466 [Google Scholar]
- Whitney, B. A., & Wolff, M. J. 2002, ApJ, 574, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S. 2003, Comput. Phys. Commun., 150, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, S., Launhardt, R., & Henning, T. 2004, Ap&SS, 292, 239 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Physical parameters for the presented ideal Bonnor−Ebert sphere setups and MHD setups.
All Figures
 |
Fig. 1 Geometrical configuration for oblate dust grains with their shorter axis perfectly aligned (PA) with the direction of the magnetic field B. The angle ϕ is defined by the projection of B into the Q− coordinate system of the Stokes vector and the inclination angle ϑ is made by the direction of propagation k and the plane of rotation perpendicular to B. |
| In the text | |
 |
Fig. 2 Geometrical configuration of a rotating oblate dust grain with angular momentum J no longer in alignment with the magnetic field B. The precession of J around B is defined by the precession angle ω and the cone angle β. The direction of propagation k is parallel to the z-axis. The inclination angle θ is not constant but varies with ω, the angle Ω between k, and magnetic field, and β. |
| In the text | |
 |
Fig. 3 3D plots for the toroidal (panel a), Eq. (17)), hourglass (panel b), Eq. (18)), quadrupole (panel c), Eq. (19)), and helical (panel d), superposition of Eq. (17) and Eq. (18)) magnetic field morphologies. |
| In the text | |
 |
Fig. 4 Linear polarization (left) and circular polarization (right) of ideal setup BEtoro with inclination angles of 3° (top), 45° (middle) and 87° (bottom), a constant dust temperature Td = 15 K, a characteristic radius Rc = 1100 AU and a density n0 = 1013 m-3 in the center. We added an offset angle of 90° to the vectors of linear polarization to match the projected magnetic toroidal field. The dust particles are perfectly aligned. |
| In the text | |
 |
Fig. 5 Same as in Fig. 4 for model BEhour2. The characteristic radii for the temperature distribution are adjusted to keep the gas temperature and dust temperature in a range of 10 K−25 K and 5 K−15 K, respectively. The dust particles are imperfectly aligned. |
| In the text | |
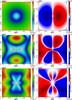 |
Fig. 6 Same as in Fig. 6 for model BEquad2. |
| In the text | |
 |
Fig. 7 Same as in Fig. 6 for model BEhelic2 with inclination angles of 0° (top), 45° (middle) and 90° (bottom). |
| In the text | |
 |
Fig. 8 Resulting degrees of linear polarization Pl (top) and circular polarization Pc (bottom) for perfectly (left) and imperfectly (right) aligned dust grains depending on inclination angle at a wavelength of 811 μm for the ideal Bonnor−Ebert sphere setups as presented in Sect. 3.1. For the degree of linear polarization Pl the mean values are plotted as solid lines and the peak values are in dashed lines. For circular polarization Pc the lowest values are plotted as solid lines, the highest values as dashed lines. The details of all model setups are listed in Table 1. |
| In the text | |
 |
Fig. 9 Resulting peak values (dashed lines) and mean values (solid lines) of intensity I, optical depth τ, and degree of linear polarization Pl for the MHD − simulation as presented in Sect. 3.2. For circular polarization polarization Pc the lowest values are plotted as solid lines and the highest values as dashed lines. The red lines correspond to the setup with perfectly aligned dust grains (MHDsim1) and the blue lines to the setup with imperfectly aligned grains (MHDsim2). |
| In the text | |
 |
Fig. 10 Resulting intensity maps (top row), optical depth maps (second top row), maps of linear (third top row) and circular (bottom row) polarization of setup MHDsim1 (left column) and MHDsim2 (right column) at a wavelength of λ = 248 μm. The intensity is in Wm-2 m-1 and the vectors of linear polarization have an offset angle of 90°. The color bar of the intensity map is on a logarithmic scale, and for the optical depth we apply an upper cut-off at 15% for illustrative purposes. The transition between optically thin and optically thick regions is indicated by the green contour lines and a marker in the color bar. |
| In the text | |
 |
Fig. 11 Resulting optical depth maps of setup MHDsim1 (left column) in comparison with setup MHDsim2 (right column) at three distinct wavelengths. The vectors of linear polarization have an offset angle of 90° to match the projected magnetic field. We adjust the color bars of the optical depth with an upper cut-off at 15% for illustrative purposes. The transition between optically thin and optically thick regions is indicated by the green contour lines and a marker in the color bar. |
| In the text | |
 |
Fig. 12 Orientation vectors of linear polarization with an inclination angle of 75° for a wavelength of λ = 46 μm (left) and λ = 811 μm (right). The parameters are identical to those of BEhour2. However, the density is n0 = 1012 m-3 in the center and the field strength is 6.0 × 10-8T. The linear polarization vectors have an offset angle of 90° to match the projected magnetic hourglass field. The orientation angles of linear polarization in the center regions differ from each other because of the 90° flip (see Appendix B). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


