| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323116 | |
| Published online | 17 June 2014 | |
Online material
Appendix A: Radiative transfer equation
Here, we provide a brief description of the equations we used to treat the radiative transfer and dichroic polarization in dusty environments. Under the assumption that no light is scattered into the line of sight, the radiative transfer equation can be written in the Stokes vector formalism as follows (Martin 1974):
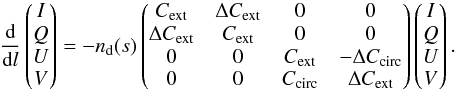 (A.1)The mechanisms of
dichroic polarization are straightforward to calculate by analytical functions since we
consider the number density \begin{lxirformule}$n_{\rm{d}}$\end{lxirformule} of the dust
to be constant in each cell. This condition is given since each cell in the model space
of MC3D operates with a set of constant physical parameter. The matrix elements
Cext and ΔCext are the
cross section for extinction and linear polarization, ΔCcirc for
circular polarization due to birefringence. With the constant number density of the dust
(nd) the system of equations decays into
two uncoupled systems (Whitney & Wolff
2002). The first system of equations solely describes the change of the
I and
Q
parameter due to dichroic extinction. It can be solved by simple substitution and
integration:
(A.1)The mechanisms of
dichroic polarization are straightforward to calculate by analytical functions since we
consider the number density \begin{lxirformule}$n_{\rm{d}}$\end{lxirformule} of the dust
to be constant in each cell. This condition is given since each cell in the model space
of MC3D operates with a set of constant physical parameter. The matrix elements
Cext and ΔCext are the
cross section for extinction and linear polarization, ΔCcirc for
circular polarization due to birefringence. With the constant number density of the dust
(nd) the system of equations decays into
two uncoupled systems (Whitney & Wolff
2002). The first system of equations solely describes the change of the
I and
Q
parameter due to dichroic extinction. It can be solved by simple substitution and
integration:
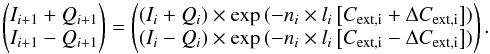 (A.2)The second system of
equations can be handled as a complex eigenvalue problem. This leads to additional
cosine and sine terms and a transfer between linear
and circular polarization
(A.2)The second system of
equations can be handled as a complex eigenvalue problem. This leads to additional
cosine and sine terms and a transfer between linear
and circular polarization 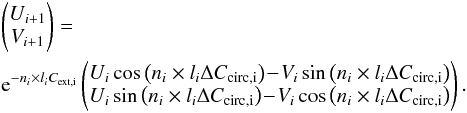 (A.3)Linear
polarization arises from linear dichroism alone, while circular polarization depends on
both a non-zero value in the U parameter and birefringence. Subsequently,
circular polarization can occur in the case of non-parallel magnetic field lines along
the line of sight.
(A.3)Linear
polarization arises from linear dichroism alone, while circular polarization depends on
both a non-zero value in the U parameter and birefringence. Subsequently,
circular polarization can occur in the case of non-parallel magnetic field lines along
the line of sight.
Appendix B: Orientation of polarization
It is possible to determine the exact conditions for the 90° flip in a single cell of the model space. In general, a threshold for
this effect does not exist along the entire line of sight. In each cell of our model
space we have the two opposing effects of dichroic extinction and thermal re-emission
adding to the linear polarization perpendicular to each other. In the reference frame of
the magnetic field the dichroic extinction provides a negative contribution to the
Q
parameter while thermal re-emission contributes positively to Q. In this orientation
the U and
V
parameter remain zero. If we solve Eq. (A.2) for the Qi + 1 parameter,
we can calculate the conditions when the two effects cancel each other out:
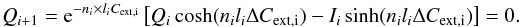 (B.1)The contribution of
thermal re-emission is determined by the temperature of the dust Td, the number
density nd, the cross sections for absorption
ΔCabs,Cabs
and the path length l. Inside each cell all the parameters and
functions nd, l, ΔCabs,
Cabs, Cext,
Bλ(T)
are positive and constant, so one can solve Eq. (B.1). As we can derive from Eqs. (2) and (3), the
contributions of Ii and
Qi in a single cell
are as follows:
(B.1)The contribution of
thermal re-emission is determined by the temperature of the dust Td, the number
density nd, the cross sections for absorption
ΔCabs,Cabs
and the path length l. Inside each cell all the parameters and
functions nd, l, ΔCabs,
Cabs, Cext,
Bλ(T)
are positive and constant, so one can solve Eq. (B.1). As we can derive from Eqs. (2) and (3), the
contributions of Ii and
Qi in a single cell
are as follows:  For
a wavelength of λ > 7 μm
one can approximate Cabs,i ≈
Cext,i. By
introducing the optical depths for extinction
For
a wavelength of λ > 7 μm
one can approximate Cabs,i ≈
Cext,i. By
introducing the optical depths for extinction
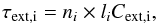 (B.4)and polarization
(B.4)and polarization
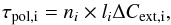 (B.5)we can derive an
inequality for the Q parameter to change its sign as a function of the
inverse hyperbolic tangent:
(B.5)we can derive an
inequality for the Q parameter to change its sign as a function of the
inverse hyperbolic tangent: 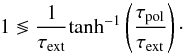 (B.6)If the right-hand side
is larger than 1, the polarization process is dominated by thermal re-emission and, in
the reverse case, by dichroic extinction. However, in the calculated synthetic
polarization maps the observed flip of 90° for the orientation of linear polarization depends
on all the physical quantities along the entire line of sight and cannot be determined
with this inequality.
(B.6)If the right-hand side
is larger than 1, the polarization process is dominated by thermal re-emission and, in
the reverse case, by dichroic extinction. However, in the calculated synthetic
polarization maps the observed flip of 90° for the orientation of linear polarization depends
on all the physical quantities along the entire line of sight and cannot be determined
with this inequality.
© ESO, 2014
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


