| Issue |
A&A
Volume 565, May 2014
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 12 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201323311 | |
| Published online | 21 May 2014 | |
Fossil group origins
III. The relation between optical and X-ray luminosities⋆
1 Dipartimento di Fisica dell’Università degli Studi di Trieste − Sezione di Astronomia, via Tiepolo 11, 34143 Trieste, Italy
e-mail: girardi@oats.inaf.it
2 INAF − Osservatorio Astronomico di Trieste, via Tiepolo 11, 34143 Trieste, Italy
3 Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna, Tenerife, Canary Islands, Spain
4 Departamento de Astrofísica, Universidad de La Laguna, Av. del Astrofísico Franciso Sánchez s/n, 38205 La Laguna (Tenerife), Canary Islands, Spain
5 INAF – Osservatorio Astronomico di Brera, via E. Bianchi 46, 23807 Merate (LC), Italy
6 Astronomy Department, University of Wisconsin, 475 Charter St., Madison, WI 53706, USA
7 Alfred P. Sloan Fellow
8 Fundación Galileo Galilei – INAF, Rambla José Ana Fernández Perez 7, 38712 Breña Baja, La Palma, Canary Islands, Spain
9 School of Physics and Astronomy, University of St Andrews (SUPA), North Haugh, St Andrews, KY16 9SS, UK
10 NRC Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, BC, V9E 2E7, Canada
11 Dipartimento di Fisica e Astronomia “G. Galilei”, Università di Padova, vicolo dell’Osservatorio 3, 35122 Padova, Italy
12 INAF – Osservatorio Astronomico di Padova, vicolo dell’Osservatorio 5, 35122 Padova, Italy
13 Instituto Nacional de Astrofísica, Óptica y Electrónica (INAOE), Aptdo. Postal 51 y 216, 72000 Puebla, Pue., Mexico
14 Instituto de Astrofísica de Andalucia – C.S.I.C., 18008 Granada, Spain
15 Centro Astronómico Hispano Alemán, C/ Jesús Durbán Remón 2-2, 04004 Almería, Spain
Received: 20 December 2013
Accepted: 28 February 2014
Aims. This study is part of the Fossil group origins (FOGO) project which aims to carry out a systematic and multiwavelength study of a large sample of fossil systems. Here we focus on the relation between the optical luminosity (Lopt) and X-ray luminosity (LX).
Methods. Out of a total sample of 28 candidate fossil systems, we consider a sample of 12 systems whose fossil classification has been confirmed by a companion study. They are compared with the complementary sample of 16 systems whose fossil nature has not been confirmed and with a subsample of 102 galaxy systems from the RASS-SDSS galaxy cluster survey. Fossil and normal systems span the same redshift range 0 <z< 0.5 and have the same LX distribution. For each fossil system, the LX in the 0.1−2.4 keV band is computed using data from the ROSAT All Sky Survey to be comparable to the estimates of the comparison sample. For each fossil and normal system we homogeneously compute Lopt in the r-band within the characteristic cluster radius, using data from the Sloan Digital Sky Survey Data Release 7.
Results. We sample the LX-Lopt relation over two orders of magnitude in LX. Our analysis shows that fossil systems are not statistically distinguishable from the normal systems through the 2D Kolmogorov-Smirnov test nor the fit of the LX-Lopt relation. Thus, the optical luminosity of the galaxy system does strongly correlate with the X-ray luminosity of the hot gas component, independently of whether the system is fossil or not. We discuss our results in comparison with previous literature.
Conclusions. We conclude that our results are consistent with the classical merging scenario of the brightest galaxy formed via merger/cannibalism of other group galaxies with conservation of the optical light. We find no evidence for a peculiar state of the hot intracluster medium.
Key words: galaxies: clusters: general / X-rays: galaxies: clusters / cosmology: observations
Tables 1 and 2 are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Several studies of galaxy systems have revealed an interesting class of objects termed fossil groups (Ponman et al. 1994). From the observational point of view, these are defined as galaxy systems with a magnitude difference of at least two magnitudes – in the R-band – between the brightest group/cluster galaxy (BCG) and the second-brightest galaxy within half the virial radius R2001 and an extended thermal X-ray halo with bolometric X-ray luminosity 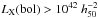 erg s -1 (see Jones et al. 2003 for the rationale). Thus, the fossil groups appear to be extreme environments devoid of typical bright galaxies while simultaneously being home to the brightest and most massive galaxies in the Universe. The first explanation was that they are old, isolated galaxy systems in which the large galaxies have merged or coalesced through dynamical friction. In this merging scenario, the magnitude gap shown by the fossil systems is a consequence of evolution rather than an initial deficit of ~L∗ galaxies (i.e., the failed group scenario; see, e.g., the discussion in the study of Mulchaey & Zabludoff 1999).
erg s -1 (see Jones et al. 2003 for the rationale). Thus, the fossil groups appear to be extreme environments devoid of typical bright galaxies while simultaneously being home to the brightest and most massive galaxies in the Universe. The first explanation was that they are old, isolated galaxy systems in which the large galaxies have merged or coalesced through dynamical friction. In this merging scenario, the magnitude gap shown by the fossil systems is a consequence of evolution rather than an initial deficit of ~L∗ galaxies (i.e., the failed group scenario; see, e.g., the discussion in the study of Mulchaey & Zabludoff 1999).
The merging scenario has been invoked to explain such observational features as the high values of X-ray luminosity (LX) and temperature (TX) of fossil systems with respect to those of normal systems with comparable optical luminosity (Lopt) or comparable velocity dispersion (σv; six fossil groups in Jones et al. 2003; seven in Khosroshahi et al. 2007) and some evidence of a high centrally concentrated dark matter halo (Khosroshahi et al. 2006). The above differences with normal systems have been generally interpreted as due to an early formation epoch of fossil groups as suggested by numerical simulations (e.g., D’Onghia et al. 2005). Accordingly, the BCGs of fossil groups should contain a fossil relic of the structure formation in the high-redshift Universe. Early observations have revealed that the BCGs of fossil groups have different observational properties than other bright elliptical galaxies, their discy isophotes (seven fossil groups; Khosroshahi et al. 2006), for example, supporting the idea that they are formed from gas-rich mergers in early times.
More recent studies have opened the discussion about the special nature of fossil groups. Alternative criteria for their definition (e.g., Dariush et al. 2007) and the concept of fossil clusters for massive systems (e.g., Cypriano et al. 2006) have been proposed. Moreover, studies based on N-body numerical simulations have suggested that many systems go through an optical fossil phase during their life (e.g., von Benda-Beckmann et al. 2008; Cui et al. 2011).
Recent observational results are often in contrast with the previous results that found no particularly high mass concentration (Democles et al. 2010) and no special X-ray properties (12 fossil systems, Voevodkin et al. 2010; 10, Proctor et al. 2011; 17, Harrison et al. 2012). Instead, Proctor et al. (2011) claim atypical richnesses and optical luminosities, but this has not been found by Voevodkin et al. (2010) and Harrison et al. (2012). Recent studies of fossil systems have also challenged the former conclusions of an early formation of their BCGs from a gas-rich merger. Analyzing the photometric and structural properties of BCGs in fossil systems, La Barbera et al. (2009, 25 fossil systems) and Méndez-Abreu et al. (2012, 20 fossil systems, hereafter Paper II) have found that they are similar to bright field ellipticals and to normal cluster BCGs, respectively. Finally, there is sparse evidence of a few fossil systems far from being dynamically relaxed (e.g., Harrison et al. 2012; La Barbera et al. 2012; Miller et al. 2012).
Summarizing, there is still an open discussion on the real nature and origin of fossil systems. For instance, on the basis of their observational results, Harrison et al. (2012) suggest that fossil systems formed rather early and their galaxies represent the end products of galaxy mergers, while Proctor et al. (2011) question the merging scenario, suggesting that the cannibalism of bright central galaxies is not a convincing explanation for the magnitude gap. Possible causes of the discrepancies among observational results reported in the literature might be connected with the use of very small samples, the presence of possible biases in the estimates of physical quantities, or inhomogeneities in the treatment of data of fossil and normal systems.
In 2008 we started a large observational program of fossil systems, the Fossil group origins (FOGO) project (Aguerri et al. 2011; hereafter Paper I). The aim of this project is to carry out a systematic, multiwavelength study of a sample of 34 fossil group candidates identified by Santos et al. (2007, hereafter S07); here each system is denoted by FGS01, FGS02, etc., according to the S07 list. The FOGO project was awarded time as International Time Programme (ITP08-4 and ITP09-1) at the Roque de los Muchachos Observatory for a total of 52 nights of observations. Most optical and NIR observations were performed during the period November 2008–May 2010 at the TNG, NOT, WHT, and INT telescopes. The spectroscopic observations went on until April 2012 thanks to additional time awarded at TNG through the Spanish and Italian Time Allocation Committees. The catalog is described in the companion study by Zarattini et al. (2014; hereafter Paper IV).
The first group we analyzed, RX J105453.3+552102 (FGS10 in the S07 catalog), is a special system, because it is already a very massive, relaxed galaxy cluster (M ~ 1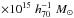 ) at z = 0.47. Contrary to the findings of previous works that claim a boost in the X-ray properties in fossil systems, FGS10 is quite normal as shown by its position in the Lopt–LX plane (see Paper I). Here we present our statistical results for 28 out of the 34 groups catalogued as fossils by S07. We have taken care to apply homogeneous procedures to the fossil and comparison systems and, in particular, we have computed consistent optical luminosities. Our present analysis is mainly based on optical data from the Sloan Digital Sky Survey Data Release 7 (hereafter SDSS-DR7, Fukugita et al. 1996; Gunn et al. 1998; Abazajian et al. 2009) and X-ray data from the ROSAT All Sky Survey (RASS, Voges et al. 1999). We have also used the results of Paper IV and, in particular, our check of the fossil classification of the S07 objects.
) at z = 0.47. Contrary to the findings of previous works that claim a boost in the X-ray properties in fossil systems, FGS10 is quite normal as shown by its position in the Lopt–LX plane (see Paper I). Here we present our statistical results for 28 out of the 34 groups catalogued as fossils by S07. We have taken care to apply homogeneous procedures to the fossil and comparison systems and, in particular, we have computed consistent optical luminosities. Our present analysis is mainly based on optical data from the Sloan Digital Sky Survey Data Release 7 (hereafter SDSS-DR7, Fukugita et al. 1996; Gunn et al. 1998; Abazajian et al. 2009) and X-ray data from the ROSAT All Sky Survey (RASS, Voges et al. 1999). We have also used the results of Paper IV and, in particular, our check of the fossil classification of the S07 objects.
This paper is organized as follows. We describe the S07 sample and the comparison sample in Sect. 2. We detail the computation of X-ray and optical luminosities in Sects. 3 and 4. We devote Sect. 5 to the comparison between fossil and normal systems in the Lopt–LX plane. We discuss our results and present our conclusions in Sect. 6.
Unless otherwise stated, we indicate errors at the 68% confidence level (hereafter c.l.). Throughout this paper, we use H0 = 70 km s-1 Mpc-1 and h70 = H0/ (70 km s-1 Mpc-1) in a flat cosmology with Ωm = 0.3 and ΩΛ = 0.7. Unless otherwise stated, all cosmology-dependent quantities that we take from the literature are rescaled to our adopted cosmology.
2. Samples of fossil and normal galaxy systems
Santos et al. (2007) list 34 galaxy systems in the range of redshifts 0.03 <z< 0.49 catalogued as fossil group candidates. These systems were obtained as the result of a cross-match of the positions of all luminous galaxies with measured spectroscopic z in the SDSS-Early Data Release (LRG catalogued by Eisenstein et al. 2001) with sources in the RASS with extended emission and having a galaxy/ROSAT source distance of less than 0.5′. Only LRGs with magnitude r< 19 and elliptical-type were considered by S07. In addition, S07 looked for the LRG companions in the SDSS-DR5, taking objects classified as galaxy within a radius of 0.5 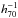 Mpc, and having the spectroscopic redshift zspec, if available, | zspec − zLRG | < Δz = 0.002 or the photometric redshift zphot, | zphot − zLRG | < Δz = 0.1. The systems so constructed were included in the S07 catalog if the magnitude difference between the LRG (i.e., the BCG of the system) and the second-brightest member was Δm12 ≥ 2 mag. The authenticity of their fossil classification is widely analyzed and discussed in Paper IV, where we used new deep r-band images and optical spectroscopy information. Out of 34 S07 objects, 15 showed to be genuine fossil groups having Δm12 ≥ 2 mag or Δm14 ≥ 2.5 mag within 0.5R200. The other 19 objects are either not fossil or their fossil nature cannot be assessed with available data. In the present study, all the S07 objects are considered, except FGS19 because it was not entirely sampled by the SDSS-DR7, and FGS11, FGS15, FGS28, FGS29, and FGS32 because a significant peak was not detected by our analysis of the 2D galaxy distribution (see Sect. 4.2). Our ALL-FGS sample includes the remaining 28 S07 systems, 12 being confirmed fossil systems (hereafter the CONF-FGS sample; the complementary sample of 16 objects is denoted by NOCONF-FGS). The NOCONF-FGS sample is used as the comparison sample.
Mpc, and having the spectroscopic redshift zspec, if available, | zspec − zLRG | < Δz = 0.002 or the photometric redshift zphot, | zphot − zLRG | < Δz = 0.1. The systems so constructed were included in the S07 catalog if the magnitude difference between the LRG (i.e., the BCG of the system) and the second-brightest member was Δm12 ≥ 2 mag. The authenticity of their fossil classification is widely analyzed and discussed in Paper IV, where we used new deep r-band images and optical spectroscopy information. Out of 34 S07 objects, 15 showed to be genuine fossil groups having Δm12 ≥ 2 mag or Δm14 ≥ 2.5 mag within 0.5R200. The other 19 objects are either not fossil or their fossil nature cannot be assessed with available data. In the present study, all the S07 objects are considered, except FGS19 because it was not entirely sampled by the SDSS-DR7, and FGS11, FGS15, FGS28, FGS29, and FGS32 because a significant peak was not detected by our analysis of the 2D galaxy distribution (see Sect. 4.2). Our ALL-FGS sample includes the remaining 28 S07 systems, 12 being confirmed fossil systems (hereafter the CONF-FGS sample; the complementary sample of 16 objects is denoted by NOCONF-FGS). The NOCONF-FGS sample is used as the comparison sample.
As a more extended comparison sample, we considered a sample of normal galaxy systems, i.e., galaxy systems not specifically selected on the basis of their Δm12 values. Specifically, we considered a subsample of 102 systems in the redshift range 0 <z< 0.5 extracted from the RASS-SDSS galaxy cluster survey (Popesso et al. 2004, hereafter P04). Following the P04 list, here each system is denoted by CL01, CL02, etc. The RASS-SDSS survey lists 114 galaxy systems in the range of redshifts 0.003 <z< 0.78 and covers a wide range of masses from groups of 1012.5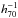 M⊙ to massive clusters of 1015
M⊙ to massive clusters of 1015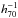 M⊙. It comprises all the X-ray selected objects already observed by the SDSS up to February 2003. The reason for using this sample for the comparison is threefold: it is quite large; it is based on the RASS and SDSS surveys, the same data sources used by S07; and it has been used by P04 to analyze optical luminosities, and thus several technical points have already been outlined and properly verified by P04 and following studies. From the 114 RASS-SDSS clusters we do not consider: the four systems classified as FGS by S07 (CL005=FGS02=Abell 267, CL017=FGS05=Abell 697; CL103=FGS30=ZwCl 1717.9+5636;CL105=FGS31), the five systems with X-ray luminosity listed as 0.00 by P04 (CL018; CL050; CL052; CL055; CL070 of which the last four have redshift z< 0.01), the other two systems with z< 0.01 (CL082; CL083), and the system with the highest redshift (CL044 at z = 0.784). We obtained a sample of 102 systems (hereafter the CL sample) with 0.01 <z< 0.46, i.e., in the same redshift range of S07 FGSs. The X-ray luminosity distributions of ALL-FGSs and CLs are not statistically different (see the Sect. 3.1 for LX computation). Since the X-ray luminosity is a proxy for the mass of galaxy systems, the FGS sample is expected to span a range of masses that is comparable to that of the CL sample. However, their z distributions differ at the >99% level according to the Kolmogorov-Smirnov test (hereafter 1DKS-test; see, e.g., Ledermann 1982). The FGS z distribution is picked at higher values (Δz ~ 0.1). Thus, we expect that FGSs are somehow less optically contrasted onto the sky than CLs.
M⊙. It comprises all the X-ray selected objects already observed by the SDSS up to February 2003. The reason for using this sample for the comparison is threefold: it is quite large; it is based on the RASS and SDSS surveys, the same data sources used by S07; and it has been used by P04 to analyze optical luminosities, and thus several technical points have already been outlined and properly verified by P04 and following studies. From the 114 RASS-SDSS clusters we do not consider: the four systems classified as FGS by S07 (CL005=FGS02=Abell 267, CL017=FGS05=Abell 697; CL103=FGS30=ZwCl 1717.9+5636;CL105=FGS31), the five systems with X-ray luminosity listed as 0.00 by P04 (CL018; CL050; CL052; CL055; CL070 of which the last four have redshift z< 0.01), the other two systems with z< 0.01 (CL082; CL083), and the system with the highest redshift (CL044 at z = 0.784). We obtained a sample of 102 systems (hereafter the CL sample) with 0.01 <z< 0.46, i.e., in the same redshift range of S07 FGSs. The X-ray luminosity distributions of ALL-FGSs and CLs are not statistically different (see the Sect. 3.1 for LX computation). Since the X-ray luminosity is a proxy for the mass of galaxy systems, the FGS sample is expected to span a range of masses that is comparable to that of the CL sample. However, their z distributions differ at the >99% level according to the Kolmogorov-Smirnov test (hereafter 1DKS-test; see, e.g., Ledermann 1982). The FGS z distribution is picked at higher values (Δz ~ 0.1). Thus, we expect that FGSs are somehow less optically contrasted onto the sky than CLs.
The FGS and CL samples are listed in Tables 1 and 2. For each FGS, Table 1 lists notes about their classification (Col. 2); the center (RA and Dec) and redshift z, as taken from S07 and referring to the BCG (Cols. 3 and 4); the X-ray luminosity, LX, in the (0.1−2.4) keV band (Col. 5); the radius R500, and the optical r-band luminosity computed within R500, Lopt( <R500) (Cols. 6 and 7); Lopt( <0.5R200) being R200 = 1.516 × R500 (Col. 8); and additional information (Col. 9). The listed values of LX, R500, Lopt are derived in the following Sections. For each CL, Table 2 lists the same properties where the CL centers and redshifts are taken from P04, as well as the X-ray luminosity values (here converted to our adopted cosmology).
3. X-ray luminosities
3.1. X-ray luminosity estimates
Our reference values for the X-ray luminosities of the CL sample are those computed by P04 and listed in their Table 12. Santos et al. (2007) list the LX values of FGSs in the (0.5−2) keV band as computed from ROSAT count rates. A quick comparison between the values of a few FGSs, which are also well-known clusters (e.g., Abell 267 = FGS02 and Abell 697 = FGS05), with the published values (e.g., Böhringer et al. 2000), shows that they are underestimated by a factor of ~2. We thus decided to recompute X-ray luminosities for the full S07 sample.
For each FGS, we considered the counts from the RASS Bright Source Catalog (RASS-BSC; Voges et al. 1999) or, alternatively, from the RASS Faint Source Catalog (RASS-FSC; Voges et al. 2000), which are in the broad band 0.1–2.4 keV. We used the total Galactic column density (NH) as taken from NASA’s HEASARC NH tool3 and the redshift z as listed by S07.
The computation of the flux was made by using an iterative procedure based on the PIMMS4 software available at NASA’s HEASARC tools (Mukai 1993). We adopted the plasma model, a metal abundance of 0.4, and, at the first step, a starting value for the temperature kTX = 2 keV. The resulting unabsorbed flux is slightly corrected to take into account the flux coming from the outer regions (× 1.08, which is the mean value in the NORAS clusters, Böhringer et al. 2000). This flux was used to compute a first estimate of the X-ray luminosity (in the 0.1−2.4 keV band). We used the X-ray luminosity to compute an estimate of the temperature through Eq. (4) in Böhringer et al. (2000) derived from the luminosity-temperature relation in Markevitch (1998) and used for the NORAS clusters 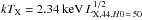 , where LX,44,H0 = 50 is the X-ray luminosity in units of 1044 erg s-1, in the 0.1−2.4 keV band, and in the Böhringer et al. (2000) cosmology. This temperature and the redshift of the system were used to compute the K-correction (Böhringer et al. 2004; see their Table 3). The K-corrected X-ray luminosity allowed us to obtain a new estimate of the temperature, which could be used as the new starting value in the PIMMS procedure. The second iteration of the procedure is enough to converge to the final luminosities and temperatures, LX and TX. Throughout the paper, these LX estimates are our reference values for the FGS sample and are listed in Table 1. The question of the level of homogeneity of these estimates with those taken from P04 for the CL sample is addressed in Sect. 3.3.
, where LX,44,H0 = 50 is the X-ray luminosity in units of 1044 erg s-1, in the 0.1−2.4 keV band, and in the Böhringer et al. (2000) cosmology. This temperature and the redshift of the system were used to compute the K-correction (Böhringer et al. 2004; see their Table 3). The K-corrected X-ray luminosity allowed us to obtain a new estimate of the temperature, which could be used as the new starting value in the PIMMS procedure. The second iteration of the procedure is enough to converge to the final luminosities and temperatures, LX and TX. Throughout the paper, these LX estimates are our reference values for the FGS sample and are listed in Table 1. The question of the level of homogeneity of these estimates with those taken from P04 for the CL sample is addressed in Sect. 3.3.
3.2. Characteristic radius estimates
In Sect. 4 we present our estimation of reference optical luminosities as computed within a radius of R500. We also estimated luminosities within 0.5R200 for useful comparison with other authors. The use of a characteristic radius is suggested in order to treat comparable regions for galaxy systems of different masses. For each system, we computed R500 using Eq. (2) in Böhringer et al. (2007), 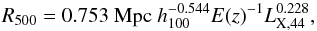 (1)where E(z) = h(z) /h0 and LX,44 is the X-ray luminosity in units of
(1)where E(z) = h(z) /h0 and LX,44 is the X-ray luminosity in units of 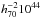 erg s-1 (in the 0.1–2.4 keV band). This equation is based on the R500–TX relation by Arnaud et al. (2005; see details in the original papers). Following Arnaud et al. (2005; see their Table 2 for whole cluster sample results), we computed R200 = 1.516 × R500, in agreement with numerical simulations where R200/R500 ~ 1.5 for the typical halo concentration parameter c = 5 (Yang et al. 2009). The median value of R500 for FGSs (and CLs) is ~0.9
erg s-1 (in the 0.1–2.4 keV band). This equation is based on the R500–TX relation by Arnaud et al. (2005; see details in the original papers). Following Arnaud et al. (2005; see their Table 2 for whole cluster sample results), we computed R200 = 1.516 × R500, in agreement with numerical simulations where R200/R500 ~ 1.5 for the typical halo concentration parameter c = 5 (Yang et al. 2009). The median value of R500 for FGSs (and CLs) is ~0.9 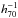 Mpc.
Mpc.
3.3. LX estimates: uncertainties and homogeneities
We adopted the value ϵLx = 20% for CLs, taken from P04 as a typical LX uncertainty. In the case of FGs, we used the count error listed by RASS-BSC/FSC and computed the relative error. The same relative error was assumed for LX (ϵLx ~ 25%; median value).
The X-ray luminosities computed by P04 were not obtained using the RASS-BSC/FSC counts, but rather with the counts estimated through the GCA method (Böhringer et al. 2000, NORAS clusters). Böhringer et al. (2000) have pointed out that RASS-BSC/FSC underestimate counts, probably because of the design of the source analysis technique used for RASS (see their Fig. 11b). To check the effect of this on our LX estimates, we recomputed X-ray luminosities for 100 out of 102 CLs following the same procedure we used for FGSs (see Sect. 3.1), these alternative estimates being labelled as LX,BSC/FSC. For two of the 102 CLs in our comparison sample we failed to find any RASS-BSC/FSC source within 5′from the P04 center and we did not consider them. We found that the difference of the two alternative estimates strongly depends on whether the system is recognized as an extended source or not by the RASS-BSC/FSC catalogs; the extended emission is one of the selection criteria required by S07. Among the 100 CLs, 67 and 33 systems are classified as extended and nonextended sources, respectively. For the 33 nonextended sources, we confirm a large systematic difference, finding LX,P04/LX,BSC/FSC = 2.6 (median value). For the 67 extended sources, the two alternative estimates are only slightly different, LX,P04/LX,BSC/FSC = 1.21. The presence of a systematic (although small) difference led us to also consider two alternative approaches when comparing FGSs and CLs (see Sect. 5): i) using LX,BSC/FSC for CLs (only the 67 extended systems are considered), and ii) applying a correction to the FGS X-ray luminosities determined in Sect. 3.1 in such a way as to more closely resemble those listed by P04 for CLs. The correction was obtained by fitting LX,P04 vs. LX,BSC/FSC for the sample of the 67 extended CLs. The direct regression line, recommended to predict the value of the y variable (see, e.g., Isobe et al. 1990), is log (LX,44,P04) = 0.136 + 0.865·log (LX,44,BSC/FSC), where LX,44 is the X-ray luminosity in units of 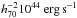 . The corrected luminosities for FGSs, hereafter LX,corr, are obtained from the values computed in Sect. 3.1 using the right-hand side of the above equation.
. The corrected luminosities for FGSs, hereafter LX,corr, are obtained from the values computed in Sect. 3.1 using the right-hand side of the above equation.
4. Optical luminosity estimates
4.1. Galaxy catalogs
The galaxy catalogs were obtained from the SDSS-DR7. For each galaxy system, we considered objects within a circular region with a radius of 30′positioned on the center listed by S07 (P04 for CLs). Only objects classified as extended and not containing one or more saturated pixels were selected. The last constraint is required to reject stars classified as bright galaxies (e.g., Yasuda et al. 2001). We always considered only objects labeled “PRIMARY” (see Yasuda et al. 2001 for more details). As a further check, we have also looked at objects classified as extended and saturated objects, but that are real galaxies having cz> 1000 km s-1. The inclusion of these (few) objects–almost always nonmember, foreground galaxies–would change the average observed luminosity for only 8 of the 136 analyzed systems. For the sake of completeness of our catalogs, we decided to include only three galaxies: the BCGs of FGS21, CL013, and CL100; other differences are negligible.
In order to compare with previous works in the literature, we considered SDSS r-band magnitudes. The SDSS photometry of point-like sources is nominally 95% complete down to a model magnitude r = 22 (Stoughton et al. 2002) and the star/galaxy classification is still reliable down to r ~ 21.5 (Lupton et al. 2001; see also Capozzi et al. 2009). Accordingly, we adopt here a limiting magnitude of r ~ 21.5 for the entire SDSS catalog.
We used dered magnitudes (hereafter mr), i.e., model magnitudes already corrected for the Galactic absorption (hereafter  ). We applied both K-dimming and evolutionary correction. We used the K-correction
). We applied both K-dimming and evolutionary correction. We used the K-correction  , supplied by Fukugita et al. (1995), for elliptical galaxies, assuming that the main population of galaxy systems in our samples are the old elliptical galaxies at the system redshift (see also P04). We also used the evolutionary correction ℰr(z) = 0.86z from Roche et al. (2009), which is typical for elliptical galaxies. The absolute magnitude is defined as
, supplied by Fukugita et al. (1995), for elliptical galaxies, assuming that the main population of galaxy systems in our samples are the old elliptical galaxies at the system redshift (see also P04). We also used the evolutionary correction ℰr(z) = 0.86z from Roche et al. (2009), which is typical for elliptical galaxies. The absolute magnitude is defined as 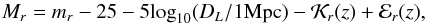 (2)where DL is the luminosity distance in
(2)where DL is the luminosity distance in 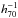 Mpc.
Mpc.
4.2. Checking the 2D galaxy distribution of S07 objects
While RASS-SDSS clusters are well-studied systems in the literature in both the X-ray and the optical wavelengths, this is not true for all S07 objects. Using NED5 we have found that 23 S07 objects have been clearly identified as galaxy systems in one or more optical cluster/group catalog(s) based on photographic plates or SDSS and few of them are well-known systems. On the contrary, 11 S07 objects have no such identification, the closest galaxy system being more distant than 4′. For each FGS object, we analyzed the galaxy distribution in the region around the BCG through the 2D DEDICA method, which is an adaptive-kernel method (Pisani 1993, 1996; see also, e.g., Girardi et al. 2011 for a recent application). This method of density reconstruction gives as output the list of density peaks, their significance, density, and richness, as well as the relative membership. To minimize the effect of foreground/background galaxies we only worked on galaxies (hereafter likely members) having a color close to that of BCG, i.e., | (r − i) − (r − i)BCG | ≤ 0.2 (see also Harrison et al. 2012), and having magnitude Mr< − 19, in order to sample the luminosity function down to ~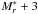 mag, if possible, but not considering fainter galaxies.
mag, if possible, but not considering fainter galaxies.
 |
Fig. 1 Projected spatial distribution and 2D-DEDICA isodensity contours of SDSS galaxies with | (r − i) − (r − i)BCG | ≤ 0.2 and Mr< − 19 in a few FGSs spanning a wide range of appearances (see text). The plots are centered on the S07 BCGs (marked with black crosses). The inner circle encloses the region within R200. The outer two circles enclose the regions within 2R200 and 3R200. The sectors used for the computation of the local field are displayed. Units on the axes are in |
For most S07 objects, there is an excellent match between the location of the BCG and the densest density peak in the whole 2R200 region [hereafter Ipeak(2R200)]. In a sample of 24 S07 systems, the median distance between the BCG and the density peak location is d ~ 80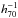 kpc ~ 0.05R200. In the above cases the presence and identification of a galaxy system is outstanding and, with the exception of FGS13, they all already have a corresponding system in one or more published optical cluster catalogs.
kpc ~ 0.05R200. In the above cases the presence and identification of a galaxy system is outstanding and, with the exception of FGS13, they all already have a corresponding system in one or more published optical cluster catalogs.
In other cases (FGS03, FGS08, FGS10, FGS32, FGS34), the BCG does not correspond to the Ipeak(2R200), but to the densest peak within R200, Ipeak(R200), often separated by a great distance, e.g., d ≲ 0.5R200 in FGS03 and FGS10. This means that these FGSs can be strongly contaminated by a very dense galaxy system that is close enough. However, FGS03, FGS08, FGS10, and FGS34 are very rich [Ipeak(R200) is richer or comparable to Ipeak(2R200)], and/or have z-data to support the existence of an extended galaxy system (see Paper IV), and appear sufficiently contrasted with respect to the field (see our local field computation in Sect. 4.3); the noticeable negative exception is thus FGS32. In other cases, no significant peak can be detected within R200 (FGS28), or Ipeak(R200) is far from the BCG, i.e., d> 0.5R200 (FGS11, FGS15, FGS18, FGS29). However, in the case of FGS18, the BCG is closely located to a significant secondary peak, IIpeak(R200), somewhat contrasted with respect to the field around it. Summarizing, we did not consider FGS11, FGS15, FGS28, FGS29, FGS32. All the rejected objects have no corresponding system in published optical cluster catalogs.
The objects listed in S07 span a wide range of morphological appearances; some are very dense, concentrated, and isolated systems, while others are very substructured and/or surrounded by a rich large scale structure. Figure 1 shows a few examples of the 2D-DEDICA contour maps: FGS05 = Abell 697, probably the most massive system in the S07 sample, is well isolated in the 2D space (but not confirmed to be a fossil system); FGS27, a massive fossil cluster; FGS03, a poor nearby fossil group, but just acceptable enough to be part of our analysis (see above); and FGS11, a S07 object not considered in this study. With the present data, we cannot be definitive about the nature of the rejected objects. We suspect that they might not correspond to an extended system (or that they are only poor subsystems). The S07 identification of extended systems based only on the RASS-BSC and FSC definition of extended sources might not always be reliable. For instance, out of six fossil groups identified by La Barbera et al. (2009) in a similar way, the following XMM X-ray data analysis shows that one does not have an extended emission, and another is at the border of a real extended system (La Barbera et al. 2012). Alternatively, the rejected objects might simply be too poorly contrasted in the sky. In either case, we were not able to perform a reliable computation of the optical luminosity.
In summary, considering the rejection of the five FGSs with no clear identification in the galaxy distribution and FGS19 (which is not fully sampled by SDSS-DR7), our working sample is formed of a sample of 28 FGSs (the ALL-FGS sample), 12 of which are confirmed fossil systems (the CONF-FGS sample), while the complementary sample of 16 objects is called NOCONF-FGS.
4.3. Computing Lopt
We computed Lopt within R500 (and 0.5R200) following standard procedures for photometric samples (e.g., Girardi et al. 2000; P04). In particular, P04 suggests that the count-based Lopt estimation has to be preferred to the fit-based one in the study of the correlation between optical and X-ray properties (see their Sect. 5.3); our procedure is of the count-based type.
Observed cluster/group luminosities, Lobs, were obtained by summing the individual absolute luminosities of all galaxies and assuming the absolute magnitude in the r-band for the Sun as M⊙ ,r = 4.68 (as listed by SDSS).
The observed luminosity needs to be corrected for foreground/background contamination, which is the largest source of uncertainty in these kinds of estimates (see, e.g., P04). Two approaches can be used for the statistical subtraction of the galaxy background: the local and the global backgrounds. The limitation of the global background is that local fluctuations of the luminosity field are not taken into account. The alternative is the local background method, which is limited by the Poisson uncertainty of the counts. As for FGSs, we decided to compute an individual local field. For each FGS we extracted from SDSS-DR7 the catalog of galaxies in the annulus between 2R200 and 3R200 in such a way that the galaxy background has been estimated outside the system, but still locally. However, one risks obtaining a local field contaminated by close companion galaxy systems. To overcome this problem, the annulus was divided into 12 sectors, each sector having an area similar to that within R500; the sectors containing 2D-DEDICA contour levels indicating a relative density >30% with respect to the FGS peak were not considered (as above, the DEDICA analysis was applied to the likely members, see Sect. 4.2). We also did not take into account those sectors not fully sampled by SDSS data. The surviving 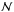 sectors were used to compute the local counts for each FGS.
sectors were used to compute the local counts for each FGS.
The local counts in the magnitude bins for each FGS were then averaged all together. These average counts, estimated using a global area of ~5 deg2, agree rather well with those of P04 (see Fig. 2). The line in Fig. 2 shows a fit to the galaxy counts-magnitude relation expected in a homogeneous universe assuming Euclidean geometry for a 3D space log [N(mr)] = log (A) + 0.6(mr − 16) (see Yasuda et al. 2001). We obtained A = 4.41 (0.5 mag)-1 deg-2 using four points in the range 16 <mr< 18 (at mr ~ 15.75 the number of galaxies is already quite small, N = 16). We define our global background as the combination of our average counts and the Euclidean fit for mr> 15.75 and mr< 15.75, respectively. A posteriori, we verified that, on average, the different corrections do not significantly affect the cluster/group luminosity estimation: we found that Lopt,loc − back/Lopt,glob − back = 1.01 ± 0.03 with rms = 0.18.
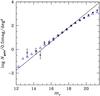 |
Fig. 2 Average field counts (squares) compared to those by P04 (blue triangles). The error bars represent 1sigma Poisson errors. The solid line is the fit for the Euclidean geometry. |
For each system, we computed the corrected luminosity, Lcorr, by subtracting the background luminosity Lback obtained from the background counts rescaled to the area of the system Lcorr = Lobs − Lback. Before the field subtraction, the field galaxies of each system were treated in the same way as the respective member galaxies, i.e., we applied the same conversion in absolute magnitudes of Eq. (2). Corrected counts Ncorr are then obtained in a similar way. As for the FGS sample, the typical correction is ~35% (median value) with the worst case having a 75% correction (FGS12).
In the case of the CL sample, we applied the above procedure adopting the global background; P04 has shown that the luminosity difference using a local or global background is smaller than the statistical error. The typical correction (~25%) is smaller than in the case of FGSs, in agreement with the fact that FGSs are expected to be somewhat less contrasted on the sky than the CLs.
In order to obtain the total optical cluster/group luminosity Lopt, we need to add the contribution of the galaxies below the magnitude completeness limit. To compute this contribution we adopted the usual Schechter (1976) form for the cluster luminosity function (LF) obtaining 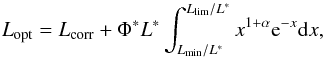 (3)
(3)
where Llim is the luminosity corresponding to the limiting magnitude; Lmin corresponds to a cutoff for the minimum galaxy luminosity (here we adopt Lmin = 10-4L∗); and L∗, α, and Φ∗ are the parameters of the LF.
We adopted the LF parameters determined by Popesso et al. (2005), i.e., the L∗ value corresponding to the absolute magnitude 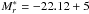 log h70 and α = −1.30 as listed in the first part of their Table 2 (second line). Following previous studies (Lumsden et al. 1997; Girardi et al. 2000), the Φ∗ parameter is determined from the (corrected) galaxy number counts in a magnitude interval around M∗ to obtain a more robust value. We used Ncorr( − 19, − 23) computed for −23 ≤ Mr ≤ − 19 to obtain
log h70 and α = −1.30 as listed in the first part of their Table 2 (second line). Following previous studies (Lumsden et al. 1997; Girardi et al. 2000), the Φ∗ parameter is determined from the (corrected) galaxy number counts in a magnitude interval around M∗ to obtain a more robust value. We used Ncorr( − 19, − 23) computed for −23 ≤ Mr ≤ − 19 to obtain 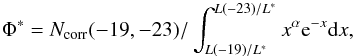 (4)
(4)
where L( − 19) and L( − 23) are the luminosities corresponding to absolute magnitudes of Mr = −19 and Mr = −23, respectively. If the absolute limiting magnitude is brighter than Mr = −19, we take Llim for the lower integration limit in Eq. (4). Owing to the extrapolation to faint magnitudes, the luminosity increases by ~10% and 5% (median values for FGSs and CLs). The obtained luminosity Lopt is considered our reference optical luminosity.
4.4. Uncertainties in Lopt estimates
The foreground/background correction is the largest correction applied to the observed luminosity and is the largest source of random error in luminosity estimates. The comparison between Lopt,loc − back and Lopt,glob − back for FGSs suggests a 20% estimate of the luminosity uncertainties. We also estimated uncertainties for each individual FGS using the field sectors adopted to compute the local background. For each FGS, we computed 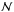 optical luminosities using the backgrounds as derived for the available
optical luminosities using the backgrounds as derived for the available 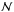 sectors: the rms of their distribution (or half of the distribution range in the case of
sectors: the rms of their distribution (or half of the distribution range in the case of 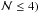 was taken as an estimate of the luminosity uncertainty for each individual FGS (on average ~20%). Conservatively, for each FGS, the largest between this individual estimate and the above global 20% estimate is assumed to be the statistical uncertainty due to the background (hereafter ϵLopt,back). As for CLs, we assumed ϵLopt,back = 20% , in agreement with that directly estimated by P04.
was taken as an estimate of the luminosity uncertainty for each individual FGS (on average ~20%). Conservatively, for each FGS, the largest between this individual estimate and the above global 20% estimate is assumed to be the statistical uncertainty due to the background (hereafter ϵLopt,back). As for CLs, we assumed ϵLopt,back = 20% , in agreement with that directly estimated by P04.
The above uncertainty has been obtained for a fixed aperture. In addition, for both FGSs and CLs, we had to take into account how the uncertainty in the estimate of R500 propagates to the Lopt computation. First, the R500 estimate is subjected to the uncertainty in the LX estimate: according to Eq. (1), the formal error is small enough, i.e., ϵR500 = 1/0.228ϵLX ~ 5% and 8% for CLs and FGSs. Second, one should consider the intrinsic scatter (i.e., not due to measurement errors) in the relations used to derive the value of R500 (Eq. (1) and those referred in the original papers) or, more generally, the intrinsic scatter between R500 values estimated from different observables. This issue is connected to the cluster mass calibration and its complete discussion is well outside the scope of this paper. In this study we have considered the result of Zhang et al. (2011), i.e., the presence of a ~ 20% intrinsic scatter in the relation between R500, as determined from X-ray observables, and velocity dispersion (see their Table 3). Adding both sources of uncertainty, a 25% error in the R500 estimate was considered. The propagated uncertainty on Lopt, ϵLopt,radius, was computed as half | Lopt,R500 + 25% − Lopt,R500 − 25% | /Lopt, where Lopt,R500 + 25% and Lopt,R500 − 25% are the luminosities in regions where the radius is 25% larger and smaller than R500. We obtained ϵLopt,radius ~ 20% (median value). Summarizing, the estimate of the total uncertainty on Lopt was then conservatively computed as ϵLopt = ϵLopt,radius + ϵLopt,back ~ 40% (median value).
5. Comparison between fossil and normal galaxy systems
Here we present the comparison between CONF-FGSs and NOCONF-FGSs in the Lopt–LX plane. We also compared CONF-FGSs (and ALL-FGSs) with CLs. The first comparison has the advantage of being only based on the S07 catalog and thus it handles a single selection function, but it has the obvious drawback of being based on two small samples. For the second comparison, we also explored the possibility of using LX,BSC/FSC for CLs or, alternatively, LX,corr for FGSs in such a way as to improve the homogeneity of the comparison (hereafter homo- and corr-cases). We note that X-ray and optical luminosity estimates have always been consistently determined, i.e., the radius used to compute Lopt is always based on the corresponding X-ray luminosity estimate. In practice, we considered the following comparisons: 12 CONF-FGSs – 16 NOCONF-FGSs; 12 CONF-FGSs – 102 CLs; 12 CONF-FGSs – 67 CLs (homo-case); 12 CONF-FGSs – 102 CLs (corr-case); 28 ALL-FGSs – 102 CLs; and 28 ALL-FGSs – 67 CLs (homo-case); 28 ALL-FGSs – 102 CLs (corr-case). We considered optical luminosities within both R500 and 0.5R200.
As a first approach we used the 2D Kolmogorov-Smirnov test (hereafter 2DKS-test, Fasano et al. 1987; Press et al. 1992), which has the advantage of being a nonparametric test. No significant difference was detected. The comparison for our reference values is shown in Fig. 3. We also performed the linear fit in the Lopt–LX logarithmic plane. We used a maximum likelihood estimate of the regression lines (see, e.g., Kendall & Stuart 1979; Press et al. 1992) to fit ![\begin{equation} {\rm log}(L_{\rm X,44})=a +b\cdot{\rm log}[L_{\rm opt,12}(<\!\!R_{500})], \end{equation}](/articles/aa/full_html/2014/05/aa23311-13/aa23311-13-eq154.png) (5)where LX,44 is the X-ray luminosity in units of
(5)where LX,44 is the X-ray luminosity in units of 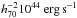 and Lopt,12 is the optical luminosity in units of
and Lopt,12 is the optical luminosity in units of 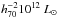 . Table 3 shows the main results. Figure 3 also shows the fitted relations for the two alternative estimates of LX. For each comparison of the above list, the 90% c.l. ellipses overlap (see also the inset plot in Fig. 3). The same result was obtained for Lopt( <0.5R200).
. Table 3 shows the main results. Figure 3 also shows the fitted relations for the two alternative estimates of LX. For each comparison of the above list, the 90% c.l. ellipses overlap (see also the inset plot in Fig. 3). The same result was obtained for Lopt( <0.5R200).
Fit parameters obtained using Eq. (5).
 |
Fig. 3 X-ray luminosity vs. r-band optical luminosity for CONF-FGSs (blue circles), NOCONF-FGSs (blue crosses), and CLs (red dots). Error bars for the CL sample are omitted. Reference values for Lopt and LX are shown. The blue solid and dotted lines indicate the fits for the CONF-FGS and ALL-FGS samples, and the red solid line is the fit for the CL sample. The magenta long-dashed and cyan dashed lines are the fits when using alternative X-ray luminosity estimates: LX,BSC/FSC values for the CL sample and LX,corr values for the CONF-FGS sample. The inset plot shows the 90% c.l. confidence ellipses corresponding to CONF-FGSs, NOCONF-FGSs, ALL-FGSs (solid, dot-dashed, and dotted blue curves), and CLs (solid red curve). Results for alternative X-ray luminosities are shown: LX,BSC/FSC for CLs (magenta long dashed curve) and LX,corr for CONF-FGSs (cyan dashed line). |
6. Discussion and conclusions
From the comparison between FGSs and CLs presented above we conclude that fossil systems are not significantly distinguishable from normal galaxy systems in the Lopt–LX plane. In particular, we find no evidence in favor of fossil systems being X-ray overluminous (by a factor of ~10, Khosroshahi et al. 2007, see their Fig. 2) or optically underluminous (by a factor of ~3, Proctor et al. 2011, see their Sect. 5.3 and their Fig. 4) than normal systems. Differences such as those suggested in previous studies are inconsistent with the plot shown in Fig. 3 (see also Fig. 4), although there is still space to accommodate modest differences. We plan some future efforts to reduce the scatter of the S07 FGSs around the LX–Lopt relation, e.g., using FOGO redshift data, to further improve the optical luminosity estimates. To improve the study of X-ray properties, we have obtained X-ray Suzaku data for ten FGSs (data under reduction).
Voevodkin et al. (2010) suggest that results might be dubious when obtained for fossil and comparison systems treated in a nonhomogeneous way. Voevodkin et al. (2010) present a remarkable homogeneous comparison, finding no difference between fossil and comparison systems. However, the fitted relation we obtained for the CL sample, log [LX,44(0.5−2.0 keV)] = (−0.59 ± 0.04) + (1.90 ± 0.09)·log [Lopt,12< (R500)], is strongly inconsistent with their Fig. 5; their optical luminosities are too small. Since Proctor et al. (2011) report the presence of a serious error in the Voevodkin et al. (2010) estimations of the optical luminosities, we no longer consider a quantitative comparison. Rather, we consider the results of Harrison et al. (2012), the most recent paper on this subject and where the data were treated in a homogeneous way. We note that their X-ray luminosity estimates are based on a different data source (XMM-Newton) and methodology. Their estimation of optical luminosities is also quite different, as it is based on galaxies in the red sequence and with no (even modest) background subtraction and no LF extrapolation. In addition, their estimation of characteristic radii is different. Figure 4 shows that the combination of data from different sources can somehow generate difficulties when pursuing precise comparisons. Thus, we stress the need to perform comparisons based on a homogeneous treatment of the data. Independently, both Harrison et al. (2012) and our study agree: there is no difference between fossil and normal systems. These are the two most recent studies on the LX–Lopt relation and treat a total of about 30 fossil systems. Thus, a definitive conclusion on this issue has likely been reached.
 |
Fig. 4 Comparison with previous literature. CONF-FGSs and CLs as in Fig. 3, but for the bolometric X-ray luminosity and the optical luminosity computed within 0.5R200. The dashed line indicates overestimates by a factor of 10 in LX(bol) or underestimates by a factor of 3 in Lopt with respect to our CL sample (red points fitted by the solid line). Large and small black triangles indicate the fossil and comparison systems in Harrison et al. (2012, see their Fig. 5). |
Regarding the formation and evolution of fossil systems, our results are consistent with the classical merging scenario where the large BCG is the product of mergers/cannibalism of other group galaxies, with the conservation of the galaxy optical light. In a general context, Lin & Mohr (2004) argue that BCGs grow in luminosity mainly by merging with other luminous galaxies as the host clusters grow hierarchically. The evidence that very luminous galaxies grow in luminosity and decrease in number as the parent cluster evolves is the result of a study based on merging vs. relaxed clusters (Barrena et al. 2012). We propose that this process was particularly efficient in fossil systems with the BCG growing at the expense of the other brightest galaxies in the system. Our Paper IV–using a subsample of S07 FGSs for which we have computed σv–shows that the main difference between fossil and normal systems of comparable mass is the fraction of optical luminosity contributed by the BCG. On the other hand, it seems that the merging/coalescing process does not cause any peculiarity in the global state of the hot intracluster medium or, alternatively, that possible peculiarities are a very short-lived phenomenon.
Online material
Properties of the FGS sample.
Properties of the CL sample.
Acknowledgments
M.G. acknowledges financial support from the PRIN-INAF/2010 and MIUR PRIN/2010-2011 (J91J12000450001). E.D. gratefully acknowledges the support of the Alfred P. Sloan Foundation. J.M.A. acknowledges support from the European Research Council Starting Grant (SEDmorph; P.I. V. Wild). EMC is supported by Padua University (grants 60A02-1283/10, 5052/11, 4807/12). J.I.P. and J.V.M. acknowledge financial support from the Spanish MINECO under grant AYA2010-21887-C04-01, and from Junta de Andalucía Excellence Project PEX2011-FQM7058. This work has been supported by the Programa Nacional de Astronomía y Astrofísica of the Spanish Ministry of Science and Innovation under grants AYA2010-21887-C04-04, AYA2007-67965-C03-01 and under the Consolider-Ingenio 2010 Program grant CSD2006-00070: First Science with the GTC (http://www.iac.es/consolider-ingenio-gtc). This work was partially funded by the local Canarian Government (grant ProID20100140). This article is based on observations made with the Telescopio Nazionale Galileo operated on the island of La Palma by the “Fundación Galileo Galilei-INAF, Fundación Canaria,” in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS Web Site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Abell, G. O., Corwin, H. G. Jr., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aguerri, J. A. L., Girardi, M., Boschin, W., et al. 2011, A&A, 527, A143 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2005, A&A, 441, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Girardi, M., Boschin, W., & Mardirossian, F. 2012, A&A, 540, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Biviano, A., Durret, F., Gerbal, D., et al. 1995, A&A, 297, 610 [NASA ADS] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capozzi, D., de Filippis, E., Paolillo, M., D’Abrusco, R., & Longo, G. 2009, MNRAS, 396, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M. 1989, MNRAS, 237, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Cypriano, E. S., Mendes de Oliveira, C. L., & Sodré, L. Jr., 2006, AJ, 132, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Cui, W., Springel, V., Yang, X., De Lucia, G., & Borgani, S. 2011, MNRAS, 416, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Democles, J., Pratt, G. W., Pierini, D., et al. 2010, A&A, 517, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feigelson, E. D., & Babu, G. J. 1992, in Statistical Challenges in Modern Astronomy, XXI (Berlin, Heidelberg, New York: Springer-Verlag), 527, 49 [Google Scholar]
- Fukugita, M., Shimasaku, K., & Ichikawa, T. 1995, PASP, 107, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Annis, J., Gunn, J. E., et al. 2001, AJ, 122, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Dariush, A., Khosroshahi, H. G., Ponman, T. J., et al. 2007, MNRAS, 382, 433 [NASA ADS] [CrossRef] [Google Scholar]
- D’Onghia, E., Sommer-Larsen, J., Romeo, A. D., et al. 2005, ApJ, 630, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] [CrossRef] [Google Scholar]
- Gal, R. R., de Carvalho, R. R., Lopes, P. A. A., et al. 2003, AJ, 125, 2064 [NASA ADS] [CrossRef] [Google Scholar]
- Girardi, M., Bardelli, S., Barrena, R., et al. 2011, A&A, 536, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girardi, M., Borgani, S., Giuricin, G., Mardirossian, F., & Mezzetti, F. 2000, ApJ, 530, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, J., McKay, T. A., Koester, B. P., 2010, ApJS, 191, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. D., Miller, C. J., Richards, J. W., et al. 2012, ApJ, 752, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Kendall, M, & Stuart, A. 1979, Advanced Theory of Statistics, eds. Buther, & Tonner Ltd (London: Griffin) [Google Scholar]
- Khosroshahi, H. G., Ponman, T., & Jones, L. R. 2006, MNRAS, 372, L68 [NASA ADS] [CrossRef] [Google Scholar]
- Khosroshahi, H. G., Ponman, T., & Jones, L. R. 2007, MNRAS, 377, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Isobe, T., Feigelson, E. D., Akritas, M. G., & Babu, G. J. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, L. R., Ponman, T. J., Horton, A., et al. 2003, MNRAS, 343, 627 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., de la Rosa, I. G., et al. 2009, AJ, 137, 3942 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., Paolillo, M., De Filippis, E., & de Carvalho, R. R. 2012, MNRAS, 422, 3010 [NASA ADS] [CrossRef] [Google Scholar]
- Ledermann, W. 1982, in Handbook of Applicable Mathematics (New York: Wiley), 6 [Google Scholar]
- Lin, Y.-T., & Mohr, J. J. 2004, ApJ, 617, 879 [NASA ADS] [CrossRef] [Google Scholar]
- Lumsden, S. L., Collins, C. A., Nichol, R. C., Eke, V. R., & Guzzo, L. 1997, MNRAS, 290, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Lupton, R., Gunn, J. E., Ivezić, Z., Knapp, G. R., & Kent, S. 2001, in Astronomical Data Analysis Software and Systems X, eds. Jr. F. R. Harnden, F. A. Primini, & H. E. Payne, ASP Conf. Ser., 238, 269 [Google Scholar]
- Markevitch, M. 1998, ApJ, 504, 27 [NASA ADS] [CrossRef] [Google Scholar]
- McConnachie, A. W., Patton, D. R., Ellison, S. L., & Simard, L. 2009, MNRAS, 395, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Méndez-Abreu, J., Aguerri, J. A. L., Barrena, R., et al. 2012, A&A, 537, A25 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, C. J., Nichol, R. C., Reichart, D., et al. 2005, AJ, 130, 969 [Google Scholar]
- Miller, E. D., Rykoff, E. S., Dupke, R. A., et al. 2012, ApJ, 747, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Mulchaey, J. S., & Zabludoff, A. I. 1999, ApJ, 514, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Mukai, K. 1993, Legacy 3, 21 [Google Scholar]
- Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] [Google Scholar]
- Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S.A., Vetterling, W. T., & Flannery, B.P. 1992, in Numerical Recipes, Second Edition (Cambridge University Press) [Google Scholar]
- Ponman, T. J., Allan, D. J., Jones, L. R., et al. 1994, Nature, 369, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Popesso, P., Böehringer, H., Brinkmann, J., Voges, W., & York, D. G. 2004, A&A, 423, 449 (P04) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popesso, P., Biviano, A., Böehringer, H., Romaniello, M., & Voges, W. 2005, A&A, 433, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Proctor, R. N., Mendes de Oliveira, C., Dupke, R., et al. 2011, MNRAS, 418, 2054 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, N., Bernardi, M., & Hyde, J. 2009, MNRAS, 398, 1549 [NASA ADS] [CrossRef] [Google Scholar]
- Santos, W. A., Mendes de Oliveira, C., & Sodré, L., Jr. 2007, AJ, 134, 1551 (S07) [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 29 [Google Scholar]
- Siegel, S. 1956, in Nonparametric Statistics for the Behavioral Sciences (New York: McGraw-Hill Book Co.), 68 [Google Scholar]
- Stoughton, C., Lupton, R. H., Bernardi, M., et al. 2002, AJ, 123, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Valotto, C. A., Nicotra, M. A., Muriel, H., & Lambas, D. G. 1997, ApJ, 479, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Voevodkin, A., Borozdin, K., Heitmann, K., et al. 2010, ApJ, 708, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 2000, IAU Circ., 7432, 1 [NASA ADS] [Google Scholar]
- von Benda-Beckmann, A. M., D’Onghia, E., Gottlöber, S., et al. 2008, MNRAS, 386, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H.-Y. K., Ricker, P. M., & Sutter, P. M. 2009, ApJ, 699, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Yasuda, N., Fukugita, M., Narayanan, V. K., et al. 2001, AJ, 122, 1104 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2009, ApJS, 183, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2010, ApJS, 187, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Zarattini, S., Barrena, R., Girardi, M., et al. 2014, A&A, 565, A116 (Paper IV) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Y.-Y., Andernach, H., Caretta, C. A., et al. 2011, A&A, 526, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwicky, F., & Kowal, C. T. 1968, Catalogue of Galaxies and of Clusters of Galaxies, vol. VI (Pasadena: California Institute of Technology) [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Projected spatial distribution and 2D-DEDICA isodensity contours of SDSS galaxies with | (r − i) − (r − i)BCG | ≤ 0.2 and Mr< − 19 in a few FGSs spanning a wide range of appearances (see text). The plots are centered on the S07 BCGs (marked with black crosses). The inner circle encloses the region within R200. The outer two circles enclose the regions within 2R200 and 3R200. The sectors used for the computation of the local field are displayed. Units on the axes are in |
| In the text | |
 |
Fig. 2 Average field counts (squares) compared to those by P04 (blue triangles). The error bars represent 1sigma Poisson errors. The solid line is the fit for the Euclidean geometry. |
| In the text | |
 |
Fig. 3 X-ray luminosity vs. r-band optical luminosity for CONF-FGSs (blue circles), NOCONF-FGSs (blue crosses), and CLs (red dots). Error bars for the CL sample are omitted. Reference values for Lopt and LX are shown. The blue solid and dotted lines indicate the fits for the CONF-FGS and ALL-FGS samples, and the red solid line is the fit for the CL sample. The magenta long-dashed and cyan dashed lines are the fits when using alternative X-ray luminosity estimates: LX,BSC/FSC values for the CL sample and LX,corr values for the CONF-FGS sample. The inset plot shows the 90% c.l. confidence ellipses corresponding to CONF-FGSs, NOCONF-FGSs, ALL-FGSs (solid, dot-dashed, and dotted blue curves), and CLs (solid red curve). Results for alternative X-ray luminosities are shown: LX,BSC/FSC for CLs (magenta long dashed curve) and LX,corr for CONF-FGSs (cyan dashed line). |
| In the text | |
 |
Fig. 4 Comparison with previous literature. CONF-FGSs and CLs as in Fig. 3, but for the bolometric X-ray luminosity and the optical luminosity computed within 0.5R200. The dashed line indicates overestimates by a factor of 10 in LX(bol) or underestimates by a factor of 3 in Lopt with respect to our CL sample (red points fitted by the solid line). Large and small black triangles indicate the fossil and comparison systems in Harrison et al. (2012, see their Fig. 5). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


