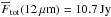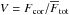| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A82 | |
| Number of page(s) | 30 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322698 | |
| Published online | 13 March 2014 | |
The dusty torus in the Circinus galaxy: a dense disk and the torus funnel⋆,⋆⋆
1 Max-Planck-Institut für Radioastronomie, auf dem Hügel 69,
53121 Bonn, Germany
e-mail:
tristram@mpifr-bonn.mpg.de
2
Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312,
Gießenbachstraße, 85741
Garching,
Germany
3
Leiden Observatory, Leiden University,
Niels-Bohr-Weg 2,
2300 CA
Leiden, The
Netherlands
4
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
5
Dark Cosmology Center, Niels Bohr Institute, University of
Copenhagen, Juliane Maries Vej
30, 2100
Copenhagen,
Denmark
6
Universitätssternwarte München, Scheinerstr. 1, 81679
München,
Germany
Received:
17
September
2013
Accepted:
26
November
2013
Context. With infrared interferometry it is possible to resolve the nuclear dust distributions that are commonly associated with the dusty torus in active galactic nuclei (AGN). The Circinus galaxy hosts the closest Seyfert 2 nucleus and previous interferometric observations have shown that its nuclear dust emission is particularly well resolved.
Aims. The aim of the present interferometric investigation is to better constrain the dust morphology in this active nucleus.
Methods. To this end, extensive new observations were carried out with the MID-infrared Interferometric instrument (MIDI) at the Very Large Telescope Interferometer, leading to a total of 152 correlated flux spectra and differential phases between 8 and 13 μm. To interpret this data, we used a model consisting of black-body emitters with a Gaussian brightness distribution and with dust extinction.
Results. The direct analysis of the data and the modelling confirm that the emission is distributed in two distinct components: a disk-like emission component with a size (FWHM) of ~0.2 × 1.1 pc and an extended component with a size of ~0.8 × 1.9 pc. The disk-like component is elongated along PA ~ 46° and oriented perpendicular to the ionisation cone and outflow. The extended component is responsible for 80% of the mid-infrared emission. It is elongated along PA ~ 107°, which is roughly perpendicular to the disk component and thus in polar direction. It is interpreted as emission from the inner funnel of an extended dust distribution and shows a strong increase in the extinction towards the south-east. We find both emission components to be consistent with dust at T ~ 300 K, that is we find no evidence of an increase in the temperature of the dust towards the centre. From this we infer that most of the near-infrared emission probably comes from parsec scales as well. We further argue that the disk component alone is not sufficient to provide the necessary obscuration and collimation of the ionising radiation and outflow. The material responsible for this must instead be located on scales of ~1 pc, surrounding the disk. We associate this material with the dusty torus.
Conclusions. The clear separation of the dust emission into a disk-like emitter and a polar elongated source will require an adaptation of our current understanding of the dust emission in AGN. The lack of any evidence of an increase in the dust temperature towards the centre poses a challenge for the picture of a centrally heated dust distribution.
Key words: galaxies: active / galaxies: nuclei / galaxies: Seyfert / galaxies: individual: Circinus / galaxies: structure / techniques: interferometric
Based on observations collected at the European Southern Observatory, Chile, programme numbers 073.A-9002(A), 060.A-9224(A), 074.B-0213(A/B), 075.B-0215(A), 077.B-0026(A), 081.B-0893(A), 081.B-0908(A/B), 383.B-0159(A), 383.B-0993(A), 087.B-0746(C), 087.B-0971(A-C), and 087.B-0266(H).
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Active galactic nuclei (AGN) are thought to play a major role in the formation and the evolution of galaxies. The AGN phase provides mechanisms for feedback from the supermassive black hole to its hosting galaxy and the intergalactic medium. Therefore, a thorough knowledge of the accretion process in AGN is required to understand their influence on the formation and evolution of galaxies. Especially little is known about the accretion process on parsec scales.
A toroidal distribution of warm molecular gas and dust surrounding the central engine, the so-called dusty torus, is a key component of AGN. First of all, the torus plays an important role in fuelling the AGN activity: it either forms the passive reservoir of material for the accretion onto the supermassive black hole or, more intriguingly, it is itself the active driver of the accretion towards the black hole (Hopkins et al. 2012). Secondly, the dusty torus is held responsible for the orientation-dependent obscuration of the central engine (e.g. Antonucci 1993; Urry & Padovani 1995): when oriented face-on, a direct view of the central engine is possible through the cavity in the torus (Type 1 AGN); when oriented edge-on, the view towards the centre is blocked by the gas and dust of the torus (Type 2 AGN). This scenario is supported by multiple observational evidence, most importantly by the detection of broad emission lines in the polarised light of several Type 2 nuclei (e.g. Antonucci & Miller 1985; Lumsden et al. 2004), indicating that Type 2 sources host the same central engine as Type 1 AGN. However, there is also a growing number of observations that challenge this simple picture, e.g. the discovery of true Type 2 sources (without broad emission lines in polarised light) and X-ray column densities discrepant with the optical classification (for a recent discussion of AGN obscuration, see e.g. Bianchi et al. 2012).
The dust in the torus is heated by the emission from the accretion disk. It re-emits this energy in the infrared (Rees et al. 1969): the innermost dust is close to its sublimation temperature and mainly emits in the near-infrared, while the dust at larger distances is at lower temperatures and emits in the mid-infrared (Barvainis 1987). Direct observations of the torus are thus best carried out at infrared wavelengths. However, the dust distributions are very compact: they are essentially unresolved by single-dish observations even with the largest currently available telescopes (e.g. Horst et al. 2009; Ramos Almeida et al. 2009). Only by employing interferometric methods in the infrared is it possible to resolve the nuclear dust distributions in AGN.
To date, several interferometric studies of the nuclear dust distributions of individual galaxies have been carried out. In the Seyfert 2 galaxy NGC 1068, the interferometric observations reveal a hot, parsec-sized disk that is surrounded by warm dust extended in polar direction (Wittkowski et al. 2004; Jaffe et al. 2004; Weigelt et al. 2004; Poncelet et al. 2006; Raban et al. 2009). A two-component structure was also found in the nucleus of the Circinus galaxy (Tristram et al. 2007, see below). In NGC 424 (Sy 2) and NGC 3783 (Sy 1) the thermal dust emission appears extended along the polar axis of the system (Beckert et al. 2008; Hönig et al. 2012, 2013). In NGC 4151, a Seyfert 1.5 galaxy, interferometric measurements in the near- and mid-infrared have provided evidence of both hot dust at the inner rim of the torus as well as warm dust farther out (Swain et al. 2003; Burtscher et al. 2009; Kishimoto et al. 2009b; Pott et al. 2010). In the radio galaxy NGC 5128 (Centaurus A) on the other hand, only half of the mid-infrared emission appears to be of thermal origin (Meisenheimer et al. 2007; Burtscher et al. 2010; Burtscher 2011). Near-infrared reverberation measurements and interferometry of several Type 1 AGN have shown that the hot inner rim of the torus scales with the square root of the AGN luminosity (Suganuma et al. 2006; Kishimoto et al. 2011a). Whether this is also true for the cooler dust in the body of the torus remains unclear after interferometric studies of small samples of galaxies in the mid-infrared (Tristram et al. 2009; Tristram & Schartmann 2011; Kishimoto et al. 2011b). Although a possible common radial structure for AGN tori has been proposed (Kishimoto et al. 2009a), the first study with a statistically significant sample of AGN shows a rather diverse picture of the dust distributions with quite large differences between the dust distributions in individual galaxies (Burtscher et al. 2013).
Because of computational limitations, initial radiative transfer calculations of geometrical torus models were carried out for smooth dust distributions (e.g. Krolik & Begelman 1988; Granato & Danese 1994; Schartmann et al. 2005). However, it was realised early on that the distribution of gas and dust is most likely clumpy (Krolik & Begelman 1988). For this reason, radiative transfer calculations of clumpy dust distributions have been carried out more recently (e.g. Nenkova et al. 2002; Schartmann et al. 2008; Hönig & Kishimoto 2010). First attempts to address the physics of the accreting nuclear material in AGN have been undertaken using hydrodynamical simulations (Wada & Norman 2002; Dorodnitsyn et al. 2008; Schartmann et al. 2009; Wada et al. 2009; Wada 2012). Nevertheless, the physical picture of the torus remains unclear. Most torus models were designed to correctly reproduce the infrared spectral energy distributions (SEDs) of AGN and the silicate feature at 10 μm. Very little can be learned about the torus itself from such comparisons: very diverse models using different assumptions and parameters can produce similar SEDs (Feltre et al. 2012). The degeneracies in the SEDs can, at least partially, be broken by resolving the dust distributions. This is, as stated above, currently only possible with infrared interferometry.
At a distance of about 4 Mpc (1 arcsec ~ 20 pc, Freeman et al. 1977), the Circinus galaxy is the closest Seyfert 2 galaxy. It is the second brightest AGN in the mid-infrared (after NGC 1068) and, hence, a prime target for detailed studies of its nuclear distribution of gas and dust. The galaxy can be considered to be a prototypical Seyfert 2 galaxy with narrow emission lines (Oliva et al. 1994), broad emission lines in polarised light (Oliva et al. 1998), a prominent ionisation cone (Veilleux & Bland-Hawthorn 1997; Maiolino et al. 2000; Wilson et al. 2000; Prieto et al. 2004), an outflow observed in CO (Curran et al. 1998, 1999), bipolar radio lobes (Elmouttie et al. 1998), a Compton thick nucleus and a reflection component in X-rays (Matt et al. 1996; Smith & Wilson 2001; Soldi et al. 2005; Yang et al. 2009). The galaxy is inclined by ~65° and the nucleus is heavily obscured by dust lanes in the plane of the galaxy so that it is only visible longward of λ = 1.6 μm (Prieto et al. 2004).
A first set of interferometric measurements with the MID-infrared Interferometric instrument (MIDI) was presented in Tristram et al. (2007). The modelling of the interferometric data showed that an extended, almost round emission region with T ≲ 300 K and a size of ~2.0 pc surrounds a highly elongated, only slightly warmer (T ~ 330 K) emission region with a size of ~0.4 pc. The latter component was found to have roughly the same orientation and size as a rotating molecular disk traced by H2O masers (Greenhill et al. 2003). The observations were interpreted as a geometrically thick dust distribution with an embedded disk component. This “torus” was found to be oriented perpendicular to the ionisation cone and outflow. The fact that the model did not reproduce all details of the observations was attributed to a more complex dust distribution. However, the properties of the dust components were poorly constrained and no evidence of hot dust was found.
In this paper, new interferometric observations of the Circinus galaxy with MIDI in the mid-infrared are presented in order to shed more light on both the small scale structure of the dust distribution as well as on the properties of the extended dust component. The paper is organised as follows: the observations and data reduction are described in Sect. 2. The results are discussed in Sect. 3. The description of our modelling of the brightness distribution and the discussion of the torus properties are given in Sects. 4 and 5, respectively. A summary of the results is given in Sect. 6.
2. Observations and data reduction
2.1. Observations
The new interferometric observations of the Circinus galaxy with MIDI were carried out in April 2008 and 2009 as well as in April and May 2011. MIDI is the mid-infrared interferometer of the Very Large Telescope Interferometer (VLTI) on Cerro Paranal in northern Chile (Leinert et al. 2003). It combines the light of two telescopes and produces spectrally dispersed interferograms in the N-band between 8 and 13 μm. All observations of the Circinus galaxy were carried out in high sensitivity ( HIGH_SENSE ) mode and with the prism (λ/δλ ≈ 30) as the dispersive element. With a few exceptions, the calibrator stars HD 120404, HD 125687 and HD 150798 were observed with the Circinus galaxy. Other calibrators observed in the same night and with the same instrumental setup were only used to determine the uncertainties of the transfer function (see Sect. 2.2).
The primary quantities measured by MIDI are the correlated flux spectra Fcor(λ) and the differential phases φdiff(λ) (differential in wavelength, therefore also called “chromatic phases”) from the interferometric measurements, as well as the masked total flux spectra Ftot(λ) from the single-dish measurements. Fcor and φdiff contain information on the source morphology and depend on the baseline vector (projected baseline length BL and position angle PA), that is on the projected separation and orientation of the two telescopes. The visibilities V(λ) commonly used in optical/IR interferometry are in principle obtained by V(λ) = Fcor(λ)/Ftot(λ) (for details on the relation of the quantities for MIDI we refer to Tristram 2007). Each interferometric measurement determines one point of the Fourier transform of the brightness distribution of the source in the so-called uv plane. The actual point measured depends on the projected baseline of the interferometer, that is on BL and PA. The basic goal of interferometry is to sample the uv plane as completely as possible in order to draw inferences on the brightness distribution. To specifically probe the small scale structures and the more extended dust in the Circinus galaxy, the new observations were carried out mainly with two long baselines using pairs of the 8.2 m Unit Telescopes (UTs) as well as with the shortest baselines of the VLTI using the 1.8 m Auxiliary Telescopes (ATs).
Including the data from Tristram et al. (2007), the Circinus galaxy was observed in a total of 18 epochs between 2004 and 2011. A summary of the observation epochs, including observing date, baseline properties and the numbers of good and bad measurements, is given in Table 1. Figure 1 shows the measurements in the uv plane, colour coded according to their observing epoch. A detailed list of the individual measurements can be found in Table A.1 in Appendix A.
To increase the sampling of the uv plane and the observing efficiency in the new observations, we continuously observed the Circinus galaxy by directly repeating the interferometry and photometry exposures. In doing so, the time-consuming acquisition and setup procedures normally performed when changing sources with MIDI are omitted. Calibrators were observed at intervals of typically 1.5 h in order to determine the variations of the instrumental and atmospheric transfer function during the night and to estimate the calibration error (see Sect. 2.2). Using this observing method, an almost continuous measurement of the correlated fluxes can be obtained along a uv track, while the projected baseline vector moves through the uv plane due to the rotation of the Earth.
List of the MIDI observation epochs for the Circinus galaxy.
 |
Fig. 1 uv plane with all MIDI measurements of the Circinus galaxy. The individual uv points are colour-coded according to the different observing epochs. Successful measurements are shown by filled circles, failed measurements by open circles. The full baseline tracks are plotted in grey for all the telescope combinations used and for a minimum elevation of the Circinus galaxy of . In the baseline names, U stands for the UTs, A1 to G0 for the stations of the ATs. Regions used for the comparison of measurements at different epochs are encircled and labelled in blue (see Sect. 2.3). Every measurement appears twice, symmetric to the centre of the uv plane, because the Fourier transform of a real valued function (such as the intensity distribution on sky) is hermitian. As a consequence, the measurements which seem covered by the figure key are identical to those on the other side of the uv plane. |
The large time span over which the observations were carried out leads to some inhomogeneity in the data. The instrumental capabilities and observing procedures evolved with time and both the UTs and ATs were used for the observations; differing integration times and chopping frequencies were used for the single-dish spectra; observations were carried out with different states of the adaptive optics and field stabilisation systems. The respective quantities and system settings are included in Table A.1 for each uv point. Any ramifications for the data resulting from these differences should be eliminated during the calibration process (see Sect. 2.2) because the calibrators were observed with the same set-up. For this reason, we combine all data into one data set in order to achieve the best possible uv coverage.
2.2. Data reduction
The data was reduced using the data reduction package EWS (Expert Work Station 1, Jaffe 2004) Version 2.0. Additional software 2 written in IDL was used to diagnose and analyse the data consistently. EWS implements the coherent integration method (e.g. Meisner et al. 2004) for the reduction of the interferometric data. In this method, the group delay and phase drifts caused by the atmosphere are determined from the data itself. Note that because of these drifts only the differential phases can be obtained with MIDI, not the “absolute” Fourier phases. After the group delay and phase drifts have been removed and the bad frames have been flagged, the interferometric signal is averaged coherently. Version 2.0 of EWS includes several improvements especially for the treatment of fainter sources (i.e. sources with correlated fluxes significantly below 1 Jy on the UTs, or 20 Jy on the ATs). For example, the group delay and water vapour phase estimation are significantly more robust and less biased than previously. A description of the improvements to the data reduction software can be found in Burtscher et al. (2012).
Values for the parameters in EWS used for the reduction of the MIDI data of the Circinus galaxy.
The parameter settings of EWS used to reduce the data of the Circinus galaxy are listed in Table 2. To extract the spectra, an optimised mask was determined for each observing epoch. The width of these masks scales with the width of the PSF and increases from 5.3 ± 1.5 pixels (0.45 arcsec for the UTs) at 8 μm to 7.4 ± 1.0 pixels (0.63 arcsec for the UTs) at 13 μm. To reduce the total flux spectra, the bands for estimating the sky background were adjusted so that they are always located symmetric with respect to the source spectra, 15 or 16 pixels (~1.33 arcsec) apart for the UTs and 11 pixels (~4.2 arcsec) apart for the ATs. The calibrator database of EWS, which is based on the database of calibrator spectra by R. van Boekel (van Boekel 2004; Verhoelst 2005), was used to calibrate the data.
In addition to the statistical errors provided by EWS, the uncertainties due to the variation of the transfer function of the atmosphere and instrument were estimated from up to five calibrators and added to the statistical errors in quadrature. In most cases, these calibration uncertainties dominate over the statistical errors. They are the main source of uncertainty in our MIDI measurements, with errors from as low as 5% to more than 20%, depending on the atmospheric conditions of the night. Similar results were obtained by e.g. Burtscher et al. (2012). The errors used in Tristram et al. (2007) are much smaller. There, only the statistical errors from EWS were used and the uncertainties were, therefore, underestimated.
Comparison of measurements at similar locations in the uv plane but from different observing epochs or baselines.
 |
Fig. 2 Comparison of the total and correlated flux spectra (first two rows), visibilities (third row) and differential phases (bottom row) at locations C4 (left column), C5 (central column) and C6 (right column). For clarity, error bars are only plotted every fifth wavelength bin. Note that for C4 and C6 the telescopes at the two epochs considered were interchanged (UT3-UT2 versus UT2-UT3). The phases of measurements #1 and #3 were corrected for this interchange in order to allow an easier comparison (see also discussion in Sect. 5.2). |
Due to the imperfect background subtraction by chopping, the uncertainties in the total flux measurements are significantly larger than those of the correlated fluxes. These uncertainties also propagate into the visibilities. Furthermore, the total flux spectra of the Circinus galaxy observed with the ATs turn out to be entirely useless. Therefore most of the following analysis is focused on the correlated fluxes and the differential phases.
2.3. Data consistency
2.3.1. Individual points in the uv plane
Unless the brightness distribution of the object has changed in intensity or shape, MIDI should always measure the same correlated flux and differential phase at the same location in the uv plane. Furthermore, we expect measurements close in uv space to be similar or to change continuously for measurements at distances less than the telescope diameters of 8.2 m for the UTs and 1.8 m for the ATs (cf. López-Gonzaga et al. 2014).
For the Circinus galaxy, several locations in the uv plane have been measured more than once in different observing epochs or using different telescope combinations. For 14 such locations we check the consistency of our measurements. The locations are marked in blue in Fig. 1 and named C1 to C14. The ratios (averaged over the N-band) of the correlated flux spectra, the total flux spectra and the visibility spectra (where available) for the 22 possible comparisons at these locations are listed in Table 3. Also indicated is whether there is an apparent change in the spectral slope of the measurements: “b” indicates that the more recent measurement shows a bluer spectrum (Fcor(13 μm)/Fcor(8 μm) decreased), “r” indicates that the more recent measurement shows a redder spectrum (Fcor(13 μm)/Fcor(8 μm) increased).
For the correlated fluxes, 14 comparisons (i.e. 64%) agree within 1σ, and 20 (i.e. 91%) agree within 2σ. This is consistent with the statistical expectation and with the results for other sources, where measurements at approximately the same location in the uv plane have been repeated (e.g. NGC 424, NGC 3783 and NGC 4593, Hönig et al. 2012, 2013; Burtscher et al. 2013). Due to the larger errors in the total flux measurements, the total fluxes and visibilities all agree within 2σ. The differential phases all agree within 1σ, when taking into account the orientation of the baseline, because the sign of the differential phase switches for an interchange of the two telescopes, i.e. φdiff(U2 - U1) = −φdiff(U1 - U2). The total and correlated flux spectra, the visibilities and differential phases for C4, C5 and C6 are plotted in Fig. 2.
C4 has the strongest discrepancy: both the correlated flux and the visibility spectra measured in 2005 are about a factor of two higher than the ones measured in 2004 (see left column in Fig. 2). These early measurements were carried out without the VLTI infrared field-stabiliser IRIS (InfraRed Image Sensor, Gitton et al. 2004). As a consequence, the beam overlap in the 2004 measurement was not optimal, which could be responsible for the lower correlated flux. In the case of C5 (middle column in Fig. 2), there is a slight increase in the correlated fluxes from 2005 to 2011. More interestingly, the (unusual) spectral shape with a dip at 12.5 μm remains essentially unchanged. Therefore, we consider this feature to be a true signal from the source (see discussion in Sect. 5.2.3). In the case of C6 (right column in Fig. 2), one measurement obtained in 2004 lies between two measurements that were obtained in 2006. This is in perfect agreement with a continuous drop of the correlated fluxes or visibilities along this uv track.
For most of the comparisons (C4 to C14), the correlated fluxes measured at later epochs are higher than those measured earlier. This is especially the case at the short wavelength end of the N-band; the more recent spectra generally appear bluer. All of the observations showing this possible increase in flux were carried out with the UTs on baselines longer than 30 m, which essentially probe spatial scales of ≲80 mas. Additionally, most of the total flux spectra observed since 2009 appear slightly (although not significantly) higher (see below). This could be interpreted as evidence of an increase in the source flux. On the other hand, the correlated fluxes obtained with the ATs, probing spatial scales of ≲170 mas, rather suggest the opposite: the correlated fluxes observed in 2009 and 2011 are slightly lower than those observed in 2008 (cf. C1, C2 and C3 in Table 3). The decrease is not significant, but an overall increase in the flux on spatial scales below 170 mas can be ruled out.
2.3.2. Total flux
 |
Fig. 3 Total flux of the Circinus galaxy at 8.2 μm (left) and 12.8 μm (right) as a function of the hour angle for four different epochs. The average fluxes at the respective wavelengths on 2008-04-18 and 2009-04-15 are indicated by the dashed lines. |
While there seem to be no significant discrepancies between the total flux spectra of the individual measurements, there are however clear trends when considering multiple measurements. In principle, MIDI should always measure the same calibrated total flux spectrum for a specific source, independent of the instrument settings and the baseline geometry. However, this is not the case for the Circinus galaxy, where significant changes in the total flux spectrum appear. Figure 3 shows the total fluxes at 8.2 μm and 12.8 μm as a function of the hour angle for four different epochs. In each of these epochs, the total flux spectrum was measured multiple times. The measurements obtained in 2005 are all consistent with each other. For the measurements obtained on 2008-04-18 and 2009-04-15, on the other hand, we find a clear decrease in the total flux with increasing hour angle at wavelengths shorter than 11.0 μm (see left panel of Fig. 3): on 2008-04-18, the flux at 8.2 μm apparently decreased from ~7 Jy at the start of the night to ~3 Jy at the end of the night, that is by more than a factor of two. At longer wavelengths, the flux levels remain more or less constant during the course of all of the observing runs (see right panel of Fig. 3). In addition, there seems to be a general increase in the total flux between 2008 and 2009. At 8.2 μm the average flux (indicated by the dashed lines in Fig. 3) increased from ~5.0 Jy to about 7.6 Jy. At 12.8 μm the increase is from ~15.6 Jy to ~19.6 Jy.
We have carried out a thorough analysis to determine the cause for these changes in the total flux measurements. We checked if (1) possible changes in the instrumental setup; (2) the different airmasses of the observation; (3) variations of the atmospheric conditions; (4) changes in the performance of the adaptive optics system; or (5) variability of the calibrator could have caused the observed flux changes, but we find none of these explanations to be conclusive (for details, see Tristram 2013).
Slit losses might be responsible for the continuous flux decreases on 2008-04-18 and 2009-04-15. Especially before 2009, the Circinus nucleus was not always perfectly centred in the slit of MIDI due to an error in the reference position. For all our observations, the 200 μm wide slit was used, corresponding to widths of 0.52 arcsec and 2.29 arcsec for the UTs and ATs respectively. Because the mid-infrared emission of the galaxy is slightly extended already in single-dish observations (e.g. Packham et al. 2005) and the field of view of MIDI rotates on the sky over the course of a night, this could have lead to a gradual decrease in the measured total fluxes. On the other hand, the resolved emission constitutes only about 20% of the total N-band emission of the Circinus nucleus (Packham et al. 2005; Reunanen et al. 2010). By consequence, slit losses due to the orientation of the extended emission cannot account for a change of the flux by up to a factor of two. Furthermore, it is unclear why such slit losses should not have played a role in 2005 and why they should only have an effect at short wavelengths, where potential slit losses should instead be reduced. A more accurate positioning of the source in the slit in 2009 could also explain the increase in the total flux for these measurements. The effect is, however, not sufficient to explain all of the observed increase.
If the light of the Circinus galaxy were significantly polarised, the rotation of the field of view together with the MIDI and VLTI optics could lead to a smooth change of the flux over the night. To obtain the observed change by a factor of 2 at 8.2 μm on 2008-04-18, this would require a degree of polarisation of 50% at the short wavelength end of the N-band. There are no polarisation measurements for the Circinus galaxy in the N-band, but in the K-band the nucleus of the Circinus galaxy has a polarisation of the order of 3 to 4% (Alexander et al. 2000). The degree of polarisation of NGC 1068 in the mid-infrared is less than 3% (Smith et al. 2000; Packham et al. 2007), that of Mrk 231, a Seyfert 1 galaxy, 8% (Siebenmorgen & Efstathiou 2001). It therefore seems unlikely that the mid-infrared emission of the nucleus of the Circinus galaxy is much higher polarised and that the degree of polarisation is strongly wavelength dependent.
A further possible explanation is that the emission from the Circinus galaxy itself has changed. As the mid-infrared emission is dominated by the emission from warm dust, variations on timescales of hours are not plausible and cannot be held responsible for the flux decrease observed in the course of a night. An increase in the flux over the period of one year, on the other hand, is very well possible physically. Indeed there is further evidence that the total flux of the Circinus galaxy has increased intrinsically between 2008 and 2009: a flux increase is also seen in single-dish photometry at 11.9 μm with VISIR and the acquisition images obtained with MIDI. There are, however, also inconsistencies with an increase in the intrinsic mid-infrared flux of the nucleus of the Circinus galaxy. Because the increase took place over a period of less than a year, the variable emission should come from a region smaller than 1 ly ≈ 0.3 pc, i.e. 15 mas on the sky. Therefore the increase in the flux should be mainly seen in the correlated fluxes on longer baselines, which probe exactly these spatial scales. Although there seems to be a slight increase in the correlated flux measurements since 2009, it is only by a few hundred mJy (see previous Sect.). This is by far not enough to explain the increase in the total flux by more than 2 Jy. Furthermore, the AT measurements do not show an increase in the correlated fluxes but rather a decrease. In summary this means we have (1) a flux increase by up to a few hundred mJy within ~80 mas; (2) a possible flux decrease within ~170 mas; and (3) an increase by more than 2Jy within ~500 mas. This is hard to explain physically. At least two “bursts” would have to be travelling outward through the dust distribution.
 |
Fig. 4 Correlated fluxes of the Circinus galaxy at 12 μm for all
uv
points containing useful interferometric data. The points are colour-coded
according to their correlated flux, Fcor(12 μm),
using a square root colour scaling as indicated in the colour bar on the right.
The uv point at the origin represents the
averaged total flux of the source, which is outside the plotted range of colours:
|
So far, no studies of the infrared variability of the Circinus galaxy have been published. Therefore, we started a more detailed investigation ourselves, including monitoring observations. A detailed discussion of the variability in the nucleus of the Circinus galaxy goes beyond the scope of this paper and will be presented in a future publication.
2.3.3. Conclusion from the data consistency checks
We conclude that the differences between the individual measurements of the correlated fluxes at the same position in the uv plane are in general consistent with the statistical expectations. On the other hand, there is no clear picture that can explain (1) the continuous decrease in the total flux during the observations on 2008-04-18 and 2009-04-15 as well as (2) the increase in the total flux between 2008 and 2009. For the following analysis, we will simply assume that the emission intrinsic to the Circinus galaxy has not changed between the interferometric measurements. We base this assumption on the fact that the correlated fluxes on the shortest baseline, i.e. within spatial scales of ~170 mas essentially remained constant. Because our further analysis and modelling is mainly based on the correlated fluxes and the differential phases, we are confident that the general results do not depend on a full discussion of possible variability. Furthermore, we find no solid basis on which to reject individual measurements that do not agree with other measurements. Therefore, we will retain all measured uv points for the following analysis.
3. Results
In total we obtained 152 useful measurements of the correlated flux spectra and differential phases and 74 useful measurements of the total flux spectra. This includes 20 correlated flux measurements already published in Tristram et al. (2007).
The new reduction of the previously published data in general increases the data quality. The positive bias of the correlated fluxes and visibilities in the ozone feature between 9.5 and 10.0 μm and at the edges of the N-band is reduced, especially for the data observed in 2004 and 2005. The more accurate group delay estimation leads to a slight increase in the correlated fluxes at the long wavelength end, but the overall spectral shape and flux levels remain unchanged. With correlated flux levels of more than 0.4 Jy at 12.0 μm in most cases, the result is robust with respect to the data reduction, and we obtain no contradictions to the values published in 2007. Due to the improved masking and sky residual estimation, the scatter of the total flux spectra is reduced significantly. The wavelength calibration of the MIDI spectra in EWS was also corrected slightly, resulting in a shift of the spectra to shorter wavelengths by about 0.1 μm. All spectra were corrected for the peculiar redshift of the Circinus galaxy of z = 0.00145 (vsys = 434 ± 3 km s-1, Koribalski et al. 2004).
All 74 useful measurements of the total flux spectra were combined by a weighted average to
obtain a single estimate for the total flux spectrum of the Circinus nucleus:
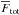 . The spectrum
agrees with the one published in 2007. It is shown as part of Fig. 10. The spectrum rises from ~6 Jy at
8 μm to
~16 Jy at 13 μm, which is quite “red”
(
. The spectrum
agrees with the one published in 2007. It is shown as part of Fig. 10. The spectrum rises from ~6 Jy at
8 μm to
~16 Jy at 13 μm, which is quite “red”
(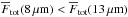 ) and indicative of emission from
warm (T ~ 290 K) dust. The spectrum is dominated by a deep
silicate absorption feature over almost the entire N-band. For the following, we
will consider the total flux spectrum as a measurement with a projected baseline length of
BL = 0 m.
) and indicative of emission from
warm (T ~ 290 K) dust. The spectrum is dominated by a deep
silicate absorption feature over almost the entire N-band. For the following, we
will consider the total flux spectrum as a measurement with a projected baseline length of
BL = 0 m.
We use all measurements of the correlated fluxes and phases individually and do not average measurements close in uv space. All useful correlated fluxes at 12 μm are listed in Table A.1 and plotted in Fig. 4. With correlated fluxes at 12 μm ranging from ~8 Jy (corresponding to V ~ 0.8) on the shortest baselines to ~0.4 Jy (V ~ 0.04) on certain long baselines, we clearly resolve the mid-infrared emission in the nucleus of the Circinus galaxy. The uv plane also shows that along certain position angles, the correlated flux is higher than along others. A very prominent example is the increase at the end of the baseline UT2-UT4, leading to cyan and green colours (corresponding to Fcor(12 μm) > 1.5 Jy) in Fig. 4. This increase will be discussed in Sect. 3.2.
Many of the correlated flux spectra (see Fig. A.1 in the appendix) have a shape similar to the total flux spectrum. Especially on short baselines, the correlated flux spectra are similar to the total flux spectrum when the spectral change due to the resolution effect at different wavelengths is taken into account.
On longer baselines, however, this is not always the case. Most noticeably, the short wavelength emission often either disappears completely or there is a downturn in the correlated flux shortward of 8.7 μm without any significant signal in the differential phases (see e.g. C6 in Fig. 2). Interestingly, a similar decrease, albeit mainly in the visibilities and for λ < 9.0 μm, might also be present in certain uv points for NGC 424 (Hönig et al. 2012) and NGC 3783 (Hönig et al. 2013). Contamination of the total flux by the wings of a spatially extended polycyclic aromatic hydrocarbon (PAH) feature at 7.7 μm was discussed as a possible reason in Hönig et al. (2012). This would, however, only affect the visibilities and not the correlated fluxes we are considering here. Furthermore, the 8.6 and 11.3 μm PAH features are completely absent in our MIDI total flux spectrum (see inset of Fig. 10) or the nuclear spectra obtained by Roche et al. (2006)3. Because the 7.7 μm feature is roughly correlated to the 8.6 μm feature (Galliano et al. 2008) and, in AGN environments, suppressed with respect to the 11.7 μm feature (Smith et al. 2007), we conclude that any contribution from the wing of the 7.7 μm feature to our nuclear fluxes is negligible. For these reasons we rule out any PAH contamination to be responsible for the downturn of the correlated flux shortward of 8.7 μm. A further possible explanation could be instrumental/calibration effects, especially correlation losses (Burtscher et al. 2012). However, this would not explain why the downturn appears so abruptly for λ < 8.7 μm. The correlation losses should instead be a smooth function of wavelength and only become significant for Fcor(12 μm) < 150 mJy (Burtscher et al. 2013). This is not the case for the measurements at hand. It seems that the emission at the shortest wavelengths is almost fully resolved out and thus comes from an extended emission region (see discussion in Sect. 5.4).
In a few measurements, also a decrease in the correlated fluxes at longer wavelengths is present (see e.g. C5 in Fig. 2). In these cases, strong gradients in the differential phases also appear. We interpret these signatures (which are also present in the visibilities) as evidence of a more complex brightness distribution with small scale structure (see discussion in Sect. 5.2.3).
3.1. Radial dependency of the correlated fluxes
The correlated fluxes (and visibilities) at 12 μm as a function of the projected baseline length BL are shown in Fig. 5. The correlated fluxes quickly drop from the total flux of 10.7 Jy to less than 2 Jy (V ≲ 20%) at BL ~ 30 m. On longer baselines, the correlated fluxes remain on more or less the same level between 0.2 Jy and 2.0 Jy. Note that the apparent scatter in the measurements at a certain baseline length is mainly due to measurements at different position angles (see next section).
The rapid drop at short baseline lengths implies that the mid-infrared emission is mostly resolved out by the interferometer. More precisely, only about 20% of the mid-infrared emission comes from structures smaller than about 70 mas in diameter. 80% of the emission is located on spatial scales between ~70 mas and ~500 mas. The new observations with the ATs (at baseline lengths of BL ~ 15 m) now also probe the majority of the flux in this extended emission region.
 |
Fig. 5 Correlated fluxes (Fcor, left ordinate) or
visibilities ( |
Because the correlated fluxes do not decrease much farther for 30 m ≲ BL ≲ 95 m (a change of the baseline length and, thus, spatial resolution by a factor of three), a single or several unresolved structures (“clumps”) with sizes below the resolution limit of the interferometer of about 15 mas must be present. The two regimes of the visibility function suggest that the corresponding brightness distribution has two distinct spatial scales: a large scale that is quickly resolved by the interferometer when increasing the baseline length and a small scale that essentially remains unresolved even at the longest baselines (i.e. at the smallest spatial scales probed by the interferometer).
3.2. Angular dependency of the correlated fluxes
 |
Fig. 6 Correlated fluxes of the Circinus galaxy at 8.5 and 12.0 μm as a function of the position angle for the baselines E0-G0 (with 13 m < BL < 16 m, left) and UT2-UT4 (with 76 m < BL < 90 m, right). Also plotted are the correlated fluxes of the three-component model discussed in Sect. 4: fit 3 by continuous lines, fit 2 and 1 by dashed lines in the left and right panels, respectively. |
There are two telescope combinations, E0-G0 4 (using the ATs) and UT2-UT4 (using the UTs), where the projected baseline lengths roughly remain the same while the position angle changes over a wide range due to the rotation of the Earth. This means the same spatial scales are probed in different directions. The correlated fluxes can therefore be directly compared to infer information on the source size in different directions under the assumption of a smooth, centrally peaked brightness distribution. The correlated fluxes at 8.5 and 12.0 μm for the two mentioned baselines are shown in Fig. 6 as a function of the position angle. On both baselines and at both wavelengths, a clear dependency of the correlated fluxes on the position angle is present.
With the E0-G0 baseline, 13 m < BL < 16 m, spatial scales of the order of 150 mas are probed. The uncertainties and scatter in the data points are relatively large because these measurements were obtained with the ATs. Nevertheless, the correlated fluxes show a clear trend with a broad minimum at at both 8.5 and 12.0 μm. This essentially means that the emission is better resolved in this direction, i.e. it is more extended along this position angle.
The UT2-UT4 baseline has projected baseline lengths between 76 m and 90 m, corresponding to spatial scales of about 25 mas. The correlated fluxes show a very pronounced peak at with correlated fluxes more than three times higher than at other position angles. This means that the source appears significantly less resolved in this direction, while it is better resolved in all other directions. Such a dependency on the position angle can be explained by an extremely elongated emission component. Furthermore there is a second, much weaker peak at in the correlated fluxes at 12.0 μm. This peak is not present at 8.5 μm. We interpret this behaviour as evidence of further small scale structure. Finally, the 12.0 μm fluxes are always above ~0.3 Jy, indicating that there is still unresolved flux at these wavelengths. The fluxes at 8.5 μm are consistent with zero at . Thus the 8.5 μm emission is completely resolved out by the interferometer.
In summary, we conclude from the direct and completely model free analysis of the data that there are two different orientations in the mid-infrared brightness distribution of the Circinus galaxy: on spatial scales of ~150 mas the emission is moderately elongated along , while on smaller spatial scales, the emission is highly elongated along .
4. Modelling
To get a better understanding of the overall structure of the emission, we model the data. Motivated by the evidence of (1) an essentially unresolved emission component; (2) a small, highly elongated component; and (3) an extended, only slightly elongated component, we expand the two-component model from Tristram et al. (2007) to three components. In the following, we will refer to these three components as i = 1 the “unresolved”, i = 2 the “disk-like” and i = 3 the “extended” components of the emission. Despite being “unresolved”, component 1 has a non-zero size because its brightness depends on its surface and temperature.
The model is not intended to directly represent any physical structure for the emission. To begin with, it is intended to capture the general morphology and spectral properties of the surface brightness distribution of the source, by fitting the interferometric data and the total flux spectrum in the wavelength range between λ = 8.0 and 13.0 μm.
The three components are modelled as black-body emitters with a Gaussian brightness
distribution. The Gaussian emitters can be elliptical and each emitter is behind an
absorption screen responsible for the silicate absorption. For each component, the
elliptical Gaussian is a function of the position on the sky
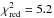 and
takes the functional form
and
takes the functional form ![\begin{equation} G_{i}(\alpha,\delta)=f_{i}\cdot\exp\left(-4\ln2\cdot\left[\left(\frac{\alpha_{i}'}{r_{i}\cdot\Delta_{i}}\right)^{2}+\left(\frac{\delta_{i}'}{\Delta_{i}}\right)^{2}\right]\right), \end{equation}](/articles/aa/full_html/2014/03/aa22698-13/aa22698-13-eq181.png) (1)where
(1)where
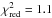 and
and
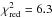 are the positional
coordinates of the Gaussians, which are offset by
are the positional
coordinates of the Gaussians, which are offset by 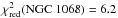 from the centre and rotated by the position angle ψi. fi specifies the maximum
surface filling and emissivity factor of this component at the position
from the centre and rotated by the position angle ψi. fi specifies the maximum
surface filling and emissivity factor of this component at the position
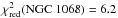 ,
Δi
is the full width half maximum (FWHM) of the Gaussian along its major axis (oriented along
ψi), and ri is the ratio of the
minor to major FWHM. A maximum surface filling factor of 1 is possible for the sum of all
three components. This was not handled entirely correctly in the modelling in Tristram et al. (2007). There, the emission of the two
components was simply added one to another, which could effectively result in a total
filling factor greater than one. This physical inconsistency, however, did not have any
consequences on the overall results. Now we take this additional, physical constraint into
account, and use modified Gaussians calculated as
,
Δi
is the full width half maximum (FWHM) of the Gaussian along its major axis (oriented along
ψi), and ri is the ratio of the
minor to major FWHM. A maximum surface filling factor of 1 is possible for the sum of all
three components. This was not handled entirely correctly in the modelling in Tristram et al. (2007). There, the emission of the two
components was simply added one to another, which could effectively result in a total
filling factor greater than one. This physical inconsistency, however, did not have any
consequences on the overall results. Now we take this additional, physical constraint into
account, and use modified Gaussians calculated as
![\begin{equation} \tilde{G}_{i}(\alpha,\delta)=\left[G_{i}(\alpha,\delta)-\left(\left(\sum_{j\,=\,1}^{i}G_{j}(\alpha,\delta)-1\right)>0\right)\right]>0. \end{equation}](/articles/aa/full_html/2014/03/aa22698-13/aa22698-13-eq189.png) (2)The final flux
density of the model at a certain wavelength λ is given by
(2)The final flux
density of the model at a certain wavelength λ is given by
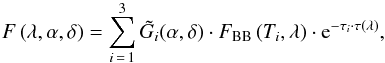 (3)where FBB is the
black-body intensity depending on the temperature Ti, and τi is the optical depth of
the silicate feature. For the extended component (i = 3), the optical depth can linearly change along
the major axis, i.e. τ3(α,δ) = τ3 + ξ3·d,
where d is the
distance from (α,δ) = (0,0) projected onto the
major axis. This gradient is a first approximation for the overall change of the silicate
absorption depth and is motivated by the gradient seen in the mid-infrared spectra by Roche et al. (2006). It will be discussed in more detail
in Sect. 5.2.2. The template absorption profile
τ(λ) is the same as in Tristram et al. (2007), i.e. it is derived from the
extinction curves of Schartmann et al. (2005) and
Kemper et al. (2004).
(3)where FBB is the
black-body intensity depending on the temperature Ti, and τi is the optical depth of
the silicate feature. For the extended component (i = 3), the optical depth can linearly change along
the major axis, i.e. τ3(α,δ) = τ3 + ξ3·d,
where d is the
distance from (α,δ) = (0,0) projected onto the
major axis. This gradient is a first approximation for the overall change of the silicate
absorption depth and is motivated by the gradient seen in the mid-infrared spectra by Roche et al. (2006). It will be discussed in more detail
in Sect. 5.2.2. The template absorption profile
τ(λ) is the same as in Tristram et al. (2007), i.e. it is derived from the
extinction curves of Schartmann et al. (2005) and
Kemper et al. (2004).
In total, the model has 25 parameters (8 for each component plus ξ3). However,
because the innermost component is assumed to be essentially unresolved, it is not
elongated, and thus ψ1 = 0 and r1 = 1.
Furthermore, because MIDI only measures differential phases and not the full Fourier phases
(see Sect. 2.2), the absolute position on the sky is
undetermined. We therefore define the disk-like component to lie at the origin of our
coordinates, that is 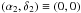 .
Furthermore, the offset of the extended component is not well constrained and it does not
lead to a significant improvement of the fit (see below). We therefore also assume the
extended component to be located at the centre,
.
Furthermore, the offset of the extended component is not well constrained and it does not
lead to a significant improvement of the fit (see below). We therefore also assume the
extended component to be located at the centre, 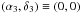 . The
coordinates of the unresolved component are therefore to be interpreted as offsets with
respect to the other components. We are then left with up to 19 free parameters in the
model. To carry out the fit, the brightness distribution of the model is calculated for
8.0 μm < λ < 13.0 μm,
then Fourier transformed to obtain the complex correlated fluxes:
. The
coordinates of the unresolved component are therefore to be interpreted as offsets with
respect to the other components. We are then left with up to 19 free parameters in the
model. To carry out the fit, the brightness distribution of the model is calculated for
8.0 μm < λ < 13.0 μm,
then Fourier transformed to obtain the complex correlated fluxes:
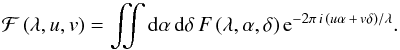 (4)The moduli of the
correlated fluxes, Fcorr = |ℱ| , and the wavelength
differential phases, φdiff, are extracted at the measured
uv points and
compared to the measurements. All calculations are carried out in IDL using custom
programmes and employ the programme mpfit (Markwardt 2009) for non-linear least squares fitting.
(4)The moduli of the
correlated fluxes, Fcorr = |ℱ| , and the wavelength
differential phases, φdiff, are extracted at the measured
uv points and
compared to the measurements. All calculations are carried out in IDL using custom
programmes and employ the programme mpfit (Markwardt 2009) for non-linear least squares fitting.
Because the components are self-similar and can become degenerate, we first fit certain parts of the uv plane separately. This approach allows us to understand the source morphology on the different spatial scales (cf. Sect. 3) first, before fitting for the entire brightness distribution. In fit 1, we fit the data from baseline U2-U4 only using the two inner components (i = 1,2); in fit 2, we fit the data with BL < 20 m (essentially baseline E0-G0) using the extended component (i = 3). The parameters of the remaining components are kept fixed. Only in fit 3, is all the data fitted by all three components, using the parameters of the previous fits as first guesses. The best fit parameters for all three fits are listed in Table 4.
Parameters of the three-component Gaussian fits.
For fit 1, the extended component is suppressed by setting f3 ≡ 0. It can be
omitted entirely because the flux from this component is almost completely resolved out
(V < 2%) for BL > 70 m.
Therefore, the correlated fluxes on the baseline U2-U4 primarily depend on the inner two
components. The two components can reproduce the general trends of the data
(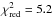 , dashed
lines in the right panel of Fig. 6). The strong
increase in the correlated flux at is well
reproduced by the strong elongation of component i = 2. For this reason, it is called “disk-like”,
which will be discussed in more detail in Sect. 5.1.1.
Due to the well measured position angle dependence of this peak, the position angle of this
elongated component is well determined. On the other hand, second order variations of the
correlated flux, such as the second peak at
(see Sect. 3.2) or changes in the spectral shape, are
not reproduced by our simple model. They require a more complex brightness distribution. The
differential phases can be at least qualitatively reproduced to some degree by an offset of
the unresolved component from the disk-like component.
, dashed
lines in the right panel of Fig. 6). The strong
increase in the correlated flux at is well
reproduced by the strong elongation of component i = 2. For this reason, it is called “disk-like”,
which will be discussed in more detail in Sect. 5.1.1.
Due to the well measured position angle dependence of this peak, the position angle of this
elongated component is well determined. On the other hand, second order variations of the
correlated flux, such as the second peak at
(see Sect. 3.2) or changes in the spectral shape, are
not reproduced by our simple model. They require a more complex brightness distribution. The
differential phases can be at least qualitatively reproduced to some degree by an offset of
the unresolved component from the disk-like component.
For fit 2, the two inner components are included in the fit because they contribute
significantly to the correlated flux. However, their parameters are held fixed at the
(approximate) values of fit 1. Because the AT data changes more smoothly as a function of
position in the uv plane and because it has larger uncertainties, both
the correlated fluxes as well as the differential phases can be well modelled by the
extended component (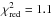 , dashed
lines in the left panel of Fig. 6). In fact, the
extended component alone is sufficient to achieve the good fit; the inner two components are
not required to model the AT data.
, dashed
lines in the left panel of Fig. 6). In fact, the
extended component alone is sufficient to achieve the good fit; the inner two components are
not required to model the AT data.
Finally, in fit 3, all free parameters are fitted using the 152 correlated flux spectra and
differential phases as well as the averaged total flux spectrum. For this fit, we obtain a
relatively high value of the reduced chi-squared, 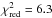 . This
means that our simple model is not a “good” fit to the full data set; it only traces the
general structure of the emission. Nonetheless the quality of our fit is comparable to the
similar fit (also using three components) of the correlated fluxes and differential phases
in NGC 1068, where
. This
means that our simple model is not a “good” fit to the full data set; it only traces the
general structure of the emission. Nonetheless the quality of our fit is comparable to the
similar fit (also using three components) of the correlated fluxes and differential phases
in NGC 1068, where 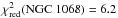 (López-Gonzaga et al. 2014). To determine a possible offset of the
extended component like in NGC 1068, we carried out a parameter scan for α3 and
δ3. Although we find a best fit for
(López-Gonzaga et al. 2014). To determine a possible offset of the
extended component like in NGC 1068, we carried out a parameter scan for α3 and
δ3. Although we find a best fit for
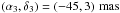 with
with
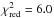 , we
also find very different offsets with similarly good values of
, we
also find very different offsets with similarly good values of
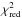 . Due to this
ambiguity and the only small improvement of the fit, we see no compelling evidence for a
particular offset of the extended component and therefore set
. Due to this
ambiguity and the only small improvement of the fit, we see no compelling evidence for a
particular offset of the extended component and therefore set
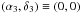 . The
correlated fluxes of fit 3 are compared to the data as a function of the position angle in
Fig. 6 (continuous curves). The dispersed correlated
fluxes and differential phases of this fit for all uv-points are plotted in red
in Figs. A.1 and A.2.
. The
correlated fluxes of fit 3 are compared to the data as a function of the position angle in
Fig. 6 (continuous curves). The dispersed correlated
fluxes and differential phases of this fit for all uv-points are plotted in red
in Figs. A.1 and A.2.
The formal fit errors calculated from the covariance matrix are very small and not representative of our fit of a smooth model to a more complex emission distribution. To determine more realistic uncertainties for the fit parameters of all three fits, we use the non-parametric bootstrap with replacement (Efron 1979). We employ a block bootstrap (Hall 1985) due to the correlation of consecutively observed uv points, i.e. we resample the data using small sequences of uv points instead of individual uv points before fitting the resampled data. The errors listed in Table 4 are directly estimated from the bootstrap distribution of the respective parameter and mark the 68.3% (1σ) confidence intervals.
Our model can fit the data on the shortest baselines very well, which means that it reproduces the low spatial frequencies of the source adequately. On longer baselines, however, the data is not well reproduced by our model. This is predominantly due to small scale variations of the correlated fluxes and differential phases at longer baselines (cf. Fig. 4), which cannot be reproduced by our smooth model. We interpret these variations as signatures for small scale structures that our model obviously cannot replicate.
Finally, a few remarks on degeneracies: several parameters of our model are not independent. The clearest example is the degeneracy between the temperature Ti and the surface filling factor fi. Because we are fitting a narrow wavelength range (8 μm < λ < 13 μm), the temperatures of our dust components are not well constrained. A small change in temperature has a direct influence on the brightness of the source, which can be compensated by changing the surface filling factor. Similar degeneracies are present between the size and the axis ratio of the source, which all change the emitted flux density. Depending on how well these parameters are constrained by the interferometric measurements, these parameters can become degenerate.
5. Discussion
5.1. Morphology
The direct analysis of the data (Sect. 3) and our modelling (Sect. 4) confirm that the mid-infrared emission in the nucleus of the Circinus galaxy comes from at least two distinct components: a highly elongated, compact “disk-like” component and a moderately elongated, extended component. To some degree, the distinction between the two components is suggested by the two different regimes of the correlated fluxes as a function of the projected baseline length (see Sect. 3.1). Primarily, however, the distinction is suggested by the different orientations of the two components: the two components are elongated roughly perpendicular to one another. Two clearly separated emission components have also been found in NGC 1068 and NGC 3783 (Raban et al. 2009; Hönig et al. 2013), and a two-component morphology in the infrared appears to be common to a large number of AGN (Kishimoto et al. 2011b; Burtscher et al. 2013).
We interpret the mid-infrared emission as emission from warm dust in the context of the hydrodynamic models of dusty tori in AGN by Schartmann et al. (2009), Wada et al. (2009) and Wada (2012). These models find a relatively cold, geometrically thin and very turbulent disk in the mid-plane of the torus, surrounded by a filamentary structure. The latter consists of long radial filaments with a hot tenuous medium in between. We associate the central, highly elongated component in the Circinus nucleus with the dense disk in these simulations, and we interpret the extended mid-infrared emission in the context of the filamentary torus structure seen in these models.
 |
Fig. 7 False-colour image of the three-component model for the mid-infrared emission of the nucleus of the Circinus galaxy (fit 3). The colours red, green and blue correspond to the model at 13.0 μm, 10.5 μm and 8.0 μm, respectively. The colour scaling is logarithmic in order to show both bright and faint features. Clearly the colour gradient of the extended component due to the increase in the silicate depth towards the south-east is visible. This colour gradient leads to a chromatic photocentre shift towards the north-west. Despite the lower surface brightness, 80% of the emission comes from the extended component. Also plotted is the trace of the water maser disk: the blue and red parts trace the approaching and receding sides of the maser disk respectively. Note that the relative offset of the mid-infrared emission with respect to the maser disk is not known (see text for details). |
A false-colour image of our best fitting model (fit 3) is shown in Fig. 7, with the model images at 13.0 μm, 10.5 μm and 8.0 μm mapped to the red, green and blue channels of the image, respectively.
When interpreting our observations, we have to take into account that the emission is dominated by the warmest dust at a certain location, which normally comes from the dust clouds directly illuminated by the central UV source. There are probably also considerable amounts of cooler dust. However, the cooler material only contributes insignificantly to the infrared emission (see also Sect. 5.3).
5.1.1. The disk-like component
The disk-like component is highly elongated and has a major axis FWHM of Δ2 ~ 1.1 pc. Due to the strong position angle dependency of the correlated fluxes for the longest baselines, the position angle of the major axis is very well constrained: . The strong elongation of this component with an axis ratio of more than 6:1 at first suggests an interpretation as a highly inclined disk, as in Tristram et al. (2007). This interpretation is supported by the close agreement in orientation and size of this component with the warped maser disk from Greenhill et al. (2003). The masers were modelled by a thin disk extending from rin ~ 0.1 pc to rout ~ 0.4 pc. The maser disk is warped with the position angle changing from at rin to at rout. With a position angle of , our disk-like component now matches this orientation much better than previously. The larger size of the mid-infrared disk as compared to the maser disk could be evidence of the disk extending out to larger radii than is probed by the maser emission. We emphasise that the agreement is only in orientation and size, not in the absolute position. With MIDI alone, no absolute astrometry is possible because the absolute phase signal is destroyed by the atmosphere (see Sect. 2.2). By consequence, the relative position between the maser disk and our disk-like component cannot be determined. In Fig. 7, the disk-like component and the maser disk are plotted centred to allow a good comparison, but the two structures might well be offset with respect to each other.
Due to the strong elongation of the disk-like component, the associated disk would have to be close to edge-on and cannot be very thick. If we assume that the emission comes directly from an infinitesimally thin and flat disk, we can use the observed axis ratio to constrain its inclination: . Or, if seen edge-on (), as suggested by the maser emission, we can derive a rough estimate for the maximum thickness of the disk: r2·Δ2 < 0.2 pc.
An interpretation as emission directly from the disk is, however, problematic. Due to the high densities required for maser emission (n(H2) ≳ 108 cm-3, Kylafis & Norman 1991), we expect the disk to be optically thick and to thus appear in absorption rather than in emission when seen close to edge-on. This is corroborated by the dense disks in the hydrodynamical torus models, which appear as dark lanes in the mid-infrared (see Fig. 8 in Schartmann et al. 2009 for an example). The effect is further enhanced by the anisotropic radiation characteristic of the accretion disk, which emits less energy in the direction of the disk plane. A dense disk, by consequence, appears dark. Our disk-like component, on the contrary, appears in emission.
Instead of the disk itself, we could be seeing the directly illuminated inner rim of a highly inclined disk, similar to what is seen for circumstellar disks (e.g. in KK Ophiuchi, Kreplin et al. 2013). However, the inner rim of the disk, where the dust sublimates, is expected to lie at rsub = rin ~ 0.03 pc for the Circinus galaxy. This is much smaller than the parsec-sized elongation we observe. In addition, the inner rim is expected to consist of hot dust close to the dust sublimation temperature, which is in disagreement with the warm dust at T ~ 300 K suggested by our observations. Only if the inner region of the disk were completely dust free and the inner rim were located at a much larger distances (rsub ≪ rin ~ 1 pc), would the size and temperature of the emission be in agreement with our interferometric observations (see also discussion in Sect. 5.4).
Therefore, two alternative explanations seem more likely: First, the emission could come from directly illuminated dusty material slightly above or below the dense disk, such as filaments of dense material swept up from the disk by turbulence. Or, the warp of the disk allows us to see a part of the disk that is directly illuminated by the central source. From the maser observations, Greenhill et al. (2003) deduce that the western side of the warped disk is oriented such that we can see its surface, which is directly illuminated by the accretion disk (see their Fig. 8). Depending on the exact geometry of the warp and the illumination characteristics of the accretion disk, this could lead to the observed highly elongated mid-infrared emission. More sophisticated radiative transfer calculations will have to be carried out to constrain the possible geometries.
5.1.2. Unresolved component
The additional unresolved emission component is required to explain the measurable correlated fluxes when the disk-like component is otherwise fully resolved out. If, in fit 3, this unresolved component is located north-east of the disk-like component, the fit quality is improved. This is mainly because of a better agreement between the differential phases of the model and the observations, especially for the strong phase signal at (u,v) ≈ (−35,35) m (dark blue points at the beginning of the U3-U4 baseline in Fig. 9). We interpret this as a sign that we are tracing smaller scale structure, e.g. an enhanced part of the disk-like component, possibly a region with less obscuration leading to the comparatively low silicate optical depth of this emission component. For the following discussion we will therefore consider the unresolved emission as a part of the disk-like emission.
5.1.3. Polar elongated dust
The extended emission component is responsible for ~80% of the emission in the N-band, independent of the wavelength. This can already be seen in Fig. 5, where the visibility quickly drops to values of ≲20% with increasing baseline length. Similarly high contributions to the total emission from extended dust have been found for NGC 1068 and NGC 3783 (Raban et al. 2009; Hönig et al. 2013). There is, however, one significant difference: in these galaxies, the contribution of the extended component depends strongly on the wavelength (e.g. from 55% to 90% between λ = 8.0 and 13.0 μm for NGC 3783). This is not the case in the nucleus of the Circinus galaxy due to the lack of any significant temperature difference between the components (see discussion in Sect. 5.4).
The extended emission is significantly elongated along , which is roughly (but not exactly) perpendicular to the disk-like component () and, thus, in polar direction. In fact, there is mounting evidence that this is a common characteristic of Seyfert galaxies: also in NGC 1068, NGC 424 and NGC 3783 the majority of the emission is extended in polar direction (Poncelet et al. 2007; Raban et al. 2008; Hönig et al. 2012, 2013). This obviously raises the question: Where is the dust responsible for this emission located?
The polar dust emission could originate from dust within the ionisation cone. Dust clouds inside the ionisation cone or, more generally, the Narrow Line Region may contribute significantly to the mid-infrared emission of AGN (e.g. Radomski et al. 2003; Poncelet et al. 2007; Schweitzer et al. 2008). A contribution of 80% in our case nevertheless appears very high for the following reason. The Circinus galaxy has a sharply delimited ionisation cone, and the central engine is fully obscured along other lines of sight. While the projected half opening angle of the visible ionisation cone onto the plane of the sky is (Wilson et al. 2000), the physical half opening angle has been estimated to be ϑcone ~ 41° from modelling of the narrow line kinematics (Fischer et al. 2013). This means that more than 70% of the sky are covered by the equatorial obscurer. Furthermore, the dusty material in the ionisation cone must have a low covering factor, typically <30%. Therefore, the total covering fraction of the dust in the ionisation cone is most likely <10%, which is consistent with the estimate by e.g. Mor et al. (2009). It is then difficult to explain why this material is responsible for 80% of the mid-infrared emission, while all the other dust intercepting most of the energy from the central engine radiates much less. Furthermore, the dust emission in the ionisation cone is expected to be optically thin and to show the silicate feature in emission. While this may be the case in NGC 424 (Hönig et al. 2012), this is certainly not the case for the Circinus galaxy: the extended emission has, on average, the highest silicate optical depth.
Deep single-dish images of the Circinus nucleus (Packham et al. 2005; Reunanen et al. 2010) already show a faint halo surrounding the nuclear point source. This halo is extended ~2 arcsec along and . It is interpreted as emission from dense dusty material which enters the ionisation cone preferentially from one direction due to a nuclear gaseous bar and is entrained outward in an outflow possibly driven by radiation pressure (Maiolino et al. 2000; Packham et al. 2005). Our extended emission component naturally appears as a continuation of this outer halo towards the nucleus. We therefore interpret the extended component as enhanced emission from the southern edge of the ionisation cone, that is from the inner funnel of the torus. The emission from the funnel most likely has smaller scale structure, such as bright regions along the cone edge or along filaments. We consider such smaller scale structures to be responsible for the irregular behaviour of the visibilities and differential phases on longer baselines (cf. Sect. 5.2.3).
In addition to an enhanced supply of material to one side of the ionisation cone, a preferential illumination of the cone edge along (and the counter cone along ) may be responsible for the enhanced emission in this direction: the best estimate for the orientation of the accretion disk comes from the innermost disk masers (see Sect. 5.1.1), suggesting a disk axis along . This value also agrees well with the position angle of the radio lobes, and (Elmouttie et al. 1998), which are most probably launched in the innermost region of the accretion disk. The flux from a thin, optically thick accretion disk depends on the polar angle ϑ as F ∝ cosϑ(1 + 2cosϑ), i.e. it emits anisotropically with the strongest emission in direction of the disk axis (Netzer 1987). This implies that the radiation towards the edges of the ionisation cone at and () are more illuminated than the opposite cone edges at and () by a factor of about two. The unobscured, western cone edge along at thus appears brighter.
5.2. Differential phases
5.2.1. Characteristics of the differential phase signal
In our MIDI data, we find relatively strong differential phases with amplitudes (peak-to-valley) of up to ~. The phase signal may be caused either by atmospheric phase residuals (mainly chromatic dispersion due to water vapour) or it may be intrinsic to the source. We are convinced that the signal is intrinsic to the source for the following reasons: (1) in several cases (especially for the measurements using the UTs), the phase measurements have a high signal to noise ratio, S/N > 5; (2) the differential phases agree or are very similar when measured twice at different epochs (cf. Sect. 2.3). This is further corroborated by a flip of the differential phase for an interchange of the telescopes. Two examples of such a flip are shown in Fig. 2 (comparisons C4 and C6: bottom row, first and last columns); (3) we see no significant differential phase signal in any other AGN (Burtscher et al. 2013, see their Fig. 63). An exception is NGC 1068, which shows strong differential phases similar to those of the Circinus galaxy (López-Gonzaga et al. 2014). It is unlikely that strong phase residuals remain after calibration only for the two brightest AGN observed with MIDI. It is more likely that we are able to detect their intrinsic phase signal more easily due to their brightness. We thus conclude that the observed differential phase signal is dominated by the intrinsic structure of the brightness distribution.
 |
Fig. 8 Examples for the two ways to produce a smooth differential phase signal: (1) a chromatic photocentre shift (blue) and (2) a purely spatial asymmetry of the brightness distribution (red). In case 1, the source is shifted to the bottom between λ ~ 10 μm and 12 μm; in case 2, the “binary” has a brightness ratio of 0.7:1.0. The resulting visibilities and phases are shown in the left panels, with the absolute Fourier phases φabs and the differential phases φdiff (as would be measured with MIDI) plotted by dotted and continuous lines, respectively. In the right panels, the two brightness distributions are shown as false-colour images, with the brightness distribution at 13.0 μm, 11.0 μm and 8.0 μm mapped to the red, green and blue channels, respectively. |
 |
Fig. 9 Amplitude of the differential phases in the uv plane: each uv point is colour-coded with the value of Δφ, the difference of the differential phase at 10 μm to those at the edges of the N-band (λ = 8.2 μm & 13.0 μm). Filled dots denote a phase signal with > 3σ significance averaged over the N-band, empty circles a phase signal with < 3σ significance, i.e. a differential phase consistent with 0. |
Differential phases appear if there is an asymmetry in the brightness distribution. This asymmetry does not necessarily have to be chromatic: due to the different spatial frequencies probed by different wavelengths, a phase signal is also introduced for non-chromatic, yet spatially asymmetric sources5. We thus distinguish two ways to produce a differential phase signal in our MIDI data (Fig. 8, see also Deroo et al. 2007):
-
1.
A chromatic photocentre shift of a brightness distribution that is otherwise point-symmetric at each wavelength (plotted blue in Fig. 8). The photocentre shift has to be nonlinear in wavenumber to produce a differential phase signal measurable with MIDI. An example of this is a point-symmetric brightness distribution that is shifted in one direction in an emission line. In this first case, the correlated fluxes (and visibilities) of the source remain unchanged with respect to a source with no photocentre shift.
-
2.
A brightness distribution that is asymmetric at each wavelength but otherwise has the same spectrum everywhere. In this case, the differential phases are caused by phase gradients (“jumps”) of the complex visibilities as they are probed at different spatial frequencies for different wavelengths. An example is a binary with unequal brightness but identical spectrum (plotted red in Fig. 8). For such a binary, the differential phases appear as a smoothed step. The amplitude and the smoothing of the step depends on the brightness ratio of the two components 6. For this second case, the phase jump occurs at a minimum of the visibilities (cf. top left panel in Fig. 8). This is in contrast to case one, where the visibilities remain unchanged.
Typically, in interferometry, a mixture of both cases occurs and it is hard to separate the two effects. For example in a binary, the two companions usually have different spectral types. Short of being able to fully reconstruct the true wavelength-dependent brightness distribution of the nuclear dust in the Circinus galaxy, we will use the discussed properties of the differential phases to derive some information on the asymmetries of the brightness distribution.
In general, the differential phases of the Circinus galaxy change smoothly over the
entire N-band, without any sharp phase jumps. Figure 9 shows the amplitude of the differential phase signal,
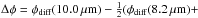 φdiff(13.0 μm)), in
the uv
plane. Differential phases with more than 3σ significance (averaged over 8.2 μm < λ < 13.0 μm)
are plotted by filled dots. Phases which are consistent with Δφ = 0 are plotted by
open circles. A negative value means the phase has a concave (∪-shaped) dependency, while positive
values mean the phase has a convex shape (i.e. ∩-shaped). To make the plot easier to
read, Δφ
was corrected for an interchange of the telescopes.
φdiff(13.0 μm)), in
the uv
plane. Differential phases with more than 3σ significance (averaged over 8.2 μm < λ < 13.0 μm)
are plotted by filled dots. Phases which are consistent with Δφ = 0 are plotted by
open circles. A negative value means the phase has a concave (∪-shaped) dependency, while positive
values mean the phase has a convex shape (i.e. ∩-shaped). To make the plot easier to
read, Δφ
was corrected for an interchange of the telescopes.
Clearly there are distinct areas in the uv plane with strong differential phases. Furthermore, we find equally strong differential phases on large spatial scales (short baselines) as on small spatial scales (long baselines). This directly implies that not only small scale structure (“clumps”) can be made responsible for the phase signal. These would only produce a phase signal on the longest baselines.
5.2.2. The phase signal of the large scale structure
On the shortest baseline (E0-G0), we measure a phase signal of up to , with a more or less smooth dependency of Δφ on the position angle. For to the differential phase is consistent with zero, then increases to reach its maximum between and . Furthermore we find that the phase signal is somewhat ∨-shaped, reminiscent of the shape of the silicate absorption feature. This and the smooth dependency with position angle strongly suggest that the phases are dominated by large scale variations of the silicate absorption strength, consistent with case 1 discussed above. Indeed, the differential phases on the shortest baselines can be very well explained by a linear gradient of the optical depth of the silicate feature over the source. In our modelling, we applied a linear gradient in the optical depth to the extended component of our three-component model (see Sect. 4): τ3(α,δ) = τ3 + ξ3·(δ·cosψ3 + α·sinψ3). Consistent with the position angle dependence of the phase signal, the gradient is oriented in direction of the major axis of this component. A gradient in the optical depth effectively leads to a shift of the emission in the direction of lower absorption (see also Fig. 7). The shift is towards the north-west, and it is non-linear in wavelength due to the specific wavelength dependency of the silicate optical depth. In fact, an enhancement of the emission towards the north-west was already suggested in Tristram et al. (2007).
From our model fit, we find a gradient of the optical depth of ξ3 ~ 27 arcsec-1. The positive value means that the silicate absorption depth increases towards the south-east, i.e. this side of the nucleus is more heavily obscured. This is consistent with observations at larger scales, where the south-eastern sides of the inclined galactic disk (Freeman et al. 1977) and a circumnuclear molecular ring (Curran et al. 1998, 1999) are located closer to us. Furthermore, the ionisation cone is one-sided towards the north-west (e.g. Marconi et al. 1994; Wilson et al. 2000), and colour maps (e.g. Prieto et al. 2004) show redder colours towards the south-east – all implying stronger obscuration towards the south-east. The highly inclined nuclear maser disk is the only structure with a size directly comparable to our dust distribution. Our results would be most consistent if the south-eastern side of the warped disk is located closer to us, similar to the galactic scale structures and as somewhat implied by Greenhill et al. (2003). It appears that the Circinus galaxy is more heavily obscured towards the south-east all the way down to the very nucleus. The disk-like obscurers on different spatial scales (the galactic disk, the circumnuclear ring and the nuclear disk) all have the north-western part of their axes slightly directed towards us.
The rather large gradient in the silicate absorption depth is necessary to obtain a significant colour change on scales of less than 100 mas. Using long-slit spectroscopy in the mid-infrared, Roche et al. (2006) mapped the strength of the silicate feature along and . They found a general trend of the optical depth along , increasing from τ9.7 μm ~ 1.0 at 1.3 arcsec west of the nucleus to τ9.7 μm ~ 2.6 at 1.3 arcsec east of the nucleus. A similar trend is not found along . These measurements further support that the south-eastern side of the nucleus is more obscured. The observed large scale trend corresponds to a gradient of ξRoche ~ 0.6 arcsec-1. This is more than one order of magnitude less than our result. Such a low gradient would not produce a significant phase signal in the interferometric measurements by far. Therefore, our gradient cannot be directly connected to the larger scale obscuration on scales of tens of parsecs. We instead interpret our strong colour gradient as evidence of more dense dusty material on scales of less than an arcsecond (i.e. less than 20 pc). This is consistent with evidence for much of the obscuration in the nucleus taking place on parsec scales (Prieto et al. 2004).
5.2.3. The phase signal for high spatial frequencies
For higher spatial frequencies (smaller scales, measured with longer baselines) the interpretation of the phase signal is more difficult. The amplitude and the shape of the differential phases change significantly between different locations in the uv plane. While some areas have a strong phase signal of up to , the measurements are consistent with no significant phase signal in other areas. In contrast to the phases on the shortest baselines, there is no preferential direction, and we find no general correlation (or anti-correlation) of Δφ with Fcor. There seem to be “patches” of stronger phases in different areas of the uv plane. In particular, we see no general trend for the phase signal to be strongest at minima in the correlated fluxes. This argues against the phase signal being caused by purely achromatic asymmetries (case 2, see Sect. 5.2.1). We therefore suspect colour gradients and especially changes in the optical depth on intermediate scales to be responsible for these phases.
 |
Fig. 10 Nuclear SED of the Circinus galaxy. Blue dots are high resolution photometry compiled by Prieto et al. (2010) plus an additional measurement with ALMA at λ = 9.3 × 10-4 m (321 GHz) by Hagiwara et al. (2013). The measurement in the J-band, which is only an upper limit, is marked with an arrow. Also shown are low resolution IRAS photometry (blue crosses), a MIDI correlated flux spectrum (cyan line), the averaged MIDI total flux spectrum (blue line) and the high resolution spectrum from Roche et al. (2006, grey line). The SED of our best fitting model is plotted in red. A possible compact hot dust component, fitted to the SED data marked by the dark red boxes, is shown by the dotted, dark red line. A zoom on the N-band region with linear scaling of the axes is shown as an inset. See text for further details. |
An exception are the uv points at (u,v) ≈ (33,14) m. These correspond to the comparison C5 (see Sect. 2.3). The correlated fluxes and differential phases for this location in the uv plane are shown in the middle column of Fig. 2. Clearly, the correlated flux (and the visibility) has a dip at λ ~ 12.4 μm which strongly deviates from the normal spectral shape of the Circinus galaxy. The dip is at the same wavelength as a strong gradient and zero-crossing of the differential phase, suggestive of case 2 discussed in Sect. 5.2.1. This means a discrete asymmetry is probed by these measurements (and only by these measurements!). A closer inspection of the data reveals that the wavelength at which the minimum occurs varies slightly from λ = 12.3 μm to λ = 12.5 μm for the individual measurements. This is roughly followed by corresponding changes of the zero-crossing of the differential phases, as we would expect for a phase jump at a visibility minimum. Assuming an unequal binary, we can directly calculate the projected separation dproj of the two components: as can be derived easily, the separation is given by dproj = λ0/BL0·(2n + 1)/2, where λ0 and BL0 are the wavelength and projected baseline length at which the minimum in the visibilities and the phase jump occur, and n ∈ N = [0,1,2,3,...]. In our case, we obtain dproj = (2n + 1)·35.5 mas. Note that only n = 0 appears likely, because separations of more than 100 mas are unlikely considering the overall size of the emission. Also, for higher values of n, we would quickly start observing more than one step in the phases within 8.0 μm < λ < 13.0 μm. In any case, the separation is intermediate between the sizes of the inner disk-like component and the extended dust component. It is certainly too large to be attributed to individual clumps of the torus. It instead indicates intermediate scale asymmetries in the brightness distribution, as could be caused by warps in the inner disk-like component or enhanced emission regions along the inner edge of the dust distribution (cf. Sect. 5.1.3).
We conclude that the strong differential phases observed on longer baselines provide evidence of intermediate scale asymmetries in the dust emission, both chromatic and achromatic, caused by the specific illumination and geometry of the dust distribution. Interferometric observations enabling image reconstruction on the one hand and more sophisticated modelling on the other hand will be required to reveal the details of the underlying brightness distribution.
5.3. Spectral energy distribution
To be meaningful, our model has to not only reproduce the interferometric data in the N-band, but also be consistent with the entire SED of the Circinus galaxy. The SED of the Circinus galaxy from Prieto et al. (2010) is shown in Fig. 10. With an angular resolution of <1.5 arcsec, these measurements represent the true nuclear SED. We add to this SED a new measurement of the continuum emission at λ = 9.3 × 10-4 m (321 GHz) obtained by Hagiwara et al. (2013) with ALMA: FALMA = 55 mJy. Low resolution measurements with IRAS (Moshir et al. 1990) are plotted as blue crosses for reference. The error bars correspond to an assumed uncertainty of 0.1 dex for all photometric data points (e.g. due to variability). A MIDI correlated flux spectrum (#41, BL = 87 m, selected for its low correlated flux and good S/N) is plotted in cyan, and the averaged total flux spectrum from MIDI is plotted in blue. The SED of our model is shown in red. For comparison, we also reproduce the high spatial resolution spectrum of the inner 0.81 arcsec from Roche et al. (2006) in grey.
Not surprisingly, the SED of our model closely resembles the Planck curve for a black body of T ~ 300 K, with some modifications due to absorption, most notably the silicate features at λ = 9.7 μm and 20 μm. Although we only fitted our model to the data obtained with MIDI, it is consistent with the entire high resolution SED: it represents the flux in the mid-infrared well while producing less or equal flux at other wavelength ranges.
At the long wavelength end of the N-band (see inset of Fig. 10) our model under-predicts the total flux spectrum for λ ≳ 12 μm. We interpret this as evidence of additional, cooler dust, which is responsible for this emission and which is not fully captured by our model. On the other hand, the measurement with ALMA sets a strong constraint on the emission from cooler dust in the innermost 1.3 arcsec (26 pc) of the Circinus galaxy. While the SED of our model is consistent with the ALMA measurement, it rules out any major contribution to the SED from additional dust in the nucleus with T < 200 K. This is consistent with the results of radiative transfer calculations of dusty tori, which in general show a steep decrease in the torus SED towards longer wavelengths.
Towards shorter wavelengths, the model SED rapidly decreases following the (absorbed) Wien tail of the black-body emission. The observed SED in the near-infrared is much higher. The observed fluxes in the J, H and K-bands are compatible with an additional compact component of hot dust (T ~ 800 K, dotted curve in Fig. 10). Such a component would not contribute significantly to the emission in the mid-infrared. It would still be (marginally) consistent with the lowest correlated fluxes measured with MIDI, which can be considered as upper limits for any contribution by a compact hot emission component (e.g. the cyan curve in Fig. 10). However, our interferometric measurements rule out a compact emitter that produces sufficient flux to explain the photometric measurements in the L and M-band. We tested this by fixing the temperature of the unresolved component to T1 = 600 K and adjusting f1 so that the near-infrared part of the SED is reasonably well reproduced. We then obtain much higher correlated fluxes than observed at the short wavelength end, unless Δ1 ≳ 15 mas. This means that most of the emission at these wavelengths must be extended by at least 0.3 pc and less than 3.8 pc (190 mas, unresolved by single dish observations). This is discussed further in Sect. 5.4.
In conclusion, we find that our model is consistent with the overall SED of the Circinus galaxy. We further conclude that the nuclear SED is dominated by emission from dust close to T ~ 300 K and that the contribution from dust at much hotter (T > 800 K) or cooler (T < 200 K) temperatures is very low on parsec scales.
5.4. Lack of a compact hot dust component
In Tristram et al. (2007), no significant temperature gradient was found in the dust distribution of the Circinus galaxy. One of the main goals of the new observations was to search for hotter dust using longer baselines, or generally for an increase in the dust temperature towards the centre, similar to what is observed in NGC 1068 (Jaffe et al. 2004; Raban et al. 2008; López-Gonzaga et al. 2014). NGC 1068 is similarly well resolved (both in terms of visibility and scales of the supposed sublimation radius) as the Circinus galaxy. In NGC 1068, the correlated fluxes are on average bluer than the total flux (Fcor(13 μm)/Fcor(8 μm) < Ftot(13 μm)/Ftot(8 μm)). This clearly indicates an increase in the dust temperature towards the centre. In the Circinus galaxy, however, the emission at the short wavelength end of the N-band is almost completely resolved out even on the longest baselines, and we see no significant difference between the temperatures of our model components (for all three components, T ~ 300 K). The new measurements thus confirm the earlier results: we find no evidence of a temperature increase towards the centre. This is unexpected, because the resolution limit of our interferometric observations, ~0.1 pc, corresponds to a few times the sublimation radius (rsub ~ 0.03 pc). We should start seeing hotter dust on these scales.
There are two possible explanations for the lack of hot dust at the centre: either we (still) cannot see it, or it is truly absent. In the first case, the hot dust component could be so highly obscured on scales of a few rsub that we simply do not see it. However, this is somewhat in contradiction with the decrease in the silicate absorption depth towards the centre unless the innermost dust contains less silicates. Full radiative transfer calculations will have to be carried out to verify if a hot dust component can be fully obscured while reproducing the other characteristics of the Circinus nucleus. In the second, more speculative case, there might simply be no hot dust at the inner rim of the torus at all. In Sect. 2.3.2, we discussed a possible variability in the Circinus galaxy. It is therefore conceivable that the active nucleus was previously in a more active state or even that an explosive event occurred some time ago (Bland-Hawthorn et al. 1997). The increased activity would lead to an increased sublimation radius. If the inner rim were to contract only slowly after the activity decreased, the innermost dust would be at much cooler temperatures for some time. Such a large and relatively cool inner rim would not only explain the lack of hot dust but also the highly elongated disk-like component (cf. Sect. 5.1.1). On the other hand, this would require very long timescales for dust formation, preventing the inner rim from quickly moving back inwards. The amplitude of variability would have to be three to four orders of magnitude to result in a significantly cooler inner rim. Moreover, the near-infrared excess of the SED with respect to our model indicates that dust at T > 500 K must exist (see Sect. 5.3).
The explanations are not very satisfactory. Furthermore, the problem is not the lack of a hot dust component alone, but rather the absence of any evidence of an increase in the dust temperature towards the centre. The interferometric measurements roughly probe spatial scales from 20 to 200 mas (0.4 to 4.0 pc). If we include our single dish measurements or the spectra observed by Roche et al. (2006), the spatial scales explored are up to 500 mas (~10 pc) or 2 arcsec (~40 pc), respectively. The temperature of directly illuminated dust 7 depends on the distance as T ∝ (L/r2)1/5.6 ∝ r−1/2.8 (Barvainis 1987). Consequently, we would expect a temperature difference by a factor of (25/170)−1/2.8 ≈ 2 in the range of the interferometric measurements, or a temperature change by a factor of more than 3 when including the single dish data. This is clearly not observed. This lack of a temperature gradient poses a challenge for the picture of a centrally heated dust distribution in the nucleus of the Circinus galaxy.
5.5. What is the “dusty torus”, and where is it?
A central question is, of course, which of the observed components can be associated with the dusty torus in unified schemes of AGN? Here we consider the “torus” defined by its role in classical unification schemes: it obscures the central engine for certain (edge-on) viewing angles while at the same time collimating the ionising radiation and outflows. Additionally, the dust in the inner funnel of the torus scatters emission from the central engine towards an observer. The Circinus galaxy certainly shows all these characteristics of a dusty torus (see Sect. 1).
One explanation for the obscuration and collimation could be a constant scale height of the inner disk, or even a puffed-up inner rim within a few rsub, similar to what has been suggested for disks around young stellar objects (Natta et al. 2001; Dullemond et al. 2001). The latter scenario has recently also been proposed for AGN (Hönig et al. 2012). However, if the obscuration and collimation already take place within a few rsub (i.e. within ~0.1 pc for the Circinus galaxy), then the material in the disk at larger radii should be shadowed and significantly colder than 300 K. This contradicts the parsec-sized, equatorially extended emission of our disk-like component as well as the requirements for the pumping of the disk masers, which require a direct line of sight to the central engine (Greenhill et al. 2003; Lo 2005). Also, such a geometry is hard to reconcile with the outflow ( opening angle) traced by water masers on sub-parsec scales, which implies that the material is still not fully collimated on these spatial scales.
We therefore argue that most of the collimation (and with it obscuration) most likely take place on scales of ~1 pc, surrounding the disk. This is consistent with the disk masers and the inner wide angle outflow not extending beyond this scale and the large scale structures having been collimated within a few parsec. In this picture, a significant part of the polar elongated emission originates from the inner funnel of the obscuring material, which is equivalent to the outer edge of the ionisation cone (see Sect. 5.1.3). Most of the obscuration and collimation is not due to the disk, but due to the material located above or below it. We therefore consider that it is this material which is commonly associated with the “obscuring torus” in AGN.
6. Summary and conclusions
We have obtained an extensive new interferometric dataset in the mid-infrared in order to study the nuclear dust distribution in the Circinus galaxy. Due to our optimised observing strategy we could increase the uv coverage from 21 uv points to 152. This allows us to more precisely determine the properties of the dust distribution in the Circinus galaxy. Using both the correlated fluxes and the differential phases measured by the interferometer, we come to the following conclusions:
-
We confirm the two-component structure previously found in the dust distribution of the Circinus galaxy, consisting of an inner dense disk-like component and an extended emission region. We interpret this as emission from warm dust in the context of an inner dense disk surrounded by a less dense, geometrically thick and filamentary dust distribution.
-
The disk-like component is highly elongated with a size (FWHM) of ~0.2 pc × 1.1 pc. Its major axis is along , which is in perfect agreement to the orientation of the nuclear maser disk and oriented perpendicular to the ionisation cone and outflow along . Because a flat, dense disk should appear in absorption rather than emission when seen close to edge-on, we interpret this component either as emission from material associated with the inner funnel of the torus directly above or below the disk or from the directly illuminated portion of a warped disk slightly oriented towards us.
-
The extended dust emission is responsible for 80% of the mid-infrared emission. It has a FWHM of ~0.8 pc × 1.9 pc and is elongated along , that is, roughly in polar direction. We see this component as the inner part of the extended emission already seen by single dish imaging. It is interpreted as the emission from the inner funnel of a more extended dust distribution and especially as emission from the funnel edge along . Dense dusty material enters the ionisation cone primarily on this side of the funnel, which is also preferentially illuminated by the inclined accretion disk.
-
We detect significant differential phases, indicating both chromatic and spatial asymmetries in the dust emission. On scales of ~1.0 pc, the differential phases are well explained by a strong increase in the silicate absorption depth towards the south-east. This strong gradient in the silicate absorption implies that a significant amount of obscuration takes place on parsec scales. It also shows that the galaxy is more obscured towards the south-east all the way to the nucleus. The more complex differential phase signal on longer baselines is most likely caused by intermediate scale asymmetries in the brightness distribution, both chromatic and achromatic. These are probably not individual clumps of a clumpy torus, but rather intermediate scale structures such as the warp of the inner disk, the sharp cone edges or large filamentary structures which are directly illuminated by the central engine.
-
We find no indications for a temperature difference in the dust distribution between ~0.1 pc to ~40 pc. On all of these scales, the mid-infrared spectrum has roughly the same slope, indicative of dust at T ~ 300 K. Because the SED shows excess emission in the near-infrared with respect to emission by 300 K dust, we argue that this emission must also be extended on scales >0.3 pc. Otherwise, the Rayleigh-Jeans part of the compact hot dust component would appear as an unresolved source in our interferometric data in the mid-infrared. This is in contrast to the results for other well studied AGN such as NGC 1068 and NGC 424, where a clear temperature increase towards the centre is observed. This result also has a consequence for MATISSE (Lopez et al. 2008), the successor to MIDI at the VLTI: we predict relatively low visibilities also in the L and M-band for the Circinus galaxy.
-
We further argue that the dense inner disk is not sufficient to provide the obscuration and collimation observed on larger scales, that is, the function normally attributed to the dusty torus in unified schemes of AGN. These must be caused by additional material above and below the disk on scales of ~1 pc. The emission from the polar component is substantially from the inner funnel of this dust distribution.
Our interferometric observations show a quite complex picture of the dust emission in the nucleus of the Circinus galaxy. To fully and unambiguously reveal the underlying brightness distribution, interferometric observations enabling image reconstruction will be necessary. Because MIDI is only a two beam interferometer, it measures no closure phases and a reliable image reconstruction is therefore not readily possible. This will, however, soon be possible with the upcoming second generation mid-infrared beam combiner for the VLTI, MATISSE, which will combine four telescopes at a time and thus provide three closure phases.
The presence of a bright disk-like component, polar elongated dust emission and the lack of a temperature difference are not expected for typical models of the centrally heated dust distributions of AGN. New sets of detailed radiative transfer calculations will be required to explain our observations and to better understand the three-dimensional dust morphology in the nuclei of active galaxies.
Online material
Appendix A: Table and plots of all uv points
Table A.1 lists all measurements of the Circinus galaxy obtained with MIDI, that is all uv points. The columns are: (1) a running number of the measurement; (2) the date and time at the start of the fringe track, i.e. the interferometric observation; (3) modified Julian date, MJD; (4) telescope combination used for the observation; (5) projected baseline length; (6) position angle of the projected baseline; (7) adaptive optics system used, either STRAP or MACAO (“_T” indicates additional usage of the technical CCD); (8) usage of IRIS with: “n/a” – IRIS not available, “off” – IRIS not used for field stabilisation, “on” – IRIS used for field stabilisation, a number – IRIS used with the integration time specified in seconds (before 2011 no IRIS integration times were stored with the data); (9) mode of the interferometric observations with: “0OPD” – tracking with a scan length of 84.2 μm at zero OPD, “OFF” – tracking with a scan length of 84.2 μm at an offset of 40 μm, “SHRT” – tracking with a reduced scan length of 53.0 μm at an offset of 40 μm; (10) detector integration time of MIDI; (11) chopping frequency for the observations of the total flux spectra with the single dishes; (12) airmass; (13) seeing; (14) coherence time; (15) name of the calibrator star; (16) time of the calibrator observation; (17) correlated flux and its error at 12 μm, if the observation was successful and is used for the further analysis. Measurements were considered successful if a fringe signal was tracked and sufficient signal was detected (mostly equivalent to more than 1500 good frames used for the averaging). No entry in the chop frequency column indicates that no photometry was observed.
All dispersed correlated fluxes are shown in Fig. A.1, the differential phases are plotted in Fig. A.2. The data is plotted in blue, the correlated fluxes and differential phases of the model from fit 3 are plotted in red. As in Table A.1, the measurements are ordered by observing date and time. The numbering is also the same as in Table A.1, however unsuccessful measurements are not plotted.
List of interferometric measurements of the Circinus galaxy obtained with MIDI.
 |
Fig. A.1 Correlated fluxes of all uv points (blue). The correlated fluxes of our three-component model (fit 3) are plotted in red. |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.2 Differential phases of all uv points (blue). The differential phases of our model (fit 3) are plotted in red. |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
The software package “MIA+EWS” can be downloaded at: http://home.strw.leidenuniv.nl/~jaffe/ews/index.html
This additional software is publicly available at: http://www.blackholes.de/downloads.html
On scales of tens of arcseconds (> 200 pc) however, the Circinus galaxy indeed shows significant PAH emission at 7.7, 8.6 and 11.3 μm (Moorwood et al. 1996; Galliano et al. 2008), most likely from the circumnuclear starburst.
In fact, even symmetric, non-chromatic brightness distributions can have a phase signal, as the examples of a ring or a uniform disk show. In these cases, however, there is a sharp phase jump by exactly 180° at the point where V = 0. This has been measured, e.g. for the star Vega (Schmitt et al. 2006). Because we do not see such sharp phase jumps in the data of the Circinus galaxy, we do not further consider these special cases here.
The dust directly illuminated by the central engine generally dominates the emission, see discussion in Sect. 5.1.
Acknowledgments
We thank the ESO staff operating the VLT(I) and the night astronomers on duty during our observations for their support. Without their assistance and help, it would not have been possible to collect this unique data set. We also thank D. Asmus and A. Kreplin for helpful discussions and their suggestions to improve the manuscript, as well as the anonymous referee for the detailed comments strengthening the manuscript. We are very grateful to K. Zelenevskiy for proof-reading the manuscript.
References
- Alexander, D. M., Heisler, C. A., Young, S., et al. 2000, MNRAS, 313, 815 , [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 , [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 , [NASA ADS] [CrossRef] [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 , [NASA ADS] [CrossRef] [Google Scholar]
- Beckert, T., Driebe, T., Hönig, S. F., & Weigelt, G. 2008, A&A, 486, L17 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., Maiolino, R., & Risaliti, G. 2012, Adv. Astron., 2012 , [Google Scholar]
- Bland-Hawthorn, J., Gallimore, J. F., Tacconi, L. J., et al. 1997, Ap&SS, 248, 9 , [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L. 2011, Ph.D. Thesis, Max-Planck-Institut für Astronomie, Heidelberg, Germany [Google Scholar]
- Burtscher, L., Jaffe, W., Raban, D., et al. 2009, ApJ, 705, L53 , [NASA ADS] [CrossRef] [Google Scholar]
- Burtscher, L., Meisenheimer, K., Jaffe, W., Tristram, K. R. W., & Röttgering, H. J. A. 2010, PASA, 27, 490 , [NASA ADS] [Google Scholar]
- Burtscher, L., Tristram, K. R. W., Jaffe, W. J., & Meisenheimer, K. 2012, in Proc. SPIE,8445, 84451G , [Google Scholar]
- Burtscher, L., Meisenheimer, K., Tristram, K. R. W., et al. 2013, A&A, 558, A149 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Curran, S. J., Johansson, L. E. B., Rydbeck, G., & Booth, R. S. 1998, A&A, 338, 863 [NASA ADS] [Google Scholar]
- Curran, S. J., Rydbeck, G., Johansson, L. E. B., & Booth, R. S. 1999, A&A, 344, 767 [NASA ADS] [Google Scholar]
- Deroo, P., van Winckel, H., Verhoelst, T., et al. 2007, A&A, 467, 1093 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dorodnitsyn, A., Kallman, T., & Proga, D. 2008, ApJ, 675, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Efron, B. 1979, Ann. Stat., 7, 1 [Google Scholar]
- Elmouttie, M., Haynes, R. F., Jones, K. L., Sadler, E. M., & Ehle, M. 1998, MNRAS, 297, 1202 , [NASA ADS] [CrossRef] [Google Scholar]
- Feltre, A., Hatziminaoglou, E., Fritz, J., & Franceschini, A. 2012, MNRAS, 426, 120 , [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., & Schmitt, H. R. 2013, ApJS, 209, 1 , [NASA ADS] [CrossRef] [Google Scholar]
- Freeman, K. C., Karlsson, B., Lynga, G., et al. 1977, A&A, 55, 445 [NASA ADS] [Google Scholar]
- Galliano, F., Madden, S. C., Tielens, A. G. G. M., Peeters, E., & Jones, A. P. 2008, ApJ, 679, 310 , [NASA ADS] [CrossRef] [Google Scholar]
- Gitton, P. B., Leveque, S. A., Avila, G., & Phan Duc, T. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, Proc. SPIE, 5491, 944 [Google Scholar]
- Granato, G. L., & Danese, L. 1994, MNRAS, 268, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Greenhill, L. J., Booth, R. S., Ellingsen, S. P., et al. 2003, ApJ, 590, 162 , [NASA ADS] [CrossRef] [Google Scholar]
- Hagiwara, Y., Miyoshi, M., Doi, A., & Horiuchi, S. 2013, ApJ, 768, L38 , [NASA ADS] [CrossRef] [Google Scholar]
- Hall, P. 1985, Stochastic Processes and their Applications, 20, 231 [Google Scholar]
- Hönig, S. F., & Kishimoto, M. 2010, A&A, 523, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Antonucci, R., et al. 2012, ApJ, 755, 149 , [NASA ADS] [CrossRef] [Google Scholar]
- Hönig, S. F., Kishimoto, M., Tristram, K. R. W., et al. 2013, ApJ, 771, 87 , [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hayward, C. C., Narayanan, D., & Hernquist, L. 2012, MNRAS, 420, 320 , [NASA ADS] [CrossRef] [Google Scholar]
- Horst, H., Duschl, W. J., Gandhi, P., & Smette, A. 2009, A&A, 495, 137 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jaffe, W. J. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, Proc. SPIE, 5491, 715 [Google Scholar]
- Jaffe, W., Meisenheimer, K., Röttgering, H. J. A., et al. 2004, Nature, 429, 47 , [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kemper, F., Vriend, W. J., & Tielens, A. G. G. M. 2004, ApJ, 609, 826 [NASA ADS] [CrossRef] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Tristram, K. R. W., & Weigelt, G. 2009a, A&A, 493, L57 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2009b, A&A, 507, L57 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2011a, A&A, 527, A121 , [CrossRef] [EDP Sciences] [Google Scholar]
- Kishimoto, M., Hönig, S. F., Antonucci, R., et al. 2011b, A&A, 536, A78 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koribalski, B. S., Staveley-Smith, L., Kilborn, V. A., et al. 2004, AJ, 128, 16 , [NASA ADS] [CrossRef] [Google Scholar]
- Kreplin, A., Weigelt, G., Kraus, S., et al. 2013, A&A, 551, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krolik, J. H., & Begelman, M. C. 1988, ApJ, 329, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Kylafis, N. D., & Norman, C. A. 1991, ApJ, 373, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Leinert, C., Graser, U., Przygodda, F., et al. 2003, Ap&SS, 286, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Lo, K. Y. 2005, ARA&A, 43, 625 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, B., Antonelli, P., Wolf, S., et al. 2008, in Proc. SPIE, 7013, 70132B , [Google Scholar]
- López-Gonzaga, N., Jaffe, W., Burtscher, L., Tristram, K. R. W., & Meisenheimer, K. 2014, A&A, submitted [arXiv:1401.3248] [Google Scholar]
- Lumsden, S. L., Alexander, D. M., & Hough, J. H. 2004, MNRAS, 348, 1451 , [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Alonso-Herrero, A., Anders, S., et al. 2000, ApJ, 531, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Moorwood, A. F. M., Origlia, L., & Oliva, E. 1994, The Messenger, 78, 20 [NASA ADS] [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Matt, G., Fiore, F., Perola, G. C., et al. 1996, MNRAS, 281, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Meisenheimer, K., Tristram, K. R. W., Jaffe, W., et al. 2007, A&A, 471, 453 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meisner, J. A., Tubbs, R. N., & Jaffe, W. J. 2004, in New Frontiers in Stellar Interferometry, ed. W. A. Traub, Proc. SPIE, 5491, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Moorwood, A. F. M., Lutz, D., Oliva, E., et al. 1996, A&A, 315, L109 [NASA ADS] [Google Scholar]
- Mor, R., Netzer, H., & Elitzur, M. 2009, ApJ, 705, 298 [NASA ADS] [CrossRef] [Google Scholar]
- Moshir, M., Kopan, G., Conrow, T., et al. 1990, in BAAS, 22, 1325 [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 2001, A&A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nenkova, M., Ivezić, Ž., & Elitzur, M. 2002, ApJ, 570, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 1987, MNRAS, 225, 55 [NASA ADS] [Google Scholar]
- Oliva, E., Salvati, M., Moorwood, A. F. M., & Marconi, A. 1994, A&A, 288, 457 [NASA ADS] [Google Scholar]
- Oliva, E., Marconi, A., Cimatti, A., & Alighieri, S. D. S. 1998, A&A, 329, L21 [NASA ADS] [Google Scholar]
- Packham, C., Radomski, J. T., Roche, P. F., et al. 2005, ApJ, 618, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Packham, C., Young, S., Fisher, S., et al. 2007, ApJ, 661, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Poncelet, A., Perrin, G., & Sol, H. 2006, A&A, 450, 483 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poncelet, A., Doucet, C., Perrin, G., Sol, H., & Lagage, P. O. 2007, A&A, 472, 823 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pott, J., Malkan, M. A., Elitzur, M., et al. 2010, ApJ, 715, 736 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, M. A., Meisenheimer, K., Marco, O., et al. 2004, ApJ, 614, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Prieto, M. A., Reunanen, J., Tristram, K. R. W., et al. 2010, MNRAS, 402, 724 , [NASA ADS] [CrossRef] [Google Scholar]
- Raban, D., Heijligers, B., Röttgering, H., et al. 2008, A&A, 484, 341 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raban, D., Jaffe, W., Röttgering, H., Meisenheimer, K., & Tristram, K. R. W. 2009, MNRAS, 394, 1325 , [NASA ADS] [CrossRef] [Google Scholar]
- Radomski, J. T., Piña, R. K., Packham, C., et al. 2003, ApJ, 587, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Levenson, N. A., Rodríguez Espinosa, J. M., et al. 2009, ApJ, 702, 1127 , [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., Silk, J. I., Werner, M. W., & Wickramasinghe, N. C. 1969, Nature, 223, 788 , [NASA ADS] [CrossRef] [Google Scholar]
- Reunanen, J., Prieto, M. A., & Siebenmorgen, R. 2010, MNRAS, 402, 879 , [NASA ADS] [CrossRef] [Google Scholar]
- Roche, P. F., Packham, C., Telesco, C. M., et al. 2006, MNRAS, 367, 1689 , [NASA ADS] [CrossRef] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., Wolf, S., & Henning, T. 2005, A&A, 437, 861 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Camenzind, M., et al. 2008, A&A, 482, 67 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schartmann, M., Meisenheimer, K., Klahr, H., et al. 2009, MNRAS, 393, 759 , [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, H. R., Pauls, T. A., Tycner, C., et al. 2006, in Advances in Stellar Interferometry, eds. J. D. Monnier, M. Schöller, et al., Proc. SPIE, 6268, 3B [Google Scholar]
- Schweitzer, M., Groves, B., Netzer, H., et al. 2008, ApJ, 679, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Siebenmorgen, R., & Efstathiou, A. 2001, A&A, 376, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, C. H., Wright, C. M., Aitken, D. K., Roche, P. F., & Hough, J. H. 2000, MNRAS, 312, 327 , [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. A., & Wilson, A. S. 2001, ApJ, 557, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. D. T., Draine, B. T., Dale, D. A., et al. 2007, ApJ, 656, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Soldi, S., Beckmann, V., Bassani, L., et al. 2005, A&A, 444, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suganuma, M., Yoshii, Y., Kobayashi, Y., et al. 2006, ApJ, 639, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Swain, M., Vasisht, G., Akeson, R., et al. 2003, ApJ, 596, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, K. R. W. 2007, Ph.D. Thesis, Max-Planck-Institut für Astronomie, Heidelberg, Germany [Google Scholar]
- Tristram, K. R. W. 2013 [arXiv:1312.3607] [Google Scholar]
- Tristram, K. R. W., & Schartmann, M. 2011, A&A, 531, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Meisenheimer, K., Jaffe, W., et al. 2007, A&A, 474, 837 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tristram, K. R. W., Raban, D., Meisenheimer, K., et al. 2009, A&A, 502, 67 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- van Boekel, R. J. H. M. 2004, Ph.D. Thesis, University of Amsterdam, The Netherlands [Google Scholar]
- Veilleux, S., & Bland-Hawthorn, J. 1997, ApJ, 479, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Verhoelst, T. 2005, Ph.D. Thesis, Institute of Astronomy, K.U. Leuven, Belgium [Google Scholar]
- Wada, K. 2012, ApJ, 758, 66 , [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., & Norman, C. A. 2002, ApJ, 566, L21 , [NASA ADS] [CrossRef] [Google Scholar]
- Wada, K., Papadopoulos, P. P., & Spaans, M. 2009, ApJ, 702, 63 , [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Wittkowski, M., Balega, Y. Y., et al. 2004, A&A, 425, 77 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, A. S., Shopbell, P. L., Simpson, C., et al. 2000, AJ, 120, 1325 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Kervella, P., Arsenault, R., et al. 2004, A&A, 418, L39 , [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, Y., Wilson, A. S., Matt, G., Terashima, Y., & Greenhill, L. J. 2009, ApJ, 691, 131 , [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Values for the parameters in EWS used for the reduction of the MIDI data of the Circinus galaxy.
Comparison of measurements at similar locations in the uv plane but from different observing epochs or baselines.
List of interferometric measurements of the Circinus galaxy obtained with MIDI.
All Figures
 |
Fig. 1 uv plane with all MIDI measurements of the Circinus galaxy. The individual uv points are colour-coded according to the different observing epochs. Successful measurements are shown by filled circles, failed measurements by open circles. The full baseline tracks are plotted in grey for all the telescope combinations used and for a minimum elevation of the Circinus galaxy of . In the baseline names, U stands for the UTs, A1 to G0 for the stations of the ATs. Regions used for the comparison of measurements at different epochs are encircled and labelled in blue (see Sect. 2.3). Every measurement appears twice, symmetric to the centre of the uv plane, because the Fourier transform of a real valued function (such as the intensity distribution on sky) is hermitian. As a consequence, the measurements which seem covered by the figure key are identical to those on the other side of the uv plane. |
| In the text | |
 |
Fig. 2 Comparison of the total and correlated flux spectra (first two rows), visibilities (third row) and differential phases (bottom row) at locations C4 (left column), C5 (central column) and C6 (right column). For clarity, error bars are only plotted every fifth wavelength bin. Note that for C4 and C6 the telescopes at the two epochs considered were interchanged (UT3-UT2 versus UT2-UT3). The phases of measurements #1 and #3 were corrected for this interchange in order to allow an easier comparison (see also discussion in Sect. 5.2). |
| In the text | |
 |
Fig. 3 Total flux of the Circinus galaxy at 8.2 μm (left) and 12.8 μm (right) as a function of the hour angle for four different epochs. The average fluxes at the respective wavelengths on 2008-04-18 and 2009-04-15 are indicated by the dashed lines. |
| In the text | |
 |
Fig. 4 Correlated fluxes of the Circinus galaxy at 12 μm for all
uv
points containing useful interferometric data. The points are colour-coded
according to their correlated flux, Fcor(12 μm),
using a square root colour scaling as indicated in the colour bar on the right.
The uv point at the origin represents the
averaged total flux of the source, which is outside the plotted range of colours:
|
| In the text | |
 |
Fig. 5 Correlated fluxes (Fcor, left ordinate) or
visibilities ( |
| In the text | |
 |
Fig. 6 Correlated fluxes of the Circinus galaxy at 8.5 and 12.0 μm as a function of the position angle for the baselines E0-G0 (with 13 m < BL < 16 m, left) and UT2-UT4 (with 76 m < BL < 90 m, right). Also plotted are the correlated fluxes of the three-component model discussed in Sect. 4: fit 3 by continuous lines, fit 2 and 1 by dashed lines in the left and right panels, respectively. |
| In the text | |
 |
Fig. 7 False-colour image of the three-component model for the mid-infrared emission of the nucleus of the Circinus galaxy (fit 3). The colours red, green and blue correspond to the model at 13.0 μm, 10.5 μm and 8.0 μm, respectively. The colour scaling is logarithmic in order to show both bright and faint features. Clearly the colour gradient of the extended component due to the increase in the silicate depth towards the south-east is visible. This colour gradient leads to a chromatic photocentre shift towards the north-west. Despite the lower surface brightness, 80% of the emission comes from the extended component. Also plotted is the trace of the water maser disk: the blue and red parts trace the approaching and receding sides of the maser disk respectively. Note that the relative offset of the mid-infrared emission with respect to the maser disk is not known (see text for details). |
| In the text | |
 |
Fig. 8 Examples for the two ways to produce a smooth differential phase signal: (1) a chromatic photocentre shift (blue) and (2) a purely spatial asymmetry of the brightness distribution (red). In case 1, the source is shifted to the bottom between λ ~ 10 μm and 12 μm; in case 2, the “binary” has a brightness ratio of 0.7:1.0. The resulting visibilities and phases are shown in the left panels, with the absolute Fourier phases φabs and the differential phases φdiff (as would be measured with MIDI) plotted by dotted and continuous lines, respectively. In the right panels, the two brightness distributions are shown as false-colour images, with the brightness distribution at 13.0 μm, 11.0 μm and 8.0 μm mapped to the red, green and blue channels, respectively. |
| In the text | |
 |
Fig. 9 Amplitude of the differential phases in the uv plane: each uv point is colour-coded with the value of Δφ, the difference of the differential phase at 10 μm to those at the edges of the N-band (λ = 8.2 μm & 13.0 μm). Filled dots denote a phase signal with > 3σ significance averaged over the N-band, empty circles a phase signal with < 3σ significance, i.e. a differential phase consistent with 0. |
| In the text | |
 |
Fig. 10 Nuclear SED of the Circinus galaxy. Blue dots are high resolution photometry compiled by Prieto et al. (2010) plus an additional measurement with ALMA at λ = 9.3 × 10-4 m (321 GHz) by Hagiwara et al. (2013). The measurement in the J-band, which is only an upper limit, is marked with an arrow. Also shown are low resolution IRAS photometry (blue crosses), a MIDI correlated flux spectrum (cyan line), the averaged MIDI total flux spectrum (blue line) and the high resolution spectrum from Roche et al. (2006, grey line). The SED of our best fitting model is plotted in red. A possible compact hot dust component, fitted to the SED data marked by the dark red boxes, is shown by the dotted, dark red line. A zoom on the N-band region with linear scaling of the axes is shown as an inset. See text for further details. |
| In the text | |
 |
Fig. A.1 Correlated fluxes of all uv points (blue). The correlated fluxes of our three-component model (fit 3) are plotted in red. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.2 Differential phases of all uv points (blue). The differential phases of our model (fit 3) are plotted in red. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.