| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A70 | |
| Number of page(s) | 13 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322404 | |
| Published online | 12 March 2014 | |
The accretion environment in Vela X-1 during a flaring period using XMM-Newton
1
Instituto Universitario de Física Aplicada a las Ciencias y las
Tecnologías, University of Alicante,
PO Box 99,
03080
Alicante,
Spain
e-mail:
silvia.martinez@ua.es
2
Departamento de Física, Ingenería de Sistemas y Teoría de la
Señal, University of Alicante, PO
Box 99, 03080
Alicante,
Spain
3
Dr. Karl Remeis-Observatory & ECAP, Universitat
Erlangen-Nürnberg, Sternwartstr.
7, 96049
Bamberg,
Germany
4 European Space Astronomy Centre (ESA/ESAC), Science
Operations Department, Villanueva de la Cañada (Madrid), Spain
5
Cahill Center for Astronomy and Astrophysics, California Institute
of Technology, Pasadena
CA
91125,
USA
6
University College Dublin, Belfield, Dublin 4, Ireland
Received:
30
July
2013
Accepted:
26
December
2013
We present analysis of 100 ks contiguous XMM-Newton data of the prototypical wind accretor Vela X-1. The observation covered eclipse egress between orbital phases 0.134 and 0.265, during which a giant flare took place, enabling us to study the spectral properties both outside and during the flare. This giant flare with a peak luminosity of 3.92+0.42-0.09 × 1037 erg s-1 allows estimates of the physical parameters of the accreted structure with a mass of ~1021 g. We have been able to model several contributions to the observed spectrum with a phenomenological model formed by three absorbed power laws plus three emission lines. After analysing the variations with orbital phase of the column density of each component, as well as those in the Fe and Ni fluorescence lines, we provide a physical interpretation for each spectral component. Meanwhile, the first two components are two aspects of the principal accretion component from the surface of the neutron star, the third component seems to be the X-ray light echo formed in the stellar wind of the companion.
Key words: X-rays: binaries / pulsars: individual: Vela X-1
© ESO, 2014
1. Introduction
Vela X-1 is an eclipsing high-mass X-ray binary discovered in 1967 (Chodil et al. 1967) at a distance of ~2 kpc (Nagase 1989). It consists of the early type supergiant HD 77581 (B0.5Iab, R ~ 34 R⊙) and a neutron star of ~1.77 M⊙ (Rawls et al. 2011), orbiting its companion with a period of 8.964 days. The distance at periastron is only 0.6 stellar radii (a ~ 53 R⊙; van Kerkwijk et al. 1995) from the stellar surface, well within the acceleration zone of the stellar wind. Despite the status of the Vela X-1 system as an archetypal wind accretor, the structure of the extended atmosphere of the supergiant and large scale structure of the stellar wind are not known in detail.
The X-ray luminosity of Vela X-1 is typically a few 1036 erg s-1, four or more orders of magnitude brighter than the intrinsic emission expected from the supergiant primary. It is well explained by wind accretion from the optical companion, with an estimated mass loss rate of 2 × 10-6 M⊙ yr-1 (Watanabe et al. 2006). Intense X-ray variability of Vela X-1, lasting from a few minutes to several hours, is commonly thought to be associated with changes in the accretion rate and to inhomogeneities in the stellar wind flow (Nagase et al. 1983; Haberl & White 1990). There have been reports, on the one hand, of reductions in the flux to less than 10% of its normal emission (“off states”), as well as of very active states, on the other, with increases in the flux by sometimes more than a factor of 10 (Kreykenbohm et al. 1999, 2008).
X-ray pulsations were discovered by McClintock et al. (1976) with a fluctuating pulse period of ~283 s. This random spin up and down does not show any apparent connection to the orbital phase of the neutron star around its supergiant companion (Nagase et al. 1984), and it is believed to be caused by the transfer of angular momentum by wind accretion onto the neutron star.
The X-ray spectrum has been described either by a power law with a high energy cut-off beyond 15−30 keV (Nagase et al. 1986; Kreykenbohm et al. 1999) or by a negative positive exponential model (NPEX; Orlandini et al. 1998; Kreykenbohm et al. 2002; Odaka et al. 2013). Below 3 keV, a soft excess is observed, which was modelled by thermal Bremsstrahlung with kT ~ 0.5 keV by Haberl (1994) using ROSAT data. Moreover, it was found that the temperature of the soft component depends on the contribution of the highly absorbed hard power-law component from the neutron star. According to Hickox et al. (2004), the observed soft excess is due to emission by photoionized or collisionally heated diffuse gas or thermal emission from the surface of the neutron star.
Above 20 keV, cyclotron resonance scattering features (CRSFs) between 25 and 32 keV (Makishima et al. 1992; Choi et al. 1996; Kreykenbohm et al. 2002) and at ~55 keV (Kendziorra et al. 1992; Orlandini et al. 1998; La Barbera et al. 2003; Attié et al. 2004) have been reported, although the interpretation of the 25 keV feature is still sometimes debated (Orlandini 2006).
Observations of the system during the eclipse of the X-ray pulsar with Tenma, ASCA, and Chandra have revealed various fluorescent lines in addition to highly ionized lines and radiative recombination continua that imply the existence of optically thick and clumped matter in addition to warm ionized plasma (Sato et al. 1986; Nagase et al. 1994; Sako et al. 1999; Schulz et al. 2002).
The structure of the wind of the system was investigated above 20 keV by Fürst et al. (2010), who suggests that a mixture of a clumpy wind, shocks, and turbulence could explain the measured mass distribution. These authors estimate a mass of the wind clumps of the order of mcl = 1021 g for the giant flares. Furthermore, in this work a log-normal distribution of the brightness was found along the orbit.
Odaka et al. (2013) report on Suzaku observations of Vela X-1 covering the orbital phase interval 0.20–0.39 for phase zero at T90. They found strong variability with LX (0.1–100 keV) ranging from ~0.5 to ~9.5 × 1036 erg s-1 and variability time scales of 1–10 ks. Assuming a clumpy wind as the source of the variations, the observed variability indicated clump radii of (2−20) × 1010 cm for a relative wind velocity of 400 km s-1. For a bright (LX = 1037 erg s-1), short (1 ks) flare this would lead to a clump mass of 4 × 1019 g and an overdensity of two orders of magnitude compared to a smooth wind model, while longer, less intense flares would be explained naturally by density variations of a factor of a few.
To study the structure of the extended atmosphere and the wind in the Vela X-1 system, a 123 ks XMM-Newton (Jansen et al. 2001) observation was performed immediately following eclipse egress. The main goal was a precise measurement of the evolution of the absorption column in this part of the orbit. From historical observations (Sato et al. 1986; Lewis et al. 1992), one expects a steep decrease in the absorption measure NH in this part of the orbit as the neutron star emerges from behind the companion’s extended atmosphere.
The remainder of the paper is structured as follows. In Sect. 2, the data and the software used are described. Section 3 describes the light curves of the observation. Spectral analysis results are presented in Sect. 4. Finally a discussion is given in Sect. 5 and a summary and conclusions in Sect. 6.
2. Observations and data reduction
XMM-Newton observed Vela X-1 on 2006 May 25−26 (MJD 53 880.452 to MJD 53 881.876) using the European Photon Imaging Camera (EPIC) and the Reflection Grating Spectrometers (RGS) during all of revolution 1183 of the satellite. For this observation (ObsID 0406430201), the EPIC-MOS1 (EPIC-Metal Oxide Semi-conductor) camera was disabled to maximize the available telemetry rate for the EPIC-pn CCD camera, which was set up in timing mode with the thin filter. In this mode, the camera provides timing information for each event with a resolution of up to 1.5 ms, as well as the standard energy resolution of about E/ΔE = 40.
Avoiding times close to the Earth’s radiation belts, we used data between MJD 53 880.613 and MJD 53 881.768 (about 100 ks), corresponding to the orbital phase interval 0.132 to 0.270 according to the ephemeris of Kreykenbohm et al. (2008) (see Table 1), where phase zero is defined as T90. When comparing our findings with other results, one should note that sometimes T90 and sometimes the mid eclipse time Tecl are used in the literature to define zero phase, where Tecl is later than T90 by 0.226 d (Kreykenbohm et al. 2008). Using Tecl as reference would shift the orbital phase of our data set by 0.0252 to earlier phases.
In this paper we focus on the EPIC-pn data and its evolution along the orbital motion of the neutron star around the supergiant companion. The RGS data will be considered in later work. The data reduction was performed using SASv11.0 and CCFs as of 2012 May starting from ODF level running rgsproc and epproc. For EPIC-pn, we applied a rate-dependent CTI correction, and to the time column a barycentric correction, as well as a correction for the Vela X-1 binary system using the ephemeris as of Bildsten et al. (1997) and Kreykenbohm et al. (2008).
Ephemeris data used for timing calculations taken from (1) Bildsten et al. (1997) and (2) Kreykenbohm et al. (2008).
2.1. Spectral extraction
Due to the high count rate (>2500 cts/s) during the flare that occurred as well as to the hard spectral emission characteristics of the source, we had to cope with two instrumental effects before extracting spectra: pile-up and the improvement of the timing mode charge transfer inefficiency due the high amount of shifted charge (rate-dependent CTI). The first can cause a change in spectral parameters, e.g. a hardening of the continuum with increasing levels of pile-up, the latter a general gain/offset shift of the complete spectrum. We mitigated the effects of pile-up by considering the pattern distribution (epatplot), the maximum count rate (<800 cts/s)1, and the stability of the spectral parameters dependent on the columns used to extract the spectra. We found that the three columns covering the central part of the point spread function (PSF) are significantly affected by pile-up, and from spectral stability analysis we got indications that their adjacent columns might still show slight and close to insignificant pile-up effects.
 |
Fig. 1 Orbit sketch of Vela X-1. The XMM-Newton 0.5−12 keV observed count rate is shown in the red curve and compared with the average light curve of the source over years of 1.5−12 keV RXTE/ASM observations (green curve). |
Restricting the analysis to the flaring period, we extracted spectra taken from the full PSF and from regions ignoring 3, 5, 7, 9, and 11 columns of the PSF centre (named PSF-# afterward) and compared their modelling of the instrumental gold edge and the relative position of the iron line, as well as general slope of the continuum.
Without correction we found a shift of the gold edge of 93 eV keeping the PSF centre, and we needed to exclude the central 11 columns (PSF-11) to be consistent with no shift of the gold edge. The Fe line-energy shift continuously decreased with increasing number of ignored columns by 132 eV from full PSF to PSF-11.
The SAS-task epfast is designed to correct for these rate-dependent CTI effects seen in EPIC-pn fast modes (but not for pile-up effects). Applying the epfast correction (using the corresponding public CCF-file EPN_CTI_0023.CCF), we still found shifts at the gold edge of 13 eV using PSF-7, 12 eV using PSF-9, and 7 eV using PSF-11, which is consistent with the systematic uncertainties of the correction2. However, the Fe line energy was consistent for all spectra of PSF-5 to PSF-11, but at an energy of about 40 eV higher compared to the uncorrected PSF-11 value.
We calculated the spectral shifts that depends on the amount of charge per column for the flare period, and with support of the XMM-Newton SOC we added the results to the calibration of the rate dependent CTI, creating a non-public EPN_CTI_0024.CCF. Using this special CCF, no more shifts at the gold edge were seen for all spectra of PSF-5 to PSF-11, and the Fe line energy was consistent with the uncorrected PSF-11 value. Also, the continuum slopes were consistent within errors, with PSF-5 slightly harder than PSF-7 to PSF-11. Finally we decided to exclude the innermost seven columns from the spectral extraction and calculated a corresponding arf response file. A comparison of the full PSF spectrum and ARF with our PSF-7 spectrum and ARF for the pre-flare period yielded a systematic error of about 3% for the PSF-7 flux normalizations. For consistency, we use the PSF-7 region for all epochs of our data set.
 |
Fig. 2 Different timing mode backgrounds. Black: closed filter; cyan: this Vela X-1 (Obs. ID 0406430201, Cols. 3−12); navy blue: Vela X-1 (Obs. ID 0111030101, Cols. 3−12); red: empty sky (Obs. ID 0406620201 Cols. 16−33, 41−58); green: final merged background. |
2.2. Background generation
Looking into the columns closest to the timing mode window border, it was obvious that the observation does not provide a local background area, since a) the light curve extracted from these columns follows the overall light curve of the source and b) its spectrum differs significantly from what is expected to be an empty sky emission, resembling the source spectrum. A background extracted from an earlier timing mode observation of Vela X-1 (Obs.ID 0111030101) showed a similar pattern but one restricted to higher energies. We therefore searched a timing mode “empty sky” and found Obs.ID 0406620201, where no source is visible in the timing mode window. Excluding again the innermost seven columns (identical PSF-7 extraction region), we extracted a spectrum of Obs.ID 0406620201 and used it as an empty sky background. Since the local background of the earlier Vela X-1 observation (Obs.ID 0111030101) shows a lower background level than this “empty sky”, we merged these two backgrounds for energies below ~2.5 keV, scaled according to exposure times and surfaces, to address the differences of absorption columns of about factor 100−1000.
 |
Fig. 3 Light curve observed during the XMM-Newton observation with the EPIC-PN camera with a binning time of 141s (~half a pulse period). The bands shown are 0.6–1, 1–3, 3–6, 6–8 and 8–10 keV. The count rate is plotted on a logarithmic scale to emphasize the variability in the different energy bands. |
 |
Fig. 4 Ratios between count rates in different energy bands to that of the 8–10 keV band. From top to bottom: 0.6–1 keV, 1–3 keV, 3–6 keV, and 6–8 keV. The time binning is 1128 s (~4 pulse periods), matching the spectra used in the time-resolved spectral analysis. In the background, the total flux evolution is plotted for comparison with the light curves. Circles mark the data points corresponding to the spectra shown in Fig. 5. |
3. Energy-resolved light curves and flux ratios
During the course of the observation, Vela X-1 displays strong variations in flux, both overall and in the relative flux in different energy bands. These variations are driven by a mix of the intrinsic variability of the X-ray source and the modulation of the X-ray flux by absorption and scattering within the system. These variations happen on all time scales studied, from tens of kilo-seconds down to fractions of the pulse period. We have not undertaken a detailed analysis of the timing behaviour on time scales below the pulse period. A corresponding study is under way and will be published separately. In this work a mostly stable pulse period of 283.389 ± 0.004 s is found. This pulse period was measured using a phase-connected technique over 10 ks intervals. The mean photon arrival times for each interval were then corrected by an empirical model and fit using a polynomial function.
To describe the overall evolution, we have generated light curves in several energy bands using the approach and corrections as described in Sect. 2. The bands used are 0.6–1, 1–3, 3–6, 6–8, and, 8–10 keV, respectively. Figure 3 shows the light curves in the different bands for comparison. The ratios between the count rates in the first four bands and the 8–10 keV band, which is least affected by the strong absorption variations, are displayed in Fig. 4.
Based on the light curves and their relative rates, several distinct intervals can be defined on the time scale of tens of kilo-seconds, as explained in the following, where we used Tobs to denote the time since the start of the observation (MJD 53 880.61305). During the first ≈10 ks the total flux varies moderately, but as Fig. 4 shows, there are opposing trends in the flux ratios below and above 3 keV. After this interval, the ratio 6–8/8–10 keV remains nearly constant despite large flux variations, indicative of a stable spectral shape for the unabsorbed source. A broad peak at all energies is evident between Tobs ≈ 10 ks and Tobs ≈ 40 ks, which is most pronounced in the 1–3 keV band.
From Tobs ≈ 40 ks to Tobs ≈ 60 ks the source flux starts to rise in all energy bands. On top of the general rise, there is flaring visible on time scales of ks between Tobs ≈ 45 ks and Tobs ≈ 55 ks, again most pronounced in the 1–3 keV band. Around Tobs ≈ 60 ks, the total source flux rises rapidly, more than an order of magnitude within a few kilo-seconds. At energies ≥6 keV, the flux actually changes only by a factor of a few, but the contribution ≤3 keV rises by several orders of magnitude, while the flux ratio 6–8 keV/8–10 keV remains stable.
Around the peak of the flare, from Tobs ≈ 62 ks to Tobs ≈ 70 ks, the overall flux is strongly variable with a series of spikes and dips. These structures are highly correlated across all bands, but variations in the flux ratios are mainly visible in the 0.6−1 and 1−3 keV bands, such that higher global flux is mainly driven by higher contributions from the low energies. From Tobs ≈ 70 ks to Tobs ≈ 78 ks the flare decays with the overall flux diminishing by an order of magnitude, similar in all bands. Around Tobs ≈ 80 ks, a smaller, but still significant flare is visible, where again any spectral variation is mainly visible at lower energies.
Beyond Tobs ≈ 82 ks, up to the end of the observation, the source seems to settle. While the flux still varies randomly in all bands, albeit less than during earlier phases, the ratios between different bands do not show a pronounced evolution.
While the short term variability appears to be mostly dominated by the intrinsic flux variations, it is important to note that the strong absorption in the circumstellar wind has a marked effect on the overall observed count rates. Moreover, the dramatic change at the onset of the flare seems to be driven by a significant variation in the absorbing and reprocessing material between the source and the observer.
 |
Fig. 5 Representative sample of the 88 EPIC-pn spectra at different relevant times marked in the inset light curve plot. The different components of the model are shown: component 1 (blue), component 2 (green) component 3 (red) and fluorescence lines modelled as Gaussian functions (grey). |
4. Orbital phase-resolved spectroscopy
To characterize the evolution of the stellar wind inhomogeneities surrounding the neutron star, a study of the flux variations in combination with the changes in the absorption column is carried out, under the hypothesis that these variations are proportional to the local Ṁ. Therefore we have divided our data in 88 EPIC-pn spectra of 1.1 ks exposure time each. The spectral time resolution was chosen as a compromise between the statistics of the data and the short term variations observed in the light curve analysis. Some of these spectra are shown in Fig. 5 at different relevant periods.
Since a fully physical model of the X-ray production mechanism in accreting X-ray pulsars does not yet exist owing to the complexity of the physical problem (significant progress has, however, been made, see e.g. Becker & Wolff 2007), an empirical model has to be used. After trying different models, we have found that there is only one continuum model that could fit all the spectra significantly well throughout the whole observation including the flare. It consists of three absorbed power-law components with a unique photon index but different normalization factors for each component. Furthermore, the spectra of the source clearly show the presence of three emission lines corresponding to Fe Kα, Fe Kβ, and Ni Kα fluorescence lines. These lines have been treated as being absorbed by the highest absorbed component and modelled by a Gaussian function even if their shapes are not perfectly Gaussian. A full description of the model is given in Eq. (1).
A similar continuum model has been used previously to characterize the spectra of several
high-mass X-ray binary systems, such as 4U 1700-37 (van der
Meer et al. 2005), Cen X-3 (Ebisawa et al.
1996), and 4U 1538-52 (Rodes-Roca et al.
2011). Our model differs from those models in two aspects: (a) we used a more
complex ISM absorption model (tbnew in Eq. (1)) and (b) we applied a non-relativistic Compton scattering correction
to the first and second spectral components because of their large measured hydrogen column
densities (cabs in Eq. (1)).
![\begin{eqnarray} \label{eq1} F(E) &=& \sum_{i=1}^{2} \left[tbnew_{i} \times \mbox{cabs}_{i} \times \mbox{Norm}_{i} \times E^{-\Gamma}\right] \nonumber \\ && +\, tbnew_{3} \times \mbox{Norm}_{3} \times E^{-\Gamma} \nonumber \\ && + \sum_{j=1}^{3} \left[tbnew_{1} \times \mbox{cabs}_{1} \times \mbox{Gaussian}_{j}\right]. \end{eqnarray}](/articles/aa/full_html/2014/03/aa22404-13/aa22404-13-eq53.png) (1)In
Eq. (1) the summation index i
refers to the three model components, and the index j refers to
the three emission lines components. Normi
are the normalization factors of each power law (photons keV-1 cm-1 s-1 at 1 keV), and Γ is the power law photon index. These
components are further modified by two effects both arising in the material between the
X-ray source and the observer with density column NH, on one hand, the photoelectric
absorption. For this purpose we use the model tbnew, an updated version of
the Tübingen-Boulder ISM absorption model (Wilms et al.
2000). The absorption cross sections are adapted from Verner et al. (1996), and the abundances are set to those of Wilms et al. (2000). On the other hand, the
non-relativistic Compton scattering effect is taken into account by using a cabs
model, which is described by
(1)In
Eq. (1) the summation index i
refers to the three model components, and the index j refers to
the three emission lines components. Normi
are the normalization factors of each power law (photons keV-1 cm-1 s-1 at 1 keV), and Γ is the power law photon index. These
components are further modified by two effects both arising in the material between the
X-ray source and the observer with density column NH, on one hand, the photoelectric
absorption. For this purpose we use the model tbnew, an updated version of
the Tübingen-Boulder ISM absorption model (Wilms et al.
2000). The absorption cross sections are adapted from Verner et al. (1996), and the abundances are set to those of Wilms et al. (2000). On the other hand, the
non-relativistic Compton scattering effect is taken into account by using a cabs
model, which is described by
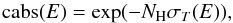 (2)where
\begin{lxirformule}$\sigma_{\rm T}(E)$\end{lxirformule} is the Thomson cross section, and
NH
is the equivalent hydrogen column that it is linked to its corresponding absorption law.
(2)where
\begin{lxirformule}$\sigma_{\rm T}(E)$\end{lxirformule} is the Thomson cross section, and
NH
is the equivalent hydrogen column that it is linked to its corresponding absorption law.
 |
Fig. 6 Contour maps (2σ confidence limits for the two selected parameters) between the free spectral parameters for the six selected spectra shown in Fig. 5. These maps demonstrate that while for some spectra the parameters cannot be constrained tightly, the observed changes of parameter values along the observation are real and significant. |
In time- or phase-resolved spectroscopy, each spectrum is usually fitted individually by minimizing the statistic, while here parameters are varied, and a minimum is sought across all 88 spectra simultaneously using the Interactive Spectral Interpretation System (ISIS) software (Houck & Denicola 2000). This novel approach allows finding a common continuum, as well as obtaining the best possible fit statistics and the best constraints of the relevant parameters. Figure 5 show the spectra and fitted models for some representative time bins throughout the observation. The inspection of this plot already reveals that the most dramatic changes are produced in components 2 and 3.
In a first analysis we left the power law index Γ free to vary among all 88 spectra. We found no significant differences
among the best-fit values of this parameter for any of the 88 spectra. Consequently, in
order to increase the precision of the other parameters, we assume a common value for
Γ, i.e. a stable continuum
slope for all 88 spectra. The best-fit value for this index is Γ = 1.595 ± 0.010 (χ2 = 14011 with
9765 d.o.f.). The absorption column 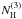 of the third component was found to be constant within errors. We therefore kept it fixed to
the average value of (0.75 ± 0.03) × 1022 cm-2. This value is in excellent agreement with the ISM
absorption towards GP Vel, the optical counterpart of Vela X-1, derived from optical data.
Finally, to pin down the fluorescence lines, we have constrained the Fe Kβ, as well as the Ni
Kα energies,
with respect to the Fe Kα centroid energy, taking theoretical calculations into
account (Kallman et al. 2004). The energy of the Fe
Kα line (left
free) turns out to be 6.435 ± 0.001 keV. The energy of the Fe Kβ line is shifted by 0.65
keV, while its flux is considered to be 13% of that of Kα. These energies are compatible with K shell
fluorescence from ionized Fe up to a maximum of Fexviii (Kallman et al. (2004), Fig. 3). In the same way, the Ni Kα centroid energy was shifted
by 1.2 keV with respect to that of Fe Kα. These ratios were kept fixed during the fitting
process.
of the third component was found to be constant within errors. We therefore kept it fixed to
the average value of (0.75 ± 0.03) × 1022 cm-2. This value is in excellent agreement with the ISM
absorption towards GP Vel, the optical counterpart of Vela X-1, derived from optical data.
Finally, to pin down the fluorescence lines, we have constrained the Fe Kβ, as well as the Ni
Kα energies,
with respect to the Fe Kα centroid energy, taking theoretical calculations into
account (Kallman et al. 2004). The energy of the Fe
Kα line (left
free) turns out to be 6.435 ± 0.001 keV. The energy of the Fe Kβ line is shifted by 0.65
keV, while its flux is considered to be 13% of that of Kα. These energies are compatible with K shell
fluorescence from ionized Fe up to a maximum of Fexviii (Kallman et al. (2004), Fig. 3). In the same way, the Ni Kα centroid energy was shifted
by 1.2 keV with respect to that of Fe Kα. These ratios were kept fixed during the fitting
process.
To estimate the possible dependence among the relevant parameters during the fits, we have computed confidence level contour maps for all 88 spectra. In Fig. 6 we show contour maps for the same selected spectra as in Fig. 5. As can be seen, the contours do not betray a systematic dependence, and therefore, the obtained parameters and their errors are considered reliable.
 |
Fig. 7 From top to the bottom: evolution of the model parameters versus time and orbital phase. Error bars are 90% confidence level. The dashed line in panel c) indicates the constant NH of component 3. The grey column marks the rise of the flare and the grey curve in panel a) shows the overall unabsorbed flux of the spectral model. |
 |
Fig. 8 A) 0.6−10 keV unabsorbed flux light curve with a binning time of 1.1 ks. Marked circles indicate the data points corresponding to the spectra shown in Figs. 5 and 6. B) Flux of the first component versus that of the second component. The inset shows an enlarged view of the first 58 ks, before the onset of the giant flare. C) Flux of the third component versus that of the second component with an inset equivalent to that in B). D) Fe Kα fluorescence line flux areas against normalization factor of second component. E) Fe Kα equivalent width against the normalization factor of the second component. All fluxes are in units of 10-9 erg cm-2 s-1. |
4.1. Evolution of the parameters
In Fig. 7 we show the evolution of the relevant parameters of our model throughout time and orbital phase. Panel a shows the unabsorbed flux evolution of each component and the overall unabsorbed flux (note the logarithmic ordinate scale). A clear progressive increase in the fluxes of components 2 and 3 can be seen, and meanwhile the flux of component 1 decreases slightly from the beginning to the end of the observation. On top of this we clearly observe two flares at φ ≈ 0.17 and 0.22 (a giant flare), respectively. A vertical grey line marks the rise of the bright flare.
In panel b we show the relative unabsorbed flux evolution of each power law against the average flux of the first component. Several characteristics can be pointed out here. On one hand, as stated before, the most dramatic changes are seen in components 2 (scattered) and 3 (low energy). During the bright flare, component 3 increases by two orders of magnitude, while component 2 increases one order of magnitude. These two components are very well correlated throughout the whole observation (except at the maximum of the bright flare). These can be clearly seen in panel C of Fig. 8. In contrast, component 1 (direct) increases only by a factor of 2 during the flare. On the other hand, while components 2 and 3 show an overall increase in flux throughout the observation, following the trend of the light curve (top panel), component 1 shows an overall decrease in flux from 1 × 10-8 erg s-1 cm-2 to 0.2 × 10-8 erg s-1 cm-2. After the flare, the flux of components 1 and 2 become identical within the errors, and in fact, the flux of all three components become very well correlated. This is clearly seen in panels B and C of Fig. 8.
In panel c of Fig. 7 we show the evolution of the
column density of the absorbing material for components 1 and 2 in units of
1022
cm-2. The
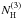 for component 3 remains constant throughout the observation at ~0.75 × 1022 cm-2, which is entirely compatible with the ISM value
(van Genderen 1981). As can be seen, the
absorption of component 1 (direct) decreases from values of
for component 3 remains constant throughout the observation at ~0.75 × 1022 cm-2, which is entirely compatible with the ISM value
(van Genderen 1981). As can be seen, the
absorption of component 1 (direct) decreases from values of
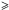 1024 cm-2 at the beginning of the
eclipse egress down to ~1.8 × 1023 cm-2 at quadrature. This reflects the decreasing amount of
stellar wind material in the line of sight towards the neutron star as it emerges from
eclipse. An enhancement is present, however, between orbital phases 0.19 and 0.23.
Remarkably, there is no dramatic change in
1024 cm-2 at the beginning of the
eclipse egress down to ~1.8 × 1023 cm-2 at quadrature. This reflects the decreasing amount of
stellar wind material in the line of sight towards the neutron star as it emerges from
eclipse. An enhancement is present, however, between orbital phases 0.19 and 0.23.
Remarkably, there is no dramatic change in 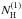 at the
moment of the flare. In contrast,
at the
moment of the flare. In contrast, 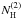 ,
which stays essentially constant throughout the observation, decreases drastically exactly
at the rise of the flare. After that, it remains constant again at ~2.5 × 1022. Since the fluxes shown before were unabsorbed
and
,
which stays essentially constant throughout the observation, decreases drastically exactly
at the rise of the flare. After that, it remains constant again at ~2.5 × 1022. Since the fluxes shown before were unabsorbed
and 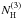 is found to be constant during the flare (during the whole observation, in fact), the
sudden flux increase of component 3 must be intrinsic. On the other hand, the flux
increase in component 2 could be either intrinsic or due to the sudden decrease in
is found to be constant during the flare (during the whole observation, in fact), the
sudden flux increase of component 3 must be intrinsic. On the other hand, the flux
increase in component 2 could be either intrinsic or due to the sudden decrease in
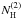 .
.
In panels d and e of Fig. 7 we show the change in the intensities and equivalent width, respectively, of the fluorescence Fe Kα and Ni Kα lines. As can be seen, the intensity of the Fe Kα line follows the overall brightness of the source well, including the sharp rise at the flares (note again the logarithmic scale in the ordinates). This is clearly seen in panel D of Fig. 8. However, the most striking fact is that the Fe Kα line is clearly less intense after the flare than before. This is also clearly seen in panel D of Fig. 8 as a hysteresis cycle. The equivalent width, in turn, which is related with the density column of the reprocessing material, follows the increase in continuum flux up to the flare, when it reaches a value of ~230 eV, and then decreases in the post flare, staying more or less constant, at a a value of 180 eV approximately, until the end of the observation (panel E, Fig. 8). This behaviour must arise from a depletion of neutral Fe in the circumsource matter after the flare. We recall that the energy of the Fe Kα lines remains constant throughout the observation and shows no sign of increasing ionization. Therefore, the depletion in neutral Fe must reflect a real depletion of circumsource matter. Regarding the Ni Kα line, its parameters show the same trend as those of the Fe Kα line, albeit with larger uncertainties.
4.2. Correlations among parameters
As mentioned in the previous section, we observe different correlations among the continuum parameters, looking in detail at panels B and C of Fig. 8, three branches are clearly identified:
-
Before the first peak, all fluxes decrease but component 1 and 3 do so more rapidly than component 2.
-
From the first peak to the pre-flare (red to blue points) all fluxes correlate.
-
During the flare and later, the fluxes correlate again, but with a different slope than before.
5. Discussion
5.1. Source brightness and variability
To put the current observation into perspective, it is instructive to compare the obtained fluxes and derived luminosities with other observations. Such comparisons, however, depend strongly on assumptions of the overall spectral shape, which for many historical data sets is not well constrained, leading quickly to systematic uncertainties of a few 10% or more.
For this reason, we assumed the spectrum of Vela X-1 above 10 keV to be modified by a
Fermi-Dirac cutoff (Tanaka 1986), as found by Kreykenbohm et al. (2008), among others. Since the
luminosity strongly depends on the parameters used to describe that high energy cutoff, we
decided to take those parameters listed in Table 5 of Kreykenbohm et al. (2008), which result in a very soft broad-band spectrum.
Choosing another set of parameters led to a harder spectrum and an increase in the
luminosity estimation at those energies, which might overestimate the real source
luminosity. The assumed parameters are therefore 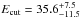 keV
and
keV
and 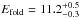 keV.
The power law photon index Γ
is consistent with the value presented here (see Sect. 4).
keV.
The power law photon index Γ
is consistent with the value presented here (see Sect. 4).
 |
Fig. 9 Distribution of X-ray luminosities for the peak of the flare in the energy range 0.5–600 keV using simulated spectra. |
To derive proper values for the uncertainty of the estimated luminosity, we have to take the uncertainties of the fit parameters into account, as well as those of the assumed FD cutoff. Based on a Monte Carlo approach, we calculated the luminosity of spectrum 56 (the peak of the flare) with varying random parameters, corresponding to their individual asymmetric uncertainties. The resulting simulated distribution of luminosities between 0.5 and 600 keV after 100 000 runs is shown in Fig. 9. The uncertainty interval of the most-likely value was chosen such, that it contains 90% of the distribution. The final value of the peak luminosity between 0.5 and 600 keV of Vela X-1 during the XMM-Newton observation is
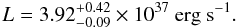 Based on hard
X-ray data from INTEGRAL observations, Fürst et al.
(2010) found a log-normal distribution of flux values, with a median absolute
luminosity ⟨ LX ⟩ = 5.1 × 1036 erg
s-1 and
multiplicative standard deviation σ ≈ 2. Even though a direct comparison with Fürst et al. (2010) is difficult because of possible
variations in the continuum, it is clear that the flare around orbital phase 0.22 is
brighter than ~99.9% of the
3.6 Ms INTEGRAL monitoring data, and thus certainly is one of the rare giant flares.
Based on hard
X-ray data from INTEGRAL observations, Fürst et al.
(2010) found a log-normal distribution of flux values, with a median absolute
luminosity ⟨ LX ⟩ = 5.1 × 1036 erg
s-1 and
multiplicative standard deviation σ ≈ 2. Even though a direct comparison with Fürst et al. (2010) is difficult because of possible
variations in the continuum, it is clear that the flare around orbital phase 0.22 is
brighter than ~99.9% of the
3.6 Ms INTEGRAL monitoring data, and thus certainly is one of the rare giant flares.
5.2. Probable origin of the spectral components
Although we have used a phenomenological model, the behaviour of the three power law components in Fig. 7 with respect to the flare immediately suggests a further unifying idea of only two physical sources: the neutron-star surface and the scattered emission by electrons in the wind. Continuum components 2 and 3 suffer parameter discontinuities across the flare with significant increases in the flux relative to component 1 coinciding with a steep decrease in component 2’s absorption such that the post-flare fluxes of components 1 and 2 are essentially identical during the subsequent decline of about an order of magnitude in brightness. This suggests that components 1 and 2 are two aspects of the same component that originates at the neutron-star surface. Absorption along the line-of-sight through the wind is complex owing to the warm ionization state of the supergiant’s expanding envelope but can be modelled successfully by the sum of two conventional cold absorption laws. The balance between these two changed across the flare because photoionization altered the ionic balance in the wind by removing electrons from the ions responsible for absorption near 1 keV. These extra free electrons were then responsible for the extra scattering that produced the increase in component 3.
As we have seen, 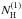 decreases from
decreases from  1024 at orbital phase
φ = 0.14 to
1024 at orbital phase
φ = 0.14 to
 1023 at orbital phase
φ = 0.26 as
the neutron star emerges from eclipse and moves along the orbit (Fig. 7, third panel). However, there is clearly a wind density enhancement
starting at φ ≈ 0.185, followed by an increase in the emission of
the neutron star due probably to the corresponding gradual accretion of more mass. The
later, more sudden increase in emission from the neutron star was probably due to the
accretion of a dense clump in the wind, although this was accompanied by
no change of spectral index. The time scale for the rise of the flare was of the order of
one time bin or trise ~ 103 s.
1023 at orbital phase
φ = 0.26 as
the neutron star emerges from eclipse and moves along the orbit (Fig. 7, third panel). However, there is clearly a wind density enhancement
starting at φ ≈ 0.185, followed by an increase in the emission of
the neutron star due probably to the corresponding gradual accretion of more mass. The
later, more sudden increase in emission from the neutron star was probably due to the
accretion of a dense clump in the wind, although this was accompanied by
no change of spectral index. The time scale for the rise of the flare was of the order of
one time bin or trise ~ 103 s.
5.3. Physical parameters of wind clumps
Our observation allows us to make direct estimates of the physical properties of the
possible clump responsible for the giant flare. Considering a spherical shape of the clump
and taking the characteristic time for the accretion of the clump into account would be
trise ~ 103 s. Assuming that
the clumps are moving with the same velocity as the bulk of the wind, they are travelling
at v(r) = v∞(1 − R∗/r)β = 0.46v∞ = 5.1 × 107
cm/s, with v∞ = 1100 km s-1, r = 1.6 R∗ and
β = 0.8.
Therefore, the size of the clump is of the order of
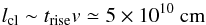 (3)or ~0.02R∗, in agreement with theoretical
expectations from massive star winds (Oskinova et al.
2011, Table 1).
(3)or ~0.02R∗, in agreement with theoretical
expectations from massive star winds (Oskinova et al.
2011, Table 1).
Using a finer time bin, as that used in Fig. 3 (141 s, half the NS spin period) we still
see four or five data points during the rise of the big flare compatible with a
trise ≲ 103 s. We can now
estimate the density of the clump from
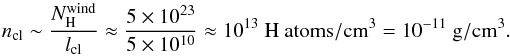 (4)On the other hand, the
characteristic volume of the clump would be Vcl ~ lcl3 ≈ 1032 cm3.
Therefore, the mass of the clump responsible of the bright flare would be mcl ~ 1021 g.
(4)On the other hand, the
characteristic volume of the clump would be Vcl ~ lcl3 ≈ 1032 cm3.
Therefore, the mass of the clump responsible of the bright flare would be mcl ~ 1021 g.
This value is two orders of magnitude greater than deduced by Odaka et al. (2013; Eq. (13)). As we have argued, however, the flare we
are analysing here is much brighter than the one seen by Suzaku. Our
estimate agrees with the one by Fürst et al. (2010)
for clumps responsible for bright flares like the one we have observed. We can also
estimate the luminosity produced by the accretion of such a clump onto the neutron star
(NS). Since this clump accretes in a characteristic time of trise ~ 103 s, the mass
accretion rate will be Ṁ ~ 1018 g/s. Now, if the mass
accretion-to-energy conversion efficiency η adopts reasonable values [0.1−0.3], the luminosity of the flare should
then be of the order of ![\begin{equation} L_{X}=\eta G \frac{M_{\rm NS}\dot{M}}{R_{\rm NS}}\approx [2-6]\times 10^{37} \ \rm erg/s \end{equation}](/articles/aa/full_html/2014/03/aa22404-13/aa22404-13-eq106.png) (5)as observed. In
conclusion the bright flare observed by XMM-Newton is consistent with the
accretion of a dense clump whose size is otherwise the one expected for the structured
stellar wind of a B0.5Ib star at r ≲ 2R∗.
(5)as observed. In
conclusion the bright flare observed by XMM-Newton is consistent with the
accretion of a dense clump whose size is otherwise the one expected for the structured
stellar wind of a B0.5Ib star at r ≲ 2R∗.
6. Summary and conclusions
The observation during eclipse egress has revealed unexpectedly rich behaviour of the Vela X-1 system. From the light curve analysis, we found strong variations in source flux (overall and relative flux in different bands) on all time scales studied from kilo-seconds down to fractions of the pulse period. At orbital phase 0.22, a giant flare took place, which was mainly driven by a change in the absorbing and reprocessing material between the source and the observer. Even though the observed short-term variability in the light curves appears to be mostly dominated by intrinsic flux variations, the spectral shape of the system remains rather stable along the observation, reflecting the marked effect of the strong absorption in the circumstellar wind on the overall observed count rates.
The observation was divided into 88 spectra of 1.1 ks exposure time each to study the spectral evolution of the system along the orbit. A phenomenological model allows us to fit all spectra well throughout the whole observation, including the flare. It consists of three continuum components formed by an absorbed power-law, with the same power-law index for each component. This continuum spectral model is complemented by three fluorescent emission lines of Fe Kα, Fe Kβ, and Ni Kα. The main results from the spectral analysis follow:
-
The power-law index remains constant along the observation with a best value of Γ = 1.595 ± 0.010.
-
The overall unabsorbed fluxes of components 2 and 3 increase during the observation, and meanwhile the overall unabsorbed flux of component 1 slightly decreases from the beginning to the end of the observation.
-
Two flares are clearly observed at φ ≈ 0.17 and 0.22 (giant flare) in the unabsorbed fluxes of the three components.
-
During the rise of the giant flare, which lasted 1.1 ks, the most dramatic changes were in components 3 and 2, with two and one order of magnitude increases in their unabsorbed fluxes, respectively.
-
The absorption column of the first component decreases from values
 1024 cm-2 at the beginning of
eclipse egress up to ~1.8 × 1023 cm-2 at quadrature. Meanwhile,
the absorption column of the second component stays constant from the beginning of the
observation until the rise of the flare, when it decreases drastically from
1023
cm-2 to
2.5 × 1022
cm-2. On the
other hand, the absorption column of the third component remains constant throughout
of the observation with a best value of (0.75 ± 0.03) × 1022 cm-2, in excellent agreement
with the ISM absorption towards HD 77581, the optical counterpart of Vela X-1.
1024 cm-2 at the beginning of
eclipse egress up to ~1.8 × 1023 cm-2 at quadrature. Meanwhile,
the absorption column of the second component stays constant from the beginning of the
observation until the rise of the flare, when it decreases drastically from
1023
cm-2 to
2.5 × 1022
cm-2. On the
other hand, the absorption column of the third component remains constant throughout
of the observation with a best value of (0.75 ± 0.03) × 1022 cm-2, in excellent agreement
with the ISM absorption towards HD 77581, the optical counterpart of Vela X-1. -
The energy of the Fe Kα line was constant during the observation with a best value of 6.435 ± 0.001 keV, reflecting no sign of increasing ionization, even during the giant flare.
-
The Fe Kα line flux follows the overall brightness of the source well, is clearly less intense after the flare. Moreover, the equivalent width of the line follows the increase in continuum flux up to the flare, reaching a maximum value of ~230 eV, and decreasing after the flare achieving a constant value of 180 eV. This observed behaviour of the line parameters clearly indicates a depletion of the neutral Fe in the circumsource matter after the giant flare.
-
The unabsorbed fluxes of three components are correlated very well during the whole observation except at the peak of the flare. We could establish three different regimes of correlation among these parameters, which are also observed between the Fe Kα flux line and the flux of the second component.
XMM_CCF_REL_256 on http://xmm2.esac.esa.int/external/xmm_sw_cal/calib/rel_notes/index.shtml
Acknowledgments
This work was supported by the Spanish Ministerio de Ciencia e Innovación through the projects AYA2010-15431 and AIB2010DE-00054. It was partly supported by the Bundesministerium für Wirtschaft und Technologie under Deutsches Zentrum für Luft- und Raumfahrt grant 50OR1113. This research was made possible in part by a travel grant from the Deutscher Akademischer Austauschdienst. JJRR acknowledges the support by the Vicerectorat d’Investigació, Desenvolupament i Innovació de la Universitat d’Alacant under grant GRE12-35. The authors acknowledge the help of the International Space Science Institute at Bern, Switzerland and support by the Faculty of the European Space Astronomy Centre. The SLXfig package, developed by John E. Davis, was used to produce some of the figures within in this paper. We thank the anonymous referee whose comments allowed us to improve this paper.
References
- Attié, D., Chernyakova, M., Kretschmar, P., & et al. 2004, in 35th COSPAR Scientific Assembly, 2862 [Google Scholar]
- Becker, P. A., & Wolff, M. T. 2007, ApJ, 654, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Bildsten, L., Chakrabarty, D., Chiu, J., et al. 1997, ApJS, 113, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Stevens, I. R., & Kallman, T. R. 1991, ApJ, 371, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Chodil, G., Mark, H., Rodrigues, R., Seward, F. D., & Swift, C. D. 1967, ApJ, 150, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, C. S., Dotani, T., Day, C. S. R., & Nagase, F. 1996, ApJ, 471, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Ebisawa, K., Day, C. S. R., Kallman, T. R., et al. 1996, PASJ, 48, 425 [NASA ADS] [Google Scholar]
- Fürst, F., Kreykenbohm, I., Pottschmidt, K., et al. 2010, A&A, 519, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haberl, F. 1994, A&A, 288, 791 [NASA ADS] [Google Scholar]
- Haberl, F., & White, N. E. 1990, ApJ, 361, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Hickox, R. C., Narayan, R., & Kallman, T. R. 2004, ApJ, 614, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 591 [Google Scholar]
- Jansen, F., Lumb, D., Altieri, B., et al. 2001, A&A, 365, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallman, T. R., Palmeri, P., Bautista, M. A., Mendoza, C., & Krolik, J. H. 2004, ApJS, 155, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Kendziorra, E., Mony, B., & Kretschmar, P. 1992, in Frontiers Science Series, Proc. Yamada Conf. XXVIII, eds. Y. Tanaka, & K. Koyama (Tokyo, Japan: Universal Academy Press), 51 [Google Scholar]
- Kreykenbohm, I., Kretschmar, P., Wilms, J., et al. 1999, A&A, 341, 141 [NASA ADS] [Google Scholar]
- Kreykenbohm, I., Coburn, W., Wilms, J., et al. 2002, A&A, 395, 129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kreykenbohm, I., Wilms, J., Kretschmar, P., et al. 2008, A&A, 492, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- La Barbera, A., Santangelo, A., Orlandini, M., & Segreto, A. 2003, A&A, 400, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lewis, W., Rappaport, S., Levine, A., & Nagase, F. 1992, ApJ, 389, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Makishima, K., Mihara, T., Nagase, F., & Murakami, T. 1992, in Frontiers Science Series, Proc. Yamada Conf. XXVIII, eds. Y. Tanaka, & K. Koyama (Tokyo, Japan: Universal Acadamy Press), 23 [Google Scholar]
- Manousakis, A., Walter, R., & Blondin, J. M. 2012, A&A, 547, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClintock, J. E., Rappaport, S., Joss, P. C., et al. 1976, ApJ, 206, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Nagase, F. 1989, PASJ, 41, 1 [NASA ADS] [Google Scholar]
- Nagase, F., Hayakawa, S., Makino, F., Sato, N., & Makishima, K. 1983, PASJ, 35, 47 [NASA ADS] [Google Scholar]
- Nagase, F., Hayakawa, S., Kunieda, H., et al. 1984, ApJ, 280, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Nagase, F., Hayakawa, S., Sato, N., Masai, K., & Inoue, H. 1986, PASJ, 38, 547 [NASA ADS] [Google Scholar]
- Nagase, F., Zylstra, G., Sonobe, T., et al. 1994, ApJ, 436, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Odaka, H., Khangulyan, D., Tanaka, Y. T., et al. 2013, ApJ, 767, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Orlandini, M. 2006, in Spectra & Timing of Compact X-ray Binaries, Adv. Space Res., 38, 2742 [Google Scholar]
- Orlandini, M., dal Fiume, D., Frontera, F., et al. 1998, A&A, 332, 121 [NASA ADS] [Google Scholar]
- Oskinova, L., Hamann, W.-R., Ignace, R., & Feldmeier, A. 2011, Bull. Soc. Roy. Sci. Liège, 80, 54 [NASA ADS] [Google Scholar]
- Rawls, M. L., Orosz, J. A., McClintock, J. E., et al. 2011, ApJ, 730, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rodes-Roca, J. J., Page, K. L., Torrejón, J. M., Osborne, J. P., & Bernabéu, G. 2011, A&A, 526, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sako, M., Liedahl, D. A., Kahn, S. M., & Paerels, F. 1999, ApJ, 525, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Sato, N., Hayakawa, S., Nagase, F., et al. 1986, PASJ, 38, 731 [NASA ADS] [Google Scholar]
- Schulz, N. S., Canizares, C. R., Lee, J. C., & Sako, M. 2002, ApJ, 564, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y. 1986, in Radiation Hydrodynamics in Stars and Compact Objects, Proc. IAU Colloq. 89, eds. D. Mihalas, & K.-H. A. Winkler (Springer-Verlag), Lect. Notes Phys., 255, 198 [Google Scholar]
- van der Meer, A., Kaper, L., di Salvo, T., et al. 2005, A&A, 432, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Genderen, A. M. 1981, A&A, 96, 82 [NASA ADS] [Google Scholar]
- van Kerkwijk, M. H., van Paradijs, J., Zuiderwijk, E. J., et al. 1995, A&A, 303, 483 [NASA ADS] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, S., Sako, M., Ishida, M., et al. 2006, ApJ, 651, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Ephemeris data used for timing calculations taken from (1) Bildsten et al. (1997) and (2) Kreykenbohm et al. (2008).
All Figures
 |
Fig. 1 Orbit sketch of Vela X-1. The XMM-Newton 0.5−12 keV observed count rate is shown in the red curve and compared with the average light curve of the source over years of 1.5−12 keV RXTE/ASM observations (green curve). |
| In the text | |
 |
Fig. 2 Different timing mode backgrounds. Black: closed filter; cyan: this Vela X-1 (Obs. ID 0406430201, Cols. 3−12); navy blue: Vela X-1 (Obs. ID 0111030101, Cols. 3−12); red: empty sky (Obs. ID 0406620201 Cols. 16−33, 41−58); green: final merged background. |
| In the text | |
 |
Fig. 3 Light curve observed during the XMM-Newton observation with the EPIC-PN camera with a binning time of 141s (~half a pulse period). The bands shown are 0.6–1, 1–3, 3–6, 6–8 and 8–10 keV. The count rate is plotted on a logarithmic scale to emphasize the variability in the different energy bands. |
| In the text | |
 |
Fig. 4 Ratios between count rates in different energy bands to that of the 8–10 keV band. From top to bottom: 0.6–1 keV, 1–3 keV, 3–6 keV, and 6–8 keV. The time binning is 1128 s (~4 pulse periods), matching the spectra used in the time-resolved spectral analysis. In the background, the total flux evolution is plotted for comparison with the light curves. Circles mark the data points corresponding to the spectra shown in Fig. 5. |
| In the text | |
 |
Fig. 5 Representative sample of the 88 EPIC-pn spectra at different relevant times marked in the inset light curve plot. The different components of the model are shown: component 1 (blue), component 2 (green) component 3 (red) and fluorescence lines modelled as Gaussian functions (grey). |
| In the text | |
 |
Fig. 6 Contour maps (2σ confidence limits for the two selected parameters) between the free spectral parameters for the six selected spectra shown in Fig. 5. These maps demonstrate that while for some spectra the parameters cannot be constrained tightly, the observed changes of parameter values along the observation are real and significant. |
| In the text | |
 |
Fig. 7 From top to the bottom: evolution of the model parameters versus time and orbital phase. Error bars are 90% confidence level. The dashed line in panel c) indicates the constant NH of component 3. The grey column marks the rise of the flare and the grey curve in panel a) shows the overall unabsorbed flux of the spectral model. |
| In the text | |
 |
Fig. 8 A) 0.6−10 keV unabsorbed flux light curve with a binning time of 1.1 ks. Marked circles indicate the data points corresponding to the spectra shown in Figs. 5 and 6. B) Flux of the first component versus that of the second component. The inset shows an enlarged view of the first 58 ks, before the onset of the giant flare. C) Flux of the third component versus that of the second component with an inset equivalent to that in B). D) Fe Kα fluorescence line flux areas against normalization factor of second component. E) Fe Kα equivalent width against the normalization factor of the second component. All fluxes are in units of 10-9 erg cm-2 s-1. |
| In the text | |
 |
Fig. 9 Distribution of X-ray luminosities for the peak of the flare in the energy range 0.5–600 keV using simulated spectra. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


