| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A92 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201322379 | |
| Published online | 14 March 2014 | |
The VIMOS Public Extragalactic Redshift Survey (VIPERS):
A quiescent formation of massive red-sequence galaxies over the past 9 Gyr⋆,⋆⋆
1
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica (IASF)
Milano, via E. Bassini
15, 20133
Milano, Italy
e-mail: afritz@iasf-milano.inaf.it
2
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astro-physique
de Marseille) UMR 7326, 13388
Marseille,
France
3
INAF – Osservatorio Astronomico di Bologna,
via Ranzani 1, 40127
Bologna,
Italy
4
Dipartimento di Fisica e Astronomia – Università di
Bologna, viale Berti Pichat
6/2, 40127
Bologna,
Italy
5
Institute of Astronomy and Astrophysics, Academia
Sinica, PO Box
23-141, 10617
Taipei,
Taiwan
6
INAF – Osservatorio Astronomico di Brera,
via Brera 28, 20122 Milano, via E. Bianchi
46, 23807
Merate,
Italy
7
Dipartimento di Fisica, Università di
Milano-Bicocca, P.zza della Scienza
3, 20126
Milano,
Italy
8
INAF – Osservatorio Astrofisico di Torino,
10025
Pino Torinese,
Italy
9
Canada-France-Hawaii Telescope, 65–1238
Mamalahoa Highway, Kamuela
HI
96743,
USA
10
Aix-Marseille Université, CNRS, CPT (Centre de Physique Théorique)
UMR 7332, 13288
Marseille,
France
11
Dipartimento di Matematica e Fisica, Università degli Studi Roma
Tre, via della Vasca Navale
84, 00146
Roma,
Italy
12
INFN, Sezione di Roma Tre, via della Vasca Navale 84, 00146
Roma,
Italy
13
INAF – Osservatorio Astronomico di Roma,
via Frascati 33, 00040
Monte Porzio Catone,
Italy
14
Laboratoire Lagrange, UMR7293, Université de Nice
Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300
Nice,
France
15
INAF – Osservatorio Astronomico di Trieste,
via G. B. Tiepolo 11,
34143
Trieste,
Italy
16
SUPA, Institute for Astronomy, University of Edinburgh, Royal
Observatory, Blackford
Hill, Edinburgh
EH9 3HJ,
UK
17
Institute of Physics, Jan Kochanowski University,
ul.Swietokrzyska 15,
25-406
Kielce,
Poland
18
Department of Particle and Astrophysical Science, Nagoya
University, Furo-cho, Chikusa-ku,
464-8602
Nagoya,
Japan
19
INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127
Bologna,
Italy
20
Institut d’Astrophysique de Paris, UMR7095 CNRS, Université Pierre
et Marie Curie, 98 bis boulevard
Arago, 75014
Paris,
France
21
Astronomical Observatory of the Jagiellonian
University, Orla
171, 30-001
Cracow,
Poland
22
National Centre for Nuclear Research, ul. Hoza 69, 00-681
Warszawa,
Poland
23
Max-Planck-Institut für Extraterrestrische Physik,
84571
Garching bei München,
Germany
24
Universitätssternwarte München, Ludwig-Maximillians
Universität, Scheinerstr.
1, 81679
München,
Germany
25
Institute of Cosmology and Gravitation, Dennis Sciama Building,
University of Portsmouth, Burnaby
Road, Portsmouth
PO1 3FX,
UK
26
INAF – Istituto di Astrofisica Spaziale e Fisica Cosmica
Bologna, via Gobetti
101, 40129
Bologna,
Italy
27
INAF – Istituto di Radioastronomia, via Gobetti 101, 40129
Bologna,
Italy
28
Università degli Studi di Milano, via G. Celoria 16, 20130
Milano,
Italy
Received:
26
July
2013
Accepted:
17
January
2014
We explore the evolution of the colour–magnitude relation (CMR) and luminosity function
(LF) at 0.4 < z < 1.3 from the VIMOS Public
Extragalactic Redshift Survey (VIPERS) using ~45 000 galaxies with precise spectroscopic redshifts down to
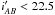 over ~10.32 deg2 in two fields. From
z = 0.5 to
z = 1.3 the
LF and CMR are well defined for different galaxy populations and
over ~10.32 deg2 in two fields. From
z = 0.5 to
z = 1.3 the
LF and CMR are well defined for different galaxy populations and
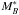 evolves by ~1.04(1.09) ± 0.06(0.10) mag for the total
(red) galaxy sample. We compare different criteria for selecting early-type galaxies: (1)
a fixed cut in rest-frame (U − V) colours, (2) an evolving
cut in (U − V) colours, (3) a rest-frame
(NUV − r′) − (r′ − K)
colour selection, and (4) a spectral-energy-distribution classification. The completeness
and contamination varies for the different methods and with redshift, but regardless of
the method we measure a consistent evolution of the red-sequence (RS). Between
0.4 < z < 1.3 we find a moderate evolution of
the RS intercept of Δ(U − V) = 0.28 ± 0.14 mag,
favouring exponentially declining star formation (SF) histories with SF truncation at
1.7 ≤ z ≤ 2.3. Together with the rise in the number
density of red galaxies by 0.64 dex since z = 1, this suggests a rapid build-up of massive
galaxies (M⋆ > 1011 M⊙)
and expeditious RS formation over a short period of ~1.5 Gyr starting before
z = 1. This
is supported by the detection of ongoing SF in early-type galaxies at 0.9 < z < 1.0, in
contrast with the quiescent red stellar populations of early-type galaxies at
0.5 < z < 0.6. There is an increase in the
observed CMR scatter with redshift, which is two times larger than observed in galaxy
clusters and at variance with theoretical model predictions. We discuss possible physical
mechanisms that support the observed evolution of the red galaxy population. Our findings
point out that massive galaxies have experienced a sharp SF quenching at z ~ 1 with only
limited additional merging. In contrast, less-massive galaxies experience a mix of SF
truncation and minor mergers which build-up the low- and intermediate-mass end of the
CMR.
evolves by ~1.04(1.09) ± 0.06(0.10) mag for the total
(red) galaxy sample. We compare different criteria for selecting early-type galaxies: (1)
a fixed cut in rest-frame (U − V) colours, (2) an evolving
cut in (U − V) colours, (3) a rest-frame
(NUV − r′) − (r′ − K)
colour selection, and (4) a spectral-energy-distribution classification. The completeness
and contamination varies for the different methods and with redshift, but regardless of
the method we measure a consistent evolution of the red-sequence (RS). Between
0.4 < z < 1.3 we find a moderate evolution of
the RS intercept of Δ(U − V) = 0.28 ± 0.14 mag,
favouring exponentially declining star formation (SF) histories with SF truncation at
1.7 ≤ z ≤ 2.3. Together with the rise in the number
density of red galaxies by 0.64 dex since z = 1, this suggests a rapid build-up of massive
galaxies (M⋆ > 1011 M⊙)
and expeditious RS formation over a short period of ~1.5 Gyr starting before
z = 1. This
is supported by the detection of ongoing SF in early-type galaxies at 0.9 < z < 1.0, in
contrast with the quiescent red stellar populations of early-type galaxies at
0.5 < z < 0.6. There is an increase in the
observed CMR scatter with redshift, which is two times larger than observed in galaxy
clusters and at variance with theoretical model predictions. We discuss possible physical
mechanisms that support the observed evolution of the red galaxy population. Our findings
point out that massive galaxies have experienced a sharp SF quenching at z ~ 1 with only
limited additional merging. In contrast, less-massive galaxies experience a mix of SF
truncation and minor mergers which build-up the low- and intermediate-mass end of the
CMR.
Key words: surveys / cosmology: observations / galaxies: evolution / galaxies: photometry / galaxies: luminosity function, mass function / galaxies: statistics
Based on observations collected at the European Southern Observatory, Cerro Paranal, Chile, using the Very Large Telescope under programs 182.A-0886 and partly 070.A-9007. Also based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT), which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. This work is based in part on data products produced at TERAPIX and the Canadian Astronomy Data Centre as part of the Canada-France-Hawaii Telescope Legacy Survey, a collaborative project of NRC and CNRS. The VIPERS website is http://www.vipers.inaf.it/.
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Early-type galaxies are a unique class with rather simple and homogeneous global properties, like morphology, structure, colours, kinematics, and stellar population content. Observationally it is well known that tight correlations exist among these properties, which are often called fundamental relations (Baum 1959; Faber & Jackson 1976; Dressler 1980; Djorgovski & Davis 1987; Dressler et al. 1987; Visvanathan & Sandage 1977)1. However, both the formation processes and the subsequent evolution of these systems with redshift are still uncertain and actively debated.
The most commonly accepted evolutionary scenario for all types of galaxies since z = 1 is the so-called downsizing scenario (Gavazzi et al. 1996; Cowie et al. 1996), with massive galaxies forming the bulk of their stars within short, highly-peaked star formation periods at earlier epochs, whereas less-massive galaxies have delayed star formation histories which are extended over a longer time period (Gavazzi et al. 1996; Thomas et al. 2005; Nelan et al. 2005; Jimenez et al. 2007; Fontanot et al. 2009). Independent evidence supports this scenario. The tight Fundamental Plane relations which exist in both cluster and field environments suggest a higher/lower formation redshift of the stellar content in massive-/less-massive E/S0s at zf > 2/zf ≲ 1 (Fritz et al. 2005, 2009a,b; di Serego Alighieri et al. 2005; Treu et al. 2005; van der Wel et al. 2008). The specific star formation rates (sSFRs) are high/low for low/high-mass galaxies at 0 < z < 2, but inverse trends are found at z > 2 (Feulner et al. 2005; Juneau et al. 2005). Furthermore, luminous E/S0s show higher mass-to-light ratios and different initial mass function (IMF) than their low-massive counterparts (e.g., Fontana et al. 2004; Cappellari et al. 2006, 2012) and there is a rapid decrease of massive post-starburst galaxies with cosmic time (Le Borgne et al. 2006; Vergani et al. 2008).
Such a downsizing scenario for galaxy evolution has some difficulties to be included within the hierarchical structure formation framework implied by the standard ΛCDM cosmological model. Simulations show that in this framework galaxies assemble their mass continously through mergers of sub-units over cosmic time, with a mass-dependent evolution of massive E/S0s which form more than half of their mass at very late epochs of z < 1. Specifically, semi-analytic models based on the hierarchical merger trees of dark-matter halos fail in matching the history of formation and abundance of massive red galaxies, unless a specific feedback mechanism is included (e.g., De Lucia et al. 2006; De Lucia & Blaizot 2007; De Lucia & Borgani 2012). Even with these ingredients, models have difficulty in reproducing the observed weak evolution since z ~ 1 of the bright and massive ends (M⋆ > 1011 M⊙) of the early-type galaxy luminosity and stellar mass functions (after correction for passive evolution), in contrast to the faster evolution of less-massive systems (Bell et al. 2004b; Borch et al. 2006; Bundy et al. 2006; Cimatti et al. 2006; Faber et al. 2007). Similarly, the number density of luminous and massive early-type galaxies remains relatively constant over the past ~8 Gyr (z ~ 0.8), whereas less-luminous (low-mass) systems show a growth over the same time period (e.g., Bundy et al. 2005; Cimatti et al. 2006; Bundy et al. 2006; Conselice et al. 2007; Scarlata et al. 2007; Cassata et al. 2011; Ilbert et al. 2013).
Since the study of fundamental relations can be very demanding in terms of observations and of telescope time, large galaxy surveys have often adopted galaxy colour as the primary parameter to use in the study of galaxy evolution via more economical photometric relations, like the colour–magnitude or the colour−stellar mass relation. It was thus discovered that galaxies exhibit a segregation in luminosity and mass between red, passive early-type (E/S0) galaxies, and blue, star forming late-type ones (Davis & Geller 1976; Sandage et al. 1985; Kauffmann et al. 2003, 2004; Baldry et al. 2004; Bell et al. 2004b), and also a strong bimodal distribution in their properties, like colour, size, star formation, luminosity/mass function (e.g., Strateva et al. 2001; Im et al. 2002; Marinoni & Hudson 2002; Hogg et al. 2002; Bell et al. 2003, 2004b; Blanton et al. 2003; Fontana et al. 2004; Baldry et al. 2004; Kauffmann et al. 2004; Weiner et al. 2005; Willmer et al. 2006; Brown et al. 2007; Wake et al. 2006; Faber et al. 2007; Cool et al. 2008; Pozzetti et al. 2010; Cool et al. 2012). However, the origin and nature of the observed bimodality and the downsizing effect in galaxy properties represents a challenge to the models. Possible galaxy evolution models that could provide some explanation for these bimodal distributions include the self-regulation of star formation processes from supernovae feedback (particularly effective in dark matter halo masses below Mh ~ 5 × 1011 M⊙), virial shock heating (Dekel & Birboim 2006; Cattaneo et al. 2006), and/or star formation quenching due to Active Galactic Nuclei (AGN) feedback (Granato et al. 2004; Menci et al. 2005, 2006; Dekel & Birboim 2006; Schawinski et al. 2006).
The bimodal distribution in optical colours of galaxies is mainly a consequence of the bulk of early-type galaxies forming a tight sequence within the colour–magnitude space, originally termed as the “red-envelope” (Visvanathan & Sandage 1977; O’Connell 1988; Ellis 1988), but now known as the “red-sequence” (RS, Gladders et al. 1998). The RS has been used as a marker in the search of clusters of galaxies in the nearby (e.g., Bower et al. 1992a,b, hereafter BLE92; Garilli et al. 1996; Scodeggio 2001; López-Cruz et al. 2004) and in the distant universe, up to z ~ 1, using optical multi-band photometry (Aragón-Salamanca et al. 1991, 1993; Stanford et al. 1995, 1998; Rakos & Schombert 1995; Garilli et al. 1996; Ellis et al. 1997; Bower et al. 1998; van Dokkum et al. 1998; Kodama et al. 1998; Gladders et al. 1998; van Dokkum et al. 2000; Blakeslee et al. 2003; Fritz et al. 2005; Tanaka et al. 2005; Yee et al. 2005; Cassata et al. 2007). Recently, the combination of optical, near-infrared (NIR) and/or mid-infrared (MIR) Spitzer photometry allowed extending the RS technique to detect high-redshift clusters at 1.2 ≲ z ≲ 2.2 (Wilson et al. 2009; Strazzullo et al. 2010; Demarco et al. 2010; Andreon & Huertas-Company 2011). The detailed properties of the RS, instead, have been used to study the formation and evolution of massive quiescent galaxies since redshift of z ~ 1 (Bell et al. 2004b; Franzetti et al. 2007; Ruhland et al. 2009; Tanaka et al. 2005; Weiner et al. 2005). The RS has been demonstrated to exist up to at least z ~ 1.5 (Franzetti et al. 2007; Williams et al. 2009; Nicol et al. 2011) and there are suggestions that it might be already in place at redshift z ~ 2, but these studies are based on multi-band photometry only (Giallongo et al. 2005; Taylor et al. 2009; Whitaker et al. 2010). Still, the most common use of the RS is in the separation of quiescent, predominantly red-coloured galaxies from the bulk of the star-forming, predominantly blue-coloured galaxies, and from galaxies in the transition zone between the blue cloud and the RS (so-called “green valley”). Unfortunately, the operational definition of the RS is not uniform in the literature. Since galaxies evolve, and the ancestors of the present-day early-type galaxies were different (types of) galaxies at high redshift (van Dokkum & Franx 2001) which underwent a number of transformations as they evolved to the final properties they have today, the definition of a selection criterion for the study of the RS is a complex task, and different RS definitions can result in rather different galaxy samples, making the comparison among various analysis a challenging task.
Another complication is that the volumes covered by deep redshift surveys have been so far too small to guarantee adequate sampling of the very rare objects on the bright (massive) end of the luminosity (mass) function. Therefore, the properties and the contribution of the global galaxy population to the RS is highly uncertain. Consequently, despite the progress described above, there is still significant uncertainty as to how and when the global RS of the overall population of galaxies integrated over all environments has emerged. The data used in this work represent a major step forward in this direction, being based on nearly 50 000 galaxies from the Public Data Release 1 (PDR-1) of the VIMOS Public Extragalactic Redshift Survey (VIPERS, Guzzo et al. 2013a). The VIPERS data are used to measure the evolution of the luminosity function (LF) and the colour–magnitude relation (CMR) of the galaxy population over the redshift range 0.5 ≲ z ≲ 1.3. Specific attention is dedicated to the properties and evolution of the red, quiescent galaxy population residing along the RS, investigating the impact of different selection criteria on the robustness of evolutionary trends that are derived from both the LF and CMR.
The paper is organised as follows. In Sect. 2 we give an overview of the data and the sample selection used for this work. We address in detail various incompleteness tests that were considered as well as the derivation of individual galaxy rest-frame properties and galaxy types. The CMR for VIPERS is presented in Sect. 3 and the different selection procedures for passive galaxies are described in Sect. 4. The evolution of the RS galaxy population is explored in Sect. 5. The LFs for VIPERS galaxies are described in Sect. 6. Section 7 compares our observational results to predictions of stellar population synthesis models. A discussion and the implications of the results for the formation and evolution of the galaxy populations is given in Sect. 8 and our main results are summarized in Sect. 9.
Throughout the paper, we assume a concordance cosmology with cosmological parameters of Ωm = 0.25, ΩΛ = 0.75, and a Hubble constant of H0 = 100 h km s-1 Mpc-1 with h = 0.7. Unless otherwise stated, the Johnson-Kron-Cousins filter system (Johnson & Morgan 1953) is used. To simplify a comparison with previous works, magnitudes and colours are given in the Vega system.
2. Data
2.1. Photometric data
The optical photometric catalogue is based on u∗g′r′i′z′
data from the T0005 release of the Canada-France-Hawaii Telescope Legacy Survey
(CFHTLS)2. The data were collected with the 3.6 m
CFH optical/infrared telescope on the Mauna Kea summit. The four independent contiguous
Wide (CFHTLS-W) patches cover between 25 to 72 deg2 resulting in a total area of
~155 deg2, of which VIPERS targets two
CFHTLS-W fields, W1 and W4. The final CFHTLS-W photometric catalog reaches in the optical
filter bands 80% completeness limit in AB for point sources of u∗ = 25.2,
g′ = 25.5,
r′ = 25.0,
i′ = 24.8,
z′ = 23.9
(Mellier et al. 2008; Goranova et al. 2009). For all bands, total apparent magnitudes were
measured in Sextractor using mag_auto in Kron-like (Kron
1980) elliptical apertures as measured from the i′-band image with a
minimum Kron radius of 1.2 arcsec (equal in all other bands). Apparent magnitudes were
corrected for Galactic extinction using the COBE dust maps by (Schlegel et al. 1998), with a median extinction of E(B − V) ~ 0.025
mag in W1 and ~0.05 mag
in W4. For VIPERS objects with 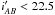 at 0 < z < 1.0, the
CFHTLS T0005 photometric redshifts have a 1σ uncertainty of σz/(1 + z) = 0.045,
whereas in the redshift range 1.0 < z < 1.5 the uncertainty is
σz/(1 + z) ~ 0.090
(Coupon et al. 2009; Scodeggio et al. 2011). For galaxies at 0.4 < z < 1.3,
typical errors in the observed u∗g′r′i′z′
CFHTLS photometry that include all measurement uncertainties (e.g., zero-point and
absolute photometric calibration, tile-to-tile offset, etc) are of the order
⟨σu∗g′r′i′z′⟩ = 0.038 ± 0.029.
There is a multitude of ancillary data available for the two VIPERS fields which will be
explored in a series of future papers. In the following, we limit the discussion to the
relevant photometric data used for the present analysis. Both W1 and W4 are covered at NIR
wavelengths by various photometric surveys. A dedicated WIRcam Ks follow-up
survey of the VIPERS fields (Arnouts et al., in prep.) was conducted for ~80% of the area in W1 and
~96% in W4 with a
5σ
completeness level for point sources of Ks ~ 22.0 mag (AB). In W1 and W4
23759 and 27371 VIPERS objects have a Ks counterpart, respectively. Further,
4591 objects (~15%) in W4
that have no WIRCAM Ks-band photometry are covered by
UKIDSS-DR9 or, when available, UKIDSS-UDS-DR8 YJHK data. For 1004 and 1500 spectroscopic sources
in W1 and W4, respectively no K-band data is available. However, only 801 out of
these 2504 VIPERS galaxies without K-band photometry and 2 ≤ zflg ≤ 9.5
are located at 0.5 < z < 1.2. Based on consistency tests with
respect to uncertainties originating from the photometric calibration (e.g., zero-point
variations or sky-subtraction errors), we conclude that the KWIRCAM
photometry is more reliable than the KUKIDSS data (e.g., Davidzon et al. 2013, hereafter D13). Thus, when both
K-band data
are available, we decided to keep the former and neglect the latter.
at 0 < z < 1.0, the
CFHTLS T0005 photometric redshifts have a 1σ uncertainty of σz/(1 + z) = 0.045,
whereas in the redshift range 1.0 < z < 1.5 the uncertainty is
σz/(1 + z) ~ 0.090
(Coupon et al. 2009; Scodeggio et al. 2011). For galaxies at 0.4 < z < 1.3,
typical errors in the observed u∗g′r′i′z′
CFHTLS photometry that include all measurement uncertainties (e.g., zero-point and
absolute photometric calibration, tile-to-tile offset, etc) are of the order
⟨σu∗g′r′i′z′⟩ = 0.038 ± 0.029.
There is a multitude of ancillary data available for the two VIPERS fields which will be
explored in a series of future papers. In the following, we limit the discussion to the
relevant photometric data used for the present analysis. Both W1 and W4 are covered at NIR
wavelengths by various photometric surveys. A dedicated WIRcam Ks follow-up
survey of the VIPERS fields (Arnouts et al., in prep.) was conducted for ~80% of the area in W1 and
~96% in W4 with a
5σ
completeness level for point sources of Ks ~ 22.0 mag (AB). In W1 and W4
23759 and 27371 VIPERS objects have a Ks counterpart, respectively. Further,
4591 objects (~15%) in W4
that have no WIRCAM Ks-band photometry are covered by
UKIDSS-DR9 or, when available, UKIDSS-UDS-DR8 YJHK data. For 1004 and 1500 spectroscopic sources
in W1 and W4, respectively no K-band data is available. However, only 801 out of
these 2504 VIPERS galaxies without K-band photometry and 2 ≤ zflg ≤ 9.5
are located at 0.5 < z < 1.2. Based on consistency tests with
respect to uncertainties originating from the photometric calibration (e.g., zero-point
variations or sky-subtraction errors), we conclude that the KWIRCAM
photometry is more reliable than the KUKIDSS data (e.g., Davidzon et al. 2013, hereafter D13). Thus, when both
K-band data
are available, we decided to keep the former and neglect the latter.
Through a collaborative effort, we have supplemented our multi-wavelength photometry with deep GALEX observations in the far-ultraviolet FUV (1350−1750 Å) and NUV (1750−2800 Å) (Arnouts et al., in prep.). A total of Texp > 30 ks/field yields a 90% completeness level of extended sources at 24.50 mag (AB) in both FUV and NUV bands. Overall, 18 838 sources (~63%) in W1 and 3688 (~13%) objects in W4 have a NUV counterpart. In W1 and W4 there are 4528 galaxies (~15%) and 1552 objects (~5%) with an associated FUV flux, respectively.
2.2. VIPERS
The VIMOS Public Extragalactic Redshift Survey (VIPERS)3, is an ongoing ESO Large Programme designed to measure in detail the spatial
distribution, clustering, and other statistical properties of the large-scale distribution
of ~105 galaxies across all galaxy
types down to  . In addition, this survey also measures
the physical parameters of galaxies, like stellar mass or star formation activity, over an
unprecedented volume of 5 × 107 h-3 Mpc3 at 0.5 < z < 1.2 (Guzzo et al. 2013a,b). The VIPERS sample selection is based on accurate optical 5-band CFHTLS
photometry, combined with a simple and robust pre-selection in the (g′ − r′)
vs. (r′ − i′) colour−colour plane to efficiently remove galaxies
with z < 0.5 (Guzzo et
al. 2013a). Spectroscopic observations have been collected with the VIsible
MultiObject Spectrograph (VIMOS; Le Fèvre et al.
2000, 2002) at the ESO Very Large
Telescope (VLT) in multi-object-spectroscopy (MOS) mode using the low-resolution red
(LR-Red) grism (λblaze = 5810 Å) at moderate resolution
(R = 210,
1′′ slit). This gives a
wavelength coverage of 5500 < λeff < 9500 Å with internal
dispersion of 7.15 Å pix-1 (Scodeggio et al.
2005). The combination of our target selection with an efficient, and aggressive
observing strategy using shorter slits (Scodeggio et al.
2009), that doubles the multiplexing of VIMOS MOS mode while at the same time
keeping the problematic effects of fringing patterns (λobs ≳ 8100 Å)
under control, allows us to double the galaxy sampling rate in the redshift range of
interest (~40%) when
compared to the sampling of a purely magnitude-limited sample.
. In addition, this survey also measures
the physical parameters of galaxies, like stellar mass or star formation activity, over an
unprecedented volume of 5 × 107 h-3 Mpc3 at 0.5 < z < 1.2 (Guzzo et al. 2013a,b). The VIPERS sample selection is based on accurate optical 5-band CFHTLS
photometry, combined with a simple and robust pre-selection in the (g′ − r′)
vs. (r′ − i′) colour−colour plane to efficiently remove galaxies
with z < 0.5 (Guzzo et
al. 2013a). Spectroscopic observations have been collected with the VIsible
MultiObject Spectrograph (VIMOS; Le Fèvre et al.
2000, 2002) at the ESO Very Large
Telescope (VLT) in multi-object-spectroscopy (MOS) mode using the low-resolution red
(LR-Red) grism (λblaze = 5810 Å) at moderate resolution
(R = 210,
1′′ slit). This gives a
wavelength coverage of 5500 < λeff < 9500 Å with internal
dispersion of 7.15 Å pix-1 (Scodeggio et al.
2005). The combination of our target selection with an efficient, and aggressive
observing strategy using shorter slits (Scodeggio et al.
2009), that doubles the multiplexing of VIMOS MOS mode while at the same time
keeping the problematic effects of fringing patterns (λobs ≳ 8100 Å)
under control, allows us to double the galaxy sampling rate in the redshift range of
interest (~40%) when
compared to the sampling of a purely magnitude-limited sample.
The data set used in the present study is based on the VIPERS PDR-1, which was made public in Fall 2013 (Garilli et al. 2014). The survey description, together with its motivation, the sample selection and the spectroscopic observations are presented in Guzzo et al. (2013a). The VIPERS data reduction pipeline (Easylife), the survey database system and its tools are described in (Garilli et al. 2012). There are several complementary scientific investigations using the VIPERS PDR-1 (D13, Bel et al. 2014; de la Torre et al. 2013; Malek et al. 2013; Marulli et al. 2013). Previous works include a CFHTLS power spectrum analysis (Granett et al. 2012) and a principal component analysis of VIPERS spectra (Marchetti et al. 2013).
The VIPERS PDR-1 contains all spectroscopic observations in the VIPERS database until the end of the 2011/2012 observing campaign and covers an effective area of ~10.32 deg2 which is 61.3% of the planned total area (~24 deg2). For 55 358 objects (93.8% of total, excluding non-extracted spectra), the automatic redshift measurement software tool EZ (Garilli et al. 2010) was able to derive an estimate of the spectroscopic redshift. All automatic measurements were validated (or corrected, if necessary) via visual inspection by two VIPERS Team members independently, who also assigned a quality flag zflg (i.e., a confidence level) to the final redshift measurement. In total, 53 608 galaxy redshifts have been measured. Finally, a comparison between the spectroscopic and the photometric redshift measurements was carried out, storing the result in the quality flag decimal value. The spectroscopic redshift measurement accuracy, reliability and flag classification system have been extensively tested and verified through repeated observations of 1215 galaxies (Scodeggio et al. 2011; Garilli et al. 2010; Guzzo et al. 2013a).
2.3. Rest-frame galaxy properties
All spectrophotometric rest-frame properties of the VIPERS galaxies were derived using the SED fitting program Hyperzmass, an updated version of the photometric redshift code Hyperz (Bolzonella et al. 2000, 2010). For the spectroscopic PDR-1 catalogue, the dust content of the galaxies was modelled with both the Prévot-Bouchet extinction law, that is based on the Small Magellanic Cloud dust properties (Prévot et al. 1984; Bouchet et al. 1985), and an extinction relation calibrated using starburst galaxies (Calzetti et al. 2000). The choice between the two extinction relations was performed on the basis of the smallest derived χ2 value. The final extinction magnitudes range between AV = 0 (no dust attenuation) to AV = 3 (strong dust attenuation).
Absolute luminosities were derived using the apparent magnitude that most closely resembles the observed photometric passband, shifted to the redshift of the galaxy under consideration. Thanks to our extensive multi-wavelength photometry (from FUV to MIR wavelengths), the k-correction factor was as small as possible and much less sensitive to the adopted SED template type than using a global filter transformation that is confined to a single specific filter passband (see Appendix A of Ilbert et al. 2005). The following analysis is restricted to rest-frame Johnson U, B, and V bands as they are covered across the whole optical to NIR observed filters over the redshift range of our main interest. Typical uncertainties in the SED fitting process that include measurement uncertainties in the zero-point, SED extrapolation, and adopted template libraries, range, for example, in the B-band from σB = 0.04 (0.4 < z < 0.7) to σB = 0.05 (0.7 < z < 0.9) and σB = 0.07 (0.9 < z < 1.1) to σB = 0.14 (1.1 < z < 1.3). These uncertainties are included in the final error budget and are used in the derivation of the intrinsic scatter of the CMR (see Sect. 5.3). In this work, we focus on exploring the differences between the two main populations of passive and star forming galaxies using the rest-frame (U − V) colours. For the U-band we adopt the original UJ-Johnson filter Johnson & Morgan 1953; hereafter U-band), which is particularly sensitive at blue wavelengths and allows a precise distinction between red and blue galaxies. One advantage is that the U-band filter response traces the 4000 Å break and therefore the U-band is a good proxy for the stellar population age of galaxies (Bruzual 1983; Kauffmann et al. 2003). In Appendix A we discuss our filter choice and provide a comparison to other U-band filters used in the literature.
 |
Fig. 1 Luminosity−redshift relation for galaxies in the VIPERS PDR-1. Galaxies are colour-coded with respect to their SED type classification. The solid line indicates the selection boundaries for 90% completeness. |
2.4. Spectrophotometric type classification
Spectrophotometric galaxy types were derived by fitting the magnitudes with a small set of spectral templates as described in (Ilbert et al. 2006). In particular, the six reference templates consist of four locally observed spectral energy distributions (SEDs; Coleman et al. 1980) and two starburst SEDs from Kinney et al. (1996). All templates were first individually extrapolated to UV and MIR wavelengths, then pairs of templates were interpolated to create a final set of 62 synthetic SEDs, and finally those were optimized with Le Phare (Arnouts et al. 1999; Ilbert et al. 2006). As our templates are constructed from real observed galaxies rather than synthetically generated templates, they already contain the typical amount of dust present for that given spectral galaxy class. The whole spectroscopic sample is then classified into four galaxy types, corresponding to early-type spheroids and spiral bulge-dominated galaxies (elliptical, lenticular and S0/Sa, hereafter E/S0), early-type spiral galaxies (hereafter Sa/Sb), late-type spiral galaxies (hereafter Sc/Sd), and starburst and irregular galaxies (hereafter SB/Irr).
Figure 1 shows the luminosity–redshift relation of
VIPERS. Galaxies are divided into their respective SED type classes. Because the flux
intensity decreases with the square of the luminosity distance
(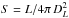 ), with increasing redshift any galaxy
sample will be incomplete at faint luminosities. The solid line denotes the selection
boundaries for a sample completeness of 90%, which was derived as in Marulli et al. (2013).
), with increasing redshift any galaxy
sample will be incomplete at faint luminosities. The solid line denotes the selection
boundaries for a sample completeness of 90%, which was derived as in Marulli et al. (2013).
In our subsequent analysis, the SED type classification serves as primary reference against which the completeness and contamination levels of each independent selection criteria of early-type galaxies are compared to. The pros are that for the SED type assessment the complete optical to NIR multi-wavelength information can be applied. The broader wavelength coverage reduces the number of possible contaminations from special objects for any given galaxy type. Our concept of using the SED type classification as a reference for selecting early-type galaxies gets independent support from a recent zCOSMOS study (Moresco et al. 2013).
 |
Fig. 2 Redshift distribution for the VIPERS PDR-1 sample used in the present study. Only galaxies with 2 ≤ zflg ≤ 9.5 are considered. The mean of the total distribution is indicated with a dashed line. The total number of galaxies and mean redshift are given for each galaxy type. |
2.5. Sample selection and redshift distribution
The sample used for the present work is composed of 44 982 galaxies (NW1 = 23 210
and NW4 = 21 772) with 2 ≤ zflg ≤ 9.5
(corresponding to a confidence level >95% in the redshift measurement) covering the redshift range
between 0.40 < z < 1.3 and look-back times of
~4.2–8.7 Gyr. An
additional 763 objects with z < 0.4 and 244 galaxies with z > 1.3 exist with the
same quality flags, but have been excluded due to sample incompleteness. The redshift
distribution of these data is presented in Fig. 2.
The mean redshift is 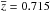 (indicated with a dashed line), and the
median is ⟨z⟩ = 0.694. Figure 2 also shows the redshift distribution of the different galaxy SED types. Using
repeated observations of 1215 galaxies with zflg ∈ 2,3,4 (excluding stars and AGNs),
the typical (root-mean-square) uncertainty in the spectroscopic redshift measurements is
δz/(1 + z) = 0.00047,
which corresponds to a radial velocity accuracy (1-σ scatter) for individual
VIPERS measurements of δv = 141(1 + z)
km s-1.
(indicated with a dashed line), and the
median is ⟨z⟩ = 0.694. Figure 2 also shows the redshift distribution of the different galaxy SED types. Using
repeated observations of 1215 galaxies with zflg ∈ 2,3,4 (excluding stars and AGNs),
the typical (root-mean-square) uncertainty in the spectroscopic redshift measurements is
δz/(1 + z) = 0.00047,
which corresponds to a radial velocity accuracy (1-σ scatter) for individual
VIPERS measurements of δv = 141(1 + z)
km s-1.
2.6. Selection function
In order to draw robust conclusions from the observed distribution of physical parameters in the VIPERS galaxy sample, we have to consider the influence of possible systematic effects which might enter our spectroscopic sample. In particular, a potential bias may arise if galaxies with extreme (e.g., colour) properties are under- or over-represented in the final spectroscopic sample. Such systematics could be either due to incompleteness in colours of the parent photometric sample, or a variable redshift measurement success rate.
2.6.1. Spectral type and colour completeness
One potential source of bias in our spectroscopic sample might be the systematic deficit of a specific class of galaxies, in particular early-type galaxies. The origin of such a selection effect might be twofold. Brighter early-type galaxies with large sizes are preferably located in dense environments and display a stronger clustering compared to their late-type counterparts. Furthermore, the number density of fainter and smaller late-type galaxies increases with increasing redshift. Because of MOS mask design restrictions, spectroscopic surveys will target only a fraction of the total galaxy population and usually select against early-type galaxies due to their increasing relative physical underabundance with redshift and their stronger clustering properties. However, the parent target sample is sufficiently sparse that the physical effect of clustering is small and can be largely accounted for during the automatic slit assignment procedure. In quantitative studies of clustering this effect can be corrected to within a few percent through a proper weighting scheme based on the angular correlation functions of the observed and full target samples.
Percentage of early- and late-type galaxies in the parent and spectroscopic VIPERS sample.
Another potential reason for a deficit of early-type galaxies might be a lower efficiency in the redshift measurement process due to the lack of prominent emission lines in the spectra. To assess this possible systematic uncertainty, we compare our spectroscopic sample to the total u∗g′r′i′z′ photometric magnitude-limited CFHTLS catalog in the VIPERS fields (Coupon et al. 2009) for which photometric redshifts could be obtained using Le Phare (Arnouts et al. 1999; Ilbert et al. 2006). For the parent sample, the same SED modelling process and photometric type classification has been conducted as described for the spectroscopic sample in Sect. 2.4. The parent sample consists of N = 345 605 galaxies with 0.4 < zphot < 1.3. We note that possible uncertainties due to photometric redshift errors are small (σzphot = 0.0387(1 + z), catastrophic outliers ≲3−4% for zflg ∈ 2,3,4; Coupon et al. 2009). In Table 1 we compare the percentage of photometrically classified early-type (E/S0) and late-type (Sa to Irr) galaxies in the parent and in the spectroscopic sample. The fractions of each galaxy type are given for different redshift intervals probed by VIPERS. Comparing the fraction of early-type galaxies in the parent and spectroscopic datasets we deduce that the incompleteness of the early-type population in the spectroscopic sample is negligible. On average, early-type galaxies are not deficient in the total spectroscopic sample. Only for the highest-redshift part (1.0 < z < 1.3) E/S0s appear to be slightly deficient by ~4.3%. Overall, we find no significant dependence of the redshift completeness on any particular galaxy type.
To establish the completeness in galaxy colours for our sample, we have estimated the
effect of the varying sampling rate using spectroscopic samples from the purely
magnitude-limited VIMOS-VLT Deep Survey (VVDS, Le Fèvre
et al. 2005, 2013). We selected galaxy
samples from the VVDS F02 and F22 fields applying an identical colour selection
criterion as the one used in VIPERS, and then derived the colour completeness (see Fig.
3). We define the Colour Sampling Rate (CSR) as
CSR(z) = NVL/NTOT,
which is the ratio of the number of galaxies in a VIPERS-like selected sample
NVL to the total number of galaxies
NTOT in the same redshift bin. Above
z = 0.6,
the CSR is independent of the redshift with CSR ~ 1 up to z ~ 1.2 and the VIPERS sample is equivalent
to a purely magnitude-limited sample with 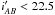 (Guzzo
et al. 2013a). If the VVDS sample is split into passive (red) and active, star
forming (blue) galaxies using a (NUV − r′) − (r′ − K)
selection (see Sect. 4.3), the completeness level
remains at a similar level, as demonstrated in Fig. 3. Below z = 0.6, a lower completeness for passive galaxies
is somewhat expected due to the sharp cut in the colour selection. However, we find only
a minor decrease in the CSR of passive galaxies. At z = 0.6, passive galaxies
have a completeness of ~94%, whereas blue galaxies are complete at ~97%. At z ~ 0.5, the CSR is
~82%, whereas at
z ~ 0.45 it is ~69%, independent of the galaxy type.
Significant biases arise when the colour completeness is ≲50% (Franzetti et al. 2007). As for z < 0.45 the CSR is still ~69%, our sample contains a large
fraction of the galaxy population between 0.4 < z < 0.5 which should not be
significantly affected by selection effects. In any case, in the subsequent analysis
this redshift range is treated separately from the rest of the sample. Overall, we
conclude that across the redshift interval probed in this work we detect no significant
dependence of the CSR on galaxy type.
(Guzzo
et al. 2013a). If the VVDS sample is split into passive (red) and active, star
forming (blue) galaxies using a (NUV − r′) − (r′ − K)
selection (see Sect. 4.3), the completeness level
remains at a similar level, as demonstrated in Fig. 3. Below z = 0.6, a lower completeness for passive galaxies
is somewhat expected due to the sharp cut in the colour selection. However, we find only
a minor decrease in the CSR of passive galaxies. At z = 0.6, passive galaxies
have a completeness of ~94%, whereas blue galaxies are complete at ~97%. At z ~ 0.5, the CSR is
~82%, whereas at
z ~ 0.45 it is ~69%, independent of the galaxy type.
Significant biases arise when the colour completeness is ≲50% (Franzetti et al. 2007). As for z < 0.45 the CSR is still ~69%, our sample contains a large
fraction of the galaxy population between 0.4 < z < 0.5 which should not be
significantly affected by selection effects. In any case, in the subsequent analysis
this redshift range is treated separately from the rest of the sample. Overall, we
conclude that across the redshift interval probed in this work we detect no significant
dependence of the CSR on galaxy type.
 |
Fig. 3 Colour completeness for VIPERS. The sample is complete in colours between 0.5 < z < 1.3, in the sense of including a proportionally correct fraction of galaxies with different colours. A NUVr′ selection to separate (red) passive (solid line) from (blue) active, star-forming (dashed line) galaxies shows that the CSR is independent of galaxy type. |
2.6.2. Statistical weights
VIPERS is based on a robust colour selection criterion in the (r′ − i′) − (u′ − g′) colour−colour plane to effectively target galaxies at z > 0.5 (Guzzo et al. 2013a). The completeness of the survey can vary as a function of different observed quantities, like galaxy redshift, magnitude, and colour, and it also varies for each targeted VIMOS quadrant. Here we describe the tools that allow us to evidence and correct for incompleteness effects in our analysis of the colour−magnitude relation (Sect. 3), the luminosity function (Sect. 6) and the GSMF (D13). A different application of the statistical weights with respect to galaxy clustering is given in de la Torre et al. (2013).
We define the Target Sampling Rate (TSR) as the fraction of all observed spectroscopic
sources with respect to the total photometric sample
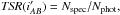 where Nphot and
Nspec are the number of potential
targets present in the parent photometric catalogue and of observed spectroscopic
sources, respectively. The TSR varies only as a function of apparent magnitude.
where Nphot and
Nspec are the number of potential
targets present in the parent photometric catalogue and of observed spectroscopic
sources, respectively. The TSR varies only as a function of apparent magnitude.
The Spectroscopic Success Rate (SSR) can be computed as
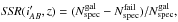 where
where
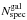 is the numberof spectroscopically
observed galaxies (excluding broad line AGNs, and spectroscopically identified stars).
is the numberof spectroscopically
observed galaxies (excluding broad line AGNs, and spectroscopically identified stars).
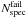 is the number of sources without a
reliable redshift confirmation (i.e., “failures” with zflg = 0, or
low confidence with zflg = 1). The SSR depends not only on
the observation details (i.e. the VIMOS quadrant) and on the redshift of the objects,
but also on their apparent magnitude, as the spectroscopic signal-to-noise ratio (S/N)
decreases with increasing magnitude.
is the number of sources without a
reliable redshift confirmation (i.e., “failures” with zflg = 0, or
low confidence with zflg = 1). The SSR depends not only on
the observation details (i.e. the VIMOS quadrant) and on the redshift of the objects,
but also on their apparent magnitude, as the spectroscopic signal-to-noise ratio (S/N)
decreases with increasing magnitude.
Finally, unobserved sources in the survey are corrected by using a statistical
weighting scheme associated to each galaxy g with a secure redshift measurement (Ilbert et al. 2005), where
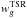 ,
, 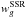 and
and
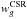 are the inverse of the TSR, SSR and CSR,
respectively. The total survey completeness weight wTOT is given
as
are the inverse of the TSR, SSR and CSR,
respectively. The total survey completeness weight wTOT is given
as 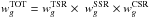 . This weighting scheme corrects for both
sources that were not observed or unidentified (i.e., objects with unknown redshifts
because of poor spectral quality). Since the VIPERS spectroscopic targets were randomly
selected from the parent sample, the TSR is independent of the apparent magnitude, being
stable at ⟨TSR⟩ ≳ 40%. In contrast, the SSR is a function
of the redshift and the i-band selection magnitude, which is connected to
the S/N of the spectrum. Hence, the SSR ranges from ~95% at
. This weighting scheme corrects for both
sources that were not observed or unidentified (i.e., objects with unknown redshifts
because of poor spectral quality). Since the VIPERS spectroscopic targets were randomly
selected from the parent sample, the TSR is independent of the apparent magnitude, being
stable at ⟨TSR⟩ ≳ 40%. In contrast, the SSR is a function
of the redshift and the i-band selection magnitude, which is connected to
the S/N of the spectrum. Hence, the SSR ranges from ~95% at
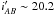 to ~75% at
to ~75% at
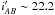 (see also de la Torre et al. 2013; Guzzo et
al. 2013a).
(see also de la Torre et al. 2013; Guzzo et
al. 2013a).
The weighting scheme was applied to all observed galaxies apart from two special object classes. First, as the spectroscopic catalogue contains a small fraction of X-ray detected sources (“compulsory” targets), the TSR for these objects is higher than the global one and therefore was computed separately. Secondly, the contribution of these “compulsory” targets to the total sample is only ~2%. In some cases, a secondary spectrum was detected within a slit assigned to a target. For these serendipitous sources the SSR would be much lower than the overall SSR as the majority of these objects are either faint or not well centred within the slit, resulting in low S/N spectra. These secondary objects have not been included in the PDR-1 and will be analysed in the future.
 |
Fig. 4 Evolution of the colour–magnitude relation for the VIPERS PDR-1 sample from z = 0.4 to z = 1.3. Galaxies are colour-coded with respect to their derived SED type. The number of galaxies for a specific SED type is shown in each slice. The lines in each panel indicate the best-fitting CMR for galaxies on the RS within the given redshift interval: classical approach (dotted), SED galaxy types (dashed). The fit for the colour-bimodality method is not shown as it coincides with the dashed line. Typical error bars (black) are shown in each redshift slice. |
3. The colour–magnitude and colour–stellar mass relations in VIPERS
Figure 4 shows the evolution of the rest-frame (U − V) vs. MV colour–magnitude relation (CMR) for the VIPERS PDR-1 sample, divided into seven redshift slices between z = 0.4 to z = 1.3. Galaxies are colour-coded according to their derived SED type classification as described in Sect. 2.4. Thanks to the large size of the survey, all redshift bins are well populated by a significant number of galaxies for each individual SED type, allowing a careful description of their relative evolutionary patterns. This is possible because of the precision of the CFHTLS photometry, as shown by the plotted colour error bars for two reference luminosities, MV − 5 log h = −23 and MV − 5 log h = −21. The CMR covers a range of about four magnitudes in the first redshift bin, which at z = 1 is reduced to 2.5 due to the apparent magnitude cut of the sample. The “blue cloud” is the part of the diagram that is less affected by such incompleteness at the faint limit (as shown in Fig. 1). Keeping these limitations in mind, a number of important trends emerge from the CMR plot. First, we note that the rest-frame colours of all galaxies become bluer with increasing redshift; this happens for all SED types. This trend cannot be the effect of a bias induced by the survey apparent magnitude cut. As demonstrated in Sect. 2.6.2, our completeness in colour remains at a very high level (>90%) across the whole redshift range, with variations from one bin to another of only ~5%. Therefore, for a given redshift slice, our sample is expected to be representative of the correct galaxy population mix present at that look-back time among relatively luminous galaxies. A second relevant feature of the diagrams is that at fixed colour, the upper luminosity limit of the distribution is higher at higher redshifts.
We can also precisely identify and measure the position of the RS and trace its evolution up to redshift z ≃ 1. In particular, the bulk of the red luminous population (hence the most massive objects) is already in place at z ~ 1. This observational evidence agrees with findings from deeper, smaller-volume surveys (e.g., Bell et al. 2004b; Cimatti et al. 2006; Bundy et al. 2007; Faber et al. 2007; Ilbert et al. 2010). However, for z > 0.7 we note the presence of a number of super-luminous red galaxies, with MV − 5 log h < −23. It is clear that these are very rare objects, which are detected in VIPERS thanks to its unprecedented volume at these redshifts. The presence of these objects on the RS is a clear indication for both a high-redshift formation epoch for the bulk of the stellar populations and an early stellar mass assembly age for these systems, contrary to speculations that the two ages could be decoupled and therefore end up being rather different from one another (Baugh et al. 1996; van Dokkum & Franx 2001).
 |
Fig. 5 Relation between galaxy colour and stellar mass for the VIPERS PDR-1 sample, within three broader redshift bins. This plot confirms that the most luminous blue galaxies observed in the CMR are in fact very massive objects. In particular, we note how a) the highest-mass edge of the blue cloud evolves with cosmic time, with a few objects as massive as log (M⋆/M⊙) ~ 11.5 displaying colours typical of star-forming galaxies; b) conversely, the corresponding highest-mass edge of the RS is substantially frozen over the explored redshift range. |
Furthermore, the ability of VIPERS to push deep into the bright end of the luminosity function also has a beneficial effect on the blue population. As we see from the same figure, a large number of green or blue very luminous galaxies is detected at all redshifts sampled by VIPERS, in particular in the highest redshift bins, where we detect galaxies with MV − 5 log h < −23 and very blue colours.
Clearly, the crucial question in terms of evolutionary patterns is whether these are objects of normal mass, experiencing an extremely active star-burst phase, or are rather massive objects going through a normal star formation phase without a strong starburst. Our results on the stellar mass function of red and blue galaxies in VIPERS (D13), show that at z ~ 1 one finds comparable abundances of blue and red galaxies with masses as large as log (M⋆/M⊙) ~ 11. The majority of these luminous blue galaxies present undisturbed morphologies without signs of interactions, tidal features, or close companions and have no strong X-ray emission. This suggests that a large fraction of the very luminous blue objects are in fact also very massive systems. To verify this more explicitly, we make use of the stellar masses computed as described in D13, to construct the corresponding (U − V) colour-mass diagram of our sample. This is shown in Fig. 5, split over three broad redshift bins. The figure confirms that the most luminous blue galaxies correspond in fact to truly massive objects that are still forming stars. Specifically, at higher redshifts (z > 0.7) we detect a higher fraction of massive galaxies with fairly blue colours (as massive as log (M⋆/M⊙) ~ 11.5) compared to the lowest redshift interval at 0.5 < z ≤ 0.7. It is quite natural to conclude that these objects are today located on the red sequence: this “migration” is in fact apparent when comparing the three diagrams, together with the overall evolution in the number density of blue and red galaxies in different mass bins (D13, Fig. 14). Figure 5 demonstrates that the build-up of the red envelope of the RS (the highest-mass edge) has been completed at z ~ 1.1 and remains constant over the whole explored redshift range (log (M⋆/M⊙) ~ 11.8), but the overall population of the RS for masses log (M⋆/M⊙) > 10.5 increases by a factor of ~2.4. We argue this represents substantial evidence for a quiet build-up of the main body of the RS, without the need of major dry merger events. Ilbert et al. (2013) showed that the overall measured star formation at z < 1 is not efficient enough to produce a population of massive star-forming galaxies. The significant population of massive blue galaxies that we have found to be already in place at z ~ 1, makes the formation of new massive blue galaxies at lower redshifts not necessary. A more detailed study of the observed evolution of the bright/massive edge of the “blue cloud” will be the subject of a future paper (Scodeggio et al., in prep.).
4. The red-sequence
An important point in all discussions about the evolution of early-type galaxies is how to select a sample of these galaxies that is sufficiently pure and complete at the same time. In this work we compare different selection procedures to construct a sample of red, old and passive galaxies of high purity, using several independent criteria to separate these galaxies from blue, star-forming ones, and we also explore the possible effects of dust obscuration in high-redshift, dusty red galaxies which are located around the RS and within the “green valley”.
4.1. The classical approach
One popular approach to distinguish the red and blue galaxy population is to use a fixed cut in galaxy colours, not-evolving with redshift (e.g., Bell et al. 2004b; Franzetti et al. 2007). When using this method, many works adopted the slope in the CMR as defined by elliptical galaxies in the Coma cluster, which is well-known and where selection effects are under control. There are two main motivations for using this criterion: (i) straightforward comparison to previous works in the literature; (ii) limiting possible uncertainties due to zero-point variations in the photometry that arise from the transformation of observed magnitudes to the rest-frame at different redshifts.
Here we follow the prescription outlined by Bell et al. (2004b), which we refer to as the “classical approach”. Galaxies that have rest-frame colours (U − V) > 1, regardless of their morphological or SED type, are considered as part of the RS. The evolution of the RS is derived by fitting a linear relation between colour and absolute magnitude, keeping the slope of the relation fixed to the Coma cluster value at all redshifts. As redshift progresses the assumption of a non-evolving selection cut with redshift becomes problematic as the number density of early-type galaxies with intermediate mass (10.8 < log (M⋆/M⊙) < 11.1) decreases by a factor of ~ 2.5 and that of high mass galaxies (log (M⋆/M⊙) ≥ 11.4) by 45% from z = 0.6 to z = 1.2 (D13). Therefore, the classical approach will select only the reddest and most luminous (hence also most massive) early-type galaxies, which are not representative of the whole early-type galaxy population. These massive early-type galaxies have formed the bulk of their stars at high redshift (z > 2) and will therefore comprise quiescent evolved stellar populations. However, any selection method using optical colours only, will contain a non-negligible contribution of dusty red galaxies (Strateva et al. 2001; Cimatti et al. 2002; Gavazzi et al. 2003; Bell et al. 2004a; Weiner et al. 2005). To disentangle the contamination of the early-type galaxy samples due to such effects, we will later on use a combination of GALEX NUV and NIR colours (Sect. 4.3).
4.2. Colour bimodality
The most evident aspect of the distribution of galaxy colours is of course the colour bimodality. In the VIPERS data, as in local surveys, this is a very general feature that is evidenced when using different rest-frame UBVRI colour combinations, spectral diagnostics such as the 4000 Å break (Garilli et al. 2014) or morphological quantities (Krywult et al. 2014, in prep.). In this work we use the (U − V) colour, as it is highly sensitive to the slope of the blue/ultraviolet continuum, representing a natural tracer for SF galaxies (see Appendix A). In particular, our U-band filter represents a good measure of the overall SF activity in our galaxies. However, similar to the classical method the colour bimodality does not take into account the contamination by AGNs or dust-obscured red galaxies (see Sect. 4.3).
 |
Fig. 6 Rest-frame U − V colour distribution in the different redshift bins, split into three broad SED galaxy types of blue galaxies (Sc/Sd and SB/Irr, blue histograms), green galaxies (Sa/Sb, green), and red (E/S0, red). The dashed line in each panel indicates the adopted separation for red and blue galaxies, defined by a fit to the local minima of the colour distributions. The colour-bimodality separation is also a good representation of the different SED types of early-type and late-type galaxies. |
4.2.1. Classification and evolution since z ~ 1.3
Another approach to segregate red and blue galaxies is to adopt a variable cut in galaxy colours that evolves with redshift (e.g., Wolf et al. 2009; Peng et al. 2010). This appears to be a more physical method to separate red from blue galaxies than assuming a fixed cut a priori without accounting for the redshift evolution.
The procedure we adopt is the following: first, we project the colour–magnitude relation onto the (U − V) colour axis, after subtracting out the slope defined by elliptical galaxies in the Coma cluster (see Sects. 4.1 and 5.1). Figure 6 illustrates the rest-frame (U − V) colour distributions, after subtracting out the Coma slope. A bimodal (U − V) colour distribution is evident across the whole redshift interval, characterized by two peaks and a well-defined minimum. The location of these three extrema depends weakly on the adopted projection method (i.e., if a reference RS slope is subtracted out or not, see Sect. 5). Next, early-type (red) galaxies are separated from late-type (blue) galaxies by measuring the local minimum in the colour distribution within each redshift bin. For the colour separation value, a simple linear evolution with redshift is assumed and by fitting the observed local minima and redshift value pairs, we derive a separation in the rest-frame (U − V) colour distribution which evolves as (U − V) = 1.1−0.25 × z, denoted with the red dashed line in Fig. 6. This partition separates well the two main populations of red and green-plus-blue galaxies. We emphasize that to measure the decrement of passive galaxies in the colour projection, the evolution of the green galaxy population needs to be considered. For this reason, we divide the rest-frame (U − V) colour distributions in Fig. 6 into the three different global SED type classes, representing the red, green and blue galaxy population. Note that for this comparison the SED types of Sc/Sd and SB/Irr were combined in order to emphasize the broader transition between the galaxy populations of the green valley and the blue cloud. Thanks to the very good statistics of VIPERS, it is possible for the first time at these redshifts to separate galaxies in the transition zone from the blue galaxy population, although this method is not corrected for possible contamination effects by dusty red galaxies.
4.3. NUVr’ classification
Red galaxy samples selected on the basis of optical colours contain a substantial contamination of ~30−40% by Seyfert 2 AGNs and/or dust obscured SF galaxies (Strateva et al. 2001; Cimatti et al. 2002; Gavazzi et al. 2003; Bell et al. 2004a; Giallongo et al. 2005; Weiner et al. 2005; Franzetti et al. 2007; Haines et al. 2008; Gallazzi et al. 2009). Dust obscuration is less significant at low redshift, where ~75% of red galaxies contain little amount of dust (Gavazzi et al. 2003; Bell et al. 2004a; Wolf et al. 2005) and for the remaining objects current space-based facilities permit a visual detection of the dust features up to z ~ 1 (e.g., McIntosh et al. 2005b; Fritz et al. 2009a,b; Tasca et al. 2009).
However, at high redshift (z > 1) the presence of dust becomes a major complication, with red galaxy samples getting significantly contaminated by dusty SF galaxies. This affects both the colour measurements and the assessment of intrinsic colour variations in the galaxies. Several alternative methods have been proposed to identify systems with colours dominated by internal dust absorption, such as mid-IR photometry (Papovich et al. 2005), an optical-NIR rest-frame colour combination, e.g., UVJ selection (Williams et al. 2009), or visual dust extinction constraints from SED modelling (Brammer et al. 2009, 2011) or a using a UV-optical-NIR colour combination (e.g., Salim et al. 2005; Arnouts et al. 2007).
 |
Fig. 7 Evolution of the rest-frame (NUV − r′) vs. (r′ − K) plane for VIPERS. A selection along the lines of of constant sSFRs (black ⟨sSFR⟩ arrow) and dust-extinction (grey SMC arrow) gives a clean separation for the majority of passive (red) and star-forming active (dusty red and blue) galaxies. The fraction of galaxies (in per cent) classified as passive and active is given in each panel. |
To explore the effects of possible dust obscuration within our early-type sample, we
introduce a combination of GALEX UV, optical and NIR fluxes. In Fig. 7 we illustrate our selection of passive red galaxies in
the rest-frame (NUV − r′) vs. (r′ − K)
plane (Arnouts et al. 2013). A similar
classification into quiescent and SF galaxies with different star formation activity level
can be obtained using (NUV − r′) vs. (r′ − J)
colours (Ilbert et al. 2010), although our
addition of the K-band permits a much sharper separation between
quiescent and galaxies with low SF activity, particularly for dust-obscured red objects at
z > 0.8
with (r′ − J) > 0.8 (AB). Further,
NUV − r′ colours represent an
excellent indicator for the current-to-past star formation ratio. This ratio decreases
with mass for star forming galaxies (Salim et al.
2005; Arnouts et al. 2007). While the NUV
passband traces stellar populations with a mean light-weighted age ⟨t⟩ ~ 108 yr, the r′ band is sensitive to
⟨t⟩ ≥ 108 yr (Martin et al. 2005) and the current to the past averaged SF rates
correlates with the birth parameter b as b = SFR(t < 108)/ ⟨SFR⟩.
Passive galaxies with de Vaucouleurs light profiles can be associated with NUV − r′ ≥ 1.70 (Vega) and
b ≤ 0.1
(Salim et al. 2005). We then define early-type
galaxies (hereafter NUVr′ selection) as all the galaxies which are redder
than 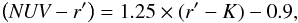 (1)which is indicated as the solid line in Fig.
7.
(1)which is indicated as the solid line in Fig.
7.
This cut is approximately equivalent to a cut at a constant star formation rate in the total galaxy sample (see e.g., Williams et al. 2009) the black ⟨sSFR⟩ arrow in the figure denotes the direction of increasing sSFR), and it is therefore quite effective at selecting galaxies with early-type SEDs. This method represents an alternative approach to the one suggested by Arnouts et al. (2007) and is a similarly powerful tool to identify dusty galaxies among the early-type galaxy population.
4.4. Completeness and contamination
In the following analysis, we adopt the SED type classification as our reference selection method (see Sect. 2.4). For each of the other selection criteria we derive their completeness in early-type galaxies (i.e., the fraction of the SED early-type galaxies which are classified as early-type galaxies with that particular selection criterion) and the contamination due to late-type galaxies (i.e., the fraction of galaxies classified as early-type with that particular selection criterion which are instead classified as late-type galaxies on the basis of the SED type classification). Figure 8 illustrates the early-type completeness and late-type contamination as a function of redshift for each selection criterion. Different lines give the completeness of red galaxies and contamination of non-red galaxies for the various selection methods, classical approach (dotted line and filled circles), colour-bimodality (solid line and blue triangles), NUVr′ selection (dashed line and open circles).
Our colour-bimodality selection of early-types proves to be highly efficient (~85%), even up to the highest redshifts. Moreover, the contamination by late-types is <10% up to z = 0.8 and reaches ~30% in the highest redshift bins. The classical approach produces a smaller contamination (~5−20%), however at the costly price of a much smaller completeness (<80% at z > 0.7). In the highest redshift bin (z > 1) its completeness is only ~45%. In terms of completeness in early-types at high redshift, the NUV − r′ selection is better than the classical approach, whereas at the same time keeping the contamination from late-type galaxies at a low level (≤20% up to z = 1.1). For the highest redshift bin, the contamination is larger and similar to that of the colour bimodality approach. Across all redshifts, the fraction of early-types in the NUV − r′ method remains quite stable at ~80−85%, even up to z = 1.3. The colour bimodality criterion has an almost constant completeness in early-type galaxies of ~90% up to z = 1, but it contains a slightly higher late-type contamination of ~5−10% than the NUV − r′ sample.
 |
Fig. 8 Completeness of early-type galaxies (lower panel) and contamination by late-type galaxies (top panel) with respect to the SED type-classified early-type galaxy population as a function of redshift for different selection methods. Classical approach (dotted line, filled circles), colour-bimodality (solid line, blue triangles), NUVr′ sample (dashed line, open circles). |
5. The evolution of the CMR since z ~ 1.3
5.1. Fitting the red sequence
For galaxies undergoing a pure passive evolution of their stellar populations it is quite simple to predict their photometric evolution in terms of luminosity and rest-frame colours. By comparing these predictions with the observed evolution of galaxies on the RS, it is therefore possible to place some constraints on the evolutionary path of the RS objects. One method often adopted to quantify the evolution in the observed properties of these galaxies is to consider the change in the best fitting linear relation between luminosity and rest-frame colour, i.e. the evolution of the average colour of the RS objects at a fixed absolute magnitude (e.g., Bell et al. 2004b; Weiner et al. 2005; Franzetti et al. 2007). The apparent simplicity of this analysis is however hiding important sources of uncertainty in the interpretation of the observed evolution. The most important one is of course the operational definition of the RS galaxies, as discussed in the previous sections, which in turn results into an uncertainty on the contaminating fraction of star-forming galaxies. We also need to consider differences in the magnitudes used to derive the observed and the rest-frame colours (aperture magnitudes versus pseudo-total ones), and also the priors used to constrain the fit. Finally, many data sets at high redshift suffer from low sample statistics that do not allow for a reliable determination of the slope of the RS relation, and therefore the fit is carried out using a fixed slope at all redshifts.
This approach was adopted in the case of the COMBO-17 photometric galaxy survey by Bell et al. (2004b), who established the following
evolution of the RS relation: 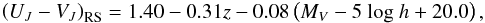 (2)where h = 0.7, assuming a fixed
slope of d(UJ − VJ)RS/d(MV) = −0.08,
as derived for elliptical galaxies in the local Coma cluster (BLE92). Another variation of
this definition is a fixed (non-evolving) parallel cut on the blue part of the CMR that
globally separates passive red (non-SF) galaxies from blue SF galaxies (e.g., Wolf et al. 2009; Ruhland et al. 2009; Brammer et al. 2009;
Whitaker et al. 2010).
(2)where h = 0.7, assuming a fixed
slope of d(UJ − VJ)RS/d(MV) = −0.08,
as derived for elliptical galaxies in the local Coma cluster (BLE92). Another variation of
this definition is a fixed (non-evolving) parallel cut on the blue part of the CMR that
globally separates passive red (non-SF) galaxies from blue SF galaxies (e.g., Wolf et al. 2009; Ruhland et al. 2009; Brammer et al. 2009;
Whitaker et al. 2010).
Local E+S0 galaxies in field and group environments display both a similar slope (d(UJ − VJ)RS/d(MV) = −0.05) and scatter (δ(UJ − VJ) = 0.06 mag (Schweizer & Seitzer 1992) across the CMR as their counterparts in clusters. However, it is still unclear if the assumption of a fixed slope holds also for field galaxies at higher redshift.
If we adopt the same methodology to fit the RS sample selected using the classical approach described in Sect. 4.1, we obtain a fit to the RS which is illustrated by the dotted red lines shown in the panels of Fig. 4. It is evident that this best-fitting relation with a fixed Coma cluster slope is somewhat too steep for the VIPERS data. We should consider that our colours are based on the CFHTLS mag_auto magnitudes that were measured in Kron-like elliptical apertures (see Sect. 2.1), and which are an approximation for total magnitudes4, while those used by BLE92 were based on fixed-aperture photometry. A difference in slope is therefore somewhat to be expected, as demonstrated by Scodeggio (2001): a CMR constructed using colour measurements within fixed apertures is steeper than a CMR based on colours established with apertures covering the effective radius of the galaxy (or pseudo-total magnitudes, for that matter).
 |
Fig. 9 Evolution of the RS using a variable slope with redshift. The CMR is divided into two redshift bins at low (0.5 < z ≤ 0.7) and high (0.7 < z ≤ 0.9) redshift. Galaxies are colour-coded with respect to their derived SED type. The number of galaxies for a specific SED type is shown in each slice. The solid line is the best-fit to the RS adopting the slope as derived from VIPERS within the selection criteria indicated with the dotted line (see text for details). |
Since the combination of large size and accurate photometry of VIPERS allows us to derive
with high precision the slope and scatter of the RS as a function of redshift, we decided
to explore the different results one would obtain with and without the fixed-slope
constraint on the fitting of the RS. Figure 9
illustrates the CMR for VIPERS for two redshift slices at 0.5 < z ≤ 0.7 and
0.7 < z ≤ 0.9. When we define RS galaxies using
the bimodality in colour distribution, as described in Sect. 4.2.1 (the partitioning colour is identified in Fig. 9 by the dotted line), we obtain the following RS
best-fitting relations at redshift ⟨z⟩ = 0.55:
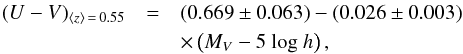 (3)and at redshift ⟨z⟩ = 0.80:
(3)and at redshift ⟨z⟩ = 0.80:
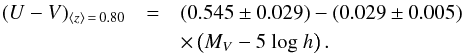 (4)For consistency with the classical method, we
fitted a free variable slope to the whole redshift interval at 0.4 < z ≤ 1.3 probed by
VIPERS, giving similar results within the uncertainties as shown for the two redshift
slices in Fig. 9. We therefore conclude that there is
no evidence of an evolving slope from z = 1 to z = 0.4.
(4)For consistency with the classical method, we
fitted a free variable slope to the whole redshift interval at 0.4 < z ≤ 1.3 probed by
VIPERS, giving similar results within the uncertainties as shown for the two redshift
slices in Fig. 9. We therefore conclude that there is
no evidence of an evolving slope from z = 1 to z = 0.4.
The slope we obtain is significantly flatter than the one obtained for the Coma cluster by BLE92, but entirely compatible with the flatter slope obtained by Scodeggio (2001) using variable apertures to cover a fixed fraction of the galaxy total light. However, the effect that the different slope might have on the observed evolution of the properties of the RS turns out to be almost negligible. The mean RS colour that is deduced from the best-fitting linear relation where the bulk of the RS galaxies are located (absolute magnitude range between − 22 and − 20), changes by less than 0.05 mag, which is significantly less than the redshift evolution discussed in the following section.
 |
Fig. 10 Evolution of the CMR intercepts in (U − V) at MV − 5 log h = −20 for red-sequence galaxies as a function of redshift. The solid line is a least-square fit to the VIPERS data including the local SDSS reference (filled black square). The blue area reflects the total observed scatter due to systematic uncertainties, whereas uncertainties due to Poisson noise are indicated with single error bars. The grey shaded area shows the observed measurement errors of the COMBO-17 data set by Bell et al. (2004b). In the bottom left corner typical uncertainties due to filter and rest-frame transformations are shown. |
5.2. Evolution of the CMR intercept
Figure 10 displays the evolution of the RS for the VIPERS sample (filled circles) as a function of redshift. To allow a fair comparison of our results with previous works, the evolution of the RS has been computed following the classical RS approach (see Sects. 4.1 and 5.1). The literature data comprise various surveys, using either spectroscopic (zsp) or photometric redshifts (zph): the COMBO-17 sample (zph, open circles, Bell et al. 2004b), a study in the Extended Chandra Deep Field South (E-CDFS, zsp, crosses, Ruhland et al. 2009), an SDSS and DEEP2 analysis (zsp, inverted triangles, Blanton 2006), the multi-wavelength medium NIR-band photometric study of NEWFIRM Medium-Band-Survey (NMBS, zph, open squares, Whitaker et al. 2010), and the results of the VVDS (zsp, triangles, Franzetti et al. 2007). The solid line is a fit to the VIPERS data but also including the SDSS measurement (filled black square, Bell et al. 2004b) as a local reference point at z = 0. Note that Blanton (2006) derived a slightly different measurement for SDSS (inverted triangle) which is consistent with the SDSS scatter. The measurement uncertainties on the RS intercepts which arise from Poissonian statistics were derived using bisector fits with the errors on the bisectors being evaluated through a bootstrap resampling of the data (Fritz et al. 2005). The total observed measurement errors including systematic uncertainties due to filter transformations and zero-point variations in the photometry are shown with the blue error corridor. For comparison purposes, the observed measurement error bars of the COMBO-17 data (Bell et al. 2004b) are shown as a grey shaded area.
(U − V) colour intercept evolution at MV − 5 log h = −20 as a function of redshift for a fixed slope of d(U − V)/d(MV) = −0.08.
The average evolution of the VIPERS RS for the classical selection criterion can be
expressed as 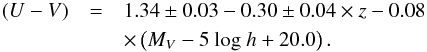 (5)Table 2 lists the (U − V) colour intercept evolution
at MV − 5 log h = −20
as a function of redshift for a fixed slope of d(U − V)/d(MV) = −0.08.
If the VIPERS sample is split into sub-samples for the W1 and W4 fields, a similar
evolution of the RS with similar uncertainties is found. Uncertainties due to cosmic
variance have only a weak influence on the derived evolution.
(5)Table 2 lists the (U − V) colour intercept evolution
at MV − 5 log h = −20
as a function of redshift for a fixed slope of d(U − V)/d(MV) = −0.08.
If the VIPERS sample is split into sub-samples for the W1 and W4 fields, a similar
evolution of the RS with similar uncertainties is found. Uncertainties due to cosmic
variance have only a weak influence on the derived evolution.
Overall, the VIPERS results themselves show a similar evolution with redshift compared to
various surveys in the literature which adopted the classical approach but with a
significantly higher precision and statistics. Galaxies located on the RS display a
moderate evolution of the intercept of Δ(U − V) = 0.44 ± 0.12 since
z ~ 1.3 up to the present day. Across the
redshift interval 0.4 < z < 1.3 the average RS intercept of
VIPERS evolves as Δ(U − V) = 0.28 ± 0.14. This
result alone is inconsistent with stellar population synthesis predictions of
Δ(U − V) = 0.09 ± 0.02 that assume a
high formation redshift for the bulk of the stars at zform = 4 and a
subsequent passive evolution of their stellar populations across the redshift range
0.4 < z < 1.3 (see Sect. 7.1). However, there could be a small systematic difference in the
adopted photometric zero-point (most likely due to the different U-band filters) which
partially contributes to the intercept evolution at z ≳ 0.8. The most
significant difference visible in Fig. 10 is at
redshift z ~ 1.1 between the VIPERS and VVDS point, but
differences in sample selection and area coverage (the VVDS being a purely magnitude
limited survey to  over ~0.7 deg2), can totally explain this
difference. At lower redshift the VIPERS data are entirely consistent with previous
measurements.
over ~0.7 deg2), can totally explain this
difference. At lower redshift the VIPERS data are entirely consistent with previous
measurements.
We have tested the impact of various systematic effects on our data. In general, possible systematic differences in the evolution of the intercept among the different surveys are most likely either due to sample statistics, differences in the filter systems or the impact of cosmic variance. In Appendices B and C we discuss the completeness of the VIPERS sample at high redshift and the systematic uncertainties introduced due to cosmic variance. VIPERS comprises the largest number of galaxies between 0.5 < z < 1.2 and at the same time covers the widest sky area in comparison to previous galaxy surveys. Therefore, both restrictions due to low number statistics or cosmic variance can be largely ruled out. Nevertheless, we have estimated the systematic effect of cosmic variance using the prescription by (Moster et al. 2011, see Appendix C for details). For RS galaxies between 0.4 < z < 1.3, the uncertainties arising from cosmic variance vary in the range 0.04 < log (M⋆/M⊙) < 0.07, with a median of ⟨log (M⋆/M⊙)⟩ = 0.05. We have also tested the impact on our findings of practical choice, e.g., using different redshift bin sizes, but our choice does not affect the results within the measured uncertainties. A quantitative comparison with previous works is complicated by the fact that many surveys do not provide the exact prescription of their used filter transmission curves. This introduces uncertainties in the adopted filter passband transformations and conversion to rest-frame magnitudes when comparing different surveys, which depend on their used spectral templates (see also Appendix A). At the left bottom of Fig. 10 the typical average uncertainty in filter transformations is indicated with an error bar. This uncertainty combines contributions from using different U and V-band filter passbands and uncertainties introduced from the conversion to absolute rest-frame colours.
 |
Fig. 11 Evolution of the RS for different selection criteria of early-type galaxies. The colour evolution of the red-sequence as described by the CMR intercepts in (U − V) at MV − 5 log h = −20 as a function of redshift. The evolution of the RS is shown for different selection criteria colour-bimodality (blue filled triangles), SED type classification (red open squares) and the classical method (black filled circles). Measurement error bars are displayed for each criteria. All relations are least-square fits to the respective VIPERS selection criteria including the local SDSS reference (filled black square). |
In Fig. 11 we compare the measured evolution of the RS with redshift for different selection criteria, but keeping a fixed, non-evolving intercept as for the classical method. The RS evolution is shown for the colour-bimodality criterion (blue filled triangles), SED type classification (green open squares), the NUVr′ selection (red open circles), and the classical method (black filled circles). In comparison to the classical approach, all other methods show a steeper evolution. It is somewhat expected that the classical approach displays a weaker evolution as this method is biased towards the few most brightest and reddest galaxies, whereas the other criteria consider the overall early-type galaxy population including also early-type galaxies with bluer colours. It is interesting to note that among the alternative selection criteria of early-type galaxies there are not large variations. The method based on the SED types produces results very similar to those obtained by the colour-bimodality and the NUVr′ selection. The good agreement among these different selection methods suggests that our early-type galaxy sample contains little amount of dust and that the effects of dust obscuration become more dominant at higher redshifts (z > 1.3).
Apart from different selection criteria, internal colour variations in the galaxies might impact the derived results. For bright, low-redshift galaxies (z ≲ 0.45), the adopted aperture in the photometry might restrict our colour measurements to the central (redder) parts of the galaxies. Internal colour gradients could change the evolution of the RS intercept at the 10% level, resulting in bluer average colours for low redshift galaxies (e.g., Peletier et al. 1990). As throughout our analysis the same aperture size is adopted in all photometric bands, possible internal colour gradients are neglected, which might give slightly steeper colour relations for brighter galaxies. In particular, the effect of internal colour gradients might cause our lowest redshift bin to display a slightly redder evolution of the RS intercept compared to the redshift evolution found for the higher redshift data.
5.3. Scatter across the CMR
Over the past years observations have found evidence for a rapid increase of the total stellar mass of passive red-sequence galaxies since z ~ 1 (e.g., Bell et al. 2004b; Brown et al. 2007; Bundy et al. 2005; Faber et al. 2007; Scarlata et al. 2007). This evolutionary process reveals itself in terms of an increase in the number density of quiescent sub-L∗ galaxies (e.g., Borch et al. 2006; Faber et al. 2007). One possible scenario is that the red-sequence population is continuously supplied with a population of massive blue galaxies that have their star-formation activity truncated or quenched over a short time scale (Bell et al. 2004b, 2007; Faber et al. 2007). Such processes would manifest themselves primarily in a larger scatter in the CMR because the continuous agglomeration of blue galaxies onto the RS will cause a broadening of the RS.
 |
Fig. 12 Intrinsic (filled symbols) and observed scatter (open symbols) in the rest-frame (U − V) colours of passive galaxies. The scatter due to measurement uncertainties is subtracted from the observed scatter in quadrature. Literature data are shown in grey. Associated data for field galaxy studies (triangles or crosses) are joined with lines, studies based on galaxy clusters are shown as stars. |
Figure 12 illustrates the evolution of the scatter of the RS galaxies as a function of redshift. We compute the intrinsic scatter (filled symbols) by subtracting the scatter due to measurement uncertainties from the observed scatter (open symbols) in quadrature. The results are shown for the classical approach (blue circles) and the SED type selection (green squares). Several interesting trends can be seen. The scatter derived from the classical method is constant up to z = 1, whereas the scatter measured on the basis of the SED type classification is increasing with redshift. Our highest-redshift measurement at z = 1.07 is partly affected by incompleteness effects and the real scatter is most likely larger by Δ(U − V) = 0.05 mag. The VIPERS sample is in good agreement with previous field galaxy surveys in the E-CDFS (Ruhland et al. 2009) and the NMBS (Whitaker et al. 2010) that use a similar computation for the scatter of the RS, whereas field galaxies from the PISCES project (Tanaka et al. 2005) display somewhat a larger scatter. Interestingly, all field galaxy surveys predict a larger scatter of the RS than the one obtained for cluster galaxies, both in the local galaxy cluster represented by the Coma cluster (open triangle, BLE92) and at higher redshift for several high-redshift galaxy clusters (star symbols). The cluster measurements comprise data for 13 clusters in the literature over the redshift range 0.18 < z ≲ 1.46 (Ellis et al. 1997; Blakeslee et al. 2003; Blanton 2006; Mei et al. 2006a,b; van Dokkum et al. 2008; Hilton et al. 2009). Despite possible differences in the colour measurements between cluster and field studies (the former usually adopt fixed apertures and restrict the RS to a few of the most luminous cluster members), the scatter in the rest-frame (U − V) colour for quiescent galaxies in the field increases with redshift and is a factor of more than two larger than in clusters at the same redshift. This points towards a dependence of the scatter and its evolution on the environment. A possibility is that field galaxies consist of younger stellar populations compared to their cluster counterparts (Bernardi et al. 1998; Fritz et al. 2009a). Alternatively, the larger scatter in the field environment could be the result of a mixed population of old and young quiescent galaxies, whereas in clusters the RS is only populated by older red galaxies that formed their bulk of stars at higher redshift.
6. The luminosity function in VIPERS
The luminosity function (LF) of field galaxies represents a fundamental diagnostic to probe the star formation history of (blue) galaxies and the gravitational mass assembly history of (red) passive galaxies. In particular, since it has been speculated that the mass assembly of red early-type galaxies could take place on different time-scales than the much earlier formation of their stellar populations (Baugh et al. 1996; van Dokkum & Franx 2001), the observed stellar mass-to-light ratios and the evolution of the CMR of passive galaxies could be non-reliable tracers of the mass assembly process, while the LF of RS galaxies would provide a much more sensitive diagnostic.
In this work the LFs were computed using the “Algorithm for Luminosity Function” (ALF) as
described in Ilbert et al. (2005). ALF was
originally developed for the VVDS project (Ilbert et al.
2004, 2005) and is a tool that implements
several standard estimators of the LF: the non-parametric 1/Vmax (Schmidt 1968), C+ (Lynden-Bell 1971; Zucca et al. 1997), and
SWML (Efstathiou et al. 1988), and the parametric STY
(Sandage et al. 1979). For the parametric STY
estimator the empirical Schechter function (Schechter
1976) was adopted: 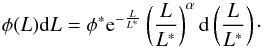 (6)While the normalisation is directly done for
the 1/Vmax estimator, the SWML, STY and
C+ estimators are
independent of the spatial density distribution and lose their normalisation. For these
three estimators we adopt the Efstathiou et al.
(1988) density estimator to recover their normalisation (see Ilbert et al. 2005, for details). The advantage of ALF is its capability
to use the same data to provide simultaneously the four different estimators, and this
allows for an easy verification of the robustness of the luminosity estimates against the
effects of binning (in absolute magnitude), of spatial inhomogeneities, or of incompleteness
in spectral type. Absolute magnitudes were derived as discussed in Sect. 2.3. For a given redshift, different galaxy types appear in
different absolute magnitude ranges because of the combination of the fixed apparent
magnitude limit used for sample selection with the k-corrections. To avoid in
particular a bias at the faint-end of the LF, the estimates of the LF are restricted to only
those galaxies within the absolute magnitude range for which the estimators are in agreement
(Ilbert et al. 2004). At magnitudes fainter than
this limit, the 1/Vmax estimator provides number densities
which are underestimated, therefore giving a lower limit of the LF slope. The
φ∗
values are computed for each point of the α − M∗ error contour at
1σ confidence
level. The uncertainty on φ∗ is derived from the maximum between
Poissonian error and error derived from the error contour.
(6)While the normalisation is directly done for
the 1/Vmax estimator, the SWML, STY and
C+ estimators are
independent of the spatial density distribution and lose their normalisation. For these
three estimators we adopt the Efstathiou et al.
(1988) density estimator to recover their normalisation (see Ilbert et al. 2005, for details). The advantage of ALF is its capability
to use the same data to provide simultaneously the four different estimators, and this
allows for an easy verification of the robustness of the luminosity estimates against the
effects of binning (in absolute magnitude), of spatial inhomogeneities, or of incompleteness
in spectral type. Absolute magnitudes were derived as discussed in Sect. 2.3. For a given redshift, different galaxy types appear in
different absolute magnitude ranges because of the combination of the fixed apparent
magnitude limit used for sample selection with the k-corrections. To avoid in
particular a bias at the faint-end of the LF, the estimates of the LF are restricted to only
those galaxies within the absolute magnitude range for which the estimators are in agreement
(Ilbert et al. 2004). At magnitudes fainter than
this limit, the 1/Vmax estimator provides number densities
which are underestimated, therefore giving a lower limit of the LF slope. The
φ∗
values are computed for each point of the α − M∗ error contour at
1σ confidence
level. The uncertainty on φ∗ is derived from the maximum between
Poissonian error and error derived from the error contour.
 |
Fig. 13 Rest-frame B-band luminosity function VIPERS from z = 0.5 to z = 1.3. The LF is shown for the total sample (black circles), for red galaxies defined using the colour-bimodality (red triangles, solid line), and for red galaxies selected using the SED criterion (red squares, dashed line). Lines indicate the fits to the luminosity function using a Schechter function. For reference, the black dotted line shows the Schechter function of a local sample by (Ilbert et al. 2005). |
 |
Fig. 14 Comparison of the VIPERS B-band LF to previous measurements. Literature data include the LF of VVDS (Ilbert et al. 2005, blue squares), the LF of DEEP2+COMBO-17 (Faber et al. 2007, dashed orange line), the LF of red early-type galaxies in the VVDS (Zucca et al. 2006, blue squares), the LF of red galaxies in the NDWFS (Brown et al. 2007, long-dashed green line) and the LF of galaxies in AGES (Cool et al. 2012, dot-dashed brown line). The numbers in the brackets denote the redshift interval of the respective LF. Left: LF for all galaxies. Right: LF for red galaxies. |
All LFs are constructed for the rest-frame Johnson B-band, which is most appropriate for the median redshift of the VIPERS sample at z ~ 0.70. This choice is driven by the fact that the dependency of the absolute magnitudes on the models is reduced and any possible bias arising from different spectral types are minimized (Ilbert et al. 2005). Furthermore, as the B-band is a common filter choice, a comparison to previous results in the literature is straightforward. Incompleteness in the survey was corrected for through the weighting scheme described in Sect. 2.6.2.
Schechter parameters and associated one sigma errors (2Δ ln ℒ = 1) of the global VIPERS LF and the LF for different sub-samples derived in the rest-frame standard B-band filter system. Parameters listed without errors are set “ad hoc” to the given value.
The VIPERS sample allows us to explore the evolution of the LF over a significant redshift range, but in particular for a large sample with homogeneous selection function over a wide area. The B-band LF of the global VIPERS sample is shown in Fig. 13. To be consistent with our analysis of the GSMF (D13), we adopt here the same redshift bins used in that work. The symbols with error bars show the results obtained with the 1/Vmax method. The solid lines are the result of the STY estimator (Sandage et al. 1979), which is independent from the adopted bin sizes, and where the likelihood of the present galaxy sample is maximized by assuming that the underlying LF can be parameterized with a Schechter (1976) function. As a reference, in all panels the dotted black line shows the Schechter fit to a local sample from the VVDS at 0.05 < z < 0.20 (Ilbert et al. 2005). This reference sample is comparable within ΔMB < 0.05 mag to the local SDSS sample of Bell et al. (2003).
The evolution of the bright part of the LFs with redshift becomes evident at high-redshift (0.8 < z < 1.2) with 1/Vmax number densities being higher than the Schechter function (see also Fig. 14).
Given our large sample, and our luminosity coverage, in the redshift range 0.5 < z < 0.8 the faint-end slope of the STY estimator was determined as part of the fitting process. Because the sample at higher redshifts becomes incomplete at faint luminosities, the slope was kept fixed at the values of α = −1.3 and α = 0.3 for the total and red sample, respectively. When the two VIPERS fields are compared, the shape and slope of the LF are very similar. At high-redshift (0.8 < z < 1.2), there is some evidence for an underabundance of red luminous galaxies in W4 compared to W1, with differences consistent with the effects of cosmic variance or environmental effects.
We have shown that the evolution of the RS depends to some extent on the selection criteria of red passive galaxies. It is interesting, therefore, to look if similar effects are observed in the LF. To explore the LF for different galaxy types, we separated red and blue galaxies on the basis of the colour-bimodality and the SED type classification. The B-band LF of the RS galaxies for the two different selection criteria are shown in Fig. 13. Both selection criteria give rise to very similar LFs, with only some differences at z ≳ 0.9. The slope of the LF is flatter for red passive galaxies compared to the global LF, while across the whole redshift interval z = 0.5 to z = 1.3 the red galaxy population contributes significantly to the bright part of the global LF. These findings are in good agreement with previous surveys covering smaller areas, based on either photometric or spectroscopic redshifts (Ilbert et al. 2004, 2005; Cimatti et al. 2006; Zucca et al. 2006, 2009; Brown et al. 2007; Faber et al. 2007). In Table 3 we give for each redshift bin the Schechter parameters and the corresponding one sigma errors measured with the STY estimator. Results are shown for the global LF and for the two separate LFs for the red galaxy samples.
6.1. Comparison with the literature
Figure 14 shows the B-band LF of the total VIPERS sample (left panel) and the LF of red galaxies (right panel) compared to LF estimates from the literature. For display purposes, only the red galaxy sample selected on the basis of the colour-bimodality is shown. The literature data include the LF of VVDS (Ilbert et al. 2005, blue squares), DEEP2+COMBO-17 data (Faber et al. 2007, orange dashed line), and the LFs of early-type galaxies in the VVDS (Zucca et al. 2006, blue squares), red galaxies in the NDWFS (Brown et al. 2007, green long-dashed line), and the LF of galaxies in AGES (Cool et al. 2012, brown dot-dashed line). As the different LFs were not constructed in exactly identical redshift intervals, the numbers in the brackets denote the redshift range of the respective LF. Overall, we find a good agreement between the different LFs across the redshift range 0.5 < z < 1.3, with possibly some differences for bright galaxies. The unique large volume probed by VIPERS at high redshift leads to a higher completeness for rare, very luminous galaxies (MV − 5 log h < −23) at high redshift (z = 0.8−1.3), extending by more than one magnitude the effective sampling of the bright-end of the LF. As demonstrated in Sect. 3, these very luminous objects are also massive systems up to masses of log (M⋆/M⊙) ≤ 11.7 at z ~ 1.
 |
Fig. 15 Comparison of RS intercept evolution with the rest-frame colour evolution of stellar population models using different burst duration time scales τ. Only PEGASE models with best-fitting models are shown. Dotted lines are for a zf = 2.5, dashed lines for zf = 3. The shaded area denotes the variation of the observed evolution in the RS intercept for different selection criteria of early-type galaxies. |
7. Stellar population modelling of the red-sequence
7.1. Imprints on the evolution of the RS
To assess the evolution of the RS as a function of redshift we confront our measurements of the CMR intercept with the predictions of stellar population synthesis modelling.
In the context of single burst models, the evolution of the CMR intercept follows the global trends of the expected passive reddening and fading of stellar populations formed at high redshift (van Dokkum & Franx 2001; Franzetti et al. 2007). Variations of the CMR intercept as a function of redshift are mainly driven by the a priori assumed star formation history. The intercept itself depends instead primarily on variations of the metallicity content of the stellar populations with minor contributions due to variations in the stellar population ages.
We have constructed stellar population (SP) models using the PEGASE2 library (Fioc & Rocca-Volmerange 1997). The SP models are parameterised by a short-burst of SF starting at an initial formation redshift in the range 1.5 < zf < 5.0 and with a duration τ in the range 0.1−3.0 Gyr. The metallicity content in the models is not held fixed but varies as the stellar population evolves with redshift.
Figure 15 shows the comparison of the predicted rest-frame colour evolution for different stellar population models with our observational VIPERS results. For display purposes, only a limited range of models, those that best reproduce the observations, are shown. The dotted lines are for a formation redshift of 2.5, while the dashed ones are for a formation redshift of 3. The VIPERS data rule out several model predictions with relatively high confidence. Models where the most-recent star formation burst in galaxies was established at zf ≤ 1.5 predict too much evolution in the RS, and do not match our data. Conversely, models with a formation redshift of zf ≥ 4 result in a much smaller evolution of the (U − V) colour across the redshift range covered by our data, giving colours at z = 1 that are already too red and allowing only for a very modest colour evolution of Δ(U − V) ~ 0.2 mag to the present day. Furthermore, the observations rule out SFHs with either a very extended burst (τ > 0.8), mainly because of the fact that the RS is already in place at z ~ 0.9, or with an extremely short one (τ < 0.3), mainly because in that case all the stars would have low metallicity and the resulting RS would be bluer than observed at z < 0.6. Our data favour SFHs with 0.5 ≤ τ ≤ 0.8, although models with 0.1 ≤ τ ≤ 0.3 and zf = 2.5 cannot be completely ruled out. These latter predictions also nicely describe the data at lower redshift down to the present-day values indicated by local SDSS reference value (black filled square). In particular, the model prescriptions with 0.7 ≤ τ ≤ 0.8 precisely end up in the SDSS measurement at z = 0. From this comparison, we conclude that assuming a starting point at z = 1.3, the build-up of the RS happened rapidly within a very short time span of only ~1.5 Gyr. In such a scenario, early-type galaxies at high redshift (0.9 ≲ z ≲ 1.1) that have not yet moved to the RS should still show signs of recent SF activity.
 |
Fig. 16 Evolution in |
7.2. The evolution of the luminosity function since z = 1.3
The evolution of the LF parameters provides important information on the evolution of the galaxy population and the different transformation processes the galaxies experience. Changes in the characteristic Schechter magnitude M∗ reflect the aging of the stellar populations in galaxies, while changes in φ∗ give information on the galaxy number density, allowing us to estimate the fraction of objects that undergo merging or fading processes.
Figure 16 shows the evolution of the Schechter
function parameters 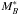 and φ∗ with redshift
for the total VIPERS sample (left panels) and for red galaxies only (right panels). In the
top panels, the dashed lines indicate the evolution in
and φ∗ with redshift
for the total VIPERS sample (left panels) and for red galaxies only (right panels). In the
top panels, the dashed lines indicate the evolution in
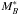 as predicted by the PEGASE models with
formation redshift zf = 2 and various burst duration
τ (see
Sect. 7.1), which were calibrated to match the local
SDSS measurements. For comparison, we also show literature data including the COMBO-17
(Bell et al. 2004b), FDF (Gabasch et al. 2004), field early-type galaxies in GOODS (Ferreras et al. 2005), VVDS (Ilbert et al. 2005), early-type galaxies from the VVDS (Zucca et al. 2006), and DEEP2 and COMBO-17 data sets
(Faber et al. 2007), red galaxies in the NDWFS
(Brown et al. 2007), and galaxies in AGES (Cool et al. 2012). Magnitudes of the different surveys
were transformed to the concordance cosmology and converted to Johnson-Cousins
B-band
magnitudes in the Vega system using MJ = MAB + 0.084
mag. For the total VIPERS galaxy population
as predicted by the PEGASE models with
formation redshift zf = 2 and various burst duration
τ (see
Sect. 7.1), which were calibrated to match the local
SDSS measurements. For comparison, we also show literature data including the COMBO-17
(Bell et al. 2004b), FDF (Gabasch et al. 2004), field early-type galaxies in GOODS (Ferreras et al. 2005), VVDS (Ilbert et al. 2005), early-type galaxies from the VVDS (Zucca et al. 2006), and DEEP2 and COMBO-17 data sets
(Faber et al. 2007), red galaxies in the NDWFS
(Brown et al. 2007), and galaxies in AGES (Cool et al. 2012). Magnitudes of the different surveys
were transformed to the concordance cosmology and converted to Johnson-Cousins
B-band
magnitudes in the Vega system using MJ = MAB + 0.084
mag. For the total VIPERS galaxy population 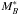 brightens by ~1.04 ± 0.06 mag over the redshift range
z = 0.5 to
z = 1.3
(see upper left panel), while RS galaxies show a brightening of
brightens by ~1.04 ± 0.06 mag over the redshift range
z = 0.5 to
z = 1.3
(see upper left panel), while RS galaxies show a brightening of
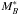 of 1.09 ± 0.10 mag. There are slight
differences in the
of 1.09 ± 0.10 mag. There are slight
differences in the 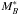 evolution between red galaxies classified
with the bimodality and the SED type classification. The SED type classification is in
better agreement with the PEGASE models as in this selection criterion galaxies with
somewhat younger ages are also considered. Overall, the number density φ∗ for red
galaxies rises over the past 9 Gyr, with a stronger increase from z = 1.3 to z ~ 0.7, followed by a
weaker rise from z < 0.7 to the present-day. This result confirms
our findings on the evolution of the RS and indicates first a rise in the build-up of
massive galaxies at 0.7 ≲ z ≲ 1.3 over a relatively short time period of
~1.5 Gyr, followed by a
continuous slower assembly over cosmic time.
evolution between red galaxies classified
with the bimodality and the SED type classification. The SED type classification is in
better agreement with the PEGASE models as in this selection criterion galaxies with
somewhat younger ages are also considered. Overall, the number density φ∗ for red
galaxies rises over the past 9 Gyr, with a stronger increase from z = 1.3 to z ~ 0.7, followed by a
weaker rise from z < 0.7 to the present-day. This result confirms
our findings on the evolution of the RS and indicates first a rise in the build-up of
massive galaxies at 0.7 ≲ z ≲ 1.3 over a relatively short time period of
~1.5 Gyr, followed by a
continuous slower assembly over cosmic time.
To probe in more detail the mass assembly of the RS, we compare in Fig. 16 the number density evolution of red, quiescent galaxies to predictions from stellar population synthesis models that involve a shut down of star formation, such as a sharp truncation or a quenching process. Sharp truncation models, resulting in a purely passive evolution of the stellar population, can reproduce quite well the evolution of M∗, but they fail to explain the build-up of the number density. An example of such a model prediction, constructed with a simple stellar population with a single metallicity formed at z = 3 is shown by the dotted line in the bottom panels of the figure. In contrast, quenching models predict a gradual increase in the RS galaxies number density with time. Here we have taken the quenching models from Harker et al. (2006), which consist of a 1 Gyr long burst of star formation at z = 5, which consumes 80%−99% of the gas reservoir, followed by progressive quenching of the star forming galaxies starting at zquench = 1.5 or zquench = 2. We notice that the resulting star formation history for these models is actually quite similar to the one we used to derive the models used in the previous section to describe the evolution of the RS colour. The φ∗ of the quenched models was normalised to the observed φ∗ of red galaxies at z = 0.5. Note that despite the simple assumptions in the models, they describe the observed trends reasonably well.
The lower right panel of Fig. 16 shows that the evolution of the red galaxy populations in VIPERS follows quite closely the tracks for quenching models with quenching onset at zquench = 1.5 (dot-dashed line), with possibly an indication that an even later onset of the quenching could better represent the highest redshift bin data. A similar picture can be drawn from other surveys (Ferreras et al. 2005; Zucca et al. 2006; Faber et al. 2007), although these data show a larger scatter because of higher measurement uncertainties. For the VIPERS colour bimodality sample the φ∗ of the RS galaxies rises by a factor of 4.4 ± 0.9 from z = 1 to the present-day, whereas for the SED-sample the φ∗ of RS galaxies increases by a factor of 5.8 ± 0.9 over the same time interval. The φ∗ of the quenching model rises by a factor of 3.8 for zquench = 2.0 and by a factor of 5.1 for zquench = 1.5. Both model values are within the observed ranges, although the VIPERS data at high redshift (z > 0.9) prefer the predictions with zquench = 1.5. We find therefore another indirect indication towards early-type galaxies at high redshift (0.9 ≲ z ≲ 1.1) still showing signs of recent SF activity.
7.3. Evidence of enhanced star formation in the spectral properties of the early-type galaxy population
To verify the indirect evidence for a recent star formation activity among redshift z ~ 1 RS galaxies, discussed in the previous sections, we analyse directly the properties of these galaxies by stacking their spectra. Figure 17 illustrates examples of (rest frame) stacked early-type galaxy spectra at low-redshift (0.5 < z < 0.6, black) and at high-redshift (0.9 < z < 1.0, red) selected on the basis of the SED type classification. Spectra of RS galaxies selected using the colour-bimodality method or the NUVr′ criteria are virtually indistinguishable from the ones shown. For the stacking process early-type galaxies within an absolute magnitude range of − 22.5 ≥ MV ≥ −23.0 were selected. The stacked spectra comprise a similar number of individual spectra (Nspec ~ 100 at 0.5 < z < 0.6, Nspec ~ 180 at 0.9 < z < 1.0) and represent the typical averaged spectra of early-type galaxies at the respective redshift range. At low-redshift the stacked spectrum is that of a purely passive, red and quiescent galaxy. However, the high-redshift counterpart displays clear signs of ongoing SF as indicated by the detection of a weak [O II] 3727 emission line.
 |
Fig. 17 Example of stacked spectra of early-type galaxies at 0.5 < z < 0.6 (black) and 0.9 < z < 1.0 (red, shifted for display purposes). All spectra should represent passive, red and quiescent galaxies. Early-type galaxies at high redshift show clear evidence of ongoing SF which is supported by weak [O II] 3727 emission. Early-type galaxies have been selected based on the SED type classification. Spectra of early-type galaxies selected using other criteria look very similar. Prominent absorption and emission features in the spectra are denoted with dotted lines. |
To quantify and constrain the recent star formation in the stacked spectra of early-type galaxies at high-redshift, the main questions of interest are the SFR, the mass fraction involved in the star formation and the duration of the star formation episode. As the individual spectra used in the stacking have been re-normalized to reproduce the total flux observed photometrically for each galaxy, we assume the measured [O II] 3727 equivalent width to be representative for the global value of the average VIPERS galaxy. Transforming the observed [O II] 3727 equivalent widths to rest-frame and assuming the relationship by Kennicutt (1992) with a global extinction correction of E(Hα) = 1 mag, we derive for the whole sample of early-type galaxies a median SFR of 1.8 M⊙ yr-1. The different stacked spectra result in similar SFRs estimates: NUVr′: median ⟨SFR⟩ = 1.9 M⊙ yr-1, colour-bimodality: ⟨SFR⟩ = 2.2 M⊙ yr-1, SED types: ⟨SFR⟩ = 1.3 M⊙ yr-1. This suggests that a fraction between 1 and 3% of the stellar mass of each galaxy is on average involved in the star formation burst which will exhaust the gas within ~0.10−0.14 Gyr, adopting a burst duration time scale of td ∝ M∗/SFR (Noeske et al. 2007).
In the nearby universe a non negligible fraction of passive galaxies on the red sequence shows signs of emission lines with characteristic line ratios of low ionisation nuclear emission-line regions (LINERs; Yan et al. 2006; Schawinski et al. 2007). Red galaxies with strong LINER features exhibit on average younger ages than their passive counterparts without emission, suggesting a connection between the local galaxy activity and internal processes (e.g., shock ionization by starburst winds, photoionization by (post-AGB) stars or AGNs) or external mechanisms that could be responsible for the emission enhancement (e.g., cooling flows, photoionization by low-luminosity-AGNs (LLAGNs), shock ionization due to gas accretion, galaxy interactions and merger activity). Because of the spectral coverage, VIPERS galaxy spectra at high redshift are restricted to the [O II] 3727 emission line as a star formation proxy. To quantify a possible contribution of LLAGNs in our red galaxy sample, we have analysed the morphologies of massive galaxies with M⊙ > 11.2. The majority of these objects appear to be indeed isolated and massive systems. There is only a small fraction (< 20%) of galaxies which shows some signs of disturbed morphologies or possible galaxy interaction with a close neighbour. This suggests that external mechanisms play only a minor rule in triggering star formation activity. It is outside the scope of the current work to speculate about possible physical triggering mechnanisms for the quenching of star formation. In the future, we will explore in more detail which processes are responsible and contribute to the star formation/AGN activity detected in our galaxies.
Our findings support the scenario for the build-up of the RS described in Sect. 7.1, where massive early-type galaxies show evidence for ongoing SF activity at z ~ 1 and subsequently experience an efficient shut-down mechanism of their SF over a short time scale of ~1.5 Gyr with a rapid exhaustion of their gas reservoirs.
8. Discussion
Our results of Fig. 16 and Table 3 indicate a modest but significant increase in the number density of luminous massive galaxies (M∗ > 1011 M⊙) by a factor of 2.4 over the past ~9 Gyr. This is in agreement with the factor of 1.8 increase between z = 1 and z = 0.6 found at corresponding masses in our analysis of the VIPERS stellar mass function (D13), with lower-mass systems increasing over the same redshift interval by a factor of 2.5. This trend is independent of the selection criteria used to define the early-type (quiescent) galaxy population, and is qualitatively consistent with the overall observed trend in the evolution of the stellar mass density since z ~ 3.5 (Ilbert et al. 2005, 2013, and references therein), while being significantly different from the predictions of a purely passive evolution model.
The shapes of the LF in Fig. 13 and the MF of D13 show that this evolution is strongly dependent on the luminosity and mass of galaxies: the higher the luminosity (mass), the smaller the evolution. The diverging faint-end slopes of the LF (shown here) and the MF (shown in D13), between the early-type and the global galaxy populations at z < 1 imply that the physical processes that switch-off star formation have to be more efficient for massive/luminous galaxies.
This effect is shown equally well by the CMR of Fig. 4, in which the bright end of the RS is already populated at z ~ 1, with only a modest increase in the number of luminous/massive red galaxies at later epochs. Models of galaxy evolution that can reproduce these trends can be roughly divided between merger-dominated models, where dry mergers between galaxies already on the RS contribute significantly to the mass growth of the brightest and most massive early-type galaxies (e.g., Hopkins et al. 2008; Skelton et al. 2012), and quenching-dominated models, where a quenching phase lasting a few Gyr can steadily transform massive star-forming galaxies into red passive ones, without the need for significant merging activity.
We have shown in Fig. 16 that a quenching model can very well reproduce the observed evolution in the RS galaxies number density, as traced by the LF φ∗ parameter, and in Fig. 5 that the luminous blue galaxies we find in the CMR across all explored redshifts (0.5 < z < 1) are in fact massive objects that provide the natural progenitors for bright red-sequence galaxies. These observations suggest that the formation of new massive quiescent galaxies through merging at z < 1 is not required, as the moderate increase in number density of this population can be explained by a few sufficiently massive objects migrating from the blue cloud. At the same time, the observed evolution of the LF shows that there must be a larger increase of the population of quiescent galaxies with M⋆ < 1011 M⊙. This scenario is also consistent with the low observed rate of dry (dissipationless) mergers for galaxies with M⋆ > 1011 M⊙, with ~0.5−1 dry merger events per galaxy estimated between z ~1 and today (van Dokkum 2005; Bell et al. 2006; López-Sanjuan et al. 2012).
Overall, the build-up of the RS can then be interpreted through a continuous supply of objects from the blue cloud through an efficient shut down of their star formation over a short time scale (~1.5 Gyr, see Sect. 7.1) for very massive objects, while at smaller masses the SF quenching has to be less efficient to explain the time delay in the population of the fainter part of the RS. Minor (gas-rich) mergers between these objects can very plausibly play a role in this process, to explain the observed differences in the internal structure of pre-quenched and post-quenched galaxies (e.g., Bell et al. 2012), and the size evolution with time of the RS galaxies (Daddi et al. 2005; Trujillo et al. 2006; Toft et al. 2007; van Dokkum et al. 2008; Saracco et al. 2009; López-Sanjuan et al. 2012; Huertas-Company et al. 2012).
Additional support for this evolutionary scenario comes from our observation of a mild
increase in the scatter of the RS with redshift (Fig. 12). If there is a regular supply of galaxies migrating from the blue cloud and
this process was more active at earlier epochs, one naturally expects the RS to appear
broader at higher redshifts. Due to a passive fading of the stellar populations which
asymptotically drives the galaxy colours to a typical value (for given metallicity), the
scatter of the RS decreases and the high mass end of the RS naturally shrinks as a function
of time, while its low-luminosity tail will be extended through a delay of star formation in
low-mass galaxies preferentially located in low-density environments (Tanaka et al. 2005). Our results show that over the range probed by
VIPERS 1 > z > 0.5, the intrinsic scatter of the CMR
decreases with time by Δ(U − V) ~ 0.06 mag at the
bright end (MV ≲ −21, i.e. roughly
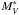 at z ~ 0.95), while
remaining constant for MV ≳ −21. This is
consistent with the luminous end of the CMR being build-up over the observed interval (at
z ~ 0.45
the scatter is independent of the luminosity), with a small number of additional massive
members migrating from the blue cloud that do not significantly alter the average asymptotic
red colours. Conversely, at fainter magnitudes there is an ongoing supply of fresh members
over the probed redshift, with the formation of the faint end being delayed due to the
extended star formation histories of lower-mass galaxies, in agreement with a downsizing
formation picture. Our scenario gets independent support by the significant buildup of the
lower luminosity end of the red sequence in clusters at 0.4 < z < 0.8, whereas
the bright end is consistent with passive evolution (Rudnick et al. 2009).
at z ~ 0.95), while
remaining constant for MV ≳ −21. This is
consistent with the luminous end of the CMR being build-up over the observed interval (at
z ~ 0.45
the scatter is independent of the luminosity), with a small number of additional massive
members migrating from the blue cloud that do not significantly alter the average asymptotic
red colours. Conversely, at fainter magnitudes there is an ongoing supply of fresh members
over the probed redshift, with the formation of the faint end being delayed due to the
extended star formation histories of lower-mass galaxies, in agreement with a downsizing
formation picture. Our scenario gets independent support by the significant buildup of the
lower luminosity end of the red sequence in clusters at 0.4 < z < 0.8, whereas
the bright end is consistent with passive evolution (Rudnick et al. 2009).
Finally, our interpretation is reinforced by the observation that the CMR scatter measured here for the general population is broader than that measured in cluster environments (Sect. 5.3) and the detection of recent SF activity in the spectra of early-type galaxies at high-redshift z ~ 1 (see Fig. 17). These results are consistent with a scenario in which a number of blue low-mass galaxies are pre-processed in denser environments (groups, e.g., Zabludoff & Mulchaey 1998; Kodama et al. 2001), before moving to the RS, strongly suggesting that the quenching mechanism in this case might be related to the environment.
The favoured scenario emerging from our data is somewhat at variance with the picture
proposed in Faber et al. (2007) and Bell et al. (2004b), in which dry mergers play an
important role within a complex formation scenario for massive red galaxies that includes a
mix of quenching and merger processes. The latest incarnation of this model is discussed in
Skelton et al. (2012). Here, the effects of
mergers on the evolution of early-type galaxies are modelled using merger trees in a
hierarchical galaxy formation framework. These authors distinguish between three models for
the evolution of a galaxy that has undergone a major merger at high redshift and a different
evolutionary path at z < 1: Model I. SF is shut-off at
z ~ 1
and no dry mergers take place afterwards. In this model the MF does not evolve because the
number density of RS galaxies does not increase because of the lack of wet mergers, and the
mix between existing RS galaxies does note change because of the lack of dry mergers.
Model II. SF is quenched at z ~ 1 and galaxies undergo on average 0.7 major
dry mergers after z = 1. Galaxies that have not yet experienced a major
merger at z > 1 fade passively up to the present.
Model III. SF continues until galaxies undergo a wet major merger. This
model is the one closest to the full semi-analytical model prescriptions and also accounts
for the effects of progenitor bias. However, the model overpredicts the local MF at high
masses (M⋆ > 1011.2 M⊙).
Contrary to the observational results discussed in Skelton
et al. (2012), our data show a significant luminosity evolution for massive RS
galaxies between z = 0.9 and today, both in the CMR and in the LF, with
Δ(U − V) = 0.33 ± 0.16 mag and
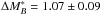 mag, respectively. Both values are in good
agreement with the predictions of Model I. (Δ(U − V) ~ 0.32 mag and
ΔMB ~ 1.15 mag),
providing further evidence against a dominant role of dry mergers for the build-up of the
RS. Of course a very sharp and highly syncronized cutoff of the SF activity as the one used
in this model cannot be considered very realistic, and if we assume to spread the cutoff
epoch over a finite amount of time we obtain an evolutionary model very similar to the
quenching one discussed in Sect. 7.2, that is also
capable of reproducing the number density evolution of RS galaxies, as discussed above,
without significantly altering the predictions on the photometric evolution of the
individual galaxies, and therefore maintainining the agreement with our observations on the
evolution of
mag, respectively. Both values are in good
agreement with the predictions of Model I. (Δ(U − V) ~ 0.32 mag and
ΔMB ~ 1.15 mag),
providing further evidence against a dominant role of dry mergers for the build-up of the
RS. Of course a very sharp and highly syncronized cutoff of the SF activity as the one used
in this model cannot be considered very realistic, and if we assume to spread the cutoff
epoch over a finite amount of time we obtain an evolutionary model very similar to the
quenching one discussed in Sect. 7.2, that is also
capable of reproducing the number density evolution of RS galaxies, as discussed above,
without significantly altering the predictions on the photometric evolution of the
individual galaxies, and therefore maintainining the agreement with our observations on the
evolution of 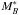 and the (U − V)
colour for the RS galaxies. Our results are in agreement with the findings by (Brown et al. 2007), who advocate that ~80% of the stellar mass of very luminous
red galaxies (4L∗) is already in place at z = 0.7 and that dry mergers
play a minor role in their evolution since z = 0.9.
and the (U − V)
colour for the RS galaxies. Our results are in agreement with the findings by (Brown et al. 2007), who advocate that ~80% of the stellar mass of very luminous
red galaxies (4L∗) is already in place at z = 0.7 and that dry mergers
play a minor role in their evolution since z = 0.9.
This scenario is also consistent with the phenomenological model by Peng et al. (2010, 2012), which supports a downsizing effect in the observed galaxy properties (Gavazzi et al. 1996; Gavazzi & Scodeggio 1996; Cowie et al. 1996). In such a picture, a “mass-quenching” process works on galaxies across all mass scales. Such a process is independent of the environment, but is proportional to the SFR of each galaxy, which in turn is proportional to the galaxy stellar mass. A second quenching process, an “environmental quenching”, is also part of the model, and is supposed to become effective at later epochs, affecting preferentially lower-mass galaxies (essentially those not yet affected by the mass-quenching). With the present analysis we cannot test the impact of the “environmental quenching” on the evolution of the RS, but we have clearly shown how a mass-quenching scenario describes with good accuracy many aspects of the evolution of the massive part of the RS.
Finally, while we provided here a consistent phenomenological scenario that agrees with the VIPERS observations, the precise physical processes that can cause the quenching of star formation are far from being understood. They include essentially two possible channels: (1) the effects of supernova feedback (effective at Mh < 5 × 1011 M⊙), virial shock heating (Dekel & Birboim 2006; Cattaneo et al. 2006); or (2) the solution favoured by semi-analytic models, i.e. “radio-mode” AGNs (Granato et al. 2004; Bower et al. 2006; Croton et al. 2006; De Lucia & Blaizot 2007). Models with a high formation redshift of early-type galaxies through gas-rich mergers that experience a phase of quasar activity (e.g., Croton et al. 2006; Bower et al. 2006; Hopkins et al. 2008) can explain the colour evolution or the MF, but fail to reproduce their combined properties for a given redshift (Stringer et al. 2009; Skelton et al. 2012; De Lucia & Borgani 2012).
9. Summary
Using a unique sample of approximately 45 000 galaxies with robust spectroscopic redshift measurements drawn from the VIPERS PDR-1, we have constructed the colour–magnitude relation (CMR), the colour−stellar mass relation, and the luminosity function (LF) for the total and for the red quiescent galaxy population across the redshift range 0.4 < z < 1.3. The combination of high-quality multi-wavelength data and of a large sample allows us to explore for the first time with high accuracy at these redshifts the contribution of the different galaxy populations to the bivariate distribution of galaxy colours and luminosities. Our main results can be summarised as follows:
-
The CMR and LF of VIPERS are well populated from z = 1.3 down to z = 0.4 with a representative number of galaxies of all galaxy types that allows us to precisely trace the photometric evolution of galaxies over a cosmic period of ~4 Gyr. We find that massive red evolved galaxies are already in place at z ~ 1, in agreement with previous studies, but the large volume covered by VIPERS at z > 0.6, and the resulting unprecedented coverage of the bright end of the LF, allows us to detect also a significant population of massive blue galaxies at high redshift (0.8 ≲ z ≲ 1.3). These objects can be considered as the natural progenitors of the late massive additions to the RS.
-
The colour and luminosity evolution of the bright part of the RS are in agreement with the predictions for a purely passively evolving old stellar population. We measure a colour evolution of Δ(U − V) = 0.33 ± 0.16 mag and an evolution of
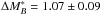 mag since z = 1. These results
are consistent with the no-merger model predictions for massive galaxies by Skelton et al. (2012), and show an evolution of
the RS galaxies significantly larger than most merger-dominated evolution models would
predict.
mag since z = 1. These results
are consistent with the no-merger model predictions for massive galaxies by Skelton et al. (2012), and show an evolution of
the RS galaxies significantly larger than most merger-dominated evolution models would
predict. -
The observed evolution of the RS favours stellar population models with exponentially declining SFHs with 0.3 ≤ τ ≤ 0.8 and a formation epoch at 2.5 < z < 3.5. Our observations rule out SFHs with τ > 0.8 and require a rapid build-up of the RS over a very short time scale of only ~1.5 Gyr; clearly, this has to happen at epochs earlier than our redshift limit of z = 1.3. The measured RS evolution gives strong constraints on the predictions of stellar population models and suggests weak star formation episodes over the redshift range 0.8 ≲ z ≲ 1.2. This claim is supported by residual star formation detected in the stacked spectra of early-type galaxies at high-redshift (0.9 < z < 1.0) which involves only a few percent of their total stellar mass. In contrast, stacked spectra of early-type galaxies at low-redshift (0.5 < z < 0.6) show the signature of a purely quiescent stellar population with no signs of recent star formation activity. Moreover, the evolution of dusty red galaxies is mild up to z = 1 and the influence of dust obscuration on the internal properties of quiescent galaxies becomes important at z > 1.3.
-
The intrinsic scatter of the RS for the galaxy sample based on the SED-type classification is increasing from z = 0.4 to z = 1.1. The total intrinsic scatter of the CMR is σ(U − V) ~ 0.11, which is a factor of two larger than the scatter of the CMR found in galaxy clusters at the same redshifts. Our observed intrinsic scatter in the field is not in agreement with theoretical model predictions (Menci et al. 2008), which suggest a scatter that is three times as large as observed.
-
The significant luminosity and number density evolution measured in the LF supports a formation scenario where massive early-type galaxies (M⋆ > 1011 M⊙) have been assembled through wet mergers at an early epoch in the universe, followed by a powerful shut-down mechanism (such as quenching) of their star formation activity at z ~ 1 over a short time-scale. Afterwards the luminosity of these systems quickly fades, and once on the RS, they evolve in a purely passive way with their stellar populations continuously becoming fainter and redder.
-
Our results imply that gas-poor (dry) major-mergers of massive galaxies are not the dominant factor in the build-up the bright, massive end of the RS since z ~ 1 and they also do not contribute to the number density of massive quiescent galaxies. Massive blue star-forming galaxies that exist at z ~ 1 can be transformed into passive quiescent RS galaxies through some quenching mechanism. Mergers however are still likely to contribute to the evolution of the internal structure and the size of galaxies on the RS.
Online material
Appendix A: The Johnson-Cousins UBVRI System
One of the most common and frequently used standard broad-band photometric systems is the photoelectric UBV system. Usually, the Johnson-Cousins UBVRI refers to the combined Johnson-Cousins UBV system (Johnson & Morgan 1953) and its red optical extension of the Cousins RI system (Cousins 1976). In this system the V-band represents an approximate measure of the visual photographic magnitude, whereas the B-band was defined to give a measure for the uncorrected photographic magnitude. In addition, the U-band probes the interesting window between the atmospheric cutoff and the B-band. However, the combination of the UBV system of having a cutoff defined by the atmosphere at low wavelengths (plus the original 1P21 glass optics) and a limit by the detector at long wavelengths (λλ ≈ 6320 ≈ VRcut) implicated that the U-band filter is sensitive to the atmospheric extinction. The original B and V bands of the UBV system could be well reproduced with current more sentitive (redder) CCD detectors (e.g., Buser 1978; Bessel 1986, for the U-band; Bessel 1990, for UBVRI). However, the characteristics of the U-band were more difficult to realise with current detector technologies, mainly because of short wavelength cutoff due to the atmosphere and the impact of temperature dependencies (Bessel et al. 1998).
In the photometric Johnson system the A0V star α Lyr (Vega) is defined to have V = 0.03 mag, whereas all other colours of Vega are equal to zero. The absolute flux of Vega can be calibrated using empirical relations (e.g., Bessel 1979, 1990), or some calibration standard stars (Landolt 1992).
For the present work, we have adopted the original 1953 UJ-Johnson filter (λc = 3499, WHM = 699, hereafter U-band) that has been reconstructed in the USA (Johnson & Morgan 1953). The original filter name is referred as Corning 9863 and was initially used in photoelectric observations. For an unreddened A0V star with V = 0.00, the U-Johnson filter gives a total flux of 3.98 × 10-9 erg cm-2 s-1 Å-1 (Lamla 1982). Our choice is primarily driven by the high filter response in the blue wavelength range compared to other U-band filters used in the literature. Because of its high sensitivity in the blue, the U-Johnson filter allow us to directly probe the luminous, hot and blue OB stars and SF associations in the stellar content of galaxies and therefore acts as a proxy for SF, although it is affected by dust extinction. However, using a combination of GALEX NUV and FUV IR colours, we demonstrate in Sect. 4.3 that we are able to perform a robust separation into red quiescent, blue star-forming galaxies as well as dust-obscured red galaxies with or without SF. Similar approaches adopting a pseudo-continuum U280 filter to split quiescent from star-forming galaxies have been used, for example, in moderate redshift clusters (Wolf et al. 2009) and for field galaxies (Nicol et al. 2011).
 |
Fig. A.1 Filter transmission curve for different popular U-band filters in the literature. The U-Johnson (dashed blue), used in VIPERS, is compared to the UBessel VVDS filter (red solid), U3 Buser filter (green), UBessel1990 (dotted cyan), u SDSS (black), u∗ CFHT MegaCam (pink), and the u⋆ CFHT MegaCam SAGEM filter (dot-dashed magenta line). |
Figure A.1 shows the filter transmission curve for the U-Johnson filter compared to other frequently used U-band filters in the literature. The U-Johnson (blue dashed) is compared to the UJKC Bessel filter (red solid), U3 Buser filter (green), UBessel 1990 (cyan dotted), u SDSS (black), u∗CFHT MegaCam (pink), and the u⋆ CFHT MegaCam SAGEM filter (dot-dashed magenta line), which is used in ALF, whereas for the SED modelling we adopt U-Johnson filter. Note that the Johnson filter has a quite different efficiency curve from the standard UJKC-Johnson-Kron-Cousins filter in the VVDS, or the U3 Buser filter as adopted in the PEGASE filter library (see Table 1 of Buser & Kurucz 1978) or in the Bruzual & Charlot (2003) models (record 12). The U-Johnson has a higher blue sensitivity than any other U-band filter and allows to obtain redder colours for red galaxies with a more prominent separation between blue and red galaxies with a minimum at (U − B) ~ 1.2 (AB). Moreover, the whole filter remains below 4000 Å and therefore is a good proxy for the 4000 Å break. The U3 filter is extended at larger wavelengths and therefore produces bluer colours compared to the U-Johnson filter and a minimum at (U3 − B) ~ 1.0 (AB).
For the BJKC filter we adopt the B3 Buser filter (Buser 1978) as commonly used in PEGASE (B3BK78) and the Bruzual & Charlot (2003) models (record 14). As the VJKC filter we define the V Buser (corresponding to VBK78 in PEGASE and record 15 in the Bruzual & Charlot (2003) models). Both the B3 and V Buser filters are also used in the Millennium simulation by De Lucia & Blaizot (2007). Table A.1 compares the main filter characteristics used in this work (U,B3,V) to the U3 filter.
Basic characteristics of different UBV filters.
We adopt the following transformation from the UJ-Johnson filter
passband to the rest-frame UJKC system (in AB):
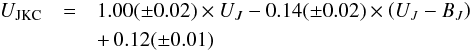 (A.1)The transformation from AB to Vega system
was performed using MJKC(AB) = MJKC(Vega) + cX(AB),
where the individual colour terms cX(AB) for each
filter were derived through the SED fitting procedure.
(A.1)The transformation from AB to Vega system
was performed using MJKC(AB) = MJKC(Vega) + cX(AB),
where the individual colour terms cX(AB) for each
filter were derived through the SED fitting procedure.
Among the literature the interpretation and application of the UBV-Johnson-Morgan-Cousins system is often inhomogeneous and ambiguous. For example, Cooper et al. (2010) used the U3 (Buser 1978) filter, whereas the B and V-band are not the corresponding Buser filters but the B2 and V filters by Asuzienis & Straizys (1969). More popular are the usage of the UBVJKC Johnson-Cousins definitions, like for the VVDS (Franzetti et al. 2007) or in the zCOSMOS survey (Cucciati et al. 2010). It is beyond the scope of the current investigation to reproduce the exact filter definitions used among works in the literature. We emphasize that that for comparisons with literature data one should always be precise and clearly describe which photometry and filter transmission curves are adopted.
Appendix B: Completeness test
In Fig. 10 we observe a change of the evolution of the RS intercept from z = 0.9 to z = 1.3. This change in the number of red galaxies could be either due to a real evolution or to sample incompleteness. To test the completeness of red galaxies in the highest redshift bin 1.0 < z < 1.3, we construct different samples of red galaxies in the lower redshift bin 0.9 < z < 1.0 (hereafter simulated samples) to verify whether the observed properties of the sample at 1.0 < z < 1.3 (hereafter real sample) are consistent with the properties of their counterparts at 0.9 < z < 1.0. Red galaxies in VIPERS are defined as those galaxies classified by SED type class 1 (see Sect. 2.4). We assume that the average observed (U − V) rest-frame distribution is the same for red galaxies at all redshifts. Because the reddest galaxies have the faintest ultra-violet magnitudes, a possible incompleteness bias would be apparent in the observed i′-band magnitude distribution with the reddest galaxies being absent.
We have computed the observed (U − V) rest-frame distribution of randomly selected red samples in the redshift bin 0.9 < z < 1.0, which were extracted from the observed (U − V) rest-frame distribution of all red galaxies within the same redshift interval. The real and randomly selected red galaxy samples at 0.9 < z < 1.0 share the same properties and the randomly selected (hence simulated) samples are always a sub-set of the total red galaxy sample. These simulated samples have the same number of galaxies as the sample at 1.0 < z < 1.3 and therefore should mimic the properties of the observed red galaxy sample at the highest redshift bin, assuming the latter is complete. We take a random set of two simulated samples at 0.9 < z < 1.0, referred to simulated 1 and simulated 2, to understand their variance and possible spread in properties. We assume the redshift bin 0.9 < z < 1.0 to be complete for all types of (red, green and blue) galaxies and we are mainly interested in possible incompleteness effects in the RS evolution at z > 1. For each galaxy in the simulated samples we derive the observed i′-band (AB) magnitudes.
For the real galaxy sample, we took the observed (U − V) rest-frame distribution of all red galaxies in the high-redshift bin 1.0 < z < 1.3 and computed for each galaxy separately the observed i′-band magnitudes. Finally, we corrected for the redshift evolution of each object as Δ(Mcorr) = Δ(Mi′)/0.3 × (zspec − 1), where Mi′ is the evolution correction from z = 1.3 to z = 0.9 derived from the LF of the VVDS (Ilbert et al. 2005) and zspec is the spectroscopic redshift of each single galaxy.
A comparison of the real and simulated red galaxy samples is shown in Fig. B.1. Two representative simulated samples of red galaxies (simulated 1 and simulated 2) are shown in blue and green, respectively. The red histogram shows the real red sample at 1.0 < z < 1.3, which was transformed to redshift 0.9 < z < 1.0. Table B.1 compares the median, first and third quartile, and the 1 σ Gaussian values of the distribution for the real and randomly selected simulated samples. The histograms display similar shapes and show consistent statistics. We therefore conclude that our red galaxy sample at z > 1 does not show any significant incompleteness of bright galaxies and that our sample is also highly complete at fainter magnitudes.
 |
Fig. B.1 Completeness test for red galaxies in the VIPERS PDR-1. The red histogram displays the observed real red galaxies at 1.0 < z < 1.3 transformed to 0.9 < z < 1.0, whereas the simulated samples are two representations of red galaxy samples at 0.9 < z < 1.0. The properties of the real sample are consistent with the properties of their simulated counterparts. |
Statistical properties of real and simulated red galaxy samples.
Appendix C: Cosmic variance
 |
Fig. C.1 Cosmic variance for the VIPERS PDR-1 sample and other surveys from the literature. Symbols denote data from AGES (Cool et al. 2012, red crosses), COMBO-17 (Bell et al. 2004b, black circles), COSMOS (Scoville et al. 2007, grey polygons), DEEP1 (Im et al. 2002, cyan stars), DEEP2 (Faber et al. 2007, orange triangles), NDWFS (Brown et al. 2007, magenta stars), and VVDS (Le Fèvre et al. 2005, 2013, green squares). |
Statistical measurements based on number counts such as the luminosity function or mass function are subjected to field-to-field variations of the number density that originate from the clustering of a particular galaxy population and from variations imprinted by the scale of the probed survey volume.
For a probability distribution function PN(V)
that denotes the probability of counting N objects within a volume V, the relative cosmic
variance is defined as 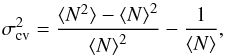 (C.1)where ⟨ N⟩ and
⟨ N2⟩ are the mean and variance of
the galaxy number counts (Somerville et al.
2004).
(C.1)where ⟨ N⟩ and
⟨ N2⟩ are the mean and variance of
the galaxy number counts (Somerville et al.
2004).
To test the impact of cosmic variance on our results, we have computed the uncertainty of cosmic variance for the VIPERS survey using the public code getcv (Moster et al. 2011). Figure C.1 shows the relative cosmic variance uncertainty in VIPERS (blue filled circles) divided into different mass ranges probed by the survey. For reference purposes, we also show the results of several other surveys taken from the literature.
For RS galaxies between 0.4 < z < 1.3, the uncertainties arising from cosmic variance vary in the range 0.04 < log (M⋆/M⊙) < 0.07, with a median of ⟨log (M⋆/M⊙)⟩ = 0.05. Note that the effective area of VIPERS is 10.32 deg2, which is about 4 deg2 larger than any other survey at intermediate redshifts (e.g., NDWFS, AGES). Figure C.1 shows that independent of the mass probed, the cosmic variance effects on VIPERS are a factor of two lower than AGES and 20% lower than NDWFS. Compared to all the other surveys, VIPERS is a factor of 4 or more less affected to cosmic variance effects. In particular, compared to DEEP2 and COMBO-17, the VIPERS data offers a huge improvement. Recent surveys like NDWFS or AGES cannot compete either with VIPERS. We emphasize that AGES has an average sampling rate of 20% in I and K-bands (Cool et al. 2012), which is a factor of two lower than the median sampling rate of VIPERS. We therefore conclude that the impact of cosmic variance has a negligible effect on our results.
CFHTLS website: http://www.cfht.hawaii.edu/Science/CFHTLS/
VIPERS website: http://www.vipers.inaf.it
Bertin & Arnouts (1996) suggest that Kron-like aperture measurements miss a somewhat uniform ~6% of the total flux for galaxies.
Acknowledgments
We would like to thank the anonymous referee for a constructive review of this manuscript. We acknowledge the crucial contribution of the ESO staff for the management of service observations. In particular, we are deeply grateful to M. Hilker for his constant help and support of this programme. Italian participation to VIPERS has been funded by INAF through PRIN 2008 and 2010 programmes. L.G. and B.R.G. acknowledge support from the European Research Council through the Darklight ERC Advanced Research Grant (# 291521). O.L.F. acknowledges support from the European Research Council through the EARLY ERC Advanced Research Grant (# 268107). Polish participants have been supported by the Polish Ministry of Science (grant N N203 51 29 38), the Polish-Swiss Astro Project (co-financed by a grant from Switzerland, through the Swiss Contribution to the enlarged European Union), the European Associated Laboratory Astrophysics Poland-France HECOLS and a Japan Society for the Promotion of Science (JSPS) Postdoctoral Fellowship for Foreign Researchers (P11802). G.D.L. acknowledges financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n. 202781. W.J.P. and R.T. acknowledge financial support from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement n. 202686. W.J.P. is also grateful for support from the UK Science and Technology Facilities Council through grant ST/I001204/1. E.B., F.M. and L.M. acknowledge support from grants ASI-INAF I/023/12/0 and PRIN MIUR 2010-2011. L.M. also acknowledges financial support from PRIN INAF 2012. Y.M. acknowledges support from CNRS/INSU (Institut National des Sciences de l’Univers) and the Programme National Galaxies et Cosmologie (PNCG). C.M. is grateful for support from specific project funding of the Institut Universitaire de France and the LABEX OCEVU. This research uses data from the VIMOS VLT Deep Survey, obtained from the VVDS database operated by Cesam, Laboratoire d’Astrophysique de Marseille, France.
References
- Andreon, S., & Huertas-Company, M. 2011, A&A, 526, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aragón-Salamanca, A., Ellis, R. S., Sharples, R. M. 1991, MNRAS, 248, 128 [NASA ADS] [Google Scholar]
- Aragón-Salamanca, A., Ellis, R. S., Couch, W. J., Carter, D. 1993, MNRAS, 262, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Cristiani, S., Moscardini, L., et al. 1999, MNRAS, 310, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Arnouts, S., Walcher, C. J., Le Fèvre, O., et al. 2007, A&A, 476, 137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnouts, S., Le Floc’h, Chevallard, J., et al. 2013, A&A, 558, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asužienis, A., & Straižys, V. 1969, Sov. Astron., 13, 316 [Google Scholar]
- Baldry, I. K., Glazebrook, K., Brinkmann, J., et al. 2004, ApJ, 600, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Baugh, C. M., Cole, S., & Frenk, C. S. 1996, MNRAS, 283, 1361 [NASA ADS] [CrossRef] [Google Scholar]
- Baum, W. A. 1959, PASP, 71, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Bel, J., Marinoni, C., Granett, B. R., et al. 2014, A&A, 563, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., et al. 2003, ApJ, 149, 289 [Google Scholar]
- Bell, E. F., McIntosh, D. H., Barden, M., et al. 2004a, ApJ, 600, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Wolf, C., Meisenheimer, K., et al. 2004b, ApJ, 608, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Naab, T., McIntosh, D. H., et al. 2006, ApJ, 640, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Zheng, X. Z., Papovich, C., et al. 2007, ApJ, 663, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., van der Wel, A., Papovich, C., et al. 2012, ApJ, 753, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardi, M., Renzini, A., da Costa, L. N., et al. 1998, ApJ, 508, L143 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bessel, M. S. 1979, PASP, 91, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, M. S. 1986, PASP, 98, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bessel, M. S., Castelli, F., & Plez, B. 1998, A&A, 333, 231 [NASA ADS] [Google Scholar]
- Blakeslee, J. P., Franx, M., Postman, M., et al. 2003, ApJ, 596, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Holden, B. P., Franx, M., et al. 2006, ApJ, 644, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M. 2006, ApJ, 648, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Blanton, M., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 592, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Bolzonella, M., Miralles, J.-M., & Pelló, R. 2000, A&A, 363, 476 [NASA ADS] [Google Scholar]
- Bolzonella, M., Kovač, K., Pozzetti, L., et al. 2010, A&A, 524, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borch, A., Meisenheimer, K., Bell, E. F., et al. 2006, A&A, 453, 869 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouchet, P., Lequeux, J., Maurice, E., Prévot, L., & Prévot-Burnichon, M. L. 1985, A&A, 149, 330 [NASA ADS] [Google Scholar]
- Bower, R. G., Lucey, J. R., & Ellis, R. S. 1992a, MNRAS, 254, 589 (BLE92) [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Lucey, J. R., & Ellis, R. S. 1992b, MNRAS, 254, 601 (BLE92) [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Kodama, T., & Terlevich, A. 1998, MNRAS, 299, 1193 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G., Whitaker, K. E., van Dokkum, P. G., et al. 2009, ApJ, 706, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Brammer, G., Whitaker, K. E., van Dokkum, P. G., et al. 2011, ApJ, 739, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, M. J. I., Dey, A., Jannuzi, B. T., et al. 2007, ApJ, 654, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G. A. 1983, ApJ, 273, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G. A., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Ellis, R. S., & Conselice, C. J. 2005, ApJ, 625, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Ellis, R. S., Conselice, C. J., et al. 2006, ApJ, 651, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Treu, T., & Ellis, R. S. 2007, ApJ, 665, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Buser, R. 1978, A&A, 62, 411 [NASA ADS] [Google Scholar]
- Buser, R., & Kurucz, R. L. 1978, A&A 70, 555 [NASA ADS] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., Bacon, R., Bureau, M., et al. 2006, MNRAS, 366, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2012, Nature, 484, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Guzzo, L., Franceschini, A., et al. 2007, ApJS, 172, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Cassata, P., Giavalisco, M., Guo, Y., et al. 2011, ApJ, 743, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Cattaneo, A., Dekel, A., Devriendt, J., et al. 2006, MNRAS, 370, 1651 [NASA ADS] [CrossRef] [Google Scholar]
- Cimatti, A., Daddi, E., Mignoli, M., et al. 2002, A&A, 381, L68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cimatti, A., Cimatti, A., Daddi, E., et al. 2006, A&A, 453, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coleman, G. D., Wu, C.-C., & Weedman, D. W. 1980, ApJS, 43, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Conselice, C. J., Bundy, K., Trujillo, I., et al. 2007, MNRAS, 381, 962 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, R. J., Eisenstein, D. J., Fan, X., et al. 2008, ApJ, 682, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, R. J., Eisenstein, D. J., Kochanek, C. S., et al. 2012, ApJ, 748, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Cooper, M. C., Coil, A. L., Gerke, B. F., et al. 2010, MNRAS, 409, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Coupon, J., Ilbert, O., Kilbinger, M., et al. 2009, A&A, 500, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cousins, A. W. J. 1976, MNRAS, 81, 25 [Google Scholar]
- Cowie, L. L., Songaila, A., Hu, E. M., & Cohen, J. G. 1996, AJ, 112, 839 [Google Scholar]
- Croton, D. J, Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Cucciati, O., Iovino, A., Kovač, K., et al. 2010, A&A, 524, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Daddi, E., Renzini, A., Pirzkal, N., et al. 2005, ApJ, 626, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Davidzon, I., Bolzonella, M., Coupon, J., et al. 2013, A&A, 558, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, M., & Geller, M. J. 1976, ApJ, 208, 13 [NASA ADS] [CrossRef] [Google Scholar]
- de la Torre, S., Guzzo, L., Peacock, J. A., et al. 2013, A&A, 557, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Lucia, G., & Blaizot, J. 2007, MNRAS, 375, 2 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., & Borgani, S. 2012, MNRAS, 426, L61 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, G., Springel, V., White, S. D. M., Croton, D., & Kauffmann, G. 2006, MNRAS, 366, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., & Birboim, Y. 2006, 368, 2 [Google Scholar]
- Demarco, R., Wilson, G., Muzzin, A., et al. 2010, ApJ, 711, 1185 [NASA ADS] [CrossRef] [Google Scholar]
- di Serego Alighieri, S., Vernet, J., Cimatti, A., et al. 2005, A&A, 442, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Djorgovski, S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1980, ApJ, 236, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Lynden-Bell, D., Burstein, D., et al. 1987, ApJ, 313, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G., Ellis, R. S., & Petersen, B. A. 1988, MNRAS, 232, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, R. S. 1988, in Towards understanding galaxies at large redshift, eds. R. Kron, & A. Renzini (Dordrecht: Kluwer Academic Publishers), 147 [Google Scholar]
- Ellis, R. S., Smail, I., Dressler, A., et al. 1997, ApJ, 483, 582 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., & Jackson, R. E. 1976, ApJ, 204, 668 [NASA ADS] [CrossRef] [Google Scholar]
- Faber, S. M., Willmer, C. N. A., Wolf, C., et al. 2007, ApJ, 665, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Ferreras, I., Lisker, T., Carollo, C. M., Lilly, S. J., & Mobasher, B. 2005, ApJ, 635, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Feulner, G., Gabasch, A., Salvato, M., et al. 2005, ApJ, 633, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fontana, A., Pozzetti, L., Donnarumma, I., et al. 2004, A&A 424, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fontanot, F., De Lucia, G., Monacao, P., et al. 2009, MNRAS, 397, 1776 [NASA ADS] [CrossRef] [Google Scholar]
- Franzetti, P., Scodeggio, M., Garilli, B., et al. 2007, A&A, 465, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fritz, A., Ziegler, B. L., Bower, R. G., Smail, I., & Davies, R. L. 2005, MNRAS, 358, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, A., Böhm, A., & Ziegler, B. L. 2009a, MNRAS, 393, 1467 [NASA ADS] [CrossRef] [Google Scholar]
- Fritz, A., Jørgensen, I., Schiavon, R. P., & Chiboucas, K. 2009b, Astron. Nachr., 330, 931 [NASA ADS] [CrossRef] [Google Scholar]
- Gabasch, A., Bender, R., Seitz, S., et al. 2004, A&A, 421, 41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallazzi, A., Bell, E. F., Wolf, C., et al. 2009, ApJ, 690, 1883 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Bottini, D., Maccagni, D., Carrasco, L., & Recillas, E. 1996, ApJS, 105, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Fumana, M., Franzetti, P., et al. 2010, PASP, 122, 827 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Paioro, L., Scodeggio, M., et al. 2012, PASP, 124, 1232 [NASA ADS] [CrossRef] [Google Scholar]
- Garilli, B., Guzzo, L., Scodeggio, M., et al. 2014, A&A, 562, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gavazzi, G., & Scodeggio, M. 1996, A&A, 400, 451 [Google Scholar]
- Gavazzi, G., Pierini, D., & Boselli, A. 1996, A&A, 312, 397 [NASA ADS] [Google Scholar]
- Gavazzi, G., Boselli, A., Donati, A., Franzetti, P., & Scodeggio, M. 2003, A&A, 400, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Giallongo, E., Salimbeni, S., Menci, N., et al. 2005, ApJ, 622, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Gladders, M. D., López-Cruz, O., Yee, H. K. C., & Kodama, T. 1998, ApJ, 501, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Goranova, Y., Hudelot, P., Magnard, F., et al. 2009, The CFHTLS T0006 Release, http://terapix.iap.fr/cplt/T0006-doc.pdf [Google Scholar]
- Granato, G., De Zotti, G., Silva, L., et al. 2004, ApJ, 600, 580 [Google Scholar]
- Granett, B. R., Guzzo, L., Coupon, J., et al. 2012, MNRAS, 421, 251 [NASA ADS] [Google Scholar]
- Guzzo, L., Scodeggio, M., Garilli, B., et al. 2013a, A&A, submitted [arXiv:1303.2623] [Google Scholar]
- Guzzo, L., and the VIPERS Team 2013b, The Messenger, 151, 41 [NASA ADS] [Google Scholar]
- Haines, C. P., Gargiulo, A., & Merluzzi, P. 2008, MNRAS, 385, 1201 [NASA ADS] [CrossRef] [Google Scholar]
- Harker, J. J., Schiavon, R. P., Weiner, B. J., et al. 2006, ApJ, 647, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Stanford, S. A., Stott, J. P., et al. 2009, ApJ, 697, 436 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D., Blanton, M., Strateva, I., et al. 2002, AJ, 124, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Kereš, D., & Hernquist, L. 2008, ApJS, 175, 390 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Huertas-Company, M., Mei, S., Shankar, F., et al. 2013, MNRAS, 428, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Arnouts, S., et al. 2004, MNRAS, 351, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., Tresse, L., Zucca, E., et al. 2005, A&A, 439, 863 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Arnouts, S., McCracken, H. J., et al. 2006, A&A, 457, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Im, M., Simard, L., Faber, S. M., et al. 2002, ApJ, 571, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Jimenez, R., Bernardi, M., Haiman, Z., et al. 2007, ApJ, 669, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, H. L., & Morgan, W. W. 1953, ApJ, 117, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Juneau, S., Glazebrook, K., Crampton, D., et al. 2005, ApJ, 619, L135 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Kauffmann, G., White, S. D. M., Heckman, T. M., et al. 2004, MNRAS, 353, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1992, ApJ, 388, 310 [NASA ADS] [CrossRef] [Google Scholar]
- Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, T., Arimoto, N., Barger, A. J., & Aragón-Salamanca, A. 1998, A&A, 334, 99 [NASA ADS] [Google Scholar]
- Kodama, T., Smail, I., Nakata, F., Okamura, S., & Bower, R. G. 2001, ApJ, 562, L9 [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Lamla, E. 1982, in Landolt-Börnstein Series, Volume 2B: “Stars and Star Clusters”, eds. K. Schaifers, & H. H. Voigt (Berlin: Springer-Verlag) [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Le Borgne, D., Abraham, R., Daniel, K., et al. 2006, ApJ, 642, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Saisse, M., Mancini, D., et al. 2000, Proc. SPIE, 4008, 546 [Google Scholar]
- Le Fèvre, O., Mancini, D., Saisse, M., et al. 2002, The Messenger, 109, 21 [NASA ADS] [Google Scholar]
- Le Fèvre, O., Vettolani, G., Garilli, B., et al. 2005, A&A, 439, 845 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Cassata, P., Cucciati, O., et al. 2013, A&A, 559, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Cruz, O., Barkhouse, W. A., & Yee, H. K. C. 2004, ApJ, 614, 679 [NASA ADS] [CrossRef] [Google Scholar]
- López-Sanjuan, C., Le Fèvre, O., Ilbert, O., et al. 2012, A&A, 548, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lynden-Bell, D. 1971, MNRAS, 155, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Małek, K., Solarz, A., Pollo, A., et al. 2013, A&A, 557, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marchetti, A., Granett, B. R., Guzzo, L., Fritz, A., & the VIPERS Team 2013, MNRAS, 428, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Marinoni, C., & Hudson, M. J. 2002, ApJ, 569, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. D., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Marulli, F., Bolzonella, M., Branchini, E., et al. 2013, A&A, 557, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McIntosh, D. H., Bell, E. F., Rix, H.-W., et al. 2005, ApJ, 632, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Blakeslee, J. P., Stanford, S. A., et al. 2006a, ApJ, 639, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Mei, S., Holden, B. P., Blakeslee, J. P., et al. 2006b, ApJ, 644, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Mellier, Y., Bertin, E., Hudelot, P., et al. 2008, The CFHTLS T0005 Release, http://terapix.iap.fr/cplt/oldSite/Descart/CFHTLS-T0005-Release.pdf [Google Scholar]
- Menci, N., Menci, N., Fontana, A., et al. 2005, ApJ, 632, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Fontana, A., Giallongo, E., et al. 2006, ApJ, 647, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Rosati, P., Gobat, R., et al. 2008, ApJ, 685, 863 [NASA ADS] [CrossRef] [Google Scholar]
- Moresco, M., Pozzetti, L., Cimatti, A., et al. 2013, A&A, 558, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moster, B. P., Somerville, R. S., Newman, J. A., & Rix, H.-W. 2011, ApJ, 731, 113 [Google Scholar]
- Nelan, J. E., Smith, R. J., Hudson, M. J., et al. 2005, ApJ, 632, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Nicol, M.-H., Nicol, M.-H., Meisenheimer, K., et al. 2011, ApJ, 727, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Faber, S. M., Weiner, B. J., et al. 2007, ApJ, 660, L47 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connell, R. W. 1988, in Towards understanding galaxies at large redshift, eds. R. Kron, & A. Renzini (Dordrecht: Kluwer Academic Publishers), 177 [Google Scholar]
- Papovich, C., Dickinson, M., Giavalisco, M., et al. 2005, ApJ, 631, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Peletier, R. F., Davies, R. L., Illingworth, G. D., et al. 1990, AJ, 100, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Kovač, K., et al. 2010, ApJ, 721, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., Lilly, S. J., Renzini, A., et al. 2012, ApJ, 757, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Pozzetti, L., Bolzonella, M., Zucca, E., et al. 2010, A&A, 523, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prévot, M. L., Lequeux, J., Prévot, L., Maurice, E., & Rocca-Volmerange, B. 1984, A&A, 132, 389 [NASA ADS] [Google Scholar]
- Rakos, K. D., & Schombert, J. M. 1995, ApJ, 439, 47 [Google Scholar]
- Rudnick, G., von der Linden, A., Pelló, R., et al. 2009, ApJ, 700, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Ruhland, C., Bell, E. F., Häußler, B., et al. 2009, ApJ, 695, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Charlot, S., Rich, R. M., et al. 2005, ApJ, 619, L39 [Google Scholar]
- Sandage, A., Tammann, G. A., & Yahil, A. 1979, ApJ, 232, 352 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandage, A., Binggeli, B., Tammann, G. A. 1985, AJ, 90, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Saracco, P., Longhetti, M., & Andreon, A. 2009, MNRAS, 392, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Scarlata, C., Carollo, C. M., Lilly, S. J., et al. 2007, ApJS, 172, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Khochfar, S., Kaviraj, S., et al. 2006, Nature, 442, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Schawinski, K., Thomas, D., Sarzi, M., et al. 2007, MNRAS, 382, 1415 [NASA ADS] [CrossRef] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Schweizer, F., & Seitzer, P. 1992, AJ, 104, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M. 2001, AJ, 121, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2005, PASP, 117, 1284 [NASA ADS] [CrossRef] [Google Scholar]
- Scodeggio, M., Franzetti, P., Garilli, B., et al. 2009, The Messenger, 135, 13 [NASA ADS] [Google Scholar]
- Scodeggio, M., Garilli, B., Fritz, A., et al. 2011, VIPERS internal report, 24/02/2011 [Google Scholar]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007, ApJS, 172, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Skelton, R. E., Bell, E. F., & Somerville, R. S. 2012, ApJ, 753, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Somerville, R. S., Lee, K., Ferguson, H. C., et al. 2004, ApJ, 600, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, S. A., Eisenhardt, P. R. M., & Dickinson, M. 1995, ApJ, 450, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Stanford, S. A., Eisenhardt, P. R., & Dickinson, M. 1998, ApJ, 492, 461 [NASA ADS] [CrossRef] [Google Scholar]
- Strateva, Ivezić, Ž., Knapp, G. R., et al. 2001, AJ, 122, 1861 [Google Scholar]
- Strazzullo, V., Rosati, P., Pannella, M., et al. 2010, A&A, 524, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stringer, M. J., Benson, A. J., Bundy, K., et al. 2009, MNRAS, 393, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, M., Kodama, T., Arimoto, N., et al. 2005, MNRAS, 362, 268 [NASA ADS] [CrossRef] [Google Scholar]
- Tasca, L., Kneib, J.-P., Iovino, A., et al. 2009, ApJ, 503, 379 [Google Scholar]
- Taylor, E., Franx, M., van Dokkum, P. G., et al. 2009, ApJ, 694, 1171 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Bender, R., & de Oliveira, C. M. 2005, ApJ, 621, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Toft, S., van Dokkum, P., Franx, M., et al. 2007, ApJ, 671, 285 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Treu, T., Ellis, R. S., Liao, T. X., et al. 2005, ApJ, 633, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Trujillo, I., Förster Schreiber, N. M., Rudnick, G., et al. 2006, ApJ, 650, 18 [NASA ADS] [CrossRef] [Google Scholar]
- van der Wel, A., Holden, B. P., Zirm, A. W., et al. 2008, ApJ, 688, 48 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G. 2005, AJ, 130, 264 [Google Scholar]
- van Dokkum, P. G., & Franx, M. 2001, ApJ, 553, 90 [Google Scholar]
- van Dokkum, P. G., Franx, M., Kelson, D. D., et al. 1998, ApJ, 500, 714 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Franx, M., Fabricant, D., Illingworth, G. D., & Kelson, D. D. 2000, ApJ, 541, 95 [NASA ADS] [CrossRef] [Google Scholar]
- van Dokkum, P. G., Franx, M., Kriek, M., et al. 2008, ApJ, 677, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Vergani, D., Scodeggio, M., Pozzetti, L., et al. 2008, A&A, 487, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visvanathan, N., & Sandage, A. 1977, ApJ, 216, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Wake, D. A., Nichol, R. C., Eisenstein, D. J., et al. 2006, MNRAS, 372, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Weiner, B., Phillips, A. C., Faber, S. M., et al. 2005, ApJ, 620, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Whitaker, K. E., van Dokkum, P. G., Brammer, G., et al. 2010, ApJ, 719, 1715 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J., Quadri, R. F., Franx, M., et al. 2009, ApJ, 691, 1879 [NASA ADS] [CrossRef] [Google Scholar]
- Willmer, C. N. A., Faber, S. M., Koo, D. C., et al. 2006, ApJ, 647, 853 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, G., Muzzin, A., Yee, H. K. C., et al. 2009, ApJ, 698, 1943 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, C., Gray, M. E., & Meisenheimer, K. 2005, A&A, 443, 435 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolf, C., Aragón-Salamanca, A., Balogh, M., et al. 2009, MNRAS, 393, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, R., Newman, J. A., Faber, S. M., et al. 2006, ApJ, 648, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Yee, H. K. C., Hsieh, B. C., Lin, H., & Gladders, M. D. 2005, ApJ, 629, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Zabludoff, A. I., & Mulchaey, J. S. 1998, ApJ, 496, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Zamorani, G., Vettolani, G., et al. 1997, A&A, 326, 477 [NASA ADS] [Google Scholar]
- Zucca, E., Ilbert, O., Bardelli, S., et al. 2006, A&A, 455, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zucca, E., Bardelli, S., Bolzonella, M., et al. 2009, A&A, 508, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Percentage of early- and late-type galaxies in the parent and spectroscopic VIPERS sample.
(U − V) colour intercept evolution at MV − 5 log h = −20 as a function of redshift for a fixed slope of d(U − V)/d(MV) = −0.08.
Schechter parameters and associated one sigma errors (2Δ ln ℒ = 1) of the global VIPERS LF and the LF for different sub-samples derived in the rest-frame standard B-band filter system. Parameters listed without errors are set “ad hoc” to the given value.
All Figures
 |
Fig. 1 Luminosity−redshift relation for galaxies in the VIPERS PDR-1. Galaxies are colour-coded with respect to their SED type classification. The solid line indicates the selection boundaries for 90% completeness. |
| In the text | |
 |
Fig. 2 Redshift distribution for the VIPERS PDR-1 sample used in the present study. Only galaxies with 2 ≤ zflg ≤ 9.5 are considered. The mean of the total distribution is indicated with a dashed line. The total number of galaxies and mean redshift are given for each galaxy type. |
| In the text | |
 |
Fig. 3 Colour completeness for VIPERS. The sample is complete in colours between 0.5 < z < 1.3, in the sense of including a proportionally correct fraction of galaxies with different colours. A NUVr′ selection to separate (red) passive (solid line) from (blue) active, star-forming (dashed line) galaxies shows that the CSR is independent of galaxy type. |
| In the text | |
 |
Fig. 4 Evolution of the colour–magnitude relation for the VIPERS PDR-1 sample from z = 0.4 to z = 1.3. Galaxies are colour-coded with respect to their derived SED type. The number of galaxies for a specific SED type is shown in each slice. The lines in each panel indicate the best-fitting CMR for galaxies on the RS within the given redshift interval: classical approach (dotted), SED galaxy types (dashed). The fit for the colour-bimodality method is not shown as it coincides with the dashed line. Typical error bars (black) are shown in each redshift slice. |
| In the text | |
 |
Fig. 5 Relation between galaxy colour and stellar mass for the VIPERS PDR-1 sample, within three broader redshift bins. This plot confirms that the most luminous blue galaxies observed in the CMR are in fact very massive objects. In particular, we note how a) the highest-mass edge of the blue cloud evolves with cosmic time, with a few objects as massive as log (M⋆/M⊙) ~ 11.5 displaying colours typical of star-forming galaxies; b) conversely, the corresponding highest-mass edge of the RS is substantially frozen over the explored redshift range. |
| In the text | |
 |
Fig. 6 Rest-frame U − V colour distribution in the different redshift bins, split into three broad SED galaxy types of blue galaxies (Sc/Sd and SB/Irr, blue histograms), green galaxies (Sa/Sb, green), and red (E/S0, red). The dashed line in each panel indicates the adopted separation for red and blue galaxies, defined by a fit to the local minima of the colour distributions. The colour-bimodality separation is also a good representation of the different SED types of early-type and late-type galaxies. |
| In the text | |
 |
Fig. 7 Evolution of the rest-frame (NUV − r′) vs. (r′ − K) plane for VIPERS. A selection along the lines of of constant sSFRs (black ⟨sSFR⟩ arrow) and dust-extinction (grey SMC arrow) gives a clean separation for the majority of passive (red) and star-forming active (dusty red and blue) galaxies. The fraction of galaxies (in per cent) classified as passive and active is given in each panel. |
| In the text | |
 |
Fig. 8 Completeness of early-type galaxies (lower panel) and contamination by late-type galaxies (top panel) with respect to the SED type-classified early-type galaxy population as a function of redshift for different selection methods. Classical approach (dotted line, filled circles), colour-bimodality (solid line, blue triangles), NUVr′ sample (dashed line, open circles). |
| In the text | |
 |
Fig. 9 Evolution of the RS using a variable slope with redshift. The CMR is divided into two redshift bins at low (0.5 < z ≤ 0.7) and high (0.7 < z ≤ 0.9) redshift. Galaxies are colour-coded with respect to their derived SED type. The number of galaxies for a specific SED type is shown in each slice. The solid line is the best-fit to the RS adopting the slope as derived from VIPERS within the selection criteria indicated with the dotted line (see text for details). |
| In the text | |
 |
Fig. 10 Evolution of the CMR intercepts in (U − V) at MV − 5 log h = −20 for red-sequence galaxies as a function of redshift. The solid line is a least-square fit to the VIPERS data including the local SDSS reference (filled black square). The blue area reflects the total observed scatter due to systematic uncertainties, whereas uncertainties due to Poisson noise are indicated with single error bars. The grey shaded area shows the observed measurement errors of the COMBO-17 data set by Bell et al. (2004b). In the bottom left corner typical uncertainties due to filter and rest-frame transformations are shown. |
| In the text | |
 |
Fig. 11 Evolution of the RS for different selection criteria of early-type galaxies. The colour evolution of the red-sequence as described by the CMR intercepts in (U − V) at MV − 5 log h = −20 as a function of redshift. The evolution of the RS is shown for different selection criteria colour-bimodality (blue filled triangles), SED type classification (red open squares) and the classical method (black filled circles). Measurement error bars are displayed for each criteria. All relations are least-square fits to the respective VIPERS selection criteria including the local SDSS reference (filled black square). |
| In the text | |
 |
Fig. 12 Intrinsic (filled symbols) and observed scatter (open symbols) in the rest-frame (U − V) colours of passive galaxies. The scatter due to measurement uncertainties is subtracted from the observed scatter in quadrature. Literature data are shown in grey. Associated data for field galaxy studies (triangles or crosses) are joined with lines, studies based on galaxy clusters are shown as stars. |
| In the text | |
 |
Fig. 13 Rest-frame B-band luminosity function VIPERS from z = 0.5 to z = 1.3. The LF is shown for the total sample (black circles), for red galaxies defined using the colour-bimodality (red triangles, solid line), and for red galaxies selected using the SED criterion (red squares, dashed line). Lines indicate the fits to the luminosity function using a Schechter function. For reference, the black dotted line shows the Schechter function of a local sample by (Ilbert et al. 2005). |
| In the text | |
 |
Fig. 14 Comparison of the VIPERS B-band LF to previous measurements. Literature data include the LF of VVDS (Ilbert et al. 2005, blue squares), the LF of DEEP2+COMBO-17 (Faber et al. 2007, dashed orange line), the LF of red early-type galaxies in the VVDS (Zucca et al. 2006, blue squares), the LF of red galaxies in the NDWFS (Brown et al. 2007, long-dashed green line) and the LF of galaxies in AGES (Cool et al. 2012, dot-dashed brown line). The numbers in the brackets denote the redshift interval of the respective LF. Left: LF for all galaxies. Right: LF for red galaxies. |
| In the text | |
 |
Fig. 15 Comparison of RS intercept evolution with the rest-frame colour evolution of stellar population models using different burst duration time scales τ. Only PEGASE models with best-fitting models are shown. Dotted lines are for a zf = 2.5, dashed lines for zf = 3. The shaded area denotes the variation of the observed evolution in the RS intercept for different selection criteria of early-type galaxies. |
| In the text | |
 |
Fig. 16 Evolution in |
| In the text | |
 |
Fig. 17 Example of stacked spectra of early-type galaxies at 0.5 < z < 0.6 (black) and 0.9 < z < 1.0 (red, shifted for display purposes). All spectra should represent passive, red and quiescent galaxies. Early-type galaxies at high redshift show clear evidence of ongoing SF which is supported by weak [O II] 3727 emission. Early-type galaxies have been selected based on the SED type classification. Spectra of early-type galaxies selected using other criteria look very similar. Prominent absorption and emission features in the spectra are denoted with dotted lines. |
| In the text | |
 |
Fig. A.1 Filter transmission curve for different popular U-band filters in the literature. The U-Johnson (dashed blue), used in VIPERS, is compared to the UBessel VVDS filter (red solid), U3 Buser filter (green), UBessel1990 (dotted cyan), u SDSS (black), u∗ CFHT MegaCam (pink), and the u⋆ CFHT MegaCam SAGEM filter (dot-dashed magenta line). |
| In the text | |
 |
Fig. B.1 Completeness test for red galaxies in the VIPERS PDR-1. The red histogram displays the observed real red galaxies at 1.0 < z < 1.3 transformed to 0.9 < z < 1.0, whereas the simulated samples are two representations of red galaxy samples at 0.9 < z < 1.0. The properties of the real sample are consistent with the properties of their simulated counterparts. |
| In the text | |
 |
Fig. C.1 Cosmic variance for the VIPERS PDR-1 sample and other surveys from the literature. Symbols denote data from AGES (Cool et al. 2012, red crosses), COMBO-17 (Bell et al. 2004b, black circles), COSMOS (Scoville et al. 2007, grey polygons), DEEP1 (Im et al. 2002, cyan stars), DEEP2 (Faber et al. 2007, orange triangles), NDWFS (Brown et al. 2007, magenta stars), and VVDS (Le Fèvre et al. 2005, 2013, green squares). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


